




















Preview text:
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC CHỨA MODUL SỐ PHỨC
DẠNG TOÁN 1. ĐIỂM VÀ ĐƯỜNG THẲNG
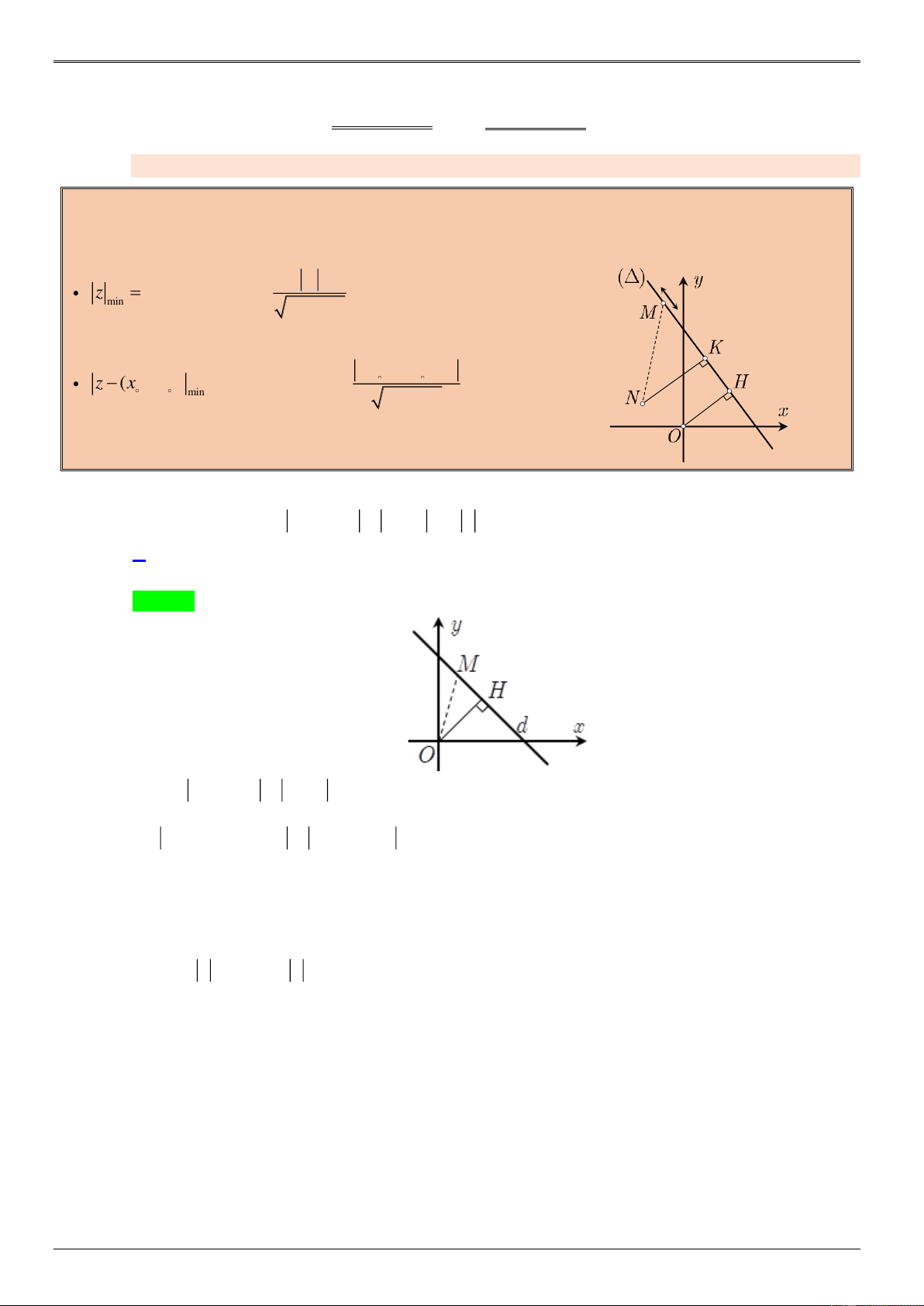
Cho đường thẳng : Ax By C 0 và điểm M .
Điểm N sao cho NM nhỏ nhất K là hình
chiếu của N lên , nghĩa là NM
NK d N, M K. min N C G z
OH d N, min 2 2 U A B YỄN
Khi đó M H và tọa độ H (OH ). H O
Ax By C À
z (x y i)
NK d N, N min 2 2 G A B VI Ệ Khi đó M
K và tọa độ K NK. T BÀI TẬP TẠI LỚP Câu 1:
Cho z x yi thỏa z 2 4i z 2i và z đạt giá trị nhỏ nhất. Tính 3x 2 y bằng A. 2. B. 3. C. 4. D. 5. Lời giải Chọn A LUY ENTHITRA
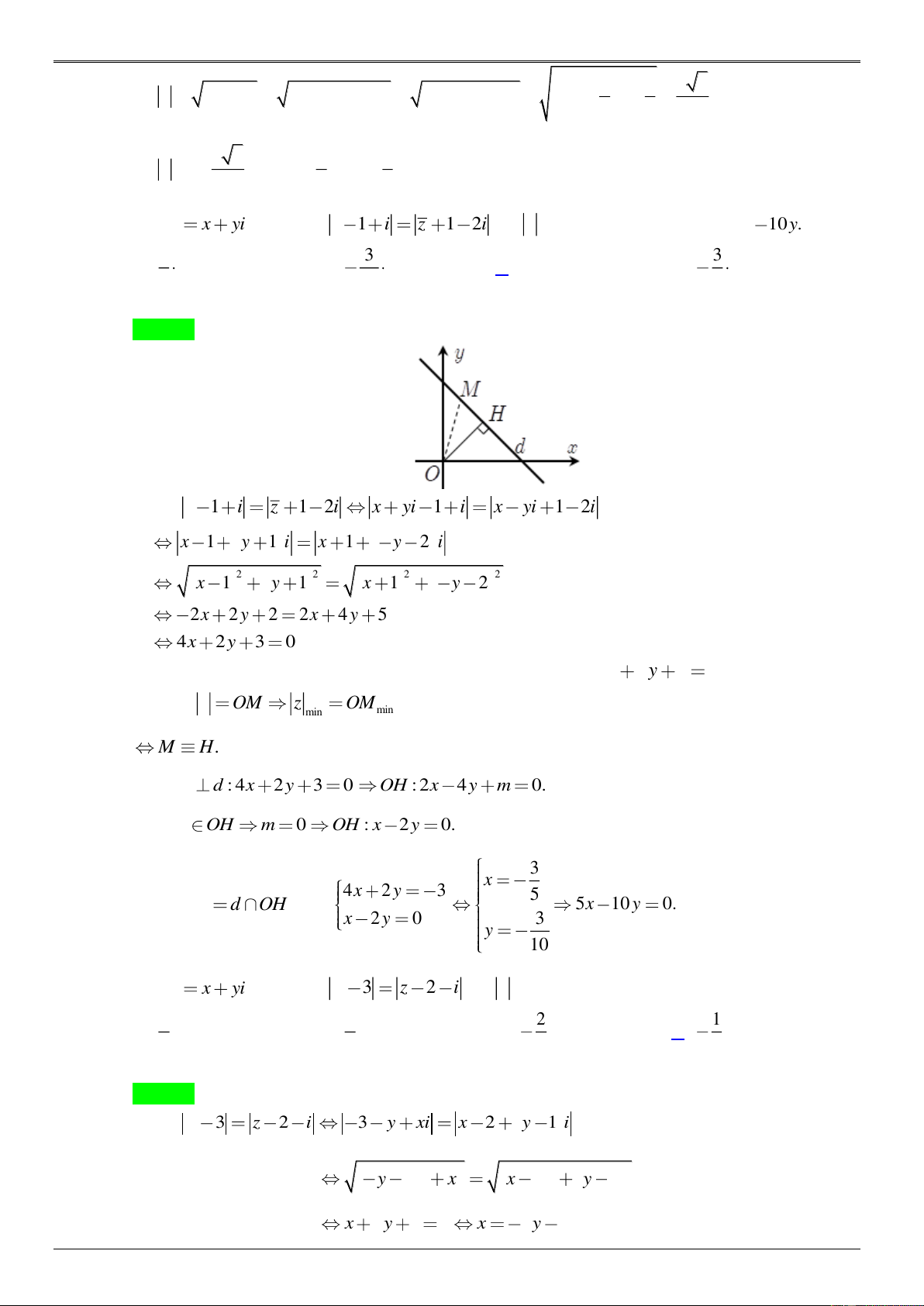
Ta có: z 2 4i z 2i C N G H
(x 2) (y 4)i x (y 2)i IEM. 2 2 2 2 V
(x 2) (y 4) x (y 2) N
x y 4 0 : là đường thẳng d.
Khi đó: z OM z OM min min M H.
Do OH d : x y 4 0
OH : x y m 0. (
O 0;0) OH m 0 OH : x y 0. x y 4
Tọa độ H d OH thỏa x y 0
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 1
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 x 2
3x 2y 2. y 2
Cách 2. Từ d : y 4 x 2 2 2 2 2
z x y x (4 x) 2(x 2) 8 8 2 2. Suy ra: z
2 2 x 2 y 2 3x 2y 2. min
Cách 3. Sử dụng Cauchy – Schwarz, có N 2 2 2 2 x y (x y) 4 G 2 2 z x y 2 2. U Y 1 1 1 1 2 ỄN H
Dấu " " khi x y và x y 4 x y 2 3x 2y 2. O ÀN G
Lưu ý. Nếu đề bài chỉ yêu cầu tính | | z , thì nó là | | z OH d( ; O d). min min VIỆT Câu 2: Cho z x
yi thỏa mãn z 1 5i z
3 i và z đạt giá trị nhỏ nhất. Tìm 3x . y 5 12 12 5 A. 12 B. 5 C. 5 D. 12 Lời giải Chọn C Ta có z 1 5i z 3 i x yi 1 5i x yi 3 i x 1 y 5 i x 3 y 1 i 2 2 2 2 x 1 y 5 x 3 y 1 LUY
2x 10y 26 6x 2y 10 x 3y 4 0 x 4 3y ENT 2 H 2 2 2 2 2 6 8 8 I Ta có z x y 4 3y y 10y 24y 16 10 y TRA 5 5 5 C N 8 6 2 12 G Suy ra z y x 3x y . H min 5 5 5 5 IEM x 2 Câu 3: Cho z x
yi thỏa mãn z 3i z
2 i và z đạt giá trị nhỏ nhất. Tìm . y .VN 1 3 A. 1 . B. 5 . C. 2 . D. 5 . Lời giải Chọn A Ta có z 3i z 2 i x y 3 i x 2 y 1 i 2 2 2 x2 y 3 x 2 y 1 x 2y 1 0 x 2y 1 2 2 2 2 2 2 2 1 1 Ta có z x y 2y 1 y 5y 4y 1 5 y 5 5 5
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 2
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 1 2 1 Suy ra z y x x 2y 1. min 5 5 5 Câu 4: Cho z x
yi thỏa mãn z 2 i z
3i và z đạt giá trị nhỏ nhất. Giá trị của 4x 2y bằng 1 5 3 A. 1 . B. 2 . C. 2 . D. 2 . Lời giải Chọn A N Ta có z 2 i z 3i x 2 y 1 i x y 3 i G U YỄ 2 2 2 2 N x 2 y 1 x y 3 HOÀ x y 1 0 x y 1 N G V 2 IỆ 2 2 2 2 2 1 1 1 T Ta có z x y y 1 y 2y 2y 1 2 y 2 2 2 1 1 1 Suy ra z y x . min 2 2 2 Vậy 4x 2y 1 . Câu 5:
Cho số phức z thỏa z 2 2i z
4i . Giá trị nhỏ nhất của iz 1 bằng 2 3 2 A. 2 2 . B. 2 . C. . D. . 2 2 LUY Lời giải ENT Chọn C H ITRA Gọi M ( ;
x y) biểu diễn số phức z x y . i C N z 2 2i z 4i (x 2) ( y 2)i x ( y 4)i G H IE x y 2
0 là đường thẳng d. M .VN Có iz 1 i z i z i AM với (0 A ;1). iz 1 AM
M là hình chiếu của A lên đường thẳng d (xem lý thuyết). Khi đó: min min 1 2 2 iz 1 AM d ( ; A d ) min min 2 2 2 1 1 Câu 6: Cho z thỏa z 1 2i z
3i 1 . Giá trị nhỏ nhất của z 2 2i bằng 3 5 A. 1. B. . C. . D. 5 . 2 2 Lời giải Chọn B Gọi M ( ;
x y) biểu diễn số phức z x y . i
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 3
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 z 1 2i z 3i 1 (x 1) ( y 2)i x 1 ( y 3)i 2y 1
0 là đường thẳng d. Có z 2 2i AM với ( A 2; 2). z 2 2i AM
M là hình chiếu của A lên đường thẳng d (xem lý thuyết). Khi đó: min min 2. 2 1 3 z 2 2i AM d ( ; A d ) N min min 2 2 G 2 0 2 U YỄN
Câu 7. Cho số phức z thỏa z 2i
z 1 2i . Tìm giá trị nhỏ nhất của (1 i)z 2 . HOÀ 5 5 N A. . B. . C. 3 . D. 5 . G 41 34 VIỆT Lời giải Chọn B Gọi M ( ;
x y) biểu diễn số phức z x y . i z 2i z 1 2i x ( y 2)i x 1 ( y 2)i 2x 8y 1
0 là đường thẳng d. Có (1 i)z 2 (1 i)z 1 i 1 i 1 i z 1 i 1 i z 1 i 2AM với ( A 1;1). LUY E (1 i)z 2 AM
M là hình chiếu của A lên đường thẳng d (xem lý thuyết). Khi đó: min N min THITRA 2. 1 8.1 1 5 (1 i)z 2 2AM 2d ( ; A d ) 2. . min min 2 2 C 2 8 34 N G H IEM BÀI TẬP VỀ NHÀ .VN Câu 1:
Cho z x yi thỏa z i z 2 3i và z đạt giá trị nhỏ nhất. Tính 3x y bằng A. 2. B. 3. C. 4. D. 5. Lời giải Chọn B
Ta có: z i z 2 3i
x y
1 i x 2 y 3i
x y 2 x 2 y 2 2 1 2 3
x 2y 3 0
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 4
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 2 6 9 3 5 2 2 2 2 2
z x y (2y 3) y 5y 12y 9 5 y 5 5 5 3 5 6 3 z
y x 3x y 3. min 5 5 5 Câu 2: Cho z x
yi thỏa mãn z 1 i z
1 2i và z đạt giá trị nhỏ nhất. Tìm 5x 10 . y 3 3 3 A. 0 D. N 5 B. 10 C. . 5 G U Lời giải YỄ Chọn C N HOÀNG VIỆT Ta có z 1 i z 1 2i x yi 1 i x yi 1 2i x 1 y 1 i x 1 y 2 i 2 2 2 2 x 1 y 1 x 1 y 2
2x 2y 2 2x 4y 5 4x 2y 3 0
Vậy tập hợp điểm M biểu diễn số phức z là đường thẳng d : 4x 2y 3 0 LUY Khi đó: z OM z OM min min ENTH M H. ITRA Do OH d : 4x 2y 3 0 OH : 2x 4y m . 0 C N G ( O ; 0 ) 0 OH m 0 OH : x 2y . 0 H IEM 3 .V x N 4x 2y 3 5 Tọa độ H d OH thỏa 5x 10y 0. x 2y 0 3 y 10 Câu 3: Cho z x
yi thỏa mãn iz 3 z
2 i và z đạt giá trị nhỏ nhất. Phần thực của z bằng 2 1 2 1 A. 5 . B. 5 . C. 5 . D. 5 . Lời giải Chọn D Ta có iz 3 z 2 i 3 y xi x 2 y 1 i 2 2 2 y x2 3 x 2 y 1 x 2y 1 0 x 2y 1
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 5
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 2 2 2 2 2 2 2 1 1 Ta có z x y 2y 1 y 5y 4y 1 5 y 5 5 5 1 2 1 Suy ra z y x . min 5 5 5 2 Câu 4:
Xét số phức z thỏa z z 2 i
4i 1 là một số thực. Giá trị nhỏ nhất của z bằng 8 16 9 7 A. 5 . B. 5 . C. 6 . D. 5 . N G U Lời giải YỄ Chọn B N H Gọi z x yi , đk , x y . Ta có z z 2 i 4i 1 x yi x yi 2 i 4i 1 O ÀNG 2 2 2 1 2 4 x y x y x y i VIỆT Vì z z 2 i
4i 1 là số thực nên x 2y 4 0 x 2y 4 2 2 2 2 2 2 8 16 16 Ta có z x y 2y 4 y 5y 16y 16 5 y 5 5 5 16 2 16 Suy ra z z min min 5 5 . Câu 5: Cho z thỏa z 1 2i z 2
i . Giá trị nhỏ nhất của z 2 3i bằng 11 121 LUY A. 10 . B. 10 . C. . D. . 10 10 ENT Lời giải H ITRA Chọn C C Gọi M ( ;
x y) biểu diễn số phức z x y . i N G H I z 1 2i z 2 i x y i x y i E 1 ( 2) 2 ( 1) M .VN x 3y
0 là đường thẳng d. Có z 2 3i AM với ( A 2;3). z 2 3i AM
M là hình chiếu của A lên đường thẳng d (xem lý thuyết). Khi đó: min min 1. 2 3.3 11 z 2 3i AM d ( ; A d ) . min min 2 2 10 1 3 Câu 6: Cho z thỏa z 1 i z 1
2i . Giá trị nhỏ nhất của (3 4i)z 5 10i bằng 7 3 15 17 25 13 A. . B. . C. . D. . 26 2 2 26 Lời giải
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 6
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 Chọn D Gọi M ( ;
x y) biểu diễn số phức z x y . i z 1 i z 1 2i x 1 ( y 1)i x 1 ( y 2)i 4x 6y 3
0 là đường thẳng d. Có (3 4i)z 5 10i (3 4i)z (3 4i) 1 2i (3 4i) z 1 2i 3 4i z 1 2i 5AM với ( A 1; 2). N G U Y (3 4i)z 5 10i AM
M là hình chiếu của A lên đường thẳng d (xem lý thuyết). min min ỄN Khi đó: H O ÀN 4. 1 6. 2 3 25 25 13 G (3 4i)z 5 10i 5AM 5d ( ; A d ) 5. . min min 2 V 2 52 26 I 4 6 ỆT Câu 7:
Cho các số phức z thỏa z z 1
2i . Giá trị nhỏ nhất của (1 2i)z 11 2i là 5 5 2 5 A. . B. . C. . D. . 2 2 5 2 Lời giải Chọn D Gọi M ( ;
x y) biểu diễn số phức z x yi z x yi . LUY z z 1 2i x yi x 1 (2 y)i EN 2x 4y 5
0 là đường thẳng d. THITRA Có (1 2i)z 11 2i (1 2i)z (1 2i) 3 4i (1 2i) z 3 4i C N 1 2i z 3 4i 5AM với ( A 3; 4). G H IE (1 2i)z 11 2i AM
M là hình chiếu của A lên đường thẳng d (xem lý thuyết). M min min .V Khi đó: N 2. 3 4.4 5 5 (1 2i)z 11 2i 5AM 5d ( ; A d ) 5. . min min 2 2 2 2 4
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 7
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
DẠNG 2: ĐIỂM VÀ ĐƯỜNG TRÒN
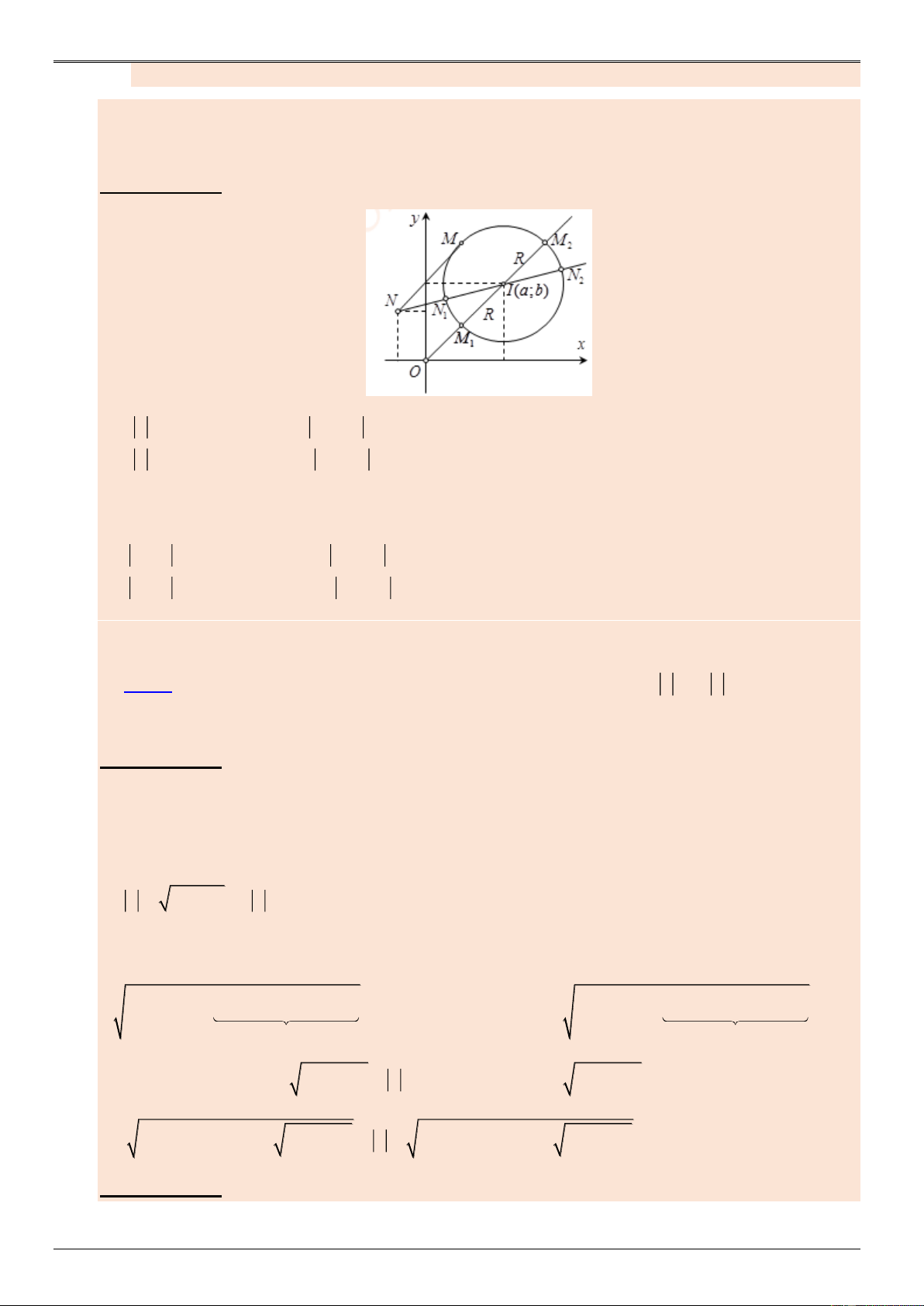
Cho tập hợp điểm M ;
x y biểu diễn các số phức z x yi là một đường tròn C có tâm I ; a b
và bán kính R . Gọi N là điểm biểu diễn số phức z .
Phương pháp 1. Hình học N G U YỄN HOÀN G VI z OM
OM OI R khi M M Ệ min 1 1 min T . z OM
OM OI R khi M M max 2 2 max
Khi đó OI C M ;M . 1 2 z z MN
NN NI R khi M N min 1 1 min . z z MN
NN NI R khi M N max 2 2 max
Khi đó NI C N ; N . 1 2 LUY
Lưu ý. Nếu đề bài yêu cầu tìm tổng phần thực, phần ảo tương ứng với z , z thì từ nhận min max E
xét I là trung điểm của M M suy ra: tổng phần thực 2a , tổng phần ảo 2 . b 1 2 N TH
Phương pháp 2. Bất đẳng thức Cauchy – Schwarz: ITRA 2 2 2 C
Giả sử tập hợp điểm là đường tròn C : x a y b R và viết lại: N G H I C 2 2 2 2
: x y 2ax 2by c 0 x y 2ax 2by c . EM.V 2 N 2 2 2 2
z x y z x y ax by c ax a b y b 2 2 2 2 2 2
2a 2b c 2 2
nhằm lợi dụng 2 x a y b
R trong bất đẳng thức Cauchy – Schwarz (điểm rơi): 2 2 a b 2 2
x a y b a x a b y b 2 2 a b 2 2 4 4 ( ) ( ) 2 . 2 . 4 4
(x a) (y b) 2 2 R R 2 Suy ra 2 2
a b c R 2 2 a b 2 2
z a b c R 2 2 2 2 2 2 2 2 a b 2 2
a b c R 2 2 a b 2 2 z
a b c R 2 2 2 2 2 2 2 2 a b .
Phương pháp 3. Lượng giác
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 8
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 2 2 2 2 x a y b
Giả sử tập hợp điểm là đường tròn C x a y b 2 : R 1 , R R
x a sint R
x a Rsin t gợi ta đến công thức 2 2
sin t cos t 1 nên đặt . y b y b R cos t cos t R Do đó 2 2 2 2 2 z
x y z x y a Rsin t 2 b R cost 2 . N G U 2 2 2 2 2 2 Y
z a b R sin t cos t 2a .
R sin t 2b . R cos t . ỄN H 2 O 2 2 2 2 2
z a b R 2R a b .sin t và luôn có 1
sint 1 ÀNG VI nên suy ra: 2 2 2 2 2 2 2 2
a b 2R a b z a b 2R a b . ỆT
Phương pháp 4. Sử dụng bất đẳng thức trị tuyệt đối z z z z z z . 1 2 1 2 1 2
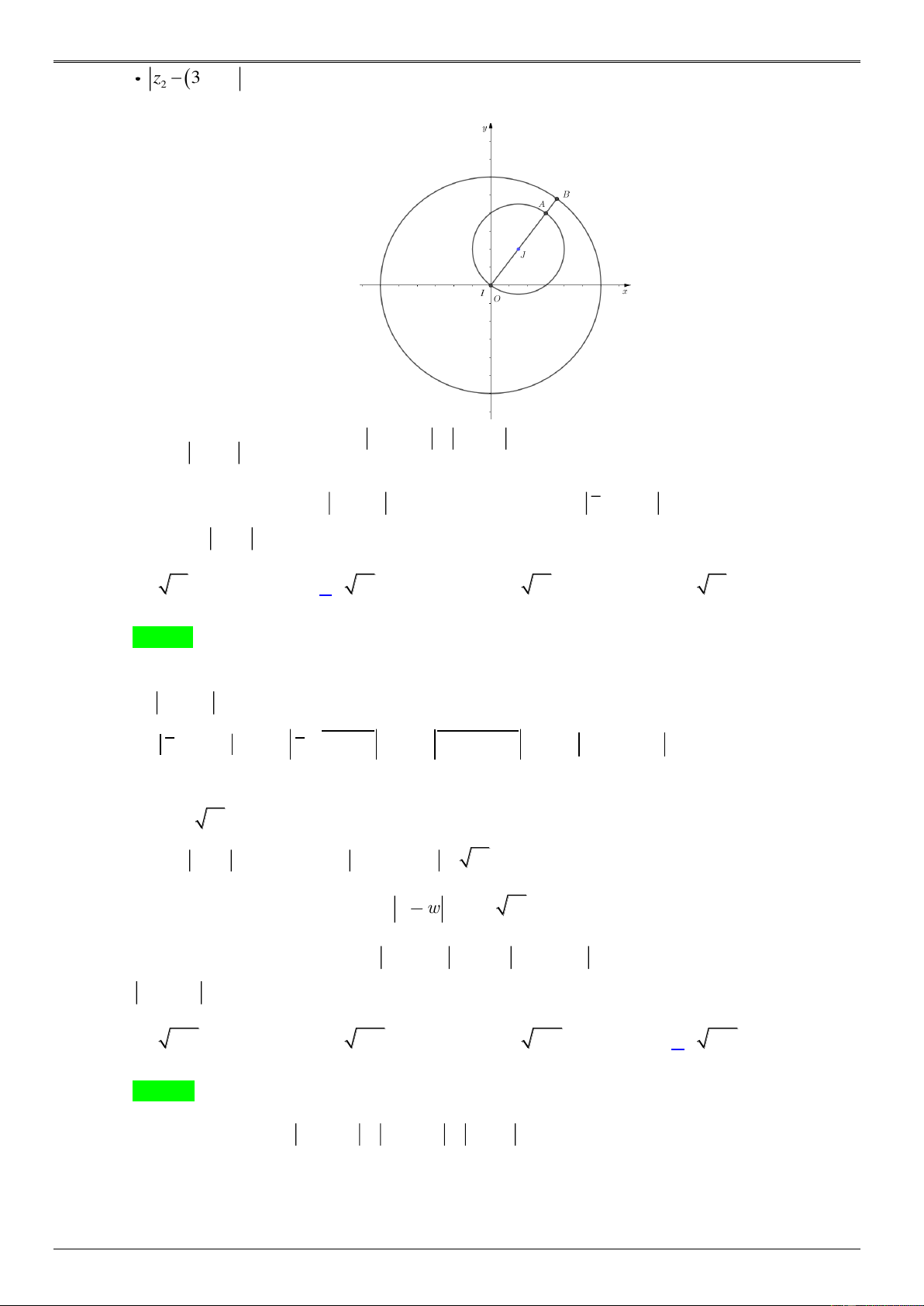
Ví dụ minh họa: Xét các số phức z x
yi thỏa mãn z 2 3i 1.
a) Giá trị nhỏ nhất và giá trị lớn nhất của z . Ứng với z
là số phức z a
bi và ứng với min z
là số phức z c d .
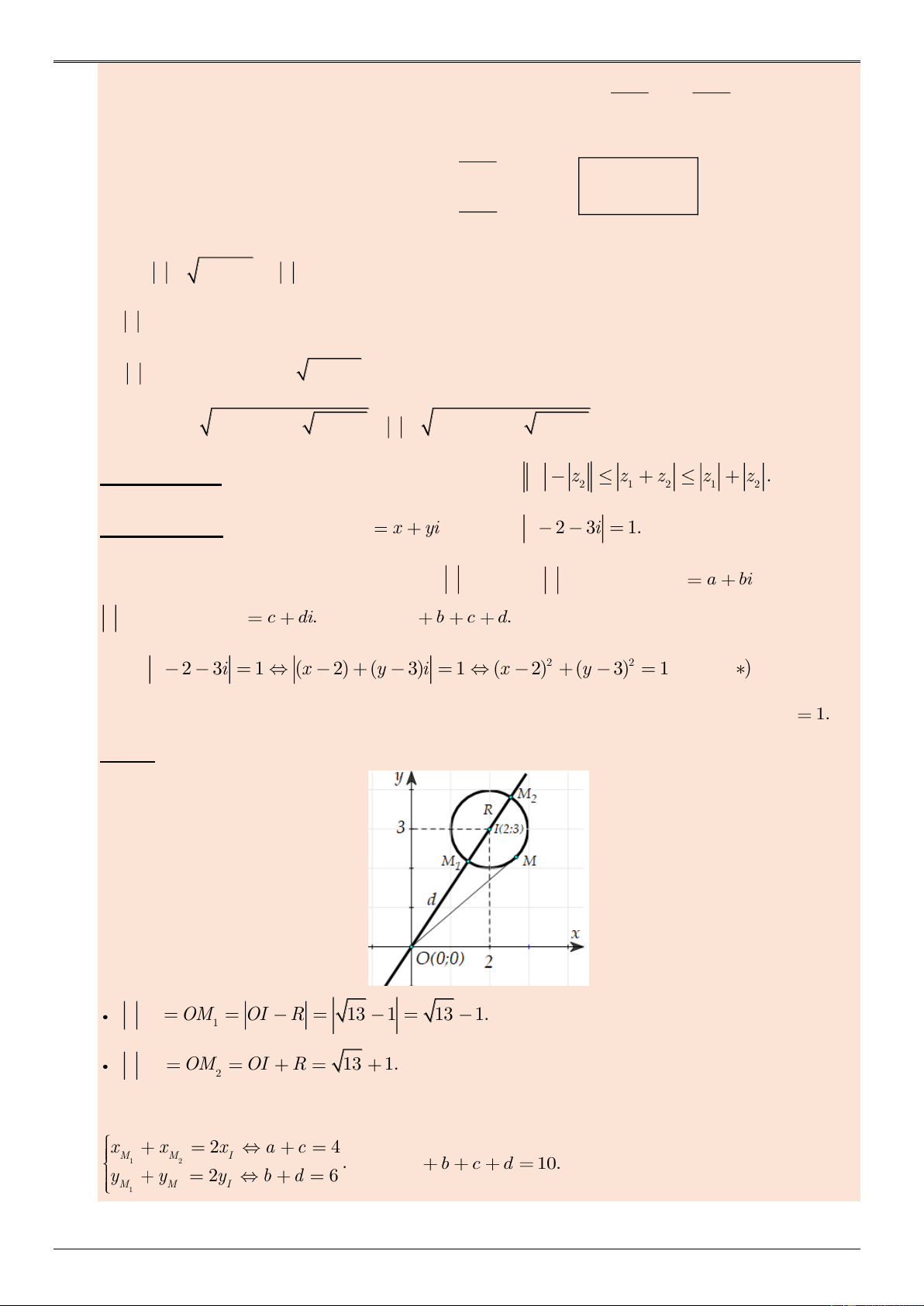
i Tìm tổng a b c d. max Ta có 2 2 z 2 3i 1 (x 2) (y 3)i 1 (x 2) (y 3) 1 ( ) LUY
Do đó tập hợp điểm biểu diễn các số phức z là đường tròn (C ) có tâm I(2;3) và bán kính R 1. ENTH Cách 1. Hình học ITRA C N G H IEM.VN z OM OI R 13 1 13 1. 1 min z OM OI R 13 1. 2 max
Vì I(2; 3) là trung điểm M M nên: 1 2 x x 2x a c 4 M M I 1 2 . Suy ra a b c d 10. y y 2y b d 6 M M I 1 2
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 9
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
Lưu ý. Nếu đề bài yêu cầu tìm số phức tương ứng với z và z
, tức là tìm hai điểm biểu diễn min max
M , M , nó cũng chính là tọa độ giao điểm của đường thẳng d
OI và đường tròn (C). 1 2
Cách 2. Bất đẳng thức Cauchy – Schwarz: Ta có: 2 2 2 2 (x 2) (y 3) 1 x y 4x 6y 12. 2 2 2 Ta lại có: z x y 4x 6y 12 4.(x 2) 6.(y 3) 14 2 2 2 2 2 2 2 2 (4 6 ) (x 2) (y 3) 4(x 2) 6(y 3) (4 6 ) (x 2) (y 3) N Mà G U Y 2 Ễ 14 2 13 z 14 2 13 13 1 z 13 1. N HO
Cách 3. Lượng giác ÀNG x 2 sint 2 2 2 V Đặt z (2 sint) (3 cost) 14 4 sint 6 cost IỆ y 3 cost T 2 2 2 z 14 4 6 .sin(t ) 14 2 13 sin(t ) và do 1 sin(t ) 1 nên: 2 14 2 13 z 14 2 13 13 1 z 13 1.
Cách 4. Sử dụng bất đẳng thức z z z z z z 1 2 1 2 1 2 Ta có z 2 3i z 2 3i z 2 3i z 13 1 z 13 1 13 z 1 13 . LUY
Nhận xét. Tùy vào cấu trúc bài toán, yêu cầu câu hỏi và sự thành thạo về kiến thức mà học sinh ENT
chọn phương pháp giải cho phù hợp. H ITRA
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P z 1 i . C N Ta có: P z 1 i (x 1) (y 1).i G H IE 2 2 (x 1) (y 1) MA với ( A 1;1). M .VN P AM AI R 13 1 min 1 Từ hình vẽ, suy ra: . P AM AI R 13 1 max 2 Kết luận: P 13 1 và P 13 1. min max
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 10
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P z 1 i . Ta có: P z 1 i (x 1) (y 1).i 2 2 (x 1) (y 1) MA với ( A 1;1). P AM AI R 13 1 min 1 Từ hình vẽ, suy ra: . P AM AI R 13 1 max 2 N G U Kết luận: P 13 1 và P 13 1. min max YỄN BÀI TẬP TẠI LỚP H O À Câu 1:
Cho các số phức z thỏa z 3 4i
4. Giá trị lớn nhất của z bằng N G VIỆT A. 9 . B. 5 . C. 12 . D. 3 . Lời giải Chọn A
Gọi M(x;y) biểu diễn số phức z x y . i z 3 4i 4 (x 3) (y 4)i 4
Suy ra tập hợp điểm M(x;y) là đường tròn tâm I(3; 4) bán kính R 4 z OI R 9 max LUY Câu 2:
Xét các số phức z thỏa z 2 4i
5. Giá trị nhỏ nhất của z bằng ENTH A. 1. B. 2. C. 5. D. 6. ITRA Lời giải C N G Chọn C H IE
Gọi M(x;y) biểu diễn số phức z x y . i M .VN z 2 4i 5 (x 2) (y 4)i 5
Suy ra tập hợp điểm M(x;y) là đường tròn tâm I(2; 4) bán kính R 5 z OI R 5 min Câu 3:
Xét các số phức z thỏa z 3 4i
2. Gọi z , z là hai số phức có môđun lớn nhất và nhỏ nhất. 1 2
Tổng phần thực của z , z bằng 1 2 A. 8. B. 6. C. 8. D. 6. Lời giải Chọn B
Gọi M(x;y) biểu diễn số phức z x y . i
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 11
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 2 2 z 3 4i 2 (x 3) (y 4)i 2 (x 3) (y 4) 4
Suy ra tập hợp điểm M(x;y) là đường tròn (C ) tâm I( 3; 4) bán kính R 2 quaO(0;0) x 3t OI : OI : u(3;4) y 4t
Tọa độ giao điểm của (C ) và OI là nghiệm của hệ phương trình 9 x N G 5 U 12 Y x 3t y ỄN 5 y 4t H 21 O 2 2 (x 3) (y 4) 4 x ÀN 5 G 28 V y IỆ 5 T 9 21
Vậy tổng phần thực của z , z bằng 6 1 2 5 5 Câu 4:
Xét các số phức z thỏa mãn iz 1 1. Gọi ,
m M lần lượt là giá trị nhỏ nhất và giá trị lớn
nhất của biểu thức P
z . Giá trị của biểu thức 2020 M m bằng A. 2014. B. 2016. C. 2018. D. 2022. Lời giải Chọn C LUY
Gọi M(x;y) biểu diễn số phức z x y . i EN 2 2 T iz 1 1 (1 y) xi 1 x (y 1) 1 H ITRA
Suy ra tập hợp điểm M(x;y) là đường tròn tâm I(0;1) bán kính R 1 C N
Tọa độ giao điểm của (C ) và OI là (0; 0),(0;2) G H IE m z 0,M z 2 M min max .VN Vậy 2020 M m 2018 Câu 5:
Xét các số phức z thỏa mãn z 2 3i 1. Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
z 1 i lần lượt là
A. 14 2, 14 2 . B. 13 1, 13 1 .
C. 13 4, 13 4 . D. 14 1, 14 1. Lời giải Chọn B
Đặt z x yi với , x y .
Khi đó z i x 2 y 2 2 3 1 2 3 1.
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 12
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
Gọi M là điểm biểu diễn hình học của số phức z ta có M I ;1 với I 2;3 . 2 2 2 2
Có z 1 i x 1 y 1 x 1 y 1 . 2 2 Gọi A 1 ;
1 suy ra z 1 i x 1 y 1 AM .
Dễ thấy AI 13 1 nên A nằm ngoài I ;1 . N G M U YỄN HO B À I C A N G VIỆT
Kẻ đường thẳng AI cắt đường tròn I
;1 tại B,C như hình vẽ.
AM AC AI IC 13 1
Có AB AM AC nên max . AM
AB AI IB 13 1 min Câu 6:
Xét các số phức z thỏa mãn z 2 . Số phức w z 3i có mô-đun nhỏ nhất và lớn nhất lần lượt
là m và M . Tổng m M bằng A. 5 . B. 7 . C. 8. D. 6 . LUY Lời giải ENT Chọn D H ITRA
Đặt z x yi với , x y . C N Khi đó 2 2 G z 2 x y 4 . H IEM
Gọi M là điểm biểu diễn hình học của số phức z ta có M ; O 2 . .VN
Xét w z i
x y 2 2 3 3 Gọi A0; 3
suy ra w z i x y 2 2 3 3 AM .
Dễ thấy AO 3 2 nên A nằm ngoài ; O 2 . M B O C A
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 13
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
Kẻ đường thẳng AO cắt đường tròn ;
O 2 tại B,C như hình vẽ. AM
AC AO OC 3 2 5 M 5
Có AB AM AC nên max
M m 6 . AM
AB AO OB 3 2 1 m 1 min Câu 7:
Xét các số phức z, w thỏamãn z 5 và w (4 3i)z 1 2 .
i Giá trị nhỏ nhất của w bằng A. 3 5. B. 4 5. C. 5 5. D. 6 5. N Lời giải G U Y Chọn B ỄN w 1 2i w 1 2i H Ta có: w (4 3i)z 1 2i z z O 4 3i 4 3i ÀNG w 1 2i VI 5 w 1 2i 5 5 ỆT 4 3i Lại có: w 1 2i w 1 2i 5 5 w 5 w 4 5 Vậy w 4 5. min Câu 8:
Cho số phức z thỏa 2 2 z 4 z
2iz . Tìm giá trị nhỏ nhất của z i . A. 1. B. 2. C. 3. D. 4. Lời giải Chọn A LUY
Giả sử z x y ; i , x y . E Ta có: N TH z 2i I 2 2 z 4 z 2iz z 2i . z 2i z . z 2i . TRA z 2i z C N Với z 2i thì z i i 1. G H I 2 E 2 2 2 M Với z 2i z x y 2 x y y 1. .VN 2 2 2 thì z i x y 1 x 4 2.
So sánh hai trường hợp ta được z i 1 đạt được khi z 2i . min BÀI TẬP VỀ NHÀ Câu 1:
Cho các số phức thỏa mãn z 2 2i
1. Giá trị lớn nhất của z bằng A. 4 2 2 . B. 2 2. C. 2 2 1. D. 3 2 1. Lời giải Chọn C
Gọi M(x;y) biểu diễn số phức z x y . i z 2 2i 1. (x 2) (y 2)i 1
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 14
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
Suy ra tập hợp điểm M(x;y) là đường tròn tâm I(2; 2) bán kính R 1 z OI R 2 2 1. max Câu 2:
Xét các số phức z thỏa iz 4 3i
1. Giá trị nhỏ nhất của z bằng A. 3. B. 4. C. 5. D. 6. Lời giải Chọn B N
Gọi M(x;y) biểu diễn số phức z x y . i G U YỄ iz 4 3i 1 ( y 4) (x 3)i 1 N 2 2 H (y 4) (x 3) 1 O ÀNG
Suy ra tập hợp điểm M(x;y) là đường tròn tâm I(4; 3) bán kính R 1 VIỆ z OI R 4 T min Câu 3:
Xét các số phức z thỏa z 2 4i
2. Gọi z , z là hai số phức có môđun lớn nhất và nhỏ nhất. 1 2
Tổng phần ảo của z , z bằng 1 2 A. 8. B. 4. C. 8. D. 4. Lời giải Chọn C
Gọi M(x;y) biểu diễn số phức z x y . i 2 2 z 2 4i 2 (x 2) (y 4)i 2 (x 2) (y 4) 4 LUY EN
Suy ra tập hợp điểm M(x;y) là đường tròn (C ) tâm I(2; 4) bán kính R 2 THI quaO(0;0) x 2t TRA OI : OI : u(2;4) y 4t C N G C H
Tọa độ giao điểm của ( ) và OI là nghiệm của hệ phương trình IEM 10 2 5 .V x N 5 20 4 5 x 2t y 5 y 4t 2 2 10 2 5 (x 2) (y 4) 4 x 5 20 4 5 y 5 20 4 5 20 4 5
Vậy tổng phần ảo của z , z bằng 8 1 2 5 5 Câu 4:
Xét các số phức z thỏa mãn điều kiện (1 i)z 1 7i 2. Gọi ,
m M lần lượt là giá trị nhỏ
nhất và giá trị lớn nhất của biểu thức P
z . Giá trị của M m bằng
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 15
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 A. 4. B. 10. C. 2. D. 24. Lời giải Chọn C
Gọi M(x;y) biểu diễn số phức z x y . i 2 2 (1 i)z 1 7i 2 x y 6x 8y 24 0
Suy ra tập hợp điểm M(x;y) là đường tròn tâm I(3; 4) bán kính R 1 N G U quaO(0;0) x 3t Y OI : OI : ỄN u(3;4) y 4t HO
Tọa độ giao điểm của (C ) và OI là nghiệm của hệ phương trình ÀNG 18 V x IỆ 5 T 24 x 3t y 5 y 4t 12 2 2 x y 6x 8y 24 0 x 5 16 y 5 m z 4,M z 6 min max M m 2 Câu 5:
Cho các số phức z thỏa mãn z 3 4i 2 và cho số phức w 2z 1 i . Khi đó w có giá trị LUY
lớn nhất bằng bao nhiêu? EN A. 16 74 . B. 2 130 . C. 4 74 . D. 4 130 . THITRA Lời giải C N Chọn D G H I
Đặt z x yi với , x y . EM.V 2 2 N
Khi đó z 3 4i 2 x 3 y 4 4.
Gọi M là điểm biểu diễn hình học của số phức z ta có M I; 2 với I 3; 4 . 2 2
w z i x y i w x 2 y 2 1 1 2 1 2 1 2 1 2 1 2 1 4 x y . 2 2 2 2 1 1 1 1 Gọi A ;
suy ra w 4 x y 2AM . 2 2 2 2 2 2 1 1 130 Dễ thấy AI 3 4 2
nên A nằm ngoài I; 2 . 2 2 2
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 16
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 M B I C A
Kẻ đường thẳng AI cắt đường tròn I; 2 tại B,C như hình vẽ. N G U
Có AM AC nên AM AC . Y max ỄN H O
Dấu “=” xẩy ra khi và chỉ khi M C khi đó 130 130 4
AC AI IC 2 . ÀN 2 2 G VI Vậy w
2AC 130 4 . Ệ max T Câu 6:
Xét các số phức z thỏa mãn z 1 3i 2 . Số phức z mà có z 1 nhỏ nhất có dạng z a bi . 0
Giá trị của tổng 2a 3b bằng A. 2 . B. 5 . C. 7 . D. 9 . Lời giải Chọn B
Đặt z x yi với , x y . 2 2 LUY
Khi đó z 1 3i 2 x
1 y 3 4. EN T
Gọi M là điểm biểu diễn hình học của số phức z ta có M
I;2 với I 1;3. H ITRA
Có z x 2 2 1 1 y . C N G H I
Gọi A1;0 suy ra z x 2 2 1
1 y AM . EM.VN
Dễ thấy AI 3 2 nên A nằm ngoài I; 2 . M B I C A
Kẻ đường thẳng AI cắt đường tròn I; 2 tại B,C như hình vẽ.
Có AM AB AM
AB AI IB 1. min
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 17
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 AB 1
Dấu “=” xẩy ra khi và chỉ khi AB AI AB
AI , với AI 0;3 suy ra AI 3 AB 0; 1 B 1; 1 . a 1
Khi đó z 1 i hay
2a 3b 5 . b 1 Câu 7:
Xét các số phức z, w thỏamãn w iz và (1 i)z 2 2i
2. Giá trị lớn nhất của z w N bằng G U Y A. 3. B. 2 3. C. 3 2. D. 3 3. ỄN H Lời giải O ÀN Chọn C G V Từ giả thiết: IỆT (1 i)z 2 2i 2 2 (1 i)z 2 2i 2 2 z 2 2 z 3. Lại có: z w z iz z . 1 i 2. z 3 2. Vậy: z w 3 2. max Câu 8: Cho 2 z 2z 5 (z 1 2i)(z
3i 1) . Giá trị nhỏ nhất của z 2 2i bằng 1 3 A. . B. 1. C. . D. 2. 2 2 Lời giải LUY Chọn B E N Giả sử z x y ; i , x y . TH Ta có: ITRA 2 z 2z 5 (z 1 2i)(z 3i 1) z 1 2i . z 1 2i z 1 2i . z 1 3i C N z 1 2i G H . I z 1 2i z 1 3i EM.V Với z 1 2i thì z 2 2i 1 1. N 2 2 2 2 1 Với z 1 2i z 1 3i x 1 y 2 x 1 y 3 y . 2 2 2 2 9 3 thì z 2 2i x 2 y 2 x 2 . 4 2
So sánh hai trường hợp ta được z 2 2i 1 đạt được khi z 1 2i . min
DẠNG TOÁN 3. ĐƯỜNG TRÒN VÀ ĐƯỜNG TRÒN Câu 1: Xét các số phức z z
z 4 1 và iz 2 1 . Giá trị nhỏ nhất của z 2z bằng 1 , 2 thỏa mãn 1 2 1 2 A. 2 5 2 B. 4 2 C. 4 2 3 D. 4 2 3 Lời giải Chọn C
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 18
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 N Đặt z 2
z , suy ra P z 2z z ( 2
z ) z z . 3 2 1 2 1 2 1 3 G U Y 1 1 Ễ Và z
z thế vào iz 2 1 iz 2 1 z 4i 2. 2 3 2 3 3 N 2 2 HO Gọi ,
A B là hai điểm biểu diễn cho hai số phức z , z . 3 1 À N G
z 4i 2 Athuộc đường tròn tâm I (0; 4), R 2. 3 3 V IỆ
z 4 1 B T
thuộc đường tròn tâm J (4;0), R 1. 1 1
P IJ R R 4 2 3 min 1 3
P z z AB . 1 3
P IJ R R 4 2 3 max 1 3 Câu 2:
Xét các số phức z , z thỏa mãn z 3i 5 2 và iz 1 2i 4. Giá trị lớn nhất của biểu thức 1 2 1 2
P 2iz 3z bằng 1 2 A. 313 16 . B. 313 . C. 313 8 . D. 313 2 5 . Lời giải Chọn A LUY E
Đặt z 2iz và z 3
z suy ra P 2iz 3z z ( 3
z ) z z . N 3 1 4 2 1 2 3 2 3 4 TH 1 1 I TRA Và z z thế vào z 3i 5 2 z 3i 5 2 z 6 10i 4. 3 1 3 2i 1 3 2i C N 1 1 G
Và z z thế vào iz 1 2i 4
iz 1 2i 4 z 6 3i 12. 4 2 4 2 4 H 3 3 IEM Gọi ,
A B là hai điểm biểu diễn cho hai số phức z , z . 3 4 . VN z 6
10i 4 A thuộc đường tròn tâm I( 6 ; 1 0), R 4. 3 3
z 6 3i 12 B thuộc đường tròn tâm J (6;3), R 12. 4 4
P IJ R R 313 16 min 3 4
P z z AB . 4 3
P IJ R R 313 16 max 3 4 Câu 3:
Xét các số phức z, w thỏa z 3 2 2 và w 4 2i 2 2. Biết z w đạt giá trị nhỏ nhất
khi z z và w w . Giá trị của 3z w bằng 0 0 0 0 A. 2 2. B. 6 2. C. 4 2. D. 1. Lời giải Chọn B Gọi ,
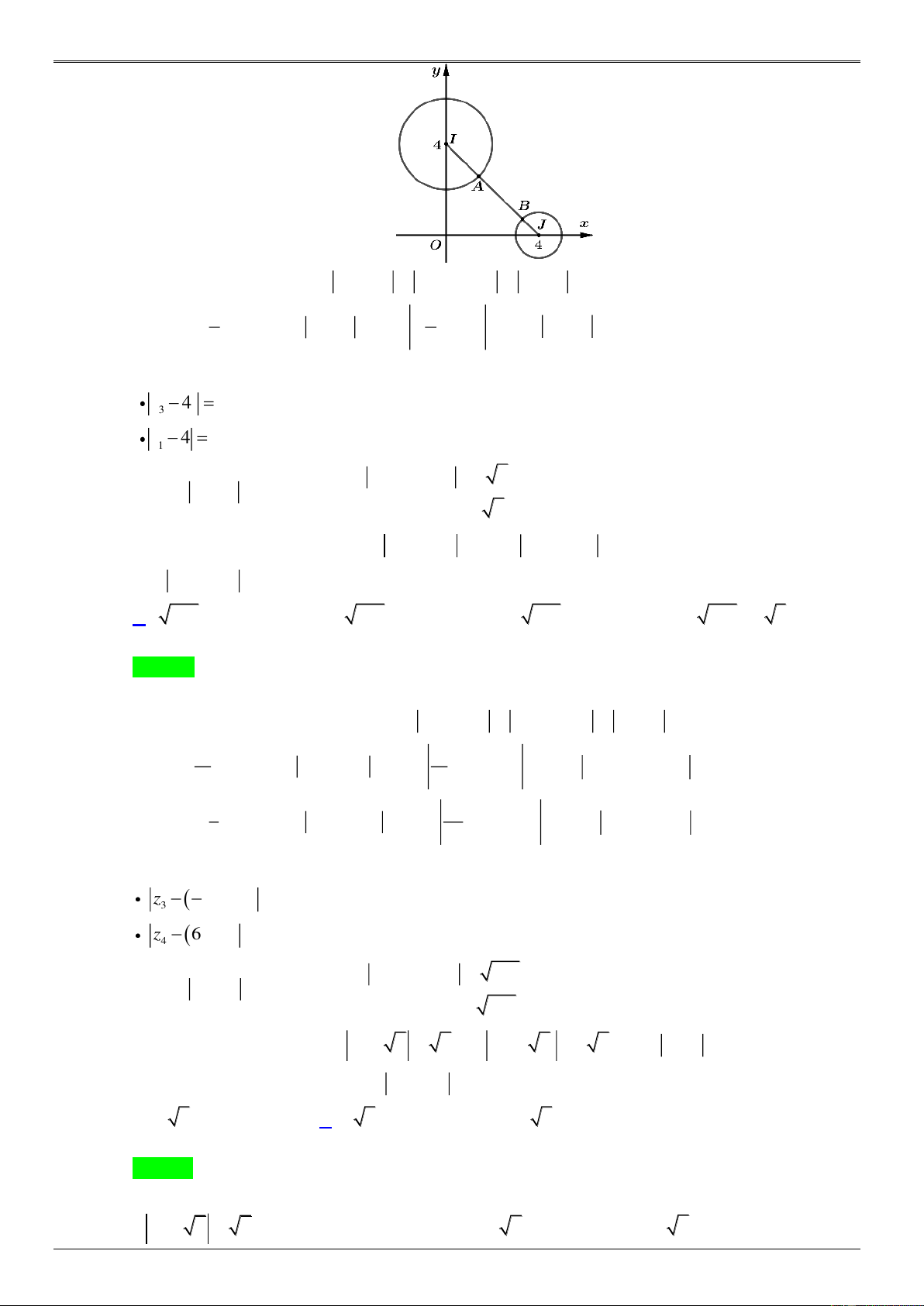
A B là hai điểm biểu diễn cho hai số phức z, w.
z 3 2 2 A thuộc đường tròn tâm I 3 2;0 , bán kính R 2 . 1 1
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 19
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
w 4 2i 2 2 B thuộc đường tròn tâm I 0;4 2 , bán kính R 2 2 . 2 2 Ta có hình vẽ: N G U YỄN HOÀNG VIỆT
Ta có: I I 9 2 16 2 5 2 . 1 2
P I I R R 2 2 min 1 2 1 2
P z w AB .
P I I R R 8 2 max 1 2 1 2 I I 3
2;4 2 , phương trình đường thẳng I I : 4x 3y 12 2 0. 1 2 1 2 12 2 4x 18 2 4 2 4 3 12 2 0 y x y x y • 3 5 5 . x 3 2 2 2 y 2 25 50 2 12 2 4 2 2 x x 48 0 x y LUY 9 3 5 5 E N 12 2 4 2 T
Điểm A là điểm nằm bên trong I I nên có toạ độ là: ; . 1 2 H 5 5 ITRA 28 2 6 2 C x y y x N 4 3 12 2 0 5 5 G • . H x y I 4 22 2 8 12 2 6 2 E y x M 5 5 .VN Điể 6 2 12 2
m B là điểm nằm bên trong I I nên có toạ độ là: ; . 1 2 5 5 Theo đó 12 2 4 2 12 2 4 2 ,
A B lần lượt biểu diễn cho z , w . Suy ra z i , w i . 0 0 0 5 5 0 5 5
Vậy: 3z w 6 2 . 0 0 Câu 4:
Xét các số phức z , z thỏa z 12 và z 3 4i 5. Giá trị nhỏ nhất của z z bằng 1 2 1 2 1 2 A. 0. B. 2. C. 7. D. 17. Lời giải Chọn B Gọi ,
A B là hai điểm biểu diễn cho hai số phức z , z . 1 2
z 12 A thuộc đường tròn tâm I (0;0), R 12. 1 1
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 20
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
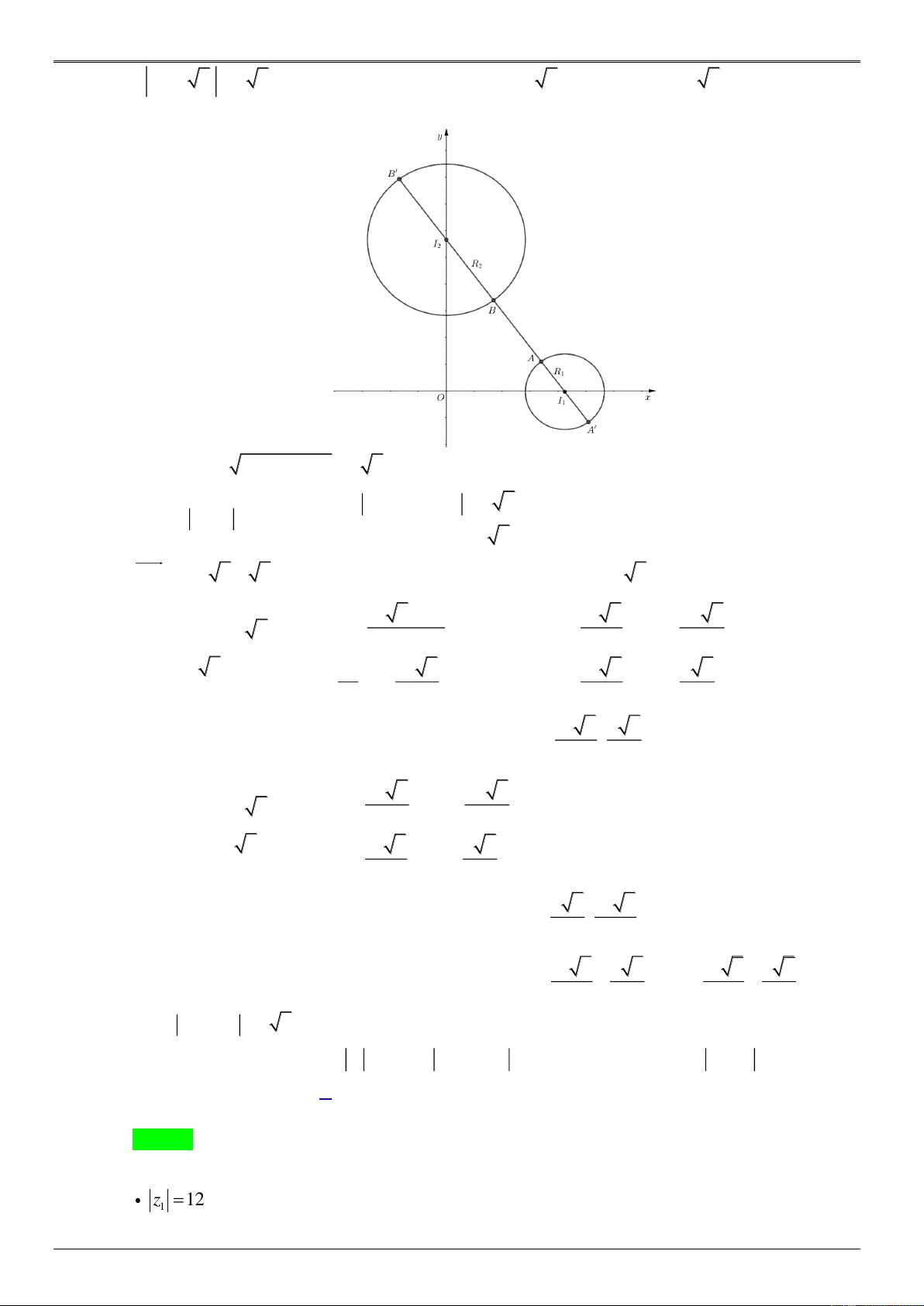
z 3 4i 5 B thuộc đường tròn tâm J (3; 4), R 5. 2 2 Ta có hình vẽ: N G U YỄN HOÀNG V IỆ
P R 2R 12 10 2 T min 1 2
P z z AB . 1 2
P 2R R 5 12 5 22 max 1 2 Câu 5:
Cho số phức z thỏa mãn z 1 i 1, số phức w thỏa mãn w 2 3i 2. Giá trị nhỏ nhất của
biểu thức z w bằng A. 13 3 . B. 17 3. C. 17 3 . D. 13 3 . Lời giải Chọn B Gọi ,
A B là hai điểm biểu diễn cho hai số phức z và w . LUY
+) z 1 i 1 A thuộc đường tròn tâm I 1
;1 , bán kính R 1. 1 ENT
+) w 2 3i 2 w 2 3i 2 w 2 3i 2 w 2 3i 2 B thuộc đường H ITRA
tròn tâm J 2; 3 , bán kính R 2 . 2 C N G
Vì IJ 17 3 R R nên hai đường tròn I; R và J; R ngoài nhau. 2 1 1 2 H IE
P z w AB P IJ R R 17 3. M min 1 2 .VN
Vậy giá trị nhỏ nhất của biểu thức z w bằng 17 3. Câu 6:
Cho các số phức z, w thỏa mãn z 5 3i 3 và iw 4 2i 2. Giá trị lớn nhất của biểu thức
3iz 2w bằng A. 554 5 . B. 578 13 . C. 578 5 . D. 554 13. Lời giải Chọn D z 3z Đặt 1
P 3iz 2w 3z 2iw z z . 1 2 z 2iw 2 Gọi ,
A B là hai điểm biểu diễn cho hai số phức z và z . 1 2
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 21
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
+) z 5 3i 3 3z 15 9i 9 z 15 9i 9 A thuộc đường tròn tâm I 15; 9 , 1 bán kính R 9 . 1
+) iw 4 2i 2 2iw 8 4i 4 z 8 4i 4 B thuộc đường tròn tâm J 8 ; 4 , 2 bán kính R 4 . 2
Vì IJ 554 13 R R nên hai đường tròn I; R và J; R ngoài nhau. 2 1 1 2
P z z AB P IJ R R 13 554 . 1 2 max 1 2 N G U Y
Vậy giá trị nhỏ nhất của biểu thức 3iz 2w bằng 13 554 . ỄN HO Câu 7:
Cho hai số phức z , z thỏa mãn z 2 3i 2 và z 1 2i 1. Giá trị lớn nhất của biểu thức 1 2 1 2 ÀNG
z z bằng 1 2 VIỆT A. 3 34 . B. 3 10 . C. 3 . D. 6 . Lời giải Chọn A Gọi ,
A B là hai điểm biểu diễn cho hai số phức z và z . 1 2
+) z 2 3i 2 A thuộc đường tròn tâm I 2
;3, bán kính R 2 . 1 1
+) z 1 2i 1 z 1 2i 1 z 1 2i 1 z 1 2i 1 B thuộc đường tròn 2 2 2 2
tâm J 1; 2 , bán kính R 1. 2 LUY
Vì IJ 34 3 R R nên hai đường tròn I; R và J; R ngoài nhau. 2 1 1 2 E N P z z AB P IJ R R 3 34 . 1 2 max 1 2 THITRA
Vậy giá trị nhỏ nhất của biểu thức z z bằng 3 34 . 1 2 C N Câu 8:
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn G H I .
z z 1 và z 3 i .
m Tổng các phần tử của S bằng EM.VN A. 2 . B. 4 . C. 2 . D. 5 . Lời giải Chọn B
Đặt z x yi, ,
x y có điểm biểu diễn là M ;
x y z x yi . +) 2 2 .
z z 1 x y 1 M thuộc đường tròn tâm O 0;0, bán kính R 1. 1
+) z 3 i m với m 0 thì điểm M thuộc đường tròn tâm I 3;
1 , bán kính R m . 2
Tồn tại duy nhất số phức z thỏa mãn yêu cầu bài toán khi và chỉ khi hai đường tròn trên tiếp xúc với nhau.
TH1: Hai đường tròn tiếp xúc ngoài OI R R m 1 2 m 1 tm . 1 2
m 3tm
TH2: Hai đường tròn tiếp xúc trong OI R R m 1 2 m 3. 1 2 m 1 l
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 22
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 S 1;
3 . Vậy tổng các phần tử của S bằng 4 .
DẠNG TOÁN 4. ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN Câu 1:
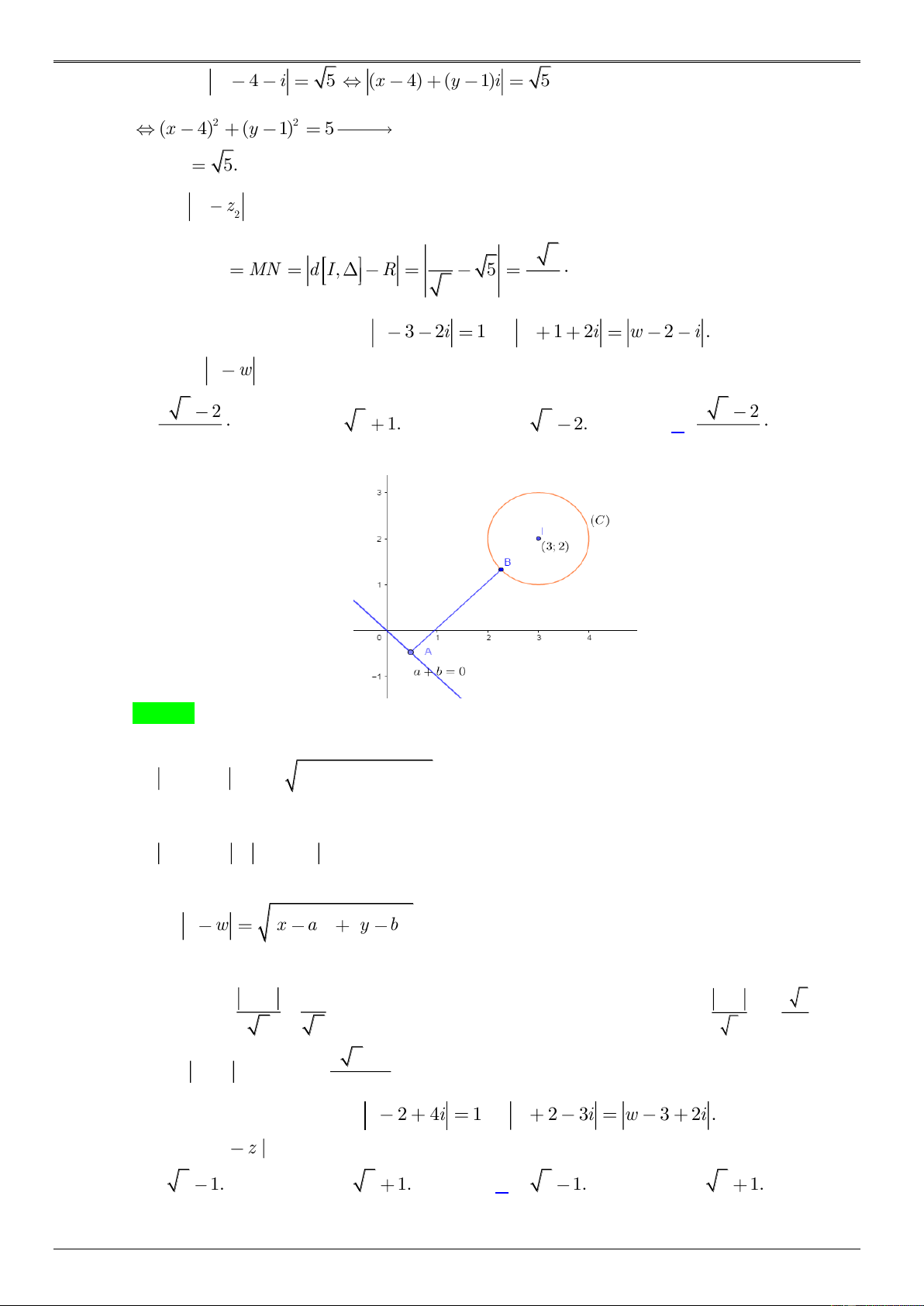
Biết rằng số phức z x yi ,
x y thỏa mãn đồng thời z 3 4i 5 và biểu thức 2 2
P z 2 z i đạt giá trị lớn nhất. Giá trị của z bằng A. 33. B. 50. C. 10. D. 5 2. Lời giải N Chọn D G U
Lời giải tham khảo 1 (hình học) YỄ 2 2 N
Có z 3 4i 5 x 3 y 4 5. HO I R À
Tập hợp các điểm biểu diễn cho số phức z là đường tròn C tâm 3; 4 , bán kính 5. N G 2 2 2 2 2 2 V Ta lại có P z 2 z i P x 2 y x y 1 IỆ T P 4x 2y 3 4x 2y 3 P
0 là đường thẳng d. 4.3 2.4 3 P
Để tồn tại z thì d và C phải có điểm chung d I, d R 5 2 2 4 2 23 P 10 13 P 33 max P 33. 4x 2y 3 33 Dấu “=” xảy ra khi 2 2 x y 5 z 5 2. x 3 y 4 5
Lời giải tham khảo 2 (đại số) LUY 2 2
Có z 3 4i 5 x 3 y 4 5. EN 2 2 2 2 2 2 T
Ta lại có P z 2 z i
P x 2 y x y 1 H ITRA P 4x 2y 3 4 x 3 2 y 4 23 C N Cauchy Schwarz 2 2 G 2 2 4 2 x 3 y 4 23 33. H IEM Dấu “=” xảy ra khi .VN x 3 y 4 2x 6 4y 16 2x 4y 10 4 2 x y 5 z 5 2. 4x 2y 30 4x 2y 30 4x 2y 3 33 Câu 2:
Xét các số phức z thỏa mãn z 1 3i 13 . Gọi ,
m M lần lượt là giá trị nhỏ nhất và giá trị lớn 2 2
nhất của biểu thức P z 2 z 3i . Tổng m M bằng A. 10. B. 25. C. 34. D. 40. Lời giải Chọn C
Đặt z x yi , x y . 2 2
Có z 1 3i 13 x 1
y 3 13.
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 23
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
Tập hợp các điểm biểu diễn cho số phức z là đường tròn C tâm I 1; 3 , bán kính R 13. 2 2 2 2 2 2 Ta lại có P z 2 z 3i P x 2 y x y 3 P 4x 6y 5 4x 6y 5 P 0 là đường thẳng .
Để tồn tại z thì và C phải có điểm chung 4.1 6.3 5 P d I, R 13 17 P 26 9 P 43. 2 2 4 6 N G m minP 9, M max P 43. U YỄN Vậy: m M 9 43 34. H O ÀN Câu 3:
Xét các số phức z x yi ;
x y thỏa mãn 1 i z 2 i 4. Giá trị lớn nhất của biểu thức G VI
P x y 3 bằng ỆT A. 4. B. 4 2 . C. 4 2 2 . D. 8 . Lời giải Chọn D 2 2 1 3 i 1 3 1
z 2 i 4 z
i 2 2 x y 8 1 . 2 2 2 2 1 3 1 3 1 3
P x y 3 x
y 4 x y 4 1 1 2 2 2 2 x y 4 8 2 2 2 2 2 2 LUY . ENT 1 3 H x y 3 ITRA 2 2 x 2
Dấu “=” xảy ra khi x y 3 8 . C N 7 G 1 3 y H x y 0 2 I 2 2 EM.VN Câu 4:
Cho số phức z thỏa mãn z 3 4i
5. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất 2 2 của biểu thức P z 2 z
i . Môđun của số phức w M mi bằng A. 1258. B. 1258. C. 2 314. D. 2 309. Lời giải Chọn B
Gọi z x yi với , x y . Có z 3 4i 5 2 2 (x 3) (y 4) 5. 2 2 Ta lại có: P z 2 z i 2 2 2 2 (x 2) y x (y 1)
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 24
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 4x 2y 3 4(x 3) 2(y 4) 23 Cauchy-Schwarz Ta có: 2 2 2 2 2 2
4(x 3) 2( y 4)
(4 2 ) (x 3) ( y 4) (4 2 ).5 10. 1
0 4(x 3) 2(y 4) 10.
13 P 33 m min P 13,M max P 33 2 2 N
W 33 13i W 33 13 1258. G U Y x 3 y 4 ỄN P đạt max khi: 4 2 H O 4x 2y 3 33 ÀNG V 2x 6 4y 16 2x 4y 10 IỆ T 4x 2y 30 4x 2y 30 x y 5. x 3 y 4 P đạt min khi: 4 2 4x 2y 3 13 2x 6 4y 16 2x 4y 10 4x 2y 10 4x 2y 10 LUY x 1,y 3. E N TH Chọn đáp án B. ITRA 2 2 Câu 5:
Xét các số phức z thỏa mãn z 2 z i
1 và các số phức z thỏa z 4 i 5. Giá trị 1 1 1 2 2 C N G nhỏ nhất của z z bằng 1 2 H IE M .VN 2 5 3 5 A. 5. B. 2 5. C. D. 5 5 Lời giải Chọn D 2 2 Ta có: 2 2 2 2 z 2 z i 1 (x 2) y x (y 1) 1 1 1 2x y 1 0
Tập hợp biểu diễn số phức z là đường thẳng d. 1
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 25
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 Ta lại có: z 4 i 5 (x 4) (y 1)i 5 2 2 2 (x 4) (y 1) 5
Tập hợp biểu diễn z là đường tròn (C ) có tâm I(4;1), bán 2 kính R 5. Khi đó z
z là khoảng cách từ 1 điểm thuộc d đến 1 điểm thuộc (C). 1 2 8 3 5 Suy ra: P MN d I, R 5 Chọn đáp án D. min N 5 5 G U YỄ Câu 6:
Cho hai số phức z, w thỏa mãn z 3 2i 1 và w 1 2i w
2 i . Giá trị nhỏ nhất của N HO biểu thức z w bằng ÀNG 3 2 2 5 2 2 VI A. B. 2 1. C. 3 5 2. D. Ệ 2 2 T Lời giải LUY Chọn D ENT
Đặt z x yi,w a b .i H ITRA
z i x 2 y 2 1 x 32 y 2 3 2 1 3 2 2
1tập hợp các số phức z là C 2 2 N
đường tròn C : x 3 y 2 1 G H 2 2 2 2 IE
w 1 2i w 2 i a 1
b 2 a 2 b 1
a b 0 tập hợp các số M .V
phức w là đường thẳng d :x y 0. N 2 2 Ta có z w x a y
b chính là khoảng cách từ một điểm A ;
a b C đến một điểm B ; x y d. Do d I d 3 2 5 ;
1 nên d không cắt C, do đó AB d I d R min 3 2 5 2 ; 1 1. 2 2 2 2 5 2 2
min z w min AB . 2 Câu 7:
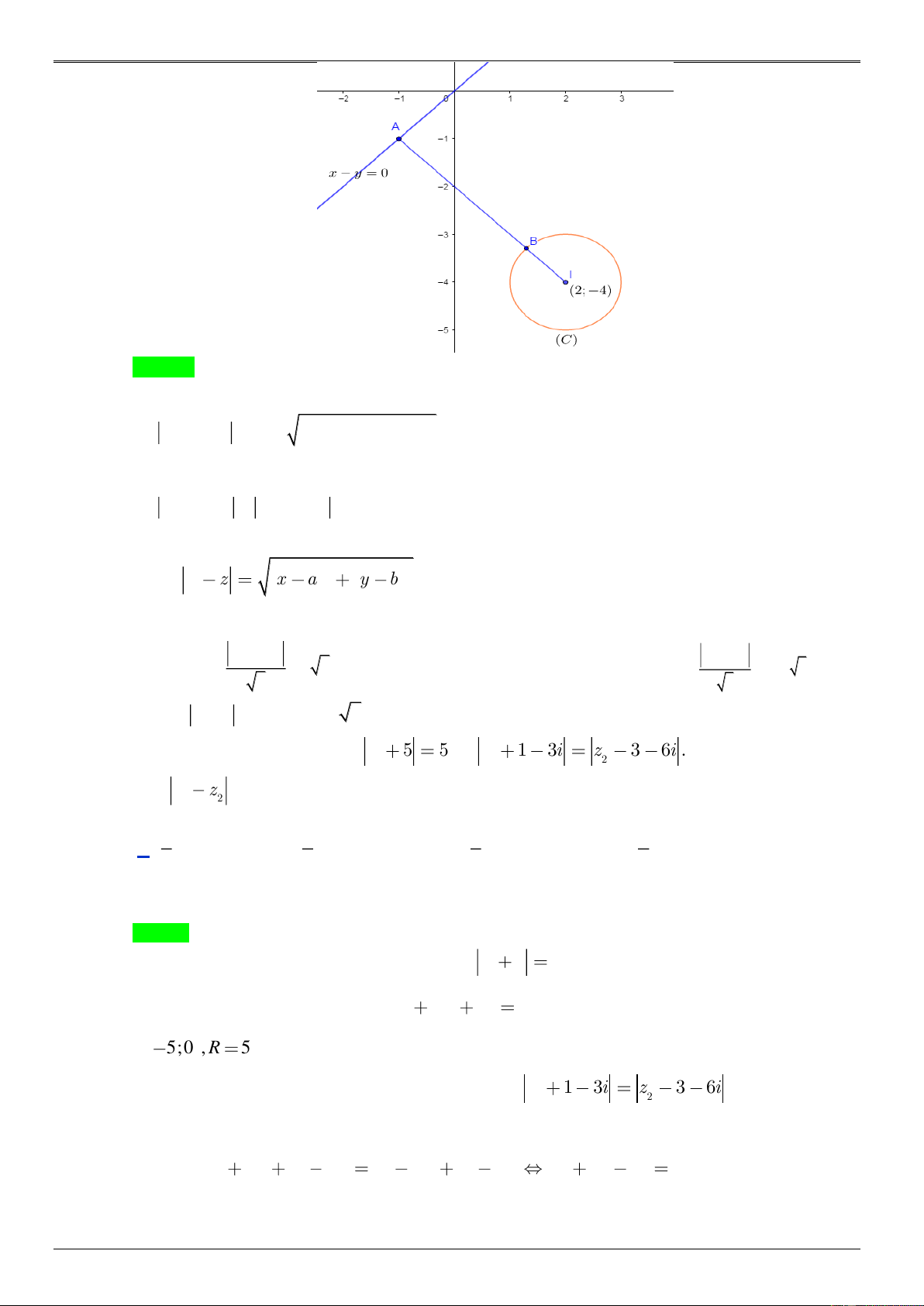
Cho hai số phức z, w thỏa mãn z 2 4i 1 và w 2 3i w 3
2i . Giá trị nhỏ nhất của biểu thức | w z | bằng A. 2 3 1. B. 2 3 1. C. 3 2 1. D. 3 2 1. Lời giải
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 26
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 N G U YỄN H O Chọn C ÀN
Đặt z x yi,w a b .i G V 2 2 2 2 IỆ
z 2 4i 1 x 2 y 4 1 x 2 y 4 1tập hợp các số phức z T là đườ 2 2
ng tròn C : x 2 y 4 1
w i w i a 2 b 2 a 2 b 2 2 3 3 2 . 2 3 3 2
a b 0 tập hợp các
số phức w là đường thẳng d :x y 0. 2 2 Ta có w z x a y
b chính là khoảng cách từ một điểm A ;
a b C đến một điểm B ; x y d. 2 4 2 4
Do d I;d
3 2 1 nên d không cắt C,do đó AB d I d R min ; 1 3 2 1. LUY 2 2 E min w z min AB 3 2 1. N TH Câu 8:
Cho hai số phức z , z thỏa mãn z 5 5 và z 1 3i z
3 6i . Giá trị nhỏ nhất của biểu 1 2 1 2 2 ITRA thức z z bằng 1 2 C N G H 5 7 1 3 I A. B. C. D. E M 2 2 2 2 .VN Lời giải Chọn A
Tập hợp các điểm biểu diễn số phức z thỏa mãn z 5
5 là tập hợp các điểm 1 1 2
M x ; y thoả mãn phương trình: 2 x 5 y 25 1 là đường tròn tâm I 5;0 , R 5
Tập hợp các điểm biểu diễn số phức z thỏa mãn z 1 3i z
3 6i là tập hợp các 2 2 2
điểm N x; y thỏa mãn phương trình 2 2 2 2 x 1 y 3 x 3 y 6 8x 6y 35 0 2
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 27
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 Khi đó z
z là khoảng cách từ một điểm thuộc d :8x 6y 35 0 tới một điểm 1 2 2 thuộc đường tròn 2 C : x 5 y 25 75 5 z z MN d I,d R 5 . 1 2 min 100 2 Câu 9:
Gọi S là tập hợp các số phức z thỏa z 1 34 và z 1 mi z m
2i . Gọi z , z là hai 1 2
số phức thuộc S sao cho z
z lớn nhất, khi đó giá trị của z z bằngP x y z bằng N 1 2 1 2 G U Y A. 2 B. 10 C. 2 D. 130 ỄN H Lời giải O ÀN Chọn B G V
Tập hợp các điểm biểu diễn số phức z thỏa mãn z 1
34 là tập hợp các điểm IỆT 2
M x ; y thoả mãn phương trình: 2 x 1 y 34 1 là đường tròn tâm I 1;0 , R 34 .
Tập hợp các điểm biểu diễn số phức z thỏa mãn phương trình z 1 mi z m 2i . là
tập hợp các điểm N x ; y thỏa mãn phương trình 2 2 2 2 x 1 y m x m y 2 2 2m x 2m 2 y 3 0 2
Tập hợp các số phức z có điểm biểu diễn thỏa mãn hệ phương trình: 2 LUY 2 x 1 y 34 EN 2 2m x 2m 2 y 3 0 T H I Khi đó z z TRA
là khoảng cách từ một điểm M thuộc tập S tới một điểm N thuộc tập S . 1 2 C Để z
z đạt giá trị lớn nhất khi MN là đường kính của đường tròn 1 2 N G H 2 2 2m 3 1 I 2 E C : x 1 y 34 d I , 0 0 m M 2 2 2 2 2m 2 2m .VN 2 2 x 1 y 34 2 2 2 2 x 1 y 34 x 1 y 34 2 2m x 2m 2 y 3 0 3x y 3 0 y 3 3x 1 m 2 2 34 3 34 2 34 3 34 ; 2 2 z i 2 2 z z 2 1 2 2 34 3 34 2 34 3 34 ; z i 2 2 2 2
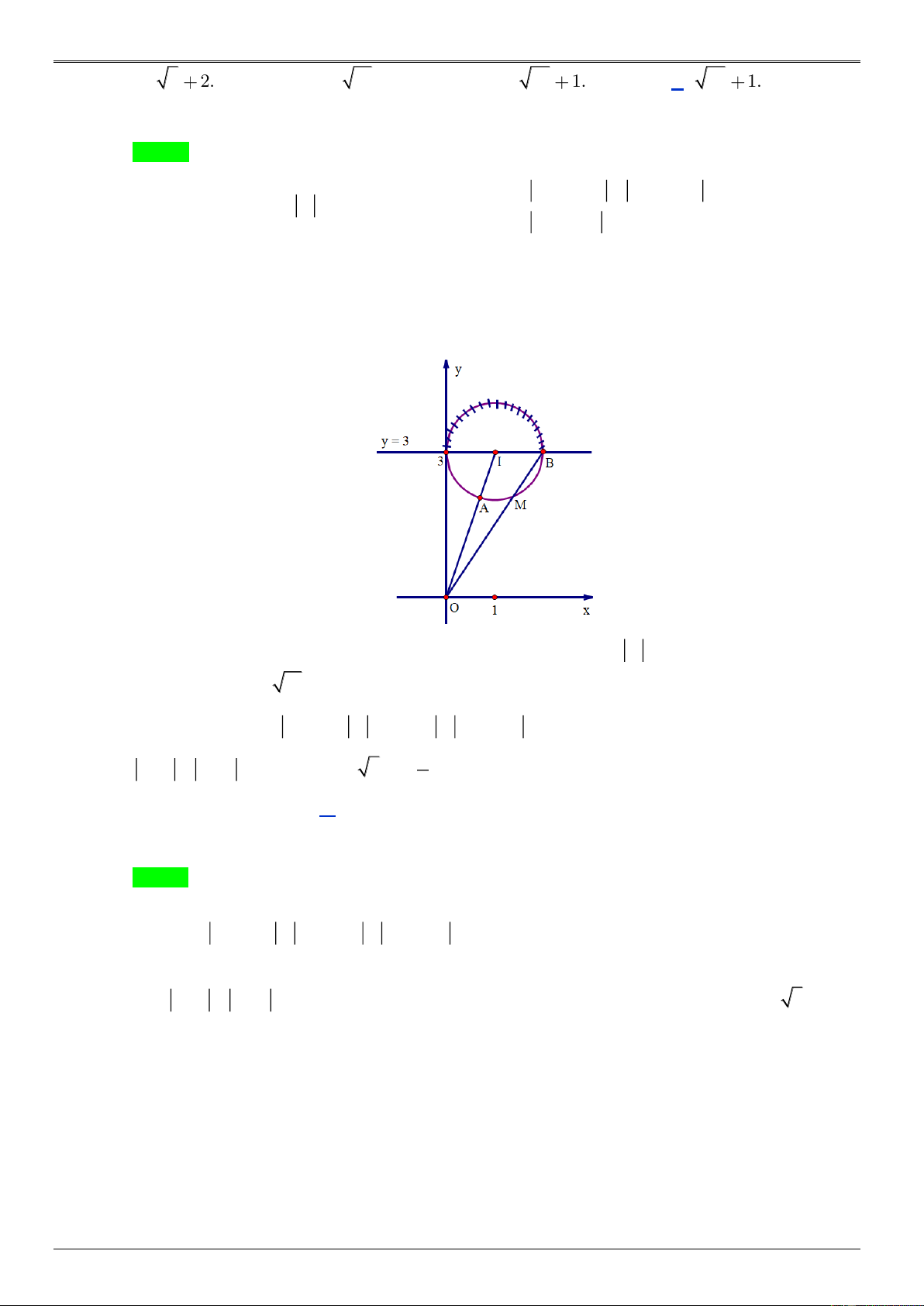
Câu 10: Xét các số thức z thỏa mãn z 2i z 4i và z 3 3i 1. Giá trị lớn nhất của biểu thức
P z 2 1 bằng
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 28
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 A. 5 2. B. 10 . C. 10 1. D. 13 1. Lời giải Chọn D
w 2 2i w 2 4i
Đặt w z 2 thì P w 1 khi ấy giả thiết trở thành w 1 3i 1 Gọi M ( ;
x y) là điểm biểu diễn của w thì giải thiết trên trở thành N G 2 2 2 2
(x 2) (y 2) (x 2) (y 4) y 3 U Y 2 2 2 2 Ễ
(x 1) (y 3) 1
(x 1) (y 3) 1 N HOÀNG VIỆT Điểm M ( ;
x y) thuộc nửa đường tròn (phần không bị gạch) P w M B max max LUY
P OB 1 13 1. Vậy chọn D. max EN
Câu 11: Cho biểu thức P z 1 2i z 3 4i z 5 6i và xét các số phức z thỏa mãn điều kiện TH a ITRA
z 2 1 2i . Biết min P a b với
là phân số tối giản. Giá trị của a b bằng b C A. 10. B. 11. C. 12. D. 12. N G H Lời giải IEM. Chọn B VN Đặt E( ;
x y) là điểm biểu diễn số phức z và ( A 1; 2), (
B 3; 4), C(5;6) .
Ta có P z 1 2i z 3 4i z 5 6i EA EB EC Mặt khác các điểm , A ,
B C thuộc đường thẳng : x y 1 0 P
E : x y 1 0. Từ giả min thiết 2 2
z 2 1 2i (x 2) y 5 E thuộc đường tròn tâm I ( 2
;0) bán kính R 5
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 29
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 y 6 C 4 B 2 A N -3 I O 1 3 5 x N G U Y -2 Ễ Δ M N H O ÀNG Từ đó suy ra P
E N E(0;1) P 2 3 2 5 2 9 2 a b 11 min min VIỆ
Vậy chọn B. T LUY ENTHITRA C N G H IEM.VN
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 30
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
DẠNG TOÁN 5. ĐOẠN THẲNG VÀ TIA
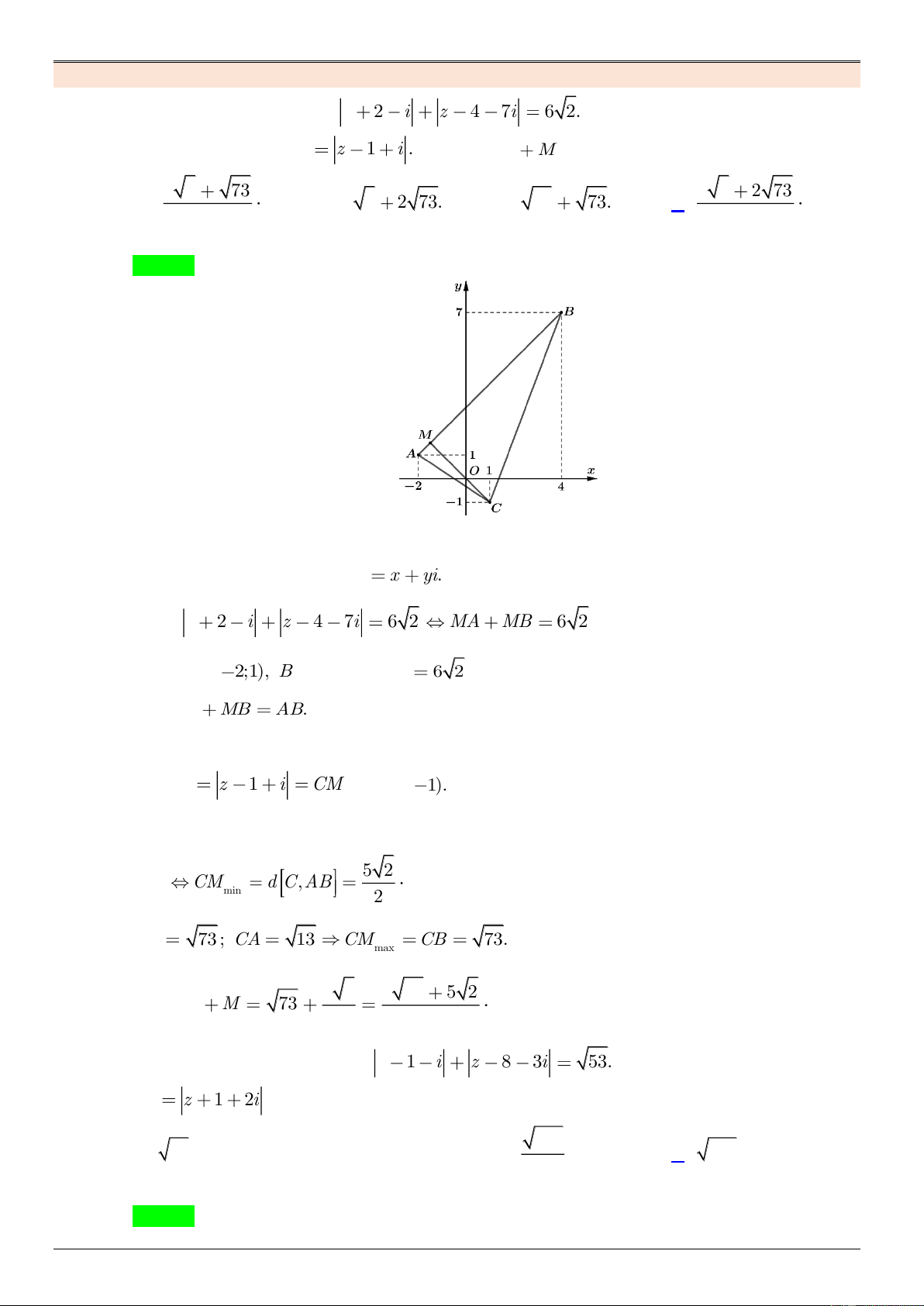
Câu 1: Xét các số phức z thỏa mãn z 2 i z 4 7i 6 2. Gọi ,
m M lần lượt là giá trị nhỏ nhất
và giá trị lớn nhất của T z
1 i . Giá trị của m M bằng 5 2 73 5 2 2 73 A. B. 5 2 2 73. C. 13 73. D. 2 2 Lời giải Chọn D N G U YỄN HOÀNG VIỆT
Gọi M(x;y) biểu diễn số phức z x y . i Ta có: z 2 i z 4 7i 6 2 MA MB 6 2 Trong đó ( A 2;1), (
B 4;7) và có AB 6 2 LUY Nên MA MB A . B ENT
Suy ra điểm M thuộc đoạn . AB H ITRA Ta có T z 1 i
CM với C(1; 1). C N G
Dựa vào hình vẽ, ta có: H IEM 5 2 .V T CM d C,AB min min N 2 CB 73 ; CA 13 CM CB 73. max 5 2 2 73 5 2 Suy ra m M 73 Chọn đáp án D. 2 2
Câu 2: Xét các số phức z thỏa mãn z 1 i z 8 3i
53. Giá trị lớn nhất của biểu thức P z 1 2i bằng. 185 A. 53. B. 53. C. . D. 106. 2 Lời giải Chọn D
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 31
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
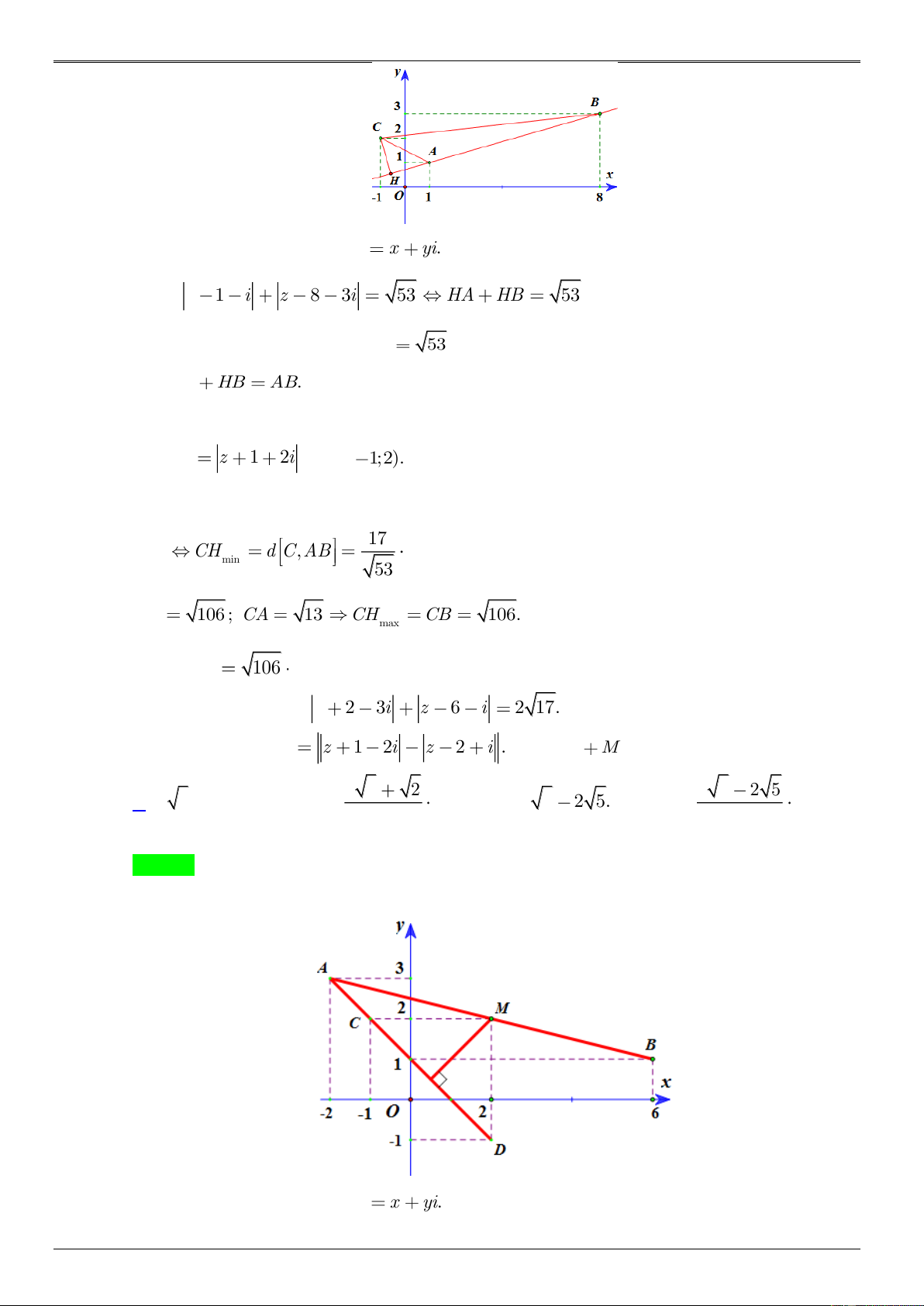
Gọi H(x;y) biểu diễn số phức z x y . i N G Ta có: z 1 i z 8 3i 53 HA HB 53 U YỄN Trong đó ( A 1;1), (
B 8;3) và có AB 53 HOÀ Nên HA HB A . B N G V
Suy ra điểm H thuộc đoạn . AB IỆT Ta có P z
1 2i với C( 1;2).
Dựa vào hình vẽ, ta có: 17 P CH d C,AB min min 53 CB 106 ; CA 13 CH CB 106. max Suy ra P 106 max Chọn đáp án D LUY
Câu 3: Xét các số phức z thỏa z 2 3i z 6 i
2 17. Gọi M, m lần lượt là giá trị lớn nhất và ENT P z i z i H giá trị nhỏ nhất của 1 2 2 . Giá trị m M bằng ITRA 3 2 2 6 2 2 5 C A. 3 2. B. C. 8 2 2 5. D. N 2 3 G H Lời giải IEM Chọn A .V N
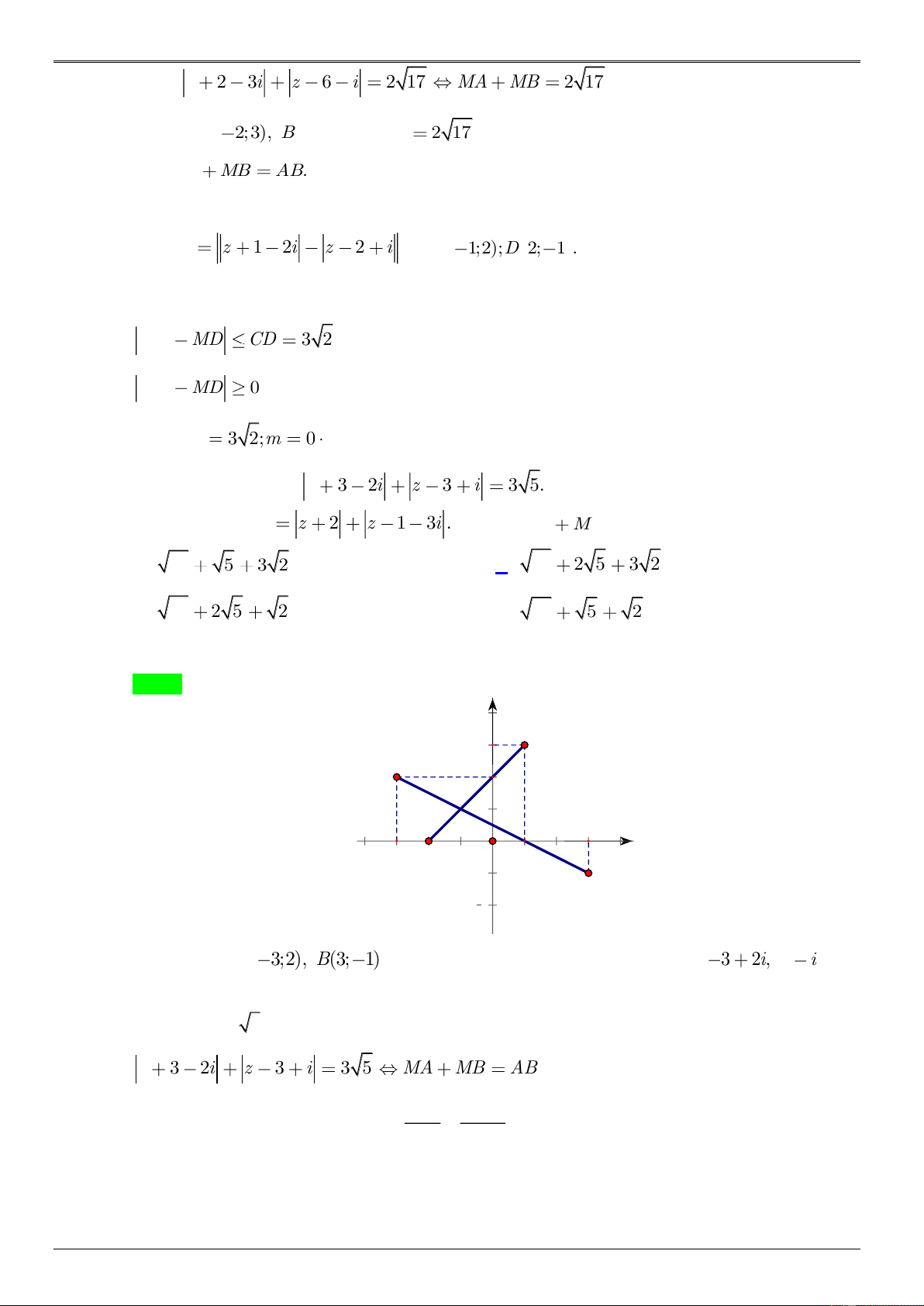
Gọi M(x;y) biểu diễn số phức z x y . i
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 32
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 Ta có: z 2 3i z 6 i 2 17 MA MB 2 17 Trong đó ( A 2;3), (
B 6;1) và có AB 2 17 Nên MA MB A . B
Suy ra điểm M thuộc đoạn . AB Ta có P z 1 2i z 2
i với C( 1;2);D 2; 1 . N G
Dựa vào hình vẽ, ta có C; D nằm về một phía của đường thẳng AB U YỄN MC MD CD 3 2 HOÀN MC MD 0 G VIỆ Suy ra M 3 2;m 0 Chọn đáp án A T Câu 4:
Xét các số phức z thỏa z 3 2i z 3 i
3 5. Gọi M, m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của P z 2 z
1 3i . Giá trị của m M bằng A. 17 5 3 2 . B. 26 2 5 3 2 . C. 26 2 5 2 . D. 17 5 2 . Lời giải LUY Chọn B 4 y ENT 3 D H ITRA 2 A C N G 3 -1 H I 10 5 -3 5 10 E O 1 x C M .V B N 2
Gọi M(x;y), ( A 3;2), (
B 3; 1) lần lượt là điểm biểu diễn các số phức z, 3 2 ,i 3 i 4
trong mặt phẳng tọa độ. Ta có: AB 3 5 z 3 2i z 3 i 3 5 MA MB
AB M nằm trên đoạn thẳng AB (1) x 3 y 2
Phương trình đường thẳng AB là:
x 2y 1 0 3 3 1 2 Gọi C 2
;0, D1;3 P MC MD
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 33
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
x 2y 1x 2y 1 2 2.0 1 1 2.3 1 1
8 0 C, D nằm về hai phía của C C D D
đường thẳng AB . (2)
Ta có: P MC MD CD 3 2
P nhỏ nhất P CD MC MD CD M nằm giữa CD (3)
Từ (1) và (3) suy ra: M là điểm chung của hai đoạn thẳng AB và CD .
M nằm trên đoạn thẳng AB M 1 2t;t ,t 0 t 3 N G
CM 3 2t;t ,CD 3;3 U YỄN 3 2t t cùng hướng tháa H
M nằm trên đoạn thẳng CD CM ,CD t 1( ) M 1; 1 O 3 3 ÀNG
Vì x x x nên điểm M nằm trên đoạn thẳng CD C M D VIỆT
Suy ra: Giá trị nhỏ nhất của là m 3 2 .
Từ (1) và (2) suy ra: P MC MD MaxAC A ; D BC B D
AC AD 5 17 BC BD 26 2 5
Do đó: Giá trị lớn nhất của P là M 26 25
M m 26 2 5 3 2 . Câu 5:
Xét các số phức z thỏa mãn iz 2i 2 z 1 3i
34. Giá trị nhỏ nhất của biểu thức P (1 i)z 2i bằng LUY 9 A. . B. 3 2 . C. 4 2.. D. 26 . E 17 N TH Lời giải ITRA Chọn C C N G H IEM.VN
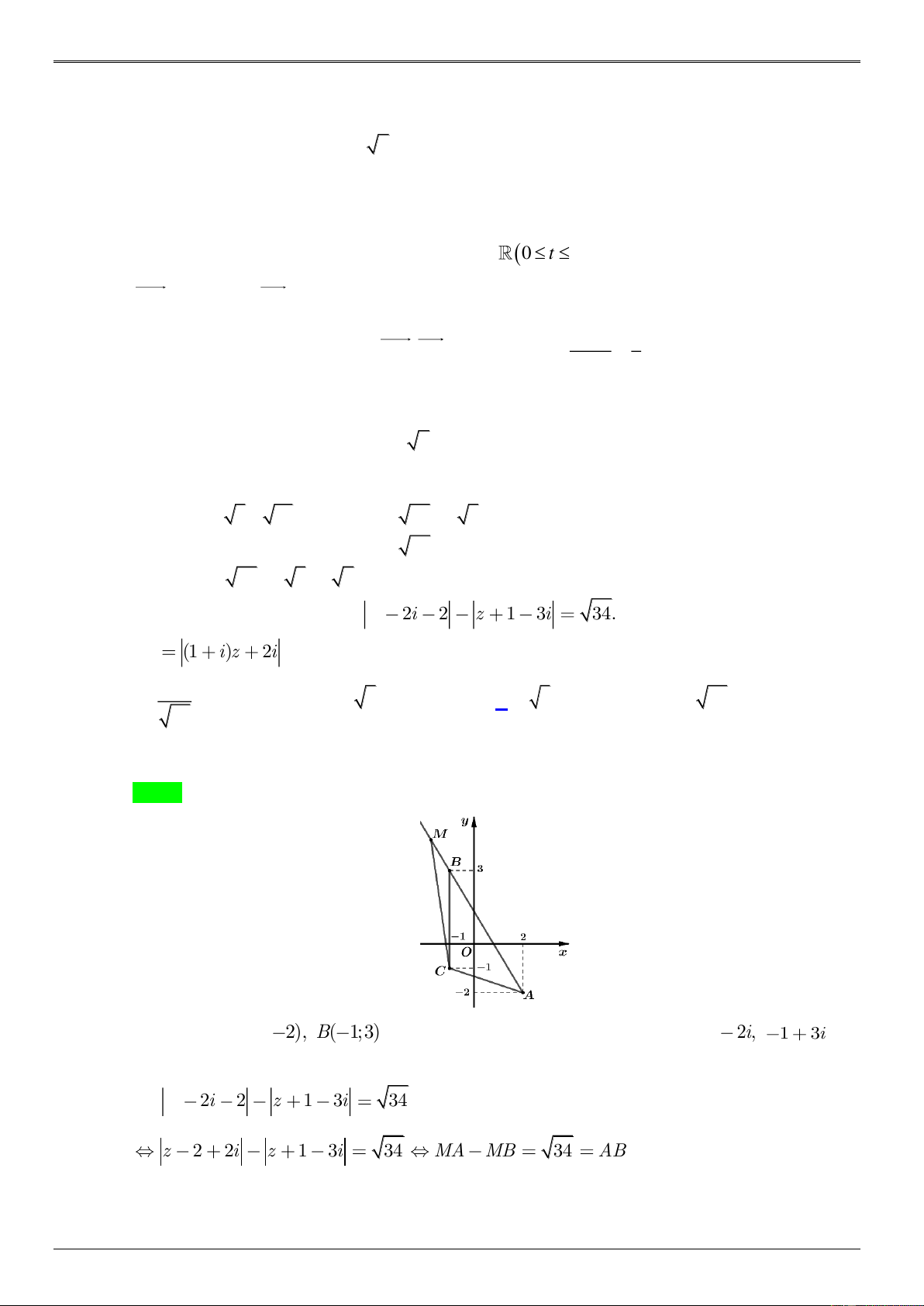
Gọi M(x;y), ( A 2; 2), (
B 1;3) lần lượt là điểm biểu diễn các số phức z, 2 2 ,i 1 3i
trong mặt phẳng tọa độ. Từ iz 2i 2 z 1 3i 34 z 2 2i z 1 3i 34 MA MB 34 AB
Suy ra M nằm trên tia đối của . BA
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 34
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 Ta có P 1 i z 2i 2 z 1 i 2MC với C 1; 1 . Có MC M B MC CB 4 P 4 2.. min min min Câu 6:
Xét các số phức z đồng thời thỏa mãn z 4 3i z 4 3i 10 và z 3 4i nhỏ nhất.
Môđun của số phức z bằng A. 5 . B. 5 2 . C. 6 2 . D. 10 . N Lời giải G U Y Chọn A 6 ỄN y H O 4 À M C N 3 G B V 2 IỆT 4 10 5 -4 3 5 10 O x 2 -3 A 4
Gọi M(x;y), ( A 4; 3), (
B 4;3) lần lượt là điểm biểu diễn các số phức z, 2 2 ,i 1 3i
trong mặt phẳng tọa độ. AB
AB 2 2 8;6 8 6 10 LUY Từ z 4 3i z 4 3i 10 EN MA MB 10 AB M , ,
A B thẳng hàng và B nằm giữa A và M THITRA Ta có z 3 4i
MC với C 3;4 . C N
Gọi H là hình chiếu của C lên đường thẳng AB . G H IE
Đường thẳng CH đi qua C và vuông góc với AB có phương trình là 4 x 3 y 0 M .VN x 4 y 3
Phương trình đường thẳng AB là
3 x 4 y 0 4 4 3 3
4 x 3y 0
Tạo độ điểm H là nghiệm của hệ phương trình
x y 0 H O0;0 3
x 4 y 0
Dễ thấy O là trung điểm của đoạn thẳng AB Do đó: z 3 4i
MC nhỏ nhất khi và chỉ khi M B
z i z 2 2 4;3 4 3 4 3 5. Câu 7: Xét các số phức z a bi ( , a b ) thỏa z 1 2i z 3i . Tính P a b khi T z 3 4i z
1 i đạt giá trị lớn nhất.
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 35
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 26 28 A. P 2 . B. P 6. C. P . D. P . 3 3 Lời giải Chọn D 2 2 2 2 z 1 2i z 3i a 1 b 2 a 3 b a b 2 0 Gọi M ;
a b là điểm biểu diễn số phức z a
bi M thuộc đường thẳng d : x y 2 0 N G U 2 2 Y
A3;4, B1; 1 AB 2 ; 5 ; AB 2 5 29 ỄN Gọi HO
Ta có: x y 2 x y ,
A B nằm về cùng phía với d (1) A A 2 B B 3 4 21 1 2 4 0 ÀNG 1 V d , A d
d B,d 2 2 (2) IỆ 2 T T z 3 4i z 1 i MA MB AB 29
Do đó: T lớn nhất khi T 29 M , ,
A B thẳng hàng và M nằm ngoài đoạn thẳng AB M , A MB cùng hướng (3)
M d b a 2 M ;
a a 2 MA 3 ; a 2 a 3 a 2 a 11
Từ (1), (2) và (3) suy ra M ,
A AB cùng hướng a 2 5 3 2 5 1 MA ; AB ( thỏa) LUY 3 3 3 11 17 28 E N a b a b T 3 3 3 H ITRA
DẠNG TOÁN 6. PARABOL C N Câu 1.
Xét hai số phức z , z thỏa mãn 2 z i z z 2i và z i 10 1 . Giá trị nhỏ nhất của biểu 1 2 1 1 1 2 G H I
thức z z bằng E 1 2 M .V A. 10 1. B. . C. . D. 3 5 1. N 101 1 101 1 Lời giải Chọn D
Gọi z a bi , a b . 1 2 Ta có 2 2 a z i z z i b . 1 1 1 4 1
Tập hợp điểm M biểu diễn z là parabol P 2 : y
x có đỉnh O 0;0 . 1 4
Ta có: z i 10 1 Tập hợp điểm N biễu diễn z là đường tròn C có tâm I 10; 1 , R 1. 2 2
Khi đó P z z MN là khoảng cách từ một điểm thuộc P đến một điểm thuộc C . 1 2
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 36
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
Ta có: MN NI MI MN MI NI MI 1 MN IM . min min 2 2 x 2 Mà 2
IM x 10 1 . 4 2 2 x 5
4 x 42 45 45 IM 45 3 5 . 4 2 N G U YỄN HOÀNG VIỆT Do đó MN 3 5 1. min Câu 2.
Xét các số phức z a bi a ,b thỏa mãn điều kiện z z i i z z 2 4 15 1 . Tính 1
P a 4b khi z
3i đạt giá trị nhỏ nhất. 2
A. P 4 .
B. P 5 .
C. P 6 .
D. P 7 . Lời giải Chọn D
z z i iz z 2 4 15 1
a bi a bi i ia bi a bi 2 4 15 1 . LUY E N
2 2 2 4 4 2 15 2 1 8 15 2 1 a a bi i i a b a b . TH 2 ITRA 2 4 C
Suy ra điểm M biểu diễn cho số phức z là Parabol có phương trình x x y . N 2 G H IE 1 M Gọi N ; 3 . .V 2 N 2 2 1 39 2 a 2 2 2 1 1
a a 10 1 2 4 39 z 3
i MN a a . 2 2 2 2 2 8 1 39 1 15 min z 3i khi a ; b
P a 4b 7 . 2 8 2 8 Câu 3.
Xét các số phức z a bi a ,b thỏa 2 z 3i z z 2i . Tính 8a 7b khi biểu thức 6 P z
i đạt giá trị nhỏ nhất. 7
A. 8a 7b 8.
B. 8a 7b 5 .
C. 8a 7b 6 .
D. 8a 7b 7 .
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 37
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 Lời giải Chọn D
Ta có: 2 z 3i z z 2i 2 a bi 3i a bi a bi 2i 2 a b 3i 2b 2i .
a b 32 b 2 1 2 2 1
b a 1. 8 Suy ra điể 1
m M biểu diễn cho số phức z là Parabol có phương trình 2 y x 1. 8 N G 6 U Gọi N 0; . Y Ễ 7 N HO 2 À 6 1 13 13 2 2 N
P z i MN a a . G 7 8 7 7 VIỆT 13 P
khi a 0, b 1 8a 7b 7 . min 7
DẠNG TOÁN 7. MỘT SỐ BÀI TOÁN KHÁC Câu 1:
Xét các số phức z thỏa mãn z
1. Giá trị lớn nhất của T z 1 2 z 1 bằng A. 2 5. B. 2 10. C. 3 2. D. 3 5. Lời giải Chọn A
Gọi số phức z x i y , với , x y . LUY E
Theo giả thiết, ta có z 1 2 2
x y 1. Suy ra 1 x 1. N THI 2 2 2 2 TRA
Khi đó, T 1 z 2 z 1 x
1 y 2 x
1 y 2x 2 2 2 2x. C N 2 2 G
Theo bất đẳng thức Bunhiacopxki: T 1 2
2x 2 2 2x
hay T 2 5 , với mọi H IE 1 x 1. M .VN 4 Vậy P
2 5 khi 2 2x 2 2 2x 3
x , y max 5 5 Câu 2:
Xét các số phức z thỏa z 1
2. Giá trị lớn nhất của T z i z 2 i bằng A. 4. B. 4 2. C. 8. D. 8 2. Lời giải Chọn A Cách 1:
Gọi số phức z x i y , với , x y
. gọi M là điểm trong mặt phẳng tọa độ biểu diễn số phức z.
Ta có z 1 2 x 2 2 1 y 2 .
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 38
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
Như vậy, tập hợp điểm M biểu diễn số phức z là đường tròn C tâm I 1;0 và bán kính R 2. Gọi A0; 1 , B 2;
1 lần lượt là các điểm biểu diễn các số phức z i
, z 2 i . Dễ thấy 1 2 ,
A B thuộc đường tròn C . Vì AB 2 2 2R nên AB là đường kính của đường tròn C 2 2 2
MA MB AB 8. Từ đó: N G 2 2 2 2 U
P z i z 2 i MA MB 1 1 MA MB 4. YỄN H MB MA MA 2 O Dấu " " xảy ra khi . À 2 2
MA MB 8 MB 2 N G VI Vậy max P 4. ỆT Cách 2.
T z i z 2 i z
1 1 i z 1 1 i .
Đặt w z 1. Ta có w 2 và T w 1 i w1 i .
Đặt w x . y i . Khi đó 2 2 2
w 2 x y . 2 2 2 2
T x 1 y
1 i x 1 y
1 i 1. x 1 y 1 1. x 1 y 1 LUY
x 2 y 2 x 2 y 2 2 2 1 1 1 1 1 1 2 2
2 2x 2 y 4 4 ENT Vậy . H maxT 4 ITRA C N Câu 3: Xét các số phức z a bi ( , a b
) có môđun bằng 2 và phần ảo dương. Tính giá trị của G H 2018 I S (5(a ) b 2) khi biểu thức P 2 z 3 2
z đạt giá trị lớn nhất. EM. A. S 0. B. S 1. C. 2018 S 2 . D. 1009 S 2 . VN Lời giải Chọn A
Gọi số phức z a i b , với a, b .
Theo giả thiết, ta có z 2 2 2
a b 4 . Suy ra 2 a 2. Khi đó, 2 2
P 2 z 3 2 z a 2 b a 2 2 3 2
b 8 4a 3 8 4a
Theo bất đẳng thức Bunhiacopxki: P 2 2 1 3
8 4a 8 4a
hay T 4 10 , với mọi 2 x 2.
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 39
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020 b 6 Vậy P
2 5 khi 3 8 4a 8 4a 8 5 a max 5 b 6 0 (lo¹i) 5 2018 8 6 2018 S (5(a b) 2) 5 2 0. 5 5
Câu 4. Xét các số phức z thỏa mãn 2 z 1 z
3i . Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất N G của P z i 2 z 4
7i . Giá trị M m bằng. U YỄN A. 10 2 5. B. 10 4 5. C. 20 2 5. D. 20 4 5. H O À Lời giải N G V Chọn D IỆT
Gọi z x yi với , x y
, gọi M là điểm trong mặt phẳng tọa độ biểu diễn số phức z . Ta có: 2 2
2 z 1 z 3i 2 x
1 yi x y 3i x 2 2 2 1 y
x y 3
x 2 y 2 2 3 20 .
Như vậy, tập hợp điểm M biểu diễn số phức z là đường tròn C tâm I 2;3 và bán kính R 2 5. Gọi A0;
1 , B 4;7 lần lượt là các điểm biểu diễn các số phức z i
, z 4 7i . Dễ thấy , A B 1 2
thuộc đường tròn C . Vì AB 4 5 2R nên AB là đường kính của đường tròn C LUY 2 2 2
MA MB AB 20 . EN Từ đó: THITRA
P z i 2 z 4 7i z i 2 z 4 7i MA MB 2 2 2 2 2 1 2
MA MB 10 . C N G MB 2MA MA 2 H Dấu " " xảy ra khi . I 2 2 E
MA MB 20 MB 4 M .VN Vậy M max P 10 .
Ta lại có P MA 2MB MA MB MB AB MB P 4 5 MB P min MB min M B m min P 4 5. Vậy M m 10 4 5.
Câu 5. Xét các số phức z thỏa z 4 z 4
10. Giá trị lớn nhất và nhỏ nhất của z lần lượt là A. 10 và 4. B. 5 và 4. C. 4 và 3. D. 5 và 3. Lời giải Chọn D Cách 1.
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 40
Max - Min Module Số Phức
NĂM HỌC 2019 – 2020
Gọi z x yi với ; x y .
Ta có 10 z 4 z 4 z 4 z 4 2z z 5 . Do đó max z 5. 2 2 Mà z z
x yi x yi x 2
y x 2 4 4 10 4 4 10 4 4 y 10.
Áp dụng bất đẳng thức Bunhiacopxki, ta có N G 2 2 2 2 2 2 2 2 2 2 U
10 1. x 4 y 1. x 4 y 1 1
x 4 y x 4 y Y ỄN H 2 2 2 2 O
10 22x 2y 32 22x 2y 32 100. ÀNG 2 2 2 2 V
x y 9 x y 3 z 3. IỆT Do đó min z 3. Cách 2. Gọi M ; x y , F 4
;0 , F 4;0 biểu diễn cho số phức z , 4 , 4. 1 1
Ta có MF MF 10 M chạy trên Elip có trục lớn 2a 10 a 5. 1 2 tiêu cự 2c F F 8 c 4. 1 2 trục nhỏ 2 2
2b 2 a c 2.3 6 b 3. LUY E
Mà z OM . Do đó giá trị lớn nhất, giá trị nhỏ nhất của z là 5 và 3. N THI TRA C N G H IEM.VN
Trên con đường thành công không có dấu chân của những kẻ lười biếng Trang 41
Document Outline
- GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC CHỨA MODUL SỐ PHỨC
- (((




