Giải chi tiết 50 câu trắc nghiệm số phức chọn lọc trong các đề thi thử – Nguyễn Thế Duy Toán 12

Giải chi tiết 50 câu trắc nghiệm số phức chọn lọc trong các đề thi thử – Nguyễn Thế Duy Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

47 24 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

20 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
CÁC CÔNG THỨC QUAN TRỌNG CẦN NẮM VỮNG
1 2 1 2
z z z z
1 2 1 2
. .z z z z
1 2 1 2
. .z z z z
1 1
2 2
z z
z z
z z z
2
.
z z z
2
1 2 1 2 1 2
. . . .z z z z z z
1
z
Re , Im
2 2
z z z z
z z
1 2 1 2 1 2
z z z z z z
1 2 1 2 1 2
z z z z z z
Re , Im
z z z z
45 CÂU TRẮC NGHIỆM + 5 CÂU VÍ DỤ MINH HỌA
Câu 1. Cho số phức
thỏa mãn điều kiện
2
2 .
4
z z
Đặt
2 2
8 12.
aP b
Mệnh đề nào dưới đây đúng?
A.
2
2
P z
. B.
2
2
4
P z
. C.
2
4
P z
. D.
2
2
2
P z
.
(THPT ĐẶNG THÚC HỨA - NGHỆ AN)
Lời giải
Cách 1. Đặt
2 2 2 2 2 2
, 2 4 4 2 .z a bi a b z a b abi z a b abi
Khi đó, giả thiết
2
2 2 2 2 2 2 2
4 2 4 4 4
z z a b a b a b
2
2 2 2 2 2 2
8 16 4
b a a b a b
2
2
4 2 2
2 2 2 2
4 4 4 4 2
P a b a b z z z
.
Cách 2. Từ giả thiết, ta có
2
2
2
2
2 2
2 4 4 4 4 .
4
z z z z z z z
2
2 2 2 2 2 2
. 4 4 16 4 . . 4. . 4 12 4
z z z z z z z z z z z z
2
22
2 2 2 2
. 2 12 4 12 4 2 1 .
z z z z z z z
Đặt
2 2 2 2
2 2 .
z a bi z a bi z z a b
Từ
1 , 2
suy ra
2
2
2 2
8 12 2 .
P b a z
Chọn D.
Câu 2. Cho các số phức
1 2
0, 0
z z
thỏa mãn điều kiện
1 2 1 2
2 1 1
.
z z z
z
Tính giá trị của biểu thức
1 2
2 1
.
z z
P
z z
TỔNG ÔN SỐ PHỨC
LỜI GIẢI CHI TIẾT 50 CÂU TRẮC NGHIỆM SỐ
PHỨC CHỌN LỌC TRONG CÁC ĐỀ
THI THỬ THPT QUỐC GIA – 2017
Tác giả - Nguyễn Thế Duy - https://www.facebook.com/theduy1995
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
A.
1
2
B.
2.
C.
2.
D.
3 2
.
2
(THPT ĐẶNGTHÚC HỨA - NGHỆ AN)
Lời giải
Cách 1. Ta có
1 2
1 2 1 2 1 2
1 2 1 2 1 2 1 2
22 1 1 1
2
z z
z z z z z z
z z z z z z z z
.
2
2 2
1 1 1
1 1 2 2
2 2 2
2. 2. 0 2. 2 0 1
z z z
z z z z i
z z z
hoặc
1
2
1
z
i
z
.
Khi đó
1 2
2 1
1 1 1 3 2
1 1 2 .
1 1 2
2
z z
P i i
z z i i
Cách 2. Chọn
1
1 2
2 2 2
2 1 1 1 3 2
2 .
2 2
zi
z i z P
i z i z z
Chọn D.
Câu 3. Cho số phức
0
z
thỏa mãn
2
3 1
1
iz i z
z
i
. Số phức
26
9
w iz
có môđun là
A.
9.
B.
26.
C.
6.
D.
5.
(THPT PHẠM HỒNG THÁI - HÀ NỘI)
Lời giải
Đặt
,z x yi x y
, khi đó giả thiết
2 2
3 1 1 .i x yi i x yi i x y
2 2 2 2
3 3 4 2 .xi y xi y x yi x y y x i x y x y i
2 2
2 2
4 1
2 2
x y x y
x y x y
. Lấy
1 2
, ta được
4 2 0 5 .x y x y x y
Thế
5x y
vào phương trình
1
, ta có
2
0 0
26 9 .
9 45
26 26
y x
y y
y x
Vậy
45 9 26 45 9
1 5 26.
26 26 9 26 26
z x yi i w i i i
Chọn C.
Câu 4. Cho số phức
z
thỏa mãn điều kiện
1 2.
z
Tìm giá trị lớn nhất của biểu thức
2 .T z i z i
A.
max 8 2.
T
B.
max 4.
T
C.
max 4 2.
T
D.
max 8.
T
(THPT CHU VĂN AN - HÀ NỘI)
Lời giải
Đặt
,z x yi x y
, ta có
2
2
1 2 1 2 1 2
z x yi x y
2
2 2 2 2 2
1 2 2 1 2 2 1x y x x y x y x
Lại có
2 1 2 1T z i z i x y i x y i
2 2 2
2 2 2 2 2
1 2 1 2 1 4 2 5
x y x y x y y x y x y
Kết hợp với
, ta được
2 2 2 6 2 2 2 2 2 2
T x y x y x y x y
Đặt
t x y
, khi đó
2 2 6 2T f t t t
với
1;1 .
t
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Ta có
max
1 1
' ; ' 0 1 1 4
2 2 6 2
f t f t t f t f
t t
. Chọn B.
Câu 5. Tìm môđun của số phức
z
biết
4 1 4 3z i z z i
.
A.
1.
z
B.
4.
z
C.
2.
z
D.
1
.
2
z
(SỞ GD&ĐT NAM ĐỊNH)
Lời giải
Cách 1. Từ giả thiết, ta có
4 4 3 1 3 4 4z z i z i zi z i z z i
Lấy môđun hai vế của
, ta được
1 3 4 4z i z z i
2 2 2 2
.1 3 4 4 10 4 4
z i z z z z z
2 2
2 2 2
10 4 4 8 32 4 2.
z z z z z z
Chọn C.
Cách 2. Ta biến đối
1 4 4
4 1 4 3
1 3
i z i
z i z z i z
i
Thử lần lượt với các đáp án, ta thấy
1 4 4 5 3 2 9 85
1 1
1 3 1 3 5 5 5
i i i
z z i z
i i
(loại).
4 1 4 4
8 4 12 4 10
4 1
1 3 1 3 5 5 5
i i
z z i z
i i
(loại).
2 1 4 4
6 2
2 2 2
1 3 1 3
i i
i
z z i z
i i
(chọn).
Câu 6. Cho số phức
0
z
sao cho
z
không phải là số thực và
2
1
z
w
z
là số thực. Tính
giá trị biểu thức
2
.
1
z
z
A.
1
.
5
B.
1
.
2
C. 2. D.
1
.
3
(THPT CHUYÊN QUỐC HỌC - HUẾ)
Lời giải
Cách 1. Tư duy nhanh.
w
là số thực
1
w
là số thực
1
z
z
là số thực.
Mà dễ thấy
z z
là số thực nên
2
2
1 1
. 1 1 1 .
2
1
z
z z z z z
z
z
Cách 2. Ta có biến đổi
2 2
2 2
. . . .
1 1
z z
z z z z z z z z z z z z
z z
2
2
0
1
. 1 1 .
. 1
2
1
z z
z
z z z
z z
z
Cách 3. Chọn
2
2
2
1 1
1 0 1 1 .
1 2 2
1
z
z
w z z z
z
z
Chọn B.
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Câu 7. Xét số phức
z
và số phức liên hợp của nó có điểm biểu diễn là
,M M
. Số phức
(4 3 )z i
và số phức liên hợp của nó có điểm biểu diễn lần lượt là
,N N
. Biết rằng
, , ,M M N N
là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của
4 5z i
A.
1
.
2
B.
2
.
5
C.
1
.
2
D.
4
.
13
(THPT CHUYÊN LÀO CAI)
Lời giải
Gọi
; ' ;
M x y M x y
và
4 3 ;3 4
4 3 4 3 3 4
' 4 3 ; 3 4
N x y x y
i z x y x y i
N x y x y
Dễ thấy
' 'MM NN
vì cùng vuông góc với
Ox
nên để
' 'MM N N
là hình chữ nhật.
Khi và chỉ khi
2 2
' '
' ' 0 4 5 5 4
MM NN
MN M N x y z x xi z i x x
MN Ox
Ta có
2 2 2
min
1 1 1 1
5 4 2 9 4 5 .
2 2 2
2
x x x z i
Chọn C.
Câu 8. Tính môđun của số phức
z
, biết
2
0
1
z
z i
iz
z i
.
A.
2
. B.
13
3
. C.
1
3
. D.
1
9
.
(THPT YÊN MÔ A - NINH BÌNH)
Lời giải
Dễ thấy
2
2
.
z
z z z z
z
, khi đó giả thiết
1
0 0
1 2
i z i
z i
iz z iz z
i
2
2 2 0 3 1 1iz z z i iz i i z z i
Đặt
,z x yi x y
suy ra
z x yi
, do đó
3 1 1.i x yi x yi i
0
3 0
3 3 1 2 3 3 1 .
1
2 3 1
3
x
x
xi y x yi x yi i x y xi i
x y
y
Vậy
1
.
3 3 3
i i
z z
Chọn C.
Câu 9. Xét số phức
z
thỏa mãn
10
1 2 2i z i
z
. Mệnh đề nào sau đây đúng?
A.
3
2
2
z
. B.
1 3
2 2
z
. C.
2
z
. D.
1
2
z
.
(THPT NHÂN CHÍNH - HÀ NỘI)
Lời giải
Cách 1. Từ giả thiết, ta có
10 10
1 2 2 1 2 2i z i i z i
z z
10 10
2 2 2 2 1z z i i z z i
z z
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Lấy môđun hai vế của
, ta được
2 2
10
2 2 1 .
z z
z
Đặt
t z
, ta có
2 2
2 2 4 2
10
2 2 1 5 5 10 2 0 1.
t t t t t t t
t
Vậy môđun của số phức
z
bằng
1 3
1 .
2 2
z
Cách 2. Sử dụng máy tính casio ( hướng dẫn chi tiết ở câu 26) để tìm
.z
Cách 3. Đặt
,z a bi a b
và
c z
, thay vào đẳng thức đã cho thì
2
2 2
10
10
1 2 2 1 2 2
10 10
2 2 1 0
a bi
Gt i c i i c i
a bi c
a b
c i c
c c
Suy ra
2 2
2
10 10
2 0 2
10 10
2 1 0 1 2
a a
c c
c c
b b
c c
c c
nên
2 2
2 2
4 2
10
10
2 1 2
a b
c c
c c
Giải ra ta có
1
c
mà
0
c
nên
1c
hay
1
z
. Do đó
1 3
.
2 2
z
Chọn B.
Câu 10. Cho số phức
z
thỏa mãn
1
3
z
z
. Tổng của giá trị lớn nhất và giá trị nhỏ nhất
của
z
là
A.
3.
B.
5.
C.
13.
D.
5.
(TOÁN HỌC & TUỔI TRẺ LẦN 8)
Lời giải
Ta có
2
2
1 1 1 1
a z a z z z
z z z z
2 2
4 2
2
2
2 2 2
2 1
1
.
z z z z z z
z
z z z
Khi đó
2 2
4 2 2
2
4 4
. 2 1 0 ;
2 2
a a a a
z z a z z z
.
Vậy
2 2
2
4 4
max ; min 4 13.
2 2
a a a a
z z M m a
Chọn C.
Câu 11. Xét số phức
z
thỏa mãn
2 1 3 2 2
z z i
. Mệnh đề nào dưới đây đúng?
A.
3
2.
2
z
B.
2.
z
C.
1
.
2
z
D.
1 3
.
2 2
z
(TOÁN HỌC & TUỔI TRẺ LẦN 8)
Lời giải
Cách 1. Sử dụng bất đẳng thức số phức, ta có
.u v u v u v
Khi đó
2 2 2 1 3 2 1 2 1
z z i z z i z i z z i z i
.
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
2 1 2 2 0 1
i z i z i z i z i z
.
Cách 2. Sử dụng hình học, giả sử điểm
,z x yi x y
có điểm biểu diễn là
;M x y
.
Số phức
1z
có điểm biểu diễn là
1;A x y
,
z i
có điểm biểu diễn là
; 1
B x y
.
Ta có
2 1 3 2 2 2. 3. 2. 1
z z i OA OB AB
vì
1; 1 2
AB AB
.
Mặt khác
2. 3. 2. 2. 2
OA OB OA OB OB AB OB
Từ
1 , 2
suy ra
0
2. 2. 0 0 0;0
1
x
AB AB OB OB OB O B z i
y
Vậy môđun của số phức
z
là
1.
z i
Chọn D.
Câu 12. Cho số phức
z
thỏa mãn
2
2 5 1 2 3 1
z z z i z i
.
Tính
min | |w
, với số phức
2 2w z i
.
A.
3
min | |
2
w
. B.
min | | 2
w
. C.
min | | 1
w
. D.
1
min | |
2
w
.
(THPT CHUYÊN LƯƠNG THẾ VINH - ĐỒNG NAI)
Lời giải
Ta có
2 2 2
2
2 5 1 4 1 2 1 2 1 2z z z z i z i z i
.
Khi đó, giả thiết
1 2
1 2 1 2 1 2 3 1
1 2 3 1
z i
z i z i z i z i
z i z i
TH1. Với
1 2z i
, ta có
2 2 1 2 2 2 1 1.
w z i i i w
TH2. Với
1 2 3 1z i z i
, đặt
,z x yi x y
, ta có
2 2 2 2
1
1 2 1 3 1 2 1 3 .
2
x y i x y i x y x y y
Do đó
2
1 3 9 3
2 2 2 2 2 2
2 2 4 2
w z i x i i x i w x
. Chọn A.
Câu 13. Cho số phức
z
thỏa mãn
1
z
. Tìm giá trị lớn nhất của biểu thức
1 2 1 .
T z z
A.
max 2 5.
T
B.
max 2 10.
T
C.
max 3 5.
T
D.
max 3 2.
T
(THPT CHUYÊN NGOẠI NGỮ - HÀ NỘI)
Lời giải
Cách 1. Gọi
,z x yi x y
;M x y
.
Và
1;0 , 1;0
A B
. Ta có
2 2
1 1 1.
z x yi x y
M
thuộc đường tròn đường kính
AB
.
2 2 2
4.
MA MB AB
Khi đó, theo Bunhiacopxki, ta có
2 2 2 2
2 1 2 5.4 2 5
T MA MB MA MB
Vậy giá trị lớn nhất của biểu thức
max 2 5
T
. Chọn A.
Cách 2. Đặt
2
2
, 1 1
z x yi x y z x y
và
2
2
1 1
z x y
.
Mặt khác
2 2 2 2
1 1 1
z x y x y
, khi đó
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
2 2
2 2
2 2
2 2 2 2
2 2
1 2 1
1 2 1 1
10 1 10.2 2 5 max 2 5.
T x y x y
x y x y
x y T
Câu 14. Cho
1
z
,
2
z
là hai số phức thỏa mãn
2 2
z i iz
, biết
1 2
1
z z
. Tính giá trị
của biểu thức
1 2
P z z
.
A.
3
.
2
P
B.
2.
P
C.
2
.
2
P
D.
3.
P
(THPT THANH CHƯƠNG I - NGHỆ AN)
Lời giải
Đặt
,z x yi x y
, ta có
2 2 2 2 1 2
z i iz x y i y xi
2 2
2 2 2 2 2 2
4 2 1 2 4 4 4 1 4 4
x y y x x y y y y x
2 2
1 2
1 1 1
x y z z z
. Sử dụng công thức (chứng minh ở câu 16)
2 2 2 2 2 2 2
1 2 1 2 1 2 1 2 1 2 1 2
2 2 3.
z z z z z z z z z z z z
Chọn D.
Câu 15. Cho ba số phức
1 2 3
; ;z z z
thỏa mãn điều kiện
1 2 3
1
z z z
và
1 2 3
0
z z z
.
Tính giá trị biểu thức
2 2 2
1 2 3
A z z z
.
A.
1
. B.
0
. C.
1
. D.
1 i
.
(THPT CHUYÊN BIÊN HÒA - HÀ NAM)
Lời giải
Ta có
2
2 2 2
1 2 3 1 2 3 1 2 2 3 3 1 1 2 2 3 3 1
2 2
A z z z z z z z z z z z z z z z z z z
1 2 3
1 2 3 1 2 3 1 2 3 1 2 3
1 2 3 1 2 3
1 1 1
2 2
z z z
z z z z z z z z z z z z
z z z z z z
Mặt khác
1 2 3 1 2 3
0 0
z z z z z z
suy ra
0.
A
Chọn B.
Câu 16. Với hai số phức
1
z
và
2
z
thỏa mãn
1 2
8 6z z i
và
1 2
2
z z
. Tìm giá trị lớn
nhất của
1 2
P z z
.
A.
5 3 5.
P
B.
2 26.
P
C.
4 6.
P
D.
34 3 2.
P
(THPT CHUYÊN KHOA HỌC TỰ NHIÊN - LẦN 4)
Lời giải
Bổ đề. Cho hai số phức
1
z
và
2
z
, ta luôn có
2 2 2 2
1 2 1 2 1 2
2z z z z z z
.
Chứng minh. Sử dụng công thức
2
1 2 1 2 1 2
z z z z z z
và
2
.
z z z
. Khi đó
2 2
1 2 1 2 1 2 1 2 1 2 1 2
1 1 1 2 1 2 2 2 1 1 1 2 1 2 2 2
2 2
1 1 2 2 1 2
. . . . . . . .
2 . . 2 .
z z z z z z z z z z z z
z z z z z z z z z z z z z z z z
z z z z z z đpcm
Áp dụng
, ta được
2
2 2 2
1 2 1 2 1 2 1 2
4 4 3 1 1.
z z z z z z z z
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Theo bất đẳng thức Bunhiacopxki, ta được
2 2
1 2 1 2
2 2 26.
P z z z z
Chọn B.
Câu 17. Cho
P z
là một đa thức với hệ số thực. Nếu số phức
z
thỏa mãn
0
P z
thì
A.
0.
P z
B.
1
0.
P
z
C.
1
0.
P
z
D.
P z
(THPT CHUYÊN TỈNH HÀ NAM)
Lời giải
Chọn hàm số
2
2 5P z z z
. Phương trình
2
1 2
0 2 5 0
1 2
z i
P z z z
z i
Xét với số phức
1 2z i
, ta có
1 2 5
z i
suy ra
2
2
2 5 5 2. 5 5 10 2 5 0.
P z z z
1 1 1 2
1 2 5 5
i
z i
suy ra
2
1 1 2 112 16
5 0.
25 25
P i
z z z
1 1 1 2
1 2 5 5
i
z i
suy ra
2
1 1 2 112 16
5 0.
25 25
P i
z z z
1 2z i
suy ra
2
2
2 5 1 2 2 1 2 5 0.
P z z z i i
Chọn D.
Câu 18. Cho số phức
z
thỏa mãn
1
z
. Đặt
2
.
2
z i
A
iz
Mệnh đề nào sau đây đúng?
A.
1.
A
B.
1.
A
C.
1.
A
D.
1.
A
(THPT CHUYÊN HÀ NAM)
Lời giải
Từ giả thiết, ta có
2
2 2 2 2
2
z i
A A iz z i A Azi z i
iz
2
2 2
2
A i
A i z Ai z
Ai
. Mà
2
1 1 2 2 .
2
A i
z A i Ai
Ai
Đặt
,A x yi x y
, khi đó
2 2 1 2
x y i y xi
2 2
2 2 2 2 2 2 2 2
4 2 1 2 4 4 4 1 4 4 1.
x y y x x y y x y y x y
Vậy môđun của
2 2
1.
A x y
Chọn A.
Câu 19. Cho số phức
z
thỏa mãn
2
2
z
và điểm
A
trong hình
vẽ bên là điểm biểu diễn của
z
. Biết rằng trong hình vẽ bên, điểm
biểu diễn của số phức
1
w
iz
là một trong bốn điểm
M
,
N
,
P
,
Q
. Khi đó điểm biểu diễn của số phức
w
là
A. điểm
Q
. B. điểm
M
.
C. điểm
N
. D. điểm
P
.
(THPT CHUYÊN ĐH VINH LẦN 1)
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Đặt
, 0
z x yi x y
, khi đó
2 2 2 2
2 1
2 2
z x y x y
và
x y
(hình vẽ)
Ta có
2 2
1
2 2 .
i x yi
i i y xi
w y x i
iz z x yi x yi x yi x y
Vì
, 0
x y
nên điểm biểu diễn số phức
w
là
2 ; 2y x
đều có hoành độ, tung độ âm.
Đồng thời
2 2 0
w w
x y y x x y
và
2 2
2 2 2w x y z
Dựa vào hình vẽ, điểm
P
chính là điểm cần tìm vì điểm
N
tuy thỏa mãn
0
w w
x y
nhưng độ dài
ON
xấp xỉ bằng độ dài
OA
. Chọn D.
Câu 20. Cho sô
phư
c
,z x yi x y
tho
a mãn
6 8 5
z i
và có môđun nhỏ nhâ
t.
Tinh tổng
.x y
A.
3.
x y
B.
1
x y
. C.
1x y
. D.
2
x y
.
(SỞ GD&ĐT QUẢNG NAM)
Lời giải
Dựa vào ví dụ, ta phát triển dạng toán Min – Max số phức như sau
Tập hợp các điểm
M z
thỏa mãn điều kiện
z a bi R
0
R
là đường tròn
C
có tâm
;I a b
và bán kính
R
.
Chứng minh. Gọi
z x yi
,
,x y
.
Theo giả thiết
z a bi R
x a y b i R
.
2 2 2 2
2
x a y b R x a y b R
Vậy tập hợp các điểm
M z
là đường tròn
C
có tâm
;I a b
và bán kính
R
.
Ví dụ 21. Trong các số phức
z
thỏa mãn điều kiện
2 4 5
z i
. Tìm
max z
.
A.
max 3 5
z
. B.
max 5
z
. C.
max 5
z
. D.
max 13
z
.
Hướng dẫn giải.
Tập hợp các điểm
M z
là đường tròn
C
có tâm
2;4
I
và bán kính
5
R
.
Vậy
2 2
max 2 4 5 3 5
z OM OI R
. Chọn A.
* Hỏi thêm:
a) Tìm
min z
.
2 2
min 2 4 5 5
z ON OI R
.
b) Tìm số phức
z
có môđun lớn nhất, nhỏ nhất.
Phương trình đường thẳng
OI
là
2y x
.
Tọa độ hai điểm
M
,
N
là nghiệm của hệ phương trình
2 2
2
2
2
1 3
; .
2 6
5 20 15 0
2 4 5
y x
y x
x x
y y
x x
x y
Số phức
z
có môđun lớn nhất là
3 6z i
tương ứng với điểm
3;6
M
.
Số phức
z
có môđun nhỏ nhất là
1 2z i
tương ứng với điểm
1;2
N
.
Ví dụ 22. Trong các số phức
z
thỏa mãn điều kiện
5 3
z i
. Nếu số phức
z
có môđun
nhỏ nhất thì phần ảo bằng bao nhiêu?
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
A.
0.
B.
3.
C.
2.
D.
4.
Hướng dẫn giải.
Tập hợp các điểm
M z
là hình tròn
C
tâm
0;5
I
và bán kính
3
R
.
Số phức
z
có môđun nhỏ nhất là
2z i
ứng với điểm
0;2
N
.
Chọn C.
Tổng quát. Trong các số phức
z
thỏa mãn
1 1
z z r
1
0
r
. Tìm giá trị lớn nhất và giá
trị nhỏ nhất của
2
P z z
.
Gọi
1
I z
;
2
N z
và
M z
. Tính
1 2 2
IN z z r
.
Khi đó,
1 1 2
max
P NM r r
và
2 1 2
min
P NM r r
.
Áp dụng.
Câu 1. (THPT CHUYÊN KHTN – LẦN 1) Trong các số phức
z
thỏa mãn điều kiện
1 1 7 2
i z i
. Tìm
max z
.
A.
max 4
z
. B.
max 3
z
. C.
max 7
z
. D.
max 6
z
.
Hướng dẫn giải.
Ta có
1 7
1 1 7 2 1 2 3 4 1
1
i
i z i i z z i
i
.
Vì
3 4 0 5
i
nên
1 2
max 1 5 6
z r r
. Chọn D.
Câu 2. Tìm giá trị lớn nhất của
z
biết rằng
z
thỏa mãn điều kiện
2 3
1 1
3 2
i
z
i
.
A.
max 1
z
. B.
max 2
z
. C.
max 2
z
. D.
max 3
z
.
Hướng dẫn giải.
Ta có
2 3 1
1 1 1 1 . 1 1
3 2
i
z iz i z z i
i i
.
Vì
0 1
i
nên
1 2
max 1 1 2
z r r
. Chọn B.
Câu 3. Trong các số phức
z
thỏa mãn điều kiện
2 4 2z i z i
. Biết rằng số phức
z x yi
,
,x y
có môđun nhỏ nhất. Tính
2 2
P x y
.
A.
10
P
. B.
8
P
. C.
16
P
. D.
26
P
.
Hướng dẫn giải.
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Gọi
z x yi
,
,x y
. Ta có
2 4 2 2 4 2z i z i x y i x y i
2 2 2
2
2 4 2
x y x y
2 2 2 2
4 4 8 16 4 4
x x y y x y y
4 4 16 0 4
x y y x
.
Do đó
2 2
2 2 2 2
4 2 8 16 2 2 8 2 2
z x y x x x x x
.
Dấu
" "
xảy ra
2 2
x y
. Vậy
2 2
2 2 8
P
. Chọn B.
Câu 4. (ĐỀ THTT LẦN 5 – 2017) Cho số phức
z
thỏa mãn
4 4 10.
z z
Giá trị lớn
nhất và giá trị nhỏ nhất của
z
lần lượt là
A.
10
và
4
B.
5
và
4
C.
4
và
3
. D.
5
và
3
.
Hướng dẫn giải.
Gọi
z x yi
,
,x y
. Theo giả thiết, ta có
4 4 10.
z z
2 2
2 2
4 4 10 4 4 10x yi x yi x y x y
Gọi
;M x y
,
1
4;0
F
và
2
4;0
F
.
Khi đó
1 2
10
MF MF
nên tập hợp các
điểm
M z
là đường elip
E
.
Ta có
4
c
;
2 10 5
a a
và
2 2 2
9
b a c
.
Do đó, phương trình chính tắc của
E
là
2 2
1
25 9
x y
.
Vậy
max ' 5
z OA OA
và
min ' 3
z OB OB
. Chọn D.
Câu 5. Biết số phức
z x yi
,
,x y
thỏa mãn đồng thời điều kiện
3 4 5
z i
và biểu thức
2 2
2
P z z i
đạt giá trị lớn nhất. Tính
z
.
A.
33
z
. B.
50
z
. C.
10
z
. D.
5 2
z
.
Hướng dẫn giải.
Tập hợp các điểm
M z
là đường tròn
C
có tâm
3;4
I
và bán kính
5
R
.
Ta có
2 2
2 2
2 2
2 1 2 1
P x yi x y i x y x y
.
4 2 3 4 2 3 0 x y x y P
.
Ta tìm
P
sao cho đường thẳng
và đường tròn
C
có điểm chung
; .d I R
12 8 3
5 23 10
20
P
P
10 23 10 13 33
P P
.
Do đó
max 33
P
. Dấu
" "
xảy ra
2 2
4 2 30 0
5
5
3 4 5
x y
x
y
x y
.
Vậy
2 2
5 5 5 2
z
. Chọn D.
Câu 23. Cho hai số phức
1
z
,
2
z
thoả mãn điều kiện
1 2 1 2
1
z z z z
.
Tính giá trị của biểu thức
2 2
1 2
2 1
z z
P
z z
.
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
A.
1P i
. B.
1P i
. C.
1P
. D.
1P i
.
(SỞ GD&ĐT QUẢNG NINH)
Lời giải
Từ giả thiết, ta có
1 1
1 2 1 2
2 2
1 1 1
z z
z z z z
z z
.
Đặt
1
2
,
z
w x yi x y
z
, khi đó
2 2
2 2
2 2
2
2
1
1
1
2
3
2
1 1
2
x
x y
x y
x y x
x y
y
Khi đó
2 2
2
2
1 1 3 1 3
1.
2 2 2 2
i i
P w
w
Chọn C.
Câu 24. Tính tích môđun của tất cả các số phức
z
thỏa mãn
2 1 1 ,z z i
đồng thời
điểm biểu diễn
z
trên mặt phẳng tọa độ thuộc đường tròn tâm
1;1
I
, bán kính
.5R
A.
5
. B.
3
. C.
53
. D.
1
.
(SỞ GD&ĐT THANH HÓA)
Lời giải
Đặt
,z x yi x y
, khi đó
2 1 1 2 1 2 . 1 1 .z z i x y i x y i
2 2 2
2 2 2
2 1 4 1 1 3 3 6 2 1 0 1 .
x y x y x y x y
Mà điểm biểu diễn
2 2
2 2
: 1 1 5 2 2 3 0 2
z
M C x y x y x y
.
Lấy
1 3. 2
, ta được
2 2 2 2
3 3 6 2 1 3 3 6 6 9 0 1
x y x y x y x y y
Thế
1
y
vào phương trình
2
, ta có
1
2
1 2
2
0
2 0 . . 2 5.
2 2
z i
x
x x z z i i
x z i
Chọn C.
Câu 25. Cho các số phức
,z w
thỏa mãn
2 2 4 , 1z i z i w iz
. Giá trị nhỏ nhất của
biểu thức
w
là
A.
2
2
. B.
2 2
. C.
2
. D.
3 2
2
.
(THPT CHUYÊN ĐH VINH - LẦN 2)
Lời giải
Đặt
,z a bi a b
, khi đó
2 2 2 2z i a b i
và
4 4z i a b i
.
Nên ta có
2 2 2
2
2 2 4 2 2
a b a b a b b a
Khi đó
2 2
2 2
1 1 1 1 1
w iz a bi i b ai w a b a a
.
Dễ thấy
2
2
2
1 1 1 2 2
1 2 min .
2 2 2 2 2
w
a a a w
Chọn A.
Câu 26. Gọi
1
z
,
2
z
là hai nghiệm của phương trình
2
1 0
z z
.
Tính giá trị của biểu thức
2017 2017
1 2
P z z
.
A.
1P
. B.
1P
. C.
0
P
. D.
2P
.
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
(THPT CHUYÊN KHOA HỌC TỰ NHIÊN - LẦN 4)
Lời giải
Ta có
2017 2017
2 3
1 2
1 3
1 0 1 1 2.
2 2
i
z z z z z P z z
Chọn D.
Câu 27. Cho số phức
z
thỏa mãn
2 3 1 2 7i z i z i
. Tìm môđun của
z
.
A.
5
z
. B.
1
z
. C.
3
z
. D.
2
z
.
(THPT CHUYÊN KHOA HỌC TỰ NHIÊN - LẦN 4)
Lời giải
Cách 1. Đặt
,z a bi a b
, khi đó giả thiết trở thành
2 3 1 2 7
5 7
5 3 7
3 1
2
2 5.
1
Gt i a bi i a bi i
a b
a b a b i i
a b
a
z i z
b
Cách 2. Xử lý bằng casio giống bài toán sau: Cho số phức
2 3 1 9z i z i
. Tích phần
thực và phần ảo của số phức
z
bằng
A.
2.
B.
1.
C.
1.
D.
2.
Đặt
z X Yi z X Yi
. Khi đó
2 3 1 9 0w X Yi i X Yi i
.
Thao tác trên máy tính
Màn hình hiển thị
Ấn
w 2
Đưa về tính số phức.
Nhập vế trái của phương trình
.
2 3 1 9X Yi i X Yi i
.
Sau đó, gán giá trị
100, 0, 01X Y
.
Ấn
r 100
r 0
q 0.01 =
.
Khi đó
10103 29097
101, 03 290, 97 .
100 100
w i i
Mặt khác, ta có
101, 03 100 1 0, 03 3 1
.
290, 97 300 9 0, 03 3 3 9
X Y
X Y
3 1 2
3 1 3 3 9 0 .
3 1
X Y X
w X Y X Y i
X Y Y
Câu 28. Có bao nhiêu số phức
z
thỏa mãn đồng thời điều kiện
. 2
z z z
và
2
z
?
A.
2.
B.
4.
C.
3.
D.
1.
(THPT CHUYÊN LAM SƠN - THANH HÓA)
Lời giải
Đặt
2 2
; . .z a bi a b z a bi z z a bi a bi a b
Khi đó, giả thiết
2 2
2 2
2 2
2
2
4
2
4
.
4 2
4 4
2
a b
a b a bi
a b
a bi
a b
a bi
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
2 2
2 2
2
2
4
2
4
2.
0
2
4 0
a b
a
a b
z
b
a
a a
Chọn D.
Câu 29. Cho số phức
w
và hai số thực
a
,
b
. Biết
1
2z w i
và
2
2 3
z w
là hai
nghiệm phức của phương trình
2
0
z az b
. Tính
1 2
T z z
.
A.
2 13
T
. B.
2 97
3
T
. C.
2 85
3
T
. D.
4 13
T
.
(THPT CHUYÊN LÊ QUÝ ĐÔN - QUẢNG TRỊ)
Lời giải
Đặt
1
2
2 2
; .
2 3 2 3 2
z w i m n i
w m ni m n
z w m ni
Ta có
1 2
3 3 3 2
z z m n i a
là số thực
2
3 2 0
.
3
3 3 0
1
n
n
m
m
Lại có
1 2
4 4
. 2 3
3 3
z z m i m i b
là số thực
4 4
. 2 3 0 3.
3 3
m m m
Do đó
1 2 1 2
4 4 2 97
3 ; 3 .
3 3 3
z i z i T z z
Chọn B.
Câu 30. Cho số phức
z
thỏa mãn
1 2z z i
là một số thuần ảo. Tập hợp điểm biểu
diễn số phức
z
là một đường tròn có diện tích bằng
A.
5
. B.
5
4
. C.
5
2
. D.
25
.
(THPT CHUYÊN NGUYỄN BỈNH KHIÊM - QUẢNG NAM)
Lời giải
Đặt
2 2
; 1 2 2 2 2 .z x yi x y z z i x y x y x y i
Theo giả thiết
1 2z z i
là số thuần ảo, suy ra
2
2
2 2
2 2
2 2 0
1 5 1 5
2 1 1 .
4 4 2 4
2 0
x y
x x y y x y
x y x y
tập hợp điểm biểu diễn số phức
z
là một đường tròn có diện tích bằng
5
.
4
Chọn B.
Câu 31. Gọi
M
là điểm biểu diễn số phức
2
1z z
w
z
, trong đó
z
là số phức thỏa mãn
1 2 2 3i z i i z
. Gọi
N
là điểm trong mặt phẳng sao cho
, 2
Ox ON
, trong đó
,
Ox OM
là góc lượng giác tạo thành khi quay tia
Ox
tới vị trí tia
OM
. Điểm
N
nằm trong góc phần tư nào?
A. Góc phần tư thứ
I
. B. Góc phần tư thứ
IV
.
C. Góc phần tư thứ
III
. D. Góc phần tư thứ
II
.
(THPT CHUYÊN NGUYỄN QUANG DIỆU - ĐỒNG THÁP)
Lời giải
Từ giả thiết, ta có
1 2 2 3 2 2 2 3i z i i z z i iz i z
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
3 6
2 3
5 5
i z i z i
2
1 33 56
.
45 45
casio
z z
w w i
z

Sử dụng lý thuyết nếu
; tan
y
z x yi P x y
x
với
là góc tạo bởi chiều dương
trục hoành với vectơ
OM
.
Khi đó
33 56 56 3696 2047
tan sin 2 ; cos 2 .
45 45 33 4225 4225
w i
Vậy điểm
N
thuộc góc phần tư thứ
.IV
Chọn B.
Câu 32. Cho số phức
z
thỏa mãn
2 3 1 z i
. Giá trị lớn nhất của
1 z i
là
A.
13 2
. B.
4
. C.
6
. D.
13 1
.
(THPT CHUYÊN PHAN BỘI CHÂU - NGHỆ AN)
Lời giải
Đặt
,z a bi a b
, ta có
2 3 1 2 3 1.
z i a b i
2 2 2 2
2 3 1 2 3 1a b a b
Đặt
2 sin
3 cos
a t
b t
(vì
2 2
sin cos 1t t
). Khi đó
1 1 1 .z i a b i
2 2
1 1a b
xét biểu thức
2 2
1 1 .P a b
Ta có
2 2 2 2
2 2
1 1 sin 3 cos 2 sin 6sin 9 cos 4cos 4a b t t t t t t
2 2
sin cos 13 6sin 4cos
14 6sin 4cos
t t t t
t t P
Theo bất đẳng thức Bunhiacopxki, ta được
2
2 2 2 2
6sin 4cos 6 4 sin cost t t t
2
6sin 4cos 52 6sin 4cos 52 2 13 14 2 13.
t t t t P
Vậy
2
2 2
1 1 1 14 2 13 13 1 13 1.
z i a b
Chọn A.
Câu 33. Có bao nhiêu số phức
z
thỏa mãn
2
z i
và
2
z
là số thuần ảo.
A. 3. B. 1. C. 4. D. 2.
(THPT CHUYÊN PHAN BỘI CHÂU - NGHỆ AN)
Lời giải
Đặt
,z x yi x y
, khi đó
2
2
2 1 2 1 2z i x y i x y
Ta có
2
2 2 2
2z x yi x y xyi
là số thuần ảo nên
2 2
0
0
0
2 0
x y
x y
x y
xy
TH1. Với
x y
, thế vào
, ta được
2
2 2
1 3
1 2 2 2 1 0 .
2
x x x x x
TH2. Với
x y
, thế vào
, ta được
2
2 2
1 3
1 2 2 2 1 0 .
2
x x x x x
Vậy có
4
số phức thỏa mãn yêu cầu bài toán. Chọn C.
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Câu 34. Cho hai số phức
1
z
,
2
z
thỏa mãn
1 2
, 0
z z
;
1 2
0
z z
và
1 2 1 2
1 1 2
z z z z
. Tính
giá trị của biểu thức
1
2
z
z
.
A.
2
2
. B.
3
2
. C.
2 3
. D.
2
3
.
(THPT CHUYÊN QUANG TRUNG)
Lời giải
Từ giả thiết, ta có
1 2
1 2 1 2 1 2
1 2 1 2 1 2 1 2
21 1 2 1
2
z z
z z z z z z
z z z z z z z z
2 2 2 2
1 2 1 1 2 1 2 2 1 1 2 2
2 2 2 2 0.
z z z z z z z z z z z z
2
1 1 1 1
2 2 2 2
1 1 2
2 2 1 0 .
2 2 2 2 2
z z z zi i
z z z z
Chọn A.
Câu 35. Cho thỏa mãn
z
thỏa mãn
10
2 1 3i z i
z
. Biết tập hợp các điểm biểu
diễn cho số phức
3 4 1 2w i z i
là đường tròn
I
, bán kính
R
. Khi đó
A.
1; 2
., 5
I R
B.
1;2 ,
.5
I R
C.
1;2 , 5.
I R
D.
1; 2 , 5.
I R
(THPT CHUYÊN QUANG TRUNG)
Lời giải
Từ giả thiết, ta có
10 10
2 1 3 2 1 3i z i z z i
z z
Lấy môđun hai vế
, ta được
2 2
10
2 1 3 1
z z z
z
.
Lại có
3 4 1 2 1 2 3 4 1 2 3 4
w i z i w i i z w i i z
1 2 3 4 . 5 5
w i i z z
tập hợp các điểm biểu diễn cho số phức
w
là đường
tròn tâm
1;2
I
và bán kính
5
R
. Chọn C.
Câu 36. Cho số phức
z
thỏa mãn
3 4 4 3 5 2 0
z i z i
. Giá trị của
z
là
A.
2
. B.
2
. C.
2 2
. D.
1
.
(THPT HÀ HUY TẬP)
Lời giải
Cách 1. Đặt
,
z x yi x y z x yi
, dựa vào giả thiết tìm nghiệm
,x y
Cách 2. Ta có, giả thiết
5 2 5 2
3 4 4 3 3 4 4 3i z i z z i
z z
Lấy môđun hai vế, ta được
2 2
5 2
3 4 4 3z z
z
mà
z z
, khi đó
2 2
2
50
3 4 4 3z z
z
đến đây có thể giải trực tiếp bằng cách đặt
t z
Hoặc sử dụng máy tính casio bằng việc thử các đáp án, để thấy được
1.
z
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Cách 3. Ta có biến đổi
2
3 4 3 4
5 2 5 2
3 4 4 3 .
5 2
i z i z
i z i z z
z z
Thử lần lượt với các đáp án, ta thấy
3 4 .4 3 4 .2
2 2 11 2
2 10
5 5
5 2
i i
z z i z
(loại).
3 4 .2 3 4 . 2
4 3 2 3 4 2
2 3
5 5
5 2
i i
z z i z
(loại).
3 4 .8 3 4 .2 2
2 2 6
5 2
i i
z z z
(loại).
3 4 3 4 2 7 2
1 2 1
10 10
5 2
i i
z z z i z
(chọn). Chọn D.
Câu 37. Cho số phức
z
thỏa mãn điều kiện
3 4 2.
z i
Trong mặt phẳng
Oxy
tập hợp
điểm biểu diễn số phức
2 1w z i
là hình tròn có diện tích bằng
A.
9
S
. B.
12
S
. C.
16
S
. D.
25
S
.
(THPT TRẦN HƯNG ĐẠO - NINH BÌNH)
Lời giải
Cách 1. Đặt
,w x yi x y
, ta có
2 1 2 1 1 1 .
x yi z i z x y i
Từ giả thiết, ta thấy rằng
3 4 2 2 . 3 4 4 2 6 8 4 2 .
z i z i z i
Từ
1 , 2
suy ra
1 1 6 8 4 7 9 4
x y i i x y i
2 2 2 2
7 9 4 7 9 16
x y x y
Vậy tập hợp điểm biểu diễn số phức
w
là hình tròn bán kính
2
4 16 .
R S R
Cách 2. Ta có
1 1
2 1 3 4 3 4
2 2
w i w i
w z i z i z i
7 9
7 9 7 9
3 4 3 4 2 7 9 4.
2 2 2
w i
w i w i
z i z i w i
tập hợp điểm biểu diễn số phức
w
là hình tròn bán kính
4 16 .
R S
Chọn C.
Câu 38. Biết số phức
, ,z x yi a b
thỏa mãn điều kiện
2 4 2z i z i
đồng
thời có môđun nhỏ nhất. Tính giá trị biểu thức
2 2
.M x y
A.
8
M
. B.
10
M
. C.
16
M
. D.
26
M
.
(THPT CHUYÊN VÕ NGUYÊN GIÁP - QUẢNG BÌNH)
Lời giải
Đặt
,z x yi x y
, ta có
2 4 2 4z i x y i
và
2 2 .z i x y i
Mặt khác
2 4 2z i z i
nên suy ra
2 2 2
2
2 4 2
x y x y
.
2 2 2 2
4 8 20 4 4 4 4 .x y x y x y y x y y x
Khi đó
2 2
2 2 2 2
4 2 8 16 2 2 8 2 2.
z x y x x x x x
Vậy môđun nhỏ nhất của
z
là
2 2.
Xảy ra
2 8.
x y M
Chọn A.
Câu 39. Gọi
H
là hình biểu diễn tập hợp các số phức
z
trong mặt phẳng tọa độ
Oxy
sao
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
cho
2 3
z z
, và số phức
z
có phần ảo không âm. Tính diện tích hình
H
.
A.
3 .
B.
3
.
4
C.
3
.
2
D.
6 .
(THPT CHUYÊN VÕ NGUYÊN GIÁP - QUẢNG BÌNH)
Lời giải
Đặt
,z x yi x y
, ta có
2 2 2 2 3z z x yi x yi x yi x yi x yi
Khi đó
2 2 2 2
2 3 3 3 9 3 9 9.
z z x yi x y x y
Mặt khác
z
có phần ảo không âm nên
0
y
. Vậy hình
H
tạo bởi
2 2
9 9
.
0
x y
y
Xét đường Elip có phương trình
2 2
2 2
: 9 9 1
9 1
x y
E x y
có độ dài hai bán trục lần
lượt là
3, 1a b
nên diện tích
E
là
3
E
S ab
.
Hình
H
giới hạn bởi hình
E
phía trên trục
0
Ox y
nên
3
.
2 2
E
S
S
Chọn C.
Câu 40. Trong các số phức
z
thỏa mãn
2 4 2
z i
, gọi
1
z
và
2
z
là số phức có môđun
lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức
1
z
và
2
z
bằng
A.
8 .i
B.
4.
C.
8.
D.
8.
(SỞ GD&ĐT HÀ TĨNH)
Lời giải
Tập hợp các điểm
M z
là đường tròn
C
có tâm
2;4
I
và bán kính
2.
R
Vậy
2 2
max 2 4 2 2 2 5.
z OM OI R
2 2
min 2 4 2 2 5 2.
z ON OI R
Tìm số phức
z
có môđun lớn nhất, nhỏ nhất.
Phương trình đường thẳng
OI
là
2 .y x
Tọa độ hai điểm
M
,
N
là nghiệm của hệ phương trình
2 2
2
2
2
2
5 20 16 0
2 4 2
y x
y x
x x
x y
2 4
; 2 ;4
5 5
x y
hoặc
2 4
; 2 ;4 .
5 5
x y
Số phức
z
có môđun lớn nhất là
2 4
2 4
5 5
z i
tương ứng
2 4
2 ;4 .
5 5
M
Số phức
z
có môđun nhỏ nhất là
2 4
2 4
5 5
z i
tương ứng
2 4
2 ;4 .
5 5
N
Vậy tổng phần ảo của hai số phức là
4 4
4 4 8.
5 5
Chọn D.
Câu 41. Cho số phức
;z w
khác 0 sao cho
2 .z w z w
Phần thực của số phức
.
z
u
w
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
A.
1
.
8
a
B.
1
.
4
a
C.
1.
a
D.
1
.
8
a
(THPT CHUYÊN ĐH VINH – LẦN 3)
Lời giải
Sử dụng công thức
1
z
với
1 2
,z z
.
Giả sử
;u a bi a b
. Từ giả thiết, suy ra
1
.
2
1 1 1.
z
z
u
w w
z w
z w z
u
w w w
2 2
2
2
2
2
1
3 3 1
4
1 1 2 .
4 4 8
1 1
a b
a a a a
a b
. Chọn D.
Câu 42. Cho số phức
z
thỏa mãn
4
3 4 8
i z
z
. Trên mặt phẳng tọa độ, khoảng cách
từ gốc tọa độ đến điểm biểu diễn số phức
z
thuộc tập nào?
A.
9
4
B.
1 5
; .
4 4
C.
1
0; .
4
D.
1 9
; .
2 4
(SỞ GD&ĐT BẮC NINH)
Lời giải
Ta có
4 4
3 4 8 3 4 8i z i z
z z
.
Lấy môđun hai vế của
và sử dụng công thức
1 2 1 2
. .z z z z
, ta được
2 2
4 1 1
3 4 8 3 4 . 4 2 5 4 2
5 4 2 1 5 8 4 0 2.
i z i z z
z z z
z z z z z
Gọi
;M x y
là điểm biểu diễn số phức
z
2 2
1 9
2 ; .
2 4
OM x y z
Chọn D.
Câu 43. Cho số phức
z
có môđun
1.
z
Giá trị lớn nhất của biểu thức
1 3 1 .P z z
A.
3 10.
B.
2 10.
C.
6.
D.
4 2.
(SỞ GD&ĐT BẮC NINH)
Lời giải
Đặt
,z x yi x y
, ta có
2 2 2 2
1 1 1
z x y x y
. Khi đó
2 2
2 2
2 2 2 2
1 3 1 1 3 1
2 1 3 2 1
2 2 3 2 2 .
P z z x y x y
x y x x y x
x x
Theo bất đẳng thức Bunhiacopxki, ta có
2
2 2
2 2 3 2 2 1 3 2 2 2 2 40
x x x x
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Suy ra
max
2 2 3 2 2 40 2 10 2 10
P x x P
. Chọn B.
Câu 44. Nếu hai số phức
1 2
,z z
thỏa mãn
1 2
1
z z
và
1 2
1
z z
thì số phức
1 2
1 2
1
z z
w
z z
có phần ảo bằng
A.
0.
B.
1.
C.
1.
D.
2.
Lời giải
Ta có
2
1 1 1 1
1
1
. 1z z z z
z
, tương tự ta cũng có
2
2
1
.
z
z
Khi đó
1 2 1 2 1 2
1 2 1 2
1 2
1 1
1 1
1 . 1
1 .
z z z z z z
w w w
z z z z
z z
là một số thực. Chọn A.
Câu 45. Cho số phức
z
thỏa mãn điều kiện
1
z
. Gọi
,M m
lần lượt là giá trị lớn nhất
của biểu thức
2
1 1
P z z z
. Tổng
M m
gần với giá trị nào sau đây nhất?
A.
3.
B.
4.
C.
6.
D.
5.
Lời giải
Đặt
1
t z
với
0;2
t
nên
2
2
2
2
1 1 1 2 2Re Re .
2
t
t z z z z z
Ta có
2 2
1 7 2z z t
, khi đó
2
7 2P f t t t
với
: 0;2 .
f
Vậy
7 7 7 7
3 .
2 2 6 6
f P f
7 7
3 5,11.
6 2
M m
Chọn D.
Đồ thị hàm số
2
7 2f t t t
như hình vẽ bên

Lời kết. Bản tài liệu làm trong thời gian ngắn, khó tránh khỏi những sai xót cũng như ý
kiến chủ quan của cá nhân tác giả, kính mong quý khán
giả tham khảo và đóng góp ý kiến với tác giả để hoàn
thiện hơn các sản phẩm về sau. Và gửi lời chúc đến các
em học sinh 99er lời chúc
“ Đỗ Đại Học nhé ;) “
Giữa thành công và thất bại có con sông
gian khổ... trên con sông đó có cây cầu tên
là sự cố gắng.
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TỔNG ÔN SỐ PHỨC
LỜI GIẢI CHI TIẾT 50 CÂU TRẮC NGHIỆM SỐ
PHỨC CHỌN LỌC TRONG CÁC ĐỀ
THI THỬ THPT QUỐC GIA – 2017
Tác giả - Nguyễn Thế Duy - https://www.facebook.com/theduy1995
CÁC CÔNG THỨC QUAN TRỌNG CẦN NẮM VỮNG
z z z z
z .z z .z
z . z z .z 1 2 1 2 1 2 1 2 1 2 1 2 z z 1 1 
z   z z 2 . z z z z z 2 2 2 z z z z z z z .z
z .z . z .z 1 1  Re  z  , Im  z  1 2  1 2   1 2  z z 2 2 2 2
z z z z z z
z z z z z z
z  Re z, Im z  z 1 2 1 2 1 2 1 2 1 2 1 2
45 CÂU TRẮC NGHIỆM + 5 CÂU VÍ DỤ MINH HỌA
Câu 1. Cho số phức z a bi thỏa mãn điều kiện 2
z  4  2 z . Đặt P   2 2
8 b a  12.
Mệnh đề nào dưới đây đúng?
A. P   z  2 2 .
B. P   z  2 2 4 .
C. P   z  2 4 .
D. P   z  2 2 2 .
(THPT ĐẶNG THÚC HỨA - NGHỆ AN) Lời giải
Cách 1. Đặt z a bi a b   2 2 2 2 2 2 ,
z a b  2abi z  4  a b  4  2ab . i 2 Khi đó, giả thiết 2 z   z   2 2 a b   2 2  a b   2 2 4 2 4 4 4 a b
 b a  
 a b   a b 2 2 2 2 2 2 2 8 16 4
P  a b   a b    z z    z  2 2 4 2 2 2 2 2 2 4 4 4 4 2 . 2 2 2
Cách 2. Từ giả thiết, ta có 2
z  4   z    2 z   2 2 4
z  4  4 z  4z.z
z z z z
z z   z z 2 2 2 2 2  z z      2 2 . 4 4 16 4 . . 4. . 4
12 4 z z  2
  z z  2     2 2
z z      2 2 . 2 12 4
12 4 z z    2 z  2   1 . Đặt 2 2
z a bi z a bi z z   2 2 2 a b  2. Từ  
1 , 2 suy ra P  b a     z  2 2 2 2 8 12 2 . Chọn D. 2 1 1
Câu 2. Cho các số phức z  0, z  0 thỏa mãn điều kiện   . 1 2 z z z z 1 2 1 2 z z
Tính giá trị của biểu thức 1 2 P   . z z 2 1
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 1 3 2 A. B. 2. C. 2. D. . 2 2
(THPT ĐẶNGTHÚC HỨA - NGHỆ AN) Lời giải 2 1 1 z  2z 1 Cách 1. Ta có 1 2       z  2z z zz z . 1 2   1 2  1 2 z z z z z z z z 1 2 1 2 1 2 1 2 2  z   z z z
  z 2  2.z z  2. z 2 1 1 1  0   2.  2  0 
i 1 hoặc 1  1   i . 1 1 2 2     z z zz 2   2  2 2 z z 1 1 1 3 2 Khi đó 1 2 P    i 1   i 1   2   . z z i 1 i 1 2 2 2 1 2 1 1 1 i z 3 2 Cách 2. Chọn 1 z i     z    2  P  . Chọn D. 1 2 i z i z 2 z 2 2 2 2
iz  3i   1 z 2 26
Câu 3. Cho số phức z  0 thỏa mãn
z . Số phức w iz có môđun là 1 i 9 A. 9. B. 26. C. 6. D. 5.
(THPT PHẠM HỒNG THÁI - HÀ NỘI) Lời giải
Đặt z x yi x, y   , khi đó giả thiết  i x yi   i   x yi    i 2 2 3 1 1 x y .
xi y xi y x yi   x y   y x 2 2
i x y   2 2 3 3 4 2
x y  .i 2 2
 x  4 y x y    1   . Lấy  
1  2 , ta được  x  4 y   2x y  0  x  5 . y 2 2
 2x y x y  2 
y  0  x  0
Thế x  5 y vào phương trình   1 , ta có 2 26 y 9 y     9 45 .  y    x    26 26 45 9 26  45 9 
Vậy z x yi    i w i  
i  1 5i  26.   Chọn C. 26 26 9  26 26 
Câu 4. Cho số phức z thỏa mãn điều kiện z 1 
2. Tìm giá trị lớn nhất của biểu thức
T z i z  2  i . A. max T  8 2. B. max T  4. C. max T  4 2. D. max T  8.
(THPT CHU VĂN AN - HÀ NỘI) Lời giải
Đặt z x yi x, y   , ta có z  
x   yi    x  2 2 1 2 1 2 1  y  2   x  2 2 2 2 2 2
1  y  2  x  2x 1 y  2  x y  2x 1 
Lại có T z i z  2  i x   y  
1 i x  2   y   1 i
x   y  2   x  2   y  2 2 2 2 2 2 1 2 1 
x y  2 y 1  x y  4x  2 y  5
Kết hợp với  , ta được T  2x  2y  2  6  2x  2 y  2 x y  2  2  2 x y
Đặt t x y , khi đó T f t   2t  2  6  2t với t 1  ;1 .
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 1 1
Ta có f 't   
; f 't   0  t  1  f t   f   1  4 . Chọn B. max 2t  2 6  2t
Câu 5. Tìm môđun của số phức z biết z  4  1 iz  4  3zi . 1 A. z  1. B. z  4. C. z  2. D. z  . 2 (SỞ GD&ĐT NAM ĐỊNH) Lời giải
Cách 1. Từ giả thiết, ta có z  4  z i z  4i  3zi z 1 3i  z  4   z  4i 
Lấy môđun hai vế của  , ta được z 1 3i  z  4   z  4i z
i   z  2   z  2  z
  z  2   z  2 . 1 3 4 4 10 4 4 2 
z   z  2   z  2 2 2 10 4 4
 8 z  32  z  4  z  2. Chọn C.
1 iz  4i  4
Cách 2. Ta biến đối z  4  1 iz  4  3zi z  1 3i
Thử lần lượt với các đáp án, ta thấy
1 i  4i  4 5  3i 2 9 85 
z  1  z      i z   1 (loại). 1 3i 1 3i 5 5 5
41 i  4i  4 8 4 12 4 10 
z  4  z     i z   1 (loại). 1 3i 1 3i 5 5 5
21 i  4i  4 6  2i
z  2  z  
  2i z  2 (chọn). 1 3i 1 3iz
Câu 6. Cho số phức z  0 sao cho z không phải là số thực và w  là số thực. Tính 2 1 z z giá trị biểu thức . 2 1 z 1 1 1 A. . B. . C. 2. D. . 5 2 3
(THPT CHUYÊN QUỐC HỌC - HUẾ) Lời giải 1 1
Cách 1. Tư duy nhanh. w là số thực 
là số thực  z  là số thực. w z 1 2 z 1
Mà dễ thấy z z là số thực nên z
z .z  1  z  1  z  1   . 2 z 1 z 2 z z Cách 2. Ta có biến đổi 2 2 
z z.z z z.z z z z z .z.z 2 2   1 z 1 z
z z  0 2 z 1   .
z z  1  z  1   .  2 . z z  1  1 z 2 z 1 z 1 Cách 3. Chọn w    z 1
 0  z  1  z  1   . Chọn B. 2  2 2 1 z 2 1 z 2
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Câu 7. Xét số phức z và số phức liên hợp của nó có điểm biểu diễn là M , M  . Số phức
z(4  3i) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N , N  . Biết rằng M , M ,
N, N  là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của z  4i  5 1 2 1 4 A. . B. . C. . D. . 2 5 2 13 (THPT CHUYÊN LÀO CAI) Lời giải N
4x  3y;3x  4y Gọi M  ;
x y   M ' ;
x y và 4  3iz  4x  3y  3x  4 yi   N ' 
4x  3y;3x  4y 
Dễ thấy MM '  NN ' vì cùng vuông góc với Ox nên để MM ' N ' N là hình chữ nhật. MM '  NN '  2 2
Khi và chỉ khi MN M ' N '  x y  0  z x xi z  4i  5   x  5   x  4 MN Ox   2 2 1 2 1 1 1
Ta có  x  5   x  4  2x  9  
z  4i  5  . Chọn C. min 2 2 2 2 2 z z i
Câu 8. Tính môđun của số phức z , biết  iz   0 . z 1 i 13 1 1 A. 2 . B. . C. . D. . 3 3 9
(THPT YÊN MÔ A - NINH BÌNH) Lời giải 2 2 z z i
1 i z i Dễ thấy .
z z z z
, khi đó giả thiết  iz z
 0  iz z   0 z 1 i 2 2
 2iz  2z z i iz i  0  3i  
1 z z i 1 
Đặt z x yi x, y   suy ra z x yi , do đó   3i  
1  x yi  x yi i 1. x  0 3  x  0 
 3xi  3y x yi x yi i 1  2x  3y  3xi i 1     1 .
2x  3y  1 y     3 i i 1 Vậy z   z   . Chọn C. 3 3 3 10
Câu 9. Xét số phức z thỏa mãn 1 2iz
 2  i . Mệnh đề nào sau đây đúng? z 3 1 3 1 A.  z  2 . B.  z
. C. z  2 . D. z  . 2 2 2 2
(THPT NHÂN CHÍNH - HÀ NỘI) Lời giải 10 10
Cách 1. Từ giả thiết, ta có 1 2iz
 2  i  1 2iz  2  i z z 10  z
z i   i
z    z   10 2 2 2 2 1 i   z z
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 2 2 10
Lấy môđun hai vế của  , ta được    z  2  2 z   1  . z 2 2 10
Đặt t z , ta có t  2  2t   2 1   t  2 5t  5 4 2
 10  t t  2  0  t  1. t 1 3
Vậy môđun của số phức z bằng 1   z  . 2 2
Cách 2. Sử dụng máy tính casio ( hướng dẫn chi tiết ở câu 26) để tìm z .
Cách 3. Đặt z a bi a,b   và c z , thay vào đẳng thức đã cho thì 10
a bi 10
Gt  1 2ic
 2  i  1 2ic   2  i 2 a bi c a 10  b 10   c
 2  i  2c  1  0 2 2 cc     a 10  a 10 c   2  0 c  2   2 2 2  2  cc 10 a b 2 2   10 Suy ra   
nên c  2  1 2c   4 2  b 10  b 10 c c 2c  1  0 1 2c  2  c    c 1 3
Giải ra ta có c  1 mà c  0 nên c  1 hay z  1. Do đó  z  . Chọn B. 2 2 1
Câu 10. Cho số phức z thỏa mãn z
 3 . Tổng của giá trị lớn nhất và giá trị nhỏ nhất z của z là A. 3. B. 5. C. 13. D. 5.
(TOÁN HỌC & TUỔI TRẺ LẦN 8) Lời giải 2 1 1  1  1  Ta có 2 a z   a z   z z      z zz  z z   z 2 4 1
z   z z 2 2 2 2  2 z 1  z    . 2 2 2 z z z 2 2   4 2 2
a a  4 a a  4
Khi đó z z . 2
a  2 1   z z   0  z   ;  . 2 2     2 2 a a  4
a a  4 Vậy 2 max z  ; min z
M m a  4  13. Chọn C. 2 2
Câu 11. Xét số phức z thỏa mãn 2 z 1  3 z i  2 2 . Mệnh đề nào dưới đây đúng? 3 1 1 3 A.  z  2. B. z  2. C. z  . D.  z  . 2 2 2 2
(TOÁN HỌC & TUỔI TRẺ LẦN 8) Lời giải
Cách 1. Sử dụng bất đẳng thức số phức, ta có u v u v u v .
Khi đó 2 2  2 z 1  3 z i  2 z 1  z i   z i  2 z 1  z i  z i .
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
 2 i 1  z i  2 2  z i z i  0  z i z  1 .
Cách 2. Sử dụng hình học, giả sử điểm z x yi x, y   có điểm biểu diễn là M  ; x y .
Số phức z 1 có điểm biểu diễn là Ax 1; y , z i có điểm biểu diễn là B  ; x y   1 . 
Ta có 2 z 1  3 z i  2 2  2.OA  3.OB  2.AB  
1 vì AB  1;   1  AB  2 .
Mặt khác 2.OA  3.OB  2.OA OB  OB  2.AB OB 2 x  0 Từ  
1 , 2 suy ra 2.AB  2.AB OB OB  0  OB  0  O B 0;0    z i y  1 
Vậy môđun của số phức z là z i  1. Chọn D.
Câu 12. Cho số phức z thỏa mãn 2
z  2z  5   z 1 2i z  3i   1 .
Tính min | w | , với số phức w z  2  2i . 3 1 A. min | w | . B. min | w | 2 . C. min | w | 1 . D. min | w | . 2 2
(THPT CHUYÊN LƯƠNG THẾ VINH - ĐỒNG NAI) Lời giải 2 2 2 Ta có 2
z  2z  5   z  
1  4   z  
1  2i   z 1 2i z 1 2i . z  1 2i
Khi đó, giả thiết   z 1 2i z 1 2i   z 1 2i z  3i   1  
z 1 2i z  3i 1 
TH1. Với z  1 2i , ta có w z  2  2i  1 2i  2  2i  1  w  1.
TH2. Với z 1 2i z  3i 1
 , đặt z x yi x, y   , ta có
  x    y  i x    y  i   x  2   y  2   x  2   y  2 1 1 2 1 3 1 2 1 3  y   . 2 1 3 9 3
Do đó w z  2  2i x
i  2  2i x  2 
i w   x  22   . Chọn A. 2 2 4 2
Câu 13. Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức
T z 1  2 z 1 . A. max T  2 5. B. max T  2 10. C. max T  3 5. D. max T  3 2.
(THPT CHUYÊN NGOẠI NGỮ - HÀ NỘI) Lời giải
Cách 1. Gọi z x yi x, y    M  ; x y .
Và A1;0, B 1;0 . Ta có 2 2
z  1  x yi  1  x y  1.
M thuộc đường tròn đường kính AB . 2 2 2
MA MB AB  4. Khi đó, theo Bunhiacopxki, ta có
T MA MB   2 2   2 2 2 1 2
MA MB   5.4  2 5
Vậy giá trị lớn nhất của biểu thức max T  2 5 . Chọn A.
Cách 2. Đặt z x yi x y    z    x  2 2 , 1
1  y và z    x  2 2 1 1  y . Mặt khác 2 2 2 2 z  1 
x y  1  x y  1, khi đó
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
T   x  2
1  y  2  x  2 2 2 1  y 1 2 x 2 1 yx 2 2 2 2 2 1 y            10  2 2 x y  
1  10.2  2 5  max T  2 5.
Câu 14. Cho z , z là hai số phức thỏa mãn 2z i  2  iz , biết z z  1. Tính giá trị 1 2 1 2
của biểu thức P z z . 1 2 3 2 A. P  . B. P  2. C. P  . D. P  3. 2 2
(THPT THANH CHƯƠNG I - NGHỆ AN) Lời giải
Đặt z x yi x, y   , ta có 2z i  2  iz  2x  2 y  
1 i  2  y xi
x   y  2    y2 2 2 2 2 2 2 4 2 1 2
x  4x  4 y  4 y 1  4  4 y y x 2 2
x y  1  z  1  z z  1. Sử dụng công thức (chứng minh ở câu 16) 1 2 2 2 z zz z  2  2 2 zz
  z z  2 2 2 zz  2  z z  3. Chọn D. 1 2 1 2 1 2 1 2 1 2 1 2
Câu 15. Cho ba số phức z ; z ; z thỏa mãn điều kiện z z z  1 và z z z  0 . 1 2 3 1 2 3 1 2 3
Tính giá trị biểu thức 2 2 2
A z z z . 1 2 3 A. 1. B. 0 . C. 1. D. 1 i .
(THPT CHUYÊN BIÊN HÒA - HÀ NAM) Lời giải 2 Ta có 2 2 2
A z z z z z z
 2 z z z z z z
  2 z z z z z z 1 2 3  1 2 3   1 2 2 3 3 1   1 2 2 3 3 1   1 1 1   z z z  1 2 3   2z z z     2z z z     z z z
z z z 1 2 3   1 2 3   1 2 3  1 2 3  z z z z z z  1 2 3   1 2 3 
Mặt khác z z z  0  z z z  0 suy ra A  0. Chọn B. 1 2 3 1 2 3
Câu 16. Với hai số phức z và z thỏa mãn z z  8  6i và z z  2 . Tìm giá trị lớn 1 2 1 2 1 2
nhất của P z z . 1 2 A. P  5  3 5. B. P  2 26. C. P  4 6. D. P  34  3 2.
(THPT CHUYÊN KHOA HỌC TỰ NHIÊN - LẦN 4) Lời giải 2 2 2 2
 Bổ đề. Cho hai số phức z và z , ta luôn có z zz z  2 zz  . 1 2 1 2  1 2    1 2 2 2
Chứng minh. Sử dụng công thức z zz z z z và .
z z z . Khi đó 1 2  1 2   1 2  2 2 z zz zz z z zz z z z 1 2 1 2  1 2   1 2   1 2   1 2 
z .z z .z z .z z .z z .z z .z z .z z .z 1 1 1 2 1 2 2 2 1 1 1 2 1 2 2 2
 2  z .z z .z   2 2 2 zzđpc . m 1 1 2 2 1 2 
 Áp dụng  , ta được z zz z
 4  z z  4   32 2 2 2
 1  z z  1. 1 2 1 2 1 2 1 2
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 2 2
Theo bất đẳng thức Bunhiacopxki, ta được P z z  2 zz  2 26. Chọn B. 1 2  1 2 
Câu 17. Cho P z là một đa thức với hệ số thực. Nếu số phức z thỏa mãn P z  0 thì  1   1 
A. P z   0. B. P  0.   C. P  0.  
D. P z  0.  z   z  (THPT CHUYÊN TỈNH HÀ NAM) Lời giải
z  1 2i
Chọn hàm số P z 2
z  2z  5 . Phương trình P z 2
 0  z  2z  5  0   z  1 2i
Xét với số phức z  1 2i , ta có
z  1 2i
5 suy ra P z   z z    2 2 2 5 5
 2. 5  5  10  2 5  0. 1 1 1 2  1  1 2 112 16     i suy ra P    5   i  0.   z 1 2i 5 5 2  z z z 25 25 1 1 1 2  1  1 2 112 16     i suy ra P    5   i  0.   z 1 2i 5 5 2  z z z 25 25 2
z  1 2i suy ra P z  2
z  2z  5  1 2i  21 2i  5  0. Chọn D. 2z i
Câu 18. Cho số phức z thỏa mãn z  1. Đặt A
. Mệnh đề nào sau đây đúng? 2  iz A. A  1. B. A  1. C. A  1. D. A  1. (THPT CHUYÊN HÀ NAM) Lời giải 2z i
Từ giả thiết, ta có A
A2  iz  2z i  2A Azi  2z i 2  iz 2 A i 2A i
 2A i z Ai  2  z  . Mà z  1 
 1  2 A i Ai  2 . Ai  2 Ai  2
Đặt A x yi x, y   , khi đó   2x  2 y  
1 i   y  2  xi
x   y  2   y  2 2 2 2 2 2 2 2 2 4 2 1 2
x  4x  4 y  4 y 1  x y  4 y  4  x y  1. Vậy môđun của 2 2 A
x y  1. Chọn A. 2
Câu 19. Cho số phức z thỏa mãn z
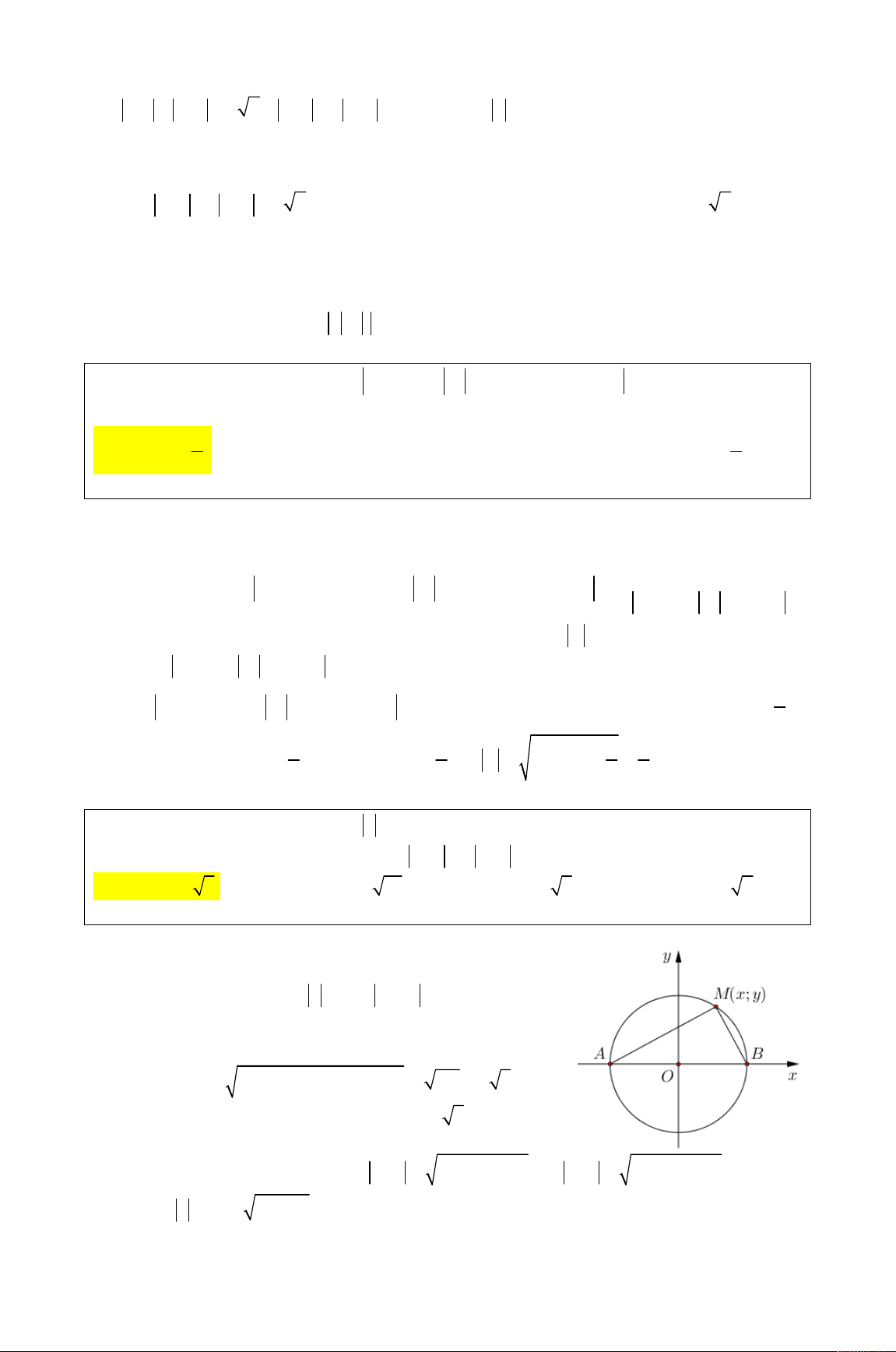
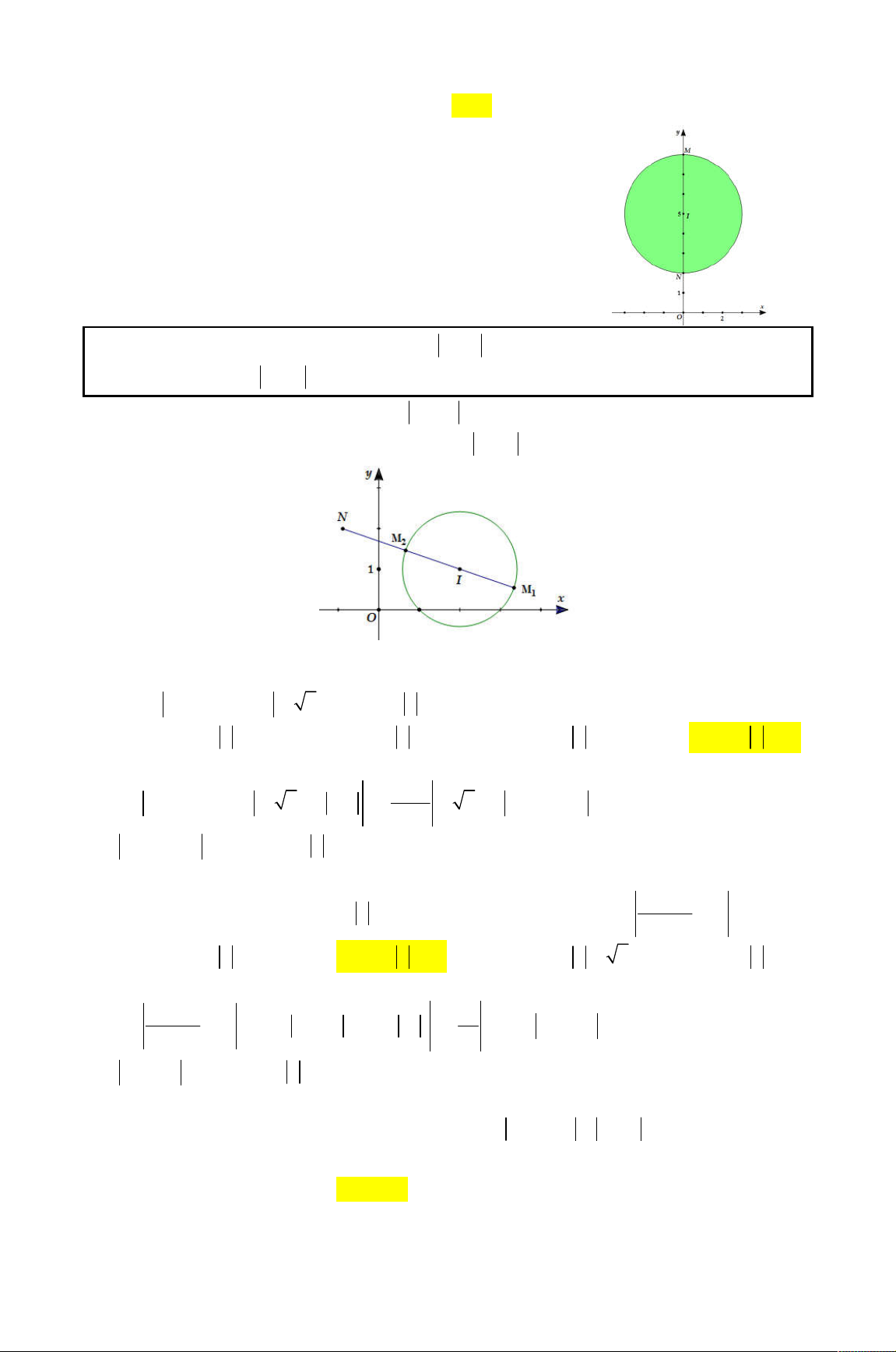
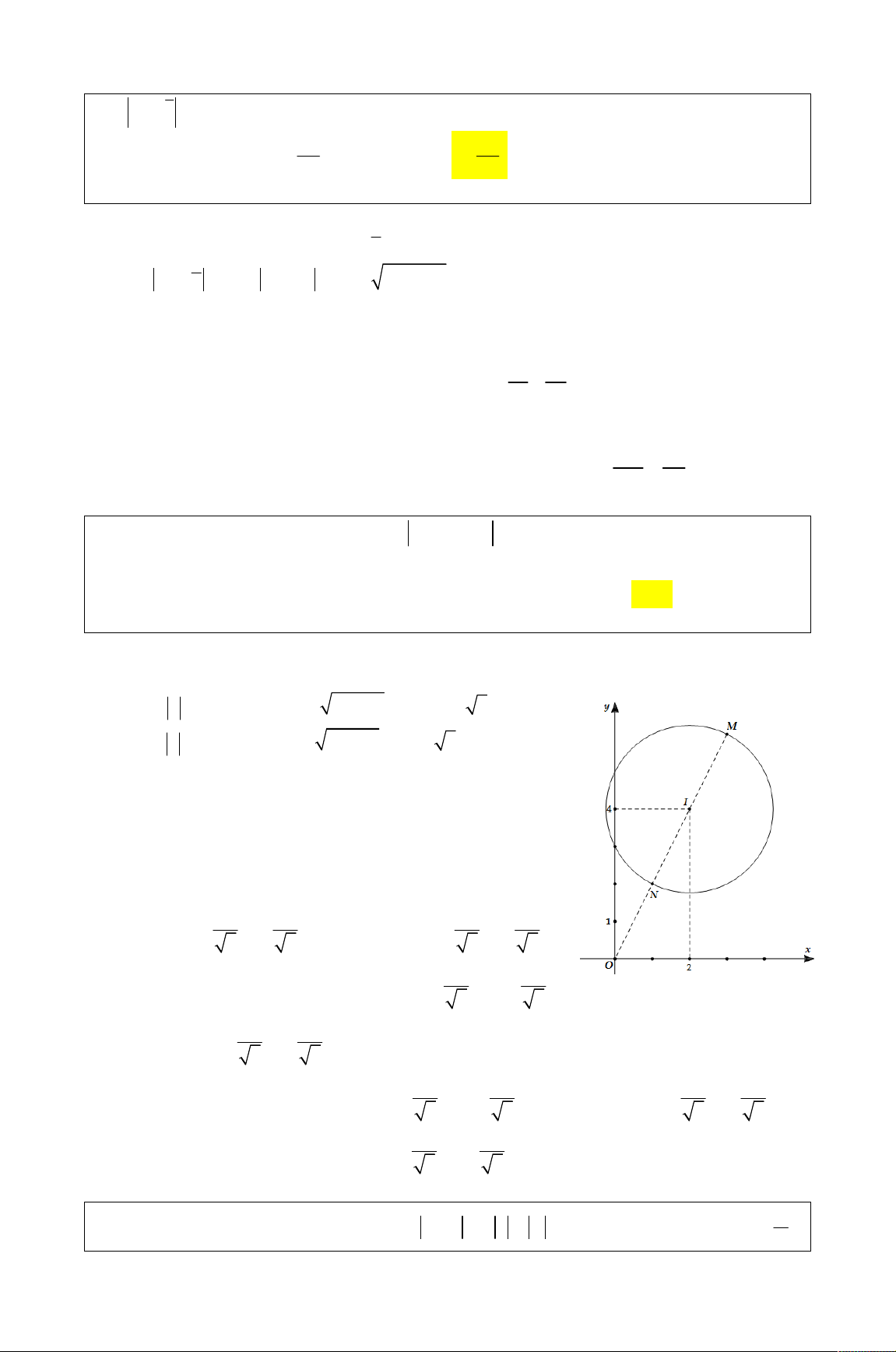
và điểm A trong hình 2
vẽ bên là điểm biểu diễn của z . Biết rằng trong hình vẽ bên, điểm 1
biểu diễn của số phức w
là một trong bốn điểm M , N , P , iz
Q . Khi đó điểm biểu diễn của số phức w là
A. điểm Q . B. điểm M .
C. điểm N . D. điểm P .
(THPT CHUYÊN ĐH VINH LẦN 1)
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 2 1
Đặt z x yi x, y  0 , khi đó 2 2 2 2 z x y   x y
và x y (hình vẽ) 2 2 1 i i
i x yiy xi Ta có w            2 y  2 . x i iz z x yi
x yi x yi 2 2 x y
Vì x, y  0 nên điểm biểu diễn số phức w là  2 y;  2x đều có hoành độ, tung độ âm.
Đồng thời x y   2 y   2x x y  0 và 2 2
w  2 x y  2  2 z w w
Dựa vào hình vẽ, điểm P chính là điểm cần tìm vì điểm N tuy thỏa mãn x y  0 w w
nhưng độ dài ON xấp xỉ bằng độ dài OA . Chọn D.
Câu 20. Cho số phức z x yi x, y   thỏa mãn z  6  8i  5 và có môđun nhỏ nhất. Tính tổng x  . y
A. x y   3. B. x y  1  .
C. x y  1.
D. x y  2 . (SỞ GD&ĐT QUẢNG NAM) Lời giải
Dựa vào ví dụ, ta phát triển dạng toán Min – Max số phức như sau
Tập hợp các điểm M z thỏa mãn điều kiện z  a bi  R R  0 là đường tròn C  có tâm I  ;
a b và bán kính R .
Chứng minh. Gọi z x yi ,  , x y   .
Theo giả thiết z  a bi  R   x a   y bi R .
   2    2 
   2    2 2 x a y b R x a y bR
Vậy tập hợp các điểm M z là đường tròn C  có tâm I  ;
a b và bán kính R .
Ví dụ 21. Trong các số phức z thỏa mãn điều kiện z  2  4i  5 . Tìm max z . A. max z  3 5 . B. max z  5 . C. max z  5 . D. max z  13 . Hướng dẫn giải.
Tập hợp các điểm M z là đường tròn C  có tâm I 2; 4 và bán kính R  5 . Vậy 2 2
max z OM OI R  2  4  5  3 5 . Chọn A. * Hỏi thêm: a) Tìm min z . 2 2
min z ON OI R  2  4  5  5 .
b) Tìm số phức z có môđun lớn nhất, nhỏ nhất.
Phương trình đường thẳng OI là y  2x .
Tọa độ hai điểm M , N là nghiệm của hệ phương trình  y  2x   y  2xx  1 x  3      ;  .  x  2 
2   y  42 2  5
5x  20x 15  0 y  2 y  6    
Số phức z có môđun lớn nhất là z  3  6i tương ứng với điểm M 3;6 .
Số phức z có môđun nhỏ nhất là z  1 2i tương ứng với điểm N 1; 2 .
Ví dụ 22. Trong các số phức z thỏa mãn điều kiện z  5i  3 . Nếu số phức z có môđun
nhỏ nhất thì phần ảo bằng bao nhiêu?
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 A. 0. B. 3. C. 2. D. 4. Hướng dẫn giải.
Tập hợp các điểm M z là hình tròn C  tâm I 0;5
và bán kính R  3 .
Số phức z có môđun nhỏ nhất là z  2i ứng với điểm N 0;2 . Chọn C.
Tổng quát. Trong các số phức z thỏa mãn z z r r  0 . Tìm giá trị lớn nhất và giá 1  1 1
trị nhỏ nhất của P z z . 2
Gọi I z ; N z và M z . Tính IN z z r . 2  1  1 2 2
Khi đó, max P NM r r và min P NM r r . 1 1 2 2 1 2 Áp dụng.
Câu 1. (THPT CHUYÊN KHTN – LẦN 1) Trong các số phức z thỏa mãn điều kiện
1 iz 1 7i  2 . Tìm max z . A. max z  4 . B. max z  3 . C. max z  7 . D. max z  6 . Hướng dẫn giải. 1 7i
Ta có 1 iz 1 7i  2  1 i z  
2  z  3  4i  1 . 1 i
Vì 3  4i  0  5 nên max z r r  1 5  6 . Chọn D. 1 2  2  3i
Câu 2. Tìm giá trị lớn nhất của z biết rằng z thỏa mãn điều kiện z 1  1 . 3  2i A. max z  1 . B. max z  2 . C. max z  2 . D. max z  3 . Hướng dẫn giải.  2  3i 1 Ta có
z 1  1   iz 1  1   i . z
 1  z   i  1. 3  2ii
Vì  i  0  1 nên max z r r  11  2 . Chọn B. 1 2
Câu 3. Trong các số phức z thỏa mãn điều kiện z  2  4i z  2i . Biết rằng số phức
z x yi ,  ,
x y   có môđun nhỏ nhất. Tính 2 2
P x y . A. P  10 . B. P  8 . C. P  16 . D. P  26 . Hướng dẫn giải.
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
Gọi z x yi ,  ,
x y   . Ta có z  2  4i z  2i   x  2   y  4i x   y  2i
  x  2   y  2  x   y  2 2 2 4 2 2 2 2 2
x  4x  4  y  8y 16  x y  4 y  4
 4x  4 y 16  0  y  4  x . 2 2 Do đó 2 2 2 z x y
x    x 2 4
 2x  8x 16  2 x  2  8  2 2 .
Dấu "  " xảy ra  x  2  y  2 . Vậy 2 2
P  2  2  8 . Chọn B.
Câu 4. (ĐỀ THTT LẦN 5 – 2017) Cho số phức z thỏa mãn z  4  z  4  10. Giá trị lớn
nhất và giá trị nhỏ nhất của z lần lượt là A. 10 và 4 B. 5 và 4 C. 4 và 3 . D. 5 và 3 . Hướng dẫn giải.
Gọi z x yi ,  ,
x y   . Theo giả thiết, ta có z  4  z  4  10.
  x    yi   x    yi
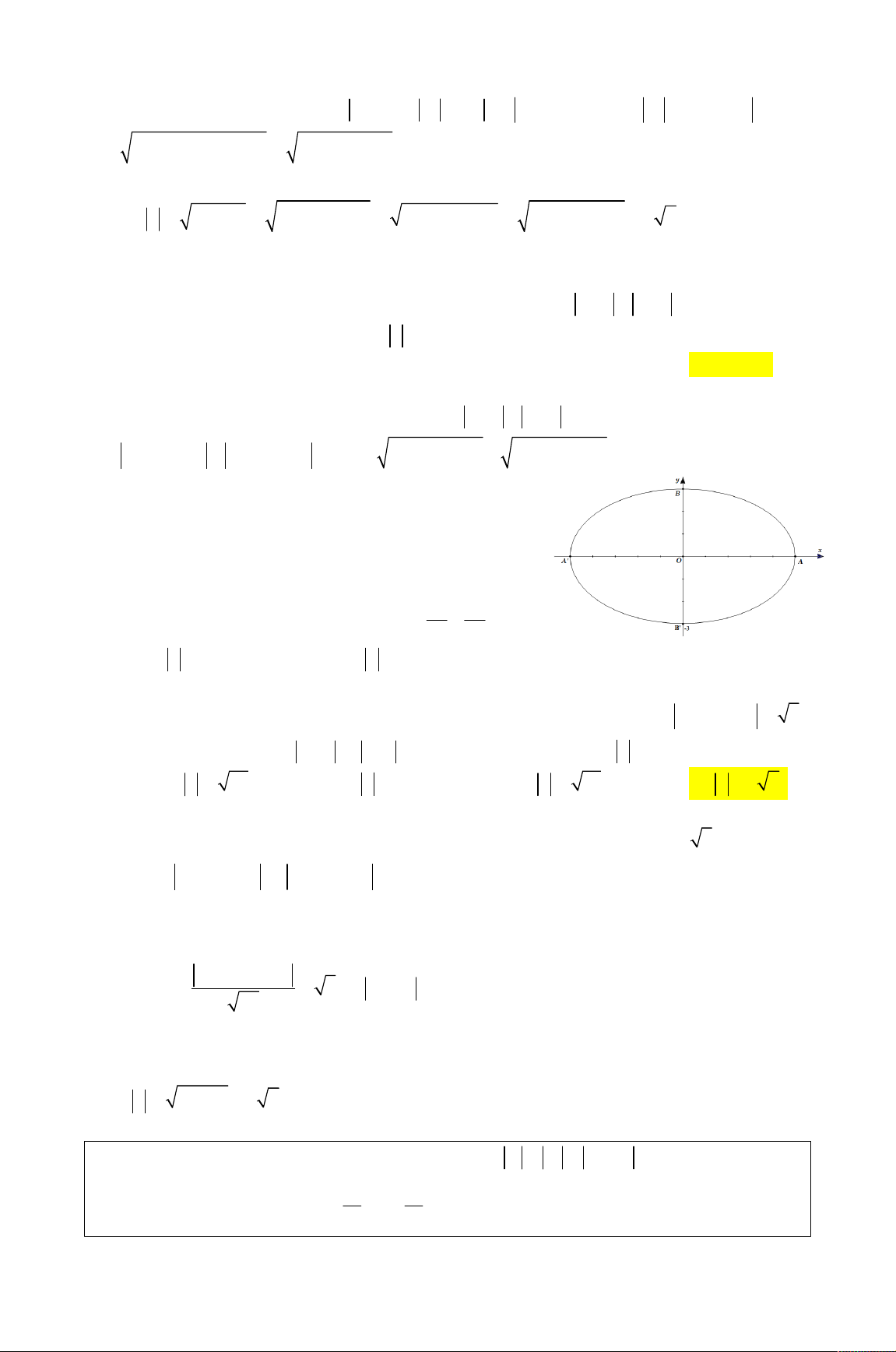
  x  2  y   x  2 2 2 4 4 10 4 4  y  10  Gọi M  ;
x y , F  4;0 và F 4;0 . 2   1  
Khi đó   MF MF  10 nên tập hợp các 1 2
điểm M z là đường elip  E .
Ta có c  4 ; 2a  10  a  5 và 2 2 2
b a c  9 . 2 2 x y
Do đó, phương trình chính tắc của  E là   1 . 25 9
Vậy max z OA OA '  5 và min z OB OB '  3 . Chọn D.
Câu 5. Biết số phức z x yi ,  ,
x y   thỏa mãn đồng thời điều kiện z  3  4i  5 2 2
và biểu thức P z  2  z i đạt giá trị lớn nhất. Tính z . A. z  33 . B. z  50 . C. z  10 . D. z  5 2 . Hướng dẫn giải.
Tập hợp các điểm M z là đường tròn C  có tâm I 3; 4 và bán kính R  5 . 2 2 2 2 Ta có Pxyi x yix  2 2 2 1 2 yxy  1              .  
 4x  2 y  3  4x  2 y  3  P  0  .
Ta tìm P sao cho đường thẳng  và đường tròn C  có điểm chung  d I;   . R 12  8  3  P
 5  23  P  10  1
 0  23  P  10  13  P  33 . 20
4x  2 y  30  0  x  5
Do đó max P  33 . Dấu "  " xảy ra     .  x  3 
2   y  42  5 y   5   Vậy 2 2
z  5  5  5 2 . Chọn D.
Câu 23. Cho hai số phức z , z thoả mãn điều kiện z z z z  1. 1 2 1 2 1 2 2 2  z   z
Tính giá trị của biểu thức 1 2 P       . z z  2   1 
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
A. P  1 i . B. P  1   i . C. P  1  .
D. P  1 i .
(SỞ GD&ĐT QUẢNG NINH) Lời giải z z Từ giả thiết, ta có 1 1
z z z z  1   1  1. 1 2 1 2 z z 2 2  1 2 2 x   z 2 2 x y  1   x y  1   2 Đặt 1 w
x yi x, y   , khi đó      z 2 2 2 2    
x y  2x 3 2  x  1 y 1    y     2 2 2 1  1 i 3   1 i 3  Khi đó 2 P w           1. Chọn C. 2 w  2 2   2 2     
Câu 24. Tính tích môđun của tất cả các số phức z thỏa mãn 2z 1  z 1 i , đồng thời
điểm biểu diễn z trên mặt phẳng tọa độ thuộc đường tròn tâm I 1; 
1 , bán kính R  5. A. 5 . B. 3 . C. 3 5 . D. 1. (SỞ GD&ĐT THANH HÓA) Lời giải
Đặt z x yi x, y   , khi đó 2z 1  z 1 i  2x 1 2 .
y i x 1  y   1 .i
  x  2  y   x  2   y  2 2 2 2 2 1 4 1 1
 3x  3y  6x  2 y 1  0   1 . 2 2
Mà điểm biểu diễn M
 C   x     y   2 2 : 1 1
 5  x y  2x  2 y  3  0 2 . z    Lấy   1  3.2 , ta được 2 2 2 2
3x  3y  6x  2 y 1 3x  3y  6x  6 y  9  0  y  1
Thế y  1 vào phương trình 2 , ta có  x  0 z   i 2 1
x  2x  0  
z . z   i . 2  i  5.   Chọn C. 1 2 x  2 z  2  i   2
Câu 25. Cho các số phức z, w thỏa mãn z  2  2i z  4i , w iz 1. Giá trị nhỏ nhất của biểu thức w là 2 3 2 A. . B. 2 2 . C. 2 . D. . 2 2
(THPT CHUYÊN ĐH VINH - LẦN 2) Lời giải
Đặt z a bi a,b   , khi đó z  2  2i a  2  b  2i và z  4i a  b  4i . 2 2 2
Nên ta có a    b   2 2 2
a  b  4  a b  2  b  2  a 2 2
Khi đó w iz   a bi 2
i    b ai w a  b   2 1 1 1 1
a  a   1 . 2 2  1  1 1 2 2 Dễ thấy 2
a  a   1  2 a     w   min  .   Chọn A.  2  2 2 2 w 2
Câu 26. Gọi z , z là hai nghiệm của phương trình 2
z z 1  0 . 1 2
Tính giá trị của biểu thức 2017 2017 P zz . 1 2 A. P  1 . B. P  1  . C. P  0 . D. P  2 .
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
(THPT CHUYÊN KHOA HỌC TỰ NHIÊN - LẦN 4) Lời giải 1 i 3 2017 2017 Ta có 2 3
z z 1  0  z   
z  1  z  1  P   zz  2. Chọn D. 1   2  2 2
Câu 27. Cho số phức z thỏa mãn 2  3iz  1 2iz  7  i . Tìm môđun của z . A. z  5 . B. z  1. C. z  3 . D. z  2 .
(THPT CHUYÊN KHOA HỌC TỰ NHIÊN - LẦN 4) Lời giải
Cách 1. Đặt z a bi a,b   , khi đó giả thiết trở thành
Gt  2  3ia bi  1 2ia bi  7  i
a  5b  7
a  5b  a  3bi  7  i   a  3b  1   a  2  
z  2  i z  5. b  1  
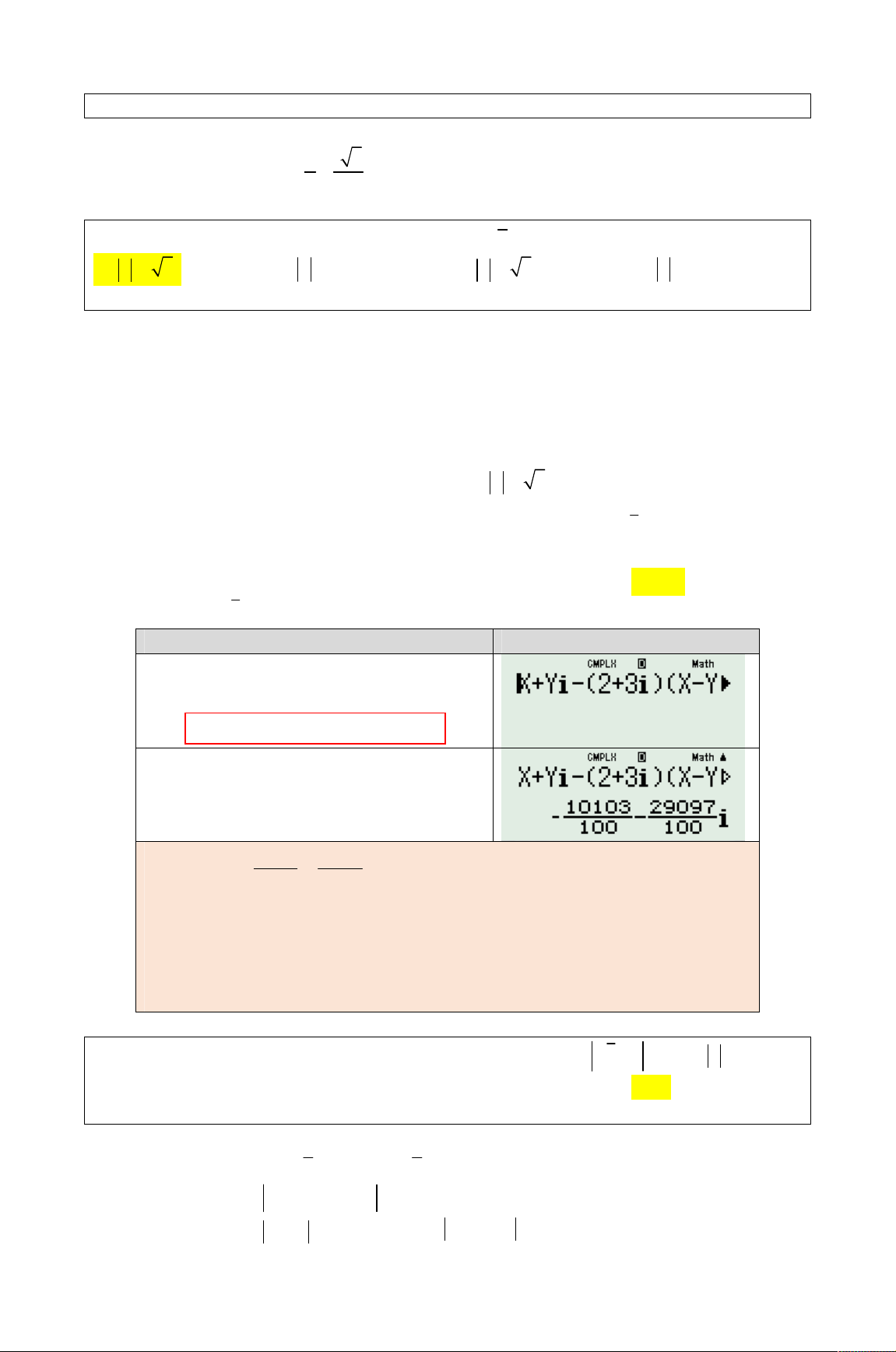
Cách 2. Xử lý bằng casio giống bài toán sau: Cho số phức z  2  3iz  1 9i . Tích phần
thực và phần ảo của số phức z bằng A. 2. B. 1. C. 1. D.  2.
Đặt z X Yi z X Yi . Khi đó w X Yi  2  3i X Yi 1 9i  0  . Thao tác trên máy tính Màn hình hiển thị
Ấn w  2  Đưa về tính số phức.
Nhập vế trái của phương trình    .
X Yi  2  3iX Yi1  9i .
Sau đó, gán giá trị X  100, Y  0, 01 . Ấn r  100  r  0  q 0.01 =. 10103 29097 Khi đó w   
i  101, 03 290, 97i. 100 100
101, 03  100  1  0, 03  X  3Y   1 Mặt khác, ta có  . 
290, 97  300  9  0, 03  3X  3Y   9    X Y X w X 3Y
1 3X 3Y 9  3  1     2         i  0     .  X Y  3 Y     1
Câu 28. Có bao nhiêu số phức z thỏa mãn đồng thời điều kiện .
z z z  2 và z  2 ? A. 2. B. 4. C. 3. D. 1.
(THPT CHUYÊN LAM SƠN - THANH HÓA) Lời giải
Đặt z a bi a b    z a bi z z  a bi a bi 2 2 ; .  a b . 2 2 2 2 2 2
a b a bi  2 a b  4 a b  4   
Khi đó, giả thiết       .
a bi  2
a  4  bi  2    a  4  2 2  b  4 
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 2 2 2 2 a b  4  a b  4 a   2      
z   2. Chọn D. a  4  2 2  a  0 a   2 b  0   
Câu 29. Cho số phức w và hai số thực a , b . Biết z w  2i và z  2w  3 là hai 1 2
nghiệm phức của phương trình 2
z az b  0 . Tính T z z . 1 2 2 97 2 85 A. T  2 13 . B. T  . C. T  . D. T  4 13 . 3 3
(THPT CHUYÊN LÊ QUÝ ĐÔN - QUẢNG TRỊ) Lời giải 
z w  2i m n  2 i 1  
Đặt w m ni  ; m n     .
z  2w  3  2m  3  2ni  2  2 3  n  2  0 n  
Ta có z z  3m  3  3n  2 i   a là số thực     3 . 1 2   3m  3  0  m  1   4  4  4 4
Lại có z . z m i 2m  3 
i b là số thực 
.2m  3  m  0  m  3. 1 2      3  3  3 3 4 4 2 97 Do đó z  3  i; z  3 
i T z z  . Chọn B. 1 2 1 2 3 3 3
Câu 30. Cho số phức z thỏa mãn  z  
1  z  2i là một số thuần ảo. Tập hợp điểm biểu
diễn số phức z là một đường tròn có diện tích bằng 5 5 A. 5 . B. . C. . D. 25 . 4 2
(THPT CHUYÊN NGUYỄN BỈNH KHIÊM - QUẢNG NAM) Lời giải
Đặt z x yi x y     z   z i 2 2 ; 1
2  x y x  2 y  2x y  2 .i
Theo giả thiết  z  
1  z  2i là số thuần ảo, suy ra 2
2x y  2  0 1 5  1  5   x x
y  2 y 1   x      y  2 2 2 1  . 2 2
x y x  2 y  0 4 4   2  4 5
 tập hợp điểm biểu diễn số phức z là một đường tròn có diện tích bằng . Chọn B. 4 z z 1
Câu 31. Gọi M là điểm biểu diễn số phức w
, trong đó z là số phức thỏa mãn 2 z 
1i z  2i  2 i  3z . Gọi N là điểm trong mặt phẳng sao cho Ox,ON   2 , trong đó   
  Ox,OM  là góc lượng giác tạo thành khi quay tia Ox tới vị trí tia OM . Điểm N
nằm trong góc phần tư nào?
A. Góc phần tư thứ  I  . B. Góc phần tư thứ  IV  .
C. Góc phần tư thứ  III  . D. Góc phần tư thứ  II  .
(THPT CHUYÊN NGUYỄN QUANG DIỆU - ĐỒNG THÁP) Lời giải
Từ giả thiết, ta có 1 i z  2i  2  i  3z z  2i iz  2  2  i  3z
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 3 6 z z 1 casio 33 56
 i  2 z  3i z   i w    w   . i 5 5 2 z 45 45 y
Sử dụng lý thuyết nếu z x yi P  ; x y  tan 
với là góc tạo bởi chiều dương x 
trục hoành với vectơ OM . 33 56 56 3696 2047 Khi đó w   i  tan    sin 2   ; cos 2   . 45 45 33 4225 4225
Vậy điểm N thuộc góc phần tư thứ  IV . Chọn B.
Câu 32. Cho số phức z thỏa mãn z  2  3i  1. Giá trị lớn nhất của z 1 i là A. 13  2 . B. 4 . C. 6 . D. 13 1 .
(THPT CHUYÊN PHAN BỘI CHÂU - NGHỆ AN) Lời giải
Đặt z a bi a,b   , ta có z  2  3i  1  a  2  b  3i  1.
 a  2  b  2   a  2  b  2 2 3 1 2 3  1 
a  2  sin t Đặt  (vì  2 2
 sin t  cos t  1). Khi đó z 1 i  a  
1  1 bi .
b  3  cos t  2 2
 a  2    b2 1 1
 xét biểu thức P  a   1  1 b . 2 2 2 2
Ta có a      b   t     t   2 2 1 1 sin 3 cos 2
 sin t  6 sin t  9  cos t  4 cos t  4   2 2
sin t  cos t  13 6sin t  4cost
 14  6sin t  4 cos t P 2
Theo bất đẳng thức Bunhiacopxki, ta được  t t    2 2   2 2 6sin 4 cos 6 4
sin t  cos t    t t 2 6sin 4 cos
 52  6sin t  4 cos t  52  2 13  P  14  2 13.
Vậy z   i  a      b      2 2 2 1 1 1 14 2 13 13 1  13 1. Chọn A.
Câu 33. Có bao nhiêu số phức z thỏa mãn z i  2 và 2
z là số thuần ảo. A. 3. B. 1. C. 4. D. 2.
(THPT CHUYÊN PHAN BỘI CHÂU - NGHỆ AN) Lời giải 2
Đặt z x yi x, y   , khi đó z i
x   y   2 2
1 i  2  x   y   1  2  2 2 x y  0
x y  0
Ta có z   x yi2 2 2 2
x y  2xyi là số thuần ảo nên    2xy  0
x   y  0   1 3
TH1. Với x y , thế vào  , ta được x   x  2 2 2 1
 2  2x  2x 1  0  x  . 2 1 3
TH2. Với x   y , thế vào  , ta được x   x  2 2 2 1
 2  2x  2x 1  0  x  . 2
Vậy có 4 số phức thỏa mãn yêu cầu bài toán. Chọn C.
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 1 1 2
Câu 34. Cho hai số phức z , z thỏa mãn z , z  0 ; z z  0 và   . Tính 1 2 1 2 1 2 z z z z 1 2 1 2 z
giá trị của biểu thức 1 . z2 2 3 2 A. . B. . C. 2 3 . D. . 2 2 3 (THPT CHUYÊN QUANG TRUNG) Lời giải 1 1 2 1 2z z Từ giả thiết, ta có 1 2    
z z  2z z z z 1 2  1 2   1 2  z z z z z z z z 1 2 1 2 1 2 1 2 2 2 2 2
z z  2z  2z z z z z  2z  2z z z  0. 1 2 1 1 2 1 2 2 1 1 2 2 2  z   z z 1 i z 1 i 2 1 1 1 1  2  2 1  0          .     Chọn A. z z z 2 2 z 2 2 2  2   2  2 2 10
Câu 35. Cho thỏa mãn z   thỏa mãn 2  iz
1 3i . Biết tập hợp các điểm biểu z
diễn cho số phức w  3  4iz 1 2i là đường tròn I , bán kính R . Khi đó A. I  1  ; 2
 , R  5. B. I 1; 2, R  5. C. I  1
 ; 2, R  5. D. I 1; 2  , R  5. (THPT CHUYÊN QUANG TRUNG) Lời giải 10 10
Từ giả thiết, ta có 2  iz 1 3i   2 z  
1   z  3i   z z 2 2 10
Lấy môđun hai vế  , ta được 2 z  
1   z  3   z  1. z
Lại có w  3  4iz 1 2i w 1 2i  3  4iz w 1 2i  3  4iz
w 1 2i  3  4i . z  5 z  5  tập hợp các điểm biểu diễn cho số phức w là đường
tròn tâm I 1; 2 và bán kính R  5 . Chọn C.
Câu 36. Cho số phức z thỏa mãn  z  3  4iz  4  3i  5 2  0  
. Giá trị của z là A. 2 . B. 2 . C. 2 2 . D. 1. (THPT HÀ HUY TẬP) Lời giải
Cách 1. Đặt z x yi x, y    z x yi , dựa vào giả thiết tìm nghiệm x, y 5 2 5 2
Cách 2. Ta có, giả thiết  3  4iz  4  3i
 3 z  4  4 z  3i z z 2 2 5 2
Lấy môđun hai vế, ta được 3 z  4  4 z  3 
mà z z , khi đó z
z  2   z  2 50 3 4 4 3 
 đến đây có thể giải trực tiếp bằng cách đặt t z 2 z
Hoặc sử dụng máy tính casio bằng việc thử các đáp án, để thấy được z  1.
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 5 2 5 2   i 2 3 4
z  3i  4 z
Cách 3. Ta có biến đổi 3  4iz  4  3i   .z z z z 5 2
Thử lần lượt với các đáp án, ta thấy
3 4i.4  3i  4.2 2 2 11 2 
z  2  z   
i z  10 (loại). 5 2 5 5
3  4i.2  3i  4. 2  4  3 2 3  4 2  z  2  z   
i z  3 (loại). 5 2 5 5
3  4i.8  3i  4.2 2 
z  2 2  z   z  6 (loại). 5 2
3  4i  3i  4 2 7 2 
z  1  z  2  z    
i z  1 (chọn). Chọn D. 5 2 10 10
Câu 37. Cho số phức z thỏa mãn điều kiện z  3  4i  2. Trong mặt phẳng Oxy tập hợp
điểm biểu diễn số phức w  2z 1 i là hình tròn có diện tích bằng A. S  9 . B. S  12 . C. S  16 . D. S  25 .
(THPT TRẦN HƯNG ĐẠO - NINH BÌNH) Lời giải
Cách 1. Đặt w x yi x, y   , ta có x yi  2z 1 i  2z x 1  y   1 i   1 .
Từ giả thiết, ta thấy rằng z  3  4i  2  2 . z  3  4i  4  2z  6  8i  4 2. Từ  
1 , 2 suy ra x 1  y  
1 i  6  8i  4  x  7   y  9i  4
  x  2   y  2    x  2   y  2 7 9 4 7 9  16
Vậy tập hợp điểm biểu diễn số phức w là hình tròn bán kính 2
R  4  S   R  16 . w 1 i w 1 i
Cách 2. Ta có w  2z 1 i   z
 3  4i z  3  4i 2 2 w  7  9i w  7  9i w  7  9i
z  3  4i
z  3  4i
 2  w  7  9i  4. 2 2 2
 tập hợp điểm biểu diễn số phức w là hình tròn bán kính R  4  S  16 . Chọn C.
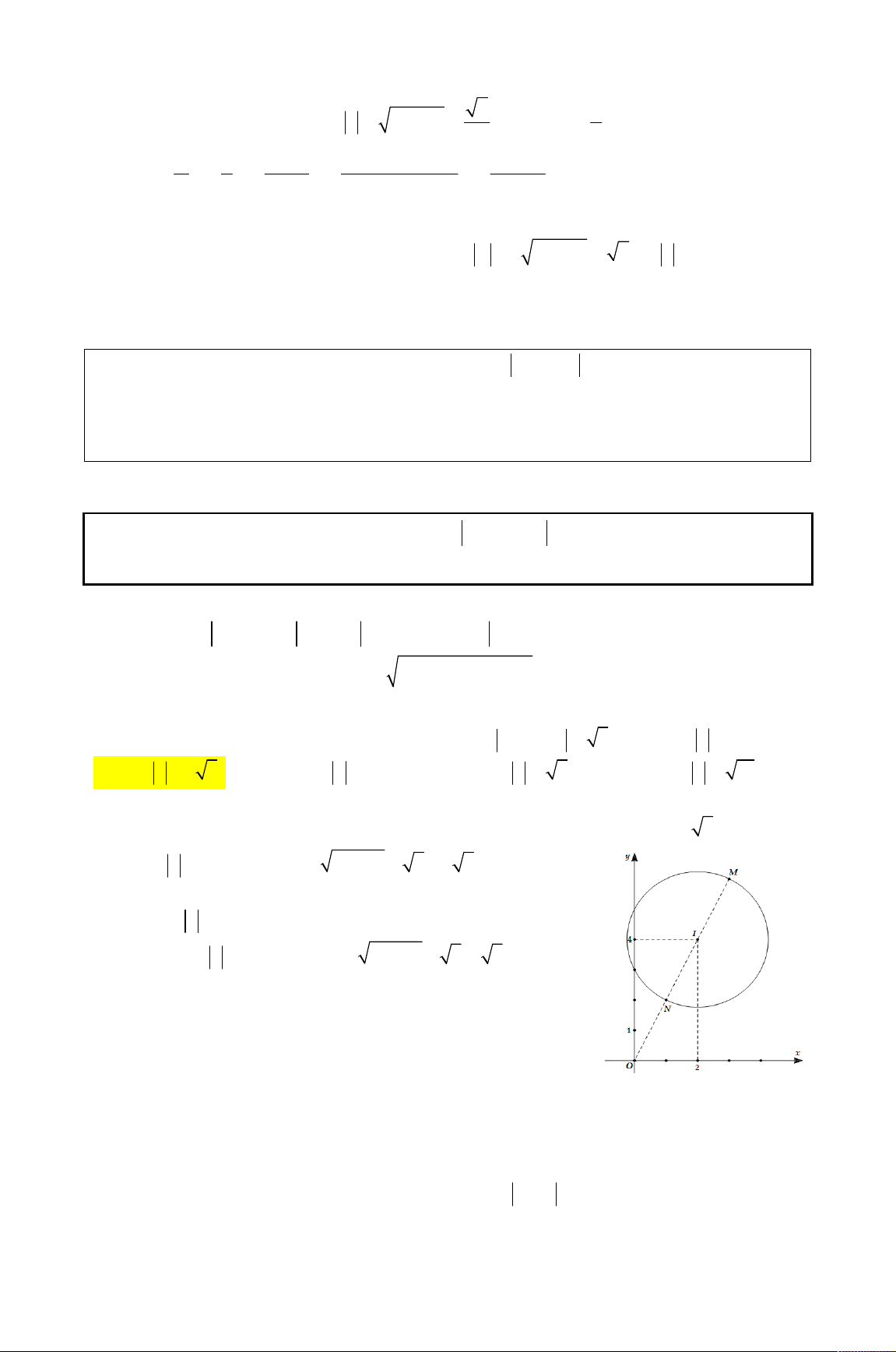
Câu 38. Biết số phức z x yi, a,b   thỏa mãn điều kiện z  2  4i z  2i đồng
thời có môđun nhỏ nhất. Tính giá trị biểu thức 2 2
M x y . A. M  8 . B. M  10 . C. M  16 . D. M  26 .
(THPT CHUYÊN VÕ NGUYÊN GIÁP - QUẢNG BÌNH) Lời giải
Đặt z x yi x, y   , ta có z  2  4i x  2   y  4 i và z  2i x   y  2 . i 2 2 2
Mặt khác z  2  4i z  2i nên suy ra  x     y   2 2 4 
x   y  2 . 2 2 2 2
x y  4x  8y  20  x y  4 y  4  x y  4  y  4  . x 2 2 Khi đó 2 2 2 z x y
x    x 2 4
 2x  8x 16  2 x  2  8  2 2.
Vậy môđun nhỏ nhất của z là 2 2. Xảy ra  x y  2  M  8. Chọn A.
Câu 39. Gọi H là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy sao
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995
cho 2z z  3 , và số phức z có phần ảo không âm. Tính diện tích hình H . 3 3 A. 3 . B. . C. . D. 6 . 4 2
(THPT CHUYÊN VÕ NGUYÊN GIÁP - QUẢNG BÌNH) Lời giải
Đặt z x yi x, y   , ta có 2z z  2 x yi   x yi  2x  2 yi x yi x  3yi Khi đó 2 2 2 2
2z z  3  x  3yi  3 
x  9 y  3  x  9 y  9. 2 2
x  9 y  9
Mặt khác z có phần ảo không âm nên y  0 . Vậy hình H tạo bởi  . y  0  2 2 x y
Xét đường Elip có phương trình  E  2 2
: x  9 y  9  
 1 có độ dài hai bán trục lần 9 1
lượt là a  3, b  1 nên diện tích  E  là S   ab  3 . ESE 3
Hình H giới hạn bởi hình  E  phía trên trục Ox y  0 nên S   . Chọn C. 2 2
Câu 40. Trong các số phức z thỏa mãn z  2  4i  2 , gọi z và z là số phức có môđun 1 2
lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức z và z bằng 1 2 A. 8 . i B. 4. C.  8. D. 8. (SỞ GD&ĐT HÀ TĨNH) Lời giải
Tập hợp các điểm M z là đường tròn C  có tâm I 2; 4 và bán kính R  2. Vậy 2 2
max z OM OI R  2  4  2  2  2 5. 2 2
min z ON OI R  2  4  2  2 5  2.
Tìm số phức z có môđun lớn nhất, nhỏ nhất.
Phương trình đường thẳng OI là y  2 . x
Tọa độ hai điểm M , N là nghiệm của hệ phương trình  y  2x   y  2x     x  2 
2   y  42 2 2  2
5x  20x 16  0    2 4   2 4    ; x y   2  ; 4    hoặc  ; x y   2  ; 4  .    5 5   5 5  2  4 
Số phức z có môđun lớn nhất là z  2   4  i   5  5   2 4  tương ứng M 2  ; 4  .    5 5  2  4   2 4 
Số phức z có môđun nhỏ nhất là z  2   4  i
 tương ứng N 2  ; 4  .   5  5   5 5  4 4
Vậy tổng phần ảo của hai số phức là 4   4   8. Chọn D. 5 5 z
Câu 41. Cho số phức z; w khác 0 sao cho z w  2 z w . Phần thực của số phức u  . w
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 1 1 1 A. a   . B. a  . C. a  1. D. a  . 8 4 8
(THPT CHUYÊN ĐH VINH – LẦN 3) Lời giải z z Sử dụng công thức 1 1 
với z , z   . z z 1 2 2 2  z z 1 u    .  w w 2 
Giả sử u a bi  ;
a b   . Từ giả thiết, suy ra  z w z w z    1  u 1  1.  w w w   1 2 2 a b   3 3 1  4   a  2 2 1  a   1 2a
a  . . Chọn D. 4 4 8   a  2 2 1  b  1  4
Câu 42. Cho số phức z thỏa mãn 3  4iz
 8 . Trên mặt phẳng tọa độ, khoảng cách z
từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?  9   1 5   1   1 9  A. ;  .   B. ; .   C. 0; .   D. ; .    4   4 4   4   2 4  (SỞ GD&ĐT BẮC NINH) Lời giải 4 4
Ta có 3  4iz
 8  3  4iz  8   . z z
Lấy môđun hai vế của  và sử dụng công thức z .z z . z , ta được 1 2 1 2 4 1 1
  3 4iz  8 
 3  4i . z  4 2   5 z  4 2  z z z 2
 5 z  4 2 z   2
1  5 z  8 z  4  0  z  2.  1 9  Gọi M  ;
x y là điểm biểu diễn số phức z 2 2  OM
x y z  2  ; .   Chọn D.  2 4 
Câu 43. Cho số phức z có môđun z  1. Giá trị lớn nhất của biểu thức P  1 z  3 1 z . A. 3 10. B. 2 10. C. 6. D. 4 2. (SỞ GD&ĐT BẮC NINH) Lời giải
Đặt z x yi x, y   , ta có 2 2 2 2 z  1 
x y  1  x y  1. Khi đó
P z 1  3 1 z   x  2
1  y  3 1 x2 2 2  y 2 2 2 2 
x y  2x 1  3 x y  2x 1 
2x  2  3 2  2x.
Theo bất đẳng thức Bunhiacopxki, ta có  x    x 2   2 2 2 2 3 2 2
1  3 2x  2  2  2x  40
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995 Suy ra P
2x  2  3 2  2x  40  2 10  P  2 10 . Chọn B. max z z
Câu 44. Nếu hai số phức z , z thỏa mãn z z  1 và z z  1 thì số phức 1 2 w  1 2 1 2 1 2 1 z z 1 2 có phần ảo bằng A. 0. B. 1. C. 1. D. 2. Lời giải 2 1 1
Ta có z .z z  1  z
, tương tự ta cũng có z  . 1 1 1 1 z 2 z 1 2 1 1  z z z z z z Khi đó 1 2 1 2 1 2 w   
w w là một số thực. Chọn A. 1 z .z 1 1 1 z z 1 2 1 2 1 . z z 1 2
Câu 45. Cho số phức z thỏa mãn điều kiện z  1. Gọi M , m lần lượt là giá trị lớn nhất của biểu thức 2
P  1 z  1 z z . Tổng M m gần với giá trị nào sau đây nhất? A. 3. B. 4. C. 6. D. 5. Lời giải 2 2 t  2
Đặt t  1 z với t 0; 2 nên 2
t  1 z  1 z1 z   2  2 Re z  Re z  . 2 Ta có 2 2 1 z z  7  2t
, khi đó P f t  2  t  7  2t
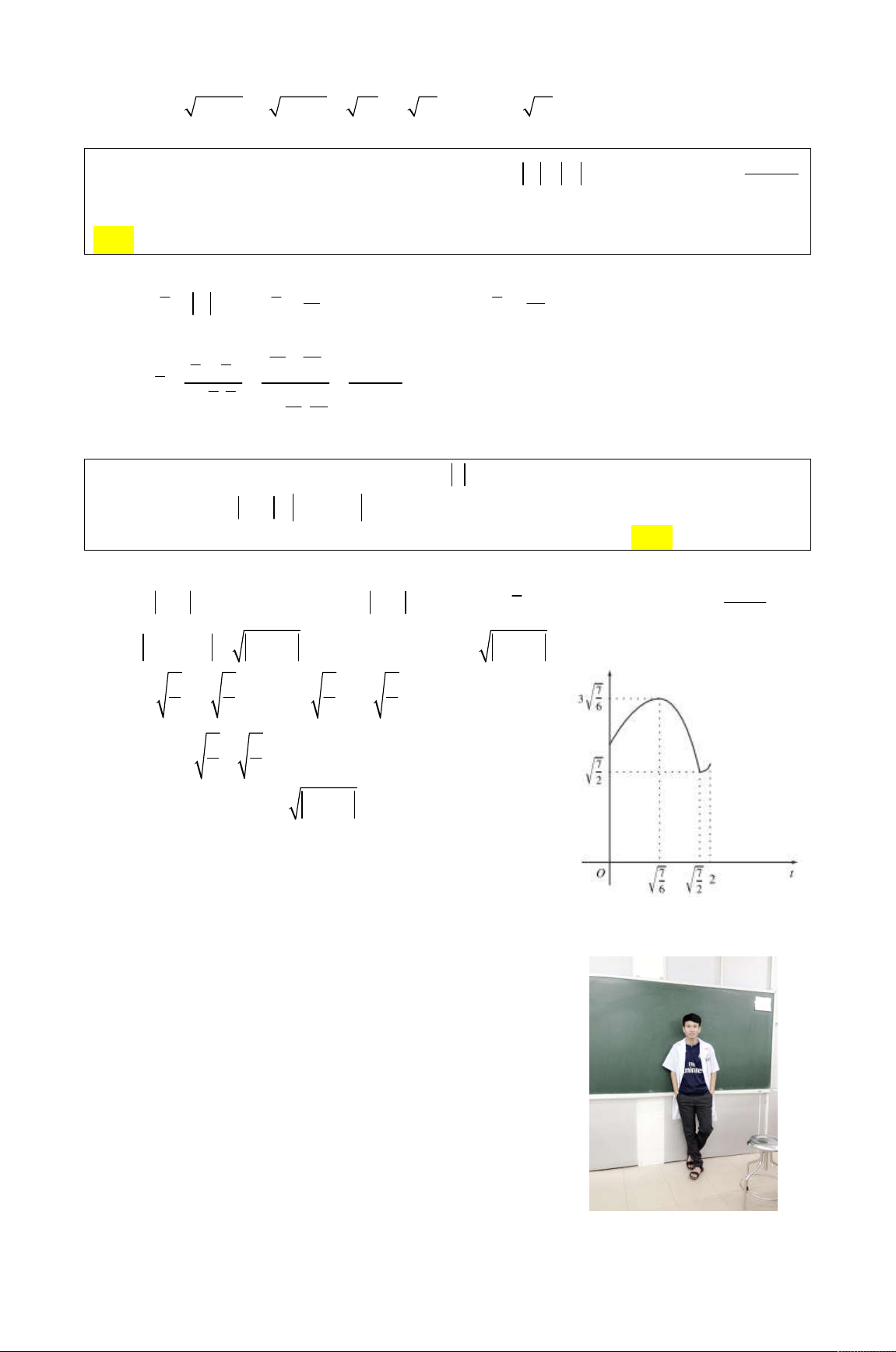
với f : 0; 2  .   7  7  7  7 Vậy f     P f    3 .  2  2  6  6     7 7
M m  3   5,11. Chọn D. 6 2
Đồ thị hàm số f t  2  t  7  2t như hình vẽ bên  
Lời kết. Bản tài liệu làm trong thời gian ngắn, khó tránh khỏi những sai xót cũng như ý
kiến chủ quan của cá nhân tác giả, kính mong quý khán
giả tham khảo và đóng góp ý kiến với tác giả để hoàn
thiện hơn các sản phẩm về sau. Và gửi lời chúc đến các
em học sinh 99er lời chúc
“ Đỗ Đại Học nhé ;) “
Giữa thành công và thất bại có con sông
gian khổ... trên con sông đó có cây cầu tên là sự cố gắng.
Không quan trọng bạn là ai, những gì bạn làm sẽ định nghĩa con người bạn – Ntd1995