Giải đề cương Hàm nhiều biến | Giải tích 2 | Đại học Bách Khoa Hà Nội
Giải đề cương Hàm nhiều biến | Giải tích 2 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!
Môn: Giải tích 2 40 tài liệu
Trường: Đại học Bách Khoa Hà Nội 2.8 K tài liệu
Tác giả:
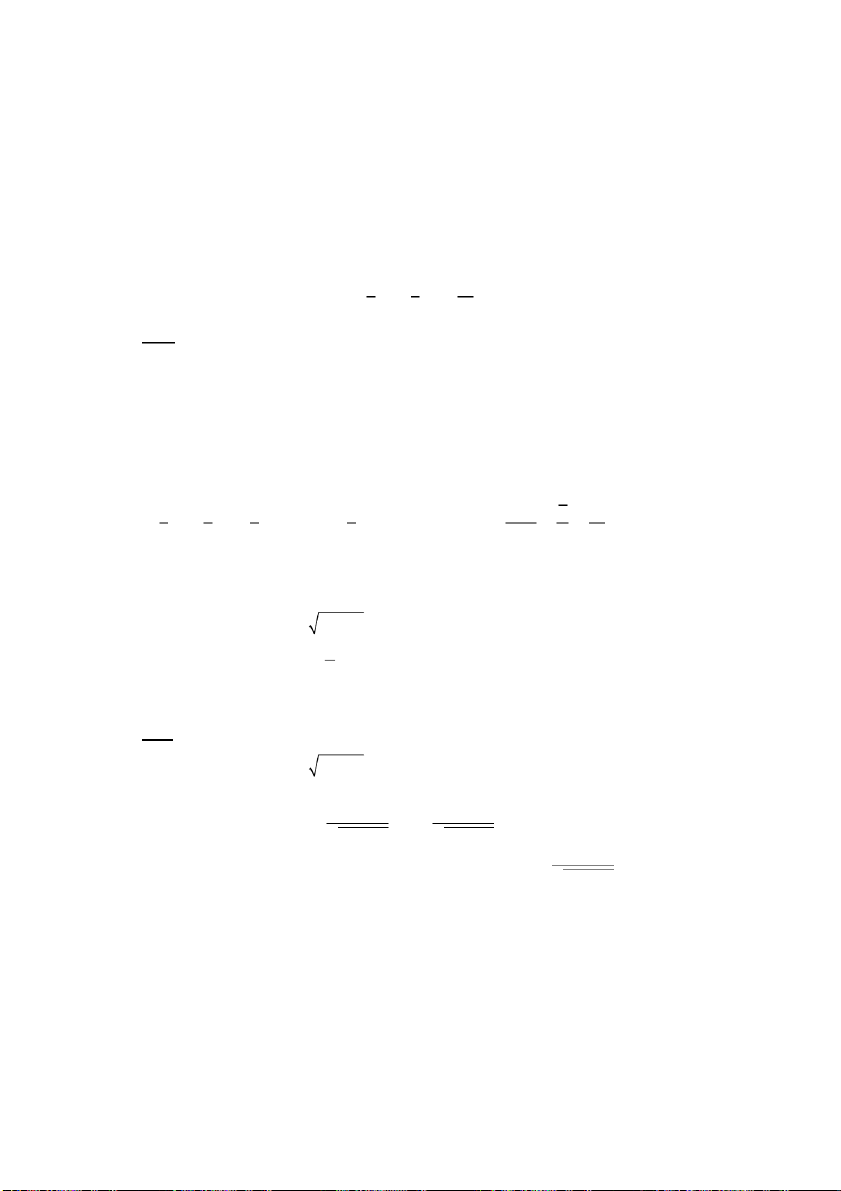
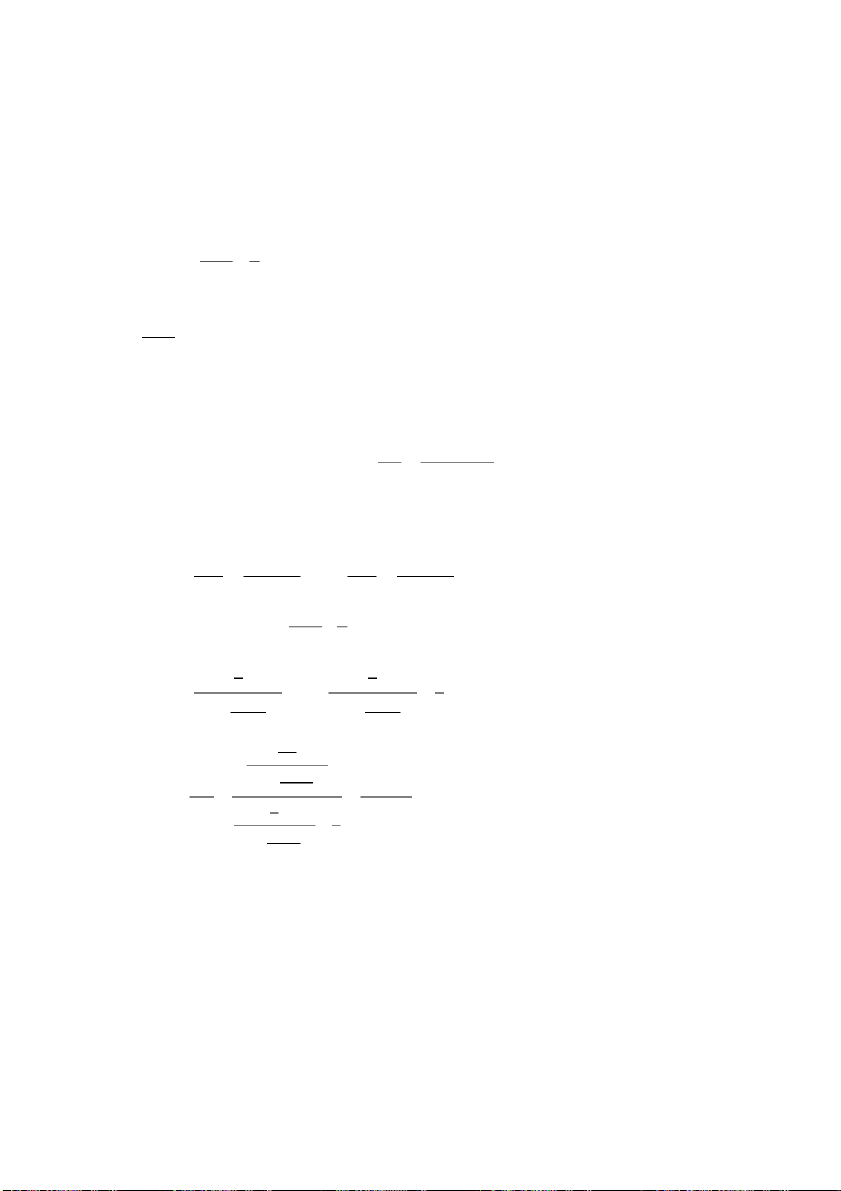
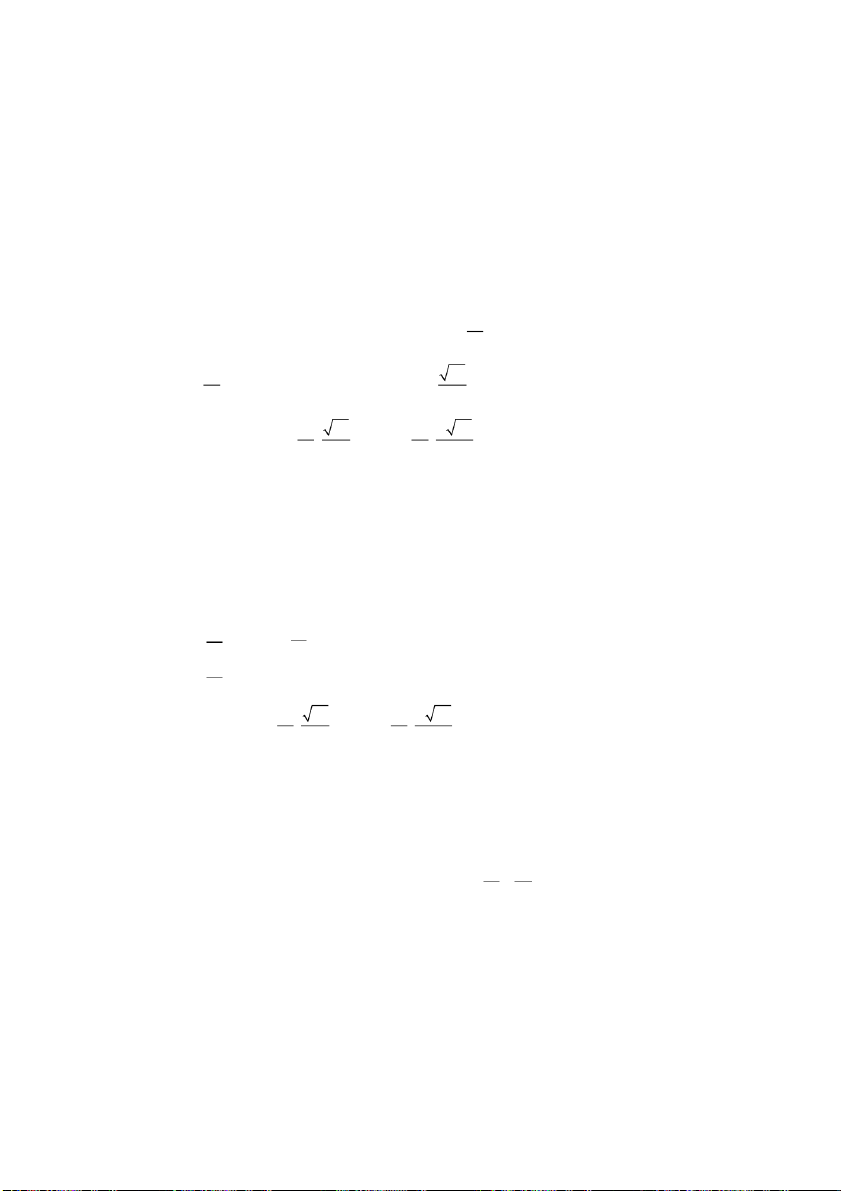
Preview text:
CHƯƠNG 1:
HÀM NHIỀU BIẾN SỐ 1
Bài 1: Tìm miền xác định của các hàm số sau z : = 2 2 x + y −1 1 y−1 a) z = c) z = arcsin 2 2 x + y −1 x d) z = s x in y b) z ( 2 2 = x y + )( 2 − x − − )2 1 4 y Giải:
a) Điều kiện xác định 𝑥2 + 𝑦2 − 1 > 0 ⇔ 𝑥2 + 𝑦2 > 1
Tập xác định: 𝐷 = {(𝑥, 𝑦) ∈ 𝑅2|𝑥2 + 𝑦2 > 1} {𝑥2 + 𝑦2 − 1 > 0 4 − 𝑥2 − 𝑦2 > 0
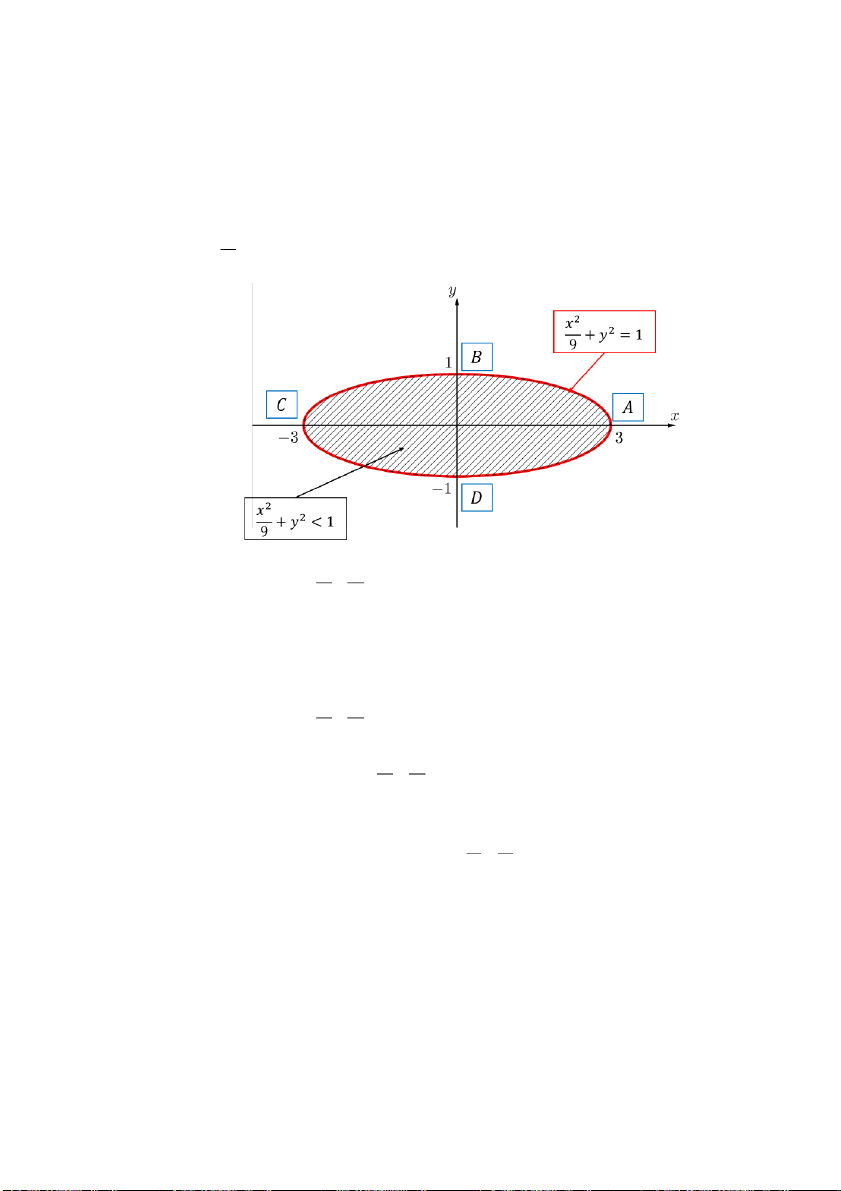
b) Điều kiện xác định (𝑥2 + 𝑦2 − 1)(4 − 𝑥2 − 𝑦2) > 0 ⇔ [{𝑥2 + 𝑦2 − 1 < 0 4 − 𝑥2 − 𝑦2 < 0 1 < 𝑥2 + 𝑦2 < 4 ⇔ [{𝑥2 + 𝑦2 < 1
𝑥2 + 𝑦2 > 4 (vô lý)
Tập xác định: 𝐷 = {(𝑥, 𝑦) ∈ 𝑅2|1 < 𝑥2 + 𝑦2 < 4} y −1
c) Điều kiện xác định 1 − 1 x
Xét với 𝑥 > 0, ta có: 𝑦 − 1
−1 ≤ 𝑥 ≤ 1 ⇔ −𝑥 ≤ 𝑦 − 1 ≤ 𝑥 ⇔ 1−𝑥 ≤ 𝑦 ≤ 1+𝑥
Xét với 𝑥 < 0, ta có: 𝑦 − 1
−1 ≤ 𝑥 ≤ 1 ⇔ −𝑥 ≥ 𝑦 − 1 ≥ 𝑥 ⇔ 1+𝑥 ≤ 𝑦 ≤ 1−𝑥 BK- i c Đạ ương môn phái PHAM THANH TUNG 1 − x y 1+ x x − 0 y 1 Vậy 1 − 1 x 1 + x y 1− x x 0
{1 − 𝑥 ≤ 𝑦 ≤ 1 + 𝑥
Tập xác định 𝐷 = {(𝑥, 𝑦) ∈ 𝑅2| [ 𝑥 > 0 }
{1 + 𝑥 ≤ 𝑦 ≤ 1 − 𝑥 𝑥 < 0 { 𝑥 ≥ 0 sin 𝑦 ≥ 0 { 𝑥 ≥ 0
𝑘2𝜋 ≤ 𝑦 ≤ 𝜋 + 𝑘2𝜋
d) Điều kiện xác định: 𝑥 sin 𝑦 ≥ 0 ⇔ [ ⇔ [ { 𝑥 ≤ 0 sin 𝑦 ≤ 0 { 𝑥 ≤ 0
−𝜋 + 𝑘2𝜋 ≤ 𝑦 ≤ 𝑘2𝜋 { 𝑥 ≥ 0
𝑘2𝜋 ≤ 𝑦 ≤ 𝜋 + 𝑘2𝜋
Tập xác định 𝐷 = {(𝑥, 𝑦) ∈ 𝑅2| [ (𝑘 ∈ 𝑍)} { 𝑥 ≤ 0
−𝜋 + 𝑘2𝜋 ≤ 𝑦 ≤ 𝑘2𝜋
Bài 2: Tìm giới hạn của các hàm số sau (nếu có): 4 y a) f ( , x )y = ( x→ 0, y→ )0 4 2 x + y 2 b) ( y f , x )y = ( x→ , y→ ) 2 x + 3 xy 2 2 1 − cos x + y c) f ( , x )y = ( x→ 0, y→ )0 2 2 x + y ( y − )1 − ( x x e y e− ) 1 d) f ( , x )y = x→ 0, y→ 0 2 2 ( ) x + y Giải: 4 4 y y 2 0 = y 4 2 2 2 y a) x + y y lim = 0 (x y)→( ) 4 2 , 0,0 x + y 2 lim y = 0 (x, y)→( 0, )0 BK- i c Đạ ương môn phái PHAM THANH TUNG
b) Xét theo phương 𝑦 = 𝑘𝑥 y (k )2 2 2 x k lim = lim = (x )y→( ) 2 x +3xy ( x )y→( ) 2 2 , , , , x +3 kx 1+ 3 k 2 y
Với mỗi một 𝑘 thì lim
tiến đến các giá trị giới hạn khác nhau (x y )→( ) 2 , , x + 3xy 2 y Vậy không tồn tại lim (x y )→( ) 2 , , x + 3xy
c) Do (𝑥, 𝑦) → (0,0) ⇒ 𝑥2 + 𝑦2 → 0 ⇒ √𝑥2 + 𝑦2 → 0 (√𝑥2 + 𝑦2)2 𝑥2 + 𝑦2
⇒ 1 − cos √𝑥2 + 𝑦2 ~ 2 = 2 𝑥2 + 𝑦2 1 − cos √𝑥2 + 𝑦2 1 ⇒ lim 2 (𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2 = lim
(𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2 = 2
d) Sử dụng khai triển Maclaurin, ta có: 2 x x e − = + x+ + (o ) 2 x 2 x − = x+ + ( 2 1 1 1 o )x với x →0 2 2 2 y y e − = + y+ + (o ) 2 y 2 y − = y+ + ( 2 1 1 1 o )y với y →0 2 2 2 2 y x x( x y + + o y − y x+ + o x y e 1) ( x y e 1) ( 2) ( 2) 2 2 − − − lim lim = ( x )y ( → ) 2 2 x + y ( x )y ( → ) 2 2 , 0,0 , 0,0 x + y 2 2 2 2 xy x y xy x xy+ − xy− − 2 2 2 2 = lim = lim ( x )y ( → ) 2 2 x + y ( x )y ( → ) 2 2 , 0,0 , 0,0 x + y 2 2 xy xy y
Theo bất đẳng thức Cauchy, ta có x:2 2 2 2 + y 2 xy = 2 2 x + y 2 xy 4 BK- i c Đạ ương môn phái PHAM THANH TUNG 2 xy y 2 2 0 xy 2 2 x + y 4 2 lim = 0(Định lý kẹp) ( x )y→( ) 2 2 , 0,0 x + y y lim = 0 (x, )y→( 0,)0 4 2 yx
Tương tự chứng minh được 2 lim = 0 (x y) ( → ) 2 2 , 0,0 x + y 2 2 2 2 xy x y xy yx − 2 2 2 2 lim = lim − lim = 0 ( x )y ( → ) 2 2 x + y ( x )y ( → ) 2 2 x + y ( x) y( → ) 2 2 , 0,0 , 0,0 , 0,0 x+ y
Bài 3: Tính đạo hàm riêng của các hàm số: a) z = ( 2 2 ln x + x + )y c) 3 y z = x 1 x y z b) 2 x z d) 2 2 2 u = e + + = y sin y Giải: a) z = ( 2 2 ln x + x + )y 1 + 𝑥 𝑦 2 2 2 2 ⇒ 𝑧′ √𝑥 + 𝑦 1 ′ √𝑥 + 𝑦 𝑦 𝑥 = = , 𝑧 = = 𝑥 + √𝑥2 + 𝑦2 √𝑥2 + 𝑦2 𝑦 𝑥 + √𝑥2 + 𝑦2
𝑥√𝑥2 + 𝑦2 + 𝑥2 + 𝑦2 x b) 2 z = y sin y 𝑥 ⇒ 𝑧′ ′ 𝑦 𝑥
𝑥 = 𝑦 cos ( 𝑦) , 𝑧𝑦 = 2𝑦sin (𝑥) − 𝑥cos (𝑦) c) 3 y z = x ⇒ 𝑧′ ′
𝑥 = 𝑦3𝑒(𝑦3−1) , 𝑧𝑦 = 𝑥𝑦3 ln(𝑥) ∙ 3𝑦2 BK- i c Đạ ương môn phái PHAM THANH TUNG 1 d) 2 2 2 x y z u e + + = 1 −2𝑥 𝑢′ 2 2
𝑥 = 𝑒 𝑥2+𝑦 +𝑧 [ (𝑥2 + 𝑦2 + 𝑧2)2] 1 −2𝑦 ⇒ 𝑢′ 2 2
𝑦 = 𝑒 𝑥2+𝑦 +𝑧 [ (𝑥2 + 𝑦2 + 𝑧2)2] 1 −2𝑧 ′ 𝑥2+𝑦2+𝑧2 {𝑢𝑧 = 𝑒 [ (𝑥 ] 2 + 𝑦2 + 𝑧2)2
Bài 4: Khảo sát sự liên tục của hàm số và sự tồn tại các đạo hàm riêng của nó: 𝑦2
a) 𝑓(𝑥, 𝑦) = {𝑥 arctan (𝑥) , nếu 𝑥 ≠ 0 0 , nếu 𝑥 = 0
𝑥 sin 𝑦 − 𝑦 sin 𝑥 b) 𝑓(𝑥, 𝑦) = { 𝑥2 + 𝑦2
, nếu (𝑥, 𝑦) ≠ (0,0)
0 , nếu (𝑥, 𝑦) = (0,0) Giải: a)
1. Khảo sát tính liên tục hàm số 𝑓(𝑥, 𝑦) 2 y
Với 𝑥 ≠ 0, 𝑦 = 𝑦0 ∈ ℝ , hàm số f ( ,x )y = a x rctan liên tục x
Xét với (𝑥, 𝑦) = (0, 𝑦0), 𝑦0 ∈ ℝ 𝑦 2 𝜋 0 ≤ |𝑥 arctan ( | ≤ | 𝑦 2 { 𝑥) 4 𝑥| 𝜋 ⇒ lim 𝑥 arctan ( = 0 (Kẹp) lim | (𝑥,𝑦)→(0,𝑦0) 𝑥)
(𝑥,𝑦)→(0,𝑦0) 4 𝑥| = 0 𝑦 2 ⇒ lim 𝑥 arctan ( = 𝑓(0, 𝑦 (𝑥,𝑦)→(0,𝑦 0) = 0 0) 𝑥)
⇒ Hàm 𝑓(𝑥, 𝑦) liên tục tại (0, 𝑦0)
Vậy 𝑓(𝑥, 𝑦) liên tục với (𝑥, 𝑦) ∈ ℝ2. BK- i c Đạ ương môn phái PHAM THANH TUNG
2. Khảo sát sư tồn tại của đạo riêng
Với 𝑥 ≠ 0, 𝑦 = 𝑦0 ∈ 𝑅, hàm số có đạo hàm riêng: 2 𝑦 2 + 𝑓′ 𝑦 −2𝑦2 1 −2𝑥2𝑦2
𝑥 = arctan ( 𝑥) + 𝑥 ∙ 𝑥3 ∙ 4 = arctan ( + 1 + (𝑦 𝑥) 𝑥) 𝑥4 + 𝑦4 1 2𝑥3𝑦 + 𝑓′ 2𝑦 𝑦 = 𝑥 ∙ 𝑥2 ∙ 4 = 1 + (𝑦𝑥) 𝑥4 + 𝑦4
Xét với (𝑥, 𝑦) = (0, 𝑦0) 2 y0 x arctan f 0 x , y f 0,0 x + − 2 y + f (0,y = lim = lim 0 = lim arctan x 0 ) ( 0 ) ( ) x→ 0 x x→ 0 x x 0 → x 2 2 2 y y y Với 0 0 0 x → 0 → + arctan → lim = f y = x (0, 0 ) x x 2 x→0 x 2 2 f 0,y + y − f 0,0 0− 0 + f (0, y + y= lim = lim = 0 y 0 ) ( 0 ) ( ) y→ 0 y y→ 0 y
⇒ Hàm số 𝑓(𝑥, 𝑦) tồn tại đạo hàm riêng tại (𝑥, 𝑦) = (0, 𝑦0) b)
1. Khảo sát tính liên tục xsin y− ysin x
Với (𝑥, 𝑦) ≠ (0,0), hàm số f ( , x )y = liên tục 2 2 x+ y
Xét với (𝑥, 𝑦) = (0,0)
Sử dụng khai triển Maclaurin, ta có: 3 x x x = − + ( 3 sin o )x với x →0 3! 3 y y y = − + ( 3 sin o )y với y →0 3! BK- i c Đạ ương môn phái PHAM THANH TUNG 3 y x y− + ( o y ) 3 x 3 − y x− + (o )3x s x in y− s y in x 3! 3! ⇒ lim lim = (x )y→( ) 2 2 x + y ( x )y→( ) 2 2 , 0,0 , 0,0 x + y 3 3 x y xy − 3 3 6 6 x y− xy = lim = lim ( x )y ( → ) 2 2 x + y ( x )y ( → ) ( 2 6 x+ y)2 , 0,0 , 0,0
Theo bất đẳng thức Cauchy, ta có: | 𝑥3𝑦
𝑥2 + 𝑦2| ≥ |2𝑥𝑦| ⇒ | 𝑥3𝑦 𝑥2
𝑥2 + 𝑦2| ≤ |2𝑥𝑦| = | 2 | 𝑥3𝑦 𝑥2
0 ≤ |𝑥2 + 𝑦2| ≤ | 2 | 𝑥3𝑦 𝑥2 ⇒ lim (𝑥,𝑦)→( 𝑥2 + 𝑦2 = 0 (Kẹp) lim | 0,0) { (𝑥,𝑦)→(0,0) 2 | = 0 3 xy
Chứng minh tương tự ta có: lim (x y) ( → ) 2 2 , 0,0 x + y 𝑥3𝑦 − 𝑥𝑦3 1 𝑥3𝑦 𝑥𝑦3 ⇒ lim
(𝑥,𝑦)→(0,0) 6(𝑥2 + 𝑦2) = 6 ( lim
(𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2 − 𝑥2 + 𝑦2) = 0 = 𝑓(0,0). ⇒ Hàm s
ố 𝑓(𝑥, 𝑦) liên t c t ụ ại (0,0) .
Vậy 𝑓(𝑥, 𝑦) liên t c v ụ ới (𝑥, 𝑦) ∈ ℝ2 .
2. Khảo sát sự tồn tại của đạo hàm riêng
Với (𝑥, 𝑦) ≠ (0,0), hàm số có đạo hàm riêng:
(sin 𝑦 − 𝑦 cos𝑥)(𝑥2 + 𝑦2) − 2𝑥(𝑥 sin𝑦 − 𝑦 sin 𝑥) + 𝑓′𝑥 = (𝑥2 + 𝑦2)2
(𝑥 cos 𝑦 − sin 𝑥)(𝑥2 + 𝑦2) − 2𝑦(𝑥 sin𝑦 − 𝑦 sin 𝑥) + 𝑓′𝑦 = (𝑥2 + 𝑦2)2
Xét với (𝑥, 𝑦) = (0,0) ) + 𝑓′
𝑓(0 + ∆𝑥, 0 − 𝑓(0,0) 0 − 0 𝑥(0,0) = lim ∆𝑥→0 ∆𝑥 = lim ∆𝑥→0 ∆𝑥 = 0 ) ( + 𝑓′
𝑓(0,0 + ∆𝑦 − 𝑓 0,0) 0 − 0 𝑦(0,0) = lim ∆𝑦→0 ∆𝑦 = lim ∆𝑥→0 ∆𝑦 = 0 BK- i c Đạ ương môn phái PHAM THANH TUNG
⇒ Hàm số tồn tại đạo hàm riêng tại (𝑥, 𝑦) = (0,0).
Vậy hàm số 𝑓(𝑥, 𝑦) có đạo hàm riêng liên tục với (𝑥, 𝑦) ∈ ℝ2.
Bài 5: Giả sử 𝑧 = 𝑦𝑓(𝑥2 − 𝑦2), trong đó 𝑓(𝑥2 − 𝑦2) là hàm khả vi. Chứng minh rằng đối ớ
v i hàm số 𝑧 hệ thức sau luôn thỏa mãn: 1 ′ 1 ′ 𝑧
𝑥 𝑧𝑥 + 𝑦 𝑧𝑦 = 𝑦2 Giải: ′ = 2𝑥
Đặt 𝑢 = 𝑥2 − 𝑦2 ⇒ { 𝑧𝑥 𝑧′𝑦 = −2𝑦 + z = y (f )u = y
(f )u+ y (f )u= 0+ y u (f ) u= 2 xy f x x x x ( ) x + z = y f ( )u = y
(f )u+ y (f )u= (f ) u+ y u ( f) u = ( ) 2 f − 2 u y f y y y y ( ) y 𝑧 1 𝑓(𝑢) ⇒ ′ 1 ′ 1 1 𝑦 𝑧
𝑥 𝑧𝑥 + 𝑦 𝑧𝑦 = 𝑥 . 2𝑥𝑦𝑓′(𝑢) + 𝑦 [𝑓(𝑢) − 2𝑦2. 𝑓′(𝑢)] = 𝑦 = 𝑦 = 𝑦2
Câu 6: Tìm đạo hàm riêng của các hàm số hợp sau: a) 2 2 u − 2v 2 2 z = e , u= cos x , v= x+ y x b) z = ( 2 2 ln u + v ) , u= x ,y v= c) z = ( x ) 3 arcsin − , y x 3= ,t y 4 = Giải: a) 2 2 u − 2v 2 2 z = e , u= cos x , v= x+ y 𝑧′ ′ ′
𝑢 = 2𝑢. 𝑒𝑢2−2𝑣2, 𝑢𝑥 = − sin 𝑥 , 𝑢𝑦 = 0 ⇒ { 𝑥 𝑧′ ′ ′ 𝑦
𝑣 = −4𝑣. 𝑒𝑢2−2𝑣2, 𝑣𝑥 = , 𝑣 = √𝑥2 + 𝑦2 𝑦 √𝑥2 + 𝑦2 𝑥 + 𝑧′ ′ ′ ′ ′ 2−2𝑣2 2−2𝑣2
𝑥 = 𝑧𝑢 . 𝑢𝑥 + 𝑧𝑣. 𝑣𝑥 = 2𝑢 ∙ 𝑒𝑢 𝑢
∙ (− sin 𝑥) − 4𝑣 ∙ 𝑒 ∙ √𝑥2 + 𝑦2 BK- i c Đạ ương môn phái PHAM THANH TUNG ⇔ 𝑧′ cos 𝑥 2−2(𝑥2+𝑦2) 𝑥
𝑥 = −2 cos 𝑥 ∙ sin 𝑥 ∙ 𝑒( ) − 4√𝑥2 + 𝑦2 ∙
. 𝑒(cos𝑥)2−2(𝑥2+𝑦2) √𝑥2 + 𝑦2 ⇔ 𝑧′ cos 𝑥)2−2(𝑥2+𝑦2) cos 𝑥 𝑥 = − sin 2𝑥 ∙ 𝑒( ) − 4𝑥 ∙ 𝑒( 2−2(𝑥2+𝑦2) ⇔ 𝑧′ 2 2)
𝑥 = 𝑒(cos 𝑥)2−2(𝑥 +𝑦 ∙ (− sin 2𝑥 − 4𝑥) 𝑦 + 𝑧′ ′ ′ ′ ′ 2−2𝑣2
𝑦 = 𝑧𝑢 . 𝑢𝑦 + 𝑧𝑣. 𝑣𝑦 = 2𝑢 ∙ 𝑒𝑢 𝑢
∙ 0 − 4𝑣 ∙ 𝑒 2−2𝑣2 ∙ √𝑥2 + 𝑦2 𝑦 ⇔ 𝑧′ 2 (cos 𝑥)2−2(𝑥2+𝑦2) cos 𝑥 2−2(𝑥2+𝑦2)
𝑦 = −4√𝑥2 + 𝑦 ∙ 𝑒 ∙ = −4𝑦𝑒( ) √𝑥2 + 𝑦2 x b) z = ( 2 2 ln u + v ) , u= x ,y v= 2𝑢 𝑧′ ′ ′
𝑢 = 𝑢2 + 𝑣2 , 𝑢𝑥 = 𝑦, 𝑢𝑦 = 𝑥 𝑧′ 2𝑣 ′ 1 ′ −𝑥
{ 𝑣 = 𝑢2 + 𝑣2 , 𝑣𝑥 = 𝑦 , 𝑣𝑦 = 𝑦2 2𝑥 2𝑢 1 + 𝑧′ ′ ′ ′ ′ 2𝑣 1 2𝑥𝑦 𝑦
𝑥 = 𝑧𝑢 . 𝑢𝑥 + 𝑧𝑣. 𝑣𝑥 = 𝑢2 + 𝑣2 .𝑦 + 𝑢2 + 𝑣2 . 𝑦 = 2 . 𝑦 + 2 . (𝑥𝑦)2 + (𝑥 𝑦 𝑦) (𝑥𝑦)2 + (𝑥𝑦) 2𝑦4 2 2(𝑦4 + 1) 2
= 𝑥(𝑦4 + 1) +𝑥(𝑦4 + 1) = 𝑥(𝑦4 + 1) = 𝑥 2𝑥 2𝑢 2𝑣 −𝑥 2𝑥𝑦 𝑦 −𝑥 + 𝑧′ ′ ′ ′ ′
𝑦 = 𝑧𝑢 . 𝑢𝑦 + 𝑧𝑣. 𝑣𝑦 = 𝑢2 + 𝑣2 . 𝑥 + 𝑢2 + 𝑣2 . 𝑦2 = 2 . 𝑥 + 2 . (𝑥𝑦)2 + (𝑥 𝑦2 𝑦) (𝑥𝑦)2 + (𝑥𝑦) 2𝑦3 −2 2 1 2(𝑦4 − 1)
= 𝑦4 +1 + 𝑦(𝑦4 +1) = 𝑦4 +1(𝑦3 − 𝑦) = 𝑦(𝑦4+1) ′ c) = 3 z = ( x ) 3 arcsin − , y x 3= ,t y 4 =⇒ { 𝑥𝑡 𝑦′𝑡 = 12𝑡2 ⇒ 𝑧′ ′ ′ ′ 3 −1 3 − 12𝑡2 𝑡 = 𝑧𝑥. 𝑥 ′ 𝑡 + 𝑧𝑦. 𝑦𝑡 = + ∙ 12𝑡2 =
√1 − (𝑥 − 𝑦)2 √1 − (𝑥 − 𝑦)2 √1 − (𝑥 − 𝑦)2 BK- i c Đạ ương môn phái PHAM THANH TUNG
Câu 7: Cho 𝑓 là hàm khả vi đến cấp hai trên ℝ . Chứng minh rằng hàm số
𝜔(𝑥, 𝑡) = 𝑓(𝑥 − 3𝑡) thỏa mãn phương trình truyền sóng: 𝜕2𝜔 𝜕2𝜔 𝜕𝑡2 = 9 𝜕𝑥2 Giải:
Đặt 𝑢 = 𝑥 − 3𝑡 ⇒ 𝑢′ ′ 𝑥 = 1, 𝑢𝑡 = −3 2 2 2 u u + = = −3 = −3 = − 3 = 9 2 2 2 t u t u t t u u t u 2 2 2 u u + = = = = = 2 2 2 x u x u
x x u u x u 2 2 = 9 2 2 2 2 t u = 9 2 2 2 2 t x = 2 2 x u
Câu 8: Tìm vi phân toàn phần của các hàm số sau: a) z = ( 2 2 sin x + ) y x+ y c) z = arctan x− y x b) z ln tan = y d) 2 y z u = x Giải: a) z = ( 2 2 sin x + ) y ⇒ 𝑑𝑧 = 𝑧′ ′
𝑥𝑑𝑥 + 𝑧𝑦𝑑𝑦 = cos(𝑥2 + 𝑦2) (2𝑥𝑑𝑥 + 2𝑦𝑑𝑦) x b) z = ln tan y 𝑥𝑑𝑦 − 𝑦𝑑𝑥 ⇒ 𝑑𝑧 = 𝑧′ ′ 2
𝑥𝑑𝑥 + 𝑧𝑦𝑑𝑦 = ∙ ( sin 2𝑦 𝑥2 ) 𝑥 x+ y c) z = arctan x− y BK- i c Đạ ương môn phái PHAM THANH TUNG ( ) ( ) ⇒ 𝑑𝑧 = 𝑧′ ′
𝑥 − 𝑦 𝑑𝑥 + 𝑥 + 𝑦 𝑑𝑦
𝑥𝑑𝑥 + 𝑧𝑦𝑑𝑦 =
(𝑥 − 𝑦)2 + (𝑥 + 𝑦)2 d) 2 y z u = x 𝑦2𝑧 ⇒ 𝑑𝑢 = 𝑢′ ′ ′
𝑥𝑑𝑥 + 𝑢𝑦𝑑𝑦 + 𝑢𝑧𝑑𝑧 = 𝑥𝑦2𝑧 ( 𝑥 𝑑𝑥 + 2𝑦𝑧 ln𝑥 𝑑𝑦 + 𝑦2 ln 𝑥 𝑑𝑧) Câu 9: Tính gần đúng:
a) 𝐴 = √(2,02)3 + 𝑒0,03 b) 𝐵 = (1,02)1,01 Giải:
a) 𝐴 = √(2,02)3 + 𝑒0,03
− Xét hàm 𝑓(𝑥, 𝑦) = √𝑥3 + 𝑒𝑦 với 𝑥0 = 2, ∆𝑥 = 0,02, 𝑦0 = 0, ∆𝑦 = 0,03 𝑒𝑦 ⇒ 𝑓′ 3𝑥2 ′ 𝑥 = , 𝑓 = 2√𝑥3 + 𝑒𝑦 𝑦 2√𝑥3 + 𝑒𝑦 − Áp dụng: 𝑓(𝑥 ′
0 + ∆𝑥, 𝑦0 + ∆𝑦) ≈ 𝑓(𝑥0; 𝑦0) + ∆𝑥 ∙ 𝑓 ′
𝑥(𝑥0, 𝑦0) + ∆𝑦 ∙ 𝑓𝑦(𝑥0, 𝑦0)
⇒ 𝑓(2 + 0,02 ; 0 + 0,03) ≈ 𝑓(2; 0) + 0,02. 𝑓′𝑥(2,0) + 0,03. 𝑓′𝑦(2,0) 0,03.1
⇒ 𝐴 = 𝑓(2,02; 0,03) ≈ 3 + 0,02.2 + 6 = 3,045 Vậy 𝐴 ≈ 3,045 b) 𝐵 = (1,02)1,01
− Xét hàm 𝑓(𝑥, 𝑦) = 𝑥𝑦 với 𝑥0 = 1, ∆𝑥 = 0,02, 𝑦0 = 1, ∆𝑦 = 0,01 ⇒ 𝑓′ ′
𝑥 = 𝑦𝑥𝑦−1 , 𝑓𝑦 = 𝑥𝑦 ∙ ln 𝑥 − Áp dụng: 𝑓(𝑥 ′
0 + ∆𝑥, 𝑦0 + ∆𝑦) ≈ 𝑓(𝑥0; 𝑦0) + ∆𝑥𝑓 ′
𝑥(𝑥0, 𝑦0) + ∆𝑦𝑓𝑦(𝑥0, 𝑦0)
⇒ 𝑓(1 + 0,02 ; 1 + 0,01) ≈ 𝑓(1; 1) + 0,02. 𝑓′ ′
𝑥(1,1) + 0,01. 𝑓𝑦(1,1)
⇒ 𝐵 = 𝑓(1,02; 1,01) ≈ 1 + 0,02.1 + 0,01.0 = 1,02 Vậy 𝐵 ≈ 1,02 BK- i c Đạ ương môn phái PHAM THANH TUNG
Câu 10: Tìm đạo hàm, đạo hàm riêng của các hàm số ẩn xác định bởi các phương trình sau: a) 3 3 4 x y y − x = a, tính 𝑦′ b) 2 3 z x y + z + +e 0 = , tính 𝑧′ ′ 𝑥, 𝑧𝑦 x+ y c) arctan = , tính 𝑦′ a a d) 3 3 3 x y + z
+ 3− xyz 0=, tính 𝑧′ ′ 𝑥, 𝑧𝑦 Giải:
a) Đặt 𝐹(𝑥, 𝑦) = 𝑥3𝑦 − 𝑦3𝑥 − 𝑎4 Ta có: 𝐹′ ′
𝑥 = 3𝑥2𝑦 − 𝑦3 , 𝐹𝑦 = 𝑥3 − 3𝑦2𝑥
Với 𝑥3 − 3𝑦2𝑥 ≠ 0 −𝐹′ −3𝑥2𝑦 + 𝑦3 𝑦′ = 𝑥
𝐹𝑦′ = 𝑥3 − 3𝑦2𝑥
b) Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑥2 + 𝑦 + 𝑧3 + 𝑒𝑧 Ta có: 𝐹′ ′ ′
𝑥 = 2𝑥 , 𝐹𝑦 = 1, 𝐹𝑧 = 3𝑧2 + 𝑒𝑧 − 𝐹′ −2𝑥 − 𝐹′ −1 ⇒ 𝑧′ 𝑥 ′ 𝑦 𝑥 = 𝐹 =
𝑧′ = 3𝑧2 + 𝑒𝑧 , 𝑧𝑦
𝐹𝑧′ = 3𝑧2 +𝑒𝑧 x+ y c) Đặt F (x, )y = arctan − a a 1 1 ⇒ 𝐹′ 𝑎 𝑎 1 𝑥 = ′ 2 , 𝐹𝑦 = 2 − 1 + (𝑥 + 𝑦 𝑎 𝑎 ) 1 + (𝑥 + 𝑦 𝑎 ) −1𝑎 2 −𝐹′ 1 + (𝑥 + 𝑦 𝑎2 ⇒ 𝑦′ = 𝑥 𝑎 ) 𝐹′ = = 𝑦 1 𝑎 (𝑥 + 𝑦)2 2 − 1 1 + (𝑥 + 𝑦 𝑎 𝑎 )
d) Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑥3 + 𝑦3 + 𝑧3 − 3𝑥𝑦𝑧 BK- i c Đạ ương môn phái PHAM THANH TUNG ⇒ 𝐹′ ′ ′
𝑥 = 3𝑥2 − 3𝑦𝑧 , 𝐹𝑦 = 3𝑦2 − 3𝑥𝑧 , 𝐹𝑧 = 3𝑧2 − 3𝑥𝑦
− 𝐹′ −3𝑥2 + 3𝑦𝑧 − 𝐹′ −3𝑦2 + 3𝑥𝑧 ⇒ 𝑧′ 𝑥 ′ 𝑦 𝑥 = 𝐹 2 =
𝑧′ = 3𝑧 − 3𝑥𝑦 , 𝑧𝑦
𝐹𝑧′ = 3𝑧2 −3𝑥𝑦
Câu 11: Cho hàm số ẩn 𝑧 = 𝑧(𝑥, 𝑦) xác định bởi phương trình
2𝑥2𝑦 + 4𝑦2 + 𝑥2𝑧 + 𝑧3 = 3 z z Tính (0, )1 , ( 0),1 x y Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑧) = 2𝑥2𝑦 + 4𝑦2 + 𝑥2𝑧 + 𝑧3 − 3 ⇒ 𝐹′ ′ ′
𝑥 = 4𝑥𝑦 + 2𝑥𝑧, 𝐹𝑦 = 2𝑥2 + 8𝑦, 𝐹𝑧 = 𝑥2 + 3𝑧2 2 z −F
−4 xy− 2 xz z − 2 x− 8 Ta có: x = = , = 2 2 2 2 x F x + 3 z y x+ 3 z z
Với 𝑥 = 0, 𝑦 = 1 thay vào 2𝑥2𝑦 + 4𝑦2 + 𝑥2𝑧 + 𝑧3 = 3 ta thu được: 4 + 𝑧3 = 3 ⇔ 𝑧 = −1
Thay 𝑥 = 0, 𝑦 = 1, 𝑧 = −1 ta thu được: 𝜕𝑧 𝜕𝑧 −8
𝜕𝑥 (0,1) = 0 ,𝜕𝑦 (0,1) = 3 x + z Câu 12: Cho u = tính 𝑢′ , 𝑢 ết rằ
𝑧 là hàm số ẩ ủa 𝑥, 𝑦 xác đị ởi phương y+ z 𝑥 𝑦′ bi ng n c nh b
trình 𝑧𝑒𝑧 = 𝑥𝑒𝑥 + 𝑦𝑒𝑦. Giải:
Đặt 𝐹(𝑥, 𝑦, 𝑧) = 𝑧𝑒𝑧 − 𝑥𝑒𝑥 − 𝑦𝑒𝑦 ⇒ 𝐹′ ′ ′
𝑥 = −𝑒𝑥 − 𝑥𝑒𝑥, 𝐹𝑦 = −𝑒𝑦 − 𝑦𝑒𝑦, 𝐹𝑧 = 𝑒𝑧 + 𝑧𝑒𝑧
−𝐹′ 𝑒𝑥 + 𝑥𝑒𝑥 −𝐹′ 𝑒𝑦 + 𝑦𝑒𝑦 ⇒ 𝑧′ 𝑥 ′ 𝑦 𝑥 = 𝐹 =
𝑧′ = 𝑒𝑧 + 𝑧𝑒𝑧 , 𝑧𝑦
𝐹𝑧′ = 𝑒𝑧 +𝑧𝑒𝑧 Ta có: BK- i c Đạ ương môn phái PHAM THANH TUNG
(1 + 𝑧′ )(𝑦 + 𝑧) − 𝑧′ ( (1 + 𝑒𝑥 + 𝑥𝑒𝑥 𝑢′ 𝑥 𝑥 𝑥 + 𝑧)
𝑒𝑧 + 𝑧𝑒𝑧 ) − (𝑥 + 𝑧) 𝑒𝑥 + 𝑥𝑒𝑥 𝑒𝑧 + 𝑧𝑒𝑧 𝑥 = (𝑦 + 𝑧)2 = (𝑦 + 𝑧)2
′ )(𝑥 + 𝑧) − 𝑧′ (𝑦 + 𝑧)
(𝑥 + 𝑧) (1 + 𝑒𝑦 + 𝑦𝑒𝑦 𝑢′ (1 + 𝑧𝑦 𝑦
𝑒𝑧 + 𝑧𝑒𝑧 ) − (𝑦 + 𝑧) 𝑒𝑦 + 𝑦𝑒𝑦 𝑒𝑧 + 𝑧𝑒𝑧 𝑦 = (𝑦 + 𝑧)2 = (𝑦 + 𝑧)2 2 Câu 13: Phương trình 2 2 2
z + = y − z xác định hàm số ẩn 𝑧 = 𝑧(𝑥, 𝑦). Chứng minh x rằng: 1 1 𝑥2𝑧′ ′ 𝑥 + 𝑦 𝑧𝑦 = 𝑧 Giải: 2 Đặt F( , x , y ) 2 2 2 z = z+ − y− z ( 2 2 x 0, y − z )0 x −2 ⇒ 𝐹′ ′ −𝑦 ′ 𝑧 𝑥 = 𝑥2 ,𝐹𝑦 = , 𝐹 = 2𝑧 + 2√𝑦2 − 𝑧2 𝑧 √𝑦2 − 𝑧2 2 𝑦 ′ −𝐹′ 2 2 ⇒ 𝑧′ −𝐹𝑥 𝑥2 ′ 𝑦 √𝑦 − 𝑧 𝑥 = 𝐹 , 𝑧𝑦 = 𝑧′ = 2𝑧 + 𝑧 𝐹′ = 2𝑧 + 𝑧 √𝑦2 − 𝑧2 𝑧 √𝑦2 − 𝑧2 1 2 + 1 1 ⇒ 𝑥2𝑧′ ′ 2 √𝑦2 − 𝑧2 √𝑦2 − 𝑧2 1 𝑥 + 𝑦 𝑧𝑦 = + = = 2𝑧 + 𝑧 2𝑧 + 𝑧 𝑧 √𝑦2 − 𝑧2 √𝑦2 − 𝑧2 𝑧 (2 + 1 ) √𝑦2 − 𝑧2
Câu 14: Tính các đạo hàm riêng cấp hai của hàm số sau: y a) 1 z = ( x + )3 2 2 y c) z = arctan 3 x b) 2 z x = ln( x + )y d) z = ( 3 3 sin x + ) y Giải: a) Ta có: BK- i c Đạ ương môn phái PHAM THANH TUNG 𝑥2 2𝑥2 + 𝑦2
𝑧′𝑥𝑥= √𝑥2 + 𝑦2 + = √𝑥2 + 𝑦2 √𝑥2 + 𝑦2 𝑧′ = 𝑥√𝑥2 + 𝑦2 𝑦2 𝑥2 + 2𝑦2 { 𝑥
⇒ 𝑧′ = √𝑥2 + 𝑦2 + = 𝑧′ 𝑦𝑦 𝑦 = 𝑦√𝑥2 + 𝑦2 √𝑥2 + 𝑦2 √𝑥2 + 𝑦2 2𝑥𝑦 𝑥𝑦 𝑧′ = = { 𝑥𝑦
2√𝑥2 + 𝑦2 √𝑥2 + 𝑦2 b) Ta có: 2𝑥 𝑥2 + 2𝑥𝑦 ′ 𝑥2
𝑧𝑥𝑥= 2 ln(𝑥 + 𝑦) + 𝑧′ 𝑥 + 𝑦 + (𝑥 + 𝑦)2
𝑥 = 2𝑥 ln(𝑥 + 𝑦) + 𝑥 + 𝑦 ′ 𝑥2 𝑥2 ⇒ 𝑧𝑦𝑦= 𝑧′ = (𝑥 + 𝑦)2 { 𝑦 𝑥 + 𝑦 𝑥2 ′ 2𝑥 {
𝑧𝑥𝑦= 𝑥 +𝑦 − (𝑥 +𝑦)2 c) Ta có: 1 −𝑦 −𝑦 ′ 2𝑥𝑦 𝑧′ 𝑧𝑥𝑥= 𝑥 = 2 ∙ (𝑥2 + 𝑦2)2 1 + (𝑦 𝑥2 = 𝑥2 + 𝑦2 𝑥) −2𝑥𝑦 ′ 1 ⇒ 𝑧𝑦𝑦= (𝑥2 + 𝑦2)2 𝑧′ 1 𝑥 𝑦 = 2 ∙ 𝑥 = 𝑥2 + 𝑦2 −(𝑥2 + 𝑦2) + 2𝑦2 𝑦2 − 𝑥2 { 1 + (𝑦𝑥) ′ = {𝑧𝑥𝑦 (𝑥2 + 𝑦2)2 = (𝑥2 + 𝑦2)2 d) Ta có: ′ ′
𝑧𝑥𝑥= 6𝑥 cos(𝑥3 + 𝑦3 3
) − 9𝑥4 sin(𝑥3 + 𝑦 )
{𝑧𝑥 = 3𝑥2 cos(𝑥3 + 𝑦3) ′ = 6𝑦 cos(𝑥3 + 𝑦3 3 ) 𝑧′ 𝑧𝑦𝑦 − 9𝑦4 sin(𝑥3 + 𝑦 )
𝑦 = 3𝑦2 cos(𝑥3 + 𝑦3) ⇒ { 𝑧′𝑥𝑦= −9𝑥2 3 𝑦2 sin(𝑥3 + 𝑦 )
Câu 15: Tính vi phân cấp hai của các hàm số sau:
a) 𝑧 = 𝑥𝑦3 − 𝑥2𝑦
b) 𝑧 = 𝑒2𝑥(𝑥 + 𝑦2) c) 𝑧 = ln (𝑥3 + 𝑦2) Giải: 𝑧′𝑥𝑥= −2𝑦
a) Ta có: { 𝑧′𝑦𝑦= 6𝑥 𝑧𝑥𝑦 ′ = 3𝑦2 − 2𝑥 BK- i c Đạ ương môn phái PHAM THANH TUNG ⇒ 𝑑2𝑧 = 𝑧′ ′ ′
𝑥𝑥𝑑𝑥2 + 2𝑧𝑥𝑦 𝑑𝑥𝑦 + 𝑧𝑦𝑦𝑑𝑦2 = −2𝑦𝑑𝑥2 + (3𝑦2 − 2𝑥)𝑑𝑥𝑦 + 6𝑥𝑑𝑦2 b) Ta có: ′ ′ 𝑧𝑥𝑥 = 4𝑒2𝑥 2𝑥 2𝑥
+ 4𝑒 (𝑥 + 𝑦2) = 4𝑒 (𝑥 + 𝑦2 + 1) {𝑧𝑥 = 𝑒2𝑥 2𝑥 + 2𝑒 (𝑥 + 𝑦2) ′ 𝑧′ 𝑧𝑦𝑦= 2𝑒2𝑥 𝑦 = 2𝑦𝑒2𝑥 ⇒ {
𝑧′𝑥𝑦= 4𝑦𝑒2𝑥 ⇒ 𝑑2𝑧 = 𝑧 ′ ′ ′ 2
𝑥𝑥𝑑𝑥2 + 2𝑧𝑥𝑦 𝑑𝑥𝑦 + 𝑧𝑦𝑦 𝑑𝑦2 = 4𝑒2𝑥 2𝑥 2𝑥
(𝑥 + 𝑦2 + 1)𝑑𝑥 + 4𝑦𝑒 𝑑𝑥𝑦 + 2𝑒 𝑑𝑦2 c) Ta có: −3𝑥2 + 6𝑥𝑦2 ′
6𝑥(𝑥3 + 𝑦2) − 3𝑥2. 3𝑥2 3𝑥2 𝑧𝑥𝑥= (𝑥3 + 𝑦2)2 = (𝑥3 + 𝑦2)2 𝑧′𝑥 = 𝑥3 + 𝑦2 −2𝑥2 + 2𝑦2 ′
2(𝑥3 + 𝑦2) − 2𝑦. 2𝑦 2𝑦 ⇒ 𝑧𝑦𝑦= 2 = 2 𝑧′ = (𝑥3 + 𝑦2) (𝑥3 + 𝑦2) { 𝑦 𝑥3 + 𝑦2 ′ −3𝑥2. 2𝑦 −6𝑥2𝑦 {
𝑧𝑥𝑦= (𝑥3 +𝑦2)2 = (𝑥3 +𝑦2)2
(−3𝑥2 + 6𝑥𝑦2)𝑑𝑥2 − 12𝑥2𝑦𝑑𝑥𝑑𝑦 + (−4𝑥2 + 4𝑦2)𝑑𝑦2 ⇒ 𝑑2𝑧 = (𝑥3 + 𝑦2)2
Câu 16: Tìm cực trị của các hàm số: a) 3 2 2
z 4= x 6+ x 4− xy − y 8− x 2+ e) 2x z e = ( 2x − xy + )2 4 2 y b) ( 2 2 2 2 ) 2 3 x y z x y e− + = + − f) = + (− + )2 3 3 z x y x y c) 4 2 z 4 = xy −x 2 − y 4 3 xy d) z = + − x y 12 Giải: ′ = 0
𝑥2 + 𝑥 − 4𝑦 − 8 = 0
𝑥2 + 𝑥 − 4𝑦 − 8 = 0 (1) a) Xét {𝑧𝑥 𝑧′𝑦 = 0 ⇔ {12 12 −4𝑥 − 2𝑦 = 0 ⇔ {12 12 𝑦 = −2𝑥 (2)
Thế (2) vào (1) ta được: 1 2
12𝑥2 + 12𝑥 + 8𝑥 − 8 = 0 ⇔ [𝑥 = 3 ⇒ 𝑦 = − 3 𝑥 = −2 ⇒ 𝑦 = 4 BK- i c Đạ ương môn phái PHAM THANH TUNG 1 − 2 ⇒
Hàm số có hai điểm tới hạn M , và M 2 − ,4 2 ( ) 1 3 3 Đặt 𝐴 = 𝑧′ ′
𝑥𝑥= 24𝑥 + 12, 𝐵 = 𝑧𝑥𝑦 = −4, 𝐶 = 𝑧𝑦𝑦′ = −2 1 −2 Tại M , ta có { 𝐴 = 20 > 0
không là điểm cực trị ủ ố 1 3 3
∆ = 𝐵2 − 𝐴𝐶 = 56 > 0 ⇒ 𝑀1 c a hàm s . Tại M 2 − ,4 ta có { 𝐴 = −36 < 0 2 ( )
∆ = 𝐵2 − 𝐴𝐶 = −56 < 0
⇒ 𝑀2 là điểm cực đại của hàm số ⇒ 𝑧𝐶Đ = 𝑧(𝑁) = 26 ′ = 0 2 2)
2𝑥[2 + 𝑒−(𝑥2+𝑦2)] = 0 b) Xét {𝑧𝑥 = 0 𝑧′ ⇔ { ⇔ {𝑥 = 0
𝑦 = 0 ⇔ {4𝑥 + 2𝑥𝑒−(𝑥 +𝑦
6𝑦 + 2𝑦𝑒−(𝑥2+𝑦2) = 0
2𝑦[3 + 𝑒−(𝑥2+𝑦2)] = 0 𝑦 = 0
⇒ Hàm số có hai điểm tới hạn 𝑀1(0,0) 𝐴 = 𝑧′ 2 2)
𝑥𝑥= 4 + 2𝑒−(𝑥 +𝑦 −(𝑥 +𝑦 ) − 4𝑥2𝑒 2 2 Đặt { 𝐵 = 𝑧′ 2 2
𝑥𝑦= −4𝑥𝑦𝑒−(𝑥 +𝑦 ) 𝐶 = 𝑧′ 2 2)
𝑦𝑦= 6 + 2𝑒−(𝑥 +𝑦 −(𝑥 +𝑦 − 4𝑦2𝑒 2 2) Tại 𝑀1(0,0), ta có { 𝐴 = 6 > 0
∆ = 𝐵2 − 𝐴𝐶 = −48 < 0
⇒ 𝑀1 là điểm cực tiểu của hàm số, 𝑧𝐶𝑇 = 𝑧(𝑀1) = −1 ′ = 0 𝑥 = 0 ⇒ 𝑦 = 0 c) Xét {𝑧𝑥 𝑧′ 𝑥 = 1 ⇒ 𝑦 = 1
𝑦 = 0 ⇔ {4𝑦 − 4𝑥3 = 0
4𝑥 − 4𝑦 = 0 ⇔ {𝑦 = 𝑥3
𝑦 = 𝑥 ⇒ 𝑥3 − 𝑥 = 0 ⇔ [ 𝑥 = −1 ⇒ 𝑦 = −1
⇒ Hàm số có ba điểm tới hạn 𝑀1(−1, −1), 𝑀2(1,1), 𝑀3(0,0) Đặt 𝐴 = 𝑧′ ′
𝑥𝑥= −12𝑥2, 𝐵 = 𝑧𝑥𝑦 = 4, 𝐶 = 𝑧𝑦𝑦′ = −4 Tại 𝑀 12 1(−1, −1), ta có { 𝐴 = − < 0
∆ = 𝐵2 − 𝐴𝐶 = −32 < 0
⇒ 𝑀1 là điểm cực đại của hàm số, 𝑧CĐ = 𝑧(𝑀1) = 1 Tại 𝑀 12 2(1,1), ta có { 𝐴 = − < 0
∆ = 𝐵2 − 𝐴𝐶 = −32 < 0
⇒ 𝑀2 là điểm cực đại của hàm số , 𝑧𝐶Đ = 𝑧(𝑀2) = 1 Tại 𝑀3(0,0), ta có { 𝐴 = 0 < 0
∆ = 𝐵2 − 𝐴𝐶 = 16 > 0 ⇒ 𝑀3 không là điểm cực trị của hàm số BK- i c Đạ ương môn phái PHAM THANH TUNG d) Xét −4 𝑦 −48 ′ 𝑦 = {𝑧𝑥 = 0 𝑥2 − 12 = 0 𝑥2 (1) 𝑧′ ⇔ 𝑦 = 0 ⇔ −3 𝑥 −36 { 𝑦2 − 12 = 0 { 𝑦2 − 𝑥 = 0 (2)
Thế (1) vào (2) ta được: −36 −1 1
2304 − 𝑥 = 0 ⇔ 64 𝑥4 − 𝑥 = 0 ⇔ 𝑥 (64 𝑥3 + 1) = 0 ⇔ [ 𝑥 = 0 (loại) 𝑥4 𝑥 = −4 ⇒ 𝑦 = −3
⇒ Hàm số có một điểm tới hạn 𝑀1(−4, −3) 8 − −1 −6 Đặt A = z = , B= z = , C= z = xx 3 xy yy 3 x 12 y 1 A = 0 8
Tại 𝑀1(−4, −3), ta có 0 1 2 B AC − = − = 48
⇒ 𝑀1 là điểm cực tiểu của hàm số, 𝑧CT = 𝑧(𝑀1) = −3 ′ = 0 𝑥𝑦 2) = 0 e) Xét {𝑧𝑥 𝑧′𝑦 = 0 ⇔ {𝑒2𝑥 2𝑥
(8𝑥 − 2𝑦) + 𝑒 (4𝑥2 − 2 + 𝑦
−2𝑥. 𝑒2𝑥 + 2𝑦𝑒2𝑥 = 0
⇔ {𝑒2𝑥(4𝑥2 − 2𝑥𝑦 + 𝑦2 + 8𝑥 − 2𝑦) = 0 𝑒2𝑥(𝑦 − 𝑥) = 0
⇔ {4𝑥2 − 2𝑥𝑦 + 𝑦2 + 8𝑥 − 2𝑦 = 0 (1) 𝑦 = 𝑥 (2)
Thế (2) vào (1) ta được: 4𝑥2 − 2𝑥2 + 𝑥2 + 6𝑥 = 0 ⇔ [ 𝑥 = 0 ⇒ 𝑦 = 0 𝑥 = −2 ⇒ 𝑦 = −2
⇒ Hàm số có hai điểm tới hạn 𝑀1(−2, −2) và 𝑀2(0,0) 𝐴 = 𝑧′ 2 𝑥𝑥= 𝑒2𝑥 2𝑥
(8𝑥 − 2𝑦 + 8) + 2𝑒 (4𝑥2 − 2𝑥𝑦 + 𝑦 + 8𝑥 − 2𝑦) Đặt {
𝐵 = 𝑧′𝑥𝑦= 𝑒2𝑥(−2𝑥 + 2𝑦 − 2) 𝐶 = 𝑧𝑦𝑦 ′ = 𝑒2𝑥 −4
Tại 𝑀1(−2, −2), ta có { 𝐴 = −4𝑒 < 0
∆ = 𝐵2 − 𝐴𝐶 = 8𝑒−8 > 0
⇒ 𝑀1 không là điểm cực trị của hàm số. BK- i c Đạ ương môn phái PHAM THANH TUNG Tại 𝑀2(0,0), ta có { 𝐴 = 8 > 0
∆ = 𝐵2 − 𝐴𝐶 = −4 < 0
⇒ 𝑀2 là điểm cực tiểu của hàm số ⇒ 𝑧𝐶𝑇 = 𝑧(𝑀2) = 0 ′ = 0 ( ) = 0 (1) f) Xét {𝑧𝑥
𝑧′𝑦 = 0 ⇔ {3𝑥2 − 2 𝑥 + 𝑦
3𝑦2 − 2(𝑥 + 𝑦) = 0 (2) 𝑦 = 𝑥
Lấy (1) trừ (2) ta được: 3𝑥2 − 3𝑦2 = 0 ⇔ [𝑦 = −𝑥
Thay 𝑦 = 𝑥 vào (1) ta thu được: 𝑥 = 0 ⇒ 𝑦 = 0 3𝑥2 − 4𝑥 = 0 ⇔ [ 4 𝑥 = 4 3 ⇒ 𝑦 =
Thay 𝑦 = −𝑥 vào (1) ta thu được: 3𝑥2 = 0 ⇔ 𝑥 = 0 ⇒ 𝑦 3= 0 4 4
⇒ Hàm số có hai điểm tới hạn M , và M 0,0 2 ( ) 1 3 3 Đặt 𝐴 = 𝑧′ ′
𝑥𝑥= 6𝑥 − 2, 𝐵 = 𝑧𝑥𝑦 = −2, 𝐶 = 𝑧𝑦𝑦′ = 6𝑦 − 2 4 4 Tại M , , ta có { 𝐴 = 6 > 0 1 3 3
∆ = 𝐵2 − 𝐴𝐶 = −32 < 0 4 4 6 − 4 ⇒ 𝑀 z = z ,
1 là điểm cực tiểu của hàm số ⇒ = CT 3 3 27
Tại 𝑀2(0,0), ta có { 𝐴 = −2 < 0 ∆ = 𝐵2 − 𝐴𝐶 = 0
Xét các điểm lân cận 𝑁(∆𝑥, ∆𝑦) với ∆𝑥 = −∆𝑦 ≠ 0 rất nhỏ. ⇒ z f(= ) N f(−M ) ( = )3 x ( + )3 y ( − x )3y + ( = )3x ( −) 3x ( − x ) 3 − x 0 2
⇒ 𝑀2(0,0) không là điểm cực trị.
Câu 17: Tìm cực trị của hàm số 𝑧 = 𝑥2 + 𝑦2 với điều kiện 3𝑥 − 4𝑦 = 5. Giải:
Điều kiện 3𝑥 − 4𝑦 = 5 ⇔ 3𝑥 − 4𝑦 − 5 = 0 Đặt hàm p ụ
h : 𝐿(𝑥, 𝑦, 𝑘) = 𝑥2 + 𝑦2 + 𝑘(3𝑥 − 4𝑦 − 5) BK- i c Đạ ương môn phái PHAM THANH TUNG Xét hệ: 𝐿′ −3𝑘 𝑥 = 0 2𝑥 + 3𝑘 = 0 𝑥 = −9𝑘 {𝐿′ 2
𝑦 = 0 ⇔ {2𝑦 − 4𝑘 = 0 ⇔ { ⇒ 𝐿′ 𝑦 = 2𝑘 2 − 4 ∙ 2𝑘 = 5 𝑘 = 0 3𝑥 − 4𝑦 = 5 3𝑥 − 4𝑦 = 5 3 −2 𝑥 = ⇒ 𝑘 = 5 5 ⇒ { −4 𝑦 = 5 − − Ta có bộ nghiệm ( x y ) 3 4 2 , , k = , , 5 5 5
Xét vi phân cấp hai: 𝑑2𝐿(𝑥, 𝑦, 𝑘) = 𝐿′ 2 2
𝑥𝑥𝑑𝑥 + 2𝐿′ 𝑥𝑦𝑑𝑥𝑑𝑦 + 𝐿′ 𝑦𝑦𝑑𝑦
⇒ 𝑑2𝐿 (𝑥, 𝑦, 𝑘) = 2𝑑𝑥2 + 2.0. 𝑑𝑥𝑑𝑦 − 4𝑑𝑦2 = 2𝑑𝑥2 + 2𝑑𝑦2 − − Với ( x y ) 3 4 2 , , k , , = 2 2 2 5 5
5 ⇒ 𝑑 𝐿 (1,0, −2) = 2𝑑𝑥 + 2𝑑𝑦 > 0 3 −4 ⇒ M ,
là điểm cực tiểu có điều kiện của hàm số, 𝑧 ( 1 5 5 CT = 𝑧 𝑀1) = 1
Câu 18: Tìm một điểm thuộc elip 4𝑥2 + 𝑦2 = 4 sao cho nó xa điểm 𝐴(1,0) nhất. Giải:
Gọi 𝑀(𝑥, 𝑦) ∈ 4𝑥2 + 𝑦2 = 4 sao cho 𝑀 xa điểm 𝐴(1,0) nhất.
Khoảng cách 𝑀𝐴 = √(𝑥 − 1)2 + 𝑦2 với 4𝑥2 + 𝑦2 = 4
⇒ 𝑀𝐴2 = (𝑥 − 1)2 + 𝑦2
Để 𝑀𝐴 đạt giá trị lớn nhất ⇔ 𝑀𝐴2 = (𝑥 − 1)2 + 𝑦2 đạt giá t ịr lớn nhất
Yêu cầu đề bài trở thành: Tìm 𝑥, 𝑦 thỏa mãn 4𝑥2 + 𝑦2 = 4 sao cho 𝑧 = (𝑥 − 1)2 + 𝑦2 đạt giá t ị r lớn nhất.
− Xét 𝑥, 𝑦 nằm trên biên của miền hình elip: 4𝑥2 + 𝑦2 = 4
Tìm điểm tới hạn của 𝑧 = (𝑥 − 1)2 + 𝑦2 với điều kiện 4𝑥2 + 𝑦2 = 4
Đặt hàm phụ 𝐿(𝑥, 𝑦, 𝑘) = (𝑥 − 1)2 + 𝑦2 + 𝑘(4𝑥2 + 𝑦2 − 4) BK- i c Đạ ương môn phái PHAM THANH TUNG 𝐿′𝑥= 0 2(𝑥 − 1) + 8𝑘𝑥 = 0 𝑥(2 + 8𝑘) = 2 (1)
Xét {𝐿′𝑦 = 0 ⇔ { 2𝑦 + 2𝑘𝑦 = 0 ⇔ { 𝑦(2 + 2𝑘) = 0 (2) 𝐿′ 2 2 𝑘 = 0 4𝑥 + 𝑦 = 4 4𝑥2 + 𝑦2 = 4 (3) (2) ⇔ [ 𝑦 = 0 𝑘 = −1
TH1: Thay 𝑦 = 0 vào (3) ⇒ 4𝑥2 = 4 ⇔ 𝑥 = ±1
⇒ Hai điểm tới hạn 𝑀1(1,0) và 𝑀2(−1,0). −
TH2: Thay 𝑘 = −1 vào (1) ⇒ 𝑥 ∙ (−6) 1 = 2 ⇒ x = 3 1 32 Thay − x =
vào (3) ⇒ 4𝑥2 + 𝑦2 = 4 ⇒y = 3 3 1 − 32 1 − − 32 ⇒ Hai điểm tới ạ h n M , và M , 3 3 3 4 3 3
− Xét 𝑥, 𝑦 nằm trong miền hình elip: 4𝑥2 + 𝑦2 < 4 ′ = 0 ) Xét {𝑧𝑥
𝑧′𝑦 = 0 ⇔ {2(𝑥 − 1 = 0 2𝑦 = 0 ⇔ {𝑥 = 1 𝑦 = 0
⇒ Điểm tới hạn 𝑀5(1,0) ≡ 𝑀1 𝑧(𝑀1) = 0 𝑧(𝑀2) = 4 16 𝑧(𝑀 16 3) = ⇒ 𝑧 ho 3
𝑚𝑎𝑥 = 3 tại 𝑀3 ặc 𝑀4 16 {𝑧(𝑀4) = 3 1 − 32 1 − − 32 Điểm cần tìm là M , và M , 3 3 3 4 3 3
Câu 19: Tính giá trị lớn nhất và bé nhất của hàm số: a) 2 2 z x = y + x
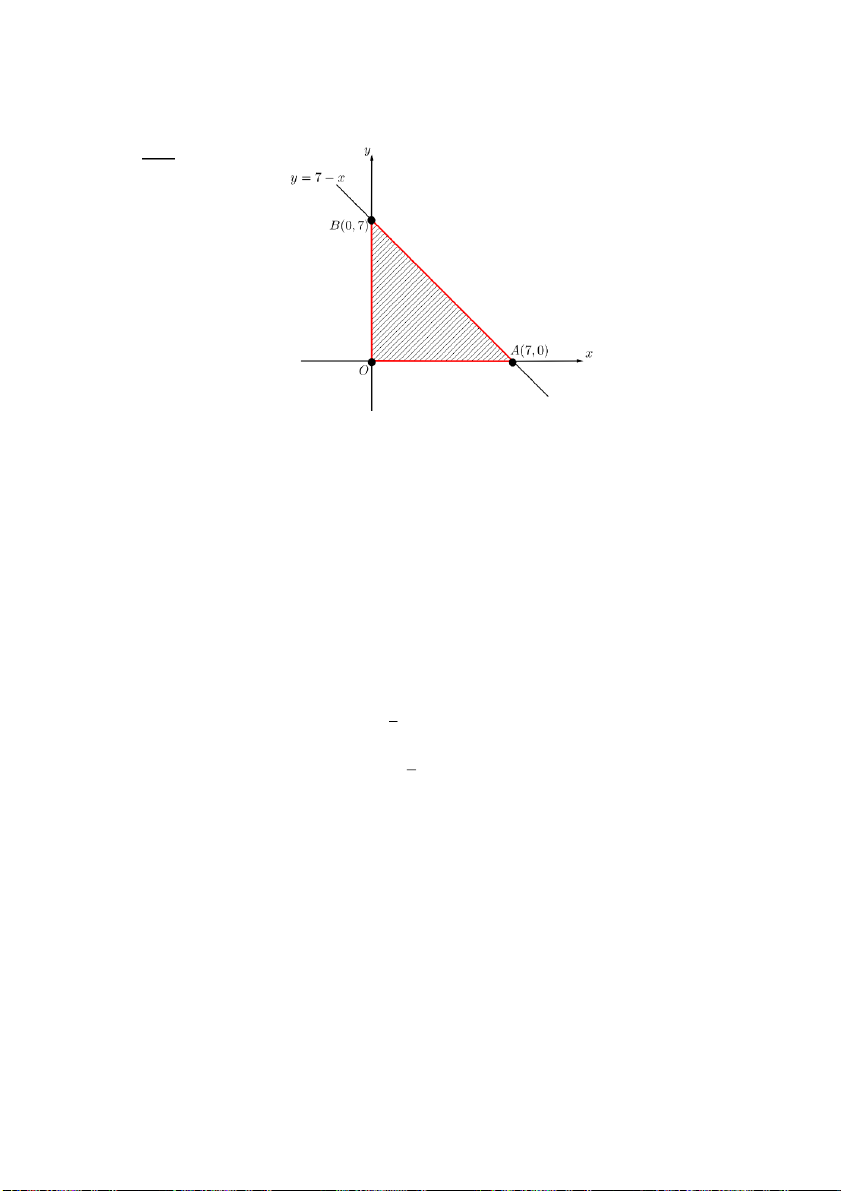
+ y 7− z 8− trong hình tam giác giới hạn bởi các đường thẳng x 0 = , y =0 và x + y =6 2 2 x y b) 2 2 z 4 = x 9
− ytrong miền giới hạn bởi đường elip + =1 9 4 BK- i c Đạ ương môn phái PHAM THANH TUNG Giải: a)
Phương trình 𝐴𝐵: 𝑦 = 6 − 𝑥 Điểm 𝐵(0,6), 𝐴(6,0)
− Xét trong miền ∆𝑂𝐴𝐵 ′ = 0 Xét hệ {𝑧𝑥
𝑧′𝑦 = 0 ⇔ {2𝑥 + 3𝑦 − 7 = 0
2𝑦 + 3𝑥 − 8 = 0 ⇔ {𝑥 = 2 𝑦 = 1
⇒ Trong miền ∆𝑂𝐴𝐵 có điểm tới hạn 𝑀1(2,1)
− Xét trên biên 𝑂𝐵 (không tính hai đầu mút): 𝑥 = 0, 0 < 𝑦 < 6
⇒ 𝑧 = 𝑦2 − 8𝑦 ⇒ 𝑧’ = 2y − 8 ⇒ 𝑧’ = 0 khi 𝑦 = 4
⇒ Trên biên 𝑂𝐵 có một điểm tới hạn 𝑀2(0; 4)
Xét trên biên 𝑂𝐴 (không tính hai đầu mút): 𝑦 = 0, 0 < 𝑥 < 6
⇒ 𝑧 = 𝑥2 − 7𝑥 ⇒ 𝑧′ 7 = 2𝑥 − 7 ⇒ 𝑥 = 2 7 ⇒
Trên biên 𝑂𝐴 có một điểm tới hạn M ,0 3 2 BK- i c Đạ ương môn phái PHAM THANH TUNG 𝑧(𝑂) = 0 𝑧(𝐴) = −6 𝑧(𝐵) = −12
𝑧(𝑀1) = −15 ⇒ 𝑧𝑚𝑖𝑛 = −16 ; 𝑧𝑚𝑎𝑥 = 0 𝑧(𝑀2) = −16 49 {𝑧(𝑀3) = − 4 b) 2 2 x y
− Xét trong miền hình elip + =1 9 4 Xét {𝑧′𝑥 = 0 𝑧′ ⇔ { 8𝑥 = 0 𝑦 = 0
−18𝑦 = 0 ⇔ 𝑥 = 𝑦 = 0
⇒ Trong miền elip có một điểm tới hạn 𝑂(0,0) 2 2 x y
− Xét ở biên của miền elip + =1 9 4 2 2 x y Tìm điểm tới ạ h n của 𝑧 với đ ề i u kiện + =1 9 4 Đặt hàm p ụ h : 𝑦2
𝐿(𝑥, 𝑦, 𝑘) = 4𝑥2 − 9𝑦2 𝑥2 + 𝑘 ( 9 + 4 −1) BK- i c Đạ ương môn phái PHAM THANH TUNG 2𝑘 2𝑘 8𝑥 + 𝑥 (8 + 𝐿′ 9 𝑥 = 0 9 ) = 0 𝑥 = 0 {𝐿′ 𝑘𝑦 𝑘 𝑦 = 0 ⇔ −18𝑦 + ⇔ 𝑦 ( 𝐿′ 2 = 0 2 − 18) = 0 𝑘 = 0 𝑥2 𝑦2 𝑥2 𝑦2 { 9 + 4 = 1 { 9 +
TH1: 𝑥 = 𝑦 = 0 ⇒ Không phải nghiệm4 = 1 của hệ
TH2: 𝑘 = −36 ⇒ 𝑦 = 0 ⇒ 𝑥 = ±3
TH3: 𝑘 = 36 ⇒ 𝑥 = 0 ⇒ 𝑦 = ±2
Với 𝑘 = −36, 𝑧 có hai điểm tới hạn 𝐴(3,0), 𝐵(−3,0)
Với 𝑘 = 36, 𝑧 có 2 điểm tới hạn 𝐶(0,2), 𝐷(0, −2) 𝑧(𝑂) = 0 𝑧(𝐴) = 36 Ta có: { 𝑧(𝐵) = 36
⇒ 𝑧𝑚𝑖𝑛 = −36, 𝑧𝑚𝑎𝑥 = 36
𝑧(𝐷) = 𝑧(𝐶) = −36 BK- i c Đạ ương môn phái PHAM THANH TUNG
TÀI LIỆU THAM KHẢO
[1] Bùi Xuân Diệu, Bài giảng Giải tích II, Bài giảng giải tích I
[2] Nguyễn Đức Trung, Bài giảng Toán cao cấp A3 - Giải tích 2
[3] Trần Bình, Bài tập giải sẵn Giải tích II, NXB Khoa học và Kỹ thuật
[4] Nguyễn Đình Trí (chủ biên), Trần Việt Dũng, Trần Xuân Hiển, Nguyễn Xuân
Thảo, Toán học cao cấp tập 2: Giải tích, NXB Giáo dục VN, 2015.
[5] James Stewart, Complete Solutions Manual for Multivariable Calculus, Seven edition
[6] Đề cương và bài tập tham khảo – Giải tích 2, ĐH Bách khoa Hà Nội
http://sami.hust.edu.vn/de-cuong/page/2/
[7] Đề thi Giải tích II các kỳ trước Đại học Bách khoa Hà Nội
Tài liệu được biên soạn dựa trên kinh nghiệm cá nhân, dù đã rất cố gắng nhưng chắc
chắn vẫn sẽ tồn tại các lỗi sai tính toán, lỗi đánh máy, … mọi ý kiến góp ý bạn đọc vui
lòng gửi qua link fb “fb.com/tungg810” hoặc email
“phamthanhtung3i.hust@gmail.com” để mình có thể kiểm tra, hoàn thiện ộ b tài liệu.
Xin chân thành cảm ơn! BK- i c Đạ ương môn phái PHAM THANH TUNG