Giải nhanh GTLN – GTNN mô đun số phức với Elip và không Elip – Lục Trí Tuyên Toán 12
Giải nhanh GTLN – GTNN mô đun số phức với Elip và không Elip – Lục Trí Tuyên Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Preview text:
Xem thêm tại: estudy.edu.vn
____________________________________________________________________________________
GIẢI NHANH GTLN-GTNN MÔ ĐUN SỐ PHỨC VỚI ELIP
Thầy Lục Trí Tuyên – ĐT: 0972177717
Bồi dưỡng KT và LTĐH Cầu Giấy – Hồ Tùng Mậu HN
Khi thấy giả thiết là Elip không chính tắc: z z z z 2a với ( z z 2a) và 1 2 1 2 z , z ;
c ci . Tìm Min, Max của P z z : 1 2 0
Tính z z 2c và 2 2 2
b a c 1 2 z z (2) Nếu thấy 1 2 z 0 max P a 0 ; min P b 2 z z z z 1 2 max P z a 1 2 z a 0 0 2 (3.1) Nếu thấy 2 z z
z z k z z 1 2 min P z a 0 1 0 2 0 2 z z 1 2 z a 0 z z (3.2) Nếu thấy 2 1 2 max P z a 0 2
z z k z z 0 1 0 2 z z
(3.3) Nếu thấy z z z z 1 2 min P z b 0 1 0 2 0 2
GIẢI THÍCH CỤ THỂ
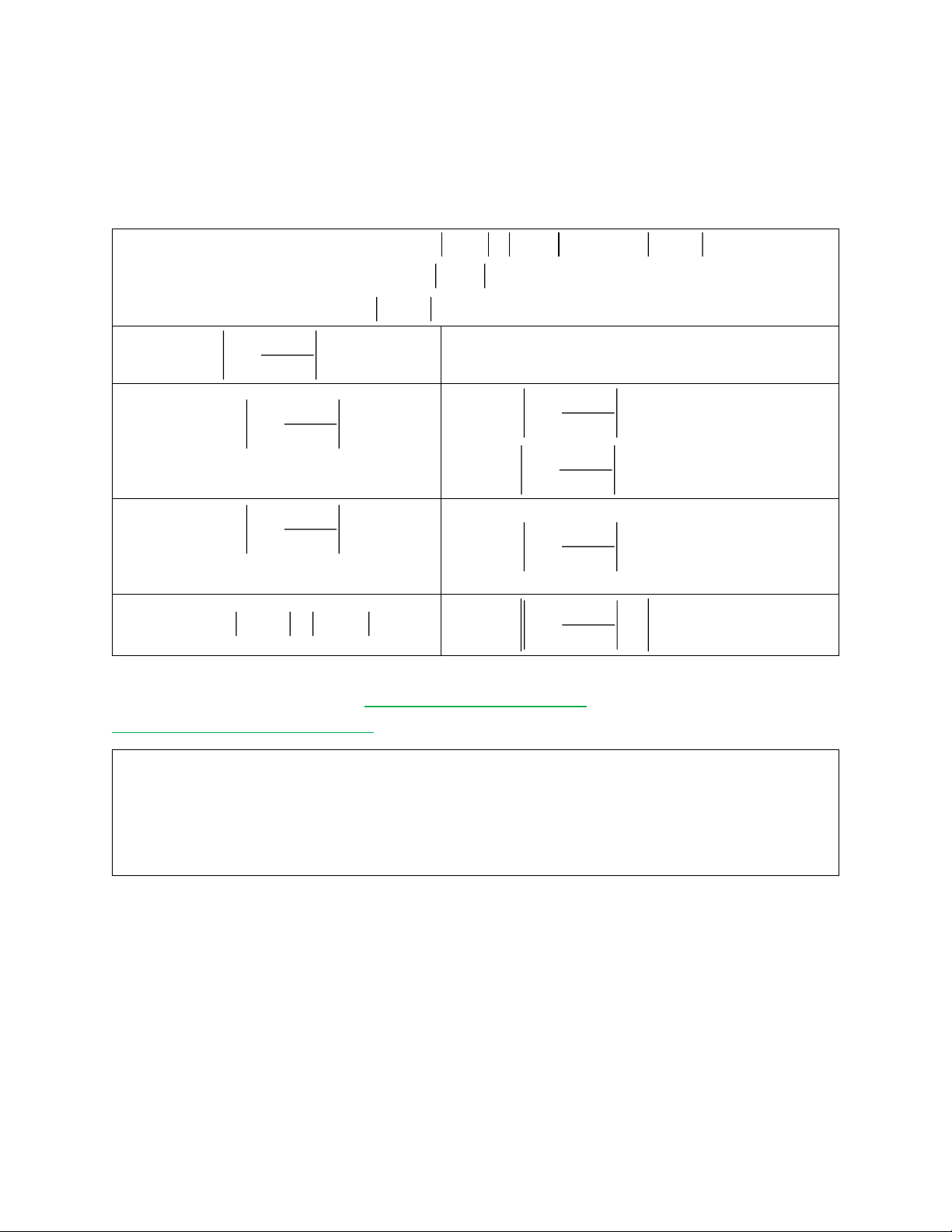
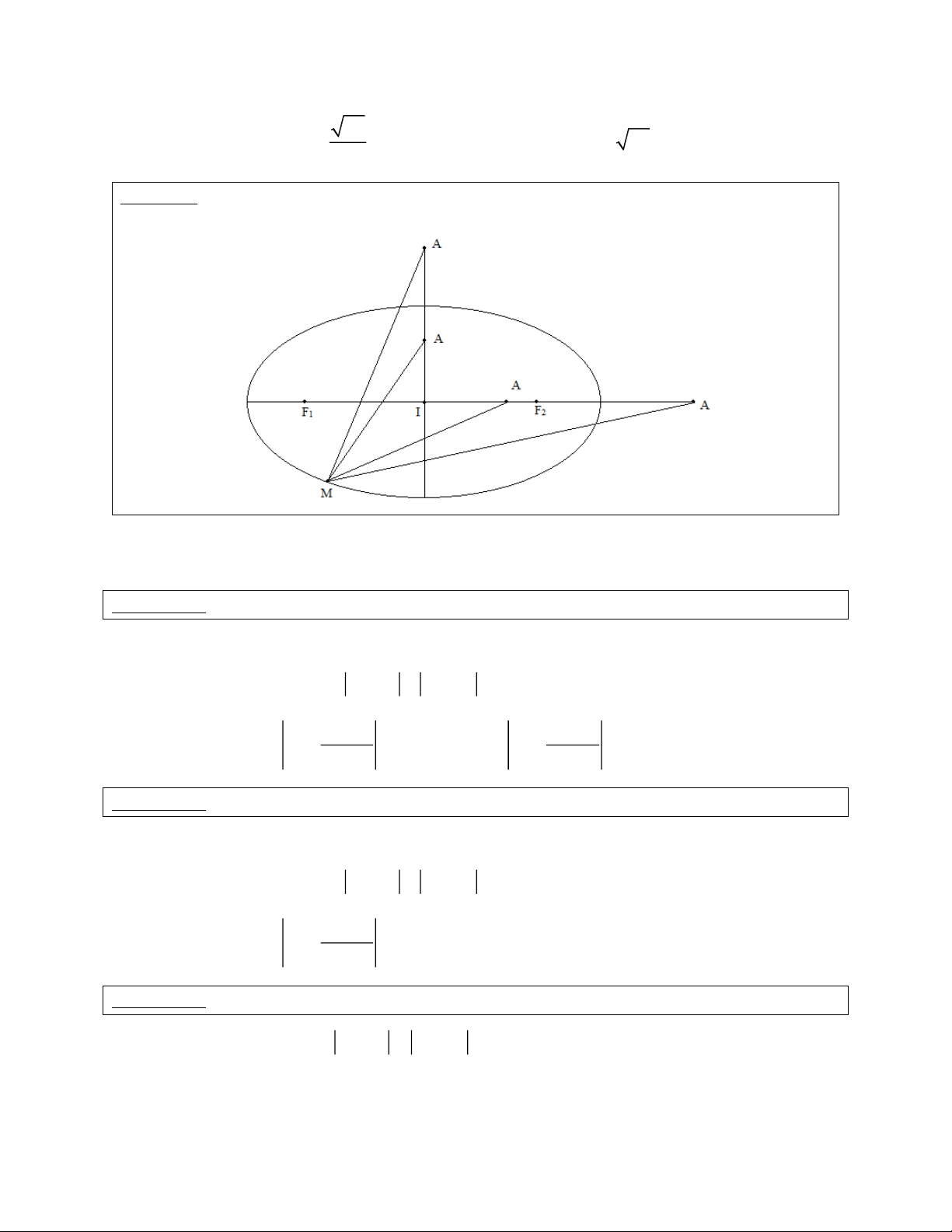
1. Hình dạng và thông số của Elip
- Định nghĩa: Cho hai điểm cố định F , F với độ dài F F 2c . Tập hợp các điểm M trong 1 2 1 2 mặt phẳng thoả mãn
MF MF 2a 1 2
Với a c 0 là số dương không đổi. - Hình dạng:
Xem thêm tại: estudy.edu.vn
_____________________________________________________________________________________
- Mối quan hệ của , a , b c : 2 2 2
a b c
2. Bài toán liên quan
Bài toán chung: Cho M chuyển động trên Elip (E) và một điểm A cố định. Tìm GTLN, GTNN của AM .
Bài toán số phức tương ứng: Cho số phức z thoả mãn z z z z 2a với 1 2
2a z z . Tìm GTLN, GTNN của P z z . 1 2 0
Sự tương ứng ở đây gồm:
- M là điểm biểu diễn z
- F , F tương ứng là điểm biểu diễn z , z . 1 2 1 2
- A là điểm biểu diễn z0
3. Các dạng giải được 2 2 x y
Bài toán 1. Phương trình (E) dạng chính tắc: 1 2 2 a b
Bài toán số phức tương ứng: Cho số phức z thoả mãn z c z c 2a hoặc
z ci z ci 2a (Elip đứng). Tìm GTLN, GTNN của P z z0 Giải: - Tính 2 2 2
b a c
Xem thêm tại: estudy.edu.vn
_____________________________________________________________________________________ 2 2 x y 2 2 x y
- Lập phương trình chính tắc của Elip:
1 với z c z c 2a . Hoặc 1 2 2 a b 2 2 b a
với z ci z ci 2a b 2 2 x y 2 2 x y
- Rút y theo x dạng: 2 2 y
a x đối với
1 (tương tự đối với 1) a 2 2 a b 2 2 b a 2 b - Thay vào P được 2 2 2 2
P (x x )
a x y , x ;
a a với z x y i 0 0 a 0 0 0
- Dùng chức năng TABLE của máy tính cầm tay Casio tìm ra GTLN, GTNN của hàm 2 P từ đó có P . Ví dụ minh hoạ:
Cho số phức z thoả mãn z 2 z 2 6 . Tìm GTLN và GTNN của P z 1 3i Giải:
- Có a 3,c 2 2 b 9 4 5 2 2 x y 5
- Phương trình chính tắc của Elip: 1 2 y 9 x 9 5 3 2 2 5 - Vậy 2
P x 2 1
9 x 3 f x 1,2 3
- Bấm TABLE các hàm f
x với x 3 ; 3 được GTLN, GTNN của 2 P 1,2
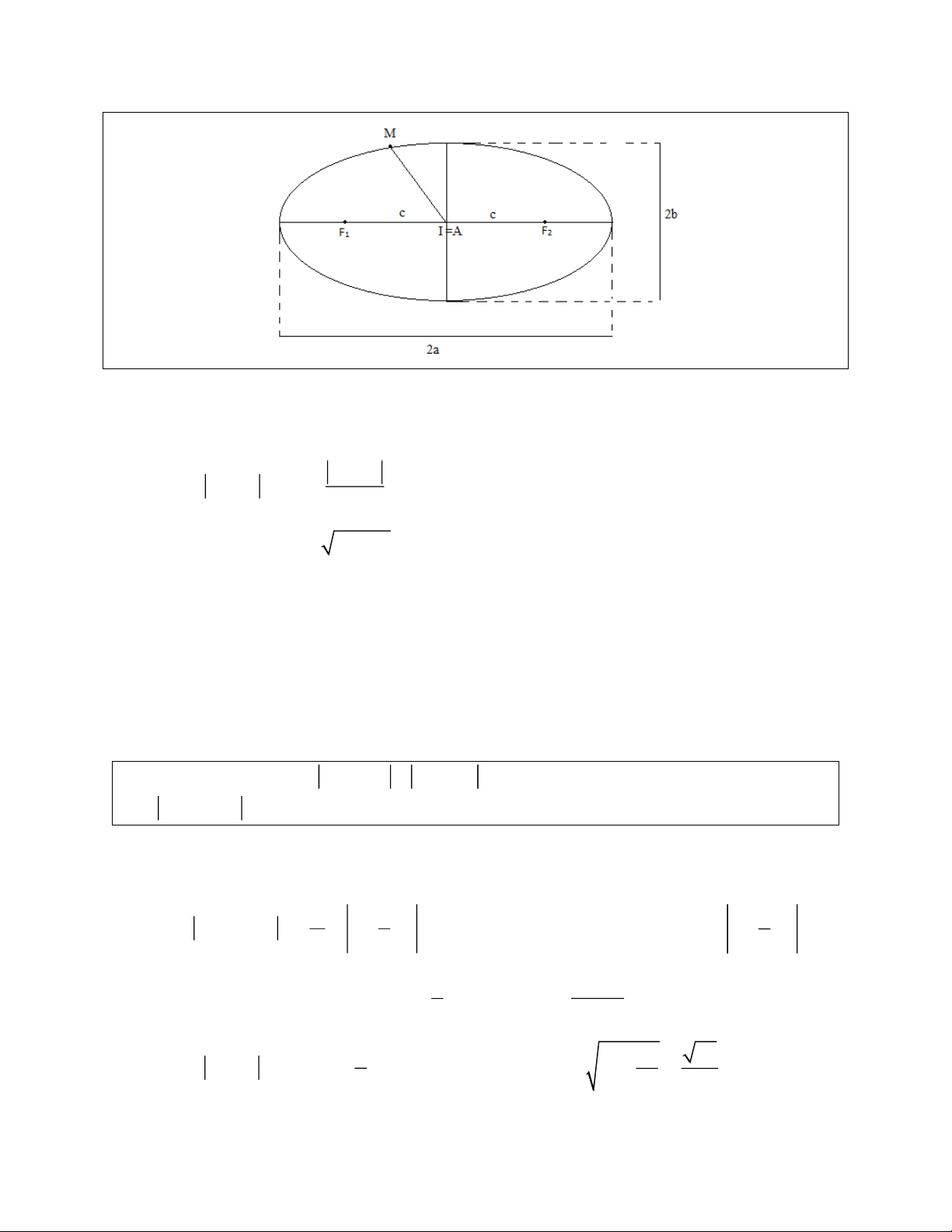
Bài toán 2. Elip không chính tắc nhưng A là trung điểm của F F tức A là tâm Elip. 1 2
Bài toán số phức tương ứng: Cho số phức z thoả mãn z z z z 2a với 2a z z . 1 2 1 2 z z
Tìm GTLN, GTNN của P z z . Với đặc điểm nhận dạng 1 2 z 0 0 2
Xem thêm tại: estudy.edu.vn
_____________________________________________________________________________________ Giải: z z
- Tính 2c z z 1 2 c 1 2 2 - Tính 2 2 2
b a c 2 2
b a c
- Vì A là tâm Elip và M di chuyển trên Elip nên:
+ AM lớn nhất bằng a hay max P a
+ AM nhỏ nhất bằng b hay min P b Ví dụ minh hoạ:
Cho số phức z thoả mãn z 1 3i z 2 i 8 . Tìm giá trị lớn nhất, giá trị nhỏ nhất của
P 2z 1 2i . Giải: P 1
Ta có P 2z 1 1 2i
z i . Ta chỉ cần tìm GTLN, GTNN của P' z i 2 2 2 1 z z
Ta thấy z 1 3i , z 2
i và z i . Do đó 1 2 z 1 2 0 2 0 2 5 25 39
- Tính 2c z z 5 c
; 2a 8 a 4 . Vậy b 16 1 2 2 4 2
Xem thêm tại: estudy.edu.vn
_____________________________________________________________________________________ 39
Vậy max P' 4 ; min P '
. Do đó max P 8 và min P 39 2
Bài toán 3. Elip không có dạng chính tắc, A không là trung điểm của F F nhưng A nằm 1 2
trên các trục của Elip
Bài toán 3.1. A nằm trên trục lớn và phía ngoài Elip:
z z k z z 0 1 0 2
- Dấu hiệu nhận biết:
z z z z 2a 0 1 0 2 z z z z - Thì 1 2 max P z a và 1 2 min P z a 0 2 0 2
Bài toán 3.2. A nằm trên trục lớn và ở phía trong Elip:
z z k z z 0 1 0 2
- Dấu hiệu nhận biết:
z z z z 2a 0 1 0 2 z z - Thì 1 2 max P z
a . Còn GTNN không xác định nhanh được. 0 2
Bài toán 3.3. A nằm trên trục nhỏ (bất kể trong hay ngoài) Elip:
- Dấu hiệu nhận biết: z z z z 0 1 0 2
Xem thêm tại: estudy.edu.vn
_____________________________________________________________________________________ z z - Thì 1 2 min P z
b . Còn GTLN không xác định nhanh được. 0 2 Ví dụ minh hoạ:
Cho số phức z thoả mãn: z i z 3 3i 6 . Tìm giá trị lớn nhất, giá trị nhỏ nhất của
P z 6 7i Giải:
z i F (0;1) ; z 3 3i F (3; 3
) ; z 6 7i ( A 6; 7
) . I là trung điểm của 1 1 2 2 0 z z 3 F F thì 1 2 I ( ; 1 ) 1 2 2 2
Có z z 6 8i ; z z 3 4i z z 2 z z
. Vậy A thuộc F F 0 1 0 2 0 1 0 2 1 2
Mặt khác z z z z 10 5 6 . Vậy A nằm ngoài Elip. 0 1 0 2 z z 21 z z 9
Vậy max P AI a 1 2 z a
; min P AI a 1 2 z a 0 2 2 0 2 2
Bấm máy: Thấy ngay a 3
- Gán z vào A; z vào B và z vào C 0 1 2 A B
- Kiểm tra A, B, C thẳng hàng: k A C
- Kiểm tra A nằm ngoài Elip: A B A C 6 B C B C
- Bấm max P A
3 ; max P A 3 2 2 ELIP SUY BIẾN
Bài toán: Cho số phức z thoả mãn: z z z z 2a nhưng có z z 2a . Tìm GTLN, 1 2 1 2
GTNN của T z z 0 Giải:
Xem thêm tại: estudy.edu.vn
_____________________________________________________________________________________
- Bài toán tương đương với bài toán hình học: MF MF F F . Tìm GTLN, GTNN của 1 2 1 2 T AM .
- Giả thiết MF MF F F tương đương với M di chuyển trong đoạn thẳng F F . Do đó: 1 2 1 2 1 2
+ Viết phương trình đường thẳng F F với x [x ; x ] (ở đây x , x lần lượt là hoành 1 2 1 2 1 2
độ của F , F ) 1 2
+ Rút y theo x từ phương trình F F vào T được T f (x) với x [x ; x ] . 1 2 1 2
+ Tìm GTLN, GTNN của f ( )
x trên đoạn x [x ; x ]. 1 2 Ví dụ minh hoạ
Cho số phức z thoả mãn z 2 i z 4 7i 10 . Tìm GTLN, GTNN của P z 1 4i Giải
Với các quy ước từ ban đầu, có F ( 2 ;1) , F (4; 7 ) và (
A 1;4) . M là điểm biểu diễn z . 1 2
Có F F 10 do đó z 2 i z 4 7i 10 M thuộc đoạn thẳng F F . 1 2 1 2 x 2 3t Có F F (6; 8
) nên phương trình tham số của F F :
. Với x [ 2; 4] 1 2 1 2 y 1 4t t [0;2] . 2 2 2 2 Có 2
P x
1 y 4 3t 3 4t 3 2
25t 6t 18 với t [0;2] . Khảo sát hàm 2
f (t) 25t 6t 18 trên [0; 2] được GTNN của f (t) bằng 18, GTLN bằng 130.
Vậy min P 3 2 và max P 130
GTLN-GTNN CỦA MÔ ĐUN SỐ PHỨC KHÔNG ELIP
Thầy Lục Trí Tuyên – ĐT: 0972177717
Ngõ 20, Hồ Tùng Mậu, Cầu Giấy, Hà Nội
Website: https://estudy.edu.vn
1. ĐỊNH NGHĨA VÀ Ý NGHĨA
Cho số phức z a bi , mô đun của z ký hiệu là z được tính bởi 2 2
| z | a b
Mỗi số phức z a bi được biểu diễn bởi điểm M ( ; a b) hay OM
Mỗi số phức z a bi có thể coi là một vecto u ( ; a ) b
Tổng (hiệu) hai số phức bằng tổng (hiệu) hai vecto | z | | u | 2. TÍNH CHẤT: 2 2 2 z . z z ; z u ;
z .z z z ; 1 2 1 2 z z n 1 1 ; z z ; n z z ; z z 2 2 z z
z z . Dấu “=” xảy ra khi z k.z ( k 0 ) 1 2 1 2 1 2
z z z z . Dấu “=” xảy ra khi z k.z ( k 0 ) 1 2 1 2 1 2
Cho M , N lần lượt biểu diễn hai số phức z , z , thì MN z z 1 2 1 2
M biểu diễn z và I biểu diễn z thì z z R M thuộc đường tròn tâm I bán kính 0 0 R.
M biểu diễn z , F biểu diễn z và F biểu diễn z thì z z z z M thuộc 1 1 2 2 1 2
đường trung trực của F F . 1 2
3. MỘT SỐ DẠNG TOÁN ÁP DỤNG
Dạng 1: Tìm z hoặc z thoả mãn phương trình z. f (| z |) g(| z |) nghĩa là phương trình bậc
nhất ẩn z chứa z . Cách giải
+ Nhận biết: Phương trình đã cho chỉ có bậc nhất với z nhưng có thể đứng nhiều nơi, còn lại là
các biểu thức chứa z .
+ Nhóm z sang một vế đưa về dạng: z. f (| z |) g(| z |) (*)
+ Lấy mô đun hai vế của (*) sử dụng tính chất z .z z z được phương trình ẩn là z . 1 2 1 2
+ Giải phương trình được z .
+ Thế z trở lại (*) giải ra z VÍ DỤ MINH HOẠ
Ví dụ 1: Cho số phức z khác 0 thỏa mãn z 3z.z 1 z 2 6iz 2
Hướng dẫn: Ta thấy trong phương trình chỉ có bậc nhất với z , còn lại là z (chú ý là . z z z ).
Vậy đây là dạng toán đang tìm hiểu!. 2
Chuyển hết z sang một vế ta được: z 3 z 1 6 z i 2 z (*). 2 2
Lấy mô đun 2 vế của (*) ta được: z
(3 z 1) 36 z 2 z 2
39 z 1 2 (do z 0 ) 1 z . 13 10
Ví dụ 2: Cho số phức z thỏa mãn (2 i) z
1 2i . Tìm z z
Hướng dẫn: Điều kiện z 0 , quy đồng ta được (2 i) z z 10 z 2iz 2 2
2 z 1 z 2i z 10 2 z
1 z 2 . z 4 2
10 5 z 5 z 10 z 1
Ví dụ 3: Cho số phức z thỏa mãn z 4 (1 i) z (4 3z)i . Tìm z
Đáp số: z 2
Hướng dẫn: Dồn z về một vế ta được z 1 3i z 4 z 4i 2 2
Lấy mô đun 2 vế, suy ra z 10 z 4 z 2 2
4 10 z 2 z 32 z 2 1
Ví dụ 4: Tìm z biết (1 i)z i 2 z
Đáp số: z 1
Hướng dẫn: Quy đồng và dồn z về một vế ta được (1 i) z z 1 2 z z i . Lấy mô đun 2 2 2 4 2
vế ta được 2 z 1 2 z 2 z 2 z 5 z 4 z 1 (chú ý z 0 )
Nhẩm thấy phương trình có nghiệm z 1, phương trình bậc 3 còn lại vô nghiệm với z 0 .
Dạng 2: Cho | z | m , | z | n và | az bz | p tính q |
cz dz |. 1 2 1 2 1 2 Cách giải
Coi z u và z v thì 2 2 2 u |
u | m , 2 2 2 v |
v | n và 2 2 ( u
a bv) p ; 2 2 ( u
c dv) p . 1 2 Khai triển: 2 2 2 2 2
p a m b n 2a . b uv (1) 2 2 2 2 2
q c m d n 2cd.uv (1)
Bây giờ khử uv là xong:
Nhân (1) với cd và nhân (2) với ab rồi trừ đi, được: 2 2
cd p ab q cd 2 2 2 2
a m b n ab 2 2 2 2 . . c m d n 2 2 2 2
cd.p a .
b q acm (ad b )
c bdn ( b c ad) 2 2 2 2
cd.p a .
b q (ad bc)(acm b n d )
Đặc biệt: Khi a b 1 và c d 1, ta có công thức hình bình hành 2 2 2 z z 2 2
z z z z 1 2 1 2 1 2 VÍ DỤ MINH HỌA
Ví dụ 1: cho các số phức thỏa mãn z 1 ; z 3 và z 3z 2 . Tính P 2z 3z 1 2 1 2 1 2
Đáp số: P 241
Hướng dẫn: coi các số phức z , z là các vector u,v ta có: 1 2 2 2 2 4 z 3z z
9 z 6u.v (1) 1 2 1 2 2 2 2 2
P 2z 3z
4 z 9 z 12u.v (2) 1 2 1 2 2 2
Nhân (1) với 2 rồi cộng với (2) ta được: 2 8 P 6 z 27 z 2
P 241 P 241 1 2
Ví dụ 2: Cho hai số phức z , z thỏa mãn z z 5 và z z 3 . Tìm GTLN của 1 2 1 2 1 2
P z z 1 2
Đáp số : max P 34
Hướng dẫn: coi các số phức z , z là các vector u,v ta có: 1 2 2 2 2 2 2 2 25 z
z 2u.v (1) và 9 z z 2u.v (2). Cộng (1) với (2) được 34 2 z z 1 2 1 2 1 2 2 2 2
. Mặt khác, theo bất đẳng thức BNC, ta có 2
P z z 2 z z 2 P 34 1 2 1 2 P 34 .
Ví dụ 3: Cho hai số phức z , z thỏa mãn z 2z 5 và 3z z 3 . Tìm GTLN của 1 2 1 2 1 2
P z z 1 2 155
Đáp số: max P 14
Hướng dẫn: coi các số phức z , z là các vector u,v ta có: 1 2 2 2 2 2 25 z
4 z 4u.v (1) và 9 9 z z 6u.v (2). Nhân (1) với 3 và nhân (2) với 2 rồi 1 2 1 2 2 2
cộng lại ta có: 93 21 z 14 z . 1 2
Bây giờ áp dụng bất đẳng thức BNC cho 2 P : 1 1 1 1 2 2 155
P z z 2 2 21 z 14 z
21 z 14 z 1 2 1 2 2 1 2 21 14 21 14 14 155 P . 14
Dạng 3. Cho số phức z thỏa mãn z z R . Tìm GTLN của P a z z b z z biết rằng 0 1 2
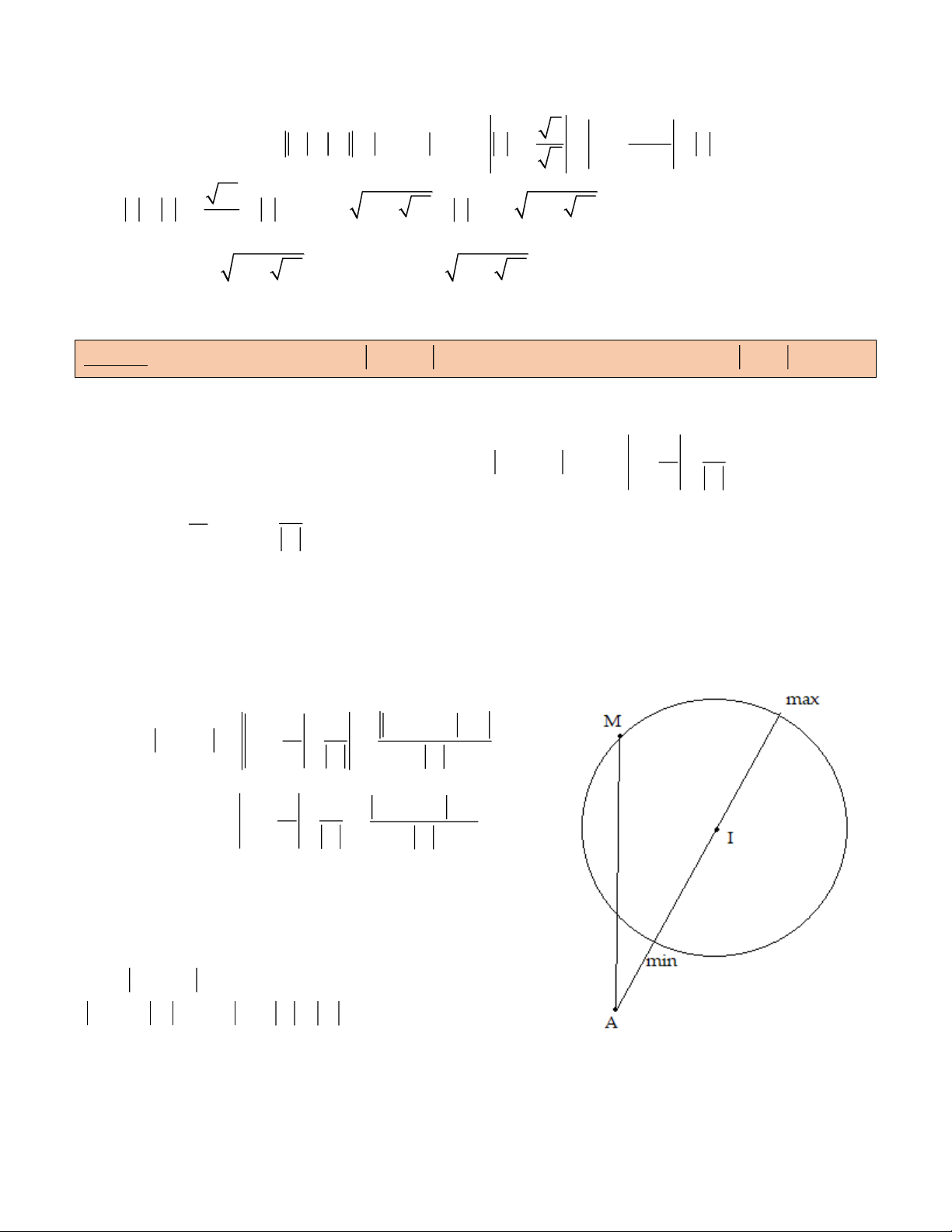
z z k z z , k 0 và , a b . 0 1 0 2 Cách giải
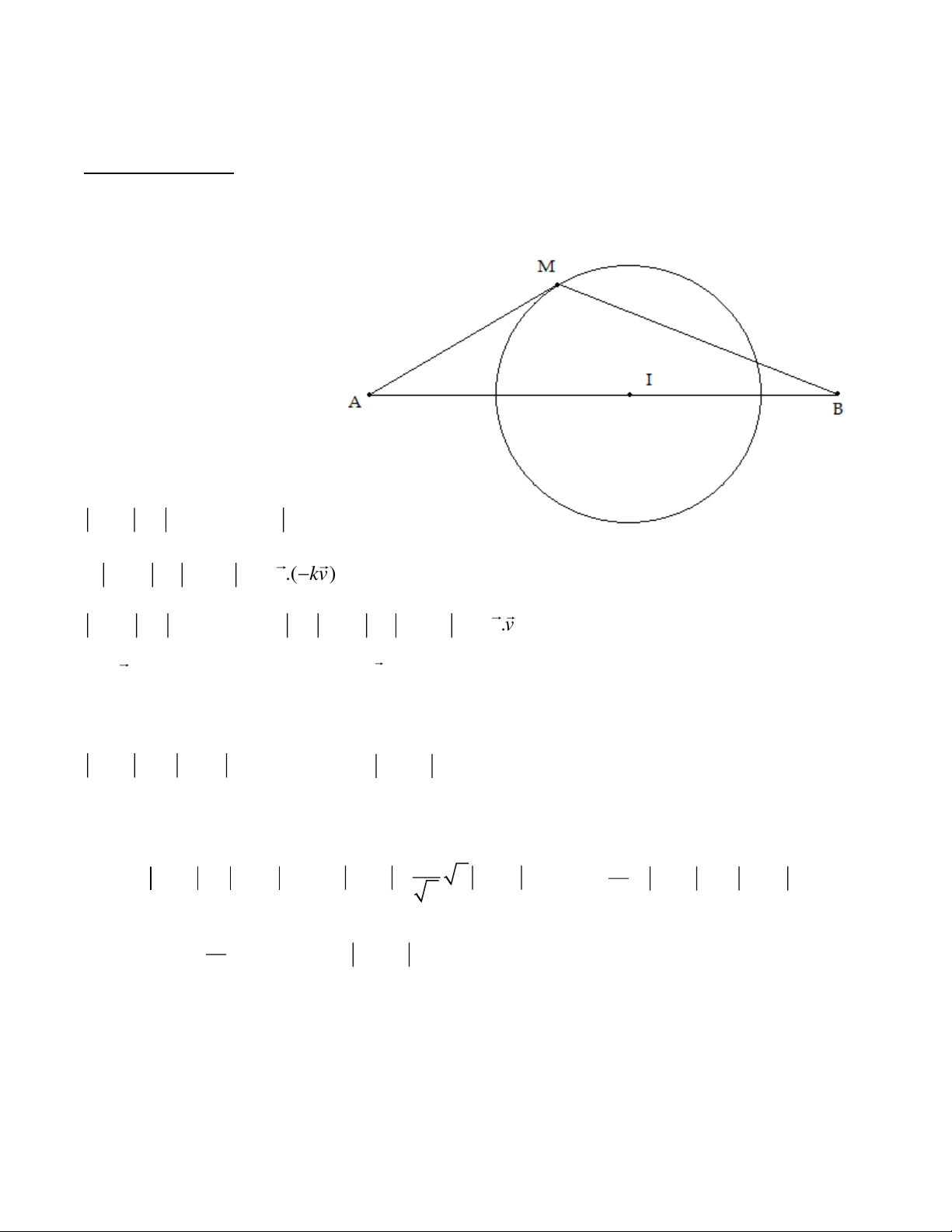
Ý nghĩa hình học: Cho điểm M chuyển động trên đường tròn tâm I bán kính R. Cho A, B là 2
điểm cố định thỏa mãn I nằm trong đoạn thẳng AB. Tìm giá trị lớn nhất của P aMA bMB .
Trừ khi I là trung điểm của AB, nếu không sử dụng
hình học để giải bài này là nhiệm vụ không hề dễ
dàng. Ta sẽ dùng các tính
chất về mô đun của số phức
để giải quyết bài toán. Ta có: 2 2 z z
z z z z 1 0 0 1 2 2
z z z z 2u.(kv) (1) 0 0 1 2 2 2 z z 2
z z z z
z z z z 2u.v (2) 2 0 0 2 0 0 2
với u là vector biểu diễn z z và v là vector biểu diễn z z với lưu ý z z k z z 0 1 0 2 0 0 2
Nhân (2) với k rồi cộng với (1) ta được: 2 2 2 z z
k z z (1 k) 2
R k z z (không đổi) 0 2 1 2
Ap dụng bất đẳng thức BNC cho 2 P , ta có: 2 b 2 b 2 2
P a z z b z z 2 2
a z z k z z 2
a z z k z z 1 2 1 2 1 2 k k 2 b P a (1 k) 2 2 2 2
R k z z . 0 2 k
Vậy, với công thức cồng kềnh như vậy rất khó nhớ, cho nên các em nên nhớ cách làm của nó. VÍ DỤ MINH HỌA
Ví dụ 1: Cho số phức z thỏa mãn z 1 2 . Tìm GTLN của T z i z 2 i
Đáp số: maxT 4
Hướng dẫn: Tâm I đường tròn trong giải thiết là z 1, bán kính r 2 . Điểm A và B ứng với 0
hai số phức z i
và z 2 i . Dễ thấy rằng z z z z . Vậy thậm chí I là trung 0 1 0 2 1 2 điểm của AB. Ta có: 2 2
z i z 11 2 2 i
z 1 1 i 2u.v (1) 2 2 2 2
z 2 i z 11 i z 1 1 i 2u.v (2). Với u,v biểu diễn z 1 và 1 i .
Cộng (1) với (2) ta được: 2 2 2
z i z 2 i 2 z 1 4 8 (không đổi) Áp dụng BNC: 2 2
T z i z i 2 2 2
2 z i z 2 i 16 T 4
Ví dụ 2: Cho số phức z thỏa mãn z 1 2i 2 . Tìm GTLN của T z z 3 6i
Đáp số: maxT 3 7
Hướng dẫn: Ta có 2 2
z z 1 2i 1 2 2 2i
z 1 2i 1 2i 2u.v (1) 2 2 2 2
z 3 6i z 1 2i 2 4i z 1 2i 4 1 2i 4u.v (2). Với u,v biểu diễn z 1 2i v 1 à 2i .
Nhân (1) với 2 rồi cộng với (2) được: 2 2
2 z z 3 6i 2 2
3 z 1 2i 6 1 2i 12 30 42
Áp dụng bất đẳng thức BNC: 2 1 1 2 2
T z z i 2 2 3 6
2 z z 3 6i 1
2 z z 3 6i 63 T 3 7 2 2 z
Dạng 4. Cho số phức z thõa mãn 0 z
k , ( k 0 ) hay dạng tương đương 2
z z k z , ( z 0
k 0 ). Tìm GTLN, GTNN của T z . Cách giải 2
Áp dụng bất đẳng thức z z
z z , ta có 2 z z
z z . Mặt khác, 2
z z k z 1 2 1 2 0 0 0 2
z k z z 0 2 0 z z 2
k z k z z z k z 0 0 2
z k z z 0 0 2 2
k k 4 z
k k 4 z 0 0 z
. Đánh giá 1 lần đối với hàm 2 biến đảm bảo dấu “=” 2 2
xảy ra. Tôi không giải chi tiết ở đây. 2
k k 4 z 2
k k 4 z Vậy 0 minT và 0 maxT 2 2 VÍ DỤ MINH HỌA 4i
Ví dụ 1: Cho số phức z thỏa mãn z
2 . Gọi M,m lần lượt là GTLN và GTNN của z . z
Tính T M m
Đáp số: T 2 5 4i
Hướng dẫn: z 2 2
z 4i 2 z . Áp dụng bất đẳng thức z z z z , ta có z 1 2 1 2 2 2 2
z 4 z 4i 2
z z 4 2 z 1
5 z 1 5 .
Vậy M 1 5 và m 1
5 . Do đó T 2 5
Ví dụ 2: Cho số phức z thỏa mãn 2
(1 i)z 1 2i 2 z . Tìm GTLN, GTNN của T z .
Hướng dẫn: Ta có thể đưa về dạng quen thuộc bằng cách chia cả hai vế cho 1 i , ta được 1 2i 2 z z . 1 i 2 5 1 2i
Áp dụng bất đẳng thức z z
z z , ta có 2 z z z 1 2 1 2 2 1 i 2 10
z z z 1
1 2 10 z 1 1 2 10 . 2
Vậy maxT 1 1 2 10 và minT 1 1 2 10
Dạng 5. Cho số phức z thỏa mãn z .z z k 0 . Tìm GTLN, GTNN của T z z 1 2 0 Cách giải z k
Ý nghĩa hình học: Gọi M là điểm biểu diễn z , có z .z z k 2 z
IM R với 1 2 z z 1 1 z k
I biểu diễn 2 và R
. Vậy M chuyển động trên đường tròn tâm I bán kính R. Gọi A là z z 1 1
điểm biểu diễn z thì T AM . Bài toán trở thành: “cho M di chuyển trên đường tròn tâm I 0
bán kính R và A là điểm cố định. Tìm GTLN, GTNN của AM”
Như vậy, nhìn vào hình vẽ ta thấy ngay: z k
z .z z k
min T AI R 2 z 1 0 2 0 z z z 1 1 1 z k
z .z z k
maxT AI R 2 z 1 0 2 0 z z z 1 1 1
(tử số như là thay z vào phương trình đường tròn 0 vậy)
Lưu ý: Không phải phương trình đường tròn nào cũng có
dạng z .z z k 0 , mà đôi khi nó ở dạng 1 2
z z z z z z với z z . Do đó, để kiểm tra điều 1 2 1 3 1 2
kiện giả thiết là phương trình đường tròn hay đường
thẳng trong trường hợp lạ, cách tốt nhất là gọi z x yi rồi thay vào giả thiết để biết ( ;
x y) thỏa mãn phương trình nào. VÍ DỤ MINH HỌA
Ví dụ 1: Cho số phức z thỏa mãn z 1 2i 4 . Tìm GTLN. GTNN của T z 1 i
Đáp số: min P 4 13 và max P 4 13
Hướng dẫn: Viết T dạng T z z thì z 1
i . Thay vào phương trình đầu ta được 0 0 z 1 2i 2 3i . 0
Vậy min P 4 13 và max P 4 13
Ví dụ 2: Cho số phức z thỏa mãn 2iz 1 3i 1. Tính GTLN, GTNN của T z 2 3i 5 2 1 5 2 1
Đáp số: min P và m x a P . 2 2
Hướng dẫn: Viết T dạng T z z thì z 2
3i . Thay z vào 2iz 1 3i ta được 0 0 0
2iz 1 3i 7 i 5 2 . 0 5 2 1 5 2 1 Vậy min P và m x a P 2 2
Ví dụ 3: Cho số phức z thỏa mãn 2z 1 z 2i . Tìm GTLN, GTNN của T z 1 2i 65 11 65 11
Đáp số: minT và maxT 3 3 3 3
Hướng dẫn: Gọi z x yi ( , x y ), và M ( ;
x y) biểu diễn z thì 2z 1 z 2i 2 2
x 2 y2 x y 2 2 2 1 2 2 2 2
3x 3y 4x 4y 3 0 2 2
x y x y 1 0. 3 3 1 1 11
Vậy M nằm trên đường tròn tâm I ; bán kính R . 3 3 3
Có T z 1 2i AM với ( A 1 ; 2 ). 65 11
Vậy minT AI R
và maxT AI 65 11 R 3 3 3 3
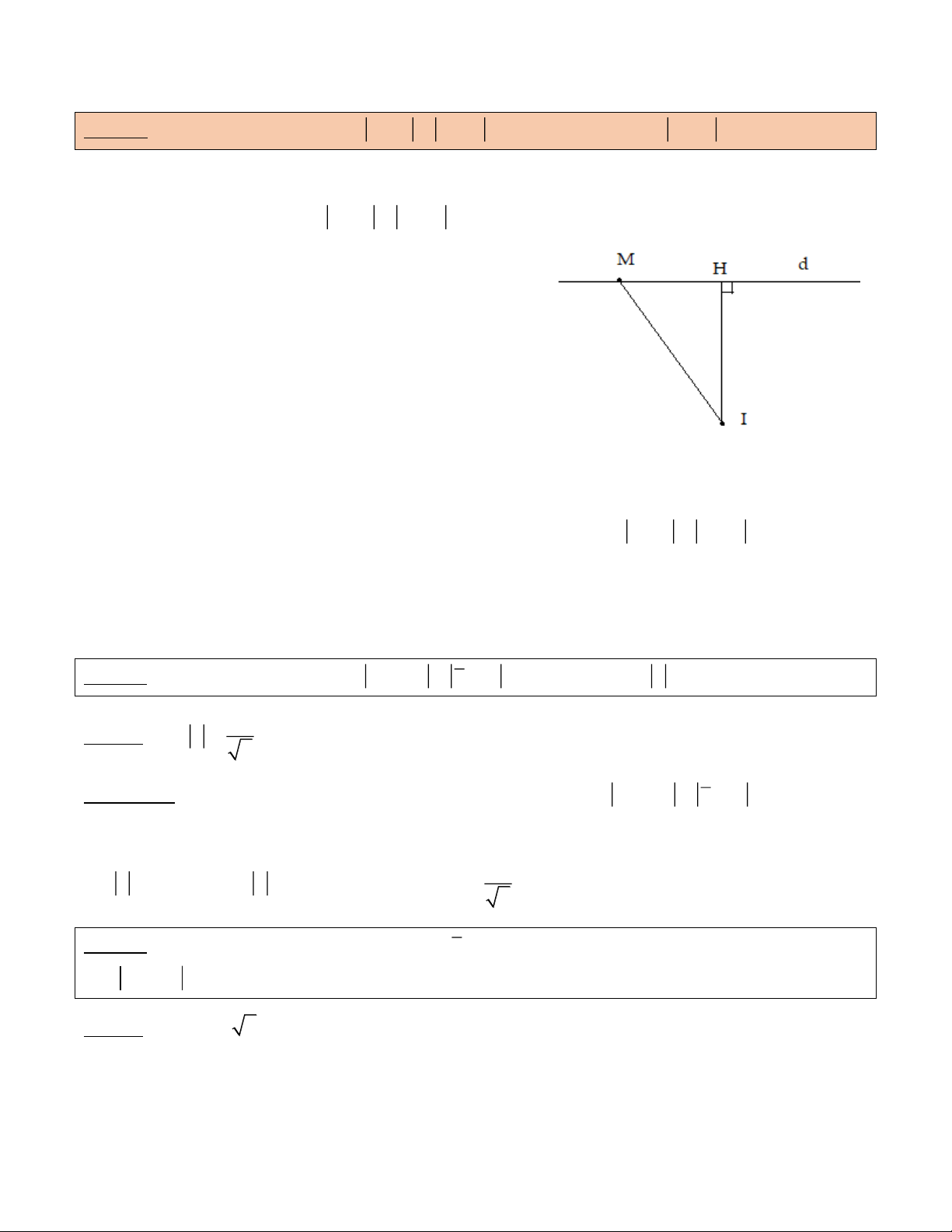
Dạng 6. Cho số phức z thỏa mãn z z z z . Tìm GTNN của T z z . 1 2 0 Cách giải
Ý nghĩa hình học: Điều kiện z z z z thực chất 1 2
là phương trình đường thẳng.
Nếu ta gọi M là điểm biểu diễn z , A là điểm biểu
diễn z và B biểu diễn z thì giả thiết tương đương với 1 2
MA MA hay M nằm trên trung trực của AB . Gọi I
là điểm biểu diễn z thì T IM . 0
Vậy IM nhỏ nhất khi M là hình chiếu vuông góc của
I lên d . Giá trị nhỏ nhất bằng min T d I, d .
Lưu ý: Không phải phương trình đường thẳng nào cũng có dạng z z z z , cho nên khi 1 2
gặp giả thiết lạ, cách tốt nhất để nhận biết giả thiết là đường thẳng hay đường tròn là gọi
z x yi rồi thay vào phương trình. VÍ DỤ MINH HỌA
Ví dụ 1: Cho số phức z thỏa mãn z i 1 z 2i . Tìm GTNN của z . 1
Đáp số: min z . 2
Hướng dẫn: Gọi z x yi thì M ( ;
x y) là điểm biểu diễn z . Từ z i 1 z 2i 2 2
(x 1) (y 1) 2 2
x (y 2) x y 1 0 (d). Vậy M di chuyển trên (d). 1
Có z OM , do đó z nhỏ nhất bằng d ( ; O d ) . 2
Ví dụ 2: Cho số phức z thỏa mãn z 3 i z 1 3i là một số thực. Tìm giá trị nhỏ nhất của
T z 1 i
Đáp số: minT 3 2
Hướng dẫn: Gọi z x yi , ta có
3 z 1 3i (x 3) (y 1)i (x 1) (y 3)i .
Tích này có phần ảo là x 3 y 3 y 1 x 1 . Phần ảo bằng 0
3x 3y 9 x y 1 0 x y 4 0 (d). Vậy nếu gọi M là điểm biểu diễn z thì M
chạy trên đường thẳng (d). Gọi ( A 1; 1
) là điểm biểu diễn 1
i thì T AM . Giá trị T nhỏ nhất bằng khoảng cách từ A 1 1 4
đến (d). Vậy min T 3 2 2
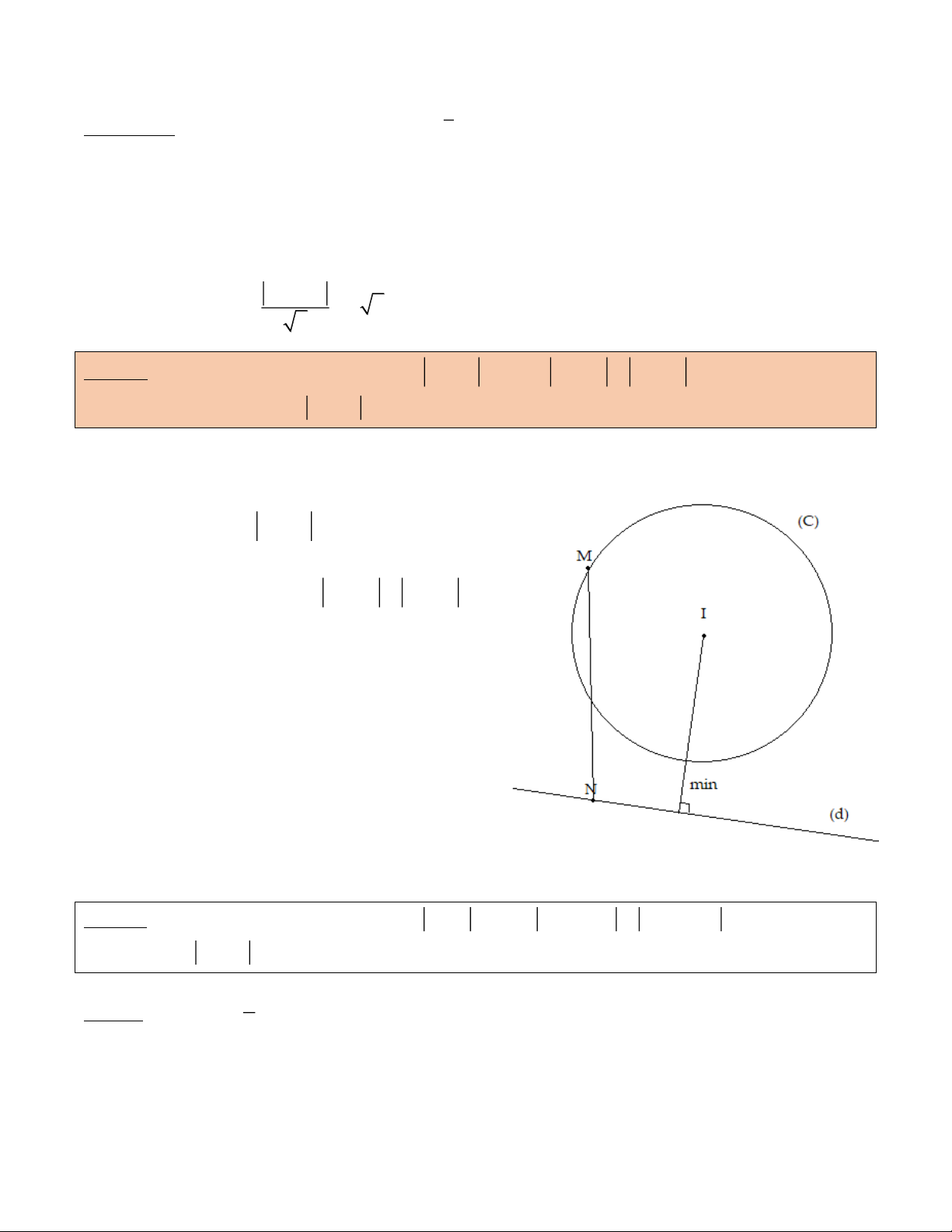
Dạng 7. Cho hai số phức z , z thỏa mãn *
z z R và * *
z z z z , với * * *
z , z , z cho 1 2 1 1 2 2 2 3 1 2 3
trước. Tìm GTNN của T z z 1 2 Cách giải
Ý nghĩa hình học: Gọi M, N là các điểm biểu
diễn z , z . Giả thiết *
z z R tương đương 1 2 1 1
với M thuộc đường tròn tâm I bán kính R (gọi
là đường tròn (C)). Giả thiết * *
z z z z 2 2 2 3
tương đương với N thuộc đường thẳng (d).
Bài toán trở thành tìm M thuộc (C) và N
thuộc (d) sao cho T MN ngắn nhất.
Từ hình vẽ ta thấy ngay giá trị nhỏ nhất của
MN bằng d(I,(d)) R
Vậy minT d I ,(d ) R . VÍ DỤ MINH HỌA
Ví dụ 1: Cho hai số phức z , z thỏa mãn z 5 5 và z 1 3i z 3 6i . Tìm giá trị nhỏ 1 2 1 2 2
nhất của T z z . 1 2 5
Đáp số: min MN . 2
Hướng dẫn: : Gọi M, N là các điểm biểu diễn z , z . Giả thiết z 5 5 tương đương M thuộc 1 2 1
đường tròn tâm I ( 5
;0) bán kính R 5. Giả thiết z 1 3i z 3 6i N thuộc đường 2 2
thẳng (d): 8x 6 y 35 0 . Vậy min MN d(I,(d)) 15 5 R 5 . 2 2
Ví dụ 2: Cho hai số phức z , z thỏa mãn z 4 3i 2 và z 2 3i z 1 2i . Tìm giá trị 1 2 1 2 2
nhỏ nhất của T z z . 1 2 23 34
Đáp số: min MN 2 34
Hướng dẫn: Gọi M, N là các điểm biểu diễn z , z . Giả thiết z 4 3i 2 tương đương M 1 2 1
thuộc đường tròn tâm I ( 4
;3) bán kính R 2 . Giả thiết z 2 3i z 1 2i N thuộc 2 2
đường thẳng (d): 3x 5y 4 0 . Vậy min MN d(I,(d)) 23 R 23 34 2 2. 34 34 Lời kết:
Các bài toán trên có thể giải bằng phương pháp đại số bằng cách rút một ẩn theo ẩn còn
lại từ giả thiết để thay vào biểu thức cần đánh giá thành hàm số dạng T f (x) . Sau đó
tìm GTLN, GTNN của f ( )
x trên miền xác định của f ( ) x .
Các đánh giá đảm bảo chặt chẽ cần chứng tỏ có đẳng thức (dấu “=”) xảy ra. Để tránh
phức tạp vấn đề tôi không trình bày ở đây. Tuy nhiên các bài toán tổng quát đã nêu đều đảm bảo điều đó.
Document Outline
- GTLN- GTNN số phức Elip- Tex
- 10. GTLN-GTNN số phức không Elip (1)