GIẢI TÍCH 12. CHƯƠNG II
A. PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LÔGARIT
B. BẤT PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LÔGARIT PHẦN 1
A. PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LÔGARIT
Bài toán 4: Giải phương trình mũ, phương trình logarit bằng phương pháp logarit hóa.
I. Giải phương trình mũ bằng phương pháp logarit hóa f  x Dạng 1: a  b.
Phương pháp giải:Điều kiện: 1  a  0 , b  0. Lấy logarit cơ số a cho hai vế, phương
trình trở thành: f  x  log b . a f  x g  x Dạng 2: a  b .
Phương pháp giải:Điều kiện: 1  a  0 , b  0. Lấy logarit cơ số a cho hai vế phương
trình trở thành: f  x  g  x.log b . a g x h x f  x b .c Dạng 3: a  . k x d
Phương pháp giải : Điều kiện: 1  a  0 ; b,c , d  0. Lấy logarit cơ số a cho hai vế,
phương trình trở thành: f x  g x.log b  hx.log c  k x.log d . a a a Các ví dụ :
A. Phương trình không có tham số: Câu 1 Giải phương trình sau: . Lời giải
Lấy logarit cơ số 2 hai vế, phương trình đã cho tương đương:  3 x  1 log 3 2 2 2 2 x  2  log
 x  2  log 31  x 1 log 3   . 2 2 2 2 x   1 log 3  2
Vậy tập nghiệm của phương trình đã cho là S   1 log 3; 1 log 3 . 2 2  Câu 2 Giải phương trình sau: . Lời giải
Điều kiện x  0 .
Phương trình đã cho tương đương:  x 1   3  x  x  3 2 7 .3  7 .3 x3 x3     x  x x 3 3 3
 7 .3 x 1  log 7 .3 x   0  x 3 log 7  log 3  0 3   3 3 x    x  3      x   1 3 log 7   0    1 . 3  x   x     log 3 7  log 7  3
Vậy tập nghiệm phương trình đã cho là S  3; log 3 . 7  Câu 3 Giải phương trình sau: . Lời giải
Điều kiện: x  0 .
Với điều kiện trên, lấy logarit cơ số 4 cho hai vế của phương trình, ta được phương trình tương đương:  log . x log x  log 10 .x  1 2020 2018 0,5 4    log x x  log 10 .x  1 log 2020 2018 2 2 2  log x x  log 10 .x 1 log 2020 2018 2 2 2 log x 1010 1009  x  10 .x  log  logx x   log 1010 1009 10 .x   log .
x log x  1010 1009 log x   1 log x  1  x  2  
 log x 1009log x 1010  0   10  . log x  1010  1010  x 10   Đố 1
i chiếu điều kiện, ta được tập nghiệm của phương trình là 1010 S   ;10  . 10  
Bài tập tương tự:
Giải các phương trình sau: 2 x3 2 log 10x 1  log 3 2 2  3  2x 5 25 x 4 x2 a) x 2 3 .4 x  18. b) . c) 2 .7 1. 1 1 d) x x x 1  x 1  x2 x3 5  3  5 3  5 3  0 . x x  e) x 2 x 1 2 2 4  3  3  2  Lời giải
a) Điều kiện: x  0.
Với điều kiện trên, phương trình đã cho tương đương:  2x3  3x6 2  2   2 3 x 2 x 2  x  2 1 x 4 2   3 .2
 3 .2  3 .2 x 1  x  4  log 2  0 3 x      x  x  2 3log 2 2 3 x  2   0   x  2    2  x 
x  2x  3log 2  0 VN  3  
b) Điều kiện: x  0 .
Với điều kiện trên, phương trình đã cho tương đương: 2 log 10 x 1  3  2xlog53 25   2 log
10x 1 .log 3  log 3.log 2x 25    5 5 5   1 2
 log 5.2x 1 log 2x  0 5   5   4 1
 log 2x  log 52 1log 2x  0 5 5 5   4  1  1 x  1 1 3 log 2x  1  2x    10 2
 log 2x  log 2x   0    5   . 5   5   5   4 2 4 log 2x  3  125  5    2x 125 x   2 c) Ta có:   2 x 2 x 4 x2 2 2 .7
1  x  4  x  2log 7  0  x  2 x  2  log 7  0  2   2  x  2   log 7  2 . d) Ta có: x x x 1  x 1  x2 x3 x x 1  x2 x x 1  x3 5  3  5  3  5  3  0  5  5  5  3  3  3   x   x x x x 5 1 2 1 5  5 5   1 3 1 3  3  3  31.5  31.3  1  x  0    3  e) Ta có: 1 1 1 1 1 x x x x   3 x x x x x x 4 2 1 2 1 2 2 2 2 2           4 3 3 2 4 2 3 3 4 . 3 . 2 3 1 x 1 x 3 3 2 3 x 4 4 3 x x x 3 3 2 2 2  4 .  3 .    4  3
 x   0  x  1 2 2 3 3 2 2 B. 2 4.4
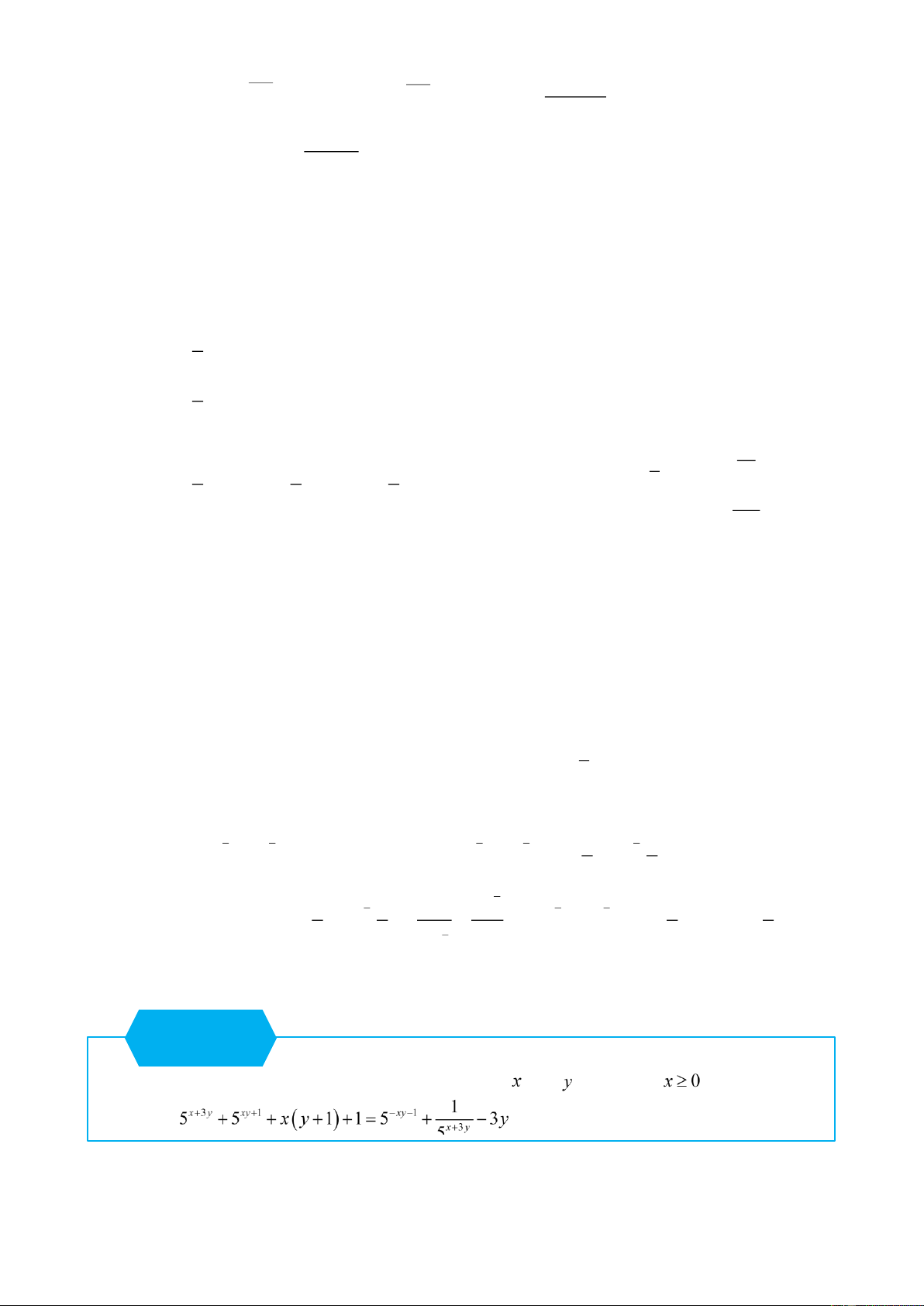
Phương trình có tham số. Câu 15 [2D2-5.5-4] Cho các số thực , với thỏa mãn
. Tìm giá trị nhỏ nhất của biểu thức Lời giải
Lấy logarit cơ số 3 hai vế, ta được: m  0  m  0    . log   2 x x 1 2 .3   2  log m
x  x log 2  log m 1  0 3 3  3 3
Để phương trình đã cho có hai nghiệm trái dấu thì m  0 m  0 1     m   . log m 1  0 log m  1    3 3 3 Câu 2 Tìm tập nghiệm của phương trình , là tham số khác 2. Lời giải 2 x2m 2 x2m x2 1  Phương trình x 1  1   x  1  2  3 .5  3.5  5  3  5  3 x x m x m x m .   *
Lấy logarit cơ số 5 hai vế của   * , ta được x  2      x 1 2 log 3  x  2  log 3  0 5   5  x  m  x  m 
Với x  2  0  x  2 (thỏa mãn). 1 1 Với
 log 3  0  x  m  
 x  m  log 5 (thỏa mãn). 5 3 x  m log 3 5
Vậy phương trình có tập nghiệm S  2;m  log 5 . 3  Câu 3
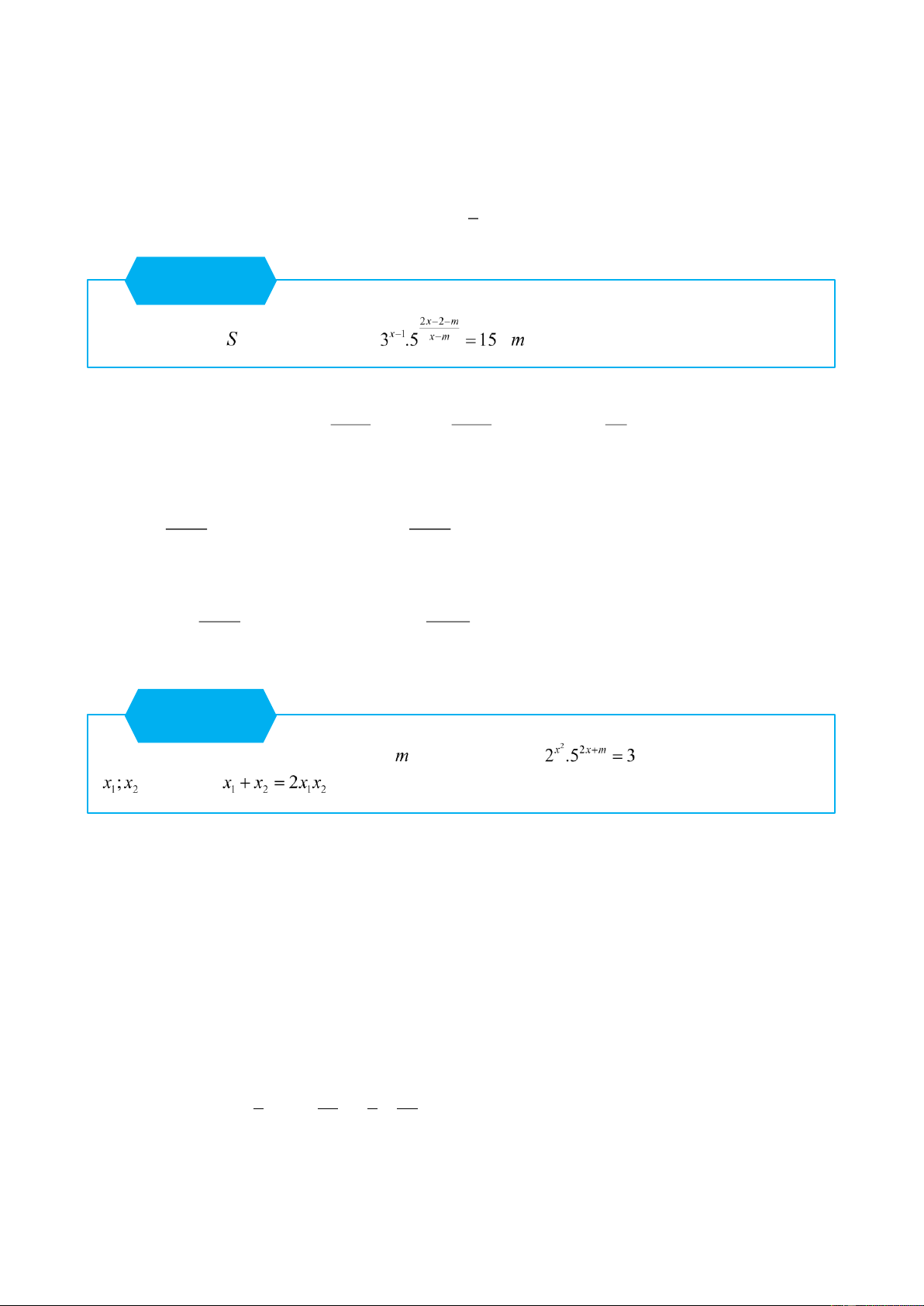
Tìm tất cả các giá trị thực của tham số để phương trình
có hai nghiệm phân biệt thỏa mãn . Lời giải
Lấy logarit cơ số 2 của hai vế phương trình đã cho ta được log  2x 2
2 .5 xm  log 3 2  2 2
 x  2x  mlog 5 log 3  0 2 2 2
 x  2log 5 x  mlog 5  log 3  0 2  2 2
Để phương trình đã cho có hai nghiệm phân biệt x ; x thỏa mãn x  x  2x x thì 1 2 1 2 1 2 2  '  0
log 5  mlog 5  log 3  0 (1) 2 2 2   
x  x  2x x  2
 log 5  2mlog 5  2log 3 (2) 1 2 1 2  2 2 2  m m 2 1 5 1 5 m 1 log log 5        3  m  1   log 3 . 2 2 5 5 3 5 3
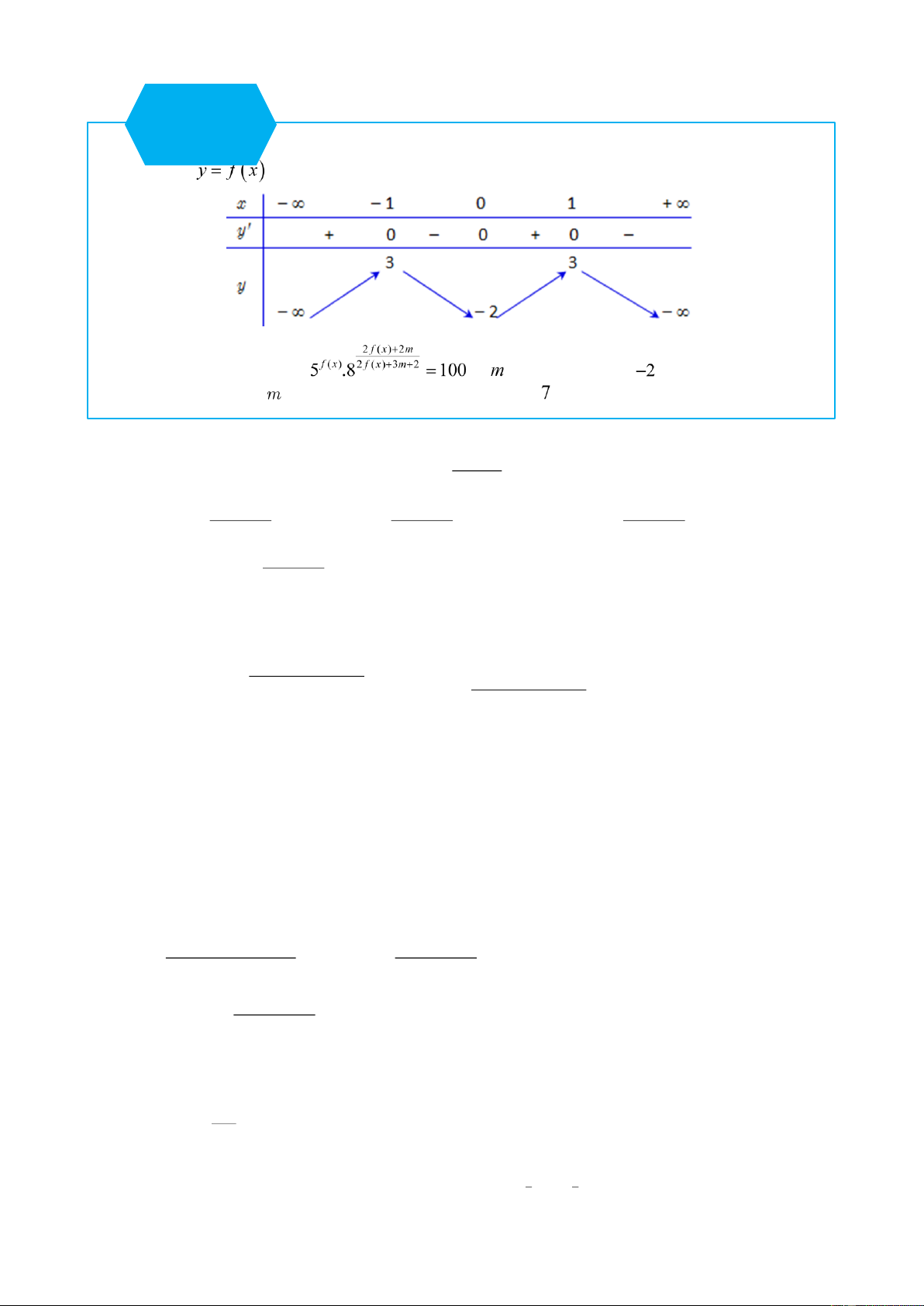
Thay m  1 log 3 vào (1) thấy thỏa mãn. Vậy m  1 log 3 là giá trị cần tìm. 5 5 Câu 4 Cho hàm số
có bảng biến thiên như sau Cho phương trình , là tham số khác . Tìm tất cả các giá trị thực của
để phương trình đã cho có đúng nghiệm phân biệt. Lời giải 
Đkxđ: f  x  m    f x 3m 2 2 3 2 0   . 2
2 f  x2m
6 f  x6m
6 f  x6m  f  x
f  x m f  x
f  x m 2 2 f x 2 2 3 2 2 3 2 2
2 f x3m2 5 .8 100  5 .2  5 .2  5  2 42 f  x f  x2
2 f  x3m2  5  2
Lấy logarit cơ số 5 của hai vế phương trình đã cho ta được  f x  2 2  f x    2  f  x    2     2 f  x log 2 5 2  3m  2 1   2 f  x log 2 5  3m  2
 f x  2 (1)  2f 
x3m  2  2  log 2 (2) 5 Với m  2
 thì phương trình (1) và (2) luôn thỏa mãn điều kiện xác định.
Dựa vào bảng biến thiên ta thấy phương trình (1) có 4 nghiệm phân biệt. Để phương trình
ban đầu có đúng 7 nghiệm phân biệt thì phương trình (2) thỏa mãn điều kiện xác định và
có 3 nghiệm phân biệt khác các nghiệm của phương trình (1).
Dựa vào bảng biến thiên để phương trình (2) có 3 nghiệm phân biệt thì 2  log 2  2  3m 2  2 log 2 5 5  2   m 
(thỏa mãn điều kiện). 2 3 2  2 log 2 Vậy 5 m 
thì phương trình đã cho có 7 nghiệm. 3
Bài tập tương tự:
Giải các phương trình sau: 2 x3 2 log 10x 1  log 3 2 2  3  2x 5 25 x 4 x2 a) x 2 3 .4 x  18. b) . c) 2 .7 1. 1 1 d) x x x 1  x 1  x2 x3 5  3  5 3  5 3  0 . x x  e) x 2 x 1 2 2 4  3  3  2  Lời giải
a) Điều kiện: x  0 .
Với điều kiện trên, phương trình đã cho tương đương:  2x3  3x6 2  2   2 3 x 2 x 2  x  2 1 x 4 2   3 .2
 3 .2  3 .2 x 1  x  4  log 2  0 3 x      x  x  2 3log 2 2 3 x  2   0   x  2    2  x 
x  2x  3log 2  0 VN  3  
b) Điều kiện: x  0 .
Với điều kiện trên, phương trình đã cho tương đương: 2 log 10 x 1  3  2xlog53 25   2 log
10x 1 .log 3  log 3.log 2x 25    5 5 5   1 2
 log 5.2x 1 log 2x  0 5   5   4 1
 log 2x  log 52 1log 2x  0 5 5 5   4  1  1 x  1 1 3 log 2x  1  2x    10 2
 log 2x  log 2x   0    5   . 5   5   5   4 2 4 log 2x  3  125  5    2x 125 x   2 c) Ta có:   2 x 2 x 4 x2 2 2 .7
1  x  4  x  2log 7  0  x  2 x  2  log 7  0  2   2  x  2   log 7  2 . d) Ta có: x x x 1  x 1  x2 x3 x x 1  x2 x x 1  x3 5  3  5  3  5  3  0  5  5  5  3  3  3   x   x x x x 5 1 2 1 5  5 5   1 3 1 3  3  3  31.5  31.3  1  x  0    3  e) Ta có: 1 1 1 1 1 x x x x   3 x x x x x x 4 2 1 2 1 2 2 2 2 2           4 3 3 2 4 2 3 3 4 . 3 . 2 3 1 x 1 x 3 3 2 3 x 4 4 3 x x x 3 3 2 2 2  4 .  3 .    4  3
 x   0  x  1 2 2 3 3 2 2 2 4.4
II. Giải phương trình logarit bằng phương pháp mũ hóa.
Dạng 1: log f x  b a  
Phương pháp giải: Sử dụng phương pháp biến đổi tương đương: 0  a  1 
Từ phương trình log f x  b   . a    f   x b  a
Dạng 2: log f x  g x a    
Phương pháp giải: Sử dụng phương pháp biến đổi tương đương: 0  a  1 
Từ phương trình log f x  g x   . a  
  f x gx  a
Dạng 3: log f x  log g x a b    f  x t  a
Phương pháp giải: Đặt log f x 
g x  t  
. Khử x trong hệ phương a   logb   g  x t  b
trình để thu được phương trình theo ẩn t, giải phương trình này tìm t, từ đó tìm x. Các ví dụ :
A. Phương trình không chứa tham số. Câu 1 Giải phương trình sau: . Lời giải
Điều kiện: 2x 1  0  2x 1  x  0. 5 Ta có: log 2x  x 2 1 2 2 1 2       x 5  2   x  log
 x  log 5  log 4 2 4 2 4 2 2
 x  2  log 5(tm) 2
Vậy phương trình có nghiệm là x  2  log 5 . 2 Câu 2 Giải phương trình sau: . Lời giải
Điều kiện: 3x 8  0  x  2log 2. 3 Ta có: x x 2 log (3 8) 2 3 8 3 x x        3 3x  1  (vn) 2
 3 x  8.3x  9  0   3x  9 x 2
 3  3  x  2 .
Vậy phương trình có nghiệm là x  2. Câu 3 Giải phương trình sau: . Lời giải
Điều kiện : x  0 . l  og t x  t  x  5t x  5 1 5    Ta có: log x  log
x  2  t       . 5 7   l  og x  2 t t t  t        7   x 2 7 5 2 7  2  t  t Từ phương trình   5 1 2   2.  1     .  7   7   t  t
Xét hàm số f t  5 1   2. ,t      .  7   7  t t
f t   5  5  1  1 '  ln  2. ln  0,t      
Hàm số f t  nghịch biến trên .  7  7  7  7
Mà f t  1  f t  f  
1 nên t  1 là nghiệm duy nhất của phương trình 2 .
Thay t  1 vào phương trình   1 ta có x  5 .
Vậy phương trình có nghiệm là x  5. Câu 4 Giải phương trình sau: . Lời giải Điều kiện x 1
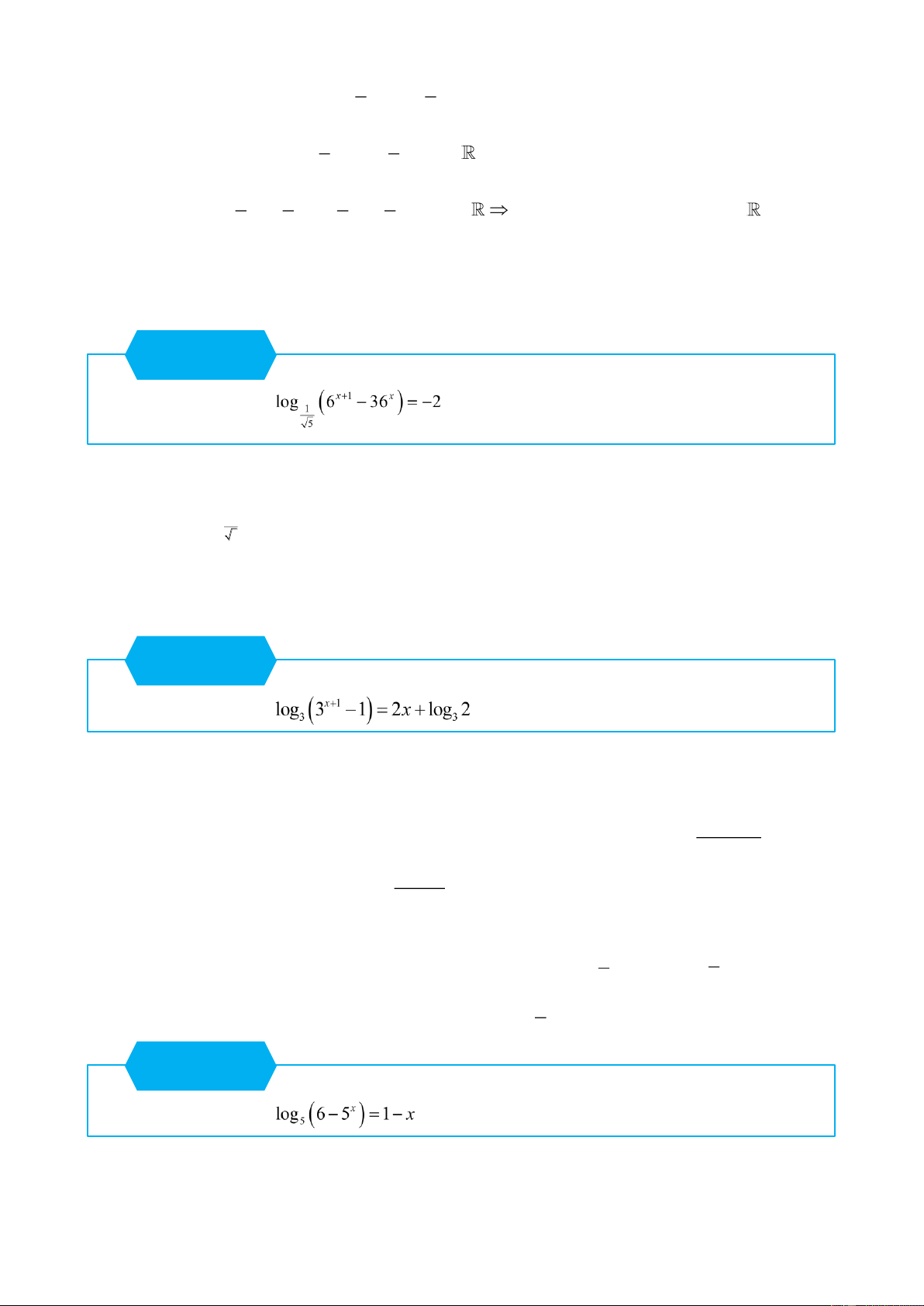
6   36x  0  x 1  2x  x  1. Ta có log  x 1 6  36x  2 2 log  x 1 6  36x  x 1 2 6           36x 5  0 1 5 5 6x 1 x  0 2
 6 x  6.6x  5  0     . 6x  5 x  log 5  6
Vậy phương trình có nghiệm là x  0 hoặc x  log 5 . 6 Câu 5 Giải phương trình sau: . Lời giải Điều kiện: x 1
3  1  0  x  1  x 1 3  1 Ta có : log  x 1 3   
1  2x  log 2  log  x 1
3  1  log 2  2x  log  2x 3 3 3    3 3 2 x 1 3  1 2 x x 1  2 
 3  3 1  2.3 x 2 3x 1 x  0 2  2.3 x 3.3x 1 0        . x 1 1 3  x  log3  2  2 1
Vậy phương trình có nghiệm là x  0 hoặc x  log . 3 2 Câu 6 Giải phương trình sau: . Lời giải
Điều kiện : 65x  0  5x  6  x  log 6 . 5 x x x x 5 Ta có log 6  5  1
1 x  6  5  5  6  5  5 5x 5x  1
x  0tm 2  5 x 
 6.5x 5  0     . 5x   5 x    1 tm
Vậy phương trình có nghiệm là x  0 hoặc x 1 . Câu 7 Giải phương trình sau: . Lời giải 9   2x  0 Điều kiện :  .  3 x  0 Ta có: log 9 2x    5 x
 log 9  2x  3 x 2   2   log53  x 8 2  9  2 
 2 x 9.2x  8  0 2x 2x  8
x  3l      x  0. 2x  1 x  0
Vậy phương trình có nghiệm là x  0 . Câu 8 Giải phương trình sau: . Lời giải Xét phương trình 2
log x  2x  log  2 x  2x  2 3 5  x  0  Điều kiện: 2
x  2x  0   . x  2 2
 x  2x  3t   1 Đặt 2
log x  2x  log  2
x  2x  2  t   3 5   2
x  2x  2  5t  2 Từ 2 thay vào   1 ta được : 5t 2 3t   t t    
Trường hợp 1: Xét 5t 2 3t   5t 3t    3 1 2  1   2       3  5   5 
Dễ thấy phương trình (3) có nghiệm t  1 . t t     t t    
Vì xét hàm số f t  3 1   2  
  có f t 3 3 1 1  .ln  2 .ln  0, t       nên hàm  5   5   5  5  5  5 số nghịch biến trên
, do đó t 1 là nghiệm duy nhất của (3).  14  2 x  2 2 2
Với t  1, ta có: x  2x  3  x  2x  3  0   (tm)  .  14  2 x   2
Trường hợp 2: 5t 2 3t    5t 2 3t    5t 3t    2 (4)
Tương tự như trường hợp 1, ta có t  0 là nghiệm duy nhất của (4)
Với t  0 , ta có: 2 2 x  2x  1
  x  2x 1 0 - phương trình vô nghiệm 14  2  14  2
Vậy phương trình có nghiệm là x  hoặc x  . 2 2
B. Phương trình chứa tham số. Câu 1
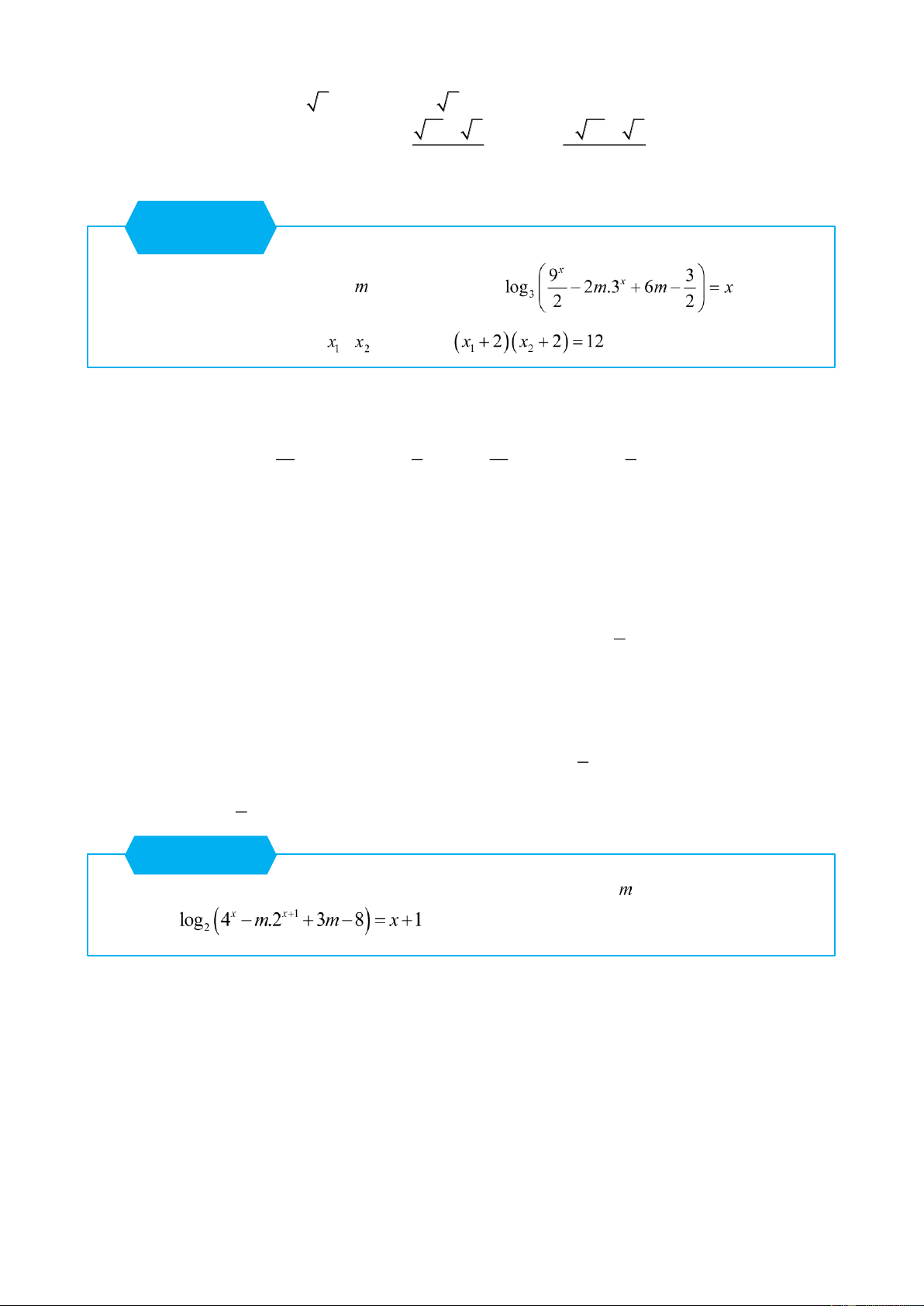
Tìm tất cả các giá trị của tham số để phương trình có hai nghiệm thực , thỏa mãn . Lời giải  9x 3  9x x x 3 Ta có : log   2 .3  6    
 2 .3  6   3x m m x m m 3  2 2  2 2
 9x  22   1 .3x m 34m  1  0 Đặt 3x t 
( t  0 ) thì phương trình đã cho trở thành 2
t  22m  
1 t  34m   1  0 (1)
Phương trình đã cho có hai nghiệm phân biệt  Phương trình (1) có hai nghiệm dương   2  0 2m   1  34m   1  0     m 1 
phân biệt  S  0  2m 1 0   1 .   m   P  0  4m 1  0   4 t  4m 1 1
3x  4m 1
x  log 4m 1 1 3   Khi đó      . t  3 2 3x  3 x  1  2
Ta có  x  2 x  2 12  log 4m 1  5 2  m 
(thỏa mãn điều kiện). 3   1  2  2 5
Vậy m  là giá trị cần tìm. 2 Câu 2 Tìm tất cả các giá trị của tham số để phương trình
có hai nghiệm trái dấu. Lời giải    Ta có : log  x x 1 4  . m 2 3m 8 x x 1 x 1  x 1 4  . m 2 3m 8  2 2  4x  2   1 .2x m 3m8  0 Đặt 2x t  , ta có phương trình 2
t  2m  
1 t  3m 8  0 (1)
Với x  0  x thì 1 x 2 0 2 1 2x   
, nên phương trình đã cho có hai nghiệm trái dấu x , 1 2 1
x khi và chỉ khi phương trình  
1 có hai nghiệm t , t sao cho 0  t  1  t . 2 1 2 1 2 Ta có   2
1  t  2t 8  m2t   3 2 . 3 2 t  2t  8 Vì t 
không là nghiệm phương trình 2 nên: 2   m 3 2 2t  . 3 t  t  3
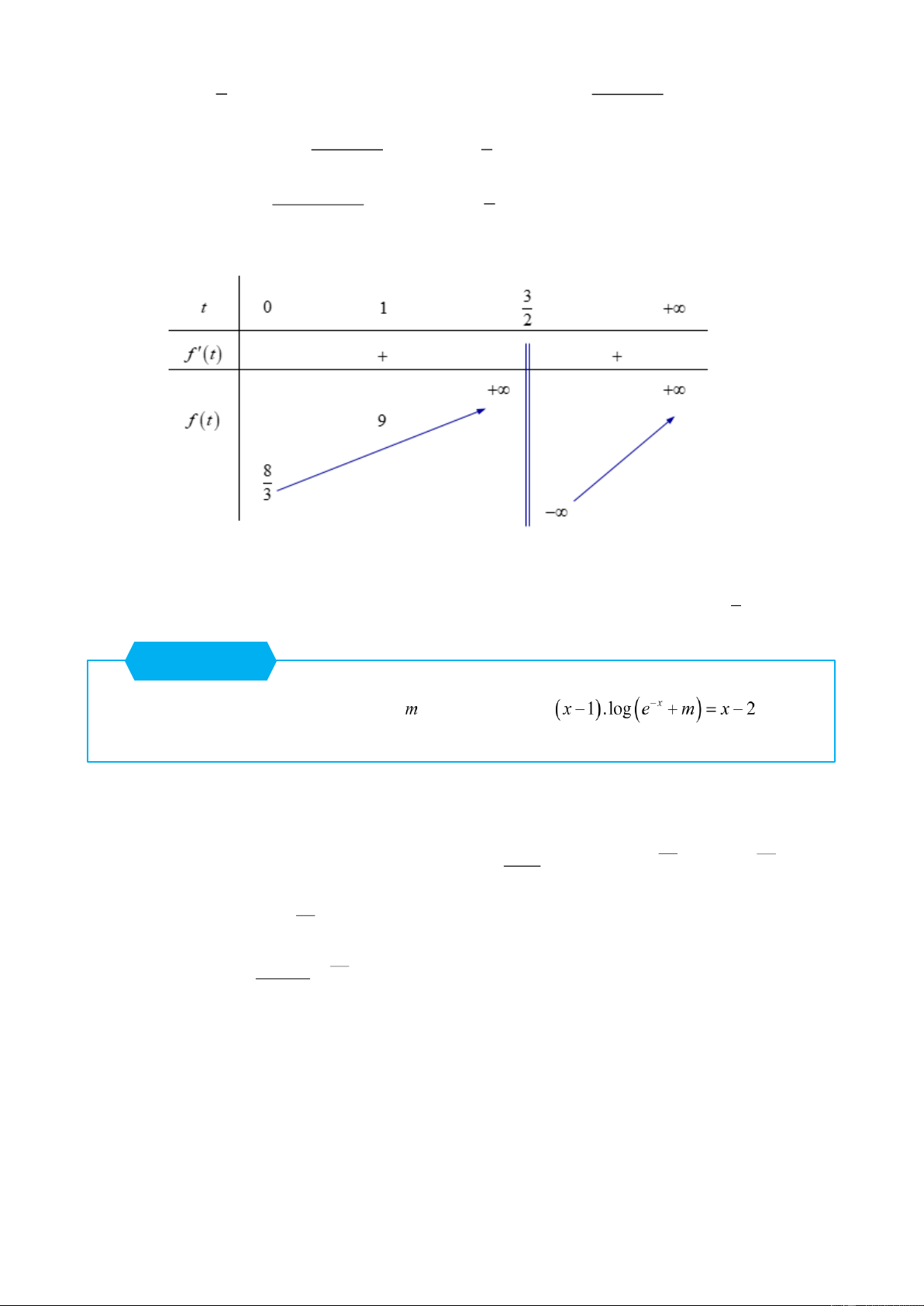
Xét hàm số f t 2 2 8  , với 0  t  . 2t  3 2 2 2t  6t  22 3
Ta có f t       với 0 t . 2t  3 0 2 2 Bảng biến thiên: Phương trình  
1 có hai nghiệm 0  t  1  t khi và chỉ khi phương trình   3 có hai 1 2 8
nghiệm 0  t  1  t . Từ bảng biến thiên ta suy ra giá trị cần tìm của m là  m  9 . 1 2 3 Câu 3
Tìm tất cả các giá trịcủa tham số để phương trình có hai nghiệm thực phân biệt. Lời giải
Vì x 1 không là nghiệm nên phương trình : x2 x2      x x 2    1 .log  x x e
 m  x  2 x x 1
 log(e  m) 
 e  m  10  1  10 x x m  e . x 1 x2 Đặ   t 1  ( ) 10 x x y g x  e . x2 1 Ta có: 1 10    ln10 x x y  e  0, x  1. 2 (x 1) Bảng biến thiên: Vậy 1
phương trình có 2 nghiệm thực phân biệt khi   m  10 . e Câu 4
Có bao nhiêu giá trị nguyên nhỏ hơn của tham số để phương trình có nghiệm. Lời giải t  x  m 
Đặt log 2020x  m  log 1010x  2020 6 t  
 2.4t   6t m 6   4   1
 010x  4t   2  .4t  6t m . Đặt   2.4t 6t f t  
 . Ta có:    6t ln62.4t f t .ln 4 . t   t  3 
Xét f t  3 2 ln 4  0       log 16    t  log log 16 . 3  6   2  ln 6 6  2  2 Bảng biến thiên:  
Phương trình f t  m có nghiệm khi và chỉ khi m  f log log 16   2  ,01. 3  6   2  m  2019  2   m  2018 Mà  nên ta có:  . m m
Vậy có 2021 giá trị nguyên của m thỏa mãn yêu cầu bài toán.