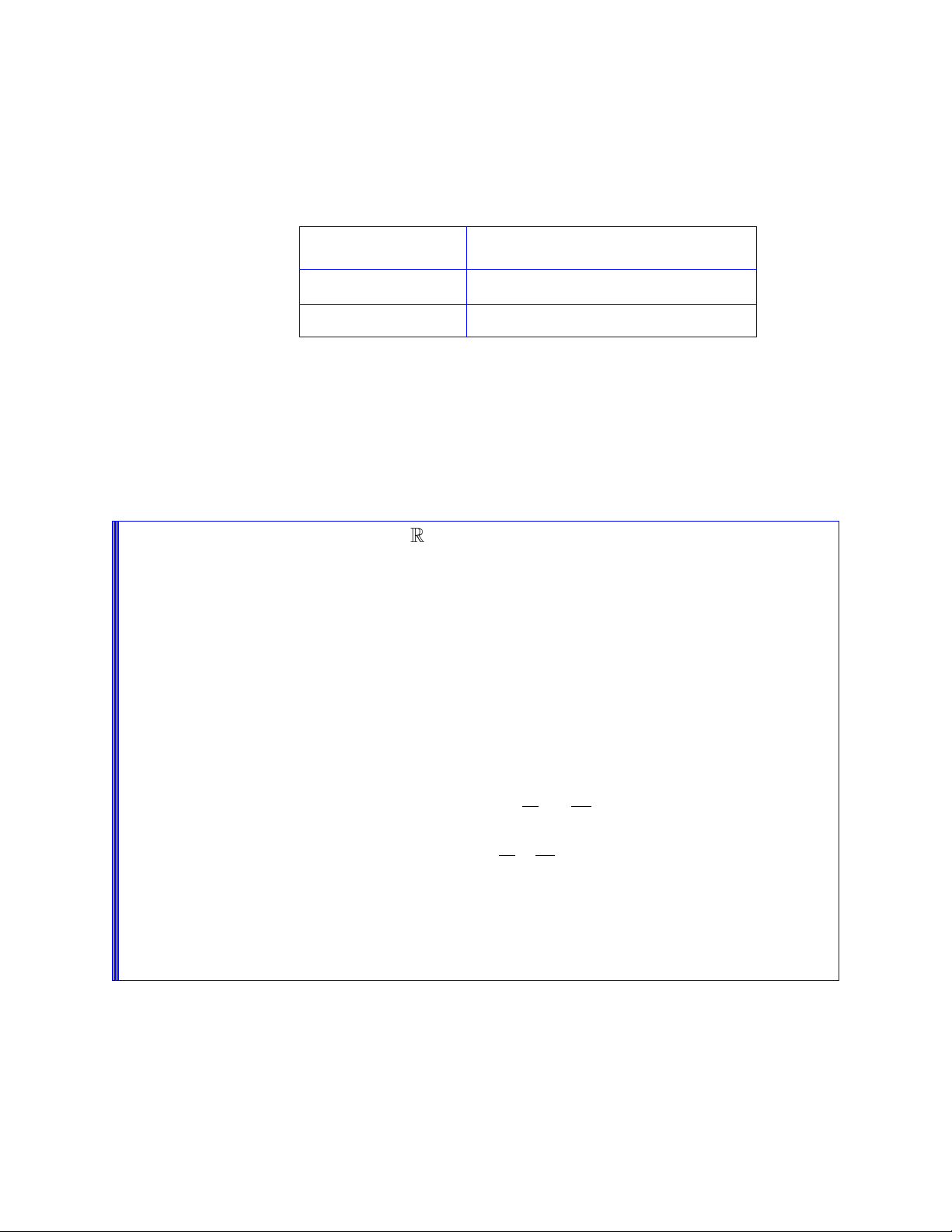
1. CỰC TRỊ CỦA HÀM SỐ BẬC 3: y  ax3  bx2  cx  d a  0.
1.1 SỐ ĐIỂM CỰC TRỊ CỦA HÀM SỐ BẬC 3 Ta có: y  2
ax  bx  c  2 3 2
Ax  Bx  C ,   2
B  4AC  4 b 3ac y'  2   Trường hợp Kết luận 2 b  3ac  0
Hàm số không có cực trị. 2 b  3ac  0
Hàm số có hai điểm cực trị.
Đối với trường hợp hàm bậc ba có hai điểm cực trị, ta có bài toán tổng quát sau đây: 1.2 BÀI TOÁN TỔNG QUÁT :
Cho hàm số y  f x m  3 ax  2 ; bx  cx  .
d Tìm tham số m để hàm số có cực đại, cực tiểu
tại x , x thỏa mãn điều kiện K cho trước? 1 2  Phương pháp:
o Bước 1: + Tập xác định: D  . + Đạo hàm: y  2
ax  bx  c  2 3 2
Ax  Bx  C
o Bước 2: Hàm số có cực trị (hai cực trị, hai cực trị phân biệt hay có cực đại và cực tiểu)  Phương trình 
y  0 có hai nghiệm phân biệt A  3a   0 a   0   m D . 2 2   
  B  4AC  4b 12ac   2 1 b ac y  0   3   0
o Bước 3: Gọi x , x là hai nghiệm của phương trình  y  0 . Khi đó: 1 2
S  x  x   B   2b  1 2  A 3a .   C c P x .x    1 2 A 3a
o Bước 4: Biến đổi điều kiện K về dạng tổng S và tích P . Từ đó giải ra tìm được m  D . 2
o Bước 5: Kết luận các giá trị m thỏa mãn: m  D  D . 1 2
1.3 MỘT SỐ DẠNG TOÁN TÌM ĐIỀU KIỆN ĐỂ HAI CỰC TRỊ CỦA HÀM SỐ THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC
Gọi x , x là các điểm cực trị của hàm số; y , y là các giá trị cực trị của hàm số. 1 2 1 2
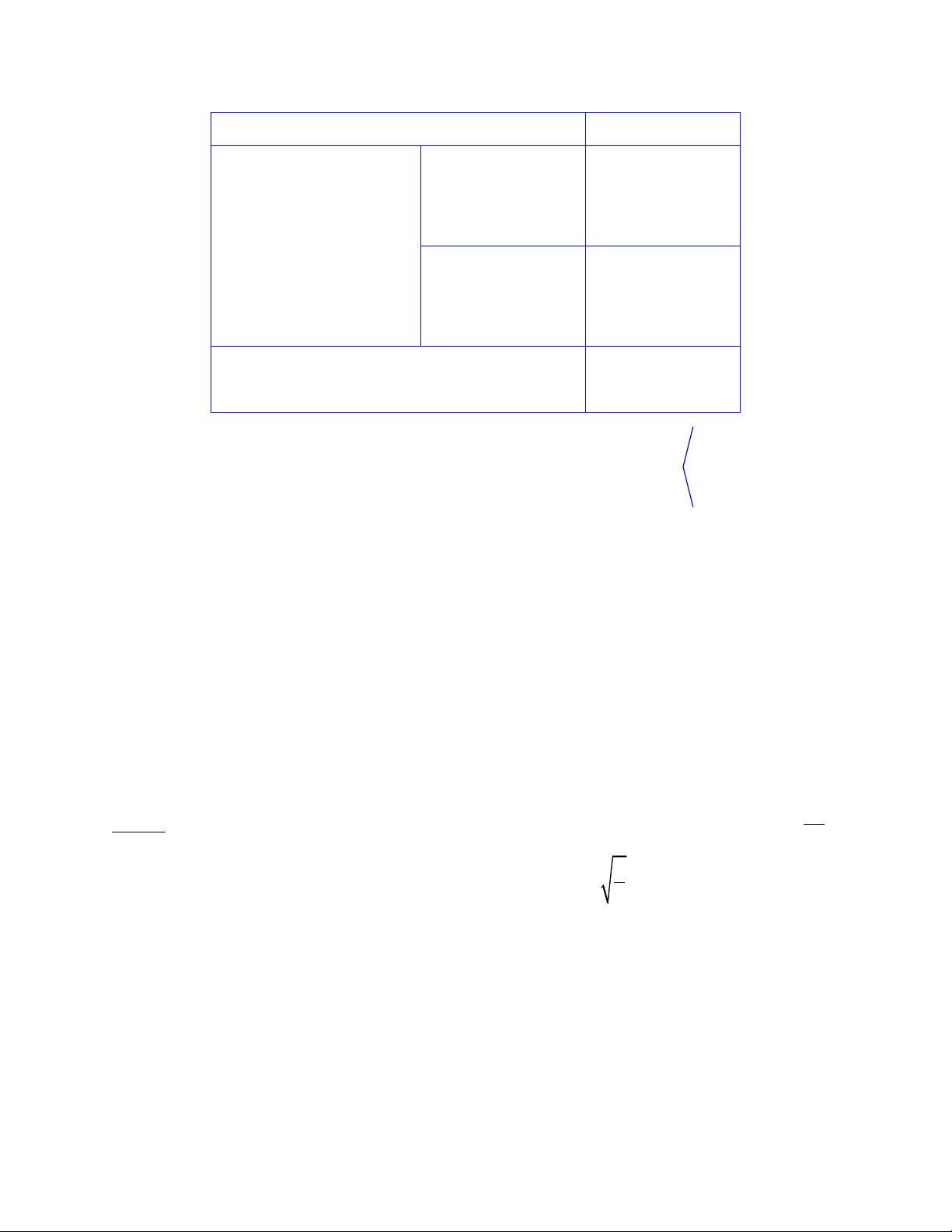
1.3.1 Điều kiện để hàm số có cực trị cùng dấu, trái dấu. Trường hợp Điều kiện   y 0  Cùng dương S  0    P   0 y 0 Cùng dấu  P   0   0  y' Cùng âm S  0 P   0   y 0 Trái dấu  P   0
x    x 1 2
1.3.2 Tìm điều kiện để hàm số có hai điểm cực trị x , x thỏa mãn: x  x   1 2 1 2
  x  x 1 2
o Hai cực trị x , x thỏa mãn x    x 1 2 1 2
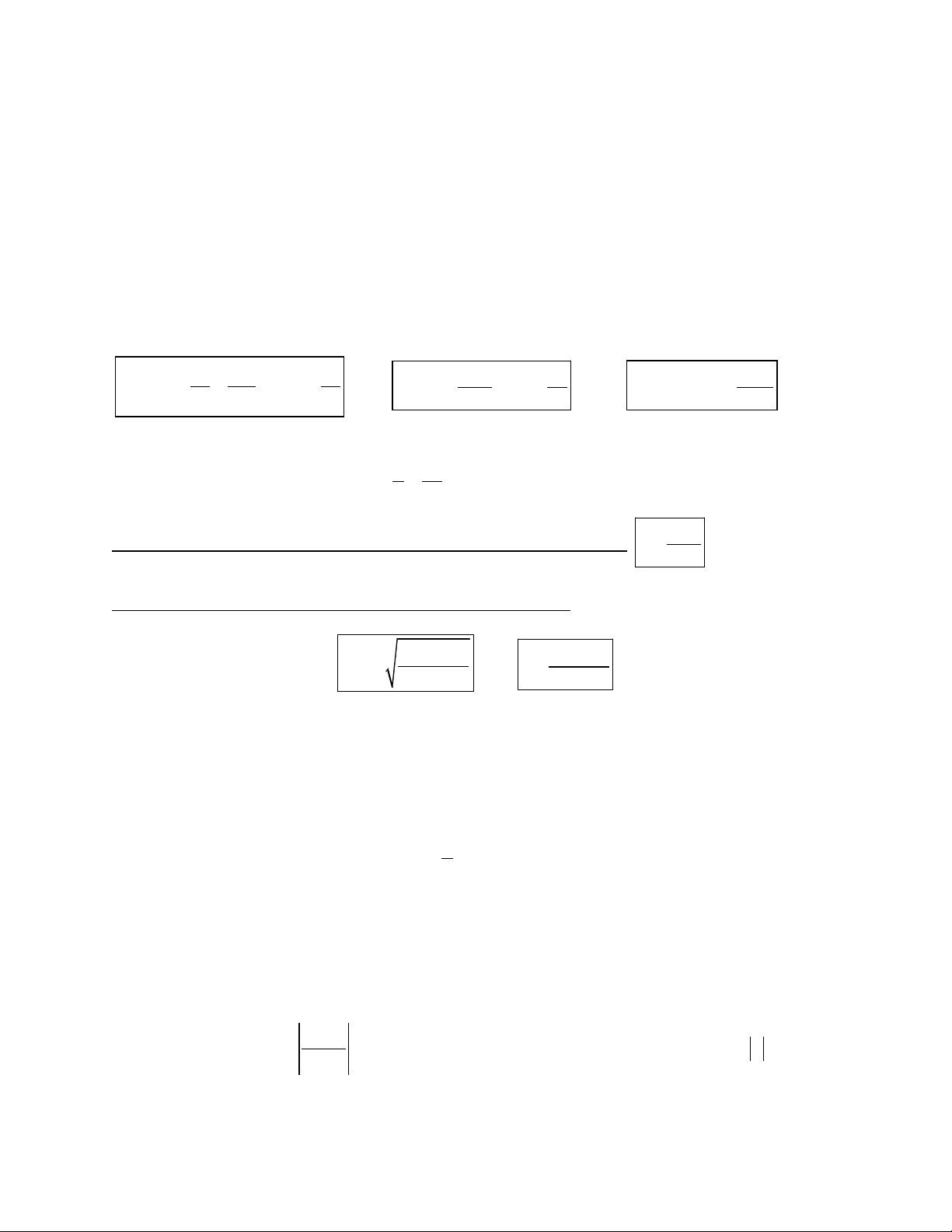
 x  x 0 x .x x x 0 1   2     1 2   1 2    2 
o Hai cực trị x , x thỏa mãn x  x   1 2 1 2
x  x 0 x .x x x 0 1   2     1 2   1 2    2     
x  x    2 x x 2 1 2      1 2
o Hai cực trị x , x thỏa mãn   x  x 1 2 1 2
x  x 0 x .x x x 0 1   2     1 2   1 2    2     
x  x    2 x x 2 1 2      1 2 b
Chú ý: Phương trình bậc 3 có 3 nghiệm lập thành cấp số cộng khi có 1 nghiệm là x  , 3a d
có 3 nghiệm lập thành cấp số nhân khi có 1 nghiệm là x   3 . a
1.3.3 Tìm điều kiện để hai hàm số có hai cực trị x , x nằm cùng phía, khác phía so với 1 2
một đường thẳng.
Cho 2 điểm A x ; y , B x ; y và đường thẳng  : ax  by  c  0. 1 1   2 2
o Nếu ax  by  cax  by  c  0 thì hai điểm A,B nằm về hai phía so với . 1 1 2 2
o Nếu ax  by  cax  by  c  0 thì hai điểm A,B nằm cùng phía so với . 1 1 2 2
1.3.4 Viết phương trình đi qua các điểm cực trị
Giả sử hàm số có cực trị, thực hiện phép chia đa thức y cho y để có:
y x  px yx  Ax  B
Như vậy, nếu x là điểm cực trị của hàm số  y x  0  y x Ax B . 0  0     0 0
Suy ra đường thẳng  : y x  Ax  B là đường thẳng đi qua tất cả các điểm cực trị của 1   C.
Đối với đường thẳng qua hai cực trị của hàm số bậc 3, ta có công thức: 2c 2b bc 2 bc y .y y x x d hay y x x d hoặc y x 9ay 1       1        1    2         3 9a  9a 9a 9a 2
Cách bấm máy tính tìm ra đường thẳng đi qua hai điểm cực trị (MODE 2) : 3  2     2 x b ax bx cx d
3ax  2bx  c  x 
i Ai  B  y  Ax    B  3 9a   
Gọi k là hệ số góc của đường thẳng đi qua các điểm cực đại, cực tiểu: k  2 9a
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bậc 3 là: 4e  3 2 b   16e 3ac AB với e  a 9a
1.3.5 Tìm điều kiện để đường thẳng đi qua các điểm cực đại, cực tiểu song song (vuông
góc) với đường thẳng d : y  px  q .
– Tìm điều kiện để hàm số có cực đại, cực tiểu.
– Viết phương trình đường thẳng đi qua các điểm cực đại, cực tiểu.
– Giải điều kiện: k  p (hoặc   1 k ). p
1.3.6 Tìm điều kiện để đường thẳng đi qua các điểm cực đại, cực tiểu tạo với đường
thẳng d : y  px  q một góc  .
– Tìm điều kiện để hàm số có cực đại, cực tiểu.
– Viết phương trình đường thẳng đi qua các điểm cực đại, cực tiểu. k  p – Giải điều kiện: 
 . (Đặc biệt nếu d  Ox, thì giải điều kiện: k  tan )  tan 1 kp
1.3.7 Tìm điều kiện để đồ thị hàm số có hai điểm cực trị A, B sao cho IAB có diện tích
S cho trước (với I là điểm cho trước).
– Tìm điều kiện để hàm số có cực đại, cực tiểu.
– Viết phương trình đường thẳng  đi qua các điểm cực đại, cực tiểu. 1
– Giải điều kiện S
 d I; AB .AB   S . IAB   2
1.3.8 Tìm điều kiện để đồ thị hàm số có hai điểm cực trị A, B đối xứng qua đường thẳng
d cho trước.
– Tìm điều kiện để hàm số có cực đại, cực tiểu.
– Viết phương trình đường thẳng  đi qua các điểm cực đại, cực tiểu.
– Gọi I là trung điểm của AB.   d – Giải điều kiện:  . I   d
1.3.9 Tìm điều kiện để đồ thị hàm số có hai điểm cực trị A, B cách đều đường thẳng d cho trước.
– Tìm điều kiện để hàm số có cực đại, cực tiểu.
– Giải điều kiện: d  A; d  dB; d
1.3.10 Tìm điều kiện để đồ thị hàm số có hai điểm cực trị A, B và khoảng cách giữa hai
điểm A, B là lớn nhất (nhỏ nhất).
– Tìm điều kiện để hàm số có cực đại, cực tiểu.
– Tìm toạ độ các điểm cực trị A, B (có thể dùng pt đường thẳng qua hai điểm cực trị).
– Tính AB. Dùng phương pháp hàm số để tìm GTLN (GTNN) của AB.