
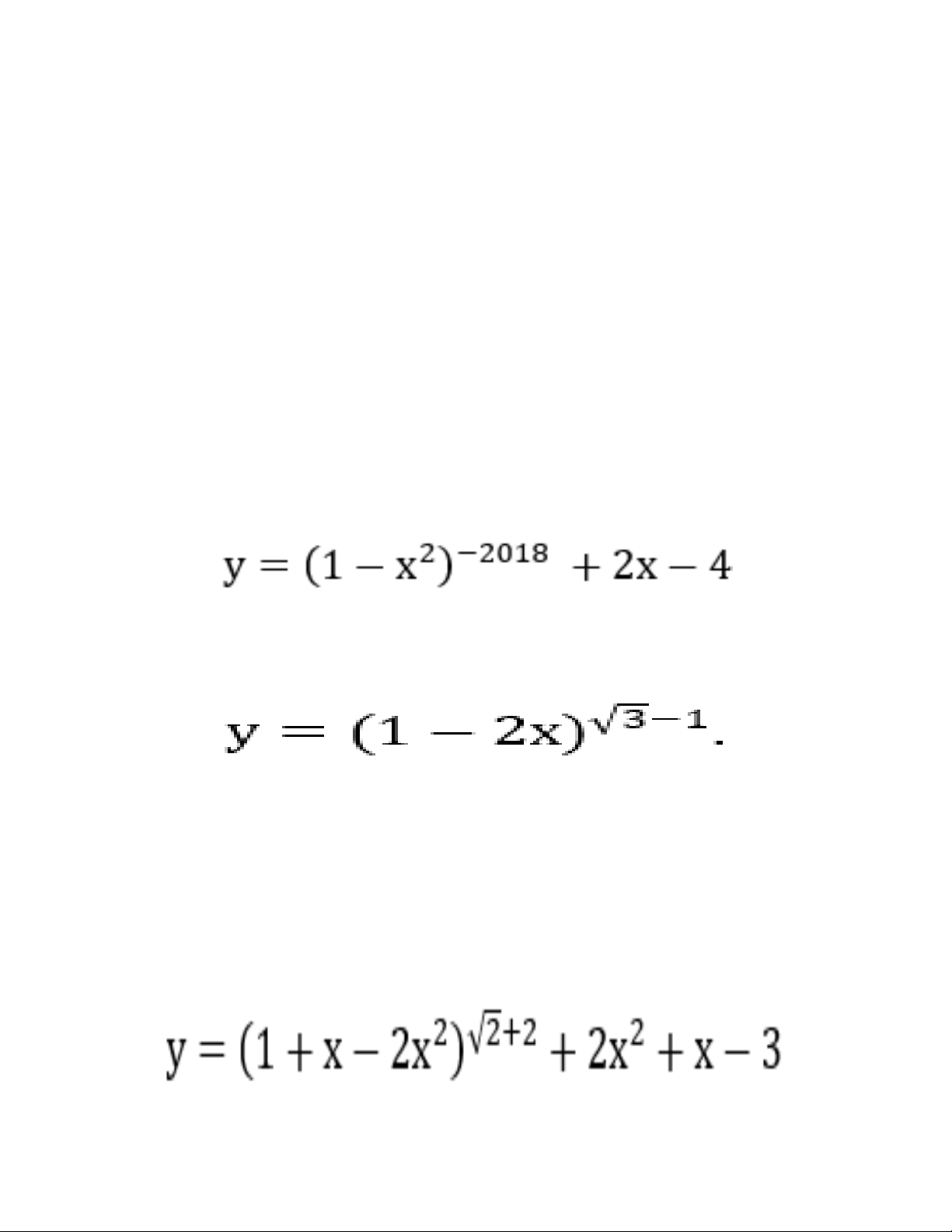
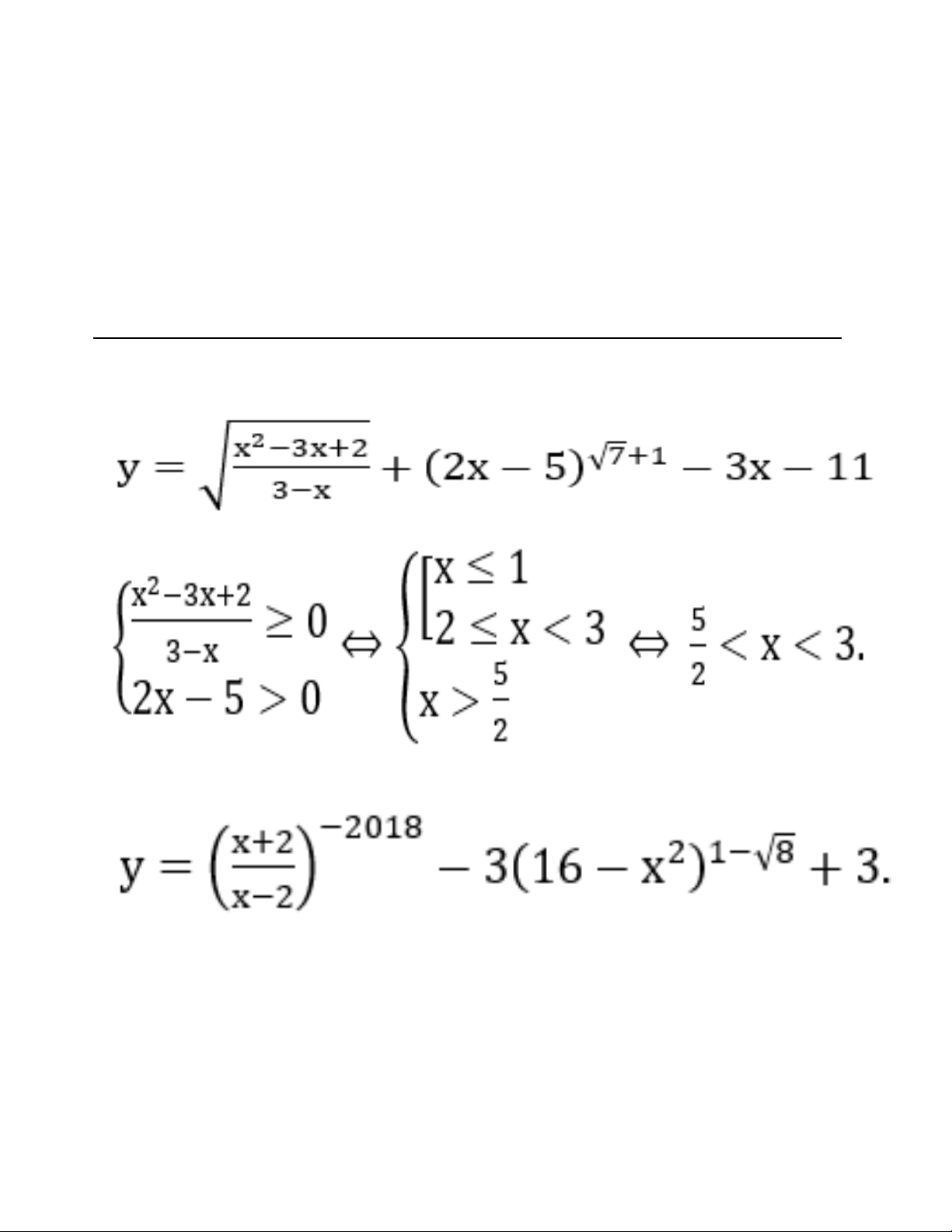
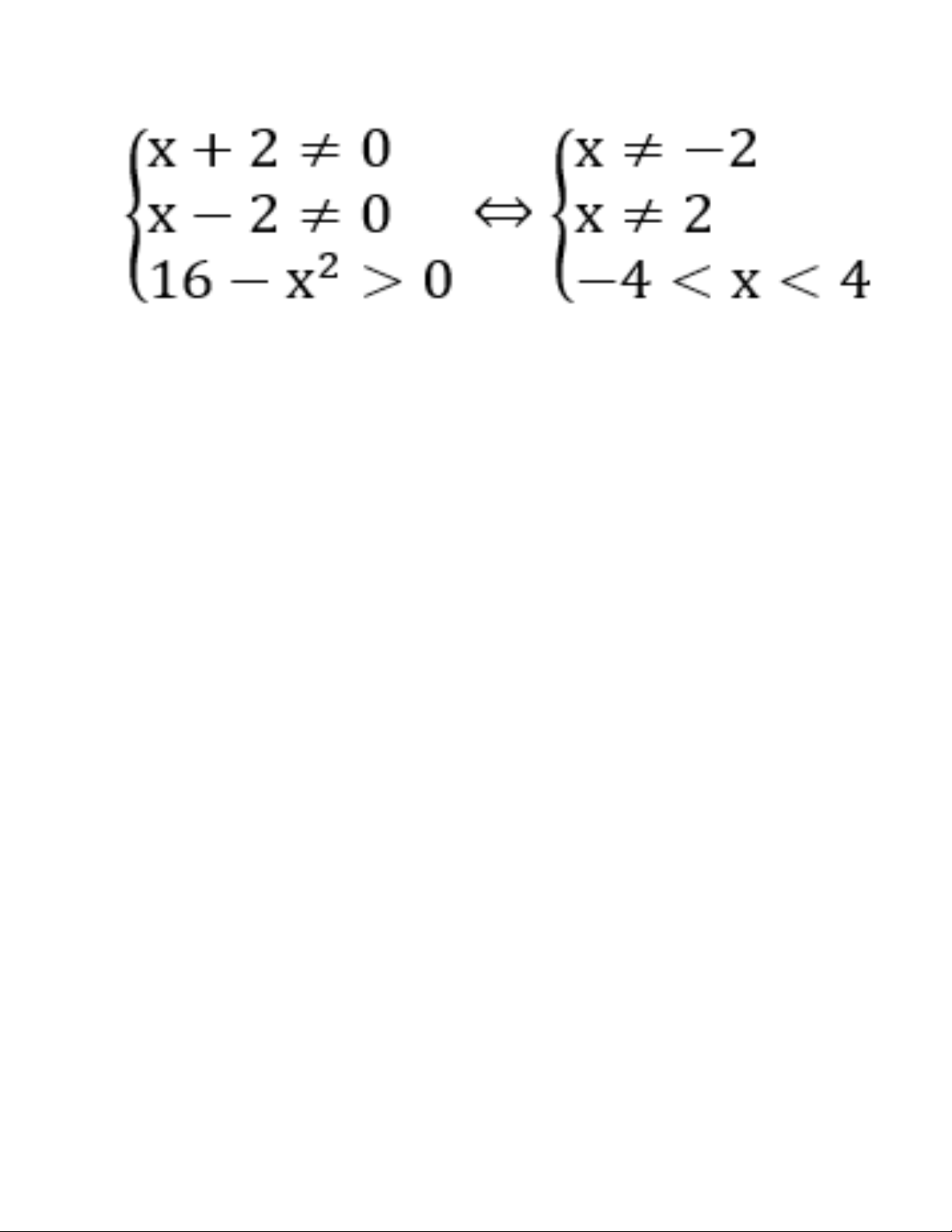

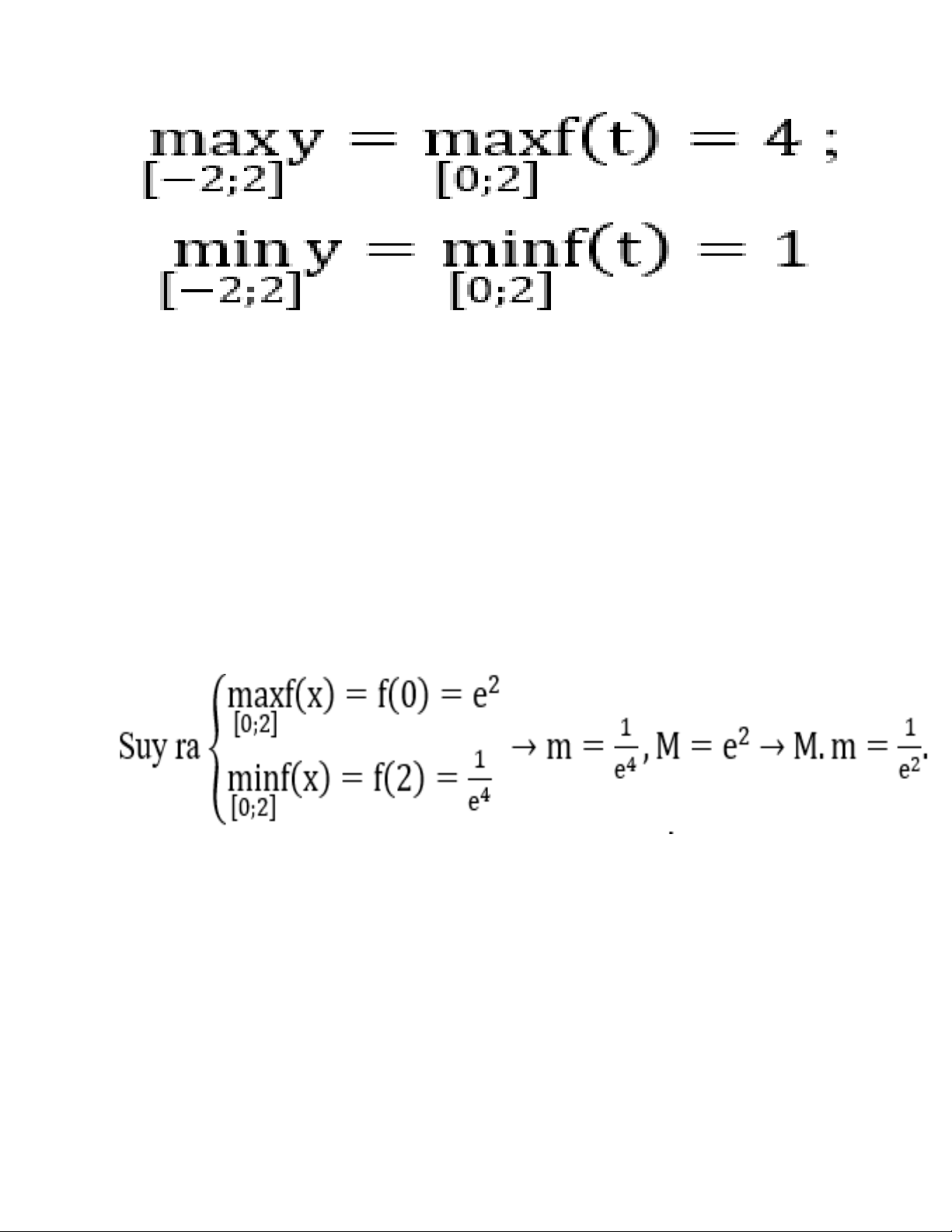
Preview text:
Bài tập về tìm tập xác định của Hàm số mũ Lũy thừa Logarit
1. Tại sao cần tìm tập xác định của hàm số mũ, lũy thừa, logarit
Theo quy ước của sách giáo khoa giải tích 12 thì hàm số lũy thừa có tập xác định phụ thuộc vào
lũy thừa. Có tất cả 3 trường hợp khác nhau về lũy thừa ảnh hưởng đến tập xác định là: Lũy thừa
với số mũ nguyên dương; Lũy thừa số mũ nguyên không dương; Lũy thừa số mũ không nguyên.
Tập xác định của một hàm số mũ là tập hợp các giá trị của biến độc lập mà hàm số có thể được
định nghĩa và hoạt động một cách hợp lệ. Tìm tập xác định của hàm số mũ là một bước quan trọng
trong việc hiểu và sử dụng hàm số này trong toán học và các ứng dụng thực tế. Dưới đây là một
số lý do tại sao cần tìm tập xác định của hàm số mũ:
- Xác định tính hợp lệ của biểu thức: Bằng cách tìm tập xác định, bạn có thể xác định xem biểu
thức mũ có thể được tính toán một cách hợp lệ hay không. Điều này giúp tránh những phép tính
không xác định hoặc vô lý.
- Tránh lỗi toán học: Trong toán học, một số phép tính có thể dẫn đến các giá trị không hợp lệ như
chia cho 0 hoặc tính căn bậc âm. Tìm tập xác định của hàm số mũ giúp tránh lỗi này và đảm bảo
tính hợp lệ của các phép tính.
- Phân tích biểu đồ: Khi vẽ biểu đồ của hàm số mũ, tập xác định giúp xác định miền giá trị của
biểu đồ, nơi mà hàm số có giá trị thực sự. Điều này hữu ích để hiểu hình dạng của đồ thị và cách nó hoạt động.
- Ứng dụng trong thực tế: Trong các ứng dụng thực tế như vật lý, kỹ thuật, và khoa học dữ liệu,
tập xác định giúp xác định miền giá trị của biến độc lập mà hàm số mũ có thể áp dụng. Điều này
quan trọng để đảm bảo tính hợp lệ của mô hình hoặc phương trình trong các vấn đề thực tế.
- Giải quyết vấn đề: Trong việc giải các phương trình hoặc bài toán có liên quan đến hàm số mũ,
việc xác định tập xác định là một bước quan trọng để giải quyết vấn đề và tìm ra nghiệm hợp lệ.
2. Bài tập về tìm tập xác định của Hàm số mũ Lũy thừa Logarit
Tập xác định của hàm số lũy thừa
Hàm số lũy thừa là các hàm số dạng y = xα (α ∈ R). Các hàm số lũy thừa có tập xác định khác nhau, tùy theo α:
- Nếu α nguyên dương thì tập các định là R
- Nếu α nguyên âm hoặc α = 0 thì tập các định là R∖{0}
- Nếu α không nguyên thì tập các định là (0; +∞). Lưu ý:
- Hàm số y = √x có tập xác định là [0; +∞).
- Hàm số y = 3√x có tập xác định R, trong khi đó các hàm y = x½, y = x1/3 đều có tập xác định (0; +∞).
Ví dụ: Tìm tập xác định của các hàm số sau: a. y=x3 b. y=x½ c. y=x-√3 d. y=e√2×2- 8
a. y=x3 vì 3 là số nguyên dương nên tập xác định của hàm số là: D = R
b. y=x½ vì 1/2 là số hữu tỉ, không nguyên nên tập xác định của hàm số là D=\left( 0,+∞ )
c. y=x-√3 vì -√3 là số vô tỉ, không nguyên nên tập xác định của hàm số là: D=( 0,+∞ )
d. Điều kiện xác định của hàm số 2x2– 8 ≥ 0 <=> x ∈ ( – ∞; -4] ∪ [4; +∞)
Vậy tập xác định của hàm số: D = R\ ( -4, 4 )
Bài 1: Tìm tâ ̣p xác đi ̣nh D của hàm số Lời giải:
Hàm số xác đi ̣nh khi và chỉ khi 1-x2 ≠ 0 ⇔ x ≠ ±1
Bài 2: Tìm tâ ̣p xác đi ̣nh D của hàm số
Lời giải: Hàm số xác đi ̣nh khi và chỉ khi 1-2x > 0 ⇔ x < 1/2
Bài 3: Tìm tâ ̣p xác đi ̣nh D của hàm số y = (2x - 4) -2018
Lời giải: Hàm số xác đi ̣nh khi và chỉ khi 2x-4 ≠ 0 ⇔ x ≠ 2
Bài 4: Tìm tâ ̣p xác đi ̣nh D của hàm số y = (4 - x) 3/11
Lời giải: Hàm số xác đi ̣nh khi và chỉ khi 4-x > 0 ⇔ x < 4
Bài 5: Tìm tâ ̣p xác đi ̣nh D của hàm số
Lời giải: Hàm số xác đi ̣nh khi và chỉ khi 1+x-2x2 > 0 ⇔ -1/2 < x < 1
Bài 6: Tìm tâ ̣p xác đi ̣nh D của hàm số
Lời giải: Hàm số xác đi ̣nh khi và chỉ khi
Vâ ̣y tâ ̣p xác đi ̣nh của hàm số là D= (5/2; 3).
Bài 7: Tìm tâ ̣p xác đi ̣nh D của hàm số
Lời giải: Hàm số xác đi ̣nh khi và chỉ khi
Vâ ̣y tâ ̣p xác đi ̣nh của hàm số là D=(-4 ; 4)\{-2 ,2}.
Bài 8: Tìm tâ ̣p xác đi ̣nh của hàm số y = log2 (5x + 2) - 125)
Lời giải: Hàm số xác đi ̣nh khi 5x+2-125 > 0 ⇔ 5x+2 > 53 ⇔ x > 1.
Vậy tập xác định D=(1;+∞).
Lời giải: Để hàm số y=log(x2-2x-m+1) có tập xác định là R
3. Trắc nghiệm về hàm số mũ, lũy thừa, lôgarit
Bài 1: Tìm mệnh đề đúng trong các mệnh đề sau:
A. Đồ thị hàm số y = ax và đồ thị hàm số y = logax đối xứng nhau qua đường thẳng y = x.
B. Hàm số y = ax với 0 < a < 1 đồng biến trên khoảng (-∞; +∞).
C. Hàm số y = axvới a > 1 nghịch biến trên khoảng (-∞; +∞)
D. Đồ thị hàm số y = ax với a > 0 và a ≠ 1 luôn đi qua điểm M (a;1). Lời giải: Đáp án: A Giải thích: Chọn A
Câu B sai vì hàm số y = ax với 0 < a < 1 nghịch biến trên khoảng (-∞; +∞).
Câu C sai vì hàm số y = ax với a > 1 đồng biến trên khoảng (-∞; +∞).
Câu D sai vì đồ thị hàm số y = ax với a < 0 và a ≠ 1 luôn đi qua điểm M(a; aa) hoặc M(0;1) chứ không phải M(a;1).
Bài 2: Với a > 0 và a ≠ 1. Phát biểu nào sau đây không đúng?
A. Hai hàm số y = ax và y = logax có cùng tính đơn điệu
B. Hai hàm số y = ax và y = logax có cùng tập giá trị
C. Đồ thị hai hàm số y = ax và y = logax đối xứng nhau qua đường thẳng y=x.
D. Đồ thị hai hàm số y = ax và y = logax đều có đường tiệm cận Lời giải: Đáp án: B Giải thích:
Tập giá trị của hàm số y = ax là (0; +∞), tập giá trị của hàm số y = logax là R.
Bài 3: Cho hàm số y=(√2-1)x. Phát biểu nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng (-∞; +∞).
B. Hàm số đồng biến trên khoảng (0; +∞)
C. Đồ thị hàm số có đường tiệm cận ngang là trục tung.
D. Đồ thị hàm số có đường tiệm cận đứng là trục hoành Lời giải: Đáp án: A Giải thích:
Vì 0 < √2-1 < 1 nên hàm số y = (√2-1)x nghịch biến trên khoảng (-∞; +∞)
Bài 4: Tìm giá trị lớn nhất của hàm số f(x)=x2 e2 trên đoạn [-1;1] A. 2e B. 1/e C. e D. 0 Lời giải: Đáp án: C Giải thích:
Trên đoạn [-1;1], ta có: f' (x)=xex (x+2); f' (x)=0 ⇔ x = 0 hoặc x = -2 (loại).
Bài 5: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=2|x| trên [-2;2] A. maxy=4; miny=-1/4 B. maxy=4; miny=1/4 C. maxy=1; miny=1/4 D. maxy=4; miny=1 Lời giải: Đáp án: D
Giải thích : Đặt t = |x|, với x ∈ [-2;2] ⇒ t ∈ [0;2]
Xét hàm f(t) = 2t trên đoạn [0;2]; f(t) đồng biến trên [0;2]
Hoặc với x ∈ [-2;2] ⇒ |x| ∈ [0;2]. Từ đây, suy ra: 20 ≤ 2|x| ≤ 22 ⇔ 1 ≤ 2|x| ≤ 4
Bài 6: Gọi m và M lần lượt là giá trị nhỏ nhất và lớn nhất của hàm số f(x)=e2-3x trên đoạn [0;2].
Mệnh đề nào sau đây là đúng? A. m+M = 1 B. M-m = e. C. M.m = 1/e2 D. M/m = e2 Lời giải: Đáp án: C Giải thích:
Hàm số f(x) xác định và liên tục trên đoạn [0;2].
Đạo hàm f'(x) = -3e2-3x < 0, ∀x ∈ R. Do đó hàm số f(x) nghịch biến trên [0;2].
Bài 7: Chọn khẳng định đúng khi nói về hàm số y=(lnx)/x
A. Hàm số không có cực trị.
B. Hàm số có một điểm cực đại
C. Hàm số có một điểm cực tiểu
D. Hàm số có một điểm cực đại và một điểm cực tiểu Lời giải: Đáp án: C Giải thích:
Hàm y' đổi dấu từ âm sang dương khi qua x=e nên x=e là điểm cực tiểu của hàm số.



