10 Đề Trắc Nghiệm Ôn Tập Chương Mũ Lôgarit Có Đáp Án

10 đề trắc nghiệm ôn tập chương mũ logarit được biên soạn dưới dạng file PDF gồm 24 trang. Tài liệu là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

76 38 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit

Môn: Toán 12

Thông tin:

24 trang 6 tháng trước

Tác giả:

Profile ha phan
Trang1
ĐỀ 1
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: Cho
log 3,log 4
ab
xx
vi
,ab
là các s thc l
log .
ab
Px
A.
12
.
7
P
B.
12.P
C.
1
.
12
P
D.
7
.
12
P
Câu 2: Gi  
b  t
2 1 , 0.
x
tt
M 
?
A.
1 2; 1 2. tt
B.
1; 1. xx
C.
2
2 2 0. tt
D.
2
2 2 1 0. tt
Câu 3: Tìm giá tr ca ca biu thc
3
3
3
3
33
daáu caên
log log .... 3 .




n
M
A.
3.
n
M
B.
.
3
n
M
C.
.Mn
D.
.
3
n
n
M
Câu 4: Vi mi s th
a
và
b
tha mãn
22
8,a b ab
m ?
A.
1
log log log .
2
a b a b
B.
1
log log log .
2
a b a b
C.
log 1 log log . a b a b
D.
1
log 1 log log .
2
a b a b
Câu 5: Cho hai s
11
10 10
2 3 2 a
và
2
log sin
7



b
. M ?
A.
0.ba
B.
0.ab
C.
0.ab
D.
0.ab
Câu 6: t
25
log 3, log 3ab
. Tính
6
log 45P
theo
,.ab
A.
2
.
a ab
P
ab b
B.
2
.
a ab
P
ab
C.
2
.
a ab
P
ab b
D.
2
.
a ab
P
ab b
Câu 7: Rút gn biu thc
1
6
3
.P x x
vi
0.x
A.
2
9
.Px
B.
1
8
.Px
C.
2
.Px
D.
.Px
Câu 8: Tìm tnh D ca hàm s
1
2
log 2 1. yx
A.
2;4 .D
B.
;2 4; .  D
C.
2;4 .D
D.
;2 . D
Câu 9: Cho hàm s
2
( ) ln 1
xx
f x e e
. M ?
A.
1 ln2.
f
B.
25
ln2 .
5
f
C.
5
2.
5
f
D.
.
f e e
Câu 10: Tìm tt c các giá tr thc ca tham s  
2
33
log log 2 7 0 x m x m
có hai
nghim thc
12
,xx
tha mãn
12
. 81.xx
A.
4.m
B.
81.m
C.
44.m
D.
4.m
Câu 11: Tìm tp nghim S ca b
2
0,2
log 4 1. x
Trang2
A.
; 2 2; .  S
B.
3;3 .S
C.
2;2 .S
D.
3; 2 2;3 . S
Câu 12: Tìm tp xác nh D ca hàm s:
2
2
4 3 .
y x x
A.
. D
B.
\ 1;3 . D
C.
( ;1) 3; .  D
D.
1;3 .D
Câu 13: Xét hàm s
2
sin5 .
x
y e x
M ?
A.
// /
4 29 0. y y y
B.
/// /
4 29 0. y y y
C.
// /
4 29 0. y y y
D.
/// /
4 29 0. y y y
Câu 14: Tìm giá tr ln nht và giá tr nh nht ca hàm s
2
( ) 4ln 3
2
x
f x x
n
2;1 .
A.
2;1
1
( ) 8ln 2
2
Max f x
và
2;1
1
( ) 4ln2.
2
Min f x
B.
2;1
1
( ) ln2
2
Max f x
và
2;1
1
( ) 4ln 2.
2
Min f x
C.
2;1
1
( ) 4ln 2
2
Max f x
và
2;1
1
( ) 8ln 2.
2
Min f x
D.
2;1
( ) 8ln2
Max f x
và
2;1
( ) 4ln2.
Min f x
Câu 15:  thành lp mt công ty. Tng s ti tr 
 ng. Bit rng c sau mng s ti tr 
viên trong c c. Hu tiên mà tng s
ti tr  ng?
A.  B.  C.  D. 
Câu 16: Cho ba s th
,,abc
 th hàm s
log , log , log
a b c
y x y x y x
c cho
trong các hình v bên. M ?
A.
.c a b
B.
.abc
C.
.abc
D.
.b c a
Câu 17: Tìm tp nghim S ca b
9 3 6 0.
xx
A.
2;3 .S
B.
1; . S
C.
3;2 .S
D.
;1 . S
Câu 18: Gi
12
;xx
là hai nghim c
22
33
log log 1 5 0 xx
. Tính
12
..P x x
A.
1.P
B.
1
.
3
P
C.
9.P
D.
3.P
Câu 19: Tính
21
1
1
2
33
3
0,001 2 .64 8 .
S
A.
95
.
4
S
B.
95
.
16
S
C.
16
.
95
S
D.
95
.
2
S
Câu 20: Tìm nghim c
2
log 1 2.x
A.
5.x
B.
3.x
C.
4.x
D.
3.x
Trang3
Đáp án
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 2
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: 
9 3.3 2 0
xx
có hai nghim
1 2 1 2
, ( )x x x x
. Tính giá tr ca
12
2 3 .A x x
A.
3
4log 2
. B.
1
. C.
3
2log 4
. D.
3
3log 2
.
Câu 2: Cho a, b > 0 và a, b 1 ; x và y là hai s n khnh sai trong các khnh sau.
A.
log
log .
log
b
a
b
x
x
a
B.
2 2 2
1
log 4log .
a
a
xx
C.
2022
log 2022log .
aa
xx
D.
log log log .
a a a
xy x y
Câu 3: Tp nghim ca b
3
2
5
11
22
x
là t
A.
; 5 .
B.
13
5; .
2



C.
13
;.
2




D.
13
;.
2




Câu 4: Gi
23
12
2
log 2log 75 0 xx
(1), mt hc sinh thc hic sau:
u kinh
0x
(II)
2
22
(1) 9log 2log 75 0 xx
(III)
2
2
log 3
25
log
9

x
x
2
log 3 8 xx
. Vy (1) có nghim duy nht là
8x
Bài gii trên sai t c nào?
A. c (III). B. c (II).
C. c (I). D. Bài gi
Câu 5: Tính tng các nghim c
5 5 5
log log 6 log 2 . x x x
A. 2. B. 2. C. 1. D. 1.
Câu 6: Gii b
21
3 10.3 3 0.
xx
A.
1 1. x
B.
1x
hoc
1.x
C.
1.x
D.
1.x
Câu 7: Giá tr nh nht ca hàm s
2
4ln 1 y x x
n
2;0
là
lna b c
(
,,abc
nguyên
ng
.abc
A. 7. B. 10. C. 8. D. 9.
Câu 8: Hàm s ng bin trên tnh ca nó?
Trang4
A.
2
.
3



x
y
B.
2
.
2




x
y
C.
.



x
y
e
D.
0,5 .
x
y
Câu 9: Tìm tnh ca hàm s
2
32
log 1 log . y x x
A.
1; . D
B.
0; . D
C.
1;0 0; . D
D.
1;0 .D
Câu 10: o hàm ca hàm s
5
8
.
xxx
y
x
A.
4
3
1
.
4
y
x
B.
4
3
1
.
4
yx
C.
4
3
4.
yx
D.
3
4
1
.
4
y
x
Câu 11: Cho hàm s
2
1
2 . .
x
y x e
Tính
50 .
y
A.
2501
10002 .e
B.
2500
10001 .e
C.
2502
10003 .e
D.
2503
10004 .e
Câu 12: Trong các m  nào sai?
A. Hàm s
1
2



x
y
nghch bin trên
.
B. Hàm s
21
x
ye
o hàm là
21
2.
x
ye
C. Hàm s
2
x
y
ng bin trên
.
D.  th hàm s
3
x
y
nhn trc Oy là tim cng.
Câu 13: Tnh ca hàm s
1
3
1yx
là t
A.
.
B.
\ 1 .
C.
;1 .
D.
;1 .
Câu 14: Cho
log 16
m
Pm
và
2
logam
, vi m là s  ?
A.
1.
4

a
P
B.
4
.
a
P
a
C.
3
.
a
P
a
D.
2
3.Pa
Câu 15: Bit
25
log 5 ; log 3 .ab
 ca
15
log 24
bng giá tr 
A.
.
1
b
ab
B.
1
.
1
a
b
C.
3
.
1
ab
ab
D.
1
.
1
a
ab
Câu 16: 
23
2
0,125.4
8




x
x
có nghim duy nht
0
.x
Giá tr  nht?
A.
0
1.x
B.
0
5.x
C.
0
10 .x
D.
0
15 .x
Câu 17: Cho hàm s
1
ln
1
y
x
. Trong các kh
A.
1.

y
xy e
B.
1.

y
xy e
C.
1.

y
xy e
D.
1.
y
xy e
Câu 18: Cho 3 s a mãn
log log log 2022.log .
a c a c
b b b
Chn khnh
nh sau.
A.
2022.ac
B.
2022.abc
C.
2022.bc
D.
2022.ab
Câu 19: Cho hàm s
ln .y x x
Tính
.

ye
A.
.e
B.
3.
C.
1
.
e
D.
2.
Câu 20: 
Trang5
A.
0 1. ab
B.
0 1 . ab
C.
0 1. ba
D.
0 1 . ba
-----------------------------------------------
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 3
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: Vi mi s tha mãn
22
6a b ab
, m nào 
A.
8 8 8
1
log ( ) (1 log log ).
2
a b a b
B.
8 8 8
log ( ) 1 log log . a b a b
C.
8 8 8
log ( ) log log . a b a b
D.
8 8 8
1
log ( ) log log .
2
a b a b
Câu 2: Tìm tnh ca hàm s
2
2
log ( 2) .yx
A.
2.x
B.
.x
C.
2.x
D.
2.x
Câu 3: o hàm ca hàm s
2 1 .
e
yx
A.
1
2 2 1 .

e
y e x
B.
1
2 2 1 .

e
yx
C.
2 2 1 .

e
yx
D.
1
2 1 .

e
y e x
Câu 4: Cho hai biu thc
9 9 9
log 15 log 18 log 10 A
và
36 1
6
1
log 2 log 3.
2
B
Giá tr ca
A
B
bng
bao nhiêu?
A.
8
. B.
4
. C.
9
. D. ...
Câu 5: o hàm cp hai ca hàm s
2
ln .yx
A.
2
2
.
x
B.
2
.
x
C.
2
2
.
x
D.
2
.
x
Câu 6: Cho hàm s
1
1 ln

y
xx
. M 
A.
ln 1 .
xy y y x
B.
ln 1 .
xy y y x
y =
log
b
x
y =
log
a
x
6
-2
1
-3
-1
4
3
2
-3
-2
-1
5
4
3
2
O
1
x
y
Trang6
C.
ln 1 .
xy y y x
D.
ln 1 .
xy y y x
Câu 7: Vit li biu thc
4
2
3
3
:aa
vii da.
A.
5
3
.a
B.
2
3
.a
C.
7
3
.a
D.
5
8
.a
Câu 8: Gii b
42
23
.
32
xx
A.
2
.
5
x
B.
2
.
3
x
C.
2
.
5
x
D.
2
.
3
x
Câu 9: n biu thc
9
3
3
1xx
c biu th
A.
3
1.xx
B.
3
1.xx
C.
3
1.xx
D.
3
1.xx
Câu 10: Tìm m trong các m sau?
A. Hàm s
log
a
yx
vi
1a
nghch bin trên khong
0; .
B. Hàm s
x
ya
vi
01a
ng bin trên khong
0; .
C. Hàm s
logyx
vinghch bin trên khong
0; .
D. Hàm s
x
ya
vi
01a
nghch bin trên khong
;. 
Câu 11: Gii b
21
2 5.2 2 0.
xx
A.
1 1. x
B.
1x
hoc
1.x
C.
1.x
D.
2.x
Câu 12: Gi
12
,xx
là hai nghim c
4 8.2 4 0
xx
. Tính giá tr biu thc
12
.P x x
A. 4. B. 4. C. 0. D. 2.
Câu 13: o hàm ca hàm s
12
ln .
1




x
x
y
xe
A.
12
ln2 1 .
1
x
x
y
xe
B.
12
ln2.
1
x
x
y
xe
C.
12
ln2 1 .
1
x
x
y
xe
D.
12
.
1
x
x
y
xe
Câu 14: 
2
12
3 .2 8.4

x x x
có hai nghim
12
,.xx
Tính
12
2.xx
A.
2
log 3.
B.
3
log 2.
C.
3
log 2 1.
D.
2
log 3 2.
Câu 15: P
33
log log 2 1 xx
có nghim
0
.x
Tính giá tr biu thc
20
1
log .
3
Ax
A.
1
.
3
A
B.
1
.
3
A
C.
4
.
3
A
D.
4
.
3
A
Câu 16: Tìm tnh ca hàm s
5
2
( ) 4 .
f x x
A.
2;2 .
B.
\ 2 .
C.
( ; 2) (2; ). 
D.
.
Câu 17: t
ln2a
và
ln5b
. Hãy biu din
ln200
theo
a
và
b
.
A.
ln200 3 2 .ba
B.
ln200 6 . ab
C.
ln200 3 2 .ab
D.
ln200 3 2 .ab
Câu 18: 
4
log 3.2 1 1
x
x
có hai nghim
12
,xx
. Tính
12
.xx
A.
6 4 2.
B.
2.
C.
2
log 6 4 2 .
D.
4.
Trang7
Câu 19: Giá tr ln nht ca hàm s
2
ln ln 1 y x x
n
1
;2
2



c t
A.
1
.
2
x
B.
1.x
C.
3
.
2
x
D.
3
.
4
x
Câu 20: Trong các m  nào sai?
A.  th các hàm s
x
ya
và
log
a
yx
(vi
01a
i xng vng thng
.yx
B. Hàm s
1
3
log ( 1)yx
nghchbin trên khong
1; 
.
C.  th hàm s
log (0 1)
a
y x a
nm phía trên trc Ox.
D. Hàm s
2
log ( 2)yx
ng bin trên khong
2;
.
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 4
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: 
2 40
22
log log 300 0 xx
có bao nhiêu nghim?
A. 1. B. 0. C. 2. D. 3.
Câu 2: Cho hàm s
.
x
y x e
. Chn h th
A.
23
y y y
. B.
23
y y y
. C.
21
yy
. D.
2
y y y
.
Câu 3: Cho hàm s
.lny m x
t giá tr ln nht bn
1;3
. Kh
A.
4m
. B.
24m
. C.
0m
. D.
02m
.
Câu 4: T
2 2 2
12
25 10 4 0

x x x
gn s nào nht?
A. 6. B. 3. C. 9. D. 12.
Câu 5: Tìm
m
 
2
33
log 2log 1 0 x x m
có nghim.
A.
2m
. B.
2m
. C.
2m
. D.
3m
.
Câu 6: B
31
3
2log 4 3 log 2 3 2 xx
có tp nghim là
;S a b
. Tính
ba
.
A.
1
2
. B.
27
8
. C.
1
4
. D.
9
4
.
Câu 7: Ch  góp ngân hàng s tin 50 tring vi lãi sut 
thì mi tháng ch i tr s tin hàng nghìn)
A. 2.396.000. B. 2.134.000. C. 2.674.000. D. 2.456.000.
Câu 8: Cho
0 và 1aa
, x và y là hai s   sau.
A.
log
a
x
i x. B.
log log
n
aa
x n x
.
C.
log log .log
a a a
xy x y
. D.
log 1 và log 0
aa
aa
.
Câu 9: Cho hàm s
2
log 2 3 y x x
có tnh
D
. Kh
Trang8
A.
3;1D
. B.
2;3D
. C.
3;2D
. D.
1;3D
.
Câu 10: Cho
22
6
2
log 3 log 5
log 75
log 3
a
b
. Tính
2
3P a ab
.
A.
5P
. B.
7P
. C.
10P
. D.
5P
.
Câu 11: Rút gn
2
1009.log 3 2018
2
P
.
A.
2018
3
2



P
. B.
1009
2P
. C.
2018
3P
. D.
1009
3
2



P
.
Câu 12: Cho các hàm s a
,,
y x y x y x
 th . Kh
A.

. B.

. C.

. D.

.
Câu 13: Tìm tnh ca hàm s
3
2
5
4yx
.
A.
( ] [ );2 2; 
. B.
R
. C.
2;2
. D.
2;2
.
Câu 14: Cho hàm s
3
32yx
. Tính
1

f
.
A.
11

f
. B.
1
1
3

f
. C.
12

f
. D.
11

f
.
Câu 15: Cho
3
4
..
m
n
a a a a
. Tính
2
2S m n
.
A.
8640S
. B.
6358S
. C.
8640S
. D.
5380S
.
Câu 16: B
2
3 4 2 10
2 3 2 3
x x x
có bao nhiêu nghi
A. 6. B. 3. C. 2. D. 4.
Câu 17: Cho
2
5 2 5 2 .
x





?
A.
2x
. B.
2
2.x
C.
2.x
D.
2.x
Câu 18: Cho
3
3
2
3
.ln2
.ln2
.
.

a x x
xx
cx
bx
. Tính
23
P a b c
.
A.
11P
. B.
13P
. C.
12P
. D.
18P
.
Câu 19: Gi
100
100
2 64
x
.
A.
20.000.x
B.
60.000.x
C.
6.000.x
D.
30.000.x
Câu 20: Cho
log2, log3ab
. Tính
2023
log 12
theo
,ab
.
A.
1
2
2023 2ab
. B.
2023
2
2
ab
. C.
2023
2
2
ab
. D.
2023
1
2
2
ab
.
-----------------------------------------------
y =
x
γ
y =
x
β
y =
x
α
1
-1
4
3
2
-1
4
3
2
O
1
x
y
Trang9
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 5
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: Cho
4
3
..
m
n
x x x x
. Tính
2
2S m n
.
A.
14S
. B.
12S
. C.
6S
. D.
13S
.
Câu 2: Cho
ln2, ln3ab
. Tính
2022
3
ln 18
theo .
,ab
..
A.
1
3
2022 2ab
. B.
2022
2
3
ab
. C.
2022
1
2
3
ab
. D.
2022
2
3
ab
.
Câu 3: Anh An gi ngân hàng 100 tring vi lãi sut 0,58%/tháng (không k hn, không rút lãi hàng
 c s tii 130 tring th anh An phi gi ít nht bao nhiêu tháng?
A. 45 tháng. B. 46 tháng. C. 47 tháng. D. 44 tháng.
Câu 4: Cho
25
log 3, log 3ab
và
20
.
log 45
.
m ab a
n b a
. Tính
22
2P m n
.
A.
5P
. B.
2P
. C.
5P
. D.
4P
.
Câu 5: Rút gn
2017
10
log
0,001. 10



P
.
A.
4029
2
P
. B.
4029
3
P
. C.
2017
10P
. D.
4039
2
P
.
Câu 6: Cho hàm s
.
x
y m e
t giá tr nh nht bn
0;2
. Kh
A.
13m
. B.
3m
. C.
01m
. D.
0m
.
Câu 7: Cho hàm s
sin .
x
y x e
. Chn h th
A.
23
y y y
. B.
22
y y y
. C.
2
y y y
. D.
23
y y y
.
Câu 8: Tính tt c các nghim c
2 2 6
33
log log 2 0 xx
.
A. 12. B. 24. C. 18. D. 35.
Câu 9:  th hai hàm s
x
ya
và
log
b
yx
. Kh
A.
01 ab
B.
01 ba
C.
1ab
D.
10 ab
Câu 10: Cho
, , , 0a b x y
và
,1ab
. Tìm m  trong các m sau.
-1
4
2
-2
-1
2
O
1
y
Trang10
A.
log
log
log



a
a
a
x
x
yy
B.
log log .log
b b a
x a x
C.
11
log
log



a
a
xx
D.
log log log
a a a
x y x y
Câu 11: 
22
22
5 2 5 2 40

xx
có bao nhiêu nghim?
A. 1. B. 4. C. 3. D. 2.
Câu 12: Gi
100
10
3 81
x
.
A.
6.000.x
B.
2.000.x
C.
4.000.x
D.
3.000.x
Câu 13: Cho hàm s
2
2
log 2 3 y x x
có tnh
D
. Kh
A.
3;1D
. B.
1;3D
. C.
1;3D
. D.
2;3D
.
Câu 14: B
log 40 log 60 2 xx
có bao nhiêu nghim nguyên?
A. 18. B. 20. C. 19. D. Vô s.
Câu 15: Tìm tt c các giá tr thc ca tham s
m
  
33
3
log log 2 log x x m
có
nghim.
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Câu 16: Tìm tp nghim ca b
1
2022
2 1 2 1
x
.
A.
1
0;
2022


. B.
1
;
2022



. C.
1
; \ 0
2022



. D.
1
;
2022




.
Câu 17: Cho
33
2
3
.
. . .
.


x
xx
ae
x e c x e
bx
. Tính
32
P a b c
.
A.
9P
. B.
11P
. C.
8P
. D.
18P
.
Câu 18: Tìm tnh ca hàm s
5
2
3
4yx
.
A.
;2 2; 
. B.
2;2
. C.
R
. D.
;2 2;
.
Câu 19: Cho
3
3 2 2 3
x
. 




?
A.
3.x
B.
3x
. C.
3.x
D.
1
3
3.x
Câu 20: Cho hàm s
2
4
2y x x
. Tính
1

f
.
A.
1
1
2

f
. B.
3
1
2

f
. C.
10

f
. D.
11

f
.
-----------------------------------------------
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
Trang11
ĐỀ 6
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: Tnh ca hàm s y =
2
2
2xx
A.
\ 1;2DR
B.
1;2D
C.
1;2D
D.
; 1 2;  D
Câu 2: Cho
7
log 25
=
a
và
2
log 5
=
b
. Tính
3
1000
5
49
log
8
theo
a
và
.b
A.
12 9
.
1000
ba
ab
B.
12 9
.
1000
ba
ab
C.
12 9
.
1000
b a ab
D.
43
.
3000
ba
ab
Câu 3:
Tng các nghim ca 
2
1 2 2
5 16
4 25

xx
bng?
A.
1
B.
2
C.
3
D.
4
Câu 4: Gi
12
;xx
là 2 nghim c
22
33
log log 1 5 0 xx
. Giá trP=
12
.xx
A.
1P
B.
3P
C.
9P
D.
1
3
P
Câu 5: Cho hai s thc a, b vi
1ab
kh
A.
10



x
a
x
b
B.
10



x
b
x
a
C.
log 1
a
b
D.
log 1
b
a
Câu 6: Cho b
1
4 5.2 16 0
xx
có tp nghin
;.ab
Tính hiu
22
log .ab
A.
0.
B.
1.
C.
1.
D.
2.
Câu 7: Tìm tt c các giá tr thc c hàm s
2
2
12
ln
13






x mx
y
xx
nh vi
x
A.
1m
B.
2 10m
C.
13m
D. 0<m<
4
3
Câu 8: Gi
1 2 1 2
, x x x x
là hai nghim thc c
21
3 4.3 1 0.
xx
Khnh nào sau

A.
21
2 2. xx
B.
12
2 0.xx
C.
12
2 2.xx
D.
12
2 2. xx
Câu 9: Cho s
4 4 23

xx
. Tìm m sai trong các m sau:
A.
log 0 1
a
x khi x
B. Nu
12
xx
thì
12
log log
aa
xx
C.
log 0 0 1
a
x khi x
D.
Tim cn ngang hàm s
y log
a
x
là trc hoành
Câu 10: Tp nghim S c
2
39
5
log ( 2) log ( 2)
4
xx
là
A.
{2}.S
B.
{1}.S
C.
8
243 2 .S
D.
.S
Câu 11: Cho
,ab
là các s a mãn
1, 1, log 3
a
a ab b
 ca
log



ab
a
b
là :
A.
8
B.
1
2
C.
2
D.
1
2
Trang12
Câu 12: Cho hàm s
lnf x x
.o hàm ca hàm s
2
3
log 'y x f x
A.
1
'.y
x
B.
1
'.
ln3
y
x
C.
ln3
'.y
x
D.
'.
ln3
x
y
Câu 13: S 



2
log 3.2 2 2
x
x
là:
A.
3.
B.
1.
C.
2.
D.
4.
Câu 14:
Tnh ca hàm s
2
1
ln
32




y
xx
là?
A.
( ;1) (2; ) 
B.
C.
[1;2]
D.
(1;2)
Câu 15: Cho
,ab
là các s      
log
a
b
là nghim c  
25 5 6 0
xx
. Trong các khnh sau, khnh nào đúng?
A.
20.ab
B.
10.ab
C.
25.ab
D.
15.ab
Câu 16: Cho
, , ,abc
là các s nguyên.Bi o hàm ca hàm s
23
22
x
y x x e
có dng
32
'.
x
y e ax bx c
Tính giá tr ca biu thc
2. S a b c
A.
2S
B.
12S
C.
48S
D.
2S
Câu 17: Cho
,,abc
là các s tha mãn
log 1, log 2. b a c b
Trong các khnh sau,
khnh nào đúng?
A.
log( ) 3. ab b c
B.
1
log( ) .
2
b
ab
c
C.
log( ) ( 1)( 2). ab b c
D.
log 1.
a
bc
b
Câu 18:
o hàm ca hàm s
sin2
x
ye
ti x = 0 là?
A.
2
B.
3
C.
1
D.
4
Câu 19: Gi M là giá tr ln nht ca hàm s
2
ln( 3) y x x
n
[2;5].
Trong các khnh
sau, khnh nào đúng?
A.
3
6.
M
e
B.
0.M
C.
5
22 0.

M
e
D.
2 0.M
Câu 20: Cho các hàm s
,,
xx
y a y b
x
yc
 th .
Kh
A.
0. c a b
B.
0. c b a
C.
0. abc
D.
0. b c a
Đáp án
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
D
B
D
A
A
B
D
D
D
C
D
B
C
D
B
A
A
A
A
B
Trang13
ĐỀ 7
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
ĐỀ 12
Câu 1:
Tnh ca hàm s
2
( 3 2)
e
y x x
là?
A.
( ; 2) ( 1; ) 
B.
( 2; 1)
C.
D.
\{ 2; 1}
Câu 2:
Tng các nghim ca 
12
1
4 lg 2 lg

xx
bng?
A.
20
B.
10
C.
1
D.
110
Câu 3:
Cho hàm s
log
a
yx
. Kh
A.
Tnh là
B.
o hàm
1
'
ln
y
xa
C.
 th hàm s không có tim cn
D.
 th hàm s không ct trc hoành
Câu 4:
Cho
1
ln
1
y
x
. Biu thc
,
.1xy
là:
A.
y
B.
y
e
C.
e
D.
1
Câu 5: o hàm ca hàm s
.
2
x
x
y
A.
' 2 ( ln2 1).

x
yx
B.
' 2 (1 ln2).

x
yx
C.
' 2 (1 ln2).
x
yx
D.
' 2 log 2.
x
e
y
Câu 6:
Số nghim c
2
33
log log (9 ) 2 0 xx
là:
A.
3
B.
1
C.
2
D.
0
Câu 7:  
4 2 .2 2 0
xx
mm
có hai nghim phân bi
A.
2m
B.
 m
C.
2m
D.
m
Câu 8: Cho các s thi
1a
. Kh
A.
1
log
log



a
a
a
bb
B.
log 1 log




aa
a
b
b
C.
log 1 log
aa
ab b
D.
2
1
log log
2

a
a
ab b
Câu 9: Cho
22
log 3,log 2 bc
. Hãy tính
2
2
log bc
.
A.
4
B.
7
C.
6
D.
9
Câu 10: B
3
3
3
3log 1 log 2 1 3 xx
có tp nghim là
A.
1;2
. B.
1;2
. C.
1
;2
2



. D.
1
;2
2


.
Câu 11:
Tng các nghim c
2 7 2 7
log 2log 2 log .log x x x x
là?
A.
-3
B.
-11
C.
11
D.
3
Câu 12: 
2
11
23

xx
có hai nghim
,ab
. Tính
.a b ab
A.
2
1.log 3
B.
2
.lo2 g31
C.
2
.lo2 g1 3
D.
1.
Câu 13: t
34
log 5;b log 5a
. Hãy biu din
15
log 20
theo a và b.
A.
15
1
log 20
aa
b a b
B.
15
1
log 20
1
ba
ab
Trang14
C.
15
1
log 20
1
bb
aa
D.
15
1
log 20
1
ab
ba
Câu 14: Tìm tnh ca hàm s
2
log 4 1 yx
A.
;4
B.
;2
C.
;2
D.
2;4
Câu 15: Bit rng
4 4 23

xx
, giá tr ca biu thc
22

xx
A
là:
A.
23A
B.
5A
C.
21A
D.
25A
Câu 16: Gi
12
,xx
là hai nghim c
4 8.2 4 0
xx
. Tính giá tr biu thc
12
.P x x
A. 4. B. 4. C. 0. D. 2.
Câu 17: Cho ba s th
, , a b c
khác
1.
 th các hàm s
,,
x x x
y a y b y c
c cho trong
hình v bên. M 
A.
1. b a c
B.
1. a c b
C.
1. b c a
D.
1. a b c
Câu 18: Cho
01 xy
, 

1
ln ln
11




yx
m
y x y x
. 


?
A.
4m
B.
1m
C.
4m
D.
2m
Câu 19: Cho các hàm s
2
21
2
3
log , , log ,
2







x
e
y x y y x y
. Trong các hàm s trên có bao nhiêu
hàms ng bin trên tnh ca hàm s 
A. 3 B. 4 C. 1 D. 2
Câu 20: Cho hàm s
2
.
x
ye
Trong các khnh sau, khnh nào đúng?
A.
" 2 ' 2 0. y xy y
B.
" ' 2 0. y xy y
C.
" 2 ' 2 0. y xy y
D.
" 2 ' 2 0. y xy y
Đáp án
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
B
D
B
B
B
C
C
A
A
A
C
D
D
C
B
D
B
A
C
C
ĐỀ 8
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: 

?
A. 
1a

log log 0.
aa
M N M N
B. 
01a

log log 0 .
aa
M N M N
C. 
,0MN

01a

log . log .log .
a a a
M N M N
D. 
01a

log 2022 log 2023.
aa
Câu 2: Tìm phát biu sai?
A.  th hàm s
0, 1
x
y a a a
nm hoàn toàn phía trên
Ox
.
B.  th hàm s
0, 1
x
y a a a
m
0;1 .A
Trang15
C.  th hàm s
1
, , 0 1



x
x
y a y a
a
i xng nhau qua trc
Ox
.
D.  th hàm s
1
, , 0 1



x
x
y a y a
a
i xng nhau qua trc
Oy
.
Câu 3: 



D

1
32
4
3 2 . y x x x
A.
0;1 2; . 
B.
\ 0,1,2 .
C.
;0 1;2 .
D.
;0 2; .
Câu 4: Gi
D
là t

3
4
2
5
2 log
3
x
yx
x
. Kh
A.
3;2 .D
B.
2;5 .D
C.
3;2 .D
D.
2;5 . D
Câu 5: 
2 3 3 2 3 3 3
4 3 3
2 1 2 2 2
.
22
A
A.
1.
B.
3
2 1.
C.
3
2 1.
D.
1.
Câu 6: Rút gn biu thc
1 log 2 1 log 3
.

ab
abP
A.
.P ab
B.
2 3 .P a b
C.
23
.P a b
D.
2 2 3 . P a b
Câu 7: Cho
7
log 25
=
a
và
2
log 5
=
b
. Tính
3
1000
5
49
log
8
theo
a
và
.b
A.
12 9
.
1000
ba
ab
B.
12 9
.
1000
ba
ab
C.
12 9
.
1000
b a ab
D.
43
.
3000
ba
ab
Câu 8: Cho hàm s
.
x
f x x e
 th ca hàm s
/
fx
 th  th sau
A. hình I B. Hình II C. Hình III D. Hình IV
Câu 9: 


'y

2
log ( ).
x
y x e
A.
1
'.
ln2
x
e
y
B.
1
'.
x
x
e
y
xe
C.
1
'.
ln2
x
y
xe
D.
1
'.
ln2
x
x
e
y
xe
Câu 10: Cho
, , ,abc
là các s nguyên. Bit o hàm ca hàm s
2
22

xx
y
có dng
-
' 2 2 .ln .
ax bx
yc
Tính giá tr ca biu thc
2. K a b c
A.
0.K
B.
2.K
C.
2.K
D.
4.K
Câu 11: Cho hàm s
..
x
y x e
ng th
A.
/
=.
x
y y e
B.
/
.
x
y y e
C.
/
.
x
y y e
D.
/
.
x
y y e
Câu 12: Mcstin100tringvàquynhgivàongân hàng vi lãi sut
7, 5% mt rng nu không rút tin ra khi ngân hàng thì c sau m tin lãi s nhp
vào vu. Nu lãi sui thì ti thic s
tin là 165 tring (tính c gc lnlãi)?
A.  B.  C.  D. 
Câu 13: 

, ab


1ab
. 




:
A.
2022
log 2023 1.
B.
2023
1 0.
2022



x
x
x
O
1
y
x
O
2
y
x
O
1
y
Hình I
x
O
2
y
Hình II
Hình III
Hình IV
Trang16
C.
2022
1 0.
2023



x
x
D.
2023
log 2022 1.
Câu 14:





2
log 2 1 2
x
có dng
log ,
b
ac

, , , abc
0, 0, 1. b c b
Tính giá tr ca biu thc
2 3 . M a b c
A.
7.M
B.
1.M
C.
11.M
D.
13.M
Câu 15: 
8.3 3.2 24 6
x x x
có tích các nghim.
A. 3. B. 0. C. 10. D. 30.
Câu 16: 

2
3
log ( 4 12) 2 xx
A. . B. .
C. . D. 
.
Câu 17: 
3
2 log
3 81
x
x
có mt nghim dng
a
b
,.ab
Tính tng
ab
A.
5.ab
B.
4.ab
C.
7.ab
D.
3.ab
Câu 18: Gii b
2
2 4.
xx
Tp nghim có dng
;.ab
Tính hiu
.ba
A.
1.ba
B.
3. ba
C.
1. ba
D.
3.ba
Câu 19: S nghim nguyên ca b
31
13
10 3 10 3 .


xx
xx
A. 1 B. 3 C. 0 D. 2
Câu 20: Gi
S
là tp nghim ca b
1
1
5
log 6 36 2.
xx
Tìm giá tr ln nht ca hàm
s
6
x
y
trên
.S
A. 4. B. 1. C. 5. D. 3.
Đáp án
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
C
C
A
B
B
B
B
D
D
B
C
C
C
D
A
C
B
D
B
C
ĐỀ 9
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: Cho
0, 1.aa
Tìm m 
A. Tnh ca hàm s
x
ya
là khong
0; .
B. Tp giá tr ca hàm s
log
a
yx
là tp
.
C. Tnh ca hàm s
log
a
yx
là tp
.
D. Tp giá tr ca hàm s
x
ya
là tp
.
Câu 2: Cho 3 s thc
,,abc
tha mãn
0, 1, 0, 0 a a b c
. Tìm phát bi
A.
log log .
aa
b c b c
B.
log log .
aa
b c b c
C.
log log .
aa
b c b c
D. C u sai.
Câu 3: Cho hàm s
2
2
log (5 2 ) . xxy
S giá tr nguyên thuc tnh ca hàm s.
A. 2. B. 1. C. 3. D. 4.
Trang17
Câu 4: 



D

3
2
10
log .
32

x
y
xx
A.
1; . D
B.
;1 2;10 .  D
C.
;10 . D
D.
2;10 .D
Câu 5: Cho s thc
0, 1.aa
Giá tr ca biu thc
2 2 4
35
3
4
. . .
log .
a
a a a a
A
a
A.
193
.
60
B.
73
.
60
C.
103
.
60
D.
43
.
60
Câu 6: Rút gn biu thc
2 4 2 2
3 9 9 9
1 1 1 .
P a a a a
A.
1
3
1.Pa
B.
4
3
1.Pa
C.
4
3
1.Pa
D.
1
3
1.Pa
Câu 7: Cho
33
log 15, log 10.ab
Biu din theo
, ab
ca
200
3
log 50 .
A.
300 1 .ab
B.
400 1 .ab
C.
100( 1).ab
D.
200 1 .ab
Câu 8:  
A.
1
.
3



x
y
B.
2
1
.
2



y
C.
3.
x
y
D.
2.
x
y
Câu 9: Cho
31
1 1 .

aa
 kt lun v a là:
A.
1 2.a
B.
2.a
C.
2
.
01

a
a
D.
1
.
2
a
a
Câu 10: o hàm
y
ca hàm s
2 1 3 .
x
yx
A.
' 3 2 2 ln3 ln3 .
x
yx
B.
' 3 2 2 ln3 ln3 .
x
yx
C.
1
' 2.3 2 1 .3 .
xx
y x x
D.
' 2.3 ln3.
x
y
Câu 11: o hàm
y
ca hàm s
.
2022
x
x
y
A.
2
/
1 ln 2022
.
2022
x
y
x
B.
/
1
.
2022 ln 2022
x
y
C.
/
1
.
2022 ln 2022
x
y
x
D.
/
1 ln 2022
.
2022
x
y
x
Câu 12: Cho hàm s
1
ln .
1
x
y
ng th
A.
yy
B.

y
ye
C.
yy
D.

y
ye
Câu 13: Mi gi ngân hàng 150 tring theo th thc lãi kép lãi sut
0,58%
trên1 tháng. Sau ít
nht bao nhiêu tháng ng?
A. 34. B. 32. C. 31. D. 30.
Câu 14: Gi
0
x
là nghim c
5
1.log x
Tìm m 
A.
0
1( ). ;  x
B.
0
. 6; 2 x
C.
0
. 0;1x
D.
0
3; .() x
Trang18
Câu 15: 
22
1
4 2 3

x x x x
có hiu các nghim
12
xx
bng:
A. 2. B. 1. C. 0. D.
1.
Câu 16: Tìm các giá tr thc ca tham s
m
 
4 2 1 .2 3 8 0
xx
mm
có hai nghim
trái du.
A.
1 9. m
B.
8
3
.m
C.
8
3
9.m
D.
9.m
Câu 17: 
33
3. log log 3 1 0 xx
có tng các nghim
A. 81. B. 77. C. 84. D. 30.
Câu 18: 



3 9.3 10

xx
:
A.
0.
B.
1.
C.
2.
D. .
Câu 19:
Tng
S
các nghim nguyên ca b
2 5 2
33
log 25log 750 0 xx
A.
925480.S
B.
38556.S
C.
378225.S
D.
388639.S
Câu 20: Tìm giá tr ln nht ca hàm s
2
2
log ( ).y x x
A.
2.
B.
1
.
4
C.
2.
D.
1
.
4
Đáp án
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
B
C
A
B
A
C
D
A
C
B
D
B
B
C
B
C
C
B
A
D
ĐỀ 10
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: Cho 3 s 
,,abc
và khác 1. Chn khnh sai?
A.
log log log .
a a a
bc b c
B.
log log b.log .
a a b
cc
C.
log
.
a
b
aa
D.
1
log .
log
a
b
b
a
Câu 2: Cho
a
và
b
là các   
1.a
   
A.
2
log 1 4log .
a
a
a ab b
B.
2
log 4 2log .
a
a
a ab b
C.
2
log 2 2log .
a
a
a ab a b
D.
Câu 3: Tnh
D
ca hàm s
10
2
2.
y x x
A.
\ 0;2 . D
B.
. D
C.
\ 0;2 . D
D.
\ 2 . D
Câu 4: T  nh
D
ca hàm s
ln 3 2

x
y
có dng
; log , 
a
Db
vi
, ab
là các s

1.a
Tính giá tr ca biu thc
2.P a b
A.
3.P
B.
7.P
C.
1.P
D.
5.P
Câu 5: Cho hàm s
9
,.
39

x
x
f x x
Bit
3.ab
Tính giá tr ca
2. K f a f b
A.
1.K
B.
2.K
C.
1
.
4
K
D.
3
.
4
K
Trang19
Câu 6: Cho 3 s 
,,abc
khác 1 và tha mãn:
log log log 2022.log .
a c a c
b b b
Chn khnh

A.
2022.ac
B.
2022.ab
C.
2022.bc
D.
2022.abc
Câu 7: Cho
log 16
m
Pm
và
2
logam
, vi
m
là s  nào ?
A.
1.
4

a
P
B.
2
3.Pa
C.
4
.
a
P
a
D.
3
.
a
P
a
Câu 8: Cho ba s th
, , a b c
khác
1.
 th các hàm s
,,
x x x
y a y b y c
c cho trong
hình v bên. M 
A.
1. b a c
B.
1. a c b
C.
1. b c a
D.
1. a b c
Câu 9: M 
A.
4
3 2 3 2 .
B.
6
11 2 11 2 .
C.
34
2 2 2 2 .
D.
34
4 2 4 2 .
Câu 10: o hàm
'y
ca hàm s
3 2022
.
x
y x e
A.
2 2022
' 3 2022 .
x
y x e
B.
2 2022
' 3 ln2022 .
x
y x e
C.
2 2022
' 3 ln2022 .
x
y x e
D.
2 2022
' 3 2021 .
x
y x e
Câu 11: Cho hàm s
lny x x
m cc tr ca hàm s thuc kho
A.
2;3
. B.
1
;1
2



. C.
1;2
. D.
1
0;
2



.
Câu 12: Anh Thành vay 20 tring c mua laptop và phi tr i
lãi sut 1,1% mi tháng. Hàng tháng anh Thành phi tr 1 s tin c nh l t
n  ng)
A. ng B. ng C. ng D. ng
Câu 13: Hàm s
.
x
y x e
tha h thc
A.
 x y x y
B.
 x y x y
C.
 x y x y
D.
 x y x y
Câu 14: 
3
24
x
có nghim thuc tp nào?
A.
;4 .
B.
;8 .
C.
;5 .
D.
;3 .
Câu 15: Gi
3
5
log log 3
2

x
x
c hai nghim
12
.xx
Kh
A.
2
1
3 0.
3

x
x
B.
2
1
3 0.
3

x
x
C.
1
2
10.
3

x
x
D.
1
2
9.
3

x
x
Câu 16: 
22
4 6.2 8 0
xx
có my nghim?
A. 3. B. 1. C. 2. D. 4.
Câu 17: Tìm tt c các giá tr ca tham s thc
m
  
6 (3 ).2 0
xx
xm
có nghim
thuc khong
0;1 .
A.
4;10 .
B.
3;4 .
C.
2;4 .
D.
3;4 .
Câu 18: Tp nghim
S
ca b
2
1 0,2
25
4log 5log 6 0. xx
Trang20
A.
. S
B.
.S
C.
11
;.
125 25



S
D.
1
;.
25




S
Câu 19: Cho hàm s
2
1
3
log 2 4 . y x x
Tp nghim ca b
' 0.y
A.
;0 .
B.
1; .
C.
;1 .
D.
2; .
Câu 20: Giá tr nh nht ca hàm s
2
.
x
ye
A. 1. B.
1.
C. e. D. 0.
Đáp án
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
C
C
A
B
A
A
C
B
C
A
D
A
A
B
B
D
A
C
C
A
ĐỀ 11
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: Cho các s thc
0.ab
M 
A.
ln ln ln .




a
ab
b
B.
2
22
ln ln ln .ab a b
C.
1
ln ln ln .
2
ab a b
D.
2
22
ln ln ln .




a
ab
b
Câu 2: Hàm s
22
ln 1 1 . y x x x x
M 
A. Hàm s có tnh là
.
.
B. Hàm s o hàm s:
/2
ln 1 . y x x
C. Hàm s ng bin trên
0; .
D. Hàm s nghch bin trên
0; .
Câu 3: Tnh
D
ca hàm s
2022
2 3 . y x x
A.
3; . D
B.
3; . D
C.
3
\ 1; .
4




D R
D.
3
; 1; .
4



D
Câu 4: 



D

0,8
21
log 1
5

x
y
x
có dng
;,


ab
D
dc
vi
, , ,a b c d
là các s
nguyên khác 0. Tính giá tr ca biu thc
2
.P a d bc
A.
2
2.P
B.
3
2.P
C.
1
3.P
D.
4
3.P
Câu 5: Rút gn biu thn biu thc :
10
6 12 2
35




K x y xy
,vi
0x
A.
0.K
B.
2
.2K xy
C.
2
. K xy
D.
2
.2 K xy
Câu 6: Giá tr ca biu thc
2
3 3 3
33
:.



ab
T ab a b
ab
A.
2.T
B.
1.T
C.
3.T
D.
1.T
Trang21
Câu 7:  th hai hàm s
x
ya
và
log
b
yx
:
Nh
A.
1, 1.ab
B.
1,0 1. ab
C.
0 1,0 1. ab
D.
0 1, 1. ab
Câu 8: Cho
22
log 5 ;log 3 .ab
Tính
3
log 135
theo
, .ab
A.
3
3
log 135 .
ab
b
B.
3
3
log 135 .
ab
b
C.
3
3
log 135 .
ab
a
D.
3
3
log 135 .
ab
a
Câu 9: Cho
, ab
là 2 s tha mãn
24
35
74
, log log
53

bb
aa
nh nào

A.
.
0 1; 1 ab
B.
1; 1.ab
C.
0 1;0 1. ab
D.
1;0 1. ab
Câu 10: o hàm
'y
ca hàm s
2
2022
log ( 1).yx
A.
'.
1011
x
y
B.
2
2
'.
( 1)ln2022
x
y
x
C.
2
1
'.
1 ln2022
y
x
D.
2
1
'.
1
y
x
Câu 11: 



sin cos 1
2 .2 .
xx
y
A.
sin cos 1
' sin .cos .2 .2 .

xx
y x x
B.
sin cos 1
' (cos sin )2 .ln2.


xx
y x x
C.
sin cos 1
' sin 2 .2 .2 .

xx
yx
D.
sin cos 1
' cos2 .2 .2 .

xx
yx
Câu 12: Theo s liu t tng cc thng kê, dân s Vii. Gi s t l
 a Vin 2015 - 2030 mi là 1,1%, tính s dân
Vi
A.
0,165
91,7.e
(trii) B.
1,65
91,7.e
(triu i);
C.
0,011
91,7.e
(trii) D.
0,11
91,7.e
(trii).
Câu 13: Cho hàm s
2
sin5 .
x
exy
ng th
A.
  y y y
B.
  y y y
C.
  y y y
D.
  y y y
Câu 14: Gi
0
x
là nghim c
32
3 27.
x
Tìm m 
A.
0
4;6 .x
B.
0
. 0;2x
C.
0
. 3;5x
D.
0
. 1;1x
Câu 15: Cho   trình
1
31
3
log 3 1 2 log 2
x
x
có hai 
1
x
và
2
x
. Tính 
12
27 27
xx
S
.
A.
180S
. B.
45S
. C.
9S
. D.
252S
.
Câu 16: Tìm các giá tr thc ca tham s
m
 
22
22
log log 3 xxm
có nghim
1;8 .x
A.
2 6.m
B.
2 3. m
C.
3 6.m
D.
6 9.m
Câu 17: Tìm các giá tr thc ca tham s
m
 
3
2
log 3x x m
có 3 nghim thc phân
bit.
A.
1.m
B.
0 1.m
C.
0.m
D.
1.m
Trang22
Câu 18: Mi nghim ca b
41
4
3 1 3
log 3 1 log
16 4



x
x
u là nghim ca b

A.
2
( 3 2) 0. x x x
B.
2
( 3 2) 0. x x x
C.
2
( 3 2) 0. x x x
D.
2
( 3 2) 0. x x x
Câu 19: S nghim nguyên ca b
22
93
log 3 4 2 1 log 3 4 2 x x x x
A. 1 B. 2 C. 0 D. 3
Câu 20: Tìm giá tr ln nht ca hàm s
2
ln 2 2 y x x
n
0;3 .
A.
0;3
ax ln17.my
B.
0;3
ax ln20.my
C.
0;3
ax ln5.my
D.
0;3
ax ln2.my
Đáp án
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
C
D
A
B
A
B
B
A
B
B
B
A
D
B
A
A
A
B
D
A
ĐỀ 12
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT
GIẢI TÍCH 12
Câu 1: Cho
2
log 3, 0aa
. Tính tng
2
2 1 2
2
2
log log log 2log . S a a a a
A.
6.S
B.
2.S
C.
3.S
D.
5.S
Câu 2: B
2
log 2 11 15 1 xx
có bao nhiêu nghim nguyên?
A. Vô s. B. 3. C. 4. D. 5.
Câu 3: Gi
1
4 2 3 0
xx
bt
2 ,( 0).
x
tt
M 
A.
4 3 0.t
B.
2
2 3 0.t
C.
2
2 3 0. tt
D.
2
3 0. tt
Câu 4: Tìm tnh D ca hàm s
2
4
1
log 3 .
27




xx
y
A.
;1 3; .  D
B.
1;3 .D
C.
1; . D
D.
1;3 .D
Câu 5: Mi gi 50 tring vào mt ngân hàng vi lãi sut rng nu không rút
tin ra khi ngân hàng thì c sau m tin lãi s c nhp vào g p theo.
Hi sau ít nhc s tin nhing, bao gm gc và lãi?
Gi nh trong sut thi gian gi, lãi sun.
A.  B.  C.  D. 
Câu 6: Bit
ln2, ln5ab
. Tính
1 2 98 99
ln ln ... ln ln
2 3 99 100
S
theo a và
.b
A.
. S a b
B.
2 2 .S a b
C.
.S a b
D.
2 2 . S a b
Câu 7: Tìm tp nghim S c
33
log (2 1) log ( 1) 1. xx
A.
4.S
B.
3;4 .S
C.
2;1 .S
D.
1.S
Câu 8: Cho
log 3,log 4
ab
xx
vi
,ab
là các s thc l
log .
ab
Px
A.
12
.
7
P
B.
7
.
12
P
C.
1
.
12
P
D.
12.P
Trang23
Câu 9: Cho
3
log 2a
và
2
1
log .
2
b
Tính
2
3 3 1
4
2log log (3 ) log .I a b
A.
4.I
B.
3
.
2
I
C.
5
.
4
I
D.
0.I
Câu 10: Tp nghim S ca b
1
1
5 0.
5

x
A.
1; . S
B.
;2 . S
C.
; 2 .  S
D.
2; . S
Câu 11: Bit
3 3 *
2
1
3 log 3 ln , ( , , )
ln
x x x x
x e a ce a b c
xb
. Tính
.
b c a
S a b c
A.
18.S
B.
40.S
C.
20.S
D.
44.S
Câu 12: Cho
a
là s th i s th
,?xy
A.
log log ( ).
aa
x
xy
y
B.
log log log .
a a a
x
xy
y
C.
log
log .
log
a
a
a
x
x
yy
D.
log log log .
a a a
x
xy
y
Câu 13: Cho hai hàm s
,
xx
y a y b
vi
,ab
là hai s tht  th là
1
C
và
2
C
 
A.
0 1. ab
B.
0 1 . ab
C.
0 1 . ba
D.
0 1. ba
Câu 14: Cho hàm s
ln
,
x
y
x
m 
A.
2
1
2.
y xy
x
B.
2
1
.
y xy
x
C.
2
1
2.
y xy
x
D.
2
1
.

y xy
x
Câu 15: Vi s th
,xy
t
33
log ,log .

xy
M 
A.
3
27
log 9 .
2








x
y
B.
3
27
log .
2





x
y
C.
3
27
log .
2





x
y
D.
3
27
log 9 .
2








x
y
Câu 16: Tp nghim S c
2 3 2 3 4
xx
là tp con ca ca t
A.
2;1;0;2 .I
B.
1;0;2 .H
C.
1;2;3;4 .K
D.
1;0;1;2 .T
Câu 17: Tìm tp nghim S ca b
2
22
log 5log 4 0. xx
A.
;1 4; .  S
B.
;2 16; .  S
C.
2;16 .S
D.
0;2 16; . S
Câu 18: o hàm ca hàm s
1
.
4
x
x
y
Trang24
A.
2
1 2( 1)ln2
.
2

x
x
y
B.
2
1 2( 1)ln2
.
2

x
x
y
C.
2
1 2( 1)ln2
.
2

x
x
y
D.
2
1 2( 1)ln 2
.
2

x
x
y
Câu 19: Tìm giá tr ln nht và giá tr nh nht ca hàm s
2
( ) ln 1 2 f x x x
n
2;0 .
A.
2;0
( ) 4
Max f x
và
2;0
1
( ) .
4
Min f x
B.
2;0
( ) 4 ln5
Max f x
và
2;0
1
( ) ln 2.
4
Min f x
C.
2;0
( ) ln5
Max f x
và
2;0
( ) ln2.
Min f x
D.
2;0
( ) 2
Max f x
và
2;0
( ) 0.
Min f x
Câu 20: Tìm tnh D ca hàm s
1
2
5
4.yx
A.
2;2 .D
B.
2;2 .D
C.
\ 2;2 .D
D.
; 2 2; .  D
Đáp án
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ 1
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT GIẢI TÍCH 12
Câu 1: Cho log x  3, log x  4 với a, b là các số thực lớn hơn 1. Tính P  log . x a b ab 12 1 7 A. P  . B. P 12. C. P  . D. P  . 7 12 12 x x x
Câu 2: Giải phương trình  2   1   2  
1  2 2  0 bằng cách đặt t   2  
1 ,t  0. Mệnh đề nào dưới đây sai?
A. t 1 2;t 1 2. B. x  1; x  1. C. 2
t t  2 2  0. D. 2
t  2 2t 1  0.  
Câu 3: Tìm giá trị của của biểu thức 3 3 3 3 M  log log  .... 3 . 3 3     n daáu caên  n A.  3n M . B. n M . C. M   . n D. M  . 3 3n
Câu 4: Với mọi số thực dương a và b thỏa mãn 2 2
a b  8ab, mệnh đề nào dưới đây đúng? 1 A. a b 1 log   log a  log . b
B. log a b  log a  log b. 2 2 1
C. log a b  1 log a  log . b
D. log a b  1 log a  log b. 2 1 1    Câu 5: Cho hai số 10 10
a  2  3  2 và b  log sin
. Mệnh đề nào dưới đây đúng? 2    7  A. b  0  . a
B. a b  0.
C. a b  0. D. a  0  . b
Câu 6: Đặt a  log 3,b  log 3 . Tính P  log 45 theo a, . b 2 5 6 a  2ab  2 a  2ab a  2ab A. P  . B. a ab P . C. P  . D. P  . ab b ab ab b ab b 1
Câu 7: Rút gọn biểu thức 3 6
P x . x với x  0. 2 1 A. 9 P x . B. 8 P x . C. 2 P x . D. P x.
Câu 8: Tìm tập xác định D của hàm số y  log x  2 1. 1   2
A. D  2;4.
B. D   ;  24;.
C. D  2; 4.
D. D   ;  2. Câu 9: Cho hàm số   x 2 ( ) ln  1 x f x e e
. Mệnh đề nào dưới đây đúng? A. f   1  ln 2. B. f   2 5 ln 2  . C. f   5 2  .
D. f e  . e 5 5
Câu 10: Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x mlog x  2m  7  0 có hai 3 3
nghiệm thực x , x thỏa mãn x .x  81. 1 2 1 2 A. m  4.  B. m  81. C. m  44. D. m  4.
Câu 11: Tìm tập nghiệm S của bấtphương trình log  2x 4  1  . 0,2  Trang1
A. S   ;  2  2;. B. S   3  ;  3 . C. S   2  ;2. D. S   3  ; 2  2;  3 . 
Câu 12: Tìm tập xác định D của hàm số: y   x x   2 2 4 3 . A. D   .
B. D   \ 1;  3 . C. D  ( ;
 1) 3;.D. D  1;3.
Câu 13: Xét hàm số 2  x y e sin 5 .
x Mệnh đề nào dưới đây đúng? A. // /
y  4 y  29 y  0. B. /// / y
 4y  29y  0. C. // /
y  4 y  29 y  0. D. /// / y
 4y  29y  0. 2 x
Câu 14: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) 
 4ln 3 x trên đoạn  2   ;1 . 2 1 1
A. Max f (x) 
 8ln 2 và Min f (x)   4ln 2. 2; 1 2  2  ;  1 2 1 1
B. Max f (x) 
 ln 2 và Min f (x)   4ln 2.  2  ;  1 2 2; 1 2 1 1
C. Max f (x) 
 4ln 2 và Min f (x)   8ln 2. 2; 1 2 2; 1 2
D. Max f (x)  8ln 2 và Min f (x)  4ln 2.  2  ;  1  2  ;  1
Câu 15: Đầu năm 2016, ông A thành lập một công ty. Tổng số tiền ông A dùng để trả lương cho nhân
viên trong năm 2016 là 1 tỷ đồng. Biết rằng cứ sau mỗi năm thì tổng số tiền dùng để trả lương cho nhân
viên trong cả năm tăng thêm 15% so với năm trước. Hỏi năm nào dưới đây là năm đều tiên mà tổng số
tiền ông A dùng để trả lương cho nhân viên trong năm lớn hơn 2 tỷ đồng? A. Năm 2023. B. Năm 2021. C. Năm 2022. D. Năm 2020.
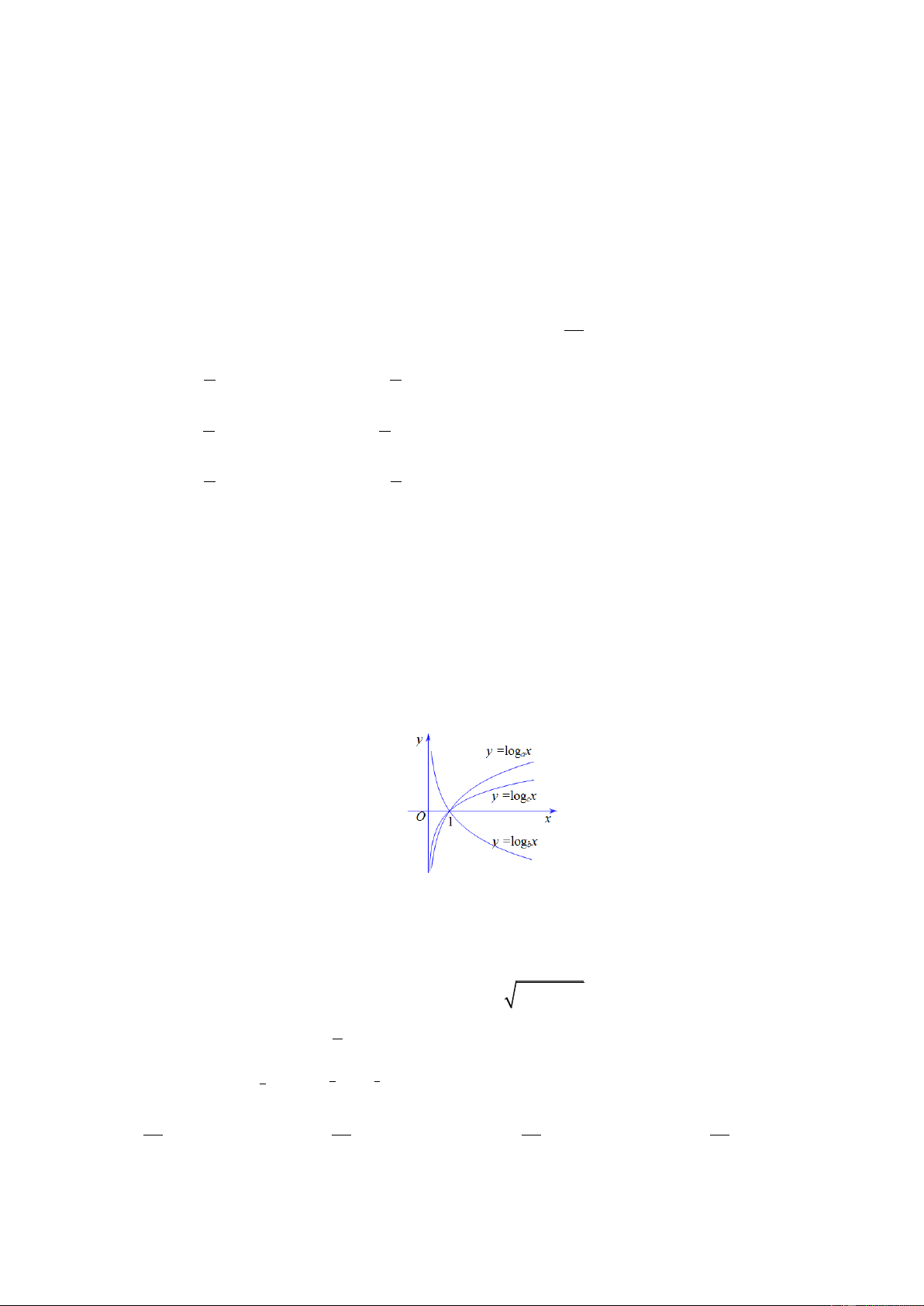
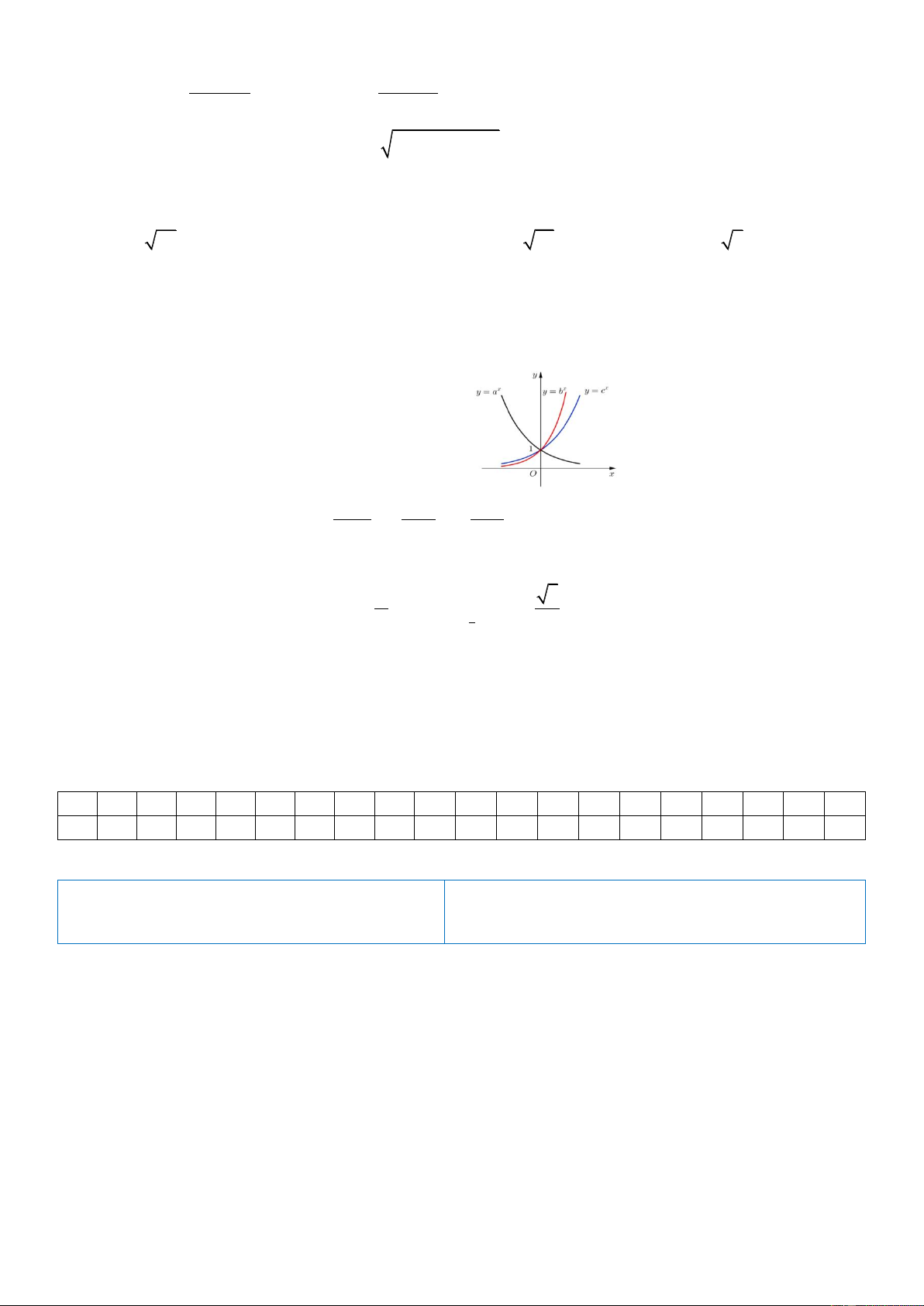
Câu 16: Cho ba số thực dương a, b, c khác 1. Đồ thị hàm số y  log x, y  log x, y  log x được cho a b c
trong các hình vẽ bên. Mệnh đề nào dưới đây là đúng?
A. c a  . b
B. a b  . c
C. a b  . c
D. b c  . a
Câu 17: Tìm tập nghiệm S của bất phương trình 9x  3x  6  0. A. S   2  ;3.
B. S  1; . C. S   3  ;2.
D. S   ;   1 .
Câu 18: Gọi x ; x là hai nghiệm của phương trình 2 2
log x  log x 1  5  0 . Tính P x .x . 1 2 3 3 1 2 1 A. P 1. B. P  . C. P  9. D. P  3. 3  
Câu 19: Tính S    2 1 1 1 2  3 3 3 0, 001  2 .64  8 . 95 95 16 95 A. S  . B. S  . C. S  . D. S  . 4 16 95 2
Câu 20: Tìm nghiệm của phương trình log 1 x  2. 2   A. x  5. B. x  3.  C. x  4.  D. x  3. Trang2 Đáp án 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 2
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12
Câu 1: Phương trình 9x  3.3x  2  0 có hai nghiệm x , x (x x ) . Tính giá trị của A  2x  3x . 1 2 1 2 1 2 A. 4 log 2 . B. 1. C. 2 log 4 . D. 3log 2 . 3 3 3
Câu 2: Cho a, b > 0 và a, b 1 ; x và y là hai số dương. Chọn khẳng định sai trong các khẳng định sau. log x A. log x b . B. 2 2 2 log x  4  log . x a log a 1 a b a C. 2022 log x  2022log . x D. log xy x y a    log log . a a a a 3 2 x5  1   1 
Câu 3: Tập nghiệm của bất phương trình   
  là tập nào sau đây?  2   2   13   13   13  A.  ;  5. B. 5; .   C.  ;  . ;  .    2   2  D.  2 
Câu 4: Giải phương trình 2 3
log x  2 log x  75  0 (1), một học sinh thực hiện theo các bước sau: 1 2 2
(I) Điều kiện xác định x  0 (II) 2
(1)  9log x  2log x  75  0 2 2 log x  3 2  (III)  25  x   x x   log 3
8 . Vậy (1) có nghiệm duy nhất là 8 2 log x   2  9
Bài giải trên sai từ bước nào? A. Bước (III). B. Bước (II). C. Bước (I).
D. Bài giải hoàn toàn đúng.
Câu 5: Tính tổng các nghiệm của phương trình log x  log x  6  log x  2 . 5 5   5   A. 2. B. –2. C. 1. D. –1.
Câu 6: Giải bất phương trình 2x 1
3  10.3x  3  0. A. 1   x 1. B. x  1  hoặc x 1. C. x  1. D. x  1. 
Câu 7: Giá trị nhỏ nhất của hàm số 2
y x  4 ln 1 x trên đoạn 2;0 là a bln c ( a,b, c nguyên
dương). Tính tổng a b  . c A. 7. B. 10. C. 8. D. 9.
Câu 8: Hàm số nào sau đây đồng biến trên tập xác định của nó? Trang3 xx x 2   2     x A. y  .   B. y    . C. y  .  
D. y  0,5 .    3  2    e
Câu 9: Tìm tập xác định của hàm số y  log  x   2 1  log x . 3 2 A. D   1  ;.
B. D  0; . C. D   1
 ;00;. D. D   1  ;0.
Câu 10: Tính đạo hàm của hàm số  x x x y . 8 5 x 1 1 1 A. y  . B. 3 4 y  x . C. 3 4 y  4 x . D. y  . 3 4 4 x 4 4 3 4 x 2 x Câu 11: Cho hàm số 1 y  2 . x e . Tính y50. A. 2501 10002e . B. 2500 10001e . C. 2502 10003e . D. 2503 10004e .
Câu 12: Trong các mệnh đề sau đây mệnh đề nào sai?  x 1 
A. Hàm số y    nghịch biến trên  .  2  B. Hàm số 2 1   x y e có đạo hàm là 2 1 2    x y e . C. Hàm số  2x y đồng biến trên  .
D. Đồ thị hàm số  3x y
nhận trục Oy là tiệm cận đứng.
Câu 13: Tập xác định của hàm số y    x13 1 là tập nào sau đây? A.  . B.  \   1 . C.  ;   1 . D.  ;   1 .
Câu 14: Cho P  log 16m và a  log m , với m là số dương khác 1. Mệnh đề nào dưới đây đúng? m 2  4  3 A.  1 a P . B. a P . C. a P . D. 2 P  3  a . 4 a a
Câu 15: Biết log 5  ; a log 3  .
b Khi đó giá trị của log 24 bằng giá trị nào sau đây? 2 5 15 b a  1 3  ab a 1 A. . B. . C. . D. . ab 1 b  1 a b   1 ab 1    x x 2
Câu 16: Phương trình 2 3 0,125.4    
 có nghiệm duy nhất x . Giá trị nào sau đây nhỏ nhất? 8 0   A. x 1 . B. x  5 . C. x 10 . D. x 15 . 0 0 0 0 1
Câu 17: Cho hàm số y  ln
. Trong các khẳng định sau đây, khẳng định nào đúng? x 1 A.   y xy e 1. B.   y xy e 1. C.   y xy e 1. D.    y xy e 1.
Câu 18: Cho 3 số dương a, b, c khác 1 và thỏa mãn log b  log b  log 2022.log .
b Chọn khẳng định a c a c
đúng trong các khẳng định sau. A. ac  2022.
B. abc  2022. C. bc  2022. D. ab  2022.
Câu 19: Cho hàm số y x ln .
x Tính ye. 1 A. . e B. 3. C. . D. 2. e
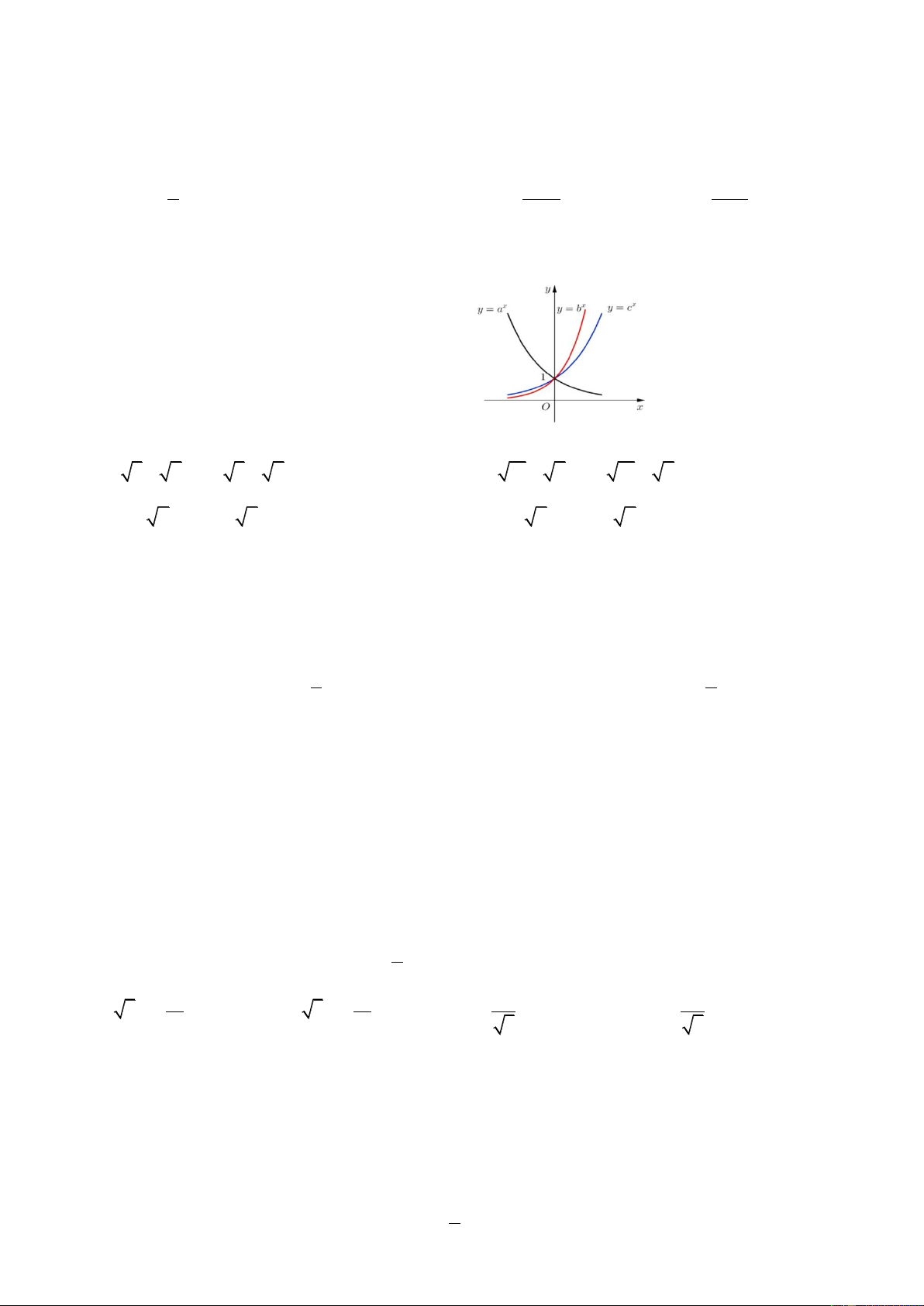
Câu 20: Cho đồ thị như hình vẽ. Mệnh đề nào sau đây là đúng? Trang4 4 y 3 y = loga x 2 1 O x -3 -2 -1 1 2 3 4 5 6 -1 -2 y = logb x -3
A. 0  a b 1.
B. 0  a 1 . b
C. 0  b a 1.
D. 0  b 1 . a
----------------------------------------------- ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 3
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12
Câu 1: Với mọi số thực dương a và b thỏa mãn 2 2
a b  6ab , mệnh đề nào dưới đây đúng? 1
A. log (a b) 
(1 log a  log b).
B. log (a b)  1 log a  log . b 8 8 8 2 8 8 8 1
C. log (a b)  log a  log . b
D. log (a b)   log a  log . b 8 8 8 8 8 8 2
Câu 2: Tìm tập xác định của hàm số 2
y  log (x  2) . 2 A. x  2. B. x  . C. x  2. D. x  2. e
Câu 3: Tính đạo hàm của hàm số y  2x   1 . eee e
A. y  e x   1 2 2 1 .
B. y   x   1 2 2 1 .
C. y  22x   1 .
D. y  ex   1 2 1 . 1 A
Câu 4: Cho hai biểu thức A  log 15  log 18  log 10 và B  log 2  log 3. Giá trị của bằng 9 9 9 36 1 2 B 6 bao nhiêu? A. 8 . B. 4 . C. 9 . D. ...
Câu 5: Tính đạo hàm cấp hai của hàm số 2 y  ln x . 2 2 2 2 A. . B. . C.  . D.  . 2 x x 2 x x 1
Câu 6: Cho hàm số y
. Mệnh đề nào sau đây đúng? 1 x  ln x
A. xy  y y ln x   1 .
B. xy y yln x   1 . Trang5
C. xy  y y ln x   1 .
D. xy y y ln x   1 . 4
Câu 7: Viết lại biểu thức 3 2 3
a : a viết dưới dạng lũy thừa. 5 2 7 5 A. 3 a . B. 3 a . C. 3 a . D. 8 a . 4 x 2  x 2   3 
Câu 8: Giải bất phương trình  .      3   2  2 2 2 2 A. x  . B. x   . C. x  . D. x  . 5 3 5 3
Câu 9: Đơn giản biểu thức x x  9 3 3 1
, ta được biểu thức nào sau đây?
A. x x  3 1 .
B. x x  3 1 .
C. x x  3 1 .
D. x x  3 1 .
Câu 10: Tìm mệnh đề đúng trong các mệnh đề sau?
A. Hàm số y  log x với a 1 nghịch biến trên khoảng 0; . a B. Hàm số  x y
a với 0  a 1 đồng biến trên khoảng 0; .
C. Hàm số y  log x vớinghịch biến trên khoảng 0; . D. Hàm số  x y
a với 0  a 1 nghịch biến trên khoảng  ;  .
Câu 11: Giải bất phương trình 2x 1
2   5.2x  2  0. A. 1   x 1. B. x  1  hoặc x 1. C. x  1. D. x  2.
Câu 12: Gọi x , x là hai nghiệm của phương trình 4x  8.2x  4  0 . Tính giá trị biểu thức P x x . 1 2 1 2 A. –4. B. 4. C. 0. D. 2.  1  2x
Câu 13: Tính đạo hàm của hàm số y  ln  .    x 1 x e 1 2x 1 2x A. y   B. y    ln 2. x  ln 2   1 . x 1 e x 1 x e 1 2x 1 2x C. y    D. y    . x  ln 2   1 . x 1 e x 1 x e
Câu 14: Phương trình 2 x 1  x x2 3 .2
 8.4 có hai nghiệm x , x . Tính x x  2 . 1 2 1 2 A. log 3. B. log 2. C. log 2 1. D. log 3  2. 2 3 3 2 1
Câu 15: Phương trình log x  log
x  2  1có nghiệm x . Tính giá trị biểu thức A  log x  . 3 3   0 2 0 3 1 1 4 4 A. A   . B. A  . C. A  . D. A   . 3 3 3 3 
Câu 16: Tìm tập xác định của hàm số f x   x   5 2 ( ) 4 . A.  2  ;2. B.  \   2 . C. ( ;  2)
  (2;). D.  .
Câu 17: Đặt a  ln 2và b  ln 5 . Hãy biểu diễn ln 200 theo a và b .
A. ln 200  3b  2 . a B. ln 200  6 . ab
C. ln 200  3a  2 . b
D. ln 200  3a  2 . b
Câu 18: Phương trình log 3.2x 1  x 1 có hai nghiệm x , x . Tính x x . 4   1 2 1 2 A. 6  4 2. B. 2. C. log 6  4 2 . D. 4. 2   Trang6 1 
Câu 19: Giá trị lớn nhất của hàm số y x   2 ln ln x   1 trên đoạn ; 2 
 đạt được tại điểm nào sau đây?  2  1 3 3 A. x  . B. x  1. C. x  . D. x  . 2 2 4
Câu 20: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Đồ thị các hàm số  x y
a và y  log x (với 0  a  1) đối xứng với nhau qua đường thẳng y  . x a
B. Hàm số y  log (x 1) nghịchbiến trên khoảng  1  ;. 1 3
C. Đồ thị hàm số y  log x (0  a  1) nằm phía trên trục Ox. a
D. Hàm số y  log (x  2) đồng biến trên khoảng 2;  . 2 ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 4
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12
Câu 1: Phương trình 2 40
log x  log x  300  0 có bao nhiêu nghiệm? 2 2 A. 1. B. 0. C. 2. D. 3. Câu 2: Cho hàm số  . x y
x e . Chọn hệ thức đúng.
A. y  2 y  3y .
B. y  2 y  3y .
C. y  2 y  1 .
D. y  2 y   y .
Câu 3: Cho hàm số y  .
m ln x đạt giá trị lớn nhất bằng 2 trên đoạn 1; 
3 . Khẳng định nào đúng? A. m  4 .
B. 2  m  4 . C. m  0 .
D. 0  m  2 . x x x
Câu 4: Tổng bình phương các nghiệm phương trình 2 2 2 1 2 25 10  4  0 gần số nào nhất? A. 6. B. 3. C. 9. D. 12.
Câu 5: Tìm m để phương trình 2
log x  2log x m 1  0 có nghiệm. 3 3 A. m  2. B. m  2 . C. m  2 .
D. m  3 .
Câu 6: Bất phương trình 2 log 4x  3  log
2x  3  2 có tập nghiệm là S   ;
a b . Tính b a . 3   1   3 1 27 1 9 A. . B. . C. . D. . 2 8 4 4
Câu 7: Chị Năm vay trả góp ngân hàng số tiền 50 triệu đồng với lãi suất 1,15%/tháng trong vòng 2 năm
thì mỗi tháng chị Năm phải trả số tiền bao nhiêu đồng? (làm tròn đến hàng nghìn) A. 2.396.000. B. 2.134.000. C. 2.674.000. D. 2.456.000.
Câu 8: Cho a  0 và a 1, x và y là hai số dương. Tìm mệnh đề đúng trong các mệnh đề sau.
A. log x có nghĩa với x. B. log n
x n log x . a a a
C. log xy  log .
x log y .
D. log 1  a và log a  0 . a a a a a
Câu 9: Cho hàm số y   2
log x  2x  3 có tập xác định D . Khẳng định nào đúng? Trang7 A. D   3  ;  1 .
B. D  2;3 . C. D   3  ;2 . D. D   1  ;3. log 3  a log 5 Câu 10: Cho 2 2 log 75  . Tính 2
P a  3ab . 6 b  log 3 2 A. P  5. B. P  7 . C. P  10. D. P  5  . 1009.log 32018 Câu 11: Rút gọn 2 P  2 . 2018  1009  3   3  A. P    . B. 1009 P  2 . C. 2018 P  3 . D. P    .  2   2    
Câu 12: Cho các hàm số lũy thừa y x , y x , y x có đồ thị như hình vẽ. Khẳng định nào đúng? y y = xα 4 y = xβ 3 2 y = xγ 1 O x -1 1 2 3 4 -1
A.      .
B.      .
C.      .
D.      .
Câu 13: Tìm tập xác định của hàm số y    x 3 2 5 4 . A. ( ;  ] 2 [2; ) . B. R .
C. 2; 2. D.  2  ;2 . Câu 14: Cho hàm số 3
y  3x  2 . Tính f   1 .
A. f    1  1.
B. f    1 1  .
C. f    1  2 .
D. f    1  1  . 3 m Câu 15: Cho 3 4 . .  n a a a a . Tính 2
S m 2  n . A. S  8640 . B. S  6358  . C. S  8640  . D. S  5380  . 2 x 3x4 2 x 1  0
Câu 16: Bất phương trình 2  3  2 3
có bao nhiêu nghiệm nguyên dương? A. 6. B. 3. C. 2. D. 4. x Câu 17: Cho       2 5 2 5
2 . Khẳngđi ̣nh nào dưới đây đúng? A. x  2 . B. 2 x  2 . C. x  2.  D. x  2.   . a ln 2x x
Câu 18: Cho  x.ln 2x 3 3   . Tính 2 3
P a b c . 3 2 . . c x b x A. P  11 . B. P  13. C. P  12 . D. P  18. x
Câu 19: Giải phương trình 100 100 2  64 .
A. x  20.000.
B. x  60.000. C. x  6.000.
D. x  30.000.
Câu 20: Cho a  log 2, b  log 3 . Tính 2023 log 12 theo a, b . 2023 2023 1 A. a b12 2023 2 . B. 2a b. C. a  2b. D.
2a b2023 . 2 2 2
----------------------------------------------- Trang8 ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 5
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12 m Câu 1: Cho 4 3 . .  n x x x
x . Tính S m 2 2  n  . A. S  14  . B. S  12  . C. S  6  . D. S 13.
Câu 2: Cho a  ln 2, b  ln 3 . Tính 3 2022 ln 18 theo . a, b .. 2022 1 2022 A. a b13 2022 2 . B. 2a b.
C. 2a b2022 . D. a  2b. 3 3 3
Câu 3: Anh An gửi ngân hàng 100 triệu đồng với lãi suất 0,58%/tháng (không kỳ hạn, không rút lãi hàng
tháng). Để có được số tiền không dưới 130 triệu đồng thỉ anh An phải gửi ít nhất bao nhiêu tháng? A. 45 tháng. B. 46 tháng. C. 47 tháng. D. 44 tháng. . m ab a
Câu 4: Cho a  log 3, b  log 3 và log 45  . Tính 2 2
P  2m n . 2 5 20 . n b a A. P  5  . B. P  2  . C. P  5. D. P  4 . 2017  10 
Câu 5: Rút gọn P  log   .  0,001. 10  4029 4029 4039 A. P  . B. P   . C. 2017 P  10 . D. P  . 2 3 2 Câu 6: Cho hàm số  . x y
m e đạt giá trị nhỏ nhất bằng 3 trên đoạn 0; 2. Khẳng định nào đúng?
A. 1 m  3. B. m  3 .
C. 0  m 1. D. m  0 . Câu 7: Cho hàm số sin .   x y
x e . Chọn hệ thức đúng.
A. y  2 y  3y .
B. y  2 y  2 y .
C. y  2 y   y .
D. y  2 y  3y .
Câu 8: Tính tổng bình phương tất cả các nghiệm của phương trình 2 2 6
log x  log x  2  0 . 3 3 A. 12. B. 24. C. 18. D. 35.
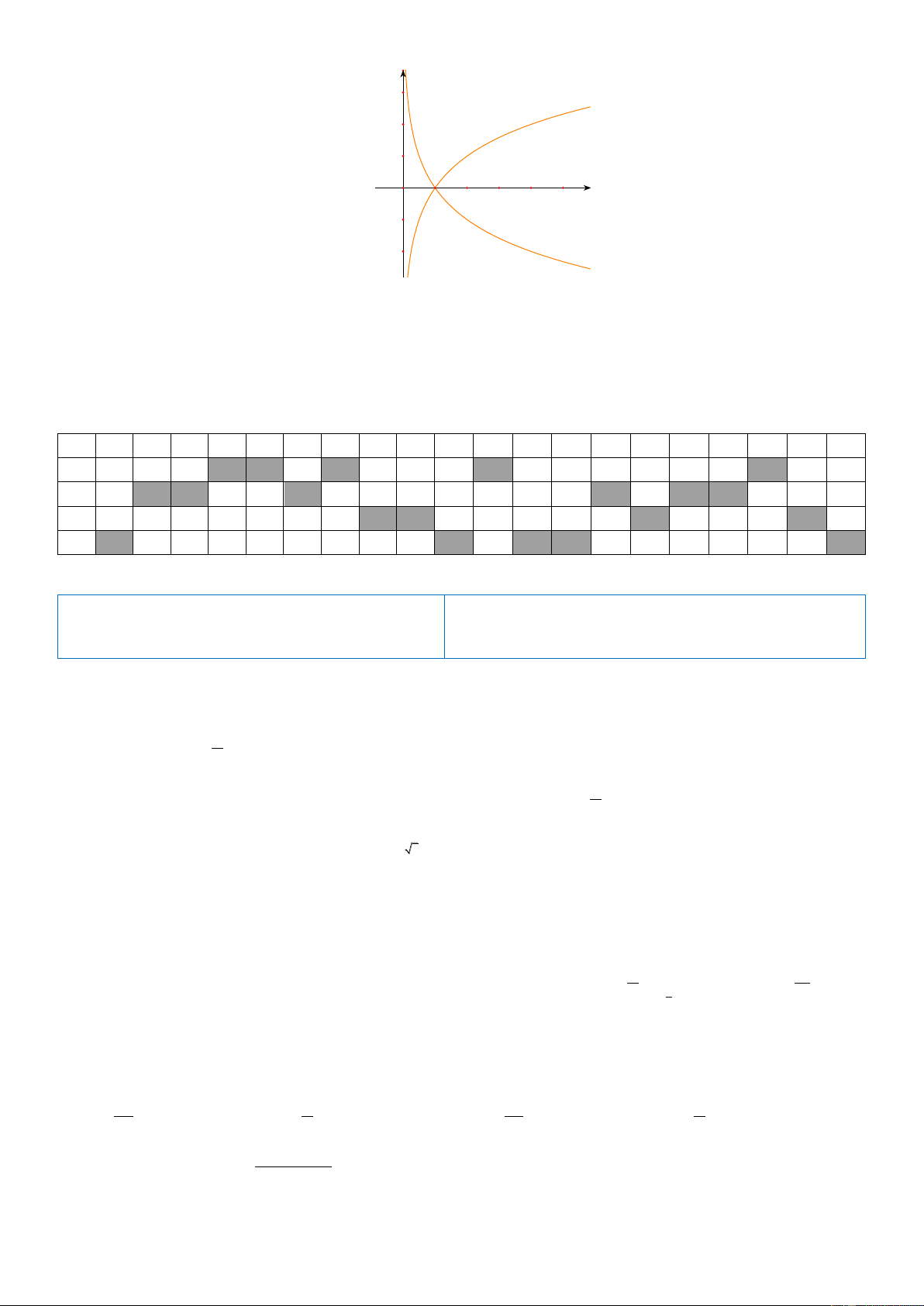
Câu 9: Cho đồ thị hai hàm số  x y
a và y  log x như hình vẽ. Khẳng định nào đúng? b y 4 2 -2 -1 O 1 2 -1
A. 0  a 1 b
B. 0  b a 1
C. a b 1
D. a 1  b  0
Câu 10: Cho a, b, x, y  0 và a, b  1. Tìm mệnh đề đúng trong các mệnh đề sau. Trang9x  log x A. log    a B. log x  log . a log x a b b a y  log y a  1  1 C. log  D. log x y x y a     log  log a    x  log x a a a 2 2 x 2 x 2
Câu 11: Phương trình  5  2   5  2
 40 có bao nhiêu nghiệm? A. 1. B. 4. C. 3. D. 2. x
Câu 12: Giải phương trình 100 10 3  81 . A. x  6.000. B. x  2.000. C. x  4.000. D. x  3.000.
Câu 13: Cho hàm số y  log  2
x  2x  3 có tập xác định D . Khẳng định nào đúng? 2  A. D   3  ;  1 . B. D   1  ;  3 . C. D   1  ;  3 .
D. D  2;3 .
Câu 14: Bất phương trình log  x  40  log 60  x  2 có bao nhiêu nghiệm nguyên? A. 18. B. 20. C. 19. D. Vô số.
Câu 15: Tìm tất cả các giá trị thực của tham số m để phương trình log x  log x  2  log m có 3 3   3 nghiệm. A. m 1. B. m 1. C. m 1. D. m 1. 1 2022
Câu 16: Tìm tập nghiệm của bất phương trình  2   1 x   2   1 .  1   1   1   1   A. 0;   . B. ;   . C. ;  \    0 . D. ;    .    2022   2022   2022   2022  xa e x  . 
Câu 17: Cho  3 x.e  3   . c x. x e . Tính 3 2
P a b c . 3 2 . b x A. P  9. B. P  11 . C. P  8 . D. P  18.
Câu 18: Tìm tập xác định của hàm số y   x  5 2 3 4 . A.  ;  22; 
  . B.  2  ;2 . C. R . D.  ;  22;    . x Câu 19: Cho       3 3 2 2
3 . Khẳng đi ̣nh nào dưới đây đúng? 1 A. x  3.  B. x  3. C. x  3.  D. 3 x  3 . Câu 20: Cho hàm số 4 2 y
2x x . Tính f    1 .
A. f   1 1   . B. f    3 1  . C. f    1  0 . D. f    1  1. 2 2
----------------------------------------------- ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D Trang10 ĐỀ 6
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12
Câu 1: Tập xác định của hàm số y =  x x   2 2 2
A. D R \  1  ;  2 B. D   1  ;2 C. D   1  ;2
D. D   ;    1  2;  49
Câu 2: Cho log 25 = a và log 5 = b . Tính 1000 log theo a và . b 7 2 3 5 8 12b  9a 12b  9a
12b  9a ab 4b  3a A. . B. . C. . D. . 1000ab 1000ab 1000 3000ab 2 1 x 2 x2    
Câu 3: Tổng các nghiệm của phương trình 5 16      bằng?  4   25  A. 1 B. 2 C. 3 D. 4
Câu 4: Gọi x ; x là 2 nghiệm của phương trình 2 2
log x  log x 1  5  0 . Giá trịP= x .x 1 2 3 3 1 2 1 A. P  1 B. P  3 C. P  9 D. P  3
Câu 5: Cho hai số thực a, b với 1 a b khẳng định nào sau đây đúng.  x x ab A. 1  x  0   B. 1  x  0  
C. log b  1
D. log a  1 a b b   a x x
Câu 6: Cho bất phương trình 1 4  5.2
16  0 có tập nghiệm l1 đoạn  ; a b. Tính hiệu  2 2
log a b . A. 0. B. 1. C. 1.  D. 2. 2
x mx 1 2 
Câu 7: Tìm tất cả các giá trị thực của m để hàm số y  ln 
  xác định với x 2  x x 1 3  4 A. m 1
B. 2  m 10 C. 1 m  3 D. 0 3
Câu 8: Gọi x , x
x x là hai nghiệm thực của phương trình 2x 1
3   4.3x 1  0. Khẳng định nào sau 1 2  1 2  đây là đúng?
A. 2x x  2  .
B. x  2x  0.
C. 2x x  2.
D. 2x x  2  . 2 1 1 2 1 2 1 2
Câu 9: Cho số 4x 4
x  23 . Tìm mệnh đề sai trong các mệnh đề sau:
A. log x  0 khi x  1 B. Nếu x x thì log x  log x a 1 2 a 1 a 2
C. log x  0 khi 0  x  1
D. Tiệm cận ngang hàm số y  log x là trục hoành a a 5
Câu 10: Tập nghiệm S của phương trình 2
log (x  2)  log (x  2)  là 3 9 4 A. S  {2}. B. S  {1}.
C. S  8 243   2 . D. S  .  a
Câu 11: Cho a, b là các số nguyên dương thỏa mãn a  1, ab  1, log b  3 , Khi đó giá trị của log a ab    b  là : 1 1 A. 8  B. C. 2  D. 2 2 Trang11
Câu 12: Cho hàm số f x  ln x .Tính đạo hàm của hàm số y  log  2 x f ' x 3   1 1 ln 3 A. y '  . B. y '  . C. y '  . D. '  x y . x x ln 3 x ln 3
Câu 13: Số nghiê ̣m của phương trình log 3.2x  2  2x là: 2   A. 3. B. 1. C. 2. D. 4.  1  
Câu 14: Tập xác định của hàm số y  ln   là? 2
x 3x  2  A. ( ;  1)  (2;) B. C. [1; 2] D. (1; 2)
Câu 15: Cho a, b là các số nguyên dương nhỏ hơn 10 và log b là nghiệm của phương trình a
25x  5x  6  0 . Trong các khẳng định sau, khẳng định nào đúng? A. ab  20. B. ab 10. C. ab  25.
D. ab 15.
Câu 16: Cho a, b, c, là các số nguyên.Biết đạo hàm của hàm số   2    3 2 2 x y x x e có dạng 3  x y e  2 '
ax bx c. Tính giá trị của biểu thức S  2a b  . c A. S  2  B. S  12  C. S  48 
D. S  2
Câu 17: Cho a, b, c là các số thực dương thỏa mãn b  log a 1, c  log b  2. Trong các khẳng định sau,
khẳng định nào đúng? b 1
A. log(ab)  b c  3. B. log(ab)  . c  2 a
C. log(ab)  (b 1)(c  2). D. log
b c 1. b
Câu 18: Đạo hàm của hàm số sin 2  x y e tại x = 0 là? A. 2 B. 3 C. 1 D. 4
Câu 19: Gọi M là giá trị lớn nhất của hàm số 2
y  ln(x  3)  x trên đoạn [2; 5]. Trong các khẳng định
sau, khẳng định nào đúng? A. 3M e  6. B. M  0. C. 5M e  22  0.
D. M  2  0.
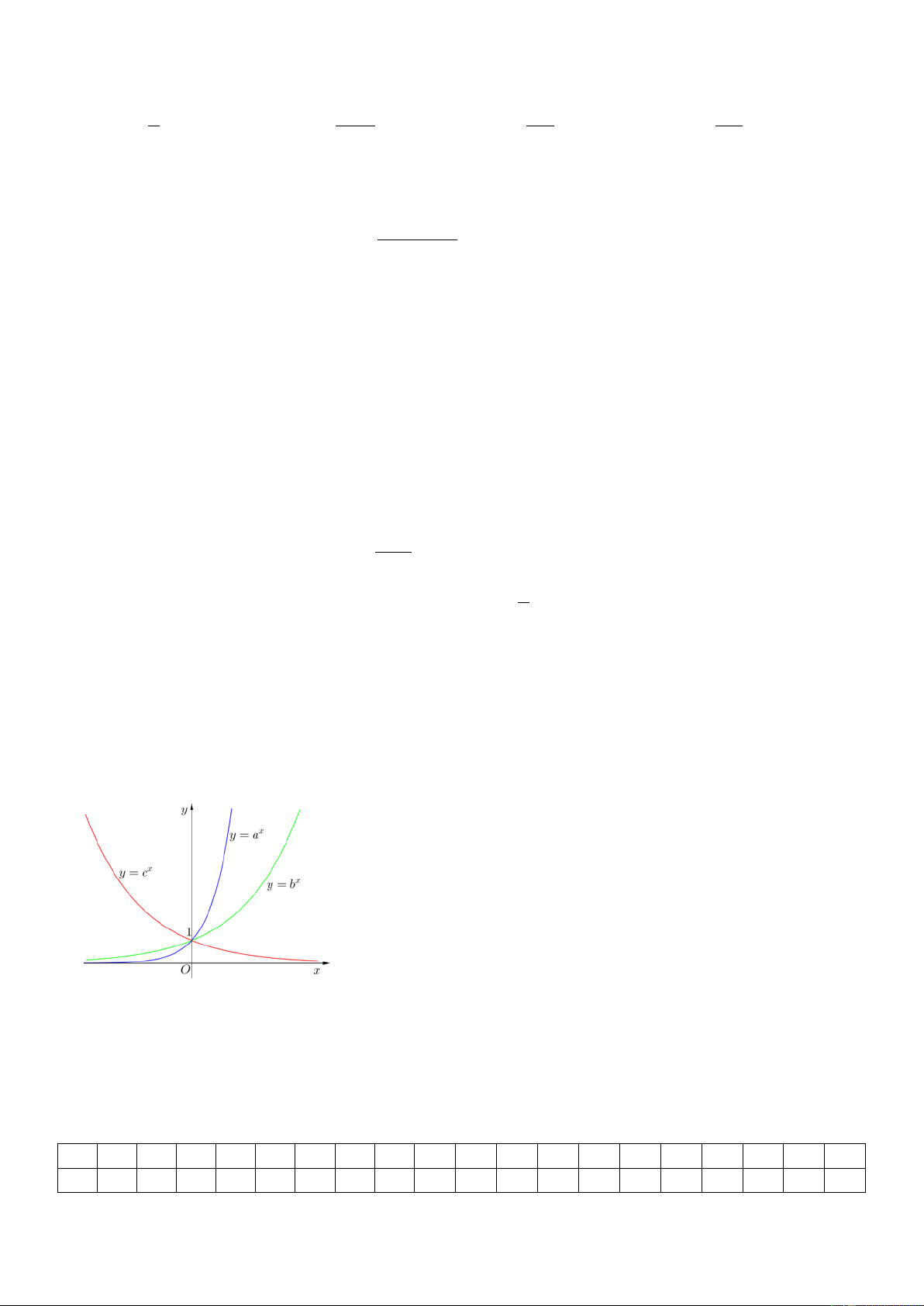
Câu 20: Cho các hàm số  x,  x y a y b ,  x y
c có đồ thị như hình vẽ.
Khẳng định nào dưới đây là đúng?
A. 0  c a  . b
B. 0  c b  . a
C. 0  a b  . c
D. 0  b c  . a Đáp án 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 D B D A A B D D D C D B C D B A A A A B Trang12 ĐỀ 7
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12 ĐỀ 12
Câu 1: Tập xác định của hàm số 2  (  3  2)e y x x là? A. ( ;  2)   ( 1
 ;) B. (2; 1) C. D.  \{  2; 1  }
Câu 2: Tổng các nghiệm của phương trình 1 2  1bằng? 4  lg x 2  lg x A. 20 B. 10 C. 1 D. 110
Câu 3: Cho hàm số y  log x . Khẳng định nào sau đây là đúng? a 1
A. Tập xác định là 
B. đạo hàm y '  x ln a
C. đồ thị hàm số không có tiệm cận
D. đồ thị hàm số không cắt trục hoành 1
Câu 4: Cho y  ln . Biểu thức , . x y 1 là: x 1 A. y B. y e C. e D. 1 x
Câu 5: Tính đạo hàm của hàm số y  . 2x A. ' 2  x y
(x ln 2 1). B. ' 2  x y
(1 x ln 2). C. '  2x y (1 x ln 2). D. y ' 2  x log 2. e
Số nghiệm của phương trình 2 log x  log (9 ) x  2  0 là: 3 3 Câu 6: A. 3 B. 1 C. 2 D. 0
Câu 7: Xác định m để phương trình: 4x  2 .2x m
m  2  0 có hai nghiệm phân biệt? Đáp án là: A. m  2 B. – 2  m  2 C. m  2 D. m
Câu 8: Cho các số thực dương a,b, với a 1. Khẳng định nào sau đây sai?  a  1  a A. log  B. log 1 log b a    a   b  log bb a a 1 C. log ab b D. log ab   log b 2   a   1loga 2 a a
Câu 9: Cho log b  3, log c  2  . Hãy tính log  2 b c . 2  2 2 A. 4 B. 7 C. 6 D. 9
Câu 10: Bất phương trình 3log  x   1  log
2x 1  3 có tập nghiệm là 3 3   3  1   1  A. 1; 2 . B. 1; 2. C.  ; 2   . D.  ; 2  .   2   2 
Câu 11: Tổng các nghiệm của phương trình log x  2 log x  2  log . x log x là? 2 7 2 7 A. -3 B. -11 C. 11 D. 3 x x
Câu 12: Phương trình 2 1 1 2
 3 có hai nghiệm a,b . Tính a b a . b A. 1 log . 3 B. 1   2log . 3 1 2 log . 3 D. 1.  2 2 C. 2
Câu 13: Đặt a  log 5; b  log 5 . Hãy biểu diễn log 20 theo a và b. 3 4 15 a 1 ab 1 aA. log 20  B. log 20  15
b a b 15 a 1 bTrang13 b 1 ba 1 bC. log 20  D. log 20  15 a 1 a 15 b 1 a
Câu 14: Tìm tập xác định của hàm số y  log 4  x 1 2   A.  ;  4 B.  ;  2 C.  ;  2 D. 2;4
Câu 15: Biết rằng 4x 4
x  23 , giá trị của biểu thức 2x 2   x A là: A. A  23 B. A  5 C. A  21 D. A  2 5
Câu 16: Gọi x , x là hai nghiệm của phương trình 4x  8.2x  4  0 . Tính giá trị biểu thức P x x . 1 2 1 2 A. –4. B. 4. C. 0. D. 2.
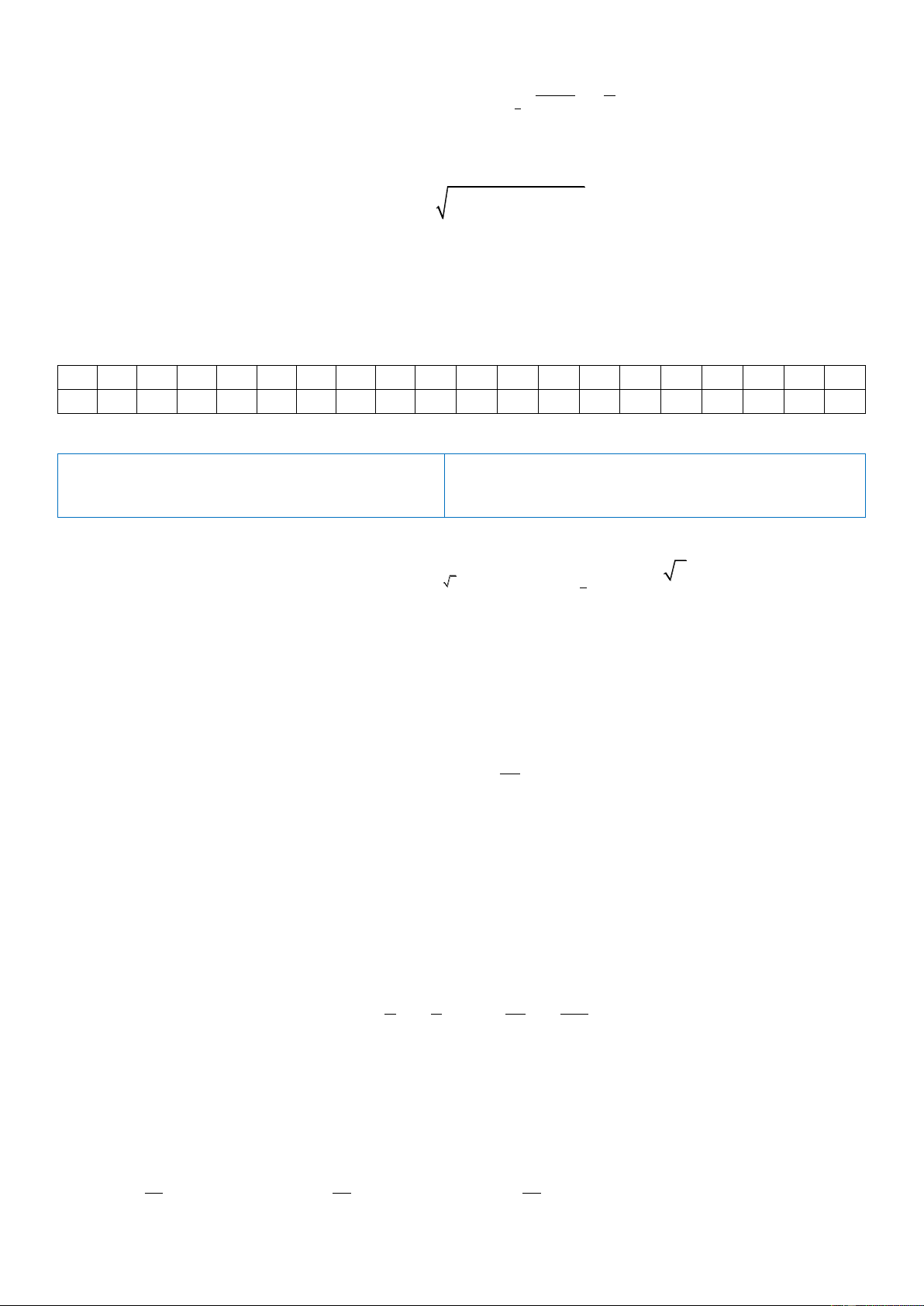
Câu 17: Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số
x,  x,  x y a y b y c được cho trong
hình vẽ bên. Mệnh đề nào dưới đây đúng?
A. b 1 a  . c
B. a 1 c  . b
C. b c a 1.
D. a 1 b  . c y x
Câu 18: Cho 0  x y  1, đă ̣t 1 m  ln  ln 
 . Mê ̣nh đề nào sau đây đúng?
y x  1 y 1 x A. m  4 B. m 1 C. m  4 D. m  2 2  x e  3 
Câu 19: Cho các hàm số y  log , x y  , y  log , x y    
 . Trong các hàm số trên có bao nhiêu 2 1      2 2  
hàmsố đồng biến trên tập xác định của hàm số đó? A. 3 B. 4 C. 1 D. 2 2 Câu 20: Cho hàm số  x y
e . Trong các khẳng định sau, khẳng định nào đúng?
A. y " 2xy ' 2 y  0.
B. y " xy ' 2 y  0.
C. y " 2xy ' 2 y  0.
D. y " 2xy ' 2 y  0. Đáp án 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 B D B B B C C A A A C D D C B D B A C C ĐỀ 8
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12
Câu 1: Tìm mê ̣nh đề nào sai?
A. Nếu a 1 thì log M  log N M N  0. a a
B. Nếu 0  a  1 thì log M  log N  0  M N. a a
C. Nếu M , N  0 và 0  a  1 thì log M N M N a  .   log .log . a a
D. Nếu 0  a 1 thì log 2022  log 2023. a a
Câu 2: Tìm phát biểu sai?
A. Đồ thị hàm số  x y
a a  0, a  
1 nằm hoàn toàn phía trên Ox .
B. Đồ thị hàm số  x y
a a  0, a  
1 luôn đi qua điểm A0;  1 . Trang14x x 1 
C. Đồ thị hàm số y a , y  , 0  a    
1 đối xứng nhau qua trục Ox .  a   x x 1 
D. Đồ thị hàm số y a , y  , 0  a    
1 đối xứng nhau qua trục Oy .  a
Câu 3: Tâ ̣p xác đi ̣nh D của hàm số y   x x x1 3 2 4 3 2 . A. 0  ;1  2; . B.  \ 0,1,  2 . C.  ;  01;2. D.  ;  02;.  5  x
Câu 4: Gọi D là tập xác định của hs y   x  2 34  log
. Khẳng định nào đúng? 2 x  3 A. D   3  ;2.
B. D  2;  5 . C.  3  ;2  . D D. 2;  5  . D  2 3 2   1  3 2 3 3 3 2  2  2 
Câu 5: Giá trị của biểu thức A  . 4 3 3 2  2 A. 1. B. 3 2 1. C. 3 2 1. D. 1. 
Câu 6: Rút gọn biểu thức 1log 2 1log 3 P ab a b .
A. P a  . b
B. P  2a  3 . b C. 2 3
P a b .
D. P  2  2a  3 . b 49
Câu 7: Cho log 25 = a và log 5 = b . Tính 1000 log theo a và . b 7 2 3 5 8 12b  9a 12b  9a
12b  9a ab 4b  3a A. . B. . C. . D. . 1000ab 1000ab 1000 3000ab Câu 8: Cho hàm số   –   x f x
x e . Đồ thị của hàm số /
f x là đồ thị nào trong các đồ thị sau y y y y 1 2 1 2 O A. hình I x B. Hình O II C. Hình O III D. Hình IV x x O Câu 9: Đa ̣o hàm x y ' của hàm số  log (  x y x e ). 2 Hình I Hình II Hình III Hình IV 1 x e 1 x e 1 1 x e A. y '  . B. y '  . C. y '  . D. y '  . ln 2 x x exxeln2 xxeln2
Câu 10: Cho a, b, c, là các số nguyên. Biết đạo hàm của hàm số  x x y 2 2 2   có dạng   ax - ' 2  2 bx y
.ln .c Tính giá trị của biểu thức K 2ab .c A. K  0. B. K  2. C. K  2.  D. K  4.  Câu 11: Cho hàm số  . x y
x e . Tìm đẳng thức đúng? A. / – =2 x y y e . B. / –  x y y e . C. / –  x y y e . D. /   x y y e .
Câu 12: Mộtgiáoviênsau10nămtíchgópđượcsốtiền100triệuđồngvàquyếtđịnhgửivàongân hàng với lãi suất
7, 5% một năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ nhập
vào vốn ban đầu. Nếu lãi suất không thay đổi thì tối thiểu sau bao nhiêu năm thì giáo viên đó có được số
tiền là 165 triệu đồng (tính cả gốc lẫnlãi)? A. 5năm. B. 6năm. C. 7năm. D. 8năm.
Câu 13: Cho hai số thực a, b với 1 a b . Khẳng đi ̣nh nào sau đây là đúng:  x 2023  A. log 2023  1. B. 1  x  0. 2022    2022  Trang15x 2022  C. 1  x  0.   D. log 2022  1.  2023  2023
Tâ ̣p nghiê ̣m của phương tri log 2x 1  2
 có dạng a  log c trong đó a,b,c  , b , Câu 14: ̀nh 2  
b  0, c  0, b  1. Tính giá trị của biểu thức M a  2b 3 . c A. M  7.  B. M  1.  C. M  11.  D. M  13. 
Câu 15: Phương trình 8.3x  3.2x  24  6x có tích các nghiệm. A. 3. B. 0. C. 10. D. 30.
Câu 16: Phương trình 2
log (x  4x 12)  2 3
A. Có hai nghiệm dương.
B. Có một nghiệm âm và một nghiệm dương.
C. Có hai nghiệm âm. D. Vô nghiê ̣m. a
Câu 17: Cho phương trình 2log3 3
x  81x có một nghiệm dạng
a,b . Tính tổng ab b
A. a b  5.
B. a b  4.
C. a b  7.
D. a b  3. x
Câu 18: Giải bất phương trình 2 2
x  4. Tập nghiệm có dạng  ;
a b. Tính hiệu b  . a
A. b a 1.
B. b a  3. 
C. b a  1. 
D. b a  3. 3 x x 1 
Câu 19: Số nghiệm nguyên của bất phương trình   x 1    x3 10 3 10 3 . A. 1 B. 3 C. 0 D. 2
Câu 20: Gọi S là tập nghiệm của bất phương trình log  x 1 6   36x  2.
 Tìm giá trị lớn nhất của hàm 1  5 số  6x y trên S. A. 4. B. 1. C. 5. D. 3. Đáp án 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 C C A B B B B D D B C C C D A C B D B C ĐỀ 9
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12
Câu 1: Cho a  0 , a  1. Tìm mệnh đề đúng?
A. Tập xác định của hàm số  x y
a là khoảng 0; .
B. Tập giá trị của hàm số y  log x là tập  . a
C. Tập xác định của hàm số y  log x là tập  . a
D. Tập giá trị của hàm số  x y a là tập  .
Câu 2: Cho 3 số thực a, b, c thỏa mãn a  0, a  1, b  0, c  0 . Tìm phát biểu đúng?
A. log b  log c b  . c
B. log b  log c b  . c a a a a
C. log b  log c b  . c
D. Cả 3 đáp án trên đều sai. a a Câu 3: Cho hàm số 2
y  log x  (5  2x) . Số giá trị nguyên thuộc tập xác định của hàm số. 2 A. 2. B. 1. C. 3. D. 4. Trang16 10  x
Câu 4: Tâ ̣p xác đi ̣nh D của hàm số y  log . 3 2 x  3x  2
A. D  1;.
B. D   
;1  2;10. C. D   ;  10.
D. D  2;10. 2 3 2 5 4
a . a. a . a
Câu 5: Cho số thực a  0, a  1. Giá trị của biểu thức A  log . a 4 3 a 193 73 103 43 A. . B. . C. . D. . 60 60 60 60 2 4 2 2    
Câu 6: Rút gọn biểu thức 3 9 9 9
P   a 1 a a 1 a 1.     1 4 4 1 A. 3 P a 1. B. 3 P a 1. C. 3 P a 1. D. 3 P a 1.
Câu 7: Cho a  log 15, b  log 10. Biểu diễn theo a, b của 200 log 50 . 3 3 3
A. 300a b   1 .
B. 400a b   1 .
C. 100(a b 1).
D. 200a b   1 .
Câu 8: Hàm số nào có đồ thị như hình vẽ ỏ bên đây?  x 1  A. y  .    3  2  1  B. y  .    2  C.  3x y . x
D. y   2 . 3  1 
Câu 9: Cho a   1  a   1
. Khi đó ta có thể kết luận về a là: a  2 a 1
A. 1 a  2. B. a  2. C. .  D. .  0  a 1 a  2
Câu 10: Tìm đạo hàm ’ y của hàm số  2   1 3 . x y x A. '  3x y 22xln3ln3. B. '  3x y
2 2xln3ln3. x xC. y    x   1 ' 2.3 2 1 . x 3 . D. '  2.3x y ln 3. x
Câu 11: Tìm đạo hàm ’
y của hàm số y  . 2022x 1 x ln 2022 1 A. / y  . B. / y  . 2 2022 x 2022x ln 2022 1 x 1 x ln 2022 C. / y  . D. / y  . 2022x ln 2022 2022x 1
Câu 12: Cho hàm số y  ln . Đẳng thức nào đúng? 1 x A. ’
y  2 y  1. B. ’  y y e  0. C. ’ yy  2  0. D. ’  4 y y e  0.
Câu 13: Một người gửi ngân hàng 150 triệu đồng theo thể thức lãi kép lãi suất 0, 58% trên1 tháng. Sau ít
nhất bao nhiêu tháng người đó có 180 triệu đồng? A. 34. B. 32. C. 31. D. 30.
Câu 14: Gọi x là nghiệm của phương trình log x  1.  Tìm mệnh đề đúng? 0 5
A. x  ( ; 1  ). B. x  6  ; 2  . C. x  0;1 . D. x  3 ( ;  . ) 0   0   0 0 Trang17
Câu 15: Phương trình 2 2 x x x x 1 4 2  
 3 có hiệu các nghiệm x x bằng: 1 2 A. 2. B. 1. C. 0. D. 1. 
Câu 16: Tìm các giá trị thực của tham số m để phương trình 4x  2   1 .2x m
 3m 8  0 có hai nghiệm trái dấu. 8 8 A. 1   m  9. B. m  . C. m  9. D. m  9. 3 3
Câu 17: Phương trình 3. log x  log 3x 1  0 có tổng các nghiệm 3 3 A. 81. B. 77. C. 84. D. 30.
Câu 18: Số nghiê ̣m nguyên của bất phương trình 3x 9.3  x  10 là: A. 0. B. 1. C. 2. D. Vô số.
Tổng S các nghiệm nguyên của bất phương trình 2 5 2
log x  25log x  750  0 Câu 19: 3 3
A. S  925480. B. S  38556.
C. S  378225.
D. S  388639.
Câu 20: Tìm giá trị lớn nhất của hàm số 2
y  log (x x ). 2 1 1 A. 2. B.  . C. 2.  D. . 4 4 Đáp án 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 B C A B A C D A C B D B B C B C C B A D ĐỀ 10
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12
Câu 1: Cho 3 số dương a, b, c và khác 1. Chọn khẳng định sai?
A. log bc  log b  log . c
B. log c  log b.log . c a a a a a b 1 C. loga b a  . a D. log b  . a log a b
Câu 2: Cho a và b là các số thực dương, a  1. Chọn khẳng định đúng? A.  2 log
a ab 1 4log . b B.  2 log
a ab  4  2log . b a a a a C. a ab a b D. a ab a b a  2 log    4log   a . a  2 log    22log   a . 
Câu 3: Tập xác định D của hàm số y   x x 10 2 2 .
A. D   \ 0;  2 . B. D   .
C. D   \ 0; 2.
D. D   \   2 .
Câu 4: Tập xác định D của hàm số ln 3  x y
 2có dạng D   ;
 log b với a, b là các số a ,
nguyên dương và a  1. Tính giá trị của biểu thức P a  2 . b A. P  3. B. P  7. C. P 1. D. P  5. x
Câu 5: Cho hàm số f x 9 
, x   . Biết a b  3. Tính giá trị của K f a  f b  2. 3  9x 1 3 A. K 1. B. K  2. C. K  . D. K  . 4 4 Trang18
Câu 6: Cho 3 số dương a, b, c khác 1 và thỏa mãn: log b  log b  log 2022.log .
b Chọn khẳng định a c a c đúng? A. ac  2022. B. ab  2022. C. bc  2022.
D. abc  2022.
Câu 7: Cho P  log 16m và a  log m , với m là số dương khác 1. Mệnh đề nào đúng? m 2  4  3 A.  1 a P . B. 2 P  3  a . C. a P . D. a P . 4 a a
Câu 8: Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số
x,  x,  x y a y b y c được cho trong
hình vẽ bên. Mệnh đề nào dưới đây đúng?
A. b 1 a  . c
B. a 1 c  . b
C. b c a 1.
D. a 1 b  . c
Câu 9: Mệnh đề nào sau đây sai? 4  6 
A.  3  2   3  2 .
B.  11  2   11  2 . 3 4 3 4
C. 2  2  2  2 .
D. 4  2  4  2 .
Câu 10: Tìm đạo hàm y ' của hàm số 3 2022   x y x e . A. 2 2022 '  3  2022 x y x e . B. 2 2022 '  3  ln 2022 x y x e . C. 2 2022 '  3  ln 2022 x y x e . D. 2 2022 '  3  2021 x y x e .
Câu 11: Cho hàm số y x ln x , điểm cực trị của hàm số thuộc khoảng nào sau đây?  1   1  A. 2;3 . B. ;1   . C. 1; 2 . D. 0;   .  2   2 
Câu 12: Anh Thành vay 20 triệu đồng của ngân hàng để mua laptop và phải trả góp trong vòng 3 năm với
lãi suất 1,1% mỗi tháng. Hàng tháng anh Thành phải trả 1 số tiền cố định là bao nhiêu để sau 3 năm hết
nợ (làm tròn đến đơn vị đồng) A. 675.807 đồng B. 673.807 đồng C. 672807 đồng D. 677807 đồng Câu 13: Hàm số .   x y x e thỏa hệ thức A. . x ’
y  1 xy  0. B. . x ’
y  1  xy  0. C. . x ’
y  1 xy  0. D. 2 . x ’
y  1 xy  0.
Câu 14: Phương trình x3 2
 4 có nghiệm thuộc tập nào? A.  ;  4. B.  ;  8. C.  ;  5. D.  ;  3. 5
Câu 15: Giải phương trình log x  log 3 
ta được hai nghiệm x x . Khẳng định nào sau đây đúng? 3 x 2 1 2 x x x x A. 2 3x   0. B. 2 3x   0.
C. 1  x  10.
D. 1  x  9. 1 3 1 3 2 2 3 3
Câu 16: Phương trình 2 2
4x  6.2x  8  0 có mấy nghiệm? A. 3. B. 1. C. 2. D. 4.
Câu 17: Tìm tất cả các giá trị của tham số thực m để phương trình 6x  (3  ).2x x
m  0 có nghiệm thuộc khoảng 0  ;1 . A. 4;10. B. 3; 4. C. 2;4. D. 3; 4.
Câu 18: Tập nghiệm S của bất phương trình: 2 4 log x  5log x  6  0. 1 0,2 25 Trang19  1 1   1  A. S   . B. S  .  C. S  ; .   D. S   ;  .   125 25   25 
Câu 19: Cho hàm số y  log
 2x 2x4 . Tập nghiệm của bất phương trình y'  0. 1  3 A.  ;  0. B. 1; . C.  ;   1 . D. 2; . 2
Câu 20: Giá trị nhỏ nhất của hàm số  x y e . A. 1. B. 1.  C. e. D. 0. Đáp án 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 C C A B A A C B C A D A A B B D A C C A ĐỀ 11
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12
Câu 1: Cho các số thực a b  0. Mệnh đề nào sau đây là sai?  a  2 A. ln
 ln a  ln b .   B.
ab   2a  2 ln ln ln b .  b  2 1  a
C. ln  ab   ln a  ln b. D. 2 2 ln
 ln a  ln b .   2  b
Câu 2: Hàm số y x  2 x   x  2 ln 1
 1 x . Mệnh đề nào sau đây sai?
A. Hàm số có tập xác định là  . .
B. Hàm số có đạo hàm số: / y   2
ln x  1 x .
C. Hàm số đồng biến trên 0; .
D. Hàm số nghịch biến trên 0; .
Câu 3: Tập xác định D của hàm số y   x x  2022 2 3 . A. D   3  ;. B. D   3  ;.  3   3 
C. D R \ 1  ; . D. D   ;     1;  .  4   4  2x 1  a b
Câu 4: Tâ ̣p xác đi ̣nh D của hàm số y  log 1 có dạng D  ;
, với a, b, c, d là các số 0,8   x  5  d c
nguyên khác 0. Tính giá trị của biểu thức 2 P a d  . bc A. 2 P  2 . B. 3 P  2 . C. 1 P  3 . D. 4 P  3 . 10  
Câu 5: Rút gọn biểu thức đơn giản biểu thức : 3 6 12 5 2 K x y  
xy  ,với x  0   A. K  0. B. 2 K  2xy . C. 2 K  xy . D. 2 K  2  xy .  a b
Câu 6: Giá trị của biểu thức T
ab : a    b 2 3 3 3 . 3 3  a bA. T  2. B. T 1. C. T  3. D. T  1.  Trang20
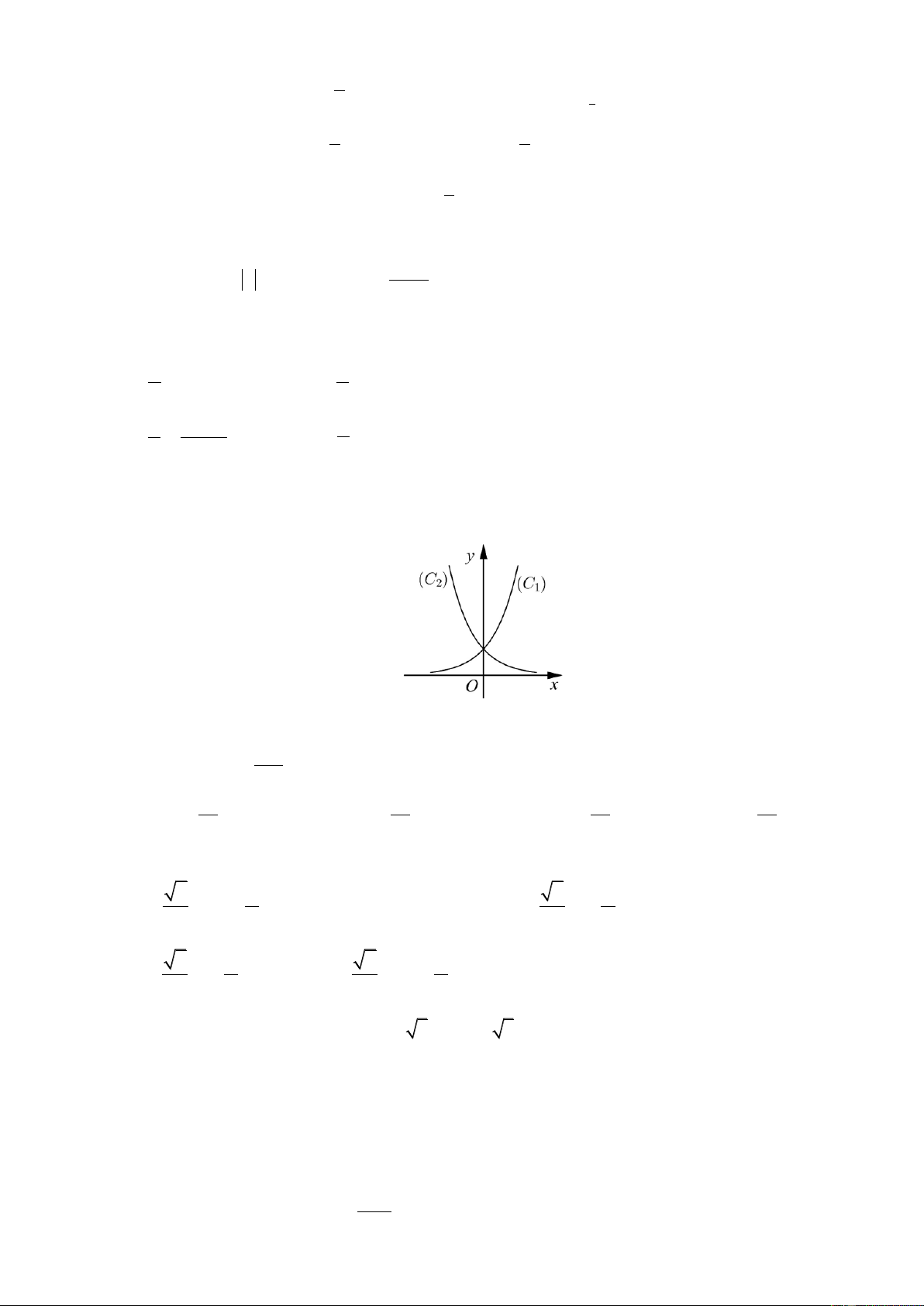
Câu 7: Cho đồ thị hai hàm số  x y
a và y  log x như hình vẽ: b Nhận xét nào đúng?
A. a  1, b  1.
B. a  1, 0  b  1.
C. 0  a  1, 0  b  1.
D. 0  a  1, b  1. Câu 8: Cho log 5  ; a log 3  .
b Tính log 135 theo a, . b 2 2 3  3 3  3   3 A. log 135  a
b . B. log 135  a b . C. log 135  a b . D. log 135  a b . 3 b 3 b 3 a 3 a 2 4 7 4
Câu 9: Cho a, b là 2 số thực dương khác 1 thỏa mãn 3 5 a a , log  log
. Khi đó khẳng định nào b 5 b 3 đúng?
A. 0  a  1;b  1
B. a  1;b  1.
C. 0  a  1; 0  b  1.
D. a  1; 0  b  1. .
Câu 10: Tính đạo hàm y ' của hàm số 2 y  log (x 1). 2022 2x A. '  x y . B. y '  . 1011 2 (x 1) ln 2022 1 1 C. y '   . D. y '  . 2 x   1 ln 2022  2x  1
Câu 11: Đa ̣o hàm của sin cos 1 2 .2   x x y . A. sin cos 1 ' sin .cos .2 .2    x x y x x . B. sin cos 1 ' (cos sin )2    x x y x x .ln 2. C. sin cos 1 ' sin 2 .2 .2    x x y x . D. sin cos 1 ' cos 2 .2 .2    x x y x .
Câu 12: Theo số liệu từ tổng cục thống kê, dân số Việt Nam năm 2015 là 91,7 triệu người. Giả sử tỉ lệ
tăng dân số hàng năm của Việt Nam trong giai đoạn 2015 - 2030 ở mức không đổi là 1,1%, tính số dân Việt Nam năm 2030. A. 0,165 91, 7.e (triệu người) B. 1,65 91, 7.e (triệu người); C. 0,011 91, 7.e (triệu người) D. 0,11 91, 7.e (triệu người). Câu 13: Cho hàm số 2 y x e sin 5 .
x Đẳng thức nào sau đây đúng?
A. y”  4 ’
y  29 y  0.
B. y”  4 ’
y  29 y  0.
C. y”  4 ’
y  29 y  0.
D. y”  4 ’
y  29 y  0.
Câu 14: Gọi x là nghiệm của phương trình 3x2 3
 27. Tìm mệnh đề đúng. 0 A. x  4;6 .
B. x  0; 2 . C. x  3;5 . D. x  1  ;1 . 0   0   0   0   x
Câu 15: Cho biết phương trình log  1 3
1  2x  log 2 có hai nghiệm x và x . Tính tổng 3  1 1 2 3 1 x 2  27  27x S . A. S 180 . B. S  45 . C. S  9 . D. S  252 .
Câu 16: Tìm các giá trị thực của tham số m để phương trình 2 2
log x  log x  3  m có nghiệm x 1;8. 2 2
A. 2  m  6.
B. 2  m  3.
C. 3  m  6.
D. 6  m  9.
Câu 17: Tìm các giá trị thực của tham số m để phương trình log  3
x  3x m có 3 nghiệm thực phân 2  biệt. A. m 1.
B. 0  m 1. C. m  0. D. m  1. Trang21  3x x 1 3
Câu 18: Mọi nghiệm của bất phương trình: log 3 1  log 
  đều là nghiệm của bất phương 4   1  16  4 4 trình nào sau đây: A. 2
x(x  3x  2)  0. B. 2
x(x  3x  2)  0. C. 2
x(x  3x  2)  0. D. 2
x(x  3x  2)  0.
Câu 19: Số nghiệm nguyên của bất phương trình: log  2
3x  4x  2 1  log  2 3x  4x  2 9 3  A. 1 B. 2 C. 0 D. 3
Câu 20: Tìm giá trị lớn nhất của hàm số y   2
ln x  2x  2 trên đoạn 0;  3 . A. a m x y  ln17. B. a
m x y  ln 20. C. a m x y  ln 5. D. a m x y  ln 2. 0; 3 0; 3 0; 3 0; 3 Đáp án 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 C D A B A B B A B B B A D B A A A B D A ĐỀ 12
ĐỀ ÔN TẬP CHƯƠNG MŨ LÔGARIT Thuvienhoclieu.Com GIẢI TÍCH 12
Câu 1: Cho log a  3, a  0 . Tính tổng 2 S  log
a  log a  log a  2log a. 2   2 1 2 2 2 A. S  6. B. S  2. C. S  3. D. S  5.
Câu 2: Bất phương trình  2
log 2x 11x 151 có bao nhiêu nghiệm nguyên? A. Vô số. B. 3. C. 4. D. 5.
Câu 3: Giải phương trình x x 1 4 2  
 3  0 bằng cách đặt  2x t
, (t  0). Mệnh đề nào dưới đây đúng?
A. 4t  3  0. B. 2 2t  3  0. C. 2
t  2t  3  0. D. 2
t t  3  0. 2  x x 1 
Câu 4: Tìm tập xác định D của hàm số 4 y  log 3  .     27 
A. D   ;   1  3;.
B. D  1;3.
C. D  1;.
D. D  1;  3 .
Câu 5: Một người gửi 50 triệu đồng vào một ngân hàng với lãi suất 6%/năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo.
Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 100 triệu đồng, bao gồm gốc và lãi?
Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền. A. 13 năm. B. 11 năm. C. 12 năm. D. 14 năm. 1 2 98 99
Câu 6: Biết a  ln 2, b  ln 5 . Tính S  ln  ln  ... ln  ln theo a và . b 2 3 99 100
A. S  a  . b
B. S  2a  2 . b
C. S a  . b
D. S   2a  2b.
Câu 7: Tìm tập nghiệm S của phương trình log (2x 1)  log (x 1)  1. 3 3 A. S    4 .
B. S  3;  4 . C. S   2  ;  1 . D. S    1 .
Câu 8: Cho log x  3, log x  4 với a, b là các số thực lớn hơn 1. Tính P  log . x a b ab 12 7 1 A. P  . B. P  . C. P  . D. P 12. 7 12 12 Trang22 1
Câu 9: Cho log a  2 và log b
. Tính I  2 log log (3a)  log b . 3  3  2 3 2 2 1 4 3 5 A. I  4. B. I  . C. I  . D. I  0. 2 4 x 1
Câu 10: Tập nghiệm S của bất phương trình 1 5   0. 5
A. S  1; .
B. S   ;  2.
C. S   ;  2  . D. S   2  ;. x x x 1 Câu 11: Biết  3
3  log x e  3x *  3 ln a
ce , (a,b,c   ) . Tính  b c a S a b c . 2 x ln b A. S 18. B. S  40. C. S  20. D. S  44.
Câu 12: Cho a là số thực dương khác 1. Mệnh đề nào dưới đây đúng với số thực dương x, y ? x x A. log
 log (x y). B. log  log x  log . y a a y a a a y x log x x C. log  a . D. log  log x  log . y a a a a y log y y a
Câu 13: Cho hai hàm số  x,  x y a y
b với a, b là hai số thực dương khác 1, lần lượt có đồ thị là C và 1 
C như hình bên. Mệnh đề nào dưới đây đúng? 2 
A. 0  a b 1.
B. 0  a 1 . b
C. 0  b 1 . a
D. 0  b a 1. ln Câu 14: Cho hàm số  x y
, mệnh đề nào dưới đây đúng? x 1 1 1 1
A. 2 y  xy  .
B. y  xy   .
C. 2 y  xy   .
D. y  xy  . 2 x 2 x 2 x 2 x
Câu 15: Với số thực dương x, y tùy ý, đặt log x   , log y  . Mệnh đề nào dưới đây đúng? 3 3 3  3 x      x   A. log    9   . B. log     . 27        y   2  27 y 2   3  3 x    x     C. log 
   . D. log    9   . 27       y 2   27  y   2  x x
Câu 16: Tập nghiệm S của phương trình 2  3  2  3  4 là tập con của của tập nào dưới đây? A. I   2  ;1;0;  2 . B. H   1  ;0;  2 .
C. K  1; 2;3;  4 . D. T   1  ;0;1;  2 .
Câu 17: Tìm tập nghiệm S của bất phương trình 2
log x  5log x  4  0. 2 2
A. S   ;  
1 4;. B. S   ;  216;.
C. S  2;16.
D. S  0; 216; . x 1
Câu 18: Tính đạo hàm của hàm số y  . 4x Trang23 1 2(x 1) ln 2 1 2(x 1) ln 2 1 2(x 1) ln 2 1 2(x 1) ln 2 A. y  . B. y  . C. y  . D. y  . 2 2 x 2 2 2 x 2x 2x 2
Câu 19: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
f (x)  x  ln 1 2x trên đoạn  2  ;0. 1 1
A. Max f (x)  4 và Min f (x)  .
B. Max f (x)  4  ln 5 và Min f (x)   ln 2.  2  ;  0  2  ;0 4   2;0  2  ;0 4
C. Max f (x)  ln 5 và Min f (x)  ln 2.
D. Max f (x)  2
 và Min f (x)  0.   2;0  2;0    2  ;  0  2  ;  0
Câu 20: Tìm tập xác định D của hàm số y    x 1 2 5 4 . A. D   2  ;2. B. D   2  ;2.
C. D   \  2  ;  2 .
D. D   ;  2  2;. Đáp án 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D Trang24