Chuyên Đề Bất Phương Trình Mũ Và Lôgarit Vận Dụng Cao Ôn Thi Tốt Nghiệp THPT Có Đáp Án Và Lời Giải
Chuyên đề bất phương trình mũ và logarit vận dụng cao ôn thi tốt nghiệp THPT có sẵn đáp án để học sinh dễ dàng đối chiếu so sánh kết quả chuẩn xác hơn. Tài liệu là kiến thức từ cơ bản đến nâng cao khác nhau. Mời các em tham khảo thêm nhé!
Chủ đề: Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit 41 tài liệu
Môn: Toán 12 3.9 K tài liệu
Tác giả:
Preview text:
DẠNG TOÁN : BẤT PHƢƠNG TRÌNH MŨ -LOGARIT VẬN DỤNG CAO
I. KIẾN THỨC CẦN NHỚ:
1. Bất phƣơng trình mũ + Nếu f x g x a 1 thì a a
f x g x. + Nếu f x g x
0 a 1 thì a a
f x g x.
+ Nếu a chứa ẩn thì f x g x a a a
1 f x g x 0 .
2. Bất phƣơng trình logarit
+ Nếu a 1 thì log f x log g x f x g x a a
+ Nếu 0 a 1 thì log f x log g x f x g x a a
log B 0 a B a 1 1 0
+ Nếu a chứa ẩn thì log A . a 0 A 1 B 1 0 log B a
II. CÁC DẠNG BÀI TẬP TƢƠNG TỰ
Lý thuyết về bất phương trình mũ – lôgarit
Nhận dạng và phát triển các dạng toán tương tự... BÀI TẬP MẪU
Câu 40.(ĐỀ MINH HỌA BGD 2020-2021) : Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có
không quá 10 số nguyên x thỏa mãn x 1
2 2 2x y 0?
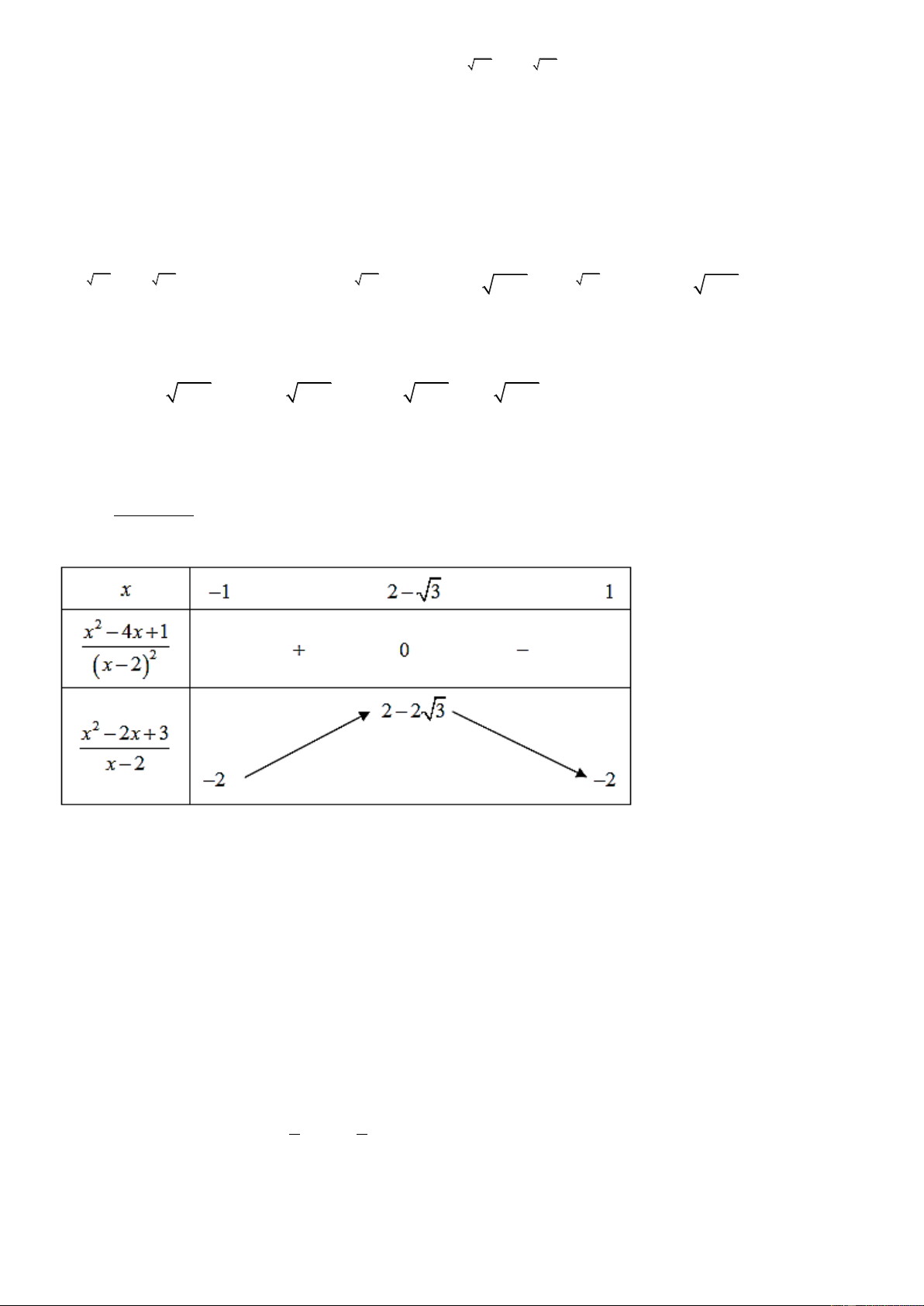
A.1024. B.2047. C. 1022. D.1023. Lời giải Chọn A Cách 1:
Ta có: y 1 log y 0 . Gọi x 1
2 2 2x y 0 (*) 2 x x 2 1 1 2 2 0 2 x +Trƣờng hợp 1: 2 2 VN 2x y 0 x 2 y 1
x log y 0 2 Trang1 x x 2 1 1 2 2 0 2 x 1 +Trƣờng hợp 2: 2 2
x log y 2 2x y 0 2 x 2 y x log y 2
Theo đề bài, ứng với mỗi số nguyên dương y có không quá 10 số nguyên x thỏa mãn bất phương trình (*)
tương đương với tập nghiệm 1 S ;log
y chứa không quá 10 số nguyên, nghĩa là: 2 2 y y 10 log y 10 y 2 1024 2
Vậy có tất cả 1024 giá trị y thỏa mãn yêu cầu đề. Cách 2: Đặt 2 2x t
0 thì ta có bất phương trình (2t 2)(t y) 0 hay (t
)(t y) 0(*). 2 2 2 2 x 1
Vì y nên y , do đó (*) t y
2 y x log . y 2 2 2 2 2
Nếu log y 10 thì x {0,1, 2,,10} đều là nghiệm nên không thỏa yêu vầu bài toán. Suy ra log y 10 2 2 hay 10
y 2 1024 , mà y nên y {1, 2,,1024}.
BÀI TẬP TƢƠNG TỰ VÀ PHÁT TRIỂN Mức độ 3
Câu 1. Giả sử x ; y là cặp nghiệm nguyên không âm có tổng S x y lớn nhất của bất phương trình 0 0 0 0 4x 2 .3 x
y 9.2x 3y 10 , giá trị của S bằng
A. 2 . B. 4 . C 3 . . D. 5 . Lời giải: Chọn C Ta có 4x 2 .
x 3y 9.2x 3y 10 2x
1 2x 3y 10 0.
Vì 2x 1 0 nên bất phương trình tương đương với 2x 3y 10 0 .
Với cặp số x, y nguyên không âm thì x, y chỉ có thể là: 0;0,0;
1 , 0; 2, 1;0, 1; 1 , 2;0;2; 1 , 3;0 . Vậy tổng S 3.
Câu 2. Có bao nhiêu cặp số nguyên dương ;
x y thỏa mãn 1 x 10 và 2 9y 3y x x
A. 10. B. 11. C. 9 . D. 8 . Trang2 Lời giải Chọn A Ta có 2 y y 2 9 3 9y 3y x x x x .
Xét hàm số đặc trưng f t 2
t t với t 0.
Ta có f t 2t 1 0,t 0 suy ra f t là hàm số đồng biến trên t 0. Suy ra 2
9y 3y 3y 3y x x f x f x .
Với giả thiết 1 x 10 ta có: 3y 10 y 2 . TH1: 1
y 1 3 x 10 x 3; 4;5;6;7;8;9;1 0 có 8 cặp nghiệm ; x y thỏa mãn. TH2: 2
y 2 3 9 x 10 x 9;1 0 có 2 cặp nghiệm ; x y thỏa mãn.
Vậy có tất cả 10 cặp nghiệm ; x y thỏa mãn.
Câu 3. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn x, y 5;50 và 2 2
x y 2y x 2 y 2y 2
A. 2 . B. 5 . C. 15. D. 11. Lời giải Chọn C Có 2 2 2 2
x y 2y x 2
y 2y 2 x x y 2y 2
y 2y 2 (2)
Xét hàm số f t t t trên khoảng 0; ta có: f t 1 1
0,t 0 f t đồng biến. 2 t
f x f 2y y 2 2 2
2 x y 2y 2.
Do x, y 5;50 nên y y y 2 2 5 2 2 50 4
1 49 1 y 6
Do y và y 5;50 nên y 5 hoặc y 6 . Với y 5 có 2
37 y 2 y 2 x 50 x 37;38;...;5 0 có 14 cặp ; x y thỏa mãn. Với y 6 có 2
50 y 2 y 2 x 50 x 50 có 1 cặp ; x y thỏa mãn.
Vậy có tất cả 15 cặp ; x y thỏa mãn. Trang3
Câu 4. Có bao nhiêu cặp số nguyên dương ;
x y thỏa mãn log 2 2y x 1
A. 10. B. 11. C. 9 . D. 8 . Lời giải Chọn D y x x y 2 2 0 log 2 2 1
2x 2y 10 (vì ;
x y nguyên dương).
2x 2y 10
;x y nguyên dương nên 2 2y 10 2y x
8 1 y 3 .
Với y 1 2x 8 x 4 x 1;2;3; 4 có 4 cặp ; x y thỏa mãn.
Với y 2 2x 6 x 3 x 1;2; 3 có 3 cặp ; x y thỏa mãn.
Với y 3 2x 2 x 1 x 1 có 1 cặp ; x y thỏa mãn.
Vậy có tất cả 8 cặp ;
x y thỏa mãn đề bài.
Câu 5. Có bao nhiêu cặp số nguyên dương ; x y thỏa mãn 2 x 2 cos 2.2 sin 2 y x y
A. 1. B. 0 . C. 2 . D. 3 . Lời giải: Chọn B 2 2 Ta có x 2 cos y x 1 cos y 2
2.2 x sin y 2 2 x 1 2 cos y . (1)
Đặt 2t 2t f t t f t
.ln 2 1 0,t 0 .
Suy ra hàm số y f t là hàm số đồng biến trên 0; .
Suy ra f x f 2 y 2 2 1 1 cos
x 1 cos y x sin y x 0 vô lí.
Vậy không tồn tại cặp số nguyên dương ;
x y nào thỏa mãn đề bài.
Câu 6. Tập các cặp số nguyên dương ;
x y thỏa mãn điều kiện y x x x 2 log 5 2
A. 6 . B. 4 . C. 5 . D. 7 . Lời giải: Chọn A Trang4
x 0, x 1
x 0, x 1 Có log y x x y x x y x x . (1) x 2 5 2 2
2 5 0 5 0 2 2
y x x 5 x y x 5 Vì ;
x y nguyên dương nên x 2;3; 4
x 0, x 1
Với x 2 có
1 y 6 5 0 y 1;2; 3 có 3 cặp ; x y thỏa mãn. y 2 5
x 0, x 1
Với x 3 có
1 y 12 5 0 y 1; 2 có 2 cặp ; x y thỏa mãn. y 3 5
x 0, x 1
Với x 4 có
1 y 20 5 0 y 1 có 1 cặp ; x y thỏa mãn. y 4 5
Vậy có tất cả 6 cặp ;
x y thỏa mãn yêu cầu đề bài. x x m
Câu 7. Có bao nhiêu m nguyên dương để bất phương trình 2 2 2 3 3 3
1 3m 0 có không quá 30 nghiệm nguyên?
A. 28. B. 29. C. 30. D. 31. Lời giải: Chọn D
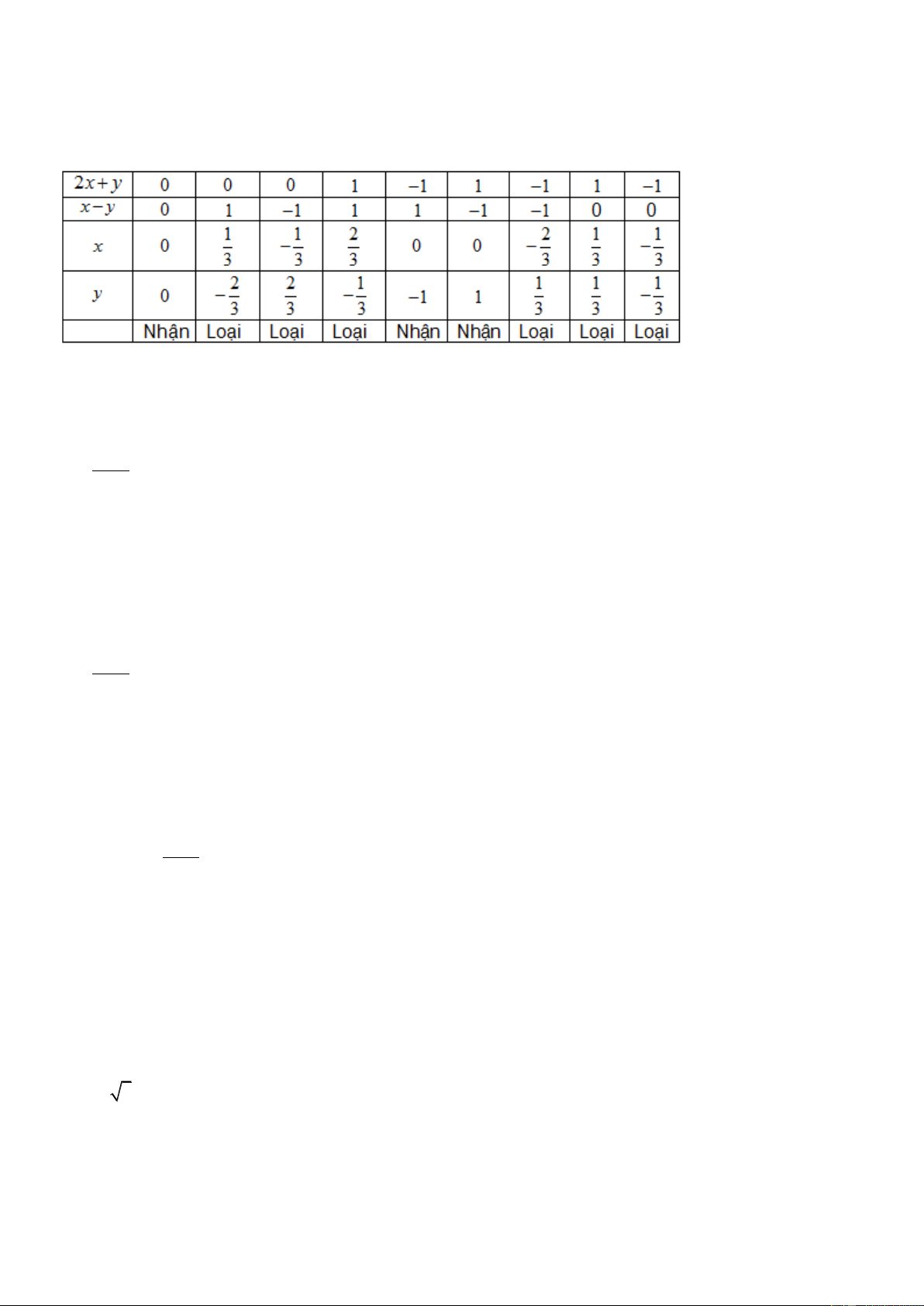
2 x2 x m2 m 2 3 3 3
1 3 0 9.3 x 9.3 .
x 3m 3x 3m 0 9.3x 3x 3m 3x 3m 0
3x 3m 9.3x 1 0
Ta có 3x 3m 0 x . m
9.3x 1 0 x 2. Bảng xét dấu
Ta có tập nghiệm S 2 ;m.
Tập hợp các nghiệm nguyên là 1 ;0;1;...;m 1 .
Để có không quá 30 nghiệm nguyên thì m 1 28 m 29. Trang5
Câu 8. Biết ;
x y là cặp nghiệm nguyên của bất phương trình log y x y thỏa x 5 1 log x 1 0
mãn y x 10 , hỏi hiệu số y x lớn nhất bằng bao nhiêu:
A. 7 . B. 5 . C. 2 . D. 9 . Lời giải: Chọn D
x 0, x 1
x 0, x 1
Điều kiện y x 5 0 . y x 5 y 0 Suy ra log y 1 x
x 0, x 1
x 0, x 1
x 0, x 1 Suy ra log y x y y x y x x 5 1 log x
1 0 5 0 5 y x y x y x x x 2 5 log 5 1 0 5
Theo giả thiết y x 10 suy ra 2x 5 y x 10 x 3 x 2; 3 .
Với x 2 9 y 12 y 10;1 1 .
Với x 3 11 y 13 y 1 2 . Trong các cặp ;
x y ta thấy hiệu y x 9 là lớn nhất.. 2 2 2 2
x xy y
Câu 9. Số cặp nghiệm ;
x y nguyên của bất phương trình x y 5 2 2 3 2 .2
x y 3 là
A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn D 2 2
Từ x y 2 2 2
5 x 2 xy2 y 9 x y x y 2 .2
x y2 3 2x y2 .2
x y2 2 3 3 0 (*)
a 2x y2 0 Đặt
khi đó (*) đưa về: .2ab 0 .2a .2 b a b a b . b
x y2 3 3
Vì a 0 b 0 .
Xét hàm số .2t f t t
,t 0; có 2t .2t f t t
.ln 2 0,t 0; .
Suy ra f a f b a b a b 0 . Trang6 2 2 2 2
Suy ra 2x y x y 3 0 2x y x y 3 .
Với giả thiết x,y là các số nguyên nên x y2 2 và x y2
chỉ có thể xẩy ra các trường hợp sau:
Vậy có tất cả 3 cặp nghiệm thỏa mãn.
Câu 10. Có bao nhiêu cặp số nguyên dương ;
x y với x 2020 thỏa mãn điều kiện x 2 2 2 log
x 4x 4y 8y 1. 2 y 1
A. 2020. B. vô số. C. 1010. D. 4040. Lời giải Chọn C x 2 log
4y x 4x 8y 1 log x 2 log y 1 4 y 2 1 x 22 2 2 1 2 2 2 y 1
log x 2x 22 log 2 y 1 2 y 1 1 . 2 2 2
Xét hàm số f t 2
log t t trên 0;. 2 1
Ta có f t
2t 0t 0; f t đồng biến trên 0;. t ln 2
1 f x 2 f 2y 2 x 2 2y 2 x 2y .
Mà 0 x 2020 0 y 1010 .
Vậy có 1010cặp số nguyên dương ; x y .
Câu 11. Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình x2 3
33x 2m 0 chứa không quá 9 số nguyên?
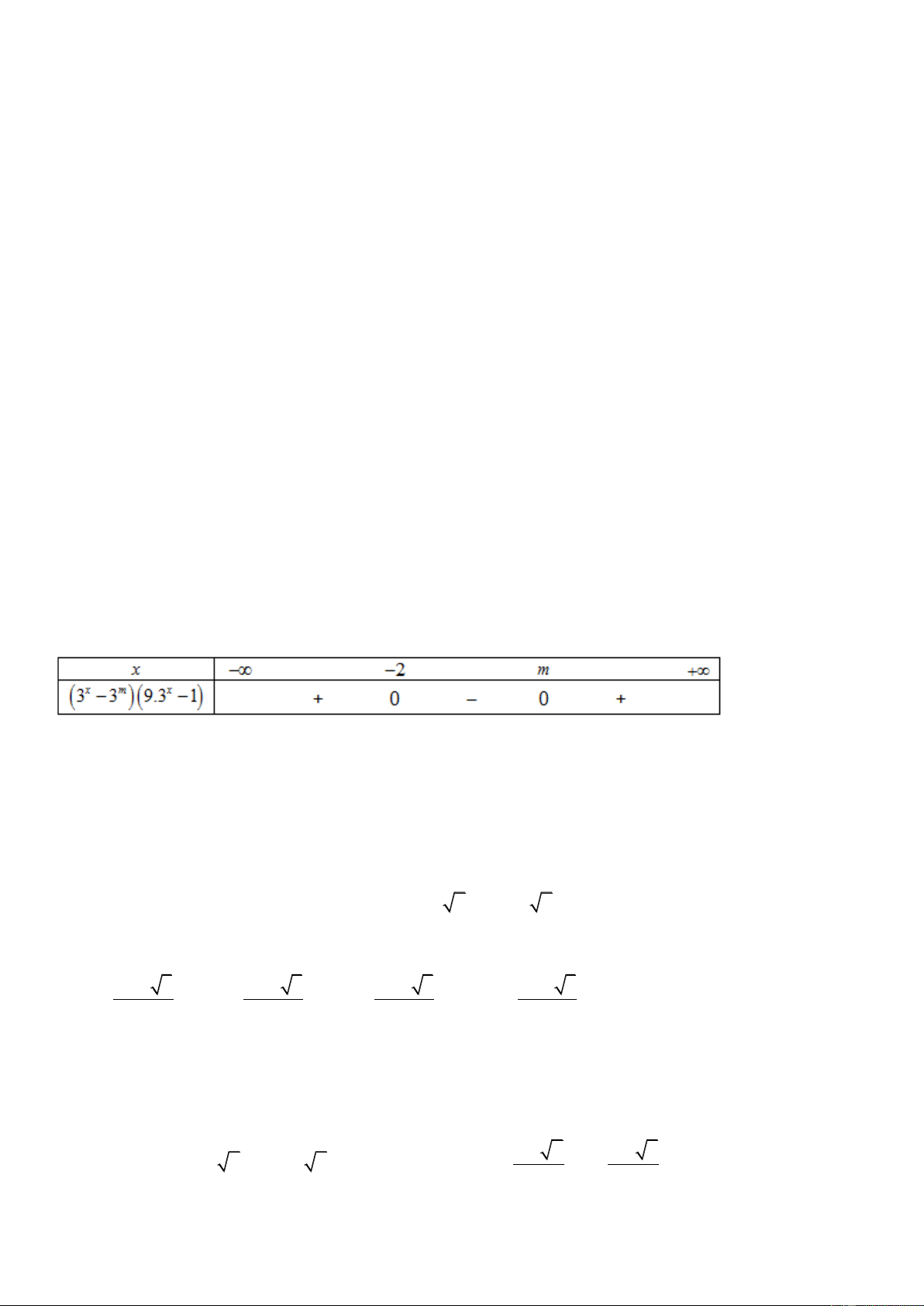
A.1094. B.3281. C.1093. D.3280. Lời giải Trang7 Chọn D Gọi x2 3
33x 2m 0 (1) Đặt 3x t
,t 0, bất phương trình (1) trở thành 9t 3t 2m 0 2 + Nếu 3 3 2m m
1 thì không có số nguyên dương m nào thỏa mãn yêu cầu bài toán. 9 18 + Nếu 3 3 2m m
thì bất phương trình 3 2 t 2m . 9 18 9
Khi đó tập nghiệm của bất phương trình 3 1 là S ;log 2 m . 3 2 Để 3
S chứa không quá 9 số nguyên thì log 2m 8 8 0 m 3 2
Vậy có 3280 số nguyên dương m thỏa mãn. 2 2 x
Câu 12. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình 3 x 92x m 0 có 5 nghiệm nguyên?
A. 65021. B. 65024 C. 65022. D. 65023. Lời giải Chọn B
Gọi 2xx 2 3
9 2x m 0 (1) x 1
Trường hợp 1: Xét 2xx 2 3
9 0 x x 2 . x 2 m 1 m 1 x Khi đó, 2 (1) 2 m 2 x log m
log m x log m 2 2 2
Nếu m 1 thì vô nghiệm.
Nếu m 1 thì (2) log m x log m . 2 2
Do đó, để bất phương trình có 5 nghiệm nguyên thì tập hợp ;
1 2; log m; log m có 5 giá trị nguyên 2 2
3 log m 4 512 m 65536. 2 Trang8
Suy ra có 65024 giá trị m nguyên thỏa mãn.
Trường hợp 2: Xét 2xx 2 3
9 0 x x 2 1
x 2 . Vì 1
;2 chỉ có hai số nguyên nên không có
giá trị m nào để bất phương trình có 5 nghiệm nguyên.
Vậy có tất cả 65024 giá trị m nguyên thỏa yêu cầu bài toán. x x m
Câu 13. Có bao nhiêu m nguyên dương để bất phương trình 2 2 2 3 3 3
1 3m 0 có không quá 30 nghiệm nguyên?
A. 28. B. 29. C. 30. D.31. Lời giải Chọn B
2 x2 x m2 m 2 3 3 3
1 3 0 9.3 x 9.3 .
x 3m 3x 3m 0
3x 3m 9.3x 1 0 Ta có 3x 3m 0
x m
9.3x 1 0 x 2. Bảng xét dấu
Ta có tập nghiệm S 2 ;m.
Tập hợp các nghiệm nguyên là 1 ;0;1;...;m 1 .
Để có không quá 30 nghiệm nguyên thì m 1 28 m 29.
Câu 14. Cho bất phương trình x 1
.3 (3 2)(4 7)x (4 7)x m m
0, với m là tham số. Tìm tất cả các
giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ;0 . 2 2 3 2 2 3 2 2 3 2 2 3 A. m . B. m . C. m . D. m . 3 3 3 3 Lời giải Chọn B x x 4 7 4 7 x 1
.3 (3 2).(4 7)x (4 7)x m m
0 3m (3m 2). 0 3 3 Trang9 x Đặt 4 7 t
, vì x 0 nên 0 t 1. 3 m 2 t BPT trở thành 3 2 2 3m
t 0,t 0; 1 3m , t 0 ;1 t t 1 2 t 2 Xét f (t) , t 0 ;1 t 1 2 t t t 2 2 f (t) t t 0 3 1 2 1 Vậy yêu cầu bài toán 2 3 6 2 2 3 3m m . 3 3
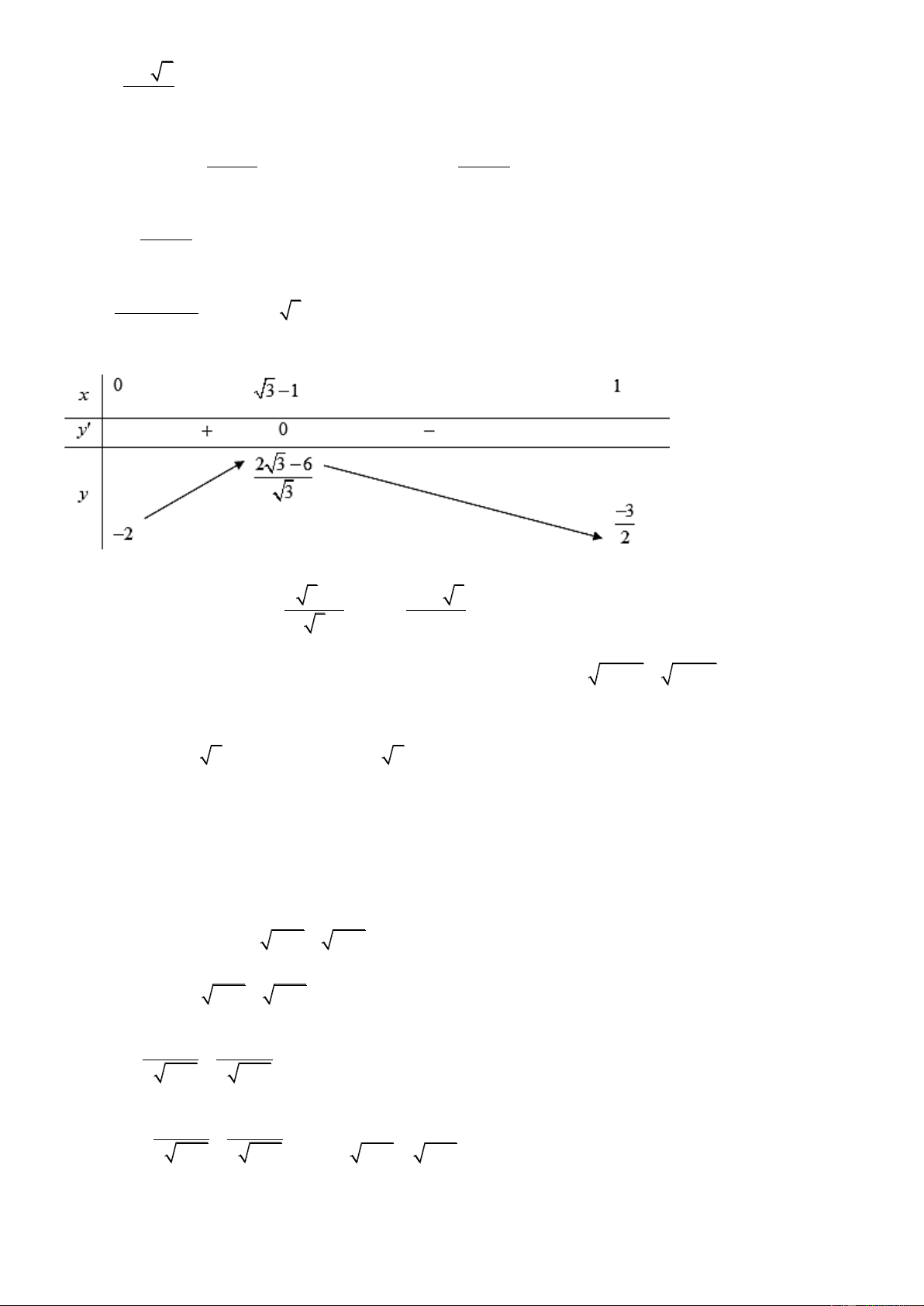
Câu 15. Tìm tất cả các giá trị thực của tham số m để bất phương trình 2x 3 5 2x m nghiệm đúng
với mọi x ;l og 5 . 2
A. m 4 . B. m 2 2 . C. m 4 . D. m 2 2 . Lời giải Chọn A
Đặt 2x t . Vì x log 5 x log 5 2 0 2 2 0 t 5. 2
Yêu cầu bài toán trở thành t 3 5 t m , t 0;5 .
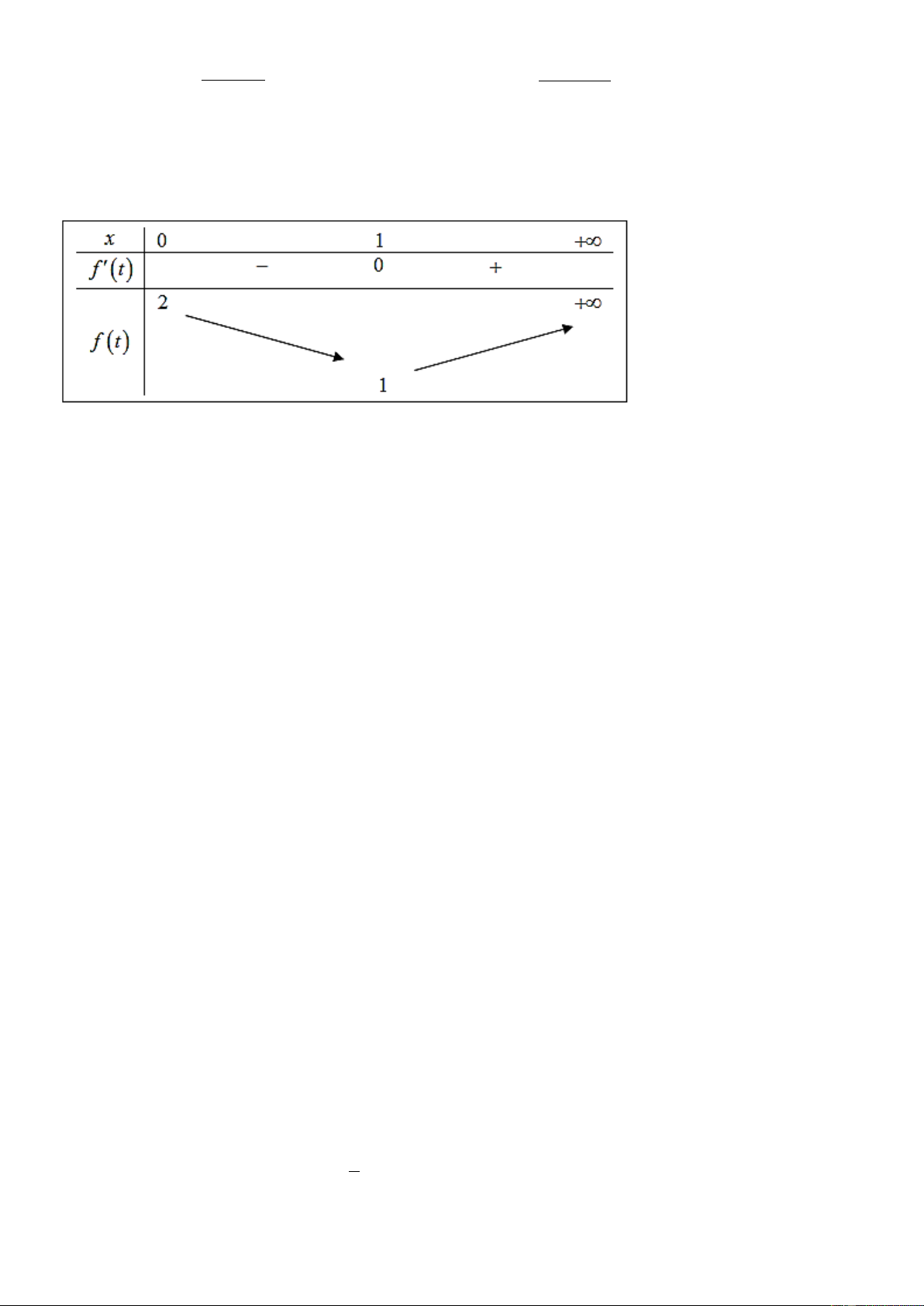
Xét hàm số f t t 3 5 t với x .
Có f t 1 1 . 2 t 3 2 5 t f t 3 t 5 1 1 0 0 t 1 2 t 3 2 5 t
t 3 5t Bảng biến thiên Trang10
Dựa vào bảng biến thiên ta có:. 2 2 2 x x x x x x
Câu 16. Tìm tất cả các giá trị của m để bất phương trình 2 1 m m 2 1 2 1 .4 1 2 .10 . m 25 0 nghiệm đúng với mọi 1 x ;2 . 2 100 1 100
A. m 0 . B. m . C. m . D. m . 841 4 841 Lời giải Chọn A 2 x x x x x x .
m 4 1 2m 2 2 1 2 1 2 1 2 1 .10 . m 25 0,x ;2 2 2 x x 2 2 1
2 x 2 x 1
m m 5 5 1 1 2 . . m 0,x ;2 1 2 2 2 2 2 x 2 x 1 x 2 x 1 Đặt 5 5 5 t t (x) .ln .
2x 2 0 x 1. 2 2 2 Bảng biến thiên
Từ bảng biến thiên ta có 4 2 t ; 25 5 t
1 m 1 2m 4 2 4 2 2 .t .
m t 0,t ; m ,t ; 2 25 5 t 2t 1 25 5 t m min (*) 2
4 2 t t ; 2 1 25 5 Xét hàm số t 4 2 f t , t ; 2 t 2t 1 25 5 t 1 l f t 2 t 1 2 f t t , 0 1 0 t 1 l
t 2t 2 2 1 Trang11 4 100 2 10 100 Ta có f , f
min f t 25 841 5 49 4 2 ; 841 25 5 100 (*) m . 841 Vậy 100 m
thì bất phương trình nghiệm đúng với mọi 1 x ;2 . 841 2
Câu 17. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 728 số nguyên y thỏa mãn log 2
x y log (x y) ? 4 3
A. 59. B. 58. C. 116. D. 115. Lời giải Chọn C
Bất phương trình đã cho tương đương log (x y) log 2
x y 0 (1) 3 4
Xét hàm số f (y) log (x y) log 2 x y . 3 4
Tập xác định D (x;) . Với mọi 1 1 x ta có 2
x x nên f ( y) x D (x y) ln 3 0, 2 x yln 4
f ( y) đồng biến trên khoảng (x;) .
Do y là số nguyên thuộc (x; ) nên y x k, k .
Giả sử y x k là nghiệm của bất phương trình (1) thì f ( y) f (x k) 0 .
Mà x 1 x 2 ...
x k và f ( y) đồng biến trên khoảng (x;) , suy ra
f (x 1) f (x 2) ...
f (x k) 0 , nên các số nguyên x 1, x 2,..., x k đều là nghiệm của
(1), hay nói cách khác bất phương trình (1) sẽ có k số nguyên y thỏa mãn yêu cầu ứng với mỗi x .
Để có không quá 728 số nguyên y thì f (x 729) 0 log 729 log 2
x x 729 0 3 4 1 13469 1 13469 2
x x 3367 0 x 2 2
Mà x nên x 5 7, 56,...,5 8 .
Vậy có 116 số nguyên x thỏa yêu cầu bài toán. Trang12 2 x x 1 2 x 1 7 7 2020x 2020
Câu 18. Điều kiện của m để hệ bất phương trình có nghiệm là : 2 x
m 2 x 2m3 0 A. m 3. B. 2
m 1. C. 1
m 2. D. m 2. Lời giải Chọn D 2x x 1 2 x 1 2 x x 1 x
x x 2 x 1 7 7 2020 2020 7 1010. 2 1 7
1010.2 x1* Hàm số ( ) 7t f t
1010.t đồng biến trên .
* f 2x x 1 f 2 x 1 2x x 1 2 x 1 1 x 1.
Hệ bất phương trình đã cho có nghiệm 2
x m 2 x 2m 3 0 có nghiệm x 1 ;1 2 x 2x 3 m
có nghiệm x 1 ;1 . x 2
Từ bảng biến thiên ta thấy m 2
là các giá trị cần tìm.
Câu 19. Có bao nhiêu giá trị nguyên dương của m để bất phương trình 2 2 2
9m x 4m x .5m x m có nghiệm?
A. 10. B. Vô số. C. 9 . D. 1. Lời giải Chọn B
Từ giả thiết, ta chỉ xét m 2 2 m x m x 2 2 2 9 4
Ta có: 9m x 4m x .5m x m m 1 5 5 Trang13 2 2 2 2 2 m x m x m x m x m x 9 4 9 4 6 Có 2 . 2 . 5 5 5 5 5 2 m x Do đó nếu 6
x là nghiệm của bất phương trình 2
m thì x cũng là nghiệm của 0 5 0 2 2 m x m x 9 4 m . 5 5 2 m x Ta xét các giá trị 6
m làm cho bất phương trình 2
m 2 có nghiệm. 5 2 2 m x m x 6 6 m Vì 2 m , m 5 5 2 m 1 m 2 m x log x log , với m . 6 2 2 6 m 2 5 5 m Vậy với 1
m thì bất phương trình 2 có nghiệm tương ứng là x log . 2 6 m 2 5
Suy ra có vô số giá trị
m làm cho bất phương trình 1 có nghiệm.
Câu 20. Có bao nhiêu giá trị nguyên của tham số m 1
0;10 để bất phương trình sau nghiệm đúng với x x
x : 6 2 7 2 3 7 1 2x m m 0
A. 10. B. 9 . C. 12. D. 11. Lời giải Chọn C Ta có: x x x x
6 2 7 2 3 7 1 2x m m
0 2x 3 7 2 3 7 1 2x m m x
x m 3 7 3 7 2 m 1 2 x Đặt 3 7 1 3 x t 7 , t 0 . 2 t t t
Yêu cầu bài toán t m 2 1 2 2
. m 1,t 0 m ,t 0 t t 1 Trang14 t t 2 t t Xét hàm số 2 3 f t 2 2
trên khoảng 0; , ta có f t t 1 t 2 1 t 3
f t 0
. Khi đó, ta có bảng biến thiên sau t 1
Từ bảng biến thiên trên ta suy ra để bất phương trình đã cho nghiệm đúng thì m 1. Suy ra trong đoạn 10
;10 có tất cả 12 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Mức độ 4
Câu 1. Có bao nhiêu cặp số nguyên dương ;
x y với x 2020 thỏa mãn log
1 2 2 1 4y x x y . 2
A. 5 . B. 1010. C. 6 . D. 2020. Lời giải Chọn A
Theo đề bài log
1 2 2 1 4y log 2 1 2 2 1 2 2 y x x y x x y 2 2 Đặt log 2 1 2 1 2t t x x . 2 Ta có t 2 2 2 y t 2y 1 .
Xét hàm số 2t f t t trên R 2t f t
.ln 2 1 0t R f t đồng biến trên R .
1 f t f 2y t 2y log 2 x 1 2y 2 2 2 1 2 y x 2 y 1 x 2 1. y 1 Mà 2 1 x 2020 2
1 2020 y 1 log 2019 . 2 2 Trang15 Vì
y Z y 1; 2;3; 4; 5 .
Vậy có 5 cặp điểm cặp số nguyên dương ; x y . 2 2
Câu 2. Xét các số thực thỏa mãn x y 1 2 2 2 2 24x x y x
. Giá trị lớn nhất của biểu thức 8x 4 P
gần với giá trị nào sau đây nhất? 2x y 1
A. 9 B. 6 . C. 7 . D. 8 . Lời giải Chọn C 2 2 x y 1 2 2 2 2 2.4x x y x 2 2
x y 2 x 1 2 2 2
x y 2x 2 x 2 2
y x 2 1 2 2 1 y 1 0 1
Đặt t x 2 2 1 y
t t t x 2 2 1 2 1 0 0 1 1 y 1 8x 4 P
2P 8.x .
P y P 4 0 2x y 1
Yêu cầu bài toán tương đương:
2P 8 P 4 1 3P 12 2P 82 2
P 5 5 P 5 5 2P 82 2 P
Câu 3. Có bao nhiêu bộ ;
x y với x,y nguyên và 1 x, y 2020 thỏa mãn
xy x y 2y 2x 1 2 4 8 log
2x 3y xy 6 log ? 3 2 y 2 x 3
A. 2017. B. 4034. C. 2 . D. 20172020 . Lời giải Chọn B * ,
x y : x, y 2020 *
x, y : x, y 2020
+ Điều kiện 2x 1 2 y . 0, 0
x 3, y 0 x 3 y 2 Trang16 x y
BPT cho có dạng x y 4 2 3 2 log
1 x 4 y 2 log 1 0 . 2 3 x 3 y 2 x 4 2
+ Xét y 1 thì thành x 3log 1 3 x 4 log
0 , rõ ràng BPT này nghiệm đúng với mọi 2 3 x 3 3 x 4 2
x 3 vì x 3 0,log
1 log 0 1 0,3 x 4 0,log 0 . 2 2 3 x 3 3
Như vậy trường hợp này cho ta đúng 2017 bộ ; x y ; x
1 với 4 x 2020, x .
+ Xét y 2 thì thành 4 x 4log 1 0 , BPT này cũng luôn đúng với mọi x mà 4 x 2020, x . 3
Trường hợp này cho ta 2017 cặp ; x y nữa.
+ Với y 2, x 3 thì VT * 0 nên không xảy ra.
Vậy có đúng 4034 bộ số ;
x y thỏa mãn yêu cầu bài toán.
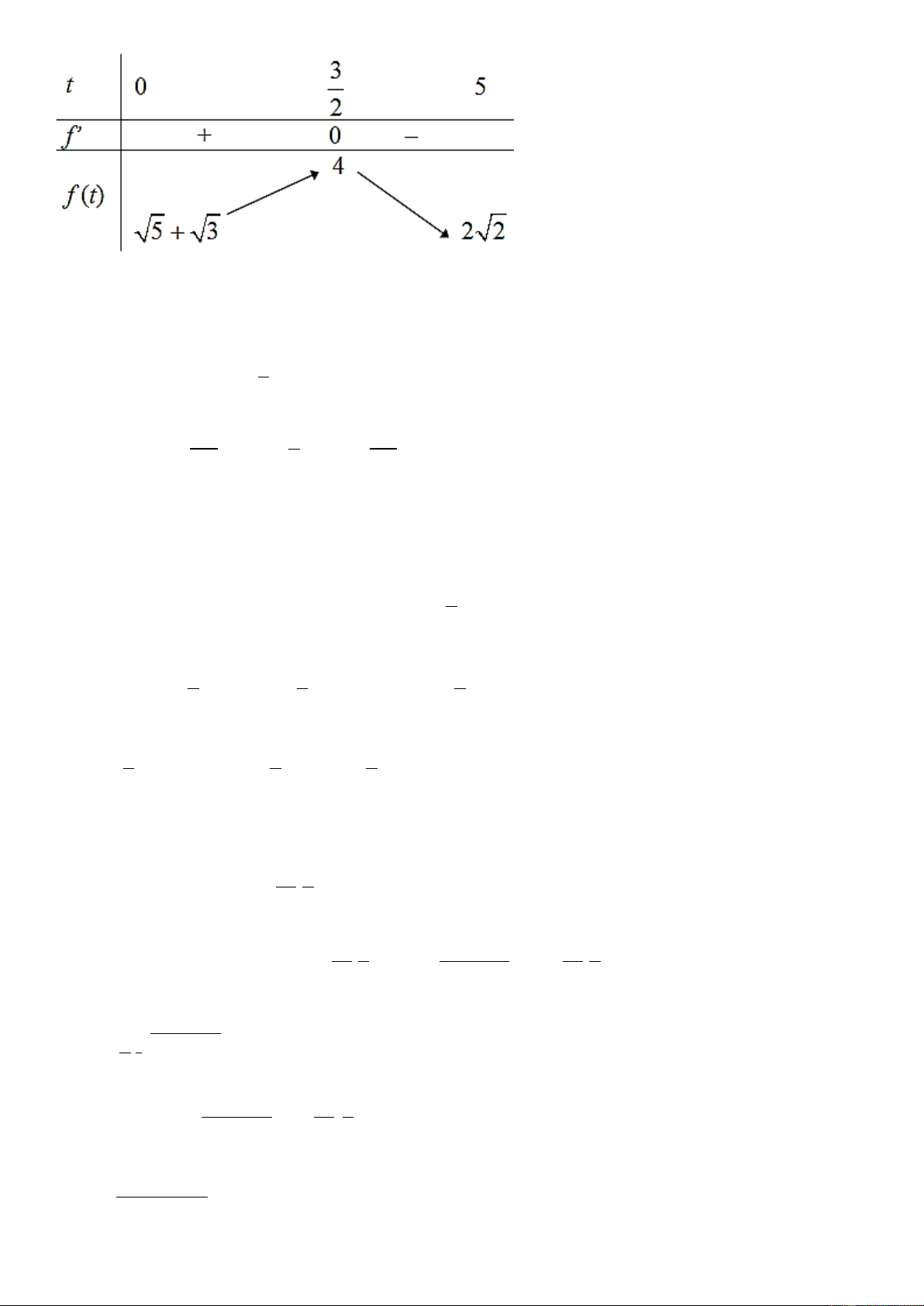
Câu 4. Cho x,y là các số thực thỏa mãn bất phương trình: log
2 2 3 8y x x y
. Biết 0 x 20 , số 2
các cặp x,y nguyên thỏa mãn bất phương trình trên là
A. 2 . B. 33. C. 35. D. 5 . Lời giải: Chọn C y x Ta có log 2 2 log 1 2 3 8 2 log 3 1 2 y x x y x 3y . (1) 2 2
Xét hàm số 2t f t
t có 2t f t
ln 2 1 0,t . Khi đó 1
log 1 3 log 3 1 3 2 y f x f y x y x 1. 2 2 Với 3 0 20 1 2 y x
21 0 y log 211,4 . 8
Vì y y 0 ;1 .
Với y 0 có x 0 nên có 21 cặp ; x y thỏa mãn.
Với y 1 có x 7 nên có 14 cặp ; x y thỏa mãn.
Vậy có tất cả 35 cặp ; x y thỏa mãn.
Câu 5. Có bao nhiêu giá trị nguyên của tham số m 1
0;10 để bất phương trình sau nghiệm đúng với x x
x : 6 2 7 2 3 7 1 2x m m 0 Trang17
A. 10. B. 9 . C. 12. D. 11. Lời giải: Chọn D Ta có: x x x x
6 2 7 2 3 7 1 2x m m
0 2x 3 7 2 3 7 1 2x m m x
x m 3 7 3 7 2 m 1 2 x Đặt 3 7 1 3 x t 7 , t 0
. Bất phương trình đã cho trở thành: 2 t 2 t t 2
t m 1 2 . m 1 m . t t 1 t t 2 t t Xét hàm số 2 3 f t 2 2
trên khoảng 0; , ta có f t t 1 t 2 1 t 3
f t 0
. Khi đó, ta có bảng biến thiên sau: t 0
Từ bảng biến thiên trên ta suy ra để bất phương trình đã cho nghiệm đúng thì m 1. Suy ra trong đoạn 10
;10 có tất cả 11 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 6. Có mấy giá trị nguyên dương của m để bất phương trình 2 2 2
9m x 4m x .5m x m có nghiệm?
A. 10. B. Vô số. C. 9 . D. 1. Lời giải: Chọn B
Từ giả thiết, ta chỉ xét m Trang18 2 2 m x m x 2 2 2 9 4
Ta có: 9m x 4m x .5m x m m 1 5 5 2 2 2 2 2 m x m x m x m x m x 9 4 9 4 6 Có 2 . 2 . 5 5 5 5 5 2 m x Do đó nếu có 6
x là nghiệm của bất phương trình 2 m 0 5 2 2 m x m x 9 4
thì x cũng là nghiệm của m . 0 5 5 2 m x Ta xét các giá trị 6
m làm cho bất phương trình 2
m 2 có nghiệm. 5 2 2 m x m x 6 6 m Vì 2 m , m 5 5 2 m 1 m 2 m x log x log , với m . 6 2 2 6 m 2 5 5 m Vậy với 1
m thì bất phương trình 2 có nghiệm tương ứng là x log . 2 6 m 2 5
Suy ra có vô số giá trị
m làm cho bất phương trình 1 có nghiệm.
Câu 7. Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình x2 3
33x 2m 0 chứa không quá 9 số nguyên?
A. 1094. B. 3281. C. 1093. D. 3280. Lời giải. Chọn D Đặt 3x t
,t 0 bất phương trình x2 3
33x 2m 0
1 trở thành 9t 3t 2m 0 2 . Nếu 3 3 2m m
1 thì không có số nguyên dương m nào thỏa mãn yêu cầu bài toán. 9 18 Nếu 3 3 2m m
thì bất phương trình 3 2 t 2m . 9 18 9
Khi đó tập nghiệm của bất phương trình 3 1 là S ;log 2 m . 3 2 Trang19 Để 3
S chứa không quá 9 số nguyên thì log 2m 8 8 0 m 3 2
Vậy có 3280 số nguyên dương m thỏa mãn.
Câu 8. Có bao nhiêu cặp số nguyên dương ;
x y thỏa mãn điều kiện x 2020 và
39y 2y x log x 3 1 2 ? 3
A. 4 . B. 2 . C. 3772. D. 3774. Lời giải: Chọn D 3
Ta có 39y 2 log 1 2 3.9y y x x
6y x 3log x 1 2 3 3 2 y 1 3 32y 1 x 1 3log x 1 . (*) 3
Xét hàm số 3t f t
3t có 3t f t
.ln 3 3 0,t .
Suy ra hàm số 3t f t
3t đồng biến trên . Do đó * f 2y
1 f log x 1 2y 1 log x 2 y 1 1 3 1 x . 3 3 y log 2021 1 Vì x 2020 nên 2 1 3 3 1 2020 y 2,9. 2
Với giả thiết y nguyên dương suy ra y 1; 2 .
Với y 1 có 26 x 2020 suy ra có 1995 cặp số ; x y thỏa mãn .
Với y 2 có 242 x 2020 suy ra có 1779 cặp số ; x y thỏa mãn .
Vậy có tất cả 3774 cặp số ;
x y thỏa mãn đề bài. 2 2 x
Câu 9. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình 3 x 92x m 0 có 5 nghiệm nguyên?
A. 65021. B. 65024 C. 65022. D. 65023. Lời giải: Chọn B
2xx 2 3
9 2x m 0 Trang20 x 2 1 Th1: Xét x x 2 3
9 0 x x 2
là nghiệm của bất phương trình. x 2 x 2 1 x Th2: Xét x 2 3
9 0 x x 2 . x 2 Khi đó, 2 x 2 (1) 2
m x log m(2) 2
Nếu m 1 thì vô nghiệm.
Nếu m 1 thì (2) log m x log m . 2 2
Do đó, có 5 nghiệm nguyên ;
1 2; log m; log m có 3 giá trị nguyên 2 2
log m 3; 4 512 m 65536 . Suy ra có 65024 giá trị m nguyên thỏa mãn. 2 2 x Th3: Xét x 2 3
9 0 x x 2 1
x 2 . Vì 1
;2 chỉ có hai số nguyên nên không có giá trị m
nào để bất phương trình có 5 nghiệm nguyên.
Vậy có tất cả 65024 giá trị m nguyên thỏa ycbt.
Câu 10. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 728 số nguyên y thỏa mãn log 2
x y log (x y) ? 4 3
A. 59. B. 58. C. 116. D. 115. Lời giải: Chọn C
Với mọi x ta có 2 x x .
Xét hàm số f (y) log (x y) log 2 x y . 3 4
Tập xác định D ( ; x ) . 1 1 f ( y) y D (x y) ln 3 0, 2 x yln 4
f ( y) tăng trên D .
Ta có f (x 1) log (x x 1) log 2
x x 1 0 . 3 4
Có không quá 728 số nguyên y thỏa mãn f y 0
f (x 729) 0 log 729 log 2
x x 729 0 3 4 Trang21 2 6
x x 729 4 0 2
x x 3367 0
57,5 x 58,5
Mà x nên x 5 7, 56,...,5 8 . Vậy có 58 ( 57
) 1 116 số nguyên x thỏa.
Câu 11. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 242 số nguyên y thỏa mãn log 2 x y log x y ? 4 3
A. 55. B. 28. C. 29. D. 56. Lời giải Chọn D 2 x y 0 Điều kiện: . x y 0 2
x y 4t 2
x x 4t 3t *
Đặt log x y t , ta có . 3
x y 3t
y 3t x
Nhận xét rằng hàm số 4t 3t f t
đồng biến trên khoảng 0; và f t 0 với mọi t 0
Gọi n thỏa n n 2
4 3 x x , khi đó * t n .
Từ đó, ta có 3t 3n x y x x .
Mặt khác, vì có không quá 242 số nguyên y thỏa mãn đề bài nên 3n 243 n log 243 5 3 Từ đó, suy ra 1 25 5 1 25 5 2 5 2
x x 4 243 x x 781 0 x 2 2
Mà x nên x 2 7, 26,...,27,2 8 .
Vậy có 56 giá trị nguyên của x thỏa yêu cầu đề bài.
Câu 12. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 127 số nguyên y thỏa mãn log 2 x y log x y ? 3 2
A. 89. B. 46. C. 45. D. 90. Lời giải Chọn D Ta có log 2 x y log x y 1 3 2 Trang22
Đặt t x y * (1) log 2
x x t log t g(t) log t log 2
x x t 0 2 3 2 2 3 Đạo hàm 1 1 g ( t)
với mọi t 0. Do đó g t đồng biến trên 0; t ln 2 0 2
x x t ln 3
Vì mỗi x nguyên có không quá 127 giá trị t * nên ta có
g(128) 0 log 128 log 2
x x 128 0 2 3 1 8236 1 8236 2 7 2
x x 128 3 x x 2059 0 x 2 2
Vậy có 90 số nguyên x thỏa yêu cầu bài toán. 2 2
Câu 13. Xét các số thực thỏa mãn x y 1 2 2 2 2 24x x y x
. Giá trị lớn nhất của biểu thức 8x 4 P
gần với giá trị nào sau đây nhất? 2x y 1
A. 9 B. 6 . C. 7 . D. 8 . Lời giải Chọn B 2 2 x y 1 2 2
x y x 2 2 x
x y 2 x 1 2 2 x 2 2
x y x y x 2 1 2 2 2 2 .4 2 2 2 2 1 y 1 0 1 Đặt
t x 2 2 1 y 0 .
t t t x 2 2 1 2 1 0 0 1 1 y 1 8x 4 P
2P 8.x .
P y P 4 0 2x y 1
2P 8 P 4
Yêu cầu bài toán tương đương
1 3P 12 2P 82 2 P 2P 82 2 P 2
P 10P 20 0 5 5 P 5 5 .
Vậy maxP 5 5 .
Câu 14. Có bao nhiêu bộ ;
x y với x,y nguyên và 1 x, y 2020 thỏa mãn
xy x y 2y 2x 1 2 4 8 log
2x 3y xy 6 log ? 3 2 y 2 x 3
A. 2017. B. 4034. C. 2 . D. 20172020 . Trang23 Lời giải Chọn B * ,
x y ; x, y 2020 *
x, y ; x, y 2020
+ Điều kiện 2x 1 2 y . 0, 0
x 3, y 0 x 3 y 2 x y
Bất phương trình x y 4 2 3 2 log
1 x 4 y 2 log 1 0 . 2 3 x 3 y 2 x 4 2
+ Xét y 1 thì thành x 3log 1 3 x 4 log
0 , rõ ràng bất phương trình này nghiệm 2 3 x 3 3 x đúng với mọi 4 2
x 3 vì x 3 0,log
1 log 0 1 0,3 x 4 0,log 0 . 2 2 3 x 3 3
Như vậy trường hợp này cho ta đúng 2017 bộ ; x y ; x
1 với 4 x 2020, x .
+ Xét y 2 thì thành 4 x 4log 1 0 , bất phương trình này cũng luôn đúng với mọi x mà 3
4 x 2020, x .
Trường hợp này cho ta 2017 cặp x; y nữa.
+ Với y 2, x 3 thì VT * 0 nên không xảy ra.
Vậy có đúng 4034 bộ số x; y thỏa mãn yêu cầu bài toán. 2
x 2 x3 log 5 y
Câu 15. Có bao nhiêu cặp số thực ;
x y thỏa mãn đồng thời điều kiện 3 ( 4) 3 5 và
y y y 2 4 1 3 8?
A. 3 . B. 2 . C. 1. D. 4 . Lời giải Chọn B Xét bảng sau: Gọi 2
4 y y 1 ( y 3) 8 (*)
+ TH1. y 0 , ta có 2 * 4
y y 1 (y 3) 8 3
y 0 , do đó 3 y 0 . Trang24
+ TH2. 0 y 1, 2
* 4 y y 1 ( y 3) 8 1
1 y 0 , do đó y 0 . 9 73 9 73 + TH3. y 1, 2
* 4 y y 1 ( y 3) 8 y , do đó loại TH3. 2 2
Vậy cả 3 trường hợp cho ta 3 y 0 , với điều này ta có y3 2 2
x 2 x3 log 5 x 2 x3 y y 1 3 ( 4) ( 3) 3 5 3 5 . 5 y3 0 2 x 2 x3 1 1 Do 3 1 và 1(y 3 ) . 5 5 2
x 2x 3 0 x 1 x 3 Dấu bằng xảy ra y 3 y 3
Vậy có 2 cặp nghiệm thỏa mãn.
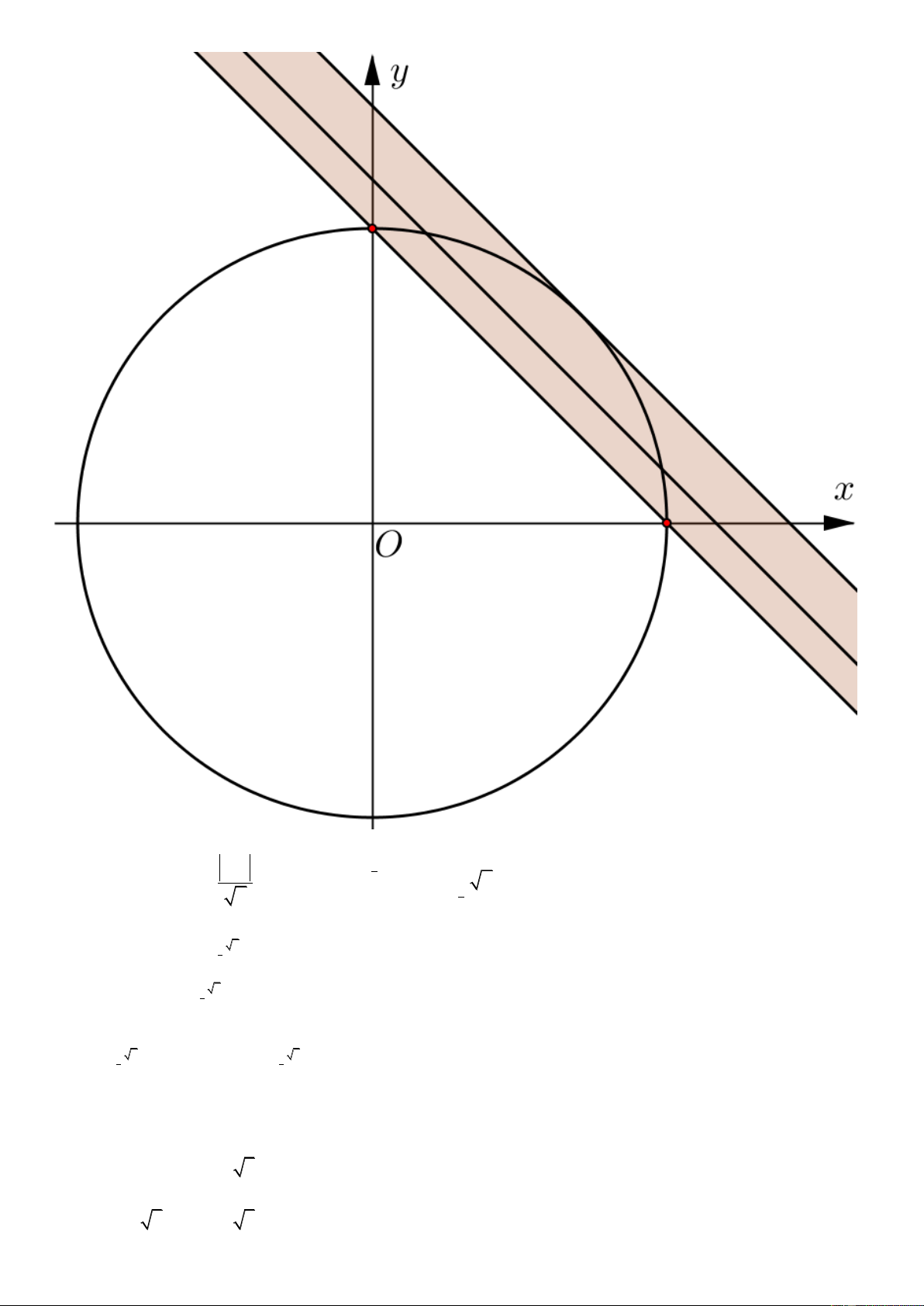
Câu 16. Trong tất cả các cặp số thực (x;y ) thỏa mãn log
2x 2 y 5 1, có bao nhiêu giá trị thực 2 2 x y 3
của m để tồn tại duy nhất cặp số thực (x;y) sao cho 2 2
x y 4x 6 y 13 m 0 .
A. 3 . B.1. C. 2 . D. 0 . Lời giải Chọn C Ta có: log
2x 2y 5 1 ⇔ 2 2
2x 2 y 5 x y 3 ⇔ 2 2
x y 2x 2 y 2 0 1 2 2 x y 3
⇒ Tập hợp các cặp số thực x, y thỏa mãn log
2x 2y 5 1 là hình tròn 2 2 x y 3 C 2 2
: x y 2x 2 y 2 0 (tính cả biên). 1 2 2 Xét 2 2
x y 4x 6y 13 m 0 x 2 y 3 . m x 2 TH1: m 0 , không thỏa mãn (1). y 3
TH2: m 0 khi đó tập hợp các cặp số thực ; x y thỏa mãn 2 2
x y 4x 6 y 13 m 0 là đường tròn C 2 2
: x y 4x 6 y 13 m 0. 2
Để tồn tại duy nhất cặp số thực ;
x y thỏa mãn yêu cầu bài toán thì hai đường tròn C và C tiếp xúc 2 1
ngoài với nhau hoặc hai đường tròn C và C tiếp xúc trong và đường tròn C có bán kính lớn hơn 2 2 1
đường tròn C .C có tâm I 1;1 , bán kính R 2. 1 1 1 1 Trang25 ( C2) có tâm I 2 ; 3
,bán kính R m m 0 . 2 2
Để C và C tiếp xúc ngoài thì I I R R . 2 1 1 2 1 2
⇔ 2 2 3 4
2 m 5 2 m m 9 tm
Để đường tròn C vàC tiếp xúc trong và đường tròn C có bán kính lớn hơn đường trònC . ⇒ 1 2 2 1
R R I I ⇔ m 2 2 2 3
4 m 49 (tm ) 2 1 1 2
Vậy có 2 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 17. Có bao nhiêu cặp số nguyên dương ;
x y với x 2020 thỏa mãn log
1 2 2 1 4y x x y . 2
A. 5 . B. 1010. C. 6 . D. 2020. Lời giải Chọn A ĐK: x 1
Theo đề bài log
1 2 2 1 4y log 2 1 2 2 1 2 2 y x x y x x y 2 2 Đặt log 2 1 2 1 2t t x x . 2 Ta có t 2 2 2 y t 2y 1 .
Xét hàm số 2t f t t trên R 2t f t
.ln 2 1 0t R f t đồng biến trên R .
1 f t f 2y t 2y log 2 x 1 2y 2 2 2 1 2 y x 2 y 1 x 2 1. y 1 Mà 2 1 x 2020 2
1 2020 y 1 log 2019 . 2 2 Vì
y Z y 1; 2;3; 4; 5 .
Vậy có 5 cặp điểm cặp số nguyên dương ; x y . Trang26
Câu 18. Có bao nhiêu cặp số nguyên dương ;
x y với x 2020 thỏa mãn điều kiện x 2 2 2 log
x 4x 4y 8y 1. 2 y 1
A. 2020. B. vô số. C. 1010. D. 4040. Lời giải Chọn C x 2 log
4y x 4x 8y 1 log x 2 log y 1 4 y 2 1 x 22 2 2 1 2 2 2 y 1
log x 2x 22 log 2 y 1 2 y 1 1 . 2 2 2
Xét hàm số f t 2
log t t trên 0;. 2 1
Ta có f t
2t 0t 0; f t đồng biến trên 0;. t ln 2
1 f x 2 f 2y 2 x 2 2y 2 x 2y .
Mà 0 x 2020 0 y 1010 .
Vậy có 1010cặp số nguyên dương ; x y .
Câu 19. Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số ; x y thỏa mãn 5 x7 y 3x5 y2 3 3
2x y
1 0 ,đồng thời thỏa mãn
2 x y m 2 ln 4 3 3
2 ln x m 1 0 ?
A. 2019. B. 6 . C. 2020. D. 4 . Lời giải Chọn D 5 x7 y 3x5 y2 x y x y 3 3
2x y 1 0 5 7 3 5 2 3
5x 7y 3
3x 5y 2
Xét hàm số 3t f t t 3t f t
ln 3 1 0, t . Suy ra hàm số 3t f t
t đồng biến trên .
Nên f 5x 7 y f 3x 5y 2 5x 7y 3x 5y 2 y 1 x 1 Điều kiện x 0 Thế 1 vào phương trình
2 x y m 2 ln 4 3 3
2 ln x m 1 0 ta được Trang27
2 x m 2 ln
2 ln x m 1 0 .
Đặt t ln x đk t , phương trình có dạng: 2
t m 2
2 t m 1 0 .
Để phương trình có nghiệm thì 2 2 7 2 2 7 0 2
3m 4m 8 0 1 ,09 m 2,43. 3 3
Vì m nên m 1 ;0;1; 2
Do đó có 4 số nguyên m thỏa mãn.
Câu 20. Cho số nguyên a , số thực b . Gọi S là tập hợp các giá trị nguyên của a để tồn tại số thực x thỏa mãn 4b x a và 2 2 3b x a
. Tổng các phần tử của tập S là
A. 7. B. -3. C. -2. D. 0. Lời giải Chọn B x 2 2 2
u x 2
u v 4b(1) Điều kiện . Đặt
;u, v 0 a 2
v a b 2
u v 3 (2) Trong đó
1 là phương trình của đường tròn tâm I (0;0) O 0;0 , bán kính 2b R và 2 là phương
trình của một đường thẳng. Trang28 3 b b
Ta phải có: dI,d 1 b b 2 2 3 2 b log 2 3 2 2 log 2 3 2 2 b 2
u v 4 4 3.27 log 2 3 b 2
u v 3 3 2.56 log 2 log 2 3 3 2 2 2 2 v 4
v a 2 4 2 a 1,27 . a {-2; 1 ;0;1} Thử lại với 2 1 3 4b a v u
3 0 b log 3. 4 b log 3 4 u 3 3 3 3 . Trang29 log 2 3 2 2
u v 2 log 3 2 2 b 4 3
3 3 3.4 trái với 2
u v 4 4 3.27 .
Vậy có 3 giá trị nguyên của a. Trang30