Giải SBT Toán 12 bài 3: Phương trình đường thẳng
Xin giới thiệu tới bạn đọc tài liệu Giải SBT Toán 12 bài 3: Phương trình đường thẳng, tài liệu kèm theo lời giải chi tiết sẽ giúp các bạn học sinh có kết quả cao hơn trong học tập. Mời các bạn học sinh và thầy cô cùng tham khảo.
Chủ đề: Chương 3: Phương pháp tọa độ trong không gian
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Phương pháp tọa độ trong không gian
Môn:
Tác giả:
Tài liệu liên quan:
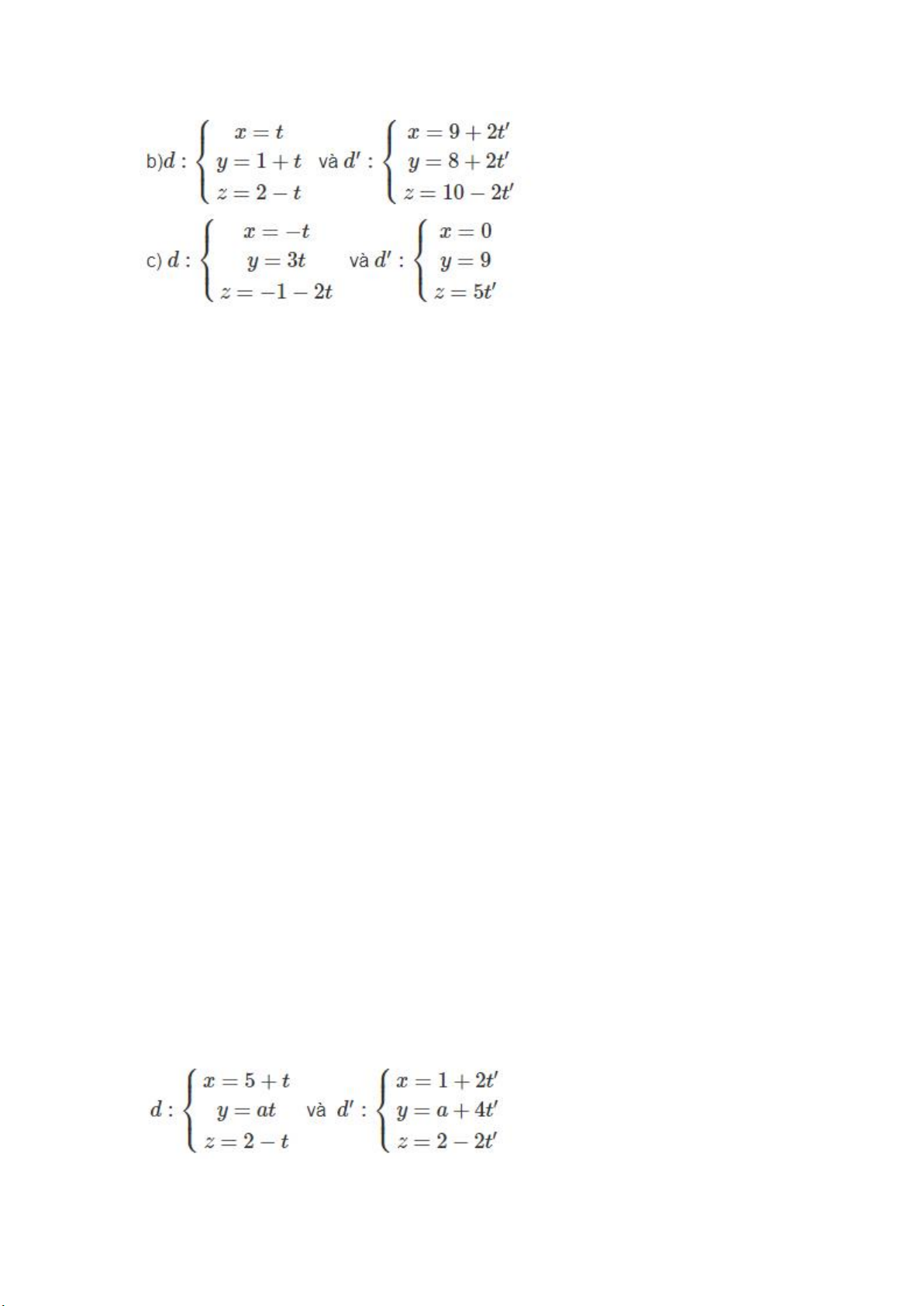
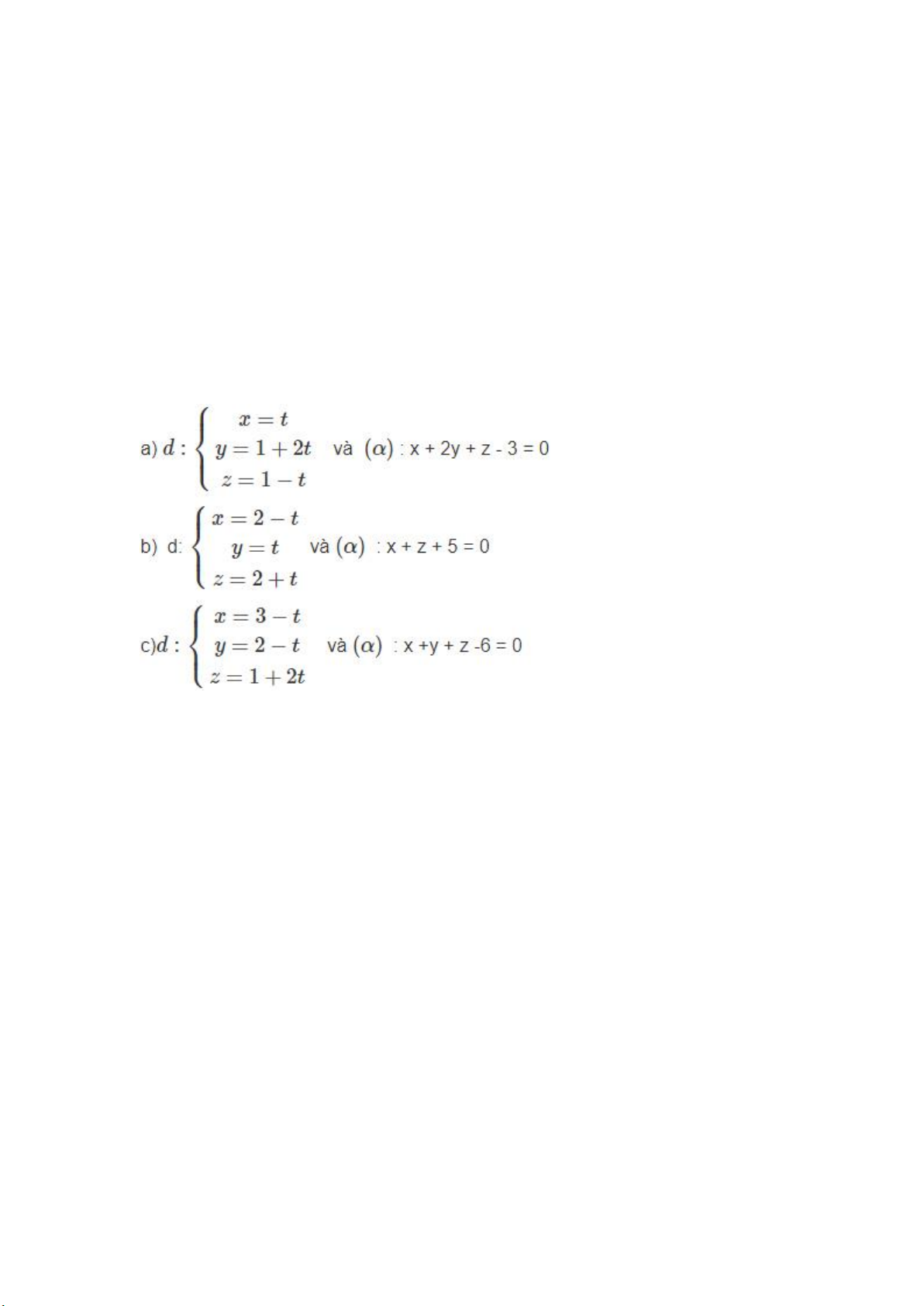
Preview text:
Giải SBT Toán 12 bài 3: Phương trình đường thẳng
Bài 3.31 trang 129 sách bài tập (SBT) – Hình học 12
Viết phương trình tham số, phương trình chính tắc của đường thẳng Δ trong các trường hợp sau:
a) Δ đi qua điểm A(1; 2; 3) và có vecto chỉ phương a→=(3;3;1);
b) Δ đi qua điểm B(1; 0; -1) và vuông góc với mặt phẳng (α): 2x – y + z + 9 = 0
c) Δ đi qua hai điểm C(1; -1; 1) và D(2; 1; 4) Hướng dẫn làm bài:
a) Phương trình tham số của đường thẳng Δ đi qua điểm A(1; 2; 3) và có vecto
chỉ phương a→=(3;3;1) là {x=1+3t;y=2+3t;z=3+t
Phương trình chính tắc của Δ là x−1/3=y−2/3=z−3/1 b) Δ⊥ (α)⇒a → → Δ =aα =(2;−1;1)
Phương trình tham số của Δ là {x=1+2t;y=−t;z=−1+t
Phương trình chính tắc của Δ là x−1/2=y/−1=z+1/1
c) Δ đi qua hai điểm C và D nên có vecto chỉ phương CD→=(1;2;3)
Vậy phương trình tham số của Δ là {x=1+t;y=−1+2t;z=1+3t
Phương trình chính tắc của Δ là x−1;1=y+1/2=z−1/3
Bài 3.32 trang 129 sách bài tập (SBT) – Hình học 12
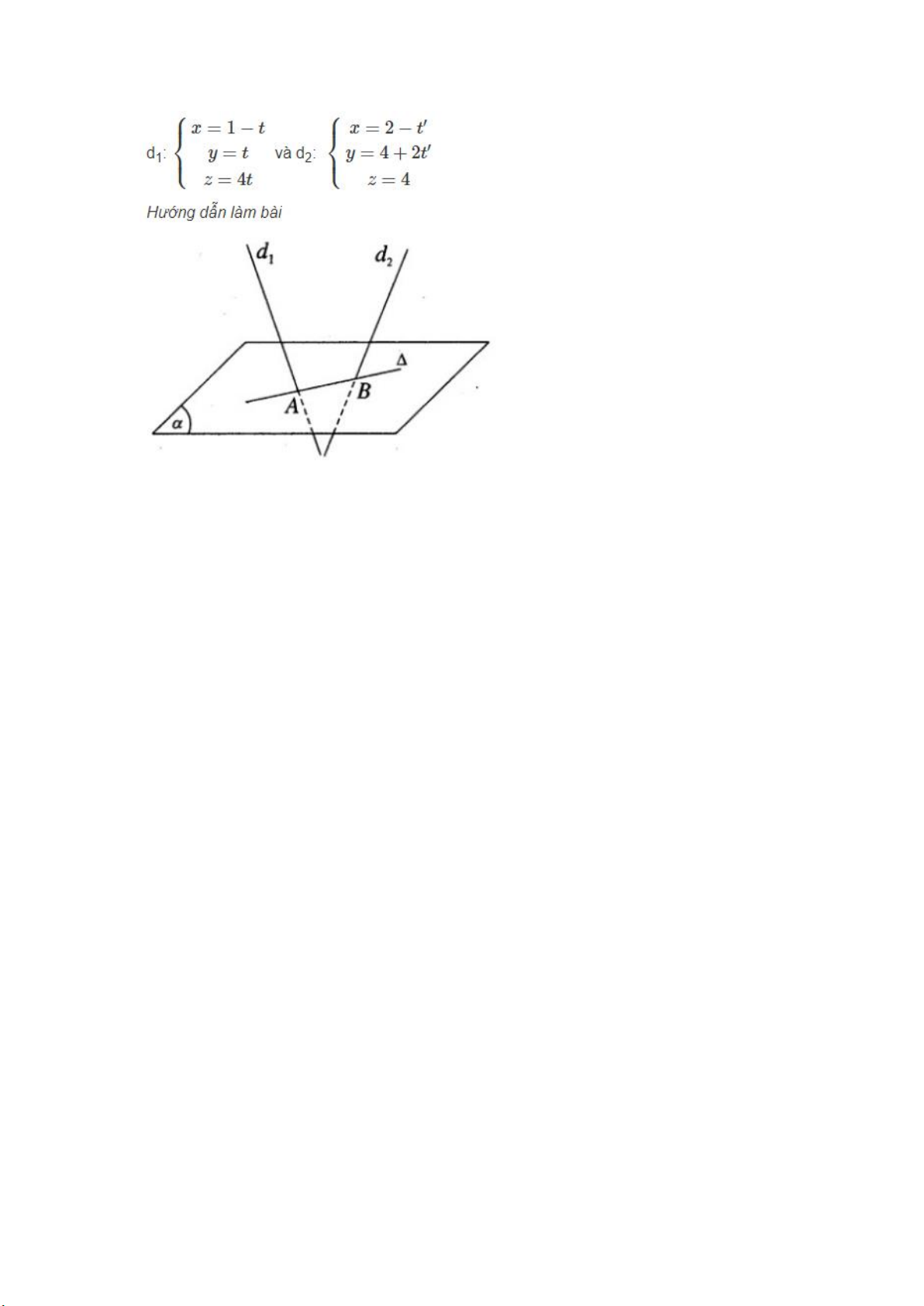
Viết phương trình của đường thẳng Δ nằm trong mặt phẳng (α): x +2z = 0 và cắt hai đường kính
Gọi A và B lần lượt là giao điểm của d1 và d2 với (α). Đường thẳng Δ cần tìm
chính là đường thẳng AB. Ta có: A(1−t;t;4t)∈ d1 A∈ (α)⇔t+4.(2t)=0⇔t=0 Suy ra: A(1; 0; 0)
Ta có: B(2−t′;4+2t′;4)∈ d2
B∈ (α)⇔4+2t′+8=0⇔t′=−6 Suy ra B(8; -8; 4)
Δ đi qua A, B nên có vecto chỉ phương a → Δ =AB→=(7;−8;4)
Phương trình chính tắc của Δ là: x−1/7=y/−8=z/4
Bài 3.33 trang 129 sách bài tập (SBT) – Hình học 12
Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau:
a) d:x+1/1=y−1/2=z+3/3 và d′:x−1/3=y−5/2=z−4/2 Hướng dẫn làm bài: a) Ta có: a → d =(1;2;3) và ad′→=(3;2;2) Suy ra n→=a → → d ∧ ad′ =(−2;7;−4)
Ta có M0(−1;1;−2)∈ d,M0′(1;5;4)∈ d′⇒M0M0′→=(2;4;6) Ta có n→.M → 0M0′
=−4+28−24=0. Vậy đường thẳng d và d’ đồng phẳng và khác
phương, nên d và d’ cắt nhau. b) Ta có a → d
=(1;1;−1) và ad′=(2;2;−2).M0(0;1;2)∈ d Vì {a → →
d′ =2ad ;M0∉ d′ (tọa độ M0 không thỏa mãn d’) nên hai đường thẳng d và d’ song song.
c) d có vecto chỉ phương a → d =(−1;3;−2)
d’ có vecto chỉ phương a → d′ =(0;0;5) Gọi n→=a → → d ∧ ad′ =(15;5;0)≠0→ Ta có M0(0;0;−1)∈ d M′ → → 0(0;9;0)∈ d′⇒M0M0′ =(0;9;1),n→.M0M0′ =45≠0
Vậy d và d’ là hai đường thẳng chéo nhau.
Bài 3.34 trang 129 sách bài tập (SBT) – Hình học 12
Tìm a để hai đường thẳng sau đây song song: Hướng dẫn làm bài: Ta có a → → d
=(1;a;−1) và ad′ =(2;4;−2)
d//d′⇒1/2=a/4=−1/−2⇒a=2
Khi đó M′0(1;2;2) thuộc d’ và M’0 không thuộc d. Vậy d // d’ ⟺ a = 2.
Bài 3.35 trang 129 sách bài tập (SBT) – Hình học 12
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau Hướng dẫn làm bài:
a) Thay x, y, z trong phương trình tham số của đường thẳng d vào phương trình
tổng quát của mặt phẳng (α) ta được: t + 2(1 + 2t) + (1 – t) – 3 = 0 ⟺ 4t = 0 ⟺ t = 0
Vậy đường thẳng d cắt mặt phẳng (α) tại M0(0; 1; 1).
b) Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của
(α) ta được: (2 – t) +(2 + t) + 5 = 0 ⟺ 0t = -9
Phương trình vô nghiệm, vậy đường thẳng d song song với (α)
c) Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của
(α) ta được: (3 – t) + (2 – t) + (1 + 2t) – 6 = 0 ⟺ 0t = 0
Phương trình luôn thỏa mãn với mọi t. Vậy d chứa trong (α)
Bài 3.36 trang 130 sách bài tập (SBT) – Hình học 12
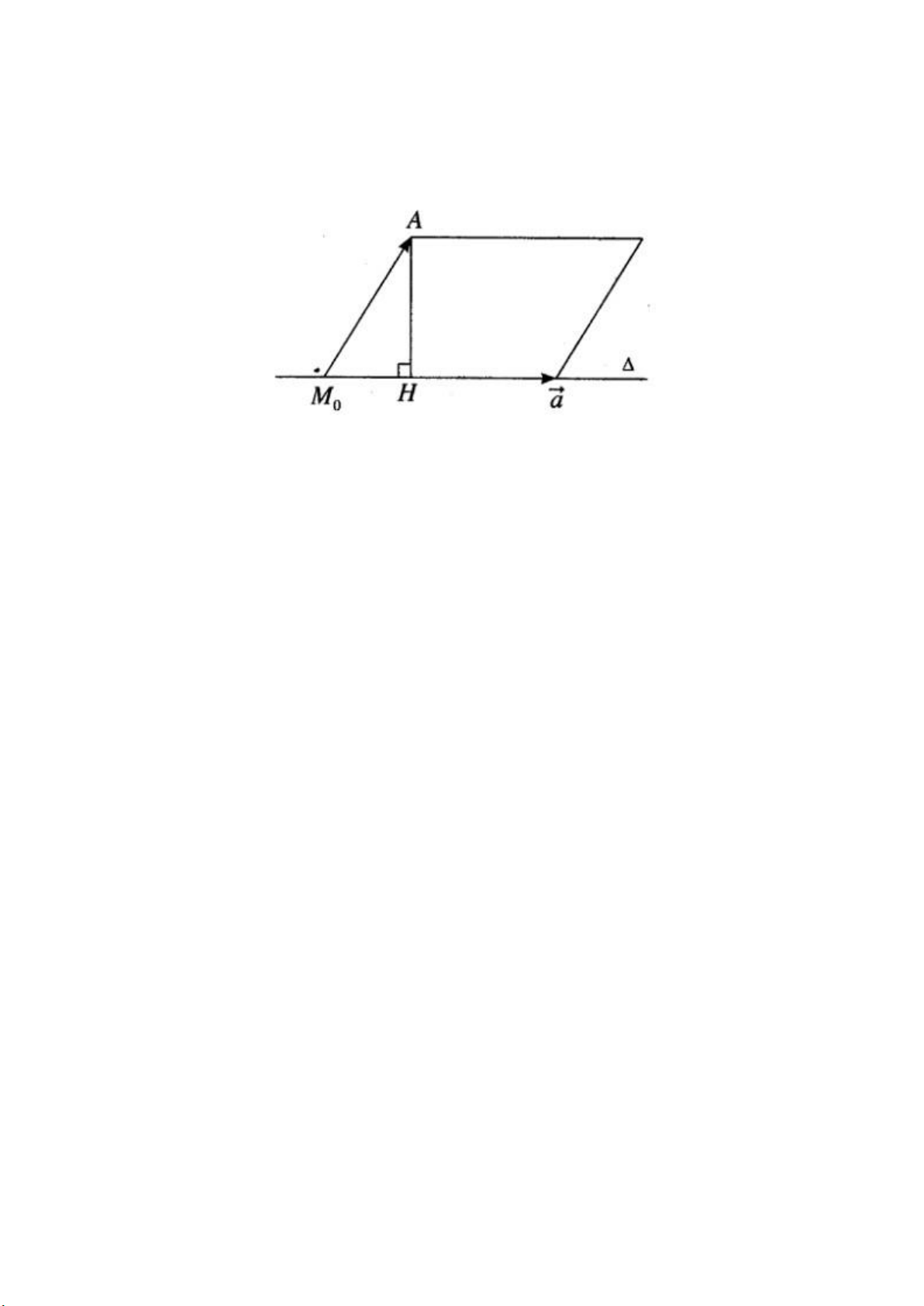
Tính khoảng cách từ điểm A(1; 0; 1) đến đường thẳng Δ:x−1/2=y/2=z/1 Hướng dẫn làm bài:
Đường thẳng Δ đi qua điểm M0(1; 0; 0) và có vecto chỉ phương a→=(2;2;1).
Ta có M0A→=(0;0;1),n→=a→∧ M0A→=(2;−2;0).
d(A,Δ)=|n→|/|a→|=√4+4+0/√4+4+1=2√2/3
Vậy khoảng cách từ điểm A đến Δ là 2√2/3
Bài 3.37 trang 130 sách bài tập (SBT) – Hình học 12
Cho đường thẳng Δ: x+3/2=y+1/3=z+1/2 và mặt phẳng (α): 2x – 2y + z + 3 = 0
a) Chứng minh rằng Δ song song với (α).
b) Tính khoảng cách giữa Δ và (α) Hướng dẫn làm bài: a) Ta có: a → →
Δ =(2;3;2) và nα =(2;−2;1) a → → Δ .nα =4−6+2=0 (1)
Xét điểm M0(-3; -1; -1) thuộc Δ, ta thấy tọa độ M0 không thỏa mãn phương trình
của (α). Vậy M0∉ (α) (2).
Từ (1) và (2) ta suy ra Δ//(α)
b) d(Δ,(α))=d(M0,(α))=|2.(−3)−2.(−1)+(−1)+3|/√4+4+1=2/3
Vậy khoảng cách giữa đường thẳng Δ và mặt phẳng (α) là 2/3.
Bài 3.38 trang 130 sách bài tập (SBT) – Hình học 12
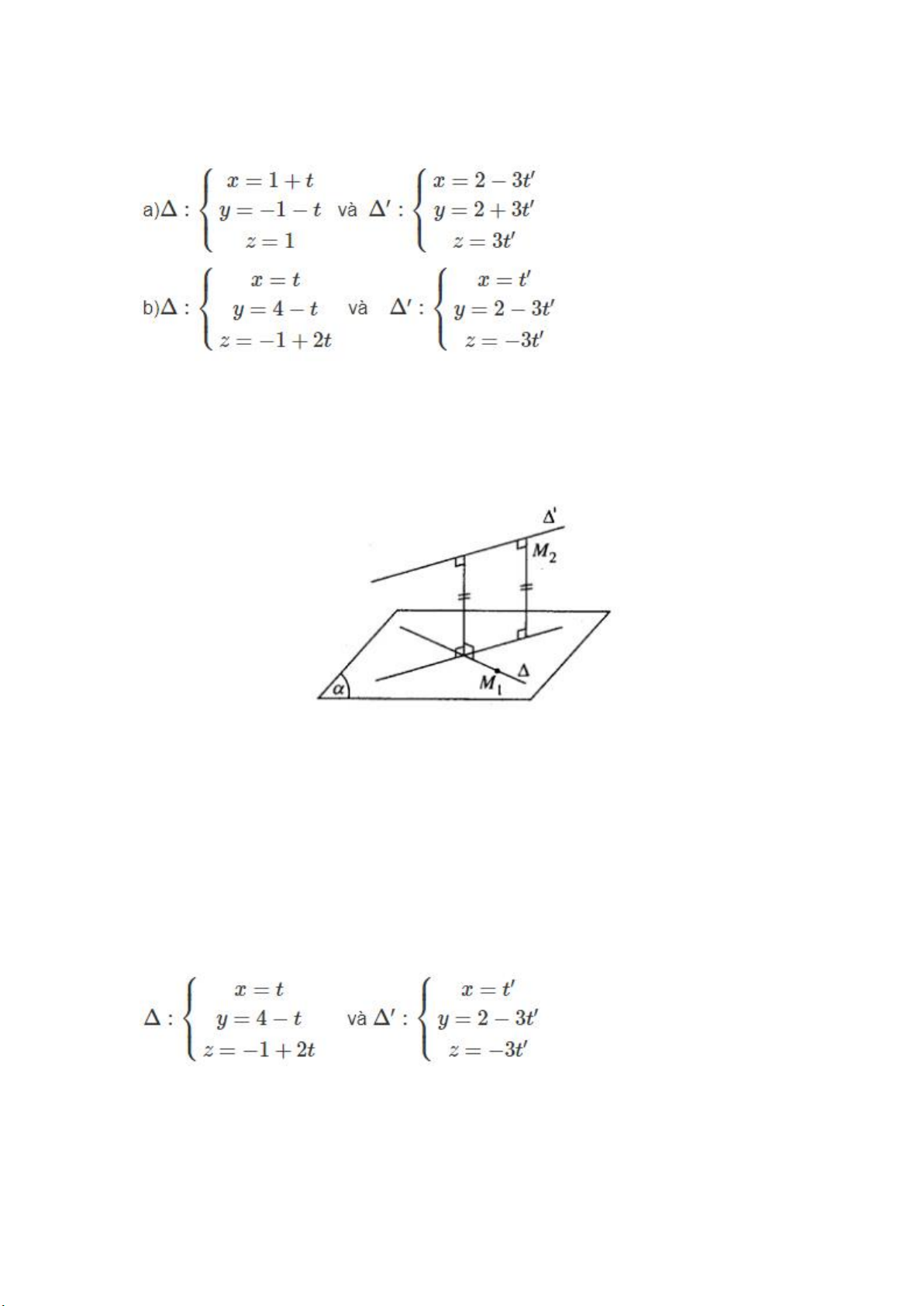
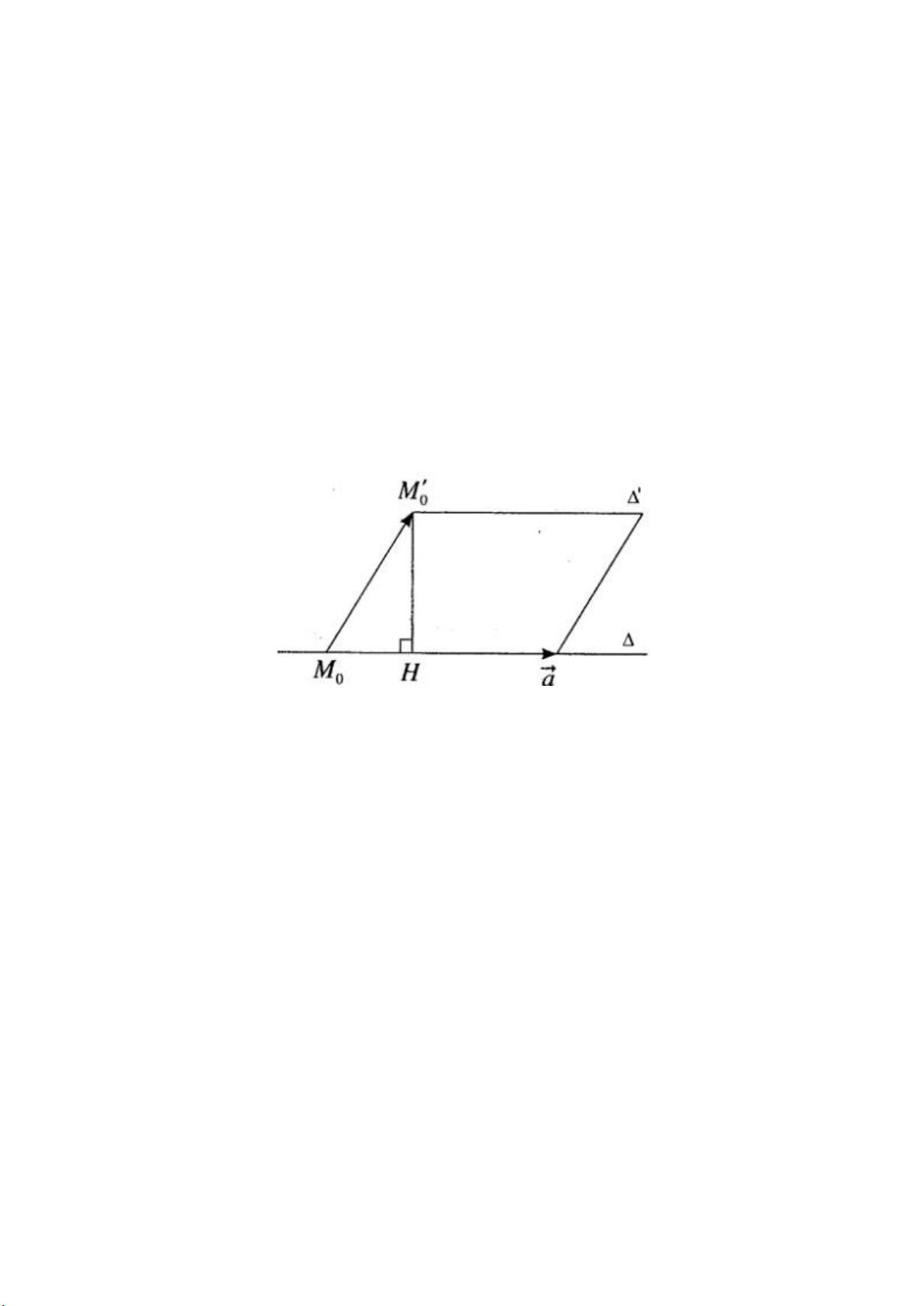
Tính khoảng cách giữa các cặp đường thẳng Δ và Δ′ trong các trường hợp sau: Hướng dẫn làm bài:
a) Gọi (α) là mặt phẳng chứa Δ và song song với Δ′. Hai vecto có giá song song
hoặc nằm trên (α) là: a→=(1;−1;0) và a→′=(−1;1;1). Suy ra n → α =(−1;−1;0) (α) đi qua điểm M →
1(1; -1; 1) thuộc Δ và có vecto pháp tuyến: nα′ =(1;1;0)
Vậy phưong trình của mặt phẳng (α) có dạng x – 1 + y + 1= hay x + y = 0
Ta có: M2((2; 2; 0) thuộc đường thẳng Δ′
d(Δ,Δ′)=d(M2,(α))=|2+2|/√1+1=2√2
b) Hai đường thẳng Δ và Δ′ có phương trình là:
Phương trình mặt phẳng (α) chứa Δ và song song với Δ′ là 9x + 5y – 2z – 22 = 0
Lấy điểm M’(0; 2; 0) trên Δ′ .
Ta có d(Δ,Δ′)=d(M′,(α))=|5.(2)−22|/√81+25+4=12/√110
Vậy khoảng cách giữa hai đường thẳng Δ và Δ′ là 12/√110
Bài 3.39 trang 130 sách bài tập (SBT) – Hình học 12
Cho hai đường thẳng Δ:x−1/2=y+3/1=z−4/−2
Δ′:x+2/−4=y−1/−2=z+1/4
a) Xét vị trí tương đối giữa Δ và Δ′;
b) Tính khoảng cách giữa Δ và Δ′. Hướng dẫn làm bài:
a) Δ đi qua điểm M0(1; -3; 4) và có vecto chỉ phương a→=(2;1;−2)
Δ′ đi qua điểm M0’(-2; 1; -1) và có vecto chỉ phương a′→=(−4;−2;4)
Ta có {a′→=2a→;M0∉ Δ′
Vậy Δ′ song song với Δ b) Ta có M → 0M0′ =(−3;4;−5) a→=(2;1;−2)
n→=M0M0′→∧ a→=(−3;−16;−11)
d(Δ,Δ′)=M′0H=|n→|/|a→|=√9+256+121/√4+1+4=√386/3
Bài 3.40 trang 130 sách bài tập (SBT) – Hình học 12
Cho điểm M(2; -1; 1) và đường thẳng Δ:x−1/2=y+1/−1=z/2
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên đường thẳng Δ;
b) Tìm tọa độ điểm M’ đối xứng với M qua đường thẳng Δ. Hướng dẫn làm bài:
a) Phương trình tham số của
a) Phương trình tham số của Δ:x=1+2t;y=−1−t;z=2t
Xét điểm H(1+2t;−1−t;2t)∈ Δ
Ta có MH→=(2t−1;−t;2t−1) a → Δ =(2;−1;2)
H là hình chiếu vuông góc của M trên Δ⇔MH→.a → Δ =0
⇔2(2t−1)+t+2(2t−1)=0⇔t=4/9
Ta suy ra tọa độ điểm H(17/9;−13/9;8/9)
b) H là trung điểm của MM’, suy ra xM’ + xM = 2xH
Suy ra xM′=2xH−xM=34/9−2=16/9
Tương tự, ta được yM′=2yH−yM=−26/9+1=−17/9 zM′=2zH−zM=16/9−1=7/9 Vậy M′(16/9;−17/9;7/9)