Giải SBT Toán 12: Đề kiểm tra - Chương 3. Phương pháp tọa độ trong không gian
Để giúp bạn đọc có kết quả cao hơn trong học tập, mời các bạn học sinh tham khảo tài liệu Giải SBT Toán 12: Đề kiểm tra - Chương 3. Phương pháp tọa độ trong không gian, đề kiểm tra kèm theo lời giải chi tiết sẽ giúp các bạn học sinh học tập tốt hơn môn Toán.
Chủ đề: Chương 3: Phương pháp tọa độ trong không gian
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Phương pháp tọa độ trong không gian
Môn:
Tác giả:
Tài liệu liên quan:
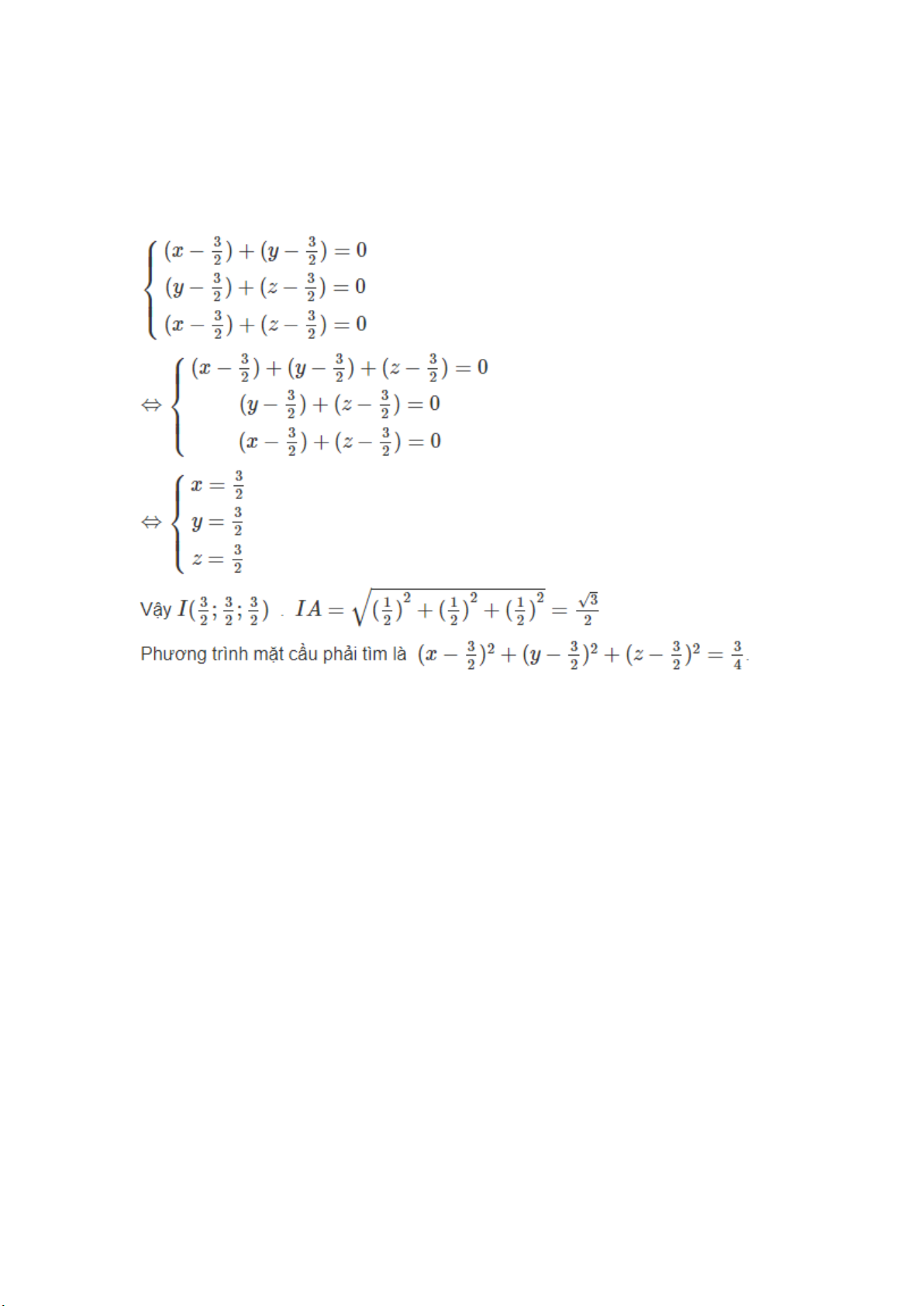
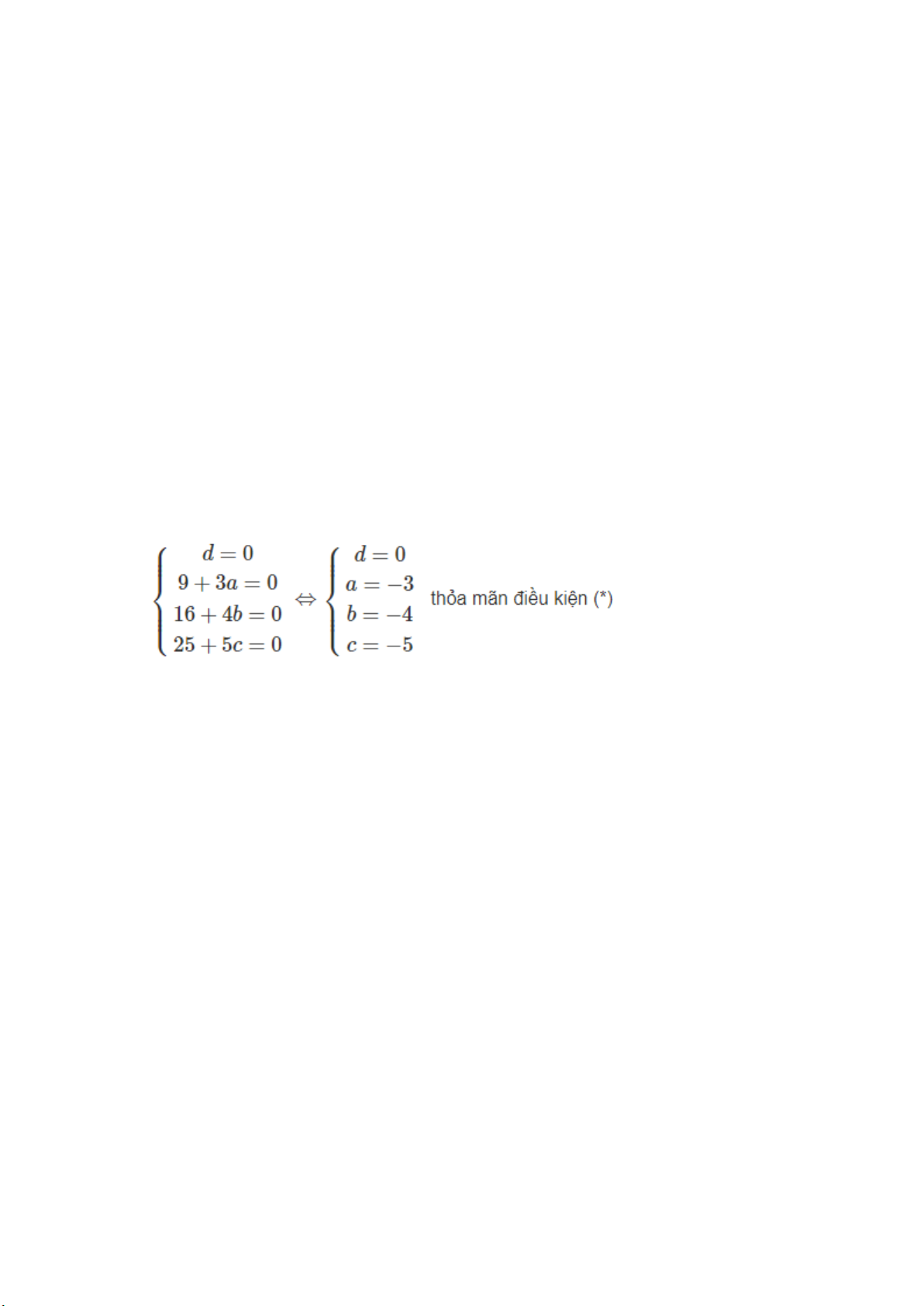
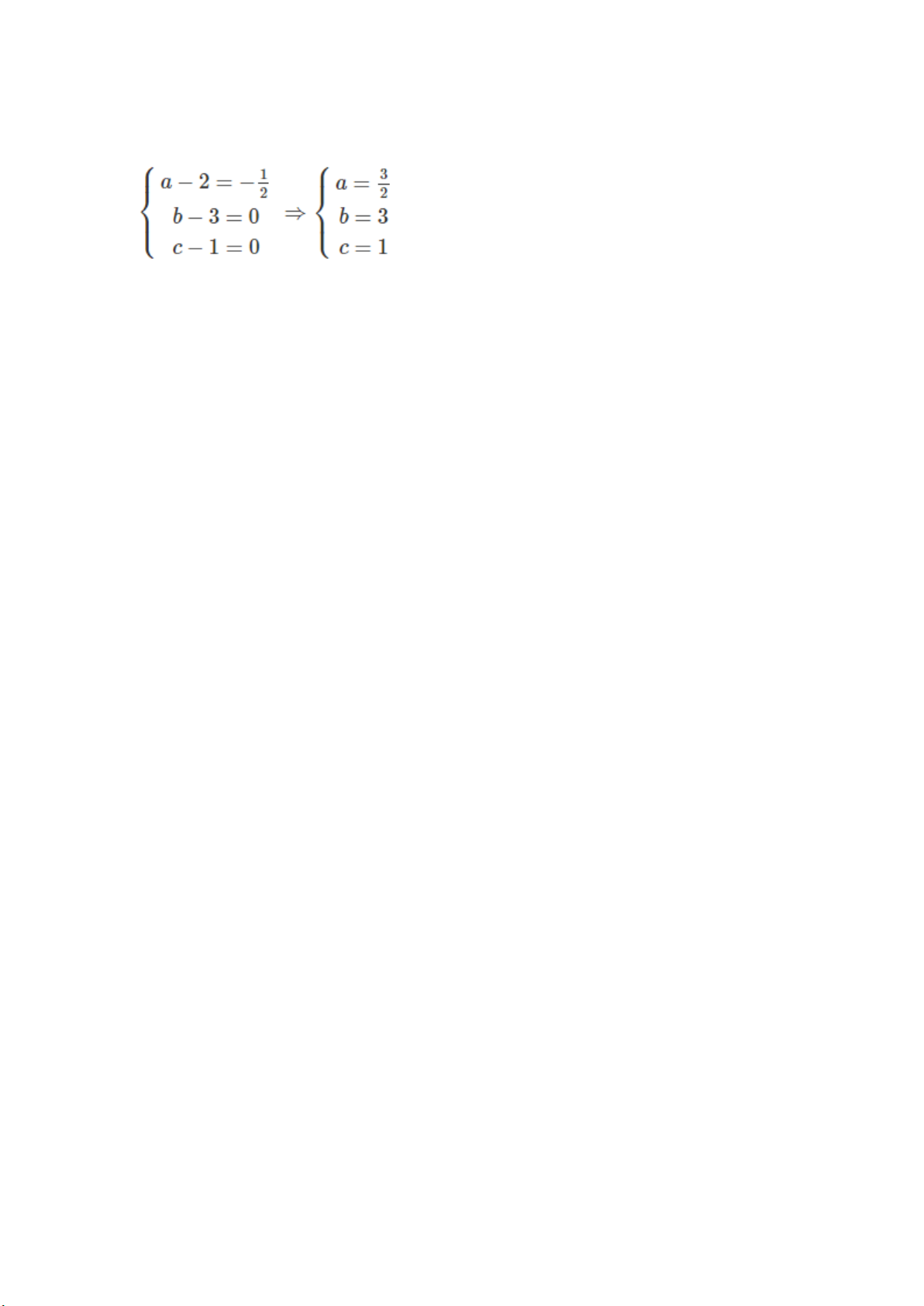
Preview text:
Giải SBT Toán 12: Đề kiểm tra - Chương 3. Phương pháp tọa độ trong không gian
Đề 1 trang 135 Sách bài tập (SBT) Hình học 12 ĐỀ 1 (45 PHÚT)
Câu 1 (6 điểm) trang 135 sách bài tập (SBT) – Hình học 12
Cho mặt phẳng (α) có phương trình tổng quát: 2x+y–z–6=0.
a) Viết phương trình mặt phẳng (β) đi qua O và song song với (α).
b) Viết phương trình tham số của đường thẳng đi qua gốc tọa độ và vuông góc với mặt phẳng (α).
c) Tính khoảng cách từ gốc tọa độ đến mặt phẳng (α). Hướng dẫn làm bài
a) Mặt phẳng (α) có phương trình: 2x+y–z–6=0
(β) đi qua O(0; 0 ;0) và (β)//(α), suy ra phương trình của (β) là 2x + y – z = 0.
b) Đường thẳng Δ đi qua O và vuông góc với mặt phẳng (α), suy ra phương
trình tham số của Δ là {x=2t;y=t;z=−t
c)d(O,(α))=|−6|/√4+1+1=√6
Câu 2 (4 điểm) trang 135 sách bài tập (SBT) – Hình học 12
Cho bốn điểm A(1;1; 1), B(2; 2; 1), C(1; 2; 2), D(2; 1; 2).
a) Chứng minh AB và CD chéo nhau.
b) Viết phương trình mặt cầu đi qua A, B, C, D. Hướng dẫn làm bài
a) Ta có: AB→(1;1;0),AC→(0;1;1),AD→(1;0;1)
AB→∧ AC→=(1;−1;1),AD→.(AB→∧ AC→)=2≠0
Do đó A, B, C, D không đồng phẳng suy ra AB và CD chéo nhau.
b) Mặt phẳng trung trực của AB đi qua trung điểm I(3/2;3/2;1) và có vecto pháp
tuyến AB→(1;1;0) nên phương trình của nó là (x−3/2)+(y−3/2)=0
Tương tự, mặt phẳng trung trực của AC là (y−3/2)+(z−3/2)=0, mặt phẳng trung
trực của AD là (x−3/2)+(z−3/2)=0
Tọa độ tâm I của mặt cầu đi qua A, B, C, D thỏa mãn hệ phương trình:
Đề 2 trang 135 Sách bài tập (SBT) Hình học 12 ĐỀ 2 (45 PHÚT)
Trang 135 sách bài tập (SBT) – Hình học 12
Cho hình hộp chữ nhật OAIB.CEDF có tọa độ các đỉnh là A(3; 0 ; 0), B(0; 4; 0), C(0; 0; 5) và O(0; 0 ;0).
a) (2 điểm) Xác định tọa độ đỉnh D. Viết phương trình tổng quát của mặt phẳng (ABD).
b) (2 điểm) Viết phương trình tham số của đường thẳng đi qua D và vuông góc với mặt phẳng (ABD).
c) (3 điểm) Viết phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD.
d) (3 điểm) Tính khoảng cách giữa hai đường thẳng AC và EF. Hướng dẫn làm bài a) D(3; 4; 5)
Ta có AD→=(0;4;5) và AB→=(−3;4;0).
Suy ra (ABD) có vecto pháp tuyến n→=AD→∧ AB→=(−20;−15;12)
Phương trình của mặt phẳng (ABD) có dạng:
20(x–3)+15y–12z=0 hay 20x+15y–12z–60=0
b) Phương trình tham số của đường thẳng Δ đi qua D và vuông góc với mặt
phẳng (ABD): x=3+20t;y=4+15t;z=5−12t
c) Mặt cầu (S) ngoại tiếp tứ diện ABCD cũng là mặt cầu ngoại tiếp tứ diện
OABC. Giả sử phương trình của (S) là x2 + y2 + z2 + ax + by + cz + d = 0.
Với điều kiện (a/2)2+(b/2)2+(c/2)2−d≥0 (*)
Vì (S) đi qua O, A, B, C nên thay tọa độ của O, A, B, C vào phương trình của (S) ta có:
Vậy phương trình của (S) là x2 + y2 + z2 – 3x – 4y – 5z = 0
d) Ta có d(EF, AC) = d(EF, (ABC)) = d(E,(ABC))
OE→=OA→+OC→=(3;0;5)⇒E(3;0;5)
AB→=(−3;4;0),AC→=(−3;0;5) AB→∧ AC→=(20;15;12)
Phương trình mặt phẳng (ABC) là 20(x–3)+15y+12z=0 hay 20x+15y+12z–60=0
Từ đó suy ra: d(EF;AC)=|60+60−60|/√769=60/√769
Đề 3 trang 135 Sách bài tập (SBT) Hình học 12 ĐỀ 3 (45 PHÚT)
Trang 135 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz cho bốn điểm A(2; 4; -1), B(1; 4; -1), C(2; 4; 3), D(2; 2; -1).
a) (2 điểm) Chứng minh rằng các đường thẳng AB, AC, AD vuông góc với nhau từng đôi một.
b) (2 điểm) Viết phương trình tham số của đường vuông góc chung Δ của hai đường thẳng AB và CD.
c) (3 điểm) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D.
d) (3 điểm) Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu (S) và song
song với mặt phẳng (ABD). Hướng dẫn làm bài
a) Ta có AB→=(−1;0;0);AC→=(0;0;4);AD→=(0;−2;0)
AB→.AC→=AC→.AD→=AD→.AB→=0 , suy ra AB⊥ AC, AC⊥ AD, AD⊥ AB
Vậy AB, AC, AD vuông góc với nhau từng đôi một.
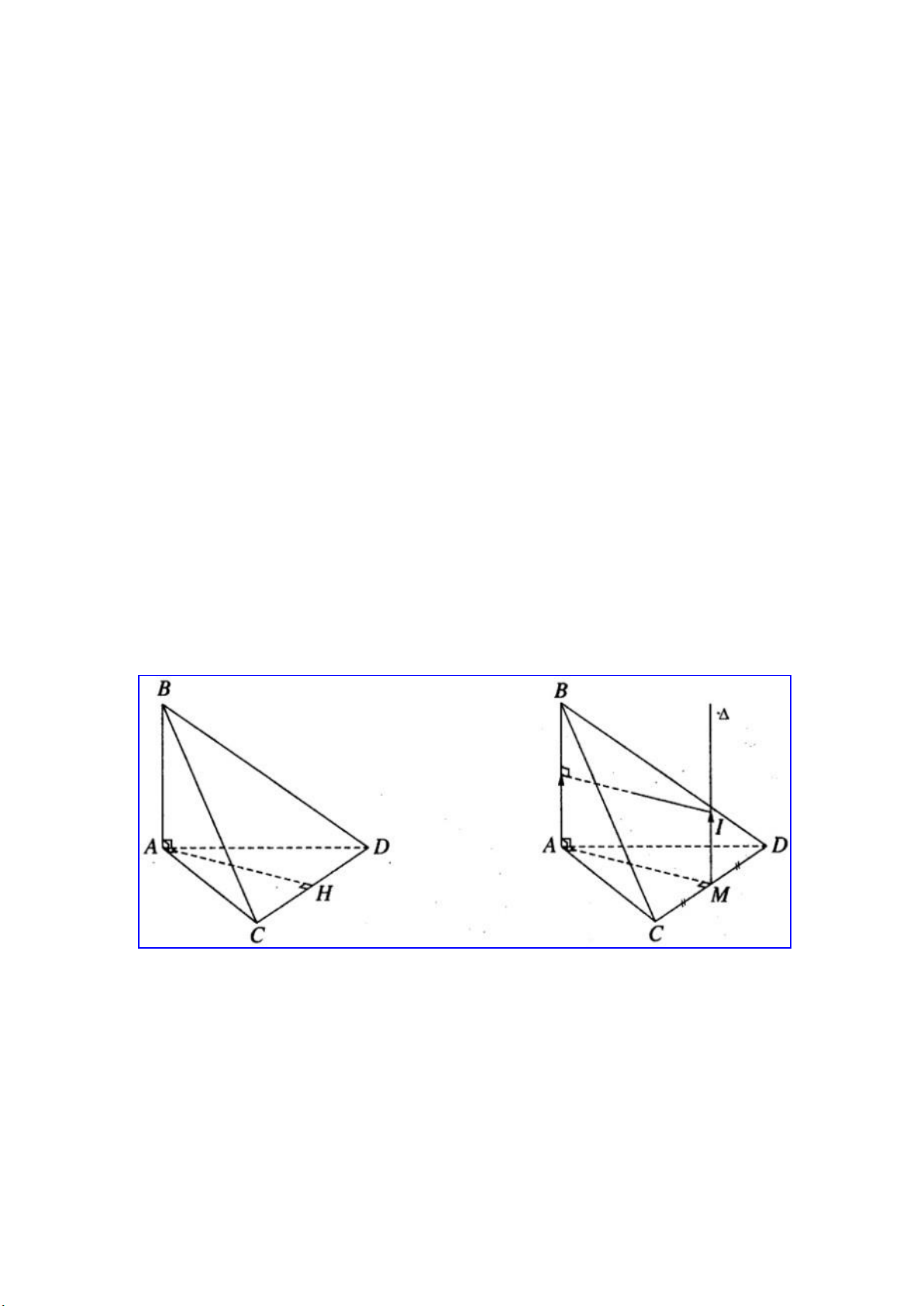
b) Gọi H là hình chiếu vuông góc của A trên CD. Ta có AH chính là đường
vuông góc chung của AB và CD (hình 3.34)
AB→=(−1;0;0); CD→=(0;−2;−4)
Vecto chỉ phương của đường thẳng AH là a→=AB→∧ CD→=(0;−4;2).
Phương trình tham số của đường thẳng AH hay Δ là {x=2;y=4−4t;z=−1+2t
c) Gọi M trung điểm của CD. Vẽ trục Δ của đường tròn (ACD), mặt phẳng
trung trực của AB cắt Δ tại I(a; b; c). Ta có I là tâm của mặt cầu (S) ngoại tiếp tứ diện ABCD (h.3.35)
Ta có M(2; 3; 1), MI→=1/2AB→ ⇒
(S) có bán kính r=IA=√1/4+1+4=√21/2
Vậy phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD là:
(x−3/2)2+(y−3)2+(z−1)2=21/4
d) Mặt phẳng (α) song song với (ABD) nên có vecto pháp tuyến là AC→=(0;0;4) hay n→=(0;0;1)
Phương trình (α) có dạng z + D = 0. Ta có:
(α) tiếp xúc với S(I, r) ⇔d(I,(α))=r⇔|1+D|=√21/2⇔[D=√21/2.−1;D=−√21/2.−1
Vậy có hai mặt phẳng (α) thỏa mãn đề bài là: (α1):z+√21/2−1=0 và (α2):z−√21/2.−1=0