Giải SBT Toán 12: Đề toán tổng hợp - Chương 1. Khối đa diện

Giải SBT Toán 12: Đề toán tổng hợp - chương 1. Khối đa diện
Bài 1.28 trang 22 sách bài tập (SBT) – Hình học 12
Hình được tạo thành từ hình lập phương ABCD.A’B’C’D’ khi ta bỏ đi các điểm
trong của mặt phẳng (ABCD) có phải là một hình đa diện không? Hướng dẫn làm bài:
Không phải là hình đa diện, vì trong hình đó có cạnh (chẳng hạn AB) không
phải là cạnh chung của đúng hai đa giác.
Bài 1.29 trang 22 sách bài tập (SBT) – Hình học 12
Chứng minh rằng mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh. Hướng dẫn làm bài:
Lấy một đỉnh B tùy ý của hình đa diện (H). Gọi M1 là một mặt của hình đa diện
(H) chứa B. Gọi A, B, C là ba đỉnh liên tiếp của M1. Khi đó AB, BC là hai cạnh
của (H). Gọi M2 là mặt khác với M1 và có chung cạnh AB với M1. Khi đó M2
còn có ít nhất một đỉnh D sao cho A, B, D là ba đỉnh khác nhau liên tiếp của M2.
Nếu D≡C thì M1 và M2 có hai cạnh chung AB và BC, điều này vô lí. Vậy D phải
khác C. Do đó qua đỉnh B có ít nhất ba cạnh BA, BC và BD.
Bài 1.30 trang 22 sách bài tập (SBT) – Hình học 12
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông cân ở C. Cạnh B’B = a
và tạo với đáy một góc bằng 600. Hình chiếu vuông góc hạ từ B’ lên đáy trùng
với trọng tâm của tam giác ABC. Tính thể tích khối lăng trụ đó theo a. Hướng dẫn làm bài:
Gọi G là trọng tâm của tam giác ABC, khi đó ˆB′BG=600,B′G=a√3/2,BG=a/2
Gọi D là trung điểm của AC, khi đó BD=3a/4
Ta có BC2 + CD2 = BD2, do đó BC2+BC2/4=5BC2/4=9a2/16
Suy ra BC2=9/20a2, SABC=BC2/2=9/40a2
VABC.A′B′C′=a√3/2.9a2/40=9√3/80.a3
Bài 1.31 trang 22 sách bài tập (SBT) – Hình học 12
Tính thể tích khối lăng trụ có chiều cao bằng h, đáy là ngũ giác đều nội tiếp
trong một đường tròn bán kính r. Hướng dẫn làm bài:
Chia đáy của hình lăng trụ đã cho thành năm tam giác cân có chung đỉnh O là
tâm đường tròn ngoại tiếp đáy. Khi đó diện tích đáy bằng 5/2r2sin720. Do đó thể
tích lăng trụ đó bằng 5/2hr2sin720
Bài 1.32 trang 22 sách bài tập (SBT) – Hình học 12
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, các mặt (SAB) và
(SAD) vuông góc với đáy. Góc giữa mặt (SAC) và đáy bằng 600, AB = 2a, BC
= a. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AB và SC theo a. Hướng dẫn làm bài:
Vì các mặt (SAB) và (SAD) vuông góc với đáy nên SA⊥ (ABCD). Ta có:
{BC⊥ AB;BC⊥ SA⇒BC⊥ (SAB)
⟹ góc((SBC),(ABCD))=ˆSBA=600 Do đó: SA=2atan600=2a√3
VS.ABCD=1/32a√3.2a.a=4√3/3.a3
Vì CD // AB nên d(AB. CD) = d(AB, (SCD)). Hạ AH⊥ SD, để ý rằng CD⊥ (SAD)⇒AH⊥ (SCD). Do đó d(AB, SC) = AH. Ta có: AH.SD=SA.AD ⇒AH=SA.AD/ =2a√3.a/ =2√3/13.a
Bài 1.33 trang 22 sách bài tập (SBT) – Hình học 12
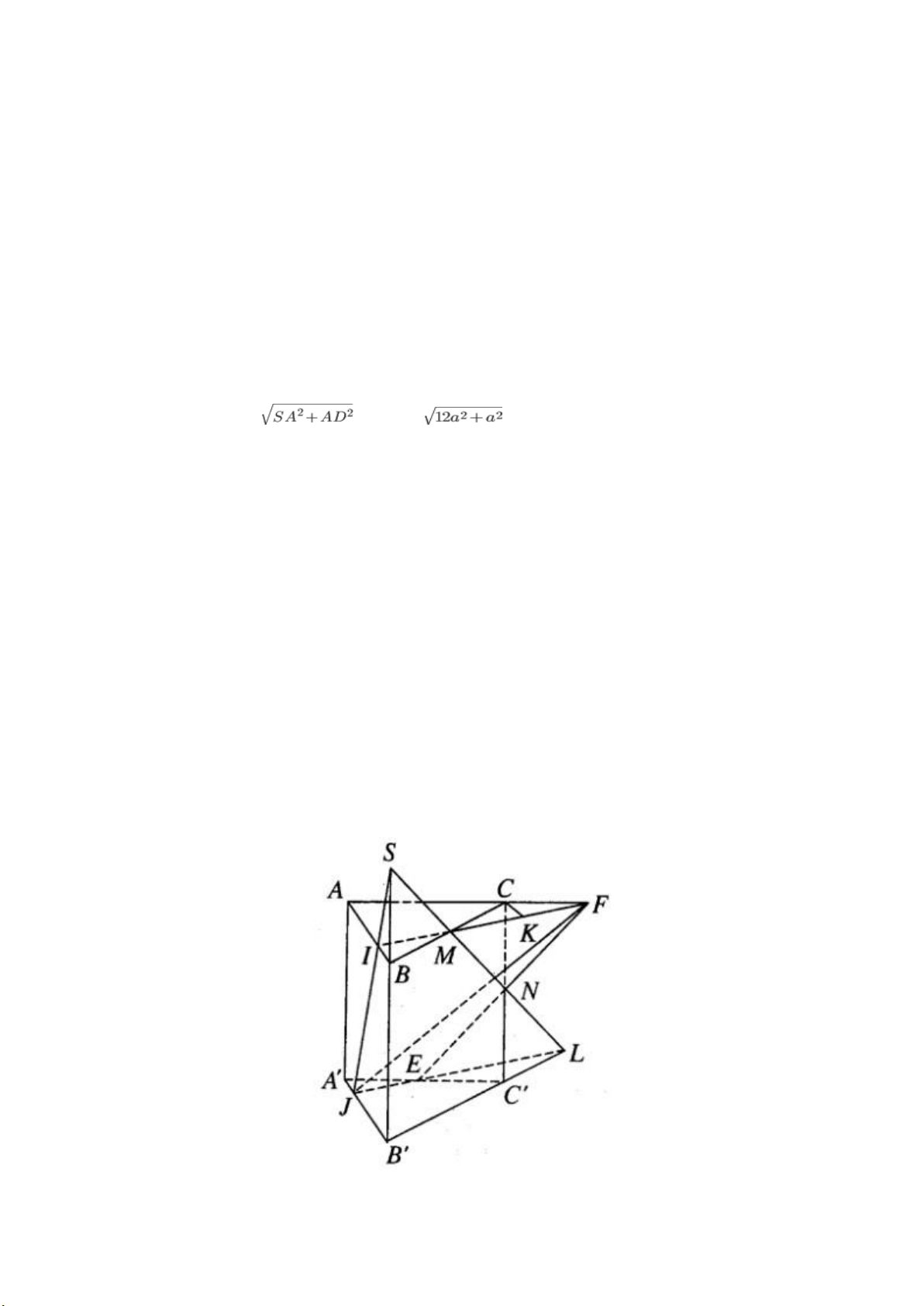
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a. Gọi M, N
và E theo thứ tự là trung điểm của BC, CC’ và C’A’. Đường thẳng EN cắt
đường thẳng AC tại F, đường thẳng MN cắt đường thẳng B’C’ tại L. Đường
thẳng FM kéo dài cắt AB tại I, đường thẳng LE kéo dài cắt A’B’ tại J.
a) Chứng minh rằng các hình đa diện IBM.JB’L và A’EJ.AFI là những hình chóp cụt.
b) Tính thể tích khối chóp F.AIJA’
c) Chứng minh rằng mặt phẳng (MNE) chia khối lăng trụ đã cho thành hai khối
đa diện có thể tích bằng nhau. Hướng dẫn làm bài:
a) Gọi S là giao của hai đường thẳng MN và BB’. Khi đó S, I, J là điểm chung
của cả hai mặt phẳng (MNE) và (ABB’A) nên chúng thẳng hàng. Do đó, ba
đường thẳng BB’, MN và IJ đồng quy nên nó là một hình chóp cụt. Tương tự,
đa diện A’EJ.AFI cũng là một hình chóp cụt.
b) Hai tam giác NCF và NC’E có ˆC=ˆC′=900, NC=NC′,ˆCNF=ˆC′NE nên chúng bằng nhau. Do đó, CF=C′E=a/2
Tương tự, C′L=CM=a/2. Từ đó suy ra tam giác MCF cân ở C.
Ngoài ra ta còn có: ˆCMF=ˆBMI=300 và ˆIBM=600 nên ˆMIB=900,
IB=BM/2=a/4 và IM=√3/2BM=√3/4.a
Vì FI⊥ AB,FI⊥ AA' nên FI⊥ (AIJA′). Ta có diện tích hình thang vuông AA’JI bằng 1/2(3a/4+a/4)b=ab/2.
Gọi K là trung điểm của MF thì do tam giác MCF cân ở C nên CK⊥ MF. Từ đó
suy ra hai tam giác vuông CMK và BMI bằng nhau.
Do đó MF = MK = MI. Từ đó suy ra FI=3√3/4.a
Vậy VF.AIJA′=1/3(ab/2)3√3/4/a=√3/8a2b
c) Tương tự câu b) ta có C′L=CM=a/2, LJ⊥ A′B′ và LJ=3√3/4a
Giả sử mặt phẳng (MNE) chia khối lăng trụ đã cho thành hai khối đa diện (H)
và (H’), trong đó (H’) là khối đa diện chứa đỉnh A, (H’) là khối đa diện chứa đỉnh B’.
Ta thấy V(H′)=VIBM.JB′L−VN.EC′L,V(H)=VJA′E.IAF−VN.FCM
Vì ΔIBM=ΔJA′E, ΔJB′L=ΔIAF, BB′=AA′ nên VIBM.JB′L=VJA′E.IAF
Ngoài ra hai hình chóp N.EC’L và N.FCM có đường cao bằng nhau và có đáy là
những tam giác bằng nhau nên chúng có thể tích bằng nhau.
Từ đó suy ra V(H) = V(H’)
Bài 1.34 trang 22 sách bài tập (SBT) – Hình học 12
Cho hai đoạn thẳng AB và CD chéo nhau, AC là đường vuông góc chung của
chúng. Biết rằng AC = h, AB = a, CD = b và góc giữa hai đường thẳng AB và
CD bằng 600. Hãy tính thể tích của khối tứ diện ABCD. Hướng dẫn làm bài:
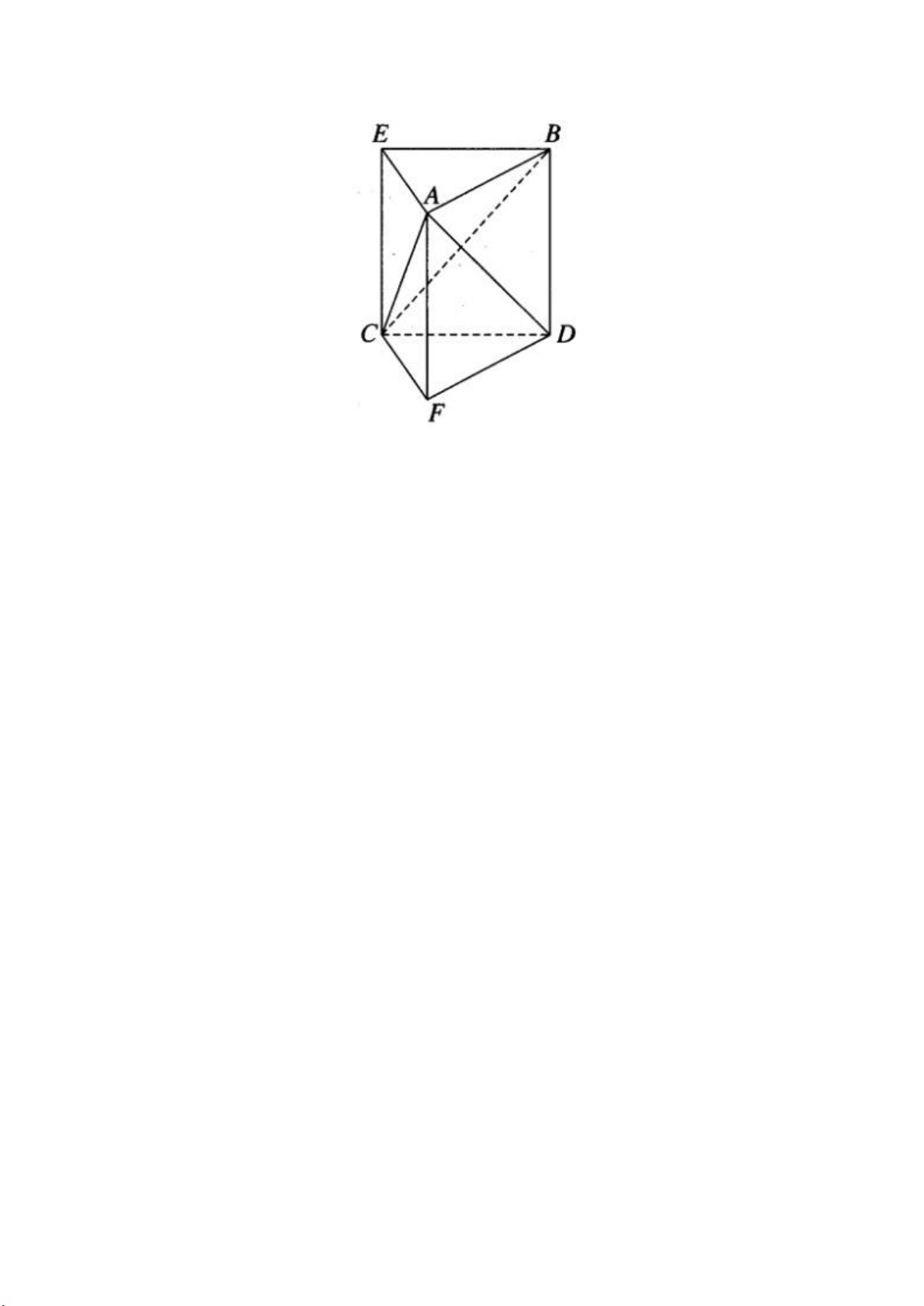
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó, ABE.FDC
là một lăng trụ đứng.
Ta có: SABE=1/2ab.sin600=ab√3/4
VC.ABE=1/3.√3/4ab.h=√3/12abh
Từ đó suy ra VA.BCD=VA.BCE=√3/12abh
Bài 1.35 trang 22 sách bài tập (SBT) – Hình học 12
Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm
các cạnh của tứ diện đều đó. Tính tỉ số V(H)/VABCD Hướng dẫn làm bài
Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là a/2.
Khi đó VABCD=a3/√2/12,V(H)=1/3(a/2)3√2=a3√2/24
Từ đó suy ra V(H)/VABCD=1/2
Bài 1.36 trang 23 sách bài tập (SBT) – Hình học 12
Cho hình lập phương ABCD.A’B’C’D’ cạnh a, M là trung điểm của BB’ Tính theo a:
a) Khoảng cách giữa AC và DC’.
b) Độ dài đoạn vuông góc chung giữa CM và AB’.
Hướng dẫn làm bài a) Gọi d(AC, DC’) = h
Ta có C’A’ // CA , do đó:
d(AC, DC’) = d(AC, (A’C’D)) = d(C, (A’C’D)) = h
Ta có: VA′.CDC′=1/3.a2/2a=a3/6
Để ý rằng tam giác A’C’D là tam giác đều cạnh bằng a√2 Do đó: SA′C′D=a2√3/2
VC.A′C′D=1/3SA′C′D.h=1/3.a2√3/2.h=VA′.CDC′=a3/6 Từ đó suy ra: h= =a/√3=a√3/3 b)
Từ A kẻ đường thẳng song song với MC’, cắt DD’ tại N và A’D’ kéo dài tại J.
Đặt h1 = d(MC’, AB’) = d(M, (AB’N))
Ta có: VM.AB′N=VN.AB′M=1/3.a2/4/a=a3/12
Để ý rằng N là trung điểm của DD’, A’J = 2A’D’ và JA = JB’
Gọi I là trung điểm của AB’, khi đó JI⊥ AB′ Ta có: = a√5;AI=a√2/2 Suy ra: IJ= = 3a/√2
SJAB′=1/2.3a/√2a√2=3a2/2
Do đó: SAB′N=1/2SJAB′=3a2/4
VM.AB′N=1/3.3a2/4.h1=a2h1/4=a3/12 Suy ra: h1=a/3
Chú ý: Có thể tính thể tích SAB’N bằng cách khác. Để ý rằng: AN=a√5/2,AB′=a√2
Gọi α=ˆNAB′. Ta có: NB2=AN2+AB2−2AN.AB.cosα
Hay 9a2/4=5a2/4+2a2−2.a√5/2.a√2cosα
⇒cosα=1/√10⇒sinα=3/√10
Do đó: SAB′N=1/2AB′.AN.sinα=1/2a√2.a√5/2.3/√10=3a2/4
Bài 1.37 trang 23 sách bài tập (SBT) – Hình học 12
Cho tứ diện ABCD. Gọi hA , hB, hC, hD lần lượt là các đường cao của tứ diện
xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh rằng: 1/hA+1/hB+1/hC+1/hD=1/r Hướng dẫn làm bài:
Gọi I là tâm mặt cầu nội tiếp tứ diện, V là thể tích tứ diện. Ta có V=VIBCD+VICDA+VIDAB+VIABC
⇒I=VIBCD/V+VICDA/V+VIDAB/V+VIABC/V =r(1/hA+1/hB+1/hC+1/hD) ⇒1/r=1/hA+1/hB+1/hC+1/hD