Toán 8 Bài 16: Đường trung bình của tam giác Kết nối tri thức
Giải Toán 8 Kết nối tri thức Tập 1 trang 83 Bài 4.6
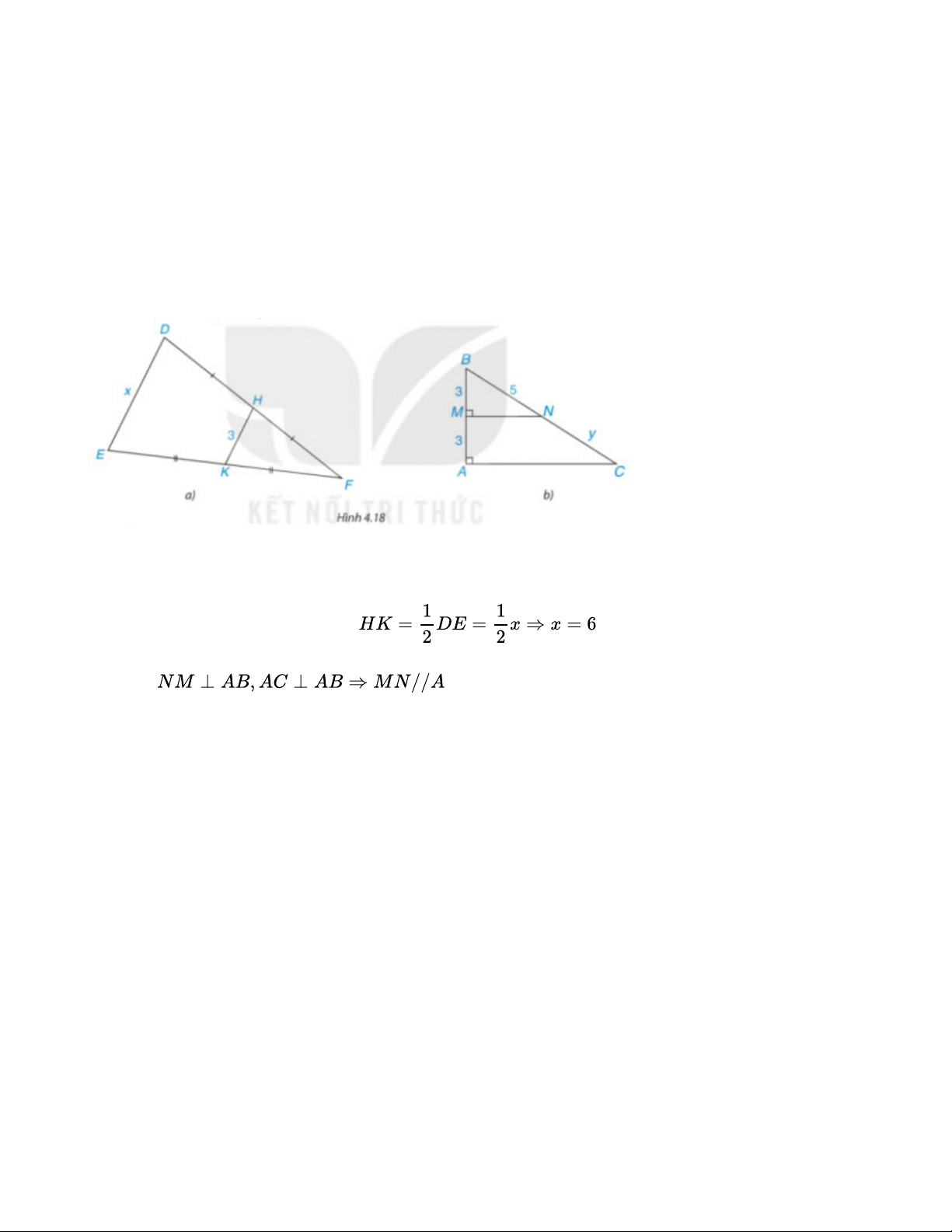
Tính các độ dài x, y trong Hình 4.18. Bài giải:
a) HK là đường trung bình suy ra b) Ta có:
Mặt khác M là trung điểm AB nên MN là đường trung bình của tam giác ABC
Suy ra N là trung điểm BC ⇒ y = BN = 5 Bài 4.7
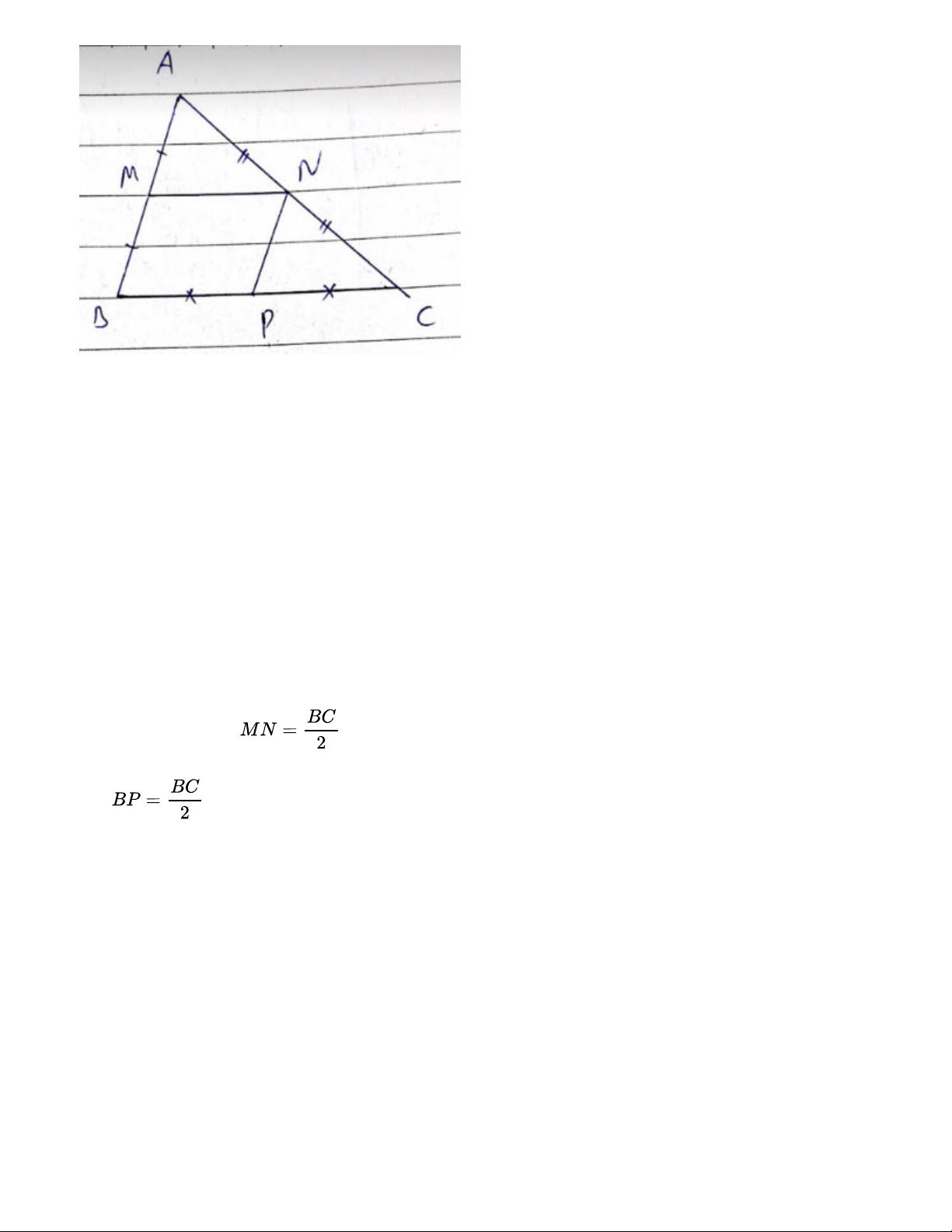
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh tứ giác BMNC là hình thang
b) Tứ giác MNPB là hình gì? Tại sao? Bài giải: a) Xét ΔABC có M là trung điểm của AB N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC suy ra MN // BC
Do đó tứ giác BMNC là hình thang
b) Ta có: MN là đường trung bình của ΔBAC Suy ra: MN//BC và mà nên MN//BP và MN=BP Xét tứ giác BMNP có MN//BP MN=BP
Do đó: BMNP là hình bình hành Bài 4.8
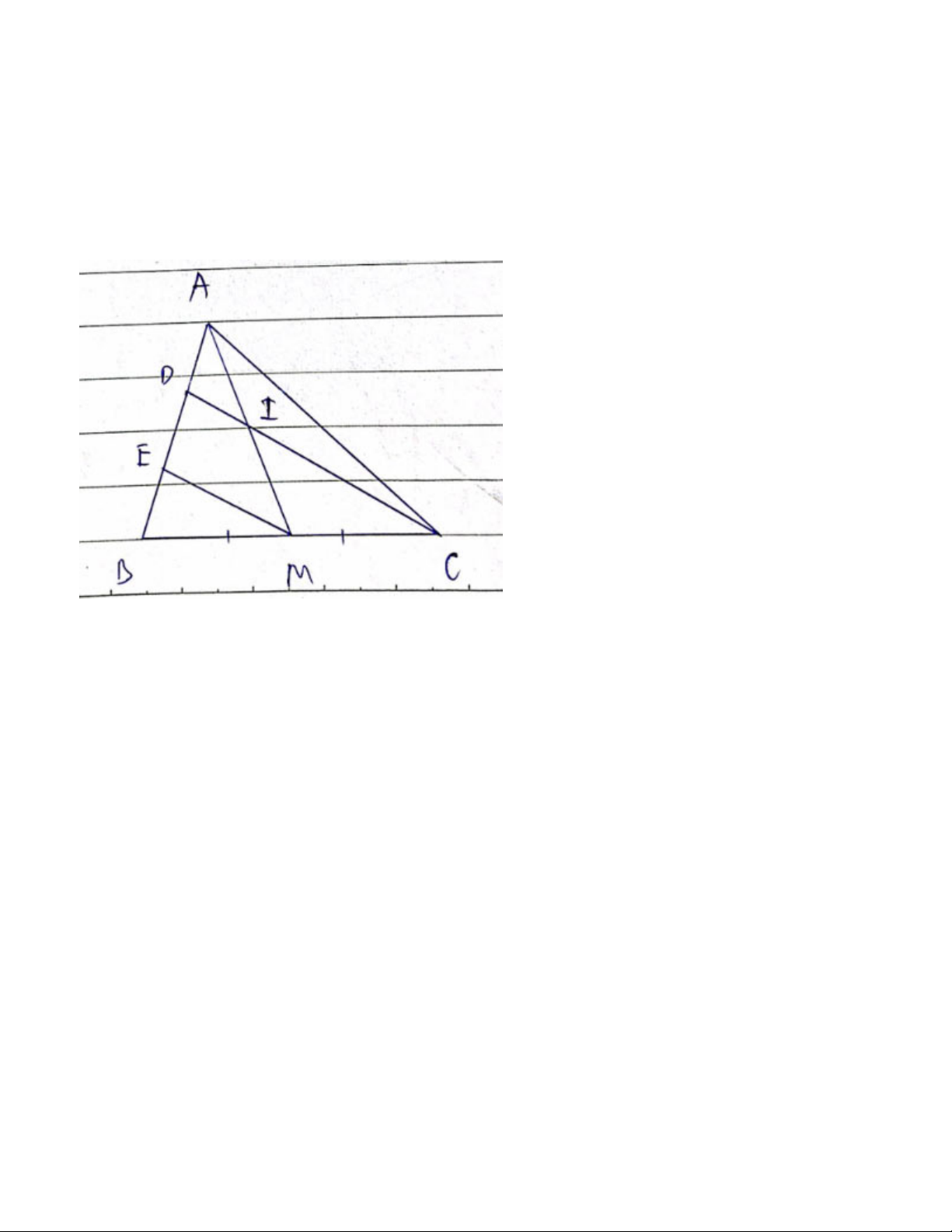
Cho tam giác ABC có trung tuyến AM. Lấy hai điểm D và E trên cạnh AB sao cho AD = DE = EB
và D nằm giữa hai điểm A, E a) Chứng minh DC // EM
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM Bài giải: a) Xét ΔBDC có
E là trung điểm của BD(BE=ED; B,E,D thẳng hàng)
M là trung điểm của BC(gt)
Do đó: EM là đường trung bình của ΔBDC (Định nghĩa đường trung bình của tam giác)
⇒ ME//CD (Định lí 2 về đường trung bình của tam giác) b) Xét ΔAEM có
D là trung điểm của AE(AD=DE; A,D,E thẳng hàng) DI//EM (cmt)
Do đó: I là trung điểm của AM (Định lí 1 về đường trung bình của tam giác) nên AI=IM (đpcm) Bài 4.9
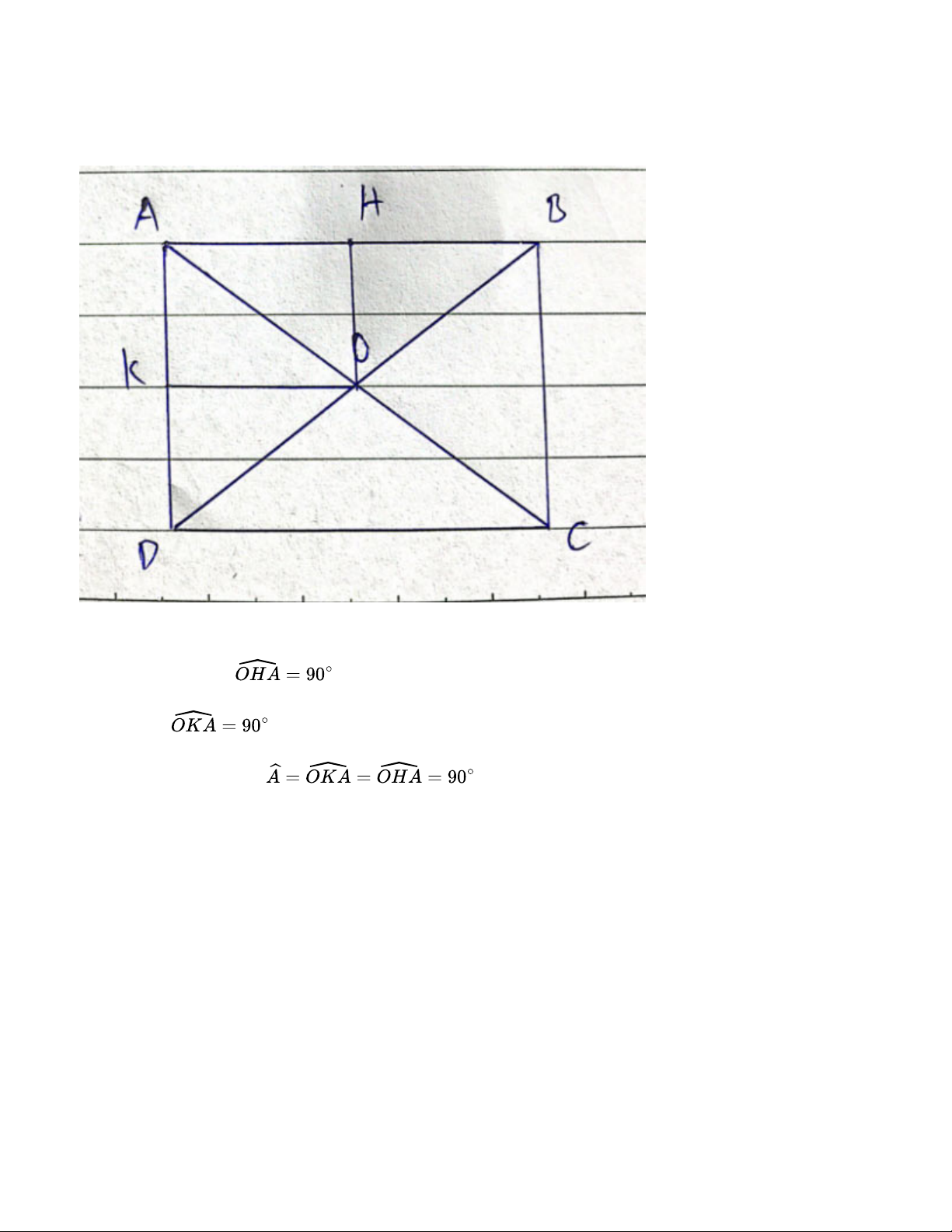
Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD.
Chứng minh rằng tứ giác AHOK là hình chữ nhật Bài giải:
Ta có: OA = OB suy ra tam giác OAB cân tại B, OH là đường trung tuyến nên OH cũng là đường cao, do đó Tương tự, Xét tứ giác AHOK có:
suy ra AHOK là hình chữ nhật