Giải Toán 8 Bài 15: Định lí Thalès trong tam giác | Kết nối tri thức
Giải Toán 8 Bài 15: Định lí Thalès trong tam giác | Kết nối tri thức. Tài liệu được biên soạn dưới dạng file PDF bao gồm 4 trang tổng hợp các kiến thức chọn lọc giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chủ đề: Chương 4: Định lý Thalès (KNTT)
Môn: Toán 8
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Toán 8 Bài 15: Định lí Thalès trong tam giác Kết nối tri thức
Giải Toán 8 Kết nối tri thức Tập 1 trang 80 Bài 4.1
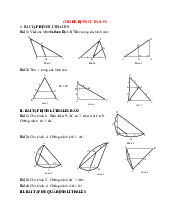
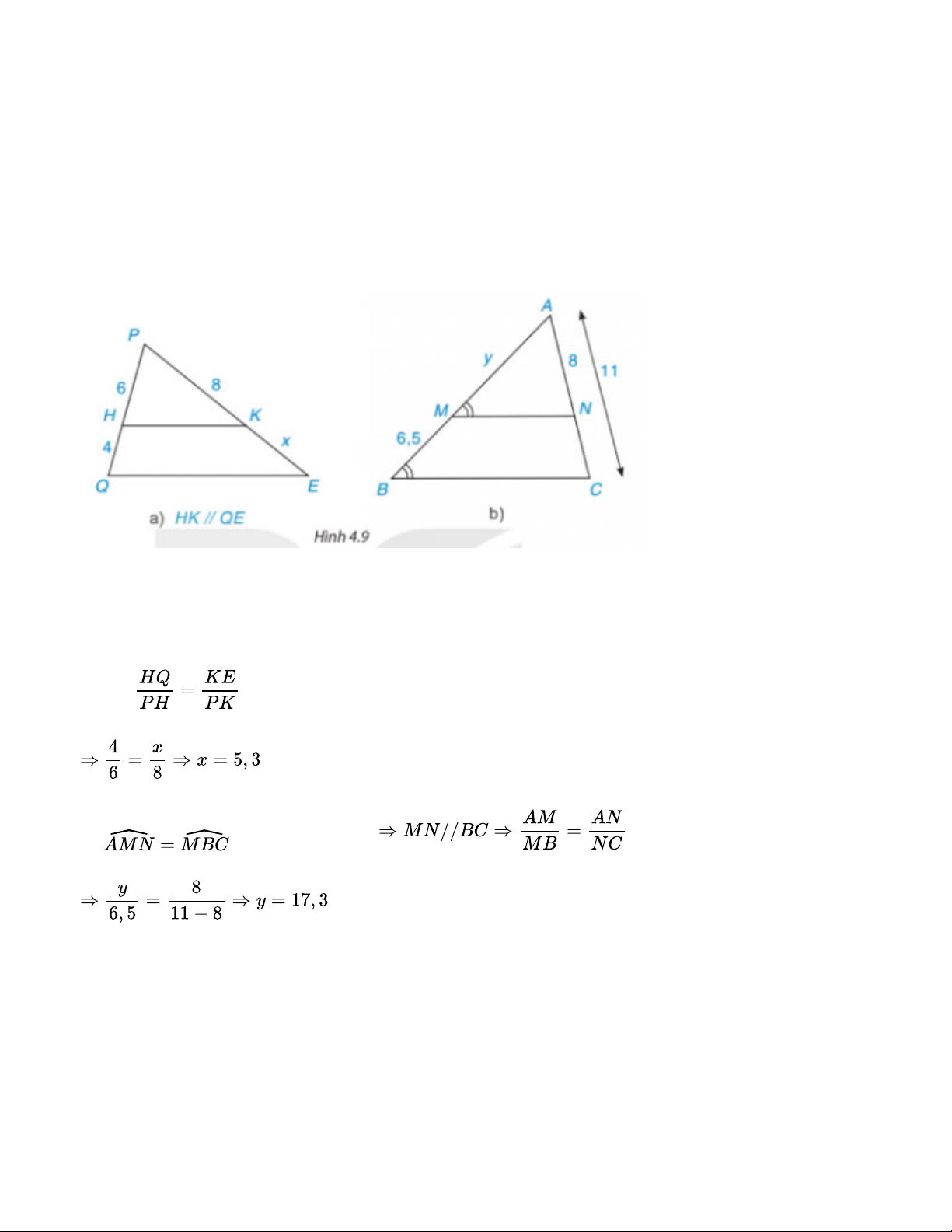
Tìm độ dài x, y trong Hình 4.9 (làm tròn kết quả đến chữ số thập phân thứ nhất) Bài giải: a) HK // QE Ta có: b) (hai góc đồng vị) Bài 4.2
Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích vì sao chúng song song với nhau Bài giải: a) Ta có: b) Ta có: Bài 4.3
Cho tam giác ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và
kẻ đường thẳng song song với AC cắt AB tại E Chứng minh rằng Bài giải:
Xét tam giác ABC có DE//AC, nên: (1)
Mặt khác, DF // AB (gt), ta có: (2)
Cộng các vế tương ứng của (1) và (2), suy ra: Bài 4.4
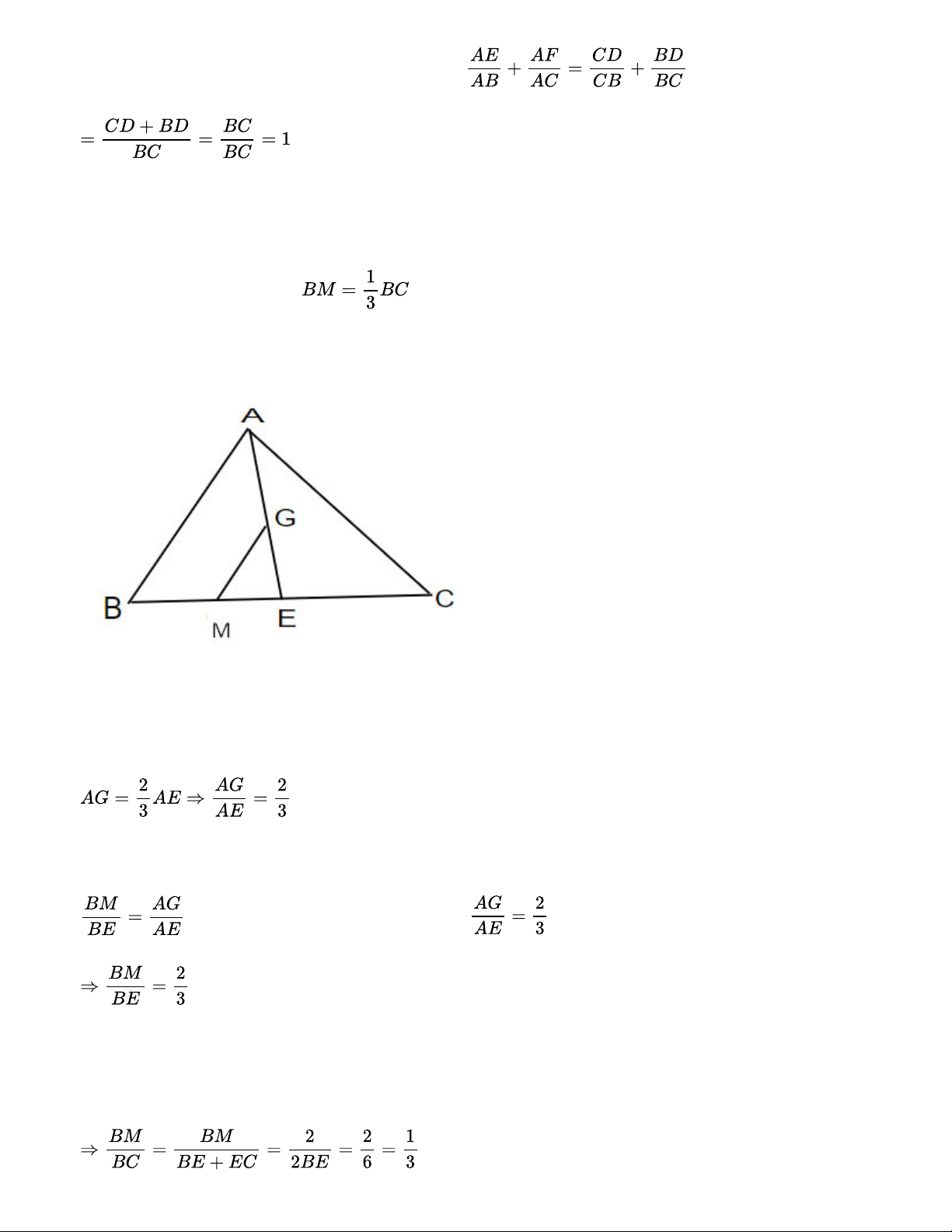
Cho tam giác ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại
điểm M. Chứng minh rằng Bài giải:
Kẻ AE là đường trung tuyến của tam giác ABC, E∈BC
Vì G là trọng tâm của tam giác ABC (gt) nên ta có:
Xét tam giác ABE có GM//AB (G∈AE; M ∈BE vì M∈BC mà E∈BC) ta có:
(áp dụng định lý Ta-lét) mà lại có: (cmt)
Mà AE là đường trung tuyến của tam giác ABC (E ∈BC) nên E là trung điểm của BC ⇒ BE = EC và BE + EC = BC (đpcm) Bài 4.5
Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí , F, C cùng
nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và
AB // EF (H.4.11). Sau đó bác An đo được khoảng cách giữa hai vị trí B và E bằng bao nhiêu? Bài giải:
Xét tam giác ABC có: AB // EF nên (cm)