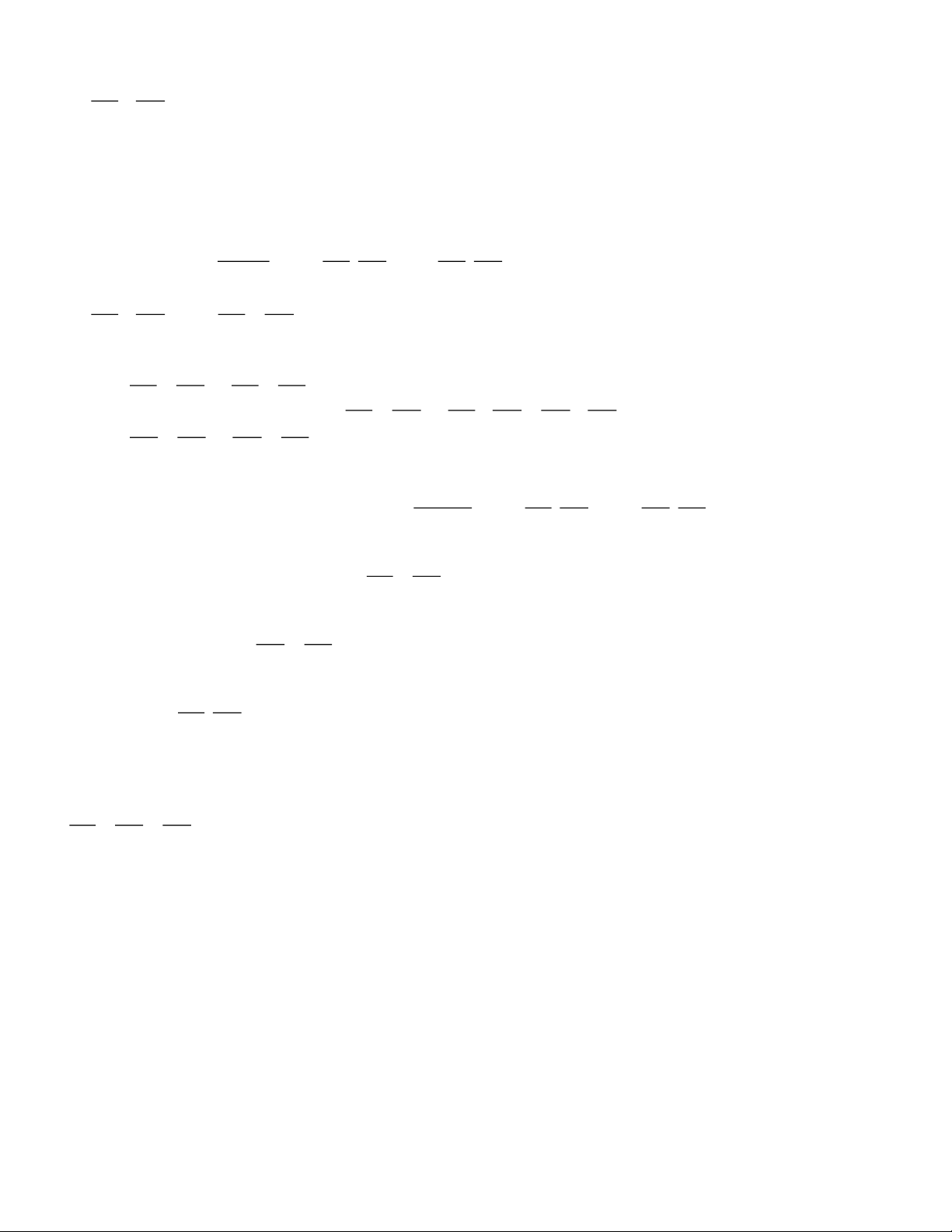


Preview text:
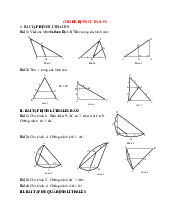
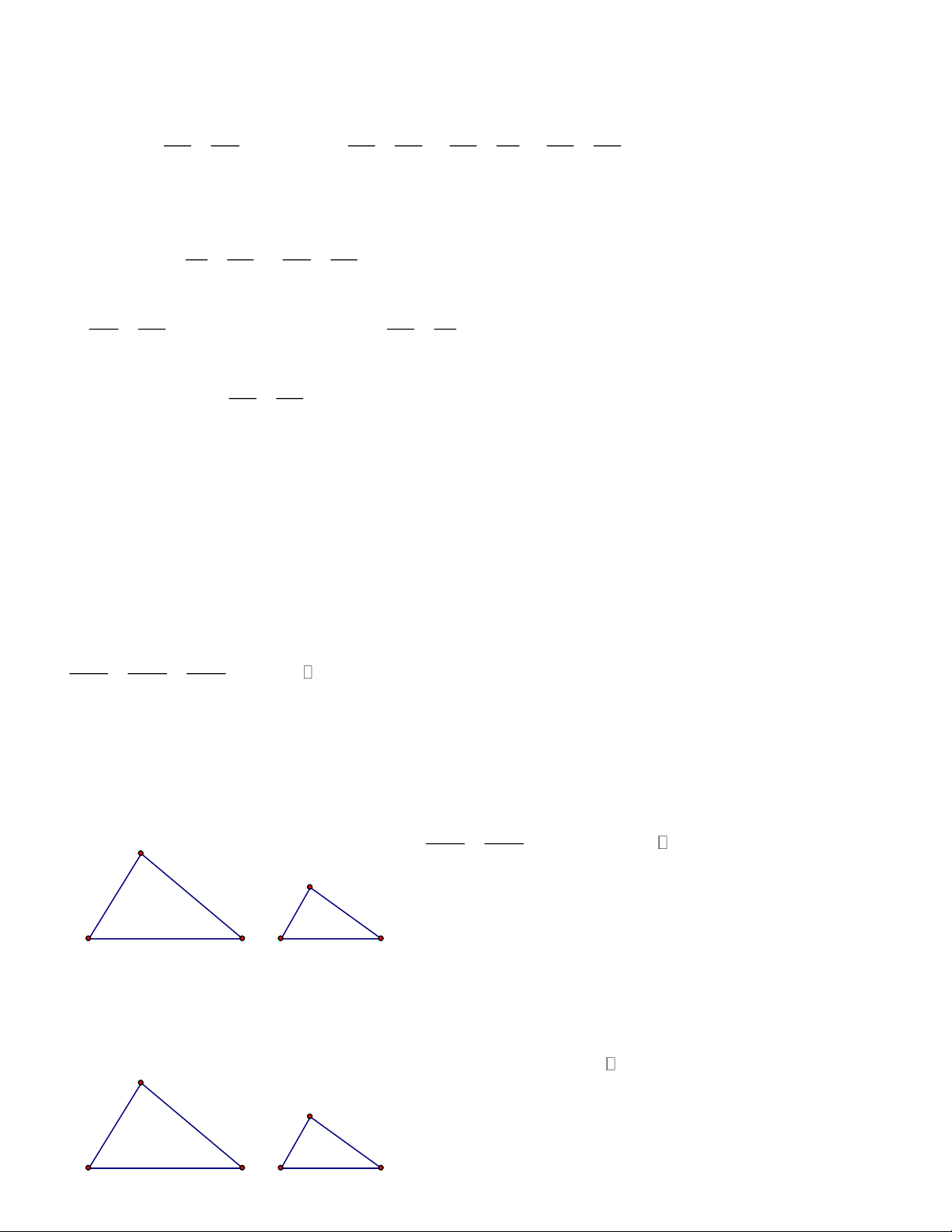
CHUYÊN ĐỀ ĐỒNG DẠNG A. ĐỊNH LÝ TALET 1. Định lý Ta Lét A ABC - AM AN AM AN → = ; = MN // BC AB AC MB NC M N
2. Hệ quả định lý Ta Let A
BC(M AB, N AC) AM AN MN = = MN // BC AB AC BC B C 3. Định lý đảo - Nếu: AM AN = → MN // BC MB NC
4. Chú ý: Định lý vẫn đúng trong các trường hợp sau C' B'
- Ta có: AB ' AC ' B 'C ' = = A AB AC BC A C B B' C' B C
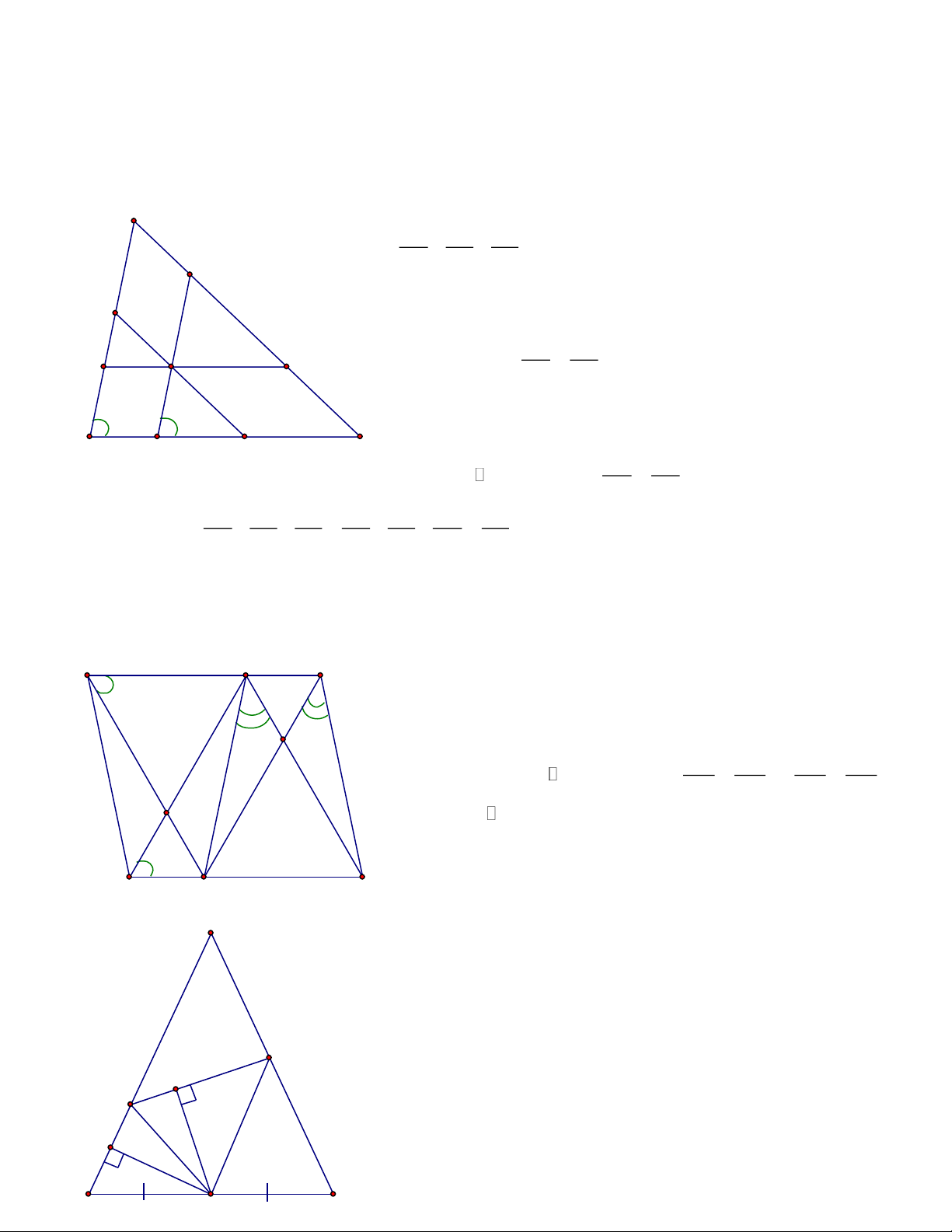
5. Định lý Ta Lét mở rộng n
a. Thuận: Nếu m cắt a, b, c tại A, B, C m
Nếu N cắt a, b, c tại A’, B’, C’ A A' a AB A' B ' AB A' B ' BC B 'C ' → = ; = ; = B' BC B 'C ' AC A'C ' AC A'C ' B b
b. Đảo: Nếu a, b, c, cắt hai cát tuyến m, n và có 1 trong 3 tỉ C' c số sau: AB A' B ' AB A' B ' BC B 'C ' → = ; = ; =
→ a // b / c C BC B 'C ' AC A'C ' AC A'C ' p Trang 1
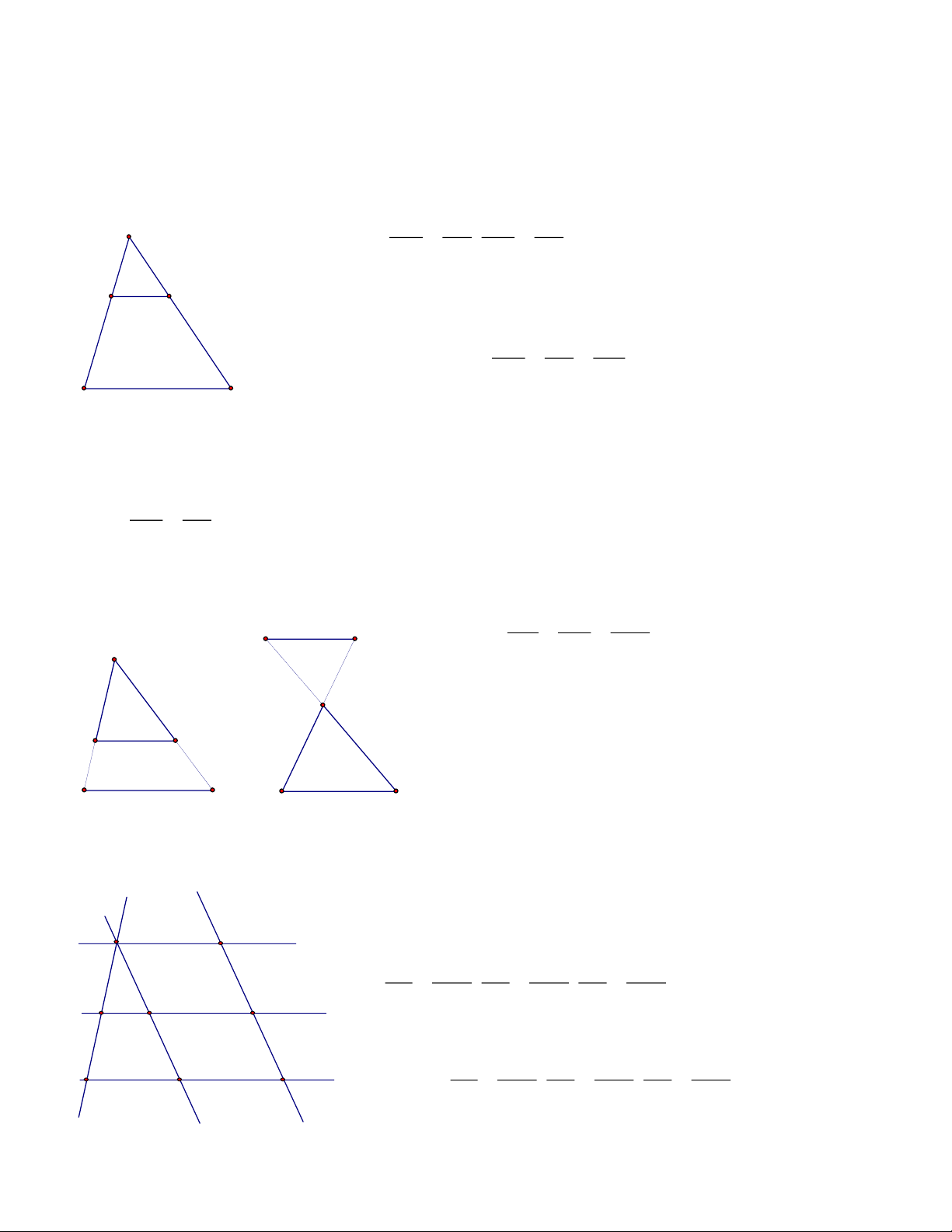
*) Hệ quả: ( các đường thẳng đồng quy cắt hai đường thẳng song song )
1. Hệ quả 1: Nhiều đường thẳng đồng quy định ra trên hai đường thẳng song song những
đoạn thẳng tương ứng tỷ lệ AB AC OA = (= ) A' B ' A'C ' OA'
2. Hệ quả 2: Nhiều đường thẳng không song song định ra trên hai đường thẳng song song các
đoạn thẳng tương ứng tỷ lệ thì chúng đồng quy tại 1 điểm O A C B a a A B C O A' C' B' b b B' C' d d d' d'' d'
- d’, d’’, d’’’ không song song cắt hai đường thẳng song song a và b tại A, B, C và A’, B’,C’ Và thảo mãn: AB AC AB = ;
1→ d ',d ',d ''O A' B '
A'C ' A' B '
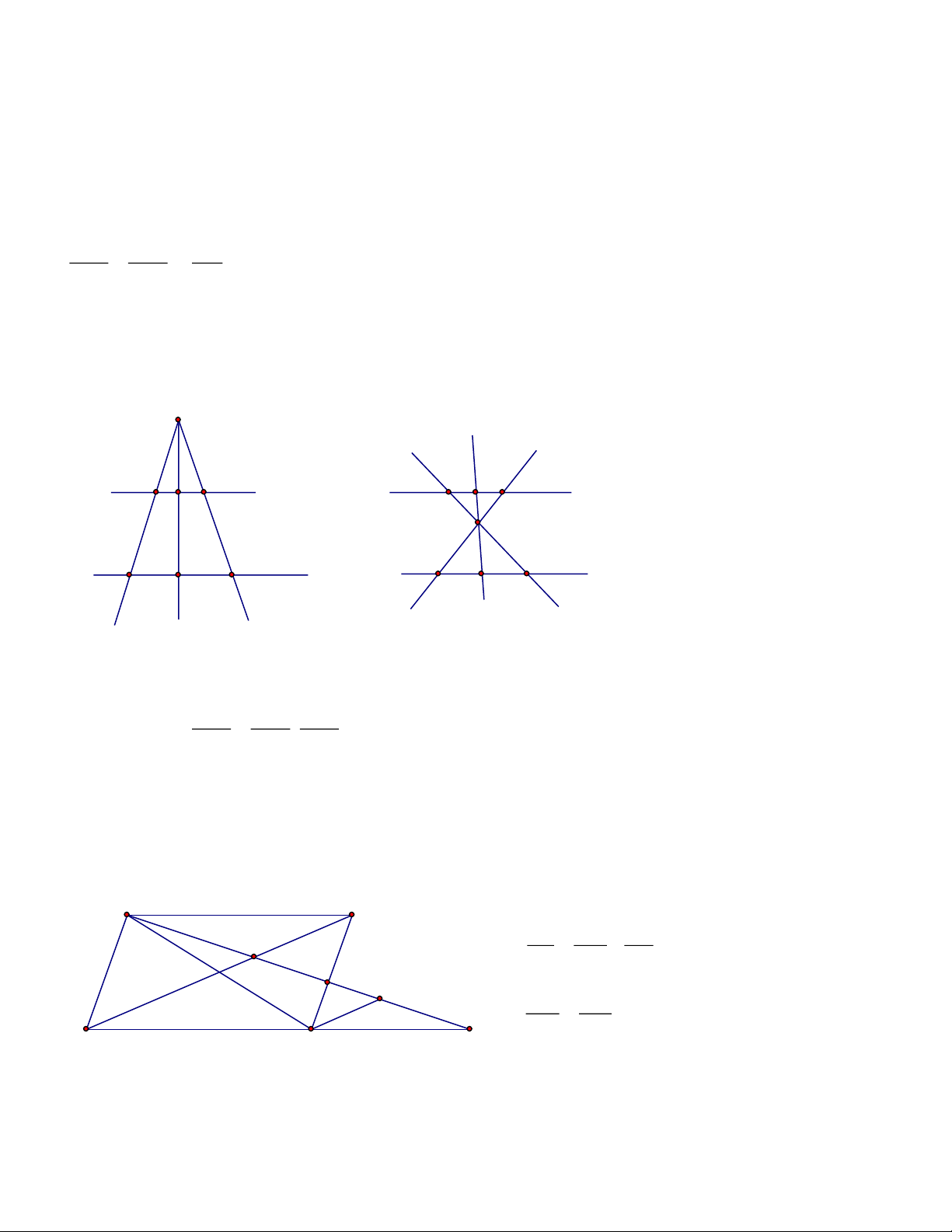
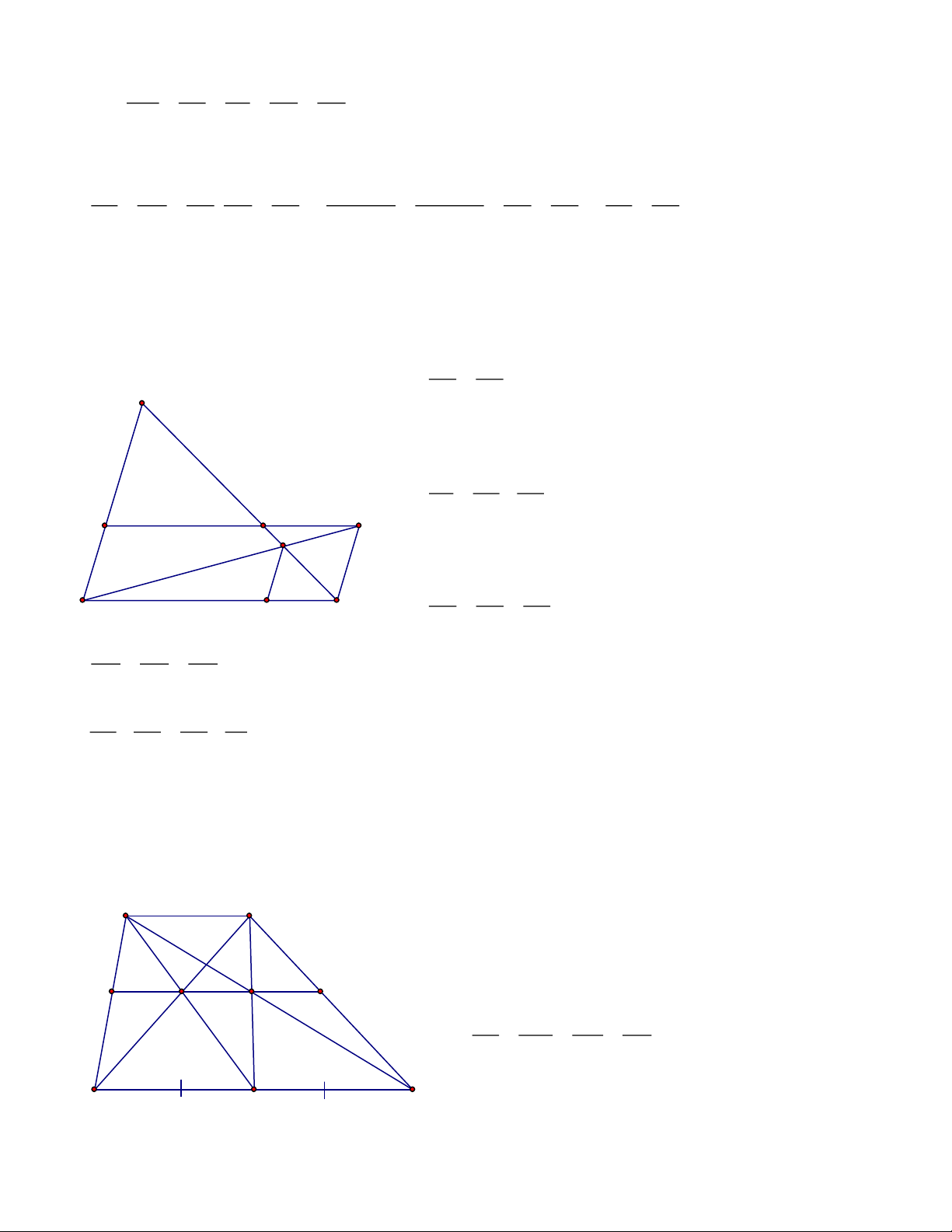
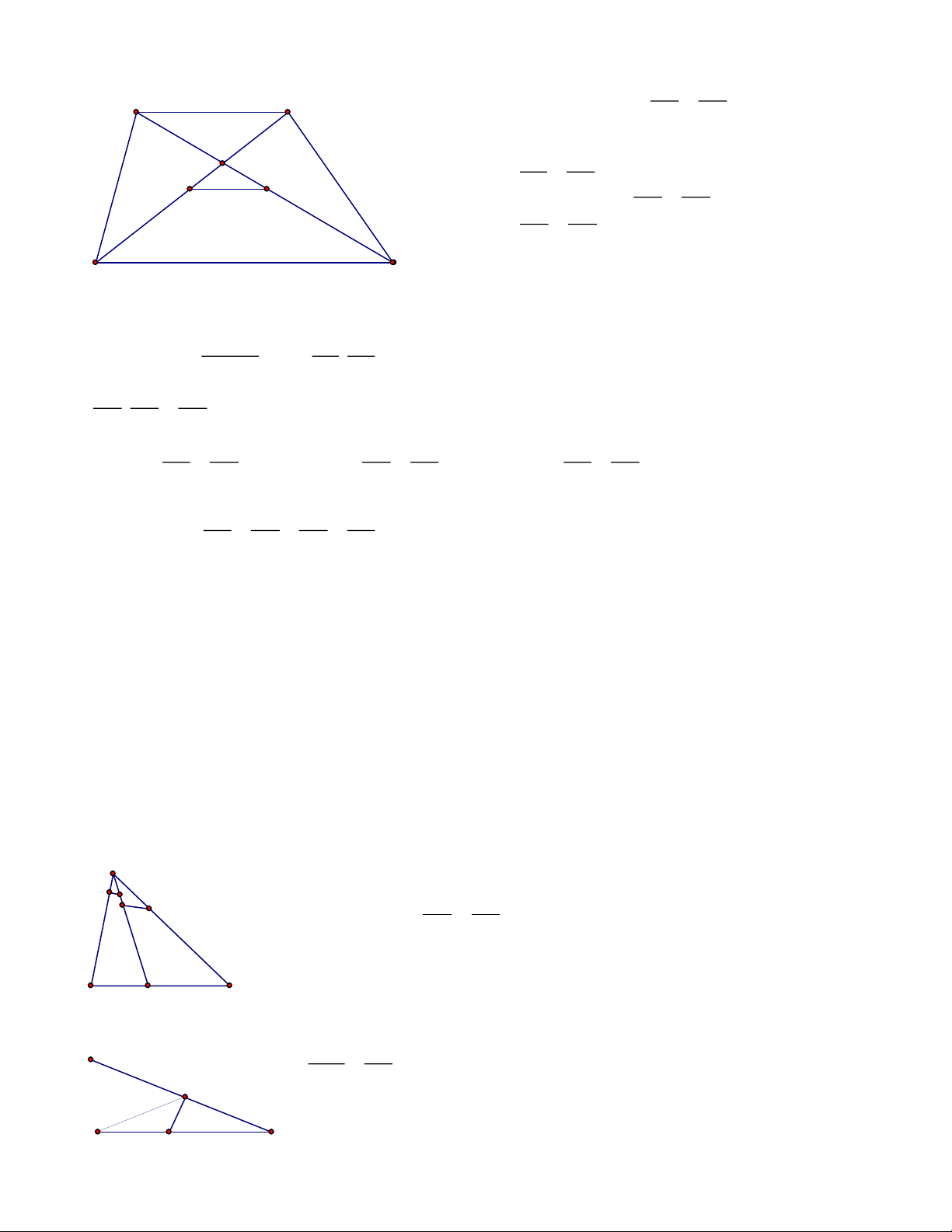
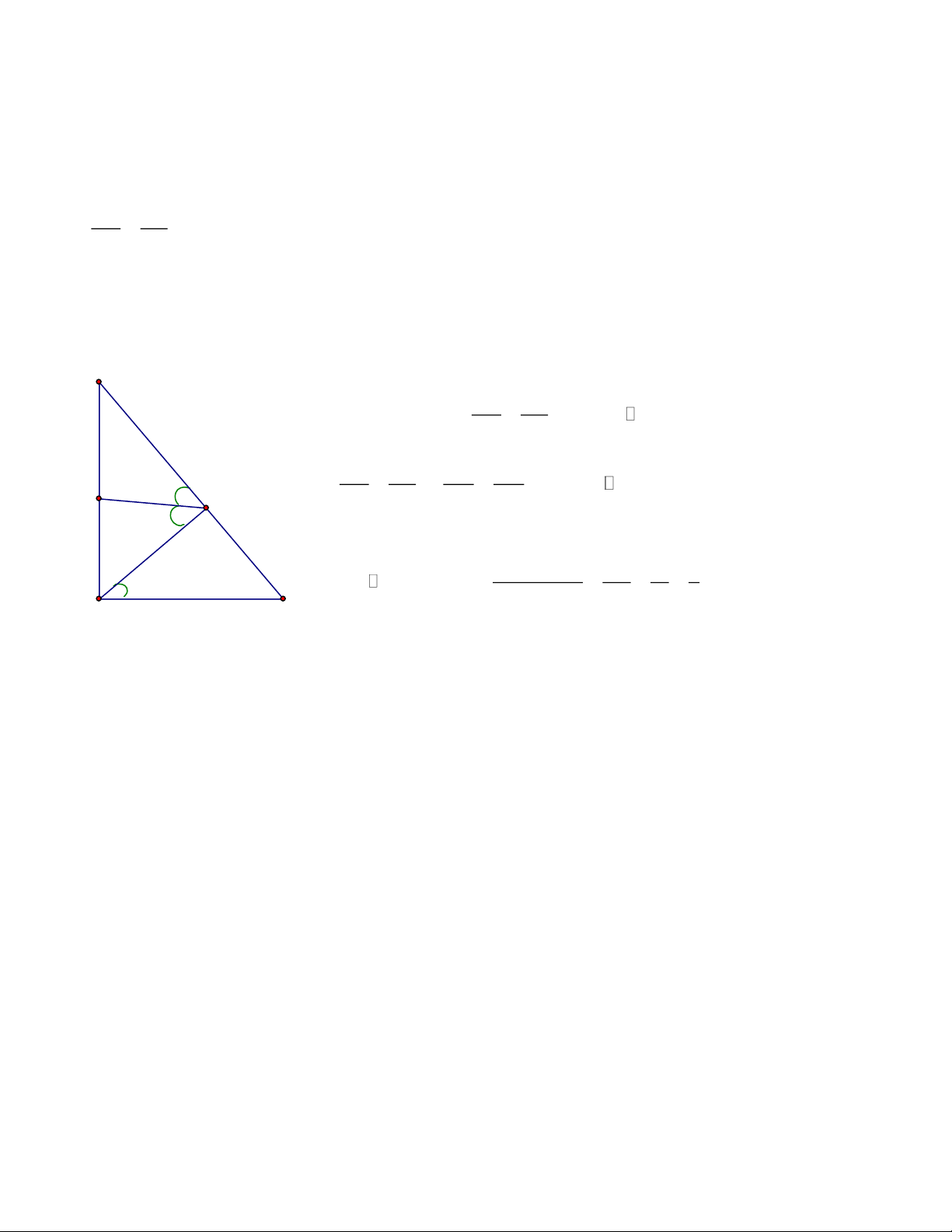
Bài 1: Cho hình bình hành ABCD và điểm E thuộc đoạn BD. Gọi M, N lần lượt là giao điểm
của BC, BD với AE. Qua C kẻ đường thẳng song song với BD cắt MN tại F. Chứng minh rằng a. 2
AE = EM .EN A D E b. 1 1 1 = + AE AM AN F N c. AM FM = AN FN B M C Lời giải Trang 2 a. EA EN 2
AE = EM.EN = EM EA Ta có: EA ED EN = =
( Các đường thẳng song song ) EM EB EA b. 1 1 1 AE AE AE = + = + AE AM AN AE AM AN + Ta có: AE DE AE BE AE AE DE EB = ; = → + = =1 AM DB AN BD AM AN BD
Chia cả hai vế cho AE, ta được: 1 1 1 = + AE AM AN FE BC FC // BE → = FM CM FE BC AN FN CN CN MN c. Ta có: → = = (1);CF // ED → = = = (2) BC AN FM CM NM FE CD AB MA AB // CD → = CM NM Từ (1)(2) FE FN AN MN FN AM → . = . = (dpc ) m FM FE MN MA FM AN
Bài 2: Cho hình thang ABCD có AB // CD, AB < CD. Kẻ đường thẳng qua A song song với
BC cắt BD ở E, đường thẳng qua B song song với AD cắt AC ở F. GỌi M, N lần lượt là giao
điểm của FE với AD, B. Chứng minh rằng: a. EM = FN A B b. 2
AB = FE.CD M N E F Lời giải
Ta phải đi chứng minh FE // AB // CD Hay AE AF = C EP FC D Q P
- Ta có: ABQD và ABCP là hình bình hành nên
AB = DQ = CP → DP = CQ +) AE AB AB FA = = = → FE // PC( .
Ta Let.Dao) → FE // CD // AB EP DP CQ FC a. Ta có: EM DE CN FN EM // AB → = = = → EM = FN AB DB CB AB Trang 3 EM AE FA BN FN = = = = Hoặc: DP AP CA BC
CQ → EM = FN DP CQ = b. FE FE BE BE AB BE AB AB BE FE AB ? = = ; = → = = = → =
→ AB = FE.CD AB DQ BD DE DP BE + DE AB + DP CD BD AB CD
Bài 3: Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB, AC tại D và
E. Qua C kẻ đường thẳng song song với AB cắt DE tại F. Gọi H là giao điểm của AC với BF.
Đường thẳng qua H song song với BC tại I. Chứng minh rằng a. DA ED = A DB FE b. 2 HC = . HA HE c. 1 1 1 = + E IH AB CF D F H Lời giải a. DA ED EA = = I B C DB FE EC b. HC HF HE = = HA HB HC c. IH IH IC BI + = + =1→ dpcm AB CF BC IC
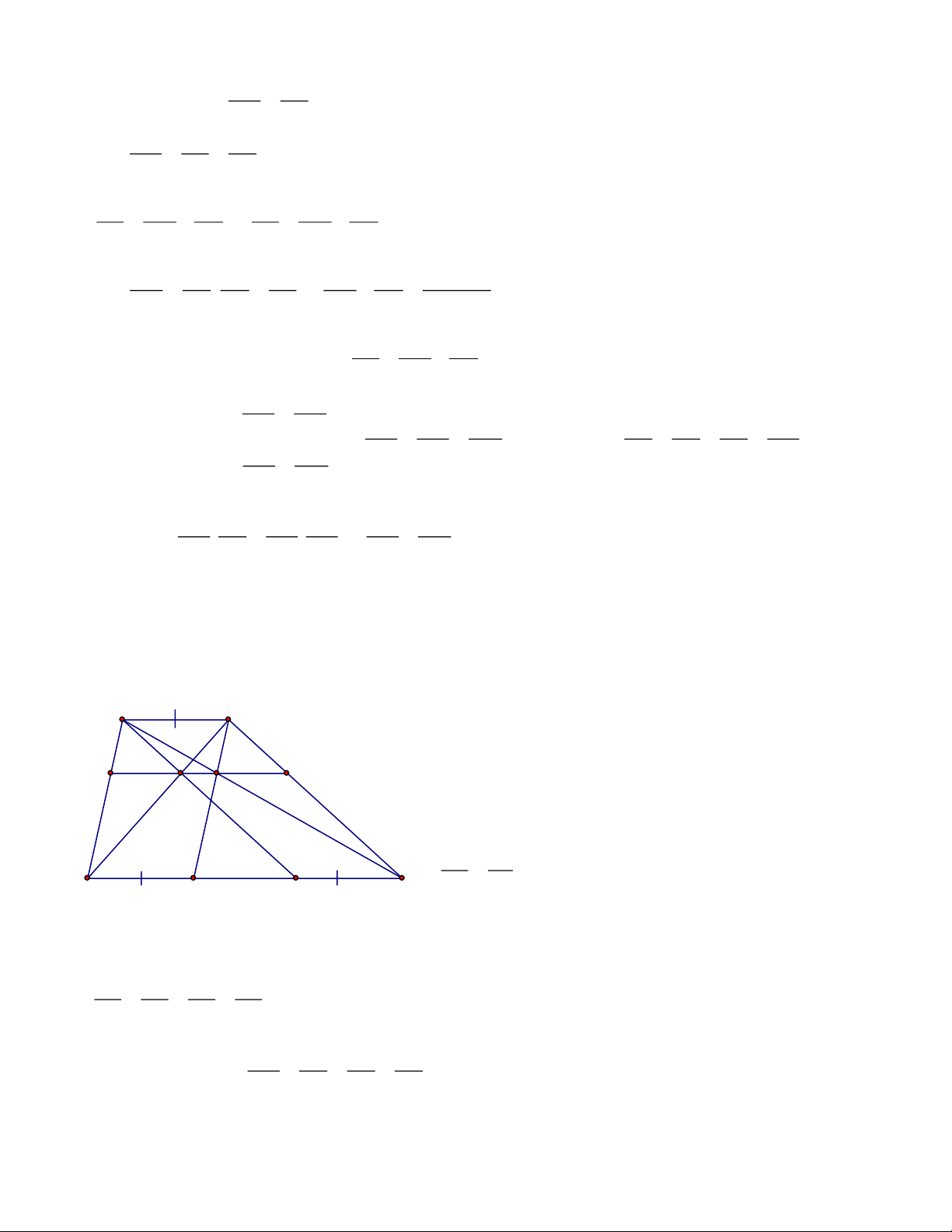
Bài 4: Cho hình thang ABCD ( AB // CD ). Gọi M là trung điểm của CD, gọi I là giao điểm
của AM với BD, K là giao điểm của BM với AC, đường thẳng IK cắt AD, BC lần lượt tại E và F. Chứng minh rằng: a. IK // AB A B b. EI = IK = KF K F Lời giải E I a. AI AB AB AK = = = → IK // MC IM DM MC KC b. Có : D M C Trang 4 IK EI DI KM CF KF = = = = =
→ EI = IK = KF AB AB DB MB CB AB
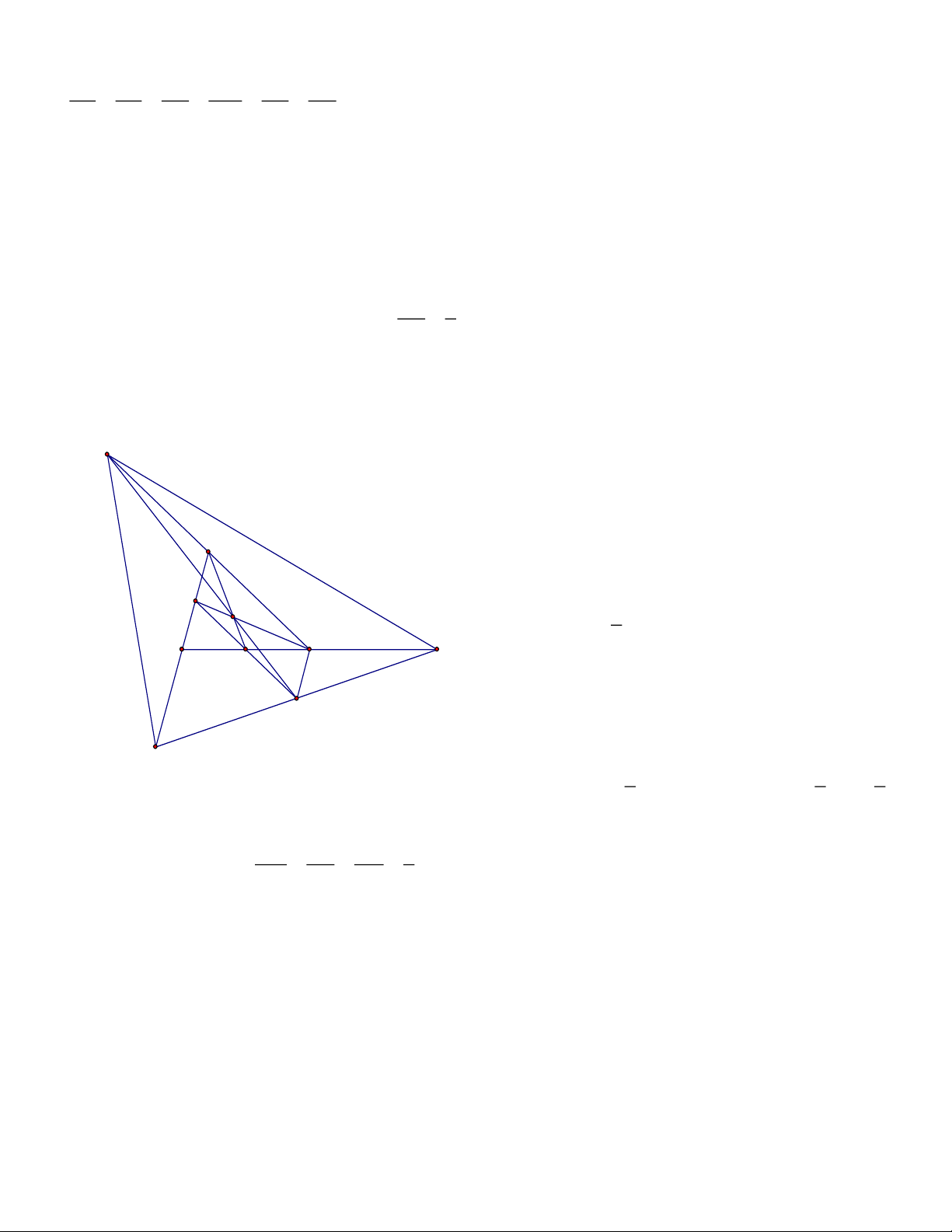
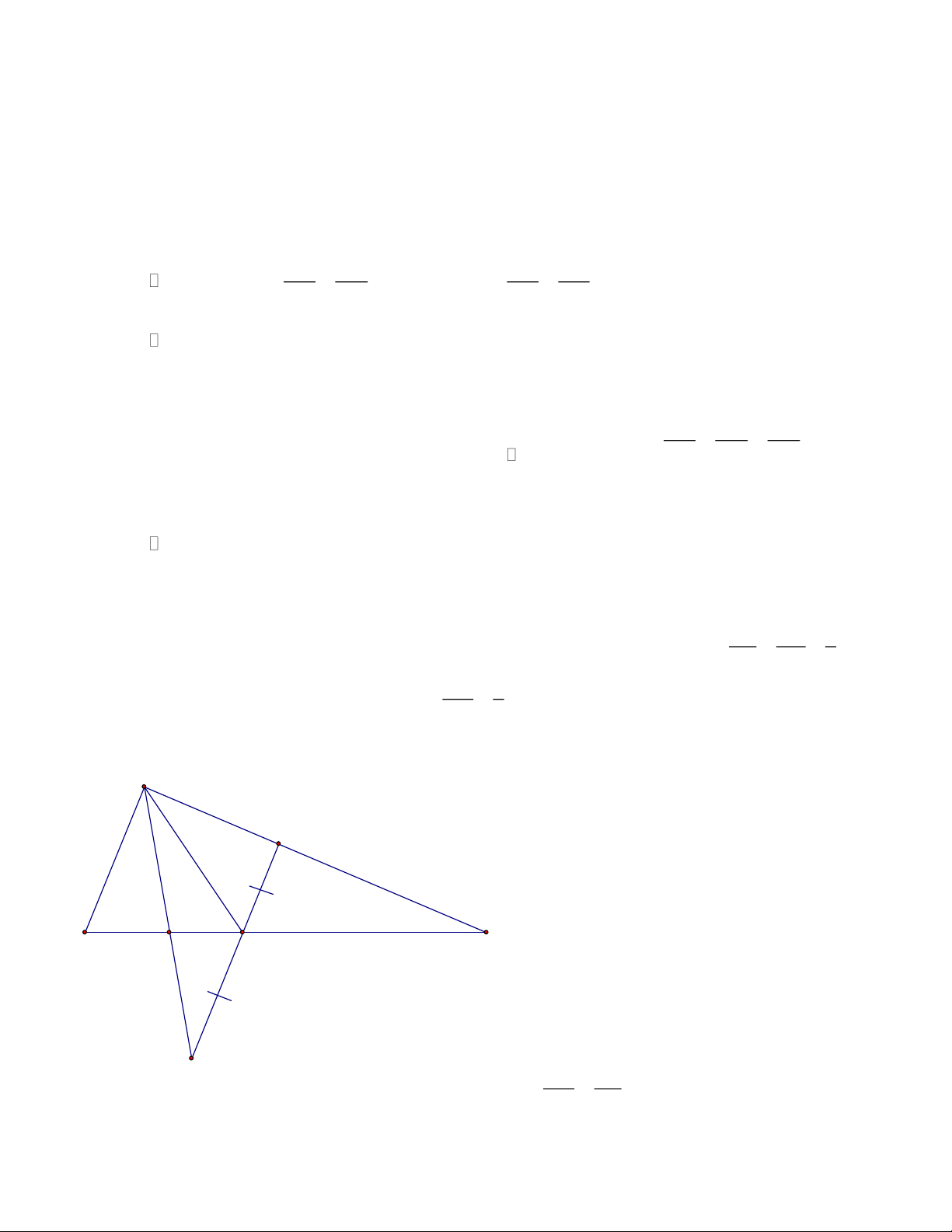
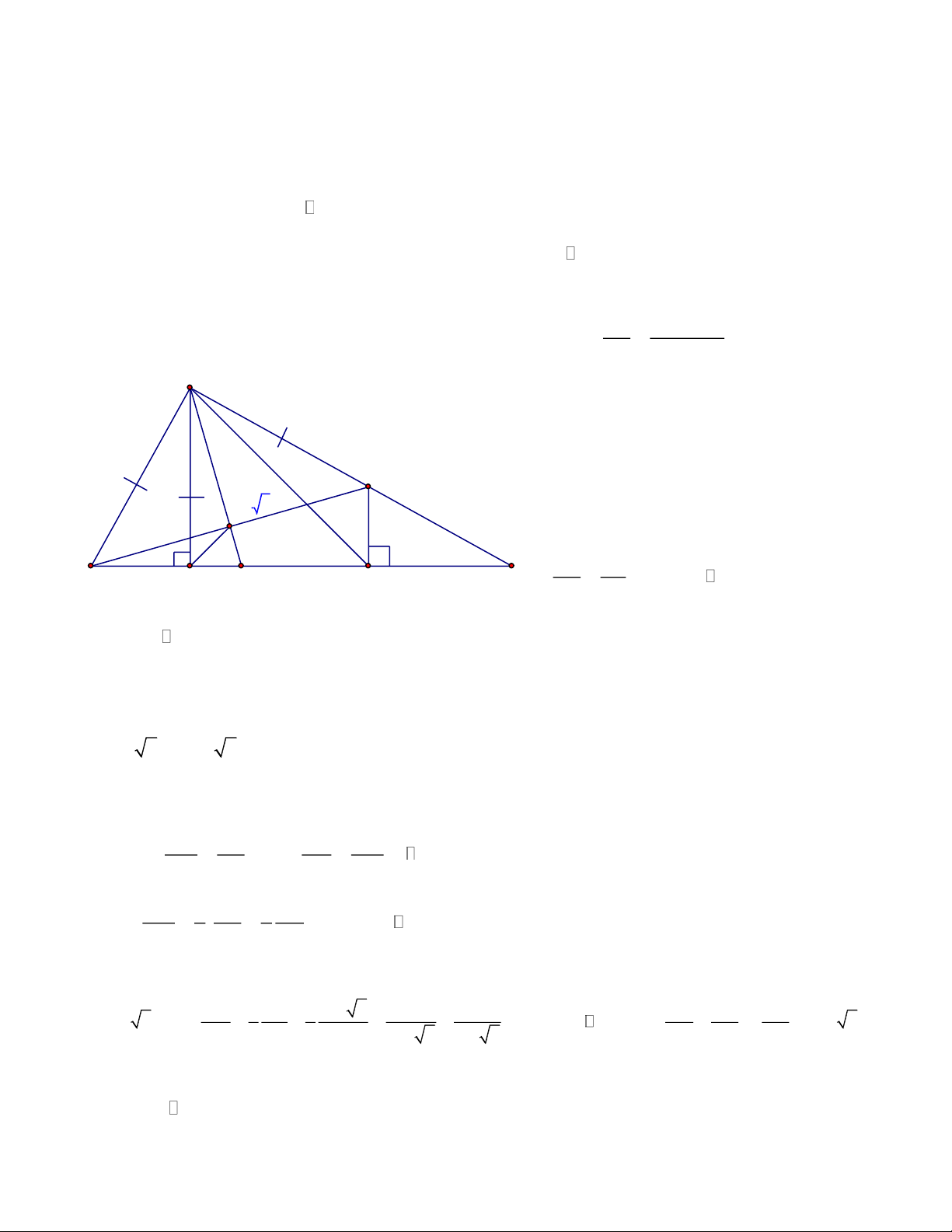
Bài 5: Cho tam giác ABC, gọi D là điểm đối xứng với A qua B, E là điểm đối xứng với B
qua C và F là điểm đối xứng với C qua A. Chứng minh rằng: ABC, DF
E có cùng trọng tâm Lời giải
- Dựa vào tâm đối xứng của hình bình hành
- Hướng dẫn: G là trọng tâm PG 1 D FE
= PM // FA PN // AC A
NPC là hình bình GF 2 hành F Giải
Gọi M, N, P lần lượt là trung điểm của BC, DE, AB A
→ CP là đường trung bình của BDE N G 1 C P // BN → CP // B ;
D CP = BD → → BNCP C 2 C B P = BN M E
Là hình bình hành → M là trung điểm NP P
+) MN là đường trung bình của ABC D 1 1 1
→ MN // AC;MN = AC → MP // AC;MP = AC = FA 2 2 2
Theo định lý Ta Lét: MG PG MP 1 = =
= → G là trọng tâm của hai tam giác. GA GF FA 2
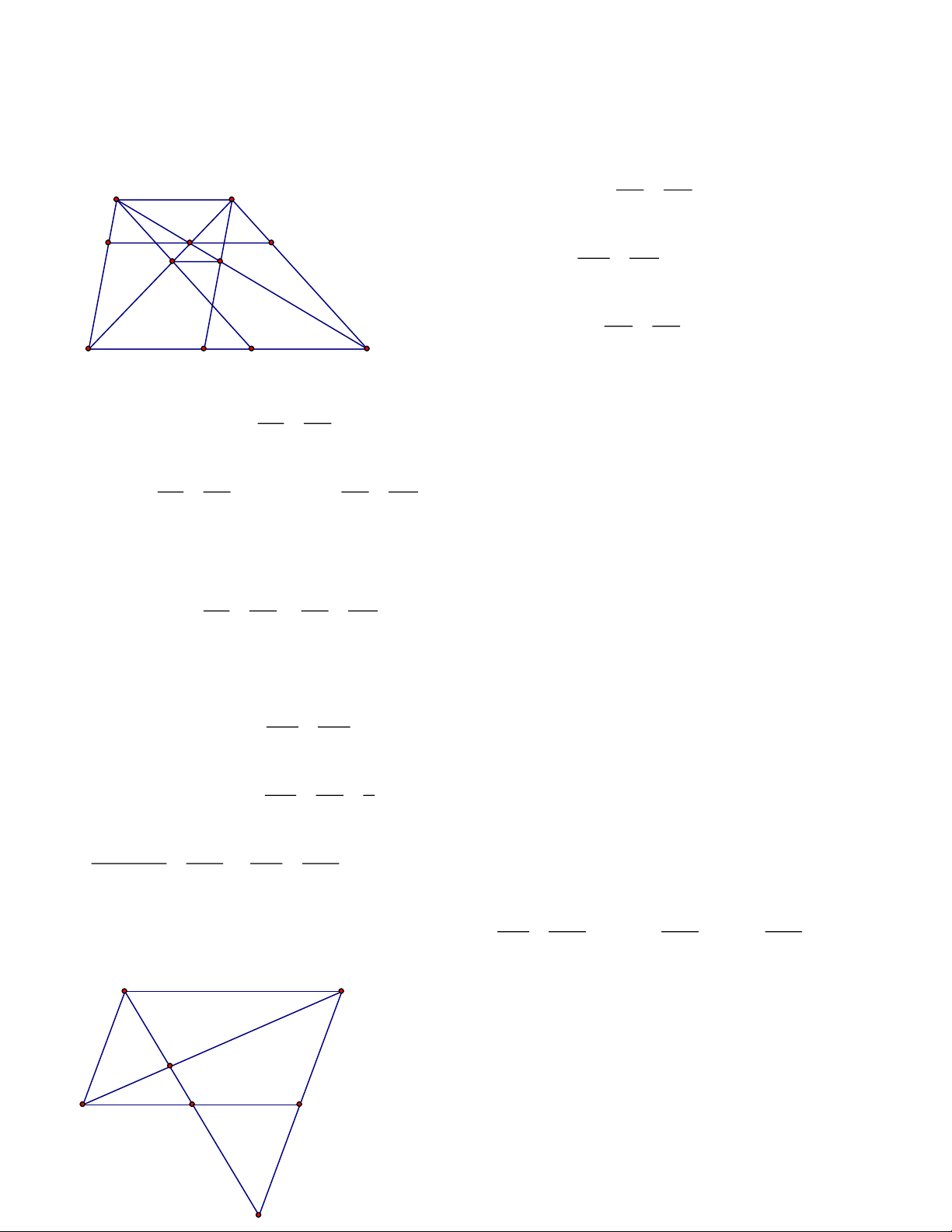
Bài 6: Cho hình thang ABCD ( AB // CD, AB < CD ). AC cắt BD tại M. Kẻ qua M đường
thẳng song song với AB cắt AD, BC lần lượt tại I và K
a. Chứng minh rằng: MI = MK
b. Kẻ Bx // AD, Bx cắt AC, CD tại E, F
Kẻ Ay // BC, Ay cắt BD, CD tại P, Q. Chứng minh rằng: DE // IK Trang 5
c. Biết AB = a, CD = b. Tính IK theo a và b Lời giải A B a. Xét IM AI A
DC, IM // CD → = ( Hệ quả TaLet) (1) CD AD M I K E
- Tương tự ta có: MK BK = (2) P CD DC Lại có: AI BK
IK // AB // CD → = ( TaLet mở rộng ) (3) AD BC D F Q C
Từ (1)(2)(3) → IM = MK
b. Ta đi chứng minh: BE BP = → PE // DF FE PD Thật vậy: BE AB BP AB = (AB // CF)(4); = (AB // DQ)(5) FE FC PD DQ AB ;
FD ABCQ là các hình bình hành → AB = DF = CQ → DQ = CF(6) Từ (4)(5)(6) BE PB AB AB → = (= =
) → PE / DF (Ta Lét đảo ) FE PD FC DQ c. Ta có: IK = 2 MI = 2 MK Xét MK BM B
CD(MK // CD) → = (H . e qu . a TaLet)(1) CD BD Xét MB AB a M
CD(AB // CD) → = = (H . e qu . a TaLet)(1) MD CD b MB a BM a → = → = (2) MB + MD a + b BD a + b Từ (1)(2) MK a ab 2ab → = → MK = → IK = CD a + b a + b a + b A B
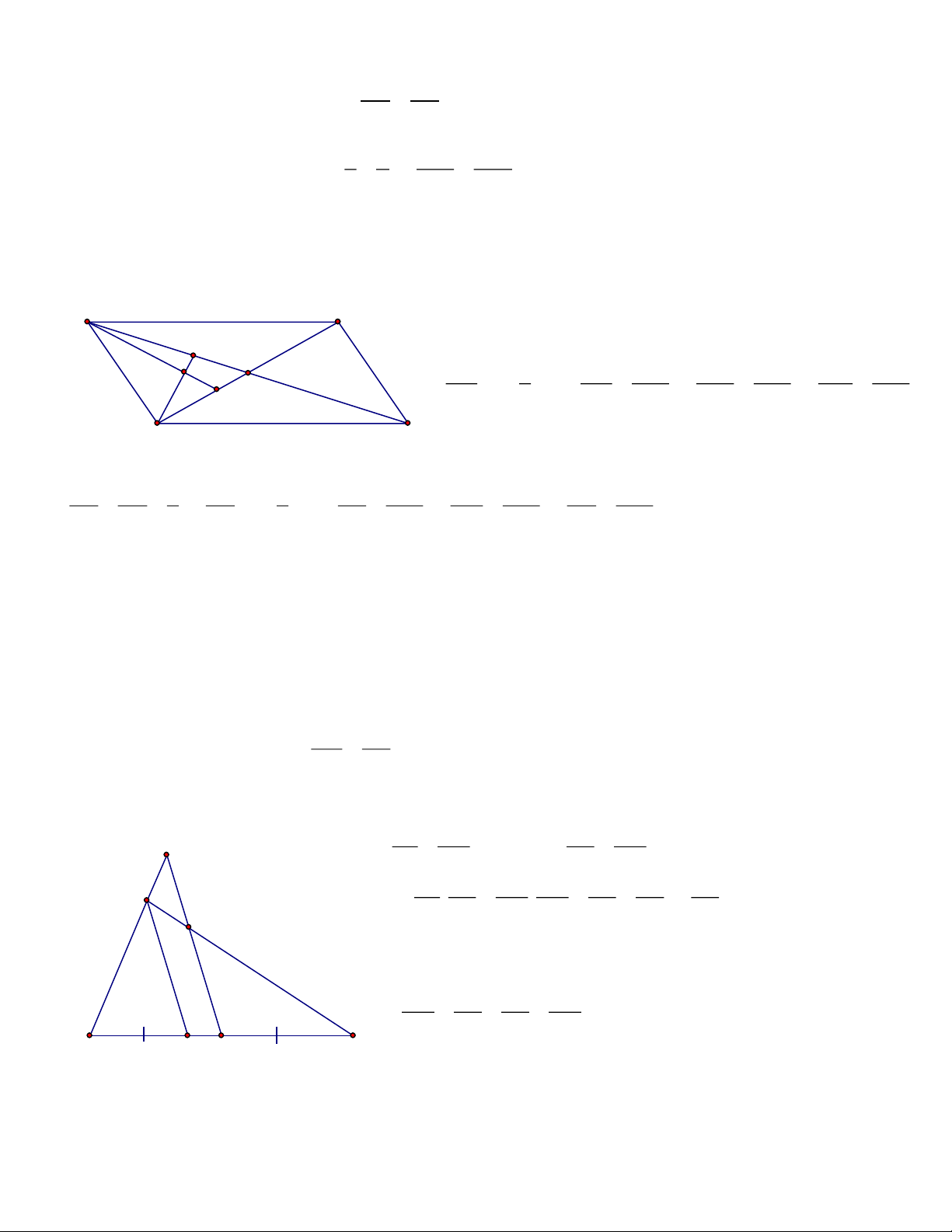
Bài 7: Cho hình hình bình ABCD, đường thẳng qua A
cắt BD, CD, BC lần lượt tại E, I, K. CMR: E a. 2
AE = EI.EK I C D Trang 6 K b. AE AE + =1 AI AK c. DI. BK không đổi Lời giải 2 a. AE AE AE BE DE 2
AE = EI.EK =1 . =1 . =1 EI.EK EI EK ED EB b. AE AE AE EK + =1 = AI AK AI AK AE BE AE BE = → = EI DE AI BD AE EK AE AE EK AE Ta có: → = + = + =1 EK EB EK BE AI AK AI AK AK AK = → = AE DE AK BD c. Ta cần chứng minh: DI.BK DI BK DE BE DI.BK=AD.AB =1 . =1 . =1 AD.AB AB AD EB ED Chứng minh: Xét DI DE D
EI, DI // AB → = (H . e qu . a . Ta Let)(1) AB EB Xét BK BE A
ED, AD // BK → = (H . e qu . a . Ta Let)(1) AD ED Từ (1)(2) DI BK → .
=1→ DI.BK = A .
B AD ( không đổi ) AB AD Hoặc cách khác: DI DE AD = =
→ DI.BK = A .
B AD ( không đổi ) AB EB BK
Bài 8: Cho Tứ giác ABCD, đường thẳng qua A song song với BC cắt BD ở E. Đường thẳng
qua B song song với AD cắt AC ở G
a. Chứng minh rằng: EG // CD
b. Giả sử AB // CD. Chứng minh rằng: 2 AB = C . D EG Lời giải Trang 7 A B a. Hướng dẫn: OE OG EG // CD = OD OC O OE OA AE // BC → = OB OC OE OG → =
→ EG // CD ( TaLet E G OB OG OD OC BG // AB → = OD OA đảo ) D C b. Hướng dẫn: 2 AB AB AB 2 AB = . CD EG =1 . =1 CD.EG GE CD Giải: OA OB OG . = (BG // AD) OG OD OA AB OA OA OD CD OD AB // EG → =
(1); AD // BD → =
(2); AB // CD → = (3) EG OG OG OB AB OB Từ (1)(2)(3) AB OA OD CD 2 → = = = → AB = C . D EG EG OG OB AB
BÌ TẬP TỰ LUYỆN: Cho tam giác ABC vuông tại A, có: AB = a, AC = b. Vẽ ra phía
ngoài tam giác đó các tam giác vuông cân ABD cân ở B và tam giác ACF vuông cân ở C. Gọi
H là giao điểm của AB và CD, K là giao điểm của AC và BF. Chứng minh rằng a. AH = AK b. 2
AH = BH.CK
B. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC
1. Định lý: Trong tam giác, đường phân giác cảu một góc chia cạnh
đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy A A
BC(D BC) DB AB = ˆ ˆ A = A DC AC 1 2
2. Chú ý: Định lý trên vẫn đúng đối với tia phân giác ngoài của tam B D C giác D ' B AB = (AB AC) D 'C AC A D B C Trang 8
3. Chú ý 2: Nếu D thuộc BC mà: DB AB =
AD là phân giác ˆ BAC DC AC
4. Chú ý tính hất của tỉ lệ thức: a c a c = → = b d a + b c + d
Bài 1: Cho hình bình hành ABCD có AB > CD. Phân giác trong các góc BAD cắt BD tại M.
Phân giác trong góc ADC cắt AC tại N. Chứng minh rằng: MN // AD Lời giải A a B N - Ta có: MB a BD a + b 2.DI a + b DM 2b +1 = +1→ = → = → = (1) b I MD b MD b DM b DI a + b M D C Lại có: NC DC a NC a AC a + b 2AI a + b AI 2b = = → +1 = +1→ = → = → = (2) NA DA b NA b NA b AN b AN a + b
Từ (1)(2) → MN // AD ( Ta Lét đảo )
Bài 2: Cho tam giác ABC, AB < AC, phân giác trong AD, M là trung điểm của BC. Đường
thẳng qua M và song song với AD cắt AB, AC lần lượt tại P và Q. Chứng minh rằng: BP = CQ Lời giải
*) Chú ý: Nếu M BC mà: MB AB =
→ AM là phân giác góc BAC MC AC a. Cách 1: BA BD CQ CM P = (AD // PM ); = (MQ // AD) BP BM CA CD BA CQ BD CM BD AB CQ A → . = . = = → =1→ CQ = BP BP CA BM CD CD AC BP Q b. Cách 2: BP BA CA CQ = = = BM BD CD
CM BP = CQ B D M C BM = CM
Bài 3: Khó: Cho tam giác vuông ABC vuông tại A có trọng tâm G, phân giác trong BD, biết
GD ⊥ AC . Tính ˆ ABC Trang 9 Lời giải B Lời giải M
Gọi M, E lần lượt là trung điểm của BC và AG G
→ DE = EA = EG = GM → EGD cân tại E E
Mặt khác, tam giác ABC vuông tại A, có AM = MB = A D C MC → ABM cân tại M - Có: ˆ ˆ ˆ ˆ ˆ ˆ
GD // AB(⊥ AC) → A = G (slt) → DGE = DEG = BAM = MBA 1 1 ˆ ˆ M = E AD AE 1 AB 1 1 → → ED // BC → = = →
= → AB = BC → AB = BM = AM ˆ ˆ M , E : . so l . e trong DC EM 2 BC 2 2
Vậy tam giác ABM là tam giác đều 0 ˆ → ABC = 60
Bài 4: Khó: Cho tam giác ABC ( AB < AC ), các phân giác BD, CE
a. Đường thẳng qua D và song song với BC cắt AB ở K. Chứng minh E nằm giữa B và K
b. Gọi M là giao điểm của DE và CB. Chứng A
minh rằng: CD > DE > BE Lời giải
a. E nằm giữa B và K KB EB K D 1 E I
Ta có: BD là phân giác góc B 2 2 1 1 C AD AB AC AE AD AE M B → = = → (1) DC BC BC EB DC EB Lại có: AD AK AK AE AK AE AB AB DK // BC → = (2) → +1 +1 DC KB KB AB KB AB KB EB
→ KB EB → E nằm giữa B và K b. Có: ˆ ˆ ˆ ˆ
KD // BC → KDB = B (slt) → B = KDB 1 2
Lại có E nằm giữa K và B ˆ ˆ ˆ ˆ
→ EDB KDB → EDB B → EB ED ( cạnh đối diện với góc lớn 2 hơn ) Trang 10 ˆ ˆ ˆ ˆ
EDB B → EDB B 2 1 +) Có: ˆ ˆ ˆ ˆ ˆ ˆ ˆ
EDB + E = B + C
→ E C = C → CD ED BE(dpcm) 1 1 1 1 1 2 ˆ ˆ EDB B1
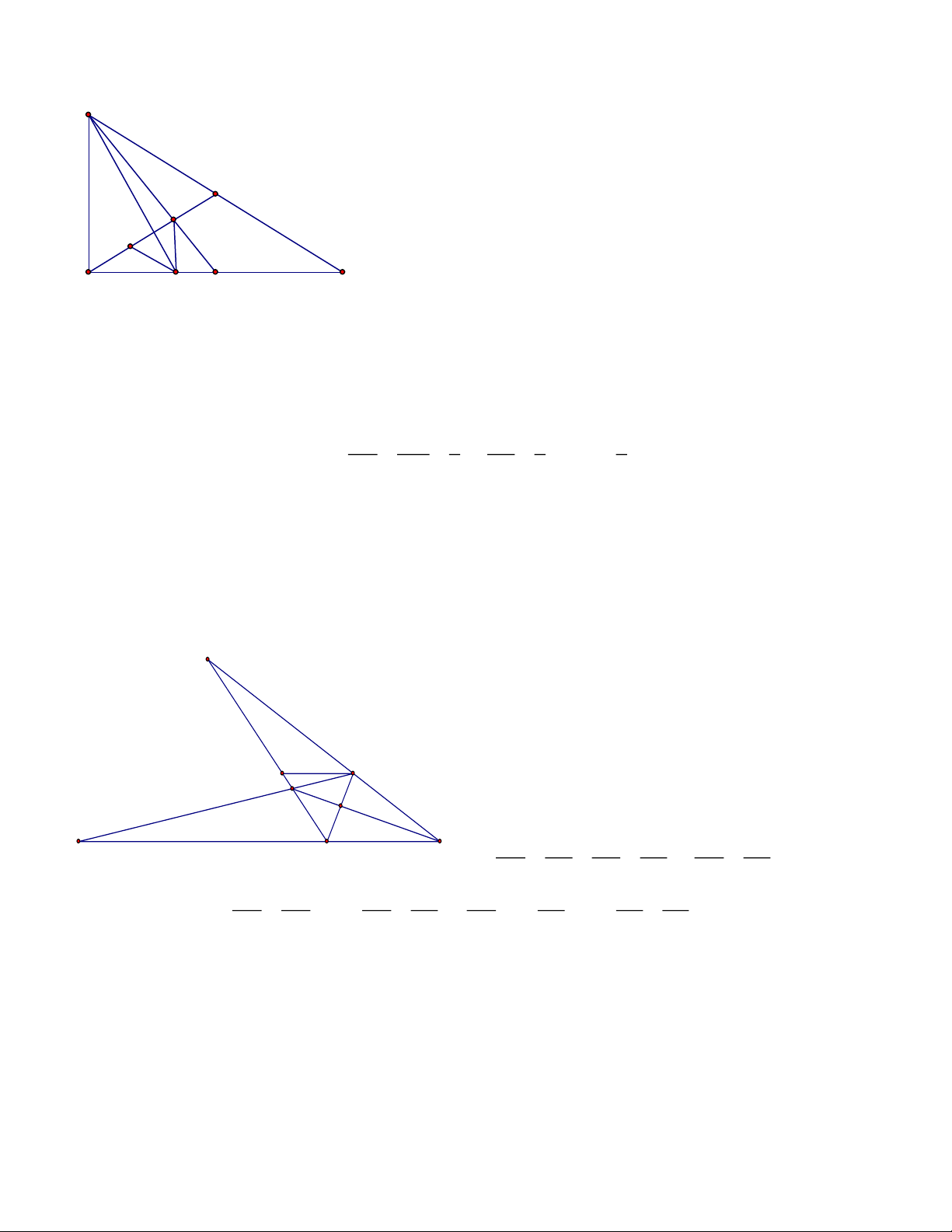
Bài 5: Cho tam giác ABC kẻ phân giác trong và phân giác ngoài của góc B cắt AC ở I và D.
Từ I và D kẻ đường thẳng song song với BC cắt AB ở M và N
a. Tính AB và MN, biết: MI = 12cm, BC = 20cm
b. Từ C kẻ đường thẳng song song với AB cắt BI tại E và cắt BD tại F,Chứng minh rằng:
BI.IC = AI.IE;CE = CF Lời giải N B 4 1 3 M 2 20 F 12 A I C D E
a. Ta có MBI cân tại M → MI = MB =12(cm) AM MI 12 3 AB − MB 3 AB −12 3 AB = 30 Do MI // BC → = = = → = = → AB BC 20 5 AB 5 AB 5 AM =18
b. Có BD là phân giác ngoài của AD AB 3 AN AD 3 30 + BN 3 ˆ CBN → = = ; BC // ND → = = →
= → BN = 60;MN = 72 DC BC 2 BN CD 2 BN 2 BI AI BI IC
c. Có: EC // AB = → .
=1→ BI.IC = IE.AI IE IC IE AI Trang 11 d. Hướng dẫn AB AD AB AB AB AI AB AB CE = CF = (CF // AB) = = = CF CD CF BC CF IC CF EC Lời giải: IA AB AD AB +) FE // AB → = (1); = (2) IC EC CD CF +) DA AB = AB IA
(tính.chat.phan.giac)(3) +) = ( ín t h.chat.phan.giac)(4) DC BC BC IC AB AB Từ (1)(2)(3)(4) → =
→ EC = FC(dpcm) EC CF
C. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC
1. Trường hợp đồng dạng thứ nhất: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam
giác kia thì hai tam giác đó đồng dạng AB BC CA = = A BC A ' B 'C '( . c . c c) A' B '
B 'C ' C ' A'
2. Trường hợp đồng dạng thứ hai: Nếu hai cạnh của tam giác này tỷ lệ với hai cạnh của
tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau AB BC ˆ ˆ A =
; B = B ' A BC A
' B 'C '(cgc) A' B ' B 'C ' A' B C B' C'
3. Trường hợp đồng dạng thứ ba: Nếu hai góc của tam giác này lần lượt bằng hai góc của
tam giác kia thì hai tam giác đó đồng dạng ˆ ˆ ˆ ˆ
A = A'; B = B ' AB C A
' B 'C '(g − g) A A' Trang 12 B C B' C'
Bài 1: Cho tam giác ABC và điểm O thuộc miền trong tam giác. Qua điểm O vẽ các đường
thẳng song song với Ca, CB, AB chúng lần lượt cắt các cạnh AB, BC, CA tại D, E, F. Chứng minh rằng: A AD BF CF + + =1 P AB BC CA D Lời giải F +) AD CN DN // AC → = (1) M AB CB
+) Tứ giác OFCN là hình bình hành → CF = CN(2) B E N C +) ON EN A BC O EN(gg) → = (3) AC BC Từ (1)(2)(3) AD BE CF CN BE ON BC → + + = + + = =1→ dpcm AB BC CA CB BC CA BC
Bài 2: Cho hai tam giác đều ABC và DEF có điểm F thuộc đoạn BC, điểm A thuộc đoạn DE,
B và E cùng phía so với đường thẳng AF. Chứng minh rằng: CD // BE A E D Lời giải 2 1 0 0 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ
CD // BE BED + EDC = 180 BEF + MDC = 60 E = A ; A = D 1 1 2 2 M ˆ ˆ MD MA MA MC
A = D AM F D MC(cgc) = = 2 2 MC MF MD MF N AM D FM
C(g − g) B F C - Chứng minh tương tự: 0 A ˆ ˆ ˆ ˆ
→ E = A → BED + CDE = 180 → BE // CD 1 1
Bài 3: Cho tam giác ABC cân tại A, M là trung điểm của
BC. Các điểm D và E thay đổi lần lượt thuộc các cạnh AB, E H AC sao cho ˆ ˆ
EMD = ABC. Chứng minh rằng khoảng cách từ D M đến DE không đổi 1 K Trang 13 1 B M C Lời giải Phân tích:
- Khoảng cách từ M đến DE bằng MH
Ta đi chứng minh: MH = MK DM là phân giác ˆ BDE MD BD ˆ ˆ MD BD B DM M DE(cgc) =
; B = DME(gt) = ME BM ME MC ˆ ˆ B DM CM
E(g − g) D = M 1 1 Giải: 0 ˆ ˆ ˆ
B + D + BMD = 180 1 MD BD BD = = Ta có: 0 ˆ ˆ ˆ ˆ ˆ
BMD + DME + M = 180 D = M → B DM CM
E(g − g) → ME CM BM 1 1 1 ˆ ˆ ˆ ˆ =
B = EMD(gt) B M1 ˆ ˆ → B DM M
DE(cgc) → EDM = BDM → MD là phân giác của ˆ BDE
- Gọi K là hình chiếu của M trên AB suy ra K cố định do M cố định → MH = MK ( cố định )
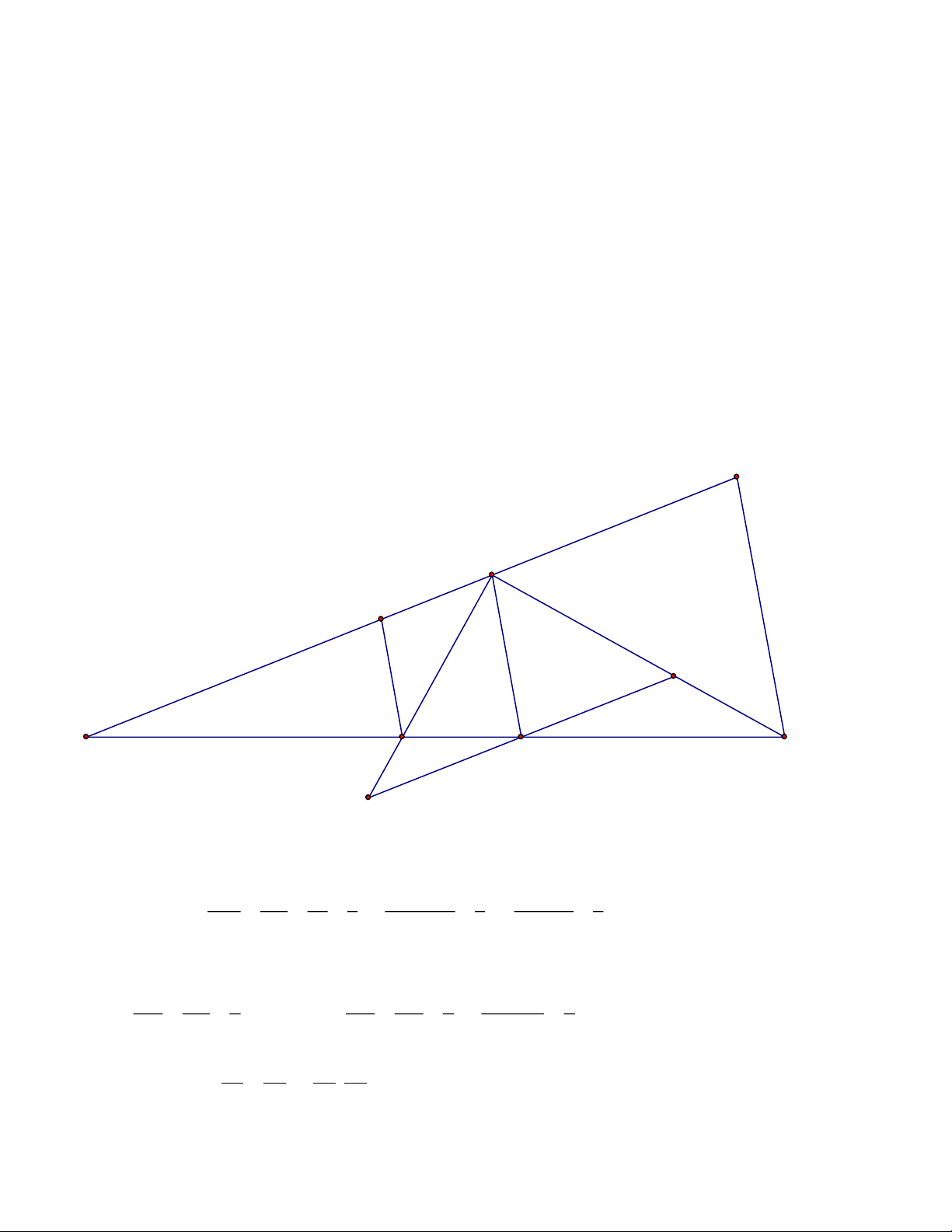
Bài 4: Trên đường thẳng d lấy bốn điểm A, B, C, D theo thứ tự ấy sao cho: BA DA 5 = = . Từ BC DC 4
điểm M nằm ngoài đường thẳng d sao cho MA 5
= , Nối M với A, B, C, D. Qua C kẻ đường MC 4
thẳng a song song với MA, đường thẳng
a cắt tia MB, MD lần lượt tại I và K M
a. Biết MB = 6cm, MD = 8cm. Tính BD K
b. Tính chu vi tam giác ADM biết chu vi 6 8
tam giác ADM bằng chu vi tam giác KCD cộng thêm 6cm A 10 B C D
c. Chứng minh rằng C là trung điểm của IK Lời giải I a. MA BA =
→ BM là phân giác ˆ AMC MC BC Trang 14 - Lại có: DA MA 5 =
= → MD là phân giác góc ngoài của ˆ
xMC → MB ⊥ MD ( hai tia phân giác DC MC 4
của hai góc kề bù ) → BMD
vuông tại M → BD =10 b. Xét chuvi DMA DA ADM , có 5
CK // AM → D CK D M ( A din . h ly) → = (tin . h chat. ) = chuvi D CK DC 4 chuvi D MA 5 chuvi D AM chuvi D CK chuvi D
AM − chuvi D CK → = → = = = 6 → ... chuvi D CK 4 5 4 1
c. C là trung điểm của IK AM AM BA DA 4 CI = CK = = = CI CK BC DC 5
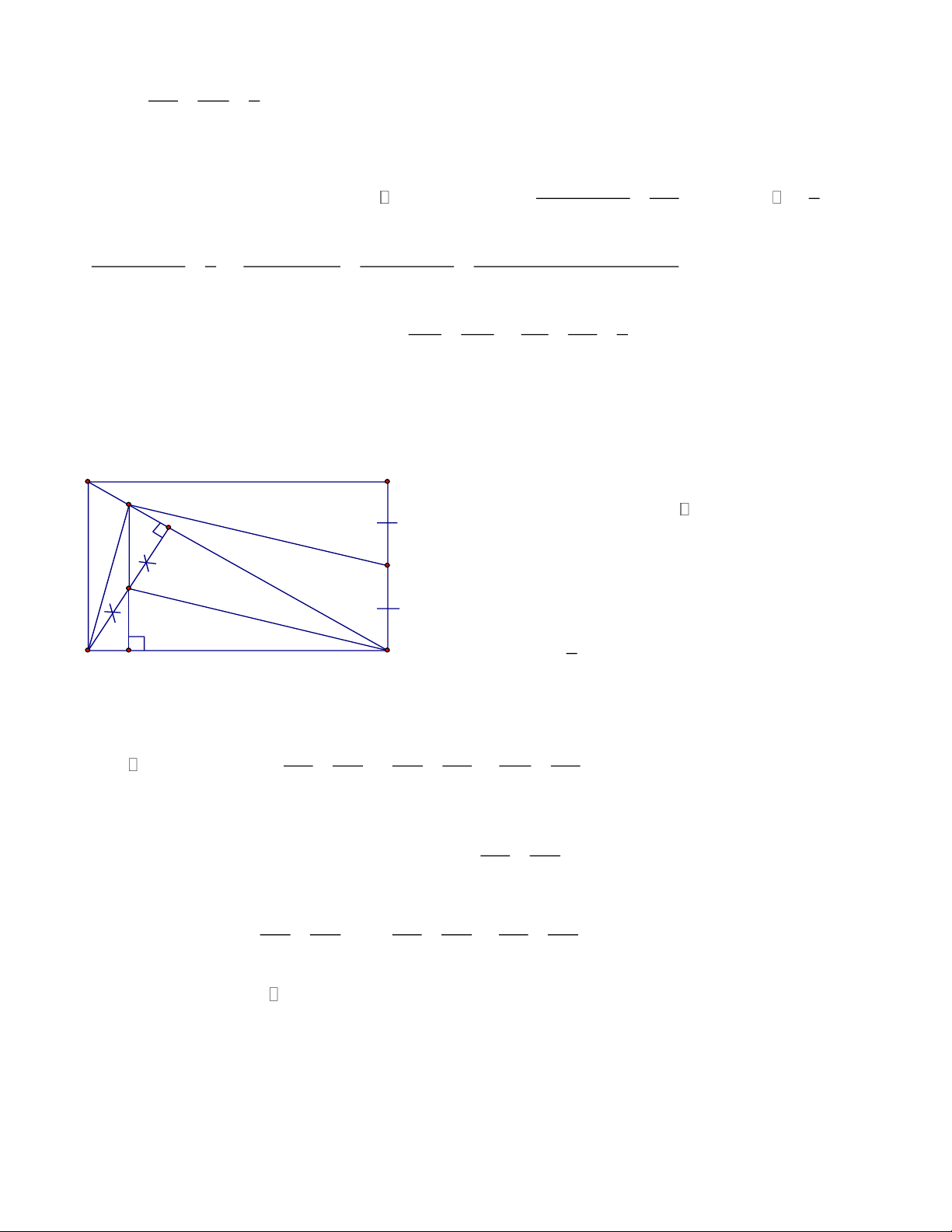
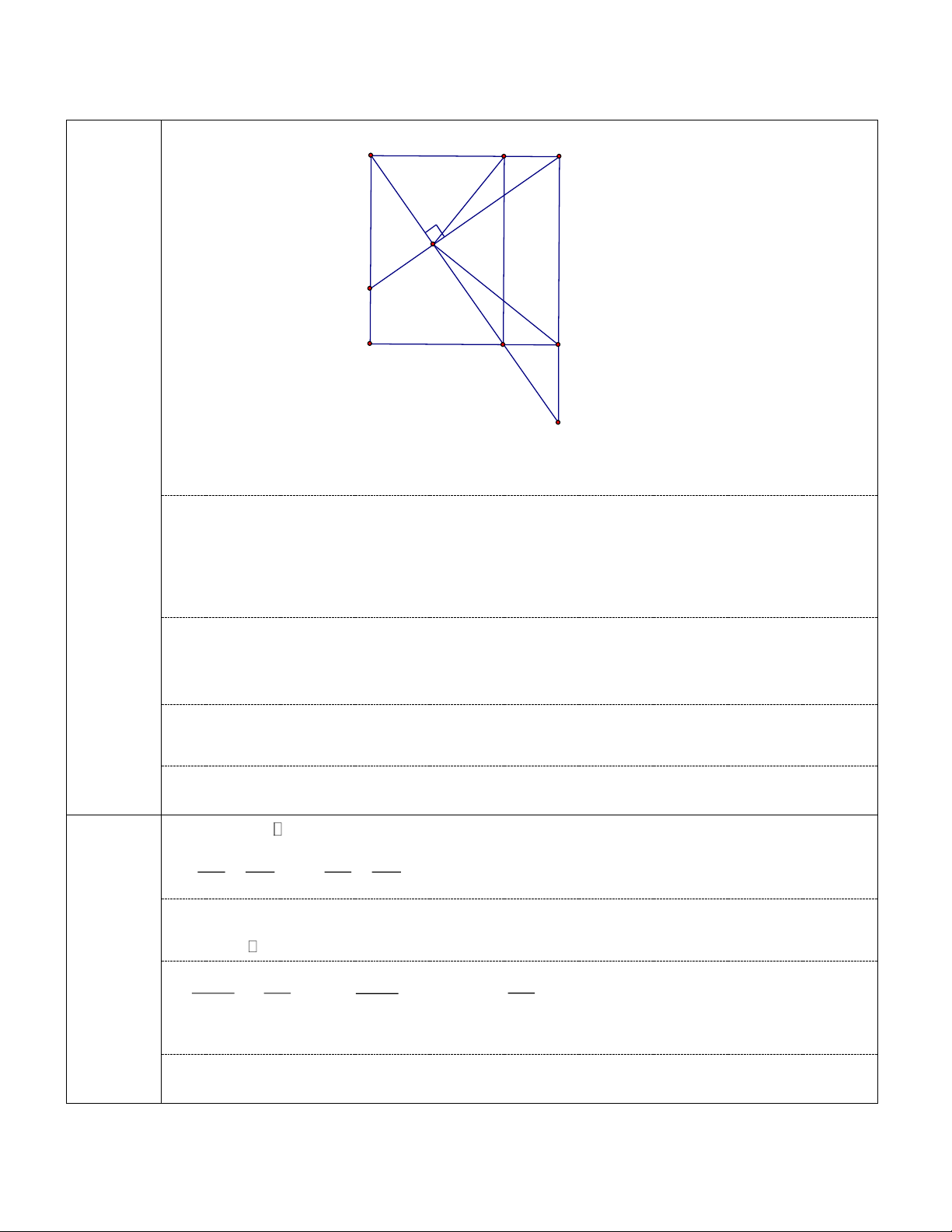
Bài 5: Cho hình chữ nhật ABCD, kẻ DH ⊥ AC H . Gọi M, N, K lần lượt là trung điểm của BC, AH, DH A
a. Tứ giác MNKC là hình gì? B 1 N
b. Chứng minh rằng: ADN C DK H
c. Chứng minh rằng: DN ⊥ MN M K 3 Lời giải 1 1 a. 1
MC // NK // = AD → MNKC D C là hình bình hành 2 b. Hướng dẫn câu b ˆ ˆ AN DK AN AD AH AD A DN C
DK A = D ; = = =
( dựa vào đồng dạng tam giác 1 1 AD DC DK DC DH DC vuông ˆA: chung AD AH
giải: Xét ADC,ADH có: → = (1) 0 ˆ ˆ ADC = AHD = 90 DC HD AN AH AD AN AD DC Xét A
HD, NK // AD → = (2) → = → = DK HD DC DK AN DK Lại có: ˆ ˆ ˆ ˆ
A = D → A DN CD
K(cgc) → D = C ( hai góc tương ứng ) 1 1 3 1 c. 0 0 ˆ ˆ ˆ ˆ ˆ ˆ ˆ
DN ⊥ MN DNM = 90 = DNK + KNM = D + KCM = C = KCM = 90 3 1
Cách khác: Chứng minh K là trực tâm D
CN → CK ⊥ DN;MN // CK → MN ⊥ DN N Trang 15
Bài 6: Cho tam giác ABC vuông tại A, AB < AC, AH ⊥ BC H, HD là phân giác ˆ
AHC(D AC) a. Chứng minh rằng: 2
AB = BH.BC b. AD AB = DC BC
c. Biết chu vi tam giác ABC là 24cm, chu vi tam giác AHC là 12cm, chu vi tam giác AHB là
9cm. Tính các cạnh của tam giác ABC Lời giải C AB BC a. 2
AB = BH.BC = A BC H B ( A gg) BH AB AD AB AH AH b. = = A BH C AH(gg) D H DC BC CH CH 12 c. chuvi A HB AB 9 3 9 * 1 A HB C H ( A gg) → = =
= = k → AB = 3k; AC = 4k(k N ) chuvi C HA AC 12 4 A B Xét 0 ˆ A
BC(A = 90 ) → BC = 5k → chuvi A
BC =12k = 24 → k = 2 → AB = 6; AC = 8; BC = 10 Trang 16
CÁC BÀI TOÁN TRONG ĐỀ THI LIÊN QUAN ĐẾN TAM GIÁC ĐỒNG DẠNG
Bài 1: Cho tam giác ABC vuông tại A ( AC > AB), đường cao AH ( H thuộc BC). Trên tia
HC lấy điểm D sao cho HD = HA. Đường vuông góc với BC tại D cắt AC tại E
a. Chứng minh rằng: BE C AD
C , tính độ dài đoạn BE theo AB = m
b. Gọi M là trung điểm của BE. Chứng minh rằng BHM BEC . Tính ˆ AHM ?
c. Tia AM cắt BC tại G. Chứng minh rằng: GB HD = BC AH + HC A Lời giải m a. BEC, A DC có: m E 1 ˆ C : chung m 2 M Cần thêm: 45° CD CA B G D = C DE C
AB(g − g) H C CE CB Vậy ˆ ˆ B EC A
DC(cgc) → BEC = ADC
+) AHD vuông cân theo giả thiết 0 0 0 ˆ ˆ ˆ
→ DAH = 45 → ADC = 135 → E = 45 → ABE vuông cân tại 1 A
→ BE = 2AB = m 2 b. BEC, A
DC có: ˆB : chung Cần thêm: BH BE BH BM = , hoac : =
→ c − g − c BM BC BE BC
- Ta có: BM 1 BE 1 AD = . = (do : B EC A DC) BC 2 BC 2 AC
+) AHD vuông cân tại H BM 1 AD 1 AH 2 AH BH AH BH BH → AD = 2AH → = = = = (do : A BH C BA = ) = (BE = 2AB) BC 2 AC 2 AC AC. 2 B . A 2 AC BA BE Vậy 0 0 ˆ ˆ B HM B
EC(cgc) → BHM = Ê
B C=135 → AHM = 45 Trang 17
c. Ta có: ABE vuông cân tại A nên AM là phân giác ˆ GB AB BAC → = GC AC mà: AB ED AH HD = ( A BC D EC) = (ED // AH ) = (AH = DH ) AC DC HC HC Vậy: GB HD GB HD GB HD = → = → = GC HC GB + BC HD + HC BC AH + HC
Bài 2: Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE, CF cắt nhau tại H a. Chứng minh rằng: .
BD DC = DH.DA HD HE HF b. + + =1 AD BE CF
c. Chứng minh H là giao điểm các đường phân giác của tam giác DEF
d. Gọi M, N, P, Q, J, K lần lượt là trung điểm của BC, CA, AB, EF, FD, DE. Chứng minh
rằng ba đường thẳng MQ, NI, PK đồng quy tại 1 điểm
Bài 3: Cho hình chữ nhật ABCD. Trên đường chéo BD lấy điểm P. Gọi M là điểm đối xứng của điểm C qua P
a. Tứ giác AMDB là hình gì?
b. Gọi E và F lần lượt là hình chiếu của điểm M lên AB. Chứng minh rằng EF // AC và ba điểm E, F, P thẳng hàng
c. Chứng minh rằng tỷ số các cạnh của hình chữ nhật MEAF không phụ thuộc vào vị trí của điểm P
d. Giả sử CP vuông góc với BD và CP = 2,4 cm, tính các cạnh của hình chữ nhật biết: PD 9 = PB 16
Bài 4: [ Việt yên – Bắc Giang – 30/04/2013 ]. Cho hình vuông ABCD, trên cạnh AB lấy
điểm E và trên cạnh AD lấy điểm F sao cho AE = AF. Vẽ AH ⊥ BF(H BF), AH cắt DC và BC tại M, N
a. Chứng minh rằng tứ giác AEMD là hình chữ nhật 1 1 1 b. Biết S = 4.S
. Chứng minh rằng: AC = 2.EF c. Chứng minh rằng: = + BCH AEH 2 2 2 AD AM AN Trang 18 Lời giải E A B H F D C M N 1 (2.0
Ta có DAM = ABF (cùng phụ BAH ) điểm) AB = AD ( gt) 0
BAF = ADM = 90 (ABCD là hình vuông) ΔADM = ΔBAF (g.c.g)
=> DM=AF, mà AF = AE (gt) Nên. AE = DM
Lại có AE // DM ( vì AB // DC )
Suy ra tứ giác AEMD là hình bình hành Mặt khác. 0 DAE = 90 (gt)
Vậy tứ giác AEMD là hình chữ nhật Ta có ΔABH ΔFAH (g.g) AB BH = = hay BC BH = ( AB=BC, AE=AF) AF AH AE AH 2
Lại có HAB = HBC (cùng phụ ABH ) (2.0 ΔCBH ΔEAH (c.g.c) điểm) 2 S BC S 2 BC ΔCBH = , mà ΔCBH = 4 (gt) = 4 nên BC2 = (2AE)2 S AE S AE ΔEAH ΔEAH
BC = 2AE E là trung điểm của AB, F là trung điểm của AD
Do đó: BD = 2EF hay AC = 2EF (đpcm) Trang 19
Do AD // CN (gt). Áp dụng hệ quả định lý ta lét, ta có: AD AM = AD CN = CN MN AM MN
Lại có: MC // AB ( gt). Áp dụng hệ quả định lý ta lét, ta có: 3 MN MC AB MC = = hay AD MC = (2.0 AN AB AN MN AN MN 2 2 2 2 điểm) 2 2 2 AD AD CN CM CN + CM MN + = + = = = 1 2 2 AM AN MN MN MN MN (Pytago) 2 2 AD AD 1 1 1 + = 1 = + = (đpcm) AM AN 2 2 2 AM AN AD
Bài 5: [ Yên Phong – 20/03/2018 ]. Cho hình vuông ABCD, trên tia đối cả tia CD lấy điểm
M bất kỳ ( CM < CD), vẽ hình vuông CMNP ( P nằm giữa B và C), DP cắt BM tại H, MP cắt BD tại K
a. Chứng minh rằng: DH ⊥ BM PC PH KP b. Tính Q = + + BC DH MK c. Chứng minh rằng: 2 M .
P MK + DK.BD = MD
Bài 6: [ Yên Phong – 2015 - 2016 ]. Cho tam giác ABC vuông tại A, đường cao AH. Gọi E,
F theo thứ tự là hình chiếu của H trên AC và AB. Cho D là 1 điểm trên BC. Gọi M, N theo
thứ tự là hình chiếu của D trên AB và AC. Chứng minh rằng 2 a. AC HC 2
AC = CH.BC; = 2 AB HB 3 b. CE AC = 3 BF AB c. . DB DC = . MA MB + N . A NC
Bài 7: [ Chương Mỹ, 2018 - 2019 ]. Cho ∆ABC có 0
BAC = 90 , AB < AC, đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên cạnh AB và AC. Trang 20