Giải Toán 8 Bài 33: Hai tam giác đồng dạng | Kết nối tri thức
Giải Toán 8 Bài 33: Hai tam giác đồng dạng | Kết nối tri thức. Tài liệu được biên soạn dưới dạng file PDF bao gồm 4 trang tổng hợp các kiến thức chọn lọc giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chủ đề: Chương 9: Tam giác đồng dạng (KNTT)
Môn: Toán 8
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
Toán 8 Bài 33: Hai tam giác đồng dạng Kết nối tri thức
Giải Toán 8 Kết nối tri thức Tập 2 Bài 33 - Luyện tập Luyện tập 1
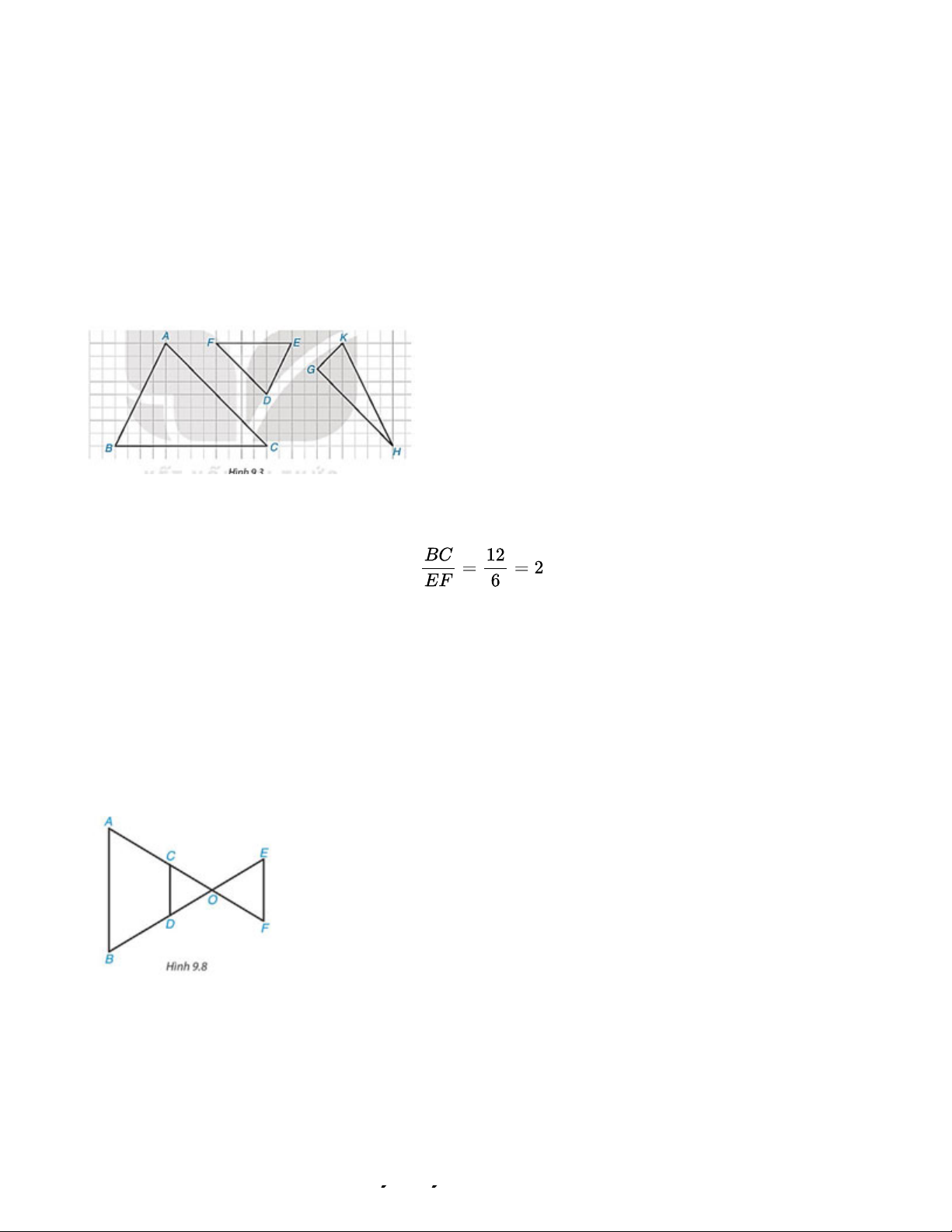
Trong các tam giác được vẽ trên ô lưới vuông (H.9.3), có một cặp tam giác đồng dạng. Hãy chỉ
ra cặp tam giác đó, viết đúng kí hiệu đồng dạng và tìm tỉ số đồng dạng của chúng. Lời giải:
Ta có ∆ABC ∽ ∆DEF với tỉ số đồng dạng
Nhìn hình vẽ ta thấy tam giác GHK vuông tại G nên không thể đồng dạng với hai tam giác còn lại. Luyện tập 2
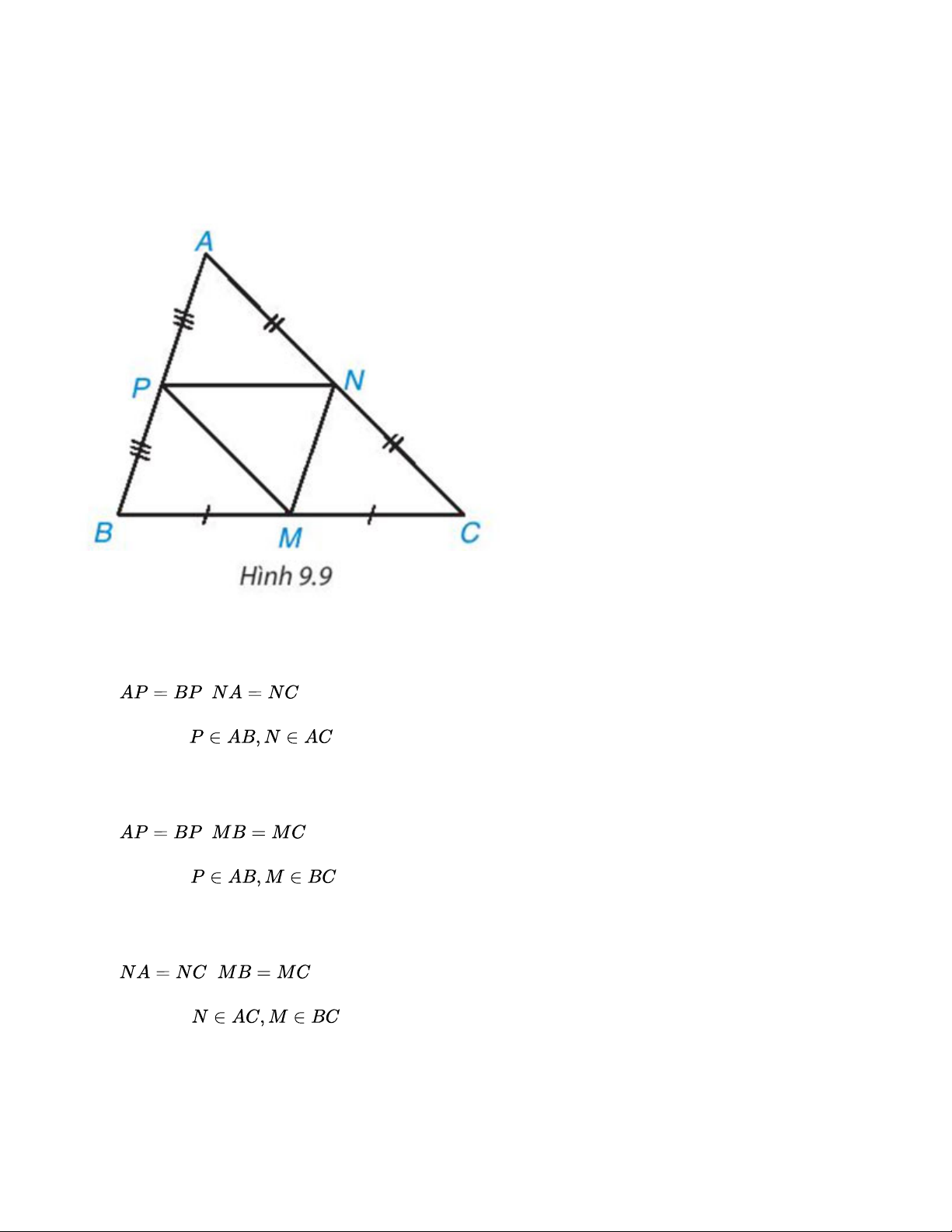
Trong Hình 9.8, các đường thẳng AB, CD, EF song song với nhau. Hãy liệt kê ba cặp tam giác (phân biệt) đồng dạng. Lời giải:
- Vì C ∊ OA, D ∊ OB và CD //AB nên ∆OCD ∽ ∆OAB.
- Vì E ∊ OB, F ∊ OA (thuộc phần kéo dài) và EF // AB nên ∆OEF ∽ ∆OBA.
- Vì F ∊ OC, E ∊ OD (thuộc phần kéo dài) và EF // CD nên ∆OEF ∽ ∆ODC. ế ố
Giải Toán 8 Kết nối tri thức Tập 2 trang 82 Bài 9.1
Cho ΔABC ~ ΔMNP, khẳng định nào sau đây không đúng? a) ΔMNP ~ ΔABC b) ΔBCA ~ ΔNPM c) ΔCAB ~ ΔPNM d) ΔACB ~ ΔMNP Lời giải:
Khẳng định d) là khẳng định không đúng => ΔACB ~ ΔMPN Bài 9.2
Khẳng định nào sau đây là đúng?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác bất kì đồng dạng với nhau
c) Hai tam giác đều bất kì đồng dạng với nhau
d) Hai tam giác vuông bất kì đồng dạng với nhau
e) Hai tam giác đồng dạng thì bằng nhau Lời giải:
Khẳng định a và c là khẳng định đúng
Khẳng định b sai vì hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau
từng đôi một và ba cặp cạnh tương ứng tỉ lệ.
Khẳng định d sai vì hai tam giác vuông mới chỉ thỏa mãn một điều kiện để xét đồng dạng, cần
thêm tỉ lệ cạnh tương ứng hoặc 1 góc tương ứng bằng nhau.
Khẳng định e sai vì hai tam giác đồng dạng chỉ có kích thước tỉ lệ với nhau, còn hai tam giác
bằng nhau là có các góc, các cạnh tương ứng bằng nhau. Bài 9.3
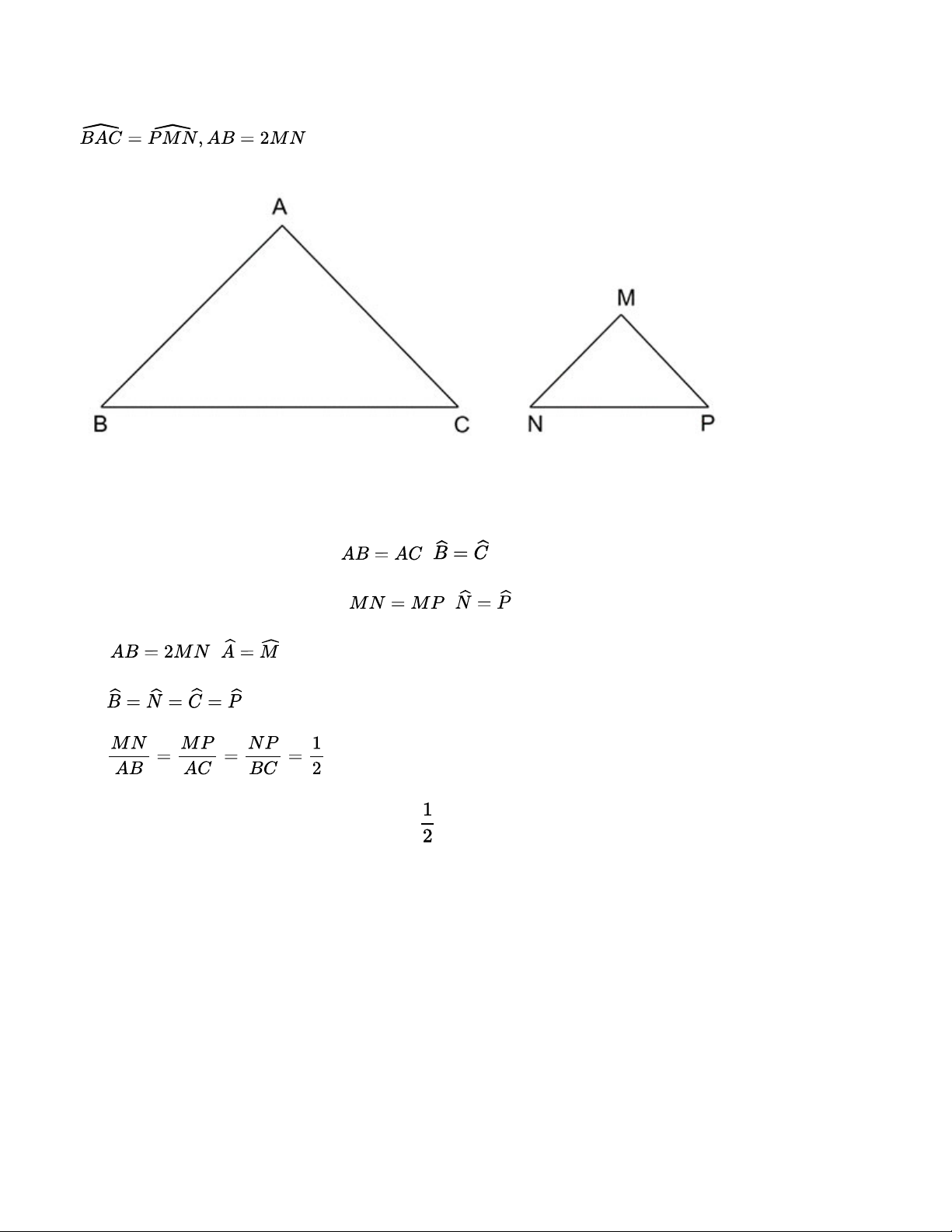
Trong hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy
tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng Lời giải: - Có , => NP // BC ( ) => ΔABC ~ ΔAPN - Có , => MP // AC ( ) => ΔABC ~ ΔPBM - Có , => MN // AB ( ) => ΔABC ~ ΔNMC
- Có ΔABC ~ ΔAPN và ΔABC ~ ΔPBM => ΔAPN ~ ΔPBM
- Có ΔABC ~ ΔNMC và ΔABC ~ ΔPBM => ΔNMC ~ ΔPBM Bài 9.4
Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng
. Chứng minh ΔMNP ~ ΔABC và tìm tỉ số đồng dạng Lời giải:
- Có tam giác ABC cân tại A => ,
- Có tam giác MNP cân tại M => , Mà , => =>
=> ΔMNP ~ ΔABC với tỉ số đồng dạng là