Giải Toán 8 Luyện tập chung trang 91 | Kết nối tri thức
Giải Toán 8 Luyện tập chung trang 91 | Kết nối tri thức. Tài liệu được biên soạn dưới dạng file PDF bao gồm 4 trang tổng hợp các kiến thức chọn lọc giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chủ đề: Chương 9: Tam giác đồng dạng (KNTT)
Môn: Toán 8
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
Toán 8 Luyện tập chung trang 91 Kết nối tri thức
Giải Toán 8 Kết nối tri thức Tập 2 trang 92 Bài 9.11 Cho ΔABC ~ ΔDEF. Biết
, hãy tính số đo các góc , , , Lời giải: Vì ΔABC ~ ΔDEF => , , Mà => => Có => Bài 9.12 Cho ΔABC ~ ΔA'B'C'. Biết ,
và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C' Lời giải: Có
=> ΔABC ~ ΔA'B'C' với tỉ số đồng dạng là
=> Chu vi tam giác ABC bằng chu vi tam giác A'B'C' => Chu vi A'B'C' là: (cm) Bài 9.13
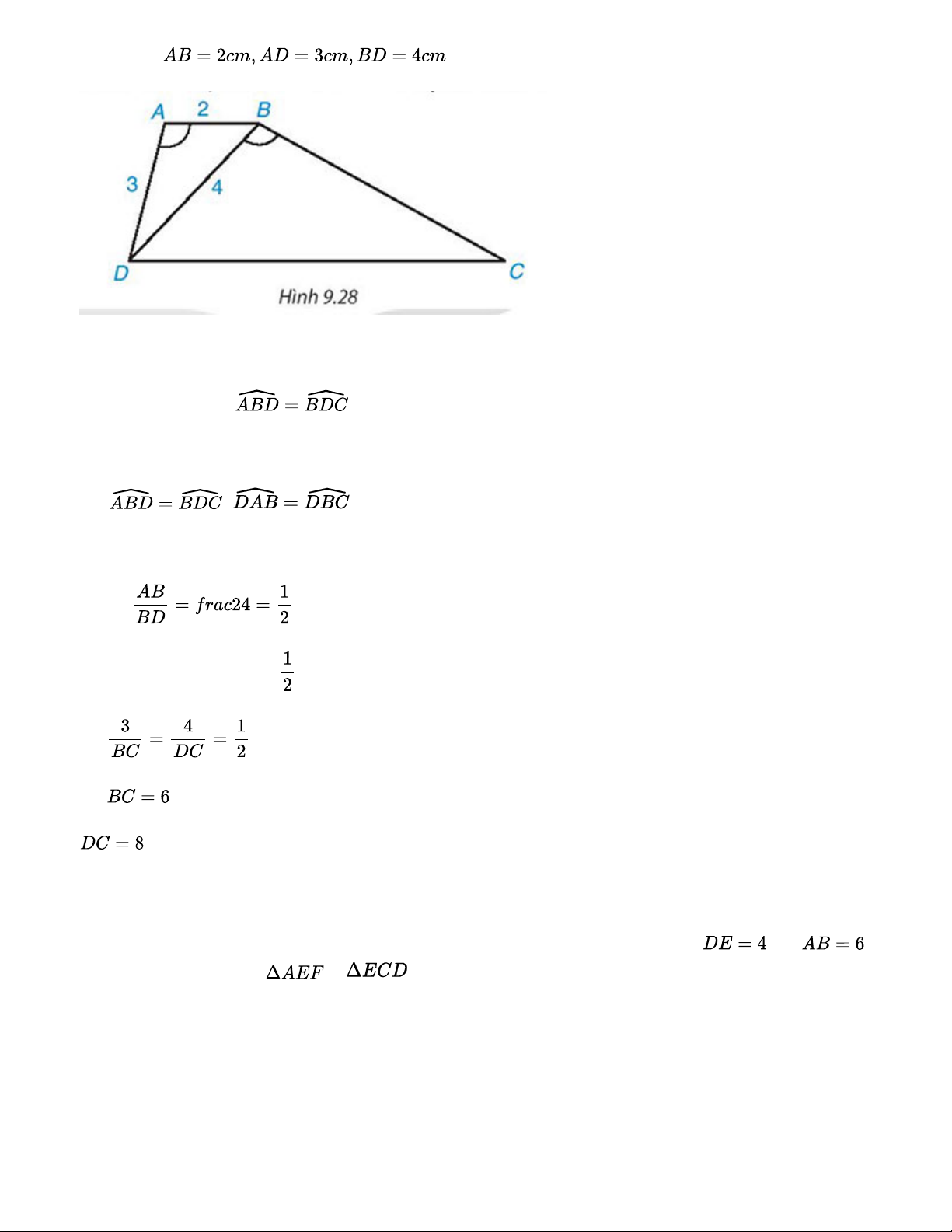
Cho hình thang ABCD (AB // CD) có
a) Chứng minh rằng ΔABD ~ ΔBDC b) Giả sử
. Tính độ dài các cạnh BC và DC Lời giải: a) Có AB // CD => - Xét ΔABD và ΔBDC Có , => ΔABD ~ ΔBDC (g.g) b) Có ΔABD ~ ΔBDC với tỉ số => => (cm) (cm) Bài 9.14
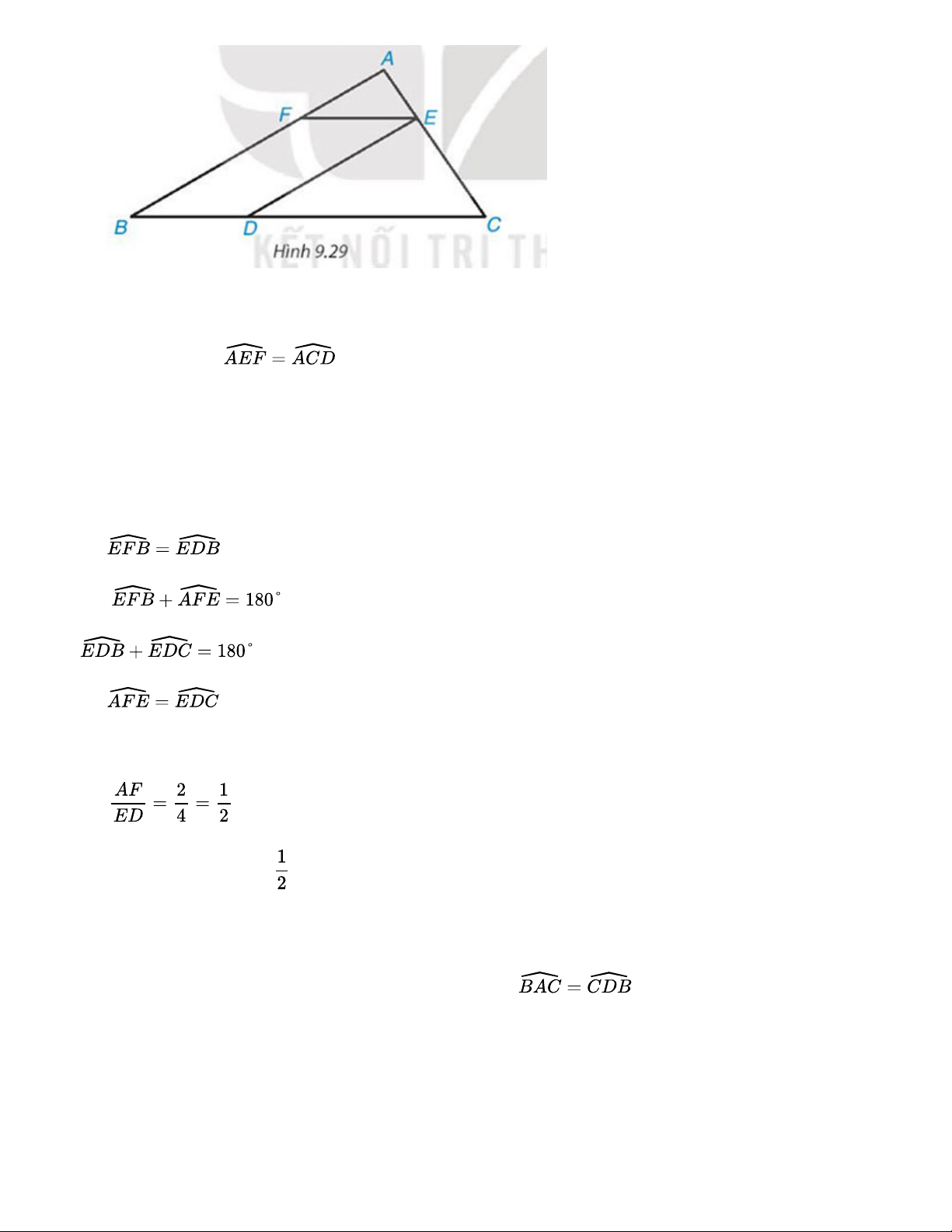
Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, cm, cm. Chứng minh rằng ~
và tính tỉ số đồng dạng Lời giải: - Có EF // BC => (2 góc đồng vị) (1) - Có EF // BD (vì EF // BC) DE // FB (vì MN // BC)
=> EFBD là hình bình hành => Mà => (2)
Từ (1) và (2) => ΔAEF ~ ΔECD (g.g) Có
=> Đồng dạng với tỉ số Bài 9.15
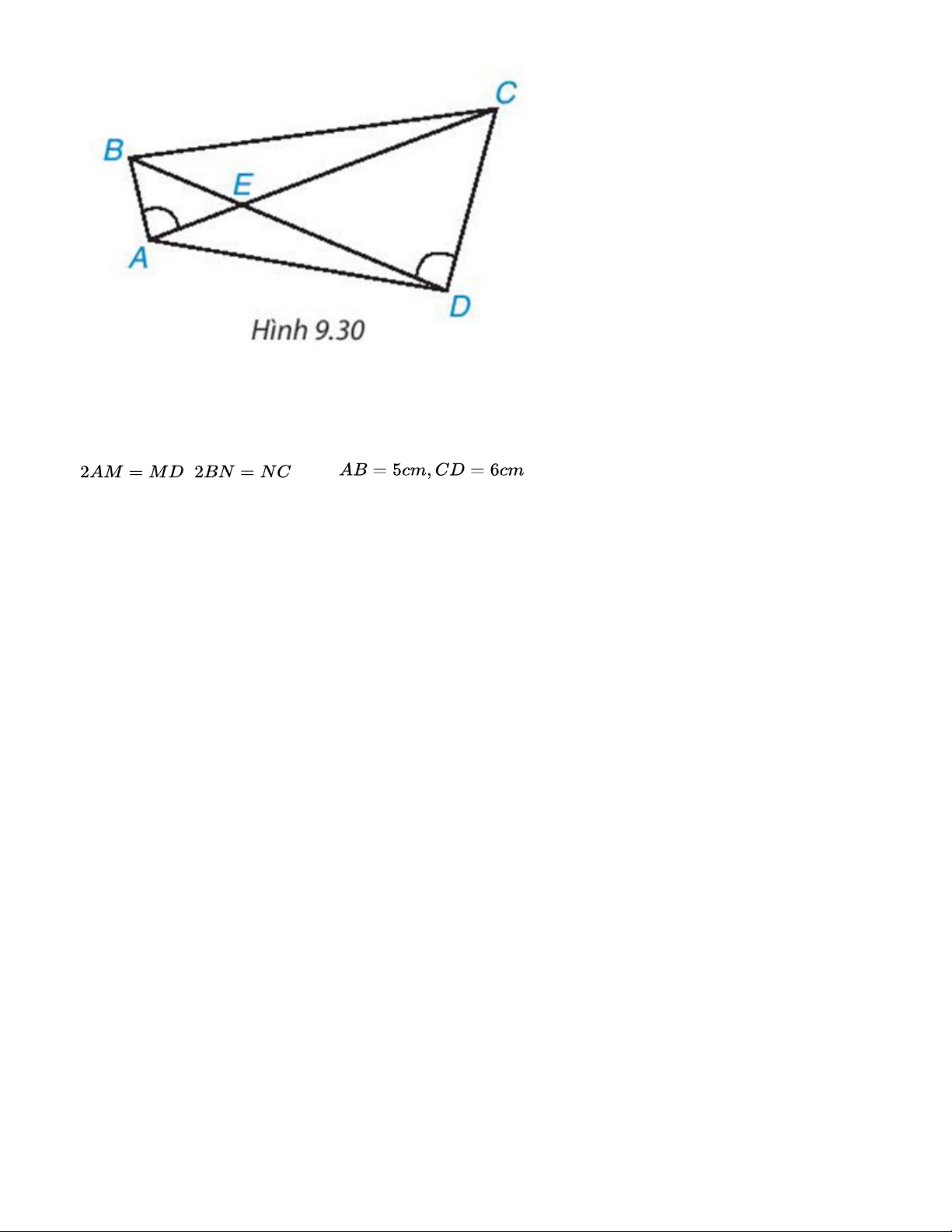
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng . Chứng minh rằng ΔAED ~ ΔBEC. Bài 9.16
Cho hình thang ABCD (AB//CD và các điểm M, N lần lượt trên cạnh AD và BC sao cho , . Biết
. Hãy tính độ dài đoạn thẳng MN.