Giải và biện luận phương trình, bất phương trình bằng phương pháp hàm số – Nguyễn Thành Trung Toán 12

Giải và biện luận phương trình, bất phương trình bằng phương pháp hàm số – Nguyễn Thành Trung Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

52 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
3
Contents
DẠNG 1: Cho đồ thị hàm số
( )
y f x=
xác định số nghiệm của phương trình
( )
( )
f t x k=
.................................................................................................................................... 4
DẠNG 2: Cho bảng biến thiên
( )
fx
tìm tham số
m
để bất phương trình
( )
,0g x m
có nghiệm thuộc
D
. .................................................................................................................... 6
DẠNG 3: Cho hàm số
( )
y f x=
có đồ thị
xác định tham số m để
( )
,0g x m
13
DẠNG 4: Cho hàm số
( )
y f x=
có đồ thị
( )
fx
xác định tham số m để
( )
,0g x m
36
DẠNG 5: Cho đồ thị hàm số
( )
y f x=
xác định tham số để phương trình có nghiệm
...................................................................................................................................................... 41
Theo bất đẳng thức Bunyakovsky ........................................................................................... 48
DẠNG 6: Cho đồ thị hàm số
( )
y f x
=
xác định số nghiệm của hàm số
( ) ( ) ( )
g x f x g x=+
...................................................................................................................... 51
DẠNG 7 : Biện luận tham số
m
của bất phương trình hoặc phương trình bằng cách
đưa về hàm số đặc trưng .......................................................................................................... 53
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
4
DẠNG 1: Cho đồ thị hàm số
( )
y f x=
xác định số nghiệm của phương trình
( )
( )
f t x k=
Ví dụ 1.
Cho hàm số
( )
fx
liên tục trên có đồ thị
( )
y f x=
như hình bên. Đặt
( ) ( )
g x f f x

=

xác định số nghiệm của
phương trình
( )
0gx
=
A.
8
.
B.
7
.
C.
6
.
D.
5
.
Lời giải
Chọn đáp án A
Ta có
( ) ( )
( )
( ) ( )
( )
( )
( )
( ) ( )
( ) ( )
1
0
2
0
11
0
22
g x f f x f x f f x
x
fx
x
gx
fx
f f x
fx


==


=−
=
=
=
=

=

=
Phương trình
( )
1
có 3 nghiệm vì đường thẳng
1y =
cắt đồ thị hàm số
( )
fx
tại 3 điểm phân
biệt.
Phương trình
( )
2
có 3 nghiệm vì đường thẳng
2y =
cắt đồ thị hàm số
( )
fx
tại 3 điểm phân
biệt.
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
5
Suy ra
( )
0gx
=
có 8 nghiệm.
Ví dụ 2.
Cho hàm số
( )
fx
liên tục trên có đồ
thị
( )
y f x=
như hình bên. Số nghiệm
thực của phương trình
( )
( )
21+=
x
f f e
là
A.
1
.
B.
2
.
C.
3
.
D.
4
.
Lời giải
Chọn đáp án B
Ta có
Theo đồ thị
( )
( )
( )
( )
( )
21
21
2 , 2 3
+ = −
+ =
+ =
x
x
x
fe
f f e
f e a a
( ) ( )
( )
loaïi
1
2 1 3 0
1
x
xx
x
e
f e f e x
eb
=
+ = − = − =
= −
( ) ( )
( )
( )
( )
loaïi
loaïi
1
2 2, 0 2 1 0 ln
2
x
x x x
x
ec
f e a f e a a e d x t
et
= −
+ = = − − = =
=
Vậy phương trình đã cho có 2 nghiệm phân biệt
Ví dụ 3.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
6
Cho hàm số
( )
fx
liên tục trên có đồ thị
( )
y f x=
như hình bên. Phương trình
( )
( )
20f f x−=
có bao tất cả bao nhiêu
nghiệm phân biệt.
A.
4
.
B.
5
.
C.
6
.
D.
7
.
Thi Thử THPT Quốc Gia Trường Yên Lạc Vĩnh Phúc Lần 4
Lời giải
Chọn đáp án B
Theo đồ thị
( 2 1)
( ) 0 (0 1)
(1 2)
x a a
f x x b b
x c c
= − −
= =
=
2 ( ) ( ) 2 (1)
(2 ( )) 0 2 ( ) ( ) 2 (2)
2 ( ) ( ) 2 (3)
f x a f x a
f f x f x b f x b
f x c f x c

− = = −

− = − = = −


− = = −

Nghiệm của phương trình
( ) ( ) ( )
1 ; 2 ; 3
là giao điểm của đường thẳng
2 ; 2 ; 2y a y b y c= − = − = −
với đồ thị hàm số
( )
fx
.
•
( 2; 1) 2 (3;4)aa − − −
suy ra phương trình
( )
1
có đúng 1 nghiệm phân biệt.
•
(0;1) 2 (1;2)bb −
suy ra phương trình
( )
2
có đúng 1 nghiệm phân biệt.
•
(1;2) 2 (0;1)cb −
suy ra nên phương trình
( )
3
có 3 nghiệm phân biệt.
Kết luận: Có tất cả 5 nghiệm phân biêt.
DẠNG 2: Cho bảng biến thiên
( )
fx
tìm tham số
m
để bất phương trình
( )
,0g x m
có
nghiệm thuộc
D
.
Ví dụ 1.
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
7
Cho hàm số
( )
y f x=
có đạo hàm trên . Bảng biến thiên của hàm số
( )
y f x
=
như hình
dưới
x
1−
1
3
3
( )
fx
1
2
Tìm
m
để bất phương trình
( )
23
1
3
m x f x x+ +
nghiệm đúng với mọi
( )
0;3x
.
A.
(0)mf
. B.
(0)mf
. C.
(3)mf
. D.
2
(1)
3
mf−
.
Lời giải
Chọn đáp án A
Ta có
( ) ( )
2 3 3 2
11
33
m x f x x m f x x x+ + + −
.
Đặt
( ) ( )
32
1
3
g x f x x x= + −
.
Ta có
( ) ( ) ( )
( )
22
22g x f x x x f x x x
= + − = − − +
.
( ) ( )
2
02g x f x x x

= = − +
.
Theo bảng biến thiên
( )
1fx
( )
0;3x
và
( ) ( )
1,
2
2
2 1 1 0;3x x x x− + = − −
nên
( ) ( )
0, 0;3g x x
.
Từ đó ta có bảng biến thiên của
()gx
:
x
0
3
( )
gx
+
( )
3g
( )
gx
( )
0g
Bất phương trình
( )
32
1
3
m f x x x + −
nghiệm đúng với mọi
( )
0;3x
( )
0 (0)m g m f
.
Ví dụ 2.
Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
x
−
1−
0
2
+
( )
fx
+
0
−
0
+
0
−
4
3
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
8
( )
fx
−
2
−
Bất phương trình
( )
( )
2
1+x f x m
có nghiệm trên khoảng
( )
1; 2−
khi và chỉ khi
A.
10m
. B.
15m
. C.
27m
. D.
15m
.
Đề thi Duyên Hải Bắc Bộ năm 2019
Lời giải
Chọn đáp án B
Yêu cầu bài toán
( )
1; 2
max
−
m g x
Với
( )
( )
( )
2
1=+g x x f x
.
Ta có:
( ) ( )
( )
( )
2
21

= + +g x x f x x f x
.
Với
( )
1;0−x
thì
( )
( )
2
0
24
0
10

+
x
fx
fx
x
( ) ( )
0, 1; 0
−g x x
.
Tại
0=x
,
( )
00
=g
.
Với
( )
0; 2x
thì
( )
( )
2
0
23
0
10

+
x
fx
fx
x
( ) ( )
0, 0;2
g x x
.
Ta có bảng biến thiên của hàm số
( )
( )
( )
2
1=+g x x f x
trên khoảng
( )
1;2−
như sau
x
1−
0
2
( )
gx
−
0
+
8
3
15
( )
gx
2
Suy ra
( )
1; 2
max 15
−
=gx
.
Kết luận:
15m
.
Ví dụ 3.
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
9
Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
x
0
1
+
4
( )
fx
−
−
Tìm
m
để bất phương trình
( )
2sinm x f x+
nghiệm đúng với mọi
( )
0;x +
.
A.
( )
0mf
.
B.
( )
1 2sin1mf−
.
C.
( )
0mf
.
D.
( )
1 2sin1mf−
.
Lời giải
Chọn đáp án C
BPT
( ) ( )
2sin 2sinm x f x m f x x+ −
.
Yêu cầu bài toán
( ) ( ) ( )
min ; 2sinm g x g x f x x = −
Ta có
( ) ( )
2cosg x f x x

=−
.
( ) ( )
0 2cosg x f x x

= =
.
Mà
( ) ( )
2, 0;f x x
+
và
( )
2cosx 2, 0;x +
nên
( ) ( )
0, 0;g x x
+
.
( )
'( ) 2
00
2cos 2
fx
g x x
x
=
= =
=
. Với
( ) ( ) ( )
0 0 2sin0 0g f f= − =
Từ đó ta có bảng biến thiên của
()gx
:
x
0
+
( )
gx
+
+
( )
gx
( )
0f
Bất phương trình
( )
0mf
nghiệm đúng với mọi
( )
0;x +
Ví dụ 4.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
10
Cho hàm số
( )
y f x=
có
( )
21fm− = +
,
( )
12fm=−
. Hàm số
( )
y f x
=
có bảng biến thiên
x
0
0
2
+
0
+
( )
fx
−
2−
Tập hợp tất cả các giá trị của tham số
m
để bất phương trình
( )
1 2 1
23
x
f x m
x
+
−
+
có
nghiệm trên
2;1x

−

là
A.
7
5;
2

−−


.
B.
( )
;0−
.
C.
( )
2;7−
.
D.
7
;
2

− +

.
Lời giải
Chọn đáp án D
Yêu cầu bài toán
( ) ( ) ( )
2; 1
1 2 1
, 2; 1 min
23
x
g x f x m x g x m
x
−

+

= − −

+
Ta có
( ) ( )
( )
2
15
2
3
g x f x
x

=−
+
.
Dựa vào bảng biến thiên của hàm số
( )
y f x
=
ta có
( ) ( )
0, 2;1f x x
−
và
( )
( )
2
5
0, 2;1
3
x
x
− −
+
. Do đó
( ) ( )
0, 2;1g x x
−
.
Bảng biến thiên của hàm số
( )
y h x=
trên khoảng
2;1

−

.
x
2−
1
( )
gx
+
( )
2g −
( )
gx
( )
1g
( ) ( )
2; 1
min 1g x g
−

=
Suy ra
( )
1gm
( )
13
1
24
fm −
23
24
m
m
−
−
27
4
m
m
−

7
2
m −
.
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
11
Ví dụ 4.
Cho hàm số
( )
y f x=
liên tục và có đồ
thị như hình vẽ. Tập các giá trị thực của
tham số
m
để phương trình
(
)
2
4f x m−=
có nghiệm thuộc nữa
khoảng
)
2 ; 3
−
là
A.
1; 3

−

.
B.
1; ( 2)f

−

.
C.
( )
(
1 ; 2f
−
.
D.
(
1;3
−
.
Đề thi thử THPT Quốc Gia Phan Bội Châu Nghệ An Lần 2 năm 2019
Lời giải
Chọn đáp án D
Đặt
2
4tx=−
,
( )
2
22
4
2 4 4
x
x
t
xx
−
−
==
−−
,
00tx= =
Bảng biến thiên
x
2−
0
3
( )
tx
2
t
2
1
Suy ra
t
(
1;2t
.
Phương trình tương đương với
( ) ( )
1f t m=
có nghiệm
(
1;2t
Nghiệm của phương trình
( )
1
là giao của đường thẳng
ym=
và đồ thị hàm số
( )
y f x=
với
(
1;2x
.
Theo đồ thị ta suy ra
13m−
. Chọn D.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
12
Ví dụ 5.
Cho hàm số
( )
y f x=
liên tục và có đồ
thị như hình vẽ. Số giá trị nguyên dương
của
m
để phương trình
( )
2
4 5 1f x x m− + + =
có nghiệm là
A.
0
.
B.
3
.
C.
4
.
D. Vô số.
8 Trường chuyên đồng bằng Sông Hồng Lần 1 năm 2019
Lời giải
Chọn đáp án B
( ) ( )
( )
22
4 5 1 4 5 1 1f x x m f x x m f t m− + + = − + = − = −
Với
( ) ) ( ) )
ñoàthò
2
2
4 5 2 1 1 1; 2;t x x x t f t

= − + = − + + ⎯⎯⎯→ +

Nên để phương trình có nghiệm
)
1 2; 1 2 3m m m
− + −
Và
1; 2; 3mm
+
. Chọn đáp án B.
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
13
DẠNG 3: Cho hàm số
( )
y f x=
có đồ thị
( )
fx
xác định tham số m để
( )
,0g x m
Ví dụ 1.
Cho hàm số
( )
y f x=
có đạo hàm trên , có đồ thị
( )
fx
như hình vẽ.
Bất phương trình
( ) sin
2
+
x
f x m
nghiệm đúng với mọi
1;3−x
khi và chỉ khi
A.
(0)mf
. B.
(1) 1−mf
. C.
( 1) 1 − +mf
. D.
(2)mf
.
Lời giải
Chọn đáp án B
( )
( ) sin sin
22

+ −
xx
f x m m f x
Để bất phương trình nghiệm đúng với mọi
1;3−x
thì
( )
1; 3
min sin
2
−

−


x
m f x
Xét hàm số
( ) ( )
sin
2
=−
x
g x f x
,
( ) ( )
cos
22


=−
x
g x f x
Nhận thấy
( )
fx
đổi dấu khi qua
1=x
gợi ý cho ta xét dấu của hàm
( )
gx
trên 2 khoảng
( )
1;1−
và
( )
1;3
• Với
( )
1;1−x
( ) ( )
1;1 0
− x f x
( đồ thị hàm số
( )
fx
nằm dưới trục hoành )
( ) ( )
1;1 ; cos 0, 1;1
2 2 2 2 2
−
− − −
xx
xx
Vậy
( ) ( ) ( )
cos 0, 1;1
22



= − −


x
g x f x x
• Với
1x =
( ) ( )
.1
1 1 cos 0
22



= − =


gf
• Với
x
( )
1;3
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
14
( ) ( )
1;3 0
x f x
(đồ thị hàm số
( )
fx
nằm trên trục hoành )
( ) ( )
3
1;3 ; cos 0, 1;3
2 2 2 2 2
−
xx
xx
Vậy
( ) ( ) ( )
cos 0, 1;3
22



= −


x
g x f x x
Ta có bảng biến thiên
x
1−
1
3
( )
gx
−
0
+
( )
11f −+
3
( )
31f +
( )
gx
( )
11f −
Suy ra
( ) ( )
1;3
11
−
=−Min g x f
Vậy
( )
11−mf
.
Ví dụ 2.
Cho hàm số
( )
fx
liên tục trên và có đồ
thị
( )
fx
như hình vẽ. Bất phương trình
( ) ( )
5
log 2 4f x m f x m

+ + + −

đúng
với mọi
( )
1; 4x−
khi và chỉ khi
A.
4 ( 1)mf − −
.
B.
3 (1)mf−
.
C.
4 - (-1)mf
.
D.
3 (4)mf−
.
Thi Thử THPT Quốc Gia Chuyên Hạ Long năm tháng 5 năm 2019
Lời giải
Chọn đáp án D
( ) ( ) ( ) ( ) ( ) ( )
5
5 5 5
log 2 4 1 log 2 2 log 5 2f x m f x m f x m f x m
+ + + − + + + + + +
Xét hàm số đặc trưng cho 2 vế của BPT
( )
2
( )
5
log
t
g t t=+
với
0t
( )
1
10
5ln
gt
t
= +
suy ra
( )
gt
đồng biến với
0t
( ) ( ) ( )
2 2 5 3f x m m f x + + −
Yêu cầu bài toán
( )
( )
( ) ( ) ( )
max 3 max 2 1; 4m f x h x x − = −
với
( ) ( )
3h x f x=−
khi đó
( )
max
hx
( )
min
fx
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
15
Từ đồ thị suy ra bảng biến thiên
x
1−
1
4
( )
fx
0
+
0
−
0
( )
1f
( )
1f −
( )
4f
( )
( )
( )
min
1
4
f
fx
f
−
=
So sánh
( )
1f −
và
( )
4f
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
14
12
11
1 1 4 1 1 4S S f x dx f x dx f f f f f f
−


− − − − − −


Suy ra
( ) ( )
min
4f x f=
và
( ) ( )
2 3 4mf −
Ví dụ 3.
Cho hàm số
( )
y f x=
có đạo hàm liên tục
trên có đồ thị khi và chỉ khi
A.
( )
11mf−
.
B.
( )
11mf+
.
C.
( )
11mf−
.
D.
( )
11mf−
.
Lời giải
Chọn đáp án D
Ta có
( ) ( )
3 2 3 2 .
xx
f x x m f x x m − + − +
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
16
Đặt
( )
( ) 3 2 .
x
g x f x x= − +
Khi đó
( )
( ) 3 ln3 2.
x
g x f x

= − +
( )
( ) 0 3 ln3 2.
x
g x f x

= = −
Đặt
( ) 3 ln3 2.
x
hx =−
Khi đó
(
2
( ) 3 ln 3 0, ; 1 .
x
h x x
= −
Bảng biến thiên
x
−
1
( )
hx
+
+
−
3ln3 2−
( )
hx
2−
(
( ) 2, ; 1 .h x x
− −
(1)
Theo đồi thị
( ),y f x
=
ta thấy
(
( ) 3, ; 1 .f x x
− −
(2)
Từ (1) và (2), ta được
(
( ) ( ), ; 1 .f x h x x
−
Nên
( ) (
( ) ( ) 0, ; 1g x f x h x x

= − −
,=suy ra
(
( )
;1
min ( ) (1) 1 1.g x g f
−
= = −
Do đó
( )
32
x
f x x m − +
có nghiệm trên
(
;1
−
khi và chỉ khi
(
( )
;1
min ( ) 1 1.m g x m f
−
−
Ví dụ 4.
Cho hàm số
( )
y f x=
có đạo hàm liên tục
trên và đồ thị như hình vẽ. Tổng tất cả
các giá trị nguyên của tham số
m
để bất
phương trình
( )
( )
( )
( )
( )
( )
22
9.6 4 .9 5 .4
f x f x f x
f x m m+ − − +
đúng với
x
là
A.
10
. B.
4
. C.
5
. D.
9
.
Lời giải
Chọn đáp án A
( )
( )
( )
( )
( )
( )
22
9.6 4 .9 5 .4
f x f x f x
f x m m+ − − +
( )
1
Đặt
( ) (
;2t f x
= − −
( theo đồ thị)
( )
1:
( ) ( )
22
9.6 4 .9 5 .4
t t t
t m m+ − − +
( )
2
22
33
9. 4 5
22
tt
t m m
+ − − +
( )
2
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
17
Đặt:
( )
( ) ( )
2
22
3 3 3 3
9. 4 . . 9 4 .
2 2 2 2
t t t t
g t t t


= + − = + −


,
(
;2t
− −
.
Xét hàm số:
( )
( )
2
3
9 4 .
2
t
h t t

= + −


với
(
;2t
− −
( )
( )
2
3 3 3
2 . 4 . .ln
2 2 2
tt
h t t t
= − + −
( )
2
33
. 2 4 .ln
22
t
tt
= − + −


.
( )
0ht
=
2
3
1 1 4 ln
2
2
3
ln
2
t

− + +


= −
(loại) hoặc
2
3
1 1 4 ln
2
2
3
ln
2
t

− − +


= −
(tm)
Ta có BBT:
x
−
2
3
1 1 4 ln
2
3
ln
2

− − +


2−
( )
ht
0
−
0
+
0
9
9
( )
ht
Từ BBT
(
( ) 9 ; 2h t t
− −
(3).
Vì
(
;2t
− −
34
0
29
t



(4).
Từ (3) và (4) suy ra
( )
( )
2
33
. 9 4 . 4
22
tt
g t t


= + −


(
;2t
− −
(
( )
4
;2
max gt
− −
=
. (Dấu "=" xảy ra khi và chỉ khi
2t =−
).
Bất phương trình (1) đúng với
x
Bất phương trình (2) đúng với
(
;2t
− −
(
( )
2
;2
5 maxm m g t
− −
− +
2
54mm − +
2
5 4 0mm − +
14m
.
Do
m
suy ra
1;2;3;4m
. Vậy tổng các giá trị nguyên của
m
là:
1 2 3 4 10+ + + =
.
Ví dụ 5.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
18
Cho hàm số
( )
y f x=
liên tục trên đoạn
1;9

−

và có đồ thị là đường cong như hình vẽ
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
( )
( ) ( )
( )
( )
( )
22
16.3 2 8 .4 3 .6
f x f x f x
f x f x m m

− + − −

nghiệm đúng với mọi giá trị
x
thuộc
đoạn
1;9

−

?
A.
32
.
B.
31
.
C.
5
.
D.
6
.
Đề thi thử THPT Quốc Gia Yên Khánh Ninh Bình Lần 4 năm 2019
Lời giải
Chọn đáp án D
Từ đồ thị ta suy ra
( )
4 2 1;9f x x

− −

.
Đặt
( )
, 4;2t f x t

= −

.
ycbt
tìm
m
sao cho bất phương trình
( )
( )
22
16.3 2 8 .4 3 .6 1
t t t
t t m m

− + − −

đúng với
4;2t

−

( )
22
16 2
1 2 8 . 3
3
2
t
t
t t m m


− + − −



với
4;2t

−

(*).
Ta có
16
4, 4;2
2
t
t

−

. Dấu bằng xảy ra khi
2t =
.
Mặt khác
2
2 8 0tt+ −
với
4;2t

−

.
Do đó
( )
2
2
2 8 . 0, 4;2
3
t
t t t


+ − −



. Dấu bằng xảy ra khi
24tt= = −
.
Như vậy
2
16 2
2 8 . 4 4; 2
3
2
t
t
t t t



− + − −




. Mà
22
16 2
2 8 . 3
3
2
t
t
t t m m


− + − −



với
4;2t

−

.
Suy ra
2
3 4 1 4m m m− −
. Như vậy có
6
giá trị nguyên của
m
thỏa mãn.
y
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
19
Ví dụ 6.
Cho hàm số
( )
=y f x
liên tục trên
1; 3−
và có đồ thị như hình vẽ. Bất
phương trình
( ) 1 7+ + + − f x x x m
có nghiệm thuộc
1; 3−
khi và chỉ khi
A.
7m
.
B.
7m
.
C.
2 2 2−m
.
D.
2 2 2+m
.
Đề thi thử THPT Quốc Gia Yên Khánh A Ninh Bình Lần 4 năm 2019
Lời giải
Chọn đáp án A
Xét hàm số
( )
17= + + −g x x x
liên tục trên
1;3−
ta có:
( ) (
11
' , 1;3
2 1 2 7
= − −
+−
g x x
xx
( )
' 0 1 7 1 7 3= + = − + = − =g x x x x x x
(nhận)
( ) ( )
( ) ( ) ( )
( ) ( )
1;3
1 2, 3 4 max max 1 , 3 3 4. 1
−
− = = = − = =g g g x g g g
Từ đồ thị hàm số
( )
=y f x
ta có:
( ) ( ) ( )
1;3
max 3 3. 2
−
==f x f
Đặt
( ) ( )
()=+h x f x g x
trên
1;3−
, kết hợp với
( )
1
và
( )
2
ta suy ra:
( )
( )
( ) ( ) ( )
1;3 1;3
max max 3 3 7
−−
+ = + =h x f x g x f g
, đẳng thức xảy ra khi
3.=x
Vậy bất phương trình
( )
m h x
có nghiệm thuộc
1;3−
khi và chỉ khi
( )
1;3
max 7.
−
=m h x
Ví dụ 7.
Cho hàm số
32
( ) 4 4f x x x x= − − +
có đồ thị như
hình vẽ. Có bao nhiêu giá trị nguyên của
m
để
phương trình sau có 4 nghiệm thuộc đoạn
0; 2


(
)
22
2019 15 30 16 15 30 16 0f x x m x x m− + − − + − =
A.
4541
.
B.
4542
.
C.
4543
.
D.
4540
.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
20
THPT Kinh Môn - Hải Dương - Lần 3 – tháng 5 – 2019
Lời giải
Chọn đáp án B
Theo đề
( ) ( )( )( )
1 1 4f x x x x
= + − −
( ) ( ) ( )
2
2
0;2 : 15 30 16 15 1 1 1; 0 2 4 1;4x t x x x t t t
= − + = − + = =
Với
1t
thì phương trình có 2 nghiệm
x
thoả mãn.
Với
1t =
có 1 nghiệm
x
thoả mãn.
BPT
( ) ( ) ( )( )( ) ( )
2019 1 2019 1 1 4 1f t m t t t t m t= + + − − = +
Xét
(
1; 4t
( ) ( )( )
( )
2
2
5 9 9
2019 1 4 2019 5 4 2019 2019 4542,75
2 4 4
m g t t t t t t


= = − − = − + = − − − = −


x
1
5
2
4
( )
gt
0
−
0
+
0
( )
gt
0
0
ym=
4542,75−
Yêu cầu bài toán
4542,75 0 45042; 45042;...; 1mm − − − −
có
45042
m
nguyên thoả
mãn.
Ví dụ 8.
Cho hàm số
( )
y f x=
liên tục trên và có đồ thị
như hình vẽ.
Tập hợp tất cả các giá trị của
m
để bất phương
trình
2
12
10
2
1
x
f f m
x


+ −


+


có nghiệm là
A.
2m
.
B.
12m
.
C.
1m
.
D.
5m −
.
Lời giải
Chọn đáp án A
Đánh giá:
2
22
2
2
1 2 1 1 1
11
x
x
xx
xx
+ −
++
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
21
Từ đồ thị thấy
1;1 2 ( ) 2x f x

− −

2;2 2 ( ) 2x f x

− −

Xét bất phương trình
2
12
1
2
1
x
f f m
x


+


+


. Đặt
2
2
1
x
t
x
=
+
;
2
2
1
x
uf
x

=

+

.
Vì
( )
1
1;1 2;2 2 ( ) 2 0 1 2
2
t u f u f u
− − − +
Vậy để bất phương trình ban đầu có nghiệm thì
2m
.
Ví dụ 9.
Cho hàm số
( )
32
f x ax bx cx d= + + +
với
, , ,a b c d
có đồ thị như hình vẽ.
S
là tập hợp
chứa tất cả
m
thuộc
10; 10

−

để
(
)
2 3 2
2 10
1 ( ) 0
33
− + − + − f x x x f m
có nghiệm
số phần tử của
S
là
A.
9
.
B.
10
.
C.
11
.
D.
12
.
Lời giải
Chọn đáp án A
(
)
( )
(
)
( )
2 3 2 2 3 2
2 1 2 1
1 ( ) 0 1
3 3 3 3
f x x x f m f m f x x x g x− + − + − − + − + =
Yêu cầu bài toán
( )
(
)
2 3 2
21
min min 1 min 1; 1
33
m g x f x x x x


= − + − + −



(vì điều kiện
2
1 0 1 1xx− −
)
•
2
0 1 1tx = −
suy ra
(
)
( )
2
1 0; 1f x f t t

− =

quan sát đồ thị ta thấy
( )
( )
0; 1
1; 1
min min 1 3f t f x


−

= − =
khi
01tx= =
.
•
( )
32
21
33
h x x x= − +
1; 1x

−

;
( ) ( ) ( )
2
2 2 2 1 ; 0 0; 1h x x x x x h x x x

= − = − = = =
( ) ( ) ( )
8
min min 0 ; 1 0 0
3
h x h h

= = = =


( )
1; 1
min gx
−

=
( )
(
)
( )
2
1; 1 1; 1
1; 1
min min 1 min 3 0 3g x f x h x
− −
−

= − + = + =
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
22
Suy ra
( )
3fm
quan sát đồ thị
0m
và
10; 10m

−

suy ra
0; 1; 2;...;10m
có
10 0 1 11− + =
giá trị.
Ví dụ 10.
Cho hàm số
( )
32
f x ax bx cx d= + + +
với
, , ,a b c d
có đồ thị như hình vẽ Có bao nhiêu
giá trị nguyên của tham số
m
để bất phương
trình
( )
2
3sin cos 1
44
2cos sin 4
xx
f f m m
xx

−−
+ +

−+

luôn đúng ?
A.
3
.
B.
4
.
C.
1
.
D.
vô số.
Lời giải
Chọn đáp án D
Đặt
3sin cos 1
2cos sin 4
xx
t
xx
−−
=
−+
( ) ( )
2 1 cos 3 sin 1 4t x t x t + − + = − −
( )
*
.
Phương trình
( )
*
có nghiệm
( ) ( ) ( )
2 2 2
2 1 3 4 1t t t + + + +
9
1
11
t −
.
Suy ra
01t
.
Từ đồ thị
( )
y f x=
ta có
( )
y f x=
đồng biến trên
x
)
0;
+
Do
( ) )
2
2
4 4 2 0;m m m
+ + = + +
;
)
0;t
+
Nên
( )
2
3sin cos 1
44
2cos sin 4
xx
f f m m
xx

−−
+ +

−+

( )
( )
2
44f t f m m + +
2
44t m m + +
Bất
phương trình luôn đúng
2
4 4 1mm + +
3
1
m
m
−
−
. Suy ra có vô số giá trị của tham số
m
.
Ví dụ 11.
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
23
Cho hàm số
( )
y f x=
liên tục trên và có
đồ thị như hình vẽ.Có bao nhiêu giá trị
nguyên dương của tham số
m
để bất
phương trình
( )
( )
( )
2
10
m
f x mf x
fx
+ − −
luôn đúng
trên đoạn
1;4

−

?
A.
3
.
B.
4
.
C.
1
.
D.
vô số.
Lời giải
Chọn đáp án D
Dựa vào đồ thị ta có
( )
1;4 1 4 0x f x m

−

Bất phương trình ban đầu tương đương với :
( )
( ) ( )
( ) ( )
( )
( )
( )
( )
( )
( )
( ) ( )
( )
( )
2
2
2
2
2
2
5
1 2 . 0
4 2 4
5
1
42
5
1
42
5
1
42
f x f x
mm
fx
f x f x
fx
m
fx
fx
fx
m
fx
fx
fx
g x f x f x m


+ − + +




+ +


+ −

= + −



Đặt
( ) ( )
12f x t t=
Bất phương trình trở thành
2
4
5
1
42
t
t t m

+ −



Yêu cầu bài toán
( )
m h t
với
( )
2
4
5
1
42
t
h t t t

= + −



( )
4
2
4
30
2
3
4
0, 1;2
2
5
21
4
t
h t t t
t
+

= −

+
( ) ( )
2 , 1;2h t h t


Để bất phương luôn đúng trên đoạn
1;4

−

ta phải có
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
24
( ) ( )
( )
2
2
2 2 2 21 4m h m h = −
Suy ra có vô số giá trị
m
thoả mãn.
Ví dụ 12.
Cho hàm số
( )
y f x=
có đồ thị như hình
vẽ.Có bao nhiêu số nguyên âm để bất
phương trình
1
1
32
x
f m x

+ −


có
nghiệm thuộc đoạn
2; 2

−

?
A.
3
.
B.
9
.
C.
8
.
D.
10
.
Lời giải
Chọn đáp án D
Ta có bất phương trình
1 6 1 3 6
22
xx
fm
+ + + +
(*)
Yêu cầu bài toán
( )
3 6 minm g t +
với
( ) ( )
6g t f t t=+
với
1
2
x
t =+
và
0; 2t


Xét hàm số
( )
6g f t t=+
với
0; 2t


Quan sát đồ thị
0; 2


hàm số
( )
ft
đồng biến suy ra
( )
0ft
Ta có
( )
' ' 6 0, 0;2g f t t

= +

suy ra hàm số
g
đồng biến
0;2t



nên
( ) ( )
0 0 4g g f = = −
( )
10
min 4 3 6 4
3
g t m m = − + − −
.
Vì
m
nguyên âm nên
3; 2; 1m − − −
.
Ví dụ 13.
Cho hàm số
( )
y f x=
liên tục trên và có
đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên âm lớn hơn
50−
của tham số
m
để
bất phương trình
( ) ( )
( )
( )
3
3
3 4 0f x f x m f x m− + − +
luôn
đúng trên đoạn
1; 4

−

?
A.
3
.
B.
5
.
C.
1
.
D.
2
.
Lời giải
m
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
25
Chọn đáp án D
BPT
( ) ( )
( )
( )
3
3
3 4 0f x f x m f x m− + − +
( ) ( )
( )
( ) ( )
( )
( ) ( )
3
3
33
33f x f x m f x f x m f x f x

− + + − + +

Đặt
( ) ( )
3
3f x f x m t− + =
Bất phương trình trở thành
( ) ( )
33
t t f x f x+ +
Xét hàm số đặc trưng cho hai vế của BPT
( )
3
g u u u=+
có
( )
2
3 1 0,g u u u
= +
Vậy hàm số
( )
gu
luôn đồng biến trên vậy ta có
( ) ( )
( )
( )
( ) ( ) ( )
( ) ( )
3
3
3
4
g t g f x
t f x
f x f x m f x
m f x f x

− +
− +
Yêu cầu bài toán
( )
minm g x
với
( ) ( ) ( )
3
4g x f x f x

= − +

Đặt
( )
f x v=
Có
( )
1;4 1 4 1 4x f x v

−

Để BPT luôn đúng trên đoạn
1; 4

−

ta phải có
( )
3
1;4
4 48m Min v v m


− + −
và
50 49; 48mm − − −
.
Ví dụ 14.
Cho hàm số
( )
=y f x
và
( )
=y g x
liên
tục trên đồ thị của hàm số
( ) ( )
=y f x g x
như sau Có bao nhiêu giá
trị nguyên thuộc
2020;2020

−

của tham
số
m
để bất phương trình
( ) ( )
22
11
10
11
+ − −
++
m
f x g x
luôn
đúng trên đoạn
1;4−
?
A.
2019
.
B.
2020
.
C.
2021
.
D.
2022
.
Lời giải
Chọn đáp án D
Ta có bất phương trình tương đương với :
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
26
( ) ( )
( )
22
11
1
11
+ + =
++
m h x
f x g x
Yều cầu bài toán
( )
1; 4
1 minm h x
−

+
Xét bất đẳng thức sau :
Nếu
1ab
, Có
( )
22
1 1 2
1
1 1 1
+
+ + +a b ab
Chứng minh:
( )( )
( )
( )
( )( )
( )
( )
( )
( )( )
( )( )
( )
( )( )
22
22
22
2 2 2 2 2 2
2 2 2 2
2
22
1 1 2
1 1 1
22
1
11
1 2 2 1
1 1 1 1 1 1
1
0
1 1 1
+
+ + +
++

+
++
+ + + + + +

+ + + + + +
−−

+ + +
a b ab
ab
ab
ab
ab a b a b a b
a b ab ab a b
ab a b
ab a b
Áp dụng
( )
1
( )
( ) ( ) ( ) ( )
22
1 1 2
1 1 1
= +
+ + +
hx
f x g x f x g x
Dựa vào đồ thị ta có
( ) ( )
( ) ( )
22
1 4 1
51
+
f x g x
f x g x
suy ra
( )
4; 1
5
min
2
hx
−

=
Vậy để thỏa mãn điều kiện đề bài ta phải có
23
1
55
−
+ mm
và
2020;2020 ; 2020; 2019;...; 1m m m

− − − −

.
Vậy có
2020
giá trị nguyên của
m
.
Ví dụ 15.
Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Có
bao nhiêu số nguyên
m
để bất phương trình
(
)
22
5 2 1 ( ) 0mx m x m f x+ − + +
có nghiệm
đúng với mọi
2; 2x

−

A.
0
.
B.
1
.
C.
3
.
D.
4
.
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
27
Đề thi thử THPT Quốc Gia Đại học Vinh Lần 2 năm 2019
Lời giải
Chọn đáp án B
Đặt
22
( ) 5 2 1g x mx m x m= + − + +
hàm số luôn xác định với
2; 2x

−

.
Vì
( )
fx
đối dấu 1 lần từ dương qua âm khi qua
1x =
2; 2x

−

Bất phương trình
( ) ( )
.0g x f x
2; 2x

−

( )
( )
0 2; 1
0 1; 2
gx
gx

−



.
Hàm số
( )
gx
liên tục trên
2; 2

−

nên
2
1
(1) 0 2 2 1 0
1
2
m
g m m m
m
=−
= + + + =
=−
.
Do
m
nên chỉ lấy
1m =−
.
Thử lại
2
1 ( ) 5 1 0 2; 1m g x x x

= − = − + − − −

và
( ) 0 [1;2]g x x
Nên
1m =−
thoả mãn. Chọn B.
Lời giải
Chọn đáp án B
Ví dụ 16.
Cho hàm số
( )
y f x=
có đồ thị như hình vẽ.
Tìm tất cả các giá trị thực của tham số
m
để
bất phương trình
2
2 ( ) 4f x x x m+ +
có
nghiệm đúng với mọi
( )
1;3x−
.
A.
3m −
.
B.
10m −
.
C.
2m −
.
D.
5m
.
Đề thi thử THPT Quốc Gia Sở Giáo Dục Ninh Bình Năm 2019 Lần 1
Lời giải
Chọn đáp án B
Bất phương trình
( ) ( )
2
24m f x x x g x + − =
Yêu cầu bài toán
( )
( )
1; 3
minm g x
−

Từ đồ thị
( )
( )
1; 3
min 3fx
−
=−
khi
2x =
( )
1
( )
( )
( )
2
22
1; 3
4 2 4 4 min 4 4x x x x x
−
− = − − − = −
khi
( )
2
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
28
Từ
( )
1
và
( )
2
suy ra
( )
( )
3; 1
min 2.3 4 10gx
−
= − − = −
10m −
Ví dụ 17.
Cho hàm số
( )
y f x=
liên tục trên có đồ thị
như hình vẽ.
Có bao nhiêu giá trị nguyên của
m
để phương
trình:
(
)
22
3 4 6 9 2f x x m− − + = −
có nghiệm
A.
4
.
B.
5
.
C.
6
.
D.
7
.
Đề thi thử THPT Quốc Gia Sở Giáo Dục Ninh Bình Năm 2019 Lần 1
Lời giải
Chọn đáp án B
Đặt
2
3 4 6 9t x x= − −
Điều kiện của t
2
2
6 9 0 0
3
x x x−
22
6 18 12(3 1)
4
2 6 9 6 9
xx
t
x x x x
−−
= − =
−−
;
1
0
3
tx= =
21
(0) 3, 1 [ 1;3]
33
t t t t
= = = − −
Suy ra
( ) ( )
22
22f t m f t m+ = − = − −
Theo đồ thị
Với
( ) ( ) ( ) )
1; 3 6; , 2; 1 6; 1t f t a a f t
= − − − − − −
để phương trình có nghiệm thì
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
29
)
2 2 2
2 6; 1 6 2 1 4 1 {0;1;2; 1; 2}m m m m
− − − − − − − − − − − − −
.
Ví dụ 18.
Cho hàm số
( )
y f x=
liên tục trên có đồ
thị như hình vẽ. Có bao nhiêu giá trị nguyên
của
m
để phương trình
( )
2 1 8f x m− + − =
có 8 nghiệm phân biệt trong khoảng
( )
5; 5−
A.
1
.
B.
5
.
C.
6
.
D.
7
.
Đề thi thử THPT Quốc Gia Sở Giáo Dục Vĩnh Phúc Lần 1Năm 2019
Lời giải
Chọn đáp án A
( ) ( )
2 1 8 2 1 8f x m f x m− + − = − + = +
Nghiệm của phương trình là giao điểm của đường
thẳng
8ym=+
và đồ thị hàm số
( )
( )
3
21y f x C= − +
Đồ thị hàm số
( )
21y f x= − +
gồm 3 bước
Bước 1. Vẽ đồ thị hàm số
( )
y f x=
Từ đồ thị
( )
y f x=
có đồ thị là
( )
C
suy ra đồ thị hàm số
( )
y f x=
có đồ thị
( )
1
C
gồm 2 phần:
• Phần 1: Giữ phần bên phải, bỏ phần bên trái đồ thị
( )
C
.
• Phần 2: Đối xứng phần 1 qua
Oy
.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
30
Bước 2. Hàm số
( )
21y f x= − +
có đồ thị là
( )
2
C
. Tịch tiến sang phải 2 đơn vị lên trên 1 đơn
vị đồ thị
( )
1
C
thu được đồ thị
( )
2
C
Bước 3. Đồ thị hàm số
( )
21y f x= − +
( )
3
C
gồm 2 phần
• Phần 1: Giữ nguyên phần bên trên trục hoành
Ox
của đồ thị
( )
2
C
.
• Phần 2: Đối xứng phần bên dưới của đồ thị
( )
2
C
qua trục
Ox
.
Yêu cầu bài toán
0 8 2 8 6mm + − −
và
7mm = −
vậy có 1 giá trị.
Nhận xét: Để đơn giản ta đặt
( )
2 7; 3t x t= − − −
ta thực hiện vẽ đồ thị hàm số
( )
1y f t=+
theo 3 bước
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
31
Bước 1. Vẽ đồ thị hàm
( )
( )
1
y f x C=
gồm 2 phần
• Phần 1: Giữ phần bên phải, bỏ phần bên trái đồ thị
( )
C
.
• Phần 2: Đối xứng phần 1 qua
Oy
.
Bước 2. Tịnh tiến lên trên 1 đơn vị đồ thị
( )
1
C
được đồ thị
( )
2
C
Bước 3. Đồ thị hàm số
( )
1y f x=+
gồm 2 phần
• Phần 1: Giữ nguyên phần bên trên trục hoành
Ox
của đồ thị
( )
2
C
.
• Phần 2: Đối xứng phần bên dưới của
( )
2
C
qua trục
Ox
.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
32
Yêu cầu bài toán
0 8 2 8 6mm + − −
và
7mm = −
vậy có 1 giá trị.
Ví dụ 19.
Cho hàm số
( )
y f x=
liên tục trên có đồ
thị như hình vẽ. Số giá trị nguyên của tham
số
m
để phương trình
( )
f x m m+=
có 4.
A.
0
.
B.
1
.
C.
2
.
D.
Vô số.
Lời giải
Chọn đáp án B
Nghiệm của phương trình
( )
f x m m+=
là hoành độ giao điểm của đồ thị hàm số
( )
y f x m=+
và đường thẳng
ym=
.
Số giao điểm của đồ thị hàm số
( )
y f x m=+
và đường thẳng
ym=
bằng số giao điểm của
đồ thị hàm số
( )
y f x=
và đường thẳng
ym=
.
Đồ thị hàm số
( )
y f x=
và vị trị có
4
nghiệm.
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
33
Từ đồ thị suy ra để phương trình có 4 nghiệm thì
3
4
1
m
m
=
=−
.
Vậy có 1 giá trị nguyên
1m =−
.
Ví dụ 20.
Cho hàm số
4 3 2
()f x ax bx cx dx e= + + + +
( , , , , )a b c d e
. Hàm số có đồ thị
( )
fx
như
hình vẽ bên. Tập nghiệm của phương trình
( )
f x e=
có số phần tử là
A.
1
.
B.
2
.
C.
3
.
D.
4
.
Lời giải
Chọn đáp án D
Xét hàm số
( ) ( ) -g x f x e=
,
( ) ( )
( )
; ( ) ( ) 0
00
g x f x
f x e g x
g

=
= =
=
Đồ thị hàm số
( ) ( )
13
( 1)
22
g x f x a x x x

= = + − −
với
0a
Ta có bảng biến thiên
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
34
x
−
1−
0
1
2
3
2
+
( )
gx
−
0
+
0
−
0
+
+
0
1
2
g



+
( )
gx
:0Ox y =
( )
1g −
3
2
g



Ta có
33
22
00
3 3 1 3 9
(0) ( ) ( 1) 0
2 2 2 2 64
g g g g x dx a x x x dx a
= − = = + − − = −

Suy ra phương trình có 4 nghiệm.
Ví dụ 21.
Cho hàm số liên tục trên
1; 9

−

và đồ thị như
hình vẽ. Có tất cả bao nhiêu giá trị nguyên của
tham số
m
để phương trình
( )
( ) ( ) ( )
22
16.3 ( ) 2 ( ) 8 4 3 .6
f x f x f x
f x f x m m

− + − −

Có nghiệm đúng với mọi
1; 9x

−

A.
22
.
B.
31
.
C.
5
.
D.
6
.
Lời giải
Chọn đáp án D
Theo đồ thị
4 ( ) 2 [ 2;9]f x x− −
. Đặt
( )
, 4; 2t f x t

= −

.
Bài toán trở thành tìm
m
để
( )
22
16.3 2 8 4 3 6
t t t
t t m m

− + − −

có nghiệm đúng với
4; 2t

−

.
( )
22
16.3 2 8 4 3 6 , [ 4;2]
t t t
t t m m t

− + − − −

( )
( )
22
16 2
2 8 3 , [ 4;2]
3
2
t
t
g t t t m m t


= − + − − −



Yêu cầu bài toán
( )
2
42
3 minm m g x
−

−
Với
16
4, [ 4;2]
2
t
t −
, dấu bằng xảy ra khi
2t =
.
0
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
35
22
2
2 8 0, [ 4;2] 2 8 0, [ 4;2]
3
t
t t t t t t


+ − − + − −



dấu bằng xảy ra khi
2t =
.
Suy ra
( ) ( )
2
4;2
16 2
2 8 4, [ 4;2] min 4
3
2
t
t
g t t t t g t
−



= − + − − =



2
3 4 1 4m m m − −
và
1; 0; 1; 2; 3; 4mm −
Kết luận: có 6 giá trị
m
.
Ví dụ 22.
Cho hàm số
( )
y f x=
liên tục trên có đồ thị
như hình vẽ. Có bao nhiêu giá trị nguyên của
1; 2025m


sao cho phương trình
(
)
2
2
2
10
1
x
f f m m
x

+ − + =

+

có nghiệm.
A.
2019
.
B.
2022
.
C.
2025
.
D.
2026
.
Lời giải
Chọn đáp án D
Theo đồ thị hàm số đối xứng với nhau qua
Ox
suy ra hàm số
hàm số lẻ.
(
)
2
2
2
10
1
x
f f m m
x

+ − + =

+

(
)
(
)
22
22
22
11
11
xx
f m m f f m m f
xx
−
− + = − − + =
++
Ta có
2 2 2
2 2 2 2 2
1 1 [ 1;1]
22
1 1 1
x x x x x
f
xx
x x x

− − − − −
= = − −

−
+ + +

đồng biến.
Mặt khác
(
)
(
)
22
1
1 ;0 1
2
m m f m m

− + − − +


đồng biến.
22
2
2
22
2
2
1 1 1 1
1
11
1 1 1 1 0
11
x
m m m m
x
mm
m m m m
mm
−
− + = − − +
+
+ +
− + + + +
− +
Nên phương trình có nghiệm với
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
36
DẠNG 4: Cho hàm số
( )
y f x=
có đồ thị
( )
fx
xác định tham số m để
( )
,0g x m
Ví dụ 1.
Cho hàm số
( )
y f x=
có đạo hàm trên .
Đồ thị hàm số
( )
'y f x=
như hình vẽ. Tìm
m
để bất phương trình
( )
2
2 2 4 3m x f x x− + + +
nghiệm đúng
với mọi
( )
3;x − +
.
A.
2 (0) 1mf+
.
B.
2 (0) 1mf−
.
C.
2 ( 1)mf−
.
D.
2 ( 1)mf−
.
Lời giải
Chọn đáp án B
Ta có
( ) ( )
22
2 2 4 3 2 2 4 3m x f x x m f x x x− + + + + + + +
.
Yêu cầu bài toán
( )
minm g x
với .
( ) ( )
2
2 2 4 3g x f x x x= + + + +
.
Ta có
( ) ( ) ( ) ( )
2 2 2 4 2


= + + + = − −

g x f x x f t t
( )
2tx=+
( ) ( ) ( )
0 2 2

= + = − +g x f x x
.
Đặt
2=+tx
ta được
( )
=−f t t
.
( )
1
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
37
Nghiệm của phương trình (1) chính là hoành độ giao điểm của đường thẳng
yt=−
và đồ thị
hàm số
( )
ft
Ta có
( )
0gx
khi đồ thị
( )
ft
nằm trên đường thẳng
yt=−
;
( )
0gx
khi đồ thị
( )
ft
nằm
dưới đường thẳng
yt=−
. Chỉ cần xét khoảng
( )
0gx
khoảng còn lại mặc nhiên sẽ làm cho
( )
0gx
( ) ( )
1 2 1 3
0
0 2 0 2
t x x
g x f t t
t x x
− + − −

−
+ −
Từ đó ta có bảng biến thiên nghiệm bội chẵn tức điểm tiếp xúc không tham gia vào quá trình
xét dấu
x
−
3−
2−
+
( )
gx
+
0
−
0
+
( )
gx
−
−
( ) ( ) ( ) ( )
min 2 2 0 1 2 0 1g x g f m f= − = − −
( )
3;x − +
( )
2 0 1mf −
Ví dụ 2.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
38
Cho hàm số
( )
y f x=
có đạo hàm trên .
Đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Tìm
m
để bất phương trình
( )
( )
2
4 2 1 2m x f x x+ + + −
nghiệm đúng
với mọi
4;2x

−

.
A.
2 (0) 1mf−
. B.
2 ( 3) 4mf − −
.
C.
2 (3) 16mf−
. D.
2 (1) 4mf−
.
Lời giải
Chọn đáp án D
( )
( )
( ) ( )
2
2
4 2 1 2 2 1 2m x f x x m f x x+ + + − + − +
Yêu cầu bài toán
( )
maxm g x
với
( ) ( ) ( )
2
2 1 2g x f x x= + − +
Đặt
1tx=+
Ta có
( ) ( ) ( ) ( ) ( )
( )
( ) ( )
2 1 2 2 2 1 2 2 1g x f x x f x x f t t

= + − + = + − + = − +

.
( ) ( )
01g x f t t

= = +
nghiệm của phương trình là hoành độ giao điểm của đường thẳng
1yt=+
và đồ thị
( )
ft
.
Từ đồ thị
( ) ( ) ( )
2 1 0g x f t t


= − +

khi đồ thị
( )
ft
nằm trên đường thẳng
1yt=+
và
( ) ( ) ( )
2 1 0g x f t t


= − +

khi đồ thị
( )
ft
nằm dưới đường thẳng
1yt=+
, ta chỉ cần xét
trường hợp
( )
3 2 3 1 2 4 1
0
3 1 3 2
t x x
gx
t x x
− − + −
+
x
4−
1
2−
( )
gx
+
0
−
0
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
39
( )
1g
( )
gx
Suy ra
( ) ( )
max 2 1 4g x f=−
4;2x

−

nên
m
( )
2 1 4f −
.
Ví dụ 3.
Cho hàm số
( )
y f x=
là hàm đa thức có hệ
số thực. Hình vẽ bên dưới là một phần đồ
thị của hai hàm số:
( )
=y f x
và
( )
=y f x
. Tập các giá trị của tham số
m
để phương trình
( )
x
f x me
luôn đúng
trên
0; 2
là ?
A.
0m
.
B.
( )
0mf
.
C.
( )
2
2f
m
e
.
D.
( )
( )
2
0+
f
mf
e
.
Lời giải
Chọn đáp án
Đồ thị hàm số
( )
fx
cắt trục hoành tại
0
x
thì
0
x
là cực trị của hàm số
( )
y f x=
. Dựa vào đồ
thị ta kí hiệu
( )
1
C
là đồ thị hàm số
( )
y f x=
,
( )
2
C
đồ thị của hàm số
( )
y f x
=
( )
x
f x me
( )

x
fx
m
e
.
Yêu cầu bài toán
( )
maxm g x
với
( )
( )
=
x
fx
gx
e
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
40
Ta có
( )
( ) ( )
−
=
x
f x f x
gx
e
.
( ) ( ) ( )
( )
1
02
1;0
=

= = =
= −
x
g x f x f x x
xa
.
( )
0gx

( ) ( )
'f x f x
khi đồ thị hàm số
( )
fx
nằm trên đồ thị
( )
0gx

( ) ( )
'f x f x
khi đồ thị hàm số
( )
fx
nằm dưới đồ thị
( )
fx
Theo đồ thị ta có bảng biến thiên.
x
0
a
1
2
( )
gx
+
0
+
0
−
( )
1g
( )
gx
Khi đó
( ) ( )
0; 2
max 1 0g x g


==
0m
Ví dụ 4.
Cho hàm số
( )
fx
liên tục trên . Hàm số
( )
y f x
=
có đồ thị như hình vẽ. Bất phương
trình
( )
2
2sin 2sinf x x m−
đúng với mọi
( )
0;x
khi và chỉ khi
A.
( )
1
1
2
mf−
.
B.
( )
1
1
2
mf−
.
C.
( )
1
0
2
mf−
.
D.
( )
1
0
2
mf−
.
Đề thi thử THPT Quốc Gia Chuyên Quang Trung Lần 5 năm 2019
Lời giải
Chọn đáp án
( ) ( )
2
2sin 2sin 1f x x m−
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
41
Ta có:
( ) (
0; sin 0;1xx
. Đặt
(
( )
2sin 0;2x t t
=
ta được bất phương trình:
( ) ( )
2
1
2
2
f t t m−
.
( )
1
đúng với mọi
( )
0;x
khi và chỉ khi
( )
2
đúng với mọi
(
0;2t
.
Xét
( ) ( )
2
1
2
g t f t t=−
với
(
0;2t
.
( ) ( )
g t f t t

=−
.
Từ đồ thị của hàm số
( )
y f x
=
và
yx=
Ta có bảng biến thiên
x
0
1
2
( )
gt
+
0
−
0
( )
1g
( )
gt
Yêu cầu bài toán
(
( ) ( )
0 ; 2
1
max 1 1
2
m g g f
= = −
.
DẠNG 5: Cho đồ thị hàm số
( )
y f x=
xác định tham số để phương trình có nghiệm
Ví dụ 5.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
42
Cho hàm số
( )
y f x=
liên tục trên . Và
có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình
( )
2 cosf f x m

=


có nghiệm
;
2
x


?
A.
2
.
B.
3
.
C.
4
.
D.
5
.
Lời giải
Chọn đáp án C
Đặt
costx=
với
;
2
x



(
1; 0t
−
.
Quan sát đồ thị trên
( )
1; 0−
hàm số nghịch biến nên
0 (0) ( ) ( 1) 2f f t f= − =
Đặt
)
2 (cos ) 0; 2u f x u
=
.
Yêu cầu bài toán tương đương với tìm
m
để phương trình
( )
f u m=
có nghiệm
)
0; 2
.
( )
)
( )
)
0; 2 0; 2
min maxf u m f u


Quan sát đồ thị
( )
)
( )
)
0; 2 0; 2
min 2; max 3 2 2f u f u m


= − = −
và
m
Nên
{ 2; 1;0;1}m − −
, có 4 giá trị
m
.
Ví dụ 6.
Số các giá trị của tham số
m
không vượt
quá
5
để phương trình
( )
2
1
0
8
x
m
f
−
−=
có 2 nghiệm phân biệt.
A.
4
.
B.
5
.
C.
6
.
D.
7
.
Lời giải
Chọn đáp án B
Đặt
0
x
t
=
. Phương trình có dạng
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
43
22
11
( ) 0 ( ) ,( 0)
88
mm
f t f t t
−−
− = =
Nghiệm phương trình phụ thuộc vào số giao điểm giữa đường thẳng
2
1
8
m
y
−
=
và đồ thị hàm
số
( )
y f t=
Quan sát đồ thị hàm số
( )
y f x=
ta có phương trình trên có 2 nghiệm phân biệt dương
2
2
1
1 1 7 9 3 3
8
m
mm
−
− − −
và
{ 2; 1;0;1;2}mm − −
.
Vậy có 5 giá trị
m
.
Ví dụ 7.
Cho hàm số bậc ba
( )
y f x=
có đồ thị
như hình vẽ. Có bao nhiêu giá trị
nguyên của tham số
m
thuộc đoạn
0; 9


sao cho bất phương trình
( ) ( ) ( ) ( ) ( )
22
2 16.2 4 16 0
f x f x m f x f x m f x+ − − −
− − +
có nghiệm
( )
1; 1x−
?
A.
6
.
B.
8
.
C.
5
.
D.
7
.
Đề thi thử THPT Quốc Gia Sở Bắc Ninh 07-05-2019
Lời giải
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
44
Chọn đáp án A
Ta có:
( ) ( ) ( ) ( ) ( )
22
2 16.2 4 16 0
f x f x m f x f x m f x+ − − −
− − +
( ) ( ) ( ) ( ) ( ) ( )
22
4 .2 16.2 4 16 0
f x f x f x m f x f x m f x− − − −
− − +
( ) ( ) ( )
(
)
( ) ( )
(
)
22
4 2 1 16 2 1 0
f x f x f x m f x f x m− − − −
− − −
( )
( )
( ) ( )
(
)
2
4 16 2 1 0
f x f x f x m−−
− −
Theo đồ thị
( )
1; 1x−
( )
22fx −
( )
22
4 4 4
fx
−
( )
( )
4 16 0 1;1
fx
x − −
Do đó
( ) ( )
( ) ( )
2
2
2 1 0 0
f x f x m
f x f x m
−−
− − −
có nghiệm
( )
1; 1x−
( ) ( )
2
f x f x m −
có
nghiệm
( )
1; 1x−
Xét
( ) ( ) ( )
2
g f x f x f x

=−

Đặt
( )
t f x=
với
( )
2;2t −
,
( )
2
g t t t=−
có đồ thị như hình vẽ
Theo đồ thị
( ) ( )
( )
2; 2
max 6g t m m g t
−
=
và
0; 9m


06m
.
Ví dụ 8.
Hình vẽ bên là đồ thị của hàm số
( )
4 3 2
f x ax bx cx dx e= + + + +
. Hỏi có bao
nhiêu
m
nguyên để phương trình
( )
f x m=
có ít nhất ba nghiệm phân
biệt?
A.
1
.
B.
2
.
C.
3
.
D.
4
.
Đề thi thử THPT Quốc Gia Sở Bắc Ninh 07-05-2019
Lời giải
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
45
Chọn đáp án C
Từ đồ thị hàm số
( ) ( )
:C y f x=
ta suy ra đồ thị hàm số
( )
( )
':C y f x=
gồm 2 phần
• Phần 1: Giữ nguyên phần đồ thị
( )
C
trên miền
, (kí hiệu phần đồ thị này là
( )
1
C
),Bỏ
phần đồ thị
( )
C
ở bên trái trục
Oy
.
• Phần 2: Đối xứng phần 1 qua
Oy
.
Theo đồ thị
( )
'C
ta có:
Phương trình
( )
f x m=
có ít nhất ba nghiệm phân biệt
3 0.m −
Vì
m
nên
2; 1;0m − −
. Vậy có 3 giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Ví dụ 9.
Cho hàm số
( )
32
= + + +f x ax bx cx d
có đồ thị
như hình vẽ, gọi
S
là tập hợp các giá trị của
( )
mm
sao cho
( ) ( ) ( ) ( )
3
1 2 1 1 0,

− − − + −

x m f x mf x f x x
. Số phần tử của tập
S
là?
A.
2
.
B.
0
.
C.
3
.
D.
1
.
Đề thi thử THPT Quốc Gia Chuyên Quang Trung Lần 5
Lời giải
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
46
Chọn đáp án A
Hướng giải 1
Từ đồ thị hàm số ta suy ra
( )
( )
( )
( )
( )
3
1
11
2
10
0
11
00
0
22
1
1
0
2
2
=
=
−=
=

= +

=
=


=
=

f
a
f
b
f x x
f
c
f
d
Theo đề
( )
3
0
1 1 0 1
1
=
= − = =
=−
m
f m m m
m
Với
0=m
, ta có:
( ) ( )
( )
( )
3
11
1 1 1 1
22

− − = − + −


x f x x x
( )
( )
( )
( )
2
32
11
1 1 1 1 0
22
= − − = − − + x x x x x x
(thoả mãn)
Với
1=m
, ta có:
( ) ( ) ( ) ( )
( ) ( )
3
1 2 1 1
11
1 2 1 1
22
− − − + −



= − − + −


x f x f x f x
xx
( )
( )
( )
( )
3 2 3 2
1
1 8 12 6 1 1 1 4 6 3 1
2
= − − + − − = − − + −x x x x x x x x
( )
( )
2
2
1 4 2 1 0= − − + x x x x
(thoả mãn)
Với
1=−m
, ta có:
( ) ( ) ( ) ( ) ( ) ( )
3
3
11
1 2 1 1 1 2 1
22

− − − + + − = − − − − +




x f x f x f x x x x
( )
( )
32
1
1 6 3 0
0
− − + −
x
x x x x
x
(Loại)
Vậy
0=m
và
1=m
.
Hướng giải 2
Để
( ) ( ) ( ) ( )
3
1 2 1 1 0,

− − − + −

x m f x mf x f x x
thì
( ) ( ) ( )
3
2 1 1

− − + −

m f x mf x f x
nhận
là nghiệm bội lẻ duy nhất và khi qua
1=x
(
( ) ( ) ( )
3
2 1 1

− − + −

m f x mf x f x
đổi dấu từ
−
sang
+
). Khi đó:
3
0
0
1
=
− =
=
m
mm
m
.
+ Thử lại, ta thấy với
0=m
thỏa.
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
47
+ Với
1=m
, ta có:
( ) ( ) ( ) ( )
3
2 1 1 2 1 1

− − + − = − −

m f x mf x f x f x
là một hàm số bậc ba có
hệ số bậc cao nhất dương.
Ta có:
( ) ( )
lim 2 1 1 , lim 2 1 1
→+ →−
− − = + − − = −
xx
f x f x
nên khi qua
hàm số sẽ đổi dấu
từ
−
sang
+
thỏa mãn.
+ Với
1=−m
, ta có:
( ) ( ) ( ) ( ) ( )
3
2 1 1 2 1 2 1

− − + − = − − + −

m f x mf x f x f x f x
là một hàm số
bậc ba có hệ số bậc cao nhất âm.
Ta có:
( ) ( )
lim 2 1 1 , lim 2 1 1
→+ →−
− − = − − − = +
xx
f x f x
nên khi qua
hàm số sẽ đổi dấu
từ
+
sang
−
không thỏa mãn.
Ví dụ 10.
Cho hàm số
( )
y f x=
liên tục trên , có
đồ thị hàm số như hình vẽ. Có bao nhiêu
giá trị nguyên dương của tham số
m
để
bất phương trình
2
(2025 ) ( ) ( ) 1 3 10 2m f x f x x x− + − + −
nghiệm đúng với mọi
[0;5]x
A.
2019
.
B.
2020
.
C.
2021
.
D.
2022
.
Lời giải
Chọn đáp án B
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
48
Để bất phương trình có nghiệm đúng với mọi
0; 5x


thì ta cần có
2
0; 5
3 10 2
2025 max
( ) ( 2) 1
xx
m
f x f x



+−

−

+ − −

Theo bất đẳng thức Bunyakovsky
3 10 2 3 2 5 (3 2)( 5 ) 5x x x x x x+ − = + − + + − =
dấu bằng “
=
” xảy ra khi và chỉ khi
3x =
. Nhìn đồ thị ta thấy rằng
( )
1fx
dấu “
=
” xảy ra khi
3; 1; 5x x x= = =
.
Suy ra
22
3 10 2 5
5 2020
( ) ( ) 1 ( ) ( ) 1
xx
m
f x f x f x f x
+−
+ − + −
.
Ví dụ 11.
Cho hàm số
( )
y f x=
có đồ thị
( )
fx
như hình vẽ.
Xét hàm số
( ) ( )
3
2 2 4 3 6 5g x f x x x m= + − − −
với
m
là số thực. Để
( )
0gx
[ 5; 5]x −
thì
điều kiện của
m
là
A.
2
( 5)
3
mf
.
B.
2
( 5)
3
mf
.
C.
2
(0) 2 5
3
mf−
.
D.
2
( 5) 4 5
3
mf − −
.
Lời giải
Chọn đáp án A
Để
33
( ) 0 ( ) 2 ( ) 2 4 3 6 5 0 3 2 ( ) 2 4 6 5g x g x f x x x m m f x x x = + − − − + − −
Với
3
( ) 2 ( ) 2 4 6 5h x f x x x= + − −
Yêu cầu bài toán
( )
5; 5
2 maxm h x

−


Xét hàm số
3
( ) 2 ( ) 2 4 6 5h x f x x x= + − −
;
2
( ) 2 ( ) 6 4h x f x x

= + −
( 5) 2 ( 5) 6.5 4 0
( 5) 2 ( 5) 6.5 4 0
(0) 2 (0) 0 4 0
(1) 2 (1) 6.1 4 0
( 1) 2 ( 1) 6.1 4 0
hf
hf
hf
hf
hf

− = − + − =

= + − =

= + − =

= + −

− = − + −
suy ra
( )
hx
đồng biến trên
5; 5

−

x
5−
5
( )
hx
+
0
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
49
( )
hx
Suy ra
( )
( ) ( )
( )
( )
5; 5
5 2 5 max 2 5h x h f f x f

−

= =
Ví dụ 12.
Cho
0 1 1a b a − −
và hàm số
( )
2
()
()
( 1)
fx
y g x
fx
==
+
có đạo hàm
)
0;
+
. Biết
đồ thị hàm số
( )
y f x=
như hình vẽ. Khẳng định
nào sau đây đúng với
[ 1; 1]x a b − −
A.
( 1)
()
fb
gx
m
−
.
B.
( 1)
()
fa
gx
n
−
.
C.
( 1)
()
fb
gx
m
−
.
D.
10 ( ) 0gx−
.
Lời giải
Chọn đáp án A
Ta có
2
[ 1; 1] ( 1) [ ; ]x a b x a b − − +
theo đồ thị có
( )
( )
2
2
1 1 1
( 1)
( 1)
m f x n
nm
fx
+
+
Với
0 1 1a b a − −
theo đồ thị hàm số
( )
fx
đồng biến trên
[ 1; 1]ab−−
( )
2
( ) ( 1)
( 1) ( ) ( 1) ( )
( 1)
f x f b
f a f x f b g x
m
fx
−
− − =
+
Ví dụ 13.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
50
Gọi
A
là tập hợp tất cả các giá trị nguyên của
tham số
m
để phương trình
( )
2sin
2
m
f x f

=


có 12 nghiệm phân biệt thuộc đoạn
;2


−

.
Tính tổng tất cả các phần tử của
A
.
A.
5
.
B.
3
.
C.
2
.
D.
6
.
Lời giải
Chọn đáp án B
Đặt
2sintx=
với
;2x


−

.
2costx
=
.
( )
0 2cos 0
2
t x x k k
= = = +
.
3
;2 ; ;
2 2 2
xx



− −



.
Bảng biến thiên
x
−
2
−
2
3
2
2
t
−
0
+
0
−
0
+
0
2
0
t
2−
2−
Từ đó, ta suy ra được bảng biến thiên của
2sinux=
là
x
−
2
−
0
2
3
2
2
u
+
0
−
0
+
0
−
0
+
0
−
2
2
2
u
0
0
0
0
Với
2u =
ta có 3 nghiệm phân biệt
;2x


−

.
Với
0u =
ta có 4 nghiệm phân biệt
;2x


−

.
Với
02u
ta có 6 nghiệm phân biệt
;2x


−

.
Yêu cầu bài toán
( )
2
m
f u f

=


có 2 nghiệm phân biệt trong khoảng
( )
0;2
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
51
02
04
27
2
0
33
16 2
22
m
m
m
f
mm



−



.
Vậy
1;2A =
. Tổng tất cả các phần tử của
A
bằng 3.
DẠNG 6: Cho đồ thị hàm số
( )
y f x
=
xác định số nghiệm của hàm số
( ) ( ) ( )
g x f x g x=+
Ví dụ 1.
Cho hàm số đa thức
( )
y f x=
có
( )
1 2018f =
và
có đồ thị
( )
y f x
=
như hình vẽ. Xét hàm số
( ) ( )
3
3 2019g x f x x x= − + −
. Phương trình
( )
20gx+=
có tất cả bao nhiêu nghiệm dương
A.
0
.
B.
1
.
C.
2
.
D.
3
.
Lời giải
Chọn đáp án
Ta có
( ) ( ) ( )
( )
22
3 3 3 3g x f x x f x x
= − + = − −
;
( ) ( )
2
0 3 3g x f x x

= = −
có nghiệm là hoành
độ giao điểm của hàm số
( )
y f x
=
và
( )
2
: 3 3P y x=−
.
Theo đồ thị ta có đồ thị hàm số
( )
0gx
khi đồ thị
( )
fx
nằm trên đồ thị
( )
P
và ngược lại
( )
0gx
khi đồ thị
( )
fx
nằm dưới đồ thị
( )
P
.
Từ đồ thị ta có :
( )
11g =
Hàm số
( )
fx
nghịch biến
( )
0; 1
suy ra
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
52
( ) ( )
0 1 2018ff =
( ) ( ) ( )
0 0 2019 1 2019 2018 2019 1g f f= − − = − = −
Phương trình
( ) ( )
2 0 2g x g x+ = = −
là giao điểm giữa đồ thị hàm số
( )
gx
và đường thẳng
2y =−
Bảng biến thiên :
x
−
1−
0
1
+
( )
gx
−
0
+
0
−
0
1
( )
gx
2y =−
( )
3g −
Kết luận : phương trình
( )
20gx+=
có 1 nghiệm dương
Ví dụ 2.
Cho hàm số
( )
y f x=
liên tục trên và có
đồ thị như hình vẽ bên. Biết rằng
( )
0fx
với mọi
( ) ( )
; 3 2;x − − +
. Số nghiệm
nguyên thuộc khoảng
( )
10;10−
của bất
phương trình
( )
( )
2
1 6 0f x x x x

+ − − −

là
A.
9
.
B.
10
.
C.
8
.
D.
7
.
Đề thi thử THPT Quốc Gia Môn Toán Trường Lương Thế Vinh lần 3 năm 2019
Lời giải
Chọn đáp án D
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
53
Đặt
( ) ( )
( )
2
16g x f x x x x

= + − − −

là hàm số liên tục trên .
( )
( ) ( )
( )
( )
22
2; 3
6 0 6 0
0
1
1
1 0 1
xx
x x x x
gx
f x x
f x x f x x

= − =
− − = − − =
=

= − +
+ − = = − +


.
Phương trình
( )
1
là phương trình hoành độ giao điểm của đồ thị hàm số
( )
y f x=
và đường
thẳng
1yx= − +
. Dựa vào đồ thị hàm số đã vẽ ở hình trên
( )
10f x x+ − =
3x =−
,
1x =−
,
0x =
và
2x =
.
Ta có bảng xét dấu
x
−
3−
2−
1−
0
2
3
+
2
6xx−−
+
|
+
0
−
|
−
|
−
|
−
0
+
( )
1f x x+−
−
0
+
|
+
0
−
0
−
0
+
|
+
( )
gx
−
0
+
0
−
0
+
0
+
0
−
0
+
( )
( )
( ) ( ) ( ) ( ) ( )
2
1 6 0 0 3; 2 1;0 0;2 3;f x x x x g x x

+ − − − − − − +

Kết hợp điều kiện
x
nguyên và
( )
10;10x−
ta có
1;4;5;6;7;8;9x
.
DẠNG 7 : Biện luận tham số
m
của bất phương trình hoặc phương trình bằng cách đưa về hàm
số đặc trưng
Ví dụ 1.
Cho hàm số
( )
53
34f x x x m= + −
. Có bao nhiêu giá trị nguyên của tham số
m
để phương
trình
( )
(
)
3
3
f f x m x m+ = −
có nghiệm thuộc đoạn
1;2


?
A.
15
. B.
16
. C.
17
. D.
18
.
Đề thi thử THPT Quốc Gia Môn Toán Trường Lương Thế Vinh lần 3 năm 2019
Lời giải
Chọn đáp án D
Đặt
( ) ( ) ( )
33
3
t f x m t f x m f x t m= + = + = −
( )
1
.
Ta có
( )
(
)
3
3
f f x m x m+ = −
, suy ra
( )
3
f t x m=−
( )
2
.
Từ
( )
1
và
( )
2
ta có
( ) ( ) ( ) ( )
3 3 3 3 5 3 5 3
44f x f t t x f x x f t t x x t t− = − + = + + = +
( )
3
.
Xét hàm số
( ) ( ) ( )
5 3 4 2
4 5 12 0g u u u g u u u u g u
= + = +
đồng biến trên .
Do đó
( ) ( ) ( )
3 g x g t x t = =
. Thay vào
( )
1
ta được
( )
3 5 3
23f x x m x x m= − + =
( )
4
.
Xét hàm số
( )
53
2h x x x=+
trên đoạn
1;2


.
Ta có
( ) ( )
42
5 6 0 1;2h x x x x h x

= +

đồng biến trên đoạn
1;2


.
Vậy ta có
( ) ( )
1; 2
min 1 3h x h


==
và
( ) ( )
1;2
max 2 48h x h


==
.
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
54
Phương trình đã cho có nghiệm thuộc
1;2


Phương trình
( )
4
có nghiệm trên
1;2


.
( ) ( )
1; 2
1; 2
min 3 max 3 3 48 1 16h x m h x m m




. Vậy có
16
giá trị nguyên của
m
.
| 1/52
| | Tải xuống

Có thể bạn quan tâm:

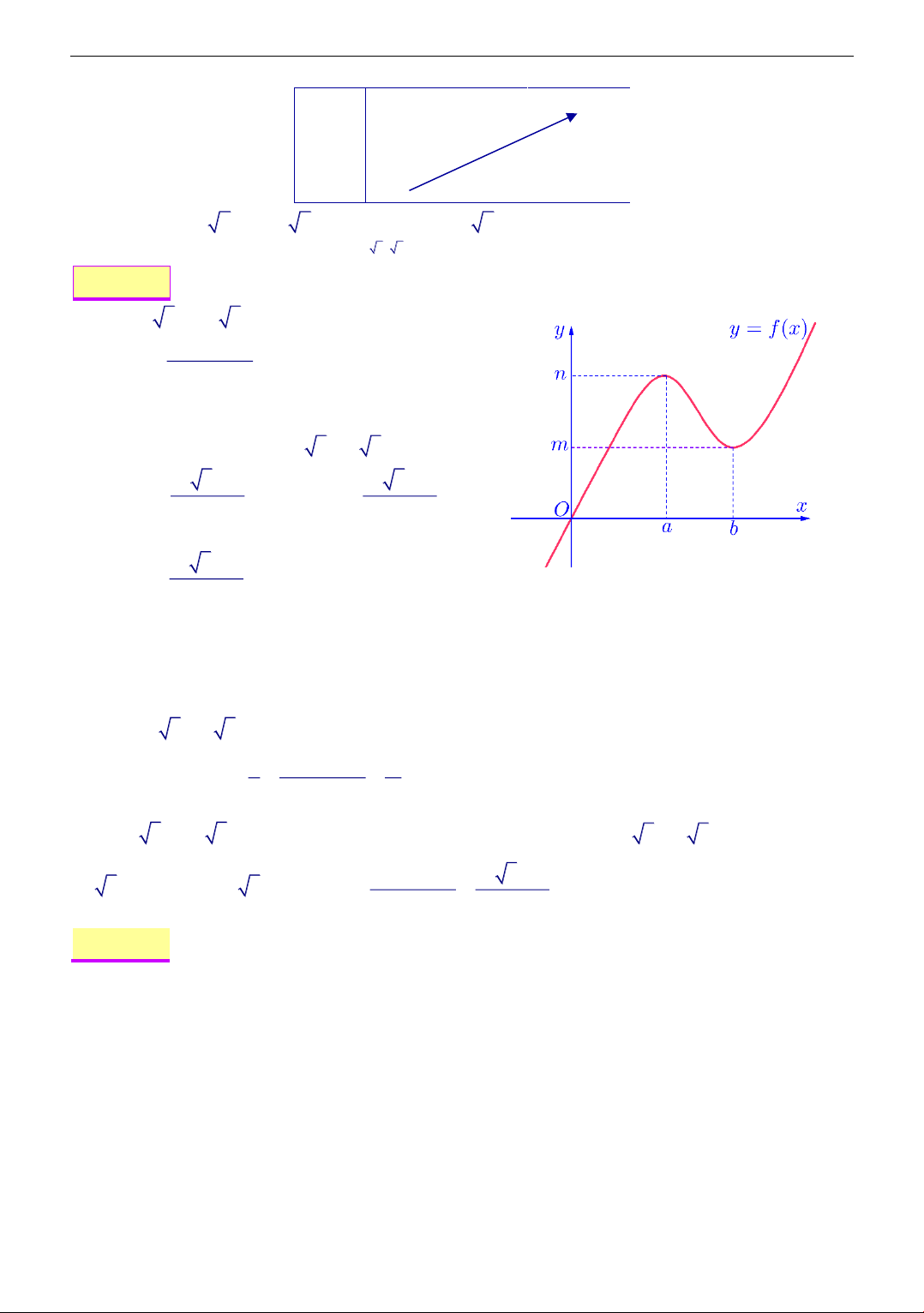
Preview text:


Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung Contents
 DẠNG 1: Cho đồ thị hàm số y = f (x) xác định số nghiệm của phương trình
f (t(x)) = k .................................................................................................................................... 4
DẠNG 2: Cho bảng biến thiên f (x) tìm tham số m để bất phương trình g(x,m)  0
có nghiệm thuộc D . .................................................................................................................... 6
 DẠNG 3: Cho hàm số y = f (x) có đồ thị f (x) xác định tham số m để g(x,m)  0 13
 DẠNG 4: Cho hàm số y = f (x) có đồ thị f (x) xác định tham số m để g(x,m)  0 36
 DẠNG 5: Cho đồ thị hàm số y = f (x) xác định tham số để phương trình có nghiệm
...................................................................................................................................................... 41
Theo bất đẳng thức Bunyakovsky ........................................................................................... 48
 DẠNG 6: Cho đồ thị hàm số y = f (x) xác định số nghiệm của hàm số
g(x) = f (x) + g(x) ...................................................................................................................... 51
 DẠNG 7 : Biện luận tham số m của bất phương trình hoặc phương trình bằng cách
đưa về hàm số đặc trưng .......................................................................................................... 53 3
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
 DẠNG 1: Cho đồ thị hàm số y = f (x) xác định số nghiệm của phương trình f (t(x)) = k Ví dụ 1.
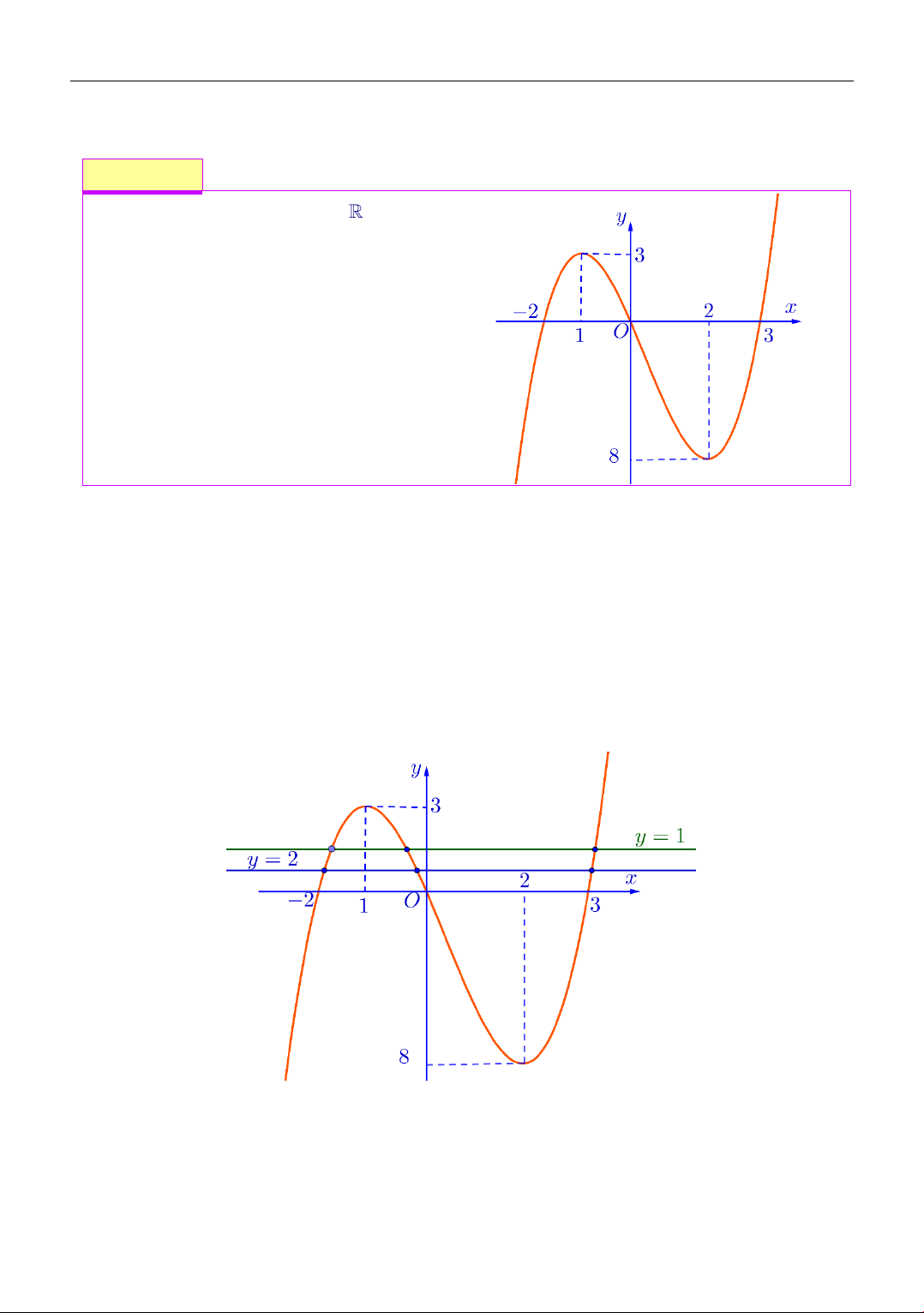
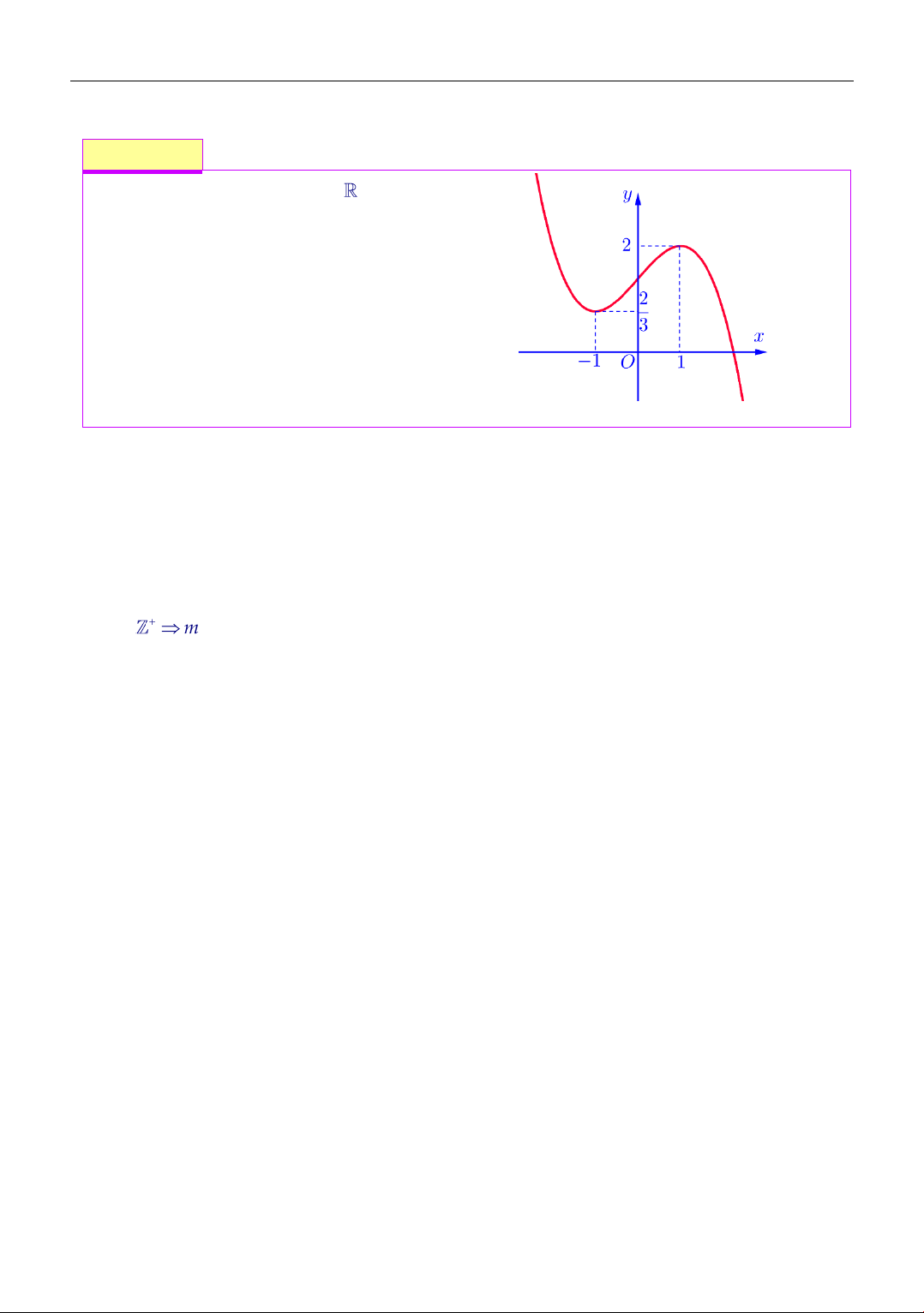
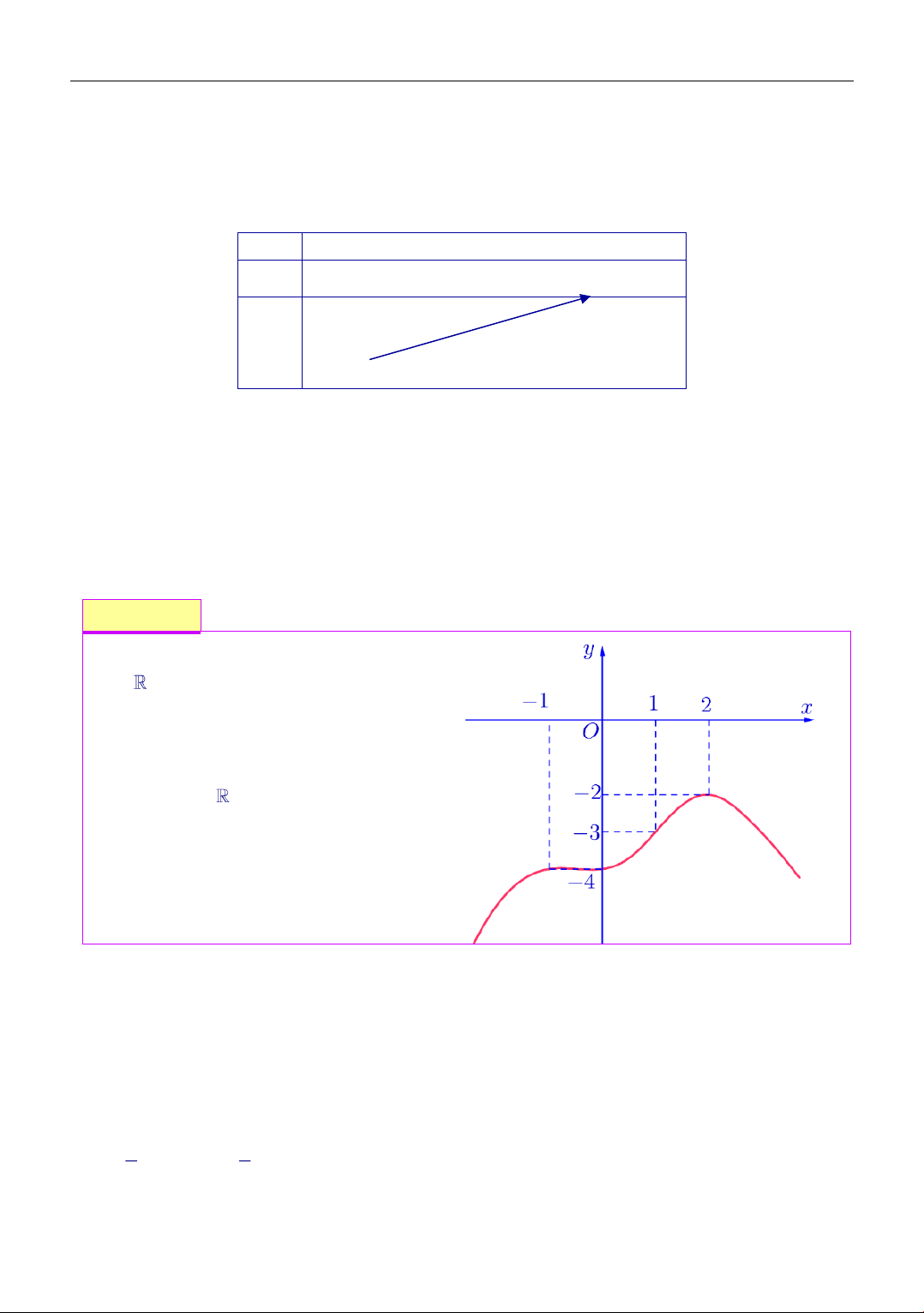
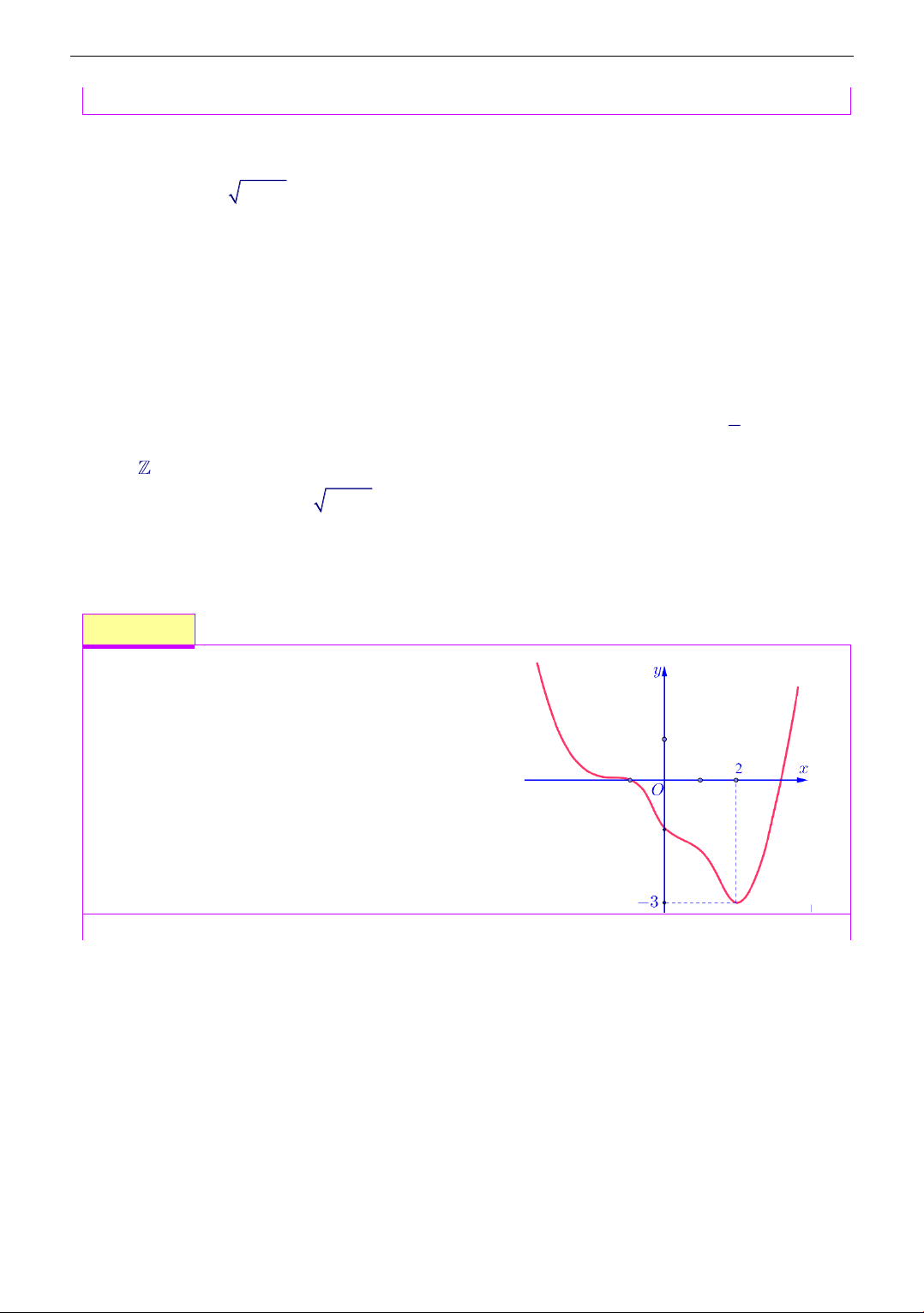
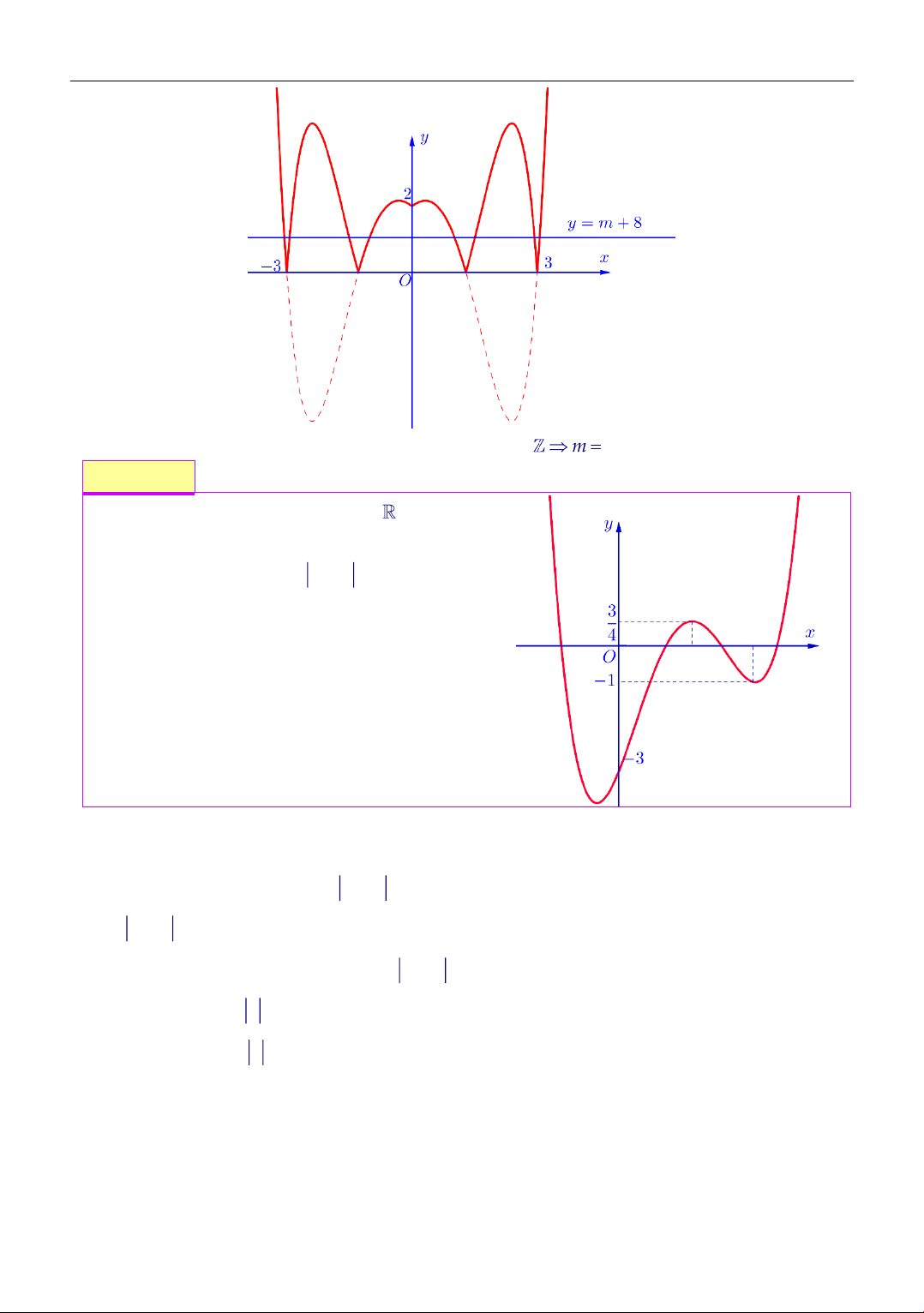
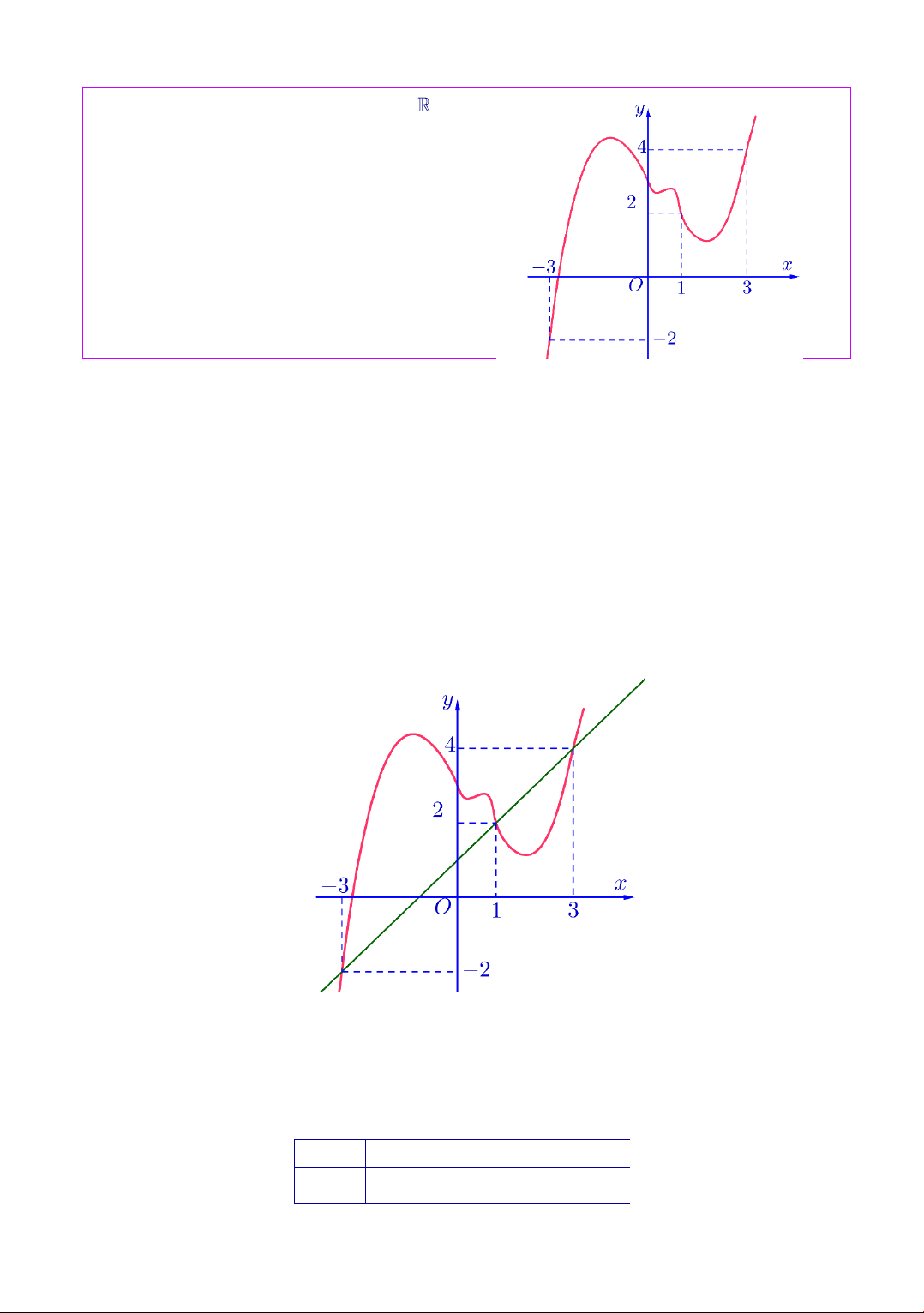
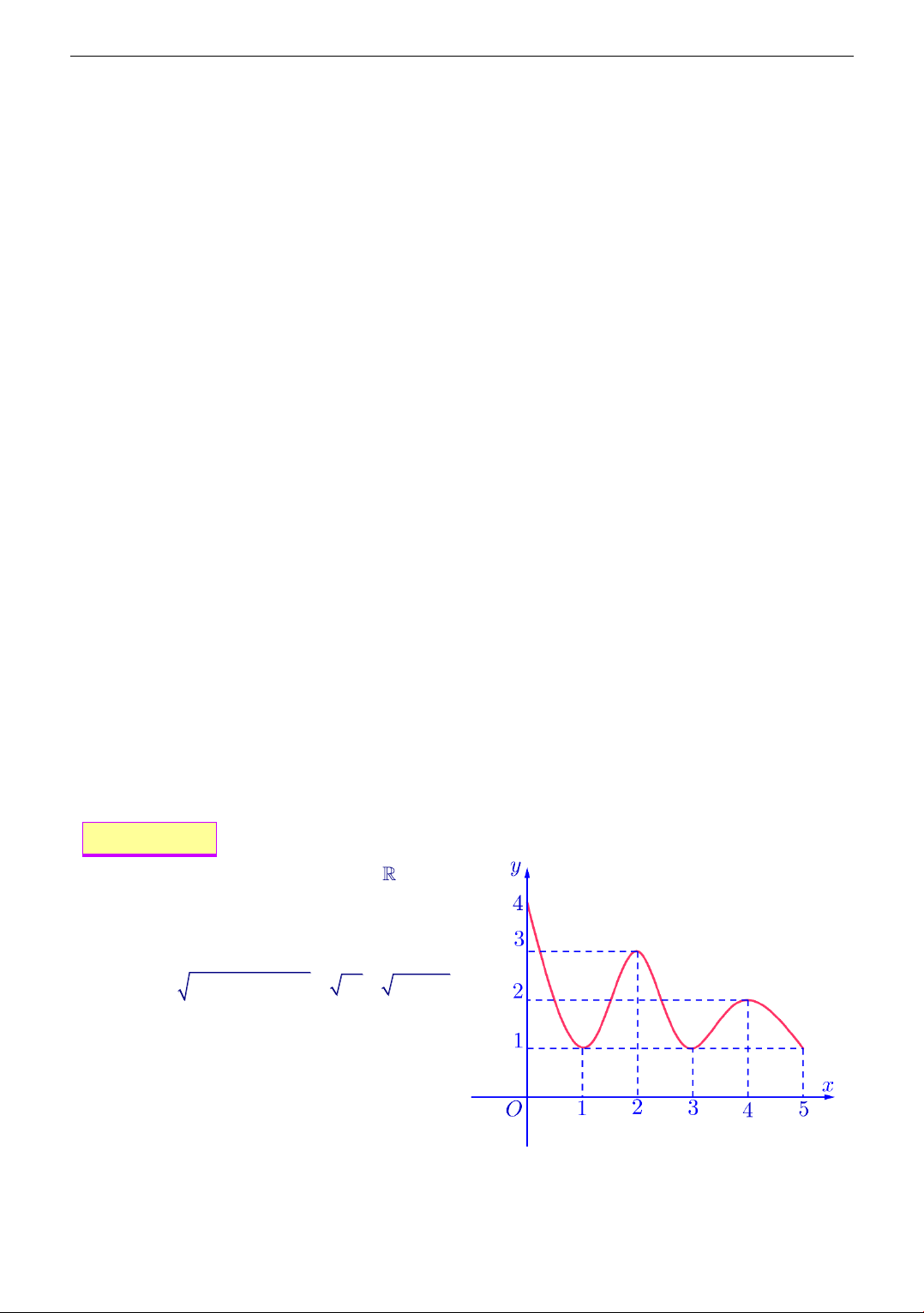
Cho hàm số f (x) liên tục trên có đồ thị
y = f (x) như hình bên. Đặt
g(x) = f f
 (x) xác định số nghiệm của
phương trình g(x) = 0 A. 8 . B. 7 . C. 6 . D. 5 . Lời giải Chọn đáp án A Ta có 
g(x) =  f
 ( f (x)) = f (x) f  f   (x) x = 1 −   f (x) = =  g(x) 0 x 2 = 0      f  f   (x) = 0 f (x) = 1 (1)    f  (x) = 2 (2)
Phương trình (1) có 3 nghiệm vì đường thẳng y = 1 cắt đồ thị hàm số f (x) tại 3 điểm phân biệt.
Phương trình (2) có 3 nghiệm vì đường thẳng y = 2 cắt đồ thị hàm số f (x) tại 3 điểm phân biệt. 4
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Suy ra g(x) = 0 có 8 nghiệm. Ví dụ 2.
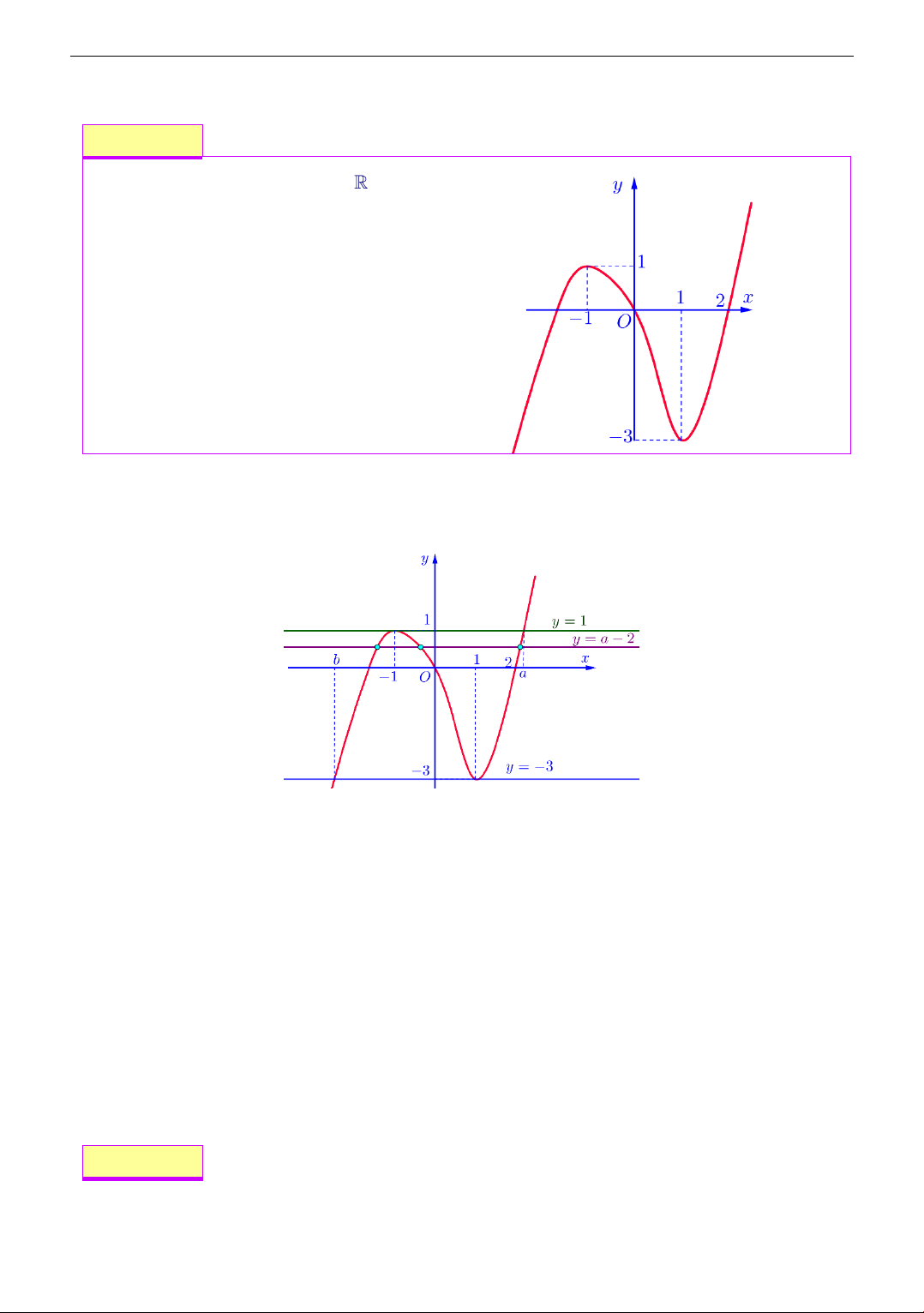
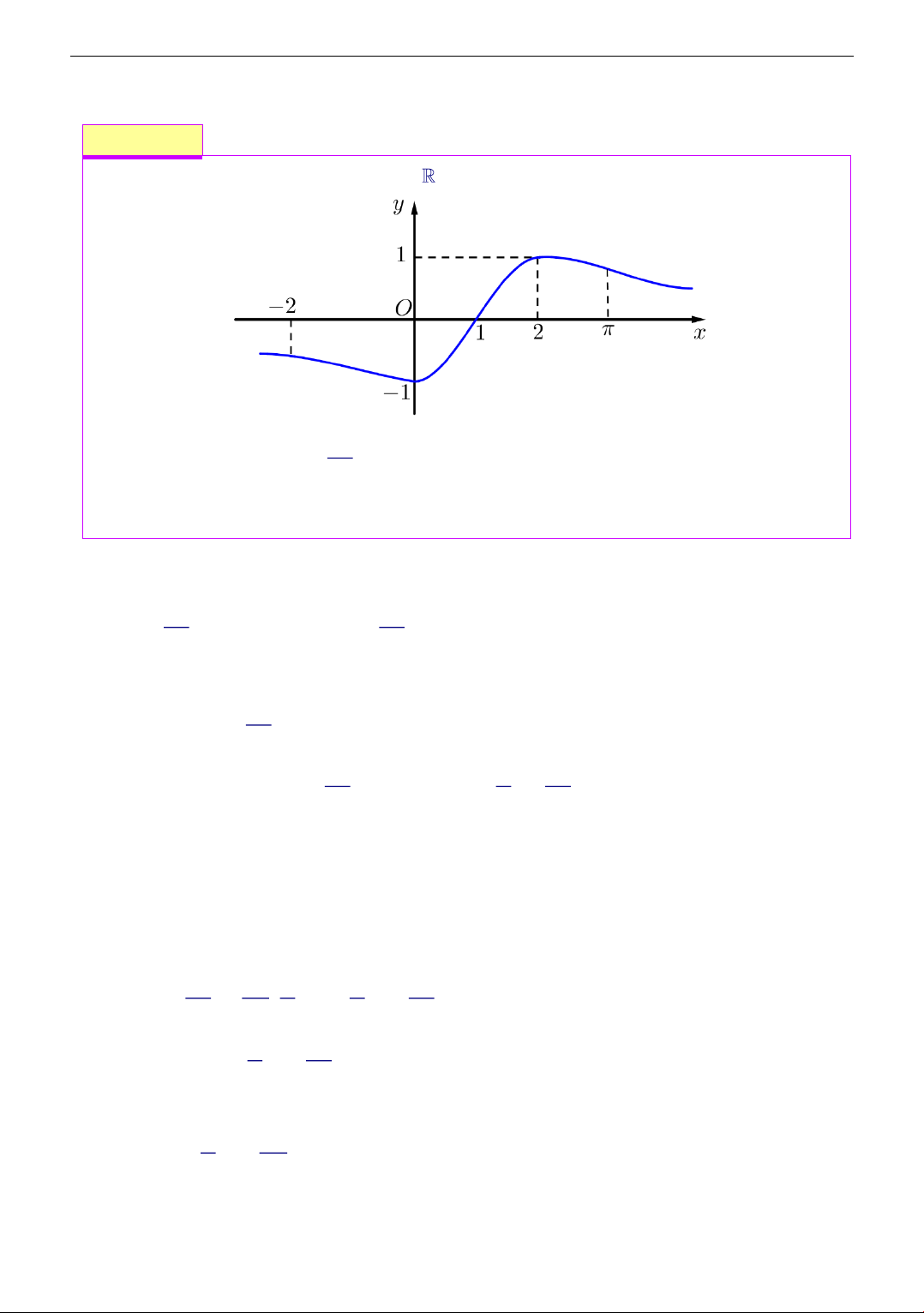
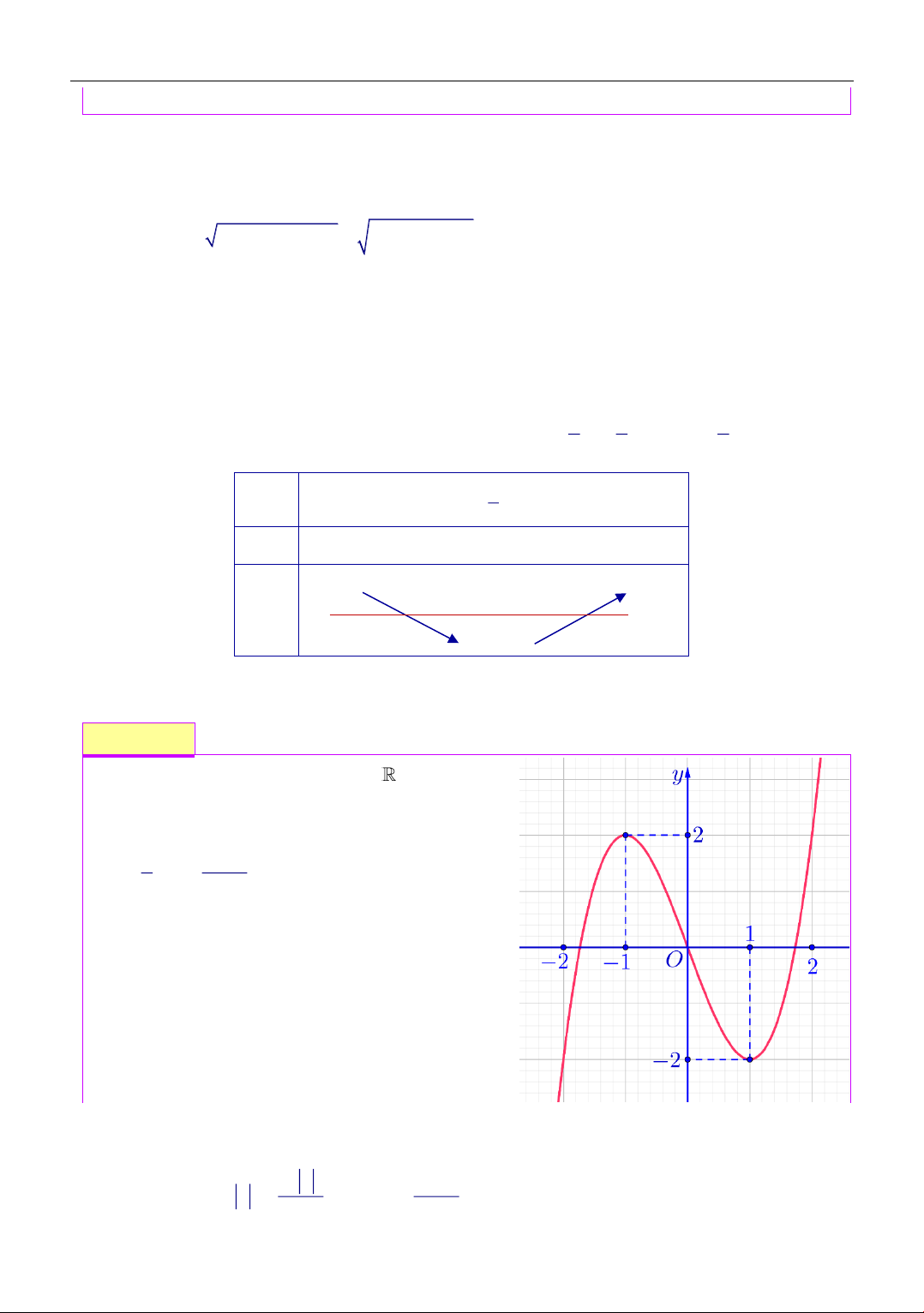
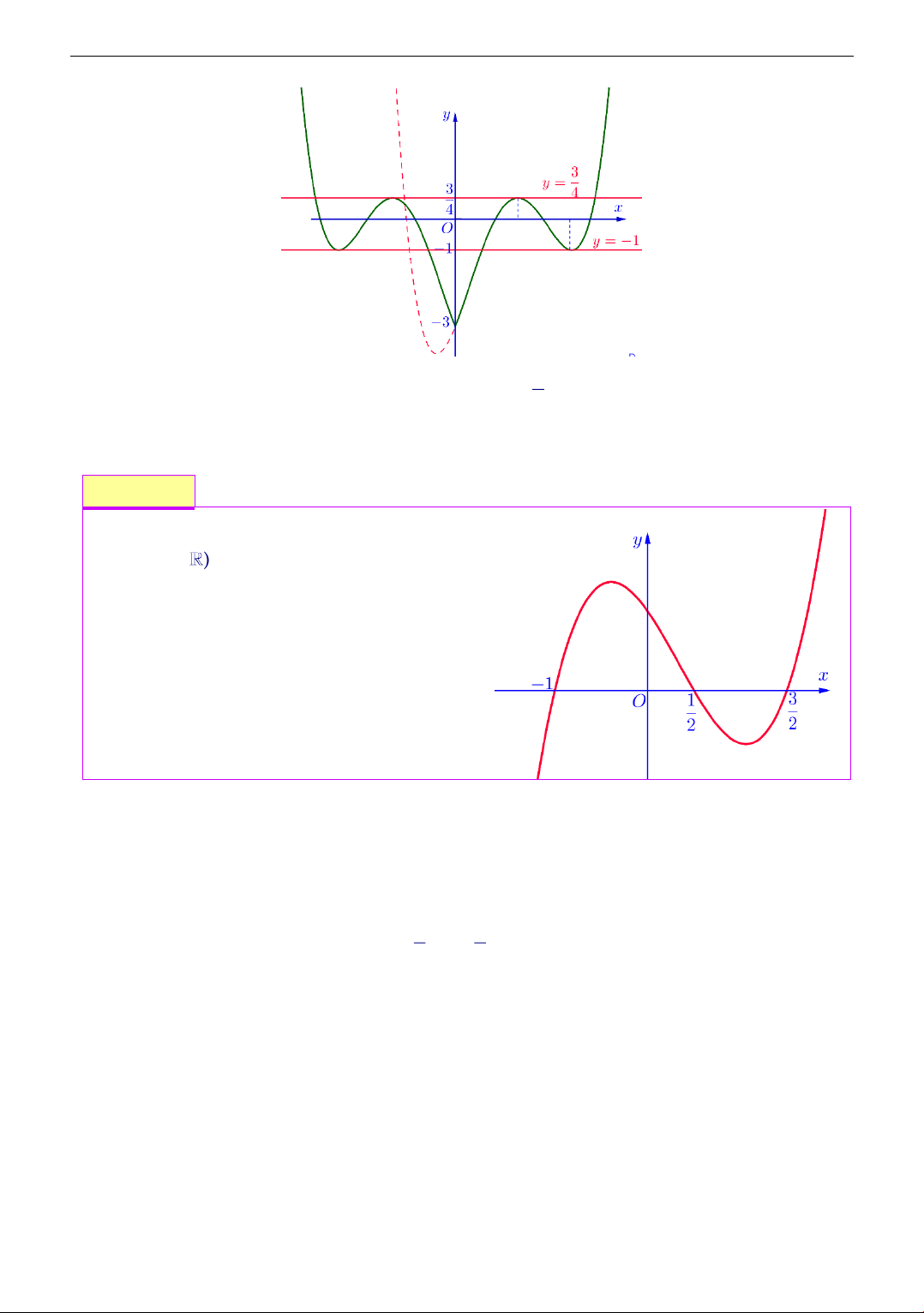
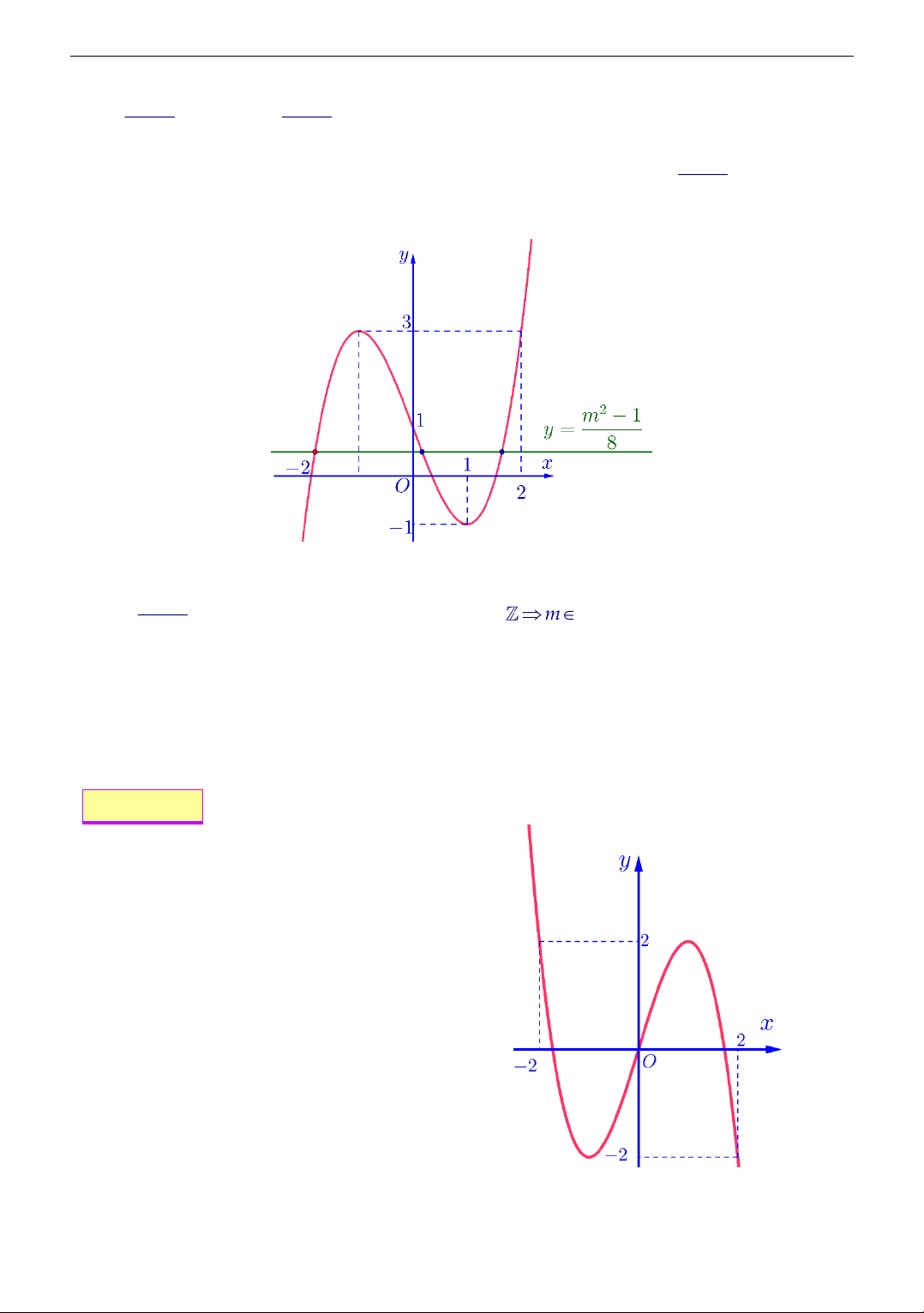
Cho hàm số f (x) liên tục trên có đồ
thị y = f (x) như hình bên. Số nghiệm thực của phương trình (2+ ( x f f e )) = 1 là A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn đáp án B Ta có Theo đồ thị (  x f e f + f ( x e ) 2 + ( ) = 1 − 2 =1   2 + x
f (e ) = a ,(2  a  3)  = + f ( e x
e ) = −  f ( x e ) x 1 2 1 = 3 −    x = xe = b  −  (loaïi) 0 1 xe = c  1 − (loaïi)  2 + f ( x
e ) = a f ( x
e ) = a − 2,(0  a − 2  1) x
 e = d  0 (loaïi)  x = lnt x e = t   2 
Vậy phương trình đã cho có 2 nghiệm phân biệt Ví dụ 3. 5
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
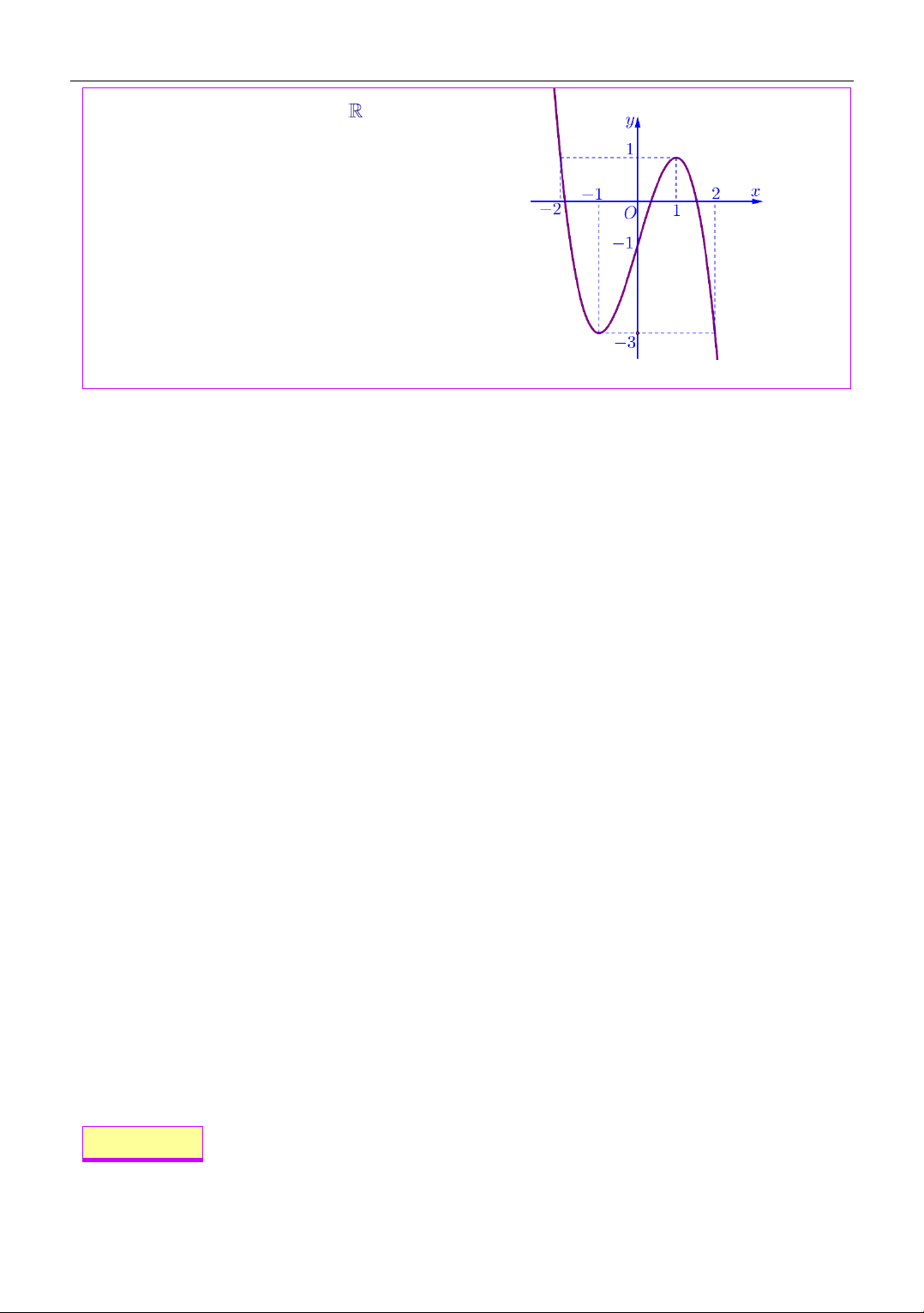
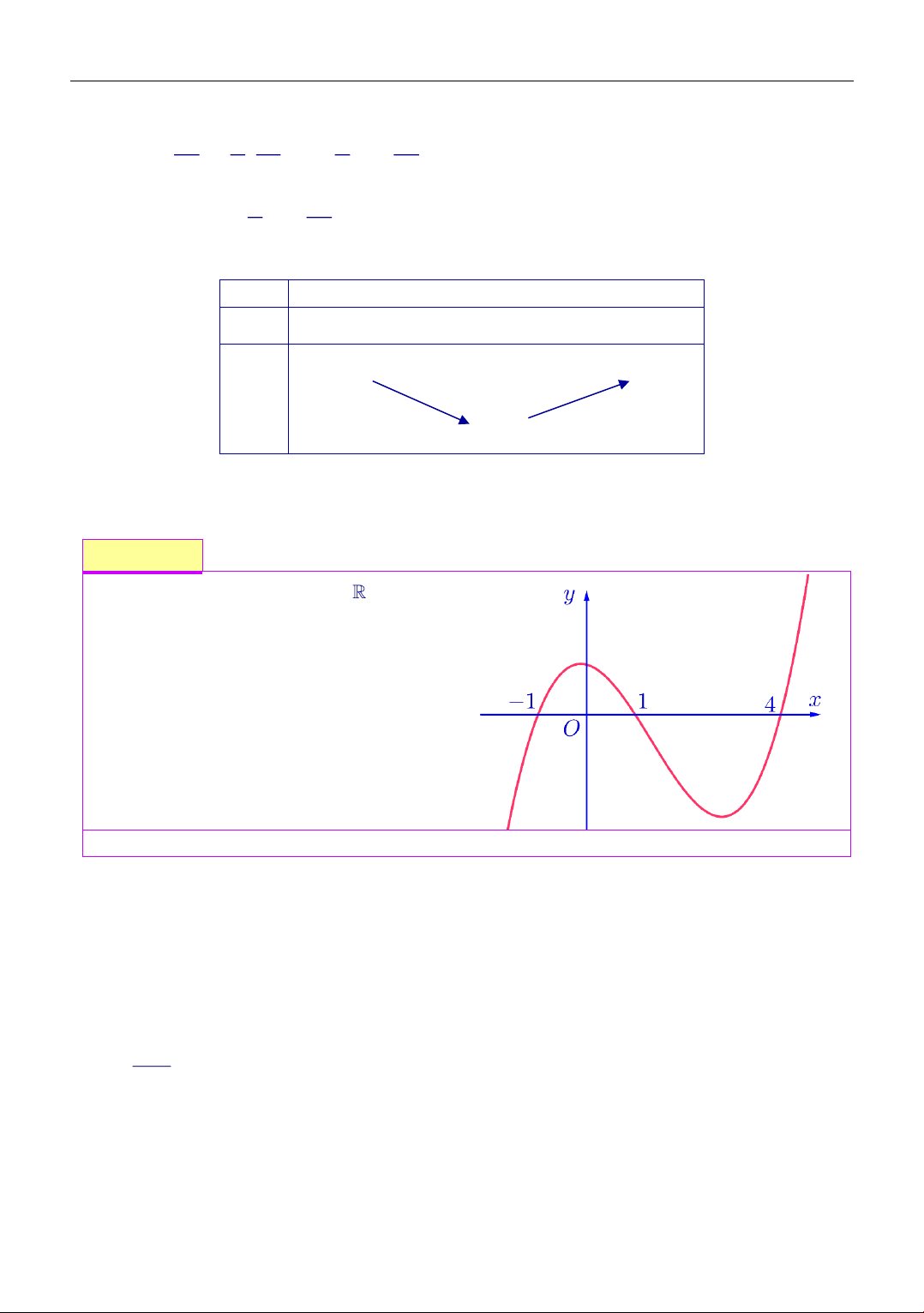
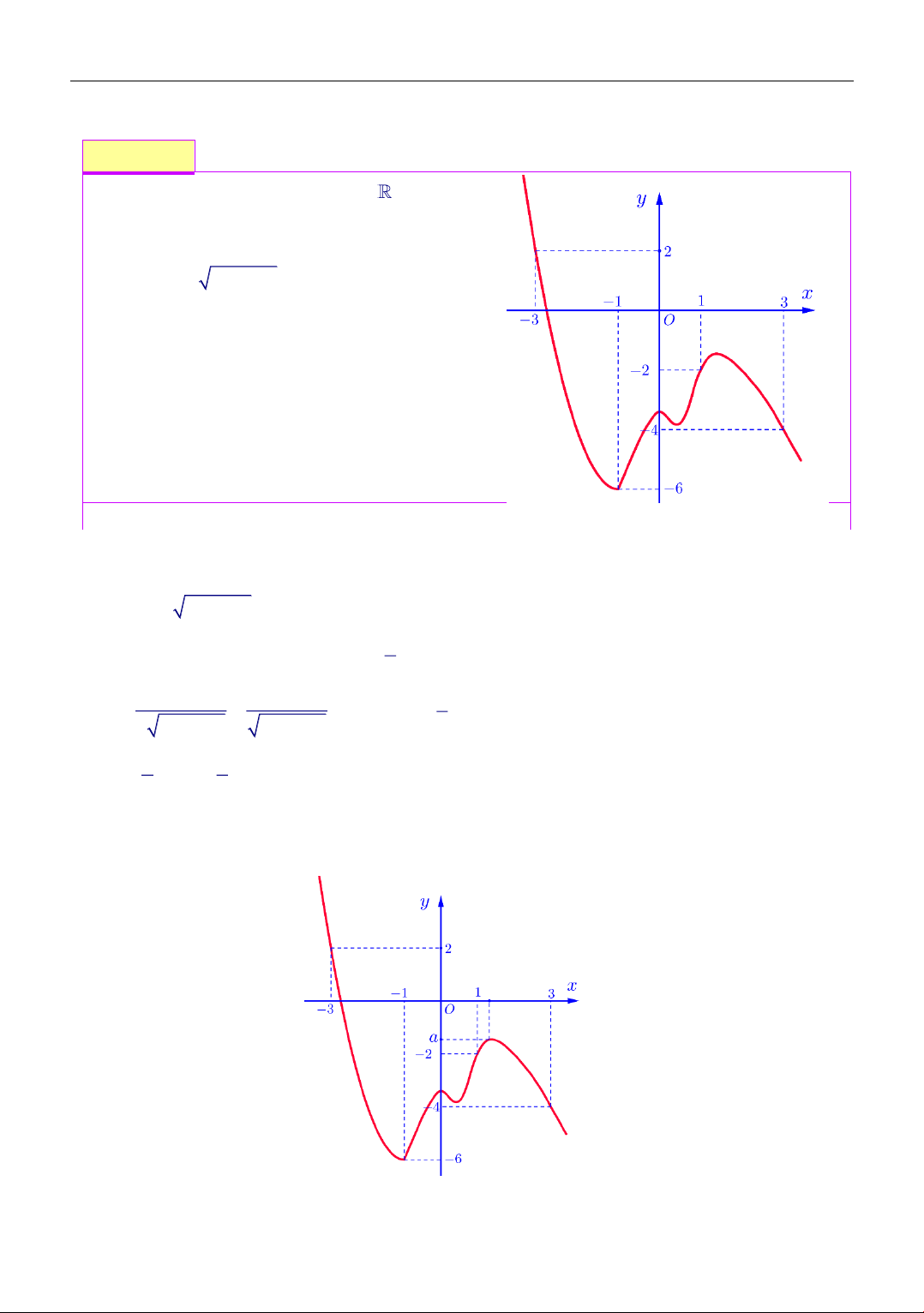
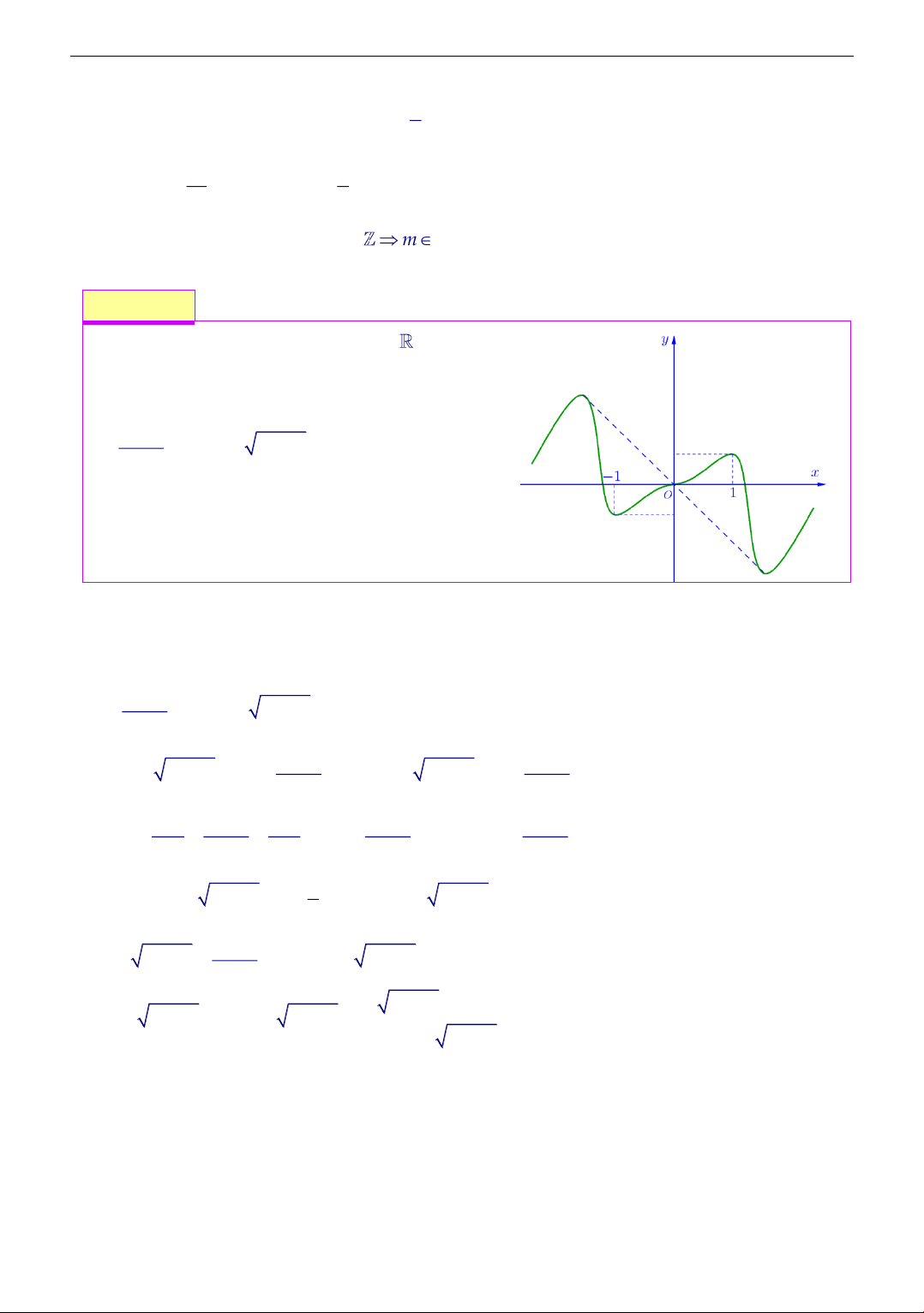
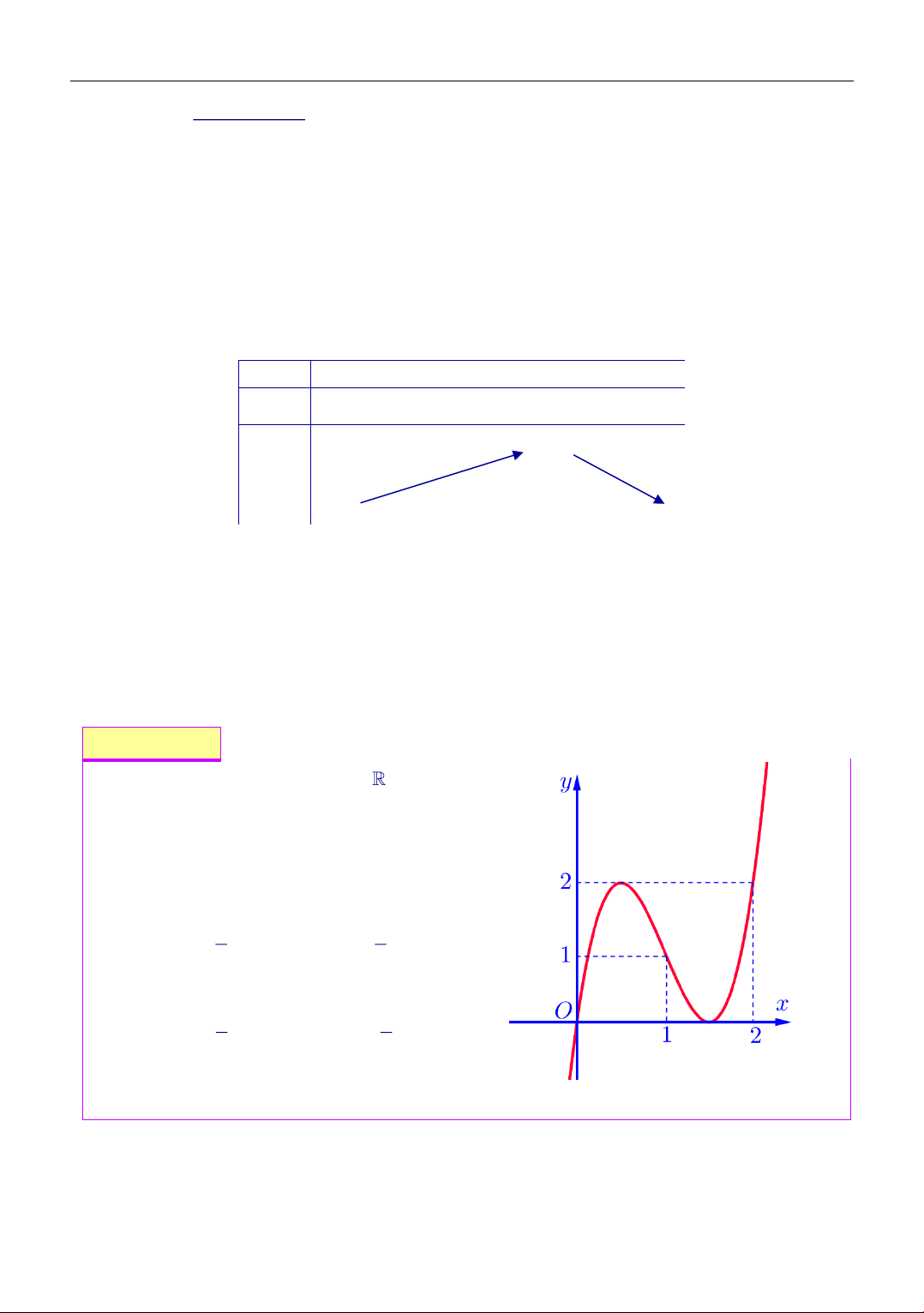
Cho hàm số f (x) liên tục trên có đồ thị
y = f (x) như hình bên. Phương trình
f (2 − f (x)) = 0 có bao tất cả bao nhiêu nghiệm phân biệt. A. 4 . B. 5 . C. 6 . D. 7 .
Thi Thử THPT Quốc Gia Trường Yên Lạc Vĩnh Phúc Lần 4 Lời giải Chọn đáp án B Theo đồ thị x = a ( 2 −  a  1 − )
2 − f (x) = a
f (x) = 2 − a (1)   
f (x) = 0  x = b (0  b  1) 
f (2 − f (x)) = 0  2 − f (x) = b f (x) = 2 − b (2)  
x = c (1  c  2) 
2 − f(x) = c
f(x) = 2 − c (3)   Nghiệm của phương trình ( ) 1 ; (2); (3) là giao điểm của đường thẳng
y = 2 − a; y = 2 − b; y = 2 − c với đồ thị hàm số f (x) . • a( 2 − ; 1
− )  2 − a(3;4) suy ra phương trình (1) có đúng 1 nghiệm phân biệt. •
b(0;1)  2 − b(1; 2) suy ra phương trình (2) có đúng 1 nghiệm phân biệt. •
c (1; 2)  2 − b(0;1) suy ra nên phương trình (3) có 3 nghiệm phân biệt.
Kết luận: Có tất cả 5 nghiệm phân biêt.
DẠNG 2: Cho bảng biến thiên f (x) tìm tham số m để bất phương trình g(x,m)  0 có nghiệm thuộc D . Ví dụ 1. 6
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
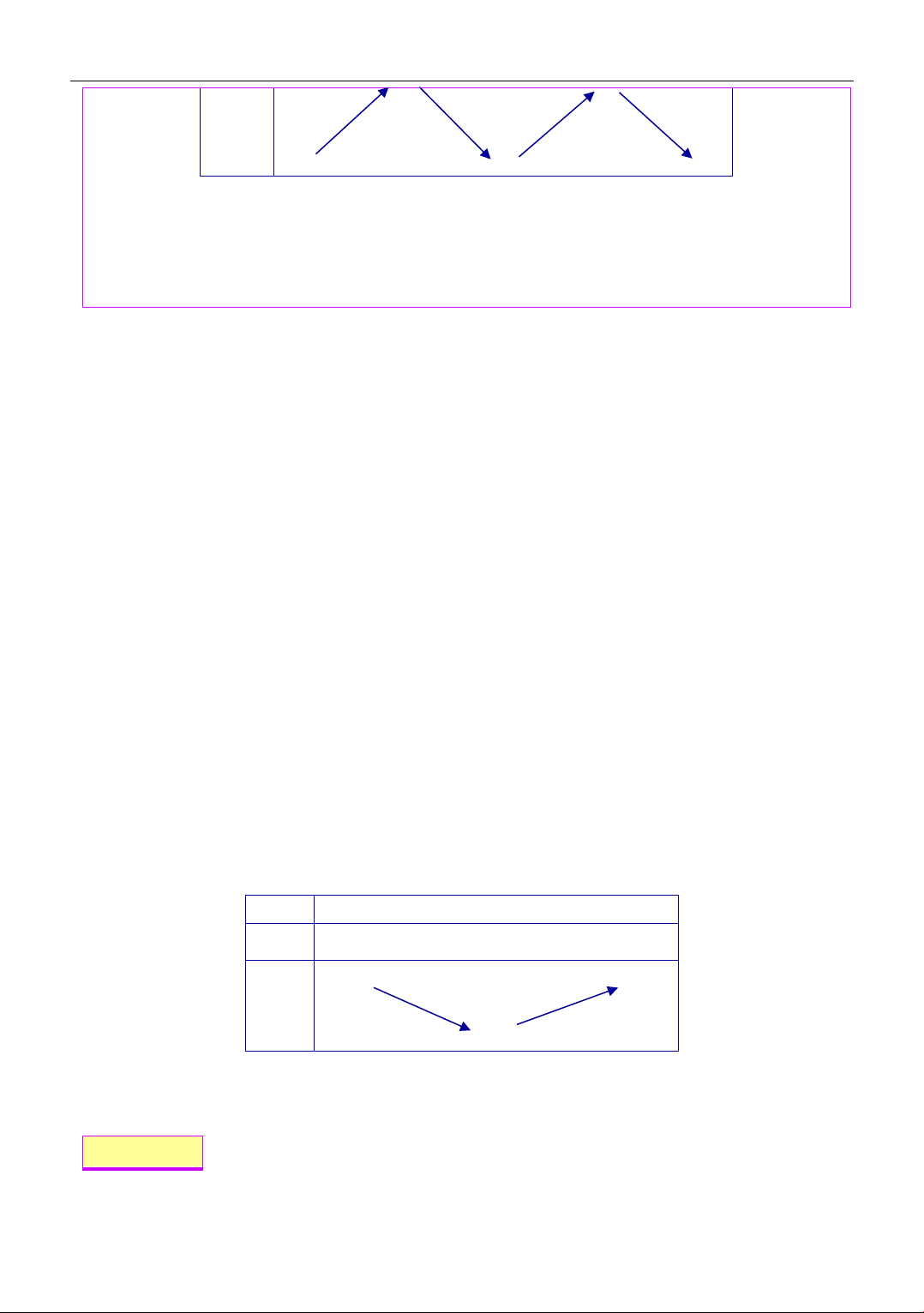
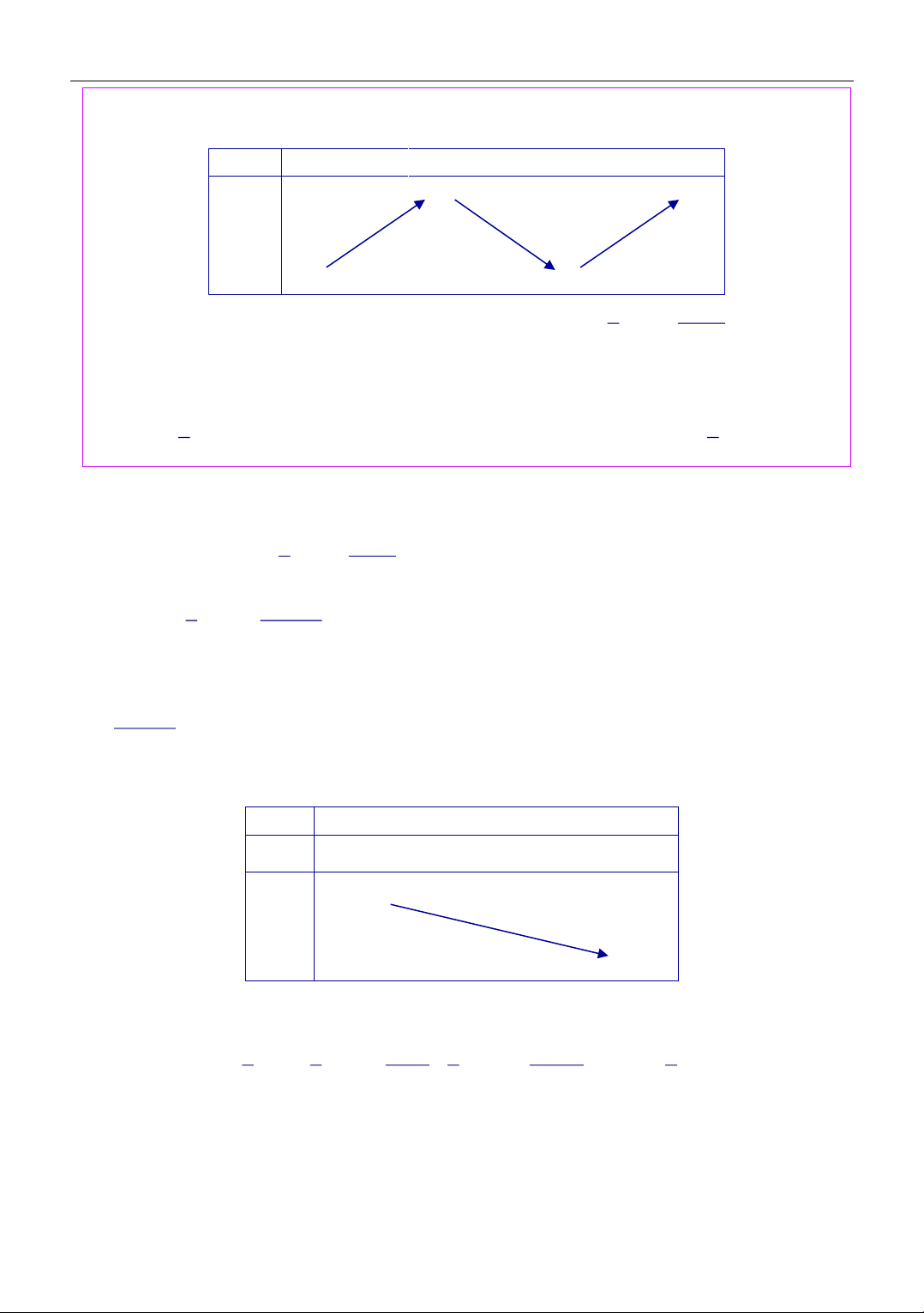
Cho hàm số y = f (x) có đạo hàm trên . Bảng biến thiên của hàm số y = f (x) như hình dưới x 1 − 1 3 3 f (x) 1 2 1
Tìm m để bất phương trình 2
m + x f (x) 3
+ x nghiệm đúng với mọi x(0;3) . 3 2
A. m f (0) .
B. m f (0) .
C. m f (3) . D. m f (1) − . 3 Lời giải
Chọn đáp án A 1 1 Ta có 2
m + x f (x) 3
+ x m f (x) 3 2 + x − x . 3 3 1
Đặt g(x) = f (x) 3 2 + x − x . 3
Ta có g(x) = f (x) 2
+ x − x = f (x) −( 2 2 −x + 2x).
g(x) =  f (x) 2 0 = −x + 2x . 2
Theo bảng biến thiên f (x)  1 x  (0;3) và 2
−x + 2x = 1− (x − ) 1  1, x  (0;3) nên
g(x)  0, x  (0;3) .
Từ đó ta có bảng biến thiên của g(x) : x 0 3 g(x) + g (3) g (x) g (0) 1
Bất phương trình m f (x) 3 2
+ x − x nghiệm đúng với mọi x(0;3) 3
m g(0)  m f (0) . Ví dụ 2.
Cho hàm số y = f (x) có bảng biến thiên như sau: x − 1 − 0 2 + f ( x) + 0 − 0 + 0 − 4 3 7
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung f (x) − 2 − Bất phương trình ( 2 x + )
1 f ( x)  m có nghiệm trên khoảng ( 1
− ; 2) khi và chỉ khi
A. m 10 .
B. m 15 . C. m  27 . D. m 15 .
Đề thi Duyên Hải Bắc Bộ năm 2019 Lời giải
Chọn đáp án B
Yêu cầu bài toán  m  max g ( x) −1; 2
Với g ( x) = ( 2 x + ) 1 f ( x) .
Ta có: g( x) = x f ( x) + ( 2 2 x + ) 1 f ( x) . x  0 2   f ( x)  4 Với x ( 1
− ; 0) thì
g(x)  0,x( 1 − ; 0) . f   ( x)  0  2 x +1  0
Tại x = 0 , g(0) = 0 . x  0 2   f ( x)  3
Với x (0; 2) thì
g(x)  0,x(0;2) . f   ( x)  0  2 x +1  0
Ta có bảng biến thiên của hàm số g ( x) = ( 2 x + )
1 f ( x) trên khoảng ( 1 − ;2) như sau x 1 − 0 2 g(x) − 0 + 8 3 15 g (x) 2
Suy ra max g ( x) = 15 .  1 − ; 2
Kết luận: m 15 . Ví dụ 3. 8
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Cho hàm số y = f (x) có bảng biến thiên như sau: x 0 1 + 4 f (x) − −
Tìm m để bất phương trình m + 2sin x f (x) nghiệm đúng với mọi x(0; +) .
A. m f (0) .
B. m f ( )
1 − 2sin1 . C. m f (0) .
D. m f ( ) 1 − 2sin1 . Lời giải
Chọn đáp án C
BPT m + 2sin x f (x)  m f (x) − 2sin x .
Yêu cầu bài toán  m  min g(x); g(x) = f (x) − 2sin x
Ta có g(x) = f (x) − 2cosx .
g(x) = 0  f (x) = 2cos x .
Mà f (x)  2, x
 (0;+) và 2cosx  2, x
 (0;+)nên g(x)  0, x  (0;+) .  = g(x) f '(x) 2 = 0  
x = 0 . Với g(0) = f (0) − 2sin0 = f (0) 2 cos x =  2
Từ đó ta có bảng biến thiên của g(x) : x 0 + g(x) + + g (x) f (0)
Bất phương trình m f (0) nghiệm đúng với mọi x(0; +) Ví dụ 4. 9
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Cho hàm số y = f (x) có f ( 2
− ) = m +1, f ( )
1 = m − 2 . Hàm số y = f (x) có bảng biến thiên x 0 0 2 + 0 + f (x) − 2 − 1 2x + 1
Tập hợp tất cả các giá trị của tham số m để bất phương trình f (x) −  m có 2 x + 3
nghiệm trên x   2 − ;1   là  7   7  A. −5; −   . B. ( ;0 − ) . C. ( 2 − ;7) . D. − ; +    .  2   2  Lời giải
Chọn đáp án D 1 2x + 1
Yêu cầu bài toán g(x) = f (x) −  m, x    2 − ; 1  min g   (x) m 2 x + 3  2 − ; 1   1 5 Ta có g(x) = f (x) − . 2 (x + 3)2
Dựa vào bảng biến thiên của hàm số y = f (x) ta có f (x)  0, x  ( 2; − )1 5 và −  0, x   2
− ;1 . Do đó g(x)  0, x  ( 2; − )1. 2 ( ) (x + 3)
Bảng biến thiên của hàm số y = h(x) trên khoảng  2 − ;1   . x 2 − 1 g(x) + g( 2 − ) g (x) g (1)
 min g(x) = g(1) −2; 1   1 3 m − 2m − 7 7 Suy ra g( ) 1  m f ( ) 1 −  2 3 m  −  m
m  −  m . 2 4 2 4 4 2 10
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung Ví dụ 4.
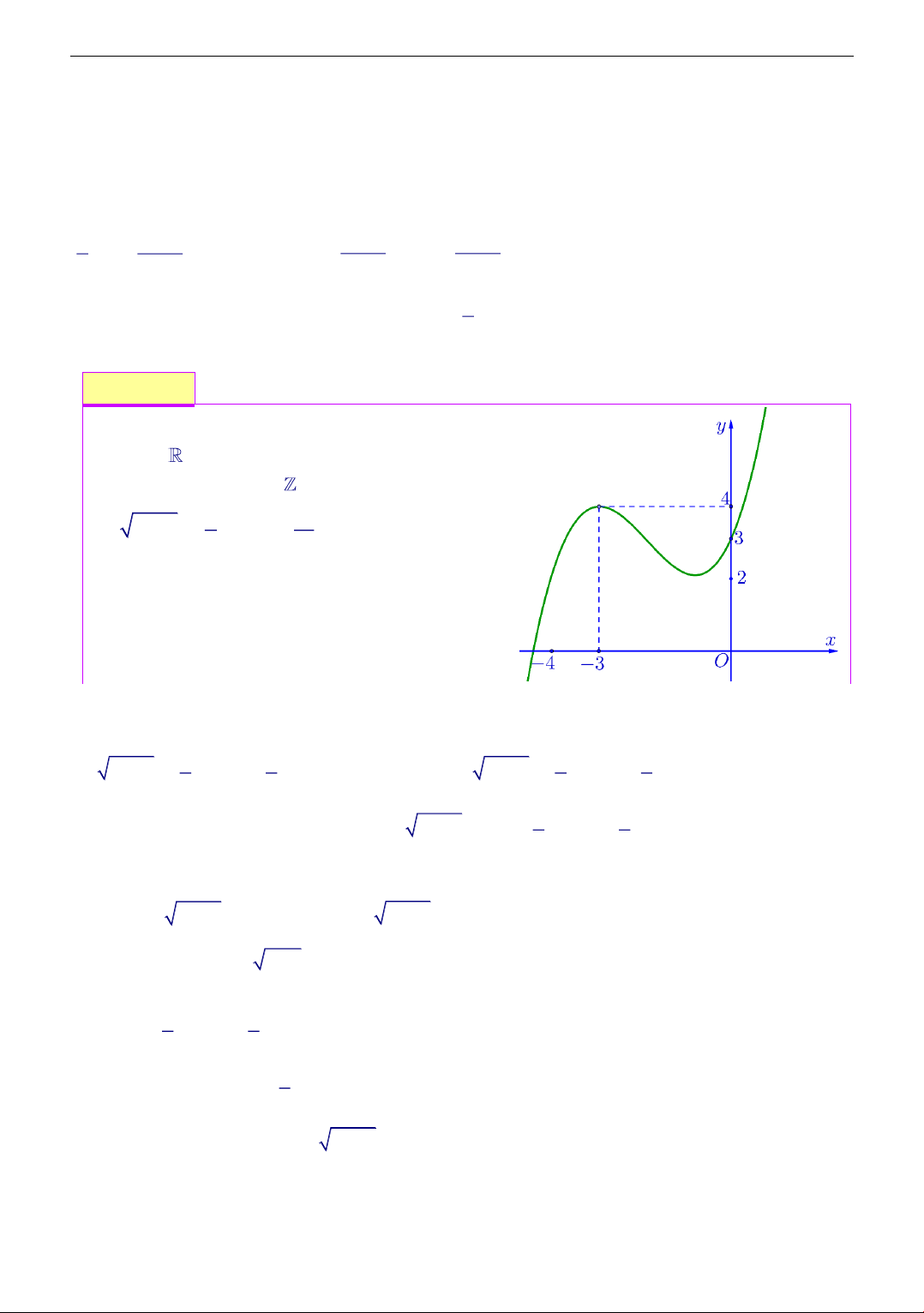
Cho hàm số y = f (x) liên tục và có đồ
thị như hình vẽ. Tập các giá trị thực của
tham số m để phương trình f ( 2
4 − x ) = m có nghiệm thuộc nữa khoảng − 2 ; 3  ) là A.  1 − ; 3 −    . B. 1; f ( 2)   .
C. ( 1 ; f ( 2) − −   . . D. ( 1;3
Đề thi thử THPT Quốc Gia Phan Bội Châu Nghệ An Lần 2 năm 2019 Lời giải
Chọn đáp án D (  2 4 − x ) −x Đặt 2
t = 4 − x , t = =
, t = 0  x = 0 2 2 2 4 − x 4 − x Bảng biến thiên x − 2 0 3 t(x) 2 t 2 1
Suy ra t t (1; 2 .
Phương trình tương đương với f (t) = m ( )
1 có nghiệm t (1; 2
Nghiệm của phương trình (1) là giao của đường thẳng y = m và đồ thị hàm số y = f (x) với x (1; 2 . Theo đồ thị ta suy ra 1
−  m  3 . Chọn D. 11
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung Ví dụ 5.
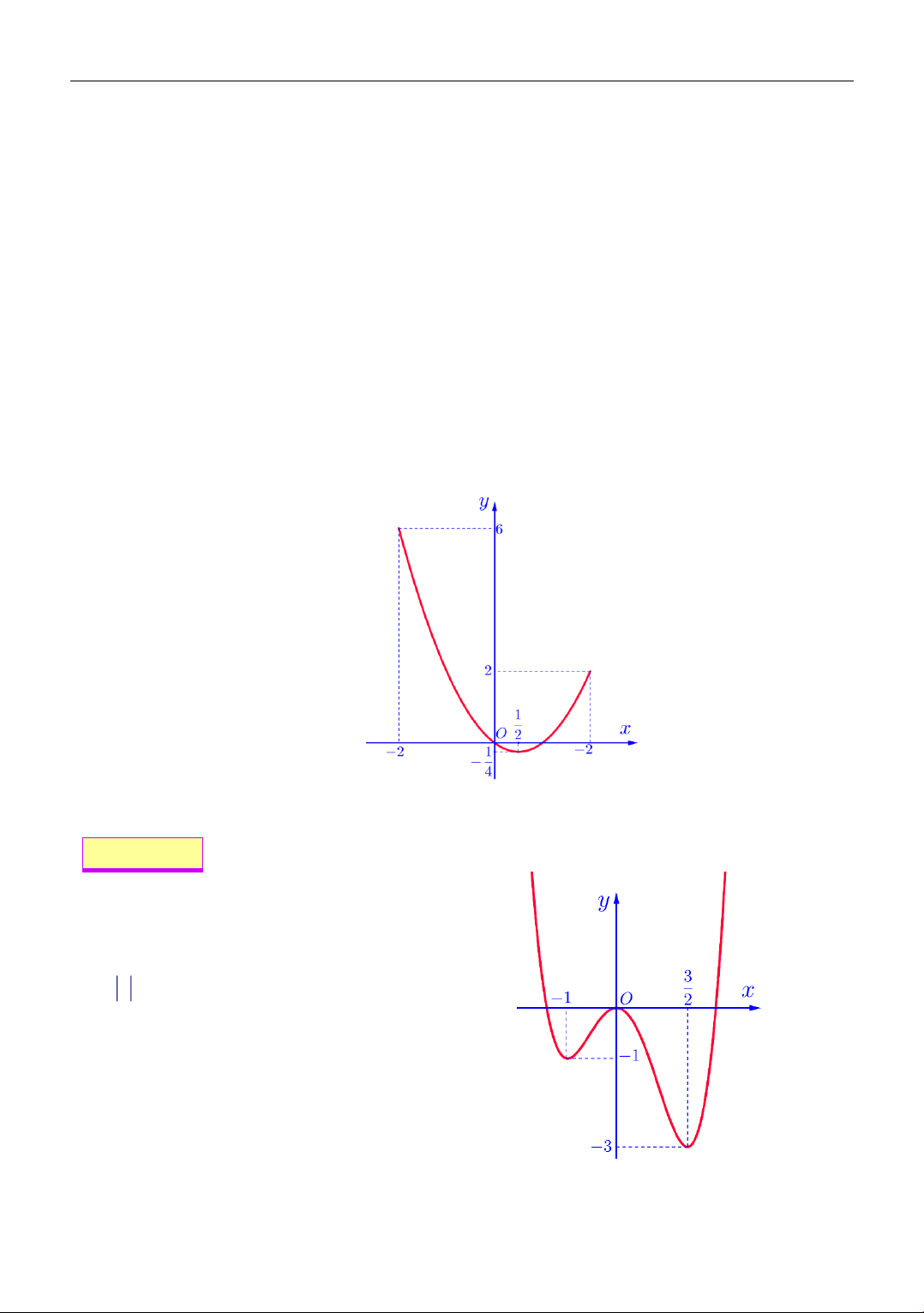
Cho hàm số y = f (x) liên tục và có đồ
thị như hình vẽ. Số giá trị nguyên dương
của m để phương trình f ( 2
x − 4x + 5) + 1 = m có nghiệm là A. 0 . B. 3 . C. 4 . D. Vô số.
8 Trường chuyên đồng bằng Sông Hồng Lần 1 năm 2019 Lời giải
Chọn đáp án B f ( 2
x − x + ) + = m f ( 2 4 5 1
x − 4x + 5) = m −1  f (t) = m −1 2 Với 2
t = x − 4x + 5 = (x − 2) + 1  1 t  1  ; + ) ñoàthò ⎯⎯⎯
→ f (t)2; +    )
Nên để phương trình có nghiệm  m − 1 2; +  
) m−1 2  m 3 Và m +   m1; 2;  3 . Chọn đáp án B. 12
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
 DẠNG 3: Cho hàm số y = f (x) có đồ thị f (x) xác định tham số m để g(x,m)  0 Ví dụ 1.
Cho hàm số y = f (x) có đạo hàm trên , có đồ thị f (x) như hình vẽ. x
Bất phương trình f (x)  sin
+ m nghiệm đúng với mọi x 1 − ;  3 khi và chỉ khi 2
A. m f (0) .
B. m f (1) −1. C. m f ( 1 − ) +1.
D. m f (2) . Lời giải
Chọn đáp án B xx f (x)  sin
+ m m f (x) − sin 2 2
Để bất phương trình nghiệm đúng với mọi x  1 − ;  3 thì   x
m  min  f ( x) − sin   −1;  3  2     Xét hàm số ( ) = ( ) − x g x f x sin , ( ) = ( ) − x g x f x cos 2 2 2
Nhận thấy f ( x) đổi dấu khi qua x =1gợi ý cho ta xét dấu của hàm g( x) trên 2 khoảng ( 1 − ; ) 1 và (1;3) • Với x ( 1 − ; ) 1 x( 1 − ; )
1  f ( x)  0 ( đồ thị hàm số f ( x) nằm dưới trục hoành ) x (  x   −      x   −1; ) 1   ;  − cos  0,x      (−1; ) 1 2  2 2  2  2     x
Vậy g( x) = f ( x) − cos  0,x    (−1; ) 1 2  2  • Với x = 1
g ( ) = f ( )   .1  1 1 − cos = 0   2  2  • Với x (1;3) 13
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
x(1;3)  f (x)  0(đồ thị hàm số f (x) nằm trên trục hoành ) x
( )  x  3     x   1;3   ;  − cos  0,x      (1;3) 2  2 2  2  2     x
Vậy g( x) = f ( x) − cos  0,x    (1;3) 2  2  Ta có bảng biến thiên x 1 − 1 3 g(x) − 0 + f (− ) 1 + 1 3 f (3) + 1 g (x) f (1) − 1
Suy ra Min g ( x) = f ( ) 1 −1  1 − ;  3
Vậy m f ( ) 1 −1. Ví dụ 2.
Cho hàm số f (x) liên tục trên và có đồ
thị f (x) như hình vẽ. Bất phương trình
log  f x + m + 2 + f x  4 − m đúng 5  ( )  ( ) với mọi x( 1 − ; 4) khi và chỉ khi
A. m  4 − f (−1) .
B. m  3 − f (1) .
C. m  4 - f (-1) .
D. m  3 − f (4) .
Thi Thử THPT Quốc Gia Chuyên Hạ Long năm tháng 5 năm 2019 Lời giải
Chọn đáp án D log  f
 (x) + m + 2 + f
(x)  4−m ( )1 log  f (x)+m+2+f   (x) 5
+ m + 2  log + 5 2 5 5  5 ( )
Xét hàm số đặc trưng cho 2 vế của BPT (2) ( ) = logt g t
+ t với t  0 5 g(t) 1 =
+ 1  0 suy ra g(t) đồng biến với t  0 5lnt
 (2)  f (x) + m + 2  5  m  3 − f (x)
Yêu cầu bài toán  m  max(3 − f (x)) = maxh(x) (2) x  ( 1
− ; 4) với h(x) = 3 − f (x) khi đó h(x)  f (x) max min 14
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Từ đồ thị suy ra bảng biến thiên x 1 − 1 4 f (x) 0 + 0 − 0 f ( ) 1 f (− ) 1 f (4)  − f (x) f ( 1) =  min  f  (4) So sánh f (− ) 1 và f (4) 1 S S f   (x) 4
dx  − f x dx f 1 − f −1  −  f 4 − f 1   f −1  f 4  1 2 ( ) ( ) ( )  ( ) ( ) ( ) ( ) 1 − 1 Suy ra f (x)
= f (4) và(2)  m  3 − f (4) min Ví dụ 3.
Cho hàm số y = f (x) có đạo hàm liên tục trên
có đồ thị khi và chỉ khi
A. m f ( ) 1 − 1.
B. m f ( ) 1 + 1 .
C. m f ( ) 1 − 1.
D. m f ( ) 1 − 1. Lời giải
Chọn đáp án D
Ta có ( )  3x − 2 +  ( ) − 3x f x x m f x + 2x  . m 15
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Đặt ( ) = ( ) − 3x g x f x + 2 . x Khi đó (  ) = ( ) − 3x g x f x ln 3 + 2. (
 ) = 0  ( ) = 3x g x f x ln 3 − 2. Đặt ( ) 3x h x = ln 3 − 2. Khi đó x 2 h (  )
x = 3 ln 3  0, x  (− ;  1.  Bảng biến thiên x − 1 h(x) + + − 3ln 3 − 2 h(x) 2 −  ( h x)  2 − , x  (−; 1.  (1)
Theo đồi thị y = f (  )
x , ta thấy f (  ) x  3 − , x  (− ;  1. (2) 
Từ (1) và (2), ta được f (  x)  ( h x), x  (− ;  1.  Nên g (  )
x = f (x) − ( h ) x  0, x  (− ;  1 ,=suy ra min ( g ) x = ( g 1) = f ( ) 1 − 1. (−; 1 Do đó ( )  3x f x
− 2x + m có nghiệm trên (−; 1 khi và chỉ khi m  min (
g x)  m f ( ) 1 − 1. (−; 1 Ví dụ 4.
Cho hàm số y = f (x) có đạo hàm liên tục trên
và đồ thị như hình vẽ. Tổng tất cả
các giá trị nguyên của tham số m để bất phương trình f (x) + ( 2
− f (x)) f(x)  ( 2 9.6 4 .9
−m + 5m) f(x) .4 đúng với x   là
A. 10 . B. 4 . C. 5 . D. 9 . Lời giải
Chọn đáp án A f (x) + ( 2
− f (x)) f(x)  ( 2 9.6 4 .9
−m + 5m) f(x) .4 (1)
Đặt t = f (x)(−; 2
−  ( theo đồ thị)  (1) : t + ( 2 − ) t  ( 2 9.6 4 .9 − + 5 ).4t t m m t t  3     9. + (4 − t ) 2 2 3 2  −m +     5m (2)  2   2  16
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung t 2t t t 3 3 3  3         
Đặt: g (t) = 9. + ( 2 4 − t ). = .9 + ( 2 4 −       t ). 
  , t (−; 2 −  .  2   2   2    2     t  3 
Xét hàm số: h(t) = 9 + ( 2
4 − t ).  với t (−; 2 −   2  t t     t  3   3  h(t) 3 = − t + ( 2 −   t ) 3 3 2 . 4 .  .ln = . 2 − t +  ( 2 4 −   t ).ln  .  2   2  2  2   2  2  2 3   3  1 − + 1+ 4ln  1 − − 1+ 4ln   2   2 
h(t) = 0  t =  2 − (loại) hoặc t =  2 − (tm) 3 3 ln ln 2 2 Ta có BBT: 2  3  1 − − 1+ 4ln  x −  2  2 − 3 ln 2 h(t) 0 − 0 + 0 9 9 h(t) Từ BBT  ( h t)  9 t
 (−;− 2 (3). t  3  4 Vì t (−; 2 −   0     (4).  2  9 t t 3  3     
Từ (3) và (4) suy ra g (t) = .9 + ( 2 4 − t ).       4 t  (−;− 2  2    2    
 max g(t) = 4. (Dấu "=" xảy ra khi và chỉ khi t = 2 − ). (−; 2 − 
Bất phương trình (1) đúng với x
   Bất phương trình (2) đúng với t  (−;− 2 2
 −m + 5m  max g(t) 2
 −m + 5m  4 2
m − 5m + 4  0  1  m  4 . (−; 2 − 
Do m suy ra m1;2; 3; 
4 . Vậy tổng các giá trị nguyên của m là: 1 + 2 + 3 + 4 = 10 . Ví dụ 5. 17
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
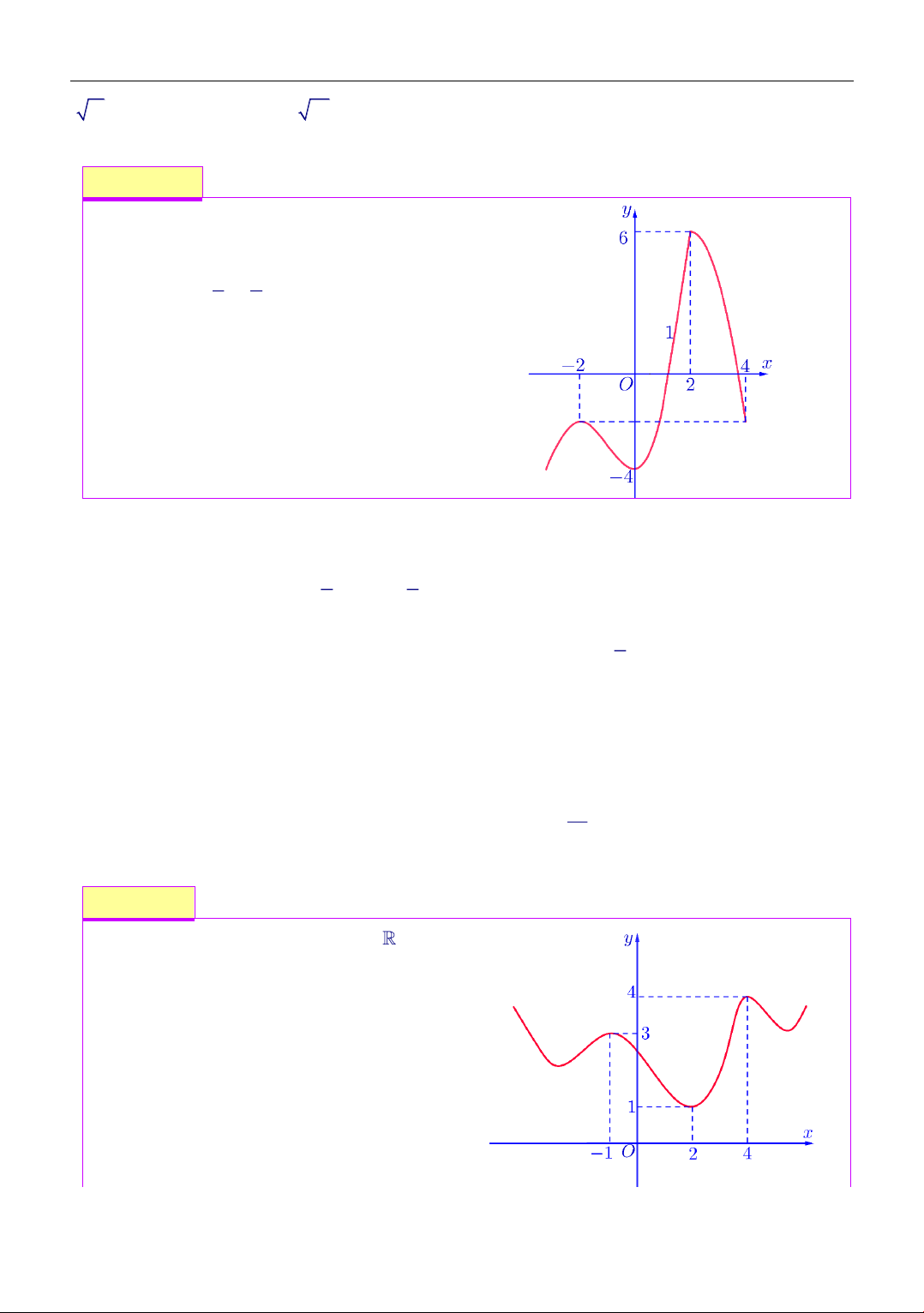
Cho hàm số y = f (x) liên tục trên đoạn  1 − ;9 
 và có đồ thị là đường cong như hình vẽ y
Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình f (x) 2 −  f
 (x) + f (x) f (x) −    ( 2 16.3 2 8 .4
m − 3m) f(x) .6
nghiệm đúng với mọi giá trị x thuộc đoạn  1 − ;9   ? A. 32 . B. 31 . C. 5 . D. 6 .
Đề thi thử THPT Quốc Gia Yên Khánh Ninh Bình Lần 4 năm 2019  Lời giải
Chọn đáp án D Từ đồ thị ta suy ra 4
−  f (x)  2 x   1 − ;9   .
Đặt t = f (x), t  4; − 2   .
ycbt  tìm m sao cho bất phương trình t 2 t −  + −     ( 2 16.3 2 8 .4 − 3 ).6t t t m m ( )1 đúng với t    4 − ;2   t (   1) 16 2 2 2 
− t + 2t − 8.  m −     3m với t    4 − ;2   (*). 2t  3  16 Ta có  4, t   −4;2 
 . Dấu bằng xảy ra khi t = 2 . 2t Mặt khác 2
t + 2t − 8  0 với t    4 − ;2   . t  2  Do đó ( 2 t + 2t − 8).  0, t    4 −   ; 2 
 . Dấu bằng xảy ra khi t = 2  t = 4 − .  3  t t 16  2  16  2  Như vậy 2
− t + 2t − 8.      4 t   4; 2 −    . Mà 2 2
− t + 2t − 8.  m −     3m với 2t  3  2t  3  t    4 − ;2   . Suy ra 2
m − 3m  4  1
−  m  4 . Như vậy có 6 giá trị nguyên của m thỏa mãn. 18
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung Ví dụ 6.
Cho hàm số y = f ( x) liên tục trên  1 − ; 
3 và có đồ thị như hình vẽ. Bất phương trình f ( )
x + x +1 + 7 − x m có nghiệm thuộc  1 − ;  3 khi và chỉ khi A. m  7 . B. m  7 . C. m  2 2 − 2 . D. m  2 2 + 2 .
Đề thi thử THPT Quốc Gia Yên Khánh A Ninh Bình Lần 4 năm 2019 Lời giải
Chọn đáp án A
Xét hàm số g ( x) = x +1 + 7 − x liên tục trên  1 − ;  3 ta có: g ( x) 1 1 ' = − , x  ( 1 − ;  3 2 x +1 2 7 − x
g '( x) = 0  x +1 = 7 − x x +1 = 7 − x x = 3 (nhận) g (− )
1 = 2, g (3) = 4  max g ( x) = maxg (− )
1 , g (3) = g (3) = 4. ( ) 1  1 − ;  3
Từ đồ thị hàm số y = f ( x) ta có: max f ( x) = f (3) = 3. (2)  1 − ;  3
Đặt h ( x) = f (x) + g ( x) trên  1 − ;  3 , kết hợp với ( ) 1 và (2) ta suy ra:
h ( x)  max f ( x) + max g ( x) = f (3) + g (3) = 7 , đẳng thức xảy ra khi x = 3.  1 − ;  3  1 − ;  3
Vậy bất phương trình m h ( x) có nghiệm thuộc  1 − ;  3 khi và chỉ khi
m  max h ( x) = 7.  1 − ;  3 Ví dụ 7. Cho hàm số 3 2
f (x) = x − 4x − x + 4 có đồ thị như
hình vẽ. Có bao nhiêu giá trị nguyên của m để
phương trình sau có 4 nghiệm thuộc đoạn 0; 2   f ( 2 x − x + ) 2 2019 15 30
16 − m 15x − 30x + 16 − m = 0 A. 4541. B. 4542 . C. 4543. D. 4540 . 19
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
THPT Kinh Môn - Hải Dương - Lần 3 – tháng 5 – 2019 Lời giải
Chọn đáp án B
Theo đề f (x) = (x + ) 1 (x − ) 1 (x − 4) 2 2 x
  0;2 : t = 15x − 30x + 16 = 15  
(x −1) +1 1; t(0) = t(2) = 4  t 1;4  
Với t  1 thì phương trình có 2 nghiệm x thoả mãn.
Với t = 1 có 1 nghiệm x thoả mãn.
BPT  2019 f (t) = m(t + ) 1  2019(t + ) 1 (t − )
1 (t − 4) = m(t + ) 1 Xét t (1; 4      
m = g(t) =
(t − )(t − ) = (t − t + ) 2 2 5 9 9 2019 1 4 2019 5 4 = 2019  t − −   2019 − = −     4542,75  2  4   4    5 x 1 4 2 g(t) 0 − 0 + 0 g(t) 0 0 y = m 4 − 542,75 Yêu cầu bài toán  4
− 542,75  m  0  m 4 − 5042; 4 − 5042;...;− 
1 có 45042 m nguyên thoả mãn. Ví dụ 8.
Cho hàm số y = f (x) liên tục trên và có đồ thị như hình vẽ.
Tập hợp tất cả các giá trị của m để bất phương 1   2x  trình f f
 + 1− m  0 có nghiệm là 2 2   x + 1  A. m  2 . B. 1  m  2 . C. m  1. D. m  5 − .  Lời giải
Chọn đáp án A 2 x 2x Đánh giá: 2
x + 1  2 x   1  1 −   1 2 2 x + 1 x + 1 20
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung Từ đồ thị thấy x   1 − ;1  2 −  f ( ) x  2   x  2; − 2  2 −  f ( ) x  2   Xét bất phương trình 1   2x  2x  2x f f
 + 1  m . Đặt t = ; u = f   . 2 2   x + 1 2 x + 1 2  x + 1  1 Vì t   1 − ;1  u 2 − ;2  2 −  f ( ) u  2  0  f     (u)+1 2 2
Vậy để bất phương trình ban đầu có nghiệm thì m  2 . Ví dụ 9. Cho hàm số ( ) 3 2
f x = ax + bx + cx + d với a, ,
b c,d có đồ thị như hình vẽ. S là tập hợp chứa tất cả m thuộc  1 − 0; 10   để f ( 2 10 2 1− x ) 3 2 + x − x +
− f (m)  0 có nghiệm 3 3
số phần tử của S là A. 9 . B. 10 . C. 11. D. 12 .  Lời giải
Chọn đáp án A f ( 2 − x ) 2 3 2 1
+ x − x + − f m   f (m)  f ( 2 − x ) 2 3 2 1 1 ( ) 0 1
+ x − x + = g(x) 3 3 3 3  2 1 
Yêu cầu bài toán m  min g (x) = min f ( 2 1 − x ) 3 2 + min x − x + x    1 −   ; 1    3 3  (vì điều kiện 2
1 − x  0  −1  x  1) • 2
0  t = 1− x  1 suy ra f ( 2
1 − x ) = f (t) t  0; 1 
 quan sát đồ thị ta thấy
min f (t) = min f ( 1 − x ) = 3 khi t = 0  x = 1. 0; 1    1 − ; 1   • 2 1 h(x) 3 2
= x − x + x    1 − ; 1   ; h(x) 2
= 2x − 2x = 2x(x − )
1 ; h(x) = 0  x = 0; x = 1 3 3   h(x) = h( ) 8 min min 0 = ; h(1) = 0 = 0  3 
min g (x) = min g(x) = min f ( 2
1 − x )+ minh(x) = 3 + 0 = 3 −1; 1    1 − ; 1  1 − ; 1    1 − ; 1     21
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Suy ra f (m)  3 quan sát đồ thị  m  0 và m 1 − 0; 10 
 suy ra m0; 1; 2;...;1  0 có 10 − 0 + 1 = 11 giá trị. Ví dụ 10. Cho hàm số ( ) 3 2
f x = ax + bx + cx + d với a, ,
b c,d có đồ thị như hình vẽ Có bao nhiêu
giá trị nguyên của tham số m để bất phương
 3sin x − cosx −1  trình f    f ( 2 m + 4m + 4)
2cos x − sin x +  4  luôn đúng ? A. 3 . B. 4 . C. 1. D. vô số.  Lời giải
Chọn đáp án D
3sin x −cos x − 1 Đặt t =  (2t + )
1 cos x − (t + 3)sinx = 1
− − 4t (*) .
2 cos x − sin x + 4 2 2 2 9
Phương trình (*) có nghiệm  (2t + )
1 + (t + 3)  (4t + ) 1  −  t  1 . 11 Suy ra 0  t  1.
Từ đồ thị y = f (x) ta có
y = f (x) đồng biến trên x   0;+  ) 2 Do 2
m + 4m + 4 = (m + 2) 0;+  ) ; t 0;+  )
 3sin x − cosx −1  Nên f    f ( 2
m + 4m + 4)  f ( t )  f ( 2 m + 4m + 4) 2
t m + 4m + 4 Bất
2cos x − sin x +  4  m  −3 phương trình luôn đúng 2
m + 4m + 4  1  
. Suy ra có vô số giá trị của tham số m . m  −  1 Ví dụ 11. 22
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Cho hàm số y = f (x) liên tục trên và có
đồ thị như hình vẽ.Có bao nhiêu giá trị
nguyên dương của tham số m để bất phương trình 2 ( ) m f x + 1 − −  luôn đúng f (x) mf (x) 0 trên đoạn  1 − ;4   ? A. 3 . B. 4 . C. 1. D. vô số.  Lời giải
Chọn đáp án D
Dựa vào đồ thị ta có x   1 − ;4  1  f  
(x) 4 m 0
Bất phương trình ban đầu tương đương với : 2 5  m m f x f x  2 f (x) ( ) ( ) + 1 −  + +  
f (x) 2 f (x). 0 4 2 4    2 5  m f x  2  f (x) ( ) + 1   +  4  f (x) 2    5 f x 2  ( ) ( ) m f x + 1 −  4 2 f (x)    g(x) 5 f x 2 =  f (x) ( ) + 1 −
f (x)  m  4 2    Đặt
f (x) = t (1  t  2)
Bất phương trình trở thành 2  5 t  4  t + 1 − t m  4 2     5 t
Yêu cầu bài toán  m h(t) với h(t) 2 4 =  t + 1 − t  4 2    30 4 + h(t) t 2 3 4 2 = − t  0, t   1  ;2   5 2 4 2 t + 1 4
h(t)  h(2), t   1  ;2  
Để bất phương luôn đúng trên đoạn  1 − ;4   ta phải có 23
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
m h( )  m h ( ) = ( − )2 2 2 2 2 21 4
Suy ra có vô số giá trị m thoả mãn. Ví dụ 12.
Cho hàm số y = f (x) có đồ thị như hình
vẽ.Có bao nhiêu số nguyên âm m để bất 1  x  phương trình f + 1  m −   x có 3  2  nghiệm thuộc đoạn  2 − ; 2   ? A. 3 . B. 9 . C. 8 . D. 10 .  Lời giải
Chọn đáp án D x   x
Ta có bất phương trình  f + 1 + 6 + 1  3m +     6 (*)  2   2  x
Yêu cầu bài toán  3m + 6  min g(t) với g(t) = f (t) + 6t với t = + 1 và t  0; 2   2
Xét hàm số g = f (t) + 6t với t  0; 2  
Quan sát đồ thị 0; 2 
 hàm số f (t) đồng biến suy ra f (t)  0
Ta có g' = f '(t) + 6  0, t  0;2 
 suy ra hàm số g đồng biến t  0;2   nên
g g(0) = f (0) = 4 −  g(t) 10 min = 4 −  3m + 6  4 −  m  − . 3
Vì m nguyên âm nên m 3 − ; 2 − ;−  1 . Ví dụ 13.
Cho hàm số y = f (x) liên tục trên và có
đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên âm lớn hơn 50
− của tham số m để bất phương trình
( f (x)− f (x)+ m)3 3 3
− 4 f (x) + m  0 luôn đúng trên đoạn  1 − ; 4   ? A. 3 . B. 5 . C. 1. D. 2 .  Lời giải 24
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Chọn đáp án D 3 BPT ( 3
f (x) − 3 f (x) + m) − 4 f (x) + m  0
 ( f (x) − f (x) + m)3 + ( f (x) − f (x) + m)   f  (x) 3 3 3 3 3  + f  (x) Đặt 3
f (x) − 3 f (x) + m = t
Bất phương trình trở thành 3 3
t + t f (x) + f (x)
Xét hàm số đặc trưng cho hai vế của BPT ( ) 3
g u = u + u có g(u) 2
= 3u + 1  0, u  
Vậy hàm số g (u) luôn đồng biến trên vậy ta có
g (t)  g( f (x))
t f (x) 3
f (x) − 3 f (x) + m f (x) 3
m  − f (x) + 4 f (x) 3
Yêu cầu bài toán  m  min g(x) với g (x) = −  f  (x) + 4 f  (x)
Đặt f (x) = v Có x   1 − ;4  1  f  
(x)  41 v  4
Để BPT luôn đúng trên đoạn  1 − ; 4   ta phải có m Min( 3
−v + 4v)  m  48 − và m  5 − 0  m 4 − 9; − 4  8 . 1  ;4   Ví dụ 14.
Cho hàm số y = f ( x) và y = g ( x) liên tục trên đồ thị của hàm số
y = f ( x) g ( x) như sau Có bao nhiêu giá trị nguyên thuộc  2 − 020;2020   của tham
số m để bất phương trình 1 1 m +1− −  0 luôn 2 1+ f ( x) 2 1+ g ( x) đúng trên đoạn  1 − ;4 ? A. 2019 . B. 2020 . C. 2021. D. 2022 .  Lời giải Chọn đáp án D
Ta có bất phương trình tương đương với : 25
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung 1 1 m +1  + = h x
1+ f ( x) 1+ g ( x) ( ) 2 2
Yều cầu bài toán  m + 1  min h (x) −1; 4  
Xét bất đẳng thức sau : Nếu ab 1, Có 1 1 2 +  ( ) 1 2 2 1+ a 1+ b 1+ ab Chứng minh: 1 1 2 +  2 2 1+ a 1+ b 1+ ab 2 2 a + b + 2 2  (  2 a + ) 1 ( 2 b + ) 1 ab +1 (ab + ) 1 ( 2 2 a + b + 2) 2 ( 2 2 2 2
a b + a + b + ) 1  (  2 a + ) 1 ( 2 b + ) 1 (ab + ) 1 (ab + ) 1 ( 2 a + ) 1 ( 2 b + ) 1 (ab − ) 1 (a − b)2  (ab )  +1 ( 0 2 a + ) 1 ( 2 b + ) 1 1 1 2
Áp dụng (1) h( x) = +  2 1+ f ( x) 2
1+ g ( x) 1+ f ( x) g ( x) Dựa vào đồ thị ta có  5
f ( x) g ( x) 2 2 1  4   = + suy ra min h(x)
f ( x) g ( x)  1 5 1 −  2 4; 1  
Vậy để thỏa mãn điều kiện đề bài ta phải có 2 3 − m +1   m  và m  2
− 020;2020;m  m 2 − 020; 2 − 019;...;−   1. 5 5
Vậy có 2020 giá trị nguyên của m . Ví dụ 15.
Cho hàm số y = f (x) có đồ thị như hình vẽ. Có
bao nhiêu số nguyên m để bất phương trình ( 2 2 mx + m
5 − x + 2m + 1) f (x)  0 có nghiệm
đúng với mọi x   2; − 2   A. 0 . B. 1. C. 3 . D. 4 . 26
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Đề thi thử THPT Quốc Gia Đại học Vinh Lần 2 năm 2019 Lời giải
Chọn đáp án B Đặt 2 2 (
g x) = mx + m
5 − x + 2m + 1 hàm số luôn xác định với x   2 − ; 2   .
Vì f (x) đối dấu 1 lần từ dương qua âm khi qua x = 1 x   2 − ; 2  
Bất phương trình  g(x). f (x)  0 x   2 − ; 2  
g(x)  0  2 − ; 1     . g  (x)  0  1  ; 2   m = 1 −
Hàm số g (x) liên tục trên  2 − ; 2    nên 2 (
g 1) = 0  m + 2m + 2m + 1 = 0  1  . m = −  2
Do m nên chỉ lấy m = 1 − . Thử lại 2 m = 1 −  ( g )
x = −x + 5 − x − 1  0  2 − ; 1   và ( g x)  0 x  [1;2] Nên m = 1 − thoả mãn. Chọn B.  Lời giải
Chọn đáp án B Ví dụ 16.
Cho hàm số y = f (x) có đồ thị như hình vẽ.
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 2 f ( )
x + x  4x + m có
nghiệm đúng với mọi x ( 1 − ; 3). A. m  3 − . B. m  10 − . C. m  2 − . D. m  5 .
Đề thi thử THPT Quốc Gia Sở Giáo Dục Ninh Bình Năm 2019 Lần 1 Lời giải
Chọn đáp án B
Bất phương trình  m f (x) 2 2
+ x − 4x = g(x)
Yêu cầu bài toán  m  min g (x) (−1; 3)
Từ đồ thị min f (x) = −3 khi x = 2 (1) (−1; 3)
x − 4x = (x − 2)2 2 − 4  4  min( 2 x − 4x) = 4 − khi x = 2 (2) ( 1 − ; 3) 27
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Từ (1) và (2) suy ra min g(x) = 2.3 − − 4 = 10 −  m  10 − ( 3 − ; 1) Ví dụ 17.
Cho hàm số y = f (x) liên tục trên có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của m để phương trình: f ( 2 − x − x ) 2 3 4 6 9
+ 2 = −m có nghiệm A. 4 . B. 5 . C. 6 . D. 7 .
Đề thi thử THPT Quốc Gia Sở Giáo Dục Ninh Bình Năm 2019 Lần 1 Lời giải
Chọn đáp án B Đặt 2
t = 3 − 4 6x − 9x Điều kiện của t 2 2
6x − 9x  0  0  x  3 6 − 18x 12(3x − 1) 1 t = 4 −  = ; t = 0  x = 2 2 2 6x − 9x 6x − 9x 3  2   1  t(0) = t = 3,t = 1 −  t [ 1 −     ; 3]  3   3  Suy ra f (t) 2
+ = −m f (t) 2 2 = −m − 2 Theo đồ thị Với t =  1
− ; 3  f (t) 6;
− a ,a( 2; − − )
1  f (t) 6; − −     
)1 để phương trình có nghiệm thì 28
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung 2 −m − − −  ) 2 2 2 6; 1  6
−  −m − 2  1 −  4 −  −m  1 −  m{0;1;2; 1 − ; 2 − } . Ví dụ 18.
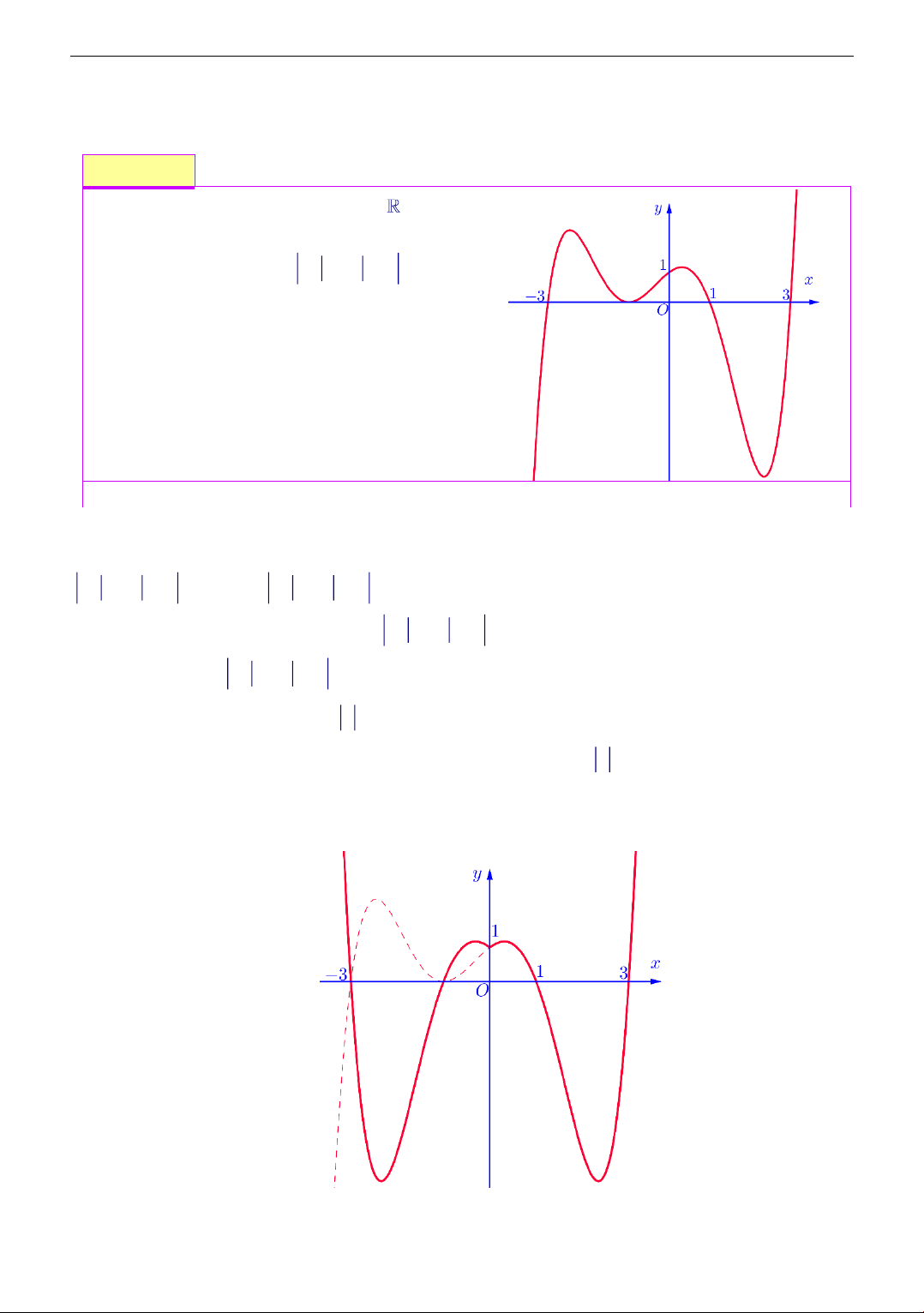
Cho hàm số y = f (x) liên tục trên có đồ
thị như hình vẽ. Có bao nhiêu giá trị nguyên
của m để phương trình f ( x − 2 ) + 1 − m = 8
có 8 nghiệm phân biệt trong khoảng ( 5 − ; 5) A. 1. B. 5 . C. 6 . D. 7 .
Đề thi thử THPT Quốc Gia Sở Giáo Dục Vĩnh Phúc Lần 1Năm 2019 Lời giải
Chọn đáp án A
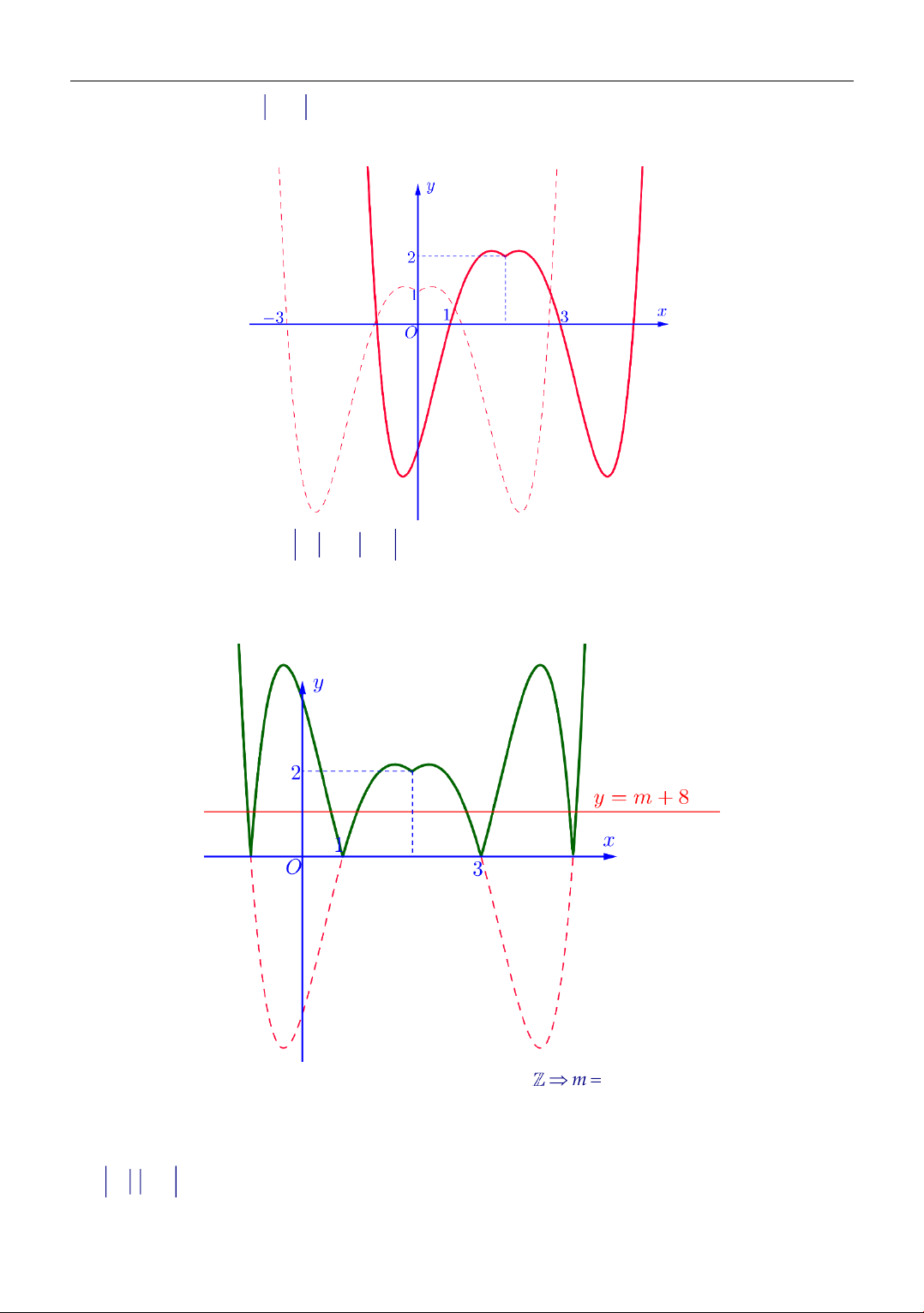
f ( x − 2 ) + 1 − m = 8  f ( x − 2 ) + 1 = m + 8 Nghiệm của phương trình là giao điểm của đường
thẳng y = m + 8 và đồ thị hàm số y = f ( x − 2 ) + 1 (C 3 )
Đồ thị hàm số y = f ( x − 2 ) + 1 gồm 3 bước
Bước 1. Vẽ đồ thị hàm số y = f ( x )
Từ đồ thị y = f (x) có đồ thị là (C) suy ra đồ thị hàm số y = f ( x ) có đồ thị (C gồm 2 phần: 1 )
• Phần 1: Giữ phần bên phải, bỏ phần bên trái đồ thị (C) .
• Phần 2: Đối xứng phần 1 qua Oy . 29
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Bước 2. Hàm số y = f ( x − 2 ) + 1 có đồ thị là (C . Tịch tiến sang phải 2 đơn vị lên trên 1 đơn 2 )
vị đồ thị (C thu được đồ thị (C 2 ) 1 )
Bước 3. Đồ thị hàm số y = f ( x − 2 ) + 1 (C gồm 2 phần 3 )
• Phần 1: Giữ nguyên phần bên trên trục hoànhOx của đồ thị (C . 2 )
• Phần 2: Đối xứng phần bên dưới của đồ thị (C qua trục Ox . 2 )
Yêu cầu bài toán  0  m + 8  2  8 −  m  6
− và m  m = 7 − vậy có 1 giá trị.
 Nhận xét: Để đơn giản ta đặt t = x − 2  t ( 7 − ; 3
− ) ta thực hiện vẽ đồ thị hàm số
y = f ( t ) + 1 theo 3 bước 30
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Bước 1. Vẽ đồ thị hàm y = f ( x ) (C gồm 2 phần 1 )
• Phần 1: Giữ phần bên phải, bỏ phần bên trái đồ thị (C) .
• Phần 2: Đối xứng phần 1 qua Oy .
Bước 2. Tịnh tiến lên trên 1 đơn vị đồ thị (C được đồ thị (C 2 ) 1 )
Bước 3. Đồ thị hàm số y = f ( x ) + 1 gồm 2 phần
• Phần 1: Giữ nguyên phần bên trên trục hoànhOx của đồ thị (C . 2 )
• Phần 2: Đối xứng phần bên dưới của (C qua trục Ox . 2 ) 31
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Yêu cầu bài toán  0  m + 8  2  8 −  m  6
− và m  m = 7 − vậy có 1 giá trị. Ví dụ 19.
Cho hàm số y = f (x) liên tục trên có đồ
thị như hình vẽ. Số giá trị nguyên của tham
số m để phương trình f ( x + m ) = m có 4. A. 0 . B. 1. C. 2 . D. Vô số.  Lời giải
Chọn đáp án B
Nghiệm của phương trình f ( x + m ) = m là hoành độ giao điểm của đồ thị hàm số
y = f ( x + m ) và đường thẳng y = m.
Số giao điểm của đồ thị hàm số y = f ( x + m ) và đường thẳng y = m bằng số giao điểm của
đồ thị hàm số y = f ( x ) và đường thẳng y = m.
Đồ thị hàm số y = f ( x ) và vị trị có 4 nghiệm. 32
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung  3 m =
Từ đồ thị suy ra để phương trình có 4 nghiệm thì  4  . m = −1
Vậy có 1 giá trị nguyên m = 1 − . Ví dụ 20. Cho hàm số 4 3 2 f ( )
x = ax + bx + cx + dx + e
(a,b,c,d,e  ) . Hàm số có đồ thị f (x) như
hình vẽ bên. Tập nghiệm của phương trình
f (x) = e có số phần tử là A. 1. B. 2 . C. 3 . D. 4 .  Lời giải
Chọn đáp án D g(x) =  f (x) Xét hàm số (
g x) = f (x) - e ,  =  = g  ( ) ; f (x) e ( g x) 0 0 =  0   
Đồ thị hàm số g(x) = f (x) 1 3 = ( a x + 1) x − x −    với a  0  2  2  Ta có bảng biến thiên 33
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung 1 3 x − 1 − 0 + 2 2 g(x) − 0 + 0 − 0 +  1  + 0 g   +  2  g (x) Ox : y = 0 0  3  g(− ) 1 g    2  3 3  3   3      1 3 9 Ta có 2 2 g = g − g(0) =
g (x)dx = a (x + 1) x − x − dx = − a           0 0 0  2   2   2  2  64
Suy ra phương trình có 4 nghiệm. Ví dụ 21.
Cho hàm số liên tục trên  1 − ; 9   và đồ thị như
hình vẽ. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình f (x) 2 f (x)
−  f x + f x −      ( 2 16.3 ( ) 2 ( ) 8 4
m − 3m) f(x) .6
Có nghiệm đúng với mọi x   1 − ; 9   A. 22 . B. 31 . C. 5 . D. 6 .  Lời giải
Chọn đáp án D Theo đồ thị 4
−  f (x)  2 x  [ 2
− ;9]. Đặt t = f (x), t 4; − 2   .
Bài toán trở thành tìm m để t 2 t −  + −      ( 2 16.3 2 8 4 − 3 )6t t t m m có nghiệm đúng với t   4; − 2   . t 2 t −  + −      ( 2 16.3 2 8 4 − 3 )6t t t m m , t  [ 4 − ;2] t    g(t) 16 2 2 =
− t + 2t − 8   m − m t   −     t ( 2 3 ), [ 4;2] 2  3  Yêu cầu bài toán 2
m − 3m  min g(x) −4 2   16 Với  4, t  [ 4
− ;2] , dấu bằng xảy ra khi t = 2 . 2t 34
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung t   2 2 2
t + 2t − 8  0, t  [ 4
− ;2]  t + 2t − 8   0, t  [ 4 −    
; 2] dấu bằng xảy ra khi t = 2 .  3  t 16  2  Suy ra g (t) 2 =
− t + 2t − 8   4, t  [ 4 − ;2] min g t =     t ( ) 4 2  3   4 − ;2   2
m − 3m  4  1
−  m  4 và m  m 1 − ; 0; 1; 2; 3;  4
Kết luận: có 6 giá trị m . Ví dụ 22.
Cho hàm số y = f (x) liên tục trên có đồ thị
như hình vẽ. Có bao nhiêu giá trị nguyên của m 1  ; 2025   sao cho phương trình  2x f + f ( 2 m − m + 1 =   0 có nghiệm. 2 )  1 + x  A. 2019 . B. 2022 . C. 2025 . D. 2026 .  Lời giải
Chọn đáp án D
Theo đồ thị hàm số đối xứng với nhau qua Ox suy ra hàm số f (x) hàm số lẻ.  2x   f + f ( 2 m − m + 1 =   0 2 )  1 + x   (    −  2 − + ) 2x = − ff ( 2 2x f m m 1 m − m + 1 =   f   2 ) 2  1 + x   1 + x  2 − x 2 − x 2 − x 2 − x  2 − x  Ta có 1 =   = 1 −  [−1;1] f   đồng biến. 2 2 2 2 − x 1 + x 2x x + 1  x + 1   1  Mặt khác ( 2
m − m + 1) − ;0  f ( 2 m − m +   1) đồng biến.  2  − 2 2x 2
m − m + 1 =  1
−  m − m + 1  1 2 x + 1  2  m + 1  m + 1 2 2  1
− + m + 1  m  1+ m + 1    m  0 2
m −1 m + 1
Nên phương trình có nghiệm với 35
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
 DẠNG 4: Cho hàm số y = f (x) có đồ thị f (x) xác định tham số m để g(x,m)  0 Ví dụ 1.
Cho hàm số y = f (x) có đạo hàm trên .
Đồ thị hàm số y = f '(x) như hình vẽ. Tìm
m để bất phương trình 2
m − x  2 f (x + 2) + 4x + 3 nghiệm đúng với mọi x( 3; − +) .
A. m  2 f (0) + 1 .
B. m  2 f (0) − 1 . C. m  2 f ( 1 − ) . D. m  2 f ( 1 − ) .  Lời giải
Chọn đáp án B Ta có 2
m − x f (x + ) + x +  m f (x + ) 2 2 2 4 3 2
2 + x + 4x + 3 .
Yêu cầu bài toán m  min g(x) với . g(x) = f (x + ) 2 2
2 + x + 4x + 3 .
Ta có g( x) = 2 f ( x + 2) + 2x + 4 = 2  f (t ) − (− 
t ) (t = x + 2)
g( x) = 0  f ( x + 2) = −( x + 2) .
Đặt t = x + 2 ta được f (t ) = −t . ( ) 1 36
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Nghiệm của phương trình (1) chính là hoành độ giao điểm của đường thẳng y = t − và đồ thị
hàm số f (t)
Ta có g(x)  0 khi đồ thị f (t) nằm trên đường thẳng y = t
− ; g(x)  0 khi đồ thị f (t) nằm
dưới đường thẳng y = t
− . Chỉ cần xét khoảng g(x)  0 khoảng còn lại mặc nhiên sẽ làm cho g(x)  0   −  +  −   −
g(x)   f (t) t 1 x 2 1 x 3 0  t −       t  0 x + 2  0 x  2 −   
Từ đó ta có bảng biến thiên nghiệm bội chẵn tức điểm tiếp xúc không tham gia vào quá trình xét dấu x − −3 2 − + g( x) + 0 − 0 + g (x) − −
min g(x) = g( 2
− ) = 2 f (0) −1 m  2 f (0) −1 x  ( 3;
− +)  m  2 f (0) −1 Ví dụ 2. 37
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Cho hàm số y = f (x) có đạo hàm trên .
Đồ thị của hàm số y = f (x) như hình vẽ.
Tìm m để bất phương trình 2
m + x + 4  2( f (x + )
1 − 2x) nghiệm đúng với mọi x  4; − 2   .
A. m  2 f (0) − 1 . B. m  2 f ( 3) − − 4 .
C. m  2 f (3) − 16 . D. m  2 f (1) − 4 . Lời giải
Chọn đáp án D
m + x +  ( f (x + ) − x)  m f (x + ) − (x + )2 2 4 2 1 2 2 1 2
Yêu cầu bài toán  m  max g(x) với g(x) = f (x + ) − (x + )2 2 1 2
Đặt t = x + 1
Ta có g(x) = 2 f (x + )
1 − 2(x + 2) = 2( f (x + )
1 − (x + 2)) = 2  f (t) − (t +  )1.
g(x) = 0  f (t) = t + 1 nghiệm của phương trình là hoành độ giao điểm của đường thẳng
y = t + 1 và đồ thị f (t) .
Từ đồ thị g(x) = 2 f
 (t) − (t + ) 1   0 
khi đồ thị f (t) nằm trên đường thẳng y = t + 1 và
g(x) = 2 f
 (t) − (t + ) 1   0 
khi đồ thị f (t) nằm dưới đường thẳng y = t + 1, ta chỉ cần xét −  t  −  x +  −  x
trường hợp g(x) 3 2 3 1 2 4 1  0       t  3 x + 1  3 x     2 x 4 − 1 2 − g(x) + 0 − 0 38
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung g (1) g (x)
Suy ra max g(x) = 2 f ( ) 1 − 4 x    4 − ;2 
 nên m  2 f ( ) 1 − 4 . Ví dụ 3.
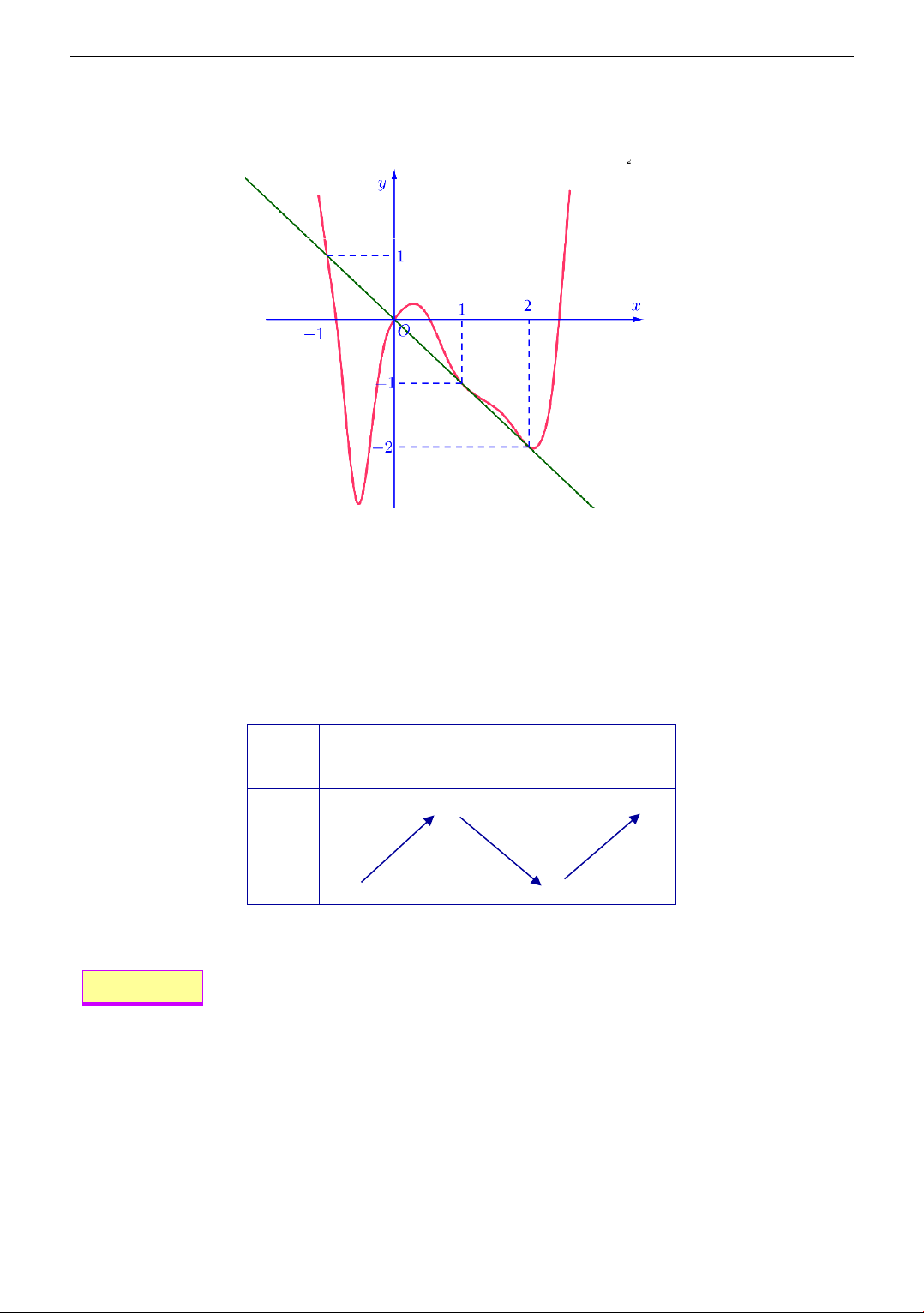
Cho hàm số y = f (x) là hàm đa thức có hệ
số thực. Hình vẽ bên dưới là một phần đồ
thị của hai hàm số: y = f ( x) và
y = f ( x) . Tập các giá trị của tham số m để phương trình ( )  x f x me luôn đúng trên 0; 2 là ?
A. m  0 . B. m f (0) . f (2) 2 C. m . D.  (0) ( ) + f m f . 2 e e Lời giải
Chọn đáp án
Đồ thị hàm số f (x) cắt trục hoành tại x thì x là cực trị của hàm số y = f (x) . Dựa vào đồ 0 0
thị ta kí hiệu (C là đồ thị hàm số y = f (x) , (C đồ thị của hàm số y = f (x) 2 ) 1 ) f ( x) ( )  x f x me m  . x e f x
Yêu cầu bài toán  m  max g(x) với g ( x) ( ) = x e 39
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
f x − f x Ta có g( x) ( ) ( ) = . x ex =1 g ( x)  
= 0  f (x) = f (x)  x = 2  . x = a  ( 1 − ;0)
g(x)  0  f '(x)  f (x) khi đồ thị hàm số f (x) nằm trên đồ thị f (x)
g(x)  0  f '(x)  f (x) khi đồ thị hàm số f (x) nằm dưới đồ thị f (x)
Theo đồ thị ta có bảng biến thiên. x 0 a 1 2 g(x) + 0 + 0 − g (1) g (x)
Khi đó max g (x) = g (1) = 0 0; 2    m  0 Ví dụ 4.
Cho hàm số f (x) liên tục trên . Hàm số
y = f (x) có đồ thị như hình vẽ. Bất phương trình f ( x) 2 2sin
− 2sin x m đúng với mọi
x (0; ) khi và chỉ khi
A. m f ( ) 1 1 − . B. m f ( ) 1 1 − . 2 2
C. m f ( ) 1
0 − . D. m f ( ) 1 0 − . 2 2
Đề thi thử THPT Quốc Gia Chuyên Quang Trung Lần 5 năm 2019 Lời giải
Chọn đáp án f ( x) 2 2sin
− 2sin x m ( ) 1 40
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Ta có: x(0; )  sin x(0;1 . Đặt 2sinx = t(t(0;2) ta được bất phương trình: f (t) 1 2
− t m (2) . 2
(1) đúng với mọi x(0; ) khi và chỉ khi (2) đúng với mọi t(0;2. 1
Xét g(t) = f (t) 2
− t với t (0;2 . 2
g(t) = f (t) − t .
Từ đồ thị của hàm số y = f (x) và y = x Ta có bảng biến thiên x 0 1 2 g(t) + 0 − 0 g (1) g(t) 1
Yêu cầu bài toán  m  max g = g (1) = f (1) − . (0 ; 2 2
 DẠNG 5: Cho đồ thị hàm số y = f (x) xác định tham số để phương trình có nghiệm Ví dụ 5. 41
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Cho hàm số y = f (x) liên tục trên . Và
có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của tham số m để phương trình  
f  2 f (cos x)  = m      có nghiệm x ;    2  ? A. 2 . B. 3 . C. 4 . D. 5 . Lời giải
Chọn đáp án C  
Đặt t = cos x với x  ;    t ( 1 − ; 0 .  2 
Quan sát đồ thị trên ( 1
− ; 0) hàm số nghịch biến nên 0 = f(0)  f(t)  f( 1 − ) = 2
Đặt u = 2 f (cos x)  u 0; 2  ) .
Yêu cầu bài toán tương đương với tìm m để phương trình f (u) = m có nghiệm 0; 2  ).
 min f (u)  m  max f (u) 0; 2  ) 0; 2  )
Quan sát đồ thị min f (u) = 2
− ; max f (u) = 3  2
−  m  2 và m 0; 2  ) 0; 2  ) Nên m{ 2 − ; 1
− ;0;1} , có 4 giá trị m . Ví dụ 6.
Số các giá trị của tham số m không vượt quá 5 để phương trình − f ( x  ) 2 m 1 −
= 0 có 2 nghiệm phân biệt. 8 A. 4 . B. 5 . C. 6 . D. 7 . Lời giải
Chọn đáp án B Đặt x
t =   0 . Phương trình có dạng 42
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung 2 2 m − 1 m − 1 f (t) − = 0  f (t) = ,(t  0) 8 8 2 m − 1
Nghiệm phương trình phụ thuộc vào số giao điểm giữa đường thẳng y = và đồ thị hàm 8
số y = f (t)
Quan sát đồ thị hàm số y = f (x) ta có phương trình trên có 2 nghiệm phân biệt dương 2 m − 1 2  1 −   1  7
−  m  9  −3  m  3 và m  m{ 2 − ; 1 − ;0;1;2}. 8
Vậy có 5 giá trị m . Ví dụ 7.
Cho hàm số bậc ba y = f (x) có đồ thị
như hình vẽ. Có bao nhiêu giá trị
nguyên của tham số m thuộc đoạn 0; 9 
 sao cho bất phương trình 2
f (x)+ f (x) 2 −m
f (x)− f (x)−m f (x) 2 − 16.2 − 4 + 16  0 có nghiệm x( 1 − ; ) 1 ? A. 6 . B. 8 . C. 5 . D. 7 .
Đề thi thử THPT Quốc Gia Sở Bắc Ninh 07-05-2019  Lời giải 43
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Chọn đáp án A 2
f (x)+ f (x) 2 −m
f (x)− f (x)−m f (x) Ta có: 2 − 16.2 − 4 + 16  0 f (x) 2
f (x)− f (x) 2 −m
f (x)− f (x)−m f (x)  4 .2 − 16.2 − 4 + 16  0 f (x) 2
f (x)− f (x)− − −  4 (2 m − 1) 2
f (x) f (x) − 16(2 m − 1)  0 f (x) ( − −  4
− 16) 2f(x) f(x) (2 m − 1)  0 2 − f (x) f (x)
Theo đồ thị x( 1 − ; ) 1  2
−  f (x)  2 2  4  4  4  4 − 16  0 x  ( 1 − ;1) 2
f (x)− f (x)− Do đó m 2 2
−1  0  f (x) − f (x) − m  0 có nghiệm x( 1 − ; ) 1 2
f (x) − f (x)  m có nghiệm x( 1 − ; ) 1 Xét  ( ) 2 g f x  = f
(x)− f (x)
Đặt t = f (x) với t ( 2; − 2) , ( ) 2
g t = t − t có đồ thị như hình vẽ
Theo đồ thị g (t)  m m  max g (t) = 6 và m0; 9 
  0  m  6 . (−2; 2) Ví dụ 8.
Hình vẽ bên là đồ thị của hàm số ( ) 4 3 2
f x = ax + bx + cx + dx + e . Hỏi có bao
nhiêu m nguyên để phương trình
f ( x ) = m có ít nhất ba nghiệm phân biệt? A. 1. B. 2 . C. 3 . D. 4 .
Đề thi thử THPT Quốc Gia Sở Bắc Ninh 07-05-2019  Lời giải 44
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Chọn đáp án C
Từ đồ thị hàm số (C) : y = f (x) ta suy ra đồ thị hàm số (C') : y = f ( x ) gồm 2 phần
• Phần 1: Giữ nguyên phần đồ thị (C) trên miền x  0 , (kí hiệu phần đồ thị này là (C ),Bỏ 1 )
phần đồ thị (C) ở bên trái trục Oy .
• Phần 2: Đối xứng phần 1 qua Oy .
Theo đồ thị (C ') ta có:
Phương trình f ( x ) = m có ít nhất ba nghiệm phân biệt  3 −  m  0.
Vì m nên m 2; − 1 − ; 
0 . Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Ví dụ 9.
Cho hàm số f ( x) 3 2
= ax + bx + cx + d có đồ thị
như hình vẽ, gọi S là tập hợp các giá trị của
m (m ) sao cho (x− ) 3
1 m f (2x − )
1 − mf ( x) + f ( x) −1  0,x   
. Số phần tử của tập S là? A. 2 . B. 0 . C. 3 . D. 1.
Đề thi thử THPT Quốc Gia Chuyên Quang Trung Lần 5 Lời giải 45
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Chọn đáp án A
Hướng giải 1 f ( )  1 1 = 1 a =    f (− ) 2 1 = 0   b = 0 1 1
Từ đồ thị hàm số ta suy ra  f (  =   f x = x + 0) ( ) 3 0 c = 0 2 2    f ( ) 1  1 0 =  d =  2  2 m = 0  Theo đề f ( ) 3
1 = 1  m − m = 0  m = 1  m = 1 −  Với m = 0, ta có:  1 1  ( x − ) 1 ( f ( x) − ) 1 = ( x − ) 3 1 x + −1    2 2  1 1 2 = (x − ) 1 ( 3 x − ) 1 = (x − ) 1 ( 2 x − x + ) 1  0 x  (thoả mãn) 2 2 Với m =1, ta có: (x − )
1  f (2x − )
1 − f ( x) + f ( x) −1   ( x )1 ( x − )3 1  = −1 2 1 + −1    2 2  1 = (x − ) 1 ( 3 2
8x −12x + 6x −1− ) 1 = ( x − ) 1 ( 3 2
4x − 6x + 3x − ) 1 2 = (x − )2 ( 2 1 4x − 2x + ) 1  0 x  (thoả mãn)  1 1  Với m = 1 − , ta có: (x − ) 1 −  f (2x − )
1 + f ( x) + f ( x) −1 =  ( x − ) 1 − (2x − )3 3 1 − +  x   2 2  (x − ) x  1 ( 1 3 2
−x + 6x − 3x)  0   (Loại) x  0
Vậy m = 0 và m =1.  Hướng giải 2 Để ( x − ) 3
1 m f (2x − )
1 − mf ( x) + f ( x) −1  0,x    thì 3 m f (2x − )
1 − mf ( x) + f ( x) −1 
 nhận x =1 là nghiệm bội lẻ duy nhất và khi qua x =1 (  m = 0 3 m f (2x − )
1 − mf ( x) + f ( x) −1 
 đổi dấu từ − sang + ). Khi đó: 3
m − m = 0   . m = 1 
+ Thử lại, ta thấy với m = 0 thỏa. 46
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung + Với m =1, ta có: 3 m f (2x − )
1 − mf ( x) + f ( x) −1 = f (2x − ) 1 −1  
là một hàm số bậc ba có
hệ số bậc cao nhất dương.
Ta có: lim  f (2x − ) 1 −1 = +, lim    f (2x − ) 1 −1 = − 
nên khi qua x =1 hàm số sẽ đổi dấu x→+ x→− từ − sang + thỏa mãn. + Với m = 1 − , ta có: 3 m f (2x − )
1 − mf ( x) + f ( x) −1 = − f (2x − )
1 + 2 f ( x) −1   là một hàm số
bậc ba có hệ số bậc cao nhất âm.
Ta có: lim  f (2x − ) 1 −1 = −, lim    f (2x − ) 1 −1 = + 
nên khi qua x =1 hàm số sẽ đổi dấu x→+ x→−
từ + sang − không thỏa mãn. Ví dụ 10.
Cho hàm số y = f (x) liên tục trên , có
đồ thị hàm số như hình vẽ. Có bao nhiêu
giá trị nguyên dương của tham số m để bất phương trình 2 (2025 − ) m
f (x) + f (x) − 1  3x + 10 − 2x
nghiệm đúng với mọi x[0; 5] A. 2019 . B. 2020 . C. 2021. D. 2022 .  Lời giải
Chọn đáp án B 47
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Để bất phương trình có nghiệm đúng với mọi x  0; 5   thì ta cần có   3x + 10 − 2x 2025 − m  max  0; 5  2   f (x) f (x 2) 1  + − −  
Theo bất đẳng thức Bunyakovsky
3x + 10 − 2x = 3 x + 2 5 − x  (3 + 2)(x + 5 − )
x = 5 dấu bằng “ = ” xảy ra khi và chỉ khi
x = 3 . Nhìn đồ thị ta thấy rằng f (x)  1 dấu “ = ” xảy ra khi x = 3; x = 1; x = 5 . 3x + 10 − 2x 5 Suy ra   5  m  2020 . 2 2
f (x) + f (x) − 1
f (x) + f (x) − 1 Ví dụ 11.
Cho hàm số y = f (x) có đồ thị f (x) như hình vẽ.
Xét hàm số g (x) = f (x) 3 2
+ 2x − 4x − 3m − 6 5
với m là số thực. Để g(x)  0 x  [− 5; 5] thì
điều kiện của m là 2 2 A. m
f ( 5) . B. m f ( 5) . 3 3 2 2 C. m
f (0) − 2 5 . D. m f (− 5) − 4 5 . 3 3  Lời giải
Chọn đáp án A Để 3 3 ( g ) x  0  ( g ) x = 2 f ( )
x + 2x − 4x − 3m − 6 5  0  3m  2 f ( )
x + 2x − 4x − 6 5 Với 3 ( h ) x = 2 f ( )
x + 2x − 4x − 6 5
Yêu cầu bài toán  2m  max h(x) − 5; 5   Xét hàm số 3 ( h ) x = 2 f ( )
x + 2x − 4x − 6 5 ; 2 h (  ) x = 2 f (  ) x + 6x − 4
h (− 5) = 2 f (− 5) + 6.5 − 4 = 0 
h ( 5) = 2 f ( 5) + 6.5 − 4 = 0    −  h (
 0) = 2 f (0) + 0 − 4 = 0
suy ra h(x) đồng biến trên 5; 5    h (
 1) = 2 f (1) + 6.1− 4  0  h ( 1 − ) = 2 f ( 1 − ) + 6.1− 4   0 x − 5 5 h( x) + 0 48
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung h(x)
Suy ra h(x)  h( 5) = 2 f ( 5)  max f (x) = 2 f ( 5) − 5; 5   Ví dụ 12.
Cho 0  a − 1  b − 1  a và hàm số f (x) y = ( g x) = có đạo hàm 0; +   ) . Biết f ( 2 (x + 1) )
đồ thị hàm số y = f (x) như hình vẽ. Khẳng định
nào sau đây đúng với x [ a − 1; b − 1] f ( b − 1) f ( a − 1) A. ( g x)  . B. ( g x)  . m n f ( b − 1) D. 10 −
g(x)  0 . C. ( g x)  . m Lời giải
Chọn đáp án A Ta có 2 x [
a −1; b −1](x +1) [ ; a ]
b theo đồ thị có m f ( 2 x + ) 1 1 1 ( 1)  n    n f ( 2 (x + 1) ) m
Với 0  a − 1  b − 1  a theo đồ thị hàm số f (x) đồng biến trên [ a − 1; b − 1] f (x) f ( b − 1)
f ( a − 1)  f (x)  f ( b − 1)  g(x) =  f ( 2 (x + 1) ) m Ví dụ 13. 49
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Gọi A là tập hợp tất cả các giá trị nguyên của  m
tham số m để phương trình f ( 2sin x ) = f    2 
có 12 nghiệm phân biệt thuộc đoạn   − ;2    .
Tính tổng tất cả các phần tử của A . A. 5 . B. 3 . C. 2 . D. 6 .  Lời giải
Chọn đáp án B
Đặt t = 2sin x với x   − ;2    . t = 2cosx .    3
t = 0  2cos x = 0  x =
+ k (k ) . x  − ;2      x   − ; ;  . 2  2 2 2  Bảng biến thiên   3 x  − − 2 2 2 2 t − 0 + 0 − 0 + 0 2 0 t 2 − 2 −
Từ đó, ta suy ra được bảng biến thiên của u = 2sin x là   3 x  − − 0  2 2 2 2 u + 0 − 0 + 0 − 0 + 0 − 2 2 2 u 0 0 0 0
Với u = 2 ta có 3 nghiệm phân biệt x   − ;2    .
Với u = 0 ta có 4 nghiệm phân biệt x   − ;2    .
Với 0  u  2 ta có 6 nghiệm phân biệt x   − ;2    .  m
Yêu cầu bài toán  f (u) = f   có 2 nghiệm phân biệt trong khoảng (0;2)  2  50
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung m 0   2 27  m    0  m  4 2  −  f    0     . 16  2  m 3  m  3   2 2 Vậy A = 1; 
2 . Tổng tất cả các phần tử của A bằng 3.
 DẠNG 6: Cho đồ thị hàm số y = f (x) xác định số nghiệm của hàm số g(x) = f (x) + g(x) Ví dụ 1.
Cho hàm số đa thức y = f (x) có f ( ) 1 = 2018 và
có đồ thị y = f (x) như hình vẽ. Xét hàm số
g(x) = f (x) 3
− x + 3x − 2019 . Phương trình
g(x) + 2 = 0 có tất cả bao nhiêu nghiệm dương A. 0 . B. 1. C. 2 . D. 3 .  Lời giải
Chọn đáp án
Ta có g(x) = f (x) 2
− x + = f (x) −( 2 3 3
3x − 3) ; g(x) =  f (x) 2 0
= 3x − 3 có nghiệm là hoành
độ giao điểm của hàm số y = f (x) và (P) 2
: y = 3x − 3 .
Theo đồ thị ta có đồ thị hàm số g(x)  0 khi đồ thị f (x) nằm trên đồ thị (P) và ngược lại
g(x)  0 khi đồ thị f (x) nằm dưới đồ thị (P) .  Từ đồ thị ta có : g (1) = 1
Hàm số f (x) nghịch biến (0; ) 1 suy ra 51
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung f (0)  f ( )
1 = 2018  g(0) = f (0) − 2019  f ( ) 1 − 2019 = 2018 − 2019 = 1 −
Phương trình g(x) + 2 = 0  g(x) = 2
− là giao điểm giữa đồ thị hàm số g(x) và đường thẳng y = −2 Bảng biến thiên : x − 1 − 0 1 + g(x) − 0 + 0 − 0 1 g (x) y = −2 g( 3 − )
Kết luận : phương trình g(x) + 2 = 0 có 1 nghiệm dương Ví dụ 2.
Cho hàm số y = f (x) liên tục trên và có
đồ thị như hình vẽ bên. Biết rằng f (x)  0
với mọi x (−;− 3)  (2;+) . Số nghiệm nguyên thuộc khoảng ( 1 − 0;10) của bất phương trình  f
 (x) + x − ( 2
1 x − x − 6)  0 là A. 9 . B. 10 . C. 8 . D. 7 .
Đề thi thử THPT Quốc Gia Môn Toán Trường Lương Thế Vinh lần 3 năm 2019  Lời giải
Chọn đáp án D 52
Tư duy giải toán Hàm Số Vận Dụng – Vận Dụng Cao Nguyễn Thành Trung
Đặt g(x) =  f
 (x) + x − ( 2
1 x − x − 6) là hàm số liên tục trên .  − − =  − − =  = − = g(x) 2 2 x x 6 0 x x 6 0 x 2; x 3 = 0       .  f
 (x) + x − 1 = 0  f
 (x) = −x + 1  f
 (x) = −x + 1 ( )1
Phương trình (1) là phương trình hoành độ giao điểm của đồ thị hàm số y = f (x) và đường
thẳng y = −x + 1 . Dựa vào đồ thị hàm số đã vẽ ở hình trên
f (x) + x − 1 = 0  x = − 3 , x = −1, x = 0 và x = 2 . Ta có bảng xét dấu x − −3 2 − 1 − 0 2 3 + 2 x − x − 6 + | + 0 − | − | − | − 0 +
f (x) + x − 1 − 0 + | + 0 − 0 − 0 + | + g(x)
− 0 + 0 − 0 + 0 + 0 − 0 +
  f (x) + x − ( 2
1 x − x − 6)  0  g(x)  0  x(−3;− 2) (−1;0) (0;2) (3;+   )
Kết hợp điều kiện x nguyên và x (−10;10) ta có x1;4;5;6;7 ;8;  9 .
 DẠNG 7 : Biện luận tham số m của bất phương trình hoặc phương trình bằng cách đưa về hàm số đặc trưng Ví dụ 1.
Cho hàm số f (x) 5 3
= x + 3x − 4m . Có bao nhiêu giá trị nguyên của tham số m để phương trình ( ( )+ ) 3 3 f f x
m = x − m có nghiệm thuộc đoạn 1  ;2   ? A. 15 . B. 16 . C. 17 . D. 18 .
Đề thi thử THPT Quốc Gia Môn Toán Trường Lương Thế Vinh lần 3 năm 2019  Lời giải
Chọn đáp án D Đặt = ( ) 3 +  = ( ) +  ( ) 3 3 t f x m t f x m
f x = t − m (1) . Ta có ( ( )+ ) 3 3 f f x
m = x − m , suy ra ( ) 3
f t = x − m (2) .
Từ (1) và (2) ta có f (x) − f (t) 3 3
= t − x f (x) 3
+ x = f (t) 3 5 3 5 3
+ t x + 4x = t + 4t (3) .
Xét hàm số g(u) 5 3
= u + u g(u) 4 2 4
= 5u + 12u  0 u
   g(u) đồng biến trên .
Do đó (3)  g(x) = g(t)  x = t . Thay vào (1) ta được f (x) 3 5 3
= x − m x + 2x = 3m (4) .
Xét hàm số h(x) 5 3
= x + 2x trên đoạn 1  ;2   . Ta có h(x) 4 2
= 5x + 6x  0 x   1  ;2  h  
(x) đồng biến trên đoạn 1;2   .
Vậy ta có min h(x) = h( )
1 = 3 và max h(x) = h(2) = 48 . 1  ;2   1  ;2   53
Tư duy giải bài toán vận dụng- vận dụng cao hàm số Nguyễn Thành Trung
Phương trình đã cho có nghiệm thuộc 1  ;2   
Phương trình (4) có nghiệm trên 1  ;2   .
 minh(x)  3m  maxh(x)  3  3m  48  1 m  16 . Vậy có 16 giá trị nguyên của m . 1  ;2 1  ;2     54