CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC HÔM NAY!
Có thể phát biểu định
lí theo các cách nào khác?
CHƯƠNG I: MỆNH ĐỀ VÀ TẬP HỢP BÀI 1: MỆNH ĐỀ NỘI DUNG
MỆNH ĐỀ, MỆNH ĐỀ CHỨA 01
03MỆNH ĐỀ CHỨA KÝ HIỆU
BIẾN, MỆNH ĐỀ PHỦ ĐỊNH ∀ ;∃
02 MỆNH ĐỀ KÉO THEO, 04 LUYỆN TẬP MỆNH ĐỀ ĐẢO,
MỆNH ĐỀ TƯƠNG ĐƯƠNG 01.
MỆNH ĐỀ, MỆNH ĐỀ CHỨA BIẾN,
MỆNH ĐỀ PHỦ ĐỊNH KĐ 1 MỆNH ĐỀ Đúng (1) 1 + 1 = 2. HĐKP 1:
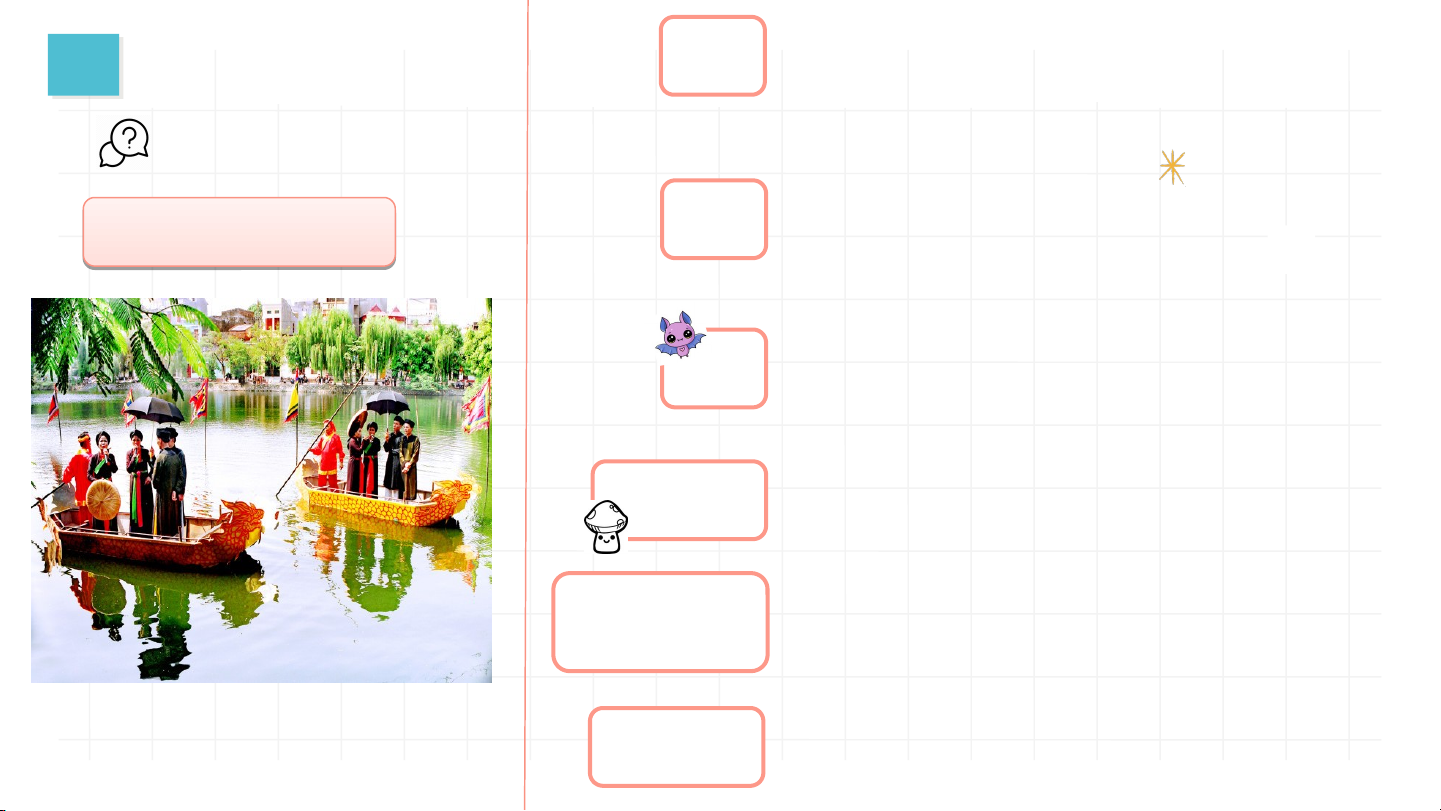
(2) Dân ca Quan họ là di sản văn hóa KĐ Thảo h ảo luận u nh n ó h m m đô đ i ô Đúng
phi vật thể đại diện cho nhân loại. KĐ Trong những câu trên, (3) Dơi là một loài chim. Sai
a) Câu nào là khẳng định đúng,
câu nào là khẳng định sai? Không phải
(4) Nấm có là một loài thực vật không? câu KĐ
b) Câu nào không phải khẳng định? Câu KĐ không xác định được
(5) Hoa hồng đẹp nhất trong các loài hoa.
c) Câu nào là khẳng định, nhưng Đúng Sai
không thể xác định nó đúng hay Không phải (6) Trời ơi, nóng quá! sai? câu KĐ 1 MỆNH ĐỀ
Mệnh đề là một khẳng định đúng hoặc sai.
Một khẳng định đúng gọi là mệnh đề đúng.
Một khẳng định sai gọi là mệnh đề sai.
Những câu không xác đinh
được tính đúng sai không phải
Một mệnh đề không thể vừa đúng vừa sai. là mệnh đề.
Chú ý: Người ta thường sử dụng các chữ cái in hoa P, Q, R, ... để biểu thị các ! mệnh đề.
Ví dụ 1: Trong các câu sau đây Trả lời: câu nào là mệnh đề: a) 3 là số lẻ; a) Là mệnh đề đúng; MỆ M NH N H ĐỀ Đ T O T Á O N N HỌ H C Ọ b) 1+2 > 3; b) Là mệnh đề sai;
c) là số vô tr phải không?;
c) Là câu hỏi, không phải mệnh đề; d) 0,0001 là số rất bé; d) Không phải mệnh đề;
e) Đến năm 2050, con người sẽ đặt e) Là mệnh đề. chân lên Sao Hỏa. Chú ý:Nhữ N n hữ g m n ệnh ệ nh đề li đ ên qu ề li an ên qu an đến t đế oán o án học đư h ợ ọc đư c ợ gọi là gọ i là mệnh đ mệ ề t nh đ oán họ oá c. n họ Thự Th c hành ực 1: hành 1: Trả lời:
Trong các câu sau, câu nào là mệnh đề? a) là số vô tỉ; a) Là mệnh đề; 1 1 1 b) + +...+ > 2 ; √2 √3 √10 b) Là mệnh đề;
c) 100 tỉ là số lớn nhất; c) Không phải mệnh đề;
d) Trời hôm nay đẹp quá! d) Không phải mệnh đề. Thực c hành 2: 2 Trả lời:
Xét tính đúng sai của mệnh đề sau: a) Là mệnh đề đúng;
a) Vịnh Hạ Long là di sản thiên nhiên thế giới; 2 b) Là mệnh đề sai;
b) √(−5) =−5 ; c) Là mệnh đề đúng. c) 52+ 122= 132 . Trả lời:
2 MỆNH ĐỀ CHỨA BIẾN
a) Không thể, vì câu này khi đúng khi sai, tùy HĐKP 2: Mệnh đề chứa biến theo giá trị của n.
Xét câu “n chia hết cho 5” (n là số tự nhiên).
b) Với n = 125 ta được câu “125 chia hết cho 5”
a) Có thể khẳng định câu trên là đúng hay
là một khẳng định đúng. sai không?
Với n = 81 ta được câu “81 chia hết cho 5” là
b) Tìm hai giá trị của n sao cho câu trên là một khẳng định sai.
khẳng định đúng,hai giá trị của n sao cho
- Mệnh đề chứa biến kí hiệu P(n)
câu trên là khẳng định sai.
- Một mệnh đề chứa biến có thể chứa
một biến hoặc nhiều biến.
Ví dụ 2: Cho các mệnh đề chứa biến Trả lời: 1
𝑎¿ 𝑃 ( 𝑥):2 𝑥 =1 ; a) Với 𝑥 = thì 𝑃 2 (12):2. {1} over {2} =1
𝑏¿ 𝑅( 𝑥, 𝑦): 2 𝑥 + 𝑦 =3 là mệnh đề đúng.
(mệnh đề này chứa hai biến x và y) Với 𝑥 =
1 thì 𝑃 (1) :2. 1 = 1
𝑐 ¿ 𝑇 (𝑛) :2 𝑛 +(n là số tự nhiên) là mệnh đề sai.
Với mỗi mệnh đề chứa biến trên, tìm những b) Với 𝑥 = 1 , 𝑦 = t
1hì 𝑅 (1,1): 2.1+1=3
giá trị của biến để đươc một mệnh đề đúng, là mệnh đề đúng. mệnh đề sai. Với 𝑥 = 1 , 𝑦
= t2hì 𝑅 (1 ,2 ):2.1+ 2 = 3 là mệnh đề sai.
Ví dụ 2: Cho các mệnh đề chứa biến Trả lời:
𝑎¿ 𝑃 ( 𝑥):2 = 𝑥 1 ;
c) Lấy số tự nhiên bất kì ta đều được là
𝑏¿ 𝑅( 𝑥, 𝑦): 2 + 𝑥 𝑦 =3 một số lẻ, nghĩa là 𝑇 (𝑛 𝑥 𝑜 ) : 2 +
(mệnh đề này chứa hai biến x và y)
là số chẵn” là mệnh đề sai.
𝑐 ¿ 𝑇 (𝑛) :2 𝑛 +(n là số tự nhiên)
Do đó không có giá trị của để là mệnh đề đúng.
Với mỗi mệnh đề chứa biến trên, tìm những 𝑇 (
𝑛 𝑜 l)à mệnh đề sau với số tự nhiên bất
giá trị của biến để đươc một mệnh đề đúng, kì. mệnh đề sai. Thực hành 3 Trả lời:
Với mỗi mệnh đề chứa biến sau, tìm
a) Khi hoặc thì đúng; sai với các giá trị
những giá trị của biến để nhận được một (thực) khác của .
mệnh đề đúng và một mệnh đề sai:
b) đúng với mọi giá trị (thực) của ;
𝑎¿ 𝑃(𝑥): { } 𝑥 ^ {2} =2;
không có giá trị của đề sai.
𝑏¿ 𝑄(𝑥): {𝑥} ^ {2} +1>0 ;
c) Với n = 1 ta được R(1): “1 + 2 chia hết cho
𝑐¿ 𝑅(𝑛): 𝑛 +chia hết cho 3”
3” là một mệnh đề đúng. (n là số tự nhiên)
Với n = 2 ta được R(2): “2 + 2 chia hết cho 3” là một mệnh đề sai.
3 MỆNH ĐỀ PHỦ ĐỊNH HĐKP 3:
Xét các cặp mệnh đề nằm cùng dòng của bảng (có hai cột và ) sau đây: Dơi là một loài chim. .
không phải là một số hữu tỉ. là một số hữu tỉ.
Nêu nhận xét về tính đúng sai của hai mệnh đề cùng cặp. Trả lời: Dơi là một loài chim. .
không phải là một số hữu tỉ. là một số hữu tỉ.
"Dơi là một loài chim" là mệnh đề sai. "Dơi không phải là một loài chim" là mệnh đề đúng.
"π không phải là một số hữu tỉ" là mệnh đề đúng. "π là một số hữu tỉ" là mệnh đề sai.
s qr t {2 } + s q r t {3 } > s q r t {5l} à mệnh đề đúng. s q r t { 2 } + s q r t {3 } ≤ s q r t {5là } mệnh đề sai. s qr t { 2} s qr t { 18} =là
6 mệnh đề đúng. s qr t { 2} s qr t { 18} ≠là 6 mệnh đề sai. Dơi là một loài chim. .
không phải là một số hữu tỉ. là một số hữu tỉ.
+ Mệnh đề và là hai phát biểu trái ngược nhau thì ta nói là mệnh đề phủ định của mệnh đề .
+ Để phủ định mệnh đề , người ta thường thêm hoặc bớt từ "không" hoặc "không phải"
vào trước vị ngữ của mệnh đề hoặc cách diễn đạt khác như: a > b thì phủ định của nó là .
Nếu P đúng thì đúng hay s
ai? Nếu P sai thì đúng hay sai? KẾT LU KẾT ẬN LU
Mỗi mệnh đề có mệnh đề phủ định, kí hiệu là .
Mệnh đề P và mệnh đề phủ định của nó có tính
đúng sai trái ngược nhau.
Nghĩa là khi P đúng thì sai, khi P sai thì đúng. Trả lời:
Ví dụ 3: Phát biểu mệnh đề phủ định của
Mệnh đề phủ định của các mệnh đề các mệnh đề sau: trên là:
P: “Tháng 12 dương lịch có 31 ngày”;
: “Không phải tháng 12 dương lịch có 31 ngày”;
𝑄: {9} ^ {10} ≥ {10} ^ {9}
𝑄: {9} ^ {10} < {10} ^ {9} R: “Phương trình 𝑥2 + 1 = c 0 ó nghiệm”. : “Phương trình 𝑥2 + 1 = vô 0 nghiệm”. Thực hành 4 Trả lời:
(Kí hiệu là mệnh đề đã cho).
Phát biểu mệnh đề phủ định của các
mệnh đề sau. Xét tính đúng sai của mỗi
a) : "Paris không phải là thủ đô của nước Anh". sai, đúng
mệnh đề và mệnh đề phủ định của nó.
b) : "23 không phải là số nguyên tố".
a) Paris là thủ đô của nước Anh; đúng, sai. b) 23 là số nguyên tố;
c) : "2021 không chia hết cho 3 ". sai, c) 2 021 chia hết cho 3; đúng.
d) Phương trình x2 – 3x + 4 = 0 vô nghiệm.
d) : "Phương trình có nghiệm". đúng, sai. 02
MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO,
MỆNH ĐỀ TƯƠNG ĐƯƠNG
4 MỆNH ĐỀ KÉO THEO HĐKP 4: Xét hai mệnh đề sau:
(1) Nếu ABC là tam giác đều thì nó là tam giác cân;
(2) Nếu 2a – 4 > 0 thì a > 2.
a) Xét tính đúng sai của mỗi mệnh đề trên.
b) Mỗi mệnh đề trên đều có dạng “Nếu P thì Q”. Chỉ ra P và Q ứng với mỗi mệnh đề đó. Trả lời:
a) (1) và (2) đều là mệnh đề đúng
b) Với mệnh đề (1), "Tam giác là tam giác đều", : "Tam giác là tam giác cân". Với mệnh đề (2), ". KẾT LUẬN
Cho hai mệnh đề P và Q. Mệnh đề "Nếu P thì Q" 𝑃 ⇒ 𝑄
được gọi là mệnh đề kéo theo, kí hiệu là 𝑄 Mệnh đề 𝑃
⇒ chỉ sai khi P đúng và Q sai. Nếu P đúng thì Nếu P đúng thì mệnh đề P Q mệnh đề P Q đúng khi nào và đúng khi nào và khi nào? sai khi nào Nhận xét: a) Mệnh đề 𝑃 ⇒
𝑄còn được phát biểu là "P kéo theo Q" hoặc "Từ P suy ra Q".
b) Để xét tính đúng sai của mệnh đề, ta chỉ cần xét trường hợp P đúng.
Khi đó, nếu Q đúng thì mệnh đề đúng, nếu Q sai thì mệnh đề sai. ĐƯỜNG LÊN ĐỈNH OLYMPIA
HOẠT ĐỘNG NHÓM ĐÔI
THI TRẢ LỜI CÂU HỎI
Với mỗi câu hỏi, trong vòng 10s
nhóm nào bấm chuông trước được
giành quyền trả lời trước. Trả lời
sai sẽ nhường quyền trả lời cho các nhóm còn lại. 1
Câu hỏi: Trong các câu sau câu nào là mệnh đề?
A. 15 là số nguyên tố B. Không được đi học muộn. 10 9 8 7 6 5 4 3 2 1 0
C. Hôm nay trời nắng. D. Bạn có đói không? ĐÁP ÁN A Answer
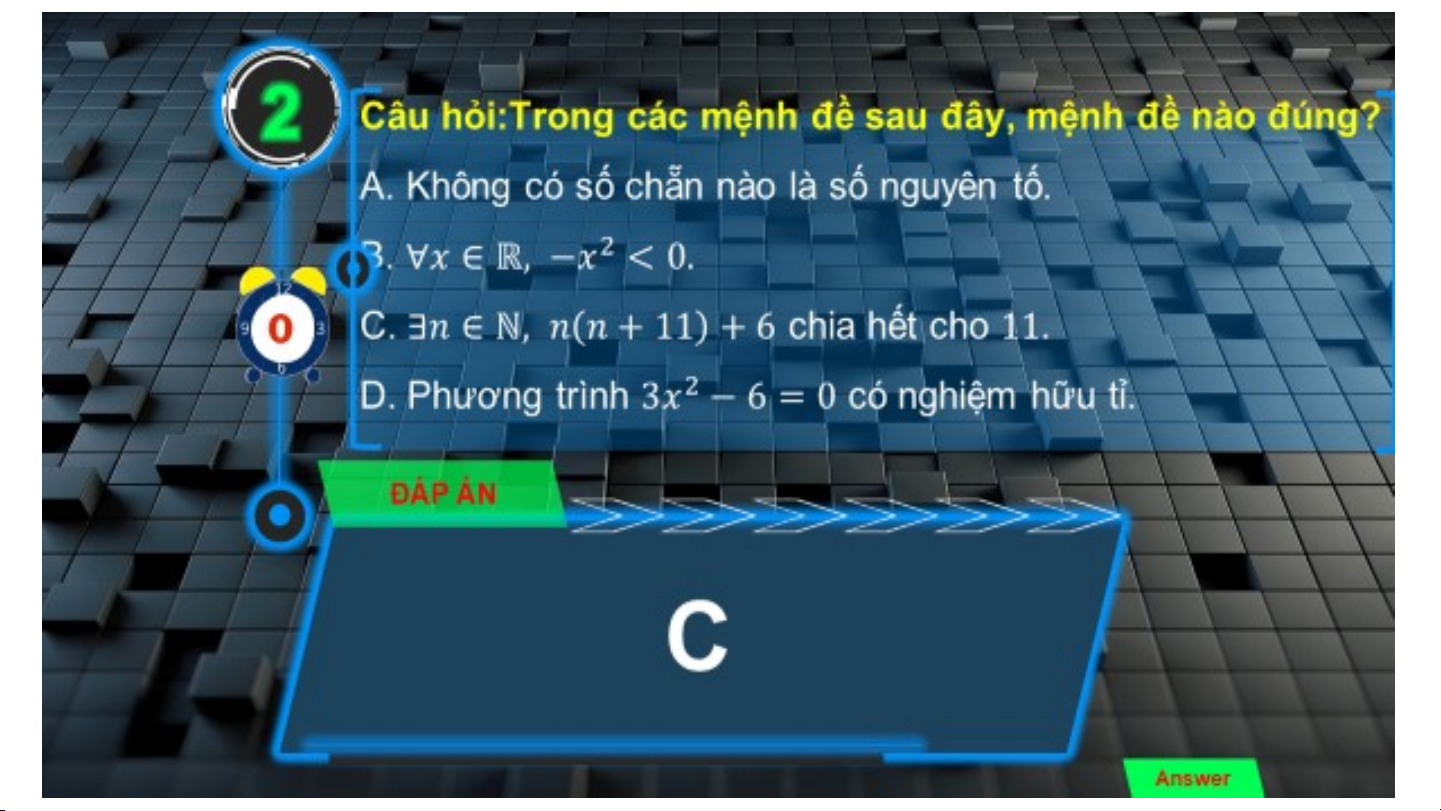
2 Câu hỏi:Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Không có số chẵn nào là số nguyên tố. B. 10 9 8 7 6 5 4 3 2 1 0 C. chia hết cho
D. Phương trình có nghiệm hữu tỉ. ĐÁP ÁN C Answer HƯỚNG DẪN Hoàn thành bài tập VỀ NHÀ trong SBT Ghi nhớ các kiến thức Đọc trước bài mới đã học Bài 2: Tập hợp
HẸN GẶP LẠI CÁC EM Ở TIẾT HỌC SAU!
Document Outline

• Slide 1
• Slide 2
• CHƯƠNG I: MỆNH ĐỀ VÀ TẬP HỢP
• LUYỆN TẬP
• MỆNH ĐỀ, MỆNH ĐỀ CHỨA BIẾN, MỆNH ĐỀ PHỦ ĐỊNH
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• 02
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33
• Slide 34