Giáo án điện tử Toán 10 Bài 2 Chân trời sáng tạo: Đường thẳng trong mặt phẳng toạ độ
Bài giảng PowerPoint Toán 10 Bài 2 Chân trời sáng tạo: Đường thẳng trong mặt phẳng toạ độ hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 10. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 10
Môn: Toán 10
Sách: Chân trời sáng tạo
Thông tin:
Tác giả:
Preview text:
BÀI 2: ĐƯỜNG THẲNG TRONG
MẶT PHẲNG TỌA ĐỘ
NHIỆT LIỆT CHÀO MỪNG
CÁC EM ĐẾN VỚI BÀI HỌC MỚI! KHỞI ĐỘNG
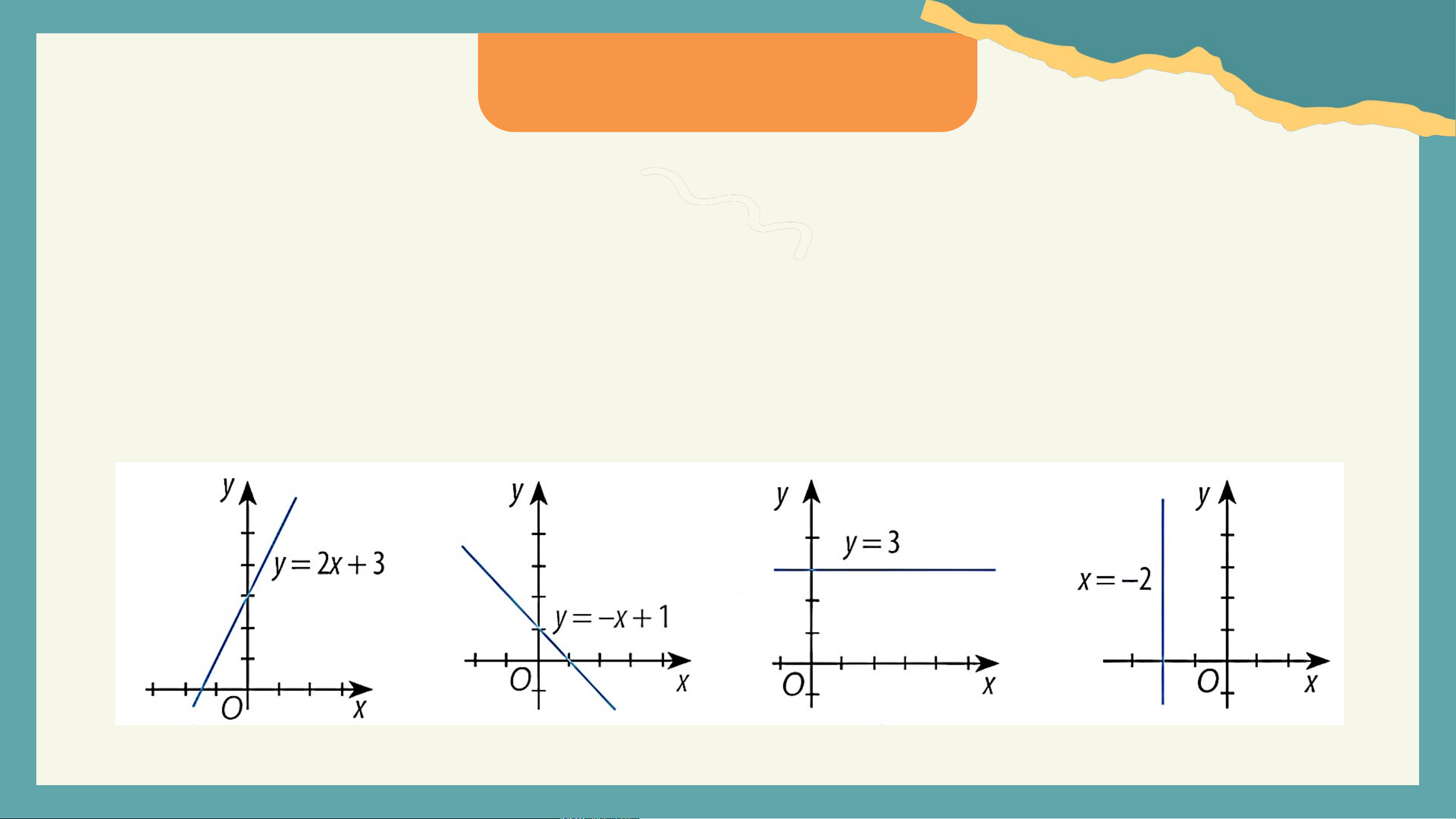
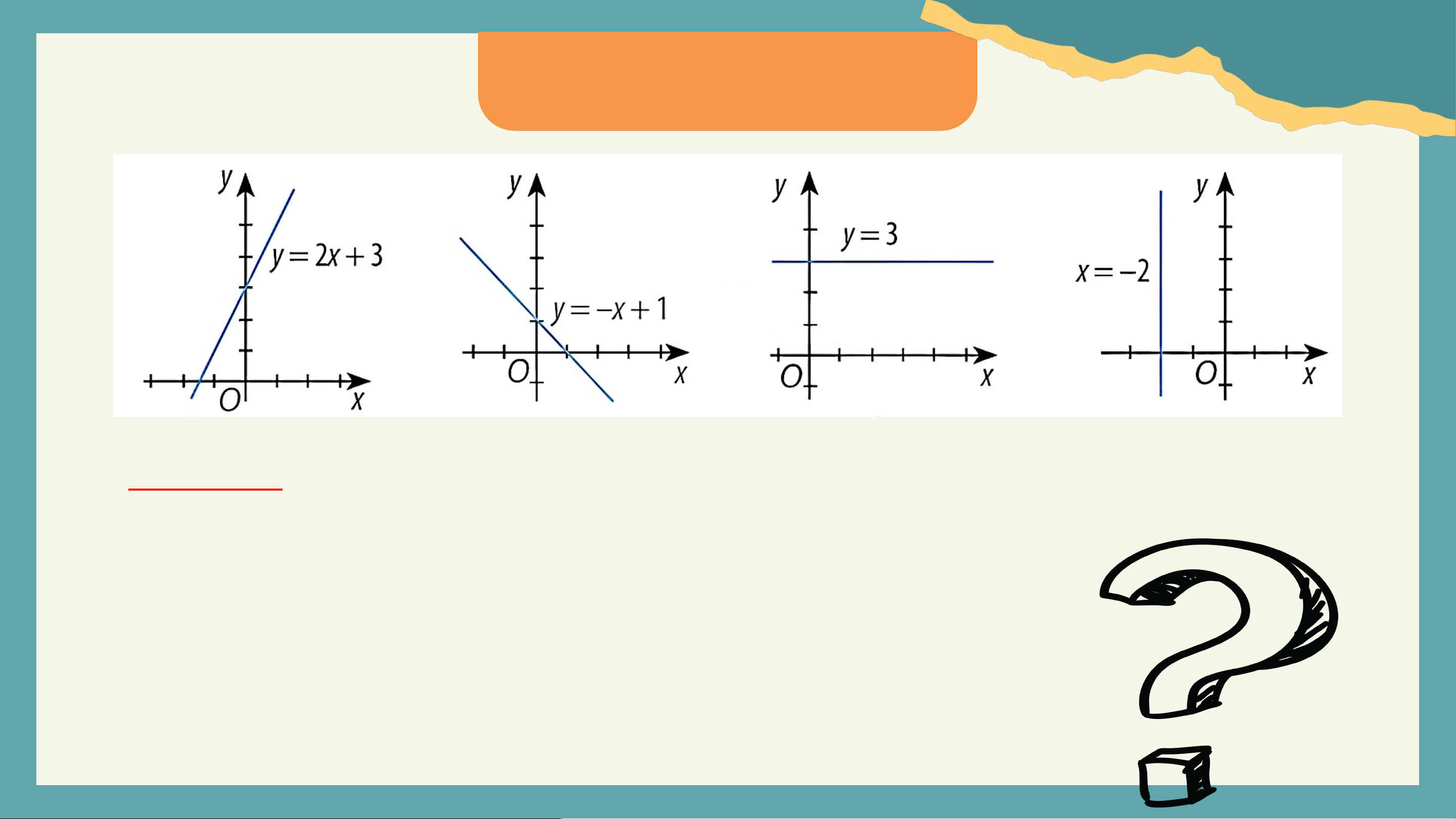
Tìm được các giá trị của tham số a, b, c để phương trình ax + by + c = 0
có thể biểu diễn được các đường thẳng trong hình dưới đây: KHỞI ĐỘNG Kết quả:
- Đường thẳng 1: a = 2; b = -1; c = 3
- Đường thẳng 2: a = -1; b = -1; c = 1
- Đường thẳng 3: a = 0; b = -1; c = -3
- Đường thẳng 4: a = 1; b = 0; c = 2
CHƯƠNG IX. PHƯƠNG PHÁP TỌA
ĐỘ TRONG MẶT PHẲNG
BÀI 2: ĐƯỜNG THẲNG TRONG
MẶT PHẲNG TỌA ĐỘ 01 NỘI DUNG
Phương trình đường thẳng BÀI HỌC 02
Vị trí tương đối của hai đường thẳng 03 NỘI DUNG
Góc giữa hai đường thẳng BÀI HỌC 04
Khoảng cách từ một điểm đến một đường thẳng
1. Phương trình đường thẳng
a) Vectơ chỉ phương và vectơ pháp tuyến của đường thẳng HĐ H K Đ P K 1
Thảo luận nhóm, hoàn thành HĐKP1.
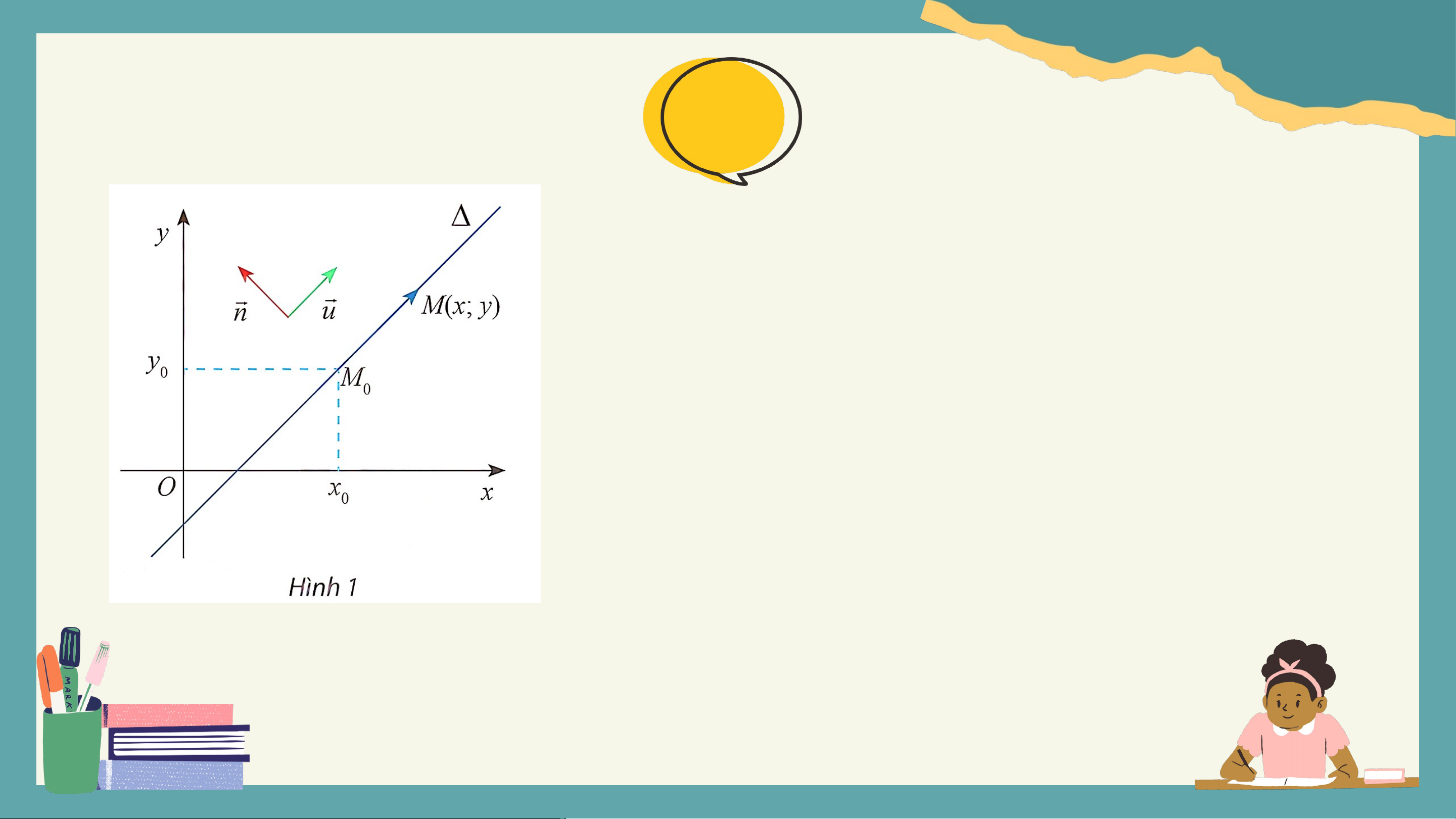
Trong mặt phẳng , cho đường thẳng đi qua điểm và cho hai vectơ
và khác vectơ-không. Cho biết có giá song song hoặc trùng với .
a) Tính tích vô hướng và nêu nhận xét về phương của hai vectơ .
b) Gọi là điểm di động trên . Chứng tỏ rằng vectơ luôn củng
phương với vectơ và luôn vuông góc với vectơ . Giải a) . = a.b + b.(-a) = 0 .
b) Vì M, thuộc đường thẳng nên chính là
vectơ chỉ phương của đường thẳng . Suy
ra, vectơ luôn cùng phương với vectơ và
luôn vuông góc với vectơ . KẾT LUẬN
- Vectơ chỉ phương của đường thẳng
Vectơ được gọi là vectơ chỉ phương của đường thẳng nếu
và giá và giá của song song hoặc trùng với .
- Vectơ pháp tuyến của đường thẳng:
Vectơ là một vectơ pháp tuyến của đường thẳng nếu
và vuông góc với vectơ chỉ phương của . Chú ý:
• Nếu đường thẳng có vectơ pháp tuyến = (a; b) thì sẽ nhận =
(b; -a) hoặc = (-b; a) là một vectơ chỉ phương.
• Nếu là một vectơ chỉ phương của đường thẳng thì vectơ ,
( cũng là một vectơ chỉ phương của đường thẳng .
• Nếu đường thẳng có vectơ chỉ phương là thì vec tơ là một
vectơ pháp tuyến của đường thẳng.
a) Cho đường thẳng có vectơ pháp tuyến . Ví V dụ 1 d
Tìm vectơ chỉ phương của .
b) Cho đường thẳng có vectơ chi phương .
Tìm hai vectơ pháp tuyến của . Giải a) có vectơ pháp tuyến
Suy ra cũng có vectơ pháp tuyến
và có vectơ chỉ phương .
b) Hai vectơ pháp tuyến của là:
b) Phương trình tham số của đường thẳng HĐ H K Đ P K 2
Thảo luận nhóm, hoàn thành HĐKP2.
Trong mặt phẳng , cho đường thẳng đi qua điểm và nhận làm
vectơ chỉ phương. Với mỗi điểm thuộc , tìm toạ độ của theo toạ độ của và . Giải Tọa độ điểm M là: KẾT LUẬN:
Trong mặt phẳng Oxy, ta gọi: (với u 2 + u 2 > 0, t) 1 2
là phương trình tham số của đường thẳng đi qua điểm M ) o (x ; y 0 0 có vectơ chỉ phương = (u ). 1; u2 Chú ý:
Cho t một giá trị cụ thể thì ta xác định được một điểm trên đường
thẳng ∆ và ngược lại. Ví dụ
dụ 2 a) Viết phương trình tham số của đường thẳng đi qua điểm và nhận làm vectơ chi phương.
b) Tìm toạ độ điểm trên , biết có hoành độ bằng . Giải .
a) Phương trình tham số của đường thẳng :
b) Thay vào phương trình , ta được , suy ra .
Thay vào phương trình , ta được . Vậy . Thự T c hự c hà h nh à nh 1
a) Viết phương trình tham số của đường thẳng đi qua điểm và nhận làm vectơ chỉ phương.
b) Tìm toạ độ điểm trên , biết có tung độ bằng 1 .
a) Phương trình tham số của đường thẳng là: Giải
b) Thay y = 1 vào phương trình y = 5 - 4t, ta được: 1 = 5 - 4t t = 1
Thay t = 1 vào phương trình x = -9 + 8t, ta được: x = -9 + 8.1 = -1 Vậy P = (-1; 1) VẬN DỤNG 1
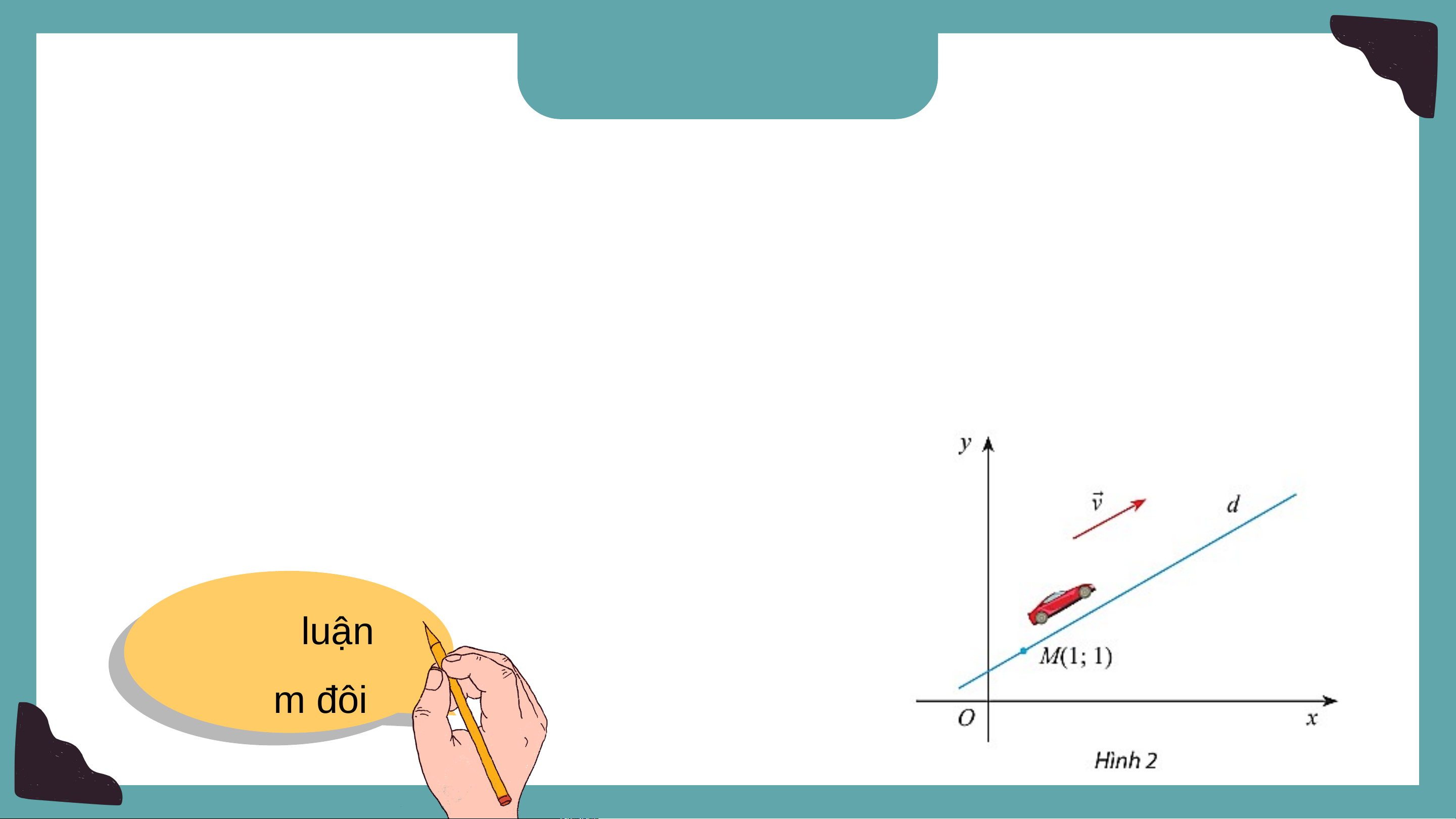
Một trò chơi đua xe ô tô vượt sa mạc trên máy tính đã xác định trước một
hệ trục toạ độ . Cho biết một ô tô chuyển động thẳng đều từ điểm với vectơ vận tốc .
a) Viết phương trình tham số của đường thẳng biểu diễn đường đi của ô tô.
b) Tìm toạ độ của xe ứng với . Th T ảhoả lou lậunậ n nh n óhm ó đ m ôđiôi Giải
a) Phương trình tham số của đường thẳng d là:
b) Thay t = 2 vào phương trình đường thẳng d, tọa độ của xe là:
Thay t = 4 vào phương trình đường thẳng d, tọa độ của xe là:
c) Phương trình tổng quát của đường thẳng HĐ H K Đ P K 3 P
Trong mặt phẳng , cho đường thẳng đi qua điểm và nhận làm vectơ
pháp tuyến. Với mỗi điểm thuộc , chứng tỏ rằng điểm có toạ độ thoả mãn phương trình:
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19