CHÀO MỪNG QUÝ THẦY CÔ ĐẾN DỰ
GIỜ TIẾT HỌC NGÀY HÔM NAY LỚP 10a3 KHỞI ĐỘNG
Em hiểu gì về hình ảnh này?
F
 θ d  KHỞI ĐỘNG
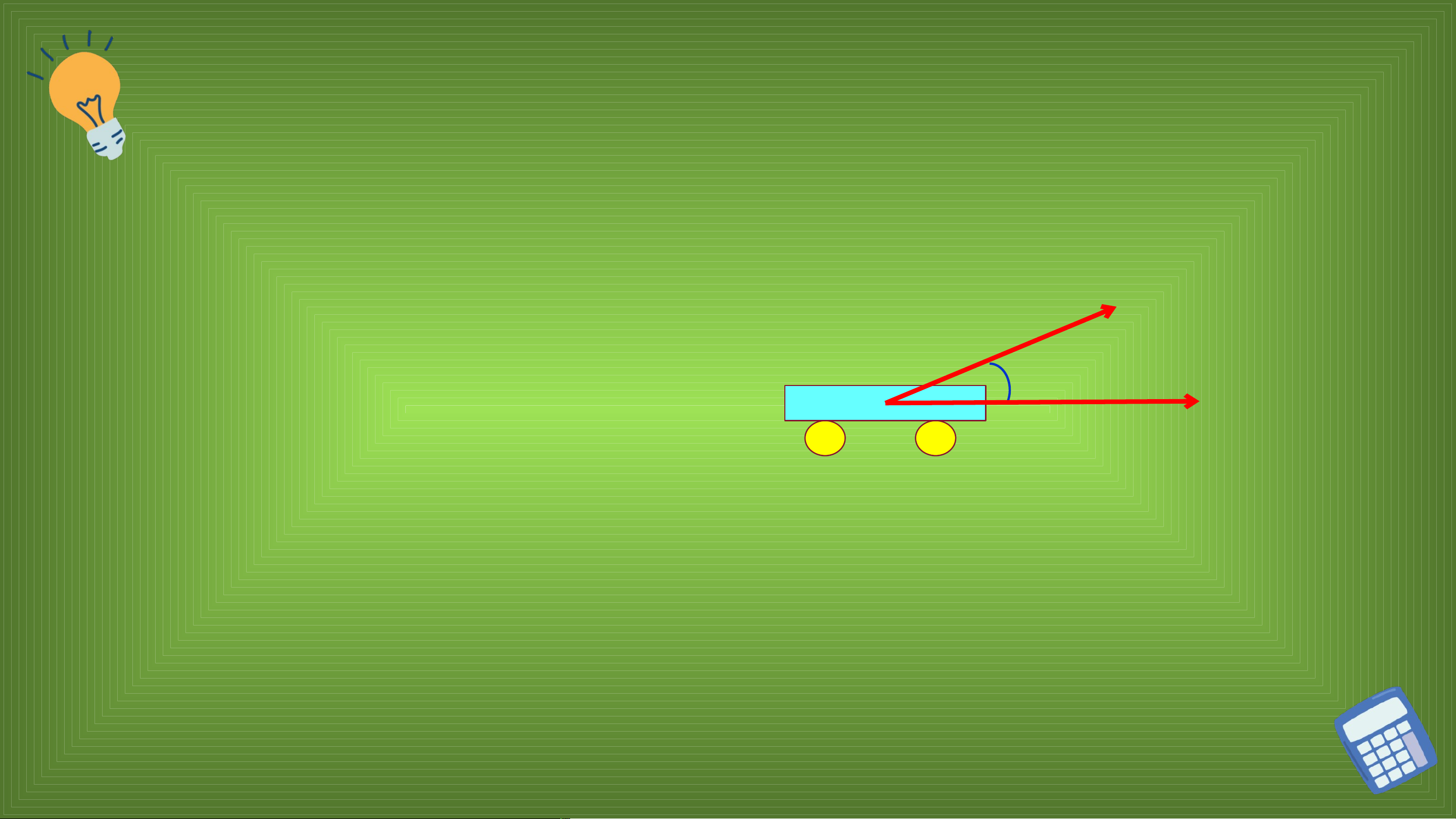
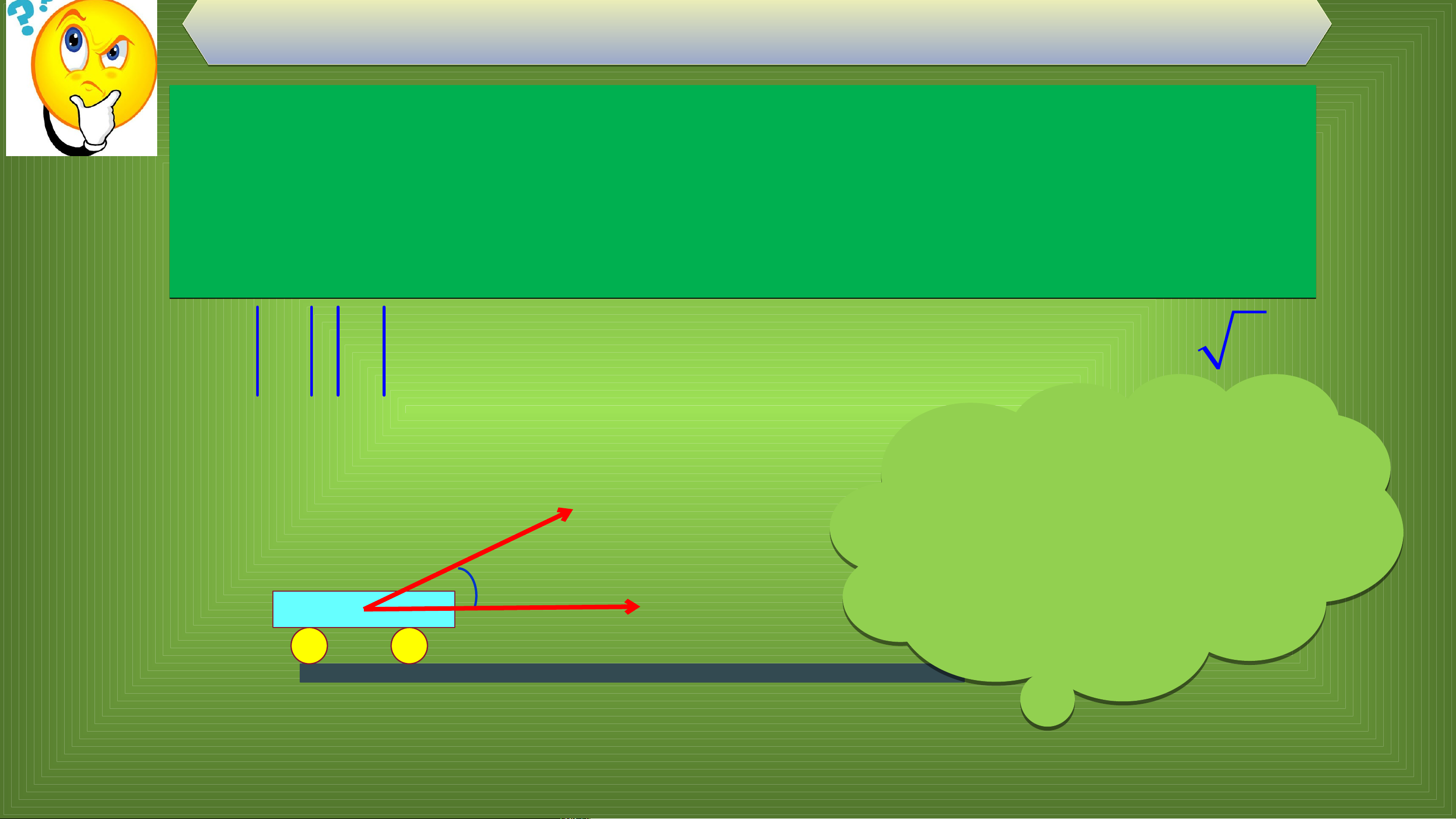
Tác dụng của một lực vào một vật làm 
cho vật đó dịch chuyển theo vectơ thì sẽ F 
sinh ra một công là A. Công A đó được θ d  tính theo công thức cos (J)
trong đó là góc giữa hai vectơ và .
TIẾT 39 - BÀI 4: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
NỘI DUNG BÀI HỌC(Tiết 1) 01 Góc giữa hai vectơ 02
Tích vô hướng của hai vectơ 01 Góc giữa hai vectơ HĐKP 1:
Các em hày trả lời các câu hỏi sau?
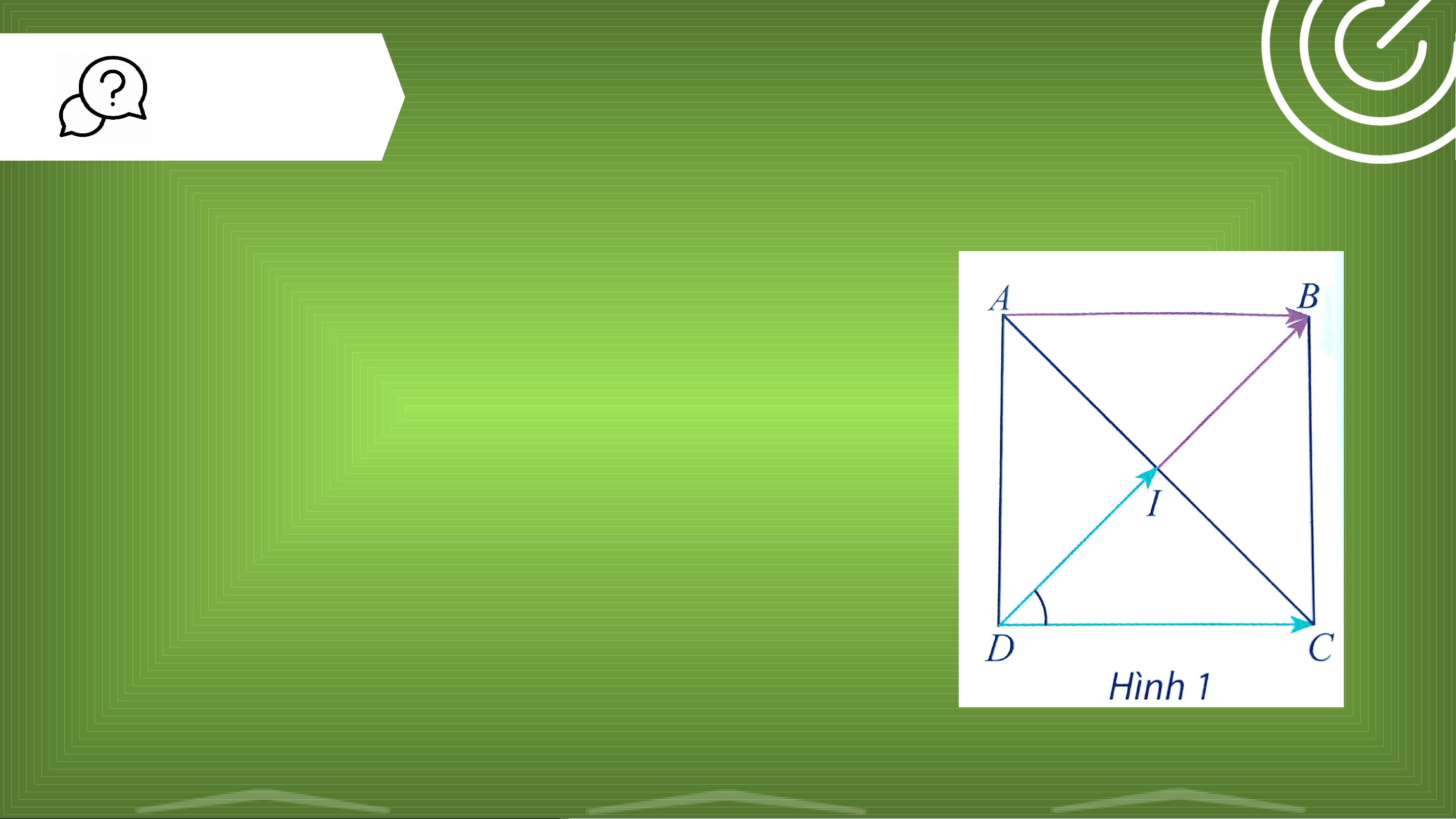
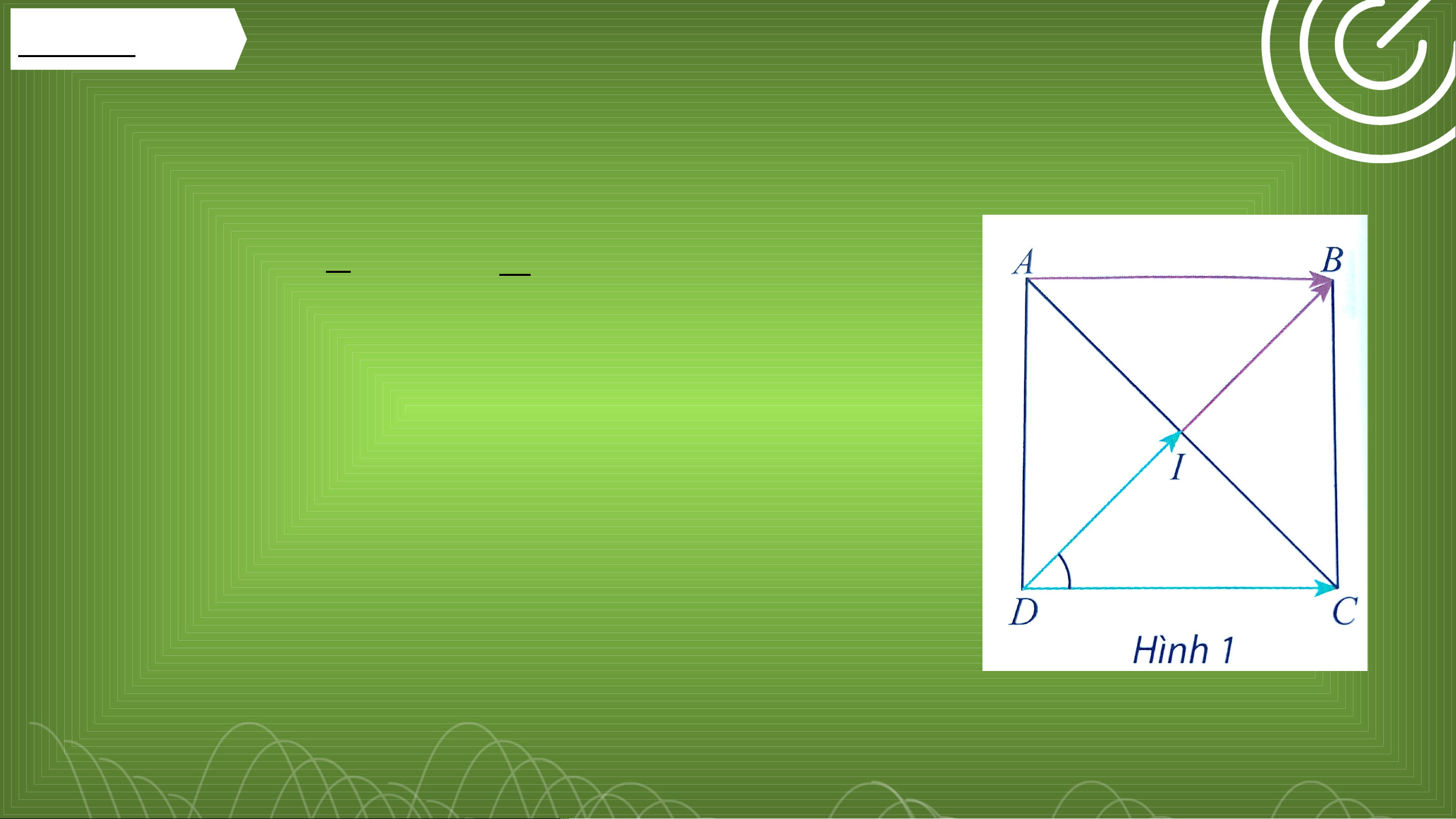
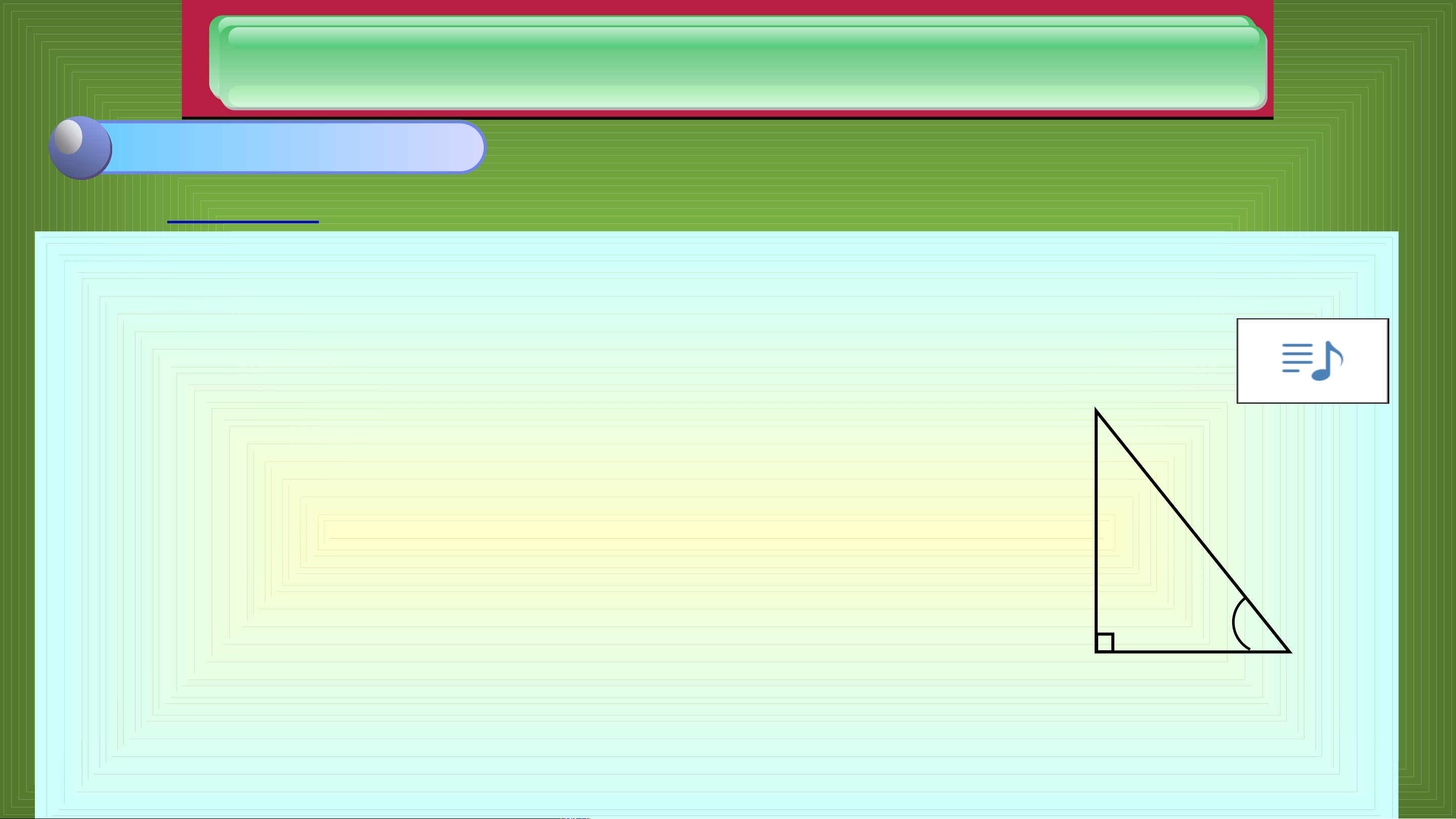
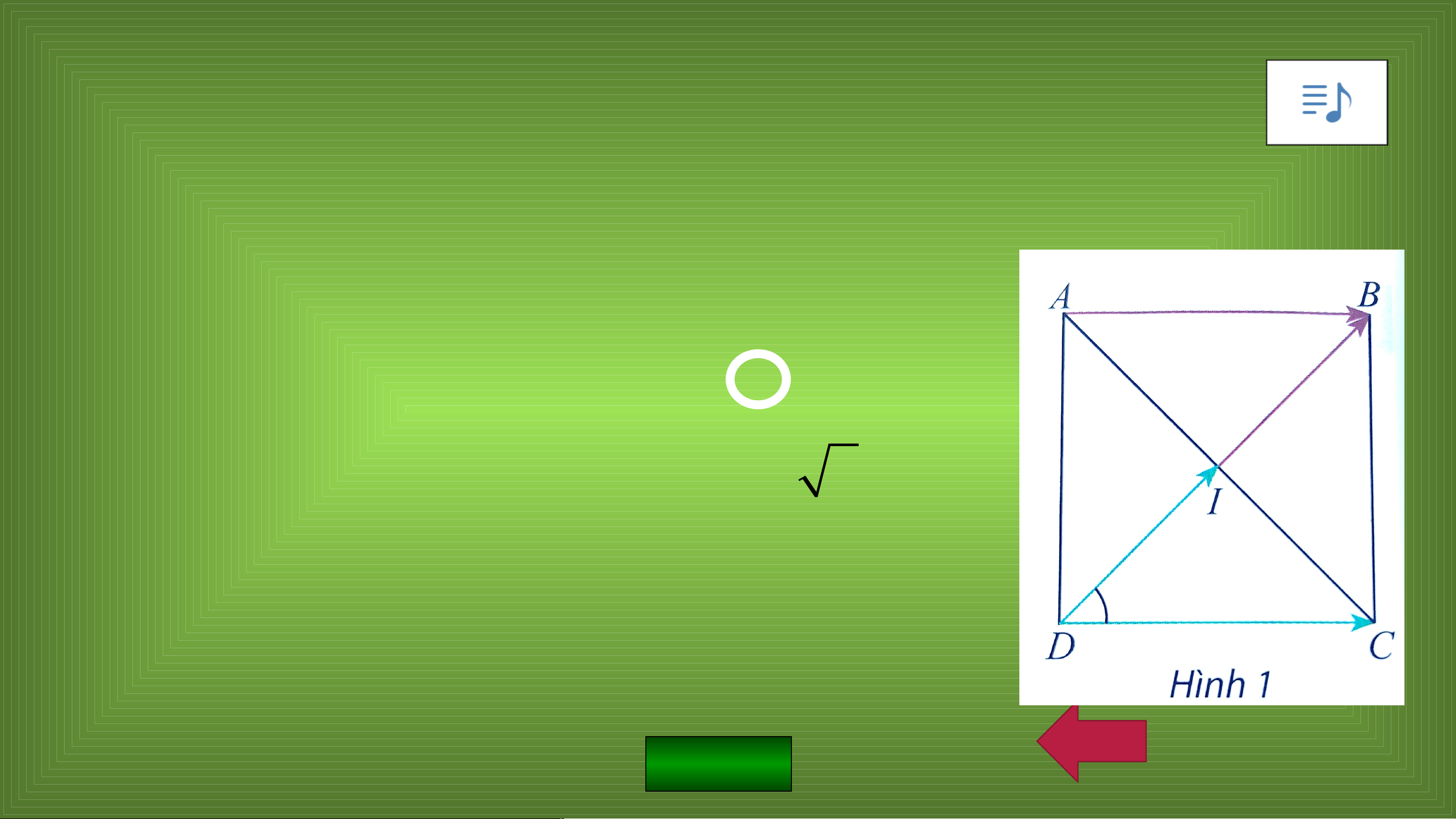
Cho hình vuông ABCD có tâm I (Hình 1). a) Tính ^ 𝐼𝐷𝐶 .
b) Tìm hai vectơ cùng có điểm đầu là D và
điểm cuối lần lượt là I và C.
c) Tìm hai vectơ cùng có điểm đầu là D và 
lần lượt bằng vectơ𝐼𝐵  và 𝐴𝐵. Trả lời
a) Vì ABCD là hình vuông nên đường chéo DB cũng là ^
phân giác của góc 𝐴𝐷𝐶 1 1 Suy ra: ^ 𝐵𝐷𝐶= ^ 𝐴𝐷𝐶 . 90𝑜 2 ¿ 2 = 45𝑜 ¿ ^ 𝐼𝐷𝐶
b) -Vectơ có điểm đầu là D và điểm cuối là I là vectơ  𝐷𝐼
- Vectơ có điểm đầu là D và điểm cuối là C là vectơ 𝐷𝐶
c) Hai véctơ lần lượt bằng là 𝐷𝐼; 𝐷𝐶
Dựa vào bài tập trên em nào có thể nêu
khái niệm góc giữa hai vectơ?
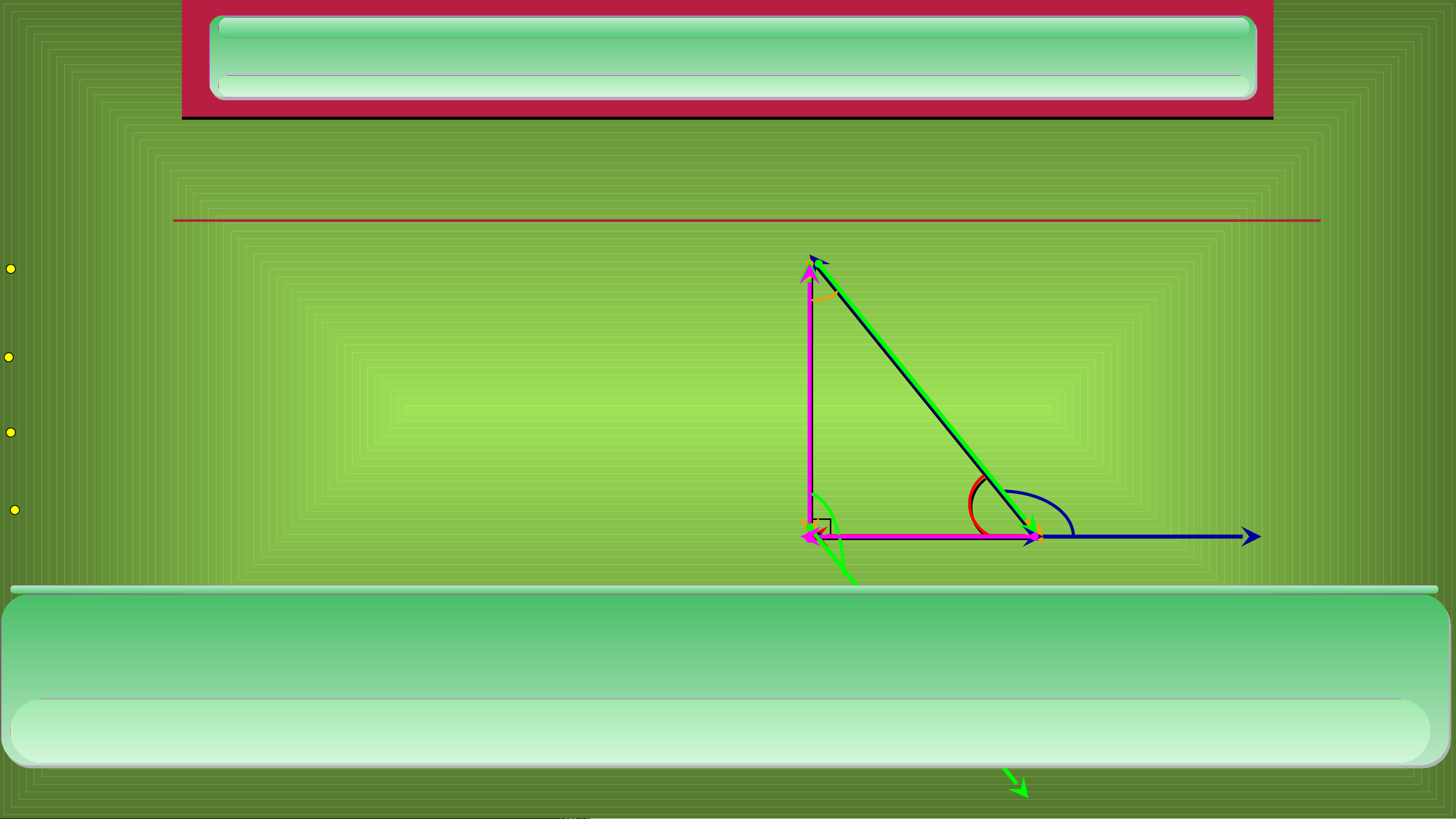
BÀI 4: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ r r r Click to add Title Góc giữa hai vectơ 2 1. Cho hai vectô a vaø b ñeà u khaù c vectô 0 uur r uur r  r vaø moä t ñieå m O baá t kì: O = A a , O = B . b A b r r a Goùc a O giöõa hai rb vectô B
BÀI 4: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ r r r Click to add Title Góc giữa hai vectơ 2 1. Cho hai vectô a vaø b ñeà u khaù c vectô 0 uur r uur r  r vaø moä t ñieå m O baá t kì: O = A a , O = B . b A b r r a Goùc a O giöõa hai rb vectô B
Góc với số đo từ đến được gọi là góc giữa hai vectơ và Ta kí hiệu góc
giữa hai vectơ và là . Nếu thì ta nói rằng và vuông góc với nhau, kí hiệu là hoặc
BÀI 4: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ Click to add Title 2
1. Góc giữa hai vectơ r O a A B rb r r b B O a A BÀI 4: : T T ÍCH óm t TVÔ ắt óm t l ắt ý th ý t u HƯỚNG CỦA HƯỚNG CỦA yết yế HAI VE HAI CTƠ 1). Góc giữa hai vectơ
 Cho hai vectơ và đều khác vectơ Từ một điểm bất kì ta vẽ và Góc với số đo
từ đến được gọi là góc giữa hai vectơ và Ta kí hiệu góc giữa hai vectơ và là .
Nếu thì ta nói rằng và vuông góc với nhau, kí hiệu là hoặc  Chú ý:
- Góc giữa hai vectơ cùng hướng và khác r
vectơ-không thì luôn bằng 00 0
- Góc giữa hai vectơ ngược hướng và khác vectơ-không thì luôn bằng 1800 §4 . T
ích vô hướng của hai vectơ
BÀI 4: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ Click to add Title Góc giữa hai vectơ 2 1.  Ví dụ 1: ˆ Cho tam giaù c ABC vuoâng taïi ,
A AB 3,AC 4,goù cB  0 60 . Hoạt động uur uuur C nhóm(2’) Nhóm 1 Tính số đo ) a  B , A BC; góc: uur uur
Nhóm 2 Tính số đo góc: b)C , A CB uur uuur 0 60
Nhóm 3 Tính số đo góc: ) c  A , B BC; A B uuur uur
Nhóm 4 Tính số đo góc: d) AC,CB
BÀI 4: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ uur uuur uur uur uur uuur uuur uur Tính: B , A BC; C , A CB; A ,
B BC;  AC,CB; uur uuur C B ,ABC · ABC  0 60 uur uur C ,ACB · ACB  0 30 uur uuur uuur uuur  · A , B BC  ' 0  '
BB ,BC BBC 120 uuur uur uuur uu  ur  · 0 AC,CB   ' AC,AC  ' 0 CAC 150 60   A B B' Nhận xét:
Góc giữa hai vectơ có chung điểm đầu hoặc điểm cuối thì điểm chung ấy chính là đinh của góc
Góc giữa hai vectơ có chung điểm giữa thì bằng 180 độ - góc có đỉnh là điểm chu C ng ' ấy
BÀI 4: TÍCH VÔ HƯỚ CH NG N CỦA HAI CỦA VE CTƠ ĐẶT ĐẶT VẤN VẤN ĐỀ Đ

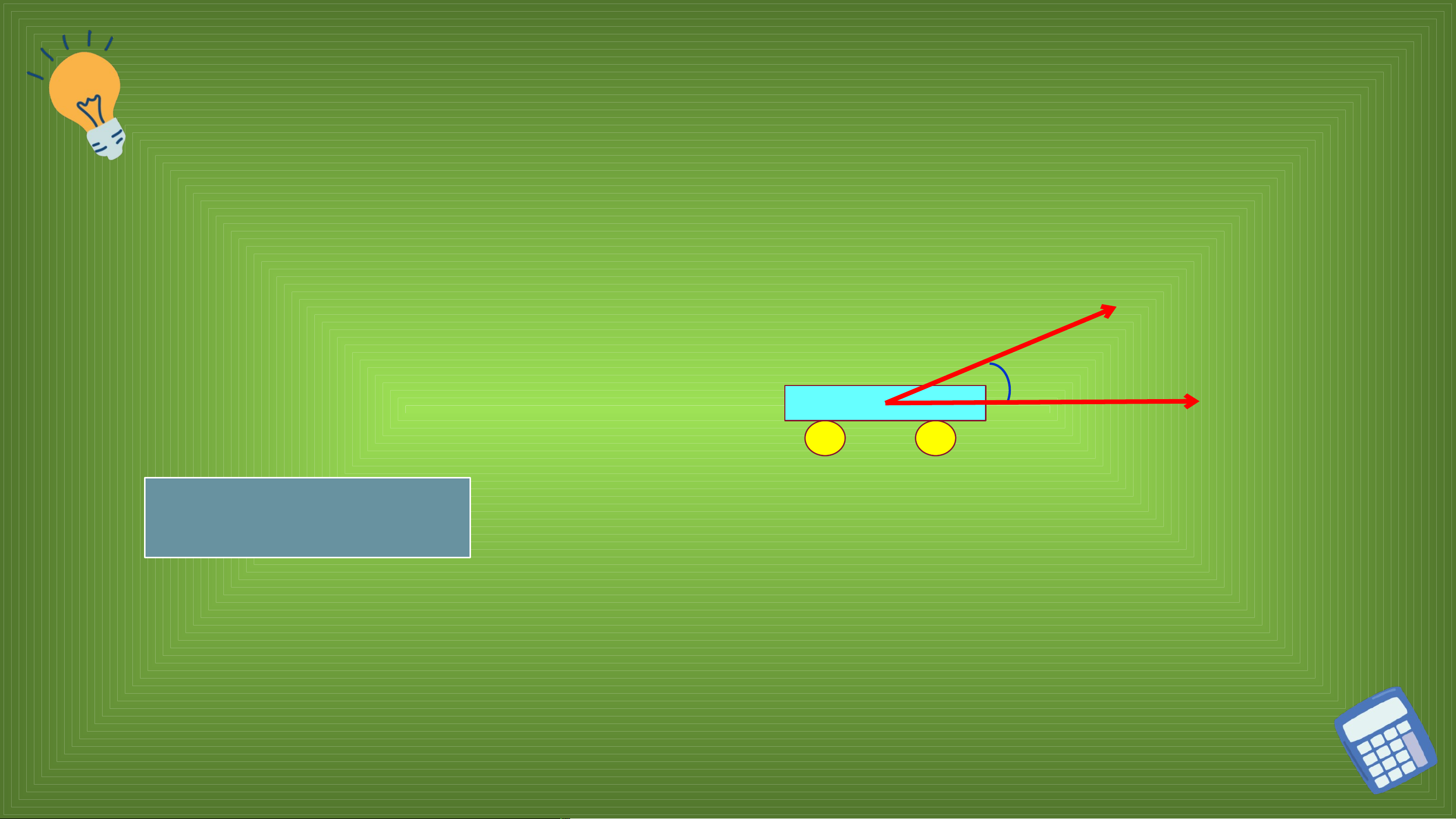
Một người dùng một lực
F có cường độ 10 N kéo một chiếc xe đi  một quảng
 đường dài 100m. Tính công sinh bởi lực F biết rằng góc giữa lực và hướ F ng di chuyển là d 450     A  F d  F d  0 . .cos , 10  .100.cos(45 ) 5  00 2(J ) Trong T toán học, giá trị trị A A
 của của biểu bi thức c trên trê gọi gọi là l F
 tích tí vô hướng
 của c hai ha
  d vectơ vec và F và d
Qua đây em nào có thể nêu khái niệm tích vô hướng của hai vectơ?
BÀI 4: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ Click 1. to Định add T ng itl hĩa e Góc giữa hai vectơ 2 1. Click to add Title
Tích vô hướng của hai vectơ 2 2.     Cho hai vectơ a và đều b
khác vectơ Tích vô hướng của a    0.
b và là một số, k. a í
b hiệu , được xác định bởi công thức:       .
a b  a . b .cos(a,b)       Nếu a  0 hoặc b  0 thì quy ước . a b 0  BÀI 4: : TÍCH VÔ ÍCH HƯỚNG CỦA HƯỚNG CỦA HAI VE HAI CTƠ       Click to add Title Góc giữa hai vectơ 2 1. .
a b  a . b .cos(a,b) Click to add Title
Tích vô hướng của hai vectơ 2 2.  a      .  . .co ? s90o a b a b 0  b Chú ý        a) Với và a b khác vectơ 0 ta có . a b  0  a  . b
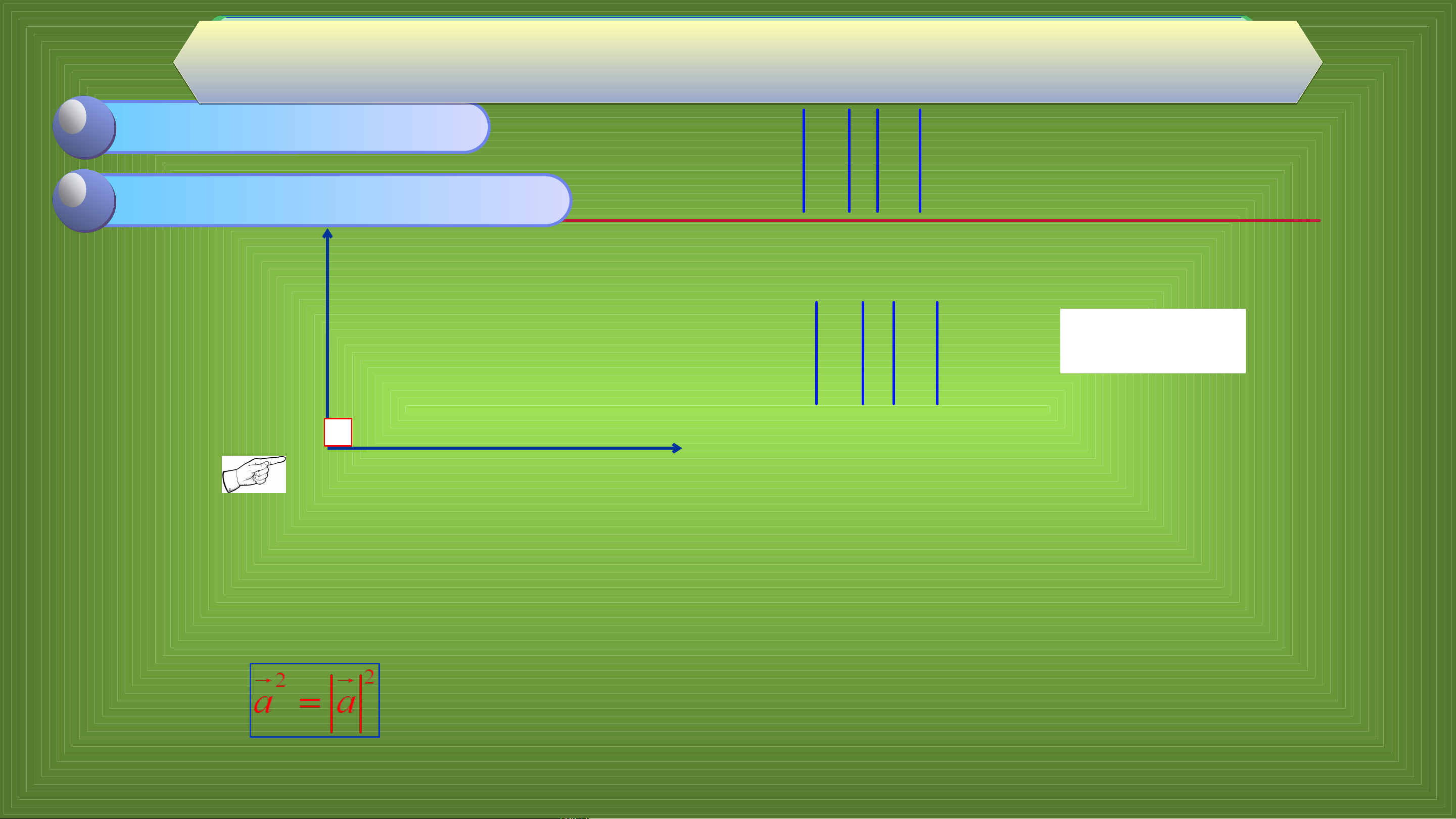
b) (Bình phương vô hướng bằng bình phương độ dài. VD 1:(SGK – tr.98) :
Hoạt động nhóm (2’) Nhóm 1 Tính: a) , , ; b) , , ; Nhóm 2 Tính: c) , , và cùng hướng; Nhóm 3 Tính: d) , , . =12 Nhóm 4 Tìm =? 2 Giải a) b) c) d) 12 2 BÀI 4: : TÍCH VÔ ÍCH HƯỚNG CỦA HƯỚNG CỦA HAI VE HAI CTƠ Click to add Title Góc giữa hai vectơ 2 1. Click to add Title 2
2. Tích vô hướng của hai vectơ  Ví dụ 2: ˆ Cho tam giaù c ABC vuoâng taïi ,
A AB 3,AC 4,goù cB  0 60 .
Hoạt động nhóm (2’)uur uuur C Nhóm 1 Tính: ) a B . A B ; C uur uur Nhóm 2 Tính: b)C . ACB uur uuur 0 Nhóm 3 Tính: 60 ) c A . B BC A B uuur uur Nhóm 4 Tính: d)AC.CB ˆ
VD2: Cho tam giaùc ABC vuoâng taïi ,
A AB 3,AC 4,goùcB  0 60 . Giải
. = ||. ||. cos(, ) = 3. 5. = 7,5 C
b) . = ||. ||. cos(, ) = 4.5. =10  2  2 34 5 4
c) . = ||. ||. cos(,) = 3.5. =-7,5 0 60 A 3 B . = ||. ||. cos(, ) = 4.5. = Bài 5:(SGK – tr.101)
Một người dùng một lực có độ lớn là 90 N làm một vật dịch chuyển một đoạn
100 m. Biết lực hợp với hướng dịch chuyển một góc 60°. Tính công sinh bởi lực . Giả i Công sinh bởi lực là:      
A F.d  F . d .cos F,d  A = 90. 100. cos60o = 4500(J) CỦNG CỐ Câu 1
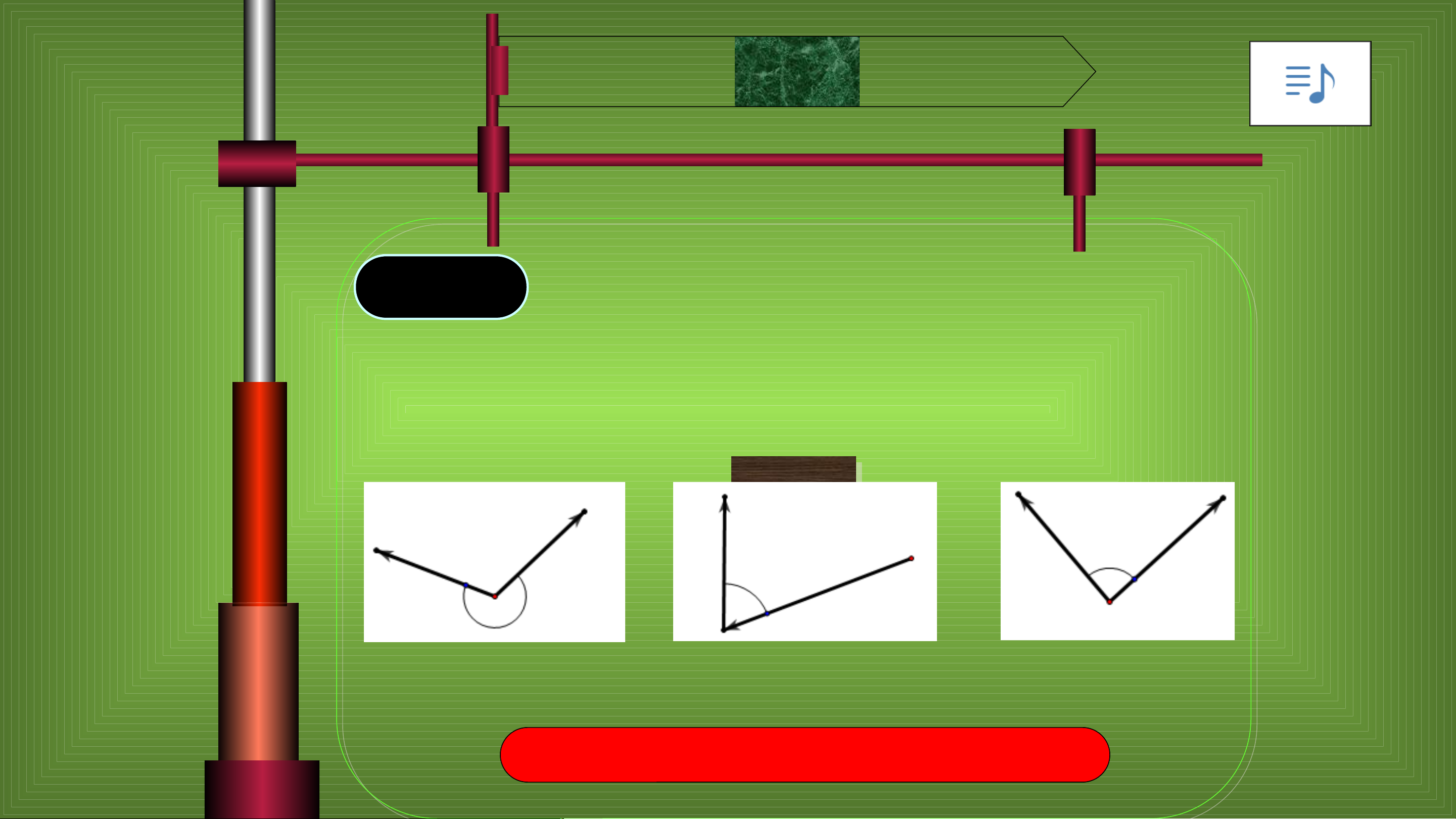
Hình nào dưới đây đánh dấu đúng góc giữa hai vectơ. A B C Câu 2:  
Cho tam giác ABC đều cạnh bằng 1, khi đó A  B,BC ?  A 0 A. 0 B. 150 90 C. 0 120 D. 0 60 B C Đáp án Câu 3:  
Cho tam giác ABC đều cạnh bằng 1, H là trung điểm BC khi đó  AH, BC ?  A 0 A. 0 B. 60 90 C. 0 30 D. 0 0 B H C Đáp án
Em nào trả lời giúp thầy: Trả lời: vectơ + vectơ = ? vectơ + vectơ = vectơ vectơ - vectơ = ? vectơ - vectơ = vectơ một số * vectơ = ? một số * vectơ = vectơ vectơ * vectơ = ?
vectơ * vectơ = 1 số thực (vô hướng)
Câu 4:Tích vô hướng của hai véc tơ là: A. Một số B. Một véc tơ
C. Tích độ dài hai véc tơ
D. Độ lớn của góc giữa đó hai véc tơ đó Đáp án Câu 5:      Cho a , b  0 khi đó . a b ?              A. .
a b  a . b .sin(a,b) B. . a b  .
a b .cos(a,b)           C. .
a b  a . b .cos(a,b) D. .
a b  a . b Đáp án Câu 6 :    Cho hai véc tơ c a,b 0  ùng hướng. Kết quả nào sau đây đúng :     A. B. . a b 0  . a b  1         C. .
a b  a . b D. .
a b  a . b (vì cos 00=1) Đáp án Câu 7:
Cho hình vuông ABCD cạnh là 1. Khi đó   A . B CD là A. B. 2  1 C. D. 1 2 Đáp án Câu 8:

Một người dùng một lực c
F ó độ lớn là 20N, kéo một vật 
dịch chuyển một đoạn 50m cùng hướng với . C F ông sinh  bởi lực là F A. 50(J ) B. 100(J ) 1000(J) C. 200(J) D. Công sinh bởi lực là:    
A  F . d .cos F,d  A = 20. 50. cos0o = 1000(J) Đáp án
CỦNG CỐ BÀI
1. Định nghĩa tích vô hướng Qua bài học,       em cần nhớ
a.b  a . b os c a;b những gì? 2   2 2. a  a     3. a . b = 0 0 (a,b) 90   a  b 
DẶN DÒ
làm bài tập 1,2,3 và 6 trang 101 SGK Chúc mừng đội chiến thắng
CẢM ƠN QUÝ THẦY CÔ VÀ CÁC EM
ĐÃ THAM GIA BÀI HỌC! 8 7 1 6 2 4 5 3 Th Thưởng Phạt KẾT Phạt THÚC ưởn g
Bài 1: (SGK – tr.101)
Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng:  𝐴𝐵 . 𝐶𝐷;  𝐴𝐵 . 𝐴𝐷 ;  𝐴𝐷 . 𝐵𝐶;  𝐴𝐶. 𝐶𝐵; 𝐴𝐶 . 𝐵𝐷 Giả
. = ||. ||. cos(, ) = a. a. = -a2 i
. = ||. ||. cos(, ) = a. a. = 0 . = ||. ||. cos(,) = a.a. = . = ||. ||. cos(, ) = a. a. =
. = ||. ||. cos(, ) = a. a. = 0
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Đặt vấn đề
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Củng cố bài
• Slide 32
• Slide 33
• Slide 34
• Slide 35
• Slide 36