Giáo án điện tử Toán 10 Chương 1 Bài 2 Cánh diều:: Tập hợp. Các phép toán trên tập hợp (3 tiết)

Bài giảng PowerPoint Toán 10 Chương 1 Bài 2 Cánh diều:: Tập hợp. Các phép toán trên tập hợp hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 10. Mời bạn đọc đón xem!

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Bài giảng điện tử Toán 10

Môn: Toán 10

Thông tin:

22 trang 4 tháng trước

Tác giả:

Profile M. Hậu
CHÀO MỪNG CÁC EM
ĐẾN VỚI BUỔI HỌC HÔM NAY!
lớp 10D


-
 !
-
"#$ !
BÀI 2: TẬP HỢP. CÁC PHÉP
TOÁN TRÊN TẬP HỢP
%&'(
I. TẬP HỢP
HĐ1
HĐ1
)$*
+
,-./0#$1

+
2$34/0#$

5 !67$8 9:;!-7-3:'
7/0:*<8=.:*
Giải
HĐ2
HĐ2
$(
>(
Giải
?$@>A*@@-37B/
0#$>C:DE>F*4>.@-37
@/0-G:*H)>C:DE>F*4
>.@-3= >C:IJ;
$(J'K<LM>A -./0#$)
>(?.:/0-G:*K
Ví dụ 1
IN.)*O$'
$(J';$ -./0#$12$3
4/0#$)
>(P>A>C:IJ;
Giải
$(

>(Q>A>C:IJ;
F<LR
HĐ3
HĐ3
$)!NSL7:=$-GINC
J=-G)/0
)M/07 /0
?.:/0#$B$:11
Giải
)/0
TT N.=)
G/0
Nhận xét:
+
-GU$/0 B%B(7
-3:
+
P*)C-G)/07V)C)*/07
)W:/07)G/0
Chú ý: B7$' -G' 
Luyện tập 1
?.:/0#$B$:
-GU$/0L
)G/0
II. TẬP CON VÀ TẬP HỢP BẰNG NHAU
1. Tập con
HĐ4
HĐ4
$(
>(PB/0#$W::*
Giải
$7
$(J'>A -./0#$
>(PB/0#$):*-GX
Kết luận:
?':/0#$W: /0#$L$) 
G#$' $@U$
Quy ướcY #$
Chú ý:
+
7$V)C'
+
?':-GZ#$7$'
Ví dụ 2
$7U[A
Giải
,4=/0:\]:*$)
JL.^)
J=
Luyện tập 2
,4=>4-L:*
$)$'W:'D!D
?=7/0#$W: /0#$
$=
Giải
$
U[A
Kết luận:
$)34$:
!
?':L
2. Tập hợp bằng nhau
HĐ5
HĐ5
$)
$(4Z/0#$W::*. 
W_
>(4Z/0#$W::*. 
W_
Giải
$7W$:)_-GX
$( >(
Kết luận:
L$)$>A$:7
' 
Chú ý:
Ví dụ 3
 $)>$>A$: 
$ )>$)>A$:<$  ) >A$:$=
-GX
Giải
^*$)>$>A$:-2-$))
>$)>A$:.$ >A$:
HOẠT ĐỘNG NHÓM ĐÔI
Z !*;)G
':>`
HƯỚNG DẪN VỀ NHÀ
a!-'
U'

<
>bQ
Chuẩn bị, đọc và
xem trước Bài tập
cuối chương I.
HẸN GẶP LẠI CÁC EM
TRONG BUỔI HỌC SAU!
| 1/22
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHÀO MỪNG CÁC EM
ĐẾN VỚI BUỔI HỌC HÔM NAY!
Khái niệm tập hợp thường gặp trong toán học và đời sống. Chẳng hạn :
- Tập hợp các học sinh lớp lớp 10D
- Tập hợp các học sinh tổ của lớp
BÀI 2: TẬP HỢP. CÁC PHÉP TOÁN TRÊN TẬP HỢP (3 tiết) I. TẬP HỢP HĐ H 1 Đ
Ở lớp 6, ta đã làm quen với khái niệm tập hợp, kí hiệu và cách viết
tập hợp, phần tử thuộc tập hợp. Hãy nêu cách cho một tập hợp. Giải
Có hai cách cho một tập hợp:
• Liệt kê các phần tử của tập hợp; Chẳng hạn:
• Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp. Chẳng hạn:
Người ta còn minh hoạ tập hợp bằng một vòng tròn kín, mỗi phần HĐ H 2 Đ
tử của tập hợp được biểu diễn bởi một chấm bên trong vòng kín,
còn phần tử không thuộc tâp hợp đó được biểu diễn bởi một chấm
bên ngoài vòng kín. Cách minh hoạ như vậy gọi là biểu đồ Ven.
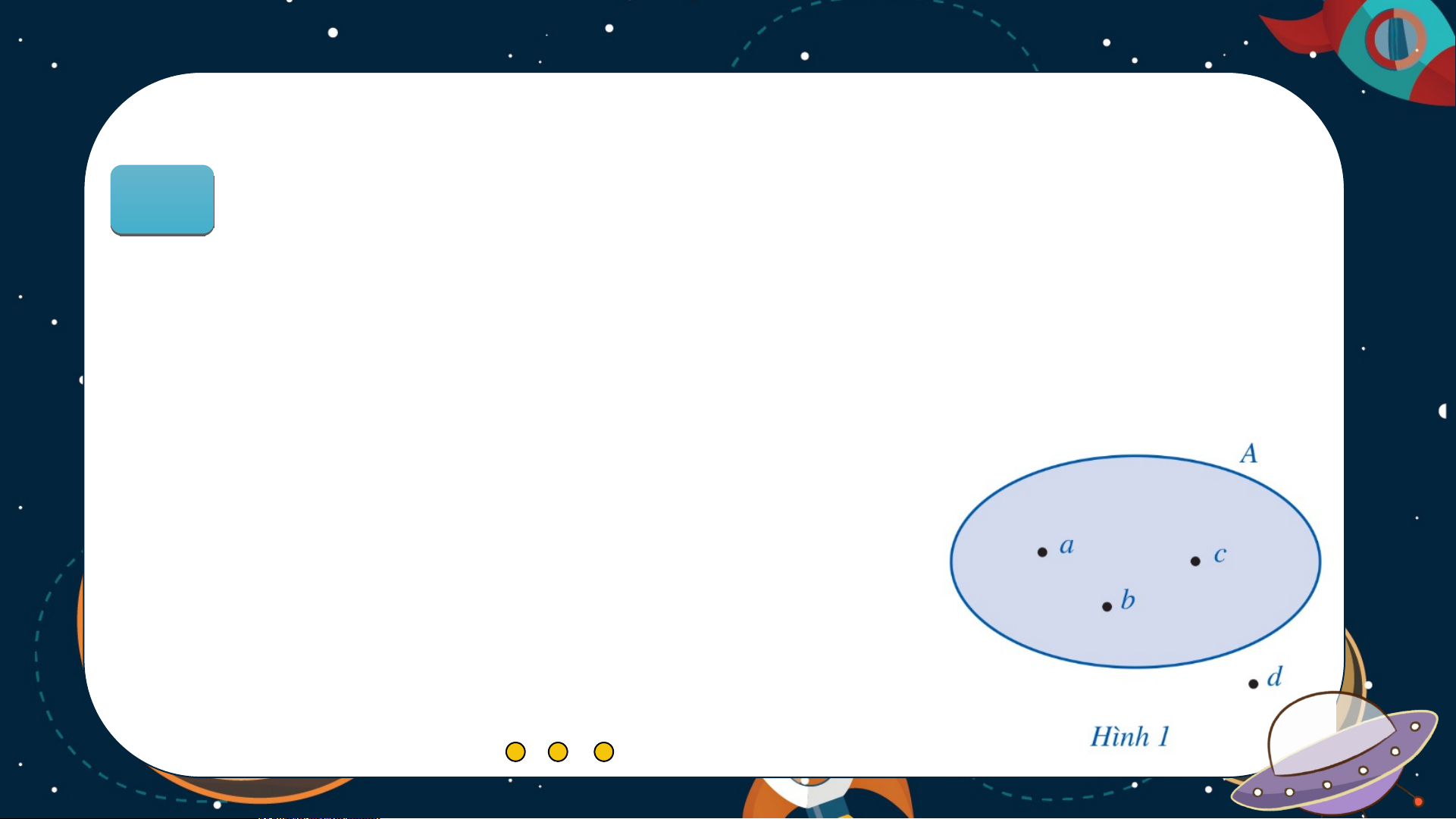
a) Viết tập hợp A trong Hình 1 bằng cách liệt kê các phần tử của tập hợp đó
b) Nêu phần tử không thuộc tập hợp A. Giải a) b) Ví dụ 1
Cho tập hợp gồm các số tự nhiên có một chữ số và chia hết cho .
a) Viết tập hợp theo hai cách: liệt kê các phần tử của tập hợp; chỉ ra tính
chất đặc trưng cho các phần tử của tập hợp đó.
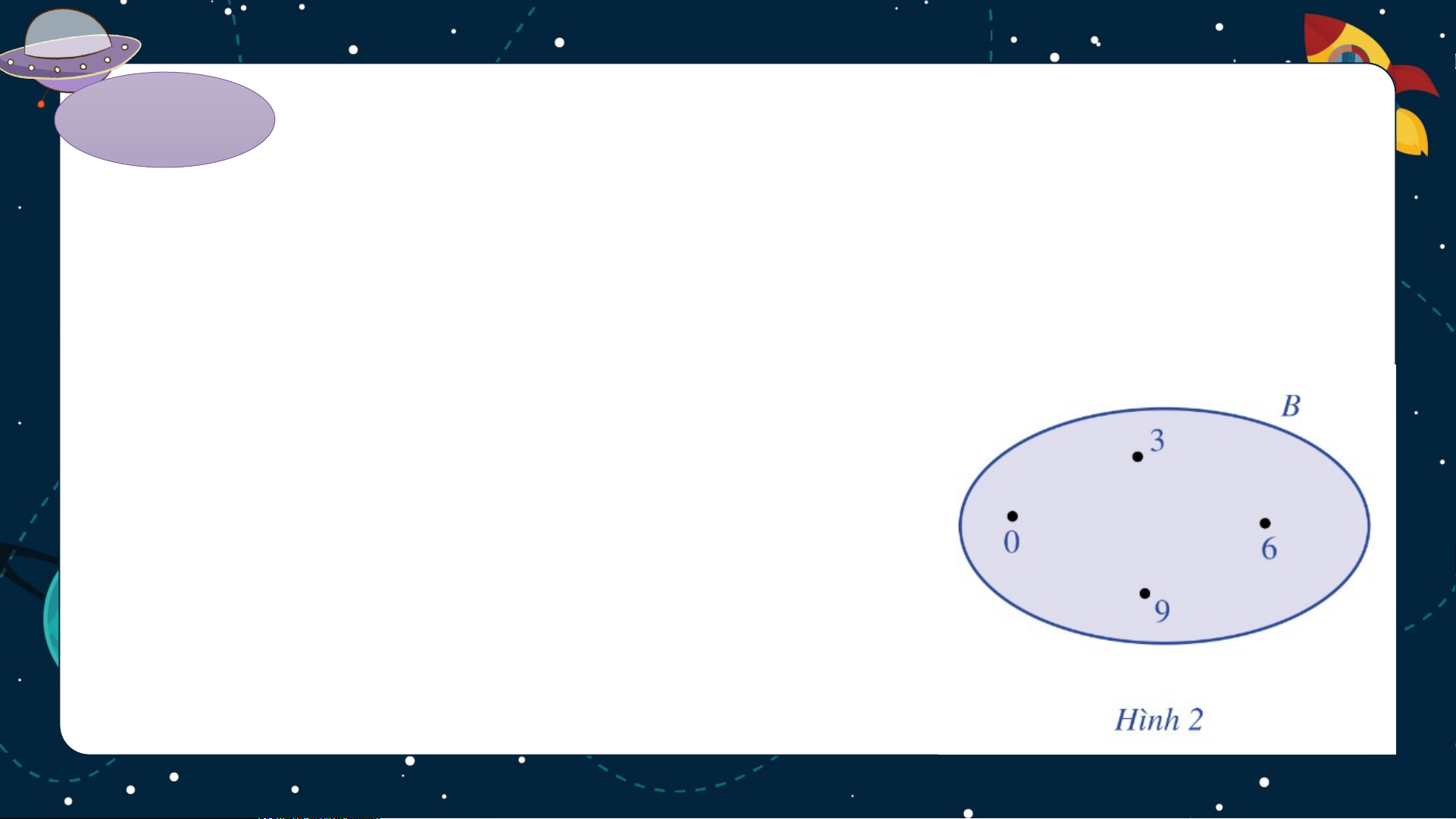
b) Minh hoạ tập hợp bằng biểu đồ Ven. . Giải a)
b) Tập hợp B được minh hoạ bằng biểu đồ Ven ở Hình 2 HĐ H 3 Đ
Nêu số phần tử của mỗi tập hợp sau:; ; và Giải
Ta có với mọi số thực x thì , suy ra không tồn tại số thực để .
Vậy tập hợp không có phần tử nào.
Tập hợp có 1 phần tử, là phần tử . Tập hợp có phần tử.
Tập hợp là tập hợp các số tự nhiên. Tập hợp này có vô số phần tử. Nhận xét:
• Tập hợp không chứa phần tử nào được gọi là tập hợp rỗng (tập rỗng), kí hiệu .
• Một tập hợp có thể không có phần tử nào, cũng có thể có một phần tử,
có nhiều phần tử, có vô số phần tử.
Chú ý: Khi tập hợp là tập hợp rỗng, ta viết và không được viết là Luyện tập 1
Nêu số phần tử của mỗi tập hợp sau
Tập hợp không chứa phần tử nào vì: .
Tập hợp có vô số phần tử.
II. TẬP CON VÀ TẬP HỢP BẰNG NHAU 1. Tập con HĐ H 4 Đ Cho hai tập hợp ,
a) Viết tập hợp bằng cách liệt kê các phần tử của tập hợp.
b) Mỗi phần tử của tập hợp có thuộc tập hợp không? Giải a)
b) Mỗi phần tử của tập hợp đều thuộc tập hợp . Kết luận:
Nếu mọi phần tử của tập hợp đều là phần tử của tập hợp thì ta nói là
môt tập hợp con của và viết là . Ta còn đọc chứa trong .
Quy ước: Tập hợp Ø được coi là tập hợp con của mọi tập hợp. Chú ý:
• Khi , ta cũng có thể viết
• Nếu không phải tập hợp con của , ta viết . Ví dụ 2
Cho hai tập hợp: , . Chứng tỏ rằng . Giải
Lấy phần tử tuỳ ý thuộc . Ta có: . Vì nên . Do đó . Vậy Cho hai tập hợp: Luyện tập 2 Chứng tỏ rằng Giải
Lấy bất kì thuộc tập hợp .
Ta có: chia hết cho đều viết được dưới dạng:
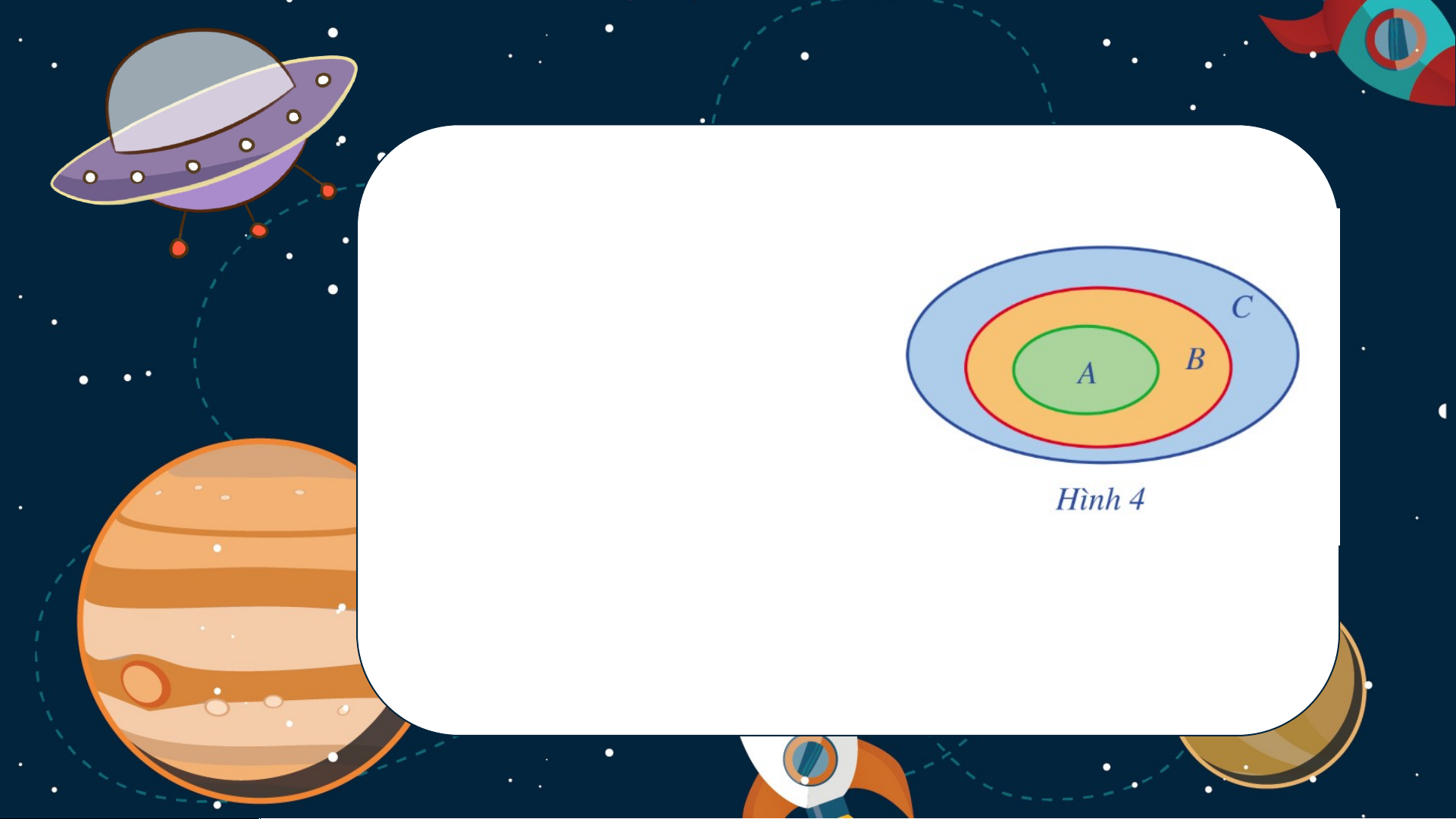
Như vậy, mọi phần tử của tập hợp đều là phần tử của tập hợp hay . Kết luận: Ta có các tính chất sau:  với mọi tập hợp  Nếu và thì .
2. Tập hợp bằng nhau HĐ H 5 Đ
Cho hai tập hợp , . Các mệnh đề sau có đúng không? a) b) Giải Ta có:
a) Tất cả các phần tử của tập đều thuộc tập nên là mệnh đề đúng.
b) Tất cả các phần tử của tập đều thuộc tập nên là mệnh đề đúng. Kết luận:
Khi và thì ta nói hai tập hợp và bằng nhau, viết là . Chú ý: Ví dụ 3
Cho là tập hợp các tam giác có ba cạnh bằng nhau và là tập hợp các
tam giác có ba góc bằng nhau. Hai tập hợp và có bằng nhau hay không? Giải
Do một tam giác có ba cạnh bằng nhau khi và chỉ khi tam giác đó có
ba góc bằng nhau nên hai tập hợp và là bằng nhau.
HOẠT ĐỘNG NHÓM ĐÔI
Cả lớp hoạt động theo nhóm đôi hoàn thành
phiếu bài tập trắc nghiệm.
HƯỚNG DẪN VỀ NHÀ Ghi nhớ kiến Hoàn thành các Chuẩn bị, đọc và thức trong tiết bài tập trong SBT
xem trước Bài tập học cuối chương I.
HẸN GẶP LẠI CÁC EM TRONG BUỔI HỌC SAU!
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Slide 22