Giáo án điện tử Toán 10 Chương 2 Bài 2 Cánh diều: Hệ bất phương trình bậc nhất hai ẩn (3 tiết)
Bài giảng PowerPoint Toán 10 Chương 2 Bài 2 Cánh diều: Hệ bất phương trình bậc nhất hai ẩn (3 tiết) hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 10. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 10
Môn: Toán 10
Sách: Cánh diều
Thông tin:
Tác giả:
Preview text:
BÀI 2: HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN (3 tiết) CHÀO MỪNG CẢ LỚP
ĐẾN VỚI BUỔI HỌC!
Theo Thông báo số 10/2019, giá quảng cáo trên VTV1 là 30 triệu
đồng cho 15 giây/1 lần quảng cáo vào khoảng 20h30; là 6 triệu
đồng cho 15 giây/1 lần quảng cáo vào khung giờ 16h00 - 17h00.
Một công ty dự định chi không quá 900 triệu đồng để quảng cáo
trên VTV1 với yêu cầu quảng cáo về số lần phát như sau: ít nhất
10 lần quảng cáo vào khoảng 20h30 và không quá 50 lần quảng
cáo vào khung giờ 16h00 -17h00. Gọi lần lượt là số lần phát
quảng cáo vào khoảng 20h30 và vào khung giờ 16h00 -17h00. Tron T g ron toán họ toá c n họ , các điều kiệ , các đi n ều kiệ ràng bu ràn ộc đối g bu ộc đối với vớ và v để để đáp đ áp ứng ứ ng nhu cầu n hu cầu trên trên của côn c g t ủa côn y đượ đư c ợ thể thể hiện h như iện thế nà như o? thế nà
Các điều kiện ràng buộc { ¿𝑥≥10 ¿ 0 ≤ 𝑦 ≤50
¿ 30 𝑥+ 6 𝑦 ≤ 900
BÀI 2: HỆ BẤT PHƯƠNG
TRÌNH BẬC NHẤT HAI ẨN (3 tiết)
I. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Cho hệ bất phương trình: HĐ H 1 Đ
a) Mỗi bất phương trình và có là bất phương trình bậc nhất hai ẩn không?
Mỗi bất phương trình và đều là bất phương trình bậc nhất hai ẩn.
b) Chỉ ra một nghiệm chung của hai bất phương trình và trong hệ trên Giải Chọn . Khi đó:
mệnh đề đúng nên là nghiệm của bất phương trình .
mệnh đề đúng nên là nghiệm của bất phương trình .
Vậy cặp số là một nghiệm chung của hai bất phương trình và trong hệ trên. Kết luận:
Hệ bất phương trình bậc nhất ẩn là một hệ gồm hai
hay nhiều bất phương trình bậc nhất hai ẩn . Mỗi
nghiệm chung các bất phương trình trong hệ được
gọi là một nghiệm của hệ bất phương trình đó. Ví V dụ d ụ 1
Cho hệ bất phương trình
{𝑥 −2 𝑦 ≤3(1) sau:
𝑥 + 𝑦 >2 (2)
Cặp số nào sau đây là nghiệm của hệ bất phương trình trên?
(3 ; 1) , (1 ; − 2), (5 ; − 3) Giải
+) Thay vào hai bất phương trình của hệ, ta có:
là mệnh đề đúng; là mệnh đề đúng;
Vậy là nghiệm chung của và nên là nghiệm của hệ bất phương trình.
+) Thay vào bất phương trình của hệ, ta có: là mệnh đề sai
Vậy không là nghiệm của nên không là nghiệm của hệ bất phương trình.
+) Thay vào bất phương trình của hệ, ta có: là mệnh đề sai
Vậy không là nghiệm của nên không là nghiệm của hệ bất phương trình. Luy u ệ y n n tập
p 1 Chỉ ra một nghiệm của {2 𝑥+𝑦>0
𝑥 −3 𝑦 <6
hệ bất phương trình sau 𝑥 − 𝑦 ≥ − 4 Giải
Thay vào bất phương trình của hệ, ta có: là mệnh đề đúng; là mệnh đề đúng; là mệnh đề đúng.
Vậy là nghiệm chung của bất phương trình nên là nghiệm của hệ bất phương trình.
II. BIỂU DIỄN MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG
TRÌNH BẬC NHẤT HAI ẨN
Miền nghiệm của hệ bất phương trình là giao các miền
nghiệm của các bất phương trình trong hệ. HĐ H 2 Đ
Cho hệ bất phương trình sau{ 𝑥−2𝑦≥−2
7 𝑥 − 4 𝑦 ≤ 1 6
2 𝑥 + 𝑦 ≥ − 4
a) Trong cùng mặt phẳng toạ độ Oxy, biểu diễn miền nghiệm của
mỗi bất phương trình bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
b) Tìm miền nghiệm của hệ bất phương trình đã cho.
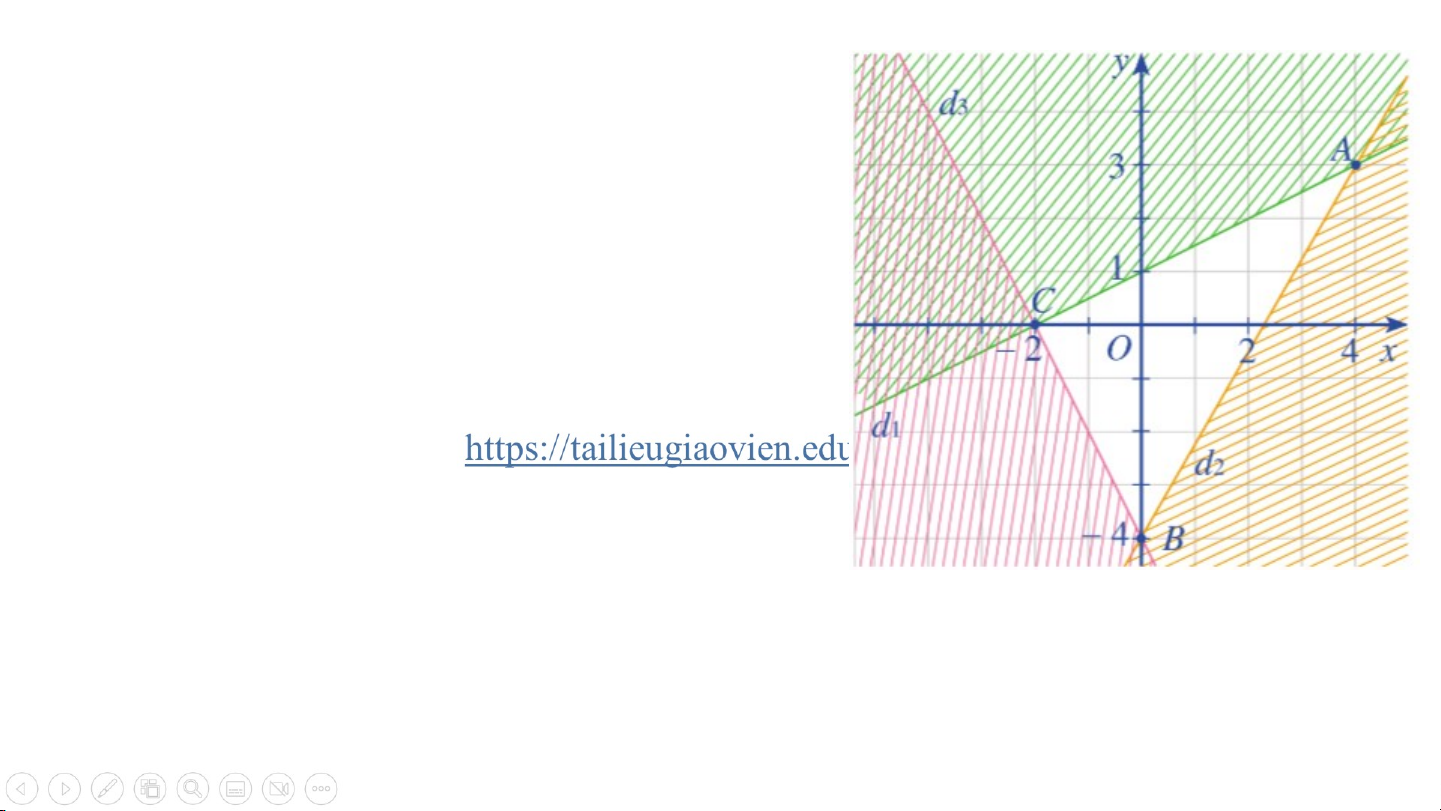
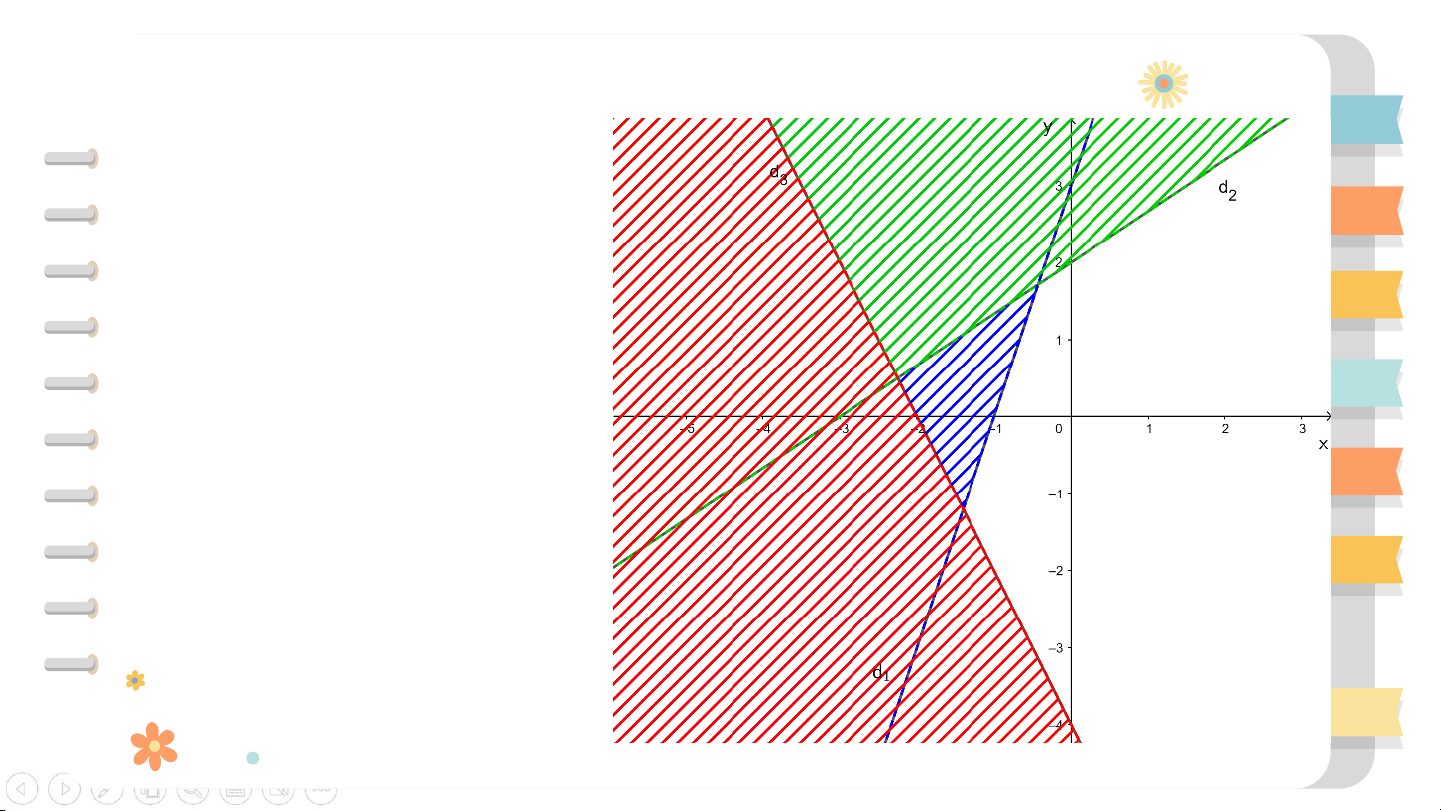
Bước 1: Trong cùng mặt phẳng toạ độ , vẽ ba đường thẳng: , , .
Vì thoả mãn các bất phương trình trong hệ
nên miền nghiệm của từng bất phương trình
trong hệ lần lượt là những nửa mặt phẳng
không bị gạch chứa điểm (kể cả đường thẳng tương ứng).
Bước 2: Phần không bị gạch là miền nghiệm của hệ bất phương trình đã
cho. Cụ thể là tam giác ABC kể cả miền trong.
Kết luận: Để biểu diễn miền nghiệm của hệ bất
phương trình hai ẩn, ta làm như sau:
+ Trong cùng mặt phẳng tọa độ, biểu diễn miền nghiệm
của mỗi bất phương trình trong hệ bằng cách gạch bỏ
phần không thuộc miền nghiệm đó.
+ Phần không bị gạch là miền nghiệm cần tìm. Ví dụ ụ 2
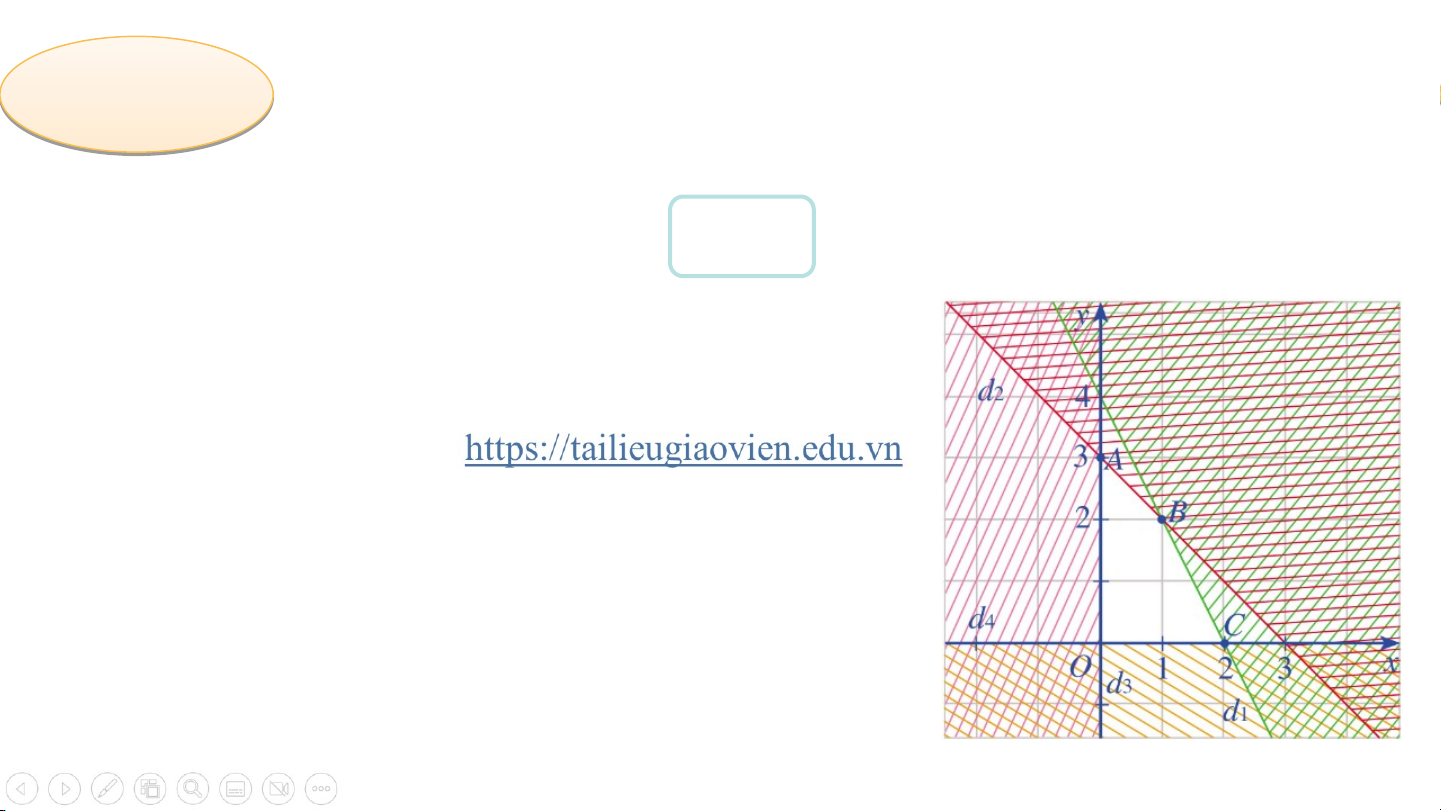
Biểu diễn miền nghiệm của hệ bất phương trình {¿2𝑥+𝑦≤4
¿ 𝑥 + 𝑦 ≤ 3 ¿ 𝑥 ≥ 0 ¿ 𝑦 ≥ 0 Giải
Vẽ các đường thẳng: , , và .
Gạch đi phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là tứ giác kể cả miền trong. Luy u ệ y n n tập ậ p 2
Biểu diễn miền nghiệm của hệ bất phương
{¿3𝑥−𝑦>−3
¿ −2 𝑥+ 3 𝑦 <6 trình
¿ 2 𝑥 + 𝑦 >− 4 Giải
Trên cùng một mặt phẳng tọa độ , vẽ đường thẳng: ; ;
Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất
phương trình là phần mặt
phẳng không bị gạch sọc không kể đường biên trong hình bên.
III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN
Tổng quát, người ta chứng minh được rằng:
Giá trị lớn nhất (hay nhỏ nhất) của biểu thức , với là tọa độ các
điểm thuộc miền đa giác , tức là các điểm nằm bên trong hay
nằm trên các cạnh của đa giác, đạt được tại một trong các đỉnh của đa giác đó.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18