Giáo án điện tử Toán 10 Chương 2 Bài 3 Kết nối tri thức: Bất phương trình bậc nhất hai ẩn
Bài giảng PowerPoint Toán 10 Chương 2 Bài 3 Kết nối tri thức: Bất phương trình bậc nhất hai ẩn hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 10. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 10
Môn: Toán 10
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
Nhân ngày Quốc tế Thiếu nhi 1-6, một rạp chiếu phim phục vụ các
khán giả một bộ phim hoạt hình. Vé được bán ra có 2 loại :
Loại 1 ( dành cho trẻ 6 – 13 tuổi) : 50.000 đồng/vé
Loại 2 ( dành cho trẻ trên 13 tuổi) : 100.000 đồng/vé
- Người ta tính toán rằng, để không
phải bù lỗ thì số tiền vé thu được ở rạp
chiếu phim này phải đạt tối thiểu 20
triệu đồng. Hỏi số lượng vé bán được
trong những trường hợp nào thì rạp
chiếu phim phải bù lỗ?
Trong tình huống mở đầu, gọi x, y lần lượt là số vé loại 1
và 2 bán được . Viết biểu thức tính số tiền bán vé thu được
( đơn vị nghìn đồng) ở rạp chiếu phim theo x, y
1 a. Các số nguyên không âm x và y phải thoả mãn điều kiện
gì để số tiền bán vé thu được đạt tối thiểu 20 triệu đồng
b. Nếu số tiền bán vé thu được nhỏ hơn 20 triệu đồng thì x
và y thoả mãn điều kiện gì ?
Số tiền bán vé thu được là :
Một hệ thức liên hệ giữa x và y thu được trong HĐ1a và
HĐ1b được gọi là bất phương trình bậc nhất hai ẩn.
Bất phương trình là bất phương trình bậc nhất hai ẩn
Bất phương trình không phải là bất phương trình bậc
nhất hai ẩn vì có chứa x2
Cặp số thoả mãn bất phương trình bậc nhất hai ẩn
trong 2 bất phương trình thu được ở HĐ1? Từ đó cho
biết rạp chiếu phim có phải bù lỗ hay không nếu bán
2 được 100 vé loại 1 và 100 vé loại 2
Trả lời câu hỏi tương tự với cặp số
Cặp số thoả mãn bất phương trình hai ẩn
Nếu rạp chiếu phim bán được 100 vé loại 1 và 100 vé loại 2 thì số
tiền thu được là 15 triệu đồng. Do đó rạp chiếu phim phải bù lỗ.
Cặp số thoả mãn bất phương trình hai ẩn
Nếu rạp chiếu phim bán được 150 vé loại 1 và 150 vé loại 2 thì số tiền
thu được là 22,5 triệu đồng. Do đó rạp chiếu phim không phải bù lỗ.
Cặp số được gọi là một nghiệm của bất phương
trình bậc nhất hai ẩn nếu bất đẳng thức đúng a. Vì :
Nên cặp số (3;4) là một nghiệm của bất phương trình đã cho. b. Vì :
Nên cặp số (0;-1) không phải là một nghiệm của bất phương trình đã cho .
a. Hai nghiệm của bất phương trình đã cho, chẳng hạn là :
b. Với , có vô số giá trị x với thoả mãn bất phương trình đã cho.
Nhận xét : Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm
Cho đường thẳng trên mặt phẳng toạ độ Oxy . Đường thẳng này
chia mặt phẳng thành hai nữa mặt phẳng
a. Các điểm O(0;0) , A(-1;3) và B(-2;-2) có thuộc cùng một nửa mặt
phẳng bờ là đường thẳng d không?
3 Tính giá trị của biểu thức tại các điểm đó và so sánh với 4. y A 3 d
Từ đồ thị : Các điểm O(0;0) , A(-1;3) và
B(-2;-2) thuộc cùng một nửa mặt phẳng 1
bờ là đường thẳng d. x -2 -1 O 2 3 4 Tại O(0;0) : -1 -2 B Tại A(-1;3) : -4 Tại và B(-2;-2) :
Cho đường thẳng trên mặt phẳng toạ độ Oxy . Đường
thẳng này chia mặt phẳng thành hai nữa mặt phẳng
b. Trả lời câu hỏi tương tự như câu a với các điểm 3 C(3;1) , D(4;-1) y d 3
Từ đồ thị : Các điểm C(3;1) , D(4;-1) thuộc
cùng một nửa mặt phẳng bờ là đường 1 C 4 x thẳng d. -2 -1 O 2 3 -1 D Tại C(3;1) : -2 Tại D(4;-1) : -4
• Trong mặt phẳng toạ độ Oxy, tập hợp các điểm có toạ độ là
nghiệm của bất phương trình được gọi là miền nghiệm của
bất phương trình đó.
• Người ta chứng minh được rằng đường thẳng d có phương
trình chia mặt phẳng toạ độ Oxy thành hai nửa mặt phẳng bờ d.
- Một nửa mặt phẳng (không kể bờ d) gồm các điểm có toạ độ (x;y) thoả mãn
- Nửa mặt phẳng còn lại (không kể bờ d) gồm các điểm có
toạ độ (x;y) thoả mãn
Bờ d gồm các điểm có toạ độ thoả mãn 𝒙+ y 𝒚=
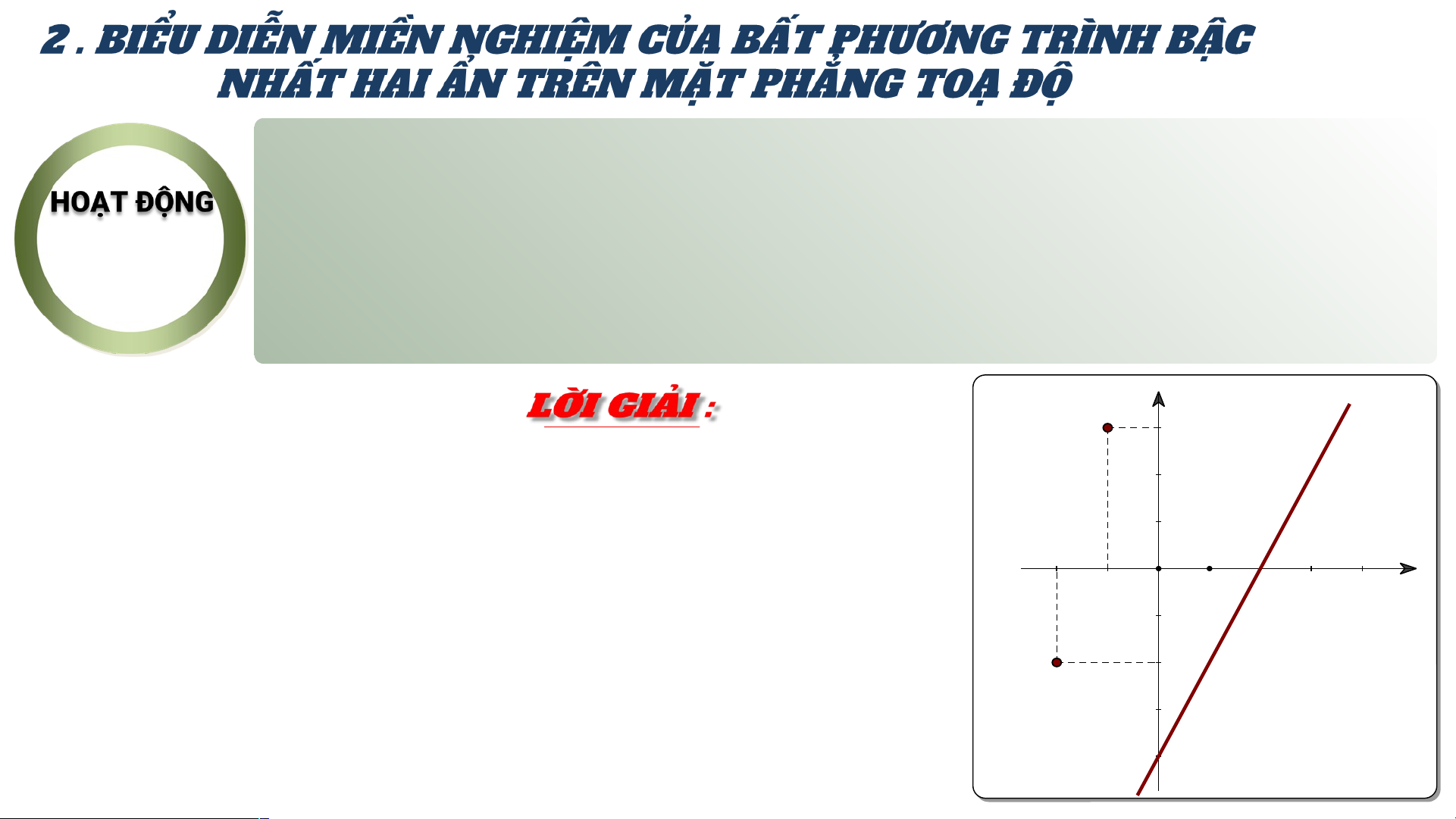
Bước 1: vẽ đường thẳng d: trên mặt 𝟏𝟎
phẳng toạ độ Oxy 𝟎 100
Bước 2: Lấy một điểm bất kì không 10
thuộc d trên mặt phẳng rồi thay vào 10 1 0 0 x biểu thức . O
Chẳng hạn : lấy O(0;0), ta có
Do đó miền nghiệm của BPT đã cho là nửa mặt phẳng bờ d
không chứa gốc toạ độ ( miền không bị gạch)
Cách biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn
• Vẽ đường thẳng trên mặt phẳng toạ độ Oxy
• Lấy một điểm không thuộc d
• Tính và so sánh với c
• Nếu thì nửa mặt phẳng bờ d chứa M là miền 0
nghệm của bất phương trình
• Nếu thì nửa mặt phẳng bờ d không chứa
M là miền nghệm của bất phương trình 0
Chú ý : + Nếu thì chọn M là gốc toạ độ 0
+ Nếu thì chọn M có toạ độ (1;0) hoặc (0;1) 0 a. Vì
Nên (5;6) là nghiệm của bất phương trình đã cho b. Vì
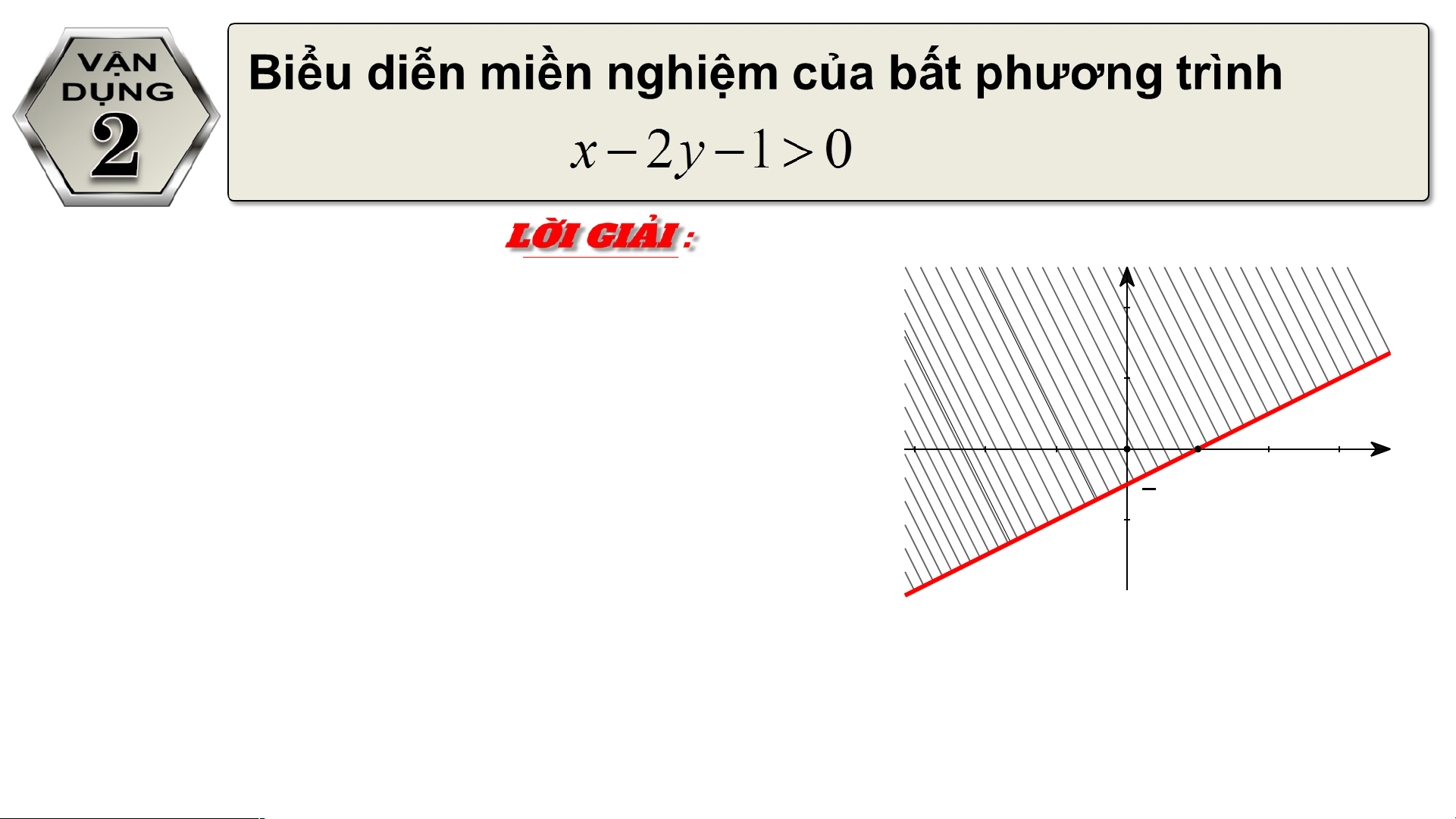
Nên (9;11) không phải là nghiệm của bất phương trình đã cho y Vẽ đường thẳng d
đi qua 2 điểm A(1;0) và O A x O
Xét gốc toạ độ O(0;0), ta thấy O không 1 B 1 B - thuộc d và 2
Nên miền nghiệm của BPT là nửa mặt
phẳng (không kể bờ d) không chứa
gốc toạ độ ( miền không gạch chéo) y
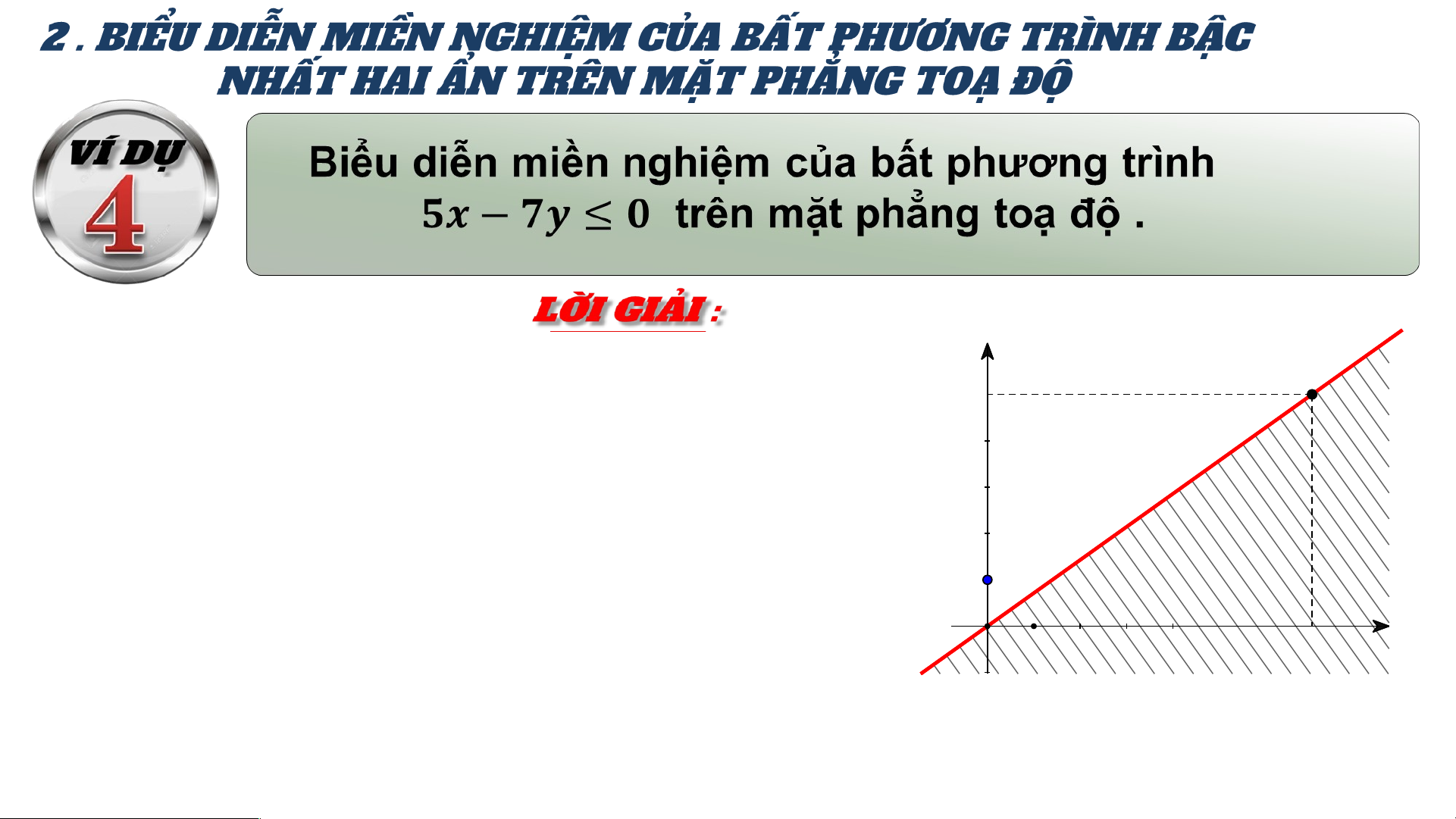
Bước 1 : Vẽ đường thẳng A 5
đi qua 2 điểm O(0;0) và A(7;5) 𝟎
Bước 2 : Xét điểm M(0;1) không thuộc
d, thay toạ độ vào biểu thức ta được
𝒅:𝟓𝒙−𝟕𝒚= M0 1 x O 7
Nên miền nghiệm của BPT là nửa mặt
phẳng (kể cả bờ d) chứa điểm M (miền không gạch chéo)
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18