Giáo án điện tử Toán 10 Chương 2 Bài 4 Kết nối tri thức: Hệ bất phương trình bậc nhất hai ẩn
Bài giảng PowerPoint Toán 10 Chương 2 Bài 4 Kết nối tri thức: Hệ bất phương trình bậc nhất hai ẩn hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 10. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 10
Môn: Toán 10
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
CHƯƠN CHƯƠNG I
G II. BẤT PHƯƠNG TRÌNH VÀ
HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN. TOÁN TOÁN ĐẠI ĐẠ S I Ố 10 S Ố 10 4
HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN 1
HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN 2
BIỂU DIỄN MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH
BẬC NHẤT HAI ẨN TRÊN MẶT PHẲNG TỌA ĐỘ 3
ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 1: Trong T các hệ bất phươn phươ g trì r nh sau sa , hệ bất ấ phương trì r nh nào là
hệ bất phương trình bậc nhất hai ẩn x y 3 x 3 A. y 1 B. B . y 2
x y x xy 2
x y y
2x 3y 4 x y 4 D. D . C. C 3 2 2 x 3 2 3y 4 2 x 3 y 1
Câu 2: Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x + 5y ≤ 10? A.(5; 2). B. (-5; 6). C. (2; 1). D. (-1; 4).
CHÚC MỪNG BẠN LÀ NGƯỜI MAY MẮN
x 3y 2 0
Câu 4: Cho hệ bất phương trinh . Trong các
2x y 1 0
điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình? A. M(-1; 1). B. N(0; 1). C. P(1; 3). D. Q(-1; 0).. Câu u 5 : : Cặp số s nào dưới d đây là nghiệm ệ của c hệ hệ bất phương trinh x y 2 x 2 y 4 x 0 A. (- 3;2) B. (4;-1) C. (0;1) D. (-2;2)
Câu 6: Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương x y 2
trinh x 2y 1 y 0 A. M(-1;2) B. N(0;1) C.P (-2;-4) D. Q(2;4)
x3. ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
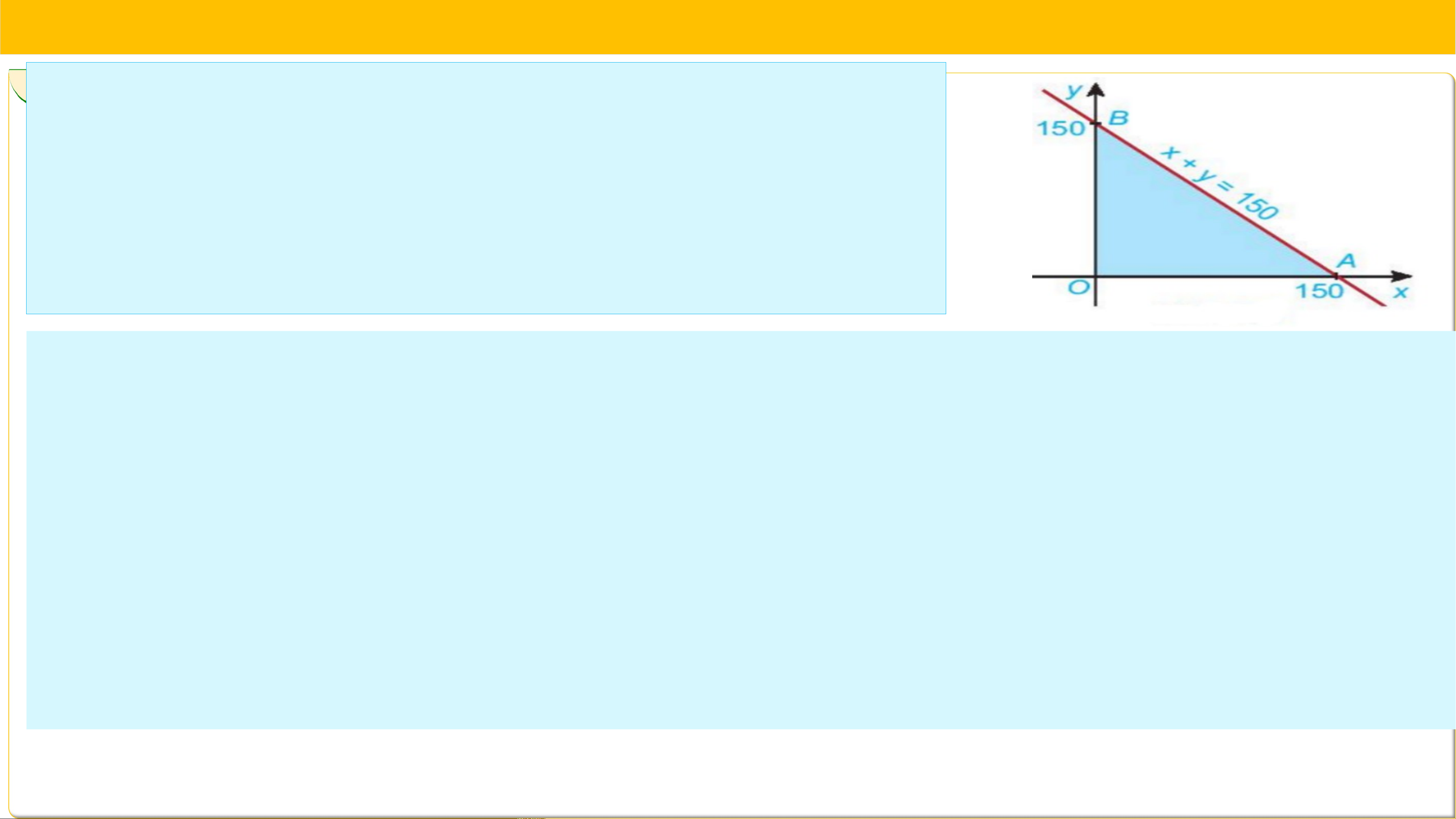
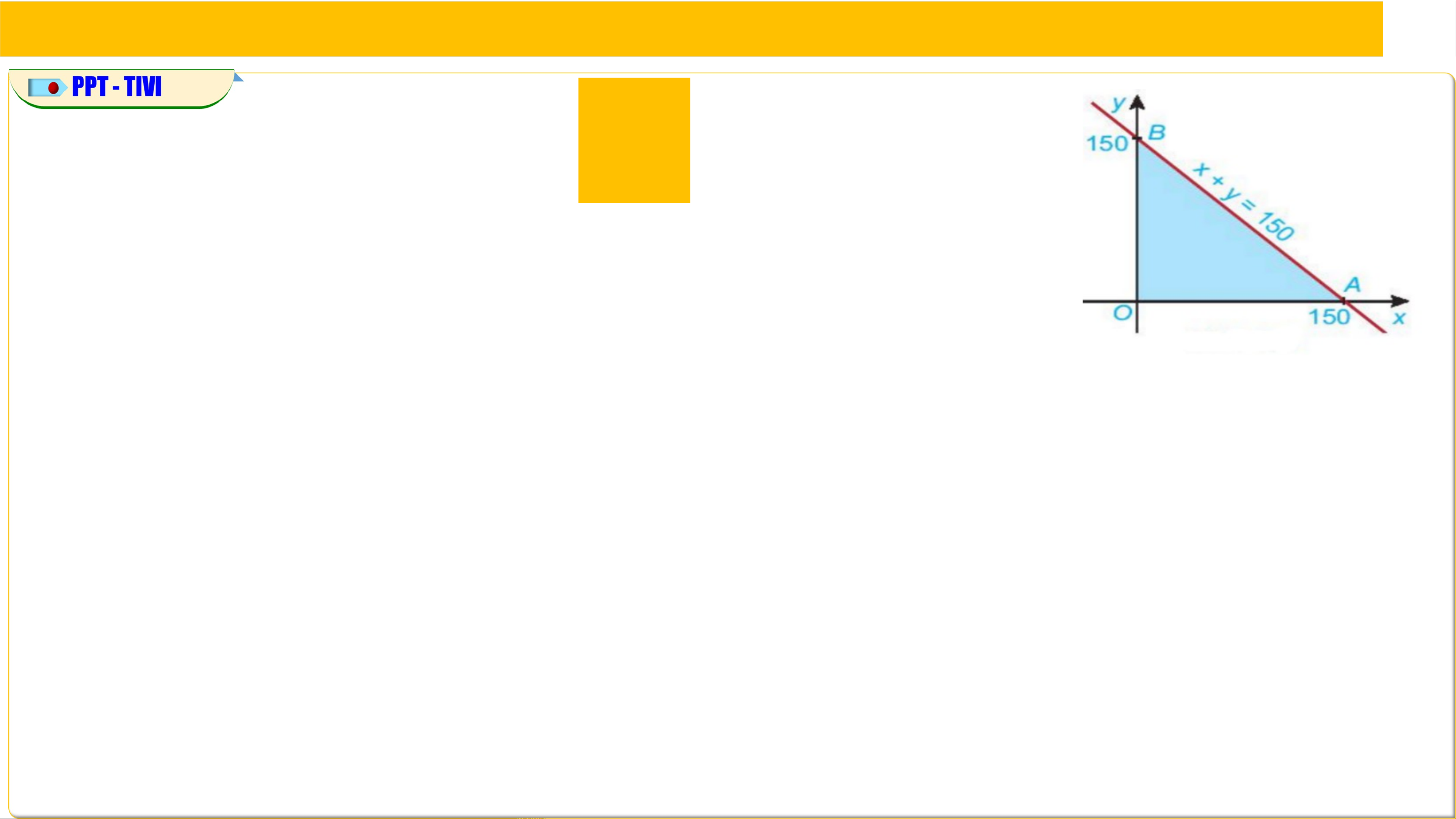
HĐ3: Xét biểu thức với thuộc miền tam
giác ở HĐ2. Tọa độ ba đỉnh là , và
a) Tính giá trị của biểu thức tại mỗi đỉnh , và .
b) Nêu nhận xét về dấu của hoành độ và tung độ của điểm x nằm
trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của
F(x;y) trên miền tam giác OAB.
c) Nêu nhận xét về tổng của điểm nằm trong miền tam giác .
Từ đó suy ra giá trị lớn nhất của trên miền tam giác .
x3. ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Giải : a)Tại đỉnh 0(0; 0) là Tại đỉnh A(150; 0) là Tại đỉnh B(0; 150) là .
b) Điểm nằm trong miền tam giác x
thì , . Do đó giá trị nhỏ nhất của trên miền tam giác là .
c) Điểm nằm trong miền tam giác thì . Từ đó suy ra giá trị lớn nhất của F(x;y) = 2x+3y
= 2(x+y) + y ≤ 2.150+150 = 450 trên miền tam giác OAB
3. ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Nhận xét: Tổng quát, người ta chứng minh được rằng
giá trị lớn nhất (hay nhỏ nhất) của biểu thức , với là tọa
độ các điểm thuộc miền đa giác , tức là các điểm nằm
bên trong hay nằm trên các cạnh của đa giác, đạt được
tại một trong các đỉnh của đa giác đó.
3. ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Ví dụ 3. Giải bài toán ở tình huống mở đầu. Giải
Giả sử cửa hàng cần nhập số máy điều hòa hai chiều là và số máy điều hòa một chiều là . Khi đó ta có , .
Vì nhu cầu của thị trường không quá 100 máy nên .
Số tiền để nhập hai loại máy điều hòa với số lượng như trên là: (triệu đồng).
Số tiền tối đa để đầu tư cho hai loại máy là 1,2 tỉ đồng, nên ta có hay .
Từ đó ta thu được hệ bất phương trình bậc nhất hai ẩn sau:
• Lợi nhuận thu được khi bán được máy điều hòa hai chiều và máy điều hòa một chiều là .
• Ta cần tìm giá trị lớn nhất của khi thỏa mãn hệ bất phương trình trên.
3. ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
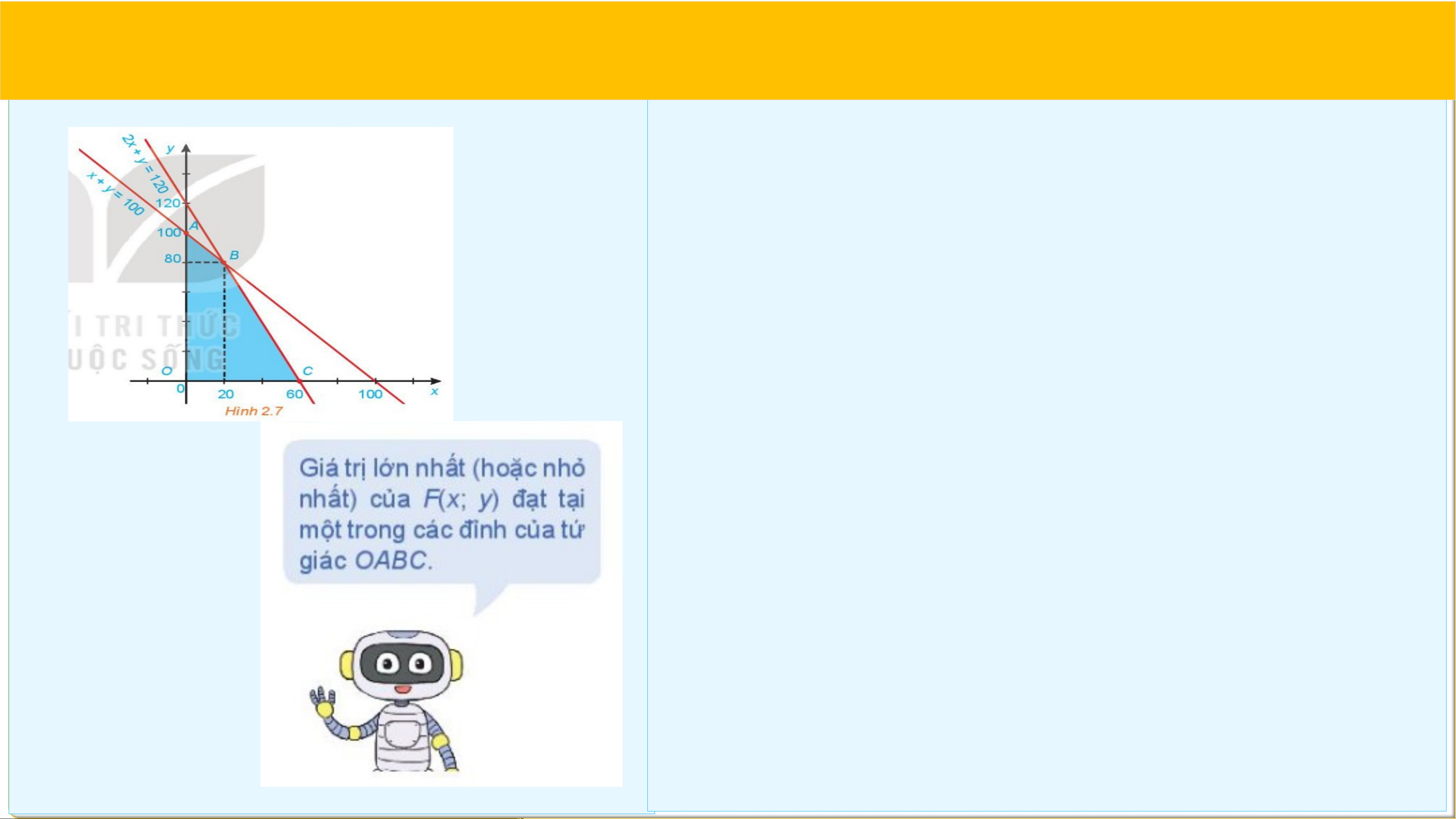
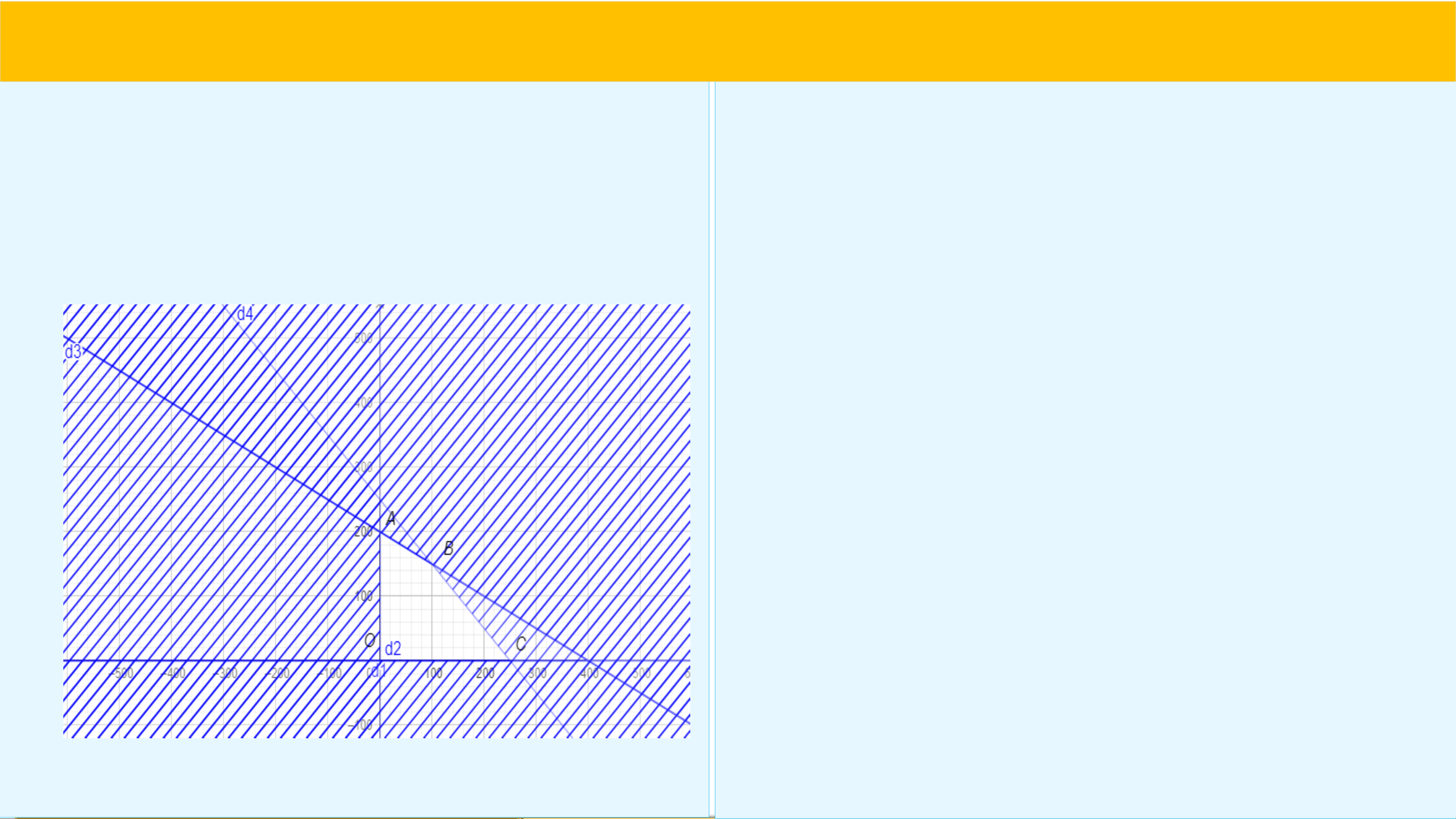
Bước 1. Xác định miền nghiệm của hệ bất
phương trình trên. Miền nghiệm là miền tứ giác
với tọa độ các đỉnh , , và (H.2.7).
Bước 2. Tính giá trị của biểu thức tại các đỉnh của tứ giác này: , , , .
Bước 3. So sánh các giá trị thu được của ở
Bước 2, ta được giá trị lớn nhất cần tìm là .
Vậy cửa hàng cần đầu tư kinh doanh 20
máy điều hòa hai chiều và 80 máy điều
hòa một chiều để lợi nhuận thu được là lớn nhất.
3. ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
• Vận dụng. Một cửa hàng có kế hoạch nhập về hai loại máy tính và , giá mỗi chiếc lần lượt là
10 triệu đồng và 20 triệu đồng với số vốn ban đầu không quá 4 tỉ đồng. Loại máy mang lại lợi
nhuận 2,5 triệu đồng cho mỗi máy bán được và loại máy mang lại lợi nhuận là 4 triệu đồng cho
mỗi máy bán được. Cửa hàng ước tính rằng tổng nhu cầu hàng tháng sẽ không vượt quá 250
máy. Giả sử trong một tháng cửa hàng cần nhập số máy tính loại là và số máy tính loại là . • Giải
a) Giả sử cửa hàng cần nhập số máy tính loại là và số máy tính loại là . Khi đó ta có , .
Số tiền để nhập hai loại máy tính với số lượng như trên là: (triệu đồng).
Số vốn ban đầu không quá 4 tỉ đồng, nên ta có hay .
Vì tổng nhu cầu hàng tháng không vượt quá 250 máy nên .
Từ đó ta thu được hệ bất phương trình bậc nhất hai ẩn sau:
3. ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
• Miền nghiệm của hệ bất phương trình trên là
b) Gọi (triệu đồng) là lợi nhuận mà cửa hàng thu
miền tứ giác với tọa độ các đỉnh , , và .
được trong tháng đó khi bán máy tính loại và máy tính loại . Khi đó .
c) Ta cần tìm giá trị lớn nhất của khi thỏa mãn hệ bất phương trình trên.
Tính giá trị của biểu thức tại các đỉnh của tứ giác : , , , .
So sánh các giá trị thu được của , ta được giá trị lớn nhất cần tìm là .
• Vậy cửa hàng mỗi tháng cần nhập 100 máy tính
loại và 150 máy tính loại để lợi nhuận thu được là lớn nhất.
Bài tập trắc nghiệm
1. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn? x y 0 x 2y 0 3 3
x y 0 3 x y 4 A. C. B. D. 2y 0 2 y 3 0 x y 3 x 2y 1 Đáp án: A
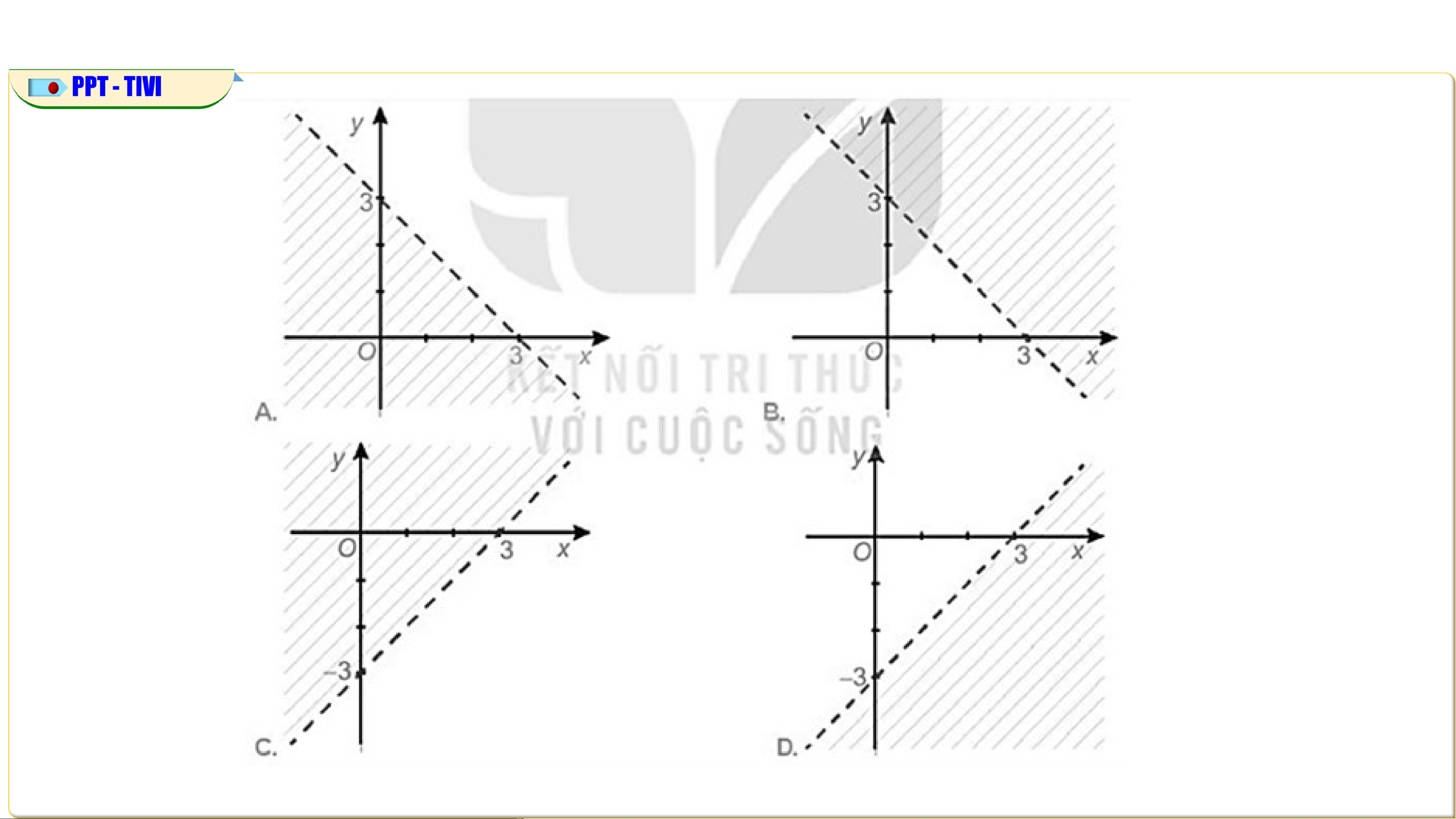
2. Hình nào dưới đây biểu diễn miền nghiệm của bất phương trình x – y < 3? Đáp án: D
Hướng dẫn học sinh học bài cũ
- Nắm cách biểu diễn miền nghiệm của hệ bất phương trình bậc nhất
hai ẩn trên mặt phẳng tọa độ.
- Làm bài tập 2.4-2.6 trang 30 SGK.
Hướng dẫn học sinh học bài mới
Ôn tập lại kiến thức, kĩ năng đã học của bài học.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19