A
 Chúng ta đã biết tỉ số lượng giác của góc
nhọn trong tam giác vuông B C
 Vậy làm thế nào để mở rộng khái niệm tỉ số lượng
giác của góc nhọn cho các góc từ 00 đến 1800 y 1 C
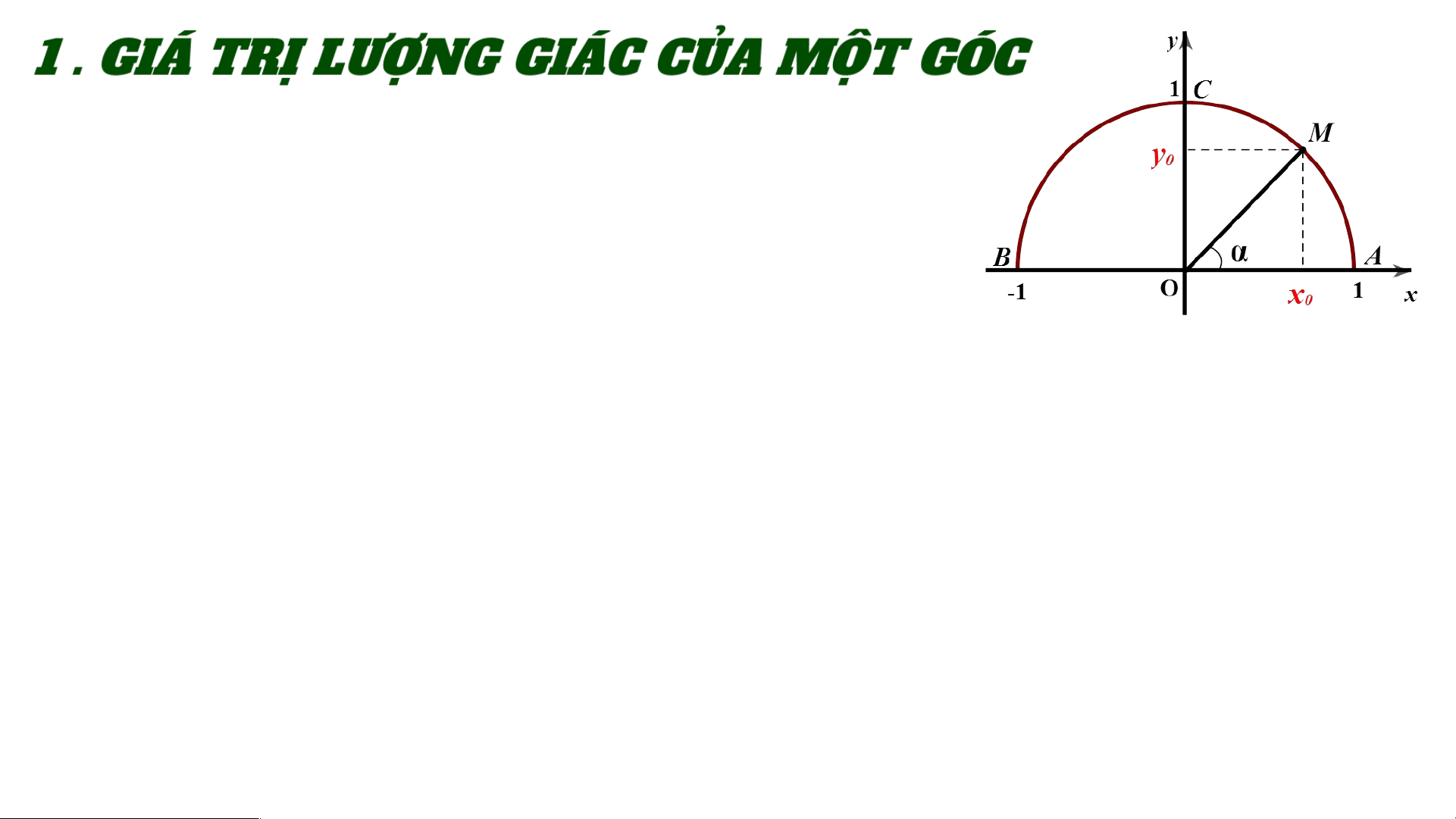
 Trong mặt phẳng toạ độ Oxy, nửa đường tròn M y0
tâm O, bán kính nằm phía trên trục hoành
được gọi là nửa đường tròn đơn vị. B α A -1 O x 1 0 x α < 900  Cho trước góc 𝛼 , . Khi đó, có y
duy nhất một điểm trên nửa đường 1 C
tròn đơn vị nói trên để M y0 α B A -1 x O 0 1 x α > 900
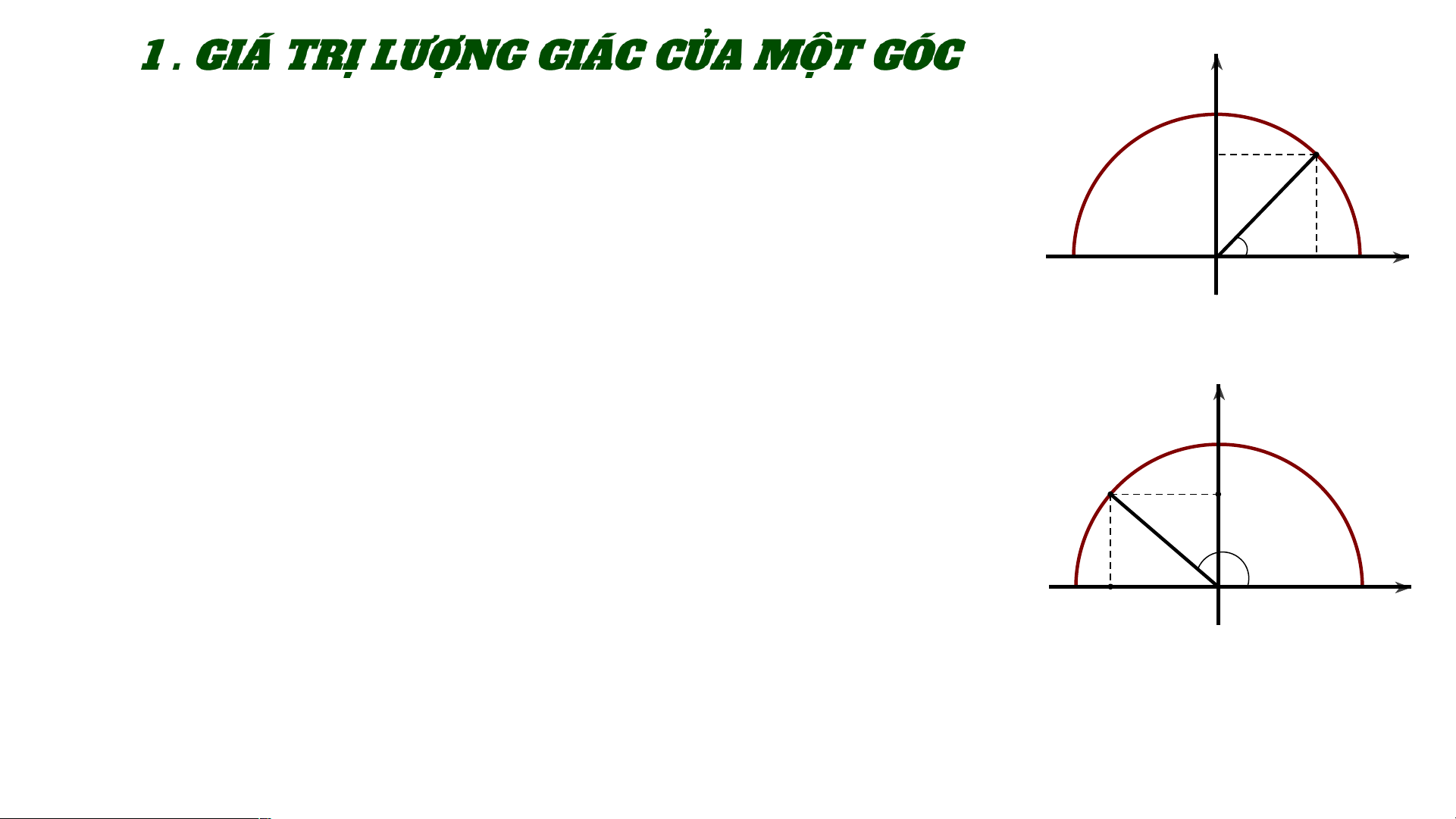
a. Nêu nhận xét về vị trí của điểm M trên nửa đường
1 tròn đơn vị trong các trường hợp sau:
b. Khi , nêu mối quan hệ giữa cos , 𝛼 sin 𝛼 với hoành
độ và tung độ của điểm M. y y y M C 1 C 1 C 1 M M y0 y y0 0 α α B A B A B α A -1 x O 0 1 x -1 x O 0 1 x -1 O x 1 0 x α > 900 α = 900 α < 900 M trùng với C M thuộc cung AC M thuộc cung CB
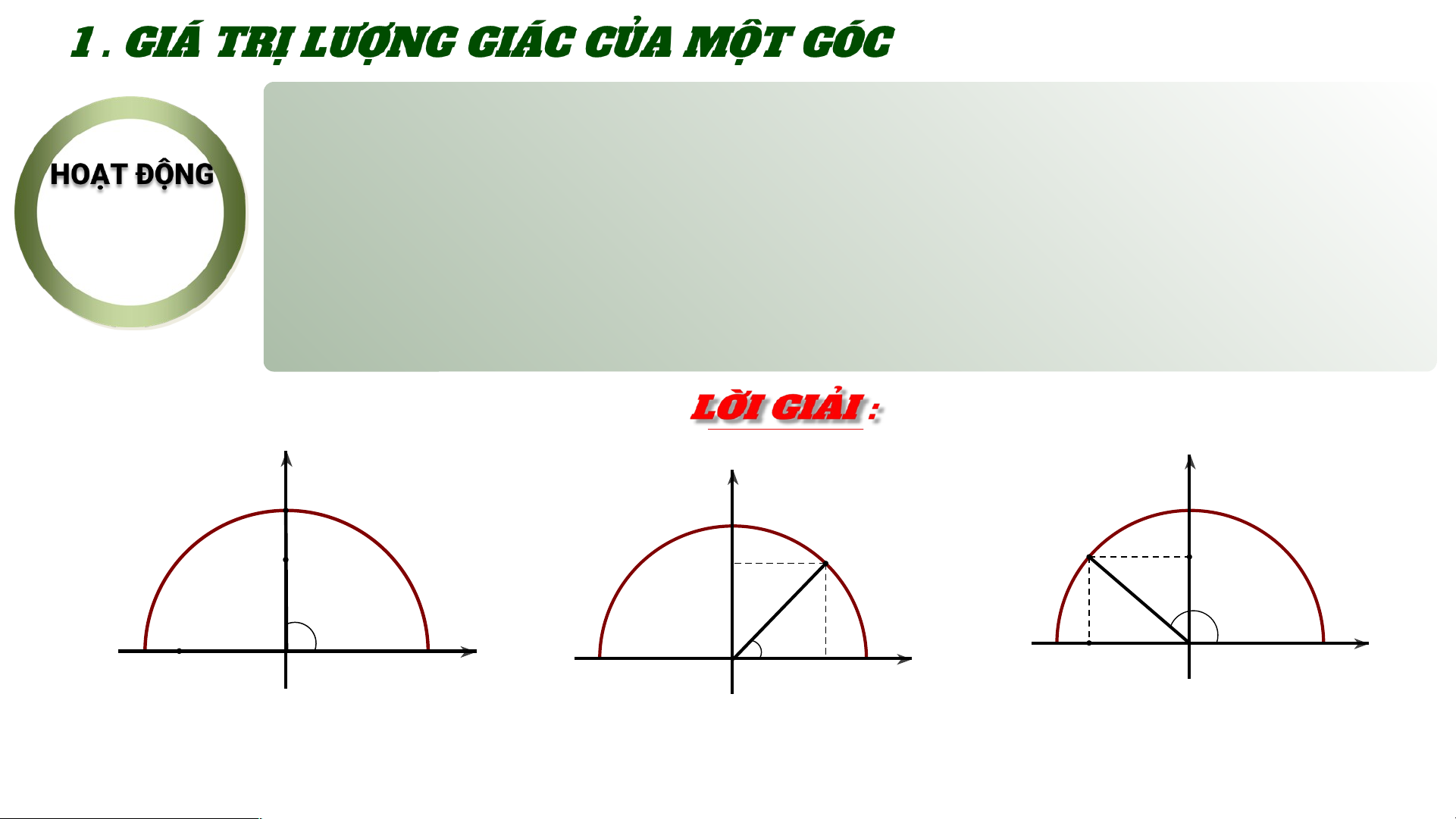
a. Nêu nhận xét về vị trí của điểm M trên nửa đường
1 tròn đơn vị trong các trường hợp sau:
b. Khi , nêu mối quan hệ giữa cos , 𝛼 sin 𝛼 với hoành
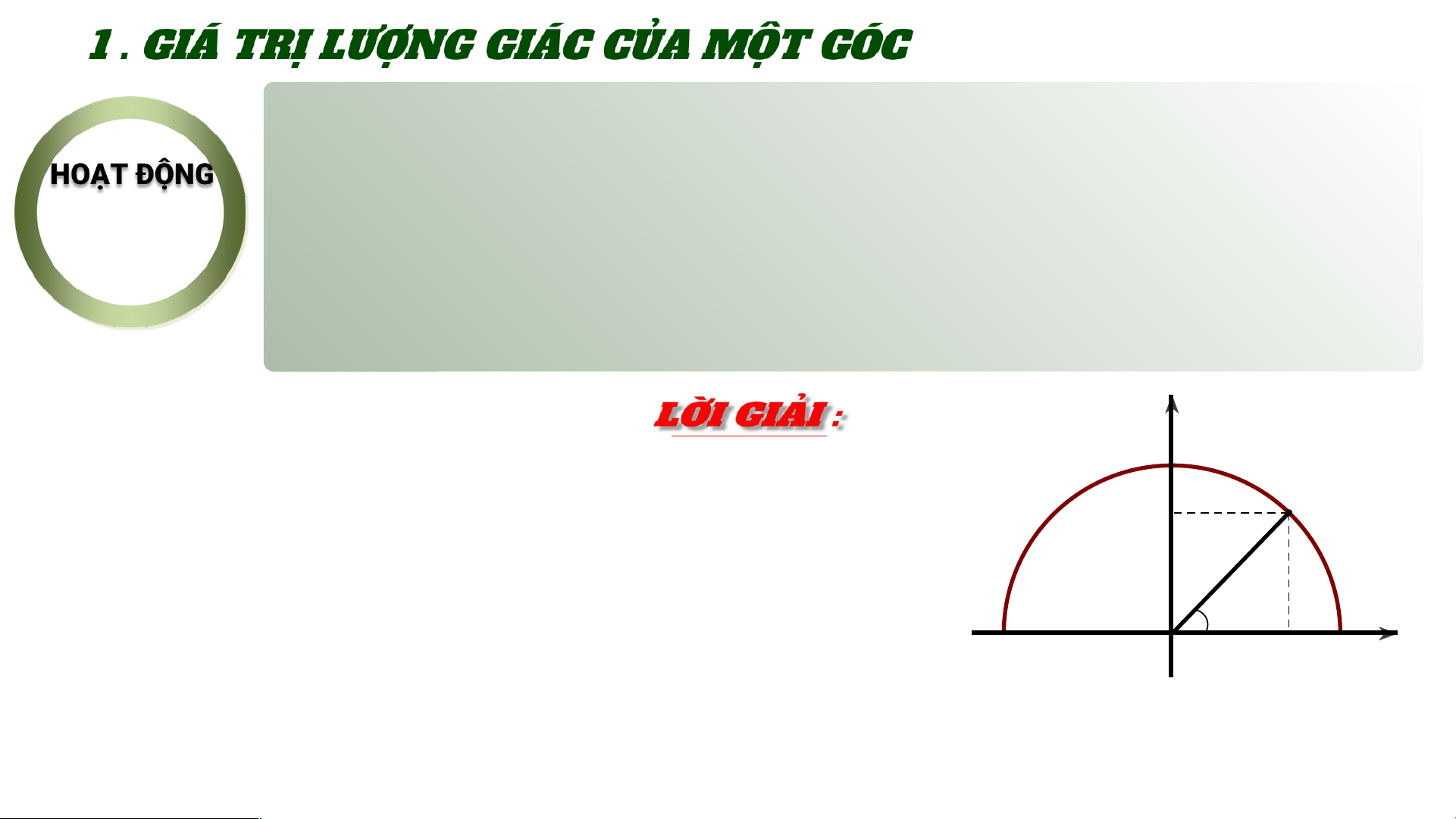
độ và tung độ của điểm M. y 1 C M b.Ta có : y0 B α A -1 O x 1 0 x α < 900 Với mỗi góc
𝛼 , gọi là điểm trên
nửa đường tròn đơn vị sao cho . Khi đó : • sin của góc
𝛼 là tung độ của điểm M . Kí hiệu là sin𝛼 • côsin của góc
𝛼 là hoành độ của điểm M . Kí hiệu là cos𝛼
• Khi ( hay ) , ta có :
• Khi ( hay ) , ta có : GTLG 00 300 450 600 900 1800 sin cos tan cot y 1
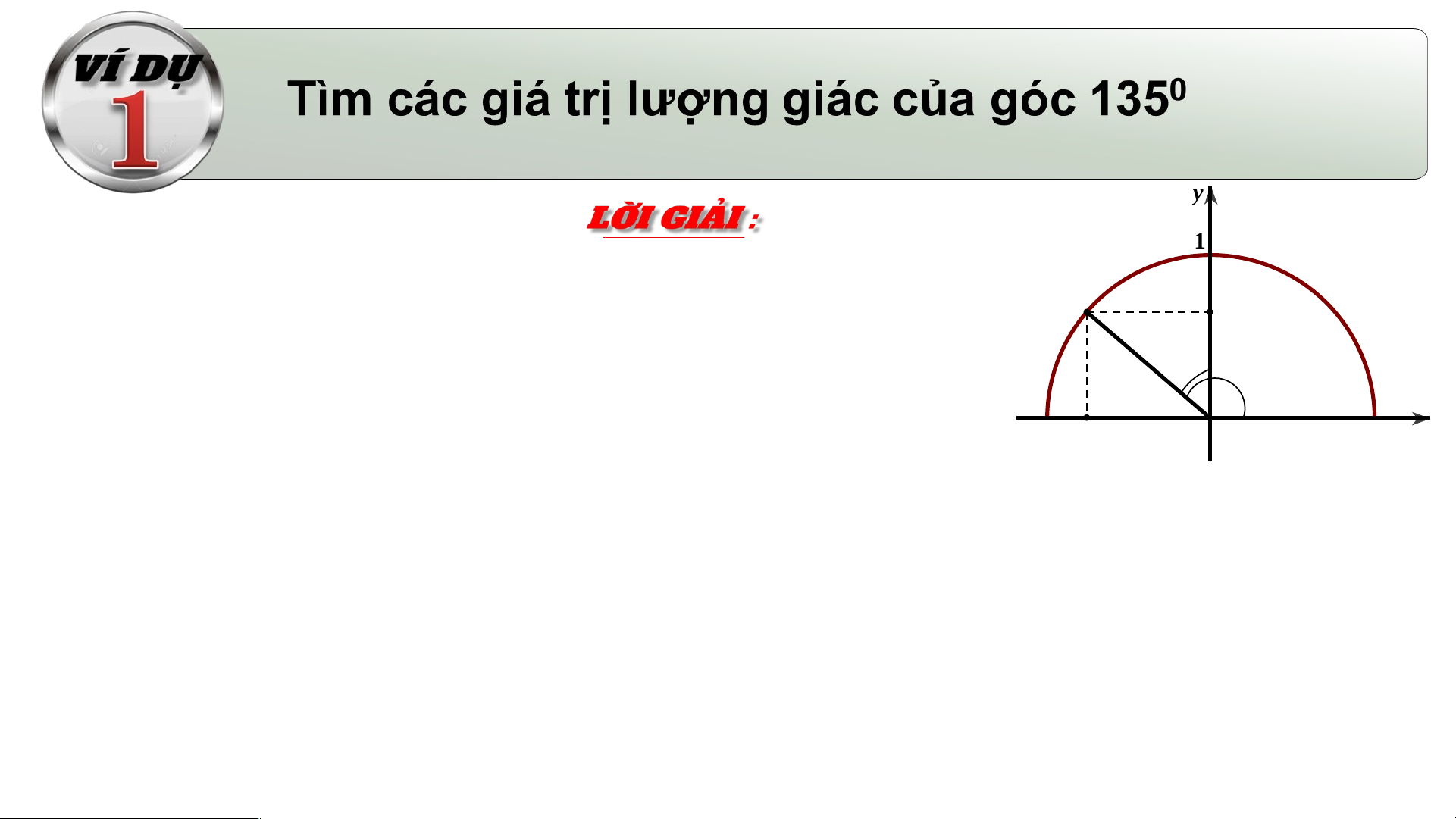
Gọi M là điểm trên nửa đường tròn đơn vị sao cho . M P 450
Gọi N, P là hình chiếu vuông góc của M 1350
lên các trục Ox, Oy. -1 N O 1 x Ta có :
Vậy các tam giác MON, MOP vuông cân với cạnh huyền
Theo định nghĩa ta có : y
Gọi M là điểm trên nửa đường tròn đơn 1 M vị sao cho . P
Gọi N, P là hình chiếu vuông góc của M 1200
lên các trục Ox, Oy. Ta có : -1 N O 1 x
Theo định nghĩa ta có :
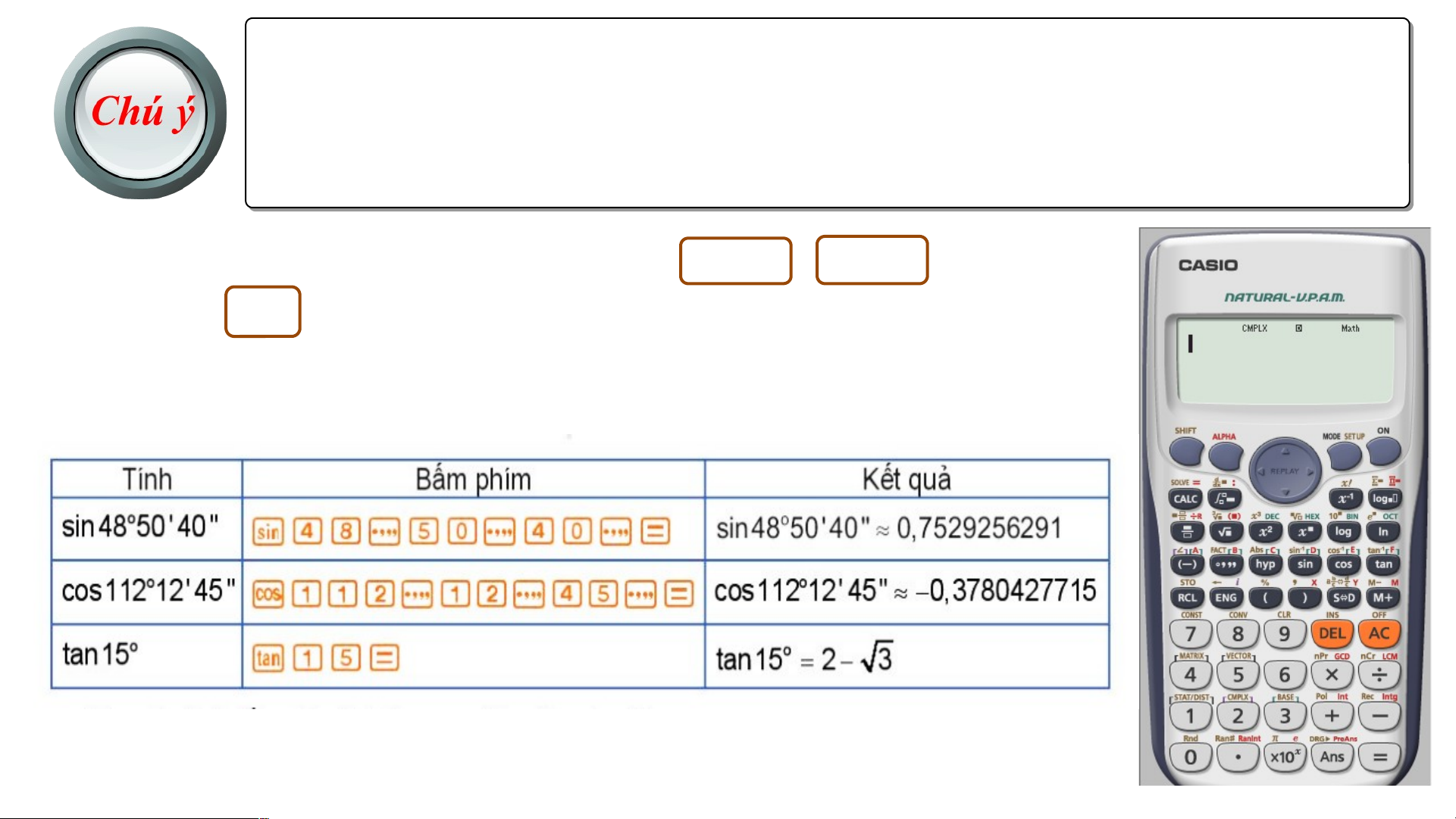
Ta có thể sử dụng máy tính cầm tay để tính các giá trị
lượng giác của một góc và tính góc khi biết giá trị
lượng giác của góc đó.
( Khi mở máy tính ta bấm phím SHI F T MO DE rồi bấm phím
3 để chọn đơn vị đo góc là “độ”)
 Tính giá trị lượng giác của một góc.
 Tính góc khi biết giá trị lượng giác của một góc nào đó. Chú ý:
• Khi tìm x biết sinx, máy tính chỉ đưa ra giá trị
• Muốn tìm x khi biết cosx, tanx ta cũng làm tương tự, chỉ thay phím si
n tương ứng bởi phím c os , tan
Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt
hay dùng MTCT ta được :
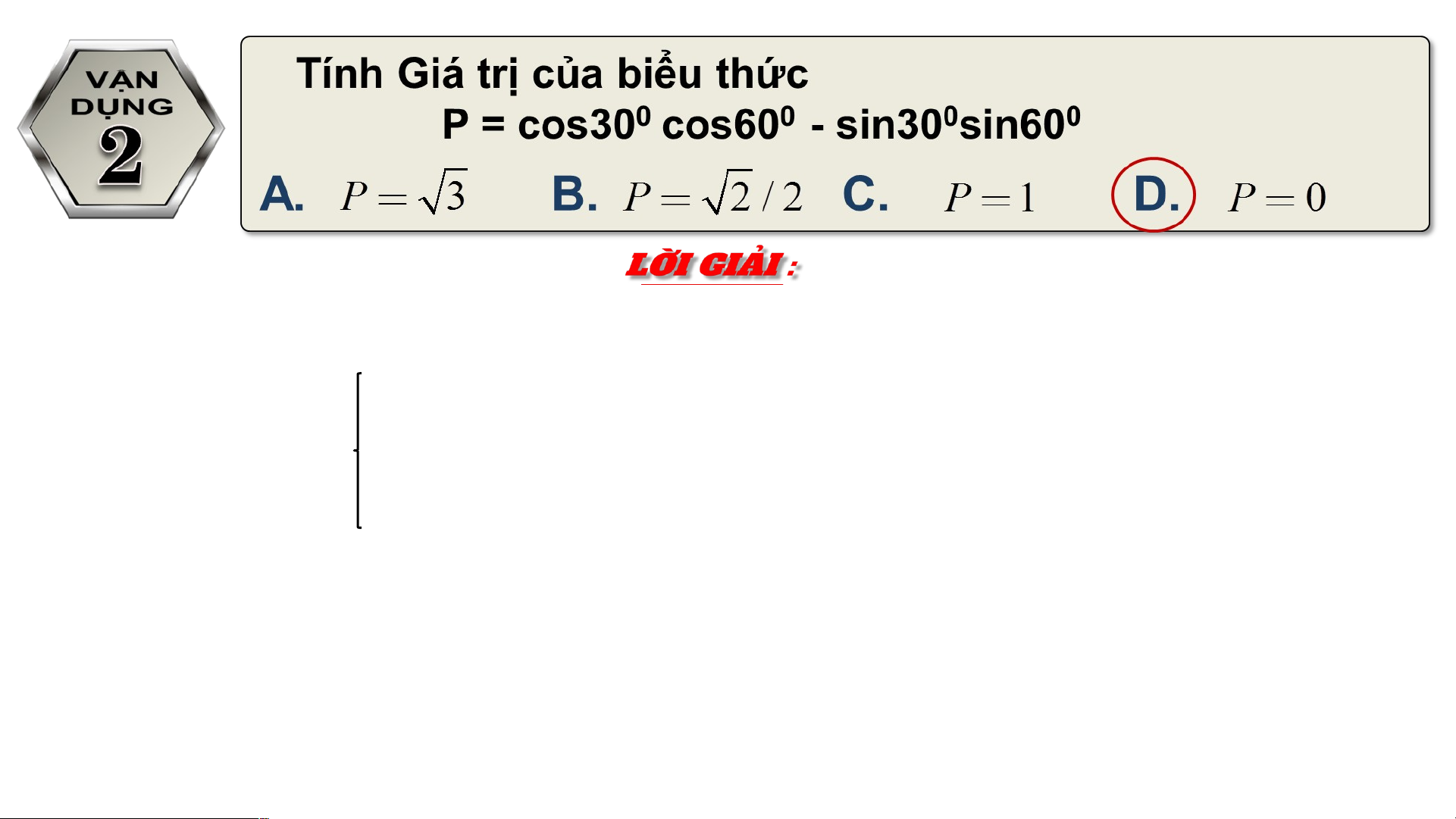
Vì 300 và 300 là 2 góc phụ nhau , nên
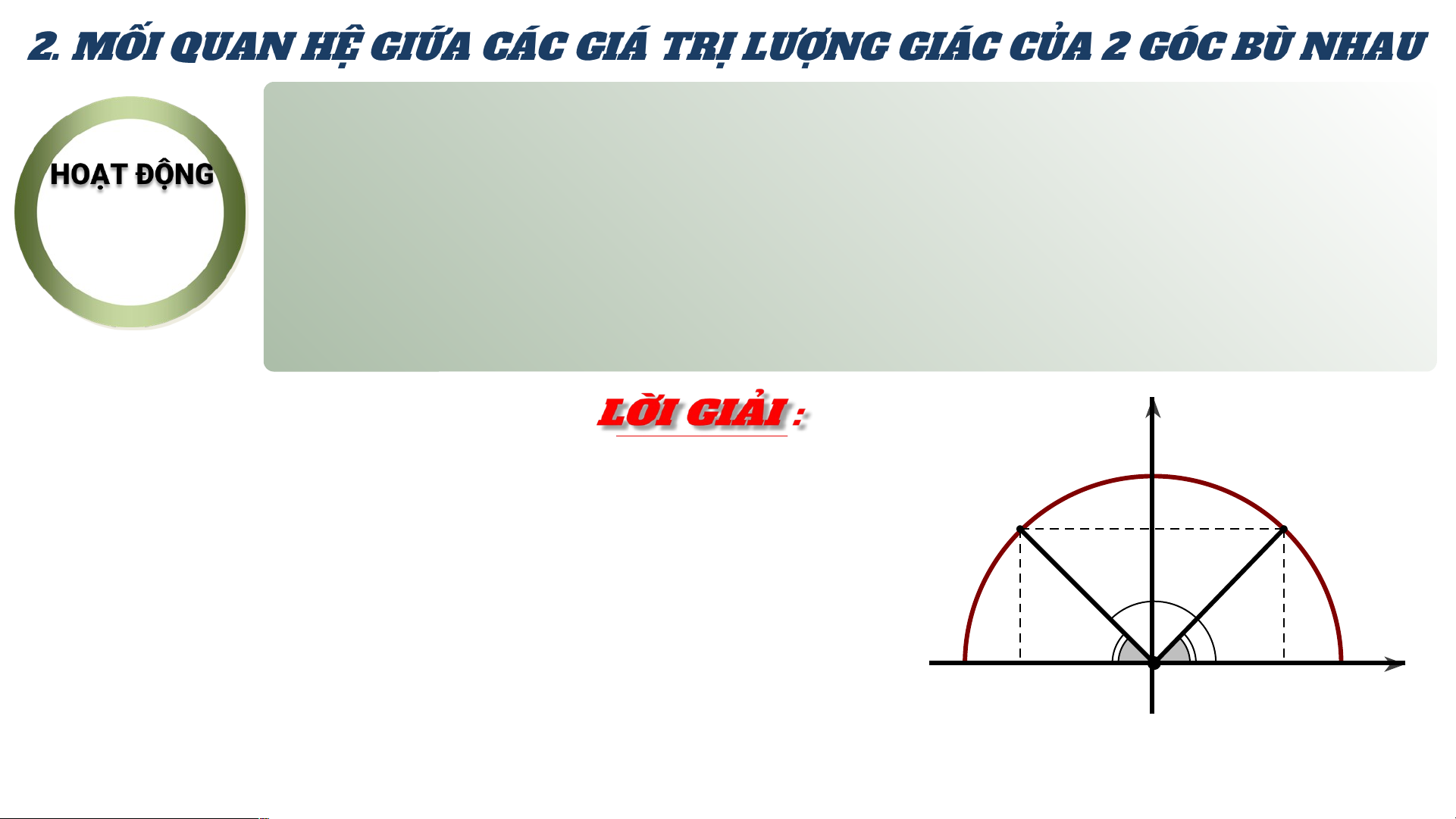
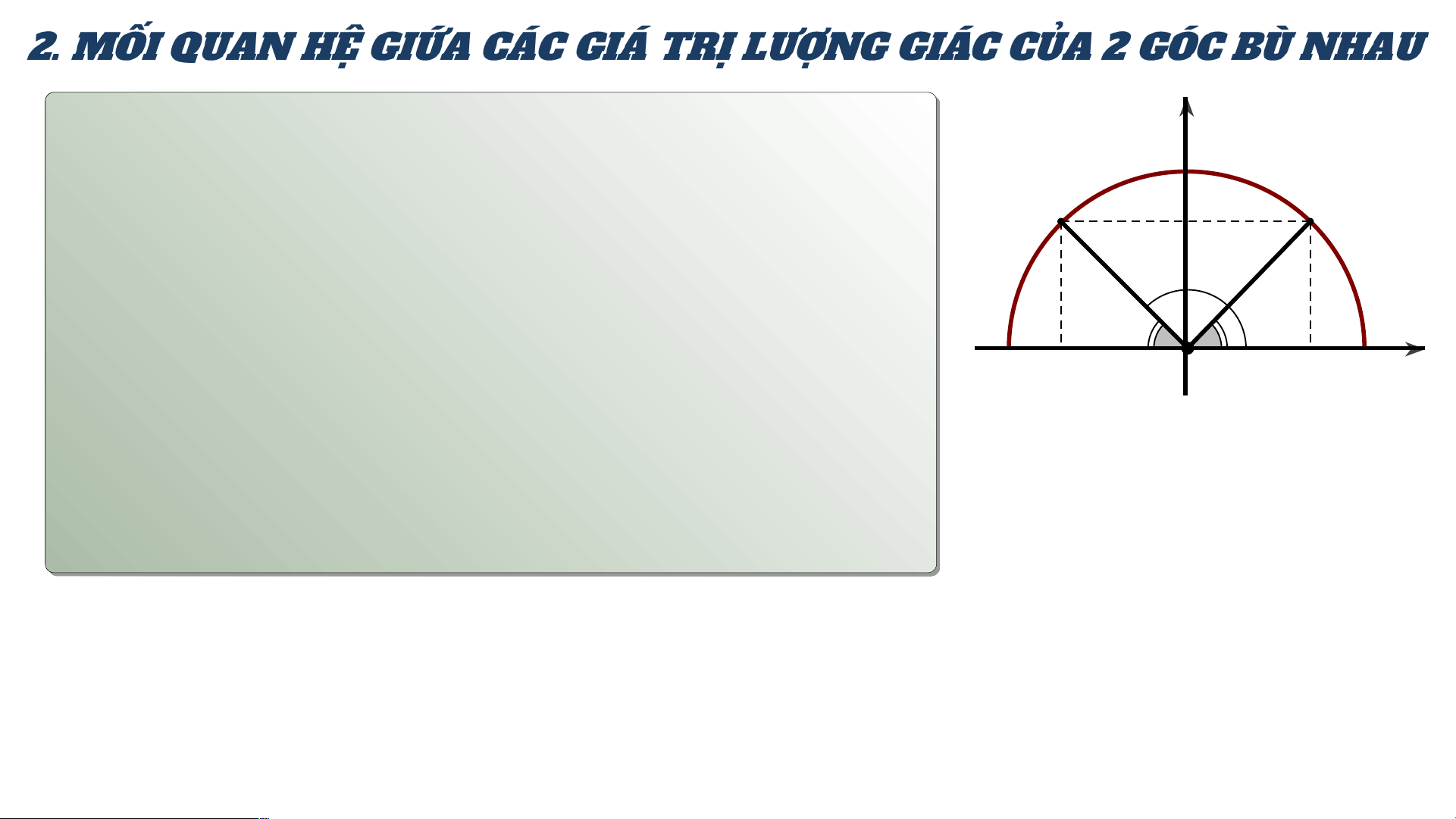
Gọi M và M’ là hai điểm trên nửa đường tròn đơn vị tương
2 ứng với hai góc bù nhau và như hình
Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy.
Từ đó nêu mối quan hệ giữa và giữa và y 1
Hai điểm M và M’ đối xứng nhau qua M' y0 M trục Oy 1800- α Khi đó : α -1 -x O x 1 x 0 0 y
Đối với hai góc bù nhau, và , ta có : 1 M' y0 M 1800- α α -1 -x O x 1 x 0 0
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15