Giáo án điện tử Toán 10 Chương 3 Bài 6 Kết nối tri thức: Hệ thức lượng trong tam giác

Bài giảng PowerPoint Toán 10 Chương 3 Bài 6 Kết nối tri thức: Hệ thức lượng trong tam giác hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 10. Mời bạn đọc đón xem!

16 8 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

BÀI 6: HỆ THỨC LƯỢNG

TRONG TAM GIÁC (4 Tiết)

CHÀO MỪNG CÁC EM ĐẾN

VỚI BÀI HỌC NGÀY HÔM NAY!

KHỞI ĐỘNG

Tháp Rùa nằm trong lòng hồ Hoàn Kiếm ở Thủ đô Hà Nội

Ngắm Tháp Rùa từ bờ, chỉ với

những dụng cụ đơn giản, dễ

chuẩn bị, ta cũng có thể xác định

được khoảng cách từ vị trí ta đứng

tới Tháp Rùa. Em có biết vì sao?

BÀI 6: HỆ THỨC LƯỢNG

TRONG TAM GIÁC (4 Tiết)

NỘI DUNG BÀI HỌC

Định lí côsin

Định lí sin

Giải tam giác và ứng dụng

thực tế

Công thức tính diện tích

tam giác

Tiết 1

1. Định lí côsin

HĐ1

 

!"# #$%&'()*+,(!!-./012 !"

)34516#$%#!7+

 81#92:!4!/!;3.0</((.()36=

7># .)36#9+

 81!3=736#9#72.0</((0

6(?)2%!@!A+

 B72(!!-&/012 )1#C:!"

)CDEFGH?I13JJ!II2%!

31("K

C#92:!4!/!;0

!)L0! L!7M02!DM1 !

N !")+O/!M!7N?'0</+

Giải

LMP&'



N!7L(&Q)0C=7

&Q()+

 ND  ER GH ?I 13 JJ #C 7  1

  2 ) C DLMN ? D #"0  D   EF

!H?I13JJ+

ND1("0)(!H?I13

)R1SK

Ghi nhớ

G%# )LMN0/(IUL0M0N?

D;)V!W:>X

00:>?!E;V!%EU

# !WL0M0NX

?Y#X

,?EUIX

Z03:>?(I!/3V7

#7)+

HĐ2

Thảo luận nhóm đôi, hoàn thành HĐ2.

O3C[+Q081=U 2!7?$

">I0#3H?-;DL+

a Tính a

theo BD

và CD

b Tính a

theo b, c và DA.

c Tính DA theo c và cos A.

d Chứng minh a

= b

+ c

-2b.c.cos A.

\EF!H?I13)#"M]N^



PM]

_N]



P]M

_]N

P

J]L

_]L_

P

_&++]L_

]LP+2`P+J2LPJ+2L

EOD^P

_&++]L_

.01]LPJ+2L

#.!-^



P

_

J&+2L+

Giải

Kết quả câu d còn đúng không khi góc A là góc vuông?

N!A0#C(L#"C2LP'0

P

_

B/a>

)!-(7b!%# 

3/-DLc+

Em hãy nhận xét mối quan hệ giữa

độ dài cạnh BC với độ dài các

cạnh BA, AC và côsin của góc A.

Định lí côsin

O3)LMN^



P

_

J&+2L



P

_

J&+2M



P

_

J&+2N

Định lí Pythagore có phải là một trường hợp đặc biệt

của định lí Cosin hay không?

GH?I13?)3/

- !d U ; !H ?I N"20

(DLPe'



GcVí dụ 1 #7^Tam giác ABC đã biết các yếu tố nào?

Để tính được BC ta dùng định lí côsin như thế nào?

Ví dụ 1

N)LMNDP.&'



#LMP<0LNPQ+OI!E

VMN+

Giải

\EF!H?I"2)LMND^

PLM

_LN

J&LM+LN+2.&'



P<

_Q

J&+<+Q+P.&e+

$1MNP

O!H?I2081#7">I2L02M0

2N!EV00;)LMN+

Luyện tập 1: N)LMNDLMP<0LNPQ#Pf<



+

OI!EV#!? D?V;)+

\EF!H?I"2)LMND^



,13MNP+

Giải

Luyện tập 1: N)LMNDLMP<0LNPQ#Pf<



+

OI!EV#!? D?V;)+

Giải

,13+

ả

ệ

9))LMN02!D!!EV02%

!DL#()3I!A!g;!H?I2V

!WL!%# )!D+

Hoạt động nhóm 4

Vận dụng 1:h]R!H?I20I(!-

!i$3G.+

LMP&'



]! !"!7

M 34 1   !" )

!7N6D+

Giải

\EF!H?I"2)LMND^

PLM

_MN

J&+LM+MN+2.[<



P&'

_.'

J&+&'+.'+jkQ&0QLNj&Q

Tiết 2

2. Định lí sin

HĐ3

O3)lCE !1081IZ#2L+

Thảo luận nhóm 4 hoàn thành HĐ3.

Bấm Tải xuống để xem toàn bộ.

| 1/22

| | Tải xuống

Preview text:

BÀI 6: HỆ THỨC LƯỢNG
TRONG TAM GIÁC (4 Tiết)
CHÀO MỪNG CÁC EM ĐẾN
VỚI BÀI HỌC NGÀY HÔM NAY! KHỞI ĐỘNG
Tháp Rùa nằm trong lòng hồ Hoàn Kiếm ở Thủ đô Hà Nội
Ngắm Tháp Rùa từ bờ, chỉ với
những dụng cụ đơn giản, dễ
chuẩn bị, ta cũng có thể xác định
được khoảng cách từ vị trí ta đứng
tới Tháp Rùa. Em có biết vì sao?
BÀI 6: HỆ THỨC LƯỢNG
TRONG TAM GIÁC (4 Tiết) NỘI DUNG BÀI HỌC 01 Định lí côsin 03
Giải tam giác và ứng dụng thực tế 02 Định lí sin 04
Công thức tính diện tích tam giác Tiết 1 1. Định lí côsin HĐ1
Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng
đông với vận tốc 20 km/h. Sau khi đi được 1 giờ, tàu chuyển sang hướng đông
nam rồi giữ nguyên vận tốc và đi tiếp.
a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1 km trên thực
tế ứng với 1 cm trên bản vẽ).
b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu
cách cảng Vân Phong bao nhiêu kilomet (số đo gần đúng).
c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hương đông
nam) thì có thể dụng Định lí Pythagore (Pi-ta-go) để tính chính xác các số đo trong câu b hay không? Giải
a) Hình vẽ thể hiển sơ đồ đường đi của tàu, tàu xuất phát từ cảng Vân
Phong (điểm A), đi theo hướng từ A đến B, sau đó từ B chuyển hướng đi
C (hướng đông nam). Thời gian đi từ B đến C là 0,5 giờ. AB = 20 BC = 10
b) Khoảng cách từ C đến A khoảng 28 cm, thì thực tế tàu cách cảng Vân Phong 28 km.
c) Có thể dùng Định lí Pythagore (Pi-ta-go) vì nếu tàu chuyển
hướng sang nam thì góc ABC là góc vuông, ta có thể áp dụng
định lí Pythagore (Pi-ta-go).
Có hay không, một kiểu định lí Pythagore cho tam giác tùy ý? Ghi nhớ
• Đối với tam giác ABC, ta thường kí hiệu A, B, C là
các góc của tam giác tại đỉnh tương ứng;
• a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; • p là nửa chu vi; • S là diện tích;
• R, r tương ứng là bán kính đường tròn ngoại tiếp và nội tiếp tam giác.
Thảo luận nhóm đôi, hoàn thành HĐ2. HĐ2
Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập
công thức tính a theo b, c và giá trị lượng giác của góc A. a) Tính a2 theo BD2 và CD2. b) Tính a2 theo b, c và DA. c) Tính DA theo c và cos A.
d) Chứng minh a2 = b2 + c2 - 2b.c.cos A. Giải
a) Áp dụng định lí Pythagore cho tam giác vuông BDC: a2 = BD2 + CD2
b) a2 = DB2 + DC2 = c2 - DA2 + (DA + b)2 = c2 + 2.b.DA + b2
c) DA = c. cos α = c. (-cosA) = -c.cosA
d) Theo b ta có: a = c2 + 2.b.DA + b2 (1), thay DA = - c. cosA vào (1) được: a2 = b2 + c2 - 2bc.cos A. Kết
t quả câu d còn đúng không khi góc A là góc vuông?
Còn đúng, vì khi A vuông thì cos A = 0, a2 = b2 + c2
Em hãy nhận xét mối quan hệ giữa Người ta cũng chứng
độ dài cạnh BC với độ dài các
minh được kết quả đối với
cạnh BA, AC và côsin của góc A. trường hợp góc A nhọn. Định lí côsin Trong tam giác ABC: a2 = b2 + c2 - 2bc.cos A b2 = c2 + a2 - 2ca.cos B c2 = a2 + b2 - 2ab.cos C
Định lí Pythagore có phải là một trường hợp đặc biệt
của định lí Cosin hay không?
Định lí Pythagore là một trường
hợp đặc biệt của định lí Côsin, khi góc A = 90o.
Đọc Ví dụ 1 và cho biết: Tam giác ABC đã biết các yếu tố nào?
Để tính được BC ta dùng định lí côsin như thế nào? Ví dụ Ví 1 dụ
Cho tam giác ABC có = 120o và AB = 5, AC = 8. Tính độ dài cạnh BC. Giải
Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 - 2AB. AC. cos120o = 52 + 82 - 2.5.8. = 129. Vậy BC =
Khám phá Từ định lí cosin, hãy viết các công thức tính cosA, cosB,
cosC theo độ dài các cạnh a, b, c của tam giác ABC.
Luyện tập 1: Cho tam giác ABC có AB = 5, AC = 8 và = 45o.
Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác.
Áp dụng định lí côsin cho tam giác ABC có: Giải Suy ra BC = .
Luyện tập 1: Cho tam giác ABC có AB = 5, AC = 8 và = 45o.
Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác. Giải Suy ra . Suy ra . Trải nghiệm Hoạt động nhóm 4
Vẽ một tam giác ABC, sau đó đo độ dài các cạnh, số
đo góc A và kiểm tra tính đúng đắn của định lí cosin tại
đỉnh A đối với tam giác đó.
Vận dụng 1: Dùng định lí cosin, tính khoảng cách được đề cập trong HĐ1b. Giải AB = 20 B
Do tàu đi theo hướng đông đến
C = 1 B rồi chuyển hướng đông nam 0 đến C nên góc .
Áp dụng định lí côsin cho tam giác ABC có:
AC2 = AB2 + BC2 - 2.AB.BC.cos 135o
= 202 + 102 - 2.20.10. ≈ 782,8 AC ≈ 28 Tiết 2 2. Định lí sin
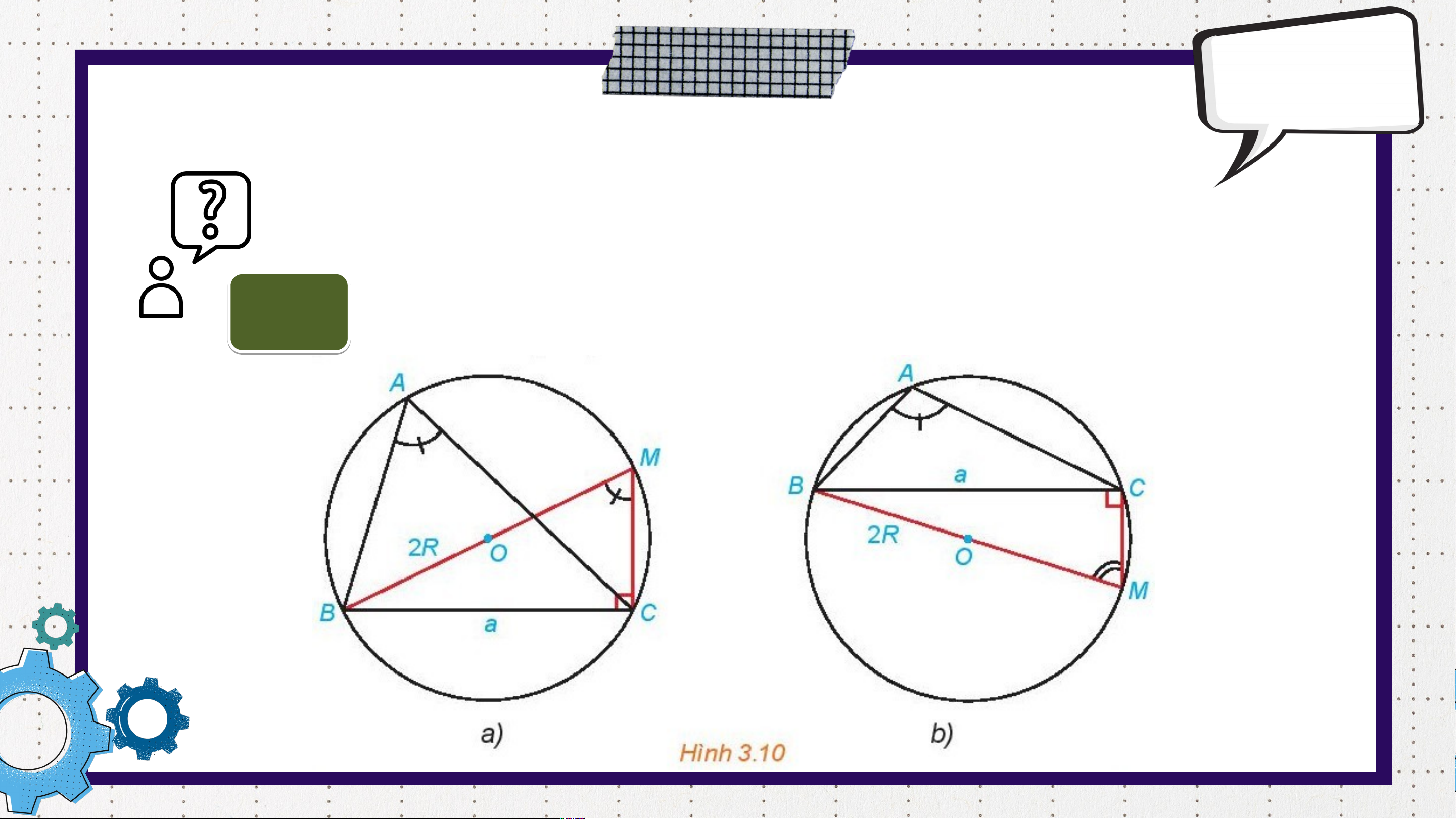
Thảo luận nhóm 4 hoàn thành HĐ3. HĐ3
Trong mỗi hình dưới đây, hãy tính R theo a và sinA.
Document Outline

Slide 1
Slide 2
Slide 3
Slide 4
Slide 5
Slide 6
Slide 7
Slide 8
Slide 9
Slide 10
Slide 11
Slide 12
Slide 13
Slide 14
Slide 15
Slide 16
Slide 17
Slide 18
Slide 19
Slide 20
Slide 21
Slide 22

Giáo án điện tử Toán 10 Chương 3 Bài 6 Kết nối tri thức: Hệ thức lượng trong tam giác

Thông tin :

Tài liệu liên quan:

Giáo án điện tử Toán 10 Chương 1 Cánh diều : Mệnh đề toán học. Tập hợp (CD)

Giáo án điện tử Toán 10 Bài 2 Chân trời sáng tạo: Tập hợp

Giáo án điện tử Toán 10 Chân trời sáng tạo: Hệ thức lượng trong tam giác

Giáo án điện tử Toán 10 Bài 1 Chân trời sáng tạo: Giá trị lượng giác của một góc từ 0° đến 180°

Giáo án điện tử Toán 10 Bài 1 Chân trời sáng tạo: Bất phương trình bậc nhất hai ẩn