Giáo án điện tử Toán 10 Chương 4 Bài 7 Kết nối tri thức: Các khái niệm mở đầu
Bài giảng PowerPoint Toán 10 Chương 4 Bài 7 Kết nối tri thức: Các khái niệm mở đầu hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 10. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 10
Môn: Toán 10
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
TRƯỜNG THPT ĐẶNG HUY TRỨ TỔ TOÁN
CHÀO MỪNG QUÝ THẦY CÔ VÀ CÁC
EM SINH VIÊN ĐẾN DỰ GIỜ THĂM LỚP LỚP 10/7
GV: LÊ THỊ HỒNG VÂN HĐ1
Nhiệt độ và gió là hai yếu tố
luôn cùng được đề cập trong các
bản tin dự báo thời tiết. Tuy
nhiên, nhiệt độ là đại lượng chỉ
có độ lớn, còn gió có cả hướng
và độ lớn. Với một đơn vị đo, ta
có thể dùng số để biểu diễn
nhiệt độ. Đối với các đại lượng
gồm hướng và độ lớn như vận
tốc gió thì sao? Ta có thể dùng
đối tượng toán học nào để biểu diễn chúng? CHƯƠNG I CHƯƠNG IV. VECTƠ
§7. Các khái niệm mở đầu
§8. Tổng và hiệu của hai vectơ
§9. Tích của một vectơ với một số
§10. Vectơ trong mặt phẳng tọa độ
§11. Tích vô hướng của hai vectơ
Bài tập cuối chương 4 CHƯƠ CH N ƯƠ G IV. N V G E C I TƠ 7
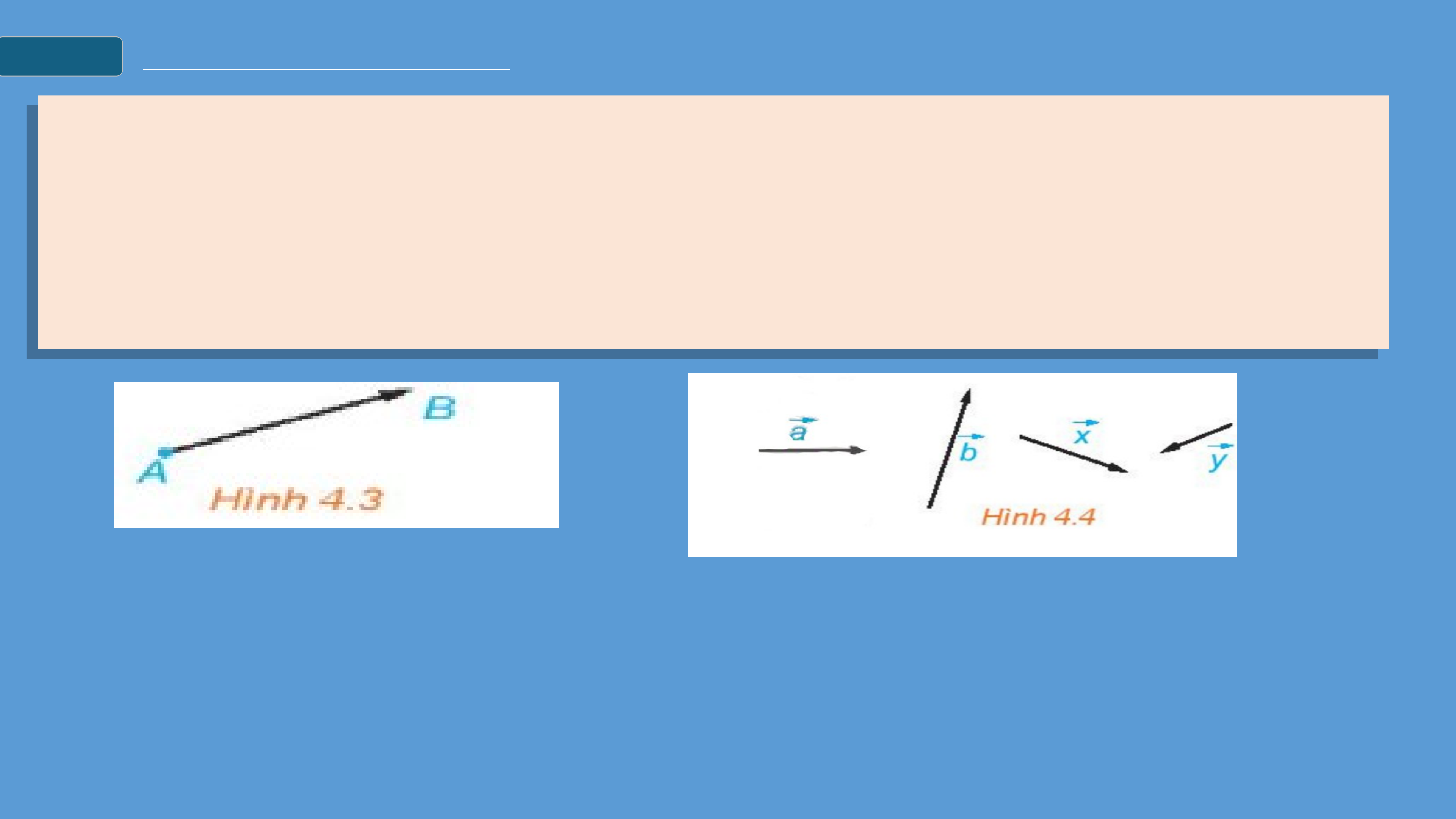
CÁC KHÁI NIỆM MỞ ĐẦU I KHÁI NIỆM VECTƠ
IIHAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU 3 I KHÁI NIỆM VECTƠ ● V ● e V c e t c ơ t ơlà l mộ à t mộ đ t o đ ạ o n ạ t n h t ẳng hẳn có g h có ướng hướ , n ng ghĩ , n a ghĩ là a , là ,t ro t ng ro ha ng i ha điể i đi m ể m m út m útcủa của đoạn đo t ạn h t ẳng h , đ ẳng ã , đ c ã hỉ c rõ hỉ rõđi ể đi m ể đ m ầu, đầ điể u, đ m iể cu m ố cu i. ối. ● V ● e V ct e ơ ct ơc ó c óđiể m điể đ m ầ đ u ầ và u đi và ể đi m ể cuố m i cuố đ i ượ đ c ượ kí c hi kí ệ hi u ệ là u là, ,đọ c đọclà ve là v c e t c ơ t ơ V e V ct e ơ ct c ơ ò c n ò đ n ượ đ c ượ kí c hi kí ệ hi u ệ là u là
● Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
● Độ dài của vectơ , tương ứng được kí hiệu là . I KHÁI NIỆM VECTƠ Ví dụ 1.
Cho hình chữ nhật với ABCD A B 3, B C 4
Hãy tính độ dài các vectơ B , A A , D AC , , . I KHÁI NIỆM VECTƠ Ví dụ 2.
Cho tam giác đều với cạnh có độ dài bằng .
Hãy chỉ ra các vectơ có độ dài bằng và có điểm đầu, điểm cuối là các đỉnh của tam giác . .
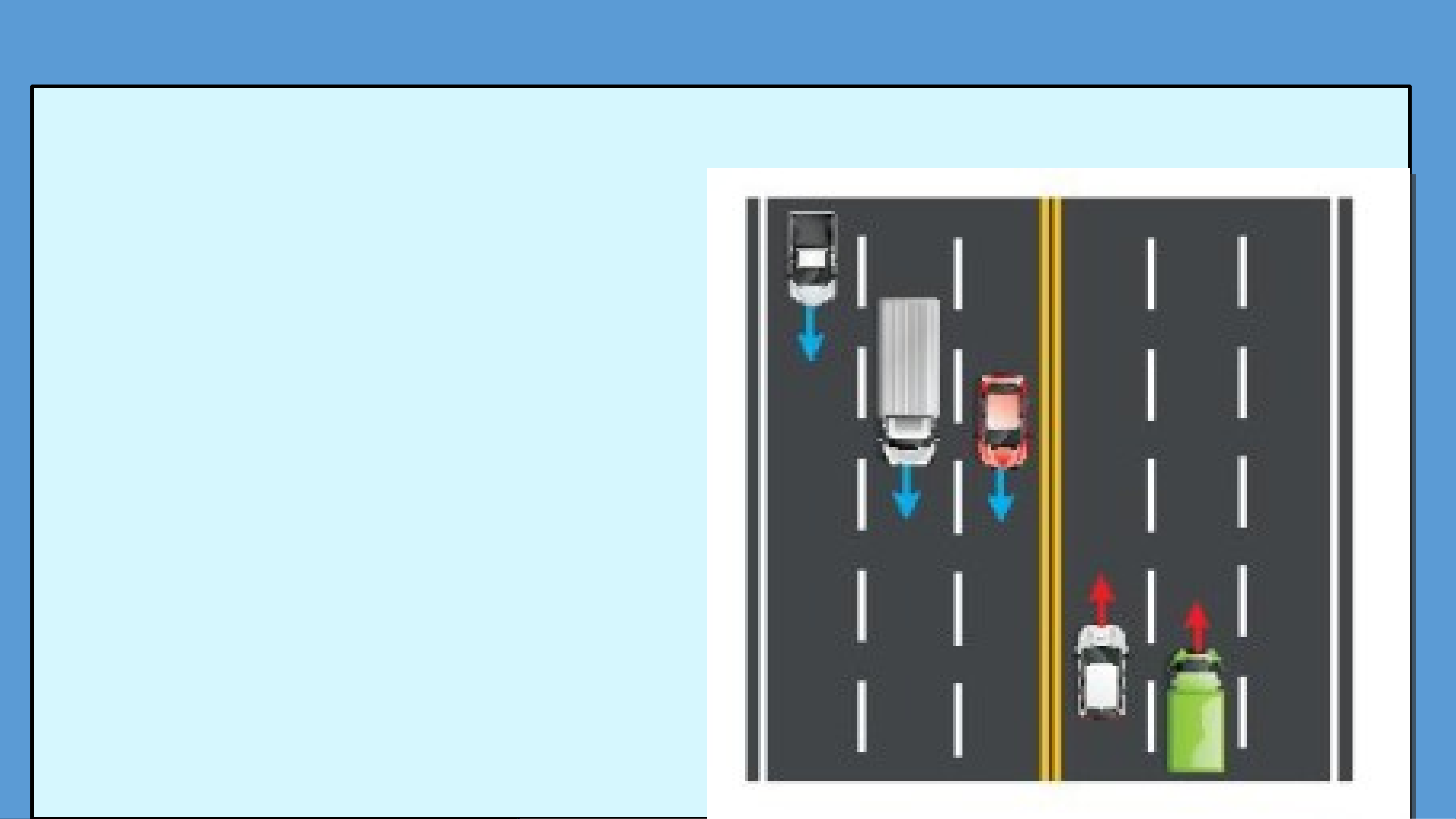
HĐ2: Quan sát các làn đường trong hình 4.5 và cho biết những nhận xét nào sau đây là đúng.
a) Các làn đường song song với nhau.
b) Các xe chạy theo cùng một hướng.
c) Hai xe bất kì đều chạy theo cùng một
hướng hoặc hai hướng ngược nhau. II
HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU
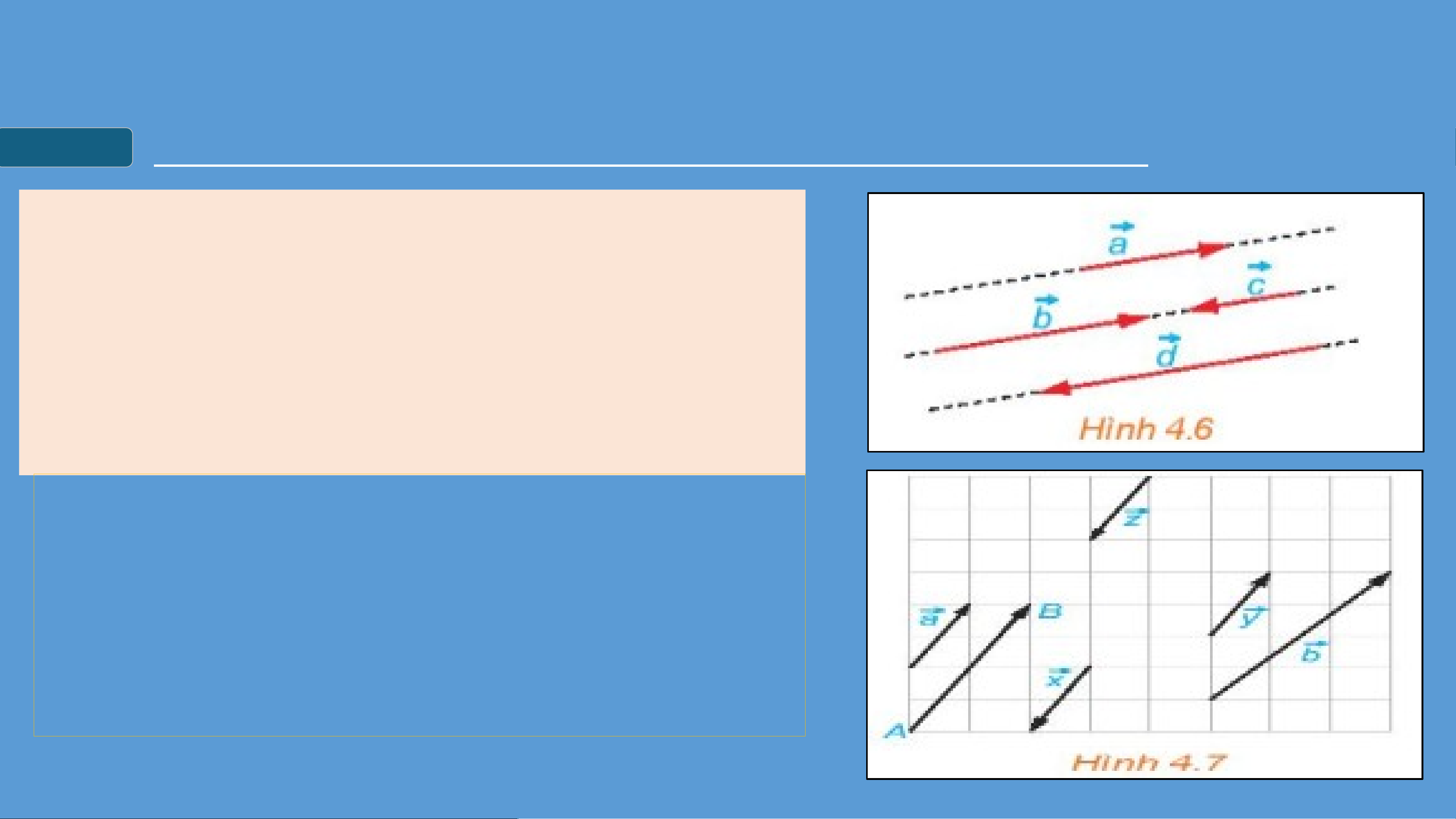
• Đường thẳng đi qua điểm đầu và điểm
cuối của một vectơ được gọi là giá của vectơ đó.
• Hai vectơ được gọi là cùng phương nếu
chúng có giá song song hoặc trùng nhau.
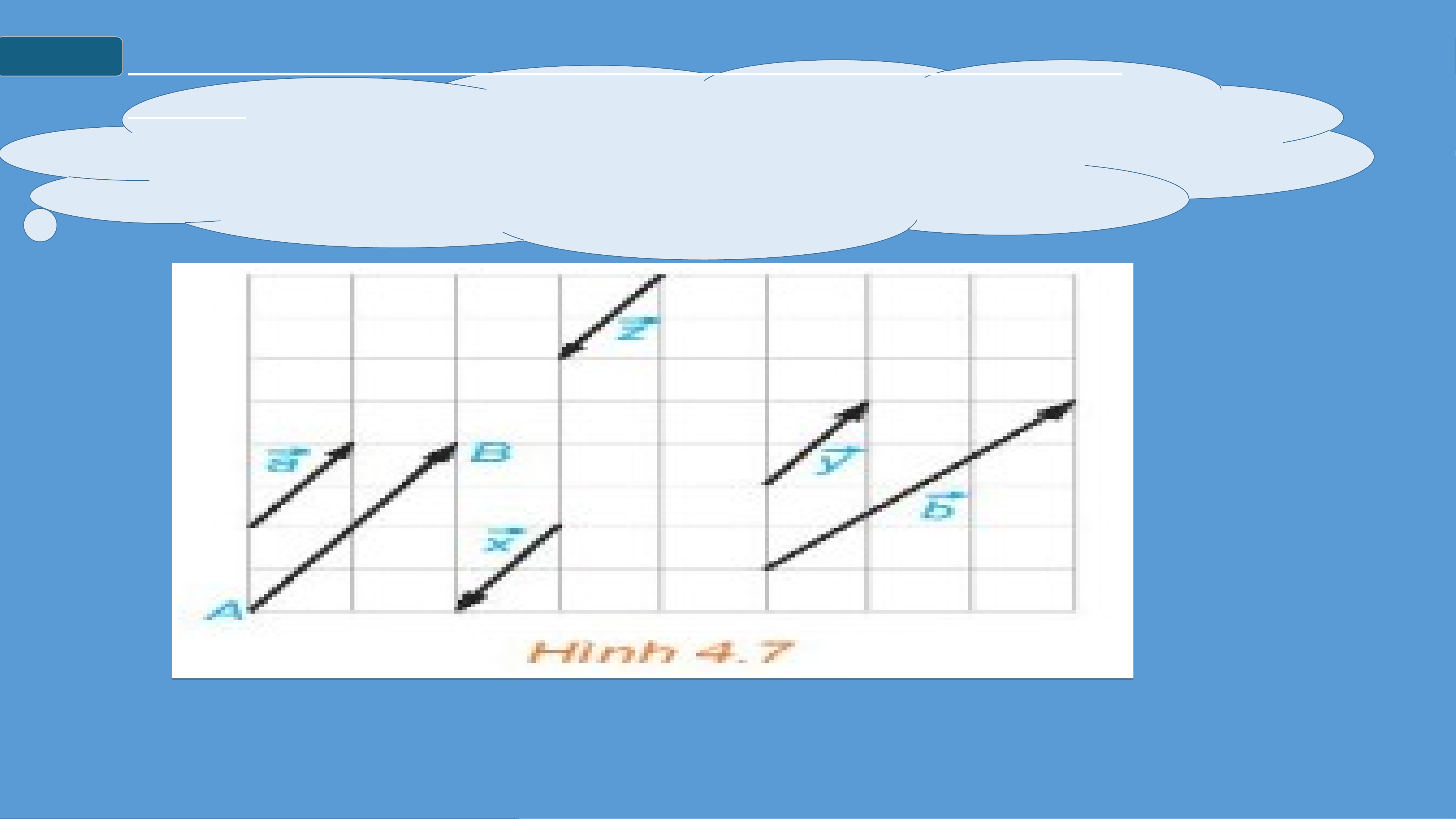
Trong cùng Hình 4.7, mỗi cặp vectơ
trong các vectơ đều cùng phương,
nhưng vectơ không cùng phương với mỗi vectơ trên. II
HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG HĐ N 3 H : A X
U ét các vectơ cùng phương trong Hình 4.7. Hai vectơ
và được gọi là cùng hướng, còn hai vectơ và được gọi là ngược hướng.
Hãy chỉ ra các vectơ cùng hướng với vectơ và các vectơ ngược hướng với vectơ . II
HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU
Đối với hai vectơ cùng phương thì
chúng cùng hướng hoặc ngược hướng. z Hai vec tơ t ơ và được
ượ gọi là bằng nhau, u kí k hiệu
ệ , nếu chúng có cùng độ dài và cùng hướng. II
HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG C NH
hú ý: AU
● Ta cũng xét các vectơ có điểm đầu và
điểm cuối trùng nhau (chẳng hạn ),
gọi là các vectơ-không. A
● Ta quy ước vectơ-không có độ dài
bằng 0, cùng hướng với mọi vectơ. ● O Hình 4.8
● Với mỗi điểm và vectơ cho trước, có
duy nhất điểm sao cho (H.4.8). II
HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG Ví dụ 3. NHAU
Cho hình bình hành . Hãy chỉ ra mối quan hệ về độ dài,
phương, hướng giữa các cặp vectơ: và , và , và .
Những cặp vectơ nào trong các cặp vectơ trên là bằng nhau? Ví dụ 4.
Chứng minh rằng ba điểm thẳng hàng khi và chỉ khi và cùng phương
Câu 1: Cho ba điểm phân biệt Có bao nhiêu vectơ
khác vectơ không có điểm đầu và điểm cuối là các điểm đã cho? A. 6 B. 5 C. 4 D. 3
Câu 2: Cho ngũ giác . Từ các đỉnh của ngũ giác đã
cho có thể lập được bao nhiêu véc tơ có điểm cuối là điểm A. 4 B. 3 C. 5 D. 6
Câu 3: Cho ba điểm thẳng hàng, trong đó điểm nằm
giữa hai điểm và . Khi đó các cặp vectơ nào sau đây cùng hướng? A. và B. và . C. và D. và
Câu 4: Cho lục giác đều ABCDEF tâm O. Số véc
tơ khác vectơ không có điểm đầu và điểm cuối là
đỉnh hoặc tâm O của lục giác và cùng phương với vectơ là A. 8 B. 6 C. 10 D. 9
Câu 5: Cho lục giác đều tâm . Các vectơ bằng vectơ là A. , , , B. , , . C. , . D. , , .
Câu 6:Cho tam giác , gọi , , lần lượt là trung điểm của
các cạnh , , . Vectơ cùng hướng với vectơ nào trong các vectơ sau đây? A. B. C. D. III. BÀI TẬP Bài 4.1
Cho ba vectơ đều khác vectơ . Những khẳng định nào sau đây là đúng?
a) đều cùng phương với vectơ .
b) Nếu không cùng hướng với thì ngược hướng với .
c) Nếu và đều cùng phương với thì và cùng phương.
d) Nếu và đều cùng hướng với thì và cùng hướng. Bài 4.3 Chứng minh rằng:
tứ giác là hình bình hành khi và chỉ khi . 𝑨 𝑫 𝑩 𝑪
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22