KHỞI ĐỘNG
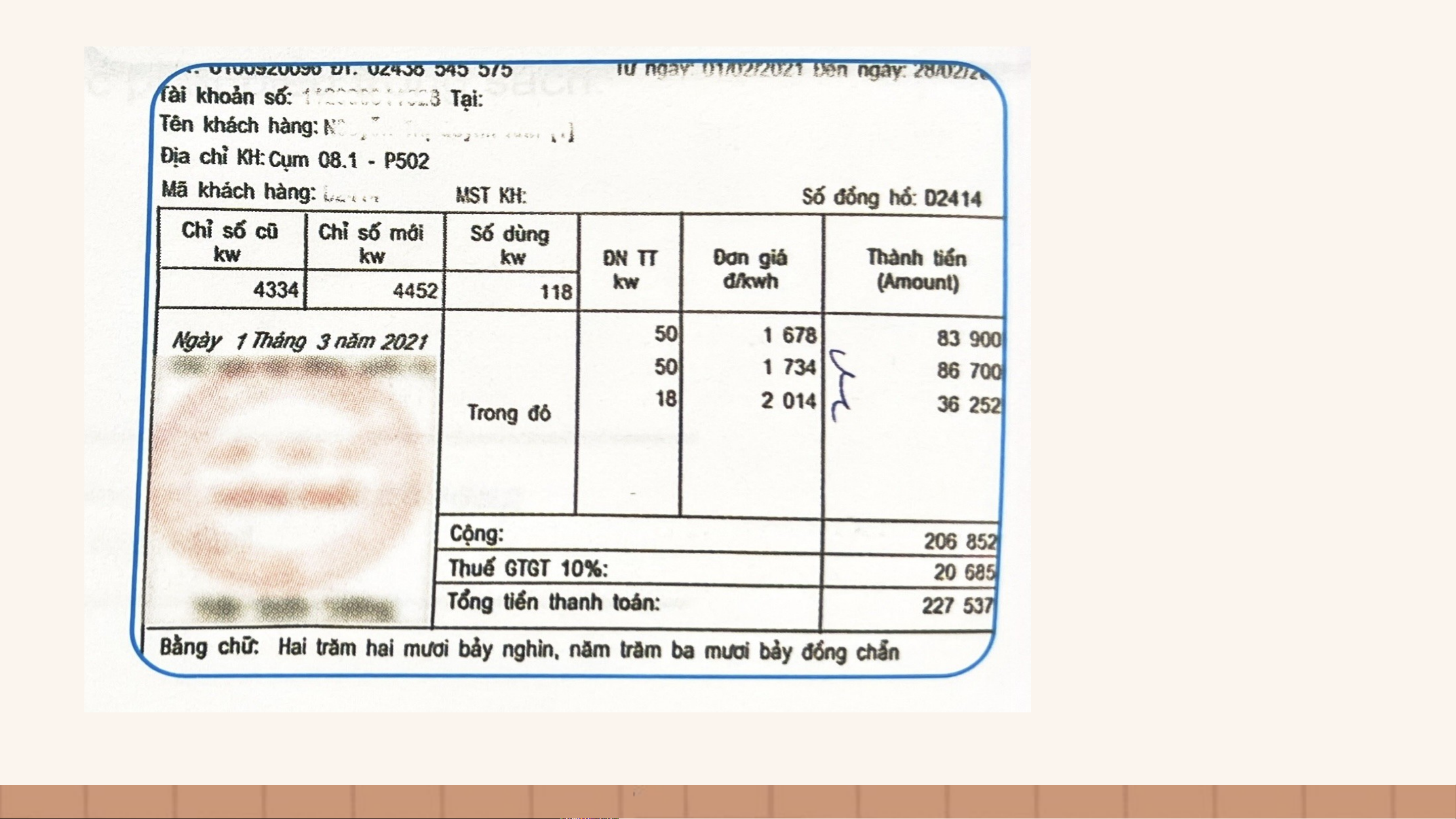
Quan sát hóa đơn tiền điện ở hình bên. Hãy cho biết tổng lượng điện tiêu thụ trong
tháng và số tiền phải trả (chưa tính thuế giá trị gia tăng). Quan sát hóa đơn tiền điện ở hình bên. Hãy cho biết tổng lượng điện tiêu thụ trong tháng và số tiền phải
trả (chưa tính thuế giá trị gia tăng). KHỞI ĐỘNG
Quan sát hóa đơn tiền điện ở hình bên. Hãy cho biết tổng lượng điện tiêu thụ trong
tháng và số tiền phải trả (chưa tính thuế giá trị gia tăng).
Có cách nào mô tả sự phụ thuộc của số
tiền phải trả vào tổng lượng điện tiêu thụ hay không? CHƯƠNG VI: HÀM SỐ,
ĐỒ THỊ VÀ ỨNG DỤNG BÀI 15: HÀM SỐ NỘI DUNG BÀI HỌC 01 Khái niệm hàm số 02 Đồ thị hàm số 03
Sự đồng biến, nghịch biến của hàm số 01 Khái niệm hàm số HĐ 1:
Bảng 6.1 cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong
ngày 25-3-2021 là một trạm quan trắc ở Thủ đô Hà Nội: THẢO LUẬN NHÓM
Các em hãy đọc nội dung của HĐ 1 và trả lời câu hỏi.
a) Hãy cho biết nồng độ bụi PM 2.5 tại mỗi thời điểm 8 giờ, 12 giờ, 16 giờ.
b) Trong Bảng 6.1, mỗi thời điểm tương ứng với bao nhiêu giá trị của nồng độ bụi PM 2.5? Gi G ải ả a) b)
• Thời điểm 8 giờ: 57,9.
Mỗi thời điểm tương ứng với một
• Thời điểm 12 giờ: 69,07.
giá trị của nồng độ bụi PM 2.5.
• Thời điểm 16 giờ: 81,78. THẢO LUẬN NHÓM
Các em hãy đọc nội dung của HĐ 2 và trả lời câu hỏi.
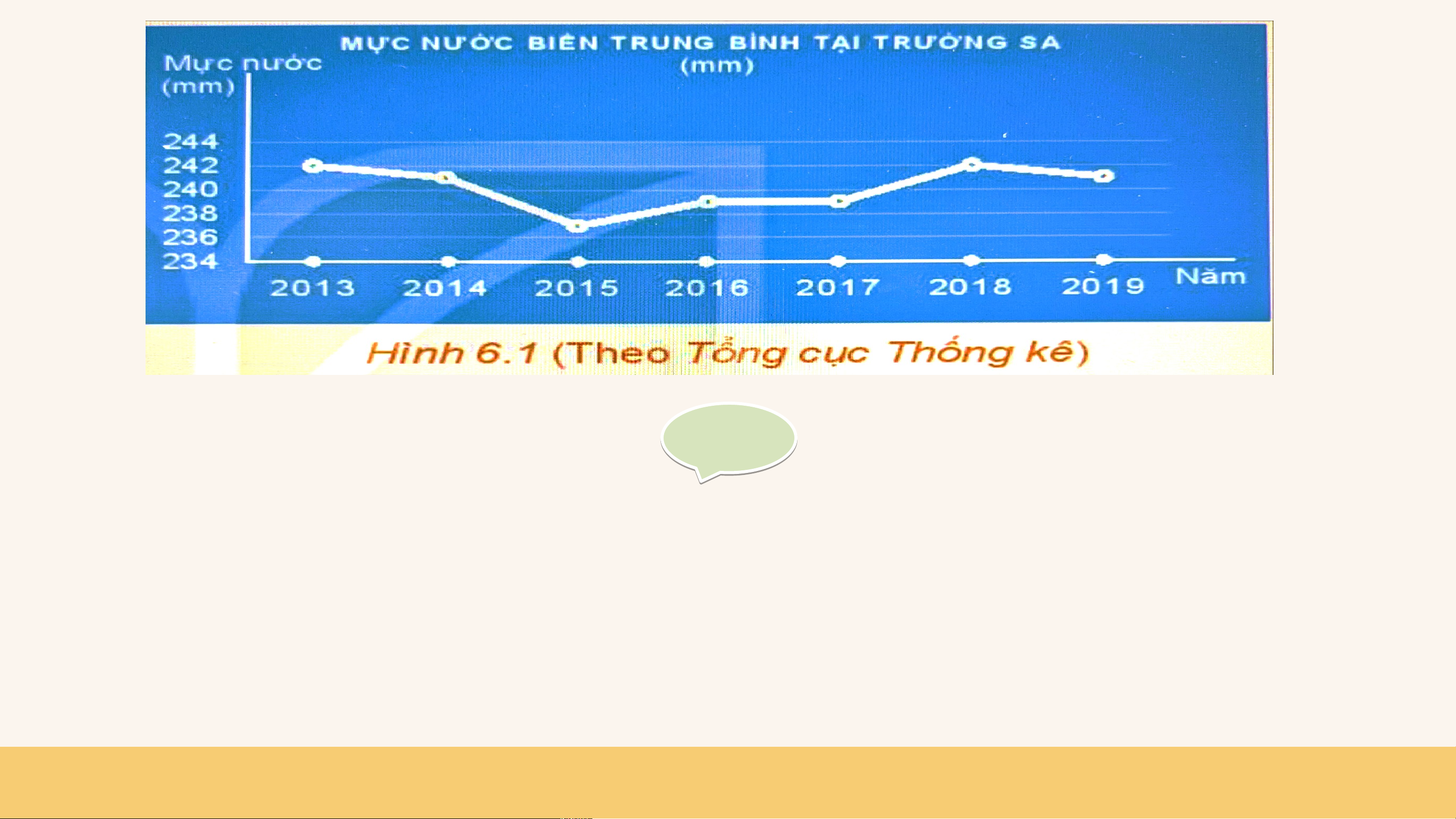
HĐ 2: Quan sát Hình 6.1
a) Thời gian theo dõi mực
nước biển ở Trường Sa được
thể hiện trong hình từ năm nào đến năm nào?
b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại
Trường Sa cao nhất, thấp nhất? Giải ả
a) Từ năm 2013 đến năm 2019.
b) Năm mực nước cao nhất: 2013 và 2018 (242mm).
Năm mực nước thấp nhất: 2015 (237mm). THẢO LUẬN NHÓM
Các em hãy đọc nội dung của HĐ 3 và trả lời câu hỏi.
HĐ 3: Tính tiền điện.
a) Dựa vào Bảng 6.2 về giá bán lẻ điện sinh hoạt, hãy tính số tiền
phải trả ứng với mỗi lượng điện tiêu thụ ở Bảng 6.3: Giải ả
a) Lượng điện tiêu thụ: Lượng điện 50 100 200 tiêu thụ (kWh) Số tiền ? ? ? (nghìn đồng) Giải ả
a) Lượng điện tiêu thụ: Lượng điện 50 100 200 tiêu thụ (kWh) Số tiền (nghìn đồng) Giải ả
a) Lượng điện tiêu thụ: Lượng điện 50 100 200 tiêu thụ (kWh) Số tiền (nghìn đồng) Giải ả
a) Lượng điện tiêu thụ: Lượng điện 50 100 200 tiêu thụ (kWh) Số tiền (nghìn đồng) THẢO LUẬN NHÓM
Các em hãy đọc nội dung của HĐ 3 và trả lời câu hỏi.
HĐ 3: Tính tiền điện.
b) Gọi x là lượng điện tiêu thụ (đơn vị kWh) và y là số tiền phải trả
tương ứng (đơn vị nghìn đồng). Hãy viết công thức mô tả sự phụ thuộc của y và x khi . Giải ả b) y = 1 = 6 1 78 7 . 8 x (với ) KẾT LUẬN
Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị
tương ứng của y thuộc tập số thực R thì ta có một hàm số.
- Ta gọi x là biến số và y là hàm số của x.
- Tập hợp D gọi là tập xác định của hàm số.
- Tập tất cả các giá trị y nhận được, gọi là tập giá tri của hàm số.
Ví dụ 1 (SGK – tr6)
Quan sát lại bảng 6.1 trong HĐ1
Nếu gọi là thời điểm, là nồng độ bụi thì là biến số và là hàm số của . Đó
là hàm số được cho bằng bảng.
- Tập xác định của hàm số là
- Tập giá trị của hàm số là .
Ví dụ 2 (SGK – tr6)
Viết hàm số mô tả sự phụ thuộc của quãng đường đi được vào thời gian của
một vật chuyển động thẳng đều với vận tốc . Tìm tập xác định của hàm số đó.
Tính quãng đường vật đi được sau . Gi G ải ả
Một vật chuyển động thẳng đều với vận tốc thì quãng đường đi được (mét) phụ
thuộc vào thời gian (giây) theo công thức , trong đó là biến số, là hàm số của .
- Tập xác định của hàm số là .
- Quãng đường vật đi được sau 5 s là: .
- Quãng đường vật đi được sau 10 s là: .
Ví dụ 3 (SGK – tr6)
Tìm tập xác định của các hàm số sau: a) b) Giải Giả
a) Biểu thức có nghĩa khi , tức là khi .
Vậy tập xác định của hàm số đã cho là .
b) Biểu thức có nghĩa khi , tức là khi .
Vậy tập xác định của hàm số đã cho là .8 LƯU Ý
Khi cho hàm số bằng công thức y = f(x) mà
không chỉ rõ tập xác định của nó thì ta quy ước
tập xác định của hàm số là tập hợp tất cả các số
thực x sao cho biểu thức f(x) có nghĩa. LUYỆN TẬP 1
a) Hãy cho biết Bảng 6.4 có cho ta một hàm số hay không. Nếu có, tìm tập
xác định và tập giá trị của hàm số đó.
b) Trở lại HDD2, ta có hàm số cho bằng biểu đồ. Hãy cho biết giá trị của hàm số tại x = 2018.
c) Cho hàm số . Tính và tìm tập xác định, tập giá trị cả hàm số này. Giải Giả
a) Bảng 6.4 có cho ta một hàm số vì mỗi giá trị của x cho ta tương ứng một
và chỉ một giá trị của y. Tập xác định: Tập giá trị:
b) Giá trị hàm số tại là . c) Tập xác định: Do nên . Tập giá trị: . NHẬN XÉT
Một hàm số có thể được cho bằng bảng,
bằng biểu đồ, bằng công thức hoặc mô tả bằng lời. 02 Đồ thị hàm số THẢO LUẬN NHÓM
Các em hãy đọc nội dung của HĐ 4 và trả lời câu hỏi.
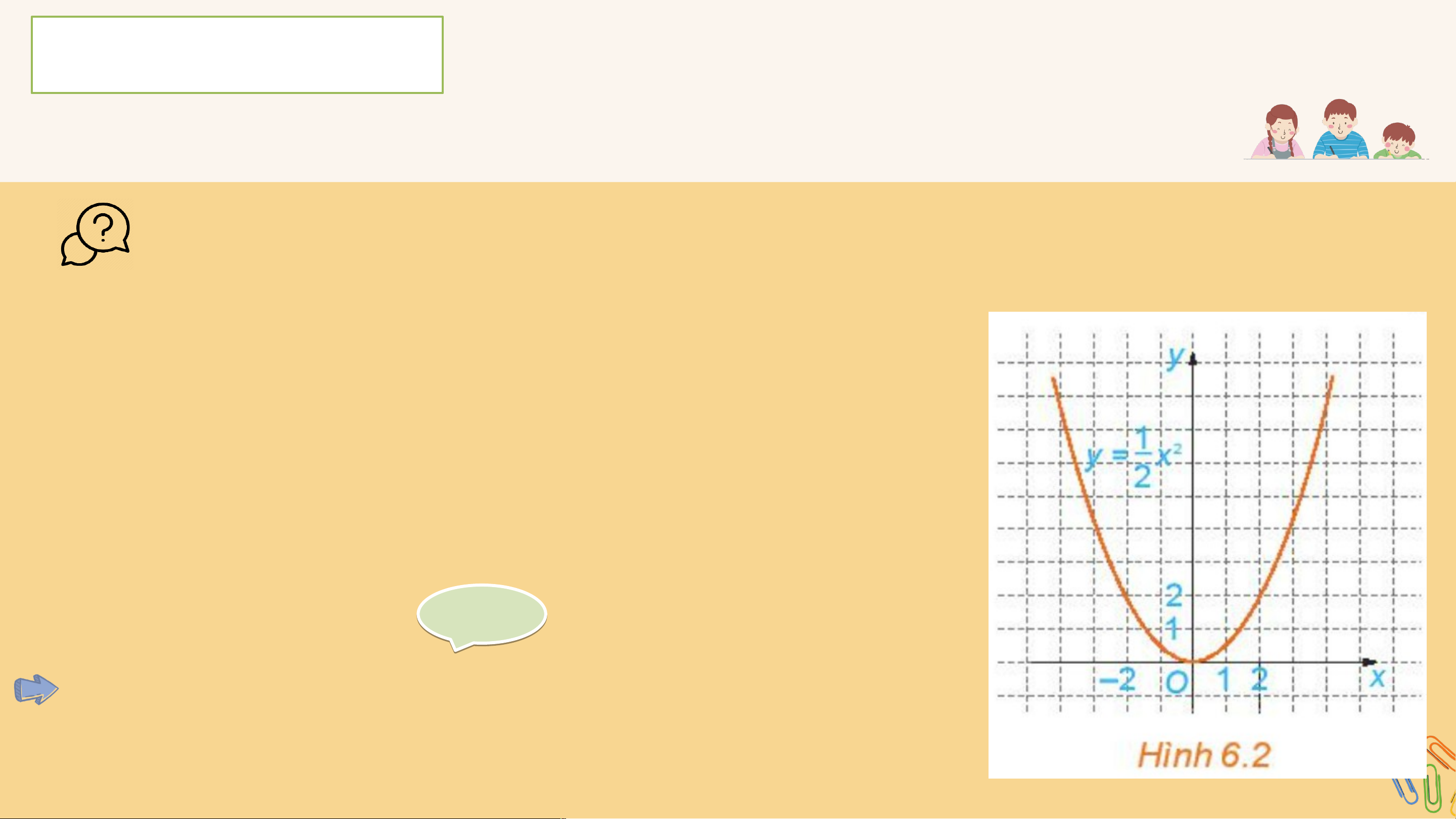
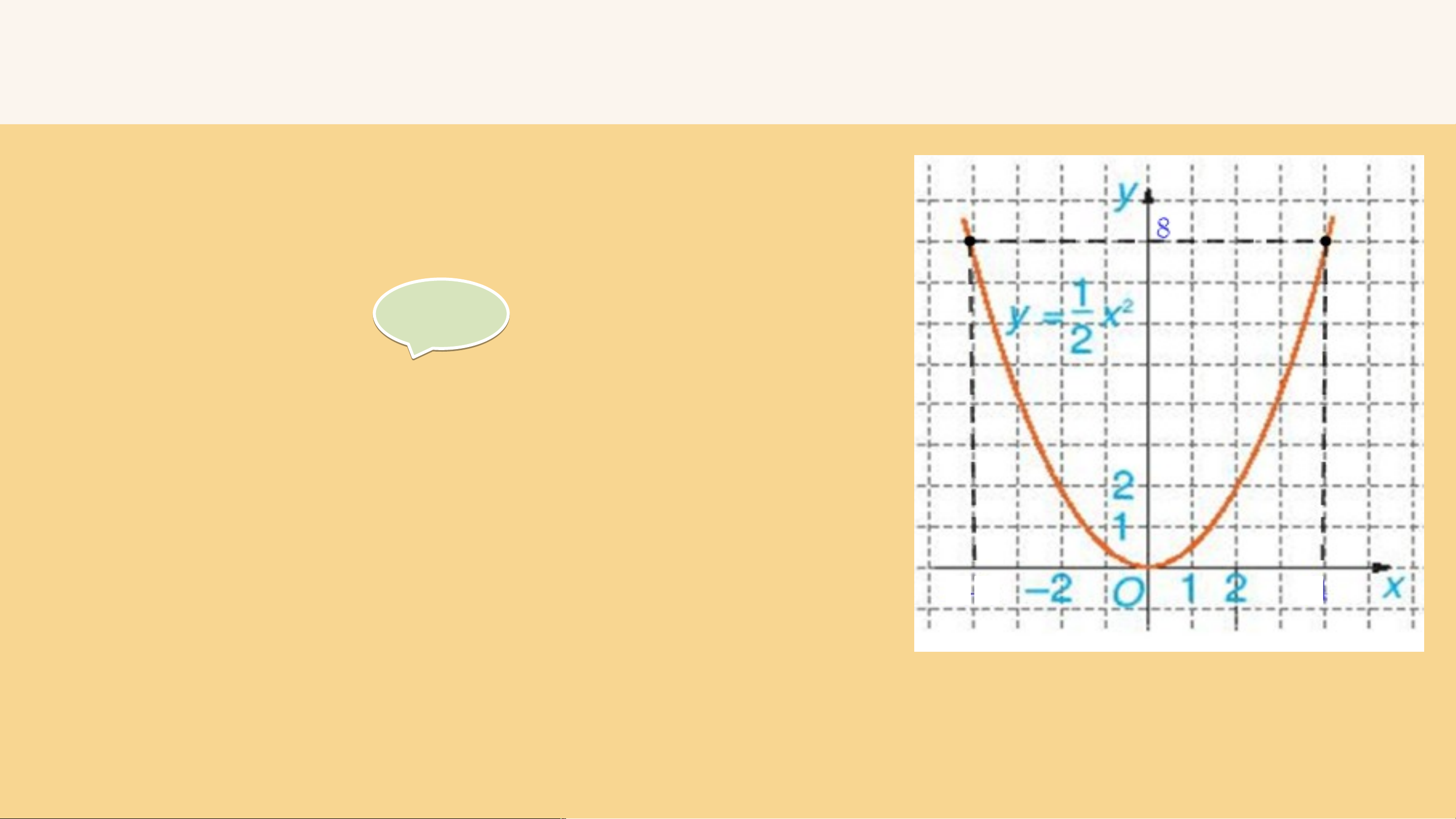
HĐ 4: Quan sát Hình và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số .
(0; 0), (2; 2), (-2; 2), (1; 2), (-1; 2).
Nêu nhận xét về mối quan hệ giữa hoành độ và
tung độ của những điểm nằm trên đồ thị. Giải ả
Những điểm nằm trên đồ thị của hàm số là: (0; 0), (2; 2), (-2; 2).
• Nhận xét: Tung độ bằng bình phương hoành độ nhân với . KẾT LUẬN
Đồ thị của hàm số xác định trên tập D là tập hợp tất cả
các điểm M(x: f(x)) trên mặt phẳng tọa độ với mọi x thuộc D.
Ví dụ 4 (SGK – tr7)
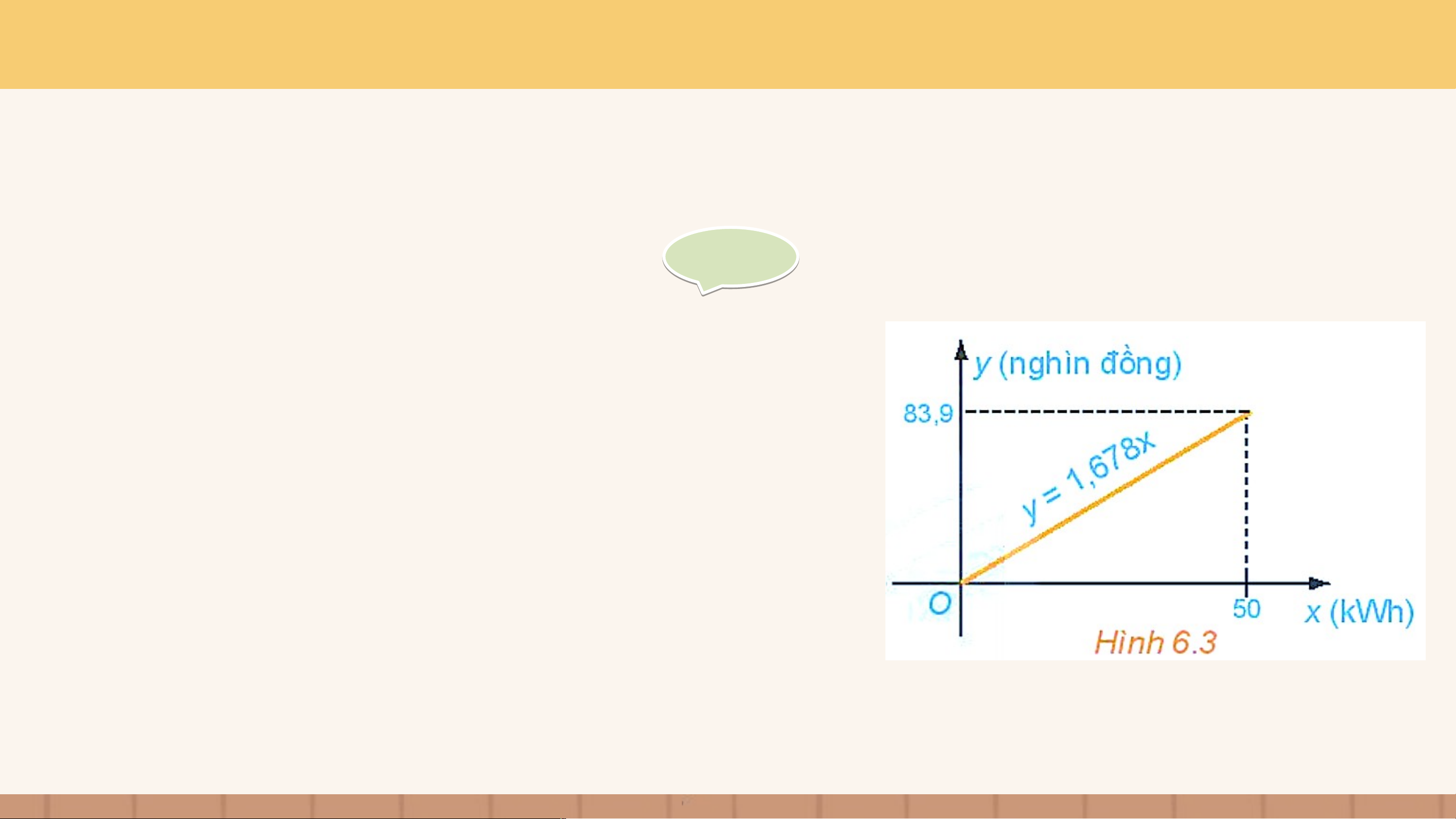
Viết công thức của hàm số cho ở HĐ3b. Tìm tập xác định, tập giá trị và vẽ đồ thị của hàm số này. Gi G ải ả
Công thức của hàm số cho ở HĐ3b là với .
Tập xác định của hàm số này là . Vì nên .
Vậy tập giá trị của hàm số là .
Đồ thị của hàm số trên là một đoạn thẳng (H.6.3). LUYỆN TẬP 2
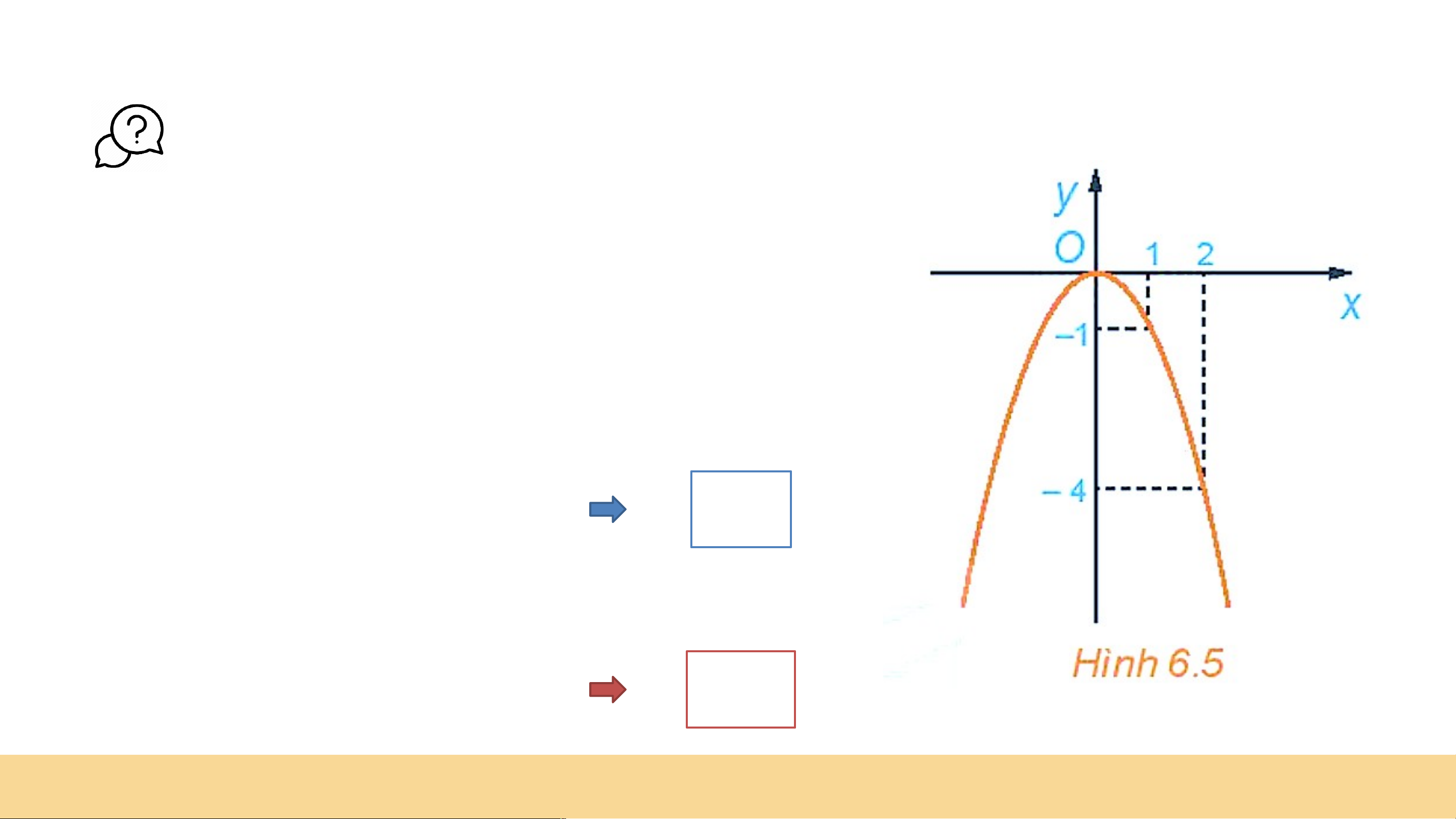
a) Dựa vào đồ thị của hàm số (H.6.2), tìm sao cho . Gi G ải ả
- Với y = 8, từ điểm 8 trên trục Oy, ta kẻ đường
thẳng song song với Ox, đường thẳng này cắt
đồ thị hàm số tại hai điểm. - 4 4
- Từ hai điểm đó hạ vuông góc xuống trục Ox, ta
thấy hai chân đường vuông góc trên Ox là điểm 4 và – 4. LUYỆN TẬP 2
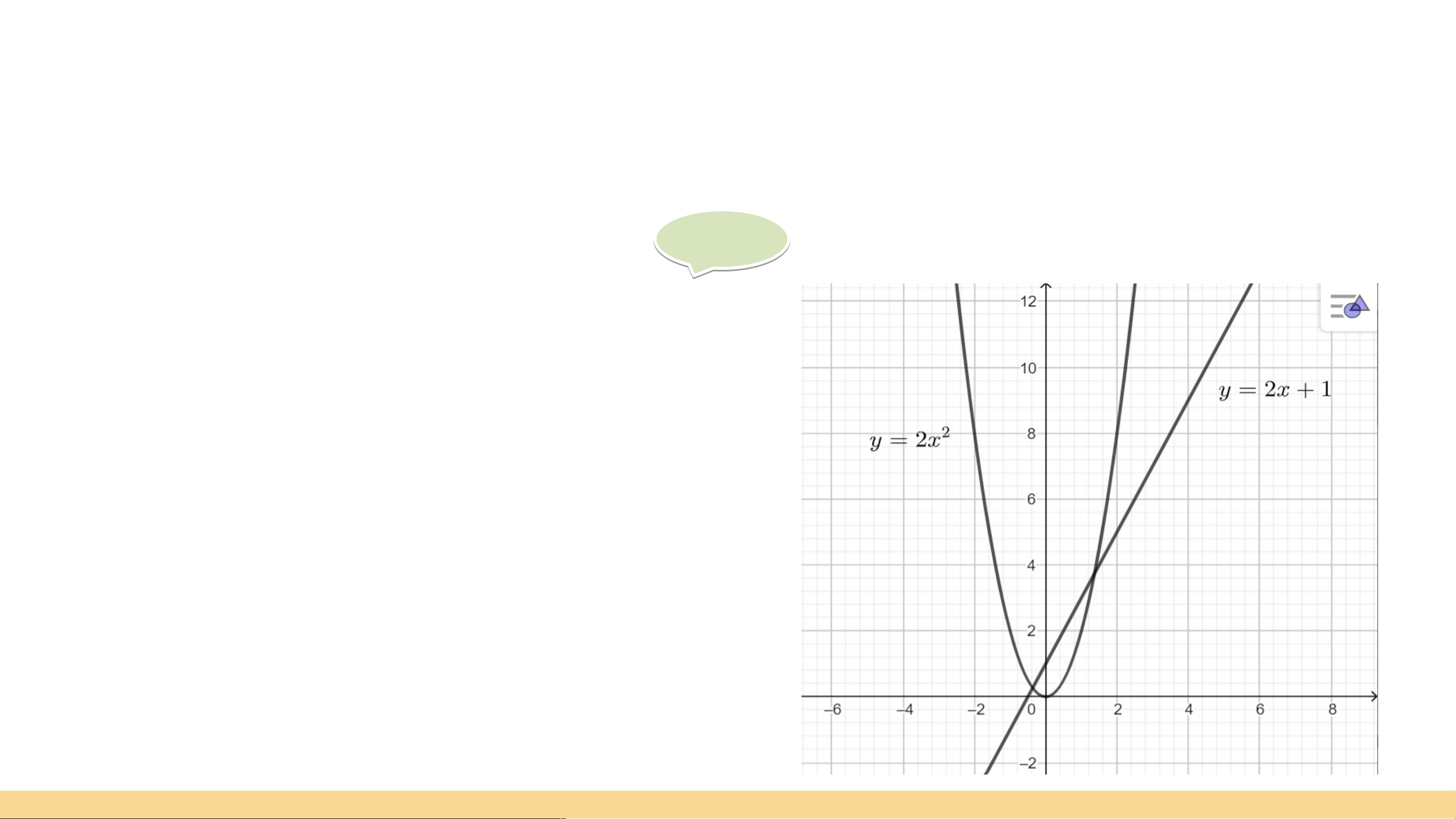
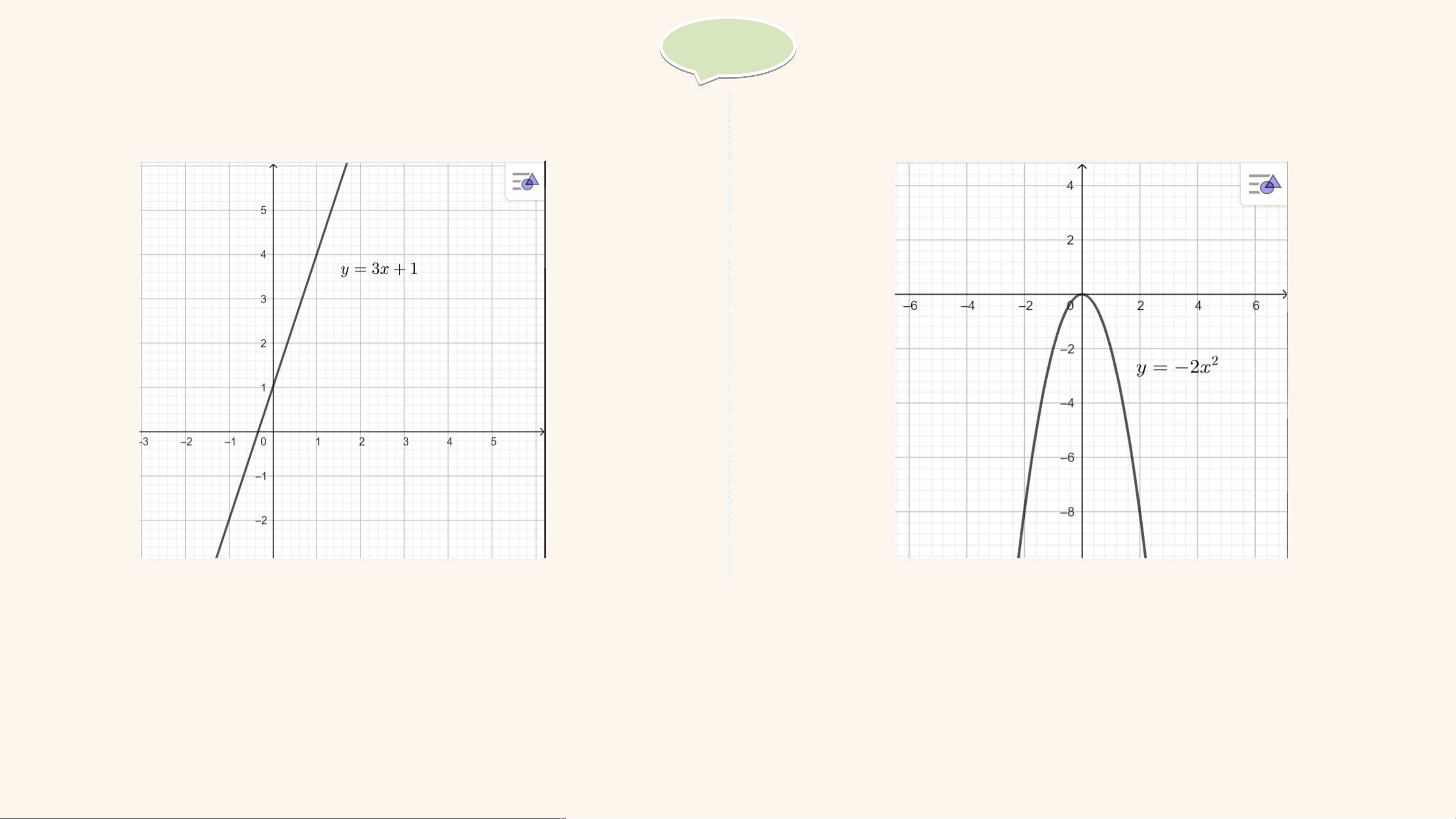
b) Vẽ đồ thị của các hàm số và trên cùng một mặt phẳng toạ độ. Giải Giả • Đồ thị hàm số
• Đồ thị hàm số y = 2x2 VẬN DỤNG 1
Nếu lượng điện tiêu thụ từ trên 50 đến thì công thức liên hệ giữa và đã
thiết lập ở không còn đúng nữa.
Theo bảng giá bán lẻ điện sinh hoạt (Bảng 6.2) thì số tiền phải trả là: , hay (nghìn đồng).
Vậy trên tập xác định , hàm số mô tả số tiền phải thanh toán có công thức là ;
tập giá trị của nó là .
Hãy vẽ đồ thị ở Hình vào vở rồi vẽ tiếp đồ thị của hàm số trên tập . Giải Giả
Đường màu đen là đồ thị ở Hình 6.3,
đường màu đỏ là đồ thị hàm số Trên tập . 03
Sự đồng biến, nghịch biến của hàm số THẢO LUẬN NHÓM
Các em hãy đọc nội dung của HĐ 5 và trả lời câu hỏi.
HĐ 5: Cho các hàm số và . Tính giá trị theo giá trị để hoàn thành bảng sau: -2 -1 0 1 2 ? ? ? ? ? ? ? ? ? ?
Khi giá trị x tăng, giá trị y tương ứng của mỗi hàm số y = -x + 1 và y = -x tăng hay giảm? Giải Giả -2 -1 0 1 2 3 2 1 0 -1 -2 -1 0 1 2
- Khi tăng, tương ứng của hàm giảm.
- Khi tăng, tương ứng của hàm tăng. HĐ 6:
Quan sát đồ thị của hàm số trên . Hỏi:
a) Giá trị của tăng hay giảm khi tăng trên khoảng ? tăng
b) Giá trị của tăng hay giảm khi tăng trên khoảng ? giảm ĐỊNH NGHĨA
Hàm số được gọi là đồng biến (tăng) trên khoảng , nếu:
Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a; b), nếu: .
Ví dụ 5 (SGK – tr8)
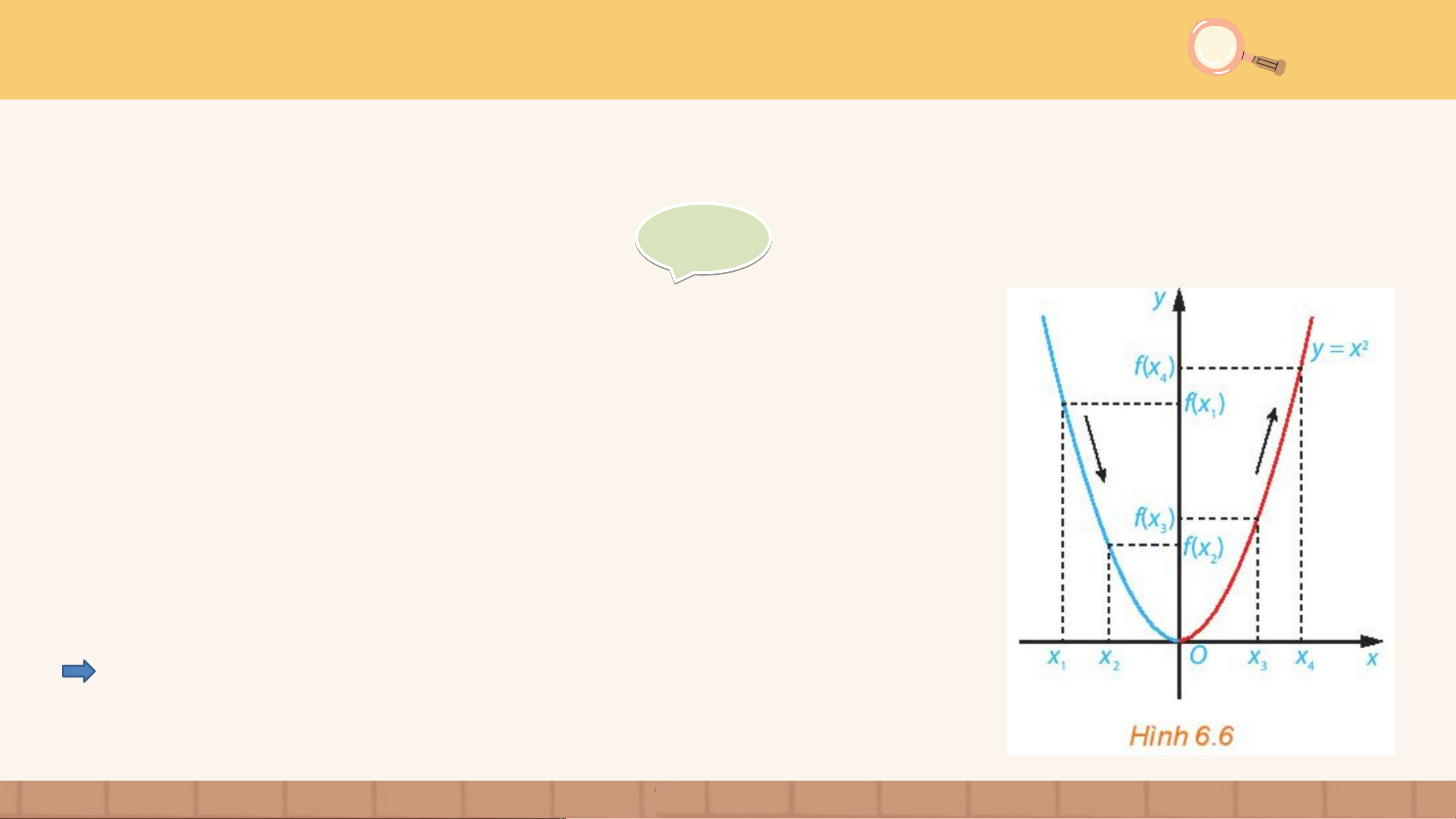
Hàm số đồng biến hay nghịch biến trên mỗi khoảng: và ? Giải Giả
Vẽ đồ thị hàm số như Hình 6.6.
- Trên khoảng đồ thị “đi xuống” từ trái sang phải và với , thì .
Như vậy, hàm số nghịch biến trên khoảng . CHÚ Ý
• Đồ thị của một hàm số đồng biến trên khoảng là đường "đi lên" từ trái sang phải.
• Đồ thị của một hàm số nghịch biến trên khoảng là đường
"đi xuống" từ trái sang phải. LUYỆN TẬP 3
Vẽ đồ thị của các hàm số và . Hãy cho biết:
a) Hàm số đồng biến hay nghịch biến trên .
b) Hàm số đồng biến hay nghịch biến trên mỗi khoảng: và . Giả G i iả Đồ thị hàm số Đồ thị hàm số
a) Hàm số đồng biến trên , vì đồ thị đi lên từ trái sang phải.
b) Hàm số đồng biến trên khoảng vì đồ thị đi lên từ trái sang phải.
Hàm số nghịch biến trên khoảng vì đồ thị đi xuống từ trái sang phải. VẬN DỤNG 2
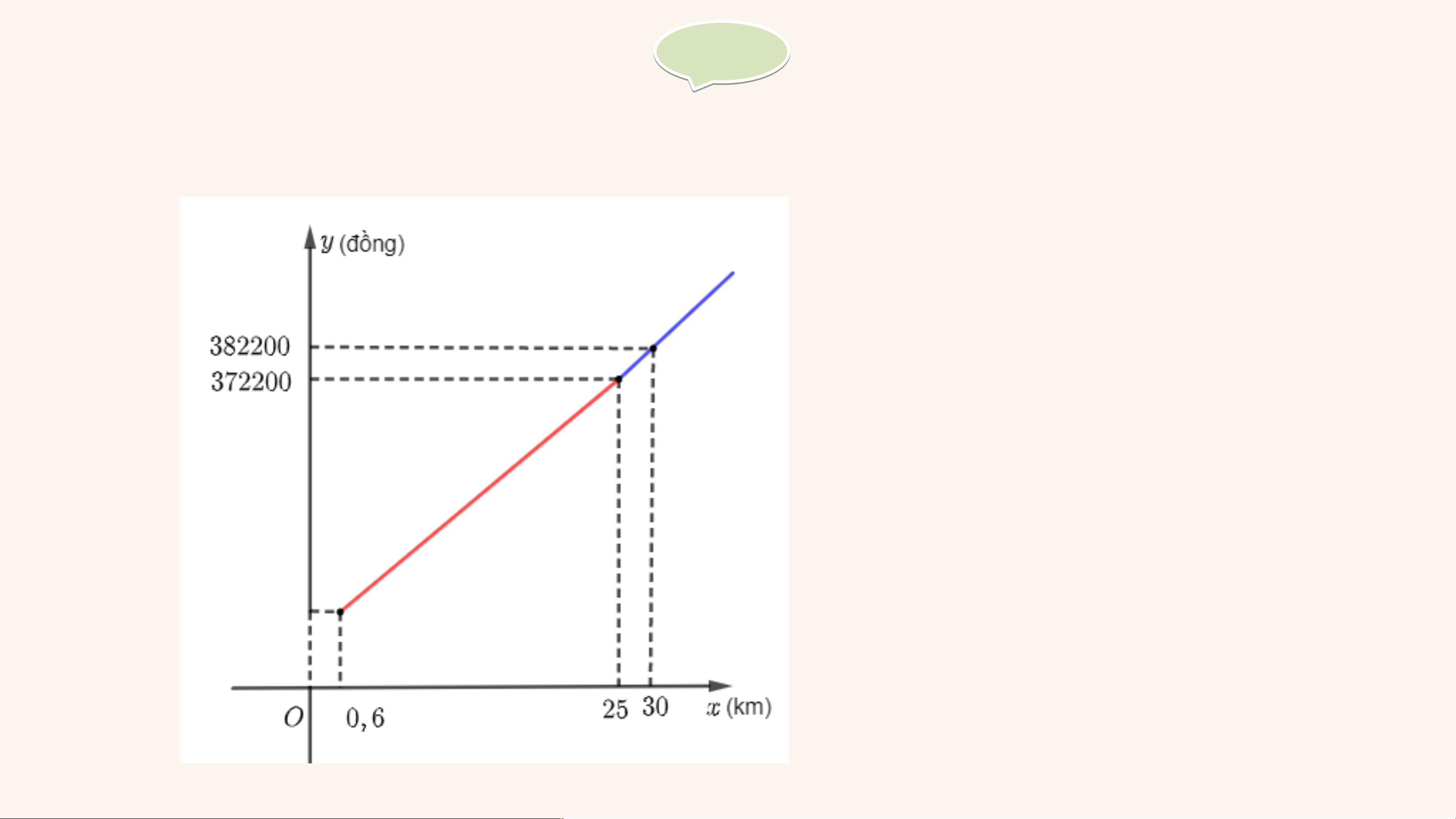
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.
a) Tính số tiền phải trả khi di chuyển .
b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.
c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào. Gi G ải ả
a) Số tiền phải trả khi di chuyển 25 km là: đồng.
b) Gọi là số kilomet mà xe taxi di chuyển. (đơn vị: km),
Gọi y là số tiền cước taxi phải trả theo kilomet di chuyển. (đơn vị: đồng), () Hay
𝑦={ ¿10000,𝑥≤0,6
¿ 13000 𝑥+2200 ;0,6<𝑥 ≤25
¿11000 𝑥 +52200 ; 𝑥>25 Gi G ải ả c)
Hàm số đồng biến trên khoảng . LUYỆN TẬP
Bài 6.1:(SGK – tr. 9)
Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây.
Những trường hợp nào thì y là hàm số của x? a) a) a x x + y + y + = 1 = . 1 c) b) b ) b d)
Bài 6.2:(SGK – tr.9)
Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra
tập xác định và tập giá trị của hàm số đó. Gi G ải ả 1 2 3 4 5 Tập xác định: -1 -2 -3 -4 -5 Tập giá trị:
Bài 6.3:(SGK – tr.9)
Tìm tập xác định của các hàm số sau: a) b) c) Giải ả a) Tập xác định: D = b) Điều kiện: Tập xác định: D = c) Điều kiện:
Tập xác định: D = [-1; 1].
Bài 6.4:(SGK – tr.9)
Tìm tập xác định và tập giá trị của mỗi hàm số sau: a) b) . Gi G ải ả a) b) . - Tập xác định: - Tập xác định: - Tập giá trị: - Có:
- Tập giá trị của hàm số: .
Bài 6.5:(SGK – tr.9)
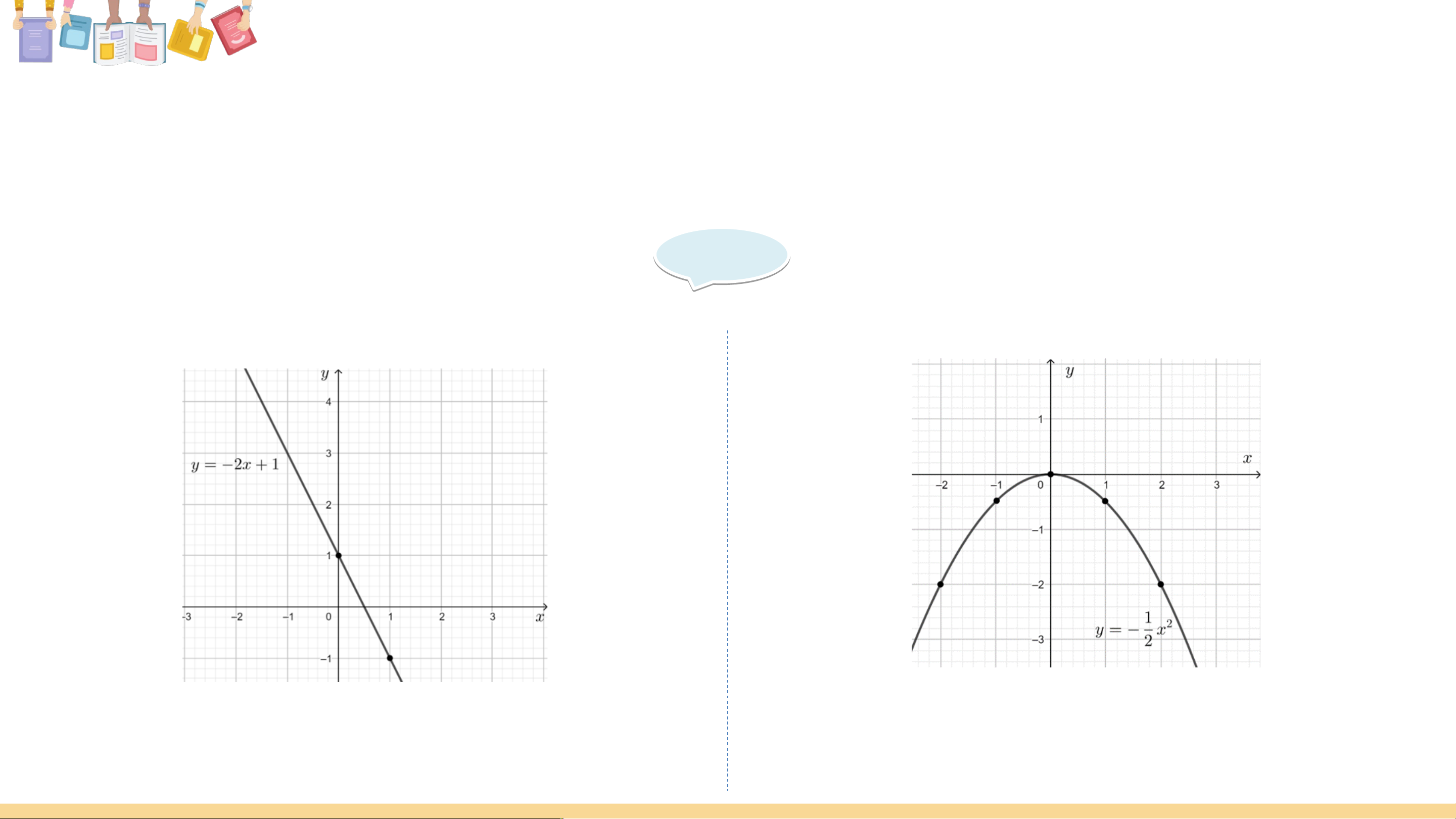
Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng. b) a) y = – 2x + 1; Giả i i ả
a) Đồ thị của hàm số . b) Đồ thị hàm số
Hàm số đồng biến trên khoảng và
Hàm số nghịch biến trên .
nghịch biến trên khoảng . VẬN DỤNG
Bài 6.6:(SGK – tr.9)
Giá thuê xe ô tự lái là 1,2 triệu đồng một ngày cho hai ngày đầu tiên và
900 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một
hàm số của số ngày x mà khách thuê xe.
a) Viết công thức của hàm số T = T(x).
b) Tính T(2), T(3), T(5) và cho biết ý nghĩa của mỗi giá trị này. Giải ả
a) Gọi T (triệu đồng) là số tiền phải trả Giải ả b) T(2) = 1,2.2 = 2,4 T(3) = 0,6 +0,9.3 = 3,3 T(5) = 0,6 + 0,9.5 = 5,1
Ý nghĩa các giá trị: T(2), T(3), T(5) lần lượt là số tiền (đơn vị : triệu đồng)
phải trả nếu khách thuê 2 ngày, 3 ngày, 5 ngày. Em E m có b ó iế b t iế ? ?
Hàm số và mô hình hóa
• HS thảo luận nhóm đôi tìm hiểu nội dung về Hàm số và mô hình hóa.
Câu hỏi: Thế nào là mô hình hóa bằng cách sử dụng hàm số ?
Trả lời: Việc tìm hàm số mô tả sự phụ thuộc của đại lượng này vào đại lượng
kia được gọi là mô hình hóa.
• Các bước mô hình hóa.
Bước 1: Diễn tả mô hình bằng lời.
Bước 2: Chọn biến số.
Bước 3: Thiết lập mô hình.
Bước 4: Sử dụng mô hình.
HƯỚNG DẪN VỀ NHÀ Ghi nhớ Hoàn thành các Chuẩn bị bài mới kiến thức trong bài. bài tập trong SBT.
“Bài 16: Hàm số bậc 2”.
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33
• Slide 34
• Slide 35
• Slide 36
• Slide 37
• Slide 38
• Slide 39
• Slide 40
• Slide 41
• Slide 42
• Slide 43
• Slide 44
• Slide 45
• Slide 46
• Slide 47
• Slide 48
• Slide 49
• Slide 50
• Slide 51
• Slide 52
• Slide 53
• Slide 54
• Slide 55