Giáo án điện tử Toán 10 Chương 7 Bài 20 Kết nối tri thức: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách
Bài giảng PowerPoint Toán 10 Chương 7 Bài 20 Kết nối tri thức: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 10. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 10
Môn: Toán 10
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
BÀI 20. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI
ĐƯỜNG THẲNG. GÓC VÀ KHOẢNG CÁCH CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI HỌC NGÀY HÔM NAY! KHỞI ĐỘNG
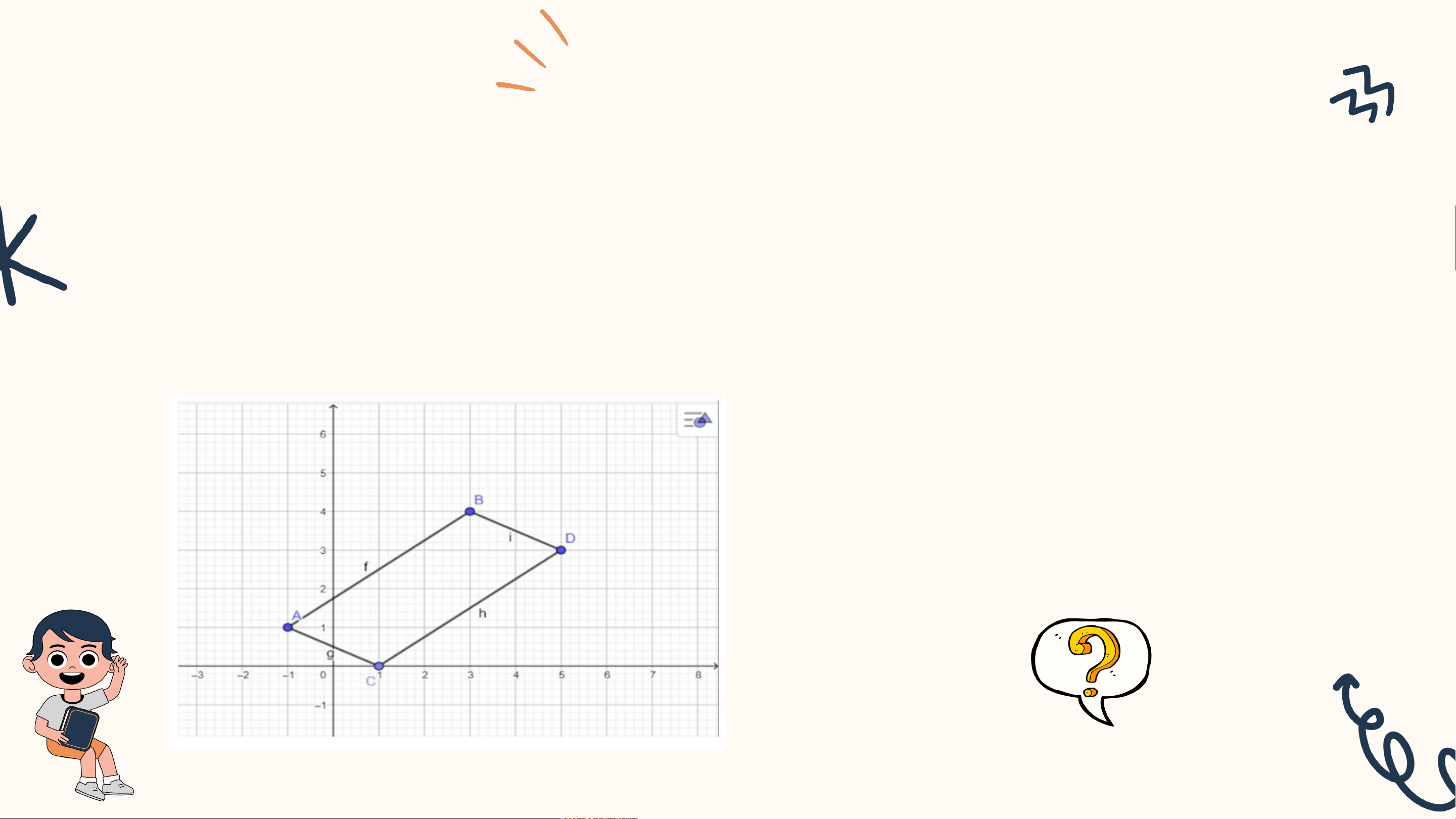
Vận động viên T chạy trên đường thẳng xuất phát từ A đến B, vận động
viên H chạy trên đường thẳng xuất phát từ C đến D (như hình vẽ).
Hỏi trên đường chạy hai vận
động viên sẽ chạy qua cùng một vị trí nào?
CHƯƠNG VII: PHƯƠNG PHÁP TOẠ
ĐỘ TRONG MẶT PHẲNG
BÀI 20: VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI
ĐƯỜNG THẲNG. GÓC VÀ KHOẢNG CÁCH NỘI DUNG BÀI HỌC 01
Vị trí tương đối giữa hai đường thẳng 02
Góc giữa hai đường thẳng 03
Khoảng cách từ một điểm đến một đường thẳng. 01
Vị trí tương đối giữa hai đường thẳng
HĐ 1: Trong mặt phẳng tọa độ, cho hai đường thẳng
𝛥 : 𝑥 – 2 𝑦 1 +3= 0 ,
𝛥2: 3 𝑥 – 𝑦 – 1=0.
a) Điểm M(1; 2) có thuộc cả hai đường thẳng nói trên hay không? b) Giải hệ
c) Chỉ ra mối quan hệ giữa tọa độ giao điểm của và với nghiệm
của hệ phương trình trên. Giải Giả
a) Thay vào phương trình đường thẳng ta được: (đúng)
Thay vào phương trình đường thẳng ta được: (đúng)
Vậy điểm thuộc cả hai đường thẳng trên. b)
⇔ {x−2 y=−3 ⇔ 3 x − y {x=1 =1 y=2
Vậy hệ phương trình có nghiệm
c) Toạ độ giao điểm của và là nghiệm của hệ phương trình trên. NH N Ậ H N Ậ N XÉ X T É
Mỗi đường thẳng trong mặt phẳng toạ độ là tập hợp những
điểm có toạ độ thoả mãn phương trình của đường thẳng đó.
Vì vậy, bài toán tìm giao điểm của hai đường thẳng được quy
về bài toán giải hệ gồm hai phương trình tương ứng. KẾ K T LU Ế Ậ T LU N Ậ
Trên mặt phẳng toạ độ, xét hai đường thẳng: và
Khi đó toạ độ giao điểm của và là nghiệm của hệ phương trình {a x y 1
+b1 + c1=0 (∗) a x y 2 +b2 + c2= 0
• cắt tại khi và chỉ khi hệ (*) có nghiệm duy nhất .
• song song khi và chỉ khi hệ (*) vô nghiệm.
• trùng khi và chỉ khi hệ (*) có vô số nghiệm. CH C Ú H Ý Ú
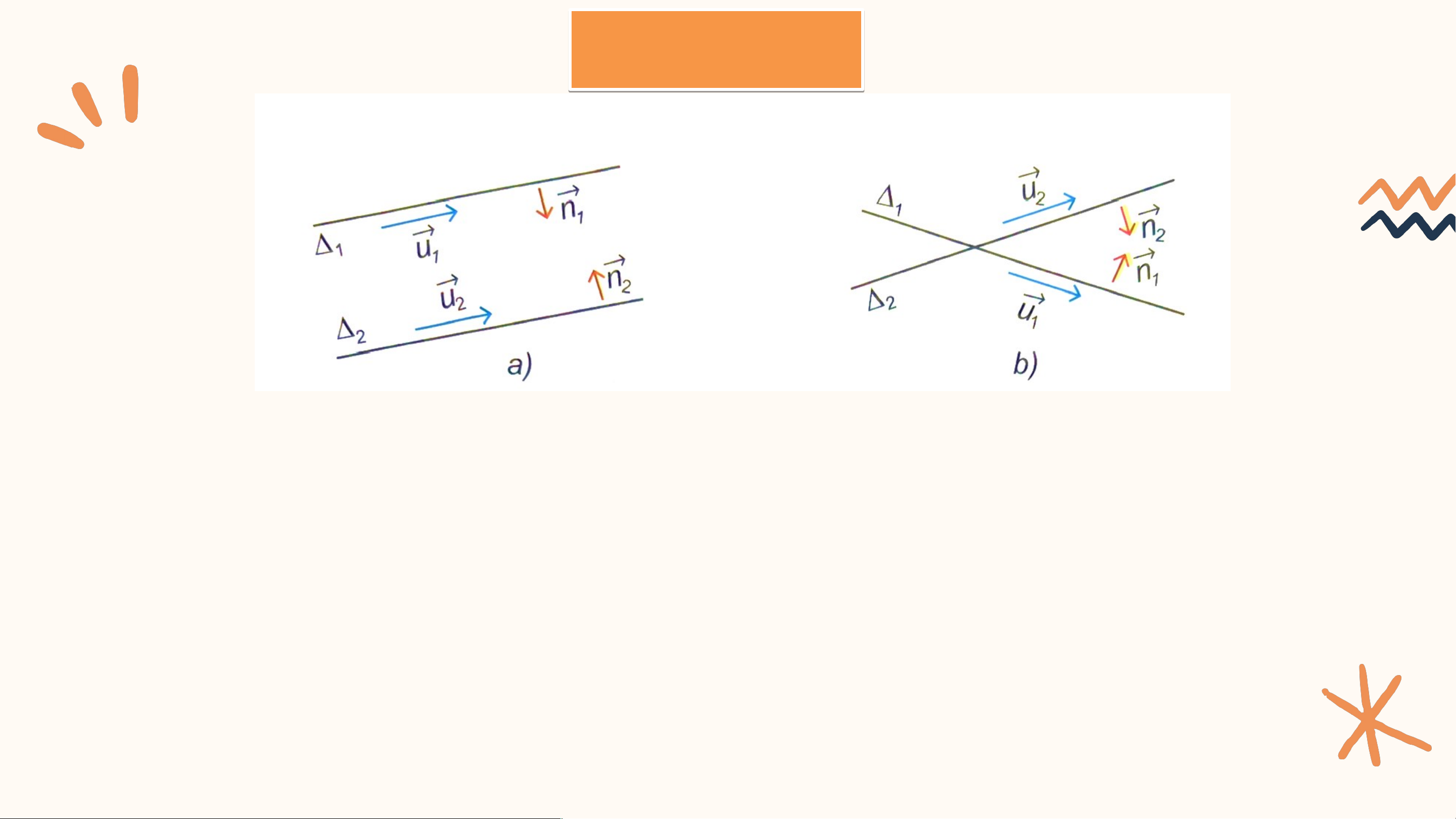
Dựa vào các vectơ chỉ phương hoặc các vectơ pháp tuyến của , ta có:
• và song song hoặc trùng nhau và cùng phương và cùng phương.
• và cắt nhau và không cùng phương và không cùng phương.
Ví dụ 1 (SGK – tr37)
Xét vị trí tương đối giữa đường thẳng và mỗi đường thẳng sau:
Δ1: √3 𝑥 − √6 𝑦 +12=0 Δ2: √2𝑥− 2 𝑦=0 Giải iả Ta có 0
⇔ √3 𝑥 −√6 𝑦 +12=0.
Vậy và là một, nói cách khác chúng trùng nhau. Giải ả
Hai đường thẳng và có hai vectơ pháp tuyến và cùng phương.
Do đó, chúng song song hoặc trùng nhau
Mặt khác, điểm thuộc đường thẳng nhưng không thuộc đường thẳng ,
nên hai đường thẳng này không trùng nhau.
Vậy và song song với nhau. NH N Ậ H N Ậ N XÉ X T É
Giả sử hai đường thẳng có hai vectơ chỉ phương (hay hai
vectơ pháp tuyến ) cùng phương. Khi đó:
- Nếu và có điểm chung thì trùng
- Nếu tồn tại điểm thuộc nhưng không thuộc thì song song với . LUY LU Ệ Y N TẬ N P TẬ 1 P
Xét vị trí tương đối giữa các cặp đường thẳng sau: a) và b) và Giải ả
a) Ta có: , do đó hai vectơ pháp tuyến không cùng phương.
Vậy hai đường thẳng và cắt nhau.
b) Ta có: , do đó hai vectơ pháp tuyến cùng phương
và song song hoặc trùng nhau.
Lấy điểm thuộc nhưng không thuộc
Vậy hai đường thẳng và song song. 02
Góc giữa hai đường thẳng HĐ 2:
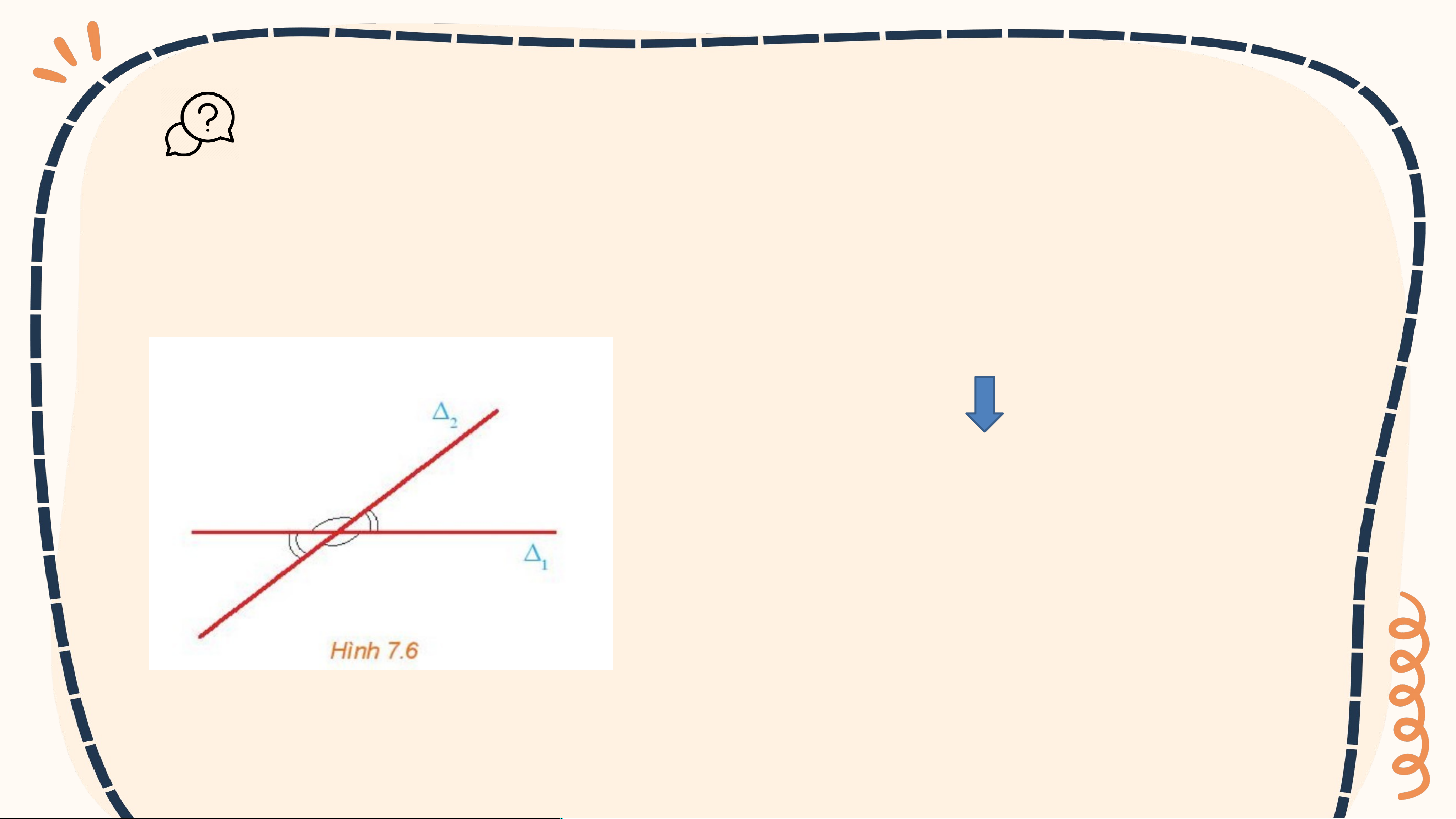
Hai đường thẳng và cắt nhau tạo thành bốn góc (H.7.6). Các số
đo của bốn góc đó có mối quan hệ gì với nhau?
Hai đường thẳng cắt nhau tạo thành
2 cặp góc đối đỉnh bằng nhau. ĐỊ Đ NH N N H GH N Ĩ GH A
- Hai đường thẳng cắt nhau tạo thành 4 góc, số đo của góc không
tù được gọi là số đo góc (hay đơn giản là góc) giữa hai đường thẳng.
- Góc giữa hai đường thẳng song song hoặc trùng nhau được quy ước bằng 0°. 50:50 50:50 Key
Câu 1: Trong mặt phẳng Oxy, tính góc giữa hai đường thẳng: A. . B. . C. . D. . 50:50 Key
Câu 2. Trong mặt phẳng Oxy, cho hai đường thẳng ,
. Khoảng cách giữa 2 hai đường thẳng là A. . B. . C. . D. . 50:50 Key
Câu 3. Trong mặt phẳng Oxy, tìm điểm nằm trên và
cách một khoảng bằng . A. (-2;1). B. (2;1). C. (2;-1). D. (-2;- 1).
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22