Giáo án điện tử Toán 10 Chương 7 Bài 21 Kết nối tri thức: Đường tròn trong mặt phẳng tọa độ
Bài giảng PowerPoint Toán 10 Chương 7 Bài 21 Kết nối tri thức: Đường tròn trong mặt phẳng tọa độ hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 10. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 10
Môn: Toán 10
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
BÀI 21: ĐƯỜNG TRÒN
TRONG MẶT PHẲNG TOẠ ĐỘ CHÀO MỪNG CÁC EM
ĐẾN TIẾT HỌC HÔM NAY! KHỞI ĐỘNG
Các hình ảnh dưới đây gợi cho em nhớ đến một hình nào đã được học? Topics Requireme nts HÌ H NH T RÒN
CHƯƠNG VII: PHƯƠNG PHÁP TOẠ ĐỘ TRONG MẶT PHẲNG
BÀI 21: ĐƯỜNG TRÒN TRONG
MẶT PHẲNG TOẠ ĐỘ NỘI DUNG BÀI HỌC 01
Phương trình đường tròn 02
Phương trình tiếp tuyến của đường tròn 01
Phương trình đường tròn HĐ 1:
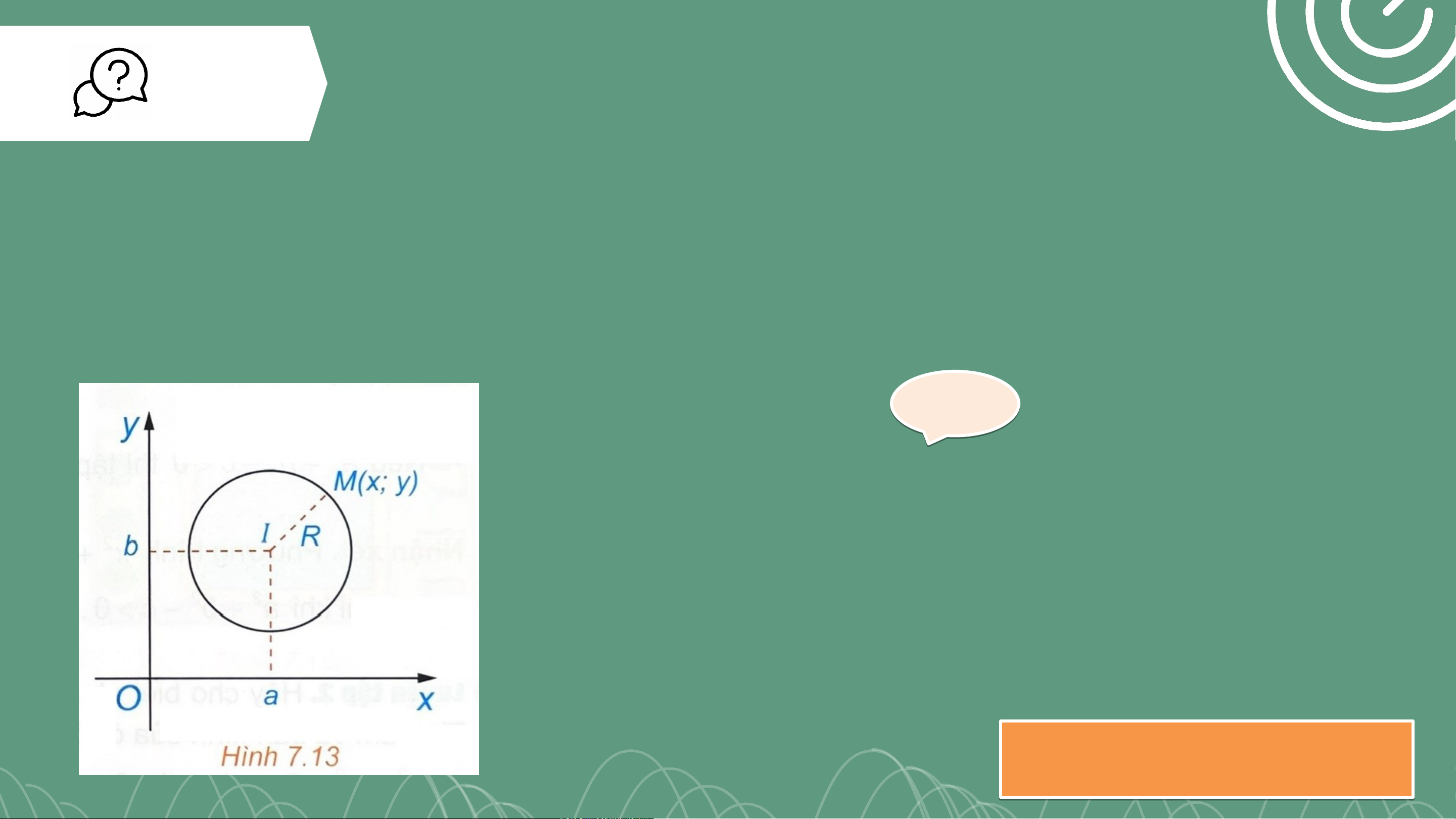
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C), tâm I(a; b), bán kính R
(H.7.13). Khi đó, một điểm M(x; y) thuộc đường tròn (C) khi và chỉ khi tọa độ
của nó thỏa mãn điều kiện đại số nào? Giải
Điểm thuộc đường tròn khi và chỉ khi khoảng cách . Hay: . THẢO L U L ẬN N NHÓM ĐỊNH NGHĨA
Điểm thuộc đường tròn , tâm , bán kính R khi và chỉ khi
Ta gọi là phương trình đường tròn
Ví dụ 1 (SGK – tr43)
Tìm tâm và bán kính của đường tròn có phương trình: .
Viết phương trình đường tròn có tâm và có bán kính gấp đôi bán kính đường tròn . Giải
Ta viết phương trình của ở dạng .
Vậy có tâm và bán kính .
Đường tròn có tâm và có bán kính , nên có phương trình LUYỆN TẬ UYỆN P TẬ 1 P
Tìm tâm và bán kính của đường tròn (C): Giải Có tâm , bán kính . NHẬN XÉT
Phương trình (1) tương đương với
Ví dụ 2 (SGK – tr44)
Cho là các hằng số. Tìm tập hợp những điểm thoả mãn phương trình Giải
Phương trình (2) tương đương với
Xét , khi đó, và phương trình trên trở thành
Ví dụ 2 (SGK – tr44)
Từ đó, ta xét các trường hợp sau:
Nếu thì tập hợp những điểm thoả mãn (2) là đường tròn tâm , bán kính .
Nếu thì (3) . Do đó, tập hợp những điểm thoả mãn (2) chỉ gồm một điểm là .
Nếu thì tập hợp những điểm là tập rỗng. NHẬN XÉT
Phương trình là phương trình của một đường tròn (C) khi và
chỉ khi . Khi đó, (C) có tâm I(a;b) và bán kính .
Hãy cho biết phương trình nào dưới đây là phương trình của LUYỆN T UYỆN ẬP T 2 ẬP
một đường tròn. Tìm tâm và bán kính của đường tròn đó. a) b) c) Giải
a) Đây không là phương trình của đường tròn vì hai hệ số của và không bằng
nhau nên ta không thể biến đổi về dạng phương trình đường tròn.
b) Phương trình đã cho không là phương trình đường tròn vì
Hãy cho biết phương trình nào dưới đây là phương trình của LUYỆN T UYỆN ẬP T 2 ẬP
một đường tròn. Tìm tâm và bán kính của đường tròn đó. a) b) c) Giả i i c) Ta có:
Phương trình đã cho là phương trình đường tròn có tâm I(-3;2) và có bán kính .
Ví dụ 3 (SGK – tr44)
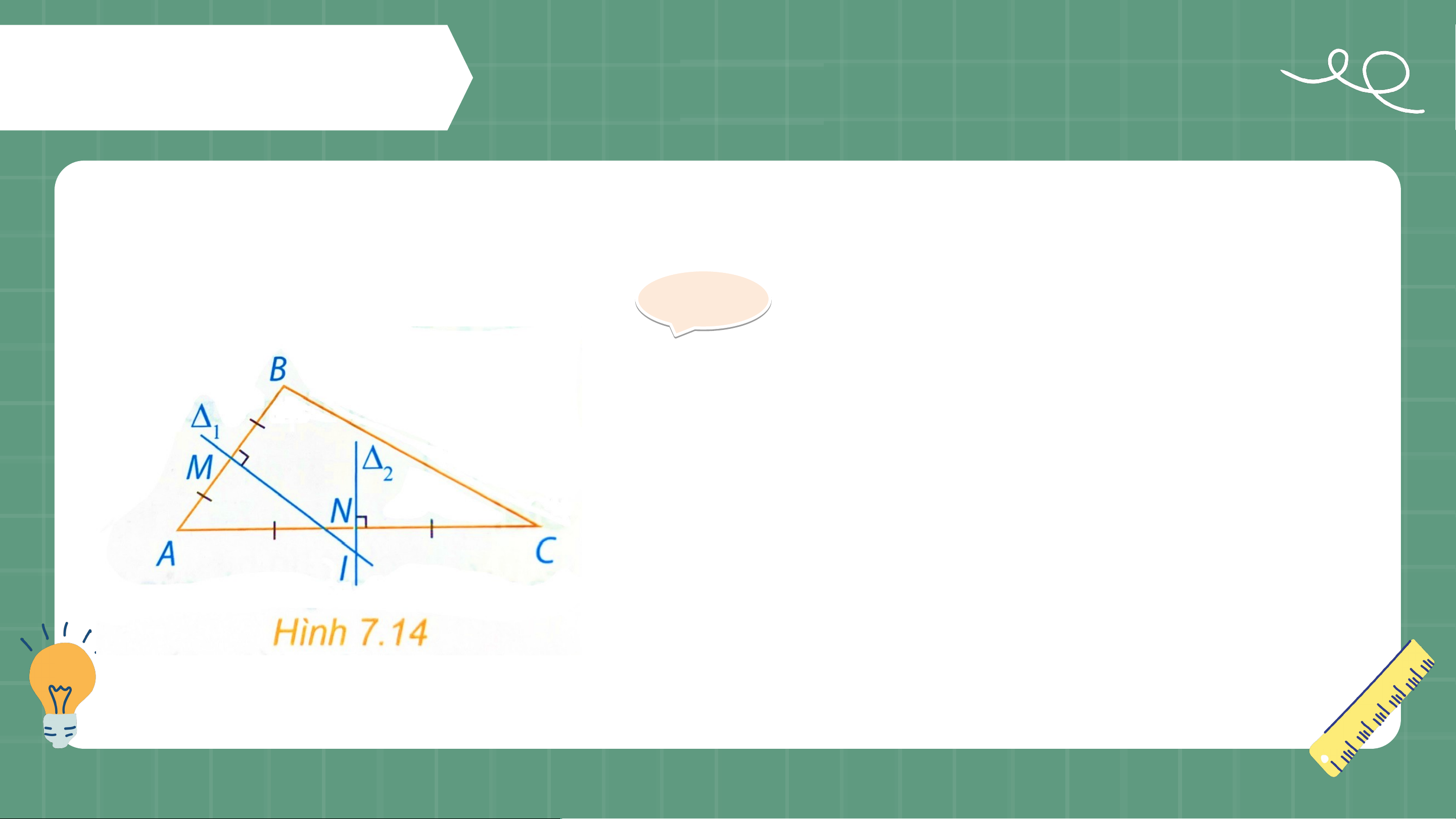
Viết phương trình đường tròn đi qua ba điểm . Giải ả
Các đoạn thẳng tương ứng có trung điểm là .
• Đường thẳng trung trực của đoạn
thẳng đi qua và có vectơ pháp tuyến .
Vì cùng phương với nên cũng nhận là vectơ pháp tuyến. Do đó, phương trình của là hay .
• Đường thẳng trung trực của đoạn thẳng AC đi qua và có vectơ pháp tuyến .
Vì cùng phương với nên cũng nhận là vectơ pháp tuyến. Do đó, phương trình của là: hay 3x – y + 9 = 0.
Tâm I của đường tròn cách đều ba điểm nên / là giao điểm của và
Vậy toạ độ của / là nghiệm của hệ phương trình .
Suy ra . Đường tròn có bán kính là . Vậy phương trình của là LUYỆN TẬ UYỆN P TẬ 3 P
Viết phương trình đường tròn (C) đi qua ba điểm M(4; – 5), N(2; – 1), P(3; – 8). Giải ả
Gọi điểm là tâm của đường tròn (C), ta có: Ta có:
Vì nên ta có hệ phương trình
{(𝑥−4)2+(𝑦+5)2=(𝑥−2)2+(𝑦+1)2
( 𝑥 −2)2+ ( 𝑦 +1)2=(𝑥 −3 )2+ ( 𝑦 + 8)2
⇔ {−4 𝑥+8 𝑦=−36 ⇔
2 𝑥 −14 𝑦 {𝑥=−1 =68 𝑦=− 5
⇒ 𝐼(−1;−5) 𝑅 2 2
=√(−1− 4) +(− 5+5) =5
Vậy phương trình đường tròn (C) là: .
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21