Giáo án điện tử Toán 11 Chương 6 Bài 3 Cánh diều: Hàm số mũ. Hàm số logarit

TOÁN 10 CÁNH DIỀU
BÀI 2: HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN (3 tiết) CHÀO MỪNG CÁC EM
ĐẾN VỚI LỚP HỌC
Nhân dịp Tết Trung thu, một doanh nghiệp dự định sản xuất hai loại bánh: bánh
nướng và bánh dẻo. Lượng đường cần cho mỗi chiếc bánh nướng, bánh dẻo
lần lượt là , . Doanh nghiệp đã nhập về đường.
"Số bánh nướng và số bánh dẻo doanh
nghiệp dự định sản xuất cần thỏa mãn
điều kiện ràng buộc gì để lượng đường
sản xuất bánh không vượt quá lượng đường đã nhập về?"
CHƯƠNG II. BẤT PHƯƠNG TRÌNH VÀ HỆ
BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
BÀI 1: BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN (2 tiết)
I. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Gọi lần lượt là số bánh nướng và số bánh dẻo doanh nghiệp dự định sản HĐ1
xuất . Nêu điều kiện ràng buộc đối với và để lượng đường sản xuất
không vượt quá lượng đường nhập về.
Điều kiện ràng buộc đối với và là:
Bất phương trình bậc nhất hai ẩn và . Kết luận:
- Bất phương trình bậc nhất hai ẩn là bất phương trình có một trong các dạng
sau: ; ; ; , trong đó: là những số thực cho trước với không đồng thời bằng và là các ẩn.
- Cho bất phương trình bậc nhất hai ẩn
Mỗi cặp số sao cho được gọi là một nghiệm của bất phương trình .
Trong mặt phẳng tọa độ , tập hợp các điểm có tọa độ là nghiệm của bất
phương trình được gọi là miền nghiệm của bất phương trình đó. Ví dụ 1
Cặp số nào sau đây là nghiệm của bất phương trình ? a) b) c) Giải
a) Thay , ta có: là mệnh đề đúng.
Vậy là nghiệm của bất phương trình.
b) Thay , ta có: là mệnh đề sai.
Vậy không là nghiệm của bất phương trình.
c) Thay , ta có: là mệnh đề đúng.
Vậy là nghiệm của bất phương trình.
Luyện tập 1 Tìm bất phương trình bậc nhất hai ẩn trong các bất phương
trình sau và chỉ ra một nghiệm của bất phương trình bậc nhất hai ẩn đó: a) b) Giải
a) là bất phương trình bậc nhất hai ẩn.
Chọn , ta có: là mệnh đề đúng.
Vậy là nghiệm của bất phương trình.
b) không phải là bất phương trình bậc nhất hai ẩn vì có ẩn ở mẫu.
II. BIỂU DIỄN MIỀN NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
1. Mô tả miền nghiệm của bất phương trình bậc nhất hai ẩn HĐ2
Trong mặt phẳng xác định điểm mà: a)
Đường thẳng chính là trục tung và chia mặt phẳng thành hai nửa.
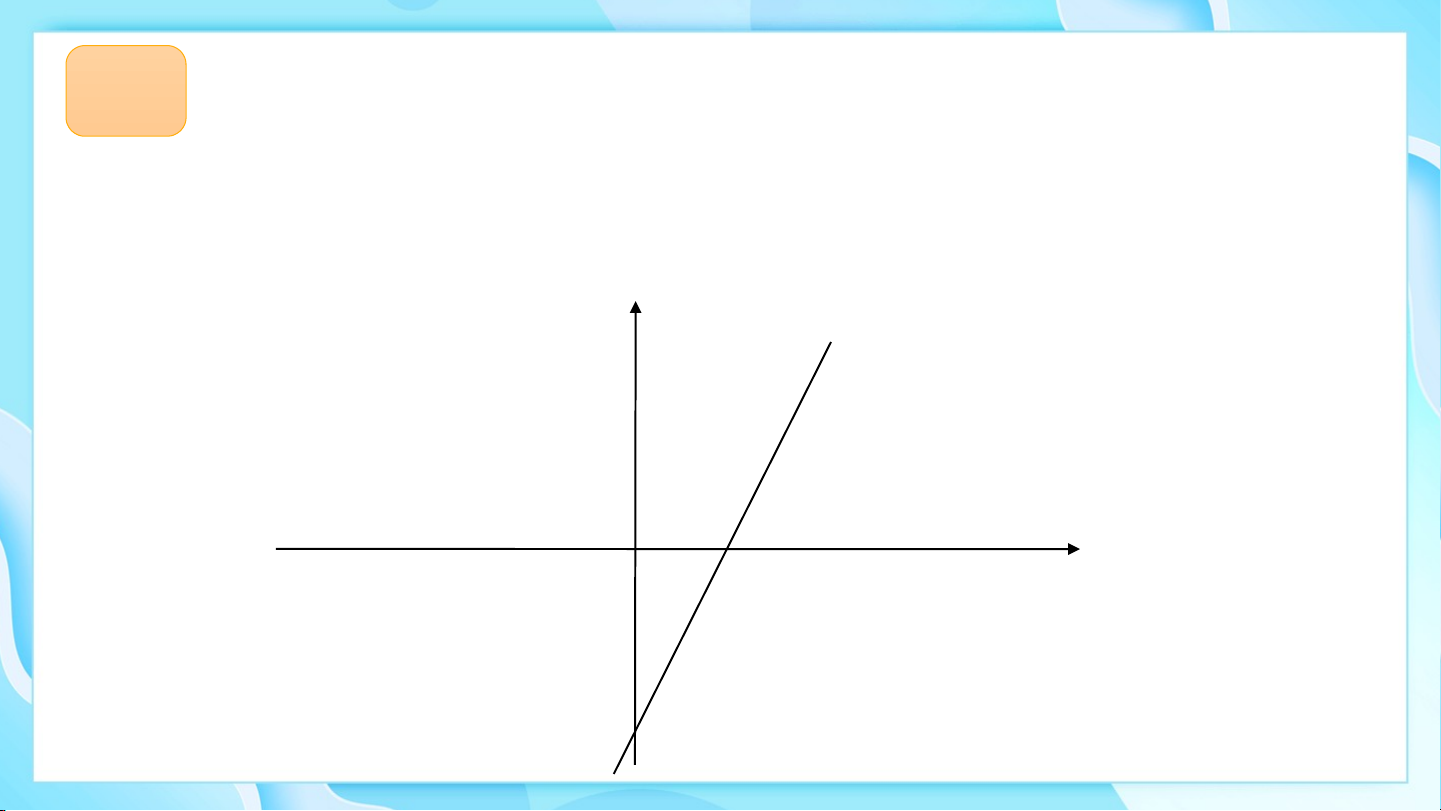
Miền nghiệm của bất phương trình là nửa bên phải trục tung. b) Vẽ đường thẳng
Đường thẳng chia mặt phẳng thành hai nửa: nửa
mặt phẳng bên trên đường thẳng và nửa mặt
phẳng nằm bên dưới đường thẳng .
Một điểm có tung độ nhỏ hơn 1 nằm ở bên dưới đường thẳng .
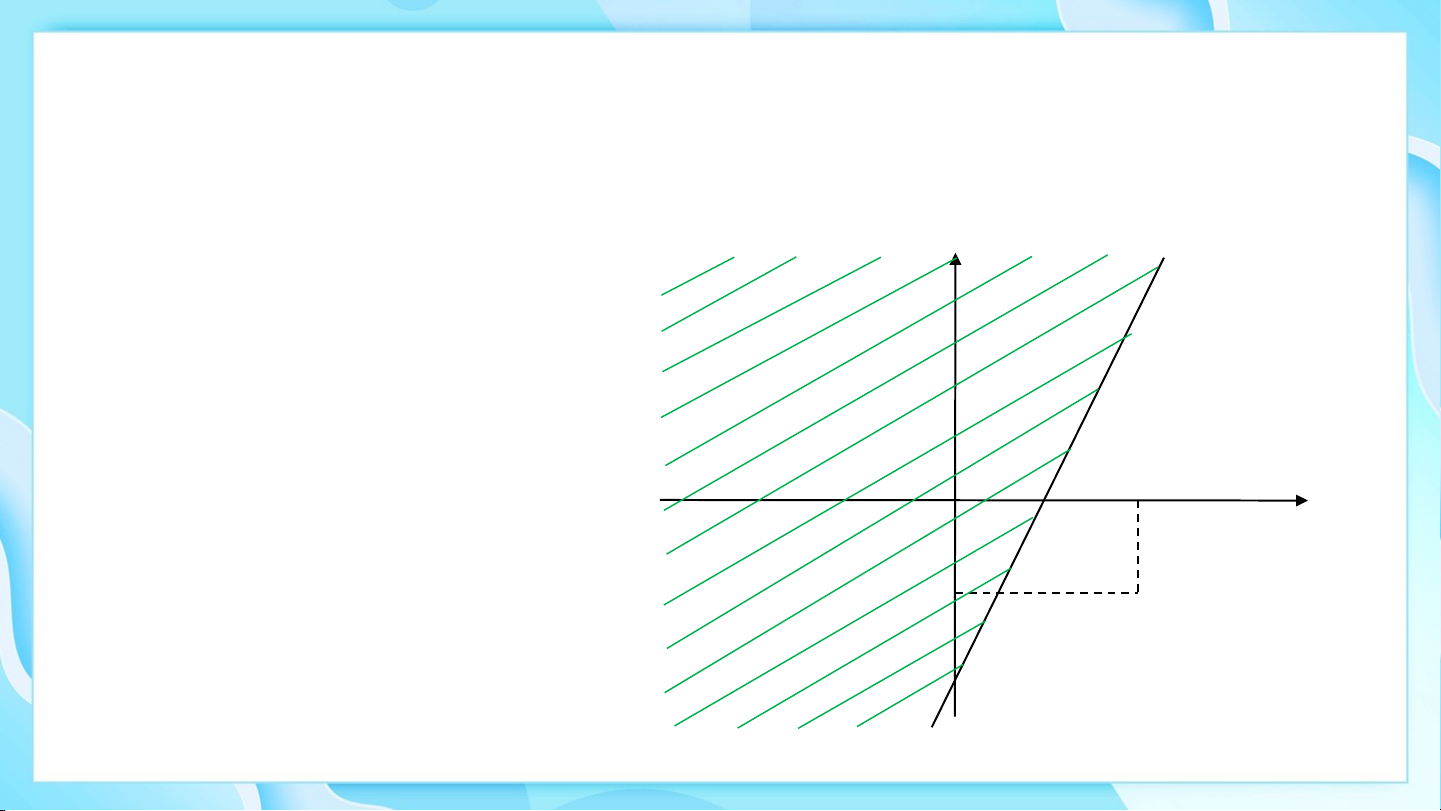
Miền nghiệm của bất phương trình là phần không bị gạch ở hình bên. HĐ3 Cho bất phương trình a) Vẽ đường thẳng
Đường thẳng đi qua hai điểm và Ta vẽ đường thẳng như sau: 2 𝑑 1 0 1 2 3 −3 −2 −1 −1 −2
b) Xét điểm . Chứng tỏ là nghiệm của bất phương trình
Thay và vào bất phương trình ta được: (luôn đúng). 2 𝑑
c) Đường thẳng chia mặt 1
phẳng tọa độ thành hai nửa
mặt phẳng. Gạch đi nửa mặt 0 1 2 3 −3 −2 −1
phẳng không chứa điểm , ta −1 𝑀(2;−1) có: −2 Kết luận:
Trong mặt phẳng tọa độ , đường thẳng chia mặt phẳng thành hai nửa mặt
phẳng. Một trong hai nửa mặt phẳng (không kể đường thẳng ) là miền
nghiệm của bất phương trình , nửa mặt phẳng còn lại (không kể đường
thẳng ) là miền nghiệm của bất phương trình .
Chú ý: Đối với bất phương trình dạng hoặc thì miền nghiệm là một trong
hai nửa mặt phẳng kể cả đường thẳng . Ví dụ 2
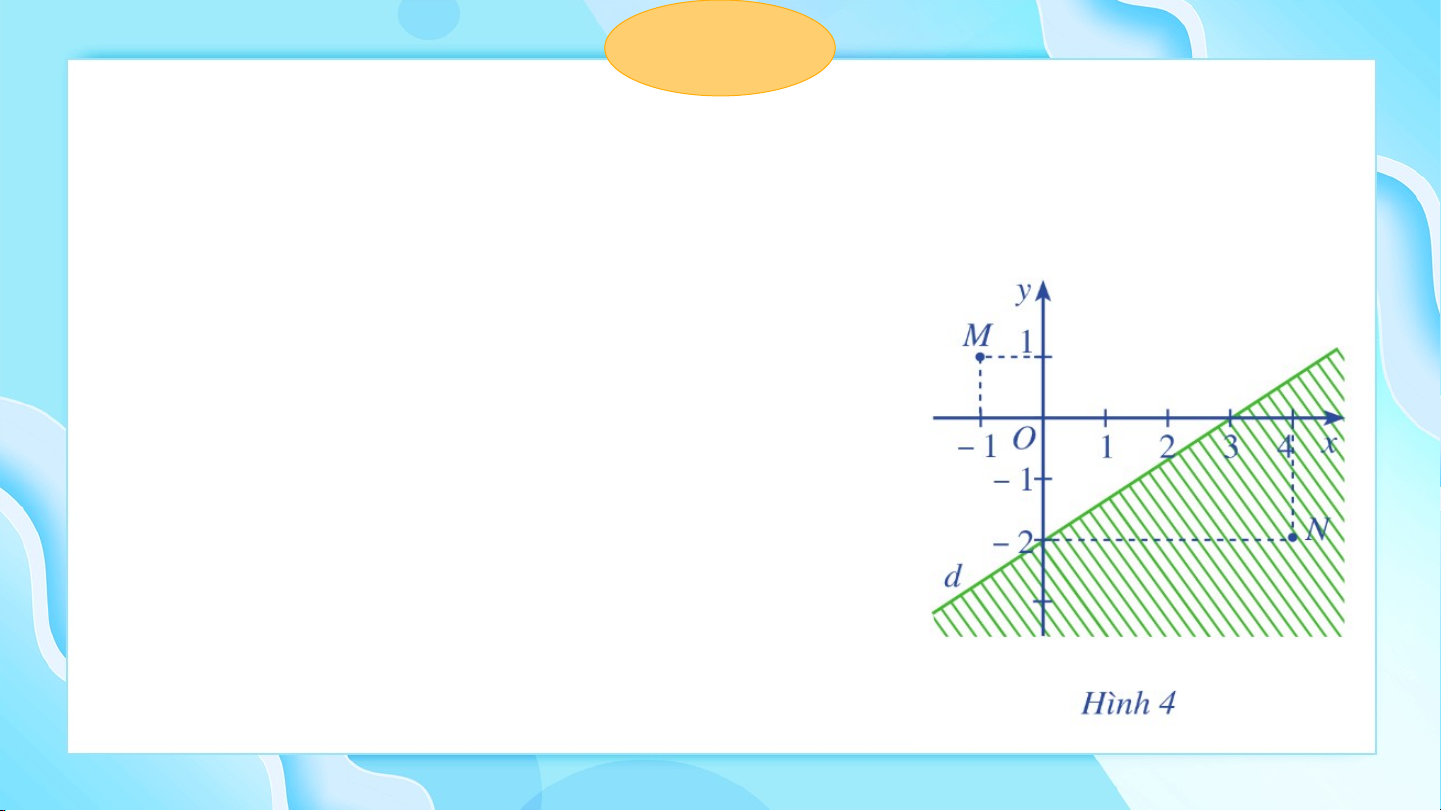
Nửa mặt phẳng không bị gạch trong Hình 4 (không kể đường thẳng ) biểu
diễn miền nghiệm của một bất phương trình bậc nhất hai ẩn. Hỏi toạ độ hai
điểm có là nghiệm của bất phương trình đó không? Giải
Điểm thuộc nửa mặt phẳng không bị gạch nên
là nghiệm của bất phương trình đó.
Điểm thuộc nửa mặt phẳng bị gạch nên không
là nghiệm của bất phương trình đó.
2. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn
Các bước biểu diễn miền nghiệm của bất phương trình trong mặt phẳng tọa độ như sau:
 Bước 1: Vẽ đường thẳng . Đường thẳng d chia mặt phẳng tọa độ thành hai nửa mặt phẳng.
 Bước 2: Lấy một điểm không nằm trên (ta thường lấy gốc tọa độ nếu ). Tính và so sánh với .
 Bước 3: Kết luận
• Nếu thì nửa mặt phẳng (không kể đường thẳng ) chứa điểm là miền
nghiệm của bất phương trình .
• Nếu thì nửa mặt phẳng (không kể đường thẳng ) không chứa điểm là
miền nghiệm của bất phương trình . Ví dụ 3
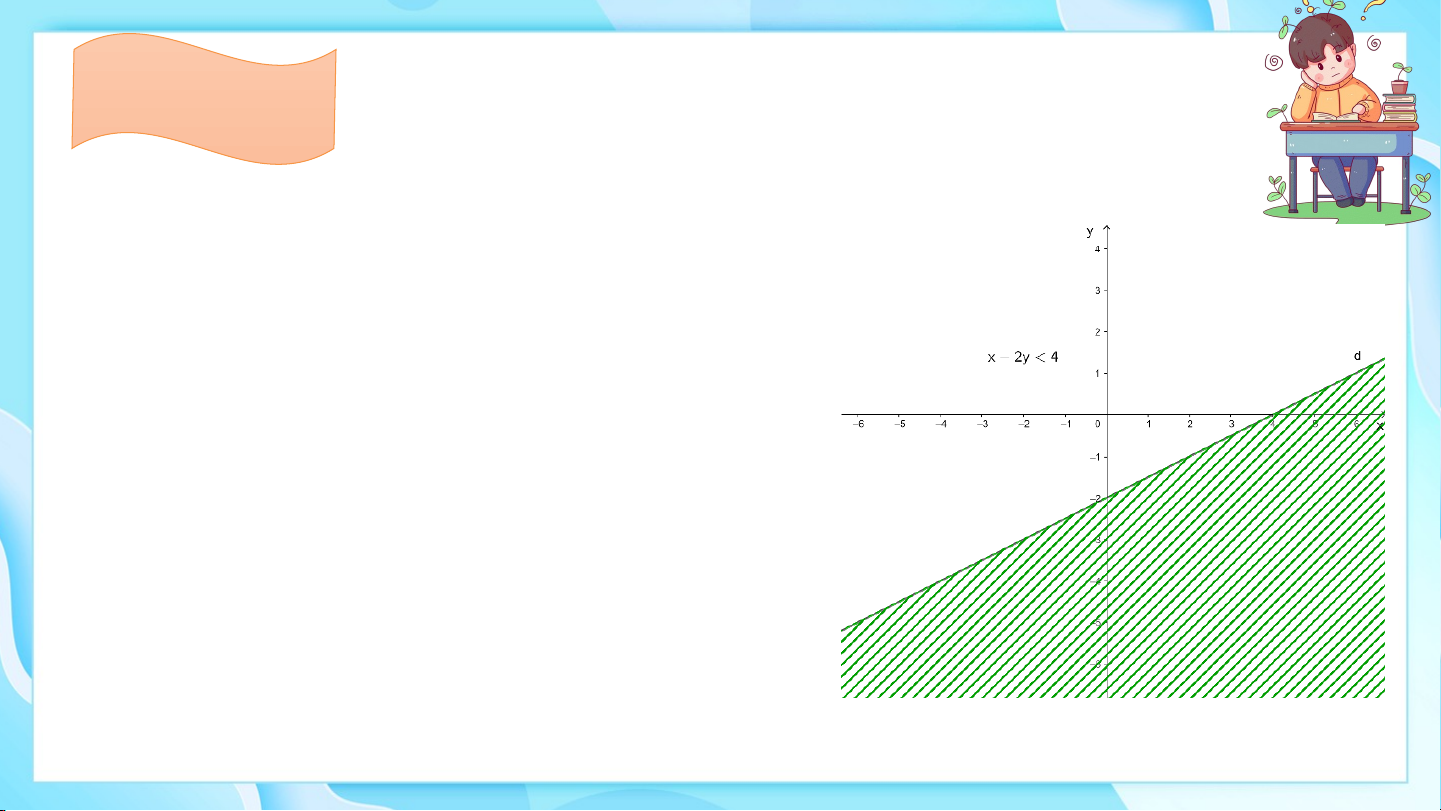
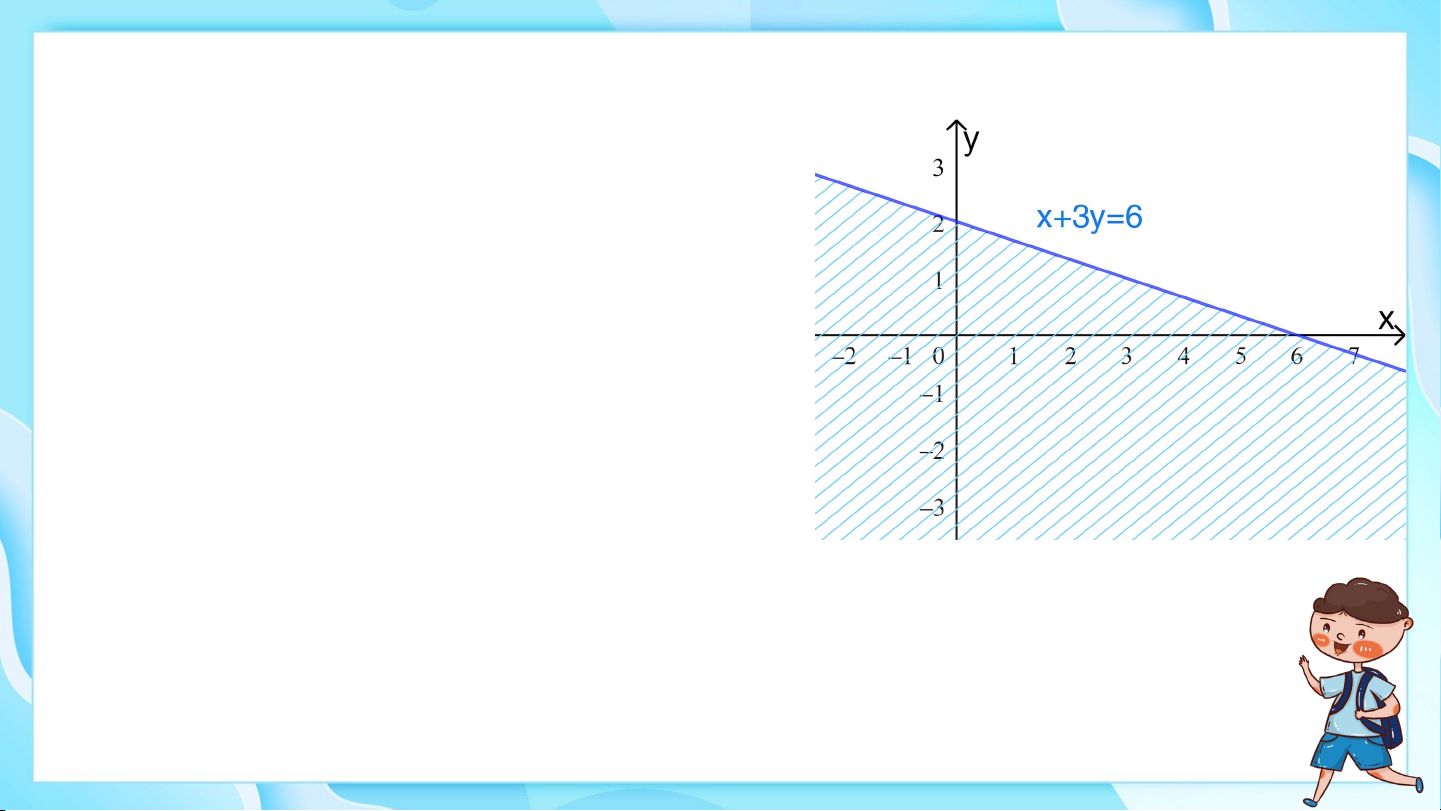
Biểu diễn miền nghiệm của bất phương trình sau: , . Giải Vẽ đường thẳng Lấy điểm Ta có:
Vậy miền nghiệm của bất phương trình là nửa mặt
phẳng không bị gạch ở Hình 5 chứa điểm không kể đường thẳng .
Tương tự, ta có: Miền nghiệm của bất phương trình là nửa mặt phẳng
không bị gạch ở Hình 5 chứa điểm kể cả đường thẳng .
Luyện tập 2 Biểu diễn miền nghiệm của mỗi bất phương trình sau a)  Vẽ đường thẳng
Cho thì , cho thì . Đường thẳng đi qua điểm và  Lấy điểm Ta có: .
Vậy miền nghiệm của bất phương trình là nửa
mặt phẳng không bị gạch chứa điểm không kể đường thẳng . b) + Vẽ đường thẳng
Cho thì , cho thì , do đó đường thẳng đi qua hai điểm và . + Lấy điểm . Ta có: .
Vậy miền nghiệm của bất phương trình
là nửa mặt phẳng không bị gạch không
chứa điểm kể cả đường thẳng .
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18