Giáo án Powerpoint bài 19 Phương trình đường thẳng sách Kết nối tri thức-Phần 1

CHƯƠNG VII. CHƯƠNG I
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG TOÁN HÌNH HỌC ➉ 19
PHƯƠNG TRÌNH ĐƯỜNG THẲNG 1 1 1 1
PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG 2
PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG 4 THUẬT NGỮ
KIẾN THỨC, KĨ NĂNG
 Mô tả được phương trình tổng quát và phương
 Vectơ chỉ phương
trình tham số của đường thẳng.
 Lập phương trình của đường thẳng khi biết một
 Vectơ pháp tuyến điểm và một
• vectơ pháp tuyến hoặc một điểm và một vectơ
 Phương trình tổng quát
chỉ phương hoặc hai điểm.
 Phương trình tham số
 Giải thích mối liên hệ giữa đồ thị hàm bậc nhất và đường thẳng.
 Vận dụng kiến thức về phương trình đường
thẳng để giải một số bài toán có liên quan đến thực tế.
Đường thẳng là một tập hợp điểm, được xác định bởi tính chất đặc trưng của
các điểm thuộc đường thẳng đó. Do vậy, ta có thể đại số hóa đường thẳng
bằng cách thể hiện tính chất đặc trưng đó bởi điều kiện đại số đối với tọa độ
của các điểm tương ứng.
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG Cho vectơ HĐ1:
𝒏 ≠ 𝟎 và điểm 𝑨. Tìm tập hợp những
điểm 𝑴 sao cho 𝑨𝑴 vuông góc với 𝒏 Giải:
Từ hình vẽ 7.1a, ta thấy tập hợp những điểm 𝑴 sao cho 𝑨𝑴 vuông góc với
𝒏 thuộc đường thẳng đi qua điểm 𝑨 và vuông góc với giá của vectơ 𝒏.
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG
Vectơ 𝒏 khác 𝟎 được gọi là vectơ pháp tuyến của
đường thẳng 𝜟 nếu giá của nó vuông góc với 𝜟. Nhận xét
Nếu 𝒏 là vectơ pháp tuyến của đường thẳng 𝜟 thì 𝒌𝒏 𝒌 ≠ 𝟎 cũng là vectơ
pháp tuyến của 𝜟
Đường thẳng hoàn toàn xác định nếu biết một điểm và một vectơ pháp tuyến của nó.
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG Ví dụ 1.
Trong mặt phẳng tọa Giải:
độ, cho tam giác có ba đỉnh là Đường trung trực của đoạn thẳng
𝑨 𝟑; 𝟏 , 𝑩 𝟒; 𝟎 , 𝑪 𝟓; 𝟑 . Hãy chỉ ra 𝑨𝑩 vuông góc với 𝑨𝑩 nên có một
một vectơ pháp tuyến của đường vectơ pháp tuyến là 𝑨𝑩 𝟏; −𝟏
trung trực của đoạn thẳng 𝑨𝑩 và một Đường cao kẻ từ 𝑨 của tam giác 𝑨𝑩𝑪
vectơ pháp tuyến của đường cao kẻ vuông góc với 𝑩𝑪 nên có một vectơ
từ A của tam giác 𝑨𝑩𝑪.
pháp tuyến là 𝑩𝑪 𝟏; 𝟑
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG
HĐ2: Trong mặt phẳng tọa độ, cho đường thẳng 𝜟 đi qua điểm 𝑨 𝒙𝒐; 𝒚𝒐
và có vectơ pháp tuyến 𝒏 𝒂; 𝒃 . Chứng minh rằng điểm 𝑴 𝒙; 𝒚 thuộc 𝜟 khi và chỉ khi
𝒂 𝒙 − 𝒙𝒐 + 𝒃 𝒚 − 𝒚𝟎 = 𝟎 (1) Giải
Ta có : 𝑨𝑴 = 𝒙 − 𝒙𝒐; 𝒚 − 𝒚𝒐
Từ hình vẽ ta thấy rằng điểm 𝑴 𝒙; 𝒚 thuộc 𝜟
khi và chỉ khi vectơ 𝑨𝑴 vuông góc với vectơ 𝒏 𝒂; 𝒃
⇔ 𝑨𝑴. 𝒏 = 𝟎 ⇔ 𝒂 𝒙 − 𝒙𝒐 + 𝒃 𝒚 − 𝒚𝒐 = 𝟎
Vậy điểm 𝑴 𝒙; 𝒚 thuộc 𝜟 khi và chỉ khi 𝒂 𝒙 − 𝒙𝒐 + 𝒃 𝒚 − 𝒚𝟎 = 𝟎
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG Nhận xét:
Trong HĐ2, nếu đặt 𝒄 = −𝒂𝒙
thì (1) còn được viết dưới dạng 𝒐 − 𝒃𝒚𝒐
𝒂𝒙 + 𝒃𝒚 + 𝒄 = 𝟎 và được gọi là phương trình tổng quát của 𝜟. Như vậy, điểm
𝑴 𝒙; 𝒚 thuộc đường thẳng 𝜟 khi và chỉ khi tọa độ của nó thỏa mãn phương
trình tổng quát của 𝜟.
Trong mặt phẳng tọa độ, mọi đường thẳng đều có phương trình tổng
quát dạng 𝒂𝒙 + 𝒃𝒚 + 𝒄 = 𝟎, với 𝒂 và 𝒃 không đồng thời bằng 𝟎. Ngược lại,
mỗi phương trình dạng 𝒂𝒙 + 𝒃𝒚 + 𝒄 = 𝟎, với 𝒂 và 𝒃 không đồng thời bằng 𝟎,
đều là phương trình của một đường thẳng, nhận 𝒏 𝒂; 𝒃 là một vectơ pháp tuyến.
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG • Ví dụ
Trong mặt phẳng tọa độ, Luyện tập Trong mặt phẳng
tọa1. độ, cho tam giác có ba đỉnh lập
2. phương trình tổng quát của 𝑨 −𝟏;𝟓 ,𝑩 𝟐;𝟑 ,𝑪 𝟔;𝟏 . Lập phương
đường thẳng 𝜟 đi qua điểm 𝑨 𝟐; 𝟏 trình tổng quát của đường cao kẻ từ
𝑨 của tam giác 𝑨𝑩𝑪.
và nhận 𝒏 𝟑; 𝟒 là một vectơ pháp Giải tuyến.
Đường cao kẻ từ 𝑨 của tam giác 𝑨𝑩𝑪
vuông góc với 𝑩𝑪 nên có một vectơ Giải
pháp tuyến là 𝑩𝑪 𝟒; −𝟐 .
Đường thẳng 𝜟 có phương trình là
Đường cao kẻ từ 𝑨 của tam
giác 𝑨𝑩𝑪có phương trình tổng quát là
𝟑 𝒙 − 𝟐 + 𝟒 𝒚 − 𝟏 = 𝟎
𝟒 𝒙 + 𝟏 − 𝟐 𝒚 − 𝟓 = 𝟎
hay 𝟑𝒙 + 𝟒𝒚 − 𝟏𝟎 = 𝟎
hay 𝟒𝒙 − 𝟐𝒚 + 𝟏𝟒 = 𝟎
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG Ví dụ
Trong mặt phẳng tọa độ, lập phương trình đường thẳng 𝜟 đi qua 𝑨 𝟎
3 ;. 𝒃 và có vectơ pháp tuyến 𝒏 𝒂; −𝟏 , với 𝒂, 𝒃 là các số thực cho trước. Hãy
chỉ ra mối liên hệ giữa đường thẳng 𝜟 với đồ thị hàm số 𝒚 = 𝒂𝒙 + 𝒃. Giải
Đường thẳng 𝜟 phương trình là 𝒂 𝒙 − 𝟎 − 𝟏 𝒚 − 𝒃 = 𝟎 hay 𝒂𝒙 − 𝒚 + 𝒃 = 𝟎.
Đường thẳng 𝜟 là tập hợp những điểm 𝑴 𝒙; 𝒚 thỏa mãn 𝒂𝒙 − 𝒚 + 𝒃 = 𝟎,
hay là 𝒚 = 𝒂𝒙 + 𝒃.
Do đó, đường thẳng 𝜟: 𝒂𝒙 − 𝒚 + 𝒃 = 𝟎 chính là đồ thị của hàm số 𝒚 = 𝒂𝒙 + 𝒃.
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG
Luyện tập Hãy chỉ ra một vectơ pháp tuyến của đường thẳng 𝜟: 𝒚 = 𝟑𝒙 + 𝟒. Giải 2.
Ta có 𝒚 = 𝟑𝒙 + 𝟒 ⇔ 𝟑𝒙 − 𝒚 + 𝟒 = 𝟎
Vậy một vectơ pháp tuyến của đường thẳng 𝜟: 𝒚 = 𝟑𝒙 + 𝟒 là 𝒏 𝟑; −𝟏 .
Nhận xét. Trong mặt phẳng tọa độ, cho đường thẳng 𝜟: 𝒂𝒙 + 𝒃𝒚 + 𝒄 = 𝟎. Nếu 𝒄
𝒃 = 𝟎 thì phương trình có thể đưa về dạng 𝒙 = 𝒎(với 𝒎 = − ) và 𝒂
𝜟 vuông góc với 𝑶𝒙.
Nếu 𝒃 ≠ 𝟎 thì phương trình có thể đưa về dạng 𝒚 = 𝒏𝒙 + 𝒑 (với 𝒂 𝒄
𝒏 = − , 𝒑 = − ). 𝒃 𝒃
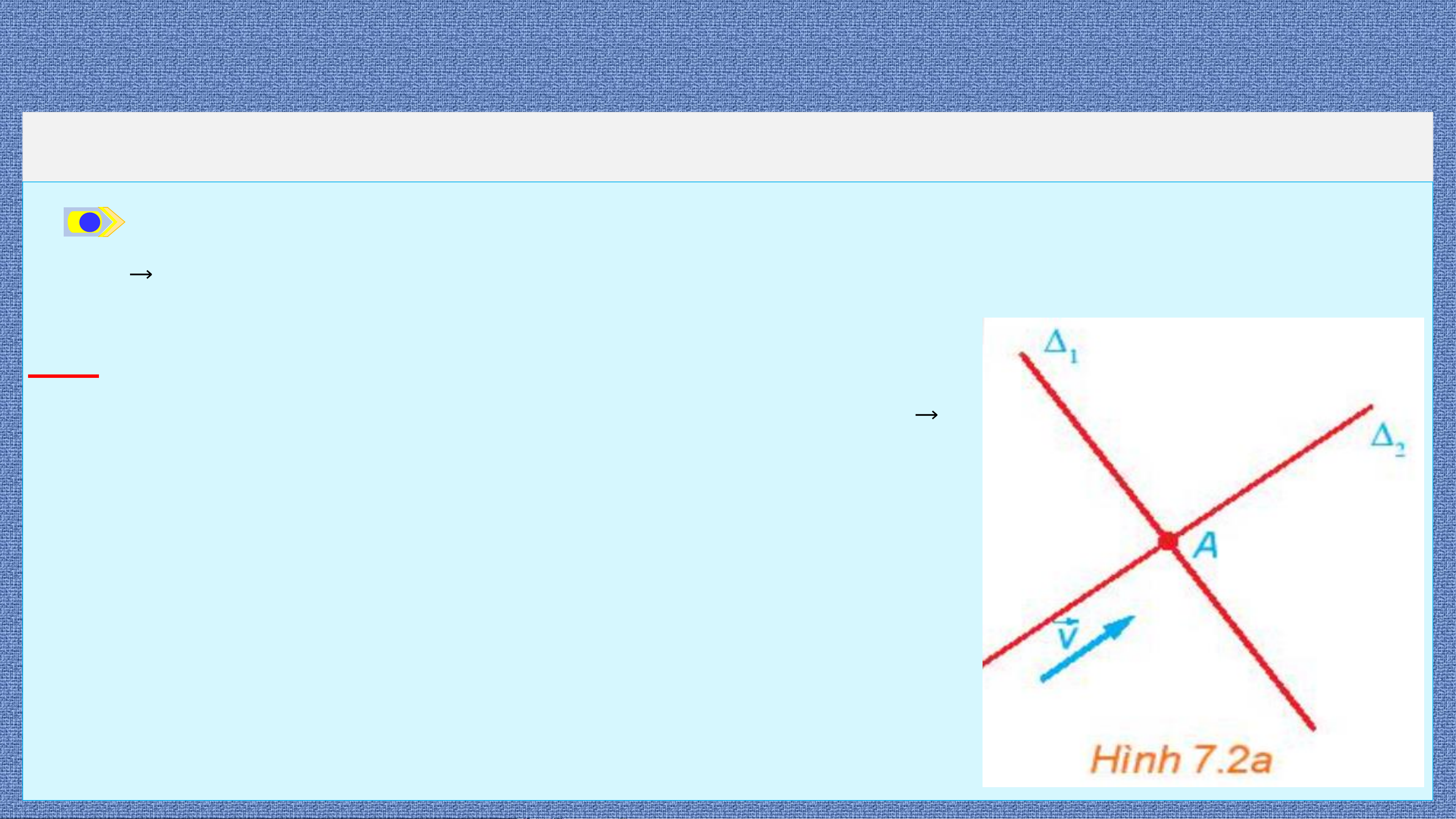
2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG Trong HĐ3:
Hình 7.2a, nếu một vật thể chuyển động với vectơ vận tốc
bằng 𝒗 đi qua 𝑨 thì nó di chuyển trên đường thẳng nào? Giải
Một vật thể chuyển động với vectơ vận tốc bằng 𝒗
đi qua 𝑨 thì nó di chuyển trên đường thẳng 𝜟 . 𝟐
2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
Vectơ 𝒖 khác 𝟎 được gọi là vectơ chỉ phương của
đường thẳng 𝜟 nếu giá của nó song song hoặc
trùng với 𝜟. Nhận xét:
 Nếu 𝒖 là vectơ chỉ phương của đường thẳng 𝜟
thì 𝒌𝒖 𝒌 ≠ 𝟎 cũng là vectơ chỉ phương của 𝜟.
 Đường thẳng hoàn toàn xác định nếu biết một điểm và một
vectơ chỉ phương của nó.
 Vec tơ 𝒏 𝒂; 𝒃 vuông góc với vec tơ 𝒖 −𝒃; 𝒂 và 𝒗 𝒃; −𝒂 nên nếu 𝒏 là vectơ
pháp tuyến của đường thẳng 𝜟 thì 𝒖, 𝒗 là hai vectơ chỉ phương của đường
thẳng đó và ngược lại.
2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG •
Ví dụ 4. Trong mặt phẳng tọa độ,
Luyện tập 3. Hãy chỉ ra một vectơ
cho 𝑨 𝟑; 𝟐 , 𝑩 𝟏; −𝟒 . Hãy chỉ ra hai chỉ phương của đường thẳng
vectơ chỉ phương của đường thẳng 𝜟:𝟐𝒙 − 𝒚 + 𝟏 = 𝟎. 𝑨𝑩. Giải Giải
Đường thẳng 𝜟 có vectơ pháp tuyến
Đường thẳng 𝑨𝑩 nhận 𝑨𝑩 −𝟐; −𝟔 là 𝒏 𝟐; −𝟏 nên có một vectơ chỉ phương
một vectơ chỉ phương. 𝒖 𝟏; 𝟐 . Lấy 𝟏
𝒖 = − 𝑨𝑩 = 𝟏; 𝟑 , khi đó 𝒖 cũng 𝟐
là một vectơ chỉ phương của đường thẳng 𝑨𝑩.
2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
HĐ4: Chuyển động của một vật thể được thể hiện trong mặt phẳng 𝑶𝒙𝒚.
Vật thể khởi hành từ 𝑨 𝟐; 𝟏 và chuyển động thẳng đều với vận tốc 𝒗 𝟑; 𝟒 .
a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm đi qua và
vectơ chỉ phương của đường thẳng đó)?
b) Chứng minh rằng tại thời điểm 𝒕(𝒕 > 𝟎) tính từ khi khởi hành, vật thể ở vị
trí có tọa độ là 𝟐 + 𝟑𝒕; 𝟏 + 𝟒𝒕 . Giải
a) Vật thể chuyển động trên đường thẳng đi qua điểm 𝑨 𝟐; 𝟏 nhận 𝒗 𝟑; 𝟒
làm vectơ chỉ phương.
b) Giả sử tại thời điểm 𝒕(𝒕 > 𝟎)tính từ khi khởi hành, vật thể ở vị trí 𝑴 𝒙; 𝒚
thuộc đường thẳng đi qua điểm𝑨 𝟐; 𝟏 nhận 𝒗 𝟑; 𝟒 làm vectơ chỉ phương. Khi
đó, hai vectơ 𝑨𝑴 và 𝒖 cùng phương nên tồn tại số thực 𝒕 sao cho 𝑨𝑴 = 𝒕𝒖
2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
Ta có 𝑨𝑴 𝒙 − 𝟐; 𝒚 − 𝟏 Do đó 𝒙 − 𝟐 = 𝟑𝒕 𝒙 = 𝟐 + 𝟑𝒕 𝑨𝑴 = 𝒕𝒖 ⇔ ⇔ 𝒚 − 𝟏 = 𝟒𝒕 𝒚 = 𝟏 + 𝟒𝒕
Vậy 𝑴 𝟐 + 𝟑𝒕; 𝟏 + 𝟒𝒕 với 𝒕 ∈ ℝ.
Cho đường thẳng 𝜟 đi qaua điểm 𝑨 𝒙
và có vectơ chỉ phương 𝟎; 𝒚𝟎 𝒖 𝒂; 𝒃 .
Khi đó điểm 𝑴 𝒙; 𝒚 thuộc đường thẳng 𝜟 khi và chỉ khi tồn tại số thực 𝒕 sao cho
𝑨𝑴 = 𝒕𝒖, hay 𝒙 = 𝒙 𝟎 + 𝒂𝒕 (2) 𝒚 = 𝒚𝟎 + 𝒃𝒕
Hệ (2) được gọi là phương trình tham số của đường thẳng 𝜟 (t là tham số).
2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG • Ví dụ Lập phương trình Luyện tập
Lập phương trình tham tham 5.
số của đường thẳng 𝜟 đi
số4.của đường thẳng 𝜟 đi qua điểm
qua điểm 𝑨 𝟐; −𝟑 và có vectơ chỉ
𝑴 −𝟏; 𝟐 và song song với đường thẳng
phương 𝒖 𝟒; −𝟏 .
𝒅: 𝟑𝒙 − 𝟒𝒚 − 𝟏 = 𝟎. Giải Giải
Đường thẳng 𝒅 có một vectơ pháp tuyến
Phương trình tham số của đường 𝒏 𝟑; −𝟒 . thẳng 𝜟 là
Đường thẳng 𝜟 song song với đường ࢛ࢗࢇ ࡭(૛; − ૜) .
thẳng 𝒅 nên 𝒅 nhận 𝒏 𝟑; −𝟒 làm vectơ vtcp 𝒖 𝟒; −𝟏
pháp tuyến, do đó 𝒅 có vectơ chỉ phương 𝒖 𝟒; 𝟑 . 𝒙 = 𝟐 + 𝟒𝒕 ⇔ .
Phương trình tham số của đường thẳng 𝜟 𝒚 = −𝟑 − 𝒕
là 𝒙 = −𝟏 + 𝟒𝒕 . 𝒚 = 𝟐 + 𝟑𝒕
2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG Ví dụ
Lập phương trình tham số của đường thẳng đi qua hai điểm 𝑨 𝟐;6𝟑 .
và 𝑩 𝟏; 𝟓 . Giải Đường thẳng 𝒒𝒖𝒂 𝑨 𝟐; 𝟑
𝑨𝑩 đi qua 𝒒𝒖𝒂 𝑩(𝟏; 𝟓) ࢛ࢗࢇ ࡭(૛;૜) ⇔ .
vtcp 𝑨𝑩 −𝟏; 𝟐 𝒙 = 𝟐 − 𝒕 ⇔ . 𝒚 = 𝟑 + 𝟐𝒕
do đó có phương trình tham số là: 𝒙 = 𝟐 − 𝒕 . 𝒚 = 𝟑 + 𝟐𝒕
2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
Luyện tập Lập phương trình tham số và phương trình tổng quát của đường 5.
thẳng đi qua hai điểm phân biệt 𝑨 𝒙 cho trước.
𝟏; 𝒚𝟏 , 𝑩 𝒙𝟐; 𝒚𝟐 Giải
+ 𝑨𝑩 = 𝒙𝟐 − 𝒙𝟏; 𝒚𝟐 − 𝒚𝟏
+ Đường thẳng 𝑨𝑩 đi qua 𝑨 𝒙 và
nên có vectơ chỉ phương 𝟏; 𝒚𝟏 𝑩 𝒙𝟐; 𝒚𝟐 𝑨𝑩 = 𝒙
, do đó có vectơ pháp tuyến là: .
𝟐 − 𝒙𝟏; 𝒚𝟐 − 𝒚𝟏
𝒏 = 𝒚𝟐 − 𝒚𝟏; 𝒙𝟏 − 𝒙𝟐
+ Phương trình tham số đường thẳng 𝒙 = 𝒙 𝑨𝑩 là
𝟏 + (𝒙𝟐 − 𝒙𝟏)𝒕.
𝒚 = 𝒚𝟏 + (𝒚𝟐 − 𝒚𝟏)𝒕
+ Phương trình tổng quát đường thẳng 𝑨𝑩 là
𝒚𝟐 − 𝒚𝟏 𝒙 − 𝒙𝟏 + 𝒙𝟏 − 𝒙𝟐 𝒚 − 𝒚` = 𝟎.