Giáo án Powerpoint bài 20 Vị trí tương đối giữa hai đường thẳng góc và khoảng cách sách Kết nối tri thức-Phần 1

CHƯƠNG VII. CHƯƠNG I
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG TOÁN HÌNH HỌC ➉ 20
VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG GÓC VÀ KHOẢNG CÁCH 1 1 1 I
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG II
GÓC GIỮA HAI ĐƯỜNG THẲNG
III KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG 4 CHƯƠNG VII. CHƯƠNG I
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG TOÁN HÌNH HỌC ➉ 20
VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG GÓC VÀ KHOẢNG CÁCH 1 1 1 THUẬT NGỮ
KIẾN THỨC, KỸ NĂNG • Góc, khoảng cách
• Nhận biết hai đường thẳng cắt nhau, song song, trùng
• Vị trí tương đối giữa hai nhau, vuông góc. đường thẳng
• Thiết lập công thức tính góc giữa hai đường thẳng.
• Tính khoảng cách từ một điểm đến một đường thẳng.
• Vận dụng các công thức tính góc và khoảng cách để giải 4
một số bài toán có liên quan đến thực tiễn.
1. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG
HĐ1: Trong mặt phẳng tọa độ, cho hai đường:
𝛥1: 𝑥 − 2𝑦 + 3 = 0 và 𝛥2: 3𝑥 − 𝑦 − 1 = 0.
a) Điểm 𝑀 1; 2 có thuộc cả hai đường thẳng nói trên hay không?
b) Giải hệ 𝑥 − 2𝑦 + 3 = 0 3𝑥 − 𝑦 − 1 = 0
c) Chỉ ra mối quan hệ giữa tọa độ giao điểm của 𝛥 và
với nghiệm của hệ phương 1 𝛥2 trình trên. Giải
a) Thay tọa độ điểm 𝑀 1; 2 vào phương trình hai đường thẳng 𝛥 và , 1 𝛥2
ta được: 1 − 2.2 + 3 = 0 (đúng) ; 3.1 − 2 − 1 = 0(đúng).
Vậy điểm 𝑀 1; 2 thuộc cả hai đường thẳng nói trên.
1. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG
HĐ1: Trong mặt phẳng tọa độ, cho hai đường:
𝛥1: 𝑥 − 2𝑦 + 3 = 0 và 𝛥2: 3𝑥 − 𝑦 − 1 = 0.
a) Điểm 𝑀 1; 2 có thuộc cả hai đường thẳng nói trên hay không?
b) Giải hệ 𝑥 − 2𝑦 + 3 = 0 3𝑥 − 𝑦 − 1 = 0
c) Chỉ ra mối quan hệ giữa tọa độ giao điểm của 𝛥 và
với nghiệm của hệ phương 1 𝛥2 trình trên. Giải b) 𝑥 − 2𝑦 + 3 = 0 𝑥 − 2𝑦 = −3 𝑥 = 1 ⇔ ⇔ . 3𝑥 − 𝑦 − 1 = 0 3𝑥 − 𝑦 = 1 𝑦 = 2
c) Giao điểm của hai đường thẳng 𝛥 và
chính là nghiệm của hệ phương trình trên. 1 𝛥2
1. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG
Nhận xét: Mỗi đường thẳng trong mặt phẳng tọa độ là tập hợp những điểm có tọa
độ thỏa mãn phương trình của đường thẳng đó. Vì vậy, bài toán tìm giao điểm của
hai đường thẳng được quy về bài toán giải hệ gồm hai phương trình tương ứng.
- Trên mặt phẳng tọa độ, xét hai đường thẳng:
𝛥1: 𝑎1𝑥 + 𝑏1𝑦 + 𝑐1 = 0 và 𝛥2: 𝑎2𝑥 + 𝑏2𝑦 + 𝑐2 = 0.
Khi đó, tọa độ giao điểm của 𝛥 và
là nghiệm của hệ phương trình: 1 𝛥2 𝑎
1𝑥 + 𝑏1𝑦 + 𝑐1 = 0. (*)
𝑎2𝑥 + 𝑏2𝑦 + 𝑐2 = 0 𝛥 cắt tại
khi và chỉ khi hệ (*) có nghiệm duy nhất . 1 𝛥2 𝑀 𝑥0; 𝑦0 𝑥0; 𝑦0 𝛥 song song với
khi và chỉ khi hệ (*) vô nghiệm. 1 𝛥2 𝛥 trùng
khi và chỉ khi hệ (*) có vô số nghiệm. 1 𝛥2
1. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG Chú ý: Hình 7.5
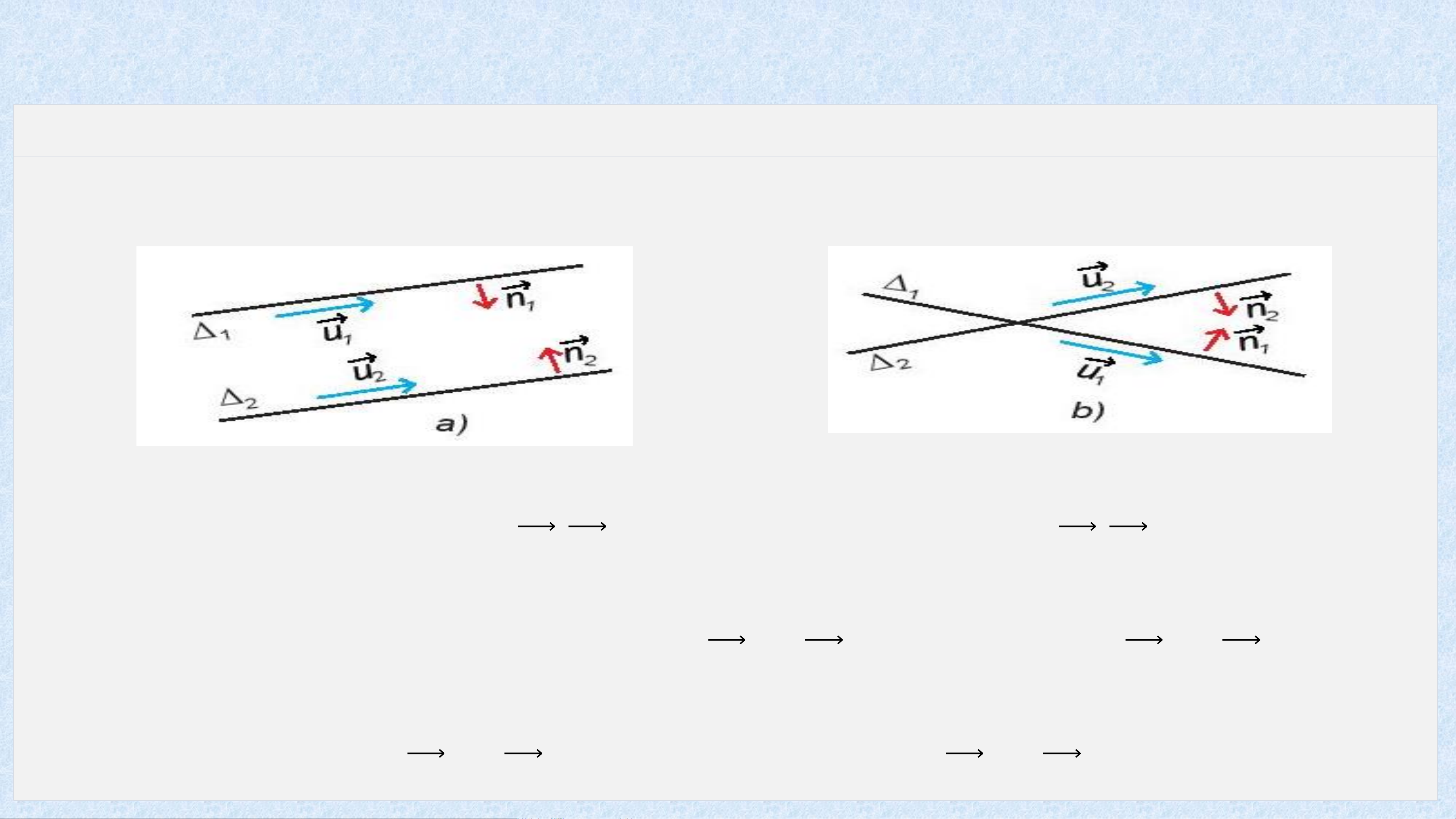
Dựa vào các vectơ chỉ phương 𝑢
hoặc các vectơ pháp tuyến của , ta 1, 𝑢2 𝑛1, 𝑛2 𝛥1, 𝛥2 có: • 𝛥 và song song hoặc trùng nhau và cùng phương và cùng 1 𝛥2 ⇔ 𝑢1 𝑢2 ⇔ 𝑛1 𝑛2 phương. • 𝛥 và cắt nhau và không cùng phương và không cùng phương. 1 𝛥2 ⇔ 𝑢1 𝑢2 ⇔ 𝑛1 𝑛2
Xét vị trí tương đối giữa đường thẳng
 : x  2y  4 3  0
và mỗi đường thẳng sau:
1. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG Ví dụ 1
Xét vị trí tương đối giữa đường thẳng 𝛥: 𝑥 − 2𝑦 + 4 3 = 0 và mỗi đường thẳng sau: 𝛥 𝛥 1: 3𝑥 − 6𝑦 + 12 = 0; 2: 2𝑥 − 2𝑦 = 0. Giải:
• Ta có 𝑥 − 2𝑦 + 4 3 = 0 ⇔ 3 𝑥 − 2𝑦 + 4 3 = 0 ⇔ 3𝑥 − 6𝑦 + 12 = 0.
Vậy 𝛥 và 𝛥 là một, tức là chúng trùng nhau. 1
Hai đường thẳng 𝛥 và 𝛥 có hai vectơ pháp tuyến 2 𝑛 1; − 2 và 𝑛2 2; −2 cùng
phương. Do đó, chúng song song hoặc trùng nhau. Mặt khác, điểm 𝑂 0; 0 thuộc
đường thẳng 𝛥 nhưng không thuộc đường thẳng 2
𝛥, nên hai đường thẳng này không trùng nhau.
Vậy 𝛥 và 𝛥 song song với nhau. 2
1. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG Nhận xét:
Giả sử hai đường thẳng 𝛥1, 𝛥2 có hai vectơ chỉ phương 𝑢1, 𝑢2 ( hay hai vectơ pháp
tuyến 𝑛1, 𝑛2) cùng phương. Khi đó:
• Nếu 𝛥1 và 𝛥2 có điểm chung thì 𝛥1 trùng 𝛥2;
• Nếu tồn tại điểm thuộc 𝛥1 nhưng không thuộc 𝛥2 thì 𝛥1 song song với 𝛥2.
1. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG
Luyện tập 1 Xét vị trí tương đối giữa các cặp đường thẳng sau:
a) 𝛥1: 𝑥 + 4𝑦 − 3 = 0 và 𝛥2: 𝑥 − 4𝑦 − 3 = 0;
b) 𝛥1: 𝑥 + 2𝑦 − 5 = 0 và 𝛥2: 2𝑥 + 4𝑦 − 3 5 = 0. Giải:
a) Hai đường thẳng 𝛥 và có hai vectơ pháp tuyến 1 𝛥2
𝑛1 = 1; 4 và 𝑛2 = 1; −4
không cùng phương. Do đó, chúng cắt nhau.
b) Hai đường thẳng 𝛥 và có hai vectơ pháp tuyến 1 𝛥2
𝑛1 = 1; 2 và 𝑛2 = 2; 4 cùng phương.
Do đó, chúng song song hoặc trùng nhau. Mặt khác, điểm 𝐴 5; 0 thuộc đường
thẳng 𝛥 nhưng không thuộc đường thẳng
, nên hai đường thẳng này không trùng 1 𝛥2 nhau. Vậy 𝛥 và song song với nhau. 1 𝛥2
2. GÓC GIỮA HAI ĐƯỜNG THẲNG HĐ2: Hai đường thẳng 𝛥 và cắt nhau tạo thành 1 𝛥2
bốn góc (H.7.6). Các số đo của bốn góc đó
có mối quan hệ gì với nhau? Hình 7.6 Giải:
Các số đo của bốn góc đó tạo ra hai cặp số đo tương ứng bằng nhau.
Hai đường thẳng cắt nhau tạo thành bốn góc, số đo của góc không tù được gọi là
số đo góc (hay đơn giản là góc) giữa hai đường thẳng.
Góc giữa hai đường thẳng song song hoặc trùng nhau được quy ước bằng 0
2. GÓC GIỮA HAI ĐƯỜNG THẲNG HĐ3:
Cho hai đường thẳng cắt nhau 𝛥 ,
tương ứng có các vectơ pháp tuyến . Gọi 1 𝛥2 𝑛1, 𝑛2 𝜑
là góc giữa hai đường thẳng đó (H.7.7). Nếu mối quan hệ giữa:
a) góc 𝜑 và góc 𝑛1, 𝑛2
b) 𝑐𝑜𝑠 𝜑 và 𝑐𝑜𝑠 𝑛1, 𝑛2 Hình 7.7 Giải: a) góc 𝜑 và góc 𝑛 bằng nhau hoặc bù nhau. 1, 𝑛2
b) 𝑐𝑜𝑠 𝜑 và 𝑐𝑜𝑠 𝑛
bằng nhau hoặc đối nhau. 1, 𝑛2
2. GÓC GIỮA HAI ĐƯỜNG THẲNG
Cho hai đường thẳng 𝛥1: 𝑎1𝑥 + 𝑏1𝑦 + 𝑐1 = 0 và 𝛥2: 𝑎2𝑥 + 𝑏2𝑦 + 𝑐2 = 0 .
Với các vectơ pháp tuyến 𝑛 và tương ứng. 1 𝑎1; 𝑏1 𝑛2 𝑎2; 𝑏2
Khi đó, góc 𝜑 giữa hai đường thẳng đó được xác định thông qua công thức : 𝑛 𝑎
𝑐𝑜𝑠 𝜑 = 𝑐𝑜𝑠 𝑛 1.𝑛2 1𝑎2+𝑏1𝑏2 . 1, 𝑛2 = = 𝑛1 . 𝑛2 𝑎2 2 2 2 1+𝑏1 . 𝑎2+𝑏2 Chú ý:
• 𝛥1 ⊥ 𝛥2 ⇔ 𝑛1 ⊥ 𝑛2 ⇔ 𝑎1𝑎2 + 𝑏1𝑏2 = 0. • Nếu 𝛥 có các vectơ chỉ phương thì góc và cũng được 1, 𝛥2 𝑢1, 𝑢2 𝜑 giữa 𝛥1 𝛥2
xác định thông qua công thức 𝑐𝑜𝑠 𝜑 = 𝑐𝑜𝑠 𝑢 . 1, 𝑢2
2. GÓC GIỮA HAI ĐƯỜNG THẲNG
Ví dụ 2 Tính góc giữa hai đường thẳng
𝛥1: 3𝑥 − 𝑦 + 2 = 0 và 𝛥2: 𝑥 − 3𝑦 − 2 = 0. Giải:
Vectơ pháp tuyến của 𝛥 là là 1 𝑛1 = 3; −1 , của 𝛥2 𝑛2 = 1; − 3 .
Gọi 𝜑 là góc giữa hai đường thẳng 𝛥 và . Ta có 1 𝛥2 𝑛 3.1+ −1 − 3 3
𝑐𝑜𝑠 𝜑 = 𝑐𝑜𝑠 𝑛 1.𝑛2 . 1, 𝑛2 = = = 𝑛1 . 𝑛2 2 2 2 3 + −1 2. 12+ − 3 Do đó, góc giữa 𝛥 và là 1 𝛥2 𝜑 = 30°.
2. GÓC GIỮA HAI ĐƯỜNG THẲNG
Luyện tập 2 Tính góc giữa hai đường thẳng:
𝛥1: 𝑥 + 3𝑦 + 2 = 0 và 𝛥2: 𝑦 = 3𝑥 + 1. Giải:
Ta có: 𝛥2: 𝑦 = 3𝑥 + 1 ⇔ 𝛥2: 3𝑥 − 𝑦 + 1 = 0
Vectơ pháp tuyến của 𝛥 là là 1 𝑛1 = 1; 3 , của 𝛥2 𝑛2 = 3; −1 .
Gọi 𝜑 là góc giữa hai đường thẳng 𝛥 và . Ta có 1 𝛥2 𝑛 1.3+3. −1
𝑐𝑜𝑠 𝜑 = 𝑐𝑜𝑠 𝑛 1.𝑛2 1, 𝑛2 = = = 0. 𝑛1 . 𝑛2 12+32. 32+ −1 2 Do đó, góc giữa 𝛥 và là 1 𝛥2 𝛥1: 𝜑 = 90°.
2. GÓC GIỮA HAI ĐƯỜNG THẲNG 𝑥 = 2 − 𝑡
Ví dụ 3 Tính góc giữa hai đường thẳng 𝛥1: 𝑥 = 3 và 𝛥2: . 𝑦 = 3 + 𝑡 Giải:
Đường thẳng 𝛥 có phương trình 1
𝑥 − 3 = 0 nên có vectơ pháp tuyến 𝑛1 = 1; 0 .
Đường thẳng 𝛥 có vectơ chỉ phương 2
𝑢2 = −1; 1 nên có véctơ pháp tuyến 𝑛 và , ta có
2 = 1; 1 . Gọi 𝜑 là góc giữa hai đường thẳng 𝛥1 𝛥2 𝑛 1.1+0.1 1
𝑐𝑜𝑠 𝜑 = 𝑐𝑜𝑠 𝑛 1.𝑛2 . 1, 𝑛2 = = = 𝑛1 . 𝑛2 12+02. 12+12 2 Do đó, góc giữa 𝛥 và là 1 𝛥2 𝜑 = 45°.
2. GÓC GIỮA HAI ĐƯỜNG THẲNG 𝑥 = 2 + 𝑡 𝑥 = 1 + 𝑡
Luyện tập 3 Tính góc giữa hai đường thẳng 𝛥 và . 1: 𝛥 𝑦 = 1 − 2𝑡 2: 𝑦 = 5 + 3𝑡 Giải:
Đường thẳng 𝛥 có VTCP 1
𝑢1 = 1; −2 nên có vectơ pháp tuyến 𝑛1 = 2; 1 .
Đường thẳng 𝛥 có VTCP 2
𝑢2 = 1; 3 nên có vectơ pháp tuyến 𝑛2 = 3; −1 .
Gọi 𝜑 là góc giữa hai đường thẳng 𝛥 và , ta có 1 𝛥2 𝑛 2.3+1. −1 1
𝑐𝑜𝑠 𝜑 = 𝑐𝑜𝑠 𝑛 1.𝑛2 . 1, 𝑛2 = = = 𝑛1 . 𝑛2 22+12. 32+ −1 2 2 Do đó, góc giữa 𝛥 và là 1 𝛥2 𝜑 = 45°.
2. GÓC GIỮA HAI ĐƯỜNG THẲNG
Xét đường thẳng 𝛥 bất kỳ cắt trục hoành 𝑂𝑥 tại một điểm 𝐴 . Điểm 𝐴 chia đường
thẳng 𝛥 thành hai tia, trong đó, gọi 𝐴𝑧 là tia nằm phía trên trục hoành. Kí hiệu 𝛼 là 𝛥 số đo của góc
𝑥𝐴𝑧 (H.7.8). Qua luyện tập sau, ta sẽ thấy ý nghĩa hình học của hệ số góc. Hình 7.8
2. GÓC GIỮA HAI ĐƯỜNG THẲNG
Cho đường thẳng 𝛥: 𝑦 = 𝑎𝑥 + 𝑏, với 𝑎 ≠ 0. Luyện tập 4
a) Chứng minh rằng 𝛥 cắt trục hoành.
b) Lập phương trình đường thẳng 𝛥 đi qua 0
𝑂 0; 0 và song song (hoặc trùng) với 𝛥.
c) Hãy chỉ ra mối quan hệ giữa 𝛼 và . 𝛥 𝛼𝛥0
d) Gọi 𝑀 là giao điểm của 𝛥 với nửa đường tròn đơn vị và là hoành độ của 0 𝑥0 𝑀.
Tính tung độ của 𝑀 theo 𝑥 và 0
𝑎. Từ đó, chứng minh rằng 𝑡𝑎𝑛 𝛼𝛥 = 𝑎. Giải:
a) Phương trình trục hoành: 𝑦 = 0 . Phương trình hoành độ giao điểm của trục hoành và −𝑏
𝛥 là: 𝑎𝑥 + 𝑏 = 0 ⇔ 𝑥 = 𝑎 ≠ 0 . 𝑎
Suy ra 𝛥 cắt trục hoành tại điểm −𝑏 ; 0 . 𝑎
2. GÓC GIỮA HAI ĐƯỜNG THẲNG Luyện tập 4
Cho đường thẳng 𝛥: 𝑦 = 𝑎𝑥 + 𝑏, với 𝑎 ≠ 0.
a) Chứng minh rằng 𝛥 cắt trục hoành.
b) Lập phương trình đường thẳng 𝛥 đi qua 0
𝑂 0; 0 và song song (hoặc trùng) với 𝛥.
c) Hãy chỉ ra mối quan hệ giữa 𝛼 và . 𝛥 𝛼𝛥0
d) Gọi 𝑀 là giao điểm của 𝛥 với nửa đường tròn đơn vị và là hoành độ của 0 𝑥0 𝑀.
Tính tung độ của 𝑀 theo 𝑥 và 0
𝑎. Từ đó, chứng minh rằng 𝑡𝑎𝑛 𝛼𝛥 = 𝑎. Giải:
b) Đường thẳng 𝛥 đi qua 0
𝑂 0; 0 và song song (hoặc trùng) với 𝛥 nên có phương trình:
𝑦 = 𝑎 𝑥 − 0 + 0 ⇔ 𝛥0: 𝑦 = 𝑎𝑥. c) 𝛼 . 𝛥 = 𝛼𝛥0
2. GÓC GIỮA HAI ĐƯỜNG THẲNG
Cho đường thẳng 𝛥: 𝑦 = 𝑎𝑥 + 𝑏, với 𝑎 ≠ 0. Luyện tập 4
a) Chứng minh rằng 𝛥 cắt trục hoành.
b) Lập phương trình đường thẳng 𝛥 đi qua 0
𝑂 0; 0 và song song (hoặc trùng) với 𝛥.
c) Hãy chỉ ra mối quan hệ giữa 𝛼 và . 𝛥 𝛼𝛥0
d) Gọi 𝑀 là giao điểm của 𝛥 với nửa đường tròn đơn vị và là hoành độ của 0 𝑥0 𝑀.
Tính tung độ của 𝑀 theo 𝑥 và 0
𝑎. Từ đó, chứng minh rằng 𝑡𝑎𝑛 𝛼𝛥 = 𝑎. Giải: d) 𝑦 𝑎𝑥 𝑀 ∈ 𝛥 . 0 0
0 ⇒ tung độ của 𝑀 là 𝑦0 = 𝑎𝑥0 𝑡𝑎𝑛 𝛼𝛥 = = = 𝑎. 0 𝑥0 𝑥0
𝛼𝛥 = 𝛼𝛥 ⇒ 𝑡𝑎𝑛 𝛼 = 𝑎. 0 𝛥 = 𝑡𝑎𝑛 𝛼𝛥0