

































































































































Preview text:
lOMoARcPSD|36086670
BỘ THÔNG TIN VÀ TRUYỀN THÔNG
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG BÀI GIẢNG
TÍN HIỆU VÀ HỆ THỐNG MÃ MÔN HỌC: TEL1368 KHOA VIỄN THÔNG 1 NHÓM BIÊN SOẠN: TS. Ngô Thị Thu Trang TS. Nguyễn Chiến Trinh TS. Nguyễn Thị Thu Nga lOMoARcPSD|36086670 i LỜI NÓI ĐẦU
Lí thuyết tín hiệu và hệ thống là các kiến thức không thể thiếu được trong
Kỹ thuật Điện tử Viễn thông và các môn học khoa học và kỹ thuật. Lí thuyết tín
hiệu và hệ thống có truyền thống phát triển lâu dài, có khả năng ứng dụng rộng rãi
trong các ngành kỹ thuật khác nhau, tạo lập nền tảng để tiếp tục học tập và phát
triển trong các lĩnh vực truyền thông, xử lí tín hiệu, thiết bị điện tử, điều khiển, . .
Ngày nay, tín hiệu và hệ thống vẫn đang được nghiên cứu và phát triển, giải quyết
các vấn đề mới liên quan đến điện tử - truyền thông, như các công nghệ IC, hệ
thống truyền thông, thiết bị công nghệ tiên tiến, và các ứng dụng khác trên mạng viễn thông.
Tài liệu này được biện soạn như Bài giảng về Tín hiệu và hệ thống với mục
tiêu cung cấp các kiến thức và hỗ trợ học tập, đặc biệt là quá trình tự học. Trong
từng chương nội dung, tài liệu trình bày các kiến thức lí thuyết cùng với các ví dụ,
giúp người đọc có thể dễ dàng hiểu và nắm bắt phương pháp luận và kĩ thuật của
tín hiệu và hệ thống. Các bài tập yêu cầu phân tích, giải quyết các vấn đề, thực
hiện tính toán trên các công cụ toán học cũng được khuyến khích thực hiện nhằm
nắm bắt, hiểu sâu hơn và vận dụng giải quyết các vấn đề trong tín hiệu và hệ thống.
Tài liệu bài giảng được bố cục trong 7 chương. Chương 1 giới thiệu về tín
hiệu và hệ thống với các đặc trưng cơ bản của các loại tín hiệu, mục tiêu và các
hoạt động chủ yếu của hệ thống, các biểu diễn toán học của tín hiệu và hệ thống.
Chương 2 phát triển quan hệ nền tảng đầu vào – đầu ra của hệ thống tuyến tính bất
biến theo thời gian LTI và các đặc trưng hệ thống, biến đổi tín hiệu trên hệ thống.
Chương 3 phân tích tín hiệu và hệ thống LTI liên tục trên miền thời gian và tần số
với chuỗi Fourrier và biến đổi Fourrier liên tục. Chương 4 cung cấp các phân tích
tín hiệu rời rạc và hệ thống LTI rời rạc, các đặc tính trên miền thời gian và tần số,
sử dụng biến đổi Fourrier rời rạc theo thời gian và biến đổi Fourrier rời rạc.
Chương 5 giới thiệu biến đổi Laplace, các tính chất và ứng dụng biến đổi Laplace
để phân tích hệ thống LTI liên tục theo thời gian. Chương 6 mô tả biến đổi z và lOMoARcPSD|36086670 i
phân tích hệ thống LTI rời rạc với biến đổi z, chuyển đổi giữa hệ thống LTI liên
tục và rời rạc. Chương 7 đưa i
ra khái niệm và phương pháp tiếp cận phân tích hệ thống cả liên tục lẫn rời rạc với không gian trạng thái.
Tài liệu bài giảng cung cấp các kiến thức cơ bản cũng như trình bày toàn
diện các vấn đề về tín hiệu hệ thống rõ ràng, mạch lạc và dễ hiểu cho người đọc.
Đồng thời cấu trúc các nội dung hợp lí, thống nhất, liên kết chặt chẽ cho cả hệ
thống liên tục và rời rạc.
Trong quá trình biên soạn tài liệu, chúng tôi đã nhận được rất nhiều ý kiến
đóng góp quí báu từ nhiều đồng nghiệp và chuyên gia trong lĩnh vực này. Chúng
tôi trân trọng cám ơn. Và chúng tôi xin gửi lời cám ơn đặc biệt tới ThS. Trần Thị
Thuỷ Bình và TS. Nguyễn Đức Nhân, những người đã đồng hành cùng chúng tôi
từ những ý tưởng đầu tiên.
Chúng tôi hy vọng cuốn tài liệu này sẽ có nhiều hữu ích cho sinh viên và
những người đọc quan tâm. Chúng tôi rất mong nhận được ý kiến đóng góp của
các quí thầy cô, các sinh viên và những bạn đọc quan tâm để hoàn thiện hơn cuốn tài liệu này.
Mọi ý kiến đóng góp xin được gửi về: trangntt1@ptit.edu.vn, trinhnc@ptit.edu.vn và ngantt@ptit.edu.vn, Nhóm biên soạn lOMoARcPSD|36086670 i ii MỤC LỤC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . i
LỜI NÓI ĐẦU . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . i
MỤC LỤC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iii
BẢNG THUẬT NGỮ VIẾT TẮT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ix
BẢNG DANH MỤC CÁC KÝ HIỆU
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xii
DANH MỤC CÁC HÌNH VẼ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xiii
DANH MỤC CÁC BẢNG . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xvi
CHƯƠNG 1: KHÁI QUÁT VỀ TÍN HIỆU VÀ HỆ THỐNG
. . . . . . . . . . . . . . . . . . . . . . 1
1.1 TÍN HIỆU VÀ PHÂN LOẠI TÍN HIỆU . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.1 Khái niệm về tín hiệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.2 Phân loại tín hiệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.1.2.1 Tín hiệu liên tục và tín hiệu rời rạc . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1.1.2.2 Tín hiệu số và tín hiệu tương
tự . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.1.2.3 Tín hiệu tuần hoàn và không tuần hoàn . . . . . . . . . . . . . . . . . . . . . . . . 5
1.1.2.4 Tín hiệu ngẫu nhiên và tín hiệu xác định . . . . . . . . . . . . . . . . . . . . . . .
5 1.1.2.5 Tín hiệu chẵn và tín hiệu
lẻ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 lOMoARcPSD|36086670 i
1.1.2.6 Tín hiệu thực và tín hiệu phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 v
1.1.2.7 Một số cách phân loại khác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.1.3 Các tín hiệu liên tục cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.1.3.1 Tín hiệu nhảy bậc đơn
vị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.1.3.2 Hàm xung đơn
vị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.1.3.3 Tín hiệu hàm mũ phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.1.3.4 Tín hiệu hình sin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.1.3.5 Một số tín hiệu liên tục cơ bản khác . . . . . . . . . . . . . . . . . . . . . . . . . 13
1.1.4 Các tín hiệu rời rạc cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.1.4.1 Chuỗi nhảy bậc đơn vị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.1.4.2 Xung đơn vị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.1.4.3 Chuỗi hàm mũ phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.1.4.4 Chuỗi xung hình sin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.2 MỘT SỐ ĐẶC TRƯNG CƠ BẢN TÍN HIỆU . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.2.1 Tính chẵn lẻ của tín hiệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.2.2 Tính nhân quả của tín hiệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 lOMoARcPSD|36086670 i
1.2.3 Năng lượng và công suất của tín hiệu . . . . . . . . . . . . . . . . . . . . . . . . . . 20
1.2.4 Giá trị trung bình, rms của tín hiệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 lOMoARcPSD|36086670 v
1.3 MỘT SỐ PHÉP CHUYỂN ĐỔI TÍN HIỆU CƠ BẢN . . . . . . . . . . . . . . . . . . . . . 25
1.3.1 Phép dịch thời gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
1.3.2 Phép đảo thời gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
1.3.3 Phép thay đổi thang thời gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.4 HỆ THỐNG VÀ PHÂN LOẠI HỆ THỐNG . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
1.4.1 Khái niệm hệ thống . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
1.4.2 Phân loại hệ thống . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
BÀI TẬP CHƯƠNG 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30 CHƯƠNG 2: HỆ THỐNG TUYẾN TÍNH BẤT BIẾN THEO THỜI GIAN . . . . . . . . . . 31 2.1 HỆ THỐNG LTI LIÊN
TỤC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.1.1 Đáp ứng của hệ thống LTI liên tục và tích chập . . . . . . . . . . . . . . . . . . 31
2.1.2 Các hệ thống LTI liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
2.1.3 Các đặc trưng của hệ thống LTI liên tục . . . . . . . . . . . . . . . . . . . . . . . . 36
2.1.3.1 Hệ thống LTI có nhớ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
2.1.3.2 Hệ thống LTI nhân quả . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 lOMoARcPSD|36086670 v
2.1.3.3 Hệ thống LTI ổn định . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
2.1.3.4 Hệ thống LTI nghịch đảo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 lOMoARcPSD|36086670 v i
2.1.4 Biểu diễn hệ thống bằng phương trình vi phân . . . . . . . . . . . . . . . . . . . 37
2.2 HỆ THỐNG LTI RỜI RẠC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
2.2.1 Đáp ứng của hệ thống LTI rời rạc và tổng chập . . . . . . . . . . . . . . . . . . 42
2.2.2 Các hệ thống LTI rời rạc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
2.2.3 Các đặc trưng của hệ thống LTI rời rạc . . . . . . . . . . . . . . . . . . . . . . . . 47
2.2.3.1 Hệ thống LTI có nhớ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
2.2.3.2 Hệ thống LTI nhân quả . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
2.2.3.3 Hệ thống LTI ổn định . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
2.2.4 Biểu diễn hệ thống bằng phương trình sai phân . . . . . . . . . . . . . . . . . . 48
BÀI TẬP CHƯƠNG 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU VÀ HỆ THỐNG LIÊN TỤC TRONG MIỀN TẦN SỐ
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
3.1 CHUỖI FOURIER . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
3.1.1 Biểu diễn tín hiệu liên tục tuần hoàn bằng chuỗi Fourier . . . . . . . . . . . 53
3.1.1.1 Biểu diễn tín hiệu liên tục tuần hoàn bằng chuỗi
Fourier . . . . . . . . . 53 lOMoARcPSD|36086670 v ii
3.1.1.2 Tính hội tụ của chuỗi Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
3.1.1.3 Phổ biên độ và phổ pha của tín hiệu tuần hoàn . . . . . . . . . . . . . . . . 59
3.1.2 Tính chất của chuỗi Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
3.2 BIẾN ĐỔI FOURIER TÍN HIỆU LIÊN TỤC THEO THỜI GIAN . . . . . . . . . . . 61
3.2.1 Biến đổi Fourier tín hiệu liên tục theo thời gian . . . . . . . . . . . . . . . . . . 62
3.2.2 Các tính chất của biến đổi Fourier tín hiệu liên tục theo thời gian . . . . 63
3.2.3 Biến đổi Fourier và phổ của một số tín hiệu cơ bản . . . . . . . . . . . . . . . 64
3.2.4 Lấy mẫu tín hiệu liên tục và định lý lấy mẫu của Shannon . . . . . . . . . 71
3.2.5 Mật độ phổ công suất và năng lượng của tín hiệu . . . . . . . . . . . . . . . . 76
3.2.5.1 Mật độ phổ năng lượng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
3.2.5.2 Mật độ phổ công suất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
3.2.5.3 Hàm tự tương quan . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
3.3 ĐÁP ỨNG TẦN SỐ CỦA HỆ THỐNG LTI . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79 3.4 MỘT SỐ VÍ DỤ VỀ ỨNG DỤNG CỦA BIẾN ĐỔI FOURIER TÍN HIỆU THỜI
GIAN LIÊN TỤC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82 lOMoARcPSD|36086670 v iii
3.4.1 Bộ lọc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
3.4.2 Băng thông . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
BÀI TẬP CHƯƠNG 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
85 CHƯƠNG 4: PHÂN TÍCH TÍN HIỆU VÀ HỆ THỐNG RỜI RẠC TRONG MIỀN TẦN SỐ
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
4.1 CHUỖI FOURIER RỜI RẠC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
4.1.1 Biểu diễn tín hiệu tuần hoàn rời rạc bằng chuỗi Fourier . . . . . . . . . . . 86
4.1.1.1 Biểu diễn tín hiệu tuần hoàn rời rạc bằng chuỗi Fourier . . . . . . . . . 86
4.1.2 Điều kiện hội tụ của chuỗi Fourier rời rạc . . . . . . . . . . . . . . . . . . . . . . 87
4.1.3 Các tính chất của chuỗi Fourier rời rạc . . . . . . . . . . . . . . . . . . . . . . . . . 87
4.2 BIẾN ĐỔI FOURIER TÍN HIỆU RỜI RẠC THỜI GIAN . . . . . . . . . . . . . . . . . . 89
4.2.1 Biến đổi Fourier của chuỗi tuần hoàn và không tuần hoàn . . . . . . . . . . 89
4.2.2 Tính chất của biến đổi Fourier tín hiệu thời gian rời rạc . . . . . . . . . . . 90
4.2.3 Các cặp biến đổi Fourier và phổ của một số tín hiệu rời rạc thời gian cơ
bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
4.3 ĐÁP ỨNG TẦN SỐ CỦA HỆ THỐNG LTI RỜI RẠC . . . . . . . . . . . . . . . . . . . .
96 4.4 MỘT SỐ VÍ DỤ VỀ ỨNG DỤNG CỦA BIẾN ĐỔI FOURIER TÍN HIỆU THỜI lOMoARcPSD|36086670 v iv
GIAN RỜI RẠC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
4.4.1 Đáp ứng hệ thống khi đầu vào là tín hiệu hình sin rời rạc . . . . . . . . . . 98
4.4.2 Mô phỏng hệ thống . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
4.5 BIẾN ĐỔI FOURIER RỜI RẠC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
4.5.1 Biến đổi Fourier rời rạc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
4.5.2 Các tính chất của biến đổi Fourier rời rạc . . . . . . . . . . . . . . . . . . . . . . 101 lOMoARcPSD|36086670 x i x
BÀI TẬP CHƯƠNG 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
102 CHƯƠNG 5: BIẾN ĐỔI LAPLACE
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103 5.1 BIẾN ĐỔI
LAPLACE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
5.1.1 Biến đổi Laplace một phía và hai phía . . . . . . . . . . . . . . . . . . . . . . . . 103
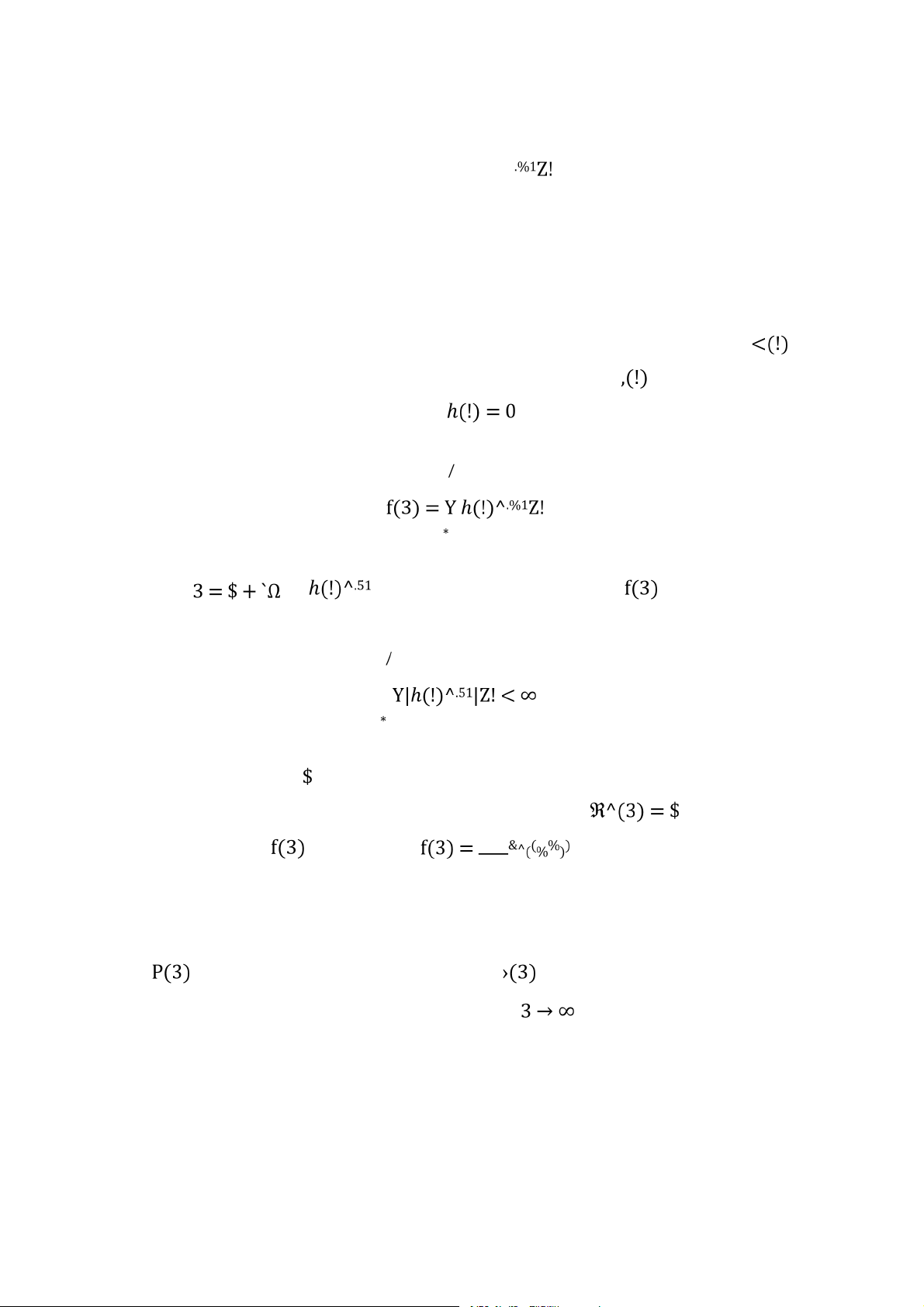
5.1.2 Điều kiện tồn tại của biến đổi Laplace . . . . . . . . . . . . . . . . . . . . . . . . 103
5.1.3 Quan hệ giữa biến đổi Laplace và biến đổi Fourier . . . . . . . . . . . . . . 104
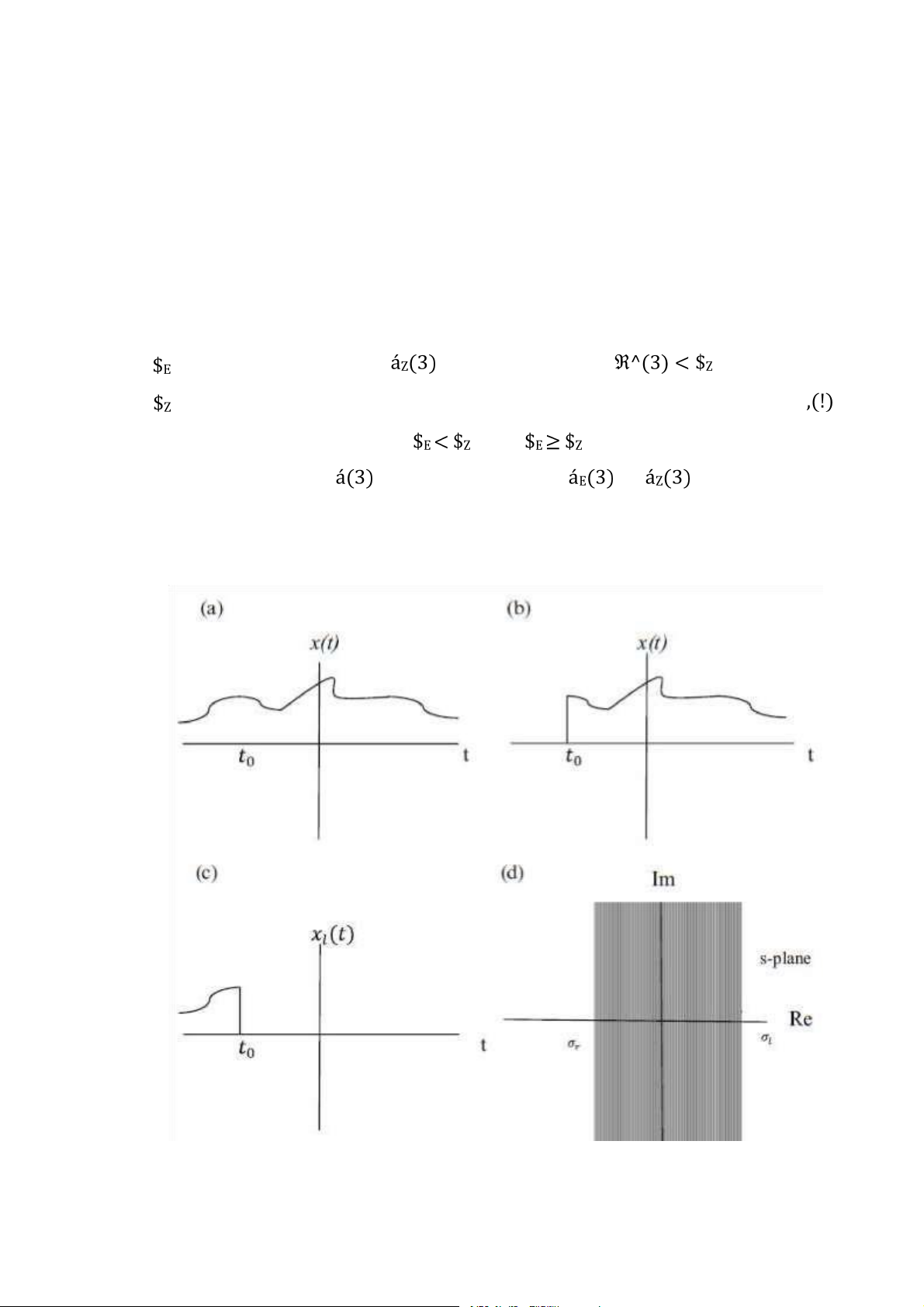
5.1.4 Biểu diễn biến đổi Laplace trong mặt phẳng s . . . . . . . . . . . . . . . . . . 105
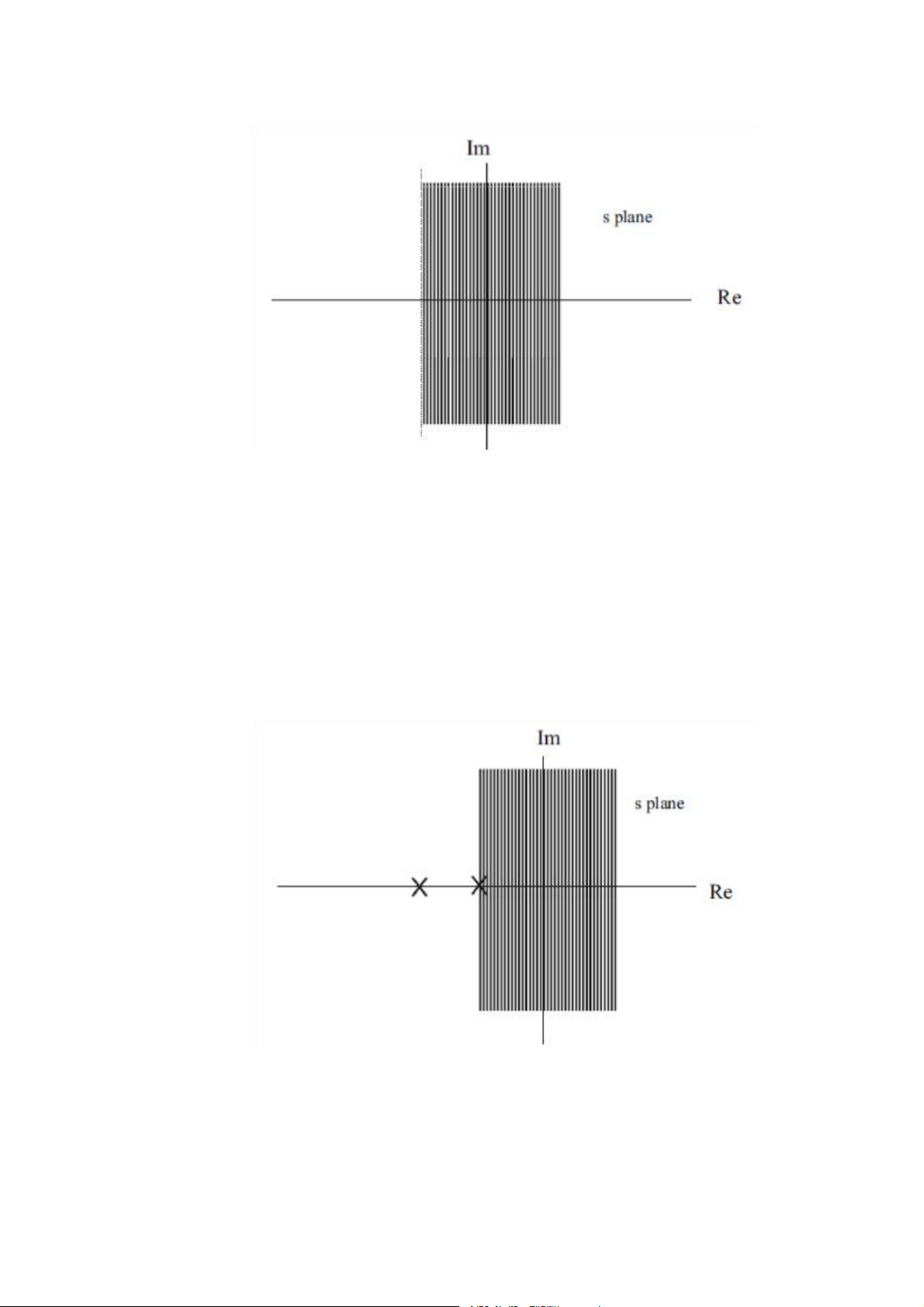
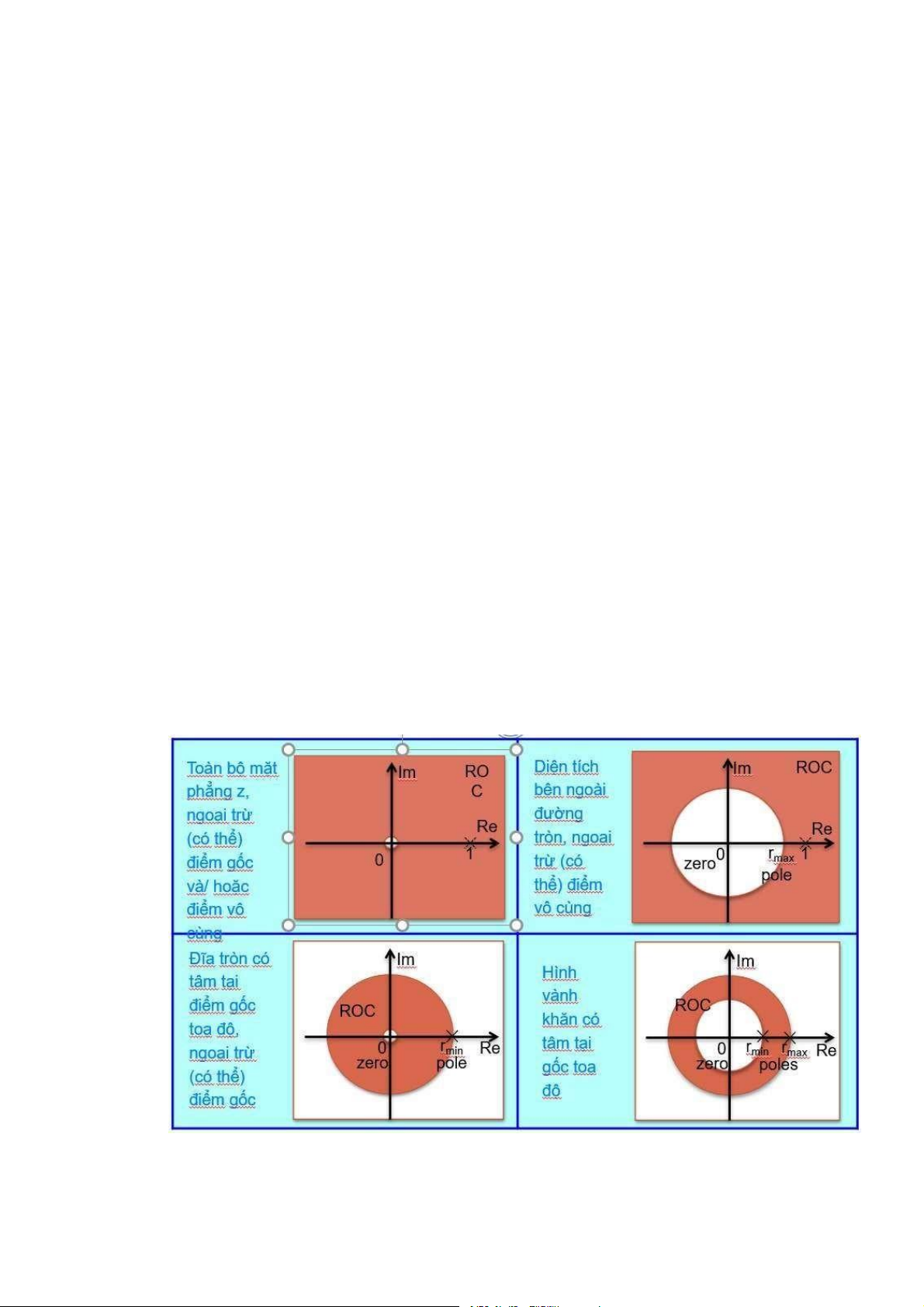
5.1.5 Các tính chất vùng hội tụ ROC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
5.1.6 Các tính chất của biến đổi Laplace . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
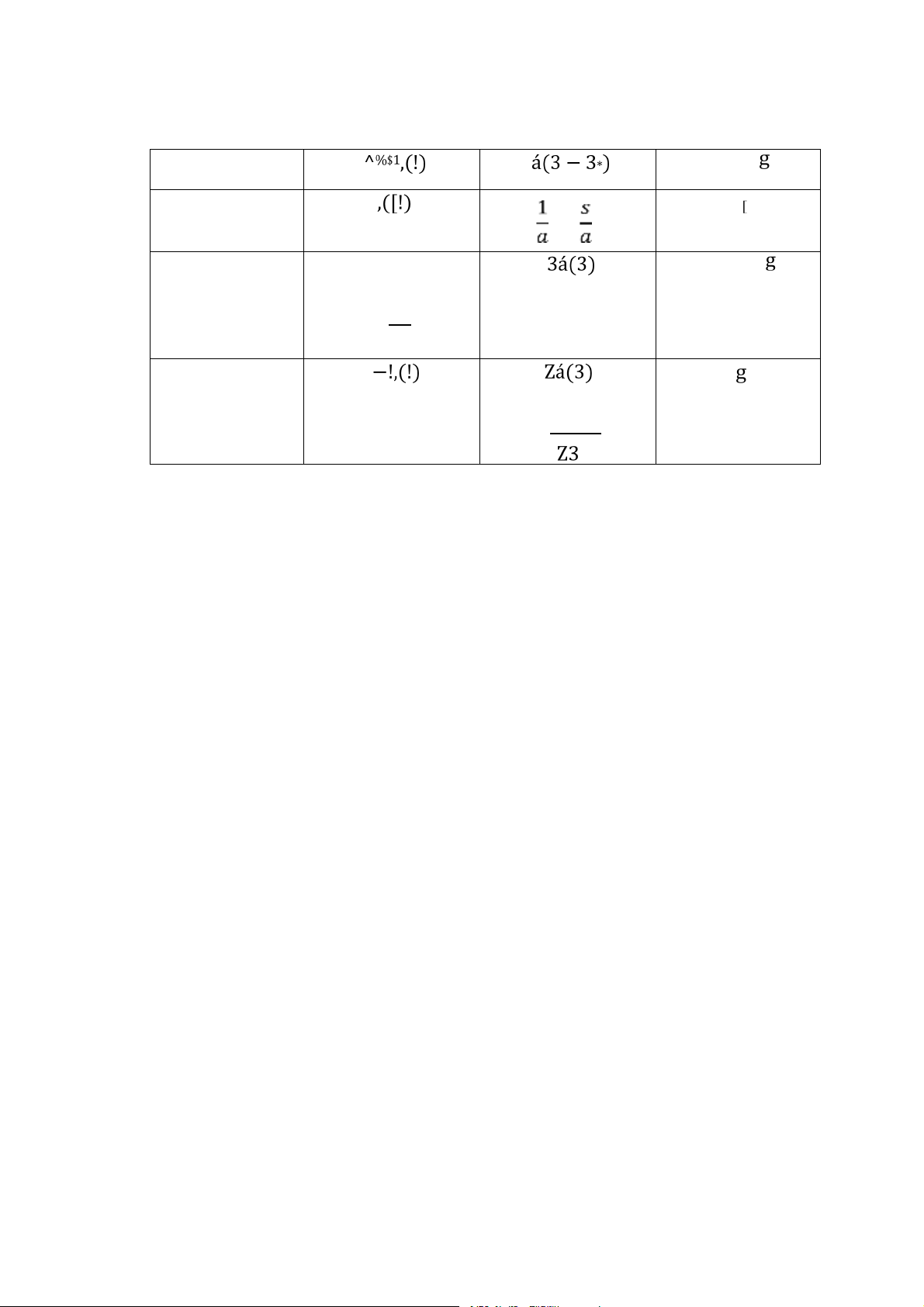
5.1.7 Một số biến đổi Laplace thông dụng . . . . . . . . . . . . . . . . . . . . . . . . . . 111
5.2 BIẾN ĐỔI LAPLACE NGƯỢC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
112 5.3 PHÂN TÍCH HỆ THỐNG LTI LIÊN TỤC BẰNG BIẾN ĐỔI LAPLACE . . . . 114
5.3.1 Hàm truyền đạt của hệ thống . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114 lOMoARcPSD|36086670
5.3.2 Điều kiện nhân quả và ổn định của hệ thống trong miền s . . . . . . . . . 115
5.3.3 Biểu diễn hệ thống trong miền s . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
Giải phương trình vi phân tuyến tính hệ số hằng sử dụng biến đổi Laplace 118
BÀI TẬP CHƯƠNG 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
119 CHƯƠNG 6: BIẾN ĐỔI z
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121 6.1 BIẾN ĐỔI
z . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
6.1.1 Biến đổi z một phía và hai phía . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
c. Biến đổi z với biến đổi Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122 6.1.2 Miền hội tụ của biến đổi Laplace
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 122 Các tính chất của ROC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125
6.1.3 Tính chất của biến đổi z . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126
6.1.4 Một số biến đổi z thông dụng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
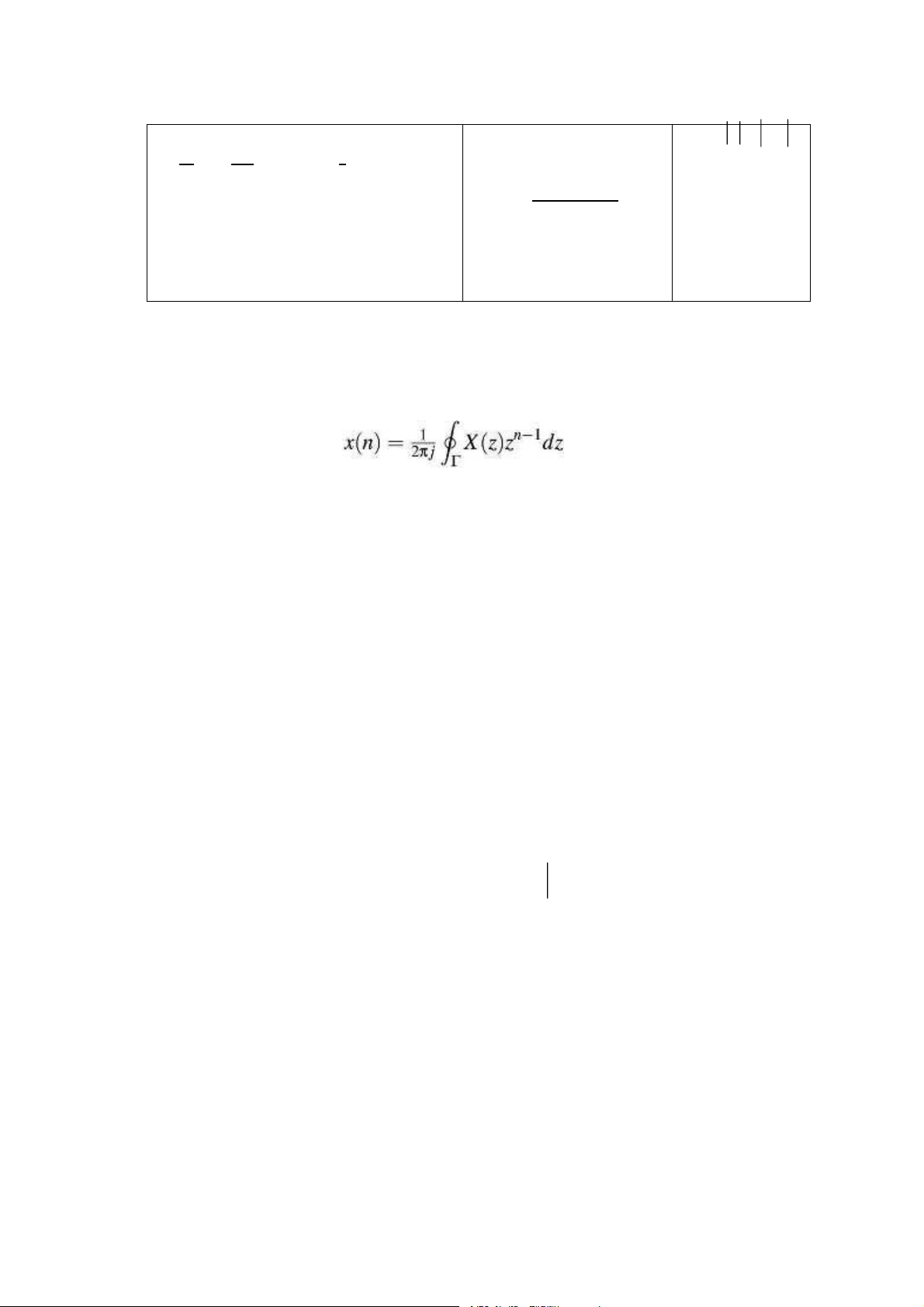
6.2 BIẾN ĐỔI z NGƯỢC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
128 6.3 PHÂN TÍCH HỆ THỐNG LTI RỜI RẠC BẰNG BIẾN ĐỔI z . . . . . . . . . . . . . 134 lOMoARcPSD|36086670 x
6.3.1 Hàm truyền đạt của hệ thống rời rạc . . . . . . . . . . . . . . . . . . . . . . . . . . 134 6.3.2
Điều kiện nhân quả và ổn định của hệ thống trong miền z . . . . . . 135
6.3.3 Biểu diễn hệ thống trong miền z . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136
6.3.4 Giải phương trình sai phân tuyến tính hệ số hằng sử dụng biến đổi z 137 lOMoARcPSD|36086670 x
i BÀITẬPCHƯƠNG6................................................
140 CHƯƠNG 7: KHÔNG GIAN TRẠNG THÁI CỦA HỆ THỐNG
. . . . . . . . . . . . . . . . . 143
7.1 KHÁI NIỆM VỀ TRẠNG THÁI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
143 7.2 PHÂN TÍCH KHÔNG GIAN TRẠNG THÁI CỦA HỆ THỐNG LTI LIÊN TỤC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144
7.2.1 Mô hình không gian trạng thái . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144
7.2.2 Nghiệm trong miền tần số của phương trình trạng thái . . . . . . . . . . . 148
7.2.3 Nghiệm trong miền thời gian của phương trình trạng thái . . . . . . . . . 149
7.2.4 Chuyển đổi tuyến tính của vector trạng thái . . . . . . . . . . . . . . . . . . . . 154
7.3 PHÂN TÍCH KHÔNG GIAN TRẠNG THÁI CỦA HỆ THỐNG LTI RỜI RẠC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
7.3.1 Mô hình không gian trạng thái . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
7.3.2 Nghiệm trong miền tần số của phương trình trạng thái . . . . . . . . . . . 157
7.3.3 Nghiệm trong miền thời gian của phương trình trạng thái . . . . . . . . . 158
7.3.4 Chuyển đổi tuyến tính của vector trạng thái . . . . . . . . . . . . . . . . . . . . 161
BÀI TẬP CHƯƠNG 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161 TÀI LIỆU THAM KHẢO
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162
BẢNG THUẬT NGỮ VIẾT TẮT lOMoARcPSD|36086670 x ii Từ viết Tiếng Anh Tiếng Việt tắt A ADC Analog to Digital Conversion
Chuyển đổi tương tự - số B C D DAC Digital-to-Analog Conversion
Chuyển đổi số - tương tự DC Direct “current” Giá trị một chiều E lOMoARcPSD|36086670 x iii F FFT Fast Fourier Transform Biến đổi Fourier nhanh G H I L M lOMoARcPSD|36086670 x iv N O P Q R lOMoARcPSD|36086670 x v S T V X W
BẢNG DANH MỤC CÁC KÝ HIỆU Ký hiệu Ý nghĩa adj
Hằng số phân biệt mức đóng góp của FWM lên từng kênh bước sóng A Hệ số nén Aeff Diện tích hiệu dụng BDC
Đại lượng dịch một chiều Bo Băng thông quang lOMoARcPSD|36086670 x vi Be Băng tần điện c
Vận tốc ánh sáng trong chân không C(.) Hàm nén C-1(.) Hàm giải nén dji Tham số walk-off D Hệ số suy biến của FWM Dc Hệ số tán sắc fj Tần số sóng mang quang FN
Hệ số hình ảnh nhiễu của bộ khuếch đại G
Hệ số khuếch đại của bộ khuếch đại quang EDFA E Trường quang !{. } Kỳ vọng Id Dòng tối kB Hằng số Boltzmann L Chiều dài sợi quang LNL Chiều dài phi tuyến Leff Chiều dài hiệu dụng Lw Chiều dài walk-off m
Chỉ số điều chế của bộ điều chế MZM M Số bậc điều chế MFWM Số sóng FWM lOMoARcPSD|36086670 x vii
DANH MỤC CÁC HÌNH VẼ
Hình 1.1: Ví dụ tín hiệu biên độ rời rạc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Hình 1.2: Ví dụ tín hiệu biên độ liên tục và biên độ rời rạc. . . . . . . . . . . . . . . . . . . 3
Hình 1.3: Chuyển đổi tín hiệu tương tự thành tín hiệu số . . . . . . . . . . . . . . . . . . . . 4
Hình 1.4: Ví dụ về tín hiệu chẵn (a, b) và tín hiệu lẻ (c, d) . . . . . . . . . . . . . . . . . . . 6
Hình 1.5: Ví dụ về tín hiệu ảnh màu gồm 2 hướng (x, y) và 3 kênh (R, G, B) . . . . 7
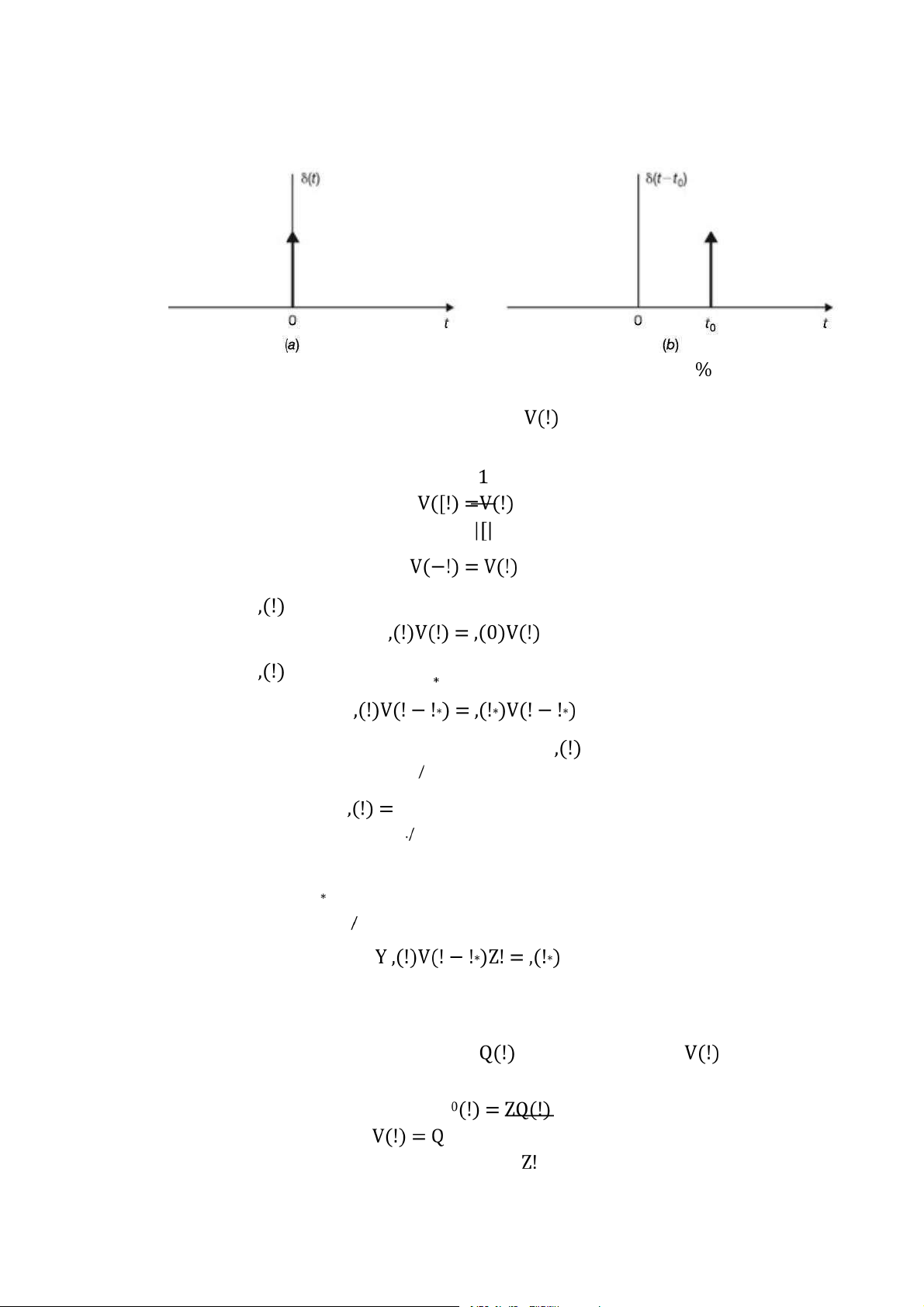
Hình 1.6: a) Tín hiệu nhảy bậc đơn vị, b) Tín hiệu nhảy bậc đơn vị dịch !0 . . . . . . 8
Hình 1.7: Biểu diễn tín hiệu đa hàm #! sử dụng tín hiệu nhảy bậc đơn vị . . . . . . . . 8
Hình 1.8: Định nghĩa hàm xung đơn vị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Hình 1.9: a) Hàm xung đơn vị, b) Hàm xung đơn vị dịch !0 . . . . . . . . . . . . . . . . . . 9
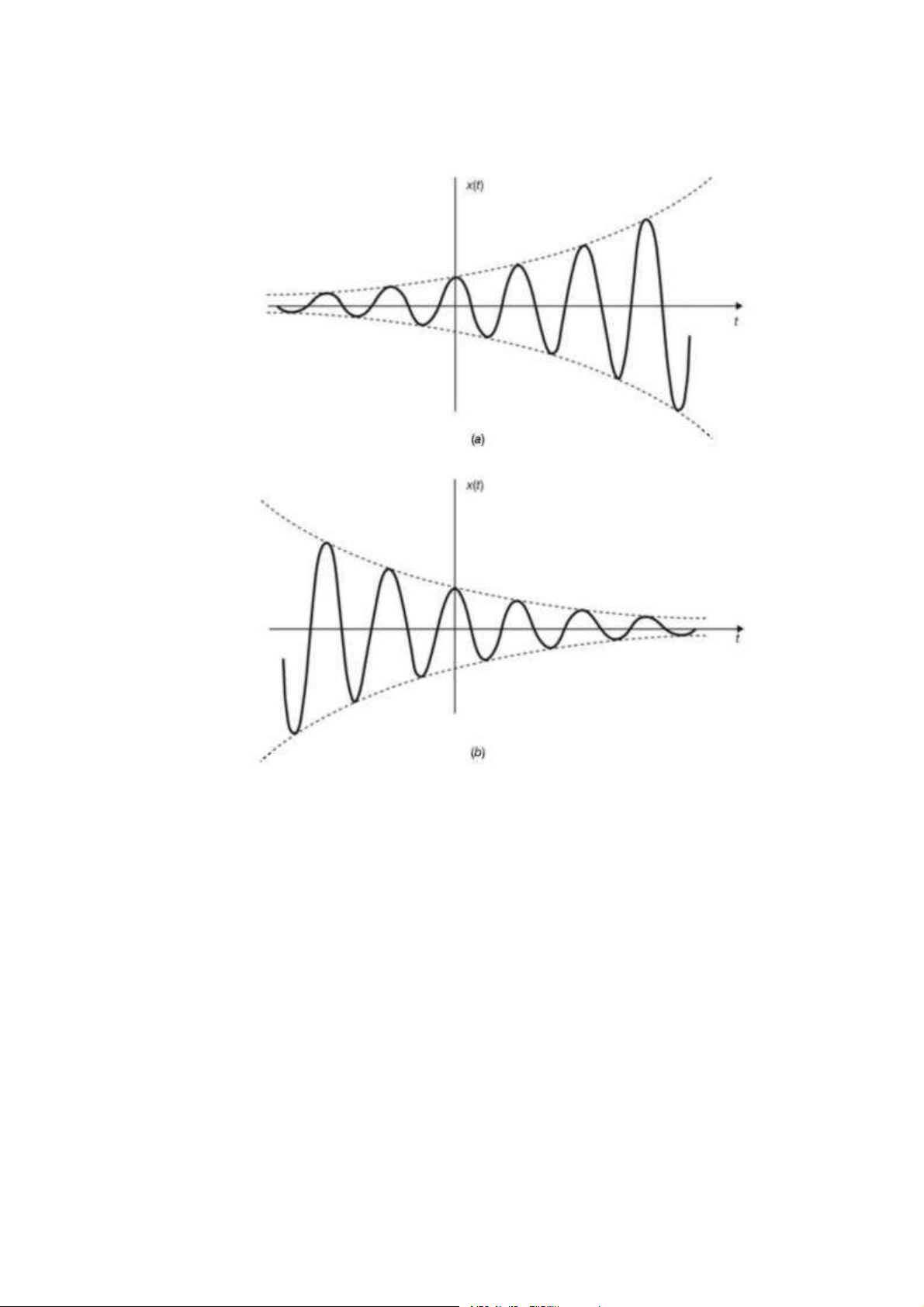
Hình 1.10: Tín hiệu sin a) tăng theo hàm mũ, b) giảm theo hàm mũ . . . . . . . . . . . 11
Hình 1.11: Tín hiệu hàm mũ thực liên tục theo thời gian a) $ > 0, b) $ < 0 . . . . 12
Hình 1.12: Tín hiệu hình sin liên tục theo thời gian . . . . . . . . . . . . . . . . . . . . . . . . 13 lOMoARcPSD|36086670 x viii
Hình 1.13: Tín hiệu hàm dốc đơn vị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Hình 1.14: Tín hiệu xung chữ nhật . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
Hình 1.15: Tín hiệu xung tam giác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
Hình 1.16: a) Chuỗi nhảy bậc đơn vị, b) Chuỗi nhảy bậc đơn vị dịch một khoảng (
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
Hình 1.17: a) Xung đơn vị, b) Xung đơn vị dịch một khoảng ( . . . . . . . . . . . . . . 15
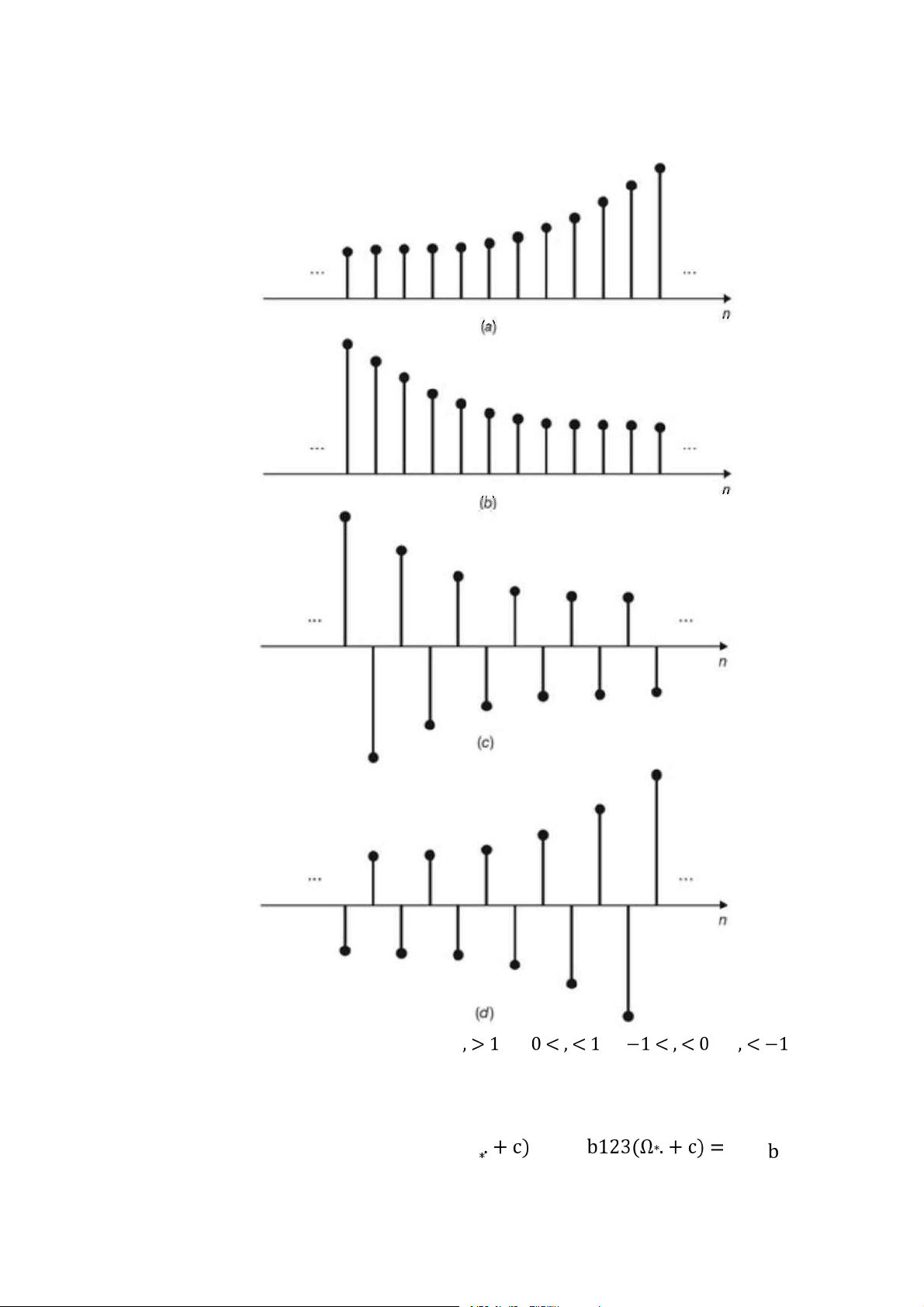
Hình 1.18: Chuỗi hàm mũ thực: a)) > 1 , b) 0 < ) < 1, c) −1 < ) < 0, d) ) <
−1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
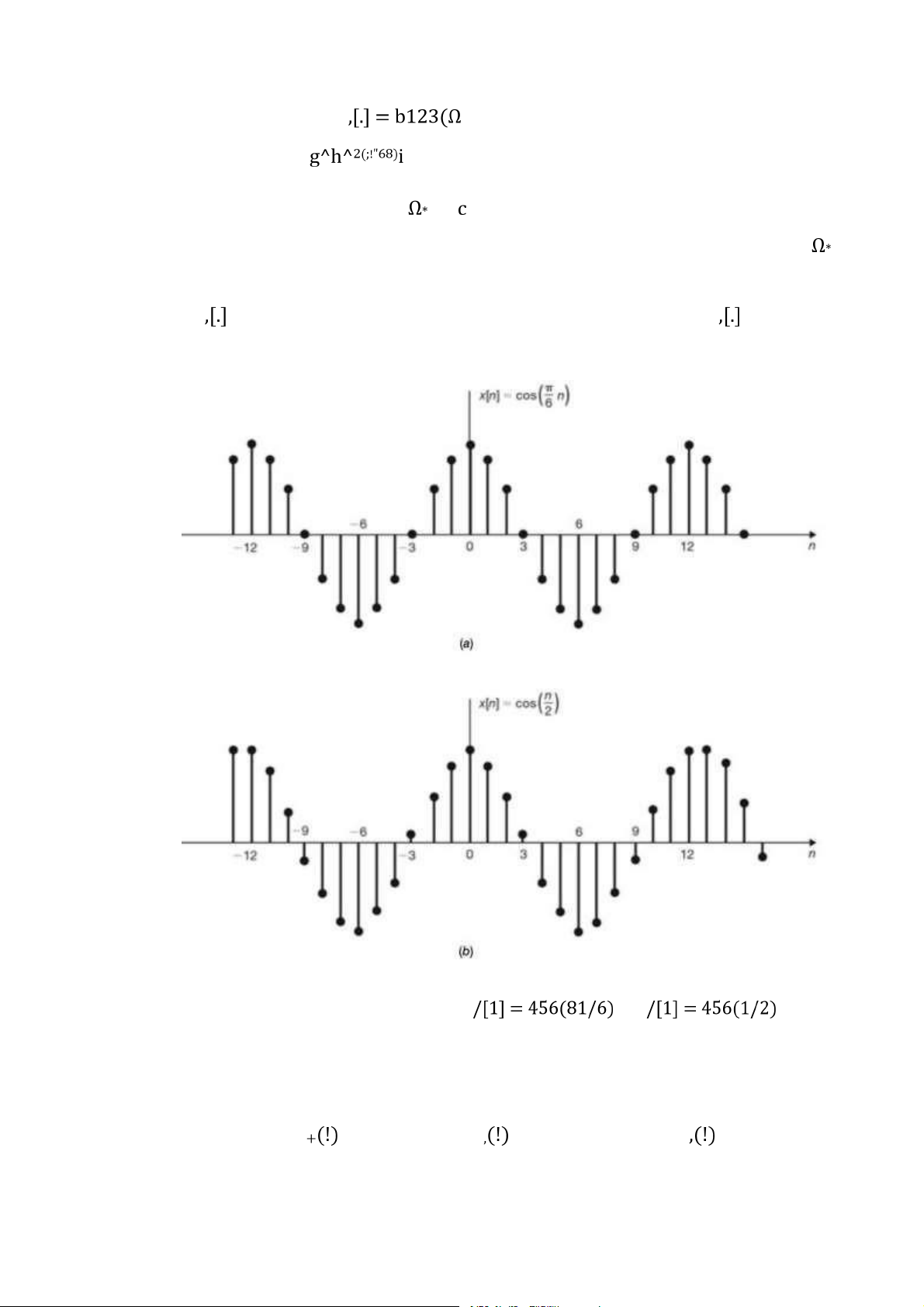
Hình 1.19: Chuỗi xung hình sin: a)
,[.] = 123(5./6) , b) ,[.] = 123(./2) . . . 19
Hình 1.20: a) Tín hiệu nhân quả, b) Tín hiệu không nhân quả . . . . . . . . . . . . . . . . 20
Hình 1.21: Giá trị trung bình theo thời gian của tín hiệu . . . . . . . . . . . . . . . . . . . . 24
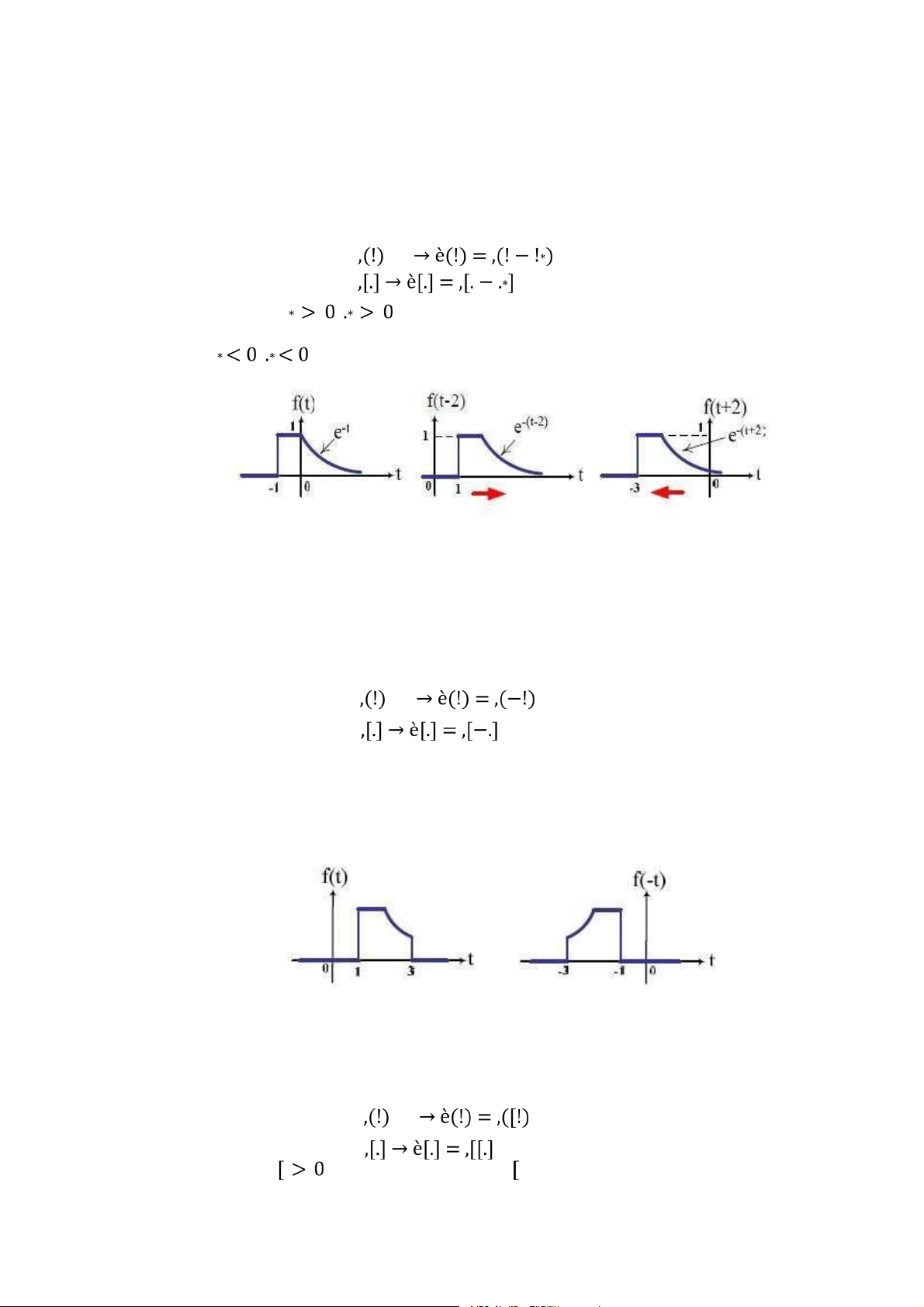
Hình 1.22: a) Tín hiệu ban đầu, b) Tín hiệu dịch phải, c) Tín hiệu dịch trái . . . . . 25
Hình 1.23: Ví dụ về phép đảo thời gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 lOMoARcPSD|36086670 x ix
Hình 1.24: Ví dụ về phép thay đổi thang thời gian . . . . . . . . . . . . . . . . . . . . . . . . . 26
Hình 1.25: Mô hình tổng quát của hệ thống . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
Hình 1.26: Biểu diễn hệ thống: a) bằng sơ đồi khối, b) bằng sơ đồ thành phần . . . 28
Hình 2.1: Hệ thống LTI liên tục theo thời gian . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
Hình 2.2: Tích chập của xung chữ nhật và xung hàm mũ . . . . . . . . . . . . . . . . . . . 34
Hình 2.2: a) Hệ thống LTI nối tiếp, b) Hệ thống LTI song song . . . . . . . . . . . . . . 35
Hình 2.3: Hệ thống LTI và hệ thống nghịch đảo của nó . . . . . . . . . . . . . . . . . . . . 37
Hình 2.4: Đáp ứng trạng thái 0 và đáp ứng đầu vào 0 . . . . . . . . . . . . . . . . . . . . . . 39
Hình 2.5: Hệ thống LTI rời rạc theo thời gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
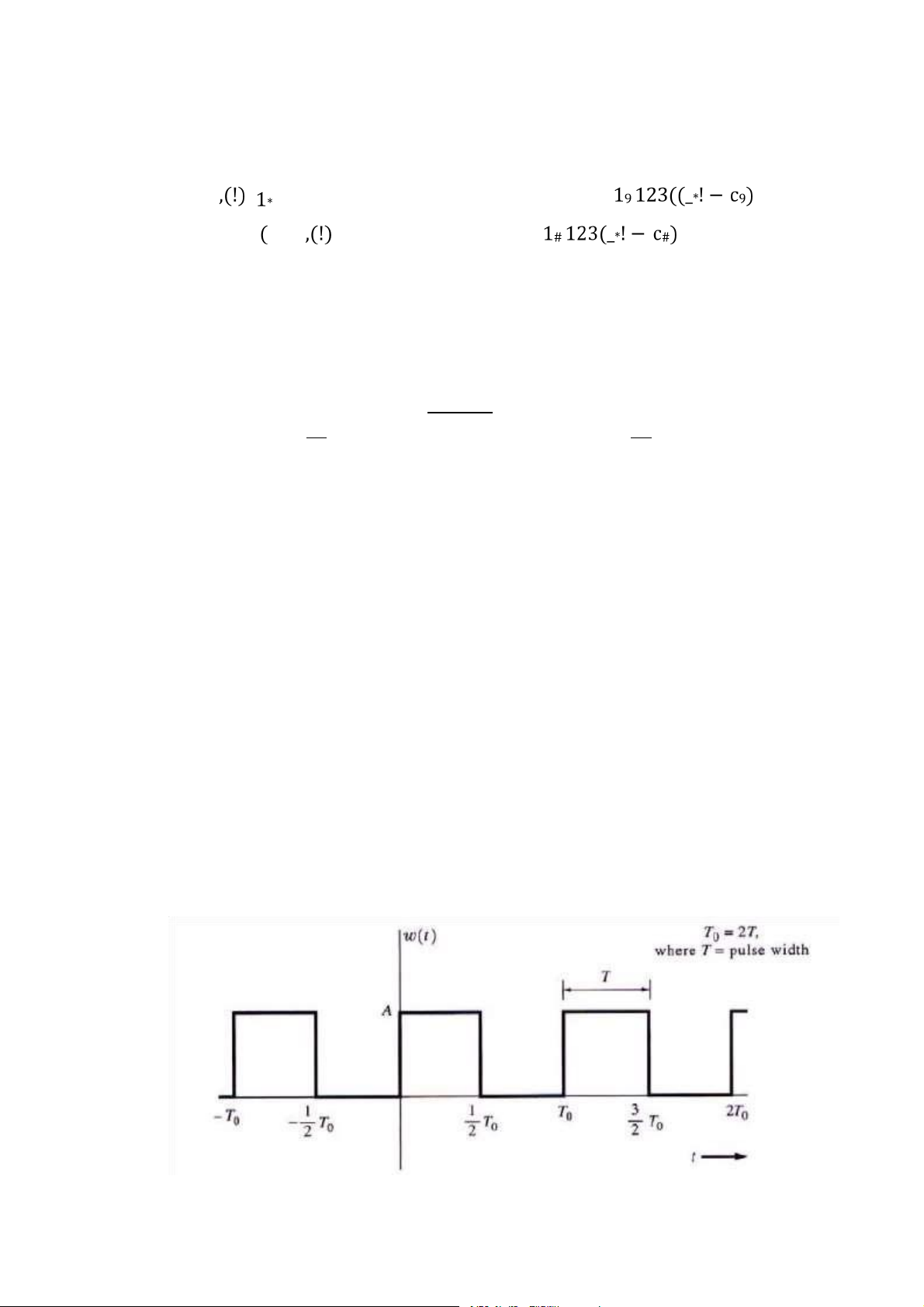
Hình 3.1: Tín hiệu xung chữ nhật tuần hoàn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
Hình 3.2: Tín hiệu vi phạm điều kiện Dirichlet . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
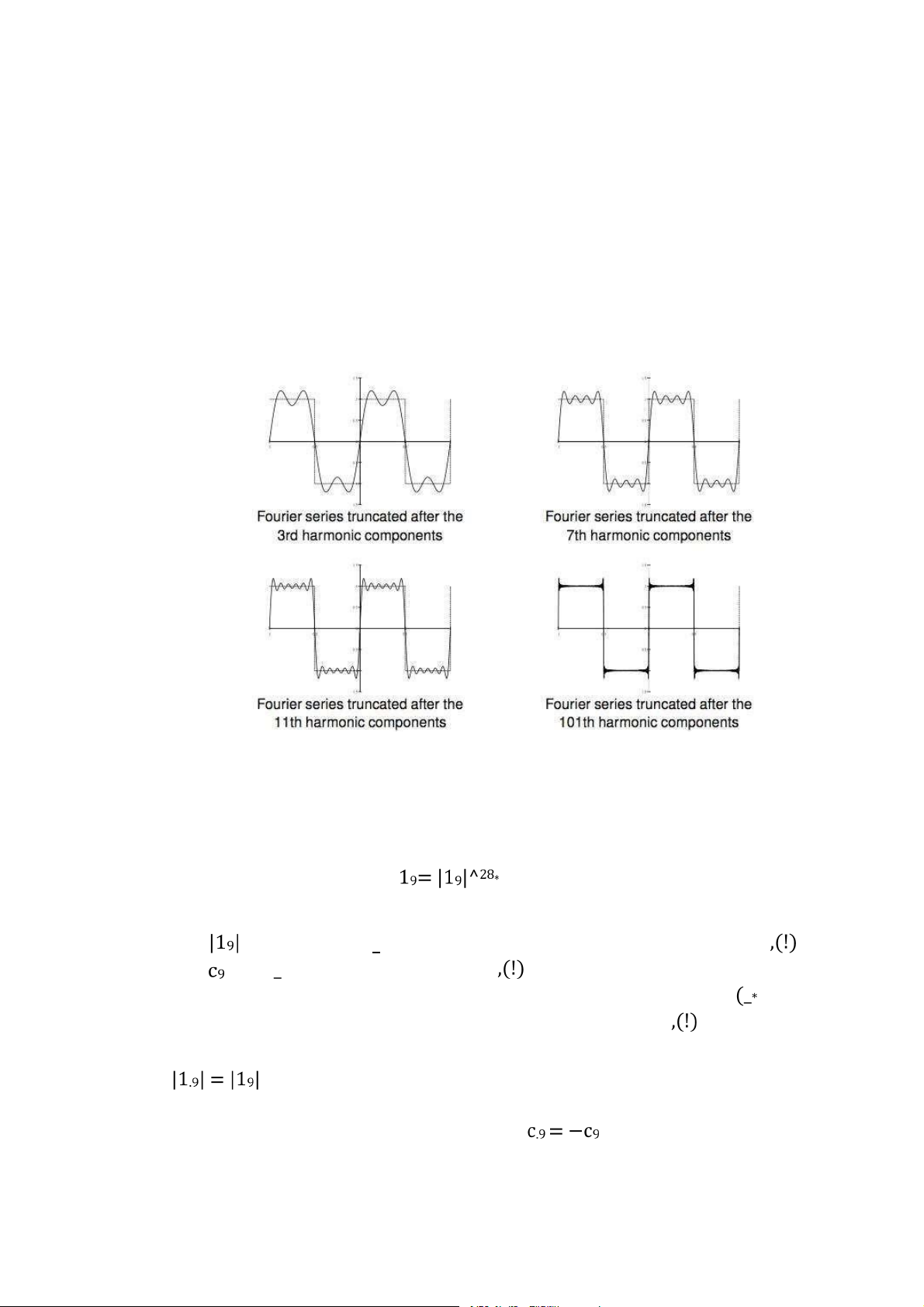
Hình 3.3: Hiện tượng Gibbs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
Hình 3.4: Phổ của tín hiệu sin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69 lOMoARcPSD|36086670 x x
Hình 3.5: Phổ của xung chữ nhật . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
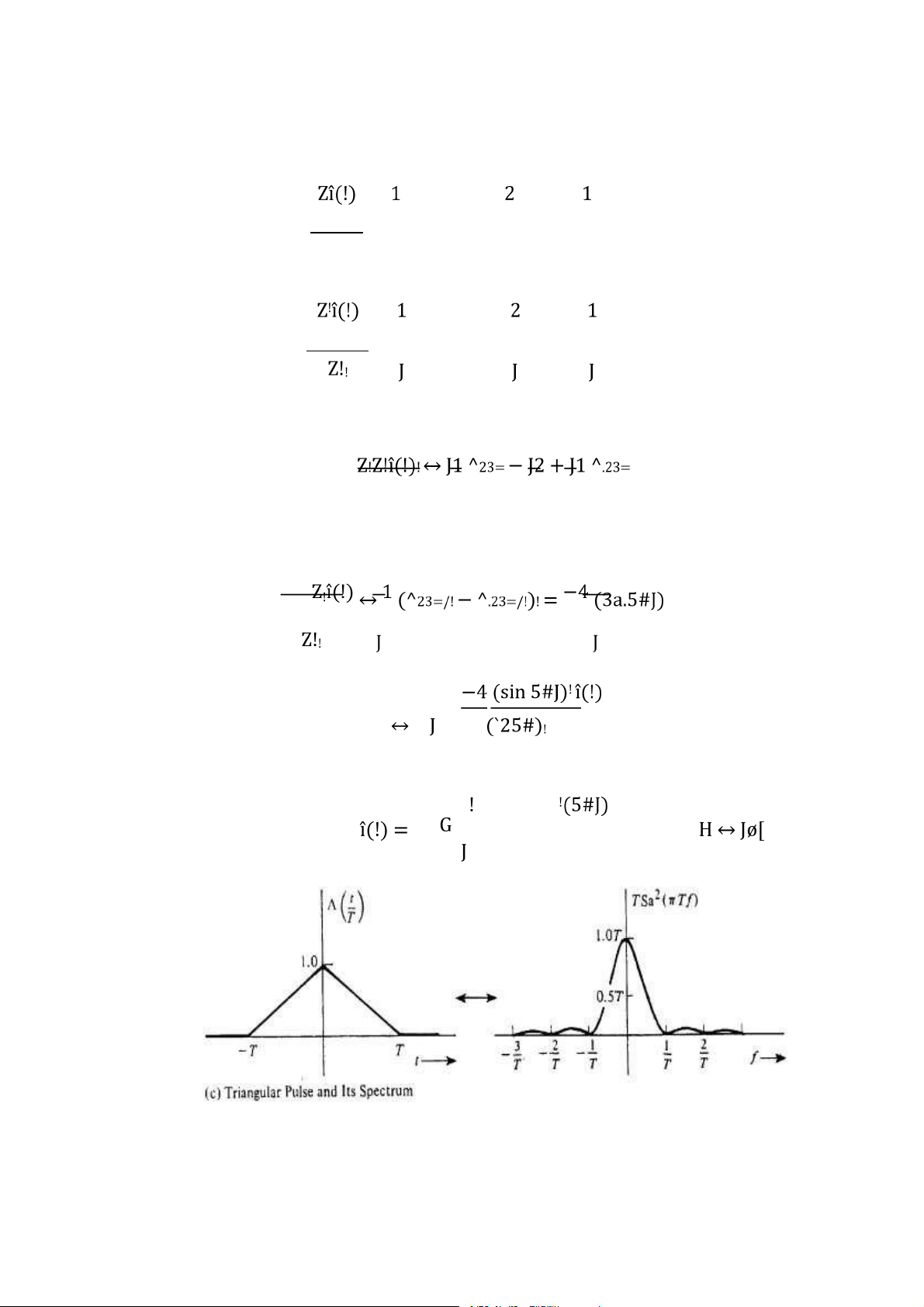
Hình 3.6: Phổ của xung tam giác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
Hình 3.7: Phổ của xung chữ nhật . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
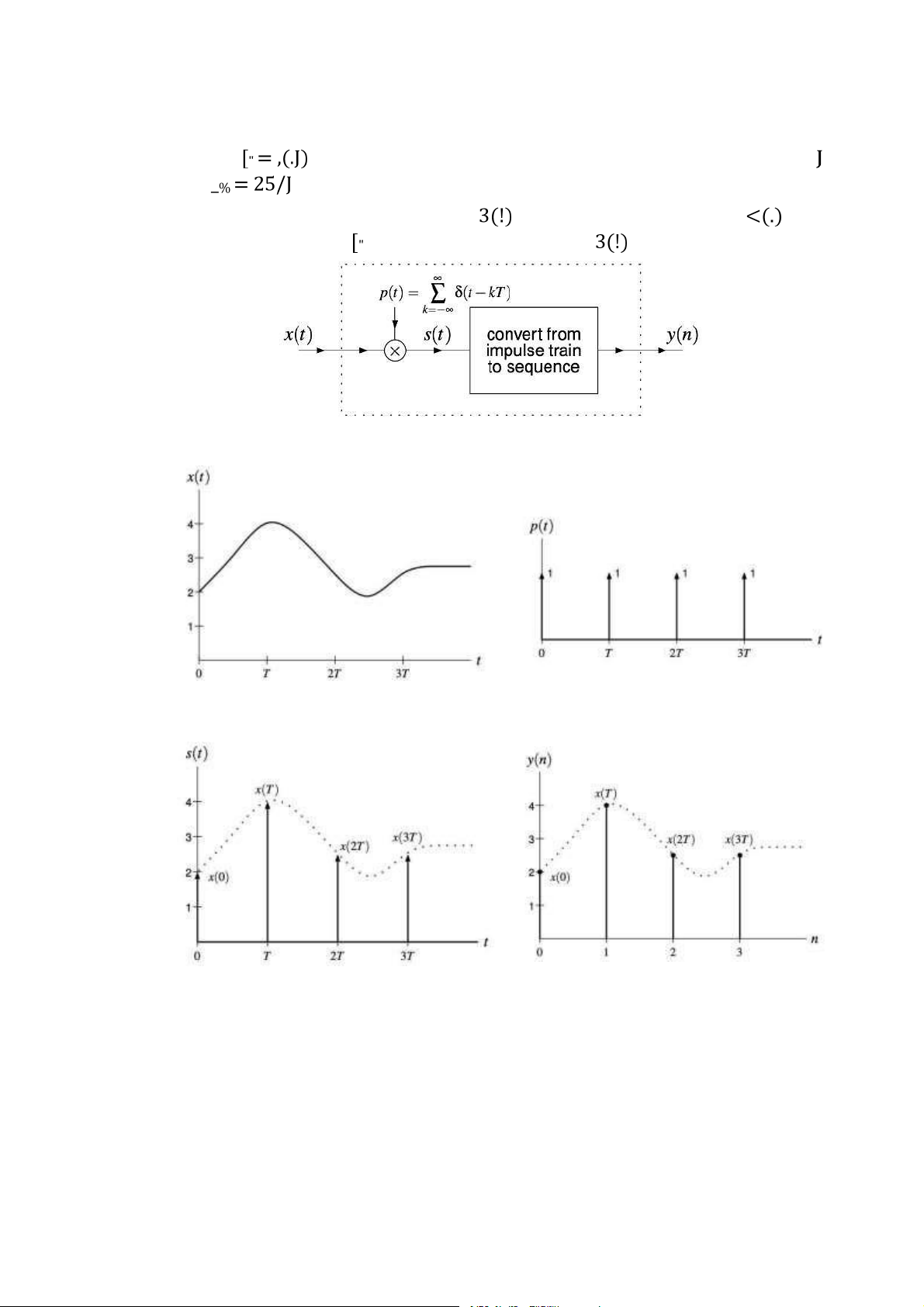
Hình 3.8: Bộ chuyển đổi tương tự - số lý tưởng . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
Hình 3.9: Quá trình chuyển đổi tương tự - số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
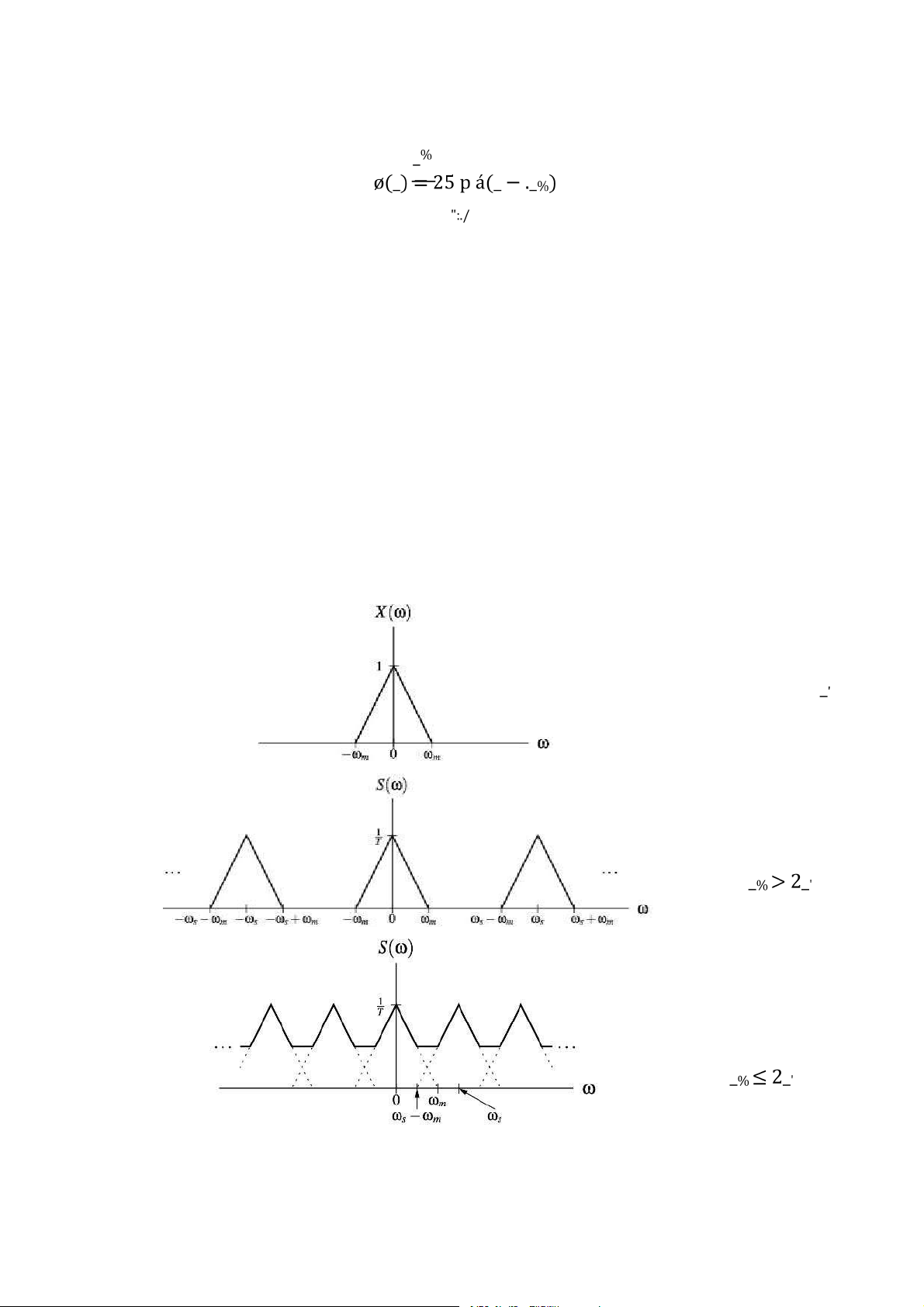
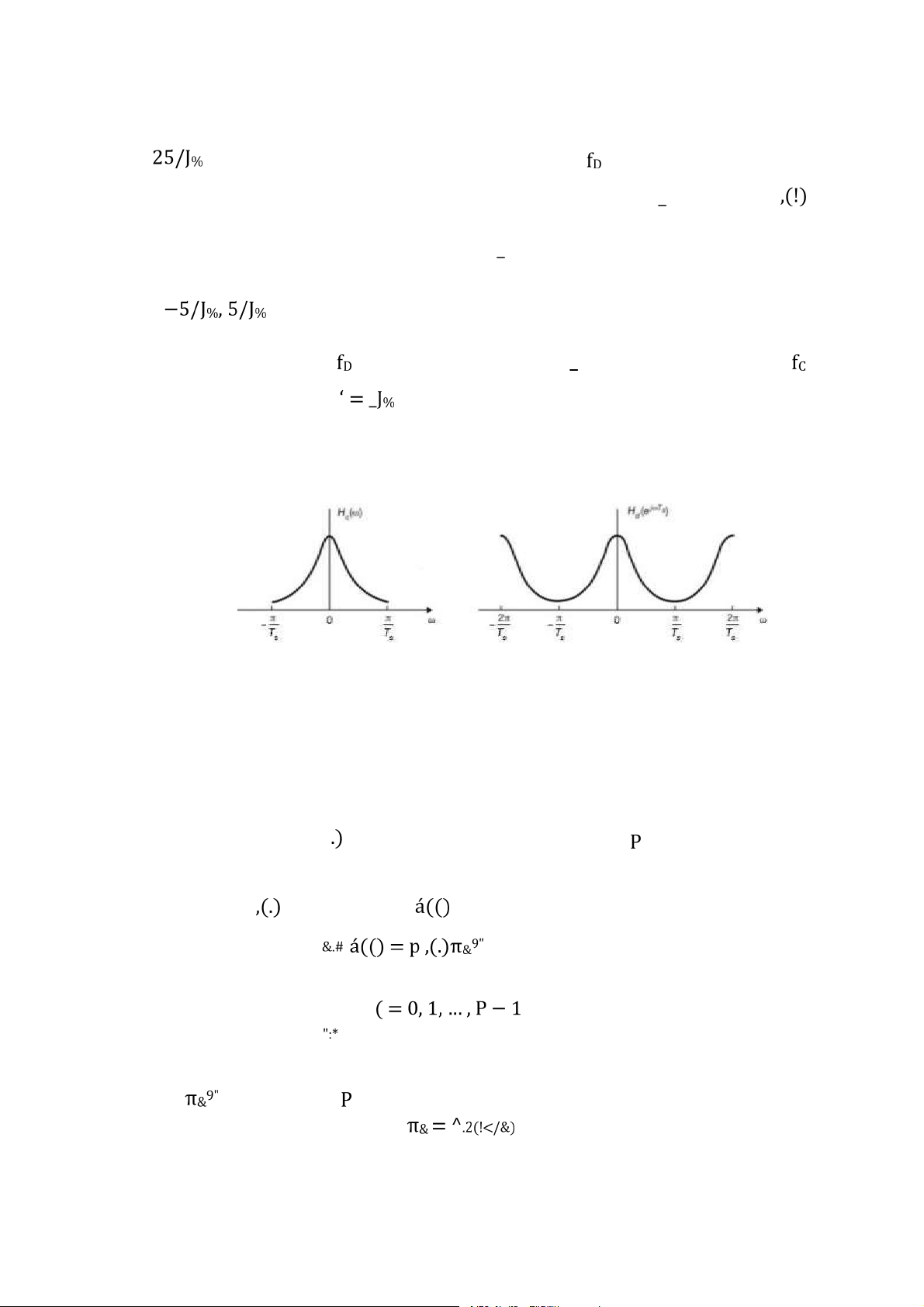
Hình 3.10: Phổ của tín hiệu sau lấy mẫu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
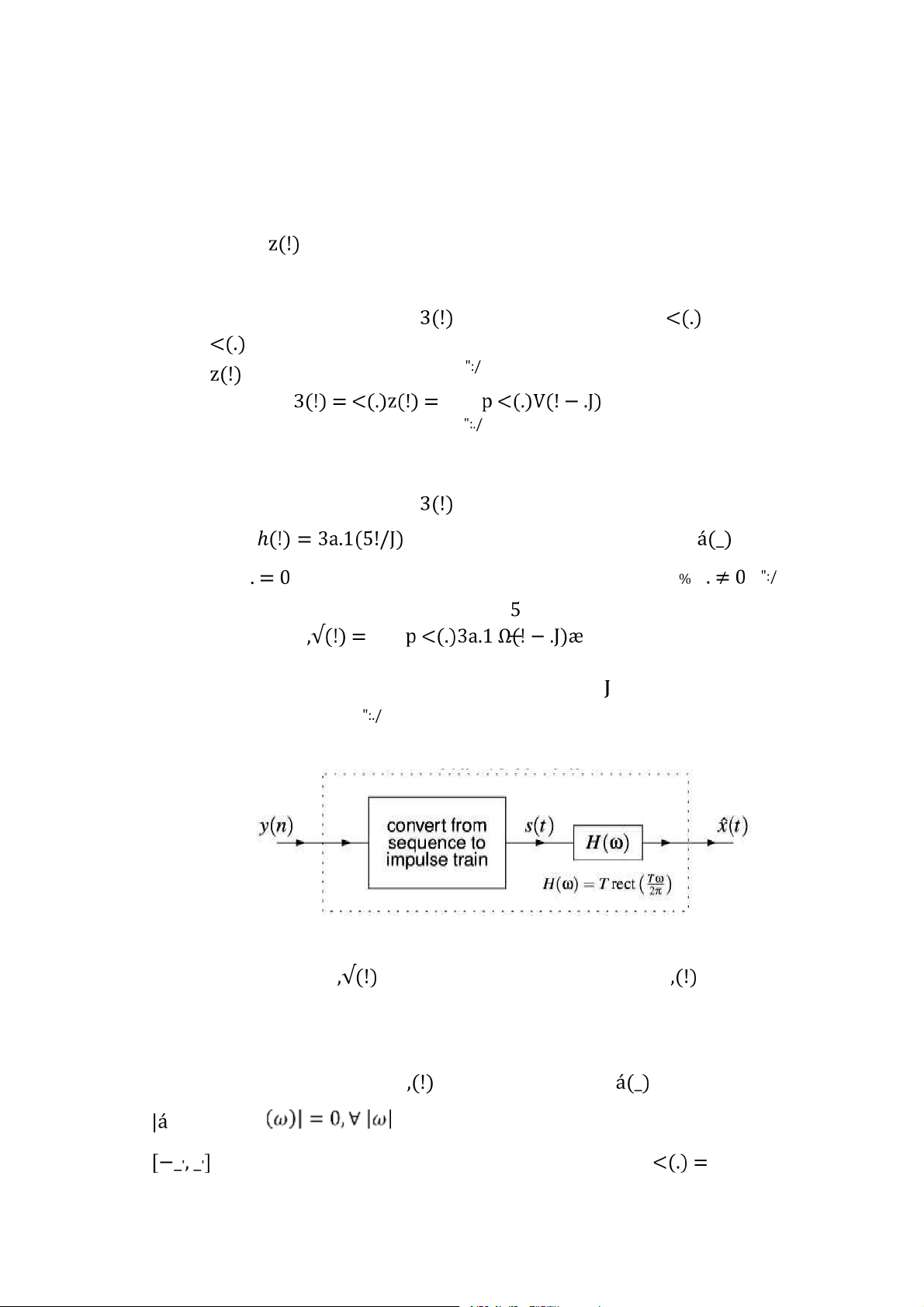
Hình 3.11: Bộ chuyển đổi số - tương tự lý tưởng . . . . . . . . . . . . . . . . . . . . . . . . . .
75 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
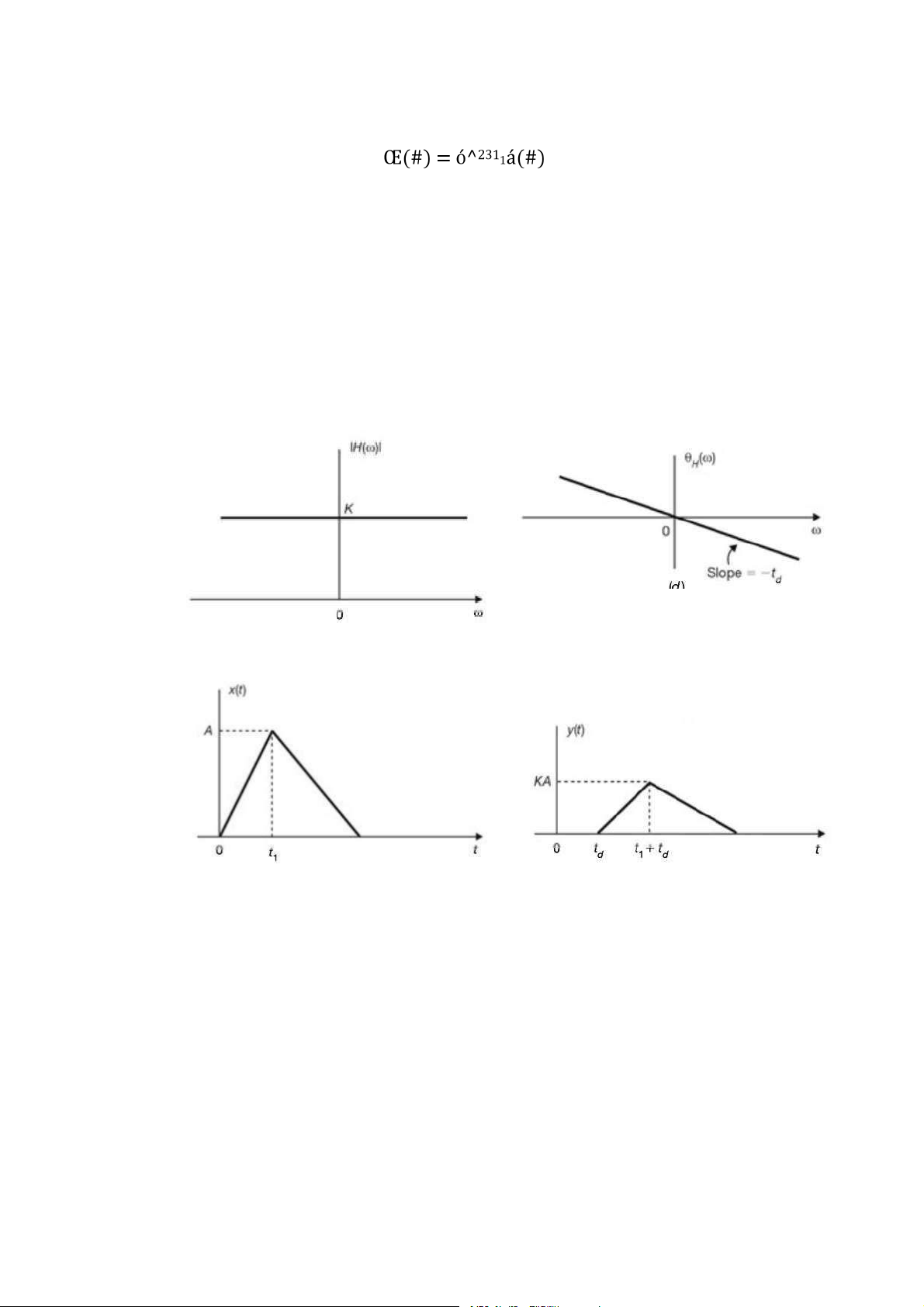
Hình 3.12: Truyền dẫn không méo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
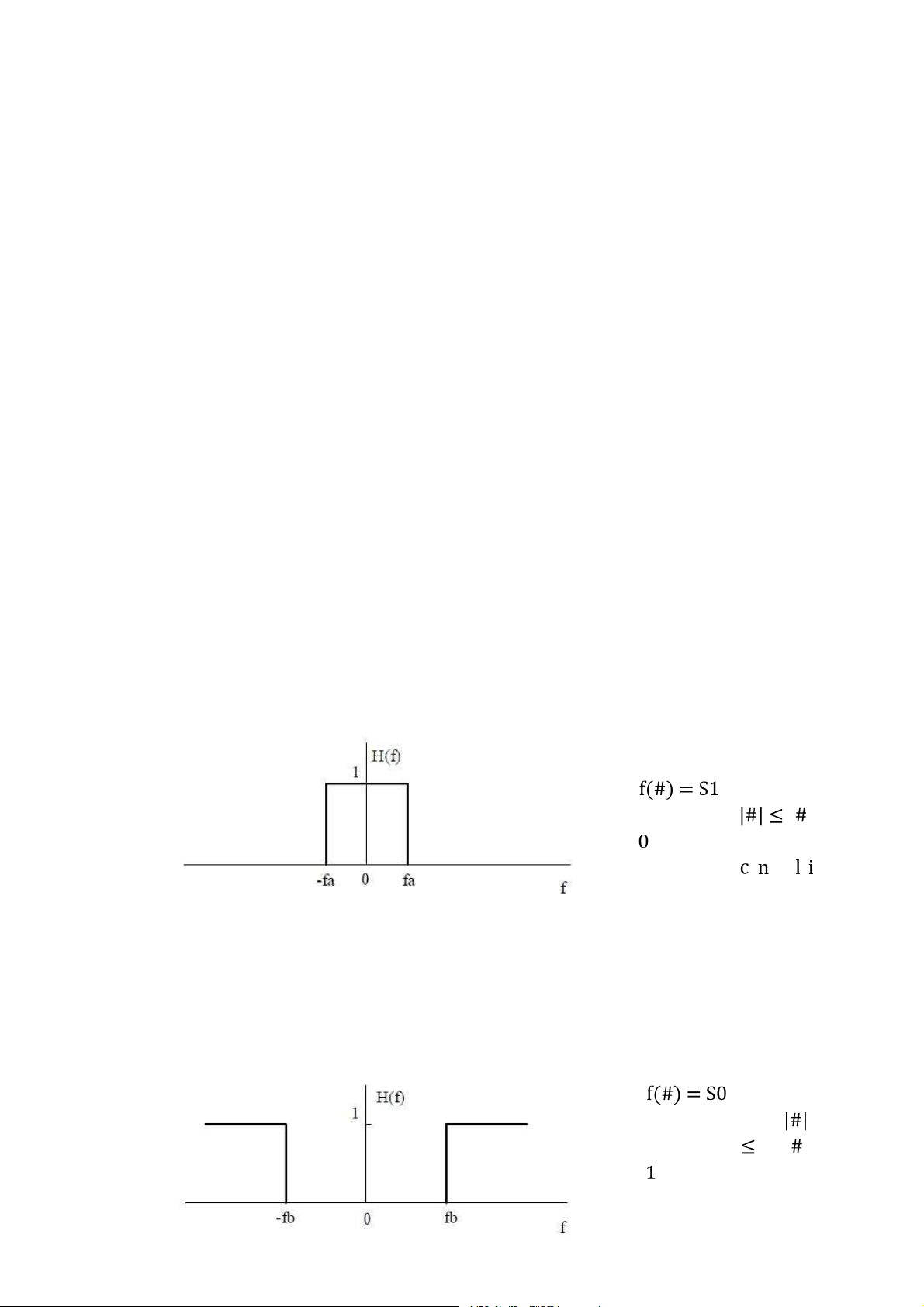
Hình 3.13: Bộ lọc thông thấp lý tưởng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
Hình 3.14: Bộ lọc thông cao lý tưởng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
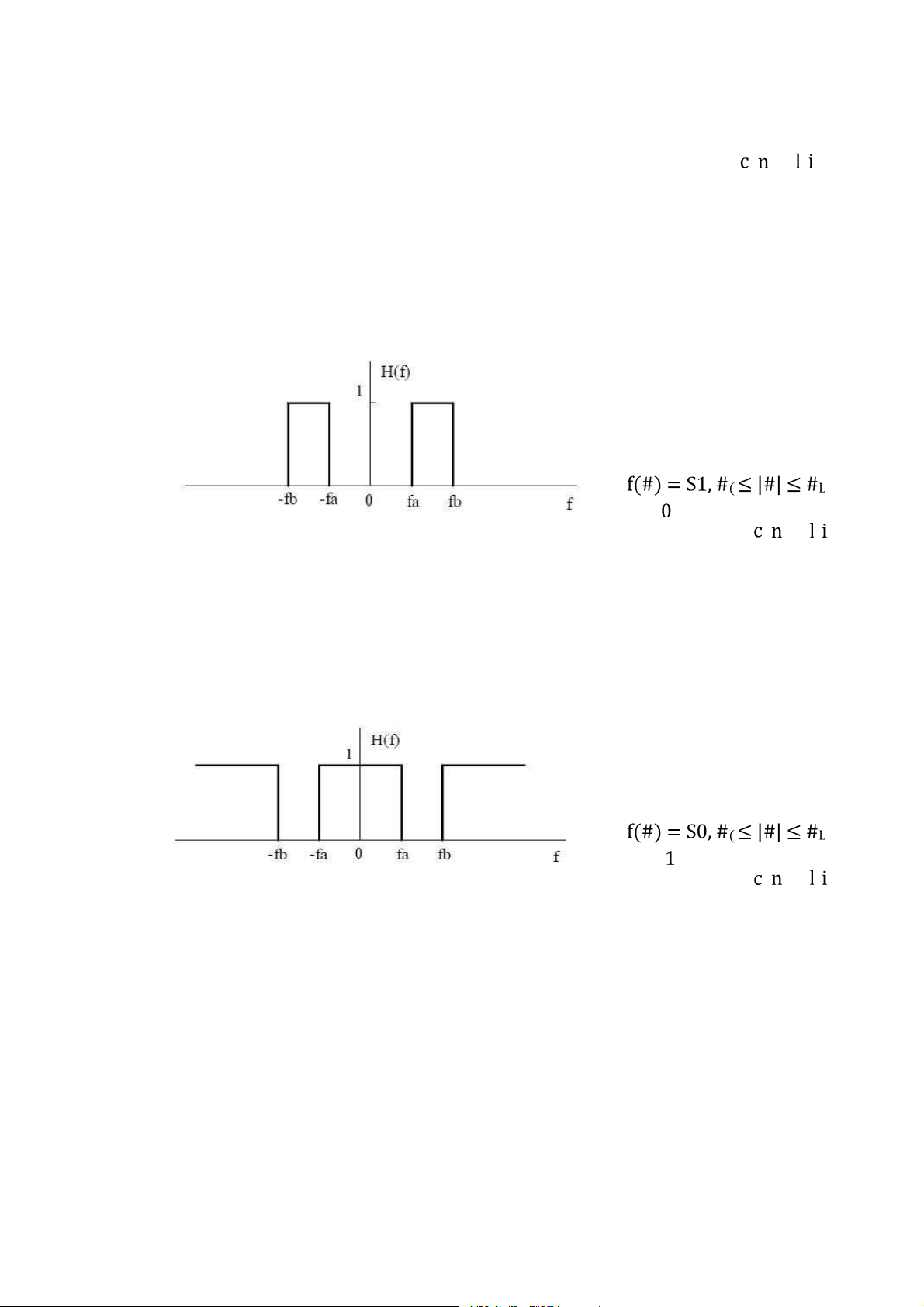
Hình 3.15: Bộ lọc thông dải lý tưởng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
Hình 3.16: Bộ lọc chặn dải lý tưởng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
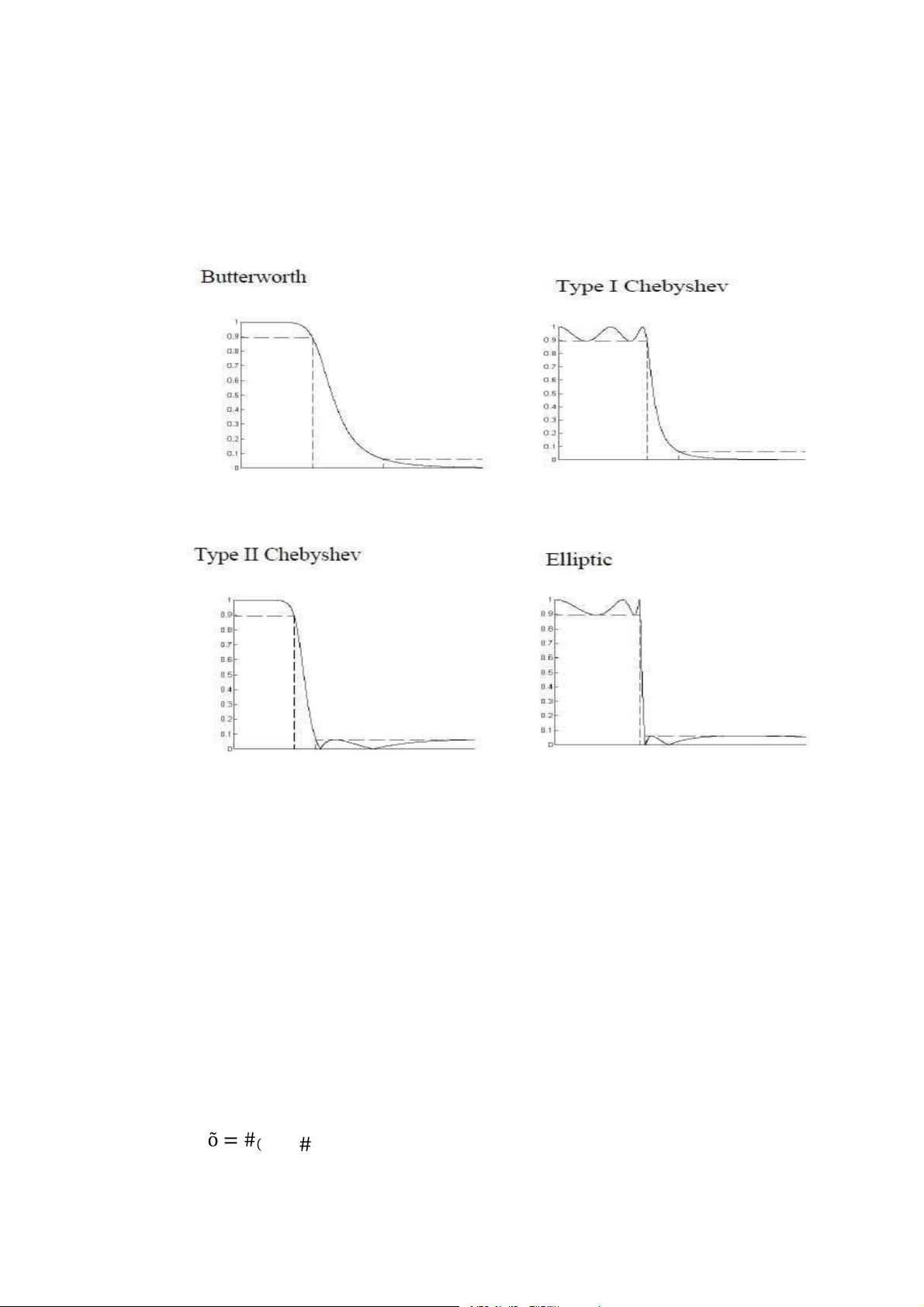
Hình 3.17: Một số bộ lọc thông thấp thực tế . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96
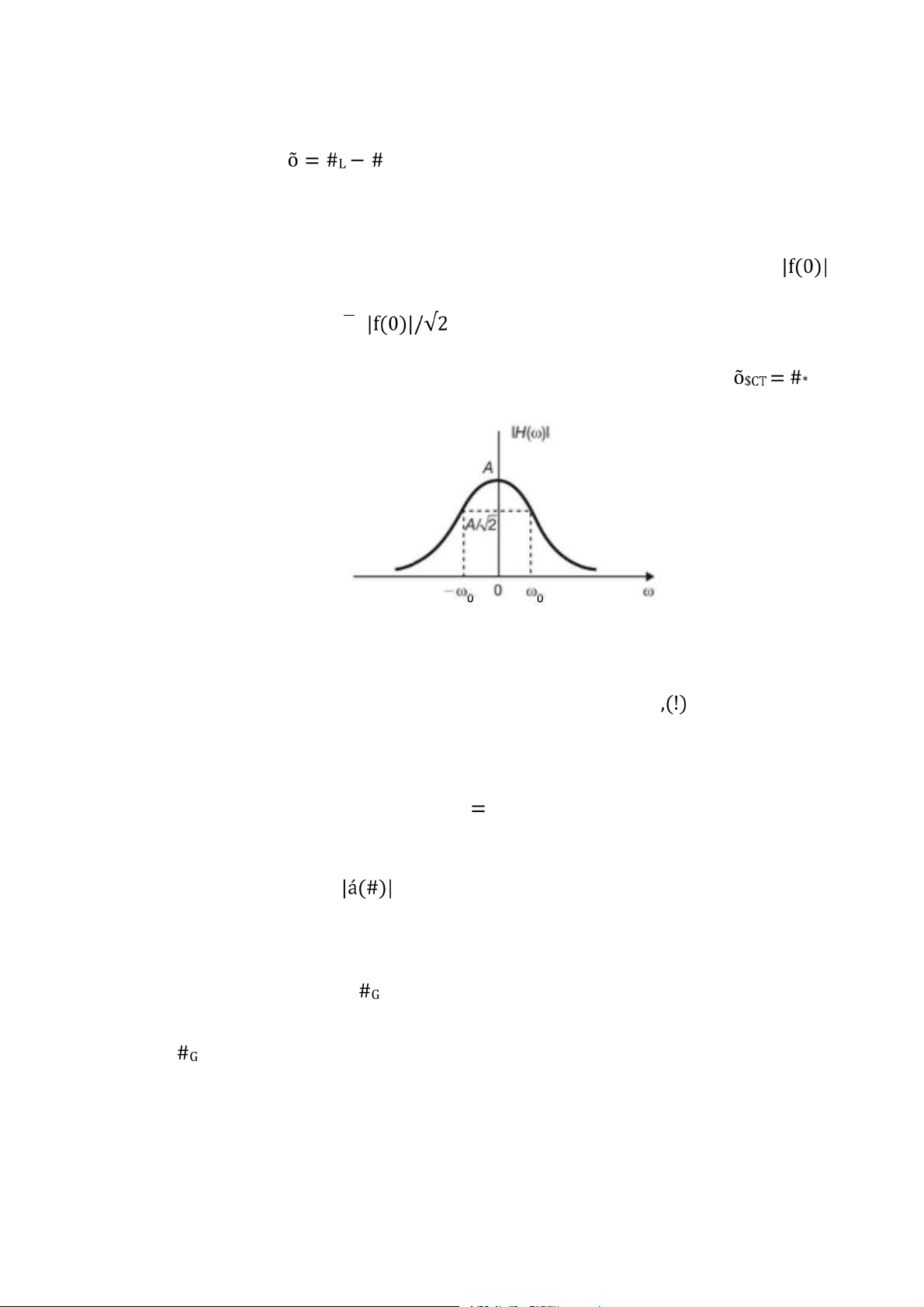
Hình 3.18: Băng thông 3 dB . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
85 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
Hình 4.1: Hàm truyền đạt của hệ thống liên tục và rời rạc thời gian. . . . . . . . . . 114
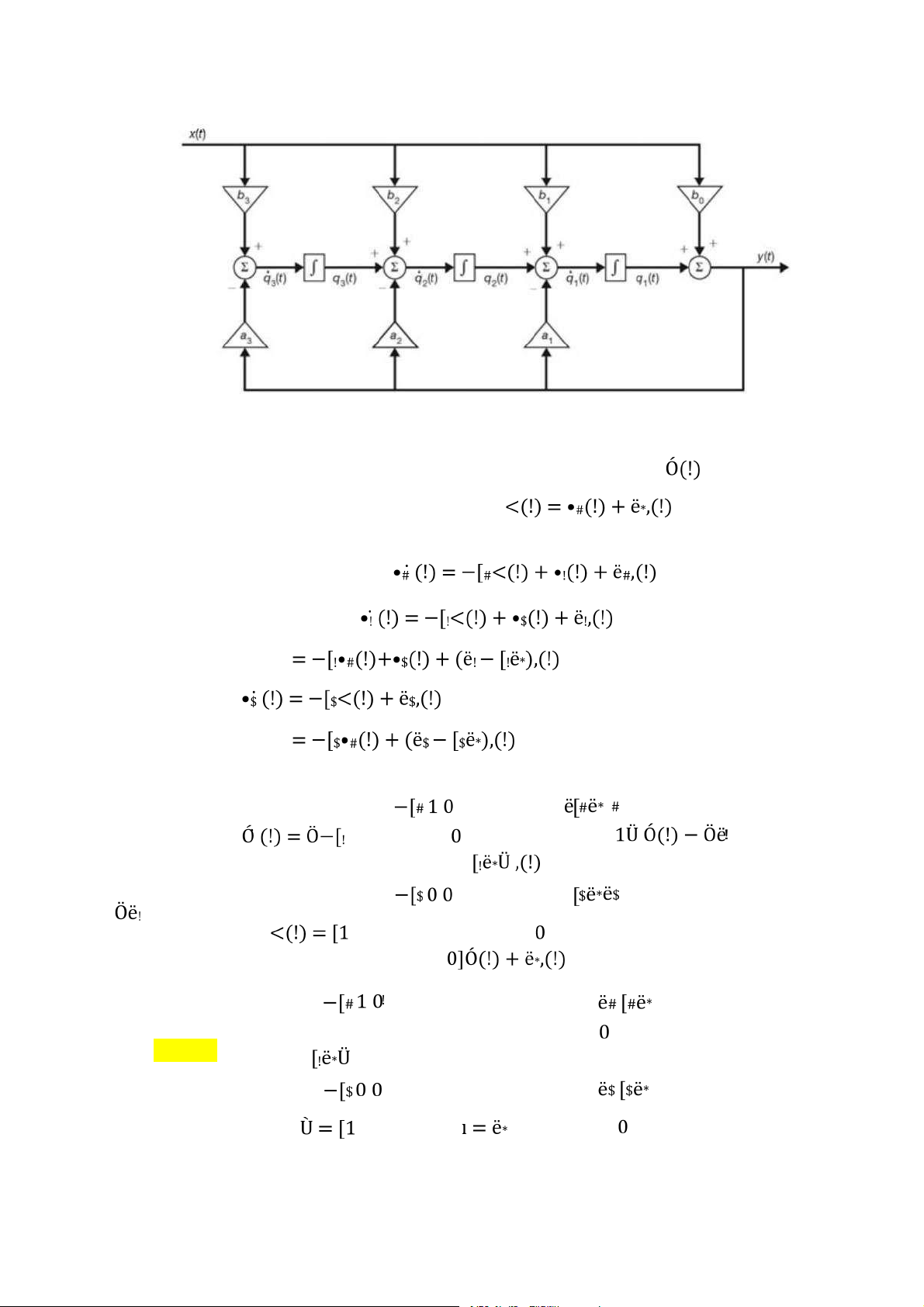
Hình 7.1: Mô hình không gian trạng thái của hệ thống thời gian liên tục (dạng 1)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147
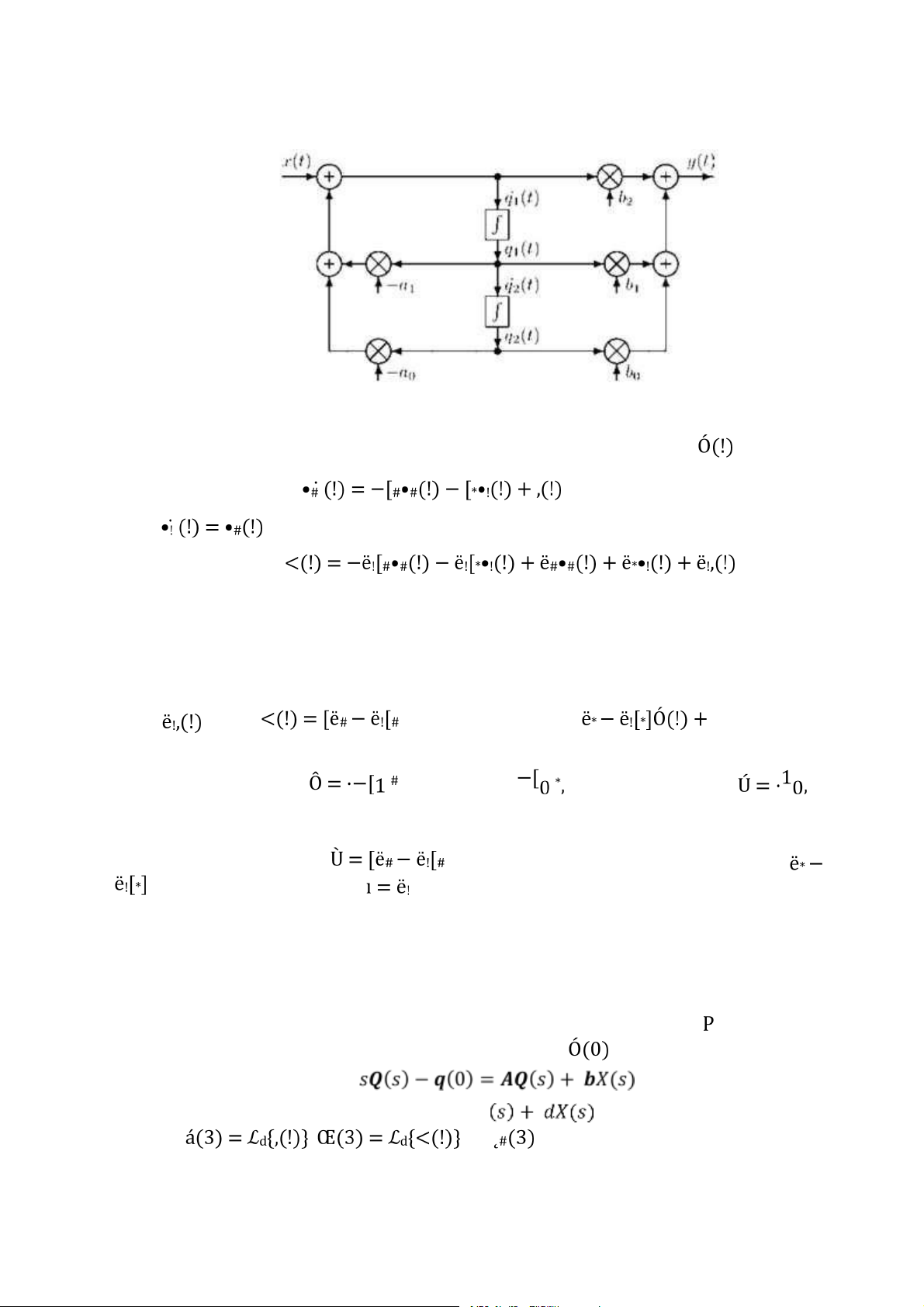
Hình 7.2: Mô hình không gian trạng thái của hệ thống thời gian liên tục (dạng 2)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148 lOMoARcPSD|36086670 x xi
DANH MỤC CÁC BẢNG Bảng 3.1: Các tính chất của chuỗi Fourier liên
tục. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Error! Bookmark not defined. Bảng 3.2: Các tính chất của biến đổi
Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
Bảng 3.3:Biến đổi Fourier của một số tín hiệu cơ bản . . . . . . . . . . . . . . . . . . . . . . 75
Bảng 4.1: Các tính chất của chuỗi Fourier rời rạc . . . . . . . . . . . . . . . . . . . . . . . . . 98
Bảng 4.2: Các tính chất của biến đổi Fourier rời rạc . . . . . . . . . . . . . . . . . . . . . . 102
Bảng 4.3: Các cặp biến đổi Fourier thời gian rời rạc. . . . . . . . . . . . . . . . . . . . . . 105
Bảng 4.4: So sánh giữa các kiểu biến đổi Fourier . . . . . . . . . . . . . . . . . . . . . . . . 113
Bảng 4.5: Các tính chất của biến đổi Fourier rời rạc . . . . . . . . . . . . . . . . . . . . . . 114 lOMoARcPSD|36086670 1
CHƯƠNG 1: KHÁI QUÁT VỀ TÍN HIỆU VÀ HỆ THỐNG
1.1 TÍN HIỆU VÀ PHÂN LOẠI TÍN HIỆU 1.1.1 Khái niệm về tín hiệu
Tín hiệu là mục tiêu nghiên cứu và xử lý trong nhiều ngành kỹ thuật và khoa học
khác nhau, trong đó đóng vai trò đặc biệt quan trọng cho tất cả các hệ thống truyền
thông và hệ thống điều khiển. Tín hiệu được định nghĩa là đại lượng vật lý có
mang thông tin về hành vi hay bản chất của một hiện tượng và biến thiên theo thời
gian, không gian hay một hoặc nhiều biến độc lập khác. Tín hiệu tràn ngập xung
quanh chúng ta, cần được xử lý, phân tích và truyền dẫn, từ đó hình thành lĩnh vực
xử lý tín hiệu, có ý nghĩa rất lớn trong kỉ nguyên số ngày nay. Một số tín hiệu xuất
phát từ cuộc sống hàng ngày của con người có thể kể đến là giọng nói, văn bản,
truyền hình, hình ảnh từ các tàu thăm dò không gian từ xa, tín hiệu từ vệ tinh GPS,
tín hiệu điện não đồ, điện tim đồ, tín hiệu từ gen người, chỉ số chứng khoán, chỉ số
giá tiêu dùng, tốc độ gió, áp suất khí quyển, nhiệt độ, độ ẩm trong các nghiên cứu
về khí tượng … và vô số tín hiệu từ nhiều ứng dụng khác nữa. Để các tín hiệu này
được truyền đi trong hệ thống truyền thông hoặc hệ thống điều khiển, chúng được
chuyển đổi thành các tín hiệu điện hoặc các sóng điện từ. Ví dụ điển hình về tín
hiệu điện đó là điện áp rơi trên tụ điện hoặc dòng điện đi qua điện trở trên một
mạch RC. Ví dụ về chuyển đổi dạng tín hiệu đó là tín hiệu âm thanh do con người
phát ra là sóng cơ học cần được đưa qua microphone để chuyển đổi thành sóng
điện trước khi truyền đi, nhịp đập của tim nhờ máy điện tim đồ chuyển thành các xung điện.
Về mặt toán học, tín hiệu được biểu diễn là một hàm của một hay nhiều
biến độc lập. Phổ biến nhất là được biểu diễn theo biến thời gian t và theo biến
không gian s. Tín hiệu điện áp và dòng điện là hàm theo một biến thời gian. Tín
hiệu hình ảnh tĩnh là hàm hai biến theo vị trí. Tín hiệu truyền hình là hàm của ba
kênh tương ứng với ba màu R, G và B. Ví dụ như, hàm số ,(!) = 4! (1.1)
mô tả tín hiệu thay đổi tuyến tính theo một biến thời gian t. Hoặc hàm 3(, <) = 4, + ,< + <!
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 2 (1.2)
mô tả tín hiệu biến đổi theo hai biến độc lập x và y, biểu diễn cho hai biến không gian trong một mặt phẳng.
1.1.2 Phân loại tín hiệu
Tín hiệu rất đa dạng với nhiều đặc trưng khác nhau. Vì thế, tuỳ thuộc vào
đặc trưng của tín hiệu mà có thể chia tín hiệu thành nhiều loại khác nhau. Tuy
nhiên, các cách phân loại này chỉ là tương đối và chỉ chính xác với từng đặc trưng
cụ thể. Ví dụ, tín hiệu rời rạc có thể là tín hiệu tuần hoàn hoặc không tuần hoàn,
hay có thể là tín hiệu ngẫu nhiên hoặc tín hiệu xác định. Sau đây trình bày một số
cách phân loại tín hiệu.
1.1.2.1 Tín hiệu liên tục và tín hiệu rời rạc
Tiêu chí phân loại dựa trên đặc trưng rời rạc của tín hiệu, bao gồm tín hiệu liên
tục và tín hiệu rời rạc theo thời gian và tín hiệu liên tục và tín hiệu rời rạc theo
biên độ. Tín hiệu có biên độ liên tục (continous-value signal) có tất cả các giá trị
trong một dải biên độ. Tín hiệu có biên độ rời rạc (discrete-value signal) chỉ lấy
một số giá trị rời rạc trong một dải biên độ. Ví dụ về tín hiệu biên độ rời rạc được chỉ ra trong hình 1.1.
Hình 1.1: Ví dụ tín hiệu biên độ rời rạc
Tín hiệu ,(!) là tín hiệu thời gian liên tục (continous-time signal) nếu biến
thời gian t là liên tục, vì thế ,(!) xác định tại mọi thời điểm. Nếu t là biến rời rạc, ,(!)
chỉ được xác định tại các điểm thời gian rời rạc, lúc này ,(!) là tín hiệu thời gian rời
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 3
rạc (discrete-time signal). Tín hiệu thời gian rời rạc thường được biểu diễn bởi một
chuỗi số, kí thiệu là {,"} hoặc ,[.] với n là số nguyên. Tín hiệu liên tục và rời rạc
trong miền thời gian sử dụng phổ biến trong kĩ thuật và thường được gọi tắt là tín
hiệu liên tục và tín hiệu rời rạc. Tín hiệu liên tục thường có bản chất tự nhiên. Tín
hiệu rời rạc thường liên quan đến các hệ thống nhân tạo và thường được biểu
diễn chủ yếu theo hai cách sau.
- Hàm rời rạc xác định qui luật tính toán giá trị thứ n của chuỗi. Ví dụ, (1.3)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 0 . < 0 1 1 1 " 4 "
{, } = @1, , , … , G H , … I 3 9 3 hoặc
Hình 1.2: Ví dụ tín hiệu biên độ liên tục và biên độ rời rạc.
- Liệt kê cụ thể các giá trị của chuỗi. Ví dụ,
"} = {… , 0, 0, 1, 2, 4, 0, −1, −3, 0, 0, … } {, (1.4) hoặc {, với
Dấu mũi tên chỉ thị vị trí
. Nếu trong trường hợp không có mũi tên, mặc định
giá trị đầu tiên của chuỗi tương ứng với vị trí
, tất cả các giá trị tại thời điểm .
đều bằng 0. Hoặc có thể liệt kê vị trí n tương ứng với các giá trị trong chuỗi.
Trong trường hợp không liệt kê vị trí n, mặc định rằng tương ứng với giá trị đầu tiên của chuỗi.
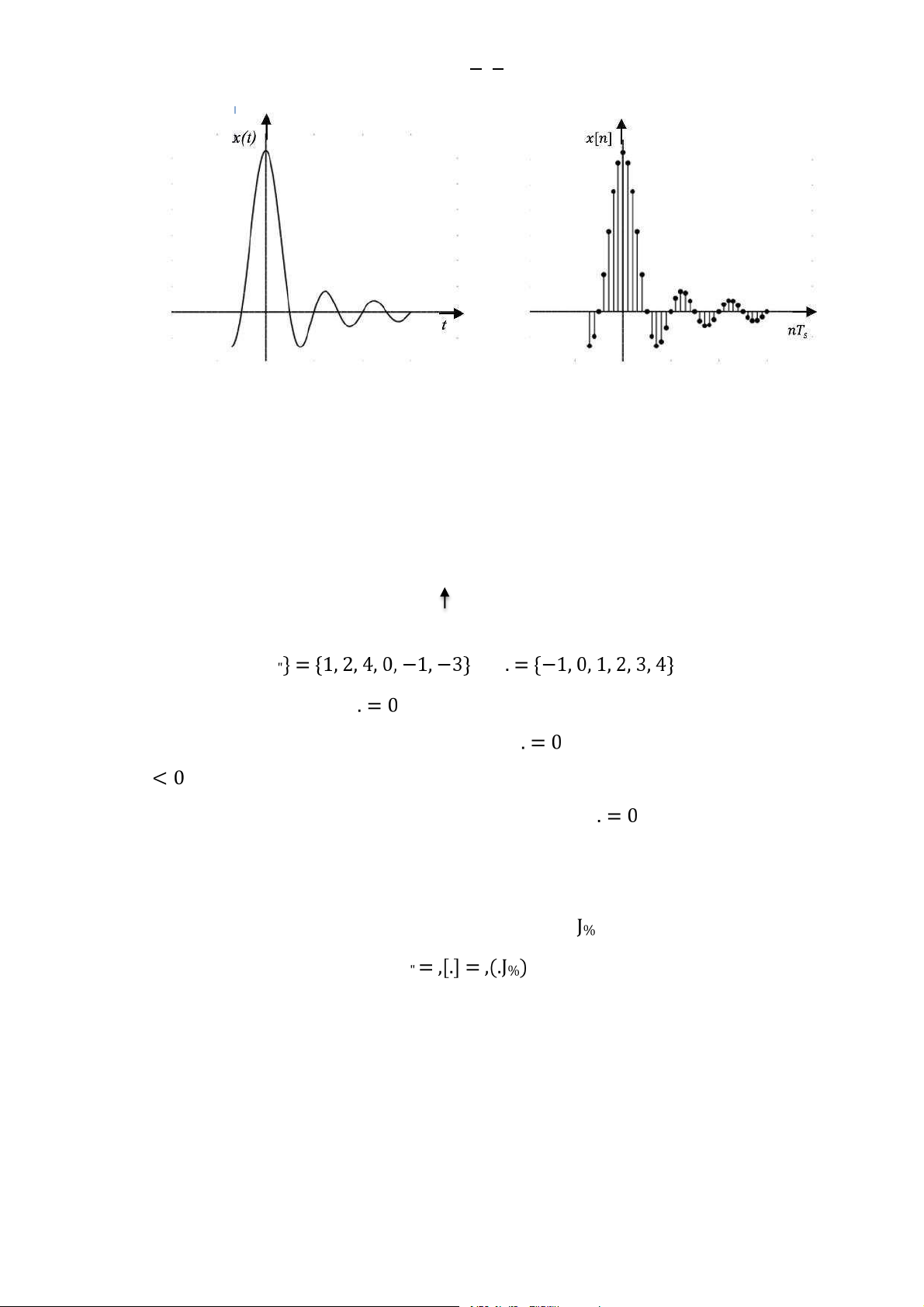
Tín hiệu rời rạc có thể thu được bằng cách lấy mẫu tín hiệu liên tục tại các khoảng
thời gian cách đều nhau, được gọi là chu kì lấy mẫu . , (1.5)
1.1.2.2 Tín hiệu số và tín hiệu tương tự
Đây là kiểu phân loại tín hiệu quan trọng trong thông tin truyền thông. Tín hiệu
tương tự là tín hiệu liên tục cả về mặt thời gian và biên độ. Tín hiệu số là tín hiệu
rời rạc cả về mặt thời gian và về mặt biên độ. Trong kĩ thuật thông tin truyền thông,
tín hiệu số nhị phân, chỉ gồm hai mức biên độ 0 và 1, được sử dụng phổ biến do dễ
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 5
dàng quyết định các mức biên độ. Tín hiệu tương tự được chuyển đổi thành tín
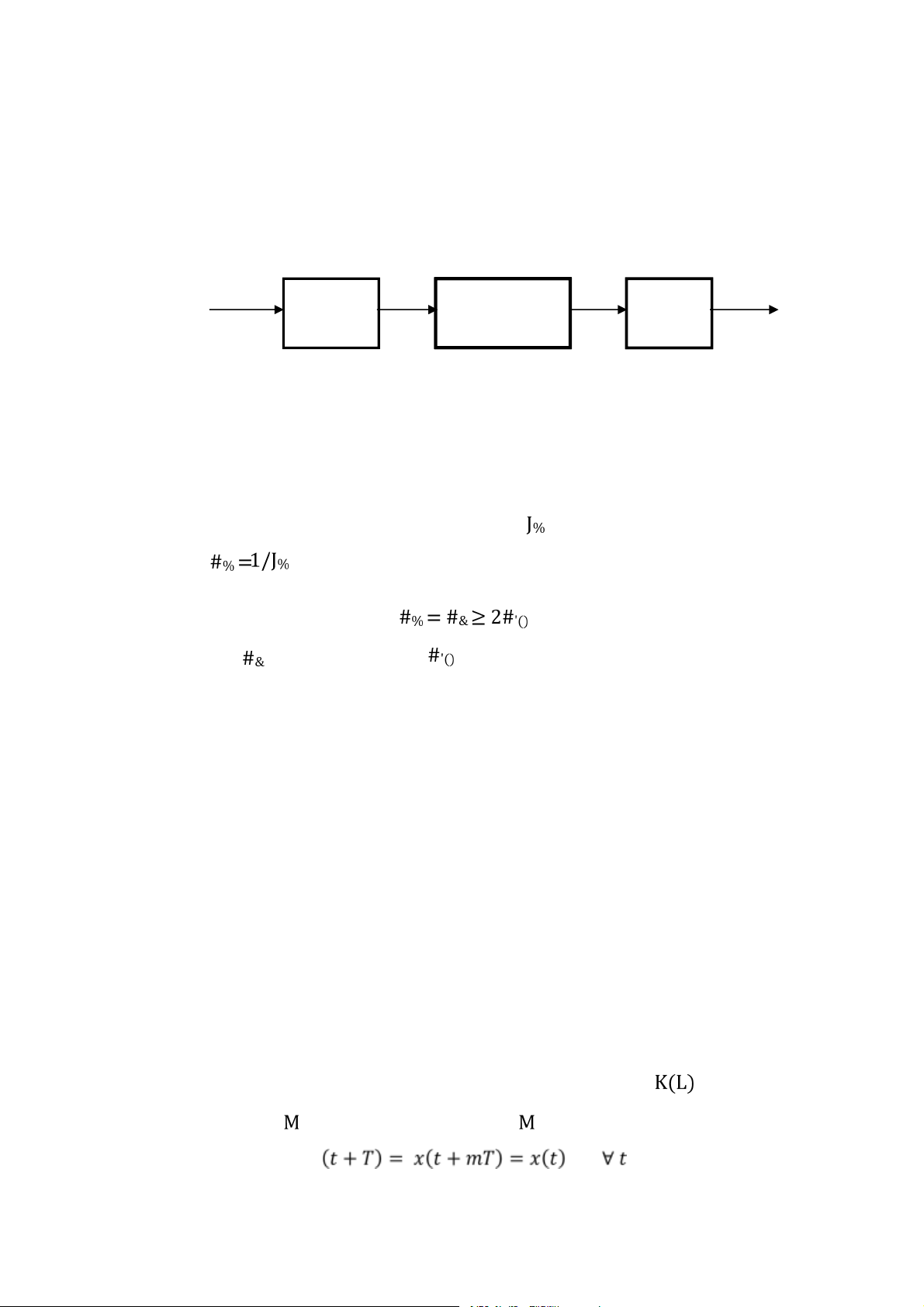
hiệu số nhị phân với sai số cho phép tuân theo ba bước sau: Tín hiệu Tín tương tự hiệu số Lấy mẫu Lượng tử hoá Mã hoá
Hình 1.3: Chuyển đổi tín hiệu tương tự thành tín hiệu số
- Lấy mẫu: Tín hiệu tương tự được lấy mẫu tại chu kì lấy mẫu xác định để thu
được tín hiệu rời rạc về mặt thời gian. Để đảm bảo tín hiệu rời rạc không làm
mất mát thông tin, chu kì lấy mẫu,
, phải đủ nhỏ, hay tần số lấy mẫu
tương ứng phải đủ lớn. (1.6) với là tần số Nyquis và
là tần số lớn nhất của tín hiệu tương tự.
- Lượng tử hoá: Tín hiệu rời rạc về mặt thời gian được lượng tử hoá, tức là gán
giá trị các mẫu về mức biên độ xác định gần nhất, để thu được tín hiệu rời rạc
về mặt biên độ. Kết quả là thu được tín hiệu số. Số lượng mức lượng tử hoá
tương ứng với số mức biên độ của tín hiệu số này.
- Mã hoá: Thực hiện mã hoá giá trị các mức biên độ ở thang thập phân về thang nhị phân.
Tín hiệu số được chuyển đổi thành tín hiệu tương tự tương ứng nhờ bộ lọc thông thấp.
1.1.2.3 Tín hiệu tuần hoàn và không tuần hoàn
Tín hiệu tuần hoàn là tín hiệu mà các giá trị (độ lớn) của nó được lặp lại liên
tục sau một khoảng quan sát nào đó. Đối với tín hiệu liên tục, được gọi là tuần
hoàn với chu kì nếu như tồn tại một giá trị dương khác 0 sao cho , (1.7)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 6
với là số nguyên bất kì. Giá trị nhỏ nhất thoả mãn phương trình (1.7), kí hiệu là
, chính là chu kì cơ bản của . Tần số là tần số cơ bản và
được gọi hài bậc n của
. Đối với tín hiệu rời rạc,
được gọi là tuần hoàn với
chu kì nếu như tồn tại một giá trị dương khác 0 sao cho (1.8)
với là số nguyên bất kì. Giá trị nhỏ nhất thoả mãn phương trình (1.8), kí hiệu là
, chính là chu kì cơ bản của .
Các tín hiệu không có chu kì được gọi là tín hiệu không tuần hoàn.
Một số lưu ý về tín hiệu tuần hoàn:
- Tín hiệu hằng số không phải là tín hiệu tuần hoàn do không xác định được chu kì nhỏ nhất.
- Tín hiệu liên tục là tuần hoàn nhưng tín hiệu lấy mẫu của nó có thể không tuần hoàn.
- Tổng của hai tín hiệu liên tục tuần hoàn có thể không tuần hoàn nhưng tổng
của hai chuỗi rời rạc tuần hoàn chắc chắn là một chuỗi tuần hoàn.
1.1.2.4 Tín hiệu ngẫu nhiên và tín hiệu xác định
Tín hiệu xác định (deterministic signal) là tín hiệu xác định được chắn chắn giá trị
(độ lớn) của tín hiệu tại mọi thời điểm. Về mặt toán học, tín hiệu xác định được
mô tả duy nhất bởi một hàm số, chuỗi số hay đồ thị, … xác định.
Tín hiệu ngẫu nhiên (random signal) là tín hiệu có giá trị (độ lớn) là ngẫu nhiên tại
mọi thời điểm, vì thế, không thể xác định chính xác giá trị (độ lớn) của tín hiệu tại
thời điểm bất kì trong tương lai. Về mặt toán học, tín hiệu ngẫu nhiên được mô tả
bởi hàm phân bố hoặc hàm mật độ phân bố và được đặc trưng bởi giá trị trung
bình, phương sai và hàm tự tương quan. Các tín hiệu có nguồn gốc tự nhiên
thường là tín hiệu ngẫu nhiên.
1.1.2.5 Tín hiệu chẵn và tín hiệu lẻ
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 7 Tín hiệu hoặc
được gọi là tín hiệu chẵn nếu (1.9) Tín hiệu hoặc
được gọi là tín hiệu lẻ nếu (1.10) Bất kì một tín hiệu hoặc
nào đều phân tích được thành tổ hợp của hai tín
hiệu, gồm một tín hiệu chẵn , hoặc , và một tín hiệu lẻ , hoặc , . (1.11) ,[.] = ,+[.] + ,,[.]
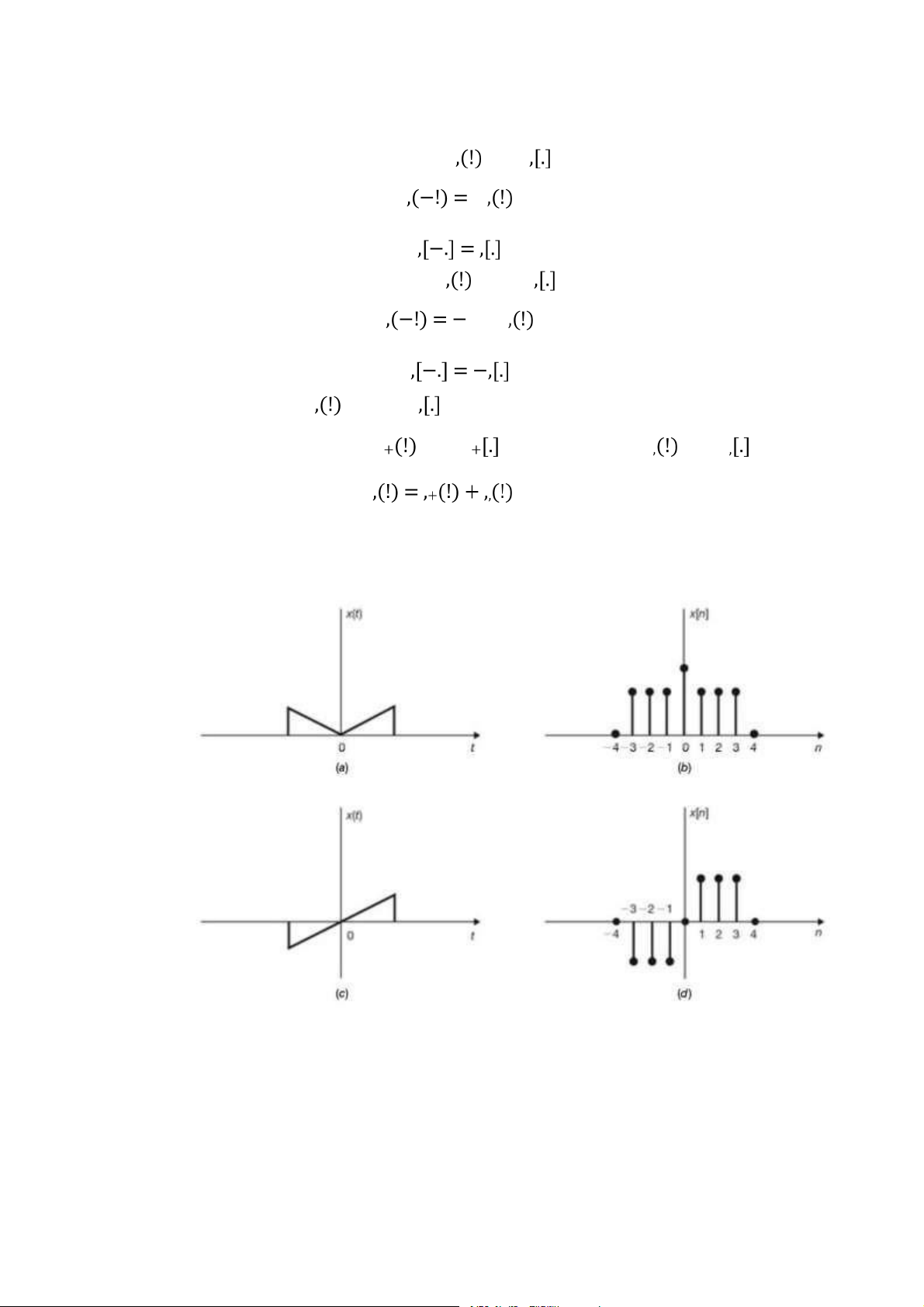
Ví dụ về tín hiệu chẵn và tín hiệu lẻ được biểu diễn trong hình 1.4.
Hình 1.4: Ví dụ về tín hiệu chẵn (a, b) và tín hiệu lẻ (c, d)
1.1.2.6 Tín hiệu thực và tín hiệu phức
Tín hiệu được gọi là thực nếu như tất cả các giá trị của nó đều là số thực. Tín hiệu
được gọi là phức nếu như tồn tại bất kì giá trị nào của nó là số phức. Các tín hiệu
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 8
có nguồn gốc tự nhiên đều là tín hiệu thực. Tín hiệu phức được tạo ra trong quá
trình phân tích, xử lý tín hiệu.
1.1.2.7 Một số cách phân loại khác
Tín hiệu đơn hàm là tín hiệu được mô tả bởi một hàm toán học duy nhất. Tín hiệu đa
hàm là tín hiệu được mô tả bởi một tập các hàm.
Tín hiệu một hướng là tín hiệu mà hàm mô tả nó chỉ phụ thuộc vào duy nhất một
biến độc lập. Tín hiệu nhiều hướng là tín hiệu mà hàm mô tả nó phụ thuộc vào nhiều biến độc lập.
Tín hiệu đơn kênh có giá trị chỉ đến từ một kênh. Tín hiệu đa kênh thường được biểu
diễn dưới dạng vector mà thành phần là các tín hiệu đơn kênh.
Hình 1.5: Ví dụ về tín hiệu ảnh màu gồm 2 hướng (x, y) và 3 kênh (R, G, B)
Tín hiệu có độ dài hữu hạn (finited signal) là tín hiệu mà tất cả các giá trị khác 0
của tín hiệu đều nằm trong một khoảng hữu hạn trên trục thời gian, ngoài khoảng
đó giá trị của tín hiệu luôn bằng 0. Tín hiệu có độ dài hữu hạn thường là tín hiệu
thực tế. Tín hiệu có độ dài vô hạn (infinited signal) là tín hiệu mà các giá trị khác 0
trên trục thời gian là vô hạn.
1.1.3 Các tín hiệu liên tục cơ bản
1.1.3.1 Tín hiệu nhảy bậc đơn vị
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 9
Tín hiệu nhảy bậc đơn vị
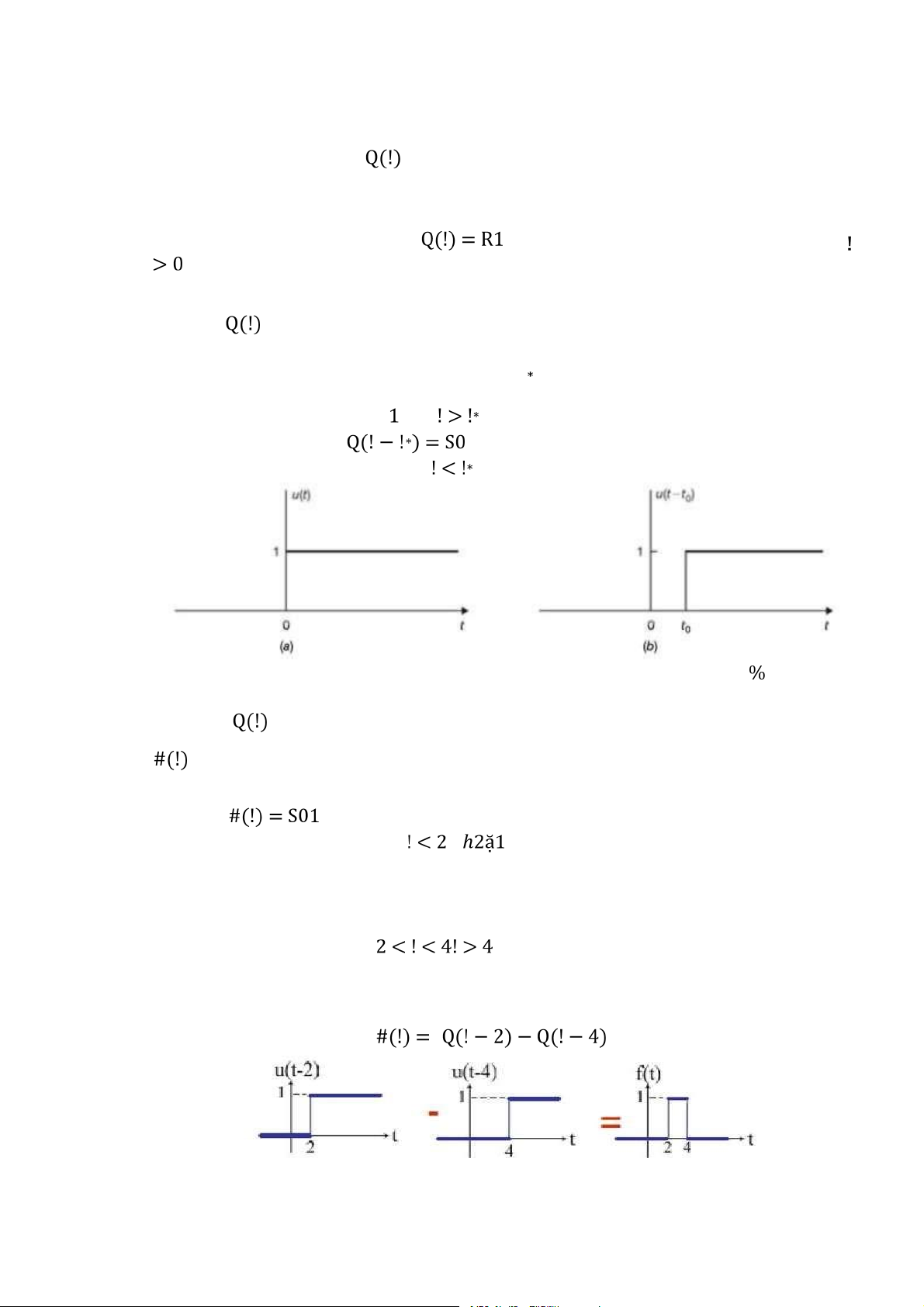
, còn được biết đến là hàm đơn vị Heaviside, được định nghĩa như sau (1.12) Tín hiệu
không liên tục tại ! = 0 và giá trị của hàm tại ! = 0 là không xác định.
Tín hiệu nhảy bậc đơn vị dịch đi một khoảng ! sẽ là
Hình 1.6: a) Tín hiệu nhảy bậc đơn vị, b) Tín hiệu nhảy bậc đơn vị dịch ! Tín hiệu
được sử dụng để biểu diễn tín hiệu đa hàm. Ví dụ, với tín hiệu đa hàm sau đây
có thể biểu diễn là tổ hợp của hàm tín hiệu nhảy bậc đơn vị như sau
Hình 1.7: Biểu diễn tín hiệu đa hàm !(#) sử dụng tín hiệu nhảy bậc đơn vị
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 10
1.1.3.2 Hàm xung đơn vị Hàm xung đơn vị
, còn được biết đến là hàm xung Dirac, đóng vai trò quan
trọng trong phân tích hệ thống. Hàm xung đơn vị
được định nghĩa là phần diện
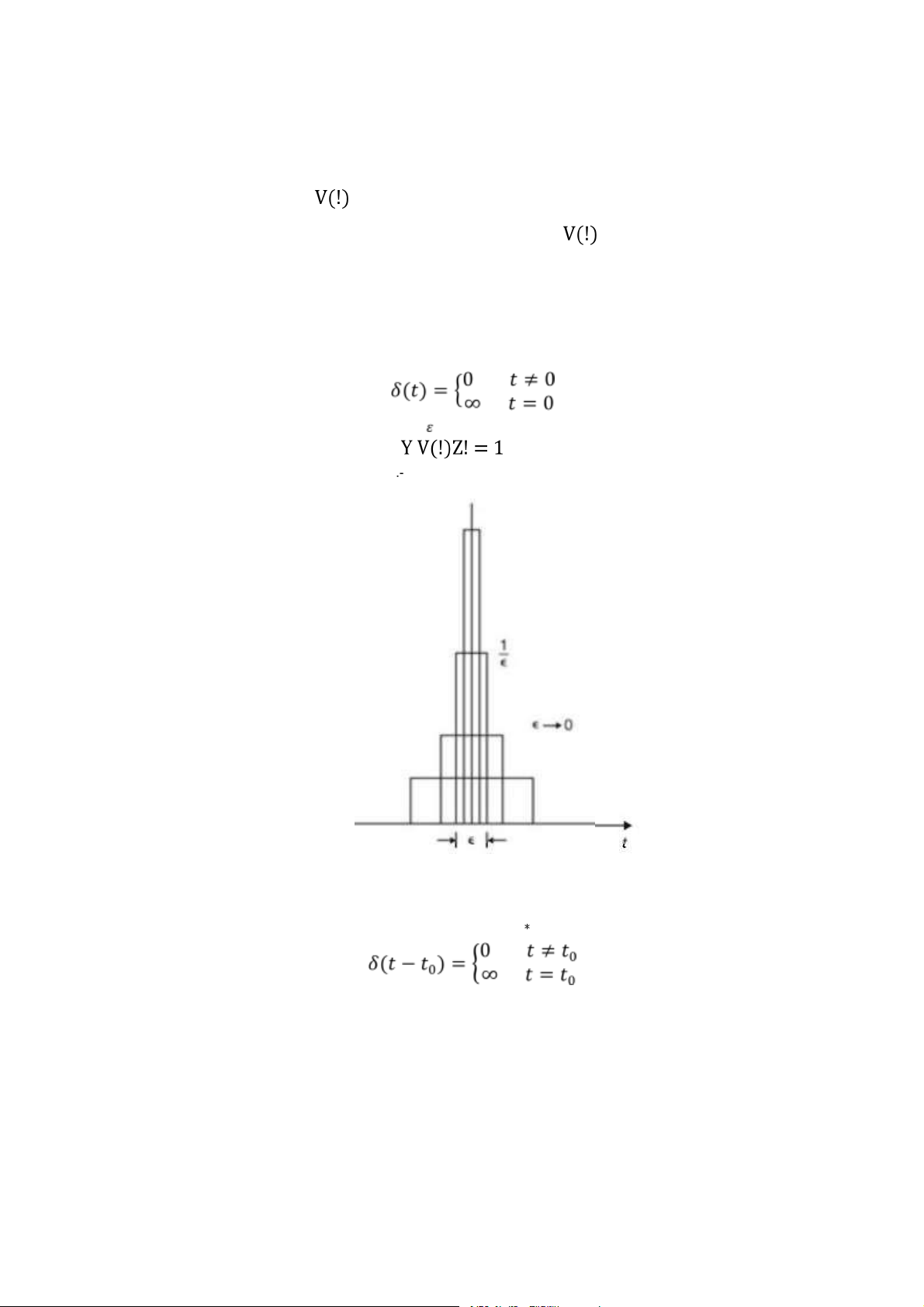
tích bằng đơn vị của hàm số đó trong khoảng thời gian rất nhỏ, được mô tả như trong hình
1.8, và có các tính chất dưới đây (1.14)
Hình 1.8: Định nghĩa hàm xung đơn vị
Hàm xung đơn vị dịch đi một khoảng ! sẽ là (1.16)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 11
Hình 1.9: a) Hàm xung đơn vị, b) Hàm xung đơn vị dịch !
Một số tính chất của hàm xung đơn vị như sau (1.17) (1.18) Nếu tín hiệu
là liên tục tại ! = 0, thì (1.19) Nếu tín hiệu
là liên tục tại ! = ! , thì (1.20)
Bất kì tín hiệu liên tục theo thời gian
nào cũng có thể biểu diễn thành
và tại thời điểm ! = ! , thì (1.22) ./
Mối quan hệ giữa xung nhảy bậc đơn vị và hàm xung đơn vị (1.23)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 12 Lưu ý, hàm
không liên tục tại ! = 0 nên phép tính tích phân tại các tính toán trên là tích phân tổng quát.
1.1.3.3 Tín hiệu hàm mũ phức Tín hiệu hàm mũ phức
là một ví dụ quan trọng của tín hiệu phức.(1.25) ! (1.26)
Biểu thức 1.25 là biểu diễn Euler của tín hiệu hàm mũ phức, trong đó ! là phần thực và
! là phần ảo. Tín hiệu hàm mũ phức
là tín hiệu tuần hoàn với
bất kì giá trị nào của , khi đó chu kì cơ bản sẽ là
(1.27) Với số phức 3 = $ + `_ thì tín hiệu hàm mũ phức tổng
quát ,(!) được định nghĩa như sau
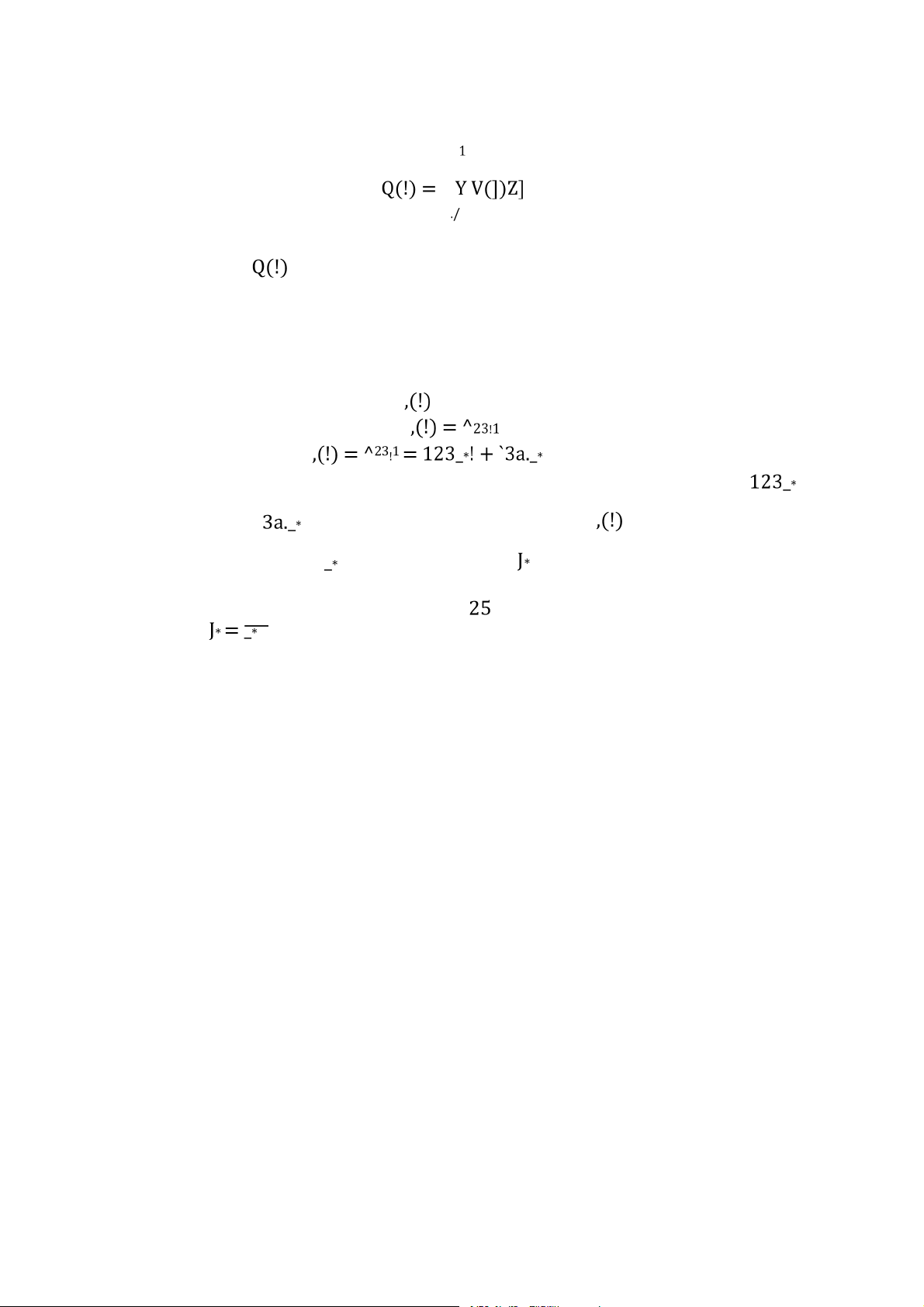
,(!) = ^%1 = ^(5623)1 = ^51(123_*! + `3a._*!) (1.28)
Trong đó, phần thực của tín hiệu là ^51123_*! và phần ảo của tín hiệu là ^513a._*! là
các hàm sin tăng theo hàm mũ nếu $ > 0 hoặc các hàm sin giảm theo hàm mũ nếu $ < 0.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 13
Hình 1.10: Tín hiệu sin a) tăng theo hàm mũ, b) giảm theo hàm mũ
Nếu 3 là số thực (3 = $) thì tín hiệu hàm mũ phức tổng quát suy biến thành tín
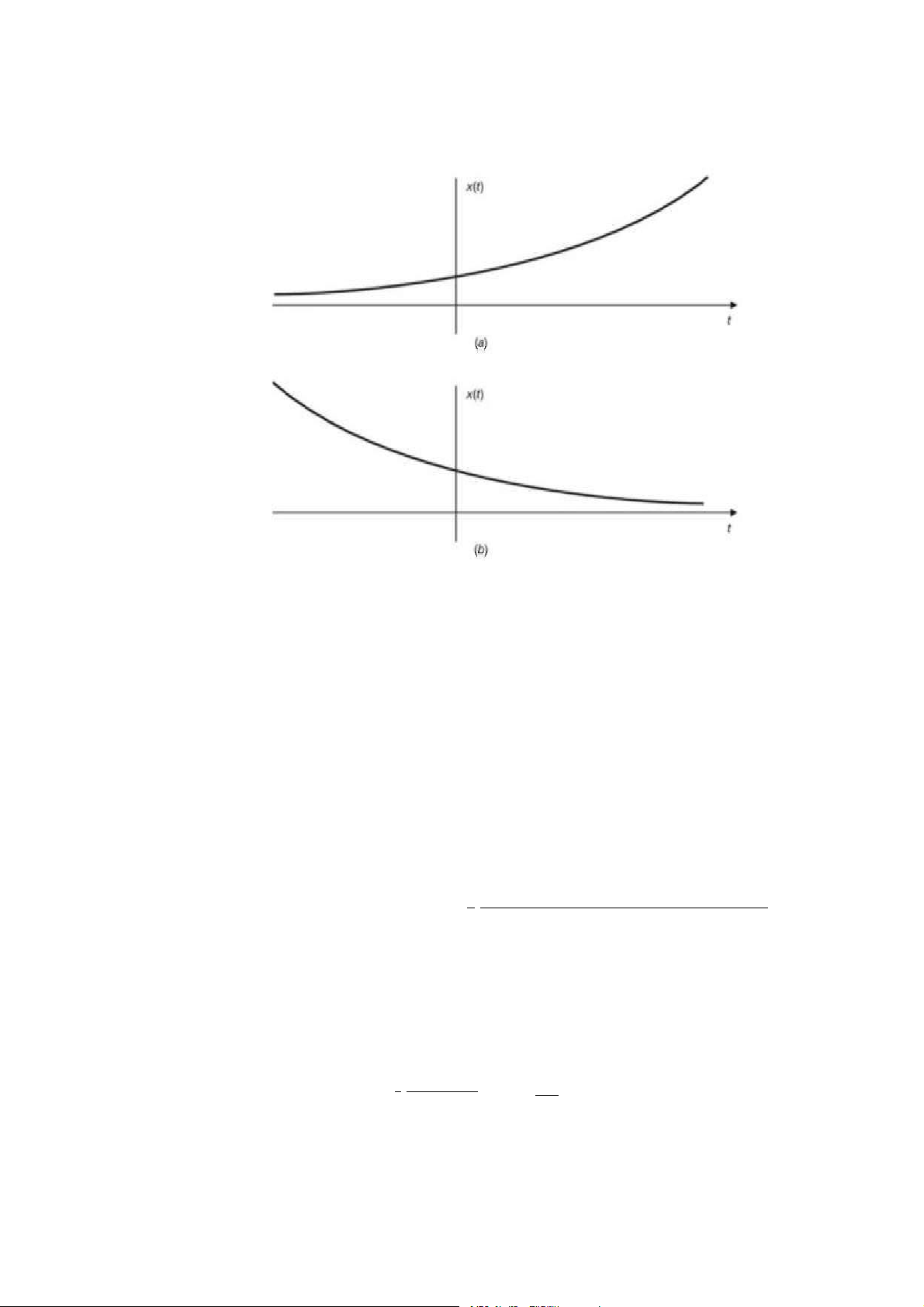
hiệu hàm mũ thực. Nếu $ > 0 thì ,(!) trở thành hàm tăng theo cấp số nhân và nếu
$ < 0 thì ,(!)trở thành hàm giảm theo cấp số nhân. ,(!) = ^51 (1.29)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 14
Hình 1.11: Tín hiệu hàm mũ thực liên tục theo thời gian a) & > 0, b) & < 0
1.1.3.4 Tín hiệu hình sin
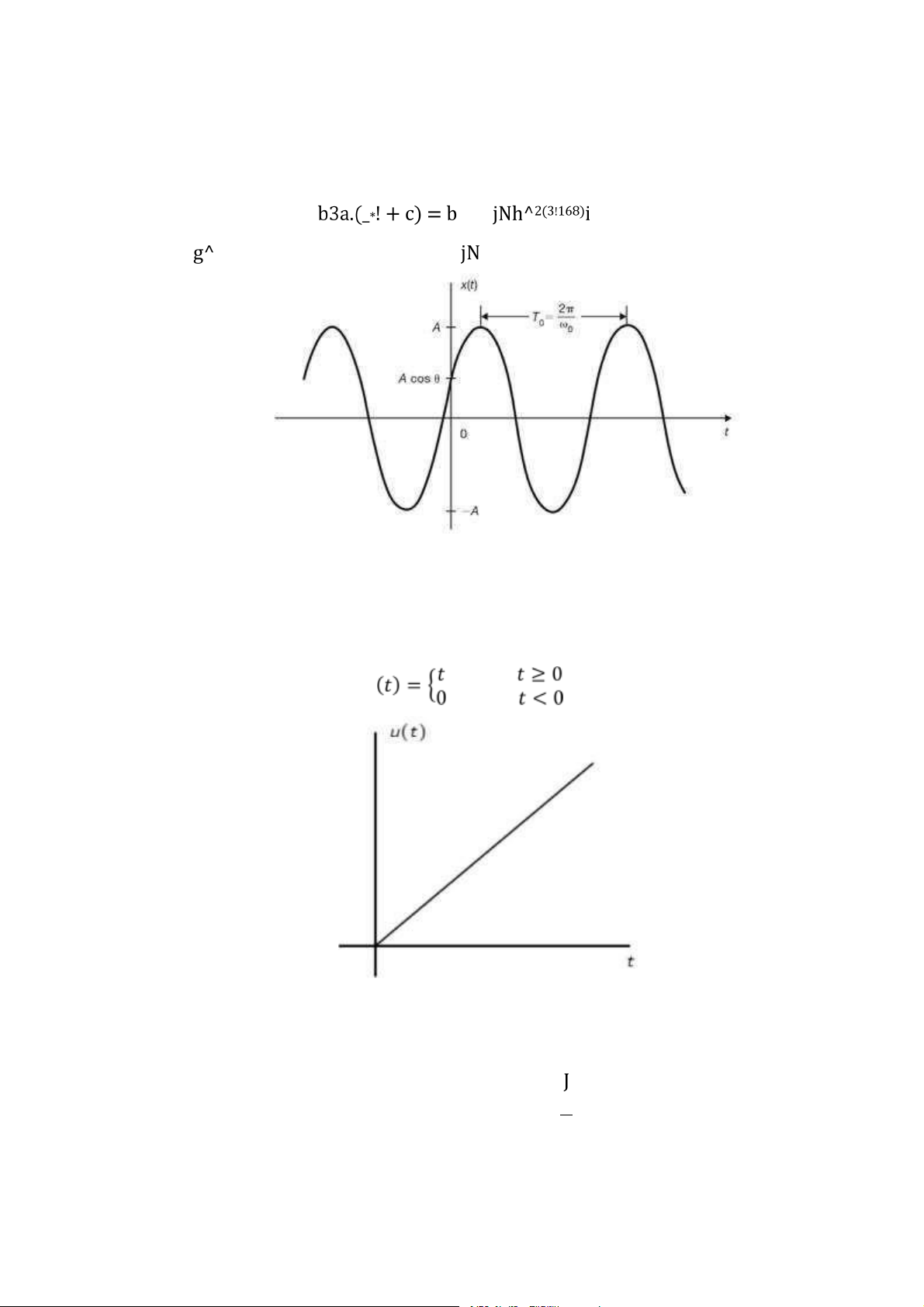
Tín hiệu hình sin liên tục được định nghĩa như sau ,(!) = b123(_*! + c) (1.30)
với b là biên độ là số thực, _* là tần số góc được tính theo đơn vị radian trong một
đơn vị thời gian (rad/s) và c là góc pha được đo ở radian. Tín hiệu hình sin là tín
hiệu tuần hoàn theo chu kì cơ bản sau 25 J* = _* (1.31)
Giá trị nghịch đảo của chu kì cơ bản J* được gọi là tần số cơ bản #* và có mối quan
hệ với tần số góc cơ bản _* như sau 1 _* #* = J* ℎ^d!e (fe) = 25 (1.32)
Sử dụng công thức Euler, tín hiệu hình sin có thể biểu diễn như sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 15 b123(_*! + c) = b g^h^2(3!168)i (1.33)
với “ ” đặc trưng cho phần thực và “ ” đặc trưng cho phần ảo của tín hiệu.
Hình 1.12: Tín hiệu hình sin liên tục theo thời gian
1.1.3.5 Một số tín hiệu liên tục cơ bản khác Tín hiệu hàm d (1.34) Q
Hình 1.13: Tín hiệu hàm dốc đơn vị
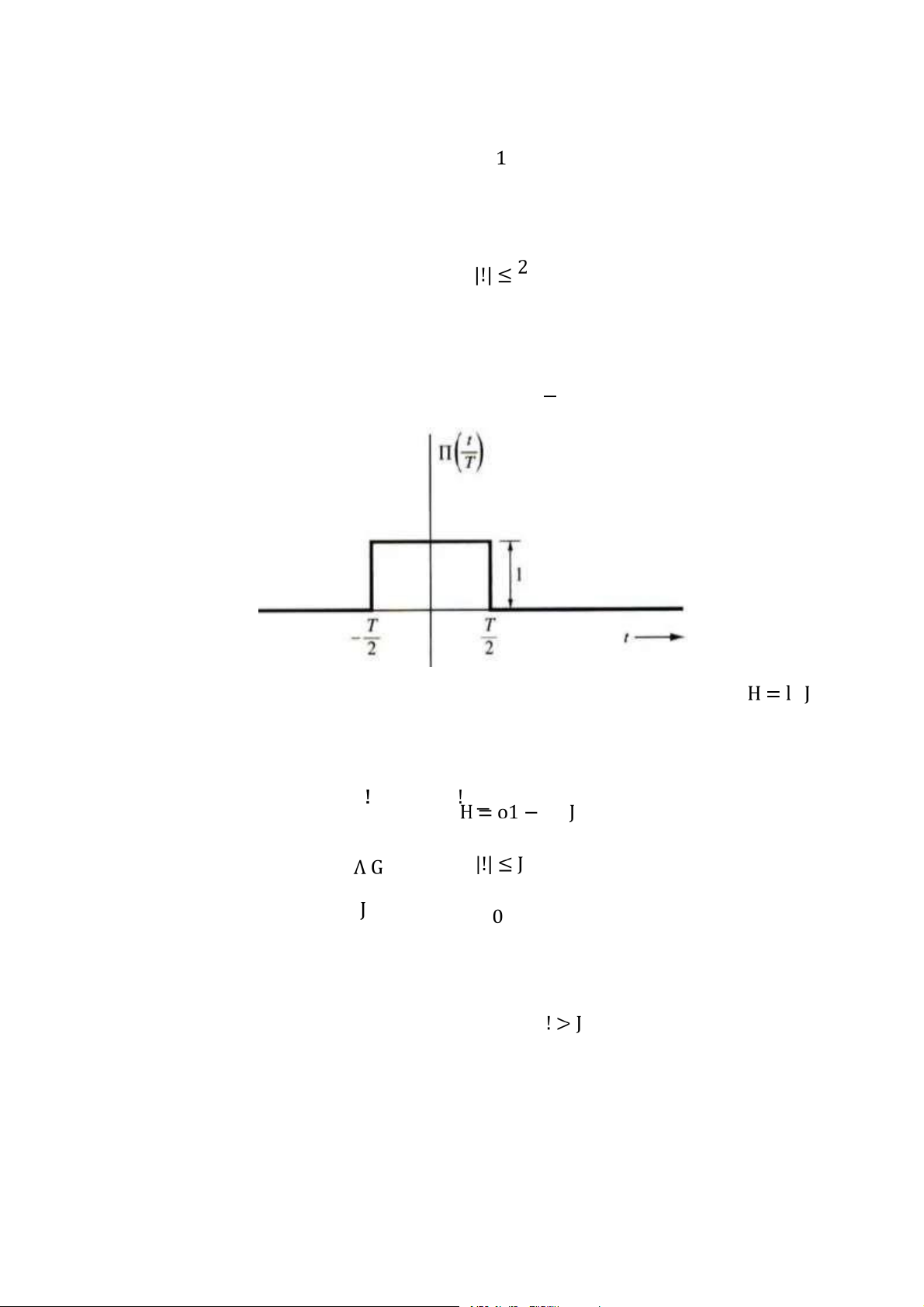
Tín hiệu xung chữ nhật được định nghĩa như sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 16 J 0 !> 2 Π G
Hình 1.14: Tín hiệu xung chữ nhật
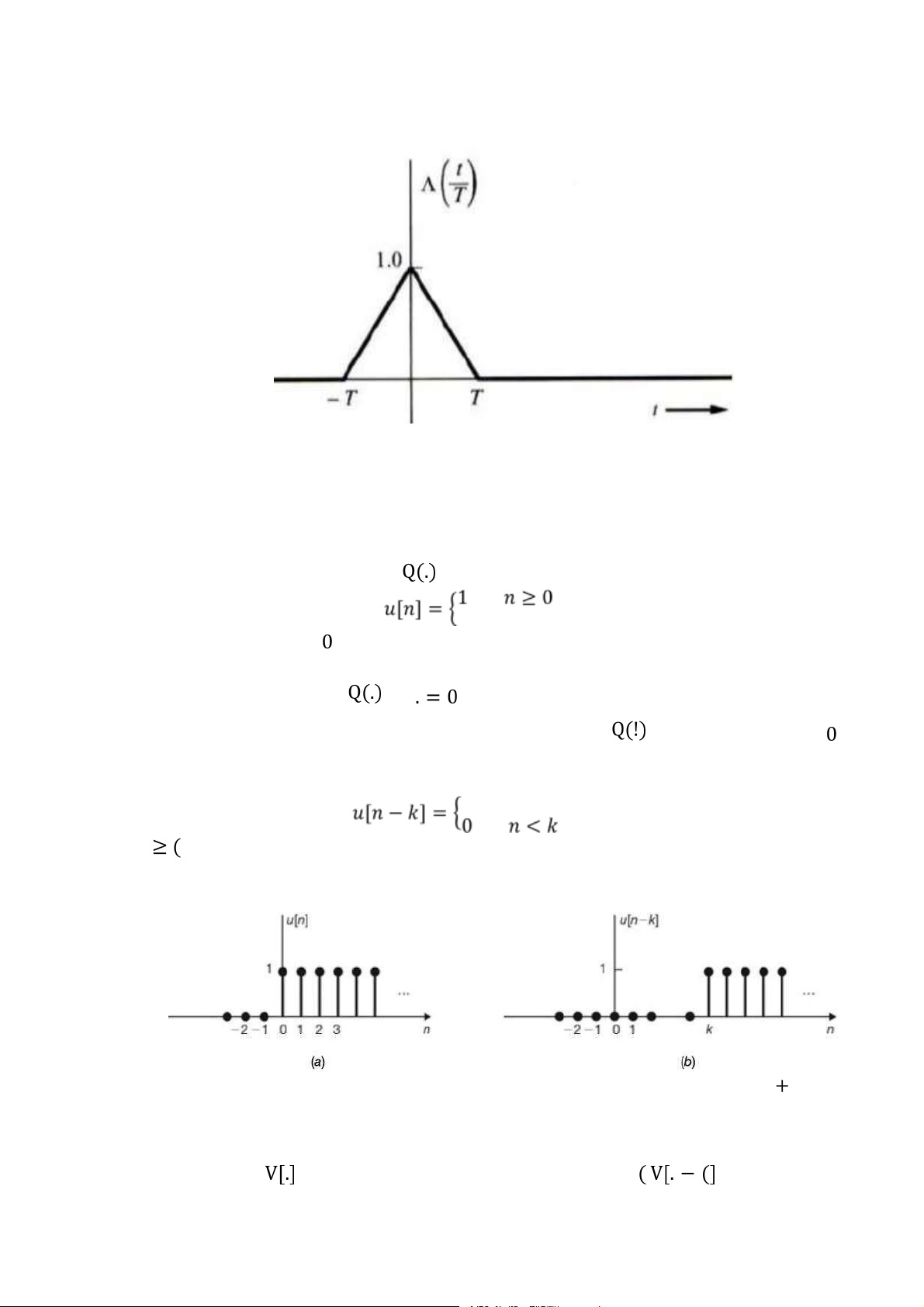
Tín hiệu xung tam giác được định nghĩa như sau (1.36)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 17
Hình 1.15: Tín hiệu xung tam giác
1.1.4 Các tín hiệu rời rạc cơ bản
1.1.4.1 Chuỗi nhảy bậc đơn vị
Chuỗi nhảy bậc đơn vị
được định nghĩa như sau (1.37)
Chú ý rằng, giá trị của tại
là xác định và bằng đơn vị, không giống như
trường hợp xung nhảy bậc đơn vị liên tục theo thời gian không liên tục tại ! = .
Chuỗi nhảy bậc đơn vị dịch đi một khoảng ( sẽ là 1 (1.38)
Hình 1.16: a) Chuỗi nhảy bậc đơn vị, b) Chuỗi nhảy bậc đơn vị dịch một khoảng
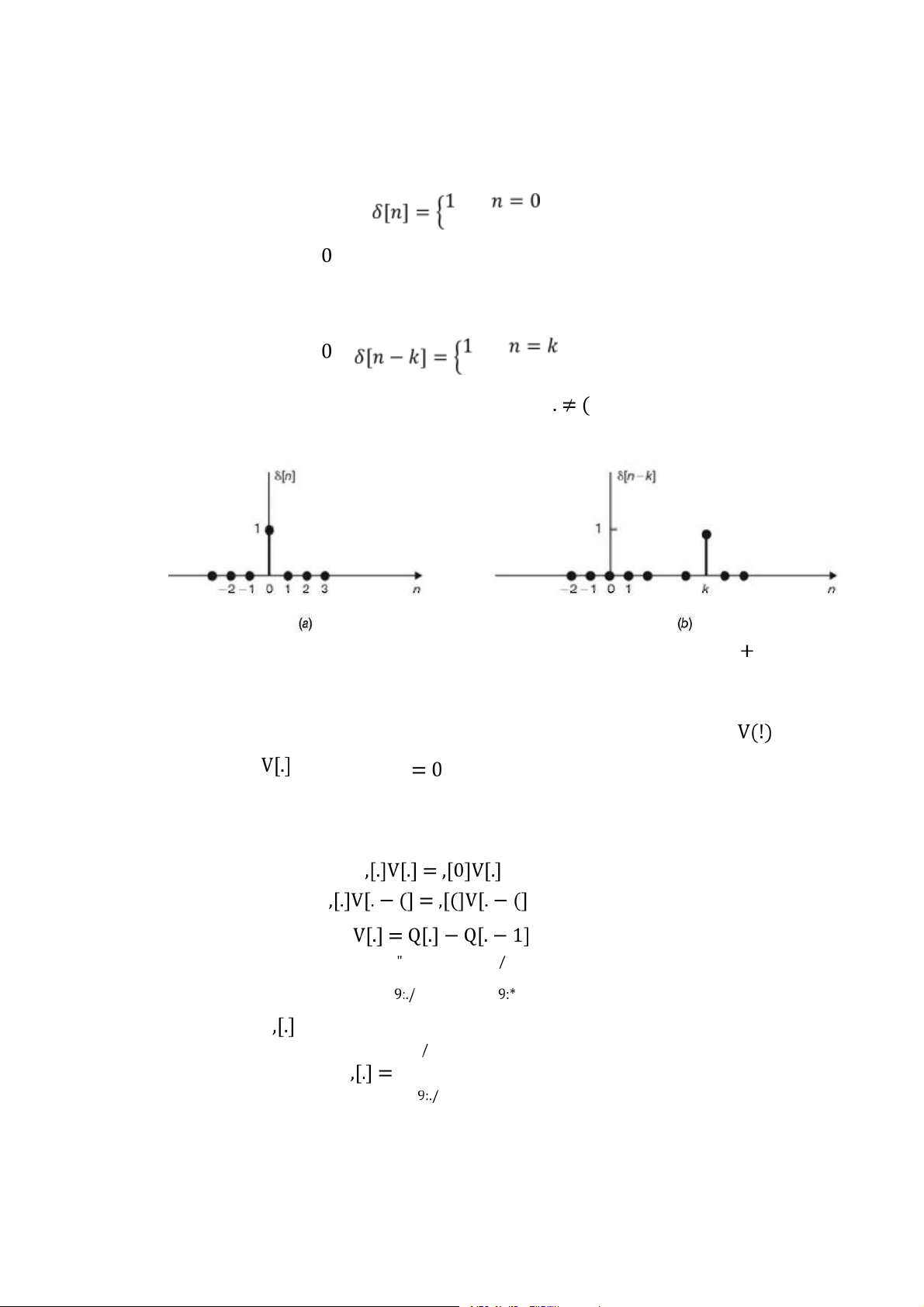
1.1.4.2 Xung đơn vị Xung đơn vị
và xung đơn vị dịch đi một khoảng được định nghĩa
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 18 như sau (1.39) (1.40)
Hình 1.17: a) Xung đơn vị, b) Xung đơn vị dịch một khoảng
Về cơ bản, xung đơn vị chính là phiên bản rời rạc hoá về mặt thời gian của hàm
xung đơn vị liên tục theo thời gian. Tuy nhiên, có điểm khác biệt với , đó là xung đơn vị xác định tại .
mà không gặp khó khăn hay phức tạp nào về mặt toán học. Sau đây
là một số tính chất của xung đơn vị. (1.40) (1.41) Bất kì chuỗi đều
biểu diễn được là tổ hợp của chuỗi xung đơn vị như sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 19
1.1.4.3 Chuỗi hàm mũ phức
Chuỗi hàm mũ phức và biểu diễn Euler của nó sẽ có dạng (1.44) . (1.45) với . là phần thực và
. là phần ảo của chuỗi.
Để chuỗi hàm mũ phức tuần hoàn với chu kì thì
phải thoả mãn điều kiện sau (1.46)
Như vậy, khác với tín hiệu hàm mũ phức liên tục theo thời gian sẽ tuần hoàn
với mọi , chuỗi hàm mũ phức
không tuần hoàn với bất kì giá trị nào của
mà chỉ tuần hoàn chỉ khi
là một số tỉ lệ. Trong trường hợp và giữa với
không có ước số chung thì chu kì cơ bản của chuỗi hàm mũ phức sẽ là (1.47)
Một điểm khác biệt quan trọng nữa giữa tín hiệu hàm mũ phức liên tục và chuỗi
hàm mũ phức rời rạc đó là tín hiệu
phân biệt với mọi giá trị phân biệt của trong khi tín hiệu
không như vậy. Xem xét chuỗi hàm mũ phức với tần số với ( là số nguyên (1.48) do
. Có thể thấy rằng chuỗi hàm mũ phức tại tần số là hoàn toàn giống
với chuỗi tại các tần số ,
, … Do vậy, đối với chuỗi hàm mũ phức chỉ cần chọn
trong khoảng . Thông thường, được chọn trong khoảng 0 hoặc .
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 20
Chuỗi hàm mũ phức tổng quát được định nghĩa như sau (1.49)
với và là các số phức. Chuỗi hàm mũ phức
là một trường hợp đặc biệt của
chuỗi hàm mũ phức tổng quát với và !.
Nếu và là các số thực thì
trở thành chuỗi hàm mũ thực và tồn tại bốn trường
hợp phân biệt ứng với giá trị của ), cụ thể là , , và . Nếu ) = 1 thì
sẽ trở thành chuỗi hằng số, còn nếu ) = −1 thì sẽ thay đổi giá trị lần lượt giữa và .
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 21
Hình 1.18: Chuỗi hàm mũ thực: a) , b) , c) , d)
1.1.4.4 Chuỗi xung hình sin
Chuỗi xung hình sin được biểu diễn như sau (1.50)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 22 (1.51)
Nếu . không có thứ nguyên thì
và đều có đơn vị là radian. Tương tự như phân
tích cho chuỗi hàm mũ phức, để chuỗi xung hình sin tuần hoàn thì tần số góc
cũng phải thoả mãn điều kiện đưa ra ở biểu thức (1.46). Như ví dụ đưa ra dưới dây, chuỗi
trong hình 1.19 a) tuần hoàn với chu kì 12 trong khi chuỗi trong hình 1.19 b) không tuần hoàn.
Hình 1.19: Chuỗi xung hình sin: a) , b)
1.2 MỘT SỐ ĐẶC TRƯNG CƠ BẢN TÍN HIỆU
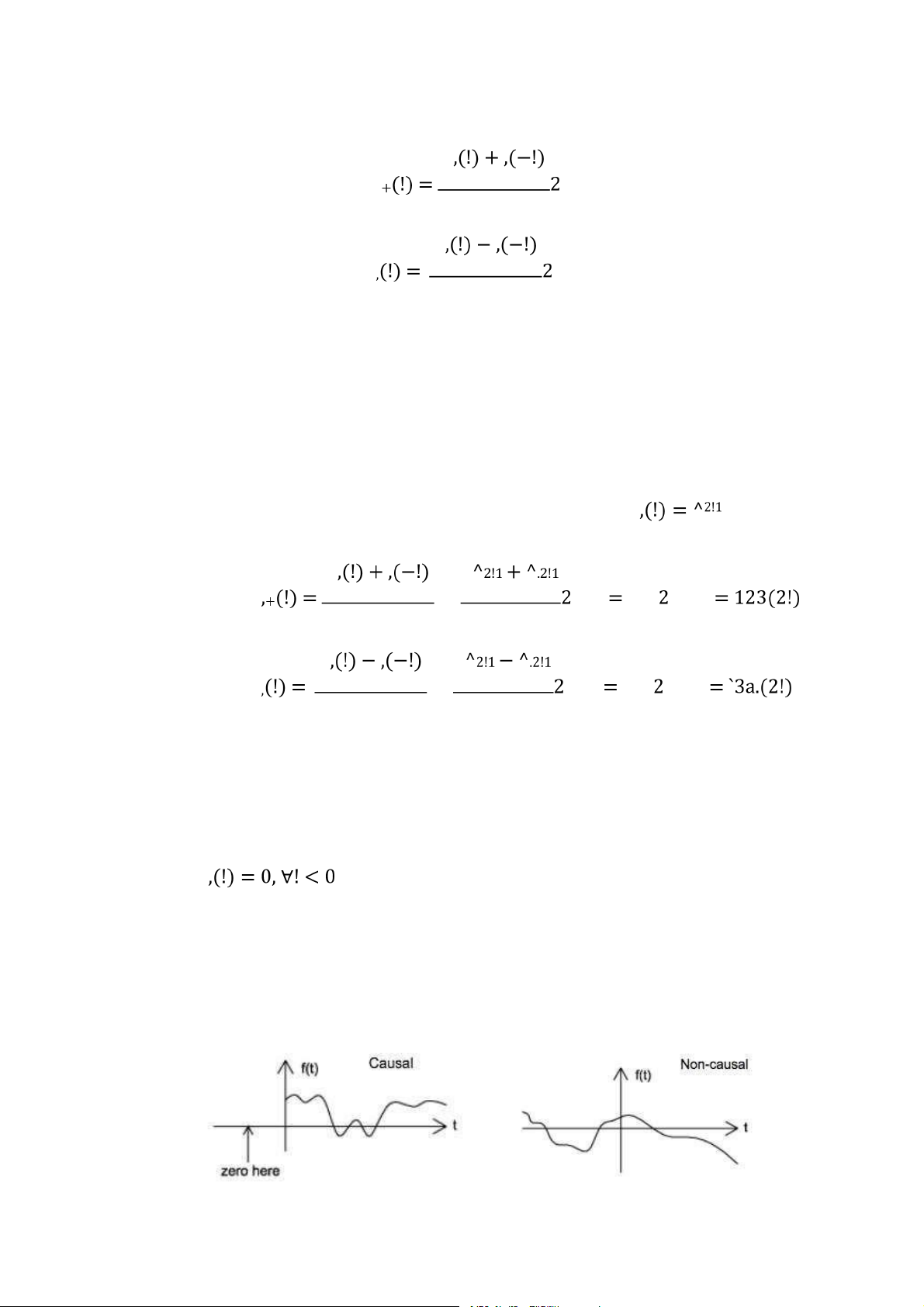
1.2.1 Tính chẵn lẻ của tín hiệu Thành phần chẵn , và thành phần lẻ , của một tín hiệu được định nghĩa như sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 23 , (1.52) ,
Định nghĩa này cũng được áp dụng cho tín hiệu rời rạc.
Một số tính chất của tín hiệu chẵn và tín hiệu lẻ
- Nhân một tín hiệu chẵn với một tín hiệu lẻ sẽ thu được tín hiệu lẻ.
- Nhân một tín hiệu chẵn với một tín hiệu chẵn sẽ thu được tín hiệu chẵn. -
Nhân một tín hiệu lẻ với một tín hiệu lẻ sẽ thu được tín hiệu chẵn.
Ví dụ 1: Tìm thành phần chẵn và thành phần lẻ của tín hiệu . Lời
giải: Áp dụng biểu thức (1.52), ta có
1.2.2 Tính nhân quả của tín hiệu
Tín hiệu được gọi là nhân quả nếu giá trị của nó bằng 0 tại mọi thời điểm ! < 0, tức là
. Tín hiệu được gọi là không nhân quả nếu giá trị của nó
khác 0 tại cả các thời điểm ! < 0 và ! > 0. Tín hiệu phản nhân quả là tín hiệu có giá trị bằng
0 tại mọi thời điểm ! > 0.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 24 a) b)
Hình 1.20: a) Tín hiệu nhân quả, b) Tín hiệu không nhân quả
1.2.3 Năng lượng và công suất của tín hiệu
Tín hiệu có thể biểu diễn cho rất nhiều hiện tượng khác nhau. Trong nhiều ứng
dụng, đặc biệt là trong các ứng dụng liên quan đến hệ thống truyền tin, tín hiệu
chính là các đại lượng vật lý được đặc trưng bởi công suất và năng lượng có mặt trên hệ
thống vật lý. Ví dụ, hệ thống vật lý là một mạch điện có điện áp và dòng điện
đi qua điện trở của mạch thì công suất tức thời của mạch sẽ là ! (1.53)
Năng lượng tổng của mạch trong khoảng thời gian ! ! là ! (1.54)
và công suất trung bình trong khoảng thời gian này là
Không mất tính tổng quát, hoàn toàn có thể giả thiết rằng điện trở trên mạch
{ℎN, khi đó công suất trung bình và năng lượng tổng của mạch chỉ phụ thuộc vào độ
lớn tín hiệu. Nói cách khác, năng lượng và công suất của tín hiệu chính là năng lượng
tổng và công suất trung bình chuẩn hoá trên một đơn vị điện trở. Áp dụng các phân
tích này cho bất kì tín hiệu liên tục hoặc rời rạc
, sẽ luôn tính được năng
lượng và công suất của nó.
Theo lý thuyết, tín hiệu có thể nhận
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 25
giá trị thực hoặc phức, vì thế trong trường hợp tổng quát cần lấy độ lớn của tín hiệu
khi tính toán công suất và năng lượng tín hiệu, đó là và . Như vậy, có thể
định nghĩa năng lượng của một tín hiệu liên tục và tín hiệu rời rạc lần lượt như sau (1.55) (1.56)
và định nghĩa công suất trung bình theo thời gian của tín hiệu liên tục và tín hiệu rời rạc lần lượt như sau (1.57) !
Cần chú ý, thuật ngữ “công suất” và “năng lượng” trong các định nghĩa này hoàn
toàn độc lập với đại lượng vật lý mà tín hiệu mang. Tức là, “công suất” và “năng
lượng” trở thành các đặc trưng cơ bản của tín hiệu. Đối với tín hiệu tuần hoàn,
công suất của tín hiệu chính bằng năng lượng trung bình của tín hiệu trong một chu kì. =/! ! (1.59)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 26 ! (1.60)
Tuỳ thuộc vào giá trị của công suất và năng lượng của tín hiệu mà có thể phân thành các loại tín hiệu sau
- Tín hiệu năng lượng: đó là các tín hiệu mà năng lượng tổng của nó là giới hạn, tức là
. Các tín hiệu năng lượng sẽ có công suất trung bình bằng 0.
Ví dụ một số tín hiệu năng lượng như tín hiệu xung chữ nhật, tín hiệu xung
tam giác, các tín hiệu giới hạn thời gian và biên độ. Thông thường, các tín
hiệu vật lý là tín hiệu năng lượng.
- Tín hiệu công suất: đó là các tín hiệu và công suất trung bình của nó là giới hạn, tức là
. Các tín hiệu công suất sẽ có năng lượng vô hạn. Ví
dụ, tín hiệu có độ lớn bằng hằng số là tín hiệu công suất.
- Tín hiệu có cả năng lượng và công suất không giới hạn. Tín hiệu là
một ví dụ về kiểu tín hiệu này.
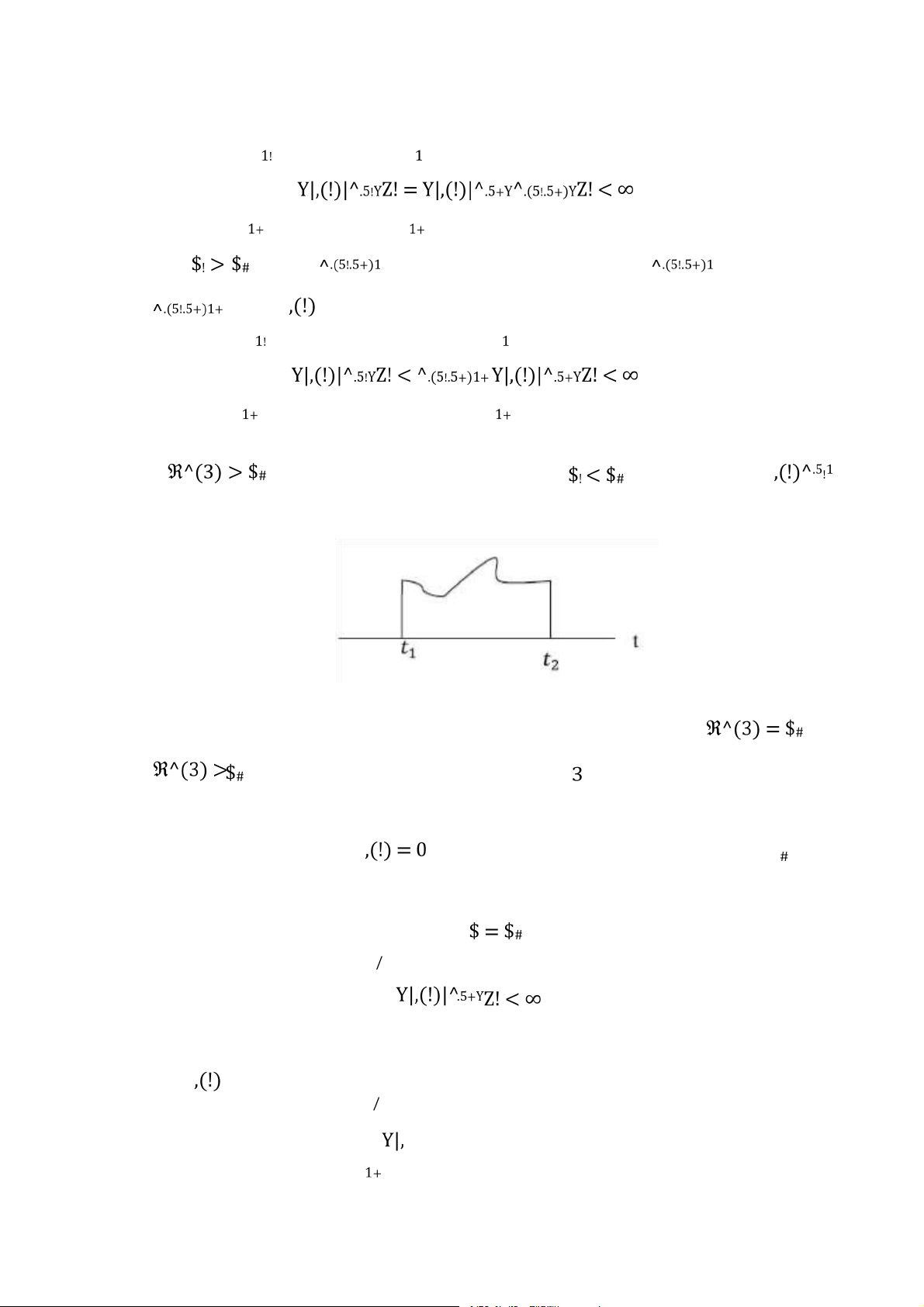
Ví dụ 2: Xác định công suất và năng lượng của tín hiệu sau , Lời giải:
Năng lượng của tín hiệu là ! | =
Y ,(!)!Z! = Y !!Z! + Y 1Z! = + 1 = Công suất của tín hiệu .
Năng lượng của tín hiệu giới hạn và công suất của tín hiệu bằng 0. Như vậy, là tín hiệu năng lượng.
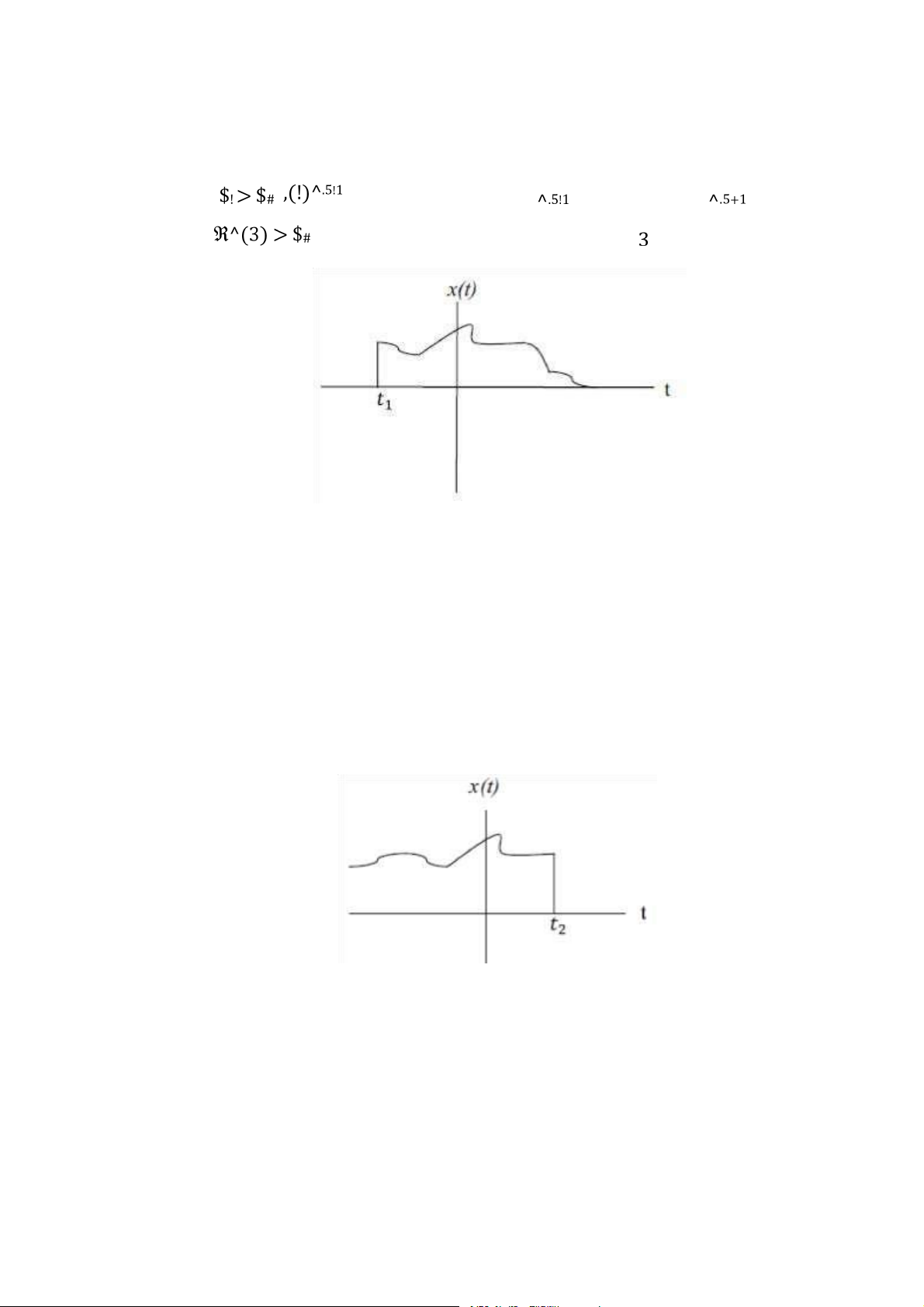
Ví dụ 3: Xác định công suất và năng lượng của tín hiệu sau Lời giải:
Năng lượng của tín hiệu là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 27 ./ ./ = + = 2
Công suất của tín hiệu là =/! =/! =/! = 4 lim 1 Y ^A1Z! + 4 lim 1 Y ^.A1Z! = 4 1 A1Ç* + 4 lim 1 ^.A1Ç=/! lim ^ 4 → = / J .=/! 4 =→/ J *
= 4 lim 1 [1 − ^.!=] + 4 lim 1 [^.!= − 1] 4 =→/ J 4 =→/ J
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 28
Năng lượng của tín hiệu giới hạn và công suất của tín hiệu bằng 0. Như vậy, là tín hiệu năng lượng.
Ví dụ 4: Xác định công suất và năng lượng của tín hiệu sau Lời giải:
Năng lượng của tín hiệu là
Công suất của tín hiệu là .=/!
Năng lượng của tín hiệu vô hạn và công suất của tín hiệu giới hạn. Như vậy, là tín hiệu công suất.
Xét tín hiệu trong không gian nhiều chiều, giả sử chiều, thì độ lớn của tín hiệu, còn
gọi là norm bậc của tín hiệu, , được định nghĩa như sau
Năng lượng của một tín hiệu chính là bình phương của norm bậc 2 của tín hiệu đó.
1.2.4 Giá trị trung bình, rms của tín hiệu
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 29
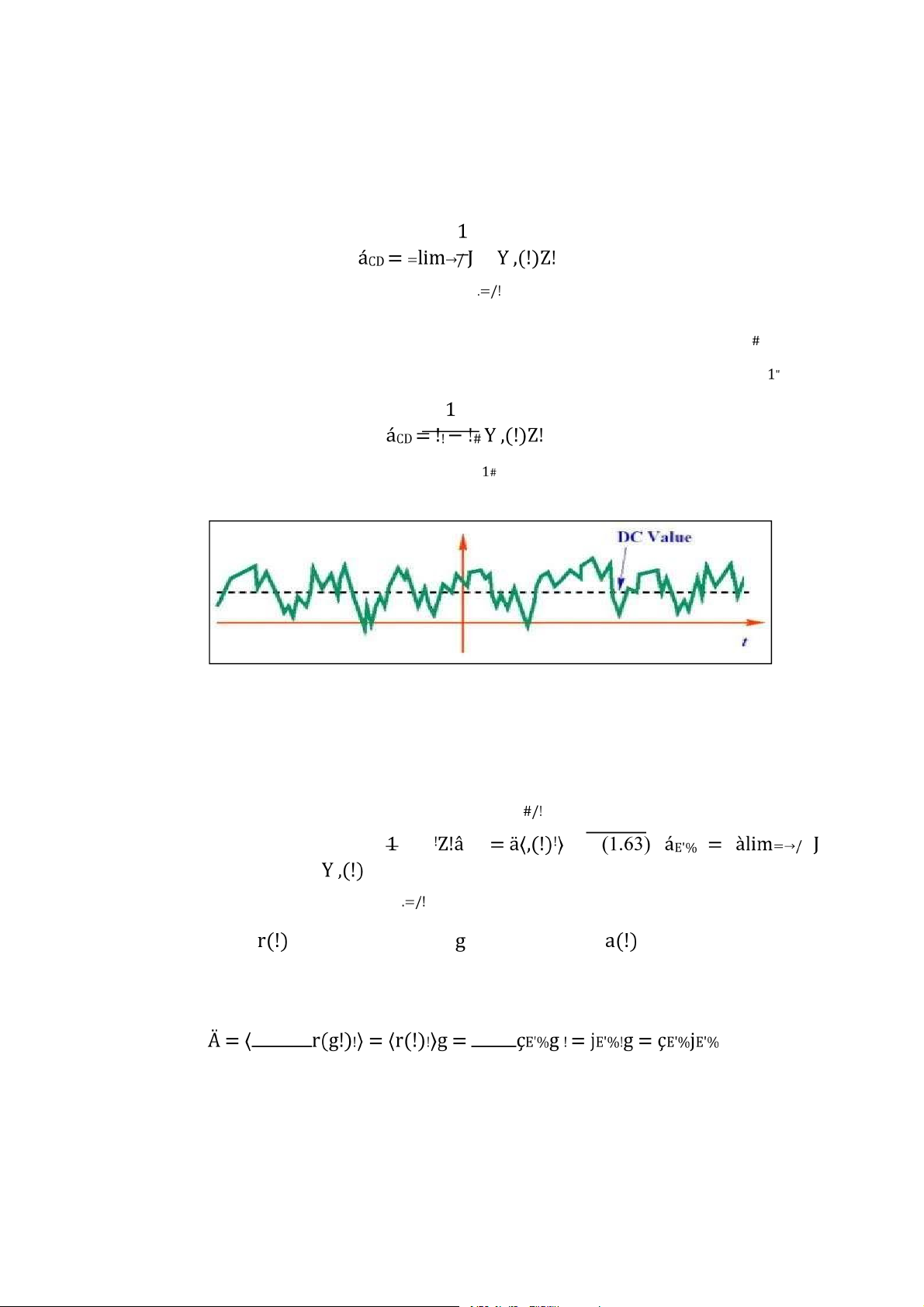
Giá trị trung bình, hay còn gọi là giá trị một chiều (DC), của tín hiệu trong miền thời
gian được tính như sau =/! (1.63)
Trong trường hợp, tín hiệu chỉ tồn tại trong khoảng thời gian hữu hạn, từ ! đến !!, thì
giá trị trung bình của tín hiệu chỉ cần tính trong khoảng thời gian tồn tại đó. (1.64)
Hình 1.21: Giá trị trung bình theo thời gian của tín hiệu
Giá trị rms (root-mean square) của tín hiệu được tính bằng căn bậc hai của trung bình
bình phương của tín hiệu. =/! Nếu điện áp
đặt trên điện trở tải sẽ có dòng điện đi qua mạch, khi đó công
suất trung bình của mạch có thể tính như sau (1.64)
1.3 MỘT SỐ PHÉP CHUYỂN ĐỔI TÍN HIỆU CƠ BẢN
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 30
1.3.1 Phép dịch thời gian
Tín hiệu được dịch sang phải (trễ) hoặc dịch sang trái (sớm) một khoảng thời gian nào đó. (1.65) (1.66) với: ! ,
: tín hiệu dịch sang phải (trễ) ! ,
: tín hiệu dịch sang trái (sớm) a) b) c)
Hình 1.22: a) Tín hiệu ban đầu, b) Tín hiệu dịch phải, c) Tín hiệu dịch trái
1.3.2 Phép đảo thời gian
Tín hiệu được lấy đối xứng qua trục tung.
Hình 1.23: Ví dụ về phép đảo thời gian
1.3.3 Phép thay đổi thang thời gian Tín hiệu được co – dãn về mặt thời gian. với:
: co thời gian với hệ số (nén)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 31
: dãn thời gian với hệ số (giãn)
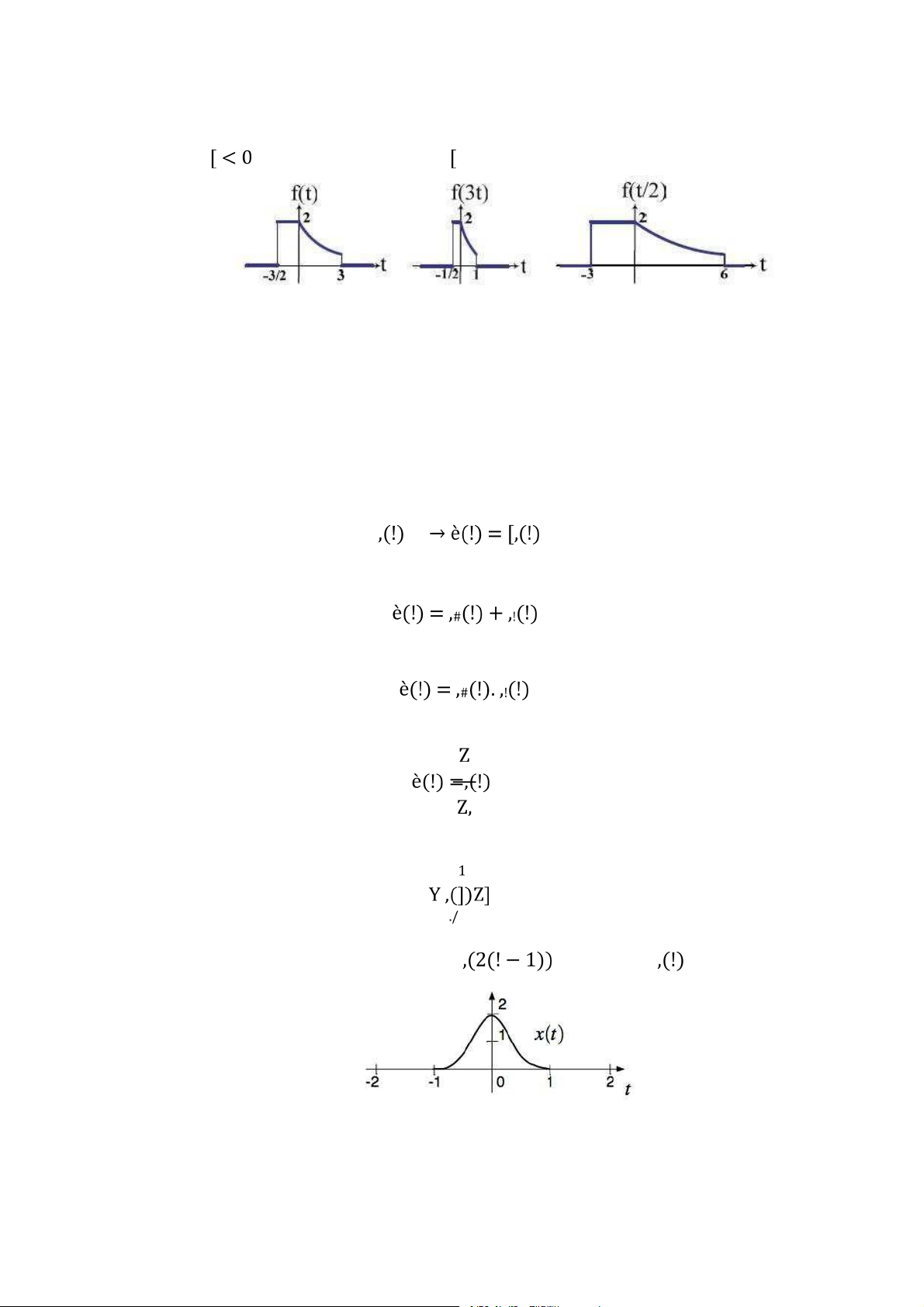
Hình 1.24: Ví dụ về phép thay đổi thang thời gian
Ngoài các phép chuyển đổi tín hiệu, các phép toán số học cũng được thực
hiện trong không gian tín hiệu. Có thể kết hợp các phép toán và các phép chuyển
đổi trên cùng một tín hiệu. Kết quả cuối cùng không phụ thuộc vào thứ tự thực
hiện các phép toán. Một số phép toán thường được sử dụng đó là -
Thay đổi biên độ tín hiệu (1.71) - Phép cộng (1.72) - Phép nhân (1.73) - Đạo hàm - Tích phân
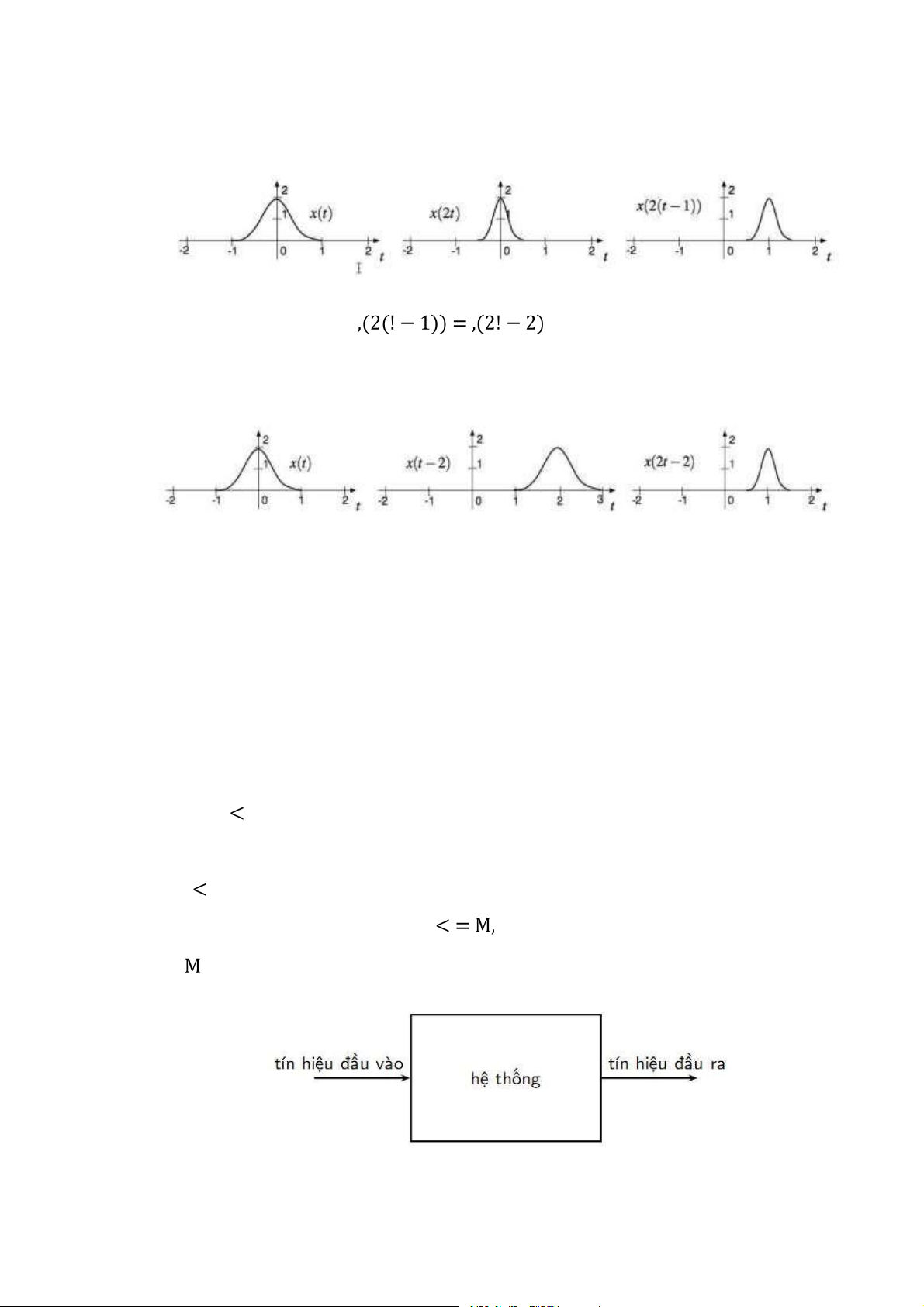
Ví dụ 5: Thực hiện các phép toán sau biết tín hiệu như sau Lời giải:
Cách 1: Thực hiện phép thay đổi thang thời gian trước, phép dịch sau -
Bước 1: Nén tín hiệu bởi 2
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 32 -
Bước 2: Dịch tín hiệu đi 1
Cách 2: Thực hiện phép dịch trước, phép thay đổi thang thời gian sau
Viết lại tín hiệu như sau -
Bước 1: Dịch tín hiệu đi 2 -
Bước 2: Nén tín hiệu bởi 2
1.4 HỆ THỐNG VÀ PHÂN LOẠI HỆ THỐNG
1.4.1 Khái niệm hệ thống
Hệ thống là một thực thể, thường là một tập hợp các đối tượng vật lý hay
còn gọi là các thành phần của hệ thống, làm thay đổi tín hiệu để thực hiện một
chức năng nào đó, trong quá trình đó, tạo ra tín hiệu mới. Về mặt toán học, hệ
thống được định nghĩa là một mô hình toán học đặc trưng cho mối quan hệ giữa tín
hiệu đầu vào và tín hiệu đầu ra của một quá trình vật lý.
Cho , và lần lượt là tín hiệu đầu vào và tín hiệu đầu ra của một hệ thống. Khi đó,
hệ thống được xem như là một bộ chuyển đổi (hoặc bộ ánh xạ) tín hiệu , thành tín
hiệu . Sự chuyển đổi này được mô tả bởi hàm toán học sau (1.76)
với là toán tử đặc trưng cho hàm chuyển đổi của hệ thống.
Hình 1.25: Mô hình tổng quát của hệ thống
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 33
Có thể biểu diễn hệ thống dưới nhiều cách thức khác nhau như sử dụng mô hình
toán học, sơ đồ khối hoặc sơ đồ thành phần. Biểu diễn hệ thống bằng mô hình toán
học chính là sử dụng hàm toán học biểu diễn mối quan hệ giữa tín hiệu đầu vào và
tín hiệu đầu ra của hệ thống. Phương thức này rất hữu ích trong việc phân tích và
thiết kế hệ thống, cho phép xác định được tín hiệu đầu ra khi biết tín hiệu đầu vào. a) b)
Hình 1.26: Biểu diễn hệ thống: a) bằng sơ đồi khối, b) bằng sơ đồ thành phần
1.4.2 Phân loại hệ thống
Phân loại hệ thống phụ thuộc vào tính chất của hệ thống. Một hệ thống có thể có
nhiều tính chất khác nhau, vì thế, việc phân loại này chỉ có tính chất tương đối.
Hệ thống tĩnh, còn gọi là hệ thống không nhớ, là những hệ thống mà tín hiệu đầu
ra chỉ phụ thuộc vào tín hiệu đầu vào ở cùng thời điểm. Các hệ thống mà tín hiệu
đầu ra phụ thuộc vào tín hiệu đầu vào ở mọi thời điểm khác nhau được gọi là hệ
thống động, hay hệ thống có nhớ.
Tuỳ thuộc vào số lượng đầu vào và đầu ra của hệ thống, sẽ có hệ thống một đầu
vào – một đầu ra (SISO), hệ thống một đầu vào – nhiều đầu ra (SIMO), hệ thống
nhiều đầu vào – một đầu ra (MISO), hệ thống nhiều đầu vào – nhiều đầu ra
(MIMO). Nếu tín hiệu đầu vào và tín hiệu đầu ra của hệ thống đều liên tục theo
thời gian thì hệ thống sẽ liên tục theo thời gian. Nếu tín hiệu đầu vào và tín hiệu
đầu ra của hệ thống đều u rời rạc theo thời gian thì hệ thống sẽ rời rạc theo thời gian.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 34
Một hệ thống được gọi là nhân quả nếu như đầu ra tại thời điểm hiện tại chỉ
phụ thuộc vào các giá trị tại thời điểm hiện tại và trong quá khứ của tín hiệu đầu vào
mà không phụ thuộc vào các giá trị ở tương lai. Như vậy, với hệ thống nhân quả, sẽ
không thể có tín hiệu đầu ra nếu chưa có tín hiệu đầu vào đưa đến. Hệ thống không
nhân quả có đầu ra phụ thuộc vào các giá trị của đầu vào trong tương lai.
Một hệ thống được gọi là tuyến tính nếu toán tử đặc trưng cho hệ thống là tuyến tính. Với , và ,
! lần lượt là các đầu vào, đầu ra thứ 1 và thứ 2
của hệ thống, toán tử sẽ là tuyến tính nếu thoả mãn điều kiện sau (1.77) hay
Như vậy, với hệ thống tuyến tính, tín hiệu đầu ra là chồng chất của nhiều tín hiệu
đầu vào, đồng thời, nếu tín hiệu đầu vào là 0 thì cũng sẽ cho tín hiệu đầu ra là 0.
Hệ thống bất biến theo thời gian sẽ có toán tử đặc trưng không đổi theo thời
gian, tức là, nếu tín hiệu đầu vào dịch đi một khoảng thời gian thì cũng gây ra một
khoảng dịch thời gian tương tự tại tín hiệu đầu ra. với ! là giá trị thực
bất kì và . là một số nguyên bất kì.
Hệ thống không thoả mãn điều kiện (1.78) đối với trường hợp liên tục theo thời
gian và không thoả mãn điều kiện (1.79) đối với trường hợp rời rạc theo thời gian
được gọi là hệ thống biến đổi theo thời gian.
Một hệ thống thoả mãn đồng thời tính tuyến tính và bất biến theo thời gian được
gọi là hệ thống tuyến tính bất biến theo thời gian (LTI). Đây là hệ thống quan
trọng trong phân tích hệ thống.
Hệ thống được gọi là ổn định nếu như tín hiệu đầu vào là hữu hạn sẽ cho tín hiệu
đầu ra cũng là hữu hạn. Hệ thống không ổn định là hệ thống không thoả mãn điều
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 35
kiện này, tức là, tín hiệu đầu vào là hữu hạn nhưng tín hiệu đầu ra không hữu hạn
hoặc ngược lại. Ví dụ, hệ thống <[.] = (. + 1)Q[.] là không ổn định do có đầu vào ,[.]
= Q[.] là hữu hạn nhưng đầu ra vô hạn.
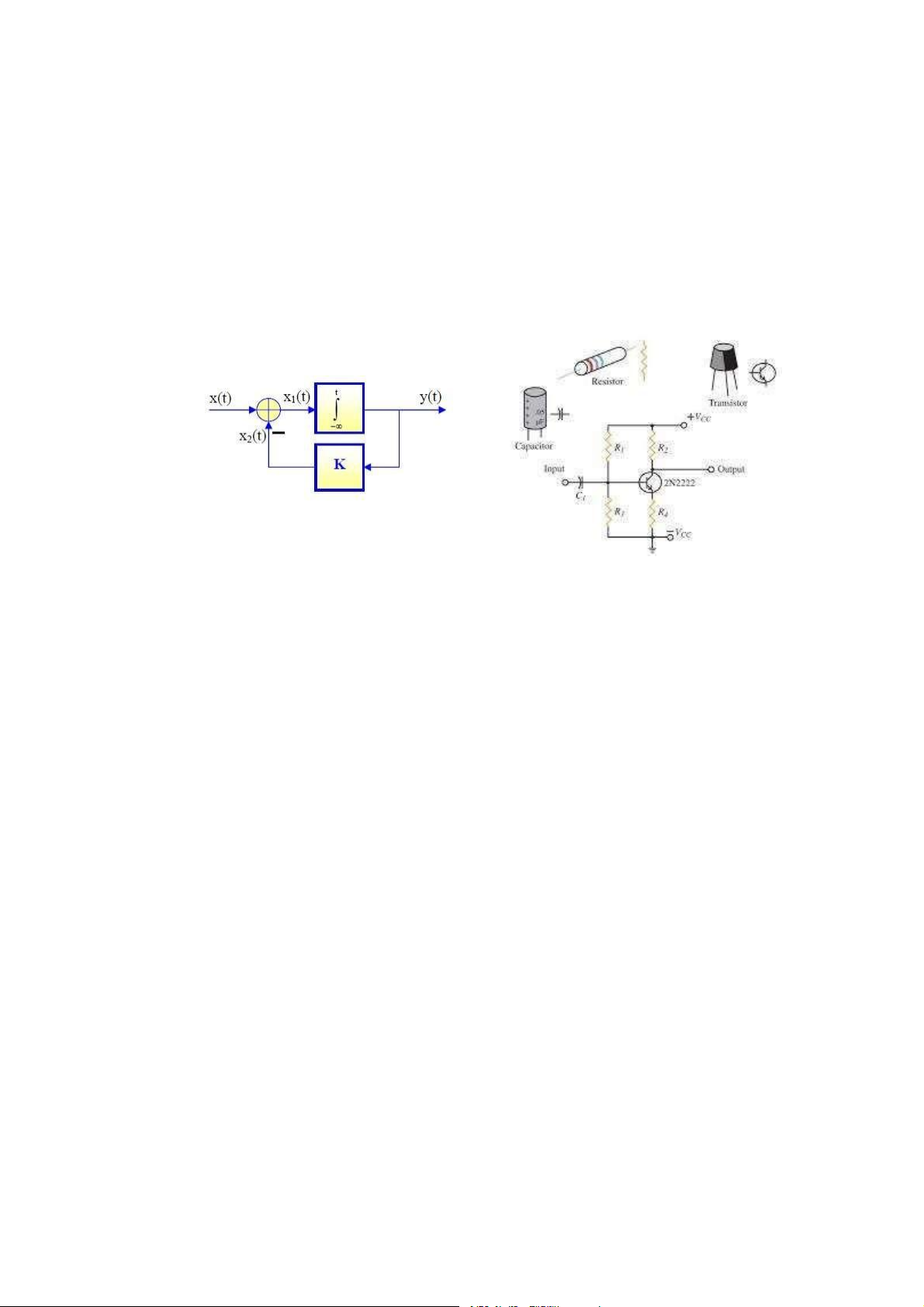
Trong ệ thống hồi tiếp, tín hiệu đầu ra được đưa trở lại đầu vào và kết hợp với tín
hiệu đầu vào của hệ thống. Đây là kiểu hệ thống quan trọng, có ứng dụng rộng rãi. BÀI TẬP CHƯƠNG 1
CHƯƠNG 2: HỆ THỐNG TUYẾN TÍNH BẤT BIẾN THEO THỜI GIAN
2.1 HỆ THỐNG LTI LIÊN TỤC
Mục 1.4 đã trình bày rất nhiều loại hệ thống với các đặc trưng cơ bản khác
nhau. Trong số đó, hệ thống tuyến tính bất biến theo thời gian (LTI) đóng vai trò
quan trọng phân tích hệ thống và xử lý tín hiệu. Thứ nhất là do rất nhiều đặc trưng
của các quá trình vật lý khác nhau đều có thể mô hình hoá dưới dạng các hệ thống
tuyến tính bất biến theo thời gian. Thứ hai là hệ thống LTI được phân tích một
cách chi tiết, cung cấp thông tin chi tiết về các thuộc tính của nó cũng như tạo ra
một bộ công cụ phân tích mạnh làm nền tảng cho hoạt động phân tích hệ thống và xử lý tín hiệu.
Một trong những đặc trưng quan trọng của tín hiệu xung đơn vị, đối với cả
tín hiệu liên tục và rời rạc theo thời gian, đó là có thể biểu diễn bất kì một tín hiệu
nào dưới dạng tổ hợp tuyến tính của tập các xung đơn vị ở các thời điểm khác
nhau. Vì thế, hoàn toàn phân tích được đầy đủ đáp ứng đầu ra của một hệ thống
LTI bất kì bằng cách coi đầu vào hệ thống là một tập các xung đơn vị chồng chất.
2.1.1 Đáp ứng của hệ thống LTI liên tục và tích chập
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 36 Đáp ứng xung
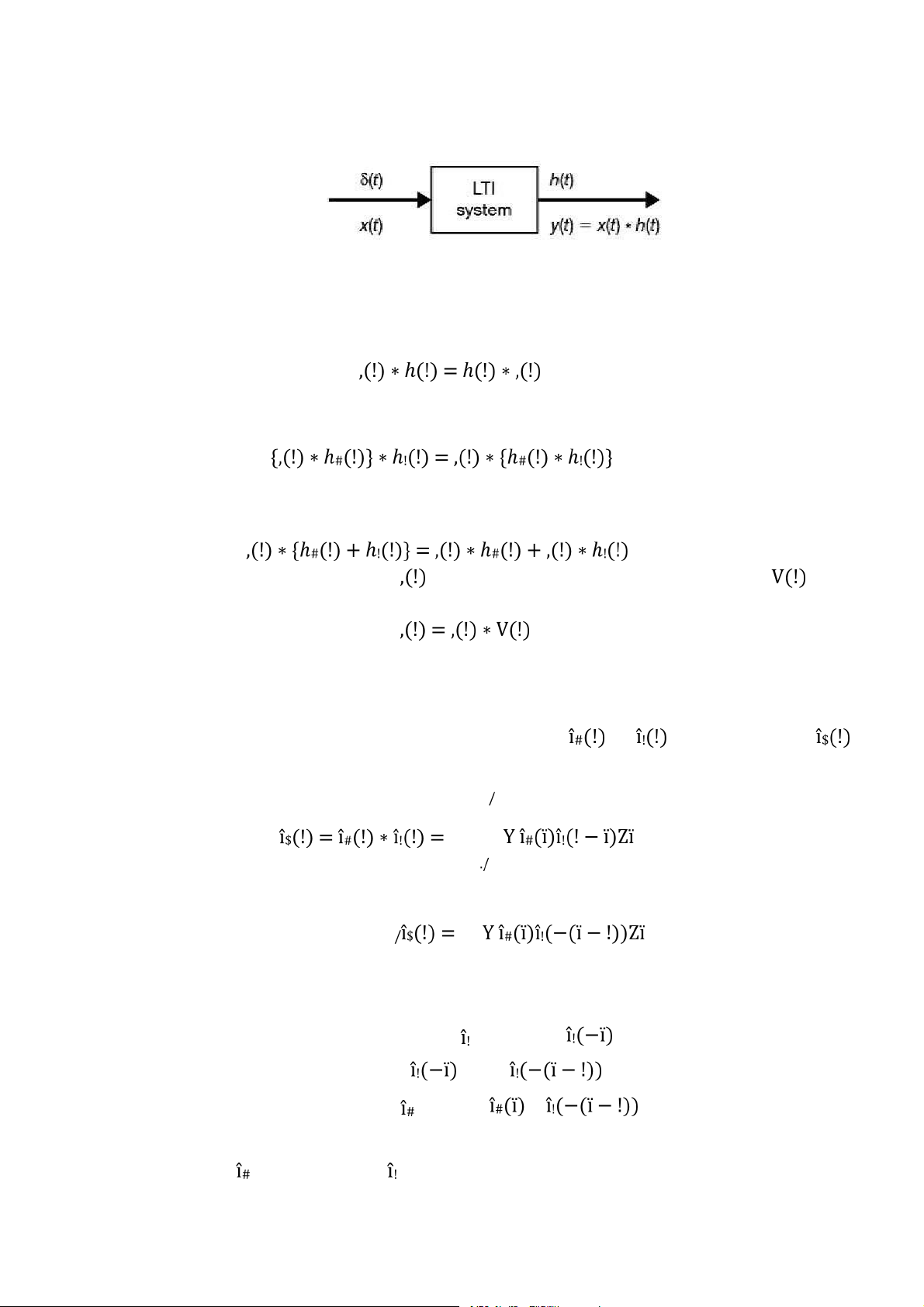
của một hệ thống LTI liên tục theo thời gian (được đặc trưng bởi
) được định nghĩa là đáp ứng của hệ thống khi đầu vào là xung đơn vị , tức là (2.1)
Khi tín hiệu đầu vào là
bất kì, áp dụng biểu thức (1.21) để biểu diễn tín hiệu thông qua
. Do hệ thống là tuyến tính, đáp ứng của hệ thống khi đầu vào là tín hiệu bất kì được biểu diễn như sau ./
Do hệ thống là bất biến, sẽ có (2.3)
Thay (2.3) vào (2.2), thu được đáp ứng
của hệ thống LTI khi đầu vào là tín hiệu bất kì có dạng
Như vậy, một hệ thống LTI liên tục theo thời gian hoàn toàn được đặc trưng bởi đáp ứng xung của nó.
Biểu thức (2.4) định nghĩa tích chập giữa hai tín hiệu liên tục theo thời gian và . Đầu ra
của một hệ thống LTI liên tục theo thời gian bất kì là tích
chập giữa tín hiệu đầu vào và hàm đáp ứng xung .
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 37
Hình 2.1: Hệ thống LTI liên tục theo thời gian
Một số tính chất của tích chập - Tính giao hoán (2.6) - Tính kết hợp (2.7) - Tính phân bố (2.8)
- Đối với bất kì tín hiệu
nào cũng đều có thể biểu diễn thông qua dưới dạng tích chập (2.9)
Tính tích chập của hai tín hiệu liên tục theo thời gian bất kì được thực hiện
theo một trong hai cách, đó là theo định nghĩa hoặc theo phương pháp đồ thị.
- Theo định nghĩa: tích chập của hai tín hiệu và sẽ tạo ra tín hiệu
được tính theo công thức sau
- Theo phương pháp đồ thị: sử dụng công thức tương đương sau (2.10) ./
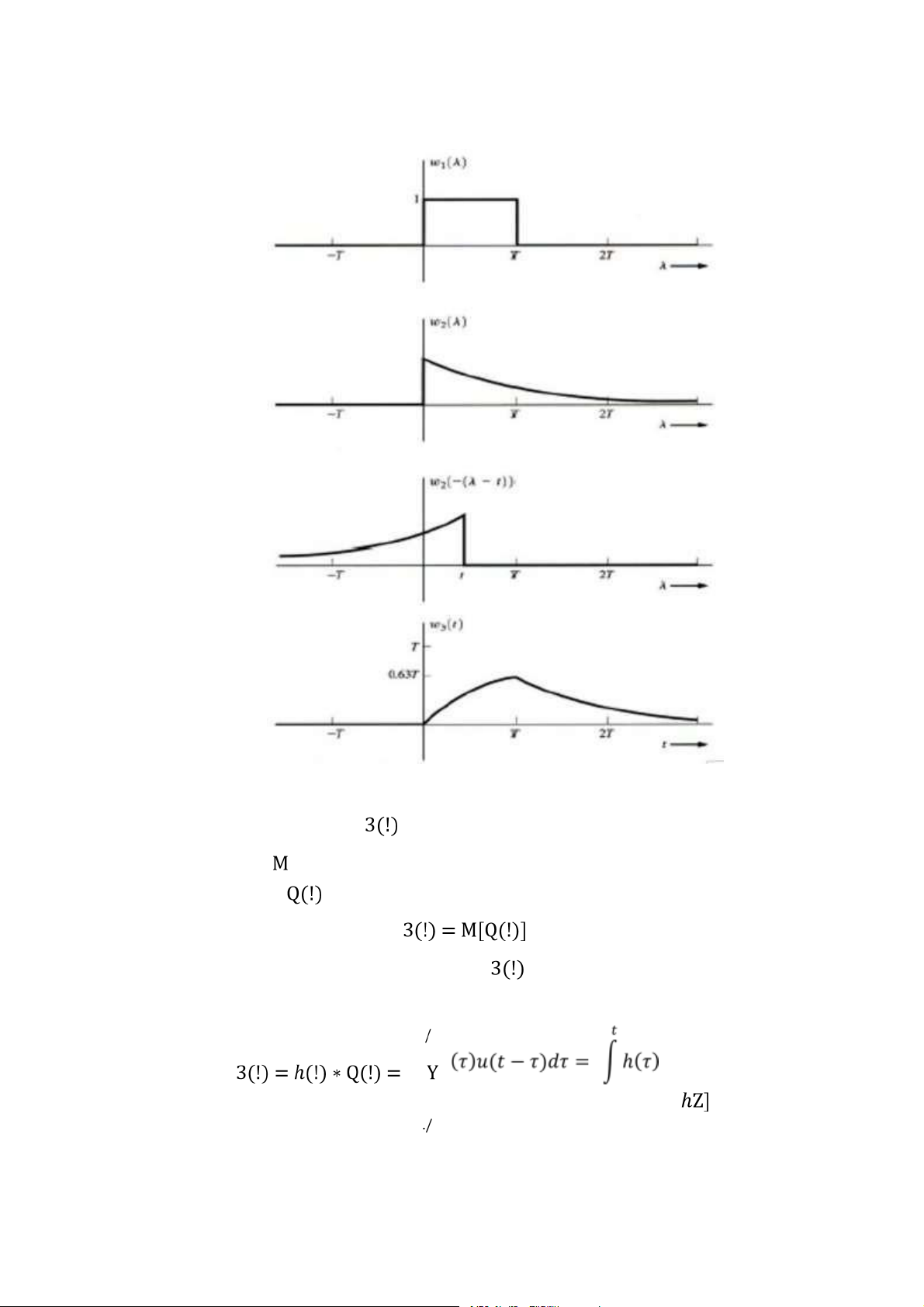
Dựa trên công thức này, thực hiện các bước sau để tính tích chập
+ Đảo ngược thời gian của (ï) để được + Dịch thời gian của để có
+ Nhân kết quả với (ï) để có
Chú ý rằng, tích chập có tính giao hoán nên hoàn toàn có thể thực hiện các
bước trên (ï) thay cho trên (ï).
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 38
Ví dụ 6: Tính tích chập của hai tín hiệu và với Lời giải: Lựa chọn
để thực hiện các bước trên Với ! < 0, Với , Với ! ≥ J, Kết quả thu được
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 39
Hình 2.2: Tích chập của xung chữ nhật và xung hàm mũ Đáp ứng nhảy bậc
của một hệ thống LTI liên tục theo thời gian (được
đặc trưng bởi ) được định nghĩa là đáp ứng của hệ thống khi đầu vào là xung nhảy bậc đơn vị , tức là (2.11)
Trong nhiều ứng dụng, đáp ứng nhảy bậc
cũng là một đăc trưng hữu ích của hệ thống và có thể được xác định bởi tích chập sau (2.12) ./
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 40
Như vậy, đáp ứng nhảy bậc 3(!) có thể thu được nhờ lấy tích phân của hàm đáp ứng
xung ℎ(!). Đạo hàm biểu thức (1.91) theo !, thu được Z3(!) (2.13)
Có thêm một cách khác nữa để xác định đáp ứng xung ℎ(!) của hệ thống, đó là lấy
đạo hàm đáp ứng nhảy bậc 3(!). Đây là giải pháp thường được sử dụng để xác
định đáp ứng xung của hệ thống trong thực tế.
2.1.2 Các hệ thống LTI liên tục
Nhờ đặc trưng tuyến và bất biến theo thời gian, các hệ thống LTI được sử dụng để
xây dựng các hệ thống phức tạp hơn bằng cách tổ hợp chúng theo nhiều cách khác
nhau như nối tiếp, song song, kết hợp.
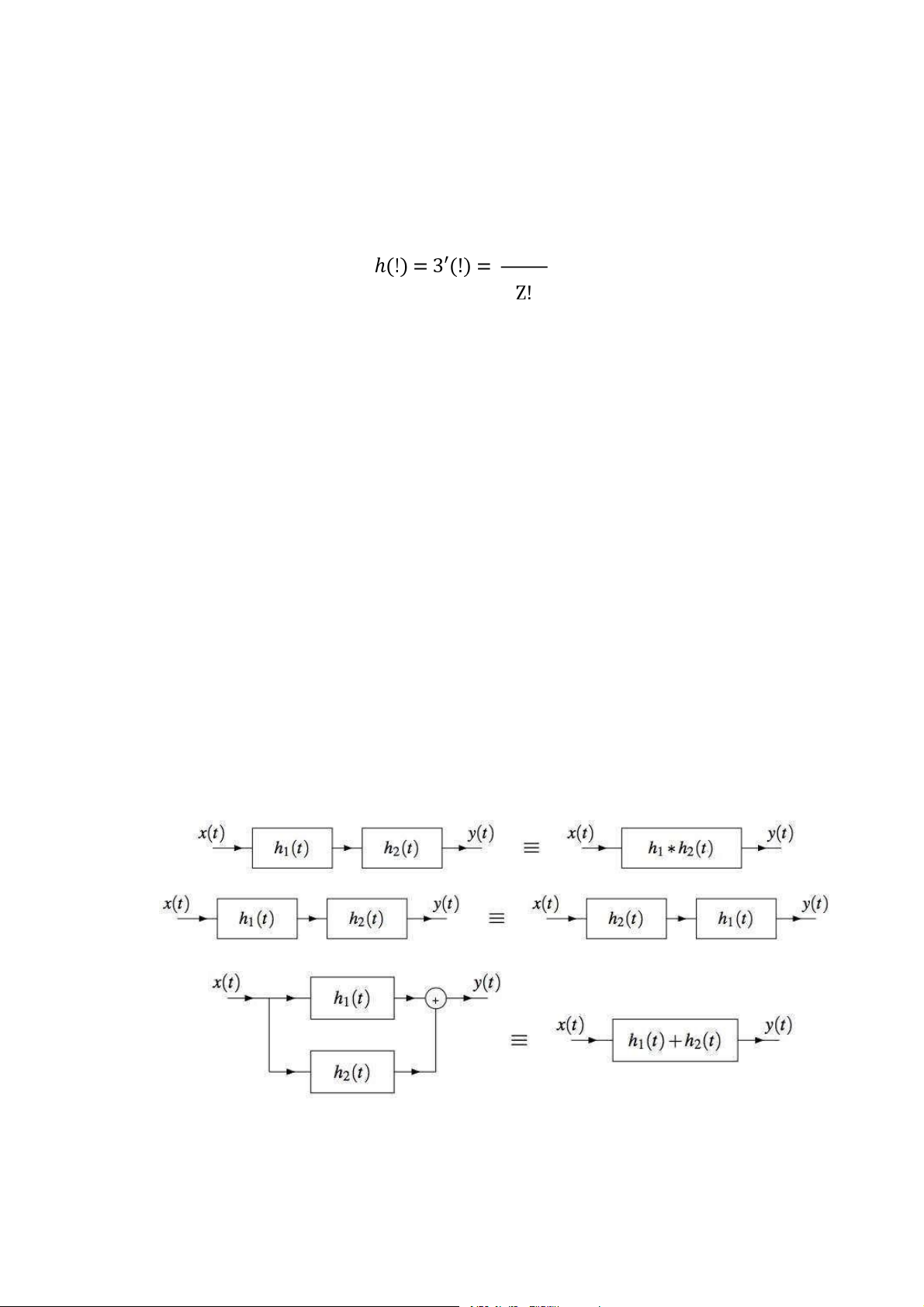
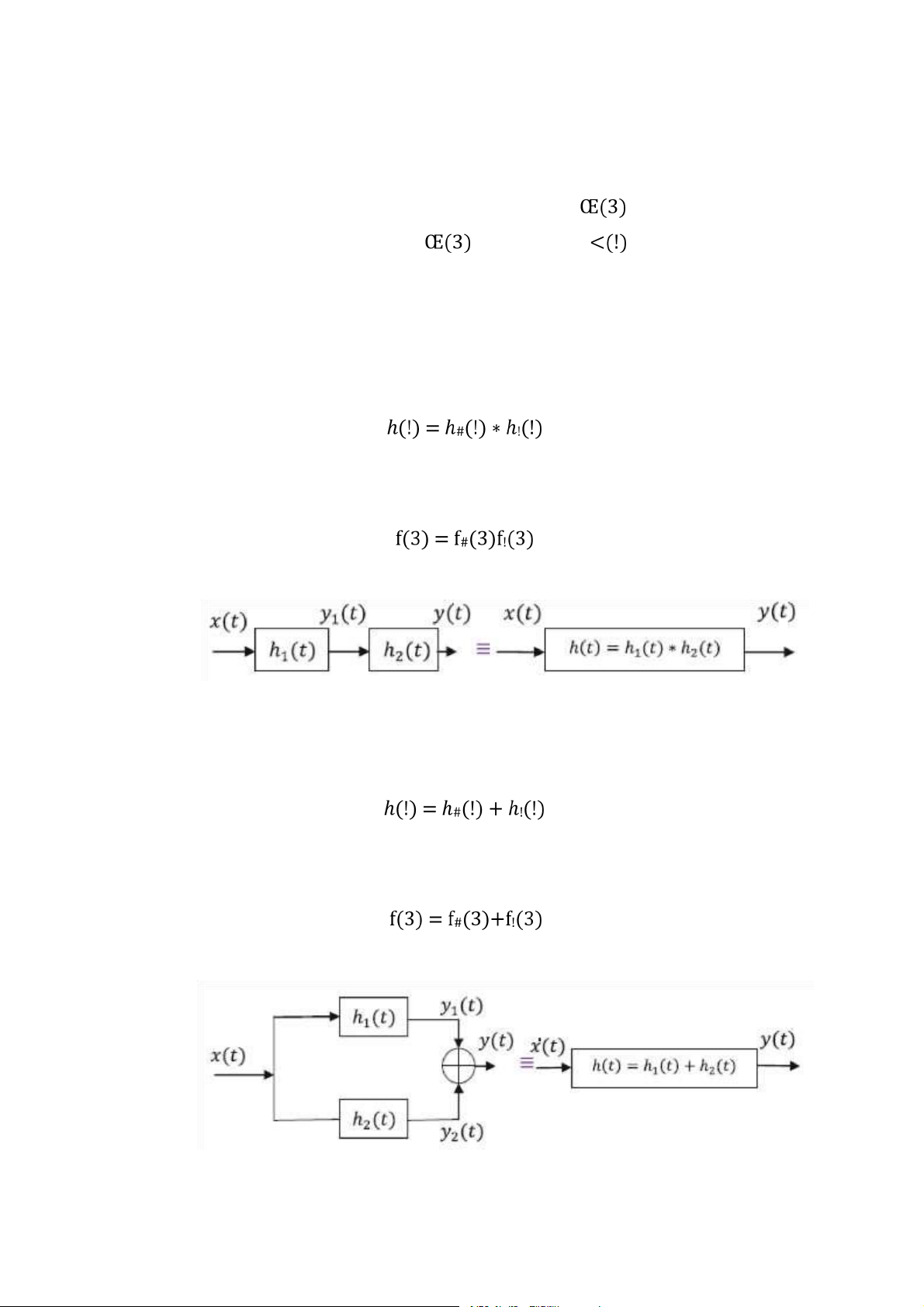
Đáp ứng xung của hệ thống gồm nhiều hệ thống LTI mắc nối tiếp là tích chập của
đáp ứng xung các hệ thống LTI thành phần. Đáp ứng xung của hệ thống gồm
nhiều hệ thống LTI mắc song song là tổng của đáp ứng xung các hệ thống LTI
thành phần. Nếu ℎ#(!) và ℎ!(!) lần lượt là đáp ứng xung của các hệ thống LTI thành phần, khi
đó đáp ứng xung của hệ thống tổ hợp được tính như sau. a) b)
Hình 2.2: a) Hệ thống LTI nối tiếp, b) Hệ thống LTI song song
2.1.3 Các đặc trưng của hệ thống LTI liên tục
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 41
2.1.3.1 Hệ thống LTI có nhớ Tín hiệu đầu ra
của hệ thống không nhớ chỉ phụ thuộc vào tín hiệu đầu vào
ở thời điểm hiện tại. Nếu hệ thống là tuyến tính và bất biến theo thời gian, thì
mối quan hệ này được biểu diễn như sau (2.14)
với là hằng số. Như vậy, đáp ứng xung
tương ứng của hệ thống sẽ là (2.15) Như vậy, nếu khi
thì hệ thống LTI liên tục theo thời gian là hệ thống có nhớ.
2.1.3.2 Hệ thống LTI nhân quả
Hệ thống LTI liên tục theo thời gian sẽ nhân quả khi đáp ứng xung thoả mãn điều kiện ! < 0 (2.16)
Áp dụng điều kiện này vào biểu thức (2.5), thu được đáp ứng đầu ra của hệ thống LTI
liên tục theo thời gian nhân quả có dạng sau (2.17)
Như vậy, chỉ những giá trị của tín hiệu đầu vào
trong khoảng ] ≤ ! được sử dụng
để tính các giá trị đầu ra .
Nếu tín hiệu đầu vào của hệ thống là nhân quả, tức là , thì tín hiệu
đầu ra của hệ thống LTI liên tục theo thời gian nhân quả sẽ là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 42
<(!) = Y ℎ(]),(! − ])Z] = Y ,(])ℎ(! − ])Z] (2.18)
2.1.3.3 Hệ thống LTI ổn định
Tính ổn định của hệ thống LTI hoàn toàn xác định được dễ dàng từ đáp ứng xung
của nó. Một hệ thống LTI liên tục theo thời gian được gọi là ổn định nếu đáp ứng xung của nó là khả tích tuyệt đối, tức là ./
2.1.3.4 Hệ thống LTI nghịch đảo
Một hệ thống được gọi là nghịch đảo nếu tín hiệu đầu vào có thể khôi phục được
khi đưa tín hiệu đầu ra của nó tới đầu vào của hệ thống. Nếu hệ thống LTI tồn tại
hệ thống nghịch đảo của nó thì hệ thống nghịch đảo cũng là LTI. Khi đưa tín hiệu
tới đầu vào hệ thống LTI có đáp ứng xung
, thì đầu ra của hệ thống nghịch đảo có đáp ứng xung sẽ là (2.21) Như vậy, tức là (2.22)
Hệ thống LTI nghịch đảo có đáp ứng xung là nghịch đảo của đáp ứng xung hệ thống LTI ban đầu.
Hình 2.3: Hệ thống LTI và hệ thống nghịch đảo của nó
2.1.4 Biểu diễn hệ thống bằng phương trình vi phân
Phương trình vi phân được sử dụng để mô hình hoá cho các hệ thống và hiện
tượng vật lý khác nhau. Đối với các hệ thống vật lý, phương trình vi phân được
thiết lập để mô tả các định luật vật lý mà hoạt động của hệ thống tuân theo. Các hệ
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 43
thống tuyến tính bất biến theo thời gian được biểu diễn bởi các phương trình vi
phân hệ số hằng. Phương trình vi phân cung cấp hiểu biết về bản chất của hệ thống,
mô tả chi tiết mối quan hệ giữa đầu vào và đầu ra của hệ thống. Phương trình vi
phân tuyến tính hệ số hằng bậc P có dạng như sau & Z9<(!) G Z9,(!) (2.23) 9:* 9:*
với [9, ë9 là các hệ số hằng. P chính là đạo hàm bậc lớn nhất của <(!). Phương
trình vi phân này biểu diễn tín hiệu lối ra như là một hàm theo tín hiệu lối vào. Vì
thế, để tìm được đáp ứng của hệ thống cần thực hiện giải phương trình vi phân
tuyến tính. Nghiệm tổng quát của phương trình (1.101) đối với tín hiệu đầu vào ,(!) cụ thể sẽ có dạng <(!) = (2.24)
trong đó, là nghiệm đồng nhất hay nghiệm bù của hệ thống.
Nghiệm đồng nhất ứng của hệ thống khi khi không có đầu vào kích thích. Nghiệm đồng nhất thu được
khi giải phương trình vi phân đồng nhất dưới đây, phương trình (2.23) khi vế phải bằng 0.
Nghiệm riêng đầu vào ,(!) cụ thể khi các điều kiện ban đầu xác định. Nghiệm riêng cùng dạng với đầu vào ,(!), đặc trưng cho đáp ứng cưỡng bức của hệ thống. Cần
chú ý rằng, không thể xác định được đầu ra <(!) theo đầu vào ,(!) nếu các điều
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 44
kiện ban đầu chưa được xác định. Mặc dù có cùng đầu vào ,(!) nhưng tùy thuộc
đặc trưng của hệ thống mà các điều kiện ban đầu có thể khác nhau vì thế nghiệm
riêng là khác nhau. Có thể nói, giá trị chính xác của nghiệm riêng phụ thuộc
vào điều kiện ban đầu của hệ thống. Nhìn chung, tập các điều kiện ban đầu chính
là các giá trị của đầu ra và các đạo hàm bậc nhỏ hơn của nó, …,
, tại một thời điểm cụ thể.
Hệ thống LTI được mô tả bởi phương trình (2.23) chỉ tuyến tính khi tất cả điều kiện
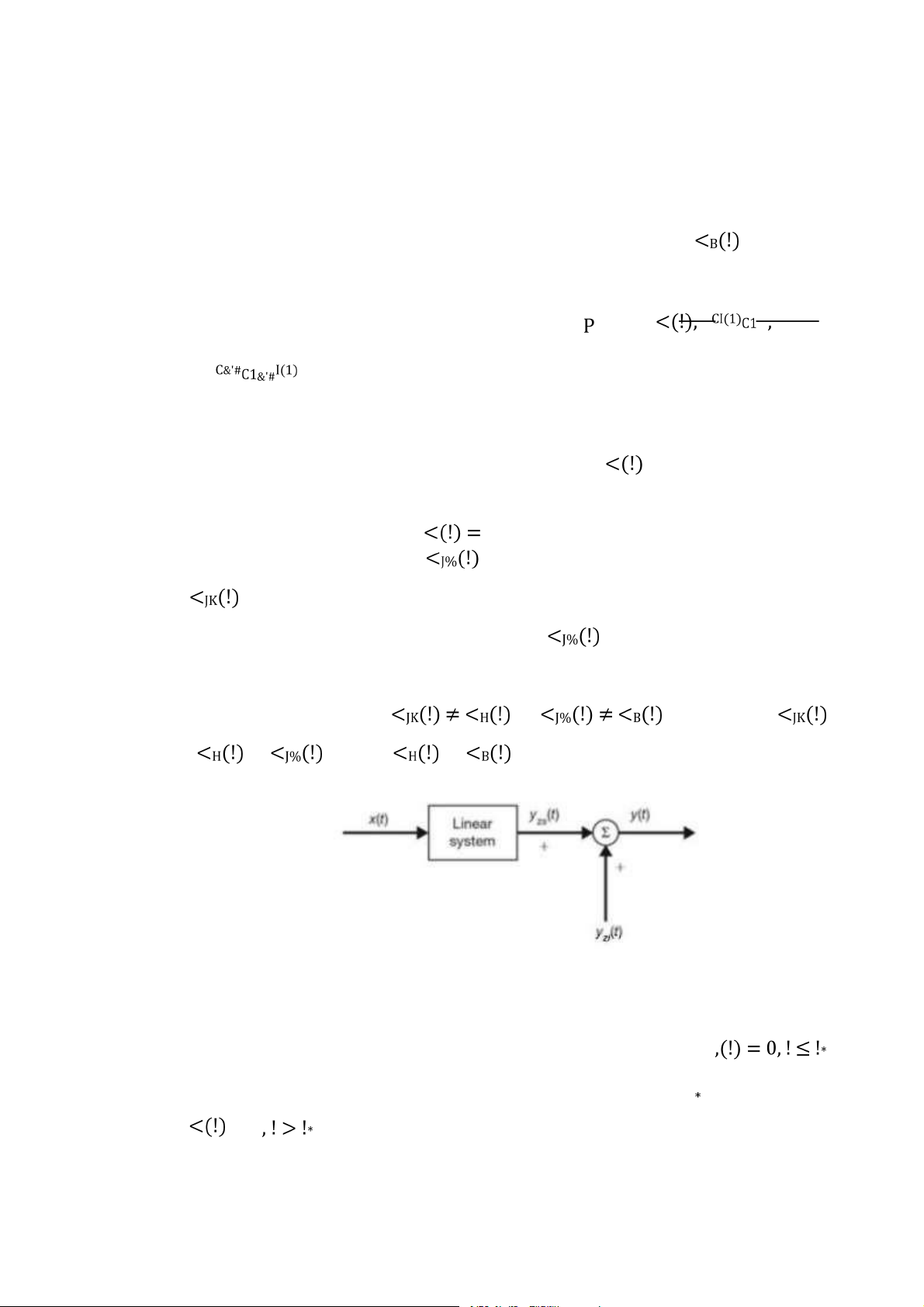
ban đầu bằng 0. Nếu điều kiện ban đầu khác 0, đáp ứng của hệ thống có thể biểu diễn như sau với,
, được gọi là đáp ứng đầu vào 0 (zero-input response), chính là đáp ứng
của hệ thống với điều kiện ban đầu hiện có, và
, được gọi là đáp ứng trạng
thái 0 (zero-state input), chính là đáp ứng của hệ thống tuyến tính khi điều kiện
ban đầu bằng 0. Chú ý rằng, và và về cơ bản chứa và chứa cả và .
Hình 2.4: Đáp ứng trạng thái 0 và đáp ứng đầu vào 0
Hệ thống LTI được mô tả bởi phương trình (2.23) sẽ nhân quả chỉ khi giả
thiết rằng điều kiện ban đầu là nghỉ (initial rest). Tức là, nếu đầu vào ,
thì giả thiết rằng đầu ra cũng thoả mãn điều kiện <(!) = 0, ! ≤ ! . Như vậy, đáp ứng khi
có thể tính được từ phương trình (1.101) với các điều kiện ban đầu như sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 45 với
Như vậy, tại điều kiện ban đầu nghỉ .
Các hệ thống LTI tuyến tính nhân quả thì nếu điều kiện ban đầu là nghỉ thì nó
cũng thoả mãn tính chất bất biến theo thời gian. Đáp ứng xung
của hệ thống LTI liên tục theo thời gian cũng thoả mãn
phương trình (2.23) nếu thoả mãn điều kiện ban đầu là nghỉ, tức là (2.28)
Giải phương trình vi phân tuyến tính hệ số hằng được thực hiện như sau:
- Tìm nghiệm đồng nhất:
Phương trình vi phân đồng nhất (vế phải bằng 0) có nghiệm dạng với là một biến phức, thay vào
phương trình đồng nhất ta có
Khi đó, là nghiệm của phương trình đại số tuyến tính bậc , hay còn được gọi là
phương trình đặc trưng, của hệ thống
Gọi các nghiệm của phương trình đặc trưng là
với ( = 1, … , P, thì nghiệm tổng
quát của phương trình đồng nhất sẽ có dạng sau
+ Nếu là các nghiệm đơn &
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 46 (2.31) K:#
+ Nếu 39là các nghiệm có bội bậc zK B(.# (2.32) K 9:#
Giá trị của các hệ số 1K được xác định tử điều kiện ban đầu. - Tìm nghiệm riêng
Để xác định nghiệm riêng có dạng tượng tự tín hiệu đầu vào ,(!) với một vài hệ số chưa biết, thay nghiệm này
vào phương trình vi phân để xác định các hệ số này. Cần lưu ý khi lựa chọn dạng
của + Nếu ^(1 không phải là một thành phần của 1^(1
+ Nếu [ là một nghiệm đơn của phương trình đặc trưng thì ^(1 là một thành
phần của + Nếu [ là một nghiệm bội bậc z của phương trình đặc trưng thì ^(1, !^(1,
…, !B.#^(1 là các thành phần của 1!B^(1
Ví dụ 7: Xác định đáp ứng của hệ thống khi đầu vào ,(!) và đầu ra <(!) của hệ thống được đặc trưng bởi
phương trình vi phân sau với điều kiện ban đầu <(0) = 0 .!1Q(!) Lời giải:
- Xác định nghiệm riêng Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 47
Do tín hiệu đầu vào ,(!) = ^.!1Q(!) nên nghiệm riêng phải có dạng Thay
vào phương trình vi phân, sẽ có ! > 0 ! > 0
- Xác định nghiệm đồng nhất
Giả thiết nghiệm đồng nhất có dạng Thay
vào phương trình vi phân, sẽ có
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 48
Khi đó, nghiệm tổng quát là
Tại điều kiện ban đầu ! = 0
Như vậy, nghiệm tổng quát của phương trình vi phân hay chính là đáp ứng đầu ra của
hệ thống với điều kiện ban đầu đã cho, sẽ là
2.2 HỆ THỐNG LTI RỜI RẠC
Biểu diễn và các đặc trưng của hệ thống LTI rời rạc theo thời gian hoàn toàn
tương tự như hệ thống LTI liên tục theo thời gian và có thể thu được từ hệ thống
LTI liên tục theo thời gian nhờ quá trình rời rạc hoá.
2.2.1 Đáp ứng của hệ thống LTI rời rạc và tổng chập
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 49 Đáp ứng xung
của một hệ thống LTI rời rạc theo thời gian (được đặc trưng bởi
) được định nghĩa là đáp ứng của hệ thống khi đầu vào là xung đơn vị , tức là (2.33)
Khi tín hiệu đầu vào là chuỗi
bất kì, áp dụng biểu thức (1.43) để biểu diễn tín hiệu thông qua
. Do hệ thống là tuyến tính, đáp ứng của hệ
thống khi đầu vào là tín hiệu
bất kì được biểu diễn như sau (2.34) 9:./
Do hệ thống là bất biến, sẽ có [. − (] = M[V[. − (]] (2.35)
Thay (2.35) vào (2.34), thu được đáp ứng
của hệ thống LTI khi đầu vào là tín hiệu bất kì có dạng
Như vậy, một hệ thống LTI rời rạc theo thời gian cũng hoàn toàn được đặc trưng bởi đáp ứng xung của nó.
Biểu thức (2.36) định nghĩa tổng chập giữa hai tín hiệu rời rạc theo thời gian và . Đầu ra
của một hệ thống LTI rời rạc theo thời gian bất kì là tổng
chập giữa tín hiệu đầu vào và hàm đáp ứng xung . (2.37) 9:./
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 50
Hình 2.5: Hệ thống LTI rời rạc theo thời gian
Một số tính chất của tổng chập - Tính giao hoán (2.38) - Tính kết hợp (2.39) - Tính phân bố (2.40)
- Đối với bất kì tín hiệu
nào cũng đều có thể biểu diễn thông qua dưới dạng tổng chập (2.41)
Tính tổng chập của hai tín hiệu rời rạc theo thời gian bất kì được thực hiện
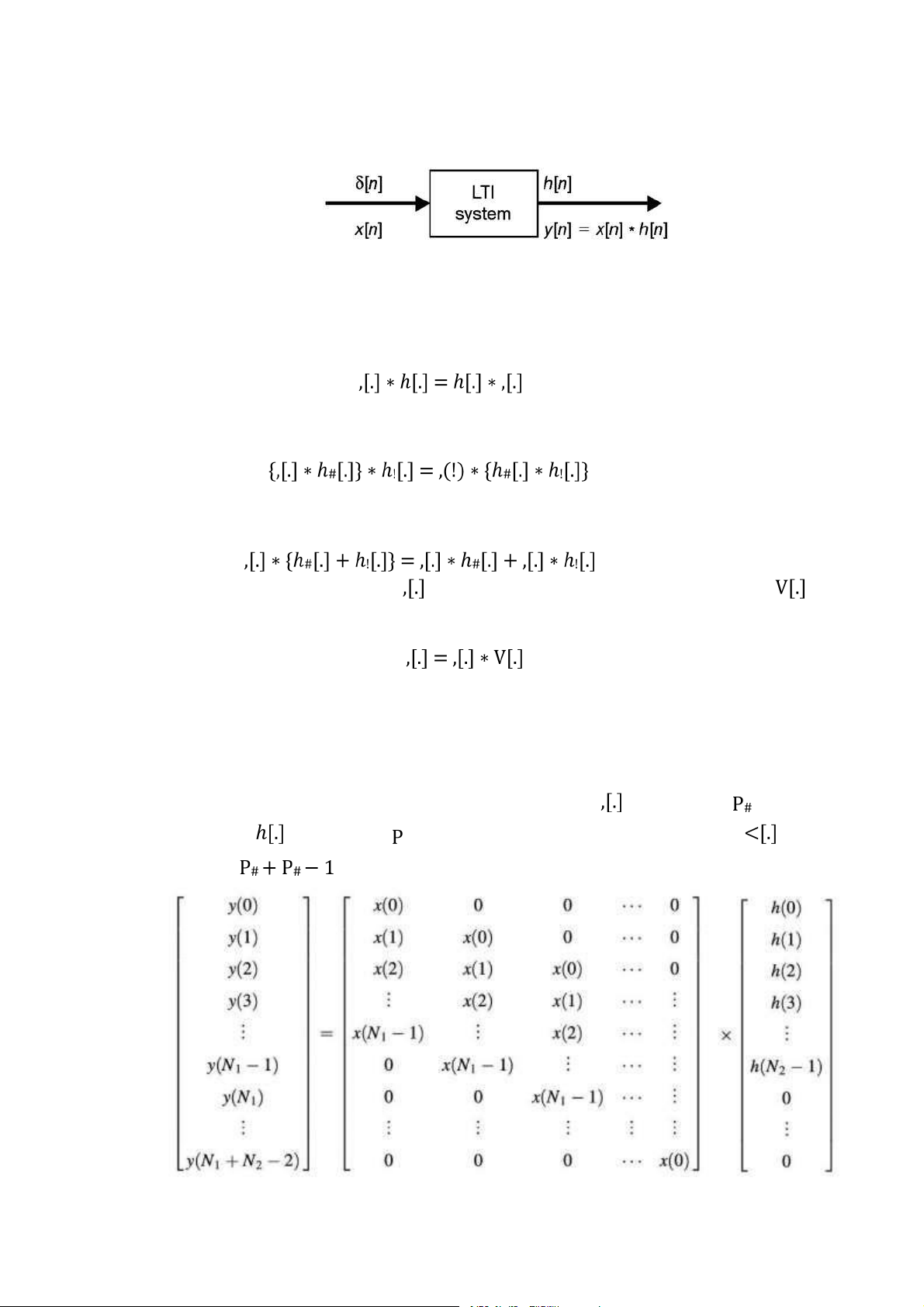
theo một trong hai cách, đó là theo phương pháp ma trận hoặc theo phương pháp đồ thị.
- Theo phương pháp ma trận: nếu chuỗi đầu vào có chiều dài và đáp ứng xung
có chiều dài ! thì tổng chập của hai tín hiệu sẽ là chuỗi có chiều dài
và được tính dưới dạng ma trận sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 51
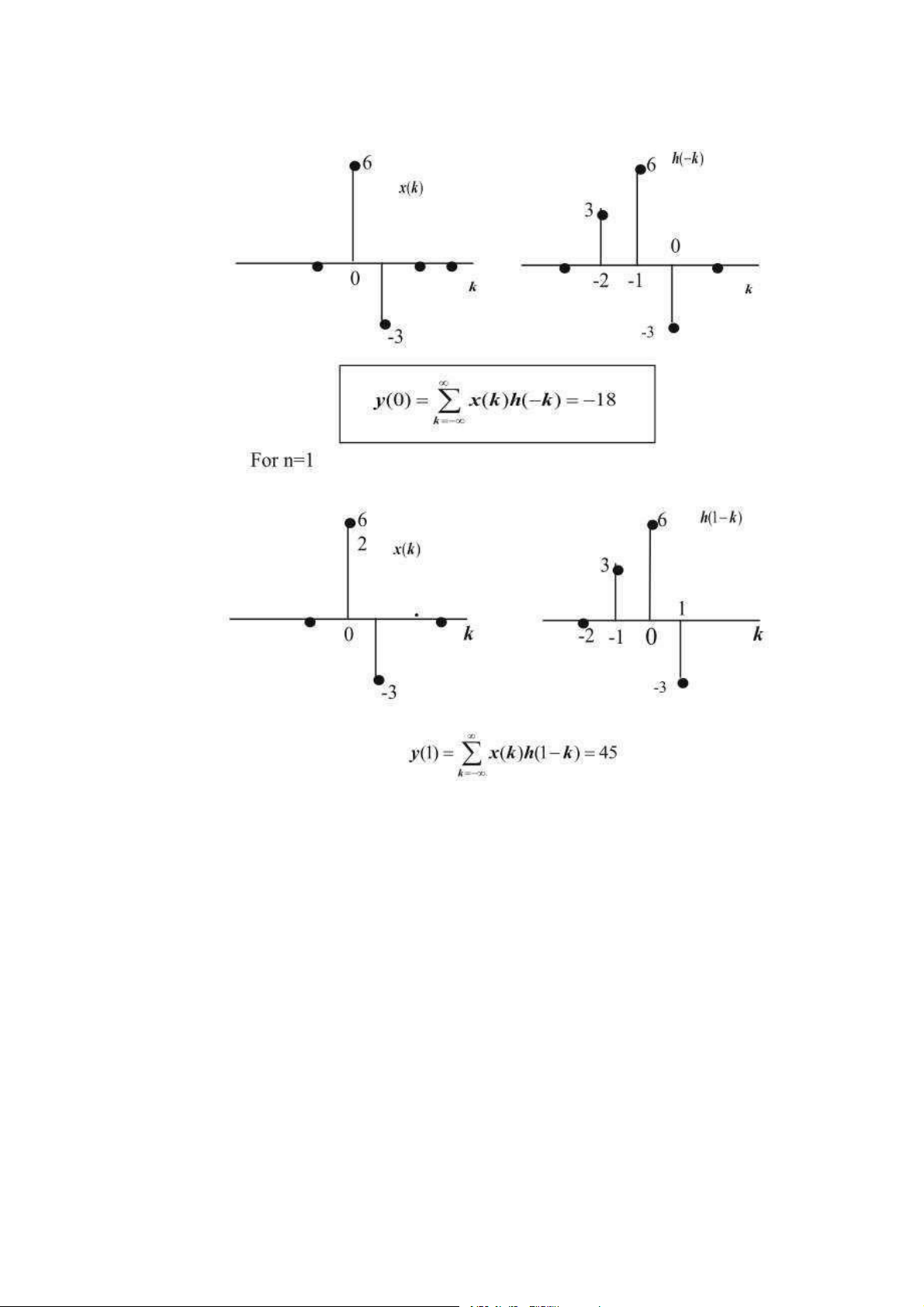
- Theo phương pháp đồ thị: nếu có chuỗi đầu vào ,[.] và đáp ứng xung ℎ[.], thực
hiện các bước sau để tính tổng chập
+ Đảo ngược thời gian của ℎ[(] để được ℎ[−(] (lấy đối xứng qua trục tung)
+ Dịch đi . để thu được ℎ[. − (] = ℎ[−(( − .)] (hàm theo (, . là tham số)
+ Nhân giá trị ,[(] với ℎ[. − (] tại từng vị trí của ( ứng với một . xác định
+ Tại một giá trị của ., thu được <[.] tương ứng bằng cách cộng tất cả các tích ,[(]ℎ[. − (]
+ Lặp lại lần lượt các bước trên với . thay đổi từ −∞ đến +∞ để thu được toàn bộ đầu ra <[.]
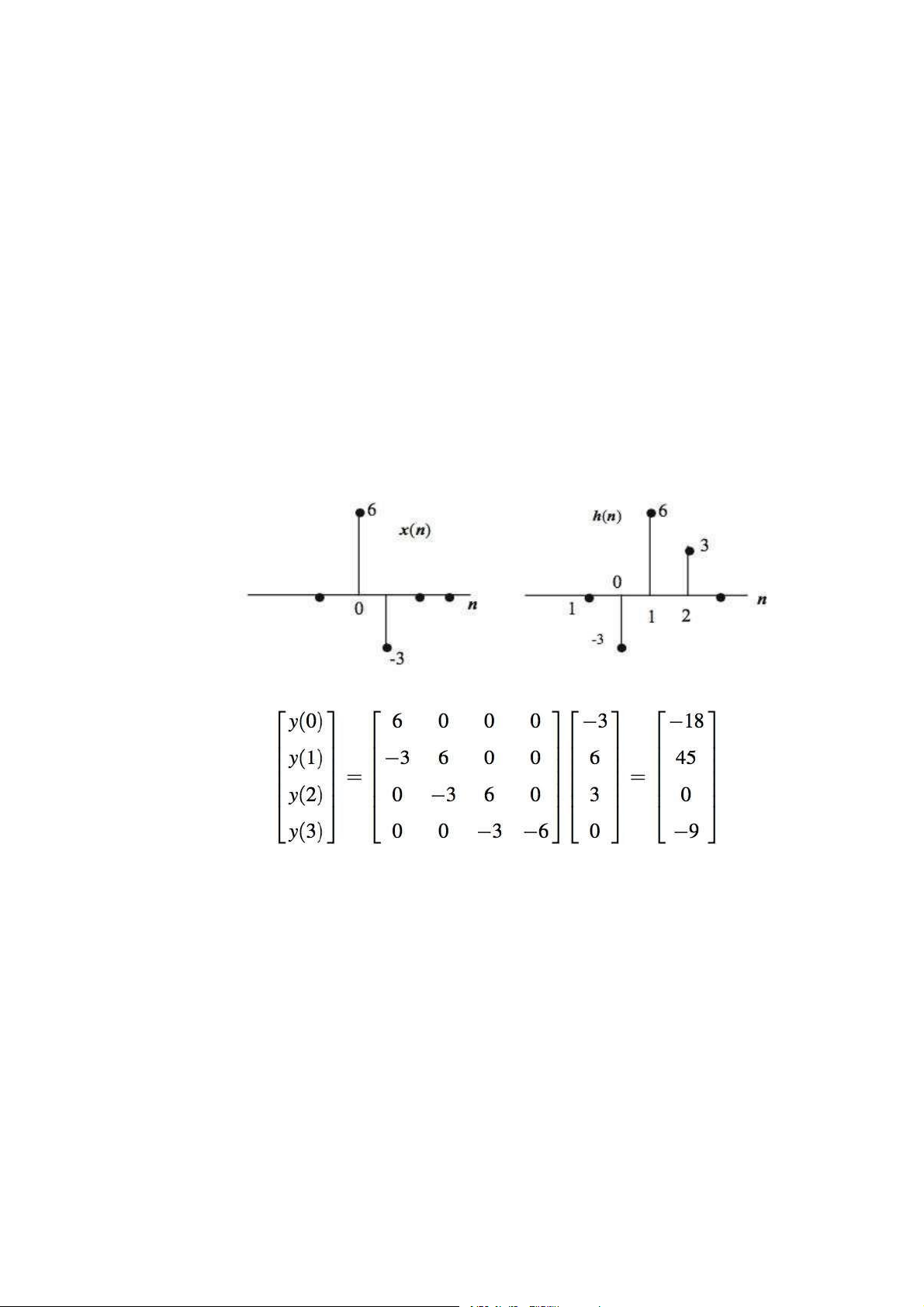
Ví dụ 8: Tính tổng chập của chuỗi ,[.] = {6, −3} và ℎ[.] = {−3, 6, 3} Lời giải:
- Theo phương pháp ma trận, thu được
Như vậy, đầu ra <[.] = {−18, 45, 0, −9}
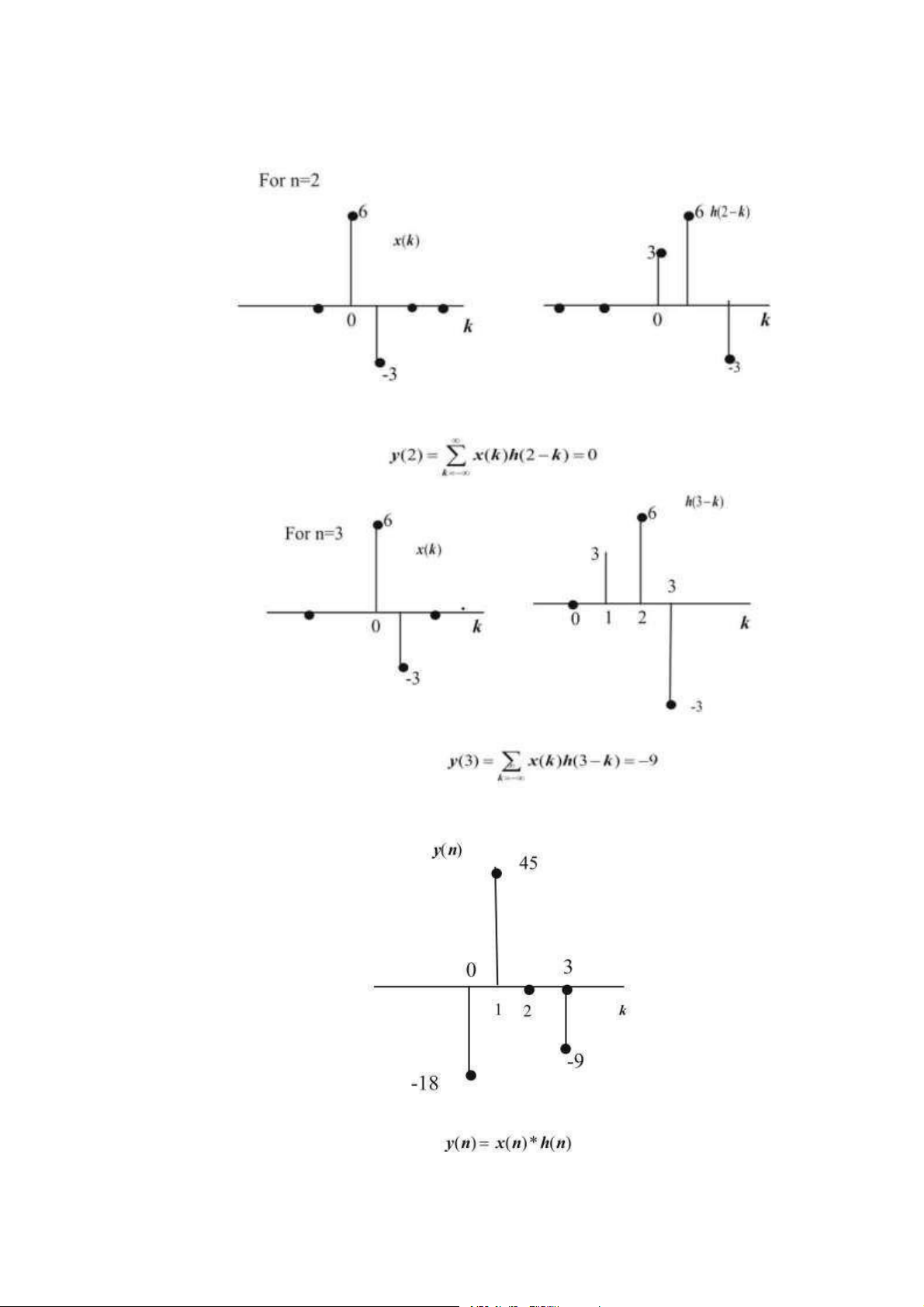
- Theo phương pháp đồ thị
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 52
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 53
Như vậy, đầu ra <[.] là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 54 Đáp ứng nhảy bậc
của một hệ thống LTI rời rạc theo thời gian (được
đặc trưng bởi ) được định nghĩa là đáp ứng của hệ thống khi đầu vào là xung nhảy bậc đơn vị , tức là
Trong nhiều ứng dụng, đáp ứng nhảy bậc
cũng là một đăc trưng hữu ích của hệ
thống và có thể được xác định bởi tổng chập sau (2.43) 9:./ 9:./
Từ phương trình (2.43) thu được (2.44)
Có thêm một cách khác nữa để xác định đáp ứng xung
của hệ thống. Các phương
trình (2.43) và (2.44) chính là rời rạc hoá các phương trình (2.12) và (2.13).
2.2.2 Các hệ thống LTI rời rạc
Nhờ đặc trưng tuyến và bất biến theo thời gian, các hệ thống LTI rời rạc được sử
dụng để xây dựng các hệ thống phức tạp hơn bằng cách tổ hợp chúng theo nhiều
cách khác nhau như nối tiếp, song song, kết hợp. Các cách kết hợp hệ thống LTI
rời rạc hoàn toàn giống với cách kết hợp hệ thống LTI liên tục theo thời gian.
2.2.3 Các đặc trưng của hệ thống LTI rời rạc
2.2.3.1 Hệ thống LTI có nhớ Tín hiệu đầu ra
của hệ thống không nhớ chỉ phụ thuộc vào tín hiệu đầu vào
ở thời điểm hiện tại. Nếu hệ thống là tuyến tính và bất biến theo thời gian, thì mối
quan hệ này được biểu diễn như sau (2.45)
với là hằng số. Như vậy, đáp ứng xung
tương ứng của hệ thống sẽ là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 55 (2.46) Như vậy, nếu khi
thì hệ thống LTI rời rạc
theo thời gian là hệ thống có nhớ.
2.2.3.2 Hệ thống LTI nhân quả
Hệ thống LTI rời rạc theo thời gian sẽ nhân quả khi đáp ứng xung thoả mãn điều kiện (2.47)
Áp dụng điều kiện này vào biểu thức (2.36), thu được đáp ứng đầu ra của hệ thống
LTI rời rạc theo thời gian nhân quả có dạng sau (2.48)
Như vậy, chỉ những giá trị của tín hiệu đầu vào
trong khoảng ( ≤ . được sử dụng
để tính các giá trị đầu ra .
Nếu tín hiệu đầu vào của hệ thống là nhân quả, tức là , thì tín hiệu
đầu ra của hệ thống LTI rời rạc theo thời gian nhân quả sẽ là
<[.] = p ℎ[(],[. − (] = p ,[(]ℎ[. − (] (2.49)
2.2.3.3 Hệ thống LTI ổn định
Tính ổn định của hệ thống LTI hoàn toàn xác định được dễ dàng từ đáp ứng xung
của nó. Một hệ thống LTI rời rạc theo thời gian được gọi là ổn định nếu đáp ứng
xung của nó có tổng tuyệt đối, tức là 9:./
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 56
2.2.4 Biểu diễn hệ thống bằng phương trình sai phân
Vai trò của phương trình sai phân trong việc mô tả các hệ thống rời rạc theo thời
gian hoàn toàn giống với vai trò của phương trình vi phân trong việc mô tả các hệ
thống liên tục theo thời gian. Các hệ thống LTI rời rạc được biểu diễn bởi các
phương trình sai phân hệ số hằng. Phương trình sai phân tuyến tính hệ số hằng bậc có dạng như sau (2.51) với ,
là các hệ số hằng. chính là độ trễ lớn nhất của . Phương trình sai phân
này có hai loại, đệ qui và không đệ qui.
Nếu như đáp ứng của hệ thống rời rạc phụ thuộc vào các giá trị hiện tại và trong quá
khứ của đầu vào cũng như các giá trị trong quá khứ của đầu ra, khi đó biểu thức
(2.23) được viết lại như sau
<[.] = [* o9:*p ë9,[. − (] − 9:p# [9<[. − (]° (2.52)
Biểu thức (2.52) được gọi là phương trình sai phân đệ qui bậc . Phương trình sai
phân đệ qui có đáp ứng xung vô hạn và yêu cầu phải có điều kiện ban đầu để giải.
Nếu như đáp ứng của hệ thống LTI rời rạc chỉ phụ thuộc vào các giá trị hiện tại và
trong quá khứ của đầu vào mà không phụ thuộc vào bất kì giá trị nào của đầu ra,
khi đó biểu thức (2.52) được viết lại như sau ( ) (2.53)
Biểu thức (2.53) được gọi là phương trình sai phân không đệ qui. Với là giá trị
giới hạn, hệ thống LTI là nhân quả. Phương trình sai phân không đệ qui có đáp
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 57
ứng xung hữu hạn, vì thế nó cũng được sử dụng để mô tả bộ lọc có đáp ứng xung hữu hạn (FIR).
Để tìm được đáp ứng của hệ thống LTI rời rạc theo thời gian cần thực hiện
giải phương trình sai phân tuyến tính hệ số hằng. Nghiệm tổng quát của phương
trình (2.51) đối với tín hiệu đầu vào cụ thể sẽ có dạng trong đó,
là nghiệm riêng hay nghiệm đặc biệt của hệ thống và được gọi
là nghiệm đồng nhất hay nghiệm bù của hệ thống. Giải phương trình vi phân tuyến
tính hệ số hằng được thực hiện như sau: - Tìm nghiệm đồng nhất Nghiệm đồng nhất
thu được khi đặt đầu vào . Khi đó, là nghiệm của phương trình sai phân đồng nhất sau với
. Để giải phương trình sai phân đồng nhất trên, giả thiết rằng (2.56)
Thay (2.56) vào (2.55) thu được phương trình sau (2.57) Rút ra được (2.58)
Biểu thức (2.58) được gọi là phương trình đặc trưng, có nghiệm được kí hiệu là
, !, …, . Nếu nghiệm là phân biệt thì nghiệm đồng nhất được biểu diễn như
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 58 sau
(2.59) với , , …, là các hằng số, sẽ
tính được từ điều kiện ban đầu của hệ thống rời rạc. Trong trường hợp phương trình
đặc trưng có nghiệm bội, nghiệm đồng nhất sẽ có dạng khác so với (2.59). Cụ thể,
nếu là nghiệm có bội bậc và , …, là các nghiệm phân biệt thì nghiệm đồng nhất có dạng sau (2.60)
Nếu phương trình đặc trưng có các nghiệm phức thì nghiệm đồng nhất có dạng với và , ! là các hằng số. - Tìm nghiệm riêng Nghiệm riêng
là nghiệm bất kì thoả mãn phương trình sai phân (2.52) với đầu vào
xác định trong điều kiện . Nghiệm riêng có dạng tượng tự tín hiệu đầu vào
với một vài hệ số chưa biết, thay nghiệm này vào phương trình
sai phân để xác định các hệ số này. Ví dụ, nếu là hằng số thì cũng là hằng số, nếu là chuỗi hình sin thì cũng có chuỗi hình sin.
Ví dụ 9: Xác định đáp ứng xung khi đầu vào
của hệ thống LTI rời rạc được
đặc trưng bởi phương trình sai phân sau Lời giải: - Tìm nghiệm đồng nhất Đặt và
, thay vào phương trình đề bài đã cho, thu được
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 59
Nhận thấy nghiệm của đa thức lần lượt là và . Như vậy,
nghiệm đồng nhất có dạng - Tìm nghiệm riêng Với đầu vào sẽ có với và . Thay vào phương trình
sai phân đề bài cho cùng giả thiết rằng nghiệm riêng có dạng giống đầu vào, tức là và , thu được
Thực hiện tương tự với để tính , thu được Thay giá trị và
tìm được vào nghiệm đồng nhất, thu được hệ phương trình
Giải hệ phương trình, tìm được và . Do đầu vào với
nên không có nghiệm riêng. Vì thế, đáp ứng xung của hệ thống là BÀI TẬP CHƯƠNG 2
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 60
CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU VÀ HỆ THỐNG LIÊN
TỤC TRONG MIỀN TẦN SỐ 3.1 CHUỖI FOURIER
Biểu diễn tín hiệu tuần hoàn dưới dạng chuỗi Fourier là một công cụ quan
trọng trong việc phân tích, biểu diễn tín hiệu và hệ thống, cung cấp các đặc trưng
của tín hiệu trong miền tần số.
3.1.1 Biểu diễn tín hiệu liên tục tuần hoàn bằng chuỗi Fourier
3.1.1.1 Biểu diễn tín hiệu liên tục tuần hoàn bằng chuỗi Fourier
Như đã định nghĩa trong 1.1.2.3, tín hiệu tuần hoàn có giá trị biên độ lặp lại
sau mỗi chu kì J. Mỗi tín hiệu tuần hoàn được đặc trưng bởi chu kì cơ bản J* và tần
số cơ bản #* = 1/J* với J* là giá trị J nhỏ nhất của tín hiệu. Hai tín hiệu tuần hoàn
cơ bản là tín hiệu hình sin ,(!) = cos (_*! + c) và tín hiệu hàm mũ phức ,(!) = ^23 1!,
với _*= 25/J*= 25#* được gọi là tần số góc cơ bản.
Biểu diễn chuỗi Fourier hàm mũ phức của một tín hiệu tuần hoàn ,(!) có chu kì cơ bản J* có dạng sau / 9:./ 293!1
với 19là hệ số Fourier phức, được tính theo công thức sau 19 = J1* YLL6=!,(!)^.293!1 Z! (3.2)
Tích phân được lấy trong một chu kì cơ bản của tín hiệu. Vì thế để thuận tiện cho tính
toán, ë thường được lấy giá trị bằng 0 hoặc −J*/2.
Tập các hàm mũ phức ^293 1! trực giao với nhau, trở thành không gian tín
hiệu cơ sở để biểu diễn cho tín hiệu tuần hoàn ,(!) bất kì. Các hàm mũ phức đều
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 61
tuần hoàn và có chu kì là một số nguyên lần của chu kì cơ bản. Như vậy, tín
hiệu ,(!) hoàn toàn được đặc trưng bởi các hệ số Fourier.
Đặt ( = 0, khi đó biểu thức (3.2) trở thành 1 L6=! 1* = J* YL ,(!) Z! (3.3)
Biểu thức (3.3) chỉ ra rằng 1* chính là giá trị trung bình của ,(!) trong một chu kì.
Biểu diễn chuỗi Fourier lượng giác của tín hiệu tuần hoàn ,(!) có chu kì cơ bản J* có dạng sau / ,(!) =
+ p([9 123 (_*! + ë9 3a. (_*!) (3.4) 9:# với [9 và ë9 là
các hệ số Fourier lượng giác. 2 L6=! (3.5) [9 = J* YL ,(!) 123 (_*! Z! 2 L6=! ë9 = J* YL ,(!) 3a. (_*! Z!
Các hệ số [9 và ë9 và hệ số Fourier phức 19 có mối quan hệ như sau = 1* [9 = 19 + 1.9 ë9 = `(19 − 1.9) (3.6) 19 = ([9 − `ë9)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 62 1.9 = ([9 − `ë9) (3.7) Nếu
là thực thì và cũng là thực và bằng (3.8) Nếu tín hiệu tuần hoàn là chẵn thì
và chuỗi Fourier của nó chỉ gồm thành phần ,(!) = 9:# (3.9) Nếu tín hiệu tuần hoàn là lẻ thì
và chuỗi Fourier của nó chỉ gồm thành phần 3a. (3.10) 9:# Có một dạng chuỗi
Fourier khác để biểu diễn tín hiệu liên tục tuần hoàn thực, đó là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 63
Biểu thức (3.11) có thể rút ra từ biểu thức (3.4) và được gọi là chuỗi Fourier dang hài của .
là thành phần một chiều của tín hiệu và là thành phần hài bậc của
. Thành phần hài bậc nhất thường được gọi
là thành phần cơ bản do chu kì của nó đúng bằng chu kì cơ bản của tín hiệu. Các hệ
số 19 được gọi là các biên độ hài và pha c9 được gọi là các góc pha, chúng có quan
hệ với các hệ số Fourier [9 và ë9 như sau 1* = [2* 19 = ´[9! + ë9! c9 = ![..# [ë99 (3.12)
Hai dạng chuỗi Fourier (3.4) và (3.12) hoàn toàn tương đương với chuỗi
Fourier dạng phức (3.1), thường được sử dụng cho tín hiệu thực. Tuy nhiên, chuỗi
Fourier dạng phức là dạng tổng quát cho tất cả các tín hiệu liên tục tuần hoàn nên
được sử dụng phổ biến.
Ví dụ 10: Hệ số Fourier của tín hiệu xung chữ nhật
Tìm hệ số Fourier cho tín hiệu xung chữ nhật tuần hoàn trong hình dưới đây. =! =2= î(!) T là độ rộng xung
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 64
Hình 3.1: Tín hiệu xung chữ nhật tuần hoàn
Sử dụng (3.2), ta có hệ số Fourier phức của tín hiệu trên như sau: 1 =!/! .293 b 19 = J* Y* b^ !1Z! = ` 25. (^.29< − 1) Suy ra ( = 0 (ℎá1
Cũng có thể dễ dàng có được các dạng khác của hệ số Fourier. Sử dụng (3.5) thu
được hệ số Fourier dạng cầu phương như sau: .
3.1.1.2 Tính hội tụ của chuỗi Fourier
Do chuỗi Fourier là tổ hợp của vô số hàm mũ phức đa hài nên vấn đề về tính hội
tụ của chuỗi cần phải được xem xét để đảm bảo độ chính xác của phương pháp
phân tích này. Giả thiết rằng tín hiệu liên tục
được biểu diễn dưới dạng chuỗi
Fourier giới hạn chỉ gồm các hài có bậc tối đa là (( ≤ P).
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 65 Khi đó, có thể thu được từ , như sau
(3.14) Như vậy, hàm lỗi xấp xỉ giữa , và và
hàm trung bình lỗi bình phương
(mean square error - MSE) được định nghĩa như sau (3.15) Nếu
(!) = 0, ∀! thì chuỗi Fourier sẽ hội tụ tới
tại mọi điểm, nếu tốc độ
hội tụ như nhau tại mọi điểm thì chuỗi Fourier sẽ hội tụ đều. Nếu thì
chuỗi Fourier sẽ hội tụ tới
theo MSE. Lưu ý rằng, chuỗi Fourier hội tụ tại
mọi điểm sẽ hội tụ theo MSE nhưng chuỗi Fourier hội tụ theo MSE chưa chắc đã
hội tụ tại mọi điểm. Như vậy, điều kiện hội tụ tại mọi điểm sẽ chặt hơn so với hội
tụ theo MSE. Nếu tín hiệu liên tục tuần hoàn
có các hệ số chuỗi Fourier có tổng tuyệt đối
thì chuỗi Fourier sẽ hội tụ đều. Trên thực tế, nhiều tín hiệu cơ bản sử
dụng phổ biến trong phân tích tín hiệu và hệ thống như xung chữ nhật, xung tam
giác, … không liên tục tại một số điểm rời rạc vì thế điều kiện hội tụ trên bị giới
hạn tại một số điểm. Nếu tín hiệu tuần hoàn
có năng lượng hữu hạn trong một chu kì
thì chuỗi Fourier của nó sẽ hội tụ theo MSE. Các tín hiệu trong
thực tế thường thoả mãn điều kiện giới hạn năng lượng trên nên hội tụ theo MSE
thường được áp dụng. Điều kiện hội tụ này được cụ thể hoá bằng các điều kiện Dirichlet sau 1.
là khả tích tuyệt đối trong một chu kì đơn,
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 66 2.
có hữu hạn các điểm cực đại và cực tiểu 3.
có hữu hạn các điểm không liên tục trong bất kì một khoảng hữu hạn nào
và mỗi điểm không liên tục này có giá trị hữu hạn.
Nếu tín hiệu tuần hoàn liên tục
thoả mãn điều kiện Dirichlet thì chuỗi Fourier sẽ
hội tụ tại mọi điểm trừ các điểm không liên tục của nó. Tại điểm không liên tục ! =
!(, chuỗi Fourier của nó sẽ hội tụ về với là giá trị của tín
hiệu ,(!) tại phía trái của !(, ,(!(.) là giá trị của tín hiệu ,(!) tại phía phải của !(. Như
vậy, điều kiện hội tụ Dirichlet được áp dụng trong thực tế. Hình 3.2 biểu diễn một số
tín hiệu vi phạm điều kiện Dirichlet. Tín hiệu đầu tiên là tín hiệu tuần hoàn có chu kì
J = 1 với ,(!) = 1/!, 0 < ! < 1, tín hiệu này vi phạm điều kiện 1. Tín hiệu thứ hai là
tín hiệu tuần hoàn có chu kì J = 1 với ,(!) = 3a.
(25/!), 0 < ! < 1, tín hiệu này vi phạm điều kiện 2. Tín hiệu thứ ba vi phạm điều kiện 3.
Hình 3.2: Tín hiệu vi phạm điều kiện Dirichlet
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 67
Tại những điểm không liên tục của ,(!), chuỗi Fourier không hội tụ đều. Tốc độ
hội tụ tại những điểm lân cận điểm không liên tục sẽ chậm hơn. Kết quả là, tại
những điểm lân cận điểm không liên tục xuất hiện các gợn sóng và đỉnh các gợn
sóng này hầu như không giảm dù số lượng các hài P tăng lên. Hiện tượng gợn
sóng tại các điểm không liên tục của tín hiệu ,(!) khi biểu diễn dưới dạng chuỗi
Fourier được gọi là hiện tượng Gibbs. Đây là một nhược điểm của chuỗi Fourier.
Hình 3.3: Hiện tượng Gibbs
3.1.1.3 Phổ biên độ và phổ pha của tín hiệu tuần hoàn
Hệ số Fourier phức có thể viết lại dưới dạng phasor như sau (3.17) Đồ thị
theo tần số góc được gọi là phổ biên độ của tín hiệu tuần hoàn , và đồ thị
theo được gọi là phổ pha của
. Do ( chỉ là các số nguyên nên phổ
biên độ và phổ pha không liên tục mà chỉ tồn tại tại các tần số rời rạc . Vì thế,
chúng được gọi là có dạng phổ tần rời rạc hay phổ vạch. Nếu là thực thì phổ
biên độ là làm chẵn và phổ pha là hàm lẻ. (3.18)
3.1.2 Tính chất của chuỗi Fourier
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 68
Biểu thức (1.59) cho phép tính công suất của tín hiệu liên tục tuần hoàn trong một chu kì. Mặt khác,
cũng được biểu diễn dưới dạng chuỗi Fourier phức, nên
hoàn toàn có thể tính công suất tín hiệu bởi các hệ số Fourier phức như sau !
(3.19) Biểu thức (3.19) được gọi là định lý Parseval cho chuỗi Fourier.
Một số tính chất khác của chuỗi Fourier được cho bởi bảng 3.1 dưới đây.
Các tính chất của chuỗi Fourier
å¥ å0¥a ek jkæç2Tpöø÷tx t( )=
a ek jkwt = è k=-¥ k=-¥ ( )= 1
ò x t e( ) -jkw0tdt = 1 ò x t e( )
- jkçæè2Tpöø÷tdt a k T T T T Các tính chất
Tín hiệu tuần hoàn Hệ số Fourier x t( )ü a
Tuần hoàn với chu kì J và ý k b y t( )þ k
tần số cơ bản _* = 25/J* Tuyến tính Ax t( )+ By t( ) Aa Bbk + k x t( -t Dịch thời gian 0)
aek - jkw0 0t =aek - jk(2p/T t)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 69 0 Dịch tần số
e jMw0t = e jM(2p/T t) x t( ) ak M- Liên hợp x t*( ) a-*k Đảo thời gian x( )-t a-k Co giãn thang đo ,([!), [ > 0, chu kì J/[ ak Tích chập
òTx( ) (t tty t - )d Ta bkk Tích thường x t y t( ) ( ) ¥ åablkl- l=-¥ Đạo hàm dx t( )
jkw0ak = jk 2pak T dt Tích phân ∫./1 ,(!)Z!
có giá trị hữu hạn vàæ 1 ö æ 1 ö tuần hoàn chỉ khi [* = 0 ç w0ø÷ak =çè
jk(2p/T)ø÷akè jk Đối xứng liên x t real( ) hợp pha khi tín
ìak =a-*k ï ïÂe a{ }k hiệu ,(!) là thực =Âe a{ } ï
-k Ám a{ }k =Ám a{ }-k í
ïak = a-k ï
ï ak= - a-k î
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 70 Tín hiệu ,(!) thực x t realand even( ) [9 là thực và chẵn và chẵn Tín hiệu ,(!) thực x t realand odd( ) [9 là ảo và lẻ và lẻ Phân tích chẵn - lẻ của một tín
ìïx te( )= Ev x t{ ( )} [x t real( Âe a{ }k j hiệu ,(!) thực ) ] í m aÁ { }k
ïîx to( )=Od x t{ ( )} [x t real( ) ]
Bảng 3.1: Các tính chất của chuỗi Fourier liên tục
3.2 BIẾN ĐỔI FOURIER TÍN HIỆU LIÊN TỤC THEO THỜI GIAN
Chuỗi Fourier cung cấp một cách hoàn toàn mới để biểu diễn tín hiệu. Thay vì
biểu diễn và phân tích tín hiệu trong miền thời gian thì chuỗi Fourier cho biết các
thông tin của tín hiệu trong miền tần số thể hiện qua phổ pha và phổ biên độ. Miền
tần số là một khái niệm nền tảng trong kĩ thuật, rất nhiều vấn đề kĩ thuật được giải
quyết trong miền tần số dễ dàng hơn trong miền thời gian. Tuy chuỗi Fourier cho
phép biểu diễn tín hiệu tuần hoàn trong miền thời gian một cách hiệu quả. Vậy, với
các tín hiệu không tuần hoàn thì sao? Thật may mắn, hầu hết tín hiệu vật lý tuy có thể
không tuần hoàn nhưng đều là các tín hiệu giới hạn thời gian. Không làm sai lệch kết
quả nếu giả thiết rằng các tín hiệu vật lý là các tín hiệu tuần hoàn với chu kì đúng
bằng thời gian tồn tại của tín hiệu. Vì thế, hoàn toàn áp dụng được biểu diễn chuỗi
Fourier cho các tín hiệu này. Với cách tiếp cận này, hoàn toàn có thể biểu diễn tín
hiệu liên tục theo thời gian bất kì sang miền tần số và được gọi là biến đổi Fourier.
Do biến đổi Fourie bắt nguồn từ chuỗi Fourier nên giữa chúng có nhiều điểm tương đồng.
3.2.1 Biến đổi Fourier tín hiệu liên tục theo thời gian
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 71 Hàm
được gọi là biến đổi Fourier của tín hiệu liên tục theo thời gian nếu Và biến đổi Fourier ngược của được định nghĩa như sau và được gọi là một cặp
biến đổi Fourier, thường được kí hiệu trong đó
là biểu diễn tín hiệu trong miền thời gian và là biểu diễn tín hiệu
trong miền tần số của cùng một tín hiệu. Cặp biến đổi Fourier là duy nhất ứng với một tín hiệu. Biến đổi Fourier của
thường có dạng phức và có thể viết dưới dạng phasor như sau (3.23)
còn được gọi là phổ của tín hiệu , với là phổ biên độ và là phổ pha của tín hiệu . Nếu tín hiệu là thực, thu được Tức là (3.25) và (3.26)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 72
Như vậy, giống như đối với tín hiệu tuần hoàn thực, nếu
là tín hiệu liên tục theo
thời gian thì phổ biên độ là hàm chẵn và phổ pha là hàm lẻ.
Tương tự như chuỗi Fourier, điều kiện hội tụ của biến đổi Fourier là tín hiệu
phải thoả mãn các điều kiện Dirichlet. Một lưu ý quan trọng, tín hiệu xung đơn vị
không thoả mãn điều kiện Dirichlet nhưng vẫn tồn tại biến đổi Fourier của nó. Nhìn
chung, tất cả các tín hiệu vật lý và tín hiệu cơ bản đều tồn tại biến đổi Fourier.
3.2.2 Các tính chất của biến đổi Fourier tín hiệu liên tục theo thời gian
Định lý Parseval đưa ra một phương pháp khác để xác định năng lượng của
tín hiệu, đó là xác định năng lượng của tín hiệu trong miền tần số dựa trên phổ của
nó. Nguyên nhân là do năng lượng được bảo toàn trong cả hai miền, thời gian và
tần số. Định lý Parseval được phát biểu như sau (_)Z# (3.27) Nếu
, thì phương trình trên trở thành (3.28)
Vế trái của biểu thức (3.28) chính là năng lượng chuẩn hoá | của tín hiệu ,(!). Như
vậy, năng lượng của tín hiệu còn có thể tính bằng tích phân bình phương phổ của
nó trong toàn bộ miền tần số. Và |á(_)|! chính là năng lượng trên một đơn vị tần số
và được định nghĩa là mật độ phổ năng lượng của tín hiệu. Biểu thức (3.28) còn được
gọi là định lý năng lượng Rayleigh.
Một số tính chất khác của biến đổi Fourier được cho bởi bảng 3.2 dưới đây.
Các tính chất của biến đổi Fourier Các tính chất Tín hiệu Biến đổi Fourier
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 73 Tuyến tính
a1 1w w( )t + a2 2( )t
aW f1 1( )+a W2 2( )f Trễ thời gian w(t -Td)
W f e( ) - j Twd Thay đổi thang 1 W æ öç ÷af đo a è ø w( )at Liên hợp w* W*(-f ) ( )t Duality W t( ) w(-f ) Tín hiệu thực
1 e W fjq ( - fc )+e- jqW f( é dịch tần số + fc )ûù 2ë [w( )t isreal]
w w q( )t cos( ct + ) Tín hiệu phức ( )t e j dịch tần số wct w W f( - fc) Tín hiệu thông dải Re{g t e( ) jw }
12 éëG f( - fc)+G*(- -f ct fc)ùû Vi phân dnw( )t
( j2pf )nW f( ) dtn Tích phân t ( W(0) ( )d
j2pf )-1W f( )+ f òwl ( )d -¥ Tích chập (#) (#) Tích thường
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 74 Luỹ thừa biến n thời gian (- j2p)-n d tnw( )t W f( )n df
Bảng 3.2: Các tính chất của biến đổi Fourier
3.2.3 Biến đổi Fourier và phổ của một số tín hiệu cơ bản
Với tín hiệu tuần hoàn, chuỗi Fourier có thể được sử dụng để biểu diễn tín hiệu
trên toàn bộ khoảng thời gian
. Do đó, phổ (hai phía) của tín hiệu
có thể được biểu diễn bằng các hệ số Fourier.
Định lý: Nếu là
tín hiệu tuần hoàn với chu kỳ thì tín hiệu sẽ có phổ như sau: (3.29) Với
và là các hệ số Fourier của tín hiệu được xác định theo (3.2). Chứng minh: Biểu diễn tín hiệu dưới
dạng chuỗi Fourier, ta có:
Thực hiện biến đổi Fourier cả 2 phía:
Định lý này chỉ ra rằng, hàm tuần hoàn luôn có phổ vạch với các vạch phổ nằm tại tần số
và có độ lớn bằng giá trị . Cũng có thể thấy rằng, hiển
nhiên không có thành phần dc vì không có vạch phổ tại tần số (tức là ).
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 75
Ngược lại, nếu hàm không chứa bất kỳ thành phần tuần hoàn nào, phổ của tín hiệu
sẽ là liên tục (không có vạch), trừ vạch tại tần số
nếu như hàm đó có thành phần một chiều.
Cũng có thể xác định các hệ số Fourier bằng cách lấy mẫu biến đổi Fourier của xung tương ứng với
trong một chu kỳ theo như định lý dưới đây: Định lý: Nếu
là hàm tuần hoàn có chu kỳ là và được biểu diễn bởi: (3.30) với (3.31)
(ℎá1 thì hệ số Fourier được xác định theo công thức sau: (3.32) với và . Chứng minh: (3.33) Suy ra
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 76
Vì xung đơn vị có thể được biểu diễn dưới dạng chuỗi Fourier như sau (3.35)
với tất cả các hệ số
. Thay (3.34) vào (3.35), ta có
Biến đổi Fourier cả hai vế của (3.36), ta có (3.37) So sánh
(3.37) và (3.29) ta có được (3.32).
Định lý này rất thuận tiện cho việc xác định hệ số Fourier khi dễ dàng biết
được biến đổi Fourier của dạng xung cơ bản đối với tín hiệu tuần hoàn, ví dụ như
chỉ đơn giản bằng cách tra bảng biến đổi Fourier 3.3).
Biến đổi Fourier của một số tín hiệu cơ bản được cho bởi bảng 3.3 dưới đây.
Một số cặp biến đổi Fourier
Biểu diễn miền thời Tín hiệu gian
Biểu diễn miền tần số
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 77 Pæ öç T Sa[ (pft)] ÷Tt Xung chữ nhật è ø Xung tam giác T Sa[(pft)]2 ì+ >1, t 0 u 1 1 d( )f + Xung nhảy bậc 2 j2pf đơn vị t( )=í < 0 î0, t ì+ >1, t 0 1 Hàm dấu
sgn( )t =í-1, t < 0 î jpf Hàm hằng số 1 d( )f
Hàm xung đơn vị d(t -to) e- j2pft0 tại t =t0 Sa(2pWt) 1 æ f ö Hàm sinc 2W Pçè2W ø÷ e j( Phasor w j0t+ )
ejjd(f - f0) cos(w jct + ) Hàm hình sin
1e jj( f - fc)+ 1e- jj( f + fc) 2 2 Tín hiệu Gauss e-p(t t/ 0)2 t e0 -p( ft0)2
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 78 T Hàm mũ một
ìe-tT/, t > 0 í phía î0, t < 0 1 2+ j pfT e-t T/ 2T Hàm mũ hai phía 1 (2+ pfT)2 k=¥
n=¥ f0 åd( f -nf0), f0 Chuỗi xung đơn vị åd(t -kT) =1/T n k=-¥ =-¥
Bảng 3.3:Biến đổi Fourier của một số tín hiệu cơ bản Ví dụ 11: Tìm phổ của tín hiệu sau 0,
Áp dụng bảng 3.3 cho tín hiệu hàm mũ một phía, thu được
Áp dụng tính chất điều chế của biến đổi Fourier với ta có
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 79
Nhìn vào phương trình trên có thể thấy rằng, phổ biên độ của tín hiệu này có đỉnh tại
. Còn phổ biên độ của tín hiệu trong ví dụ 2-2 có đỉnh tại . Điều này có nghĩa là,
đã làm đỉnh của phổ dịch từ tần số đến .
Ví dụ 12: Tìm phổ của tín hiệu hình sin sau !
Thực hiện biến đổi Fourier ta có: (b sin _*!) ^.231Z! ./ Z! ./ 2`
.2!<(M.M!)1Z! − b Y ^.2!<(M6M!)1Z!
Lưu ý rằng: phổ của tín hiệu sin là ảo vì
là hàm thực và và là hàm lẻ. Ngoài ra,
) không phải là hàm có năng lượng hữu hạn và không khả tích tuyệt đối (không
thỏa mãn đầy đủ các điều kiện của Dirichlet) nhưng trong trường hợp này ta thấy
vẫn có thể thực hiện được biến đổi Fourier.
Phổ biên độ của tín hiệu là:
Với A là số dương. Do chỉ tồn tại 2 thành phần phổ tại nên phổ biên độ của
tín hiệu sin có dạng như sau:
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 80 A/2 b. Phổ biên độ a. Phổ pha
Hình 3.4: Phổ của tín hiệu sin
Ví dụ 13: Tìm phổ của xung chữ nhật Π A B
Thực hiện biến đổi Fourier ta có: π(#) = Y 1. ^ .=/! −`_ sin(_J/2) = J= Jø[(5J#) _J/2 Vậy: ! Π Miền thời gian Miền tần số
Hình 3.5: Phổ của xung chữ nhật
Ví dụ 14: Tìm phổ của xung tam giác Λ A B
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 81 Ta có: Và:
Thực hiện biến đổi Fourier cả 2 vế, ta có: Hay: !
Áp dụng định lý tích phân hai lần ta có: Vậy: Λ
Hình 3.6: Phổ của xung tam giác
3.2.4 Lấy mẫu tín hiệu liên tục và định lý lấy mẫu của Shannon
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 82
Các tín hiệu trong thực tế thường ở dạng liên tục và vì thế các hệ thống liên tục
theo thời gian được nghiên cứu và phát triển rộng rãi ở thời kì đầu của ngành điện
tử truyền thông. Tuy nhiên, từ khi các hệ thống truyền thông số ra đời, các tín hiệu
liên tục cần được chuyển đổi sang miền số để phù hợp với các hệ thống này. Quá
trình lấy mẫu và nội suy cho phép chuyển đổi tín hiệu từ dạng liên tục sang rời rạc
và ngược trở lại. Quá trình lấy mẫu có thể được thực hiện theo nhiều cách khác
nhau nhưng lấy mẫu tuần hoàn được sử dụng phổ biến trong thực tế nhờ sự dễ
dàng khi thực hiện. Tín hiệu liên tục ,(!) được lấy mẫu tuần hoàn theo chu kì lấy
mẫu J sẽ tạo ra một chuỗi <(.) gồm các mẫu thu được từ tín hiệu ,(!) tại các thời điểm .J khác nhau, cụ thể <(.) = ,(.J) với . nguyên (3.38)
trong đó, chu kì lấy mẫu J phải là một hằng số thực dương và _% = 25/J được gọi
là tần số lấy mẫu. Một ví dụ về quá trình lấy mẫu tuần hoàn được mô tả trong hình
3.7 dưới đây. Tín hiệu liên tục theo thời gian ,(!) (hình 3.7 a) được lấy mẫu với chu
kì J = 10 và thu được chuỗi <(.) (hình 3.7b). a) Tín hiệu liên tục b) Tín hiệu lấy mẫu
Hình 3.7: Phổ của xung chữ nhật
Ví dụ 15: Thực hiện lấy mẫu hai tín hiệu sau với chu kì lấy mẫu J = 1
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 83 !
Lời giải: Lấy mẫu mỗi tín hiệu với chu kì
thu được chuỗi tín hiệu tương ứng Nhận thấy, trong khi không nguyên. Như vậy,
câu hỏi đặt ra là liệu có thể khôi phục tín hiệu liên tục từ các mẫu của nó hay
không? Thật may mắn, điều này hoàn toàn thực hiện được nếu như quá trình lấy
mẫu đáp ứng được một số điều kiện cụ thể.
Để thực hiện lấy mẫu
tuần hoàn, sử dụng chuỗi xung lấy mẫu với chu kì như sau
Quá trình lấy mẫu tín hiệu liên tục bằng chuỗi xung gồm hai bước: - Bước 1: Nhân tín hiệu
với chuỗi xung tuần hoàn , thu được chuỗi xung . Lưu ý, chuỗi xung vẫn là tín hiệu liên tục theo thời gian. (3.40)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 84 với
hay còn gọi là trọng số của các xung cách đều nhau chu kì và là tần số lấy mẫu.
- Bước 2: Chuyển đổi chuỗi xung
thành chuỗi tín hiệu rời rạc bằng
cách lấy trọng số của các xung liên tiếp trong .
Hình 3.8: Bộ chuyển đổi tương tự - số lý tưởng a) Tín hiệu liên tục b) Chuỗi xung lấy mẫu
c) Chuỗi xung tín hiệu liên tục
d) Chuỗi tín hiệu rời rạc
Hình 3.9: Quá trình chuyển đổi tương tự - số
Thực hiện biến đổi Fourier cho chuỗi xung 3(!), thu được phổ của nó như sau ":/
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 85 (3.41)
Nhận thấy, phổ của chuỗi xung 3(!) là một tổng với tỉ lệ _%/25 của vô số các bản sao
được dịch đi một số nguyên lần tần số lấy mẫu _% của phổ tín hiệu ban đầu. Tuỳ
thuộc vào độ rộng của phổ tín hiệu ban đầu và độ lớn của tần số lấy mẫu mà có thể
xảy ra sự chồng lấn hoặc không của các bản sao phổ.
- Trong trường hợp xảy ra sự chồng lấn, một phần của các bản sao phổ bị
chồng lấn lên nhau dẫn đến dạng phổ của tín hiệu ban đầu bị mất đi. Hiện
tượng này được gọi là chồng phổ. Khi có hiện tượng chồng phổ xảy ra,
không thể khôi phục tín hiệu ban đầu từ các mẫu của nó.
- Trong trường hợp không xảy ra chồng phổ, các bản sao phổ giữ nguyên
được dạng phổ ban đầu, vì thế sẽ khôi phục được tín hiệu ban đầu từ các mẫu của nó. Phổ của tín hiệu ban đầu (có băng tần ) Phổ của chuỗi xung trong trường hợp không chồng phổ ( ) Phổ của chuỗi xung trong trường hợp chồng phổ ( )
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 86
Hình 3.10: Phổ của tín hiệu sau lấy mẫu
Quá trình nội suy cho phép chuyển đổi tín hiệu rời rạc thành tín hiệu liên tục. Chuỗi xung lấy mẫu
cũng được sử dụng để khôi phục tín hiệu liên tục ban đầu từ các
mẫu của nó. Quá trình nội suy gồm hai bước
- Bước 1: Tạo chuỗi xung
từ chuỗi tín hiệu rởi rạc bằng cách nhân với chuỗi xung lấy mẫu
- Bước 2: Đưa chuỗi xung
thu được đi qua bộ lọc thông thấp có đáp ứng xung
để giữ lại thành phần phổ cơ bản tại băng tần gốc (
) và loại bỏ tất cả các bản sao của nó tại tần số ._ , ( ). (3.43)
Hình 3.11: Bộ chuyển đổi số - tương tự lý tưởng Để tín hiệu khôi phục
giống với tín hiệu liên tục ban đầu thì không được
xảy ra hiện tượng chồng phổ khi lấy mẫu tín hiệu. Từ đó, định lý lấy mẫu được rút ra và phát biểu như sau
Định lý lấy mẫu: Nếu tín hiệu có biến đổi Fourier là , và giả thiết rằng > _', tức là tín hiệu
bị giới hạn băng tần trong khoảng , thì
sẽ được xác định duy nhất bởi các mẫu của nó
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 87 , nguyên nếu (3.44)
Biểu thức (3.44) còn được gọi là điều kiện Nyquist, được gọi là tần số
Nyquist và được gọi là chu kì lấy mẫu Nyquist.
3.2.5 Mật độ phổ công suất và năng lượng của tín hiệu
3.2.5.1 Mật độ phổ năng lượng
Định lý năng lượng Rayleigh (biểu thức 3.28) cho thấy vế phải chính là năng
lượng chuẩn hoá của tín hiệu được tính trong miền tần số. Mật độ phổ năng lượng
(ESD – Energy Spectral Density) được định nghĩa là năng lượng của tín hiệu trên
một đơn vị tần số, biểu diễn như sau ! (3.45)
Khi đó, năng lượng của tín hiệu được tính thông qua hàm mật độ phổ năng lượng sẽ là
3.2.5.2 Mật độ phổ công suất
Để đưa ra được công thức xác định mật độ phổ công suất của tín hiệu, trước tiên cần định nghĩa hàm cửa sổ của tín hiệu !),
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 88 á = ,(!)Π (3.47)
Sử dụng công thức (1.50) ta có công suất trung bình chuẩn hóa của tín hiệu
được tính như dưới đây: ∞ (3.48) .=/!./
Áp dụng định lý Parseval, công thức trên được biến đổi thành dạng dưới đây ∞ ∞ ∞ ∞ =(J#)|!æ Z# (3.49) với .
Như vậy, từ công thức (3.49), với tín hiệu công suất ta có khái niệm mật độ phổ công
suất (PSD – Power Spectral Density) được định nghĩa như sau ∞ (3.50) với ,
(#) là mật độ phổ công suất của tín hiệu có đơn vị là W/Hz.
Lưu ý rằng PSD luôn là một hàm thực, không âm theo tần số. Ngoài ra, PSD không nhạy với phổ pha của
Từ công thức (3.49) ta có công suất trung bình của tín hiệu được tính theo công thức sau Z# (3.51) ./
Điều này có nghĩa là phần diện tích nằm dưới hàm PSD sẽ là công suất trung bình
chuẩn hóa của tín hiệu.
3.2.5.3 Hàm tự tương quan
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 89 Hàm =/! (3.52) .=/!
Định lý Wiener-Khintchine: Hàm tự tương quan và PSD của tín hiệu là một cặp biến đổi Fourier (#) (3.53) Trong đó .
Như vậy, có thể xác định PSD bằng một trong hai cách sau:
- Sử dụng phương pháp trực tiếp, tính theo công thức định nghĩa (3.50) - Sử
dụng phương pháp gián tiếp bằng cách: đầu tiên xác định hàm tương quan, sau
đó thực hiện biến đổi Fourier của hàm tương quan, ta sẽ có PSD.
Ngoài ra, công suất chuẩn hóa trung bình đối với tín hiệu
có thể được xác định
theo một trong bốn cách sau ! Z# = g)(0) (3.54) ./
Ví dụ 16: Xác định PSD của tín hiệu hình sin Lời giải:
Ở đây ta sử dụng phương pháp gián tiếp để xác định DSP. ]) Z! .=/!
Thực hiện biến đổi lượng giác ta có: .=/!.=/! Rút gọn, ta có:
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 90
PSD được xác định như sau: !
Công suất chuẩn hóa trung bình có thể được xác định theo (3.53):
Hoặc xác định theo công thức: (ta cũng có kết quả tương tự).
Có thể thấy rằng tín hiệu và
! có cùng PSD (và hàm tương quan) do
pha không ảnh hưởng đến PSD. Dễ dàng chứng minh được đều này nếu ta áp dụng
cách tính trên cho tín hiệu !
Tóm lại, chúng ta đã xem xét các đặc trưng của một tín hiệu liên tục theo thời gian
như phổ, công suất trung bình, mật độ phổ công suất, mật độ phổ
năng lượng, giá trị rms … Vấn đề còn lại là làm thế nào đế biểu diễn tín hiệu.
Phương pháp trực tiếp là sử dụng một phương trình toán học có dạng gần đúng để
biểu diễn tín hiệu. Một số phương pháp tương đương khác dùng để biểu diễn tín
hiệu cũng rất hữu ích, ví dụ như sử dụng khai triển chuỗi Taylor xung quanh điểm a cho tín hiệu dưới đây .! với , (3.56) ! = [
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 91
Trong trường hợp này, nếu biết đạo hàm tại ! = [, , thuật toán này có
thể được sử dụng để tái tạo lại tín hiệu. Một kiểu biểu diễn tín hiệu khác hay được
sử dụng trong các bài toán liên quan đến hệ thống viễn thông hơn, đó là sử dụng
các chuỗi trực giao. Vấn đề này đã được trình bày cụ thể trong 3.1.
3.3 ĐÁP ỨNG TẦN SỐ CỦA HỆ THỐNG LTI
Đối với hệ thống LTI liên tục theo thời gian có đáp ứng xung thì đầu ra
chính là tích chập giữ đáp ứng xung và tín hiệu đầu vào , như trình bày tại
2.1.1. Áp dụng bảng tích chất biến đổi Fourier 3.2, thu được (3.57) với , và
lần lượt là biến đổi Fourier của , và . Từ biểu thức (3.57) rút ra (3.58) Hàm
được gọi là đáp ứng tần số của hệ thống, được biểu diễn dưới dạng phasor như sau (3.59)
được gọi là đáp ứng biên độ và
được gọi là đáp ứng pha của hệ thống.
Nếu tín hiệu đầu vào của hệ thống là hàm mũ phức , với biến đổi Fourier
, thì đầu ra của hệ thống sẽ là (3.60)
Lấy biến đổi Fourier ngược cho , thu được (3.61)
Biểu thức (3.61) cho thấy tín hiệu hàm mũ phức là hàm riêng của hệ thống LTI với
giá trị riêng tương ứng là .
Nếu đầu vào của hệ thống là tín hiệu
tuần hoàn được biểu diễn dưới dạng chuỗi
Fourier thì đầu ra tương ứng
cũng là tín hiệu tuần hoàn được biểu diễn dưới
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 92 dạng chuỗi Fourier "f(.#*)^2"3!1 (3.62) ∞
Nếu đầu vào của hệ thống là tín hiệu
không tuần hoàn thì đầu ra tương ứng được biểu diễn như sau
Như vậy, hệ thống LTI liên tục theo thời gian hoàn toàn được đặc trưng bởi đáp ứng tần số
của nó. Biểu điễn phổ tín hiệu đầu vào và tín hiệu đầu ra dưới dạng phasor (3.64)
Từ biểu thức (3.57), thu được (3.65)
Phổ biên độ và phổ pha của tín hiệu đầu ra được xác định thông qua phổ biên độ và
phổ pha của tín hiệu đầu vào và đáp ứng xung của hệ thống theo biểu thức (3.65).
Nếu mật độ phổ công suất của tín hiệu đầu vào là (#) thì hàm mật độ phổ công
suất của tín hiệu đầu ra (#) của hệ thống LTI sẽ là (#) (3.66)
Hàm truyền đạt công suất của hệ thống sẽ là œH I)|! (3.67)
Truyền dẫn không méo qua hệ thống LTI yêu cầu dạng tín hiệu đầu vào phải được
giữ nguyên vẹn tại đầu ra mặc dù biên độ có thể thay đổi và trễ đi một lượng thời
gian nhất định. Nếu tín hiệu đầu vào thì đầu ra phải có dạng <(!) = ó,(! − ! (3.68)
với ! là độ trễ thời gian và
là hằng số. Lấy biến đổi Fourier cả hai về của (3.68) thu được
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 93 (3.69)
Để hệ thống LTI truyền không méo, hàm đáp ứng tần số phải thoả mãn điều kiện sau f(#)= |f(#)|^28+(-)= ó^2311 (3.70) Tức là, |f(#)| = ó (3.71) cQ(M) = ^2311
Nói cách khác, đáp ứng biên độ phải là hằng số trên toàn bộ miền tần số và đáp ứng
pha phải là hàm tuyến tính trong toàn bộ miền tần số. a) Đáp ứng biên độ b) Đáp ứng pha c) Tín hiệu đầu vào d) Tín hiệu đầu ra
Hình 3.12: Truyền dẫn không méo
Khi phổ biên độ của hệ thống không phải là hằng số trong vùng tần số quan tâm thì
được gọi là méo biên độ. Lúc này, các thành phần tần số của tín hiệu đầu vào được
khuếch đại hay suy giảm với các mức độ khác nhau. Khi phổ pha của hệ thống
không phải là tuyến tính trong vùng tần số quan tâm thì được gọi là méo pha. Lúc
này, các thành phần tần số của tín hiệu đầu vào bị trễ đi một lượng không đều nhau
khi đi qua hệ thống làm biến dạng tín hiệu.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 94
3.4 MỘT SỐ VÍ DỤ VỀ ỨNG DỤNG CỦA BIẾN ĐỔI FOURIER TÍN HIỆU THỜI GIAN LIÊN TỤC 3.4.1 Bộ lọc
Một trong các hoạt động cơ bản nhất của hệ thống xử lý tín hiệu là quá trình
lọc. Quá trình lọc chỉnh sửa dạng phổ của tín hiệu bằng cách tăng cường hoặc làm
suy giảm một số thành phần tần số xác định. Hệ thống LTI đóng vai trò giống một bộ
lọc cho tín hiệu đầu vào.
Bộ lọc lựa chọn tần số cho phép một dải tần số đi qua hầu như không méo hoặc
méo rất nhỏ, trong khi làm suy giảm hầu hết các thành phần tần số còn lại. Dải tần
số được đi qua bộ lọc hầu như không méo được gọi là băng tần truyền qua. Dải tần
số gần như bị loại bỏ hoàn toàn khi đi qua bộ lọc được gọi là băng tần chặn của bộ
lọc. Bộ lọc được ứng dụng rộng rãi trong các hệ thống viễn thông, làm nhiệm vụ
sửa phổ, sửa dạng xung, tối thiểu hoá nhiễu và méo. Tuỳ thuộc dải tần cho đi qua
mà bộ lọc lựa chọn tần số được chia làm bốn loại. Dưới đây là hàm truyền của bốn
loại bộ lọc lựa chọn tần số lý tưởng. ( ò ạ a) Đáp ứng biên độ b) Hàm truyền đạt
Hình 3.13: Bộ lọc thông thấp lý tưởng (
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 95 ò ạ a) Đáp ứng biên độ b) Hàm truyền đạt
Hình 3.14: Bộ lọc thông cao lý tưởng ò ạ a) Đáp ứng biên độ b) Hàm truyền đạt
Hình 3.15: Bộ lọc thông dải lý tưởng ò ạ a) Đáp ứng biên độ b) Hàm truyền đạt
Hình 3.16: Bộ lọc chặn dải lý tưởng
Các bộ lọc lý tưởng có đáp ứng biên độ bằng hằng số và có sự thay đổi đột ngột giá
trị tại các tần số cắt #(, #L. Điều này không thể thực hiện được trong thực tế. Các bộ
lọc lựa chọn tần số lý tưởng không phải là hệ thống nhân quả.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 96
Các bộ lọc thực tế được thiết kế dựa trên các linh kiện điện tử hoặc các vi mạch, vì
thế đáp ứng tần số của nó không hoàn toàn là hằng số trong dải tần quan tâm nên có
gây ra méo tín hiệu khi truyền qua. a) Bộ lọc Butterworth
b) Bộ lọc Chebyshev loại I
c) Bộ lọc Chebyshev loại II d) Bộ lọc elip
Hình 3.17: Một số bộ lọc thông thấp thực tế 3.4.2 Băng thông
Một khái niệm quan trọng đó là băng thông của hệ thống LTI. Có rất nhiều định
nghĩa khác nhau cho băng thông hệ thống, tuy nhiên, hai định nghĩa sau đây được dùng phổ biến
- Băng thông tuyệt đối là khoảng tần số từ tần số có biên độ phổ lớn nhất đến
tần số dương lớn nhất sao cho biên độ phổ bắt đầu từ tần số đó trở đi đều
bằng 0. Băng thông tuyệt đối chỉ tồn tại ở các hệ thống lý tưởng. Đối với bộ
lọc thông thấp lý tưởng như hình 3.13 thì băng thông tuyệt đối của hệ thống
với ( chính là tần số cắt của bộ lọc. Bộ lọc thông dải có băng thông
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 97 tuyệt đối
(. Trong khi các bộ lọc thông cao và bộ lọc chặn dải
không tồn tại băng thông tuyệt đối
- Băng thông 3 dB được ứng dụng phổ biến cho các bộ lọc thực tế và nhân
quả. Băng thông 3 dB được định nghĩa là dải tần số dương mà biên độ phổ
của các thành phần tần số đó thay đổi từ giá trị biên độ phổ lớn nhất về giá trị
. Băng thông 3 dB còn được gọi là băng thông
nửa công suất do tương ứng tại tần số cắt công suất tín hiệu giảm đi một
nửa. Trong hình 3.18 dưới dây, băng thông 3 dB của hệ thống là . Hình 3.18: Băng thông 3 dB
Băng thông của tín hiệu được định nghĩa là dải tần số mà năng lượng và công suất
của tín hiệu tập trung chủ yếu. Băng thông 3 dB của tín hiệu được định nghĩa
tương tự như băng thông 3 dB của hệ thống. Một tín hiệu được gọi là có băng tần giới hạn nếu như (3.72) và
cũng được định nghĩa là băng thông của tín hiệu. BÀI TẬP CHƯƠNG 3
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 98
CHƯƠNG 4: PHÂN TÍCH TÍN HIỆU VÀ HỆ THỐNG RỜI
RẠC TRONG MIỀN TẦN SỐ
Phân tích Fourier cho tín hiệu và hệ thống rời rạc đóng vai trò quan trọng tương tự
như phân tích Fourỉe cho tín hiệu và hệ thống tương tự. Có rất nhiều sự tương
đồng giữa các kĩ thuật phân tích tín hiệu và hệ thống rời rạc theo thời gian và liên tục theo thời gian.
4.1 CHUỖI FOURIER RỜI RẠC
4.1.1 Biểu diễn tín hiệu tuần hoàn rời rạc bằng chuỗi Fourier
4.1.1.1 Biểu diễn tín hiệu tuần hoàn rời rạc bằng chuỗi Fourier
Như đã định nghĩa trong 1.1.2.3, tín hiệu rời rạc tuần hoàn có tập các giá trị
lặp lại sau mỗi chu kì . Mỗi tín hiệu tuần hoàn được đặc trưng bởi chu kì cơ bản với
là giá trị nhỏ nhất của tín hiệu. Tín hiệu tuần hoàn rời rạc cơ bản là chuỗi mũ phức với
là tần số cơ bản. Có một điểm
khác biệt quan trọng giữa các tín hiệu mũ phức liên tục và rời rạc theo thời gian.
Đó là, hàm mũ phức liên tục
là phân biệt với mọi giá trị phân biệt, trong khi chuỗi mũ phức rời rạc
là hoàn toàn giống nhau nếu như tần số của nó khác
nhau một số nguyên lần của . Tức là, (4.1) Đặt
thay vào biểu thức (4.1) thu được (4.3) Tổng quát, sẽ có
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 99 với N là số nguyên (4.4)
Như vậy, chuỗi Ψ9(.) chỉ phân biệt trong khoảng P* giá trị liền nhau của (. Biểu
diễn chuỗi Fourier rời rạc của một tín hiệu tuần hoàn ,(.) có chu kì cơ bản P* có dạng sau &!.# 9:* 29;!"
với 19là hệ số Fourier phức, được tính theo công thức sau &!.# 1 .29;!" (4.6) 19 = P* ":*p ,(.)^
Đặt ( = 0, khi đó biểu thức (4.6) trở thành (4.7)
Biểu thức (4.7) chỉ ra rằng 1* chính là giá trị trung bình của ,(.) trong một chu kì.
Biểu diễn chuỗi Fourier lượng giác khi tín hiệu tuần hoàn rời rạc ,(.) là thực sẽ có có dạng sau ⎧[* &!/! 25 25 + [&!/! 123 5. , P* chẵn
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 100 (4.8)
với và là các hệ số Fourier lượng giác. Các hệ số và và hệ số Fourier phức có mối quan hệ như sau
4.1.2 Điều kiện hội tụ của chuỗi Fourier rời rạc
Do chuỗi Fourier phức rời rạc là chuỗi hữu hạn, ngược lại với trường hợp chuỗi
Fourier phức liên tục, nên chuỗi Fourier rời rạc luôn hội tụ.
4.1.3 Các tính chất của chuỗi Fourier rời rạc
Biểu thức (1.60) cho phép tính công suất của tín hiệu tuần hoàn rời rạc
trong một chu kì. Mặt khác,
cũng được biểu diễn dưới dạng chuỗi Fourier phức,
nên hoàn toàn có thể tính công suất tín hiệu bởi các hệ số Fourier phức như sau
Biểu thức (4.10) được gọi là định lý Parseval cho chuỗi Fourier phức rời rạc.
Một số tính chất khác của chuỗi Fourier rời rạc được cho bởi bảng 4.1 dưới đây.
Các tính chất của chuỗi Fourier rời rạc
x n( )¬¾¾®DTFSa and y nk( )¬¾¾®DTFSbk Tính chất
Tín hiệu tuần hoàn Hệ số Fourier
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 101 Tuyến tính
a bx n( )+ y n( ) a bak+ bk Dịch thời gian x n n( - 0)
e- jk(2p/N n) a 0 k e x n( ) Dịch tần số j(2p/N k n) 0 a k k- 0 Phép đảo x n(- ) a-k Liên hợp phức x n*( ) a*-k 1 x Duality an k(- ) N Tổng chập Nabk k Tích Tín hiệu chẵn Tín hiệu lẻ Tín hiệu thực a ak = -*k
Bảng 4.1: Các tính chất của chuỗi Fourier rời rạc
4.2 BIẾN ĐỔI FOURIER TÍN HIỆU RỜI RẠC THỜI GIAN
4.2.1 Biến đổi Fourier của chuỗi tuần hoàn và không tuần hoàn
Tương tự như chuỗi Fourier liên tục, các hệ số Fourier phức của chuỗi
Fourier rời rạc cũng biểu diễn phổ của tín hiệu tuần hoàn rời rạc theo thời gian. Do
( chỉ là các số nguyên nên phổ biên độ và phổ pha không liên tục mà chỉ tồn tại tại các tần số rời rạc
nên được gọi là có dạng phổ tần rời rạc hay phổ vạch.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 102
Biến đổi Fourier là một công cụ cho phép biểu diễn tín hiệu rời rạc thời gian
bất kì, có thể tuần hoàn hoặc không tuần hoàn, sang miền tần số. Giữa biến đổi
Fourie cho tín hiệu thời gian rời rạc và chuỗi Fourier rời rạc có nhiều điểm tương đồng. Hàm
được gọi là biến đổi Fourier của tín hiệu rời rạc thời gian nếu Và biến đổi Fourier ngược của được định nghĩa như sau (4.12) và được gọi là một cặp
biến đổi Fourier, thường được kí hiệu trong đó
là biểu diễn trong miền thời gian và
là biểu diễn trong miền tần
số của cùng một tín hiệu rời rạc. Cặp biến đổi Fourier là duy nhất ứng với một tín hiệu. Biến đổi Fourier của
thường có dạng phức và có thể viết dưới dạng phasor như sau (4.14)
còn được gọi là phổ của tín hiệu không tuần hoàn rời rạc , với là phổ biên độ và
là phổ pha của tín hiệu . Nếu tín hiệu là thực thì phổ biên độ là hàm chẵn và phổ pha là hàm lẻ.
Do biến đổi Fourier của tín hiệu thời gian rời rạc là tổng của vô số hàm mũ phức vì
thế vấn đề về tính hội tụ của biến đổi Fourier cần phải được xem xét để đảm bảo sự
tồn tại của phép biến đổi này. Tương tự như chuỗi Fourier liên tục, điều kiện hội tụ
của biến đổi Fourier thời gian rời rạc là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 103
- Biến đổi Fourier thời gian rời rạc sẽ hội tụ đều khi và chỉ khi có tổng tuyệt đối hữu hạn (4.15)
- Biến đổi Fourier thời gian rời rạc sẽ hội tụ theo MSE khi và chỉ khi có tổng
bình phương hữu hạn, tức là, tín hiệu
là tín hiệu năng lượng. (4.16) Nếu phổ
là giới hạn thì biến đổi Fourier ngược thời gian rời rạc luôn luôn hội tụ
do tích phân được lấy trong khoảng giới hạn.
4.2.2 Tính chất của biến đổi Fourier tín hiệu thời gian rời rạc
Định lý Parseval đưa ra một phương pháp khác để xác định năng lượng của
tín hiệu, đó là xác định năng lượng của tín hiệu trong miền tần số dựa trên phổ của
nó. Định lý Parseval cho tín hiệu thời gian rời rạc được phát biểu như sau (4.17) Nếu ,
thì phương trình trên trở thành
Biểu thức (4.18) cho thấy năng lượng của tín hiệu trong miền thời gian và trong miền
tần số được bảo toàn.
Giữa biến đổi Fourier thời gian rời rạc (DTFT) và chuỗi Fourier liên tục
(CTFS) có mối quan hệ tương hỗ với nhau. DTFS hoàn toàn giống với CTFS khi
hoán đổi vai trò của các hàm trong miền thời gian cho miền tần số và ngược lại.
Nhắc lại, cặp biến đổi Fourier thời gian rời rạc gồm biến đổi Fourier thuận và
ngược được lần lượt mô tả như sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 104
Chuỗi Fourier thời gian liên tục cho tín hiệu tuần hoàn chu kì , còn được gọi là biểu
thức tính tổng hợp và biểu thức phân tích, lần lượt được biểu diễn như sau
có thể được viết lại như sau
Từ (4a) và (4c) nhận thấy, biểu thức tổng hợp của CTFS với sẽ tương ứng
với biến đổi Fourier thời gian rời rạc thuận khi đặt , và . Biểu
thức phân tích của CTFS với
sẽ tương ứng với biến đổi Fourier thời gian rời rạc ngược khi đặt và
. Kết quả là, biến đổi Fourier thời gian rời rạc của chuỗi rời rạc
có thể được xem như biểu diễn chuỗi Fourier thời gian liên tục của phổ tín hiệu với chu kì .
Một số tính chất khác của biến đổi Fourier thời gian rời rạc được cho bởi bảng 4.2 dưới đây.
Các tính chất của biến đổi Fourier thời gian rời rạc Tính chất Tín hiệu rời rạc Biến đổi Fourier , ,
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 105 Tuần hoàn X(W+2 )p=X( )W Tuyến tính ax n a x n1 1[ ]+ 22[ ]
aX1 1( )W +a X2 2( )W Dịch thời gian xn n[ - 0]
e- j nW X( ) 0 W Dịch tần số e xnjW0n [ ] X(W-W0) Liên hợp phức x n*[ ] X*(-W) Phép đảo x n[- ] X(-W)
ìx n m[ /] x( )m [ ]n if n = km Co dãn thang đo =í î0
if n ¹ km X m( W) dX( )W j Frequency differentiation nxn[ ] dW Sai phân bậc 1 xn xn[ ]- -[1]
(1-e- jW) ( )X W ¥ p dX ( ) ( )0 W + 1- Tổng vô hạn å jW X ( )W x k[ ] 1-e k=-¥ W£p Tổng chập , Tích , X1( )WÄ WX2( ) Tín hiệu thực
xn x n x n[ ]= e[ ]+ o[ ]
X( )W = A( )W + jB( )W Tín hiệu chẵn x ne[ ]
Re[ ( )]X W =A( )W Tín hiệu lẻ x no[ ]
jIm[ ( )]X W = jB( )W
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 106
Bảng 4.2: Các tính chất của biến đổi Fourier rời rạc
4.2.3 Các cặp biến đổi Fourier và phổ của một số tín hiệu rời rạc thời gian cơ bản
Từ tín hiệu thời gian rời rạc
tuần hoàn với chu kì , định nghĩa một tín hiệu rời rạc , như sau , (4.19) tức là, ,
tương ứng với tín hiệu
trong một chu kì và bằng 0 tại các thời điểm còn lại. Đặt và
lần lượt là biến đổi Fourier của và
thì giữa chúng có mối quan hệ như sau Ta có,
là hệ số chuỗi Fourier của tín hiệu rời rạc có chu kì (4.21) Thay vào (4.20), thu được (4.22)
Nhận thấy, hệ số chuỗi Fourier có thể thu được bằng cách lấy mẫu tại các
số nguyên lần của tần số cơ bản với hệ số tỉ lệ . Cách này rất thuận
tiện cho việc xác định hệ số Fourier
khi dễ dàng biết được biến đổi Fourier của
tín hiệu rời rạc tuần hoàn cơ bản, ví dụ như chỉ đơn giản bằng cách tra bảng biến
đổi Fourier 4.3. Biểu thức (4.22) chỉ ra rằng, tín hiệu thời gian rời rạc tuần hoàn
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 107
luôn có phổ vạch với các vạch phổ nằm tại tần số
và có độ lớn bằng giá trị .
Biến đổi Fourier của một số tín hiệu cơ bản được cho bởi bảng 3.3 dưới đây.
Một số cặp biến đổi Fourier tín hiệu rời rạc cơ bản x n[ ] X( )W d[ ]n 1 d(n n- 0) e- j nW 0 xn[ ] 1= 2pd( )W W£,p e jW0n 2pd(W-W W W £0), , 0p cosW0n
pd[ (W-W0)+d(W+W W W £0)], , 0p sinW0n
-jpd[ (W-W - W0) d( +W W W £0)], 0 p un[ ]
pd( )W + 1-jW, W£p 1-e - - -u n[1]
-pd( )W + 1- jW, W£p 1-e aun an [ ],<1 1 1-ae- jW
-au nn [- -1], a >1 1 1-ae- jW
(n+1)a un an [ ],<1
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 108 a an,<1 1-a2 1 2- acosW+a2 ì xn[ ]=ïí1 n é 1 ù
N£ 1 ïî0 n N> 1 + sinêWæçèN1 2öø÷úû ë sin(W / 2) sinWn ì
,0 < <W p pn
X( )W =íï1 0£W£N1ïî0 0£W >N1 ¥ ¥ åd[n kN- 0] W0 åd(W-W W0), 0= 2p k=-¥ N k=-¥ 0
Bảng 4.3: Các cặp biến đổi Fourier thời gian rời rạc
Ví dụ 17: Tìm DTFT của tín hiệu xung đơn vị
. Lời giải: Áp dụng định nghĩa của DTFT, sẽ có
Ví dụ 18: Tìm DTFT của tín hiệu hàm mũ thực một phía . Lời giải:
Áp dụng định nghĩa của DTFT, sẽ có
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 109
Một số tín hiệu rời rạc cơ bản không thoả mãn điều kiện hội tụ, tức là không có cả
tổng tuyệt đối và tổng bình phương hữu hạn, thì biến đổi Fourier thời gian rời rạc
của nó phải được tính toán thông qua việc lấy giới hạn của các tín hiệu phù hợp để
chúng suy biến về các tín hiệu cơ bản cần tính DTFT. Như vậy, giới hạn của biến
đổi Fourier tương ứng chính là biến đổi Fourier cần tính của tín hiệu ban đầu dưới
điều kiện đang xét. Tìm DTFT của xung nhảy bậc là một ví dụ cụ thể. Ví dụ 19:
Tìm DTFT của tín hiệu xung nhảy bậc
Lời giải: Tín hiệu xung nhảy bậc không có cả tổng tuyệt đối và tổng bình phương
hữu hạn, vì thế DTFT của nó được tính khi lấy giới hạn của tín hiệu khi [ → .
Phần thực của phổ tín hiệu là hàm chẵn và phần ảo của phổ tín hiệu là hàm lẻ. Phần
diện tích giới hạn bởi phần thực của phổ tín hiệu luôn bằng
với bất kì giá trị nào
của [, đây là tính chất cơ bản của hàm mũ. Thực hiện lấy biến đổi Fourier ngược cho và tính giá trị tại . 1 − 2[123Ω + [
Nhận thấy, phổ của tín hiệu liên tục tại các thành phần tần số ngoại trừ tại tần số
. Phần diện tích không đổi
được chia đôi, giảm còn ½ với khi [ →
. Kết quả là, thu được phổ của tín hiệu nảy bậc như sau
Ví dụ 20: Tìm DTFT của tín hiệu xung nhảy bậc
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 110 Lời giải:
Tín hiệu một chiều có thể viết lại như sau .
Áp dụng bảng tính chất của biến đổi Fourier thời gian rời rạc, bảng 4.2, để tính DTFT của
, kết hợp với kết quả của ví dụ 17 và ví dụ 19, thu được DTFT của tín hiệu như sau
5V(Ω) + 1 − [^.2; + 5V(−Ω) + 1 − [^2; − 1 = 25V(Ω)
Hiển thị tính tuần hoàn theo chu kì
của phổ tín hiệu rời rạc, thu được Ví dụ 21: DTDF
của một tín hiệu có dạng Tìm tín hiệu rời rạc tương ứng. Lời giải:
Do phổ tín hiệu là hàm chẵn, áp dụng định nghĩa sẽ thu được 3a.
là tín hiệu sinc, là hàm chẵn theo . Tín hiệu sinc rời rạc có tồn tại tổng bình
phương hữu hạn nhưng không tồn tại tổng tuyệt đối hữu hạn, và là tín hiệu năng lượng.
4.3 ĐÁP ỨNG TẦN SỐ CỦA HỆ THỐNG LTI RỜI RẠC
Đối với hệ thống LTI rời rạc theo thời gian có đáp ứng xung thì đầu ra
chính là tổng chập giữa đáp ứng xung và tín hiệu đầu vào , như trình bày tại
2.2.1. Áp dụng bảng tích chất biến đổi Fourier 4.2, thu được (4.23) với , và
lần lượt là biến đổi Fourier của , và . Từ biểu thức (4.23) rút ra (4.24)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 111 Hàm
được gọi là đáp ứng tần số của hệ thống, được biểu diễn dưới dạng phasor như sau (4.25)
được gọi là đáp ứng biên độ và
được gọi là đáp ứng pha của hệ thống.
Nếu tín hiệu đầu vào của hệ thống là chuỗi mũ phức , thu được tín hiệu đầu ra như sau (4.26)
Biểu thức (4.26) cho thấy chuỗi mũ phức là hàm riêng của hệ thống LTI với giá trị riêng tương ứng là .
Nếu đầu vào của hệ thống là tín hiệu
tuần hoàn được biểu diễn dưới dạng
chuỗi Fourier thì đầu ra tương ứng
cũng là tín hiệu tuần hoàn được biểu diễn dưới dạng chuỗi Fourier
Nếu đầu vào của hệ thống là tín hiệu
không tuần hoàn thì đầu ra tương ứng
được biểu diễn như sau (4.28)
Nếu hệ thống LTI thời gian rời rạc được dặc trưng bởi phương trình sai phân như
mô tả bởi biểu thức (2.23). Lấy biến đổi Fourier thời gian rời rạc cho cả hai vế, thu được (4.29)
Như vậy, thu được hàm truyền đạt tương ứng của hệ thống như sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 112 (4.30)
Không giống với đáp ứng tần số của hệ thống LTI liên tục, đáp ứng tần số của hệ
thống LTI rời rạc cũng tuần hoàn với chu kì . Vì thế, chỉ cần quan sát đáp ứng tần
số của hệ thống trong phạm vi hoặc .
4.4 MỘT SỐ VÍ DỤ VỀ ỨNG DỤNG CỦA BIẾN ĐỔI FOURIER TÍN HIỆU THỜI GIAN RỜI RẠC
4.4.1 Đáp ứng hệ thống khi đầu vào là tín hiệu hình sin rời rạc Giả thiết rằng , và
lần lượt là đáp ứng đầu ra của hệ thống khi đầu là , và . Do , áp dụng các tính chất của hệ thống LTI, thu được Nếu tín hiệu
thu được bằng cách lấy mẫu tín hiệu hình sin liên tục theo thời gian (_!) với chu kì lấy mẫu , tức là (4.32) Đặt
và áp dụng cho tất cả các tính toán trong tiểu mục này.
Tín hiệu hình sin liên tục theo thời gian
sẽ có dạng sóng duy nhất ứng với
mỗi giá trị của trong phạm vi 0 đến . Giá trị càng tăng thì hình sin có tần số
ngày càng lớn. Ngược lại, tín hiệu hình sinh rời rạc chỉ có dạng sóng duy
nhất với các giá trị của trong khoảng 0 đến do (4.33)
với là số nguyên. Khoảng giá trị này còn được giới hạn hơn nữa vì lý do sau (4.34) Do vậy,
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 113 (4.35)
Biểu thức (4.35) chỉ ra rằng tín hiệu hình sin rời rạc ở tần số (5 + Ω) có cùng dạng
với tín hiệu ở tần số (5 − Ω). Vì thế, tín hiệu hình sin ở bất kì giá trị nào nằm ngoài khoảng 0 đến
sẽ hoàn toàn giống với hình sin có tần số nằm trong
khoảng 0 đến . Như vậy, rút ra kết luận rằng đối với tín hiệu hình sinh rời rạc
chỉ có dạng sóng duy nhất với các giá trị của trong khoảng 0 đến , chỉ
cần quan sát đáp ứng tần số của hệ thống trong khoảng tần số này.
4.4.2 Mô phỏng hệ thống
Xét hệ thống LTI thời gian liên tục với đầu vào và đầu ra , cần tìm hệ thống LTI thời gian rời rạc với đầu vào và đầu ra sao cho (4.36) với là chu kì lấy mẫu. Gọi
và (‘) lần lượt là hàm truyền đạt của hệ thống
liên tục và hệ thống rời rạc. Nếu đưa vào hai hệ thống tín hiệu đầu vào dạng hàm mũ phức sẽ thu được các đầu ra tương ứng (4.38) Để thu được thì các hàm truyền
của hai hệ thống phải thoả mãn điều kiện sau (4.39) Tức là (4.40)
Chú ý rằng hàm truyền đạt của hệ
thống rời rạc (‘) là tuần hoàn theo với chu kì
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 114
, nhưng hàm truyền đạt của hệ thống liên tục (_) không như vậy. Vì thế,
nhìn chung, biểu thức (4.40) không đúng với mọi giá trị của . Nhưng nếu là
tín hiệu có băng tần giới hạn thì biểu
thức (4.40) có thể xảy ra. Về nguyên
tắc, biểu thức (4.40) có thể thoả mãn nếu như các giá trị nằm trong khoảng ( ). Tuy
nhiên, hàm truyền đạt (_) là hàm phân thức theo trong khi hàm truyền đạt (‘) là hàm phân thức theo
nên biểu thức (4.40) không thể thoả mãn. Vì thế, chỉ
có thể xác định hệ thống rời rạc thời gian tương đương với hệ thống thời gian liên
tục với độ chính xác nhất định khi tín hiệu đầu vào có băng tần giới hạn.
Hình 4.1: Hàm truyền đạt của hệ thống liên tục và rời rạc thời gian
4.5 BIẾN ĐỔI FOURIER RỜI RẠC 4.5.1 Biến đổi Fourier rời rạc
Biến đổi Fourier rời rạc (DFT – Discrete Fourier Transform) thực hiện
chuyển đổi tín hiệu thời gian rời rạc có độ dài giới hạn sang miền tần số. Tín hiệu
thu được trong miền tần số cũng là rời rạc và có cùng độ dài với tín hiệu trong
miền thời gian. Nếu ,( là chuỗi thời gian rời rạc có độ dài , tức là thì DFT của , được kí hiệu là
, được định nghĩa như sau với
là nghiệm bậc của giá trị đơn vị, có dạng (4.43)
Biến đổi DFT người được định nghĩa như sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 115
Một số đặc trưng cơ bản của biến đổi Fourier rời rạc là
- DFT là ánh xạ duy nhất giữa và và ngược lại
- DFT có liên quan chặt chẽ với chuỗi Fourier rời rạc và biến đổi Fourier
- DFT phù hợp thực hiện trên máy tính vì biểu diễn tín hiệu rời rạc và hữu hạn
cả trong miền thời gian và miền tần số
- DFT có thuật toán tính toán cực nhanh, được gọi là biến đổi Fourier nhanh
(FFT – Fast Fourier Transform)
Chú ý rằng, lựa chọn giá trị cho chuỗi
không cần cố định. Nếu có
Cặp biến đổi DFT được kí hiệu (4.45) chiều dài
nhưng vẫn muốn thực hiện DFT với chiều dài thì chỉ cần thêm vào
mẫu có giá trị 0 vào chuỗi
. Quá trình thêm các mẫu không có ý
nghĩa vào một chuỗi được gọi là zero padding. Như vậy, chuỗi mới này được coi là chuỗi mẫu và
cũng có mẫu và biến đổi Fourier rời rạc được gọi là
DFT điểm. Trong thực tế, thường được chọn là luỹ thừa của 2 để đạt được hiệu quả tính toán cao.
So sánh giữa DFT và chuỗi Fourier thời gian rời rạc cho thấy của một chuỗi hữu hạn
có thể tính toán thông qua các hệ số Fourier phức của chuỗi Fourier
thời gian rời rạc bằng cách, mở rộng chu kì của chuỗi rời rạc thành và nhân
với một hệ số tỉ lệ là . Tức là, (4.46)
Áp dụng biến đổi Fourier
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 116
So sánh (4.47) với (4.42), nhận thấy (4.48) Vậy, tương ứng với được
lấy mẫu đều tại các tần số cách đều nhau với k nguyên. Biến đổi
Biến đổi Tín hiệu miền Tín hiệu thuận ngược thời gian miền tần số Biến đổi Fourier thời Liên tục Liên tục Liên tục Liên tục gian liên tục (CTFT) Biến đổi Fourier thời Rời rạc Liên tục Rời rạc Liên tục gian rời rạc (DTFT) Biến đổi Fourier rời Rời rạc Rời rạc Rời rạc Rời rạc rạc (DFT)
Bảng 4.4: So sánh giữa các kiểu biến đổi Fourier
4.5.2 Các tính chất của biến đổi Fourier rời rạc
Định lý Parseval áp dụng cho DFT có dạng sau !
Một số tính chất của biến đổi Fourier rời rạc được cho bởi bảng 4.5 dưới đây.
Các tính chất của DFT Tính chất Tín hiệu rời rạc DFT Tuyến tính ax n bx n1[ ]+ 2[ ] aX k bX k1( )+ 2( ) Dịch thời gian xn m[ - ]
e- j2pkmX k( )
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 117 Dịch tần số
e- j2pk n N0/ xn[ ] X k k( - 0) Đảo x n[- ] X k(- ) Liên hợp phức x n*[ ] X*(-k) Tổng chập x n1[ ]Äx n2[ ] X k X k1[ ] 2[ ] Tích x n x n1[ ] [ ]2 1 X k[ ]ÄX k[ ] N 1 2
Bảng 4.5: Các tính chất của biến đổi Fourier rời rạc BÀI TẬP CHƯƠNG 4 .
CHƯƠNG 5: BIẾN ĐỔI LAPLACE
5.1 BIẾN ĐỔI LAPLACE
Biến đổi Laplace là trường hợp tổng quát của biến đổi Fourier cho tín hiệu liện
tục. Biến đổi Laplace có thể chuyển đổi các tín hiệu mà biến đổi Fourier không thực
hiện được. Do vậy, biến đổi Laplace là công cụ hữu hiệu trong phân tích và thiết kế
các hệ thống liên tục theo thời gian.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 118
5.1.1 Biến đổi Laplace một phía và hai phía Biến đổi Laplace của tín hiệu là được định nghĩa (5.1) Biến số phức có dạng
với phần thực và phần ảo . Biến đổi Laplace
được định nghĩa trên phương trình (5.1) được gọi là biến đổi laplace hai phía. Biến
đổi Laplace một phía đóng vai trò quan trọng trong phân tích các hệ thống nhân
quả được mô tả bằng phương trình vi phân tuyến tính hệ số hằng với điều kiện ban đầu. Biến đổi Laplace
một phía được định nghĩa toán học như sau (5.2)
Khác biệt trong phương trình (5.1) và (5.2) là cận dưới của phép tích phân. Biến đổi
Laplace hai phía phụ thuộc vào toàn bộ tín hiệu, còn biến đổi Laplace một phía phụ
thuộc phần bên phải của tín hiệu, tức là với ! < 0.
5.1.2 Điều kiện tồn tại của biến đổi Laplace
Biến đổi Laplace tồn tại nếu như độ lớn của biến đổi là hữu hạn, tức là .
Liên tục từng phần: Hàm số
là liên tục từng phần trên đoạn giới hạn [ ≤ , ≤ ë
nếu , là liên tục trên [[, ë] ngoại trừ một số hữu hạn các điểm tại đó , có giới hạn
phải hoặc giới hạn trái hữu hạn.
Điều kiện đủ: Điều kiện đủ để tồn tại biến đổi Laplace là nếu liên tục từng phần
trên (0, ∞) và tồn tại hằng số và sao cho thì tồn tại với 3 > (. Chứng minh: Vì
là liên tục từng phần trên (0, ∞),
là khả tích trên (0, ∞),
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 119 )|^.%1Z! (5.3) với , {,(!)} < ∞.
5.1.3 Quan hệ giữa biến đổi Laplace và biến đổi Fourier
Khi biến phức chỉ có phần ảo, tức là
, phương trình (5.1) trở thành
Phương trình (5.4) là biến đổi Fourier của , (5.5)
Nếu không chỉ có phần ảo, phương trình (5.1) có thể được viết như sau (5.6) ./ Viết lại (5.6) ta có
Vế phải của (5.7) là biến đổi Fourier của
. Do vậy, biến đổi Laplace có thể
được diễn giải như biến đổi Fourier của
sau khi lấy tích với tín hiệu hàm mũ phần thực.
5.1.4 Biểu diễn biến đổi Laplace trong mặt phẳng s
Biến đổi Laplace là tỉ số của đa thức đại số biến phức có thể biểu diễn như sau (5.8)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 120 Trong đó
là đa thức tử số và đó
là là đa thức mẫu số. Phương trình (5.8)
được xem như là một tỉ số. Các nghiệm của đa thức tử số được gọi là điểm không của
vì tại các giá trị này của
bằng 0. Các nghiệm của đa thức mẫu số
được gọi là các điểm cực của
, do tại các giá trị này của . Biến
đổi Laplace cho đa thức tỉ số có thể được xác định bằng vị trí các điểm cực x và
điểm không o trên mặt phẳng s, gọi là các đường cực-không của biến đổi Laplace.
Đối với các tín hiệu, biến đổi Laplace hội tụ cho một khoảng giá trị của . Khoảng
giá trị này được gọi là vùng hội tụ (ROC), được đưa ra như một vùng giới hạn bởi đường cực-không.
5.1.5 Các tính chất vùng hội tụ ROC
Tính chất 1: ROC của
chứa các dải song song với trục . ROC của chứa các giá trị
trên đó biến đổi Fourrier của hội tụ. Vì vậy, ROC của
xác định trên phần thực của , chứ không phải trên tần số . Như vậy, ROC của
chứa các dải song song với trục .
Tính chất 2: Biến đổi Laplace của đa thức tỉ số không chứa các cực. Trong ROC
phải hữu hạn cho tất cả , do
là vô hạn tại các điểm cực và
phương trình (5.1) không hội tụ tại các điểm cực. Do đó, ROC không chứa các điểm cực.
Tính chất 3: ROC là toàn bộ mặt phẳng s đối với một khoảng hữu hạn nếu có ít
nhất một giá trị tại đó biến đổi Laplace hội tụ. Chứng minh
Tín hiệu trên một khoảng hữu hạn sẽ bằng không bên ngoài đoạn giới hạn như trong Hình 5.1. Giả sử
là khả tích tuyệt đối cho giá trị nào đó Thì đường nằm trong ROC. Đường ! cũng nằm trong ROC nếu
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 121 ! (5.10) Nếu sao cho
giảm dần, thì giá trị lớn nhất của trở thành đối với
khác không trên đoạn này. ! (5.11)
Vế phải của phương trình (5.11) là hữu hạn, và do đó vế trái cũng vậy. Vì vậy
phải nằm trong ROC. Tương tự, nếu có thể chỉ ra rằng
là khả tích tuyệt đối. Do vậy, ROC là toàn bộ mặt phẳng s.
Hình 5.1. Tín hiệu trên khoảng hữu hạn.
Tính chất 4: Nếu ROC của tín hiệu bên phải chứa đường thì
sẽ nằm trong ROC cho tất cả giá trị của . Chứng minh
Đối với tín hiệu bên phải
cho tất cả các giá trị trước một thời điểm ! nào đó như Hình 5.2.
Nếu biến đổi Laplace hội tụ cho giá trị nào đó, thì (5.12) ./ Nếu là tín hiệu bên phải thì
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 122 Đối với ,
là khả tích tuyệt đối do giảm nhanh hơn khi ! → ∞ là. Do đó,
sẽ nằm trong ROC cho tất cả giá trị của . .
Hình 5.2. Tín hiệu bên phải.
Tính chất 5: Nếu ROC của tín hiệu bên trái chứa đường ℜ^(3) = $# thì ℜ^(3) < $#
sẽ nằm trong ROC cho tất cả giá trị của 3.
Đối với tín hiệu bên trái ,(!) = 0 cho tất cả các giá trị sau một thời điểm !# nào đó như
Hình 5.3. Tính chất này có thể chứng minh dễ dàng với các lập luận như tính chất 4.
Hình 5.3. Tín hiệu bên trái.
Tính chất 6: Nếu ROC của tín hiệu hai phía chứa đường ℜ^(3) = $* thì ROC sẽ
chứa một dải, bao gồm cả các đường biên dải. Chứng minh
Tín hiệu hai phía trải vô hạn cho cả ! > 0 và ! < 0 như Hình 5.4 (a).
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 123
Chọn thời điểm bất kì !* chia tín hiệu thành tổng của tín hiệu phải và tín hiệu trái
như Hình 5.4 (b) và (c). Biến đổi Laplace của ,(!) hội tụ tại các giá trị của 3 tại đó
cả tín hiệu bên phải và bên trái đều hội tụ. Như đã biết từ Tính chất 4 ROC biến
đổi Laplace của tín hiệu bên phải áE(3) chứa nửa mặt phẳng ℜ^(3) > $E đối với giá trị
nào đó, và từ Tính chất 5 chứa nửa mặt phẳng đối với giá trị
nào đó. Chồng của hai nửa mặt phẳng này chính là ROC của tín hiệu hai phía
như Hình 5.4 (d) với giả thiết . Nếu
thì sẽ không có miền chồng, trong trường hợp này không tồn tại mặc dù và vẫn tồn tại đồng thời riêng biệt.
Hình 5.4. (a) Tín hiệu hai phía (b) Tín hiệu bên phải. (c) Tín hiệu bên trái. (d) ROC của tín hiệu hai phía.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 124
5.1.6 Các tính chất của biến đổi Laplace Tuyến tính: Nếu và
và là hai tín hiệu với biến đổi Laplace và , cùng ROC
và ! tương ứng, thì biến đổi Laplace tổ hợp tuyến tính của , và là
(5.14) Trong đó ROC ít nhất là
, và ! là các hằng số bất kì.
Dịch thời gian: Nếu
là tín hiệu với biến đổi Laplace và ROC , thì với bất kì hằng số !
nào biến đổi Laplace của sẽ là (5.15)
Với ROC giữ nguyên như đối với .
Dịch trên miền s: Nếu
là tín hiệu với biến đổi Laplace và ROC , thì biến
đổi Laplace của tín hiệu sẽ là (5.16) Với ROC là .
Tỉ lệ thời gian: Nếu
là tín hiệu với biến đổi Laplace và ROC , thì biến đổi Laplace của
cho bất kì hằng số [ thực hoặc phức là ℒ{,([!)} = á A B (5.17) Với ROC là .
Vi phân trên miền thời gian: Nếu
là tín hiệu với biến đổi Laplace và ROC , thì (5.18) Với ROC chứa .
Vi phân trên miền s: Nếu
là tín hiệu với biến đổi Laplace , thì (5.19)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 125 Tích phân: Nếu
là tín hiệu với biến đổi Laplace và ROC , thì Với ROC chứa . Chia cho t: Nếu
là tín hiệu với biến đổi Laplace , thì (5.21) Với điều kiện tồn tại.
Tích chập trên miền thời gian: Nếu , và
và là hai tín hiệu với biến đổi Laplace và và ROC và ! tương ứng, thì (5.22) Với ROC chứa .
Tích chập trên miền tần số: Nếu , và
và là hai tín hiệu với biến đổi Laplace và thì (5.23)
Tính chất hàm chẵn: Nếu là hàm số chẵn thì .
Tính chất hàm lẻ: Nếu là hàm số lẻ thì .
Bảng 5.1. Các tính chất của biến đổi Laplace Tính chất Tín hiệu Biến đổi Laplace ROC Tuyến tính It nhất Dịch thời gian , Giữ nguyên
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 126 Dịch trên miền s Dịch Tỉ lệ thời gian ( á A B Vi phân trên Z, Ít nhất miền thời gian Z! Vi phân trên miền s
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 111 Tích phân Tích chập , !
Tính chất vi phân của biến đổi Laplace một phía
Phần lớn các tính chất của biến đổi Laplace hai phía (Bảng 5.1) đều đúng cho biến
đổi Laplace một phía. Cụ thể, đặc tính vi phân của biến đổi Laplace một phía có sự khác biệt do nó yêu cầu
với ! < 0 và không bao hàm các xung và điểm kì dị bậc cao. Nếu
là tín hiệu với biến đổi Laplace
, thì biến đổi Laplace một phía của
có thể thực hiện bằng cách tích phân từng phần như
Tiếp tục quá trình n lần, biến đổi Laplace một phía CC1,,) nhận được là (5.25) Trong đó ,̇ là tính tại ! = 0 , và là )C1!)! tính tại ! = 0 .
Định lí giá trị ban đầu Cho tín hiệu với biến đổi Laplace và khi ! < 0 thì (5.26)
Định lí giá trị cuối Cho tín hiệu với biến đổi Laplace và khi ! < 0 thì (5.27)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 128
5.1.7 Một số biến đổi Laplace thông dụng
Một số biến đổi Laplace của các hàm số cơ bản được đưa ra trong Bảng 5.2 dưới đây.
Bảng 5.2. Các hàm số phổ biến và biến đổi Laplace Tín hiệu Biến đổi Laplace ROC Tất cả Tất cả . − 1)! (3 + )) ! (3 + )) !
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670
5.2 BIẾN ĐỔI LAPLACE NGƯỢC
5.2.1 Biến đổi Laplace ngược
Từ phương trình (5.6) chúng ta biết rằng biến đổi Laplace giá trị của tín hiệu được tính 125 (5.28) ./
Áp dụng biến đổi Fourier ngược đẳng thức trên nhận được ,(!)^.5Y = ℱ.#á($ + `Ω) = Y á($ + `Ω)^2;YZ Ω (5.29)
Nhân cả hai vế (5.29) với nhận được ,(!) = Y á($ + `Ω)^(562;)YZ Ω ./ Do , là hằng số,
. Thay thế vào phương trình (5.30), thay đổi
biến tích phân từ sang chúng ta nhận được biến đổi Laplace ngược như sau (5.31)
5.2.2 Tính toán biến đổi Laplace ngược sử dụng triển khai phân số từng phần
Biến đổi Laplace ngược của hàm số tỉ số
có thể dễ dàng tính được bằng cách
sử dụng triển khai phân số từng phần
Triển khai phân số từng phần với các cực đơn
Xét biến đổi Laplace tỉ số có dạng (5.32)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 130 Với bậc của
nhỏ hơn bậc của đa thức mẫu số. Các cực , !, . ., phân biệt.
Biến đổi Laplace của hàm tỉ số
có thể triển khai sử dụng triển khai phân số từng phần như sau (5.33)
Các hệ số , , . ., được gọi là phần dư của triển khai phân số từng phần. Các phần dư được tính bằng (5.34)
Khi đã biết các hệ số , , . ., biến đổi ngược của từng số hạng có thể được tính
dựa trên vị trí của mỗi cực tương ứng với ROC. Triển khai phân số từng phần với đa cực
Xét biến đổi Laplace tỉ số
với các cực được lặp lại có dạng (5.35) Với đa cực bậc tại . Hàm số
với đa cực có thể triển khai như sau (5.36)
Các hệ số , . ., có thể được tính sử dụng công thức phần dư của triển khai phân
số từng phần cho hàm số đơn cực ở trên. Các hệ số , , . ., được tính như sau (5.37) 127 (5.38)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670
Và cứ tiếp tục như vậy cho các hệ số còn lại.
5.3 PHÂN TÍCH HỆ THỐNG LTI LIÊN TỤC BẰNG BIẾN ĐỔI LAPLACE
5.3.1 Hàm truyền đạt của hệ thống
Hệ thống LTI liên tục theo thời gian có thể được đặc tính hóa hoàn toàn bằng đáp ứng xung . Tín hiệu đầu ra
của hệ thống LTI và tín hiệu đầu vào liên hệ bằng tích chập (5.40)
Sử dụng tính chất tích chập, nhận được (5.41)
Công thức này chỉ ra rằng biến đổi Laplace của tín hiệu đầu ra là tích của biến
đổi Laplace xung đáp ứng và tín hiệu đầu vào . Biến đổi được gọi là
hàm truyền đạt của hệ thống hay hàm hệ thống và được biểu diễn như sau (5.42)
Các nghiệm của đa thức mẫu số của hàm truyền đạt được gọi là các điểm cực. Các
nghiệm của đa thức tử số được gọi là các điểm không. Các vị trí mà hàm truyền
đạt vô hạn (các cực) xác định vùng hội tụ.
5.3.2 Điều kiện nhân quả và ổn định của hệ thống trong miền s
Hệ thống LTI ổn định
Hệ thống LTI liên tục theo thời gian là ổn định khi và chỉ khi đáp ứng xung khả tích tuyệt đối, tức là ./
Biến đổi Laplace của đáp ứng xung được biết như hàm hệ thống, và được biểu diễn bằng
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 132 (5.44)
Hệ thống LTI liên tục theo thời gian là ổn định khi và chỉ khi hàm truyền đạt có ROC
bao gồm trục ảo (đường trên mặt phẳng phức tại đó phần thực bằng không).
Hệ thống LTI nhân quả
Hệ thống LTI liên tục theo thời gian là nhân quả khi và chỉ khi đầu ra phụ
thuộc chỉ vào thời điểm hiện tại và qúa khứ của đầu vào , mà không phụ thuộc
vào đầu vào trong tương lai. Do đó, với ! < ∞.
Đối với hệ thống nhân quả, hàm hệ thống có thể được viết như sau (5.45) Nếu và
là khả tích tuyệt đối hội tụ của
dẫn đến điều kiện hội tụ sau (5.46)
Với bất cứ giá trị nào đủ lớn để thỏa mãn phương trình trên. Do vậy, ROC chính
là vùng bên phải của đường thẳng đứng đi qua điểm như trên Hình 5.5. Đặc biệt, nếu là hàm tỉ số,
thì hệ thống là nhân quả khi và chỉ khi
ROC là nửa mặt phẳng bên phải từ cực nằm xa bên phải nhất và bậc của hàm tử số
không lớn hơn bậc của hàm mẫu số
, sao cho ROC là nửa mặt phẳng bên
phải không chứa bất cứ cực nào (thâm chí tại ).
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 133
Hình 5.5. ROC của hệ thống LTI nhân quả.
Hệ thống LTI ổn định và nhân quả
ROC của hệ thống nhân quả nằm bên phải của cực bên phải xa nhất và đối với hệ
thống ổn định cực bên phải xa nhất phải nằm tại nửa bên trái của mặt phẳng s và
phải chứa trục `Ω. Dẫn đến tất cả các cực của hệ thống phải nằm trên nửa bên trái
của mặt phẳng s (phần thực của tất cả các cực là âm, ℜ^…3BÀ < 0 cho tất cả 3B)
trong hệ thống nhân quả và ổn định như Hình 5.6.
Hình 5.6. ROC của hệ thống LTI ổn định và nhân quả.
Hệ thống LTI ổn định và nhân quả nghịch đảo
Đối với hệ thống ổn định nhân quả các cực phải nằm trên nửa bên trái của mặt phẳng s.
Nhưng các cực của hệ thống nghịch đảo là điểm không của hệ thống gốc ban đầu.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 134
Do đó, các điểm không của hệ thống gốc phải nằm trên nửa trái của mặt phẳng s.
5.3.3 Biểu diễn hệ thống trong miền s
Hàm hệ thống được đặc trưng hóa bằng phương trình tuyến tính hệ số hằng có thể
nhận được bằng cách áp dụng các tính chất của biến đổi Laplace. Biến đổi Laplace
chuyển đổi phương trình vi phân thành phương trình đại số trên miền s để dễ dàng
giải phương trình vi phân trên miền thời gian.
Xét phương trình vi phân tuyến tính hệ số hằng tổng quát có dạng [" Z!" + [".# Z!".# Z! Z! (5.47) Z!+ ë# Z!
Thực hiện biến đổi Laplace cả hai vế của phương trình sử dụng tính chất vi phân và tuyến tính nhận được (5.48) = (ë'3' + ë'.# Hàm hệ thống nhận được là
(3) = Œ(3) = ë'3' + ë'.#(5.49) (3)
[ " 3" +[ ".# 3".# + ⋯+ [ ! 3! +[ #3+ [ * á f
Hàm hệ thống là tỉ số đối với hệ thống được đặc trưng hóa bằng phương trình vi
phân với các nghiệm của đa thức tử số là các điểm không và các nghiệm của đa
thức mẫu số là các điểm cực.
Phương trình (5.49) không xác định bất cứ ROC nào, do bản thân phương trình vi
phân không bị ràng buộc bởi bất cứ vùng hội tụ nào. Tuy nhiên, với các nhận biết
về tính ổn định và nhân quả, có thể xác định ROC.
Giải phương trình vi phân tuyến tính hệ số hằng sử dụng biến đổi Laplace
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 135
Trình tự giải phương trình vi phân tuyến tính như sau:
Bước 1: Biến đổi Laplace cả hai vế của phương trình.
Bước 2: Rút gọn phương trình đại số nhận được cho trên miền s.
Bước 3: Tìm biến đổi ngược của để nhận được
, là lời giải của phương trình vi phân.
5.3.4 Hàm truyền đạt kết nối các hệ thống LTI Kết
nối nối tiếp hai hệ thống LTI
Đáp ứng xung của hai hệ thống LTI nối tiếp là (5.50)
Và từ tính chất tích chập của biến đổi Laplace hàm hệ thống kết nối nối tiếp là (Hình 5.7) (5.51)
Hình 5.7. Kết nối nối tiếp hai hệ thống LTI
Kết nối song song hai hệ thống LTI
Đáp ứng xung của hai hệ thống LTI kết nối song song là (5.52)
Và từ tính chất tuyến tính của biến đổi Laplace hàm hệ thống kết nối song song là (Hình 5.8) (5.53)
Hình 5.8. Kết nối song song hai hệ thống LTI.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 136 BÀI TẬP CHƯƠNG 5
1. Tìm biến đổi Laplace của các hàm số sau: a)
,(!) = ^.!1Q(!) + ^$1Q(−!) b) ,(!) = ^1Q(!) + ^.$1Q(−!)
2. Tìm biến đổi Laplace của %K"!1 1
3. Tìm biến đổi Laplace của _`aA1._`ab1 1
4. Chứng minh rằng ROC của biến đổi Laplace tín hiệu không nhân quả là vùng bên
trái của đường thẳng đứng trên mặt phẳng s.
5. Tìm biến đổi Laplace của tín hiệu tuần hoàn chu kì T.
6. Xác định ,(!), kiểm tra bằng định lí giá trị cuối cho á(3) = % # ! 6#
7. Cho hàm truyền đạt của hệ thống LTI là f(3) =
# . Tìm đáp ứng xung và vùng %6\
hội tụ và giá trị định ) để hệ thống là nhân quả và ổn định.
8. Cho hệ thống LTI liên tục được mô tả bằng phương trình vi phân sau Z$< Z!< Z< $ + 6 Z!! + 11 Z! + 6< = , Z!
a) Tìm hàm truyền đạt của hệ thống;
b) Xác định ℎ(!) cho các trường hợp sau: (i) hệ thống là nhân quả, (ii) hệ thống ổn
định, (iii) hệ thống không nhân quả và không ổn định.
9. Giải phương trình vi phân sử dụng biến đổi Laplace Z!< Z< ! − 2 Z! + 2< = cos ! <(0) = 1, < (0) = 0 Z!
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 137
CHƯƠNG 6: BIẾN ĐỔI z
Trong chương 5 đã giới thiệu phép biến đổi Laplace. Trong chương 6 sẽ trình bày
phép biến đổi z, là bản sao thời gian rời rạc của phép biến đổi Laplace. Phép biến
đổi z được giới thiệu để biểu diễn tín hiệu rời rạc thời gian (hoặc chuỗi) trong
miền z ( với z là một biến phức). 6.1 BIẾN ĐỔI z
Biến đổi z có thể xem là tổng quát hoá biến đổi Fourier thời gian rời rạc.
Biến đổi z áp dụng cho đa dạng các tín hiệu rời rạc khác nhau, bao gồm cả các tín
hiệu không thực hiện được biến đổi Fourier.
Phép biến đổi Laplace chuyển đổi các phương trình vi phân tích phân thành
phương trình đại số. Theo cách tương tự, phép biến đổi z chuyển đổi các phương
trình sai phân thành phương trình đại số, do đó đơn giản hóa việc phân tích các hệ
thống thời gian rời rạc.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 138
Biến đổi z có thể coi là biến đổi Laplace rời rạc. Biến đổi z và biến đổi Laplace có
nhiều đặc trưng tương tự. Tuy nhiên, giữa chúng vẫn tồn tại một số khác biệt cơ
bản do chúng mô tả cho hai kiểu tín hiệu và hệ thống khác nhau: rời rạc và liên tục
Các thuộc tính của phép biến đổi z song song với các tính chất của phép biến đổi
Laplace. Tuy nhiên, chúng ta sẽ thấy một số điểm khác biệt quan trọng giữa phép
biến đổi z và phép biến đổi Laplace.
6.1.1 Biến đổi z một phía và hai phía a. Biến đổi z hai phía
(Bilateral z transform) của tín hiệu x(n) (6.1)
ở đây z là một biến số phức có dạng biểu diễn lượng giác: z = re jω
Biến đổi Z thực hiện biến đổi tín hiệu x[n] trong miền biến số độc lập tự nhiên n
thành tín hiệu X(Z) trong miền Z. Miền Z là mặt phẳng phức Z. b. Biến đổi z một phía (Bilateral z
transform) của tín hiệu x(n) (6.2)
Biến đổi Z một phía và 2 phía có sự khác biệt:
- Biến đổi z một phía ứng dụng cho tín hiệu và hệ thống nhân quả x(n) = 0 với n < 0.
- Không biểu diễn được tín hiệu x[n] đối với miền biến số độc lập âm (n < 0).
- Biến đổi z một phía và hai phía của tín hiệu nhân quả là như nhau.
c. Biến đổi z với biến đổi Fourier Nếu biến phức z
có biên độ r = 1, z = e jω, biến đổi z của x(n) là (6.3)
Khi đó biến đổi Z chính là biến đổi Fourier thời gian rời rạc. Nếu biến phức z có
biên độ r ≠ 1, z = re jω, biến đổi z của x(n) là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 139 (6.4)
Khi đó biến đổi Z chính là biến đổi Fourier thời gian rời rạc của x(n)r –n
6.1.2 Miền hội tụ của biến đổi Laplace
Đối với một tín hiệu, biến đổi z hội tụ tại một vùng giá trị của z, được gọi là vùng
hội tụ (ROC – Range of Convergence). Để biến đổi z hội tụ thì biến đổi Fourier
của tín hiệu x(n)r –n phải hội tụ. (6.5)
Với mỗi tín hiệu x(n), điều kiện hội tụ xảy ra với một số giá trị r nhất định. z được
biểu diễn dưới dạng toạ độ cực, đặc trưng bởi bán kính r và tần số góc ω. Vùng hội tụ
trên mặt phẳng z là tập các đường tròn tâm tại gốc toạ độ và bán kính r thoả mãn điều
kiện xác định . Đây chính là điểm khác biệt so với biến đổi Laplace.
Biến đổi z suy biến thành biến đổi Fourier khi vùng hội tụ là đường tròn đơn vị trên
mặt phẳng z, tức là r=1.
Phương trình đại số mô tả biến đổi z X(z) của hai tín hiệu x(n) khác nhau có thể
hoàn toàn giống nhau ngoại trừ vùng hội tụ khác nhau. Vùng hội tụ là thành phần
không thể thiếu của biến đổi z để đảm bảo biến đổi z là ánh xạ duy nhất.
Ví dụ 1: Cho tín hiệu x(n) = a nu(n) với a thực (tín hiệu phía phải). Tìm biến đổi z và vùng hội tụ của x(n).
Lời giải: Áp dụng công thức (6.1) ta có Để X(z) hội tụ thì
|az –1| <1 |z| > |a| r > |a|
• |a| = 1 x(n) là xung nhảy bậc đơn vị Fourier transform
• |a| > 1: ROC không chứa đường tròn đơn vị FT của x(n) không hội tụ • |a|
< 1: ROC có chứa đường tròn đơn vị FT của x(n) có hội tụ
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 140
Hình 6.1 Miền hội tụ của tín hiệu x(n) = a nu(n) với a thực (tín hiệu phía phải) Ví dụ
2: Cho tín hiệu x(n) = – a –nu(– n – 1) với a thực (tín hiệu phía trái). Tìm biến
đổi z và vùng hội tụ của x(n). Lời giải: Áp dụng công thức (6.1) ta có
Để X(z) hội tụ thì |a –1z| < 1 |z| < |a| r < |a|
Hình 6.2 Miền hội tụ của tín hiệu x(n) = - a –nu(- n -1) với a thực (tín hiệu phía trái) Ví
dụ 3: Tìm biến đổi z và vùng hội tụ của x(n).
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 141
Lời giải: Áp dụng công thức (6.1) ta có
Vùng hội tụ của X(Z) là |1/5| < |z| và |z| > |1/3|
Hình 6.3 Miền hội tụ của tín hiệu x(n) 2 phía
Các tính chất của ROC
1. ROC của X(z) gồm các đường tròn đồng tâm có tâm tại gốc của mặt phẳng phức
2. ROC không chứa bất kì điểm cực nào.
3. Với x(n) là tín hiệu giới hạn, tức là x(n) ≠ 0 với N1 ≤ n ≤ N2, và X(z) hội tụ tại
một vài giá trị của z thì ROC là toàn bộ mặt phẳng z ngoại trừ (có thể) z = 0 và/ hoặc z = ∞
4. Với x(n) là tín hiệu phía trái, tức là x(n) = 0 với t > N1 > -∞, và X(z) hội tụ tại
một vài giá trị của z thì ROC là phần diện tích bên trong đường tròn |z| = rmin
của mặt phẳng z ngoại trừ (có thể) z = 0, tức là ROC có dạng:
|z| < rmin hoặc 0 < |z| < rmin với rmin = min{abs(poles)}
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 142
5. Với x(n) là tín hiệu phía phải, tức là x(n) = 0 với t < N2 < ∞, và X(z) hội tụ tại
một số giá trị của z thì ROC là phần diện tích bên ngoài đường tròn |z| = rmax
của mặt phẳng z ngoại trừ (có thể) z = ∞, tức là ROC có dạng:
|z| > rmax hoặc ∞ > |z| > rmax với rmax = max{abs(poles)}
6. Với x(n) là tín hiệu hai phía và X(z) hội tụ tại một số giá trị của z thì ROC là
phần diện tích hình vành khăn trên mặt phẳng z nằm giữa hai đường tròn |z|
= rmax và |z| = rmin và không chứa bất kì điểm cực nào, tức là ROC sẽ có dạng:
rmin < |z| < rmax với rmax,min = abs(poles)
Nếu X(z) của x(n) có dạng phân số thì ROC của x(n) có các tính chất sau:
1. ROC bị giới hạn bởi các điểm cực hoặc mở rộng tới vô cùng
2. Nếu x(n) là tín hiệu phía phải thì ROC là vùng diện tích bên ngoài đường tròn
có bán kính là điểm cực lớn nhất. Và nếu x(n) là nhân quả, x(n) = 0, n < 0, thì ROC có chứa z = ∞
3. Nếu x(n) là tín hiệu phía trái thì ROC là vùng diện tích bên trong đường tròn
có bán kính là điểm cực nhỏ nhất. Và nếu x(n) là phản nhân quả, tức là x(n)
= 0, n > 0, thì ROC có chứa z = 0 Các dạng của ROC
6.1.3 Tính chất của biến đổi z
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 143
Các tính chất của biến đổi Z được đưa ra trong bảng 6.1 sau Bảng
6.1 Các tính chất của biến đổi Z TT Tính chất Miền n Miền z 1 Định nghĩa ò x n( )= 2p1 j C X z z dz( )
X z( )= å¥x n z( ) -n -1 n=-¥ 2 Tuyến tính ax n bx n aX z 1( )+ 2( ); a,b là hằng 1( )+bX z2( ) số 3 Trễ thời gian n x n n( - 0) z X z-n0( ) 4 Thay đổi tỷ lệ a x nn ( ) trong miền Z X a z( -1) 5 Vi phân trong nx n( ) miền Z dX z( ) -z dz 6 Dãy liên hợp
x*(n) ; (*: liên hợp phức) X*(z*) phức 7 Đảo biến x n(- ) æ ö1 X ç ÷z è ø 8 Tích chập x n x n1( )* 2( ) X z X z1( ). 2( ) trong miền n 9 Tích chập x n x n trong miền Z 1( ). 2( ) X 2p1 j
òC1( )v X2æ öç ÷è øvz v dv-1 10 Tương quan tín x n x hiệu 1( )* 2(-n)
X z X1( ). 2æ öç ÷1z è ø
6.1.4 Một số biến đổi z thông dụng
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 144
Một số biến đổi Z thông dụng được đưa ra trong bảng 6.2 sau.
Bảng 6.2 Một số biến đổi Z thông dụng Miền n Miền z ROC d( )n 1 Toàn bộ mặt phẳng z z-n0 Toàn bộ mặt phẳng z, d(n n- 0) trừ tại 0 nếu n0 > 0, trừ tại ¥ nếu n0 < 0 u n( ) z >1 u n(- -1) z <1 nu n( ) z-1 z >1 ( -1)2 1-z a u nn ( ) z > a nau nn ( ) az-1 z > a ( - )12 1-az
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 145 -au nn (- -1) z < a -nau nn (- -1) az-1 z < a ( - )12 1-az cos(w z >1 0n u n) ( ) 1-z c-1 osw0
1 2- z c-1osw0+z-2 sin(w z >1 0n u n) ( ) z-1sinw0
1 2- z c-1osw0+z-2 a cn os(w z > a 0n u n) ( ) 1-az c-1 osw0
1 2- az c-1osw0+a z2 2- ansin(w z > a 0n u n) ( ) az-1sinw0
1 2- az c-1osw0+a z2 2- (z z > zpk pk )n u n( ) 1 1-z zpk-1 - 1 z < zpk
(z )pkn1u n( -1) 1-z zpk-1 z z > zpk ) ( ) n n( -1 . .
m!n m- +1 (zpk)nm-u n( m+1 ) (z z- )pk
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 146 z
n n( -1 . .) (m!n m- +1)(z z < zpk
pk )n m- u n(- -1) m+1 (z z- )pk
6.2 BIẾN ĐỔI z NGƯỢC Biến đổi z ngược
(Inverse – z transform) của tín hiệu X(z) được định nghĩa như sau: (6.6)
Với Γ cho biết tích phân được tính theo đường bao tròn khép kín ngược chiều kim
đồng hồ có tâm tại gốc và bán kính r sao cho Γ nằm trong ROC của X(z). Thực tế,
để tìm x(n) từ X(z) thì công thức biến đổi z ngược ít được sử dụng.
Nếu X(z) có dạng phân số thì triển khai phân số từng phần được áp dụng để thực hiện biến đổi z ngược.
Có 3 cách tính biến đổi z ngược
a. Phương pháp ap dụng lý thuyết phần dư Cauchy (Cauchy’s residue theorem)
Theo lý thuyết phần dư Cauchy, trong trường hợp X(z) có dạng tỉ số thì biến đổi z ngược của X(z) sẽ là:
x n( )=åRes X z .éë ( ) zn-1 zz= ùû (6.7) pk k
Res[X(z)zn – 1]: phần dư của hàm [X(z)zn – 1], với zpk: cực của X(z). zn-1 nằm trong đường cong khép kín C.
Z– 1[X(z)] = x(n) = tổng của các phần dư của hàm [X(z)zn – 1] tại tất cả các cực pi được
bao bởi đường tròn C nằm trong ROC của X(z) và có chứa gốc.
Phần dư tại một điểm cực đơn có dạng
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 147 (6.8)
Phân dự tại một điểm cực có bội bậc m có dạng (6.9)
Ví dụ 4: Cho x(n) là tín hiệu nhân quả có
Tìm biến đổi ngược của X(Z) Lời giải:
Do tín hiệu nhân quả nên n > 0.
X(z)zn –1 có hai cực đơn tại z = 0.8 và z = –0.4 Tại
n = 0, có thêm cực tại gốc. Với n > 0
Ví dụ 5: Cho x(n) là tín hiệu nhân quả có
Tìm biến đổi ngược của X(Z) Lời giải:
Do tín hiệu nhân quả, n > 0 và X(z)zn –1 có cực bội bậc 3 tại z = 1 nên
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 148
b. Khai triển phân số từng phần khi X(z) có dạng tỉ số
Khi X(Z) có dạng hữu tỉ ta có thể viết biến đổi Z thành X(Z)= N(Z)/D(Z). Phương
pháp này tiến hành khai triển biến đổi Z thành các phân thức tối giản và tìm biến
đổi Z ngược của các phân thức này sau đó cộng các kết quả sẽ thu được biến đổi Z ngược của X(Z).
Các bước thực hiện biến đổi Z ngược bằng khai triển phân số từng phần như sau:
- Bước 1: Chia hai vế của X(z) cho z.
- Bước 2: Đưa đa thức thu được ở bước 1 về dạng tổng của các đa thức tỉ lệ bậc thấp có dạng cơ bản.
- Bước 3: Tra bảng để tìm dạng tín hiệu trong miền thời gian của từng đa thức thành phần.
- Bước 4: Tổ hợp các kết quả để thu được tín hiệu trong miền thời gian cần tìm. Biểu thức X(z)
với các điểm cực đơn có dạng sau (6.10) Áp dụng khai triển phân số từng phần, X(z) được viết lại (6.11) Khi đó, X(z) sẽ là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 149 (6.12)
Biểu thức X(z) có điểm cực kép bậc r thì khai triển X(z)/z sẽ bao gồm các đa thức bậc thấp sau (6.13) Với (6.14)
Biểu thức X(z) có bậc của tử số lớn hơn bậc của mẫu số thì X(z) vẫn được áp dụng
khai triển phân số từng phần và có dạng sau (6.15)
Ví dụ 6: Tìm biến đổi Z ngược của H(Z) Lời giải:
- Chia 2 vế của H(Z) cho Z ta có
- Đưa về tổng các đa thức có bậc thấp
Với A= -1,78, B= 0,033 và C= 2,75 - Nhân cả 2 vế với Z
- Tra bảng các cặp biến đổi Z ta có:
Ví dụ 7: Tìm biến đổi Z ngược của X(Z)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 150 Lời giải:
- Chia 2 vế của X(Z) cho Z và đưa về tổng các đa thức có bậc thấp ta có
- Với A= 0, B= 1và C= 2 - Nhân cả 2 vế với Z:
- Tra bảng các cặp biến đổi Z ta có:
c. Phương pháp khai triển chuỗi công suất
Biểu thức xác định cho phép biến đổi z (6.1) cho thấy X(Z) là một chuỗi lũy thừa theo
z-1 hoặc z trong đó các giá trị thứ tự x [n] là hệ số của z-n. Do đó, nếu X (z) được cho là một chuỗi lũy thừa ở dạng(6.16)
chúng ta có thể xác định bất kỳ giá trị cụ thể nào của dãy bằng cách tìm hệ số lũy thừa thích hợp của z-1.
Ví dụ 8: Tìm biến đổi Z ngược của
Lời giải: Do |e|<# nên x[n] là tín hiệu phía trái. Do đó, ta thực hiện chia tử số của !
X(Z) cho mẫu của X(Z) như sau.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 151
Và ta viết lại X(Z) dưới dạng
Theo (6.1) ta có chuỗi x[n] là
Ví dụ 9: Tìm biến đổi Z ngược của
Lời giải: Do |e| > 1 nên x[n] là tín hiệu phía phải. Do đó, ta thực hiện chia tử số của
X(Z) cho mẫu của X(Z) như sau.
Và ta viết lại X(Z) dưới dạng
Theo (6.1) ta có chuỗi x[n] là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 152
6.3 PHÂN TÍCH HỆ THỐNG LTI RỜI RẠC BẰNG BIẾN ĐỔI z
6.3.1 Hàm truyền đạt của hệ thống rời rạc
Trong chương 2, ta đã biết rằng một hệ thống DT-LTI có mối quan hệ giữa đầu ra y(n)
với đầu vào x(n) và đáp ứng ứng h(n) như sau. y(n) = x(n) * h(n) (6.17)
Áp dụng biết đổi Z cả 2 vế của (6.x) ta có: Y(z) = X(z) H(z) (6.18) Và (6.19)
H(z): hàm truyền đạt hay hàm hệ thống (system function) của hệ thống
DTLTI. Công thức (6.19) cho thấy hàm truyền đạt hay hàm hệ thống H(z) được
định nghĩa là tỉ số của biến đổi Z đầu ra y(n) với đầu vào x(n).
Đáp ứng xung H(z) và hàm truyền đạt h(n) là một cặp biến đổi z.
Hình 6.4 Mối quan hệ giữa đáp ứng xung và hàm truyền đạt
6.3.2 Điều kiện nhân quả và ổn định của hệ thống trong miền z
Nhiều đặc tính của hệ thống DT-LTI rời rạc có mối quan hệ chặt chẽ với các đặc
tính của H(z) trong mặt phẳng Z và đặc biệt với các vị trí cực và miền hội tụ Z. -
Hệ thống DT-LTI là nhân quả thì h(n) = 0 n < 0
Khi đó h(n) phải là tín hiệu phải nên ROC của H(z) phải là phần diện tích bên ngoài
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 153
đường tròn rmax trên mặt phẳng z và |z| > rmax -
Hệ thống là không nhân quả nghĩa là h(n) = 0 n ≥ 0
Khi đó h(n) phải là tín hiệu trái nên ROC của H(z) phải là phần diện tích bên trong
đường tròn rmax trên mặt phẳng z và |z| -
Hệ thống DT-LTI là ổn định thì
Nên miền hội tụ ROC của H(z) phải chứa đường tròn đơn vị (|z| = 1) -
Nếu hệ thống LTI thời gian rời rạc muốn là nhân quả và ổn định thì tất
cả các điểm cực của H(z) phải nằm bên trong đường tròn đơn vị, tức là rmax < 1 với rmax = max(Re(poles))
6.3.3 Biểu diễn hệ thống trong miền z
Từ các cách biểu diễn các phần tử trong miền n ta thực hiện biến đổi Z đầu vào đầu
ra của các phần tử này sẽ thu được biểu diễn trong miền Z. a. Phần tử trễ:
Gọi x(n) là tín hiệu đầu vào, y(n) là tín hiệu đầu ra. Quan hệ giữa đầu vào và đầu ra
của phần tử trễ như sau: y(n) = x(n-1) (6.20)
Lấy biến đổi Z hai vế ta có Y(Z) = Z-1 X (Z) (6.21)
Phép trễ trong miền n được thay bằng phép nhân với Z-1 trong miền Z. b. Phần tử cộng
Gọi x(n) là tín hiệu đầu vào, y(n) là tín hiệu đầu ra. Quan hệ giữa đầu vào và đầu ra
của phần tử cộng như sau: G (6.22) <(.) = p ,K(.)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 154 K:#
Lấy biến đổi Z 2 vế ta có G (6.23) Œ(Ë) = p áK(Ë) K:#
c. Phần tử nhân với hằng số
Gọi x(n) là tín hiệu đầu vào, y(n) là tín hiệu đầu ra. Quan hệ giữa đầu vào và đầu ra
của phần tử cộng như sau: y(n) = αx(n) (6.24)
Lấy biến đổi Z 2 vế ta có Y(Z) = α X (Z) (6.25)
Các phần tử này trong miền Z được thể hiện như sau: -1 Z X(Z Y(Z)= Z -1 α X(Z Y(Z)= αX(Z)
Hình 6.5 Các phần tử trong miền Z
6.3.4 Giải phương trình sai phân tuyến tính hệ số hằng sử dụng biến đổi z
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 155
Như phần mở đầu chương 6 ta đã biết rằng phương trình sai phân tuyến tính có thể
được giải bằng biến đổi Z. Hệ thống DT-
LTI được đặc trưng bởi phương trình sai phân hệ số hằng (6.26) Áp dụng biến đổi
Z hai vế phương trình (6.26) ta thu được (6.27) Từ (6.21) ta rút ra
hàm truyền đạt của hệ thống (6.28)
Các bước giải phương trình sai phân sử dụng biến đổi z:
1. Áp dụng biến đổi z cho cả hai phía của phương trình
2. Đưa ra phương trình đại số đặc trưng cho Y(z) trong miền z
3. Tìm biến đổi ngược của Y(z) để thu được y(n)
Ví dụ 10: Hệ thống DT – LTI nhân quả được mô tả bởi phương trình sai phân a. Xác định H(z) b. Tìm đáp ứng xung h(n)
c. Tìm đáp ứng nhảy bậc u (n) của hệ thống Lời giải:
a. Thực hiện biến đổi Z của phương trình sai phân ta có
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 156 Hay Hàm truyền đạt H(z) là
b. Để tìm đáp ứng xung h(n) ta sử dụng phương pháp khai triển phân số từng phần Với và H(z) là
Thực hiện biến đổi ngược H(z) ta có
c. Khi đầu vào x(n) là xung nhảy bậc. Biến đổi Z của tín hiệu đầu vào xung nhảy bậc là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 157
Do đó ta có hàm truyền đạt H(z) của hệ thống
Để tìm đáp ứng xung h(n) ta sử dụng phương pháp khai triển phân số từng phần Với và H(z) là
Thực hiện biến đổi ngược H(z) ta có BÀI TẬP CHƯƠNG 6
Bài 6.1: Tìm biến đổi z và vẽ giản đồ cực – không của các tín hiệu sau: a) x(n) = an + 1u(n + 1)
b) x(n) = (1/2)nu(n) + (1/3)nu(n)
c) x(n) = (1/3)nu(n) + (1/2)nu(– n – 1) Bài 6.2 Cho tín hiệu x(n) = a|n| a > 0
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 158
a) Vẽ tín hiệu x(n) với a > 1 và a < 1
b) Tìm X(z) và vẽ giản đồ cực - không và ROC với a > 1 và a < 1 Bài 6.3
Tính tích chập x(n) của các tín hiệu sau bằng cách sử dụng biến đổi z: x
n1( )=æ öç ÷è ø12 nu n( ) và x n2( )=æ öç ÷è ø15 nu n( ) Bài 6.4
Hãy tìm biến đổi z ngược của X(z) như sau: a) X z( )= 4 z +8z 2 2 với |"| >1 4z -5 1z+ b) X z( )= z 2
với |"| >2 (z-1) (z-2) Bài 6.5
Hệ thống DT-LTI khi đưa u(n) tới đầu vào thì thu được đáp ứng đầu ra y(n) = 2(1/3)n u(n). a) Tìm đáp ứng xung h(n)
b) Tìm y(n) khi đầu vào là (1/2)n u(t) Bài 6.6
Sử dụng biến đổi z để giải phương trình sai phân sau:
a) y(n) – (1/2)y(n – 1) = x(n) với y(– 1) = 1 khi x(n) = (1/3)n
b) 3y(n) – 4y(n – 1) + y(n – 2) = x(n) với y(–1) = 1, y(–2) = 2 khi x(n) = (1/2)n Bài 6.7
Cho sơ đồ hệ thống như hình vẽ. Tìm giá trị của k để hệ thống ổn định.
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 159
CHƯƠNG 7: KHÔNG GIAN TRẠNG THÁI CỦA HỆ THỐNG
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 160
Ba công cụ quan trọng mô hình hoá hệ thống gồm biểu diễn hệ thống bằng
phương trình vi phân/ sai phân, mô hình tích chập/ tổng chập và biểu diễn hệ thống
bằng hàm truyền đạt cho biết mô tả bên ngoài của hệ thống. Các phương pháp này
tập trung xác định mối quan hệ giữa đầu vào và đầu ra nên hiệu quả cho các hệ
thống tuyến tính bất biến theo thời gian và phù hợp với hệ thống một đầu vào một
đầu ra. Để hiểu rõ các mô tả bên trong của hệ thống, phương pháp không gian
trạng thái được đề xuất. Phương pháp này có các ưu điểm nổi bật sau: - Cung cấp
cái nhìn sâu sắc về bên trong hệ thống thông qua việc xác định mối quan hệ bên
trong của hệ thống nhờ các biến trung gian
- Hiệu quả trong việc mô hình hoá các hệ thống phi tuyến và biến đổi theo thời gian
- Phù hợp cho các hệ thống nhiều đầu vào, nhiều đầu ra
7.1 KHÁI NIỆM VỀ TRẠNG THÁI
Đối với hệ thống nhân quả, trạng thái của hệ thống tại một thời điểm !*, hoặc
.* được định nghĩa là thông tin tối thiểu đủ để xác định trạng thái và đầu ra của hệ
thống tại mọi thời điểm ! ≥ ! hoặc
khi biết trước đầu vào hệ thống tại mọi thời
điểm ! ≥ ! . Các biến chứa thông tin này được gọi là biến trạng thái.
Xem xét một mạch điện LTI một đầu vào, một đầu ra với cấu trúc mạch cho
trước, thì toàn bộ thông tin của đầu vào trong khoảng từ đến ! là đủ để xác định đầu ra
trong cùng khoảng thời gian này. Tuy nhiên, nếu thông tin của đầu vào
chỉ được biết trong khoảng từ ! đến ! thì dòng đi qua cuộn cảm và điện
áp rơi trên tụ tại các thời điểm ! phải được biết để xác định đầu ra trong
khoảng từ ! đến !. Các giá trị dòng và điện áp này tạo thành trạng thái của mạch
tại thời điểm ! . Trong trường hợp này, trạng thái của mạch liên quan đến bộ nhớ của nó. Nói cách khác, đầu ra
cần đến thông tin của các biến trung gian (dòng, điện
áp, …) tại thời điểm ! để xác định. Các biến trung gian này được gọi là trạng thái
của hệ thống tại thời điểm ! .
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 161
Chú ý rằng, việc lựa chọn các biến trạng thái của hệ thống không phải là
duy nhất. Có rất nhiều cách chọn biến trạng thái ứng với một hệ thống cho trước.
Do các biến trạng thái của hệ thống có thể coi là chính các phần tử nhớ của hệ
thống nên đối với các hệ thống thời gian rời rạc được tổ hợp bởi các bộ trễ, bộ
khuếch đại và bộ cộng thì đầu ra của bộ trễ thường được chọn làm biến trạng thái.
Đối với các hệ thống thời gian liên tục được tổ hợp bởi các bộ tích phân, bộ
khuếch đại và bộ cộng thì đầu ra của các bộ tích phân được lựa chọn làm biến
trạng thái. Nếu các hệ thống thời gian liên tục có chứa các phần tử lưu trữ năng
lượng thì đầu ra của các phần tử này được lựa chọn làm biến trạng thái. Nếu hệ
thống được đặc trưng bởi phương trình vi phân/ sai phân thì biến trạng thái thường
được lựa chọn là đầu ra của các bộ vi phân/ sai phân.
7.2 PHÂN TÍCH KHÔNG GIAN TRẠNG THÁI CỦA HỆ THỐNG LTI LIÊN TỤC
7.2.1 Mô hình không gian trạng thái
Giả thiết rằng hệ thống LTI thời gian liên tục một đầu vào, một đầu ra được
biểu diễn bởi phương trình sai phân bậc sau Z!& + [# Z!&.#
+ ⋯ + [&<(!) = ,(!) (7.1) Với một đầu vào cho trước với
yêu cầu cần phải có điều kiện ban đầu cụ thể để xác định được duy nhất đầu ra với
. Tức là, trạng thái của hệ thống chỉ được xác định tại bất kì thời điểm
nào nếu tồn tại điều kiện ban đầu. Mỗi tập giá trị của điều kiện ban đầu khác nhau sẽ
cho mô hình của trạng thái khác nhau, dẫn đến đầu ra
khác nhau. Một trong số tập
điều kiện ban đầu có thể là , , …, với
. Định nghĩa biến trạng thái , , …, như sau (7.2)
Từ biểu thức (7.2) và (7.1), thu được
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 162 •#̇ •̇! (7.3a) và (7.3b) với (!)/Z!.
Các biểu thức (7.3a) và (7.3b) được viết lại dưới dạng ma trận biểu diễn mối
quan hệ giữa các biến trạng thái, đầu ra và đầu vào như sau Î (7.4b) •&(!)
Như vậy, định nghĩa được ma trận P × 1 (hay vector P chiều) Ó(!), được gọi là vector trạng thái như sau •#(!) Ó Î (7.5) •&(!)
Đạo hàm của ma trận là đạo hàm của từng phần tử trong ma trận, áp dụng cho (7.5) (7.6) Z! ⋮ •&̇ (!)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 163
Lúc này, biểu thức (7.4a) và (7.4b) có thể viết ngắn gọn lại thành Ó̇ (!) = ÔÓ(!) + ,(!) (7.7a) <(!) = ÒÓ(!) (7.7b) với 0 0 00Î Ô = Í ⋮ ⋮ Î = Í⋮
−[& −[&.# −[&.! ⋯ −[# 1
Biểu thức (7.7a) và (7.7b) được gọi là biểu diễn không gian trạng thái P chiều, hay
hệ phương trình trạng thái, của hệ thống. Ma trận Ô kích thước P × P được gọi là
ma trận hệ thống. Một cách tổng quát, khi phương trình vi phân (7.1) có vế phải
đầy đủ, thì hệ phương trình trạng thái của hệ thống LTI thời gian liên tục một đầu
vào, một đầu ra sẽ được định nghĩa như sau Ó̇ (!) = ÔÓ(!) + ,(!) (7.8a) <(!) = ÒÓ(!) + Z,(!) (7.8b)
Nếu hệ thống LTI thời gian liên tục có đầu vào, đầu ra và biến trạng thái thì
biểu diễn không gian trạng thái của hệ thống sẽ là Ó̇ (7.9b) (7.9b) với ,#(!)Î
Û(!) = ⎡⎢⎢<<#!⋮((!!))⎥⎤⎥ •&(!) ,
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 164 ! và [ [&! ⋯ [&& #& !⋮# 1!!⋮ ⋯⋱ 1!⋮& Î 1 B×&
Như vậy, có thêm một phương pháp nữa để mô hình hoá hệ thống ngoài 3
phương pháp đã biết. Với mỗi tập điều kiện ban đầu khác nhau của hệ thống mà
ma trận hệ thống sẽ khác nhau. Để xác định đầu ra của hệ thống từ đầu vào và ma trận hệ thống
cần giải phương trình trạng thái. Tuỳ thuộc vào ma trận hệ
thống mà cùng với một đầu vào sẽ thu được đầu ra khác nhau.
Ví dụ : Phương trình vi phân biểu diễn mối quan hệ giữa đầu vào và đầu ra của hệ
thống thời gian liên tục sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 165
Hình 7.1: Mô hình không gian trạng thái của hệ thống thời gian liên tục (dạng 1)
Lời giải: Chọn đầu ra của các bộ tích phân làm biến trạng thái , thu được Viết lại dưới dạng ma trận với 0] Ví dụ : Phương
trình vi phân biểu diễn mối quan hệ giữa đầu vào và đầu ra của hệ thống thời gian liên tục sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 166
Hình 7.2: Mô hình không gian trạng thái của hệ thống thời gian liên tục (dạng 2) Lời giải:
Chọn đầu ra của các bộ tích phân làm biến trạng thái , thu được và đầu ra
Viết lại dưới dạng ma trận với
7.2.2 Nghiệm trong miền tần số của phương trình trạng thái
Thực hiện giải phương trình trạng thái trong miền tần số sẽ thu được
nghiệm trong miền tần số của hệ thống. Áp dụng biến đổi Laplace một phía cho
biểu thức (7.8a) và (7.8b), đây là biểu diễn không gian trạng thái chiều của hệ
thống LTI thời gian liên tục, với trạng thái ban đầu sẽ có (7.10a) Œ(3) = Ò˝ (7.10b) với , và
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 167
Sắp xếp lại (7.10a), thu được (7.11)
Nhân phía trước hai vế của (7.11) với (3ˇ − Ô) sẽ có (7.12)
Thay (7.12) vào (7.10b), xác định được phổ của đáp ứng đầu ra của hệ thống (7.13)
Thực hiện biến đổi Laplace ngược biểu thức (7.13) sẽ thu được đầu ra của hệ thống
trong miền thời gian. Trong biểu thức (7.13), số hạng đầu tiên của vế phải được gọi
là đáp ứng với đầu vào bằng 0, kí hiệu là
, và số hạng thứ hai được gọi là
đáp ứng trạng thái 0, kí hiệu là , của đáp ứng đầu ra của hệ thống.
Hàm truyền đạt của hệ thống LTI thời gian liên tục được định nghĩa là
với điều kiện ban đầu bằng 0. Đặt Ó(0) = ! thì biểu thức (7.13) trở thành (7.14)
Như vậy, xác định được hàm truyền đạt của hệ thống là (7.15)
7.2.3 Nghiệm trong miền thời gian của phương trình trạng thái
Thực hiện giải phương trình trạng thái trong miền thời gian sẽ thu được nghiệm
trong miền thời gian của hệ thống, tức là tìm được đầu ra của hệ thống trong miền
thời gian ứng với đầu vào và tập điều kiện ban đầu xác định. Chuỗi vô hạn xác
định hàm mũ của số vô hướng [ có dạng (7.16)
Áp dụng phân tích (7.16) cho hàm mũ của ma trận , thu được (7.17)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 168
Nếu ! = 0 thì (7.17) suy biến thành (7.18)
với ! là ma trận toàn 0 kích thước . Do , áp dụng cho , thu được (7.19)
Đặt ! = ] trong (7.19) sẽ có (7.20) Như vậy, (7.21)
Biểu thức (7.11) chỉ ra rằng là nghịch đảo của
. Lấy đạo hàm hai vế của (7.17) theo ! được viết lại thành (7.22) Z!
Áp dụng công thức tính tích phân từng phần cho và áp dụng biểu thức (7.22), thu được (7.23)
Z [^.e1Ó(!)] = " Z ^e1# Ó(!) + ^.e1Ó̇ (!)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 169
Nhân phía trước cả hai vế của (7.8a) với sẽ có
^.e1Ó̇ (!) = ^.e1ÔÓ(!) + ^.e1 ,(!) hoặc (7.24)
Áp dụng biểu thức (7.23), biểu thức (7.24) có thể viết lại như sau (7.25) Z! Tích phân cả hai vế
của (7.25) trong khoảng từ 0 đến !, thu được 1
^.e1Ó(!) = Ó(0) + Y ^.eg ,(]) Z] * Nhân phía trước
cả hai vế của (7.26) với và áp dụng (7.19) và 1 (7.20), sẽ có
Ó(!) = ^e1Ó(0) + Y ^e(1.g) ,(]) Z] *
Trong biểu thức (7.27), số hạng đầu tiên của vế phải được gọi là thành phần với
đầu vào bằng 0 và số hạng thứ hai được gọi là thành phần trạng thái 0 của vector trạng thái
. Chúng được kí hiệu lần lượt là và . Có thể nhận thấy rằng thành phần chính là tích chập giữa và .
Nếu như trạng thái ban đầu là
và biết được đầu vào
với ! ≥ ! thì sẽ thu được
bằng cách lấy tích phân của (7.13) từ ! đến , thu được
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 170 Hàm ma trận
được gọi là ma trận chuyển trạng thái của hệ thống thời gian liên tục. Thay biểu thức (7.27) vào (7.8b) sẽ xác định 1 được đầu ra của hệ thống là
<(!) = Ò^e1Ó(0) + Y Ò^e(1.g) ,(]) Z] + Z,(!) * (7.29)
Trong biểu thức (7.29), số hạng đầu tiên của vế phải được gọi là thành phần với
đầu vào bằng 0, kí hiệu là
, và số hạng thứ hai được gọi là thành phần trạng thái 0, kí hiệu là , của đáp ứng đầu ra
của hệ thống. Có thể thấy đáp ứng
đầu vào bằng 0 của hệ thống chỉ phụ thuộc vào ma trận chuyển trạng thái .
Có bốn phương pháp để xác định ma trận chuyển trạng thái .
Phương pháp 1: dựa trên định lý Cayley - Hamilton
Nếu là ma trận kích thước
thì phương trình đặc trưng của ma trận sẽ là với
chính là định thức của ma trận và là ma trận đơn vị bậc . Các nghiệm của
được gọi là các giá trị riêng của .
Dựa vào định lý Cayley-Hamilton, ta có (7.30)
Nếu tất cả các giá trị riêng
của là phân biệt, các hệ số có thể xác
định được nhờ điều kiện sau ( = 1, 2, … , P (7.31a)
Biểu thức (7.31a) được viết lại dưới dạng ma trận là
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 171 (7.31b)
Giả thiết rằng hệ thống có
và trong số các giá trị riêng của có là giá trị riêng kép bậc 2 thì các hệ số sẽ được xác định như sau (7.32)
Nhận thấy, hàng 2 của ma trận trong biểu thức (7.32) là đạo hàm của hàng 1 theo .
Phương pháp 2: dựa trên đường chéo hoá ma trận
Nếu tất cả các giá trị riêng của là phân biệt, sẽ có ^F ^e1 = $ Í (7.33)
với là ma trận đường chéo hoá và
là các vector riêng của và
được định nghĩa lần lượt là $ = [K# K! (7.34)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 172 ( = 1, 2, … , P với
, được gọi là các ma trận cấu thành, được tính bằng
Phương pháp 3: dựa trên phân tích phổ của ma trận
Nếu tất cả các giá trị riêng
của là phân biệt, có thể viết lại thành Khi đó, thu được (7.38) (7.37)
Phương pháp 4: dựa trên biến đổi Laplace
So sánh giữa nghiệm trong miền thời gian (7.27) và nghiệm trong miền tần số (7.13), nhận thấy (7.39)
Nếu tất cả các giá trị riêng
của có phần thực âm, tức là ( = 1, 2, … , P (7.40)
thì hệ thống được gọi là tiệm cận ổn định. Nếu tất cả các giá trị riêng là phân biệt
và thoả mãn điều kiện (7.40) thì hệ thống sẽ ổn định và giới hạn đầu vào, giới hạn đầu ra (BIBO). Ví dụ 3 Ví dụ 4
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 173 Ví dụ 5 Ví dụ 6
7.2.4 Chuyển đổi tuyến tính của vector trạng thái
Như đã phân tích ở 7.1, một hệ thống LTI thời gian liên tục cho trước có vô số
cách lựa chọn biến trạng thái. Nói cách khác, với một hệ thống dù mối quan hệ
giữa đầu vào và đầu ra được xác định cụ thể thì vẫn có thể có nhiều kiểu cấu trúc
bên trong khác nhau, dẫn đến có nhiều ma trận trạng thái khác nhau của cùng một
hệ thống. Biến đổi tuyến tính của vector trạng thái cho phép xác định một vector
trạng thái mới từ vector trạng thái đã có.
Cùng xác định mô hình không gian trạng thái của một hệ thống có vector trạng thái
sử dụng một vector trạng thái mới sao cho và với
là một ma trận biến đổi kích thước
và tồn tại ma trận nghịch đảo.
Với vector trạng thái mới, phương trình trạng thái (7.9a) được viết lại thành (7.41)
Nhân trước cả hai vế của (7.41) với thu được (7.42) Đặt và
, phương trình trạng thái (7.42) trở thành (7.43) Đặt
phương trình đầu ra lúc này sẽ trở thành (7.44)
Định thức của các cặp ma trận và , và là như nhau. Tổng
đường chéo của cặp ma trận và
cũng như nhau. Vì thế, phương trình đặc trưng của hai ma trận và
là không đổi. Từ các tính chất này, hoàn toàn có thể
xác định được Ô), ma trận hệ thống mới. Và
được gọi là phép biến đổi tuyến tính của vector trạng thái. Ví dụ 7
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 174
7.3 PHÂN TÍCH KHÔNG GIAN TRẠNG THÁI CỦA HỆ THỐNG LTI RỜI RẠC
7.3.1 Mô hình không gian trạng thái
Giả thiết rằng hệ thống LTI thời gian rời rạc một đầu vào, một đầu ra được biểu
diễn bởi phương trình sai phân bậc sau (7.45)
Định nghĩa biến trạng thái , , …, như sau (7.46)
Từ biểu thức (7.46) và (7.45), thu được •# ! (7.47a) và (7.47b)
Các biểu thức (7.47a) và (7.47b) được viết lại dưới dạng ma trận biểu diễn mối
quan hệ giữa các biến trạng thái, đầu ra và đầu vào như sau ! Î ,(.) (7.48a)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 175 ] (7.49b)
Như vậy, định nghĩa được ma trận (hay vector chiều)
, được gọi là vector trạng thái như sau Î (7.50)
Lúc này, biểu thức (7.48a) và (7.48b) có thể viết ngắn gọn lại thành (7.51a) = ÍÎ
Biểu thức (7.51a) và (7.51b) được gọi là biểu diễn không gian trạng thái chiều, hay
hệ phương trình trạng thái, của hệ thống. Ma trận kích thước được gọi là ma trận hệ thống.
Một cách tổng quát, khi phương trình sai phân (7.45) có vế phải đầy đủ, thì hệ
phương trình trạng thái của hệ thống LTI thời gian liên rời rạc đầu vào, đầu
ra sẽ được định nghĩa như sau (7.52a) (7.52b) với Ó
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 176 ,#(.)Î
Û(.) = ⎡⎢⎢<<#!((⋮. ))⎥⎤⎥ •&(.) , ! và #&
7.3.2 Nghiệm trong miền
tần số của phương trình trạng thái
Thực hiện giải phương trình trạng thái trong miền tần số sẽ thu được
nghiệm trong miền tần số của hệ thống. Áp dụng biến đổi z một phía cho biểu thức
(7.51a) và (7.51b), đây là biểu diễn không gian trạng thái chiều của hệ thống LTI
thời gian rời rạc, với trạng thái ban đầu cho trước sẽ có (7.53a) (7.53b) với , và (e)
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 177 (e)
Sắp xếp lại (7.53a), thu được (7.54)
Nhân phía trước hai vế của (7.54) với (eˇ − Ô) sẽ có (7.55)
Thay (7.55) vào (7.51b), xác định được phổ của đáp ứng đầu ra của hệ thống (7.56)
Thực hiện biến đổi z ngược biểu thức (7.56) sẽ thu được đầu ra của hệ thống trong
miền thời gian. Trong biểu thức (7.56), số hạng đầu tiên của vế phải được gọi là
đáp ứng với đầu vào bằng 0, kí hiệu là
(e), và số hạng thứ hai được gọi là đáp
ứng trạng thái 0, kí hiệu là
(e), của đáp ứng đầu ra của hệ thống. Hàm
truyền đạt của hệ thống LTI thời gian rời rạc được định nghĩa là
với điều kiện ban đầu bằng 0. Đặt
thì biểu thức (7.56) trở thành (7.57)
Như vậy, xác định được hàm truyền đạt của hệ thống là (7.58)
7.3.3 Nghiệm trong miền thời gian của phương trình trạng thái
Thực hiện giải phương trình trạng thái trong miền thời gian sẽ thu được
nghiệm trong miền thời gian của hệ thống, tức là tìm được đầu ra của hệ thống
trong miền thời gian ứng với đầu vào và tập điều kiện ban đầu xác định. Một trong các giải pháp xác định từ điều kiện ban đầu
cho trước đó là giải phương trình (7.51a) theo cách sau
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 178
Tiếp tục quá trình như vậy, thu được
Nếu trạng thái ban đầu là và được xác định với , thì, thực hiện quá
trình tương tự như trên, sẽ có Ma trận
là ma trận được nhân . lần (7.61) n
được gọi là ma trận chuyển trạng thái của hệ thống thời gian rời rạc. Thay biểu thức
(7.60) vào (7.51b) thu được đáp ứng đầu ra của hệ thống rời rạc theo thời gian ứng
với điều kiện ban đầu (7.62)
Trong biểu thức (7.62), số hạng đầu tiên của vế phải được gọi là đáp ứng với đầu vào bằng 0, kí hiệu là
, và số hạng thứ hai được gọi là đáp ứng trạng thái 0, kí hiệu là , của đáp ứng đầu ra của hệ thống.
Có bốn phương pháp để xác định ma trận chuyển trạng thái .
Phương pháp 1: dựa trên định lý Cayley-Hamilton
Dựa vào định lý Cayley-Hamilton, ta có
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 179 (7.63)
Nếu tất cả các giá trị riêng
của là phân biệt, các hệ số có thể xác
định được nhờ điều kiện sau ( = 1, 2, … , P (7.64a)
Biểu thức (7.64a) được viết lại dưới dạng ma trận là ⋮ ⋮ ⋮ ⋱ (7.64b)
Giả thiết rằng hệ thống có
và trong số các giá trị riêng của có là giá trị riêng
kép bậc 2 thì các hệ số
sẽ được xác định như sau !
Nhận thấy, hàng 2 của ma trận trong biểu thức (7.65) là đạo hàm của hàng 1 theo .
Phương pháp 2: dựa trên đường chéo hoá ma trận N
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 180
với là ma trận đường chéo hoá và
là các vector riêng của và
được định nghĩa lần lượt là $ = [K# K! (7.67) ( = 1, 2, … , P (7.68)
Phương pháp 3: dựa trên phân tích phổ của ma trận
Nếu tất cả các giá trị riêng
của là phân biệt, có thể viết lại thành
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 với
, được gọi là các ma trận cấu thành, được tính bằng 177 (7.70) Khi đó, thu được (7.71)
Phương pháp 4: dựa trên biến đổi z
So sánh giữa nghiệm trong miền thời gian (7.62) và nghiệm trong miền tần số (7.56), nhận thấy (7.72)
Nếu tất cả các giá trị riêng
của nhỏ hơn đơn vị, tức là ( = 1, 2, … , P (7.73)
thì hệ thống được gọi là tiệm cận ổn định, tức là, các trạng thái của hệ thống có xu
hướng tiến đến 0 từ bất kì trạng thái ban đầu giới hạn
nào. Nếu tất cả các giá
trị riêng là phân biệt và thoả mãn điều kiện (7.73) thì hệ thống sẽ ổn định và giới
hạn đầu vào, giới hạn đầu ra (BIBO). Ví dụ 3 Ví dụ 4 Ví dụ 5 Ví dụ 6
7.3.4 Chuyển đổi tuyến tính của vector trạng thái
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 182
Một hệ thống LTI thời gian rời rạc cho trước có vô số cách lựa chọn biến
trạng thái. Biến đổi tuyến tính của vector trạng thái cho phép xác định một vector
trạng thái mới từ vector trạng thái đã có.
Mô hình không gian trạng thái của một hệ thống có vector trạng thái hoàn toàn
xác định được từ một vector trạng thái mới sao cho và
với là một ma trận biến đổi kích thước
và tồn tại ma trận nghịch đảo.
Với vector trạng thái mới, phương trình trạng thái (7.52a) được viết lại thành (7.74)
Nhân trước cả hai vế của (7.74) với thu được (7.75) Đặt và
, phương trình trạng thái (7.75) trở thành (7.76) Đặt
phương trình đầu ra (7.52b) lúc này sẽ trở thành (7.77)
Định thức của các cặp ma trận và ,
và (eˇ − Ô)) là như nhau. Tổng
đường chéo của cặp ma trận và
cũng như nhau. Vì thế, phương trình đặc trưng của hai ma trận và
là không đổi. Từ các tính chất này, hoàn toàn có thể
xác định được Ô), ma trận hệ thống mới. Và
được gọi là phép biến đổi tuyến tính của vector trạng thái. Ví dụ 7 BÀI TẬP CHƯƠNG 7
Downloaded by Dung Tran (tiendungtr12802@gmail.com) lOMoARcPSD|36086670 TÀI LIỆU THAM KHẢO
[1]. A. V. Oppenheim, A.S Willsky, S.H. Nawab, Signals and Systems, Prentice Hall, 1997, 2nd Edition. 179
[2]. D. Sundararajun, A Practical Approach to Signals and Systems, Wiley and Son Inc, 2008. [3].
H. P. Hsu, Signals and Systems, Mc Graw Hill, Third Edition, 2013.
[4]. K. D. Rao, Signals and Systems, Springer International Publishing AG, 2018.
[5]. A. Papoulis, Probability, Random Variables, and Stochastic Processes, McGraw Hill, 3rd edition, 1991. [6].
Downloaded by Dung Tran (tiendungtr12802@gmail.com)
Document Outline
- Hình 3.10: Phổ của tín hiệu sau lấy mẫu
- Hình 3.11: Bộ chuyển đổi số - tương tự lý tưởng
- 3.3 ĐÁP ỨNG TẦN SỐ CỦA HỆ THỐNG LTI
- Hình 3.12: Truyền dẫn không méo
- Hình 3.13: Bộ lọc thông thấp lý tưởng
- Hình 3.14: Bộ lọc thông cao lý tưởng
- Hình 3.15: Bộ lọc thông dải lý tưởng
- Hình 3.16: Bộ lọc chặn dải lý tưởng
- Hình 3.17: Một số bộ lọc thông thấp thực tế
- Hình 3.18: Băng thông 3 dB
- Hình 4.1: Hàm truyền đạt của hệ thống liên tục và




