



























































































Preview text:
TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN KHOA THỐNG KÊ NỘI DUNG
GIỚI THIỆU CHUNG VỀ THỐNG KÊ 1 2
THU THẬP DỮ LIỆU THỐNG KÊ 3 TỔNG HỢP THỐNG KÊ
CÁC MỨC ĐỘ THỐNG KÊ MÔ TẢ 4 5 ĐIỀU TRA CHỌN MẪU 6
PHÂN TÍCH HỒI QUY VÀ TƯƠNG QUAN 7
PHÂN TÍCH DÃY SỐ THỜI GIAN 8 PHƯƠNG PHÁP CHỈ SỐ ĐÁNH GIÁ HỌC PHẦN
• Điểm đánh giá của GV: 10% • Kiểm tra: 30%
• Thi kết thúc học phần: 60%
(Điều kiện được tham dự thi: Điểm đánh giá của GV từ
5 điểm trở lên và Điểm kiểm tra từ 3 điểm trở lên) THI KẾT THÚC HỌC PHẦN
Thời gian làm bài: 90 phút (SV được sử dụng tài liệu)
I. PHẦN TRẮC NGHIỆM (10 câu x 0,4 = 4 điểm)
(Lựa chọn 1 phương án trả lời đúng nhất) Lý thuyết + Bài tập
II. PHẦN TỰ LUẬN (6 điểm)
Bài tập 1: Dựa vào kết quả phần mềm SPSS (3 điểm)
Bài tập 2: Tự tính toán (3 điểm)
CHƯƠNG I: GIỚI THIỆU CHUNG VỀ THỐNG KÊ I II III IV ĐỐI TƯỢNG CÁC KHÁI NIỆM THANG ĐO QUÁ TRÌNH NGHIÊN CỨU THƯỜNG DÙNG TRONG NGHIÊN CỨU CỦA TRONG THỐNG KÊ THỐNG KÊ THỐNG KÊ THỐNG KÊ
I. Đối tượng nghiên cứu của thống kê Thốngkê là gì?
Sơlượclịch sửphát triểnthốngkê
Đốitượngnghiên cứu của thốngkê 1. Thống kê là gì?
Thống kê học là khoa học nghiên cứu hệ thống các
phương pháp thu thập, xử lý và phân tích các con số
(mặt lượng) nhằm để tìm hiểu bản chất và tính quy
luật vốn có của chúng (mặt chất).
2. Sơ lược về sự ra đời và phát triển của thống kê công cụ quản lý vĩ mô Thể hiện quan hệ lượng chất Phân tích đánh giá theo thời gian, không giain Ghi chép các con số
3. Đối tượng nghiên cứu của thống kê II. Một ts ố khái niệm ệm thường ường dùng trong th ống kê 1
Tổng thể thống kê và đơn vị tổng thể 2 Tiêu thức thống kê 3 Chỉ tiêu thống kê
có 3 cách phân loại : + t ng th ổ ể b c l ộ (có ranh gi ộ ới rõ ràng, có thể ậ nh n biết dc) + t ng th ổ ể tiềm ẩn.
1. Tổng thể thống kê và đơn vị tổng thể
Tổng thể thống kê là hiện tượng số lớn bao gồm các
đơn vị hoặc phần tử cần quan sát và phân tích mặt
lượng. Các đơn vị hoặc phần tử này được gọi là đơn vị tổng thể. (trong kien th đ
ời gian cụ thể, k phải chân lý) VD: m c ti ứ ền lương c a nh ủ
ững năm 2000 và 2022, có m t s
ộ ự chênh lệch rất lớn
Các loại tổng thể thống kê Theo sự nhận biết các đơn vị Tổng thể Tổng thể bộc lộ tiềm ẩn
Các loại tổng thể thống kê Theo mục đích nghiên cứu Tổng thể Tổng thể không đồng chất đồng chất
Các loại tổng thể thống kê Theo phạm vi nghiên cứu Tổng thể Tổng thể bộ phận chung 2. Tiêu thức thống kê
Tiêu thức thống kê là đặc điểm của đơn vị tổng thể
được chọn ra để nghiên cứu tuỳ theo mục đích nghiên cứu khác nhau.
khái niệm: là hiện tượng số lớn, bao g m t ồ ất cả các đơ ị n v cần đ ứ c nghiên c u
và phân tích và mỗi đơn vị dc nghiên cứu dc g i là 1 t ọ ng th ổ ể
Các loại tiêu thức thống kê Tiêu thức thống kê T iê u thứckhônggian Tiêu thức thực thể Nêu lên bản chất của đơn vị tổng thể Tiêu thức Số lượng Tiêu thức Tiêu thức Biểu hiện trực tiếp thuộc tính Thay phiên thông qua con số Biểu hiện không Là tiêu thức có hai (lượng biến) trực tiếp bằng con biểu hiện không số, mà bằng các trùng nhau trên đặc điểm, tính chất cùng một đơn vị khác nhau tổng thể Tiêu thức thời gian
Phản ánh thời gian của hiện tượng nghiên cứu Tiêu thức không gian Nêu lên phạm ạ m vi lãnh thổ hổ của hiện ệ n tượng ợ ng nghiên cứu ứ 3. Chỉ tiêu thống kê
Chỉ tiêu thống kê phản ánh mặt lượng gắn với chất của
các hiện tượng trong điều kiện thời địa điểm cụ thể
Các loại chỉ tiêu thống kê Theo hình thức biểu hiện Chỉ tiêu Chỉ tiêu hiện vật giá trị
Các loại chỉ tiêu thống kê Theo tính chất biểu hiện Chỉ tiêu Chỉ tiêu tuyệt đối tương đối
Các loại chỉ tiêu thống kê Theo đặc điểm thời gian Chỉ tiêu Chỉ tiêu thời điểm thời kỳ
Các loại chỉ tiêu thống kê Theo nội dung Chỉ tiêu Chỉ tiêu chất lượng Số lượng (khối lượng)
III. THANG ĐO TRONG THỐNG KÊ 1. Thang đo định danh 2. Thang đo thứ bậc 3. Thang đo khoảng 4. Thang đo tỷ lệ
MÔ HÌNH MÔ TẢ CÁC THANG ĐO Đánh số các biểu hiện
cùng loại của tiêu thức
THANG ĐO ĐỊNH DANH Biểu hiệu có (Nominal Scale) thứ tự hơn kém Tiêu thức thuộc tính THANG ĐO THỨ BẬC Có khoảng cách (Ordinal Scale) bằng nhau THANG ĐO KHOẢNG (Interval Scale) Có gốc 0 Tiêu thức Số lượng THANG ĐO TỶ LỆ (Ratio Scale)
VI. S¬ ®å chung cña qu¸ trình nghiª n cøu PH P ÂN  N TÍ T CH C H VÀ V DỰ Ự ĐOÁN Á N ĐI Đ ỀU Ề U TR T A R THỐ H NG N G KÊ K TỔ T NG N G HỢ H P Ợ TH T ỐNG N G KÊ K TH T ỐN Ố G N G KÊ (Thu T thập ậ thông tin) (Xử X lý l tài ililệ i u) (Phâ P n hâ tíc í h c dữ lilệ i u) Xâ X y dựng hệ thống ch c ỉ ỉtitêu thống kê Tr T ình ì bày kết tquả ả nghiê hi n ê cứu (Xá X c á c địn ị h nhu cầ c u thông tin) i - Xác đị đ n ị h h m ụ m c ụ đíc í h c ngh g iê i n n cứu u - Ph P ân â tích đ ặ đ c ặ điể i m m h i h ệ i n n tượ ư ng n ỨNG DỤNG SPSS TRONG QUẢN LÝ VÀ XỬ LÝ DỮ LIỆU THỐNG KÊ
1. Giới thiệu chung về SPSS
SPSS (Statistical Package for Social Sciences) Là
phần mềm chuyên dụng xử lý thông tin sơ cấp.
(thông tin được thu thập trực tiếp từ đối tượng
nghiên cứu thông qua bảng hỏi được thiết kế sẵn) 29
Các màn hình chính trong SPSS
- Màn hình quản lý dữ liệu - Màn hình quản lý biến
- Màn hình hiển thị kết quả 30 Các menu chính
File: tạo file mới, mở file sẵn có, ghi file, in, thoát,…
Edit: undo, cắt, dán, tìm kiếm thay thế, xác lập các mặc định,…
View: hiện dòng trạng thái, thanh công cụ, chọn font chữ,…
Data: các vấn đề liên quan đến dữ liệu,…
Transform: chuyển đổi dữ liệu, tính toán, mã hóa lại các biến,…
Analyze: các phân tích thống kê,…
Graphs: biểu đồ và đồ thị,…
Utilities: thông tin về các biến và file,…
Window: sắp xếp và di chuyển các cửa sổ làm việc Help: trợ giúp 31 2. Quản lý dữ liệu
Cơ sở dữ liệu (định nghĩa kiểu kĩ thuật): là một tập hợp thông tin có cấu trúc.
Chú ý: Trong SPSS tại một thời điểm, chỉ có 1 CSDL được mở. Thành phần của CSDL
• Quan sát (Observation): chứa thông tin về 1 đối tượng điều tra:
• Biến (variable): thể hiện các thuộc tính của quan sát 32 Khai báo biến trong SPSS
Variable Name (tên biến)
Variable Type (Kiểu biến) Labels (nhãn biến)
Value (giá trị của từng mã hoá)
Missing (giá trị khuyết) Measure (thang đo)
Width (Xác định số lượng ký tự hiện thị)
Decimals (số lượng số hiện thị sau dấu phẩy)
Column format (Định kích cỡ cho cột- độ rộng của cột)
Align (Định ra vị trí hiện thị các giá trị - căn phải/trái/giữa) 33
CHƯƠNG II: THU THẬP DỮ LIỆU THỐNG KÊ I II III ĐIỀU TRA BÁO CÁO KHAI THÁC THỐNG KÊ THỐNG KÊ DỮ LIỆU HỒ SƠ ĐỊNH KỲ HÀNH CHÍNH I. ĐIỀU TRA THỐNG KÊ
Khái niệm chung về điều tra thống kê 1 2 Phân loại 3
Phương án điều tra thống kê 4
Sai số trong điều tra thống kê
1. Khái niệm điều tra thống kê Khái niệm:
Điều tra thống kê là tổ chức một cách khoa học và
theo mộtkế hoạchthống nhấtviệcthu thậptài liệuvề
các hiệntượngnghiên cứu. Yêu cầu: - Chính xác - Kịpthời.
- Đầyđủ(nộidung, phạmvi).
2. Các loại điều tra thống kê Theo tính chất liên tục của việc ghi chép Điều tra thường Điều tra không xuyên thường xuyên
+số trung bình cộng giản đơn: (c ng h ộ ết vào r chia) 1/9/2020 +trung bình c ng gia quy ộ
ền: khi mà tài liệu ã phân t đ ổ: có x, y, f(x),... * Các loại số bình quân
a. Số bình quân cộng (áp dụng khi các lượng biến có quan hệ tổng)
Tổng lượng biến của tiêu thức Số trung bình = Tổng số đơn vị a. Số bình quân cộng
Số bình quân cộng giản đơn (khi dữ liệu chưa phân tổ) x x .. x x x 1 2 n i n n 10 1/9/2020 a. Số bình quân cộng Số cộng quyền x f x f .. x f 1 1 2 2 n x n f1 f .. f 2 n f x x d i d i i i fi quyền s : có m ố ặt ở cả tử s và m ố ẫu s . ố * Các loại số bình quân (trung bình nhân) Số dụng lượng biến hệ
+ khi các lượng biến có mqh tích (t c ố đ phát tri ộ ển) sd khi ây là kq c đ a ủ
Số bình quân nhân giản đơn + tính chỉ s t ố ng h ổ ợp phần mềm x n x 1 x 2 ... xn n xi
Số bình quân nhân gia quyền khi có bảng s li ố ệu i f f f f 1 2 f i n fi x x x ... x x 1 2 n i * lượng biến đ t xu ộ ất. 11 chỉ s GNI. ố
số trung bình - đại diện mang tính t ng th ổ ể c a hi ủ ện tượng số lớn. 1/9/2020
* Đặc điểm của số bình quân
•Mang tính tổng hợp, khái quát.
•San bằng các chênh lệch giữa các đơn vị về trị số của tiêu thức nghiên cứu.
* Điều kiện vận dụng số bình quân
• Số bình quân chỉ nên tính ra từ tổng thể đồng chất.
• Số bình quân chung cần được vận dụng kết hợp
với các số bình quân tổ hoặc dãy số phân phối. 12 1/9/2020 2. Mốt (Mode) Khái niệm Cách xác định Tác dụng Khái niệm Mốt biểu hiện của
thức phổ biến nhất gặp nhiềunhất một tổng thể một số phối biểu hiện c a t
ủ ần số lớn nhất ( dãy s thu ố c tính ho ộ ặc dãy s có l ố
ượng biến k có khoangr cách tổ)
dãy số lượng biến có khoảng cách t b ổ ằng nhau: + tổ chưa m t (có t ố ần s f l ố ớn nhất) 13 1/9/2020 Cách xác định
Đối với trường hợp phân tổ không có khoảng cách tổ,
mốt là lượng biến có tần số lớn nhất. M x ( f o i i max) Cách xác định
Đối với trường hợp phân tổ có khoảng cách tổ
Bước1: Xác định tổ có mốt Tổ có f => Phân i=max
tổ có khoảng cách bằng nhau Tổ có m => Phân i=max
tổ có khoảng cách không bằng nhau 14 1/9/2020 Cách xác định
Bước 2: Xác định trị số gần đúng của mốt: 1 M o x (min ) h M M o o 1 2 1 f f Mo Mo 1 Khoảng cách bằng nhau 2 f f Mo Mo 1 1 m m Mo Mo 1
Khoảng cách không bằng nhau 2 m m Mo Mo 1 Tác dụng
• Có thể thay thế hoặc bổ sung cho trung bình cộng trong
trường hợp tính trung bình gặp khó khăn
• Có ý nghĩa hơn số bình quân cộng trong trường hợp dãy số có lượng biến đột xuất
• Là một trong những tham số nêu lên đặc trưng phân phối của dãy số
• Có tác dụng trong phục vụ nhu cầu hợp lý 15 1/9/2020 3. Trung vị (Median) Khái niệm Cách xác định Tác dụng Khái niệm 16 1/9/2020 Cách xác định
Trường hợp phân tổ không có khoảng cách tổ
+ Nếu số đơn vị tổng thể lẻ ( fi = 2m + 1): Me xm 1 x m xm 1
+ Nếu số đơn vị tổng thể chẵn ( fi = 2m): Me 2 Cách xác định
Trường hợp phân tổ có khoảng cách tổ:
- Bước 1: Xác định tổ chứa Me (tổ chứa đơn vị ở vị trí giữa trong dãy số)
- Bước 2: Xác định trị số gần đúng fi - S(M -e1) Me x h 2 Me (min) Me M f e
Cách nhận xét: có ít nhất 50% có ... từ .... trở lên 17 1/9/2020 Tác dụng
• Có thể thay thế hoặc bổ sung cho trung bình cộng trong
trường hợp tính trung bình gặp khó khăn
• Có ý nghĩa hơn số bình quân cộng trong trường hợp dãy số có lượng biến đột xuất
• Là một trong những tham số nêu lên đặc trưng phân phối của dãy số
• Có tác dụng trong phục vụ công cộng vì x Me f i i min - s trung v ố
ị k san bằng, bù trừ hay chênh lệch.
- kém nhạy bén về sự biến thiên của tiêu thức.
- k chịu ảnh hưởng c a l ủ ượng biến đ t xu ộ ất.
* Đặc trưng phân phối của dãy số quan tâm đến ĐUÔI c a ủ đ th
ồ ị. (Đuôi nào dài hơn thì lệch sang bên ó) đ (dựa vào s trung v ố ị Me) X = Me = Mo Đối xứng Mo Me X Lệch phải X Me Mo Lệch trái 18 1/9/2020
III. Các tham số đo độ phân tán (biến thiên) Khoảng biến thiên 1 2
Độ lệch tuyệt đối bình quân 3 Phương sai 4 Độ lệch tiêu chuẩn 5 Hệ số biến thiên 1. Khoảng biến thiên • Công thức tính: R = Xmax - Xmin 19 1/9/2020
2. Độ lệch tuyệt đối bình quân • Công thức tính x - x x - x f d i i i d (cã quyÒn sè) n fi 3. Phương sai Công thức tính: 2 2 (x - x) f 2 (x - x) i 2 i S i S (có quyềnsố) n 1 f 1 i
Công thức thực hành (khi có quyền số): 2 2 2 2 2 x f x f f x f x f S i i i i i i i i i f 1 f f 1 f 1 f f i i i i i i 2 fi 2 2 S x x f 1 i 20 1/9/2020 4. Độ lệch tiêu chuẩn • Công thức tính: 2 S S 5. Hệ số biến thiên • Công thức tính: S V 100 x 21 1/9/2020 Thực hiện bằng SPSS
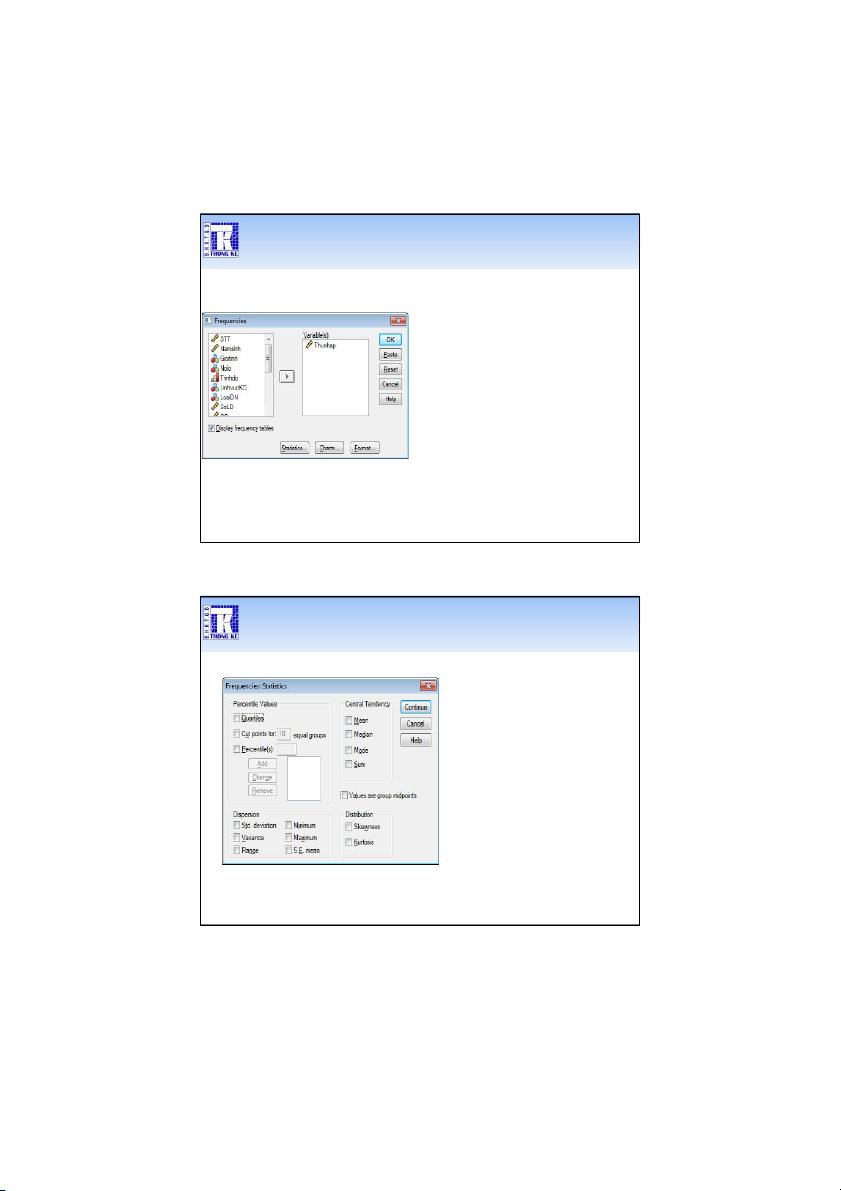
ChọnAnalyze > Descriptive Statistics > Frequencies…
Đưacác biếncầntính toán các tham sốsang Variable(s) NhấnStatistic… 43 Thực hiện bằng SPSS
ChọnAnalyze > Descriptive Statistics > Frequencies…
Chọncác thốngkê cầntính toán 44 22 1/9/2020
CHƯƠNG V: ĐIỀU TRA CHỌN MẪU I II III IV NHỮNG VẤN CƠ SỞ ƯỚC ƯỚC LƯỢNG KIỂM ĐỊNH GIẢ ĐỀ CHUNG VỀ LƯỢNG VÀ KẾT QUẢ ĐIỀU THUYẾT THỐNG KÊ ĐIỀU TRA KIỂM ĐỊNH TRA CHỌN CHỌN MẪU MẪU I. Những vấn đề chung Khái niệm 1 2 Ưu điểm 3 Hạn chế 4 Trường hợp vận dụng 5
Tổng thể chung và tổng thể mẫu 6 Cách chọn mẫu 1 1/9/2020 Khái niệm Ưu điểm
+ Tiết kiệm (chi phí, nhân lực, thời gian)
+ Mở rộng nội dung điều tra
+ Tài liệu có độ chính xác cao + Tổ chức đơn giản 2 1/9/2020 Hạn chế
+ Không cho biết thông tin đầy đủ về tổng thể + Sai số khi suy rộng
+ Kết quả điều tra không thể tiến hành phân tổ theo mọi phạm vi nghiên cứu Trường hợp vận dụng
• Thay thế cho điều tra toàn bộ
• Kết hợp với điều tra toàn bộ
• Kiểm định giả thuyết thống kê 3 1/9/2020
Tổng thể chung và tổng thể mẫu Chỉ tiêu
Tổng thể chung Tổng thể mẫu Quy mô N n fi Số bình quân x Tỷ lệ theo một tiêu thức p f 2 2 S Phương sai p 1 ( p) f 1 ( f ) Cách chọn mẫu
Chọn hoàn lại (Chọn nhiều lần, chọn lặp) n k N 4 1/9/2020 Cách chọn mẫu
Chọn không hoàn lại, (Chọn 1 lần, chọn không lặp) ! N k ! n N n ! II. CƠ C SỞ ƯỚC Ớ LƯ L ỢN Ợ G N G KIỂM Ể M ĐỊ Đ NH H GIẢ I Ả THU H YẾ Y T Ế T THỐN Ố G N G KÊ 1 Biến ngẫu nhiên 2
Quy luật phân phối biến ngẫu nhiên 5 1/9/2020 BIẾN NGẪU NHIÊN
• Biến ngẫu nhiên là biến nhận một trong các giá trị
có thể có của nó tuỳ thuộc vào sự tác động của các
nhân tố ngẫu nhiên trong một phép thử.
• Biến ngẫu nhiên là biến mà các giá trị không được
xác định trước qua mỗi lần thực nghiệm (phép thử). Xác suất?
Xác suất của một biến cố là một con số đặc
trưng khả năng khách quan xuất hiện biến cố
đó khi thực hiện phép thử 6 1/9/2020
Quy luật phân phối xác suất
• Quyluật phânphối xácsuất của biến ngẫu nhiênlàsự
tươngứnggiữagiátrịcóthểcócủanóvàxácsuấttương ứngvớigiátrịđó. 13
Quy luật phân phối chuẩn • NếuX~N(µ, 2) 2 (x ) 1 • Hàmmậtđộxácsuất 2 2 f ( ) x e 2 14 µ 7 1/9/2020
Quy luật phân phối chuẩn µ 68,26% 95,44% 99,74% 15
Quy luật phân phối chuẩn hoá • NếuX~N(0,1) 2 x • Hàmmậtđộxácsuất 1 2 f ( ) x e 2 0 -1,96 1,96 95% 16 8 1/9/2020
Quy luật phân phối chuẩn hoá
• NếuXphânphốichuẩn: X~N(µ, 2) • Thìbiếnngẫunhiên x Z ~ N s 0 ( ,ẽp ) 1 hânphốichuẩn hóa 0 -1,96 1,96 95% 17
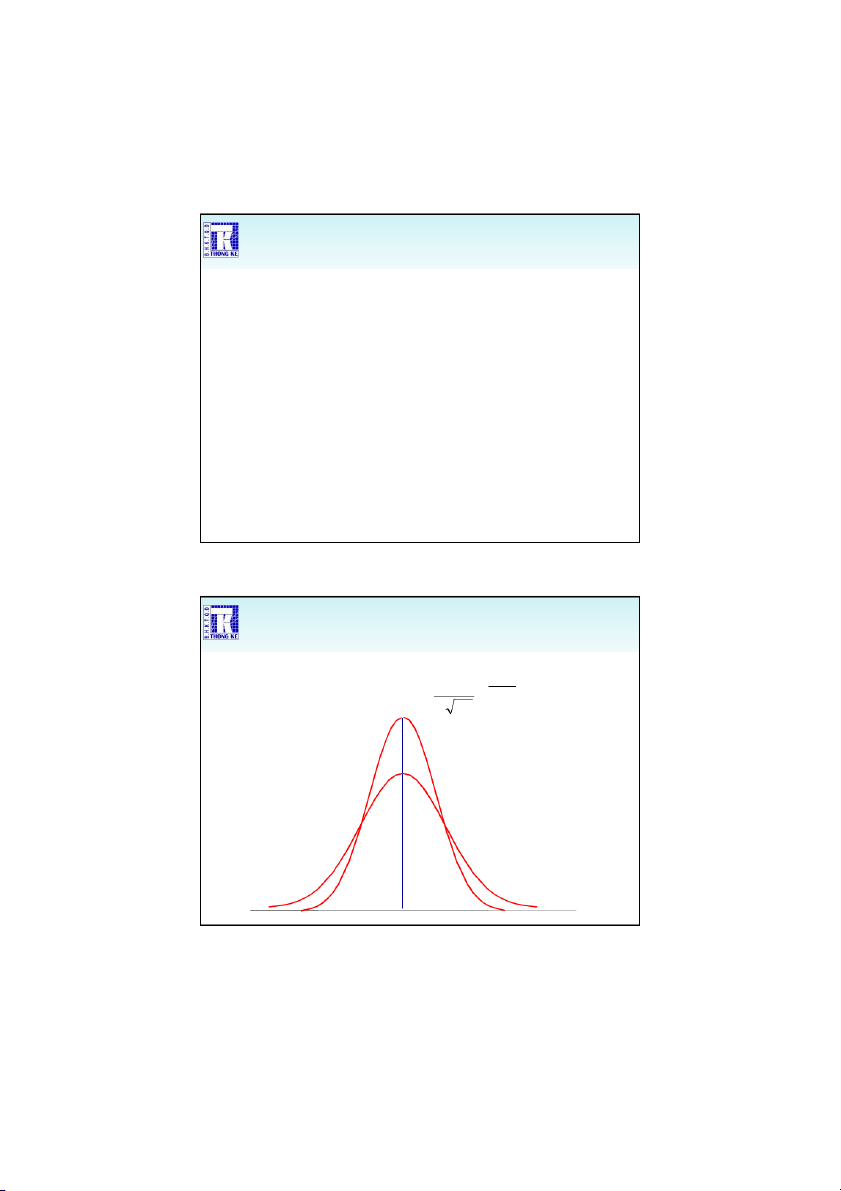
Định lý giới hạn trung tâm • Nếu 2 X ~ N ,
• Thì với mẫu ngẫu nhiên kích thước n 2 x ~ N , x x Z ~ N( , 0 ) 1 x 9 1/9/2020
Định lý giới hạn trung tâm
• Nếu tổng thể có phân phối chuẩn thì phân
phối của trung bình mẫu cũng có phân phối chuẩn
• Với kích thước mẫu đủ lớn thì phân phối
trung bình và tỷ lệ mẫu sẽ xấp xỉ phân phối chuẩn II. Ướ Ư c ớ c lượn ợ g g kết ế tquả uả điều ề u tra 1
Ước lượng (suy rộng) kết quả điều tra 2
Xác định kích thước (quy mô) mẫu 10 1/9/2020
1. Ước lượng kết quả điều tra • Công thức chung '
: tham số của tổng thể chung ' : thống kê mẫu
: phạm vi sai số chọn mẫu
Các nguyên nhân sai số trong ĐTCM
- Vi phạm nguyên tắc chọn mẫu ngẫu nhiên
- Số lượng đơn vị mẫu không đủ lớn
- Kết cấu tổng thể mẫu khác với kết cấu tổng thể chung
- Sai số do đăng ký, ghi chép 11 1/9/2020
Ước lượng kết quả điều tra • Với mức ý nghĩa α
• Ước lượng trung bình
Khi biết phương sai tổng thể chung (hoặc chưa biết phương
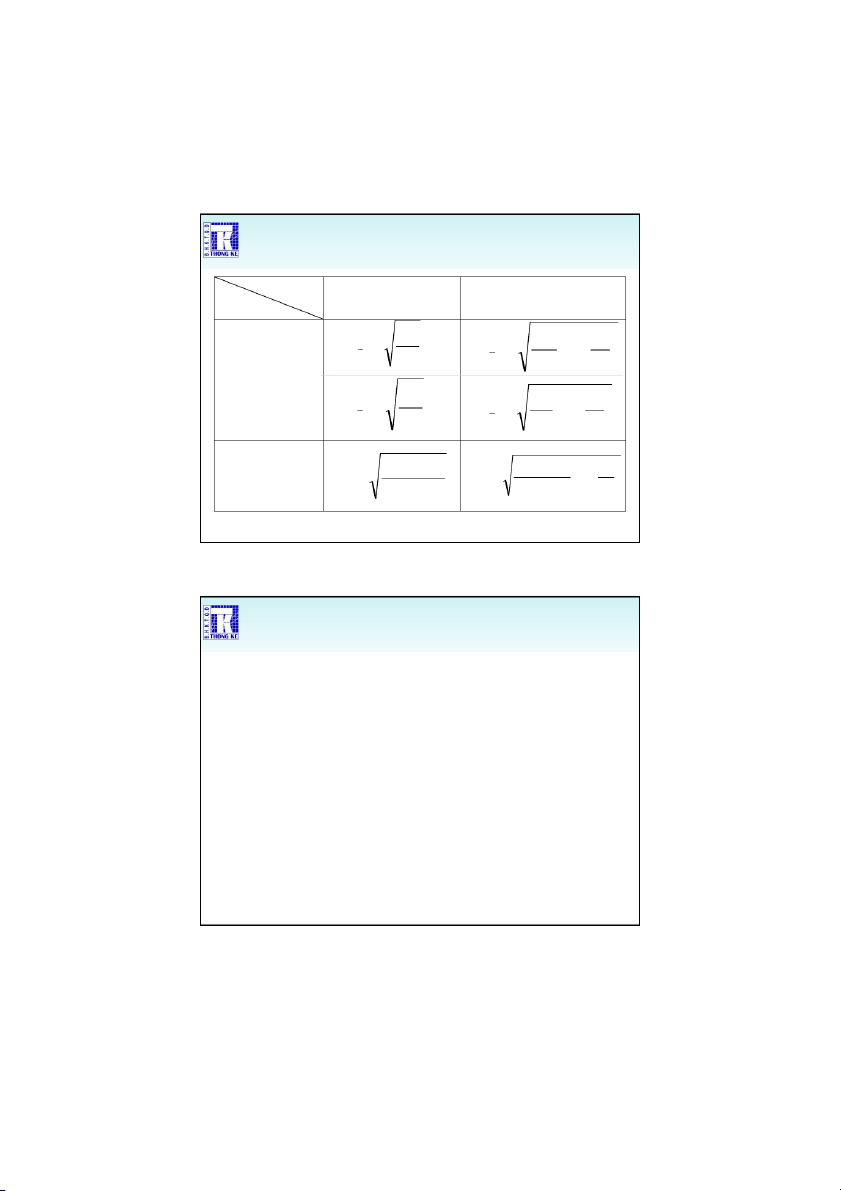
sai tổng thể chung & mẫu lớn) Hai phía x z . / 2 x z . x / 2 x Vế phải x z . x Vế trái x z . x
Khi chưa biết phương sai tổng thể chung n 1 n Hai phía x t /2 . x t 1 / 2 . x x Vế phải n x t 1 . x Vế trái n x t 1. x
Ước lượng kết quả điều tra • Với mức ý nghĩa α • Ước lượng tỷ lệ Hai phía f z . p f z . / 2 f / 2 f Vế phải f z. p f Vế trái p x z . f 12 1/9/2020
Ước lượng kết quả điều tra Trong đó
được gọi là hệ số tin cậy (giá trị tới hạn mức α z , t
của phân phối chuẩn hoá và phân phối Student) • α – mức ý nghĩa
• (1-α) là xác suất hay trình độ tin cậy
Ước lượng kết quả điều tra
Mộtsốgiátrịđặc biệt củaphânphốichuẩnhoá Z Xác suất tin cậy /2 1 0,6826 2 0,9544 3 0,9974
Xác suất tin cậy Mức ý nghĩa Z /2 0,900 0,100 1,645 0,950 0,050 1,960 0,975 0,025 2,326 0,990 0,010 2,576 ,
được gọi là sai số bình quân chọn mẫu x f 13 1/9/2020
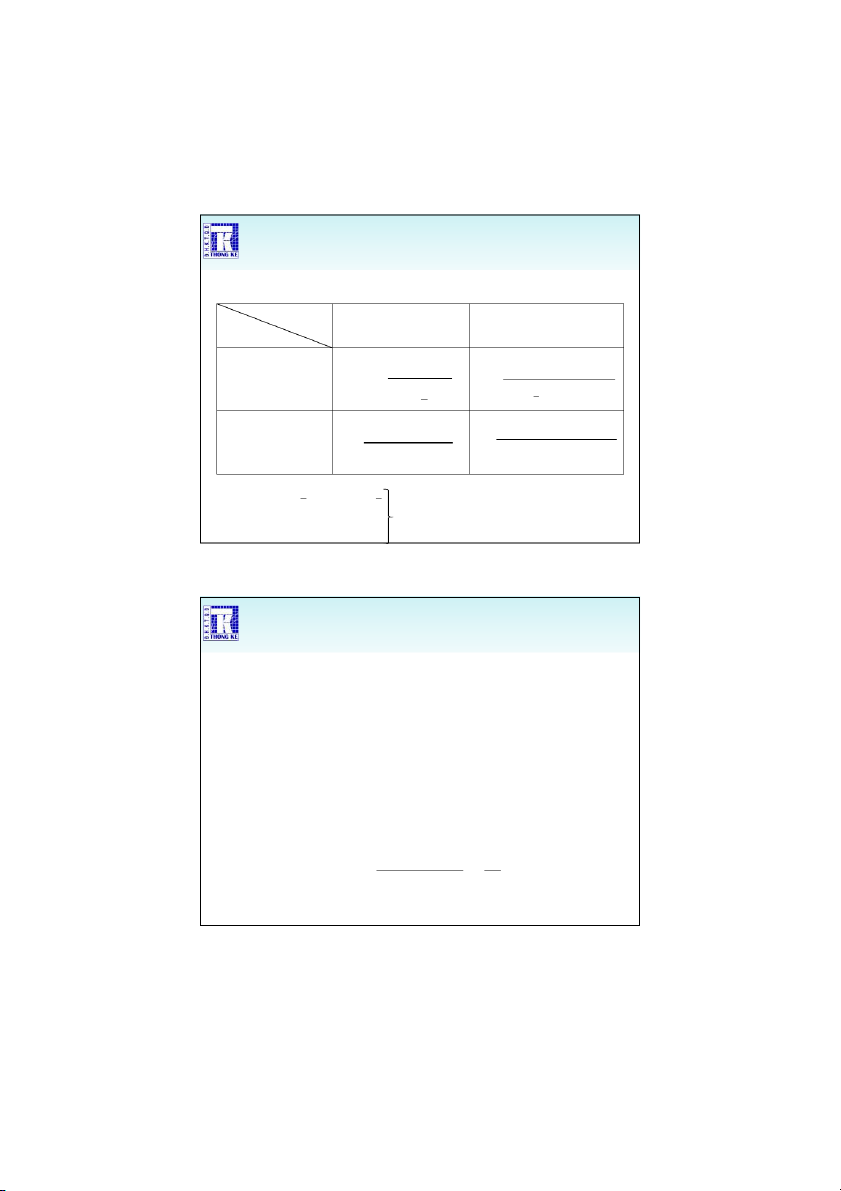
Sai số bình quân chọn mẫu Cách chọn Hoàn lại Không hoàn lại Suy rộng (chọn nhiều lần) (chọn một lần) 2 2 n x 1 ( ) n x Số bình quân n N S2 2 S n x x 1 ( ) n n N Tỷ lệ f 1 ( f ) f 1 ( f ) n 1 ( ) f n f n N
2. Xác định số đơn vị mẫu điều tra • Yêu cầu: + Sai số nhỏ nhất + Chi phí thấp nhất 14 1/9/2020 Cách xác định Cách chọn Chọn hoàn lại Chọn không hoàn lại Suy rộng (chọn nhiều lần) (chọn một lần) 2 2 z 2 2 N.z . Bình quân / 2 n / 2 n 2 2 2 2 . N z . x x / 2 2 z .p 1 ( ) p . 2 Nz .p 1 ( ) p Tỷ lệ /2 n /2 n 2 2 2 f .N z /2 .p 1 ( p ) f z x / 2 x
Phạm vi sai số chọn mẫu z f / 2 f
Một số phương pháp xác định
phương sai tổng thể chung giảm dần về đ
ộ ưu tiên (ít dùng cách thứ 4 nhất)
+ Lấy phương sai lớn nhất hoặc tỷ lệ gần 0,5 nhất
trong các lần điều tra trước
+ Lấy phương sai hoặc tỷ lệ của các cuộc điều tra khác có tính chất tương tự.
+ Điều tra thí điểm để xác định phương sai hoặc tỷ lệ.
+ Ước lượng phương sai dựa vào khoảng biến thiên x x R max min 6 6 15 1/9/2020 IV I . Kiểm ể m định h giả ả thuy u ế y t ế tthốn ố g n g kê
Những vấn đề chung về kiểm định giả thuyết thống kê 1 2
Kiểm định giá trị trung bình của 1 tổng thể Giả thuyết thống kê
Là giả thuyết về một vấn đề nào đó của tổng thể
chung (về các tham số như trung bình, tỷ lệ,
phương sai, dạng phân phối,…) 16 1/9/2020 Giả thuyết thống kê
Giả thuyết mà ta muốn kiểm định (H ) 0
Giả thuyết đối lập (H1, H , H) a Giả thuyết thống kê
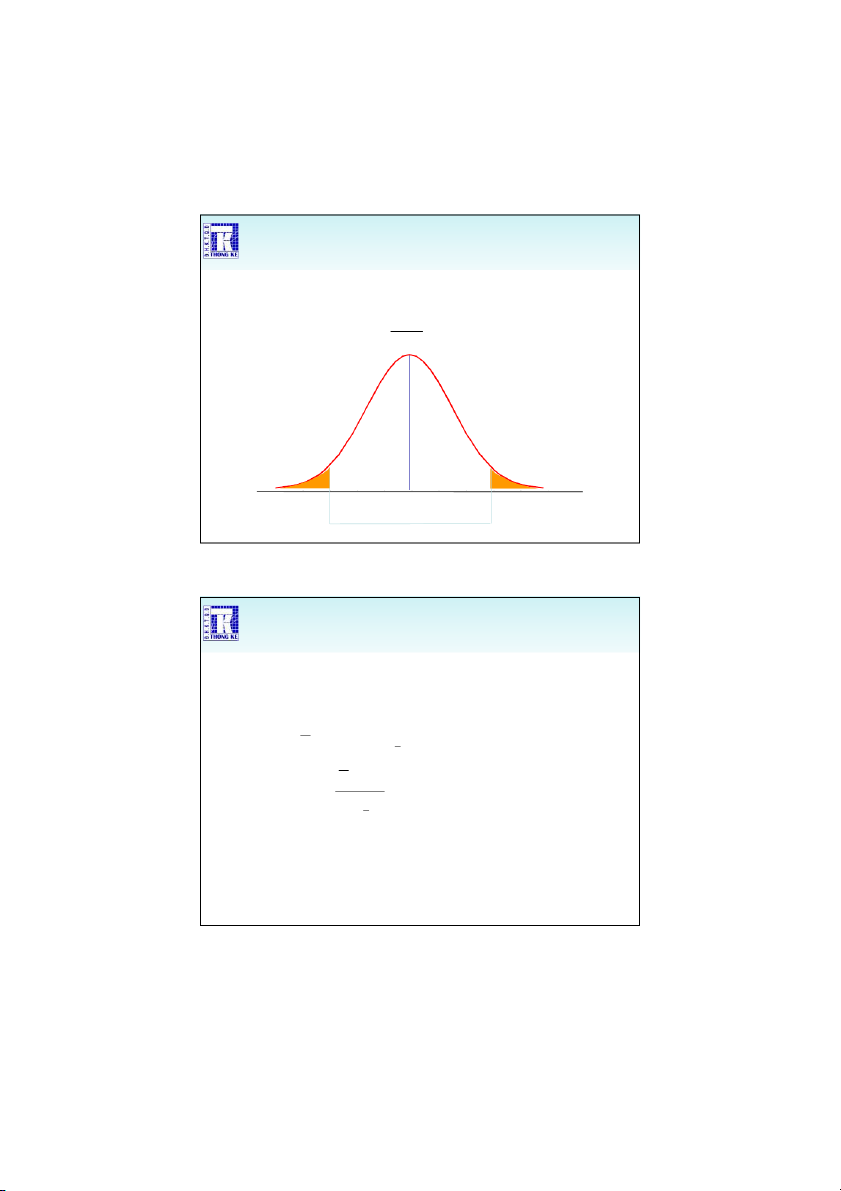
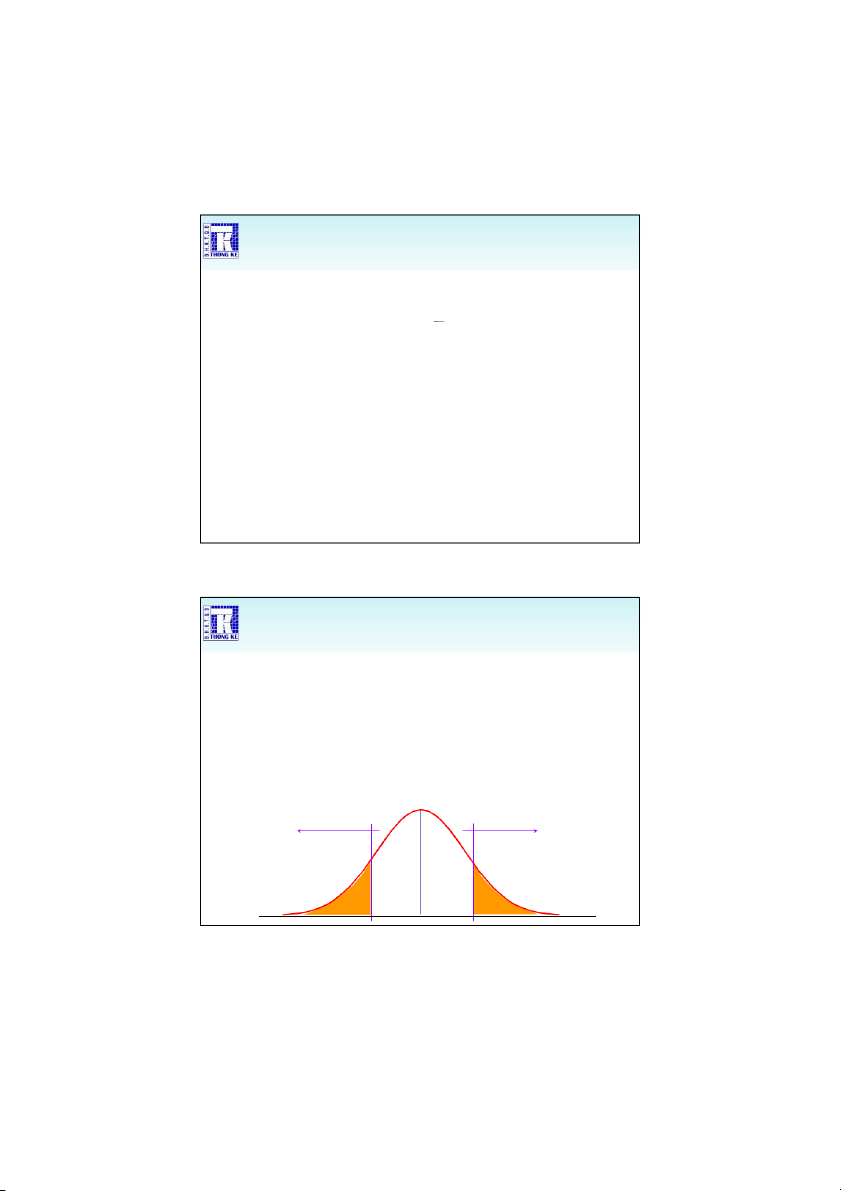
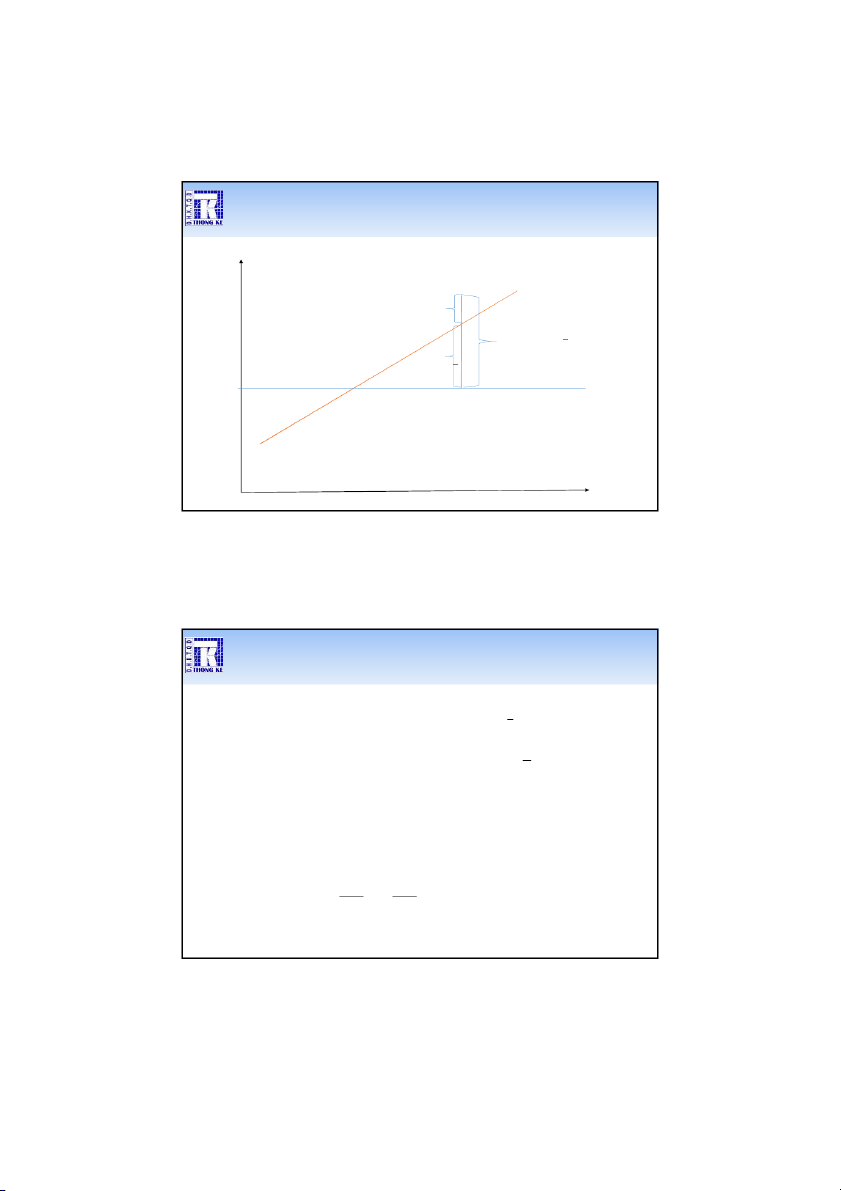
Kiểm định 2 phía, kiểm định phía trái/phải Ví dụ: H0: = 0 H1: 0 Bác bỏ H0 Bác bỏ H0 0
nằm trong vùng cam: bác b H0 ỏ
nằm trong vùng trắng: chưa đủ cơ sở để bác b H0. ỏ 17 1/9/2020
Sai lầm và mức ý nghĩa trong kiểm định
- Sai lầm loại I là bác bỏ H khi H 0 0 đúng
- Sai lầm loại II là chấp nhận H khi H sai 0 0 Kết luận Thực tế Chấp nhận H bỏ H 0 Bác 0 H0 đúng Kết luận đúng Sai lầm loại I H0 sai Sai lầm loại II Kết luận đúng
Sai lầm và mức ý nghĩa trong kiểm định
Mức ý nghĩa của kiểm định ( ) là xác suất mắc sai lầm loại I 18 1/9/2020 Tiêu chuẩn kiểm định
Tiêu chuẩn kiểm định là quy luật phân phối
xác suất nào đó dùng để kiểm định.
Trong tập hợp các kiểm định thống kê có cùng
mức ý nghĩa , kiểm định nào có xác suất mắc
sai lầm loại 2 nhỏ nhất được xem là “tốt nhất”. alpha là Sai lầm loại I.
Các bước tiến hành kiểm định
- Xây dựng giả thuyết H và giả thuyết đối H 0 1
- Xác định mức ý nghĩa
- Chọn tiêu chuẩn kiểm định
- Tính giá trị của tiêu chuẩn kiểm định từ mẫu quan sát - Kết luận 19 1/9/2020 Kết luận
Quy tắc kiểm định giả thuyết thống kê
- Nếu giá trị tiêu chuẩn kiểm định thuộc miền bác
bỏ (W ), có cơ sở để bác bỏ H0
- Nếu giá trị của tiêu chuẩn kiểm định không
thuộc miền bác bỏ, chưa đủ cơ sở để bác bỏ H0
Phương pháp tiếp cận P-value trong kiểm định giả thuyết
• P-value là xác suất lớn nhất để có thể bác bỏ giả thuyết H0.
• Các nguyên tắc ra quyết định để bác bỏ
giả thuyết H0 với P-value là:
• Nếu p-value lớn hơn hoặc bằng α, chưa
đủ cơ sở để bác bỏ giả thuyết H0.
• Nếu p-value nhỏ hơn α, bác bỏ giả thuyết H0. 20 1/9/2020
2. Kiểm định giá trị trung bình của 1 tổng thể
- Giả sử nghiên cứu X N( , 2) - Chưa biết
song có cơ sở để giả định nó bằng 0 (H0: = 0)
- Để kiểm định giả thuyết trên, lấy ngẫu nhiên n
đơn vị từ đó tính các thống kê mẫu. - Tiêu chuẩn kiểm định
2. Kiểm định giá trị trung bình của 1 tổng thể
Khi đã biết phương sai tổng thể chung Tiêu chuẩn kiểm định (x ) Z 0 / n
Nếu H0 đúng -> Thống kê Z sẽ tuân theo quy luật phân phối chuẩn hoá 21 1/9/2020
2. Kiểm định giá trị trung bình của 1 tổng thể Miền bác bỏ W - Hai phía: Z > z qs /2 - Vế phải: Z > z qs - Vế trái: Z < -z qs
2. Kiểm định giá trị trung bình của 1 tổng thể
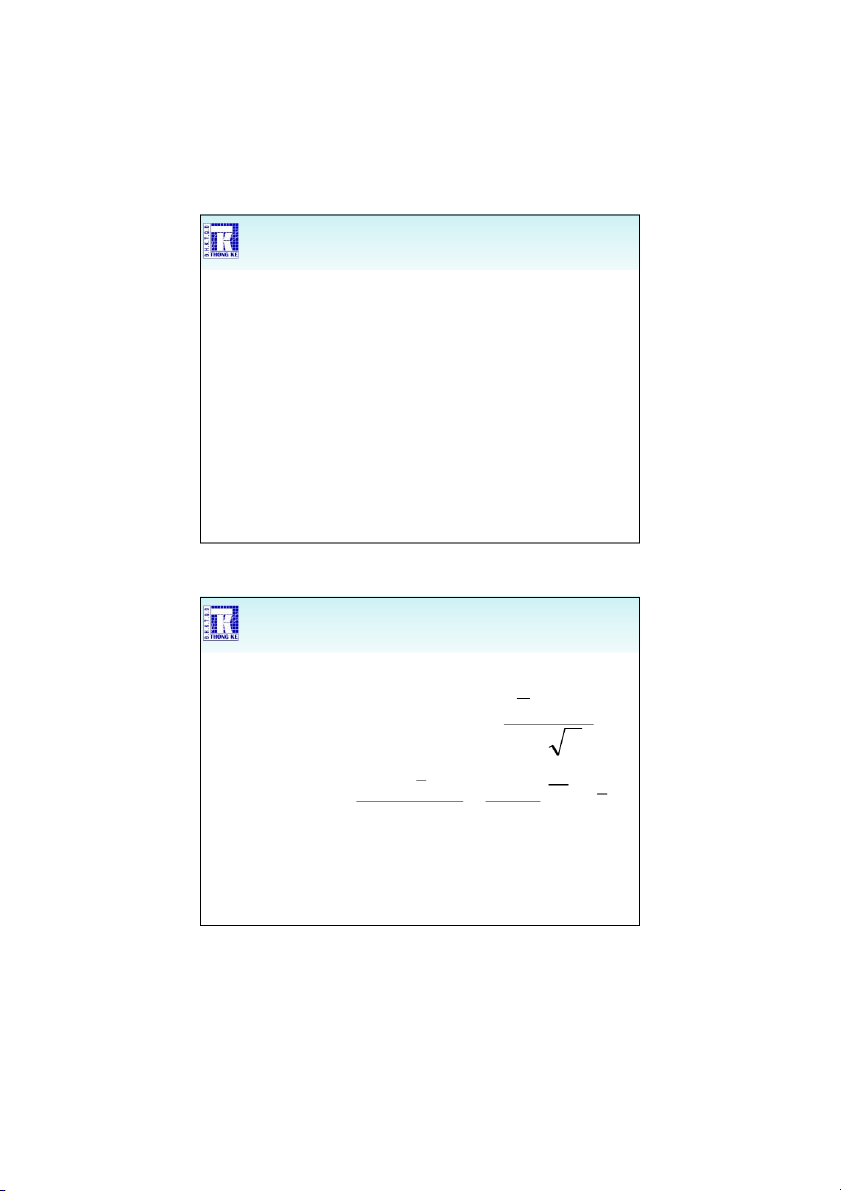
Khi chưa biết phương sai tổng thể chung Tiêu chuẩn kiểm định (x ) T 0 S / n 2 Trong đó 2 ( x ) x f f i i i 2 2 S x (x ) f 1 f 1 i i
Nếu H0 đúng -> Thống kê T sẽ tuân theo quy luật
phân phối Student với bậc tự do là (n-1) 22 1/9/2020
2. Kiểm định giá trị trung bình của 1 tổng thể Miền bác bỏ W - Hai phía: T > t qs /2(n-1) - Vế phải: T > t qs (n-1) - Vế trái: T < -t qs (n-1) ỨNG DỤNG SPSS
TRONG ƯỚC LƯỢNG VÀ KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 23 1/9/2020 Ước lượng thống kê
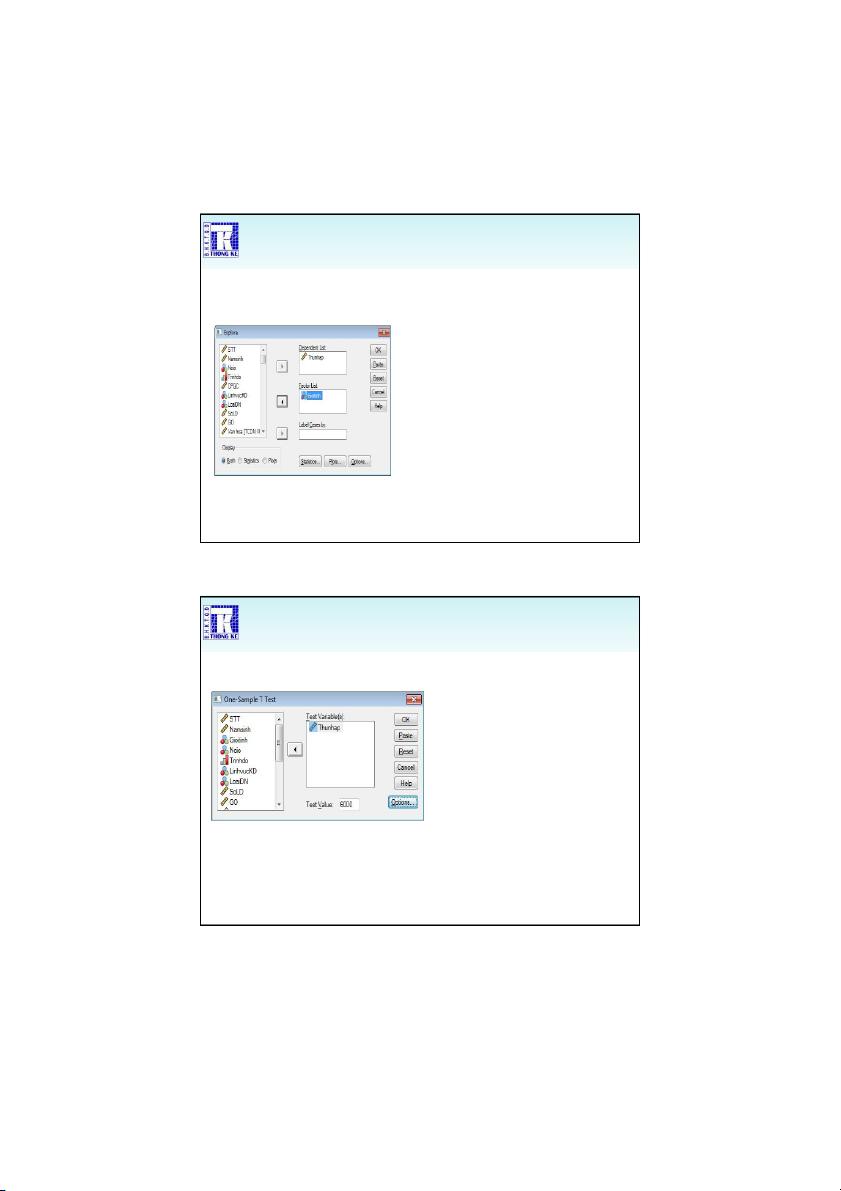
Chọn Analyze > Descriptive Statistics > Explore …
Đưa các biến cần tính toán các tham số sang Dependent List
Muốn phân tích theo biến nào
đó thì đưa sang biến sang Factor List Trong mục Display chọn Statistics hoặc Both 47
Kiểm định giả thiết về giá trị trung bình của một tổng thể
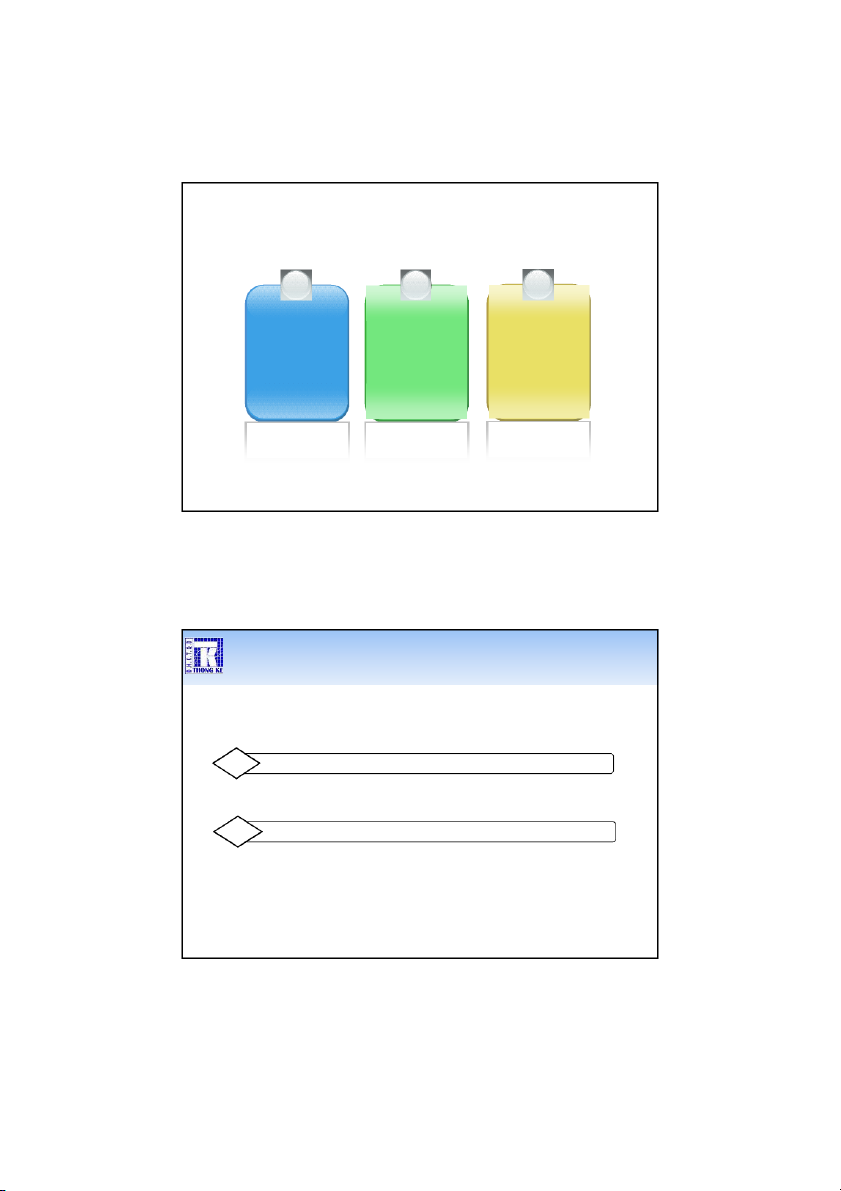
Analyze > Compare Means > One-Sample T Test…
Đưa các biến cần kiểm định giá trị
trung bình vào Test Variable(s)
Nhập giá trị cần kiểm định trung bình vào Test Value Nhấn Options... 48 24 1/9/2020
Kiểm định giả thiết về giá trị trung bình của một tổng thể
Analyze > Compare Means > One-Sample T Test…
Nhập độ tin cậy của kiểm định vào Confidence Interval
Chỉ kiểm định đối với các quan sát
có ý nghĩa của biến chọn Exclude
cases analysis by analysis
Chỉ kiểm định đối với các quan sát
có đầy đủ trong các biến chọn
Exclude cases listwise (n như nhau) 49 25
CHƯƠNG VI: PHÂN TÍCH HỒI QUY VÀ TƯƠNG QUAN I II III NHỮNG VẤN ĐỀ PHÂN TÍCH HỒI PHÂN TÍCH HỒI CHUNG VỀ QUY TUYẾN QUY TUYẾN PHÂN TÍCH TÍNH ĐƠN TÍNH BỘI HỒI QUY VÀ TƯƠNG QUAN
I. Những vấn đề chung về phân tích hồi quy và tương quan
Mối liên hệ của các hiện tượng kinh tế xã hội 1 2
Nhiệm vụ của phân tích hồi quy và tương quan
1. Mối liên hệ của các hiện tượng kinh tế xã hội Liên hệ hàm số Liên hệ tương quan Liên hệ hàm số
• Khái niệm: liên hệ hàm số là mối liên hệ hoàn toàn chặt chẽ
• Đặc điểm: Liên hệ được biểu hiện trên từng đơn vị cá biệt Liên hệ tương quan
• Khái niệm: liên hệ tương quan là mối liên hệ không hoàn toàn chặt chẽ.
• Đặc điểm: Liên hệ không được biểu hiện trên từng
đơn vị cá biệt mà phải quan sát số lớn
2. Nhiệm vụ của phân tích hồi quy và tương quan
Xây dựng phương trình hồi quy.
Đánh giá trình độ chặt chẽ của mối liên hệ
II. Hồi quy – tương quan đơn
Xây dựng phương trình hồi quy 1 2
Đánh giá phương trình hồi quy 1. Phương trình hồi quy
Đường hồi quy lý thuyết: là đường điều chỉnh bù trừ các chênh
lệch ngẫu nhiên nêu ra mối liên hệ cơ bản của hiện tượng.
Phương trình hồi quy: là phương trình xác định vị trí của đường hồi quy lý thuyết y
Đường hồi quy lý thuyết 0 x
Phương trình hồi quy tổng thể
Tham số tự do (hệ số chặn)
Hệ số hồi quy (hệ số góc) Y 0 x i 1i i Biến độc lập Biến phụ thuộc Nguyên nhân Kết quả Biến giải thích Biến được giải thích Công cụ dự báo Dự báo Ngoại sinh Nội sinh Tác nhân kích thích Câu trả lời Ý nghĩa các tham số
• β0: phản ánh ảnh hưởng của các nguyên nhân khác
(ngoài nguyên nhân x) tới kết quả y
• β1: phản ánh ảnh hưởng trực tiếp của nguyên nhân x tới
kết quả y. Cụ thể, khi x tăng thêm 1 đơn vị thì y thay đổi bình quân là β1 đơn vị
β1 > 0: x và y có mối liên hệ thuận (cùng chiều)
β1 < 0: x và y có mối liên hệ nghịch (ngược chiều)
Phương trình hồi quy mẫu
Với một mẫu ngẫu nhiên kích thước n, chúng ta có phương
trình hồi quy mẫu như sau: yˆ b b x i 0 1 i
Ước lượng của tham số β
Ước lượng của tham số β 0 1 Giả thiết OLS
+ Giả thiết 1: Mô hình được ước lượng trên cơ sở mẫu ngẫu nhiên
+ Giả thiết 2: Kỳ vọng toán của sai số bằng không
+ Giả thiết 3: Sai số tuân theo quy luật phân bố chuẩn
+ Giả thiết 4: Phương sai của sai số bằng nhau (không đổi)
+ Giả thiết 5: Không có tương quan giữa các phần dư (không có tự tương quan)
+ Giả thiết 6: Giữa các biến độc lập không có tương quan tuyến tính hoàn
hảo (đa cộng tuyến) - Đối với hồi quy bội. Nội dung phương pháp OLS
Tìm các tham số sao cho tổng bình phương các
chênh lệch giữa giá trị thực tế và giá trị lý thuyết của
tiêu thức kết quả là nhỏ nhất. S ( y ˆ y i )2i min S ( y b b x i )2i min 0 1 S ( 2 y b b x i 0 1 . i )( ) 1 0 b y . n b b. x 0 i 0 1 i S 2 ( 2 y b b x x y. x b x b . x i 0 .1 i )( i ) 0 b i i 0 i 1 i 1
Kiểm định hệ số hồi quy • Giả thuyết: H 0 : j 0 bj
• Tiêu chuẩn kiểm định: T s ( e b ) j n x2 2 i 2 se b ( ) i se b 1 ( ) . 1 n 0 n 2 n x x 2 x x i i i 1 i 1 n y ˆ 2 i y SSE i 2 i 1 n 2 n 2
• Nếu H0 đúng thống kê T sẽ tuân theo quy luật phân phối
student với (n-2) bậc tự do.
Kiểm định hệ số hồi quy
Miền bác bỏ giả thuyết H0 (W )
- Hai phía: Tqs > t /2 ,(n-2)
- Vế phải: Tqs > t (n-2)
- Vế trái: Tqs < -t (n-2)
Ước lượng hệ số hồi quy n 2 n • Hai phía: b t se b b t se b j ( ) 2 ( ) 2 j j j 2 j • Phái trái: n 2 b t se b j j ( ) j • Phái phải: n b t 2 se(b ) j j j Hệ số xác định y n SSE 2 i y i yˆ i 1 n SST 2 i y y n i 1 SSR 2 ˆiy y 1 x 0 Hệ số xác định n
Toàn bộ biến thiên của biến phụ thuộc SST 2 i y y i 1n
Biến thiên được giải thích bởi hồi quy SSR y y 2 ˆi i 1 n Biến thiên do phần dư SSE 2 i y ˆ iy i 1 SST = SSR + SSE 2 SSR SSE Hệ số xác định R 1 SST SST
Phản ánh phần trăm thay đổi của biến phụ thuộc được giải thích bởi biến độc lập
Kiểm định ý nghĩa mô hình H : Mô h ình khôngc ó n ý ghia H : 2 R 0 Cặp giả thuyết o o H : Mô h ình c ó n ý ghia 2 1 H : R 0 1 2 SSR R n 2 Tiêu chuẩn kiểm định F 2 SSE 1 R n 2
Nếu H0 đúng, thống kê F sẽ tuân theo quy luật phân phối Fisher với bậc tự do (1, n-2)
Với mức ý nghĩa α, Miền bác bỏ giả thuyết H0 khi, F > fα(1.n-2)
Hệ số tương quan tuyến tính Công thức tính 2 2 xi xi y x . x y n n r b x b 1 1 2 2 x y y yi yi n n
Hệ số tương quan tuyến tính Tác dụng
- Xác định chiều hướng của mối liên hệ
- Đánh giá mức độ chặt chẽ của liên hệ tương quan tuyến tính
Tính chất của hệ số tương quan Liên hệ hàm số Không có mối liên hệ Liên hệ hàm số -1 0 +1
Tính chất của hệ số tương quan Y R2 = 1,r = +1 Y R2 = 1, r = -1 ^ Y = b + b X i 0 1 i ^ Y = b + b X i 0 1 iX X Y R2 < 1, r <1 Y R2 = 0, r = 0 ^ ^ Y = b + b X Y = b + b X i 0 1 i i 0 1 i X X
Kiểm định hệ số tương quan H : 0 Cặp giả thuyết o H : 0 1 r Tiêu chuẩn kiểm định T 1 2 r n 2
Nếu H0 đúng, thống kê T sẽ tuân theo quy luật phân phối student với bậc tự do (n-2)
Với mức ý nghĩa α, Miền bác bỏ giả thuyết H n 2 0 khi T t 2
III. Hồi quy – tương quan bội
Xây dựng phương trình hồi quy 1 2 Đán á h n hgiá phương trình
Phương trình hồi quy tổng thể Y 0 1 x 1 2 x .... 2 x i i i k ki i
β0 - Tham số tự do (hệ số chặn)
βj (j=1-k) Hệ số hồi quy riêng Ý nghĩa hệ số hồi quy
• βj: phản ánh ảnh hưởng thuần của nguyên nhân xj tới
kết quả y (khi các yếu tố khác không đổi). Cụ thể, khi xj
tăng thêm 1 đơn vị thì y thay đổi trung bình là βj đơn vị
Phương trình hồi quy mẫu
Với một mẫu ngẫu nhiên kích thước n, chúng ta có phương
trình hồi quy mẫu như sau: y ˆ b b x b x ..... b x i 0 1 1i 2 2 i k ki
bj: Ước lượng của tham số βj
Kiểm định hệ số hồi quy • Giả thuyết: 0 H : 0 j bj
• Tiêu chuẩn kiểm định: T se(b ) j
• Nếu H0 đúng thống kê T sẽ tuân theo quy luật phân phối
student với (n-k-1) bậc tự do.
Kiểm định hệ số hồi quy
Miền bác bỏ giả thuyết H (W ) 0
- Hai phía: Tqs > t /2 ,(n-k-1)
- Vế phải: Tqs > t (n-k-1)
- Vế trái: Tqs < -t (n-k-1)
Ước lượng hệ số hồi quy • Hai phía: n k 1 n k b t se b b t se b j 2 ( j ) 1 j j 2 ( j ) • Phái trái: n k 1 b t se b j j ( j ) n k 1 • Phái phải: b t se(b ) j j j
Hệ số hồi quy chuẩn hoá • Công thức: xj Bêta b j j y
• Biểu hiện vai trò của từng biến độc lập tới biến thuộc Hệ số xác định n
Toàn bộ biến thiên của biến phụ thuộc SST 2 i y y i 1 n
Biến thiên được giải thích bởi hồi quy SSR y y 2 ˆi i 1 n Biến thiên do phần dư SSE 2 i y ˆiy i 1 SST = SSR + SSE 2 SSR SSE Hệ số xác định R 1 SST SST
Phản ánh phần trăm thay đổi của biến phụ thuộc được giải thích bởi các biến độc lập
Hệ số xác định điều chỉnh SSE 1 ( 2 2 R )(n ) 1
Hệ số xác định điều chỉnh n k 1 R 1 1 adj SST n k 1 n 1
Dùng để so sánh, đánh giá độ phù hợp của mô hình khi số lượng biến trong mô hình hồi quy khác nhau
Khi k >1 thì R2adj ≤ R2≤1 K càng lớn R2 càng nhỏ so với R2 adj
R2adj có thể âm, sẽ quy ước R2 = 0 adj
Kiểm định ý nghĩa mô hình H : 2 R 0 Cặp giả thuyết o H : 2 1 R 0 SSR 2 R n k 1 Tiêu chuẩn kiểm định k F 2 SSE k 1 R n k 1
Nếu H0 đúng, thống kê F sẽ tuân theo quy luật phân phối Fisher với bậc tự do (k, n-k-1)
Với mức ý nghĩa α, Miền bác bỏ giả thuyết H0 khi, F > fα(k, n-k-1) Hệ số tương quan chung SSE SSR Công thức 2 R 1 R SST SST
Ứng dụng SPSS trong phân tích HQ
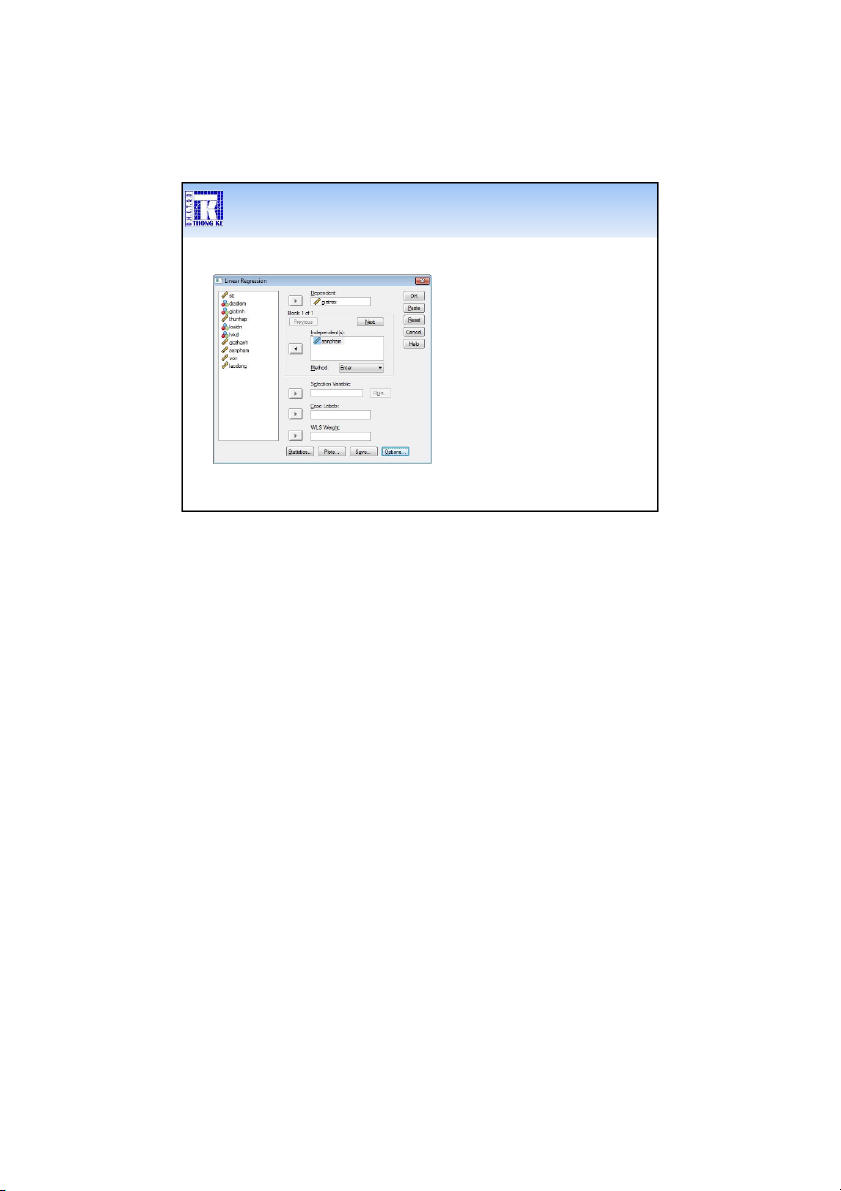
Analyze > Regression > Linear…
Đưa biến phụ thuộc sang Dependent
Đưa các biến độc lập sang Independent(s) 37
CHƯƠNG VII : PHÂN TÍCH DÃY SỐ THỜI GIAN I II III IV KHÁI NIỆM PHÂN TÍCH ĐẶC BIỂU DIỄN XU DỰ ĐOÁN CHUNG VỀ DÃY ĐIỂM BIẾN HƯỚNG BIẾN THỐNG KÊ SỐ THỜI GIAN ĐỘNG CỦA HIỆN ĐỘNG CỦA HIỆN NGẮN HẠN TƯỢNG QUA TƯỢNG THỜI GIAN
I. KHÁI NIỆM CHUNG VỀ DÃY SỐ THỜI GIAN 1 Khái niệm 2 Cấu tạo 3 Các loại 4 Các thành phần 5 Tác dụng 6 Yêu cầu 1. Khái niệm
Dãy số thời gian là một dãy trị số của chỉ tiêu
thống kê được sắp xếp theo thứ tự thời gian 2. Cấu tạo
Thời gian: ngày, tháng, quý,năm,… Độ dài
giữahai thờigian là khoảngcách thờigian
Chỉ tiêu về hiện tượng nghiên cứu: tên chỉ
tiêu, đơn vịtính và trị số chỉtiêu yi (i=1,n) là
mứcđộcủadãy sốthờigian 3. Các loại Dãy sốtuyệtđối Thờiđiểm Dãy số tươngđối DS-TG Thờikỳ Dãy sốbình quân 4. Các thành phần Thời vụ/chu kỳ (S) Các yếu tố ngẫu nhiên (I) Xu hướng (T) Mô hình kết hợp cộng Y T S I Mô hình kết hợp nhân Y T S I 5. Tác dụng
Nghiên cứu các đặc điểm biến động của hiện
tượng,và xác địnhxu hướngvà tính quy luậtcủasự phát triển.
Là cơsởdựđoáncác mứcđộcủahiệntượng. 6. Yêu cầu
Đảm bảo tính chất có thể so sánh được
giữa các mức độ của dãy số thời gian
Thống nhất về nội dung và phương pháp tính. Thống nhất về phạm vi.
Khoảng cách thời gian trong dãy số thời kỳ phải bằng nhau.
II. Các chỉ tiêu phân tích đặc điểm biến
động của hiện tượng qua thời gian 1
Mức độ bình quân qua thời gian 2
Lượng tăng (giảm) tuyệt đối 3 Tốc độ phát triển 4 Tốc độ tăng (giảm) 5
Giá trị tuyệt đối của 1% của tốc độ tăng (giảm)
1. Mức độ bình quân qua thời gian
Ý nghĩa: Mức độ bình quân theo thời gian phản ánh
mức độ đại biểu của tất cả các mức độ của dãy số. n Cách tính y y . . 1 y2 yn 1 y i
* Đối với dãy số thời kỳ: y n i 1 n n
1. Mức độ bình quân qua thời gian
* Đối với dãy số thời điểm: y y DK CK
- Dãy số biến động đều: y 2
* Đối với dãy số thời điểm:
- Dãy số biến động không đều
+ Có số liệu tại thời điểm có khoảng cách thời gian bằng nhau: y y 1 y y n 2 ... 2 n 1 2 y n 1
1. Mức độ bình quân qua thời gian
* Đối với dãy số thời điểm:
- Dãy số biến động không đều
+ Có số liệu tại thời điểm có khoảng cách thời gian không bằng nhau: y tii y ti
2. Lượng tăng (giảm) tuyệt đối
Ý nghĩa: Phản ánh sự biến động về trị số tuyệt đối của chỉ tiêu qua thời gian - Liên hoàn y y 1 i i i - Định gốc y y i i 1 i - Mối liên hệ i i i 2 n i y y - Bình quân i 2 n n 1 n 1 n 1 n 1 3. Tốc độ phát triển
Ý nghĩa: tốc độ và xu hướng biến động của hiện tượng qua thời gian y - Liên hoàn i ti 1 ( 00) yi 1 y - Định gốc T i i 1 ( 00) 1 y i - Mối liên hệ T t i i i 2 n y - Bình quân n 1 n n 1 t t T 1 n i n i 2 y1 4. Tốc độ tăng (giảm)
Ý nghĩa: mức độ của hiện tượng qua thời gian tăng (giảm) đi bao nhiêu lần hoặc % y y - Liên hoàn i i 1 a 1 ( 00) i 1 ( 00) t i i (%) 1 ( 1 00) y y i 1 i 1 - Định gốc y y i 1 A 1 ( 0 ) 0 i 1 ( 00) T( i i %) 1 ( 1 00) y y 1 1
- Mối liên hệ: Không có mối liên hệ - Bình quân a t (%) 10 ( 1 0)
5. Giá trị tuyệt đối của 1% của tốc độ tăng (giảm)
Ý nghĩa: 1% tăng/giảm của tốc độ tăng/giảm thì tương ứng
với một trị số tuyệt đối là bao nhiêu - Liên hoàn i i y i1 g i ai (%) i 100 100 yi 1 y - Định gốc G i i 1 i const --> Không tính A (%) 100 i i 100 y1
- Mối liên hệ: Không có mối liên hệ - Bình quân: không tính
III. Một số phương pháp biểu diễn xu
hướng phát triển cơ bản của hiện tượng
Mở rộng khoảng cách thời gian 1 2 Số bình quân trượt 3 Hàm xu thế
1. Mở rộng khoảng cách thời gian Điều kiện Nội dung Hạn chế vận dụng Khi DSTG có Mởrộng thêm khoảngcách tương khoảngcách thời - Mấtđiảnh đốingắncó quá gian bằngcách hưởngcủanhững nhiềumứcđộ mà ghép mộtsốthời nhân tốcơ bản chưaphảnánh -Mấtđi tính chất gian liềnnhau vào đượcxu hướng thờivụcủahiện mộtkhoảngthời phát triểncơbản gian dài hơn tượng củahiệntượng
2. Phương pháp bình quân trượt
Giảsửcó dãy số thờigian: y1, y2, y3,… yn y ... y ... y k i k i , 0 5 i , 0 5 Nếuk lẻ: y 2 2 k k i ( ; 5 , 0 n ) 5 , 0 i k 2 2 y ... y ... k i y k i i 1 k k Nếuk chẵn: y 2 2 i ( ; 1 n ) 1 i k 2 2 3. Xây dựng hàm xu thế Khái niệm Một số dạng hàm xu thế yˆ b b t i 0 1 i Hàm số biểu hiện các 2 ˆy b b t b t mức độ của hiện i 0 1 i 2 i tượng qua thời gian b yˆ b 1 i 0 ˆy f t i ( i ) ti
Tiêu chuẩn lựa chọn hàm xu thế
Bước1: Lựachọn dạnghàm có ý nghĩa: Căncứ vào giá
trịSighoặcp_valuecủacác hệsốtrong từnghàm xu thế.
Bước2: Lựachọn dạnghàm tốtnhất: n y ˆ 2 i y SSE i i 1 SE min n p n p
SửdụngSPSS trong việcxây dựnghàm xu thế
Địnhnghĩathờigian: Dữliệuthờigian (dữliệuchuỗi) là dữliệumà mỗi
dòng (quan sát) là sốliệu ởmột thời gian nhấtđịnh(tháng, quý, năm,...) Data>Define Dates.. 22 Xây dựnghàm xu thế
Analyze>Regression > Curve Estimation… 23
IV. Một số phương pháp dự
đoán thống kê đơn giản
Dự đoán dựa vào lượng tăng (giảm) tuyệt đối bình quân 1 2
Dự đoán dựa vào tốc độ phát triển bình quân 3
Dự đoán dựa vào hàm xu thế Khái niệm chung
• Dự đoán thống kê là xác định mức độ của hiện
tượng trong tương lai bằng cách sử dụng tài liệu
thống kê và áp dụng các phương pháp phù hợp
• Tài liệuthốngkê thường được sử dụng trong dự
đoán thống kê là dãy số thời gian
1. Dự đoán dựa vào lượng tăng (giảm) tuyệt đối bình quân • Công thức: yˆ y h . n h n Trong đó: n i y
y Lượng tăng (giảm) tuyệt đối bình i 2 n n 1 n 1 n 1 n 1 quân
Điều kiện áp dụng: Dãy số có các lượng tăng (giảm)
tuyệt đối liên hoàn xấp xỉ nhau
2. Dự đoán dựa vào tốc độ phát triển bình quân • Công thức: h yˆ y t ( ) n h n Trong đó: n y n 1 n n 1 n t t T 1 i n
Tốc độ phát triển bình quân i 2 1 y
Điều kiện áp dụng: Dãy số có các tốc độ phát triển liên hoàn xấp xỉ nhau
3. Dự đoán dựa vào hàm xu thế • Mô hình dự đoán: ˆy f (t ) i i Trong đó: ti: thứ tự thời gian
CHƯƠNG VIII: PHƯƠNG PHÁP CHỈ SỐ I II III NHỮNG VẤN ĐỀ PHƯƠNG PHÁP HỆ THỐNG CHUNG VỀ TÍNH CHỈ SỐ CHỈ SỐ PHƯƠNG PHÁP CHỈ SỐ
I Những vấn đề chung về phương pháp chỉ số Khái niệm 1 2 Các loại chỉ số 3 Đặc điểm 1 Khái niệm
Chỉ số là số tương đối (tính bằng lần hoặc %) biểu
hiện quan hệ so sánh giữa haimức độcủa cùng một hiện tượng nghiên cứu
Chỉ số trong thống kê là phương pháp biểu hiện quan
hệ so sánh giữa hai mức độ cùng loại 2 Phân loại CHỈ SỐ Theo đặc điểm Theo phạm vi Theo nội dung quan hệ thiết lập chỉ tiêu Chỉ số Chỉ số Chỉ số Chỉ số Chỉ số Chỉ số chỉ Chỉ số chỉ phát không kế đơn (cá tổng tiêu chất tiêu số triển gian hoạch thể) hợp lượng lượng (chung)
3. Đặc điểm của phương pháp chỉ số
- Khi phản ánh sự biến động của hiện tượng gồm
nhiều phần tử -> chuyển chúng về dạng giống nhau
để có thể trực tiếp so sánh được với nhau
- Khi có nhiều nhân tố tham gia vào tính toán thì giả
định chỉ có một nhân tố nghiên cứu thay đổi còn các
nhân tố khác cố định (không thay đổi)
II Phương pháp tính chỉ số Chỉ số phát triển 1 2 Chỉ số không gian 3 Chỉ số kế hoạch 1 Chỉ số phát triển Chỉ số đơn Chỉ số tổng hợp 1.1 Chỉ số đơn
Chỉ số đơn của chỉ tiêu chất lượng (lấy giá bán làm ví dụ): p1 ip 1 ( 0 ) 0 p o
Chỉ số đơn của chỉ tiêu số lượng (lấy lượng
hàng tiêu thụ làm ví dụ): q1 i ) 100 ( q q o 1.2 Chỉ số tổng hợp
Chỉ số tổng hợp của chỉ tiêu chất lượng (lấy giá làm ví dụ): p1 q Ip p q o 1.2 Chỉ số tổng hợp
– Chỉ số tổng hợp của Laspeyres (quyền số ở kỳ gốc) p q L 1 o I p p q o o
- Biến đổi theo chỉ số đơn về giá: ip p1 p q0o p q p i .p q p q L 1 o 0 p 0 o 0 o I i .d trong đó d p p o p q p q p q 0 p q o o o o o o o o 1.2 Chỉ số tổng hợp
- Chỉ số tổng hợp của Paasche (quyền số ở kỳ nghiên cứu) p q p 1 1 I p p q o 1
- Biến đổi theo chỉ số đơn về giá: ip p q p q p q P 1 1 1 1 1 1 1 1 p q 1 1 I trđ :d p 1 p q p p q p q d o 1 1 1 1 1 p q o 1 1 1 p q 1 1 p i p q .i i 1 p 1 1 p p 1.2 Chỉ số tổng hợp
- Chỉ số tổng hợp của Fisher (khi có sự chênh lệch
lớn giữa chỉ số của Laspayres và Passche) p q p q F L 1 0 1 1 I I . P I . p p p p q p q o 0 o 1 1.2 Chỉ số tổng hợp
Chỉ số tổng hợp của chỉ tiêu số lượng (lấy lượng làm ví dụ): pq1 Iq pq 0 1.2 Chỉ số tổng hợp
- Chỉ số tổng hợp của Laspeyres (quyền số ở kỳ gốc) p q L 0 1 Iq p q o o
- Biến đổi theo chỉ số đơn về lượng: iq q1 p q0o p q q i .p q L 0 1 q 0 o 0 I i .d q q o p q p q p q o o o o o o 1.2 Chỉ số tổng hợp
- Chỉ số tổng hợp của Paasche (quyền số ở kỳ nghiên cứu) p q p 1 1 Iq p q 1 0
- Biến đổi theo chỉ số đơn về lượng: iq p q p q p q P 1 1 1 1 1 1 1 1 Iq p q q p q p q d o 1 1 1 1 1 1 0 p q 1 1 q i p q .i i 1 q 1 1 q q 1.2 Chỉ số tổng hợp
- Chỉ số tổng hợp của Fisher (khi có sự chênh lệch
lớn giữa chỉ số của Laspayres và Passche) p q p q F L 0 1 1 1 I I . P I . q q q p q p q o 0 1 0 2 Chỉ số không gian Chỉ số đơn Chỉ số tổng hợp Bài toán tổng quát
Giả sử nghiên cứu biến động về giá bán và khối lượng
tiêu thụ của các mặt hàng ở hai thị trường A và B Ký hiệu: p - giá bán q - lượng hàng tiêu thụ A, B – Thị trường A, B Chỉ số đơn Chỉ số đơn về giá pA 1 i (A p /B) p i B (B p /A) Chỉ số đơn về lượng qA 1 iq( A/B) q i B ( q B/A) Chỉ số tổng hợp
Chỉ số tổng hợp về giá p q A I ( pA/B) p q B p (q q ) p Q A A B A I Trong đó Q q q p ( A/B) A B p (q q ) p Q B A B B Chỉ số tổng hợp
Chỉ số tổng hợp về lượng p qA I ( q A/B) p B q
- Lấy giá do cố định (p ) do nhà nước quy định) n p nqA I ( qA/B) p q n B
- Lấy giá trung bình của hai thị trường pq p q p q A I A A B B ví i p ( q A/B) pq q q B A B 2.3. Chỉ số kế hoạch
• Nếu căn cứ vào sản lượng thực tế của
doanh nghiệp ở các kỳ, ta có 2 loại chỉ số:
+ Chỉ số kế hoạch giá thành: z q k 0 Iz z q o 0
+ Chỉ số thực hiện kế hoạch giá thành: z q 1 1 I z z q k 1 2.3 Chỉ số kế hoạch
• Nếu căn cứ vào sản lượng kế hoạch của doanh nghiệp:
+ Chỉ số kế hoạch giá thành: z q k k I z z q o k
+ Chỉ số thực hiện kế hoạch giá thành: z qk I 1 z z q k k III Hệ thống chỉ số
Khái niệm chung về hệ thống chỉ số 1 2
Phương pháp xây dựng hệ thống chỉ số tổng hợp Khái niệm
• Hệ thống chỉ số là một dãy các chỉ số có liên hệ với
nhau, hợp thành một phương trình cân bằng • Ví dụ: Ipq Ip Iq
Cấu thành của một hệ thống chỉ số thường bao gồm
một chỉ số toàn bộ và các chỉ số nhân tố Tác dụng
Phân tích biến động (tuyệt đối, tương đối) của
hiện tượng do ảnh hưởng biến động của các nhân tố.
Tính ra 1 chỉ số chưa biết khi đã biết các chỉ
số còn lại trong hệ thống Quy tắc xây dựng
Sắp xếp các nhân tố theo trình tự tính chất lượng
giảm dần, tính số lượng tăng dần
Khi phân tích sự biến động của nhân tố chất lượng
sử dụng quyền số là nhân tố số lượng ở kỳ nghiên
cứu, khi phân tích sự biến động của nhân tố số lượng,
sử dụng quyền số là nhân tố chất lượng ở kỳ gốc
2. Hệ thống chỉ số tổng hợp
Vậndụngphân tích sựbiếnđộngdoanh thu do ảnh
hưởng biếnđộng củagiá và lượng Biến động tương đối: Ipq = Ip x Iq p q p q p q 1 1 1 1 0 1 x p q p q p q 0 0 0 1 0 0 Biến động tuyệt đối: p q p q p q p q p q p q 1 1 0 0 1 1 0 1 0 1 0 0 p q pq pq pq




