





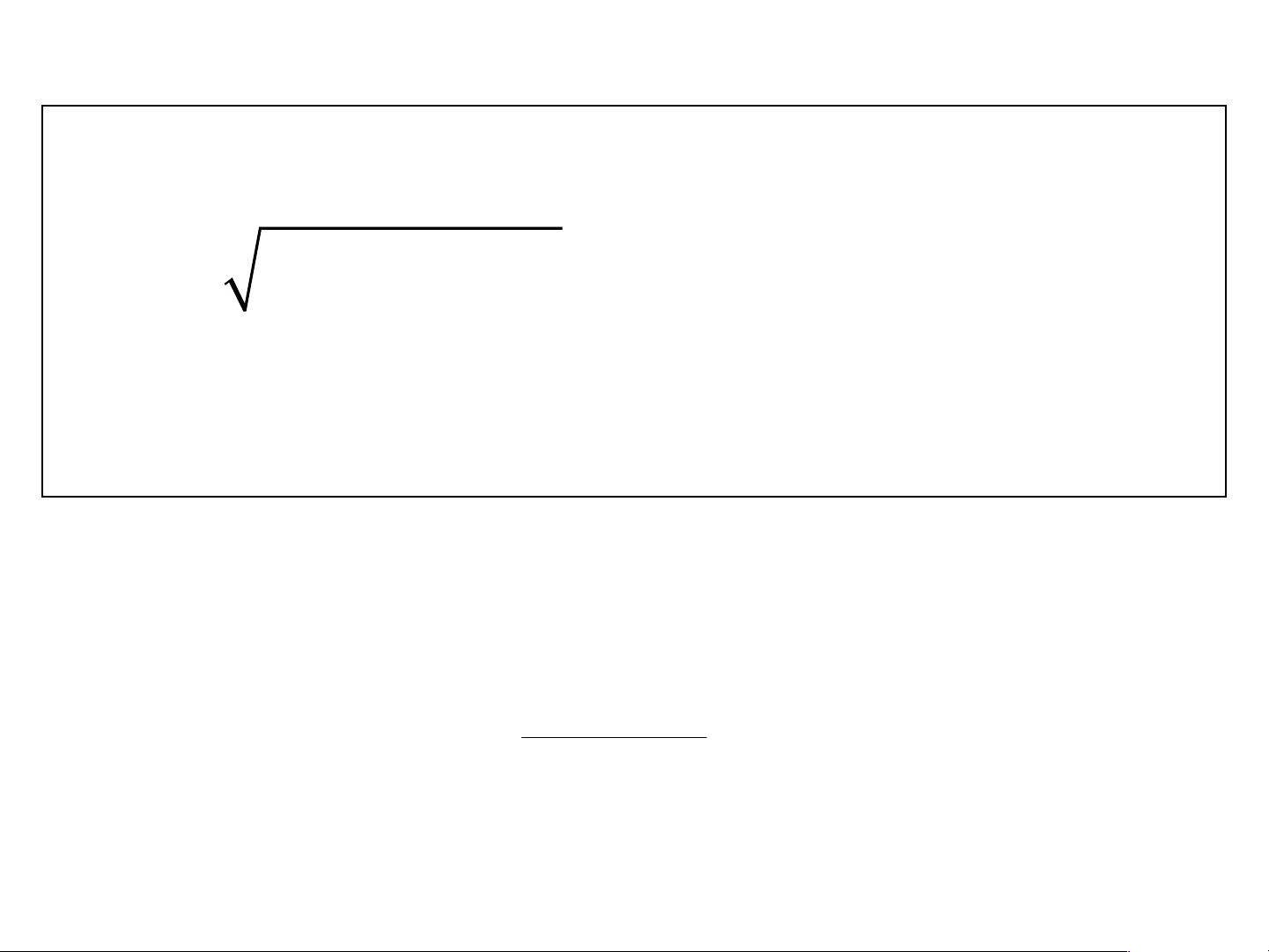
Preview text:
TÍCH PHÂN MẶT LOẠI 2
PHÁP TUYẾN CỦA MẶT CONG.
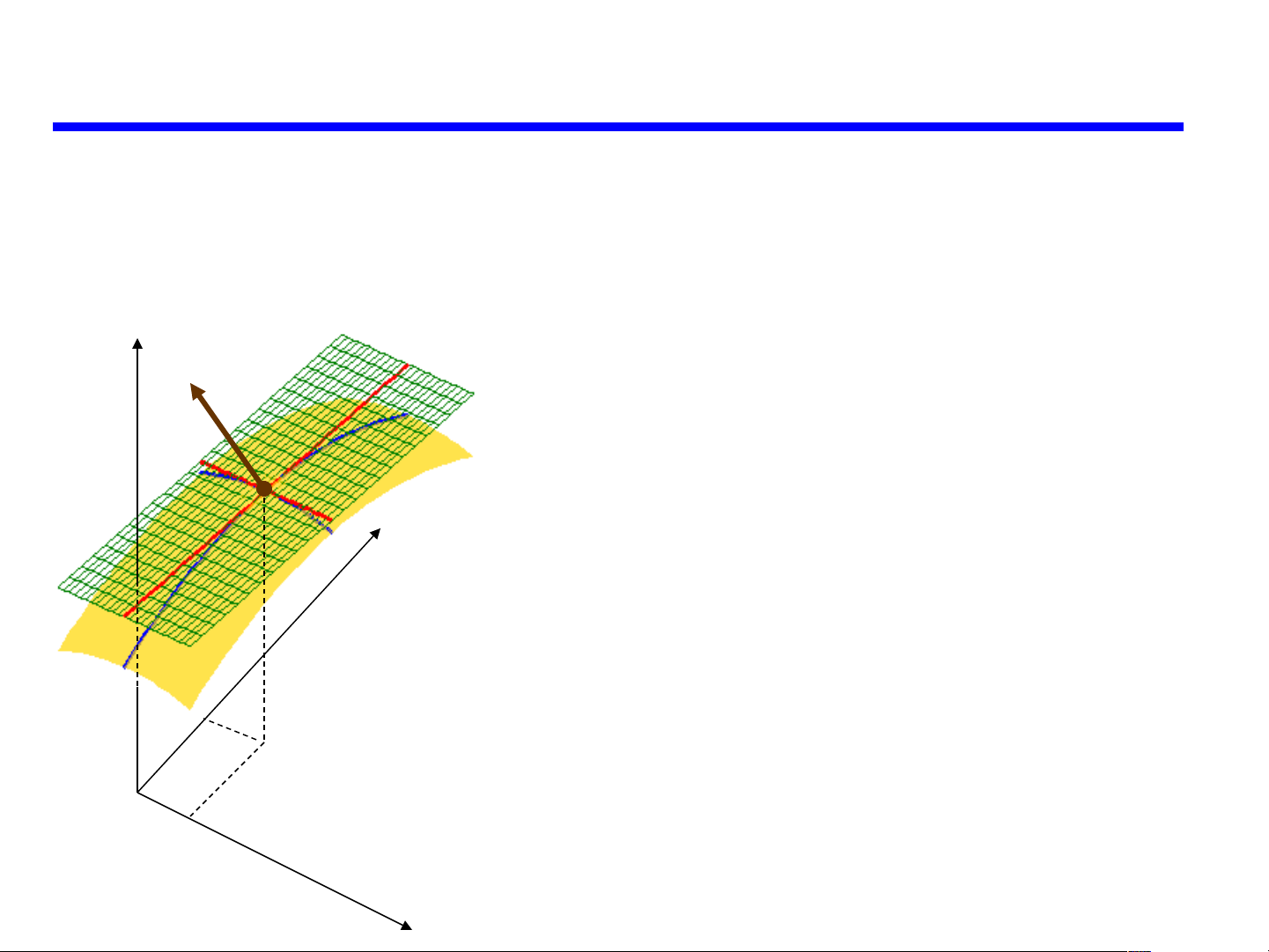
Cho mặt cong S: F(x, y, z) = 0, M(x ,y ,z ) 0 0 0 S
•L là đường cong trong S đi
qua M. Tiếp tuyến của L tại M n
gọi là tiếp tuyến của S tại M.
•Các tiếp tuyến này cùng thuộc
1 mặt phẳng gọi là mặt tiếp diện của S tại M.
•Pháp tuyến của mặt tiếp
diện tại M gọi là pháp tuyến của S tại M. PHÁP TUYẾN MẶT CONG
Giả sử L S có pt: x = x(t), y = y(t), z = z(t) M = (x(t ), y(t ), z(t )) 0 0 0 L
Vt chỉ phương của tiếp tuyến tại M là : u x (
t0),y (y0),z (t0) M S: F(x,y,z) = 0, ta có:
F(M)x (
t0) F(M)y (t0) F ( M)z ( t0) 0 x y z x (
t0),y (t0),z (t0)
F(M),F(M),F ( M) x y z x (
t0),y (t0),z (t0)
F(M),F(M),F ( M) x y z
(đúng với mọi đường cong trong S và qua M) n =
F(M ),F(M ),F ( M) x y z và các vector tỷ lệ
là pháp vector của S tại M Một ký hiệu khác: gradF(M)
F(M),F(M),F ( M) x y z (gradient của F tại M)
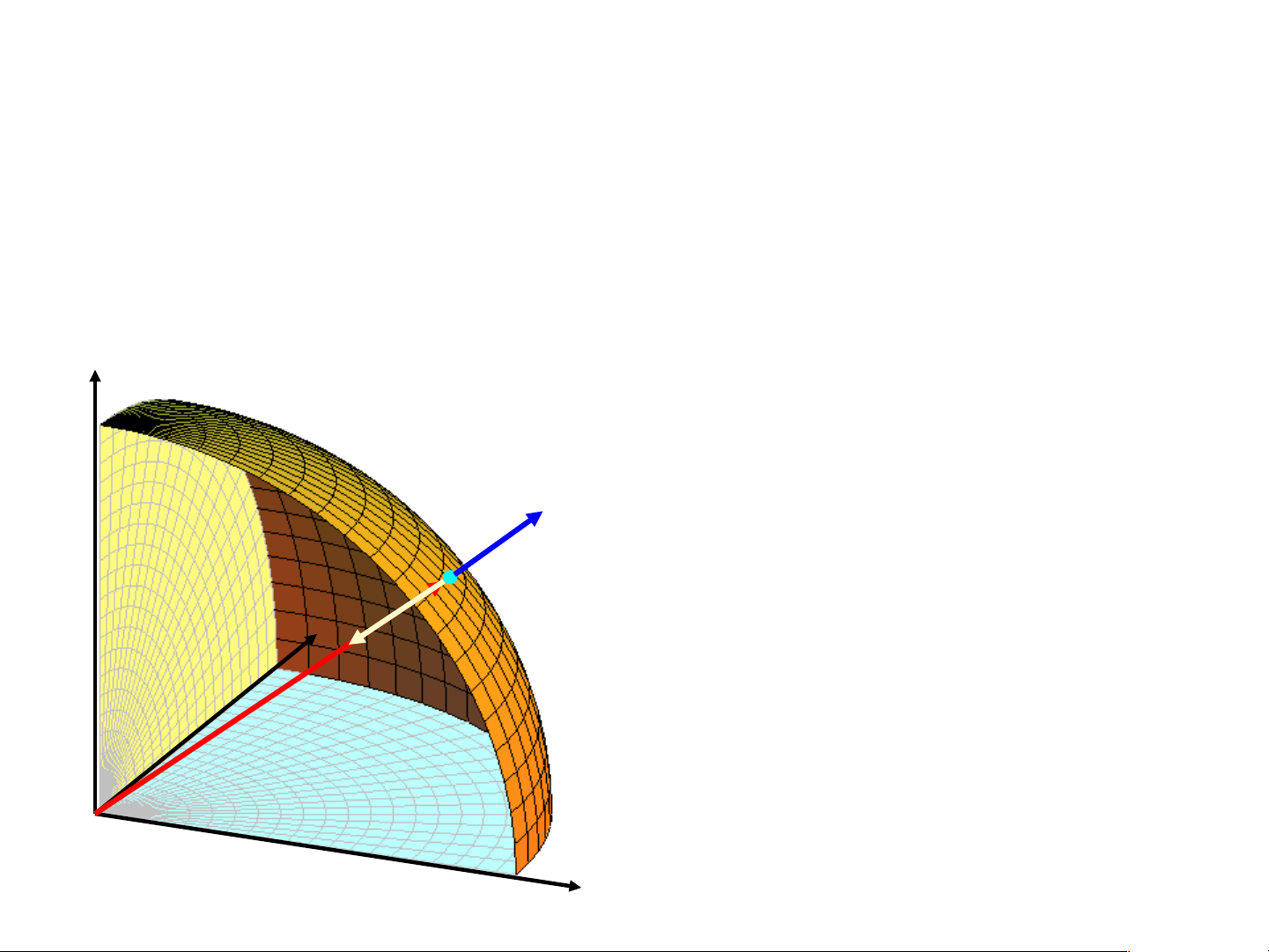
Một số ví dụ tìm pháp vector 2 2 2 2
a/ Mặt cầu S : x y z R
M(x0,y0, 0
z ) S, n(M) 2x0,2y0,2 0 z (và các vector tỷ lệ)
n n
OM(x0,y0, 0z)
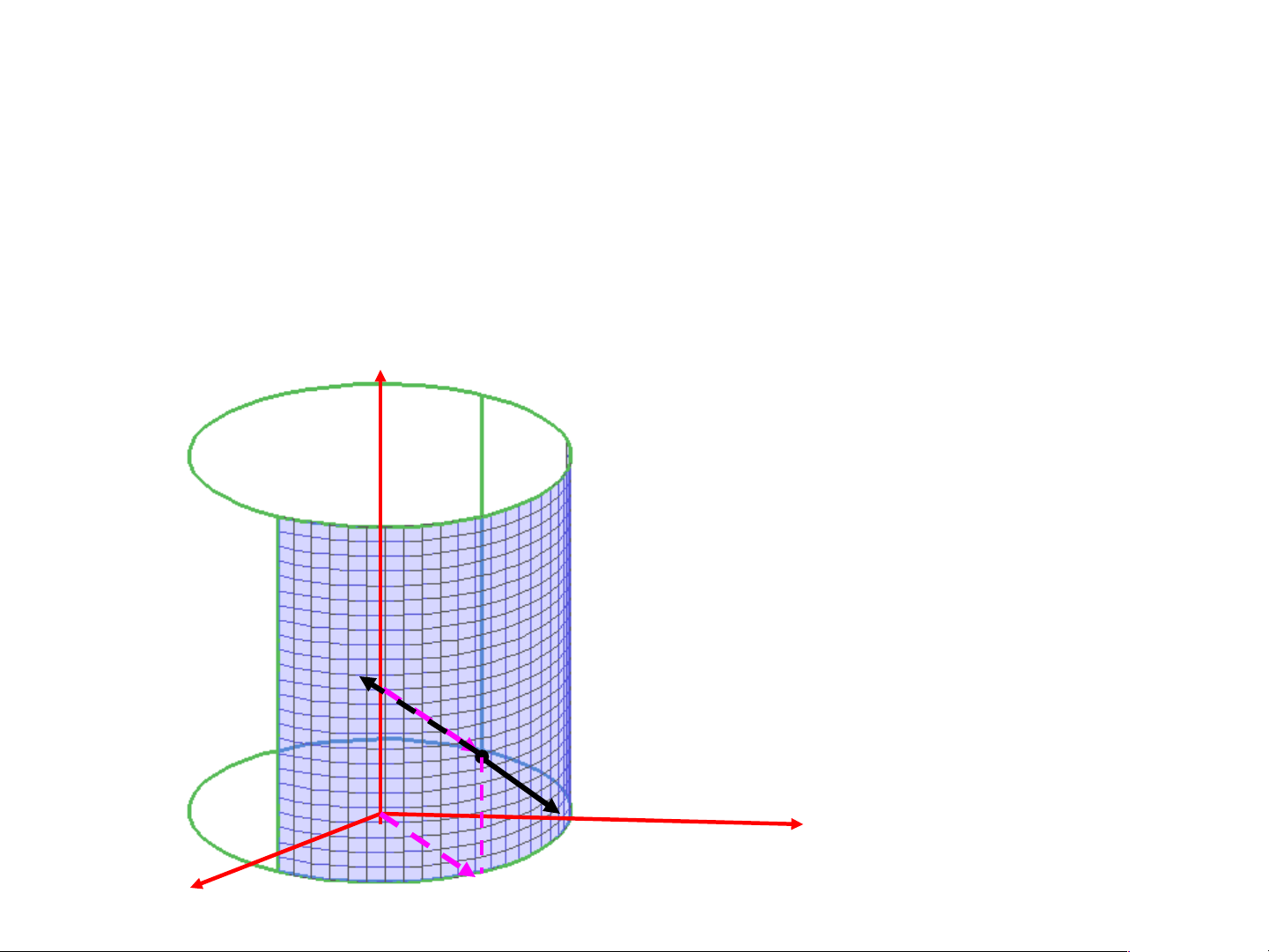
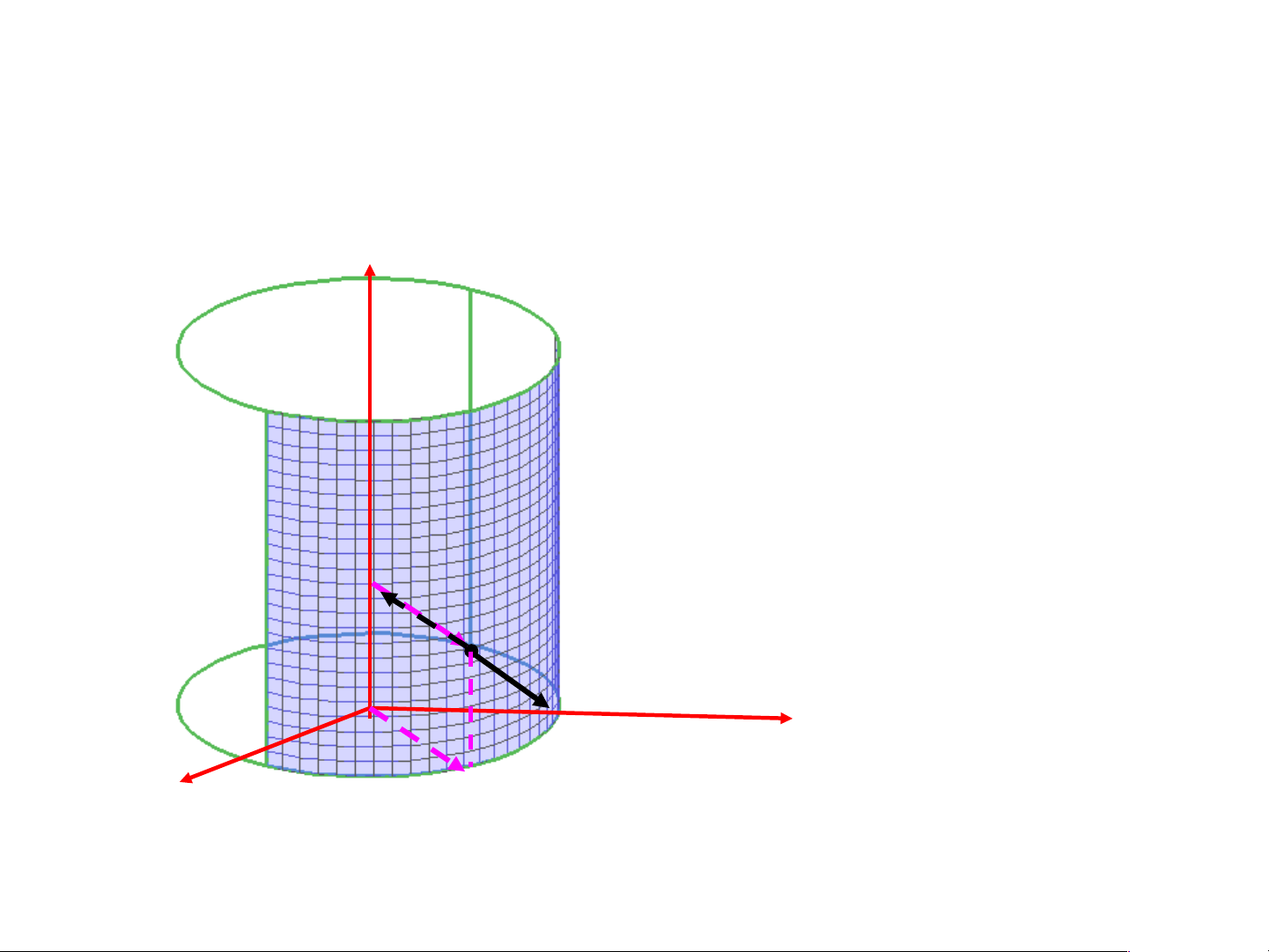
Một số ví dụ tìm pháp vector 2 2 2
a/ Mặt trụ S : x y R
M(x0,y0, 0 z ) S, n(M) 2x0,2y0,0 (và các vector tỷ lệ)
M n
OM ( x0, y0,0)
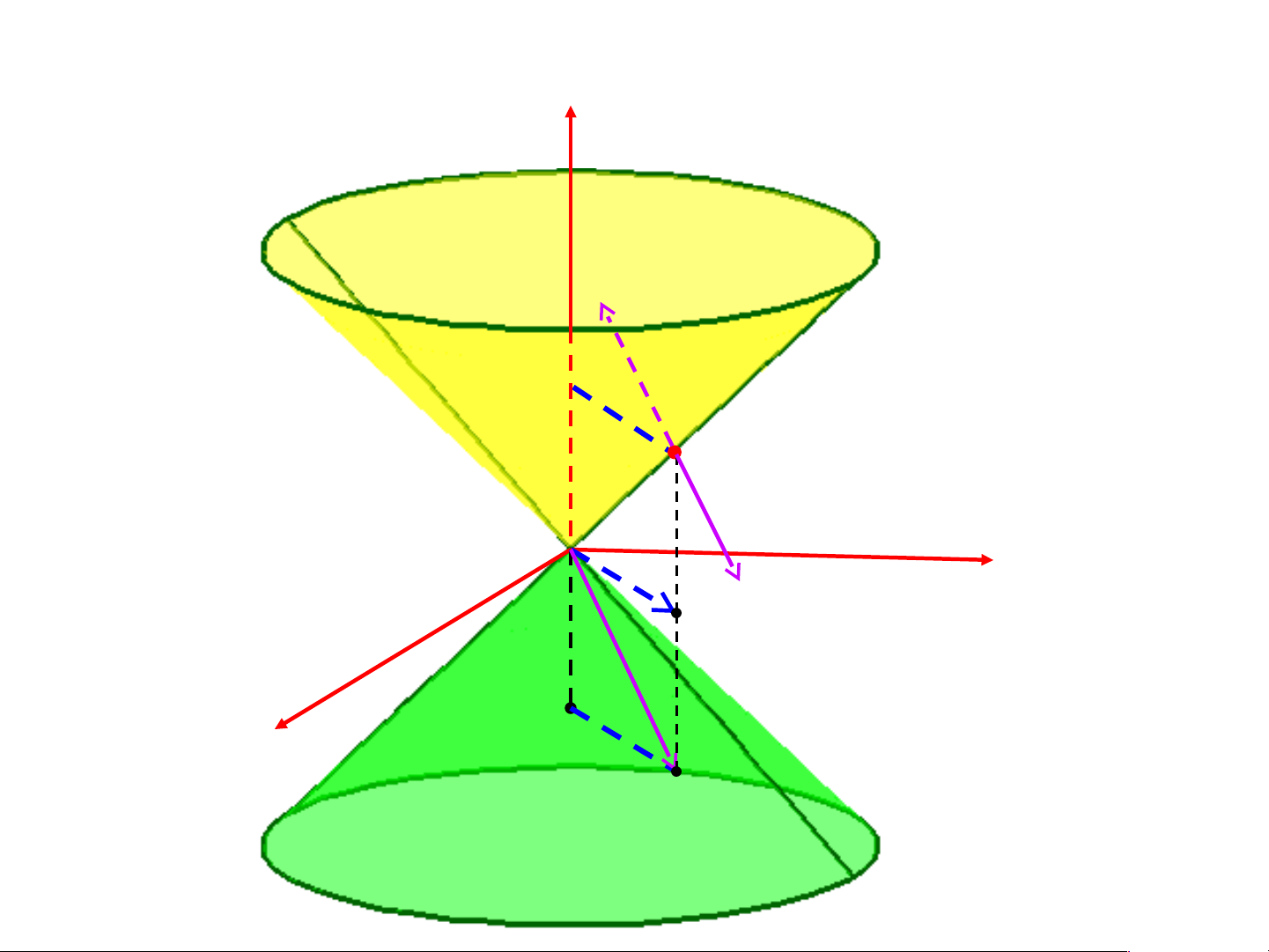
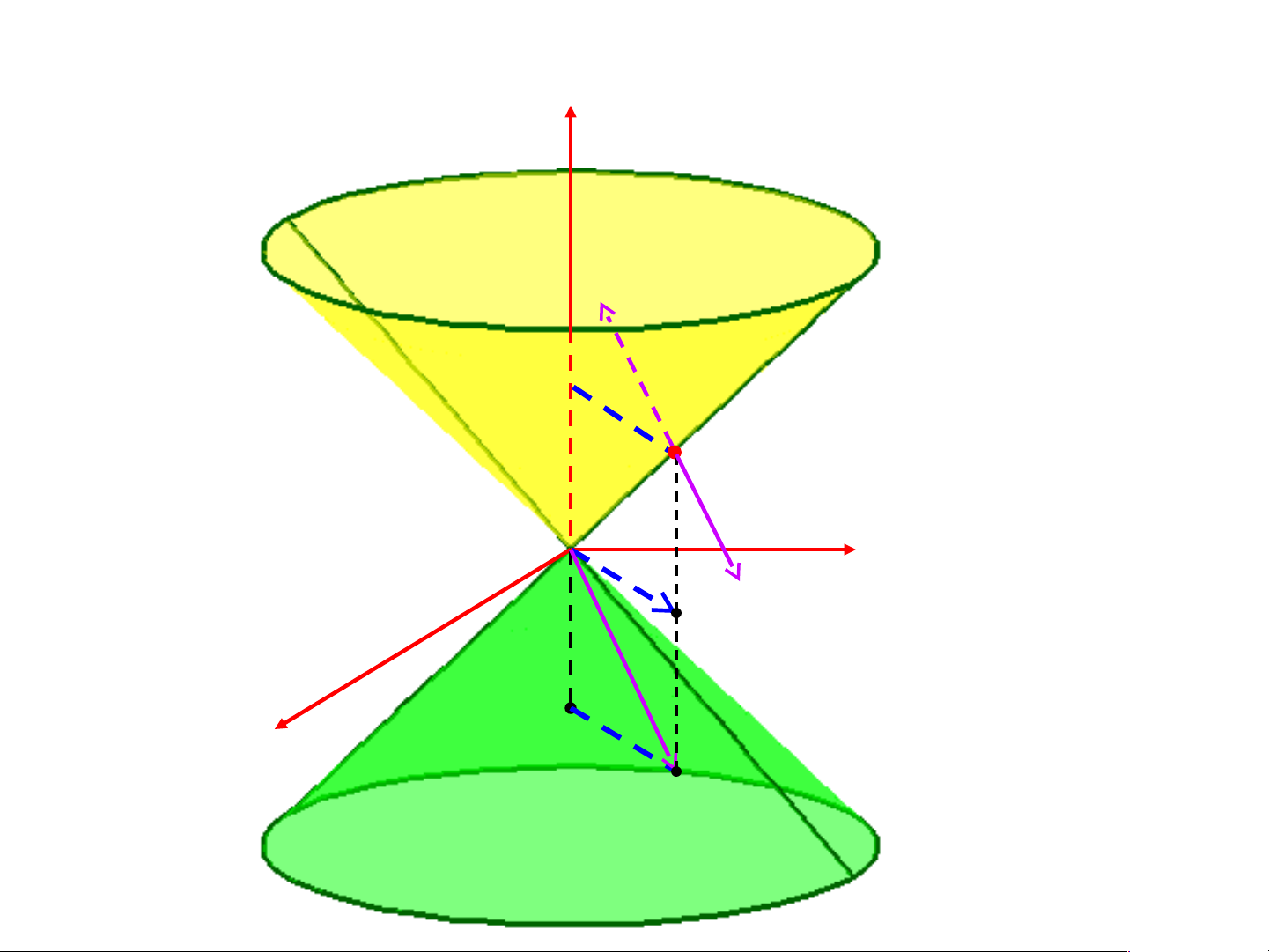
Một số ví dụ tìm pháp vector 2 2 2
a/ Mặt nón S : x y z 2 2
z x y
M(x0,y0, 0
z ) S, n(M)
2x0,2y0, 2 0 z
n(M) 0 z
M(x0,y0, 0 z ) M ( x0, y0,0) 0 z (x0,y0, 0 z ) MẶT ĐỊNH HƯỚNG
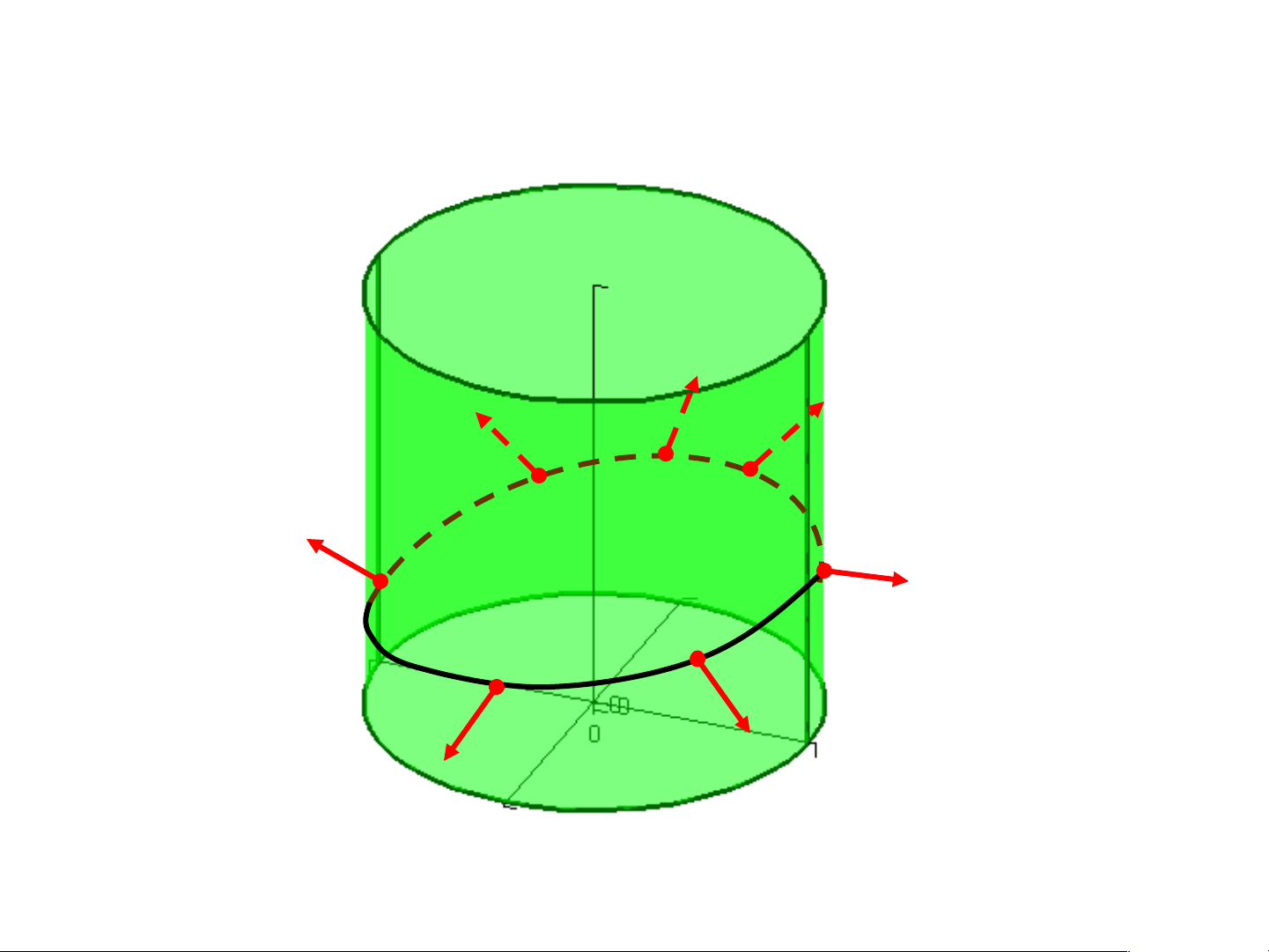
S được gọi là mặt định hướng (mặt 2 phía) nếu
cho pháp vector tại MS di chuyển dọc theo 1
đường cong kín không cắt biên, khi quay về điểm
xuất phát vẫn không đổi chiều.
Ngược lại, pháp vector đảo chiều, thì S được gọi
là mặt không định hướng (mặt 1 phía ).
Phía của S là phía mà đứng trên đó, pháp vector
hướng từ chân lên đầu.
(Chương trình chỉ xét mặt 2 phía) Mặt một phía Mặt hai phía
Ví dụ tìm PVT tương ứng với phía mặt cong 2 2 2 2
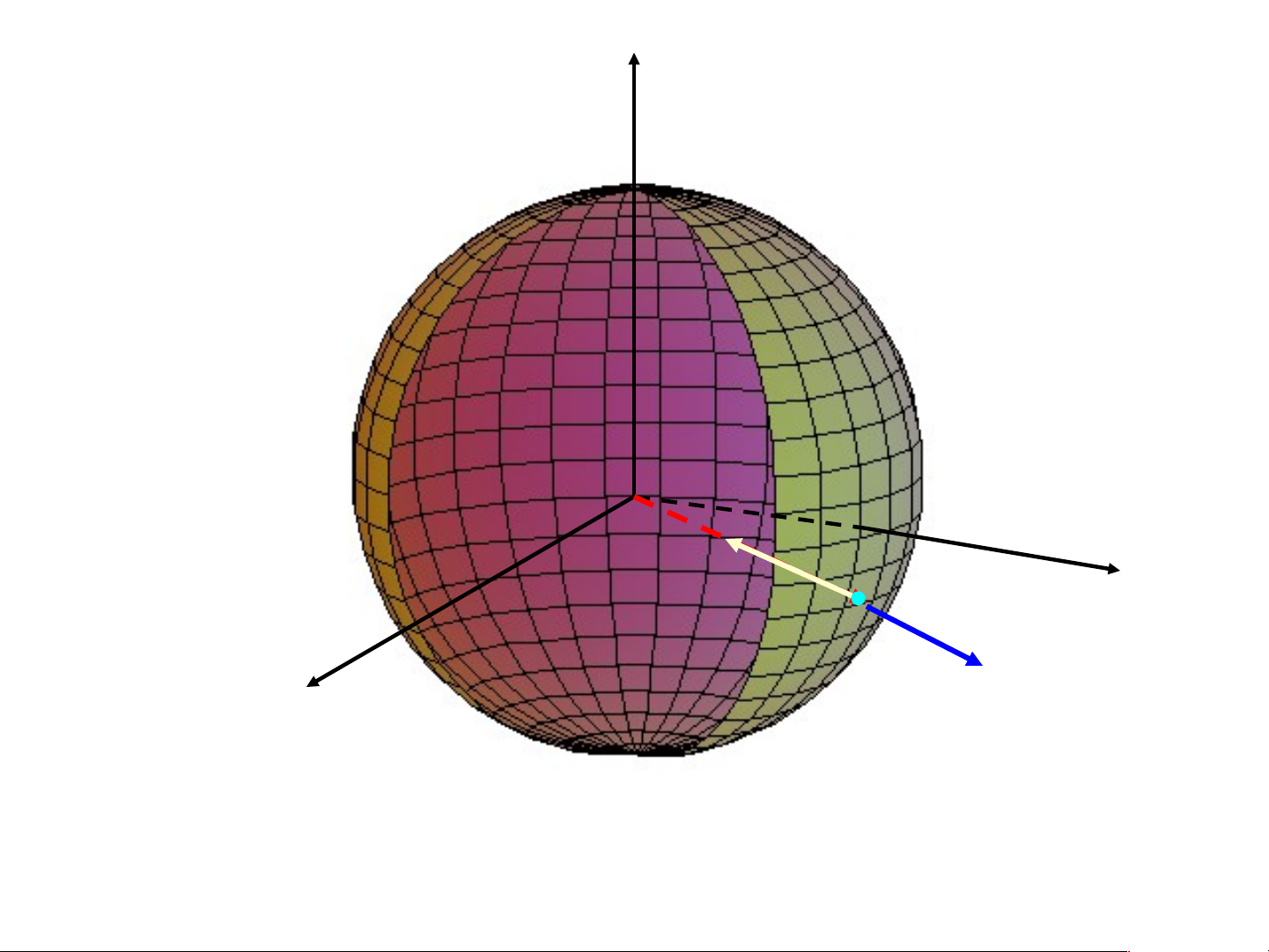
a/ Mặt cầu S : x y z R
M(x0,y0, 0 z ) S,
n ( x0,y0, 0 z )
pháp VT ngoài n
n (x0,y0, 0 z )
OM(x0,y0, 0 z ) pháp VT trong 2 2 2
b/ Mặt trụ S : x y R
M(x0,y0, 0 z ) S, n(M) 2x0,2y0,0 PVT trong
M n (
x0, y0,0) PVT ngoài c/ Mặt nón
M(x0,y0, 0 z ) S, PVT trong 0 z
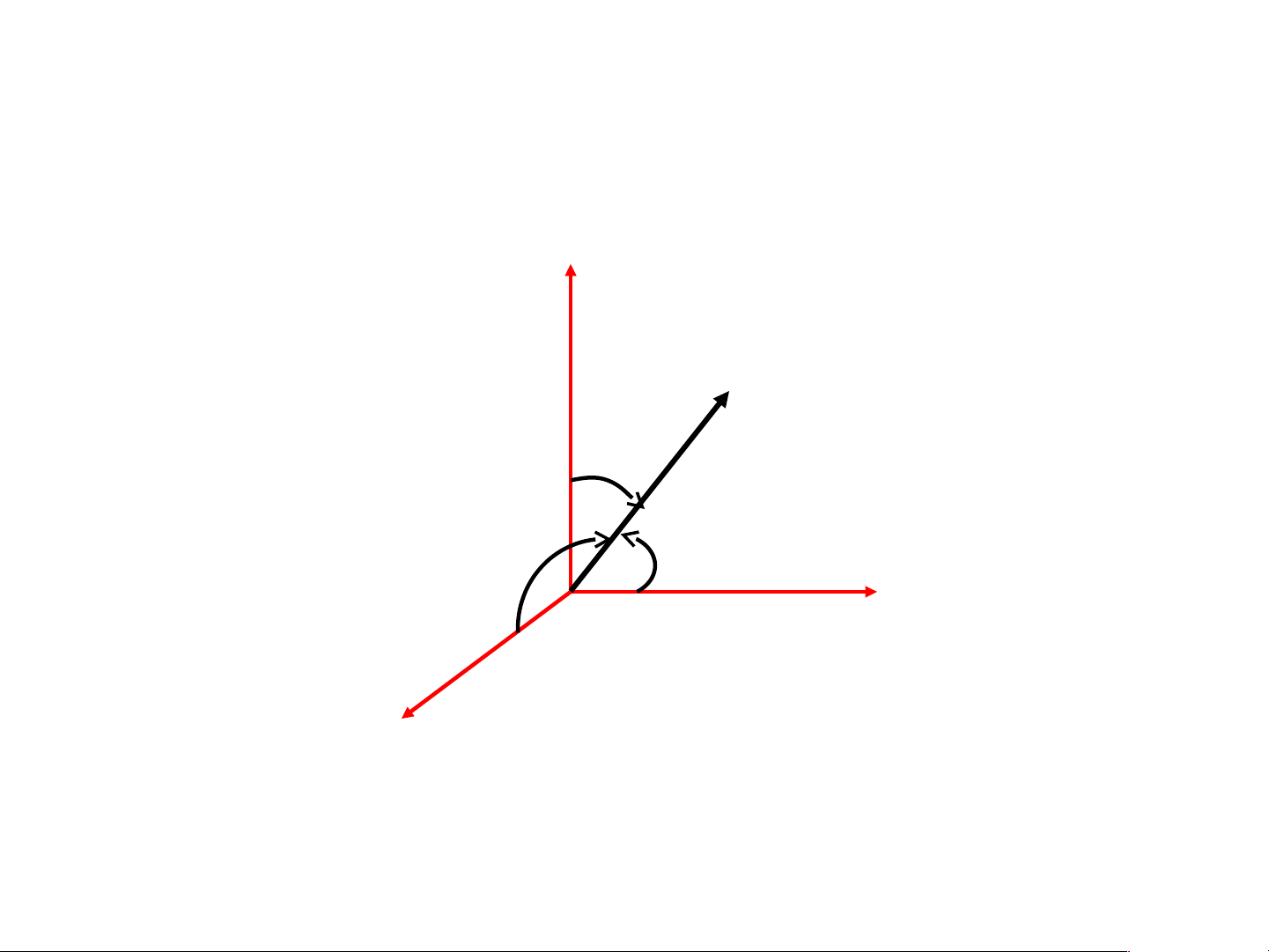
n ( x0,y0, 0 z ) PVT ngoài 0 z Pháp vector đơn vị z
n y x n ( cos ,cos ,cos)
ĐỊNH NGHĨA TÍCH PHÂN MẶT LOẠI 2
Cho các hàm P, Q, R liên tục trên mặt định
hướng S.Gọi pháp vector đơn vị của S là n ( cos ,cos ,cos)
Tích phân mặt loại 2 của P, Q, R trên S định nghĩa bởi
Pdydz Qdzdx Rdxdy (P,Q,R).nds S S
Pdydz Qdzdx Rdxdy S
(P cos Qcos R cos)ds S VÍ DỤ
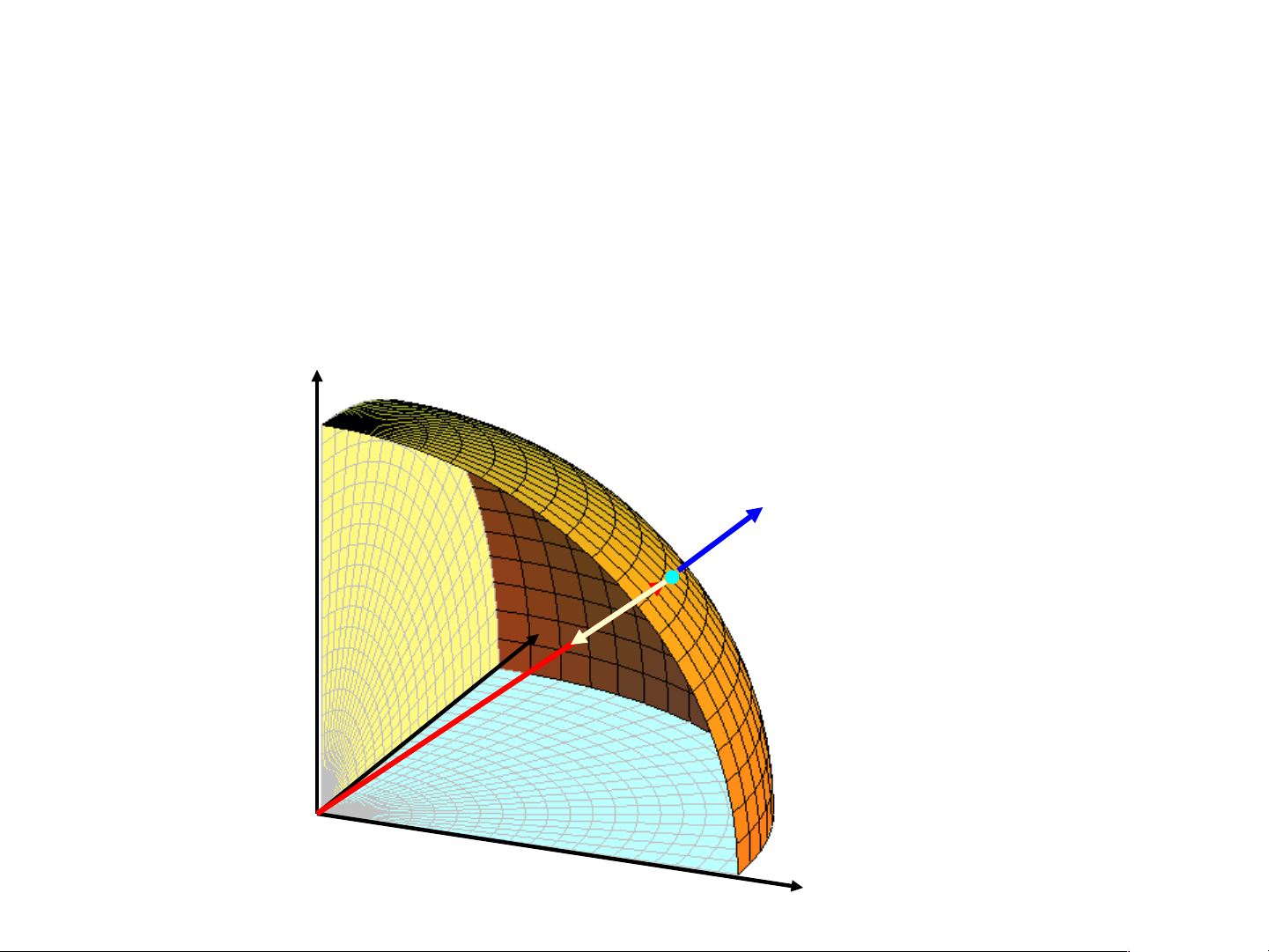
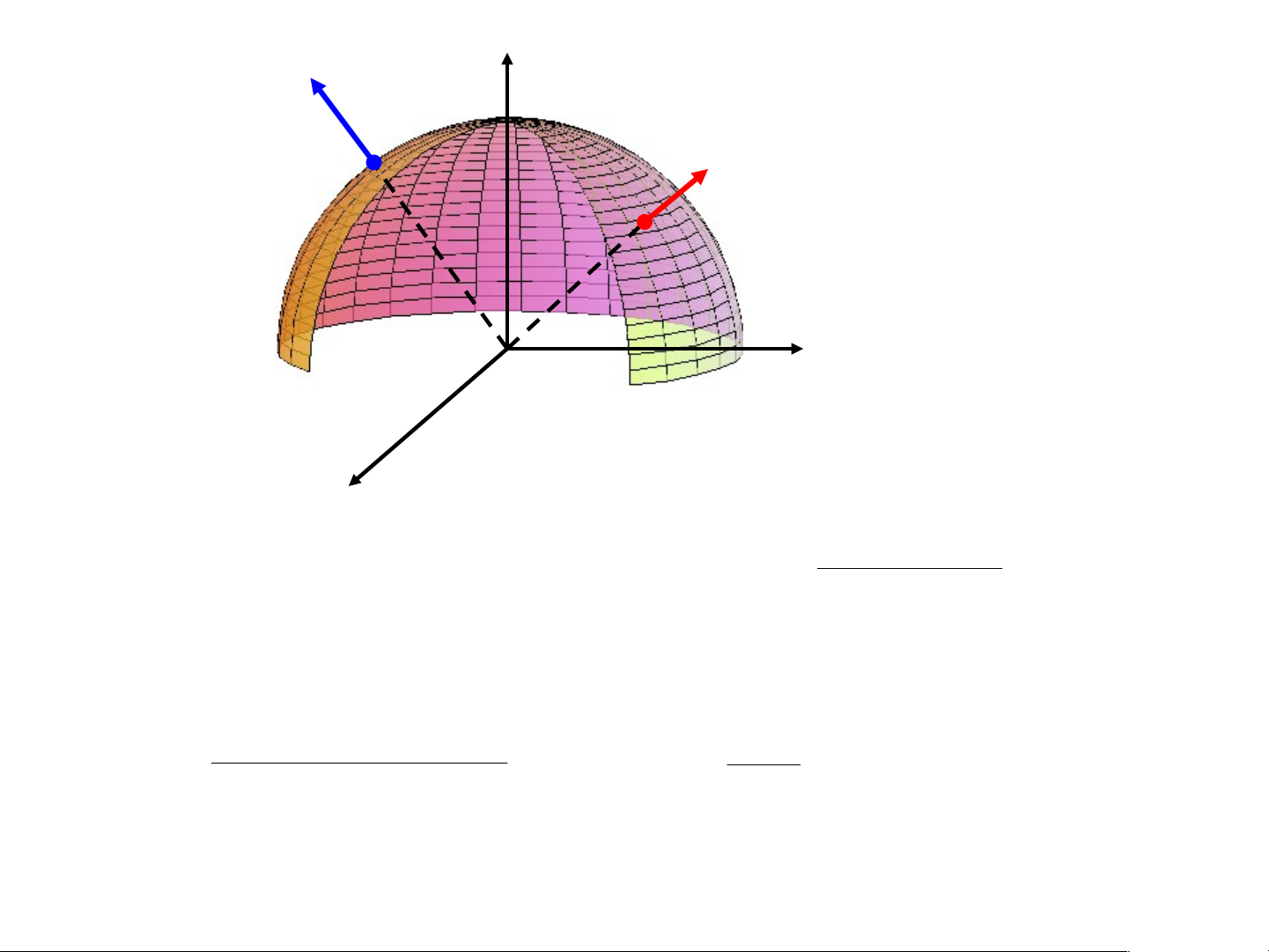
1/ Cho S là phía ngoài của nửa mặt cầu 2 2 2
z R x y , tính
I xdydz ydzdx zdxdy S
Tại M (x, y, z) trên S, pháp vector đơn vị là
(x, y,z) n R (x, y,z)
I (P,Q,R).nds (x,y,z). ds S S R 2 2 2
x y z 2 R ds ds R ds R R S S S 3 2 R




