-
Thông tin
-
Hỏi đáp
[GIÁO TRÌNH] XÁC SUẤT THỐNG KÊ | Trường đại học Hải Phòng
Xác suất thống kê là lĩnh vực có rất nhiều ứng dụng trong nghiên cứu, trong thực tiễn, vì vậy nó là học phần bắt buộc ở bậc cao đẳng, đại học và sau đại học cho các ngành kĩ thuật, kinh tế, công nghệ và cả ngành xã hội học. Hiện nay, có rất nhiều sách Xác suất thống kê đã được xuất bản - đó là tài liệu tự đọc, tự học và giảng dạy phong phú đối với sinh viên, giảng viên trường Đại học Hải Phòng. Tuy nhiên, do quy mô đào tạo, do trình độ toán học của sinh viên các ngành không đồng đều, nên chúng tôi biên soạn giáo trình "Xác suất thống kê" này nhằm cung cấp các kiến thức cơ bản nhất, cần thiết nhất đối với các ngành đào tạo không chuyên Toán (ngoài Đại học sư phạm Toán, Đại học Toán) trong trường Đại học Hải Phòng. Tài liệu giúp bạn tham khảo, ôn tập đạt kết quả cao. Mời đọc đón xem!
Kinh doanh - quản lý 22 tài liệu
Đại học Hải Phòng 164 tài liệu
[GIÁO TRÌNH] XÁC SUẤT THỐNG KÊ | Trường đại học Hải Phòng
Xác suất thống kê là lĩnh vực có rất nhiều ứng dụng trong nghiên cứu, trong thực tiễn, vì vậy nó là học phần bắt buộc ở bậc cao đẳng, đại học và sau đại học cho các ngành kĩ thuật, kinh tế, công nghệ và cả ngành xã hội học. Hiện nay, có rất nhiều sách Xác suất thống kê đã được xuất bản - đó là tài liệu tự đọc, tự học và giảng dạy phong phú đối với sinh viên, giảng viên trường Đại học Hải Phòng. Tuy nhiên, do quy mô đào tạo, do trình độ toán học của sinh viên các ngành không đồng đều, nên chúng tôi biên soạn giáo trình "Xác suất thống kê" này nhằm cung cấp các kiến thức cơ bản nhất, cần thiết nhất đối với các ngành đào tạo không chuyên Toán (ngoài Đại học sư phạm Toán, Đại học Toán) trong trường Đại học Hải Phòng. Tài liệu giúp bạn tham khảo, ôn tập đạt kết quả cao. Mời đọc đón xem!
Môn: Kinh doanh - quản lý 22 tài liệu
Trường: Đại học Hải Phòng 164 tài liệu
Thông tin:
Tác giả:
Preview text:
lOMoARcPSD|50202050
ỦY BAN NHÂN DÂN THÀNH PHỐ HẢI PHÒNG
TRƯỜNG ĐẠI HỌC HẢI PHÒNG
GIÁO TRÌNH CẤP TRƯỜNG NĂM HỌC 2017 - 2018 XÁCSUẤTTHỐNGKÊ Mã số : GT.TN.2018.01 Chủ biên:
TS. Nguyễn Thị Quyên Đơn vị : Khoa Toán
Hải Phòng, tháng 6 năm 2018 lOMoARcPSD|50202050 1 LỜI NÓI ĐẦU
Xác suất thống kê là lĩnh vực có rất nhiều ứng dụng trong nghiên cứu, trong thực tiễn,
vì vậy nó là học phần bắt buộc ở bậc cao đẳng, đại học và sau đại học cho các ngành kĩ
thuật, kinh tế, công nghệ và cả ngành xã hội học. Hiện nay, có rất nhiều sách Xác suất thống
kê đã được xuất bản - đó là tài liệu tự đọc, tự học và giảng dạy phong phú đối với sinh
viên, giảng viên trường Đại học Hải Phòng. Tuy nhiên, do quy mô đào tạo, do trình độ toán
học của sinh viên các ngành không đồng đều, nên chúng tôi biên soạn giáo trình "Xác suất
thống kê" này nhằm cung cấp các kiến thức cơ bản nhất, cần thiết nhất đối với các ngành
đào tạo không chuyên Toán (ngoài Đại học sư phạm Toán, Đại học Toán) trong trường Đại học Hải Phòng.
Giáo trình được viết theo quan điểm thực hành, chú trọng việc áp dụng xác suất thống
kê vào thực tiễn. Các khái niệm được trình bày dễ hiểu dưới dạng biểu thức, công thức và
được nêu rõ ý nghĩa, nhận xét cùng các ví dụ minh họa được trình bày cẩn thận, rõ ràng.
Sau mỗi chương đều có hệ thống bài tập kèm theo hướng dẫn, đáp số để sinh viên dễ
dàng luyện tập, kiểm tra thêm. Trong Chương 2, 4, 7 chúng tôi có đưa thêm phần Hướng
dẫn sử dụng máy tính bỏ túi để hỗ trợ đắc lực sinh viên trong việc tính toán, tránh nhầm
lẫn. Cuối giáo trình là Phụ lục các bảng giá trị tới hạn phục vụ việc tra cứu.
Giáo trình gồm 7 chương, phù hợp với thời lượng 3 tín chỉ, trong đó: Chương 1, 2 do
Ths. Trần Thị Hồng An biên soạn, Chương 3, 4, 5 do TS. Nguyễn Thị Quyên biên soạn và
Ths. Nguyễn Đức Trường biên soạn Chương 6, 7. Đối với thời lượng 2 tín chỉ, sinh viên có
thể bỏ qua Chương 3, và Chương 7. Chúng tôi lưu ý rằng, trong một số chương, kí hiệu *
trước mục, phần,...là phần dành cho sinh viên tự học.
Chúng tôi xin chân thành cảm ơn các thầy, cô trong tổ Giải tích và Toán ứng dụng, cũng
như các thầy cô, sinh viên Khoa Toán- trường Đại học Hải Phòng đã cho những đóng góp
quý báu về cấu trúc, văn phạm, thuật ngữ và đọc kĩ bản thảo, chỉnh sửa các lỗi chế bản.
Tuy nhiên, trong quá trình biên soạn, hoàn thiện, giáo trình không thể tránh khỏi những
thiếu sót. Chúng tôi mong nhận được các đóng góp ý kiến của đồng nghiệp, sinh viên để
giáo trình được hoàn thiện hơn nữa. Các tác giả MỤC LỤC Lời nói đầu 1 Chương 1
Biến cố ngẫu nhiên và xác suất 5 1.1
Quy tắc đếm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 1.1.1
Quy tắc cộng, quy tắc nhân . . . . . . . . . . . . . . . . . . . . . . 5 1.1.2
Hoán vị, chỉnh hợp, tổ hợp . . . . . . . . . . . . . . . . . . . . . . 6 1.2
Định nghĩa xác suất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 lOMoARcPSD|50202050 2 1.2.1
Phép thử và biến cố . . . . . . . . . . . . . . . . . . . . . . . . . . 7 1.2.2
Xác suất của biến cố . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.3 Các định lý xác suất
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.3.1 Mối quan hệ giữa các biến cố
. . . . . . . . . . . . . . . . . . . . 12 1.3.2
Công thức cộng xác suất . . . . . . . . . . . . . . . . . . . . . . . 13 1.3.3
Công thức nhân xác suất . . . . . . . . . . . . . . . . . . . . . . . 14 1.3.4 Công thức Bernoulli
. . . . . . . . . . . . . . . . . . . . . . . . . 17 1.3.5
Công thức xác suất đầy đủ và Bayes . . . . . . . . . . . . . . . . . 18
Bài tập Chương 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 Hướng dẫn, đáp số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 Chương 2
Biến ngẫu nhiên và quy luật phân bố xác suất 26 2.1
Định nghĩa và phân loại biến ngẫu nhiên . . . . . . . . . . . . . . . . . . . 26 2.1.1 Định nghĩa
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 2.1.2
Phân loại và ví dụ . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 2.2
Quy luật phân bố xác suất của biến ngẫu nhiên . . . . . . . . . . . . . . . . 27 2.2.1 Định nghĩa
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 2.2.2
Bảng phân bố xác suất . . . . . . . . . . . . . . . . . . . . . . . . 27
2.2.3 Hàm phân bố xác suất
. . . . . . . . . . . . . . . . . . . . . . . . 27 2.2.4
Hàm mật độ xác suất . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.3 Các tham số đặc trưng của biến ngẫu nhiên
. . . . . . . . . . . . . . . . . 30 2.3.1
Kỳ vọng toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 2.3.2 Phương sai
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 2.3.3
Độ lệch chuẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 2.3.4
Một số tham số khác . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.4 Một số quy luật phân bố xác suất thông dụng
. . . . . . . . . . . . . . . . 34
2.4.1 Quy luật phân bố nhị thức
. . . . . . . . . . . . . . . . . . . . . . 34
2.4.2 Quy luật phân bố Poisson
. . . . . . . . . . . . . . . . . . . . . . 36
2.4.3 Quy luật phân bố chuẩn
. . . . . . . . . . . . . . . . . . . . . . . 37 2.4.4
Một số quy luật phân bố xác suất khác . . . . . . . . . . . . . . . . 39 lOMoARcPSD|50202050 3
Bài tập Chương 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 Hướng dẫn, đáp số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 Chương 3
Biến ngẫu nhiên hai chiều 46 3.1
Khái niệm về biến ngẫu nhiên hai chiều và hàm phân bố . . . . . . . . . . . 46 3.1.1
Khái niệm và phân loại . . . . . . . . . . . . . . . . . . . . . . . . 46 3.1.2
Hàm phân bố của biến ngẫu nhiên hai chiều . . . . . . . . . . . . . 47 3.2
Biến ngẫu nhiên hai chiều rời rạc . . . . . . . . . . . . . . . . . . . . . . . 48 3.2.1
Bảng phân bố xác suất đồng thời
. . . . . . . . . . . . . . . . . . 48
3.2.2 Bảng phân bố xác suất biên
. . . . . . . . . . . . . . . . . . . . . 49
3.2.3 Bảng phân bố xác suất có điều kiện
. . . . . . . . . . . . . . . . . 50
3.3 Biến ngẫu nhiên hai chiều liên tục
. . . . . . . . . . . . . . . . . . . . . . 51 3.3.1
Hàm mật độ xác suất đồng thời . . . . . . . . . . . . . . . . . . . . 51
3.3.2 Hàm mật độ xác suất biên
. . . . . . . . . . . . . . . . . . . . . . 53 3.3.3
Hàm mật độ xác suất có điều kiện . . . . . . . . . . . . . . . . . . 53
3.4 Các tham số đặc trưng
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 3.4.1
Kỳ vọng, phương sai, kỳ vọng có điều kiện . . . . . . . . . . . . . 54
3.4.2 Hiệp phương sai và hệ số tương quan
. . . . . . . . . . . . . . . . 55
3.4.3 Phân bố chuẩn hai chiều
. . . . . . . . . . . . . . . . . . . . . . . 57 3.5
Các định lý giới hạn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 3.5.1
Bất đẳng thức Chebyshev . . . . . . . . . . . . . . . . . . . . . . . 58 3.5.2
Định lý Chebyshev . . . . . . . . . . . . . . . . . . . . . . . . . . 58 3.5.3 Định lý Bernoulli
. . . . . . . . . . . . . . . . . . . . . . . . . . 59
Bài tập Chương 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 Hướng dẫn, đáp số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
Chương 4 Cơ sở lý thuyết mẫu 64 4.1
Một số khái niệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
4.1.1 Tổng thể nghiên cứu
. . . . . . . . . . . . . . . . . . . . . . . . . 64 4.1.2
Mẫu ngẫu nhiên và các phương pháp chọn mẫu . . . . . . . . . . . 65 4.2 Thống kê
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70 4.2.1 Định nghĩa
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70 lOMoARcPSD|50202050 4
4.2.2 Một số thống kê đặc trưng của mẫu
. . . . . . . . . . . . . . . . . 70
Bài tập Chương 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75 Hướng dẫn, đáp số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
Chương 5 Ước lượng các tham số của biến ngẫu nhiên 77 5.1
Phương pháp ước lượng điểm . . . . . . . . . . . . . . . . . . . . . . . . . 77 5.1.1
Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77 5.1.2
Các tiêu chuẩn lựa chọn hàm ước lượng . . . . . . . . . . . . . . . 77
5.2 Phương pháp ước lượng khoảng
. . . . . . . . . . . . . . . . . . . . . . . 80 5.2.1
Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80 5.2.2
Phương pháp xây dựng khoảng tin cậy . . . . . . . . . . . . . . . . 80
5.2.3 Ước lượng cho kỳ vọng của phân bố chuẩn . . . . . . . . . . . . . 81 5.2.4
*Ước lượng phương sai của biến ngẫu nhiên phân bố chuẩn . . . . . 86
5.2.5 Ước lượng xác suất tổng thể
. . . . . . . . . . . . . . . . . . . . . 87
Bài tập Chương 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89 Hướng dẫn, đáp số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91 Chương 6
Kiểm định giả thuyết thống kê 94 6.1 Khái niệm chung
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94 6.1.1 Các khái niệm
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 94 6.1.2
Các bước tiến hành . . . . . . . . . . . . . . . . . . . . . . . . . . 95 6.2 Kiểm định tham số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
6.2.1 Kiểm định giả thuyết về kỳ vọng của phân phối chuẩn . . . . . . . 95
6.2.2 *Kiểm định giả thuyết về phương sai của phân phối chuẩn . . . . . 97
6.2.3 Kiểm định giả thuyết về tỷ lệ
. . . . . . . . . . . . . . . . . . . . 98 6.2.4
*So sánh hai kỳ vọng . . . . . . . . . . . . . . . . . . . . . . . . . 99
6.2.5 *So sánh hai tỷ lệ . . . . . . . . . . . . . . . . . . . . . . . . . . . 102 Bài tập Chương 6 . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103 Hướng dẫn, đáp số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106 Chương 7
Phân tích tương quan và hồi quy 109
7.1 Phân tích tương quan tuyến tính
. . . . . . . . . . . . . . . . . . . . . . . 109
7.1.1 Hệ số tương quan và hệ số tương quan mẫu . . . . . . . . . . . . . 109 7.1.2
Kiểm định về sự tương quan của hai biến ngẫu nhiên . . . . . . . . 111 lOMoARcPSD|50202050 5 7.2
Phân tích hồi quy tuyến tính đơn . . . . . . . . . . . . . . . . . . . . . . . 111 7.2.1
Hàm hồi quy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111 7.2.2
Bài toán kiểm định . . . . . . . . . . . . . . . . . . . . . . . . . . 113
7.2.3 Bài toán ước lượng và dự báo
. . . . . . . . . . . . . . . . . . . . 114 Bài tập
Chương 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117 Hướng dẫn, đáp số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
Tài liệu tham khảo 121 CHƯƠNG1
BIẾN CỐ NGẪU NHIÊN VÀ XÁC SUẤT 1.1 Quy tắc đếm 1.1.1
Quy tắc cộng, quy tắc nhân a. Quy tắc cộng
Giả sử một công việc A có thể được thực hiện theo một trong k phương án: A1,A2,...,Ak, trong đó: -
Phương án A1 có n1 cách thực hiện. -
Phương án A2 có n2 cách thực hiện không trùng với bất kì cách thực hiện
nào của phương án A1. ... -
Phương án Ak có nk(k > 2) cách thực hiện không trùng với bất kì cách
thực hiện nào của các phương án trước đó.
Khi đó, công việc A có thể được thực hiện theo (n1 +n2 +···+nk) cách.
Ví dụ 1.1. Trong một hộp có sáu quả cầu trắng được đánh số từ 1 đến 6 và ba quả cầu đen
được đánh số 7, 8, 9. Hỏi có bao nhiêu cách chọn một quả cầu?
Giải. Vì các quả cầu trắng hoặc đen được đánh số phân biệt nên mỗi lần lấy ra một quả
bất kỳ là một lần chọn.
+) Nếu chọn quả trắng có 6 cách.
+) Nếu chọn quả đen có 3 cách.
Vậy số cách chọn một quả cầu là: 6 + 3 = 9(cách). b. Quy tắc nhân lOMoARcPSD|50202050 6
Giả sử một công việc A được hoàn thành bởi k bước liên tiếp. -
Bước 1 có n1 cách thực hiện. -
Bước 2 có n2 cách thực hiện. ... - Bước i (i = 3
,k) có ni cách thực hiện.
Khi đó số cách để hoàn thành công việc A đó là: (n1.n2 ...nk) cách.
Ví dụ 1.2. Từ các chữ số 1,2,3,4,5 có thể lập được bao nhiêu số gồm 4 chữ số đôi một khác nhau.
Giải. Gọi số phải tìm là abcd, (a =6 0,a =6 b =6 c =6 d).
Ta có: a có 5 cách chọn,
b có 4 cách chọn (vì chỉ còn 4 số sau khi đã chọn a), c có
3 cách chọn (vì chỉ còn 3 số sau khi đã chọn a, b), d có 2
cách chọn (vì chỉ còn 2 số sau khi đã chọn a, b, c).
Vậy có: 5.4.3.2 = 120 cách lập số thỏa mãn đề bài. 1.1.2
Hoán vị, chỉnh hợp, tổ hợp a. Hoán vị
Cho tập A gồm n phần tử khác nhau (n ≥ 1). Kết quả của việc sắp xếp n phần tử đó
theo một thứ tự nhất định được gọi là một hoán vị các phần tử của A (gọi tắt là hoán vị
của A). Kí hiệu Pn là số các hoán vị của tập A gồm n phần tử khác nhau thì
Pn = n! = n(n−1)...2.1.
Ví dụ 1.3. Cho tập A = {1,2,3,4,5}. Hỏi có bao nhiêu số có 5 chữ số đôi một khác nhau được
tạo nên từ tập A?
Giải. Số cách tạo nên số có 5 chữ số đôi một khác nhau từ A là số các hoán vị của các
phần tử của A: P5 = 5! = 120. b. Chỉnh hợp
Cho tập hợp A gồm n phần tử khác nhau (n ≥ 1). Kết quả của việc lấy k phần tử (0 ≤ k
≤ n) khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được lOMoARcPSD|50202050 7
gọi là một chỉnh hợp chập k của n phần tử đã cho. Kí hiệu: Akn là số các chỉnh hợp chập k
của n phần tử của A thì k n! An = . (n−k)!
Ví dụ 1.4. Cho tập A = {1,2,3,4,5}. Hỏi có bao nhiêu số có bốn chữ số đôi một khác nhau
được tạo nên từ tập A?
Giải. Từ tập A chọn ra bốn chữ số và sắp xếp chúng theo một thứ tự nhất định ta được
một số có bốn chữ số thỏa mãn đề bài. Vì vậy, số các số tạo thành thỏa mãn là số các chỉnh
hợp chập 4 của 5 hay: A . c. Tổ hợp
Cho tập hợp A gồm n phần tử khác nhau (n≥1). Mỗi tập con gồm k phần tử (0≤k ≤n)
của A được gọi là một tổ hợp chập k của n phần tử của A. Kí hiệu: C k
n là số các tổ hợp chập k của n phần tử của A thì k n! Cn =
. k!(n−k)!
Ví dụ 1.5. Cho tập A = {1,2,3,4,5}. Hỏi có bao nhiêu tập con có bốn chữ số được tạo nên từ tập A?
Giải. Vì các phần tử của tập con không phân biệt thứ tự nên số các tập con có 4 chữ
số được tạo ra từ tập A là: C
. 1.2 Định nghĩa xác suất
1.2.1 Phép thử và biến cố a. Định nghĩa
Việc thực hiện một nhóm các điều kiện cơ bản để quan sát một hiện tượng nào đó có
thể xảy ra hay không được gọi là phép thử. Hiện tượng có thể xảy ra trong kết quả của
phép thử được gọi là biến cố.
Ví dụ 1.6. Tung một con xúc xắc xuống đất, thấy mặt ngửa lên có 3 chấm. Khi đó, phép thử
là "tung một con xúc xắc xuống đất" và biến cố là "mặt ngửa lên có 3 chấm". lOMoARcPSD|50202050 8
b. Các loại biến cố
Biến cố sơ cấp: Là biến cố không có trường hợp riêng, nó là kết quả đơn giản nhất của phép thử, kí hiệu: ω.
Không gian mẫu: Là tập hợp tất cả các biến cố sơ cấp của phép thử, kí hiệu: Ω.
Biến cố chắc chắn: Là biến cố chắc chắn xảy ra khi thực hiện phép thử, kí hiệu: Ω.
Biến cố không thể : Là biến cố không bao giờ xảy ra khi thực hiện phép thử, kí hiệu: 0/.
Biến cố ngẫu nhiên: Là biến cố có thể xảy ra hoặc không xảy ra khi thực hiện một phép thử, kí hiệu: A,B,C...
Tập hợp tất cả các kết quả làm cho biến cố A xảy ra được gọi là tập các kết quả thuận lợi
cho A, kí hiệu: ΩA.
Ví dụ 1.7. Tung một con xúc xắc, khi đó:
Biến cố " Xuất hiện mặt có số chấm nhỏ hơn hoặc bằng 6" là biến cố chắc chắn Ω.
Biến cố " Xuất hiện mặt có số chấm lớn hơn 6" là biến cố không thể có 0/.
Biến cố " Xuất hiện mặt có số chấm chẵn" là biến cố ngẫu nhiên. Biến cố này gồm 3 biến
cố sơ cấp thuận lợi cho nó nên ΩA có 3 phần tử.
1.2.2 Xác suất của biến cố
Như vậy, việc biến cố ngẫu nhiên xảy ra hay không trong phép thử là kết quả không thể
đoán trước được. Tuy nhiên, bằng trực quan ta có thể thấy rằng các biến cố khác nhau có
thể có khả năng xảy ra khác nhau, hay khi lặp đi lặp lại phép thử thì mật độ xuất hiện của
một số biến cố là khác nhau. Để định lượng khả năng xuất hiện của biến cố nào đó, ta sẽ
nghiên cứu các khái niệm về xác suất. Trước hết, người ta đưa ra khái niệm "xác suất của
biến cố": Xác suất của một biến cố là một con số đặc trưng khả năng xuất hiện khách quan
của biến cố đó khi thực hiện phép thử. Để tính toán được xác suất của biến cố, người ta có
các định nghĩa sau đây.
a. Định nghĩa cổ điển của xác suất Giả sử với phép thử nào đó có hữu hạn kết cục và các
kết cục là đồng khả năng thì xác suất xuất hiện biến cố A, kí hiệu: P(A), là tỷ số giữa số kết
cục thuận lợi cho A và tổng số kết cục đồng khả năng đó, tức là: P .
Nhận xét. Như vậy, định nghĩa cổ điển của xác suất được sử dụng khi số kết cục là hữu
hạn, đồng khả năng.
Từ định nghĩa cổ điển, ta dễ dàng suy ra được các tính chất sau của xác suất. Tính chất. lOMoARcPSD|50202050 9
i) 0 ≤ P(A) ≤ 1, với mọi biến cố A bất kì.
ii) P(Ω) = 1, P(0/) = 0.
Ví dụ 1.8. Tung một đồng tiền xu cân đối và đồng chất 2 lần. Tính xác suất của các biến cố sau:
a) Mặt sấp xuất hiện 2 lần.
b) Mặt sấp xuất hiện đúng 1 lần.
c) Mặt sấp xuất hiện ít nhất 1 lần.
Giải. Ta có Ω = {SS,NN,SN,NS} suy ra |Ω| = 4.
a) Gọi A là biến cố mặt sấp xuất hiện 2 lần, ta có ΩA = {SS} suy ra |ΩA| = 1 nên P .
b) Gọi B là biến cố mặt sấp xuất hiện đúng 1 lần, ta có ΩB = {SN,NS} suy ra |ΩB| = 2, nên P .
c) GọiC là biến cố mặt sấp xuất hiện ít nhất 1 lần, ta có ΩC ={SN,NS,SS} suy ra |ΩC|=3, nên P .
Ví dụ 1.9. Trong một hộp có 7 chính phẩm và 3 phế phẩm. Lấy ngẫu nhiên ra 3 sản phẩm.
Tính xác suất của các biến cố sau:
a) Cả 3 sản phẩm lấy ra đều là chính phẩm.
b) Trong 3 sản phẩm lấy ra có đúng 1 chính phẩm.
Giải. Số cách lấy ra 3 sản phẩm từ 10 sản phẩm là .
a) Gọi A là biến cố cả 3 sản phẩm lấy ra đều là chính phẩm thì nên: C73 7
P(A) = 3 = C10 24
b) Gọi B là biến cố trong 3 sản phẩm lấy ra có đúng 1 chính phẩm thì nên: P . C
*b. Định nghĩa hình học của xác suất lOMoARcPSD|50202050 10
Tiếp tục, ta xét trường hợp kết quả của phép thử là vô hạn, không đếm được. Cụ thể,
giả sử mỗi biến cố sơ cấp được biểu diễn bởi một điểm trong một miền H nào đó, biến cố
A được biểu diễn bởi miền A là một phần nằm trong miền H . Khi đó, xác suất của A được định nghĩa: m(A ) P(A) = , m(H )
với m(A ),m(H ) là độ đo của miền A ,H (độ đo thông thường là độ dài, diện tích, thể tích,..).
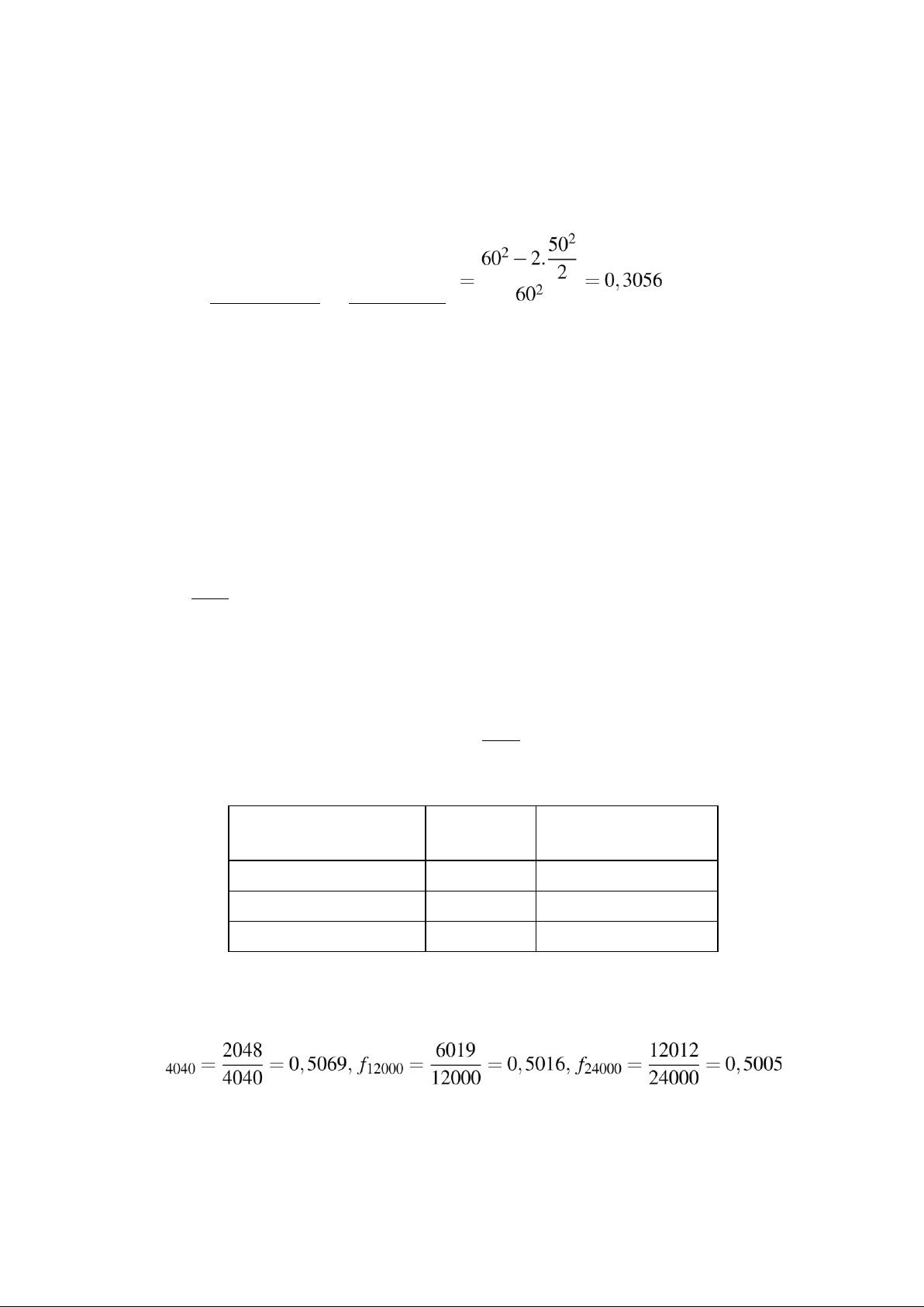
Ví dụ 1.10. Hai người bạn hẹn gặp nhau tại một địa điểm trong khoảng thời gian từ 18 giờ
đến 19 giờ để cùng đi xem phim. Hai người đến chỗ hẹn độc lập với nhau và quy ước rằng
người đến trước sẽ chỉ đợi người đến sau 10 phút, nếu không gặp thì sẽ đi trước. Tính xác
suất để hai người gặp nhau. Giải. Gọi A là biến cố hai người gặp nhau. Coi gốc thời gian là lúc 18 giờ.
Gọi x, y là thời điểm (phút) người thứ nhất, thứ hai đến điểm hẹn. Khi đó
0 ≤ x ≤ 60, 0 ≤ y ≤ 60.
Như vậy thời điểm đến chỗ hẹn của hai người được biểu diễn bởi
Hình 1.1: Biểu diễn các biến cố Ω, ΩA.
Ω = {(x,y) : 0 ≤ x ≤ 60;0 ≤ y ≤ 60}.
Thời điểm để hai người gặp nhau được biểu diễn
ΩA = {(x,y) ∈ Ω : |x−y| ≤ 10} lOMoARcPSD|50202050 11 hay
ΩA = {(x,y) ∈ Ω : x−10 ≤ y ≤ x+10}.
Biểu diễn trên hệ trục tọa độ Oxy (xem Hình 1.1) thì Ω được biểu diễn bởi hình vuông
OBDF và ΩA được biểu diễn bởi lục giác OACDEG, nên theo định nghĩa hình học của xác suất: S(OBDEFH) P(A) = . S(OEFG)
c. Định nghĩa thống kê của xác suất
Nhận thấy, nếu các kết quả có thể của phép thử là vô hạn hoặc hữu hạn nhưng không
đồng khả năng thì cách tính theo xác suất cổ điển, xác suất hình học như trên không còn
đúng nữa. Tính xác suất theo thống kê là một giải pháp trong trường hợp này.
Giả sử một phép thử ngẫu nhiên được thực hiện lặp lại n lần trong những điều kiện
giống hệt nhau. Nếu trong n lần thực hiện phép thử, biến cố A xuất hiện n(A) lần thì tỷ số n(A) fn(A) =
được gọi là tần suất xuất hiện của biến cố A trong n lần thử. n
Người ta nhận thấy rằng, khi n tăng ra vô hạn thì tần suất trên dao động quanh một
giá trị xác định - giá trị đó được định nghĩa là xác suất của biến cố A, tức là n(A) P(A) = lim . n→∞ n
Ví dụ 1.11. Để nghiên cứu khả năng xuất hiện mặt sấp khi tung một đồng tiền xu, Pearson
và Buffon tiến hành tung một đồng tiền xu nhiều lần thu được bảng sau đây: Người làm thí
Số lần tung Số lần được mặt nghiệm sấp Buffon 4040 2048 Pearson 12000 6019 Pearson 24000 12012
Hãy tính các tần suất mẫu và cho nhận xét.
Giải. Tần suất xuất hiện mặt sấp của đồng tiền xu cho các trường hợp trên lần lượt là: f .
Nhận thấy, khi số lần tung tăng lên thì tần suất xuất hiện mặt sấp gần về giá trị 0,5.
d. *Phương pháp tiên đề để định nghĩa xác suất lOMoARcPSD|50202050 12
Các định nghĩa cổ điển, hình học, thống kê của xác suất có nhiều hạn chế để xây dựng
một lí thuyết tổng quát. Định nghĩa cổ điển không dùng được trong trường hợp các kết
quả là vô hạn, định nghĩa hình học không dùng được khi các kết quả không đồng khả năng,
định nghĩa bằng thống kê chỉ đưa ra một giá trị xấp xỉ để đánh giá xác suất và đòi hỏi số
quan sát phải rất lớn. Để khắc phục nhược điểm này, nhà toán học người Nga - Komogorov
- đã xây dựng hệ tiên đề làm cơ sở cho việc định nghĩa một cách hoàn chỉnh khái niệm xác
suất về mặt lí thuyết. Cách xác định xác suất theo tiên đề sẽ chứa trong nó các định nghĩa
cổ điển, hình học hay thống kê của xác suất như là các trường hợp riêng.
Định nghĩa 1.1. Giả sử Ω 6= 0/ bất kì, và F là họ các tập con nào đó của Ω. Khi đó F được
gọi là một đại số nếu nó thỏa mãn:
i) Ω ∈ F. ii) A ∈ F thì Ac = Ω\A
∈ F. iii) ∀A, B ∈ F thì A∪B ∈ F.
Như vậy, F đóng kín với phép toán hợp, giao hữu hạn được.
Định nghĩa 1.2. Giả sử F là một đại số các tập con của Ω. Xác suất trên F là hàm tập P : F →
[0,1] thỏa mãn ba tiên đề sau:
TĐ1) P(A) ≥ 0, ∀A ∈ F. TĐ2) P(Ω) = 1.
TĐ3) Với các tập Ai ∈ F, i = 1,2,..., đôi một không giao nhau: Ai.Aj = 0/, ∀i =6 j mà F, thì: P . i=1 i=1 Khi đó, người ta gọi:
Ω là không gian mẫu, mỗi phần tử ω ∈ Ω là một biến cố sơ cấp.
Mỗi tập con A ∈ F là một biến cố ngẫu nhiên (biến cố.
P(A) là xác suất của biến cố A.
*e. Nguyên lý xác suất lớn và xác suất nhỏ
Trong nhiều bài toán thực tế ta thường gặp các biến cố có xác suất nhỏ, tức là gần bằng
0. Tuy nhiên qua nhiều lần quan sát, người ta thấy rằng các biến cố có xác suất nhỏ gần
như sẽ không xảy ra khi tiến hành một phép thử. Trên cơ sở đó có thể đưa ra"Nguyên lý lOMoARcPSD|50202050 13
thực tế không thể có của các biến cố có xác suất nhỏ" sau đây: Nếu một biến cố có xác suất
nhỏ thì thực tế có thể cho rằng trong một phép thử biến cố đó sẽ không xảy ra.
Hiển nhiên là việc quy định một mức xác suất được coi là rất nhỏ tùy thuộc vào từng
bài toán cụ thể. Chẳng hạn, xác suất để một chuyến bay chở khách bị nạn là 0,01 thì không
thể coi là nhỏ. Trái lại, xác suất để máy bay đến trễ quá 15 phút là 0,05 thì hoàn toàn có
thể coi là nhỏ, có thể xem như máy bay đến đúng giờ!
Tương tự, ta có thể đưa ra "Nguyên lý thực tế chắc chắn xảy ra của các biến cố có xác
suất lớn" như sau: Nếu biến cố ngẫu nhiên có xác suất gần bằng 1 thì thực tế có thể cho
rằng biến cố đó sẽ xảy ra trong một phép thử. Việc quy định một mức xác suất coi là lớn
tùy thuộc vào từng bài toán cụ thể. 1.3 Các định lý xác suất
1.3.1 Mối quan hệ giữa các biến cố
Về mặt tập hợp, mỗi biến cố là một tập con của không gian mẫu, nên giữa các biến cố
cũng có các phép toán như của tập hợp (hợp, giao, phần bù). Tuy nhiên, các phép toán này
được gọi theo thuật ngữ riêng của lí thuyết xác suất.
a. Tổng của các biến cố
Tổng của hai biến cố A và B, kí hiệu: A+B, là biến cố xảy ra khi có ít nhất một trong hai
biến cố A hoặc B xảy ra.
Tổng quát ta được: Tổng của n biến cố A1, A2, . ., An, kí hiệu: n
A1 +A2 +...+An = ∑Ai, i=1
là biến cố xảy ra khi và chỉ khi có ít nhất một trong n biến cố nói trên xảy ra.
b. Tích của các biến cố
Tích của hai biến cố A và B, kí hiệu: A.B (hoặc AB), là biến cố xảy ra khi và chỉ khi cả hai
biến cố A và B cùng xảy ra.
Trong trường hợp A.B = 0/ thì A,B được gọi là xung khắc với nhau.
Tổng quát: Tích của n biến cố A1, A2, . .An, kí hiệu: n
A1.A2...An = ∏Ai, i=1
là biến cố xảy ra khi và chỉ khi cả n biến cố nói trên cùng xảy ra. c. Biến cố đối lOMoARcPSD|50202050 14
Biến cố đối của biến cố A, kí hiệu: A , là biến cố xảy ra khi và chỉ khi biến cố A không xảy ra. Như vậy, ta có
A.A = 0/, A+A = Ω, A = A.
Nhận xét. Từ các quan hệ trên và tương tự như công thức đối ngẫu De Morgan của tập
hợp, ta có các phép toán với biến cố như sau:
A1 +A2 +...+An = A1.A2...An.
A1.A2....An = A1 +A2 +...+An.
Ví dụ 1.12. Hai người cùng bắn vào một bia, gọi A1, A2 lần lượt là biến cố người thứ nhất,
người thứ hai bắn trúng. Xét các biến cố sau:
A: chỉ có người thứ nhất bắn trúng.
B: có đúng một người bắn trúng.
C: bia bị trúng đạn. Khi đó
A = A1.A2;B = A1.A2 +A1.A2.
Để mô tả biến cố C ta có thể mô tả trực tiếp, hoặc sử dụng biến cố đối
C = A1 +A2 = A1.A2.
1.3.2 Công thức cộng xác suất
Cho hai biến cố A và B, xác suất của biến cố tổng A+B được tính theo công thức:
P(A+B) = P(A)+P(B)−P(AB).
Việc chứng minh công thức này là dễ dàng khi sử dụng biểu đồ Venn.
Đặc biệt, nếu A và B là hai biến cố xung khắc thì
P(A+B) = P(A)+P(B).
Chú ý. Từ công thức trên, xét với B = A, ta được công thức sau:
P(A)+P(A) = 1.
Hoàn toàn tương tự, ta có công thức cộng cho ba biến cố: lOMoARcPSD|50202050 15
P(A+B+C) = P(A)+P(B)+P(C)+P(AB)+P(BC)+P(AC)−P(ABC).
Nếu 3 biến cố A,B,C đôi một xung khắc thì
P(A+B+C) = P(A)+P(B)+P(C).
Như vậy, nếu n biến cố A1, A2,...,An đôi một xung khắc thì n n
P(∑Ai) = ∑P(Ai). i=1 i=1
Ví dụ 1.13. Trong một hộp đựng 6 quả cầu đỏ, 5 quả cầu xanh. Lấy ngẫu nhiên 2 quả cầu. Tính xác suất để:
a) Lấy được 2 quả cầu cùng màu.
b) Lấy được 2 quả cầu khác màu.
Giải. a) Gọi A là biến cố lấy được 2 quả xanh. B
là biến cố lấy được 2 quả đỏ.
C là biến cố lấy được 2 quả cùng màu.
Khi đó: C = A+B và A.B = 0/ nên C52 C62 5 P(C)
= P(A+B) = P(A)+P(B) = + = . C
b) Gọi D là biến cố lấy được 2 quả khác màu thì D =C nên P . 1.3.3
Công thức nhân xác suất
a. Xác suất điều kiện
Xác suất của biến cố B được tính với điều kiện biến cố A đã xảy ra (P(A) > 0), được gọi
là xác suất điều kiện của B với điều kiện A, kí hiệu: P(B/A), được xác định bởi: P(AB) P(B/A) = . P(A)
Như vậy, nếu sử dụng định nghĩa cổ điển để tính xác suất thì ta có công thức: P . lOMoARcPSD|50202050 16
Hơn nữa, từ định nghĩa dễ dàng suy ra rằng xác suất điều kiện cũng có đầy đủ các tính
chất của xác suất thông thường. Tính chất.
i) 0 ≤ P(B/A) ≤ 1,P(Ω/A) = 1.
ii) P(B/A) = 1−P(B/A).
Ví dụ 1.14. Trong một hộp có 5 quả cầu trắng và 3 quả cầu đen. Lấy ngẫu nhiên lần lượt
không hoàn lại 2 quả cầu. Tìm xác suất để:
a) Lần thứ hai lấy được quả cầu trắng nếu biết lần thứ nhất đã lấy được quả cầu trắng.
b) Lần thứ nhất lấy được quả cầu trắng nếu biết lần thứ hai lấy được quả cầu trắng
Giải. a)Nhận thấy, nếu lần đầu đã lấy được cầu trắng thì trong hộp còn lại 4 quả trắng
và 3 quả đen. Khi đó, xác suất để lần thứ hai lấy được cầu trắng là: .
b) Trong tình huống này, ta không thể tính trực tiếp được, vì biến cố đã biết là biến cố xảy
ra sau. Ta sẽ tính bằng công thức.
Gọi A1 là biến cố: Lần thứ nhất lấy được quả cầu trắng.
A2 là biến cố: Lần thứ hai lấy được quả cầu trắng.
Xác suất cần tính P(A1/A2) = P (A1A2). P(A2)
Phép thử: lấy ngẫu nhiên lần lượt không hoàn lại 2 quả cầu nên: , và . Do vậy P , suy ra P(A1A2) 20/56 4
P(A1/A2) = = = . P(A2) 35/56 7
Nhận thấy, rõ ràng ta cũng có thể tính P .
b. Công thức nhân xác suất
Cho 2 biến cố A, B, nếu P(A), P(B) > 0, thì từ công thức xác suất có điều kiện ta thu được công thức nhân: lOMoARcPSD|50202050 17
P(A.B) = P(A).P(B/A) = P(B).P(A/B).
Trong trường hợp ba biến cố A, B,C ta có:
P(ABC) = P(AB).P(C/AB) = P(A).P(B/A).P(C/AB).
Bằng qui nạp, ta thu được công thức nhân tổng quát:
P(A1A2...An) = P(A1).P(A2/A1)...P(An/A1.A2. .An−1).
Chú ý. Hai biến cố A và B được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của
biến cố này không làm thay đổi xác suất xảy ra hay không xảy ra của biến cố kia, tức là
P(A/B) = P(A/B) = P(A);P(B/A) = P(B/A) = P(B).
Khi đó, trong trường hợp hai biến cố A, B độc lập ta thu được công thức
P(A.B) = P(A).P(B)
Ví dụ 1.15. Tung một con xúc xắc cân đối và đồng chất hai lần. Tính xác suất sao cho tổng
số chấm trong hai lần tung là chẵn.
Giải. Gọi A là biến cố lần đầu xuất hiện mặt chẵn.
B là biến cố lần hai xuất hiện mặt chẵn.
C là biến cố tổng số chấm trong hai lần tung là chẵn.
Khi đó C = A.B+A.B
Vì các cặp biến cố A,B và A,B độc lập, hơn nữa A.B;A .B xung khắc nên P .
Ví dụ 1.16. Hai công ty X và Y cùng doanh một mặt hàng. Xác suất để công ty X,Y thua lỗ
lần lượt là 0,1 và 0,15. Giả sử hai công ty này hoạt động độc lập với nhau. Tìm xác suất để:
a) Chỉ có một công ty thua lỗ.
b) Có ít nhất một công ty không thua lỗ.
Giải. a) Gọi A1 là biến cố công ty X bị thua lỗ.
A2 là biến cố công ty Y bị thua lỗ. lOMoARcPSD|50202050 18
A là biến cố chỉ có một công ty bị thua lỗ.
Ta có A = A1.A2 +A1.A .
Vì các cặp (A1,A2) và (A1,A2) độc lập. Hơn nữa,A1.A2,A1.A 2 xung khắc nên
P(A) = P(A1.A2 +A1.A2) = P(A1).P(A2)+P(A1).P(A2) =
0,1.0,85+0,9.0,15 = 0,22.
b) Gọi B là biến cố có ít nhất 1 công ty không thua lỗ
Ta có B = A1.A2 +A1.A2 +A1.A2 nên
P(B) = P(A1.A2 +A1.A2 +A1.A2)
= 0,1.0,85+0,9.0,15+0,9.0,85 = 0,985.
1.3.4 Công thức Bernoulli
Hai phép thử độc lập nếu hệ biến cố sơ cấp của phép thử này độc lập với hệ biến cố
sơ cấp của phép thử kia.
Xét một dãy gồm n phép thử độc lập, giống nhau. Trong mỗi phép thử biến cố A xảy ra
với xác suất như nhau: P(A) = p. Khi đó, dãy phép thử đó được gọi là dãy phép thử
Bernoulli; Bài toán thỏa mãn yêu cầu trên được gọi là tuân theo lược đồ Bernoulli.
Gọi Pk(n,p) là xác suất để trong n phép thử Bernoulli, có đúng k phép thử xảy ra biến
cố A, ta có công thức Bernoulli: Pk .
Ngoài ra, người ta cũng hay xét trường hợp số phép thử xảy ra biến cố A "ít hơn",
"nhiều hơn", "trong khoảng" nào đó,... . Khi đó, ta cũng thường sử dụng kí hiệu:
P≥k(n,p) = Pk(n,p)+Pk+1(n,p)+...+Pn(n,p) = 1−P(n,p).
Ví dụ 1.17. Bắn 6 viên đạn vào bia. Xác suất trúng đích của mỗi viên đạn đều bằng nhau
và bằng 0,7. Tính xác suất để có đúng 3 viên đạn trúng bia.
Giải. Nếu coi mỗi lần bắn là một phép thử, thì ta có 6 phép thử độc lập. Hơn nữa, trong
mỗi phép thử chỉ có hai trường hợp: viên đạn trúng đích hoặc không trúng đích; xác suất
trúng đích của mỗi viên bằng p = 0,7.
Như vậy bài toán thỏa mãn lược đồ Bernoulli, nên xác suất để chỉ có 3 viên đạn trúng bia
được tính bằng công thức Bernoulli: lOMoARcPSD|50202050 19 P . 1.3.5
Công thức xác suất đầy đủ và Bayes
a. Nhóm đầy đủ các biến cố
Nhóm các biến cố H1,H2,...,Hn (n ≥ 2) của một phép thử tạo thành một nhóm đầy đủ các
biến cố nếu thỏa mãn hai điều kiện sau:
i) Hi.Hj = 0/, ∀i =6 j. ii) H1
+H2 +...+Hn = Ω.
Như vậy, với phép thử đang xét nào đó, nếu H1,H2,...,Hn là một nhóm đầy đủ các biến cố thì
kết quả của phép thử sẽ xảy ra một và chỉ một trong các biến cố đó.
b. Công thức xác suất đầy đủ
Giả sử n biến cố H1,H2,...,Hn lập thành nhóm đầy đủ, biến cố A có thể xảy ra đồng thời
với một trong các biến cố H1,H2,...,Hn. Khi đó xác suất của biến cố A được tính theo công
thức xác suất đầy đủ (toàn phần) sau đây: n
P(A) = ∑P(Hi)P(A/Hi). i=1
Ví dụ 1.18. Có 3 hộp giống nhau. Hộp thứ nhất đựng 10 sản phẩm trong đó có 6 chính
phẩm, hộp thứ hai đựng 15 sản phẩm trong đó có 10 chính phẩm. Hộp thứ ba đựng 20
sản phẩm trong đó có 15 chính phẩm. Lấy ngẫu nhiên một hộp và từ đó lấy ngẫu nhiên
một sản phẩm. Tính xác suất để lấy được chính phẩm.
Giải. Gọi A là biến cố lấy được chính phẩm.
Hi là biến cố lấy được sản phẩm ở hộp thứ i (i = 1,2,3). Khi
đó H1,H2,H3 tạo thành nhóm đầy đủ và
P(H1) = P(H2) = P(H3) = ; P .
Theo công thức xác suất đầy đủ, ta có: P i=1