Hệ thống dạng toán và bài tập chuyên đề thể tích khối đa diện

Tuyển tập hệ thống dạng toán và bài tập chuyên đề thể tích khối đa diện trong chương trình môn Toán 12 phần Hình học..Mời bạn đọc đón xem.

40 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

123 trang 8 tháng trước

Tác giả:

Profile Lan Tường
THỂ TÍCH KHỐI ĐA DIỆN
TOÁN 12
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
HỆ THỐNG DẠNG TOÁN- ĐỀ ÔN TẬP
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <1 >
TỔNG HỢP MỘT SỐ DẠNG TÍNH THỂ TÍCH CẦN LƯU Ý
Dạng 1: Hình chóp tam giác có cạnh bên vuông góc với đáy
Mức 1: Cho hình chóp
có đáy là tam giác đều
cạnh
,a SA
vuông góc với đáy và
2.SA a
(tham khảo
hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Mức 2: Cho hình chóp
có đáy là tam giác đều
cạnh
,a SA
vuông góc với đáy và diện tích tam giác
SAB
bằng
2
2a
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Mức 3: Cho hình chóp
có đáy là tam giác đều
cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SB
và mặt
đáy
bằng
60
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <2 >
Mức 4: Cho hình chóp
có đáy là tam giác đều
cạnh
,a SA
vuông góc với đáy. Biết góc giữa mặt phẳng
SBC
và mặt đáy
bằng
60
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Mức 5: Cho hình chóp
có đáy là tam giác đều
cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SC
và
SAB
bằng
30
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Mức 6: Cho hình chóp
có đáy là tam giác đều
cạnh
2,a SA
vuông góc với đáy. Biết khoảng cách từ điểm
A
đến
SBC
bằng
a
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <3 >
Dạng 2: Hình chóp tứ giác có cạnh bên vuông góc với đáy
Mức 1: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy và
2.SB a
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 2: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy và diện tích tam giác
SAC
bằng
2
22a
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 3: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SC
và mặt đáy
ABCD
bằng
30
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <4 >
Mức 4: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SBC
và mặt đáy
ABCD
bằng
30
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 5: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SBD
và mặt đáy
ABCD
bằng
30
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 6: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SC
và
SAB
bằng
30
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <5 >
Mức 7: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SA
và
SBD
bằng
30
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 8: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
3,a SA
vuông góc với đáy. Gọi
M
là trung điểm
SD
và
khoảng cách từ
M
đến
SBC
bằng
a
(tham khảo hình
vẽ).
M
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Dạng 3: Hình chóp tam giác đều
Mức 1: Cho hình chóp tam giác đều
có cạnh đáy
bằng
,a
cạnh bên bằng
2a
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <6 >
Mức 2: Cho hình chóp tam giác đều
có cạnh đáy
bằng
,a
diện tích một mặt bên bằng
2
2a
(tham khảo hình
vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Mức 3: Cho hình chóp tam giác đều
có cạnh đáy
bằng
,a
cạnh bên hợp với đáy một góc
60
(tham khảo hình
vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Mức 4: Cho hình chóp tam giác đều
có cạnh đáy
bằng
,a
mặt bên hợp với đáy một góc
60
(tham khảo hình
vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <7 >
Mức 5: Cho hình chóp tam giác đều
có cạnh đáy
bằng
4.a
Biết khoảng cách từ điểm
A
đến
SBC
bằng
a
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Dạng 4: Hình chóp tứ giác đều
Mức 1: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
,a
cạnh bên bằng
2a
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 2: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
,a
diện tích tam giác
SAC
bằng
2
2a
(tham khảo hình
vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <8 >
Mức 3: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
,a
cạnh bên hợp với đáy một góc
60
(tham khảo hình
vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 4: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
,a
mặt bên hợp với đáy một góc
60
(tham khảo hình
vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 5: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
2.a
Biết khoảng cách từ điểm
A
đến
SBC
bằng
a
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <9 >
Mức 6: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
2.a
Biết góc giữa hai mặt phẳng
SAB
và
SCD
bằng
90
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Dạng 5: Hình chóp tam giác có mặt bên là tam giác cân tại S và nằm trong mặt phẳng
vuông góc với đáy
Mức 1: Cho hình chóp
có đáy là tam giác đều có
cạnh bằng
,a
mặt bên
SAB
là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy (tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Mức 2: Cho hình chóp
có đáy là tam giác đều có
cạnh bằng
,a
mặt bên
SAB
là tam giác vuông cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy (tham khảo hình
vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <10 >
Mức 3: Cho hình chóp
có đáy là tam giác đều có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SC
và
mặt đáy bằng
60
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Mức 4: Cho hình chóp
có đáy là tam giác đều có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SC
và
SAB
bằng
30
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Mức 5: Cho hình chóp
có đáy là tam giác đều có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SBC
và mặt đáy bằng
60
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <11 >
Dạng 6: Hình chóp tứ giác có mặt bên là tam giác cân tại S và nằm trong mặt phẳng vuông
góc với đáy
Mức 1: Cho hình chóp
.S ABCD
có đáy là hình vuông có
cạnh bằng
,a
mặt bên
SAB
là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy (tham khảo hình vẽ).
S
A
B
C
D
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 2: Cho hình chóp
.S ABCD
có đáy là hình vuông có
cạnh bằng
,a
mặt bên
SAB
là tam giác vuông cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy (tham khảo hình
vẽ).
S
A
B
C
D
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 3: Cho hình chóp
.S ABCD
có đáy là hình vuông có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SC
và
mặt đáy bằng
60
(tham khảo hình vẽ).
S
A
B
C
D
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <12 >
Mức 4: Cho hình chóp
.S ABCD
có đáy là hình vuông có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SC
và
SAB
bằng
30
(tham khảo hình vẽ).
S
A
B
C
D
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Mức 5: Cho hình chóp
.S ABCD
có đáy là hình vuông có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SAC
và mặt đáy bằng
60
(tham khảo hình vẽ).
S
A
B
C
D
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
Trình bày:
Dạng 7: Hình lăng trụ đều
Mức 1: Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
,a
cạnh bên bằng
2a
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <13 >
Mức 2: Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
,a
AB
hợp với đáy một góc
60
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Mức 3: Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
,a
A BC
hợp với
ABC
một góc
60
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Mức 4: Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
,a
AB
hợp với
BCC B

một góc
30
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <14 >
Mức 5: Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
,a
A BC
hợp với
BCC B

một góc
60
(tham khảo hình
vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Dạng 8: Hình lăng trụ đứng
Mức 1: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Diện tích tứ giác
ABB A

bằng
2
2a
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Mức 2: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Diện tích tam giác
A BC
bằng
2
2a
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <15 >
Mức 3: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
, 2 .B CC a
Biết khoảng cách từ
A
đến
BCC B

bằng
a
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Mức 4: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Biết góc giữa
AC
và
bằng
45
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Mức 5: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Biết góc giữa
BC
và
ABB A

bằng
60
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <16 >
Mức 6: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Biết góc giữa
ABC
và
ABB A

bằng
60
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Mức 7: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Gọi
I
là trung điểm
CC
và khoảng cách từ
I
đến
AB C

bằng
2
4
a
(tham
khảo hình vẽ).
I
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Dạng 9: Hình lăng trụ có đường cao khác cạnh bên
Mức 1: Cho lăng trụ
.ABC A B C
có đáy
ABC
là tam giác
vuông cân tại
,.B AB a
Cạnh bên
2BB a
và hợp với
đáy một góc
30
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <17 >
Mức 2: Cho lăng trụ
.ABC A B C
có mặt bên
BCC B

là
hình vuông cạnh
2.a
Biết khoảng cách từ
A
đến
BCC B

bằng
a
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Mức 3: Cho lăng trụ
.ABC A B C
có mặt bên
BCC B

là
hình vuông cạnh
2 , , 60 .AA a BC a B BC

Biết khoảng
cách từ
A
đến
BCC B

bằng
a
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Mức 4: Cho lăng trụ
.ABC A B C
có đáy là tam giác đều
cạnh
.a
Hình chiếu của
A
trên
là trung điểm
H
của
.AB
Biết góc giữa
AC
và
bằng
60
(tham
khảo hình vẽ)
H
C'
B'
A'
A
B
C
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <18 >
Mức 5: Cho lăng trụ
.ABC A B C
có đáy là tam giác đều
cạnh
.a
Hình chiếu của
A
trên
là trung điểm
H
của
.AB
Biết góc giữa
ACC A

và
bằng
60
(tham khảo hình vẽ)
H
C'
B'
A'
A
B
C
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Mức 6: Cho lăng trụ
.ABC A B C
có đáy là tam giác đều
cạnh
.a
Hình chiếu của
A
trên
là trọng tâm
G
của tam giác
.AB
Biết góc giữa
AA
và
bằng
60
(tham khảo hình vẽ)
G
M
A'
B'
C'
A
B
C
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Mức 7: Cho lăng trụ
.ABC A B C
có đáy là tam giác đều
cạnh
.a
Hình chiếu của
A
trên
là trọng tâm
G
của tam giác
.AB
Biết góc giữa
AA B B

và
bằng
60
(tham khảo hình vẽ)
G
M
A'
B'
C'
A
B
C
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <19 >
TỔNG HỢP MỘT SỐ DẠNG TÍNH THỂ TÍCH CẦN LƯU Ý
LỜI GIẢI CHI TIẾT
Dạng 1: Hình chóp tam giác có cạnh bên vuông góc với đáy
Mức 1: Cho hình chóp
có đáy là tam giác đều
cạnh
,a SA
vuông góc với đáy và
2.SA a
(tham khảo
hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
3
6
a
Trình bày:
Ta có:
2
3
.
4
ABC
a
S
Vậy
23
.
1 1 3 3
. .2 . .
3 3 4 6
S ABC ABC
aa
V SA S a
Mức 2: Cho hình chóp
có đáy là tam giác đều
cạnh
,a SA
vuông góc với đáy và diện tích tam giác
SAB
bằng
2
2a
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
3
3
a
Trình bày:
Ta có:
2
3
.
4
ABC
a
S
Ta có:
2
1
. 4 .
2
SAB
SAB
S
S SA AB SA a
AB
Vậy
23
.
1 1 3 3
. .4 . .
3 3 4 3
S ABC ABC
aa
V SA S a
Mức 3: Cho hình chóp
có đáy là tam giác đều
cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SB
và mặt
đáy
bằng
60
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Trình bày:
S
A
B
C
Ta có:
2
3
.
4
ABC
a
S
Do
;.SA ABC SB ABC SBA
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <20 >
Đáp án:
3
4
a
Ta có:
tan 3.
SA
SBA SA a
AB
Vậy
23
.
1 1 3
. . 3. .
3 3 4 4
S ABC ABC
aa
V SA S a
Mức 4: Cho hình chóp
có đáy là tam giác đều
cạnh
,a SA
vuông góc với đáy. Biết góc giữa mặt phẳng
SBC
và mặt đáy
bằng
60
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
3
8
a
Trình bày:
M
C
B
A
S
Ta có:
2
3
.
4
ABC
a
S
Gọi
M
là trung điểm
BC
;SBC ABC SMA
Ta có:
3
tan .tan .
2
SA a
SMA SA AM SMA
AM
Vậy
23
.
1 1 3 3 3
. . . .
3 3 2 4 8
S ABC ABC
a a a
V SA S
Mức 5: Cho hình chóp
có đáy là tam giác đều
cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SC
và
SAB
bằng
30
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
6
12
a
Trình bày:
M
C
B
A
S
Ta có:
2
3
.
4
ABC
a
S
Gọi
M
là trung điểm
;.AB SC SAB CSM
Ta có:
sin 3.
CM
CSM SC a
SC
Suy ra:
22
2.SA SC AC a
Vậy
23
.
1 1 3 6
. . 2. .
3 3 4 12
S ABC ABC
aa
V SA S a
Mức 6: Cho hình chóp
có đáy là tam giác đều
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <21 >
cạnh
2,a SA
vuông góc với đáy. Biết khoảng cách từ điểm
A
đến
SBC
bằng
a
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
2
2
a
H
S
A
B
C
M
Ta có:
2
2
32
3.
4
ABC
a
Sa
Gọi
M
là trung điểm
.BC
Dựng
;.AH SM AH d A SBC a
Ta có:
2 2 2
1 1 1
AH SA AM

2 2 2 2
1 1 1 2 6
.
2
3
a
SA
SA AH AM a
Vậy
3
2
.
1 1 6 2
. . . 3 .
3 3 2 2
S ABC ABC
aa
V SA S a
Dạng 2: Hình chóp tứ giác có cạnh bên vuông góc với đáy
Mức 1: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy và
2.SB a
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
3
3
a
Trình bày:
Ta có:
2
.
ABCD
Sa
Ta có:
22
3.SA SB AB a
Vậy
3
2
.
1 1 3
. . 3. .
3 3 3
S ABCD ABCD
a
V SA S a a
Mức 2: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy và diện tích tam giác
SAC
bằng
2
22a
(tham khảo hình vẽ).
Trình bày:
Ta có:
2
.
ABCD
Sa
Ta có:
2
1
. . 4 .
2
SAC
SAC
S
S SA AC SA a
AC
Vậy
3
2
.
1 1 4
. .4 . .
3 3 3
S ABCD ABCD
a
V SAS a a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <22 >
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
4
3
a
Mức 3: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SC
và mặt đáy
ABCD
bằng
30
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
6
9
a
Trình bày:
D
C
A
S
B
Ta có:
2
.
ABCD
Sa
Do
;.SA ABCD SC ABCD SCA
Ta có:
6
tan .
3
SA a
SCA SA
AC
Vậy
3
2
.
1 1 6 6
. . . .
3 3 3 9
S ABCD ABCD
aa
V SA S a
Mức 4: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SBC
và mặt đáy
ABCD
bằng
30
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
3
9
a
Trình bày:
B
S
A
C
D
Ta có:
2
.
ABCD
Sa
Ta có:
;.SBC ABCD SBA
Ta có:
3
tan .
3
SA a
SBA SA
AB
Vậy
3
2
.
1 1 3 3
. . . .
3 3 3 9
S ABCD ABCD
aa
V SA S a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <23 >
Mức 5: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SBD
và mặt đáy
ABCD
bằng
30
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
6
18
a
Trình bày:
O
D
C
A
S
B
Ta có:
2
.
ABCD
Sa
Gọi
O
là tâm hình vuông
.ABCD
Ta có:
;.SBD ABCD SOA
Ta có:
6
tan .
6
SA a
SOA SA
AO
Vậy
3
2
.
1 1 6 6
. . . .
3 3 6 18
S ABCD ABCD
aa
V SA S a
Mức 6: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SC
và
SAB
bằng
30
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
2
3
a
Trình bày:
D
C
A
S
B
Ta có:
2
.
ABCD
Sa
Do
;.BC SAB SC SAB BSC
Ta có:
tan 3.
BC
BSC SB a
SB
Suy ra:
22
2.SA SB AB a
Vậy
3
2
.
1 1 2
. . 2. .
3 3 3
S ABCD ABCD
a
V SA S a a
Mức 7: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a SA
vuông góc với đáy. Biết góc giữa
SA
và
SBD
bằng
30
(tham khảo hình vẽ).
Trình bày:
B
S
A
C
D
O
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <24 >
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
6
6
a
Ta có:
2
.
ABCD
Sa
Gọi
O
là tâm hình vuông
.ABCD
Ta có:
;.SA SBD ASO
Ta có:
6
tan .
2
AO a
ASO SA
SA
Vậy
3
2
.
1 1 6 6
. . . .
3 3 2 6
S ABCD ABCD
aa
V SA S a
Mức 8: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
3,a SA
vuông góc với đáy. Gọi
M
là trung điểm
SD
và
khoảng cách từ
M
đến
SBC
bằng
a
(tham khảo hình
vẽ).
M
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
18 5
5
a
Trình bày:
H
M
B
S
A
C
D
Ta có:
2
.
ABCD
Sa
Ta có:
11
; ; ;
22
d M SBC d D SBC d A SBC
; 2 .d A SBC a
Dựng
; 2 .AH SB d A SBC AH a
Ta có:
2 2 2
1 1 1 6 5
.
5
a
SA
AH SA AB
Vậy
3
2
.
1 1 6 5 18 5
. . . .
3 3 5 5
S ABCD ABCD
aa
V SAS a
Dạng 3: Hình chóp tam giác đều
Mức 1: Cho hình chóp tam giác đều
có cạnh đáy
bằng
,a
cạnh bên bằng
2a
(tham khảo hình vẽ).
Trình bày:
C
B
A
S
G
M
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <25 >
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
11
12
a
Ta có:
2
3
.
4
ABC
a
S
Gọi
M
là trung điểm
,BC G
là trọng tâm tam
giác
.ABC
Ta có:
2
2 2 2
2 33
33
AM a
SG SA AG SA



.
Vậy
23
.
1 1 33 3 11
. . . .
3 3 3 4 12
S ABC ABC
a a a
V SG S
Mức 2: Cho hình chóp tam giác đều
có cạnh đáy
bằng
,a
diện tích một mặt bên bằng
2
2a
(tham khảo hình
vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
191
24
a
Trình bày:
C
B
A
S
G
M
Ta có:
2
3
.
4
ABC
a
S
Gọi
M
là trung điểm
,BC G
là trọng tâm tam
giác
.ABC
Ta có:
2
1
. 4 .
2
SBC
SBC
S
S SM BC SM a
BC
Suy ra:
22
573
.
6
a
SG SM GM
Vậy
23
.
1 1 573 3 191
. . . .
3 3 6 4 24
S ABC ABC
a a a
V SG S
Mức 3: Cho hình chóp tam giác đều
có cạnh đáy
bằng
,a
cạnh bên hợp với đáy một góc
60
(tham khảo hình
vẽ).
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <26 >
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
3
12
a
M
G
S
A
B
C
Ta có:
2
3
.
4
ABC
a
S
Gọi
M
là trung điểm
,BC G
là trọng tâm tam
giác
.ABC
Ta có:
;.SA ABC SAG
Ta có:
tan .
SG
SAG SG a
AG
Vậy
23
.
1 1 3 3
. . . .
3 3 4 12
S ABC ABC
aa
V SG S a
Mức 4: Cho hình chóp tam giác đều
có cạnh đáy
bằng
,a
mặt bên hợp với đáy một góc
60
(tham khảo hình
vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
3
24
a
Trình bày:
M
G
S
A
B
C
Ta có:
2
3
.
4
ABC
a
S
Gọi
M
là trung điểm
,BC G
là trọng tâm tam
giác
.ABC
Ta có:
;.SBC ABC SMG
Ta có:
tan .
2
SG a
SMG SG
MG
Vậy
23
.
1 1 3 3
. . . .
3 3 2 4 24
S ABC ABC
a a a
V SG S
Mức 5: Cho hình chóp tam giác đều
có cạnh đáy
bằng
4.a
Biết khoảng cách từ điểm
A
đến
SBC
bằng
a
(tham khảo hình vẽ).
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <27 >
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
8 11
33
a
H
C
B
A
S
G
M
Ta có:
2
3
.
4
ABC
a
S
Gọi
M
là trung điểm
,BC G
là trọng tâm tam
giác
.ABC
Ta có:
3 ; 3 ;
AM
d A SBC d G SBC
GM
;.
3
a
d G SBC
Dựng
;.GH SM GH d G SBC
Ta có:
2 2 2
1 1 1 2 33
.
33
a
SG
GH GS GM
Vậy
23
.
1 1 2 33 3 8 11
. . . .
3 3 33 4 33
S ABC ABC
a a a
V SG S
Dạng 4: Hình chóp tứ giác đều
Mức 1: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
,a
cạnh bên bằng
2a
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
14
6
a
Trình bày:
O
S
A
B
C
D
Ta có:
2
.
ABCD
Sa
Gọi
O
là tâm hình vuông
.ABCD
Ta có:
22
14
.
2
a
SO SD OD
Vậy
3
2
.
1 1 14 14
. . . .
3 3 2 6
S ABCD ABCD
aa
V SOS a
Mức 2: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
,a
diện tích tam giác
SAC
bằng
2
2a
(tham khảo hình
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <28 >
vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
22
3
a
O
S
A
B
C
D
Ta có:
2
.
ABCD
Sa
Gọi
O
là tâm hình vuông
.ABCD
Ta có:
2
1
. . 2 2 .
2
SAC
SAC
S
S SO AC SO a
AC
Vậy
3
2
.
1 1 2 2
. .2 2 . .
3 3 3
S ABCD ABCD
a
V SO S a a
Mức 3: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
,a
cạnh bên hợp với đáy một góc
60
(tham khảo hình
vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
6
6
a
Trình bày:
D
C
B
A
S
O
Ta có:
2
.
ABCD
Sa
Gọi
O
là tâm hình vuông
.ABCD
Ta có:
;.SB ABCD SBO
Ta có:
6
tan .
2
SO a
SBO SO
BO
Vậy
3
2
.
1 1 6 6
. . . .
3 3 2 6
S ABCD ABCD
aa
V SO S a
Mức 4: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
,a
mặt bên hợp với đáy một góc
60
(tham khảo hình
vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Trình bày:
M
D
C
B
A
S
O
Ta có:
2
.
ABCD
Sa
Gọi
O
là tâm hình vuông
,ABCD M
là trung
điểm
.CD
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <29 >
Đáp án:
3
3
6
a
Ta có:
;.SCD ABCD SMO
Ta có:
3
tan
2.
SO a
SMO SO
OM
Vậy
3
2
.
1 1 3 3
. . . .
3 3 2 6
S ABCD ABCD
aa
V SO S a
Mức 5: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
2.a
Biết khoảng cách từ điểm
A
đến
SBC
bằng
a
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
43
9
a
Trình bày:
H
M
D
C
B
A
S
O
Ta có:
2
4.
ABCD
Sa
Gọi
O
là tâm hình vuông
,ABCD M
là trung
điểm
.BC
Ta có:
; 2 ; .d A SBC d O SBC
Dựng
;.OH SM d O SBC OH
Ta có:
2 2 2
1 1 1 3
.
3
a
SO
OH OM SO
Vậy
3
2
.
1 1 3 4 3
. . .4 .
3 3 3 9
S ABCD ABCD
aa
V SO S a
Mức 6: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
2.a
Biết góc giữa hai mặt phẳng
SAB
và
SCD
bằng
90
(tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
4
3
a
Trình bày:
N
M
D
C
B
A
S
O
Ta có:
2
4.
ABCD
Sa
Gọi
,MN
lần lượt là trung điểm
,.AB CD
Ta có:
; 90 .SAB SCD MSN
Suy ra:
1
.
2
SO MN a
Vậy
3
2
.
1 1 4
. . .4 .
3 3 3
S ABCD ABCD
a
V SO S a a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <30 >
Dạng 5: Hình chóp tam giác có mặt bên là tam giác cân tại S và nằm trong mặt phẳng
vuông góc với đáy
Mức 1: Cho hình chóp
có đáy là tam giác đều có
cạnh bằng
,a
mặt bên
SAB
là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy (tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
8
a
Trình bày:
S
A
B
C
H
Ta có:
2
3
.
4
ABC
a
S
Gọi
H
là trung điểm
.AB SH ABC
Ta có:
23
.
1 1 3 3
. . . .
3 3 2 4 8
S ABC ABC
a a a
V SH S
Mức 2: Cho hình chóp
có đáy là tam giác đều có
cạnh bằng
,a
mặt bên
SAB
là tam giác vuông cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy (tham khảo hình
vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
3
24
a
Trình bày:
S
A
B
C
H
Ta có:
2
3
.
4
ABC
a
S
Gọi
H
là trung điểm
.AB SH ABC
Ta có:
23
.
1 1 3 3
. . . .
3 3 2 4 24
S ABC ABC
a a a
V SH S
Mức 3: Cho hình chóp
có đáy là tam giác đều có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SC
và
mặt đáy bằng
60
(tham khảo hình vẽ).
Trình bày:
H
C
B
A
S
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <31 >
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
3
8
a
Ta có:
2
3
.
4
ABC
a
S
Gọi
H
là trung điểm
.AB SH ABC
Ta có:
;.SC ABC SCH
Ta có:
3
tan .
2
SH a
SCH SH
HC
Ta có:
23
.
1 1 3 3 3
. . . .
3 3 2 4 8
S ABC ABC
a a a
V SH S
Mức 4: Cho hình chóp
có đáy là tam giác đều có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SC
và
SAB
bằng
30
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Đáp án:
3
3
8
a
Trình bày:
S
A
B
C
H
Ta có:
2
3
.
4
ABC
a
S
Gọi
H
là trung điểm
.AB SH ABC
Ta có:
;.SC SAB HSC
Ta có:
3
tan .
2
HC a
HSC SH
SH
Ta có:
23
.
1 1 3 3 3
. . . .
3 3 2 4 8
S ABC ABC
a a a
V SH S
Mức 5: Cho hình chóp
có đáy là tam giác đều có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SBC
và mặt đáy bằng
60
(tham khảo hình vẽ).
C
B
A
S
Thể tích khối chóp
bằng
Trình bày:
M
N
H
C
B
A
S
Ta có:
2
3
.
4
ABC
a
S
Gọi
H
là trung điểm
.AB SH ABC
Gọi
,MN
lần lượt là trung điểm
BC
và
.BM
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <32 >
Đáp án:
3
3
16
a
Ta có:
;.SBC SAB SNH
Ta có:
3
tan .
4
SH a
SNH SH
HN
Ta có:
23
.
1 1 3 3 3
. . . .
3 3 4 4 16
S ABC ABC
a a a
V SH S
Dạng 6: Hình chóp tứ giác có mặt bên là tam giác cân tại S và nằm trong mặt phẳng vuông
góc với đáy
Mức 1: Cho hình chóp
.S ABCD
có đáy là hình vuông có
cạnh bằng
,a
mặt bên
SAB
là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy (tham khảo hình vẽ).
S
A
B
C
D
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
3
6
a
Trình bày:
H
B
S
A
C
D
Ta có:
2
.
ABCD
Sa
Gọi
H
là trung điểm
.AB SH ABCD
Vậy
3
2
.
1 1 3 3
. . . . .
3 3 2 6
S ABCD ABCD
aa
V SH S a
Mức 2: Cho hình chóp
.S ABCD
có đáy là hình vuông có
cạnh bằng
,a
mặt bên
SAB
là tam giác vuông cân tại
S
và
nằm trong mặt phẳng vuông góc với đáy (tham khảo hình
vẽ).
S
A
B
C
D
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
6
a
Trình bày:
H
B
S
A
C
D
Ta có:
2
.
ABCD
Sa
Gọi
H
là trung điểm
.AB SH ABCD
Vậy
3
2
.
11
. . . . .
3 3 2 6
S ABCD ABCD
aa
V SH S a
Mức 3: Cho hình chóp
.S ABCD
có đáy là hình vuông có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SC
và
mặt đáy bằng
60
(tham khảo hình vẽ).
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <33 >
S
A
B
C
D
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
15
6
a
D
C
A
S
B
H
Ta có:
2
.
ABCD
Sa
Gọi
H
là trung điểm
.AB SH ABCD
Suy ra:
;.SC ABCD SCH
Ta có:
15
tan .
2
SH a
SCH SH
CH
Vậy
3
2
.
1 1 15 15
. . . . .
3 3 2 6
S ABCD ABCD
aa
V SH S a
Mức 4: Cho hình chóp
.S ABCD
có đáy là hình vuông có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SC
và
SAB
bằng
30
(tham khảo hình vẽ).
S
A
B
C
D
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
11
6
a
Trình bày:
D
C
A
S
B
H
Ta có:
2
.
ABCD
Sa
Gọi
H
là trung điểm
.AB SH ABCD
Do
BC SAB
nên
;.SC SAB BSC
Ta có:
tan 3.
BC
BSC SB a
SB
Suy ra:
22
11
.
2
a
SH SB BH
Vậy
3
2
.
1 1 11 11
. . . . .
3 3 2 6
S ABCD ABCD
aa
V SH S a
Mức 5: Cho hình chóp
.S ABCD
có đáy là hình vuông có
cạnh bằng
,a
mặt bên
SAB
là tam giác cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa
SAC
và mặt đáy bằng
60
(tham khảo hình vẽ).
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <34 >
S
A
B
C
D
Thể tích khối chóp
.S ABCD
bằng
Đáp án:
3
6
12
a
K
O
D
C
A
S
B
H
Ta có:
2
.
ABCD
Sa
Gọi
H
là trung điểm
.AB SH ABCD
Gọi
O
là tâm hình vuông
,ABCD K
là trung
điểm
.AO
Suy ra:
;.SAC ABCD SKH
Ta có:
6
tan .
4
SH a
SKH SH
HK
Vậy
3
2
.
1 1 6 6
. . . . .
3 3 4 12
S ABCD ABCD
aa
V SH S a
Dạng 7: Hình lăng trụ đều
Mức 1: Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
,a
cạnh bên bằng
2a
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
3
2
a
Trình bày:
Ta có:
2
3
.
4
ABC
a
S
Suy ra:
3
.
3
..
2
ABC A B C ABC
a
V AA S

Mức 2: Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
,a
AB
hợp với đáy một góc
60
(tham khảo hình vẽ).
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <35 >
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
3
4
a
C'
B'
A'
A
B
C
Ta có:
2
3
.
4
ABC
a
S
Ta có:
;.A B ABC A BA

Ta có:
tan 3.
AA
A BA AA a
AB

Suy ra:
3
.
3
..
4
ABC A B C ABC
a
V AA S

Mức 3: Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
,a
A BC
hợp với
ABC
một góc
60
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
33
8
a
Trình bày:
M
C
B
A
A'
B'
C'
Ta có:
2
3
.
4
ABC
a
S
Gọi
M
là trung điểm
.BC
Ta có:
;.A BC ABC A MA

Ta có:
3
tan .
2
AA a
A MA AA
AM

Suy ra:
3
.
33
..
8
ABC A B C ABC
a
V AA S

Mức 4: Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
,a
AB
hợp với
BCC B

một góc
30
(tham khảo hình vẽ).
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <36 >
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
6
4
a
M
C
B
A
A'
B'
C'
Ta có:
2
3
.
4
ABC
a
S
Gọi
M
là trung điểm
.BC

Ta có:
;.A B BCC B A BM
Ta có:
sin 3.
AM
A BM A B a
AB

Suy ra:
2.BB a
Suy ra:
3
.
6
..
4
ABC A B C ABC
a
V AA S

Mức 5: Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
,a
A BC
hợp với
BCC B

một góc
60
(tham khảo hình
vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
3
8
a
Trình bày:
N
M
C'
B'
A'
A
B
C
Ta có:
2
3
.
4
ABC
a
S
Gọi
,MN
lần lượt là trung điểm
,.BC B C

Ta có:
;.A BC BCC B A MN
Ta có:
tan .
2
A N a
A MN MN
MN
Suy ra:
.
2
a
AA
Suy ra:
3
.
3
..
8
ABC A B C ABC
a
V AA S

Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <37 >
Dạng 8: Hình lăng trụ đứng
Mức 1: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Diện tích tứ giác
ABB A

bằng
2
2a
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
a
Trình bày:
Ta có:
2
.
2
ABC
a
S
Ta có:
. 2 .
ABB A
S AA AB AA a


Suy ra:
3
.
..
ABC A B C ABC
V AA S a

Mức 2: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Diện tích tam giác
A BC
bằng
2
2a
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
15
2
a
Trình bày:
C
B
A
A'
B'
C'
Ta có:
2
.
2
ABC
a
S
Do
.BC ABB A BC A B
Ta có:
1
. 4 .
2
A BC
S A B BC A B a

Suy ra:
22
15 .AA A B AB a

Suy ra:
3
.
15
..
2
ABC A B C ABC
a
V AA S

Mức 3: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
, 2 .B CC a
Biết khoảng cách từ
A
đến
BCC B

bằng
a
(tham khảo hình vẽ).
Trình bày:
Ta có:
;.d A BCC B A B a

Suy ra:
2
1
. . .
22
ABC
a
S BA BC
Vậy
3
.
..
ABC A B C ABC
V AA S a

Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <38 >
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
a
Mức 4: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Biết góc giữa
AC
và
bằng
45
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
2
2
a
Trình bày:
C'
B'
A'
A
B
C
Ta có:
2
.
2
ABC
a
S
Ta có:
;.A C ABC A CA

Ta có:
tan 2.
AA
A CA AA a
AC

Suy ra:
3
.
2
..
2
ABC A B C ABC
a
V AA S

Mức 5: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Biết góc giữa
BC
và
ABB A

bằng
60
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
3
6
a
Trình bày:
C
B
A
A'
B'
C'
Ta có:
2
.
2
ABC
a
S
Do
;.B C ABB A BC ABB A C BB
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <39 >
Ta có:
3
tan .
3
B C a
C BB BB
BB

Suy ra:
3
.
3
..
6
ABC A B C ABC
a
V AA S

Mức 6: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Biết góc giữa
ABC
và
ABB A

bằng
60
(tham khảo hình vẽ).
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
3
6
a
Trình bày:
C
B
A
A'
B'
C'
Ta có:
2
.
2
ABC
a
S
Do
;.AB BCC B C AB ABB A C BB
Ta có:
3
tan .
3
B C a
C BB BB
BB

Suy ra:
3
.
3
..
6
ABC A B C ABC
a
V AA S

Mức 7: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác vuông cân tại
,.B AB a
Gọi
I
là trung điểm
CC
và khoảng cách từ
I
đến
AB C

bằng
2
4
a
(tham
khảo hình vẽ).
I
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
2
a
Trình bày:
H
I
C'
B'
A'
A
B
C
Ta có:
2
.
2
ABC
a
S
Ta có:
11
; ; ; .
22
d I AB C d C AB C d A AB C

Dựng
2
;.
2
a
A H AB A H d A AB C
Ta có:
2 2 2
1 1 1
.AA a
A H AA A B
Suy ra:
3
.
..
2
ABC A B C ABC
a
V AA S

Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <40 >
Dạng 9: Hình lăng trụ có đường cao khác cạnh bên
Mức 1: Cho lăng trụ
.ABC A B C
có đáy
ABC
là tam giác
vuông cân tại
,.B AB a
Cạnh bên
2BB a
và hợp với
đáy một góc
30
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
2
a
Trình bày:
Ta có:
2
.
2
ABC
a
S
Gọi
H
là hình chiếu vuông góc của
B
trên
;.ABC BB ABC B BH


Ta có:
sin .
BH
B BH B H a
BB

Suy ra:
3
.
..
2
ABC A B C ABC
a
V B H S

Mức 2: Cho lăng trụ
.ABC A B C
có mặt bên
BCC B

là
hình vuông cạnh
2.a
Biết khoảng cách từ
A
đến
BCC B

bằng
a
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
2a
Trình bày:
Ta có:
2
4.
BCC B
Sa

Ta có:
3
.
14
; . .
33
A B C CB BCC B
a
V V d A BCC B S
Mặt khác:
.
2
3
ABC A B C
VV
3
.
3
2.
2
ABC A B C
V V a
Mức 3: Cho lăng trụ
.ABC A B C
có mặt bên
BCC B

là
hình vuông cạnh
2 , , 60 .AA a BC a B BC

Biết khoảng
cách từ
A
đến
BCC B

bằng
a
(tham khảo hình vẽ)
C
B
A
A'
B'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
3
2
a
Trình bày:
Ta có:
2
1
2 2. . sin60 3 .
2
BCC B BB C
S S BB BC a
Ta có:
3
.
13
; . .
33
A B C CB BCC B
a
V V d A BCC B S
Mặt khác:
.
2
3
ABC A B C
VV
3
.
33
.
22
ABC A B C
a
VV
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <41 >
Mức 4: Cho lăng trụ
.ABC A B C
có đáy là tam giác đều
cạnh
.a
Hình chiếu của
A
trên
là trung điểm
H
của
.AB
Biết góc giữa
AC
và
bằng
60
(tham
khảo hình vẽ)
H
C'
B'
A'
A
B
C
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
33
8
a
Trình bày:
H
C
B
A
A'
B'
C'
Ta có:
2
3
.
4
ABC
a
S
Ta có:
;.A C ABC A CH

Ta có:
3
tan .
2
A H a
A CH A H
HC

Suy ra:
3
.
33
..
8
ABC A B C ABC
a
V A H S

Mức 5: Cho lăng trụ
.ABC A B C
có đáy là tam giác đều
cạnh
.a
Hình chiếu của
A
trên
là trung điểm
H
của
.AB
Biết góc giữa
ACC A

và
bằng
60
(tham khảo hình vẽ)
H
C'
B'
A'
A
B
C
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
33
16
a
Trình bày:
N
M
C'
B'
A'
A
B
C
Ta có:
2
3
.
4
ABC
a
S
Gọi
,MN
lần lượt là trung điểm
,.AC AM
Ta có:
;.A C CA ABC A NH
Ta có:
3
tan .
4
A H a
A NH A H
HN

Suy ra:
3
.
33
..
16
ABC A B C ABC
a
V A H S

Mức 6: Cho lăng trụ
.ABC A B C
có đáy là tam giác đều
cạnh
.a
Hình chiếu của
A
trên
là trọng tâm
G
của tam giác
.AB
Biết góc giữa
AA
và
bằng
60
(tham khảo hình vẽ)
Trình bày:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <42 >
G
M
A'
B'
C'
A
B
C
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
3
4
a
G
M
A'
B'
C'
A
B
C
Ta có:
2
3
.
4
ABC
a
S
Ta có:
;.AA ABC A AG

Ta có:
tan .
AG
A AG A G a
AG

Suy ra:
3
.
3
..
4
ABC A B C ABC
a
V A G S

Mức 7: Cho lăng trụ
.ABC A B C
có đáy là tam giác đều
cạnh
.a
Hình chiếu của
A
trên
là trọng tâm
G
của tam giác
.AB
Biết góc giữa
AA B B

và
bằng
60
(tham khảo hình vẽ)
G
M
A'
B'
C'
A
B
C
Thể tích khối lăng trụ
.ABC A B C
bằng
Đáp án:
3
3
8
a
Trình bày:
N
C
B
A
C'
B'
A'
M
G
Ta có:
2
3
.
4
ABC
a
S
Gọi
N
là trung điểm
.AB
Ta có:
;.AA B B ABC A NG
Ta có:
tan .
2
A G a
A NG A G
AG

Suy ra:
3
.
3
..
8
ABC A B C ABC
a
V A G S

_____________________HẾT_____________________
Huế, 11h00’ Ngày 20 tháng 7 năm 2022
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU HỌC TẬP SỐ 01_TrNg 2021
CHUY£N §Ò TR¾C NGHIÖM
M«n:
To¸n 12
Chuyên đề:
THỂ TÍCH KHỐI ĐA DIỆN
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Cho khối lăng trụ đứng có diện tích đáy bằng
2
2a
và cạnh bên bằng
3a
. Thể tích khối lăng trụ
đã cho bằng
A.
3
2.a
B.
3
3.a
C.
3
18 .a
D.
3
6.a
Câu 2: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
bằng
A.
3
3
12
a
. B.
3
3
6
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Câu 3: Cho hnh lăng trụ đứng
. ' ' 'ABC A B C
c đáy
ABC
l tam giác vuông cân tại
A
vi
BC a
v
mt bên
''AA B B
l hnh vuông. Thể tích của khối lăng trụ
. ' ' 'ABC A B C
bằng
A.
3
2
.
8
a
B.
3
2
.
4
a
C.
3
.
4
a
D.
3
.
12
a
Câu 4: Cho hình chóp
c đường cao
,SA
tam giác
ABC
vuông tại
A
có
2AB
,
4AC
. Gọi
H
l trung điểm của
BC
(tham khảo hình vẽ).
H
C
B
A
S
Biết diện tích tam giác
SAH
bằng 2, thể tích của khối chóp
bằng
A.
16 5
5
. B.
16 5
15
. C.
45
9
. D.
45
3
.
Câu 5: Cho hình chóp tứ giác đều có cạnh đáy bằng
x
(tham khảo hình vẽ).
O
A
D
B
C
S
Biết diện tích xung quanh của hnh chp đ gấp đôi diện tích đáy. Khi đ thể tích của khối
chóp đã cho bằng
A.
3
3
.
12
x
B.
3
3
.
2
x
C.
3
3
.
3
x
D.
3
3
.
6
x
Câu 6: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
2a
, cạnh bên bằng
3a
(tham khảo hình
vẽ).
O
A
D
B
C
S
Thể tích
V
của khối chp đã cho l
A.
3
47Va
. B.
3
47
9
a
V
. C.
3
4
3
a
V
. D.
3
47
3
a
V
.
Câu 7: Cho khối chóp
có thể tích
V
. Gọi
,BC

lần lượt l trung điểm của
,AB AC
(tham khảo
hình vẽ).
C'
B'
C
B
A
S
Tính theo
V
thể tích khối chóp
.S AB C

.
A.
1
3
V
. B.
1
2
V
. C.
1
12
V
. D.
1
4
V
.
Câu 8: Cho tứ diện
có thể tích bằng
V
, hai điểm
,MP
lần lượt l trung điểm của
AB
,
CD
;
N
l điểm thuộc đoạn
AD
sao cho
3AD AN
(tham khảo hình vẽ).
N
A
B
C
D
M
P
Thể tích tứ diện
BMNP
bằng
A.
4
V
. B.
12
V
. C.
8
V
. D.
6
V
.
Câu 9: Cho hnh lăng trụ
.ABC A B C
có thể tích bằng
V
. Gọi
M
l trung điểm cạnh
BB
, điểm
N
thuộc cạnh
CC
sao cho
2CN C N
(tham khảo hình vẽ).
N
M
C'
A'
B'
A
B
C
Thể tích khối chóp
.A BCNM
là
A.
.
7
12
A BCNM
V
V
. B.
.
7
18
A BCNM
V
V
. C.
.
5
18
A BCNM
V
V
. D.
.
3
A BCNM
V
V
.
Câu 10: Cho hình chóp
.S ABCD
c đáy l hnh bnh hnh. Gọi
,MN
l trung điểm của
,SA SB
(tham
khảo hình vẽ).
N
C
B
A
S
D
M
Mt phẳng
()MNCD
chia hnh chp đã cho thnh hai phần. Tỉ số thể tích hai phần (số bé chia
số ln) là
A.
3
.
5
B.
3
.
4
C.
1
.
3
D.
4
.
5
Câu 11: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều cạnh
a
,
3
2
a
AA
. Biết rằng hình chiếu
vuông góc của
A
lên
l trung điểm
BC
(tham khảo hình vẽ).
C'
B'
A'
B
A
C
Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
2
8
a
. B.
3
32
8
a
. C.
3
6
2
a
. D.
3
2
3
a
.
Câu 12: Cho lăng trụ
. ' ' 'ABC A B C
c đáy
ABC
là tam giác vuông tại
B
, đường cao
BH
. Biết
'A H ABC
và
1, 2, ' 2AB AC AA
(tham khảo hình vẽ).
H
C
B
A
C'
B'
A'
Thể tích của khối lăng trụ đã cho bằng
A.
21
12
. B.
7
4
. C.
21
4
. D.
37
4
.
Câu 13: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều cạnh
a
, độ dài cạnh bên bằng
2
3
a
, hình
chiếu của đỉnh
A
trên mt phẳng
trùng vi trọng tâm của tam giác
ABC
(tham khảo
hình vẽ).
M
G
C
B
A
B'
A'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
3
36
a
. B.
3
3
6
a
. C.
3
3
12
a
. D.
3
3
24
a
.
Câu 14: Cho hình chóp
.S ABCD
c đáy
là hình thang vuông tại
A
và
,B
1
2
AB BC AD a
.
Tam giác
SAB
đều và nằm trong mt phẳng vuông góc vi đáy (tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ACD
là
A.
3
.
2
S ACD
a
V
. B.
3
.
3
6
S ACD
a
V
. C.
3
.
3
S ACD
a
V
. D.
3
.
2
6
S ACD
a
V
.
Câu 15: Cho hnh lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
2a
, góc giữa hai đường thẳng
AB
và
BC
bằng
o
60
(tham khảo hình vẽ).
C
B
A
C'
B'
A'
Thể tích của khối lăng trụ đ l
A.
3
26Va
. B.
3
23
3
a
V
. C.
3
26
3
a
V
. D.
3
23Va
.
Câu 16: Cho khối tứ diện
ABCD
có thể tích
V
. Gọi
E
,
F
,
G
lần lượt l trung điểm của
,,BC BD CD
,và
, , ,M N P Q
lần lượt là trọng tâm của các tam giác
,,ABC ABD
,ACD BCD
(tham khảo hình
vẽ).
G
F
E
Q
P
N
M
D
A
B
C
Thể tích của khối tứ diện
MNPQ
bằng
A.
9
V
. B.
3
V
. C.
2
9
V
. D.
27
V
.
Câu 17: Cho khối chóp
.S ABCD
có thể tích bằng 1, đáy
là hình thang vi đáy ln
AD
và
3AD BC
. Gọi
M
l trung điểm của cạnh
SA
,
N
l điểm thuộc
CD
sao cho
3ND NC
(tham
khảo hình vẽ).
N
M
D
C
B
S
A
Mt phẳng
BMN
cắt
SD
tại
P
. Thể tích khối chóp
AMBNP
bằng
A.
3
.
8
B.
5
.
12
C.
5
.
16
D.
9
.
32
Câu 18: Cho hnh lập phương
.ABCD A B C D
cạnh bằng 1. Gọi
M
l trung điểm cạnh
BB
(tham
khảo hnh vẽ).
M
D
A
B
C
D'
A'
B'
C'
Mt phẳng
MA D
cắt cạnh
BC
tại
K
. Thể tích của khối đa diện
A B C D MKCD
bằng
A.
7
.
24
B.
7
.
17
C.
1
.
24
D.
17
.
24
Câu 19: Xét khối chóp
c đáy l tam giác vuông cân tại
A
,
SA
vuông góc vi mt phẳng đáy,
khoảng cách từ
A
đến mt phẳng
SBC
bằng 3 (tham khảo hình vẽ).
C
B
A
S
Gọi
là góc giữa hai mt phẳng
SBC
và
, giá trị
cos
khi thể tích khối chóp
.S ABC
nhỏ nhất là
A.
2
2
. B.
2
3
. C.
3
3
. D.
6
3
.
Câu 20: Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật c đáy l hnh vuông sao
cho thể tích của khối hộp được tạo thành là
3
dm8
và diện tích toàn phần đạt giá trị nhỏ nhất
(tham khảo hình vẽ).
Độ dài cạnh đáy của mỗi hộp muốn thiết kế là
A.
2.dm
B.
3
2 2 .dm
C.
4.dm
D.
2 2 .dm
_______________HẾT_______________
Huế, 15h40 ngày 14 tháng 9 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU HỌC TẬP SỐ 01_TrNg 2021
CHUY£N §Ò TR¾C NGHIÖM
M«n:
To¸n 12
Chuyên đề:
THỂ TÍCH KHỐI ĐA DIỆN
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Cho khối lăng trụ đứng có diện tích đáy bằng
2
2a
và cạnh bên bằng
3a
. Thể tích khối lăng trụ
đã cho bằng
A.
3
2.a
B.
3
3.a
C.
3
18 .a
D.
3
6.a
Lời giải:
Ta có:
23
. 2 .3 6V B h a a a
.
Chọn đáp án D.
Câu 2: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
bằng
A.
3
3
12
a
. B.
3
3
6
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Lời giải:
Ta có
23
.
33
..
44
ABC A B C ABC
aa
V S AA a
.
Chọn đáp án D.
Câu 3: Cho hnh lăng trụ đứng
. ' ' 'ABC A B C
c đáy
ABC
l tam giác vuông cân tại
A
vi
BC a
v
mt bên
''AA B B
l hnh vuông. Thể tích của khối lăng trụ
. ' ' 'ABC A B C
bằng
A.
3
2
.
8
a
B.
3
2
.
4
a
C.
3
.
4
a
D.
3
.
12
a
Lời giải:
Tam giác
ABC
vuông cân tại
A
c
BC a
nên
2
a
AB AC
.
2
11
. . . .
2 2 4
22
ABC
a a a
S AB AC
.
Do mt bên
''AA B B
l hnh vuông nên
'
2
a
AA AB
.
V
. ' ' 'ABC A B C
l lăng trụ đứng nên
23
. ' ' '
2
. ' .
48
2
ABC A B C ABC
a a a
V S AA
.
Chọn đáp án A.
Câu 4: Cho hình chóp
c đường cao
,SA
tam giác
ABC
vuông tại
A
có
2AB
,
4AC
. Gọi
H
l trung điểm của
BC
(tham khảo hình vẽ).
H
C
B
A
S
Biết diện tích tam giác
SAH
bằng 2, thể tích của khối chóp
bằng
A.
16 5
5
. B.
16 5
15
. C.
45
9
. D.
45
3
.
Lời giải:
H
A
C
B
S
Xét tam giác
ABC
vuông tại
A
:
2 2 2 2
2 4 2 5BC AB AC
.
Suy ra
11
.2 5 5
22
AH BC
.
Xét tam giác
SAH
vuông tại
A
:
1 1 4 5
. 2 . 5
2 2 5
SAH
S SA AH SA SA
.
Diện tích tam giác
ABC
:
11
. .2.4 4
22
ABC
S AB AC
.
Thể tích khối chóp
:
.
1 1 4 5 16 5
. . .4
3 3 5 15
S ABC ABC
V SA S
.
Chọn đáp án B.
Câu 5: Cho hình chóp tứ giác đều có cạnh đáy bằng
x
(tham khảo hình vẽ).
O
A
D
B
C
S
Biết diện tích xung quanh của hnh chp đ gấp đôi diện tích đáy. Khi đ thể tích của khối
chóp đã cho bằng
A.
3
3
.
12
x
B.
3
3
.
2
x
C.
3
3
.
3
x
D.
3
3
.
6
x
Lời giải:
Gọi
M
l trung điểm của cạnh
BC
. Đt
SM h
. Do diện tích xung quanh gấp đôi diện tích
đáy nên ta c:
22
1
4. 2 4. . 2 2. . 2
2
SBC ABCD
S S SM BC x h x x h x
Tam giác
SOM
vuông tại
M
nên ta có:
2
2 2 2
3
22
xx
SO SM OM x



.
Vậy
23
.
1 1 3 3
. . . .
3 3 2 6
S ABCD ABCD
x
V SO S x x
.
Chọn đáp án D.
Câu 6: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
2a
, cạnh bên bằng
3a
(tham khảo hình
vẽ).
O
A
D
B
C
S
Thể tích
V
của khối chp đã cho l
A.
3
47Va
. B.
3
47
9
a
V
. C.
3
4
3
a
V
. D.
3
47
3
a
V
.
Lời giải:
Diện tích đáy
2
2
24
ABCD
S a a
.
.S ABCD
là hình chóp tứ giác đều nên
SO ABCD
.
2 2 2 2
9 2 7h SO SA AO a a a
(vi
11
2 2 2
22
AO AC a a
).
Vậy
3
.
1 4 7
33
S ABCD
a
V Sh
.
Chọn đáp án D.
Câu 7: Cho khối chóp
có thể tích
V
. Gọi
,BC

lần lượt l trung điểm của
,AB AC
(tham khảo
hình vẽ).
C'
B'
C
B
A
S
Tính theo
V
thể tích khối chóp
.S AB C

.
A.
1
3
V
. B.
1
2
V
. C.
1
12
V
. D.
1
4
V
.
Lời giải:
C'
B'
A
C
B
S
Ta có tỷ số thể tích
.
.
1 1 1
..
2 2 4
A SB C
A SBC
V
AB AC
V AB AC


. Do đ
..
1
4
A SB C A SBC
VV

hay
.
1
4
S AB C
VV

.
Chọn đáp án D.
Câu 8: Cho tứ diện
có thể tích bằng
V
, hai điểm
,MP
lần lượt l trung điểm của
AB
,
CD
;
N
l điểm thuộc đoạn
AD
sao cho
3AD AN
(tham khảo hình vẽ).
N
A
B
C
D
M
P
Thể tích tứ diện
BMNP
bằng
A.
4
V
. B.
12
V
. C.
8
V
. D.
6
V
.
Lời giải:
N
A
B
C
D
M
P
Ta có:
P
l trung điểm của
CD
nên
1
, , ,
2
d P BMN d P ABD d C ABD
.
1
3. 6. .
6
ABD ABN BMN BMN ABD
S S S S S
.
Khi đ:
1 1 1 1
. , . . . , .
3 3 2 6
PBMN BMN ABD
V d P BMN S d C ABD S


1 1 1
. . , .
12 3 12
ABD
d C ABD S V

.
Chọn đáp án B.
Câu 9: Cho hnh lăng trụ
.ABC A B C
có thể tích bằng
V
. Gọi
M
ltrung điểm cạnh
BB
, điểm
N
thuộc cạnh
CC
sao cho
2CN C N
(tham khảo hình vẽ).
N
M
C'
A'
B'
A
B
C
Thể tích khối chóp
.A BCNM
là
A.
.
7
12
A BCNM
V
V
. B.
.
7
18
A BCNM
V
V
. C.
.
5
18
A BCNM
V
V
. D.
.
3
A BCNM
V
V
.
Lời giải:
N
M
C'
A'
B'
A
B
C
Cách 1:
Vì
BCNM
là hình thang nên:
12
.;
.;
23
77
. . ;
2 2 12 12
BCNM BCC B
CC CC d B CC
BM CN d B CC
S CC d B CC S





.
Khi đ:
. . .
7 7 7 1 7 1 7
. ; .
12 12 12 3 12 3 18
A BCNM A BCC B A A B C A B C
V
V V V V V d A A B C S V V
Cách 2: Dùng công thức giải nhanh
Ta có:
.
.
1 1 2 1 7 7 7
0
3 3 3 2 18 18 18
ABCMN
ABCNM ABC A B C
ABC A B C
V
CN BM AA V
VV
V CC BB AA
.
Chọn đáp án B.
Câu 10: Cho hình chóp
.S ABCD
c đáy l hnh bnh hnh. Gọi
,MN
l trung điểm của
,SA SB
(tham
khảo hình vẽ).
N
C
B
A
S
D
M
Mt phẳng
()MNCD
chia hnh chp đã cho thnh hai phần. Tỉ số thể tích hai phần (số bé chia
số ln) là
A.
3
.
5
B.
3
.
4
C.
1
.
3
D.
4
.
5
Lời giải:
N
C
B
A
S
D
M
Giả sử thể tích của khối chóp
.S ABCD
là
.V
Ta có
.
.
1
. . ;
2
S MDC
S ADC
V
SM SD SC
V SA SD SC

.
.
1
. . ;
4
S MNC
S ABC
V
SM SN SC
V SA SB SC

. . . . .
..
1 1 3
1 1 1
2 4 4
2 2 2
S MDC S MNC S MDC S MNC S MNCD
S ADC S ABC
V V V V V
VV
V V V
.
.
3 3 5 3
.
8 8 8 5
S MNCD
S MNCD MNABCD
MNABCD
V
V V V V V V
V
Cách khác: Dùng công thức giải nhanh.
Ta có:
..
..
.
.
3
2 2 1 1 3 3
8
.
5
4 4.2.2.1.1 8 5
8
S MNCD S ABCD
S MNCD S MNCD
S ABCD ABNMDC
ABNMDC S ABCD
VV
VV
a b c d
V abcd V
VV
Chọn đáp án A.
Câu 11: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều cạnh
a
,
3
2
a
AA
. Biết rằng hình chiếu
vuông góc của
A
lên
l trung điểm
BC
(tham khảo hình vẽ).
C'
B'
A'
B
A
C
Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
2
8
a
. B.
3
32
8
a
. C.
3
6
2
a
. D.
3
2
3
a
.
Lời giải:
H
C'
B'
A'
B
A
C
Gọi
M
l trung điểm
BC
, khi đ
A M ABC
. Tam giác
ABC
đều cạnh
a
nên
AM BC
và
3
2
a
AM
. Xét tam giác vuông
A AM
vuông tại
M
có
2 2 2
A M AM AA


.
2
2
22
3 3 6
2 2 2
a a a
A M AA AM








.
23
.
6 3 3 2
.S .
2 4 8
ABC A B C ABC
a a a
V A M
.
Chọn đáp án B.
Câu 12: Cho lăng trụ
. ' ' 'ABC A B C
c đáy
ABC
là tam giác vuông tại
B
, đường cao
BH
. Biết
'A H ABC
và
1, 2, ' 2AB AC AA
(tham khảo hình vẽ).
H
C
B
A
C'
B'
A'
Thể tích của khối lăng trụ đã cho bằng
A.
21
12
. B.
7
4
. C.
21
4
. D.
37
4
.
Lời giải:
Độ dài của đường cao
BH
:
.3
2
AB BC
BH
AC

. Suy ra
31
:3
22
AH 
.
Khi đ độ di đường cao
'AH
của hnh lăng trụ bằng :
22
17
' ' 2
42
A H AA AH
.
Thể tích khối lăng trụ đã cho bằng :
1 1 7 21
. . ' .1. 3
2 2 2 4
V AB BC A H
.
Chọn đáp án C.
Câu 13: Cho lăng trụ
.ABC A B C
c đáy
ABC
l tam giác đều cạnh
a
, độ dài cạnh bên bằng
2
3
a
, hình
chiếu của đỉnh
A
trên mt phẳng
trùng vi trọng tâm của tam giác
ABC
(tham khảo
hình vẽ).
M
G
C
B
A
B'
A'
C'
Thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
3
36
a
. B.
3
3
6
a
. C.
3
3
12
a
. D.
3
3
24
a
.
Lời giải:
M
G
C
B
A
B'
A'
C'
Gọi
G
là trọng tâm của tam giác
ABC
. Ta có:
23
33
a
AG AM
;
2
2
2
2 2 2
23
.
3 3 9 3
a a a a
A G A A AG A G







Suy ra:
23
33
..
4 3 12
a a a
V B h
.
Chọn đáp án C.
Câu 14: Cho hình chóp
.S ABCD
c đáy
là hình thang vuông tại
A
và
,B
1
2
AB BC AD a
.
Tam giác
SAB
đều và nằm trong mt phẳng vuông góc vi đáy (tham khảo hình vẽ).
D
C
B
A
S
Thể tích khối chóp
.S ACD
là
A.
3
.
2
S ACD
a
V
. B.
3
.
3
6
S ACD
a
V
. C.
3
.
3
S ACD
a
V
. D.
3
.
2
6
S ACD
a
V
.
Lời giải:
H
C
E
A
D
B
S
Gọi
H
l trung điểm
AB
. Do tam giác
SAB
đều nên
SH AB
.
Lại có:
mp SAB
vuông góc
mp ABCD
theo giao tuyến
AB
nên
SH ABCD
.
Gọi
E
l trung điểm
AD
.
Ta có:
AECB
là hình vuông cạnh
a
,
ECD
là tam giác vuông cân tại
E
.
Ta thấy: tam giác
ACD
có trung tuyến
CE
bằng nửa cạnh đối diện
AD
nên tam giác
ACD
vuông tại
C
mà
2AC CD a
nên tam giác
ACD
vuông cân tại
C
.
Thể tích khối chóp
.S ACD
là:
3
2
1 1 3 1 3
. . . 2
3 3 2 2 6
ACD
aa
V SH S a
.
Chọn đáp án B.
Câu 15: Cho hnh lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
2a
, góc giữa hai đường thẳng
AB
và
BC
bằng
o
60
(tham khảo hình vẽ).
C
B
A
C'
B'
A'
Thể tích của khối lăng trụ đ l
A.
3
26Va
. B.
3
23
3
a
V
. C.
3
26
3
a
V
. D.
3
23Va
.
Lời giải:
D
C
B
B'
C'
A'
A
Dựng hình bình hành
B C BD

, suy ra
//BC DB

, do đ gc giữa hai đường thẳng
AB
và
BC
bằng góc giữa hai đường thẳng
AB
và
DB
.
Xét tam giác
ACD
có trung tuyến
AB
bằng nửa cạnh đối diện
CD
nên
ACD
vuông tại
A
.
2 2 2 2
16 4 2 3AD DC AC a a a
.
Lại do
.ABC A B C
l lăng trụ tam giác đều nên
AB BC

hay
AB DB

B DA
cân tại
B
,
mà
o
, 60AB DB

nên tam giác
B DA
đều cạnh bằng
23a
.
2 2 2 2
12 4 2 2BB AB AB a a a

.
Thể tích
V
của khối lăng trụ đã cho l
2
3
23
. 2 2. 2 6
4
ABC
a
V BB S a a
.
Chọn đáp án A.
Câu 16: Cho khối tứ diện
ABCD
có thể tích
V
. Gọi
E
,
F
,
G
lần lượt là trung điểm của
,,BC BD CD
,và
, , ,M N P Q
lần lượt là trọng tâm của các tam giác
,,ABC ABD
,ACD BCD
(tham khảo hình
vẽ).
G
F
E
Q
P
N
M
D
A
B
C
Thể tích của khối tứ diện
MNPQ
bằng
A.
9
V
. B.
3
V
. C.
2
9
V
. D.
27
V
.
Lời giải:
Do
//MNP BCD
nên:
1
, E, A,
2
d Q MNP d MNP d MNP
( Vì
2MA ME
).
Suy ra:
1
.
2
QMNP AMNP
VV
(1)
Mt khác áp dụng công thức tỷ số thể tích ta có
2 2 2 8
. . . . .
3 3 3 27
AMNP
AEFG
V
AM AN AP
V AE AF AG
(2)
Lại có:
1
4
AEFG
ABCD
V
V
. (3)
Từ (1), (2), (3) ta có:
1 8 1
. . .
2 27 4 27
MNPQ ABCD
V
VV
. Vậy
27
MNPQ
V
V
.
Cách khác: Đc biệt hóa, tứ diện
là tứ diện đều cạnh bằng
2
1.
12
ABCD
V
Lúc đ, tứ diện
MNPQ
là tứ diện đều vi cạnh
MN
được tính bởi:
2 2 2 1 1
..
3 3 3 2 3
MN
MN EF
EF
Suy ra:
3
2 1 1 2 1
. . .
12 3 27 12 27
MNPQ ABCD
VV



Chọn đáp án D.
Câu 17: Cho khối chóp
.S ABCD
có thể tích bằng 1, đáy
là hình thang vi đáy ln
AD
và
3AD BC
. Gọi
M
l trung điểm của cạnh
SA
,
N
l điểm thuộc
CD
sao cho
3ND NC
(tham
khảo hình vẽ).
N
M
D
C
B
S
A
Mt phẳng
BMN
cắt
SD
tại
P
. Thể tích khối chóp
AMBNP
bằng
A.
3
.
8
B.
5
.
12
C.
5
.
16
D.
9
.
32
Lời giải:
E
P
N
M
S
D
C
B
A
Gọi
E
l giao điểm của
BN
và
.AD
Đt
1 AMBNP
VV
.
Ta có:
BC
//
AD
nên
33
DE ND
DE BC AD
BC NC
D
là trung điểm của
AE
P
là trọng tâm của tam giác
SAE
2
3
EP
EM

,
3
4
EN
EB
Ta có
.
.
1 2 3 1
. . . .
2 3 4 4
E DNP
E MAB
V
ED EP EN
V EA EM EB
Mt khác,
. ( ,( )) ( ,( )) ( ,( ))
1 1 1 1
. . . .
3 3 3 9
E NDP P DEN DEN S ABCD DNE S ABCD DNE
V d S d S d S
( , )
1 1 3 3
. . . .
2 2 4 8
AND DNE N AD
S S AD d AD h AD h
(h l đường cao của hình thang)
Ta lại có:
1 1 4 2 3
( ). . . . .
2 2 3 3 2
ABCD ABCD
S AD BC h AD h AD h AD h S
3 3 9
.
8 2 16
AND ABCD ABCD
S S S
. ( ,( )) . .
1 9 3 3 3 3 3 3 3
. . ; 4. .
9 16 16 8 16 4 4 8 8
E NDP S ABCD ABCD AENP E ABM A BMPC
V d S V V V
Chọn đáp án A.
Câu 18: Cho hnh lập phương
.ABCD A B C D
cạnh bằng 1. Gọi
M
l trung điểm cạnh
BB
(tham
khảo hnh vẽ).
M
D
A
B
C
D'
A'
B'
C'
Mt phẳng
MA D
cắt cạnh
BC
tại
K
. Thể tích của khối đa diện
A B C D MKCD
bằng
A.
7
.
24
B.
7
.
17
C.
1
.
24
D.
17
.
24
Lời giải:
*Ta có
'
1
1 .1
'.
2
3
2 2 4
A MBA
A A MB AB
S



Nên
' '.
11
..
31
..
3 43
1
4
A MBD A M AAB
VSAD 
* Dễ thấy
.
.CB'D
1 1 1
..
' 2 2 4
B MKD
B
BM BK
BV B BC
V
Suy ra
. .CB'D
1 1 1 1 1 1 1 1 1 1
. . . ' . . . . . ' . . .1.1.1
4 4 3 4 3 2 4 3 2 24
DBB MKD CB
S BB DC BCV BBV
*Vậy
' ' ' '. . ' .
1 1 17
1 1 .
4 24 24
A B C D MKCD D A AB BDM MK
VVV
Chọn đáp án D.
Câu 19: Xét khối chóp
c đáy l tam giác vuông cân tại
A
,
SA
vuông góc vi mt phẳng đáy,
khoảng cách từ
A
đến mt phẳng
SBC
bằng 3 (tham khảo hình vẽ).
C
B
A
S
Gọi
là góc giữa hai mt phẳng
SBC
và
, giá trị
cos
khi thể tích khối chóp
.S ABC
nhỏ nhất là
A.
2
2
. B.
2
3
. C.
3
3
. D.
6
3
.
Lời giải:
H
M
C
B
A
S
Đt
,SA h AB AC a
. Ta có:
,SBC ABC SMA

.
Ta có
2
3
2 2 2 2 2 2 2 4 2
1 1 1 1 1 1 1 1 1
; 3; 3 6
9
d A SBC AH a h
AH SA AB AC a a h a h
.
Suy ra:
2
.
1
1
6
S ABC
V a h
.
Thể tích nhỏ nhất bằng 1 khi
3
2
a h SM a
os
2 2 3
23
3
AM a
c
SM
a
Chọn đáp án C.
Câu 20: Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật c đáy l hnh vuông sao
cho thể tích của khối hộp được tạo thành là
3
dm8
và diện tích toàn phần đạt giá trị nhỏ nhất
(tham khảo hình vẽ).
Độ dài cạnh đáy của mỗi hộp muốn thiết kế là
A.
2.dm
B.
3
2 2 .dm
C.
4.dm
D.
2 2 .dm
Lời giải:
Gọi cạnh đáy hnh vuông l
x
0x
thì chiều cao của khối hộp là
2
8
h
x
.
Ta có diện tích toàn phần của khối hộp là
2
24
tp
S x xh
2
32
2x
x

22
3
16 16 16 16
2 3 2 . .xx
x x x x
24
tp
S
. Dấu bằng xảy ra khi
2x
.
Vậy độ dài cạnh đáy của mỗi hộp muốn thiết kế là
dm2
.
Chọn đáp án A.
_______________HẾT_______________
Huế, 15h40 ngày 14 tháng 9 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU HỌC TẬP SỐ 02_TrNg 2021
CHUY£N §Ò TR¾C NGHIÖM
M«n:
To¸n 12
Chuyên đề:
THỂ TÍCH KHỐI ĐA DIỆN
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Tính thể tích
V
của khối lập phương
.ABCD A B C D
có tổng diện tích tất cả các mặt bằng
2
24 .cm
A.
3
8.V cm
B.
3
16 .V cm
C.
3
24 .V cm
D.
3
12 .V cm
Câu 2: Cho hình lập phương
.ABCD A B C D
có
23BD
(tham khảo hình vẽ).
D'
C'
B'
A'
D
C
B
A
Thể tích của hình lập phương đó bằng
A.
16.
B.
64.
C.
8.
D.
512.
Câu 3: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
mặt bên
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với
ABCD
(tham khảo hình vẽ).
A
B
C
D
S
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
3
.
6
a
V
B.
3
.
12
a
V
C.
3
3
.
8
a
V
D.
3
3
.
24
a
V
Câu 4: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
hai mặt phẳng
SAB
và
SAD
cùng
vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc bằng
o
30
(tham khảo hình vẽ).
A
B
C
D
S
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
6
.
3
a
V
B.
3
2
.
3
a
V
C.
3
6
.
6
a
V
D.
3
2.Va
Câu 5: Cho khối chóp
.S ABCD
có đáy
là hình chữ nhật,
,
3AD a
,
SA
vuông góc
với mặt phẳng đáy và mặt phẳng
SBC
tạo với đáy một góc
60
(tham khảo hình vẽ).
A
B
C
D
S
Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
3Va
. B.
3
3
3
a
V
. C.
3
Va
. D.
3
3
a
V
.
Câu 6: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
hình chiếu vuông góc của
S
trên mặt
phẳng
là trung điểm của
BC
và
SA
hợp với đáy một góc
o
60
(tham khảo hình vẽ).
S
A
B
C
Tính thể tích
V
của khối chóp
..S ABC
A.
3
3
.
8
a
V
B.
3
3
.
24
a
V
C.
3
5
.
8
a
V
D.
3
3
.
12
a
V
Câu 7: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
(tham khảo
hình vẽ).
A'
B'
C
A
B
C'
Biết
2BC a
và thể tích lăng trụ bằng
3
2,a
khoảng cách
d
từ
A
đến mặt phẳng
'A BC
bằng
A.
35
.
5
a
B.
5a
. C.
5
.
5
a
D.
25
.
5
a
Câu 8: Cho hình chóp
có đáy là tam giác đều cạnh bằng
a
và
SA
vuông góc với
.ABC
Biết
góc giữa
SC
và
SAB
bằng
o
30
(tham khảo hình vẽ).
S
A
B
C
Thể tích khối chóp
.S ABC
bằng
A.
3
6
.
12
a
B.
3
3
.
16
a
C.
3
.
12
a
D.
3
.
6
a
Câu 9: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác vuông tại
A
,
o
, 60AC a ACB
(tham
khảo hình vẽ).
B'
A'
C
B
A
C'
Đường thẳng
'BC
tạo với mặt phẳng
''ACC A
một góc
0
30
. Tính thể tích
V
của khối lăng
trụ
. ' ' '.ABC A B C
A.
3
3Va
. B.
3
3
3
a
V
. C.
3
3Va
. D.
3
6Va
.
Câu 10: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
mặt bên
SAB
là tam giác cân tại
S
và
nằm trong mặt vuông góc với đáy,
SC
tạo với mặt đáy một góc bằng
o
60
(tham khảo hình
vẽ).
A
B
C
D
S
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
15
.
2
a
V
B.
3
3.Va
C.
3
15
.
6
a
V
D.
3
3
.
3
a
V
Câu 11: Cho hình chóp
.S ABCD
có đáy
là hình thoi cạnh bằng
30
o
,a CBD
và
SA
vuông góc
với đáy (tham khảo hình vẽ).
A
B
C
D
S
Biết góc giữa hai đường thẳng
SB
và
CD
bằng
60
o
,
tính thể tích
V
của khối chóp
..S ABCD
A.
3
2
.
a
V
B.
3
6
.
a
V
C.
3
3
2
.
a
V
D.
3
3
6
.
a
V
Câu 12: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,,A AB a AB C

hợp với mặt đáy một góc
o
30
(tham khảo hình vẽ).
C
B'
A'
C'
B
A
Tính thể tích
V
của khối lăng trụ
.ABC A B C
A.
3
6
.
6
a
V
B.
3
6
.
36
a
V
C.
3
6
.
12
a
V
D.
3
6
.
4
a
V
Câu 13: Cho hình lăng trụ
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
,a
hình chiếu vuông góc của
A
trên
ABC
là trọng tâm tam giác
,ABC
AA
hợp với mặt đáy một góc
o
60
(tham khảo
hình vẽ).
M
G
C
B
A
B'
A'
C'
Tính thể tích
V
của khối lăng trụ
..ABC A B C
A.
3
3
.
4
a
V
B.
3
33
.
4
a
V
C.
3
3
.
12
a
V
D.
3
33
.
8
a
V
Câu 14: Cho hình lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
,a AC
hợp với mặt phẳng
ABB A

một góc
o
45
(tham khảo hình vẽ).
C
B'
A'
C'
B
A
Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
6
.
24
a
B.
3
3
.
4
a
C.
3
6
.
8
a
D.
3
6
.
4
a
Câu 15: Gọi
V
là thể tích khối chóp
..S ABC
Gọi
,MN
lần lượt là trung điểm của các cạnh
,SB SC
(tham khảo hình vẽ).
M
S
A
B
C
N
Tính thể tích khối
.AMNCB
A.
.
4
V
B.
.
8
V
C.
.
2
V
D.
3
.
4
V
Câu 16: Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau;
6AB a
,
7AC a
và
4AD a
. Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB (tham khảo hình vẽ).
P
N
M
C
B
A
D
Tính thể tích V của tứ diện AMNP.
A.
3
7
.
2
Va
B.
3
14 .Va
C.
3
28
.
3
Va
D.
3
7.Va
Câu 17: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
,MN
lần lượt là trung điểm
của các cạnh
,SA SD
(tham khảo hình vẽ).
N
M
A
S
D
C
B
Mặt phẳng
chứa
MN
và cắt các tia
,SB SC
lần lượt tại
,PQ
. Đặt
SP
x
SC
,
1
V
là thể tích
khối chóp
.S MNQP
và
V
là thể tích khối chóp
.S ABCD
. Tìm
x
để
1
2VV
.
A.
1
2
x
. B.
1 33
4
x

. C.
1 41
2
x

. D.
2x
.
Câu 18: Cho hình chóp
.S ABCD
có đáy là hình thang với
AB
song song với
CD
,
7CD AB
. Gọi
M
trên cạnh
SA
sao cho
SM
k
SA
,
01k
(tham khảo hình vẽ).
M
D
C
B
A
S
Giá trị của
k
để
CDM
chia khối chóp thành hai phần có thể tích bằng nhau là.
A.
7 53
.
2
k

B.
7 65
.
2
k

C.
7 71
.
4
k

D.
7 53
.
4
k

Câu 19: Cho khối lăng trụ
.ABC A B C
có thể tích bằng 2. Gọi
M
,
N
lần lượt là hai điểm nằm trên hai
cạnh
AA
,
BB
sao cho
M
là trung điểm cạnh
AA
và
2
3
BN BB
(tham khảo hình vẽ).
N
M
A
B
C
C'
A'
B'
Đường thẳng
CM
cắt đường thẳng
CA

tại
P
và đường thẳng
CN
cắt đường thẳng
CB

tại
Q
. Thể tích khối đa diện
A MPB NQ

bằng:
A.
13
18
. B.
23
9
. C.
7
18
. D.
7
9
.
Câu 20: Cho hình chóp
.S ABCD
có cạnh
SA x
còn tất cả các cạnh khác có độ dài bằng
2
(tham khảo
hình vẽ).
S
D
C
B
A
Tính thể tích
max
V
lớn nhất của khối chóp
.S ABCD
.
A.
max
1.V
B.
max
1
.
2
V
C.
max
3.V
D.
max
2.V
_______________HẾT_______________
Huế, 15h40 ngày 15 tháng 9 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU HỌC TẬP SỐ 02_TrNg 2021
CHUY£N §Ò TR¾C NGHIÖM
M«n:
To¸n 12
Chuyên đề:
THỂ TÍCH KHỐI ĐA DIỆN
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Tính thể tích
V
của khối lập phương
.ABCD A B C D
có tổng diện tích tất cả các mặt bằng
2
24 .cm
A.
3
8.V cm
B.
3
16 .V cm
C.
3
24 .V cm
D.
3
12 .V cm
Lời giải:
Gọi cạnh của hình lập phương đã cho là
0.tt
Diện tích một mặt của hình lập phương bằng
2
.t
Theo giả thiết:
2
6 24 2.tt
Vậy
3
8.Vt
Chọn đáp án A.
Câu 2: Cho hình lập phương
.ABCD A B C D
có
23BD
(tham khảo hình vẽ).
D'
C'
B'
A'
D
C
B
A
Thể tích của hình lập phương đó bằng
A.
16.
B.
64.
C.
8.
D.
512.
Lời giải:
D'
C'
B'
A'
D
B
A
Gọi cạnh của lập phương là
a
22
2 2 2 2
2 2 3 2.B D D D B D a a a
Vậy thể tích khối lập phương đó bằng
3
2 8.
Chọn đáp án C.
Câu 3: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
mặt bên
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với
ABCD
(tham khảo hình vẽ).
A
B
C
D
S
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
3
.
6
a
V
B.
3
.
12
a
V
C.
3
3
.
8
a
V
D.
3
3
.
24
a
V
Lời giải:
S
A
B
C
D
H
+) Ta có:
2
.
ABCD
Sa
+) Dựng
.SH AB
Ta có:
.
SH AB
SH ABCD
SAB ABCD

Vậy
3
2
.
1 1 3 3
. . . .
3 3 2 6
S ABCD ABCD
aa
V SH S a
Chọn đáp án A.
Câu 4: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
hai mặt phẳng
SAB
và
SAD
cùng
vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc bằng
o
30
(tham khảo hình vẽ).
A
B
C
D
S
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
6
.
3
a
V
B.
3
2
.
3
a
V
C.
3
6
.
6
a
V
D.
3
2.Va
Lời giải
Ta có:
.
SAB ABCD
SA ABCD
SAD ABCD

và
;.
BC AB
BC SAB SC SAB BSC
BC SA
Xét tam giác
SBC
vuông tại
:B
tan
BC
BSC
SB
22
3 2.
tan
BC
SB a SA SB AB a
BSC
và
2
.
ABCD
Sa
Vậy
3
.
12
..
33
S ABCD ABCD
a
V SA S
Chọn đáp án B.
a
30
0
A
B
C
D
S
Câu 5: Cho khối chóp
.S ABCD
có đáy
là hình chữ nhật,
,
3AD a
,
SA
vuông góc
với mặt phẳng đáy và mặt phẳng
SBC
tạo với đáy một góc
60
(tham khảo hình vẽ).
A
B
C
D
S
Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
3Va
. B.
3
3
3
a
V
. C.
3
Va
. D.
3
3
a
V
.
Lời giải:
Ta có
2
3
ABCD
Sa
. Vì
SBC ABCD BC
BC SB SBC
BC AB ABCD



,SBC ABCD SBA
. Vậy
60 .SBA 
Xét tam giác vuông
SAB
có:
tan tan 3
SA
SBA SA AB SBA a
AB
Vậy
3
.
1
.
3
S ABCD ABCD
V S SA a
.
Chọn đáp án C.
B
S
D
C
A
60
0
Câu 6: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
hình chiếu vuông góc của
S
trên mặt
phẳng
là trung điểm của
BC
và
SA
hợp với đáy một góc
o
60
(tham khảo hình vẽ).
S
A
B
C
Tính thể tích
V
của khối chóp
..S ABC
A.
3
3
.
8
a
V
B.
3
3
.
24
a
V
C.
3
5
.
8
a
V
D.
3
3
.
12
a
V
Lời giải:
H
C
B
A
S
+) Ta có:
2
3
.
4
ABC
a
S
+) Dựng
SH BC H
là trung điểm
.BC
Ta có:
;.
SH BC
SH ABC SA ABC SAH
SBC ABC
Xét tam giác
SAH
vuông tại
3
: tan .tan .
2
SH a
H SAH SH AH SAH
AH
Vậy
23
.
1 1 3 3 3
. . . .
3 3 2 4 8
S ABC ABC
a a a
V SH S
Chọn đáp án A.
Câu 7: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
(tham khảo
hình vẽ).
A'
B'
C
A
B
C'
Biết
2BC a
và thể tích lăng trụ bằng
3
2,a
khoảng cách
d
từ
A
đến mặt phẳng
'A BC
bằng
A.
35
.
5
a
B.
5a
. C.
5
.
5
a
D.
25
.
5
a
Lời giải:
H
K
A'
C'
B'
2a
A
B
C
Do tam giác
ABC
là tam giác vuông cân tại
A
và
2BC a
nên suy ra
2AB AC a
,
2
1
.
2
ABC
S AB AC a
.
Lúc đó lăng trụ đã cho có thể tích là:
'.
ABC
V AA S
.
Theo giả thiết:
23
'. 2 ' 2 .AA a a AA a
Gọi H là trung điểm BC
.AH a
Ta có:
'.AH BC BC A AH
Dựng
''AK A H AK A BC
. Vậy
; ' .d A A BC AK
Xét
'A AH
vuông tại
A
:
2 2 2
1 1 1 2 5
.
5
'
a
AK
AK A A AH
Chọn đáp án D.
Câu 8: Cho hình chóp
có đáy là tam giác đều cạnh bằng
a
và
SA
vuông góc với
.ABC
Biết
góc giữa
SC
và
SAB
bằng
o
30
(tham khảo hình vẽ).
S
A
B
C
Thể tích khối chóp
.S ABC
bằng
A.
3
6
.
12
a
B.
3
3
.
16
a
C.
3
.
12
a
D.
3
.
6
a
Lời giải:
H
C
B
A
S
Gọi
H
là trung điểm
HC AB
AB HC SAB
HC SA
0
; 60 .SC SAB HSC
Xét tam giác
SHC
vuông tại
: sin 3.
CH
H HSC SC a
SC
Ta có:
22
2.SA SC AC a
Ta có:
2
3
.
4
ABC
a
S
Suy ra:
3
.
16
..
3 12
S ABC ABC
a
V SA S
Chọn đáp án A.
Câu 9: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác vuông tại
A
,
o
, 60AC a ACB
(tham
khảo hình vẽ).
B'
A'
C
B
A
C'
Đường thẳng
'BC
tạo với mặt phẳng
''ACC A
một góc
0
30
. Tính thể tích
V
của khối lăng
trụ
. ' ' '.ABC A B C
A.
3
3Va
. B.
3
3
3
a
V
. C.
3
3Va
. D.
3
6Va
.
Lời giải:
Ta có
''AB ACC A
nên
0
', ' ' ' 30 .BC ACC A BC A
0
.tan60 3.AB AC a
0 2 2
' .cot30 3 ' 9 2 2 .AC AB a CC a a a
Vậy
3
. ' ' "
1
. . ' 6
2
ABC A B C
V AB AC AA a




.
Chọn đáp án D.
C'
A'
B
C
A
B'
Câu 10: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
,a
mặt bên
SAB
là tam giác cân tại
S
và
nằm trong mặt vuông góc với đáy,
SC
tạo với mặt đáy một góc bằng
o
60
(tham khảo hình
vẽ).
A
B
C
D
S
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
15
.
2
a
V
B.
3
3.Va
C.
3
15
.
6
a
V
D.
3
3
.
3
a
V
Lời giải
Dựng
SH AB H
là trung điểm
.AB
Do
.SAB ABCD SH ABCD
Vậy
0
; 60 .SC ABCD SCH
Xét tam giác
SHC
vuông tại
15
: tan
2
SH a
H SCH SH
HC
và
2
.
ABCD
Sa
Vậy
3
.
1 15
..
36
S ABCD ABCD
a
V SH S
Chọn đáp án C.
A
B
C
D
S
H
60
0
a
Câu 11: Cho hình chóp
.S ABCD
có đáy
là hình thoi cạnh bằng
30
o
,a CBD
và
SA
vuông góc
với đáy (tham khảo hình vẽ).
A
B
C
D
S
Biết góc giữa hai đường thẳng
SB
và
CD
bằng
60
o
,
tính thể tích
V
của khối chóp
..S ABCD
A.
3
2
.
a
V
B.
3
6
.
a
V
C.
3
3
2
.
a
V
D.
3
3
6
.
a
V
Lời giải:
Do
ABCD
là hình thoi cạnh bằng
0
30,a CBD
ΔABC
là tam giác đều cạnh bằng
.a
Suy ra:
22
33
22
42
..
ABCD ABC
aa
SS
Do
/ / ; ;CD AB SB CD SB AB SBA
(do
ΔSAB
vuông tại
A
).
Xét
SAB
vuông tại
A
:
3tan tan .
SA
SBA SA AB SBA a
AB
Vậy
23
1 1 3
3
3 3 2 2
.
. . . .
S ABCD ABCD
aa
V SA S a
Chọn đáp án A.
Câu 12: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
,,A AB a AB C

hợp với mặt đáy một góc
o
30
(tham khảo hình vẽ).
C
B'
A'
C'
B
A
Tính thể tích
V
của khối lăng trụ
.ABC A B C
A.
3
6
.
6
a
V
B.
3
6
.
36
a
V
C.
3
6
.
12
a
V
D.
3
6
.
4
a
V
Lời giải:
M
C'
B'
A'
A
B
C
+) Ta có:
2
1
..
22
ABC
a
S AB AC
+) Gọi
M
là trung điểm
.
B C A M
B C B C AA M B C AM
B C AA
Suy ra:
;.AB C A B C AMA
Xét tam giác
AA M
vuông tại
: tan
AA
A AMA
AM

16
tan . .tan .
26
a
AA A M AMA B C AMA
Vậy
3
.
6
..
12
ABC A B C ABC
a
V AA S

Chọn đáp án C.
Câu 13: Cho hình lăng trụ
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
,a
hình chiếu vuông góc của
A
trên
ABC
là trọng tâm tam giác
,ABC
AA
hợp với mặt đáy một góc
o
60
(tham khảo
hình vẽ).
M
G
C
B
A
B'
A'
C'
Tính thể tích
V
của khối lăng trụ
..ABC A B C
A.
3
3
.
4
a
V
B.
3
33
.
4
a
V
C.
3
3
.
12
a
V
D.
3
33
.
8
a
V
Lời giải:
M
G
C
B
A
B'
A'
C'
+) Ta có:
2
3
.
4
ABC
a
S
+) Gọi
M
là trung điểm
,B C G

là trọng tâm tam giác
.A B C
Do
AG A B C
nên
;.AA A B C AA G
Xét tam giác
A AG
vuông tại
: tan tan .
AG
G AA G AG A G AA G a
AG
Vậy
3
.
3
..
4
ABC A B C ABC
a
V A G S

Chọn đáp án A.
Câu 14: Cho hình lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
,a AC
hợp với mặt phẳng
ABB A

một góc
o
45
(tham khảo hình vẽ).
C
B'
A'
C'
B
A
Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
6
.
24
a
B.
3
3
.
4
a
C.
3
6
.
8
a
D.
3
6
.
4
a
Lời giải:
H
45
0
A
B
C
B'
C'
A'
a
a
a
Ta có:
2
3
.
4
A B C
a
S
Dựng
C H A B C H ABB A
0
; 45 .AC ABB A C AH
Suy ra
AHC
vuông cân tại
3
.
2
a
H HC AH
Xét tam giác
A AH
vuông tại
22
2
:.
2
a
A A A AH A H
Vậy
3
6
..
8
A B C
a
V AA S

Chọn đáp án C.
Câu 15: Gọi
V
là thể tích khối chóp
..S ABC
Gọi
,MN
lần lượt là trung điểm của các cạnh
,SB SC
(tham khảo hình vẽ).
M
S
A
B
C
N
Tính thể tích khối
.AMNCB
A.
.
4
V
B.
.
8
V
C.
.
2
V
D.
3
.
4
V
Lời giải:
M
S
A
B
C
N
Ta có:
.
. . .
.
1 1 3 3
..
4 4 4 4
S AMN
S AMN S ABC ABCNM S ABC
S ABC
V
SM SN
V V V V V
V SB SC
Chọn đáp án D.
Câu 16: Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau;
6AB a
,
7AC a
và
4AD a
. Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB (tham khảo hình vẽ).
P
N
M
C
B
A
D
Tính thể tích V của tứ diện AMNP.
A.
3
7
.
2
Va
B.
3
14 .Va
C.
3
28
.
3
Va
D.
3
7.Va
Lời giải
Ta có:
3
1
. . 28 .
6
ABCD
V AB AC AD a
Dễ thấy
MNP
được tạo nên bởi các đường trung bình của
BCD
chúng đồng dạng với nhau theo tỉ số
1
2
3
1 1 1 1
. 7 .
2 2 4 4
AMNP MNP
AMNP ABCD
ABCD BCD
VS
V V a
VS
Chọn đáp án D.
M
N
P
D
A
B
C
Câu 17: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
,MN
lần lượt là trung điểm
của các cạnh
,SA SD
(tham khảo hình vẽ).
N
M
A
S
D
C
B
Mặt phẳng
chứa
MN
và cắt các tia
,SB SC
lần lượt tại
,PQ
. Đặt
SP
x
SC
,
1
V
là thể tích
khối chóp
.S MNQP
và
V
là thể tích khối chóp
.S ABCD
. Tìm
x
để
1
2VV
.
A.
1
2
x
. B.
1 33
4
x

. C.
1 41
2
x

. D.
2x
.
Lời giải:
Q
P
N
M
A
S
D
C
B
Dễ thấy
//MN PQ
nên
1
;
2
SM SN SP SQ
x
SA SA SB SC
Ta có:
2
1
11
. . .
1 1 1
22
22
4 8 4 2
xx
V
xx
V x x



1 33
4
x


.
Chọn đáp án B.
Câu 18: Cho hình chóp
.S ABCD
có đáy là hình thang với
AB
song song với
CD
,
7CD AB
. Gọi
M
trên cạnh
SA
sao cho
SM
k
SA
,
01k
(tham khảo hình vẽ).
M
D
C
B
A
S
Giá trị của
k
để
CDM
chia khối chóp thành hai phần có thể tích bằng nhau là.
A.
7 53
.
2
k

B.
7 65
.
2
k

C.
7 71
.
4
k

D.
7 53
.
4
k

Lời giải:
Kẻ
/ / / / .MN AB CD
Gọi
1 2 3 4
; ; ;
SDMN SABD SDNC SDBC
V V V V V V V V
Ta có
24
1
7
VV
;
2
22
14
12
2
. . .
7
V k V
SM SN
k k k V k V
V SA SB
3
34
4
V
SN
k V kV
V SB
2
. . . 1 3 4
.
7
S DMNC S DMN S DNC
k
V V V V V V k



Mà
4
.
8
7
S ABCD
V
V
2
4
.
4
.
7
11
8
22
7
S DMNC
S ABCD
k
Vk
V
V
V



2
7 4 0kk
7 65
2
7 65
2
kN
kL


Chọn đáp án B.
Câu 19: Cho khối lăng trụ
.ABC A B C
có thể tích bằng 2. Gọi
M
,
N
lần lượt là hai điểm nằm trên hai
cạnh
AA
,
BB
sao cho
M
là trung điểm cạnh
AA
và
2
3
BN BB
(tham khảo hình vẽ).
N
M
A
B
C
C'
A'
B'
Đường thẳng
CM
cắt đường thẳng
CA

tại
P
và đường thẳng
CN
cắt đường thẳng
CB

tại
Q
. Thể tích khối đa diện
A MPB NQ

bằng:
A.
13
18
. B.
23
9
. C.
7
18
. D.
7
9
.
Lời giải:
P
Q
M
C
B
A'
B'
C'
A
N
Ta có:
.
.
C ABNM
C ABB A
dt ABNM
V
V
dt ABB A


1
2
AM BN
AA
1
2
AM BN
AA BB





1 1 2 7
2 2 3 12



.
..
7
12
C ABNM C ABB A
VV


.
72
..
12 3
ABC A B C
V
7 2 7
. .2
12 3 9

.
Mặt khác,
' ' 1 2 1
..
2 3 3
dt C A B
C A C B
C P C Q
dt C PQ


.
Do đó:
.
.
.
1
3 3. 1
1
3
..
3
ABC A B C
C C PQ
h dt C A B dt C A B
V
V
dt C PQ
h dt C PQ
hay
..C C PQ ABC A B C
VV
.
Suy ra:
.A MPB NQ C C PQ CMNC A B
V V V

.ABC A B C CMNC A B
VV

.C ABNM
V
7
9
.
Chọn đáp án D.
Câu 20: Cho hình chóp
.S ABCD
có cạnh
SA x
còn tất cả các cạnh khác có độ dài bằng
2
(tham khảo
hình vẽ).
S
D
C
B
A
Tính thể tích
max
V
lớn nhất của khối chóp
.S ABCD
.
A.
max
1.V
B.
max
1
.
2
V
C.
max
3.V
D.
max
2.V
Lời giải:
Gọi
O
là giao điểm của
AC
và
BD
. Ta có:
BAD BSD BCD
nên
AO SO CO
1
2
SO AC
SAC
vuông tại
S
Do đó:
2 2 2
4AC SA SC x
22
22
4 12
4
42
xx
OD AD AO

2
12BD x
,
0 2 3x
Ta thấy:
BD AC
BD SAC
BD SO

Trong
SAC
hạ
SH AC
. Khi đó:
SH AC
SH ABCD
SH BD

2 2 2
1 1 1
SH SA SC

2 2 2
. 2.
4
SA AC x
SH
SA SC x

2 2 2
.
2
1 1 2 1
. 4. 12 . . . 12
3 2 3
4
S ABCD
x
V x x x x
x
22
max
1 12
2 2.
32
xx
V

Dấu
""
xảy ra khi
22
12 6x x x
.
Chọn đáp án D.
_______________HẾT_______________
Huế, 15h40 ngày 15 tháng 9 năm 2021
S
A
B
C
D
O
H
a
a
x
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
TUYỂN TẬP ĐỀ THI THPT QUỐC GIA 2007 – 2022
THỂ TÍCH KHỐI ĐA DIỆN
NỘI DUNG ĐỀ BÀI
Câu 1: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh
12
cm. Người
ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x
(cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm
x
để hộp nhận được có thể tích lớn nhất.
A.
6x
B.
3x
C.
2x
D.
4x
Câu 2: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tính thể tích
V
của khối lập phương
.ABCD A B C D
, biết
3AC a
.
A.
3
Va
. B.
3
36
4
a
V
. C.
3
33Va
. D.
3
1
3
Va
.
Câu 3: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là
hình vuông cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng đáy và
2SA a
. Tính thể tích
V
của khối chóp
.S ABCD
A.
3
2
6
a
V
B.
3
2
4
a
V
C.
3
2Va
D.
3
2
3
a
V
Câu 4: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho tứ diện
DABC
có các cạnh
AB
,
AC
và
AD
đôi
một vuông góc với nhau;
6AB a
,
7AC a
và
4AD a
. Gọi
M
,
N
,
P
tương ứng là trung
điểm các cạnh
BC
,
CD
,
DB
. Tính thể tích
V
của tứ diện
AMNP
.
A.
3
7
2
Va
B.
3
14Va
C.
3
28
3
Va
D.
3
7Va
Câu 5: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác
.S ABCD
có đáy là hình
vuông cạnh bằng
2a
. Tam giác
SAD
cân tại
S
và mặt bên
SAD
vuông góc với mặt phẳng
đáy. Biết thể tích khối chóp
.S ABCD
bằng
3
4
3
a
. Tính khoảng cách
h
từ
B
đến mặt phẳng
SCD
A.
2
3
ha
B.
4
3
ha
C.
8
3
ha
D.
3
4
ha
Câu 6: (ĐTN BGD&ĐT NĂM 2016-2017) Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
2a
và
thể tích bằng
3
a
. Tính chiều cao
h
của hình chóp đã cho.
A.
3
6
a
h
B.
3
2
a
h
C.
3
3
a
h
D.
3ha
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Câu 7: (ĐTN BGD&ĐT NĂM 2016-2017) Cho tứ diện
ABCD
có thể tích bằng 12 và
G
là trọng tâm
của tam giác
BCD
. Tính thể tích
V
của khối chóp
.AGBC
A.
3V
B.
4V
C.
6V
D.
5V
Câu 8: (ĐTN BGD&ĐT NĂM 2016-2017) Cho lăng trụ tam giác
.
ABC A B C
có đáy
ABC
là tam giác
vuông cân tại
A
, cạnh
22AC
. Biết
AC
tạo với mặt phẳng
ABC
một góc
60
và
4
AC
. Tính thể tích
V
của khối đa diện

ABCB C
.
A.
8
3
V
B.
16
3
V
C.
83
3
V
D.
16 3
3
V
Câu 9: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Thể tích của khối lăng trụ tam giác đều có tất cả
các cạnh bằng
a
.
A.
3
3
.
6
a
V
B.
3
3
.
12
a
V
C.
3
3
.
2
a
V
D.
3
3
.
4
a
V
Câu 10: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hình chóp
.S ABCD
có đáy là hình vuông
cạnh
a
,
SA
vuông góc với mặt đáy,
SD
tạo với mặt phẳng
SAB
một góc bằng
30
. Tính
thể tích
V
của khối chóp
.S ABCD
.
A.
3
6
18
a
V
B.
3
3Va
C.
3
6
3
a
V
D.
3
3
3
a
V
Câu 11: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho khối tứ diện có thể tích bằng
V
. Gọi
V
là
thể tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho,
tính tỉ số
V
V
.
A.
1
2
V
V
. B.
1
4
V
V
. C.
2
3
V
V
. D.
5
8
V
V
.
Câu 12: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh
bên gấp hai lần cạnh đáy. Tính tích V của khối chóp tứ giác đã cho.
A.
3
2
.
2
a
V
B.
3
2
.
6
a
V
C.
3
14
.
2
a
V
D.
3
14
.
6
a
V
Câu 13: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho khối chóp S. ABCD có đáy là hình vuông cạnh a,
SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc
30
. Tính thể tích V của khối
chóp đã cho.
A.
3
6
.
3
a
V
B.
3
2
.
3
a
V
C.
3
2
.
3
a
V
D.
3
2.Va
Câu 14: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần
lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE)
chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích
V. Tính V.
A.
3
72
.
216
a
V
B.
3
11 2
.
216
a
V
C.
3
13 2
.
216
a
V
D.
3
2
.
18
a
V
Câu 15: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng
.ABC A B C
có
BB a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
.Va
B.
3
.
3
a
V
C.
3
.
6
a
V
D.
3
.
2
a
V
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Câu 16: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ
nhật,
AB a
,
3AD a
,
SA
vuông góc với mặt phẳng đáy và mặt phẳng
SBC
tạo với đáy
một góc
60
o
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
.
3
a
V
B.
3
3
.
3
a
V
C.
3
.Va
D.
3
.3Va
Câu 17: (MĐ 102 BGD&ĐT NĂM 2016-2017) Xét khối tứ diện
ABCD
có cạnh
AB x
và các cạnh
còn lại đều bằng
23
. Tìm
x
để thể tích khối tứ diện
ABCD
đạt giá trị lớn nhất.
A.
6.x
B.
14.x
C.
3 2.x
D.
2 3.x
Câu 18: (MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp
.S ABC
có
SA
vuông góc với đáy,
4SA
,
6AB
,
10BC
và
8CA
. Tính thể tích khối chóp
.S ABC
.
A.
40V
. B.
192
. C.
32V
. D.
24V
.
Câu 19: (MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy và khoảng cách từ
A
đến mặt phẳng
SBC
bằng
2
2
a
. Tính thể tích
V
của khối chóp đã cho.
A.
3
2
a
V
. B.
3
Va
. C.
3
3
9
a
V
. D.
3
3
a
V
.
Câu 20: (MĐ 103 BGD&ĐT NĂM 2016-2017) Xét khối chóp
.S ABC
có đáy là tam giác vuông cân tại
A
,
SA
vuông góc với đáy, khoảng cách từ
A
đến mặt phẳng
SBC
bằng
3
. Gọi
là góc
giữa mặt phẳng
SBC
và
ABC
, tính
cos
khi thể tích khối chóp
.S AB C
nhỏ nhất.
A.
1
cos .
3
B.
3
cos .
3
C.
2
cos .
2
D.
2
cos .
3
Câu 21: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2a
. Tính thể tích
V
của khối chóp
.S ABC
A.
3
13
12
a
V
. B.
3
11
12
a
V
. C.
3
11
6
a
V
. D.
3
11
4
a
V
.
Câu 22: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác cân với
AB AC a
,
120BAC 
. Mặt phẳng
AB C

tạo với đáy một góc
60
.
Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
3
8
a
V
. B.
3
9
8
a
V
. C.
3
8
a
V
. D.
3
3
4
a
V
.
Câu 23: (MĐ 104 BGD&ĐT NĂM 2016-2017) Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu
có bán kính bằng 9, tính thể tích
V
của khối chóp có thể tích lớn nhất.
A.
144V
. B.
576V
. C.
576 2V
. D.
144 6V
.
Câu 24: (ĐTK BGD&ĐT NĂM 2017-2018) Thể tích của khối chóp có chiều cao bằng
h
và diện tích
đáy bằng
B
là:
A.
1
3
V Bh.
B.
1
6
V Bh.
C.
V Bh.
D.
1
2
V Bh.
Câu 25: (ĐTK BGD&ĐT NĂM 2017-2018) Cho hình vuông
ABCD
và
ABEF
có cạnh bằng
1
, lần
lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi
S
là điểm đối xứng của
B
qua đường
thẳng
DE
. Thể tích của khối đa diện
ABCDSEF
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
A.
7
.
6
B.
11
.
12
C.
2
.
3
D.
5
.
6
Câu 26: (MĐ 101 BGD&ĐT NĂM 2017-2018) Cho khối chóp có đáy là hình vuông cạnh
a
và chiều
cao bằng
2a
. Thể tích của khối chóp đã cho bằng
A.
3
4a
B.
3
2
3
a
C.
3
2a
D.
3
4
3
a
Câu 27: (MĐ 101 BGD&ĐT NĂM 2017-2018) Ông
A
dự định dùng hết
2
6,5m
kính để làm một bể cá
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng . Bể cá có dung tích lớn
nhất bằng bao nhiêu?
A.
3
2,26 .m
B.
3
1,61 .m
C.
3
1,33 .m
D.
3
1,50 .m
Câu 28: (MĐ 101 BGD&ĐT NĂM 2017-2018) Cho khối lăng trụ
.ABC A B C
, khoảng cách từ
C
đến
đường thẳng
BB
bằng
2
, khoảng cách từ
A
đến các đường thẳng
BB
và
CC
lần lượt bằng
1
và
3
, hình chiếu vuông góc của
A
lên mặt phẳng
ABC
là trung điểm
M
của
BC

và
23
3
AM
. Thể tích của khối lăng trụ đã cho bằng
A.
2
B.
1
C.
3
D.
23
3
Câu 29: (ĐTK BGD&ĐT NĂM 2018-2019) Thể tích của khối lập phương cạnh
2a
bằng
A.
3
8a
. B.
3
2a
. C.
3
a
. D.
3
6a
.
Câu 30: (ĐTK BGD&ĐT NĂM 2018-2019) Cho khối chóp tứ giác đều có tất cả các cạnh bằng
2a
. Thể
tích của khối chóp đã cho bằng
A.
3
42
3
a
. B.
3
8
3
a
. C.
3
82
3
a
. D.
3
22
3
a
.
Câu 31: (ĐTK BGD&ĐT NĂM 2018-2019) Cho khối lăng trụ
.ABC A B C
có thể tích bằng 1. Gọi
,MN
lần lượt là trung điểm các đoạn thẳng
AA
và
BB
. Đường thẳng
CM
cắt đường thẳng
CA

tại
P
, đường thẳng
CN
cắt đường thẳng
CB

tại
Q
. Thể tích của khối đa diện lồi
A MPB NQ

bằng
A.
1
. B.
1
3
. C.
1
2
. D.
2
3
.
Câu 32: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam
giác đều cạnh
a
và
'3AA a
. Thể tích của lăng trụ đã cho bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
4
a
. D.
3
2
a
.
Câu 33: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho lăng trụ
' ' 'ABC A B C
có chiều cao bằng
8
và đáy
là tam giác đều cạnh bằng
6
. Gọi
,MN
và
P
lần lượt là tâm của các mặt bên
''ABB A
,
''ACC A
và
''BCC B
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng:
A.
27 3
. B.
21 3
. C.
30 3
. D.
36 3
.
Câu 34: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối lập phương có cạnh bằng 6. Thể tích của
khối lập phương đã cho bằng
A. 216. B. 18. C. 36. D. 72.
Câu 35: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối lăng trụ đứng
.
ABCD A B C D
có đáy là
hình thoi cạnh
,3a BD a
và
4
AA a
(minh họa như hình bên dưới). Thể tích của khối
lăng trụ đã cho bằng
A.
3
2 3 .a
B.
3
4 3 .a
C.
3
23
.
3
a
D.
3
43
.
3
a
Câu 36: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối chóp
.S ABC
có đáy
ABC
là tam giác
vuông cân tại
, , 90 ,A AB a SBA SCA
góc giữa hai mặt phẳng
SAB
và
SAC
bằng
60
. Thể tích khối chóp đã cho bằng
A.
3
a
. B.
3
3
a
. C.
3
2
a
. D.
3
6
a
.
Câu 37: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Thể tích của khối lập phương cạnh
2
bằng
A.
6
. B.
8
. C.
4
. D.
2
.
Câu 38: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Cho khối chóp có diện tích đáy
3B
và chiều cao
4h
. Thể tích của khối chóp đã cho bằng
A.
6
. B.
12
. C.
36
. D.
4
.
Câu 39: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Cho hình hộp
. ' ' ' 'ABC D A B C D
có chiều cao bằng
8
và diện tích đáy bằng
9.
Gọi
,,M N P
và
Q
lần lượt là tâm của các mặt bên
' ', ' ', ' 'ABB A BCC B CDD C
và
''DAA D
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , , ,A B C D M N P
và
Q
bằng
A. 27. B. 30. C. 18. D. 36
Câu 40: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho khối hộp chữ nhật có 3 kích thước
3;4;5
. Thể tích
của khối hộp đã cho bằng?
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
A.
10
. B.
20
. C.
12
. D.
60
.
Câu 41: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho khối chóp có diện tích đáy
6B
và chiều cao
2h
. Thể tích của khối chóp đã cho bằng:
A.
6
. B.
3
. C.
4
. D.
12
.
Câu 42: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
a
, cạnh
bên bằng
2a
và
O
là tâm của đáy. Gọi
M
,
N
,
P
,
Q
lần lượt là các điểm đối xứng với
O
qua
trọng tâm của các tam giác
SAB
,
SBC
,
SCD
,
SDA
và
'S
là điểm đối xứng với
S
qua
O
. Thể
tích của khối chóp
'.S MNPQ
bằng
A.
3
20 14
81
a
. B.
3
40 14
81
a
. C.
3
10 14
81
a
. D.
3
2 14
9
a
.
Câu 43: (ĐỀ THAM KHẢO 2021) Một khối chóp có diện tích đáy bằng 6 và chiều cao bằng 5. Thể tích
của khối chóp đó bằng
A. 10. B. 30. C. 90. D. 15.
Câu 44: (ĐỀ THAM KHẢO 2021) Thể tích của khối hộp chữ nhật có ba kích thước 2; 3; 7 bằng
A. 14. B. 42. C. 126. D. 12.
Câu 45: (ĐỀ THAM KHẢO 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh a, cạnh
bên SA vuông góc với mặt phẳng đáy, góc giữa
SA
và mặt phằng
()SBC
bằng
45
(tham
khảo hình bên). Thể tích của khối chóp
.S ABC
bằng
A.
3
8
a
. B.
3
3
8
a
. C.
3
3
12
a
. D.
3
4
a
.
Câu 46: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Thể tích của khối lập phương cạnh
5a
bằng
A.
3
5a
. B.
3
a
. C.
3
125a
. D.
3
25a
.
Câu 47: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Cho khối chóp có diện tích đáy
2
5Ba
và chiều
cao
ha
. Thể tích của khối chóp đã cho bằng
A.
3
5
6
a
. B.
3
5
2
a
. C.
3
5a
. D.
3
5
3
a
.
Câu 48: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy
là hình vuông,
2BD a
, góc giữa hai mặt phẳng
'A BD
và
ABC D
bằng
0
30
. Thể tích của
khối hộp chữ nhật đã cho bằng
A.
3
63a
. B.
3
23
9
a
. C.
3
23a
. D.
3
23
3
a
.
Câu 49: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối chóp có diện tích đáy
B
và chiều cao
h
. Thể tích
V
của khối chóp đã cho được tính theo công thức nào dưới đây ?
A.
1
3
V Bh
. B.
4
3
V Bh
. C.
V Bh
. D.
3V Bh
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Câu 50: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối lăng trụ có diện tích đáy
2
5Ba
và
chiều cao
ha
. Thể tích của khối lăng trụ đã cho bằng
A.
3
5
3
a
. B.
3
5a
. C.
3
5
6
a
. D.
3
5
2
a
.
Câu 51: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối lăng trụ tam giác đều
ABCA B C
có
cạnh bên bằng
4a
, góc giữa hai mặt phẳng
A BC
và
ABC
bằng
30
. Thể tich của khối
lăng trụ đã cho bằng
A.
3
64 3a
. B.
3
64 3
3
a
. C.
3
64 3
27
a
. D.
3
64 3
9
a
.
Câu 52: (ĐỀ THAM KHẢO 2022) Cho khối chóp có diện tích đáy
7B
và chiều cao
6h
. Thể tích
của khối chóp đã cho bằng
A.
42
. B.
126
. C.
14
. D.
56
.
Câu 53: (ĐỀ THAM KHẢO 2022) Cho khối lăng trụ có diện tích đáy
B
và chiều cao
h
. Thể tích
V
của
khối lăng trụ đã cho được tính theo công thức nào dưới đây?
A.
1
3
V Bh
. B.
4
3
V Bh
. C.
6V Bh
. D.
V Bh
.
Câu 54: (ĐỀ THAM KHẢO 2022) Cho khối chóp đều
.S ABCD
có
4AC a
, hai mặt phẳng
SAB
và
SCD
vuông góc với nhau. Thể tích khối chóp đã cho bằng
A.
3
16 2
3
a
. B.
3
82
3
a
. C.
3
16a
. D.
3
16
3
a
.
______________________HẾT______________________
Huế, 16h00 Ngày 27 tháng 6 năm 2022
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
LỜI GIẢI CHI TIẾT
Câu 1: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh
12
cm. Người
ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x
(cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm
x
để hộp nhận được có thể tích lớn nhất.
A.
6x
B.
3x
C.
2x
D.
4x
Li gii:
Ta có :
h x cm
là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là:
12 2x cm
Vậy diện tích đáy hình hộp
2
2
12 2S x cm
. Ta có:
00
0;6
12 2 0 6
xx
x
xx




Thể tích của hình hộp là:
2
.1. 22VS xh x
Xét hàm số:
2
. 12 2 0;6y x x x
Ta có :
2
' 12 2 4 12 2 12 2 12 6y x x x x x
;
' 0 12 2 . 12 6 0 2y x x x
hoặc
6x
(loại).
Suy ra với
2x
thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là
2 128y
.
Câu 2: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tính thể tích
V
của khối lập phương
.ABCD A B C D
, biết
3AC a
.
A.
3
Va
. B.
3
36
4
a
V
. C.
3
33Va
. D.
3
1
3
Va
.
Li gii:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Giả s khối lập phương có cạnh bằng
;0xx
Xt tam giác
' ' 'A B C
vuông cân tại
'B
ta có:
2 2 2
' ' ' ' ' 'A C A B B C
2 2 2
2x x x
' ' 2A C x
Xt tam giác
''A A C
vuông tại
'A
ta có
2 2 2
' ' ' 'AC A A A C
2 2 2
32a x x
xa
Thể tích của khối lập phương
.ABCD A B C D
là
3
Va
.
Câu 3: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là
hình vuông cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng đáy và
2SA a
. Tính thể tích
V
của khối chóp
.S ABCD
A.
3
2
6
a
V
B.
3
2
4
a
V
C.
3
2Va
D.
3
2
3
a
V
Li gii:
A
B
D
C
S
Ta có
SA ABCD SA
là đường cao của hình chóp
Thể tích khối chóp
.S ABCD
:
3
2
1 1 2
. . 2.
3 3 3
ABCD
a
V SA S a a
.
Câu 4: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho tứ diện
DABC
có các cạnh
AB
,
AC
và
AD
đôi
một vuông góc với nhau;
6AB a
,
7AC a
và
4AD a
. Gọi
M
,
N
,
P
tương ứng là trung
điểm các cạnh
BC
,
CD
,
DB
. Tính thể tích
V
của tứ diện
AMNP
.
A.
3
7
2
Va
B.
3
14Va
C.
3
28
3
Va
D.
3
7Va
Li gii:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Ta có
3
1 1 1
. . 6 .7 .4 28
3 2 6
ABCD
V AB AD AC a a a a
Ta nhận thấy
3
1 1 1
7
2 4 4
MNP MNPD BCD AMNP ABCD
S S S V V a
.
Câu 5: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác
.S ABCD
có đáy là hình
vuông cạnh bằng
2a
. Tam giác
SAD
cân tại
S
và mặt bên
SAD
vuông góc với mặt phẳng
đáy. Biết thể tích khối chóp
.S ABCD
bằng
3
4
3
a
. Tính khoảng cách
h
từ
B
đến mặt phẳng
SCD
A.
2
3
ha
B.
4
3
ha
C.
8
3
ha
D.
3
4
ha
Li gii:
Gọi
I
là trung điểm của
AD
. Tam giác
SAD
cân tại
S
SI AD
Ta có
SI AD
SI ABCD
SAD ABCD

SI
là đường cao của hình chóp.
Theo giả thiết
32
.
1 4 1
. . .2 2
3 3 3
S ABCD ABCD
V SI S a SI a SI a
Vì
AB
song song với
SCD
, , 2 ,d B SCD d A SCD d I SCD
Gọi
H
là hình chiếu vuông góc của
I
lên
SD
.
Mặt khác
SI DC
IH DC
ID DC

. Ta có
,
IH SD
IH SCD d I SCD IH
IH DC
Xt tam giác
SID
vuông tại
2 2 2 2 2
1 1 1 1 4 2
:
4 2 3
a
I IH
IH SI ID a a
4
, , 2 ,
3
d B SCD d A SCD d I SCD a
.
Câu 6: (ĐTN BGD&ĐT NĂM 2016-2017) Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
2a
và
thể tích bằng
3
a
. Tính chiều cao
h
của hình chóp đã cho.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
A.
3
6
a
h
B.
3
2
a
h
C.
3
3
a
h
D.
3ha
Li gii:
Do đáy là tam giác đều cạnh
2a
nên
2
2
23
3
4

ABC
a
Sa
.
Mà
1
.
3
ABC
V S h
3
2
33
3
3
ABC
Va
ha
S
a
.
Câu 7: (ĐTN BGD&ĐT NĂM 2016-2017) Cho tứ diện
ABCD
có thể tích bằng 12 và
G
là trọng tâm
của tam giác
BCD
. Tính thể tích
V
của khối chóp
.AGBC
A.
3V
B.
4V
C.
6V
D.
5V
Li gii:
Cách 1:
Phân tích: tứ diện
ABCD
và khối chóp
.AGBC
có cùng đường cao là khoảng cách từ
A
đến
mặt phẳng
BCD
. Do
G
là trọng tâm tam giác
BCD
nên ta có

BGC BGD CGD
S S S
3


BCD BGC
SS
(xem phần chứng minh).
Áp dụng công thức thể tích hình chóp ta có:
.
.
1
1
.
.
3
3
3
1
1
.
.
3
3
ABCD BCD
BCD
ABCD BCD
A GBC GBC
GBC
A GBC GBC
V h S
hS
VS
VS
hS
V h S
.
11
.12 4
33
A GBC ABCD
VV
.
Chứng minh: Đặt
;DN h BC a
.
+)
11
//
2 2 2
MF CM h
MF ND MF DN MF
DN CD
.
+)
2 2 2
// .
3 3 3 2 3
GE BG h h
GE MF GE MF
MF BM
A
B
C
D
G
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
+)
11
.
22
33
11
.
2 2 3

BCD
BCD GBC
GBC
DN BC ha
S
SS
h
S
GE BC a
+) Chứng minh tương tự có
33

BCD GBD GCD
S S S
BGC BGD CGD
S S S
Cách 2:
Ta có
;
11
;;
33
;
d G ABC
GI
d G ABC d D ABC
DI
d D ABC
.
Nên
.
11
; . . 4
33
G ABC ABC DABC
V d G ABC S V
G
I
D
B
C
A
H
1
H
Câu 8: (ĐTN BGD&ĐT NĂM 2016-2017) Cho lăng trụ tam giác
.
ABC A B C
có đáy
ABC
là tam giác
vuông cân tại
A
, cạnh
22AC
. Biết
AC
tạo với mặt phẳng
ABC
một góc
60
và
4
AC
. Tính thể tích
V
của khối đa diện

ABCB C
.
A.
8
3
V
B.
16
3
V
C.
83
3
V
D.
16 3
3
V
Li gii:
Phân tích: Tính thể tích của khối đa diện

ABCB C
bằng thể tích khối của lăng trụ
.
ABC A B C
trừ đi thể tích của khối chóp
.
A A B C
.
Giả s đường cao của lăng trụ là
CH
. Khi đó góc giữa
AC
mặt phẳng
ABC
là góc
60
C AH
.
B’
B
A
C
H
C’
A’
22
4
0
60
23
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Ta có:
sin60 2 3; 4
ABC
CH
C H S
AC
;
2
.
1
. 2 3. . 2 2 8 3
2
ABC A B C ABC
V C H S
.
..
1 1 8 3
..
3 3 3
A A B C ABC ABC A B C
V C H S V
;
..
8 3 16 3
83
33
ABB C C ABC A B C A A B C
V V V
.
Câu 9: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Thể tích của khối lăng trụ tam giác đều có tất cả
các cạnh bằng
a
.
A.
3
3
.
6
a
V
B.
3
3
.
12
a
V
C.
3
3
.
2
a
V
D.
3
3
.
4
a
V
Li gii:
3
2
3
.
3
4
4
ha
a
V h S
a
S
.
Câu 10: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hình chóp
.S ABCD
có đáy là hình vuông
cạnh
a
,
SA
vuông góc với mặt đáy,
SD
tạo với mặt phẳng
SAB
một góc bằng
30
. Tính
thể tích
V
của khối chóp
.S ABCD
.
A.
3
6
18
a
V
B.
3
3Va
C.
3
6
3
a
V
D.
3
3
3
a
V
Li gii:
A
B
D
C
S
Góc giữa SD và mp là
0
30DSA
.
Ta có
0
3
tan30
AD
SA a
. Suy ra:
3
2
13
.3
33
a
V a a
.
Câu 11: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho khối tứ diện có thể tích bằng
V
. Gọi
V
là
thể tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho,
tính tỉ số
V
V
.
A.
1
2
V
V
. B.
1
4
V
V
. C.
2
3
V
V
. D.
5
8
V
V
.
Li gii:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Cách 1. Đặc biệt hóa tứ diện cho là tứ diện đều cạnh
a
. Hình đa diện cần tính có được bằng
cách cắt
4
góc của tứ diện, mỗi góc cũng là một tứ diện đều có cạnh bằng
2
a
.
Do đó thể tích phần cắt bỏ là
4.
82
VV
V


.
Vậy
1
22
VV
V
V
.
Cách 2. Khối đa diện là hai khối chóp tứ giác có cùng đáy là hình bình hành úp lại. Suy ra:
. . .
1 1 1
2 4. 4. 4. .
2 4 2
N MEPF N MEP P MNE
V V V V V V
Cách 3. Ta có
. . . .
'
AQEP B QMF C MNE D NPF
V V V V V
V
VV
..
..
1
AQEP B QMF
C MNE D NPF
VV
VV
V V V V
1 1 1 1 1 1 1 1 1 1 1 1 1
1 . . . . . . . .
2 2 2 2 2 2 2 2 2 2 2 2 2
.
Câu 12: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh
bên gấp hai lần cạnh đáy. Tính tích V của khối chóp tứ giác đã cho.
A.
3
2
.
2
a
V
B.
3
2
.
6
a
V
C.
3
14
.
2
a
V
D.
3
14
.
6
a
V
Li gii:
.S ABCD
là khối chóp tứ giác đều
ABCD
là hình vuông và
, SO ABCD O
là tâm của
hình vuông.
Q
P
N
M
D
C
B
A
E
F
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
2
2 2 2
1 2 2 14
;4
2 2 2 2
aa
OD BD SO SD OD a a




23
1 1 14 14
. . . .
3 3 2 6
ABCD
V SO S a a a
.
Câu 13: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho khối chóp S. ABCD có đáy là hình vuông cạnh a,
SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc
30
. Tính thể tích V của khối
chóp đã cho.
A.
3
6
.
3
a
V
B.
3
2
.
3
a
V
C.
3
2
.
3
a
V
D.
3
2.Va
Li gii:

lµ hinh vu«ngBC BA ABCD
BC SA SA ABCD
, 30BC SAB SC SAB BSC
SBC
vuông tại B:
0
0
tan30 3
tan30
BC BC
SB a
SB
SAB
vuông tại A:
2 2 2 2
32SA SB AB a a a
C
B
D
A
S
a
30
0
C
B
D
A
S
O
a
2a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
23
1 1 2
. . 2 .
3 3 3
ABCD
V SA S a a a
Câu 14: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần
lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE)
chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích
V. Tính V.
A.
3
72
.
216
a
V
B.
3
11 2
.
216
a
V
C.
3
13 2
.
216
a
V
D.
3
2
.
18
a
V
Li gii:
MNE
chia khối tứ diện ABCD thành 2 khối đa diện
1
:.AC MNPQ
và
2
:.BD MNPQ
MNE
cắt AD tại Q, cắt CD tại P.
. . .AC MNPQ E AMNC E ACPQ
V V V








.
1
,.
3
1
,.
3
11
,.
34
1 3 3
.2. D, .
3 4 2
E AMNC AMNC
ABC BMN
ABC ABC
ABC ABCD
V d E AMNC S
d E ABC S S
d E ABC S S
d ABC S V
.
1 1 1 8 8
, . B, . B, .
3 3 3 9 9
E ACPQ ACPQ ACD DPQ ACD ABCD
V d E ACPQ S d ACD S S d ACD S V
33
.
3 8 11 11 2 11 2
.
2 9 18 18 12 216
AC MNPQ ABCD ABCD ABCD
V V V V a a
.
Câu 15: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng
.ABC A B C
có
BB a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
.Va
B.
3
.
3
a
V
C.
3
.
6
a
V
D.
3
.
2
a
V
Li gii:
A
B
C
D
Q
P
E
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
a
a
2
C'
B'
A
B
C
A'
Tam giác
ABC
vuông cân tại
B
2
AC
AB BC a
. Suy ra:
2
1
2
ABC
Sa
.
Khi đó:
3
2
.
1
..
22
ABC A B C ABC
a
V S BB a a
.
Câu 16: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ
nhật,
AB a
,
3AD a
,
SA
vuông góc với mặt phẳng đáy và mặt phẳng
SBC
tạo với đáy
một góc
60
o
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
.
3
a
V
B.
3
3
.
3
a
V
C.
3
.Va
D.
3
.3Va
Li gii:
60
a
a
3
D
A
B
C
S
Ta có
2
3
ABCD
Sa
.
Vì
,;
SBC ABCD BC
BC SB SBC SBC ABCD SB AB SBA
BC AB ABCD


.
Vậy
60
o
SBA
Xét tam giác vuông
SAB
có:
tan60 .tan60 3
oo
SA
SA AB a
AB
Vậy
23
.
11
. 3. 3
33
S ABCD ABCD
V S SA a a a
.
Câu 17: (MĐ 102 BGD&ĐT NĂM 2016-2017) Xét khối tứ diện
ABCD
có cạnh
AB x
và các cạnh
còn lại đều bằng
23
. Tìm
x
để thể tích khối tứ diện
ABCD
đạt giá trị lớn nhất.
A.
6.x
B.
14.x
C.
3 2.x
D.
2 3.x
Li gii:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
2
3
2
3
2
3
2
3
2
3
x
M
N
A
D
C
B
Gọi
,MN
lần lượt là trung điểm của
CD
và
AB
.
Ta có
CD MB CD MN
CD MAB
CD MA CD AB





.
Tam giác
MAB
cân tại
M
nên
MN AB
.
11
. . , .sin , .2 3. .sin90
66
ABCD
V ABCD d AB CD AB CD x MN
22
2
22
36
1 3 3
.2 3. 3 . 36 . 3 3
6 2 6 6 2
xx
x
x x x








.
Dấu
""
xảy ra
2
36 3 2x x x
.
Vậy với
32x
thì
ABCD
V
đạt giá trị lớn nhất bằng
33
.
Câu 18: (MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp
.S ABC
có
SA
vuông góc với đáy,
4SA
,
6AB
,
10BC
và
8CA
. Tính thể tích khối chóp
.S ABC
.
A.
40V
. B.
192
. C.
32V
. D.
24V
.
Li gii:
8
6
10
4
A
C
B
S
Ta có
2 2 2
AB AC BC
suy ra tam giác
ABC
vuông tại
A
,do đó diện tích tam giác
ABC
là:
11
. .6.8 24
22
S AB AC
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Ta có
11
. . .4.24 32
33
SABC ABC
V SA S
.
Câu 19: (MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy và khoảng cách từ
A
đến mặt phẳng
SBC
bằng
2
2
a
. Tính thể tích
V
của khối chóp đã cho.
A.
3
2
a
V
. B.
3
Va
. C.
3
3
9
a
V
. D.
3
3
a
V
.
Li gii:
Kẻ
AH
vuông góc
SB
.
Ta có
()AH SBC
nên
AH
chính là khoảng cách từ
A
đến mp
SBC
.
Ta có
2 2 2 2 2 2 2
1 1 1 1 1 1 1
AH SA AB SA AH AB a
.
Suy ra
SA a
. Thể tích cần tính là
3
1
..
33

a
V a a a
.
Câu 20: (MĐ 103 BGD&ĐT NĂM 2016-2017) Xét khối chóp
.S ABC
có đáy là tam giác vuông cân tại
A
,
SA
vuông góc với đáy, khoảng cách từ
A
đến mặt phẳng
SBC
bằng
3
. Gọi
là góc
giữa mặt phẳng
SBC
và
ABC
, tính
cos
khi thể tích khối chóp
.S ABC
nhỏ nhất.
A.
1
cos .
3
B.
3
cos .
3
C.
2
cos .
2
D.
2
cos .
3
Li gii:
Gọi
M
là trung điểm
BC
,
H
là giao điểm của đường thẳng qua
A
và vuông góc với
SM
. Ta
được:
Góc giữa mặt phẳng
SBC
và
ABC
là
SMA
.
3
;
sin
AM
3
cos
SA
;
1
.
2
AM BC
Suy ra
2
.
2
19
..
3 sin .cos
S ABC
V AM SA


.
Thể tích khối chóp nhỏ nhất khi
2
sin .cos

lớn nhất.
Xét hàm số
23
f sin .cos cos cosx x x x x
với
0
2
x

sin 3cos .sinf x x x x
,
sin 0
( ) 0
3
cos
3
x
fx
x


Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Suy ra
2
sin .cos

lớn nhất khi
3
cos .
3
Câu 21: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2a
. Tính thể tích
V
của khối chóp
.S ABC
A.
3
13
12
a
V
. B.
3
11
12
a
V
. C.
3
11
6
a
V
. D.
3
11
4
a
V
.
Li gii:
O
I
A
C
B
S
Do đáy là tam giác đều nên gọi
I
là trung điểm cạnh
BC
, khi đó
AI
là đường cao của tam
giác đáy. Theo định lý Pitago ta có
2
2
3
42
aa
AI a
, và
2 2 3 3
3 3.2 3
aa
AO AI
.
Trong tam giác
SOA
vuông tại
O
ta có
2
2
11
4
3
3
aa
SO a
Vậy thể tích khối chóp
.S ABC
là
3
1 1 3 11 11
..
3 2 2 12
3
a a a
Va
.
Câu 22: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng
.ABC A B C
có đáy
ABC
là
tam giác cân với
AB AC a
,
120BAC 
. Mặt phẳng
AB C

tạo với đáy một góc
60
.
Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
3
8
a
V
. B.
3
9
8
a
V
. C.
3
8
a
V
. D.
3
3
4
a
V
.
Li gii:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Gọi
I
là trung điểm của
BC

.
Trong
2 2 2 2
: 2 . .cos 3A B C B C A B A C A B A C B A C a
2
13
. .sin120
24
ABC
a
S a a
;
2
23
2
23
ABC
S a a
AI
BC
a

Ta có :
60
AB C A B C B C
AI B C AIA
A I B C

Trong tam giác vuông
AIA
có
3
.tan60
2
a
AA A I

.
Vậy thể tích
23
3 3 3
.
4 2 8
a a a
V 
.
Câu 23: (MĐ 104 BGD&ĐT NĂM 2016-2017) Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu
có bán kính bằng 9, tính thể tích
V
của khối chóp có thể tích lớn nhất.
A.
144V
. B.
576V
. C.
576 2V
. D.
144 6V
.
Li gii:
Gọi độ dài cạnh đáy, chiều cao của hình chóp tứ giác đều lần lượt là
; ( , 0)x h x h
. Ta có đáy
là hình vuông với độ dài na đường chéo bằng
2
x
suy ra độ dài cạnh bên
2
2
2
x
lh
.
Ta có bán kính mặt cầu ngoại tiếp hình chóp
2
2
2
22
2
9 36 2
22
x
h
l
R x h h
hh
.
Diện tích đáy của hình chóp
2
Sx
nên
22
11
. 36 2
33
V h x h h h
Ta có
3
2
1 1 1 36 2
. 36 2 . . 36 2 . 576 576
3 3 3 3
h h h
h h h h h h V



, dấu bằng xảy ra
khi
36 2 12, 12h h h h x
vậy
576
max
V
.
Câu 24: (ĐTK BGD&ĐT NĂM 2017-2018) Thể tích của khối chóp có chiều cao bằng
h
và diện tích
đáy bằng
B
là:
A.
1
3
V Bh.
B.
1
6
V Bh.
C.
V Bh.
D.
1
2
V Bh.
Li gii:
Thể tích của khối chóp có chiều cao bằng
h
và diện tích đáy bằng
B
là:
V Bh
1
3
.
Câu 25: (ĐTK BGD&ĐT NĂM 2017-2018) Cho hình vuông
ABCD
và
ABEF
có cạnh bằng
1
, lần
lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi
S
là điểm đối xứng của
B
qua đường
thẳng
DE
. Thể tích của khối đa diện
ABCDSEF
bằng
A.
7
.
6
B.
11
.
12
C.
2
.
3
D.
5
.
6
Li gii:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
S
F
E
D
C
B
A
Ta có:ADF.BCE là hình lăng trụ đứng có đáy là tam giác vuông cân
Dựa vào hình vẽ ta có :
. ....
2
ABCDSEF ADF BCE ADFS CDFE B CDFEBCE AD E B DEF ABC
V V V V V V V
.
1 1 1 1 1 5
. ; . 2.
2 3 6 2 6 6

ADF BCE BCE BADE ABE ABCDSEF
V AB S V AD S V
.
Câu 26: (MĐ 101 BGD&ĐT NĂM 2017-2018) Cho khối chóp có đáy là hình vuông cạnh
a
và chiều
cao bằng
2a
. Thể tích của khối chóp đã cho bằng
A.
3
4a
B.
3
2
3
a
C.
3
2a
D.
3
4
3
a
Li gii:
Khối chóp có đáy là hình vuông cạnh
a
nên có diện tích đáy:
2
đáy
Sa
.
Chiều cao
2ha
.
Vậy thể tích khối chóp đã cho là
1
..
3
đáy
V S h
2
1
. .2
3
aa
3
2
3
a
.
Câu 27: (MĐ 101 BGD&ĐT NĂM 2017-2018) Ông
A
dự định dùng hết
2
6,5m
kính để làm một bể cá
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng . Bể cá có dung tích lớn
nhất bằng bao nhiêu?
A.
3
2,26 .m
B.
3
1,61 .m
C.
3
1,33 .m
D.
3
1,50 .m
Li gii:
c
b
a
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Giả s hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá:
V abc
Mặt khác theo giả thiết ta có:
2 2 6,5
2
ab bc ac
ab
2
2 6 6,5
2

b bc
ab
2
6,5 2
6
2
b
c
b
ab
Khi đó
2
2
6,5 2
2.
6
b
Vb
b
3
6,5 2
3

bb
V
.
Xét hàm số:
3
6,5 2
3
bb
fb
. Có BBT
Vậy bể cá có dung tích lớn nhất là :
3
39
1,50
6




fm
.
Câu 28: (MĐ 101 BGD&ĐT NĂM 2017-2018) Cho khối lăng trụ
.ABC A B C
, khoảng cách từ
C
đến
đường thẳng
BB
bằng
2
, khoảng cách từ
A
đến các đường thẳng
BB
và
CC
lần lượt bằng
1
và
3
, hình chiếu vuông góc của
A
lên mặt phẳng
ABC
là trung điểm
M
của
BC

và
23
3
AM
. Thể tích của khối lăng trụ đã cho bằng
A.
2
B.
1
C.
3
D.
23
3
Li gii:
T
M
B
2
H
C
2
A'
C
1
A
B
1
A
A'
T
B'
C'
M
H
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Cắt lăng trụ bởi một mặt phẳng qua
A
và vuông góc với
AA
ta được thiết diện là tam giác
11
A B C
có các cạnh
1
1AB
;
1
3AC
;
11
2BC
.
Suy ra tam giác
11
A B C
vuông tại
A
và trung tuyến
AH
của tam giác đó bằng
1
.
Gọi giao điểm của
AM
và
AH
là
T
.
Ta có:
23
3
AM
;
1AH
1
3
MH
. Suy ra
30MA H

.
Do đó
60MA A

4
3
cos
AM
AA
MA A
.
Thể tích khối lăng trụ
.ABC A B C
bằng thể tích khối lăng trụ
1 1 2 2
.A B C AB C
và bằng
11
43
.2
2
3
A B C
V AA S
.
Câu 29: (ĐTK BGD&ĐT NĂM 2018-2019) Thể tích của khối lập phương cạnh
2a
bằng
A.
3
8a
. B.
3
2a
. C.
3
a
. D.
3
6a
.
Li gii:
Thể tích của khối lập phương cạnh
2a
bằng
3
3
28aa
.
Câu 30: (ĐTK BGD&ĐT NĂM 2018-2019) Cho khối chóp tứ giác đều có tất cả các cạnh bằng
2a
. Thể
tích của khối chóp đã cho bằng
A.
3
42
3
a
. B.
3
8
3
a
. C.
3
82
3
a
. D.
3
22
3
a
.
Li gii:
O
A
D
B
C
S
Xét khối chóp tứ giác đều
.S ABCD
có đáy là hình vuông tâm
O
, suy ra
SO ABCD
.
Ta có:
+
22AC a
2AO a
;
22
SO SA AO
22
42aa
2a
.
+
2
2
24
ABCD
S a a
.
Vậy
1
..
3
ABCD
V SO S
2
1
. 2.4
3
aa
3
42
3
a
.
Câu 31: (ĐTK BGD&ĐT NĂM 2018-2019) Cho khối lăng trụ
.ABC A B C
có thể tích bằng 1. Gọi
,MN
lần lượt là trung điểm các đoạn thẳng
AA
và
BB
. Đường thẳng
CM
cắt đường thẳng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
CA

tại
P
, đường thẳng
CN
cắt đường thẳng
CB

tại
Q
. Thể tích của khối đa diện lồi
A MPB NQ

bằng
A.
1
. B.
1
3
. C.
1
2
. D.
2
3
.
Li gii:
N
M
A
C
B
A'
B'
C'
P
Q
+) Ta có
A
là trung điểm
PC
;
B
là trung điểm
QC
. Do đó
44
C PQ
C PQ C A B
C A B
S
SS
S
.
+)
. . . .
14
. 4 4 .
33
C PQ
C C PQ C A B C C A B C ABC A B C
C A B
S
V V V V
S



+) Mặt khác
. . .
1 1 1 1 2
. . 1 .
3 3 2 2 3
A B C MNC ABC A B C ABC A B C
A M B N C C
V V V
A A B B C C
+) Do đó
..
4 2 2
.
3 3 3
A MPB NQ C C PQ A B C MNC
V V V
Câu 32: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam
giác đều cạnh
a
và
'3AA a
. Thể tích của lăng trụ đã cho bằng
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
4
a
. D.
3
2
a
.
Li gii:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Ta có:
ABC
là tam giác đều cạnh
a
nên
2
3
4
ABC
a
S
.
Ta lại có
. ' ' 'ABC A B C
là khối lăng trụ đứng nên
'3AA a
là đường cao của khối lăng trụ.
Vậy thể tích khối lăng trụ đã cho là:
23
. ' ' '
33
'. 3.
44
ABC A B C ABC
aa
V AA S a
.
Câu 33: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho lăng trụ
' ' 'ABC A B C
có chiều cao bằng
8
và đáy
là tam giác đều cạnh bằng
6
. Gọi
,MN
và
P
lần lượt là tâm của các mặt bên
''ABB A
,
''ACC A
và
''BCC B
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , ,A B C M N P
bằng:
A.
27 3
. B.
21 3
. C.
30 3
. D.
36 3
.
Li gii:
Gọi
1 1 1
,,A B C
lần lượt là trung điểm của các cạnh
', ', 'AA BB CC
.
Khối lăng trụ
1 1 1
.ABC A B C
có chiều cao là
4
là tam giác đều cạnh
6
.
Ba khối chóp
1
.A A MN
,
1
BB MP
,
1
CC NP
đều có chiều cao là 4 và cạnh là tam giác đều cạnh
3
Ta có:
1 1 1 1 1 1
. . . . .ABC MNP ABC A B C A A MN B B MP C C NP
V V V V V
2
6 3 1 9 3
4 3 4 27 3
4 3 4
.
Câu 34: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối lập phương có cạnh bằng 6. Thể tích của
khối lập phương đã cho bằng
A. 216. B. 18. C. 36. D. 72.
Li gii:
Thể tích khối lập phương đã cho là
3
6 216.V 
Câu 35: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối lăng trụ đứng
.
ABCD A B C D
có đáy là
hình thoi cạnh
,3a BD a
và
4
AA a
(minh họa như hình bên dưới). Thể tích của khối
lăng trụ đã cho bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
A.
3
2 3 .a
B.
3
4 3 .a
C.
3
23
.
3
a
D.
3
43
.
3
a
Li gii:
Vì
ABCD
là hình thoi cạnh
22
3
, 3 2 2
4
a BD a AC AO a a a
Vậy
2
3
3
. 2 3
2
ABCD ABCD
a
S V AA S a
.
Câu 36: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối chóp
.S ABC
có đáy
ABC
là tam giác
vuông cân tại
, , 90 ,A AB a SBA SCA
góc giữa hai mặt phẳng
SAB
và
SAC
bằng
60
. Thể tích khối chóp đã cho bằng
A.
3
a
. B.
3
3
a
. C.
3
2
a
. D.
3
6
a
.
Li gii:
Cách 1:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Ta có
2
1
.
22
ABC
a
S AB AC

.
Gọi
D
là hình chiếu vuông góc của
S
lên mặt phẳng
ABC
.
Ta có
AB SB
AB SBD AB BD
AB SD
.
Tương tự, ta có
AC CD
ABDC
là hình vuông cạnh
a
.
Đăt
,0SD x x
.
Gọi
H
là hình chiếu vuông góc của
D
lên
2 2 2 2
.DB DS ax
SB DH
DB DS a x

.
Ta có
22
,
DH SB
ax
DH SAB d D SAB DH
DH AB
ax
.
Lại có
// // , ,CD AB CD SAB d C SAB d D SAB DH
.
SCA
vuông tại
,C
có
22
,AC a SC x a
.
Kẻ
22
2 2 2 2
..
2
CACS a x a
CK SA CK
CA CS x a

.
Vì
,
sin ,
,
d C SAB
DH
SAB SAC SA SAB SAC
d C SA CK
22
22
2
2 2 2 2 2
22
22
22
32
sin60 3 4 2
2
2
ax
x x a
ax
x a x x a x a
xa
a x a
xa
.
DH a
.
Vậy
3
.
1
.
36
S ABC ABC
a
V S SD

.
Cách 2:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Dựng hình vuông
ABCD
SD ABCD
.
Đặt
,0SD x x
.
Kẻ
,DH SB H SB DH SAB
và
22
ax
DH
xa
.
Kẻ
,DK SC K SC DK SAC
và
22
ax
DK
xa
.
Ta có
2 2 2 2
2 2 2 2 2 2 2
// . 2
SH SK SD x x x
HK BD HK BD a
SB SC
SB x a x a x a
.
Ta có
2 2 2
cos , cos
2.
DH DK HK
SAB SAC HDK
DH DK


2 2 2 4
2 2 2
22
2
2 2 2 2
22
22
11
22
2
x a a x
xa
xa
a
xa
x a x a
xa
.
.SD a
Lại có
2
1
.
22
ABC
a
S AB AC

.
Vậy
3
.
1
.
36
S ABC ABC
a
V S SD

.
Cách trình bày khác
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
a
a
2
A
B
C
S
I
Hai tam giác vuông
SAB
và
SAC
bằng nhau chung cạnh huyền
SA
.
Kẻ
BI
vuông góc với
SA
suy ra
CI
cũng vuông góc với
SA
và
IB IC
.
,SA IC SA IB SA IBC
tại
I
.
. . .
1 1 1 1
3 3 3 3
S ABC A IBC S IBC IBC IBC IBC IBC
V V V S AI S SI S AI SI S SA
.
00
, , , 60 60SAB SAC IB IC IB IC BIC
hoặc
0
120BIC
.
Ta có
IC IB AB a
mà
2BC a
nên tam giác
IBC
không thể đều suy ra
0
120BIC
.
Trong tam giác
IBC
đặt
0IB IC x x
có:
2
2
2 2 2
0
2
22
1 6 6
cos120
2 . 2 3 3
2
xa
IB IC BC a a
x IB IC
IB IC
x

.
Trong tam giác
ABI
vuông tại
I
có:
2
2 2 2
63
33
aa
AI AB IB a




.
Trong tam giác
SAB
vuông tại
B
đường cao
BI
có:
22
2
.3
3
3
AB a
AB IA SA SA a
IA
a
.
Vậy
2
3
0
.
1 1 1 1 6
. . sin a 3sin120
3 3 2 6 3 6
S ABC IBC
aa
V S SA IB IC SA BIC





.
Cách trình bày khác
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Gọi
H
là hình chiếu của
S
lên
ABC
.
Theo bài ra, ta có
,HC CA HB BA ABHC
là hình vuông cạnh
a
.
Gọi
O H A BC
,
E
là hình chiếu của
O
lên
SA
.
Ta dễ dàng chứng minh được
,EC SA EB SA
.
Từ đó, ta được: góc giữa
SAC
và
SAB
là góc giữa
EB
và
EC
.
Vì
0
90CAB
nên
00
90 120 .BEC BEC
Ta dễ dàng chỉ ra được
0
60OEB OEC
.
Đặt
22
22
.2
2
22
AO SH xa
SH x SA x a OE
SA
xa
.
0
22
22
tan60 : 3
2
22
OC a xa
xa
OE
xa
.
Vậy
3
2
..
1 1 1
. . .
2 2 3 6
S ABC S HBAC
a
V V a a
.
Cách trình bày khác
S
B
D
C
A
I
Ta có
SAB SAC
và chung cạnh huyền SA. Kẻ
BI SA CI SA
và góc giữa
hai mặt phẳng
SAB
và
SAC
là góc giữa hai đường thẳng
BI
và
; 60CI BI CI
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Có
2BC a
,
BIC
cân tại I. Do
2BI CI AC a a BC
nên
BIC
không đều
6
120
3
a
BIC BI CI
. Từ đó
3
3
a
AI
;
2
. 3.AB AI SA SA a
Dựng hình vuông
ABDC
SD ABDC
.
Có :
3
2 2 2
.
1
; . .
36
ABC S ABC ABC
a
SD SA AD a S a V S SD

HOẶC CÁCH KHÁC PPTHỂ TÍCH
.
11
..
33
S ABC IBC IBC
V S SI AI S SA

.
Với
2 2 3
.
1 3 1 3
. . . 120 . . 3 .
2 6 3 6 6
IBC S ABC
a a a
S IB IC sin V a
Câu 37: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Thể tích của khối lập phương cạnh
2
bằng
A.
6
. B.
8
. C.
4
. D.
2
.
Li gii:
Ta có
3
28V 
.
Câu 38: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Cho khối chóp có diện tích đáy
3B
và chiều cao
4h
. Thể tích của khối chóp đã cho bằng
A.
6
. B.
12
. C.
36
. D.
4
.
Li gii:
Thể tích khối chóp đã cho là
11
. . .3.4 4
33
V B h
.
Câu 39: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Cho hình hộp
. ' ' ' 'ABC D A B C D
có chiều cao bằng
8
và diện tích đáy bằng
9.
Gọi
,,M N P
và
Q
lần lượt là tâm của các mặt bên
' ', ' ', ' 'ABB A BCC B CDD C
và
''DAA D
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , , , ,A B C D M N P
và
Q
bằng
A. 27. B. 30. C. 18. D. 36
Li gii:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Mặt
MNPQ
cắt các cạnh
AA',BB',CC', DD'
tại
1 1 1 1
, , ,A B C D
. Thể tích khối đa diện cần tìm là
V
, thì:
1 1 1 1 1 1 1 1
. ' ' ' ' '. '. '. '.
8.9
4
2 24
30
A B C D A B C D A QMA B MNB C PNC D QPD
V V V V V V
V
V

.
Câu 40: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho khối hộp chữ nhật có 3 kích thước
3;4;5
. Thể tích
của khối hộp đã cho bằng?
A.
10
. B.
20
. C.
12
. D.
60
.
Li gii:
Thể tích của khối hộp đã cho bằng
3.4.5 60V 
.
Câu 41: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho khối chóp có diện tích đáy
6B
và chiều cao
2h
. Thể tích của khối chóp đã cho bằng:
A.
6
. B.
3
. C.
4
. D.
12
.
Li gii:
Thể tích của khối chóp
1
4
3
V Bh
.
Câu 42: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
a
, cạnh
bên bằng
2a
và
O
là tâm của đáy. Gọi
M
,
N
,
P
,
Q
lần lượt là các điểm đối xứng với
O
qua
trọng tâm của các tam giác
SAB
,
SBC
,
SCD
,
SDA
và
'S
là điểm đối xứng với
S
qua
O
. Thể
tích của khối chóp
'.S MNPQ
bằng
A.
3
20 14
81
a
. B.
3
40 14
81
a
. C.
3
10 14
81
a
. D.
3
2 14
9
a
.
Li gii:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Gọi
1 2 3 4
, , ,G G G G
lần lượt là trọng tâm
, , ,SAB SBC SCD SDA
.
, , ,E F G H
lần lượt là trung điểm của các cạnh
, , ,AB BC CD DA
.
Ta có
1 2 3 4
2
4 4 1 8
4 4. 4. . .
9 9 2 9
MNPQ G G G G EFGH
a
S S S EG HF
.
1 2 3 4
, , ,
, 2 ,
2
,,
3
5 5 14
,
36
d S MNPQ d S ABCD d O MNPQ
d S ABCD d O G G G G
d S ABCD d S ABCD
a
d S ABCD





Vậy
23
.
1 5 14 8 20 14
3 6 9 81
S MNPQ
a a a
V
.
Câu 43: (ĐỀ THAM KHẢO 2021) Một khối chóp có diện tích đáy bằng 6 và chiều cao bằng 5. Thể tích
của khối chóp đó bằng
A. 10. B. 30. C. 90. D. 15.
Câu 44: (ĐỀ THAM KHẢO 2021) Thể tích của khối hộp chữ nhật có ba kích thước 2; 3; 7 bằng
A. 14. B. 42. C. 126. D. 12.
Câu 45: (ĐỀ THAM KHẢO 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh a, cạnh
bên SA vuông góc với mặt phẳng đáy, góc giữa
SA
và mặt phằng
()SBC
bằng
45
(tham
khảo hình bên). Thể tích của khối chóp
.S ABC
bằng
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
A.
3
8
a
. B.
3
3
8
a
. C.
3
3
12
a
. D.
3
4
a
.
Li gii:
Gọi
M
là trung điểm
BC
thì
AM BC
và
SA BC
nên
( ).BC SAM
Từ đây dễ thấy góc
cần tìm là
45ASM
. Do đó,
SAM
vuông cân ở
A
và
3
.
2
a
SA AM
Suy ra
23
.
1 3 3
.
3 2 4 8
S ABC
a a a
V
Câu 46: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Thể tích của khối lập phương cạnh
5a
bằng
A.
3
5a
. B.
3
a
. C.
3
125a
. D.
3
25a
.
Li gii:
Thể tích của khối lập phương cạnh
5a
là
3
3
5 125V a a
.
Câu 47: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Cho khối chóp có diện tích đáy
2
5Ba
và chiều
cao
ha
. Thể tích của khối chóp đã cho bằng
A.
3
5
6
a
. B.
3
5
2
a
. C.
3
5a
. D.
3
5
3
a
.
Li gii:
Thể tích của khối chóp đã cho
23
1 1 5
. . .5 .
3 3 3
V B h a a a
.
Câu 48: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy
là hình vuông,
2BD a
, góc giữa hai mặt phẳng
'A BD
và
ABC D
bằng
0
30
. Thể tích của
khối hộp chữ nhật đã cho bằng
A.
3
63a
. B.
3
23
9
a
. C.
3
23a
. D.
3
23
3
a
.
Li gii:
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Gọi
O
là tâm hình vuông
ABCD
. Vì
BD OA
và
'BD AA
nên
''BD A OA BD OA
Lại có
'A BD ABCD BD
. Do đó
0
' , ' 30A BD ABCD A OA
(Hình vẽ trên).
Vì tứ giác
ABCD
là hình vuông có
2BD a
nên
OA a
và
2AB AD a
.
Xét tam giác
'A AO
vuông tại
A
có
OA a
và
0
' 30A OA
nên
0
3
' .tan30
3
a
AA OA
.
Vậy thể tích khối hộp chữ nhật
3
3 2 3
. . ' a 2. 2.
33
a
V AB AD AA a a
.
Câu 49: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối chóp có diện tích đáy
B
và chiều cao
h
. Thể tích
V
của khối chóp đã cho được tính theo công thức nào dưới đây ?
A.
1
3
V Bh
. B.
4
3
V Bh
. C.
V Bh
. D.
3V Bh
.
Câu 50: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối lăng trụ có diện tích đáy
2
5Ba
và
chiều cao
ha
. Thể tích của khối lăng trụ đã cho bằng
A.
3
5
3
a
. B.
3
5a
. C.
3
5
6
a
. D.
3
5
2
a
.
Li gii:
Thể tích của khối lăng trụ
23
. 5 . 5V B h a a a
.
Câu 51: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối lăng trụ tam giác đều
ABCA B C
có
cạnh bên bằng
4a
, góc giữa hai mặt phẳng
A BC
và
ABC
bằng
30
. Thể tich của khối
lăng trụ đã cho bằng
A.
3
64 3a
. B.
3
64 3
3
a
. C.
3
64 3
27
a
. D.
3
64 3
9
a
.
Li gii:
30
°
I
A'
C'
B'
A
C
B
Gọi
I
là trung điểm của
BC BC AI
(vì
ABC
đều).
Ta có
BC AI
BC A AI BC A I
BC AA

Suy ra
, , 30A BC ABC A I AI A IA
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Tam giác
A AI
vuông tại
A
có
44
tan 4 3
tan30
3
3
AA a a
A AI AI a
AI
Vì
ABC
đều nên
3 2 2.4 3
8
2
33
BC AI a
AI BC a
.
Diện tích
ABC
là
22
2
3
3 64 3
16
4 4
ABC
BC a
Sa
.
Thể tich khối lăng trụ
23
. 4 .16 3 64 3
ABC
V AA S a a a
.
Câu 52: (ĐỀ THAM KHẢO 2022) Cho khối chóp có diện tích đáy
7B
và chiều cao
6h
. Thể tích
của khối chóp đã cho bằng
A.
42
. B.
126
. C.
14
. D.
56
.
Câu 53: (ĐỀ THAM KHẢO 2022) Cho khối lăng trụ có diện tích đáy
B
và chiều cao
h
. Thể tích
V
của
khối lăng trụ đã cho được tính theo công thức nào dưới đây?
A.
1
3
V Bh
. B.
4
3
V Bh
. C.
6V Bh
. D.
V Bh
.
Câu 54: (ĐỀ THAM KHẢO 2022) Cho khối chóp đều
.S ABCD
có
4AC a
, hai mặt phẳng
SAB
và
SCD
vuông góc với nhau. Thể tích khối chóp đã cho bằng
A.
3
16 2
3
a
. B.
3
82
3
a
. C.
3
16a
. D.
3
16
3
a
.
Li gii:
Gọi
O
là tâm của hình vuông
ABCD
.
Do
.S ABCD
là hình chóp đều nên
SO ABCD
SO AB
.
Ta có:
S
là một điểm chung của hai mặt phẳng
SAB
và
SCD
.
AB SAB
;
CD SCD
;
//AB CD
.
Suy ra hai mặt phẳng
SAB
và
SCD
cắt nhau theo giao tuyến là đường thẳng
đi qua
S
,
song song với
AB
và
CD
.
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Gọi
H
;
K
lần lượt là trung điểm của
AB
và
CD
HK
đi qua
O
và
HK AB
.
Ta có:
SO AB
HK AB
AB SHK
SHK
(Do
//AB
).
; ; 90SAB SCD SH SK
SH SK
Tam giác
SHK
vuông tại
S
.
22
2
AC
AB a
;
11
2
22
SO HK AB a
.
22
8
ABCD
S AB a
.
Vậy thể tích khối chóp
.S ABCD
là:
23
.
1 1 8 2
. 2.8
3 3 3
S ABCD ABCD
V SO S a a a
.
______________________HẾT______________________
Huế, 16h00 Ngày 27 tháng 6 năm 2022
| 1/123
| | Tải xuống

Có thể bạn quan tâm:

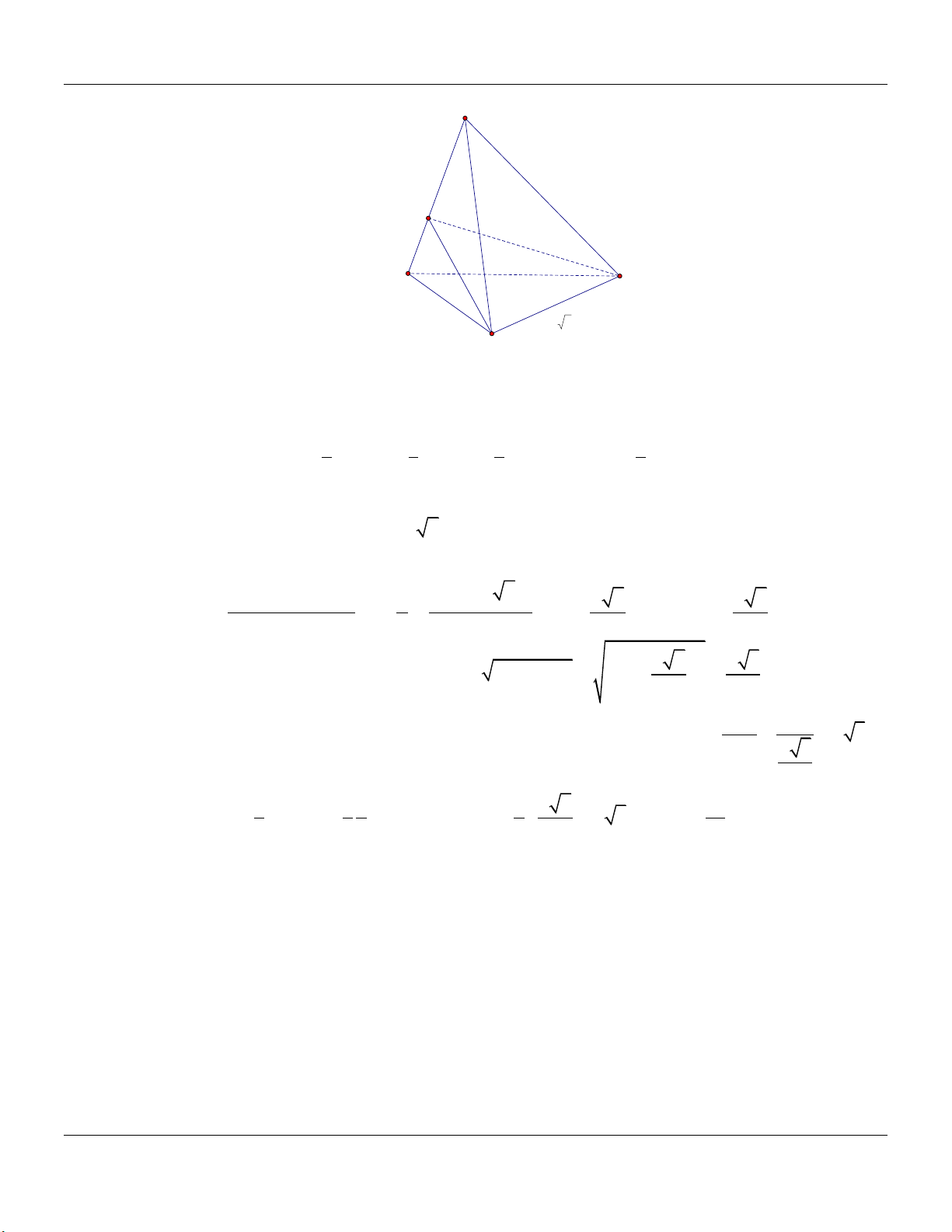
Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 12 THỂ TÍCH KHỐI ĐA DIỆN
HỆ THỐNG DẠNG TOÁN- ĐỀ ÔN TẬP
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
TỔNG HỢP MỘT SỐ DẠNG TÍNH THỂ TÍCH CẦN LƯU Ý
Dạng 1: Hình chóp tam giác có cạnh bên vuông góc với đáy
Mức 1: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
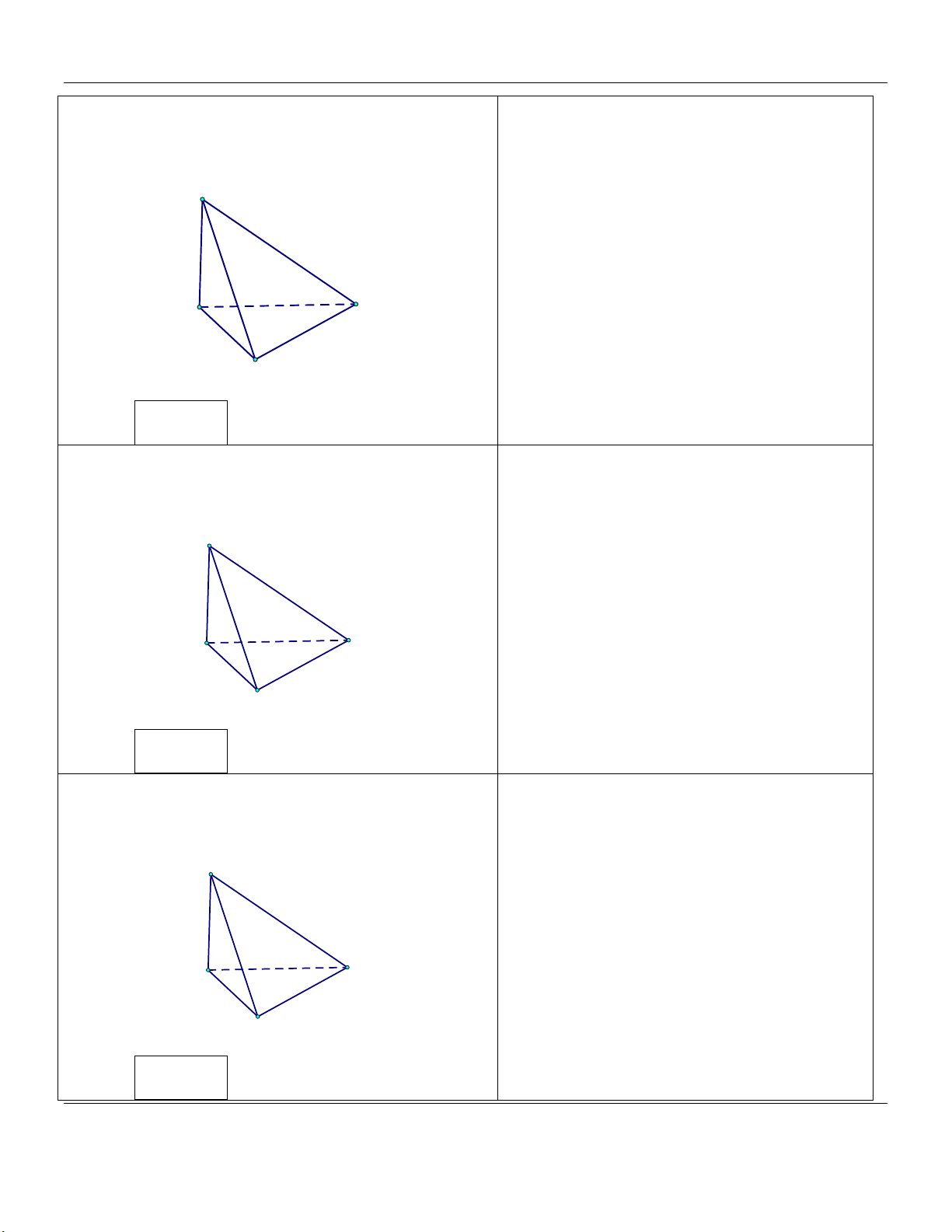
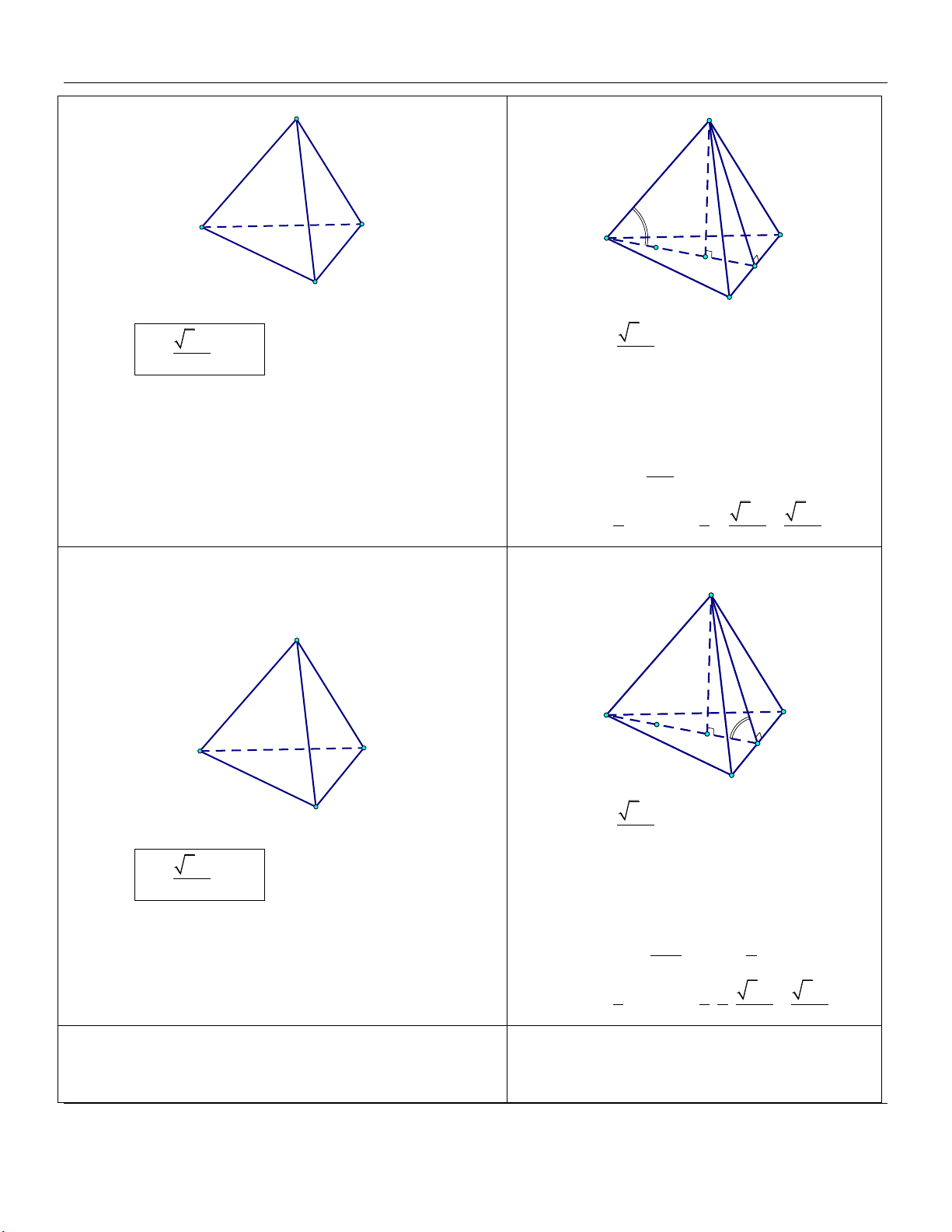
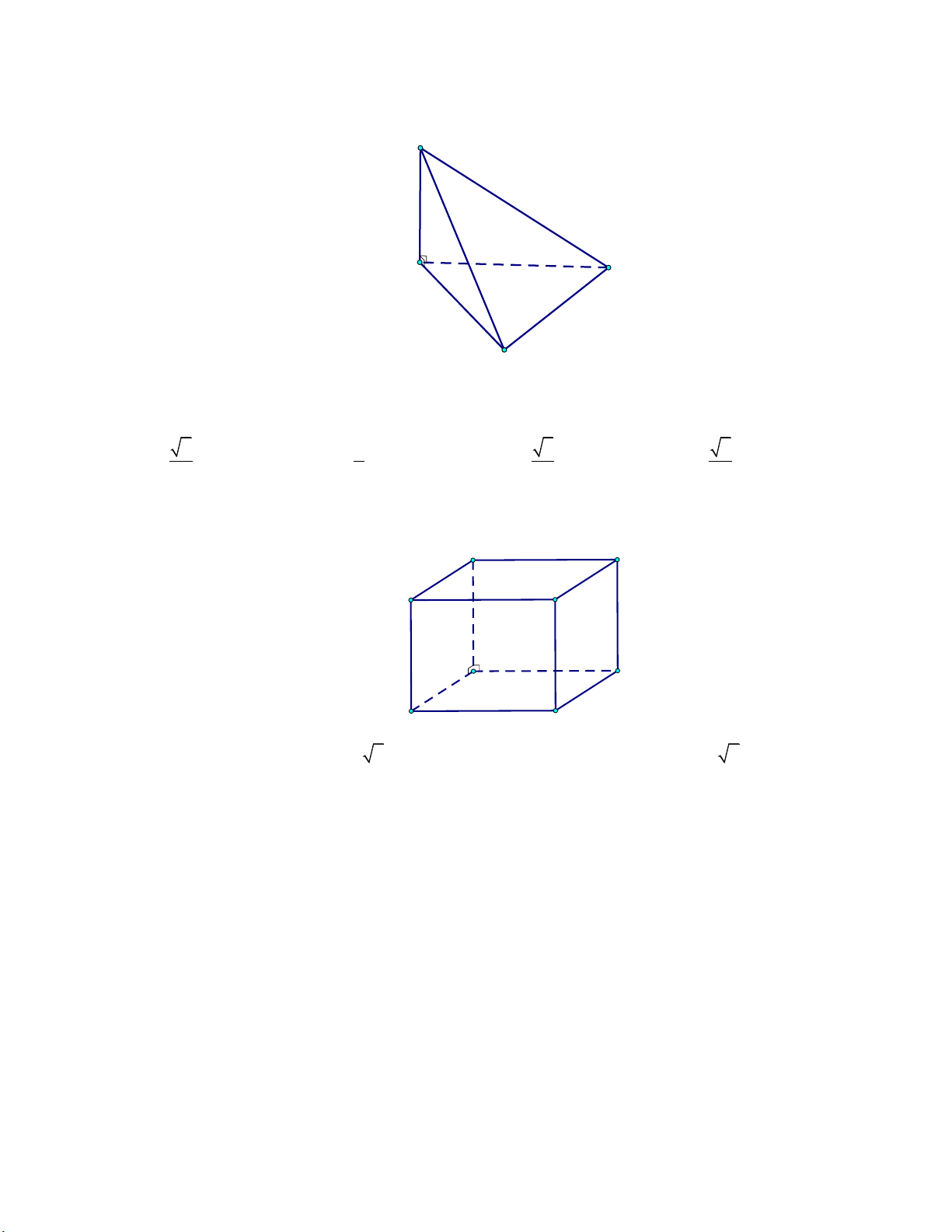
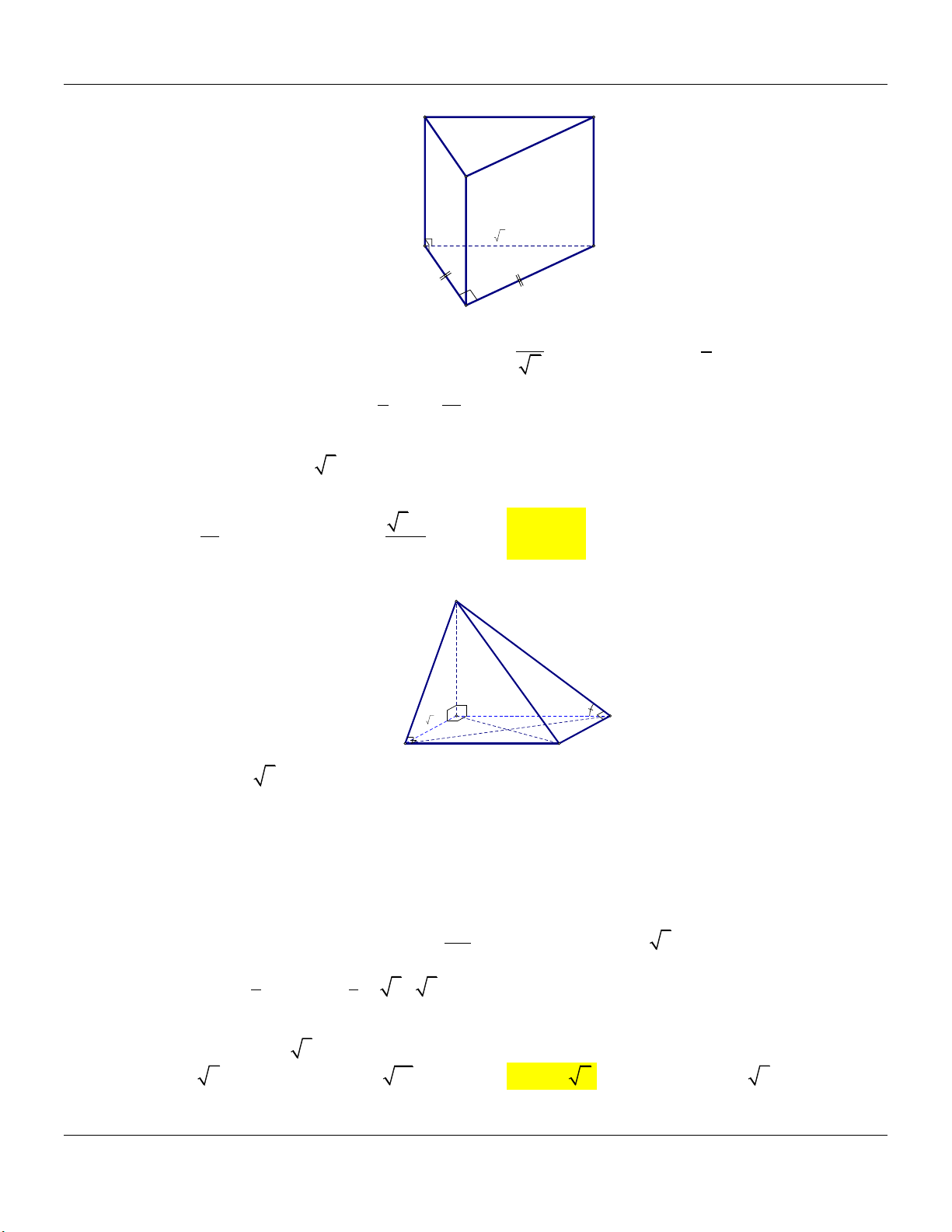
cạnh a,SA vuông góc với đáy và SA  2 . a (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Mức 2: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
cạnh a,SA vuông góc với đáy và diện tích tam giác SAB bằng 2
2a (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Mức 3: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
cạnh a,SA vuông góc với đáy. Biết góc giữa SB và mặt
đáy ABC bằng 60 (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <1 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 4: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
cạnh a,SA vuông góc với đáy. Biết góc giữa mặt phẳng
SBC và mặt đáy ABC bằng 60 (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Mức 5: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
cạnh a,SA vuông góc với đáy. Biết góc giữa SC và
SAB bằng 30 (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Mức 6: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
cạnh 2a,SA vuông góc với đáy. Biết khoảng cách từ điểm
A đến SBC bằng a (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <2 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Dạng 2: Hình chóp tứ giác có cạnh bên vuông góc với đáy
Mức 1: Cho hình chóp .
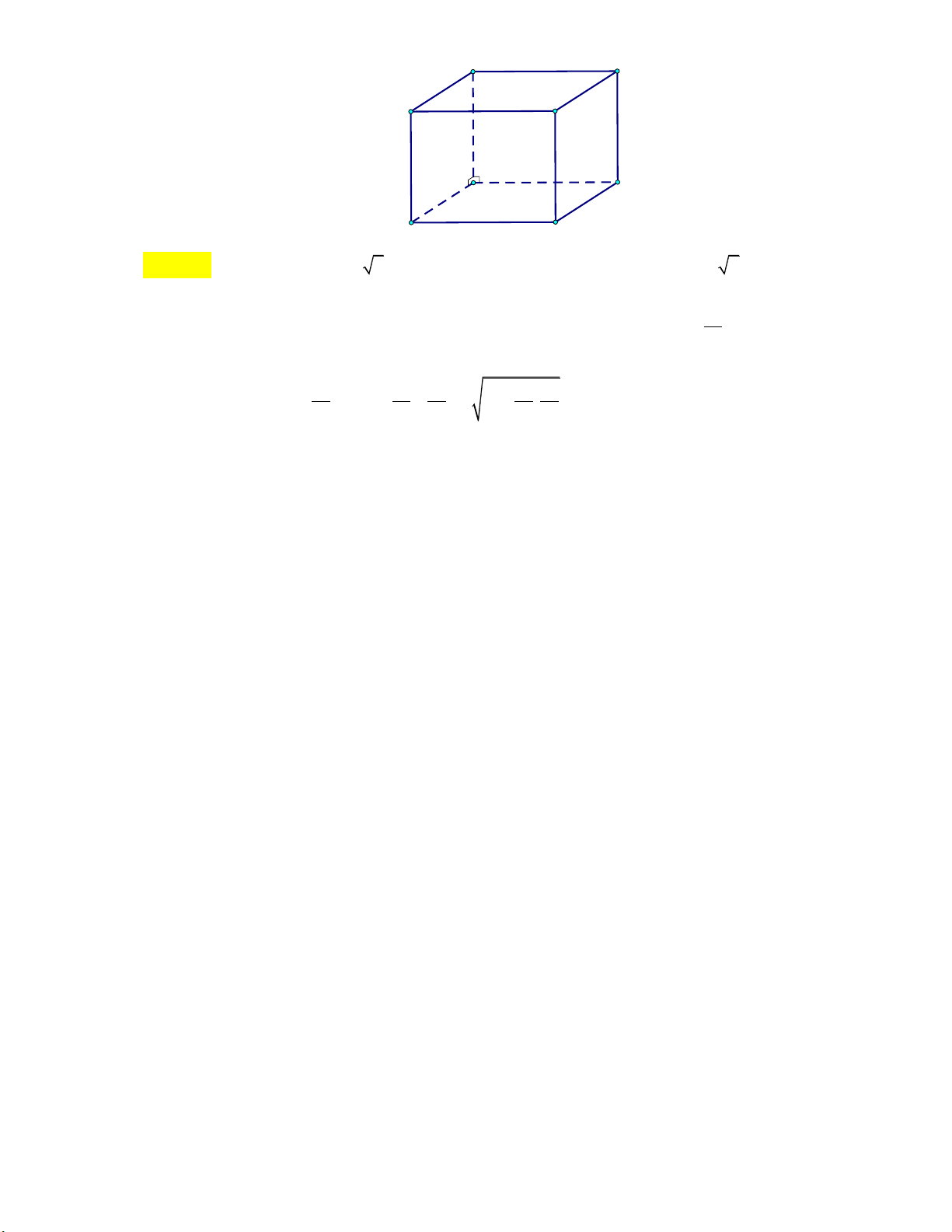
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy và SB  2 .
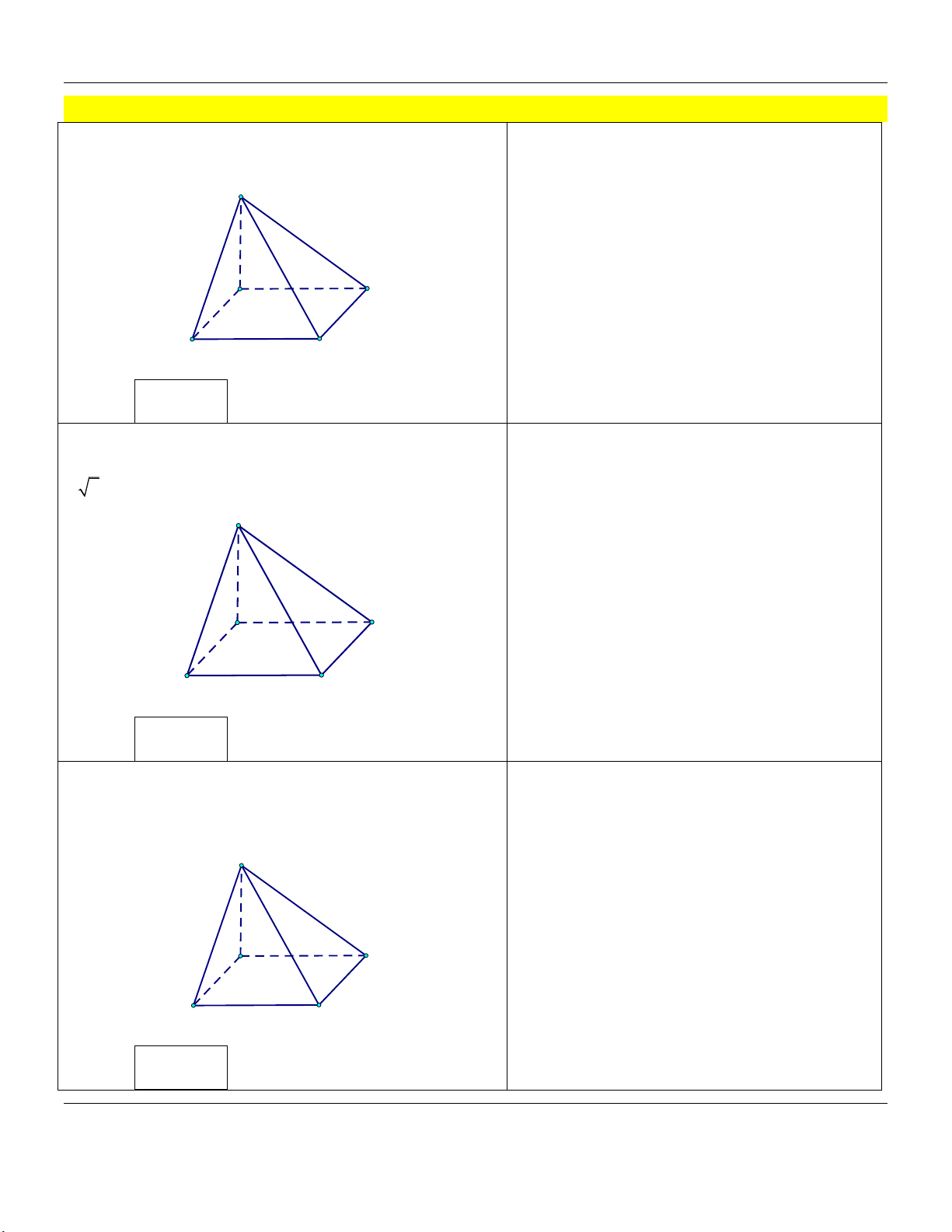
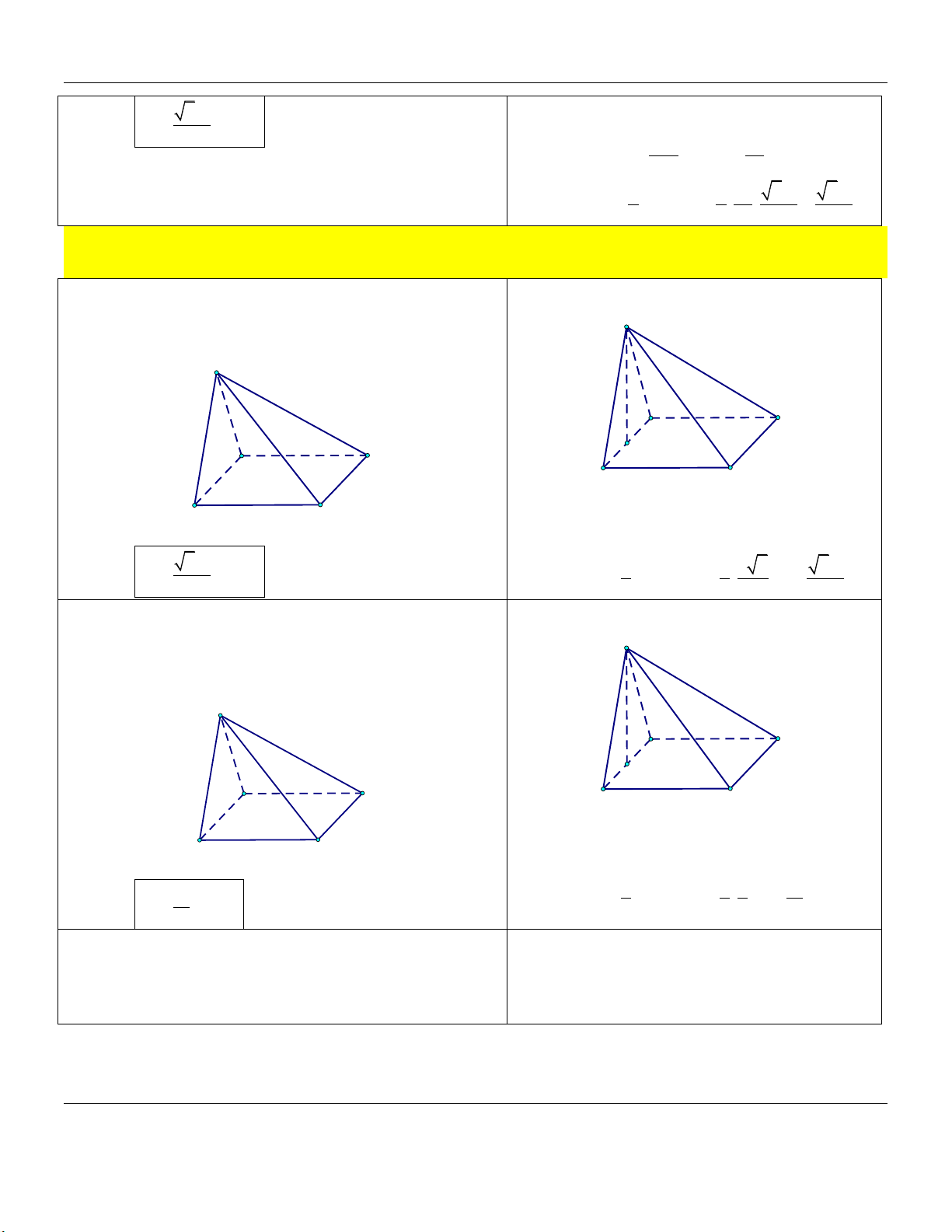
a (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 2: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy và diện tích tam giác SAC bằng 2
2 2a (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 3: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy. Biết góc giữa SC và mặt đáy
ABCD bằng 30 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <3 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 4: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy. Biết góc giữa SBC và mặt đáy
ABCD bằng 30 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 5: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy. Biết góc giữa SBD và mặt đáy
ABCD bằng 30 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 6: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy. Biết góc giữa SC và SAB bằng
30 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <4 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 7: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy. Biết góc giữa SA và SBD bằng
30 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 8: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
3a,SA vuông góc với đáy. Gọi M là trung điểm SD và
khoảng cách từ M đến SBC bằng a (tham khảo hình vẽ). S M A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
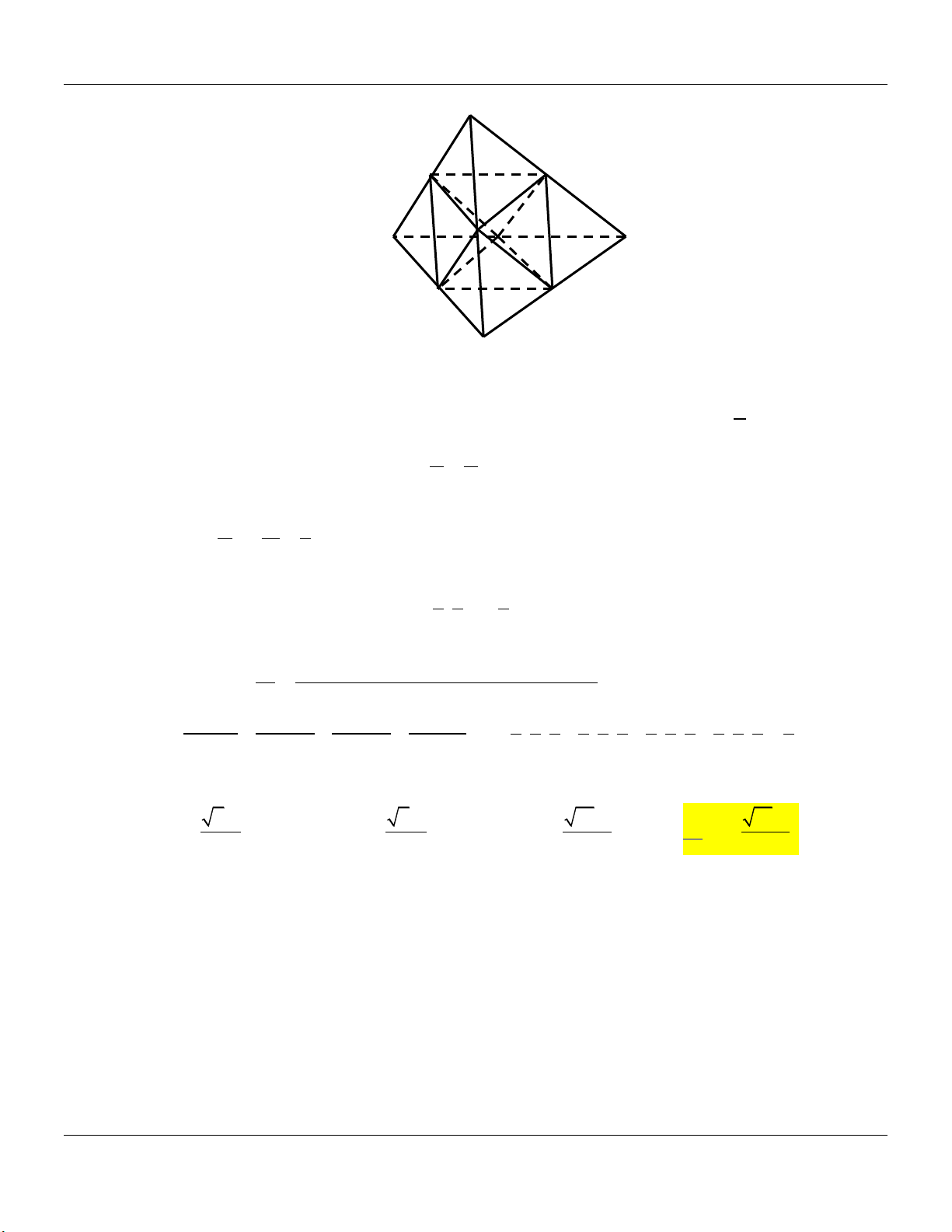
Dạng 3: Hình chóp tam giác đều
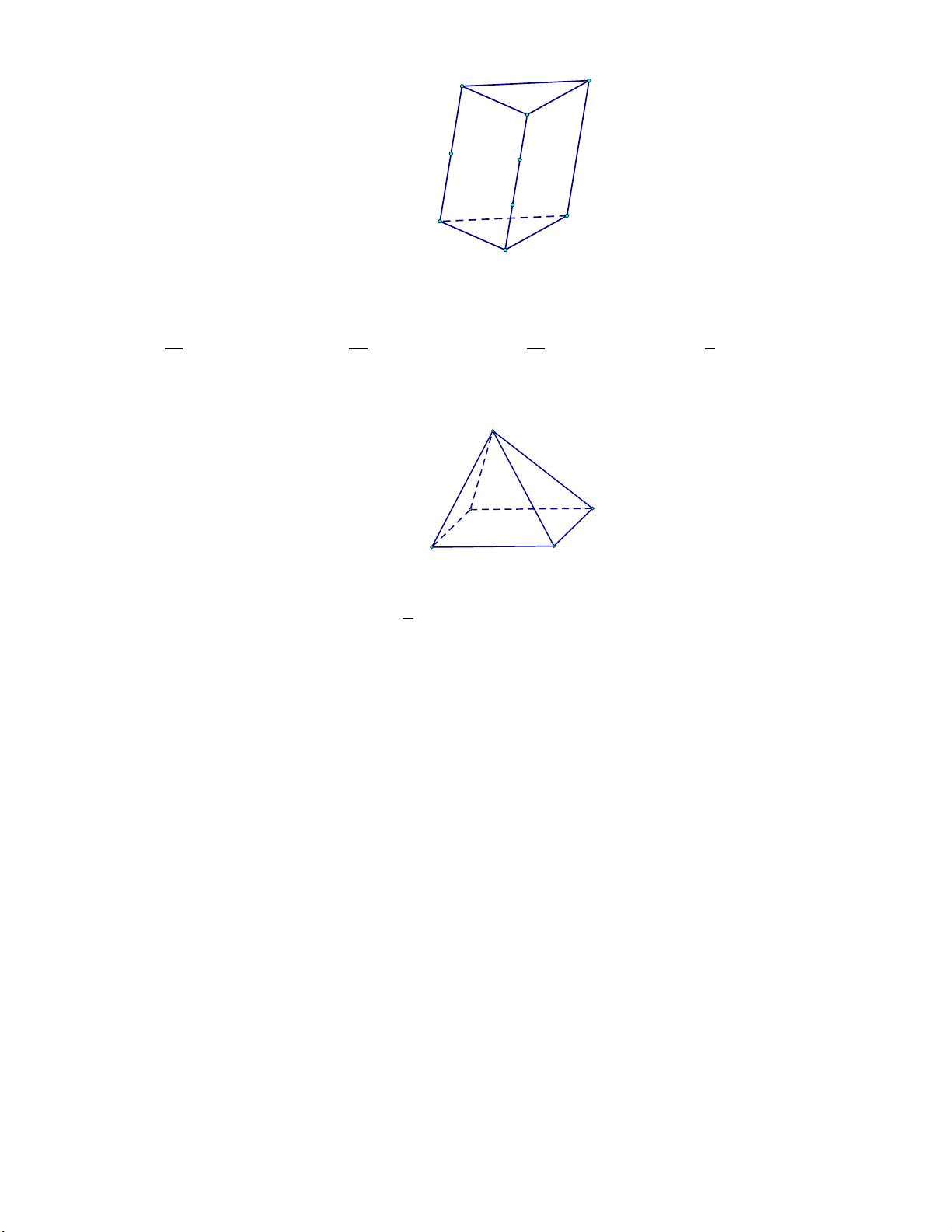
Mức 1: Cho hình chóp tam giác đều .
S ABC có cạnh đáy Trình bày:
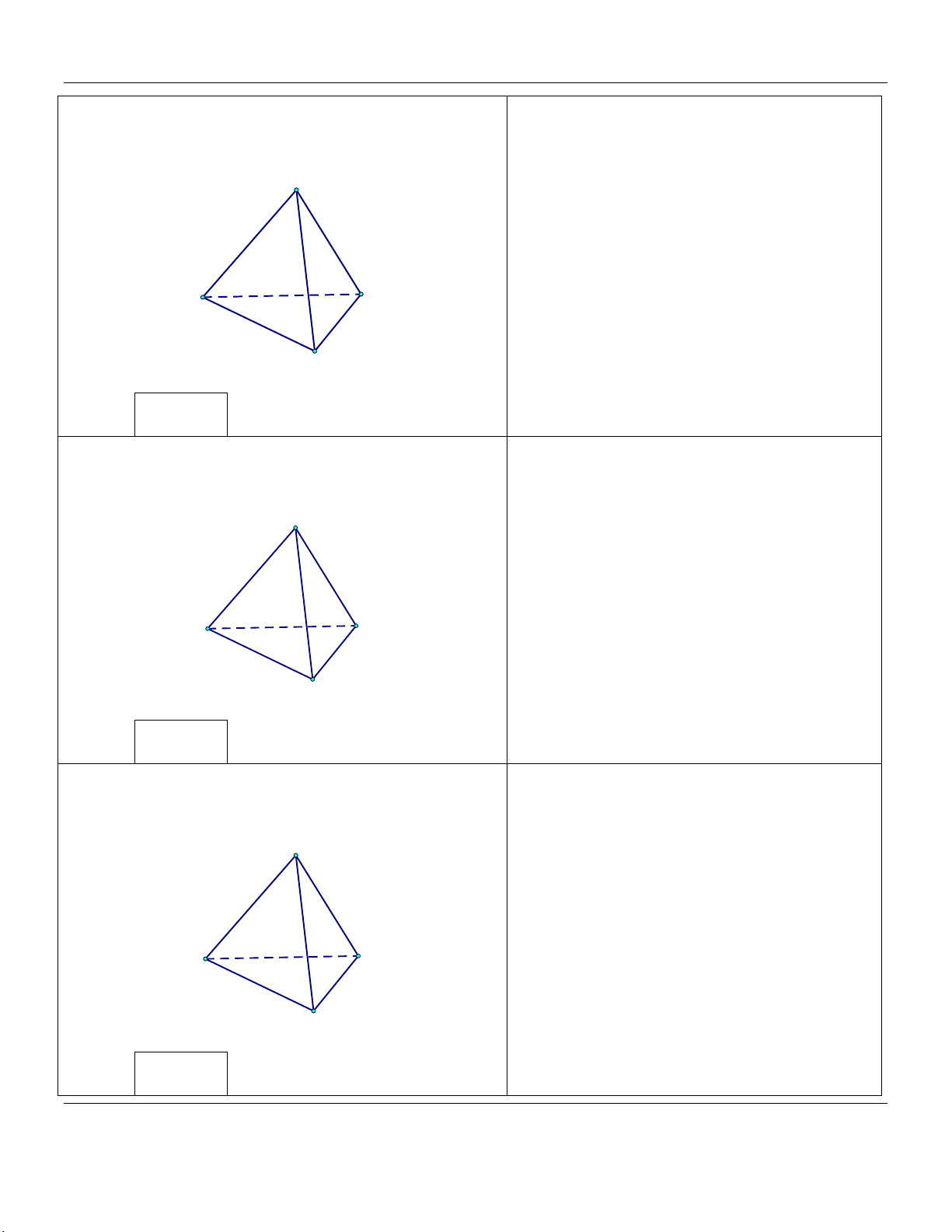
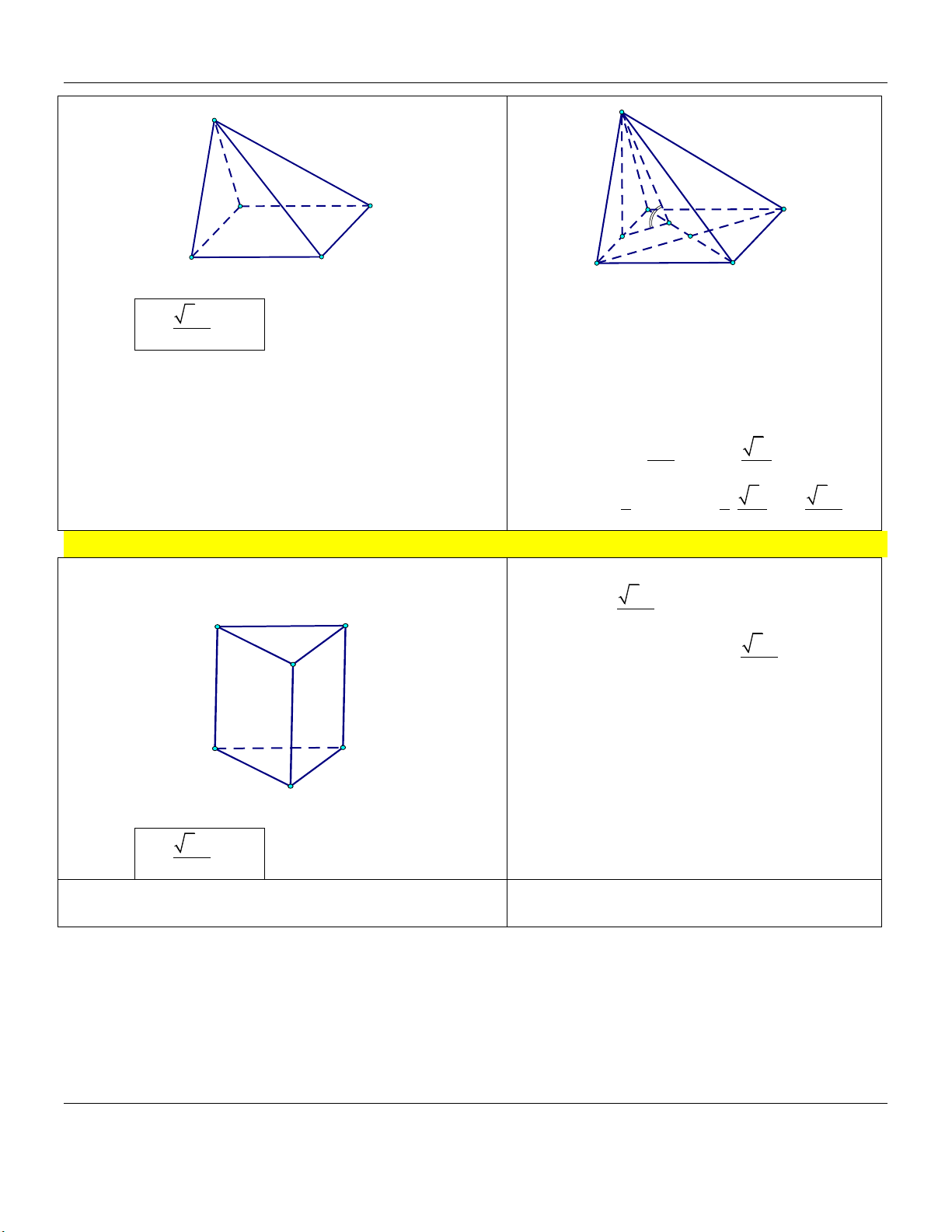
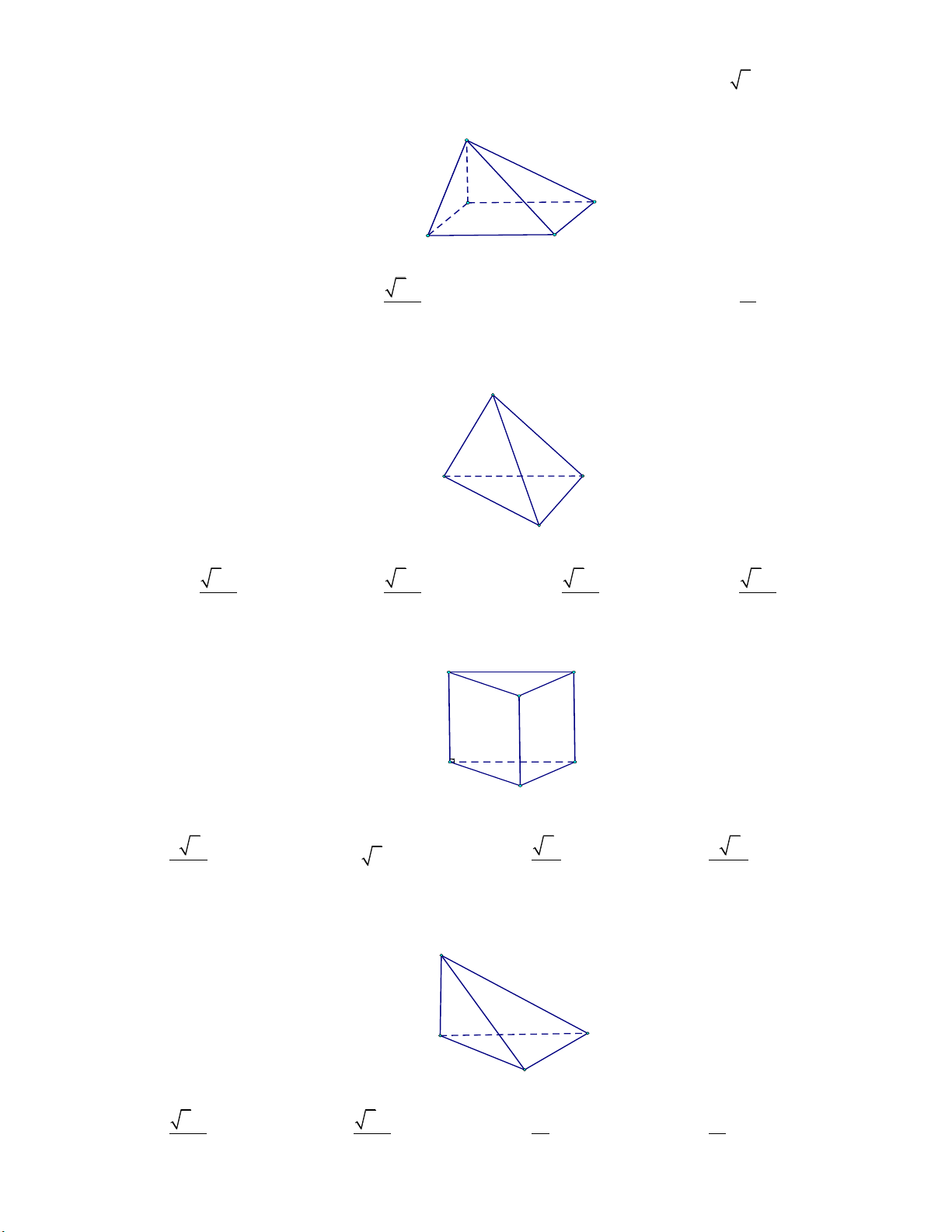
bằng a, cạnh bên bằng 2a (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <5 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 2: Cho hình chóp tam giác đều .
S ABC có cạnh đáy Trình bày:
bằng a, diện tích một mặt bên bằng 2 2a (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Mức 3: Cho hình chóp tam giác đều .
S ABC có cạnh đáy Trình bày:
bằng a, cạnh bên hợp với đáy một góc 60 (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Mức 4: Cho hình chóp tam giác đều .
S ABC có cạnh đáy Trình bày:
bằng a, mặt bên hợp với đáy một góc 60 (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <6 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 5: Cho hình chóp tam giác đều .
S ABC có cạnh đáy Trình bày: bằng 4 .
a Biết khoảng cách từ điểm A đến SBC bằng a
(tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
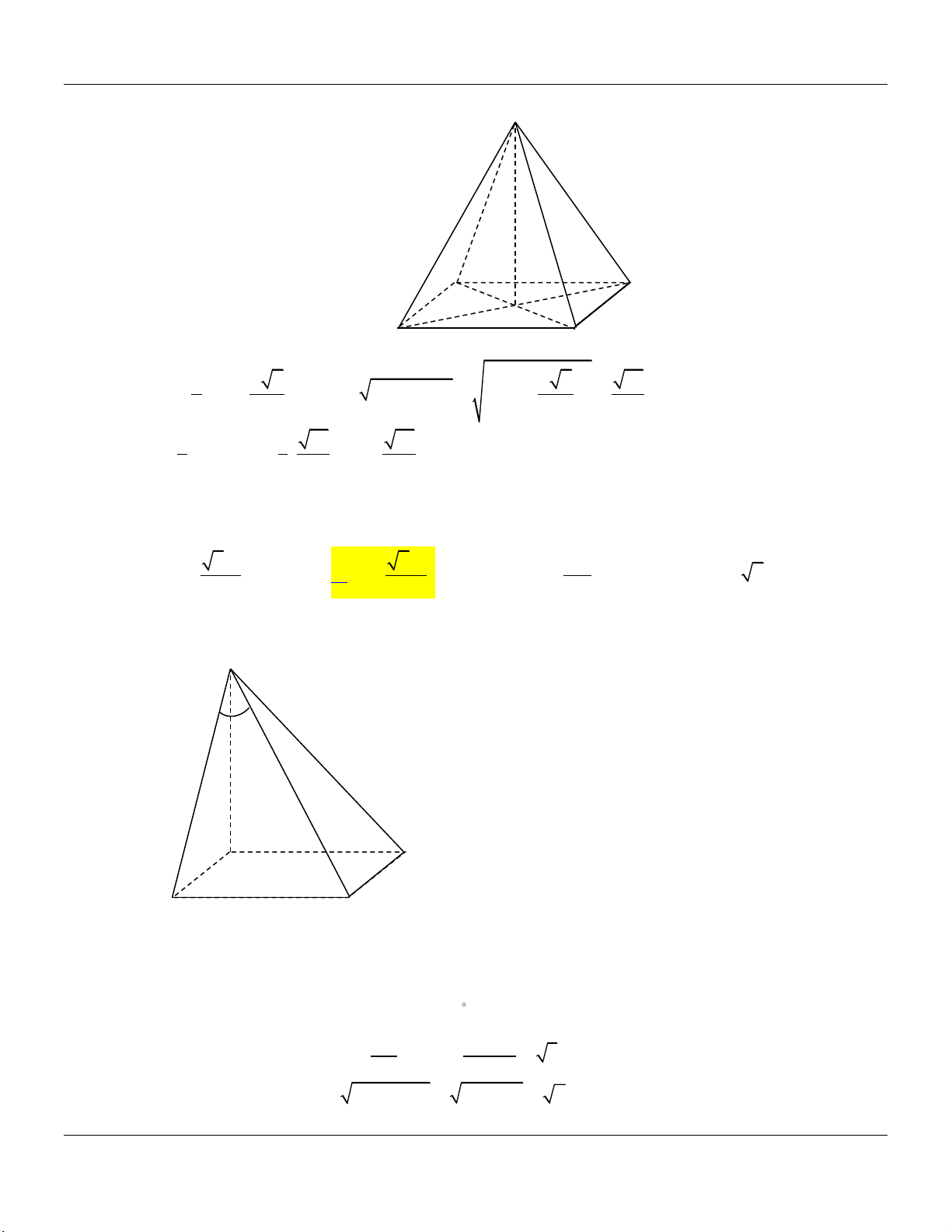
Dạng 4: Hình chóp tứ giác đều
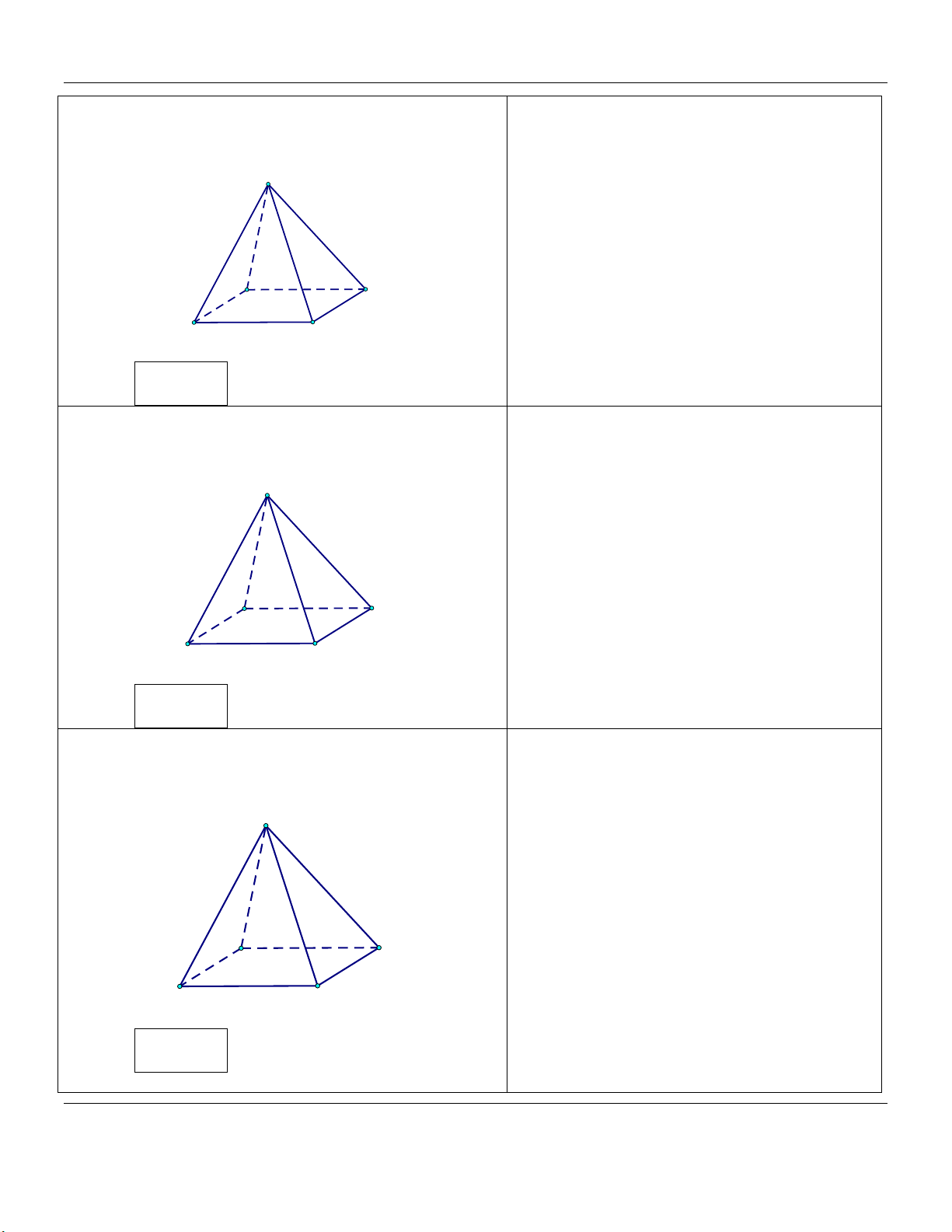
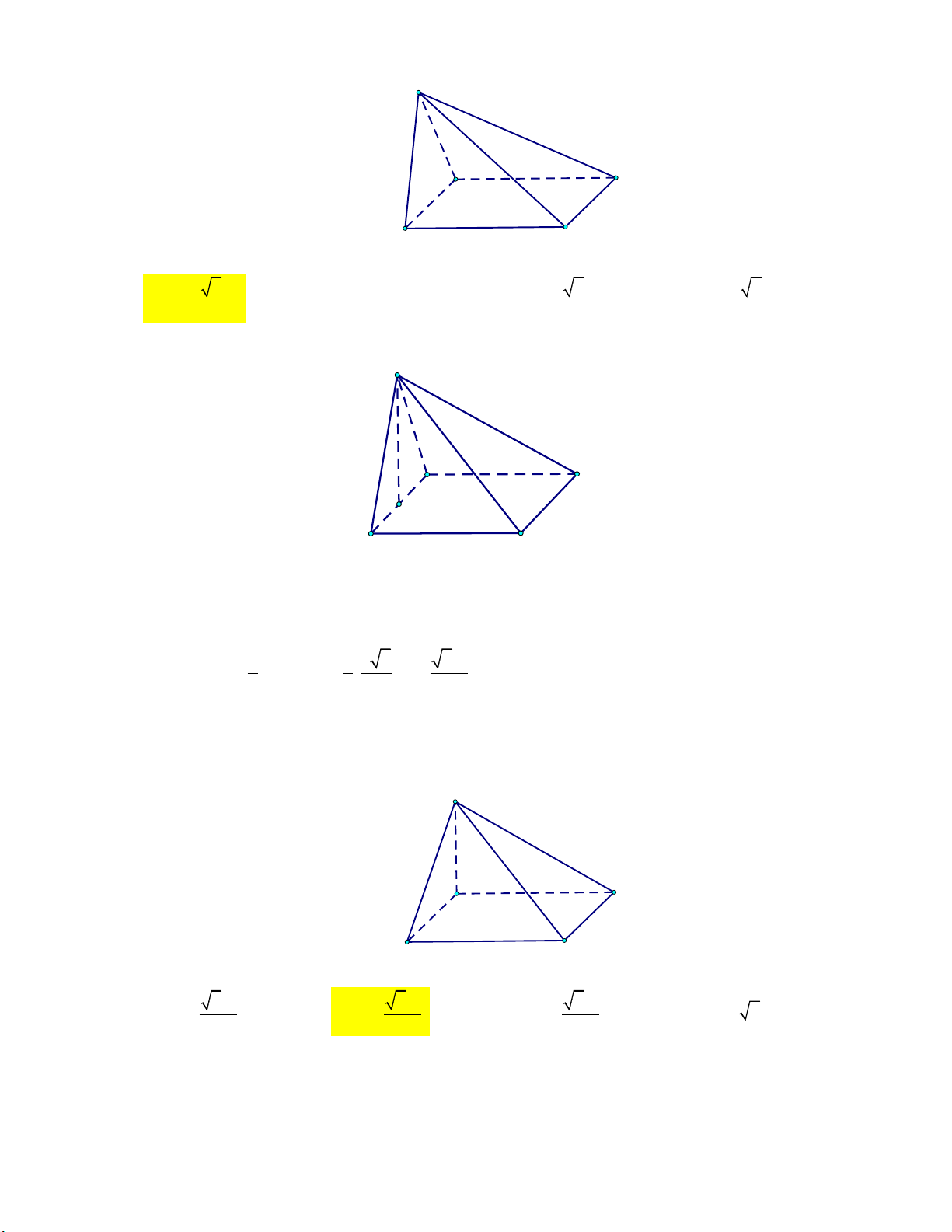
Mức 1: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày:
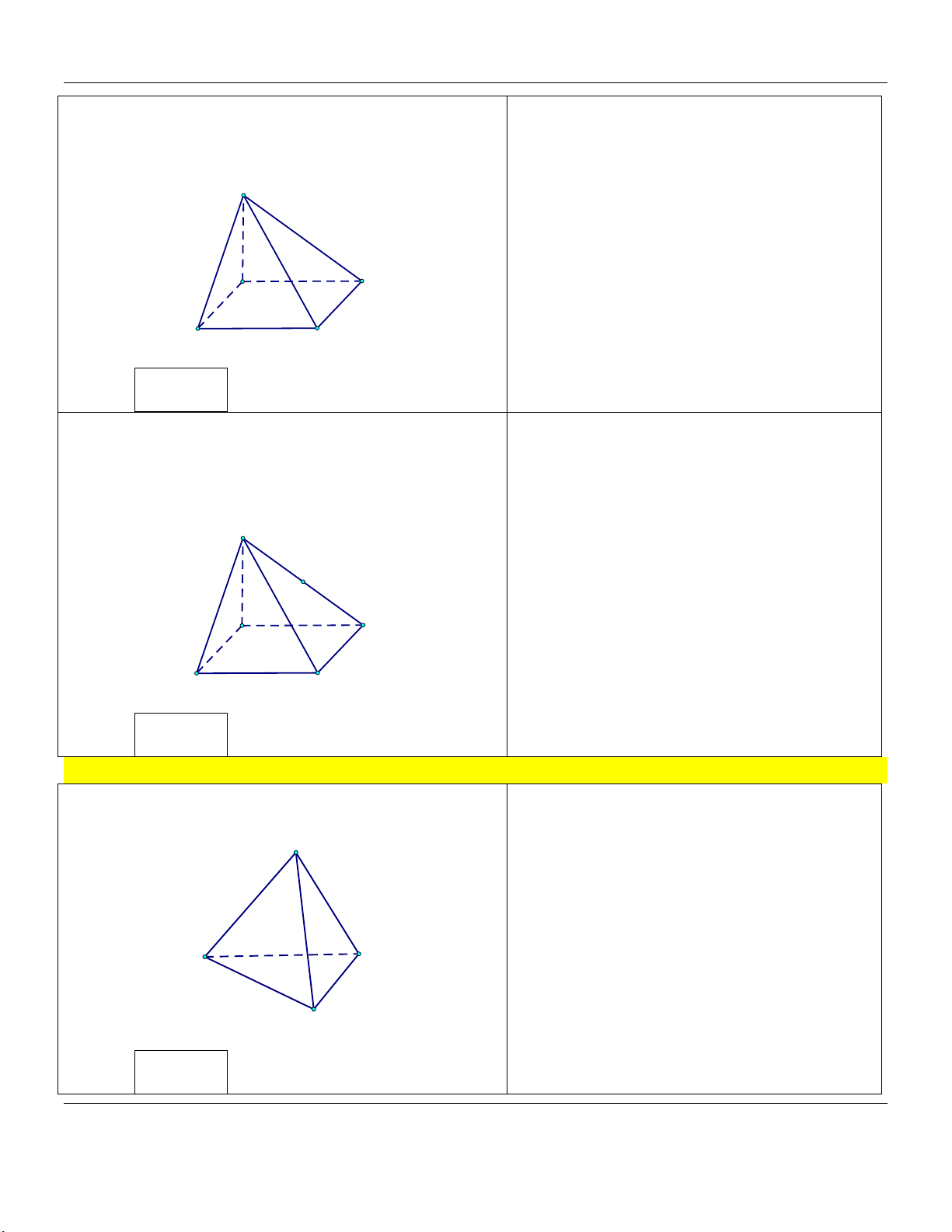
bằng a, cạnh bên bằng 2a (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 2: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày:
bằng a, diện tích tam giác SAC bằng 2 2a (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <7 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
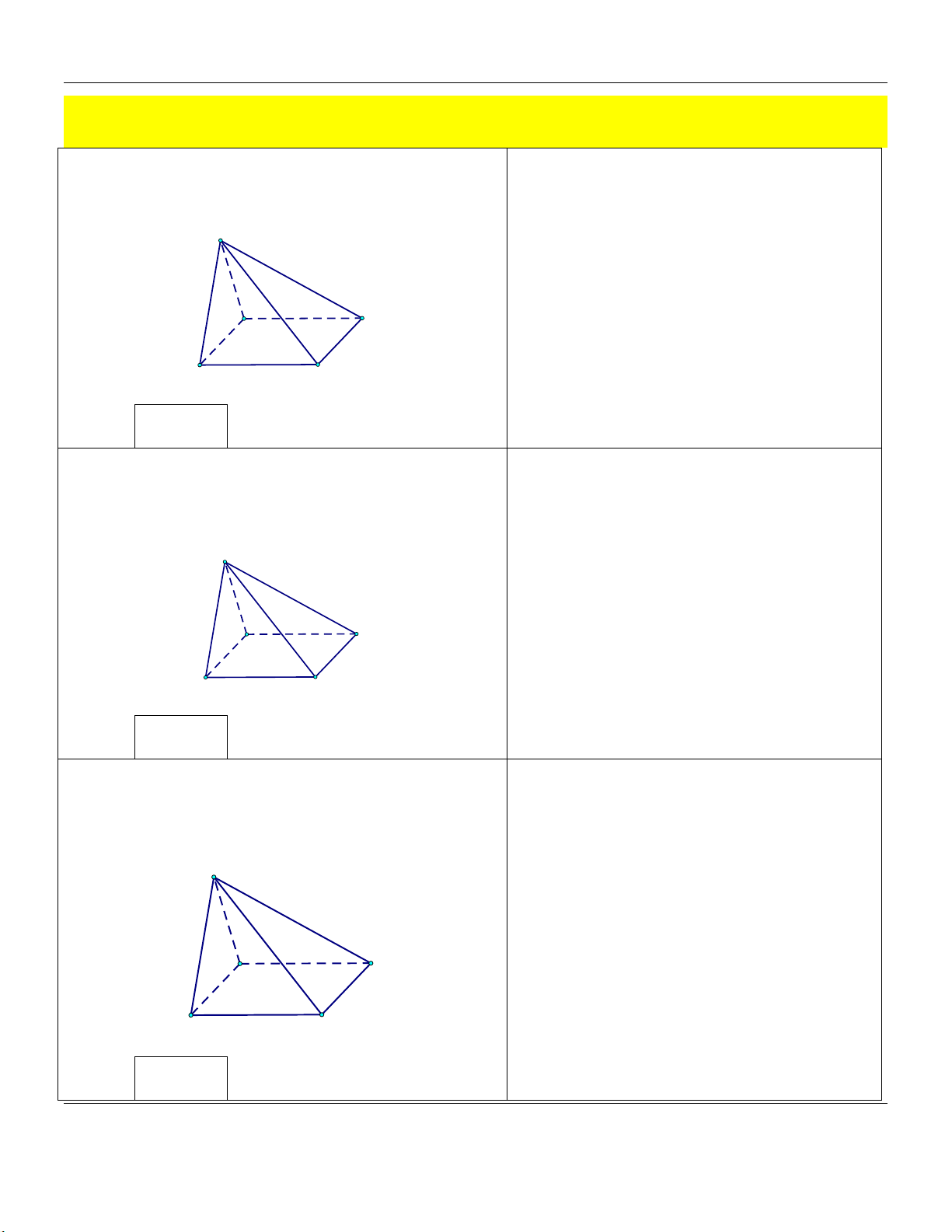
Mức 3: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày:
bằng a, cạnh bên hợp với đáy một góc 60 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 4: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày:
bằng a, mặt bên hợp với đáy một góc 60 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 5: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày: bằng 2 .
a Biết khoảng cách từ điểm A đến SBC bằng a
(tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <8 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 6: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày: bằng 2 .
a Biết góc giữa hai mặt phẳng SAB và SCD
bằng 90 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
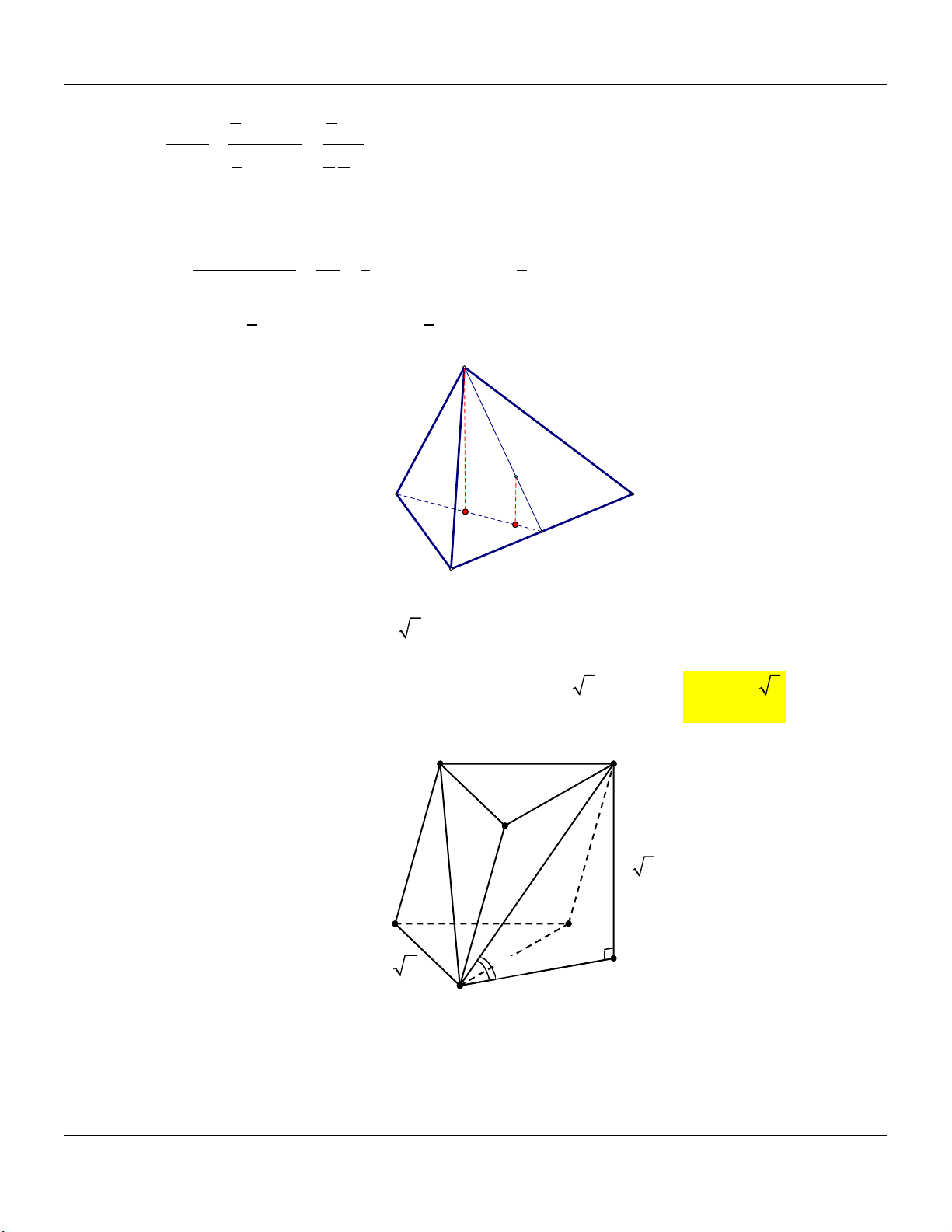
Dạng 5: Hình chóp tam giác có mặt bên là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy
Mức 1: Cho hình chóp .
S ABC có đáy là tam giác đều có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Mức 2: Cho hình chóp .
S ABC có đáy là tam giác đều có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác vuông cân tại S và
nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <9 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 3: Cho hình chóp .
S ABC có đáy là tam giác đều có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa SC và
mặt đáy bằng 60 (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Mức 4: Cho hình chóp .
S ABC có đáy là tam giác đều có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa SC và
SAB bằng 30 (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Mức 5: Cho hình chóp .
S ABC có đáy là tam giác đều có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa SBC
và mặt đáy bằng 60 (tham khảo hình vẽ). S A C B
Thể tích khối chóp . S ABC bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <10 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Dạng 6: Hình chóp tứ giác có mặt bên là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy
Mức 1: Cho hình chóp .
S ABCD có đáy là hình vuông có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 2: Cho hình chóp .
S ABCD có đáy là hình vuông có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác vuông cân tại S và
nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 3: Cho hình chóp .
S ABCD có đáy là hình vuông có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa SC và
mặt đáy bằng 60 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <11 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 4: Cho hình chóp .
S ABCD có đáy là hình vuông có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa SC và
SAB bằng 30 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Mức 5: Cho hình chóp .
S ABCD có đáy là hình vuông có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa SAC
và mặt đáy bằng 60 (tham khảo hình vẽ). S A D B C
Thể tích khối chóp . S ABCD bằng Đáp án:
Dạng 7: Hình lăng trụ đều
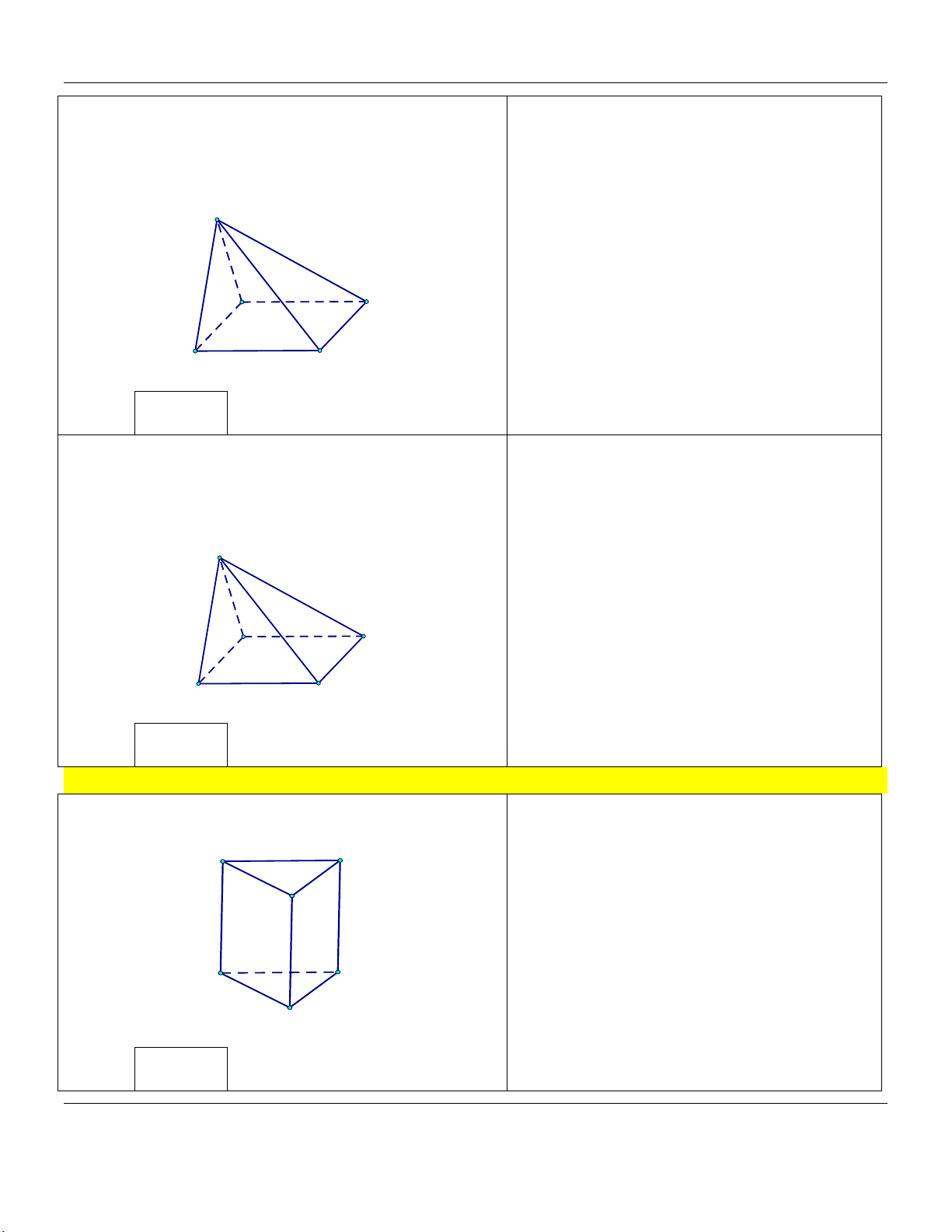
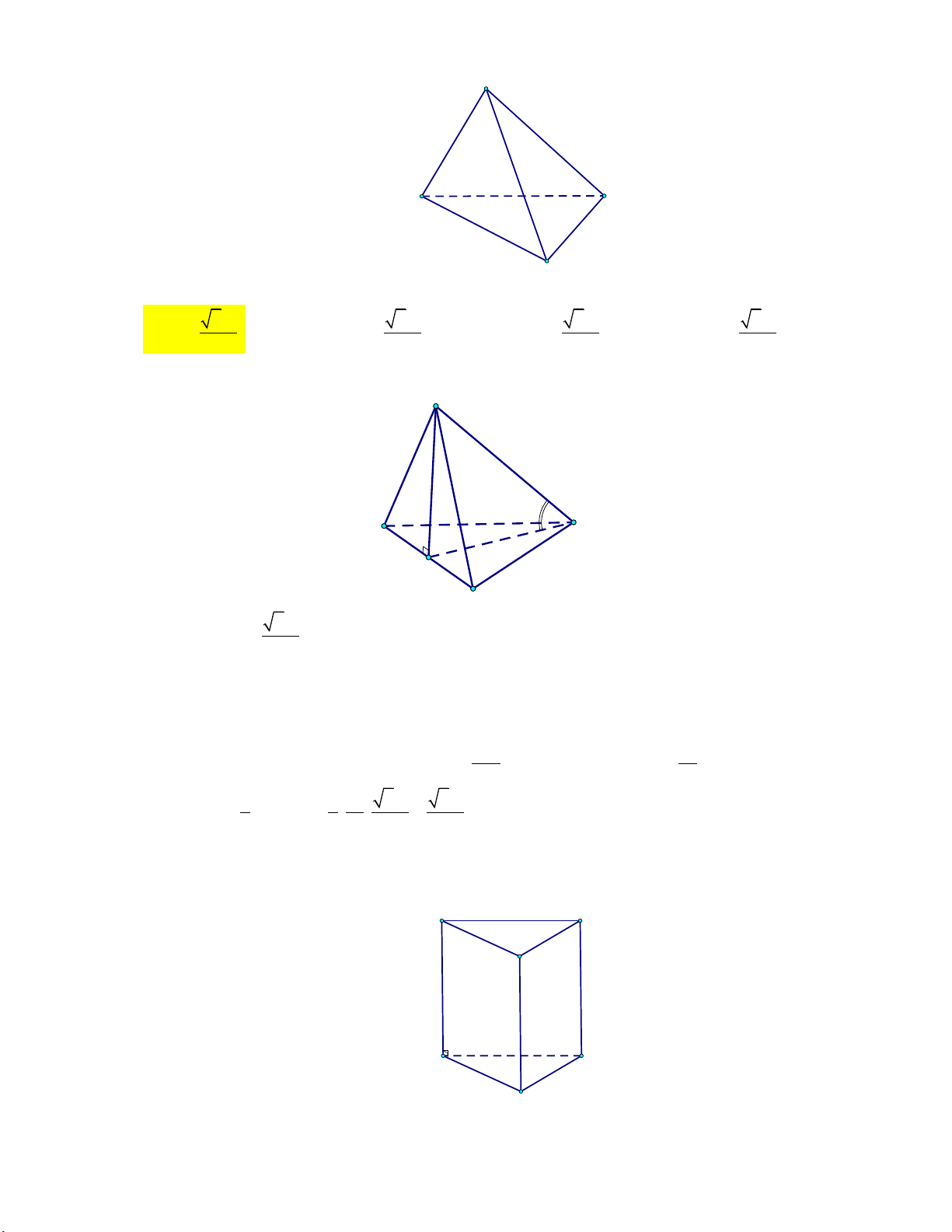
Mức 1: Cho lăng trụ đều ABC.A BC
  có cạnh đáy bằng a, Trình bày:
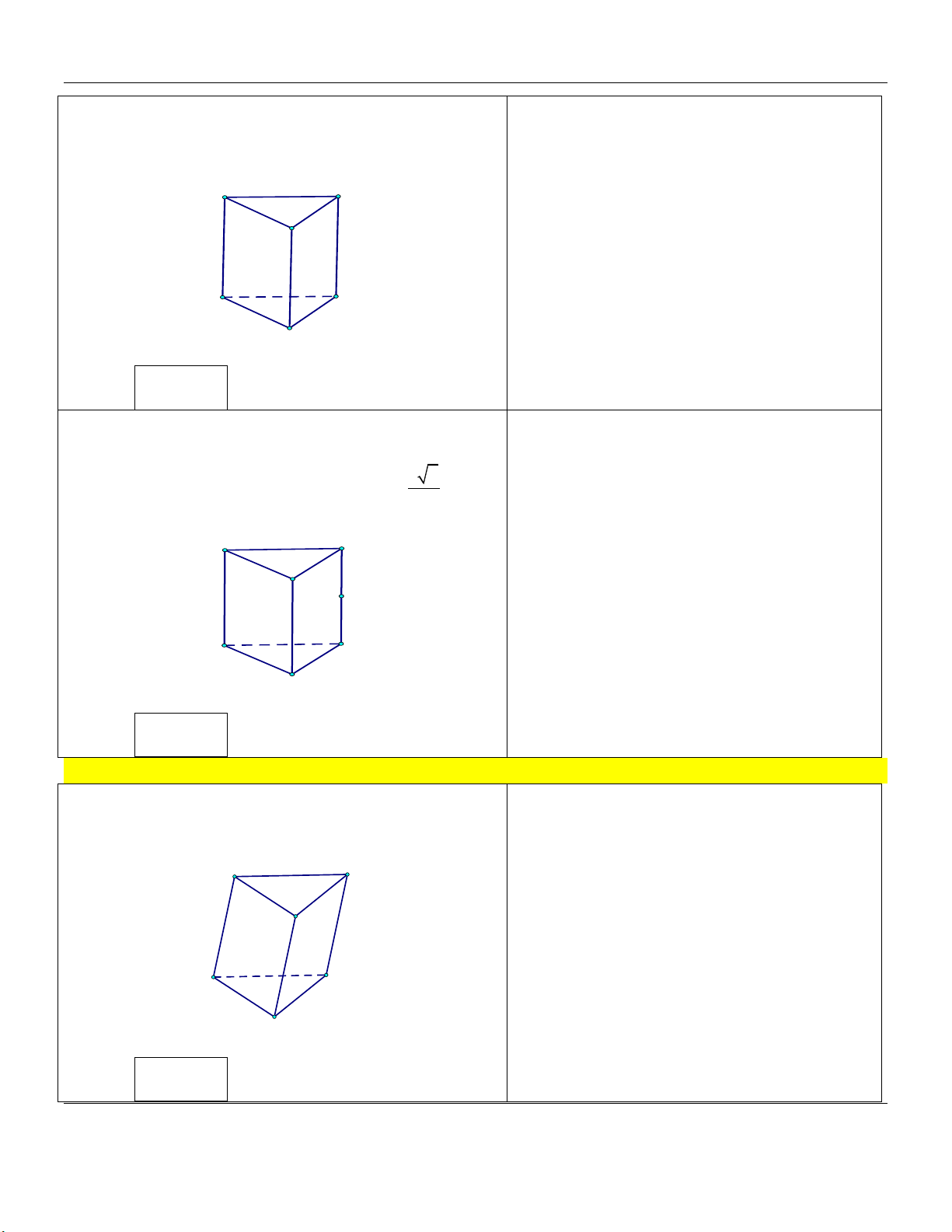
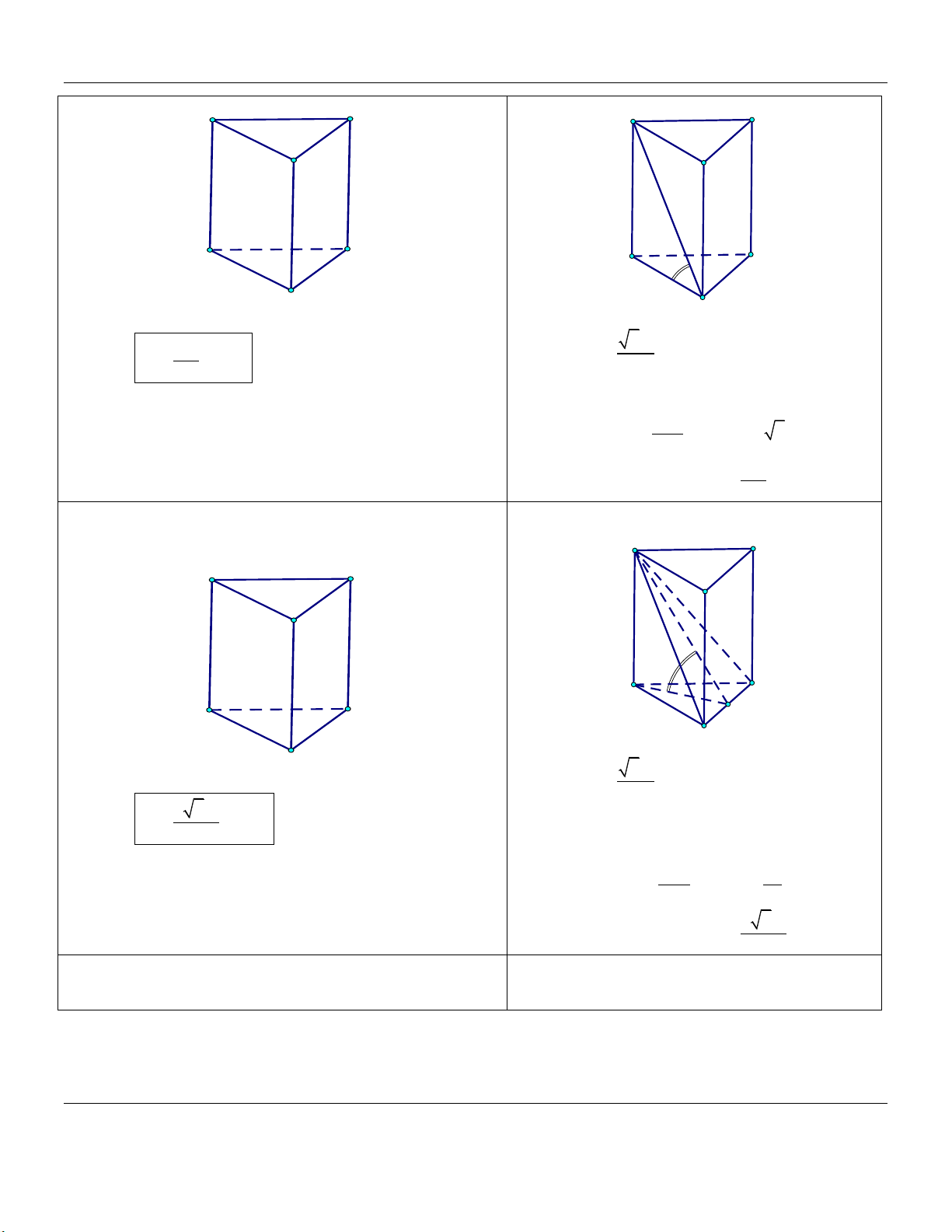
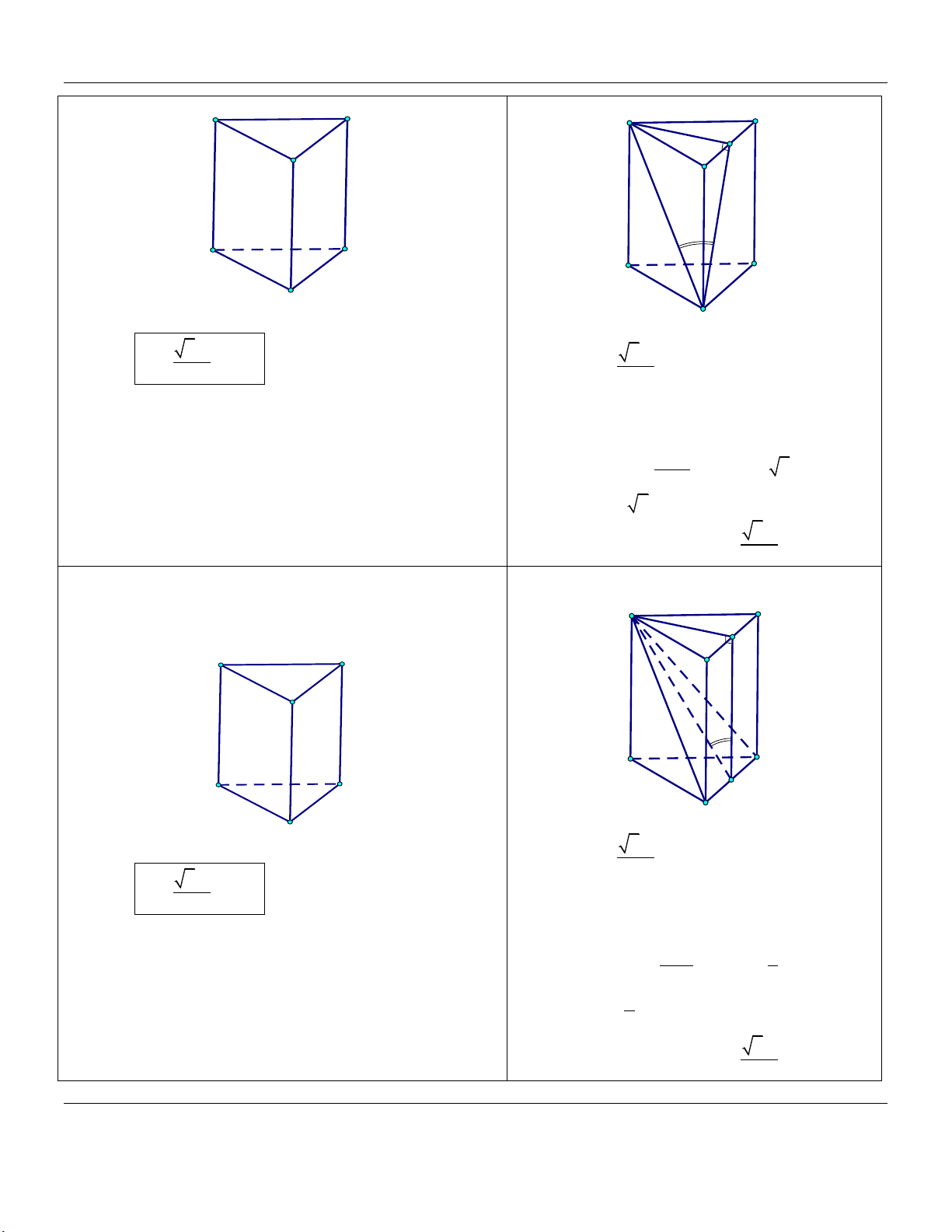
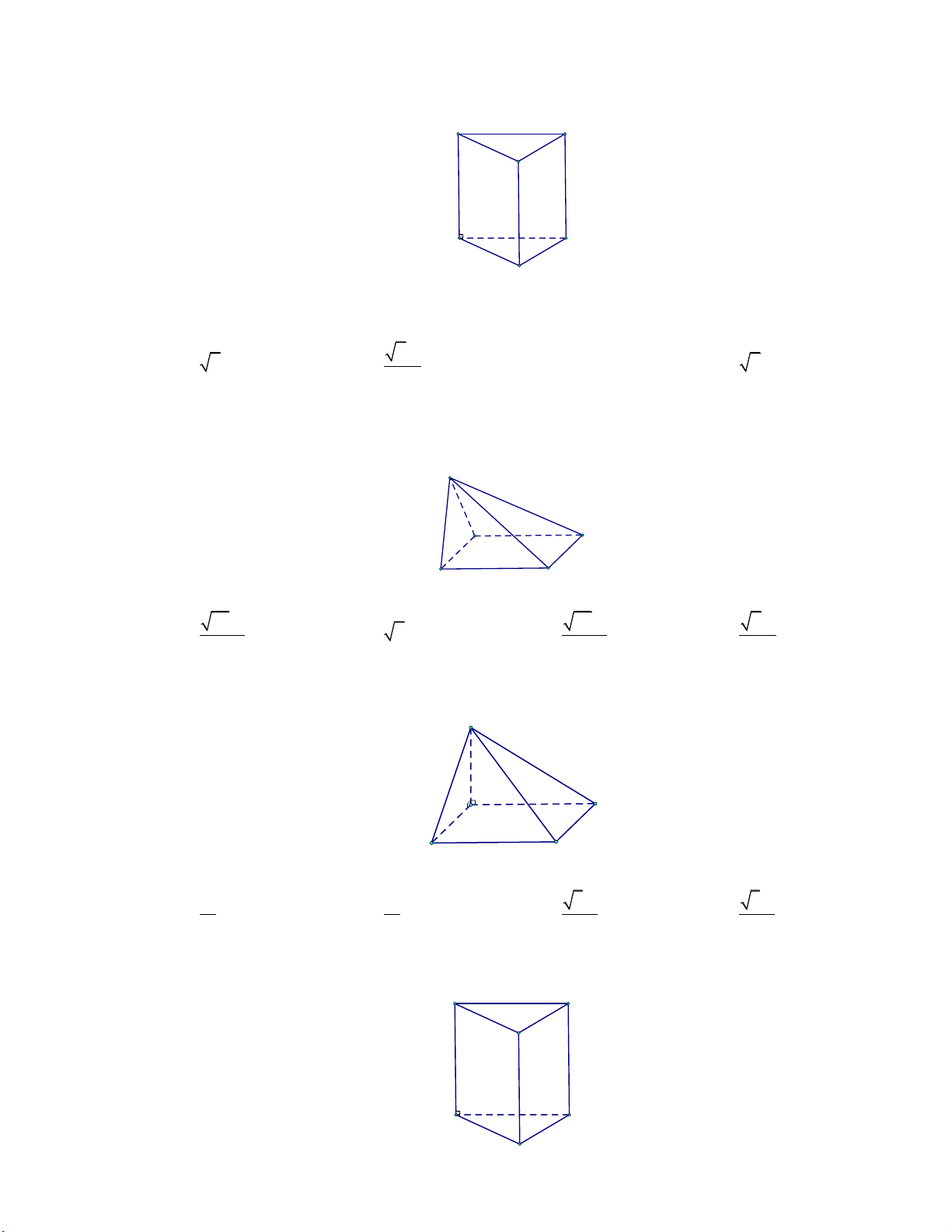
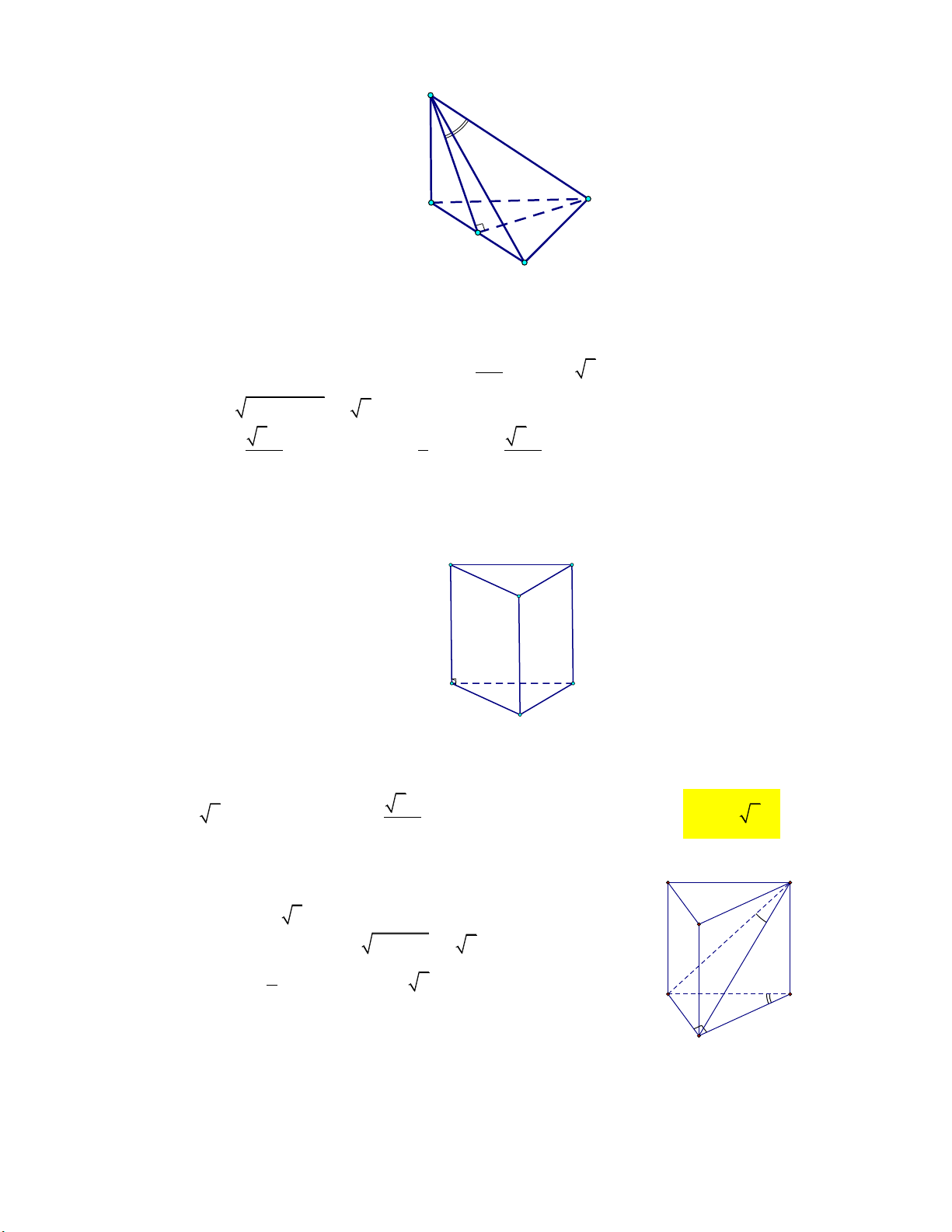
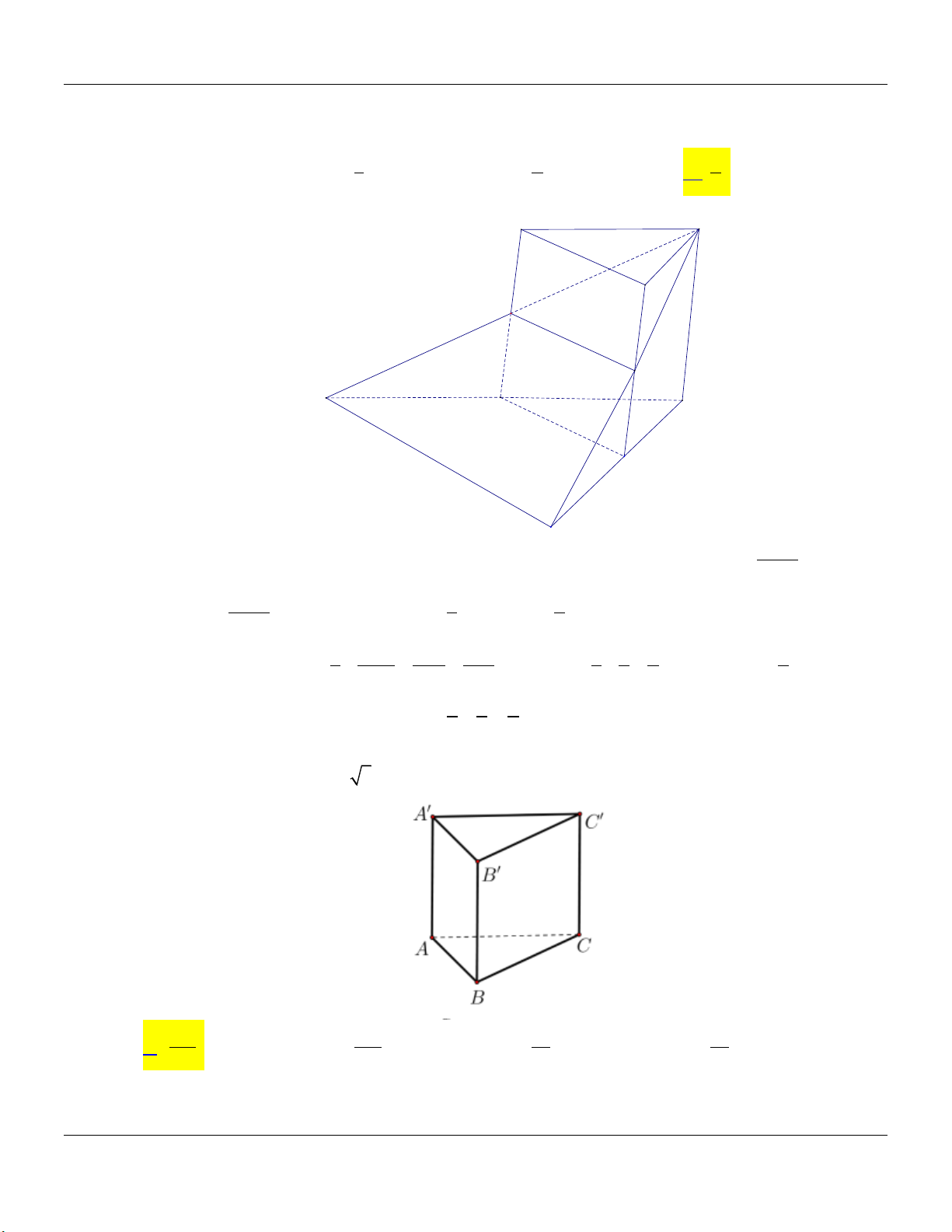
cạnh bên bằng 2a (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <12 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
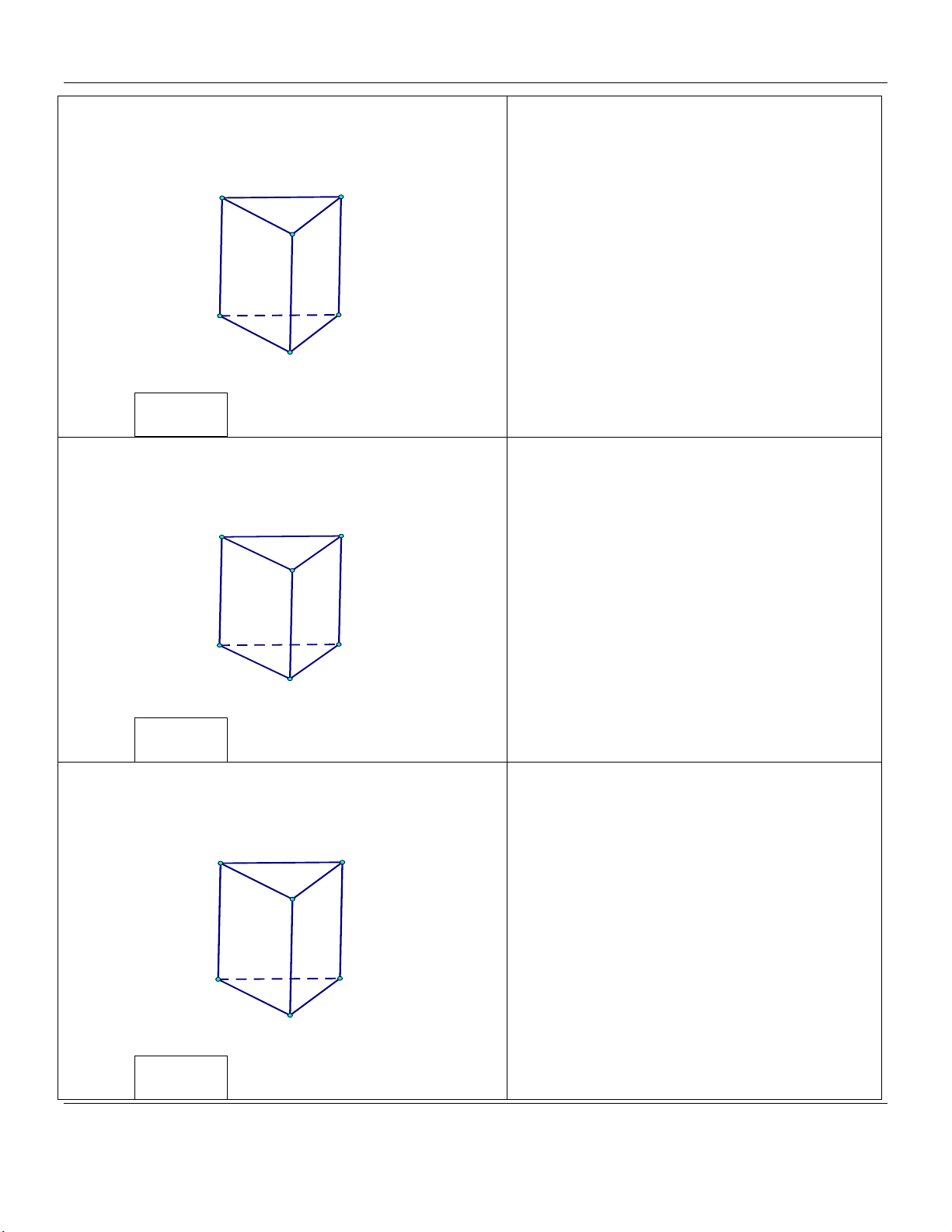
Mức 2: Cho lăng trụ đều ABC.A BC
  có cạnh đáy bằng a, Trình bày: A B
hợp với đáy một góc 60 (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Mức 3: Cho lăng trụ đều ABC.A BC
  có cạnh đáy bằng a, Trình bày:
A BC hợp với ABC một góc 60 (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Mức 4: Cho lăng trụ đều ABC.A BC
  có cạnh đáy bằng a, Trình bày: A B
hợp với BCC B
  một góc 30 (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <13 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 5: Cho lăng trụ đều ABC.A BC
  có cạnh đáy bằng a, Trình bày:
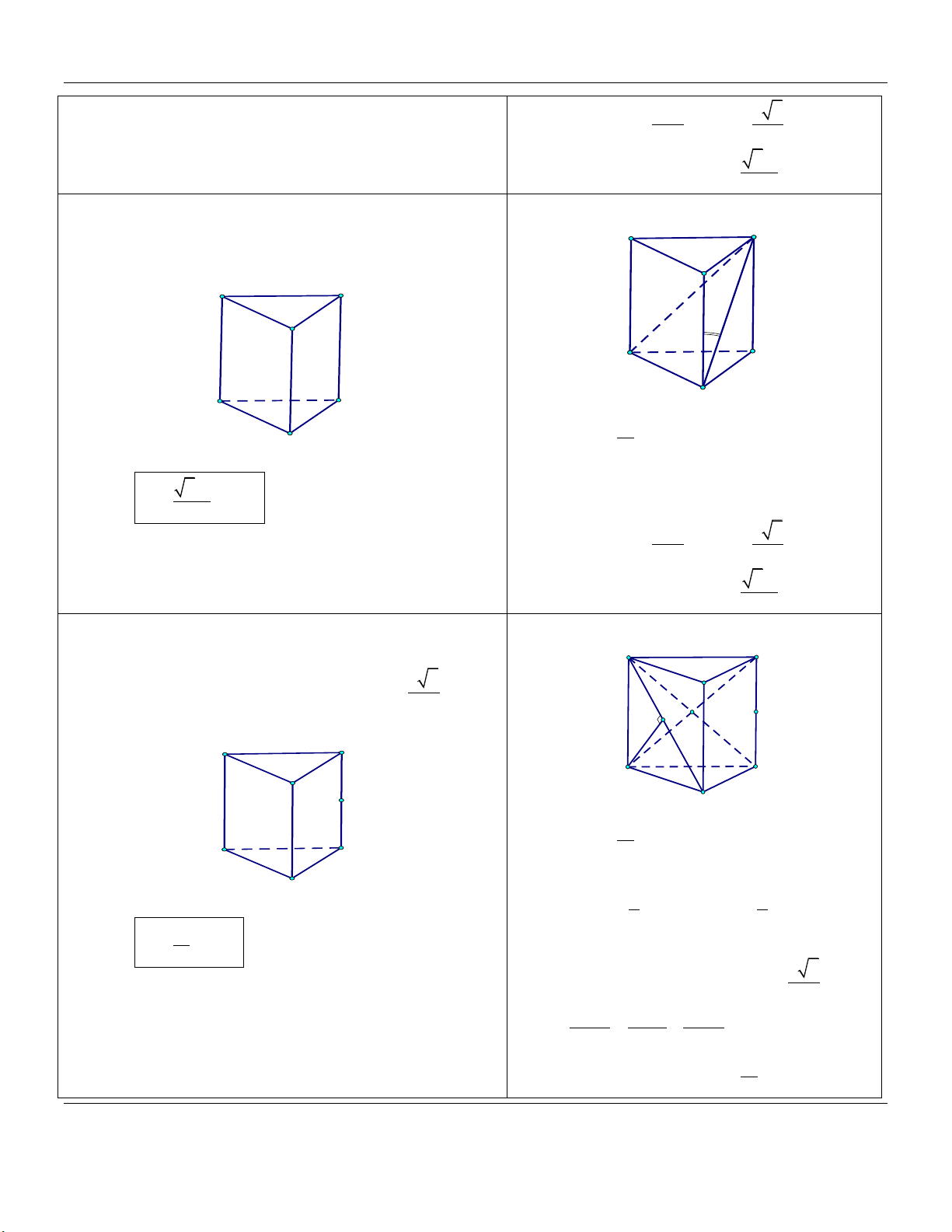
A BC hợp với BCC B một góc 60 (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Dạng 8: Hình lăng trụ đứng
Mức 1: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Diện tích tứ giác ABB A   bằng 2
2a (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Mức 2: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Diện tích tam giác A BC bằng 2
2a (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <14 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 3: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B,CC  2 .
a Biết khoảng cách từ
A đến BCC B
  bằng a (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Mức 4: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Biết góc giữa A C và
ABC bằng 45 (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Mức 5: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Biết góc giữa BC và ABB A
  bằng 60 (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <15 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 6: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Biết góc giữa ABC và ABB A
  bằng 60 (tham khảo hình vẽ). A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Mức 7: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Gọi I là trung điểm a 2
CC và khoảng cách từ I đến AB C   bằng (tham 4 khảo hình vẽ). A C B I A' C' B'
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
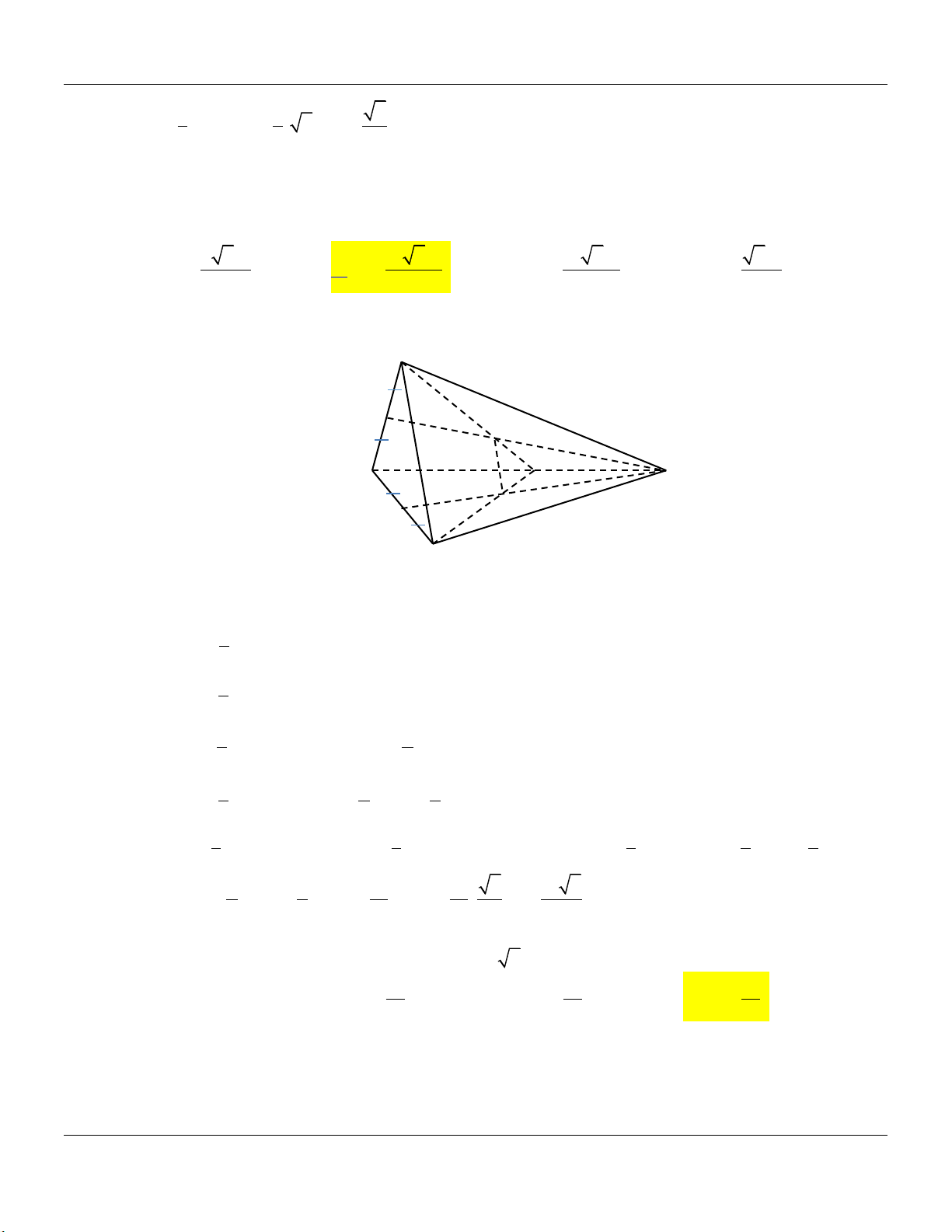
Dạng 9: Hình lăng trụ có đường cao khác cạnh bên
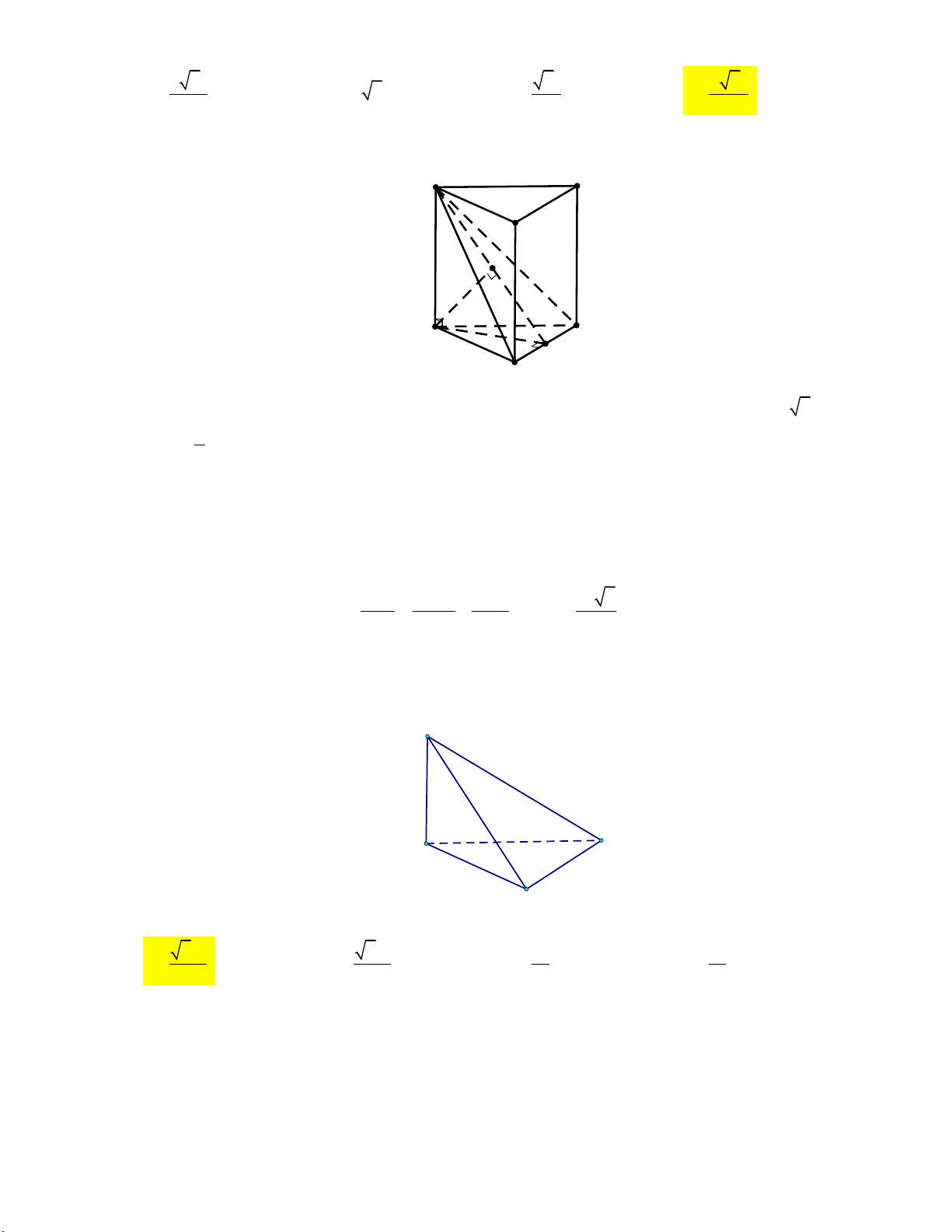
Mức 1: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác Trình bày:
vuông cân tại B, AB  .
a Cạnh bên BB  2a và hợp với
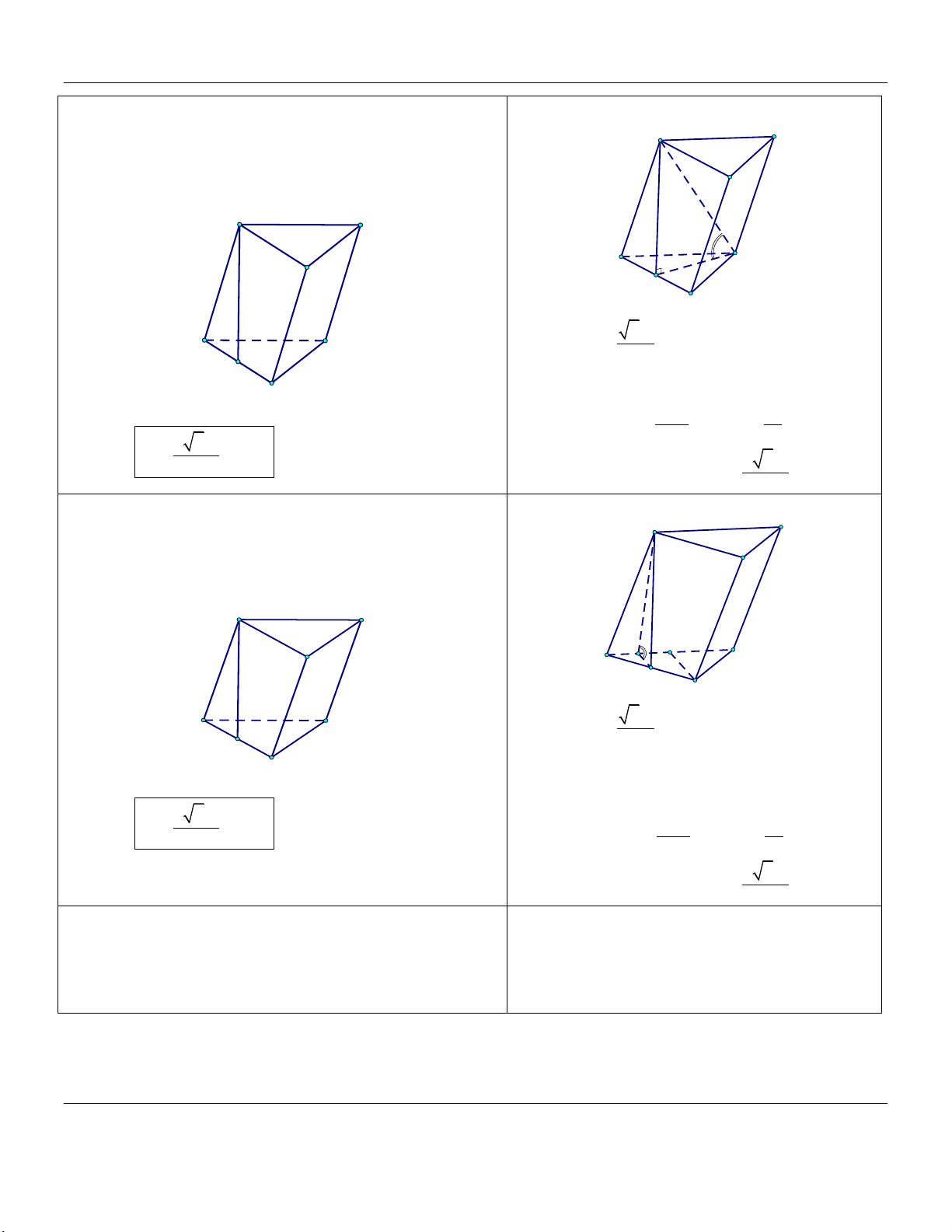
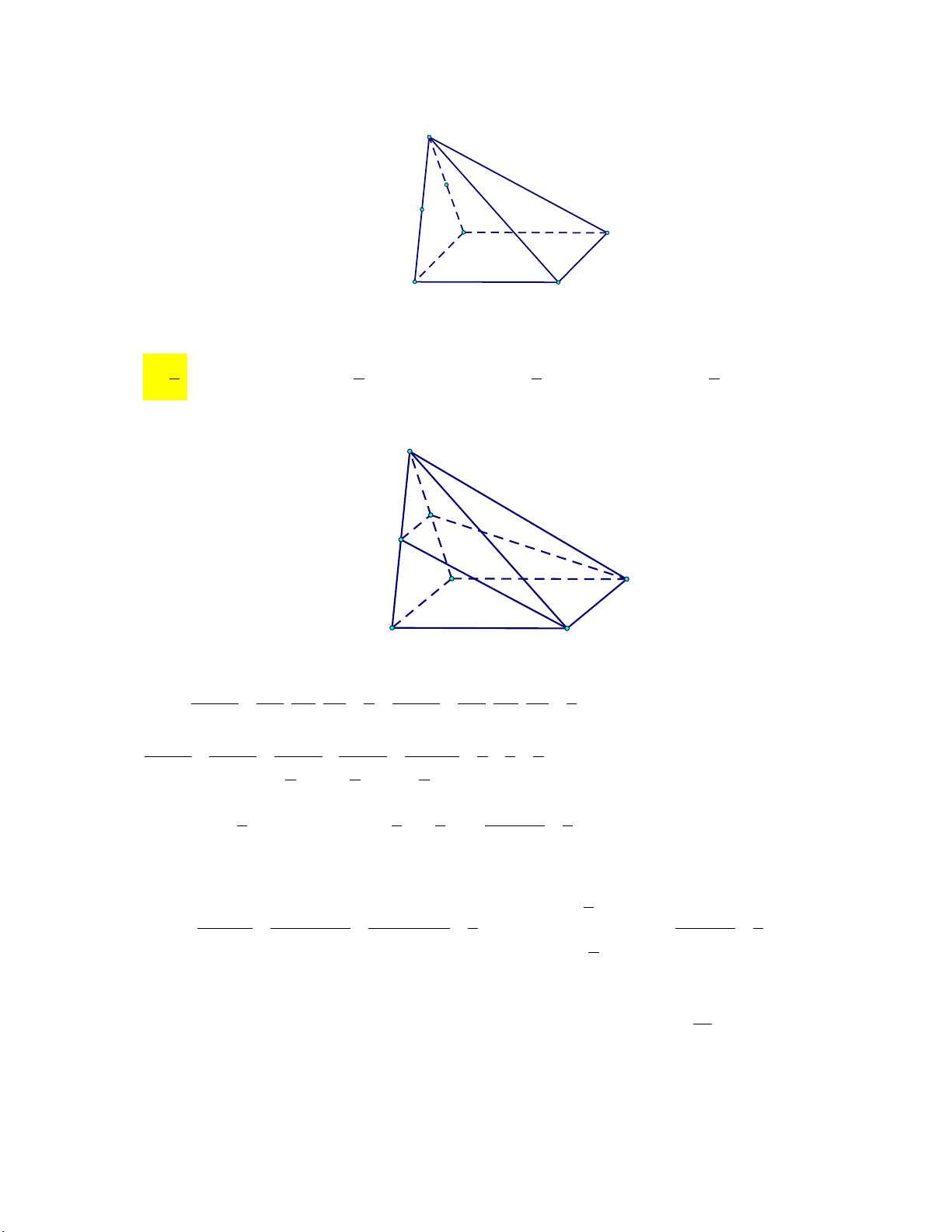
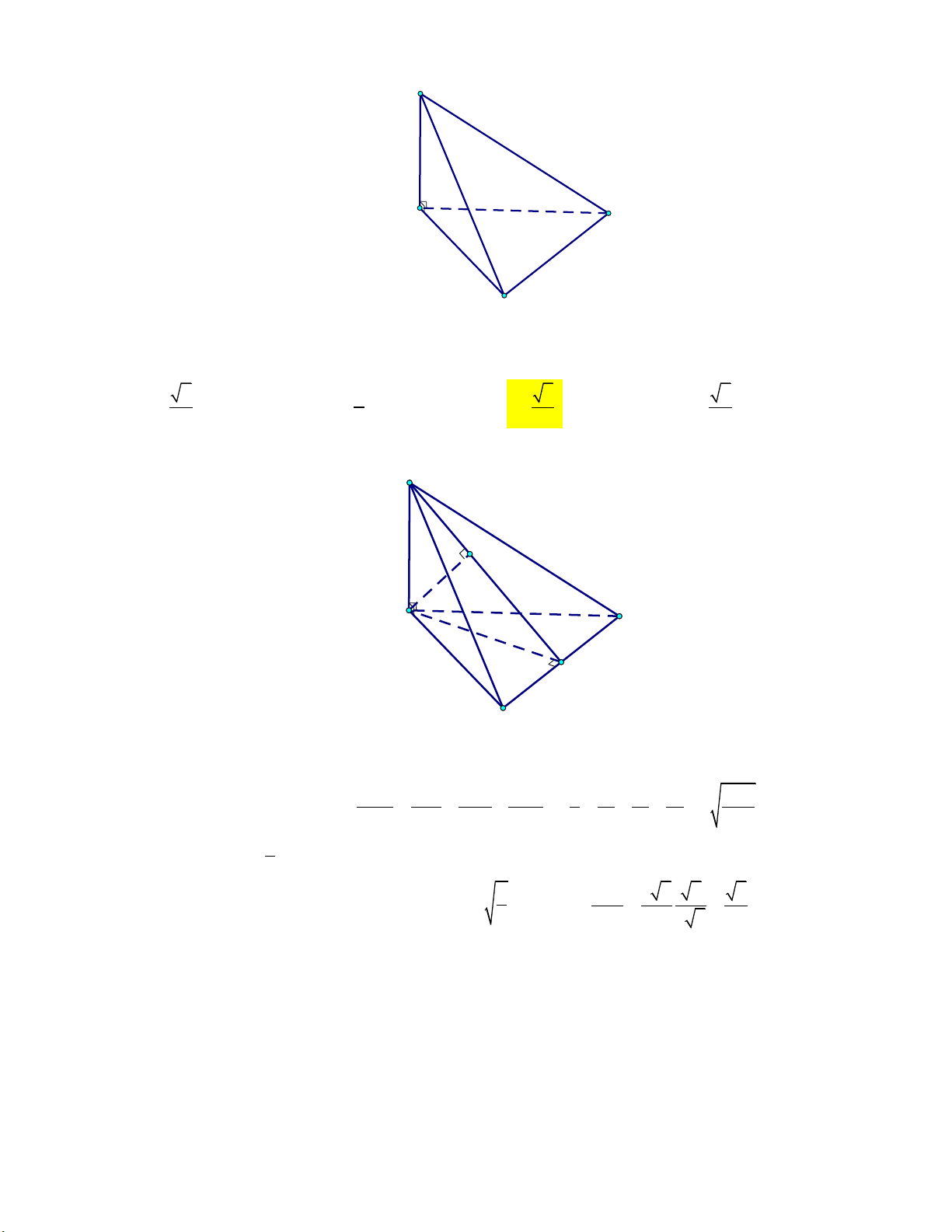
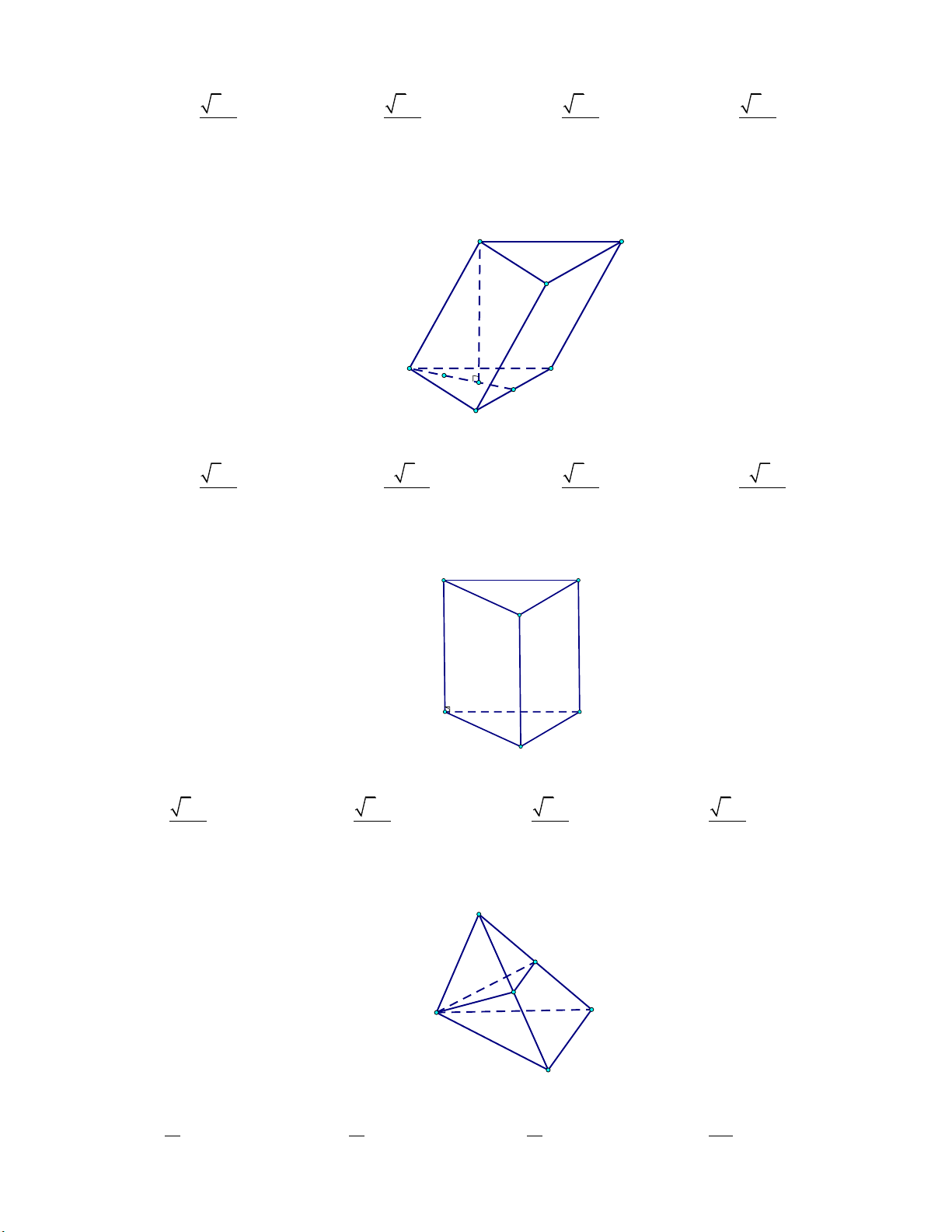
đáy một góc 30 (tham khảo hình vẽ) A' B' C' B A C
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <16 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 2: Cho lăng trụ ABC.A BC
  có mặt bên BCC B
  là Trình bày: hình vuông cạnh 2 .
a Biết khoảng cách từ A đến BCC B  
bằng a (tham khảo hình vẽ) A' B' C' B A C
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Mức 3: Cho lăng trụ ABC.A BC
  có mặt bên BCC B
  là Trình bày:
hình vuông cạnh AA  2a,BC a,B B
C  60 . Biết khoảng
cách từ A đến BCC B
  bằng a (tham khảo hình vẽ) A' B' C' B A C
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Mức 4: Cho lăng trụ ABC.A BC
  có đáy là tam giác đều Trình bày: cạnh .
a Hình chiếu của A trên ABC là trung điểm H của .
AB Biết góc giữa A C
và ABC bằng 60 (tham khảo hình vẽ) A' C' B' A C H B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <17 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 5: Cho lăng trụ ABC.A BC
  có đáy là tam giác đều Trình bày: cạnh .
a Hình chiếu của A trên ABC là trung điểm H của .
AB Biết góc giữa ACC A
  và ABC bằng 60
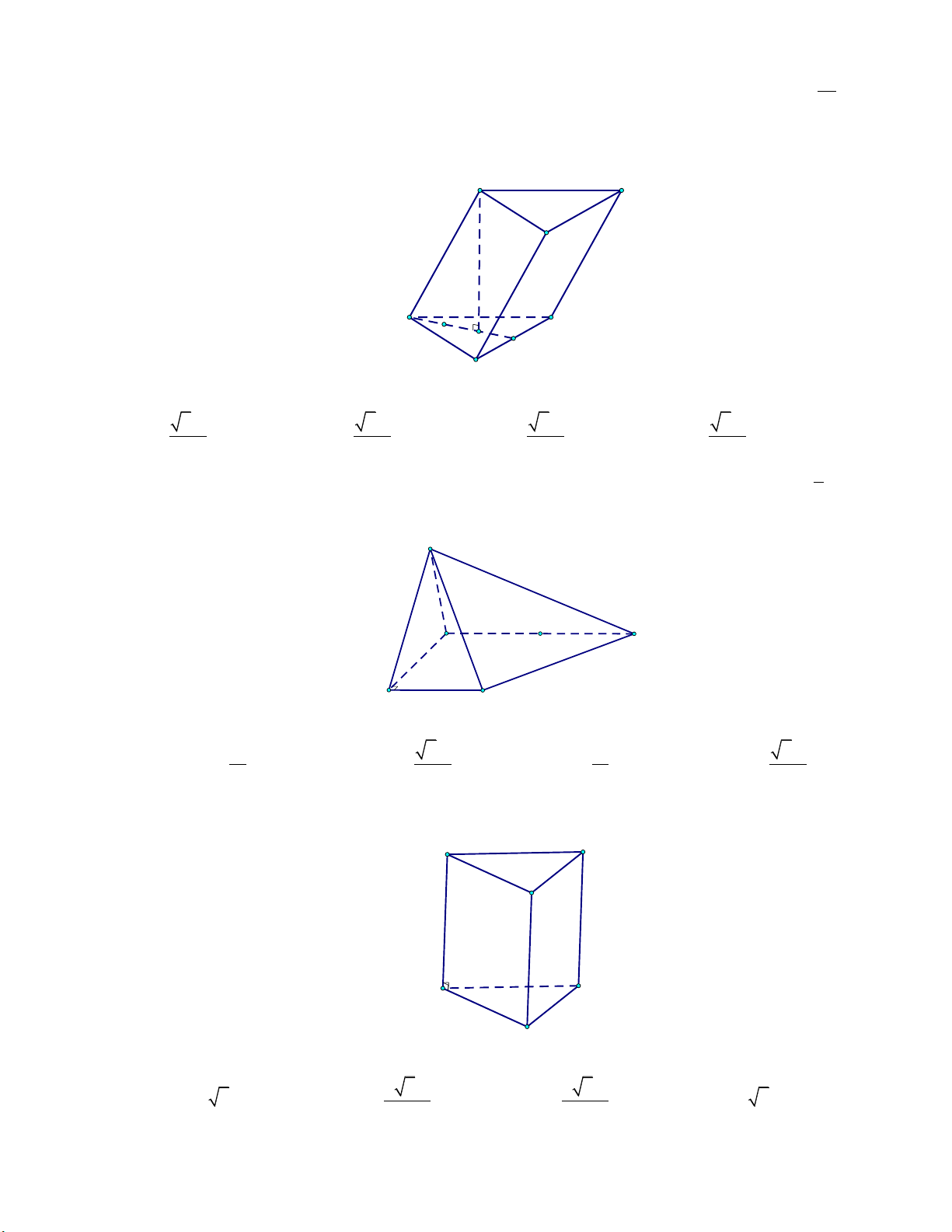
(tham khảo hình vẽ) A' C' B' A C H B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Mức 6: Cho lăng trụ ABC.A BC
  có đáy là tam giác đều Trình bày: cạnh .
a Hình chiếu của A trên ABC là trọng tâm G của tam giác .
AB Biết góc giữa AA và ABC bằng 60
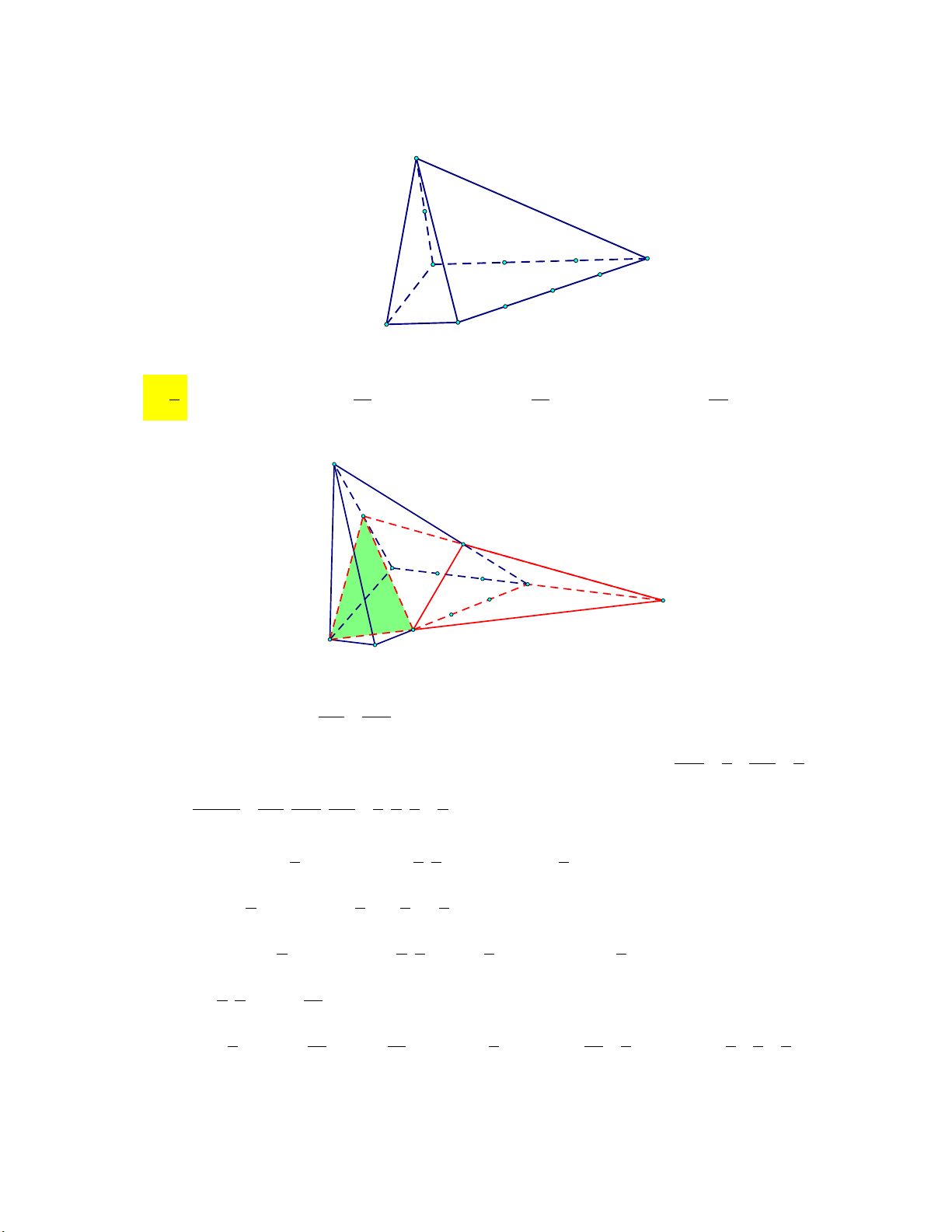
(tham khảo hình vẽ) A' C' B' A C G M B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Mức 7: Cho lăng trụ ABC.A BC
  có đáy là tam giác đều Trình bày: cạnh .
a Hình chiếu của A trên ABC là trọng tâm G của tam giác .
AB Biết góc giữa AA BB
  và ABC bằng
60 (tham khảo hình vẽ) A' C' B' A C G M B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <18 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
TỔNG HỢP MỘT SỐ DẠNG TÍNH THỂ TÍCH CẦN LƯU Ý
LỜI GIẢI CHI TIẾT
Dạng 1: Hình chóp tam giác có cạnh bên vuông góc với đáy
Mức 1: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
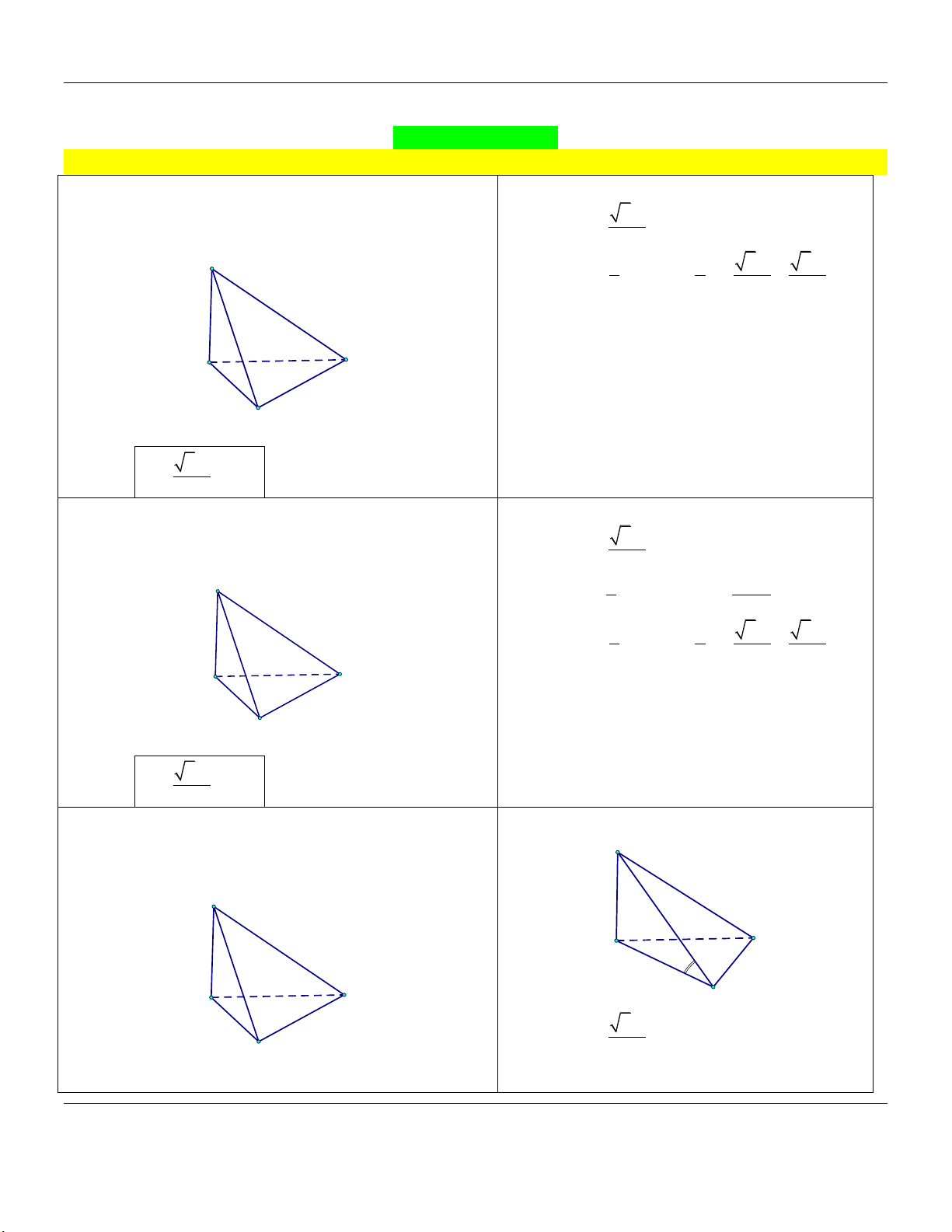
cạnh a,SA vuông góc với đáy và SA  2 . a (tham khảo 2 3a Ta có: S  . hình vẽ). ABC 4 S 2 3 1 1 3a 3a Vậy VS . A S  .2 . a  . S.ABC 3 ABC 3 4 6 A C B
Thể tích khối chóp . S ABC bằng 3 3a Đáp án: 6
Mức 2: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
cạnh a,SA vuông góc với đáy và diện tích tam giác SAB 2 3a Ta có: S  . bằng 2
2a (tham khảo hình vẽ). ABC 4 S 1 2S Ta có: S  . SAB SA AB SA   4 . a SAB 2 AB 2 3 1 1 3a 3a Vậy VS . A S  .4 . a  . S.ABC 3 ABC 3 4 3 A C B
Thể tích khối chóp . S ABC bằng 3 3a Đáp án: 3
Mức 3: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
cạnh a,SA vuông góc với đáy. Biết góc giữa SB và mặt S
đáy ABC bằng 60 (tham khảo hình vẽ). S A C A C B 2 3a Ta có: S  . B ABC 4
Thể tích khối chóp . S ABC bằng
Do SA   ABC  SB;ABC  SB . A
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <19 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 a SA Đáp án: Ta có: tanSBA   SA a 3. 4 AB 2 3 1 1 3a a Vậy VS . A S  .a 3.  . S.ABC 3 ABC 3 4 4
Mức 4: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
cạnh a,SA vuông góc với đáy. Biết góc giữa mặt phẳng S
SBC và mặt đáy ABC bằng 60 (tham khảo hình vẽ). S A C M A C B 2 3a Ta có: S  . ABC 4 B
Gọi M là trung điểm BC
Thể tích khối chóp . S ABC bằng
  SBC;ABC  SMA 3 3a Đáp án: 8 Ta có: SA 3a tanSMA
SA AM.tanSMA  . AM 2 2 3 1 1 3a 3a 3a Vậy VS . A S  . .  . S.ABC 3 ABC 3 2 4 8
Mức 5: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
cạnh a,SA vuông góc với đáy. Biết góc giữa SC và S
SAB bằng 30 (tham khảo hình vẽ). S A C M A C B 2 3a Ta có: S  . ABC B 4
Thể tích khối chóp
Gọi M là trung điểm . S ABC bằng
AB  SC;SAB  3 6a CSM. Đáp án: 12 CM Ta có: sinCSM   SC a 3. SC Suy ra: 2 2
SA SC AC a 2. 2 3 1 1 3a 6a Vậy V  . SA S  .a 2.  . S.ABC 3 ABC 3 4 12
Mức 6: Cho hình chóp .
S ABC có đáy là tam giác đều Trình bày:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <20 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
cạnh 2a,SA vuông góc với đáy. Biết khoảng cách từ điểm S
A đến SBC bằng a (tham khảo hình vẽ). S H A C A C M B B 3 2a2 2
Thể tích khối chóp . S ABC bằng Ta có: S   3a . ABC 4 3 2a Đáp án: Gọi M là trung điểm BC. Dựng 2
AH SM AH dA;SBC  . a 1 1 1 Ta có:   2 2 2 AH SA AM 1 1 1 2 6a      SA  . 2 2 2 2 SA AH AM 3a 2 3 1 1 a 6 2a Vậy 2 V  . SA S  . . 3a  . S.ABC 3 ABC 3 2 2
Dạng 2: Hình chóp tứ giác có cạnh bên vuông góc với đáy
Mức 1: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy và SB  2 .
a (tham khảo hình vẽ). Ta có: 2 Sa . ABCD S Ta có: 2 2
SA SB AB a 3. 3 1 1 3a Vậy 2 VS . A S  .a 3.a  . S.ABCD 3 ABCD 3 3 A D B C
Thể tích khối chóp . S ABCD bằng 3 3a Đáp án: 3
Mức 2: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy và diện tích tam giác SAC bằng Ta có: 2 Sa . ABCD 2
2 2a (tham khảo hình vẽ). 1 2S Ta có: S  . . SAC SA AC SA   4 . a SAC 2 AC 3 1 1 4a Vậy 2 V  . SA S  .4 . a a  . S.ABCD 3 ABCD 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <21 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S A D B C
Thể tích khối chóp . S ABCD bằng 3 4a Đáp án: 3
Mức 3: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy. Biết góc giữa SC và mặt đáy S
ABCD bằng 30 (tham khảo hình vẽ). S A D A D C B Ta có: 2 Sa . ABCD B C
Do SA   ABCD  SC;ABCD  SC . A
Thể tích khối chóp . S ABCD bằng SA 6a 3 6a Ta có: tanSCA   SA  . Đáp án: AC 3 9 3 1 1 6a 6a Vậy 2 VS . A S  . .a  . S.ABCD 3 ABCD 3 3 9
Mức 4: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy. Biết góc giữa SBC và mặt đáy S
ABCD bằng 30 (tham khảo hình vẽ). S A D C B A D Ta có: 2 Sa . ABCD
Ta có:  SBC;ABCD  SB . A B C
Thể tích khối chóp . S ABCD bằng SA 3a Ta có: tanSBA   SA  . AB 3 3 3a Đáp án: 3 1 1 3a 3a 9 Vậy 2 VS . A S  . .a  . S.ABCD 3 ABCD 3 3 9
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <22 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 5: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy. Biết góc giữa SBD và mặt đáy S
ABCD bằng 30 (tham khảo hình vẽ). S A D O A C D B Ta có: 2 Sa . ABCD
Gọi O là tâm hình vuông ABCD. B C
Thể tích khối chóp
SBD ; ABCD  . S ABCD bằng Ta có:     . SOA 3 6a SA 6a Đáp án: Ta có: tanSOA   SA  . 18 AO 6 3 1 1 6a 6a Vậy 2 VS . A S  . .a  . S.ABCD 3 ABCD 3 6 18
Mức 6: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy. Biết góc giữa SC và SAB bằng S
30 (tham khảo hình vẽ). S A D A C D B Ta có: 2 Sa . ABCD
BC SAB  SC; SAB   B C Do     BSC.
Thể tích khối chóp . S ABCD bằng BC Ta có: tan BSC   SB a 3. 3 2a SB Đáp án: 3 Suy ra: 2 2
SA SB AB a 2. 3 1 1 2a Vậy 2 VS . A S  .a 2.a  . S.ABCD 3 ABCD 3 3
Mức 7: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
a,SA vuông góc với đáy. Biết góc giữa SA và SBD bằng S
30 (tham khảo hình vẽ). A D O C B
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <23 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S Ta có: 2 Sa . ABCD
Gọi O là tâm hình vuông ABCD.
Ta có: SA;SBD  A . SO A AO 6a D Ta có: tan ASO   SA  . SA 2 3 1 1 6a 6a Vậy 2 VS . A S  . .a  . B C S.ABCD 3 ABCD 3 2 6
Thể tích khối chóp . S ABCD bằng 3 6a Đáp án: 6
Mức 8: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh Trình bày:
3a,SA vuông góc với đáy. Gọi M là trung điểm SD và S
khoảng cách từ M đến SBC bằng a (tham khảo hình M vẽ). H S A D M C B Ta có: 2 Sa . ABCD A D Ta có:
dM SBC 1
dD SBC 1 ; ;
dA;SBC B C 2 2
Thể tích khối chóp . S ABCD bằng
dA;SBC  2 .a 3 18 5a
AH SB dA; SBC    Đáp án: Dựng   AH 2 . a 5 1 1 1 6 5a Ta có:    SA  . 2 2 2 AH SA AB 5 Vậy 3 1 1 6 5a 2 18 5a V  . SA S  . .a  . S.ABCD 3 ABCD 3 5 5
Dạng 3: Hình chóp tam giác đều
Mức 1: Cho hình chóp tam giác đều .
S ABC có cạnh đáy Trình bày:
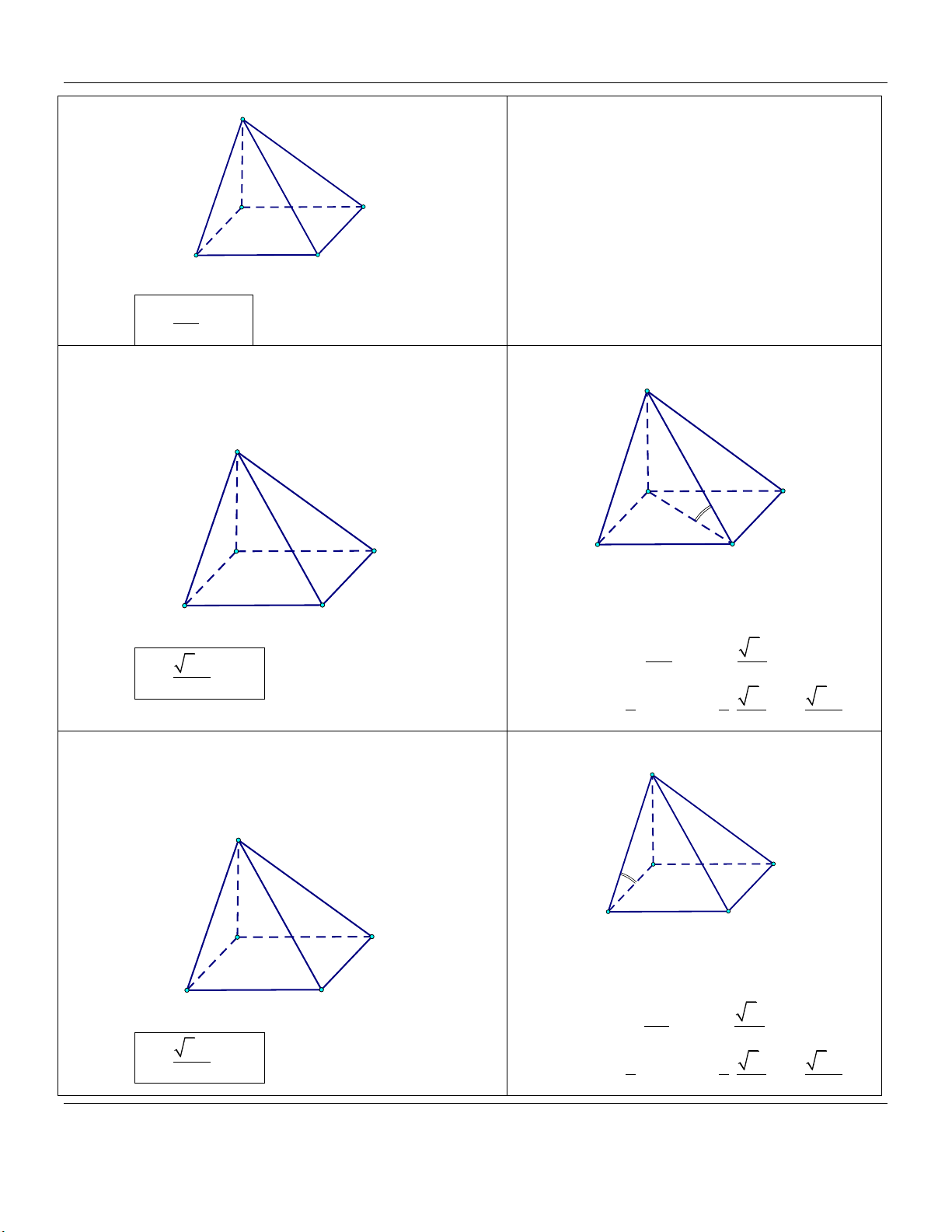
bằng a, cạnh bên bằng 2a (tham khảo hình vẽ). S A C G M B
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <24 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S 2 3a Ta có: S  . ABC 4
Gọi M là trung điểm BC,G là trọng tâm tam giác ABC. Ta có: A C 2   2 2 2 2AM 33a
SG SA AG SA     .  3  3 2 3 B 1 1 33a 3a 11a Vậy V  . SG S  . .  .
Thể tích khối chóp S.ABC ABC . S ABC bằng 3 3 3 4 12 3 11a Đáp án: 12
Mức 2: Cho hình chóp tam giác đều .
S ABC có cạnh đáy Trình bày:
bằng a, diện tích một mặt bên bằng 2 2a (tham khảo hình S vẽ). S A C G A C M B 2 B 3a Ta có: S  . ABC
Thể tích khối chóp . S ABC bằng 4
Gọi M là trung điểm BC,G là trọng tâm tam 3 191a Đáp án: giác ABC. 24 1 2S Ta có: SSM. SBC BC SM   4 . a SBC 2 BC a Suy ra: 2 2 573
SG SM GM  . 6 Vậy 2 3 1 1 573a 3a 191a VS . G S  . .  . S.ABC 3 ABC 3 6 4 24
Mức 3: Cho hình chóp tam giác đều .
S ABC có cạnh đáy Trình bày:
bằng a, cạnh bên hợp với đáy một góc 60 (tham khảo hình vẽ).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <25 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S S A C A C G M B B
Thể tích khối chóp . S ABC bằng 2 3 3a 3a Đáp án: Ta có: S  . ABC 12 4
Gọi M là trung điểm BC,G là trọng tâm tam giác ABC.
Ta có: SA;ABC  SA . G SG Ta có: tanSAG   SG  . a AG 2 3 1 1 3a 3a Vậy VS . G S  . . a  . S.ABC 3 ABC 3 4 12
Mức 4: Cho hình chóp tam giác đều .
S ABC có cạnh đáy Trình bày:
bằng a, mặt bên hợp với đáy một góc 60 (tham khảo hình S vẽ). S A C A C G M B 2 B 3a Ta có: S  .
Thể tích khối chóp ABC . S ABC bằng 4 3
Gọi M là trung điểm BC,G là trọng tâm tam 3a Đáp án: 24 giác ABC.
Ta có:  SBC; ABC  SM . G SG a Ta có: tanSMG   SG  . MG 2 2 3 1 1 a 3a 3a Vậy VS . G S  . .  . S.ABC 3 ABC 3 2 4 24
Mức 5: Cho hình chóp tam giác đều .
S ABC có cạnh đáy Trình bày: bằng 4 .
a Biết khoảng cách từ điểm A đến SBC bằng a (tham khảo hình vẽ).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <26 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S S H A A C C G M B B 2
Thể tích khối chóp . S ABC bằng 3a Ta có: S  . ABC 3 4 8 11a Đáp án:
Gọi M là trung điểm BC,G là trọng tâm tam 33 giác ABC. AM Ta có:  3  d ;
A SBC  3dG;SBC GM   a
d G;SBC  . 3
Dựng GH SM GH dG;SBC. 1 1 1 2 33a Ta có:    SG  . 2 2 2 GH GS GM 33 Vậy 2 3 1 1 2 33a 3a 8 11a VS . G S  . .  . S.ABC 3 ABC 3 33 4 33
Dạng 4: Hình chóp tứ giác đều
Mức 1: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày:
bằng a, cạnh bên bằng 2a (tham khảo hình vẽ). S S A D A D O B CB C Ta có: 2 S a . ABCD
Thể tích khối chóp . S ABCD bằng
Gọi O là tâm hình vuông ABCD. 3 14a a Đáp án: Ta có: 2 2 14
SO SD OD  . 6 2 3 1 1 14a 14a Vậy 2 V  . SO S  . .a  . S.ABCD 3 ABCD 3 2 6
Mức 2: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày:
bằng a, diện tích tam giác SAC bằng 2 2a (tham khảo hình
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <27 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia vẽ). S S A D A D O B CB C Ta có: 2 S a . ABCD
Thể tích khối chóp . S ABCD bằng
Gọi O là tâm hình vuông ABCD. 3 2 2a 1 2SSAC Đáp án: Ta có: S  .S . O AC SO   2 2 . a SAC 3 2 AC 3 1 1 2 2a Vậy 2 V  . SO S  .2 2 . a a  . S.ABCD 3 ABCD 3 3
Mức 3: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày:
bằng a, cạnh bên hợp với đáy một góc 60 (tham khảo hình S vẽ). S A D O B C A D Ta có: 2 Sa . ABCD
Gọi O là tâm hình vuông ABCD. B C S ;B ABCD
Thể tích khối chóp  . S ABCD bằng Ta có:   SB . O 3 6a SO a 6 Đáp án: Ta có: tanSBO   SO  . 6 BO 2 3 1 1 a 6 6a Vậy 2 VS . O S  . .a  . S.ABCD 3 ABCD 3 2 6
Mức 4: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày:
bằng a, mặt bên hợp với đáy một góc 60 (tham khảo hình S vẽ). S A D O M B C A D Ta có: 2 Sa . ABCD
Gọi O là tâm hình vuông ABCD, M là trung B C điểm . CD
Thể tích khối chóp . S ABCD bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <28 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 3a
Ta có:  SCD;ABCD  SM . O Đáp án: 6 SO a 3 Ta có: tanSMO   SO OM 2. 3 1 1 a 3 3a Vậy 2 VS . O S  . .a  . S.ABCD 3 ABCD 3 2 6
Mức 5: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày: bằng 2 .
a Biết khoảng cách từ điểm A đến SBC bằng a S
(tham khảo hình vẽ). S H A D O B M C A D Ta có: 2 S  4a . ABCD
Gọi O là tâm hình vuông ABCD, M là trung B C điểm BC.
Thể tích khối chóp . S ABCD bằng
Ta có: dA;SBC  2dO;SBC. 3 4 3a Đáp án: 9
Dựng OH SM dO;SBC  OH. 1 1 1 a 3 Ta có:    SO  . 2 2 2 OH OM SO 3 3 1 1 a 3 4 3a Vậy 2 V  . SO S  . .4a  . S.ABCD 3 ABCD 3 3 9
Mức 6: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy Trình bày: bằng 2 .
a Biết góc giữa hai mặt phẳng SAB và SCD S
bằng 90 (tham khảo hình vẽ). S A D M N O A D B C Ta có: 2 S  4a . ABCD B C
Gọi M, N lần lượt là trung điểm AB,CD.
Thể tích khối chóp . S ABCD bằng 3 4a
Ta có:  SAB;SCD  MSN  90 .  Đáp án: 3 1
Suy ra: SO MN  . a 2 3 1 1 4a Vậy 2 V  . SO S  . . a 4a  . S.ABCD 3 ABCD 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <29 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Dạng 5: Hình chóp tam giác có mặt bên là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy
Mức 1: Cho hình chóp .
S ABC có đáy là tam giác đều có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác đều và nằm trong S
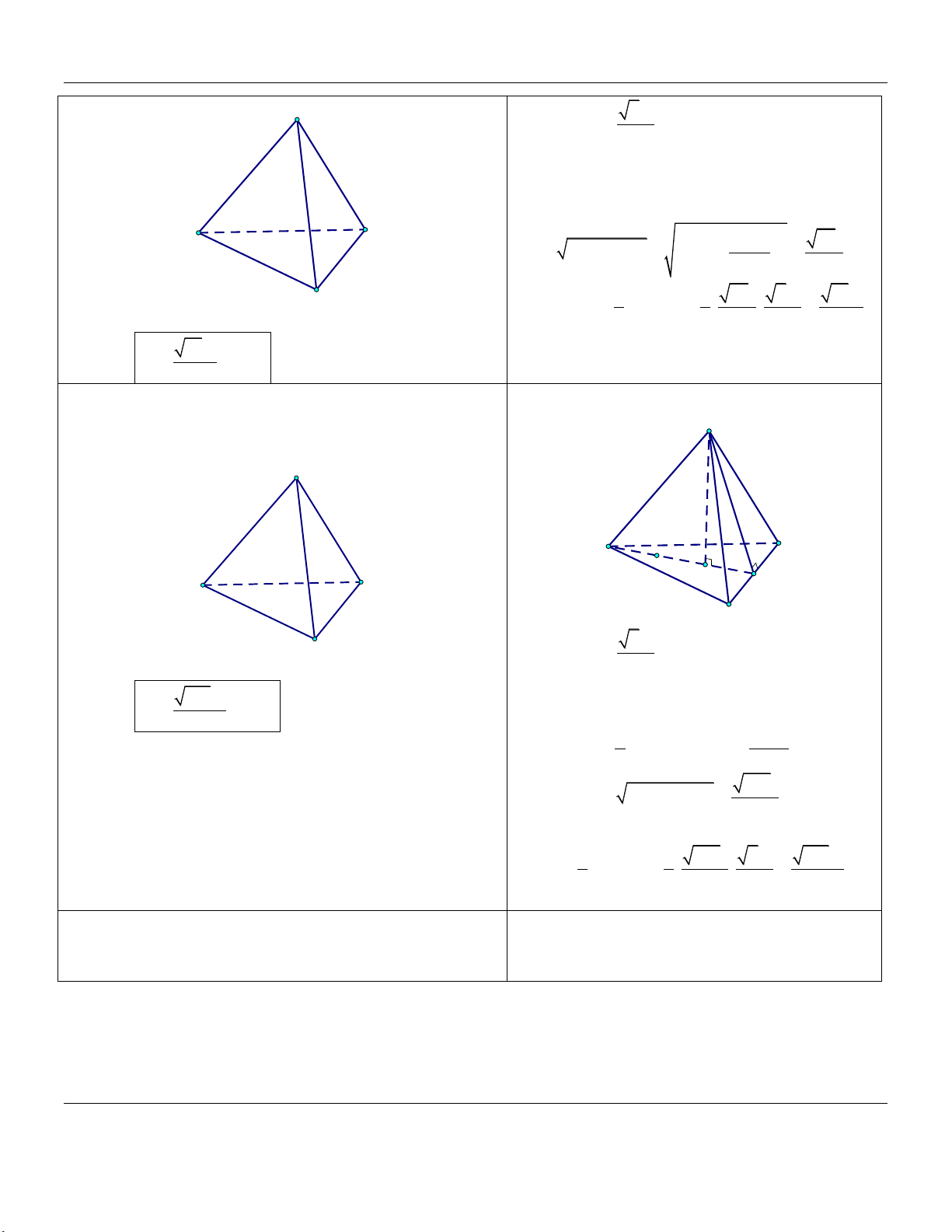
mặt phẳng vuông góc với đáy (tham khảo hình vẽ). S A C A C H B 2 3a B Ta có: S  . ABC 4
Thể tích khối chóp . S ABC bằng
Gọi H là trung điểm AB SH   ABC. 3 a Đáp án: 2 3 8 1 1 a 3 3a a Ta có: VSH.S  . .  . S.ABC 3 ABC 3 2 4 8
Mức 2: Cho hình chóp .
S ABC có đáy là tam giác đều có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác vuông cân tại S và S
nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). S A C H A C B 2 3a Ta có: S  . ABC 4 B
Gọi H là trung điểm AB SH   ABC.
Thể tích khối chóp . S ABC bằng 2 3 3 3a 1 1 a 3a 3a    Đáp án: Ta có: V SH.S . . . S.ABC ABC 24 3 3 2 4 24
Mức 3: Cho hình chóp .
S ABC có đáy là tam giác đều có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm S
trong mặt phẳng vuông góc với đáy. Biết góc giữa SC và
mặt đáy bằng 60 (tham khảo hình vẽ). C A H B
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <30 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S 2 3a Ta có: S  . ABC 4
Gọi H là trung điểm AB SH   ABC.
Ta có: SC;ABC  SCH. A C SH 3a Ta có: tanSCH   SH  . HC 2 B 2 3 1 1 3a 3a 3a
Thể tích khối chóp . S ABC bằng Ta có: VSH.S  . .  . S.ABC 3 ABC 3 2 4 8 3 3a Đáp án: 8
Mức 4: Cho hình chóp .
S ABC có đáy là tam giác đều có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm S
trong mặt phẳng vuông góc với đáy. Biết góc giữa SC và
SAB bằng 30 (tham khảo hình vẽ). S A C H B A C 2 3a Ta có: S  . ABC 4 B
Gọi H là trung điểm AB SH   ABC.
Thể tích khối chóp . S ABC bằng
Ta có: SC;SAB  HSC. 3 3a Đáp án: 8 HC 3a Ta có: tan HSC   SH  . SH 2 2 3 1 1 3a 3a 3a Ta có: VSH.S  . .  . S.ABC 3 ABC 3 2 4 8
Mức 5: Cho hình chóp .
S ABC có đáy là tam giác đều có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm S
trong mặt phẳng vuông góc với đáy. Biết góc giữa SBC
và mặt đáy bằng 60 (tham khảo hình vẽ). S C A M H N B A C 2 3a Ta có: S  . ABC 4 B  
Gọi H là trung điểm AB SHABC.
Thể tích khối chóp . S ABC bằng
Gọi M, N lần lượt là trung điểm BC và BM.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <31 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 3a
Ta có:  SBC;SAB  SNH. Đáp án: 16 SH 3a Ta có: tanSNH   SH  . HN 4 2 3 1 1 3a 3a 3a Ta có: VSH.S  . .  . S.ABC 3 ABC 3 4 4 16
Dạng 6: Hình chóp tứ giác có mặt bên là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy
Mức 1: Cho hình chóp .
S ABCD có đáy là hình vuông có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác đều và nằm trong S
mặt phẳng vuông góc với đáy (tham khảo hình vẽ). S A D A H D C B B C Ta có: 2 S a . ABCD
Thể tích khối chóp . S ABCD bằng
Gọi H là trung điểm AB SH   ABCD. 3 3a 3 Đáp án: 1 1 a 3 3a Vậy 2 V  .SH.S  . .a  . 6 S.ABCD 3 ABCD 3 2 6
Mức 2: Cho hình chóp .
S ABCD có đáy là hình vuông có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác vuông cân tại S và S
nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). S A D H A D C B Ta có: 2 Sa . ABCD B C
Gọi H là trung điểm AB SH   ABCD.
Thể tích khối chóp . S ABCD bằng 3 3 1 1 a a a Vậy 2 V  .SH.S  . .a  . Đáp án: S.ABCD 3 ABCD 3 2 6 6
Mức 3: Cho hình chóp .
S ABCD có đáy là hình vuông có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa SC và
mặt đáy bằng 60 (tham khảo hình vẽ).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <32 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S S A A D D H B C C B
Thể tích khối chóp . S ABCD bằng Ta có: 2 Sa . ABCD 3 15a   Đáp án:
Gọi H là trung điểm AB SHABCD. 6
Suy ra: SC;ABCD  SCH. SH 15a Ta có: tanSCH   SH  . CH 2 3 1 1 15a 15a Vậy 2 V  .SH.S  . .a  . S.ABCD 3 ABCD 3 2 6
Mức 4: Cho hình chóp .
S ABCD có đáy là hình vuông có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm S
trong mặt phẳng vuông góc với đáy. Biết góc giữa SC và
SAB bằng 30 (tham khảo hình vẽ). S A D H A C D B Ta có: 2 Sa . ABCD
Gọi H là trung điểm AB SH   ABCD. B C
Thể tích khối chóp . S ABCD bằng
Do BC  SAB nên SC;SAB  BSC. 3 11a BC Đáp án: Ta có: tan BSC   SB a 3. 6 SB a Suy ra: 2 2 11
SH SB BH  . 2 3 1 1 11a 11a Vậy 2 V  .SH.S  . .a  . S.ABCD 3 ABCD 3 2 6
Mức 5: Cho hình chóp .
S ABCD có đáy là hình vuông có Trình bày:
cạnh bằng a, mặt bên SAB là tam giác cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Biết góc giữa SAC
và mặt đáy bằng 60 (tham khảo hình vẽ).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <33 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S S A D A D K H O B C C B
Thể tích khối chóp . S ABCD bằng Ta có: 2 Sa . 3 6a ABCD Đáp án:
Gọi H là trung điểm AB SH   ABCD. 12
Gọi O là tâm hình vuông ABCD,K là trung điểm . AO
Suy ra:  SAC;ABCD  SKH. SH 6a Ta có: tanSKH   SH  . HK 4 3 1 1 6a 6a Vậy 2 V  .SH.S  . .a  . S.ABCD 3 ABCD 3 4 12
Dạng 7: Hình lăng trụ đều
Mức 1: Cho lăng trụ đều ABC.A BC
  có cạnh đáy bằng a, Trình bày:
cạnh bên bằng 2a (tham khảo hình vẽ). 2 3a Ta có: S  . A' ABC C' 4 3 3a Suy ra: V       AA .S . ABC.A B C ABC B' 2 C A B
Thể tích khối lăng trụ ABC.A BC   bằng 3 3a Đáp án: 2
Mức 2: Cho lăng trụ đều ABC.A BC
  có cạnh đáy bằng a, Trình bày: A B
hợp với đáy một góc 60 (tham khảo hình vẽ).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <34 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A' C' A' C' B' B' C A C A B B
Thể tích khối lăng trụ ABC.A BC   bằng 2 3 3a 3a Đáp án: Ta có: S  . ABC 4 4 Ta có:  A ;
B ABC  A B  . A AA Ta có: tan A BA
AA  a 3. AB 3 3a Suy ra: V       AA .S . ABC.A B C ABC 4
Mức 3: Cho lăng trụ đều ABC.A BC
  có cạnh đáy bằng a, Trình bày:
A BC hợp với ABC một góc 60 (tham khảo hình vẽ). A' C' A' C' B' B' C A C M A B B 2 3a
Thể tích khối lăng trụ ABC.A BC   bằng Ta có: S  . ABC 4 3 3 3a Đáp án:
Gọi M là trung điểm BC. 8 Ta có:  A B
C;ABC  A M  . A AA 3a Ta có: tan A MA   AA  . AM 2 3 3 3a Suy ra: V       AA .S . ABC.A B C ABC 8
Mức 4: Cho lăng trụ đều ABC.A BC
  có cạnh đáy bằng a, Trình bày: A B
hợp với BCC B
  một góc 30 (tham khảo hình vẽ).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <35 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A' C' A' C' M B' B' C A C A B
Thể tích khối lăng trụ ABC.A BC   bằng B 3 6a 2 Đáp án: 3a Ta có: S  . 4 ABC 4
Gọi M là trung điểm B C  . Ta có: A ; B BCC B    A BM. A M  Ta có: sin A BM   A B   a 3. A B
Suy ra: BB  a 2. 3 6a Suy ra: V       AA .S . ABC.A B C ABC 4
Mức 5: Cho lăng trụ đều ABC.A BC
  có cạnh đáy bằng a, Trình bày:
A BC hợp với BCC B một góc 60 (tham khảo hình A' C' vẽ). N A' C' B' B' A C C A M B B 2
Thể tích khối lăng trụ ABC.A BC   bằng 3a Ta có: S  . ABC 3 4 3a Đáp án:
Gọi M, N lần lượt là trung điểm BC, B C  . 8 Ta có:  A B
C;BCC B    A MN. A Na Ta có: tan A MN   MN  . MN 2 a Suy ra: AA  . 2 3 3a Suy ra: V       AA .S . ABC.A B C ABC 8
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <36 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Dạng 8: Hình lăng trụ đứng
Mức 1: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Diện tích tứ giác 2 a Ta có: S  . ABC ABB A   bằng 2
2a (tham khảo hình vẽ). 2      A' Ta có: S   AA .AB AA 2 . a C' ABB A Suy ra: 3 V       AA .S a . ABC.A B C ABC B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án: 3 a
Mức 2: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Diện tích tam giác A' C' A BC bằng 2
2a (tham khảo hình vẽ). A' C' B' B' C A C A B B 2
Thể tích khối lăng trụ ABC.A BC   bằng a Ta có: S  . ABC 3 15a 2 Đáp án:
Do BC   ABB A
   BC A . B 2 1 Ta có: S       A . B BC A B 4 . a A BC 2 Suy ra: 2 2 AA  A B   AB  15 . a 3 15a Suy ra: V       AA .S . ABC.A B C ABC 2
Mức 3: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B,CC  2 .
a Biết khoảng cách từ Ta có: dA ;BCC B    A B    . a
A đến BCC B
  bằng a (tham khảo hình vẽ). 2 1 a Suy ra: S  .B . A BC  . ABC 2 2 Vậy 3 V       AA .S a . ABC.A B C ABC
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <37 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A' C' B' C A B
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án: 3 a
Mức 4: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Biết góc giữa A C và A' C'
ABC bằng 45 (tham khảo hình vẽ). A' B' C' B' C A C A B 2 a B Ta có: S  . ABC 2
Thể tích khối lăng trụ ABC.A BC   bằng Ta có:  A C
 ;ABC  A . CA 3 2a Đáp án:  2 AA Ta có: tan A CA
AA  a 2. AC 3 2a Suy ra: V       AA .S . ABC.A B C ABC 2
Mức 5: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Biết góc giữa BC và A' C'ABB A
  bằng 60 (tham khảo hình vẽ). A' C' B' B' C A C A B 2 B a Ta có: S  .
Thể tích khối lăng trụ ABC.A BC   bằng ABC 2 3 3a Do B C    ABB A
   BC ;ABB A    C BB . Đáp án: 6
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <38 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia B C   a 3 Ta có: tanC BB   BB  . BB 3 3 3a Suy ra: V       AA .S . ABC.A B C ABC 6
Mức 6: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Biết góc giữa ABC A' C' và ABB A
  bằng 60 (tham khảo hình vẽ). B' A' C' B' C A C B A 2 a B Ta có: S  . ABC 2
Thể tích khối lăng trụ ABC.A BC   bằng Do 3 3a Đáp án: AB  BCC B     C A
B;ABB A    C BB . 6 B C   a 3 Ta có: tanC BB   BB  . BB 3 3 3a Suy ra: V       AA .S . ABC.A B C ABC 6
Mức 7: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là Trình bày:
tam giác vuông cân tại B, AB  .
a Gọi I là trung điểm A C a 2 B
CC và khoảng cách từ I đến AB C   bằng (tham 4 H I khảo hình vẽ). A C C' A' B I B' 2 a Ta có: S  . A' C' ABC 2 Ta có: B' 1 1
Thể tích khối lăng trụ ABC.A BC   bằng
dI;AB C
   dC;AB C
   dA ;AB C  . 2 2 3 a Đáp án: Dựng 2 A H
  AB  A H
  dA AB C   a 2 ;  . 2 1 1 1 Ta có:    AA  . a 2 2 2 A HAAA B   3 a Suy ra: V       AA .S . ABC.A B C ABC 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <39 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Dạng 9: Hình lăng trụ có đường cao khác cạnh bên
Mức 1: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác Trình bày:
vuông cân tại B, AB  .
a Cạnh bên BB  2a và hợp với 2 a Ta có: S  .
đáy một góc 30 (tham khảo hình vẽ) ABC 2
Gọi H là hình chiếu vuông góc của B trên A' B'
ABC BB ;ABC  B BH. C' B H  Ta có: sin B BH   B H   . a BB 3 a    B Suy ra: V    B H.S . A ABC.A B C ABC 2 C
Thể tích khối lăng trụ ABC.A BC   bằng 3 a Đáp án: 2
Mức 2: Cho lăng trụ ABC.A BC
  có mặt bên BCC B
  là Trình bày: hình vuông cạnh 2 .
a Biết khoảng cách từ A đến BCC B   Ta có: 2 S    4a . BCC B
bằng a (tham khảo hình vẽ) Ta có: A' B' 1 a V   V         d A BCC B S A B C CB    3 4 ; .   . . 3 BCC B 3 C' 2
Mặt khác: V   V .    3 ABC A B C 3 3     B V    V 2a . A ABC.A B C 2 C
Thể tích khối lăng trụ ABC.A BC   bằng Đáp án: 3 2a
Mức 3: Cho lăng trụ ABC.A BC
  có mặt bên BCC B
  là Trình bày:
hình vuông cạnh AA  2a,BC a,B B
C  60 . Biết khoảng 1 Ta có: 2 S        2S  2. BB .BC sin 60 3a . BCC B BB C
cách từ A đến BCC B
  bằng a (tham khảo hình vẽ) 2 Ta có: A' B' 1 3a V   V         d A ; BCC B .S   . A .B C CB    3 C' 3 BCC B 3 2
Mặt khác: V   V .    3 ABC A B C B A 3 3 3aV       V . ABC.A B C 2 2 C
Thể tích khối lăng trụ ABC.A BC   bằng 3 3a Đáp án: 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <40 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mức 4: Cho lăng trụ ABC.A BC
  có đáy là tam giác đều Trình bày: cạnh .
a Hình chiếu của A trên ABC là trung điểm H A' C' của .
AB Biết góc giữa A C
và ABC bằng 60 (tham B' khảo hình vẽ) A' C' A C B' H B 2 3a A Ta có: C S  . ABC 4 H Ta có: A C
 ;ABC  A CH  . B
Thể tích khối lăng trụ ABC.A BC   bằng A H  3a Ta có: tan A CH   A H   . 3 3 3a HC 2 Đáp án: 3 8 3 3a Suy ra: V       A H.S . ABC.A B C ABC 8
Mức 5: Cho lăng trụ ABC.A BC
  có đáy là tam giác đều Trình bày: cạnh .
a Hình chiếu của A trên ABC là trung điểm H A' C' của .
AB Biết góc giữa ACC A
  và ABC bằng 60 B'
(tham khảo hình vẽ) A' C' N M A C B' B 2 3a A C Ta có: S  . ABC H 4 B
Gọi M, N lần lượt là trung điểm AC, AM.
Thể tích khối lăng trụ ABC.A BC   bằng Ta có:  A CCA
;ABC  A NH  . 3 3 3a Đáp án: A H  3a 16 Ta có: tan A NH   A H   . HN 4 3 3 3a Suy ra: V       A H.S . ABC.A B C ABC 16
Mức 6: Cho lăng trụ ABC.A BC
  có đáy là tam giác đều Trình bày: cạnh .
a Hình chiếu của A trên ABC là trọng tâm G của tam giác .
AB Biết góc giữa AA và ABC bằng 60
(tham khảo hình vẽ)
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <41 >
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A' C' A' C' B' B' A C G A C M G B M
Thể tích khối lăng trụ ABC.A BC   bằng B 3 2 3a 3a Đáp án: Ta có: S  . ABC 4 4
Ta có: AA ; ABC  A A  . G A G  Ta có: tan A AG   A G   . a AG 3 3a Suy ra: V       A . G S . ABC.A B C ABC 4
Mức 7: Cho lăng trụ ABC.A BC
  có đáy là tam giác đều Trình bày: cạnh .
a Hình chiếu của A trên ABC là trọng tâm G A' C' của tam giác .
AB Biết góc giữa AA BB
  và ABC bằng B'
60 (tham khảo hình vẽ) A' C' B' A C N G M B 2 3a A Ta có: S  . C ABC 4 G M
Gọi N là trung điểm . AB B
Thể tích khối lăng trụ ABC.A BC   bằng Ta có:  AA BB
 ;ABC  A . NG 3 3aĐáp án: A G a Ta có: tan A NG   A G   . 8 AG 2 3 3a Suy ra: V       A . G S . ABC.A B C ABC 8
_____________________HẾT_____________________
Huế, 11h00’ Ngày 20 tháng 7 năm 2022
Lớp Toán thầy Lê Bá Bảo TP Huế 0935.785.115 <42 >
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 12 Chuyên đề:
THỂ TÍCH KHỐI ĐA DIỆN
PHIẾU HỌC TẬP SỐ 01_TrNg 2021 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Cho khối lăng trụ đứng có diện tích đáy bằng 2
2a và cạnh bên bằng 3a . Thể tích khối lăng trụ đã cho bằng A. 3 2a . B. 3 3a . C. 3 18a . D. 3 6a .
Câu 2: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a bằng 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 12 6 2 4
Câu 3: Cho hình lăng trụ đứng ABC.A' B'C ' có đáy ABC là tam giác vuông cân tại A với BC a và
mặt bên AA'B'B là hình vuông. Thể tích của khối lăng trụ ABC.A' B'C ' bằng 3 2a 3 2a 3 a 3 a A. . B. . C. . D. . 8 4 4 12
Câu 4: Cho hình chóp .
S ABC có đường cao SA, tam giác ABC vuông tại A có AB  2 , AC  4 . Gọi
H là trung điểm của BC (tham khảo hình vẽ). S C A H B
Biết diện tích tam giác SAH bằng 2, thể tích của khối chóp . S ABC bằng 16 5 16 5 4 5 4 5 A. . B. . C. . D. . 5 15 9 3
Câu 5: Cho hình chóp tứ giác đều có cạnh đáy bằng x (tham khảo hình vẽ). S A D O B C
Biết diện tích xung quanh của hình chóp đó gấp đôi diện tích đáy. Khi đó thể tích của khối chóp đã cho bằng 3 3 3 3 A. 3 x . B. 3 x . C. 3 x . D. 3 x . 12 2 3 6
Câu 6: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng 2a , cạnh bên bằng 3a (tham khảo hình vẽ). S A D O B C
Thể tích V của khối chóp đã cho là 3 4 7a 3 4a 3 4 7a A. 3 V  4 7a . B. V  . C. V  . D. V  . 9 3 3
Câu 7: Cho khối chóp .
S ABC có thể tích V . Gọi B,C lần lượt là trung điểm của AB, AC (tham khảo hình vẽ). S C' C A B' B
Tính theo V thể tích khối chóp . S AB C   . 1 1 1 1 A. V . B. V . C. V . D. V . 3 2 12 4
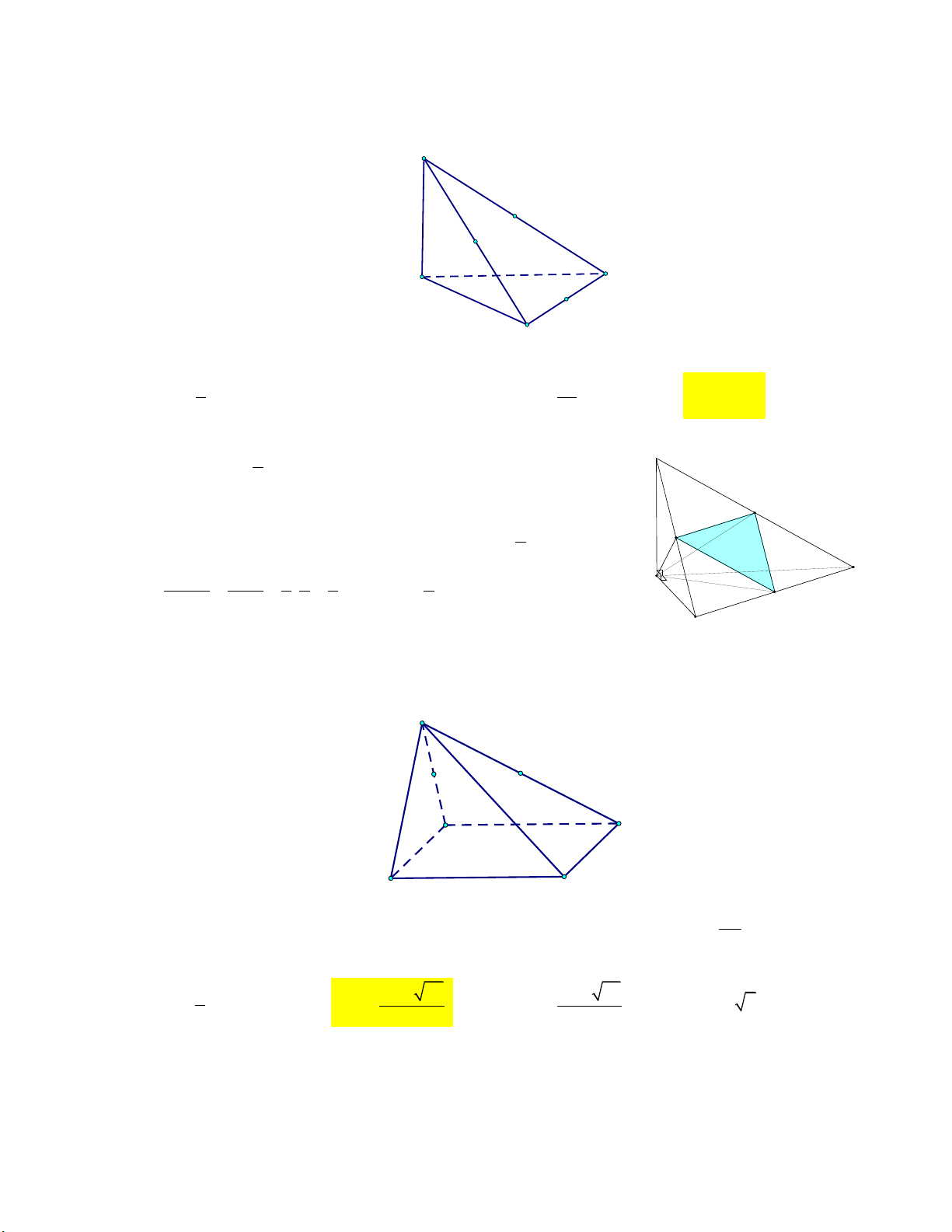
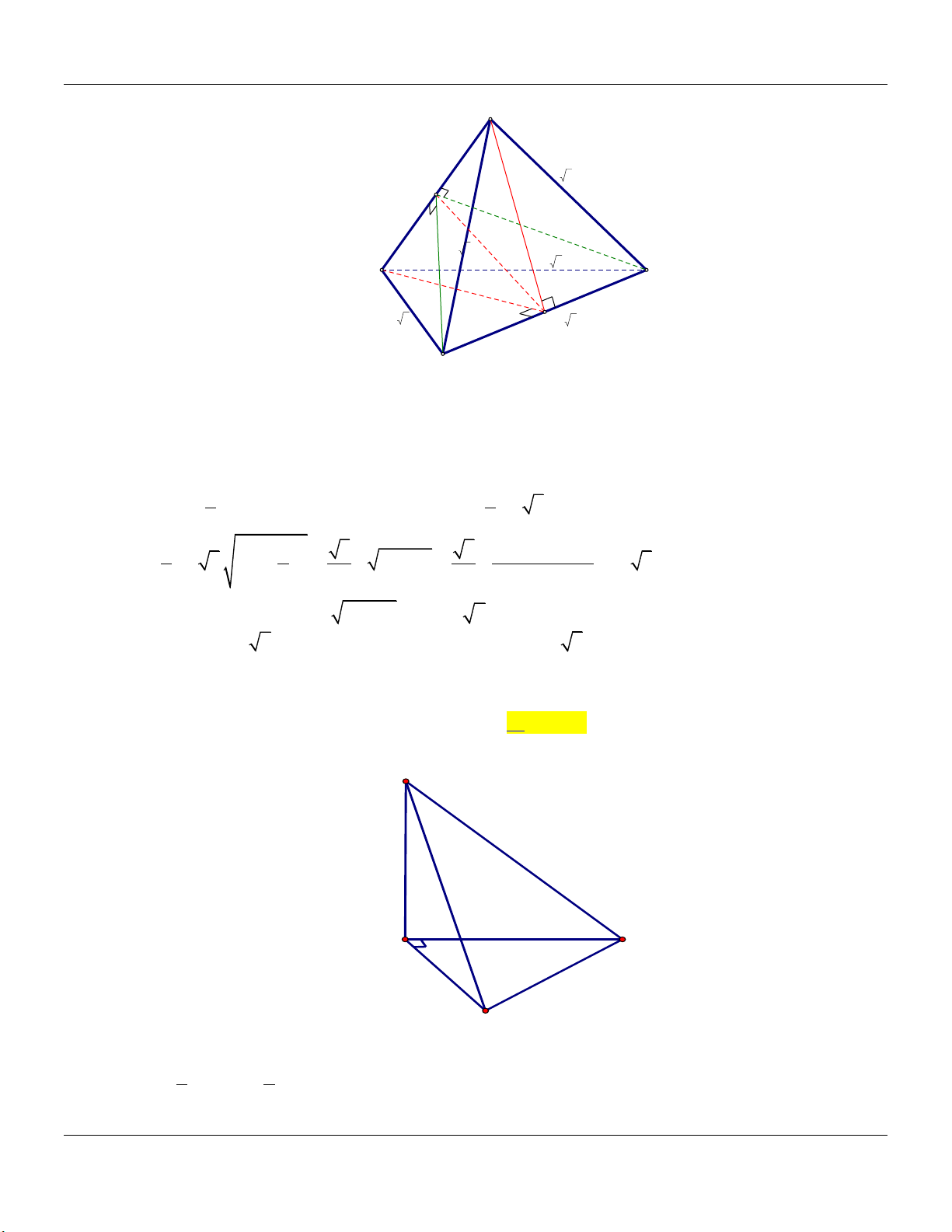
Câu 8: Cho tứ diện ABCD có thể tích bằng V , hai điểm M, P lần lượt là trung điểm của AB , CD ;
N là điểm thuộc đoạn AD sao cho AD  3AN (tham khảo hình vẽ). A N M B D P C
Thể tích tứ diện BMNP bằng V V V V A. . B. . C. . D. . 4 12 8 6
Câu 9: Cho hình lăng trụ ABC.A BC
  có thể tích bằng V . Gọi M là trung điểm cạnh BB , điểm N
thuộc cạnh CC sao cho CN  2C N  (tham khảo hình vẽ). A C B N M C' A' B' Thể tích khối chóp . A BCNM là 7V 7V 5V V A. V  . B. V  . C. V  . D. V  . A.BCNM 12 A.BCNM 18 A.BCNM 18 A.BCNM 3
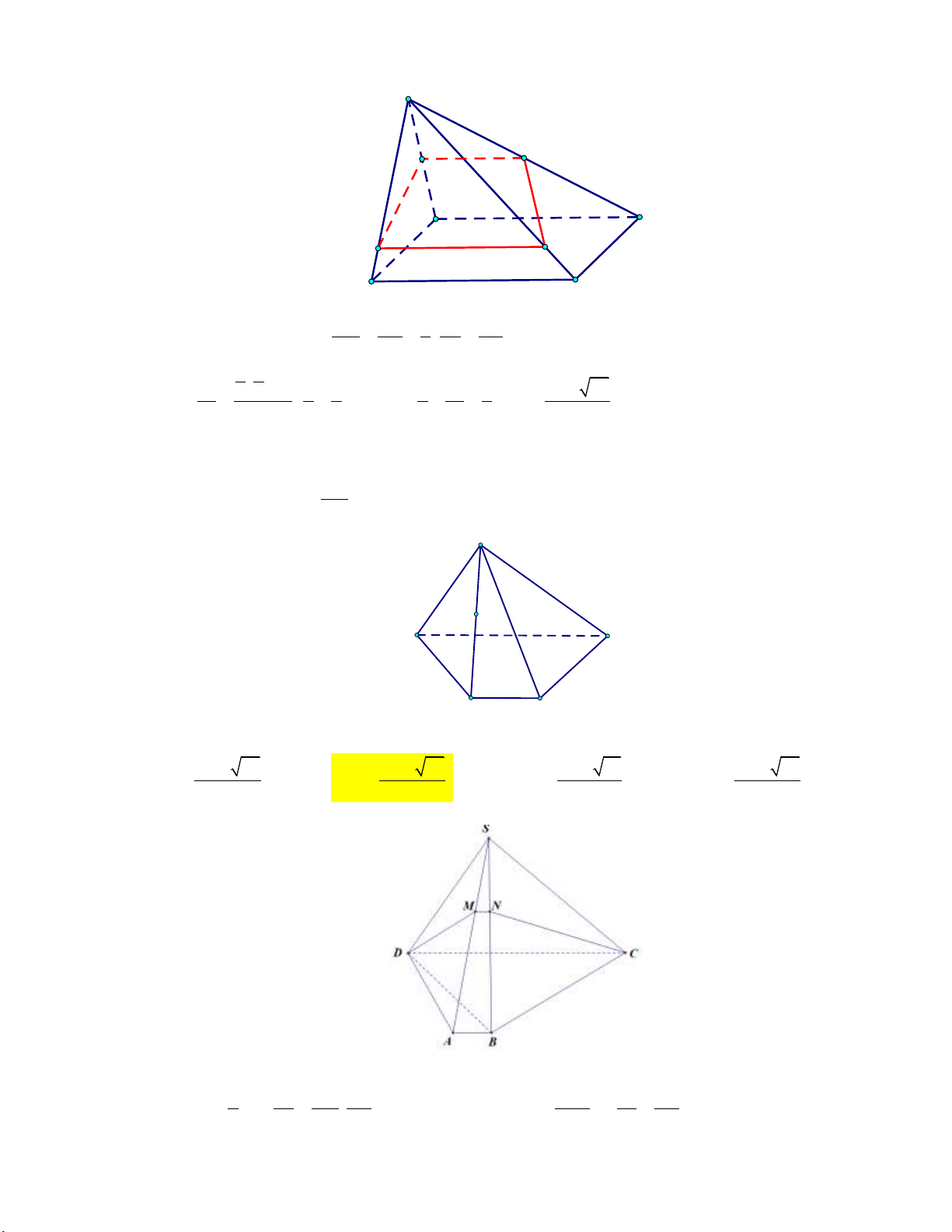
Câu 10: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi M , N là trung điểm của SA,SB (tham khảo hình vẽ). S M N D A B C
Mặt phẳng (MNCD) chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần (số bé chia số lớn) là 3 3 1 4 A. . B. . C. . D. . 5 4 3 5 3a
Câu 11: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác đều cạnh a , AA  . Biết rằng hình chiếu 2
vuông góc của A lên  ABC là trung điểm BC (tham khảo hình vẽ). A' C' B' A C B
Thể tích của khối lăng trụ ABC.A BC   bằng 3 2a 3 3 2a 3 6a 3 2a A. . B. . C. . D. . 8 8 2 3
Câu 12: Cho lăng trụ ABC.A' B'C ' có đáy ABC là tam giác vuông tại B , đường cao BH . Biết
A' H   ABC  và AB  1, AC  2, AA'  2 (tham khảo hình vẽ). A' C' B' H A C B
Thể tích của khối lăng trụ đã cho bằng 21 7 21 3 7 A. . B. . C. . D. . 12 4 4 4 2a
Câu 13: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác đều cạnh a , độ dài cạnh bên bằng , hình 3
chiếu của đỉnh A trên mặt phẳng  ABC trùng với trọng tâm của tam giác ABC (tham khảo hình vẽ). A C B A' C' G M B'
Thể tích khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 36 6 12 24 1
Câu 14: Cho hình chóp .
S ABCD có đáy ABCD là hình thang vuông tại A và B, AB BC AD a . 2
Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). S D A B C Thể tích khối chóp . S ACD là 3 a 3 3a 3 a 3 2a A. V  . B. V  . C. V  . D. V  . S.ACD 2 S.ACD 6 S.ACD 3 S.ACD 6
Câu 15: Cho hình lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng 2a , góc giữa hai đường thẳng
AB và BC bằng o 60 (tham khảo hình vẽ). B' C' A' C B A
Thể tích của khối lăng trụ đó là 3 2 3a 3 2 6a A. 3 V  2 6a . B. V  . C. V  . D. 3 V  2 3a . 3 3
Câu 16: Cho khối tứ diện ABCD có thể tích V . Gọi E , F , G lần lượt là trung điểm của BC, BD,CD ,và
M, N, P,Q lần lượt là trọng tâm của các tam giác ABC, ABD, AC
D, BCD (tham khảo hình vẽ). A N M P B D F Q E G C
Thể tích của khối tứ diện MNPQ bằng V V 2V V A. . B. . C. . D. . 9 3 9 27
Câu 17: Cho khối chóp .
S ABCD có thể tích bằng 1, đáy ABCD là hình thang với đáy lớn AD và
AD  3BC . Gọi M là trung điểm của cạnh SA , N là điểm thuộc CD sao cho ND  3NC (tham khảo hình vẽ). S M D A N B C
Mặt phẳng BMN  cắt SD tại P . Thể tích khối chóp AMBNP bằng 3 5 5 9 A. . B. . C. . D. . 8 12 16 32
Câu 18: Cho hình lập phương A . BCD A BCD
  cạnh bằng 1. Gọi M là trung điểm cạnh BB (tham khảo hình vẽ). A' B' D' C' M A B D C Mặt phẳng  MA D
  cắt cạnh BC tại K . Thể tích của khối đa diện A BCDMKCD bằng 7 7 1 17 A. . B. . C. . D. . 24 17 24 24
Câu 19: Xét khối chóp .
S ABC có đáy là tam giác vuông cân tại A , SA vuông góc với mặt phẳng đáy,
khoảng cách từ A đến mặt phẳng SBC bằng 3 (tham khảo hình vẽ). S A C B
Gọi  là góc giữa hai mặt phẳng SBC và  ABC , giá trị cos khi thể tích khối chóp . S ABC
nhỏ nhất là 2 2 3 6 A. . B. . C. . D. . 2 3 3 3
Câu 20: Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật có đáy là hình vuông sao
cho thể tích của khối hộp được tạo thành là 3
8 dm và diện tích toàn phần đạt giá trị nhỏ nhất (tham khảo hình vẽ).
Độ dài cạnh đáy của mỗi hộp muốn thiết kế là A. 2 . dm B. 3 2 2 . dm C. 4 . dm D. 2 2 . dm
_______________HẾT_______________
Huế, 15h40 ngày 14 tháng 9 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 12 Chuyên đề:
THỂ TÍCH KHỐI ĐA DIỆN
PHIẾU HỌC TẬP SỐ 01_TrNg 2021 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Cho khối lăng trụ đứng có diện tích đáy bằng 2
2a và cạnh bên bằng 3a . Thể tích khối lăng trụ đã cho bằng A. 3 2a . B. 3 3a . C. 3 18a . D. 3 6a . Lời giải: 2 3 Ta có: V  .
B h  2a .3a  6a .
Chọn đáp án D.
Câu 2: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a bằng 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 12 6 2 4 Lời giải: 2 3 a 3 3a Ta có V        S .AA .a . ABC.A B C ABC 4 4
Chọn đáp án D.
Câu 3: Cho hình lăng trụ đứng ABC.A' B'C ' có đáy ABC là tam giác vuông cân tại A với BC a và
mặt bên AA'B'B là hình vuông. Thể tích của khối lăng trụ ABC.A' B'C ' bằng 3 2a 3 2a 3 a 3 a A. . B. . C. . D. . 8 4 4 12 Lời giải: a
Tam giác ABC vuông cân tại A có BC a nên AB AC  . 2 2 1 1 a a aS  .A . B AC  . .  . ABC 2 2 2 2 4 a
Do mặt bên AA'B'B là hình vuông nên AA'  AB  . 2 2 3 a a a 2
Vì ABC.A' B'C ' là lăng trụ đứng nên VS .AA'  .  .
ABC.A' B'C ' ABC 4 2 8
Chọn đáp án A.
Câu 4: Cho hình chóp .
S ABC có đường cao SA, tam giác ABC vuông tại A có AB  2 , AC  4 . Gọi
H là trung điểm của BC (tham khảo hình vẽ). S C A H B
Biết diện tích tam giác SAH bằng 2, thể tích của khối chóp . S ABC bằng 16 5 16 5 4 5 4 5 A. . B. . C. . D. . 5 15 9 3 Lời giải: S A C H B
Xét tam giác ABC vuông tại A : 2 2 2 2
BC AB AC  2  4  2 5 . 1 1
Suy ra AH BC  .2 5  5 . 2 2 1 1 4 5
Xét tam giác SAH vuông tại A : S  . SA AH  2  . SA 5  SA  . SAH 2 2 5 1 1
Diện tích tam giác ABC : SA . B AC  .2.4  4 . ABC 2 2 1 1 4 5 16 5 Thể tích khối chóp . S ABC : VS . A S  . .4  . S.ABC 3 ABC 3 5 15
Chọn đáp án B.
Câu 5: Cho hình chóp tứ giác đều có cạnh đáy bằng x (tham khảo hình vẽ). S A D O B C
Biết diện tích xung quanh của hình chóp đó gấp đôi diện tích đáy. Khi đó thể tích của khối chóp đã cho bằng 3 3 3 3 A. 3 x . B. 3 x . C. 3 x . D. 3 x . 12 2 3 6 Lời giải:
Gọi M là trung điểm của cạnh BC . Đặt SM h . Do diện tích xung quanh gấp đôi diện tích 1 đáy nên ta có: 2 2 4.S  2S
 4. SM.BC  2x  2. .
h x  2x h x SBC ABCD 2 2  x x
Tam giác SOM vuông tại M nên ta có: 2 2 2 3
SO SM OM x     .  2  2 1 1 x 3 3 Vậy 2 3 V  . . SO S  . .x x . S.ABCD 3 ABCD 3 2 6
Chọn đáp án D.
Câu 6: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng 2a , cạnh bên bằng 3a (tham khảo hình vẽ). S A D O B C
Thể tích V của khối chóp đã cho là 3 4 7a 3 4a 3 4 7a A. 3 V  4 7a . B. V  . C. V  . D. V  . 9 3 3 Lời giải: Diện tích đáy S   a2 2 2  4a . ABCD .
S ABCD là hình chóp tứ giác đều nên SO  ABCD . 2 2 2 2 1 1
h SO SA AO  9a  2a a 7 (với AO
AC  2a 2  a 2 ). 2 2 3 1 4a 7 Vậy VSh  . S.ABCD 3 3
Chọn đáp án D.
Câu 7: Cho khối chóp .
S ABC có thể tích V . Gọi B,C lần lượt là trung điểm của AB, AC (tham khảo hình vẽ). S C' C A B' B
Tính theo V thể tích khối chóp . S AB C   . 1 1 1 1 A. V . B. V . C. V . D. V . 3 2 12 4 Lời giải: S C' A C B' B V     AB AC 1 1 1 1 1
Ta có tỷ số thể tích A.SB C  .  .  . Do đó V     V hay V   V . V AB AC 2 2 4 A.SB C A. 4 SBC S.AB C 4 A.SBC
Chọn đáp án D.
Câu 8: Cho tứ diện ABCD có thể tích bằng V , hai điểm M, P lần lượt là trung điểm của AB , CD ;
N là điểm thuộc đoạn AD sao cho AD  3AN (tham khảo hình vẽ). A N M B D P C
Thể tích tứ diện BMNP bằng V V V V A. . B. . C. . D. . 4 12 8 6 Lời giải: A N M B D P C 1
Ta có: P là trung điểm của CD nên dP,BMN  dP,ABD  dC,ABD . 2 1 S  3.S  6.SS  .S . ABD ABN BMN BMN 6 ABD 1 1 1 1 Khi đó: V  .d P BMN Sd C ABD S PBMN  , . . . BMN  , . 3 3 2 6 ABD 1 1 
dC ABD 1 . . , .SV . 12 3 ABD 12
Chọn đáp án B.
Câu 9: Cho hình lăng trụ ABC.A BC
  có thể tích bằng V . Gọi M là trung điểm cạnh BB , điểm N
thuộc cạnh CC sao cho CN  2C N  (tham khảo hình vẽ). A C B N M C' A' B' Thể tích khối chóp . A BCNM là 7V 7V 5V V A. V  . B. V  . C. V  . D. V  . A.BCNM 12 A.BCNM 18 A.BCNM 18 A.BCNM 3 Lời giải: A C B N M C' A' B' Cách 1:
Vì BCNM là hình thang nên:  1 2     CC  
CC d B CC
BM CN .dB;CC .  ;   2 3  7 S   
CCd B CC  S . BCNM   7 . . ;   2 2 12 12 BCC B Khi đó: 7 7 7  1  7  1  7V VV             V V    V .d A; A B C .S     V V A.BCNM A.BCC BA.A B C     12 12 12  3 A B C  12  3  18
Cách 2: Dùng công thức giải nhanh V 1  CN BM AA  1  2 1  7 7 7V Ta có: ABCMN       0   VV      . ABCNM ABC.    V       3  CC BB AA  3  3 2  18 18 A B C 18 ABC.A B C
Chọn đáp án B.
Câu 10: Cho hình chóp .
S ABCD có đáy là hình bình hành. Gọi M , N là trung điểm của SA,SB (tham khảo hình vẽ). S M N D A B C
Mặt phẳng (MNCD) chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần (số bé chia số lớn) là 3 3 1 4 A. . B. . C. . D. . 5 4 3 5 Lời giải: S M N D A B C
Giả sử thể tích của khối chóp . S ABCD là V . V SM SD SC 1 V SM SN SC 1 Ta có S.MDC  . .  ; S.MNC  . .  ; V SA SD SC 2 V SA SB SC 4 S.ADC S.ABC V V V V V 1 1 3 S.MDC S.MNC S.MDC S.MNC S.MNCD        V V 1 1 1 2 4 4 S.ADC S.ABC V V V 2 2 2 3 3 5 V 3 S.MNCDVV V
V V V   . S.MNCD 8 MNABCD 8 8 V 5 MNABCD
Cách khác: Dùng công thức giải nhanh.  3 VVS.MNCD S. V
a b c d 2  2  1  1 3  V S MNCD 8 ABCD 3 Ta có: . S.MNCD        . V 4abcd 4.2.2.1.1 8 5 V 5 S.ABCDABNMDC VV ABNMDC S.  8 ABCD
Chọn đáp án A. 3a
Câu 11: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác đều cạnh a , AA  . Biết rằng hình chiếu 2
vuông góc của A lên  ABC là trung điểm BC (tham khảo hình vẽ). A' C' B' A C B
Thể tích của khối lăng trụ ABC.A BC   bằng 3 2a 3 3 2a 3 6a 3 2a A. . B. . C. . D. . 8 8 2 3 Lời giải: A' C' B' A C H B
Gọi M là trung điểm BC , khi đó A M
  ABC . Tam giác ABC đều cạnh a nên AM BC và a 3 AM
. Xét tam giác vuông A A
M vuông tại M có 2 2 2     2 2 2 a a a A M
AM AA . 2 2 3 3 6  A M
  AA  AM        . 2  2    2   2 3 a 6 a 3 3 2aV        A M.S . . ABC.A B C ABC 2 4 8
Chọn đáp án B.
Câu 12: Cho lăng trụ ABC.A' B'C ' có đáy ABC là tam giác vuông tại B , đường cao BH . Biết
A' H   ABC  và AB  1, AC  2, AA'  2 (tham khảo hình vẽ). A' C' B' H A C B
Thể tích của khối lăng trụ đã cho bằng 21 7 21 3 7 A. . B. . C. . D. . 12 4 4 4 Lời giải: A . B BC 3 3 1
Độ dài của đường cao BH : BH   . Suy ra AH  : 3  . AC 2 2 2
Khi đó độ dài đường cao A'H của hình lăng trụ bằng : 2 2 1 7
A' H AA'  AH  2   . 4 2 1 1 7 21
Thể tích khối lăng trụ đã cho bằng : V A .
B BC.A' H  .1. 3  . 2 2 2 4
Chọn đáp án C. 2a
Câu 13: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác đều cạnh a , độ dài cạnh bên bằng , hình 3
chiếu của đỉnh A trên mặt phẳng  ABC trùng với trọng tâm của tam giác ABC (tham khảo hình vẽ). A C B A' C' G M B'
Thể tích khối lăng trụ ABC.A BC   bằng 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 36 6 12 24 Lời giải: A C B A' C' G M B'
Gọi G là trọng tâm của tam giác ABC . Ta có: 2 2 2 a 3 2  a   a a a AG AM  ; 2 2 2 2 3 A G   A A   AG         A G   . 3 3 3  3    9 3   2 3 a 3 a a 3
Suy ra: V B.h  .  . 4 3 12
Chọn đáp án C. 1
Câu 14: Cho hình chóp .
S ABCD có đáy ABCD là hình thang vuông tại A và B, AB BC AD a . 2
Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). S D A B C Thể tích khối chóp . S ACD là 3 a 3 3a 3 a 3 2a A. V  . B. V  . C. V  . D. V  . S.ACD 2 S.ACD 6 S.ACD 3 S.ACD 6 Lời giải: S A E D H B C
Gọi H là trung điểm AB . Do tam giác SAB đều nên SH AB .
Lại có: mpSAB vuông góc mpABCD theo giao tuyến AB nên SH   ABCD .
Gọi E là trung điểm AD .
Ta có: AECB là hình vuông cạnh a , ECD là tam giác vuông cân tại E .
Ta thấy: tam giác ACD có trung tuyến CE bằng nửa cạnh đối diện AD nên tam giác
ACD vuông tại C mà AC CD a 2 nên tam giác ACD vuông cân tại C . a a Thể tích khối chóp .
S ACD là: V SH Sa  . ACD   3 2 1 1 3 1 3 . . . 2 3 3 2 2 6
Chọn đáp án B.
Câu 15: Cho hình lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng 2a , góc giữa hai đường thẳng
AB và BC bằng o 60 (tham khảo hình vẽ). B' C' A' C B A
Thể tích của khối lăng trụ đó là 3 2 3a 3 2 6a A. 3 V  2 6a . B. V  . C. V  . D. 3 V  2 3a . 3 3 Lời giải: B' C' A' D C B A
Dựng hình bình hành B CB
D , suy ra BC// DB , do đó góc giữa hai đường thẳng AB và BC
bằng góc giữa hai đường thẳng AB và DB .
Xét tam giác ACD có trung tuyến AB bằng nửa cạnh đối diện CD nên ACD vuông tại A . 2 2 2 2
AD DC AC  16a  4a  2a 3 . Lại do ABC.A BC
  là lăng trụ tam giác đều nên AB  BC hay AB  DB  B DA  cân tại B ,
mà  ABDB o ,
 60 nên tam giác B D
A đều cạnh bằng 2a 3 . 2 2 2 2
BB  AB  AB  12a  4a  2a 2 . 2a2 3
Thể tích V của khối lăng trụ đã cho là 3
V BB .S  2a 2.  2 6a . ABC 4
Chọn đáp án A.
Câu 16: Cho khối tứ diện ABCD có thể tích V . Gọi E , F , G lần lượt là trung điểm của BC, BD,CD ,và
M, N, P,Q lần lượt là trọng tâm của các tam giác ABC, ABD, AC
D, BCD (tham khảo hình vẽ). A N M P B D F Q E G C
Thể tích của khối tứ diện MNPQ bằng V V 2V V A. . B. . C. . D. . 9 3 9 27 Lời giải: 1
Do MNP // BCD nên: dQ,MNP  dE,MNP  dA,MNP ( Vì MA  2ME ). 2 1 Suy ra: VV . (1) QMNP 2 AMNP V AM AN AP 2 2 2 8
Mặt khác áp dụng công thức tỷ số thể tích ta có AMNP  . .  . .  . (2) V AE AF AG 3 3 3 27 AEFG V 1
Lại có: AEFG  . (3) V 4 ABCD 1 8 1 V V
Từ (1), (2), (3) ta có: V  . . .V  . Vậy V  . MNPQ 2 27 4 ABCD 27 MNPQ 27 2
Cách khác: Đặc biệt hóa, tứ diện ABCD là tứ diện đều cạnh bằng 1  V  . ABCD 12
Lúc đó, tứ diện MNPQ là tứ diện đều với cạnh MN được tính bởi: 3 MN 2 2 2 1 1 2  1  1 2 1
  MN EF  .  . Suy ra: V  .  .    V . EF 3 3 3 2 3 MNPQ 12  3  27 12 27 ABCD
Chọn đáp án D.
Câu 17: Cho khối chóp .
S ABCD có thể tích bằng 1, đáy ABCD là hình thang với đáy lớn AD và
AD  3BC . Gọi M là trung điểm của cạnh SA , N là điểm thuộc CD sao cho ND  3NC (tham khảo hình vẽ). S M D A N B C
Mặt phẳng BMN  cắt SD tại P . Thể tích khối chóp AMBNP bằng 3 5 5 9 A. . B. . C. . D. . 8 12 16 32 Lời giải: S M P A E D N B C
Gọi E là giao điểm của BN và .
AD Đặt V V . 1 AMBNP DE ND
Ta có: BC // AD nên 
 3  DE  3BC AD BC NCEP 2 EN 3
D là trung điểm của AE P là trọng tâm của tam giác SAE   ,  EM 3 EB 4 V ED EP EN 1 2 3 1 Ta có E.DNP  . .  . .  V EA EM EB 2 3 4 4 E.MAB 1 1 1 1 Mặt khác, Vd .S  . d .Sd .S E.NDP ( P ,( DEN )) DEN (S,( ABCD)) DNE (S,( ABCD)) 3 3 3 9 DNE 1 1 3 3 SS  .A . D dA . D h A .
D h (h là đường cao của hình thang) AND DNE ( N ,AD) 2 2 4 8 1 1 4 2 3 Ta lại có: S
 (AD BC).h  . A . D h A . D h A . D h S ABCD 2 2 3 3 2 ABCD 3 3 9  S  . SS AND 8 2 ABCD 16 ABCD 1 9 3 3 3 3 3 3 3  Vd . .S   V  ;V  4.   V    . E.NDP (S,( ABCD)) ABCD AENP E.ABM A. 9 16 16 8 16 4 BMPC 4 8 8
Chọn đáp án A.
Câu 18: Cho hình lập phương A . BCD A BCD
  cạnh bằng 1. Gọi M là trung điểm cạnh BB (tham khảo hình vẽ). A' B' D' C' M A B D C Mặt phẳng MA D
  cắt cạnh BC tại K . Thể tích của khối đa diện A BCDMKCD bằng 7 7 1 17 A. . B. . C. . D. . 24 17 24 24 Lời giải:  1    A A MB 1 .1 ' .AB  2  3 *Ta có S    A' MBA 2 2 4 1 1 3 1 Nên V  .S .AD  . .1  D.A' A M B A' 3 MBA 3 4 4 V BM BK 1 1 1
* Dễ thấy B.MKD  .  .  V BB' BC 2 2 4 B.CB'D 1 1 1 1 1 1 1 1 1 1 Suy ra VV  . .S
.BB'  . . .DC.BC.BB'  . . .1.1.1  B.MKD B.CB'D 4 4 3 DBC 4 3 2 4 3 2 24 1 1 17 *Vậy V  1 VV  1   .
A' B'C ' D'.MKCD D.A' ABM B. D MK 4 24 24
Chọn đáp án D.
Câu 19: Xét khối chóp .
S ABC có đáy là tam giác vuông cân tại A , SA vuông góc với mặt phẳng đáy,
khoảng cách từ A đến mặt phẳng SBC bằng 3 (tham khảo hình vẽ). S A C B
Gọi  là góc giữa hai mặt phẳng SBC và  ABC , giá trị cos khi thể tích khối chóp . S ABC
nhỏ nhất là 2 2 3 6 A. . B. . C. . D. . 2 3 3 3 Lời giải: S H A C M B
Đặt SA h, AB AC a . Ta có:  SBC,ABC  SMA   . 1 1 1 1 1 1 1 1 1
Ta có dA;SBC 2           3 AH 3; 3  a h  6 . 2 2 2 2 2 2 2 4 2 AH SA AB AC 9 a a h a h 1 Suy ra: 2 Va h  1. S.ABC 6 3 AM a 2 2 3
Thể tích nhỏ nhất bằng 1 khi a h SM a  os c     2 SM 2 a 3 3
Chọn đáp án C.
Câu 20: Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật có đáy là hình vuông sao
cho thể tích của khối hộp được tạo thành là 3
8 dm và diện tích toàn phần đạt giá trị nhỏ nhất (tham khảo hình vẽ).
Độ dài cạnh đáy của mỗi hộp muốn thiết kế là A. 2 . dm B. 3 2 2 . dm C. 4 . dm D. 2 2 . dm Lời giải: 8
Gọi cạnh đáy hình vuông là x x  0 thì chiều cao của khối hộp là h  . 2 x
Ta có diện tích toàn phần của khối hộp là 2 16 16 16 16
S  2x  4xh 2 32  2x  2 2 3  2x    3 2x . . tp x x x x x
S  24 . Dấu bằng xảy ra khi x  2 . tp
Vậy độ dài cạnh đáy của mỗi hộp muốn thiết kế là 2 dm .
Chọn đáp án A.
_______________HẾT_______________
Huế, 15h40 ngày 14 tháng 9 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 12 Chuyên đề:
THỂ TÍCH KHỐI ĐA DIỆN
PHIẾU HỌC TẬP SỐ 02_TrNg 2021 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Tính thể tích V của khối lập phương A . BCD A BCD
  có tổng diện tích tất cả các mặt bằng 2 24 cm . A. V   3 8 cm . B. V   3 16 cm . C. V   3 24 cm . D. V   3 12 cm .
Câu 2: Cho hình lập phương A . BCD A BCD   có B D
  2 3 (tham khảo hình vẽ). D C A B D' C' A' B'
Thể tích của hình lập phương đó bằng A. 16. B. 64. C. 8. D. 512.
Câu 3: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với  ABCD (tham khảo hình vẽ). S A D B C
Tính thể tích V của khối chóp . S ABCD. 3 3a 3 a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 6 12 8 24
Câu 4: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, hai mặt phẳng SAB và SAD cùng
vuông góc với đáy, SC tạo với mặt phẳng SAB một góc bằng o 30 (tham khảo hình vẽ). S D A B C
Tính thể tích V của khối chóp . S ABCD. 3 6a 3 2a 3 6a A. V  . B. V  . C. V  . D. 3 V  2a . 3 3 6
Câu 5: Cho khối chóp .
S ABCD có đáy ABCD là hình chữ nhật, AB a , AD a 3 , SA vuông góc
với mặt phẳng đáy và mặt phẳng SBC tạo với đáy một góc 60 (tham khảo hình vẽ). S D A B C
Tính thể tích V của khối chóp . S ABCD . 3 3a 3 a A. 3 V  3a . B. V  . C. 3 V a . D. V  . 3 3
Câu 6: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S trên mặt
phẳng  ABC là trung điểm của BC và SA hợp với đáy một góc o 60 (tham khảo hình vẽ). S A C B
Tính thể tích V của khối chóp . S ABC. 3 3a 3 3a 3 5a 3 3a A. V  . B. V  . C. V  . D. V  . 8 24 8 12
Câu 7: Cho hình lăng trụ đứng ABC.A' B'C ' có đáy ABC là tam giác vuông cân tại A (tham khảo hình vẽ). A' C' B' C A B
Biết BC  2a và thể tích lăng trụ bằng 3
2a , khoảng cách d từ A đến mặt phẳng  A'BC  bằng 3 5a 5a 2 5a A. . B. a 5 . C. . D. . 5 5 5
Câu 8: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng a và SA vuông góc với  ABC. Biết
góc giữa SC và SAB bằng o 30 (tham khảo hình vẽ). S C A B Thể tích khối chóp . S ABC bằng 3 6a 3 3a 3 a 3 a A. . B. . C. . D. . 12 16 12 6
Câu 9: Cho hình lăng trụ đứng ABC.A' B'C ' có đáy là tam giác vuông tại A , o
AC a, ACB  60 (tham khảo hình vẽ). B' C' A' C B A
Đường thẳng BC ' tạo với mặt phẳng  ACC' A' một góc 0
30 . Tính thể tích V của khối lăng
trụ ABC.A' B'C '. 3 3a A. 3 V  3a . B. V  . C. 3 V  3a . D. 3 V  6a . 3
Câu 10: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và
nằm trong mặt vuông góc với đáy, SC tạo với mặt đáy một góc bằng o 60 (tham khảo hình vẽ). S A D B C
Tính thể tích V của khối chóp . S ABCD. 3 15a 3 15a 3 3a A. V  . B. 3 V  3a . C. V  . D. V  . 2 6 3
Câu 11: Cho hình chóp .
S ABCD có đáy ABCD là hình thoi cạnh bằng a CBD  30o , và SA vuông góc
với đáy (tham khảo hình vẽ). S A D B C
Biết góc giữa hai đường thẳng SB và CD bằng 60o , tính thể tích V của khối chóp . S ABCD. 3 a 3 a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 2 6 2 6
Câu 12: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại
A, AB a,  AB C
  hợp với mặt đáy một góc o 30 (tham khảo hình vẽ). A C B A' C' B'
Tính thể tích V của khối lăng trụ ABC.A BC   3 6a 3 6a 3 6a 3 6a A. V  . B. V  . C. V  . D. V  . 6 36 12 4
Câu 13: Cho hình lăng trụ ABC.A BC
  có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của A trên  A BC
  là trọng tâm tam giác A BC  , A A
 hợp với mặt đáy một góc o 60 (tham khảo hình vẽ). A C B A' C' G M B'
Tính thể tích V của khối lăng trụ ABC.A BC  . 3 3a 3 3 3a 3 3a 3 3 3a A. V  . B. V  . C. V  . D. V  . 4 4 12 8
Câu 14: Cho hình lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng a, AC hợp với mặt phẳng ABB A   một góc o 45 (tham khảo hình vẽ). A C B A' C' B'
Thể tích của khối lăng trụ ABC.A BC   bằng 3 6a 3 3a 3 6a 3 6a A. . B. . C. . D. . 24 4 8 4
Câu 15: Gọi V là thể tích khối chóp .
S ABC. Gọi M, N lần lượt là trung điểm của các cạnh SB, SC (tham khảo hình vẽ). S N M A C B
Tính thể tích khối AMNC . B V V V 3V A. . B. . C. . D. . 4 8 2 4
Câu 16: Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; AB  6a , AC  7a
và AD  4a . Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB (tham khảo hình vẽ). D N P C A M B
Tính thể tích V của tứ diện AMNP. 7 28 A. 3 V a . B. 3 V  14a . C. 3 V a . D. 3 V  7a . 2 3
Câu 17: Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm
của các cạnh SA,SD (tham khảo hình vẽ). S N M D A C B SP
Mặt phẳng   chứa MN và cắt các tia SB,SC lần lượt tại P,Q . Đặt
x , V là thể tích SC 1 khối chóp .
S MNQP và V là thể tích khối chóp .
S ABCD . Tìm x để V  2V . 1 1 1   33 1   41 A. x  . B. x  . C. x  . D. x  2 . 2 4 2
Câu 18: Cho hình chóp .
S ABCD có đáy là hình thang với AB song song với CD , CD  7 AB . Gọi M SM
trên cạnh SA sao cho
k , 0  k  1 (tham khảo hình vẽ). SA S M D C A B
Giá trị của k để CDM chia khối chóp thành hai phần có thể tích bằng nhau là. 7   53 7   65 7   71 7   53 A. k  . B. k  . C. k  . D. k  . 2 2 4 4
Câu 19: Cho khối lăng trụ ABC.A BC
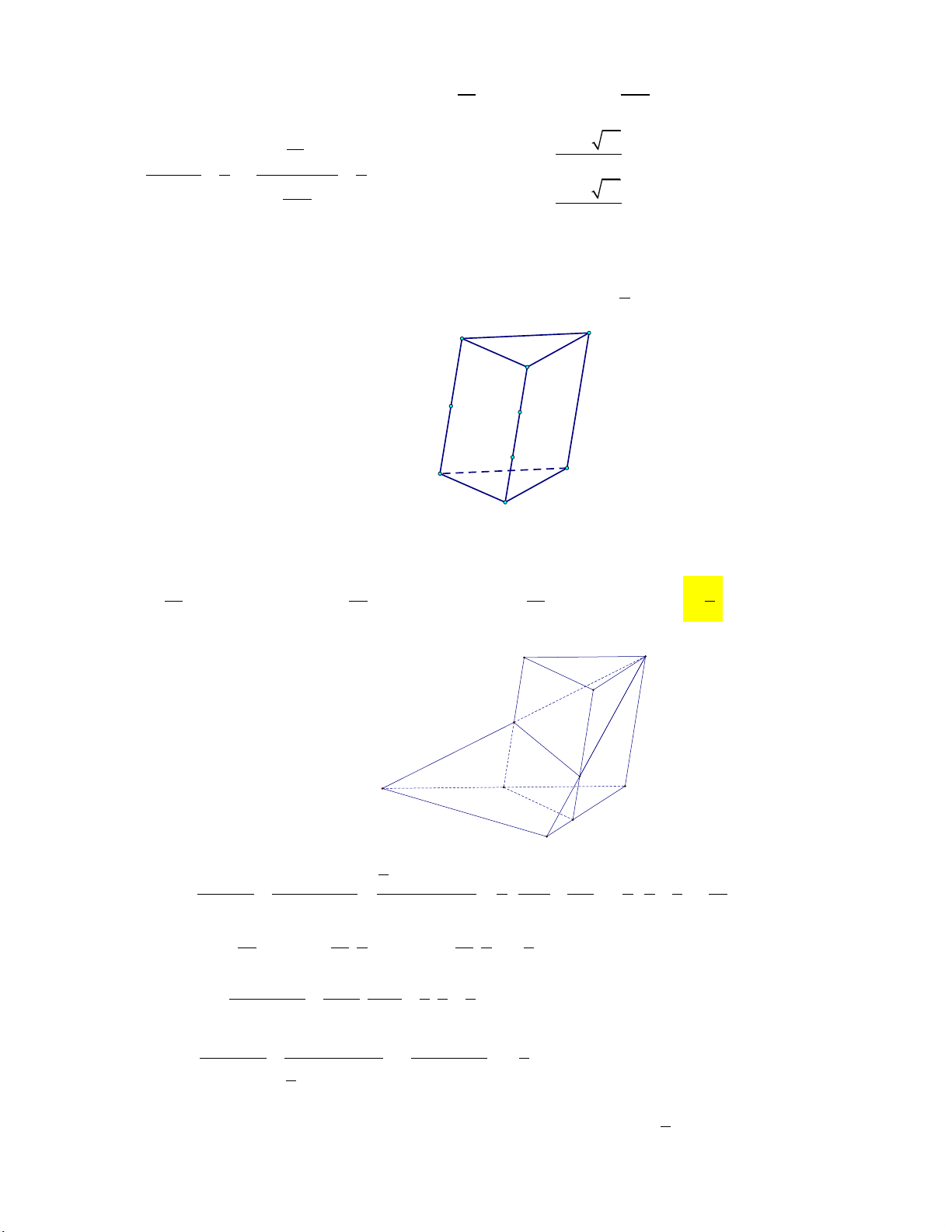
  có thể tích bằng 2. Gọi M , N lần lượt là hai điểm nằm trên hai 2
cạnh AA , BB sao cho M là trung điểm cạnh AA và BN BB (tham khảo hình vẽ). 3 A C B M N C' A' B'
Đường thẳng CM cắt đường thẳng C A
  tại P và đường thẳng CN cắt đường thẳng C B   tại
Q . Thể tích khối đa diện A MPB NQ bằng: 13 23 7 7 A. . B. . C. . D. . 18 9 18 9
Câu 20: Cho hình chóp .
S ABCD có cạnh SA x còn tất cả các cạnh khác có độ dài bằng 2 (tham khảo hình vẽ). S B C D A Tính thể tích V
lớn nhất của khối chóp . S ABCD . max 1 A. V  1. B. V  . C. V  3. D. V  2. max max 2 max max
_______________HẾT_______________
Huế, 15h40 ngày 15 tháng 9 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 12 Chuyên đề:
THỂ TÍCH KHỐI ĐA DIỆN
PHIẾU HỌC TẬP SỐ 02_TrNg 2021 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Tính thể tích V của khối lập phương A . BCD A BCD
  có tổng diện tích tất cả các mặt bằng 2 24 cm . A. V   3 8 cm . B. V   3 16 cm . C. V   3 24 cm . D. V   3 12 cm . Lời giải:
Gọi cạnh của hình lập phương đã cho là t t  0. Diện tích một mặt của hình lập phương bằng 2 t . Theo giả thiết: 2
6t  24  t  2. Vậy 3 V t  8.
Chọn đáp án A.
Câu 2: Cho hình lập phương A . BCD A BCD   có B D
  2 3 (tham khảo hình vẽ). D C A B D' C' A' B'
Thể tích của hình lập phương đó bằng A. 16. B. 64. C. 8. D. 512. Lời giải: D A B D' C' A' B' 2 2
Gọi cạnh của lập phương là a  2 2 2 B D    D D   B D   a  2 2
a  2 3  a  2.
Vậy thể tích khối lập phương đó bằng 3 2  8.
Chọn đáp án C.
Câu 3: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với  ABCD (tham khảo hình vẽ). S A D B C
Tính thể tích V của khối chóp . S ABCD. 3 3a 3 a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 6 12 8 24 Lời giải: S A D H B C +) Ta có: 2 Sa . ABCD SH    AB +) Dựng SH  . AB Ta có:    SAB  
ABCDSH ABCD. 3 1 1 a 3 3a Vậy 2 VSH.S  . .a  . S.ABCD 3 ABCD 3 2 6
Chọn đáp án A.
Câu 4: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, hai mặt phẳng SAB và SAD cùng
vuông góc với đáy, SC tạo với mặt phẳng SAB một góc bằng o 30 (tham khảo hình vẽ). S D A B C
Tính thể tích V của khối chóp . S ABCD. 3 6a 3 2a 3 6a A. V  . B. V  . C. V  . D. 3 V  2a . 3 3 6 Lời giải SAB   ABCDS Ta có:    SAD  
ABCDSA ABCD. 300 BC AB và 
BC  SAB  SC;SAB  BSC. BC   SA BC
Xét tam giác SBC vuông tại B : tan BSC D SB A BC 2 2  SB
a 3  SA SB AB a 2. tan BSC B a C 3 1 2a và 2 Sa . Vậy V  . SA S  . ABCD S.ABCD 3 ABCD 3
Chọn đáp án B.
Câu 5: Cho khối chóp .
S ABCD có đáy ABCD là hình chữ nhật, AB a , AD a 3 , SA vuông góc
với mặt phẳng đáy và mặt phẳng SBC tạo với đáy một góc 60 (tham khảo hình vẽ). S D A B C
Tính thể tích V của khối chóp . S ABCD . 3 3a 3 a A. 3 V  3a . B. V  . C. 3 V a . D. V  . 3 3 Lời giải:
SBCABCD  BCS  Ta có 2 S
 3a . Vì BC SB  SBCABCDBC AB   ABCD
  SBC,ABCD  SBA . Vậy SBA  60 .
Xét tam giác vuông SAB có: D SA tanSBA
SA ABtanSBA a 3 A 600 AB 1 Vậy 3 VS .SA a . B C S.ABCD 3 ABCD
Chọn đáp án C.
Câu 6: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S trên mặt
phẳng  ABC là trung điểm của BC và SA hợp với đáy một góc o 60 (tham khảo hình vẽ). S A C B
Tính thể tích V của khối chóp . S ABC. 3 3a 3 3a 3 5a 3 3a A. V  . B. V  . C. V  . D. V  . 8 24 8 12 Lời giải: S B A H C 2 3a +) Ta có: S  . ABC 4
+) Dựng SH BC H là trung điểm BC. Ta có: SH    BC      SBC  
ABCSH ABC  ;
SA ABC SAH. SH 3a
Xét tam giác SAH vuông tại H : tanSAH
SH AH.tanSAH  . AH 2 2 3 1 1 3a 3a 3a Vậy VSH.S  . .  . S.ABC 3 ABC 3 2 4 8
Chọn đáp án A.
Câu 7: Cho hình lăng trụ đứng ABC.A' B'C ' có đáy ABC là tam giác vuông cân tại A (tham khảo hình vẽ). A' C' B' C A B
Biết BC  2a và thể tích lăng trụ bằng 3
2a , khoảng cách d từ A đến mặt phẳng  A' BC bằng 3 5a 5a 2 5a A. . B. a 5 . C. . D. . 5 5 5 Lời giải: A' C' B' 2a K A C H B
Do tam giác ABC là tam giác vuông cân tại A và BC  2a nên suy ra AB AC a 2 , 1 2 SA . B AC a . ABC 2
Lúc đó lăng trụ đã cho có thể tích là: V AA'.S . ABC Theo giả thiết: 2 3
AA'.a  2a AA'  2 . a
Gọi H là trung điểm BC AH  .
a Ta có: AH BC BC   A' AH .
Dựng AK A' H AK   A'BC . Vậy dA;A'BC  AK. 1 1 1 2a 5 Xét A
 ' AH vuông tại A :    AK  . 2 2 2 AK A' A AH 5
Chọn đáp án D.
Câu 8: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh bằng a và SA vuông góc với  ABC. Biết
góc giữa SC và SAB bằng o 30 (tham khảo hình vẽ). S C A B Thể tích khối chóp . S ABC bằng 3 6a 3 3a 3 a 3 a A. . B. . C. . D. . 12 16 12 6 Lời giải: S A C H B HC AB
Gọi H là trung điểm AB  
HC  SAB  SC SAB 0 ;  HSC  60 . HC   SA CH
Xét tam giác SHC vuông tại H : sin HSC   SC a 3. SC Ta có: 2 2
SA SC AC a 2. 2 3a 3 1 6a Ta có: S  . Suy ra: V  . SA S  . ABC 4 S.ABC 3 ABC 12
Chọn đáp án A.
Câu 9: Cho hình lăng trụ đứng ABC.A' B'C ' có đáy là tam giác vuông tại A , o
AC a, ACB  60 (tham khảo hình vẽ). B' C' A' C B A
Đường thẳng BC ' tạo với mặt phẳng  ACC' A' một góc 0
30 . Tính thể tích V của khối lăng
trụ ABC.A' B'C '. 3 3a A. 3 V  3a . B. V  . C. 3 V  3a . D. 3 V  6a . 3 Lời giải:
Ta có AB   ACC' A' nên BC ACC A  0 ',
' '  BC' A  30 . B' C' 0
AB AC.tan 60  a 3. A' 0 2 2 AC '  A .
B cot 30  3a CC '  9a a  2 2 . a  1  Vậy 3 VA . B AC .AA'    a 6 .
ABC.A' B'C "  2  B C
Chọn đáp án D. A
Câu 10: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và
nằm trong mặt vuông góc với đáy, SC tạo với mặt đáy một góc bằng o 60 (tham khảo hình vẽ). S A D B C
Tính thể tích V của khối chóp . S ABCD. 3 15a 3 15a 3 3a A. V  . B. 3 V  3a . C. V  . D. V  . 2 6 3 Lời giải
Dựng SH AB H là trung điểm . AB S
Do SAB   ABCD  SH   ABCD.
Vậy SC ABCD 0 ;  SCH  60 . Xét tam giác SHC vuông tại A SH 15a D H : tanSCH   SH  và 2 Sa . Vậy H HC 2 ABCD 600 3 1 15a B a C VSH.S  . S.ABCD 3 ABCD 6
Chọn đáp án C.
Câu 11: Cho hình chóp .
S ABCD có đáy ABCD là hình thoi cạnh bằng a CBD  30o , và SA vuông góc
với đáy (tham khảo hình vẽ). S A D B C
Biết góc giữa hai đường thẳng SB và CD bằng 60o , tính thể tích V của khối chóp . S ABCD. 3 a 3 a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 2 6 2 6 Lời giải:
Do ABCD là hình thoi cạnh bằng 0 a, CBD  30
 ΔABC là tam giác đều cạnh bằng . a 2 2 3a 3a Suy ra: S  2S  2.  . ABCD ABC 4 2
Do CD / / AB   ; SB CD   ;
SB AB  SBA
(do ΔSAB vuông tại A ).
Xét SAB vuông tại A : SA tanSBA
SA ABtanSBA  3 . a AB 2 3 1 1 3a a Vậy VS . A S  . 3 . a  . S.ABCD 3 ABCD 3 2 2
Chọn đáp án A.
Câu 12: Cho hình lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại
A, AB a,  AB C
  hợp với mặt đáy một góc o 30 (tham khảo hình vẽ). A C B A' C' B'
Tính thể tích V của khối lăng trụ ABC.A BC   3 6a 3 6a 3 6a 3 6a A. V  . B. V  . C. V  . D. V  . 6 36 12 4 Lời giải: A C B C' A' M B' 2 1 a +) Ta có: SA . B AC  . ABC 2 2 B C    A M
+) Gọi M là trung điểm B C      B C    AA M    B C    AM. B C     AA Suy ra:  AB C  ;A BC
   AMA . AA Xét tam giác AA M
 vuông tại A : tan AMA  A M  1 a 6
AA  A M
 tan AMA  .B C  .tan AMA  . 2 6 3 6a Vậy V       AA .S . ABC.A B C ABC 12
Chọn đáp án C.
Câu 13: Cho hình lăng trụ ABC.A BC
  có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của A trên  A BC
  là trọng tâm tam giác A BC  , A A
 hợp với mặt đáy một góc o 60 (tham khảo hình vẽ). A C B A' C' G M B'
Tính thể tích V của khối lăng trụ ABC.A BC  . 3 3a 3 3 3a 3 3a 3 3 3a A. V  . B. V  . C. V  . D. V  . 4 4 12 8 Lời giải: A C B A' C' G M B' 2 3a +) Ta có: S  . ABC 4
+) Gọi M là trung điểm B C
 , G là trọng tâm tam giác A BC  .
Do AG   A BC
  nên AA ;A BC
   AA . G AG Xét tam giác A A
G vuông tại G : tan AA G    AG A G  tan AA G   a. A G  3 3a Vậy V       A . G S . ABC.A B C ABC 4
Chọn đáp án A.
Câu 14: Cho hình lăng trụ tam giác đều ABC.A BC
  có cạnh đáy bằng a, AC hợp với mặt phẳng ABB A   một góc o 45 (tham khảo hình vẽ). A C B A' C' B'
Thể tích của khối lăng trụ ABC.A BC   bằng 3 6a 3 3a 3 6a 3 6a A. . B. . C. . D. . 24 4 8 4 Lời giải: A C B 450 a A' C' a H a B' 2 3a Ta có: S               . Dựng C H A B C HABB A A B C 4   a 3 AC  ABB A   0 ;  C A
H  45 .Suy ra AHC vuông cân tại H HC  AH  . 2 a 3 6a Xét tam giác A AH vuông tại 2 2 2 A : A A
  AH A H  
. Vậy V AA .S      . 2 A B C 8
Chọn đáp án C.
Câu 15: Gọi V là thể tích khối chóp .
S ABC. Gọi M, N lần lượt là trung điểm của các cạnh SB, SC (tham khảo hình vẽ). S N M A C B
Tính thể tích khối AMNC . B V V V 3V A. . B. . C. . D. . 4 8 2 4 Lời giải: S N M A C B V SM SN 1 1 3 3
Ta có: S.AMN  .   VVVVV. S.AMN S.ABC ABCNM S. V SB SC 4 4 4 ABC 4 S.ABC
Chọn đáp án D.
Câu 16: Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; AB  6a , AC  7a
và AD  4a . Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB (tham khảo hình vẽ). D N P C A M B
Tính thể tích V của tứ diện AMNP. 7 28 A. 3 V a . B. 3 V  14a . C. 3 V a . D. 3 V  7a . 2 3 Lời giải 1 D Ta có: 3 VA .
B AC.AD  28a . ABCD 6
Dễ thấy MNP được tạo nên bởi các đường trung bình của N 1 P BC
D  chúng đồng dạng với nhau theo tỉ số 2 V S C 1 1 1 1 A AMNP MNP 3    .   VV  7a . M V S 2 2 4 AMNP 4 ABCD ABCD BCD
Chọn đáp án D. B
Câu 17: Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm
của các cạnh SA,SD (tham khảo hình vẽ). S N M D A C B SP
Mặt phẳng   chứa MN và cắt các tia SB,SC lần lượt tại P,Q . Đặt
x , V là thể tích SC 1 khối chóp .
S MNQP và V là thể tích khối chóp .
S ABCD . Tìm x để V  2V . 1 1 1   33 1   41 A. x  . B. x  . C. x  . D. x  2 . 2 4 2 Lời giải: S N M D Q A P C B SM SN 1 SP SQ
Dễ thấy MN / /PQ nên   ;   x SA SA 2 SB SC 1 1 . . . x x 2 V  1 1  x x 1 1   33 Ta có: 1 2 2    2  2       x  . V 4  x x  8 4 2 4
Chọn đáp án B.
Câu 18: Cho hình chóp .
S ABCD có đáy là hình thang với AB song song với CD , CD  7 AB . Gọi M SM
trên cạnh SA sao cho
k , 0  k  1 (tham khảo hình vẽ). SA S M D C A B
Giá trị của k để CDM chia khối chóp thành hai phần có thể tích bằng nhau là. 7   53 7   65 7   71 7   53 A. k  . B. k  . C. k  . D. k  . 2 2 4 4 Lời giải:
Kẻ MN / / AB / /C .
D Gọi V V ; V V ; V V ; V V 1 SDMN 2 SABD 3 SDNC 4 SDBC 1 2 V SM SN k V V SN
Ta có V V ; 1 2 2 4  .
k.k k V k .V   3 
k V kV 2 4 7 1 2 V SA SB 7 3 4 V SB 2 4 2  k   8V VVV
V V V   k . Mà 4 VS.DMNC S.DMN S.DNC 1 3 4  7  S.ABCD 7 2  k   V   k  7   65 k  N 4 V 1  7  1 S.DMNC    2
k  7k  4  0   2 V 2 8V 2    S.ABCD 4 7 65 k  L 7  2
Chọn đáp án B.
Câu 19: Cho khối lăng trụ ABC.A BC
  có thể tích bằng 2. Gọi M , N lần lượt là hai điểm nằm trên hai 2
cạnh AA , BB sao cho M là trung điểm cạnh AA và BN BB (tham khảo hình vẽ). 3 A C B M N C' A' B'
Đường thẳng CM cắt đường thẳng C A
  tại P và đường thẳng CN cắt đường thẳng C B   tại
Q . Thể tích khối đa diện A MPB NQ bằng: 13 23 7 7 A. . B. . C. . D. . 18 9 18 9 Lời giải: A C B M N P A' C' B' Q
1 AM BNV dt ABNM 1  AM BN  1  1 2  7
Ta có: C.ABNM  2           . V        dt ABB A AA 2  AA BB  2  2 3  12 C.ABB A   7  7 2 VV  7 2 7 . .V  . .2  . C.ABNM C.      12 ABB A . 12 3 ABC A B C 12 3 9 dt C AB
  C'AC'B 1 2 1 Mặt khác,    dt C P  . Q . . C PC Q  2 3 3 V . h dt          C A B dt C A B  1
Do đó: ABC.A B C   3  3.  1 hay V   V    . V 1  C.C PQ ABC.A B Cdt C PQ 3 C.C PQ . . h dt C PQ   3 Suy ra: V      7    V V V    V V . A MPB NQ C.C PQ CMNC AB   ABC.A B C CMNC AB   C.ABNM 9
Chọn đáp án D.
Câu 20: Cho hình chóp .
S ABCD có cạnh SA x còn tất cả các cạnh khác có độ dài bằng 2 (tham khảo hình vẽ). S B C D A Tính thể tích V
lớn nhất của khối chóp . S ABCD . max 1 A. V  1. B. V  . C. V  3. D. V  2. max max 2 max max Lời giải: S a x B C a O H D A
Gọi O là giao điểm của AC và BD . Ta có: BAD   BSD BC
D nên AO SO  1 CO SO
AC  SAC vuông tại S 2 Do đó: 2 2 2
AC SA SC x  4 2 2   2 2 4 x 12 x
OD AD AO  4   2
BD  12  x , 0  x  2 3 4 2 BD AC Ta thấy: 
BD  SACBD   SO SH   AC
Trong SAC hạ SH AC . Khi đó: 
SH  ABCDSH   BD 1 1 1   S . A AC 2.xSH   2 2 2 SH SA SC 2 2 2 SA SC 4  x 1 1 2x 1 2 2 1 x  12  x 2 2 2  V  .
x  4. 12  x .  . . x 12  x   2  V  2. S.ABCD 2 3 2  3 max x 4 3 2 Dấu "  " xảy ra khi 2 2
x  12  x x  6 .
Chọn đáp án D.
_______________HẾT_______________
Huế, 15h40 ngày 15 tháng 9 năm 2021
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
TUYỂN TẬP ĐỀ THI THPT QUỐC GIA 2007 – 2022
THỂ TÍCH KHỐI ĐA DIỆN NỘI DUNG ĐỀ BÀI Câu 1:
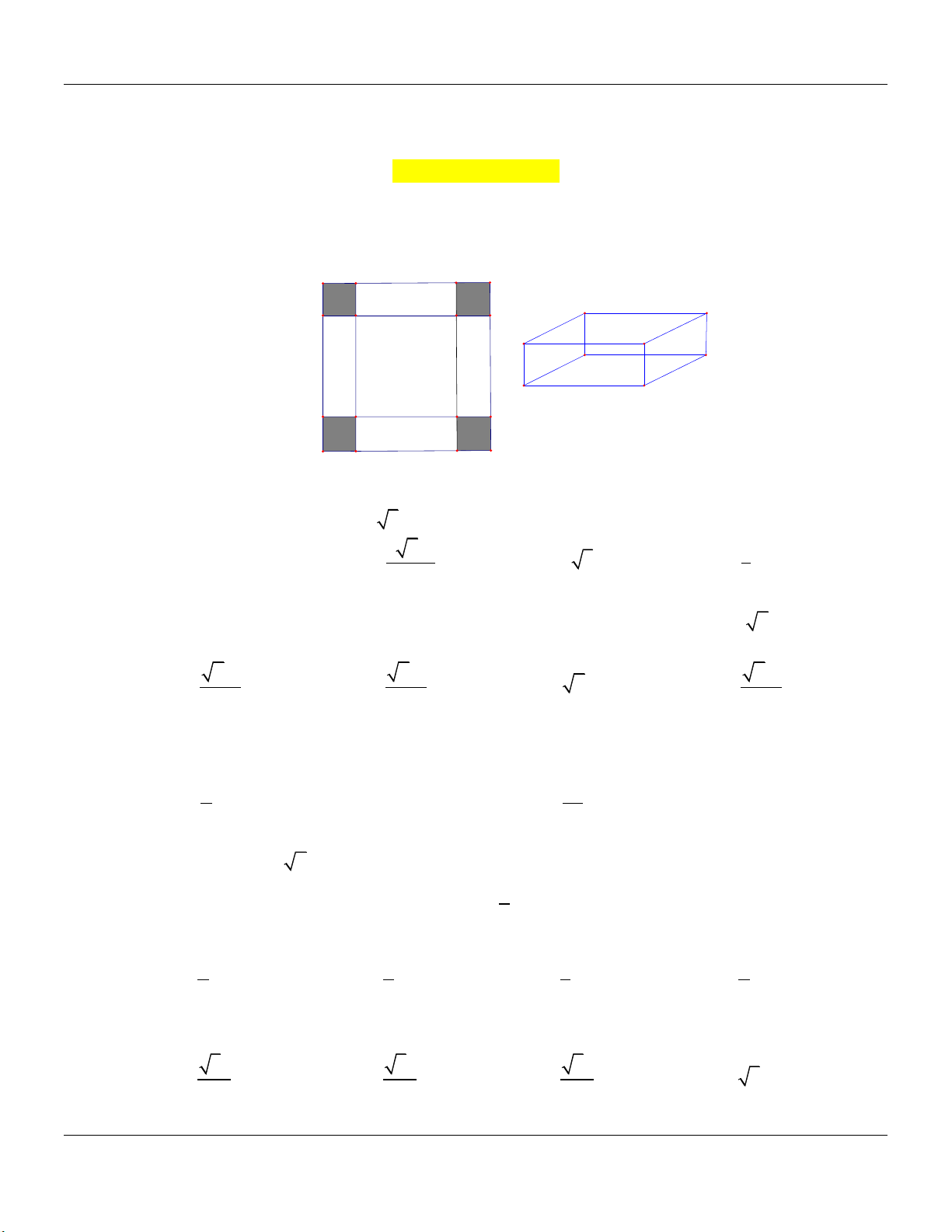
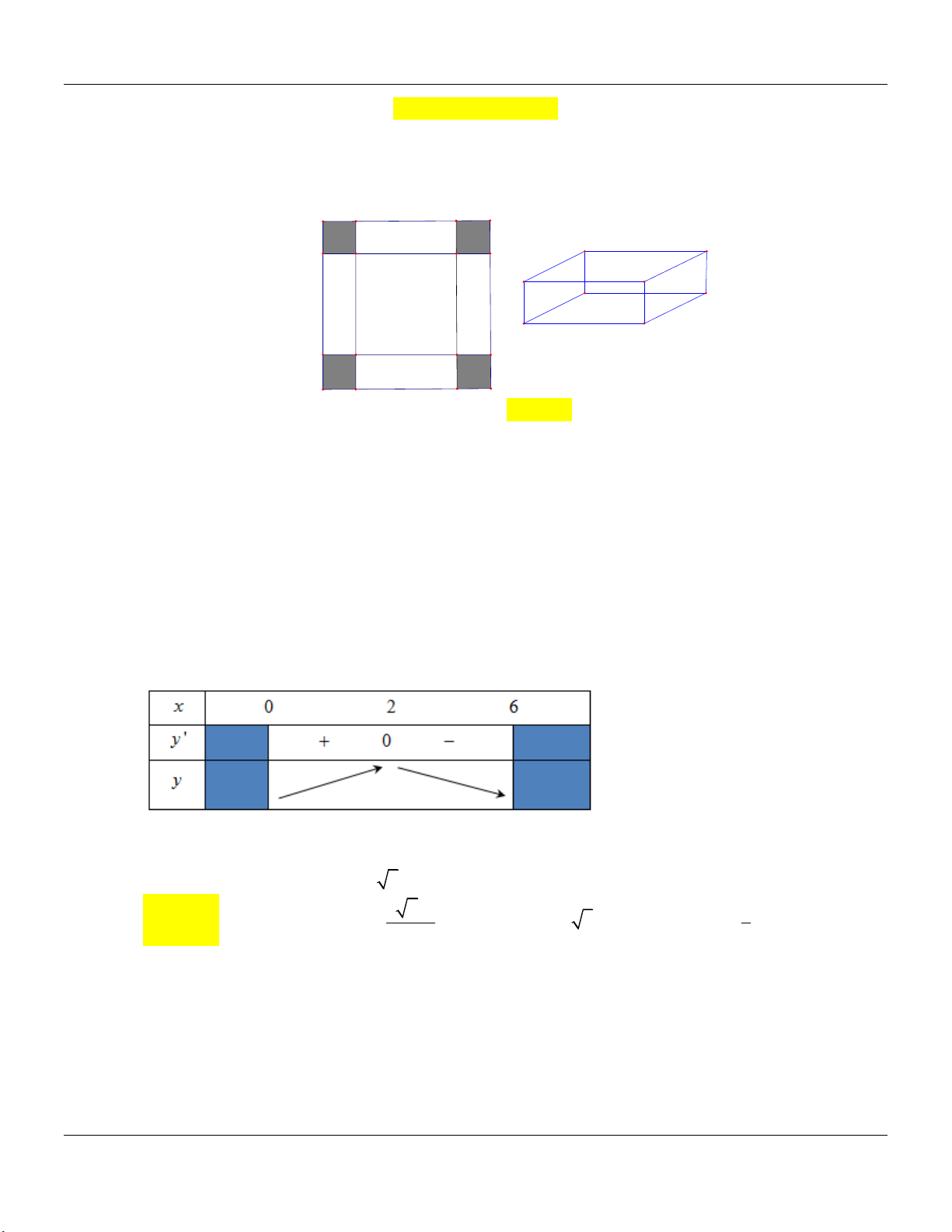
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh 12 cm. Người
ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x
để hộp nhận được có thể tích lớn nhất. A. x  6 B. x  3 C. x  2 D. x  4 Câu 2:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tính thể tích V của khối lập phương ABC . D AB CD
  , biết AC  a 3 . 3 3 6a 1 A. 3 V a . B. V  . C. 3 V  3 3a . D. 3 V a . 4 3 Câu 3:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác S.ABCD có đáy ABCD là
hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy và SA a 2 . Tính thể tích
V của khối chóp S.ABCD 3 2a 3 2a 3 2a A. V B. V C. 3 V  2a D. V  6 4 3 Câu 4:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho tứ diện ABCD có các cạnh AB , AC và AD đôi
một vuông góc với nhau; AB  6a , AC  7a và AD  4a . Gọi M , N , P tương ứng là trung
điểm các cạnh BC , CD , DB . Tính thể tích V của tứ diện AMNP . 7 28 A. 3 V a B. 3 V  14a C. 3 V a D. 3 V  7a 2 3 Câu 5:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác S.ABCD có đáy là hình
vuông cạnh bằng 2a . Tam giác SAD cân tại S và mặt bên SAD vuông góc với mặt phẳng 4
đáy. Biết thể tích khối chóp S.ABCD bằng 3
a . Tính khoảng cách h từ B đến mặt phẳng 3 SCD 2 4 8 3 A. h a B. h a
C. h a D. h a 3 3 3 4 Câu 6:
(ĐTN BGD&ĐT NĂM 2016-2017) Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3
a . Tính chiều cao h của hình chóp đã cho. 3 3 3 A. a h B. a h C. a h
D. h  3a 6 2 3
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia Câu 7:
(ĐTN BGD&ĐT NĂM 2016-2017) Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm
của tam giác BCD . Tính thể tích V của khối chóp . A GBC A. V  3 B. V  4 C. V  6 D. V  5 Câu 8:
(ĐTN BGD&ĐT NĂM 2016-2017) Cho lăng trụ tam giác ABC. 
A BC có đáy ABC là tam giác
vuông cân tại A , cạnh AC  2 2 . Biết AC tạo với mặt phẳng  ABC  một góc 60 và
AC  4 . Tính thể tích V của khối đa diện ABCBC . 8 16 8 3 16 3 A. V B. V C. V D. V  3 3 3 3 Câu 9:
(ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a . 3 3 3 3 3 3 3 3 A.a V . B.a V . C.a V . D.a V . 6 12 2 4
Câu 10: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hình chóp S.ABCD có đáy là hình vuông
cạnh a , SA vuông góc với mặt đáy, SD tạo với mặt phẳng SAB một góc bằng 30 . Tính
thể tích V của khối chóp S.ABCD . 3 6a 3 6a 3 3a A. V B. 3 V  3a C. V D. V  18 3 3
Câu 11: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho khối tứ diện có thể tích bằng V . Gọi V  là
thể tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, V  tính tỉ số . V V  1 V  1 V  2 V  5 A.  . B.  . C.  . D.  . V 2 V 4 V 3 V 8
Câu 12: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh
bên gấp hai lần cạnh đáy. Tính tích V của khối chóp tứ giác đã cho. 3 2 3 2 3 14 3 14 A. a V . B. a V . C. a V . D. a V . 2 6 2 6
Câu 13: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho khối chóp S. ABCD có đáy là hình vuông cạnh a,
SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc 30 . Tính thể tích V của khối chóp đã cho. 3 6 3 2 3 2 A.a V . B.a V . C.a V . D. 3 V  2a . 3 3 3
Câu 14: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần
lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE)
chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V. 3 7 2 3 11 2 3 13 2 3 2 A.a V . B.a V . C.a V . D.a V . 216 216 216 18
Câu 15: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng ABC.AB C
  có BB  a , đáy
ABC là tam giác vuông cân tại B và AC a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 3 3 A. 3
V a . B. a V . C. a V . D. a V . 3 6 2
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 16: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho khối chóp S.ABCD có đáy ABCD là hình chữ
nhật, AB a , AD a 3 , SA vuông góc với mặt phẳng đáy và mặt phẳng  SBC  tạo với đáy
một góc 60o . Tính thể tích V của khối chóp S.ABCD . 3 3 3 A. a V . B. a V . C. 3 V a . D. 3 V  3a . 3 3
Câu 17: (MĐ 102 BGD&ĐT NĂM 2016-2017) Xét khối tứ diện ABCD có cạnh AB x và các cạnh
còn lại đều bằng 2 3 . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất. A. x  6. B. x  14. C. x  3 2. D. x  2 3.
Câu 18: (MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp S.ABC có SA vuông góc với đáy,
SA  4 , AB  6, BC  10 và CA  8 . Tính thể tích khối chóp S.ABC . A. V  40 . B. 192 . C. V  32 . D. V  24 .
Câu 19: (MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , a 2
SA vuông góc với đáy và khoảng cách từ A đến mặt phẳng SBC  bằng . Tính thể tích 2
V của khối chóp đã cho. 3 3 3 3 A. a V . B. 3 V a . C. a V . D. a V . 2 9 3
Câu 20: (MĐ 103 BGD&ĐT NĂM 2016-2017) Xét khối chóp S.ABC có đáy là tam giác vuông cân tại
A , SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng  SBC  bằng 3 . Gọi  là góc
giữa mặt phẳng SBC  và  ABC  , tính cos khi thể tích khối chóp S.ABC nhỏ nhất. 1 3 2 2 A. cos  . B. cos  . C. cos  . D. cos  . 3 3 2 3
Câu 21: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng
a và cạnh bên bằng 2a . Tính thể tích V của khối chóp S.ABC 3 13a 3 11a 3 11a 3 11a A. V  . B. V  . C. V  . D. V  . 12 12 6 4
Câu 22: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là
tam giác cân với AB AC a , BAC  120 . Mặt phẳng  AB C
  tạo với đáy một góc 60 .
Tính thể tích V của khối lăng trụ đã cho. 3 3a 3 9a 3 a 3 3a A. V  . B. V  . C. V  . D. V  . 8 8 8 4
Câu 23: (MĐ 104 BGD&ĐT NĂM 2016-2017) Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu
có bán kính bằng 9, tính thể tích V của khối chóp có thể tích lớn nhất. A. V  144 . B. V  576 .
C. V  576 2 .
D. V  144 6 .
Câu 24: (ĐTK BGD&ĐT NĂM 2017-2018) Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là: 1 1 1 A. V Bh. B. V Bh.
C. V Bh. D. V Bh. 3 6 2
Câu 25: (ĐTK BGD&ĐT NĂM 2017-2018) Cho hình vuông ABCD và ABEF có cạnh bằng 1, lần
lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng của B qua đường
thẳng DE . Thể tích của khối đa diện ABCDSEF bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 7 11 2 5 A. . . C. . D. . 6 B. 12 3 6
Câu 26: (MĐ 101 BGD&ĐT NĂM 2017-2018) Cho khối chóp có đáy là hình vuông cạnh a và chiều
cao bằng 2a . Thể tích của khối chóp đã cho bằng 2 4 A. 3 4a B. 3 a C. 3 2a D. 3 a 3 3
Câu 27: (MĐ 101 BGD&ĐT NĂM 2017-2018) Ông A dự định dùng hết 2
6, 5m kính để làm một bể cá
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng . Bể cá có dung tích lớn nhất bằng bao nhiêu? A. 3 2, 26 m . B. 3 1, 61 m . C. 3 1, 33 m . D. 3 1, 50 m .
Câu 28: (MĐ 101 BGD&ĐT NĂM 2017-2018) Cho khối lăng trụ ABC.AB C
  , khoảng cách từ C đến
đường thẳng BB bằng 2 , khoảng cách từ A đến các đường thẳng BB và CC lần lượt bằng
1 và 3 , hình chiếu vuông góc của A lên mặt phẳng  AB C
  là trung điểm M của B C   và 2 3 AM
. Thể tích của khối lăng trụ đã cho bằng 3 2 3 A. 2 B. 1 C. 3 D. 3
Câu 29: (ĐTK BGD&ĐT NĂM 2018-2019) Thể tích của khối lập phương cạnh 2a bằng A. 3 8a . B. 3 2a . C. 3 a . D. 3 6a .
Câu 30: (ĐTK BGD&ĐT NĂM 2018-2019) Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a . Thể
tích của khối chóp đã cho bằng 3 4 2a 3 8a 3 8 2a 3 2 2a A. . B. . C. . D. . 3 3 3 3
Câu 31: (ĐTK BGD&ĐT NĂM 2018-2019) Cho khối lăng trụ ABC.AB C
  có thể tích bằng 1. Gọi
M , N lần lượt là trung điểm các đoạn thẳng AA và BB . Đường thẳng CM cắt đường thẳng C A
  tại P , đường thẳng CN cắt đường thẳng C B
  tại Q . Thể tích của khối đa diện lồi A MPB NQ bằng 1 1 2 A. 1 . B. . C. . D. . 3 2 3
Câu 32: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho khối lăng trụ đứng ABC.A ' B 'C ' có đáy là tam
giác đều cạnh a và AA'  3a . Thể tích của lăng trụ đã cho bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 3a 3 3a 3 a 3 a A. . B. . C. . D. . 4 2 4 2
Câu 33: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho lăng trụ ABC A ' B 'C ' có chiều cao bằng 8 và đáy
là tam giác đều cạnh bằng 6 . Gọi M , N và P lần lượt là tâm của các mặt bên ABB ' A ' ,
ACC ' A ' và BCC ' B '. Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B, C, M , N , P bằng: A. 27 3 . B. 21 3 . C. 30 3 . D. 36 3 .
Câu 34: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối lập phương có cạnh bằng 6. Thể tích của
khối lập phương đã cho bằng A. 216. B. 18. C. 36. D. 72.
Câu 35: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối lăng trụ đứng ABC . D
A BCD có đáy là
hình thoi cạnh a, BD a 3 và 
AA  4a (minh họa như hình bên dưới). Thể tích của khối
lăng trụ đã cho bằng 2 3 4 3 A. 3 2 3a . B. 3 4 3a . C. 3 a . D. 3 a . 3 3
Câu 36: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại , A AB a, SBA SCA
90 , góc giữa hai mặt phẳng SAB và SAC  bằng
60 . Thể tích khối chóp đã cho bằng 3 a 3 a 3 a A. 3 a . B. . C. . D. . 3 2 6
Câu 37: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Thể tích của khối lập phương cạnh 2 bằng A. 6 . B. 8 . C. 4 . D. 2 .
Câu 38: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Cho khối chóp có diện tích đáy B  3 và chiều cao
h  4 . Thể tích của khối chóp đã cho bằng A. 6 . B. 12 . C. 36 . D. 4 .
Câu 39: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Cho hình hộp ABC .
D A' B 'C ' D ' có chiều cao bằng
8 và diện tích đáy bằng 9. Gọi M , N , P và Q lần lượt là tâm của các mặt bên
ABB ' A ', BCC ' B ', CDD 'C ' và DAA ' D '. Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B, C, D, M , N , P và Q bằng A. 27. B. 30. C. 18. D. 36
Câu 40: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho khối hộp chữ nhật có 3 kích thước 3; 4;5 . Thể tích
của khối hộp đã cho bằng?
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A. 10 . B. 20 . C. 12 . D. 60 .
Câu 41: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho khối chóp có diện tích đáy B  6 và chiều cao
h  2 . Thể tích của khối chóp đã cho bằng: A. 6 . B. 3 . C. 4 . D. 12 .
Câu 42: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh
bên bằng 2a và O là tâm của đáy. Gọi M , N , P , Q lần lượt là các điểm đối xứng với O qua
trọng tâm của các tam giác SAB , SBC , SCD , SDA và S ' là điểm đối xứng với S qua O . Thể
tích của khối chóp S '.MNPQ bằng 3 20 14a 3 40 14a 3 10 14a 3 2 14a A. . B. . C. . D. . 81 81 81 9
Câu 43: (ĐỀ THAM KHẢO 2021) Một khối chóp có diện tích đáy bằng 6 và chiều cao bằng 5. Thể tích
của khối chóp đó bằng A. 10. B. 30. C. 90. D. 15.
Câu 44: (ĐỀ THAM KHẢO 2021) Thể tích của khối hộp chữ nhật có ba kích thước 2; 3; 7 bằng A. 14. B. 42. C. 126. D. 12.
Câu 45: (ĐỀ THAM KHẢO 2021) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh
bên SA vuông góc với mặt phẳng đáy, góc giữa SA và mặt phằng (SBC) bằng 45 (tham
khảo hình bên). Thể tích của khối chóp S.ABC bằng 3 a 3 3a 3 3a 3 a A. . B. . C. . D. . 8 8 12 4
Câu 46: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Thể tích của khối lập phương cạnh 5a bằng A. 3 5a . B. 3 a . C. 3 125a . D. 3 25a .
Câu 47: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Cho khối chóp có diện tích đáy 2
B  5a và chiều
cao h a . Thể tích của khối chóp đã cho bằng 5 5 5 A. 3 a . B. 3 a . C. 3 5a . D. 3 a . 6 2 3
Câu 48: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Cho khối hộp chữ nhật ABC .
D A' B ' C ' D ' có đáy
là hình vuông, BD  2a , góc giữa hai mặt phẳng  A' BD và  ABCD bằng 0 30 . Thể tích của
khối hộp chữ nhật đã cho bằng 2 3 2 3 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. a . 9 3
Câu 49: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối chóp có diện tích đáy B và chiều cao
h . Thể tích V của khối chóp đã cho được tính theo công thức nào dưới đây ? 1 4
A. V Bh . B. V Bh .
C. V Bh .
D. V  3Bh . 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Câu 50: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối lăng trụ có diện tích đáy 2 B  5a và
chiều cao h a . Thể tích của khối lăng trụ đã cho bằng 5 5 5 A. 3 a . B. 3 5a . C. 3 a . D. 3 a . 3 6 2
Câu 51: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối lăng trụ tam giác đều ABCAB C   có
cạnh bên bằng 4a , góc giữa hai mặt phẳng  ABC  và  ABC  bằng 30 . Thể tich của khối lăng trụ đã cho bằng 64 3 64 3 64 3 A. 3 64 3a . B. 3 a . C. 3 a . D. 3 a . 3 27 9
Câu 52: (ĐỀ THAM KHẢO 2022) Cho khối chóp có diện tích đáy B  7 và chiều cao h  6 . Thể tích
của khối chóp đã cho bằng A. 42 . B. 126 . C. 14 . D. 56 .
Câu 53: (ĐỀ THAM KHẢO 2022) Cho khối lăng trụ có diện tích đáy B và chiều cao h . Thể tích V của
khối lăng trụ đã cho được tính theo công thức nào dưới đây? 1 4 A. V Bh . B. V Bh .
C. V  6Bh .
D. V Bh . 3 3
Câu 54: (ĐỀ THAM KHẢO 2022) Cho khối chóp đều S.ABCD có AC  4a , hai mặt phẳng  SAB và
SCD vuông góc với nhau. Thể tích khối chóp đã cho bằng 16 2 8 2 16 A. 3 a . B. 3 a . C. 3 16a . D. 3 a . 3 3 3
______________________HẾT______________________
Huế, 16h00 Ngày 27 tháng 6 năm 2022
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
LỜI GIẢI CHI TIẾT Câu 1:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho một tấm nhôm hình vuông cạnh 12 cm. Người
ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x
để hộp nhận được có thể tích lớn nhất. A. x  6 B. x  3 C. x  2 D. x  4 Lời giải:
Ta có : h x cm là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là: 12  2x cm     2 x 0 x 0
Vậy diện tích đáy hình hộp S    x  2 12 2 cm . Ta có:     x 0;6 1  2  2x  0 x  6
Thể tích của hình hộp là: V S.h x  2  2x2 . 1 2 Xét hàm số: y  .
x 12  2xx  0;6 2
Ta có : y '  12  2x  4x 12  2x  12  2x12  6x ;
y '  0  12  2x.12  6x  0  x  2 hoặc x  6 (loại).
Suy ra với x  2 thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là y 2  128 . Câu 2:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tính thể tích V của khối lập phương ABC . D AB CD
  , biết AC  a 3 . 3 3 6a 1 A. 3 V a . B. V  . C. 3 V  3 3a . D. 3 V a . 4 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Giả sử khối lập phương có cạnh bằng ;
x x  0
Xét tam giác A ' B 'C ' vuông cân tại B ' ta có: 2 2 2
A 'C '  A ' B '  B 'C ' 2 2 2
x x  2x A'C '  x 2
Xét tam giác A ' AC ' vuông tại A ' ta có 2 2 2
AC '  A ' A A 'C ' 2 2 2
 3a x  2x x a
Thể tích của khối lập phương ABC . D AB CD   là 3 V a . Câu 3:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác S.ABCD có đáy ABCD là
hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy và SA a 2 . Tính thể tích
V của khối chóp S.ABCD 3 2a 3 2a 3 2a A. V B. V C. 3 V  2a D. V  6 4 3 Lời giải: S B A D C
Ta có SA   ABCD  SA là đường cao của hình chóp 3 1 1 a 2
Thể tích khối chóp S.ABCD : 2 V S . A S  .a 2.a  . 3 ABCD 3 3 Câu 4:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho tứ diện ABCD có các cạnh AB , AC và AD đôi
một vuông góc với nhau; AB  6a , AC  7a và AD  4a . Gọi M , N , P tương ứng là trung
điểm các cạnh BC , CD , DB . Tính thể tích V của tứ diện AMNP . 7 28 A. 3 V a B. 3 V  14a C. 3 V a D. 3 V  7a 2 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 1 1 1 Ta có 3 VA . B A . D AC  6 . a 7 .
a 4a  28a ABCD 3 2 6 1 1 1 Ta nhận thấy 3 SSSVV  7a . MNP 2 MNPD 4 BCD AMNP 4 ABCD Câu 5:
(ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Cho hình chóp tứ giác S.ABCD có đáy là hình
vuông cạnh bằng 2a . Tam giác SAD cân tại S và mặt bên SAD vuông góc với mặt phẳng 4
đáy. Biết thể tích khối chóp S.ABCD bằng 3
a . Tính khoảng cách h từ B đến mặt phẳng 3 SCD 2 4 8 3 A. h a B. h a
C. h a D. h a 3 3 3 4 Lời giải:
Gọi I là trung điểm của AD . Tam giác SAD cân tại S SI AD SI AD  Ta có     SAD
  ABCDSI ABCD
SI là đường cao của hình chóp. Theo giả thiết 1 4 1 3 2 V  .SI.S
a SI.2a SI  2a S . ABCD 3 ABCD 3 3
Vì AB song song với SCD
d B,SCD  d  ,
A SCD  2d I,SCD
Gọi H là hình chiếu vuông góc của I lên SD . SI DCIH SD Mặt khác 
IH DC . Ta có 
IH  SCD  d I,SCD  IH ID DCIH DC 1 1 1 1 4 2a
Xét tam giác SID vuông tại I :      IH  2 2 2 2 2 IH SI ID 4a 2a 3
d B SCD  d A SCD  d I SCD 4 , , 2 ,  a . 3 Câu 6:
(ĐTN BGD&ĐT NĂM 2016-2017) Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3
a . Tính chiều cao h của hình chóp đã cho.
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 3 3 A. a h B. a h C. a h
D. h  3a 6 2 3 Lời giải: 2a2 3
Do đáy là tam giác đều cạnh 2a nên 2 S   a 3  . ABC 4 1 3 3V 3a Mà V S .h      h 3a . 3 ABC 2 Sa ABC 3 Câu 7:
(ĐTN BGD&ĐT NĂM 2016-2017) Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm
của tam giác BCD . Tính thể tích V của khối chóp . A GBC A. V  3 B. V  4 C. V  6 D. V  5 Lời giải: A B D G C Cách 1:
Phân tích: tứ diện ABCD và khối chóp .
A GBC có cùng đường cao là khoảng cách từ A đến mặt phẳng
BCD . Do G là trọng tâm tam giác BCD nên ta có SS   S   S 3S (xem phần chứng minh). BGCBGDCGDBCDBGC
Áp dụng công thức thể tích hình chóp ta có: 1  1 V  . h S ABCDBCD .  h S 3   V 3 BCD S 1 1 ABCD    
BCD  3 VV  .12  4 . 1 V 1 . A GBC ABCDS 3 3 . V  . A GBC h S . GBC h S .   GBC A GBC 3 GBC  3
Chứng minh: Đặt DN  ; h BC a . MF CM 1 1 h +) MF // ND  
  MF DN MF  . DN CD 2 2 2 GE BG 2 2 2 h h +) GE // MF  
  GE MF  .  MF BM 3 3 3 2 3
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 1 1 DN.BC ha S +) BCD 2 2    3  S  3S S 1 1 BCDGBC hGBC GE.BC a 2 2 3
+) Chứng minh tương tự có S  3S  3     S S S S BCDGBDGCD BGC BGD CGD Cách 2: d  ; G ABC  GI 1 1 Ta có . d     d  ;
G ABC   d  ; D ABC  ; D ABC      DI 3 3 1 1 Nên V
d G; ABC .S  .V  4 G.ABC     3 ABC 3 DABC D G A C H1 H I B Câu 8:
(ĐTN BGD&ĐT NĂM 2016-2017) Cho lăng trụ tam giác ABC. 
A BC có đáy ABC là tam giác
vuông cân tại A , cạnh AC  2 2 . Biết AC tạo với mặt phẳng  ABC  một góc 60 và
AC  4 . Tính thể tích V của khối đa diện ABCBC . 8 16 8 3 16 3 A. V B. V C. V D. V  3 3 3 3 Lời giải: B’ C’ A’ 4 2 3 B C 0 H 2 2 60 A
Phân tích: Tính thể tích của khối đa diện ABCBC bằng thể tích khối của lăng trụ ABC. 
A BC trừ đi thể tích của khối chóp . A A BC .
Giả sử đường cao của lăng trụ là CH . Khi đó góc giữa AC mặt phẳng  ABC  là góc
CAH  60 .
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia CH 1 Ta có: sin 60 
CH  2 3; S  4 VCH S    ; . ABCA BC . 2 3. . 2 2 8 3 . ABC  2 ACABC 2 1 1 8 3 8 3 16 3 VCH SV  ; VVV    .
ABBCC ABCA BCAA BC 8 3 AA BC . . . ABC ABC.  A BC 3 3 3 . . 3 3 Câu 9:
(ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a . 3 3 3 3 3 3 3 3 A.a V . B.a V . C.a V . D.a V . 6 12 2 4 Lời giải: h a 3  a 3 2   V  . 3 h S a  . S  4  4
Câu 10: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hình chóp S.ABCD có đáy là hình vuông
cạnh a , SA vuông góc với mặt đáy, SD tạo với mặt phẳng  SAB một góc bằng 30 . Tính
thể tích V của khối chóp S.ABCD . 3 6a 3 6a 3 3a A. V B. 3 V  3a C. V D. V  18 3 3 Lời giải: S A B D C
Góc giữa SD và mp là 0 DSA  30 . AD 3 1 a 3 Ta có SA   a 3 . Suy ra: 2 V a .a 3  . 0 tan 30 3 3
Câu 11: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho khối tứ diện có thể tích bằng V . Gọi V  là
thể tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, V  tính tỉ số . V V  1 V  1 V  2 V  5 A.  . B.  . C.  . D.  . V 2 V 4 V 3 V 8 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A Q P B E F D M N C
Cách 1. Đặc biệt hóa tứ diện cho là tứ diện đều cạnh a . Hình đa diện cần tính có được bằng a
cách cắt 4 góc của tứ diện, mỗi góc cũng là một tứ diện đều có cạnh bằng . 2 V V
Do đó thể tích phần cắt bỏ là V   4.  . 8 2 V V  1 Vậy V     . 2 V 2
Cách 2. Khối đa diện là hai khối chóp tứ giác có cùng đáy là hình bình hành úp lại. Suy ra: 1 1 1 V   2V  4.V  4.V
 4. . V V N .MEPF N .MEP P.MNE 2 4 2 ' V V    . A QEP V . B QMF C V .MNE V V . D NPF Cách 3. Ta có  V V V . A QEP V . B QMF C V .MNE V . 1 D NPF     1 1 1 1 1 1 1 1 1 1 1 1 1
1 . .  . .  . .  . .  . V V V V 2 2 2 2 2 2 2 2 2 2 2 2 2
Câu 12: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh
bên gấp hai lần cạnh đáy. Tính tích V của khối chóp tứ giác đã cho. 3 2 3 2 3 14 3 14 A. a V . B. a V . C. a V . D. a V . 2 6 2 6 Lời giải:
S.ABCD là khối chóp tứ giác đều  ABCD là hình vuông và SO  ABCD, O là tâm của hình vuông.
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S 2a A D O a B C 2 1 a 2  a 2  14 2 2 2 OD BD  ; SO SD OD  4a     a 2 2  2  2   1 1 14 14 2 3 V  .S . O S  . . a a a . 3 ABCD 3 2 6
Câu 13: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho khối chóp S. ABCD có đáy là hình vuông cạnh a,
SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc 30 . Tính thể tích V của khối chóp đã cho. 3 6 3 2 3 2 A.a V . B.a V . C.a V . D. 3 V  2a . 3 3 3 Lời giải: S 300 A D a B C BC  
BA ABCD lµ hinh vu«ng  BC   SA SA   ABCD
BC  SAB  S ,
C SAB  BSC  30 BC BC
SBC vuông tại B: 0 tan 30   SB   3a 0 SB tan 30
SAB vuông tại A: 2 2 2 2 SA SB AB  3a a  2a
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 1 1 2 2 3 V S . A S  . 2 . a a a 3 ABCD 3 3
Câu 14: (MĐ 101-BGD&ĐT NĂM 2016-2017) Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần
lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE)
chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V. 3 7 2 3 11 2 3 13 2 3 2 A.a V . B.a V . C.a V . D.a V . 216 216 216 18 Lời giải:
MNE chia khối tứ diện ABCD thành 2 khối đa diện  : A . C MNPQ và  : . BD MNPQ 2  1  A Q D E B P C
MNE cắt AD tại Q, cắt CD tại P. VVV AC. MNPQ E. AMNC E. ACPQ V
 1 d E, AMNC .S E. AMNC    3 AMNC
 1 d E,  ABC.S   S ABCBMN  3
1 d E, ABC  1   . S    S ABCABC  3  4 
 1 d   ABC 3 S  3 .2. D, .  V 3 4 ABC 2 ABCD 1 1 1 8 8 V
d E, ACPQ .S
d B, ACD . SS
d B, ACD . SV E. ACPQ    ACPQ  
  ACD DPQ      3 3 3 9 ACD 9 ABCD 3 8 11 11 2 11 2 3 3 VVVV  . a a . AC. MNPQ 2 ABCD 9 ABCD 18 ABCD 18 12 216
Câu 15: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng ABC.AB C
  có BB  a , đáy
ABC là tam giác vuông cân tại B và AC a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 3 3 A. 3
V a . B. a V . C. a V . D. a V . 3 6 2 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A' C' a B' a 2 A C B AC 1
Tam giác ABC vuông cân tại B AB BC   a . Suy ra: 2 Sa . ABC 2 2 3 1 a Khi đó: 2 V        S .BB a .a . ABC.A B C ABC 2 2
Câu 16: (MĐ 102 BGD&ĐT NĂM 2016-2017) Cho khối chóp S.ABCD có đáy ABCD là hình chữ
nhật, AB a , AD a 3 , SA vuông góc với mặt phẳng đáy và mặt phẳng  SBC  tạo với đáy
một góc 60o . Tính thể tích V của khối chóp S.ABCD . 3 3 3 A. a V . B. a V . C. 3 V a . D. 3 V  3a . 3 3 Lời giải: S a 60 B A a 3 D C Ta có 2 S  3a . ABCD
SBC  ABCD  BC
Vì BC SB  SBC
 SBC, ABCD  S ;
B AB  SBA . BC AB   ABCD Vậy 60o SBA SA
Xét tam giác vuông SAB có: tan 60o   SA A .
B tan 60o a 3 AB 1 1 Vậy 2 3 VS .SA a 3.a 3  a . S . ABCD 3 ABCD 3
Câu 17: (MĐ 102 BGD&ĐT NĂM 2016-2017) Xét khối tứ diện ABCD có cạnh AB x và các cạnh
còn lại đều bằng 2 3 . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất. A. x  6. B. x  14. C. x  3 2. D. x  2 3. Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia A 2 3 N x 2 3 2 3 B C 2 3 2 3 M D
Gọi M , N lần lượt là trung điểm của CD và AB . CD MBCD MN Ta có
  CD  MAB   . CD MACD AB
Tam giác MAB cân tại M nên MN AB . 1 VAB CD d AB CD AB CD x MNABCD     1 . . , .sin , .2 3. .sin 90 6 6 2 2  x  36   1   3 3 x x 2 2  2   .2 x 3. 3   . x 36  x  .    3 3   . 6  2  6 6  2    Dấu "  " xảy ra 2
x  36  x x  3 2 .
Vậy với x  3 2 thì V
đạt giá trị lớn nhất bằng 3 3 . ABCD
Câu 18: (MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp S.ABC có SA vuông góc với đáy,
SA  4 , AB  6, BC  10 và CA  8 . Tính thể tích khối chóp S.ABC . A. V  40 . B. 192 . C. V  32 . D. V  24 . Lời giải: S 4 8 A C 6 10 B Ta có 2 2 2
AB AC BC suy ra tam giác ABC vuông tại A ,do đó diện tích tam giác ABC là: 1 1 S A . B AC  .6.8  24 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 1 1 Ta có V  .S . A S  .4.24  32 . SABC 3 ABC 3
Câu 19: (MĐ 103 BGD&ĐT NĂM 2016-2017) Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , a 2
SA vuông góc với đáy và khoảng cách từ A đến mặt phẳng SBC  bằng . Tính thể tích 2
V của khối chóp đã cho. 3 3 3 3 A. a V . B. 3 V a . C. a V . D. a V . 2 9 3 Lời giải:
Kẻ AH vuông góc SB .
Ta có AH  (SBC) nên AH chính là khoảng cách từ A đến mp SBC  . 1 1 1 1 1 1 1 Ta có       . 2 2 2 2 2 2 2 AH SA AB SA AH AB a 3 1
Suy ra SA a . Thể tích cần tính là  . .  a V a a a . 3 3
Câu 20: (MĐ 103 BGD&ĐT NĂM 2016-2017) Xét khối chóp S.ABC có đáy là tam giác vuông cân tại
A , SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng  SBC  bằng 3 . Gọi  là góc
giữa mặt phẳng SBC  và  ABC  , tính cos khi thể tích khối chóp S.ABC nhỏ nhất. 1 3 2 2 A. cos  . B. cos  . C. cos  . D. cos  . 3 3 2 3 Lời giải:
Gọi M là trung điểm BC , H là giao điểm của đường thẳng qua A và vuông góc với SM . Ta được:
Góc giữa mặt phẳng  SBC  và  ABC  là SMA . 3 3 1 AM ; SA  ; AM BC. sin cos 2 1 9 Suy ra 2 V  .AM .SA  . S . ABC 2 3 sin .cos
Thể tích khối chóp nhỏ nhất khi 2 sin .cos lớn nhất.  Xét hàm số  x 2 3 f  sin .
x cos x  cos x  cos x với 0  x  2 sin x  0 
f  x   sin x  3cos .
x sin x , f (  x)  0  3  cos x    3
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 Suy ra 2
sin .cos lớn nhất khi cos  . 3
Câu 21: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng
a và cạnh bên bằng 2a . Tính thể tích V của khối chóp S.ABC 3 13a 3 11a 3 11a 3 11a A. V  . B. V  . C. V  . D. V  . 12 12 6 4 Lời giải: S A C O I B
Do đáy là tam giác đều nên gọi I là trung điểm cạnh BC , khi đó AI là đường cao của tam 2 a a 3 2 2a 3 a 3
giác đáy. Theo định lý Pitago ta có 2 AI a   , và AO AI   . 4 2 3 3.2 3 2 a 11a
Trong tam giác SOA vuông tại O ta có 2 SO  4a   3 3 3 1 1 a 3 11a 11a
Vậy thể tích khối chóp S.ABC là V  . a .  . 3 2 2 3 12
Câu 22: (MĐ 104 BGD&ĐT NĂM 2016-2017) Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là
tam giác cân với AB AC a , BAC  120 . Mặt phẳng  AB C
  tạo với đáy một góc 60 .
Tính thể tích V của khối lăng trụ đã cho. 3 3a 3 9a 3 a 3 3a A. V  . B. V  . C. V  . D. V  . 8 8 8 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Gọi I là trung điểm của B C   . Trong 2 2 2 2 A  B C   : B C
   AB  AC  2AB .AC .cos B A
 C  3a 2 1 a 3 2 2S    a 3 a S    A B C        . a . a sin120 ; A I A B C 2 4 B C   2a 3 2   AB C
   AB C    B C   
Ta có : AI B C    AIA  60
AI B C    a 3
Trong tam giác vuông AIA có AA  A I  .tan 60  . 2 2 3 a 3 a 3 3a Vậy thể tích V  .  . 4 2 8
Câu 23: (MĐ 104 BGD&ĐT NĂM 2016-2017) Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu
có bán kính bằng 9, tính thể tích V của khối chóp có thể tích lớn nhất. A. V  144 . B. V  576 .
C. V  576 2 .
D. V  144 6 . Lời giải:
Gọi độ dài cạnh đáy, chiều cao của hình chóp tứ giác đều lần lượt là ;
x h (x, h  0) . Ta có đáy x 2 x
là hình vuông với độ dài nửa đường chéo bằng
suy ra độ dài cạnh bên 2 l h  . 2 2 2 x 2  2 h l
Ta có bán kính mặt cầu ngoại tiếp hình chóp 2 2 2 R  
 9  x  36h  2h . 2h 2h 1 1
Diện tích đáy của hình chóp 2 S x nên 2 V  . h x h  2 36h  2h  3 3 3 1 1
1  h h  36  2h  Ta có . h  2
36h  2h   . .
h h 36  2h  .  576  V  576   , dấu bằng xảy ra 3 3 3  3 
khi h h  36  2h h  12, x  12 vậy V  576 . max
Câu 24: (ĐTK BGD&ĐT NĂM 2017-2018) Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là: 1 1 1 A. V Bh. B. V Bh.
C. V Bh. D. V Bh. 3 6 2 Lời giải:
Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là: V  1 Bh . 3
Câu 25: (ĐTK BGD&ĐT NĂM 2017-2018) Cho hình vuông ABCD và ABEF có cạnh bằng 1, lần
lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng của B qua đường
thẳng DE . Thể tích của khối đa diện ABCDSEF bằng 7 11 2 5 A. . . C. . D. . 6 B. 12 3 6 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S F E D A C B
Ta có:ADF.BCE là hình lăng trụ đứng có đáy là tam giác vuông cân
Dựa vào hình vẽ ta có : VVVVV  2VV ABCDSEF ADF .BCE S .CDFE ADF .BCE B.CDFE ADF . E BC B D A E 1 1 1 1 1 5 VA . B S  ;VA . D S   V  2.   . ADF .BCEBCE BADE  2 3 ABE 6 ABCDSEF 2 6 6
Câu 26: (MĐ 101 BGD&ĐT NĂM 2017-2018) Cho khối chóp có đáy là hình vuông cạnh a và chiều
cao bằng 2a . Thể tích của khối chóp đã cho bằng 2 4 A. 3 4a B. 3 a C. 3 2a D. 3 a 3 3 Lời giải:
Khối chóp có đáy là hình vuông cạnh a nên có diện tích đáy: 2 Sđáy a .
Chiều cao h  2a . 1 1 2
Vậy thể tích khối chóp đã cho là V  .S . 2  3  đáy h .a .2a a . 3 3 3
Câu 27: (MĐ 101 BGD&ĐT NĂM 2017-2018) Ông A dự định dùng hết 2
6, 5m kính để làm một bể cá
có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng . Bể cá có dung tích lớn nhất bằng bao nhiêu? A. 3 2, 26 m . B. 3 1, 61 m . C. 3 1, 33 m . D. 3 1, 50 m . Lời giải: a c b
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Giả sử hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá: V abc 2    6, 5 2b
ab  2bc  2ac  6,5 2
2b  6bc  6,5 c
Mặt khác theo giả thiết ta có:      6ba  2ba  2b a  2b 2 6,5  2 3 6,5  2 Khi đó 2  b V 2b .   b b V . 6b 3  Xét hàm số:   3 6,5 2  b b f b . Có BBT 3  39 
Vậy bể cá có dung tích lớn nhất là : 3 f   1,50   m . 6  
Câu 28: (MĐ 101 BGD&ĐT NĂM 2017-2018) Cho khối lăng trụ ABC.AB C
  , khoảng cách từ C đến
đường thẳng BB bằng 2 , khoảng cách từ A đến các đường thẳng BB và CC lần lượt bằng
1 và 3 , hình chiếu vuông góc của A lên mặt phẳng  AB C
  là trung điểm M của B C   và 2 3 AM
. Thể tích của khối lăng trụ đã cho bằng 3 2 3 A. 2 B. 1 C. 3 D. 3 Lời giải: A C2 B2 C' A M M B' A' C A' 1 H T H B1 T
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Cắt lăng trụ bởi một mặt phẳng qua A và vuông góc với AA ta được thiết diện là tam giác
AB C có các cạnh AB  1; AC  3 ; B C  2 . 1 1 1 1 1 1
Suy ra tam giác AB C vuông tại A và trung tuyến AH của tam giác đó bằng 1. 1 1
Gọi giao điểm của AM và AH là T . 2 3 1
Ta có: AM
; AH  1  MH
. Suy ra MAH  30 . 3 3 A M
Do đó MAA  60 4  AA   . cos MA A  3
Thể tích khối lăng trụ ABC.AB C
  bằng thể tích khối lăng trụ AB C .AB C và bằng 1 1 2 2 4 3
V AA .S     2 . A B C 1 1 3 2
Câu 29: (ĐTK BGD&ĐT NĂM 2018-2019) Thể tích của khối lập phương cạnh 2a bằng A. 3 8a . B. 3 2a . C. 3 a . D. 3 6a . Lời giải:
Thể tích của khối lập phương cạnh 2a bằng  a3 3 2  8a .
Câu 30: (ĐTK BGD&ĐT NĂM 2018-2019) Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a . Thể
tích của khối chóp đã cho bằng 3 4 2a 3 8a 3 8 2a 3 2 2a A. . B. . C. . D. . 3 3 3 3 Lời giải: S A D O B C
Xét khối chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O , suy ra SO   ABCD . Ta có:
+ AC  2a 2  AO a 2 ; 2 2 SO SA AO 2 2
 4a  2a a 2 . + S   a2 2 2  4a . ABCD 1 1 3 4 2a Vậy V  . . SO S 2  .a 2.4a  . 3 ABCD 3 3
Câu 31: (ĐTK BGD&ĐT NĂM 2018-2019) Cho khối lăng trụ ABC.AB C
  có thể tích bằng 1. Gọi
M , N lần lượt là trung điểm các đoạn thẳng AA và BB . Đường thẳng CM cắt đường thẳng
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia C A
  tại P , đường thẳng CN cắt đường thẳng C B
  tại Q . Thể tích của khối đa diện lồi A MPB NQ bằng 1 1 2 A. 1 . B. . C. . D. . 3 2 3 Lời giải: A C B M N P A' C' B' Q S +) Ta có 
A là trung điểm PC ; B là trung điểm QC . Do đó S     4 C PQ S    4 . C PQ C A B SC ABS   C PQ 1 4 +) V      .V    4V    4 V     . C.C PQ C. A B C C. A B C ABC.  S     3 A B C  3 C A B 1  A MB NC C   1  1 1  2 +) Mặt khác V           . V      . 1 V      . A B C .MNC ABC. A B C ABC. 3  A AB BC C   3  2 2 A B C  3 4 2 2 +) Do đó V        VV    . A MPB NQ C.C PQ A B C .MNC 3 3 3
Câu 32: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho khối lăng trụ đứng ABC.A ' B 'C ' có đáy là tam
giác đều cạnh a và AA'  3a . Thể tích của lăng trụ đã cho bằng 3 3a 3 3a 3 a 3 a A. . B. . C. . D. . 4 2 4 2 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 a 3
Ta có: ABC là tam giác đều cạnh a nên S  . ABC  4
Ta lại có ABC.A ' B 'C ' là khối lăng trụ đứng nên AA'  3a là đường cao của khối lăng trụ. 2 3 a 3 3a
Vậy thể tích khối lăng trụ đã cho là: VAA'.Sa 3.  .
ABC. A' B 'C ' ABC 4 4
Câu 33: (MĐ 101 BGD&ĐT NĂM 2018-2019) Cho lăng trụ ABC A ' B 'C ' có chiều cao bằng 8 và đáy
là tam giác đều cạnh bằng 6 . Gọi M , N và P lần lượt là tâm của các mặt bên ABB ' A ' ,
ACC ' A ' và BCC ' B '. Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B, C, M , N , P bằng: A. 27 3 . B. 21 3 . C. 30 3 . D. 36 3 . Lời giải:
Gọi A , B ,C lần lượt là trung điểm của các cạnh AA', BB ',CC ' . 1 1 1
Khối lăng trụ ABC.A B C có chiều cao là 4 là tam giác đều cạnh 6 . 1 1 1 Ba khối chóp .
A A MN , BB MP , CC NP đều có chiều cao là 4 và cạnh là tam giác đều cạnh 3 Ta có: 1 1 1 2 6 3 1 9 3 VVVVV   4  3   4  27 3 . ABC.MNP ABC. 1 A 1 B 1 C
 .A 1AMN B. 1BMP C. 1CNP 4 3 4
Câu 34: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối lập phương có cạnh bằng 6. Thể tích của
khối lập phương đã cho bằng A. 216. B. 18. C. 36. D. 72. Lời giải:
Thể tích khối lập phương đã cho là 3 V  6  216.
Câu 35: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối lăng trụ đứng ABC . D
A BCD có đáy là
hình thoi cạnh a, BD a 3 và 
AA  4a (minh họa như hình bên dưới). Thể tích của khối
lăng trụ đã cho bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 3 4 3 A. 3 2 3a . B. 3 4 3a . C. 3 a . D. 3 a . 3 3 Lời giải: 3
Vì ABCD là hình thoi cạnh 2 2
a, BD a 3  AC  2AO  2 a a a 4 2 a 3 Vậy 3 S
V AA .S  2 3a . ABCD 2 ABCD
Câu 36: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại , A AB a, SBA SCA
90 , góc giữa hai mặt phẳng  SAB và  SAC  bằng
60 . Thể tích khối chóp đã cho bằng 3 a 3 a 3 a A. 3 a . B. . C. . D. . 3 2 6 Lời giải: Cách 1:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 2 1 a Ta có SA . B AC  . ABC  2 2
Gọi D là hình chiếu vuông góc của S lên mặt phẳng  ABC  . AB SB Ta có 
AB  SBD  AB BD . AB SD
Tương tự, ta có AC CD
ABDC là hình vuông cạnh a .
Đăt SD x, x  0 . D . B DS ax
Gọi H là hình chiếu vuông góc của D lên SB DH   . 2 2 2 2 DB DS a xDH SB ax Ta có 
DH  SAB  d D,SAB  DH  .   2 2 DH AB a x
Lại có CD // AB CD // SAB  d C,SAB  d D,SAB  DH .
SCA vuông tại C, có 2 2
AC a, SC x a . 2 2 C . A CS . a x a
Kẻ CK SA CK   . 2 2 2 2 CA CS x  2a
d C, SAB DH
Vì SAB SAC   SA  sin SAB,SAC    
d C, SACK ax 2 2 2 2 a x 3 x x  2a  sin 60   
 3x a 2 2 2 2  4x  2 2 x  2ax a . 2 2  2 2 2  x a a x a 2 2 x  2aDH a . 3 1 a Vậy VS .SD  . S.ABC  3 ABC 6 Cách 2:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Dựng hình vuông ABCD SD   ABCD .
Đặt SD x, x  0 . ax
Kẻ DH SB, H SB  DH  SAB và DH  . 2 2 x a ax
Kẻ DK SC, K SC   DK  SAC  và DK  . 2 2 x a 2 2 2 2 SH SK SD x x x Ta có   
HK // BD HK BD  .a 2 . 2 2 2 2 2 2 2 SB SC SB x a x a x a
DH DK HK Ta có
SAB SAC 2 2 2 cos ,  cos HDK  2DH.DK 2 2 2 4 2x a 2a x  2 2 x a  1 x a 2 2 2 2 1 a      x a . 2 2 2 2 2 2x a 2 x a 2 2 x aSD  . a 2 1 a Lại có S A . B AC ABC    . 2 2 3 1 a Vậy VS .SD  . S.ABC  3 ABC 6
Cách trình bày khác
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia S I A C a a 2 B
Hai tam giác vuông SAB và SAC bằng nhau chung cạnh huyền SA .
Kẻ BI vuông góc với SA suy ra CI cũng vuông góc với SA và IB IC .
SA IC, SA IB SA   IBC  tại I . 1 1 1 1 VVVS AI S SI S AI SI S SA . S . ABC . A IBC S .IBC IBC IBC IBC    3 3 3 3 IBC
SAB SAC  IB IC  IB IC 0 0 , , ,
 60  BIC  60 hoặc 0 BIC  120 .
Ta có IC IB AB a mà BC a 2 nên tam giác IBC không thể đều suy ra 0 BIC  120 .
Trong tam giác IBC đặt IB IC xx  0 có: 2x
IB IC BCa 2 1 2 2 2 2 2 a 6 a 6 0 cos120      x
IB IC  . 2 2I . B IC 2 2x 3 3 2  a 6  a 3
Trong tam giác ABI vuông tại I có: 2 2 2 AI AB IB a       . 3 3   2 2 AB a
Trong tam giác SAB vuông tại B đường cao BI có: 2 AB I . A SA SA    a 3 . IA a 3 3 2 3 1 1 1 1  a 6  a Vậy 0 V  S SA I .
B IC.SAsin BIC    a 3 sin120  . S . ABC    3 IBC 3 2 6 3 6  
Cách trình bày khác
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Gọi H là hình chiếu của S lên  ABC  .
Theo bài ra, ta có HC C ,
A HB BA ABHC là hình vuông cạnh a .
Gọi O HA BC , E là hình chiếu của O lên SA .
Ta dễ dàng chứng minh được EC  , SA EB SA .
Từ đó, ta được: góc giữa  SAC  và  SAB là góc giữa EB và EC . Vì 0 CAB  90 nên 0 0
BEC  90  BEC  120 .
Ta dễ dàng chỉ ra được 0
OEB OEC  60 . A . O SH xa 2 Đặt 2 2
SH x SA
x  2a OE   . 2 2 SA 2 x  2a OC a 2 xa 2 0 tan 60   :
 3  x a . 2 2 OE 2 2 x  2a 3 1 1 1 a Vậy 2 VV  . . . a a  . S . ABC S . 2 HBAC 2 3 6
Cách trình bày khác S I D C B A
Ta có   SAB    SAC và chung cạnh huyền SA. Kẻ BI  SA  CI  SA và góc giữa
hai mặt phẳng  SAB và  SAC  là góc giữa hai đường thẳng BI và CI   BI;CI   60 .
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Có BC a 2 , BIC cân tại I. Do BI CI AC a a 2  BC nên BIC không đều a 6 a 3 BIC 120 BI CI . Từ đó AI  ; 2
AB AI.SA SA a 3. 3 3
Dựng hình vuông ABDC SD   ABDC  . 3 1 a Có : 2 2 2
SD SA AD  ; a Sa VS .SD  . ABC S .ABC  3 ABC 6
HOẶC CÁCH KHÁC PPTHỂ TÍCH 1 1 VS . SI AI S .SA . S . ABC IBC    3 3 IBC 2 2 3 1 a 3 1 a 3 a Với S  .I . B IC.s 1 in 20  V  . .a 3  . IBC S . 2 6 ABC 3 6 6
Câu 37: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Thể tích của khối lập phương cạnh 2 bằng A. 6 . B. 8 . C. 4 . D. 2 . Lời giải: Ta có 3 V  2  8 .
Câu 38: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Cho khối chóp có diện tích đáy B  3 và chiều cao
h  4 . Thể tích của khối chóp đã cho bằng A. 6 . B. 12 . C. 36 . D. 4 . Lời giải: 1 1
Thể tích khối chóp đã cho là V  . . B h  .3.4  4 . 3 3
Câu 39: (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Cho hình hộp ABC .
D A' B 'C ' D ' có chiều cao bằng
8 và diện tích đáy bằng 9. Gọi M , N , P và Q lần lượt là tâm của các mặt bên
ABB ' A ', BCC ' B ', CDD 'C ' và DAA ' D '. Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B, C, D, M , N , P và Q bằng A. 27. B. 30. C. 18. D. 36 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Mặt MNPQ cắt các cạnh AA', BB', CC', DD'tại A , B ,C , D . Thể tích khối đa diện cần tìm là 1 1 1 1 V , thì: V VVVVV 1 A 1 B 1 C 1
D .A ' B ' C ' D ' A '.QM 1 A B '.M 1 NB C '.P 1 NC D '.QP 1 D 8.9 V   4 . 2 24  V  30
Câu 40: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho khối hộp chữ nhật có 3 kích thước 3; 4;5 . Thể tích
của khối hộp đã cho bằng? A. 10 . B. 20 . C. 12 . D. 60 . Lời giải:
Thể tích của khối hộp đã cho bằng V  3.4.5  60 .
Câu 41: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho khối chóp có diện tích đáy B  6 và chiều cao
h  2 . Thể tích của khối chóp đã cho bằng: A. 6 . B. 3 . C. 4 . D. 12 . Lời giải: 1
Thể tích của khối chóp V Bh  4 . 3
Câu 42: (MĐ 101 BGD&ĐT NĂM 2019-2020) Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh
bên bằng 2a và O là tâm của đáy. Gọi M , N , P , Q lần lượt là các điểm đối xứng với O qua
trọng tâm của các tam giác SAB , SBC , SCD , SDA và S ' là điểm đối xứng với S qua O . Thể
tích của khối chóp S '.MNPQ bằng 3 20 14a 3 40 14a 3 10 14a 3 2 14a A. . B. . C. . D. . 81 81 81 9 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Gọi G ,G ,G ,G lần lượt là trọng tâm SAB  , SBC  , SCD, SDA . 1 2 3 4
E, F, G, H lần lượt là trung điểm của các cạnh AB, BC,CD, DA . 2 4 4 1 8a Ta có S  4S  4. S  4. . E . G HF  . MNPQ 1 G 2 G 3 G 4 G 9 EFGH 9 2 9
d S ,MNPQ  d S , ABCD  d O,MNPQ
d S, ABCD  2d O,G G G G 1 2 3 4  
d S ABCD 2 ,
d S, ABCD 3 5
d S ABCD 5a 14 ,  3 6 2 3 1 5a 14 8a 20a 14 Vậy V     . S .  MNPQ 3 6 9 81
Câu 43: (ĐỀ THAM KHẢO 2021) Một khối chóp có diện tích đáy bằng 6 và chiều cao bằng 5. Thể tích
của khối chóp đó bằng A. 10. B. 30. C. 90. D. 15.
Câu 44: (ĐỀ THAM KHẢO 2021) Thể tích của khối hộp chữ nhật có ba kích thước 2; 3; 7 bằng A. 14. B. 42. C. 126. D. 12.
Câu 45: (ĐỀ THAM KHẢO 2021) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh
bên SA vuông góc với mặt phẳng đáy, góc giữa SA và mặt phằng (SBC) bằng 45 (tham
khảo hình bên). Thể tích của khối chóp S.ABC bằng
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia 3 a 3 3a 3 3a 3 a A. . B. . C. . D. . 8 8 12 4 Lời giải:
Gọi M là trung điểm BC thì AM BC và SA BC nên BC
(SAM ). Từ đây dễ thấy góc a 3 cần tìm là ASM
45 . Do đó, SAM vuông cân ở A và SA AM . 2 2 3 1 a 3 a 3 a Suy ra V . S. ABC 3 2 4 8
Câu 46: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Thể tích của khối lập phương cạnh 5a bằng A. 3 5a . B. 3 a . C. 3 125a . D. 3 25a . Lời giải:
Thể tích của khối lập phương cạnh 5a là V   a3 3 5 125a .
Câu 47: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Cho khối chóp có diện tích đáy 2
B  5a và chiều
cao h a . Thể tích của khối chóp đã cho bằng 5 5 5 A. 3 a . B. 3 a . C. 3 5a . D. 3 a . 6 2 3 Lời giải: 1 1 5
Thể tích của khối chóp đã cho 2 3 V  . .
B h  .5a .a a . 3 3 3
Câu 48: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 1) Cho khối hộp chữ nhật ABC .
D A' B ' C ' D ' có đáy
là hình vuông, BD  2a , góc giữa hai mặt phẳng  A' BD và  ABCD bằng 0 30 . Thể tích của
khối hộp chữ nhật đã cho bằng 2 3 2 3 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. a . 9 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Gọi O là tâm hình vuông ABCD . Vì BD OA và BD AA ' nên BD   A'OA  BD OA'
Lại có  A' BD   ABCD  BD . Do đó  A BD  ABCD 0 ' ,
A'OA  30 (Hình vẽ trên).
Vì tứ giác ABCD là hình vuông có BD  2a nên OA a và AB AD a 2 . a 3
Xét tam giác A ' AO vuông tại A có OA a và 0
A 'OA  30 nên 0 AA'  O . A tan 30  . 3 a 3 2 3
Vậy thể tích khối hộp chữ nhật 3 V A . B A .
D AA '  a 2.a 2.  a . 3 3
Câu 49: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối chóp có diện tích đáy B và chiều cao
h . Thể tích V của khối chóp đã cho được tính theo công thức nào dưới đây ? 1 4
A. V Bh . B. V Bh .
C. V Bh .
D. V  3Bh . 3 3
Câu 50: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối lăng trụ có diện tích đáy 2 B  5a và
chiều cao h a . Thể tích của khối lăng trụ đã cho bằng 5 5 5 A. 3 a . B. 3 5a . C. 3 a . D. 3 a . 3 6 2 Lời giải:
Thể tích của khối lăng trụ 2 3 V  .
B h  5a .a  5a .
Câu 51: (MĐ 101 BGD&ĐT NĂM 2020-2021 Lần 2) Cho khối lăng trụ tam giác đều ABCAB C   có
cạnh bên bằng 4a , góc giữa hai mặt phẳng  ABC  và  ABC  bằng 30 . Thể tich của khối lăng trụ đã cho bằng 64 3 64 3 64 3 A. 3 64 3a . B. 3 a . C. 3 a . D. 3 a . 3 27 9 Lời giải: A' C' B' A C 30° I B
Gọi I là trung điểm của BC BC AI (vì ABC đều). BC AI Ta có 
BC   A A
I   BC A I BC AA Suy ra  A B
C, ABC  AI, AI  AIA  30.
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia AA 4a 4a
Tam giác AAI vuông tại A có tan AAI   AI    4a 3 AI tan 30 3 3 BC 3 2AI 2.4a 3
Vì ABC đều nên AI   BC    8a . 2 3 3 2 2 BC 3 64a 3
Diện tích ABC là 2 S   16a 3 . ABC  4 4 Thể tich khối lăng trụ 2 3
V AA .S  4 .1 a 6a 3  64 3a . ABC
Câu 52: (ĐỀ THAM KHẢO 2022) Cho khối chóp có diện tích đáy B  7 và chiều cao h  6 . Thể tích
của khối chóp đã cho bằng A. 42 . B. 126 . C. 14 . D. 56 .
Câu 53: (ĐỀ THAM KHẢO 2022) Cho khối lăng trụ có diện tích đáy B và chiều cao h . Thể tích V của
khối lăng trụ đã cho được tính theo công thức nào dưới đây? 1 4 A. V Bh . B. V Bh .
C. V  6Bh .
D. V Bh . 3 3
Câu 54: (ĐỀ THAM KHẢO 2022) Cho khối chóp đều S.ABCD có AC  4a , hai mặt phẳng  SAB và
SCD vuông góc với nhau. Thể tích khối chóp đã cho bằng 16 2 8 2 16 A. 3 a . B. 3 a . C. 3 16a . D. 3 a . 3 3 3 Lời giải:
Gọi O là tâm của hình vuông ABCD .
Do S.ABCD là hình chóp đều nên SO   ABCD  SO AB .
Ta có: S là một điểm chung của hai mặt phẳng  SAB và  SCD .
AB   SAB ; CD  SCD ; AB / /CD .
Suy ra hai mặt phẳng  SAB và  SCD cắt nhau theo giao tuyến là đường thẳng  đi qua S ,
song song với AB và CD .
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà
Chuyên đề THỂ TÍCH KHỐI ĐA DIỆN Luyện thi THPT Quốc gia
Gọi H ; K lần lượt là trung điểm của AB và CD HK đi qua O và HK AB . SO AB Ta có: 
AB  SHK     SHK  (Do  / / AB ). HK AB
 SAB;SCD  SH ;SK   90  SH SK Tam giác SHK vuông tại S .  AC 1 1 AB
 2 2a ; SO HK AB a 2 . 2 2 2 2 2 SAB  8a . ABCD 1 1 8 2
Vậy thể tích khối chóp S.ABCD là: 2 3 VS . O Sa 2.8a a . S . ABCD 3 ABCD 3 3
______________________HẾT______________________
Huế, 16h00 Ngày 27 tháng 6 năm 2022
Lớp Toán thầy Lê Bá Bảo TP Huế Số 4 Kiệt 116 Nguyễn Lộ Trạch, TP Huế – Trung tâm KM 10 Hương Trà