































Preview text:
Chuyên đề 12: Hình học giải tích trong không gian Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam Email : dangnamneu@gmail.com Yahoo: changtraipkt Mobile: 0976266202 CHUYÊN ĐỀ 12:
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN 690 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Chuyên đề 12: Hình học giải tích trong không gian 691 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam Email : dangnamneu@gmail.com Yahoo: changtraipkt Mobile: 0976266202
CÁC CÔNG THỨC CẦN NHỚ
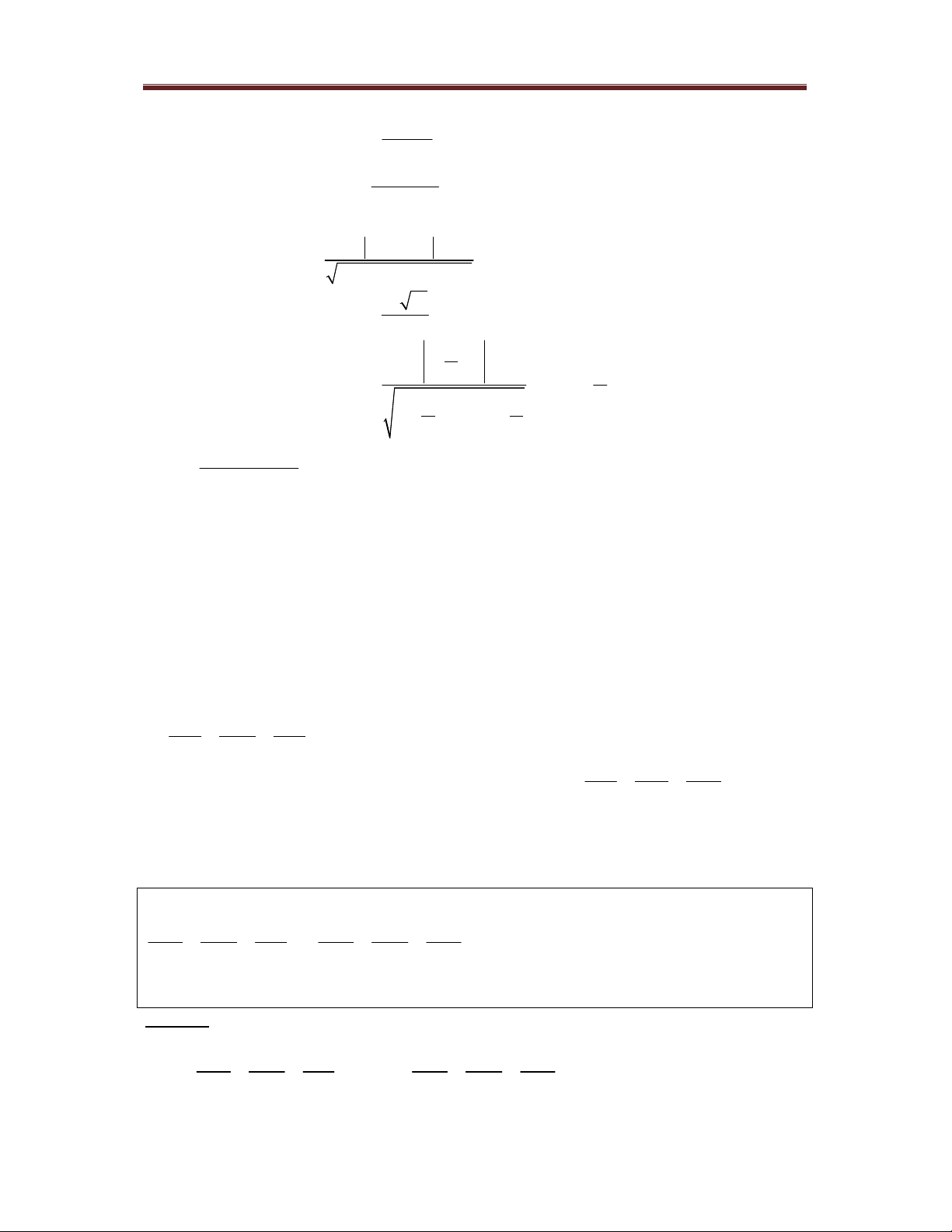
Tích vô hướng của hai véc tơ v (x , y , z ) và véc tơ v (x , y , z ) là một số 1 1 1 1 2 2 2 2
v .v x x y y z z . 1 2 1 2 1 2 1 2
Tích có hướng của hai véc tơ là một véc tơ được xác định bởi y z z x x y 1 1 1 1 1 1
v ,v , , . 1 2 y z z x x y 2 2 2 2 2 2
Có v v ,v ; v v ,v ; v ,v v . v .sin . 1 1 2 2 1 2 1 2 1 2
Diện tích của tam giác tạo bởi ba điểm ,
A B, C không thẳng hang 1 S AB, AC . ABC 2 x y z 1 1 1
Tích hỗn tạp của ba véc tơ (v , v , v ) là một số và được ký hiệu là D v ,v ,v x y z 1 2 3 1 2 3 2 2 2 x y z 3 3 3
Ba véc tơ đồng phẳng khi và chỉ khi D v ,v ,v 0 . 1 2 3
Thể tích tứ diện tạo bởi 4 đỉnh ,
A B,C, D được tính bởi công thức 1
1 V D( , AB AC, AD) , AB AC .AD ABCD 6 6
Thể tích của hình hộp dựng trên ba véc tơ v , v , v được xác định bởi công thức 1 2 3
V D(v , v , v ) D(v , v ).v . 1 2 3 1 2 3
Cho đường thẳng d có véc tơ chỉ phương u (a, ,
b c) và mặt phẳng (P) có véc tơ pháp tuyến n ( ,
A B, C) , khi đó góc tạo bởi d , P được xác định bởi u.n
Aa Bb Cc sin = . 2 2 2 2 2 2 u . n
A B C . a b c
Cho hai đường thẳng d có véc tơ chỉ phương u a, ,
b c và đường thẳng d có véc tơ 2 1
chỉ phương v (a ',b ', c ') , khi đó góc giữa d , d được xác định bởi 1 2 u.v
aa ' bb ' cc '
cos . 2 2 2 2 2 2 u . v
a b c . a ' b ' c '
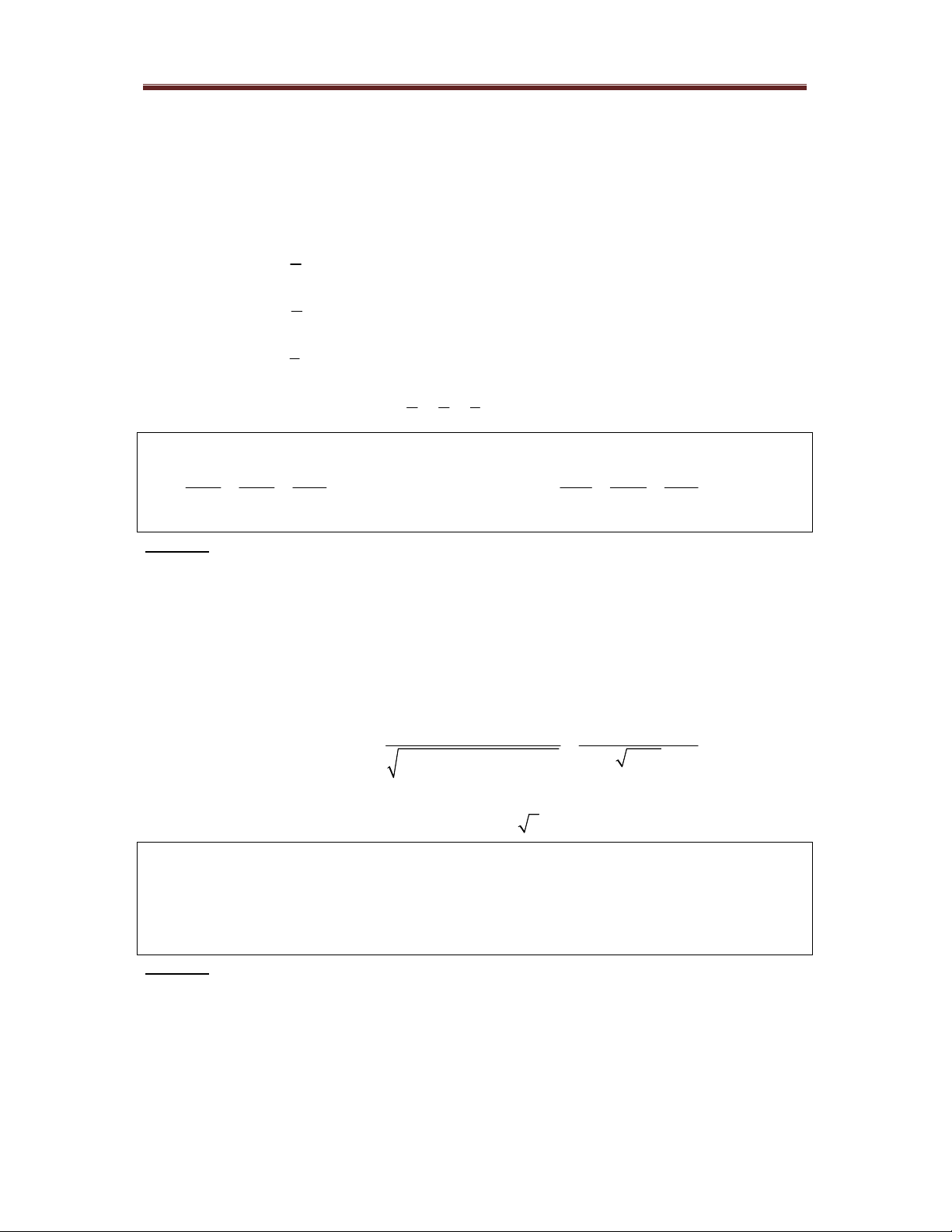
Khoảng cách từ điểm M đến đường thẳng d đi qua điểm M và có véc tơ chỉ phương u 0 được xác định bởi 692 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN MM ,u
d M ;d 0
( lưu ý là tử thức là độ dài véc tơ không phải trị tuyệt đối). u
Khoảng cách giữa hai đường thẳng chéo nhau d đi qua điểm M , có véc tơ chỉ phương u 1
và đường thẳng d đi qua điểm N , có véc tơ chỉ phương v được xác định bởi 2
u, v.MN
d d , d
( lưu ý dưới mẫu là độ dài véc tơ, tử thức là giá trị tuyệt đối). 1 2 u , v
Tất cả các công thức trên đều được áp dụng tính trực tiếp trong bài thi.
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG, GIỮA ĐƯỜNG THẲNG VÀ MẶT
PHẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN
Cho đường thẳng d có véc tơ chỉ phương a và mặt phẳng P có véc tơ pháp tuyến n và
cặp véc tơ chỉ phương a , a . 1 2
+ Đường thẳng d và mặt phẳng P không có điểm chung ta nói d / / P .
Vậy d / / P xảy ra khi thỏa mãn một trong các điều kiện:
(i). Hệ phương trình tạo bởi đường thẳng d và mặt phẳng P vô nghiệm.
(ii). a n và tồn tại một điểm Ad , A P .
(iii). a là một véc tơ chỉ phương của P và tồn tại một điểm Ad nhưng không thuộc P .
+ Đường thẳng d và mặt phẳng P có hai điểm chung phân biệt ta nói d P , xảy ra
khi thỏa mãn một trong các điều kiện:
(i). Hệ phương trình tạo bởi đường thẳng d và mặt phẳng P vô số nghiệm.
(ii). Mặt phẳng P đi qua hai điểm phân biệt ,
A B d .
(iii). Mặt phẳng P đi qua điểm Ad và nhận a làm một véc tơ chỉ phương.
+ Đường thẳng d có một điểm chung duy nhất với P ta nói d cắt P , xảy ra khi hệ
phương trình tạo bởi đường thẳng d và mặt phẳng P có nghiệm duy nhất.
Đường thẳng d P a / /n .
Cho hai đường thẳng d , d phân biệt theo thứ tự có các véc tơ chỉ phương là a , a . Lấy 1 2 1 2
hai điểm Ad , B d ; A B . 1 2
Khi đó xét tích hỗn tạp của 3 véc tơ D(a ,a , AB) 1 2
(i). Nếu D(a ,a , AB) 0 thì d và d đồng phẳng. 2 1 1 2
(ii). Nếu D(a ,a , AB) 0 thì d và d chéo nhau. 2 1 1 2 693 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
+ Giữa hai đường thẳng song song d , d trong không gian có các dạng bài toán sau: 1 2
(i). Viết phương trình mặt phẳng P chứa hai đường thẳng song song d , d 1 2
(ii). Viết phương trình đường thẳng d song song, cách đều d , d và thuộc mặt phẳng 1 2
chứa d , d . 1 2
(iii). Tính khoảng cách giữa hai đường thẳng d , d . 1 2
+ Giữa hai đường thẳng cắt nhau d , d trong không gian có các dạng bài toán sau: 1 2
(i). Viết phương trình mặt phẳng P chứa d , d . 1 2
(ii). Viết phương trình đường phân giác tạo bởi d , d . 1 2
+ Giữa hai đường thẳng chéo nhau d , d trong không gian có các dạng bài toán sau: 1 2
(i). Viết phương trình đường vuông góc chung của d , d . 1 2
(ii). Tính khoảng cách giữa hai đường thẳng d , d . 1 2
(iii). Viết phương trình của mặt phẳng cách đều d , d . 1 2
(iv). Viết phương trình hai mặt phẳng P, Qsong song với nhau và lần lượt chứa d , d . 1 2
(v). Viết phương trình mặt phẳng P cách đều d , d . 1 2
(vi). Viết phương trình đường thẳng d đi qua điểm M cho trước và cắt cả d , d . 1 2 BÀI TẬP MẪU
Bài 1. Cho mặt phẳng P và đường thẳng d có phương trình lần lượt là 5
x 3 y 2z 5 0
P : 4x 3y 7z 7 0 và d :
2x y z 1 0
Chứng minh rằng d P . Lời giải:
Cách 1: Xét hệ phương trình tạo bởi d và P . 5
x 3y 2z 5 0 5
x 3y 2z 5 0 5
x 3y 2z 5 0
2x y z 1 0 9
x 5 y 7 0
hệ này vô số nghiệm, do
9x 5y 7 0
4x 3y 7z 7 0
18x 10 y 14 0
đó d P đpcm. 7 5 7 2
Cách 2: Lấy hai điểm phân biệt A , 0, ; B 0, ,
d thay tọa độ của , A B vào 9 9 5 5
phương trình của P ta được: 7 5 4. 3.0 7. 7 0 9 9
thỏa mãn, dó đó d P . 7 2 4.0 3. 7. 7 0 5 5 694 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Bài 2. Biện luận theo tham số m vị trí tương đối của mặt phẳng P và đường thẳng d , biết: P 2
: m x 2 y z 1 3m 0 , x t
d : y 1 t ,t
z 3 2t Lời giải:
Thay x, y, z từ phương trình của d vào phương trình của P ta được phương trình: 2
m 4t 3m 6(*) + Nếu 2
m 4 0 m 2 -
Với m 2 (*) vô số nghiệm, khi đó d P . - Với m 2
(*) vô nghiệm, khi đó d / / P . 3 m 1 3m
+ Nếu m 2 (*) có nghiệm duy nhất, khi đó d P A , , .
m 2 m 2 m 2
x mz m 0
Bài 3. Cho đường thẳng d m là tham số m : , 1 m
x my 0
Chứng minh rằng d
luôn đi qua một điểm cố định và nằm trong một phẳng cố định. m Lời giải:
Giả sử điểm M x , y , z là điểm cố định mà d luôn đi qua, khi đó m 0 0 0 x 0
x mz m 0 x z 0 1 m 0 0 0 0 0 , m , m y 0 1 m
x my 0 x m x y 0 0 0 0 0 0 0 z 1 0 Vậy d
luôn đi qua điểm cố định M 0, 0, 1 . m
Từ phương trình đường thẳng d , ta suy ra m
mx my mz m 0 x y z 1 0 P : x y z 1 0 là mặt phẳng mà d luôn m thuộc P . 3
x y 2z 4 0
Bài 4. Cho mặt phẳng P : 2x my z 5 0 , d :
x y 2z 7 0
Tìm giá trị của m để:
a. d / / P .
b. d P . Lời giải: 1 2 23 31
Đường thẳng d có véc tơ chỉ phương a , , 4, 4 , 4 12 21 1 1
Mặt phẳng P có véc tơ pháp tuyến n 2, , m 1 .
a. d / / P a n .
a n 0 4.2 4.m 4.1 0 m 1. 695 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN 2 m 1
b. d P a / /n
vô lý. Vậy không tồn tại m để d P . 4 4 4 3
x y 4z 27 0
Bài 5. Cho đường thẳng d :
và mặt phẳng P : 2x 5y z 17 0.
6x 3y z 7 0
Xác định phương trình đường thẳng đi qua giao điểm A của d và P và vuông góc với
d , nằm trong mặt phẳng P . Lời giải:
+ Xét hệ phương trình tạo bởi d và P
2x y 4z 27 0 x 2
6x 3y z 7 0 y 5
d P A 2, 5, 4 . 2x 5y z 17 0 z 4
+ Gọi a là véc tơ chỉ phương của d , ta được a 11, 27,15
Gọi Q là mặt phẳng qua A và vuông góc với d , khi đó Q nhận a làm véc tơ pháp
tuyến, nên Q : 11 x 2 27 y 5 15 z 4 0 Q : 11x 27 y 15z 97 0 .
Khi đó, đường thẳng cần tìm chính là giao của hai mặt phẳng P và Q .
2x 5 y z 17 0
Vậy đường thẳng cần tìm là :
11z 27 y 15z 97 0 x 2t 1 x u 2
Bài 6. Cho hai đường thẳng d : y t 2 và d : y 3 2u 2 1
z 3t 3 z 3u 1
Chứng minh rằng d và d chéo nhau và xác định phương trình mặt phẳng P song song 2 1
và các đều d , d . 1 2 Lời giải:
+ d có véc tơ chỉ phương a 2,1,3 và d có véc tơ chỉ phương a 1, 2,3 . 2 2 1 1
Lấy điểm A1, 2, 3
d ; B 2,3,1 d suy ra AB 1, 5, 4 1 2 21 3
Ta có D a ,a , AB 12 3 24 0 . Vậy d và d chéo nhau. 2 1 1 2 1 5 4 3 1
+ Gọi I là trung điểm của AB I , , 1
khi đó mặt phẳng cần tìm đi qua I và có cặp 2 2 3 x 2t t 1 2 2 1
véc tơ chỉ phương a , a P : y t 2t t ,t . 1 2 1 2 1 2 2
z 1 3t 3t 1 2 696 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Bài 7. Viết phương trình đường thẳng d song song, cách đều hai đường thẳng x 2 y 5 z 9 x y 3 z 7 d : , d :
và thuộc mặt phẳng chứa d , d . 1 2 2 1 3 1 4 3 1 4 Lời giải :
+ d / / d , d có véc tơ chỉ phương a 3, 1 , 4 1 1 2 Lấy điểm A 2
,5,9 d ; B 0; 3 ; 7 d
suy ra trung điểm của AB là I 1 ,1, 1 . Khi 1 2
đó đường thẳng cần tìm đi qua I và có véc tơ chỉ phương là a x 1 y 1 z 1 Vậy d : . 3 1 4 x 0
x 2u 2
Bài 8. Cho hai đường thẳng d : y 1
và d : y 1 2 1 z 1 t z 0
Chứng mỉnh rằng d và d cắt nhau. Xác định tọa độ giao điểm của chúng. Viết phương 2 1
trình đường phân giác tạo bởi d , d . 1 2 Lời giải :
+ Xét hệ phương trình tạo bởi d , d , ta có 1 2 0 2u 2 u 1 1 1 d d I 0,1, 0 1 2 t 1 1 t 0
+ Lấy điểm A0,1, 2 d , B 2u 2,1, 0 d sao cho 1 2 IA IB u 2 2 2 4 2 2
u 0 u 2
+ Với u 0 B 2
,1, 0 , ta có tọa độ trung điểm của AB là I 1
,1,1 II 1, 0,1 , 1 1 1 1
khi đó đường phân giác cần tìm là đi qua I và có véc tơ chỉ phương II : 1 x t : y 1 1 z t x t
+ Với u 2 B 2,1, 0 tương tự ta có đường phân giác : y 1 2 2 z t x 2 y z 1 x 7 y 2 z
Bài 9. Cho hai đường thẳng d : và d : 2 1 4 6 8 6 9 12
Chứng minh rằng d song song với d , viết phương trình mặt phẳng P chứa d , d 1 2 2 1
và tính khoảng cách giữa d , d . 1 2 Lời giải : 697 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
+ Đường thẳng d có véc tơ chỉ phương u 4, 6, 8 và đường thẳng d có véc tơ chỉ 2 1 phương v 6
, 9,12 , suy ra u / /v . Lấy điểm A2, 0,
1 d thay vào phương trình của 1 2 7 0 2 1 d
vô lý. Từ đó suy ra d / / d Ta có đpcm. 1 2 2 6 9 12
+ Lấy điểm B 7, 2, 0 d . Mặt phẳng P chứa d , d nên P đi qua điểm A và có 1 2 2
cặp véc tơ chỉ phương u, AB nên
x 2 2u 5v
P : y 3u 2v
z 1 4u v AB, v 854
+ Do d / / d nên d d , d d , A d 1 2 2 1 2 v 29 x 1 t x 1 y 2 z 4
Bài 10. Cho hai đường thẳng d :
và d : y t 2 1 2 1 3
z 2 3t
Chứng minh rằng d và d cắt nhau và xác định tọa độ giao điểm I của chúng. Viết 2 1
phương trình mặt phẳng chứa d , d . 1 2 Lời giải :
+ Thay x, y, z ở phương trình của d vào phương trình của d ta được 1 2 1 t 1 t 2 2 3t 4
t 2 , thay vào phương trình của d I 1, 2 , 4 2 2 1 3
Vậy d d I 1, 2 , 4 . Ta có đpcm. 1 2
+ Đường thẳng d có véc tơ chỉ phương u 2,1,3 và d có véc tơ chỉ phương 2 1 v 1, 1,3
Khi đó mặt phẳng P chứa d , d đi qua điểm I và có véc tơ pháp tuyến 1 2 1 3 3 2 2 1
n u, v , , 6,9, 1 1 3 31 1 1
Vậy P : 6 x
1 9 y 2 z 4 0 P : 6x 9 y z 8 0 .
x y z 3 0
Bài 11. Trong không gian Oxyz , cho hai đường thẳng d : và 1
y z 1 0
x 2 y 2z 9 0 d : 2
y z 1 0
Viết phương trình đoạn vuông góc chung của d , d . 1 2 Lời giải : 11 11 11
Đường thẳng d có véc tơ chỉ phương u , , 0, 1 , 1 1 11 10 01 698 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
22 21 1 2
Đường thẳng d có véc tơ chỉ phương v , , 4,1, 1 2 1 1 1 0 01
Gọi d là đương vuông góc chung của d , d khi đó d có véc tơ chỉ phương a thỏa 1 2 11 10 0 1
mãn a u, v , ,
2,4, 4 , chọn a 1 , 2, 2 1 1 14 41
+ Gọi P là mặt phẳng chứa d ,d , khi đó P có véc tơ pháp tuyến 1 1 1 1 0 0 1
n u, a , , 4 , 1,
1 , lấy điểm A2,1, 0 d 1 2 2 2 1 12
Khi đó P : 4 x 2 y
1 z 0 P : 4x y z 9 0
+ Gọi Q là mặt phẳng chứa d ,d , khi đó Q có véc tơ pháp tuyến 2 1 1 1 4 4 1
n ' v, a , ,
0,9,9 , lấy điểm B 3 , 2, 1 d 2 2 2 2 1 12
Khi đó Q : y 2 z
1 0 Q : y z 1 0
Và d là giao tuyến của hai mặt phẳng P, Q
Vậy phương trình đoạn vuông góc chung của d , d là 1 2
4x y z 9 0 d :
y z 1 0 x 2t 1 x u 2
Bài 12. Cho hai đường thẳng d : y t 2 và d : y 3 2u 2 1
z 3t 3 z 3u 1
Viết phương trình đường vuông góc chung của d , d . 1 2 Lời giải :
Đường thẳng d có véc tơ chỉ phương u 2,1,3 và đường thẳng d có véc tơ chỉ 2 1
phương v 1, 2,3 .
Lấy điểm A2t 1, t 2, 3t
3 d ; B u 2, 3 2u,3u 1 d suy ra 1 2
AB u 2t 1, 2u t 5,3u 3t 4 , và AB là đoạn vuông góc chung của A . B u 0
d , d 1 2 A . B v 0 25 u 2
u 2t
1 2u t 5 33u 3t 4 0 9
u 2t 1 2
2u t 5 33u 3t 4 0 29 t 9 67 47 20 43 23 84 24 24 24 24 Từ đó suy ra A , , ; B , , ; AB , , 1,1, 1 9 9 3 9 9 9 9 9 9 9 699 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Vậy phương trình đoạn vuông góc chung của d , d đi qua A và có véc tơ chỉ phương 1 2 1 , 1 , 1 67 x t 9 47
Vậy AB : y t 9 20 z t 3
BÀI TẬP ĐỀ NGHỊ
x 4mz 3m 0
Bài 1. Cho đường thẳng d m : 1 m
x my 0
Chứng minh rằng d
luôn thuộc một mặt phẳng cố định và luôn đi qua một điểm cố định. m x 1 y z 2
Bài 2. Cho đường thẳng d :
và mặt phẳng P : 2x y z 0 2 1 3
Xác định phương trình đường thẳng đi qua giao điểm A của d và P và vuông góc với
d , nằm trong mặt phẳng P .
Bài 3. Trong không gian Oxyz cho mặt phẳng P : 2x y 2 0và đường thẳng 2m
1 x 1 m y m 1 0 d
m : mx 2m
1 z 4m 2 0
Xác định m để d / / P . m x 5 y 1 z 5
Bài 4. Trong không gian Oxyz cho hai đường thẳng d : 1 2 1 1
x 3 2t
Và d : y 3 t 2 z 1 t
Chứng minh rằng d / / d . Viết phương trình đường thẳng song song, cách đều và nằm 1 2
trong mặt phẳng chứa d , d . 1 2 x 3 2t
4x y 19 0
Bài 5. Cho hai đường thẳng d : y 2
3t và d : 2 1
x z 15 0 z 6 4t
Chứng minh rằng d cắt d . Viết phương trình đường phân giác tạo bởi góc nhọn giữa 2 1 d , d . 1 2
x 8z 23 0
x 2z 3 0
Bài 6. Cho hai đường thẳng d : và d : 2 1
y 4z 10 0
y 2z 2 0 700 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Chứng minh rằng d và d chéo nhau. Viết phương trình mặt phẳng P song song và các 2 1
đều d , d . 1 2 x 3 y 1 z 2
4x y 2 0
Bài 7. Cho hai đường thẳng d : và d : 2 1 1 4 3 3x z 0
Chứng minh rằng d song song với d . Viết phương trình tổng quát của mặt phẳng P 2 1
chứa d , d . Viết phương trình đường thẳng d nằm trong P và các đều d , d . 1 2 1 2
Tính khoảng cách giữa d , d . 1 2
2x y 1 0 3
x y z 3 0
Bài 8. Cho hai đường thẳng d : và d : 2 1
x y z 1 0
2x y 1 0
Chứng minh rằng d và d cắt nhau, xác định tọa độ giao điểm của chúng. Viết phương 2 1
trình mặt phẳng chứa d , d . 1 2 x t 3
x y z 3 0
Bài 9. Cho điểm A1, 1,
1 và hai đường thẳng d :
và d : y 1 2t 2 1
2x y 1 0 z 3t
Chứng minh rằng d , d , A cùngg thuộc một mặt phẳng. 1 2
Bài 10. Trong không gian Oxyz cho hai đường thẳng d : x y 1 z 1 và 1
d : x 1 y 1 z . 2
Tìm tọa độ điểm Ad và điểm B d sao cho đường thẳng AB vuông góc với cả 2 1 d , d . 1 2
x 2 2t
x y 2z 0
Bài 11. Cho hai đường thẳng d :
và d : y 5t 2 1
x y z 1 0 z 2 t
Chứng minh rằng d , d chéo nhau. Tính khoảng cách giữa d , d . Viết phương trình 1 2 1 2
đoạn vuông góc chung của d , d . Viết phương trình mặt phẳng P chứa d và song 1 1 2
song với d . Viết phương trình đường thẳng đi qua điểm M 1,1,
1 và cắt cả d , d . 1 2 2
ĐIỂM, ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Xét các dạng bài toán sau
Dạng 1: Đường thẳng cắt cả hai đường thẳng d , d và thỏa mãn điều kiện cho trước. 1 2
(i). Viết phương trình đường thẳng đi qua một điểm A và cắt cả hai đường thẳng d , d . 1 2 Phương pháp: Cách 1: 701 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Viết phương trình mặt phẳng P đi qua A và chứa d . 1
Viết phương trình mặt phẳng Q đi qua A và chứa d . 2
+ Nếu P Q , bài toán có vô số nghiệm.
+ Nếu P / / Q , bài toán vô nghiệm.
+ Nếu P Q d , đây chính là đường thẳng cần tìm. Cách 2:
Viết phương trình mặt phẳng P đi qua A và chứa d . 1
Xác định giao điểm B của P và d 2
+ Nếu vô nghiệm thì bài toán vô nghiệm.
+ Nếu có vô số nghiệm thì bài toán có vô số nghiệm.
+ Nếu có nghiệm duy nhất thì phương trình đường thẳng d cần tìm chính là AB , đi qua A
và có véc tơ chỉ phương AB . Cách 3:
Áp dụng khi cả hai đường thẳng cho ở dạng tham số
Giả sử đường thẳng cần tìm cắt d tại B và cắt d tại C , với tọa độ của B,C cho ở dạng 2 1 tham số. Xét điều kiện ,
A B, C thẳng hàng.
(ii). Viết phương trình đường thẳng d song song với đường thẳng và cắt cả hai đường
thẳng d , d . 1 2 Phương pháp:
(iii). Viết phương trình đường thẳng d vuông góc với mặt phẳng P và cắt cả hai đường
thẳng d , d . 1 2 Phương pháp: BÀI TẬP MẪU Bài 1.
Dạng 2: Đường thẳng đi qua một điểm và vuông góc với cả hai đường thẳng cho trước.
(i). Viết phương trình đường thẳng d đi qua điểm A và vuông góc với cả hai đường thẳng d , d . 1 2 Cách 1:
Viết phương trình mặt phẳng P đi qua A và vuông góc d . 1
Viết phương trình mặt phẳng Q đi qua A và vuông góc d . 2
Khi đó d chính là giao tuyến của P, Q . Cách 2:
Xác định các véc tơ chỉ phương u,v của d , d , khi đó véc tơ chỉ phương a của d thỏa 1 2
mãn a u, a v a u, v
Đường thẳng d sẽ đi qua điểm A và có véc tơ chỉ phương a . BÀI TẬP MẪU Bài 1. 702 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Dạng 3: Đường thẳng đi qua một điểm và vuông góc với một đường thẳng và căt một đường thẳng.
(i). Viết phương trình đường thẳng d đi qua điểm A và vuông góc với đường thẳng d và 1
cắt đường thẳng d . 2 Phương pháp: Cách 1:
Viết phương trình mặt phẳng P đi qua A và vuông góc với d . 1
Viết phương trình mặt phẳng Q đi qua A và chứa d . 2
Khi đó đường thẳng d cần tìm là giao của P, Q . Cách 2:
Viết phương trình mặt phẳng P đi qua A và vuông góc với d . 1
Xác định giao điểm B của P và d , khi đó đường thẳng d cần tìm chính là AB , đi qua 2
A và có véc tơ chỉ phương AB . BÀI TẬP MẪU Bài 1.
Dạng 4: Hình chiếu vuông góc của điểm lên mặt phẳng
(i). Tìm tọa độ hình chiếu vuông góc H của một điểm A lên mặt phẳng P . Phương pháp:
Viết phương trình đường tham số của đường thẳng d đi qua điểm A và vuông góc với mặt phẳng P
Tọa độ hình chiếu H chính là giao điểm của d và P .
(ii). Tìm điểm đối xứng của điểm A qua mặt phẳng P . Phương pháp:
Tìm tọa độ hình chiếu H của A trên P .
Tìm điểm A đối xứng với A qua H . 1
(iii). Xác định phương trình đường thẳng đối xứng với đường thẳng d qua mặt phẳng P . Phương pháp:
Lấy hai điểm phân biệt ,
A B d .
Tìm tọa độ hai điểm A , B lần lượt đối xứng với ,
A B qua mặt phẳng P . 1 1
Khi đó đường thẳng cần tìm chính là đường thẳng đi qua hai điểm A , B . 1 1 BÀI TẬP MẪU
Bài 1. Cho điểm A2,3,
1 và mặt phẳng P : 2x y z 5 0 . Xác định tọa độ điểm A 1
đối xứng với A qua P . Lời giải:
Đường thẳng d đi qua A và vuông góc với P sẽ nhận véc tơ pháp tuyến n 2, 1, 1
của P làm véc tơ chỉ phương, nên 703 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
x 2 2t
d : y 3 t
z 1 t
Thay tọa độ x, y, z từ phương trình của d vào phương trình của P ta được 1 5 3
2 2 2t 3 t 1 t 5 0 t
d P H 3, , 2 2 2
Tọa độ điểm A sẽ đối xứng với A qua H , suy ra A 4, 2, 2 . 1 1
x y 7z 14 0
Bài 2. Cho mặt phẳng P : 3x 6y z 2 0 và đường thẳng d :
x y z 2 0
Xác định tọa độ giao điểm A của d , P . Viết phương trình đường thẳng đối xứng với
d qua P . Lời giải:
Xét hệ tạo bởi d , P , ta có:
x y 7 z 14 0 x 0
x y z 2 0
y 0 d P A0, 0, 2 3 x 6y z 2 0 z 2
Lấy điểm B 3, 6, 0 d , ta tìm tọa độ điểm B đỗi xứng với B qua P , khi đó đường 1
thẳng cần tìm chính là AB . 1 10 210 58
10 210 104 2 Tìm được B , , AB , , 5, 1 05,52 1 1 23 23 23 23 23 23 23 x 5t
Vậy : y 105t z 2 52t
Bài 3. Viết phương trình mặt phẳng Q đi qua A 2
, 4, 3 và song song với mặt phẳng
P : 2x 3y 6z 19 0 . Tính khoảng cách giữa hai mặt phẳng P,Q. Hạ AH P ,
Xác định tọa độ điểm H . Lời giải :
Mặt phẳng Q sẽ nhận véc tơ pháp tuyến n 2, 3, 6 của P làm véc tơ pháp tuyến, nên
Q : 2 x 2 3 y 4 6 z
3 0 Q;2x 3y 6z 2 0.
Đường thẳng d đi qua A và vuông góc với P nhận n làm véc tơ chỉ phương nên,
x 2 2t
d : y 4 3t
z 3 6t
Khi đó tọa độ điểm H là nghiệm của hệ tạo bởi d , P . 704 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN 20 x x 2 2t 7
y 4 3t 37 20 37 3 y H , , z 3 6t 7 7 7 7 3 2x 3y 6z 19 0 z 7
BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho bốn điểm A4,1, 4; B 3,3,
1 ;C 1,5,5 ; D1,1, 1 .
Xác định tọa độ hình chiếu của D trên mặt phẳng ABC , tính thể tích tứ diện ABCD . Viết
phương trình đường vuông góc chung của AC, BD .
Bài 2. Cho bốn điểm Aa, 0, 0; B 0,b, 0;C 0, 0, c , a,b,c 0 . Dựng hình hộp chữ nhật nhận , O ,
A B, C làm bốn đỉnh và gọi D là đỉnh đối diện với O của hình hộp đó.
(i). Tính khoảng cách từ C đến mặt phẳng ABD .
(ii). Tính tọa độ hình chiếu vuông góc của C xuống mặt phẳng ABD. Tìm điều kiện của a, ,
b c để hình chiếu đó nằm trong mặt phẳng xOy .
Bài 3. Cho điểm A2,3,5 và mặt phẳng P : 2x 3y z 17 0 .
(i). Lập phương trình đường thẳng d đi qua A và vuông góc với P .
(ii). Chứng minh rằng d cắt trục Oz , tìm giao điểm M của chúng.
(iii). Xác định tọa độ điểm A đối xứng với A qua P . 1
Dạng 5: Hình chiếu vuông góc của đường thẳng lên mặt phẳng.
(i). Xác định phương trình hình chiếu vuông góc của đường thẳng d lên mặt phẳng P . Phương pháp:
Viết phương trình mặt phẳng Q chứa d và vuông góc với P .
Khi đó đường thẳng chính là giao tuyến của hai mặt phẳng P, Q . BÀI TẬP MẪU
x y z 5 0
Bài 1. Cho đường thẳng d :
và mặt phẳng P : 2x 3y z 4 0 .
3x 2 y z 15 0
Viết phương trình hình chiếu vuông góc của d trên mặt phẳng P . Lời giải:
Mặt phẳng P có véc tơ pháp tuyến n 2, 3, 1 1 1 1 1 1 1
Đường thẳng d có véc tơ chỉ phương u , , 3, 4, 1 2 1 13 3 2 Lấy điểm A 2 5, 3 0, 0d
Gọi Q là mặt phẳng chứa d và vuông góc với P , khi đó Q đi qua A và có véc tơ pháp tuyến 705 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN 31 12 2 3 n ' , n u , , 7 ,5, 1 4 1 13 3 4
Vậy Q : 7 x 25 5 y 30 z 0 Q : 7x 5y z 25 0
Khi đó đường thẳng cần tìm chính là giao tuyến của P, Q
7x 5 y z 25 0 :
2x 3y z 4 0
x my z m 0
Bài 2. Cho đường thẳng d
m : mx y mz 1 0
(i). Viết phương trình hình chiếu vuông góc của d
trên mặt phẳng xOy m
(ii). Chứng minh rằng khi m thay đổi, đường thẳng luôn tiếp xúc với một đường tròn cố
địnhnằm trong mặt phẳng xOy . Lời giải:
(i). Khử z từ hai phương trình của d
ta được mx 2 m 2 2 1 y m 1 m
Khi đó hình chiếu vuông góc của d
trên mặt phẳng xOy là m mx 2 m 2 2
1 y m 1 0 : z 0 2 m 1
(ii). Trong mặt phẳng xOy , Ta có d O, 1
4m m 2 2 2 1
Từ đó suy ra đường thẳng luôn tiếp xúc với đường tròn tâm O0, 0 bán kính R 1 nằm
trong mặt phẳng xOy (đpcm). x 1 y 1 z 3
Bài 3. Cho đường thẳng d :
và mặt phẳng P : 2x 2y z 3 0 . 1 2 2
(i). Tìm tọa độ giao điểm A của d , P . Tính góc giữa d , P .
(ii). Viết phương trình hình chiếu vuông góc của d lên mặt phẳng P . Lấy điểm B AB AM
thuộc đường thẳng d sao cho AB a 0 . Xét tỷ số
với M di động trên mặt BM
phẳng P . Chứng minh rằng tồn tại một vị trí của M để tỷ số đó đạt giá trị lớn nhất và tìm giá trị lớn nhất đó. Lời giải:
(i). Tọa độ giao điểm A d P là nghiệm hệ phương trình
2x 2 y z 3 0 x 2 y 1 A x y z 2 , 1,5 1 1 3 1 2 2 z 5 1.2 2.2 2 .1 4
Góc giữa d , P được xác định bởi sin 2 2 2 2 2 2 9 1 2 2 . 2 2 1 706 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
2x 5 y 6z 21 0
(ii). Xác định được :
2x 2 y z 3 0
Lấy điểm B d ; AB a 0và điểm M P . AB AM
2R sin M 2R sin B sin M sin B
Xét tam giác ABM , ta có BM 2R sin A sin A M B M B M B 2sin cos o c s 1 1 2 2 2 A A A A 2 sin o c s sin sin sin 2 2 2 2 2 M B cos 1 2
Dấu bằng xảy ra khi và chỉ khi
A , M B A 2 s in sin 2 2 AB AM 1
Vậy giá trị lớn nhất của bằng . BM sin 2
BÀI TẬP ĐỀ NGHỊ
x z 3 0
Bài 1. Cho đường thẳng d :
và mặt phẳng P : x y z 3 0 2 y 3z 0
Lập phương trình hình chiếu vuông góc của d trên P .
Bài 2. Cho ba mặt phẳng P : 3x y z 2 0;Q : x 4y 5 0; R : 2x z 7 0
Viết phương trình đường thẳng là hình chiếu vuông góc của đường thẳng d trên mặt
phẳng R , trong đó d là giao tuyến của hai mặt phẳng P, Q .
2x z 1 0
Bài 3. Cho mặt phẳng P : x y z 1 0 và hai đường thẳng d : và 1
x 2y 0 3
y z 12 0 d : 2
x z 2 0
(i). Viết phương trình mặt phẳng Q chứa d và vuông góc với mặt phẳng P . 1
(ii). Viết phương trình hình chiếu vuông góc , lần lượt của d , d trên mặt phẳng 1 2 1 2
P . Tìm tọa độ giao điểm I của , . 1 2 x 5 y 2 z 6
2x y 11 0
Bài 4. Cho hai đường thẳng d : và d : 2 1 2 1 3
x y z 5 0
Chứng minh rằng d , d đồng phẳng. Viết phương trình mặt phẳng đó. 1 2
Viết phương trình chính tắc của đường thẳng là hình chiếu song song của d theo 2
phương của d trên mặt phẳng P : 3x 2 y 2z 1 0 . 1
Bài 5. Cho tứ diện có 4 đỉnh O 0, 0, 0; A6,3, 0; B 2, 9, 1 ; S 0,5, 8 .
(i). Chứng minh rằng SB vuông góc với OA . 707 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
(ii). Chứng minh rằng hình chiếu của cạnh SB trên mặt phẳng OAB vuông góc với cạnh OA
. Gọi K là giao điểm của hình chiếu đó với OA . Xác định tọa đôk điểm K .
(iii). Gọi P, Q lần lượt là trung điểm của các cạnh SO, AB . Tìm tọa độ điểm M trên SB sao
cho PQ và KM cắt nhau.
Dạng 6: Hình chiếu vuông góc của điểm lên đường thẳng.
(i). Tìm tọa độ hình chiếu H của điểm A lên đường thẳng d . Phương pháp: Cách 1:
Viết phương trình mặt phẳng P đi qua A và vuông góc với d
Khi đó tọa độ giao điểm H của d , P chính là điểm cần tìm. Cách 2:
Lấy điểm H thuộc d , tọa độ dưới dạng tham số và H là hình chiếu của A trên d khi và
chỉ khi AH d AH.u 0 H .
(ii). Tìm điểm A đối xứng với A qua d . 1 Phương pháp:
Tìm tọa độ hình chiếu vuông góc H của A trên d
Điểm A cần tìm đối xứng với A qua H . 1
(iii). Viết phương trình đường thẳng đối xứng với một đường thẳng d qua một đường 1
thẳng d cho trước. 2 Phương pháp:
Lấy hai điểm phân biệt , A B d 1
Tìm tọa độ điểm A , B lần lượt đối xứng với , A B qua d . 2 1 1
Khi đó đường thẳng vần tìm chính là đường thẳng đi qua hai điểm A , B . 1 1
(iv). Viết phương trình đường thẳng đi qua A vuông góc với đường thẳng d và cắt d . Phương pháp:
Xác định tọa độ hình chiếu vuông góc H của A trên d .
Đường thẳng cần tìm là đường thẳng đi qua hai điểm , A H . BÀI TẬP MẪU
Bài 1. Cho điểm A1, 2,
1 và đường thẳng d có phương trình
x y z 3 0 d :
y z 1 0
Xác định tọa độ hình chiếu vuông góc của A lên đường thẳng d và tạo độ điểm A đối xứng 1
với A qua d . Lời giải: 11 11 11
Đường thẳng d có véc tơ chỉ phương u , , 0, 1 , 1 11 10 01 708 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Gọi P là mặt phẳng đi qua A và vuông góc với d khi đó P nhận u làm véc tơ pháp
tuyến, nên P : y 2 z
1 0 P : y z 3 0
Xét hệ tọa bởi d , P :
x y z 3 0 x 2
y z 1 0 y 2 y z 3 0 z 1
Vậy tọa độ hình chiếu của A trên d là điểm H 2, 2, 1 .
Điểm A đối xứng với A qua d nhận H làm trung điểm của AA nên A 3, 2, 1 . 1 1 1 x 1 t
Bài 2. Cho điểm A1, 2,
1 và đường thẳng d : y t z 1
Xác định tọa độ hình chiếu vuông góc của A lên đường thẳng d . Lời giải:
Đường thẳng d có véc tơ chỉ phương u 1,1, 0
Gọi H là hình chiếu vuông góc của điểm A lên d , do
H d H 1 t, t,
1 AH t, t 2,0 . Do
AH u AH.u 0 t .
1 t 2 0 t 1 H 0,1, 1 . x 1 y 2 z 2
Bài 3. Cho điểm M 1, 2,
1 và đường thẳng d : 3 2 2
Gọi N là điểm đối xứng của điểm M qua đường thẳng d . Tính độ dài đoạn MN . Lời giải:
Đường thẳng d có véc tơ chỉ phương u 3, 2, 2 x 1 3t
Phương trình của d dạng tham số là d : y 2 2t
z 2 2t Gọi H 1
3t, 2 2t, 2 2t d là hình chiếu vuông góc của M trên d , ta có
MH 3t 2, 2t, 2t 3
Do MH u MH.u 0
33t 2 2 2
t 22t 3 0 t 0 MH 2, 0,3
Điểm N đối xứng với M qua H nên MN 2 MH 2 13 . x y z 3
Bài 4. Cho điểm A2,3,
1 và đường thẳng d : 2 4 1
Viết phương trình đường thẳng đi qua A vuông góc với d và cắt d . Lời giải:
Đường thẳng d có véc tơ chỉ phương u 2, 4, 1 709 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN x 2t
Đường thẳng d ở dạng tham số là d : y 4t x 3 t
Gọi H 2t, 4t,3 t d là hình chiếu vuông góc của A trên d , ta có AH
2t 2, 4t 3,4 t 4
2 2t 2 44t 3 4 t 0 t 7 AH u 6 5 32 Suy ra AH , , 7 7 7
Vậy đường thẳng cần tìm đi qua điểm A và có véc tơ chỉ phương AH nên 6 x 2 t 7 5
: y 3 t 7 32 z 1 t 7 x t
2x y 1 0
Bài 5. Cho hai đường thẳng d :
và d : y 1 2t 2 1
x y z 1 0
z 4 5t
Gọi B, C lần lượt là các điểm đối xứng của A1, 0, 0qua d , d . Tính diện tích tam giác 1 2 ABC . Lời giải: 1 0 02 21
Đường thẳng d có véc tơ chỉ phương u , , 1, 2 , 3 . 1 11 1 1 1 1
Đường thẳng d có véc tơ chỉ phương v 1, 2, 5 2
+ Gọi H là hình chiếu vuông góc của A trên d 1 1
Gọi P là mặt phẳng đia qua A và vuông góc với d P có véc tơ pháp tuyến u , nên 1
P : x
1 2 y 3z 0 P : x 2 y 3z 1 0 .
Khi đó tọa độ H d P là nghiệm của hệ 1 1 710 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN 1 x 14
2x y 1 0 12 1 12 3
15 12 3
x y z 1 0 y H , , AH , , + Gọi 1 1 14 14 14 14 14 14 14
x 2y 3z 1 0 3 z 14 H
t,1 2t, 4 5t d
là hình chiếu vuông góc của A trên d , khi đó 2 2 2
AH t 1,1 2t, 4 5t 2 AH v 2 7 17 4 5 t
1 2 1 2t 54 5t 0 t AH , , 2 10 10 10 10
Các điểm B,C đối xứng với A qua H , H 1 2
5904 Ta có S 4S
2 AH , AH . ABC A 1 H H2 1 2 35 x z 0
Bài 6. Cho đường thẳng d : y 0
(i). Với mỗi điểm M x , y , z trong không gian viết phương trình mặt phẳng P đi qua M 0 0 0 0
và vuông góc với d . Tính khoảng cách từ M đến d .
(ii). Chứng minh rằng quỹ tích các điểm trong mặt phẳng Oxy mà khoảng cách từ điểm đó
đến d bằng 2 là một elip. Xác định tọa độ tiêu điểm của elip đó. Lời giải : 0 1 1 1 1 0
(i). Đường thẳng d có véc tơ chỉ phương u , , 1, 0, 1 1 0 0 0 01
Mặt phẳng P cần tìm sẽ nhận u làm véc tơ pháp tuyến, nên 0
P : x x z z 0 P : x z x z 0. 0 0 0 0 0
Khi đó tọa độ giao điểm H của P , d là nghiệm hệ phương trình 0 x z 0 0 x x z 0 2 x z x z 0 0 0 0 y 0 y 0 H , 0, 2 2 x z x z 0 x z 0 0 0 0 z 2
Khoảng cách từ M đến d chính là 2 2 x z x z x z 0 0 2 0 0 0 0 2 2 MH x y z y 0 0 0 0 2 2 2
(ii). Điểm M Oxy M , x y, 0 711 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Theo đề bài và áp dụng câu trên ta có, 2 2 2 2 2 x x y x y d M d 2 , y 2
1 M E : 1(đpcm). 2 8 4 8 4
Ta có tọa độ tiêu điểm F 2, 0 , F 2, 0 . 1 2
BÀI TẬP ĐỀ NGHỊ
x 2 y 2z 9 0
Bài 1. Cho điểm A1, 2,3 và đường thẳng d :
y z 1 0
Xác định tọa độ hình chiếu vuông góc H của A trên d . Xác định đọ độ điểm A đối xứng 1
với A qua d . Tính độ dài đoạn AA . 1
y z 4 0
Bài 2. Cho đường thẳng d :
2x y z 2 0
(i). Viết phương trình mặt phẳng P đi qua điểm A2, 1 ,
1 và vuông góc với d .
(ii). Viết phương trình đường thẳng đi qua A và vuông góc, cắt d .
(iii). Xác định tọa độ điểm A đối xứng với A qua d . 1 x 1 y 2 z 3
Bài 3. Cho điểm A2,1, 3 và đường thẳng d : 1 2 1
(i). Tính khoảng cách từ A đến d .
(ii). Xác định tọa độ điểm A đối xứng với A qua d . Tính độ dài đoạn thẳng AA . 1 1
(iii). Viết phương trình đường thẳng đi qua A và vuông góc , cắt đường thẳng d .
Bài 4. Cho bốn đường thẳng
mx y 0
mx y 0
mx y 0
mx y 0 d : , d : , d : , d : 1 2 3 4 z h z h z h z h
Chứng minh rằng bốn điểm A , A , A , A đối xứng với A lần lượt qua d , d , d , d 1 2 3 4 1 2 3 4
đồng phẳng. Viết phương tình mặt phẳng đi qua bốn điểm đó.
BÀI TOÁN VỀ GÓC VÀ KHOẢNG CÁCH -
Thường xác định mặt phẳng dưới dạng tổng quát 2 2 2
Ax By Cz D 0, A B C 0 -
Sau đó dựa vào giả thiết bài toán, biểu diễn được C, D theo , A B -
Cuối cùng là giải phương trình với hai ẩn là , A B BÀI TẬP MẪU
Bài 1. Trong không gian với hệ toạ độ Oxyz cho điểm A 1
, 2, 3 và B 2, 1,6 và mặt
phẳng P : x 2 y z 3 0 . Viết phương trình mặt phẳng Q chứa AB vào tạo với mặt 3
phẳng P một góc thỏa mãn cos . 6 Lời giải: 712 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Giả sử phương trình mặt phẳng cần tìm Q ax by cz d 2 2 2 :
0 a b c 0
Mặt phẳng Q chứa AB nên ,
A B Q, từ đó suy ra
a 2b 3c d 0
c a b (*)
2a b 6c d 0
d 4a b
Mặt phẳng P có véc tơ pháp tuyến n 1, 2,
1 . Từ đó suy ra góc giữa hai mặt phẳng này là
a 2b c 3 cos
2 a 2b c2 2 2 2
a b c 2 2 2 2 2 2 6
a b c . 1 2 1
Ta thay c, d ở hệ (*) vào phương trình trên ta suy ra:
a b2 a b a b2 2 2 2 2 2 2 3
3a 11ab 8b 0 a b
c 0, d 3b 8b 5 29b a c , b d 3 3 3
Vậy có hai phương trình mặt phẳng cần tìm
Q : x y 3 0; Q :8x 3y 5z 29 0 . 1 2 x y 3 z 1
Bài 2. Cho hai điểm A2, 1, 1 , B 0,1, 2
và đường thẳng d : . Viết 1 1 2
phương trình đường thẳng đi qua giao điểm của d , OAB và nằm trong mặt phẳng 5
OAB hợp với đường thẳng d một góc thỏa mãn cos . 6 Lời giải: Ta có OA 2, 1 , 1 ;OB 0,1, 2
suy ra mặt phẳng OAB có véc tơ pháp tuyến 11 1 2 2 1 n , , 1, 4, 2 1 2 2 0 01
Vậy OAB : x 4 y 2z 0 . Gọi M là giao điểm của d ,OAB khi đó tọa độ điểm M là nghiệm của hệ x y 3 z 1 x 1 0 1 1
2 y 13 M 10,13, 2 1
x 4y 2z 0 z 21
Giả sử đường thẳng cần tìm có véc chỉ phương v a, ,
b c , điều kiện 2 2 2
a b c 0 .
Do OAB n v a 4b 2c 0(1)
Đường thẳng d có véc tơ chỉ phương u 1, 1, 2
Yêu cầu bài toán tương đương với
a b 2c 5 cos
6a b 2c2 25 2 2 2
a b c (2)
a b c 2 2 2 2 2 2 6 . 1 1 2 713 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN b
c a 6 c
Rút a 4b 2c từ (1) thay vào (2) ta được: 2 2 11b 16bc 5c 0 5 42 b c a c 11 11
Vậy có hai phương trình cần tìm là: 42 x 10 t 11 x 1 0 6t 5
: y 13 t
và : y 13 t 2 1 11
z 21 t z 21 t
Bài 3. Trong không gian Oxyz . Viết phương trình đường thẳng đi qua điểm A0,1, 2 x 3 y 2 z
vuông góc với đường thẳng d :
và tạo với mặt phẳng 1 1 1
P : 2x y z 5 0 một góc 0 30 . Lời giải:
Giả sử đường thẳng có véc tơ chỉ phương u a,b, c với 2 2 2
a b c 0
Đường thẳng d có véc tơ chỉ phương v 1, 1,
1 và mặt phẳng P có véc tơ pháp tuyến n 2,1, 1 . Theo đề bài ta có u v
a b c 0 . u n 2 1
a b c 1 sin 2 2 2 2 2 2 u . n 2 2
a b c . 2 1 1 x y z x 1 y 1 z 1
Bài 4. Cho hai đường thẳng d : và d : 2 1 1 2 1 1 1 3
(i). Chứng minh rằng hai đường thẳng d , d chéo nhau. 1 2
(ii). Viết phương trình mặt phẳng P chứa đường thẳng d và tạo với đường thẳng d1 2 một góc 0 30 . Lời giải:
(i). Đường thẳng d đi qua điểm O0, 0,0 và có véc tơ chỉ phương u 1, 2, 1 1
Đường thẳng d đi qua điểm A1, 1,
1 và có véc tơ chỉ phương v 1, 1,3 2 2 1 11 12 Ta có u , v , , 5, 2 , 1 và OA 1, 1 , 1 1 3 31 11 Suy ra u
, v.OA 5.1 2.
1 1.1 2 0 . Từ đó suy ra d , d chéo nhau. 1 2
(ii). Giả sử mặt phẳng P : ax by cz d 0có véc tơ pháp tuyến n a,b, c với 2 2 2
a b c 0
Đường thẳng d đi qua điểm B 0, 0, 2 . 2 714 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN b a c a b c d 0 3
Do d P nên ,
A B P (*) 2
2c d 0 2 b a d 3
Đường thẳng d và P tạo với nhau một góc 0 30 nên 1
a 2b c 1 sin 30
2a 2b c2 0 3 2 2 2
a b c
a b c 2 2 2 2 2 2 2 . 1 2 1 a 2b b a Thay c
từ (*) vào biểu thức trên ta được : 2 2 11a 17ab 10b 0 5 3 a b 11 Với a 2
b c ,
b d 2b . Từ đó suy ra P : 2x y z 2 0 . 1 5 2 4 Với a b c , b d
b . Từ đó suy ra P : 5x 11y 2z 4 0 . 2 11 11 11
Vậy có hai mặt phẳng cần tìm thỏa mãn :
P : 2x y z 2 0 và P : 5x 11y 2z 4 0 . 2 1
Bài 5. Cho tứ diện ABCD có A1, 2,
1 ; B 2,1,3;C 2, 1 , 1 ; D 0,3, 1 . Viết phương trình
mặt phẳng P đi qua hai điểm ,
A B sao cho khoảng cách từ điểm C đến P bằng khoảng
cách từ D đến P . Lời giải:
Giả sử mặt phẳng P 2 2 2
: ax by cz d 0, a b c 0 .
a 2b c d 0 Do ,
A B P nên (*) 2
a b 3c d 0 Theo giả thiết ta có:
2a b c d
3b c d
d C, P d ,
D P 2 2 2 2 2 2
a b c
a b c a b
2a b c d 3b c d
a b c d 0
(i). Với a b , kết hợp với (*) ta có hệ phương trình:
a 2b c d 0 a b 0 2
a b 3c d 0
P : cz c 0 P : z 1 0 . d c a b
(ii). Với a b c d 0 , kết hợp với (*) ta có hệ phương trình:
a 2b c d 0 b 0 2
a b 3c d 0 c a
P : ax az 2a 0 P : x z 2 0 . a b c d 0 d 2 a
Vậy có hai mặt phẳng cần tìm: P : z 1 0; P : x z 2 0 . 1 2 715 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN x y 3 z 1
Bài 6. Trong không gian Oxyz cho đường thẳng d : và hai điểm 1 1 2 A2, 1, 1 , B 0,1, 2
. Tìm tọa độ điểm M d sao cho tam giác ABM có diện tích nhỏ nhất. Lời giải:
Giả sử điểm M t,3 t, 2t
1 d là điểm cần tìm. AM
t 2,4 t,2t 2 Ta có:
BM t, 2 t, 2t 1
4 t 2t 2 2t 2 t 2 t 2 4 t
AM , BM , ,
t 8, t 2, 4
2 t 2t 1 2t 1 t t 2 t
1 1 2 2 1 2 34 Khi đó S
AM , BM t t t ABM 8 2 16 2 5 34 2 2 2 2
Dấu bằng xảy ra khi và chỉ khi t 5 M 5,8, 1 1 . Vậy M 5 ,8, 1 1 là điểm cần tìm.
Bài 7. Cho hai điểm A4, 9, 9, B 1 0,13,
1 và mặt phẳng. Tìm tọa độ điểm
M P : x 5y 7z 5 0 sao cho 2 2
MA MB nhỏ nhất. Lời giải:
Giả sử điểm M ,
x y, z P x 5y 7z 5 0, khi đó
MA MB x 2 y 2 z 2 x
2 y 2 z 2 2 2 4 9 9 10 13 1 x 2 y 2 z 2 2 3 11 4 156
Ta có x 5 y 7z 5 0 x 3 5 y 1
1 7 z 4 75
Theo bất đẳng thức Cauchyshar ta có:
2 x y z 2
x 2 y 2 z 2 75 3 5 11 7 4 1 25 49 3 11 4
x 2 y 2 z 2 3 11 4 75. Từ đó suy ra 2 2
MA MB 2.75 156 306 .
Dấu bằng xảy ra khi và chỉ khi x 3 y 11 z 4 50 192 75 50 192 75 x ; y ; z M , , 1 5 7 17 17 17 17 17 17 Là điểm cần tìm.
Bài 8. Cho ba điểm A4,1,5; B 3, 0, 1 ;C 1
, 2, 0 . Tìm tọa độ điểm M thuộc mặt phẳng
P : 3x 3y 2z 37 0 để biểu thức M . A MB M .
B MC MC.MA đạt giá trị nhỏ nhất. Lời giải: Gọi M ,
x y, z P 3x 3y 2z 37 0 . Khi đó
MA x 4, y 1, z 5 ; MB x 3, y, z
1 ; MC x 1, y 2, z
Từ đó suy ra: MA MB MB MC MC MA 2 2 2 . . .
3 x y z 4x 2 y 4z 4 716 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN x 2 y 2 z 2 3 2 1 2 5 .
Mặt khác theo bất đẳng thức Cauchyshart ta có: 2 x y z 2 x 2 y 2 z 2 44 3 2 3 1 2 2 9 9 4 2 1 2 2 2 2
Suy ra x 2 y 1
z 2 88 . Suy ra
M . A MB M .
B MC MC.MA 388 5 249 . Dấu bằng xảy ra khi và chỉ khi x 2 y 1 z 2
x 4; y 7; z 2 M 4,7, 2
là điểm cần tìm. 3 3 2
Bài 9. Cho hai điểm A0,1, 2; B1,1, 0 . Tìm điểm M thuộc mặt phẳng P : x y z 0
sao cho tam giác MAB vuông cân tại B . Lời giải:
Giả sử điểm M ,
x y, z P là điểm cần tìm suy ra x y z 0(*)
Ta có: BA 1, 0, 2; BM x 1, y 1, z . Tam giác MAB vuông cân tại B khi và chỉ khi B . A BM 0 5 x 2 1 y 2 2 1 z
kết hợp với (*) ta có hệ phương trình: 2 2 BA BM
y z 1 0 1 10 4 10 x x
x 2 y 2 2 3 3 5 1 1 z 4 10 2 10
y z 1 0 y y 6 6 x y z 0 2 10 2 10 z z 6 6 x 1 2t x 1 y 1 z 3
Bài 10. Cho hai đường thẳng d :
và d : y 1 2 1 1 1 1 z t IA
Đường thẳng đi qua điểm I 0,3,
1 cắt d tại A và cắt d tại B . Tính . 2 1 IB Lời giải:
Do Ad A 1 t ', 1
t ',3 t ' và B d B 1
2t,1, t 2 1 Ta có: IA 1
t ', t ' 4, 4 t '; IB 1 2t, 2, t 1 . Do ,
A I , B thẳng hàng nên
1 t ' k 1 2t t 1 IA
IA k IB t ' 4 2 k t ' 6 k 5 . IB
4 t ' k t 1 k 5 x 3
Bài 11. Cho mặt phẳng P : x 2 y z 5 0 và đường thẳng d :
y 1 z 3 và 2 điểm A 2
,3, 4 . Gọi là đường thẳng nằm trong P và đi qua giao điểm của d , P
và vuông góc với d . Tìm điểm M sao cho khoảng cách AM nhỏ nhất. Lời giải: 717 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Giả sử d P B , khi đó tọa độ của B là nghiệm của hệ x 3 x 1
y 1 z 3 2
y 0 B 1, 0, 4 x 2y z 5 0 z 4
Mặt phẳng P có véc tơ pháp tuyến n 1, 2,
1 và đường thẳng d có véc tơ chỉ phương u 2,1, 1 . 2 1 11 1 2 Ta có: , n u , , 3, 3, 3 . 1 1 1 2 21
Do P và vuông góc với d nên có véc tơ chỉ phương u / / ,
n u u 1, 1, 1 .
Vậy có véc tơ chỉ phương u và đi qua điểm B .
x 1 t
Vậy : y t z 4 t
Giả sử điểm cần tìm M 1 t, t
, 4 t , khi đó 2
MA t 2 t 2 t 2 1 26 26 2 2 1 3 t 3 3 3 1 2 1 11
Dấu bằng xảy ra khi và chỉ khi t M , , là điểm cần tìm. 3 3 3 3
BÀI TẬP ĐỀ NGHỊ x 1 y 1 z
Bài 1. Cho hai điểm A1,5, 0, B 3,3, 6và đường thẳng d : . Tìm tọa độ 2 1 2
điểm M thuộc đường thẳng d để tam giác MAB có diện tích nhỏ nhất.
Bài 2. Cho điểm A1, 4, 2; B1, 2, 4 . Tìm điểm M thuộc đường thẳng x 1 y 2 z d : sao cho 2 2
MA MB 28 . 1 1 2
Bài 3. Cho ba điểm A0,1, 2; B 2, 2 , 1 ;C 2 , 0,
1 . Viết phương trình mặt phẳng ABC và
tìm điểm M thuộc mặt phẳng P : 2x 2 y z 3 0 sao cho MA MB MC . x t
Bài 4. Cho điểm A1, 0,
1 và đường thẳng d : y 2t . Tìm tọa độ hai điểm M , N thuộc z 1
d sao cho tam giác AMN đều.
Bài 5. Cho mặt phẳng (P) : 2x 3y z 7 0 . Viết phương trình mặt phẳng ( ) đi qua (
A 1;1;0) và B(1; 2;7) và vuông góc với mặt phẳng (P) . y 2
Bài 6. Trong không gian Oxyz , xác định mặt phẳng (P) chứa đường thẳng d : x z 1 x 2 z 5
và tạo với đường thẳng ' d : y 3 một góc 0 30 . 2 1 718 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Bài 7. Trong không gian Oxyz viết phương trình mặt phẳng (P) chứa đường thẳng
x y 2 0 d :
sao cho giao tuyến của mặt phẳng (P) và mặt cầu
2x z 6 0 2 2 2
(S ) : x y z 2x 2 y 2z 1 0 là đường tròn có bán kính bằng 1.
Bài 8. Trong không gian Oxyz cho ba điểm (
A 1; 2; 0), B(0; 4;0), C(0; 0;3) . Viết phương trình
mặt phẳng (P) chứa OA sao cho khoảng cách từ B đến (P) bằng khoảng cách từ C đến (P) .
BÀI TOÁN CỰC TRỊ TRONG HÌNH HỌC GIẢI TÍCH KHÔNG GIAN
Dưới dây xin đề cập một số bài toán cực trị lien quan đến phương trình tổng quát của mặt phẳng Phương pháp:
Giả sử phương trình mặt phẳng cần tìm có dạng: 2 2 2
Ax By Cz D 0, A B C 0
Khi đó dựa vào điều kiện bài toán để tìm ra mối lien hệ giữa ,
A B,C, D
Thường thỉ biểu diễn được ,
A D theo B, C . BÀI TẬP MẪU
Bài 1. Trong không gian Oxyz cho hai điểm M 0;1; 2; N 1
;1;3 . Viết phương trình mặt
phẳng (P) đi qua M , N sao cho khoảng cách từ K (0; 0; 2) đến mặt phẳng (P) là lớn nhất. Lời giải:
Giả sử mặt phẳng (P) có dạng: 2 2 2
Ax By Cz D 0, A B C 0
Do (P) đi qua M , N nên ta có:
B 2C D 0
A 2B C
(P) : (2B C) x By Cz B 2C 0
A B 3C D 0
D B 2C B
Khi đó khoảng cách từ K đến mặt phẳng (P) là d K, (P) 2 2
4B 2C 4BC
Nếu B 0 d K,(P) 0 . 1 1
Nếu B 0 d K, (P) 2 2 C 2 1 2 B
Dấu bằng xảy ra khi và chỉ khi C B , chọn C 1; B 1 ; A 1 ; D 3 .
Vậy mặt phẳng cần tìm là (P) : x y z 3 0 .
Bài 2. Trong không gian Oxyz cho đường thẳng (d ) và mặt phẳng (P) lần lượt có phương x 1 trình: d :
y 1 z 3 và (P) : x 2 y z 5 0 . Viết phương trình mặt phẳng (Q) 2
chứa đường thẳng (d ) và tạo với mặt phẳng (P) một góc nhỏ nhất. Lời giải: - Giả sử mặt phẳng 2 2 2
(Q) : Ax By Cz D 0, A B C 0 -
Chọn hai điểm M (1; 1;3); N (1; 0; 4) (d )
A B 3C D 0 C 2 A B -
Mặt phẳng (Q) chứa (d ) nên M , N (Q)
A 4C D 0
D 7 A 4B 719 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Suy ra mặt phẳng (Q) có véc tơ pháp tuyến n ( ;
A B; 2 A B) và mặt phẳng (P) có véc tơ Q
pháp tuyến n (1; 2; 1) . Khi đó góc giữa hai mặt phẳng (P),(Q) là P 3 A B cos . 2 2 6
5 A 2B 4 AB 3
Nếu A 0 cos . 2 6 B 1 3 A B
Nếu A 0 cos . , đặt x xét hàm số 2 6 B B A 5 2 4 A A 2 9 x 2x 1 f (x) . , dễ thấy 2
cos f (x) . Góc lớn nhất ứng với cos nhỏ nhất. 2
6 5 2x 4x
Khảo sát tính đơn điệu của hàm số này suy ra min f (x) f ( 1 ) 0 . Suy ra x min 0 . cos 2 6 Vậy
và A 0 chọn B 1 C 1; D 4 . 6
Vậy mặt phẳng cần tìm (Q) : y z 4 0 . x 1 t
Bài 3. Trong không gian Oxyz cho đường thẳng d : y 2 t z 2t
Viết phương trình mặt phẳng (P) chứa đường thẳng d và tạo với trục Oy một góc lớn nhất. Lời giải: - Giả sử mặt phẳng 2 2 2
(P) : Ax By Cz D 0, A B C 0 -
Chọn hai điểm M (1; 2; 0); N (0; 1; 2) d A B
A 2B D 0 C -
Mặt phẳng (P) chứa d nên M , N (P) 2
B 2C D 0
D A 2B A B -
Suy ra mặt phẳng (P) có véc tơ pháp tuyến n ( ; A B;
) . Gọi là góc giữa mặt P 2
phẳng (P) và trục Oy , ta có B 2 B sin 2 2 2 A B
5A 5B 2 AB 2 2 A B 2 Góc 0;
lớn nhất ứng với sin lớn nhất. 2
Nếu B 0 0 . 720 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN 2 2 5
Nếu B 0 sin 2 2 6 A A A 1 24 5 5 2 5 B B B 5 5 A 1
Dấu bằng xảy ra khi và chỉ khi , chọn B 5
A 1; B 5 C 2; D 9 (P) : x 5 y 2z 9 0 là mặt phẳng cần tìm. x 1 y z 2
Bài 4. Trong không gian Oxyz cho điểm (
A 2;5;3) và đường thẳng d : . Viết 2 1 2
phương trình mặt phẳng (P) chứa đường thẳng d sao cho khoảng cách từ A đến (P) lớn nhất. Lời giải: - Giả sử mặt phẳng 2 2 2
(P) : Ax By Cz D 0, A B C 0 có véc tơ pháp tuyến n ( ; A ; B C) . P -
Đường thẳng d đi qua điểm M (1; 0; 2) và có véc tơ chỉ phương u (2;1; 2) . Do (P) d chứa d nên ta có 2 A B n .u 0
2 A B 2C 0 C P d 2 M (P)
A 2C D 0
D A B
Suy ra mặt phẳng (P) : 2 Ax 2By (2A B)z 2 A 2B 0
Nếu B 0 (P) : x z 1 0 d ,
A (P) 0 .
Nếu B 0 , chọn B 1 , khi đó (P) : 2 Ax 2 y (2 A 1)z 2 A 2 0 9 9 Khi đó d , A (P) 3 6 2 2 8A 4 A 5 1 3 2 2 A 2 2 1 1 3
Dấu bằng xảy ra khi và chỉ khi A
C ; D . 4 4 4
Vậy mặt phẳng cần tìm (P) : x 4 y z 3 0 . x 1 2t
Bài 5. Trong không gian Oxyz cho đường thẳng d : y t
. Viết phương trình mặt phẳng z 1 3t (P) chứa điểm (
A 10; 2; 1) song song với d và cách d một khoảng lớn nhất. Lời giải: - Giả sử mặt phẳng 2 2 2
(P) : Ax By Cz D 0, A B C 0 có véc tơ pháp tuyến n ( ; A ; B C) . P -
Đường thẳng d đi qua điểm M (1; 0;1) và có véc tơ chỉ phương u (2;1;3) . Do (P) d
song song với d và chứa A nên ta có 721 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN 2 A B C 1
0 A 2B C D 0 3
2 A B 3C 0 32 A 7B D 3
Khi đó mặt phẳng (P) : 3Ax 3By (2 A B)z 32 A 7B 0 và ta có 33A 6B
d d, (P) d M , (P) 2 2
13A 10B 4 AB 33 13
Nếu B 0 d d, (P) 13 A 33 6 B A
Nếu B 0 d d, (P) , đặt x và xét hàm số 2 A A B 13 10 4 B B 2 (33x 6) f (x)
suy ra m ax f (x) f (7) . Từ đó chọn A 7, B 1 C 5; D 77 . 2 13x 4x 10 x
Vậy mặt phẳng cần tìm (P) : 7x y 5z 77 0 .
BÀI TẬP ĐỀ NGHỊ
Bài 1. Trong các mặt phẳng đi qua hai điểm ( A 1; 2; 1 ) và B( 1
;1; 2) . Tìm mặt phẳng tạo với
mặt phẳng (xOy) một góc nhỏ nhất.
Bài 2. Trong các mặt phẳng đi qua (
A 1;1; 1) và vuông góc với mặt phẳng
(P) : 2x y z 2 0 . Tìm mặt phẳng tạo với Oy một góc lớn nhất.
Bài 3. Trong các mặt phẳng đi qua điểm ( A 2; 1
;0) và song song với đường thẳng x 1 y 2 z 1 d :
. Xác định mặt phẳng tạo với mặt phẳng (xOy) một góc nhỏ nhất. 1 1 1 x 1 y 1 z 2
Bài 4. Viết phương trình mặt phẳng ( ) chứa đường thẳng d : sao cho 2 1 5 khoảng cách từ (
A 5;1; 6) đến ( ) là lớn nhất.
TAM GIÁC TRONG KHÔNG GIAN BÀI TẬP MẪU
Bài 1. Cho tam giác ABC , đỉnh A1, 2,5 và phương trình hai đường trung tuyến: x 3 y 6 z 1 x 4 y 2 z 2 và . 2 2 1 1 4 1
(i). Viết phương trình chính tắc các cạnh của tam giác ABC .
(ii). Viết phương trình chính tắc của đường phân giác trong góc A . Lời giải:
(i). Nhận thấy A không thuộc hai đường trung tuyến, nên ta giả sử đó là: x 3 y 6 z 1 x 4 y 2 z 2 BN : và CP : . 2 2 1 1 4 1 722 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Từ đó suy ra B 2
t 3, 2t 6, t
1 ;C u 4, 4
u 2,u 2
Tọa độ trọng tâm G BN CP là nghiệm của hệ: x 3 y 6 z 1 x 3 2 2 1
y 6 G 3, 6, 1 x 4 y 2 z 2 z 1 1 4 1
Ta có GA 2, 4, 4;GB 2
t, 2t, t ;GC u 1, 4u 4, u 1
2 2t u 1 0
t 2
Do GA GB GC 0 4
2t 4u 4 0 u 3
4 t u 1 0 B 7, 2, 1 AB 6,0,6 C 1,14, 1 AC 0,12, 6 x 1 y 2 z 5
Cạnh AB đi qua A và có véc tơ chỉ phương AB AB : . 1 0 1
Một cách tương tự, ta có: x 1 y 2 z 5 x 7 y 2 z 1 AC : ; BC : . 0 2 1 1 2 0
(ii). Lấy điểm C 1, 2v 2, v 5 AC AC 0, 2v, v sao cho AC k AC, k 0 . Và 1 1 1
AB AC . Điều này tương đương với 1 2v 12k
v 6k 6 10
10 12 10 25 6 10 v C 1, , 1 k 0 5 5 5 2 5v 6 2
Tọa độ trung điểm M của BC là M 4, 1
Đường phân giác trong của góc A chính là đường thẳng AM .
Bài 2. Cho hai điểm A0, 0, 3, B 2, 0,
1 và mặt phẳng P : 3x 8y 7z 1 0 .
(i). Tìm tọa độ giao điểm I của đường thẳng đi qua hai điểm ,
A B với mặt phẳng P .
(ii). Tìm tọa độ điểm C nằm trên mặt phẳng P sao cho tam giác ABC đều. Lời giải:
(i). Đường thẳng AB đi qua A và có véc tơ chỉ phương AB 2, 0, 2 , nên x 2t
AB : y 0
z 3 2t
Thay x, y, z từ phương trình của AB vào phương trình của P , ta được: 11 11 4
3.2t 8.0 7 3 2t 1 0 t
AB P I , 0, . 10 5 5 723 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
(ii). Gọi C ,
x y, z P sao cho tam giác ABC đều, khi đó 3
x 8 y 7z 1 0 3
x 8y 7z 1 0 AC BC
x y z 32 x 22 y z 2 2 2 2 2 2 1 2 2 AC AB x y z 32 2 2 2 2 2 2 2 x 3 x 2 2 y 2 y 3 z 3 1 z 3 2 2 1
Vậy có hai điểm C 2, 2, 3 ;C , ,
thỏa mãn yêu cầu bài toán. 1 2 3 3 3
Bài 3. Cho tam giác ABC có đỉnh C 3, 2,3 và phương trình đường cao x 2 y 3 z 3 x 1 y 4 z 3 AH :
và đường phân giác trong BM : 1 1 2 1 2 1
Tính độ dài các cạnh của tam giác ABC . Lời giải:
A 2 t, 3 t, 3 2t AH Ta có
B 1 u, 4 2u,3 u BM BC u 2, 2u 2, u
Do AH BC BC.AH 0 2
u 2 2u 2u 0 u 0 B1, 4, 3 .
Ta có BA 1 t, 1 t, 2t ; BM 1, 2,
1 ; BC 2, 2,0
Vì BM là đường phân giác trong của góc B , do đó t t t t cos B ,
A BM cos BM , BC 1 2 1 2 1.2 2. 2 1.0 0 + 1 t2 1 t 2 2 4 4 t 1 4t
với t 0 A2,3, 3 ,
A B,C thẳng hang, nên loại. + Với t 1
A1, 2,5 , khi đó AB AC BC 2 2 .
Bài 4. Cho ba điểm A1, 4,5; B 0,3,
1 ;C 2, 1, 0 và mặt phẳng P : 3x 3y 2z 15 0 .
Gọi G là trọng tâm của tam giác ABC . Chứng minh rằng điều kiện cần và đủ để điểm M
thuộc mặt phẳng P có tổng các bình phương khoảng cách đến các điểm ,
A B, C nhỏ nhất là
điểm M phải là hình chiếu vuông góc của G trên mặt phẳng P . Xác định tọa độ điểm đó. Lời giải: 2 2 2 Ta có 2 2 2
MA MB MC MG GA MG GB MG GC
2 MG 2 2 2
GA GB GC MG GA GB GC 2 MG 2 2 2 3 2 . 3
GA GB GC Từ đó suy ra 2 2 2
MA MB MC nhỏ nhất, khi và chỉ khi MG nhỏ nhất, điều này tương đương với
M là hình chiếu vuông góc của G trên P . Ta có đpcm. 724 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Dễ thấy G 1, 2, 2
Đường thẳng d đi qua G và vuông góc với mặt phẳng P nhận véc tơ pháp tuyến
n 3, 3, 2 của P làm véc tơ chỉ phương, nên x 1 3t
d : y 2 3t
z 2 2t
Khi đó điểm M cần tìm chính là giao điểm của d , P M 4, 1, 0 .
BÀI TẬP ĐỀ NGHỊ Bài 1. MẶT CẦU
Phương trình chính tắc của mặt cầu S có tâm I a, ,
b cvà bán kính R là
S x a2 y b2 z c2 2 : R .
Phương trình tổng quát của mặt cầu S 2 2 2
: x y z 2ax 2by 2cz d 0 . Các dạng bài toán
Dạng 1: Viết phương trình mặt cầu ngoại tiếp, nội tiếp khối đa diện hoặc có tâm thỏa mãn điều kiện nào đó.
(i). Mặt cầu ngoại tiếp tứ diện ABCD . Phương pháp:
Giả sử mặt cầu ngoại tiếp tứ diện ABCD có phương trình là S 2 2 2
: x y z 2ax 2by 2cz d 0 . Từ điều kiện ,
A B, C, D thuộc S , ta thay tọa độ của ,
A B,C, D lần lượt vào phương trình
của S , giải hệ 4 ẩn a, , b c, d .
(ii). Mặt cầu nội tiếp tứ diện ABCD .
(iii). Mặt cầu có đường kính là đoạn vuông góc chung của hai đường thẳng chéo nhau d , d . 1 2 Phương pháp:
Tìm tọa độ trung điểm của đoạn vuông góc chung của d , d và độ dài đoạn vuông góc 1 2 chung. BÀI TẬP MẪU
Bài 1. Viết phương trình mặt cầu đi qua ba điểm A0,1, 0, B 1, 0, 0 , C 0, 0, 1 và có tâm I
nằm trên mặt phẳng P : x y z 3 0 . Lời giải:
Giả sử mặt cầu S có phương trình: S 2 2 2
: x y z 2ax 2by 2cz d 0 .
Điểm A0,1, 0 S 1 2b d 0(1) . 1
2a d 0(2) Tương tự có : 1
2c d 0(3)
a b c 3 0(4)
Giải hệ phương trình tạo bởi (1),(2),(3),(4) ta được: a b c d 1. 725 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN Vậy S 2 2 2
: x y z 2x 2 y 2z 1 0. x 2t 1 x u 2
Bài 2. Cho hai đường thẳng d : y t 2 và d : y 3 2u 2 1
z 3t 3 z 3u 1
Viết phương trình đường vuông góc chung của d , d . Và viết phương trình mặt cầu S 1 2
có đường kính là đoạn vuông góc chung của d , d . 1 2 Lời giải :
(i). Đường thẳng d có véc tơ chỉ phương u 2,1,3 và đường thẳng d có véc tơ chỉ 2 1
phương v 1, 2,3 .
Lấy điểm A2t 1, t 2, 3t
3 d ; B u 2, 3 2u,3u 1 d suy ra 1 2
AB u 2t 1, 2u t 5,3u 3t 4 , và AB là đoạn vuông góc chung của A . B u 0
d , d 1 2 A . B v 0 25 u 2
u 2t
1 2u t 5 33u 3t 4 0 9
u 2t 1 2
2u t 5 33u 3t 4 0 29 t 9 67 47 20 43 23 84 24 24 24 24 Từ đó suy ra A , , ; B , , ; AB , , 1,1, 1 9 9 3 9 9 9 9 9 9 9
Vậy phương trình đoạn vuông góc chung của d , d đi qua A và có véc tơ chỉ phương 1 2 1 , 1 , 1 67 x t 9 47
Vậy AB : y t 9 20 z t 3 55 35 8 3
(ii). Tọa độ trung điểm I của AB là I , ,8 và AB 9 9 3 2 2 55 35 2 48
Khi đó mặt cầu cần tìm là S : x y z 8 . 9 9 9
Dạng 2: Vị trí tương đối của điểm, đường thẳng, mặt phẳng, mặt cầu với mặt cầu và các bài toán liên quan.
(i). Mặt cầu tiếp xúc với mặt phẳng.
(ii). Mặt cầu cắt mặt phẳng.
(iii). Mặt cầu cắt, tiếp xúc với đường thẳng.
BÀI TẬP ĐỀ NGHỊ 726 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
2x 4 y z 7 0
Bài 1. Viết phương trình mặt cầu có tâm thuộc đường thẳng d : và tiếp
4x 5 y z 14 0
xúc với hai mặt phẳng P : x 2 y 2z 2 0 và Q : x 2 y 2z 4 0. x 1 y 2 z
Bài 2. Cho đường thẳng d :
và mặt phẳng P : 2x y 2z 2 0 . 3 1 1
Viết phương trình mặt cầu S có tâm nằm trên d , tiếp xúc với P và có bán kính bằng 1.
x y 2z 3 0
Bài 3. Cho đường thẳng d :
và hai mặt phẳng P : 5x 4 y z 6 0 và
x 3y z 0
Q : 2x y z 7 0 .
Viết phương trình mặt cầu S có tâm tại giao điểm của d , P , biết Q cắt S theo thiết
diện là hình tròn có diện tích 2 20 .
Bài 4. Viết phương trình mặt cầu S có tâm I 3, 2, 4 và tiếp xúc với đường thẳng x y z 3 d : . 2 4 1
x 2 y z 9 0
Bài 5. Viết phương trình mặt cầu tâm I 1,1,
1 cắt đường thẳng d : tại hai
2 y z 5 0 điểm phân biệt ,
A B sao cho độ dài AB 16 .
Bài 6. Cho mặt cầu S 2 2 2
: x y z 2x 2z 2 0 và mặt phẳng P : 2x 2y z 6 0 .
Tìm điểm M S sao cho khoảng cách từ M đến P đạt giá trị nhỏ nhất.
Bài 7. Chứng minh rằng mặt cầu 2 2 2
x y z 4 x 6 y 6z 17 0 cắt mặt phẳng
x 2 y 2z 1 0 theo giao tuyến là một đường tròn C . Viết phương trình mặt cầu S
chứa C và có tâm thuộc mặt phẳng P : x y z 3 0 .
Bài 8. Viết phương trình mặt phẳng P tiếp xúc với mặt cầu S 2 2 2
: x y z 10x 2 y 26z 113 0, đồng thời song song với hai đường thẳng x 5 y 1 z 13 x 7 y 1 z 8 d : và d : . 2 1 2 3 2 3 2 0 8
x 11y 8z 30 0
Bài 9. Viết phương trình mặt phẳng chứa đường thẳng d : và tiếp
x y 2z 0
xúc với mặt cầu S 2 2 2
: x y z 2x 6 y 4z 15 0 .
BÀI TẬP TỔNG HỢP 3
x 2 y 11 0
Bài 1. Cho hai điểm A2,1,
1 ; B 0,1,3 và đường thẳng d :
y 3z 8 0
(i). Viết phương trình mặt phẳng P đi qua trung điểm I của AB và vuông góc với AB . Gọi
K là giao điểm của d , P . Chứng minh rằng IK vuông góc với d .
(ii). Viết phương trình hình chiếu vuông góc của d trên mặt phẳng Q : x y z 1 0 . 727 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN x 1 2t x y z
Bài 2. Cho hai đường thẳng d :
và d : y t 2 1 1 2 2 z 1 t
(i). Chứng minh rằng d , d chéo nhau. 1 2
(ii). Tìm điểm M d , N d sao cho MN song song với mặt phẳng P : x y z 0 và 1 2 độ dài MN 2 .
Bài 3. Cho hình lập phương ABC .
D A B C D có A0, 0, 0; B 2, 0, 0; D 0, 2, 2 . Gọi M là 1 1 1 1 1
trung điểm của BC . Chứng minh rằng tỷ số khoảng cách từ điểm N AC , N A tới hai mặt 1
phẳng AB D , AMB không phụ thuộc vào vị trí của điểm N . 1 1 1
Bài 4. Cho hai điểm A4, 0, 0; B0, 4, 0 và mặt phẳng P : 3x 2 y z 4 0 . Gọi I là
trung điểm của AB . Tìm điểm K cách đều gốc tọa độ và mặt phẳng P sao cho IK P . x 1 t x 3 y 1 z
Bài 5. Cho hai đường thẳng d : y 1 t và d : 2 1 1 2 1 z 2
Tìm điểm Ad , B d sao cho độ dài AB nhỏ nhất. 1 2 x 3 y 2 z 1
Bài 6. Cho đường thẳng d :
và mặt phẳng P : x y z 2 0 . 2 1 1
Xác định giao điểm M của d , P . Viết phương trình đường thẳng nằm trong mặt
phẳng P , vuông góc với d sao cho khoảng cách từ M đến bằng 42 . x 1 y 3 z x 5 y z 5
Bài 7. Cho hai đường thẳng d : và d : và mặt phẳng 2 1 2 3 2 6 4 5
P : x 2y 2z 1 0. Tìm tọa độ điểm M d , N d sao cho MN song song với P 1 2
và cách P một khoảng bằng 2.
Bài 8. Viết phương trình mặt phẳng P đi qua điểm M 4 , 9
,12 và cắt các trục tọa độ O
C OA OB O ,
x Oy, Oz lần lượt tại ,
A B, C sao cho 4 1 1 . OC OA OB x 3 y 3 z 3
Bài 9. Cho điểm I 0,1,3 và hai đường thẳng d : và 1 2 2 1 5
x 6 y 6z 13 0 d : 2
x 6y 6z 7 0
(i). Chứng minh rằng d , d chéo nhau. 1 2 41
(ii). Tìm điểm Ad , B d sao cho tam giác IAB có diện tích bằng . 1 2 42 728 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN x 1 t x y 1 z 1
Bài 10. Cho điểm A0,1, 2 và hai đường thẳng d :
và d : y 1 2t 2 1 2 1 1 z 2 t
Tìm tọa độ điểm M d , N d sao cho ,
A M , N thẳng hàng. 1 2 x 1 y 2 z 3
Bài 11. Cho điểm A0,1, 0; B 2, 2, 2;C 2, 3,
1 và đường thẳng d : . 2 1 2
(i). Tìm điểm M d để thể tích tứ diện MABC bằng 3.
(ii). Tìm điểm N d để cho diện tích tam giác NAB nhỏ nhất.
Bài 12. Cho mặt phẳng P : 2x y z 5 0 . Viết phương trình mặt phẳng Q đi qua giao
tuyến của P và mặt phẳng xOy và Q tạo với ba mặt phẳng tọa độ một tứ diện có thể 125 tích bằng . 36 x 1 y z 2
Bài 13. Tìm trên đường thẳng Ox điểm A cách đều đường thẳng d : và 1 2 2
mặt phẳng P : 2x y 2z 0 .
Bài 14. Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu S 2 2 2
: x y z 4x 2 y 4 0 và mặt phẳng (P) : x 2 y 2z 9 0 . Viết phương trình
đường thẳng tiếp xúc với mặt cầu S , nằm trên (P) và cắt trục hoành.
Bài 15. Trong không gian với hệ trục tọa độ Oxyz cho điểm (
A 3; 2;1) , 2 điểm B, D nằm trên x 1 y 2 z 2 đường thẳng :
, điểm C nằm trên mặt phẳng (P) : 2x y z 3 0 . 1 2 1
Tìm tọa độ điểm B biết tứ giác ABCD là hình chữ nhật.
Bài 16. Trong không gian với hệ trục tọa độ Oxyz cho hai mặt phẳng P , P có các 1 2
phương trình tuuowng ứng là 2x y 2z 1 0 và 2x y 2z 5 0 và điểm A 1 ;1; 1 nằm
trong khoảng giữa hai mặt phẳng đó. Gọi S là mặt cầu bất kỳ qua A và tiếp xúc với cả hai
mặt phẳng P , P . Gọi I là tâm của mặt cầu S . Chứng tỏ rằng I thuộc một đường tròn 1 2
cố định. Xác định tọa độ tâm và tính bán kính của đường tròn đó.
MỘT SỐ BÀI TOÁN HÌNH HỌC KHÔNG GIAN GIẢI BẰNG PHƯƠNG PHÁP TỌA
ĐỘ TRONG KHÔNG GIAN
Bài 1. Cho hình lập phương ABC .
D A B C D cạnh bằng a. 1 1 1 1
(i). Tính theo a khoảng cách giữa A B và B D . 1 1
(ii). Gọi M , N , P theo thứ tự là trung điểm các cạnh BB , CD, A D . Tính góc giữa MP và 1 1 1 C N . 1
Bài 2. Cho hình lập phương ABC .
D A B C D cạnh bằng a. Gọi M , N theo thứ tự là trung điểm 1 1 1 1 các cạnh A ,
D CD . Lấy điểm P BB , BP 3PB . Tính diện tích thiết diện do mặt phẳng 1 1
MNP cắt hình lập phương. 729 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
Bài 3. Cho hình hộp chữ nhật ABC .
D A B C D có AB a, AD 2a, AA a . 1 1 1 1 1
(i). Tính theo a khoảng cách giữa AD , B C . 1 1 AM
(ii). Gọi M là điểm chia đoạn AD theo tỷ số
3 . Tính khoảng cách từ M đến mặt MD phẳng AB C . 1
(iii). Tính thể tích tứ diện AB D C . 1 1
Bài 4. Cho tứ diện ABCD có AD vuông góc với mặt phẳng ABC . Và có
AC AD 4, AB 3, BC 5 . Tính khoảng cách từ A đến mặt phẳng BCD .
Bài 5. Cho hình lập phương ABC .
D A B C D cạnh bằng a. Gọi M , N lần lượt là trung điểm 1 1 1 1 của BC, DD . 1
(i). Chứng minh rằng MN / / A BD . 1
(ii). Tính khoảng cách giữa BD và MN theo a.
Bài 6. Cho hình lập phương ABC .
D A B C D cạnh bằng 1. Lấy M , N , P theo thứ tự thuộc 1 1 1 1
BB , CD, A D sao cho B M CN D P a(0 a 1) . 1 1 1 1 1
Chứng minh rằng MN a AB AD a
1 AA và AC vuông góc với mặt phẳng MNP . 1 1
Bài 7. Cho hình hộp chữ nhật ABC .
D A B C D . Gọi H , K theo thứ tự là hình chiếu vuông góc 1 1 1 1 của ,
A C xuống mặt phẳng CB D . Chứng minh rằng AH 2KC . 1 1 1 1 730 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN 731 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam




