42 trang 98 lượt tải

Hình không gian thể tích từ cơ bản đến nâng cao – Nguyễn Tiến Đạt Toán 12

195

Tài liệu gồm 42 trang tóm tắt lý thuyết, công thức tính và hướng dẫn giải các dạng toán về thể tích của khối đa diện. Tài liệu phù hợp để các học sinh bị “mất gốc” ôn lại kỹ năng giải toán hình học không gian.Mời các bạn đón xem.

Chủ đề: Chương 1: Khối đa diện 172 tài liệu

Môn: Toán 12 4.3 K tài liệu

Tác giả:

Lan Tường

1 năm trước

Danh sách Quiz

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



HINH KHÔNG GIAN THÊ TICH

TƯ CƠ BAN ĐÊN NÂNG CAO FULL

Giáo viên: Nguyễn Tiến Đạt

HÌNH KHÔNG GIAN THỂ TÍCH

ÔN TẬP 1: KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 9 – 10

1. Hệ thức lượng trong tam giác vuông: Cho

ABC

vuông ở

. Ta có:

a) Định lý Pitago :

222

BC AB AC

.; .BA BH BC CA CH CB

..AB AC BC AH

222

111

AH AB AC



2BC AM

sin ,cos , tan ,cot

bcbc

BBBB

aacb



.sin .cos , .sin .cos ,

sin cos

ba Ba Cca

Ca   

.tan .cotbc Bc C

2. Hệ thức lượng trong tam giác thường



Định lý hàm số côsin:

222

2.cosabc bc A



Định lý hàm số sin:

sin sin sin

abc

ABC



3. Các công thức tính diện tích

Công thức tính diện tích tam giác













.sin

22 4

abc

SabCprppaapbpc

h

với

abc





Đặc biệt:

ABC

vuông ở

SABAC

ABC

đều cạnh

ABC

S 

b) Diện tích hình vuông:

S 

cạnh x cạnh

c) Diện tích hình chữ nhật:

S 

dài x rộng

d) Diện tích hình thoi:

S 

(chéo dài x chéo ngắn)

c b

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



e) Diện tích hình thang:

S 

(đáy lớn + đáy nhỏ) x chiều cao

f) Diện tích hình bình hành:

S 

đáy x chiều cao

g) Diện tích hình tròn:





ÔN TẬP 2: KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 11

A. QUAN HỆ SONG SONG

§1.ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG

1. Định nghĩa

Đường thẳng và mặt phẳng gọi là

song song với nhau nếu chúng

không có điểm nào chung.









aP aP 

2.Các định lý:

Định lý 1: Nếu đường thẳng

không nằm trên mặt phẳng







và

song song với một đường thẳng

nào đó nằm trên







thì

song

song với

















ba a





















Định lý 2: Nếu đường thẳng

song song với mặt phẳng





P thì

mọi mặt phẳng





Q chứa

mà

cắt





P thì cắt theo giao tuyến

song song với











()

aQ ba

PQb

















Định lý 3: Nếu hai mặt phẳng cắt

nhau cùng song song với một

đường thẳng thì giao tuyến của

chúng cũng song song với đường

thẳng đó.











PQb

Pa ba















§2.HAI MẶT PHẲNG SONG SONG

1. Định nghĩa:

Hai mặt phẳng được gọi là song

song với nhau nếu chúng không có

điểm nào chung.

















PQ PQ 

(P)

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



2. Các định lý:

Định lý 1: Nếu mặt phẳng





chứa hai đường thẳng a, b cắt nhau

và cùng song song với mặt phẳng





thì





và





song song

với nhau.



















ab P

ab I P Q

aQbQ







 







Định lý 2: Nếu một đường thẳng

nằm một trong hai mặt phẳng song

song thì song song với mặt phẳng

kia.





























Định lý 3: Nếu hai mặt phẳng





và





song song thì mọi mặt

phẳng





đã cắt





thì phải cắt





và các giao tuyến của chúng

song song.

 

















RPa ab

RQb















B. QUAN HỆ VUÔNG GÓC

§1.ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

1. Định nghĩa:

Một đường thẳng được gọi là

vuông góc với một mặt phẳng nếu

nó vuông góc với mọi đường thẳng

nằm trên mặt phẳng đó.









,aP accP

2. Các định lý:

Định lý 1: Nếu đường thẳng

vuông góc với hai đường thẳng cắt

nhau

và b cùng nằm trong mặt

phẳng





P thì đường thẳng

vuông góc với mặt phẳng





P .









dadb

ab P d P



















Định lý 3: (Ba đường vuông góc)

Cho đường thẳng

không vuông

góc với mặt phẳng





P và đường

thẳng

b nằm trong





P . Khi đó,

 

aPbP

ba ba





http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



điều kiện cần và đủ để b vuông góc

với

là b vuông góc với hình

chiếu

'a của

trên





P .

§2.HAI MẶT P

Ẳ

VUÔNG GÓC

1. Định nghĩa:

Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90

2. Các

định

lý:

Định lý 1: Nếu một mặt phẳng

chứa một đường thẳng vuông góc

với một mặt phẳng khác thì hai mặt

phẳng đó vuông góc với nhau.































Định lý 2: Nếu hai mặt phẳng





và





Q vuông góc với nhau thì bất

cứ đường thẳng

nào nằm trong





P , vuông góc với giao tuyến của





P và





Q đều vuông góc với

mặt phẳng





Q .

 

















PQd aQ

aPad

















Định lý 3: Nếu hai mặt phẳng





và





Q vuông góc với nhau và

là

một

iểm

trong





P thì đường

thẳng

đi qua điểm A và vuông

góc với





Q sẽ nằm trong

















































Định lý 4: Nếu hai mặt phẳng cắt

nhau và cùng vuông góc với mặt

phẳng thứ ba thì giao tuyến của

chúng vuông góc với mặt phẳng

thứ ba.























PQa

PR aR

















§3.K

ẢNG

CÁCH

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



1. Khoảng cách từ 1 điểm tới 1 đường thẳng, đến 1

mặt phẳ

ng:

Khoảng

cách từ điểm

M đến đường thẳng

(hoặ

đến mặt phẳng





P ) là khoảng cách giữa hai điểm

và

H , trong đó H là hình chiếu của điểm M trên

đường thẳng

( hoặc trên mặt phẳng





P )













;;;dOa OHdO P OH

2. Khoảng cách giữa đường thẳng và mặt phẳng

song

song:

Khoảng cách giữa đường thẳng

và mặt phẳng





song song

với

là khoảng cách từ một điểm nào đó

của

đến mặt phẳng





P .









;da P OH

3. Khoảng cách giữa hai mặt phẳng song song:

là khoảng cách từ một điểm bất kỳ trên mặt phẳng này

đến mặt phẳng kia.













;dP Q OH

4.Khoảng cách giữa hai đường thẳng chéo nhau:

là

độ dài đoạn vuông góc chung của hai đường thẳng

đó.





;dab AB

§4.G

ÓC

1. Góc giữa hai

đường thẳng

và b

là

óc

iữa hai đường thẳng

'a và 'b cùng đi qua một

điểm và lần lượt cùng phương với

và b .

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



2. Góc giữa đường thẳng

không vuông góc với

mặt phẳng





là góc g

iữa

và hình chiếu 'a của nó trên mặt phẳng





P .

Đặc b

iệt: Nếu

vuông góc với mặt phẳng





P thì ta

nói rằng góc giữa đường thẳng

và mặt phẳng





là

90 .

3. Góc giữa hai mặt phẳng

là góc giữa hai đường thẳng lần lượt vuông góc với hai

mặt phẳng

đó.

Hoặc là góc giữa 2 đường thẳng nằm trong 2 mặt

phẳng cùng vuông góc với giao tuyến tại 1 điểm

4. Diện tích hình chiếu: Gọi S là diện tích của đa

giác





H trong mặt phẳng





P và

là diện tích

hình chiếu





'H của





H trên mặt phẳng





'P thì:

'cosSS





trong đó



là góc giữa hai mặt phẳng





P và





P .

ÔN TẬP

IẾN

THỨC CƠ BẢN HÌNH HỌC LỚP 12

A. CÁC CÔNG THỨC THỂ TÍCH CỦA KHỐI ĐA DIỆN:

1. Thể tích khối lăng trụ:

.VSh

Trong đó:

: Diện tích đa giác đáy.

: Đường cao của hình lăng trụ.

a) Thể tích khối hộp chữ nhật:

..V abc

với

,,abc

là ba kích thước

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



b) Thể tích khối lập phương:

Va

với

là độ dài cạnh

2. Thể tích khối chóp:

VSh

Trong đó:

: Diện tích đa giác đáy.

: Đường cao của hình chóp.

3. Tỉ số thể tích tứ diện:

Hai

khối chóp

.S ABC

và

.SMNP

có chung đỉnh

và các

óc

ở đỉn

. Khi đó:

SMNP

SABC

SM SN SP

VSASBSC



4. Thể tích khối chóp cụt:





VBBBB

Trong đó:

,'BB

: Diện tích hai đáy.

: Chiều cao.

Chú ý:

1/ Đường chéo của hình vuông cạnh

là

2da

Đường chéo của hình lập phương cạnh

là

3da

Đường chéo của hình hộp chữ nhật có ba kích thước

,,abc

là

222

abdc

2/ Đường cao của tam giác đều cạnh

là



3/ Hình chóp đều

là hình chóp có đáy là đa giác đều và các cạnh bên đều bằng nhau ( hoặc có đáy là đa giác đều,

hình chiếu của đỉnh trùng với tâm của đáy).

4/ Lăng trụ đều là lăng trụ đứng có đáy là đa giác đều.

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



PHÂN DẠNG BÀI TẬP

A. LOẠI 1: THỂ

TÍCH LĂNG TRỤ

1. Dạng 1: Khối lăng trụ đứng có chiều cao hay cạnh đáy

Ví dụ 1. Cho ()H là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng

. Thể tích của ()H bằng:

. B.

. C.

. D.

Hướng dẫn giải:

SBC

VS AA

Ví dụ 2. Cho lăng trụ đứng

.ABCABC



có

AA a





, tam giác

ABC

đều cạnh

. Tính theo

thể tích của

khối lăng trụ

.ABCABC



ABC A B C





. B.

ABC A B C





. C.

ABC A B C





. D.

ABC ABC





Hướng dẫn giải:

,' .

ABC ABC

ShAAaVSh

Ví dụ 3. Cho lăng trụ đứng

.ABCABC



có đáy

ABC

là tam giác vuông, BA BC a, 2AA a



 . Tính theo

thể tích của khối lăng trụ

.ABCABC



ABC A B C





. B.

ABC A B C





. C.

ABC A B C





. D.

ABC ABC





Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



..'

VABBCAA

Ví dụ 4. Lăng trụ đứng

.' ' 'ABC A B C

có đáy

ABC

là tam giác vuông tại ,A 2,BC a

AB a

. Mặt bên





’’BB C C

là hình vuông. Khi đó thê



tı



ch lăng trụ là:

. B.

2a . C.

23a

. D.

Hướng dẫn giải:

Ta có:

''BB C C

là hình vuông

.’’’

ABC A B C

ABC

hBB a

AC BC AB a

SABAC

VBBSa

















 





Ví dụ 5. Đáy của lăng trụ đứng tam giác .'' 'ABC A B C là tam giác ABC vuông cân tại A có cạnh

2BC a

và biết '3AB a . Tính thể tích khối lăng trụ.

a . B.

. C.

. D.

2a .

Hướng dẫn giải:

ABC

 vuông cân tại A nên AB AC a

.'' 'ABC A B C là lăng trụ đứng

'' 22

2..'

ABC

VBh

AA AB

AA A B

Sa 

 







http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Ví dụ 6. Đáy của lăng trụ đứng tam giác .'' 'ABC A B C là tam giác đều cạnh 4a  và biết diện tích tam giác

'ABC bằng 8. Tính thể tích khối lăng trụ.

. B.

. C.

. D. 8 .

Hướng dẫn giải:

Gọi

I là trung điểm BC .Ta có:

ABC đều nên



.'''

23; '

.' ' 4

'' 2

.'83

ABC

ABC A B C ABC

AI AI BC A I BC

SBCAIAI

AA ABC AA AI

AA A I AI

VSAA

 









Ví dụ 7. Cho lăng trụ tứ giác đều .' ' ' 'ABCDABCD có cạnh bên bằng 4a và đường chéo 5a . Tính thể tích

khối lăng trụ này.

9a . B. 9 . C.

3a . D. 3 .

Hướng dẫn giải:

.'' ' 'ABCDABCD là lăng trụ đứng nên

''3

BD BD DD a



ABCD là hình vuông

AB

Suy ra

ABCD

BS

..'9

ABCD

V BhS AA a 

Ví dụ 8. Cho hình hộp đứng

.ABCD A B C D



có đáy

ABCD

là hình vuông, tam giác

AAC



vuông cân và

AC a





. Tính theo

thể tích của khối hộp

.ABCD A B C D



ABCD A B C D





. B.

ABCD A B C D





. C.

ABCD A B C D





. D.

ABCD A B C D





Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



ABCD

AC a AC AA AB

VS AA

    

 

Ví dụ 9. Cho hình hộp đứng có đáy là hình thoi cạnh a và có góc nhọn bằng 60. Đường chéo lớn của đáy

bằng đường chéo nhỏ của hình hộp. Tính thể tích hình hộp .

. B.

. C.

. D.

Hướng dẫn giải:

Ta có tam giác

ABD đều nên BD a và

ABCD ABD

S 

Theo đề bài

'3BD AC a

.'''

ABCD

VS DDDD BD BD a 

Ví dụ 10. Một tấm bìa hình vuông có cạnh 44cm , người ta cắt bỏ đi ở mỗi góc tấm bìa một hình vuông cạnh

12cm rồi gấp lại thành một cái hộp chữ nhật không có nắp. Tính thể tích cái hộp này.

1200cm . B.

1600cm . C.

2400cm . D.

4800cm .

Hướng dẫn giải:

Theo đề bài, ta có:

''' '12

AA BB CC DD cm

 

nên

ABCD là hình vuông.

44 24 20 ; 12

. 4800

ABCD

AB cm cm cm h cm

VS h cm

 

 

2. Dạng 2: Lăng

ụ

đứ

ng có góc giữa đường thẳng và mặt phẳ

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Ví dụ 1. Cho lăng trụ đứng

.ABCABC



có đáy

ABC

là tam giác vuông cân tại B ,

BA BC a

, AB



hợp

với mặt đáy một góc

60

. Tính theo

thể tích của khối lăng trụ

.ABCABC



ABC A B C





. B.

ABC A B C





. C.

.ABC A B C



 . D.

ABC A B C





Hướng dẫn giải:

















'',','60

'.tan60 3 ...'

AA ABC AA ABC A B AB ABA

AA AB a V AB BC AA

  

   

Ví dụ 2. Cho lăng trụ đứng

.ABCABC



có đáy

ABC

là tam giác cân tại

, góc giữa



và





ABB A



bằng

60

AB AA a





. Tính theo

thể tích của khối lăng trụ

.ABCABC



15.

ABC A B C





. B.

18.

ABC A B C





. C.

ABC A B C





. D.

ABC A B C





Hướng dẫn giải:

Gọi

là trung điểm của













''' '''

', ' ' ', ' 60

' ' ' .tan 60

15 15

ABC ABC

C M ABB AC

BC ABB A BC BM MBC

MC BB MB

SVSAA





  

  

Ví dụ 3. Cho lăng trụ đứng

.ABCABC



có đáy

ABC

là tam giác vuông tại A ,

,60AC a ACB

, góc giữa



và mặt phẳng





AA C C



bằng

30

. Tính theo

thể tích của khối lăng trụ

.ABCABC



ABC ABC





. B.

ABC A B C





. C.

ABC A B C





. D.

ABC A B C





Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ

















3, 2

', ' ' ', ' ' 30

'3 ' ' 2 2

..' 6

AC a AB a BC a

AB AA C C

BC AA C C BC AC AC B

AC a CC AC AC a

VABACCCa

  





  

 

Ví dụ 4. Cho lăng trụ đứng

.ABCD A B C D



có đáy

ABCD

là hình vuông cạnh

và đường chéo BD



của

lăng trụ hợp với đáy





ABCD

một góc

30

. Tính thể tích của khối lăng trụ

.ABCD A B C D



ABCD A B C D





. B.

ABCD A B C D





. C.

ABCD A B C D





. D. Kết quả khác.

Hướng dẫn giải:

















'; ', ' 30

' .tan 30

ABCD

DD ABCD

BD ABCD BD BD DBD

DD BD

VS DD





 

 

Ví dụ 5. Cho hình hộp đứng

.ABCD A B C D



có đáy

ABCD

là hình thoi cạnh

và

BAD  . Biết AB



hợp

với đáy





ABCD

một góc 30. Tính theo

thể tích của khối lăng trụ .ABCD A B C D



ABCD A B C D





. B.

ABCD A B C D





. C.

.ABCD A B C D





. D.

ABCD A B C D





Hướng dẫn giải:

















', ', ' 30

' .tan30

.'2 .'

ABCD ABD

BB ABCD

AB ABCD AB AB BAB

BB AB

V S BB S BB





 

  

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Ví dụ 6. Cho lăng trụ tứ giác đều .ABCD A B C D



có cạnh đáy bằng

, góc giữa 'AC và mặt phẳng



BCC B



bằng 30. Tính theo

thể tích của khối lăng trụ .ABCD A B C D



ABC A B C





. B.

ABC A B C





. C.

ABC A B C





. D.

.ABC A B C





Hướng dẫn giải:

















', ' ' ', ' ' 30

' .cot 30 3

''''2

.' 2

ABCD

AB BCC B

AC BCC B AC BC AC B

BC AB a

BB BC B C a

VS BBa





 

  

 

Ví dụ 7. Cho lăng trụ tứ giác đều .ABCD A B C D



có cạnh đáy bằng

, đường chéo 'AC tạo với mặt bên



BCC B



một góc





045





. Khi đó, thể tích khối lăng trụ bằng:

cot 1a



 . B.

cot 2a



. C.

cot 1a



 . D.

tan 1a



 .

Hướng dẫn giải:













', ' ' ', ' '

' .cot ' cot 1

.' cot 1

ABCD

AB BCC B

AC BCC B AC BC AC B

BC AB BB a

V S BB a











  

  

3. Dạng 3: Lăng

ụ

đứ

ng có góc giữa hai mặt phẳng

Ví dụ 1. Cho lăng trụ đứng .ABC A B C



có đáy ABC là tam giác vuông cân tại B , BA BC a, AB



hợp

với mặt đáy một góc 60. Tính theo

thể tích của khối lăng trụ .ABC A B C



ABC A B C





. B.

ABC A B C





. C.

.ABC ABC





. D.

ABC A B C





Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



















'',','60

'.tan60 3 ...'

AA ABC AA ABC A B AB ABA

AA AB a V AB BC AA

  

   

Ví dụ 2. Cho lăng trụ đứng .ABC A B C



có đáy ABC là tam giác cân tại A ,

2,AC a

120CAB , góc giữa



ABC



và mặt phẳng



ABC

bằng 45. Tính theo

thể tích của khối lăng trụ .ABC A B C



ABC A B C





. B.

ABC A B C





. C.

ABC ABC





. D.

ABC A B C





Hướng dẫn giải:

Gọi

M là trung điểm của BC .

















.cos60

2 . .cos120 2 3

', ', '45

'..'3

AM AC a

BC AC AB AB AC a

A M BC AM BC

A BC ABC A M AM AMA

AA AM a V BC AM AA a



 





  

Ví dụ 3. Cho lăng trụ đứng .' ' 'ABCABC có đáy là tam giác đều cạnh

. Mặt phẳng



''AB C

tạo với mặt đáy

góc

. Tính theo

thể tích lăng trụ .' ' 'ABCABC.

V 

. B.

V 

. C.

V 

. D.

V 

Hướng dẫn giải:

Gọi

M là trung điểm ''BC

















'''

60 '', ''' ,' '

';''.tan'

333

ABC ABC

AM BC

AB C A B C AM A M AMA

A M AA A M AMA

SVSAA





  

 

 

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Ví dụ 4. Cho lăng trụ tam giác đều .ABC A B C



có cạnh đáy bằng

. Góc giữa hai mặt phẳng



ABC



và



ABC

bằng 30. Tính theo

thể tích của khối lăng trụ .ABC A B C



ABC A B C





. B.

ABC A B C





. C.

ABC A B C



 . D.

ABC A B C





Hướng dẫn giải:

Gọi

M là trung điểm của BC .

















', ', ' 30

' .tan30 . '

ABC

A M BC AM BC

A BC ABC A M AM A MA

AA AM V S AA

 



  

Ví dụ 5. Cho hình lăng trụ đứng .' ' 'ABCABC có đáy ABC là tam giác vuông tại B , BC a , mặt phẳng



'ABC

tạo với đáy một góc

30 và tam giác 'ABC có diện tích bằng

3a . Tính thể tích khối lăng

trụ .'' 'ABCABC.

. B.

. C.

. D.

Hướng dẫn giải:

































,' ,' '

12.3

'. ' 2 3

ABC

BC AB

BC A B

BC AA

BC AB ABC

BC A B A BC

BC ABC A BC

ABC A BC AB A B ABA

SABBCAB a

BC a







































n n

.'''

' .cos ' 2 3.cos30 3 ; ' ' .sin ' 2 3.sin30 3

1133

. .'...'.3..3

222

ABC A B C ABC

AB A B ABA a a AA A B ABA a a

V B h S AA AB BC AA a a a



   

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Ví dụ 6. Cho lăng trụ tứ giác đều .ABCD A B C D



có cạnh đáy bằng

, mặt phẳng





'BC D

hợp với đáy





ABCD

một góc

60

. Tính theo

thể tích của khối lăng trụ .ABCD A B C D



ABCD A B C D





. B.

ABCD A B C D





. C.

ABCD A B C D





. D. Kết quả khác.

Hướng dẫn giải:

Gọi

I là trung điểm của BD .

























'; ,' '60

12 6

'.tan60

22 2

ABCD

AC BD C I BD

BC D ABCD BD

BC D ABCD AC C I CIC

CI AC CC CI

VS CC



 













 

 

Ví dụ 7. Cho hình hộp chữ nhật

.' ' ' 'ABCDABC D

. Mặt phẳng



'ABC

hợp với đáy



ABCD

một góc

'AC hợp với đáy



ABCD

một góc

và '3AA a . Tính theo

thể tích khối hộp.

26Va . B.

V 

. C.

22Va . D.

Va

Hướng dẫn giải:

































22 2

.''' '

30 ', ', '

60 ' , ' , '

tan ' tan '

22; . 2 2

.'2 6

ABCD

ABCD A B C D ABCD

AA ABCD

AC ABCD AC AC ACA

A BC ABCD A B AB A BA

AA AA

AB a AC a

ABA ACA

BC AC AB a S AB BC a

V S AA a



  



  



4. Dạng 4: Khối lăng trụ xiên

Ví dụ 1. Cho lăng trụ .ABC A B C



có đáy ABC là tam giác đều cạnh

. Biết cạnh bên bằng 3a và hợp với

đáy



ABC

một góc 60. Tính theo

thể tích của khối lăng trụ .ABC A B C



ABC A B C





. B.

ABC A B C





. C.

ABC A B C





. D. Đáp án khác.

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Kẻ



'AH ABC













', ', ' 60AA ABC AA AH A AH

' '.sin 60 . '

ABC

AH AA V S A

H  

Ví dụ 2. Cho lăng trụ .ABC A B C



có đáy ABC là tam giác đều cạnh

, điểm 'A cách đều ba điểm

,,ABC

Góc giữa 'AA và



ABC

bằng 60. Tính theo

thể tích của khối lăng trụ .ABC A B C



ABC A B C





. B.

ABC A B C





. C.

ABC A B C





. D.

ABC A B C





Hướng dẫn giải:

Gọi

G là trọng tâm của



'ABC A G ABC













', ', ' 60

'.tan60 .'

ABC

AA ABC AA AG GAA

A G AG a V S A G



  

Ví dụ 3. Cho lăng trụ .ABC A B C



có đáy ABC là tam giác vuông cân tại B , 2AC a ; cạnh bên 2AA a





. Hình chiếu vuông góc của A



trên mặt phẳng

()ABC

là trung điểm cạnh AC . Tính thể tích V của

khối lăng trụ .ABC A B C



Va

. B.

V 

. C.

Va

. D.

V 

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Vì ABC là tam giác vuông cân tại B nên trung tuyến

BH cũng là đường cao của nó và

HB HA HC AC a 

22 22

'' 2

ABC A B C ABC

AH AA AH a a a

V A H S A H BH AC a







Ví dụ 4. Cho lăng trụ .ABC A B C



có đáy ABC là tam giác đều cạnh

, hình chiếu vuông góc của 'A lên mặt

phẳng



ABC

trùng với tâm O của tam giác ABC . Tính theo

thể tích của khối lăng trụ

.ABC A B C



, biết khoảng cách giữa 'AA và BC là

ABC A B C





. B.

ABC A B C





. C.

ABC A B C





. D. Kết quả khác.

Hướng dẫn giải:

Gọi

M là trung điểm của





BC BC AA M



Gọi

H là hình chiếu của M lên 'AA





sin '

AA BC

aHM

HM d A AO

    

' 30 ' .tan '

ABC

AAO AO AO AAO

VS AO

 

 

Ví dụ 5. Cho lăng trụ .ABC A B C



có đáy ABC là tam giác đều cạnh

. Hình chiếu vuông góc của 'A trên



ABC

là trung điểm của BC , góc giữa cạnh bên và mặt đáy bằng 30. Tính theo

thể tích của

khối lăng trụ

.ABCABC



ABC A B C





. B.

ABC A B C





. C.

ABC A B C





. D.

ABC A B C





Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Gọi M là trung điểm của

















', ', ' 30

' .tan30 . '

ABC

AM ABC

AA ABC AA AM A AM

AM AM V S AM





  

Ví dụ 6. Cho lăng trụ

.ABCABC



có đáy

ABC

là tam giác đều cạnh

. Hình chiếu vuông góc của 'A trên





ABC

là trung điểm của AB , góc giữa mặt phẳng





AA C C



và mặt đáy bằng

60

. Tính theo

thể tích của khối lăng trụ

.ABCABC



ABC A B C





. B.

ABC A B C





. C.

ABC A B C





. D.

ABC A B C





Hướng dẫn giải:

Gọi

M là trung điểm của AB , kẻ

MH AC













'', ', ' 60

11 3

3; .

222

' .tan 60

ABC AMC ABC

ABC

A M ABC

ACC A ABC A H HM A HM

SaS ACMHS

MH A M MH

VS AM







   



Ví dụ 7. Cho lăng trụ

.ABCABC



có

, 2,,135

AA AC a BC a ACB





. Hình chiếu vuông góc của



lên mặt phẳng





ABC

trùng với trung điểm M của AB . Tính theo

thể tích của khối lăng trụ

.ABCABC



.ABC A B C



 . B.

ABC A B C





. C.

ABC ABC





. D.

ABC A B C





Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ







22 2

2..cos 5

. .sin135 . '

AB AC BC AC BC ACB a

AC BC AB

MC CC MC

VACBC MC

 



 

  

  

Ví dụ 8. Cho lăng trụ

.ABCABC



có độ dài cạnh bên bằng

, đáy

ABC

là tam giác vuông tại

BAC 

, góc giữa 'BB và





ABC

bằng

60

. Hình chiếu vuông góc của 'B lên





ABC

trùng với trọng tâm

của tam giác

ABC

. Tính theo

thể tích của khối lăng trụ

.ABCABC



208

ABC A B C





. B.

280

ABC A B C





. C.

208

ABC A B C





. D.

802

ABC A B C





Hướng dẫn giải:

Gọi

là trọng tâm

ABC

, M là trung điểm AC





B G ABC















22 2

', ', ' 60

' '.sin 60 , '.cos60

.cos60 , .sin 60

3 3 13 3

24 4 4

93 27

104 208

ABC

ABC ABC

BB ABC BB BG B BG

B G BB BG BB

AB AB

AC AB BC AB

AB BC AC

aABa

BM BG AB

SVSBG



   







  

  

Ví dụ 9. Cho hình hộp

.ABCD A B C D



có đáy

ABCD

là hình chữ nhật với

3, 7AB AD

. Hai mặt bên





''ABB A và





''ADD A lần lượt tạo với đáy các góc 45 và 60. Tính theo thể tích của khối hộp

.ABCD A B C D



biết cạnh bên bằng 1.

A. 1. B. 3. C. 6. D. 9.

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Kẻ





',,A H ABCD HM AB HN AD

' , ' ' 45 , ' 60A M AB A N AD A MH A NH   

Đặt

'AH x . Khi đó:

342

';''

sin 60

A N AN AA A N HM











Mà .cot 45HM x x

.''' '

34 3

..3

ABCD A B C D

VABADx



 



Ví dụ 10. Cho lăng trụ

.' ' ' 'ABCD A B C D

có đáy

ABCD

là hình chữ nhật tâm

và

,3AB a AD a

;

'AO

vuông góc với đáy





ABCD

. Cạnh bên 'AA hợp với mặt đáy





ABCD

một góc

45

. Tính theo

thể tích khối lăng trụ đã cho.

V 

. B.

V 

. C.

V 

. D.

3Va

Hướng dẫn giải:













.''' '

45 ', ', '

'.'3

ABCD

ABCD A B C D ABCD

SABADa

AC AB AD a AO a

A O ABCD

AA ABCD AA AO A AO

AO AO a V S AO a







  

  

B. LO

ẠI 2:

Ể T

ÍCH

KHỐI CHÓP

Một số hình chóp đặc biệt:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ





Hình chóp tam giác đều:

‒ Đáy là tam giác đều.

‒ Các mặt bên là các tam giác cân.

Hình tứ diện đều:

‒ Đáy là tam giác đều.

‒ Các mặt bên là các tam giác đều.

Cách vẽ:

‒ Vẽ đáy

ABC .

‒ Vẽ trung tuyến

AI .

‒ Dựng trọng tâm

H .

‒ Vẽ





SH ABC .

Ta có:

‒

SH là chiều cao của hình chóp.

‒ Góc giữa cạnh bên và mặt đáy:

SAH



 .

‒ Góc giữa mặt bên và mặt đáy:

SIH



 .



Hình chóp tứ giác đều:

‒ Đáy là hình vuông.

‒ Các mặt bên là các tam giác cân.

Cách vẽ:

‒ Vẽ đáy

ABCD .

‒ Dựng giao điểm

H của hai đường chéo AC và BD .

‒ Vẽ





SH ABCD .

Ta có:

‒

SH là chiều cao của hình chóp.

‒ Góc giữa cạnh bên và mặt đáy:

SAH



 .

‒ Góc giữa mặt bên và mặt đáy:

SIH



 .



Hình chóp có một cạnh bên vuông góc với đáy:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



‒





SA ABC .

‒ Góc giữa cạnh bên

SB và mặt đáy:

SBA



 .

‒ Góc giữa cạnh bên

SC và mặt đáy:

SCA



 .

‒





SA ABCD .

‒ Góc giữa cạnh bên

SB và mặt đáy:

SBA



 .

‒ Góc giữa cạnh bên

SC và mặt đáy:

SCA



 .

‒ Góc giữa cạnh bên

SD và mặt đáy:

SDA



 .

Chú ý:

a) Đường chéo củ

a hình vuông cạnh

là

2da

Đường chéo của hình lập phương cạnh

là

3da

Đường chéo của hình hộp chữ nhật có 3 kích thước

,,abc là

222

dabc.

b) Đường

cao của tam giác đều cạnh

là

h 

c) Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên đều bằng nhau ( hoặc có đáy là đa giác

đều, hình chiếu của đỉnh trùng với tâm của đáy).

1. Dạng 1: Khối chóp có cạnh bên vuông góc với đáy

Ví dụ 1. Cho hình chóp

.S ABC

SB SC BC CA a

. Hai mặt





ABC

và





ASC

cùng vuông góc với





SBC

. Thể tích khối chóp

.S ABC

bằng:

SABC

V 

. B.

SABC

V 

. C.

SABC

V 

. D.

SABC

V 

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



  

,ABC SBC ASC SBC AC SBC

SB SC BC SBC

đều

312

SBC

VSCA 

Ví dụ 2. Cho hình chóp

.S ABC

có đáy là tam giác vuông tại B ,

,3AB a AC a

, cạnh bên

vuông góc

với mặt phẳng đáy,

2SA a

. Tính theo

thể tích của khối chóp

.S ABC

SABC

V 

. B.

SABc

V 

. C.

SABM

V 

. D.

SABM

V 

Hướng dẫn giải:

2....

32 3

BC AC AB a V AB BC SA  

Ví dụ 3. Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh

, cạnh bên

vuông góc với đáy và

2SB a

Tính theo

thể tích của khối chóp

.S ABC

SABC

V 

. B.

SABC

V 

. C.

SABC

V 

. D.

SABC

V 

Hướng dẫn giải:

113

.. . .3

3344

ABC

SA SB AB a

V S SA a



  

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Ví dụ 4. Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại B , AC a . Biết bên

vuông góc với đáy

và SB hợp với đáy một góc 60. Tính thể tích của khối chóp

.S ABC

. B.

. C.

. D.

Hướng dẫn giải:

















,,60

22 4

61 6

.tan 60 .

23 24

ABC

SA ABCD

SB ABCD SB AB SBA

AB BC S AB BC

SA AB V S SA





  



Ví dụ 5. Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

. Biết SA vuông góc với đáy





ABC và





SBC hợp với đáy





ABC một góc 60. Tính thể tích hình chóp.

. B.

. C.

. D.

Hướng dẫn giải:

Gọi

M là trung điểm BC .Ta có:

ABC đều nên

 





,60

31 3

.tan 60 .

23 8

ABC

AM BC SA BC

SBC ABC SMA

SA AM V S SA







Ví dụ 6. Cho hình chóp

.S ABC

có mặt bên

SBC

là tam giác đều cạnh

, cạnh bên

vuông góc với mặt

phẳng đáy, góc

BAC

bằng

120

. Tính theo

thể tích của khối chóp

.S ABC

SABC

V 

. B.

SABC

V 

. C.

SABC

V 

. D.

SABC

V 

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Hướng dẫn giải:

SB SC AB AC ABC 

cân tại A .

Có

222

2. . .cos120BC AB AC AB AC 

;

11 2

.. . .sin120.

32 36

AB AC SA SB AB

VABAC SA

   

  

Ví dụ 7. Cho hình chóp

.SABCD

có đáy là hình chữ nhật,

2, , 60AB a BC a SCA

, cạnh bên

vuông

góc với đáy. Tính theo

thể tích của khối chóp

.SABCD

SABCD

Va

. B.

SABCD

Va

. C.

SABCD

Va

. D.

S ABCD

Va

Hướng dẫn giải:

;60

.tan 60 3

... 2

AC AB BC SCA

SA AC a

VABBCSAa

 

 

 

Ví dụ 8. Cho hình chóp

.SABCD

có

ABCD

là hình vuông cạnh

vuông góc với mặt phẳng đáy



ABCD

và mặt bên





SCD hợp với đáy một góc

60

. Tính thể tích hình chóp

.SABCD

. B.

. C.

. D.

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



















;

,60

.tan60 3

ABCD

SA ABCD CD AD CD SD

SCD ABCD SDA

SA AD a

VSSA







 

Ví dụ 9. Cho hình chóp

.SABCD

có

ABCD

là hình vuông cạnh

vuông góc với mặt phẳng đáy



ABCD

. Biết góc giữa

và mặt phẳng



ABCD

bằng

60

. Tính thể tích khối chóp

.SABCD

. B.

. C.

. D.

Hướng dẫn giải:













,60

tan 60 tan 60 6

11 6

..6

33 3

ABCD

AC AB BC a

SA ABCD SA AC

SC ABCD SCA

SA AC a

VSSAaa







 

  

Ví dụ 10. Cho hình chóp

.SABCD

có đáy là hình thang vuông tại A và D , ,AD CD a

3AB a

, cạnh bên

vuông góc với mặt phẳng đáy. Góc giữa

với mặt đáy bằng

45

. Tính theo

thể tích của khối

chóp

.SABCD

SABCD

V 

. B.

SABCD

V 

. C.

S ABCD

V 

. D.

SABCD

V 

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ























,,45

11 2 2

.. . .

32 3

SA ABCD SC ABCD SC AC SCA

SA AC AD CD a

VABCDADSA

  

   

  

2. Dạng 2: K

hối

óp

có một mặt bên vuông góc

với đáy

Ví dụ 1. Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

2, 30

AC a ACB

. Hình chiếu vuông góc

của

lên mặt đáy là trung điểm

của cạnh

và

2SH a

. Tính theo

thể tích của khối chóp

.S ABC

SABC

V 

. B.

SABC

V 

. C.

SABC

V 

. D.

SABC

V 

Hướng dẫn giải:

.sin30 3

11 6

.. . .

32 6

AB AC a BC a

VABACSH



 

Ví dụ 2. Cho tứ diện

ABCD

có ABC là tam giác đều, BCD là tam giác vuông cân tại D ,









ABC BCD

và AD hợp với





BCD một góc 60. Tính thể tích của khối tứ diện

ABCD

V 

. B.

ABCD

V 

. C.

ABCD

V 

. D.

ABCD

aV  .

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Gọi H là trung điểm của BC .

Ta có tam giác

ABC đều nên





AH BCD

















.tan 60 3

323

.cot 60 ; 2

BCD

ABC BCD AH BCD

AH HD AH AD a

HD AD BC HD

VSAH



 



 

Ví dụ 3. Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại A ,

25SC a

. Hình chiếu vuông góc của

lên





ABC

là trung điểm M của cạnh AB , góc giữa đường thẳng

với mặt phẳng đáy bằng

. Tính theo

thể tích của khối chóp

.S ABC

215

S ABC

V 

. B.

SABC

V 

. C.

SABC

V 

. D.

315

SABC

V 

Hướng dẫn giải:

 







,, 60

.cos60 5; 15

SM ABC SC ABC SC CM SCM

CM SC a SM a

  

  

Tam giác

MAC

vuông tại

11 2 15

2....

32 3

AACaV ABACSM 

Ví dụ 4. Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại B , BC a . Mặt bên SAC vuông góc với

đáy, các mặt bên còn lại đều tạo với mặt đáy một góc 45. Tính thể tích của khối chóp

.S ABC

SABC

V 

. B.

SABC

V 

. C.

SABC

V 

. D.

SABC

V 

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Kẻ SH BC . Gọi ,IJ lần lượt là hình chiếu của

trên

AB và BC .

 







,45

SAC ABC SH ABC

SI AB SJ BC SIH SJH

SHI SHJ HI HJ







BH là đường phân giác của ABC

H

là trung điểm của AC .

2312

S ABC ABC

HI HJ SH V S SH  

Ví dụ 5. Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại A ,









,AB a SBC ABC

. Hai mặt bên còn

lại hợp với đáy một góc

. Tính theo

thể tích của khối chóp

.S ABC

SABC

V 

. B.

SABC

V 

. C.

SABC

V 

. D.

SABC

V 

Hướng dẫn giải:

Kẻ

SH BC

. Do













SBC ABC SH ABC

Kẻ

,60HD AB HE AC SDH SEH

Do tam giá

ABC

vuông cân tại

nên

HD HE H

là trung điểm của

311 3

.tan60 . . . .

232 12

SH HD V AB AC SH   

Ví dụ 6. Cho hình chóp

.SABCD

có đáy

ABCD

là hình vuông cạnh

, mặt bên

SAB

là tam giác đều và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp

.SABCD

. B.

. C.

. D.

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Hướng dẫn giải:

Gọi

H là trung điểm của AB

SAB đều SH AB













33 1 3

22 3 6

ABCD

SAB ABCD SH ABCD

AB a a

SH V S SH



 

Ví dụ 7. Cho hình chóp

.SABCD

có mặt bên

SAB

vuông góc với mặt phẳng đáy và tam giác

SAB

cân tại

Tính theo

thể tích của khối chóp

.SABCD

, biết rằng: đáy

ABCD

là hình vuông cạnh

, góc giữa

mặt





SBD

và mặt đáy bằng

60

SABCD

Va

. B.

SABCD

V 

. C.

SABCD

V 

. D.

SABCD

V 

Hướng dẫn giải:

Gọi

là trung điểm của













SAB ABCD SM ABCD

Gọi

là giao điểm của

và

là trung điểm của





















,,60

61 6

.tan60 . .

43 12

MN BD

BD SMN BD SN

SM BD

SBD ABCD SN MN SNM

SM MN V AB SM







 











   

Ví dụ 8. Cho hình chóp

.SABCD

có mặt bên

SAB

vuông góc với mặt phẳng đáy và tam giác

SAB

cân tại

Tính theo

thể tích của khối chóp

.SABCD

, biết rằng: đáy

ABCD

là hình chữ nhật,

,2AB a AD a

, góc giữa mặt

SAC

và mặt đáy bằng

60

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



SABCD

V 

. B.

SABCD

V 

. C.

SABCD

V 

. D.

SABCD

V 

Hướng dẫn giải:

Gọi

là trung điểm của













SAB ABCD SM ABCD

Kẻ

vuông góc với

, gọi

là trung điểm của

AH MN AC





















222

,,60

111 6 6

326

.tan 60 . . .

23 3

MN AC

AC SMN AC SN

SM AC

SAC ABCD SN MN SNM

aBHa

BH MN

BH AB BC

SM MN V AB AD SM







 













   

Ví dụ 9. Cho hình chóp

.SABCD

có đáy là hình thoi,

AB BC BD a

, mặt bên

SAB

là tam giác đều và

nằm trong mặt phẳng vuông góc với đáy. Tính thể tích của khối chóp

.SABCD

SABCD

V 

. B.

SABCD

V 

. C.

SABCD

V 

. D.

SABCD

V 

Hướng dẫn giải:

Gọi

là trung điểm của

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ















SAB ABCD SM ABCD

331

,2 ..

2234

ABCD ABD ABCD

aa a

SM S S V S SM 

Ví dụ 10. Cho hình chóp

.SABCD

có đáy

ABCD

là hình thang vuông tại A và D, 3, 2,AB a AD a CD a,

tam giác

SAD

cân tại

, mặt phẳng





SAD

vuông góc với đáy, góc giữa mặt phẳng





SBC

và mặt

đáy bằng

60

. Tính thể tích của khối chóp

.SABCD

S ABCD

V 

. B.

S ABCD

V 

. C.

SABCD

V 

. D.

SABCD

V 

Hướng dẫn giải:

Gọi

là trung điểm của





































, , 60 .tan 60 6

11 4 6

.. . .

32 3

SAD ABCD SM ABCD SM BC

BC SMC BC SC

MC BC

SBC ABCD SC MC SCM SM MC a

VABCDADSM







 











  

3. Dạng 3: Khối chóp

đều

Ví dụ 1. Cho H là khối tứ diện đều cạnh

. Thể tích của H bằng bao nhiêu?

. B.

. C.

. D.

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Gọi

là trọng tâm tam giác



SGCBAB A C

23 3 6

32 3 3

11362

.. . .

334312

ABC

aa a

AG SG SA AG

aa a

VSSG



  

Ví dụ 2. Cho hình chóp tam giác đều

.S ABC

có cạnh đáy bằng

, cạnh bên bằng

. Tính thể tích của khối

chóp .S ABC .

. B.

. C.

. D.

Hướng dẫn giải:

Gọi

là trọng tâm tam giác



SGCBAB A C

22 3

33 1 11

44 3 12

ABC S ABC ABC

AB a

AG SA a

SG SA AG

AB a a

SVSSG

 

  

 

13 3

343 36

aaa

V 

Ví dụ 3. Cho khối tứ diện đều ABCD có cạnh bằng

, M là trung điểm của CD . Tính thể tích hình chóp

.M ABC .

MABC

V 

. B.

MABC

V 

. C.

MABC

V 

. D.

MABC

V 

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Gọi G là trọng tâm ABC . Kẻ MH DG









22 3

11 6

22 3

33 1 3

44 3 24

ABC ABC

DG ABC MH ABC

MH DG CD GC

AB a a

SVSMH

  

 

 

Ví dụ 4. Cho hình chóp tam giác đều

.S ABC

có cạnh đáy bằng

, cạnh bên bằng

. Gọi I là trung điểm của

cạnh

. Tính theo

thể tích của khối chóp

.S ABI

SABC

V 

. B.

SABC

V 

. C.

SABC

V 

. D.

SABC

V 

Hướng dẫn giải:

Gọi

là trọng tâm tam giác



ABC SG ABC

22 2

333

111 11

.. .

223 24

S ABI S ABC ABC

AB a

SG SA AG SA

VV SSG





    





  

Ví dụ 5. Cho hình chóp tứ giác đều

.SABCD

tất cả các cạnh đều bằng

. Tính theo

thể tích của khối chóp

.SABCD

V 

. B.

V 

. C.

V 

. D.

V 

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Gọi O là giao điểm của AC và BD





12 2

;

22 2

11 2

...

33 6

ABCD

SO ABCD

AO AC SO SA AO

V S SO AB BC SO



 

 

Ví dụ 6. Cho hình chóp tứ giác đều

.SABCD

cạnh đáy bằng

, góc giữa mặt bên và mặt đáy bằng 60. Tính

theo

thể tích của khối chóp

.SABCD

SABCD

V 

. B.

SABCD

V 

. C.

SABCD

V 

. D.

SABCD

V 

Hướng dẫn giải:

Gọi

là giao điểm của

và

là trung điểm của

















,,60

.tan 60

ABCD

OM CD SM CD

SCD ABCD OM SM SMO

SO OM

VSSO

 



 

 

Ví dụ 7. Cho một hình chóp tứ giác đều có cạnh đáy bằng

và diện tích xung quanh gấp đôi diện tích đáy.

Khi đó thể tích của khối chóp là:

. B.

. C.

. D.

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Gọi

là giao điểm của

và

là trung điểm của

44...2.;

22.2

xq SCD d

xq d

ABCD

S S CD SM a SM S AB a

SS aSMaSMa

SO SM OM

VSSO

  

 

  



4. Dạng 4: Khối chóp

và phương pháp tỉ số thể tích

Ví dụ 1. Cho tứ diện

ABCD

. Gọi 'B và

lần lượt là trung điểm của AB và

. Khi đó tỉ số thể tích của

khối tứ diện

''AB C D

và khối tứ diện

ABCD

bằng:

. B.

. C.

. D.

Hướng dẫn giải:

'' 1

AB C D

ABCD

AB AC AD

VABACAD



Ví dụ 2. Cho hình chóp tam giác

.S ABC

. Gọi

,AB



lần lượt là trung điểm của

và

. Mặt phẳng



ABC



chia hình chóp thành hai phần. Tỉ số thể tích của hai phần đó bằng:

. B.

. C.

. D.

Hướng dẫn giải:

.'' .''

.''

'' 1 1

SABD SABD

S ABC ABCDA B

SA SB SC

VSASBSCV



http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Ví dụ 3. Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại B ,

2AC a

, cạnh bên

vuông góc với

đáy,

SA a

. Gọi G là trọng tâm tam giác ABC . Mặt phẳng







qua AG và song song với BC , cắt

,SC SB lần lượt tại ,MN. Tính thể tích của khối chóp

.SAMN

SAMN

V 

. B.

SAMN

V 

. C.

SAMN

V 

. D.

SAMN

V 

Hướng dẫn giải:

Gọi

I là trung điểm của BC





4411 2

.. . .

9 932 27

SAMN

S ABC

SAMN SABC

AC a AB BC a

SM SN SG

BC MN BC

SB SC SI

SM SN

VSBSC

V V AB BC SA





  

 

  

Ví dụ 4. Cho tam giác

ABC

vuông cân tại

, AB a . Trên đường thẳng qua C và vuông góc với mặt phẳng





ABC lấy điểm D sao cho

CD a

. Mặt phẳng qua C vuông góc với BD , cắt BD tại F và cắt

AD tại E . Tính theo

thể tích khối tứ diện

CDEF

. B.

. C.

. D.

Hướng dẫn giải:

22 2

6636

ABCD ABC

CDEF

CDEF ABCD

ABCD

VSCD

DE DA DC DE DC

DE DA DC

DA DA DA DA

DF DC

CMTT

DB DB

DE DF a

VDADB



   



  

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Ví dụ 5. Cho hình chóp

.SABCD

có đáy

ABCD

là hình vuông cạnh

, cạnh bên

vuông góc với mặt phẳng

đáy. Gọi M và

lần lượt là trung điểm của

và

. Tính tỉ số thể tích của hai khối chóp

.SAMN

và

.SABD

. B.

. C.

. D.

Hướng dẫn giải:

SAMN

SABD

SA SM SN

VSASBSD



Ví dụ 6. Cho hình chóp

.SABCD

có đáy

ABCD

là hình vuông cạnh

. Gọi ', ', ', 'ABCD lần lượt là trung điểm

của ,,,SA SB SC SD . Khi đó tỉ số thể tích của hai khối chóp

.' ' ' 'SABC D

và

.SABCD

là:

. B.

. C.

. D.

Hướng dẫn giải:

.''' .' ''

.''' .' '' .''' .' '' .''' '

.. .. .

' ' '1 ' ' '1

.. ; ..

SABC SADC

S ABC S ADC

SABC SADC SABC SADC SABCD

SA SB SC SA SD SC

V SA SB SC V SA SD SC

VVVVV

VV VV V





  



Ví dụ 7. Cho khối chóp tứ giác đều .S ABCD . Mặt phẳng







đi qua ,AB và trung điểm M của

. Tỉ số

thể tích của hai phần khối chóp bị phân chia bởi mặt phẳng đó là:

. B.

. C.

. D.

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



Kẻ





MN CD N CD

, suy ra hình thang

ABMN

là thiết diện của khối chóp.

...

....

;

11 3

48 8

SABM

S ABMN S ABM S AMN

SABC

SABM SABC SABCD

SAMN

SAMN SABCD

S ACD

S ABMN S ABCD S ABCD S ABCD

SABMN

ABMNDC S ABCD

ABMNDC

VVV

VSC

VVV

SM SN

VSCSD

VVVV

 

 



  

 

Ví dụ 8. Cho hình chóp tứ giác đều .S ABCD có đáy ABCD là hình vuông cạnh

, cạnh bên tạo với đáy góc

60

. Gọi M là trung điểm của SC . Mặt phẳng đi qua AM và song song với BD cắt SB tại E và

cắt SD tại F . Tính theo

thể tích khối chóp .S AEMF .

. B.

. C.

. D.

Hướng dẫn giải:

Gọi

ISOAM





...

... . .

61 6

.tan 60 .

236

111

336

318

S ABCD ABCD

S AMF

SAMF SACD SABCD

S ACD

S AEMF S AMF S AME S AMF S ABCD

AEMF BD EF BD

SO OA V S SO

SM SF

VVV

VSCSD

VVV V V



 



  

Ví dụ 9. Cho hình chóp .S ABCD có đáy ABCD là hình vuông cạnh

, SA vuông góc với đáy, 2SA a .

Gọi ', 'BD lần lượt là hình chiếu của A lên ,SB SD . Mặt phẳng





''AB D cắt SC tại 'C . Tính theo

thể tích khối chóp .'''SABC D.

. B.

. C.

. D.

Hướng dẫn giải:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan



N KHÔNG THÊ



THAY

ĐÔ



I ĐI



CH ĐÊ



N NÊ





N KHÔNG

ĐÔ



I THAY CON ĐƯƠ



.''

.'' .

. ''' . '' . '' . '' .

'2'1

;

''1 1

222

SABC

SABC SABC

SABC

S AB C D S AB C S AC D S AB C S ABC

SB SA SC

SB SB SC

SB SC

VSBSC

VVVV V

 



  

Ví dụ 10. Cho hình chóp tứ giác

.SABCD

có thể tích bằng

với đáy là hình bình hành. Gọi

là trung điểm

cạnh

. Mặt phẳng qua

'AC

và song song với BD cắt các cạnh ,SB SD lần lượt tại ', 'BD. Khi đó

thể tích của khối chóp

.' ' ' 'SABC D

bằng:

. B.

. C.

. D.

Hướng dẫn giải:

Gọi

là giao điểm của

và

, gọi

là giao điểm của

và

Qua

kẻ

''BD

song song với

. Khi đó mặt phẳng qua

'AC

và song song

với

là mặt phẳng



'''AB C D

Ta dễ dàng nhận thấy rằng

là trọng tâm của tam giác

SAC

nên



Theo định lí Ta lét ta có

''2

SD SI SB

SD SO SB

 

''' '' ''

''211

.. 1..

32 3

''211

.. 1..

32 3

.2.

22 3

SAD C

SADC

SAB C

SABC

SADC SABC SABCD

SAD C B SAD C SAB C SABCD

SA SD SC

VSASDSC

SA SB SC

VSASBSC

VV V

VVV V





 

Bấm Tải xuống để xem toàn bộ.

Preview text:

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
HÌNH KHÔNG GIAN THỂ TÍCH
TỪ CƠ BẢN ĐẾN NÂNG CAO FULL
Giáo viên: Nguyễn Tiến Đạt HÌNH KHÔNG GIAN THỂ TÍCH
ÔN TẬP 1: KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 9 – 10
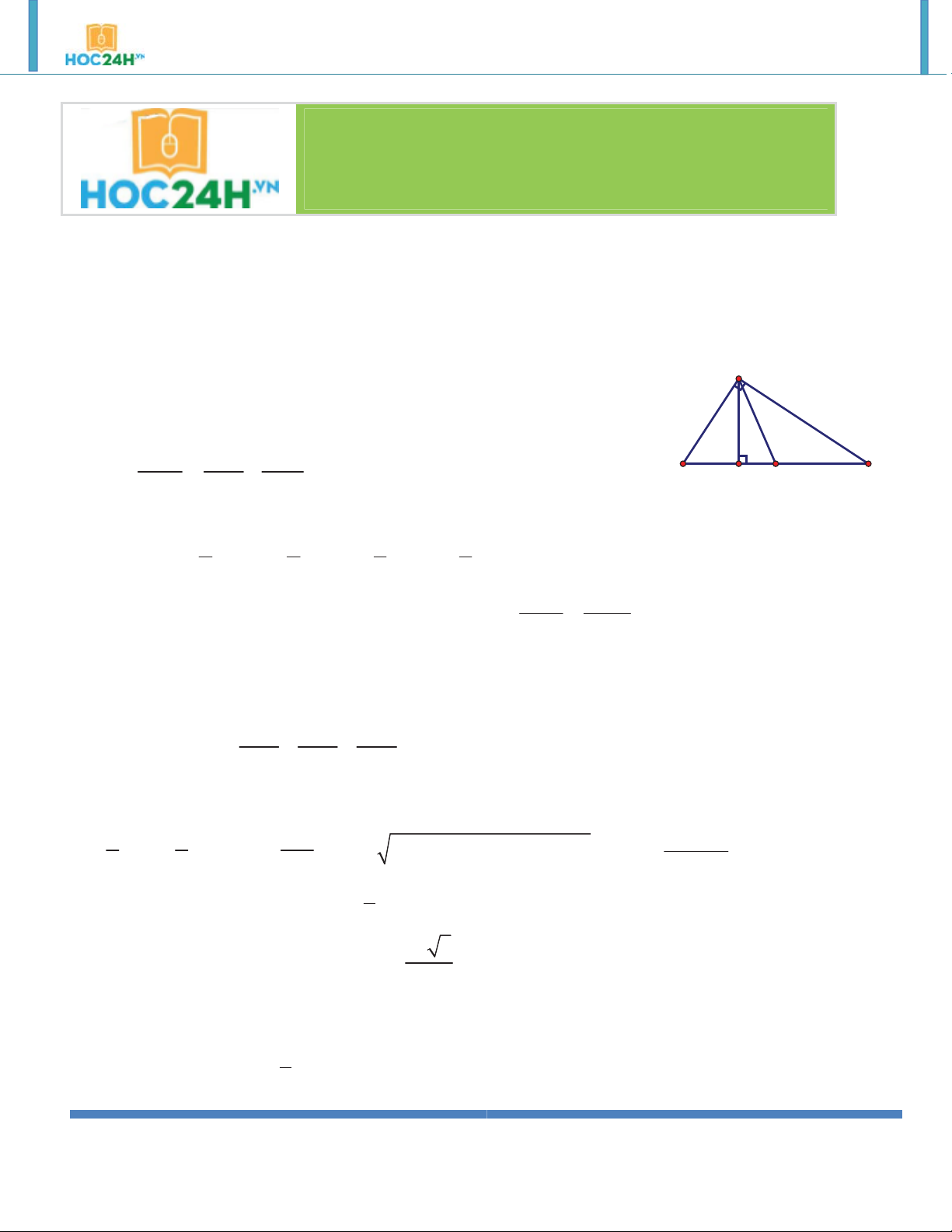
1. Hệ thức lượng trong tam giác vuông: Cho AB 
C vuông ở A . Ta có: a) Định lý Pitago : 2 2 2
BC  AB  AC A b) 2 2
BA  BH.BC;CA  CH.CB c b c) .
AB AC  BC.AH 1 1 1 d)   B C 2 2 2 AH AB AC H M a e) BC  2 AM b c b c f) sin B 
,cos B  , tan B  ,cot B  a a c b b b g) b  . a sin B  .
a cos C, c  . a sin C  .
a cos B, a   sin B cosC b  .t c an B  . c cot C
2. Hệ thức lượng trong tam giác thường
Định lý hàm số côsin: 2 2 2
a  b  c  2b . c cos A a b c Định lý hàm số sin:    2R sin A sin B sin C
3. Các công thức tính diện tích
a) Công thức tính diện tích tam giác 1 1 abc S a b c  . a h  . a bsin C   pr 
p p  a p  b p  c p   a     với  2 2 4R 2 1 Đặc biệt: AB 
C vuông ở A : S  A . B AC 2 2 a 3 AB 
C đều cạnh AB  C : S  4
b) Diện tích hình vuông: S  cạnh x cạnh
c) Diện tích hình chữ nhật: S  dài x rộng 1
d) Diện tích hình thoi: S  (chéo dài x chéo ngắn) 2
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 1 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan 1
e) Diện tích hình thang: S  (đáy lớn + đáy nhỏ) x chiều cao 2
f) Diện tích hình bình hành: S  đáy x chiều cao
g) Diện tích hình tròn: 2 S   R
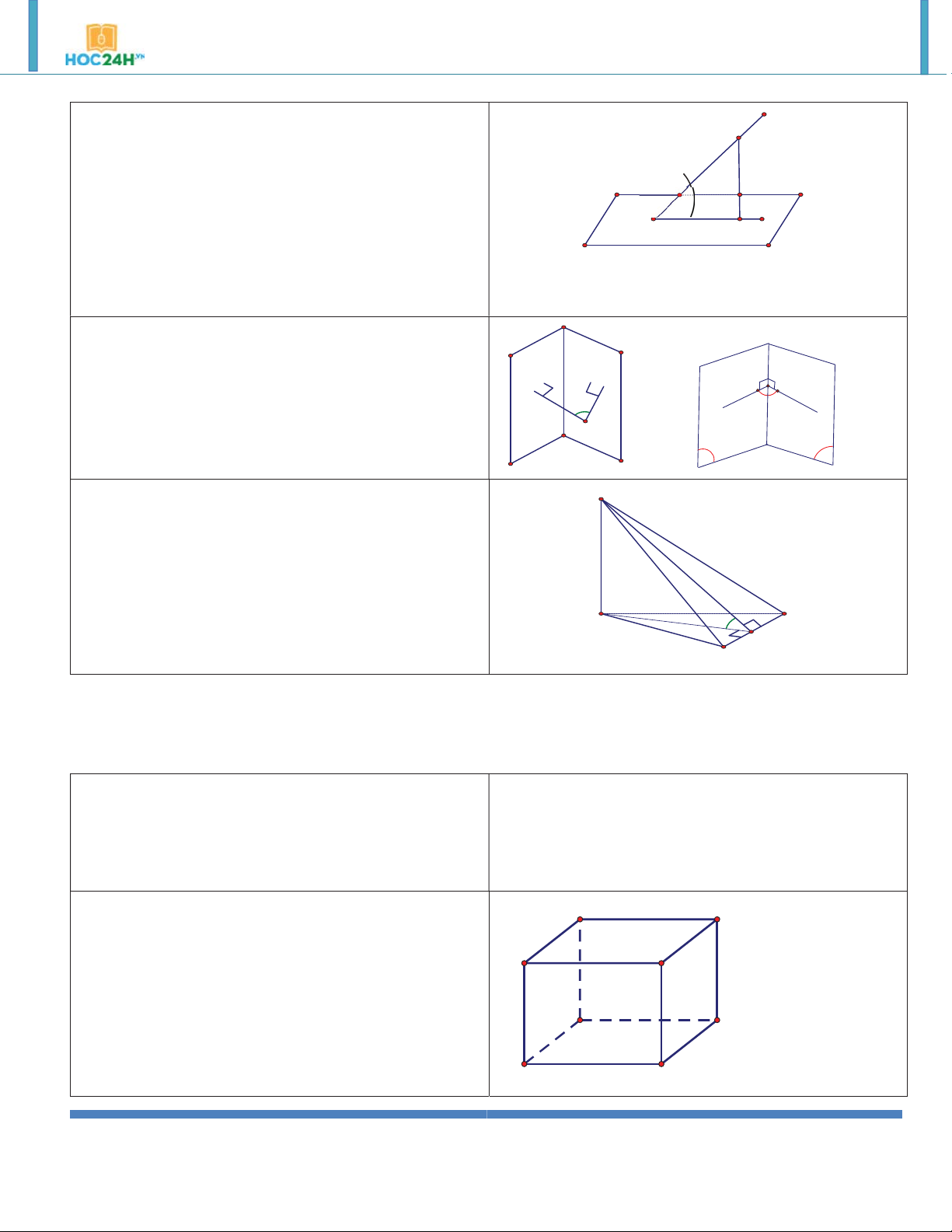
ÔN TẬP 2: KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 11 A. QUAN HỆ SONG SONG
§1.ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG 1. Định nghĩa
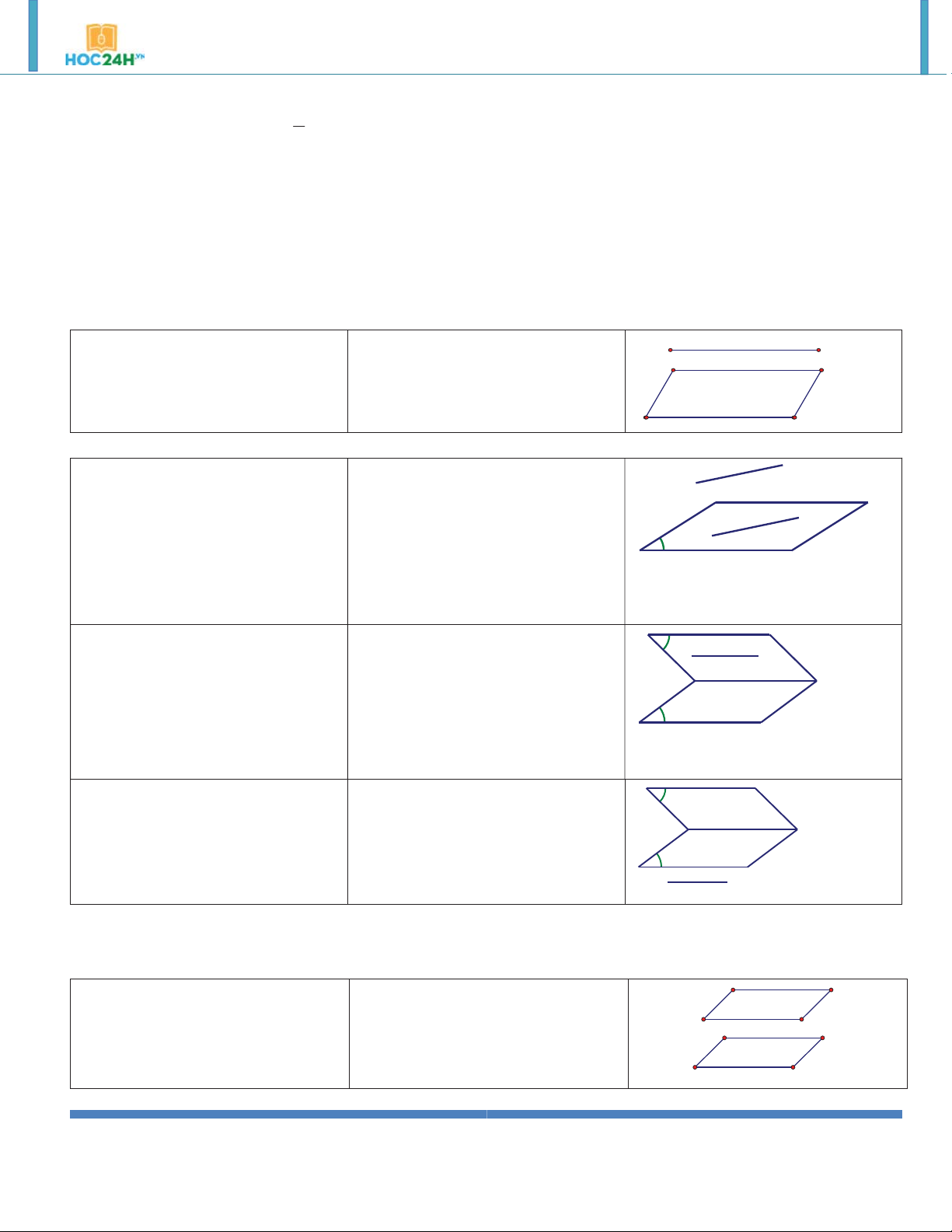
Đường thẳng và mặt phẳng gọi là a & PaP   a
song song với nhau nếu chúng
không có điểm nào chung. (P) 2.Các định lý:
Định lý 1: Nếu đường thẳng a a   a  
không nằm trên mặt phẳng  và b & a   a &  
song song với một đường thẳng b   b  α
nào đó nằm trên  thì a song song với  .
Định lý 2: Nếu đường thẳng a
a & P Q 
song song với mặt phẳng P thì  a a  (Q)  b & a  b
mọi mặt phẳng Q chứa a mà   P 
Q  b P cắt  
P thì cắt theo giao tuyến song song với a .
Định lý 3: Nếu hai mặt phẳng cắt 
 PQ  b Q
nhau cùng song song với một  P & a  b & a
đường thẳng thì giao tuyến của    b
chúng cũng song song với đường     Q & a P thẳng đó. a
§2.HAI MẶT PHẲNG SONG SONG 1. Định nghĩa:
Hai mặt phẳng được gọi là song   P &   Q   P   Q  
song với nhau nếu chúng không có P điểm nào chung. Q
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 2 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan 2. Các định lý:
Định lý 1: Nếu mặt phẳng   P a,b    P   a
chứa hai đường thẳng a, b cắt nhau a b I   
  P & Q P I b
và cùng song song với mặt phẳng 
a & Q,b & Q   Q thì   P và   Q song song Q với nhau.
Định lý 2: Nếu một đường thẳng P& Q a
nằm một trong hai mặt phẳng song
  a & Q a  P  P
song thì song song với mặt phẳng    kia. Q
Định lý 3: Nếu hai mặt phẳng   P
P& Q  R  và  
Q song song thì mọi mặt RP  a  a & b  a phẳng   R đã cắt  
P thì phải cắt R  Q  b P   
Q và các giao tuyến của chúng b Q song song. B. QUAN HỆ VUÔNG GÓC
§1.ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG 1. Định nghĩa:
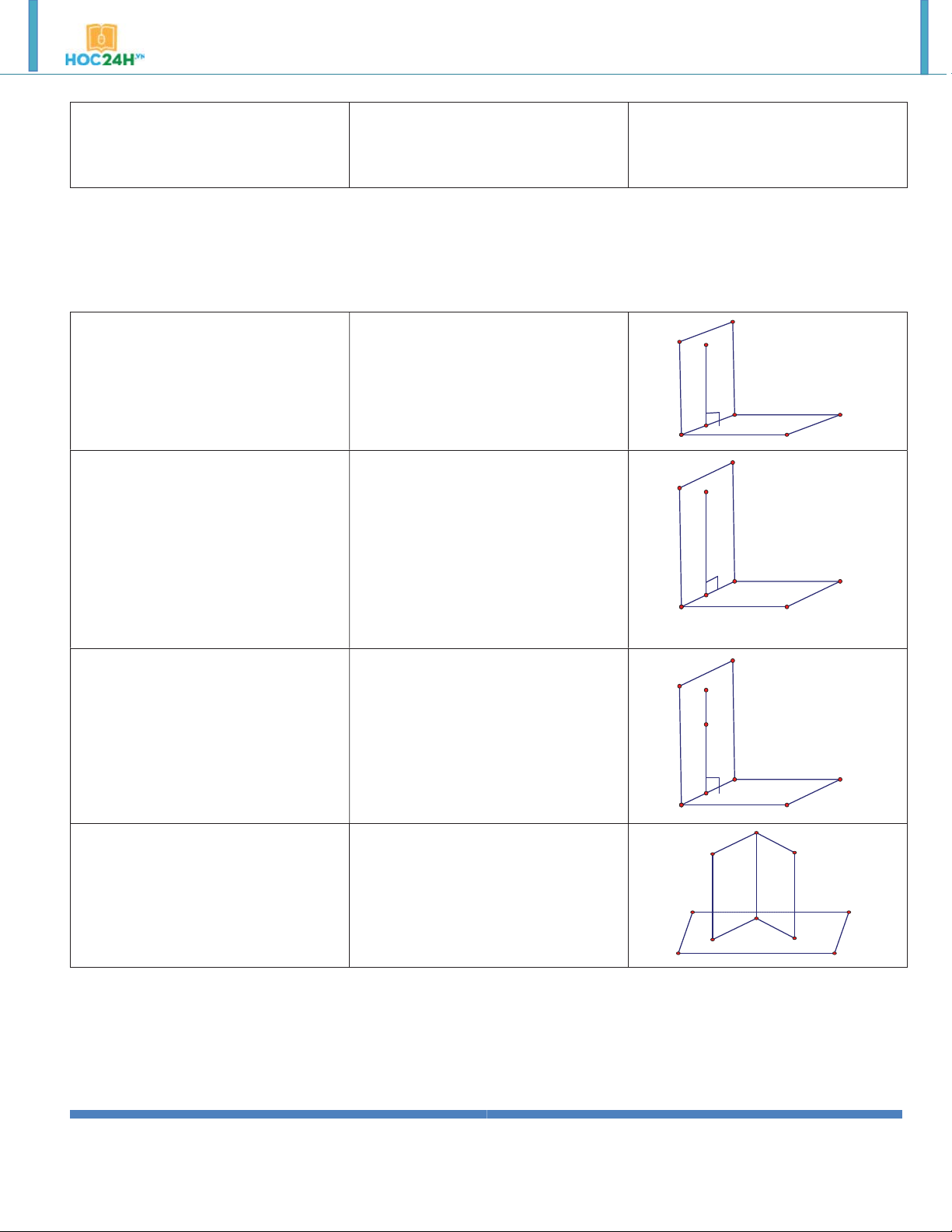
Một đường thẳng được gọi là a   
P  a  c, c     P
vuông góc với một mặt phẳng nếu a
nó vuông góc với mọi đường thẳng
nằm trên mặt phẳng đó. P c 2. Các định lý:
Định lý 1: Nếu đường thẳng d d  a , d  b
vuông góc với hai đường thẳng cắt  d a ,b   P  
  d  P
nhau a và b cùng nằm trong mặt  ab  
phẳng P thì đường thẳng d  b
vuông góc với mặt phẳng P. P a
Định lý 3: (Ba đường vuông góc) a    P ,b    P
Cho đường thẳng a không vuông b  ab  a'
góc với mặt phẳng   P và đường
thẳng b nằm trong   P . Khi đó,
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 3 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
điều kiện cần và đủ để b vuông góc
với a là b vuông góc với hình
chiếu a ' của a trên   P .
§2.HAI MẶT PHẲNG VUÔNG GÓC 1. Định nghĩa:
Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 900. 2. Các định lý:
Định lý 1: Nếu một mặt phẳng a  P Q
chứa một đường thẳng vuông góc
  Q  P a  Q  a
với một mặt phẳng khác thì hai mặt  
phẳng đó vuông góc với nhau. P
Định lý 2: Nếu hai mặt phẳng P   P    Q   P 
và Q vuông góc với nhau thì bất  
P Q  d   a   Q  a
cứ đường thẳng a nào nằm trong a  P,a  d
P, vuông góc với giao tuyến của
P và Q đều vuông góc với d Q mặt phẳng Q.
Định lý 3: Nếu hai mặt phẳng P   P    Q  P
và Q vuông góc với nhau và A A P   
  a  P a
là một điểm trong P thì đường Aa  A 
thẳng a đi qua điểm A và vuông a  Q 
góc với Q sẽ nằm trong P Q
Định lý 4: Nếu hai mặt phẳng cắt PQ a
nhau và cùng vuông góc với mặt  Q P R  P    a  R a
phẳng thứ ba thì giao tuyến của       
chúng vuông góc với mặt phẳng  
Q  R  thứ ba. R §3.KHOẢNG CÁCH
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 4 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
1. Khoảng cách từ 1 điểm tới 1 đường thẳng, đến 1 O mặt phẳng:
Khoảng cách từ điểm M đến đường thẳng a (hoặc đến mặt phẳng  
P ) là khoảng cách giữa hai điểm M O
và H , trong đó H là hình chiếu của điểm M trên H H
đường thẳng a ( hoặc trên mặt phẳng P) a P d  ;
O a  OH;d  ; O   P   OH
2. Khoảng cách giữa đường thẳng và mặt phẳng song song: a O
Khoảng cách giữa đường thẳng a và mặt phẳng   P
song song với a là khoảng cách từ một điểm nào đó
của a đến mặt phẳng   P . H P d a;  P   OH
3. Khoảng cách giữa hai mặt phẳng song song:
là khoảng cách từ một điểm bất kỳ trên mặt phẳng này O P đến mặt phẳng kia. d   
P ;Q  OH H Q
4.Khoảng cách giữa hai đường thẳng chéo nhau: A
là độ dài đoạn vuông góc chung của hai đường thẳng a đó. d  ; a  b  AB b B §4.GÓC
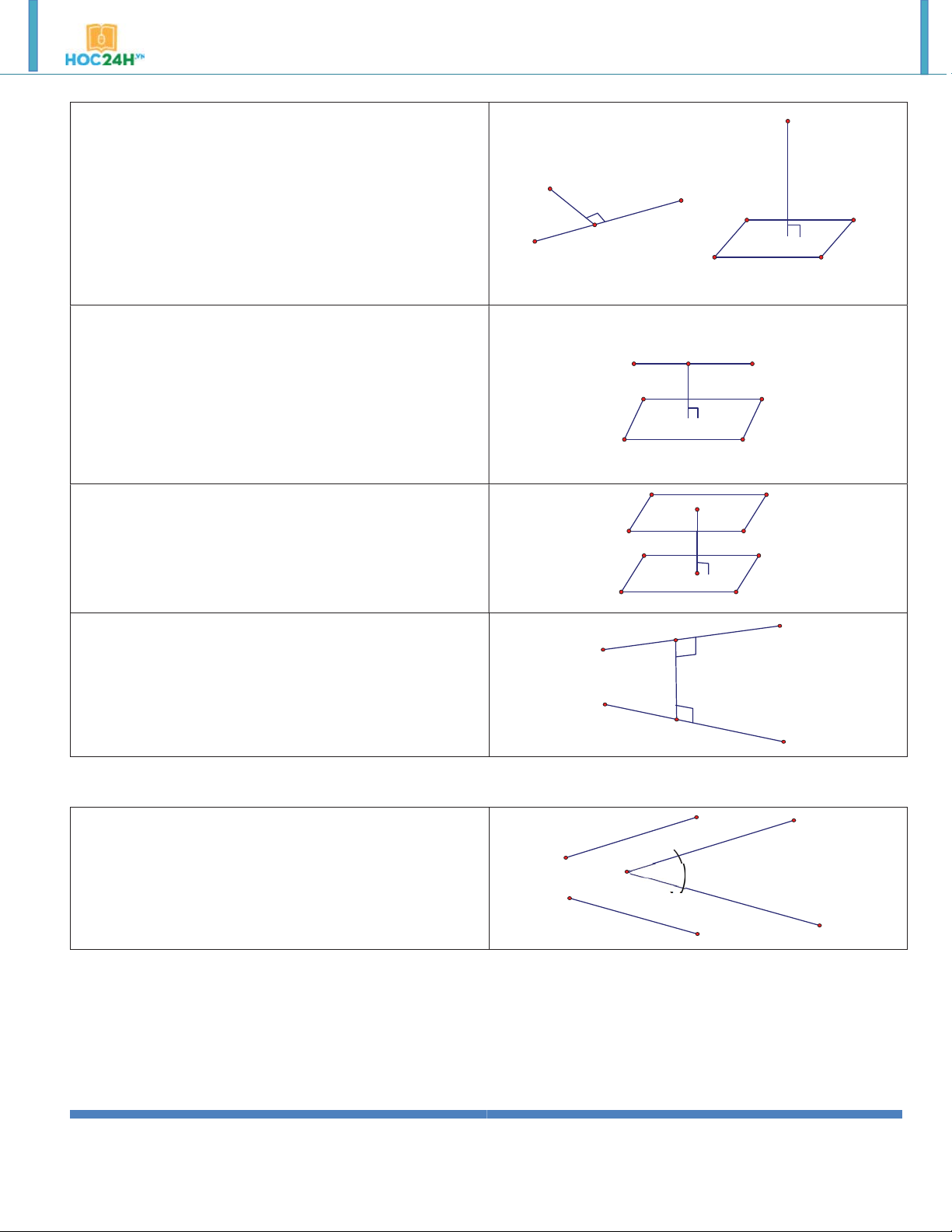
1. Góc giữa hai đường thẳng a và b
là góc giữa hai đường thẳng a ' và b ' cùng đi qua một a a'
điểm và lần lượt cùng phương với a và b . b' b
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 5 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
2. Góc giữa đường thẳng a không vuông góc với a mặt phẳng P
là góc giữa a và hình chiếu a ' của nó trên mặt phẳng P.
Đặc biệt: Nếu a vuông góc với mặt phẳng P thì ta a' P
nói rằng góc giữa đường thẳng a và mặt phẳng   P là 90 .
3. Góc giữa hai mặt phẳng
là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Hoặc là góc giữa 2 đường thẳng nằm trong 2 mặt a b a b
phẳng cùng vuông góc với giao tuyến tại 1 điểm P Q P Q
4. Diện tích hình chiếu: Gọi S là diện tích của đa S
giác H trong mặt phẳng  
P và S ' là diện tích
hình chiếu H ' của H trên mặt phẳng P ' thì:
S '  S cos
trong đó  là góc giữa hai mặt phẳng P và P '. A M C B
ÔN TẬP 3: KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 12
A. CÁC CÔNG THỨC THỂ TÍCH CỦA KHỐI ĐA DIỆN:
1. Thể tích khối lăng trụ:
V  S.h Trong đó:
S : Diện tích đa giác đáy.
h : Đường cao của hình lăng trụ.
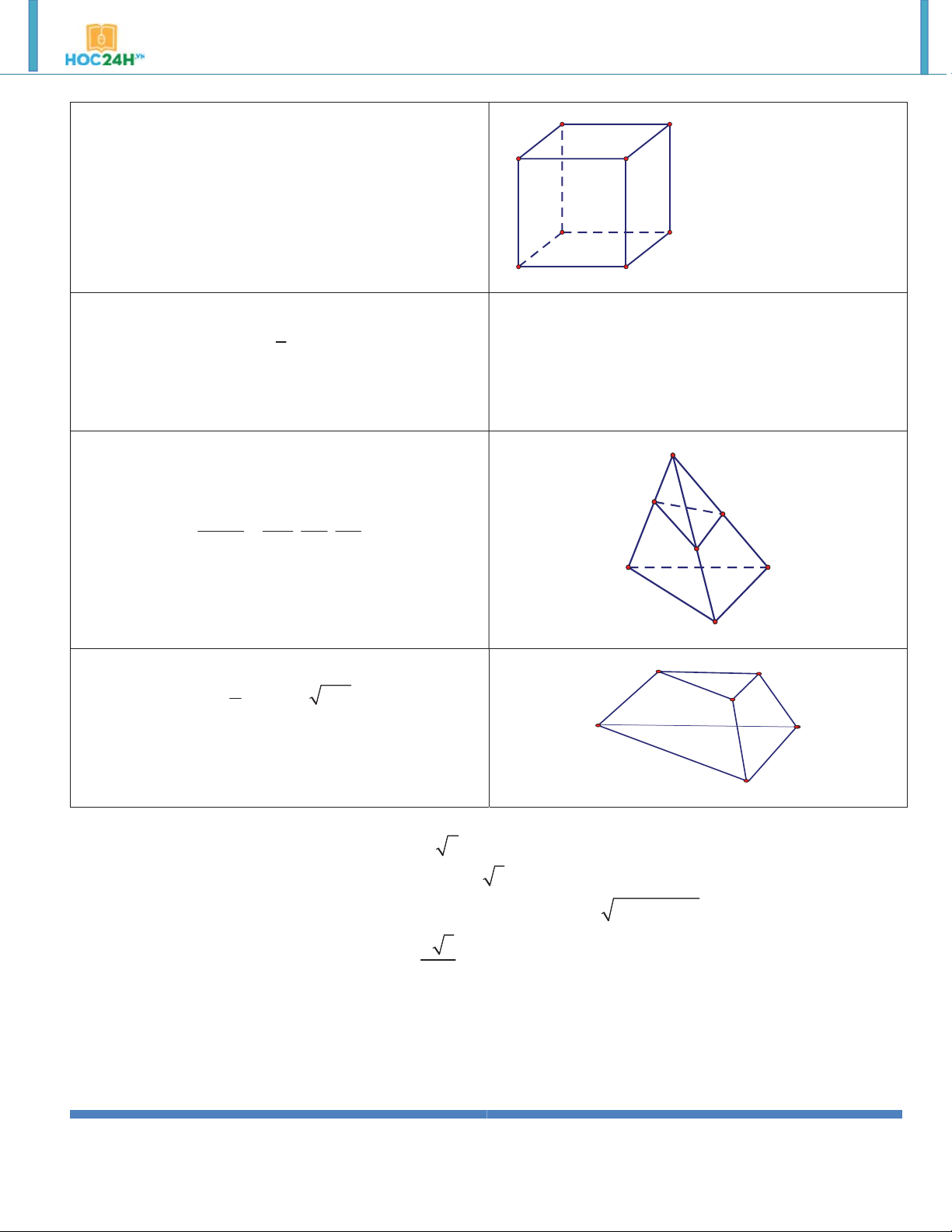
a) Thể tích khối hộp chữ nhật: A' D' V  a. . b c
với a,b, c là ba kích thước B' C' A D B C
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 6 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
b) Thể tích khối lập phương: A' D' 3 V  a B' C'
với a là độ dài cạnh A D B C 2. Thể tích khối chóp: 1 V  S.h 3 Trong đó:
S : Diện tích đa giác đáy.
h : Đường cao của hình chóp.
3. Tỉ số thể tích tứ diện: S
Hai khối chóp S.ABC và S.MNP có chung đỉnh S
và các góc ở đỉnh S . Khi đó: M P V SM SN SP S.MNP  . . V SA SB SC S.ABC N A C B
4. Thể tích khối chóp cụt: A' B' h
V  B  B' BB' C' 3  Trong đó:
B, B ' : Diện tích hai đáy. A B h : Chiều cao. C Chú ý:
1/ Đường chéo của hình vuông cạnh a là d  a 2 ,
Đường chéo của hình lập phương cạnh a là d  a 3 ,
Đường chéo của hình hộp chữ nhật có ba kích thước a,b, c là 2 2 2
d  a  b  c , a 3
2/ Đường cao của tam giác đều cạnh a là h  2
3/ Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên đều bằng nhau ( hoặc có đáy là đa giác đều,
hình chiếu của đỉnh trùng với tâm của đáy).
4/ Lăng trụ đều là lăng trụ đứng có đáy là đa giác đều.
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 7 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan PHÂN DẠNG BÀI TẬP
A. LOẠI 1: THỂ TÍCH LĂNG TRỤ
1. Dạng 1: Khối lăng trụ đứng có chiều cao hay cạnh đáy
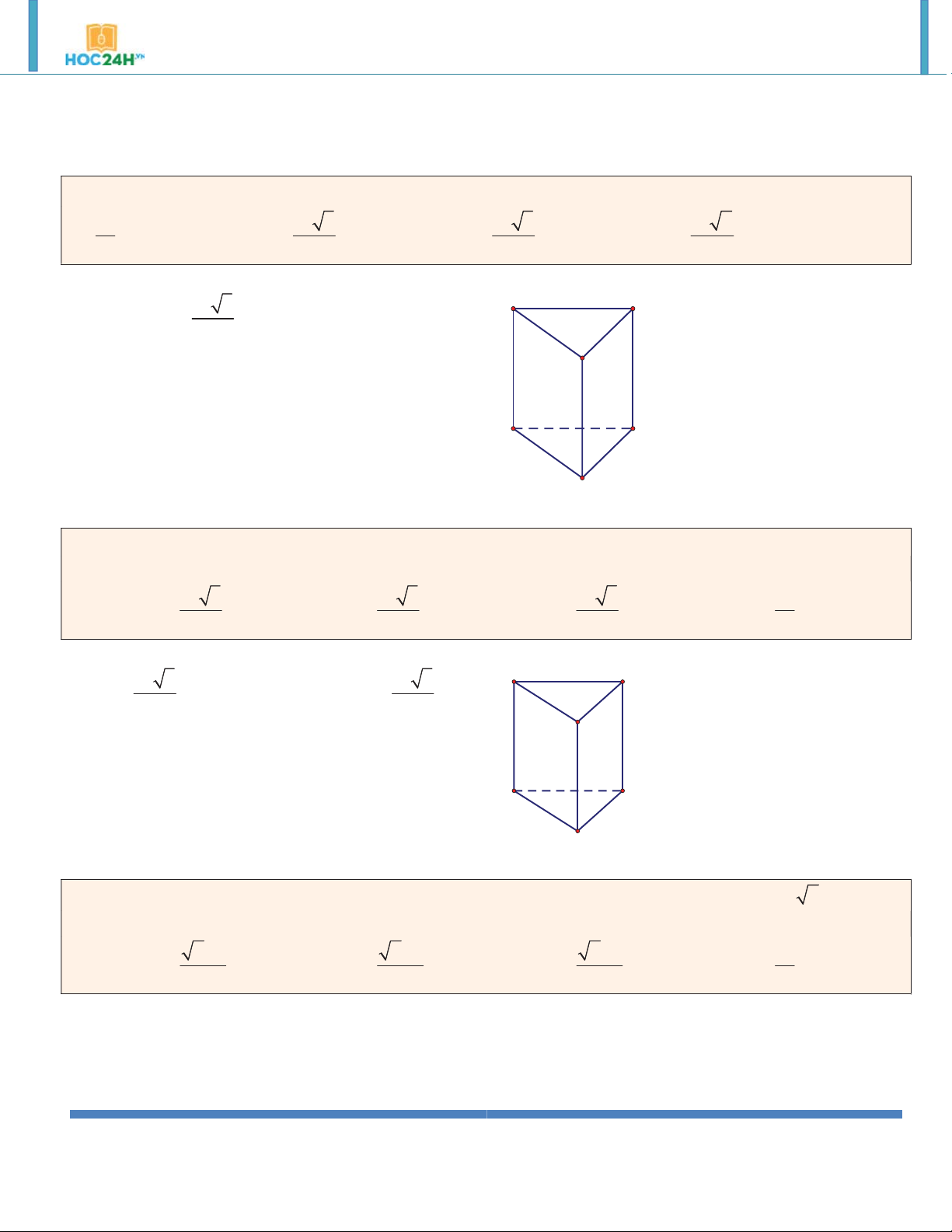
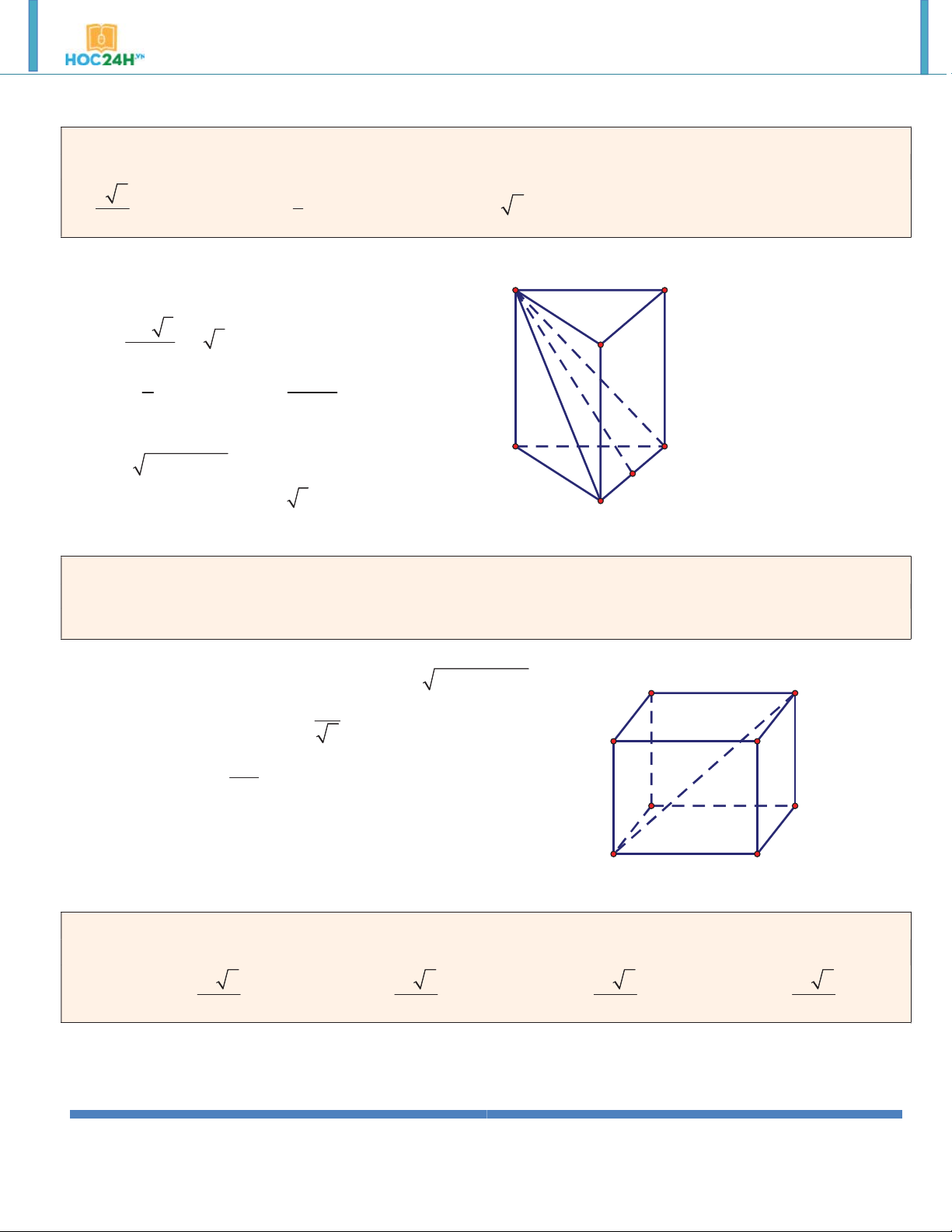
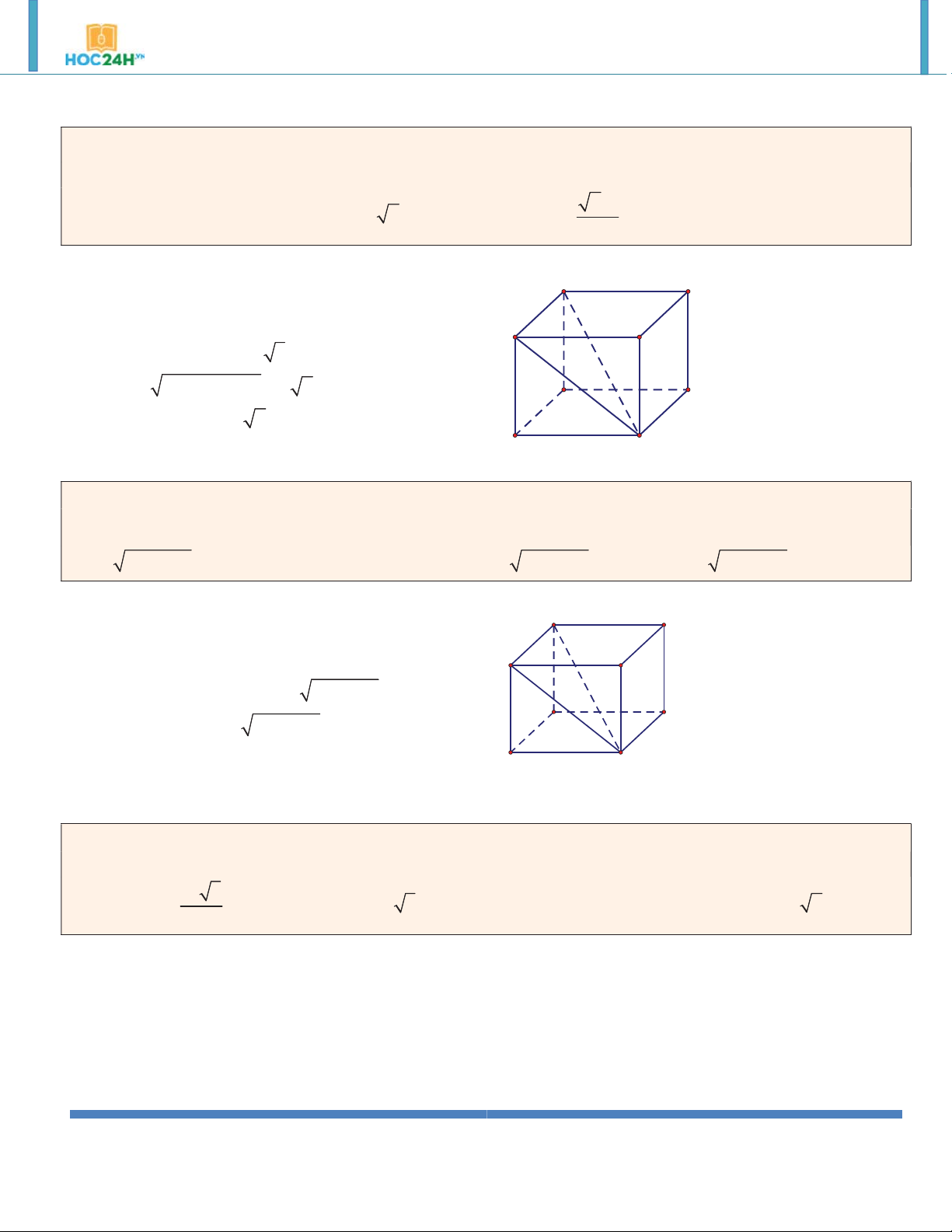
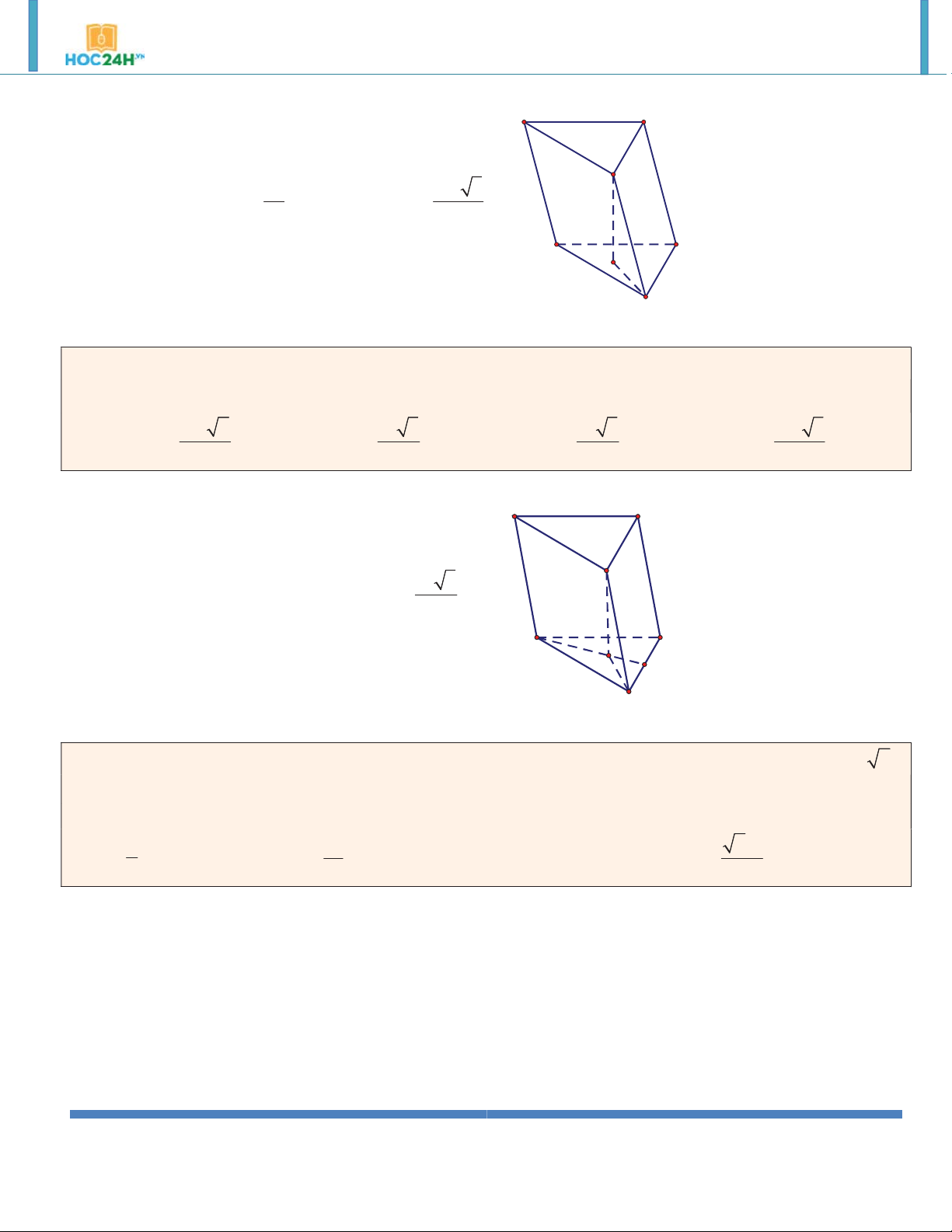
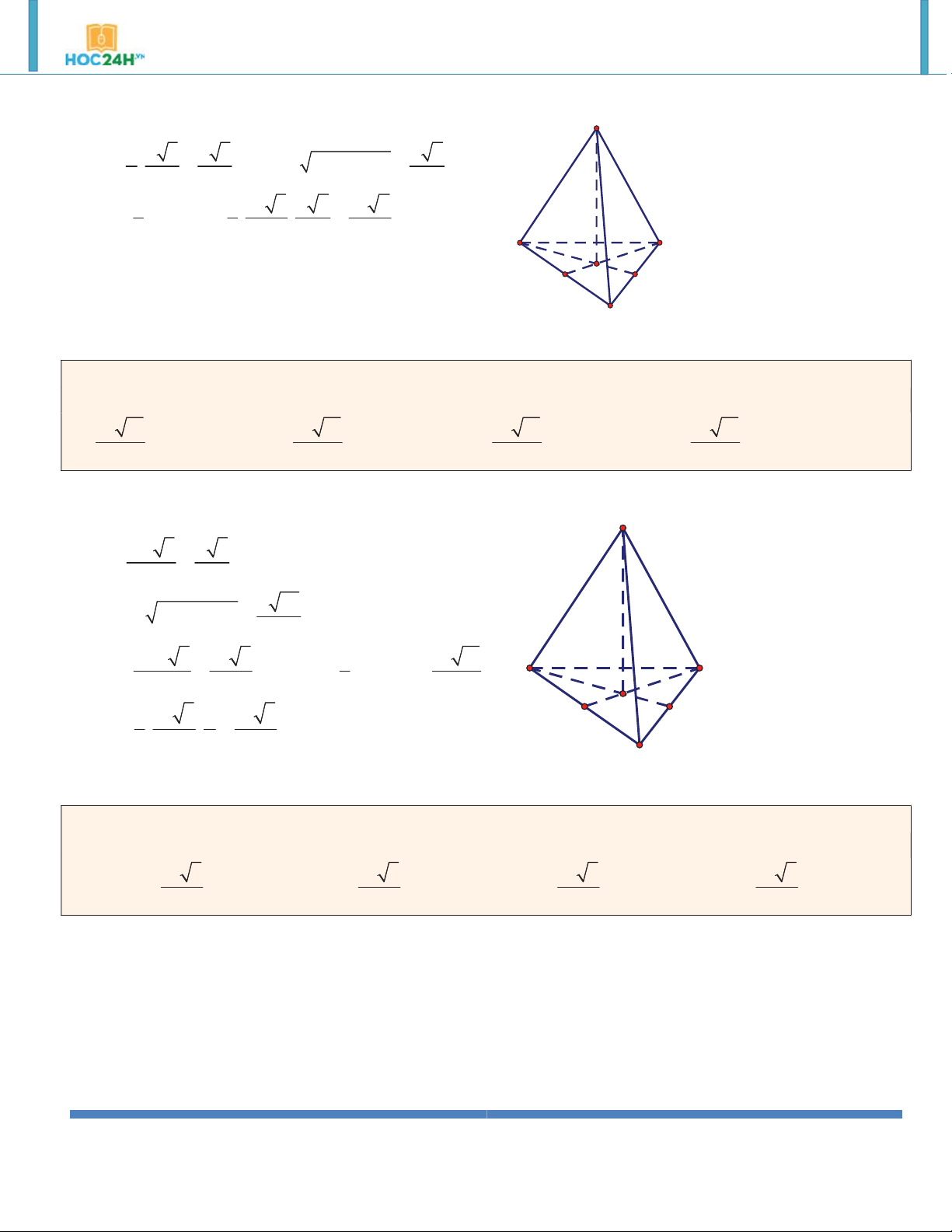
Ví dụ 1. Cho (H ) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a . Thể tích của (H ) bằng: 3 a 3 a 3 3 a 3 3 a 2 A. . B. . C. . D. . 2 2 4 3 Hướng dẫn giải: 3 a 3 A' C' V  S .AA' SBC  4 B' A C B
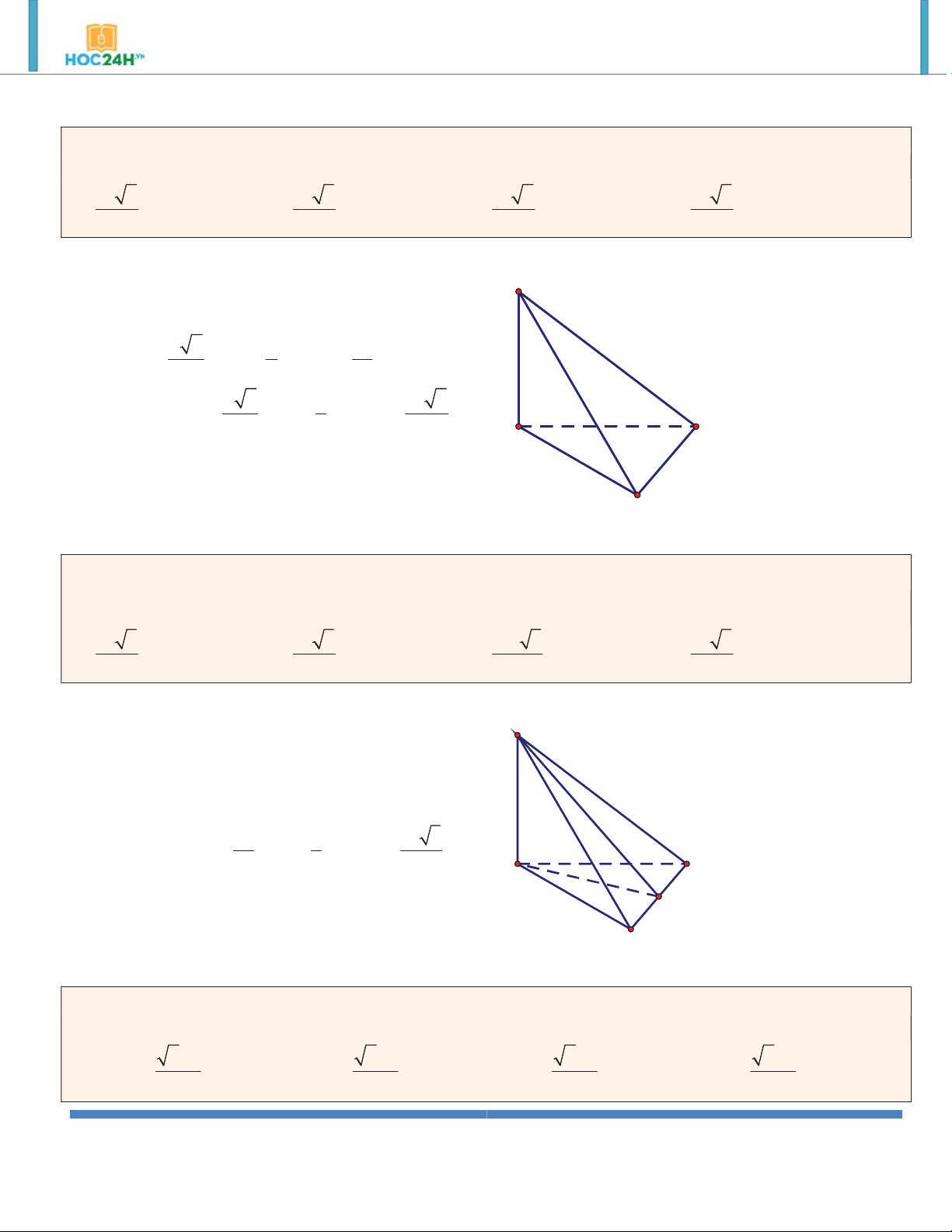
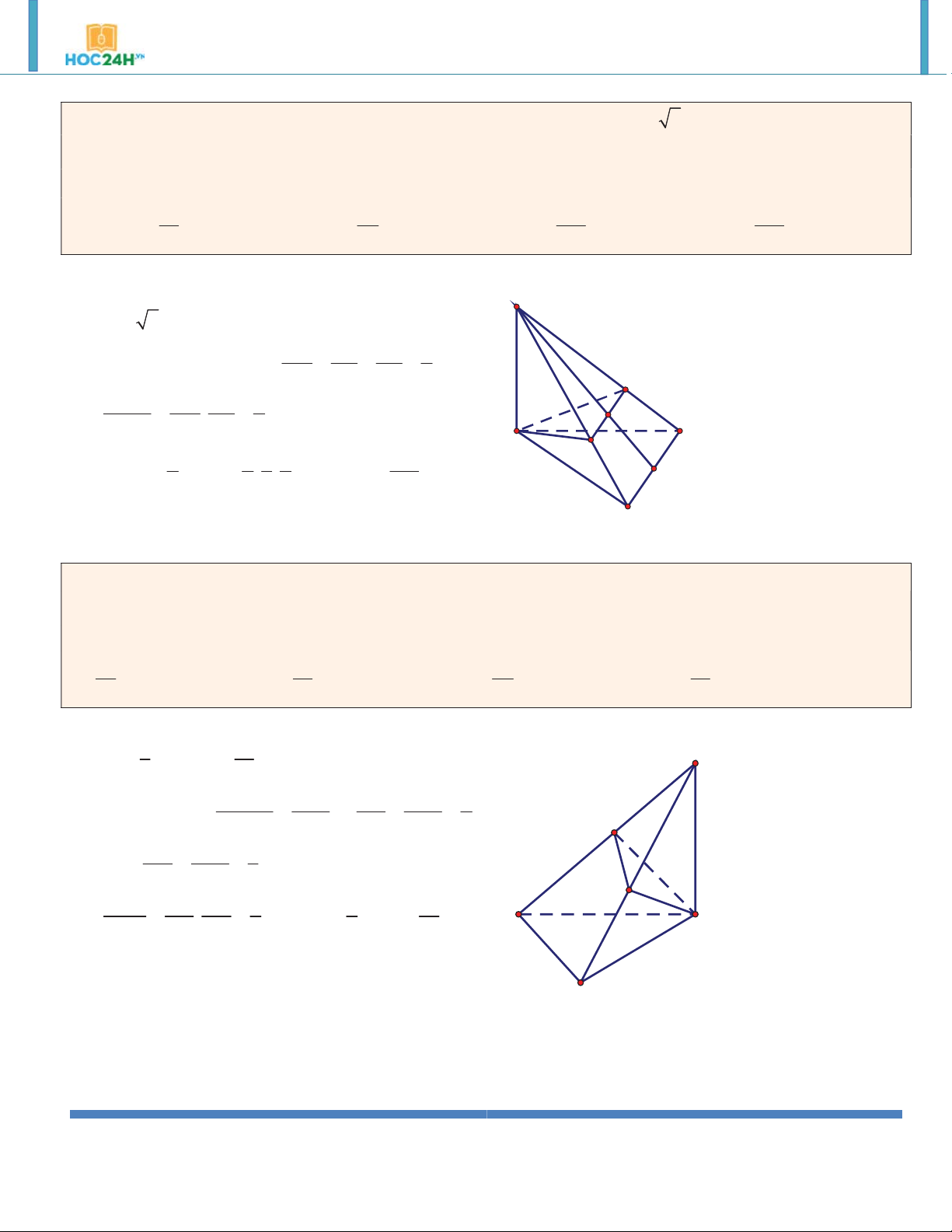
Ví dụ 2. Cho lăng trụ đứng ABC.A B  C
  có AA  a , tam giác ABC đều cạnh a . Tính theo a thể tích của
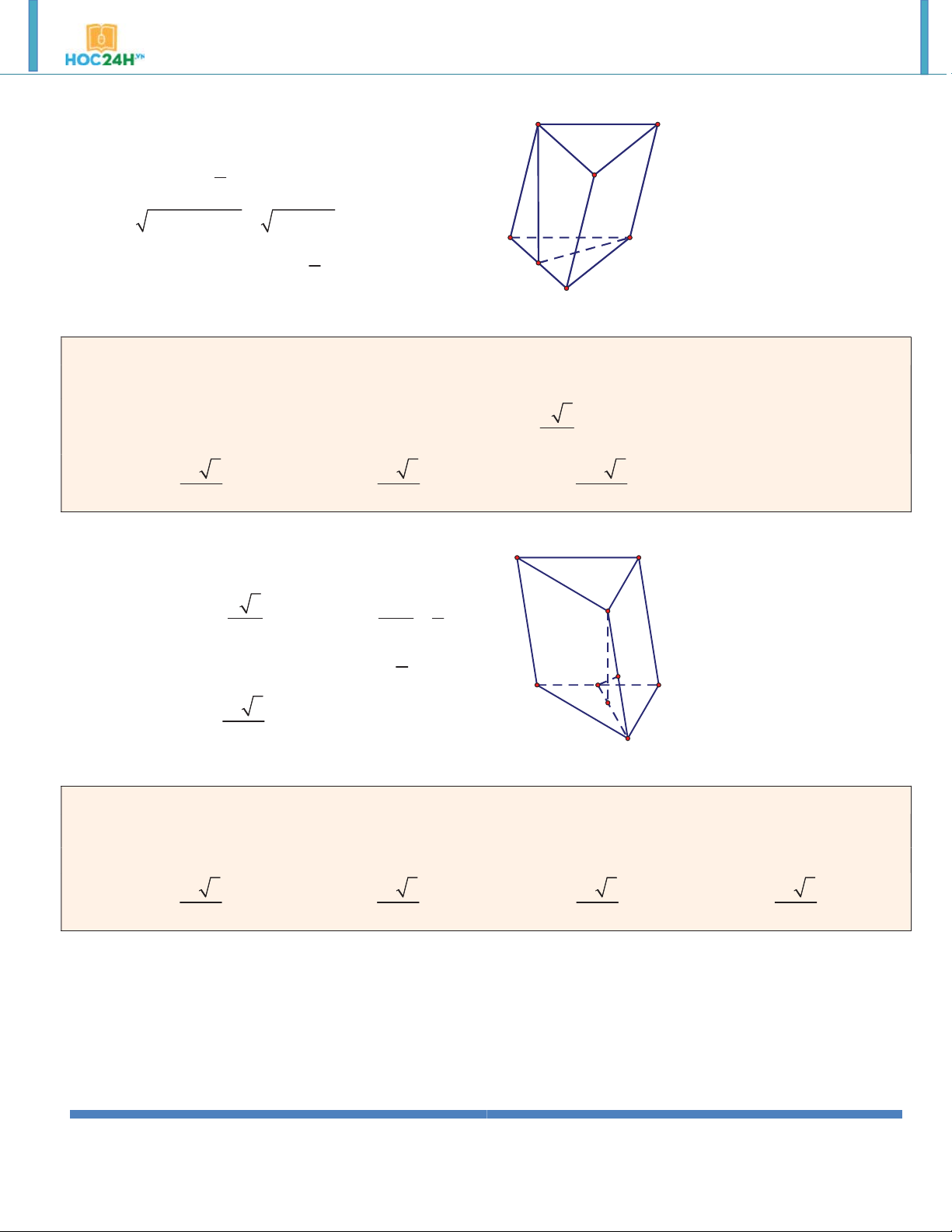
khối lăng trụ ABC.A B  C   . 3 a 3 3 a 3 3 a 3 3 a A. V V V V ABC. A B  C    . B. 12 ABC. A B  C    . C. 8 ABC. A B  C    . D. 4 ABC.A B  C    . 6 Hướng dẫn giải: 2 3 a 3 a 3 A B S 
, h  AA'  a  V  S .h ABC  4 ABC 4 C A' B' C'
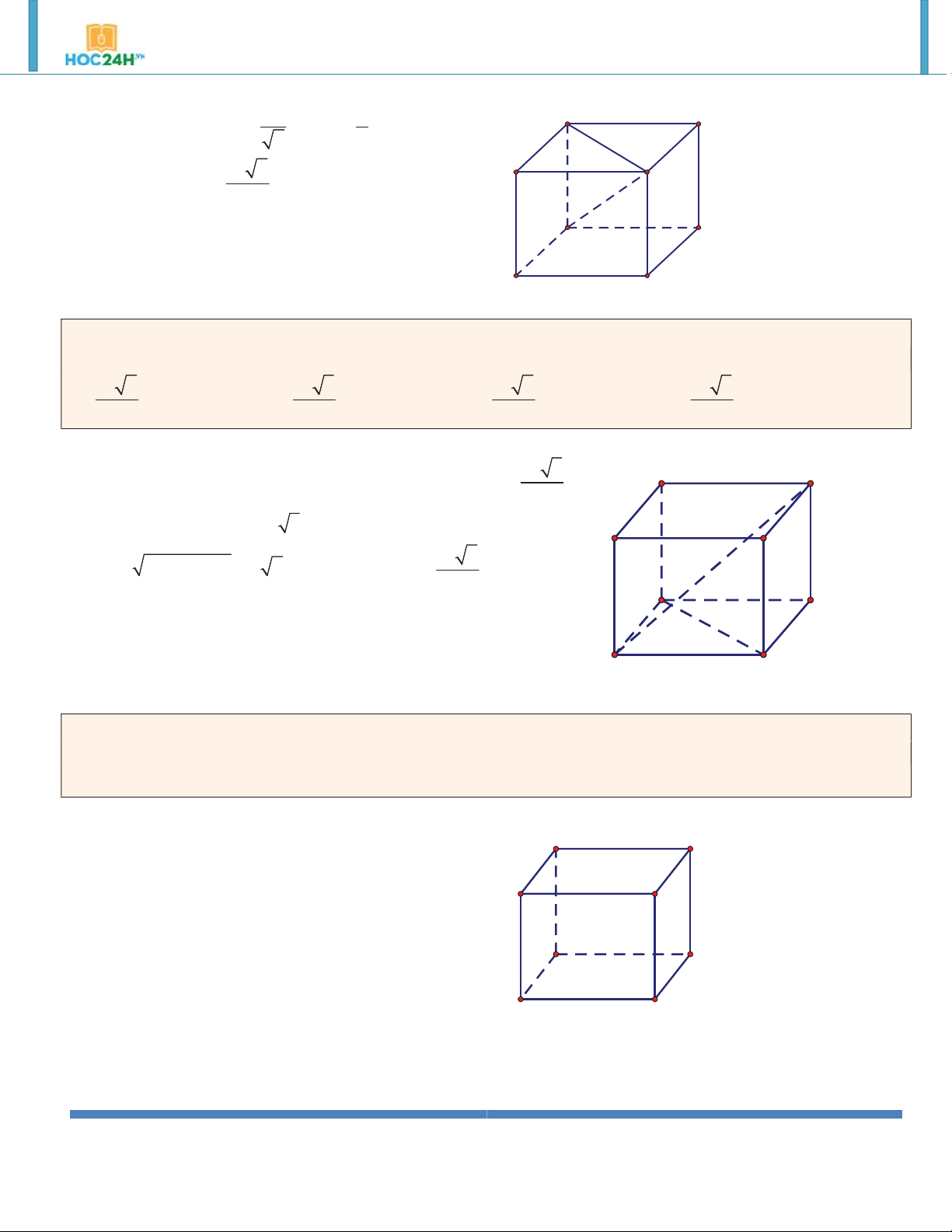
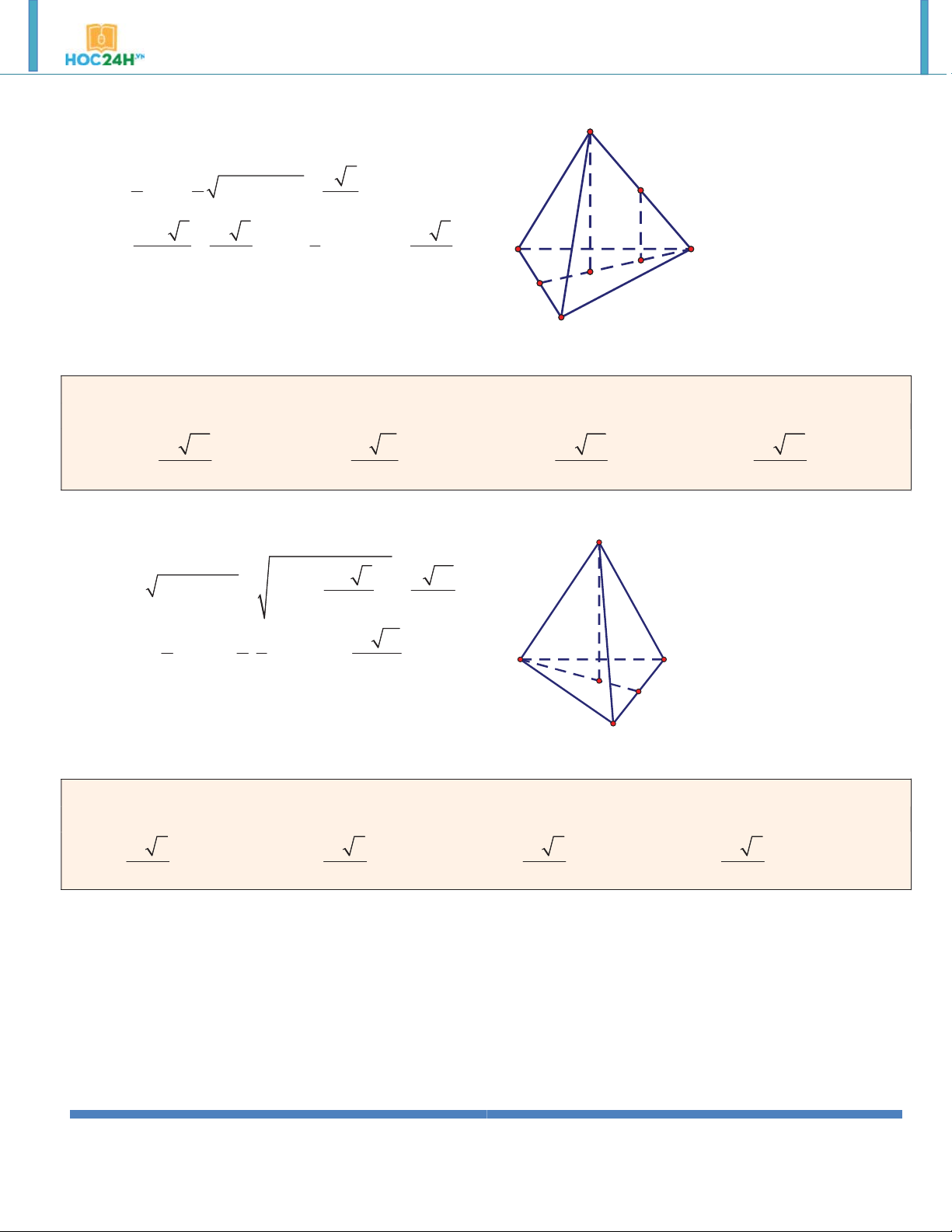
Ví dụ 3. Cho lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác vuông, BA  BC  a , AA  a 2 . Tính theo
a thể tích của khối lăng trụ ABC.A B  C   . 3 2.a 3 2.a 3 2.a 3 a A. V V V V ABC.A B  C    . B. 3 ABC.A B  C    . C. 2 ABC.A B  C    . D. 4 ABC.A B  C    . 3 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 8 ĐÔI THAY CON ĐƯƠNG
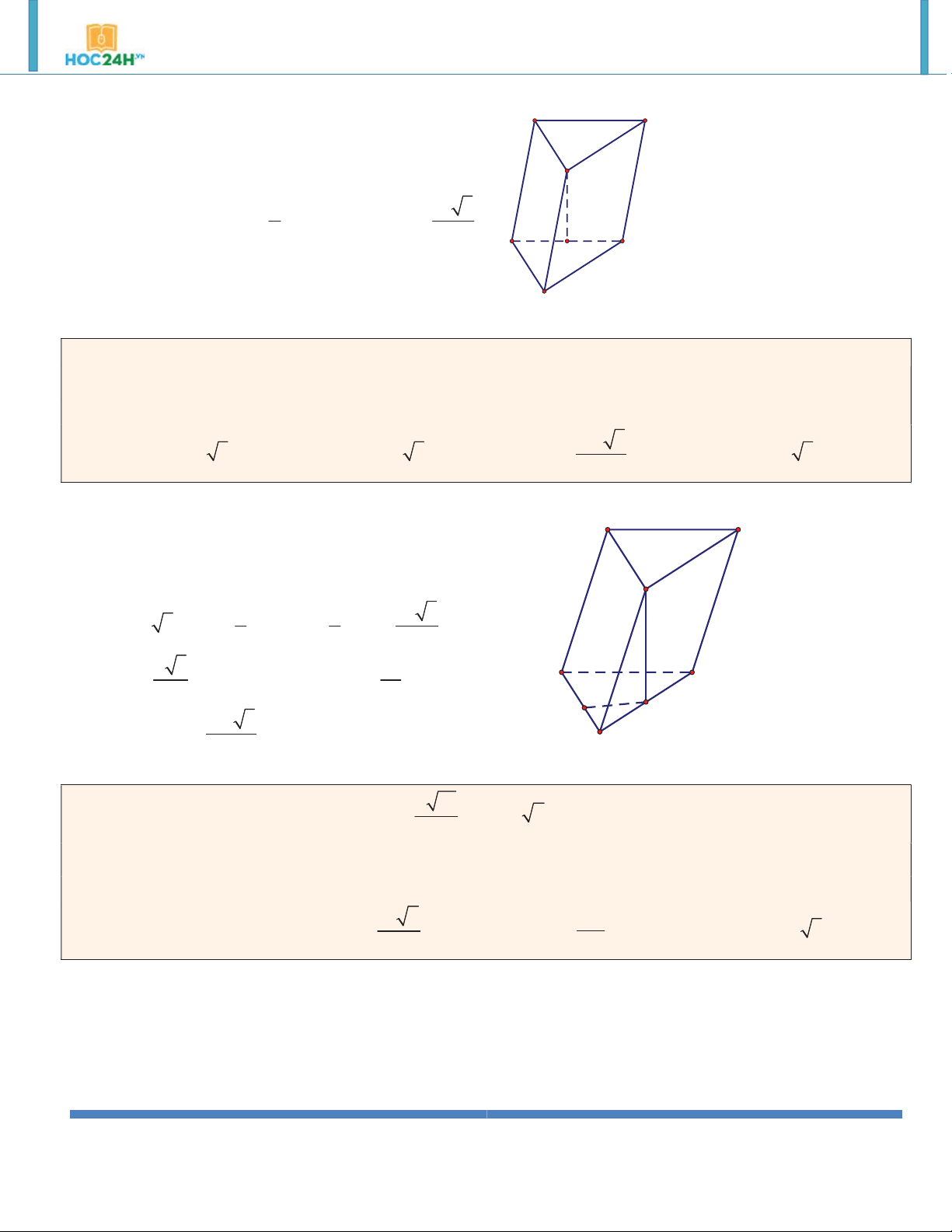
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan 3 1 a 2 B' C' V  A . B BC.AA'  2 2 A' B C A
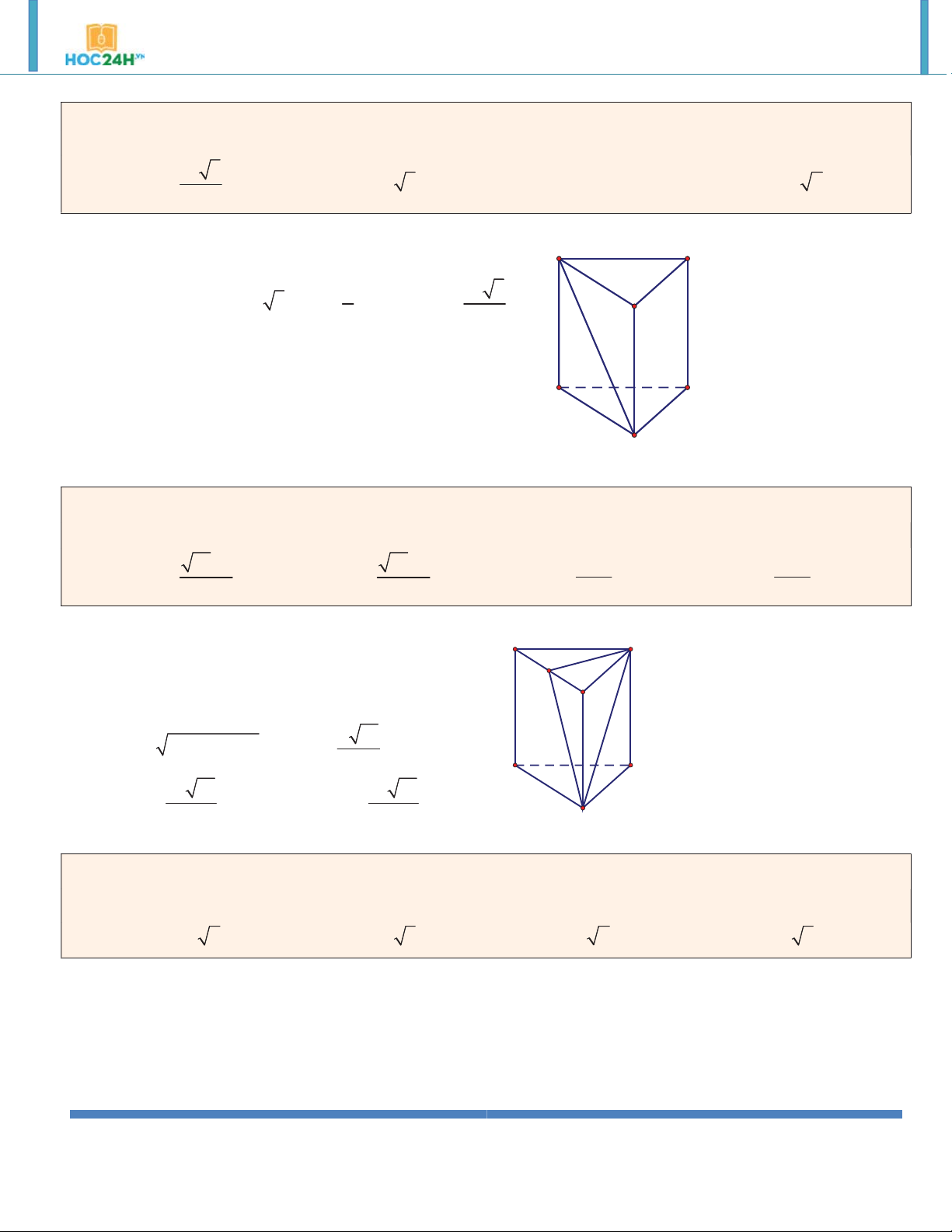
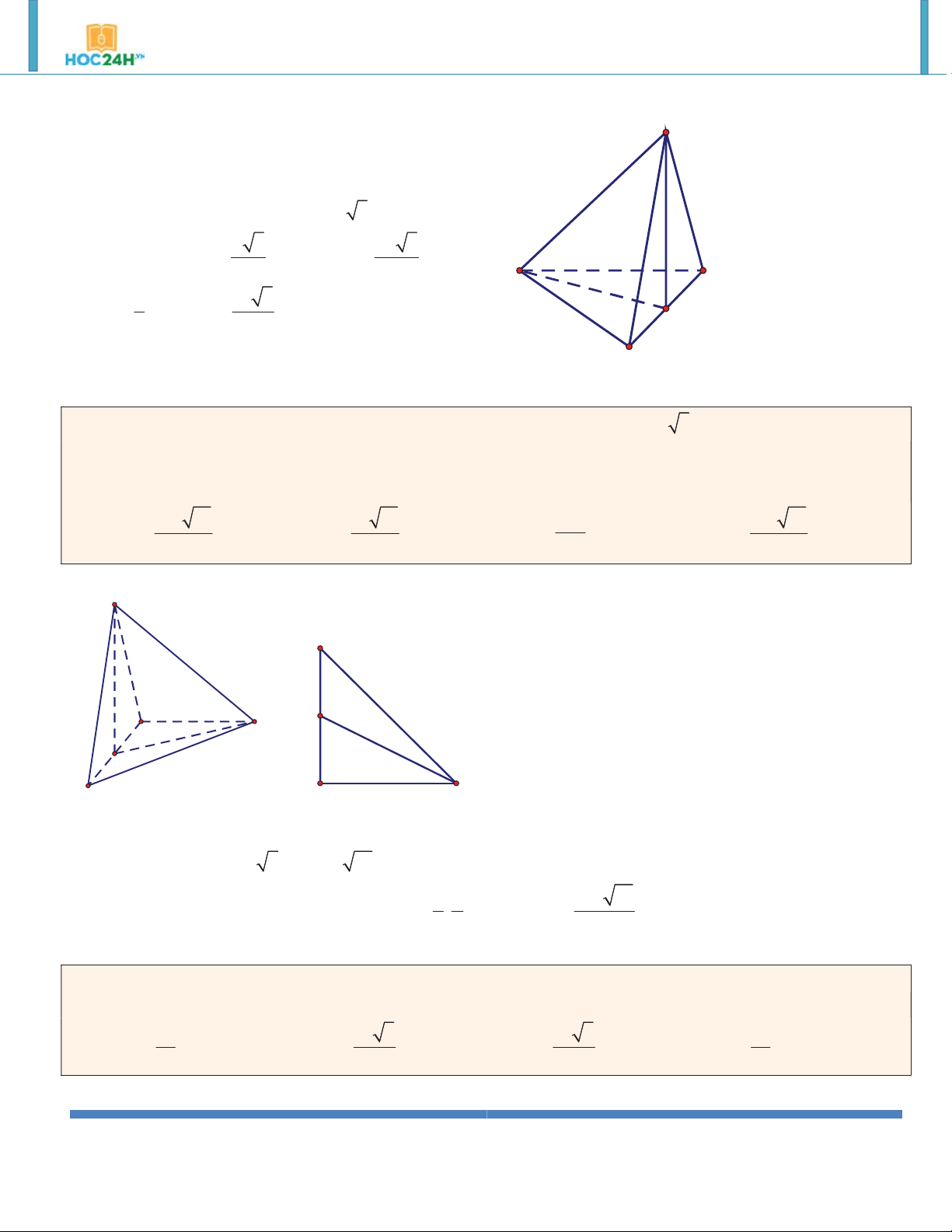
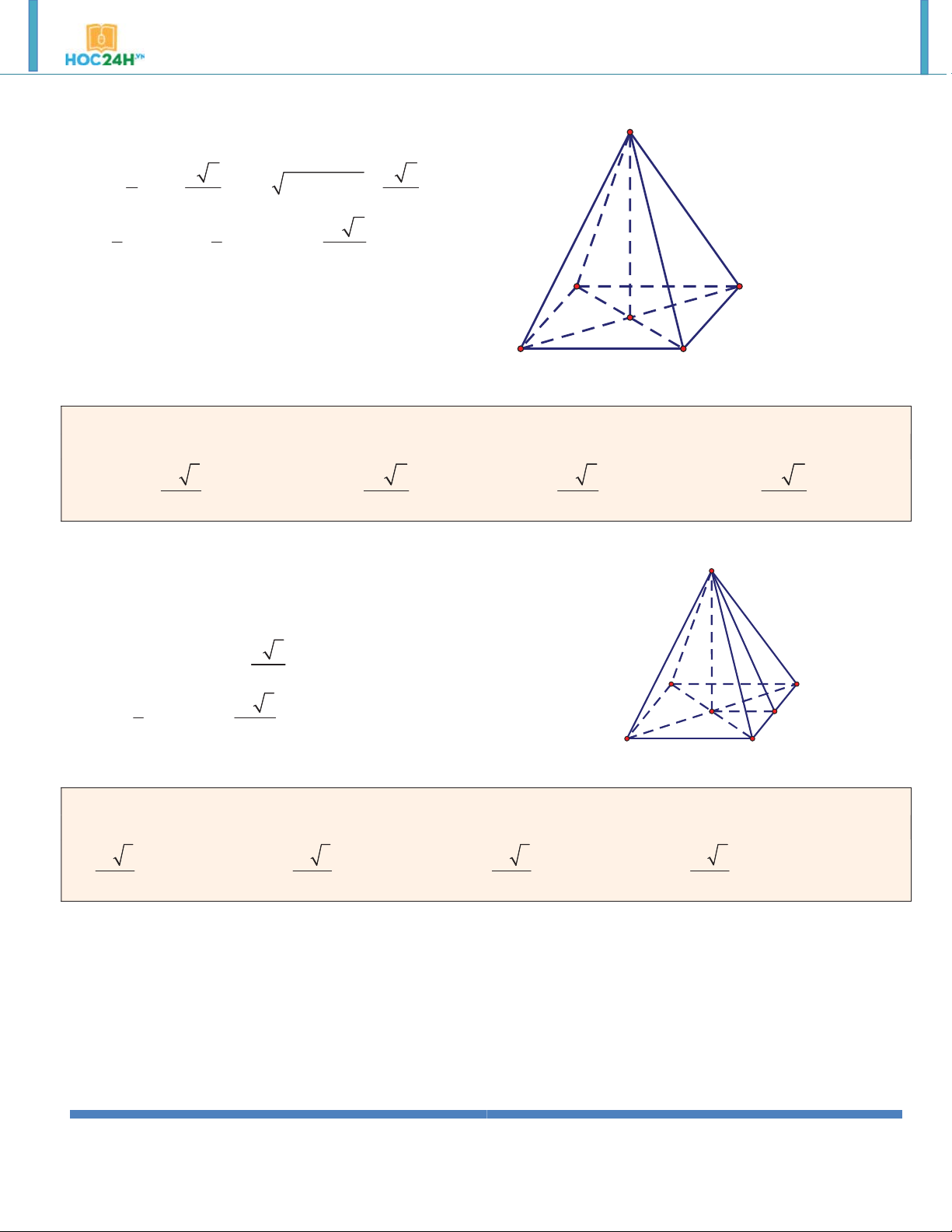
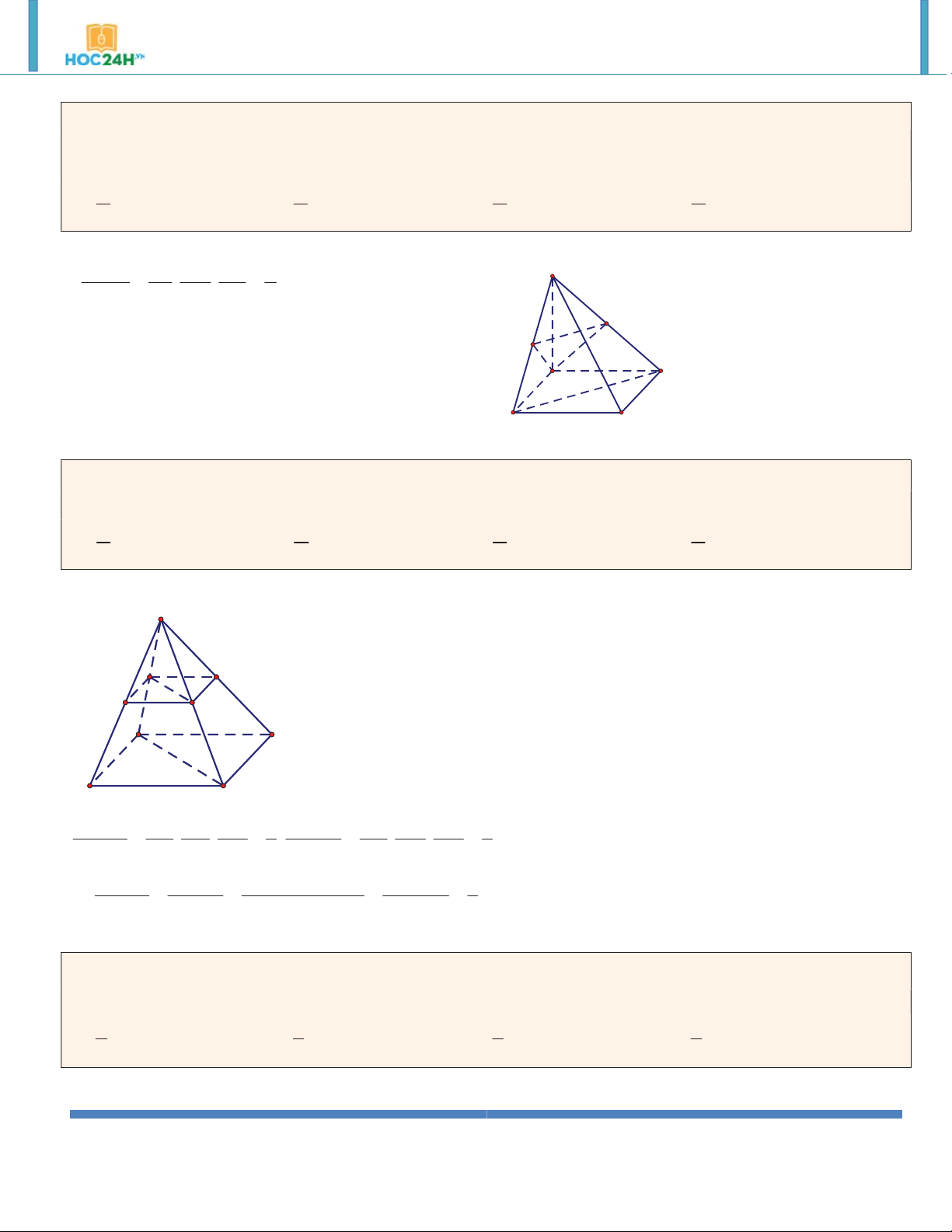
Ví dụ 4. Lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác vuông tại , A BC  2 ,
a AB  a . Mặt bên  ’
BB C’C là hình vuông. Khi đó thể tı́ch lăng trụ là: 3 a 3 A. . B. 3 a 2 . C. 3 2a 3 . D. 3 a 3 . 3 Hướng dẫn giải:
Ta có: BB 'C 'C là hình vuông B' C'
h  BB  2a  2 2
AC  BC  AB  a 3 A' 2 1 a 3  S  A . B AC ABC  2 2 B C 3 V BB .   S  a 3 ABC. ’ A B’C’ ABC A
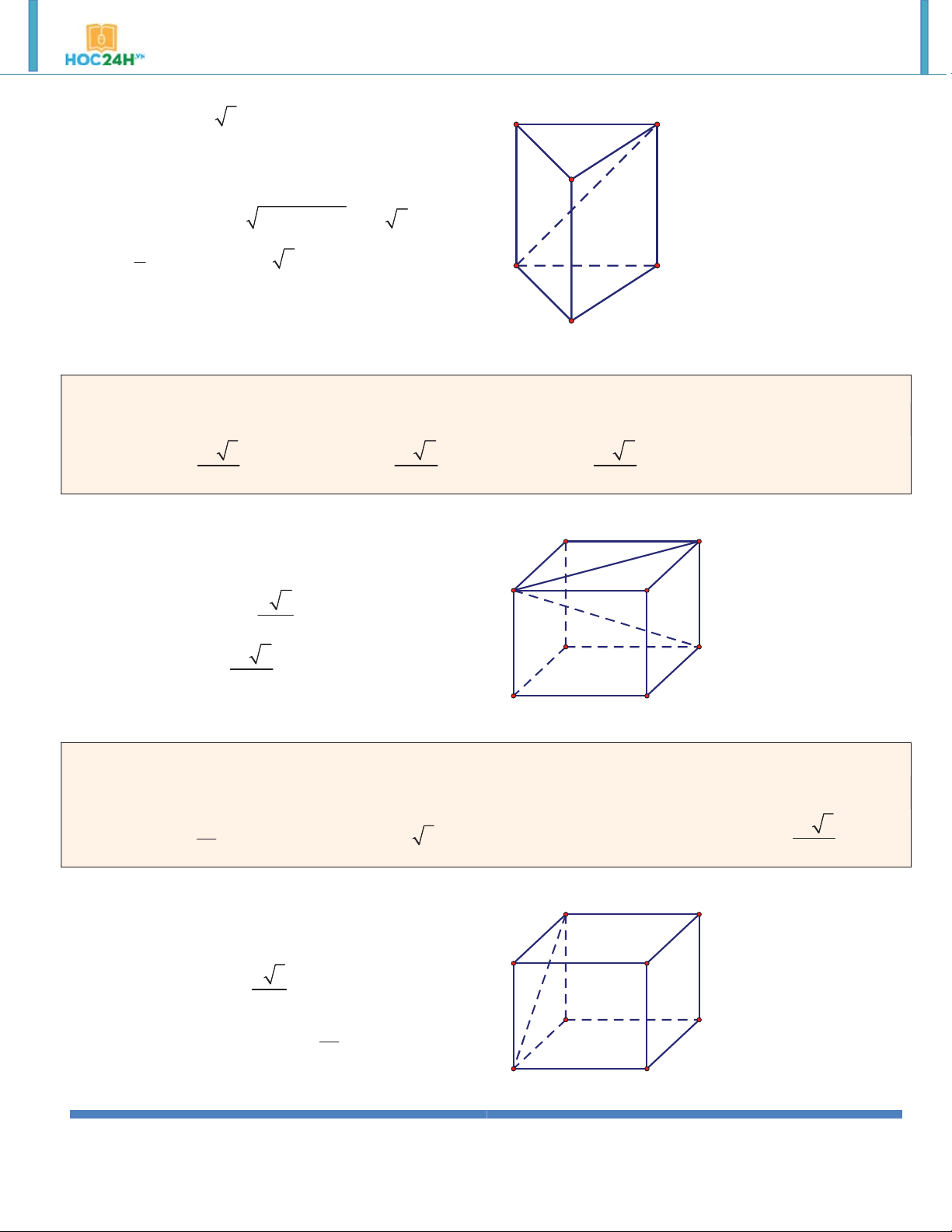
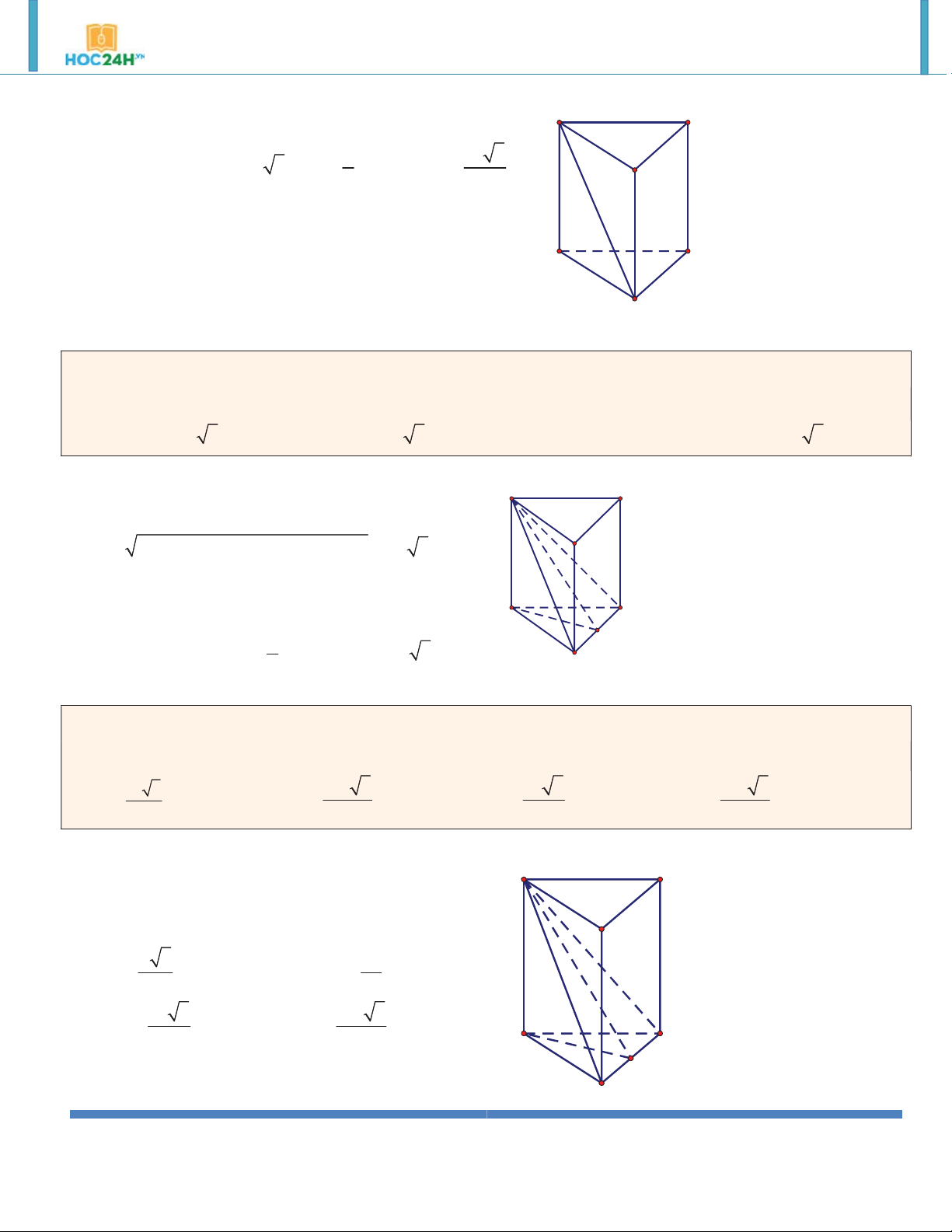
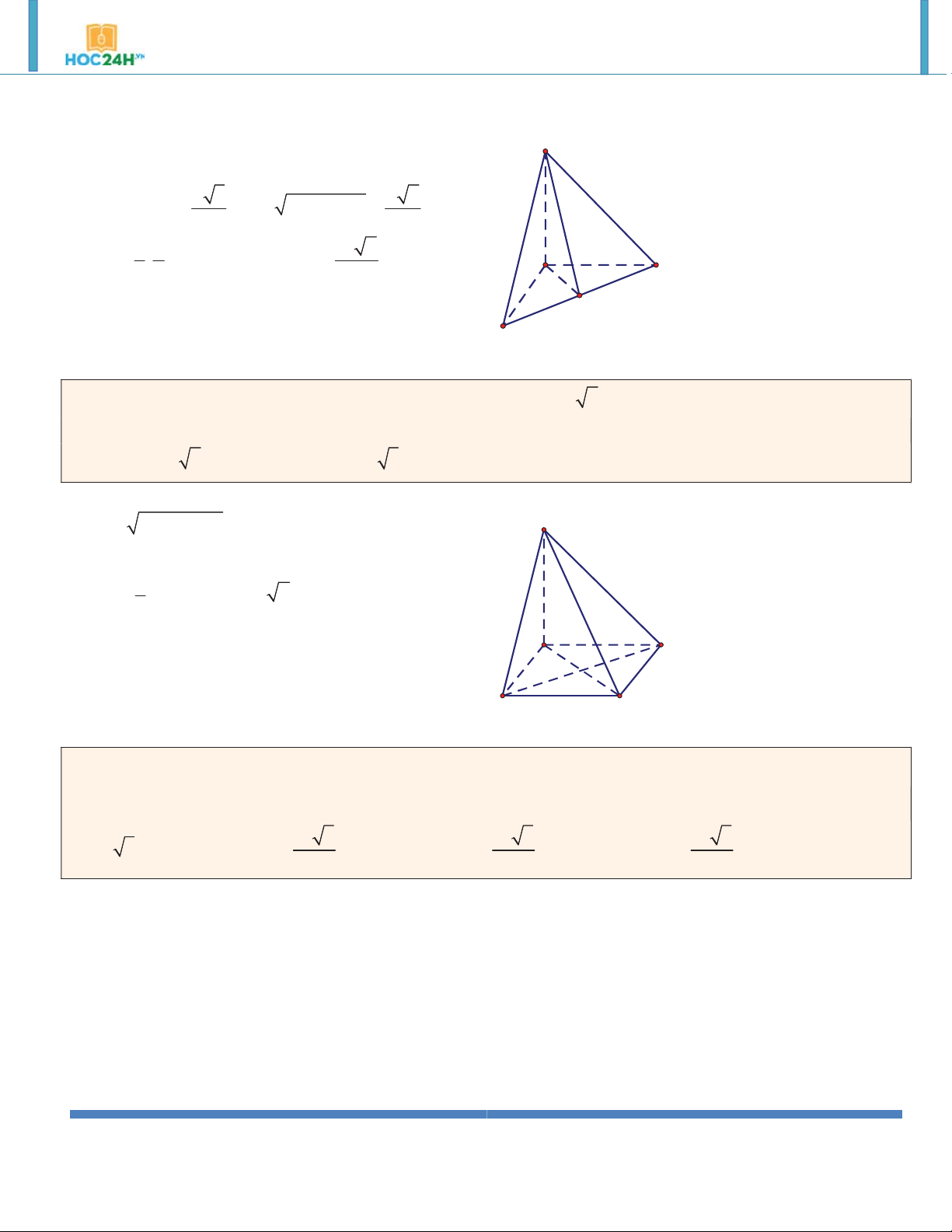
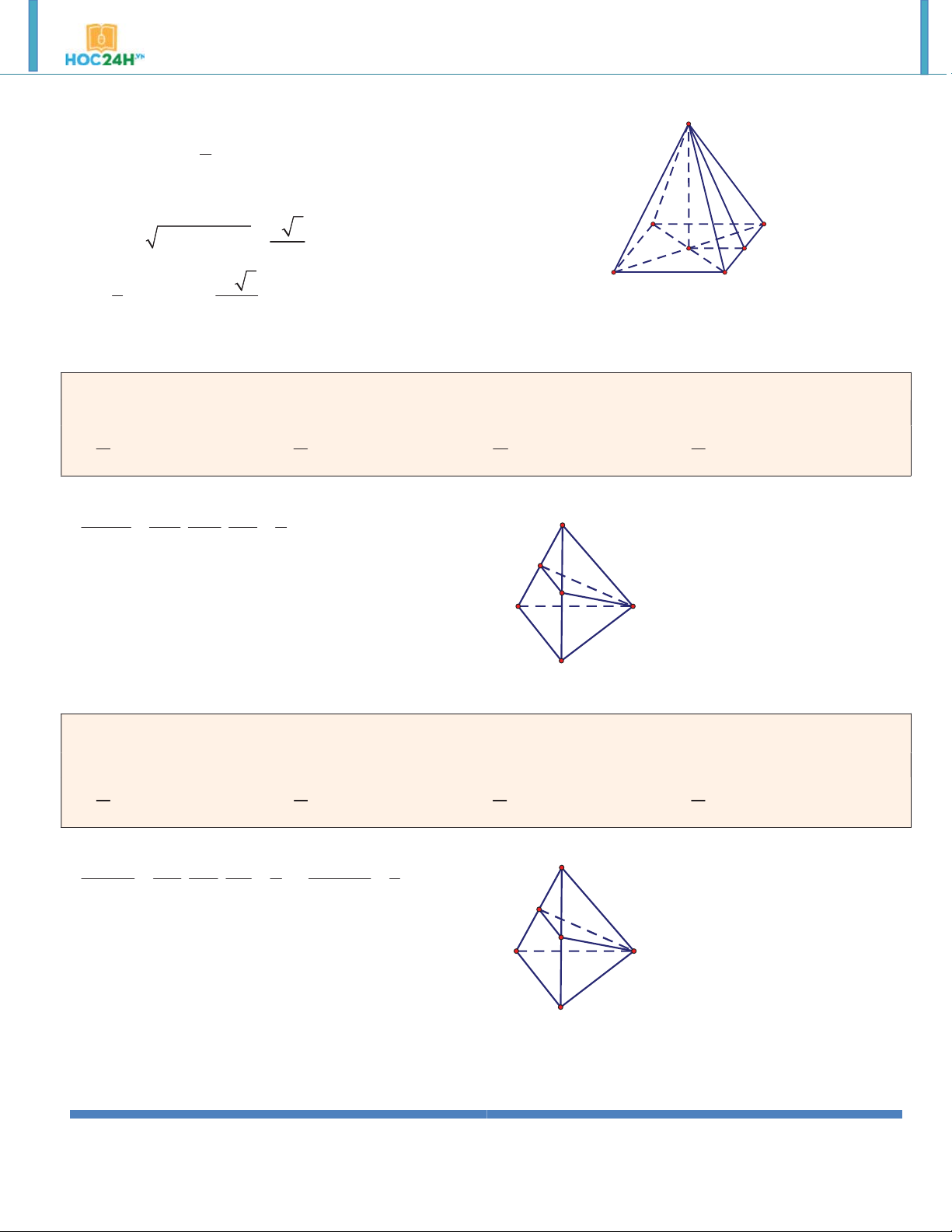
Ví dụ 5. Đáy của lăng trụ đứng tam giác ABC.A' B 'C ' là tam giác ABC vuông cân tại A có cạnh BC  a 2
và biết A' B  3a . Tính thể tích khối lăng trụ. A. 3 a . B. 3 a 2 . C. 3 a 3 . D. 3 2a . Hướng dẫn giải:
ABC vuông cân tại A nên AB  AC  a A' C'
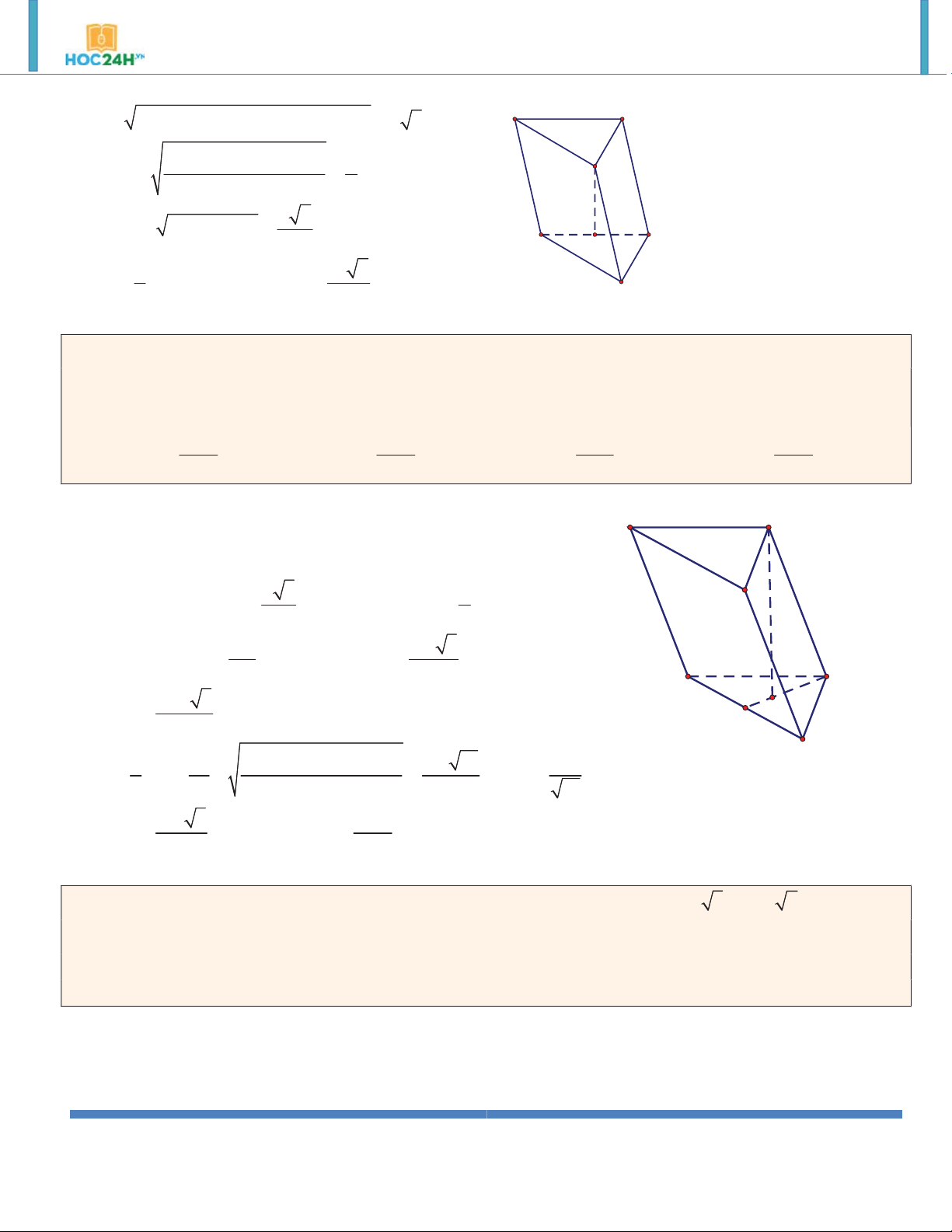
ABC.A' B 'C ' là lăng trụ đứng  AA'  AB B' 2 2  AA' 
A' B  AB  2a 2 3  V  . B h  S .AA'  a 2 ABC A C B
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 9 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
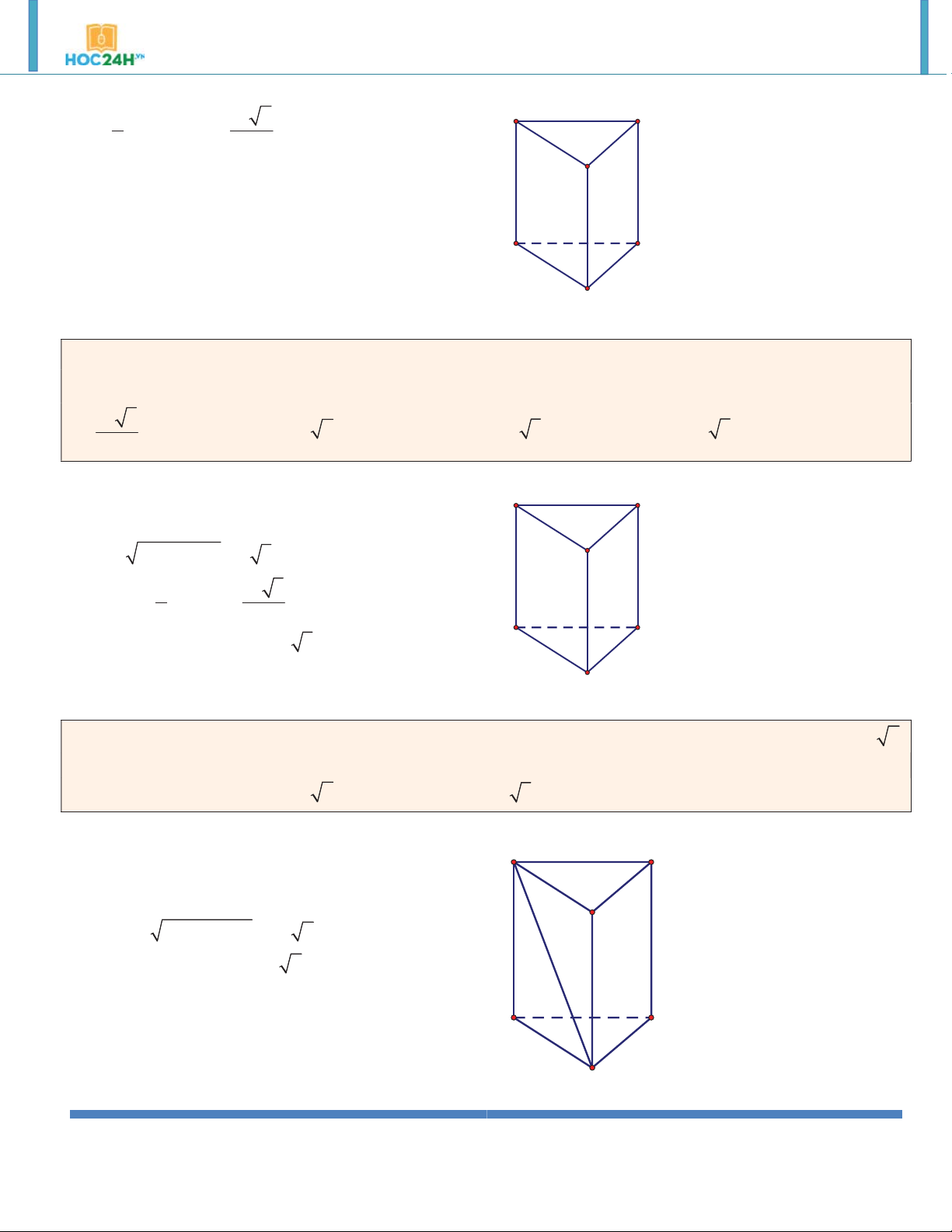
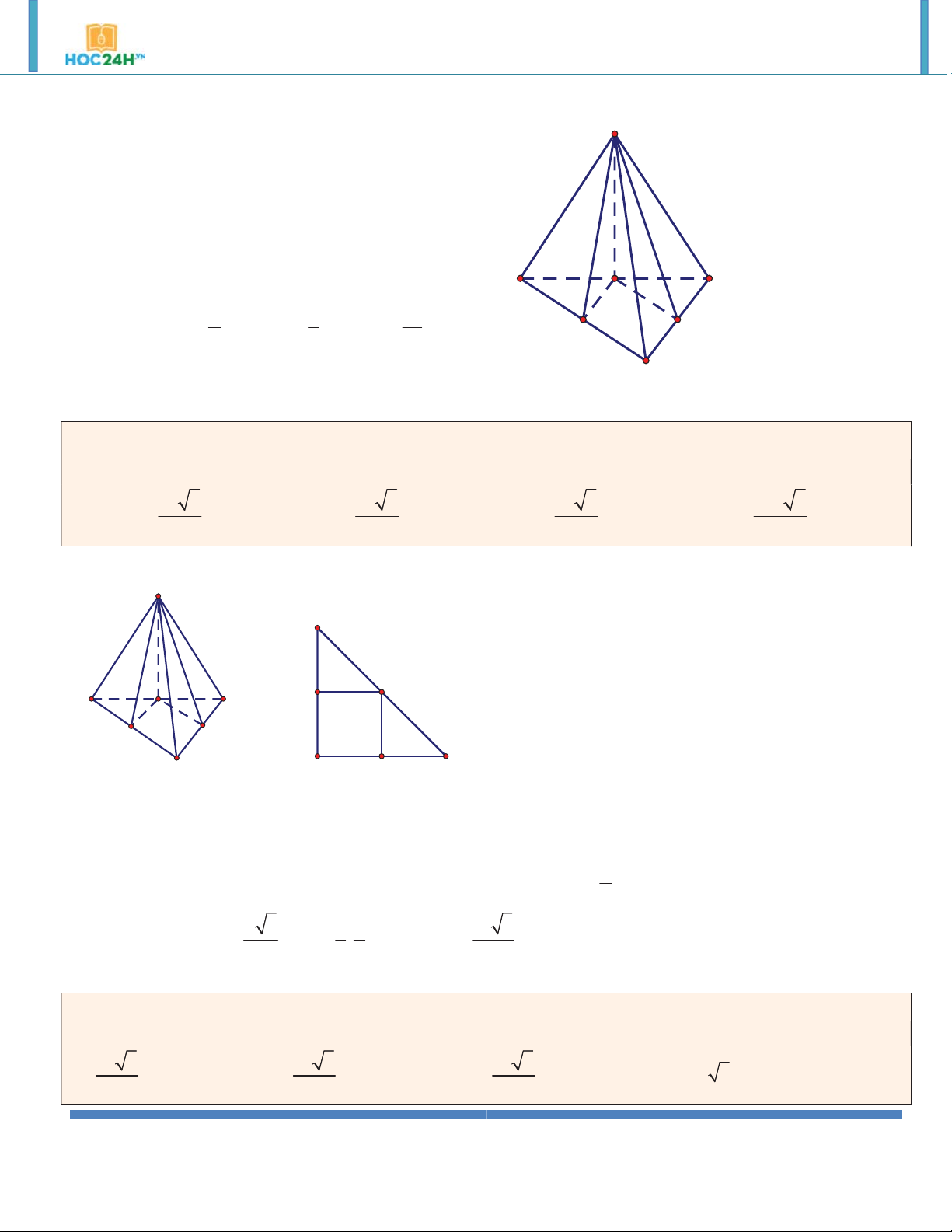
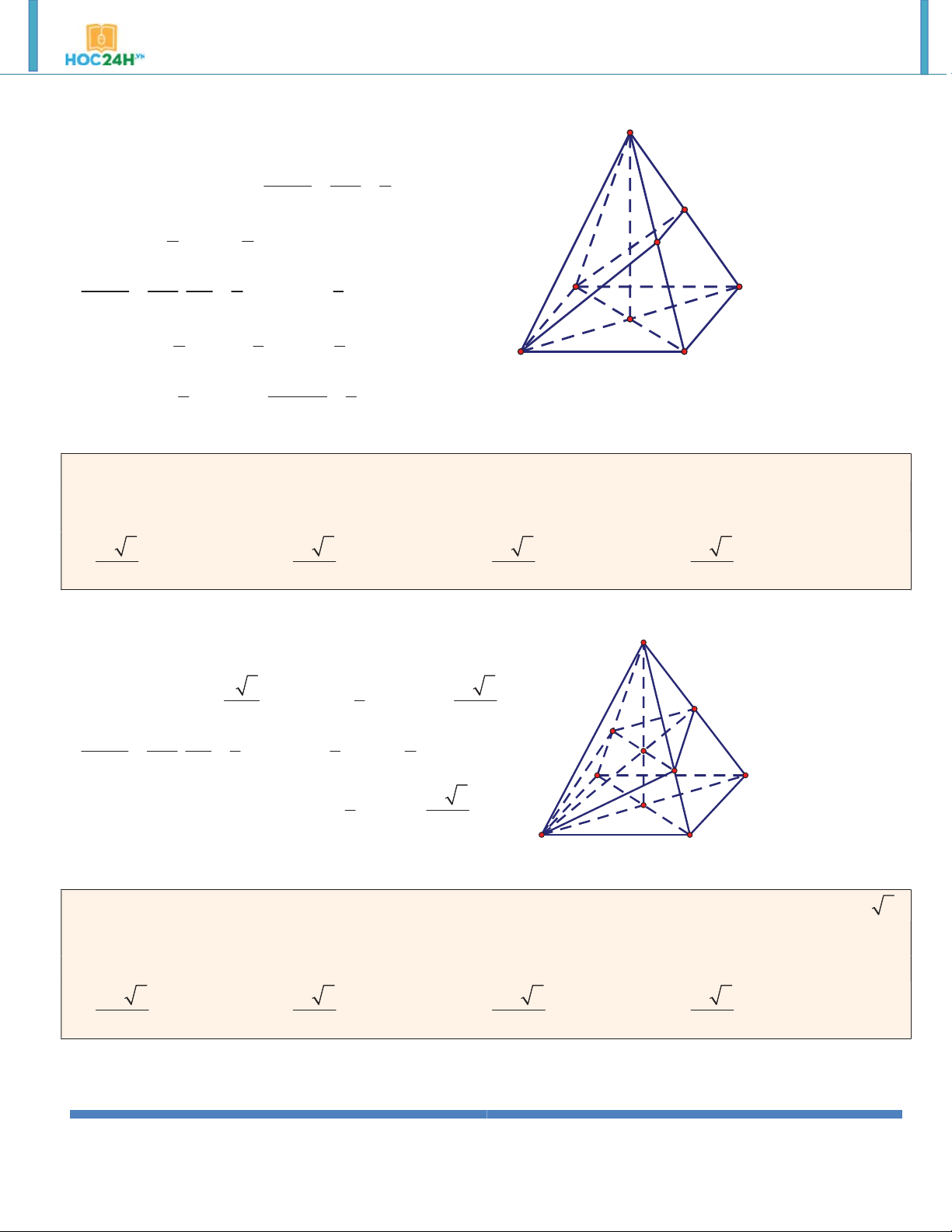
Ví dụ 6. Đáy của lăng trụ đứng tam giác ABC.A' B 'C ' là tam giác đều cạnh a  4 và biết diện tích tam giác
A' BC bằng 8. Tính thể tích khối lăng trụ. 8 2 8 A. . B. . C. 8 2 . D. 8 . 3 3 Hướng dẫn giải:
Gọi I là trung điểm BC .Ta có: A' C' ABC đều nên AB 3 AI 
 2 3; AI  BC  A' I  BC 2 B' 1 2SA' S 
BC.A' I  A' BC I   4 A' BC 2 BC
AA'  ABC AA'  AI 2 2 AA' A C 
A' I  AI  2 I  V  S .AA'  8 3
ABC.A' B 'C ' ABC B
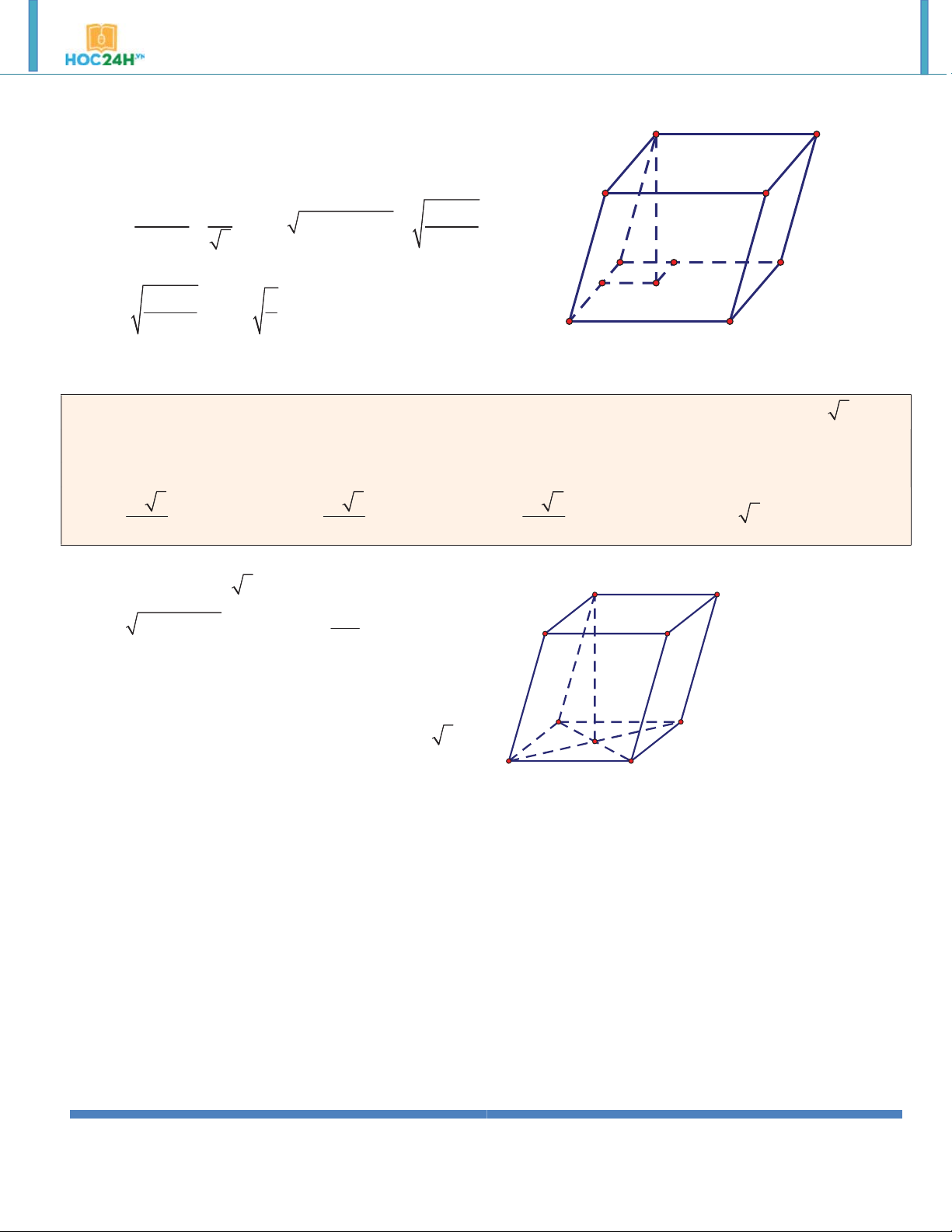
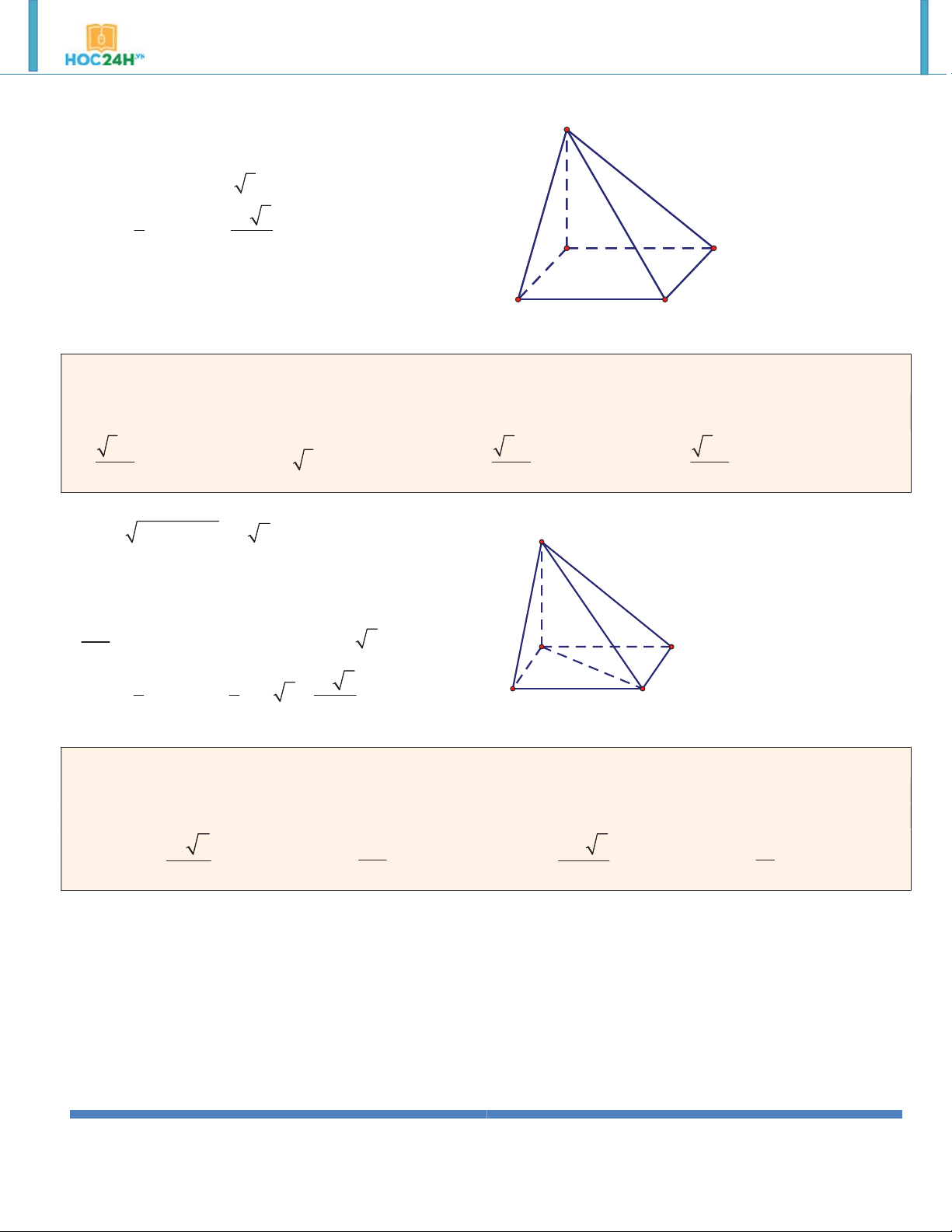
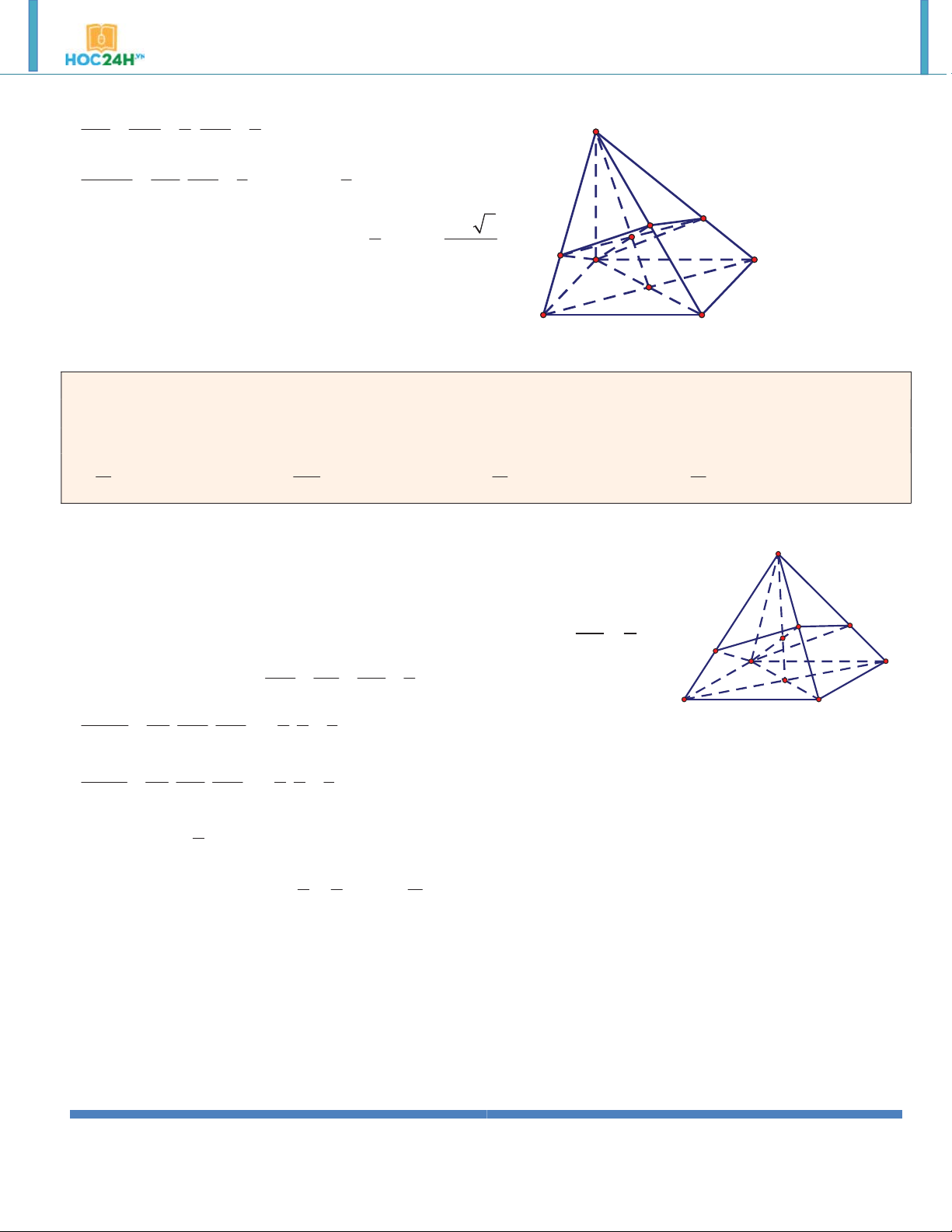
Ví dụ 7. Cho lăng trụ tứ giác đều ABC .
D A' B 'C ' D ' có cạnh bên bằng 4a và đường chéo 5a . Tính thể tích khối lăng trụ này. A. 3 9a . B. 9 . C. 3 3a . D. 3 . Hướng dẫn giải: ABC .
D A' B 'C ' D ' là lăng trụ đứng nên 2 2
BD  BD '  DD '  3a A' D' 3a
ABCD là hình vuông  AB  2 B' C' 2 9a
Suy ra B  SABCD  4 A 3 D  V  . B h  S .AA'  9a ABCD B C
Ví dụ 8. Cho hình hộp đứng AB . CD A B  C  D
  có đáy ABCD là hình vuông, tam giác A A  C vuông cân và A C
  a . Tính theo a thể tích của khối hộp AB . CD A B  C  D  . 3 a 2 3 a 2 3 a 2 3 a 2 A. V V V V ABCD.A B  C  D    . B. 24 ABCD.A B  C  D    . C. 48 ABCD.A B  C  D    . D. 16 ABCD.A B  C  D    . 8 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 10 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan a a A A'C D
 a  AC  AA'   AB  2 2 3 a 2 C B  V  S .AA' ABCD  8 A' D' B' C'
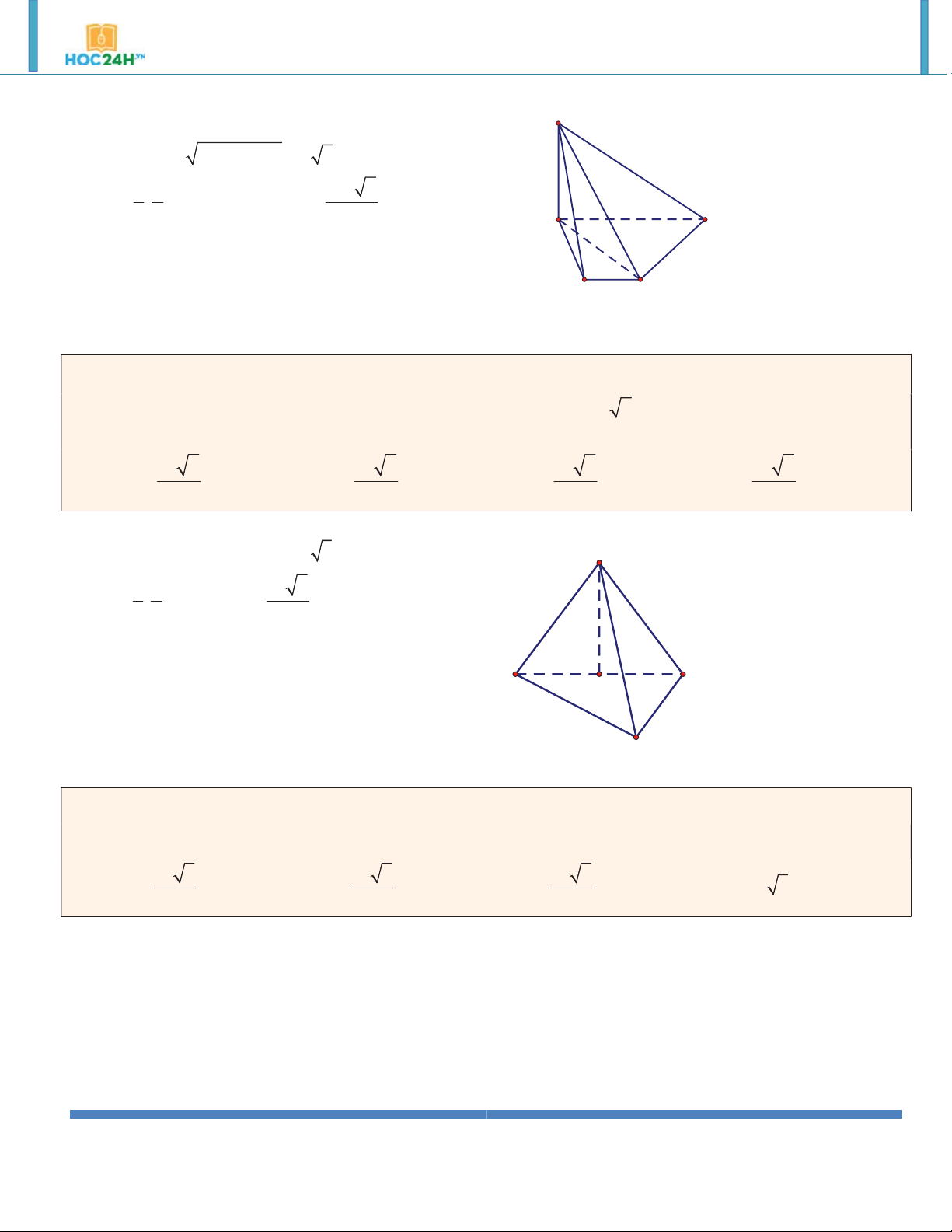
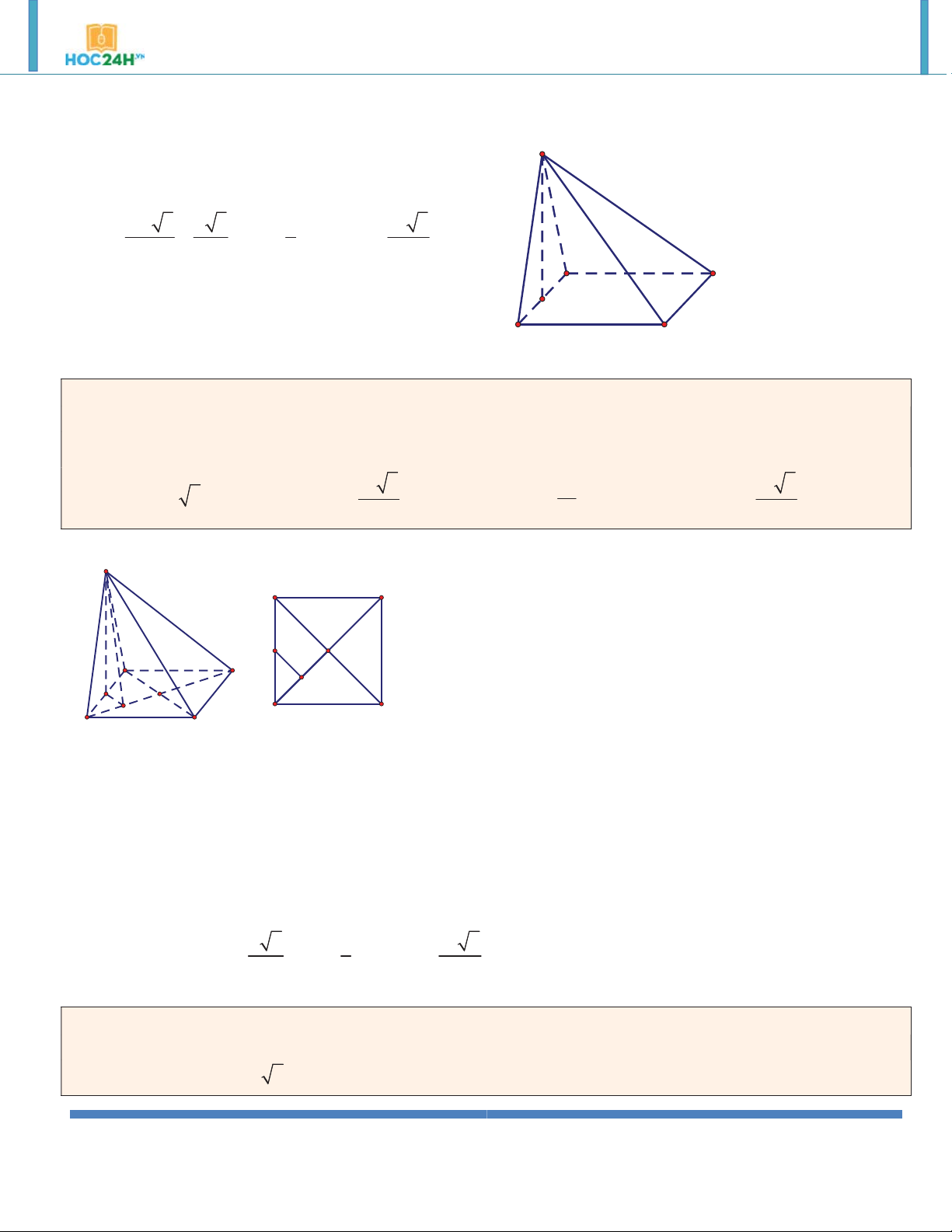
Ví dụ 9. Cho hình hộp đứng có đáy là hình thoi cạnh a và có góc nhọn bằng 60. Đường chéo lớn của đáy
bằng đường chéo nhỏ của hình hộp. Tính thể tích hình hộp . 3 a 6 3 a 3 3 a 6 3 a 3 A. . B. . C. . D. . 2 2 6 6 Hướng dẫn giải: 2 a 3 A'
Ta có tam giác ABD đều nên BD D'  a và S  2S ABCD ABD  2
Theo đề bài BD '  AC  a 3 B' 3 a 6 C' 2 2
DD '  BD '  BD  a 2  V  S .DD ' ABCD  2 A D B C
Ví dụ 10. Một tấm bìa hình vuông có cạnh 44cm , người ta cắt bỏ đi ở mỗi góc tấm bìa một hình vuông cạnh
12cm rồi gấp lại thành một cái hộp chữ nhật không có nắp. Tính thể tích cái hộp này. A. 3 1200cm . B. 3 1600cm . C. 3 2400cm . D. 3 4800cm . Hướng dẫn giải:
Theo đề bài, ta có: AA'  BB '  CC '  DD '  12cm A' D'
nên ABCD là hình vuông.
AB  44 cm  24 cm  20 ; cm h  12 cm B' 3 C'  V  S .h  4800cm ABCD A D B C
2. Dạng 2: Lăng trụ đứng có góc giữa đường thẳng và mặt phẳng
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 11 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
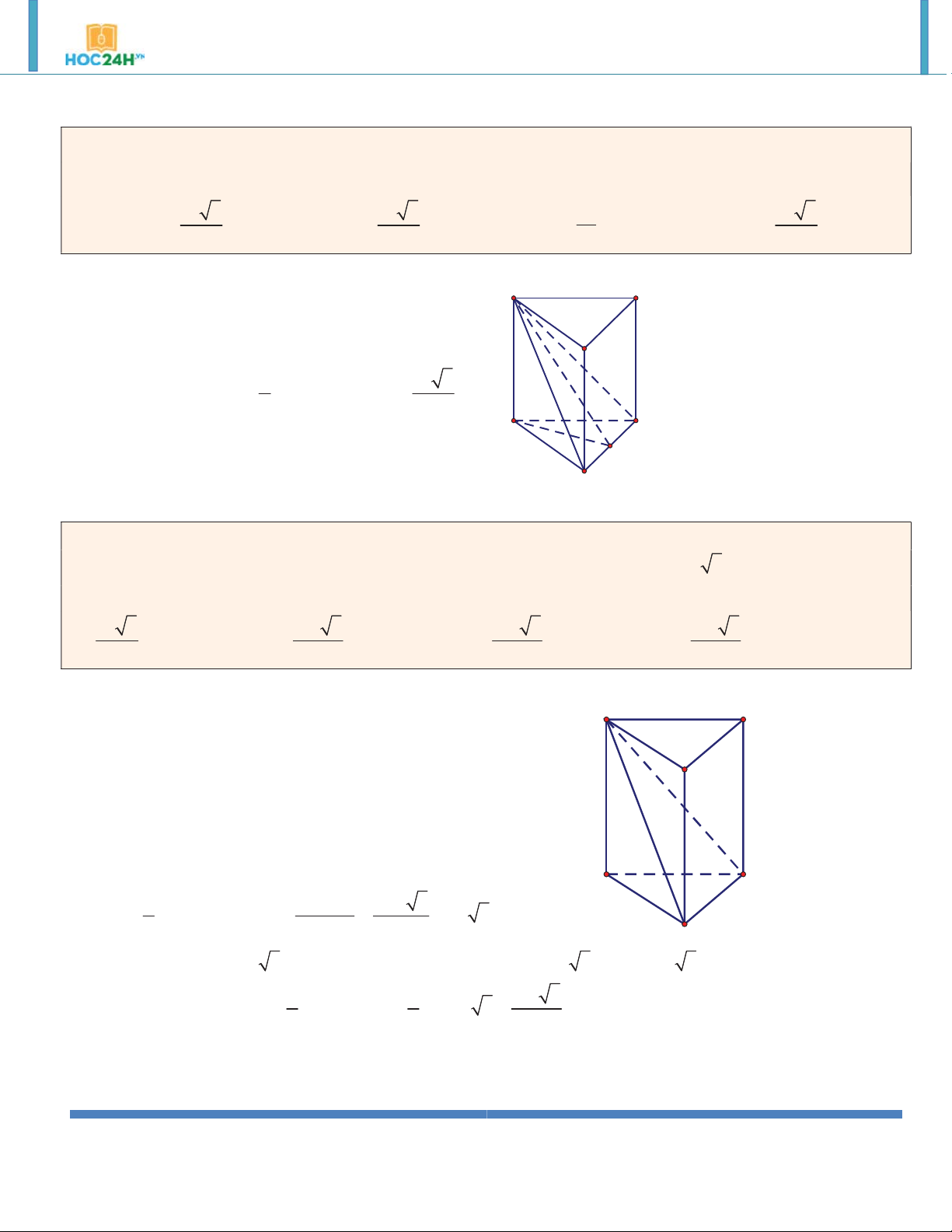
Ví dụ 1. Cho lăng trụ đứng AB . C A B  C
  có đáy ABC là tam giác vuông cân tại B , BA  BC  a , A B  hợp
với mặt đáy một góc 60. Tính theo a thể tích của khối lăng trụ AB . C A B  C   . 3 a 3 A. V V . C. 3 V . D. 3 V .     5a 2     a     a 3 ABC. A B  C    . B. 3 2 ABC.A B C ABC.A B C ABC.A B C Hướng dẫn giải:
AA'  ABC AA',ABC A'B, AB n  ABA '  60 A' C' 3 1 a 3  AA'  .
AB tan 60  a 3  V  . . AB BC.AA'  2 2 B' A C B
Ví dụ 2. Cho lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác cân tại C , góc giữa BC và ABB A   bằng
60, AB  AA  a . Tính theo a thể tích của khối lăng trụ ABC.A B  C   . 3 15.a 3 18.a 3 15a 3 18a A. V V V V ABC.A B  C    . B. 4 ABC.A B  C    . C. 4 ABC.A B  C    . D. 4 ABC.A B  C    . 4 Hướng dẫn giải:
Gọi M là trung điểm của A' B ' . A' C'
 C ' M  ABB ' AC M
 BC ',ABB' A '  BC ', BM n  MBC '  60 B' a 15 2 2
 MC '  BB '  MB ' . tan 60  2 A C 2 3 a 15 a 15  S   V  S .AA' A'B 'C ' A' B 'C '  4 4 B
Ví dụ 3. Cho lăng trụ đứng AB . C A B  C
  có đáy ABC là tam giác vuông tại A , n
AC  a, ACB  60 , góc giữa
BC và mặt phẳng AA C  C
  bằng 30. Tính theo a thể tích của khối lăng trụ AB . C A B  C   . A. 3 V . B. 3 V . C. 3 V . D. 3 V .     a 5     2 2a     a 3     a 6 ABC.A B C ABC.A B C ABC.A B C ABC.A B C Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 12 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
AC  a  AB  a 3, BC  2a B' C'
AB  AA'C 'C A'
 BC ',AA'C 'C  BC ', AC  n
'  AC ' B  30 2 2
 AC '  3a  CC ' 
AC '  AC  2a 2 1 3  V  A .
B AC.CC '  a 6 2 B C A
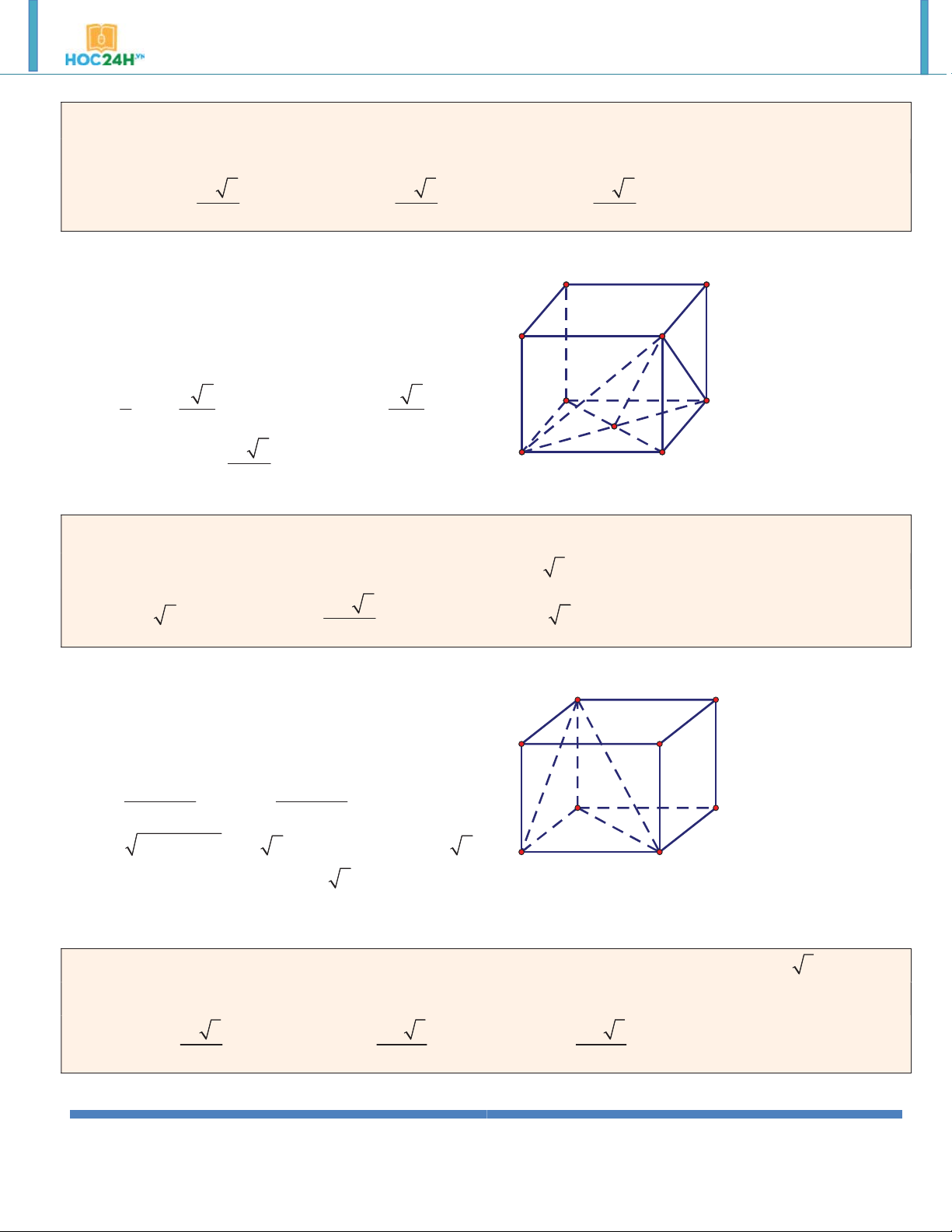
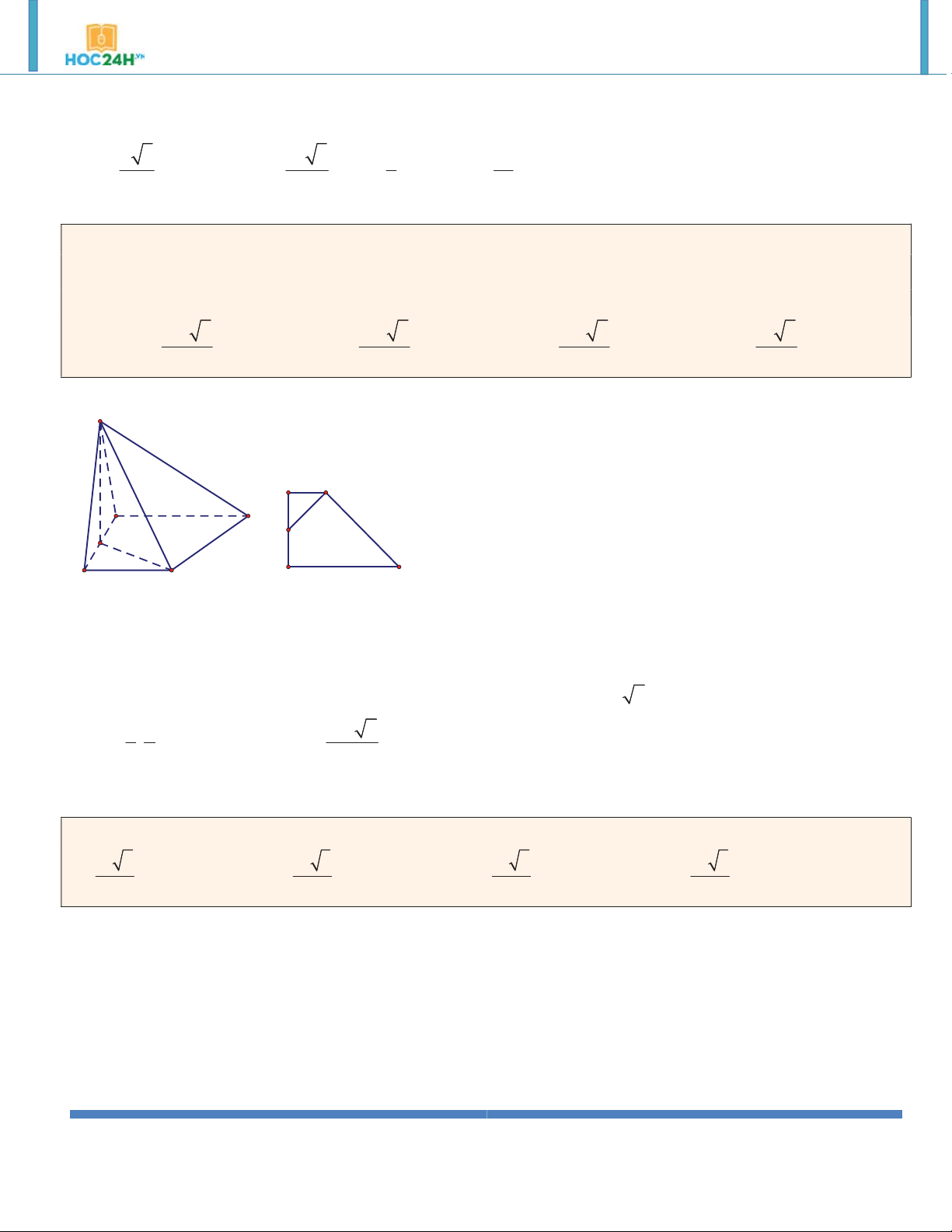
Ví dụ 4. Cho lăng trụ đứng AB . CD A B  C  D
  có đáy ABCD là hình vuông cạnh a và đường chéo BD của
lăng trụ hợp với đáy ABCD một góc 30. Tính thể tích của khối lăng trụ AB . CD A B  C  D  . 3 a 3 3 a 2 3 a 6 A. V V V ABCD.A B  C  D    . B. 3 ABCD.A B  C  D    . C. 2 ABCD.A B  C  D    . D. Kết quả khác. 3 Hướng dẫn giải:
DD '  ABCD A D
 BD';ABCD  BD ', BD n  DBD '  30 C B a 6  DD '  . BD tan 30  3 3 a 6 A' D'  V  S .DD ' ABCD  3 B' C'
Ví dụ 5. Cho hình hộp đứng AB . CD A B  C  D
  có đáy ABCD là hình thoi cạnh a và n 60o BAD  . Biết AB hợp
với đáy ABCD một góc 30. Tính theo a thể tích của khối lăng trụ AB . CD A B  C  D  . 3 a 3 a 3 A. V V . C. 3 V . D. V      a      a 5 ABCD.A B  C  D    . B. 3 2 ABCD.A B C D ABCD.A B C D ABCD.A B  C  D    . 2 Hướng dẫn giải:
BB '  ABCD A D
 AB',ABCD  AB', AB n  BAB '  30 C B a 3  BB '  . AB tan 30  3 3 a A' D'  V  S .BB '  2S .BB ' ABCD ABD  2 B' C'
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 13 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Ví dụ 6. Cho lăng trụ tứ giác đều AB . CD A B  C  D
  có cạnh đáy bằng a , góc giữa AC ' và mặt phẳng BCC B  
bằng 30. Tính theo a thể tích của khối lăng trụ AB . CD A B  C  D  . 3 2a A. 3 V . B. 3 V . C. V V .     a     2a     2a ABC.A B C ABC.A B C ABC.A B  C    . D. 3 2 ABC.A B C Hướng dẫn giải:
AB  BCC 'B ' A D
 AC ',BCC 'B '  AC ',BC  n
'  AC ' B  30 C B  BC '  .
AB cot 30  a 3 2 2
 BB '  BC '  B 'C '  a 2 A' D' 3  V  S .BB '  a 2 ABCD B' C'
Ví dụ 7. Cho lăng trụ tứ giác đều AB . CD A B  C  D
  có cạnh đáy bằng a , đường chéo AC ' tạo với mặt bên BCC B
  một góc 0   45o  
. Khi đó, thể tích khối lăng trụ bằng: A. 3 2 a cot  1 . B. 3 a cot 2 . C. 3 2 a cot  1 . D. 3 2 a tan  1 . Hướng dẫn giải:
AB  BCC 'B ' A D
 AC ',BCC 'B '  AC ', BC  n
'  AC ' B   C B 2  BC '  A .
B cot  BB '  a cot  1 3 2 A' D'  V  S
.BB '  a cot  1 ABCD B' C'
3. Dạng 3: Lăng trụ đứng có góc giữa hai mặt phẳng
Ví dụ 1. Cho lăng trụ đứng . ABC A B  C
  có đáy ABC là tam giác vuông cân tại B , BA  BC  a , A B  hợp
với mặt đáy một góc 60. Tính theo a thể tích của khối lăng trụ . ABC A B  C   . 3 a 3 A. V V . C. 3 V . D. 3 V .     5a 2     a     a 3 ABC.A B  C    . B. 3 2 ABC.A B C ABC.A B C ABC.A B C Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 14 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
AA'  ABC AA',ABC A'B, AB n  ABA '  60 A' C' 3 1 a 3  AA '  .
AB tan 60  a 3  V  . . AB BC.AA'  2 2 B' A C B
Ví dụ 2. Cho lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác cân tại A , AC  2 , a n
CAB  120, góc giữa A B
 C và mặt phẳng ABC bằng 45. Tính theo a thể tích của khối lăng trụ ABC.A B  C   . A. 3 V . B. 3 V . C. 3 V . D. 3 V .     2a 3     3a     3a 3     a 3 ABC.A B C ABC.A B C ABC.A B C ABC.A B C Hướng dẫn giải:
Gọi M là trung điểm của BC . A' C'
AM  AC.cos 60  a B' 2 2
BC  AC  AB  2A .
B AC.cos120  2a 3
A' M  BC, AM  BC  
 A'BC,ABC  A'M, AM n  AMA'  45 A C 1 M 3
 AA'  AM  a  V 
BC.AM .AA'  a 3 2 B
Ví dụ 3. Cho lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác đều cạnh a . Mặt phẳng AB 'C ' tạo với mặt đáy góc 0
60 . Tính theo a thể tích lăng trụ ABC.A' B 'C '. 3 3 3a 3 3 a 3 3 3a 3 A. a 3 V . B. V  . C. V  . D. V  . 2 4 8 8 Hướng dẫn giải:
Gọi M là trung điểm B 'C ' A C
 A' M  B 'C ' 0  60  
 AB'C ',A'B'C ' AM, A'M n  AMA' B a 3 n 3a A' M 
; AA'  A' M.tan AMA'  2 2 2 3 a 3 3a 3 S   V  S .AA' 
A'B 'C ' 4 ABC 8 C' A' M B'
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 15 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Ví dụ 4. Cho lăng trụ tam giác đều ABC.A B  C
  có cạnh đáy bằng a . Góc giữa hai mặt phẳng A B  C và
ABC bằng 30. Tính theo a thể tích của khối lăng trụ ABC.A B  C   . 3 a 3 3 a 3 3 a 3 a 3 A. V V V V ABC.A B  C    . B. 8 ABC.A B  C    . C. 4 ABC.A B  C    . D. 2 ABC.A B  C    . 2 Hướng dẫn giải:
Gọi M là trung điểm của BC . A' C'
 A' M  BC, AM  BC  
 A'BC,ABC A'M, AM n
 A' MA  30 B' 3 a a 3
 AA'  AM .tan 30   V  S .AA'  2 ABC 8 A C M B
Ví dụ 5. Cho hình lăng trụ đứng ABC.A' B 'C ' có đáy ABC là tam giác vuông tại B , BC  a , mặt phẳng
A'BC tạo với đáy một góc 30 và tam giác A'BC có diện tích bằng 2 a
3 . Tính thể tích khối lăng
trụ ABC.A' B 'C ' . 3 a 3 3 3a 3 3 3a 3 3 3a 3 A. . B. . C. . D. . 8 4 8 2 Hướng dẫn giải: BC  AB  A' C'
  BC  A' B BC  AA'
BC  AB  ABC   B' BC
A' B A'BC     
BC  ABCA'BC  
 ABC,A'BC AB, A'B n  ABA' A C 2 1 2.S 2.a 3 A' S  A' . B BC  A' BC B    2a 3 A'BC 2 BC a B n 0 n 0 AB  A' .
B cos ABA'  2a 3.cos30  3 ; a AA'  A' .s
B in ABA'  2a 3.sin 30  a 3 3 1 1 3a 3 V  . B h  S .AA'  .A .
B BC.AA'  .3 . a . a a 3
ABC.A'B'C ' ABC  2 2 2
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 16 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Ví dụ 6. Cho lăng trụ tứ giác đều AB . CD A B  C  D
  có cạnh đáy bằng a , mặt phẳng BC '  D hợp với đáy AB 
CD một góc 60. Tính theo a thể tích của khối lăng trụ AB . CD A B  C  D  . 3 a 6 3 a 3 3 a 6 A. V V V ABCD.A B  C  D    . B. 6 ABCD.A B  C  D    . C. 2 ABCD.A B  C  D    . D. Kết quả khác. 2 Hướng dẫn giải:
Gọi I là trung điểm của BD . A' D'
 AC  BD,C ' I  BD 
BC 'DABCD  BD B' C'  
 BC 'D;ABCD AC,C 'I n  CIC '  60 1 a 2 a 6 A CI  AC 
 CC '  CI.tan 60  D 2 2 2 3 I a 6  V  S .CC ' B ABCD  C 2
Ví dụ 7. Cho hình hộp chữ nhật ABCD.A' B 'C ' D ' . Mặt phẳng A'BC hợp với đáy ABCD một góc 0 60 ,
A'C hợp với đáy ABCD một góc 0
30 và AA'  a 3 . Tính theo a thể tích khối hộp. 3 2a 6 A. 3 V  2a 6 . B. V  . C. 3 V  2a 2 . D. 3 V  a . 3 Hướng dẫn giải:
AA'  ABCD A' D' 0
 30  A'C,ABC 
D   A'C, AC n  A'CA B' C' 0  60  
 A'BC,ABCD A'B, A  n
B  A' BA AA' AA' AB  n  a; AC  n  3a A tan A' BA tan A'CA D 2 2 2
BC  AC  AB  2a 2; S  . AB BC  2a 2 ABCD B C 3  V  S .AA'  2a 6
ABCD.A' B 'C ' D' ABCD
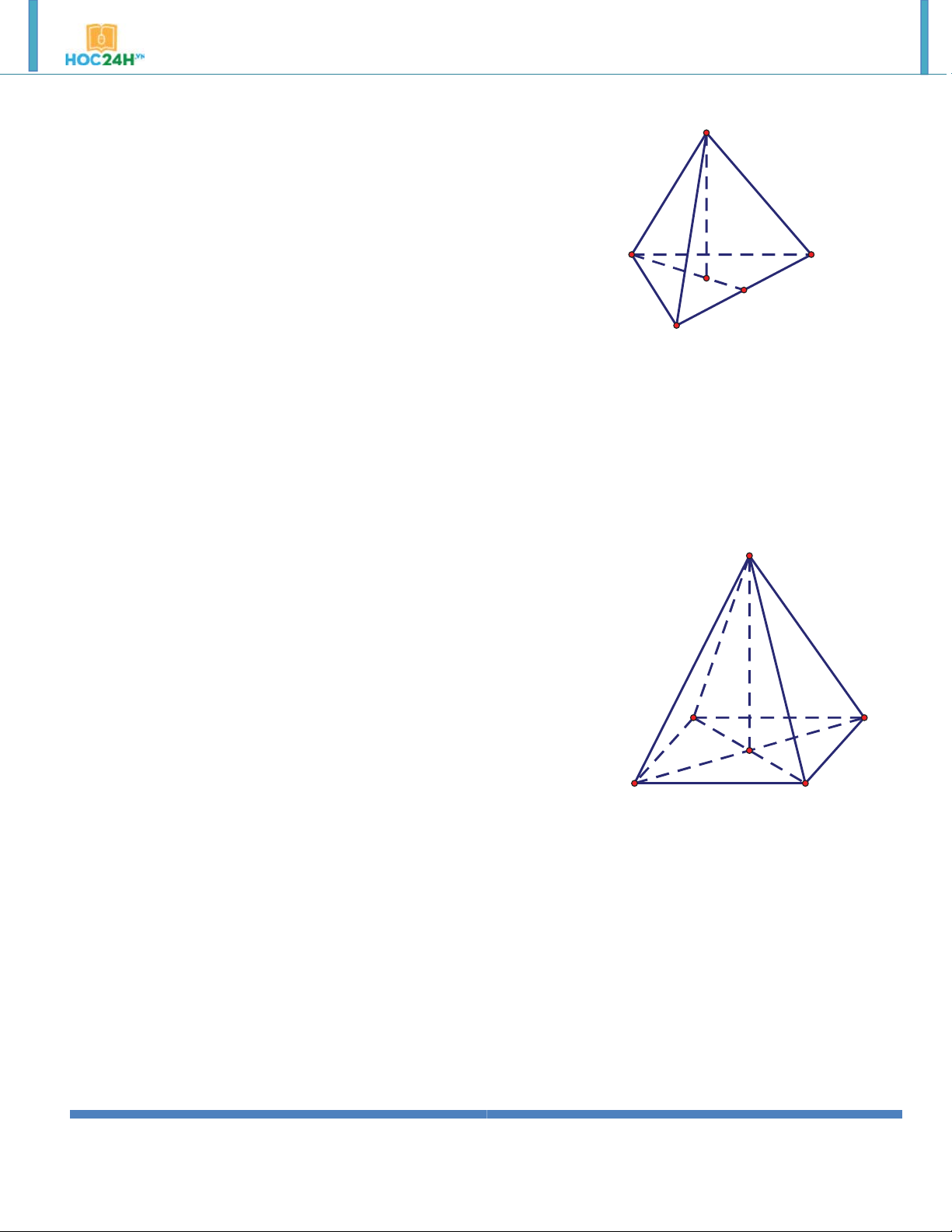
4. Dạng 4: Khối lăng trụ xiên Ví dụ 1. Cho lăng trụ . ABC A B  C
  có đáy ABC là tam giác đều cạnh a . Biết cạnh bên bằng a 3 và hợp với
đáy ABC một góc 60. Tính theo a thể tích của khối lăng trụ . ABC A B  C   . 3 a 3 3 3a 3 3 5a 3 A. V V V ABC.A B  C    . B. 8 ABC.A B  C    . C. 8 ABC.A B  C    . D. Đáp án khác. 8 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 17 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Kẻ A' H  ABC C' B'
 AA ABC  AA AH n ', ',
 A ' AH  60 A' 3 3a 3a 3
 A' H  AA'.sin 60   V  S .A' H  2 ABC 8 C B H A Ví dụ 2. Cho lăng trụ . ABC A B  C
  có đáy ABC là tam giác đều cạnh a , điểm A' cách đều ba điểm , A , B C .
Góc giữa AA' và ABC bằng 60. Tính theo a thể tích của khối lăng trụ . ABC A B  C   . 3 3a 4 3 a 3 3 a 3 3 5a 3 A. V V V V ABC.A B  C    . B. 4 ABC.A B  C    . C. 2 ABC.A B  C    . D. 4 ABC.A B  C    . 4 Hướng dẫn giải:
Gọi G là trọng tâm của ABC  A 'G  ABC C' B'
 AA',ABC  AA', AG n  GAA '  60 3 a 3 A'
 A'G  AG. tan 60  a  V  S .A'G ABC  4 C G B A
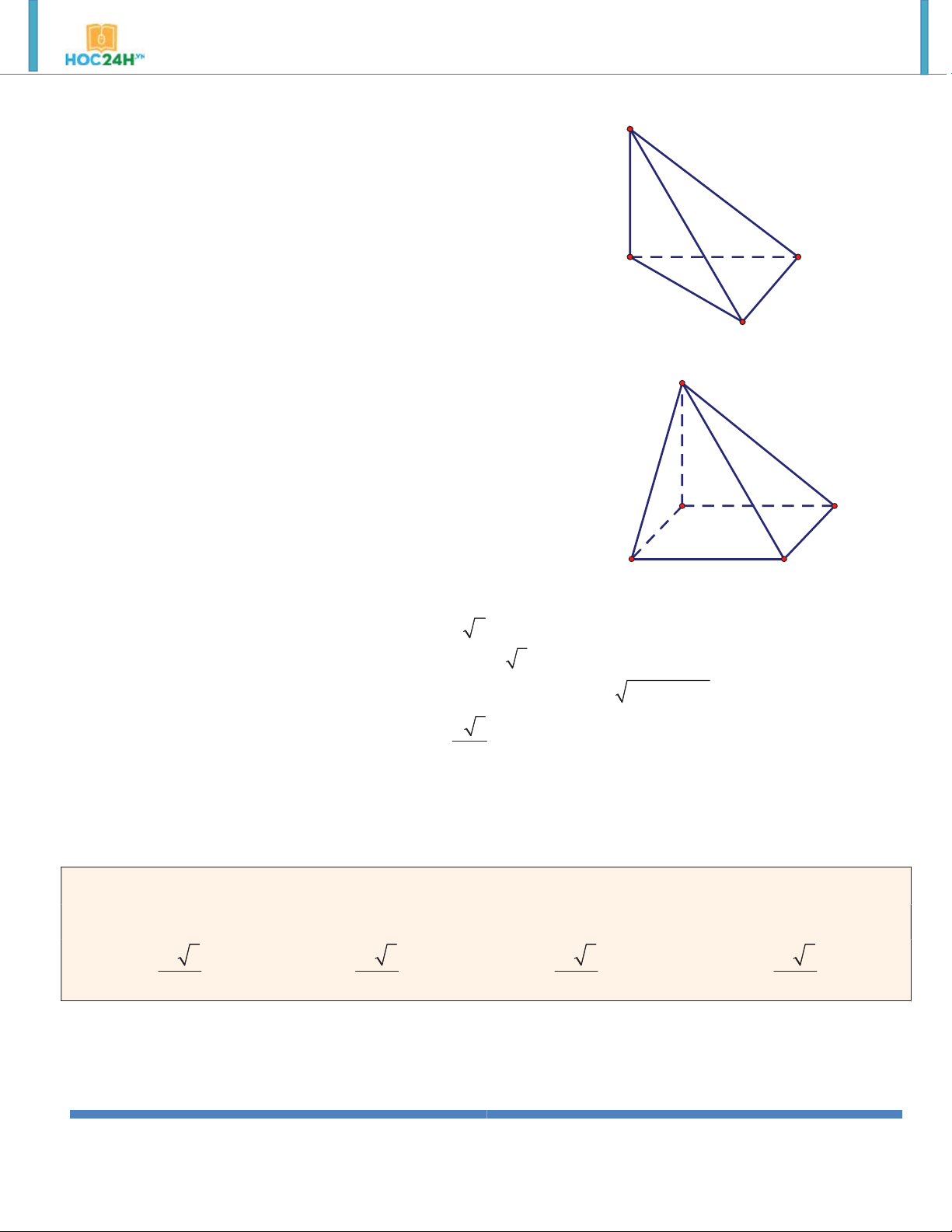
Ví dụ 3. Cho lăng trụ ABC.A B  C
  có đáy ABC là tam giác vuông cân tại B , AC  2a ; cạnh bên AA  2a
. Hình chiếu vuông góc của A trên mặt phẳng (ABC) là trung điểm cạnh AC . Tính thể tích V của
khối lăng trụ ABC.A B  C   . 1 3 a 3 2a A. 3 V  a . B. V  . C. 3 V  a . D. V  . 2 3 3 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 18 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Vì ABC là tam giác vuông cân tại B nên trung tuyến A' C' BH cũng là đường cao của nó và 1
HB  HA  HC  AC  a . 2 B' 2 2 2 2
A' H  A' A  AH  2a  a  a 1 A B 3 V
    A ' H  S
 A' H  BH  AC  a ABC.A B C ABC 2 H C
Ví dụ 4. Cho lăng trụ ABC.A B  C
  có đáy ABC là tam giác đều cạnh a , hình chiếu vuông góc của A' lên mặt
phẳng ABC trùng với tâm O của tam giác ABC . Tính theo a thể tích của khối lăng trụ a 3 ABC.A B  C
  , biết khoảng cách giữa AA' và BC là . 4 3 a 3 3 a 3 3 4a 3 A. V V V ABC.A B  C    . B. 12 ABC.A B  C    . C. 4 ABC.A B  C    . D. Kết quả khác. 5 Hướng dẫn giải:
Gọi M là trung điểm của BC  BC  AA'M  C' B'
Gọi H là hình chiếu của M lên AA' a 3 n HM 1  HM  d 
 sin A' AO   A' AA',BC 8 AM 2 n n a
 A' AO  30 A'O  A .
O tan A' AO  3 M H C B 3 a 3  V  S .A'O O ABC  12 A
Ví dụ 5. Cho lăng trụ ABC.A B  C
  có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của A' trên
ABC là trung điểm của BC , góc giữa cạnh bên và mặt đáy bằng 30. Tính theo a thể tích của
khối lăng trụ ABC.A B  C   . 3 a 3 3 a 3 3 a 3 3 a 3 A. V V V V ABC. A B  C    . B. 4 ABC. A B  C    . C. 3 ABC. A B  C    . D. 12 ABC. A B  C    . 8 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 19 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Gọi M là trung điểm của BC C' B'
 A' M  ABC
 AA',ABC  AA', AM n
 A' AM  30 A' 3 a a 3
 A' M  AM . tan 30   V  S .A' M  2 ABC 8 C M B A
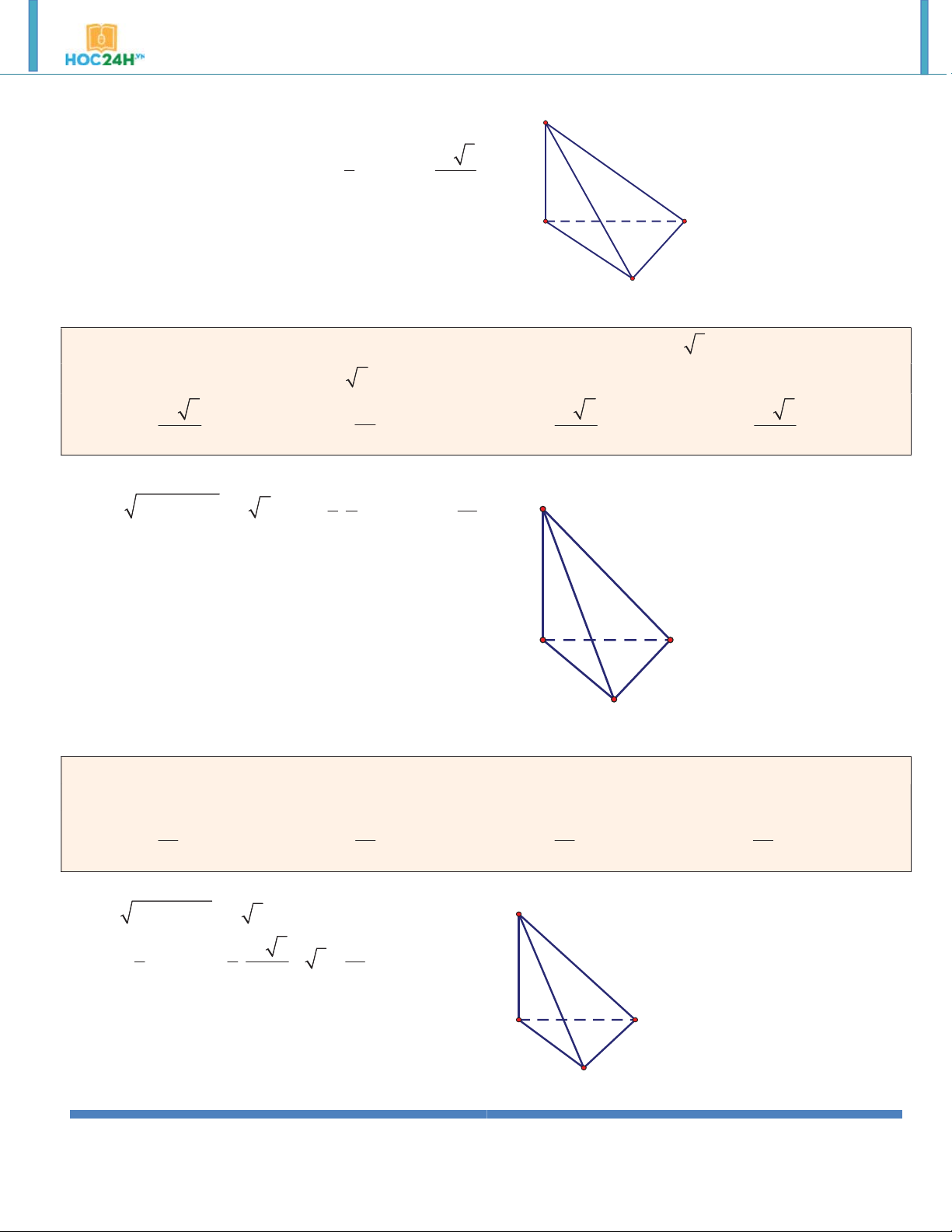
Ví dụ 6. Cho lăng trụ ABC.A B  C
  có đáy ABC là tam giác đều cạnh 2a . Hình chiếu vuông góc của A' trên
ABC là trung điểm của AB , góc giữa mặt phẳng AAC C
  và mặt đáy bằng 60. Tính theo a
thể tích của khối lăng trụ ABC.A B  C   . 3 3a 3 A. 3 V . B. 3 V . C. V V .     a 3     3a 3     2a 3 ABC.A B C ABC.A B C ABC.A B  C    . D. 3 2 ABC.A B C Hướng dẫn giải:
Gọi M là trung điểm của AB , kẻ MH  AC C' B'
 A' M  ABC  
 ACC ' A ',ABC A'H,HM n
 A' HM  60 A' 2 1 1 a 3 2 S  a 3; S 
AC.MH  S ABC AMC  2 2 ABC 2 a 3 3a  MH 
 A' M  MH. tan 60  C B 2 2 3 3a 3 H M V  S .A' M ABC  2 A a 10
Ví dụ 7. Cho lăng trụ ABC.A B  C   có  n AA 
, AC  a 2, BC  a, ACB  135o . Hình chiếu vuông góc của 4
C lên mặt phẳng ABC trùng với trung điểm M của AB . Tính theo a thể tích của khối lăng trụ ABC.A B  C   . 3 a 6 3 3a A. 3 V . B. V V V .     3a 3     a ABC.A B C ABC.A B  C    . C. 8 ABC.A B  C    . D. 3 8 ABC.A B C Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 20 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan 2 2 n AB A' B' 
AC  BC  2AC.BC.cos ACB  a 5 2 2 2 AC  BC  2  AB a  MC   C' 4 2 a 6 2 2
 MC '  CC '  MC  4 A M B 3 1 a 6  V 
AC.BC.sin135.MC '  2 8 C
Ví dụ 8. Cho lăng trụ ABC.A B  C
  có độ dài cạnh bên bằng a , đáy ABC là tam giác vuông tại C , n 60o BAC 
, góc giữa BB ' và ABC bằng 60. Hình chiếu vuông góc của B' lên ABC trùng với trọng tâm
của tam giác ABC . Tính theo a thể tích của khối lăng trụ ABC.A B  C   . 3 27a 3 27a 3 73a 3 27a A. V V V V ABC.A B  C    . B. 208 ABC.A B  C    . C. 280 ABC.A B  C    . D. 208 ABC.A B  C    . 802 Hướng dẫn giải:
Gọi G là trọng tâm AB 
C , M là trung điểm AC  B 'G  ABC A' B'
 BB',ABC  BB', BG n
 B ' BG  60 a 3 a C'
 B 'G  BB '.sin 60 
, BG  BB '.cos 60  2 2 AB AB 3 AC  . AB cos 60  , BC  . AB sin 60  2 2 A B 2 AB 3  S G ABC  8 M C 3 3a 2 2 2 AB  BC  2  AC AB 13 3a BM  BG     AB  2 4 4 4 13 2 3 9a 3 27a  S   V  S .B 'G ABC  104 ABC 208
Ví dụ 9. Cho hình hộp AB . CD A B  C  D
  có đáy ABCD là hình chữ nhật với AB  3, AD  7 . Hai mặt bên
ABB' A ' và ADD' A ' lần lượt tạo với đáy các góc 45 và 60. Tính theo thể tích của khối hộp AB . CD A B  C  D
  biết cạnh bên bằng 1. A. 1. B. 3. C. 6. D. 9. Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 21 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Kẻ A' H  ABCD, HM  AB, HN  AD A' D' n n
 A' M  AB, A' N  AD  A' MH  45 ,
 A' NH  60
Đặt A' H  x . Khi đó: B' 2 x 2x 3 C'  4x 2 2 A' N  
; AN  AA'  A' N   HM sin 60 3 3 A N Mà HM  .
x cot 45  x M D 2 3  4x 3 H  x   x  3 7 B C  V  A . B A . D x  3
ABCD.A' B'C 'D '
Ví dụ 10. Cho lăng trụ ABC .
D A' B 'C ' D ' có đáy ABCD là hình chữ nhật tâm O và AB  a, AD  a 3 ; A'O
vuông góc với đáy ABCD. Cạnh bên AA' hợp với mặt đáy ABCD một góc 45. Tính theo a
thể tích khối lăng trụ đã cho. 3 a 3 3 a 3 3 a 6 A. V  . B. V  . C. V  . D. 3 V  a 3 . 6 3 2 Hướng dẫn giải: 2 S  A . B AD  a 3 A' D' ABCD AC 2 2
AC  AB  AD  2a  AO   a B' C' 2
A'O  ABCD
 45  AA', 
ABCD   AA',  n
AO  A' AO A 3 D
A'O  AO  a  V  S
.A'O  a 3
ABCD.A'B 'C 'D ' ABCD O B C
B. LOẠI 2: THỂ TÍCH KHỐI CHÓP
Một số hình chóp đặc biệt:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 22 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Hình chóp tam giác đều: S
Hình chóp tam giác đều:
‒ Đáy là tam giác đều.
‒ Các mặt bên là các tam giác cân.
Hình tứ diện đều:
‒ Đáy là tam giác đều.
‒ Các mặt bên là các tam giác đều. A C Cách vẽ: H
‒ Vẽ đáy ABC . I
‒ Vẽ trung tuyến AI . B
‒ Dựng trọng tâm H .
‒ Vẽ SH  ABC. Ta có:
‒ SH là chiều cao của hình chóp.
‒ Góc giữa cạnh bên và mặt đáy: n SAH   .
‒ Góc giữa mặt bên và mặt đáy: n SIH   .
Hình chóp tứ giác đều: S
Hình chóp tứ giác đều: ‒ Đáy là hình vuông.
‒ Các mặt bên là các tam giác cân. Cách vẽ:
‒ Vẽ đáy ABCD .
‒ Dựng giao điểm H của hai đường chéo AC và BD .
‒ Vẽ SH  ABCD. A D Ta có:
‒ SH là chiều cao của hình chóp. O
‒ Góc giữa cạnh bên và mặt đáy: n SAH B   . C
‒ Góc giữa mặt bên và mặt đáy: n SIH   .
Hình chóp có một cạnh bên vuông góc với đáy:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 23 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
‒ SA  ABC. S
‒ Góc giữa cạnh bên SB và mặt đáy: n SBA   .
‒ Góc giữa cạnh bên SC và mặt đáy: n SCA   . A C B
‒ SA  ABCD. S
‒ Góc giữa cạnh bên SB và mặt đáy: n SBA   .
‒ Góc giữa cạnh bên SC và mặt đáy: n SCA   .
‒ Góc giữa cạnh bên SD và mặt đáy: n SDA   . A D B C Chú ý:
a) Đường chéo của hình vuông cạnh a là d  a 2 .
Đường chéo của hình lập phương cạnh a là d  a 3 .
Đường chéo của hình hộp chữ nhật có 3 kích thước a, , b c là 2 2 2
d  a  b  c . a 3
b) Đường cao của tam giác đều cạnh a là h  . 2
c) Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên đều bằng nhau ( hoặc có đáy là đa giác
đều, hình chiếu của đỉnh trùng với tâm của đáy).
1. Dạng 1: Khối chóp có cạnh bên vuông góc với đáy
Ví dụ 1. Cho hình chóp S.ABC SB  SC  BC  CA  a . Hai mặt ABC và ASC cùng vuông góc với SB 
C . Thể tích khối chóp S.ABC bằng: 3 a 3 3 a 3 3 a 3 3 a 3 A. V V V V S.ABC  . B.  . C.  . D.  . 12 S.ABC 2 S.ABC 6 S.ABC 3 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 24 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan AB  C S  BC ,AS  C S 
BC  AC S  BC A 3 1 a 3
SB  SC  BC  SBC 
đều V  .S .CA  3 SBC 12 B C S
Ví dụ 2. Cho hình chóp S.ABC có đáy là tam giác vuông tại B , AB  ,
a AC  a 3 , cạnh bên SA vuông góc
với mặt phẳng đáy, SA  a 2 . Tính theo a thể tích của khối chóp S.ABC . 3 a 3 3 a 3 a 2 3 a 3 A. V V  V V S.ABC  . B. . C.  . D.  . 3 S.ABc 3 S.ABM 3 S.ABM 2 Hướng dẫn giải: 3 1 1 a 2 2 S
BC  AC  AB  a 2 V  . .A . B . BC SA  3 2 3 A C B
Ví dụ 3. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy và SB  2a .
Tính theo a thể tích của khối chóp S.ABC . 3 a 3 a 3 a 3 a A. V V V V S.ABC  . B.  . C.  . D.  . 4 S.ABC 3 S.ABC 2 S.ABC 7 Hướng dẫn giải: 2 2 S
SA  SB  AB  a 3 2 3 1 1 a 3 a  V  .S .SA  . .a 3  3 ABC 3 4 4 A C B
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 25 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Ví dụ 4. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AC  a . Biết bên SA vuông góc với đáy
và SB hợp với đáy một góc 60. Tính thể tích của khối chóp S.ABC . 3 a 6 3 a 3 3 a 6 3 a 3 A. . B. . C. . D. . 8 8 24 24 Hướng dẫn giải:
SA  ABCD S
 SB,ABCD  SB, AB n  SBA  60 2 a 2 1 a AB  BC  ; S  . AB BC  2 ABC 2 4 3 a 6 1 a 6 SA  A . B tan 60   V  S .SA  2 3 ABC 24 A C B
Ví dụ 5. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Biết SA vuông góc với đáy ABC và
SBC hợp với đáy ABC một góc 60. Tính thể tích hình chóp. 3 a 3 3 a 3 3 3a 3 3 a 3 A. . B. . C. . D. . 8 4 8 2 Hướng dẫn giải:
Gọi M là trung điểm BC .Ta có: S ABC đều nên
AM  BC  SA  BC  
 SBC,ABC n  SMA  60 3 3a 1 a 3
SA  AM .tan 60  V  S .SA  2 3 ABC 8 A C M B
Ví dụ 6. Cho hình chóp S.ABC có mặt bên SBC là tam giác đều cạnh a , cạnh bên SA vuông góc với mặt
phẳng đáy, góc BAC bằng 120. Tính theo a thể tích của khối chóp S.ABC . 3 2.a 3 2.a 3 2.a 3 2.a A. V V V V S.ABC  . B.  . C.  . D.  . 36 S.ABC 12 S.ABC 6 S.ABC 3
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 26 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan Hướng dẫn giải:
SB  SC  AB  AC  A
 BC cân tại A . S Có 2 2 2
BC  AB  AC  2.A . B . AC cos120 a 3 a 6 2 2
 AB  AC 
; SA  SB  AB  3 3 3 1 1 a 2
 V  . .AB.AC.sin120.SA  3 2 36 A C M B Ví dụ 7. Cho hình chóp .
S ABCD có đáy là hình chữ nhật, n
AB  a 2, BC  ,
a SCA  60, cạnh bên SA vuông
góc với đáy. Tính theo a thể tích của khối chóp . S ABCD . A. 3 V  a 2 . B. 3 V  a 3 . C. 3 V  3a . D. 3 V  2a . S.ABCD S.ABCD S.ABCD S.ABCD Hướng dẫn giải: 2 2 n
AC  AB  BC ; SCA  60 S
 SA  AC. tan 60  3a 1 3  V  .A .
B BC.SA  a 2 3 A D B C
Ví dụ 8. Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy ABC  D
và mặt bên SCD hợp với đáy một góc 60 . Tính thể tích hình chóp S.ABCD. 3 a 3 3 a 3 3 a 3 A. 3 a 3 . B. . C. . D. . 2 3 4 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 27 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
SA  ABCD;CD  AD  CD  SD S  
 SCD,ABCD n  SDA  60 SA  A .t
D an 60  a 3 3 1 a 3  V  S .SA  3 ABCD 3 A D B C Ví dụ 9. Cho hình chóp .
S ABCD có ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy AB  CD
. Biết góc giữa SC và mặt phẳng AB 
CD bằng 60 . Tính thể tích khối chóp . S ABCD . 3 3a 3 2a 3 6a A. . B. 3 3a . C. . D. . 6 3 3 Hướng dẫn giải: 2 2
AC  AB  BC  a 2 S
SA  ABCD SA  AC
 SC,ABCD n  SCA  60
SA  tan60 SA  AC tan60 a 6 A AC B 3 1 1 a 6 2  V  S
.SA  a .a 6  D C 3 ABCD 3 3 Ví dụ 10. Cho hình chóp .
S ABCD có đáy là hình thang vuông tại A và D , AD  CD  a, AB  3a , cạnh bên
SA vuông góc với mặt phẳng đáy. Góc giữa SC với mặt đáy bằng 45. Tính theo a thể tích của khối chóp . S ABCD . 3 a 2 3 2a 3 2a 2 3 a A. V V  V V  S.ABCD  . B. . C.  . D. . 3 S.ABCD 3 S.ABCD 3 S.ABCD 3 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 28 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan SA  AB 
CD  SC,ABC 
D   SC, AC n  SCA  45 S 2 2
 SA  AC  AD  CD  a 2 3 1 1 2a 2
 V  . .AB C  D .A . D SA  3 2 3 A B D C
2. Dạng 2: Khối chóp có một mặt bên vuông góc với đáy
Ví dụ 1. Cho hình chóp S.ABC có đáy là tam giác vuông tại B , n  2 ,  30o AC a ACB . Hình chiếu vuông góc
của S lên mặt đáy là trung điểm H của cạnh AC và SH  a 2 . Tính theo a thể tích của khối chóp S.ABC . 3 a 6 3 a 6 3 a 6 3 a 6 A. V V V V S.ABC  . B.  . C.  . D.  . 17 S.ABC 3 S.ABC 5 S.ABC 6 Hướng dẫn giải: AB  A .s
C in30 a  BC  a 3 S 3 1 1 a 6 V  . .A . B A . C SH  3 2 6 A H C B
Ví dụ 2. Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông cân tại D , ABC  BCD
và AD hợp với BCD một góc 60. Tính thể tích của khối tứ diện ABCD. 3 a 3 3 a 3 3 a 3 A. V V V V  a . ABCD  . B.  . C.  . D. 3 3 9 ABCD 6 ABCD 3 ABCD Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 29 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Gọi H là trung điểm của BC . A
Ta có tam giác ABC đều nên AH  BC  D 
 ABC,BCD AH BCD
AH  HD  AH  A .
D tan 60  a 3 a 3 2a 3 HD  . AD cot 60  ; BC  2HD  3 3 D C 3 1 a 3  V  S .AH  3 BCD 9 H B
Ví dụ 3. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A , SC  2a 5 . Hình chiếu vuông góc của
S lên AB 
C là trung điểm M của cạnh AB , góc giữa đường thẳng SC với mặt phẳng đáy bằng
60 o . Tính theo a thể tích của khối chóp S.ABC . 3 2a 15 3 a 15 3 2a 3 3a 15 A. V V V  V S.ABC  . B.  . C. . D.  . 3 S.ABC 3 S.ABC 3 S.ABC 2 Hướng dẫn giải: S B M C A M B A C
SM  ABCSC ABC  SC CM n , ,  SCM  60
 CM  SC.cos 60  a 5; SM  a 15 3 1 1 2a 15
Tam giác MAC vuông tại A  AC  2a V  . .A . B A . C SM  3 2 3
Ví dụ 4. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , BC  a . Mặt bên SAC vuông góc với
đáy, các mặt bên còn lại đều tạo với mặt đáy một góc 45. Tính thể tích của khối chóp S.ABC . 3 a 3 a 3 3 a 3 3 a A. V V V V S .ABC  . B.  . C.  . D.  . 4 S.ABC 4 S.ABC 2 S .ABC 12 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 30 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Kẻ SH  BC . Gọi I, J lần lượt là hình chiếu của H S
trên AB và BC . 
 SAC,ABC SH ABC n n
SI  AB, SJ  BC  SIH  SJH  45 SHI   SHJ   HI  HJ
 BH là đường phân giác của ABC H
 H là trung điểm của AC . A C 3 a 1 a
HI  HJ  SH   V  S .SH S .  2 ABC 3 ABC 12 I J B
Ví dụ 5. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A , AB  , a SB 
C ABC. Hai mặt bên còn
lại hợp với đáy một góc 60 o . Tính theo a thể tích của khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 7a 3 A. V V V V S.ABC  . B.  . C.  . D.  . 12 S.ABC 5 S.ABC 18 S.ABC 12 Hướng dẫn giải: S B H D B C H D E A A C E
Kẻ SH  BC . Do S  BC  
ABC  SH AB  C Kẻ n n HD  ,
AB HE  AC  SDH  SEH  60
Do tam giác ABC vuông cân tại A nên a HD  HE 
 H là trung điểm của BC 2 3 a 3 1 1 a 3  SH  H .t D an60 V  . .A . B A . C SH  . 2 3 2 12
Ví dụ 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp S.ABCD . 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. 3 a 3 . 6 4 2
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 31 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan Hướng dẫn giải:
Gọi H là trung điểm của AB S
SAB đều  SH  AB
SABABC 
D  SH  ABCD 3 AB 3 a 3 1 a 3 SH    V  S .SH  2 2 3 ABCD 6 A D H B C Ví dụ 7. Cho hình chóp .
S ABCD có mặt bên SAB vuông góc với mặt phẳng đáy và tam giác SAB cân tại S .
Tính theo a thể tích của khối chóp .
S ABCD , biết rằng: đáy ABCD là hình vuông cạnh a , góc giữa mặt SB 
D và mặt đáy bằng 60. 3 a 6 3 a 3 a 6 A. 3 V  a 6 . B. V V  . D. V S.ABCD S.ABCD  . C.  . 5 S.ABCD 12 S.ABCD 12 Hướng dẫn giải: S A D M O A D N M N O B B C C
Gọi M là trung điểm của AB . SA  B ABC 
D  SM ABC  D
Gọi O là giao điểm của AC và BD , N là trung điểm của OB .
 MN  BD BD SMN BD  SN SM  BD    
 SBD,ABCD  SN,MN n  SNM  60 3 a 6 1 a 6 2
 SM  MN.tan 60 
 V  .AB .SM  4 3 12 Ví dụ 8. Cho hình chóp .
S ABCD có mặt bên SAB vuông góc với mặt phẳng đáy và tam giác SAB cân tại S .
Tính theo a thể tích của khối chóp .
S ABCD , biết rằng: đáy ABCD là hình chữ nhật, AB  ,
a AD  a 2 , góc giữa mặt SAC và mặt đáy bằng 60.
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 32 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan 3 a 3 a 3 a 3 a A. V V V V S.ABCD  . B.  . C.  . D.  . 3 S.ABCD 6 S.ABCD 2 S.ABCD 8 Hướng dẫn giải: S A D N H M A D M H N B B C C
Gọi M là trung điểm của AB . SA  B ABC 
D  SM ABC  D
Kẻ BH vuông góc với AC , gọi N là trung điểm của AH  MN  AC
 MN  AC AC SMN AC SN SM  AC    
 SAC,ABCD SN,MN n  SNM  60 1 1 1 a 6 BH a 6    BH   MN   2 2 2 BH AB BC 3 2 6 3 a 2 1 a
 SM  MN.tan 60   V  .A . B . AD SM  2 3 3 Ví dụ 9. Cho hình chóp .
S ABCD có đáy là hình thoi, AB  BC  BD  a , mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích của khối chóp . S ABCD 3 a 3 5a 3 5a 3 11a A. V V V V S.ABCD  . B.  . C.  . D.  . 4 S.ABCD 6 S.ABCD 2 S.ABCD 8 Hướng dẫn giải: S A D A D M B C B C
Gọi M là trung điểm của AB .
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 33 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan SA  B ABC 
D  SM ABC  D 2 3 a 3 a 3 1 a SM  , S  2S  V  .S .SM  2 ABCD ABD 2 3 ABCD 4 Ví dụ 10. Cho hình chóp .
S ABCD có đáy ABCD là hình thang vuông tại A và D, AB  3 , a AD  2 , a CD  a ,
tam giác SAD cân tại S , mặt phẳng SA 
D vuông góc với đáy, góc giữa mặt phẳng SBC và mặt
đáy bằng 60. Tính thể tích của khối chóp . S ABCD . 3 4a 6 3 2a 6 3 5a 6 3 a 6 A. V V V V S.ABCD  . B.  . C.  . D.  . 3 S.ABCD 3 S.ABCD 3 S.ABCD 3 Hướng dẫn giải: S D C A B M M D C A B
Gọi M là trung điểm của AD .
SAD ABCD SM  ABCD SM  BC  BC SMC BC  SC MC  BC    
 SBC,ABCD  SC,MC n
 SCM  60  SM  MC. tan 60  a 6 3 1 1 4a 6
 V  . .AB  CD.AD.SM  3 2 3
3. Dạng 3: Khối chóp đều
Ví dụ 1. Cho H là khối tứ diện đều cạnh a . Thể tích của H bằng bao nhiêu? 3 a 2 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 6 12 12 4 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 34 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Gọi G là trọng tâm tam giác C
AB  SG  B A  C S 2 a 3 a 3 a 6 2 2 AG  . 
 SG  SA  AG  3 2 3 3 2 3 1 1 a 3 a 6 a 2  V  .S .SG  . .  3 ABC 3 4 3 12 A C G B
Ví dụ 2. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , cạnh bên bằng 2a. Tính thể tích của khối chóp S.ABC . 3 a 11 3 a 11 3 a 11 3 a 11 A. . B. . C. . D. . 36 12 6 24 Hướng dẫn giải:
Gọi G là trọng tâm tam giác C
AB  SG  B A  C S AB 3 a 3 AG   ; SA  2a 3 3 a 33 2 2
 SG  SA  AG  3 2 2 3 AB 3 a 3 1 a 11 S    V  S .SG A C ABC S.  4 4 ABC 3 ABC 12 2 3 1 a 3 a a 3 G V  . .  3 4 3 36 B
Ví dụ 3. Cho khối tứ diện đều ABCD có cạnh bằng a , M là trung điểm của CD . Tính thể tích hình chóp M .ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. V V V V M .ABC  . B.  . C.  . D.  . 24 M .ABC 16 M .ABC 12 M .ABC 8 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 35 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Gọi G là trọng tâm ABC . Kẻ MH & DG D
 DG  ABC MH ABC 1 1 a 6 2 2 MH M  DG  CD  GC  2 2 3 2 2 3 AB 3 a 3 1 a 3 S    V  S .MH ABC  A C 4 4 3 ABC 24 H G B
Ví dụ 4. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , cạnh bên bằng 2a. Gọi I là trung điểm của
cạnh BC . Tính theo a thể tích của khối chóp S.ABI . 3 a 41 3 a 11 3 a 31 3 a 21 A. V V V V S.ABC  . B.  . C.  . D.  . 24 S.ABC 24 S.ABC 24 S.ABC 24 Hướng dẫn giải:
Gọi G là trọng tâm tam giác ABC  SG   ABC S 2  AB 3  a 33 2 2 2 SG SA AG SA          3  3   3 1 1 1 a 11  V  V  . .S .SG S.ABI S.  2 ABC 2 3 ABC 24 A C G I B
Ví dụ 5. Cho hình chóp tứ giác đều S.ABCD tất cả các cạnh đều bằng a . Tính theo a thể tích của khối chóp S.ABCD . 3 a 2 3 a 2 3 a 2 3 a 2 A. V  . B. V  . C. V  . D. V  . 2 3 4 6 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 36 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Gọi O là giao điểm của AC và BD S
 SO  AB  CD 1 a 2 a 2 2 2 AO  AC 
; SO  SA  AO  2 2 2 3 1 1 a 2 V  S .SO  . AB BC.SO  3 ABCD 3 6 A D O B C
Ví dụ 6. Cho hình chóp tứ giác đều .
S ABCD cạnh đáy bằng a , góc giữa mặt bên và mặt đáy bằng 60. Tính
theo a thể tích của khối chóp . S ABCD . 3 a 3 2 a 6 3 a 6 2 a 6 A. V V V V S.ABCD  . B.  . C.  . D.  . 6 S.ABCD 6 S.ABCD 5 S.ABCD 5 Hướng dẫn giải:
Gọi O là giao điểm của AC và BD , M là trung điểm của CD . S
 OM  CD, SM  CD  
 SCD,ABCD  OM,SM n  SMO  60 a 3
 SO  OM .tan 60  2 A 3 D 1 a 3  V  .S .SO  3 ABCD 6 O M B C
Ví dụ 7. Cho một hình chóp tứ giác đều có cạnh đáy bằng a và diện tích xung quanh gấp đôi diện tích đáy.
Khi đó thể tích của khối chóp là: 3 a 3 3 a 3 3 a 3 3 a 2 A. . B. . C. . D. . 3 12 6 3 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 37 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Gọi O là giao điểm của AC và BD , M là trung điểm của CD . S 1 2 2 S  4S  4. . . CD SM  2 .
a SM ; S  AB  a xq SCD 2 d 2 S  2S  2 .
a SM  2a  SM  a xq d A a 3 2 2
 SO  SM  OM  D 2 O M B 3 1 a 3 C V  .S .SO  3 ABCD 6
4. Dạng 4: Khối chóp và phương pháp tỉ số thể tích
Ví dụ 1. Cho tứ diện ABCD . Gọi B ' và C ' lần lượt là trung điểm của AB và AC . Khi đó tỉ số thể tích của
khối tứ diện AB 'C ' D và khối tứ diện ABCD bằng: A. 1 . B. 1 . C. 1 . D. 1 . 2 4 6 8 Hướng dẫn giải: V
AB' AC' AD 1 AB'C'D A  . .  V AB AC AD 4 ABCD B' C' B D C
Ví dụ 2. Cho hình chóp tam giác S.ABC . Gọi A , B lần lượt là trung điểm của SA và SB. Mặt phẳng A B    C
chia hình chóp thành hai phần. Tỉ số thể tích của hai phần đó bằng: A. 1 . B. 1 . C. 1 . D. 2 . 2 3 4 3 Hướng dẫn giải: V
SA' SB' SC 1 V 1
S.A'B'D S.A'B' S  . . D    V SA SB SC 4 V 3 S.ABC ABCDA'B' A' B' A C B
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 38 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Ví dụ 3. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AC  a 2 , cạnh bên SA vuông góc với
đáy, SA  a . Gọi G là trọng tâm tam giác ABC . Mặt phẳng  qua AG và song song với BC , cắt
SC, SB lần lượt tại M , N . Tính thể tích của khối chóp S.AMN . 3 a 3 a 3 2a 3 2a A. V V V V S.AMN  . B.  . C.  . D.  . 9 S.AMN 27 S.AMN 27 S.AMN 9 Hướng dẫn giải:
Gọi I là trung điểm của BC S
AC  a 2  AB  BC  a SM SN SG 2
& BC  MN & BC     SB SC SI 3 N V SM SN 4 S. AMN   .  G V SB SC 9 S.ABC A C 3 4 4 1 1 2a M  V  V  . . A . B BC.SA S.AMN S.  9 ABC 9 3 2 27 I B
Ví dụ 4. Cho tam giác ABC vuông cân tại A , AB  a . Trên đường thẳng qua C và vuông góc với mặt phẳng
ABC lấy điểm D sao cho CD  a. Mặt phẳng qua C vuông góc với BD , cắt BD tại F và cắt
AD tại E . Tính theo a thể tích khối tứ diện CDEF . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 36 18 24 12 Hướng dẫn giải: 3 1 a V D  S .CD ABCD  3 ABC 6 2 2 DE.DA DC DE DC 1 2
DE.DA  DC      2 2 2 DA DA DA DA 2 E 2 DF DC 1 CMTT :   2 DB DB 3 F 3 V DE DF 1 1 a CDEF   .   V  V  A C V DA DB 6 CDEF 6 ABCD 36 ABCD B
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 39 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan Ví dụ 5. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng
đáy. Gọi M và N lần lượt là trung điểm của SB và SD . Tính tỉ số thể tích của hai khối chóp S.AMN và . S ABD . A. 1 . B. 3 . C. 1 . D. 1 . 4 4 2 5 Hướng dẫn giải: V SA SM SN 1 S S.AMN  . .  V SA SB SD 4 S.ABD N M A D B C Ví dụ 6. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a . Gọi A', B',C', D' lần lượt là trung điểm của , SA , SB ,
SC SD. Khi đó tỉ số thể tích của hai khối chóp S.A' B 'C ' D ' và . S ABCD là: A. 1 . B. 1 . C. 1 . D. 1 . 8 6 4 2 Hướng dẫn giải: S A' D' B' C' A D B C V
SA' SB' SC ' 1 V
SA' SD' SC ' 1
S.A'B'C '
S.A'D'C '  . .  ;  . .  V SA SB SC 8 V SA SD SC 8 S.ABC S.ADC V V V V V 1
S.A'B'C '
S.A'D'C '
S.A'B'C '
S.A'D'C '
S.A'B'C 'D'      V V V V V 8 S.ABC S.ADC S.ABC S.ADC S.ABCD
Ví dụ 7. Cho khối chóp tứ giác đều S.ABCD . Mặt phẳng  đi qua ,
A B và trung điểm M của SC . Tỉ số
thể tích của hai phần khối chóp bị phân chia bởi mặt phẳng đó là: 1 3 5 3 A. . B. . C. . D. . 4 8 8 5 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 40 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan
Kẻ MN & CDN CD, suy ra hình thang ABMN S
là thiết diện của khối chóp. V SM 1 S. V  V V ; ABM S.ABMN S.ABM S.AMN   V SC 2 S.ABC N 1 1  V  V  V S.ABM S .ABC S. 2 4 ABCD M V SM SN 1 1 A S.AMN  .   V  V D S.AMN S. V SC SD 4 8 ABCD S.ACD 1 1 3 O  V  V  V  V S.ABMN S.ABCD S .ABCD S . 4 8 8 ABCD B C 5 V 3 S.ABMN  V  V ABMNDC S .   8 ABCD V 5 ABMNDC
Ví dụ 8. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên tạo với đáy góc
60. Gọi M là trung điểm của SC . Mặt phẳng đi qua AM và song song với BD cắt SB tại E và
cắt SD tại F . Tính theo a thể tích khối chóp S.AEMF . 3 a 6 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. . 36 18 9 6 Hướng dẫn giải:
Gọi I  SO  AM S
AEMF& BD  EF & BD 3 a 6 1 a 6 SO  O . A tan 60   V  S .SO S.  M 2 ABCD 3 ABCD 6 E V SM SF 1 1 1 I S.AMF  .   V  V  V S.AMF S.ACD S. V SC SD 3 3 6 ABCD B S.ACD F C 3 1 a 6 V  V V  2V  V S.AEMF S.AMF S .AME S.AMF S.  3 ABCD 18 O A D
Ví dụ 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy, SA  a 2 .
Gọi B ', D ' lần lượt là hình chiếu của A lên ,
SB SD . Mặt phẳng AB'D ' cắt SC tại C '. Tính theo
a thể tích khối chóp S.AB 'C ' D '. 3 2a 2 3 a 2 3 2a 2 3 a 2 A. . B. . C. . D. . 9 9 27 18 Hướng dẫn giải:
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 41 ĐÔI THAY CON ĐƯƠNG
http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan 2 SB ' SA 2 SC ' 1 S   ;  2 SB SB 3 SC 2 V SB ' SC ' 1 1
S.AB 'C '  .   V  V S.AB 'C ' S. V SB SC 3 3 ABC S.ABC D' 3 C' 2 2a 2 V  V V  2V  V
S.AB 'C 'D ' S.AB 'C ' S.AC 'D' S.AB 'C ' S.  3 ABC 9 B' A D B C
Ví dụ 10. Cho hình chóp tứ giác .
S ABCD có thể tích bằng V với đáy là hình bình hành. Gọi C ' là trung điểm
cạnh SC . Mặt phẳng qua AC' và song song với BD cắt các cạnh ,
SB SD lần lượt tại B', D' . Khi đó
thể tích của khối chóp S.A' B 'C ' D ' bằng: A. V . B. 2V . C. V . D. V . 3 3 4 2 Hướng dẫn giải:
Gọi O là giao điểm của AC và BD , gọi I là giao điểm của SO và AC'. S
Qua I kẻ B' D' song song với BD . Khi đó mặt phẳng qua AC' và song song
với BD là mặt phẳng AB'C'D '. C' D'
Ta dễ dàng nhận thấy rằng I là trọng tâm của tam giác SAC nên SI 2  SO 3 B' I
Theo định lí Ta lét ta có SD ' SI SB ' 2    A D SD SO SB 3 O V SA SD' SC ' 2 1 1 B C SAD'C '  . .  1. .  V SA SD SC 3 2 3 SADC V SA SB' SC ' 2 1 1 SAB'C '  . .  1. .  V SA SB SC 3 2 3 SABC 1 V  V  V SADC SABC 2 SABCD 1 1 V V  V V  .2. V SAD'C 'B' SAD'C ' SAB'C '  2 2 SABCD 3
BẠN KHÔNG THÊ THAY ĐÔI ĐICH ĐÊN NÊU BẠN KHÔNG 42 ĐÔI THAY CON ĐƯƠNG

Hình không gian thể tích từ cơ bản đến nâng cao – Nguyễn Tiến Đạt Toán 12

Tài liệu liên quan:

Bảng khối đa diện đều | Toán 12

Lăng trụ đều là gì? Lăng trụ tam giác đều, lăng trụ tứ giác đều là gì? | Toán 12

Chuyên Đề Thể Tích Khối Đa Diện Có Yếu Tố Góc Ôn Thi Tốt Nghiệp THPT Có Đáp Án Và Lời Giải

10 Đề Trắc Nghiệm Ôn Tập Chương Khối Đa Diện Hình 12 Có Đáp Án

TOP 600 bài tập chọn lọc khối tròn xoay – Lê Minh Tâm Toán 12