



Preview text:
Homework #3.
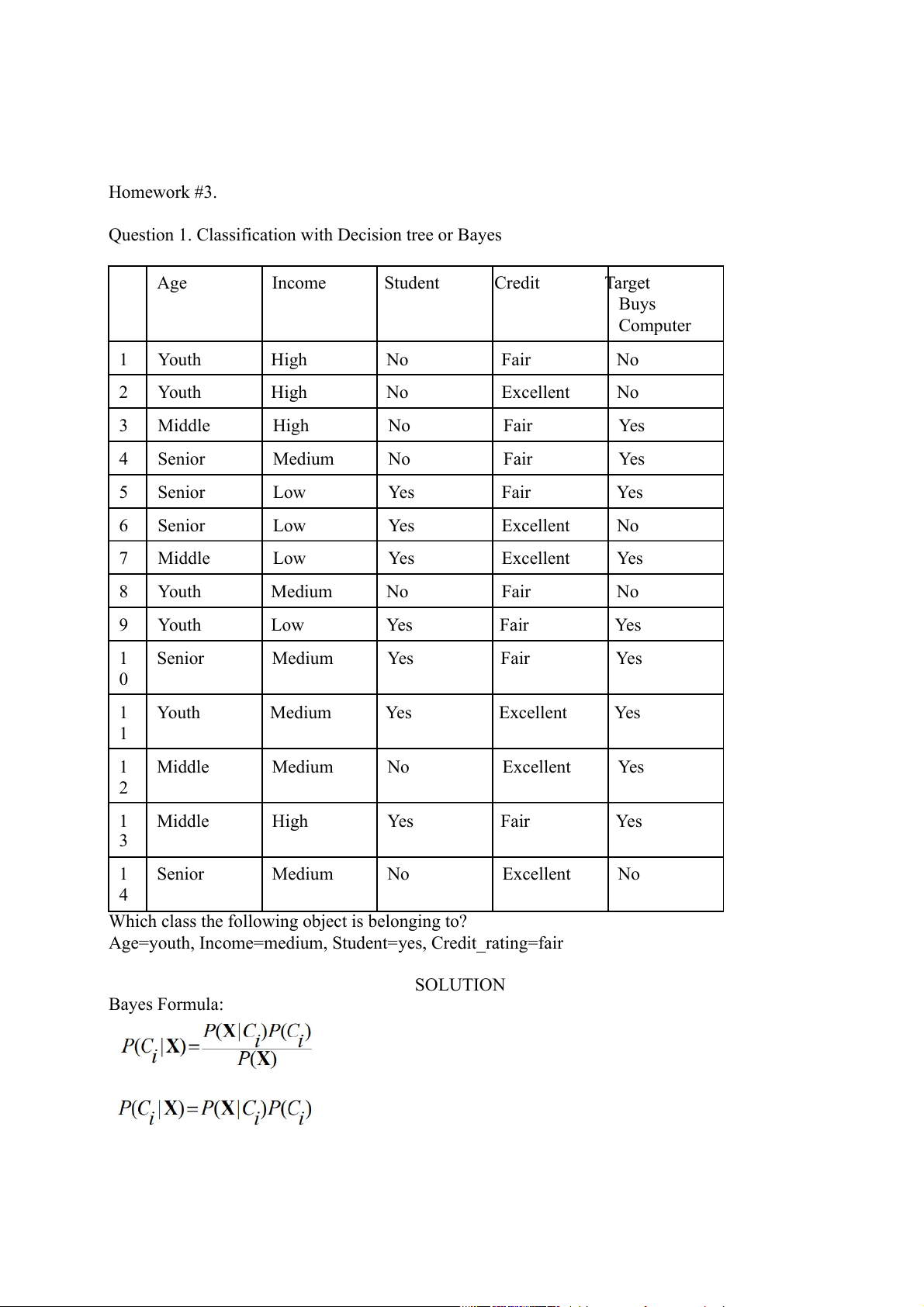
Question 1. Classification with Decision tree or Bayes Age Income Student Credit Target Buys Computer 1 Youth High No Fair No 2 Youth High No Excellent No 3 Middle High No Fair Yes 4 Senior Medium No Fair Yes 5 Senior Low Yes Fair Yes 6 Senior Low Yes Excellent No 7 Middle Low Yes Excellent Yes 8 Youth Medium No Fair No 9 Youth Low Yes Fair Yes 1 Senior Medium Yes Fair Yes 0 1 Youth Medium Yes Excellent Yes 1 1 Middle Medium No Excellent Yes 2 1 Middle High Yes Fair Yes 3 1 Senior Medium No Excellent No 4
Which class the following object is belonging to?
Age=youth, Income=medium, Student=yes, Credit_rating=fair SOLUTION Bayes Formula:
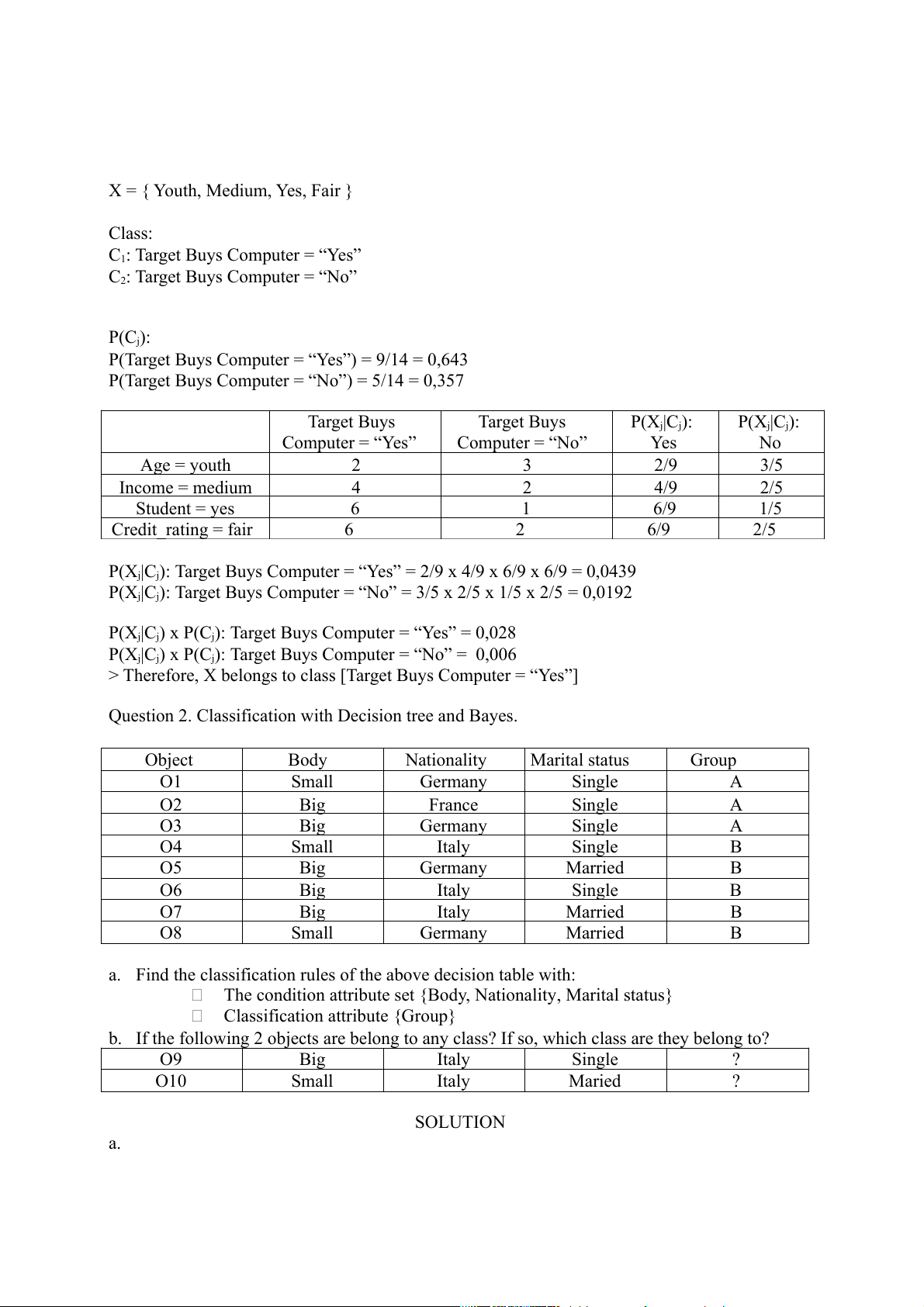
X = { Youth, Medium, Yes, Fair } Class:
C1: Target Buys Computer = “Yes”
C2: Target Buys Computer = “No” P(Cj):
P(Target Buys Computer = “Yes”) = 9/14 = 0,643
P(Target Buys Computer = “No”) = 5/14 = 0,357 Target Buys Target Buys P(Xj|Cj): P(Xj|Cj): Computer = “Yes” Computer = “No” Yes No Age = youth 2 3 2/9 3/5 Income = medium 4 2 4/9 2/5 Student = yes 6 1 6/9 1/5 Credit_rating = fair 6 2 6/9 2/5
P(Xj|Cj): Target Buys Computer = “Y 2/9 es” = 4/9 x 6/9 x 6/9 x = 0,0439
P(Xj|Cj): Target Buys Computer = “No” = 3/5 2/5 x 1/5 x 2/5 x = 0,0192
P(Xj|Cj) x P(Cj): Target Buys Computer = “Yes” = 0,028
P(Xj|Cj) x P(Cj): Target Buys Computer = “No” = 0,006
> Therefore, X belongs to class [Target Buys Computer = “Yes”]
Question 2. Classification with Decision tree and Bayes. Object Body Nationality Marital status Group O1 Small Germany Single A O2 Big France Single A O3 Big Germany Single A O4 Small Italy Single B O5 Big Germany Married B O6 Big Italy Single B O7 Big Italy Married B O8 Small Germany Married B
a. Find the classification rules of the above decision table with:
The condition attribute set {Body, Nationality, Marital status}
Classification attribute {Group}
b. If the following 2 objects are belong to any class? If so, which class are they belong to? O9 Big Italy Single ? O10 Small Italy Maried ? SOLUTION a. Gini Formula: | D 1| Gini | A(D) = D 2| ¿ D∨¿ gini (D 1)+ ¿ ¿ D∨¿ gini ( D2) ¿ Nationalit Body y Marital status Small 3 Italy 3 Single 5 Germany & Marrie Big 5 France 5 d 3 8 8 8 Class: C1: A C2: B
Gini(Small) = 1− (1)2− (2)2 3 3 = 4/9 Gini(Big) = 1− (2)2− (3)2 5 5 = 12/25 3 5 > Gini( ) = Body
gini(Small)+ gini(Big ) = 7/15 = 0,47 8 8
Gini(Italy) = 1− (0)2− (3)2 3 3 = 0
Gini(Germany & France) = 1− (3)2− (2)2 = 12/25 = 0,48 5 5 3 5 > Gini( ) = Nationality
gini ( Italy )+ gini( Germany∧France ) = 3/10 = 0,3 8 8
Gini(Single) = 1− (3)2− (2)2 5 5 = 12/25 = 0,48
Gini(Married) = 1− (0)2− (3)2 3 3 = 0 5 3 > Gini(Marital status) =
gini (Single)+ gini (Married ) = 0,3 8 8
Em chỉ biết tính tới đây thôi thầy ơi, em xin lỗi ☹ b. Class: C1: Group = “A” C2: Group = “B” X09 = { Big, Italy, Single } P(Cj):
P(Group = “A”) = 3/8 = 0,375
P(Group = “B”) = 5/8 = 0,625 Group = “A” Group = “B” P(Xj|Cj): A P(Xj|Cj): B Body = Big 2 3 2/3 3/5 Nationality = Italy 0 3 0/3 3/5 Marital status = Single 3 2 3/3 2/5 P(Xj|Cj): A = 2/3 0/3 x 3/3 x = 0 P(Xj|Cj): B = 3/5 3/5 x 2/5 x = 0,144
P(Xj|Cj) x P(Cj): Group = “A” = 0
P(Xj|Cj) x P(Cj): Group = “B” = 0,09
> Therefore, X belongs to class [Group = “B”] 09
X10 = { Small, Italy, Married } Group = “A” Group = “B” P(Xj|Cj): A P(Xj|Cj): B Body = Small 1 2 1/3 2/5 Nationality = Italy 0 3 0/3 3/5 Marital status = Married 0 3 0/3 3/5 P(Xj|Cj): A = 1/3 0/3 x 0/3 x = 0 P(Xj|Cj): B = 2/5 3/5 x 3/5 x = 0,144
P(Xj|Cj) x P(Cj): Group = “A” = 0
P(Xj|Cj) x P(Cj): Group = “B” = 0,09
> Therefore, X belongs to class [Group = “B”] 10 Question 3. Given data set
If X= (O = Sunny, Temp = Hot, Humidity = Normal, Wind = Weak),
Which answer should be? Yes or No SOLUTION Bayes Formula: Class: C1: Play = “Yes” C2: Play = “No”
X = { Sunny, Hot, Normal, Weak } P(Cj):
P(Play = “Yes”) = 9/14 = 0,643
P(Play = “No”) = 5/14 = 0,357 Play= “Yes” Play = “No” P(Xj|Cj): Yes P(Xj|Cj): No Outlook = Sunny 2 3 2/9 3/5 Temp = Hot 2 2 2/9 2/5 Humidity = Normal 5 1 5/9 0/5 Wind = Weak 6 2 6/9 2/5 P(Xj|Cj): Yes = 2/9 2/9 x 5/9 x 6/9 x = 0,0183 P(Xj|Cj): No = 3/5 2/5 x 1/5 x 2/5 x = 0,0192
P(Xj|Cj) x P(Cj): Play = “Yes” = 0,012
P(Xj|Cj) x P(Cj): Play = “No” = 0,006
> Therefore, X belongs to class [Play = “Yes”]




