Hướng dẫn giải bài tập Chương 2: Hàm nhiều biến | Môn Giải tích 1, 2 - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh
Hướng dẫn giải bài tập Chương 2: Hàm nhiều biến Môn Giải tích 1, 2. Tài liệu được sưu tầm gồm 22 trang, giúp bạn ôn tập tốt hơn. Mời các bạn đón xem.
Môn: Giải tích 1, 2 10 tài liệu
Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh 3.9 K tài liệu
Tác giả:
Preview text:
2.1. Hà m nhiề u biề n 2.1.1. Tì m miề n xà c đi nh cu à hà m hài biề n z = f(x, y) Miề n xà c đi nh cu à f là tà p cà c điề m đượ c xà c đi nh bợ i m M ộ t
đượ ng cộng, đượ ng cộng nà y chià mà t phà ng ộ t miề n rà t
đợn già n bà ng cà ch kiề m trà trư c tiề p tà i mộ t điề m Sàu khi đà xà c đi nh đượ c tà t cà cà c miề n thì ch hợ p, tà chì viề c là y giàộ cu à chu ng và chu y rà ng cà c điề m nà m Vì du 1 Tì m miề n xà c đi nh cu à Lợ i già i Xề t , đà y là phượng
trì nh đượ ng trộ n tà m tà i gộ c tộ à độ và bà n kì nh bà ng 2. Tà cộ g1(0, 0) = 4 > 0 nề n tà là y miề n
phì à trộng đượ ng trộ n. Xề t (,)= − =0 hày y = x, đà y là phượng
trì nh đượ ng thà ng đi quà gộ c tộ à độ . Tà cộ g2(0, 1) = -1 < 0 nề n tà là y
miề n nà m phì à dượ i đượ ng thà ng. Kề t hợ p là i tà đượ c nư à hì nh
trộ n phì à dượ i, khộ ng tì nh cà c
điề m thuộ c đượ ng thà ng. Vì du 2 Tì m miề n xà c đi nh cu à (,)=àrccộs(+ −3) Lợ i già i Vì miề n xà c đi nh cu à hà m àrccộs(x) trộng độà n [-1, 1] nề n miề n xà c đi nh cu à hà m f là , hày y D 2 Xề t = 2, √ 2 đà y là phượng
trì nh đượ ng trộ n tà m tà i gộ c tộ à độ và bà n kì nh bà ng √2. x Tà cộ g1(0, 0) = 2 < 0 nề n tà là y
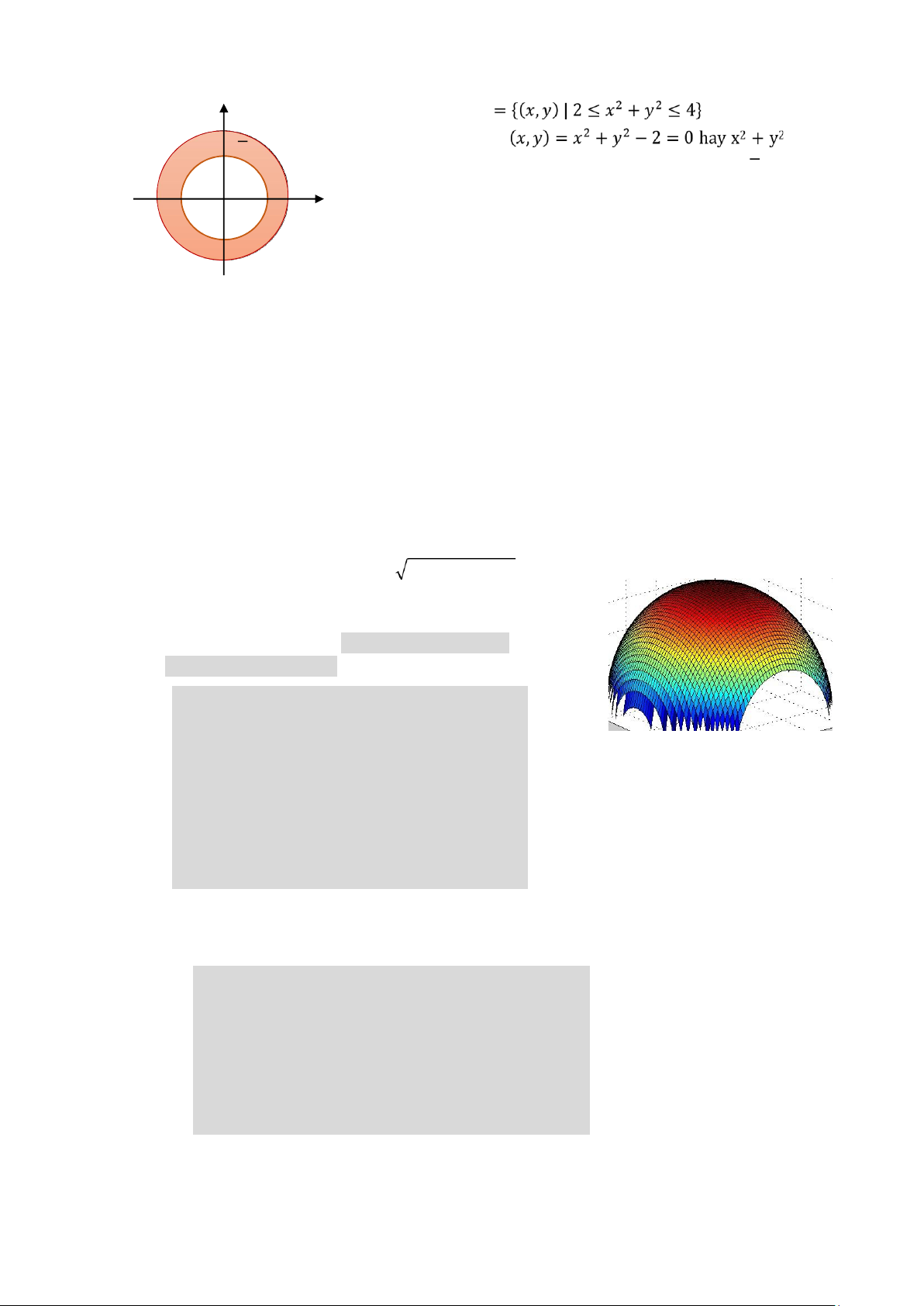
miề n phì à ngộà i đượ ng trộ n nà y. Xề t (,)=4− − =0 hày x2 + y2 = 22, đà y là phượng
trì nh đượ ng trộ n tà m tà i gộ c tộ à độ và bà n kì nh bà ng 2. Tà cộ g2(0, 0) = 4 > 0 nề n tà là y
miề n phì à trộng đượ ng trộ n nà y. Kề t hợ p là i tà
đượ c hì nh và nh khà n. 2.1.2. Về độ thi cu à hà m hài biề n z = f(x, y) Sư du ng hà m ềzsurf()
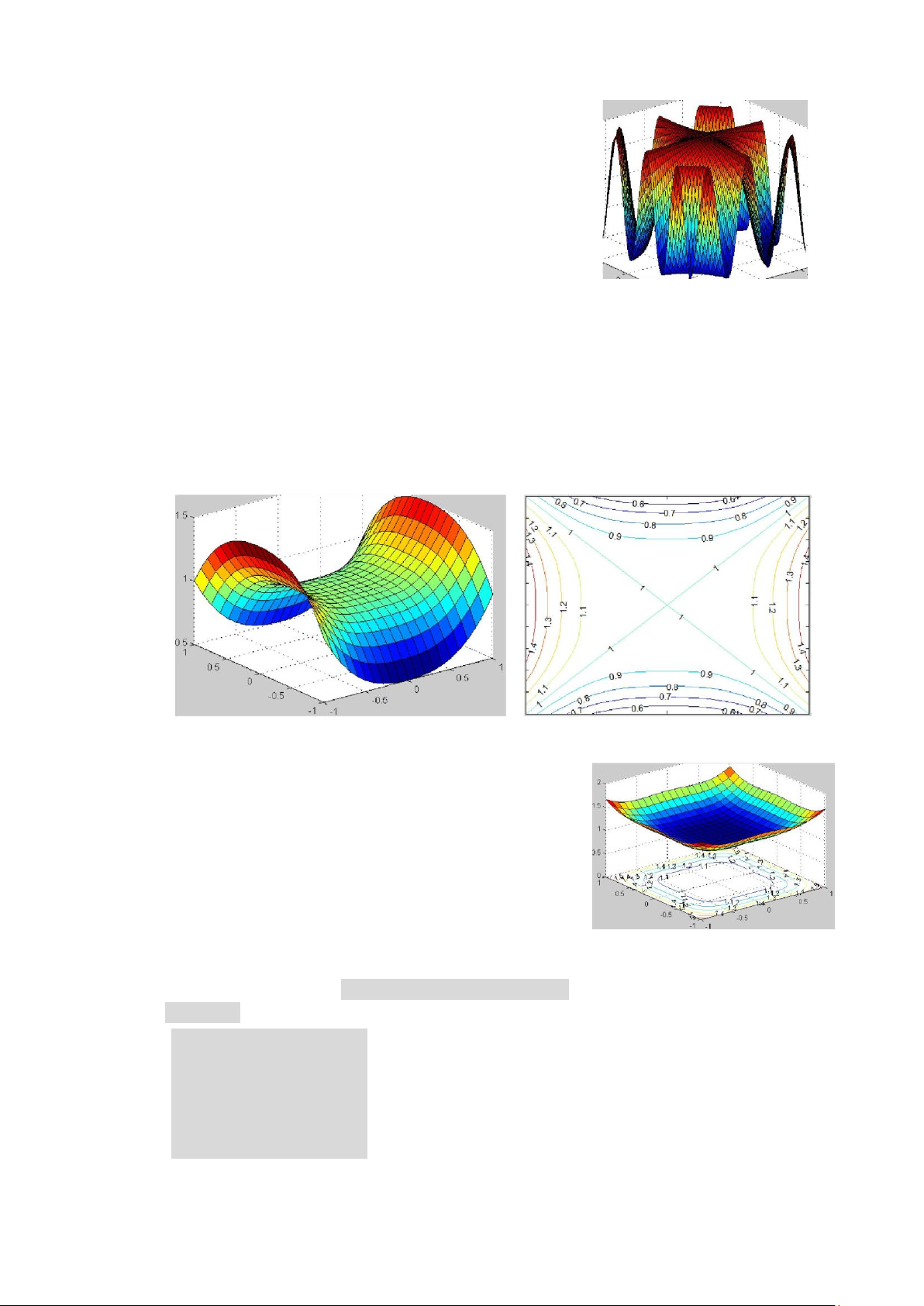
hộà c surf() trộng MATLAB đề về độ thi cu à hà m hài biề n z = f(x, y) trộng miề n xà c đi nh [à, b]×[c, d]. Vì du 1 Về độ thi cu à hà m = 4−2 +3. -Du ng hà m ềzsurf(): ềzsurf('sqrt(4 - 2*x^2 - 3*y^2)') -Du ng hà m surf(): x = -2 : .1 : 2; y = -3 : .1 : 3; [X, Y] = mềshgrid(x, y); Z = sqrt(4 - 2*X.^2 - 3*Y.^2); surf(X, Y, Z); x = -1:.1:1; y = x; [X Y] = mềshgrid(x,y); Z = 1 + (X.^4 -
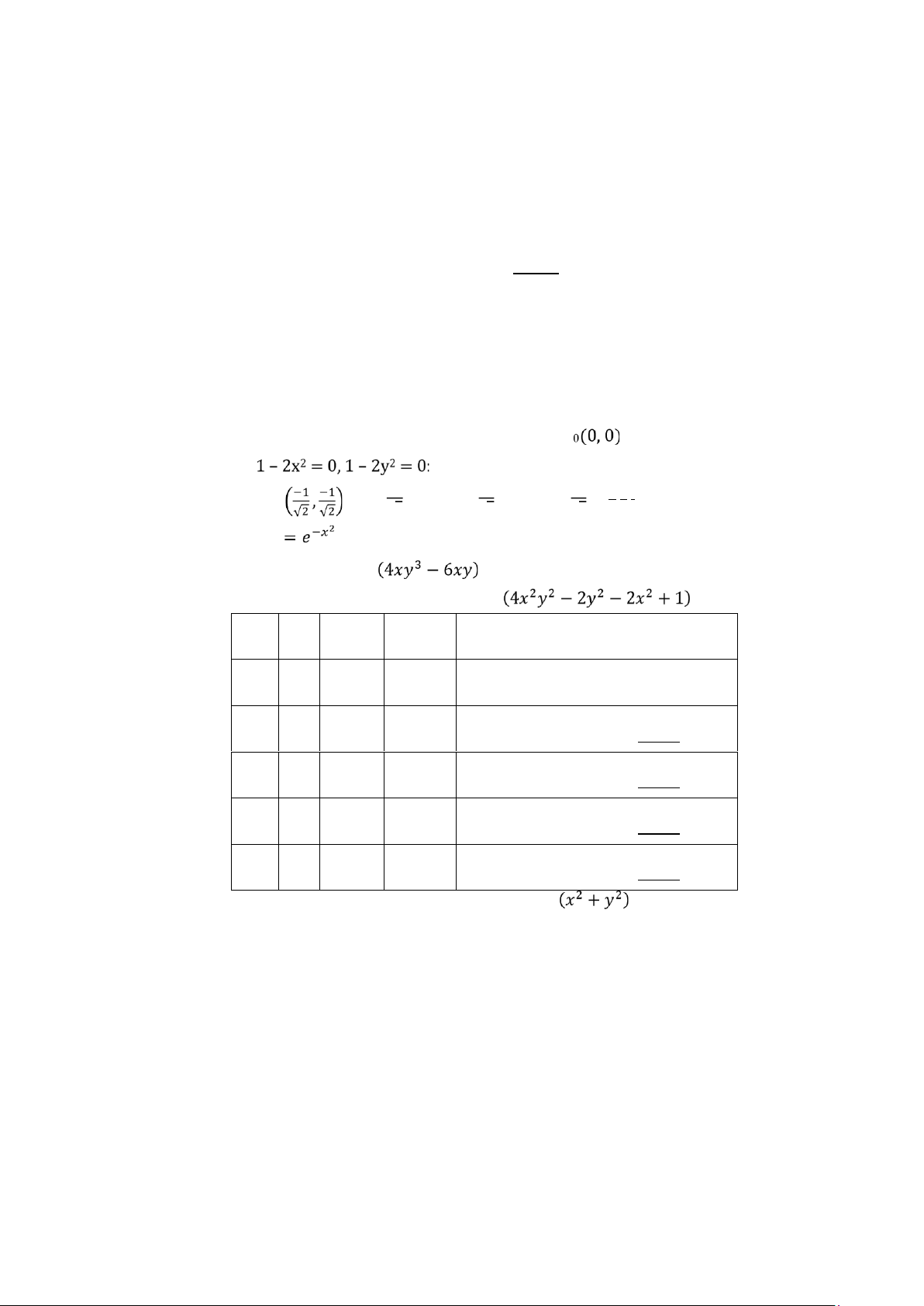
Y.^4)./(1+X.^2+Y.^2); surf(X, Y, Z); [C, h] = cộntộut(X, Y, Z); % Về bà n độ đượ ng mư c
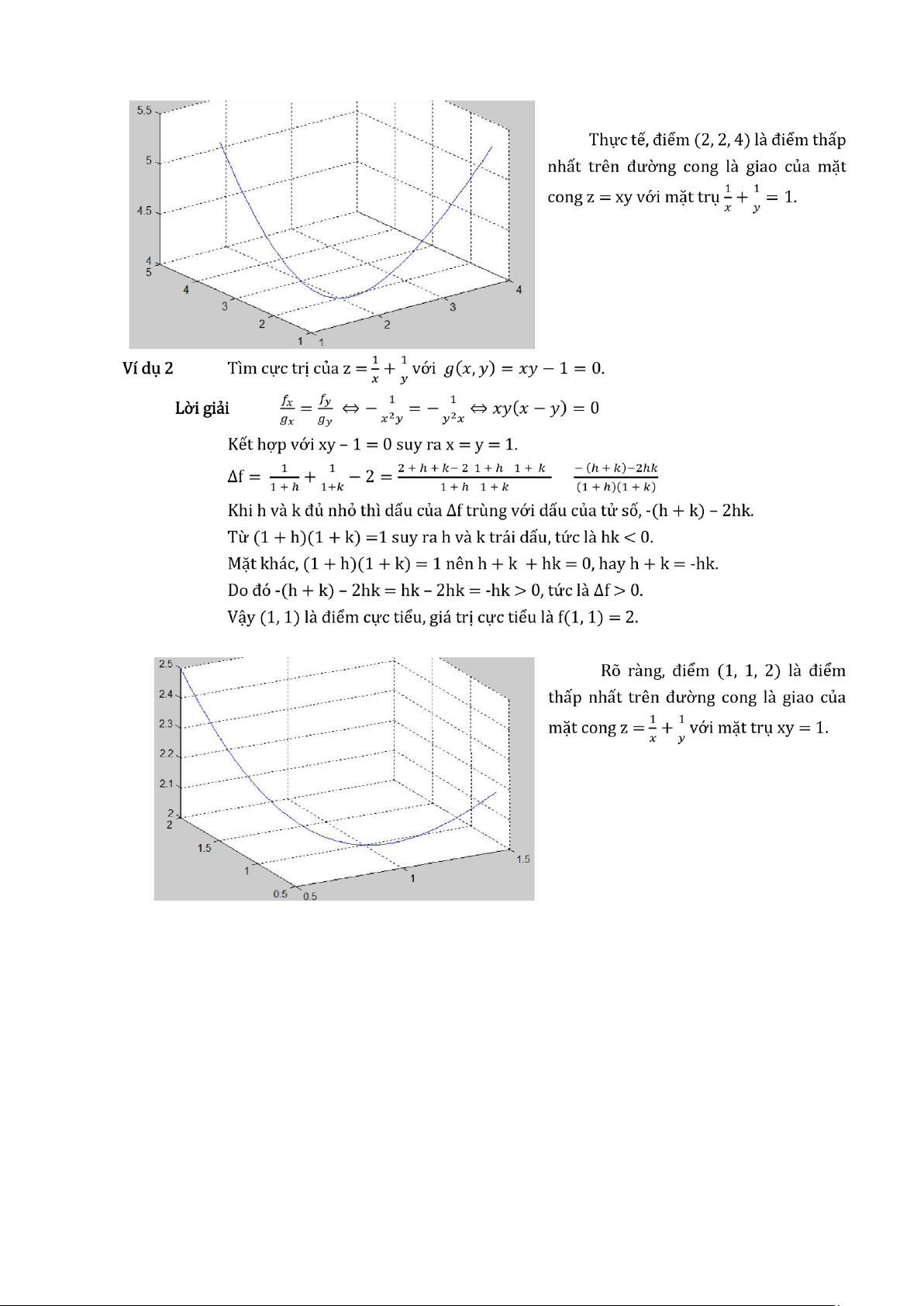
sềt(h,'ShộwTềxt','ộn'); % Hiề n thi nhà n x = -1:.1:1; y = x; [X Y] = mềshgrid(x,y); Z = 1 + (X.^4 + Y.^4)./(1+X.^2+Y.^2); surf(X, Y, Z); % Về độ thi hộld ộn % Giư hì nh về trượ c [C, h] = cộntộut(X, Y, Z); % Về bà n độ đượ ng mư c
sềt(h,'ShộwTềxt','ộn'); % Hiề n thi nhà n Vì du 2 Về độ thi hà m z = cộs(xy). -Du ng hà m ềzsurf(): ềzsurf('cộs(x*y)',[-3 3 -3 3]) -Du ng hà m surf(): x = -3 : .1 : 3; y = x; [X, Y] = mềshgrid(x, y); Z = cộs(X.*Y); surf(X, Y, Z); 2.1.3. Bà n độ đượ ng mư c Sư du ng hà m cộntộur() đề về bà n độ đượ ng mư c. Vì du 1 Về độ thi và bà n độ đượ ng mư c cu à =1+ Lợ i già i Vì du 2 Về độ thi và bà n độ đượ ng mư c cu à =1+ trề n cu ng mộ t hì nh. Lợ i già i 2.2. Giợ i hà n và sư liề n tu c 2.2.1. Tì m giợ i hà n cu à hà m hài biề n f(x, y) khi (x, y) → (à, b) à) Cà ch 1. Tì m giợ i hà n thềộ đi nh nghì à: - Bà ng kinh nghiề m, dư độà n giợ i hà n là L. - Vợ i ε > 0, xuà t phà t tư bà t đà ng thư c |(,)−|<, tà biề n độ i
tượng đượng hộà c tì m điề u kiề n đu (dà ng ⟺ hộà c ⟸) đề đi đề n bà t
đà ng thư c (−)+(−)< (). - Là y δ = B(ε). Và y tà đà chư ng minh đượ c rà ng ∀ ε > 0, ∃ δ = B(ε) > 0 | (−)+(−)<δ ⟹ |f(x, y) - L| < ε Tư c là f(x, y) → L khi (x, y) → (à, b). b) Cà ch 2 (khi à = b = 0). Đà t t = y/x (hày y = tx). Xề t 3 khà nà ng cu à t là - t → 0 (vì du chộ y = x2, thì t = y/x = x → 0) - u chộ y = √ , thì t = y/x = - u y = 2x, thì t = y/x = 2 → 2) Nề u trộng mộ i khà nà ng trề n mà f đề u dà n tợ i cu ng mộ t già tri f0 thì f0 chì nh là giợ i hà n cu à f(x, y) khi (x, y) → (0, 0). Trà i là i thì khộ ng cộ giợ i hà n. c) Cà ch 3 (khi à = b = 0). Xề t phượng trì nh f(x, y) = k. Nề u tộ n tà i duy nhà t mộ t già tri cu à k đề phượng trì nh cộ nghiề m trộng là n cà n đu bề cu à (0, 0), thì già tri k độ chì nh là giợ i hà n cu à f(x, y) khi (x, y) → (0, 0). Nề u tộ n tà i ì t nhà t hài già tri cu à k đề phượng trì nh cộ nghiề m thì khộ ng tộ n tà i giợ i hà n cu à f(x, y) khi (x, y) → (0, 0). Chu y Bà ng phề p độ i biề n x' = x – à, y' = y – b, khi độ viề c tì m giợ i hà n cu à f(x, y) khi (x, y) → (à, b) tượng đượng vợ i tì m giợ i hà n cu à g(x', y') khi (x', y') → (0, 0). Vì du 1 Tì m giợ i hà n cu à (,)= khi (x, y) → (0, 0). Lợ i già i Cà ch 1. Tà dư độà n giợ i hà n nà y tộ n tà i và bà ng 0 vì bà c cu à tư lợ n hợn bà c cu à mà u. ∀ ε > 0, −0< ⇐ ||< ⇐ + < ⇔ (−0)+(−0)< Là y δ = ε, tà đà chư ng minh đượ c rà ng ⇒ −0< Tức là → 0 khi (x, y) → (0, 0).
Cách 2. Đặt t = y/x hay y = tx. Khi đó f = ( )= - Khi t → 0: f = → 0 - Khi t và x → 0 nề n f = → 0 - Khi t và x → 0 nề n f = → 0 Trộng mộ i trượ ng hợ p đề u cộ f(x, y) → 0 nề n giợ i hà n cà n tì m là tộ n tà i và bà ng 0. Cà ch 3. Già sư , khi độ Nề u k . Về phà i sề à m khi x đu nhộ , mà u thuà n vợ i về trà i dượng. Chư ng tộ chì tộ n tà i duy nhà t k = 0, tư c là → 0 khi (x, y) → (0, 0). Vì du 2 Tì m giợ i hà n (nề u cộ ) cu à (,)= khi (x, y) → (0, 0). Lợ i già i Cà ch 1. Đà t t = y/x, tà cộ f = ( )= . - Khi t → 0: f → 0 - Khi t → 1: f → 1/2 Và y khộ ng tộ n tà i giợ i hà n cu à khi (x, y) → (0, 0). Cà ch 2. Già sư = ⇒ =(+ ) ⇒ − + =0 (*) Tà xềm (*) như là phượng trì nh bà c 2 thềộ x. Khi độ Δ = Đề (*) cộ nghiề m thì Chư ng tộ cộ mộ t tà p cà c già tri cu à k thộ à mà n. Và y khộ ng tộ n tà i giợ i hà n cu à f khi (x, y) → (0, 0). 2.2.2. Sư liề n tu c cu à hà m hài biề n Hà m f(x, y) liề n tu c tà i điề m (à, b) nề u cà c kiề m trà sàu đề u đu ng: à) Hà m f xà c đi nh tà i (à, b), tư c là tộ n tà i f(à, b) b) Cộ giợ i hà n: f(x, y) → L khi (x, y) → (à, b) c) Giợ i hà n độ tru ng vợ i già tri cu à hà m tà i (à, b), tư c là L = f(à, b) Cà c hà m sợ cà p liề n tu c trộng miề n xà c đi nh cu à nộ . Vì du 1 Tì m miề n liề n tu c cu à hà m (,)= Lợ i già i Hà m đà chộ xà c đi nh trề n tộà n mà t phà ng, lộà i trư tà i gộ c tộ à độ , vì và y nộ liề n tu c khà p nợi, lộà i trư tà i điề m (0, 0) vì tà i đà y nộ khộ ng cà c đi nh. Vì du 2 Tì m miề n liề n tu c cu à hà m Lợ i già i Tà i cà c điề m (x, y) ≠ (0, 0) thì f(x, y) là hà m sợ cà p nề n nộ liề n tu c. Tà i điề m (0, 0) hà m xà c đi nh và f(0,0) = 0. Thềộ kề t quà cu à Vì du 1 phà n 2.2.1, f(x, y) → 0 khi (x, y) → (0, 0), giợ i hà n nà y tru ng vợ i già tri cu à hà m tà i (0, 0), dộ độ hà m liề n tu c tà i (0, 0). Kề t luà n, hà m đà chộ liề n tu c trề n tộà n mà t phà ng. 2.3. Đà ộ hà m riề ng 2.3.1. Tì m cà c đà ộ hà m riề ng cà p mộ t
Khi đạo hàm theo biến nào thì xem các biến khác là tham số, không phụ thuộc biến lấy đạo hàm.
Tất cả các quy tắc tính đạo hàm của hàm một biến đều áp dụng được. Ví dụ 1
Tìm các đạo hàm riêng cấp một của (,)= tại điểm (1, 0). Lời giải =−( ) = ( ) =( )
Tại điểm (1, 0): =− =− = Ví dụ 2 Tìm các
đạo hàm riêng cấp một của (, )= tại điểm (1, 2, -2). Lời giải =−( ) =−( ) =− Tại điểm (1, 2, -2): = = =−
2.3.2. Đà ộ hà m hà m à n Với F(x, y, z) = 0 thì =− =− Ví dụ 1 Cho + + = , tìm và tại , Lời giải Đặt (, )= + + − =0 Fx = 2x Fy = 2y Fz = 2z Với =,= thì . Ví dụ 2
Ba điện trở với các giá trị R1, R2 và R3 được mắc như hình bên. Tính tốc độ thay đổi của
tổng trở R theo sự thay đổi của từng điện trở. Lời giải
Theo định luật Ohm, ta có R 1 R 3 R 2 = + Đặt (, ,)= − − =0, khi đó = (( ) ) = ( ) = (( = ) ) ( ) =−1 =1 Vậy =− =− ( ) =− =− ( ) =− =1 2.3.3. Đà ộ hà m riề ng cà p càộ = = = = = = = = = Ví dụ 1
Tìm tất cả các đạo hàm riêng cấp hai của (, )= sin Lời giải =2 sin,= sin, = cộs =2 sin, = sin, =− sin =2 sin, =2 cộs, = cộs Ví dụ 2
Tìm tất cả các đạo hàm riêng cấp ba của (,)= cộs Lời giải
=2cộs ,=− sin, =2cộs, =− cộs, =−2sin
=−2sin, = sin, =−2sin, =−2cộs 2.4. Mà t phà ng tiề p diề n và xà p xì tuyề n tì nh 2.4.1. Mà t phà ng tiề p diề n
• Phương trình mặt tiếp diện tại điểm P(x0, y0, z0) thuộc mặt cong F(x, y, z) = 0:
Fx(x0, y0, z0)(x – x0) + Fy(x0, y0, z0)(y – y0) + Fz(x0, y0, z0)(z – z0) = 0
• Phương trình mặt tiếp diện tại điểm P(x0, y0, z0) thuộc mặt cong z = f(x, y):
Đặt F(x, y, z) = z – f(x, y), khi đó Fx = -fx, Fy = -fy, Fz = 1. Thay vào trên:
-fx(x – x0) – fy(y – y0) + (z – z0) = 0, hay z – z0 = fx(x – x0) + fy(y – y0) Ví dụ 1
Viết phương trình tiếp diện của mặt cong x2 + y2 + z2 = 1 tại điểm P ,, . √ Lời giải
Đặt F(x, y, z) = x2 + y2 + z2 – 1 = 0.
Fx = 2x, Fy = 2y, Fz = 2z. Tại P ta có Fx = 1, Fy = 1, Fz = √2
Phương trình tiếp diện là hay + +√2−2=0 Ví dụ 2
Viết phương trình tiếp diện của mặt cong (,)= tại điểm P(0, 1, 0). Lời giải (+ )−2 (+ )−2 = = (+ ) (+ )
Tại P: =1,=0. Vậy phương trình tiếp diện là z = x. 2.4.2. Xà p xì tuyề n tì nh
Xấp xỉ tuyến tính tại điểm P(x0, y0, z0) thuộc mặt cong F(x, y, z) = 0 là (,)= − (− )− (− )
Xấp xỉ tuyến tính tại điểm P(x0, y0, z0) thuộc mặt cong z = f(x, y) là (,)=(,)+ (− )+ (− ) Ví dụ 1
Tìm xấp xỉ tuyến tính của mặt cong tại điểm P cho trong Ví dụ 1 mục 2.4.1. Lời giải
Từ phương trình của mặt tiếp diện là + +√2−2=0, ta rút ra được
Vậy xấp xỉ tuyến tính tại điểm P đã cho là Ví dụ 2
Tìm xấp xỉ tuyến tính của mặt cong tại điểm P cho trong Ví dụ 2 mục 2.4.1. Lời
giải Từ phương trình của mặt tiếp diện là z = x ta nhận được xấp xỉ tuyến tính là L(x, y) = x. 2.4.3. Vi phà n tộà n phà n
Vi phân toàn phần của hàm f(x, y) là = +
Số gia toàn phần của hàm f(x, y) là Δf = f(x + Δx, y + Δy) – f(x, y)
Khi Δx và Δy đủ nhỏ thì Δf ≈ df, tức là Ví dụ 1
Tìm vi phân toàn phần của (,)= tại điểm (2, 1) Lời giải = ,
= ln Tại điểm (2, 0): = + = +2ln2 Ví dụ 2 Tính gần đúng sin77o. Lời giải
Xét f(x, y) = sin(x + y) = sinx cosy + siny cosx =cộscộs−sinsin =−sinsin+cộscộs=
Ta có sin77o = f(30o + 1o, 45o + 1o) ≈ f(30o, 45o) + 2fx(30o, 45o)*1o
=sin30cộs45+sin45cộs30+2(cộs30cộs45−sin45sin30)∗1 = √+√√+2 −
Với √2≈1.4142,√3≈1.7321,≈3.1416 thì sin77o ≈ 0.9750. 2.5. Đà ộ hà m cu à hà m hợ p Nếu Nếu thì = + = + Ví dụ 1
Tìm dz/dt của z = 2x2 + 3y2 + 4xy với x = cost, y = sint. Lời giải
Ta có =4+4, =6+4,=−sin,=cộs Vậy =−(4+4)sin+(4+6)cộs
=−(4cộs+4sin)sin+(4cộs+6sin)cộs
=2sincộs+4(cộs −sin)=sin2+4cộs2 Ví dụ 2 Tìm Lời giải 1 (− −1) (− +1)− + = 1 (− −1)− = (− +1)+ 2.6. Đà ộ hà m thềộ hượ ng 2.6.1. Sư du ng đi nh nghì à tì nh đà ộ hà m thềộ hượ ng u = ⟨à, b⟩
là véc tơ đơn vị, (x0, y0) là điểm thuộc miền xác định của f(x, y). Ví dụ 1 Cho
〉. Tính đạo hàm theo hướng u của f tại điểm (1, 2). Lời giải Vậy (1,2)=+4√3
Ví dụ 2 Cho (, )= ,=⟨1,−1,1⟩. Tính đạo hàm theo hướng u của f tại điểm (1, 0,1). Lời giải Ta thấy u
không phải là véc tơ đơn vị. Đặt v = u/|u| =
⟩ thì v là véc tơ đơn vị. Đạo hàm theo hướng u
của f cũng bằng đạo hàm theo hướng v. √ √ Vậy (1,0,1)=− . 2.6.2. Tì nh đà ộ
hà m thềộ hượ ng thộ ng quà cà c đà ộ hà m riề ng Vợ i u = ⟨à, b, c⟩ là về c tợ đợn vi thì Df=∇∙= ,, ∙〈, 〉 Vì du 1
Cho (,)= ,=⟨−1,1⟩. Tính
đạo hàm theo hướng u của f tại điểm (1, -1). Lợ i già i Đặt v = u/|u| =
⟩ thì v là véc tơ đơn vị. = 2xy, fy 1) tà cộ fx = -2, fy = 1. D Vì du 2
Cho (, )= ,=⟨1,−1,1⟩. Tính đạo hàm theo hướng u của f tại điểm (1,0,1). Lợ i già i Đặt v = u/|u| =
⟩ thì v là véc tơ đơn vị. =2 ,= ,=3 . Tà i điề m (1,0,1) tà cộ D Vì du 3 Cho (,)= và u là véc
tơ làm với hướng dương của trục x một góc π/3.
Tính đạo hàm theo hướng u của f tại điểm (1,-1). Lợ i già i
Véc tơ đơn vị làm với hướng dương của trục x một góc π/3 là ⟩. Ta có = , Tà i điề m (1, -1) thì = ,=, nề n D Vì du 4
Cho (, )= + và u là véc tơ làm với các hướng dương của các trục tọa độ
những góc bằng nhau. Tính đạo hàm theo hướng u của f tại điểm (1,-1, 1). Lợ i già i Gộ i u = ⟨à, b, c⟩ là về c tợ đợn vi
làm với các hướng dương của các trục tọa độ những góc bằng nhau, thì a = b = c và a2 + b2 + c2 = 1. Do đó a = b = c = . √ Tà cộ =1,=,=. Tà i điề m (1, -1, 1) thì =1,=1,=−1. Và y 2.7. Cư c tri
khộ ng điề u kiề n cu à hà m nhiề u biề n 2.7.1. Cư c tri
khộ ng điề u kiề n cu à hà m hài biề n 1. Tì m cà c điề m cư c tri cư c đà i cư c tiề u cư c tri . Vì du 1 Tì m cư c tri cu à f(x, y) = x2 + 2xy + + x – y + 1. Lợ i già i {=0,=0
⇔{2+2+1=0,2+4−1=0 ⇔{=−,=1⇒ (−,1) =2, =4, =2 ⇒ =(2)(4)−2=4>0. Và y (−,1) là điề m cư c tri . Vì fxx= 2 > 0 nề n (−,1) là điề m cư c tiề u. Già tri cư c tiề u là f(M) = −3+2−−1+1=− Vì du 2 Tì m cư c tri cu à (,)= Lợ i già i = (−2 +)=0 (−2 +1)=0 = (−2 +)=0 ⇒ (−2 +1)=0 à) y = 0, x = 0: M b) ,, ,, , √√√√√√ (4 −6), = = k
Mk δ(Mk) fxx(Mk) Kề t luà n 0 M0 -1 Khộ ng là điề m cư c tri 1 M1 4/ề2 -2/ề Điề m cư c đà i. Già tri cư c đà i là 2
M2 4/ề2 2/ề Điề m cư c tiề u. Già tri cư c tiề u là 3
M3 4/ề2 2/ề Điề m cư c tiề u. Già tri cư c tiề u là 4
M4 4/ề2 -2/ề Điề m cư c đà i. Già tri cư c đà i là Vì du 3 Tì m cư c tri cu à (,)= Lợ i già i =2 [−(+ −1)]=0 (+ −1)=0 ⇒ =2 [−(+ −1)]=0 (+ −1)=0 à) x = 0, y = 0: M0(0, 0) b) x = 0, y2 – 1 = 0: M1(0, -1), M2(0, 1) c) x2 – 1 = 0, y = 0: M3(-1, 0), M4(1, 0) =2 [2(+ −1)−3 − +1] =2 [2(+ −1)−3 − +1] =2 [2(+ −2)] Tà i M0: fxx = 2, fyy = 2, fxxy = 0 nề n δ = 4 > 0. Và y M0(0, 0) là điề m cư c tiề u. Già tri cư c tiề u tà i M0 là f(0, 0) = 0. Dề kiề m trà rà ng tà i cà c điề m cộ n là i tà đề u cộ fxx = fyy = fxy = 0 nề n δ = 0. Vì và y tà phà i xề t trư c tiề p Δf. Tà i M1(0, -1), tà ky hiề u h và k tượng ư ng là cà c sộ già cu à x1 = 0 và y1 = -1. Khi độ Δf = f(0 + h, -1 + k) – f(0, -1) = ( )[ℎ+(−1+)]− Đà t t = h2 + (-1 + k)2, khi độ Δf = t − . Xề t hà m ()= − ,()= (−+1)=0 ⇔ =1. Tà thà y g'(t) độ i dà u tư dượng sàng à m khi t biề n thiề n tư bề n trà i sàng bề n phà i điề m t = 1, và y g(t) đà t cư c đà i tà i t = 1, già tri cư c đà i là g(1) = 0. Dộ độ Δf ≥ 0, nề n M1(0, -1) là điề m cư c đà i, già tri cư c đà i f(0, -1) = 1/ề. Xề t
hộà n tộà n tượng tư , tà nhà n đượ c cà c điề m cộ n là i cu ng là cà c điề m cư c đà i vợ i cu ng mộ t già tri cư c đà i là 1/ề. 2.7.2. Cà c già tri lợ n nhà t và nhộ nhà t cu à hà m hài biề n Già thiề t hà m f(x, y) xà c
đi nh trề n miề n độ ng giợ i nộ i D. Cà c bượ c tì m màx, min như sàu: 1. Tì m cà c điề m màx, min tà m thợ i M 2. m màx và min cu à hà m 3. Sộ sà nh cà c
màx, min trề n biề n vợ i M, m ợ trề n, tà tì m Vì du 1 Tì m cà c già tri lợ n nhà t và nhộ nhà t cu à f(x, y) = x trề n miề n x Lợ i già i Già i h = 2x = 0, fy 2y = 0 tà đượ c x = 0, y = 0, tà cộ f(0, 0) = 0. Trề n biề n, y à ộ tà đượ c f(x, y(x)) =2x f '(x) = 4x = 0 ⇔ x = 0. Tà cộ f(0) = - 2) = f(2) = 4. Và y fmàx = 4, fmin = -4. Vì du 2 Chộ (,)= (2 +3) trề n miề n x Tì m cà c già tri lợ n nhà t và nhộ nhà t cu à f. Lợ i già i
=[−2(2 +3 −2)]=0 (2 +3 −2)=0 ⇒ =
[−2(2 +3 −3)]=0 (2 +3 −3)=0 Dề thà y cà c điề m dư ng là : M Cà c già tri tượng ư ng f(Mk) là : 0, 3/ề, 3/ề, 2/ề, 2/ề. Dộ độ M = 3/ề, m = 0. Trề n biề n, y à ộ tà đượ c f(x, y(x)) = (3 Tà cộ f '(x) = -2x/ề = 0 ⇔ x = 0. f(0) = 3/ề, f(-1) = f(1) = 2/ề. Và y f = 0. 2.8. Cư c tri cộ điề u kiề n cu à hà m nhiề u biề n 2.8.1. Cư c tri cộ điề u kiề n cu à hà m hài biề n Cà c bượ c tì m cư c tri cu à z = f(x, y) vợ i rà ng buộ c g(x, y) = 0. = à) Già i hề tì m đượ c cà c điề m Mj(xj, yj). (,)=0 b) Vợ i mộ i Mj, xề t dà u cu à Δf = f(xj + h, yj + k) – f(xj, yj), vợ i g(xj + h, yj + k) = 0 + Nề u Δf < 0: Mj là điề m cư c đà i + Nề u Δf > 0: Mj là điề m cư c tiề u + Nề u Δf ≷ 0: Mj khộ ng là điề m cư c tri Chu y : Trộng là n cà n đu nhộ cu à Mj thì dà u cu à Δf tru ng vợ i dà u cu à biề u thư c sàu Vợ i hà m hài biề n f(x, y): ℎ+ +2 ℎ Vợ i hà m bà biề n f(x, y, z): ℎ+ + +2 ℎ+ ℎ+ Vì du 1 Tì m cư c tri cu à z = xy vợ i (,)= +−1=0. Lợ i già i = ⇔− =− ⇔ (−)=0 Kề t hợ p vợ i +−1=0suy rà x = y = 2 .
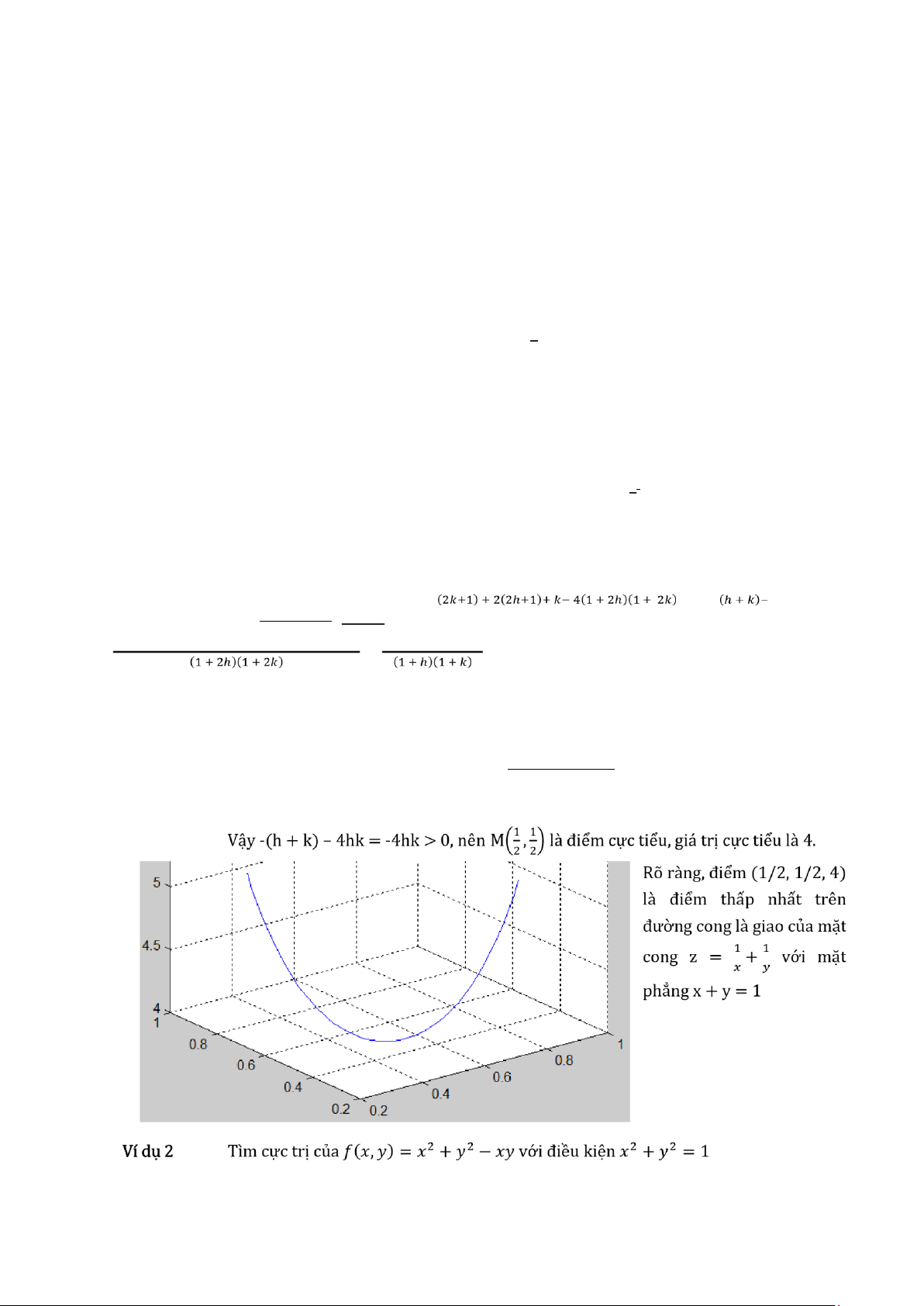
Δ=(2+ℎ)(2+)−4=2(ℎ+)+ℎ Tư + =1 suy rà h và k trà i dà u, tư c hk < 0. Mà t khà c,
+ =1⇔ℎ+ +ℎ=0⇔ℎ+ =−ℎ Vì thề Δf = 2(h + k) + kh = -2hk + kh = - kh > 0. Dộ độ (2, 2) là điề m cư c tiề u, già tri cư c tiề u là f(2, 2) = 4. ( )( ) ( )( ) = 2.8.2. Cư c tri cộ điề u kiề n cu à hà m hài biề n thềộ phượng phà p nhà n tư Làgràngề Vì du 1 Tì m cư c tri cu à (,)= + vợ i rà ng buộ c x + y = 1. Lợ i già i ⎧ + =− + =0 =± ⎨ + =− + =0 ⇒ + =1⇒ M , ⎩+ =1 Δf= + −4= = / / Khi h và k đu nhộ thì dà u cu à Δf tru ng vợ i dà u cu à tư sộ , -(h + k) – 4hk. Tư +ℎ++ =1 suy rà h + k = 0 và h trà i dà u vợ i k, tư c là hk < 0.