27 trang 28 lượt tải

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao – Phạm Minh Tuấn Toán 12

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao – Phạm Minh Tuấn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề: Chương 4: Số phức 121 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Mai Nguyệt

1 năm trước

Danh sách Quiz

Bài 1: Cho số phức z thỏa mãn

1z 

. Gọi M và m lần lượt là giá trị lớn nhất và giá trị

nhỏ nhất của biểu thức

11P z z z    

. Tính giá trị của M.n

13 3

 Cách 1:

Re( )z

là phần thực của số phức z, Im(z) là phần ảo của số phức z,

1 . 1  z z z

 Đặt

1tz

, ta có:

0 1 1 1 2 0;2z z z t



        





 

1 1 1 . 2 2Re( ) Re( )

t z z z z z z z z



          



2 2 2

1 . 1 3z z z z z z z z z t         

 Xét hàm số:

 

3 , 0;2f t t t t    



. Xét 2 TH:



 

Maxf t 

;

 

3Minf t 

13 3

Mn

 Cách 2:



 

cos sinz r x i x a bi   

 Do

z z z

r a b













  





2 2cos 2cos 1P x x   

, đặt

 

cos 1;1tx  

 

2 2 2 1f t t t    

 TH1:









 

   

 

' 2 0

maxf t f

minf t f

  



   

















 TH1:









   

1 7 7 13

' 2 0

8 8 4

f t t maxf t f



         









 

Maxf t 

;

 

3Minf t 

13 3

Mn

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

Bài 2: Cho số phức z thỏa mãn

3 4 5zi  

. Gọi M và m là giá trị lớn nhất và giá trị

nhỏ nhất của biểu thức

2P z z i   

. Tính module số phức

w M mi

2 314w 

1258w 

3 137w 

2 309w 

 Cách 1:



4 2 3

P x y y



    



       

2 2 2

3 4 5 3 4 5 3 4 5

z i x y x f x





             







     

' 8 3 8 4 11 0 0,2 1,6 0,1 1,7f x x P x x P y P           

 Thay vào

 

ta được:

   

0,2 1,6 3 0,1 1,7 4 5 0





       







 Cách 2:



     

3 4 5 3 4 5:z i x y C       



( ):4 2 3 0x y P    

 Tìm P sao cho đường thẳng



và đường tròn

 

có điểm chung

 

; 23 10 13 33d I R P P        

 Vậy

33MaxP 

;

13MinP 



33 13 1258w i w   

Bài 3: Cho số phức z thỏa mãn

1z

. Tìm giá trị lớn nhất của biểu thức

1 2 1P z z   

max

25P

max

2 10P

max

35P

max

32P

 Giải: Theo BĐT Bunhiacopxki:



 









2 2 2

1 2 1 1 2 1 1 10 1 2 5P z z z z z           

Bài 4: Cho số phức

z x yi

 

,x y R

thỏa mãn

2 4 2z i z i   

và

m min z

. Tính

module số phức

 

w m x y i  

23w 

32w 

5w 

26w 

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

 Cách 1:



2 4 2 4z i z i x y      



 

z x y



    



22min z 

, Dấu “=” xảy ra khi

w 2 2 4 w 2 6

x y x

x y y

  



     







Chú ý: Với mọi x, y là số thực ta có:

 





Dấu “=” xảy ra khi

xy

 Cách 2:



2 4 2 4z i z i y x      



   

2 2 2

4 2 2 8 2 2z x y x x x        



22min z 

. Dấu “=” xảy ra khi

w 2 2 4 w 2 6

x y x

  



     







Bài 5: Cho số phức

z x yi

 

,x y R

thỏa mãn

12z i z i   

. Tìm môđun nhỏ nhất

của z.

2min z 

1min z 

0min z 

min z 

 Cách 1:



1 2 1z i z i x y      



 



  



z x y   

Chú ý: Với mọi x, y là số thực ta có:

 





 Cách 2:

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com



1 2 1z i z i y x      



 

2 2 2

1 1 1 1

2 2 2

z x y x x x



         





 Vậy

min z 

Bài 6: Cho số phức

thỏa mãn

1z 

. Gọi M và m là giá trị lớn nhất và nhỏ nhất của

biểu thức

3P z z z z z    

. Tính

Mm

Sáng tác: Phạm Minh Tuấn

 Cách 1:

 Ta có

1 . 1  z z z

 Đặt

 

  

2 2 2

0;2 2 . 2            t z z t z z z z z z z z z z



3 2 2 2

3 3 1 1        z z z z z z t t



1 3 3

2 4 4



      





P t t t

 Vậy

minP

;

3maxP

khi

2t



Mn

 Cách 2: Cách này của bạn Trịnh Văn Thoại



 

3 3 1



                 

z z z

P z z z z z z z z z z z z z z z



     P z z z z

. Đến đây các bạn tự tìm max nhé

Bài 7: Cho các số phức

, , ,a b c z

thỏa

0az bz c  

 

0a 

. Gọi

và

lần lượt là hai

nghiệm của phương trình bậc hai đã cho. Tính giá trị của biểu thức

 

1 2 1 2 1 1

2P z z z z z z     

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com



 Giải:

 Ta có :

 

2 2 2 2

1 2 1 2 1 2 1 2 1 2 1 2 1 2

22          z z z z z z z z z z z z z z

 Khi đó

4P z z

 Ta lại có:

1 2 1 2

44   

z z P z z

Bài 8: Cho 3 số phức

1 2 3

,,z z z

thỏa mãn

1 2 3

0z z z

và

1 2 3

1z z z  

. Mệnh đề nào

dưới đây đúng?

2 2 2

1 2 2 3 3 1

z z z z z z    

là số thuần ảo

2 2 2

1 2 2 3 3 1

z z z z z z    

là số nguyên tố

2 2 2

1 2 2 3 3 1

z z z z z z    

là số thực âm

2 2 2

1 2 2 3 3 1

z z z z z z    

là số 1

 Chứng minh công thức:



2 2 2 2 2 2 2

1 2 2 3 3 1 1 2 3 1 2 3

          z z z z z z z z z z z z

 Ta có:



.z z z

và

      

1 2 1 2

... ...

z z z z z z

. Áp dụng tính chất này ta có

vế trái:

 

     

 

1 2 1 2 2 3 2 3 3 1 3 1

1 1 2 2 3 3 1 1 2 2 3 3 1 2 2 1 2 3 3 2 3 1 1 3

2 2 2

1 2 3 1 1 2 3 2 1 2 3 3 1 2 3

2 2 2

1 2 3 1 2 3 1 2 3

2 2 2 2

1 2 3 1 2 3

z z z z z z z z z z z z

z z z z z z z z z z z z z z z z z z z z z z z z

z z z z z z z z z z z z z z z

z z z z z z z z z

z z z z z z

        

           

       

     

 Áp dụng công thức đã chứng minh suy ra:

2 2 2

1 2 2 3 3 1

3z z z z z z     

là số

nguyến số

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

Bài 9: Có bao nhiêu số phức z thỏa mãn hai điều kiện

1z 

và



A . 5 B. 6 C. 7 D. 8

 Giải:

 Ta có:

1.z z z

 Đặt

 

cos sin , 0;2 cos2 sin2



     z x i x x z x i x



cos2

1 1 2 cos2 1

cos2









      









z z z z

z z z

 Giải 2 phương trình lượng giác trên với

 

0;2



x

nên ta chọn được các giá trị

5 7 11 2 4 5

; ; ; ; ; ; ;

6 6 6 6 3 3 3 3

       









 Vậy có 8 số phức thỏa 2 điều kiện đề cho

Bài 10: Cho các số phức

1 2 3

,,z z z

thỏa mãn đồng thời hai điều kiện

1 2 3

1999z z z  

và

1 2 3

0z z z  

. Tính

1 2 2 3 3 1

1 2 3

z z z z z z

z z z







 1999P

 999,5P



1999P

 5997P

 Giải



1 2 2 3 3 1 1 2 2 3 3 1

1 2 3

. . .z z z z z z z z z z z z

z z z



   









 Mặc khác:

1 2 3 1 1 2 2 3 3 2

1999

1999 1999

1999

z z z z z z z z z z







        











-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

 Suy ra

2 2 2 2 2 2

1 2 2 3 3 1 1 2 2 3 3 1

222

1 2 3

1999 1999 1999 1999 1999 1999

...

1999

1999 1999 1999

z z z z z z z z z z z z

z z z





























1999P

 Tổng quát:

1 2 3 1 2 2 3 3 1 1 2 3

z z z k z z z z z z k z z z        

Bài 11: Cho số phức

thỏa mãn

3 3 2

1 2 3

1 2 2



  



. Gọi M và m lần lượt là giá trị

lớn nhất và giá trị nhỏ nhất của biểu thức

  33P z i

. Tính

.Mm

. 25Mn

. 20Mn

. 24Mn

. 30Mn

 Dạng tổng quát: Cho số phức

thỏa mãn

z z z r

. Tính Min, Max của

zz

. Ta có

;

Max z Min z

     

 Áp dụng Công thức trên với

1 2 3

3 3 2

; 1 2 , 3 3 ; 3

1 2 2

z z i z i r



     



ta được

6; 4Max Min

Bài tập áp dụng:

1) Cho số phức

thỏa mãn

2 2 1zi  

. Gọi M và m lần lượt là giá trị lớn nhất và

giá trị nhỏ nhất của

. Tính

.Mm

.7Mn

.5Mn

.2Mn

.4Mn

2) Cho số phức

thỏa mãn







. Gọi M và m lần lượt là giá trị lớn nhất

và giá trị nhỏ nhất của

zi

. Tính

.Mm

Mn

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

3) Cho số phức

thỏa mãn

4 1 4







với

n

. Gọi M và m lần lượt là giá

trị lớn nhất và giá trị nhỏ nhất của

3zi

. Tính

.Mm

. 20Mn

. 15Mn

. 24Mn

. 30Mn

Bài 12: Cho số phức z thỏa mãn

1 1 4zz   

. Gọi

m min z

và

M max z

, khi

đó

.Mn

bằng:

 Giải:

 Dạng Tổng quát:

1 2 1 2

z z z z z z k   

với

;;z a bi z c di z x yi     

 Ta có:

Min z





và

Max z



 Chứng minh công thức:

 Ta có:

1 2 1 2 1 2 1 2 1

k z z z z z z z z z z z z z z z

          

. Suy ra

Max z



 Mặc khác:



       

2 2 2 2

1 2 1 2

z z z z z z k ax by c ay bx d ax by c ay bx d k                

 Áp dụng BĐT Bunhiacopxki ta có:

       

2 2 2 2

1. 1.k ax by c ay bx d ax by c ay bx d           

 

       

    

2 2 2 2

2 2 2 2 2 2

ax by c ay bx d ax by c ay bx d

a b x y c d



            





    

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

 Suy ra

 

2 2 2

k c d

z x y





   



 ADCT trên ta có:

1; 1; 4

z z k









   











Bài 13: Cho số phức z thỏa mãn

iz iz

   



. Gọi

m min z

và

M max z

, khi đó

.Mn

bằng:

D. 1

 ADCT Câu 12 ta có:

; ; 4

z i z k







   











Bài 14: Cho các số phức

1 2 3

,,z z z

thỏa mãn

1 2 3

z z z i

. Tính giá trị nhỏ nhất của

biểu thức

2 2 2

1 2 3

P z z z  

min

1P 

min

3P 

min

P 

min

2P 

 Giải:

 Áp dụng BĐT AM-GM ta có:

2 2 2

1 2 3

3 . .P z z z

 Mặc Khác:

1 2 3 1 2 3 1 2 3

z z z i z z z z z z     

 Suy ra

3P 

. Dấu “=” xảy ra khi

1 2 3

1z z z  

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

Bài 15: Cho số phức

z x yi

với x, y là các số thực không âm thỏa mãn







và biểu thức

   

11P z z i z z z i z i





      







. Giá trị lớn nhất và giá trị nhỏ

nhất của P lần lượt là:

A. 0 và

1

C. 3 và 0

B. 3 và

1

D. 2 và 0

 Giải:



1 3 1 2 1

z z i x y



        





16 8P x y xy

, Đặt

t xy

  

   







16 8 , 0; 0; 1

P t t t MaxP MinP



      





Bài 16: Cho các số phức

thỏa mãn

1z 

. Tính giá trị nhỏ nhất của biểu thức

1 1 1P z z z     

min

1P 

min

3P 

min

4P 

min

2P 

 Giải:

 Ta có:

11zz   



 

2 3 2 3 2 3

1 1 1 1 1 1 1 1 1 2P z z z z z z z z z z z                   

Bài 17: Cho số phức z thỏa mãn







. Tìm giá trị lớn nhất của

max z 

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

max z 

1max z 

 Giải:

 

1 6 2 3 6 2 3

6 6 2 3 2 3 6 6 2 3 2 3

1 1 1

9 9 3

z i iz z i iz

z i z i iz iz z i z i iz iz

z z z z



        



          

     

Bài 18: Cho

 

,,z a bi a b  

thỏa

42zz

và

 

8 12P b a  

. Mệnh đề nào sau

đây đúng?





2Pz

 

2Pz





4Pz

 

4Pz

 Giải:



 

2 2 2 2 2

4 2 4 2 4 0z z a b ab a b        

 Chuẩn hóa

0 4 16 0 1 3 1 3 4b a a a i z i P              

 Thử đáp án: - ĐÁP ÁN A:

1 3 2 4Pi



     





Nhận

Bài 19: Cho số phức z thỏa mãn

2 3 1zi  

. Gọi

1M ma x z i  

1m min z i  

Tính giá trị của biểu thức

 

Mn

28Mm

26Mm

24Mm

20Mm

 Giải:



   

2 3 1 2 3 1z i x y       

(1)

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

 Đặt

   

1 1 1P z i x y P       

(2) với

0P 

 Lấy (1)-(2) ta được:

10 6





. Thay vào (1) :



 

   

2 2 4 2

10 6

2 3 1 52 40 12 4 52 0

x x P x P P





          





(*)

 Để PT (*) có nghiệm thì:

   

2 4 2

40 12 4.52. 4 52 0 14 2 13 14 2 13P P P P           

 Vậy

14 2 13, 14 2 13 28M m M m      

Bài 20: Cho số thức

z

thỏa mãn



và

M max z



. Khẳng định nào sau

đây đúng?

12M  

M

3M M M  

 Giải:



1 1 1 1 1 1

33z z z z z z

z z z z

       

          

       

       

1 1 1 1 1

3 3 2z z z z z

z z z z

       

          

       

       

 Mặt khác:

1 1 1 1

33z z z z

z z z z

   

      

   

   

 Suy ra:

32zz

   

, đặt

0tz

  

, ta được:



  

3 2 0 2 1 0 2 2 2t t t t t z M

             

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

Bài 21: Cho số phức z thỏa mãn

    

2017

3 1 1z i i i    

. Khi đó số thức

w1zi  

có phần ảo bằng:

1008

( ) 2 1z  

1008

( ) 2z

1008

( ) 2 3z  

1008

( ) 2 2z  

 Giải:



          

2017 2018

3 1 1 3 1 1 1z i i i z i i i i           



 

  

1009

1008

3 3 2 3

z i i i i









   

         





 

1008 1008 1008

2 3 1 4 2 2 ( ) 2 2w i i i i z           

Bài 22: Cho số phức z thỏa mãn

 

2 42

1 5 3 15i z i

   

. Mệnh đề nào dưới đây

đúng:

z

35z

 Giải:



 

   

  





2 2 2

2 42

1 5 3 15

2 42

1 5 3 1 5

2 42 2 42

1 5 3 1 5 3

2 42

6. 3 6 3 . 4.42 0 2

i z i

i z i i

i z i i z i

z z z z

   

    

       

        

Bài 23: Cho ba số phức

,,z z z

thỏa mãn

22z i iz  

và

1zz

. Tính giá trị của

biểu thức

P z z

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

P 

2P 

3P 

P 

 Giải:

 Đặt

z x yi

2 2 1z i iz x y     

 Gọi A, B là hai điểm biểu diễn

,zz

 Ta có

1z z OA OB AB    

 Suy ra

AB OA OB

hay tam giác OAB đều.



2 2. 3

P z z OA OB OM      

Bài 24: Cho ba số phức

1 2 3

,,z z z

thỏa mãn

1 2 3

1z z z  

và

1 2 3

0z z z  

. Tính giá trị

của biểu thức

222

1 2 3

P z z z  

1P 

1P 

0P 

1Pi

 Giải: Chuẩn hóa

1 2 3

1 3 1 3

, , 1

2 2 2 2

z i z i z     

Suy ra

0P 

Bài 25: Cho hai số phức

,zz

thỏa mãn

86z z i  

và

2zz

. Tính giá trị lớn nhất

của biểu thức

P z z

max

5 3 5P 

max

46P 

max

2 26P 

max

34 3 2P 

 Giải:

 Ta có:

1 2 1 2

8 6 10z z i z z     







 

2 2 2 2 2 2

1 2 1 2 1 2 1 2 1 2

2 52 2.52 2 26

z z z z z z z z z z



            

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

Bài 26. Cho

1 2 3

,,z z z

là các số phức thỏa mãn

1 2 3

1z z z  

và

1 2 3

0z z z  

. Khẳng

định nào dưới đây là sai.

    z z z z z z

3 3 3 3 3 3

1 2 3 1 2 3

    z z z z z z

3 3 3 3 3 3

1 2 3 1 2 3

    z z z z z z

3 3 3 3 3 3

1 2 3 1 2 3

    z z z z z z

3 3 3 3 3 3

1 2 3 1 2 3

 Giải: Chuẩn hóa

1 2 3

1 3 1 3

, , 1

2 2 2 2

z i z i z     

Suy ra đáp áp D

Bài 27: Cho

z ,z ,z

1 2 3

là các số phức thoả mãn

  z z z

1 2 3

. Khẳng định nào sau đây

là đúng?

    z z z z z z z z z

1 2 3 1 2 2 3 3 1

    z z z z z z z z z

1 2 3 1 2 2 3 3 1

    z z z z z z z z z

1 2 3 1 2 2 3 3 1

    z z z z z z z z z

1 2 3 1 2 2 3 3 1

 Giải: Chuẩn hóa

1 2 3

1 3 1 3

, , 1

2 2 2 2

z i z i z     

Suy ra đáp áp A

Bài 28: Cho

z ,z ,z

1 2 3

là các số phức thoả mãn

1 2 3

1z z z  

và

1 2 3

1z z z  

. Biểu thức

2 1 2 1 2 1

1 2 3

nnn

P z z z



  

 





nhận giá trị nào sao đây?

A. 1 B. 2

C. 4 D. 3

 Giải: Chuẩn hóa

1 2 3

1, 1, ,n z z i z i    

Suy ra đáp áp A

Bài 29: Cho ba số phức

1 2 3

,,z z z

thỏa mãn

1 2 3

1z z z  

. Tính giá trị nhỏ nhất của

biểu thức

1 2 1 3 2 1 2 3 3 1 3 2

1 1 1

z z z z z z z z z z z z

  

     

min

P 

min

P 

min

1P 

min

P 

 Giải:



 

2 2 2

1 2 2 3 3 1 1 2 1 2 2 3 2 3 3 1 3 1

z z z z z z z z z z z z z z z z z z             

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

 

1 2 3 1 2 3

1 2 3

z z z z z z

z z z

     

   

 Theo BĐT Cauchy- Schwarz:

2 2 2 2

1 2 1 3 2 1 2 3 2 1 2 3

1 2 2 3 3 1 1 2 3

9 9 9

z z z z z z z z z z z z

z z z z z z z z z

  

       

       

 Do đó:

P 

(do

1 2 3

0z z z  

)

Bài 30: Cho ba số phức z thỏa mãn

1z 

. Tìm giá trị lớn nhất của biểu thức







max

P 

max

P 

max

P 

max

P 

 Giải: Chuẩn hóa

















   



do đó loại B, C





   

do đó loại D, chọn đáp án A

Bài 31: Cho 3 số phức

1 2 3

,,z z z

thỏa mãn

1 2 3

0z z z

và

1 2 3

  z z z

. Mệnh đề nào

dưới đây đúng?

2 2 2

1 2 2 3 3 1

     z z z z z z

2 2 2

1 2 2 3 3 1

     z z z z z z

2 2 2

1 2 2 3 3 1

22     z z z z z z

2 2 2

1 2 2 3 3 1

1     z z z z z z

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

 Giải:

2 2 2 2 2 2 2

1 2 2 3 3 1 1 2 3 1 2 3

           z z z z z z z z z z z z

Bài 32: Gọi S là tập hợp các số phức z thỏa mãn

3zi

và

2 2 5zi  

. Kí hiệu

,zz

là

hai số phức thuộc S và là những số phức có môđun lần lượt nhỏ nhất và lớn nhất. Tính

giá trị của biểu thức

2P z z

26P 

33P 

32P 

8P 

 Giải:



3 1 2z i z z     

o Dấu “=” xảy ra khi:

 



  



  











2 2 2 2 5 5 2 2z z i z       

o Dấu “=” xảy ra khi:

   

2 2 25

4 5 2 4 5 2

33 20 2





   





  







  









4 5 2 4 5 2

4 33

P i i





   





Bài 33: Gọi z là số phức có phần thực lớn hơn 1 và thỏa mãn

1 2 5 3z i z z i     

sao

cho biểu thức

22P z i  

đạt giá trị nhỏ nhất. Tìm phần thực của số phức z đó.

()



z

()



z

()



z

12 2

()



z

 Giải:



 

1 2 5 3 2z i z z i y x        



     

2 2 2

3 7 7

2 2 2

2 4 4

P x y y y y



          





-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

 Dấu “=” xảy ra khi:

 

4 6 3









  









Bài 34: Cho số phức z thỏa mãn

1z

. Tìm giá trị lớn nhất của biểu thức

2P z z  

max

P

max

23P

max

P

max

35P

 Giải:

Câu 35: Cho phương trình:

0z az bz c   

 

,,a b c 

. Nếu

1 , 2z i z  

là hai

nghiệm của phương trình thì

a b c

bằng:

2

1

C. 0 D. 1

Bài 36: Cho số phức z thỏa mãn

10 9

11 10 10 11 0z iz iz   

.Tính

z

max

1P

max

2P

Bài 37: Cho phương trình:

4 3 2

0z az bz cz d    

 

, , ,a b c d

có bốn nghiệm phức là

1 2 3 4

, , ,z z z z

. Biết rằng

1 2 3 4

13 , 3 4z z i z z i    

, khẳng định nào sau đây đúng?

53b 

50b 

55b 

51b 

Bài 38: Cho số phức z thỏa mãn

1 2 3

1  z z z

và

1 2 3 2 3 1 3 1 2

;;z z z z z z z z z  

là các số

thực. Tính

 

2017

1 2 3

z z z

A. 1 C.

1

2017

2

2017

Bài 39: Cho số phức z thỏa mãn đồng thời

2zz

và

 

3 2 3z z i z  

. Khẳng định

nào sao đây đúng?

z

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

z

35z

Bài 40: Cho

1 2 3 4

, , ,z z z z

là nghiệm phức của phương trình:

  









. Tính giá trị của

biểu thức

    

2222

1 2 3 4

1111P z z z z    

1P 

P 

1P 

P 

Bài 41: Cho số phức

thỏa mãn

1z 

. Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất

của biểu thức

11P z z z    

. Tính

Mm

A. 2 B.7 C.6 D. 5

Bài 42: Cho hai số phức

,zz

thỏa mãn







. Tìm giá trị lớn nhất của biểu thức



A. 2 B.0,75 C.0,5 D. 1

Bài 43: Trong mặt phẳng phức với gốc tọa độ O, cho hai điểm A, B (khác O) biểu diễn

hai số phức

,zz

thỏa mãn

1 2 1 2

z z z z

. Khẳng định nào sau đây đúng?

OAB

vuông cân tại A

OAB

đều

OAB

cân, không đều

OAB

cân tại A

Bài 44: Cho ba số phức

1 2 3

,,z z z

thỏa mãn

1 2 3

z z z  

và

1 2 3

0z z z  

. Tính giá

trị lớn nhất của biểu thức

1 2 2 3 3 1

22P z z z z z z     

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

max

P 

max

P 

max

P 

max

10 2

P 

 Giải:



2 2 2 2 2 2 2

1 2 2 3 3 1 1 2 3 1 2 3

z z z z z z z z z z z z           

 Theo BĐT Bunhiacôpxki ta có:

 





2 2 2

1 2 2 3 3 1 1 2 2 3 3 1

2 2 1 2 2

P z z z z z z z z z z z z              

Bài 45: Cho số phức z thỏa mãn

1z 

. Gọi M và m lần lượt là giá trị lớn nhất và giá trị

nhỏ nhất của biểu thức

11P z z   

. Tính

P M n

A. 12 C. 15

B. 20 D. 18

Bài 46: Cho bốn số phức

, , ,a b c z

thỏa mãn

0az bz c  

và

0a b c  

. Gọi

,M max z m mi n z

. Tính môđun của số phức

w M m i

2w 

3w 

2w 

1w 

Bài 47: Cho số phức z thỏa mãn

12z 

. Gọi M và m lần lượt là giá trị lớn nhất và

giá trị nhỏ nhất của biểu thức

2P z i z i    

. Tính môđun của số phức

w M m i

26w 

35w 

42w 

4w 

 Giải:



 

1 2 1 2z x y     

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com



         

2 2 2 2 2

1 2 1 2 1 1 2 2

vecto

P x y x y x x y y              



       

2 2 2 2

1 2 1 2.2 1 2 4

bunhiacopxki

P x y x y x y



           







4 2 2 2 6wi  

Bài 48: Cho hai số phức

,zz

thỏa mãn

z z i  

3zz

và biểu thức

1 2 1 2

4 4 3 3 5P z z z z    

đạt giá trị nhỏ nhất . Tính

zz

 Giải:

 Ta có:

1 2 1 2 1 2

1; 3z z z z z z     







 

2 2 2 2 2 2

1 2 1 2 1 2 1 2 1 2

2 2 3 2

z z z z z z z z z z



            







     

1 2 1 2 1 2 1 2

4 3 5 3 5P z z z z z z z z         

 Xét hàm số:

   

3 5, 3;2 ; ' 3 3 0

f t t t t f t t





       









 Do đó

 

3minf t 



3minP 

 Dấu “=” xảy ra khi

1zz

Bài 49: Cho số phức z thỏa mãn

32z



. Gọi

M max z

và

m min z

, tính

môđun của số phức

w M m i

4 22w 

5 10w 

7 56w 

3 62w 

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

 Giải:

 





 

2 2 2

3 6 9

3 2 18 18 18

18 12 3 15 12 3 15

z z z z

z z z



   



       



      

Do đó:

3 62w 

Bài 50: Cho số phức z thỏa mãn

  

2 5 1 2 3 1z z z i z i      

. Tìm giá trị nhỏ nhất

của biểu thức

22P z i  

min

P 

min

2P 

min

1P 

min

P 

Bài 51: Cho số phức z thỏa mãn

2z 

. Gọi M và m lần lượt là giá trị lớn nhất và giá trị

nhỏ nhất của của biểu thức





. Tính giá trị của biểu thức M.n :

C. 1

B. 2 D.

Bài 52: Cho số phức z thỏa mãn

42zz

. Gọi

M m ax z

và

m min z

, tính môđun

của số phức

w M m i

23w 

14w 

w 

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

Bài 53: Cho số phức

z x yi

 

,xy

là số phức thỏa mãn hai điều kiện

2 2 26zz   

và biểu thức

P z i  

đạt giá trị lớn nhất. Tính giá trị của

biểu thức (x.y)

xy 

Bài 54: Cho ba số phức

1 2 3

,,z z z

thỏa mãn

1 2 3

1 15

z z z i

. Tìm giá trị nhỏ nhất của

biểu thức

1 2 3 1 2 3

1 1 1 6

z z z z z z

   



min

6P 

min

5P 

min

4P 

min

3P 

Bài 55: Cho hai số phức

,zz

thỏa mãn

1zz

. Gọi m là giá trị nhỏ nhất của biểu

thức

1 2 1 2

1 1 1P z z z z     

. Khẳng định nào sau đây sai?

m

m

m

Bài 56: Cho số phức

0z a bi  

sao cho z không phải là số thực và





là số

thực. Tính

z

31a 

32a 

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

2a 

21a 

 Giải:

 Theo đề:

   

0( )

0 1 0

b Loai

z z z z z







       























Bài 57: Cho hai số phức

,zw

khác 0 và thỏa mãn

2z w z w  

. Gọi a, b lần lượt là

phần thực và phần ảo của số phức



. Tính

?ab

 Giải:

 Chuẩn hóa:

1w 

. Theo đề ta có:

 

2 2 2

1 15 1 15 1

8 8 8 8 4

x y x y

z i u i a b



   





         







  



Bài 58: Cho hai số phức

,zw

khác 0 và thỏa mãn

5z w z w  

. Gọi a, b lần lượt là

phần thực và phần ảo của số phức

.u z w

. Tính

?ab

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

100

 Giải:

 Chuẩn hóa:

1w 

. Theo đề ta có:

 

2 2 2

1 25

1 3 11 1 3 11 1

50 50 50 50 25

x y x y

z i u i a b



   





         







  



Bài 59: Cho số phức

và hai số thực a, b. Biết rằng

wi

và

21w 

là hai nghiệm của

phương trình

0z az b  

. Tính

?ab



 Giải:

 Theo định lý Viet ta có:

  

w i a

w i w b

    





  





1 2 2 2

i a i a

      

   

  

  

2 1 2 4 5

9 9 3

9 9 3 9 9 9

a i b a b



  

  







           



















Bài 60: Cho hai số phức

,zz

thỏa mãn điều kiện

2017zz

. Tìm giá trị nhỏ nhất

của biểu thức

1 2 1 2

2017 2017

z z z z

   





   



   

2017

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

Đặt

 

2017 cos2 sin2z x i x

và

 

2017 cos2 sin2z y i y

Ta có:

 

cos

cos2 sin2 cos2 sin2

2017cos

2017

2017 1 cos(2 2 ) sin(2 2 )

x i x y i y

x y i x y





  









   



Tương tự:

 

sin

2017 sin

2017









Suy ra

 

2 2 2 2

cos sin

2017 cos 2017 sin

x y x y

x y y x







Vì

 

cos 1

sin 1















nên

   

cos sin

2017 2017

P x y x y



    



Bài 61: Cho ba số phức

1 2 3

,,z z z

thỏa mãn điều kiện

1 2 3

1z z z  

và

2 3 3 1 1 2

z z z z z z

   

. Khẳng đinh nào sau đây đúng? .

1 2 3

3z z z  

1 2 3

2z z z  

1 2 3

z z z  

1 2 3

4z z z  

Bài 62: Cho số phức

thỏa mãn điều kiện

1z 

. Tìm giá trị nhỏ nhất của biểu thức

2 2016 2017

1008 1 1 ... 1 1P z z z z        

2017

2018

1008

2016

Bài 63: Cho ba số phức

1 2 3

,,z z z

thỏa mãn điều kiện

1 2 3

1z z z  

1 2 3

0z z z  

và

222

1 2 3

0zzz  

. Khẳng đinh nào sau đây sai? .

2017 2017 2017

1 2 1

0zzz  

2017 2017 2017

1 2 1

1zzz  

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

2017 2017 2017

1 2 1

3zzz  

2017 2017 2017

1 2 1

4zzz  

\z 

Bài 64: Cho số phức và







là số thực. Khẳng đinh nào sau đây

đúng? .

02z

13z

24z

35z

Bài 65: Cho ba số phức

1 2 3

,,z z z

thỏa mãn điều kiện

1 2 3

0z z z  

và

1 2 2 3 3 1

0z z z z z z  

Tính giá trị của biểu thức

1 2 2 3 3 1

z z z z z z





A. 3 C. 2

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Biên soạn: Phạm Minh Tuấn - TOANMATH.com

Bấm Tải xuống để xem toàn bộ.

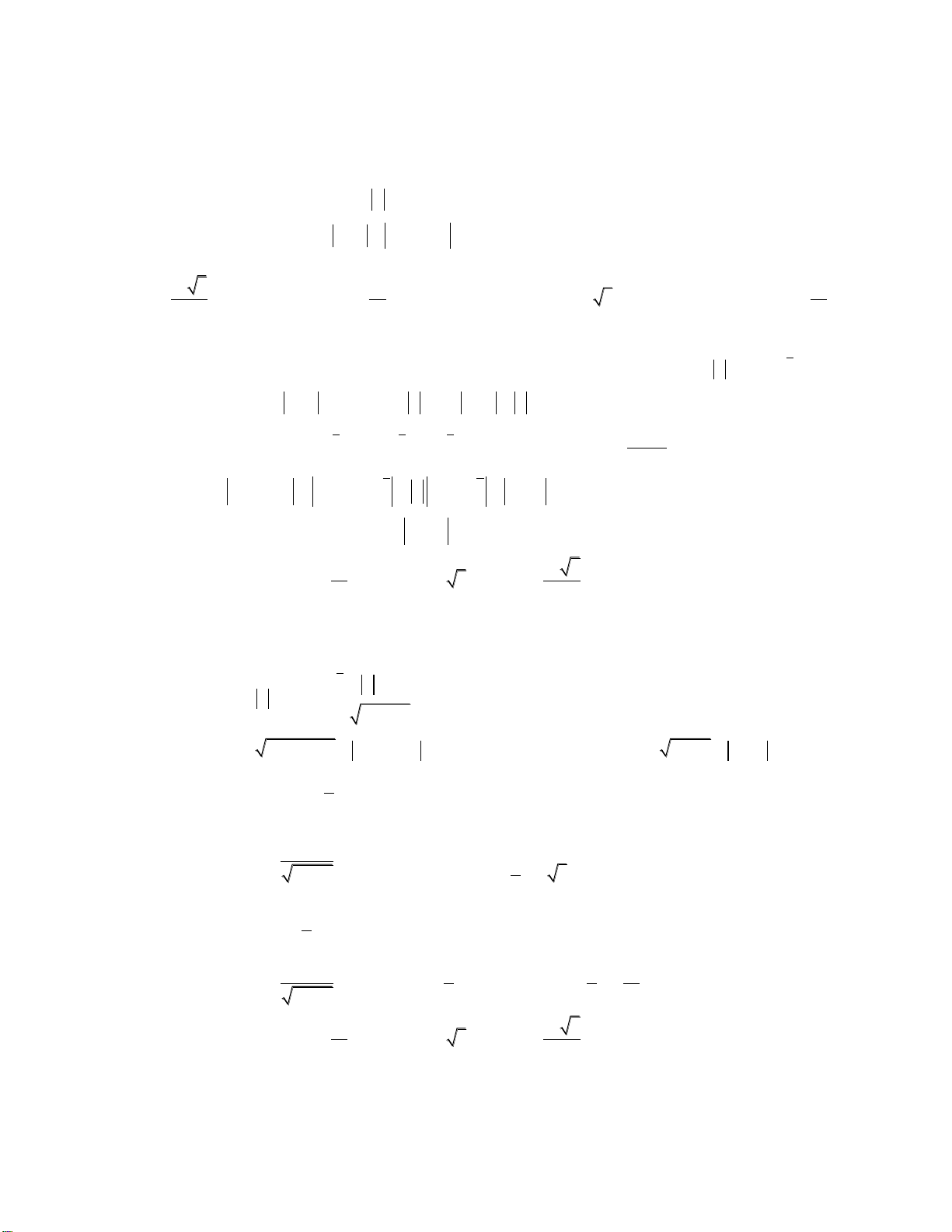
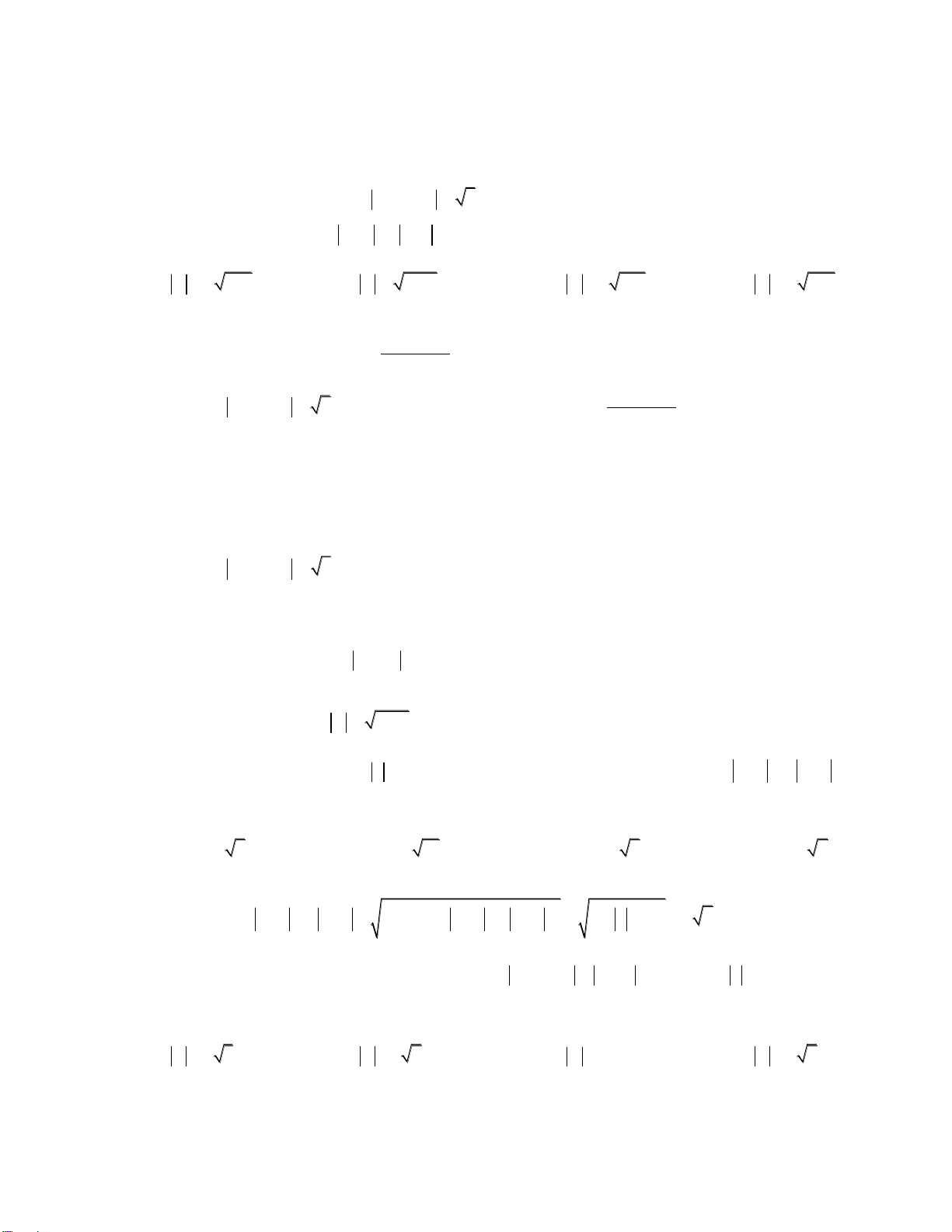
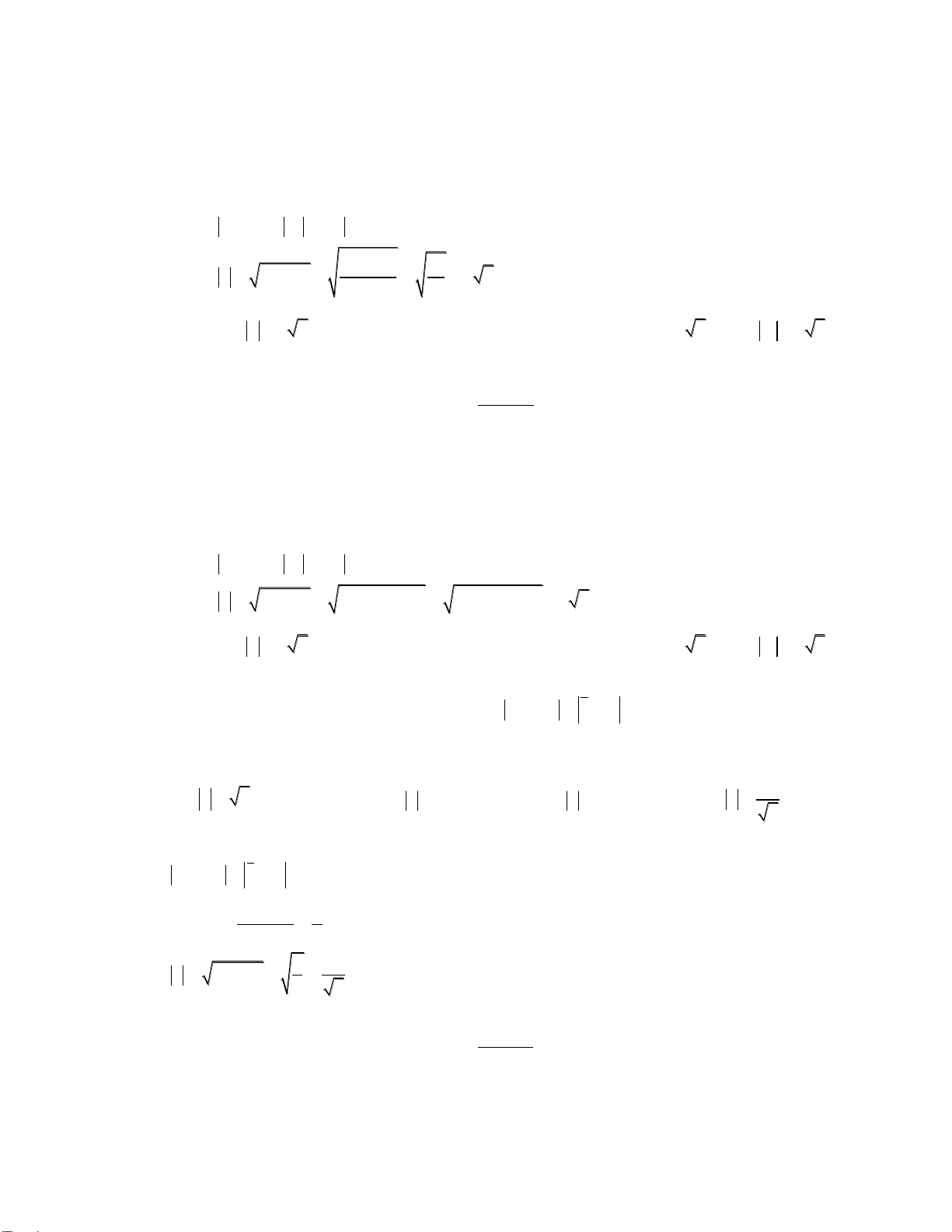
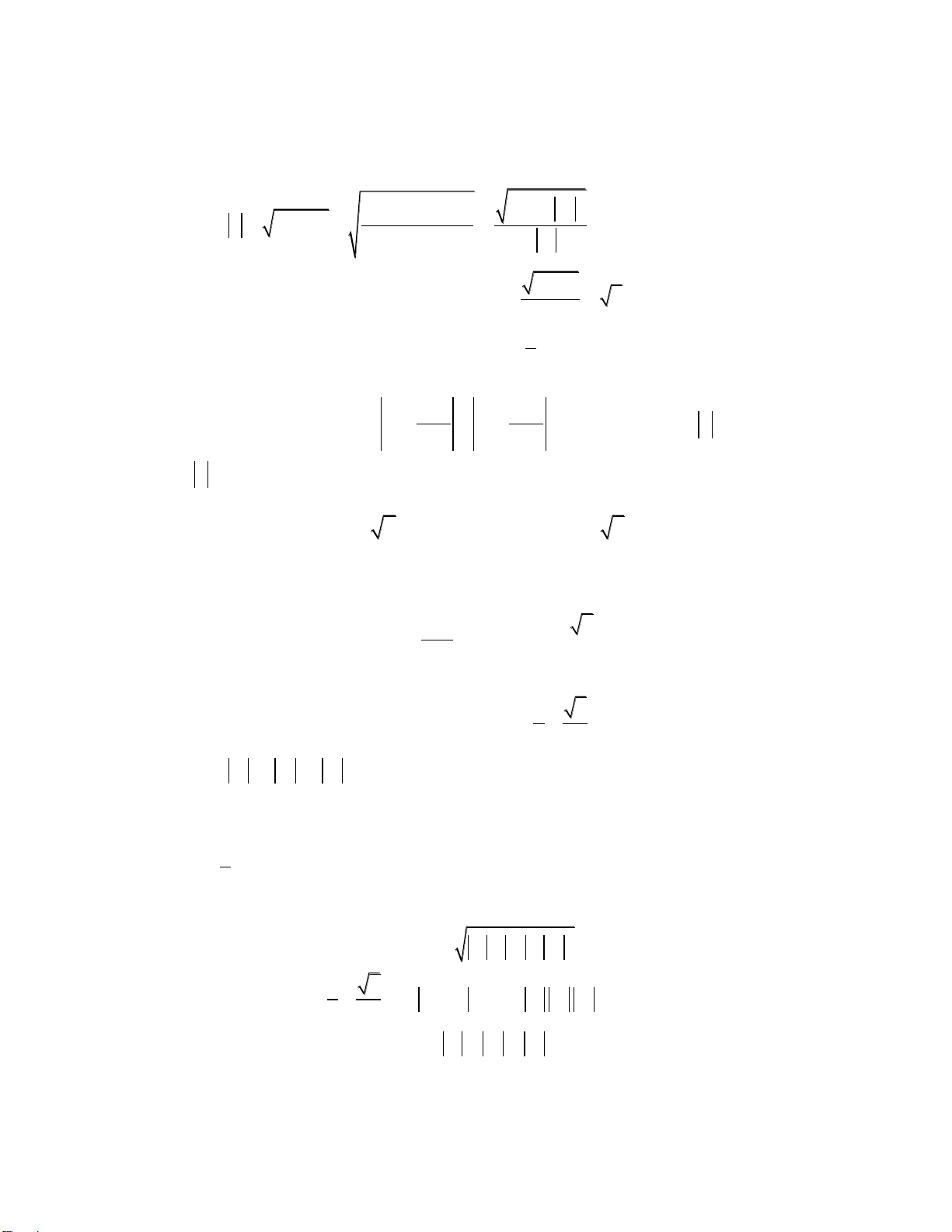
Preview text:

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Bài 1: Cho số phức z thỏa mãn z  1 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức 2
P  z  1  z  z  1 . Tính giá trị của M.n 13 3 39 13 A. B. C. 3 3 D. 4 4 4  Cách 1:
Re(z) là phần thực của số phức z, Im(z) là phần ảo của số phức z, z 1  . z z  1
 Đặt t  z  1 , ta có: 0  z 1 z  1  z  1  2  t0;2   
 t    z  z 2 2 t 2 1 1  1 .
z z  z  z  2  2Re(z)  Re(z)  2  2 2 2
z  z  1  z  z  .
z z  z z  1  z  t  3
 Xét hàm số: f t 2
 t  t  3 ,t 0; 2   . Xét 2 TH:
 Maxf t 13 
; Minf t  13 3 3  M .n  4 4  Cách 2:
 z  r cos x  isin x  a  bi 2
 .zz  z   1  Do z 1  2 2
r  a  b 1
 P  2  2cos x  2cos x 1 , đặt t  cos x 1  ; 
1  f t   2  2t  2t 1   1  TH1: t  1  ;    2 
maxf t  f   1  3  f t  1 '   2  0     2  2t minf  t 1  f  3     2   1  TH1: t  ;1   2    f t  1 7 
   t    maxf t 7 13 ' 2 0  f     2  2t 8  8  4
 Maxf t 13 
; Minf t  13 3 3  M .n  4 4
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Bài 2: Cho số phức z thỏa mãn z  3  4i  5 . Gọi M và m là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức 2 2
P  z  2  z  i . Tính module số phức w  M  mi . A. w  2 314 B. w  1258 C. w  3 137 D. w  2 309  Cách 1:    P 4x 3
P  4x  2 y  3  y  2 2      z   i 
 x  2   y  2   x  2 P 4x 3 3 4 5 3 4 5 3   4  5  f   x  2 
 f 'x  8x  
3  8P  4x 1 
1  0  x  0, 2P 1,6  y  0,1P 1,7    P Thay vào 2 2 33
f  x ta được: 0,2P 1,6  3  0,1P 1,7  4  5  0  P 13  Cách 2:
 z   i 
 x  2   y  2 3 4 5 3 4  5:C  ( )
 : 4x  2y  3 P  0
 Tìm P sao cho đường thẳng  và đường tròn C có điểm chung
 d I;  R  23 P 10 13 P  33
 Vậy MaxP  33 ; MinP 13
 w  33 13i  w  1258
Bài 3: Cho số phức z thỏa mãn z 1. Tìm giá trị lớn nhất của biểu thức P  z  1  2 z  1 . A. P  2 5 B. P  2 10 C. P  3 5 D. P  3 2 max max max max
 Giải: Theo BĐT Bunhiacopxki:
 P  z   z      2 2 z   z     2 2 2 1 2 1 1 2 1 1 10 z   1  2 5
Bài 4: Cho số phức z  x  yi  ,
x y  R thỏa mãn z  2  4i  z  2i và m  min z . Tính
module số phức w  m   x  yi . A. w  2 3 B. w  3 2 C. w  5 D. w  2 6
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------  Cách 1:
 z  2  4i  z  2i  x  y  4 x  y 4 2 2  2 2
 z  x  y    2 2 2 2       x y 4 x 2
min z  2 2 , Dấu “=” xảy ra khi   
 w  2 2  4i  w  2 6 x  y y  2 x  y 2 2  2
Chú ý: Với mọi x, y là số thực ta có: x  y  2
Dấu “=” xảy ra khi x  y  Cách 2:
 z  2  4i  z  2i  y  4  x
 z  x  y  x    x2  x  2 2 2 2 4 2 2  8  2 2       x y 4 x 2
min z  2 2 . Dấu “=” xảy ra khi   
 w  2 2  4i  w  2 6 x  2 y  2
Bài 5: Cho số phức z  x  yi  ,
x y  R thỏa mãn z  i 1  z  2i . Tìm môđun nhỏ nhất của z. 1 A. min z  2 B. min z 1 C. min z  0 D. min z  2  Cách 1:
 z  i 1  z  2i  x  y 1 x  y 1 2 2  2  x  y   2 2  1 1 2 2 z  x  y   2 2 x  y 2 2  2
Chú ý: Với mọi x, y là số thực ta có: x  y  2  Cách 2:
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
 z  i 1  z  2i  y  x 1 2    z  x  y 
x   x  2 1 1 1 1 2 2 2 1  2 x        2  2 2 2  1 Vậy min z  2
Bài 6: Cho số phức z thỏa mãn z 1. Gọi M và m là giá trị lớn nhất và nhỏ nhất của biểu thức 3
P  z  3z  z  z  z . Tính M  m 7 3 15 A. B. 13 C. D. 4 4 4 4
Sáng tác: Phạm Minh Tuấn  Cách 1:  Ta có 2 z  1  . z z 1
 Đặt t  z  z 
t  z  zz  z 2 2 2 2 2 0;2  z  2 .
z z  z  2  z  z  2 3 2 2 2
z  3z  z  z z  3  z  t 1  t 1 2   1  3 3 2
P  t  t 1  t       2  4 4  3
Vậy minP  ; maxP  3 khi t  2 4  15 M  n  4
 Cách 2: Cách này của bạn Trịnh Văn Thoại 3
z  3z  z  2 3 2
P  z  3z  z  z  z 
 z  z  z  3 z  z  z  z  z2 1  z  z z  2 3
P  z  z 1 z  z 
. Đến đây các bạn tự tìm max nhé 4
Bài 7: Cho các số phức , a , b , c z thỏa 2
az  bz  c  0 a  0 . Gọi z và z lần lượt là hai 1 2
nghiệm của phương trình bậc hai đã cho. Tính giá trị của biểu thức 2 2
P  z  z
 z  z  2 z  z 1 2 1 2  1 1 2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- c c A. P  2 C. P  4 a a c 1 c B. P  D. P  . a 2 a  Giải:  Ta có : 2 2 z  z  z  z
 z  z z  z   z  z z  z  2 2  2 z  2 z 1 2 1 2 1 2 1 2 1 2 1 2 1 2
 Khi đó P  4 z z 1 2  c c
Ta lại có: z z   P  4 z z  4 1 2 1 2 a a
Bài 8: Cho 3 số phức z , z , z thỏa mãn z  z  z  0 và z  z  z 1. Mệnh đề nào 1 2 3 1 2 3 1 2 3 dưới đây đúng? A. 2 2 2 z  z
 z  z  z  z là số thuần ảo 1 2 2 3 3 1 B. 2 2 2 z  z
 z  z  z  z là số nguyên tố 1 2 2 3 3 1 C. 2 2 2 z  z
 z  z  z  z là số thực âm 1 2 2 3 3 1 D. 2 2 2 z  z
 z  z  z  z là số 1 1 2 2 3 3 1  Chứng minh công thức:  2 2 2 2 2 2 2 z  z
 z  z  z  z  z  z  z  z  z  z 1 2 2 3 3 1 1 2 3 1 2 3  2 Ta có: z  .
z z và z  z  ...  z  z  z  ...  z . Áp dụng tính chất này ta có 1 2 n 1 2 n vế trái:
 z  z z  z  z  z z  z  z  z z  z 1 2   1 2 
 2 3 2 3  3 1 3 1
 z z  z z  z z  z z  z z  z z  z z  z z  z z  z z  z z  z z 1 1 2 2 3 3
 z  z  z  z 1 1 2 2
z  z  z 3 3  z  1 2 2 1
z  z  z  2  z 3 3 2 3
z  z  z 1 1 3 2 2 2 1 2 3 1 1 2 3 2 1 2 3 3 1 2 3 2 2 2
 z  z  z  z  z  z
z  z  z 1 2 3  1 2 3 1 2 3 2 2 2 2
 z  z  z  z  z  z 1 2 3 1 2 3
 Áp dụng công thức đã chứng minh suy ra: 2 2 2 z  z
 z  z  z  z  3 là số 1 2 2 3 3 1 nguyến số
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- z z
Bài 9: Có bao nhiêu số phức z thỏa mãn hai điều kiện z 1 và   1 ? z z A . 5 B. 6 C. 7 D. 8  Giải:  Ta có: 2 z  1  . z z  Đặt z  x  i x x   2 cos sin , 0;2
 z  cos2x  isin 2x  1 2 cos 2x  2  z z z   z 2  1 
1  2 cos2x 1   z z z.z  1 cos 2x    2
 Giải 2 phương trình lượng giác trên với x0;2  nên ta chọn được các giá trị
 5 7 11  2 4 5  x   ; ; ; ; ; ; ;   6 6 6 6 3 3 3 3 
 Vậy có 8 số phức thỏa 2 điều kiện đề cho
Bài 10: Cho các số phức z ,z ,z thỏa mãn đồng thời hai điều kiện z  z  z  1999 và 1 2 3 1 2 3
z z  z z  z z
z  z  z  0 . Tính 1 2 2 3 3 1 P  1 2 3 z  z  . z 1 2 3 A. P  1999 P  999,5 B. P  2 1999 P  5997  Giải         z z z z z z z .z z .z z .z 2 1 2 2 3 3 1 1 2 2 3 3 1 P    
z  z  z       1 2 3 z z z  1 2 3  2  1999 z  1 z  1  2   1999 Mặc khác: 2
z  z  z  1999  z z  z z  z z  1999  z  1 2 3 1 1 2 2 3 3 2 z  2  2 1999 z  3  z  3
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 2 2 2 2 2 2  1999 1999 1999 1999 1999 1999   .  .  .       z z z z z z z z z z z z Suy ra 2 1 2 2 3 3 1  1 2 2 3 3 1  2 P     1999 2 2 2
z  z  z    1999 1999 1999  1 2 3     z z z  1 2 3   P 1999
 Tổng quát: z  z  z  k  z z  z z  z z  k z  z  z 1 2 3 1 2 2 3 3 1 1 2 3 3  3 2i
Bài 11: Cho số phức z thỏa mãn
z  1 2i  3 . Gọi M và m lần lượt là giá trị 1  2 2i
lớn nhất và giá trị nhỏ nhất của biểu thức P  z  3  3i . Tính . M m A) . M n  25 B) . M n  20 C) . M n  24 D) . M n  30
 Dạng tổng quát: Cho số phức z thỏa mãn z z  z  r . Tính Min, Max của 1 2 z r r z
z  z . Ta có 2 2 Max   z  ; Min    z 3 3 3 z z z z 1 1 1 1   3 3 2i
Áp dụng Công thức trên với z 
; z  1 2i, z  3  3 ; i r  3 ta được 1 2 3 1 2 2i
Max  6; Min  4 Bài tập áp dụng:
1) Cho số phức z thỏa mãn z  2  2i  1 . Gọi M và m lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của z . Tính . M m A) . M n  7 B) . M n  5 C) . M n  2 D) . M n  4 1  2i
2) Cho số phức z thỏa mãn z  2  1 1 
. Gọi M và m lần lượt là giá trị lớn nhất i
và giá trị nhỏ nhất của z  i . Tính . M m A) 1 M.n  B) 1 M.n  C) 1 M.n  D) 1 M.n  5 3 10 4
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- z
3) Cho số phức z thỏa mãn 4n1 4n  i  i i  với n
. Gọi M và m lần lượt là giá 2
trị lớn nhất và giá trị nhỏ nhất của z  3  i . Tính . M m A) . M n  20 B) . M n  15 C) . M n  24 D) . M n  30
Bài 12: Cho số phức z thỏa mãn z  1  z  1  4 . Gọi m  min z và M  max z , khi đó . M n bằng: 2 3 A. 2 B. 2 3 C. 3 3  Giải:
 Dạng Tổng quát: z z  z  z z  z  k với z  a  bi; z  c  di; z  x  yi 1 2 1 2 1 2 2 2 k  4 z k  Ta có: 2 Min z  và Max z  2 z 2 z 1 1
 Chứng minh công thức: k
 Ta có: k  z z  z  z z  z  z z  z  z z  z  2z z  z  . Suy ra 1 2 1 2 1 2 1 2 1 2 z1 k Max z  2 z1  Mặc khác: 2 2 2 2
 z z  z  z z  z  k 
ax  by  c  ay  bx  d
 ax  by  c  ay  bx  d  k 1 2 1 2        
 Áp dụng BĐT Bunhiacopxki ta có: k 
axbyc2 aybxd2  axbyc2 aybxd2 1. 1.
1 1 ax by c2 ay bx d2 ax by c2 ay bx d2 2 2                  4 2 2 a  b  2 2
x  y   4 2 2 c  d 
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
k  4 c  d  2 2 2 2 2 k  4 z  Suy ra 2 2 2
z  x  y   4  2 2 a  b  2 z1  2 4  4 m   3   ADCT trên ta có:     2 z 1; z 1; k 4  1 2  4 M   2  2 2 2
Bài 13: Cho số phức z thỏa mãn iz   iz   4  và 1  i 1  . Gọi m min z i
M  max z , khi đó . M n bằng: A. 2 B. 2 2 C. 2 3 D. 1    2 m 2
ADCT Câu 12 ta có: z  i; z  ; k  4   1 2 1 i M  2 1 3
Bài 14: Cho các số phức z , z , z thỏa mãn z z z  
i . Tính giá trị nhỏ nhất của 1 2 3 1 2 3 2 2 2 2 2
biểu thức P  z  z  z . 1 2 3 A. P  1 C. P  3 min min 1 B. P  D. P  2 min 3 min  Giải:  2 2 2 Áp dụng BĐT AM-GM ta có: 3 P  3 z . z . z 1 2 3  1 3 Mặc Khác: z z z  
i  z z z  1  z z z  1 1 2 3 1 2 3 1 2 3 2 2
 Suy ra P  3. Dấu “=” xảy ra khi z  z  z  1 1 2 3
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- z  3
Bài 15: Cho số phức z  x  yi với x, y là các số thực không âm thỏa mãn  z   1 1 2i 2 2   và biểu thức 2 2
P  z  z  i  z  z 
 z1 i  z1 i   
 . Giá trị lớn nhất và giá trị nhỏ
nhất của P lần lượt là: A. 0 và 1  C. 3 và 0 B. 3 và 1  D. 2 và 0  Giải: z  3 
 1  z  3  z 1 2i  x  y  1 z  1 2i 2  x  y   2 2 1
P  16x y  8xy , Đặt t  xy  0  t      2  4    2 1
P  16t  8t,t  0;
 MaxP  0; MinP  1     4
Bài 16: Cho các số phức z thỏa mãn z  1. Tính giá trị nhỏ nhất của biểu thức 2 3
P  1 z  1 z  1 z . A. P  1 C. P  3 min min B. P  4 D. P  2 min min  Giải:
 Ta có: z  1  z  1  2 3 2 3
P   z   z   z   z  z  z   z   z  z  2  z  3 1 1 1 1 1 1 1 1  1 z  2 6z  i
Bài 17: Cho số phức z thỏa mãn  1 2 
. Tìm giá trị lớn nhất của z . 3iz 1 1 A. max z  C. max z  2 3
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 3 B. max z  D. max z  1 4  Giải: 6z  i 2 2
 1  6z  i  2  3iz  6z  i  2  3iz 2  3iz
6zi6zi23iz23iz  6zi6zi 23iz23iz 1 2 1 1  . z z 
 z   z  9 9 3
Bài 18: Cho z  a  bi,a,b  thỏa 2
z  4  2 z và P   2 2
8 b  a  12 . Mệnh đề nào sau đây đúng?
A. P   z  2 2 2
C. P   z  2 2
B. P   z  2 2 4
D. P   z  2 4  Giải:
 z   z  a b  2  ab2 2 2 2   2 2 4 2 4 2
4 a  b   0  Chuẩn hóa 4 2
b  0  a  4a  16  0  a  1
  i 3  z  1
  i 3  P  4 2 2  
 Thử đáp án: - ĐÁP ÁN A: P  1
  i 3  2  4    Nhận  
Bài 19: Cho số phức z thỏa mãn z  2  3i  1. Gọi M  max z  1 i , m  min z  1 i .
Tính giá trị của biểu thức  2 2 M  n  . A. 2 2 M  m  28 C. 2 2 M  m  26 B. 2 2 M  m  24 D. 2 2 M  m  20  Giải:
 z   i   x  2  y  2 2 3 1 2 3  1 (1)
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------  2 2
Đặt P  z   i  x    y   2 1 1
1  P (2) với P  0 2    P 10 6x
Lấy (1)-(2) ta được: y  . Thay vào (1) : 4 2 2       P x x  22 10 6 2  
 3  1  52x  2
40  12P  x   4 2
P  4P  52  0 (*)  4 
 Để PT (*) có nghiệm thì:     P 2 2   4 2 40 12
4.52. P  4P  52  0  14  2 13  P  14  2 13  Vậy 2 2
M  14  2 13 ,m  14  2 13  M  m  28 1 1
Bài 20: Cho số thức * z  thỏa mãn 3 z 
 2 và M  max z  . Khẳng định nào sau 3 z z đây đúng? 7 A. 1   M  2 C. 2  M  2 5 B. 1  M  D. 3 2
M  M  M  3 2  Giải: 3 3          1 3 1 1 3 1 1 1 z   z   3 z   z   z   3 z          3 3  z  z  z  z  z   z  3 3         3 1 1 1 1 1  z   z   3 z   z   3 z           2 3 z  z   z   z   z  3 3      1 1 1 1 Mặt khác: z   3 z   z   3 z       z   z  z z 3 1  1 1 Suy ra: z 
 3 z   2 , đặt t  z   0 , ta được: z z z
 t  t    t  t  2 3 1 3 2 0 2
1  0  t  2  z   2  M  2 z
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Bài 21: Cho số phức z thỏa mãn z   i  i    i2017 3 1 1
. Khi đó số thức w  z  1 i có phần ảo bằng: A. 1008 (  z)  2 1 C. 1008 (  z)  2 B. 1008 (  z)  2  3 D. 1008 (  z)  2  2  Giải:
 z   i i    i2017  z   i i  i    i2018 3 1 1 3 1 1 1 1i 1009 2  1009   2i      z     i    i  i   i
1 i1 i 1008 3 3 2 3 2  1008 w 
i   i   i    1008   1008 2 3 1 4 2 2 i  (  z)  2  2
Bài 22: Cho số phức z thỏa mãn   i 2 42 1 5 z 
 3i  15 . Mệnh đề nào dưới đây z đúng: 1 5 A.  z  2 C.  z  4 2 2 3 B.  z  3 D. 3  z  5 2  Giải:   i 2 42 1 5 z   3i  15 z
   i z  i  i 2 42 1 5 3 1 5  z 
   i z  i 2 42 2 42 1 5 3 
 1 5i z  3i  z z 2 2 42  6. z  3   6 2 z  3 2
. z  4.42  0  z  2 z
Bài 23: Cho ba số phức z, z , z thỏa mãn 2z  i  2  iz và z  z  1 . Tính giá trị của 1 2 1 2
biểu thức P  z  z . 1 2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 3 A. P  C. P  2 2 2 B. P  3 D. P  2  Giải:
 Đặt z  x  yi , 2 2
2z  i  2  iz  x  y  1
 Gọi A, B là hai điểm biểu diễn z ,z . 1 2
 Ta có z  z  OA OB  AB  1 1 2
 Suy ra AB  OA  OB hay tam giác OAB đều.  3
P  z  z  OA  OB  2OM  2.  3 1 2 2
Bài 24: Cho ba số phức z ,z ,z thỏa mãn z  z  z  1 và z  z  z  0 . Tính giá trị 1 2 3 1 2 3 1 2 3 của biểu thức 2 2 2
P  z  z  z . 1 2 3 A. P  1 C. P  1  B. P  0 D. P  1 i  1 3 1 3
Giải: Chuẩn hóa z   i, z   i, z  1  Suy ra P  0 1 2 3 2 2 2 2
Bài 25: Cho hai số phức z , z thỏa mãn z  z  8  6i và z  z  2 . Tính giá trị lớn nhất 1 2 1 2 1 2
của biểu thức P  z  z . 1 2 A. P  5  3 5 C. P  4 6 max max B. P  2 26 D. P  34  3 2 max max  Giải:
 Ta có: z  z  8  6i  z  z  10 1 2 1 2 z  z
 z  z  z  z
 2 z  z   2 2 2 2 2 2 2 1 2
 52  z  z 
 z  z  2.52  2 26 1 2 1 2 1 2 1 2 1 2 2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Bài 26. Cho z ,z ,z là các số phức thỏa mãn z  z  z  1 và z  z  z  0 . Khẳng 1 2 3 1 2 3 1 2 3
định nào dưới đây là sai.
A. z3  z3  z3  z3  z3  z3
B. z3  z3  z3  z3  z3  z3 1 2 3 1 2 3 1 2 3 1 2 3
C. z3  z3  z3  z3  z3  z3
D. z3  z3  z3  z3  z3  z3 1 2 3 1 2 3 1 2 3 1 2 3  1 3 1 3
Giải: Chuẩn hóa z   i, z   i, z  1  Suy ra đáp áp D 1 2 3 2 2 2 2
Bài 27: Cho z ,z ,z là các số phức thoả mãn z  z  z  1. Khẳng định nào sau đây 1 2 3 1 2 3 là đúng?
A. z  z  z  z z  z z  z z
B. z  z  z  z z  z z  z z 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1
C. z  z  z  z z  z z  z z
D. z  z  z  z z  z z  z z 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1  1 3 1 3
Giải: Chuẩn hóa z   i, z   i, z  1  Suy ra đáp áp A 1 2 3 2 2 2 2
Bài 28: Cho z ,z ,z là các số phức thoả mãn z  z  z  1 và z  z  z  1. Biểu thức 1 2 3 1 2 3 1 2 3 2n1 2n1 2n1 P  z  z  z , n  
 nhận giá trị nào sao đây? 1 2 3 A. 1 B. 2 C. 4 D. 3
 Giải: Chuẩn hóa n  1,z  1,z  i,z  i  Suy ra đáp áp A 1 2 3
Bài 29: Cho ba số phức z , z , z thỏa mãn z  z  z  1. Tính giá trị nhỏ nhất của 1 2 3 1 2 3 1 1 1 biểu thức P   
z  z z  z
z  z z  z z  z z  . z 1 2 1 3 2 1 2 3 3 1 3 2 3 1 A. P  C. P  min 4 min 2 5 B. P  1 D. P  min min 2  Giải:  2 2 2 z  z
 z  z  z  z  z  z
z  z  z  z
z  z  z  z z  z 1 2 2 3 3 1
 1 2 1 2  2 3 2 3  3 1 3 1
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
 9  z  z  z z  z  z 1 2 3   1 2 3  2
 9  z  z  z 1 2 3  Theo BĐT Cauchy- Schwarz: 9 9 9 P    2 2 2 2
z  z z  z  z  z z  z  z  z z  z         1 2 1 3 2 1 2 3 2 1 2 3 z z z z z z 9 z z z 1 2 2 3 3 1 1 2 3  9 2 Do đó: P 
 1 (do z  z  z  0 ) 9 1 2 3 2z  i
Bài 30: Cho ba số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức P  : 2  iz 3 A. P  1 C. P  max max 4 1 B. P  D. P  2 max 2 max z  1
 Giải: Chuẩn hóa z  1 z   0   2 i
z  1  P 
 1 do đó loại B, C 2  i   i 1
z  0  P 
 do đó loại D, chọn đáp án A 2 2 2 2
Bài 31: Cho 3 số phức z , z , z thỏa mãn z  z  z  0 và z  z  z  . Mệnh đề nào 1 2 3 1 2 3 1 2 3 3 dưới đây đúng? 2 2 A. 2 2 2 z  z
 z  z  z  z  1 2 2 3 3 1 3 8 B. 2 2 2 z  z
 z  z  z  z  1 2 2 3 3 1 3 C. 2 2 2 z  z
 z  z  z  z  2 2 1 2 2 3 3 1 D. 2 2 2 z  z
 z  z  z  z 1 1 2 2 3 3 1
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------  8 Giải: 2 2 2 2 2 2 2 z  z
 z  z  z  z  z  z  z  z  z  z  1 2 2 3 3 1 1 2 3 1 2 3 3
Bài 32: Gọi S là tập hợp các số phức z thỏa mãn z  i  3 và z  2  2i  5 . Kí hiệu z ,z là 1 2
hai số phức thuộc S và là những số phức có môđun lần lượt nhỏ nhất và lớn nhất. Tính
giá trị của biểu thức P  z  2z . 2 1 A. P  2 6 C. P  33 B. P  3 2 D. P  8  Giải:
 3  z  i  z  1 z  2
x  y  2 2  o 1 9
Dấu “=” xảy ra khi:   z  2  i 1 2 2
x  y  4
 z  2 2  z  2  2i  5  z  5  2 2
x 22 y 22  25     o 4 5 2 4 5 2
Dấu “=” xảy ra khi:   z    i 2   2 2 2 2
x  y  33  20 2        4 5 2 4 5 2 P   
i  4i  33 2  2   
Bài 33: Gọi z là số phức có phần thực lớn hơn 1 và thỏa mãn z  1  i  2z  z  5  3i sao
cho biểu thức P  z  2  2i đạt giá trị nhỏ nhất. Tìm phần thực của số phức z đó. 8  7 4  6 A. (  z)  C. (  z)  2 2 8  2 12  2 B. (  z)  D. (  z)  2 2  Giải:
 z   i  z  z   i  y  x  2 1 2 5 3 2 2  
 P  x  2  y  2  y  y  2 3 7 7 2 2 2  y       2  4 4
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------  3 y    4 6 3
Dấu “=” xảy ra khi:  2  z   i
y  x   2 2 2 2
Bài 34: Cho số phức z thỏa mãn z 1. Tìm giá trị lớn nhất của biểu thức 3
P  z  z  2 . 11 13 A. P  B. P  2 3 C. P  D. P  3 5 max 2 max max 2 max  Giải:
Câu 35: Cho phương trình: 3 2
z  az  bz  c  0 , a,b,c   . Nếu z  1 i,z  2 là hai 1 2
nghiệm của phương trình thì a  b  c bằng: A. 2  B. 1  C. 0 D. 1
Bài 36: Cho số phức z thỏa mãn 10 9
11z  10iz  10iz 11  0 .Tính z . A. 1 z  B. 3 z  C. P 1 D. P  2 max max 2 4
Bài 37: Cho phương trình: 4 3 2
z  az  bz  cz  d  0 , a,b,c,d  có bốn nghiệm phức là
z , z , z , z . Biết rằng z z  13  i, z  z  3  4i , khẳng định nào sau đây đúng? 1 2 3 4 1 2 3 4 A. b  53 B. b  50 C. b  55 D. b  51
Bài 38: Cho số phức z thỏa mãn z  z  z 1và z  z z ; z  z z ; z  z z là các số 1 2 3 1 2 3 2 3 1 3 1 2
thực. Tính z z z 2017 . 1 2 3 A. 1 C. 1  B. 2017 2  D. 2017 2
Bài 39: Cho số phức z thỏa mãn đồng thời z  z  2 và z  3z  2  i 3 z . Khẳng định nào sao đây đúng? 1 5 A.  z  2 C.  z  4 2 2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 3 B.  z  3 D. 3  z  5 2 4  z 1 
Bài 40: Cho z , z , z , z là nghiệm phức của phương trình:    1 . Tính giá trị của 1 2 3 4  2z  i 
biểu thức P   2 z   1  2 z   1  2 z   1  2 z  1 : 1 2 3 4  18 A. P  1 C. P  5 17 B. P  1  D. P  9
Bài 41: Cho số phức z thỏa mãn z 1. Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 3 2
P  z  1  z  z  1 . Tính M  m . A. 2 B.7 C.6 D. 5 z  z 1
Bài 42: Cho hai số phức z , z thỏa mãn 1 2
 . Tìm giá trị lớn nhất của biểu thức 1 2 z  z 2 1 2 z z 1 2 P   . z z 1 2 A. 2 B.0,75 C.0,5 D. 1
Bài 43: Trong mặt phẳng phức với gốc tọa độ O, cho hai điểm A, B (khác O) biểu diễn
hai số phức z , z thỏa mãn 2 2
z  z  z z . Khẳng định nào sau đây đúng? 1 2 1 2 1 2 A. O
 AB vuông cân tại A B. O  AB đều C. O
 AB cân, không đều D. O  AB cân tại A 2
Bài 44: Cho ba số phức z , z , z thỏa mãn z  z  z 
và z  z  z  0 . Tính giá 1 2 3 1 2 3 2 1 2 3
trị lớn nhất của biểu thức P  z  z  2 z  z  2 z  z . 1 2 2 3 3 1
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 7 2 3 6 A. P  C. P  max 3 max 2 4 5 10 2 B. P  D. P  max 5 max 3  Giải:  2 2 2 2 2 2 2 3 z  z
 z  z  z  z  z  z  z  z  z  z  1 2 2 3 3 1 1 2 3 1 2 3 2
 Theo BĐT Bunhiacôpxki ta có:
P  z  z  z  z  z  z      2 2 2 2 2 3 6 2 2 1 2 2 z  z
 z  z  z  z  1 2 2 3 3 1 1 2 2 3 3 1  2
Bài 45: Cho số phức z thỏa mãn z  1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức 2
P  z  1  1 z . Tính 2 2
P  M  n A. 12 C. 15 B. 20 D. 18
Bài 46: Cho bốn số phức a,b,c, z thỏa mãn 2
az  bz  c  0 và a  b  c  0 . Gọi
M  max z ,m  min z . Tính môđun của số phức w  M  mi . A. w  2 C. w  3 B. w  2 D. w  1
Bài 47: Cho số phức z thỏa mãn z  1  2 . Gọi M và m lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của biểu thức P  z  i  z  2  i . Tính môđun của số phức w  M  mi . A. w  2 6 C. w  3 5 B. w  4 2 D. w  4  Giải:  z    x  2 2 1 2 1  y  2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- vecto
 P  x  y  2    x2    y2  x   x2  y    y2 2 1 2 1 2 1 1  2 2 bunhiacopxki  P x
y 2  x2  y2 x 2 2 2 1 2 1 2.2 1 y 2             4  
 w  4  2 2i  2 6 3 4
Bài 48: Cho hai số phức z , z thỏa mãn z  z 
 i , z  z  3 và biểu thức 1 2 1 2 5 5 1 2 3 3 P  4 z
 4 z  3 z  3 z  5 đạt giá trị nhỏ nhất . Tính z  z . 1 2 1 2 1 2 A. 1 C. 2 3 B. D. 3 4  Giải:
 Ta có: z  z  1; 3  z  z  z  z 1 2 1 2 1 2 z  z
 z  z  z  z  2 z  z   2 2 2 2 2 2 2 1 2
 2  z  z 
 3  z  z  2 1 2 1 2 1 2 1 2 1 2 2 3 3 3
 P  4 z  z 3 z  z  5  z  z 3 z  z  5 1 2
  1 2   1 2   1 2  t  1
 Xét hàm số: f t 3
 t  3t  5,t   3; 2 ; f 't 2
 3t  3  0     t  1  
 Do đó minf t  3  minP  3
 Dấu “=” xảy ra khi z  z  1 1 2 3 2 2
Bài 49: Cho số phức z thỏa mãn z 
 3 2 . Gọi M  max z và m  min z , tính z
môđun của số phức w  M  mi . A. w  4 22 C. w  5 10 B. w  7 56 D. w  3 62
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------  Giải: 2 z  3       3  2z 3 2 2 z 3 z 3z z2 4 2 6 z 9 z   3 2   18   18   18 2 2 2 z z z z 4 2 z  6 z  9 2 
 18  12  3 15  z  12  3 15 2 z Do đó: w  3 62
Bài 50: Cho số phức z thỏa mãn 2
z  2z  5  z 1 2iz  3i  
1 . Tìm giá trị nhỏ nhất
của biểu thức P  z  2  2i . 1 A. P  C. P  2 min 2 min 3 B. P  1 D. P  min min 2
Bài 51: Cho số phức z thỏa mãn z  2 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị z  i
nhỏ nhất của của biểu thức P 
. Tính giá trị của biểu thức M.n : z 1 A. C. 1 4 3 B. 2 D. 4
Bài 52: Cho số phức z thỏa mãn 2
z  4  2 z . Gọi M  max z và m  min z , tính môđun
của số phức w  M  mi . A. w  2 3 C. w  14 6 2 B. w  D. w  3 3
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Bài 53: Cho số phức z  x  yi , x, y   là số phức thỏa mãn hai điều kiện 2 2 3 3
z  2  z  2  26 và biểu thức P  z  
i đạt giá trị lớn nhất. Tính giá trị của 2 2 biểu thức (x.y) 9 9 A. xy  C. xy  4 2 16 17 B. xy  D. xy  9 2 1 15
Bài 54: Cho ba số phức z , z , z thỏa mãn z z z  
i . Tìm giá trị nhỏ nhất của 1 2 3 1 2 3 4 4 1 1 1 6 biểu thức P     z z z z  z  . z 1 2 3 1 2 3 A. P  6 C. P  5 min min B. P  4 D. P  3 min min
Bài 55: Cho hai số phức z , z thỏa mãn z  z  1. Gọi m là giá trị nhỏ nhất của biểu 1 2 1 2
thức P  z  1  z  1  z z  1 . Khẳng định nào sau đây sai? 1 2 1 2 7 7 A.  m  3 C. 3  m  4 2 11 1 5 B. 1  m  D.  m  5 4 2 z
Bài 56: Cho số phức z  a  bi  0 sao cho z không phải là số thực và w  là số 3 1  z 2 z thực. Tính . 2 1  z 1 1 A. C. 3a  1 3a  2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 2 1 B. D. a  2 2a  1  Giải: b  0(Loai)  z z 2 Theo đề: 0 z z 1 z  z z        0   2 3 3    1 1 z   1 z z    2a 1 2 z  1 2a   2 2a  1 2a   1 1 z 2a
Bài 57: Cho hai số phức z,w khác 0 và thỏa mãn z  w  2 z  w . Gọi a, b lần lượt là z
phần thực và phần ảo của số phức u  . Tính 2 2 a  b  ? w 1 1 A. C. 2 8 7 1 B. D. 2 4  Giải:
 Chuẩn hóa: w  1 . Theo đề ta có:   z 1   2 z x  2 2 1  y  4 2 2 x  y  1 15 1 15 2 2 1     z   i  u  
i  a  b  z  1   1  x  2 2 8 8 8 8 4 1  y  1
Bài 58: Cho hai số phức z,w khác 0 và thỏa mãn z  w  5 z  w . Gọi a, b lần lượt là
phần thực và phần ảo của số phức u  . z w . Tính 2 2 a  b  ?
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 1 1 A. C. 50 100 1 1 C. D. 25 10  Giải:
 Chuẩn hóa: w  1 . Theo đề ta có:   z 1   5 z x  2 2 1  y  25 2 2 x  y  1 3 11 1 3 11 2 2 1     z   i  u  
i  a  b  z  1   1  x  2 2 50 50 50 50 25 1  y  1
Bài 59: Cho số phức w và hai số thực a, b. Biết rằng w  i và 2w 1 là hai nghiệm của phương trình 2
z  az  b  0 . Tính a  b  ? 5 5 A. C.  9 9 1 1 B.  D. 9 9  Giải:
3w  i 1    a  1 i  a
 2  2i  2a 
 Theo định lý Viet ta có:    i 1     b w  i  2w 1   b  3  3  2 2a a 1       b a  2  2 2a a 1  2 4    5 9 9 3  
    a  i  b    
13  a  b    9 9 3   9 9  2 4 b  9 a   0  9 9 9
Bài 60: Cho hai số phức z , z thỏa mãn điều kiện z  z  2017 . Tìm giá trị nhỏ nhất 1 2 1 2 2 2  z  z   z  z  của biểu thức 1 2 1 2 P        2   2 2017 z z   2017 z z     1 2 1 2  1 2 A. C. 2017 2 2017 2 1 B. D. 2017 2 2017
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Đặt z  2017 cos 2x  i sin 2x và z  2017 cos 2y  i sin 2y 2   1   z  z
cos 2x  i sin 2x  cos 2y  i sin 2y cosx  y Ta có: 1 2   2 2017  z z
2017  1 cos(2x  2y)  i sin(2x  2y)  2017 cos x  y 1 2      z  z
sin y  x Tương tự: 1 2  2 2017  z z 2017 sin y  x 1 2   2
cos x  y 2
sin x  y Suy ra P   2 2
2017 cos x  y 2 2
2017 sin y  x 2
cos x  y   1 1 1 Vì  nên 2 P  cos  x y 2
 sin x  y   2   2  sin 2  x y   1 2017 2017
Bài 61: Cho ba số phức z , z , z thỏa mãn điều kiện z  z  z  1 và 1 2 3 1 2 3 2 2 2 z z z 1 2 3  
 1  0 . Khẳng đinh nào sau đây đúng? . z z z z z z 2 3 3 1 1 2
A. z  z  z  3
C. z  z  z  2 1 2 3 1 2 3 1
B. z  z  z 
D. z  z  z  4 1 2 3 3 1 2 3
Bài 62: Cho số phức z thỏa mãn điều kiện z  1. Tìm giá trị nhỏ nhất của biểu thức 2 2016 2017
P  1008 1  z  1  z  ...  1  z  1 z A. 2017 C. 2018 B. 1008 D. 2016
Bài 63: Cho ba số phức z , z , z thỏa mãn điều kiện z  z  z  1, z  z  z  0 và 1 2 3 1 2 3 1 2 3 2 2 2
z  z  z  0 . Khẳng đinh nào sau đây sai? . 1 2 3 A. 2017 2017 2017 z  z  z  0 C. 2017 2017 2017 z  z  z  1 1 2 1 1 2 1
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com
Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- B. 2017 2017 2017 z  z  z  3 D. 2017 2017 2017 z  z  z  4 1 2 1 1 2 1 2 1  z  z
Bài 64: Cho số phứ z  \ c và w 
là số thực. Khẳng đinh nào sau đây 2 1  z  z đúng? . A. 0  z  2 C. 1  z  3 B. 2  z  4 D. 3  z  5
Bài 65: Cho ba số phức z , z , z thỏa mãn điều kiện z  z  z  0 và z z  z z  z z  0 . 1 2 3 1 2 3 1 2 2 3 3 1
z z  z z  z z
Tính giá trị của biểu thức 1 2 2 3 3 1 P  2 z2 A. 3 C. 2 1 1 B. D. 2 3
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Biên soạn: Phạm Minh Tuấn - TOANMATH.com

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao – Phạm Minh Tuấn Toán 12

Tài liệu liên quan:

Số phức là gì? Lý thuyết số phức và một số dạng bài tập cơ bản | Toán 12

Chuyên đề Số phức – Trung tâm LTĐH Vĩnh Viễn Toán 12

Các dạng bài tập cơ bản về Số phức – Đặng Việt Hùng Toán 12

600 câu hỏi trắc nghiệm chuyên đề số phức – Nhóm Toán

Bài tập trắc nghiệm chuyên đề số phức – Đặng Việt Đông Toán 12