Hướng dẫn giải một số bài tập tọa độ trong không gian nâng cao – Phạm Minh Tuấn Toán 12
Hướng dẫn giải một số bài tập tọa độ trong không gian nâng cao – Phạm Minh Tuấn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Chủ đề: Chương 3: Phương pháp tọa độ trong không gian
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Phương pháp tọa độ trong không gian
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________
Câu 1: Tìm m để góc giữa hai vectơ: u 1; 1 log lo l g o 5; 5 log lo l g o 2,v 3;log 3;4 3 là góc nhọn. Chọn m 5
phương án đúng và đầy đủ nhất. 1 1
A. m ! ,m z 1
B. m !1 hoặc 0 m 2 2 1 C. 0 m D. m !1 2 ¾ Giải: . u v 3 log 5.log 3 4log 2 Ta có cosu,v 3 5 m
. Do mẫu số luôn lớn hơn 0 nên ta u . v u . v
đi tìm điều kiện để tử số dương.
Mặt khác 3 log 5.log 3 4log 2 ! 0 4log 2 ! 4 ! ! 1 log 2 1 log 2 log 3 5 m m m m m m 1 1 Với 0 m 1 thì
! 2 m . Kết hợp với điều kiện suy ra m 1 0 . m 2 2 1 1 Với m ! 1 thì
2 m ! . Kết hợp điều kiện suy ra m !1. m 2 1
Vậy m !1 hoặc 0 m 2
Câu 2: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 3x 3y 2z 37 0 các
điểm A4;1;5 , B3;0; 1 , C 1 ;2;0 . Điểm M ; a ;
b c thuộc (P) sao cho biểu thức P M . A MB M .
B MC MC.MA đạt giá trị nhỏ nhất, khi đó a b c bằng: A. 10 B. 13 C. 9 D. 1 ¾ Giải:
M a b c P
ª a 2 b 2 c 2 ; ; 3 2 1 2 5º ¬ ¼
M P 3a 3b 2c 37 0 3a 2 3b 1 2c 2 4 4
Áp dụng BĐT Bunhiacốpxki ta có: 4 42 ª3 ¬ a 2 3b 1 2c 2 2 º d ¼ 3 3 2 ªa22 b 2 1 c 22 2 2 2 º ¬ ¼ 2 a 22 b 2 1 c 22 44 t 88 2 2 2 3 3 2 a b c 2 1 2
Dấu “=” xảy ra khi và chỉ khi: M 4; 7; 2
a b c 1 3 3 2
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________
Câu 3: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x y 2 0 và 2m °
1 x 1 m y m 1 0 đường thẳng d :
( m là tham số ). Tìm m để đường m ® °mx ¯ 2m 1 z 4m 2 0
thẳng d song song với mặt phẳng (P). m 1 1 A. m B. m 1 C. m D. m 1 2 2 ¾ Giải: 2x y 2 0 °
d // P hệ PT ẩn x , y, z sau vô nghiệm: ® 2m
1 x 1 m y m 1 0 m °mx ¯
2m 1z 4m 2 0 m m 1 2 4
(1) y 2x 2 . Thay vào (2) ta được: x y 3 3 1
Thay x, y vào (3) ta được: 2m 1 z 2
m 11m 6 . Để PT này vô nghiệm thì 3 1 m 2
Câu 4: Trong không gian với hệ tọa độ Oxyz, một mặt phẳng đi qua điểm M 1;3;9 và
cắt các tia Ox, Oy, Oz lần lượt tại A ;0 a ;0 , B0; ;
b 0 , C 0;0;c với a, b, c là các số thực
dương. Tìm giá trị của biểu thức P a b c để thể tích tứ diện OABC đạt giá trị nhỏ nhất. A. P 44 B. P 39 C. P 27 D. P 16 ¾ Giải: 1 1 V O . A O . B OC abc OABC 6 6 x y z
Phương trình mặt phẳng đi qua A, B ,C : 1 a b c Vì M ABC 1 3 9 1 a b c 1 3 9 1 3 9 27.27 1 Áp dụng BĐT Côsi: 3 1 t 3 . . 1t abc t121,5 minV a b c a b c abc 6 OABC
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ 1 3 9 1 a 3 ° ° °
Dấu “=” xảy ra khi và chỉ khi: a b c ® b
® 9 a b c 39 1 3 9 ° ° c 27 ¯ °¯a b c x 1 y z 1
Câu 5: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ' : và ba 1 2 1 điểm A3;2; 1 , B 3; 2 ;3 , C5;4; 7
. Gọi tọa độ điểm M ; a ;
b c nằm trên ' sao cho
MA MB nhỏ nhất, khi đó giá trị của biểu thức P a b c là: 16 6 6 42 6 6 A. P B. P 5 5 16 6 6 16 12 6 C. P D. P 5 5 ¾ Giải
M ' nên M 1 t;2t; 1 t
AM t 2;2t 2; t 2
AM 6t 12t 8
BM t 4;2t 2; t 4 2
BM 6t 24t 36 ª º « » MA MB t t t t « t2 1 6 12 8 6 24 36 6 1 t 22 2 2 2» 3 « » «¬ f x »¼ 2 2 § · § · 2 1 1
Áp dụng BĐT Vectơ ta có: f x t 1 t t 2 2 9 2 ¨ ¸ ¨ ¸ © 3 ¹ © 3 ¹ 1 t t 2 8 3 6
Dấu “=” xảy ra khi và chỉ khi: 1 t 2 5 3 § · 13 3 6 16 6 6 3 6 13 16 6 6 Do đó: M ¨ ; ; ¸ P ¨ 5 5 5 ¸ 5 © ¹
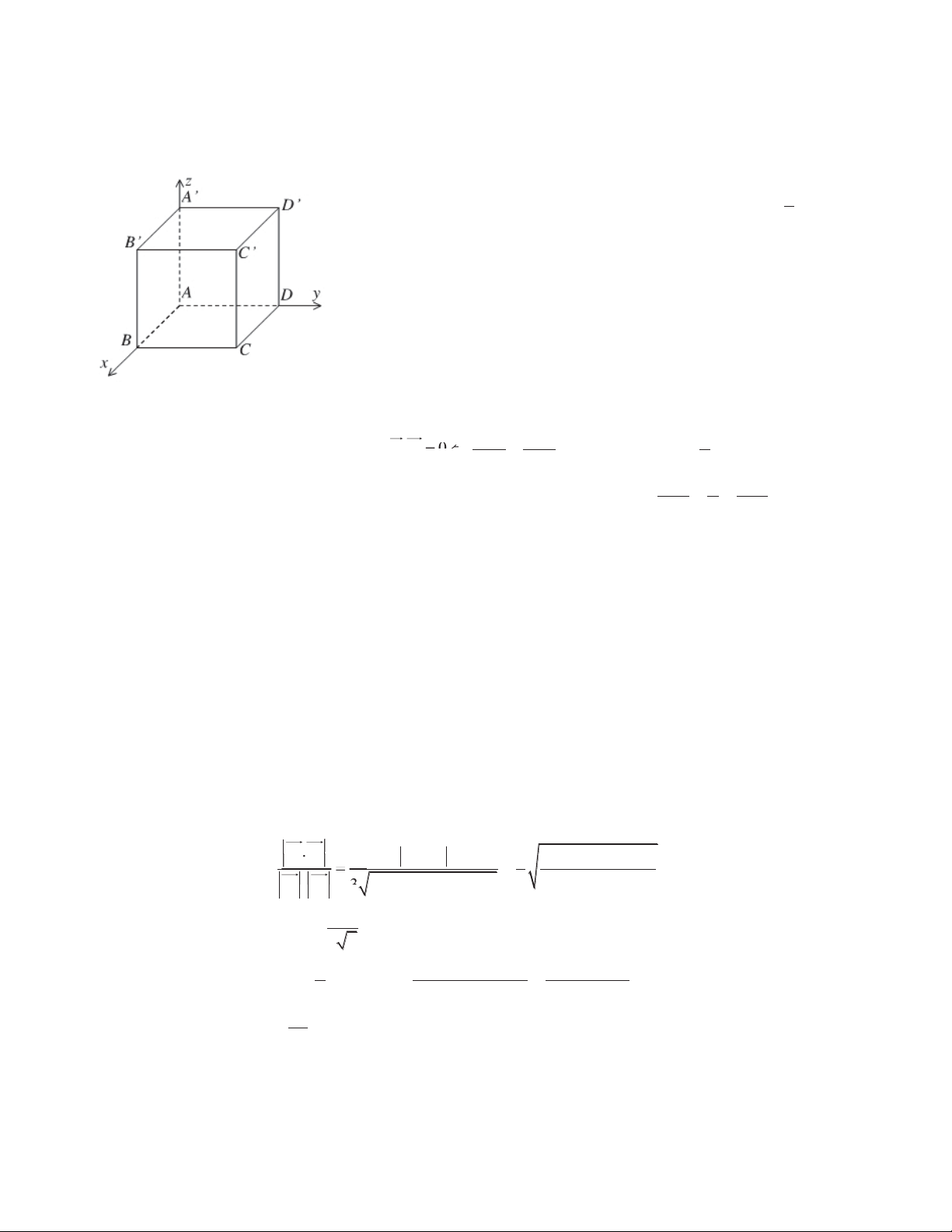
Câu 6: Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật . ABCD '
A B' C' D' có
A trùng với gốc của hệ tọa độ. Cho B ;0 a ;0 , D0; ;
a 0 , A'0;0;b với , a b ! 0 . Gọi M là a
trung điểm của cạnh CC’. Xác định tỉ số để hai mặt phẳng A'BD và BDM vuông b góc với nhau. a a 1 a a A. 2 B. C. 3 D. 1 b b 2 b b
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ § b ·
-Từ giả thiết ta có: C ; a ; a 0 ; C ; a ; a b M ; a ; ¨ a ¸ © 2 ¹
- Mặt phẳng (BDM) có VTPT là: § ab ab 2 · n ªBD BM º 1 ª 1 , ; ; ¬ ¼ ¨ a ¸ © 2 2 ¹
- Mặt phẳng (A’BD) có VTPT là: n ªB , D BA'º ¬ ¼ 2 a ;ba ; 2 b a
-Yêu câu của bài toán tương đương với: 2 2 2 2 a b a b 4 . 0 0 a n n a a b 1 1 2 2 2 b x 1 y z 1
Câu 7: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ' : và mặt 2 1 1
phẳng (P): 2x y 2z 1 0. Mặt phẳng (Q) chứa ' và tạo với (P) một góc D nhỏ nhất,
khi đó góc D gần với giá trị nào nhất sau đây? A. 0 6 B. 0 8 C. 0 10 D. 0 5 ¾ Giải: x 1 2t ' ° : ® y t Chọn 2 điểm 1;0; 1 và 3;1; 2 với t 1 °z 1 t ¯
(Q) chứa ' suy ra Q: ax
1 by cz
1 0 ax by cz a c 0 Và 3;1; 2
Q 3a b 2c a c 0 2a b c 0 c 2a b
Vậy (Q): ax by 2a b z a b 0 . Gọi D 0 ( ),( ) ,D 0 ª ;90o P Q º ¬ ¼ 2 2 n .n P Q b 6a 1 b 12ab 36 a Ta có: cosD 2 2 2 2 2 n . n 3 b ab a a b a b P Q (2 ) 3 2 4 5 1 Nếu a 0 cosD 3 2 2 2 2 b ab a t t 12 36 12 36
Nếu a z 0 , đặt b t thì ta có: f t 2 2 2 a
2b 4ab 5a 2t 4t 5 ª 7 t « f 't 0 10 «
. Từ bảng biến thiến ta có thể dễ nhận thấy: «¬t 6
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ § · § · maxf t 7 53 1 53 1 0 f D cos ¨ ¸ ¨ ¸ | 8 10 6 ¨ 3 6 ¸ © ¹ © ¹
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho điểm A0;1; 1 , B1;0; 3 , C 1 ; 2 ; 3 và mặt cầu (S): 2 2 2
x y z 2x 2z 2 0 . Điểm D ; a ;
b c trên mặt cầu (S) sao cho tứ diện
ABCD có thể tích lớn nhất, khi đó a b c bằng: 2 2 4 A. B. C. 1 D. 3 3 3 ¾ Giải: Tâm I 1;0;
1 , bán kính R=2. (ABC): 2x 2y z 1 0 2 1 V d D ABD S khi đó V
max khi và chỉ khi d ; D ABC max ABCD ; . 3 ABC ABCD Gọi 1 D 2
D là đường kính của (S) vuông góc với (ABC). Ta thấy với D là điểm bất
kỳ thuộc (S) thì d ;
D ABC d max^d D ; ABC ,d D ; 1 2 ABC`
Dấu “=” xảy ra khi D trùng với 1 D hoặc 2 D ª 2 x 1 2t t « ° 3 § 7 4 1 · § 1 4 5 · D D : ® y 2 thay vào (S) ta suy ra: « D ; ; , D ; ; 1 2 t 1 ¨ ¸ 2 ¨ ¸ ° « 2 © 3 3 3 ¹ © 3 3 3 ¹ z 1 ¯ t t «¬ 3 § 7 4 1 · 2
Vì d D ; ABC ! d D ; D ; ;
a b c 1 2 ABC nên ¨ ¸ © 3 3 3 ¹ 3 x 2 t °
Câu 9: Cho mặt cầu S 2 2 2
: x y z 2x 4z 1 0 và đường thẳng d : ® y t . Tìm m để °z m t ¯
d cắt S tại hai điểm phân biệt ,
A B sao cho các mặt phẳng tiếp diện của S tại A và
tại B vuông góc với nhau. A. m 1 hoặc m 4
B. m 0 hoặc m 4 C. m 1 hoặc m 0
D. Cả A, B, C đều sai ¾ Giải:
¾ Bình luận: Ta có nếu hai mặt phẳng tiếp diện của S tại A và B vuông góc với
nhau thì hai vtpt của hai mặt phẳng này cũng vuông góc với nhau. Mà hai vtpt
của hai mặt phẳng này chính là IA, IB . Với I 1; 0; 2
là tâm của mặt cầu S .
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________
Vậy ta có hai điều kiện sau:
1. d cắt S tại hai điểm phân biệt. 2. . IA IB 0 .
Để thỏa mãn yêu cầu đề bài thì trước tiên d phải cắt mặt cầu, tức là phương trình
t2 t m t2 2 2
2.2 t 4.m t 1 0 có hai nghiệm phân biệt. 2 t m 2 3 2
1 t m 4m 1 0
Phương trình có hai nghiệm phân biệt khi ' ! m 2 2 ' 0 1 3m 12m 3 ! 0 2 m 5m 1 0 .
Với phương trình có hai nghiệm phân biệt , áp dụng định lí Viet ta có 2 m 4m 1 2 t t ; t t m 1 1 2 1 2 3 3
Khi đó IA 1t ;t ;m 2 t ,IB 1t ;t ;m 2 t . 1 1 1 2 2 2 Vậy . IA IB 1 t
1 t t t m 2 t m 2 t 0 1 2 1 2 1 2 3t t m
1 t t m 22 1 0 1 2 1 2 ª m
m m m 2 m 2 2 2 4 1 1 2 1 1 0 « (TM). 3 m 4 ¬
Câu 10: Trong không gian Oxyz cho ba điểm A1;1;1,B 1; 2;0,C3; 1; 2 . Điểm x 1 y z 1 M a; ;
b c thuộc đường thẳng ' : sao cho biểu thức 2 1 1 2 2 2
P 2MA 3MB 4MC đạt giá trị nhỏ nhất. Tính a b c ? 5 11 A. C. 3 3 16 B. 0 D. 3 ¾ Giải:
Gọi Dx; y;z là điểm thỏa 2DA
A 3DB 4DC 0
2DA 3DB 4DC 0 2DA 3DA AB 4DA AC 0 DA 4AC A 3AB A 1 x 4.2 3.2 ° 1 ® y 4 .2 3.1 D 13; 12; 6 °1 z 4.1 3.1 ¯ 2 2 2
Khi đó: P 2MD DA 3MD DB 4MD DC
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ 2
MD 2MD2DAA 3DB 4DCC 2 2 2 2AD A 3BD 4DC 2 2 2 2
MD 2AD 3BD 4DC Do 2 2 2
2AD 3BD 4DC không đổi nên P nhỏ nhất khi MD nhỏ nhất. Mà M thuộc
' nên MD nhỏ nhất khi M là hình chiếu của D lên ' § · 11 8 11 5 11
M1 2t;t; 1
t . Ta có: DM.u 0 t M ¨ ; ; ¸ a b c ' 6 © 3 6 6 ¹ 3
Câu 11: Trong không gian Oxyz cho ba điểm A1;1;1,B 1; 2;0,C3; 1; 2 . Điểm M a; ;
b c thuộc mặt phẳng D : 2x y 2z 7 0 sao cho biểu thức P 3MA MA 5MB MB 7MC
MC đạt giá trị nhỏ nhất. Tính a b c ? A. 4 C. 13 B. 5 D. 7 ¾ Giải:
Gọi Fx; y;z là điểm thỏa 3FA
A 5FB 7FC C 0 CF C 3C 3 A C 5C 5 B C F 23; 20; 1 1
Khi đó: P 3MF FA 5MF FB 7MF FC MF M
Do đó P nhỏ nhất khi M là hình chiếu của F lên D . Điểm M 23 2t;20 t; 1
1 2t. Vì M thuộc D nên: 2 2 3 2t 20 t 2 1
1 2t 7 0 t 9 M 5
;11;7 a b c 13
Câu 12: Trong không gian Oxyz cho ba điểm A1;1; 1 , B 1; 2;0,C3; 1; 2 . Điểm 2 2 M a; ;
b c thuộc mặt cầu S x 2 : 1 y z 1 861 sao cho biểu thức 2 2 2
P 2MA 7MB 4MC đạt giá trị nhỏ nhất. Tính a b c ? A. 8 C. 5 B. 5 D. 3 ¾ Giải:
Gọi Kx; y;z là điểm thỏa 2KA
A 7KB 4KC C 0 K 21 ;16;10 Khi đó: 2 2 2 2
P MK 2KA 7KB 4KC
Do đó P nhỏ nhất khi MK lớn nhất. Mặt cầu (S) có tâm I 1;0; 1 KI 22; 1 6; 1 1
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ x 1 22t °
Phương trình đường thẳng KI: ®y 16 t
. Thay x, y, z vào (S) ta được: °z 1 11t ¯ t2 t2 t2 22 16 11 861 t 1
r . Suy ra KI cắt (S) tại hai điểm ªK 23; 16 ; 1 2 1 « «K 21 ;16;10 ¬ 2
Vì KK ! KK nên MK lớn nhất khi và chỉ khi M { K 23; 16 ; 1 2 . Vậy 1 1 2 M 23; 1 6; 12
Câu 13: Trong không gian Oxyz cho hai điểm A1;1; 1 , B 3
;5;5. Điểm Ma; ; b c thuộc
mặt phẳng D : 2x y 2z 8 0 sao cho biểu thức P MA MB đạt giá trị nhỏ nhất.
Tính a b c ? A. 7 C. 2 B. 3 D. 4 ¾ Giải: Ma; ;
b c . Đặt f M 2a b 2c 8
Ta có f A. f B ! 0 , nên A, B ở về cùng một phía so với D . Gọi A’ là điểm đối xứng của A qua D x 1 2t °
Phương trình đường thẳng AA’: ®y 1 t
. Tọa độ giao điểm I của AA’ và D °z 1 2t ¯ x 1 2t ° °y 1 t là nghiệm của hệ: ® I 3;0;1 z 1 2t °
°2x y 2z 8 ¯ 0
Vì I là trung điểm AA’ nên A'5; 1
;3 và A’, B nằm khác phía so với D . Khi đó
với mọi điểm M thuộc D ta luôn có:
MA MB A' M MB t A'B . Đẳng thức xảy ra khi M A' B D
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ x 5 4t ° A' B 8
;6;2 A'B : ®y 1
3t . Tọa độ giao điểm M của A’B và D là nghiệm °z 3 t ¯ x 5 4t ° °y 1 3t của hệ: ® M1;2;4 z 3 t °
°2x y 2z 8 ¯ 0
Câu 14: Trong không gian Oxyz cho hai điểm A1;1; 1 ,C7; 4
;4 . Điểm Ma; ; b c thuộc
mặt phẳng D : 2x y 2z 8 0 sao cho biểu thức P MA MC đạt giá trị lớn nhất.
Tính a b c ? A. 7 C. 2 B. 3 D. 4 ¾ Giải: Ma; ;
b c . Đặt f M 2a b 2c 8
Ta có f A. f C 0 nên A và C nằm về hai phía so với D
Gọi A’ là điểm đối xứng của A qua D x 1 2t °
Phương trình đường thẳng AA’: ®y 1 t
. Tọa độ giao điểm I của AA’ và D °z 1 2t ¯ x 1 2t ° °y 1 t là nghiệm của hệ: ® I 3;0;1 z 1 2t °
°2x y 2z 8 ¯ 0
Vì I là trung điểm AA’ nên A'5; 1
;3 . Khi đó với mọi điểm M thuộc D ta luôn có:
MA MC MA' MC d A'C . Đẳng thức xảy ra khi M A'C D
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ x 5 2t ° A'C 2; 3
;1 A'C : ®y 1
3t . Tọa độ giao điểm M của A’C và D là nghiệm °z 3 t ¯ x 5 2t ° °y 1 3t của hệ: ® M3;2;2 z 3 t °
°2x y 2z 8 ¯ 0 x 1 y 1 z
Câu 15: Trong không gian Oxyz cho đường thẳng ' : và mặt phẳng 1 2 2
P:axby cz 3 0 chứa ' và cách O một khoảng lớn nhất. Tính abc ? A. 2 C. 1 B. 3 D. 1 ¾ Giải:
Gọi K là hình chiếu vuông góc của O lên ' , suy ra K1 t;1 2t;2t ,
OK 1 t;1 2t;2t § 2 1 2 · °K ¨ ; ; ¸ 1 ° © 3 3 3 ¹
Vì OK A ' nên OK.u 0 t ' ® 3 § 2 1 2 · °OK ¨ ; ; ¨ ¸ °¯ © 3 3 3 ¹
Gọi H là hình chiếu của O lên (P), ta có: d ;
O P OH d OK 1. Đẳng thức xảy ra
khi H { K . Do đó (P) cách O một khoảng lớn nhất khi và chỉ khi (P) đi qua K và
vuông góc với OK. Từ đó ta suy ra phương trình của (P) là:
2x y 2z 3 0 a b c 1 x 1 y 1 z
Câu 15: Trong không gian Oxyz cho đường thẳng ' : và mặt phẳng 1 2 2
D:x2y 2z5 0. Mặt phẳng Q:axby cz 3 0 chứa ' và tạo với D một góc
nhỏ nhất. Tính a b c ? A. 1 C. 5 B. 3 D. 1 ¾ Giải:
¾ Công thức giải nhanh: ªª º º n ª «¬¬
n D ,n ,n Q ' ' ¼ »¼
¾ Chứng minh công thức:
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________
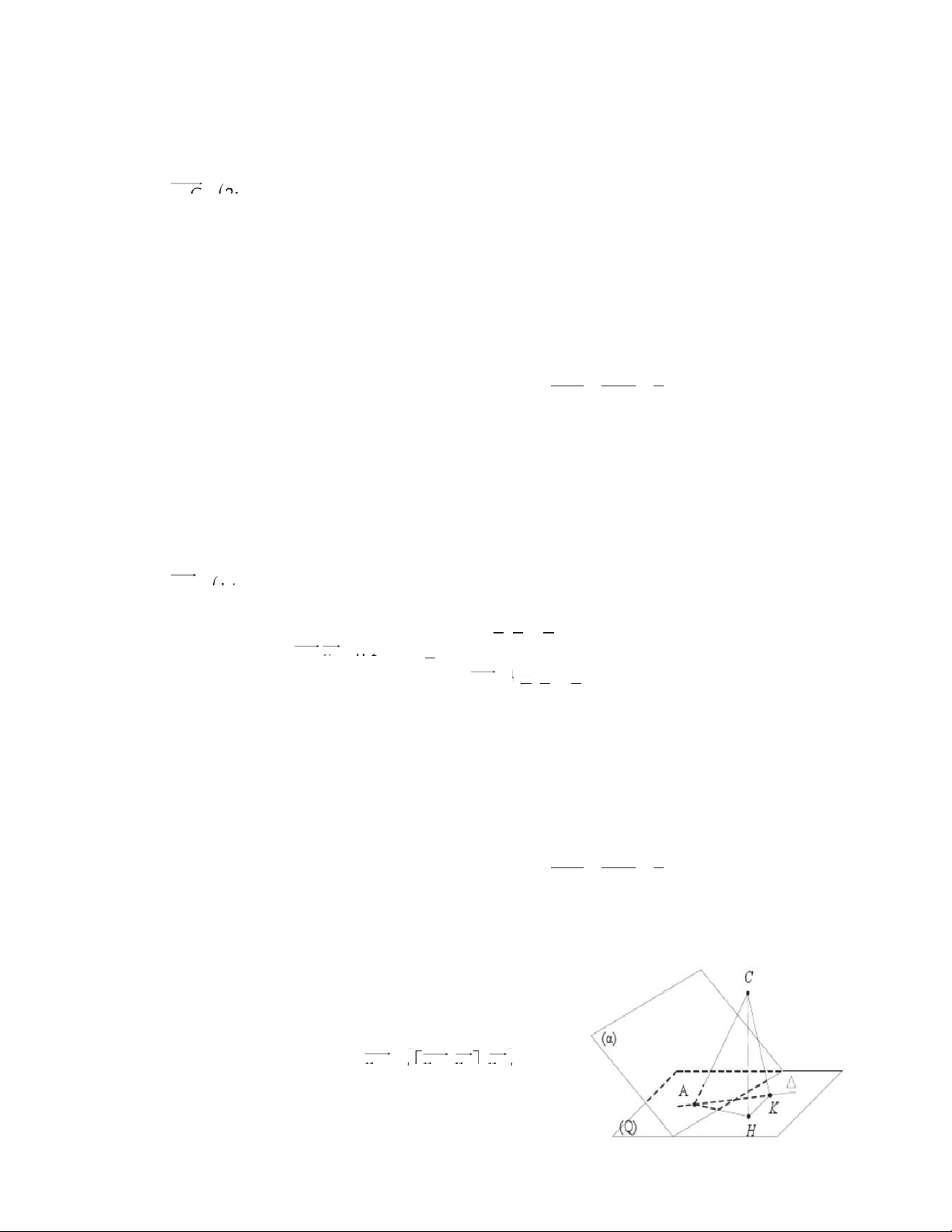
A1;1;0' . Gọi d là đường thẳng đi qua A và vuông góc với D , x 1 t °
suy ra d : ®y 1 2t , chọn C2; 1
;2d,C z A . Gọi H, K lần lượt là hình chiếu của °z 2t ¯ AH AK AK
C lên Q và ' , khi đó M ACH và sinM sinACH t . Mà không đổi AC AC AC
nên suy ra M nhỏ nhất H { K hay Q là mặt phẳng đi qua ' và vuông góc với mặt phẳng ACK
Mặt phẳng ACK đi qua ' và vuông góc với D nên: ª º n ª ¬ n D ,n ACK ' ¼
Do Q đi qua ' và vuông góc với mặt phẳng ACK nên: ª º ªª º º n ª ¬ n ,n ' ¼ «¬¬
n D ,n ,n Q ACK ' ' ¼ »¼
Áp dụng công thức trên ta có n 8; 20; 1 6 suy ra: Q Q: 8 x 1 20y
1 16z 0 2x 5y 4z 3 0 a b c 1 x 1 y 1 z
Câu 16: Trong không gian Oxyz cho đường thẳng ' : và hai điểm 1 2 2 M1;2; 1 ,N 1
;0;2 . Mặt phẳng E : ax by cz 43 0 đi qua M, N và tạo với ' một
góc lớn nhất. Tính a b c ? A. 22 C. 33 B. 3 3 D. 11 ¾ Giải:
¾ Công thức giải nhanh: ª n ª º º n n ,n ,n E « NM ' NM ¬¬ ¼ »¼
Chứng mình tương tự câu 15: n E 1;10; 22 suy ra
E:1x 110y222z 1 0 x10y22z43 0abc 33
Câu 17: Trong không gian Oxyz cho ba điểm A1;2;3,B 1 ;0; 3 ,C2; 3 ; 1 . Điểm M a; ;
b c thuộc mặt phẳng D : 2x y 2z 1 0 sao cho biểu thức 2 2 2
P 3MA 4MB 6MC đạt giá trị nhỏ nhất. Tính a b c ? A. 15 C. 20
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ B. 12 D. 7 ¾ Giải: M ; a ;
b cD 2a b 2c 1 0
P a b c a b c a 2 b 2 c 2 2 2 2 26 48 6 2 11 25
1 22a b 2c 1 747 t 747
Dấu “=” xảy ra khi: a 11
;b 25;c 1 a b c 15
Câu 18: Trong không gian Oxyz cho ba điểm A1;2;3,B 1 ;0; 3 ,C2; 3 ; 1 . Điểm x 1 y 1 z 1 M a; ;
b c thuộc đường thẳng ' : sao cho biểu thức 2 3 1 P MA MA 7MB MB 5MC
M đạt giá trị lớn nhất. Tính a b c ? 31 12 A. C. 4 5 11 55 B. D. 3 7 ¾ Giải:
M' M1 2t; 1 3t;1 t
MA 7MB 5MC 2t 2 19; 3t 14; t 20 2 § ·
P t 2 t 2 t2 12 6411 6411 2 19 3 14 20 14 t t ¨ ¸ © 7 ¹ 7 7 12 55
Dấu “=” xảy ra khi: t
a b c 7 7
Câu 19: Trong không gian Oxyz cho ba điểm A1;2;3,B 1 ;0; 3 ,C2; 3 ; 1 . Điểm 2 2 2 283 M a; ;
b c thuộc mặt cầu S : x 2 y 2 z 8 sao cho biểu thức 2 2 2 2
P MA 4MB 2MC đạt giá trị lớn nhất. Tính a b c ? C. 28 C. 6 D. 7 D. 3 ¾ Giải:
Gọi Ex; y;z là điểm thỏa EA 4EB
E 2EC 0 E 9 ;4; 1 3 Khi đó: 2 2 2 2
P EM EA 4EB 2EC
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________
P lớn nhất khi EM nhỏ nhất. Mặt cầu (S) có tâm x 2 11t ° 1 I 2; 2;8 IE 1 1;2; 2
1 IE : ®y 2 2t . Thay x, y, z vào (S) ta được t r . ° 2 z 8 21t ¯ ª § 7 5 · «E ¨ ; 3; ¸ 1 « © 2 2 ¹
Suy ra IE cắt (S) tại hai điểm « § 15 37 · «E ¨ ;1; ¸ 2 ¬ © 2 2 ¹ § · 7 5
Vì EE EE nên EM nhỏ nhất khi và chỉ khi M { E ¨ ; 3; , suy ra 1 2 ¸ 1 © 2 2 ¹ M 6;0;12 x y 1 z 2
Câu 20: Trong không gian Oxyz cho đường thẳng d : cắt đường thẳng a b c x 1 y z 2 d' :
sao cho khoảng cách từ điểm B2;1;1 đến đường thẳng d là nhỏ nhất. 2 1 1
Tính a b c ? A. 28 C. 6 B. 7 D. 18 ¾ Giải: M d ° d' ªAB,AMº AB AM ° 1t;1;4 2t Gọi ® , suy ra ¬ ¼ ® ¯
M t t t A 0; 1 ;2 1 2 ; ;2 ° d u ° AM A AM ¯
2t2 1;t 1; t d ªABB,AMº AB AM AM 2 ¬ ¼ dB d 5t 18t 18 , f t 2 AM 6t 2t 2 ª f t t 0 «
minf t f 1 ' 0 2 u 3;3; 2
a b c 4 t ¬ 2 11 d x y 1 z 2
Câu 21: Trong không gian Oxyz cho đường thẳng d : cắt đường thẳng a b c x 1 y z 2 x 5 y z d' :
sao cho khoảng cách giữa d và ' : là lớn nhất. Tính 2 1 1 2 2 1
a b c ? A. 8 C. 1 B. 1 D. 12
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ ¾ Giải: M d ° d' Gọi ® , suy ra u AM A AM 2t 2 1;t 1; t d ¯
M t t t A 0; 1 ;2 1 2 ; ;2 ° d
N5;0;0 , u 2; 2; 1 u ª ,AMº A
t 1;4t 1;6t ' ' ¬ ¼ ª º 2 u , AM A .AN ' A ¼ 2 ¬ ¼ t dd,' 3 3 f t 2 ª º 53t 10t 2 u , AM ' ¬ A ¼ ª 4 § · t « 1 f t 37 minf t 4 ' 0 f u
a b c ¨ ¸ d 29; 41;4 8 « © 37 ¹ 37 «¬t 2
Câu 22: Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng P : x 2y 2z 1 0,
Q: x y 2z 1 0 và điểm I 1;12.Mặt cầu S tâm I, tiếp xúc với P và mặt
phẳng D : ax by cz m 0 vuông góc với P,Q sao cho khoảng cách từ I đến (α)
bằng 29 . Biết rằng tổng hệ số a b c m dương .
Cho các mệnh đề sau đây:
(1) Điểm A1;1;0 và B 1 ;1; 2
thuộc mặt cầu S .
(2) Mặt phẳng (α) đi qua C 0; 5 ; 3 . x 2t °
(3) Mặt phẳng (α) song song với đường thẳng (d) ®y 5 t °z 3 ¯
(4) Mặt cầu S có bán kính R 2.
(5) Mặt phẳng (α) và Mặt cầu S giao nhau bằng một đường tròn có bán kính lớn hơn 2.
Hỏi có bao nhiêu mệnh đề sai ? A . 1 B . 3 C . 2 D . 4
¾ Giải: Chọn đáp án C 2 2 2
R dI,P 2 . Phương trình mặt cầu: x 1 y 1 z 2 4.
n 2;3;4 D : 2x 4y 3z m 0 d I; D r D . 29 m 29
Vậy D : 2x 4y 3z r 29 0 chọn D : 2x 4y 3z 29 0 do a b c m ! 0. Đối chiếu:
(1) Đúng: Thay tọa độ điêm vào mặt cầu ta thấy .
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________
(2) Đúng: Thay tọa độ điêm vào mặt phẳng
(3) Sai: Thực chất ta tưởng lầm rằng mặt phẳng phẳng (α) song song (d) nhưng
thực chất là (d) thuộc phẳng phẳng (α), các em kiểm tra bằng cách tính khoảng
cách 2 điểm bất kỳ đến (α) đều bằng 0 . (4) Đúng
(5) Sai: Do khoảng cách từ tâm mặt cầu đến mặt phẳng lớn hơn bán kính mặt cầu
nên hai mặt không giao nhau .
Câu 23: Trong không gian Oxyz, cho các điểm A2; 3;0 ,B0; 2; 0 và đường thẳng d x t °
có phương trình ®y 0 . Điểm Ca; ;
b c trên đường thẳng d sao cho tam giác ABC có °z 2 t ¯
chu vi nhỏ nhất. Tính a b c ? A. 2 C. 1 B. 3 D. 4 ¾ Giải:
Vì AB không đổi nên tam giác ABC có chu vi nhỏ nhất khi CA+CB nhỏ nhất 2 2
Gọi Ct;0;2 t . Ta có CA t 2 CB t 2 2 2 3 , 2 1 2
Đặt u 2t 2;3 v 21t;2 u v 2;5
Áp dụng tính chất u v t u v . Dấu “=’’ xảy ra khi u cùng hướng với v
CA CB u v t u v 2 25 3 3 2 t 2 3 7 Dấu “=” xảy ra khi
t a b c 2 1 t 2 2 5
Câu 24: Trong không gian Oxyz, cho điểm Ma; ;
b c với c 0 thuộc mặt cầu
S x 2 y 2 z 2 : 2 1
1 9 sao cho biểu thức P a 2b 2c đạt giá trị lớn nhất. Khi
đó a b c ? A. 1 C. 1 B. 9 D. 3 ¾ Giải
Ma b cS a 2 b 2 c 2 ; ; 2 1 1 9
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ P a b c
ªa 2 b 2 c 2 2 2 1 2 1 6 1 4 4 2 1 1 º d 9 6 15 «¬ »¼ b 1 a 2 ° 2 ° ° c 1
Dấu “=” xảy ra khi: ®a 2
a b c 1 2
°°a22 b12 c12 9 °¯
Câu 25: Trong không gian Oxyz, cho 4 điểm A2; 4; 1 , B1;4; 1 , C 2; 4; 3 , D2; 2; 1 và điểm M ; a ;
b c sao cho biểu thức 2 2 2 2
P MA MB MC MD đạt giá
trị nhỏ nhất, khi đó a b c ? 7 21 A. C. 4 4 23 3 B. D. 4 4 ¾ Giải: § · 7 14
Gọi G là trong tâm của ABCD suy ra G ¨ ; ; 0 ¸ © 4 4 ¹ 2 2 2 2 2
P 4MG GA GB GC GD . Vì 2 2 2 2
GA GB GC GD không đổi nên P § 7 14 ·
nhỏ nhất khi MG nhỏ nhất hay M { G ¨ ; ; 0 ¸ © 4 4 ¹
Câu 26: Trong không gian Oxyz, cho mặt cầu S 2 2 2
: x y z 4x 2y 6z 5 0 và
mặt phẳng P : 2x 2y z 16 0 . Điểm M ; a ;
b c di động trên (S) và điểm N ; m ; n p
di động trên (P) sao cho độ dài đoạn thẳng MN là ngắn nhất, khi đó
a b c m n p ? A. 3 C. 0 B. 2 D. 1 ¾ Giải:
Mặt cầu (S) có tâm I 2; 1
; 3 và bán kính R 3
dI;P 5 ! R. Do đó (S) và (P) không có điểm chung. Suy ra minMN 5 3 2
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________
Trong trường hợp này, M ở vị trí M và N ở vị trí N . Dễ thấy N là hình chiếu 0 0 0
vuông góc của I lên mặt phẳng (P) và M là giao điểm của đoạn thẳng IN với 0 0
mặt cầu (S). Gọi d là đường thẳng đi qua I và vuông góc với (P) thì N d P , 0 y 2 2t °
khi đó d : ®y 1
2t . Tọa độ N là nghiệm của hệ: ° 0 z 3 t ¯ y 2 2t ° °y 1 2t § 4 13 14 · ® N ¨ ; ; ¸ 0 z 3 t ° © 3 3 3 ¹
°2x 2y z 16 ¯ 0 3
IM IN M 0; 3
;4 a b c m n p 0 0 0 5
Câu 27: Trong không gian Oxyz, cho mặt cầu S 2 2 2
: x y z 6x 8y 2z 23 0 và
mặt phẳng P : x y z 3 0 . Điểm M ; a ;
b c nằm trên mặt cầu (S) sao cho khoảng
cách từ M đến mặt phẳng (P) là lớn nhất, khi đó a b c ? A. 1 C. 7 B. 5 D. 9 ¾ Giải:
Mặt cầu (S) có tâm I 3; 4; 1 và bán kính R 3 y 3 t °
Gọi d là đường thẳng đi qua I và vuông góc với (P), d : ®y 4 t . Khi đó °z 1t ¯
M d S hay tọa độ M là nghiệm của hệ: y 3 t ° °y 4 t ªM 4;5;0 1 d : ® « z 1 t ° «M 2;3;2 ¬ 2 2 2 2
°x y z 6x 8y 2z 23 ¯ 0
Ta thấy dM ; P ! d M ; P . Do đó M4;5;0 a b c 9 1 2
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________
Câu 28: Trong không gian Oxyz, cho mặt cầu S 2 2 2
: x y z 4x 6y m 0 và đường
thẳng d là giao tuyến của hai mặt phẳng P : 2x 2y z 1 0 , Q : x 2y 2z 4 0 .
Tìm m để mặt cầu (S) cắt đường thẳng d tại hai điểm M, N sao cho MN 8 A. m 12 C. m 3 B. m 5 D. m 12 ¾ Giải:
Mặt cầu (S) có tâm I 2;
3;0 và bán kính R 13 m IMm 13
Gọi H là trung điểm của MN suy ra MH 4 . IH dI;d m 3 . (d) qua A có ªu; AIº ¬ AI AI ¼ VTCP u dI d ; 2;1; 2 ; 3 . Vậy m 3 3 m 1 2 u
Câu 29: Trong không gian Oxyz, cho hai điểm E2;1; 5 , F4;3;9 . Gọi ' là giao tuyến
của hai mặt phẳng P : 2x y z 1 0 , Q : x y 2z 7 0 . Điểm I a; ; b c thuộc '
sao cho biểu thức P IE IF lớn nhất. Tính a b c ? A. 4 C. 3 B. 1 D. 2 ¾ Giải: x 1 t x 2 t' ° °
' : ®y 5t , EF : ®y 1 t' ° ° z 3 3t ¯ z 5 2t ' ¯ 1 t 2 t' ° ªt 0 Xét hệ: ® 5 t 1 t' «
EF cắt ' tại A1;0;3 t ' 1 ° ¬ 3 3t 5 2t ' ¯
Trong mặt phẳng '; EF mọi điểm I thuộc ' ta có IE IF d EF
Dấu “=” xảy ra khi I, E, F thẳng hàng, suy ra I { A1;0;3
Câu 30: Trong không gian Oxyz, cho hai điểm A 1; 1; 2 , B 2; 2; 1 và mặt phẳng
P: x3yz2 0. Gọi (Q) là mặt phẳng trung trực của đoạn AB, ' là giao tuyến của
(P) và (Q). Điểm Ma; ;
b c thuộc ' sao cho độ dài đoạn thẳng OM là nhỏ nhất, khi đó
a b c ?
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ 3 A. C. 1 2 3 B. D. 4 2 ¾ Giải: § · 3 3 3
Gọi I là trung điểm AB suy ra I ; ¨ ; ¸ , Q 3
: x y z 0 © 2 2 2 ¹ 2 7 x 2t ° 4 ° § · ' 7 1
là giao tuyến của (P) và (Q) suy ra ' : ®y t M ¨ 2t; t ; t ¸ ° © 4 4 ¹ 1 °z t ¯ 4 2 § · 5 25 25 OM 6 t t ¨ ¸ © 8 ¹ 32 32 § · 5 1 5 3
Dấu “=” xảy ra khi t M ; ; ¨ ¸ 8 © 2 8 8 ¹
Câu 31: Trong không gian Oxyz, cho điểm A 2;
3;4 , mặt phẳng P : x 2y z 5 0 x 3 y 1 z 3
và đường thẳng d :
. Gọi ' là đường thẳng nằm trên (P) đi qua giao 2 1 1
điểm của d và (P) đồng thời vuông góc với d. Điểm Ma; ;
b c thuộc ' sao cho độ dài
đoạn thẳng AM là nhỏ nhất, khi đó a b c ? 13 7 A. C. 3 2 3 B. D. 0 2 ¾ Giải:
Gọi I d P suy ra I 1 ;0; 4 x 1 t ° u u ª ,n º u ' ® ' 3;3;3 suy ra : y t
M 1 t;t; 4 t d P ¬ ¼ °z 4t ¯
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________ 4
AM ngắn nhất khi và chỉ khi AM A ' AM.u 0 t ' 3 § · 7 4 16 Vậy M ¨ ; ; ¸ © 3 3 3 ¹
Câu 32: Trong không gian Oxyz, cho ba điểm A5;8; 11 , B3;5; 4 , C2;1; 6 và x 1 y 2 z 1 đường thẳng d : . Điểm Ma; ;
b c thuộc d sao cho biểu thức 2 1 1 P MA M MB M MC
M đạt giá trị nhỏ nhất, khi đó a b c ? 15 7 A. C. 4 2 14 B. D. 2 9 ¾ Giải:
M1 2t;2 2t;1td 2 § ·
P t 2 t 2 2 10 53 53 2 1 2 4 t 9 t t ¨ ¸ © 9 ¹ 9 9 § · 10 11 2 1
Dấu “=” xảy ra khi t M ; ; ¨ ¸ 9 © 9 9 9 ¹
Câu 33: Trong không gian Oxyz, cho hai điểm A1; 5;0 , B3; 3; 6 và đường thẳng x 1 y 1 z d :
. Điểm Ma; ;bc thuộc d sao cho MA '
B có diện tích nhỏ nhất, khi đó 2 1 2
a b c ? A. 3 C. 4 B. 1 D. 2 ¾ Giải: M 1
2t;1t; 2td 1 S ªAM, ABº AM AB 18 t t MA ' B 2 1 198 198 2 ¬ ¼
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________
Dấu “=” xảy ra khi t 1 M1;0;2
Câu 34: Trong không gian Oxyz, cho hai điểm A1; 1; 2, B3; 4; 2 và đường thẳng x 2 4t ° d : ®y 6 t . Điểm I a; ;
b c thuộc d sao cho IA IB đạt giá trị nhỏ nhất, khi đó °z 1 8t ¯
a b c ? 43 65 A. C. 29 29 23 21 B. D. 58 58 ¾ Giải: AB 2; 3 ; 4
AB / /d . Gọi A’ là điểm đối xứng của A qua d
IA IB IA' IB t A' B. Dấu “=” xảy ra khi A’, I, B thẳng hàng suy ra I A' Bd .
Vì AB//d nên I là trung điểm của A’B. § · § · 36 33 15 43 95 28
Gọi H là hình chiếu của A lên d suy ra H ¨ ; ; ¸ suy ra A' ; ; ¨ ¸ . © 29 29 29 ¹ © 29 29 29 ¹ § · 65 21 43
Vì I là trung điểm của A’B nên I ; ; ¨ ¸ © 29 58 29 ¹ x 1 t °
Câu 35: Trong không gian Oxyz, cho hai đường thẳng d : ®y 1 t và °z 2 ¯ x 3 y 1 z d' :
. Điểm A ;a ;
b cd và B ; m ;
n pd' sao cho đoạn AB có độ dài 1 2 1
ngắn nhất, khi đó a b c m n p ? C. 4 C. 6 D. 1 D. 5 ¾ Giải: A1 t; 1
t; 2 và B3t';1 2t';t' suy ra AB 2 t t';2 t 2t';t' 2
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com
HчԒng dӢn giӚi mԐt sԈ bài tӤp tԄa ¶Ԑ trong không gian nâng cao
_____________________________________________________________________________________________________________________________
AB có độ dài nhỏ nhỏ nhất khi AB là đoạn vuông góc chung của d và d’ hay: ° . AB u 0 d ®
t t' 0 A1; 1; 2,B3;1;0 ° . AB u 0 ¯ d'
_____________________________________________________________________________________________________________________________
Tác giӚ: PHӗM MINH TUӛN - TOANMATH.com