Hướng dẫn giải một số câu hỏi số phức khó trong các đề thi thử – Lê Hồng Quốc Toán 12

Hướng dẫn giải một số câu hỏi số phức khó trong các đề thi thử – Lê Hồng Quốc Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

22 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 1
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
Câu 1. (Đề khảo sát của Bộ dành cho 50 trường) Xét số phức
z
thỏa
13
z
i
. Tìm giá trị nhỏ nhất
T
của
9
5z i
.
A.
2
13
T
. B
.
3
13
T
. C.
13
T
. D.
4
13
T
.
H
ướng dẫn giải.
Chọn A.
Đặt
z
x yi
(với
,x
y
). Khi đó
13
z i
2
2
x
y
.
Cách 1. Đại số.
Chọn
13 sin
13
cos 1
x t
y
t
.
T
a có
2
2
2
2 2
9
5 9 5 13 sin 9 13 cos 6
P
z i x y t t
2
2
1
3 sin cos 18 13 sin 12 13 cos 117 130 6 13 3sin 2cost t t t t t
1
30 78sin 52 208
t
P
, với
3
s
in
13
2
co
s
1
3
.
Vậy
2
13
T
.
Cá
ch 2. Hình học.
Đặt
9
5 9 5w z i w z i
2
2 2
9
5
w
x y
su
y ra tập hợp các số phức
w
nằm
trên
đường tròn
1
C
có
tâm là
9;
5
A
, b
án kính
1
R
.
Mà
13
z
i
2
2
x
y
suy
ra tập hợp các số phức
w
nằm
trên đường tròn
2
C
có
tâm
là
0;
1
B
, b
án kính
2
1
3
R
.
Gọi
C
là
điểm thuộc đường tròn
1
C
,
suy
A
C w
,
mà
C
th
uộc
2
C
,
suy ra
2
2
A
B R AC AB R
,
ta có
9
; 6 117 3 13
AB
AB
s
uy ra
2
13 4 13
AC
. Vậy
2 13
T
.
Câu 2. Có bao nhiêu giá trị thực của
m
để p
hương trình
2 2
4
4 1 3 0
z
m z m m
có
hai nghiệm
phức thỏa
1
2
2
z
z
.
A.
0
. B
.
1
. C.
2
. D.
4
.
H
ướng dẫn giải.
Chọn C.
Cách 1:
'
4 4m
.
T
rường hợp 1:
'
0
1m
. Khi đó phương trình
2
2
4 4 1 3 0
z m z m m
có hai nghiệm là
1
z
a bi
,
2
z
a bi
với
,a b
.
T
a có
2
2
1 2
2
1
z
z a b
1
.
T
heo định lí Vi-ét ta có
2
1
2
3
4
m
m
z
z
2
,
từ
1
v
à
2
su
y ra
1
4
m
m
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Trang
2
Sưu tầm và biên soạn:
Lê Hồng
Quốc ĐT: 0898.244.454
Suy
ra
m
3
.
Trư
ờng hợp 2:
' 0 1m
ph
ương trình đã cho có hai nghiệm
1 2
1
z z
, suy
ra
1 2
2
z z
.
Suy
ra
1m
thỏa
4
.
Trư
ờng hợp 3:
' 0
1m
. Khi đó phương trình có hai nghiệm thực
1 2
,z z
thảo hệ thức Vi-ét
1 2
2
1
2
1
3
4
z z
m
m m
z z
.
Theo đề ta có
1 2
2
z z
2 2
1
2 1 2
2 4
z z z z
2
1 2
1 2 1 2
2 2 4
z z z z z z
2 2
2
3 3
1 4
2 2
m
m m m
m
2
2
2
1 4 3 0
3
3 3
0
m khi m m
m
m khi m m
5
.
Vậy
từ
3
,
4
,
5
suy
ra
3m
,
1m
thỏa.
Cá
ch 2:
Phư
ơng trình
2 2
4 4 1 3 0
z m z m m
lu
ôn có hai nghiệm phức
1 2
,z z
, theo
định lí Vi-ét ta có
1 2
2
1
2
1
3
4
z z
m
m m
z z
. Theo
yêu cầu bài toán ta có
1 2
2
z z
2 2
1
2 1 2
2 4
z z
z z
2 2
1
2 1 2
1 2
2 4
2
z z z z
z z
2 2
1
2 1 2 1 2 1 2
4 4
8
z z
z z z z z z
2 2
2 2
1 1 3 3 8
m m m m m m
2
2
1 1
3 8
m m
m m
2
2
2
2
2
2
1 1
3 8 1
1 1 3 8 1;0 3;
1 1 3 8 0 3
m m m m khi m
m m m m khi m
m m m m khi m

2
2
2 6
8 0 1
2 4 6 0 1;0 3;
2 6 0 0 3
m m khi m
m m khi m
m khi m

1 3m
m
.
Vậy
3m
,
1m
th
ỏa.
Câu 3. (THPT chuyên Quang Trung – Bình Phước) Cho
z
th
ỏa mãn
10
2 1
2i z i
z
. B
iết
tập hợp các điểm biểu diễn cho số phức
3 4
1 2w i z i
là
đường tròn tâm
I
,
bán kính
R
. K
hi đó
A.
1;
2
5
I
R
. B.
1;
2
5
I
R
. C.
1;
2
5
I
R
. D.
1;
2
5
I
R
.
Hư
ớng dẫn giải
Chọn
Nhận xét. Ở đây đề cho lỗi, vì chỉ có 1 số phức
z
thỏa
10
2 1
2i z i
z
, nên tập hợp điểm
biểu di
ễn số phức
w
cũng
chỉ có 1 điểm chứ không phải là 1 đường tròn.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 3
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
*
Lời
giải sai.
T
a có
2
10
10
2 1 2 2 1 2
i z i z z i z
z
z
.
Lấy
môđun hai vế ta được
2
2
2
10
2
2 1z z
z
(Do
z
z
).
2
2
2
10
2
2 1z z
z
2
2
10
5
5 1 1 2 (3 4 ) . 5
z
z w i i z
z
.
Do đó tập hợp điểm biểu diễn w là đường tròn
1
;2
5
I
R
.
*
*
Lời
giải đúng.
Ta có
2
10 10
2
1 2 2 1 2
i
z i z z i z
z
z
.
Lấy môđun hai vế ta được
2
2
2
10
2
2 1z z
z
(D
o
z
z
).
2
2
2
10
2
2 1z z
z
2
2
10
5
5 1
z
z
z
. Thay
1
z
vào
10
2 1 2i z i
z
ta được
1
0 10 10 3 10
2
1 2
1 3 10 10
i i z i
z i
su
y ra
1
0 9 10 20 13 10
10 10
w i
,
suy ra điểm
biểu diễn của số phức
w
là 1 điểm.
Câu 4. (THPT chuyên Lương Thế Vinh – Đồng Nai – L1) Cho số phức
z
thỏa mãn
2
2
5 1 2 1 3z z z i z i
. Tìm
giá trị nhỏ nhất của
w
,
biết rằng
2
2w z i
.
A
.
min
3
2
w
. B
.
min
2
w
. C
.
min
1
w
. D.
min
1
2
w
.
H
ướng dẫn giải.
Chọn C.
Cách 1: Đại số.
2
2
5 1 2 1 3z z z i z i
2
2
1
4 1 2 1 3z i z i z i
1 2 1 2 1 2 1 3z i z i z i z i
1
2 0 1
1 2 1 3 2
z
i
z i z i
.
+)
1 1 2z i
1 1
w w
3
.
+)
Đặt
z a bi
, với
,a
b
. Khi đó ta có
2
1 2 1 3a b i a b i
2
2 2 2
1
2 1 3
a
b a b
4 4 6 9b b
1
2
b
,
suy ra
3
2
2
w
a i
2
9
3
2
4 2
w
a
4
. Từ
3
,
4
ta
suy ra
m
in
1
w
.
Cá
ch 2: Hình học.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 4
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
2
2
5 1 2 1 3z z z i z i
2
2
1
4 1 2 1 3z i z i z i
1
2 1 2 1 2 1 3z i z i z i z i
1
2 0 1
1 2 1 3 2
z
i
z i z i
.
+)
1
1 2z i
1w
1
w
3
.
+)
Đặt
z a bi
,
với
,a
b
.
Khi đó ta có
2
1 2 1 3a b i a b i
2
2 2 2
1
2 1 3
a
b a b
1
4 4 6 9
2
b b b
,
suy ra
3
2
2
w
a i
,
suy ra tập
hợp các số phức
w
nằm trên đường thẳng
3
2
y
, suy ra
;
3
2
O
w
d
.
Câu 5. (Chuyên ĐH Vinh – L3) Cho hai số phức
z
,
w
kh
ác
0
và
thỏa
2
z
w z w
.
Phần thực
z
u
w
là
A
.
1
8
. B
.
1
4
. C.
1
. D.
1
8
.
H
ướng dẫn giải.
Chọn D.
Ta có
2
z
w z w
1
2
1
z
w
z w
w
1
2
1
z
w
z w
w
1
2
1
1
u
u
, đặt
u
a bi
, với
,a
b
, khi đó
ta được hệ phương trình
2
2
2
2
1
4
1
1
a b
a b
3
1
2
1
4
8
a
a
.
Câu 6. Biết rằng khi
m
a
,
với
a
v
à
m
là
các số thực, thì phương trình
2
1 1 0
i x m i x
kh
ông
có nghiệm thựC. Chọn mệnh đề đúng.
A.
1;1
a
. B.
1;5
a
. C.
3;6
a
. D.
3;1
a
.
Hướng dẫn giải.
Chọn D.
Giả sử phương trình có nghiệm thực là
x
b
,
khi đó ta có
2
1 1 0
i b m i b
2
2
1
0b mb b b i
2
2
1
0
0
b
mb
b b
1
2
b
m
,
suy ra
2m
thì
phương trình
2
1
1 0
i
x m i x
k
hông có nghiệm thực.
Câu 7. (THPT chuyên Quang Trung – Bình Phước) Cho hai số phức
1
z
,
2
z
khác thỏa
0
,
1
2
0
z
z
và
1
2 1 2
1 1 2
z z z z
.
Tính giá trị biểu thức
1
2
z
z
.
A.
2
2
. B
.
3
2
. C.
2
3
. D.
2
3
.
H
ướng dẫn giải.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 5
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
C
họn A.
Theo đề, ta có
1
2 1 2
1
1 2
z z z z
1 2 1 2 1 2
2z
z z z z z
2
2
1 1 2 2
2
2 0z z z z
1
2
1
1
2 2
z
i
z
1
2
2
2
z
z
.
C
âu 8. (THPT chuyên Nguyễn Quang Diêu – Đồng Tháp – L2) Gọi
M
là
điểm biểu diễn số phức
2
1z
z
w
z
,
trong đó
z
là
số phức thỏa mãn
1
2 2 3i z i i z
.
Gọi
N
l
à điểm trong mặt phẳn
g
sao
cho
,
2Ox ON
,
trong đó
,Ox
OM
l
à góc tạo thành khi quay tia
Ox
tứi
vị trí của tia
OM
.
Đ
iểm
N
nằm ở góc phầ tư nào?
A. G
óc phần tư thứ nhất. B. Góc phần tư thứ tư.
C. góc phần
tư thứ ba.
D. G
óc phần tư thứ hai.
Hướng dẫn giải.
Chọn B.
Theo đề, ta có
1
2 2 3i z i i z
3
6
5 5
z i
11
56
15 45
w i
,
suy ra
56
tan
3
3
,
ta có
2
2
2
56
1089 3696
sin2 2sin .cos 2tan .cos 2. .
33 4225 4225
2 1089 2047
cos2 2cos 1 .2. 1
4225 4225
tan 1
.
C
âu 9. (THPT Thanh Chương 1 – Nghệ An – L2) Cho số phức
1
z
thỏa
2
2
2
1z z i
và
số phức
2
z
thỏa
4
5z i
. Tìm
giá trị nhỏ nhất của
1
2
z
z
?
A.
2
5
5
. B
.
5
. C.
2
5
. D.
3
5
5
.
H
ướng dẫn giải.
Chọn D.
Đặt
1
z a bi
,
2
z c di
(
,
, ,a b c d
)
.
Ta có số phức
1
z
t
hỏa
2
2
2
1z z i
su
y ra
2
2
2 2
2 1 1a b a b
2
1a b
,
suy ra tập hợp
điểm biểu diễn số phức
1
z
nằm
trên đường thẳng
2
1x y
.
Lại
có số phức
2
z
thỏa
4
5z i
suy
ra
2
2
4
1 5c b
,
suy ra tập hợp điểm biểu diễn số phức
2
z
nằm
trên đường tròn
C
có
tâm
4;1I
,
bán kính
5r
.
B
iểu diễn
C
và
lên
mặt phẳng tọa độ, ta suy ra
1
2
;
min
3 5
5
I
z
z d r
.
C
âu 10. (THPT chuyên Biên Hòa – Hà Nam) Cho ba số phức
1
z
,
2
z
,
3
z
thảo
mãn điều kiện
1
2 3
1z z z
v
à
1 2 3
0z
z z
.
Tính
2
2 2
1 2 3
A
z z z
.
A.
1
. B.
0
. C.
1
. D.
1 i
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 6
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
H
ướng dẫn giải.
Chọn B.
2
2
2 2
1
2 3 1 2 3 1 2 2 3 3 1 1 2 2 3 3 1
2 2
A z z z z z z z z z z z z z z z z z z
2 2 2
1 2 3
1
2 3 1 2 3 1 2 3 1 2 3
1
2 3 1 2 3
1
1 1
2 2 2
z z z
z
z z z z z z z z z z z
z
z z z z z
Mà
1
2 3 1 2 3
0
0
z
z z z z z
.
Vậy
0A
.
Câu
11. (THPT chuyên Lê Hồng Phong – TP.HCM) Cho
1
2
,z
z
là
hai số phức khác
0
thỏa
2
2
1 1 2 2
2
2 0
z
z z z
.
Biết
1
2
,z
z
có
điểm biểu diễn lần lượt là
M
,
N
.
Tính góc
OM
N
A
.
o
30
. B
.
o
45
. C.
o
60
. D.
o
90
.
H
ướng dẫn giải.
Chọn B.
1
2
2
2
1 1 2 2
1
2
1
2
2 0
1
z
i z
z
z z z
z
i z
.
Vì hai trường hợp này là như nhau nên tối chỉ trình bày một
trường hợp như sau.
Với
1
2
1
z
i z
,
đặt
1
z
a bi
,
2
z
c di
(với
,
, ,a b c d
) v
à
1
z
,
2
z
lần
lượt có điểm biểu diễn là
;M
a b
,
c;N
d
.
Khi đó
1
1
2
2 2 2 2
2
1
1 1
z
a
c bd bc ad
z
i z i i i
z
c d c d
2
2
2
2
1
ac bd
ac bd z
c d
,
mà
1
1
2
2
1
2
z
i
z z
z
.
Ta có
;O
M a b
,
;
NM
a c b d
.
2
2
2 2 2 2 2 2
c
os cos ,
. 2
a b ac bd
OMN OM NM
a
b a b c d ac bd
2
2 2
1 2 2
2 2
2 2
1 1 2
1
2
2
z
z z
z z
z z z
, suy ra
o
45O
MN
.
Câu 12. (Đề minh họa – L3) Xét các số phức
z
thỏa
mãn
2
4 7 6 2
z
i z i
.
Gọi
m
,
M
lần
lượt
là giá trị nhỏ nhất, giá trị lớn nhất của
1
z i
. T
ính
P
m M
.
A.
1
3 73
P
. B
.
5
2 2 73
2
P
. C
.
5
2 73
P
. D.
5
2 73
2
P
.
H
ướng dẫn giải.
Chọn B.
Cách 1. Đại số.
Đặt
z
a bi
,
với
,a
b
.
Khi đó ta có
2 4 7 6 2
z i z i
2
2 2 2
2
1 4 7 6 2
a
b a b
, xét các điểm
;N
a b
,
2;
1
A
,
4;
7
B
, khi đó ta
được
6
2NA NB AB
,
suy ra
N
,
A
,
B
t
hẳng hàng (
N
nằm
giữa
A
và
B
).
Phương trình
đường thẳng
:
3 0AB x y
, suy ra
;
3
N
a a
(
2
4a
).
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 7
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
T
heo đề
2
2
1
1 1z i a b
2
2
1
4a a
2
2 6 17a a f a
.
/
2
2
3
6 17
a
f a
a a
;
/
3
0
2
f a a
.
Ta có bảng biến
thiên như hình bên.
Dựa vào bảng biến thiên ta suy ra
5
2
2
m
,
73M
.
Vậy
5
2 2 73
2
P
.
Cá
ch 2. Bất đẳng thức.
Đặt
z
a bi
,
với
,a b
.
Khi đó ta có
2
4 7 6 2z i z i
2
2 2 2
2
1 4 7 6 2a b a b
1
,
áp dụng bất đẳng thức Mincopxki ta có
2
2
1 2 4 1 7 6 2VT a a b b
,
dấu
"
"
xảy
ra
2
7 4 1
3
2;4 , 1;7
2;4 , 1;7
a b a b
b a
a b
a b
.
Theo đề
2
2
1
1 1z i a b
2
2
1
4a a
2
2
6 17a a f a
.
/
2
2
3
6 17
a
f a
a a
;
/
3
0
2
f
a a
. Ta có bảng biến
thiên như hình bên.
Dựa vào bảng biến thiên ta suy ra
5
2
2
m
,
7
3M
. Vậy
5
2 2 73
2
P
.
Cách 3. Hình học.
Đặt
z
a bi
,
với
,a
b
.
Khi đó ta có
2
4 7 6 2z i z i
2
2 2 2
2 1 4 7 6 2a b a b
,
xét các điểm
;N
a b
,
2;
1A
,
4;
7B
,
khi đó ta
được
6
2NA NB AB
, suy ra
N
,
A
,
B
thẳng hàng (
N
nằm giữa
A
và
B
). Phương trình
đường thẳng
:
3 0AB x y
.
T
heo đề
2
2
1
1 1z i a b
, xét điểm
1
; 1I
suy ra
2
2
1
1IN a b
,
khi đó
;
;
mi
n ; ;d ; ;d
I
AB I AB
IA
IB IN Max IA IB
min
;
max
5
2
d
2
73
I
AB
m
IN
M IN IB
.
Vậy
5
2 2 73
2
P m M
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 8
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
Câu
13. (THPT Thị xã Quảng Trị) Cho số phức
z a bi
(
,a
b
)
thỏa mãn
z
kh
ông là số thực và
2
2
1
1
z
z
z
z
l
à số thựC. Tính
4
4
6 6
1
1
a
b
M
a
b
.
A.
1
2
. B.
2
3
. C.
4
3
. D.
1
3
.
Hướng dẫn giải.
Chọn B.
z
a bi
,
với
,a
b
.
Vì
z
k
hông là số thực nên
0b
.
T
a có
2
2
2
2
2 2
1
2
1
1
1 2
a
b a ab b i
z
z
w
z z
a b a ab b i
,
suy ra phần ảo của số phức
w
là
2
3
2
2
2
2
2
2 2
1 2
b a b b
a
b a ab b
,
mà
2
2
1
1
z
z
z
z
là
số thực suy ra
4
4
2
2 2 2
1
1
2
a
b
a
b a b
,
ta có
4
4 4 4 4 4
6 6
2 2 4 4 2 2
4 4
1
1 1 2
3
3
1
1
1
2
a
b a b a b
M
a b
a b a b a b
a b
.
Câu
14. (Thầy Trần Trọng Trị - THPT Gia Định – TP.HCM) Cho hai số phức
1
z
,
2
z
thỏa
mãn điều kiện
1
1 1
2
2z i z z i
và
2
1
0 1
z
i
. Tì
m giá trị nhỏ nhất của
1
2
z
z
?
A.
3 5 1
. B
.
101 1
. C.
101 1
. D.
10 1
.
H
ướng dẫn giải.
Chọn A.
Cách 1.
T
a có
1
1 1
2
2z i z z i
suy
ra tập hợp điểm biểu diễn số phức
1
z
nằm
trên parabol
2
:
4
x
P
y
.
Và
2
1
0 1
z
i
su
y ra tập hợp điểm biểu diễn số phức
2
z
nằm
trên đường tròn
2
2
:
10 1 1
C
x y
.
Xét đường tròn
2
2
:
10 1
x
y k
với
0;k
tiếp
xúc vớ
i
P
. Giải
điều kiện tiếp xúc
và
P
T
a có
2
2
10 1
x y k
2
2
2
2
10
'
1
10 10
10
1
10
'
10
x
y
y k x k x
x
y k x
y
k x
.
và
P
tiếp xúc nhau khi hệ phương trình sau có nghiệm
TH1:
2
2
2
2
1
10
4
10
0
4 45
10
2
1
2
4
10
x
k x
x
x
x k
x
x
x
k x
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 9
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
TH
2:
2
2
2
2
1 10
4
10
0 4 45
10
2
1
2
4
10
x
k x
x
x
x k
x
x
x
k x
.
Ta
suy ra
45k
. Vậy
1
2
M
in 3 5 1
z
z
.
Cá
ch 2.
T
a có
1
1 1
2 2z i z z i
suy
ra tập hợp điểm biểu diễn số phức
1
z
nằm
trên parabol
2
:
4
x
P
y
.
Và
2
1
0 1z i
su
y ra tập hợp điểm biểu diễn số phức
2
z
nằm
trên đường tròn
2
2
:
10 1 1C x y
.
Đường tròn
C
có
tâm là
1
0; 1I
bán k
ính
1R
.
X
ét điểm
2
;
4
a
A
a P
,
khi đó
4
2
2
20
101
16 2
a a
IA f a a
;
3
/
2
0
4
a
f a a
;
/
0 4f a a
, lập
BBT suy ra
Min 45f a
su
y ra
M
in 3 5IA
.
Vậy
1 2
M
in 3 5 1
z
z
.
Câu 15. Cho số phức
z
thỏa
2 2 6z z
. Tìm giá trị nhỏ nhất của biểu thức
3
3P
z z
A.
3
. B.
2
. C.
1
. D.
4
.
H
ướng dẫn giải.
Chọn A.
Đặt
z x yi
,
với
,a b
.
Khi đó ta có
2
2
2 2
2 2 6 2 2 6z z x y x y
.
Xét
điểm
1
2;
0F
,
2
2
; 0F
v
à
;M
x y
,
suy ra ta có biểu thức
1
2
6
2.3MF MF
, su
y ra tập hợp điểm biểu diễn số phức
z
nằm
trên đường elip có phương trình
2
2
1
9
5
y
x
(với
3
, 5, 2a b c
). Tọa độ các đỉnh trên trục lớn là
1
3; 0A
,
2
3; 0A
, các đỉnh nằm trên trục bé là
1
0
; 5B
,
2
0
; 5B
.
T
a có
2
2
1
3
3z x y MA
,
z
MO
(
O
l
à gốc tọa độ). Suy ra
3
1
P
MA MO
.
Lại có
1
1
1 2
M
in
Max
MA M A
MO M A hay M A
1
1
2
M
in 0
Max 3
MA
MO OA OA
.
Vậy
m
in
3P
.
C
âu 16. (THPT chuyên Hưng Yên –L3) Cho số phức z thoả mãn
3
4 5z i
.
Gọi M và m lần lượt là
gia trị lớn nhất và giá trị nhỏ nhất của biểu thức
2 2
2P
z z i
.
Tính modun của số phức
w M mi
A.
2
314w
. B
.
2
309w
. C.
1258w
. D.
3
137w
.
H
ướng dẫn giải
Chọn C.
Đặt
z
x yi
. Ta có
2 2
2 2
2
1 4 2 3P x y x y x y
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 10
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
Mặt
khác
2
2
3
4 5 3 4 5
z
i x y
,
đặt
3
5 sin ; 4 5 cosx t y t
.
Suy
ra
4
5 sin 2 5 cos 23
P
t t
,
ta có
10
4 5 sin 2 5 cos 10
t
t
.
D
o đó
1
3 33 1258
P
w
.
Câu
17. (THPT chuyên Hưng Yên –L3) Cho số phức w, biết rằng
1
2z
w i
và
2
2
4
z
w
là hai nghiệm
của phương trình
2
0z
az b
với
a,b là các số thựC. Tính
1 2
T
z z
.
A
.
8 10
3
T
. B
.
2 3
3
T
. C.
5T
. D.
2 37
3
T
.
H
ướng dẫn giải
Chọn A.
Đặt
w
x yi
.
Theo Viet ta có:
1
2
3 2 4 3 4 3 2z z a w i x y i
là
số thực nên
2
3
y
.
Lại
có
1
2
2
4
2
2 4
3 3
z z b x i i x i
l
à số thực.
Suy ra
4
4 4 16
2
4 2 4 4
3 3 3 9
x
i x i x x i x
l
à số thực suy ra
4x
D
o đó
1
2
4
4
2 4
3
3
z i i i
,
2
4
8 10
4
3 3
z
i T
.
Câu
18. (THPT Thái Nguyên – L2) Tập hợp các số phức
1
1w i z
với
z
l
à số phức thỏa
mãn
1
1
z
l
à hình tròn. Tính diện tích hình tròn đó.
A.
4
. B
.
2
. C.
3
. D.
.
H
ướng dẫn giải
Chọn B
Đặt
w x yi
, với
,x y
thì
1
1 1 1 2 2 1 1
w
i z w i z i w i z i z
2
2 2
2
1 1 2 1 2 1 2
w
i z i z x y z
, suy ra tập hợp số phức cần tìm nằm
trên hình tròn bán kính
2R
có tính biên.
2
2S
R
.
Câu
19. (THPT Thái Nguyên – L2) Cho số phức
z
có
môđun là
3
,
biết tập hợp các điểm biểu diễn số
phức
3
2 2
w
i i z
là một đường tròn thì có bán kính là?
A.
3
2
. B
.
3
5
. C.
3
3
. D.
3
7
.
H
ướng dẫn giải
Chọn B
Đặt
w x yi
, với
,x y
thì
3
2
3
2 2
2
x
yi i
x
yi i i z z
i
2
1 2 8
2
2 6 4 3 2
5
5
i
x y x y
x yi i xi y i
z z
2 2
2 2
3 2 1 2 8 25.9 5 5 30 20 65 29.5
z x y x y x y x y
2
2
2 2
6
4 13 45 3 2 45 3 5
x
y x y x y R
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 11
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
Câu
20. (THPT Thái Nguyên – L2) Cho số phức
z
a bi
,
với
,a
b
thỏa
mãn
1
1
1
z iz
i
z
z
.
Tính
2
2
a
b
?
A.
3
2 2
. B
.
2
2 2
. C.
3
2 2
. D.
4
.
H
ướng dẫn giải
Chọn A
Điều kiện
0
1
z
z
.
Khi
đó
1
1
1
z iz
i
z
z
1
1z iz z i
2
1z
i z z i
2
1
z
z z i
2
2
1
1
z z z
z z z
2
2
1 0
z
z z
1
2
z
2
3
2 2
z
.
Câu
21. (THPT chuyên KHTN – Hà Nội – L5) Cho
1
2
,z
z
là 2 số phức bất kỳ, giá trị biểu thức:
2 2
1 2
2
2
1
2 1 2
z
z
a
z
z z z
bằn
g?
A.
2a
. B
.
1
2
a
. C.
1a
. D.
3
2
a
.
H
ướng dẫn giải
Chọn B
Cách 1.
Đặt
1
z
a bi
,
2
z
c di
, với
, , ,a b c d
. Khi đó
2
2
2 2 2 2
1 2
2 2 2 2 2 2
1 2 1 2
1
2
a
b c d
z z
a
z z z z a c b d a c b d
Cá
ch 2.
N
goài ra ta có thể chọn
2
2
1 2
1 2
2 2 2
2 2
1 2 1 2
1
1 1
1
2
2
0
z z
z z
z z z z
.
Câu
22. Cho số phức
z
t
hỏa
2
2 17
z
i
.
Gọi
M
,
m
lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất
của
1999 2 2017 6 3P z i z i
.
Tính
M m
.
A
.
8
302 17M m
. B.
4
034 17M m
.
C.
2
2
1
7 1999 2017 1999
M
m
. D.
2
2
2
17 1999 2017 1999
M
m
.
H
ướng dẫn giải
Chọn D
Cách 1.
2
2 17
z
i
suy
ra tập hợp số phức
z
nằm
trên đường tròn tâm
2;2
I
bá
n kính
17
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 12
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
X
ét các điểm
2;
1
A
,
6;
3
B
,
;C
x y
.
Khi đó
1
999 2017P CA CB
.
Ta có
A
B
là
đường kính củ
a
đườn
g tròn tâm
I
nê
n
2
1999
68 2017P CB CB
.
X
ét hàm số
2
1
999 68 2017f x x x
với
0
;2 17
x
su
y ra
min
1
999.2 17
P
,
2
2
ma
x
2
17 1999 2017
P
. Vậy
2
2
2
17 1999 2017 1999
M
m
.
Cá
ch 2.
2
2
2
2 17 4 4 9
z
i a b a b
2
2 2 2
1999 2 2017 6 3 1999 4 2 5 2017 12 6 45
P z i z i a b a b a b a b
2
2
19
99 8 2 14 2017 8 2 54 2 17 1999 2017
P
a b a b
Suy ra
2 2
ma
x
2
17 1999 2017
P
.
m
in
1
999.2 17
P
(sử dụng xét hàm)
Vậy
2
2
2
17 1999 2017 1999
M
m
.
C
hú ý: ở cách hai ta có có thể xét hàm số
1
999 14 2017 54
f
t t t
(
với
8
2t a b
v
à
14
54t
)
.
Câu 23. (THPT Chu Văn An – Hà Nội – L2) Cho sô phưc z thoa man điêu kiên
1 2
z
.
Tim gia tri
lơn nhât cua
2
T
z i z i
A.
m
ax 8 2T
. B
.
max 4T
. C.
m
ax 4 2T
. D.
max 8T
.
H
ướng dẫn giải
Chọn B
Đặt
z x yi
. Ta co:
2
2
1
2 1 2 1 2
z
x yi x y
Khi đo:
2
2 2
2
1
2 2 1 2 1
T
z z i x yi i x yi i x y x y
2
2 2
2
2 2
1
1 . 1 2 1
x
y x y
2
2
2 2
2
2 4 4 2 2 2 2. 1 4 2. 4 4 4
x
x y x y
Vâ
y
m
ax 4T
.
Câu
24. (THPT Quốc Học – Huế - L2) Cho số phức
0z
sao
cho
z
kh
ông phải là số thực và
2
1
z
w
z
là
số thựC. Tính
2
.
1
z
z
A.
1
.
5
B.
1
.
2
C.
2.
D.
1
.
3
H
ướng dẫn giải
Chọn B
Cách 1.
T
heo giả thiết ta có
2
1
z
w
z
là
số thực nên ta có thể chọn
w
là
số thực bất kỳ sao cho
z
kh
ông
phải là số thực.
Một s
ố câu hỏi số phức khó trong các đề thi thử 2017
Trang 1
3
Sưu tầm và biên soạn:
Lê Hồng
Quốc ĐT: 0898.244.454
Chọn
2
2 2
1 3 1
1 1 1 .
2 2
1
1
z
z i
w z z
z z
z
z
Cách 2
.
Ta
có
2
1
z
w
z
là số
thực suy ra
2
1 1 1
z
z
w z z
là s
ố thực suy ra
1
z
là
số phức liên hợp của
z
suy r
a
2
2
1 1 1
.
. 1 1 .
1 1 2
1
z
z z z
z z
z
z
Câu 25. (Chuyên ĐH Vinh – Nghệ An – L3) Cho sô phưc
z
thay đôi, luôn co
2
z
. Khi đo tâp hơp
điêm biêu diên sô phưc
1 2 3w
i z i
la:
A. Đươ
ng tron
2
2
3 2 5
x y
. B. Đương
tron
2
2
3 20
x y
.
C. Đương
tron
2
2
3 20
x y
. D. Đương
tron
2
2
3 2 5
x y
.
Hướ
ng dẫn giải
Chọn B
Gia sư
, 1 2
3w a bi a b a bi i z i
3 1 2
3 2 3
2 3
1 2 5 5
a b i
i
a b i a
b a b i
z
i
2
2 2 2
1
2 3 2
3 2 2 6 2 3 100
5
z z a
b a b a b a b
2 2
2 2 12
2 6 2 55
a b a
b a b a b
2
2 2 2 2 2
5 5 30
55 6 11 3 20
a b b
a b b a b
.
Câu 26
. (THPT chuyên Vị Thanh – Hậu Giang) Biết số phức
z
thỏa mãn
phương trình
1
1.
z
z
Tính
2016
2016
1
.
P z
z
A.
0
. B.
1
. C.
2
. D.
3
.
Hướ
ng dẫn giải
Chọn C
Ta có
1
1
z
z
3
3
3
1 1 1
1 3 1
z z z
z z
z
3
3
1
2 0
z
z
2
3
1 0
z
3
1z
672
3
672
3
1
1 1 2.
P z
z
Câu 27
. (THPT Kim Liên – Hà Nội) Cho hai số thực
b
và
c
0 .
c
Ký
hiệu
A
,
B
là
hai điểm của mặt
phẳng phức biểu diễn hai nghiệm của phương trình
2
2 z 0
.z b c
Tìm
điều kiện của
b
và
c
sao cho
OAB
là tam giác vuông (
O
là gốc tọa độ).
A.
2
2 .b c
B.
2
2 .c b
C.
.b c
D.
2
.b c
Hướ
ng dẫn giải
Chọn B
Theo yêu cầu bài toán suy ra phương trình không có nghiệm thực.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 14
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
T
a có:
2
2
2 2 2
1
2
2
2
z 0
z b i c b
z
b c z b b c c b
z
b i c b
.
Khi đó
2
;
A
b c b
,
2
;
B
b c b
,
suy ra
2
;
O
A b c b
,
2
;
O
B b c b
.
Ta có
,A
B
là
hai điểm đối xứng nhua
qua trục
Oy
. Suy
ra tam giác
OAB
vu
ông tại
O
.
T
heo giả thiết ta có:
2
2 2
0 2 .b b c c b
Câu 28
. (Chuyên Ngữ – Hà Nội) Trên mặt phẳng tọa độ
O
xy
,
tìm tập hợp các điểm biểu diễn các số
phức
z
thỏa
mãn điều kiện số phức
w
2 3 5z i i
là
số thuần ảo.
A. Đ
ường tròn
2
2
5
.
x
y
B. Đườn
g thẳng
2
3 5 0.x y
C. Đườn
g tròn
2
2
3
2 5.
x
y
D. Đường
thẳng
3
2 1 0.x y
H
ướng dẫn giải
Chọn B
Đặt
z
x yi
, với
,x
y
2 3 5 2 3 5 3 2 1w x yi i i x y x y i
.
W là số thuần ảo khi và chỉ khi
2
3 5 0
2
3 5 0
3
2 1 0
x y
x y
x y
Tập
hợp các điểm biểu diễn số
phức z là đường thẳng
2
3 5 0.x y
Câu
29. (Chuyên Ngữ – Hà Nội) Cho số phức z thỏa mãn
1
.
z
T
ìm giá trị lớn nhất của biểu thức
1
2 1
T
z z
.
A.
a
x 2 5.
M
T
B
.
a
x 2 10.
M
T
C.
a
x 3 5.
M
T
D.
a
x 3 2.M T
Hướng dẫn giải
Chọn A
Cách 1.
2
2 2
2
1
2 1 1 2 1 1 5.2 1 2 5
T
z z z z z
(
BĐT Bunhiacopxki)
Chú ý:
2
2 2
2 2
1
1 2 2 2 2 1
z
z x y z
với
z x yi
,
,x y
.
Cá
ch 2.
Đặt
z
x yi
, với
,x
y
ta
có:
2
2
2
2
1 2 1 1 2 1
T x yi x yi x y x y
Lại
có
2
2
1
2 2 2 2 2
x
y T x x f x
Ta có
ma
x
1
2 6
'
0 2 5
10
2 2 2 2
f x x T
x x
.
Câu 30. (Sở GD – Đồng Tháp) Trong các số phức
z
t
hỏa mãn điều kiện
|
1 2 | | |z i z i
,
tìm số phức
có mô-đun nhỏ nhất.
A
.
1
3
5 5
z i
. B
.
3
1
5 5
z i
. C
.
2
16
5 5
z i
. D.
1
6 2
5 5
z i
.
H
ướng dẫn giải
Chọn A
Gọi
z a bi
,
,
a
b R
. T
a có
1 2 1 2
z i z i a b i a b i i
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 15
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
2
2 2
2 2 2 2 2
1
2 1 2 1 4 4 2 1a b a b a a b b a b b
2
6 4 3 2a b a b
D
o đó
2
2
2
2 2 2
3
2 10
3
2 10 12 4 10
5
5 5
z
a b b b b b b
.
Dấu
"
"
xảy
ra
3 1
5 5
b
a
. Vậy
1 3
.
5 5
z i
Câu 31. (THPT Nguyễn Bỉnh Khiêm) Cho số phức z thỏa mãn
1 2w z z i
là một số thuần ảo.
Tập
hợp điểm biểu diễn số phức
z
là
một đường tròn có diện tích bằng bao nhiêu?
A.
5
.
B.
5
.
4
C.
5
.
2
D.
25
.
H
ướng dẫn giải
Chọn B
Đặt
z
a bi
, với
,a
b
2
2
1
2 2 2 2w a bi a bi i a b a b a b i
.
w
là số thuần ảo suy ra
2
2
2
2
2 2
2
0
1 5
2 0 1 .
2 4
2a
2 0
a b a b
a b a b a b
b
Suy
ra tập hợp điểm biểu diễn số phức
z
là
một đường tròn có diện tích bằng
5
.
4
Câu 32. (THPT Nguyễn Bỉnh Khiêm) Cho số phức
,
.
z
x yi x y
Khi đó phần thực
a
và phần
ảo
b
của
số phức
2
z
i
iz
l
à:
A.
2
2
2 2
2 2
2
1
2
,
.
2 2
x y
y y x
a b
y x y x
B.
2
2
2 2
2 2
2
1
2
,
.
2 2
x y
y y x
a b
y x y x
C.
2 2
2 2
2 2
2
1
2
, .
2 2
x y
y y x
a b
y x y x
D.
2 2
2 2
2 2
2
1
2
, .
2 2
x y
y y x
a b
y x y x
H
ướng dẫn giải
Chọn B
Ta có:
2
2
2
2
2
x 2
2
2
2
2 2
2
x y i y y x
x yi i xi y
x yi i x yi i
xi y
i x yi xi y xi y
x y
2
2
2 2
2 2
2 2
2 2
2
2
2
1
2 1
2
2
2
2
2
2
x
y
a
x y
y
x
y
y x
i
y y x
y x x y
b
x y
.
Câu
31. (THPT Lam Sơn – Thanh Hóa) Cho số phức
z
,
tìm giá trị lớn nhất của
z
b
iết
z
thỏa
mãn điều
kiện
2
3
1
1.
3
2
i
z
i
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 16
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
A.
3
. B
.
2
. C.
1
. D.
2.
H
ướng dẫn giải
Chọn B
Tổng quát: Cho số phức
z
t
hỏa mãn
z
a bi R
tìm
modun lớn nhất và nhỏ nhất của số phức
.z
Đ
iểm biểu diễn số phức
z
l
à đường tròn
2
2
2
.x
a y b R
Khi đ
ó:
2
2
max
z OI R a b R
,
2
2
min
z OI R a b R
.
Áp dụng: Ta có:
2
2
2
3
1
1 1 1 1 1.
3
2
z
x yi
i
z
iz y x
i

Khi đ
ó:
max
1
1 2.
z
OI R
Câu
32. (THPT Thanh Chương –Nghệ An – L1) Cho
1
2
,z
z
l
à hai số phức thỏa mãn phương trình
2
2 ,z i iz
biết
1 2
1
.
z
z
Tính giá trị của biểu thức
1 2
.P
z z
A
.
3
.
2
P
B
.
2
.P
C
.
2
.
2
P
D.
3
.
P
Hướng dẫn giải
Chọn D
Cách 1.
T
a có
2
2
z
i iz
2
2
2 2
z i iz
(
2 )(2. ) (2 )(2 . )z i z i iz i z
2 2
4 . 2 2 4 2 2 .z z iz iz i iz iz i z z
5
. 5z z
.
1z z
2
1
1
z
z
1
1
z
và
2
1
.
z
Chú ý:
2
2
.
2 (2 ).(2 ) (2 )(2 ).a a a z i z i z i z i z i
Tập
hợp điểm biểu diễn số phức
1 2
,z
z
là
đường tròn tâm
O
,
1.R
Gọi
1 1 2 2 1 2
,
1.
M
z M z OM OM
T
a có
1
2 1 2 2 1 1 2
1
z z OM OM M M OM M
đều.
Mà
1
2 1 2
z z OM OM OM OM
với
M
là
điểm thỏa mãn
1
2
OM
MM
là
hình thoi cạnh
1
3
3.
O
M P
Cá
ch 2.
Đặt
(
, ),z x yi x y
ta
có
2
2 2( 1)z i x y i
v
à
2
2 .iz y xi
Khi đ
ó
1
2
2 2 2 2 2
2
1
2
2 4 (2 1) ( 2) 1 1
1
z
z
i iz x y y x x y z
z
.
Sử dụn
g công thức
2
2
2 2 2
1 2 1 2 1 2 1 2 1 2
2
3 3.
z
z z z z z z z z z
Câu
33. (Sở GD Phú Thọ) Cho hai số phức
1
z
v
à
2
z
thỏa
mãn
1
3
z
,
2
4
z
,
1
2
37
z
z
.
Xét số
phức
1
2
z
z
a bi
z
.
Tìm
b
.
A
.
3
3
8
b
. B
.
3
9
8
b
. C
.
3
8
b
. D.
3
8
b
.
H
ướng dẫn giải
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 17
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
Chọn
A.
Đặt
1
z x yi
,
2
z c di
, , ,x y c d
.
Ta có:
2
2
1
3 9
z x y
;
2
2
2
4 16
z c d
;
2
2
2 2 2 2
1 2
37
37 2 2 37 6
z
z x c y d x y c d xc yd xc yd
.
Lại
có:
1
2
2 2 2 2 2 2 2
2
x
yi c di xc yd yc xd i
z
x yi xc yd yc xd
i
a bi
z
c di
c d c d c d c d
3
8
b
i
.
Mà
2
1
2 2 2 2 2
1
2
2
3
9 9 3 27 3 3
4 16 16 8 64 8
z
z
a
b a b b b
z
z
.
Vậy
3 3
8
b
.
Câu 34. (Chuyên ĐH Vinh – Nghệ An – L4) Cho số phức
z
thỏa
mãn
z
kh
ông phải số thực và
2
2
z
w
z
l
à số thựC. Giá trị lớn nhất của biểu thức
1
P
z i
l
à
A.
2
2
. B.
2
. C.
2
. D.
8
.
Hướng dẫn giải
Chọn A.
Cách 1.
2
2
z
w
z
là
số thực
w
w
2
2
2
2
2
. 2
2
2
z
z
z
z z z zz
z z
2
.z z z z z z
z
z
(loại
do
z
khô
ng là số thực) hoặc
2
. 2
z
z z
.
Suy
ra:
2OM
với
M
là
điểm biểu diễn của
z
,
M
thuộc
đường tròn
C
tâm
O
,
2R
Ta có:
1
P
z i MA
, với
1
;1
A
. Ta có:
A
C
nên
M
A
lớn nhất bằng
2
2 2R
.
Cách 2.
Vì
z
k
hông là số thực nên
0z
. Suy
ra
0w
.
T
a có
2
2
2
1
2
2 0 *
2
z
w
w z z z z
w
z
.
*
là
phương trình bậc hai với hệ số thực
1
w
nê
n có nghiệm
2
phức
1
z
,
2
z
li
ên hợp của nhau.
Theo Viet ta có:
1
2 1 2 1 2 1 1
.
2 . 2 2 2 2
z
z z z z z z z z
.
Suy ra
1
1 2 2 2 2
P
z i z i
.
Cá
ch 3.
T
a có
2
1
2
2
z
w
z
w
z
z
,
mà
w
s
uy ra
1
w
,
suy ra
2
z
l
à số phức liên hợp của
z
.
Suy
ra
.
2 2
z
z z
.
Ta có
1
1 2 2 2 2
P
z i z i
.
Câu
35. (Chuyên ĐH Vinh – Nghệ An – L4) Cho hai số phức
1
z
v
à
2
z
thỏa
mãn
1
2 1 2
1
z
z z z
.
Tính
1
2
z z
A.
3
. B.
1
. C.
2
3.
D.
3
2
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 18
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
H
ướng dẫn giải
Chọn A
Cách 1.
Ta
có
2 2 2 2
1
2 1 2 1 2
2z
z z z z z
.
Khi đó
2
1
2 1 2
2
1 1 1 3 3
z
z z z
.
Cá
ch 2.
C
họn
1
1
z
từ đ
ó suy ra
2
z
từ hệ
2
2
1
1
1
z
z
. Tha
y vào
1
2
z
z
ta
cũng được kết quả
1
2
3
z
z
.
Câu
36. (THPT Chuyên Võ Nguyên Giáp – Quảng Bình) Gọi
H
là
hình biểu diễn tập hợp các số
phức
z
t
rong mặt phẳng tọa đọ
O
xy
để
2
3
z
z
số phức
z
có
phần thực không âm. Tính
diện tích hình
H
.
A.
3
. B
.
3
2
. C.
3
4
. D.
6
.
H
ướng dẫn giải
Chọn B
Đặt
0
z
x yi x
,
,a
b
2
2
2
3 3 3 9 9
z
z x yi x y
.
2
2
1
9
1
y
x
. D
o hình
H
l
à nửa hình Elip có
3, 1a b
.
Khi đó
1
1 3
.
2 2 2
el
ip
S
S ab
.
Câu
37. (THPT Hoằng Hóa 4 – Thanh Hóa) Cho số phức
z
thỏa
điều kiện
1
z
z i
.
Tìm số phức
2
3w z i
có
môđun nhỏ nhất.
A
.
1
3
2 2
i
. B
.
1
1
2 2
i
. C
.
1
1
2 2
i
. D.
1
3
2 2
i
.
H
ướng dẫn giải
Chọn B.
Cách 1. Đại số
Đặt
z a bi
với
,
ba
.
T
a có
1
1 1 1z z i a bi a bi i a bi a b i
2
2
2 2
1 1 0
a b a b a b
Khi đó
2
3 3 2 3 2w a bi i a b i a a i
2
2
2 2
2 2
2
5 1 5 1 1
3
2 2 10 13 2 5 2
4
2 2 2 2
w
a a a a a a a
min
2
2
w
k
hi
5
5 5 5 1 1
2 2 2 2 2 2
a b z i w i
.
Cá
ch 2. Hình học
Đặt
z
a bi
với
,
ba
.
T
a có
1
1 1 1z z i a bi a bi i a bi a b i
2
2
2 2
1 1 0
a b a b a b
,
suy ra tập hợp các số phức
z
nằm
trên đường thẳng
: y
x
. Xét điểm
3
; 2
I
. Ta có
2
3 2 3
w
z i w z i IM
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tran
g 19
Sưu tầm và biên soạn:
Lê Hồng
Quốc ĐT: 0898.244.454
Ta
có
min
IM
khi
M
là
hình chiếu vuông góc của
I
trên
,
;M m m
suy
ra
2;
3IM m m
,
5
. 0 2 3 0
2
IM u m m m
. V
ậy
1 1
2 2
w i
là
số phức có môđun nhỏ nhất.
Câu 38. (THPT Đống Đa – Hà Nội) Cho số phức
z
thỏa mã
n
2
2 2 1z z z i
. Bi
ểu thức
z
có giá
trị lớn nhất là
A.
2 1
. B.
2
. C.
2 2
. D.
2 1
.
Hư
ớng dẫn giải.
Chọn A.
Cách 1: Đại số.
2
2 2
1z z z i
2
2
1 1z
i z i
1 1 1z i z i z i
1 0
1
1 1 2
z i
z i
.
+)
1 1 2z
i z
3
.
+)
Đặt
z a
bi
, v
ới
,a b
.
Khi đó ta có
2 1
1 1a b i
2 2
1 1 1a b
2 2
2 2
1a b a b
, theo
bất đẳng thức Bunhiacopxki ta có:
2 2
2 2
1 8 1a b a b
2
2 2
1 0z z
2 1
2 1z
4
.
Từ
3
,
4
suy ra
max
2 1z
.
Các
h 2: Hình học.
2
2 2
1z z z i
2
2
1 1z
i z i
1 1
1z i z i z i
1 0
1
1 1 2
z i
z i
.
+)
1 1 2z
i z
3
.
+) Đ
ặt
z a bi
,
với
,a b
.
Khi đó ta có
2 1
1 1a b i
2 2
1 1
1a b
, suy ra tập hợp
các số phức cần tìm nằm trên đường tròn tâm
1;
1I
, b
án kính
1R
. Suy ra
OI
R z OI R
2 1
2 1z
. Vậy
max
2 1z
.
Câu 39. (Sở GD Bắc Giang – L1) Cho số phức z thay đổi và luôn thỏa mãn
3 4
4z i
. Tìm
giá trị lớn
nhất
Max
P
của
biểu thức
P z
A.
12
Max
P
. B.
5
Max
P
. C.
9
Max
P
. D.
3
Max
P
.
Hư
ớng dẫn giải
Chọn C
Cho số phức z thõa mãn
z a bi R
tìm
modun lớn nhất và nhỏ nhất
của số phức
z
. Điểm biểu diễn số phức z là đường tròn:
2 2
2
x a
y b R
Khi đó
2 2
m
ax
z O
I R a b R
,
2 2
m
in
z O
I R a b R
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 20
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
Áp
dụng:
2
2
3
4 4 9
M
ax
P
.
Câu
40 (Sở GD Quảng Ninh) Cho hai số phức
1
2
,z
z
thỏa
mãn
1
2 1 2
1
z
z z z
.
Tính giá trị của
biểu thức
2
2
1
2
2 1
z
z
P
z
z
A.
1P
i
. B
.
1P
i
. C.
1P
. D.
1P
i
.
H
ướng dẫn giải
Chọn C
Cách 1.
Ta có
1
1 2
1 1
2 2
2 2
1
1 1
z
z z
z z
GT
z z
z z
.
Đặt
1
2
z
a bi
z
ta
có:
2
2
2 2
1
1
a
b a b
2
2
3
1
3 1
2
1
2 2
1
2
b
w P w
w
a
.
Cá
ch 2.
Chọn
1
2
1
3 1 3
;
1
2 2 2 2
i
i
z z P
.
Cá
ch 3. Dùng dạng lượng giác của số phức (đọc thêm).
Gọi
1
2 1 2
;
;
A
z B z AB z z OAB
là
tam giác đều cạnh 1
Khi đó
2
2 2
0
0 0
1
1 1 1
1 2 1 2
2 2 2 2
1
2 2 1 120 cos120 sin120
z
r r
i
z r r
Tư
ơng tự
2
0
0
1
2
cos
120 sin 120 1
z
i
P
z
.
Câu
41. (THPT chuyên Hà Giang – L1) Cho sô phưc z thoa man điêu kiên
2
2 1
z
i
.
Tim gia tri lơn
nhât cua
z
A.
max 2 2 1
z
. B
.
max 2 2
z
. C
.
max 2 2 2
z
. D.
max 2 2 1
z
.
H
ướng dẫn giải
Chọn A
Cách 1. Đại số
G
ia sư
z
a bi
,
với
,a
b
.
T
a co:
2
2 1 2 2 1 2 2 1
z
i a bi i a b i
2
2
2
2 1
a
b
.
Đ
ăt
2
sin
2 cos
a t
b t
.
Kh
i đo:
2
2
2
2
2
sin 2 cos
z
a b t t
9
4 sin cost t
2
2
max
9
4 sin cos 9 4 2 2 2 1 2 2 1
t
t z
kh
i
sin
cost t
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 21
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
Ca
ch 2. Hình học
C
ho sô phưc z thoa man
z
a bi R
ti
m mô đun lơn nhât va nho nhât
cua sô phưc
z
.
Điêm biêu diên sô phưc
z
la
đương tron:
2
2
2
x
a y b R
Khi đ
o
2
2
max
z
OI R a b R
,
2
2
min
z
OI R a b R
.
A
p dung:
2
2
max
2
2 1 2 2 1P
.
C
âu 42. (Chuyên KHTN – Hà Nội – L4) Gọi
1
z
,
2
z
là
2 nghiệm của phương trình
2
1 0z z
.
Tính giá
trị
2017
2017
1 2
P
z z
.
A.
1P
. B.
1P
. C.
0P
. D.
2P
.
H
ướng dẫn giải
Chọn B
Vì
1
z
là
nghiệm của phương trình
2
1
0z z
n
ên ta có
2
3 3 2016 2017
1 1 1 1 1 1 1
1 0 1 0 1 1z z z z z z z
C
hứng minh tương tự:
20
17
2 2
z
z
.
Vậy
1 2
1P
z z
.
Câu 43. (Chuyên KHTN – Hà Nội – L4) Với hai số phức
1
z
v
à
2
z
t
hỏa mãn
1
2
8
6z z i
v
à
1 2
2z
z
.
Tìm giá trị lớn nhất của
1
2
P
z z
.
A.
5
3 5P
. B
.
2
26P
. C.
4
6P
. D.
34 3 2P
.
H
ướng dẫn giải
Chọn B
Đặt
1
2
,O
A z OB z
(
với
O
l
à gốc tọa độ,
,A B
là
điểm biểu diễn của
1
2
,z
z
)
.
Dựng hình bình hành
O
ACB
,
khi đó ta có
1
2
2AB z z
,
2 1
1
0OC z z
,
5OM
.
T
heo định lý đường trung tuyến ta có
2
2 2
2 2
2 2 2
1 2
2
52
52
4
OA OB AB
OM OA OB z z
T
a có
2
2
1 2 1 2
2
2 26z z z z
(B
ĐT Bunhiacopxki). Vậy
m
ax
2
26P
.
C
âu 44. (Sở GD Hải Dương) Cho số phức z thỏa mãn
.
1z z
. Tì
m giá trị nhỏ nhất của biểu thức:
3
|
3 | | |P z z z z z
.
A.
1
5
4
. B.
3
4
. C.
1
3
4
. D.
3
.
H
ướng dẫn giải
Chọn B
Gia sư
z
a bi z a bi
, với
,a
b
.
.
1z z
suy ra
2
2
1b a
.
Một
số câu hỏi số phức khó trong các đề thi thử 2017
Tra
ng 22
Sưu tầm và biên soạn:
Lê Hồn
g Quốc ĐT: 0898.244.454
3
| 3 | | |P z z z z z
su
y ra
2
2
2
2 2 2 2 2 2
3
4 3 2 4P a a b b a b a
2
1P f x x x
với
0; 4
x
. Lập
bảng biến thiên ta suy ra
min
3
4
P
.
T
rong quá trình biên soạn tôi cũng khó có thể tránh khỏi sai sót. Mong nhận được sự góp ý từ các bạn và
quí thầy cô. Mọi góp ý xin inbox trực tiếp cho tôi theo địa chỉ https://www.facebook.com/lehong.quoc.12
.Chân
thành cảm ơn và chúc các bạn học tốt!
| 1/22
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 1 Câu 1.
(Đề khảo sát của Bộ dành cho 50 trường) Xét số phức z thỏa z i  13 . Tìm giá trị nhỏ nhất
T của z  9  5i . A. T  2 13 . B. T  3 13 . C. T  13 . D. T  4 13 . Hướng dẫn giải. Chọn A.
Đặt z x yi (với x, y   ). Khi đó z i  13  x  y  2 2 1  13 . Cách 1. Đại số.
x  13 sin t Chọn  .
y  13 cos t  1  2 2 2 2 2
Ta có P z  9  5i  x  9  y  5   13 sint  9   13 cost  6   2 2
13 sin t  cos t  18 13 sint  12 13 cost  117  130  6 13 3sint  2cost  3 sin    13
 130  78 sint    52  P  208 , với  . 2 cos    13 Vậy T  2 13 . Cách 2. Hình học. 2 2 2
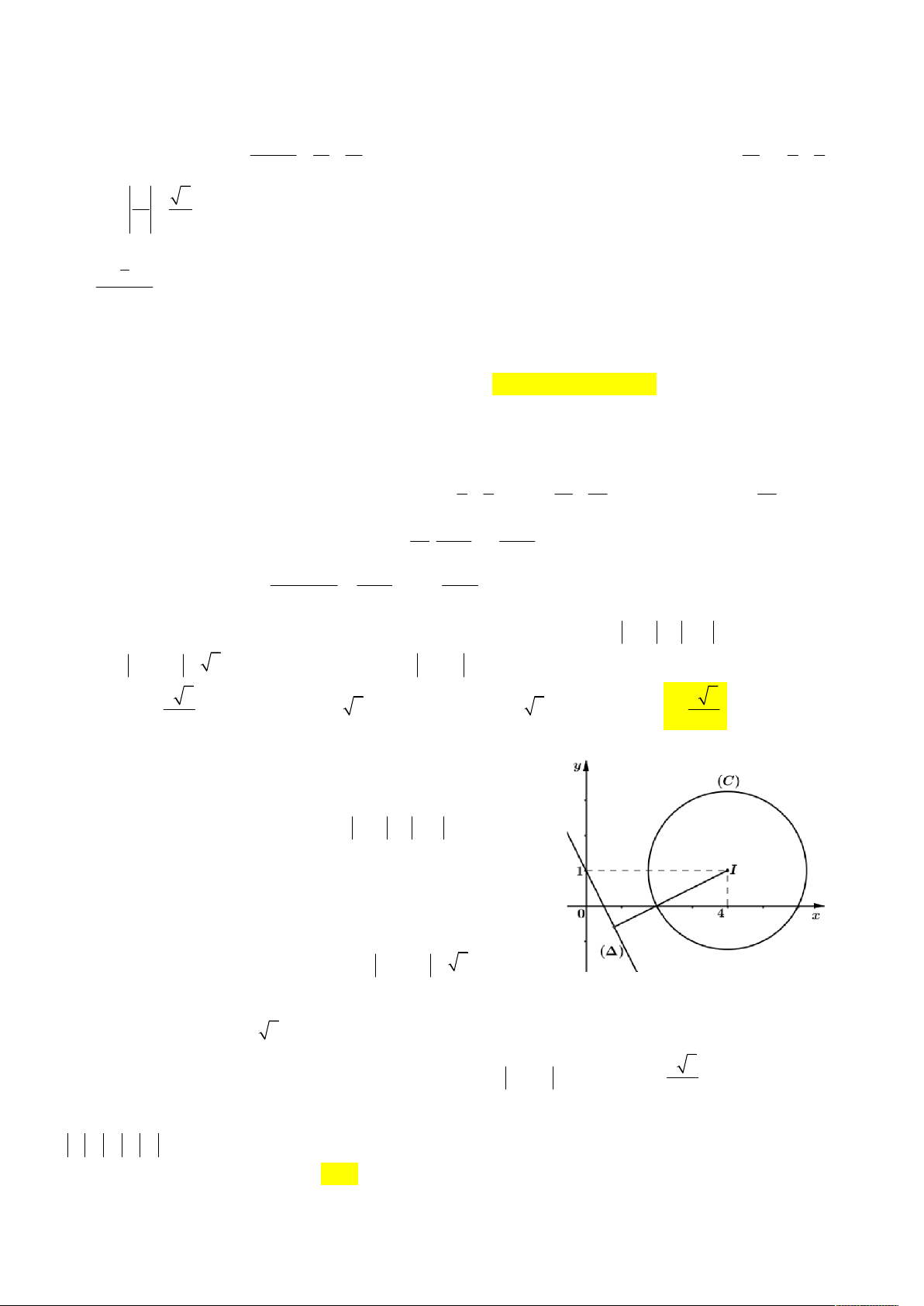
Đặt w z  9  5i w z  9  5i w  x  9  y  5 suy ra tập hợp các số phức w nằm trên
đường tròn C có tâm là A9; 5 , bán kính R . 1  1
Mà z i  13  x  y  2 2
1  13 suy ra tập hợp các số phức w nằm trên đường tròn C có tâm 2  là B0; 1
  , bán kính R  13 . 2
Gọi C là điểm thuộc đường tròn C , suy AC w , mà C thuộc C , suy ra 2  1  
AB R AC AB R , ta có AB  9; 6
   AB  117  3 13 suy ra 2 13  AC  4 13 . Vậy 2 2 T  2 13 . Câu 2.
Có bao nhiêu giá trị thực của m để phương trình 2
z  m   2 4 4
1 z m  3m  0 có hai nghiệm
phức thỏa z z  2 . 1 2 A. 0 . B. 1 . C. 2 . D. 4 . Hướng dẫn giải. Chọn C. Cách 1: '  4m  4 .
Trường hợp 1: '  0  m  1
 . Khi đó phương trình 2
z  m   2 4 4
1 z m  3m  0 có hai nghiệm là
z a bi , z a bi với a,b . 1 2 Ta có 2 2
z z  2  a b  1 1 . 1 2 2 m  3mm  1
Theo định lí Vi-ét ta có z z
2 , từ 1 và 2 suy ra . 1 2  4 m  4 
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 2
Suy ra m  3 .
Trường hợp 2: '  0  m  1
 phương trình đã cho có hai nghiệm z z  1 , suy ra z z  2 . 1 2 1 2 Suy ra m  1  thỏa 4 .
Trường hợp 3: '  0  m  1. Khi đó phương trình có hai nghiệm thực z , z thảo hệ thức Vi-ét 1 2
z z  1  m 1 2  2  m  3m . z z   1 2  4 2 2 Theo đề ta có
z z  2  zz
 2 z z  4  z z
 2z z  2 z z  4 1 2 2 1 2 1 2 1 2 1 2 1 2 2 2 m  12 2
 4 khi m  3m  0    2 m  3m m  3m m 1    4    m  3 5 . 2 2 2 m  3
khi m  3m  0 
Vậy từ 3 , 4 , 5 suy ra m  3 , m  1  thỏa. Cách 2: Phương trình 2
z  m   2 4 4
1 z m  3m  0 luôn có hai nghiệm phức z , z , theo định lí Vi-ét ta có 1 2
z z  1  m 1 2  2 2 2 
m  3m . Theo yêu cầu bài toán ta có z z  2  zz  2 z z  4 z z 1 2 1 2 1 2   1 2  4 2 2 z zz z 1 2 1 2 2 2 
 2 z z  4  z zz z
 4z z  4 z z  8 1 2  1 2  1 2 2 1 2 1 2
 m  2  m  2 2 2 1
1  m  3m m  3m  8  m  2 2
1  m  1  m  3m  8
m 12  m  1   2
m  3m  8 khi m  1  
 m  12  m  1    2
m  3m  8 khi m  1  ; 0  3;      
m  12  m  1   2
m  3m  8 khi 0  m  3  2
2m  6m  8  0 khi m  1   2
 2m  4m  6  0 khi m   1  ; 0  3;     
  m  1 m  3 . 2m  6  0
khi 0  m  3 
Vậy m  3 , m  1  thỏa. Câu 3.
(THPT chuyên Quang Trung – Bình Phước) Cho z   thỏa mãn   i 10 2 z   1  2i . Biết z
tập hợp các điểm biểu diễn cho số phức w  3  4iz  1 2i là đường tròn tâm I , bán kính R . Khi đó I   1  ; 2  I  1; 2 I   1  ; 2 I  1; 2 A.  . B.  . C.  . D.  .  R  5  R  5   R  5   R  5  Hướng dẫn giải Chọn
Nhận xét. Ở đây đề cho lỗi, vì chỉ có 1 số phức z   thỏa   i 10 2 z
 1  2i , nên tập hợp điểm z
biểu diễn số phức w cũng chỉ có 1 điểm chứ không phải là 1 đường tròn.
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 3
* Lời giải sai. 10 10
Ta có 2  iz
 1  2i  2 z  1   z  2i z . 2 z z 2 2 10
Lấy môđun hai vế ta được  z  2  2 z   1  (Do z z ). 2 z  2 10
z  2   z  2 10 2 2 1   5 z  5 
z  1  w  1  2i  (3  4i) . z  5 . 2 2 z z  I  1  ; 2
Do đó tập hợp điểm biểu diễn w là đường tròn  .  R  5 
* * Lời giải đúng. 10 10
Ta có 2  iz
 1  2i  2 z  1   z  2i z . 2 z z 2 2 10
Lấy môđun hai vế ta được  z  2  2 z   1  (Do z z ). 2 z  2 10
z  2   z  2 10 2 2 1   5 z  5 
z  1 . Thay z  1 vào   i 10 2 z
 1  2i ta được 2 2 z z z  10  9 10 20  13 10  i 10 10 10 3 10 2 
 1  2i z    i suy ra w   i , suy ra điểm z 1  3i 10 10 10 10
biểu diễn của số phức w là 1 điểm. Câu 4.
(THPT chuyên Lương Thế Vinh – Đồng Nai – L1) Cho số phức z thỏa mãn 2
z  2z  5  z  1  2iz  1  3i . Tìm giá trị nhỏ nhất của w , biết rằng w z  2  2i . 3 1 A. w  . B. w  2 . C. w  1 . D. w  . min 2 min min min 2 Hướng dẫn giải. Chọn C. Cách 1: Đại số. 2 2
z  2z  5  z  1  2iz  1  3i  z   2
1  4i  z  1  2iz  1  3i
z  1  2i  0 1
 z  1  2iz  1  2i  z  1  2iz  1  3i   .
z  1  2i z  1  3i 2  +)  
1  z  1  2i w  1
  w  1 3 .
+) Đặt z a bi , với a, b   . Khi đó ta có 2  a  1  b  2i  a  1  b  3i 1 3
 a  2  b  2  a  2  b  2 1 2 1 3
 4b  4  6b  9  b   , suy ra
w a  2  i 2 2
w  a  2 9 3 2  
4 . Từ 3 , 4 ta suy ra w  1 . 4 2 min Cách 2: Hình học.
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 4 2 2
z  2z  5  z  1  2iz  1  3i  z   2
1  4i  z  1  2iz  1  3i
z  1  2i  0 1
 z  1  2iz  1  2i  z  1  2iz  1  3i   .
z  1  2i z  1  3i 2  +)  
1  z  1  2i w  1
  w  1 3 .
+) Đặt z a bi , với a, b   . Khi đó ta có 2  a  1  b  2i  a  1  b  3i 1 3
 a  2  b  2  a  2  b  2 1 2 1 3
 4b  4  6b  9  b   , suy ra w a  2  i , suy ra tập 2 2 3 3
hợp các số phức w nằm trên đường thẳng y
 , suy ra w d  . 2 O; 2 Câu 5.
(Chuyên ĐH Vinh – L3) Cho hai số phức z , w khác 0 và thỏa z w  2 z w . Phần thực z u  là w 1 1 1 A.  . B. . C. 1 . D. . 8 4 8 Hướng dẫn giải. Chọn D.  z 1  z 1      1  w 2  w 2  u
Ta có z w  2 z w       2
, đặt u a bi , với a, b   , khi đó z wz w    1  1 u  1  1   ww    2 2 1 a b   3 1
ta được hệ phương trình 4   2a  1   a  .   4 8 a  12 2  b  1  Câu 6.
Biết rằng khi m a , với a và m là các số thực, thì phương trình   i 2 1
x  m ix  1  0 không
có nghiệm thựC. Chọn mệnh đề đúng. A. a 1  ;  1 . B. a1; 5 . C. a3;6 . D. a 3  ;  1 . Hướng dẫn giải. Chọn D.
Giả sử phương trình có nghiệm thực là x b , khi đó ta có   i 2 1
b  m ib  1  0 2 
b mb  1  0 b  1  2
b mb    2 1
b bi  0    
, suy ra m  2 thì phương trình 2 b b  0  m  2     i 2 1
x  m ix  1  0 không có nghiệm thực. Câu 7.
(THPT chuyên Quang Trung – Bình Phước) Cho hai số phức z , z khác thỏa 0 , z z  0 và 1 2 1 2 1 1 2 z  
. Tính giá trị biểu thức 1 . z z z z z 1 2 1 2 2 2 3 2 A. . B. . C. 2 3 . D. . 2 2 3 Hướng dẫn giải.
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 5 Chọn A. 1 1 2 z 1 1 Theo đề, ta có  
z z z z 2z z 2 2
 2z  2z z z  0 1     i 1 2  1 2   1 2  z z z z 1 1 2 2 z 2 2 1 2 1 2 2 z 2 1   . z 2 2 Câu 8.
(THPT chuyên Nguyễn Quang Diêu – Đồng Tháp – L2) Gọi M là điểm biểu diễn số phức z z  1 w
, trong đó z là số phức thỏa mãn 1 iz  2i  2  i  3z . Gọi N là điểm trong mặt phẳng 2
z    
sao cho Ox,ON  2 , trong đó   Ox,OM là góc tạo thành khi quay tia Ox tứi vị trí của tia OM .
Điểm N nằm ở góc phầ tư nào?
A. Góc phần tư thứ nhất. B. Góc phần tư thứ tư. C. góc phần tư thứ ba. D. Góc phần tư thứ hai. Hướng dẫn giải. Chọn B. 3 6 11 56 56
Theo đề, ta có 1 iz  2i  2  i  3z z   i w  
i , suy ra tan   , ta có 5 5 15 45 33  2 56 1089 3696
sin 2  2 sin.cos  2 tan.cos   2.  .     33 4225 4225  . 2 2 1089 2047
cos2  2cos   1  .2.  1   2  tan    1 4225 4225 2 2 Câu 9.
(THPT Thanh Chương 1 – Nghệ An – L2) Cho số phức z thỏa z  2  z i  1 và số phức 1
z thỏa z  4  i  5 . Tìm giá trị nhỏ nhất của z z ? 2 1 2 2 5 3 5 A. . B. 5 . C. 2 5 . D. . 5 5 Hướng dẫn giải. Chọn D.
Đặt z a bi , z c di ( a, b, c, d   ). 1 2 2 2
Ta có số phức z thỏa
z  2  z i  1 suy ra 1 a 2 bab 2 2 2 2 1      
 1  2a b  1 , suy ra tập hợp  
điểm biểu diễn số phức z nằm trên đường thẳng 2x y  1 1  . Lại có số phức z thỏa
z  4  i  5 suy ra 2
c  2  b  2 4
1  5 , suy ra tập hợp điểm biểu diễn số phức z nằm trên đường tròn C có tâm 2 I 4; 
1 , bán kính r  5 . 3 5
Biểu diễn C và  lên mặt phẳng tọa độ, ta suy ra z zdr  . 1 2 min I; 5
Câu 10. (THPT chuyên Biên Hòa – Hà Nam) Cho ba số phức z , z , z thảo mãn điều kiện 1 2 3
z z z  1 và z z z  0 . Tính 2 2 2
A z z z . 1 2 3 1 2 3 1 2 3 A. 1 . B. 0 . C. 1  . D. 1  i .
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 6 Hướng dẫn giải. Chọn B.
A z z z  z z z 2 2 2 2
 2 z z z z z z  2 z z z z z z 1 2 3 1 2 3  1 2 2 3 3 1   1 2 2 3 3 1  2 2 2    1 1 1  z z z 1 2 3 2z z z   2z z z            2
z z z z z z 1 2 3 1 2 3 1 2 3  1 2 3  z z zz z z   1 2 3  1 2 3  
Mà z z z  0  z z z  0 . Vậy A  0 . 1 2 3 1 2 3
Câu 11. (THPT chuyên Lê Hồng Phong – TP.HCM) Cho z , z là hai số phức khác 0 thỏa 1 2 2 2 
z  2z z  2z  0 . Biết z , z có điểm biểu diễn lần lượt là M , N . Tính góc OMN 1 1 2 2 1 2 A. o 30 . B. o 45 . C. o 60 . D. o 90 . Hướng dẫn giải. Chọn B.
z  1  i z 2 2 1   2
z  2z z  2z  0  
. Vì hai trường hợp này là như nhau nên tối chỉ trình bày một 1 1 2 2
z  1  i z  1   2 trường hợp như sau.
Với z  1  i z , đặt z a bi , z c di (với a, b, c, d   ) và z , z lần lượt có điểm biểu diễn là 1   2 1 2 1 2 z ac bd bc ad
M a; b , N c; d . Khi đó
z  1  i 1 z   1  i   i  1  i 1 2 2 2 2 2 z c d c d 2 ac bd   2 z
 1  ac bd z , mà
1  1  i z  2 z . Ta có OM  a; b , NM  a c; b d . 2 2 2 c d 1 2 z2 2 2
  2 2 2 
a b ac bd zz z 1
cosOMN  cosOM,NM    1 2 2    2 2 2 2 2 2
a b . a b c d  2ac bd 2 2 2 z z 2 z zz 2 2 1 1 2  , suy ra o OMN  45 .
Câu 12. (Đề minh họa – L3) Xét các số phức z thỏa mãn z  2  i z  4  7i  6 2 . Gọi m , M lần lượt
là giá trị nhỏ nhất, giá trị lớn nhất của z  1  i . Tính P m M . 5 2  2 73 5 2  73 A. P  13  73 . B. P  . C. P  5 2  73 . D. P  . 2 2 Hướng dẫn giải. Chọn B. Cách 1. Đại số. Đặt
z a bi , với a, b   . Khi đó ta có
z  2  i z  4  7i  6 2
 a  2  b  2  a  2  b  2 2 1 4 7
 6 2 , xét các điểm N  ; a b , A 2;  
1 , B4;7 , khi đó ta
được NA NB  6 2  AB , suy ra N , A , B thẳng hàng ( N nằm giữa A và B ). Phương trình
đường thẳng AB : x y  3  0 , suy ra N a; a  3 ( 2  a  4 ).
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 7 2 2 2 2
Theo đề z  1  i  a   1  b   1  a   1  a  4 2
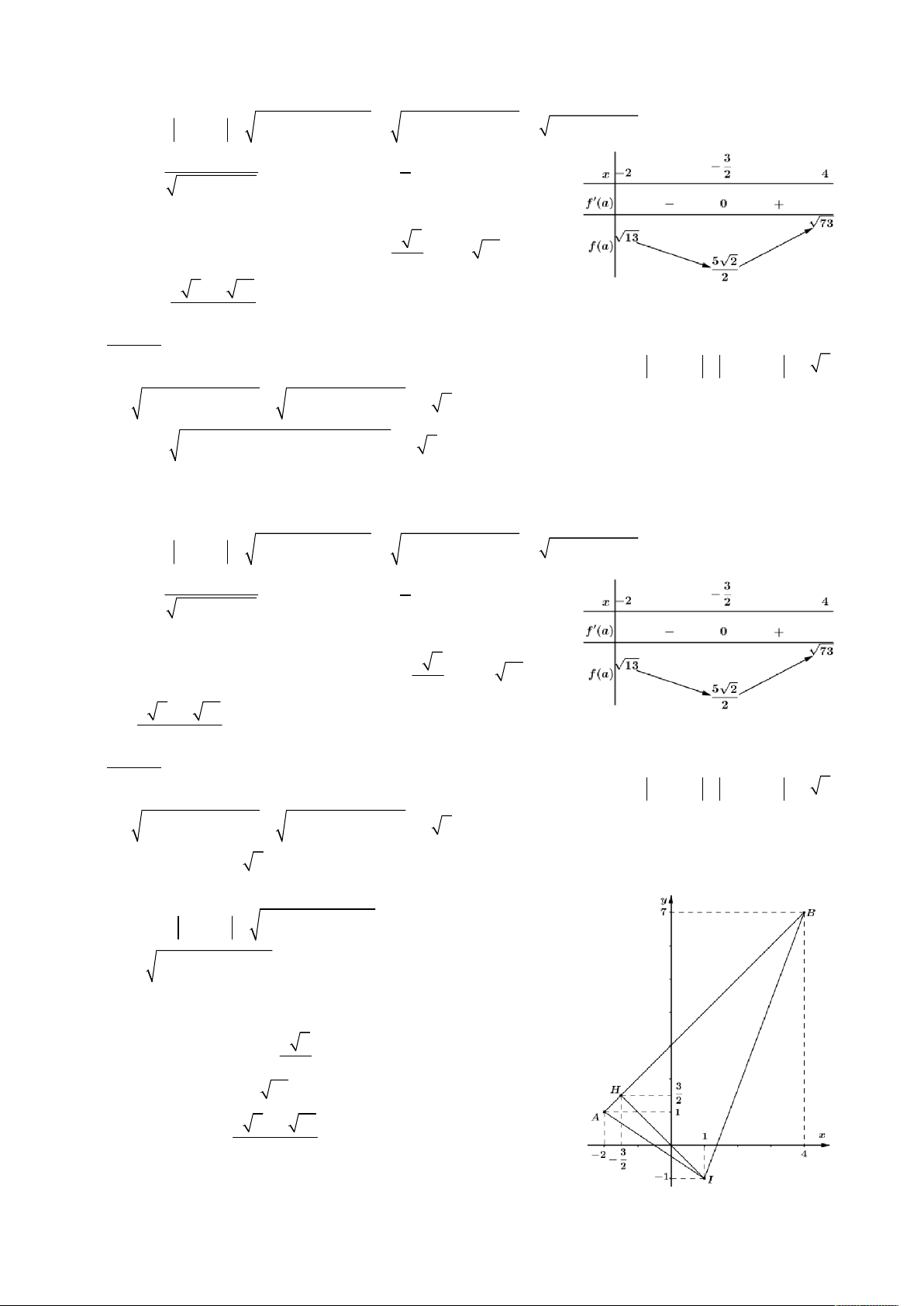
 2a  6a  17  f a . /  3 f a 2a 3  ; /
f a  0  a   . Ta có bảng biến 2 a  6a  17 2 thiên như hình bên. 5 2
Dựa vào bảng biến thiên ta suy ra m  , M  73 . 2 5 2  2 73 Vậy P  . 2
Cách 2. Bất đẳng thức. Đặt
z a bi , với a, b   . Khi đó ta có
z  2  i z  4  7i  6 2
 a  2  b  2  a  2  b  2 2 1 4 7  6 2
1 , áp dụng bất đẳng thức Mincopxki ta có
VT    a    a2  b    b2 1 2 4 1 7  6 2 , dấu "  " xảy ra   a  2 
7  b  4  ab  1 b a  3      .
a  2; 4 , b  1  ; 7 a   2  ; 4 , b  1  ; 7             2 2 2 2
Theo đề z  1  i  a   1  b   1  a   1  a  4 2
 2a  6a  17  f a . /  3 f a 2a 3  ; /
f a  0  a   . Ta có bảng biến 2 a  6a  17 2 thiên như hình bên. 5 2
Dựa vào bảng biến thiên ta suy ra m  , M  73 . Vậy 2 5 2  2 73 P  . 2 Cách 3. Hình học. Đặt
z a bi , với a, b   . Khi đó ta có
z  2  i z  4  7i  6 2
 a  2  b  2  a  2  b  2 2 1 4 7
 6 2 , xét các điểm N  ; a b , A 2;
 1 , B4;7 , khi đó ta
được NA NB  6 2  AB , suy ra N , A , B thẳng hàng ( N nằm giữa A và B ). Phương trình
đường thẳng AB : x y  3  0 . 2 2
Theo đề z  1  i  a   1  b  
1 , xét điểm I 1; 1   suy ra
IN  a  2  b  2 1 1 , khi đó minIA; IB;d
IN Max IA; I ; B d I ; AB   I ; AB       5 2 m IN  d  min I;AB   2 . M INIB  73  max 5 2  2 73
Vậy P m M  . 2
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 8
Câu 13. (THPT Thị xã Quảng Trị) Cho số phức z a bi ( a, b   ) thỏa mãn z không là số thực và 2 z z  1 4 4 1  a b
là số thựC. Tính M  . 2 z z  1 6 6 1  a b 1 2 4 1 A. . B. . C. . D. . 2 3 3 3 Hướng dẫn giải. Chọn B.
z a bi , với a, b   . Vì z không là số thực nên b  0 .    2 2 2
a b a  1  2 1
ab bi z z Ta có w  
, suy ra phần ảo của số phức w là 2 z z  1  2 2
a b a  1  2ab bi 2 3
2b  2a b  2b 2 z z  1 4 4  a b , mà là số thực suy ra 2 2 2 2 1
a b  1  a b  , ta có  2
a b a  12  2ab b2 2 2 z z  1 2 4 4 4 4 4 4 1  a b 1  a b 1  a b 2 M     . 6 6 1  a b 1   2 2 a b  4 4 2 2
a b a b  3  4 4
1  a b  3 2
Câu 14. (Thầy Trần Trọng Trị - THPT Gia Định – TP.HCM) Cho hai số phức z , z thỏa mãn điều kiện 1 2
2 z i z z  2i và z  10  i  1 . Tìm giá trị nhỏ nhất của z z ? 1 1 1 2 1 2 A. 3 5  1 . B. 101  1 . C. 101  1 . D. 10  1 . Hướng dẫn giải. Chọn A. Cách 1. 2 x
Ta có 2 z i z z  2i suy ra tập hợp điểm biểu diễn số phức z nằm trên parabol P : y  . 1 1 1 1 4
Và z  10  i  1 suy ra tập hợp điểm biểu diễn số phức z nằm trên đường tròn 2 2  2 2 C  x  2  y  2 : 10
1  1. Xét đường tròn   : x  10  y  1  k với k 0;   tiếp xúc với
P. Giải điều kiện tiếp xúc   và P  x  10 y'   y 1 k x 102     
k  x  102 2 2 Ta có x
 10   y  1  k     . 
y  1  k  x  102 x  10  y'  
k  x  102 
  và P tiếp xúc nhau khi hệ phương trình sau có nghiệm 2  x
1  k  x  102   4 xx   10 TH1:  x    
 0  x  4  k  45 10 x . 2 2 x    1 
k  x  102 2 4 
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 9 2  x
1  k  x  102   4 xx   10 TH2:  x    
 0  x  4  k  45 10 . 2 x 2 x   1 
k  x  102 2 4 
Ta suy ra k  45 . Vậy Min  3 5  1 .  1 z z2 Cách 2. 2 x
Ta có 2 z i z z  2i suy ra tập hợp điểm biểu diễn số phức z nằm trên parabol P : y  . 1 1 1 1 4
Và z  10  i  1 suy ra tập hợp điểm biểu diễn số phức z nằm trên đường tròn 2 2
C x  2  y  2 : 10
1  1 . Đường tròn C có tâm là I 10; 1 bán kính R  1 . 2  a  4 2 a a 3 a Xét điểm A 2 /  a;    P , khi đó
IA f a    20a  101 ; f a   a  20 ; 4   16 2 4 /
f a  0  a  4 , lập BBT suy ra Minf a  45 suy ra MinIA  3 5 . Vậy Min  3 5  1 . z z 1 2 3
Câu 15. Cho số phức z thỏa z  2  z  2  6 . Tìm giá trị nhỏ nhất của biểu thức P z  3  z A. 3 . B. 2 . C. 1  . D. 4  . Hướng dẫn giải. Chọn A. 2 2
Đặt z x yi , với a, b   . Khi đó ta có z   z    x   2 2 2 2 6
2  y x  y  2  6 . Xét điểm F 2; 
0 , F 2; 0 và M x; y , suy ra ta có biểu thức 2   1  
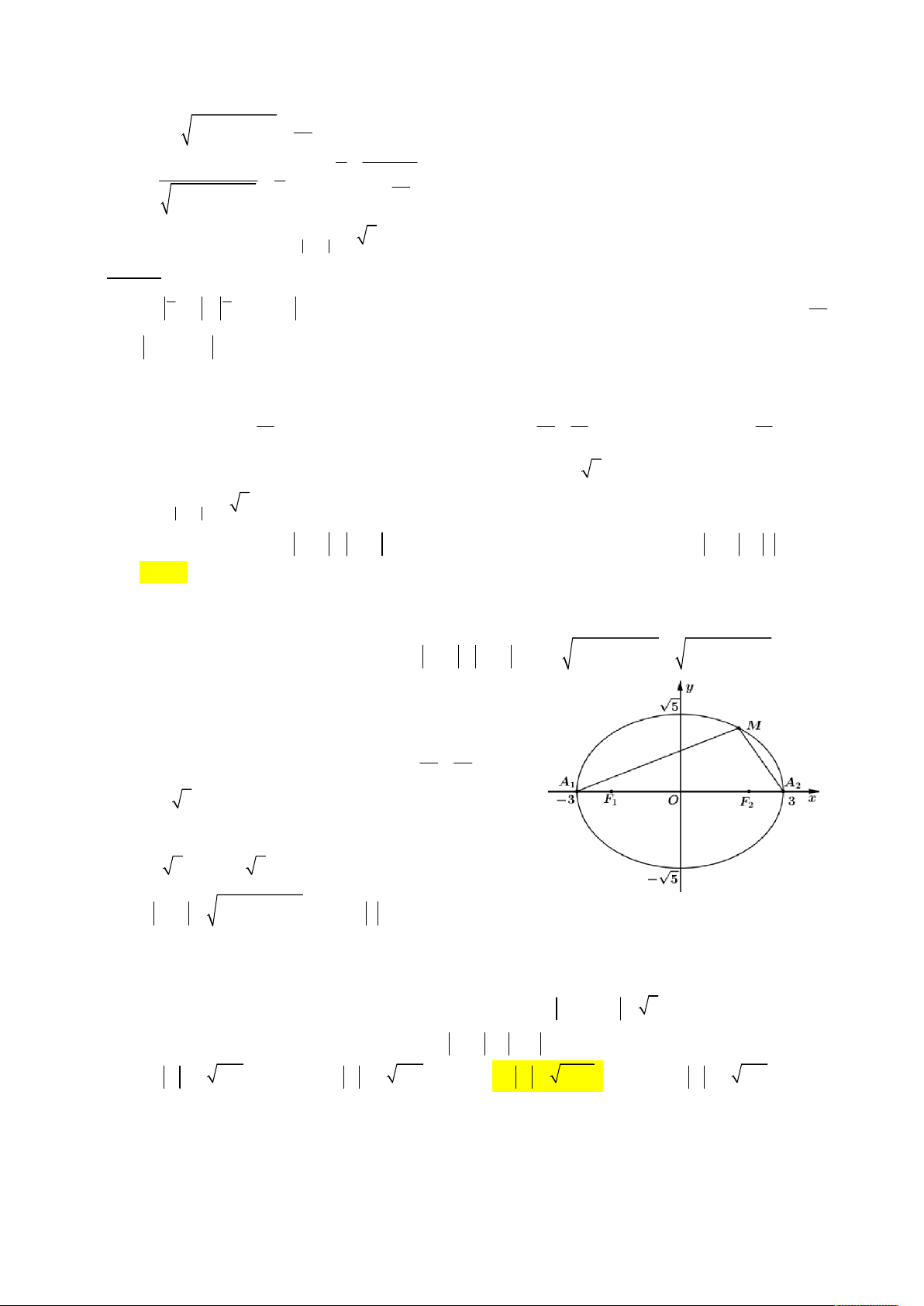
MF MF  6  2.3 , suy ra tập hợp điểm biểu diễn số phức 1 2 2 2 x y
z nằm trên đường elip có phương trình   1 (với 9 5
a  3,b  5, c  2 ). Tọa độ các đỉnh trên trục lớn là A 3
 ; 0 , A 3; 0 , các đỉnh nằm trên trục bé là 2   1  
B 0;  5 , B 0; 5 . 2   1  
Ta có z  3  x  32 2
y MA , z MO ( O là gốc tọa độ). Suy ra 3
P MA MO . 1 1
MinMA M   A  MinMA  0 Lại có 1 1  1   . Vậy P  3 . min
Max MO M A hay M A
MaxMO OA OA  3 1 2  1 2
Câu 16. (THPT chuyên Hưng Yên –L3) Cho số phức z thoả mãn z  3  4i  5 . Gọi M và m lần lượt là 2 2
gia trị lớn nhất và giá trị nhỏ nhất của biểu thức P z  2  z i . Tính modun của số phức w M mi A. w  2 314 . B. w  2 309 . C. w  1258 . D. w  3 137 . Hướng dẫn giải Chọn C. 2 2
Đặt z x yi . Ta có P x  2  2 2 y xy 1       
 4x  2y  3  
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 10 2 2
Mặt khác z  3  4i  5  x  3   y  4  5 , đặt x  3  5 sint; y  4  5 cost .
Suy ra P  4 5 sint  2 5 cost  23 , ta có 10 
 4 5 sin t  2 5 cost  10 .
Do đó 13  P  33  w  1258 .
Câu 17. (THPT chuyên Hưng Yên –L3) Cho số phức w, biết rằng z w  2i và z  2w  4 là hai nghiệm 1 2 của phương trình 2
z az b  0 với a,b là các số thựC. Tính T z z . 1 2 8 10 2 3 2 37 A. T  . B. T  . C. T  5 . D. T  . 3 3 3 Hướng dẫn giải Chọn A. 2
Đặt w x yi . Theo Viet ta có: z z  a  3w  2i  4  3x  4  3y  2 i là số thực nên y  . Lại 1 2     3  2  4 
có z z b x i  2i
2x i  4 là số thực. 1 2     3  3   4  4  4 16 Suy ra x i
2x  4  i x2x  4  i x  4    
là số thực suy ra x  4  3  3  3 9 2 4 4 8 10
Do đó z  4  i  2i  4  i , z  4  i T  . 1 3 3 2 3 3
Câu 18. (THPT Thái Nguyên – L2) Tập hợp các số phức w  1 iz  1 với z là số phức thỏa mãn
z  1  1 là hình tròn. Tính diện tích hình tròn đó. A. 4 . B. 2 . C. 3 . D.  . Hướng dẫn giải Chọn B
Đặt w x yi , với x, y   thì
w  1  iz  1  w  1  iz  
1  i  2  w i  2  z  
1  iz   1  w i
 z    iz    x  2  y  2  z  2 2 1 1 2 1 2
1  2 , suy ra tập hợp số phức cần tìm nằm
trên hình tròn bán kính R  2 có tính biên. 2
S   R  2 .
Câu 19. (THPT Thái Nguyên – L2) Cho số phức z có môđun là 3 , biết tập hợp các điểm biểu diễn số
phức w  3  2i  2  iz là một đường tròn thì có bán kính là? A. 3 2 . B. 3 5 . C. 3 3 . D. 3 7 . Hướng dẫn giải Chọn B
x yi   i
Đặt w x yi , với x, y   thì x yi   i    i 3 2 3 2 2 z z  2  i
2x  2yi  6  4i xi y  3i  2
i x  2y  1  2x y  8  z   z  5 5
z   x y  2   x y  2 2 2 3 2 1 2 8
 25.9  5x  5y  30x  20y  65  29.5
x y x y  
 x  2  y  2 2 2 6 4 13 45 3 2  45  R  3 5 .
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 11
z 11 iz
Câu 20. (THPT Thái Nguyên – L2) Cho số phức z a bi , với a, b   thỏa mãn  i . Tính 1 z z 2 2 a b ? A. 3  2 2 . B. 2  2 2 . C. 3  2 2 . D. 4 . Hướng dẫn giải Chọn A  z  0  Điều kiện  . z  1  
z 11 iz 2 2 Khi đó
i z 1  iz   z  1i  z i z    z  1i z   z  1 z i 1 z z 2  2
z  1  z z 1   z  0  2   
z  1  2  z  3  2 2 . 2  2
z  1  z   z  
z  2 z  1  0 
Câu 21. (THPT chuyên KHTN – Hà Nội – L5) Cho z , z là 2 số phức bất kỳ, giá trị biểu thức: 1 2 2 2 zz 1 2 a  bằng? 2 2 z zz z 1 2 1 2 1 3 A. a  2 . B. a  . C. a  1 . D. a  . 2 2 Hướng dẫn giải Chọn B Cách 1.
Đặt z a bi , z c di , với a, b, c, d   . Khi đó 1 2 2 2 zz  2 2
a b    2 2 c d 1 2  1 a    2 2 z zz z
a c2  b d2  a c2  b d2 2 1 2 1 2 Cách 2. 2 2 zz 1  1 1 Ngoài ra ta có thể chọn 1 2
z z  1    . 1 2 2 2 z zz z  2 2 2 2 2 1 2 1 2  0
Câu 22. Cho số phức z thỏa z  2  2i  17 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của P  1999 z  2  i  2017 z  6  3i . Tính M m .
A. M m  8302 17 .
B. M m  4034 17 . C. M m   2 2 17 1999  2017  1999 . D. M m   2 2 2 17 1999  2017  1999 . Hướng dẫn giải Chọn D Cách 1.
z  2  2i  17 suy ra tập hợp số phức z nằm trên đường tròn tâm I 2; 2 bán kính 17 .
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 12
Xét các điểm A 2;  
1 , B6;3 , Cx; y . Khi đó P  1999CA  2017CB . Ta có AB là đường kính của
đường tròn tâm I nên 2
P  1999 68  CB  2017CB . Xét hàm số f x 2
 1999 68  x  2017x với x 0; 2 17   suy ra P  1999.2 17 ,   min 2 2 P
 2 17 1999  2017 . Vậy M m   2 2 2 17 1999  2017  1999 . max Cách 2. 2 2
z  2  2i  17  a b  4a  4b  9 2 2 2 2
P  1999 z  2  i  2017 z  6  3i  1999 a b  4a  2b  5  2017 a b  12a  6b  45 2 2
P  1999 8a  2b  14  2017 8
a  2b  54  2 17 1999  2017 Suy ra 2 2 P
 2 17 1999  2017 . P
 1999.2 17 (sử dụng xét hàm) max min
Vậy M m   2 2 2 17 1999  2017  1999 .
Chú ý: ở cách hai ta có có thể xét hàm số f t  1999 14  t  2017 t
  54 (với t  8a  2b và 14  t  54 ).
Câu 23. (THPT Chu Văn An – Hà Nội – L2) Cho số phức z thỏa mãn điều kiện z  1  2 . Tìm giá trị
lớn nhất của T z i z  2  i A. maxT  8 2 . B. maxT  4 . C. maxT  4 2 . D. maxT  8 . Hướng dẫn giải Chọn B
Đặt z x yi . Ta có: z    x yi    x  2 2 1 2 1 2 1  y  2 2 2 2 Khi đó: 2
T z  1  z  2  i x yi i x yi  2  i x   y  
1  x  2  y   1 
 x y 2 x 2 y 2 2 2 2 1 1 . 1 2 1            
x x   y      x  2 2 2 2 2 2 4 4 2 2 2 2.
1  y   4  2.4  4  4 Vậy maxT  4 . z
Câu 24. (THPT Quốc Học – Huế - L2) Cho số phức z  0 sao cho z không phải là số thực và w  2 1  z z là số thựC. Tính . 2 1  z 1 1 1 A. . B. . C. 2. D. . 5 2 3 Hướng dẫn giải Chọn B Cách 1. z
Theo giả thiết ta có w
là số thực nên ta có thể chọn w là số thực bất kỳ sao cho z không 2 1  z phải là số thực.
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 13 z 1  i 3 z 1 Chọn 2 w
 1  z  1  z z   z  1   . 2 2 1  z 2 2 1  z Cách 2. z 2 1 z  1 1 1 Ta có w  là số thực suy ra   z  là số thực suy ra
là số phức liên hợp của z 2 1  z w z z z 2 1 z 1 1 suy ra . z z z  . z  1  z  1    . 2 z 1  1 2 1  z
Câu 25. (Chuyên ĐH Vinh – Nghệ An – L3) Cho số phức z thay đổi, luôn có z  2 . Khi đó tập hợp
điểm biểu diễn số phức w  1  2iz  3i là:
A. Đường tròn x   y  2 2 3  2 5 .
B. Đường tròn x   y  2 2 3  20 .
C. Đường tròn x  y  2 2 3  20 .
D. Đường tròn x  2 2 3  y  2 5 . Hướng dẫn giải Chọn B
Giả sử w a bi a,b   a bi  1  2iz  3i
a  b  3i
a  b  3i1  2ia  2  
b  3  2a b  3iz    1  2i 5 5 1  z z
a  2b  3 2
  2a b  32  2  a  2b  62  2a b  32  100 5  
 a b2   a b2 2 2
 12a  2b  62a b  55  a b b
a b b
a  b  2 2 2 2 2 2 5 5 30 55 6 11 3  20 . 1
Câu 26. (THPT chuyên Vị Thanh – Hậu Giang) Biết số phức z thỏa mãn phương trình z   1. Tính z 2016 1 P z  . 2016 z A. 0 . B. 1. C. 2 . D. 3 . Hướng dẫn giải Chọn C 3 1  1  1  1  1 Ta có z   1 3  z   1  z   3 z   1 3 3      z
 2  0  z  2 3 1  0  z  1 z 3 3  z zz z
P  z 672 3 1   1  1  2. z 672 3
Câu 27. (THPT Kim Liên – Hà Nội) Cho hai số thực b và c c  0. Ký hiệu A , B là hai điểm của mặt
phẳng phức biểu diễn hai nghiệm của phương trình 2
z  2bz  c  0. Tìm điều kiện của b và c
sao cho OAB là tam giác vuông ( O là gốc tọa độ). A. 2 b  2 . c B. 2 c  2b . C. b c. D. 2 b c. Hướng dẫn giải Chọn B
Theo yêu cầu bài toán suy ra phương trình không có nghiệm thực.
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 14 2  2
z  b i c b Ta có: 2
z  2bz  c  0  z b 2 1
b c    2
c b  . Khi đó A 2  ; b c b , 2
z  b i c b  2   B 2  ;
b c b  , suy ra OA   2  ;
b c b , OB 2  ;
b c b  . Ta có A, B là hai điểm đối xứng nhua
qua trục Oy . Suy ra tam giác OAB vuông tại O . Theo giả thiết ta có: 2 2 2
b b c  0  c  2b .
Câu 28. (Chuyên Ngữ – Hà Nội) Trên mặt phẳng tọa độ Oxy , tìm tập hợp các điểm biểu diễn các số
phức z thỏa mãn điều kiện số phức w  z2  3i  5  i là số thuần ảo. A. Đường tròn 2 2 x y  5.
B. Đường thẳng 2x  3y  5  0. 2 2
C. Đường tròn x  3   y  2  5.
D. Đường thẳng 3x  2y  1  0. Hướng dẫn giải Chọn B
Đặt z x yi , với x, y    w  x yi2  3i  5  i  2x  3y  5  3x  2y   1 i .
2x  3y  5  0
W là số thuần ảo khi và chỉ khi 
 2x  3y  5  0  Tập hợp các điểm biểu diễn số
3x  2y  1  0 
phức z là đường thẳng 2x  3y  5  0.
Câu 29. (Chuyên Ngữ – Hà Nội) Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức
T z  1  2 z  1 .
A. M axT  2 5.
B. M axT  2 10.
C. M axT  3 5.
D. M axT  3 2. Hướng dẫn giải Chọn A Cách 1.
T z   z      2 2 z   z     2 2 1 2 1 1 2 1 1 5.2 z  
1  2 5 (BĐT Bunhiacopxki) 2 2 2 Chú ý: 2 2
z  1  z  1  2x  2y  2  2 z  1 với z x yi , x, y  . Cách 2.
Đặt z x yi , với x, y   ta có:
T x yi   x yi   x  2  y  x  2 2 2 1 2 1 1 2 1  y Lại có 2 2
x y  1  T  2x  2  2 2x  2  f x 1 2 6
Ta có f 'x    0  x   T  2 5 . max 2x  2 2  2x 10
Câu 30. (Sở GD – Đồng Tháp) Trong các số phức z thỏa mãn điều kiện|z  1  2i| |
z i| , tìm số phức có mô-đun nhỏ nhất. 1 3 3 1 2 16 16 2 A. z   i .
B. z    i . C. z   i . D. z   i . 5 5 5 5 5 5 5 5 Hướng dẫn giải Chọn A
Gọi z a bi , a, bR . Ta có z  1  2i z i  a  1  b  2i ab ii
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 15
 a  2  b  2  a  b  2 2 2 2 2 2 1 2 1
a  2a  1  b  4b  4  a b  2b  1
 2a  6b  4  a  3b  2 2 2   Do đó 2 2
z a b   b   2 2 3 2 10 3 2
b  10b  12b  4  10 b      .  5  5 5 3 1 1 3
Dấu "  " xảy ra b    a  . Vậy z   i. 5 5 5 5
Câu 31. (THPT Nguyễn Bỉnh Khiêm) Cho số phức z thỏa mãn w  z  1z  2i là một số thuần ảo.
Tập hợp điểm biểu diễn số phức z là một đường tròn có diện tích bằng bao nhiêu? 5 5 A. 5 . B. . C. . D. 25 . 4 2 Hướng dẫn giải Chọn B
Đặt z a bi , với a, b    w  a   bia bi i 2 2 1
2  a b a  2b  2a b  2i . 2 2 2 
a b a  2b  0  1  2 5
w là số thuần ảo suy ra 2 2 
a b a  2b  0  a     b   1  . 2a  b  2  0   2  4 5
Suy ra tập hợp điểm biểu diễn số phức z là một đường tròn có diện tích bằng . 4
Câu 32. (THPT Nguyễn Bỉnh Khiêm) Cho số phức z x yi x, y . Khi đó phần thực a và phần z i
ảo b của số phức   là: iz  2 x2y  1 2 2
y y x  2
x2y  1 2 2
y y x  2 A. a  , b  . B. a  , b  .  2 2
y  22  xy  22 2 2  xy  2 2  xy  2 2  x x2y  1 2 2
y y x  2
x2y  1 2 2
y y x  2 C. a  , b  . D. a  , b  .  2 2
y  22  xy  22 2 2  xy  2 2  xy  2 2  x Hướng dẫn giải Chọn B
x yi i
x yi i
x yi ixi y  2 x  2xy i 2 2
y y x  2 Ta có:     
i x yi  2 xi y  2
xi y  2xi y  2
x  y  22 2 
x2y  1 a
x2y  1 2 2
y y x  2   y  22 2  x     i   .
y  22  x
x  y  22 2 2 2 2 
y y x  2 b   x   y  22 2 
Câu 31. (THPT Lam Sơn – Thanh Hóa) Cho số phức z , tìm giá trị lớn nhất của z biết z thỏa mãn điều 2   3i kiện z  1  1. 3  2i
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 16 A. 3 . B. 2 . C. 1. D. 2. Hướng dẫn giải Chọn B
Tổng quát: Cho số phức z thỏa mãn z a bi R tìm modun lớn nhất và nhỏ nhất của số phức z . 2 2
Điểm biểu diễn số phức z là đường tròn x a   y b 2  R . Khi đó: 2 2 z
OI R a b R , 2 2 z
OI R a b R . max min 2  3i Áp dụng: Ta có:
z  1  1  iz  1  1
zxyi
y  12 2  x  1. 3  2i Khi đó: z
OI R  1  1  2. max
Câu 32. (THPT Thanh Chương –Nghệ An – L1) Cho z , z là hai số phức thỏa mãn phương trình 1 2
2z i  2  iz , biết z z  1. Tính giá trị của biểu thức P z z . 1 2 1 2 3 2 A. P  . B. P  2. C. P  . D. P  3. 2 2 Hướng dẫn giải Chọn D Cách 1. 2 2
Ta có 2z i  2  iz  2z i  2  iz  (2z i)(2.z i)  (2  iz)(2  i.z) 2 2 2
 4z.z  2iz  2iz i  4  2iz  2iz i z.z  5z.z  5  .
z z  1  z  1  z  1
z  1 và z  1. 1 2 2 Chú ý: 2 .
a a a  2z i  (2z i).(2z i)  (2z i)(2z i).
Tập hợp điểm biểu diễn số phức z , z là đường tròn tâm O , R  1. 1 2
Gọi M z , M z OM OM  1. 1  1  2  2  1 2
  
Ta có z z OM OM M M  1  OMM đều. 1 2 1 2 2 1 1 2
  
Mà z z OM OM OM OM với M là điểm thỏa mãn OM MM là hình thoi cạnh 1 1 2 1 2 1 2
OM  3  P  3. Cách 2.
Đặt z x yi (x, y  ), ta có 2z i  2x  2(y  1)i và 2  iz  2  y xi.  z  1  Khi đó 2 2 2 2 2 2 1
2z i  2  iz  4x  (2y  1)  (y  2)  x x y  1  z  1   . z  1   2 2 2 Sử dụng công thức 2 2 z zz z
 2 z z  2  z z
 3  z z  3. 1 2 1 2 1 2 1 2 1 2
Câu 33. (Sở GD Phú Thọ) Cho hai số phức z và z thỏa mãn z  3 , z  4 , z z  37 . Xét số 1 2 1 2 1 2 z phức 1 z
a bi . Tìm b . z2 3 3 39 3 3 A. b  . B. b  . C. b  . D. b  . 8 8 8 8 Hướng dẫn giải
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 17 Chọn A.
Đặt z x yi ,
z c di x, y,c,d . Ta có: 2 2
z  3  x y  9 ; 2 2
z  4  c d  16 ; 1 2 1 2
z z  37  x c2  y d2 2 2 2 2
 37  x y c d  2xc  2yd  37  xc yd  6 . 1 2 z x yi
x yic dixc yd  yc xdi xc yd yc xd 3 Lại có: 1     
i a bi    bi . 2 2 2 2 2 2 2 2 z c di c d c d c d c d 8 2 2 z z 3 9 9  3  27 3 3 Mà 1 1 2 2 2 2 2  
a b a b   b      b     . z z 4 16 16  8  64 8 2 2 3 3 Vậy b  . 8
Câu 34. (Chuyên ĐH Vinh – Nghệ An – L4) Cho số phức z thỏa mãn z không phải số thực và z w
là số thựC. Giá trị lớn nhất của biểu thức P z  1  i là 2 2  z A. 2 2 . B. 2 . C. 2 . D. 8 . Hướng dẫn giải Chọn A. Cách 1. z z z w
là số thực w w 2 2    2z  .
z z  2z zz 2 2  z 2 2 2  z 2  z
 2z z   .
z z z z   z z (loại do z không là số thực) hoặc 2  .
z z z  2 .
Suy ra: OM  2 với M là điểm biểu diễn của z , M thuộc đường tròn C tâm O , R  2 Ta có:
P z  1  i MA , với A 1  ; 
1 . Ta có: A C nên MA lớn nhất bằng 2R  2 2 . Cách 2.
Vì z không là số thực nên z  0 . Suy ra w  0 . z 1 Ta có w   w  2 2  z  2  z z z  2  0 * . 2   2  z w   1 
* là phương trình bậc hai với hệ số thực  
  nên có nghiệm 2 phức z , z liên hợp của nhau. 1 2  w  Theo Viet ta có:
z .z  2  z .z  2  z z  2  z z  2  z  2 . 1 2 1 2 1 2 1 1
Suy ra P z  1  i z  1  i  2  2  2 2 . Cách 3. z 1 2 1 2 Ta có w    z  , mà w   suy ra   , suy ra
là số phức liên hợp của z . 2 2  z w z w z Suy ra .
z z  2  z  2 . Ta có P z  1  i z  1  i  2  2  2 2 .
Câu 35. (Chuyên ĐH Vinh – Nghệ An – L4) Cho hai số phức z và z thỏa mãn z z z z  1 . 1 2 1 2 1 2 Tính z z 1 2 3 A. 3 . B. 1 . C. 2 3. D. . 2
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 18 Hướng dẫn giải Chọn A Cách 1. 2 2 2 2 2 Ta có z zz z  2 zz
. Khi đó z z
 2 1  1  1  3  z z  3 . 1 2   1 2 1 2  1 2  1 2 Cách 2.  z  1 
Chọn z  1 từ đó suy ra z từ hệ 2
. Thay vào z z ta cũng được kết quả z z  3 . 1 2  z 1 2 1 2  1  1   2
Câu 36. (THPT Chuyên Võ Nguyên Giáp – Quảng Bình) Gọi  H  là hình biểu diễn tập hợp các số
phức z trong mặt phẳng tọa đọ Oxy để 2z z  3 số phức z có phần thực không âm. Tính
diện tích hình  H  . 3 3 A. 3 . B.  . C.  . D. 6 . 2 4 Hướng dẫn giải Chọn B
Đặt z x yi x  0 , a,b 2 2
 2z z  3  x  3yi  3  x  9y  9 . 2 2 x y 1 1 3  
 1 . Do hình  H  là nửa hình Elip có a  3,b  1. Khi đó S S  .  ab   . elip   9 1 2 2 2
Câu 37. (THPT Hoằng Hóa 4 – Thanh Hóa) Cho số phức z thỏa điều kiện z  1  z i . Tìm số phức
w z  2i  3 có môđun nhỏ nhất. 1 3 1 1 1 1 1 3 A.    i . B.     i . C.    i . D.     i . 2 2 2 2 2 2 2 2 Hướng dẫn giải Chọn B. Cách 1. Đại số
Đặt z a bi với a,b  .
Ta có z  1  z i a bi  1  a bi i  a  1  bi a  b  1i
 a  2  b a  b  2 2 2 1
1  a b  0
Khi đó w a bi  2i  3  a  3  b  2i  a  3  a  2i 2 2    
w  a  2  a  2 2 2 25 1 5 1 1 3 2
 2a  10a  13  2 a  5a    2 a         4  2  2  2 2 2 5 5 5 5 1 1  w  khi a   b    z  
i w    i . min 2 2 2 2 2 2 2 Cách 2. Hình học
Đặt z a bi với a,b  .
Ta có z  1  z i a bi  1  a bi i  a  1  bi a  b  1i
 a  2  b a  b  2 2 2 1
1  a b  0 , suy ra tập hợp các số phức z nằm trên đường thẳng
 : y  x . Xét điểm I 3; 2
  . Ta có w z  2i  3  w z  2i  3  IM .
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 19  Ta có IM
khi M là hình chiếu vuông góc của I trên  , M ;
m m suy ra IM  m  2; 3  m , min   5 1 1
IM.u  0  m  2  m  3  0  m
. Vậy w    i là số phức có môđun nhỏ nhất.  2 2 2
Câu 38. (THPT Đống Đa – Hà Nội) Cho số phức z thỏa mãn 2
z  2z  2  z  1  i . Biểu thức z có giá trị lớn nhất là A. 2  1 . B. 2 . C. 2  2 . D. 2  1. Hướng dẫn giải. Chọn A. Cách 1: Đại số.
z  1  i  0 1 2
z  2z  2  z  1  i  z  2 2
1  i z  1  i z  1  i z  1  i z  1  i   .
z  1  i  1 2  +) 1  z  1
  i z  2 3 . 2 2
+) Đặt z a bi , với a, b   . Khi đó ta có 2  a  1  b  1i  1  a  1  b  1  1 2 2
a b  2a  2b  1 , theo bất đẳng thức Bunhiacopxki ta có:  a b    2 2 2 2 1
8 a b   1 2
z  2 2 z  1  0  2  1  z  2  1 4 .
Từ 3 , 4 suy ra z  2  1 . max Cách 2: Hình học. 2
z  2z  2  z  1  i  z  2 2
1  i z  1  i
z  1  i  0 1
z  1  i z  1  i z  1  i   .
z  1  i  1 2  +) 1  z  1
  i z  2 3 . +) Đặt
z a bi , với a, b   . Khi đó ta có  2 2
2  a  1  b  1i  1  a  1  b  1  1, suy ra tập hợp
các số phức cần tìm nằm trên đường tròn tâm I  1  ; 1   , bán kính
R  1 . Suy ra OI R z OI R  2  1  z  2  1 . Vậy z  2  1 . max
Câu 39. (Sở GD Bắc Giang – L1) Cho số phức z thay đổi và luôn thỏa mãn z  3  4i  4 . Tìm giá trị lớn nhất P
của biểu thức P z Max A. P  12 . B. P  5 . C. P  9 . D. P  3 . Max Max Max Max Hướng dẫn giải Chọn C
Cho số phức z thõa mãn z a bi R tìm modun lớn nhất và nhỏ nhất
của số phức z . Điểm biểu diễn số phức z là đường tròn:   2    2 2 x a y bR Khi đó 2 2 z
OI R a b R , 2 2 z
OI R a b R . max min
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 20 Áp dụng: 2 2 P  3  4  4  9 . Max Câu 40
(Sở GD Quảng Ninh) Cho hai số phức z , z thỏa mãn z z z z  1 . Tính giá trị của 1 2 1 2 1 2 2 2  z   z  biểu thức 1 2 P       z z  2   1 
A. P  1  i .
B. P  1  i . C. P  1 .
D. P  1  i . Hướng dẫn giải Chọn C Cách 1. z z z z z Ta có 1 1 2 1 1 GT   1    1   1 . z z z z 2 2 2 2  3 zb    1 3 1
Đặt 1  a bi ta có: a b   a  2 2 2 2 1 1  b 2 2    w    P w   1  . z 2  1 2 2 w 2 a    2 Cách 2. 1 i 3 1 i 3 Chọn z   ; z     P  1 . 1 2 2 2 2 2
Cách 3. Dùng dạng lượng giác của số phức (đọc thêm). 
Gọi Az ; B z ; AB z z  OAB là tam giác đều cạnh 1 1   2   1 2  2 2 2  z   r     r  Khi đó 1 1 1 1             1 2  2  1 1
 20  cos120  i sin120 1 2   1 2  0  0 0  z r   r  2   2 2   2  2  z  Tương tự 1    cos 0 1  20   i sin 0 120    P  1  . z  2 
Câu 41. (THPT chuyên Hà Giang – L1) Cho số phức z thỏa mãn điều kiện z  2  2i  1 . Tìm giá trị lớn nhất của z
A. max z  2 2  1 . B. max z  2 2 .
C. max z  2 2  2 .
D. max z  2 2  1. Hướng dẫn giải Chọn A Cách 1. Đại số
Giả sử z a bi , với a,b . 2 2
Ta có: z  2  2i  1  a bi  2  2i  1  a  2  b  2i  1  a  2  b  2  1 .
a  2  sin t Đặt  . b  2   cost  2 2 Khi đó: 2 2
z a b  2  sint   2
  cost  9  4sint  cost  9  4 2 2
sin t  cos t  9  4 2  2 2  1  z
 2 2  1 khi sin t   cost . max
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 21 Cách 2. Hình học
Cho số phức z thỏa mãn z a bi R tìm mô đun lớn nhất và nhỏ nhất
của số phức z . Điểm biểu diễn số phức z là đường tròn:   2    2 2 x a y bR Khi đó 2 2 z
OI R a b R , 2 2 z
OI R a b R . max min Áp dụng: 2 2 P
 2  2  1  2 2  1 . max
Câu 42. (Chuyên KHTN – Hà Nội – L4) Gọi z , z là 2 nghiệm của phương trình 2
z z  1  0 . Tính giá 1 2 trị 2017 2017 P zz . 1 2 A. P  1 . B. P  1 . C. P  0 . D. P  2 . Hướng dẫn giải Chọn B
Vì z là nghiệm của phương trình 2
z z  1  0 nên ta có 1 2 3 3 2016 2017
z z  1  0  z  1  0  z  1  z  1  zz 1 1 1 1 1 1 1
Chứng minh tương tự: 2017 z
z . Vậy P z z  1 . 2 2 1 2
Câu 43. (Chuyên KHTN – Hà Nội – L4) Với hai số phức z và z thỏa mãn z z  8  6i và z z  2 1 2 1 2 1 2
. Tìm giá trị lớn nhất của P z z . 1 2 A. P  5  3 5 . B. P  2 26 . C. P  4 6 . D. P  34  3 2 . Hướng dẫn giải Chọn B
Đặt OA z ,OB z ( với O là gốc tọa độ, A,B là điểm biểu diễn của 1 2 z , z ). 1 2
Dựng hình bình hành OACB , khi đó ta có AB z z  2 , 1 2
OC z z  10 , OM  5 . 2 1 Theo định lý đường trung tuyến ta có 2 2 2 OA OB  2  AB 2 2 2 2 2 OM
OA OB  52  zz  52 1 2 4 2 2
Ta có z z  2 zz
 2 26 (BĐT Bunhiacopxki). Vậy P  2 26 . 1 2  1 2  max
Câu 44. (Sở GD Hải Dương) Cho số phức z thỏa mãn .
z z  1 . Tìm giá trị nhỏ nhất của biểu thức: 3
P |z  3z z ||z z |. 15 3 13 A. . B. . C. . D. 3 . 4 4 4 Hướng dẫn giải Chọn B
Giả sử z a bi z a bi , với a,b . . z z  1 suy ra 2 2 b  1  a .
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454
Một số câu hỏi số phức khó trong các đề thi thử 2017 Trang 22 2 2 3
P |z  3z z||z z| suy ra 2 P a  2 2 a b   2  b  2 2 a b   2 3 4 3 2  4a 3
P f x 2
x x  1 với x  0; 4 
 . Lập bảng biến thiên ta suy ra P  . min 4
Trong quá trình biên soạn tôi cũng khó có thể tránh khỏi sai sót. Mong nhận được sự góp ý từ các bạn và
quí thầy cô. Mọi góp ý xin inbox trực tiếp cho tôi theo địa chỉ https://www.facebook.com/lehong.quoc.12
.Chân thành cảm ơn và chúc các bạn học tốt!
Sưu tầm và biên soạn: Lê Hồng Quốc ĐT: 0898.244.454