






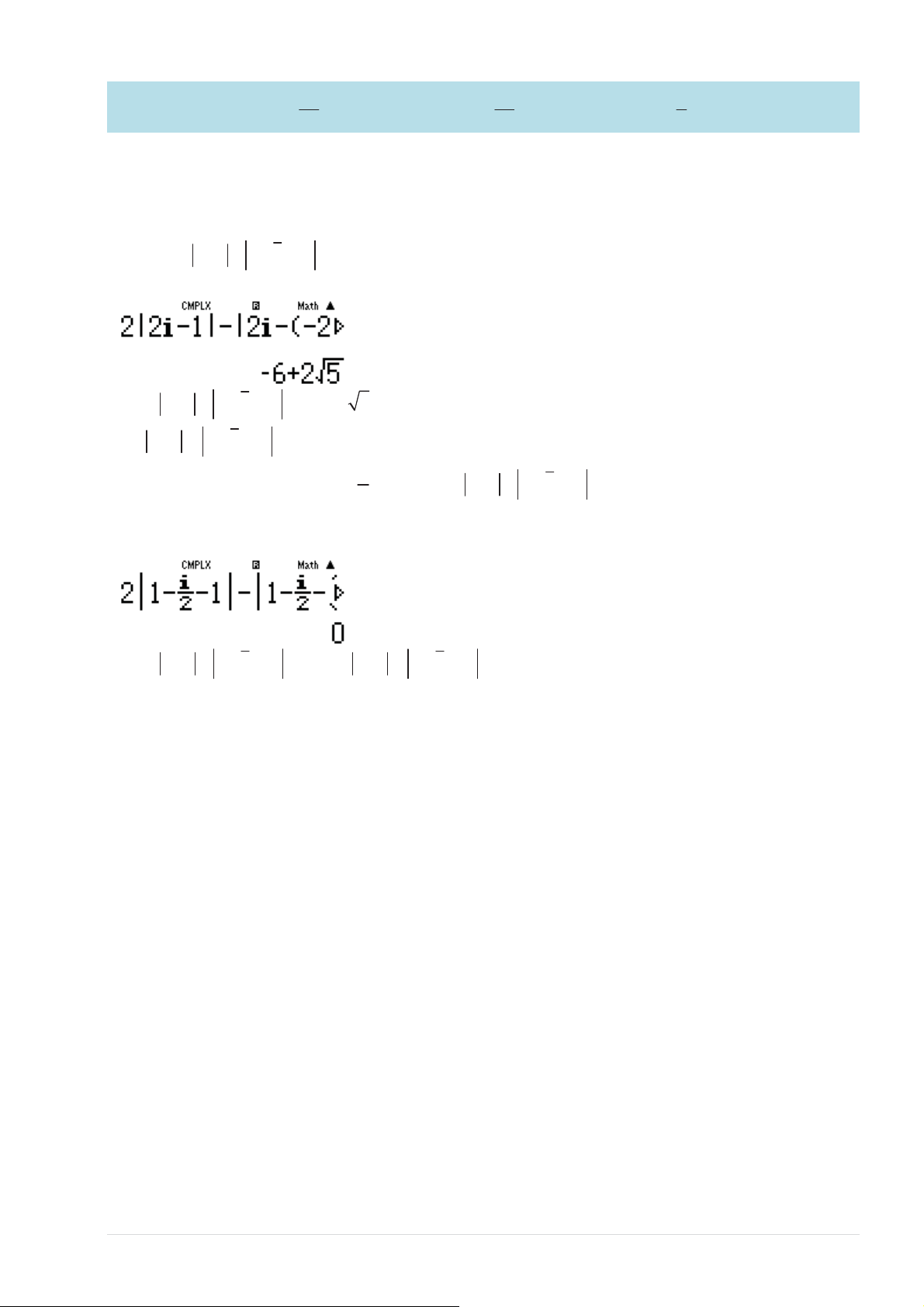


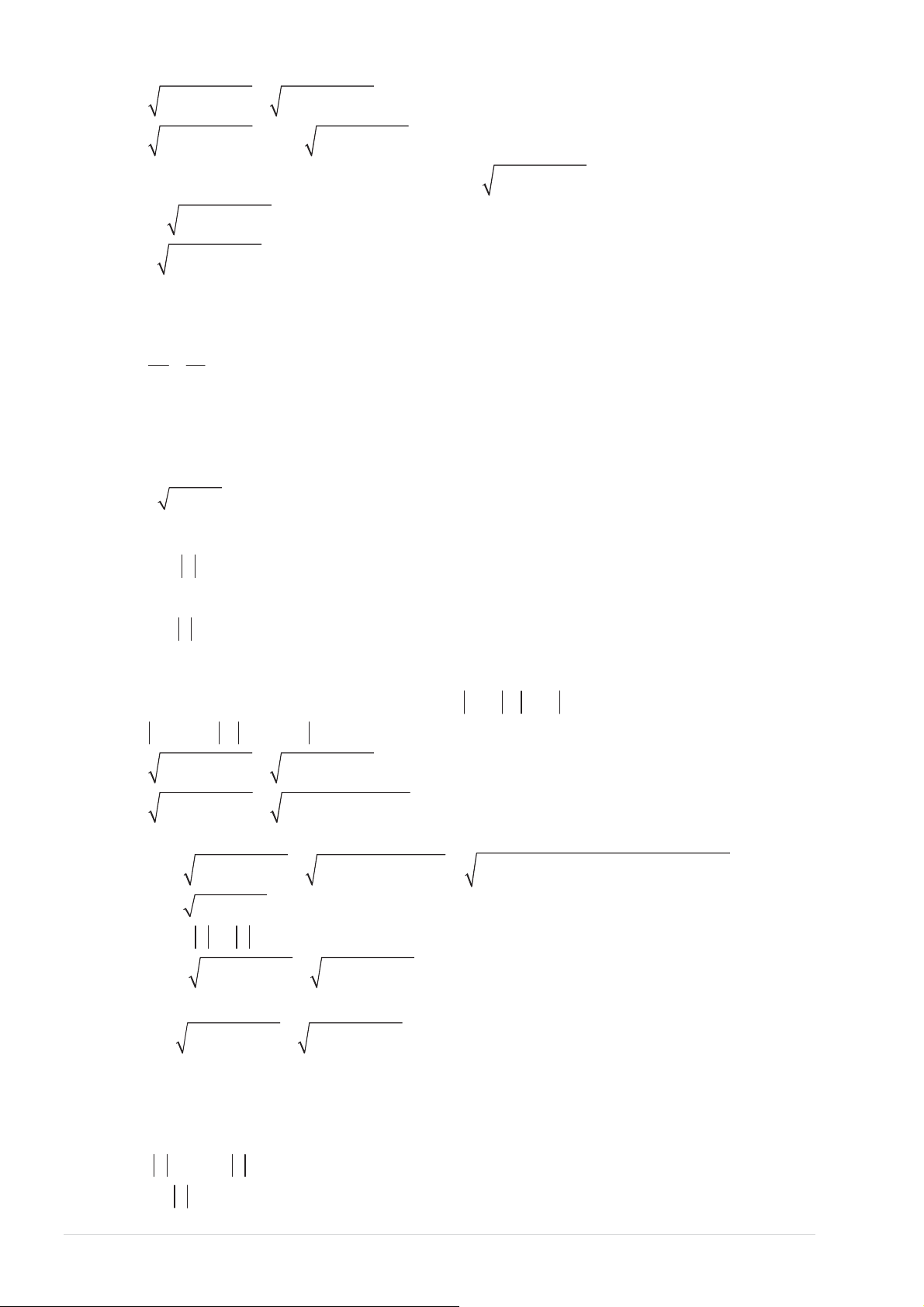




Preview text:
ЎЇϮБЌȂ
GIẢI NHANH BÀI TOÁN SỐ PHỨC A2ІϪЁЏǤ I) KIӂN THӬC NӄN TҦNG
1. Các khái niӋm thѭӡng gһp
ҿŶǀҷңŽůăŵҾƚĜҢŝůӇӄŶŐĜӇӄĐŬşŚŝҵƵ i ǀăĐſƚşŶŚĐŚҤƚ 2 i = −1
^ҺƉŚӈĐůăŵҾƚďŝҳƵƚŚӈĐĐſĚҢŶŐ a + bi ƚƌŽŶŐĜſ a,b ůăĐĄĐƐҺƚŚӌĐ͘dƌŽŶŐĜſ a ĜӇӄĐŐҸŝůă
ƉŚҥŶƚŚӌĐǀă b ĜӇӄĐŐҸŝůăƐҺңŽ
^ҺƉŚӈĐůŝġŶŚӄƉĐӆĂƐҺƉŚӈĐ z = a + bi ůăƐҺƉŚӈĐ z = a − bi 1 1
^ҺƉŚӈĐŶŐŚҷĐŚĜңŽĐӆĂƐҺƉŚӈĐ z = a + bi ůăƐҺƉŚӈĐ 1 z− = = z a + bi
DƀĚƵůĐӆĂƐҺƉŚӈĐ z = a + bi ĜӇӄĐŬşŚŝҵƵůă z ǀăĐſĜҾůӀŶ 2 2 z = a + b 2. LӋnh Caso
ҳdžӊůljƐҺƉŚӈĐƚĂƐӊĚӅŶŐůҵŶŚƚşŶŚƐҺƉŚӈĐDKϮ
>ҵŶŚƚşŶŚDƀĜƵŶĐӆĂƐҺƉŚӈĐůă^,/&d,zW
>ҵŶŚƚşŶŚƐҺƉŚӈĐůŝġŶŚӄƉ z ůă^,/&dϮϮ
>ҵŶŚƚşŶŚĐŐƵŵĞŶƚĐӆĂƐҺƉŚӈĐůă^,/&dϮϭ II) VÍ DӨ MINH HӐA
VD1-[ĈӅ minh hӑa THPT Quӕc Gia lҫn 1 năm 2017]
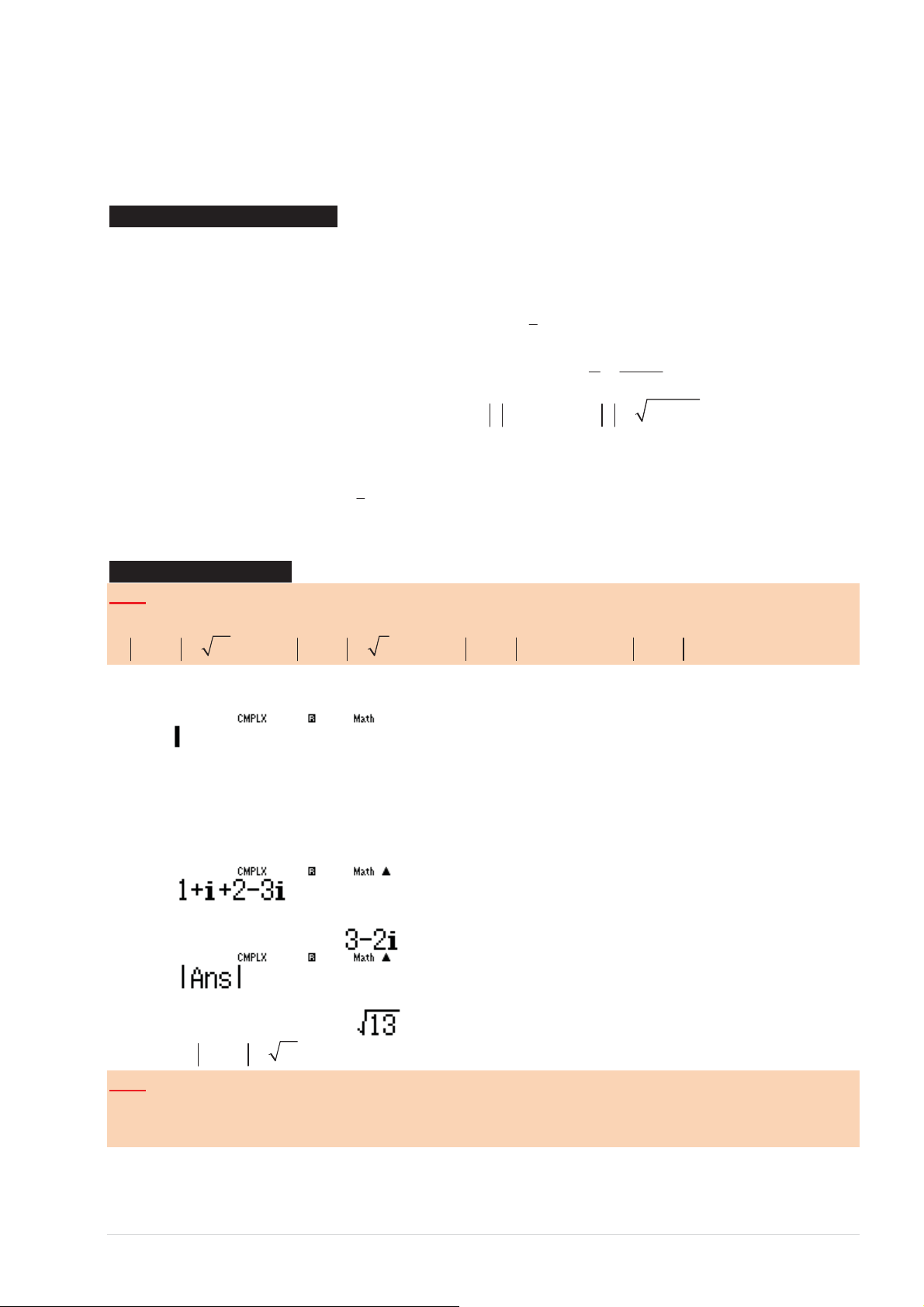
Cho hai sӕ phӭc z = 1+ i và z = 2 − 3i .Tính Môÿun cӫa sӕ phӭc z + z 1 2 1 2
A. z + z = 13
B. z + z = 5
C. z + z = 1
D. z + z = 5 1 2 1 2 1 2 1 2 GIҦI ¾
ĉŶŐŶŚҨƉůҵŶŚƐҺƉŚӈĐZ
;<ŚŝŶăŽŵĄLJƚşŶŚŚŝҳŶƚŚҷĐŚӋDW>yƚŚŞďҩƚĜҥƵƚşŶŚƚŽĄŶƐҺƉŚӈĐĜӇӄĐͿ ¾
ҳƚşŶŚDƀĜƵŶĐӆĂƐҺƉŚӈĐƚĂŶŚҨƉďŝҳƵƚŚӈĐǀăŽŵĄLJƚşŶŚƌһŝƐӊĚӅŶŐůҵŶŚ^,/&d,zW ESE TF0
sҨLJ z + z = 13 ĄƉƐҺĐŚşŶŚdžĄĐůă 1 2
VD2-[Thi thӱ báo Toán hӑc tuәi trҿ lҫn 3 năm 2017] 2 2
Sӕ phӭc liên hӧp vӟi sӕ phӭc z = (1+ i) − 3(1+ 2i) là : A. 9 − −10i B. 9 +10i C. 9 −10i D. 9 − +10i GIҦI ¾
^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽƚşŶŚ z EGSEG TOANMATH.com
Tác giả: Trần Bá Hưng z = 9 −10i ¾
^ҺƉŚӈĐůŝġŶŚӄƉĐӆĂ z = a + bi ůă z = a − bi ͗
sҨLJ z = 9 +10i ĄƉĄŶůăĐŚşŶŚdžĄĐ
VD3-[Thi thӱ trung tâm DiӋu HiӅn – Cҫn thѫ lҫn 1 năm 2017]
Cho sӕ phӭc z = a + bi . Sӕ phӭc 2 z có phҫn ҧo là : A. 2 2 a b B. 2 2 2a b C. 2ab D. ab GIҦI ¾
sŞĜҲďăŝĐŚŽӂĚҢŶŐƚҼŶŐƋƵĄƚŶġŶƚĂƚŝұŶŚăŶŚ͞ĐĄďŝҵƚŚſĂ͟ďăŝƚŽĄŶďҪŶŐĐĄĐŚĐŚҸŶŐŝĄƚƌҷĐŚŽ
a, b ;ůӇƵljŶġŶĐŚҸŶĐĄĐŐŝĄƚƌҷůүĜҳƚƌĄŶŚdžңLJƌĂƚƌӇӁŶŐŚӄƉĜҭĐďŝҵƚͿ͘
ŚҸŶ a = 1.25 ǀă b = 2.1ƚĂĐſ z = 1.25 + 2.1i ¾
^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽƚşŶŚ 2 z EG 21 sҨLJƉŚҥŶңŽůă 4 21 ¾
yĞŵĜĄƉƐҺŶăŽĐſŐŝĄƚƌҷůă
ƚŚŞĜĄƉĄŶĜſĐŚşŶŚdžĄĐ͘dĂĐſ͗ 4 21 Vұy 2ab =
Ĉáp án C là chính xác 4
VD4-[Thi thӱ báo Toán hӑc tuәi trҿ lҫn 4 năm 2017]
ĈӇ sӕ phӭc z = a + (a − )
1 i ( a là sӕ thӵc) có z = 1 thì : 1 3 ªa = 0 A. a = B. a = C. « D. a = 1 ± 2 2 ¬a = 1 GIҦI ¾
ҳdžӊůljďăŝŶăLJƚĂƐӊĚӅŶŐƉŚĠƉƚŚӊ͕ƚƵLJŶŚŝġŶƚĂĐŚҸŶ a ƐĂŽĐŚŽŬŚĠŽůĠŽŶŚҤƚĜҳƉŚĠƉƚŚӊƚŞŵ
ĜĄƉƐҺŶŚĂŶŚŶŚҤƚ͘dĂĐŚҸŶ a = 1ƚƌӇӀĐ͕ŶұƵ a = 1ĜƷŶŐƚŚŞĜĄƉĄŶĜƷŶŐĐŚҶĐſƚŚҳů㌎ҭĐ͕
ŶұƵ a = 1ƐĂŝƚŚŞǀăĜҲƵƐĂŝ͘ ¾
sӀŝ a = 1^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽƚşŶŚ z SE TF0 TOANMATH.com
Tác giả: Trần Bá Hưng
sҨLJ z = 1 ĄƉĄŶĜƷŶŐĐŚҶĐſƚŚҳů㌎ҭĐ ¾
dŚӊǀӀŝ a = 0 ^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽƚşŶŚ z ͗ SE TF0
sҨLJ z = 1 ĄƉĄŶĐŚşŶŚdžĄĐůă
VD5-[Thi thӱ THPT Phҥm Văn Ĉӗng – Ĉҳc Nông lҫn 1 năm 2017] 2 20
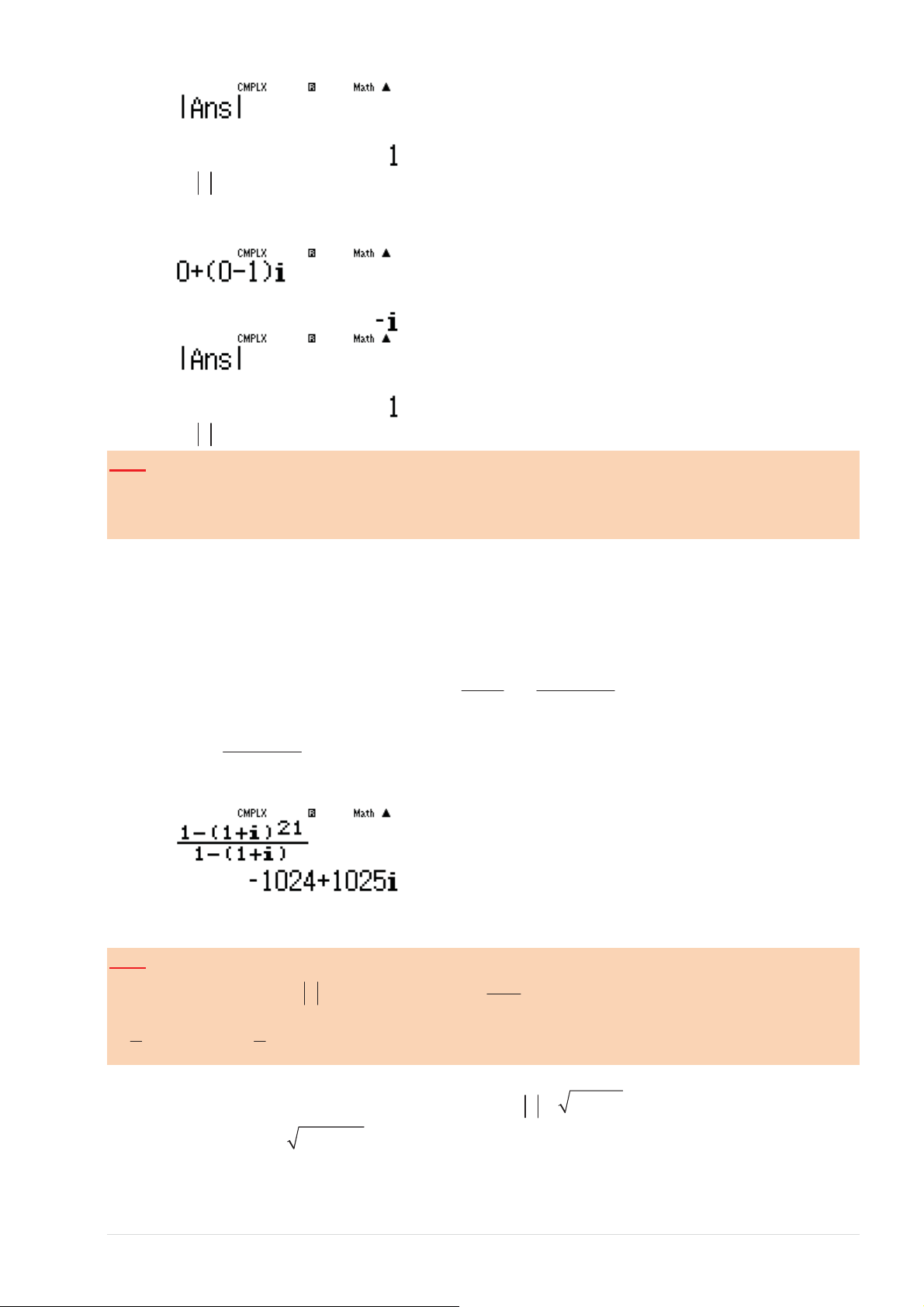
Sӕ phӭc z = 1+ (1+ i) + (1+ i) + ...+ (1+ i) có giá trӏ bҵng : A. 20 −2 B. 10 − + ( 20 2 2 + ) 1 i C. 10 + ( 10 2 2 + ) 1 i D. 10 10 2 + 2 i GIҦI ¾ 2 20
EұƵƚĂŶŚҨƉĐңďŝҳƵƚŚӈĐ1+ (1+ i) + (1+ i) + ...+ (1+ i) ǀăŽŵĄLJƚşŶŚĂƐŝŽƚŚŞǀҧŶĜӇӄĐ͕
ŶŚӇŶŐŵҤƚŶŚŝҲƵƚŚĂŽƚĄĐƚĂLJ͘ҳƌƷƚŶŐҩŶĐƀŶŐĜŽҢŶŶăLJƚĂƚŝұŶŚăŶŚƌƷƚŐҸŶďŝҳƵƚŚӈĐ
dĂƚŚҤLJĐĄĐƐҺŚҢŶŐƚƌŽŶŐĐƶŶŐďŝҳƵƚŚӈĐĜҲƵĐſĐŚƵŶŐŵҾƚƋƵLJůƵҨƚ͞ƐҺŚҢŶŐƐĂƵďҪŶŐƐҺŚҢŶŐ
ƚƌӇӀĐŶŚąŶǀӀŝĜҢŝůӇӄŶŐ1+ i ͞ǀҨLJĜąLJůăĐҤƉƐҺŶŚąŶǀӀŝĐƀŶŐďҾŝ1+ i 21 n − q − − i
1+ (1+ i) + (1+ i)2 + ...+ (1+ i)20 1 1 (1 ) = U =1. 1 1−1 1− (1− i) − ( + i)21 1 1 ¾ sӀŝ z =
^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽƚşŶŚ z 1− (1+ i) DSEA5SE dĂƚŚҤLJ 10 z = − + i = − + ( 10 1024 1025 2 2 + ) 1 i ĄƉĄŶĐŚşŶŚdžĄĐůă
VD6-[Thi thӱ chuyên KHTN lҫn 1 năm 2017] 1
NӃu sӕ phӭc z thӓa mãn z = 1 thì phҫn thӵc cӫa bҵng : 1 − z 1 1 A. B. − C. 2 D.Mӝt giá trӏ khác 2 2 GIҦI ¾
ҭƚƐҺƉŚӈĐ z = a + bi ƚŚŞDƀĜƵŶĐӆĂƐҺƉŚӈĐnjůă 2 2
z = a + b = 1 ¾ ŚҸŶ a = 0.5 2 2
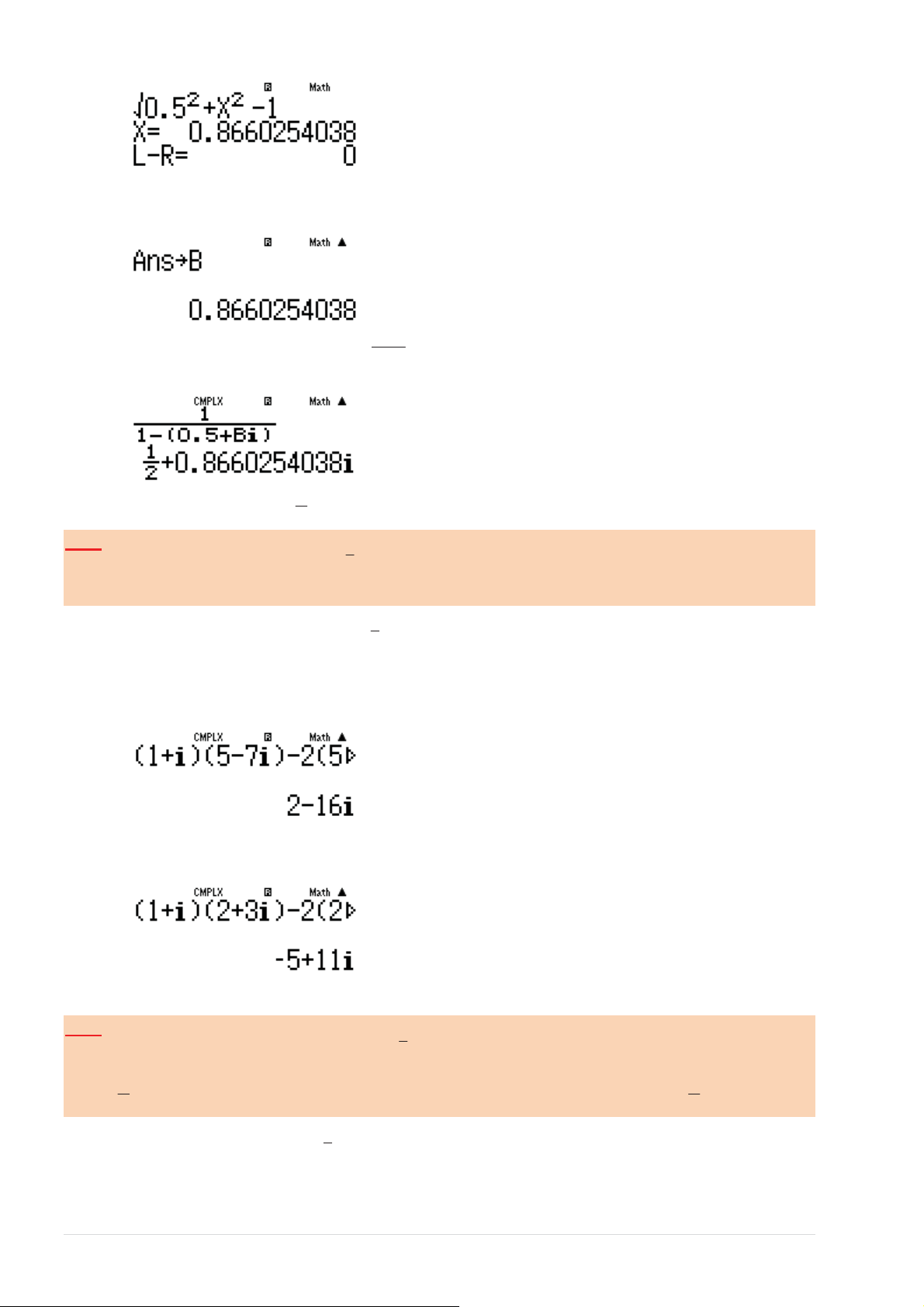
0.5 + b =1͘^ӊĚӅŶŐĐŚӈĐŶĉŶŐĚžŶŐŚŝҵŵ^,/&d^K>sĜҳƚŞŵb ZVG4GSTU TOANMATH.com
Tác giả: Trần Bá Hưng
>ӇƵŐŝĄƚƌҷŶăLJǀ㎠b T-[ 1 ¾
dƌӂůҢŝĐŚұĜҾDW>yĜҳƚşŶŚŐŝĄƚƌҷ ͗ 1 − z ZD5S4[E 1
sҨLJƉŚҥŶƚŚӌĐĐӆĂ z ůă ĄƉĄŶĐŚşŶŚdžĄĐůă 2
VD7-[Thi thӱ nhóm toán Ĉoàn Trí DNJng lҫn 3 năm 2017]
Tìm sӕ phӭc z biӃt rҵng : (1+ i) z − 2z = 5 − +11i
A. z = 5 − 7i B. z = 2 + 3i C. z = 1+ 3i
D. z = 2 − 4i GIҦI ¾
sӀŝ z = 5 − 7i ƚŚŞƐҺƉŚӈĐůŝġŶŚӄƉ z = 5 + 7i ͘EұƵĜĄƉĄŶĜƷŶŐƚŚŞƉŚӇҿŶŐƚƌŞŶŚ͗
(1+i)(5−7i)−2(5+7i) = 5 − +11i ;ϭͿ ¾
^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽŶŚҨƉǀұƚƌĄŝĐӆĂ;ϭͿ ESESE sŞ 2 −16i ≠ 5
− +11i ŶġŶĜĄƉĄŶƐĂŝ ¾
dӇҿŶŐƚӌŶŚӇǀҨLJǀӀŝĜĄƉĄŶ EESSE
ҴƚŚҤLJǀұƚƌĄŝ;ϭͿсǀұƉŚңŝ;ϭͿс 5 − +11i ĄƉƐҺĐŚşŶŚdžĄĐůă
VD8-[ĈӅ minh hӑa cӫa bӝ GD-ĈT lҫn 2 năm 2017]
Cho sӕ phӭc z = a + bi thӓa mãn (1+ i) z + 2z = 3 + 2i . Tính P = a + b 1 1 A. P = B. P = 1 C. P = −1 D. P = − 2 2 GIҦI ¾
WŚӇҿŶŐƚƌŞŶŚ ⇔ (1+ i) z + 2z − 3 − 2i = 0 ;ϭͿ͘<ŚŝŶŚҨƉƐҺƉŚӈĐůŝġŶŚӄƉƚĂŶŚҤŶůҵŶŚ T TOANMATH.com
Tác giả: Trần Bá Hưng ¾
^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽŶŚҨƉǀұƚƌĄŝĐӆĂ;ϭͿ E4T4SSE ¾
X ůăƐҺƉŚӈĐŶġŶĐſĚҢŶŐ X = a + bi ͘EŚҨƉ X = 1000 +100i ;ĐſƚŚҳƚŚĂLJ a;b ůăƐҺŬŚĄĐͿ UE
2897 = 3.1000 −100 − 3 = 3a − b − 3
sҨLJǀұƚƌĄŝĐӆĂ;ϭͿďҪŶŐ 2897 + 898i ͘dĂĐſ͗ ®898 ¯
=1000 −100 − 2 = a − b − 2 3
a − b − 3 = 0 1 −3
DҭƚŬŚĄĐĜĂŶŐŵƵҺŶǀұƚƌĄŝ = 0 ® ⇔ a = ;b = a ¯ − b − 2 = 0 2 2 sҨLJ a + b = 1 − ĄƉƐҺĐŚşŶŚdžĄĐůă 5 + 3i 3
VD9-Sӕ phӭc z = có mӝt Acgument là : 1− 2i 3 π π π 8π A. B. C. D. 6 4 2 3 GIҦI ¾
dŚƵŐҸŶ z ǀҲĚҢŶŐƚҺŝŐŝңŶ z = −1+ 3i DEV5SEV ¾
dŞŵĐŐƵŵĞŶƚĐӆĂ z ǀӀŝůҵŶŚ^,/&dϮϭ TSVE 2π 2π
sҨLJ z ĐſϭĐŐƵŵĞŶƚůă
͘dƵLJŶŚŝġŶŬŚŝƐŽƐĄŶŚŬұƚƋƵңƚĂůҢŝŬŚƀŶŐƚŚҤLJĐſŐŝĄƚƌҷŶăŽůă ͘ 3 3
<ŚŝĜſƚĂŶŚӀĜұŶƚşŶŚĐŚҤƚ͞EұƵŐſĐα ůăŵҾƚĐŐƵŵĞŶƚƚŚŞŐſĐα + 2π ĐƹŶŐůăŵҾƚĐŐƵŵĞŶƚ͟ 2π 8π
ĄƉƐҺĐŚşŶŚdžĄĐůăǀŞ + 2π = 2 3 III) BÀI TҰP TӴ LUYӊN
Bài 1-[Thi thӱ chuyên Lam Sѫn – Thanh Hóa lҫn 2 năm 2017]
Cho hai sӕ phӭc z = 1+ i, z = 2 + 3i . Tìm sӕ phӭc w = ( z .z 1 )2 1 2 2
A. w = 6 + 4i B. w = 6 − 4i C. w = −6 − 4i
D. w = −6 + 4i
Bài 2-[Thi thӱ THPT Phan Chu Trinh – Phú Yên lҫn 1 năm 2017] TOANMATH.com
Tác giả: Trần Bá Hưng
Cho sӕ phӭc z = a + bi . Sӕ phӭc 1
z− có phҫn thӵc là : a b − A. a + b B. C.
D. a − b 2 2 a + b 2 2 a + b
Bài 3-[Thi thӱ nhóm toán Ĉoàn Trí DNJng lҫn 1 năm 2017] § 1 ·
Tìm môÿun cӫa sӕ phӭc z = 2 − 3i ¨ + 3i ¸ là : © 2 ¹ 103 3 103 5 103 A. B. C. D. Ĉáp án khác 2 2 2
Bài 4-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 3 năm 2017] 2 3 22
Cho sӕ phӭc z = (1+ i) + (1+ i) + ...+ (1+ i) . Phҫn thӵc cӫa sӕ phӭc z là : A. 11 2 − B. 11 2 − + 2 C. 11 2 − − 2 D. 11 2
Bài 5-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 3 năm 2017]
Cho sӕ phӭc z = 2 − 3i . Phҫn ҧo cӫa sӕ phӭc w = (1+ i) z − (2 − i) z là : A. −9i B. −9 C. −5 D. −5i
Bài 6-[ĈӅ thi Ĉҥi hӑc –Cao ÿҷng khӕi A năm 2009]
Cho sӕ phӭc z = a + bi thӓa mãn ÿiӅu kiӋn ( − i) z + ( + i) z = −( + i)2 2 3 4 1 3
. Tìm P = 2a + b A. 3 B. −1 C.1 D. Ĉáp án khác
Bài 7-[Thi thӱ chuyên Lam Sѫn – Thanh Hóa lҫn 2]
Cho sӕ phӭc z = a + bi thӓa mãn ÿiӅu kiӋn ( − i) z + ( + i) z = −( + i)2 2 3 4 1 3
. Tìm P = 2a + b A. 3 B. −1 C.1 D. Ĉáp án khác
LӠI GIҦI BÀI TҰP TӴ LUYӊN
Bài 1-[Thi thӱ chuyên Lam Sѫn – Thanh Hóa lҫn 2 năm 2017]
Cho hai sӕ phӭc z = 1+ i, z = 2 + 3i . Tìm sӕ phӭc w = ( z .z 1 )2 1 2 2
A. w = 6 + 4i B. w = 6 − 4i C. w = −6 − 4i
D. w = −6 + 4i GIҦI
^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽǀӀŝĐŚӈĐŶĉŶŐDKϮ;DW>yͿ EG2E Vұy w = 6
− + 4i ta chӑn D là ÿáp án chính xác
Bài 2-[Thi thӱ THPT Phan Chu Trinh – Phú Yên lҫn 1 năm 2017]
Cho sӕ phӭc z = a + bi . Sӕ phӭc 1
z− có phҫn thӵc là : a b − A. a + b B. C.
D. a − b 2 2 a + b 2 2 a + b GIҦI
sŞĜҲďăŝŵĂŶŐƚşŶŚĐŚҤƚƚҼŶŐƋƵĄƚŶġŶƚĂƉŚңŝĐĄďŝҵƚŚſĂ͕ƚĂĐŚҸŶ a = 1;b = 1.25͘ 1 sӀŝ −1 z
= ^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽ z D5E TOANMATH.com
Tác giả: Trần Bá Hưng 16
Ta thҩy phҫn thӵc sӕ phӭc 1 z− là :
ÿây là 1 giá trӏ dѭѫng. Vì ta chӑn b > a > 0 nên ta thҩy ngay 41
ÿáp sӕ C và D sai. 9 16
Thӱ ÿáp sӕ A có a + b = 1+1.25 = ≠
vұy ÿáp sӕ A cNJng sai Ĉáp án chính xác là B 4 41
Bài 3-[Thi thӱ nhóm toán Ĉoàn Trí DNJng lҫn 1 năm 2017] § 1 ·
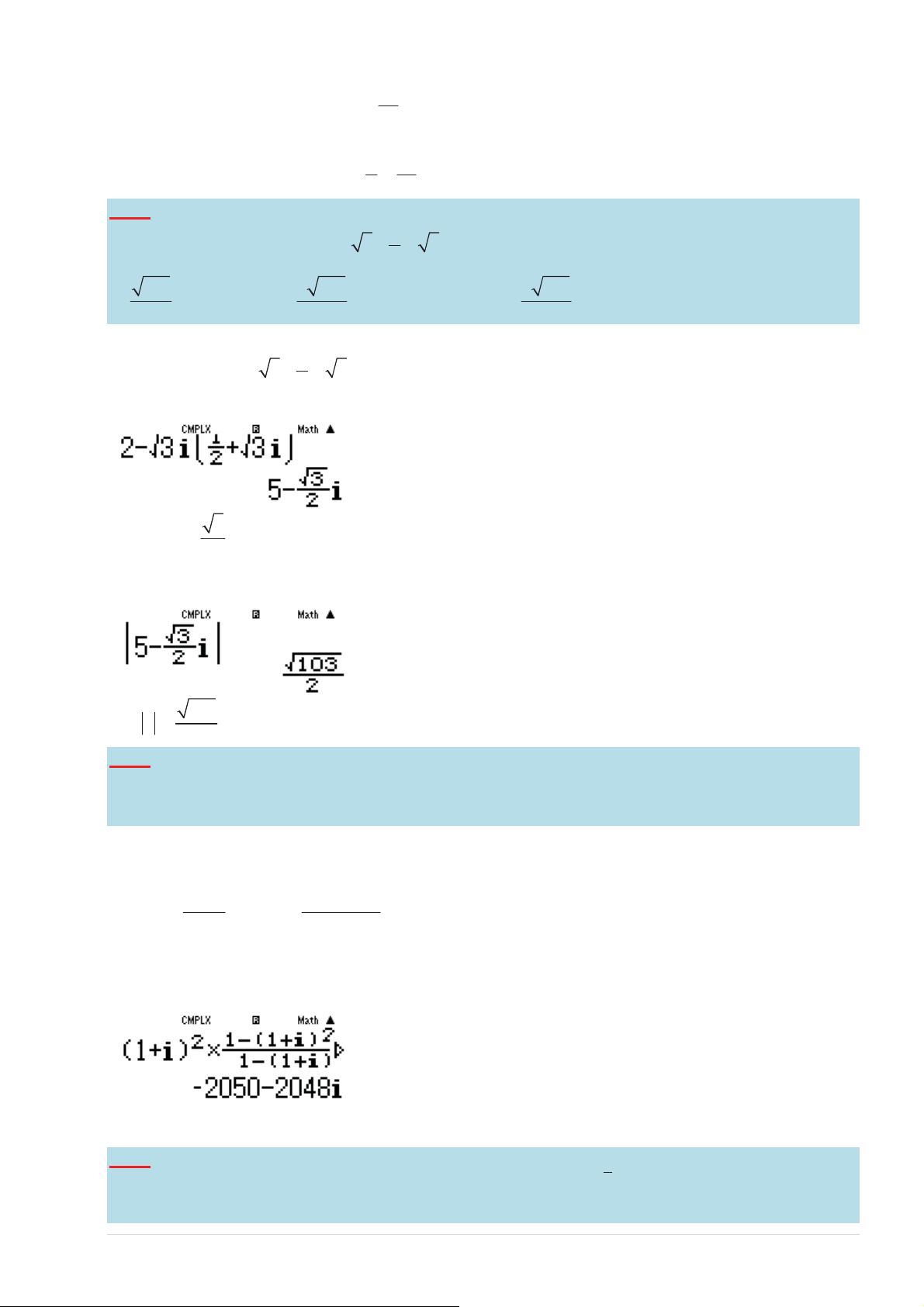
Tìm môÿun cӫa sӕ phӭc z = 2 − 3i ¨ + 3i ¸ là : © 2 ¹ 103 3 103 5 103 A. B. C. D. Ĉáp án khác 2 2 2 '/ѵ/ § 1 ·
dşŶŚƐҺƉŚӈĐ z = 2 − 3i ¨ + 3i ¸ © 2 ¹ SVED5VE 3 Vұy z = 5 − i 2
ƶŶŐůҵŶŚ^,/&d,zWƚşŶŚDƀĜƵŶĐӆĂƐҺƉŚӈĐ z ƚĂĜӇӄĐ TFSDV5E 103 sҨLJ z = ĄƉƐҺĐŚşŶŚdžĄĐůă 2
Bài 4-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 3 năm 2017] 2 3 22
Cho sӕ phӭc z = (1+ i) + (1+ i) + ...+ (1+ i) . Phҫn thӵc cӫa sӕ phӭc z là : A. 11 2 − B. 11 2 − + 2 C. 11 2 − − 2 D. 11 2 '/ѵ/
ĆLJƐҺƚƌġŶůăŵҾƚĐҤƉƐҺŶŚąŶǀӀŝU = (1+ i)2 ͕ƐҺƐҺŚҢŶŐůă 21ǀăĐƀŶŐďҾŝůă1+ i ͘dŚƵŐҸŶ z ƚĂĜӇӄĐ 1 21 1 n − q − + 2 1 1 i ͗ z = U . = 1+ i . 1 ( ) ( ) 1− q 1− (1+ i)
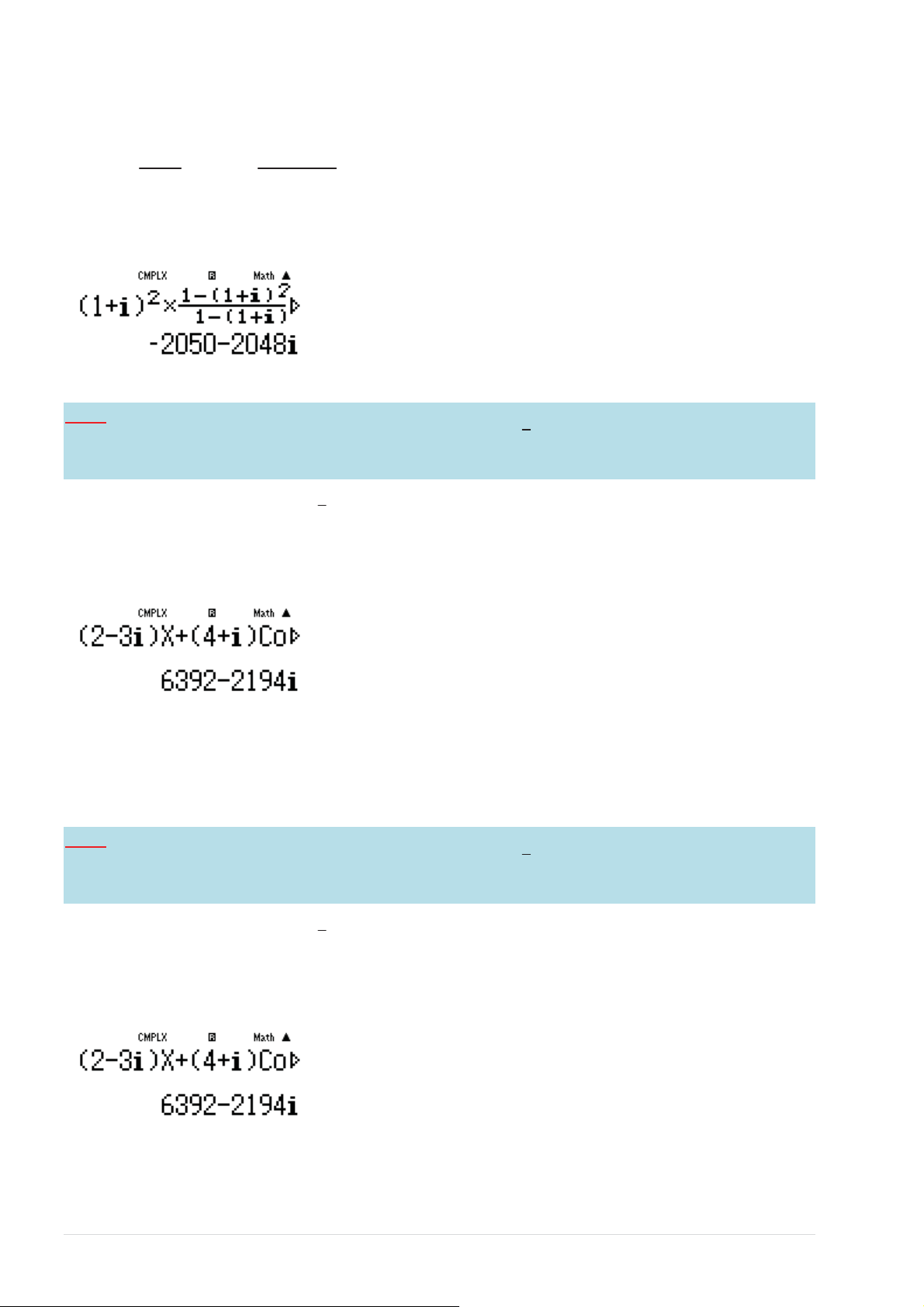
^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽƚşŶŚ z EG2DSEA5S E Vұy z = 2050 − − 2048i
WŚҥŶңŽƐҺƉŚӈĐ z ůă 11
−2050 = −2 − 2 ĄƉƐҺĐŚşŶŚdžĄĐůă
Bài 5-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 3 năm 2017]
Cho sӕ phӭc z = 2 − 3i . Phҫn ҧo cӫa sӕ phӭc w = (1+ i) z − (2 − i) z là : A. −9i B. −9 C. −5 D. −5i TOANMATH.com
Tác giả: Trần Bá Hưng '/ѵ/
ĆLJƐҺƚƌġŶůăŵҾƚĐҤƉƐҺŶŚąŶǀӀŝU = (1+ i)2 ͕ƐҺƐҺŚҢŶŐůă 21ǀăĐƀŶŐďҾŝůă1+ i ͘dŚƵŐҸŶ z ƚĂĜӇӄĐ 1 21 1 n − q − + 2 1 1 i ͗ z = U . = 1+ i . 1 ( ) ( ) 1− q 1− (1+ i)
^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽƚşŶŚ z EG2DSEA5S E Vұy z = 2050 − − 2048i
WŚҥŶңŽƐҺƉŚӈĐ z ůă 11
−2048 = −2 ĄƉƐҺĐŚşŶŚdžĄĐůă
Bài 6-[ĈӅ thi Ĉҥi hӑc –Cao ÿҷng khӕi A năm 2009]
Cho sӕ phӭc z = a + bi thӓa mãn ÿiӅu kiӋn ( − i) z + ( + i) z = −( + i)2 2 3 4 1 3
.Tìm P = 2a + b A. 3 B. −1 C.1 D. Ĉáp án khác '/ѵ/
WŚӇҿŶŐƚƌŞŶŚ ⇔ ( − i) z + ( + i) z + ( + i)2 2 3 4 1 3 = 0
EŚҨƉǀұƚƌĄŝǀăŽŵĄLJƚşŶŚĂƐŝŽǀă>ǀӀŝ X = 1000 +100i SE4ET4 EGUE
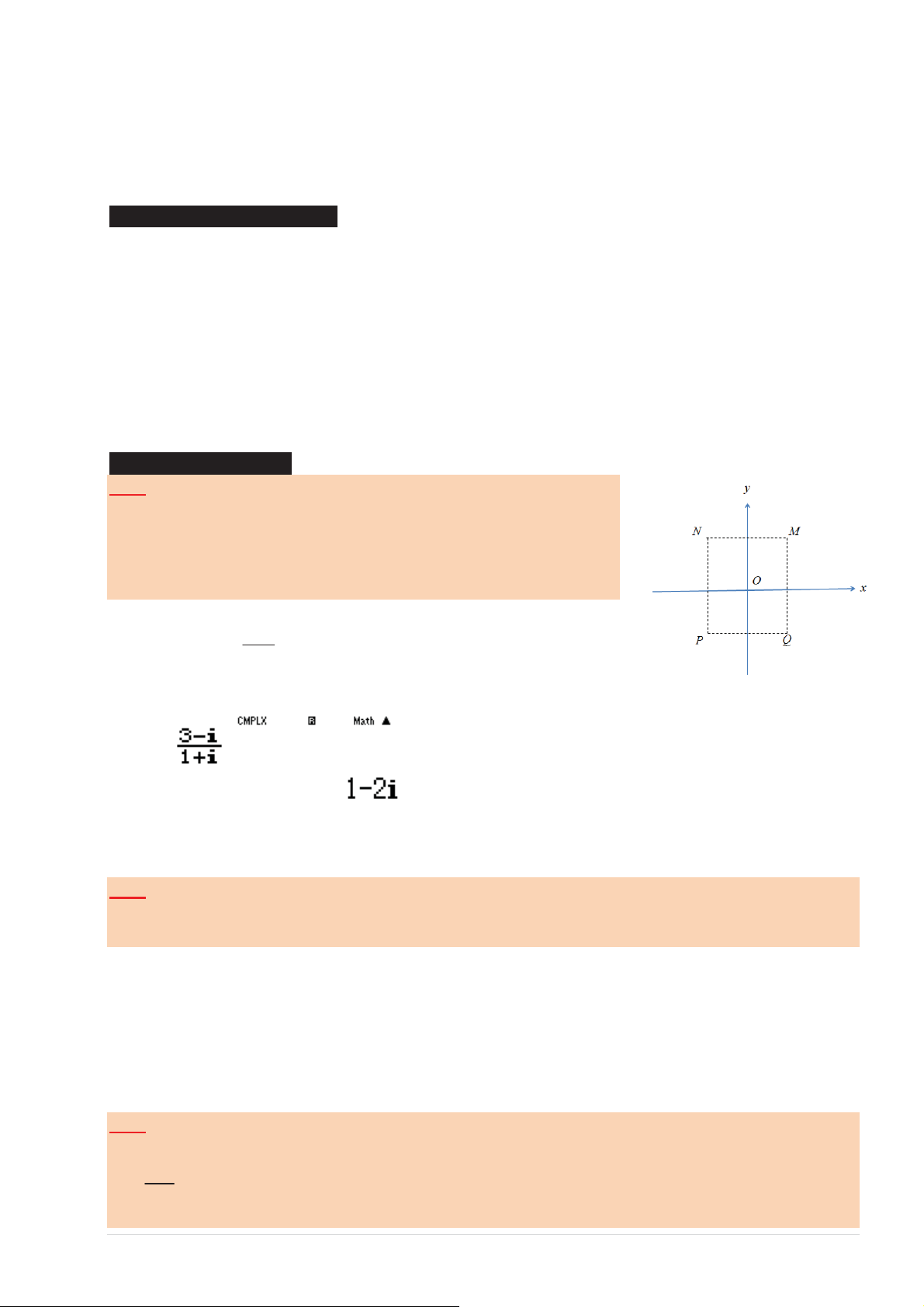
6392 = 6.1000 + 4.100 − 8 = 6a + 4b − 8
Vұy vӃ trái = 6392 − 2194i vӟi ®¯2194 = 2.1000+ 2.100−6 = 2a +2b−6
6a + 4b −8 = 0 ҳǀұƚƌĄŝ = 0 ƚŚŞ ®
⇔ a = −2;b = 5
¯2a + 2b − 6 = 0
sҨLJ z = −2 + 5i P = 2a + b = 1 ĄƉƐҺĐŚşŶŚdžĄĐůă
Bài 7-[Thi thӱ chuyên Lam Sѫn – Thanh Hóa lҫn 2]
Cho sӕ phӭc z = a + bi thӓa mãn ÿiӅu kiӋn ( − i) z + ( + i) z = −( + i)2 2 3 4 1 3
. Tìm P = 2a + b A. 3 B. −1 C.1 D. Ĉáp án khác '/ѵ/
WŚӇҿŶŐƚƌŞŶŚ ⇔ ( − i) z + ( + i) z + ( + i)2 2 3 4 1 3 = 0
EŚҨƉǀұƚƌĄŝǀăŽŵĄLJƚşŶŚĂƐŝŽǀă>ǀӀŝ X = 1000 +100i SE4ET4 EGUE
6392 = 6.1000 + 4.100 − 8 = 6a + 4b − 8
Vұy vӃ trái = 6392 − 2194i vӟi ®¯2194 = 2.1000+ 2.100−6 = 2a +2b−6 TOANMATH.com
Tác giả: Trần Bá Hưng ЎІȂ Ϻϻ@ϿЍЁЏ I) KIӂN THӬC NӄN TҦNG
1. Các khái niӋm thѭӡng gһp
,ҵƚƌӅĐƚŚӌĐңŽŐһŵĐſϮƚƌӅĐǀƵƀŶŐŐſĐǀӀŝŶŚĂƵ͗dƌӅĐŶҪŵŶŐĂŶŐůăƚƌӅĐƚŚӌĐ͕ƚƌӅĐĜӈŶŐĚҸĐůă ƚƌӅĐңŽ
^ҺƉŚӌĐ z = a + bi ŬŚŝďŝҳƵĚŝҴŶƚƌġŶŚҵƚƌӅĐƚŚӌĐңŽůăĜŝҳŵ M ( ; a b) JJJJG
DƀĜƵŶĐӆĂƐҺƉŚӈĐ z = a + bi ůăĜҾůӀŶĐӆĂǀĞĐƚŽ OM 2. LӋnh Caso
ҳdžӊůljƐҺƉŚӈĐƚĂƐӊĚӅŶŐůҵŶŚƚşŶŚƐҺƉŚӈĐDKϮ
>ҵŶŚŐŝңŝƉŚӇҿŶŐƚƌŞŶŚďҨĐŚĂŝDKϱϯ
>ҵŶŚŐŝңŝƉŚӇҿŶŐƚƌŞŶŚďҨĐďĂDKϱϰ II) VÍ DӨ MINH HӐA
VD1-[Câu 31 ĈӅ minh hӑa THPT Quӕc Gia lҫn 1 năm 2017]
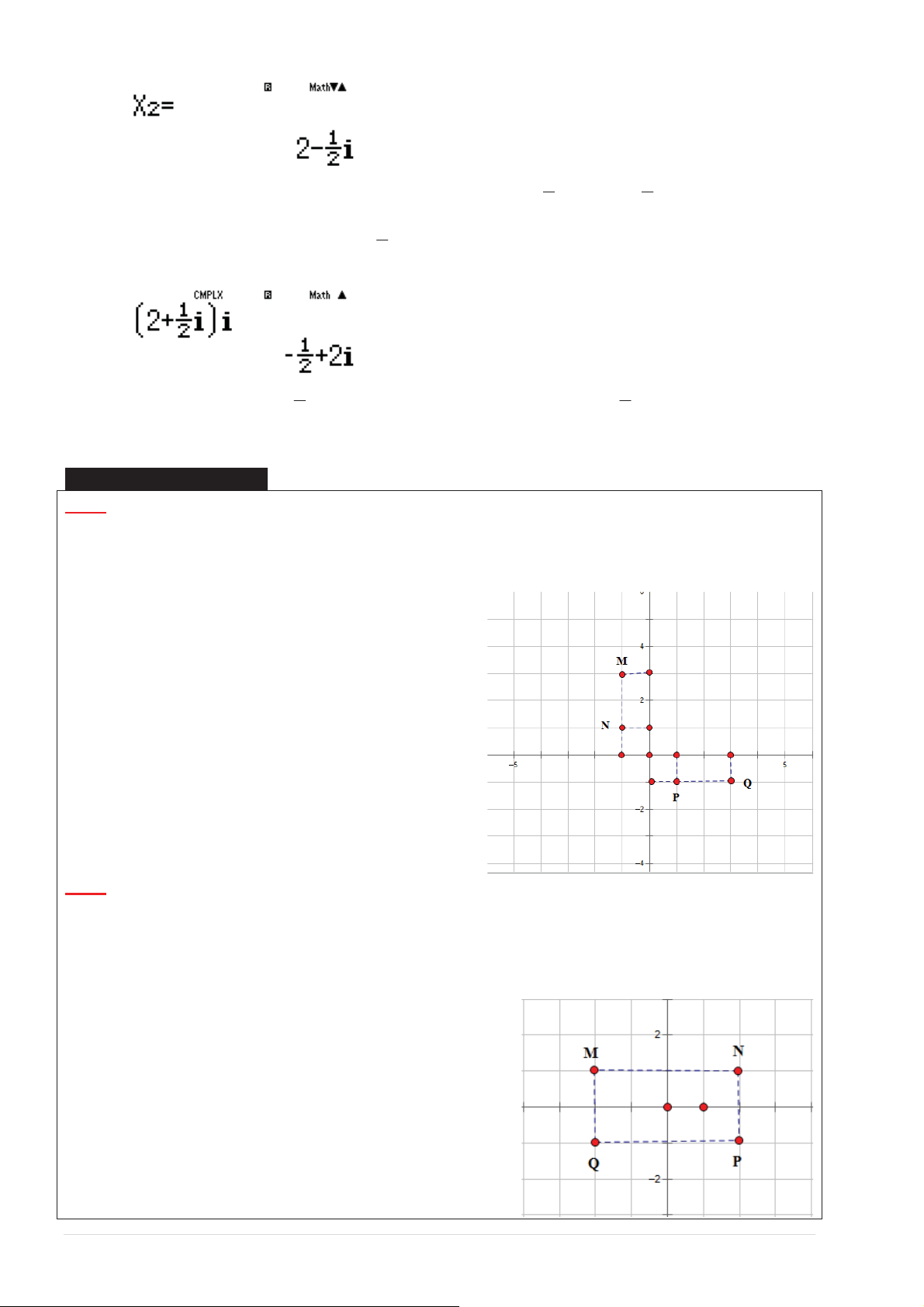
Cho sӕ phӭc z thӓa mãn (1+ i) z = 3− i . Hӓi ÿiӇm biӇu diӉn sӕ
phӭc z là ÿiӇm nào trong các ÿiӇm M , N , P, Q A.ÿiӇm P B.ÿiӇm Q
C.ÿiӇm M D.ÿiӇm N GIҦI 3 −1 ¾ ƀůҨƉ z = 1+i
^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽƚƌŽŶŐŵƀŝƚƌӇӁŶŐDW>yĜҳƚŞŵ z ZDSE5E
z =1− 2i ǀăĜŝҳŵďŝҳƵĚŝҴŶ z ƚƌŽŶŐŚҵƚƌӅĐƚŚӌĐңŽĐſƚҸĂĜҾ(1; 2
− ) ͘ŝҳŵĐſƚŚӌĐĚӇҿŶŐǀă
ңŽąŵƐҰŶҪŵӂŐſĐƉŚҥŶƚӇƚŚӈ/s
ŝҳŵƉŚңŝƚŞŵůăQ ǀăĜĄƉĄŶĐŚşŶŚdžĄĐůă
VD2-[Thi thӱ trung tâm DiӋu HiӅn – Cҫn thѫ lҫn 1 năm 2017]
ĈiӇm biӇu diӉn sӕ phӭc z = 7 + bi vӟi b∈ R , nҵm trên ÿѭӡng thҷng có phѭѫng trình là : A. x = 7 B. y = x
C. y = x + 7 D. y = 7 GIҦI ¾
ŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ z = 7 + bi ůăĜŝҳŵ M ĐſƚҸĂĜҾ M (7;b)
dĂďŝұƚĜŝҳŵ M ƚŚƵҾĐĜӇӁŶŐƚŚҫŶŐ d ŶұƵƚҸĂĜҾĜŝҳŵ M ƚŚҹĂŵĆŶƉŚӇҿŶŐƚƌŞŶŚĜӇӁŶŐƚŚҫŶŐ d ¾
dŚӊĜĄƉĄŶƚĂĐſ x = 7 ⇔ 1.x + 0.y − 7 = 0 ͘dŚұƚҸĂĜҾĜŝҳŵ M ǀăŽƚĂĜӇӄĐ͗
1.7 + 0.b − 7 = 0 ;ĜƷŶŐͿ
Vұy ÿiӇm M thuӝc ÿѭӡng thҷng x = 7 Ĉáp án A là chính xác
VD3-[Thi thӱ Group Nhóm toán – Facebook lҫn 5 năm 2017]
Các ÿiӇm M , N , P lҫn lѭӧt là ÿiӇm biӇu diӉn cho các sӕ phӭc 4i z =
; z = 1− i 1+ 2i ; z = 1 − + 2i 2 ( )( ) 1 i −1 3 A. Tam giác vuông B.Tam giác cân
C.Tam giác vuông cân D.Tam giác ÿӅu TOANMATH.com
Tác giả: Trần Bá Hưng GIҦI ¾
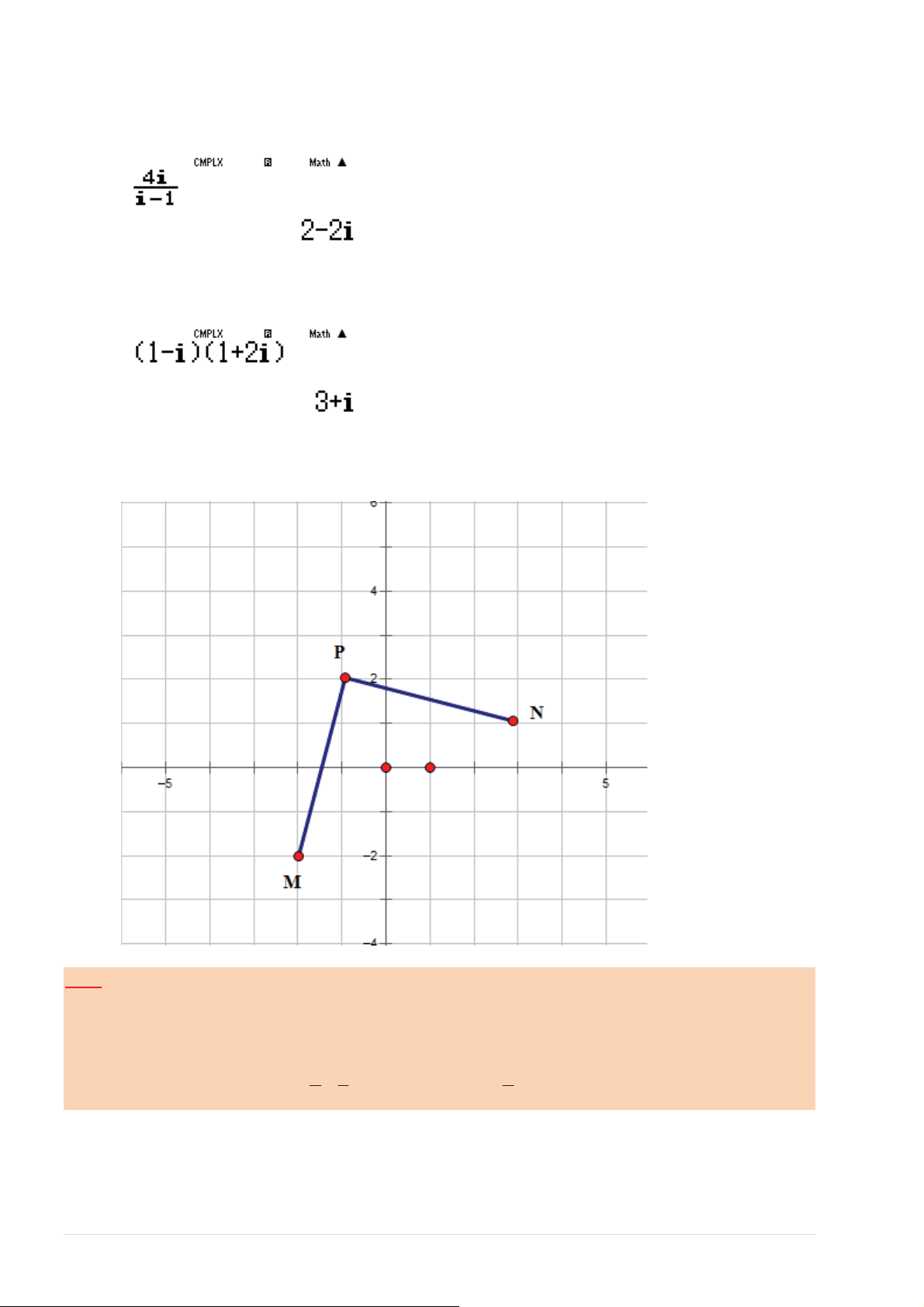
ZƷƚŐҸŶ z ďҪŶŐĂƐŝŽ 1 DE5ES
dĂĜӇӄĐ z = 2 − 2i ǀҨLJĜŝҳŵ M (2; 2 − ) 1 ¾
ZƷƚŐҸŶ z ďҪŶŐĂƐŝŽ 2 SEE
dĂĜӇӄĐ z = 3 + i ǀҨLJĜŝҳŵ N (3; ) 1 2 dӇҿŶŐƚӌ z = 1
− + 2i ǀăĜŝҳŵ P( 1 − ;2) 2 ¾
ҳƉŚĄƚŚŝҵŶƚşŶŚĐŚҤƚĐӆĂƚĂŵŐŝĄĐ MNP ƚĂŶġŶďŝҳƵĚŝҴŶϯĜŝҳŵ M , N , P ƚƌġŶŚҵƚƌӅĐƚҸĂĜҾ
DӉ thҩy tam giác MNP vuông cân tҥi P ÿáp án C chính xác
VD4-[Thi thӱ báo Toán hӑc Tuәi trҿ lҫn 4 năm 2017]
Trong mһt phҷng Oxy , gӑi các ÿiӇm M , N lҫn lѭӧt là ÿiӇm biӇu diӉn sӕ phӭc z = 1− i, z = 3 + 2i . 1 2
Gӑi G là trӑng tâm tam giác OMN , vӟi O là gӕc tӑa ÿӝ. Hӓi G là ÿiӇm biӇu diӉn cӫa sӕ phӭc nào sau ÿây. 4 1 1 A. 5 − i B. 4 + i C. + i D. 2 + i 3 3 2 GIҦI ¾
ŝҳŵ M ďŝҳƵĚŝҴŶƐҺƉŚӈĐ z = 1− i ƚҸĂĜҾ M (1;− ) 1 1
ŝҳŵ N ďŝҳƵĚŝҴŶƐҺƉŚӈĐ z = 3 + 2i ƚҸĂĜҾ N (3;2) 2 'ҺĐƚҸĂĜҾ O (0;0) TOANMATH.com
Tác giả: Trần Bá Hưng
§ x + x + x y + y + y · § 4 1 · ¾ dҸĂĜҾĜŝҳŵ M N O G ; M N O ¨ ¸ = ; ¨ ¸ © 3 3 ¹ © 3 3 ¹ 4 1
sҨLJ G ůăĜŝҳŵďŝҳƵĚŝҴŶĐӆĂƐҺƉŚӈĐ
+ i ůăĜĄƉĄŶĐŚşŶŚdžĄĐ 3 3
VD5-[Thi thӱ THPT Hàm Rӗng – Thanh Hóa lҫn 1 năm 2017]
Trong mһt phҷng tӑa ÿӝ Oxy , gӑi M là ÿiӇm biӇu diӉn sӕ phӭc z = 3 − 4i , ÿiӇm M ' là ÿiӇm biӇu 1+ i diӉn sӕ phӭc z ' =
z . Tính diӋn tích OMM Δ ' 2 25 25 15 15 A. S = B. S = C. S = S = OM Δ M ' Δ Δ D. OM Δ M ' 4 OMM ' 2 OMM ' 4 2 GIҦI ¾
ŝҳŵ M ďŝҳƵĚŝҴŶƐҺƉŚӈĐ z = 3 − 4i ƚҸĂĜҾ M (3; 4 − ) 1 1+ i § 7 1 ·
ŝҳŵ M ' ďŝҳƵĚŝҴŶƐҺƉŚӈĐ z ' = z ƚҸĂĜҾ N ; ¨ − ¸ 2 © 2 2 ¹ DE52SE
'ҺĐƚҸĂĜҾ O (0;0) ¾
ҳƚşŶŚĚŝҵŶƚşĐŚƚĂŵŐŝĄĐ OMM ' ƚĂӈŶŐĚӅŶŐƚşĐŚĐſŚӇӀŶŐĐӆĂϮǀĞĐƚŽƚƌŽŶŐŬŚƀŶŐŐŝĂŶ͘dĂƚŚġŵ
ĐĂŽĜҾϬĐŚŽƚҸĂĜҾŵҽŝĜŝҳŵ O, M , M ' ůădžŽŶŐ JJJJG JJJJJG § 7 1 · 1 JJJJG JJJJJG
OM (3;−4;0) ͕OM ' ; ¨
− ;0¸ S = ªOM ;OM 'º © ¬ ¼ 2 2 ¹ 2 JJJJG JJJJJG
dşŶŚ ªOM ;OM 'º ¬ ¼ Z S T3 S 3 &TTT JJJJG JJJJJG 25 1 JJJJG JJJJJG 25
sҨLJ ªOM ;OM 'º = 12.5 = S = ªOM ;OM 'º = OMM ' ¬ ¼ ¬ ¼ 2 2 4
ůăĜĄƉĄŶĐŚşŶŚdžĄĐ
VD6-[ĈӅ thi minh hӑa bӝ GD-ĈT lҫn 2 năm 2017]
Kí hiӋu z là nghiӋm phӭc có phҫn ҧo dѭѫng cӫa phѭѫng trình 2
4z −16z +17 = 0 . Trên mһt phҷng 0
tӑa ÿӝ, ÿiӇm nào dѭӟi ÿây là ÿiӇm biӇu diӉn sӕ phӭc w = iz0 § 1 · § 1 · § 1 · § 1 · A. M ; 2 ¨
¸ B. M ¨ − ; 2¸ C. ¨ − ;1¸ D. M ;1 ¨ ¸ © 2 ¹ © 2 ¹ © 4 ¹ © 4 ¹ GIҦI ¾
^ӊĚӅŶŐůҵŶŚŐŝңŝƉŚӇҿŶŐƚƌŞŶŚďҨĐŚĂŝDKϱϯĜҳŐŝңŝƉŚӇҿŶŐƚƌŞŶŚ 2
4z −16z +17 = 0 Z S TOANMATH.com
Tác giả: Trần Bá Hưng 1 1 sҨLJƉŚӇҿŶŐƚƌŞŶŚ 2
4z −16z +17 = 0 ĐſŚĂŝŶŐŚŝҵŵ z = 2 + i ǀă z = 2 − i 2 2 1 ¾
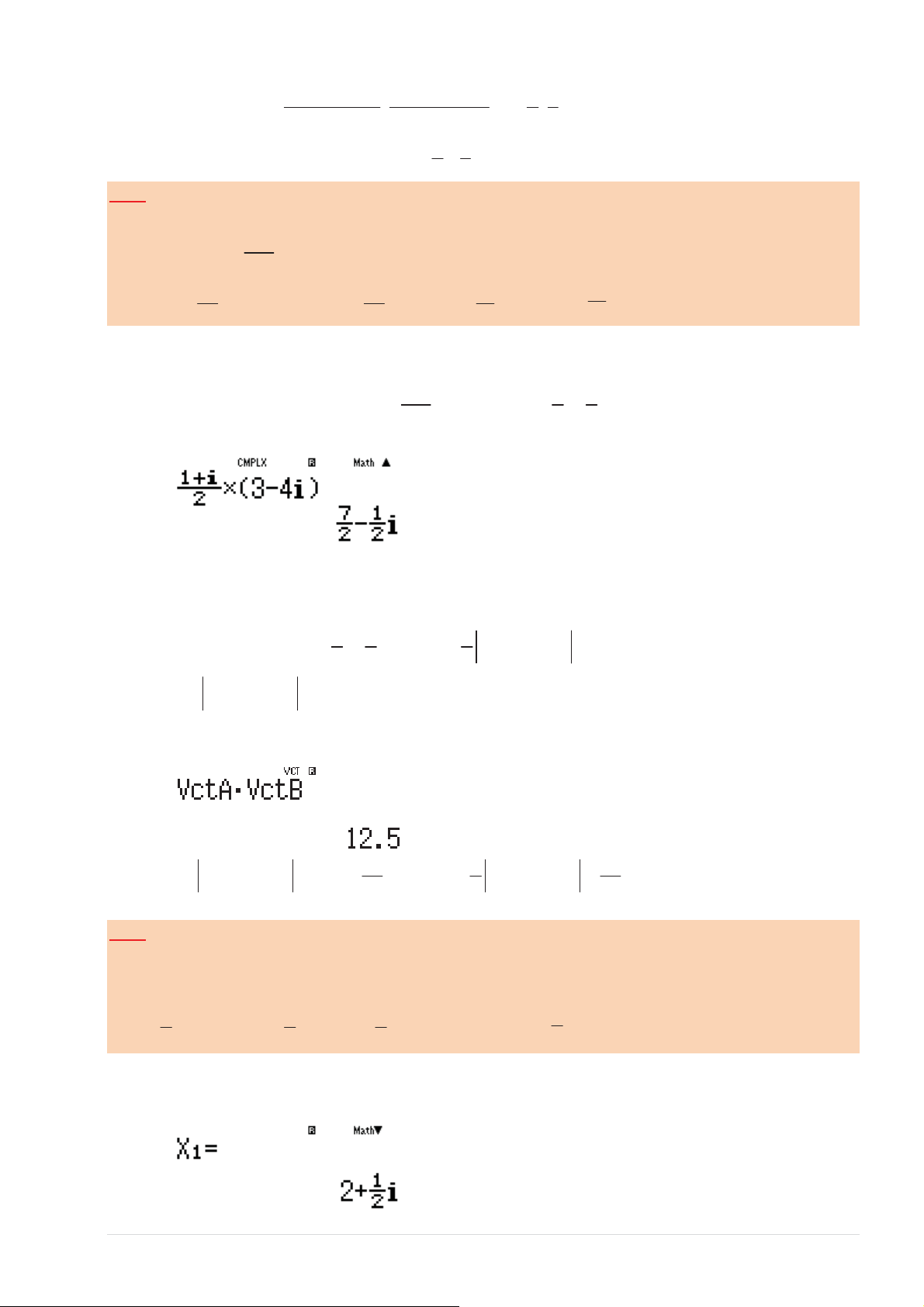
ҳ z ĐſƉŚҥŶңŽĚӇҿŶŐ z = 2 − i ͘dşŶŚ w = z i 0 2 0 ZD5EE 1 § 1 ·
sҨLJƉŚӇҿŶŐƚƌŞŶŚ w = − + 2i ŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ w ůă M ¨ − ;2¸ 2 © 2 ¹
ůăĜĄƉĄŶĐŚşŶŚdžĄĐ II) BÀI TҰP TӴ LUYӊN
Bài 1-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 2 năm 2017]
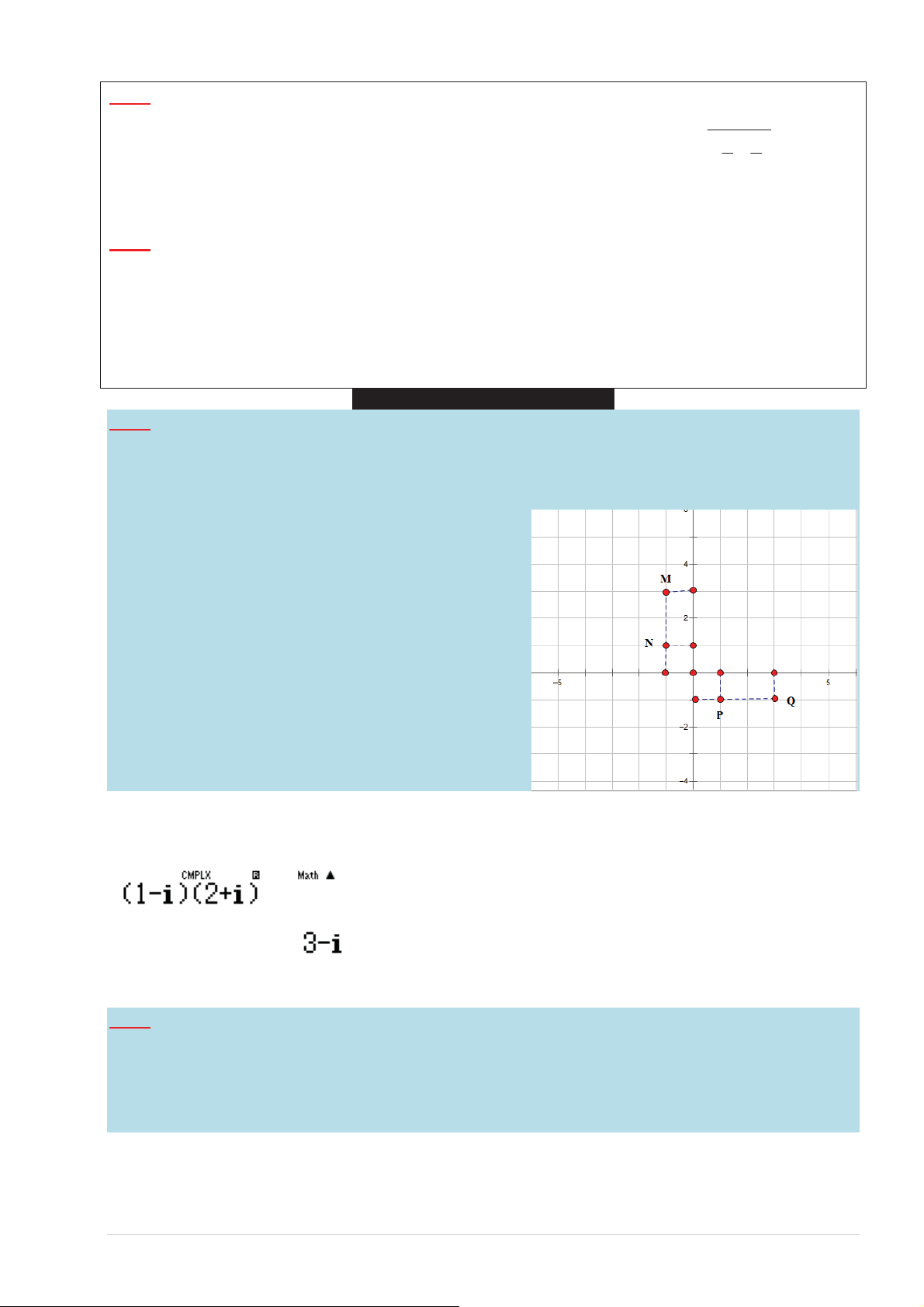
Cho sӕ phӭc z = 2 + i . Hãy xác ÿӏnh ÿiӇm biӇu diӉn hình hӑc cӫa sӕ phӭc w = (1− i) z A.ĈiӇm M B.ĈiӇm N C.ĈiӇm P D. ĈiӇm Q
Bài 2-[Thi thӱ facebook nhóm toán lҫn 5 năm 2017]
Cho sӕ phӭc z thӓa mãn (2 − i) z = 4z + 5 . Hӓi ÿiӇm biӇu diӉn cӫa z là ÿiӇm nào trong các ÿiӇm
M , N , P, Q ӣ hình bên . A.ĈiӇm N B.ĈiӇm P
C.ĈiӇm M D. ĈiӇm Q TOANMATH.com
Tác giả: Trần Bá Hưng
Bài 3-[Thi thӱ báo Toán hӑc tuәi trҿ lҫn 4 năm 2017] 4
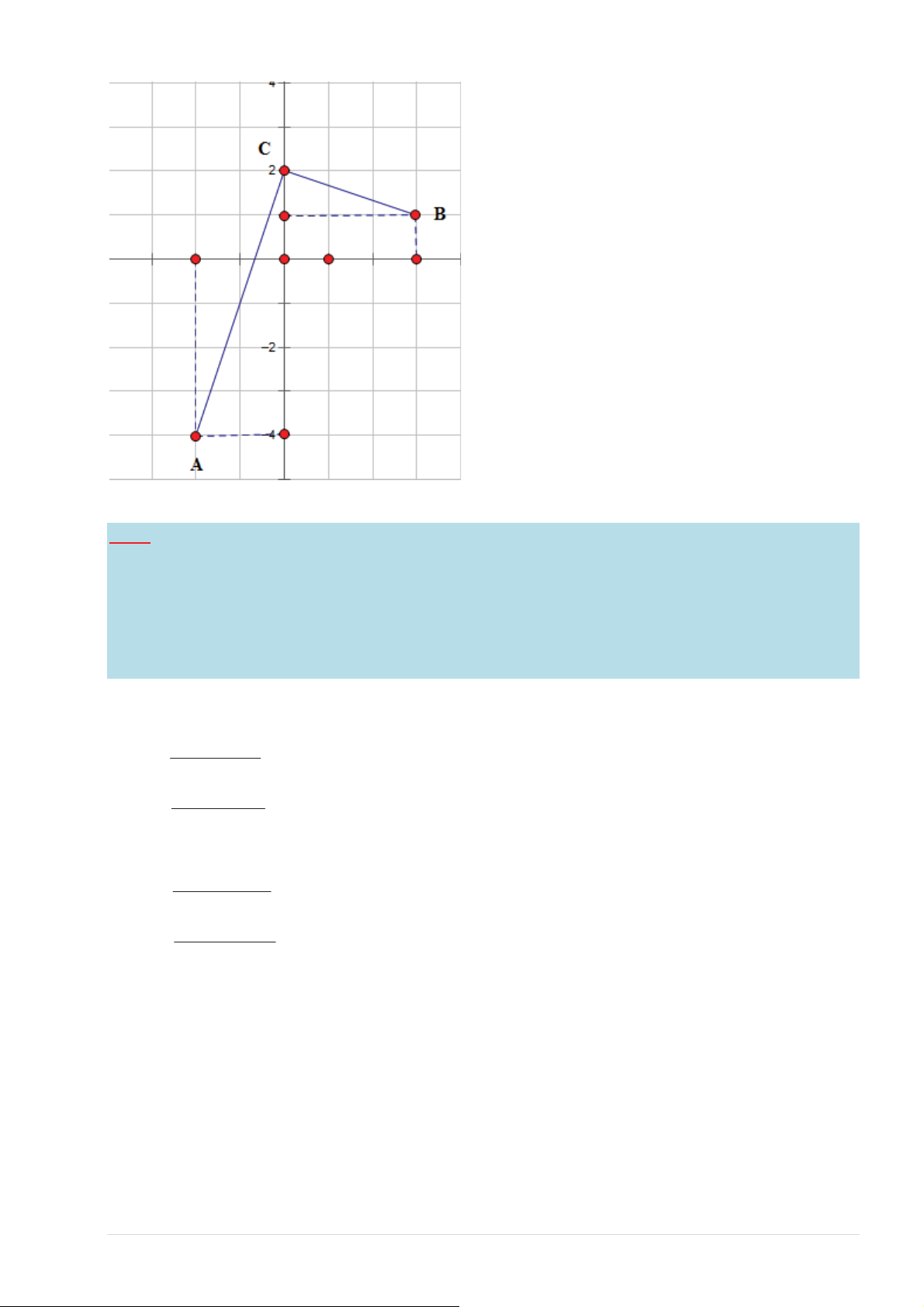
Trên mһt phҷng tӑa ÿӝ các ÿiӇm ,
A B, C lҫn lѭӧt là ÿiӇm biӇu diӉn cӫa sӕ phӭc , 2 4 − + i 5 5 (1−i)(1+ 2i), 3
−2i Khi ÿó tam giác ABC
A.Vuông tҥi C
B.Vuông tҥi A
C.Vuông cân tҥi B D. Tam giác ÿӅu Bài 4-Các ÿiӇm ,
A B, C , A ', B ', C ' trong mһt phҷng phӭc theo thӭ tӵ biӇu diӉn các sӕ :
1− i, 2 + 3i,3 + i và
3i, 3 − 2i,3 + 2i có G, G ' lҫn lѭӧt là trӑng tâm tam giác ABC và A' B 'C ' . Khҷng ÿӏnh nào sau ÿây ÿúng JJJJG
A. G trùng G '
B. Vecto GG ' = (1;− ) 1 JJJG JJJG
C. GA = 3GA'
D. Tӭ giác GAG ' B lұp thành mӝt hình bình hành
LӠI GIҦI BÀI TҰP TӴ LUYӊN
Bài 1-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 2 năm 2017]
Cho sӕ phӭc z = 2 + i . Hãy xác ÿӏnh ÿiӇm biӇu diӉn hình hӑc cӫa sӕ phӭc w = (1− i) z A.ĈiӇm M B.ĈiӇm N C.ĈiӇm P D. ĈiӇm Q '/ѵ/
dşŶŚƐҺƉŚӈĐ w = (1−i) z ďҪŶŐŵĄLJƚşŶŚĂƐŝŽ SEE
Vұy tӑa ÿӝ cӫa ÿiӇm thӓa mãn sӕ phӭc w là (3; ) 1
− . Ĉây là tӑa ÿӝ ÿiӇm Q ĄƉƐҺĐŚşŶŚdžĄĐůă
Bài 2-[Thi thӱ facebook nhóm toán lҫn 5 năm 2017]
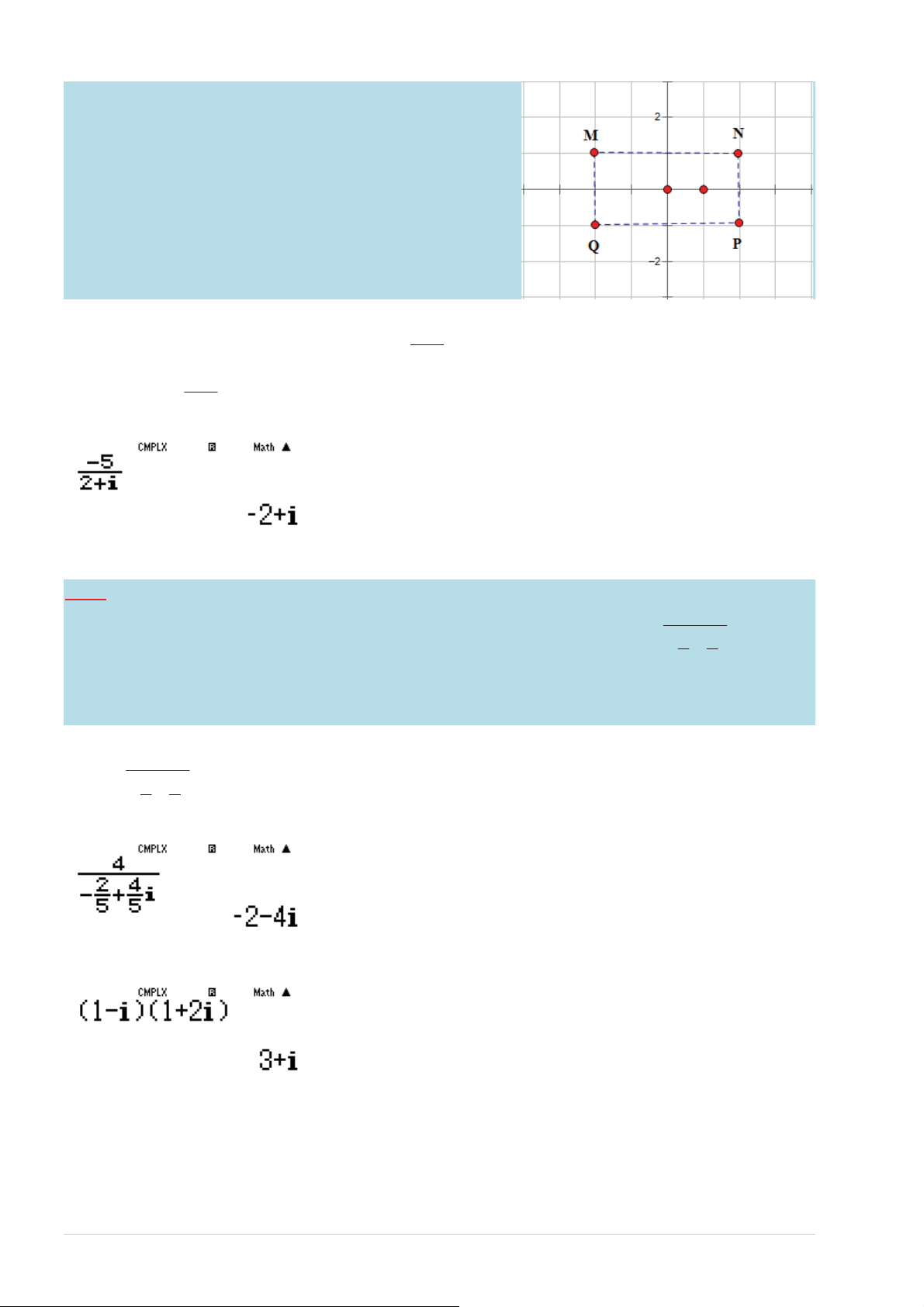
Cho sӕ phӭc z thӓa mãn (2 − i) z = 4z + 5 . Hӓi ÿiӇm biӇu diӉn cӫa z là ÿiӇm nào trong các ÿiӇm
M , N , P, Q ӣ hình bên . A.ĈiӇm N B.ĈiӇm P
C.ĈiӇm M D. ĈiӇm Q TOANMATH.com
Tác giả: Trần Bá Hưng '/ѵ/ −
ƀůҨƉ ( − i) z − = ⇔ −( + i) 5 2 4z 5 2
z = 5 ⇔ z = 2+i 5 −
dŞŵƐҺƉŚӈĐ z = 2+i DS5E
Vұy tӑa ÿӝ cӫa ÿiӇm thӓa mãn sӕ phӭc z là ( 2; − )
1 . Ĉây là tӑa ÿӝ ÿiӇm M ĄƉƐҺĐŚşŶŚdžĄĐůă
Bài 3-[Thi thӱ báo Toán hӑc tuәi trҿ lҫn 4 năm 2017] 4
Trên mһt phҷng tӑa ÿӝ các ÿiӇm ,
A B, C lҫn lѭӧt là ÿiӇm biӇu diӉn cӫa sӕ phӭc , 2 4 − + i 5 5 (1−i)(1+ 2i), 3
−2i Khi ÿó tam giác ABC
A.Vuông tҥi C B.Vuông tҥi A C.Vuông cân tҥi B D. Tam giác ÿӅu '/ѵ/ 4 ZƷƚŐҸŶ ĜӇӄĐ 2
− − 4i ǀҨLJƚҸĂĜҾĜŝҳŵ A( 2; − 4 − ) 2 4 − + i 5 5 D5SD5D5E
ZƷƚŐҸŶ (1−i)(1+ 2i) ĜӇӄĐ3+ i ǀҨLJƚҸĂĜҾĜŝҳŵ B(3; ) 1 SEE ZƷƚŐҸŶ 3 2
−2i = −2 .ii = 2i ǀҨLJƚҸĂĜҾĜŝҳŵC (0;2)
ҳƉŚĄƚŚŝҵŶƚşŶŚĐŚҤƚĐӆĂƚĂŵŐŝĄĐ ABC ƚĂĐŚҶĐҥŶďŝҳƵĚŝҴŶƚƌġŶŚҵƚƌӅĐƚҸĂĜҾůăƚŚҤLJŶŐĂLJ TOANMATH.com
Tác giả: Trần Bá Hưng
DӉ thҩy tam giác ABC vuông tҥi C ĄƉƐҺĐŚşŶŚdžĄĐůă Bài 4-Các ÿiӇm ,
A B, C , A ', B ', C ' trong mһt phҷng phӭc theo thӭ tӵ biӇu diӉn các sӕ :
1− i, 2 + 3i,3 + i và
3i, 3 − 2i,3 + 2i có G, G ' lҫn lѭӧt là trӑng tâm tam giác ABC và A' B 'C ' . Khҷng ÿӏnh nào sau ÿây ÿúng JJJJG
A. G trùng G '
B. Vecto GG ' = (1;− ) 1 JJJG JJJG
C. GA = 3GA'
D. Tӭ giác GAG ' B lұp thành mӝt hình bình hành '/ѵ/
dĂĐſƚҸĂĜҾĐĄĐĜҶŶŚ A(1;− )
1 , B (2;3), C (3; )
1 dҸĂĜҾƚƌҸŶŐƚąŵ G (2; ) 1 x + x + x A B C x = = 2 ° G ° 3 ® y ° + y + y A B C y = = 1 G °¯ 3
dĂĐſƚҸĂĜҾĐĄĐĜҶŶŚ A'(0;3), B'(3; 2
− ), C '(3;2) dҸĂĜҾƚƌҸŶŐƚąŵG(2; ) 1 x + x + x A' B ' C ' x = = 2 ° G' ° 3 ® y ° + y + y A' B ' C ' y = =1 G ' °¯ 3
Rõ ràng G ≡ G ' Ĉáp sӕ chính xác là A TOANMATH.com
Tác giả: Trần Bá Hưng ЎЇϮБЌȂ ЖA0ϺϺϻЍЁЏ I) KIӂN THӬC NӄN TҦNG 1. Mҽo giҧi nhanh
ăŝƚŽĄŶƋƵӎƚşĐŚůƵƀŶĜŝůġŶƚӉĜҷŶŚŶŐŚšĂ͘dĂůƵƀŶĜҭƚ z = x + yi ͕ďŝҳƵĚŝҴŶƐҺƉŚӈĐƚŚĞŽLJġƵĐҥƵ
ĜҲďăŝ͕ƚӉĜſŬŚӊ i ǀăƚŚƵǀҲŵҾƚŚҵƚŚӈĐŵӀŝ͗
EұƵŚҵƚŚӈĐĐſĚҢŶŐ Ax + By + C = 0 ƚŚŞƚҨƉŚӄƉĜŝҳŵůăĜӇӁŶŐƚŚҫŶŐ 2 2
EұƵŚҵƚŚӈĐĐſĚҢŶŐ ( − ) + ( − ) 2 x a y b
= R ƚŚŞƚҨƉŚӄƉĜŝҳŵůăĜӇӁŶŐƚƌžŶƚąŵ I ( ; a b) ďĄŶ ŬşŶŚ R 2 2 x y EұƵŚҵƚŚӈĐĐſĚҢŶŐ +
=1ƚŚŞƚҨƉŚӄƉĜŝҳŵĐſĚҢŶŐŵҾƚůŝƉ 2 2 a b 2 2 x y EұƵŚҵƚŚӈĐĐſĚҢŶŐ −
=1ƚŚŞƚҨƉŚӄƉĜŝҳŵůăŵҾƚ,LJƉĞƌďŽů 2 2 a b EұƵŚҵƚŚӈĐĐſĚҢŶŐ 2
y = Ax + Bx + C ƚŚŞƚҨƉŚӄƉĜŝҳŵůăŵҾƚWĂƌĂďŽů 2. Phѭѫng pháp Caso
dŞŵĜŝҳŵĜҢŝĚŝҵŶƚŚƵҾĐƋƵӎƚşĐŚĐŚŽӂĜĄƉĄŶƌһŝƚŚұŶŐӇӄĐǀăŽĜҲďăŝ͕ŶұƵƚŚҹĂŵĆŶƚŚŞůăĜƷŶŐ II) VÍ DӨ MINH HӐA
VD1-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 3 năm 2017]
Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z thӓa mãn z − 2 − i = z + 2i
A. 4x − 2 y +1 = 0
B. 4x − 2y −1 = 0
C. 4x + 2y −1 = 0 D. 4x − 6 y −1 = 0 GIҦI ĄĐŚĂƐŝŽ ¾
'ҸŝƐҺƉŚӈĐ z ĐſĚҢŶŐ z = a + bi ͘dĂŚŝҳƵ͗Ĝŝҳŵ M ďŝҳƵĚŝҴŶƐҺƉŚӈĐ z ƚŚŞ M ĐſƚҸĂĜҾ M ( ; a b) ͘
'ŝңƐӊĜĄƉĄŶĜƷŶŐƚŚŞ M ƚŚƵҾĐĜӇӁŶŐƚŚҫŶŐ 4x − 2 y +1 = 0 ƚŚŞ 4a − 2b +1 = 0 5
ŚҸŶ a = 1ƚŚŞ b =
z =1+ 2.5i ͘^ҺƉŚӈĐ z ƚŚҹĂŵĆŶ z − 2 − i = z + 2i ƚŚŞ 2
z − 2 − i − z + 2i = 0 ¾
^ӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽĜҳŬŝҳŵƚƌĂ TFESSESTFS EE
dĂƚŚҤLJƌĂŵҾƚŬұƚƋƵңŬŚĄĐϬǀҨLJ z − 2 − i − z + 2i = 0 ůăƐĂŝǀăĜĄƉĄŶƐĂŝ ¾
dӇҿŶŐƚӌǀӀŝĜĄƉƐҺĐŚҸŶ a = 1ƚŚŞ b = 1.5 ǀă z = 1+1.5i TFESSESTFS EE TOANMATH.com
Tác giả: Trần Bá Hưng
dĂƚŚҤLJŬұƚƋƵңƌĂϬǀҨLJ z − 2 − i − z + 2i = 0 ůăĜƷŶŐǀăĜĄƉĄŶĐŚşŶŚdžĄĐůă ĄĐŚŵҮŽ ¾
ҭƚ z = x + yi ;ƚĂůƵƀŶĜŝůġŶƚӉĜҷŶŚŶŐŚšĂͿ͘ ¾
dŚұǀ㎠z − 2 − i = z + 2i ƚĂĜӇӄĐ
(x − )+( y − ) 2 2
1 i = x + (− y + 2)i
⇔ (x − )2 + ( y − )2 = x +(−y + )2 2 2 1 2
⇔ (x − )2 + ( y − )2 = x + (−y + )2 2 2 1 2 2 2 2 2
⇔ x − 4x + 4 + y − 2y +1 = x + y − 4y + 4
⇔ 4x − 2y −1 = 0
sҨLJƚҨƉŚӄƉĐĄĐĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ z ůăĜӇӁŶŐƚŚҫŶŐ 4x − 2 y −1 = 0
ĜĄƉĄŶůăĐŚşŶŚdžĄĐ ŞŶŚůƵҨŶ ¾
dƌŽŶŐĚҢŶŐƚŽĄŶŶăLJƚĂŶġŶӇƵƚŝġŶĚƶŶŐŵҮŽǀŞƚşŶŚŶŚĂŶŚŐҸŶĐӆĂŶſ ¾
EŚҩĐůҢŝŵҾƚůҥŶŶӋĂ͕ůƵƀŶĜҭƚ z = x + yi ƌһŝďŝұŶĜҼŝƚŚĞŽĜҲďăŝ
VD2-[Thi thӱ sӣ GD-ĈT Hà Tƭnh lҫn 1 năm 2017]
Cho sӕ phӭc z thӓa mãn 2 + z = 1− i . Chӑn phát biӇu ÿúng
A.Tұp hӧp ÿiӇm biӇu diӉn sӕ phӭc z là mӝt ÿѭӡng thҷng
B.Tұp hӧp ÿiӇm biӇu diӉn sӕ phӭc z là mӝt ÿѭӡng Parabol
C.Tұp hӧp ÿiӇm biӇu diӉn sӕ phӭc z là mӝt ÿѭӡng tròn
D.Tұp hӧp ÿiӇm biӇu diӉn sӕ phӭc z là mӝt ÿѭӡng Elip GIҦI ĄĐŚŵҮŽ ¾
ҭƚ z = x + yi ͘ ¾
dŚұǀ㎠2 + z = 1− i ƚĂĜӇӄĐ
x + 2 + yi = 1− i
⇔ (x + )2 + y = + (− )2 2 2 2 1 1
⇔ (x + ) + y = ( )2 2 2 2 2
sҨLJƚҨƉŚӄƉĐĄĐĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ z ůăĜӇӁŶŐƚƌžŶƚąŵ I ( 2;
− 0) ďĄŶŬşŶŚ R = 2
sҨLJĜĄƉĄŶůăĐŚşŶŚdžĄĐ
VD3-[ĈӅ thi minh hӑa cӫa bӝ GD-ĈT lҫn 1 năm 2017]
Cho các sӕ phӭc z thӓa mãn z = 4 . BiӃt rҵng tұp hӧp các ÿiӇm biӇu diӉn các sӕ phӭc
w = (3+ 4i) z + i là mӝt ÿѭӡng tròn. Tính bán kính r cӫa ÿѭӡng tròn ÿó. A. r = 4 B. r = 5
C. r = 20 D. r = 22 GIҦI ĄĐŚĂƐŝŽ ¾
ҳdžąLJĚӌŶŐϭĜӇӁŶŐƚƌžŶƚĂĐҥŶϯĜŝҳŵďŝҳƵĚŝҴŶĐӆĂ w ͕ǀŞ z ƐҰƐŝŶŚƌĂ w ŶġŶĜҥƵƚŝġŶƚĂƐҰ
ĐŚҸŶϯŐŝĄƚƌҷĜҢŝĚŝҵŶĐӆĂ z ƚŚҹĂŵĆŶ z = 4 ¾
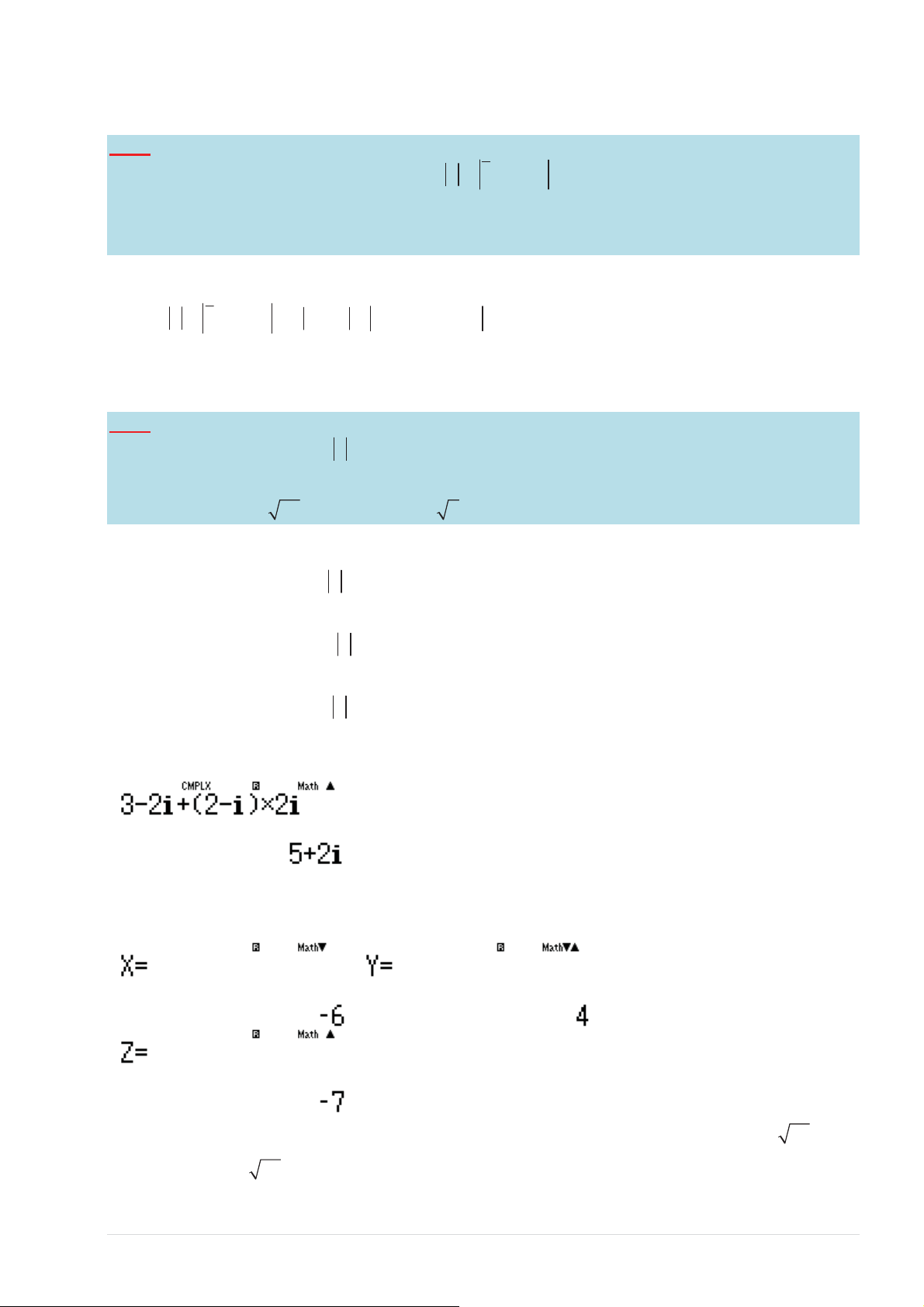
ŚҸŶ z = 4 + 0i ;ƚŚҹĂŵĆŶ z = 4 Ϳ͘dşŶŚ w = 3 + 4i 4 + 0i + i 1 ( )( ) E2E TOANMATH.com
Tác giả: Trần Bá Hưng
dĂĐſĜŝҳŵďŝҳƵĚŝҴŶĐӆĂ z ůă M (12;17) 1 ¾
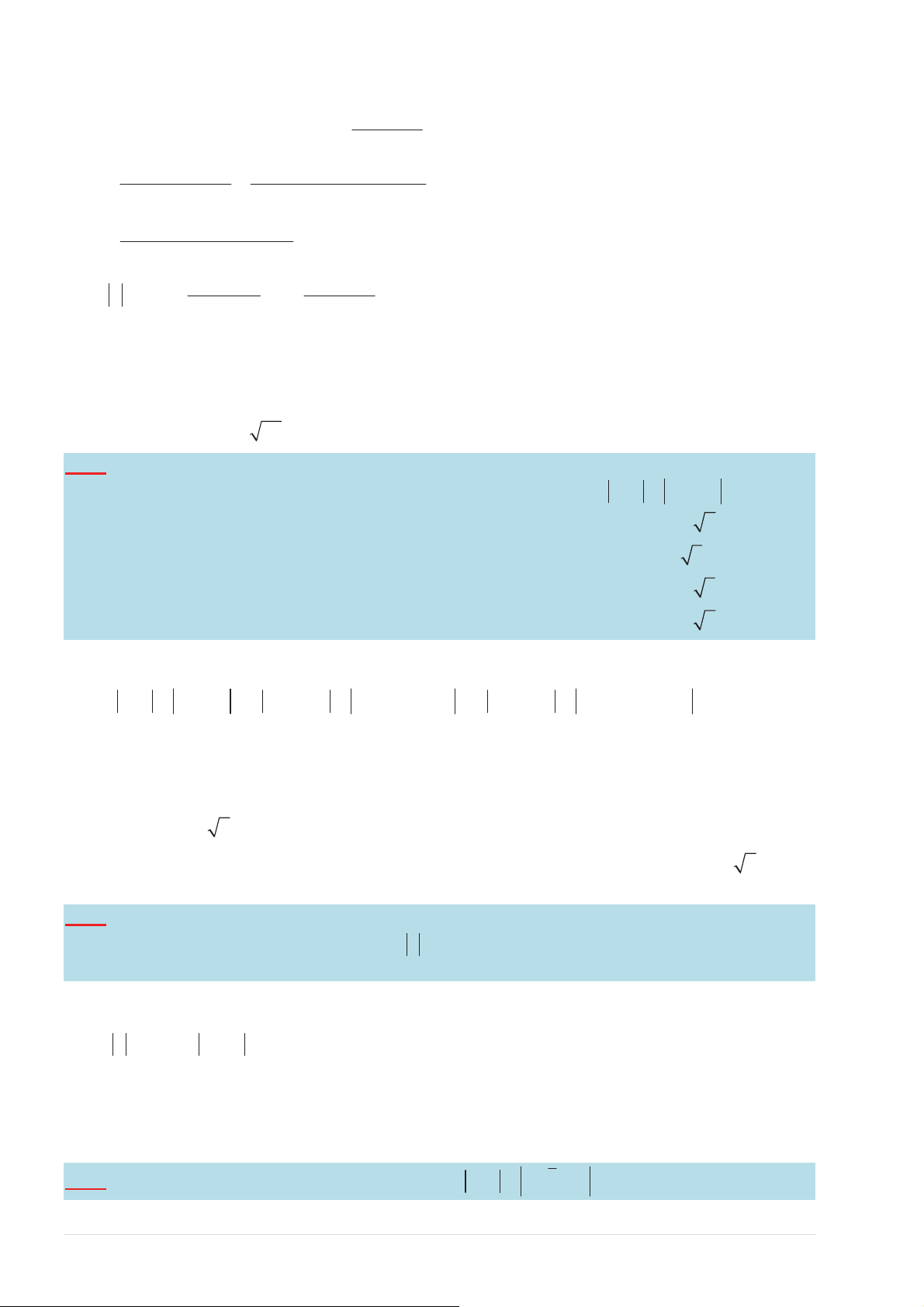
ŚҸŶ z = 4i ;ƚŚҹĂŵĆŶ z = 4 Ϳ͘dşŶŚ w = 3 + 4i 4i + i 2 ( )( ) E2EE
dĂĐſĜŝҳŵďŝҳƵĚŝҴŶĐӆĂ z ůă N ( 16 − ;13) 2 ¾ ŚҸŶ z = 4
− i ;ƚŚҹĂŵĆŶ z = 4Ϳ͘dşŶŚ w = 3+ 4i 4 − i + i 3 ( )( ) ESEE
dĂĐſĜŝҳŵďŝҳƵĚŝҴŶĐӆĂ z ůă P (16; 1 − ) 1 3
sҨLJƚĂĐſϯĜŝҳŵ M , N , P ƚŚƵҾĐĜӇӁŶŐƚƌžŶďŝҳƵĚŝҴŶƐҺƉŚӈĐ w ¾
ӇӁŶŐƚƌžŶŶăLJƐҰĐſĚҢŶŐƚҼŶŐƋƵĄƚ 2 2
x + y + ax + by + c = 0 ͘ҳƚŞŵ a,b, c ƚĂƐӊĚӅŶŐŵĄLJ
ƚşŶŚĂƐŝŽǀӀŝĐŚӈĐŶĉŶŐDKϱϯ ¾ Z SGSG S SGSG S SGSG
sҨLJƉŚӇҿŶŐƚƌŞŶŚĜӇӁŶŐƚƌžŶĐſĚҢŶŐ x + y − y −
= ⇔ x + ( y − )2 2 2 2 2 2 399 0 1 = 20
ĄŶŬşŶŚĜӇӁŶŐƚƌžŶƚҨƉŚӄƉĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ w ůăϮϬ ĄƉĄŶĐŚşŶŚdžĄĐůă ĄĐŚŵҮŽ ¾
ҲďăŝLJġƵĐҥƵƚŞŵƚҨƉŚӄƉĐĄĐĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ w ǀҨLJƚĂĜҭƚ w = x + yi ͘ w − i
x + y − i ¾
dŚұǀ㎠w = ( + i) ( )1
3 4 z + i ⇔ z = =
͘dŝұƉƚӅĐƌƷƚŐҸŶƚĂĜӇӄĐ 3 + 4i 3 + 4i ªx ¬ + ( y − )
1 iº¼ (3 − 4i) 3x + 4y − 4 + (−4x + 3y − 3)i z = ( =
3 + 4i)(3 − 4i) 25 2 2 2
§ 3x + 4y − 4 ·
§ −4x + 3y − 3 ·
z = 4 ⇔ z = 16 ⇔ ¨ ¸ + ¨ ¸ = 16 © 25 ¹ © 25 ¹ 2 2
25x + 25y + 25 − 50 y ⇔ =16 2 25 2 2
⇔ x + y − 2y = 399
⇔ x + ( y − )2 2 2 1 = 20
sҨLJƚҨƉŚӄƉĐĄĐĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ w ůăĜӇӁŶŐƚƌžŶďĄŶŬşŶŚ r = 20
ĜĄƉĄŶůăĐŚşŶŚdžĄĐ ŞŶŚůƵҨŶ TOANMATH.com
Tác giả: Trần Bá Hưng ¾
ŚӈĐŶĉŶŐDKϱϮĜҳƚŞŵƉŚӇҿŶŐƚƌŞŶŚĜӇӁŶŐƚƌžŶĜӇӄĐŐŝңŝƚŚşĐŚŶŚӇƐĂƵ͗ ӇӁŶŐƚƌžŶĐſĚҢŶŐ 2 2
x + y + ax + by + c = 0
sӀŝ M ƚŚƵҾĐĜӇӁŶŐƚƌžŶƚŚŞ 2 2
12a +17b + c = −12 −17
sӀŝ N ƚŚƵҾĐĜӇӁŶŐƚƌžŶƚŚŞ 2 2
−16a +13b + c = −16 −13
sӀŝ P ƚŚƵҾĐĜӇӁŶŐƚƌžŶƚŚŞ 2 2
16a −11b + c = −16 −11 2 2 1
2a +17b + c = 12 − −17 °
sҨLJƚĂůҨƉĜӇӄĐŚҵƉŚӇҿŶŐƚƌŞŶŚϯҦŶďҨĐŶŚҤƚ 2 2 ® 16
− a +13b + c = 16 − −13 ° 2 2
16a −11b + c = 16 − −11 ¯
săƚĂƐӊĚӅŶŐĐŚӈĐŶĉŶŐŐŝңŝŚҵƉŚӇҿŶŐƚƌŞŶŚϯҦŶďҨĐŶŚҤƚDKϱϮĜҳdžӊůlj ¾
,ĂŝĐĄĐŚĜҲƵŚĂLJǀăĐſӇƵĜŝҳŵƌŝġŶŐ͕ƚӌůƵҨŶƐҰƚŝұƚŬŝҵŵƚŚӁŝŐŝĂŶŵҾƚĐŚƷƚŶŚӇŶŐǀŝҵĐƚşŶŚƚŽĄŶ
ƌƷƚŐҸŶĚҴŶŚҥŵůҧŶ͕ĐžŶĐĂƐŝŽĐſǀүďҤŵŵĄLJŶŚŝҲƵŚҿŶŶŚӇŶŐƚƵLJҵƚĜҺŝŬŚƀŶŐƐĂŝ͘
VD4-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 3 năm 2017] z −1
Tұp hӧp các ÿiӇm biӇu diӉn các sӕ phӭc z thӓa mãn phҫn thӵc cӫa
bҵng 0 là ÿѭӡng tròn tâm z − i
I bán kính R (trӯ ÿi mӝt ÿiӇm) § 1 1 · 1 § 1 1 · 1
A. I ¨ − ;− ¸ , R = B. I ; ¨ ¸ , R = © 2 2 ¹ 2 © 2 2 ¹ 2 § 1 1 · 1 § 1 1 · 1 C. I ; ¨ ¸ , R =
D. I ¨ − ;− ¸ , R = © 2 2 ¹ 2 © 2 2 ¹ 2 GIҦI ĄĐŚŵҮŽ ¾
ҭƚ z = x + yi ͘ z −1 x 1 yi
(x−1+ yi)ªx −( y − )1iº − + ¬ ¼ ¾ dŚұǀ㎠ƚĂĜӇӄĐ = z − i x + ( y − ) 1 i ªx + ( y − )
1 iº ªx − ( y − ) 1 iº ¬ ¼ ¬ ¼ 2 2
x − x + y − y + xyi − ( x − ) 1 ( y − ) 1 i = x + ( y − )2 2 1 2 2 z −1 § 1 · § 1 · 1 ҳƉŚҥŶƚŚӌĐĐӆĂ ďҪŶŐϬƚŚŞ 2 2
x − x + y − y = 0 ⇔ x ¨ − ¸ + y ¨ − ¸ = z − i © 2 ¹ © 2 ¹ 2 § 1 1 · 1
sҨLJƚҨƉŚӄƉĜŝҳŵĐҥŶƚŞŵůăĜӇӁŶŐƚƌžŶƚąŵ I ; ¨ ¸ ďĄŶŬşŶŚ R =
ĜĄƉĄŶůăĐŚşŶŚdžĄĐ © 2 2 ¹ 2 III) BÀI TҰP TӴ LUYӊN
Bài 1-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 2 năm 2017]
Cho các sӕ phӭc z thӓa mãn z +1− i = z −1+ 2i . Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z trên mһt
phҷng tӑa ÿӝ là mӝt ÿѭӡng thҷng. ViӃt phѭѫng trình ÿѭӡng thҷng ÿó.
A. 4x + 6 y − 3 = 0
B. 4x − 6 y − 3 = 0
C. 4x + 6 y + 3 = 0
D. 4x − 6 y + 3 = 0
Bài 2-[Thi thӱ THPT TriӋu Sѫn – Thanh Hóa lҫn 1 năm 2017]
Tұp hӧp các ÿiӇm M biӇu diӉn sӕ phӭc z : z = z − 3 + 4i là phѭѫng trình có dҥng
A. 6x + 8y − 25 = 0
B. 3x + 4 y − 3 = 0 C. 2 x + y = 25 2 2
D. ( x − 3) + ( y − 4) = 25
Bài 3-[Thi thӱ THPT NguyӉn Ĉình ChiӇu – Bình Ĉӏnh lҫn 1 năm 2017]
Cho các sӕ phӭc z thӓa mãn z = 2 . BiӃt rҵng tұp hӧp các ÿiӇm biӇu diӉn các sӕ phӭc
w = 3 − 2i + (2 − i) z là mӝt ÿѭӡng tròn. Tính bán kính r cӫa ÿѭӡng tròn ÿó. A. r = 20 B. r = 20 C. r = 7 D. r = 7 TOANMATH.com
Tác giả: Trần Bá Hưng
Bài 4-[Thi thӱ THPT Hàm Rӗng – Thanh Hóa lҫn 1 năm 2017]
Trong mһt phҷng Oxy , tìm tұp hӧp ÿiӇm biӇu diӉn sӕ phӭc z thӓa mãn z −1 = (1+ i) z
A.Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng tròn tâm I (2;− ) 1 , bán kính R = 2
A.Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng tròn tâm I (1;0) , bán kính R = 3
A.Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng tròn tâm I (0;− ) 1 , bán kính R = 3
A.Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng tròn tâm I (0;− ) 1 , bán kính R = 2
Bài 5-[Thi thӱ THPT Quҧng Xѭѫng I – Thanh Hóa lҫn 1 năm 2017] 2
Tұp hӧp ÿiӇm biӇu diӉn sӕ phӭc z thӓa mãn 2 z = z là : A.Cҧ mһt phҷng B.Ĉѭӡng thҷng
C.Mӝt ÿiӇm D.Hai ÿѭӡng thҷng
Bài 6-Tұp hӧp ÿiӇm biӇu diӉn sӕ phӭc z thӓa mãn 2 z −1 = z − z + 2i là mӝt Parabol có dҥng: 2 x 2 x 1 A. 2
y = 3x − 6x + 2 B. y = − x C. y = − 4 D. 2
y = x + 2x + 2 3 3
LӠI GIҦI BÀI TҰP TӴ LUYӊN
Bài 1-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 2 năm 2017]
Cho các sӕ phӭc z thӓa mãn z +1− i = z −1+ 2i . Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z trên mһt
phҷng tӑa ÿӝ là mӝt ÿѭӡng thҷng. ViӃt phѭѫng trình ÿѭӡng thҷng ÿó.
A. 4x + 6 y − 3 = 0
B. 4x − 6 y − 3 = 0
C. 4x + 6 y + 3 = 0
D. 4x − 6 y + 3 = 0 '/ѵ/ ĄĐŚϭ͗ĂƐŝŽ
'ŝңƐӊĜĄƉĄŶĜƷŶŐ͕ĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ z = x + yi ƚŚƵҾĐĜӇӁŶŐƚŚҫŶŐ 4x + 6 y − 3 = 0 1 1
Chӑn x = 1 thì y = − và sӕ phӭc z = 1− i . 6 6
yĠƚŚŝҵƵ z +1− i − z −1+ 2i ͘EұƵŚŝҵƵƚƌġŶ = 0 ƚŚŞĜĄƉĄŶĜƷŶŐ͘ҳůăŵǀŝҵĐŶăLJƚĂƐӊĚӅŶŐŵĄLJƚşŶŚ ĂƐŝŽ TFSD5ESESTFSD5 ESE
HiӋu trên khác 0 vұy ÿáp án A sai 1 1
dŚӊǀӀŝĜĄƉĄŶ͘ŚŽŶ x =1ƚŚŞ y = ǀăƐҺƉŚӈĐ x = 1+ i ͘yĠƚŚŝҵƵ͗ 6 6 TFD5ESESTFD5 ESE
Vұy hiӋu z +1− i − z −1+ 2i = 0 ⇔ z +1− i = z −1+ 2i Ĉáp án chính xác là B ĄĐŚϮ͗dӌůƵҨŶ
sŞĜҲďăŝLJġƵĐҥƵƚŞŵƚҨƉŚӄƉĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ z ŶġŶƚĂĜҭƚ z = x + yi
dŚĞŽĜҲďăŝ z +1− i = z −1+ 2i x +1+ ( y − )
1 i = x −1+ ( y + 2)i
⇔ (x + )2 + ( y − )2 = (x − )2 + ( y + )2 1 1 1 2 TOANMATH.com
Tác giả: Trần Bá Hưng 2 2 2 2
⇔ x + 2x +1+ y − 2y +1 = x − 2x +1+ y + 4y + 4
⇔ 4x − 6y − 3 = 0 . Vұy ÿáp án chính xác là B
Bài 2-[Thi thӱ THPT TriӋu Sѫn – Thanh Hóa lҫn 1 năm 2017]
Tұp hӧp các ÿiӇm M biӇu diӉn sӕ phӭc z : z = z − 3 + 4i là phѭѫng trình có dҥng
A. 6x + 8y − 25 = 0
B. 3x + 4 y − 3 = 0 C. 2 x + y = 25 2 2
D. ( x − 3) + ( y − 4) = 25 '/ѵ/
ҭƚƐҺƉŚӈĐ z = x + yi ͘ 2 2
Ta có : z = z − 3 + 4i ⇔ x + yi = x − 3 + (4 − y)i 2 2
⇔ x + y = (x − 3) + (4 − y) 2 2 2 2
⇔ x + y = x − 6x + 9 + y −8y +16 ⇔ 6x + 8y − 25 = 0
Vұy tұp hӧp các ÿiӇm M biӇu diӉn sӕ phӭc z là ÿѭӡng thҷng 6x + 8 y − 25 = 0
Ĉáp án chính xác là A
Bài 3-[Thi thӱ THPT NguyӉn Ĉình ChiӇu – Bình Ĉӏnh lҫn 1 năm 2017]
Cho các sӕ phӭc z thӓa mãn z = 2 . BiӃt rҵng tұp hӧp các ÿiӇm biӇu diӉn các sӕ phӭc
w = 3 − 2i + (2 − i) z là mӝt ÿѭӡng tròn. Tính bán kính r cӫa ÿѭӡng tròn ÿó. A. r = 20 B. r = 20 C. r = 7 D. r = 7 '/ѵ/ ĄĐŚϭ͗ĂƐŝŽ
ŚҸŶƐҺƉŚӈĐ z = 2 ƚŚҹĂŵĆŶ z = 2ǀҨLJ w = 3− 2i + 2 − i .2 = 7 − 4i ͘dĂĐſĜŝҳŵďŝҳƵĚŝҴŶĐӆĂ w ůă 1 ( ) 1 M (7; 4 − )
ŚҸŶƐҺƉŚӈĐ z = −2 ƚŚҹĂŵĆŶ z = 2ǀҨLJ w = 3− 2i + 2 − i . 2 − = 1
− + 0i ͘dĂĐſĜŝҳŵďŝҳƵĚŝҴŶƐҺ 2 ( ) ( )
ƉŚӈĐ w ůă N ( 1 − ;0) 2
ŚҸŶƐҺƉŚӈĐ z = 2i ƚŚҹĂŵĆŶ z = 2ǀҨLJ w = 3− 2i + 2 − i . 2i = 5 + 2i ͘dĂĐſĜŝҳŵďŝҳƵĚŝҴŶƐҺ 3 ( ) ( )
ƉŚӈĐ w ůă P (5;2) 3 SESE2E
^ӊĚӅŶŐŵĄLJƚşŶŚƚŞŵƉŚӇҿŶŐƚƌŞŶŚĜӇӁŶŐƚƌžŶĚŝƋƵĂϯĜŝҳŵ M , N , P Z S SGSG S SG SGSG
Vұy phѭѫng trình ÿѭӡng tròn cҫn tìm là x + y − x + y − = ⇔ ( x − ) + ( y + ) = ( )2 2 2 2 2 6 4 7 0 3 2 20 sӁ
có bán kính là r = 20
Ĉáp án chính xác là B ĄĐŚϮ͗dӌůƵҨŶ TOANMATH.com
Tác giả: Trần Bá Hưng
sŞĜҲďăŝLJġƵĐҥƵƚŞŵƚҨƉŚӄƉĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ w ŶġŶƚĂĜҭƚ w = x + yi w − + i
dŚĞŽĜҲďăŝ w = 3 − 2i + (2 − 3 2 i) z z = 2 − i
x − 3 + ( y + 2)i ªx
¬ − 3 + ( y + 2)iº¼ (2 + i) ⇔ z = = 2 − i (2−i)(2+i)
2x − y − 8 + ( x + 2y + ) 1 ⇔ z = 3 2 2
§ 2x − y −8 · § x + 2y +1· dĂĐſ z = 2 ¨ ¸ + ¨ ¸ = 4 © 5 ¹ © 5 ¹
⇔ ( x − y − )2 + (x + y + )2 2 8 2 1 = 100 2 2
⇔ 5x + 5y − 30x + 20y + 65 =100 2 2
⇔ x + y − 6x + 4y = 7
⇔ (x − ) + ( y + ) = ( )2 2 2 3 2 20
Bài 4-[Thi thӱ THPT Hàm Rӗng – Thanh Hóa lҫn 1 năm 2017]
Trong mһt phҷng Oxy , tìm tұp hӧp ÿiӇm biӇu diӉn sӕ phӭc z thӓa mãn z −1 = (1+ i) z
A.Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng tròn tâm I (2;− ) 1 , bán kính R = 2
A.Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng tròn tâm I (1;0) , bán kính R = 3
A.Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng tròn tâm I (0;− ) 1 , bán kính R = 3
A.Tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng tròn tâm I (0;− ) 1 , bán kính R = 2 '/ѵ/
ҭƚƐҺƉŚӈĐ z = x + yi ͘
dĂĐſ͗ z −1 = (1+ i) z ⇔ x + yi −1 = (x + yi)(1+ i) ⇔ x −1+ yi = x − y + (x + y)i
⇔ (x − )2 + y = (x − y)2 + (x + y)2 2 1 2 2 2 2 2 2
⇔ x − 2x +1+ y = x − 2xy + y + x + 2xy + y 2 2
⇔ x + y + 2x −1 = 0
⇔ (x + ) + y = ( )2 2 2 1 2
Vұy tұp hӧp các ÿiӇm M biӇu diӉn sӕ phӭc z là ÿѭӡng tròn tâm I ( 1
− ;0) , bán kính R = 2
Ĉáp án chính xác là D
Bài 5-[Thi thӱ THPT Quҧng Xѭѫng I – Thanh Hóa lҫn 1 năm 2017] 2
Tұp hӧp ÿiӇm biӇu diӉn sӕ phӭc z thӓa mãn 2 z = z là : A.Cҧ mһt phҷng B.Ĉѭӡng thҷng
C.Mӝt ÿiӇm D.Hai ÿѭӡng thҷng '/ѵ/
ҭƚƐҺƉŚӈĐ z = x + yi ͘ 2 2 2 dĂĐſ 2
z = z ⇔ x + yi = ( x + yi) ⇔ x + y = x + xyi + ( yi)2 2 2 2 2 ª y = 0 2
2 y − 2xyi = 0 ⇔ y ( y − xi) ⇔ « y ¬ − ix = 0
Vұy tұp hӧp các ÿiӇm M biӇu diӉn sӕ phӭc z là hai ÿѭӡng thҷng y = 0 và y − ix = 0
Ĉáp án chính xác là D
Bài 6-Tұp hӧp ÿiӇm biӇu diӉn sӕ phӭc z thӓa mãn 2 z −1 = z − z + 2i là mӝt Parabol có dҥng: TOANMATH.com
Tác giả: Trần Bá Hưng 2 x 2 x 1 A. 2
y = 3x − 6x + 2 B. y = − x C. y = − 4 D. 2
y = x + 2x + 2 3 3 '/ѵ/
ҭƚƐҺƉŚӈĐ z = x + yi ͘
EұƵĜĄƉƐҺĜƷŶŐƚŚŞĜƷŶŐǀӀŝŵҸŝ z = x + yi ƚŚҹĂŵĆŶ 2
y = 3x − 6x + 2 ͘ Chӑn mӝt cһp ( ; x y) bҩt kì thӓa 2
y = 3x − 6x + 2 ví dө A(0;2) z = 2i
Xét hiӋu 2 z −1 − z − z + 2i TFESSTFESSEE
Vұy 2 z −1 − z − z + 2i = 6 − + 2 5 ≠ 0
2 z −1 ≠ z − z + 2i Ĉáp sӕ A sai 1
dӇҿŶŐƚӌǀӀŝĜĄƉƐҺĐŚҸŶ z = 1− i ͘yĠƚŚŝҵƵ 2 z −1 − z − z + 2i 2 TFSDE5SSTFSDE5 SDE5E
Vұy 2 z −1 − z − z + 2i = 0 2 z −1 = z − z + 2i Ĉáp sӕ B chính xác TOANMATH.com
Tác giả: Trần Bá Hưng ЎІȂ ГϾЍЁЏ I) KIӂN THӬC NӄN TҦNG
1. Bҩt ÿҷng thӭc thѭӡng gһp
ҤƚĜҫŶŐƚŚӈĐƵŶŚŝĂĐŽƉdžŬŝ͗ŚŽĐĄĐƐҺƚŚӌĐ a, b, x, y ƚĂůƵƀŶĐſ ( + )2 ≤ ( a b 2 2 + )( 2 2 ax by a b
x + y )͘ҤƵсdžңLJƌĂ ⇔ = x y G G G G JJJJG
ҤƚĜҫŶŐƚŚӈĐsĞĐƚҿ͗ŚŽϮǀĞĐƚŽ u ( x; y) ǀă v ( x '; y ') ƚĂůƵƀŶĐſ u + v ≥ u + v
⇔ x + y + x + y ≥ (x − x )2 +( y − y )2 2 2 2 2 ' ' ' ' x y ҤƵсdžңLJƌĂ ⇔ = < 0 x ' y '
2. Phѭѫng pháp mҽo sӱ dөng sӱ tiӃp xúc
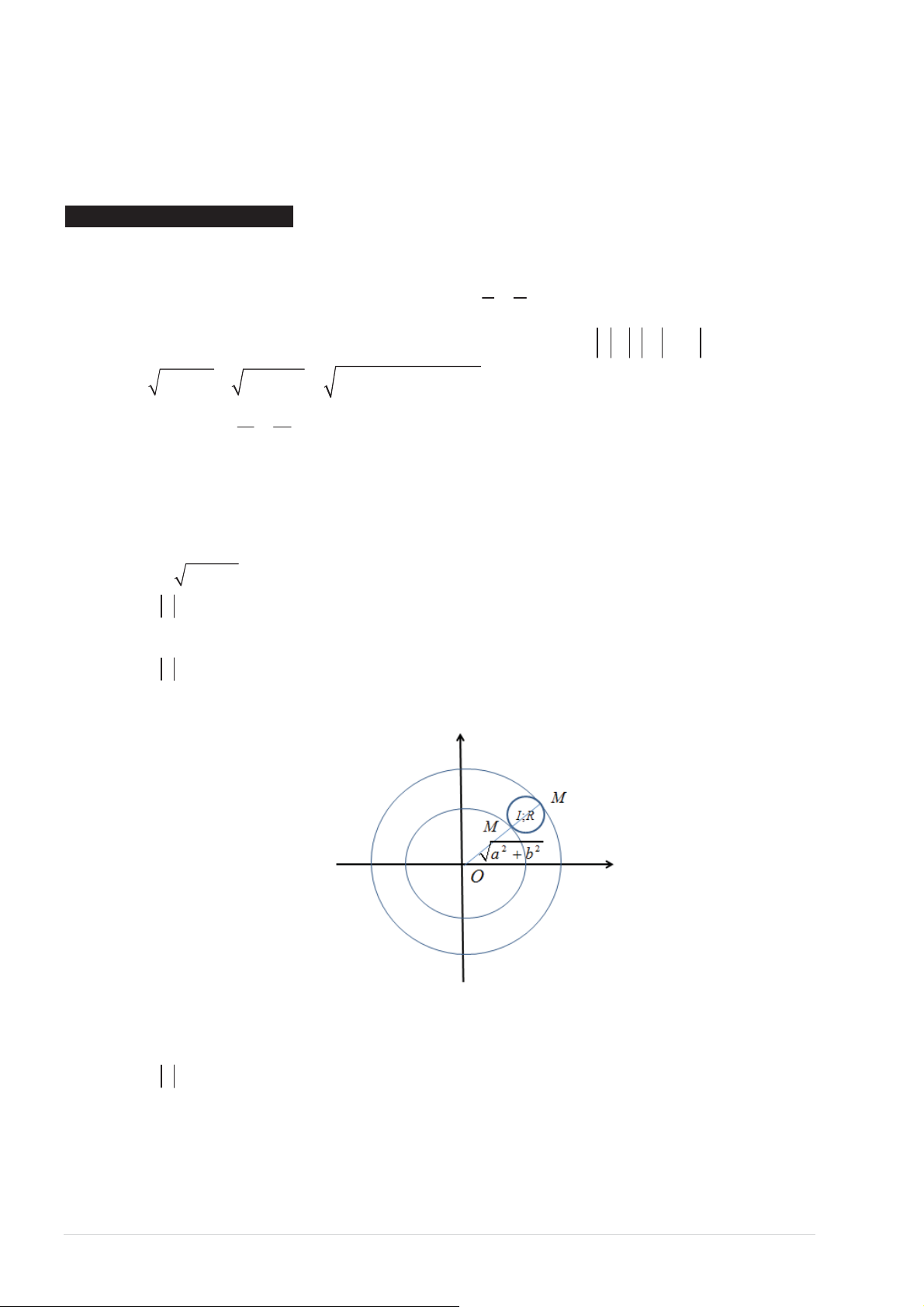
ҢŶŐϭ͗ŚŽƐҺƉŚӈĐ z ĐſƚҨƉŚӄƉĐĄĐĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ z ůăĜӇӁŶŐƚƌžŶ (C) ďĄŶŬşŶŚZ͘
sӀŝŵҽŝĜŝҳŵ M ƚŚƵҾĐĜӇӁŶŐƚƌžŶ (C) ƚŚŞĐƹŶŐƚŚƵҾĐĜӇӁŶŐƚƌžŶ(C ') ƚąŵŐҺĐƚҸĂĜҾďĄŶŬşŶŚ 2 2
OM = a + b ͘
нͿҳ z ůӀŶŶŚҤƚƚŚŞ OM ůӀŶŶŚҤƚĜҢƚĜӇӄĐŬŚŝĜӇӁŶŐƚƌžŶ (C ') ƚŝұƉdžƷĐƚƌŽŶŐǀӀŝĜӇӁŶŐƚƌžŶ
(C)ǀăOM = OI + R
нͿҳ z ŶŚҹŶŚҤƚƚŚŞ OM ŶŚҹŶŚҤƚĜҢƚĜӇӄĐŬŚŝĜӇӁŶŐƚƌžŶ (C ') ƚŝұƉdžƷĐŶŐŽăŝǀӀŝĜӇӁŶŐƚƌžŶ
(C)ǀăOM = OI − R
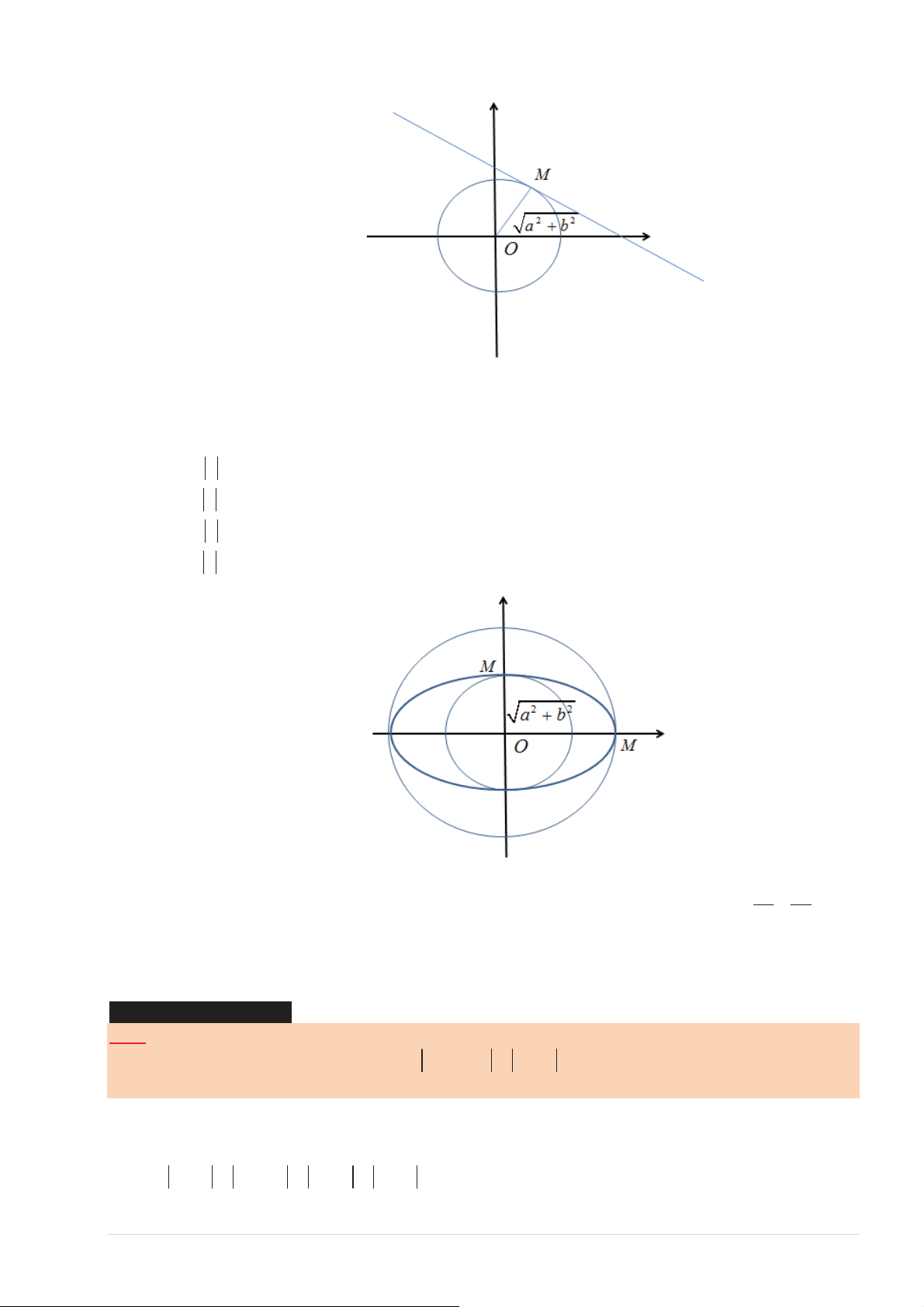
ҢŶŐϮ͗ŚŽƐҺƉŚӈĐ z ĐſƚҨƉŚӄƉĐĄĐĜŝҳŵďŝҴƵĚŝҴŶƐҺƉŚӈĐ z ůăĜӇӁŶŐƚŚҫŶŐ (d ) ͘sӀŝŵҽŝ
Ĝŝҳŵ M ƚŚƵҾĐ (d ) ƚŚŞĐƹŶŐƚŚƵҾĐĜӇӁŶŐƚƌžŶ(C ')
нͿҳ z ŶŚҹŶŚҤƚƚŚŞ OM ŶŚҹŶŚҤƚŬŚŝĜſ OM ǀƵƀŶŐŐſĐǀӀŝ (d ) ǀăOM = d ( ; O (d )) TOANMATH.com
Tác giả: Trần Bá Hưng
ҢŶŐϯ͗ŚŽƐҺƉŚӈĐ z ĐſƚҨƉŚӄƉĐĄĐĜŝҳŵďŝҴƵĚŝҴŶƐҺƉŚӈĐ z ůăůŝƉĐſĜҶŶŚƚŚƵҾĐƚƌӅĐůӀŶ A( ;
a 0) ǀăĜҶŶŚƚŚƵҾĐƚƌӅĐŶŚҹ B(0;b) ͘sӀŝŵҽŝĜŝҳŵ M ƚŚƵҾĐ(d ) ƚŚŞĐƹŶŐƚŚƵҾĐĜӇӁŶŐƚƌžŶ (E)
нͿҳ z ůӀŶŶŚҤƚƚŚŞ OM ůӀŶŶŚҤƚŬŚŝĜſ M ƚƌƶŶŐǀӀŝĜҶŶŚƚŚƵҾĐƚƌӅĐůӀŶǀă
max z = OM = OA
нͿҳ z ŶŚҹŶŚҤƚƚŚŞ OM ŶŚҹŶŚҤƚŬŚŝĜſ M ƚƌƶŶŐǀӀŝĜҶŶŚƚŚƵҾĐƚƌӅĐŶŚҹǀă
max z = OM = OB 2 2 x y
ҢŶŐϰ͗ŚŽƐҺƉŚӈĐ z ĐſƚҨƉŚӄƉĐĄĐĜŝҳŵďŝҴƵĚŝҴŶƐҺƉŚӈĐ z ůă,LJƉĞƌďŽů ( H ) : − =1Đſ 2 2 a b
ŚĂŝĜҶŶŚƚŚƵҾĐƚƌӅĐƚŚӌĐ A'(− ; a 0), A( ;
a 0) ƚŚŞƐҺƉŚӈĐ z ĐſŵƀĜƵŶŶŚҹŶŚҤƚŶұƵĜŝҳŵďŝҳƵĚŝҴŶ
ƐҺƉŚӈĐ z ŶăLJƚƌƶŶŐǀӀŝĐĄĐĜҶŶŚƚƌġŶ͘;ŵƀĜƵŶůӀŶŶŚҤƚŬŚƀŶŐƚһŶƚҢŝͿ II) VÍ DӨ MINH HӐA
VD1-[Thi thӱ THPT Vƭnh Chân – Phú Thӑ lҫn 1 năm 2017]
Trong các sӕ phӭc z thӓa mãn ÿiӅu kiӋn z − 2 − 4i = z − 2i . Tìm sӕ phӭc z có môÿun nhӓ nhҩt. A. z = 1
− + i B. z = 2
− + 2i C. z = 2 + 2i
D. z = 3 + 2i GIҦI ĄĐŚĂƐŝŽ ¾
dƌŽŶŐĐĄĐƐҺƉŚӈĐӂĜĄƉĄŶ͕ƚĂƐҰƚŝұŶŚăŶŚdžҩƉdžұƉĐĄĐƐҺƉŚӈĐƚŚĞŽƚŚӈƚӌŵƀĜƵŶƚĉŶŐĚҥŶ͗ 1 − + i < 2
− + 2i = 2 + 2i < 3+ 2i TOANMATH.com
Tác giả: Trần Bá Hưng ¾
dŝұƉƚŚĞŽƐҰƚŝұŶŚăŶŚƚŚӊŶŐŚŝҵŵƚӉŶŐƐҺƉŚӈĐƚŚĞŽƚŚӈƚӌŵƀĜƵŶƚĉŶŐĚҥŶ͕ƐҺƉŚӈĐŶăŽƚŚҹĂ
ŵĆŶŚҵƚŚӈĐĜŝҲƵŬŝҵŶ z − 2 − 4i = z − 2i ĜҥƵƚŝġŶƚŚŞůăĜƷŶŐ sӀŝ z = 1
− + i yĠƚŚŝҵƵ͗ (−1+ i) − 2 − 4i − (−1+ i) − 2i TFSESSESTFSE SE
ZĂŵҾƚŐŝĄƚƌҷŬŚĄĐϬǀҨLJ z = 1
− + i ŬŚƀŶŐƚŚҹĂŵĆŶŚҵƚŚӈĐ͘ ĄƉĄŶƐĂŝ ¾
dӇҿŶŐƚӌŶŚӇǀҨLJǀӀŝ z = 2 + 2i TFESSESTFES E
sҨLJƐҺƉŚӈĐ z = 2 + 2i ƚŚҹĂŵĆŶŚҵƚŚӈĐ ĄƉƐҺůăĜĄƉƐҺĐŚşŶŚdžĄĐ ĄĐŚŵҮŽ
'ҸŝƐҺƉŚӈĐ z ĐſĚҢŶŐ z = a + bi ͘ z ƚŚҹĂŵĆŶ z − 2 − 4i = z − 2i
⇔ a − 2 + (b − 4)i = a + (b − 2)i
⇔ (a − )2 + (b − )2 = a + (b − )2 2 2 4 2 2 2 2 2
⇔ a − 4a + 4 + b − 8b +16 = a + b − 4b + 4 ⇔ 4a + 4b =16
⇔ a + b − 4 = 0
dƌŽŶŐĐĄĐĜĄƉĄŶĐŚҶĐſĜĄƉĄŶƚŚҹĂŵĆŶ a + b − 4 = 0 ĄƉĄŶĐŚşŶŚdžĄĐůă ĄĐŚƚӌůƵҨŶ
'ҸŝƐҺƉŚӈĐ z ĐſĚҢŶŐ z = a + bi ͘ z ƚŚҹĂŵĆŶ z − 2 − 4i = z − 2i
⇔ a − 2 + (b − 4)i = a + (b − 2)i
⇔ (a − )2 + (b − )2 = a + (b − )2 2 2 4 2 2 2 2 2
⇔ a − 4a + 4 + b − 8b +16 = a + b − 4b + 4 ⇔ 4a + 4b =16 ⇔ a + b = 4
dŚĞŽďҤƚĜҫŶŐƚŚӈĐƵŶŚŝĂĐŽƉdžŬŝ͗
= (a +b)2 ≤ ( 2 2 + )( 2 2 a + b ) 2 2 2 16 1 1
z = a + b ≥ 8 z ≥ 2 2 a b ° = ҤƵсdžңLJƌĂ ⇔ ®1 1
⇔ a = b = 2 z = 2 + 2i °¯a +b = 4
VD2-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 2 năm 2017]
Vӟi các sӕ phӭc z thӓa mãn (1+ i) z +1− 7i = 2 . Tìm giá trӏ lӟn nhҩt cӫa z
A. max z = 4 B. max z = 3 C. max z = 7 D. max z = 6 GIҦI ĄĐŚŵҮŽ TOANMATH.com
Tác giả: Trần Bá Hưng ¾
'ҸŝƐҺƉŚӈĐ z ĐſĚҢŶŐ z = a + bi ͘ z ƚŚҹĂŵĆŶ (1+ i) z +1− 7i = 2
⇔ (a + bi)(1+ i) +1− 7i = 2
⇔ a − b +1+ (a + b − 7)i = 2
⇔ (a − b + )2 + (a + b − )2 1 7 = 2 2 2
⇔ 2a + 2b + 50 −12a −16b = 2 2 2
⇔ a + b − 6a − 8b + 25 = 1
⇔ (a − )2 + (b − )2 3 4 = 1
sҨLJƋƵӎƚşĐŚĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ z ůăĜӇӁŶŐƚƌžŶƚąŵ I (3;4) ďĄŶŬşŶŚ R = 1͘dĂŐҸŝĜąLJůă ĜӇӁŶŐƚƌžŶ (C) ¾
sӀŝŵҽŝĜŝҳŵ M ďŝҳƵĚŝҴŶƐҺƉŚӈĐ z = a + bi ƚŚŞ M ĐƹŶŐƚŚƵҾĐĜӇӁŶŐƚƌžŶƚąŵ O (0;0) ďĄŶ ŬşŶŚ 2 2
a + b ͘dĂŐҸŝĜąLJůăĜӇӁŶŐƚƌžŶ (C ') ͕DƀĜƵŶĐӆĂ z ĐƹŶŐůăďĄŶŬşŶŚĜӇӁŶŐƚƌžŶ(C ') ¾
ҳďĄŶŬşŶŚ (C ') ůӀŶŶŚҤƚƚŚŞO, I, M ƚŚҫŶŐŚăŶŐ;ŶŚӇŚŞŶŚͿǀă(C ') ƚŝұƉdžƷĐƚƌŽŶŐǀӀŝ(C)
<ŚŝĜſ OM = OI + R = 5 +1 = 6 ĄƉƐҺĐŚşŶŚdžĄĐůă ĄĐŚƚӌůƵҨŶ ¾
'ҸŝƐҺƉŚӈĐ z ĐſĚҢŶŐ z = a + bi ͘ z ƚŚҹĂŵĆŶ (1+ i) z +1− 7i = 2
⇔ (a + bi)(1+ i) +1− 7i = 2
⇔ a − b +1+ (a + b − 7)i = 2
⇔ (a − b + )2 + (a + b − )2 1 7 = 2 2 2
⇔ 2a + 2b + 50 −12a −16b = 2 2 2
⇔ a + b − 6a − 8b + 25 = 1
⇔ (a − )2 + (b − )2 3 4 = 1 ¾ 2 dĂĐſ 2 2
z = a + b = 6a + 8b − 24 = 6(a − 3) + 8(b − 4) + 26
dŚĞŽďҤƚĜҫŶŐƚŚӈĐƵŶŚŝĂĐŽƉdžŬŝƚĂĐſ͗ 6 (a − 3) + 8(b − 4) ≤ 6(a − 3) + 8(b − 4) ( )ª¬(a )2 (b )2 2 2 6 8 3 4 º ≤ + − + − = 10 ¼ 2
sҨLJ z ≤ 36 ⇔ z ≤ 6
ĜĄƉĄŶůăĐŚşŶŚdžĄĐ ŞŶŚůƵҨŶ ¾
sŝҵĐƐӊĚӅŶŐďҤƚĜҫŶŐƚŚӈĐĜҳĜĄŶŚŐŝĄ z ůăƌҤƚŬŚſŬŚĉŶ͕ĜžŝŚҹŝŚҸĐƐŝŶŚƉŚңŝŶҩŵƌҤƚǀӋŶŐďҤƚ
ĜҫŶŐƚŚӈĐƵŶŚŝĂĐŽƉdžŬŝǀăĐĄĐďŝұŶĚҢŶŐĐӆĂŶſ ¾
dƌŽŶŐƚŞŶŚŚƵҺŶŐĐӆĂďăŝƚŽĄŶŶăLJ͕ŬŚŝƐŽƐĄŶŚϮĐĄĐŚŐŝңŝƚĂƚŚҤLJĚƶŶŐŵҮŽƚŝұƉdžƷĐƚҹƌĂĜҿŶŐŝңŶ
ĚҴŚŝҳƵǀăƚŝұƚŬŝҵŵƚŚӁŝŐŝĂŶŚҿŶ͘
VD3-[Thi thӱ báo Toán hӑc tuәi trҿ lҫn 5 năm 2017]
Cho sӕ phӭc z thӓa mãn z − 4 + z + 4 = 10 , giá trӏ lӟn nhҩt và giá trӏ nhӓ nhҩt cӫa z lҫn lѭӧt là : A.10 và 4 B. 5 và 4
C. 4 và 3D. 5 và 3 GIҦI ĄĐŚŵҮŽ ¾
'ҸŝƐҺƉŚӈĐ z ĐſĚҢŶŐ z = a + bi ͘ z ƚŚҹĂŵĆŶ z − 4 + z + 4 = 10
⇔ a − 4 + bi + a + 4 + bi = 10 TOANMATH.com
Tác giả: Trần Bá Hưng
⇔ (a − )2 + b + (a + )2 2 2 4 4 + b = 10
⇔ (a + )2 + b = − (a − )2 2 2 4 10 4 + b
⇔ a + a + + b =
+ a − a + + b − (a − )2 2 2 2 2 2 8 16 100 8 16 20 4 + b ⇔ (a − )2 2 20 4 + b = 100 −16a ⇔ (a − )2 2 5 4 + b = 25 − 4a ⇔ ( 2 2 a − a + + b ) 2 25 8 16
= 625 − 200a +16a 2 2
⇔ 9a + 25b = 225 2 2 a b ⇔ + = 1 25 9
sҨLJƋƵӎƚşĐŚĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ z ůăĜӇӁŶŐůŝƉĜҶŶŚƚŚƵҾĐĜĄLJůӀŶůă A(5;0) ͕ĜҶŶŚƚŚƵҾĐ
ĜĄLJŶŚҹůă B (0;3) ¾
sӀŝŵҽŝĜŝҳŵ M ďŝҳƵĚŝҴŶƐҺƉŚӈĐ z = a + bi ƚŚŞ M ĐƹŶŐƚŚƵҾĐĜӇӁŶŐƚƌžŶƚąŵ O (0;0) ďĄŶ ŬşŶŚ 2 2
a + b ͘dĂŐҸŝĜąLJůăĜӇӁŶŐƚƌžŶ (C ') ͕DƀĜƵŶĐӆĂ z ĐƹŶŐůăďĄŶŬşŶŚĜӇӁŶŐƚƌžŶ(C ') ¾
ҳďĄŶŬşŶŚ (C ') ůӀŶŶŚҤƚƚŚŞ M ƚƌƶŶŐǀӀŝĜҶŶŚƚŚƵҾĐƚƌӅĐůӀŶǀă M ≡ A(5;0) OM = 5 max z = 5 ¾
ҳďĄŶŬşŶŚ (C ') ůӀŶŶŚҤƚƚŚŞ M ƚƌƶŶŐǀӀŝĜҶŶŚƚŚƵҾĐƚƌӅĐŶŚҹǀă M ≡ B (0;3) OM = 3 min z = 3 ĄƉƐҺĐŚşŶŚdžĄĐůă ĄĐŚƚӌůƵҨŶ ¾
'ҸŝƐҺƉŚӈĐ z ĐſĚҢŶŐ z = a + bi ͘ z ƚŚҹĂŵĆŶ z − 4 + z + 4 = 10
⇔ a − 4 + bi + a + 4 + bi = 10
⇔ (a − )2 + b + (a + )2 2 2 4 4 + b = 10
⇔ (a + )2 + b + (−a + )2 + (−b)2 2 4 4 = 10
dŚĞŽďҤƚĜҫŶŐƚŚӈĐǀĞĐƚŽƚĂĐſ͗ ⇔
= (a + )2 + b + (−a + )2 + (−b)2 2 10 4 4
≥ ª(a + 4) −(−a + 4) 2º + ªb −(−b) 2º ¬ ¼ ¬ ¼ 2 2 ⇔ 10 ≥ 4a + 4b
⇔ 10 ≥ 2 z z ≤ 5 ¾ 2 2 dĂĐſ ⇔ (a − ) 2 + b + (a + ) 2 4 4 + b = 10
dŚĞŽďҤƚĜҫŶŐƚŚӈĐƵŶŚŝĂĐŽƉdžŬŝƚĂĐſ͗ 2 (a )2 b (a ) ( 2 b ) (
)ª(a )2 b (a )2 2 2 2 2 2 2 100 4 4 1 1 4 4 b º = − + + + + ≤ + − + + + + ¬ ¼ ⇔ ≤ ( 2 2 100 2 2a + 2b + 32) 2 2
⇔ 2a + 2b + 32 ≥ 50 2 2 ⇔ a + b ≥ 9 2
sҨLJ z ≥ 9 ⇔ z ≤ 3
3 ≤ z ≤ 5 ĜĄƉĄŶůăĐŚşŶŚdžĄĐ TOANMATH.com
Tác giả: Trần Bá Hưng
VD4-Trong các sӕ phӭc z thӓa mãn z − 2 − z + 2 = 2 , tìm sӕ phӭc z có môÿun nhӓ nhҩt.
A. z = 1− 3i B. z = 1
− + 3i C. z = 1
D. z = 3 + i GIҦI ĄĐŚŵҮŽ ¾
'ҸŝƐҺƉŚӈĐ z ĐſĚҢŶŐ z = x + yi ͘ z ƚŚҹĂŵĆŶ z − 2 − z + 2 = 2
⇔ x − 2 + yi − x + 2 + yi = 2
⇔ (x − )2 + y − (x + )2 2 2 2 2 + y = 2
⇔ (x − )2 + y = + (x + )2 2 2 2 2 2 + y
⇔ (x − )2 + y = + (x + )2 + y +(x + )2 2 2 2 2 4 4 2 2 + y ⇔ − − § · x = ( x + )2 2 1 2 2 + 1
y ¨ −1− 2x ≥ 0 ⇔ x ≤ − ¸ © 2 ¹ 2 2 2
⇔ 1+ 4x + 4x = x + 4x + 4 + y 2 y 2 ⇔ x − =1 3 2 y
sҨLJƚҨƉŚӄƉĜŝҳŵďŝҳƵĚŝҴŶƐҺƉŚӈĐ z ůă,LJƉĞďŽů (H ) 2 : x −
=1ĐſϮĜҶŶŚƚŚƵҾĐƚŚӌĐůă 3 A'( 1 − ;0),B(1;0) ¾
^ҺƉŚӈĐ z = x + yi ĐſĜŝҳŵďŝҳƵĚŝҴŶ M ( ;
x y) ǀăĐſŵƀĜƵŶůă 2 2
OM = a + b ͘ҳ OM ĜҢƚŐŝĄ
ƚƌҷŶŚҹŶŚҤƚƚŚŞ M ƚƌƶŶŐǀӀŝŚĂŝĜҶŶŚĐӆĂ ( H )
M ≡ A M (1;0) z =1
Ĉáp án chính xác là C
II) BÀI TҰP TӴ LUYӊN
Bài 1-Cho các sӕ phӭc z thӓa mãn 2z − 2 + 2i = 1. Môÿun z nhӓ nhҩt có thӇ ÿҥt ÿѭӧc là bao nhiêu : 1 − + 2 2 1+ 2 2 A. B. C. 2 +1 D. 2 −1 2 2
Bài 2-Trong các sӕ phӭc z thӓa mãn z − 3i + iz + 3 = 10 . Hai sӕ phӭc z và z có môÿun nhӓ 1 2
nhҩt. Hӓi tích z z là bao nhiêu 1 2 A. 25 B. −25 C.16 D. −16
Bài 3-Trong các sӕ phӭc z thӓa mãn iz − 3 = z − 2 − i . Tính giá trӏ nhӓ nhҩt cӫa z . 1 1 1 1 A. B. C. D. 2 2 5 5
LӠI GIҦI BÀI TҰP TӴ LUYӊN
Bài 1-Cho các sӕ phӭc z thӓa mãn 2z − 2 + 2i = 1. Môÿun z nhӓ nhҩt có thӇ ÿҥt ÿѭӧc là bao nhiêu : 1 − + 2 2 1+ 2 2 A. B. C. 2 +1 D. 2 −1 2 2 '/ѵ/ ĄĐŚŵҮŽ
'ҸŝƐҺƉŚӈĐ z = x + yi ƚŚҹĂŵĆŶ 2z − 2 + 2i =1 ⇔ 2x − 2 + 2yi + 2i = 1 TOANMATH.com
Tác giả: Trần Bá Hưng
⇔ ( x − )2 + ( y + )2 2 2 2 2 = 1
⇔ (x − )2 + ( y + )2 1 1 1 = 4 1
Vұy tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng tròn (C) có tâm I (1;− ) 1 bán kính R = 2
sӀŝŵҽŝĜŝҳŵ M ( ;
x y) ďŝҳƵĚŝҴŶƐҺƉŚӈĐ z = x + yi ƐҰƚŚƵҾĐĜӇӁŶŐƚƌžŶƚąŵO ďĄŶŬşŶŚ 2 2
R ' = z = x + y ͘sŞǀҨLJĜҳ R = z ŶŚҹŶŚҤƚƚŚŞĜӇӁŶŐƚƌžŶ (C ') ƉŚңŝƚŝұƉdžƷĐŶŐŽăŝǀӀŝĜӇӁŶŐ (C') −1+ 2 2
Khi ÿó ÿiӇm M sӁ là tiӃp ÿiӇm cӫa ÿѭӡng tròn (C) và (C ') và z = OM = OI − R = 2 VSGSSGSD5
Ĉáp sӕ chính xác là A
Bài 2-Trong các sӕ phӭc z thӓa mãn z − 3i + iz + 3 = 10 . Hai sӕ phӭc z và z có môÿun nhӓ 1 2
nhҩt. Hӓi tích z z là bao nhiêu 1 2 A. 25 B. −25 C.16 D. −16 '/ѵ/ ĄĐŚŵҮŽ
'ҸŝƐҺƉŚӈĐ z = x + yi ƚŚҹĂŵĆŶ z − 3i + iz + 3 = 10
⇔ x + ( y −3)i + y + 3+ xi =10
⇔ x + ( y − )2 + ( y + )2 2 2 3 3 + x = 10
⇔ ( y + )2 + x = − x + ( y − )2 2 2 3 10 3
⇔ ( y + )2 + x = −
x + ( y − )2 + x + ( y − )2 2 2 2 3 100 20 3 3 ⇔ x + ( y − )2 2 20 3 = 100 −12y 2 2
⇔ 25x +16y = 400 2 2 x y ⇔ + =1 16 25 2 2 x y
Vұy tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng Elip (E) : +
=1có 2 ÿӍnh thuӝc trөc nhӓ 16 25 là A( 4; − 0), A'(4;0)
sӀŝŵҽŝĜŝҳŵ M ( ;
x y) ďŝҳƵĚŝҴŶƐҺƉŚӈĐ z = x + yi ƐҰƚŚƵҾĐĜӇӁŶŐƚƌžŶƚąŵO ďĄŶŬşŶŚ 2 2
R ' = z = x + y ͘sŞĞůŝƉ (E) ǀăĜӇӁŶŐƚƌžŶ(C) ĐſĐƶŶŐƚąŵO ŶġŶĜҳOM ŶŚҹŶŚҤƚƚŚŞ M ůă
ĜҶŶŚƚŚƵҾĐƚƌӅĐŶŚҹ
M ≡ A' z = 4
− , M ≡ A z = 4 1 2
Tәng hӧp z .z = 4 − .4 = 1 − 6 1 2 ( )
Ĉáp sӕ chính xác là D DӂƌҾŶŐ TOANMATH.com
Tác giả: Trần Bá Hưng
EұƵĜҲďăŝŚҹŝƚşĐŚ z z ǀӀŝ z , z ĐſŐŝĄƚƌҷůӀŶŶŚҤƚƚŚŞŚĂŝĜŝҳŵ M ďŝҳƵĚŝҴŶŚĂŝƐҺƉŚӈĐƚƌġŶůăŚĂŝ 1 2 1 2
ĜҶŶŚƚŚƵҾĐƚƌӅĐůӀŶ B (0; 5 − ), B'(0;5)
M ≡ B ' z = 5
− i , M ≡ A z = 5i 1 2
Tәng hӧp z z = 5 .i( 5 − i) 2 = 2 − 5i = 25 1 2
Bài 3-Trong các sӕ phӭc z thӓa mãn iz − 3 = z − 2 − i . Tính giá trӏ nhӓ nhҩt cӫa z . 1 1 1 1 A. B. C. D. 2 2 5 5 '/ѵ/ ĄĐŚŵҮŽ
'ҸŝƐҺƉŚӈĐ z = x + yi ƚŚҹĂŵĆŶ iz − 3 = z − 2 − i
⇔ − y − 3 + xi = x − 2 + ( y − ) 1 i
⇔ (−y − )2 + x = (x − )2 + ( y − )2 2 3 2 1 2 2 2 2
⇔ y + 6y + 9 + x = x − 4x + 4 + y − 2y +1
⇔ x + 2y +1 = 0 ⇔ x + ( y − )2 2 20 3 = 100 −12y
Vұy tұp hӧp các ÿiӇm biӇu diӉn sӕ phӭc z là ÿѭӡng thҷng (d ) : x + 2y +1 = 0
sӀŝŵҽŝĜŝҳŵ M ( ;
x y) ďŝҳƵĚŝҴŶƐҺƉŚӈĐ z = x + yi ƚŚŝ z = OM ≥ OH ǀӀŝ H ů㌪ŶŚĐŚŝұƵǀƵƀŶŐŐſĐ
ĐӆĂ O ůġŶĜӇӁŶŐƚŚҫŶŐ (d ) ǀăOH ůăŬŚŽңŶŐĐĄĐŚƚӉĜŝҳŵO ůġŶĜӇӁŶŐƚŚҫŶŐ (d ) 1.0 + 2.0 +1 1
Tính OH = d (O;(d )) = = 2 2 1 + 2 5 1 Vұy z ≥ 5
Ĉáp sӕ chính xác là D 2 2 3 2 2 3 2 1
x − y +1+ 2xyi
x − xy + x + x yi + y i − yi + 2xy x + yi + = = 2 2 x + yi x + yi x + y TOANMATH.com
Tác giả: Trần Bá Hưng ЎІȂ ЎІ@ЁЏ I) KIӂN THӬC NӄN TҦNG
1. ChuyӇn sӕ phӭc vӅ dҥng lѭӧng giác
ҢŶŐůӇӄŶŐŐŝĄĐĐӆĂƐҺƉŚӈĐ͗ŚŽƐҺƉŚӈĐ z ĐſĚҢŶŐ z = r (cosϕ + i sinϕ ) ƚŚŞƚĂůƵƀŶĐſ͗ n n
z = r (cos nϕ + isin nϕ )
>ҵŶŚĐŚƵLJҳŶƐҺƉŚӈĐ z = a + bi ǀҲĚҢŶŐůӇӄŶŐŐŝĄĐ͗>ҵŶŚ^,/&dϮϯ
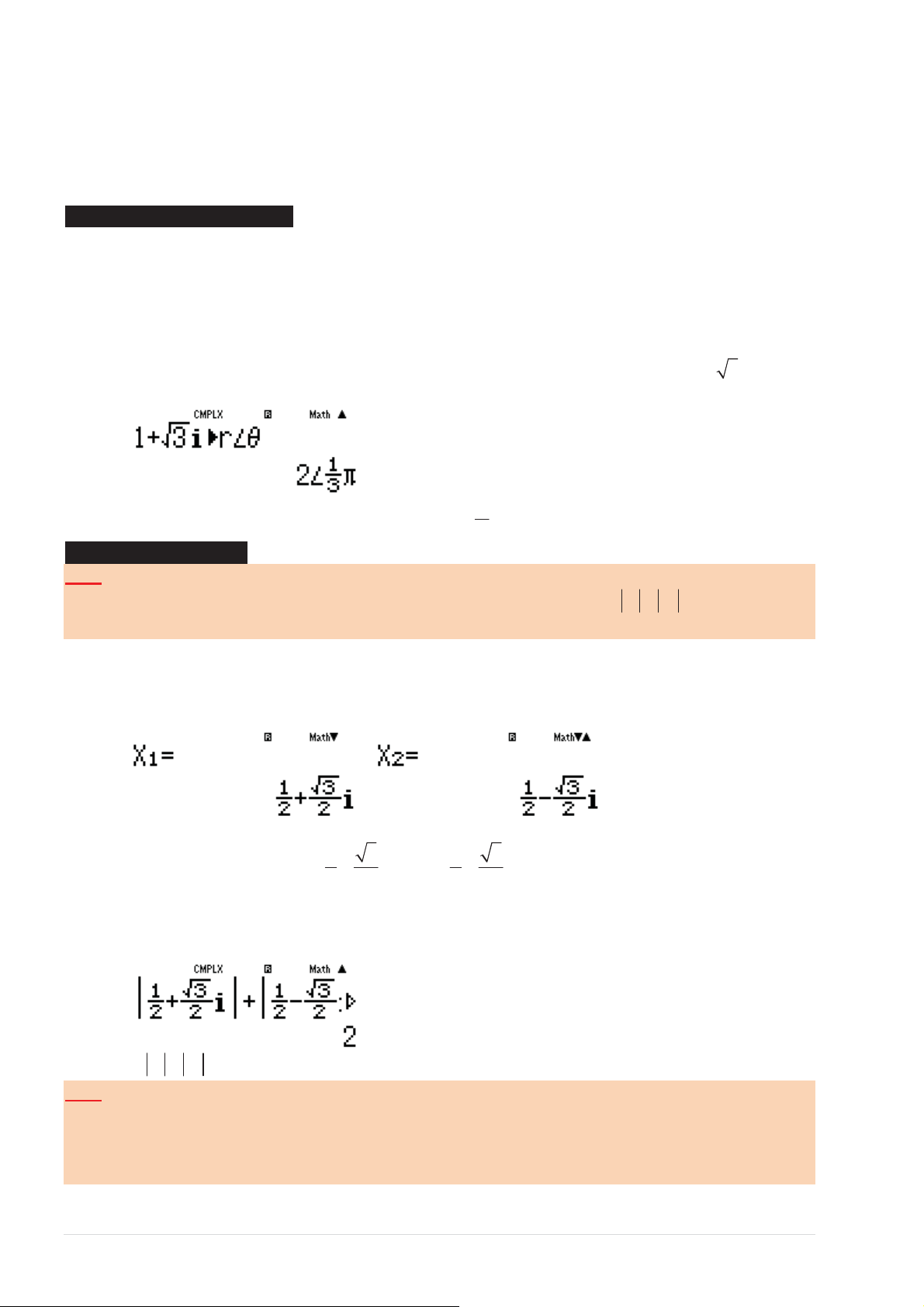
ӇӀĐϭ͗EŚҨƉƐҺƉŚӈĐ z = a + bi ǀăŽŵăŶŚŞŶŚƌһŝĚƶŶŐůҵŶŚ^,/&dϮϯ;sşĚӅ z = 1+ 3i Ϳ VET π
ӇӀĐϮ͗dӉďңŶŐŬұƚƋƵңƚĂĜҸĐŚŝҳƵ r = 2 ǀăϕ = 3 II) VÍ DӨ MINH HӐA
VD1-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 1 năm 2017]
Gӑi z , z là hai nghiӋm phӭc cӫa phѭѫng trình 2
z − z +1 = 0 . Giá trӏ cӫa z + z bҵng : 1 2 1 2 A. 0 B.1 C. 2 D. 4 GIҦI ĄĐŚĂƐŝŽ ¾
dşŶŚŶŐŚŝҵŵĐӆĂƉŚӇҿŶŐƚƌŞŶŚďҨĐŚĂŝ 2
z − z +1 = 0 ďҪŶŐĐŚӈĐŶĉŶŐDKϱϯ Z S 1 3 1 3 ¾
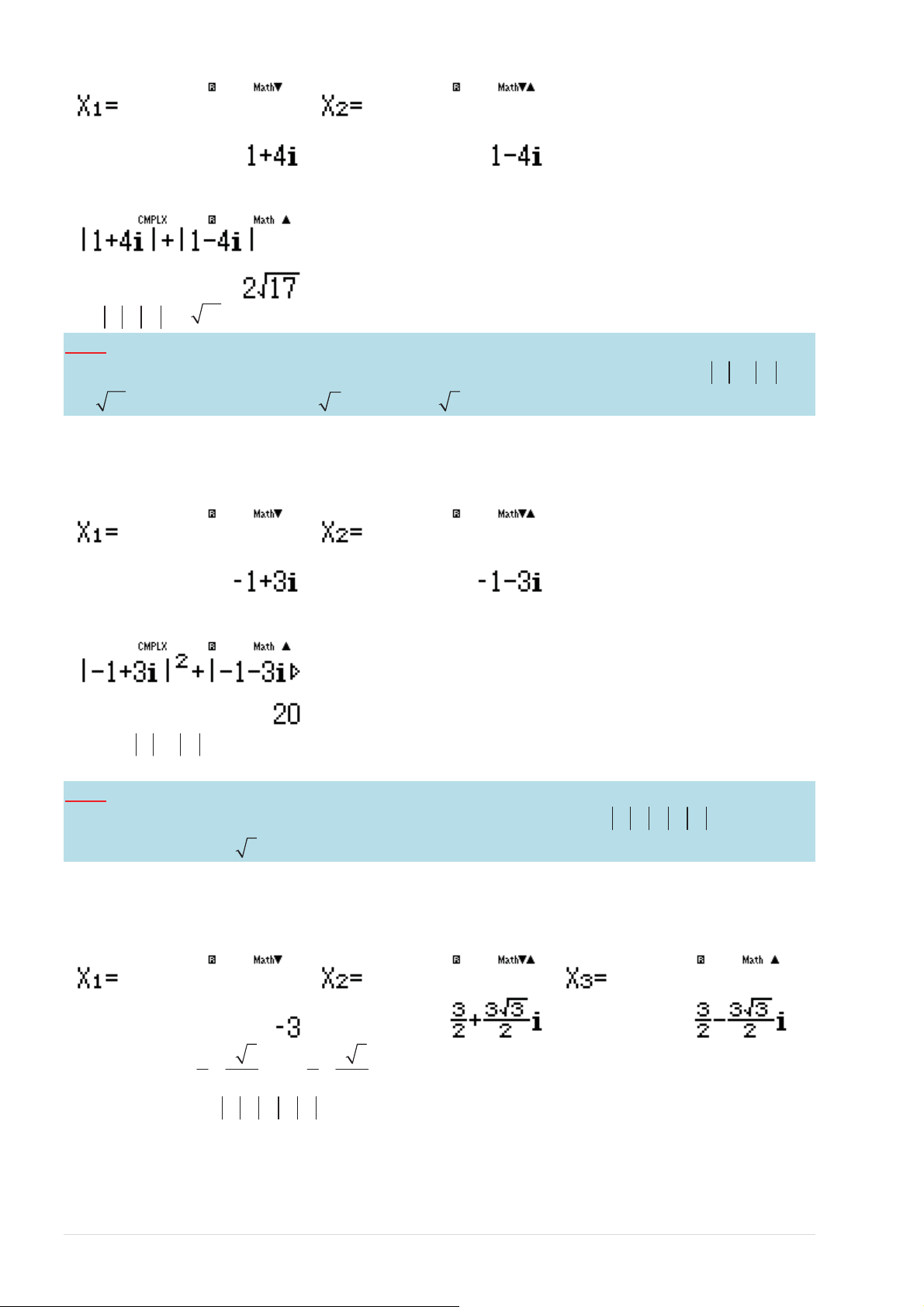
sҨLJƚĂĜӇӄĐŚĂŝŶŐŚŝҵŵ z = + i ǀă z = −
i ͘dşŶŚƚҼŶŐDƀĜƵŶĐӆĂŚĂŝƐҺƉŚӈĐƚƌġŶƚĂ 1 2 2 2 2 2
ůҢŝĚƶŶŐĐŚӈĐŶĉŶŐ^,/&d,zW ZTFD5DV5ETF D5SDV5E
z + z = 2 ƚĂƚŚҤLJůăĜĄƉĄŶĐŚşŶŚdžĄĐ 1 2
VD2-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 2 năm 2017]
Gӑi z , z là hai nghiӋm phӭc cӫa phѭѫng trình 2
z + 2z + 2 = 0 . Tính giá trӏ cӫa biӇu thӭc 1 2 2016 2016 P = z + z : 1 2 A. 1009 2 B. 0 C. 2017 2 D. 1008 2 GIҦI ĄĐŚĂƐŝŽϭ TOANMATH.com
Tác giả: Trần Bá Hưng ¾
dşŶŚŶŐŚŝҵŵĐӆĂƉŚӇҿŶŐƚƌŞŶŚďҨĐŚĂŝ 2
z + 2z + 2 = 0 ďҪŶŐĐŚӈĐŶĉŶŐDKϱϯ Z ¾
dĂƚŚƵĜӇӄĐŚĂŝŶŐŚŝҵŵ z = −1+ i ǀă z = 1
− − i ͘sӀŝĐĄĐĐӅŵĜҭĐďŝҵƚ 1 − + i ͕ 1
− − i ƚĂĐſĜŝҲƵ 1 2
ĜҭĐďŝҵƚƐĂƵ͗ (− + i)4 1 = −4 ͕(− − i)4 1 = 4 − ZSEA 504 504 2016 2016 4 4 sҨLJ 2016 2016 P z z 1 i 1 i ª 1 i º ª 1 i º = + = − + + − − = − + + − − 1 2 ( ) ( ) ¬( ) ¼ ¬( ) ¼ = (− )504 + (− )504 504 504 1008 1008 1008 1009 4 4 = 4 + 4 = 2 + 2 = 2.2 = 2 2016 2016 1009 P = z + z = 2
ƚĂƚŚҤLJůăĜĄƉĄŶĐŚşŶŚdžĄĐ 1 2 ĄĐŚĂƐŝŽϮ ¾
EŐŽăŝĐĄĐŚƐӊĚӅŶŐƚşŶŚĐŚҤƚĜҭĐďŝҵƚĐӆĂĐӅŵ (− ± )4 1 i ƚĂĐſƚŚҳdžӊůlj 1
− ± i ďҪŶŐĐĄĐŚĜӇĂǀҲ
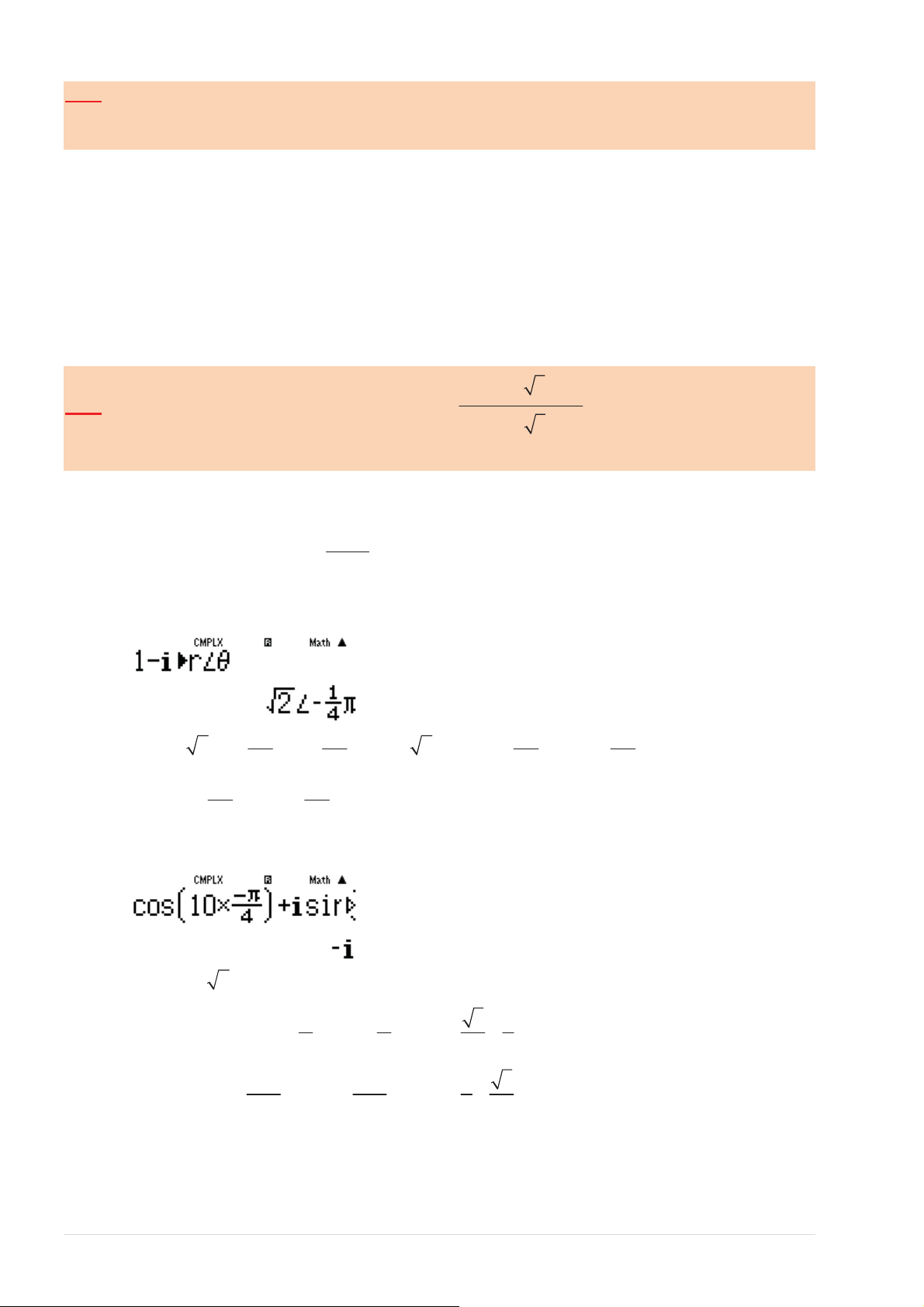
ĚҢŶŐůӇӄŶŐŐŝĄĐďҪŶŐůҵŶŚ^,/&dϮϯ sӀŝ z = 1
− + i = r cosϕ + isinϕ 1 ( ) SET 3π
dĂŶŚҨŶĜӇӄĐ r = 2 ǀăŐſĐϕ = 4 § 3π 3π · § π π · z = 2 cos ¨ + i sin z ¸ = ( 2)2016 3 3 2016 cos 2016. ¨ + i sin 2016. 1 1 ¸ © 4 4 ¹ © 4 4 ¹ § 3π · § 3π · ¾ dşŶŚ cos 2016. ¨ ¸ + .isin 2016. ¨ ¸ © 4 ¹ © 4 ¹ N2DT.5E2M 2DT.5R z = ( 2)2016 2016 1008 = 2 1 ¾ dӇҿŶŐƚӌ 2016 1008 1009 z = 2 T = 2 2
VD3-[ĈӅ minh hӑa bӝ GD-ĈT lҫn 1 năm 2017]
Kí hiӋu z , z , z và z là bӕn nghiӋm phӭc cӫa phѭѫng trình 4 2
z − z −12 = 0 . Tính tәng : 1 2 3 4
T = z + z + z + z 1 2 3 4 A. T = 4
B. T = 2 3 C. T = 4 + 2 3 D. T = 2 + 2 3 GIҦI TOANMATH.com
Tác giả: Trần Bá Hưng ĄĐŚĂƐŝŽ ¾
ҳƚşŶŚŶŐŚŝҵŵĐӆĂƉŚӇҿŶŐƚƌŞŶŚƚĂĚƶŶŐĐŚӈĐŶĉŶŐDKϱ͘dƵLJŶŚŝġŶŵĄLJƚşŶŚĐŚҶƚşŶŚĜӇӄĐ
ƉŚӇҿŶŐƚƌŞŶŚďҨĐϮǀăϯŶġŶĜҳƚşŶŚĜӇӄĐƉŚӇҿŶŐƚƌŞŶŚďҨĐϰƚƌƶŶŐƉŚӇҿŶŐ 4 2
z − z −12 = 0 ƚŚŞƚĂ ĐŽŝ 2
z = t ŬŚŝĜſƉŚӇҿŶŐƚƌŞŶŚƚƌӂƚŚăŶŚ 2
t − t −12 = 0 Z S S ªt = 4 2 ªz = 4 sҨLJ « ŚĂLJ « t ¬ = 3 − 2 z ¬ = −3 ¾ sӀŝ 2 z = 4 z = ±2 ¾ sӀŝ 2
z = −3 ƚĂĐſƚŚҳĜӇĂǀҲ 2 2
z = 3i ⇔ z = ± 3i ǀӀŝ 2 i = 1
− ͘,ŽҭĐƚĂĐſƚŚҳƚŝұƉƚӅĐƐӊĚӅŶŐ
ĐŚӈĐŶĉŶŐDKϱĐŚŽƉŚӇҿŶŐƚƌŞŶŚ 2 2
z = −3 ⇔ z + 3 = 0 Z
Tóm lҥi ta sӁ có 4 nghiӋm z = 1, ± z = ± 3i ¾
dşŶŚ T ƚĂůҢŝƐӊĚӅŶŐĐŚӈĐŶĉŶŐƚşŶŚŵƀĜƵŶ^,/&d,zW ZTFTFSTFVE TFSVE
Ĉáp án chính xác là C
VD4-[Thi thӱ nhóm toán Ĉoàn Trí DNJng lҫn 3 năm 2017]
Giҧi phѭѫng trình sau trên tұp sӕ phӭc : 3 z + (i + ) 2 1 z + (i + ) 1 z + i = 0 1 3 1 3 A. z = i − B. z = − +
i C. z = − − i
D.Cҧ A, B, C ÿӅu ÿúng 2 2 2 2 GIҦI ĄĐŚĂƐŝŽ ¾
ҳŬŝҳŵƚƌĂŶŐŚŝҵŵĐӆĂϭƉŚӇҿŶŐƚƌŞŶŚƚĂƐӊĚӅŶŐĐŚӈĐŶĉŶŐ> 4AE4GE4 EUSE
sҨLJ z = −i ůăŶŐŚŝҵŵ 1 3 ¾
dŝұƉƚӅĐŬŝҳŵƚƌĂ z = − +
i ŶұƵŐŝĄƚƌҷŶăLJůăŶŐŚŝҵŵƚŚŞĐңĜĄƉĄŶǀăĜҲƵĜƷŶŐĐſŶŐŚšĂůă 2 2
ĜĄƉĄŶĐŚşŶŚdžĄĐ͘EұƵŐŝĄƚƌҷŶăLJŬŚƀŶŐůăŶŐŚŝҵŵƚŚŞĐŚҶĐſĜĄƉĄŶĜƷŶŐĚƵLJŶŚҤƚ͘ US3V3E TOANMATH.com
Tác giả: Trần Bá Hưng 1 3 Vұy z = − +
i tiӃp tөc là nghiӋm có nghƭa là ÿáp án A và B ÿӅu ÿúng 2 2
Ĉáp án chính xác là D ĄĐŚƚӌůƵҨŶ ¾
ҳŐŝңŝƉŚӇҿŶŐƚƌŞŶŚƐҺƉŚӈĐdžƵҤƚŚŝҵŶƐҺ i ƚƌŽŶŐĜſƚĂŬŚƀŶŐƚŚҳƐӊĚӅŶŐĐŚӈĐŶĉŶŐDKϱ
ĜӇӄĐŵăƉŚңŝƚŝұŶŚăŶŚŶŚſŵŶŚąŶƚӊĐŚƵŶŐ WŚӇҿŶŐƚƌŞŶŚ 3 2
⇔ z + z + z + ( 2z + z + )1i = 0 ⇔ ( ª = − z + i)( z i 2 z + z + ) 1 = 0 ⇔ « 2 z ¬ + z +1 = 0 ¾ WŚӇҿŶŐƚƌŞŶŚ 2
z + z +1 = 0 ŬŚƀŶŐĐŚӈĂƐҺ i ŶġŶƚĂĐſƚŚҳƐӊĚӅŶŐŵĄLJƚşŶŚĂƐŝŽǀӀŝĐŚӈĐŶĉŶŐ
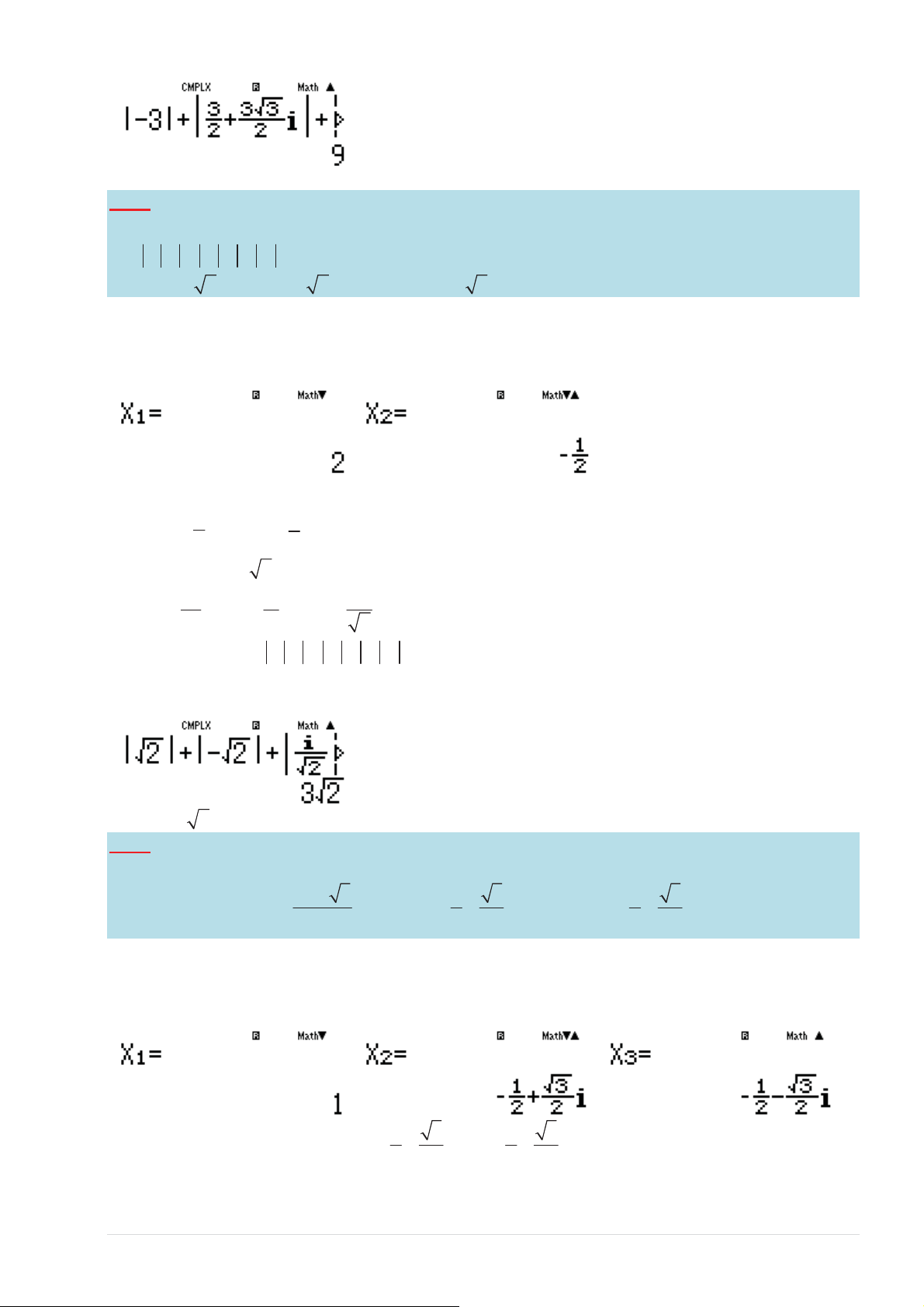
ŐŝңŝƉŚӇҿŶŐƚƌŞŶŚDKϱ Z 1 3 1 3
dſŵůҢŝƉŚӇҿŶŐƚƌŞŶŚĐſϯŶŐŚŝҵŵ z = i − ; z = − + i ; z = − − i 2 2 2 2
ůăĜĄƉĄŶĐŚşŶŚdžĄĐ
VD5-[Thi thӱ báo Toán hӑc tuәi trҿ lҫn 3 năm 2017]
Trong các phѭѫng trình dѭӟi ÿây, phѭѫng trình nào có hai nghiӋm z = 1+ 3 ; z = 1− 3 1 2 A. 2
z + i 3z +1 = 0 B. 2
z + 2z + 4 = 0 C. 2
z − 2z + 4 = 0 D. 2 z − 2z − 4 = 0 GIҦI ¾
dĂŚŝҳƵƉŚӇҿŶŐƚƌŞŶŚďҨĐŚĂŝ 2
ax + bx + c = 0 ŶұƵĐſŚĂŝŶŐŚŝҵŵƚŚŞƐҰƚƵąŶƚŚĞŽĜҷŶŚůljsŝͲĞƚ;Ŭҳ
ĐңƚƌġŶƚҨƉƐҺƚŚӌĐŚĂLJƚҨƉƐҺƉŚӈĐͿ b z + z = − ° 1 2 ° a ® c °z z = 1 2 °¯ a ¾
dşŶŚ z + z = 2 1 2 ZVESVE dşŶŚ z z = 4 1 2 VESVE b c
Rõ ràng chӍ có phѭѫng trình 2
z − 2z + 4 = 0 có − = 2 và = 4 a a
Ĉáp sӕ chính xác là C TOANMATH.com
Tác giả: Trần Bá Hưng
VD6-[Thi thӱ chuyên Khoa hӑc tӵ nhiên lҫn 1 năm 2017] Phѭѫng trình 2
z + iz +1 = 0 có bao nhiêu nghiӋm trong tұp sӕ phӭc : A. 2
B.1C. 0 D.Vô sӕ GIҦI ¾
dĂƉŚąŶďŝҵƚ͗dƌġŶƚҨƉƐҺƚŚӌĐƉŚӇҿŶŐƚƌŞŶŚďҨĐŚĂŝ 2
ax + bx + c = 0 ƐҰĐſŚĂŝŶŐŚŝҵŵƉŚąŶďŝҵƚ
ŶұƵ Δ > 0 ͕ĐſŚĂŝŶŐŚŝҵŵŬĠƉŶұƵ Δ = 0 ͕ǀƀŶŐŚŝҵŵŶұƵ Δ < 0 ͘dƵLJŶŚŝġŶƚƌġŶƚҨƉƐҺƉŚӈĐ
ƉŚӇҿŶŐƚƌŞŶŚďҨĐŚĂŝ 2
ax + bx + c = 0 ĐſϭŶŐŚŝҵŵĚƵLJŶŚҤƚŶұƵ Δ = 0 ͕ĐſŚĂŝŶŐŚŝҵŵƉŚąŶďŝҵƚ ªΔ > 0 ŶұƵ «¬Δ < 0 ¾
sҨLJƚĂĐŚҶĐҥŶƚşŶŚ Δ ůădžŽŶŐ͘sӀŝƉŚӇҿŶŐƚƌŞŶŚ 2
z + iz +1 = 0 ƚŚŞ 2
Δ = i − 4 = −5 ůăŵҾƚĜҢŝ
ůӇӄŶŐ < 0 ǀҨLJƉŚӇҿŶŐƚƌŞŶŚƚƌġŶĐſϮŶŐŚŝҵŵƉŚąŶďŝҵƚ
Ĉáp sӕ chính xác là A (1−i) ( 3 +i)5 10
VD7-Phҫn thӵc cӫa sӕ phӭc z là bao nhiêu biӃt z = ( 1−−i 3)10 A. 1 − + i B.1 C. 3 − 2i D. 5 2 i GIҦI ¾
ҳdžӊůljƐҺƉŚӈĐďҨĐĐĂŽ (> 3) ƚĂƐӊĜӇĂƐҺƉŚӈĐǀҲĚҢŶŐůӇӄŶŐŐŝĄĐǀăƐӊĚӅŶŐĐƀŶŐƚŚӈĐDŽĂͲ 10 5 z .z
ǀҿ͘săĜҳĚҴŶŚŞŶƚĂĜҭƚ 1 2 z = 10 z3 ¾
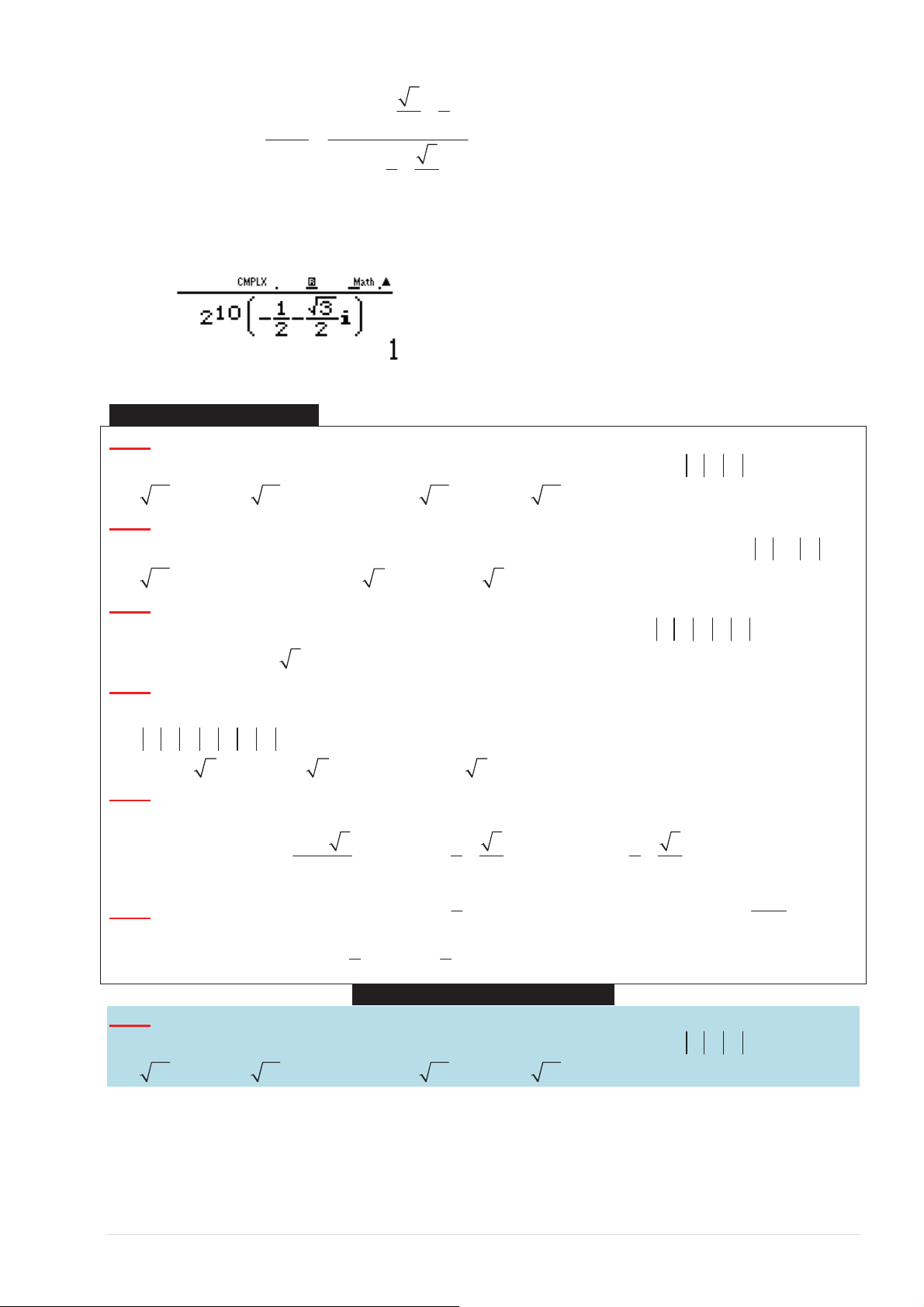
dşŶŚ z = 1− i = r cosϕ + i sinϕ ͘ҳƚşŶŚ r ǀăϕ ƚĂůҢŝƐӊĚӅŶŐĐŚӈĐŶĉŶŐ^,/&Ϯϯ 1 ( ) SET § π − π − · § π − π − · sҨLJ z = 2 cos ¨ + isin z = 2 cos10. ¨ + i sin10. 1 ( )10 10 1 ¸ ¸ © 4 4 ¹ © 4 4 ¹ π − π − dşŶŚ cos10. + isin10. 4 4 N2DST.5EM2DST .5 Vұy z = ( 2)10 10 5 .i = 2 .i 1 § π π · § 3 1 · ¾ dӇҿŶŐƚӌ 5 5 5 z = 2 cos 5. ¨ + i sin 5. ¸ = 2 ¨− + i ¸ 2 6 6 ¨ 2 2 ¸ © ¹ © ¹ § 2π 2π · § 1 3 · − − 10 10 10 z = 2 cos10. ¨ + i sin10. ¸ = 2 ¨ − − i ¸ 3 3 3 ¨ 2 2 ¸ © ¹ © ¹ TOANMATH.com
Tác giả: Trần Bá Hưng § · 5 5 3 1 2 . i 2 ¨ − + i ¸ 10 5 z .z 2 2 © ¹ dҼŶŐŚӄƉ 1 2 z = = 10 z § · 3 10 1 3 2 ¨ − − i ¸ 2 2 © ¹ DAE2ASDV5D 5E5ASD5SDV 5E
sҨLJ z = 1 ĄƉƐҺĐŚşŶŚdžĄĐůă III) BÀI TҰP TӴ LUYӊN
Bài 1-[Thi thӱ chuyên Lam Sѫn – Thanh Hóa lҫn 2 năm 2017] Cho phѭѫng trình 2
z − 2z +17 = 0 có hai nghiӋm phӭc z và z . Giá trӏ cӫa z + z là : 1 2 1 2 A. 2 17 B. 2 13 C. 2 10 D. 2 15
Bài 2-[ĈӅ thi toán Ĉҥi hӑc – Cao ÿҷng khӕi A năm 2009] 2 2
Gӑi z , z là hai nghiӋm cӫa phѭѫng trình 2
z + 2z +10 = 0 . Tính giá trӏ biӇu thӭc A = z + z 1 2 1 2 A. 2 10 B. 20 C. 5 2 D.10 3
Bài 3-[Thi thӱ Group Nhóm toán lҫn 5 năm 2017]
Kí hiӋu z , z , z là nghiӋm cӫa phѭѫng trình 3
z + 27 = 0 . Tính tәng T = z + z + z 1 2 3 1 2 3 A.T = 0 B.T = 3 3 C.T = 9 D.T = 3
Bài 4-[Thi thӱ THPT Bҧo Lâm – Lâm Ĉӗng lҫn 1 năm 2017]
Gӑi z , z , z , z là bӕn nghiӋm phӭc cӫa phѭѫng trình 4 2
2z − 3z − 2 = 0 . Tính tәng sau : 1 2 3 4
T = z + z + z + z 1 2 3 4 A. 5 B. 5 2 C. 3 2 D. 2
Bài 5-[Thi thӱ THPT Bҧo Lâm – Lâm Ĉӗng lҫn 1 năm 2017] Xét phѭѫng trình 3
z = 1 trên tұp sӕ phӭc . Tұp nghiӋm cӫa phѭѫng trình là : ° 1 3 ½ − ± ° ° 1 3 ½ ° ° 1 3 ½ ° A. S = { } 1 B. S = 1 ® ; ¾ C. S = 1 ® ; − ± i¾ D. S = ®− ± i¾ ° 2 ¯ °¿ ° 2 2 ¯ °¿ ° 2 2 ¯ °¿ 1 1
Bài 6-BiӃt z là nghiӋm cӫa phѭѫng trình z + = 1 . Tính giá trӏ biӇu thӭc 2009 P = z + z 2009 z 5 7 A. P = 1
B. P = 0 C. P = − D. P = 2 4
LӠI GIҦI BÀI TҰP TӴ LUYӊN
Bài 1-[Thi thӱ chuyên Lam Sѫn – Thanh Hóa lҫn 2 năm 2017] Cho phѭѫng trình 2
z − 2z +17 = 0 có hai nghiӋm phӭc z và z . Giá trӏ cӫa z + z là : 1 2 1 2 A. 2 17 B. 2 13 C. 2 10 D. 2 15 '/ѵ/ ĄĐŚĂƐŝŽ
dŞŵŚĂŝŶŐŚŝҵŵĐӆĂƉŚӇҿŶŐƚƌŞŶŚ 2 z − 2z +17 = 0 Z S TOANMATH.com
Tác giả: Trần Bá Hưng
dşŶŚƚҼŶŐŚĂŝŵƀĜƵŶďҪŶŐůҵŶŚ^,/&d,zW ZTFETFSE
Vұy z + z = 2 17 Ĉáp sӕ chính xác là A 1 2
Bài 2-[ĈӅ thi toán Ĉҥi hӑc – Cao ÿҷng khӕi A năm 2009] 2 2
Gӑi z , z là hai nghiӋm cӫa phѭѫng trình 2
z + 2z +10 = 0 . Tính giá trӏ biӇu thӭc A = z + z 1 2 1 2 A. 2 10 B. 20 C. 5 2 D.10 3 '/ѵ/ ĄĐŚĂƐŝŽ
dŞŵŚĂŝŶŐŚŝҵŵĐӆĂƉŚӇҿŶŐƚƌŞŶŚ 2 z + 2z +10 = 0 Z
dşŶŚƚҼŶŐďŞŶŚƉŚӇҿŶŐŚĂŝŵƀĜƵŶďҪŶŐůҵŶŚ^,/&d,zW ZTFSEGTFSSEG 2 2 Vұy A = z
+ z = 20 Ĉáp sӕ chính xác là B 1 2
Bài 3-[Thi thӱ Group Nhóm toán lҫn 5 năm 2017]
Kí hiӋu z , z , z là nghiӋm cӫa phѭѫng trình 3
z + 27 = 0 . Tính tәng T = z + z + z 1 2 3 1 2 3 A.T = 0 B.T = 3 3 C.T = 9 D.T = 3 '/ѵ/ ĄĐŚĂƐŝŽ
dşŶŚŶŐŚŝҵŵĐӆĂƉŚӇҿŶŐƚƌŞŶŚ 3
z + 27 = 0 ďҪŶŐĐŚӈĐŶĉŶŐDKϱϰ Z 3 3 3 3 3 3
Vұy z = −3, z = + i, z = − i 1 2 3 2 2 2 2
dşŶŚƚҼŶŐŵƀĜƵŶT = z + z + z 1 2 3 Z ZZTFS TFD5DV5ETFD 5SDV5E TOANMATH.com
Tác giả: Trần Bá Hưng
Vұy T = 9 Ĉáp sӕ chính xác là C
Bài 4-[Thi thӱ THPT Bҧo Lâm – Lâm Ĉӗng lҫn 1 năm 2017]
Gӑi z , z , z , z là bӕn nghiӋm phӭc cӫa phѭѫng trình 4 2
2z − 3z − 2 = 0 . Tính tәng sau : 1 2 3 4
T = z + z + z + z 1 2 3 4 A. 5 B. 5 2 C. 3 2 D. 2 '/ѵ/ ĄĐŚĂƐŝŽ ҭƚ 2
t = z ͘dŞŵŶŐŚŝҵŵĐӆĂƉŚӇҿŶŐƚƌŞŶŚ 2
2t − 3t − 2 = 0 Z S S 2 ªt = 2 ªz = 2 « « Vұy 1 1 2 «t « = − z = − ¬ 2 «¬ 2 sӀŝ 2 z = 2 z = ± 2 2 1 − i i Vӟi 2 2 z = z = z = ± 2 2 2
dşŶŚƚҼŶŐŵƀĜƵŶT = z + z + z + z 1 2 3 4 ZTFVTFSVTFDE5 VTFDSE5V
Vұy T = 3 2 Ĉáp sӕ chính xác là C
Bài 5-[Thi thӱ THPT Bҧo Lâm – Lâm Ĉӗng lҫn 1 năm 2017] Xét phѭѫng trình 3
z = 1 trên tұp sӕ phӭc . Tұp nghiӋm cӫa phѭѫng trình là : ° 1 3 ½ − ± ° ° 1 3 ½ ° ° 1 3 ½ ° A. S = { } 1 B. S = 1 ® ; ¾ C. S = 1 ® ; − ± i¾ D. S = ®− ± i¾ ° 2 ¯ °¿ ° 2 2 ¯ °¿ ° 2 2 ¯ °¿ '/ѵ/ ĄĐŚĂƐŝŽ
'ŝңŝƉŚӇҿŶŐƚƌŞŶŚďҨĐďĂ 3
z −1 = 0 ǀӀŝĐŚӈĐŶĉŶŐDKϱϰ Z S 1 3 1 3
WŚӇҿŶŐƚƌŞŶŚĐſϯŶŐŚŝҵŵ x = 1, x = − + i, x = − − i 1 2 3 2 2 2 2
Ĉáp sӕ chính xác là C TOANMATH.com
Tác giả: Trần Bá Hưng 1 1
Bài 6-BiӃt z là nghiӋm cӫa phѭѫng trình z + = 1 . Tính giá trӏ biӇu thӭc 2009 P = z + z 2009 z 5 7 A. P = 1
B. P = 0 C. P = − D. P = 2 4 '/ѵ/ ĄĐŚĂƐŝŽ 1
YƵLJĜһŶŐƉŚӇҿŶŐƚƌŞŶŚ z + = 0 ƚĂĜӇӄĐƉŚӇҿŶŐƚƌŞŶŚďҨĐŚĂŝ 2
z − z +1 = 0 ͘dşŶŚŶŐŚŝҵŵƉŚӇҿŶŐƚƌŞŶŚ z
ŶăLJǀӀŝĐŚӈĐŶĉŶŐDKϱϯ Z S
dĂƚŚƵĜӇӄĐŚĂŝŶŐŚŝҵŵ z ŶŚӇŶŐŚĂŝŶŐŚŝҵŵŶăLJĐſǀĂŝƚƌžŶŚӇŶŚĂƵŶġŶĐŚҶĐҥŶůҤLJŵҾƚŶŐŚŝҵŵ z ĜҢŝ ĚŝҵŶůăĜӇӄĐ 1 3 § π π · sӀŝ z = −
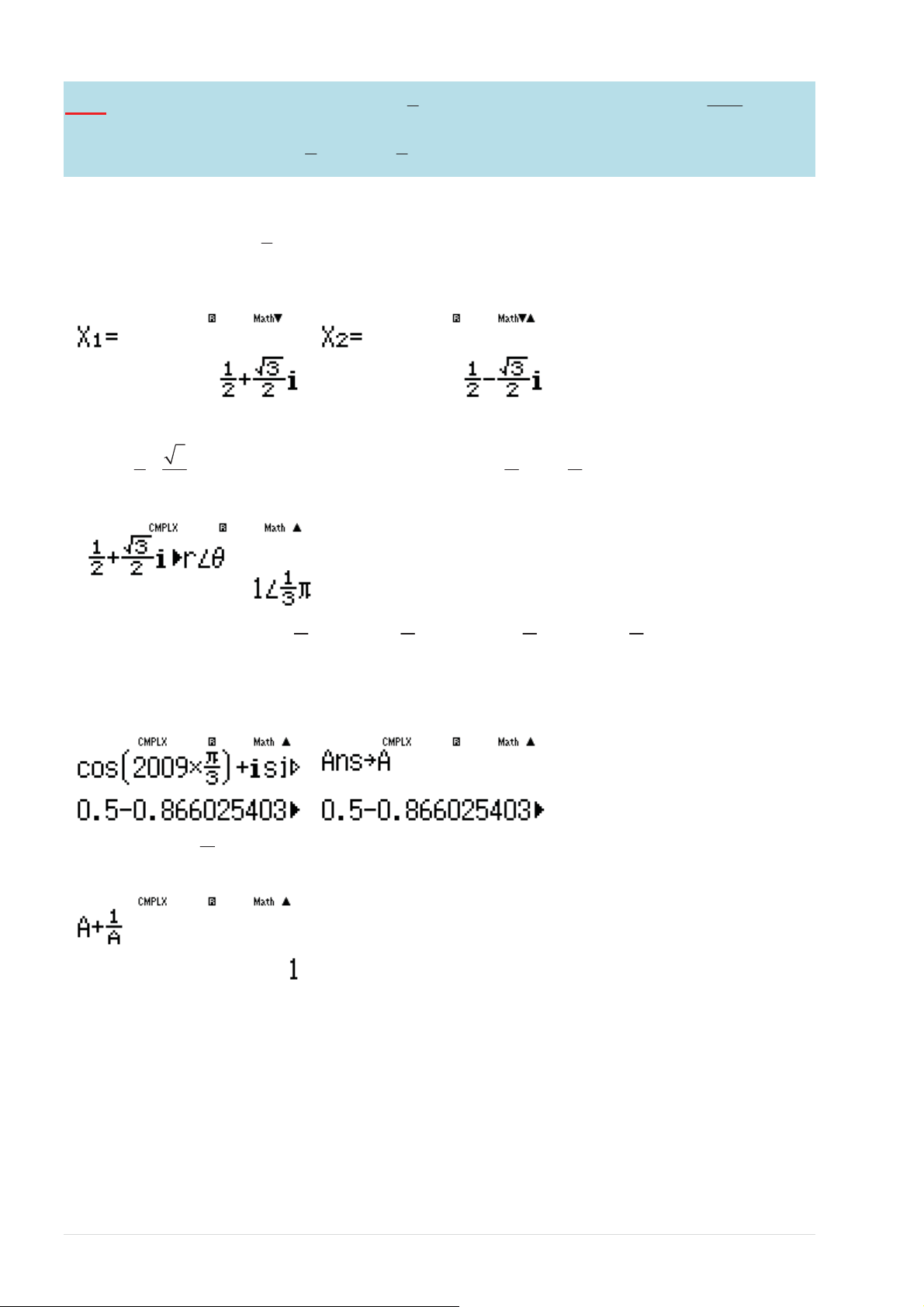
i ƚĂĐŚƵLJҳŶǀҲĚҢŶŐůӇӄŶŐŐŝĄĐ z = 1 cos ¨ + i sin ¸ 2 2 © 3 3 ¹ D5DV5ET § π π · § π π · sҨLJ 2009 2009 z =1 cos 2009. ¨
+ i sin 2009. ¸ = cos2009. ¨ + i sin 2009. ¸ © 3 3 ¹ © 3 3 ¹ dşŶŚ 2009 z
ǀăůӇƵǀăďŝұŶ A :N2DT.5EM2D T.5 T-] 1
Tәng kӃt P = A + = 1 A 4]D54]
Ĉáp sӕ chính xác là A TOANMATH.com
Tác giả: Trần Bá Hưng




