Kĩ thuật thế hằng số trong bài toán số phức – Vũ Quốc Triệu Toán 12

PHIẾU HỌC TẬP-SỐ PHỨC
NĂM HỌC 2020 – 2021
KĨ THUẬT THẾ HẰNG SỐ TRONG TOÁN PHỨC
Vũ Quốc Triệu , Hà Nội tháng 6.2021
Trong Toán học nói chung và toán Phức nói riêng, ngoài các phép toán thông thường V
ta còn có một phép toán ‘ thế hằng số’, nghĩa là thay một hằng số bởi một biểu thức chứa Ũ Q
biến. Phép toán này giúp giảm sự phức tạp trong tính toán, rút gọn các biểu thức số phức U Ố
bậc cao hoặc đôi khi nó còn là điểm mấu chốt để giải quyết vấn đề. Một hằng số nếu chỉ C T
nhìn nó ở góc độ số học thì đó là điều rất bình thường, thế nhưng khi thay thế nó bởi một RI Ệ
biểu thức chứa biến phù hợp lại tạo ra điều bất ngờ trong việc giải quyết bài toán. U
A. KIẾN THỨC SỬ DỤNG
1. Cho số phứ z  a  bi a,b   .Khi đó : 2 2 +) 2 2
z.z  z  z  a  b . n 2 n n +) 2n        .  n k z k z z z
 z .z k  0.
2. Với hai số phức bất kì z và w ,ta luôn có : n +) .
z w  z . w ; n z  z . z z +)  w  0. w w
+) z  w  z  w ; z  w  z  w  z  w . V
3. Bất đẳng thức môđun Ũ Q U         Ố +) z w z
w . Dấu bằng xảy ra k , k 0 sao cho z k.w . C T RI
+) z  w  z  w . Dấu bằng xảy ra  k  , k  0 sao cho z  k.w . ỆU B. ÁP DỤNG
BÀI TOÁN 1 ( Trích đề thi thử THPT QG – SGD Thái Bình 2021 ) : Cho các số phức z ; z ; z thoả 1 2 3
mãn z  4 ; z  5 ; z  2 và 4z z 16z z  25z z  80 . Giá trị của biểu thức 1 2 3 1 2 2 3 1 3
P  z  z  z bằng 1 2 3 A. 8 . B. 2 . C. 1. D. 6 .
Nhận xét : Quan sát các hệ số trong giả thiết 4z z 16z z  25z z  80 ta thấy 1 2 2 3 1 3 2 2 2 2 16  4  z  z .z ; 2 25  5  z  z .z ; 2 4  2  z  z .z . 1 1 1 2 2 2 3 3 3 Lời giải Chọn B.
Từ giả thiết z  4 , z  5 , z  2 ta có, z .z  4 ; z .z  16 ; z .z  25 . 1 2 3 3 3 1 1 2 2
https://www.facebook.com/bank.trieu Trang 1
PHIẾU HỌC TẬP-SỐ PHỨC
NĂM HỌC 2020 – 2021
Thay các hệ số 4; 16 và 25 bởi các biểu thức tương ứng ở trên vào giả thiết
4z z 16z z  25z z  80 , ta được : 1 2 2 3 1 3
 z .z z z  z .z z z  z .z z z  80 3 3  1 2  1 1 2 3  2 2 1 3 VŨ
  z z z z  z  z  80  z z z z  z  z  80 1 2 3  Q  1 2 3 1 2 3 1 2 3 U Ố C         T
z . z . z . z z z 80 4.5.2. z z z 80 1 2 3 1 2 3 1 2 3 RI ỆU
 z  z  z  2 . 1 2 3
BÀI TOÁN 2 ( Trích đề thi thử THPT QG – THPT Trần Hưng Đạo, Nam Định 2021 ) :
Cho các số phức z; w thoả mãn z  4 , iw  5  2i  1. Giá trị nhỏ nhất của biểu thức 2
P  z  wz 16 bằng A. 16 . B. 14 . C. 18 . D. 17 . Lời giải Chọn B. Ta có :
*) iw  5  2i  1  w  5i  2  1  tập hợp điểm biểu diễn tất cả các số phức w là đường tròn
C x  2  y  2 : 2 5 1 *) 2
P  z  wz  z.z  z . z  w  z  4 z  z  w . VŨ Q
Đặt z  a  bi  ; a b 
 . Vì z  4  2 2
a  b  16 . U Ố C Khi đó :   T P 4 2a w . RI ỆU
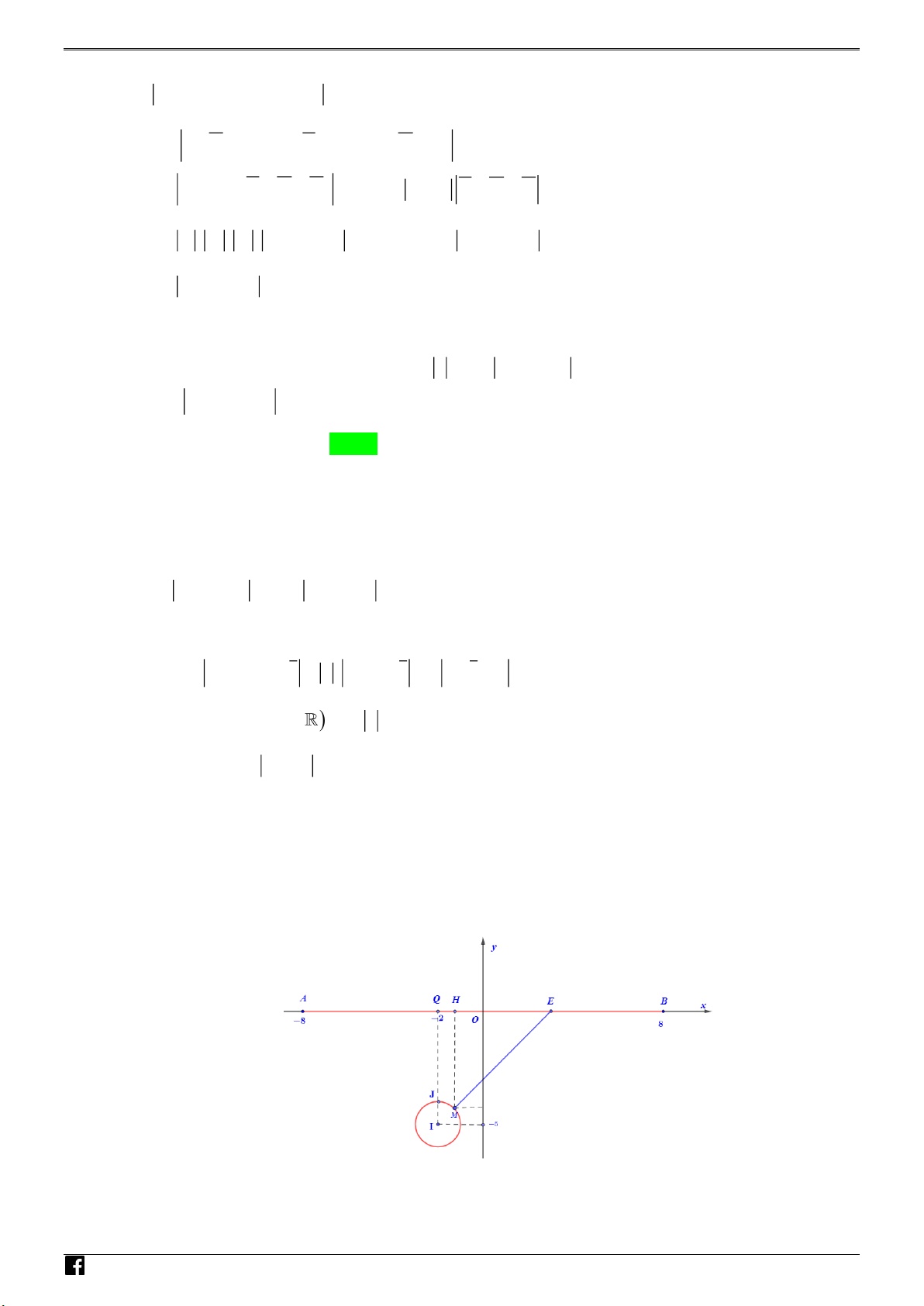
Gọi M w  M C . Chọn điểm E 2 ;
a 0 thì P  4ME . Vì 2 2 2
a  b  16  a  16  4   a  4  8   2a  8. Chọn A 8
 ;0; B8;0 thì điểm E thuộc đoạn thẳng AB .
Từ hình vẽ suy ra ME  MH  JQ  IQ  IJ  5 1  4  P  4ME 16 .
https://www.facebook.com/bank.trieu Trang 2
PHIẾU HỌC TẬP-SỐ PHỨC
NĂM HỌC 2020 – 2021 Vậy P 16 . min 2
Nhận xét: Mấu chốt để giải quyết bài toán là ta nhận ra: 2 16  4  z  . z z .  
BÀI TOÁN 3: Cho hai số phức z; w thay đổi thoả mãn z  3 , w  2 và z . w z 3 5 . Giá trị lớn nhất V Ũ Q của biểu thức 2 P  .
w z  38  i bằng U Ố C T RI A. 19 . B. 19 2 . C. 19 5 . D. 19 3 . ỆU 2 2 2 2
Nhận xét: Ta có 9  3  z  .
z z; 16  4  w  .
w w .Từ đó ta nghĩ đến 36  z. . w z.w . Lời giải Chọn B. Giả thiết  2 2 P  .
w z  38  i  .
w z  36  2  i .
Áp dụng bất đẳng thức môđun : z  z  z  z , ta có : 1 2 1 2 2 P  . w z    i 2 36 2  .
w z  36  2  i . Vì :
* 2  i  5 . * 2 2 2 . w z  36  . w z  9.4  .
w z  z z.ww  wz  z  z.w  w . z . z  z.w  3.2.3 5 .
Suy ra P  18 5  5  P  19 5 . VŨ Q
Dễ thấy khi z  3 ;
i w  2i ( thỏa mãn các giả thiết ) thì P  19 5 . U Ố C
Vậy M ax P  19 5 . T RI Ệ
BÀI TOÁN 4 ( Trích đề thi thử THPT QG –Cụm liên trường, SGD Quảng Nam 2021 ) : Cho số phức U
z thay đổi và thoả mãn z  1. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của 3 biểu thức 5 4
P  z  z  6z  2 z 1 . Khi đó M  m bằng
A. M  m 1.
B. M  m  3.
C. M  m  6 .
D. M  m  7 . 2 2 2 2 2 2 Nhận xét: Ta có: 2
  z  z z
  2    z  2 1 1 . ; 1 1
 z .z . Lời giải Chọn A.
P  z  z
 z  z   2  z  z z z  z  z z z 2 5 3 2 4 2 5 3 4 1 6 2 1 . . 6 2 . 4 4 2 2 2 4 4 2 2
 z . z  z  6  2 z . z  z  z  z  6  2 z  z 2 2   2 2 z  z  2 2 2 2
 z z   z  z   2 2 z  z  2 2 2 . 6 2
 4  2 z  z
https://www.facebook.com/bank.trieu Trang 3
PHIẾU HỌC TẬP-SỐ PHỨC
NĂM HỌC 2020 – 2021
Đặt z  x  yi,  ; x y  . +) 2 2 2 2
z  1  x  y  1  y  1 x . 2 2 2 2 2 2 2 2 2 2
+) P  4 x  y   4  2 2x  y   4 x  y  1  4 x  y V    Ũ Q U Ố   =  x  2 2 2 4 2 1 1  4 2x 1 C   . T RI 2 Ệ 2 x   0;  1 U
Lại đặt t  2x 1  t  0;1 . 2      2 x 1  1;  1
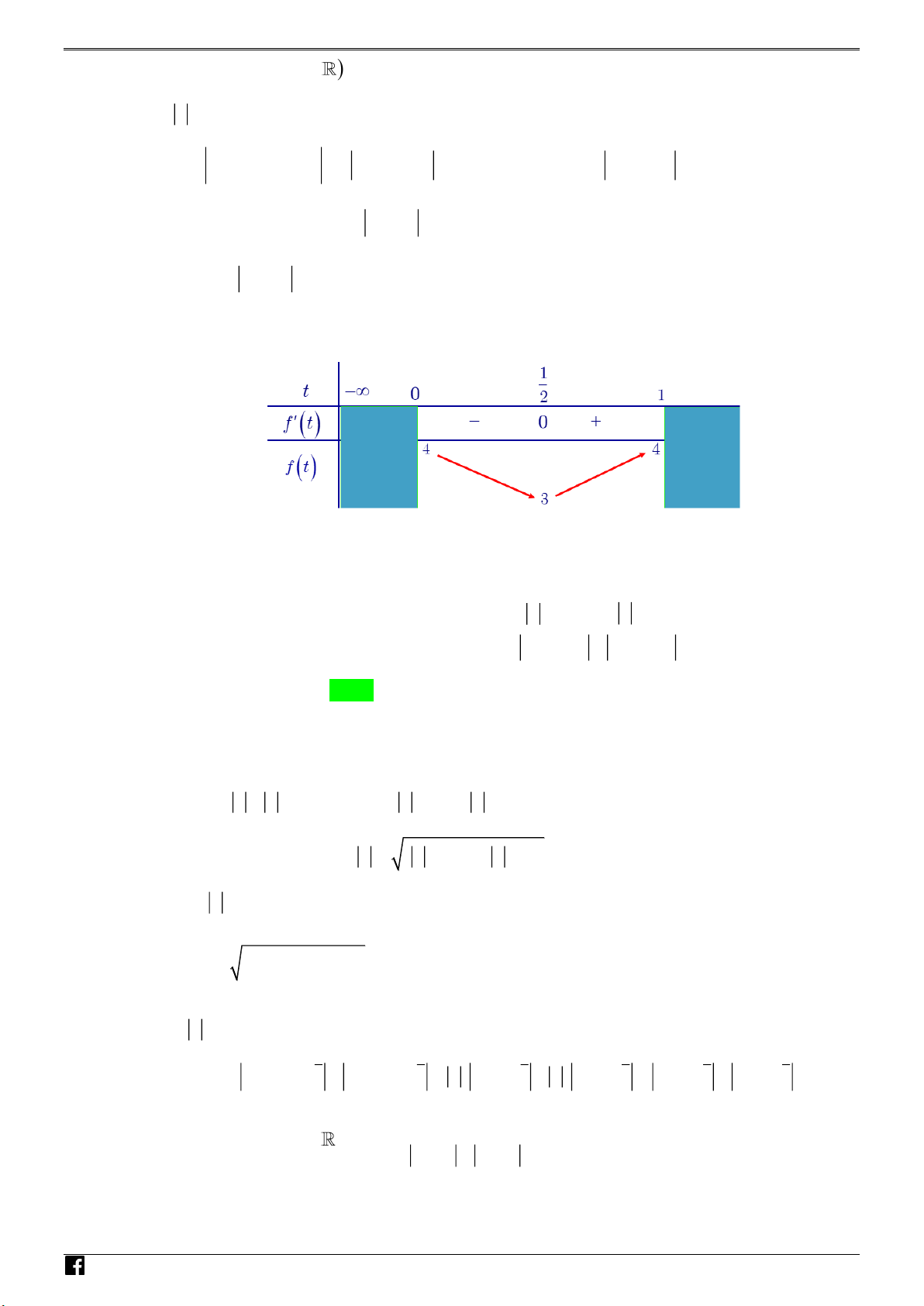
Khi đó: P  f t   2t   2
 t  t   t   2 4 1 4 4 4 4
4 t  t   1 .
Từ bảng biến thiên suy ra M ax P  4; M in P  3 .
Vậy M  m 1.
BÀI TOÁN 5: Cho số phức z thay đổi, thoả mãn z  2  i  z 1 i và z  5 . Gọi M , m lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P  z  z 1  z  z 1 . Tổng M  m bằng A. 2 . B. 6 . C. 1. D. 4 . V Ũ Q Lời giải U Ố C Chọn B T RI Ệ          U Ta có: z z z i 2 i z
 z 2  z 1i . 2 2
Lấy môdun hai vế ta được: z   z  2   z   1 .
Đặt t  z t  0 t 1 nhaän 2 2
Suy ra t  t  2  t     2 2 2 2 1
 t  t  4t  4 t  2t 1 t  6t  5  0   . t  5  loaïi Vậy z  1. Lại có: 2 2
P  z  z  z.z  z  z  z.z  z . z 1 z  z . z 1 z  z 1 z  z 1 z . 2 2
x  y 1
Đặt z  x  yi  ; x y    .
P  2x 1  2x 1  Vì 2 2 2 2
x  y  1  y  1 x và 2 x 0  ;1 .
https://www.facebook.com/bank.trieu Trang 4
PHIẾU HỌC TẬP-SỐ PHỨC
NĂM HỌC 2020 – 2021 Ta có: 2 2 2
P  8x  2  2 4x 1 Đặt 2
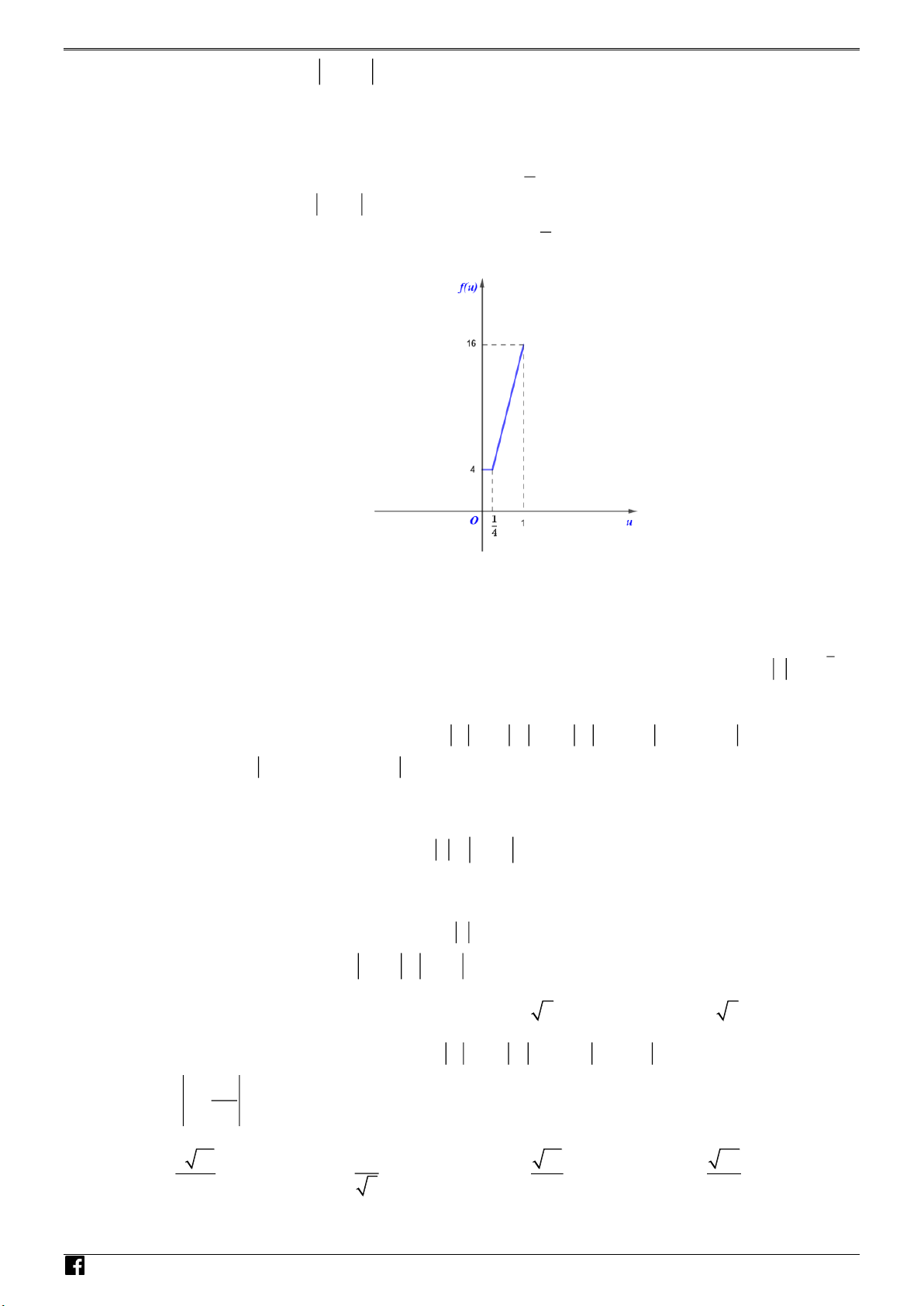
u  x  u 0  ;1 .  1  V 16u ; u  ;1 Ũ    Q   4  2       U Suy ra P 8u 2 2 4u 1 f u  . Ố   1  C 4 ; u  0;    T   4 RI ỆU
Từ đồ thị hàm số f u  f u   2
4;16  P 4;16  P 2;4 .
Vậy M ax P  4; M in P  2 . 2
Nhận xét: Mấu chốt để giải quyết nhanh việc rút gọn biểu thức là sử dụng: 2 1  1  z  . z z . VŨ
C. BÀI TẬP TỰ LUYỆN Q U
BÀI TẬP 1: Cho các số phức z , z , z thoả mãn z  1, z  2 , z  3 và z  z  z  4 . Giá trị của 1 2 3 1 2 3 1 2 3 Ố C T
biểu thức P  9z z  z z  4z z bằng 1 2 2 3 3 1 RI ỆU A. 27 . B. 31. C. 35 . D. 24 .
BÀI TẬP 2: Có bao nhiêu số phức z thoả mãn 4
z  z 1  1. A. 0 . B. 1. C. 4 . D. 8 .
BÀI TẬP 3: Cho số phức z thay đổi và thoả mãn z  1. Gọi M , m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức 4 4
P  z 1  z 1 . Tích M.m bằng A. 2 . B. 4 . C. 2 . D. 4 2 .
BÀI TẬP 4 : Cho hai số phức z , z thỏa mãn z  2, z  1 và z  2z  2 . Giá trị của biểu thức 1 2 1 2 1 2 3 2  2  z T bằng z1 3 10 8 19 37 A. . B. . C. . D. . 2 3 2 2
https://www.facebook.com/bank.trieu Trang 5
PHIẾU HỌC TẬP-SỐ PHỨC
NĂM HỌC 2020 – 2021
BÀI TẬP 5: Cho hai số phức z; w thay đổi thoả mãn z  1, w  2 và w.z  .
w z  1 . Giá trị lớn nhất của biểu thức 2 2
P  w .z 1 3i bằng A.  . D. 7 2  7 . 3 . B. 5 . C. 2 7 2 V Ũ Q
BÀI TẬP 6: ( Trích đề thi thử THPT QG –Cụm liên trường, SGD Quảng Nam 2021 ) : Cho các số U Ố        C
phức z ; z ; z thoả mãn z z z k 0 và z z z
0 . Giá trị của biểu thức 1 2 3 1 2 3 1 2 3 T RI
z z  z z  z z 1 2 2 3 3 1 Ệ P  bằng U   z z z 1 2 3 A. k . B. 2 k . C. 1. D. 3 k . HƯỚNG DẪN GIẢI 1.D 2.D 3.B 4.A 5.C 6.A
BÀI TẬP 1: Cho các số phức z , z , z thoả mãn z  1, z  2 , z  3 và z  z  z  4 . Giá trị của 1 2 3 1 2 3 1 2 3
biểu thức P  9z z  z z  4z z bằng 1 2 2 3 3 1 A. 27 . B. 31. C. 35 . D. 24 . Lời giải Chọn D. VŨ
Ta có : P = z .z .z .z  z .z .z .z  z .z .z .z 1 2 3 3 1 1 2 3 2 2 3 1 Q U Ố C
= z .z .z . z  z  z 1 2 3  3 1 2  T RI ỆU
= z . z . z . z  z  z  z . z
z . z  z  z  z . z
z . z  z  z  24 1 2 3 3 1 2 1 2 3 1 2 3 1 2 3 1 2 3
BÀI TẬP 2: Có bao nhiêu số phức z thoả mãn 4
z  z 1  1. A. 0 . B. 1. C. 4 . D. 8 . Lời giải Chọn D.
Đặt z  x  yi,  ; x y  . Ta có: +) 2 2 2 2
z  1  a  b  1  a  1 b .
+) z    z   2 2 2 4 4 2 4 2 2 2 1 1 1
1  z  z .z 1  z . z  z 1
https://www.facebook.com/bank.trieu Trang 6
PHIẾU HỌC TẬP-SỐ PHỨC
NĂM HỌC 2020 – 2021  1 2 2 a  b   2 2 2 2 2
 z  z 1  2 a  b 1   . 1  2 2 a  b    2 VŨ  3  Q 2 3  1  2 2 a     a   U a b  4  Ố Trường hợp 1: 2  2    
 có 4 số phức thỏa mãn. C 1 T 2 2 2 1        RI a b 1 b b    4  Ệ 2 U  1  1 2  1 a  a   2 2
a  b       Trườ 4 2 ng hợp 2:  2    
 có 4 số phức thỏa mãn. 3 2 2 2 3    2 a  b 1 b  b    4  2
Vậy có tất cả 8 số phức z thỏa mãn yêu cầu bài toán. 2 2 2 2
Nhận xét: Mấu chốt để giải quyết nhanh việc rút gọn là sử dụng:   2    z  2 1 1
 z .z .
BÀI TẬP 3: Cho số phức z thay đổi và thoả mãn z  1. Gọi M , m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức 4 4
P  z 1  z 1 . Tích M.m bằng A. 2 . B. 4 2 . C. 2 . D. 4 . Lời giải Chọn B V 2 2 Ũ 2 2 2 2 Q
Ta có: 1  1   z    .zz  z .z . U Ố C 2 2 2 2 T Khi đó: 4 2 4 2 2 2 2 2
P  z  z .z  z  z .z  z z  z  z z  z RI     ỆU 2 2 2 2 2 2 2 2 2 2
 z z  z  z z  z  z  z  z  z .
Đặt z  x  yi,  ; x y  . +) 2 2 2 2
z  1  x  y  1  y  1 x . +) 2 2
P  2 x  y  4xy
Bình phương hai vế, ta được P  x  y 2 2 2 2 2 2 2 2 4
16x y 16 xy x  y 2 2 2 2
  x  y  x  y 2 2 4
16x y 16 xy x  y .x  y
   xy  xy 2 2 4 1 2 1 2
16x y 16 xy 1 2xy1 2xy 2 2
 4 16 xy 1 4x y .
https://www.facebook.com/bank.trieu Trang 7
PHIẾU HỌC TẬP-SỐ PHỨC
NĂM HỌC 2020 – 2021 2 2    Đặ x y 1 1
t t  xy .Vì 0  xy    t  0;   2 2  2 Suy ra: 2 2
P  4 16t 1 4t  f t  . VŨ 2  Q 161 8t  1  1 f  t  f  U Ta có   ;
t  0  t   0;   . 2 Ố 1 4t 2 2  2 C T RI     Ệ f  f  f    U Mà   1 1 0 4; 4; 8    
. Từ đó M ax f t  8; M in f t  4 .  2   2 2 
Vậy M  2 2; m  2 .
BÀI TẬP 4 : Cho hai số phức z , z thỏa mãn z  2, z  1 và z  2z  2 . Giá trị của biểu thức 1 2 1 2 1 2 3 2  2  z T bằng z1 37 8 19 3 10 A. . B. . C. . D. . 2 3 2 2 Lời giải Chọn A. 2
Ta có 4  z  2z  z  2z z  2z  z  2z z  2z 1 2  1 2   1 2   1 2   1 2  2 2  z
 4 z  2 z .z  z .z  8  2 z .z  z .z . 1 2  1 2 1 2  1 2 1 2 VŨ Q
Suy ra z .z  z .z  2  U 1 2 1 2 Ố C T 3z 2z  3z 2z  3z RI Lại có 2 1 2 1 2 T  2    Ệ z z 2 U 1 1 2 Suy ra 2
4T  2z  3z  2z  3z 2z  3z 1 2  1 2   1 2  2 2
 2z  3z 2z  3z
 4 z  9 z  6 z .z  z .z  25  6 z .z  z .z  37 1 2   1 2  1 2  1 2 1 2  1 2 1 2 37 Vậy T  . 2
BÀI TẬP 5: Cho hai số phức z; w thay đổi thoả mãn z  1, w  2 và w.z  .
w z  1 . Giá trị lớn nhất của biểu thức 2 2
P  w .z 1 3i bằng A. 3 . B. 5 . C. 2 7  2 . D. 7 2  7 . 2 2 Nhận xét: Ta có 2 2 1  1  z  .
z z; 4  2  w  .
w w .Từ đó ta nghĩ đến 4  1.4  z. . w z.w . Lời giải Chọn C.
https://www.facebook.com/bank.trieu Trang 8
PHIẾU HỌC TẬP-SỐ PHỨC
NĂM HỌC 2020 – 2021 Giả thiết  2 2 2 2
P  w .z 1 3i  w .z  4  5  3i .
Áp dụng bất đẳng thức môđun : z  z  z  z , ta có : 1 2 1 2 2 2
P  w .z     i  2 2 4 5 3
 w .z  4  5   3i . VŨ QU Vì : Ố C T *) 5
  3i  2 7 . RI ỆU *) 2 2 2 2 2 2
w .z  4  w .z 1.4  w .z  z.z. . w w  .
w z.wz  z.w  w . z . w.z  z.w  2. 1 1.  2 .
Suy ra P  2 7  2 . 3 1 Dễ thấy khi z   ;
i w  2i ( thỏa mãn các giả thiết ) thì P  2 7  2 . 2 2
Vậy M ax P  2 7  2 . BÀI TẬP 6
( Trích đề thi thử THPT QG –Cụm liên trường, SGD Quảng Nam 2021 ) : Cho các số
phức z ; z ; z thoả mãn z  z  z  k  0 và z  z  z  0 . Giá trị của biểu thức 1 2 3 1 2 3 1 2 3
z z  z z  z z 1 2 2 3 3 1 P  bằng
z  z  z 1 2 3 A. k . B. 2 k . C. 1. D. 3 k . 2 2 2 Nhận xét : 2 k  z  z
 z  z .z  z .z  z .z . 1 2 3 1 1 2 2 3 3 VŨ Q Lời giải U Ố C Chọn A. T RI 2 2 2 2 Ệ
Từ giả thiết suy ra k  z  z
 z  z .z  z .z  z .z . 1 2 3 1 1 2 2 3 3 U
z z  z z  z z 2 2 2
1 z z .k  z z .k  z z .k Ta có 1 2 2 3 3 1 P  = 1 2 2 3 3 1
z  z  z 2 k
z  z  z 1 2 3 1 2 3
1 z z .z .z  z z .z .z  z z z .z = 1 2 3 3 2 3 1 1 3 1 2 2 2 k
z  z  z 1 2 3 1
z  z  z = z z z  3 1 2 . 2 1 2 3 k
z  z  z 1 2 3 1   1
z  z  z z z z 3 1 2 = 3 1 2 z z z . 
z . z . z . 2 1 2 3 2 1 1 1 k
z  z  z k
z  z  z 1 2 3 1 2 3 1
z  z  z   1 2 3 1 z z z = 1 2 3
z . z . z . 
z . z . z . 2 1 1 1 2 1 1 1 k
z  z  z k
z  z  z 1 2 3 1 2 3
https://www.facebook.com/bank.trieu Trang 9
PHIẾU HỌC TẬP-SỐ PHỨC
NĂM HỌC 2020 – 2021 1 1 =
z . z . z 
.k.k.k  k . 2 1 1 1 2 k k 2 2 2   Lưu ý : k k k
Cách trắc nghiệm nhanh, có thể chọn z  z  z  k  P   k . 1 2 3
k  k  k VŨ QU Ố C
…………………………………………………HẾT………………………………………………… T RI ỆU VŨ QUỐC TRIỆU
https://www.facebook.com/bank.trieu Trang 10