Kỹ thuật giải nhanh chuyên đề hình giải tích không gian – Trần Đình Cư Toán 12

Kỹ thuật giải nhanh chuyên đề hình giải tích không gian – Trần Đình Cư Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Phương pháp tọa độ trong không gian

Môn: Toán 12

Thông tin:

83 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
TRUNG TÂM LUYỆN THI VÀ GIA SƯ CHẤT LƯỢNG CAO
SĐT: 01234332133. ĐC: Phòng 5, dãy 22 Tập thể xã tắc.TP HUẾ
Biên soạn: Ths. Trần Đình Cư
KĨ THUẬT GIẢI NHANH
Dành cho học sinh luyện thi THPT Quốc Gia.
Bồi dưỡng học sinh giỏi 10, 11, 12.
Giáo viên giảng dạy, dạy thêm và luyện thi Quốc gia
TÀI LIỆU DÀNH TẶNG
HỌC SINH LỚP TOÁN THẦY CƯ
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 1
MỤC LỤC
CHỦ ĐỀ 1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN ..................................................... 3
VẤN ĐỀ 1. Các bài toán điển hình thường gặp .............................................................. 5
VẤN ĐỀ 2. Ứng dụng tọa độ giải toán hình học không gian........................................... 9
CHỦ ĐỀ 2. MẶT PHẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN ............................... 10
VẤN ĐỀ 1. Viết phương trình mặt phẳng ................................................................ 11
VẤN ĐỀ 2. Vị trí tương đối của hai mặt phẳng ............................................................ 14
VẤN ĐỀ 3. Khoảng cách từ một điểm đến một mặt phẳng, khoảng cách giữa hai mặt
phẳng song song. Hính chiếu và điểm đối xứng ............................................................. 16
VẤN ĐỀ 4. Góc của hai mặt phẳng............................................................................... 17
VẤN ĐỀ 5. Ứng dụng giải toán hình học không gian ................................................... 18
CHỦ ĐỀ 3. MẶT CẦU VÀ CÁC BÀI TOÁN LIÊN QUAN ..................................... 20
VẤN ĐỀ 1. Viết phương trình mặt cầu ........................................................................ 20
VẤN ĐỀ 2. Vị trí tương đối của mặt phẳng và mặt cầu................................................ 20
CHỦ ĐỀ 4. ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN ........................ 28
VẤN ĐỀ 1. Viết phương trình đường thẳng .................................................................. 28
Dạng 1. Viết phương trình đường thẳng
(
()P
hoặc
/ / ( )P
) qua điểm A và
vuông góc với đường thẳng d ..................................................................................... 30
Dạng 2. Viết phương trình đường thẳng
qua A, vuông góc với
1
d
và cắt
2
d
........ 30
Dạng 3. Viết phương trình đường thẳng
qua A, song song với (P) và cắt d ......... 31
Dạng 4. Viết phương trình đường thẳng d nằm trong mặt phẳng (P) và cắt cả hai
đường thẳng d1, d2...................................................................................................... 31
VẤN ĐỀ 2. Vị trí tương đối của 2 đường thẳng trong không gian ........................ 32
Dạng 1. Viết phương trình đường thẳng đi qua điểm M và cắt cả hai đường thẳng
12
,dd
.......................................................................................................................... 32
Dạng 2. Viết phương trình đường thẳng d song song với đường thẳng
và cắt hai
đường thẳng
12
,dd
..................................................................................................... 33
Dạng 3. Viết phương trình đường vuông góc chung d của hai đường thẳng chéo nhau
................................................................................................................................... 34
VẤN ĐỀ 3. Khoảng cách từ một điểm đến một đường thẳng và khoảng cách
giữa hai đường thẳng chéo nhau ............................................................................... 34
Dạng 1. Khoảng cách từ một điểm đến một đường thẳng .......................................... 34
Dạng 2. Khoảng cách giữa hai đường thẳng chéo nhau ............................................. 35
Dạng 3. Ứng dụng tọa độ giải toán không gian ......................................................... 35
VẤN ĐỀ 4. Các bài toán liên quan giữa đường thẳng và mặt phẳng ............................ 36
Dạng 1. Đường thẳng song song với mặt phẳng ....................................................... 37
Dạng 2. Hình chiếu vuông góc của một điểm lên mặt phẳng ..................................... 38
Dạng 3. Hình chiếu vuông góc của một đường thẳng lên mặt phẳng ........................ 40
Dạng 4. Hình chiếu của một điểm lên đường thẳng .................................................. 43
VẤN ĐỀ 5. Các bài toán liên quan giữa đường thẳng và mặt cầu ................................. 53
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 2
CHỦ ĐỀ 5. GÓC TRONG KHÔNG GIAN ............................................................... 57
VẤN ĐỀ 1. Góc và các bài toán liên quan ................................................................ 57
VẤN ĐỀ 2 . Sử dụng tọa độ giải toán hình học không gian ........................................... 58
CHỦ ĐỀ 6. MỘT SỐ PHƯƠNG PHÁP GIẢI TOÁN CỰC TRỊ HÌNH HỌC
KHÔNG GIAN ............................................................................................................... 59
VẤN ĐỀ 1. Giải toán cực trị hình học bằng cách sử dụng bất đẳng thức hình học ....... 59
VẤN ĐỀ 2. Giải toán cực trị bằng phương pháp hàm số hoặc bằng cách sử dụng bất
đẳng thức đại số ............................................................................................................. 60
VẤN ĐỀ 3. Giải toán cực trị bằng phương pháp ứng dụng tâm tỉ cự .................. 62
Dạng 1. Cực trị độ dài vectơ...................................................................................... 62
Dạng 2. Cực trị độ dài bình phương vô hướng của vectơ .......................................... 63
Dạng 3. Cực trị dựa vào tính chất hình học ............................................................... 63
PHỤ LỤC ......................................................................................................................... 65
PHỤ LỤC 1. MỘT SỐ BÀI TẬP RÈN LUYỆN HÌNH HỌC GIẢI TÍCH TRƯỚC KHI
THI ................................................................................................................................ 65
PHỤ LỤC 2. GIẢI BÀI TOÁN HÌNH HỌC KHÔNG GIAN BÀNG HAI CÁCH ...... 76
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 3
CHỦ ĐỀ 1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
A. CƠ SỞ LÝ THUYẾT
2 2 2
1 1 2 2 3 3
1 2 3
222
1 2 3
11
22
33
1 1 2 2 3 3
1. ( , , )
2.
3. , ,
4. k.a , ,
5. a
6. a
7. a. . . . | |.| | os a
B A B A B A
B A B A B A
AB x x y y z z
AB AB x x y y z z
a b a b a b a b
ka ka ka
aaa
ab
b a b
ab
b a b a b a b a b c
3
12
1 2 3
1 1 2 2 3 3
2 3 3 1
12
2 3 3 1
12
,
8. a/ / . , 0
9. a . 0 . . . 0
10. [a, ] , ,
b
a
aa
b a k b a b
b b b
b a b a b a b a b
a a a a
aa
b
b b b b
bb





Trong không gian
cho
; ; ; ; ; ; ; ;
A A A B B B C C C
A x y z B x y z C x y z
. Ta có:
2 2 2
;;
B A B A B A
B A B A B A
AB x x y y z z
AB AB x x y y z z
I là trung điểm của AB thì
2
2
2
AB
I
AB
I
AB
I
xx
x
yy
y
zz
z
G là trọng tâm của tam giác ABC thì
3
3
3
A B C
G
A B C
G
A B C
G
x x x
x
y y y
y
z z z
z



Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 4
Tính chất tích có hướng
1. a, ,
2. a, . .sin a,
3. a, ; a,
b b a
b a b b
b a b b




Ứng dụng của tích có hướng
1.
,,a b c
đồng phẳng
, . 0a b c



2. Diện tích tam giác ABC:
1
,
2
S AB AC


3. Diện tích hình bình hành ABCD:
,S AB AD


4. Thể tích tứ diện ABCD:
1
,.
6
V AB AC AD


5. Thể tích hình hộp
. ' ' ' 'ABCD A B C D
:
, . 'V AB AC AA


Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 5
VẤN ĐỀ 1. Các bài toán điển hình thường gặp
Ví dụ 1:
1; ;2 ; 2;2;1 ; 0; 2;2a m b m c m
a) Tìm
m
để
ab
b) Tìm m để
,,a b c
đồng phẳng
c) Tìm m để
a b c
ĐS:
42
) ; ) ; ) 6 3 3
35
a m b m c m
Ví dụ 2: Tìm
,xy
để ba điểm
2;0;2 ; 1;2;3 ; ; 3;7A B C x y
thẳng hàng
ĐS:
13, 13xy
Ví dụ 3. Cho tam giác ABC có A(1;2;1), B(5;3;4); C(8;-3;2)
a) Chứng minh rằng
ABC
vuông
b) Tìm điểm M sao cho
2 2 2
nhoû nhaátMA MB MC
Hướng dẫn
) . 0
) ( ; , )...; 4, 4, 1
a AB BC
b M x y z x y z
Ví dụ 4. Cho 3 điểm A(1;-1;2), B(2;1;0); C(0;1;-1). Tìm điểm M thuộc trục
Oz
sao cho
2 2 2
nhoû nhaátMA MB MC
Hướng dẫn:
1
(0;0; );...,
3
M t t
BTTT: Cho 3 điểm A(1;-1;2), B(-1;2;0); C(3;-1;0). Tìm điểm M thuộc trục
Oz
sao cho
2 2 2
nhoû nhaátMA MB MC
Hướng dẫn:
1
(0;0; );...,
3
M t t
Ví dụ 5. Cho 3 điểm A(1;-1;1), B(2;1;-2); C(0;0;1). Tìm tọa độ trực tâm của
ABC
Hướng dẫn:
.0
5 4 8
. 0 . : ; ;
9 9 9
, , ñoàng phaúng
. ; 0
AH BC AH BC
BH AC BH AC ÑS H
BC AC CH
CH BC AC









BTTT: Cho 3 điểm A(4;-2;-1), B(1;4;-1); C(1;-2;-7). Tìm tọa độ trực tâm của
ABC
.
Đáp số: H(3;-1;-2)
Ví dụ 6. Cho 2 điểm A(1;2;-1), B(-2;1;3). Tìm M thuộc trục
Ox
sao cho
có diện tích nhỏ
nhất.
Hướng dẫn
2
1 1 1
( ;0;0). ; 17 2 75,....
2 2 17
AMB
M t S AM AB t t t


Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 6
Ví dụ 7. Cho tam giác ABC có A(-1;0;2), B(0;4;3); C(-2;1;2). Tính độ dài đường phân giác trong AD
của tam giác ABC,
D BC
.
Hướng dẫn:
roài suy ra . Suy ra toïa ñoä cuûa D, sau ñoù tính DA.
3 7 9 3 6
: ; ;
2 4 4 4
DB AB
k DB kDC
DC AC
ÑS D AD



BTTT: Cho tam giác ABC có A(1;2;-1), B(2;-1;3); C(-4;7;5). Tính độ dài đường phân giác trong góc
B.
Đáp số:
17 26
; ;7
33



Ví dụ 8. Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC biết A(0;0;-2), B(1;-4;1); C(2;2;-1)
Hướng dẫn:
22
22
59 14 13
: ; ;
30 15 30
; ; ñoàng phaúng
; . 0
IA IB
IA IB IC
IA IC ÑS I
AB AC MA
AB AC MA








BTTT: Cho điểm
15
2 ;3 ; 2
22
M x x x



và tam giác ABC với A(1;1;3), B(0;5;2);C(-1;3;4).
a) Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC
b) Chứng minh rằng với mọi
0x
, đường thẳng MI vuông góc với (ABC)
Hướng dẫn:
)Tam giaùc ABC vuoâng taïi C taâm laø trung ñieåm cuûa AB
.0
b)
.0
a
MI AB
MI AC
Ví dụ 9. Cho 4 điểm A(-2;2;-1); B(-3;-2;-4); C(5;1;2);
OxDz
.
Tìm D biết DA=DB và
37
6
ABCD
V
.
Hướng dẫn:
22
( ) neân D(x;0;z).
37
V 15 29 35 37; 3 10
6
: ( 1;0; 3) hoaëc ( 4;0; 2)
ABCD
D Oxz
x z DA DB DA DB x z
ÑS D D
Ví dụ 10.
a) Cho hai điểm A(1;2;-1); B(4;3;5). Xác định M thuộc Ox sao cho M cách đều A và B
b) Cho hai điểm A(-4;-1;2); B(3;5;-1). Tìm C biết trung điểm của AC thuộc Oy và trung điểm
của BC thuộc (Oxz)
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 7
Hướng dẫn:
) (0;0;4)
) ( ; ; ).... : 4; 5; 2
aM
b C a b c ÑS a b c
Ví dụ 11. Cho 4 điểm A(1;2;4); B(2;-1;0); C(-2;3;-1);
( ; ; )M x y z ABC
. Tìm hệ thức liên hệ
giữa x, y, z. Tìm tọa độ D biết ABCD là hình bình hành và diện tích hình bình hành ABCD.
Hướng dẫn:
; . 0 19 17 8 29 0
( 1;0; 5); 714
ABCD
M ABC AB AC AM x y z
DS


Ví dụ 12. Cho tứ diện ABCD, có A(2;3;1); B(1;1;-2); C(2;1;0); D(0;-1;2). Đường cao AH. Tìm tọa độ
chân đường cao
Hướng dẫn:
31
..... 3; ;
22
; . 0
AH BC
AH BD H
BC BD BH





Ví dụ 13. Cho 3 điểm A(3;2;-5); B(-2;1;-3); C(5;1;-1).
a) Chứng minh rằng
ABC
nhọn
b) Tìm điểm D thuộc (xOy) sao cho tứ diện ABCD là tứ diện trực tâm ( có các cặp cạnh đối
vuông góc với nhau)
Hướng dẫn:
2 2 2 2 2 2 2 2 2
)*Chöùng minh A, B, C laø ba ñænh cuûa tam giaùc
* Chöùng minh AB , ,
) ( ; ;0)
. ; 0
Ñieàu kieän laø töù dieän tröïc taâm . 0
.
a
BC CA AB CA BC BC CA AB
b D x y
AB AC AD
ABCD AB CD
AB BD


31 19
..... ; ;0
77
0
D



Ví dụ 14. Tam giác ABC có các đỉnh A, B, C lần lượt thuộc các trục Ox, Oy, Oz và có trọng tâm
G(1;2;-1). Tính diện tích tam giác đó.
Hướng dẫn:
3
( ;0;0); (0; ;0); (0;0; ).G laø troïng taâm cuûa tam giaùc ABC neân 7
3
3
27
(h laø khoaûng caùch töø O ñeán (ABC))
2
OABC
ABC
x
A x B y C z y
z
V
S
h


Ví dụ 15. Cho ba điểm A(2;0;0), B(1;1;2), C(3;-1;1).
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 8
a) Chứng minh rằng tam giác ABC là một tam giác vuông
b) Biết ABC.A’B’C’ là một hình lăng trụ đứng có các cạnh bên AA’, BB’, CC’ và A’ ở trên mặt
phẳng
Oyz
. Tìm tọa độ của A’,B’,C’
Hướng dẫn và đáp số
) laø tam giaùc vuoâng taïi A
b)A' '(0; ; )
ABC.A'B'C' laø hình laêng truï ñöùng neân
a ABC
Oyz A m p

'. 0 2
' ........ '( 1; 1;2) '(1; 3;1)
0
'. 0
AB AA AB m
AA B vaøC
AC p
AA AC


Ví dụ 16. Cho hình hộp ABCD.A’B’C’D’ có A(1;2;-1); C(3;-4;1), B’(2;-1;3)., D’(0;3;5)
a) Tính tọa độ các đỉnh của hình hộp
b) Tính thể tích hình hộp
Hướng dẫn và đáp số:
. ' ' ' '
)AC coù trung ñieåm I(2;-1;0). B'D' coù trung ñieåm laø I'(1;1;4); A'(x;y;z).
' ' '(0;4;3); ' ' (3; 3; 1)
'(2; 2;5); (1;1;1;)
) '. , 6
ABCD A B C D
a
AA II A BB II B
CD
b V AA AB AD



BTTT: Cho hình hộp ABCD.A’B’C’D’ có A(1;0;1); B’(2;1;1), C(4;5;-5),
D’(1;-1;1). Tính tọa độ các đỉnh của hình hộp.
Đáp số:
7 3 3 5 5 9 5 3
3; ; ; 2; ; ; ' 0; ; ; ' 3; ; ;
2 2 2 2 2 2 2 2
B D A C
Ví dụ 17. Cho 3 điểm A(2;-1;-4); B(-2;3;-4), C(2;m+1;-8)
a) Tìm m để tam giác ABC là tam giác đều
b) Với giá trị m tìm được, hãy xác định tọa độ điểm S thuộc (Oyz) sao cho S.ABC là hình
chóp đều.
Đáp số: a) m=2; b) S(0;1;-6)
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 9
VẤN ĐỀ 2. Ứng dụng tọa độ giải toán hình học không gian
Bài 1. Cho
.S ABCD
có ABCD là hình chữ nhật với
, 2 , ( ),AB a AD a SA ABCD
góc giữa
SB với mặt phẳng (ABCD) bằng 60
0
. Lấy
3
,
2
a
M SA AM
, (BCM) cắt SD tại N. Tính
.S BCNM
V
.
Bài 2. Cho
.S ABCD
có
là hình vuông cạnh bằng
,a
SAD
đều,
SAD ABCD
.
Gọi M, N, P lần lượt là trung điểm của SB, BC, CD. Chứng minh
AM BP
và
CMNP
V
.
Bài 3. Cho
có
SA ABC
, tam giác
ABC
vuông tại B,
,2AB a BD SA a
. Gọi M
là trung điểm của SC. Chứng minh
AMB
cân tại M. Tính
AMB
S
.
Bài 4. Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác vuông,
, ' 2AB AC a AA a
.
Gọi M, N lần lượt là trung điểm của AA’, BC’. Chứng minh MN là đường vuông góc chung của
AA’ và BC’. Tính
. ' 'M A BC
V
Bài 5. Cho lăng trụ đứng
. ' ' ' 'ABCD A B C D
có đáy ABCD là hình bình thoi cạnh a,
0
60BAD
.
Gọi M, N theo thứ tự là trung điểm của AA’, CC’. Chứng minh bốn điểm B’, M, D, N cùng thuộc
một mặt phẳng. Tính AA’ theo a để B’MDN là hình vuông.
Bài 6. D2010. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, cạnh bên SA=a;
hình chiếu vuông góc của đỉnh S trên (ABCD) là điểm H thuộc AC,
4
AC
AH
. Gọi CM là đường
cao của tam giác SAC. Chứng minh M là trung điểm của SA và tính thể tích khối tứ diện
SMBC
theo a
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 10
CHỦ ĐỀ 2. MẶT PHẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN
A. CƠ SỞ LÝ THUYẾT
1. Vectơ pháp tuyến của mp: Vectơ
0n
được gọi là véctơ pháp tuyến của nếu giá của
n
vuông góc với
()
2. Cặp véctơ chỉ phương của mp: Cho hai vectơ
,ab
không cùng phương và khác
0
. Nếu giá
của
,ab
song song hoặc nằm trên
()
thì
,ab
được gọ là cặp vectơ chỉ phương của
()
. Lúc
đó:


,n a b
3. Phương trình mặt phẳng: Có dạng
0Ax By Cz D
với
;;n A B C
là vectơ pháp
tuyến của mặt phẳng.
Phương trinh mặt phẳng
()
đi qua điểm
0 0 0 0
;;M x y z
và có vectơ pháp tuyến
;;n A B C
sẽ có dạng
0 0 0
0A x x B y y C z z
Phương trình mặt phẳng đi qua A(a,0,0) B(0,b,0) ; C(0,0,c) có dạng
1
x y z
a b c
Phương trình các mặt phẳng tọa độ
(Oyz) : x = 0 ; (Oxz) : y = 0 ; (Oxy) : z = 0
4. Vị trí tương đối của hai mp (1) và (2) :
Cho hai mặt phẳng
1 1 1 1
2 2 2 2
( ): 0
( ): 0
A x B y C z D
A x B y C z D


1 1 1 2 2 2
: : : :caét A B C A B C
2
1
2
1
2
1
2
1
//
D
D
C
C
B
B
A
A
2
1
2
1
2
1
2
1
D
D
C
C
B
B
A
A
0
212121
CCBBAA
5. Khoảng cách từ một điểm đến mặt phẳng
Cho
0 0 0
( ; ; )M x y z
và
( ): 0Ax By Cz D
. Lúc đó

2 2 2
( , )
o o o
Ax By Cz D
dM
A B C
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 11
6. Góc giữa hai mặt phẳng :



.
cos( , )
.
nn
nn
VẤN ĐỀ 1. Viết phương trình mặt phẳng
Phương pháp chung: Để lập phương trình mặt phẳng () ta cần xác định một điểm thuộc () và
một VTPT của nó.
TH 1: (
) đi qua điểm
0 0 0
M x ; y ;z
có VTPT
n A;B;C
:
(
):
0 0 0
0A x x B y y C z z
TH 2: () đi qua điểm
0 0 0
M x ; y ;z
có cặp VTCP
,ab
. Khi đó một VTPT của () là
n a b,
.
TH 3: () đi qua điểm
0 0 0
M x ; y ;z
và song song với (): Ax + By + Cz + D = 0:
(
):
0 0 0
0A x x B y y C z z
TH 4: () đi qua 3 điểm không thẳng hàng A, B, C:
Khi đó ta có thể xác định một VTPT của () là:
,n AB AC


TH 5: Phương trình mặt phẳng đi qua A(a,0,0) B(0,b,0) ; C(0,0,c) có dạng
1
x y z
a b c
TH 6: () đi qua điểm M và vuông góc với hai mặt phẳng cắt nhau (), ():
Xác định các VTPT
,nn

của () và ().
Một VTPT của () là:
,nn



.
Ví dụ 1. Trong mỗi trường hợp sau, viết phương trình mặt phẳng
a) Đi qua ba điểm A(-1;2;3),B(2;-4;3),C(4;5;6)
b) Đi qua điểm M(1;2;-2) và vuông góc với trục Oy
c) Đi qua điểm M(1;3;-2) và vuông góc với đường thẳng BC với B(0;2;-3), C(1;-4;1)
d) Đi qua M(1;3;-2) và song song với
( ):2 3 4 0x y z
e) Đi qua điểm A(3;1;-1),B(2;-1;4) và vuông góc với mặt phẳng 2x-y+3z+4=0
f) Đi qua điểm M(2;-1;2), song song với Oy và vuông góc với mặt phẳng
2 3 4 0x y z
.
g) Đi qua điểm M(-2;3;1) và vuông góc với hai mặt phẳng
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 12
( ):2 2 5 0; ( ):3 2 3 0x y z x y z

h) Đi qua
1;1; 1 ; 5;3;1AB
và song song với trục
Oz
i) Mặt phẳng trung trực
()
của đoạn thẳng AB, biết
1;2; 1 ; 5;3;2AB
Ví dụ 2. Viết phương trình mặt phẳng
()
trong mỗi trường hợp sau:
a) Đi qua điểm M(2;1;-1) và qua giao tuyến của hai mặt phẳng
4 0; 3 1 0x y z x y z
b) Qua giao tuyến của hai mặt phẳng
2 4 0; 3 0y z x y z
đồng thời song song
với mặt phẳng
20x y z
c) Qua giao tuyến của hai mặt phẳng
3 2 0; 4 5 0x y z x y
đồng thời vuông góc
với mặt phẳng
2 7 0xz
Ví dụ 3. Cho điểm H(-1;4;2). Mặt phẳng
()
đi qua H và cắt các trục toạ độ tại A, B, C (không
trùng với O). Biết H là trực tâm của tam giác ABC. Viết phương trình mặt phẳng
()
Hướng dẫn:
chöùng minh: ( )
( ) ( ): H vaø nhaän laøm vtpt
( ): 4 2 21
OH AB
OH ABC
OH BC
ABC Qua OH
x y z

BTTT: Viết phương trình
()
đi qya
(2;1;1)H
và cắt các trục tọa độ tại các điểm
,,A B C
sao cho
H là trục tâm của tam giác ABC. Đáp số:
2 6 0x y z
Ví dụ 4. Cho mặt phẳng
()
đi qua điểm M(-4;1;-3) và cắt ba trục toạ độ Ox, Oy, Oz tại A,B,C
(Khác O). Biết M là trọng tâm của tam giác ABC. Viết phương trình của mặt phẳng
()
Hướng dẫn:
Goïi A(a;0;0);B(0;b;0);C(0;0;c).
Phöông trình maët phaúng ( ): 1.
00
4
3
00
M laø troïng taâm cuûa ABC neân 1 12, 3, 9
3
00
3
3
x y z
a b c
a
b
a b c
c





BTTT: Viết phương trình
()
đi qua
1;2;3G
và cắt các trục tọa độ tại các điểm A, B, C sao cho
G là trọng tâm của tam giác ABC. Đáp số:
6 3 2 18 0x y z
Ví dụ 5. Cho điểm M(4;1;2). Gọi (P) là mặt phẳng qua M và cắt các tia Ox, Oy, Oz theo chiều
dương lần lượt tại A,B,C. Viết phương trình của (P) khi khối tứ diện OABC có thể tích nhỏ nhất.
Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 13


Goïi ( ;0;0); (0; ;0); (0;0; ). ( 0, 0, 0)
Phöông trình maët phaúng (P): 1.
4 1 2
( ) ñi qua ñieåm M(4;1;2) neân 1. (1)
11
. . (2)
66
4 1 2
Theo baát ñaúng thöùc Cauchy, ta coù:
OABC
A a B b C c a b c
x y z
a b c
P
a b c
V OA OB OC abc
ab
3
3
4 1 2
3 . . (3)
8 4 1 2 1
Töø (1),(2),(3) 3 36. Ñaúng thöùc xaûy ra
63
12; 3; 6
c a b c
V
V a b c
a b c
BTTT: Viết phương trình mặt phẳng đi qua điểm M(1;1;1) cắt các trục Ox, Oy, Oz tại A, B, C sao
cho thể tích của OABC có giá trị nhỏ nhất. Đáp số:
30x y z
Ví dụ 6. Trong không gian Oxyz cho mặt phẳng
( ):2 5 0x y x
. Viết phương trình mặt
phẳng (P) qua giao tuyến
()
và mặt phẳng (xOy) và (P) tạo với 3 mặt phẳng tọa độ một tứ diện
có thể tích bằng
36
125
Hướng dẫn:
Phương trình (xOy): z = 0
m(2x – y + z – 5) – nz = 0
(P): 2mx my (m n)z 5m 0
(P) cắt Ox, Oy, Oz lần lượt là
5 5m
A ; 0; 0 , B(0; 5; 0), C 0; 0;
2 m n
1 1 5 5m 125
V .OA.OB.OC . .5.
6 6 2 m n 36
m 1, n 2
m 1, n 4

Vậy có 2 mặt phẳng (P):
1
2
(P ): 2x y 3z 5 0 (m 1; n 2)
(P ): 2x y 3z 5 0 (m 1; n 4)
Ví dụ 7. Viết phương trình mặt phẳng
()
đi qua điểm
0
(1;2;4),M
cắt các trục tọa độ Ox, Oy,
Oz lần lượt tại các điểm A,B,C sao cho OA=OB=OC
0
Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 14




2 2 2
2 2 2 2 2 2
( ): 1 2 4 0, 0 (1)
ax 2 4
2 4 2 4
( ) caét Ox, Oy, Oz laàn löôït A ;0;0 ; 0; ;0 ;
22
24
0;0; vôùi a+2b+4c 0.
2
Ta coù: OA=OB=OC OA =OB =OC
a x b y c z a b c
by cz a b c
a b c a b c
B
abc
C
a b c
Neá
, , (1) -7 0
, - (1) - 1 0
, -
u a b c cuøng daáu thì a b c vaø trôû thaønh x y z
Neáu a b cuøng daáu vaø khaùc daáu vôùi c thì a b c vaø trôû thaønh x y z
Neáu a c cuøng daáu vaø khaùc daáu vôùi b thì a c b vaø 
(1) - -3 0
, - (1) - -5 0
trôû thaønh x y z
Neáu c b cuøng daáu vaø khaùc daáu vôùi a thì a b c vaø trôû thaønh x y z
Ví dụ 8. Cho
0;1;2 ; 2; 2;1 ; 2;0;1A B C
a) Viết phương trình mặt phẳng đi qua A, B, C
b) Tìm
( ):2 2 3 0M x y z
sao cho MA=MB=MC
Đáp số:
) : 2 4 6 0; ) 2;3; 7a ABC x y z b M
BTTT: Cho
0;0;3 ; 2;0; 1 ;AB
và
( ):3 8 7 1 0P x y z
. Tìm
()CP
sao cho tam giác
ABC đều. ĐS:
2 2 1
2; 2; 3 ; ; ;
3 3 3
CC



Ví dụ 9. Viết phương trình mặt phẳng
()
đi qua điểm
4; 1;1M
và cắt các tia
Ox, ,Oy Oz
lần
lượt tại A, B, C sao cho
23OA OB OC
ĐS:
2 3 5 0x y z
Ví dụ 10. Cho hai điểm A(-1;3;2), B(2;3;-1) và
( ):2 3 5 0x y z
. Tìm điểm C thuộc
()
sao cho tam giác ABC đều.
VẤN ĐỀ 2. Vị trí tương đối của hai mặt phẳng
Phương pháp:
Cho hai mặt phẳng
1 1 1 1
2 2 2 2
( ): 0
( ): 0
A x B y C z D
A x B y C z D


1 1 1 2 2 2
: : : :caét A B C A B C
2
1
2
1
2
1
2
1
//
D
D
C
C
B
B
A
A
2
1
2
1
2
1
2
1
D
D
C
C
B
B
A
A
0
212121
CCBBAA
Ví dụ 1: Cho hai mặt phẳng
( ): 2 0;( ):2 3 2 0P x y z Q x y z
a) Chứng tỏ
( ) ( )PQ
. Chỉ ra phương trình giao tuyến
d
của (P) và (Q)
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 15
b) Lập phương trình mặt phẳng
()R
chứa d và qua M(1;2;3).
Đáp số: b)
7 13 3 10 0x y z
Ví dụ 2: Cho ba mặt phẳng
( ): 2 0;( ): 3 2 0;( ):4 2 0P x y z Q x y z R y z
a) Chứng tỏ (P) và (R) cắt nhau theo giao tuyến (d)
b) Lập phương trình mặt phẳng (T) chứa d và song song với (Q)
Đáp số: b)
30x y z
Ví dụ 3: Cho hai mặt phẳng
( ):2 2 1 0; ( ): 2 0x y z x y z

a) Chứng tỏ
( ),( )

cắt nhau theo giao tuyến d
b) Lập phương trình mặt phẳng
()
chứa d và cắt các trục tọa độ theo thứ tự các điểm M, N,
P sao cho
1
6
OMNP
V
Đáp số: b)
10x y z
Ví dụ 4: Xác định k và m để ba mặt phẳng sau đây cùng đi qua một đường thẳng :
5 4 0; 3 7 3 0; 9 2 5 0x ky z m x y z x y z
Hướng dẫn:
Goïi laø giao tuyeán cuûa 2 maët phaúng 3x-7y+z-3=0; x-9y-2z+5=0
1 18 31 9
Laáy A ;0; ; ; ;0
7 7 10 10
ieåm A,B thuoäc : 5x+ky+4z+m=0 k=-5;m=-11
B
Ñ

Ví dụ 5: Xác định m để ba mặt phẳng sau đây đôi một cùng vuông góc với nhau, tìm giao điểm
chung của 3 mặt phẳng đó.
( ):5 4 0;
( ):3 7 3 0;
( ): 9 2 5 0
P x ky z m
Q x y z
R x y z
Hướng dẫn:
.0
Ba maët phaúng ñoâi moät vuoâng goùc nhau . 0 1
.0
Goïi I(x;y;z) laø nghieäm chung cuûa 3 maët phaúng, toïa ñoä I laø nghieäm cuûa heä 3 phöông
trình ba maët p
PQ
PR
RQ
nn
n n m
nn
haúng treân. I(1;2;3)
BTTT:Xác định m để ba mặt phẳng sau đây đôi một cùng vuông góc với nhau, tìm giao điểm
chung của 3 mặt phẳng đó.
( ): 6 0;
( ): 2 1 0;
( ): 1 2 0
P x y z
Q mx y z m
R mx m y z m
Đáp số: I(1;2;3)
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 16
VẤN ĐỀ 3. Khoảng cách từ một điểm đến một mặt phẳng, khoảng cách giữa hai mặt phẳng song
song. Hính chiếu và điểm đối xứng
Phương pháp
Khoảng cách từ điểm M0(x0; y0; z0) đến mặt phẳng (): Ax + By + Cz + D = 0
0 0 0
0
2 2 2
,( )
Ax By Cz D
dM
A B C

Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì trên mặt phẳng
này đến mặt phẳng kia.
Chú ý: Nếu hai mặt phẳng không song song thì khoảng cách giữa chúng bằng 0.
Điểm H là hình chiếu của điểm M trên (P)
MH n cuøng phöông
HP
,
()
Điểm M
đối xứng với điểm M qua (P)
2MM MH
Ví dụ 1: Cho
( ):6 2 1 0; ( ):6 2 3 0P x y z Q x y z
. Tính khoảng cách giữa (P) và
(Q).
Ví dụ 2: Viết phương trình tổng quát của (P) cách (Q) một khoảng
14k
với
( ):3 2 3 0Q x y x
.
Ví dụ 3: Viết phương trình mặt phẳng
( )/ /( ): 2 2 5 0x y z

và cách
(2; 1;4)A
một
khoảng
4k
Ví dụ 4:Tìm
M Ox
và cách đều hai mặt phẳng
( ),( )

với
( ): 2 2 1 0x y z
và
( ):2 2 5 0x y z
.
Ví dụ 5: Tìm
M Oy
và cách đều
1; 4; 2N 
và
( ): 14 0x y z
.
Ví dụ 6: Cho
1;1;1A
. Tìm
M Oz
sao cho
3 ,(Ox )MA d A y
Ví dụ 7: Cho
( ): 5 14 0; (1; 4; 2)P x y z M
a) Tính
( ,( ))d M P
b) Tìm tọa độ hình chiếu của M trên (P). Từ đó suy ra tọa độ M’ là điểm đối xứng của M trên
(P).
BÀI TẬP ÁP DỤNG
Bài 1. Cho hai mặt phẳng
( ):2 2 4 0; ( ): 4 2 4 9 0x y z x y z

a) Tính
,d

b) Viết phương trình mặt phẳng (P) cách đều hai mặt phẳng
( ),( )

Đáp số:
1 17
) ; )2 2 0
64
a b x y z
Bài 2. B2009. Cho
1;2;1 ; 2;1;3 ; 2; 1;1 ; 0;3;1A B C D
. Viết phương trình mặt phẳng
()
qua A, B và
,( ) ,( )d C d D

Đáp số:
12
( ): 4 2 7 15 0; ( ):2 3 5 0;x y z x z

Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 17
Bài 3. Cho
1;2;1 ; 0;4;0 ; 0;0;4 ;A B C
. Viết Phương trình mặt phẳng
()
chứa đường
thẳng OA và cách đều hai điểm B, C.
Đáp số:
12
( ):3 0; ( ): 0;x y z x y z

Bài 4. B2010. Cho
1;0;0 ; 0; ;0 ; 0;0; , , 0A B b C c b c
và
( ): 1 0P y z
. Xác định b, c
biết
( ) ( )ABC P
và
1
( ;( ))
3
d O ABC
.
Đáp số:
1
2
bc
Bài 5. Cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là những số dương thay đổi sao cho
2 2 2
3a b c
. Xác định a, b, c để khoảng cách từ O đến (ABC) lớn nhất
Đáp số:
1a b c
VẤN ĐỀ 4. Góc của hai mặt phẳng
Phương pháp
Cho hai mặt phẳng (
), (
) có phương trình: (
):
1111
0A x B y C z D
(
):
2222
0A x B y C z D
Góc giữa (
), (
) bằng hoặc bù với góc giữa hai VTPT
12
nn,
.
1 2 1 2 1 2 1 2
2 2 2 2 2 2
12
1 1 1 2 2 2
.
cos ( ),( )
.
.
n n A A B B C C
nn
A B C A B C


Chú ý:
00
0 90( ),( )


.
1 2 1 2 1 2
0A A B B C C( ) ( )

Ví dụ 1: Viết phương trình mặt phẳng
()
đi qua
3;0;0 , 0;0;1AC
và cắt trục tung tại điểm
B sao cho
ABC
có
7
2
S
Ví dụ 2: Viết phương trình mặt phẳng
()
đi qua
0;0;3 , 0;0;1AC
, cắt trục hoành tại điểm
B và
()
tạo với (Oxy) một góc 30
0
.
Ví dụ 3: Viết phương trình mặt phẳng (P) đi qua
3;0;0 , 2;1;0AB
và tạo với (Oxy) một góc
0
60
.
Hướng dẫn:
6
( ): 3 0
3
P x y z
Ví dụ 4: Cho
( ): 2 3 6 0; ( ): 1 2 4 6 0x y z m x m y m

. Tìm m để
5
cos ( ),( )
27
PQ
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 18
Hướng dẫn:
7
1;
2
mm
Ví dụ 5: Tìm m để góc giữa hai mặt phẳng sau bằng :
0
2 12 0
70
45
mx y mz
x my z
VẤN ĐỀ 5. Ứng dụng giải toán hình học không gian
Ví dụ 1: A2003. Cho hình chóp
có tam giác ABC đều cạnh a,
6
, ( ).
2
a
SA SA ABC
Tính
,( )d A SBC
. Đáp số:
2
2
a
d
Ví dụ 2: B2004. Cho
0
, 3 , ( ), 2 , 120SA a SA ABC AB BC a ABC
. Tính
,( )d A SBC
. Đáp số:
Ví dụ 3: A2007. Cho lăng trụ đứng
. ' ' 'ABC A B C
có
, 2 , AA' 2 5,AB a AC a a
0
120BAC
. M là trung điểm của CC’. Chứng minh:
'MB MA
và
,( 'd A A BM
.
Đáp số:
5
,( '
3
a
d A A BM
Ví dụ 4: DB A2003. Cho lăng trụ đứng
. ' ' 'ABC A B C
có
ABC
cân
AB AC a
',BB a
0
120BAC
. I là trung điểm của CC’. Chứng minh:
'AB I
vuông và tính
cos ( ),( ' )ABC AB I
. Đáp số:
30
cos ( ),( ' )
10
ABC AB I
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,
3SA a
,
SA ABCD
.Tính
d,A SBC
và khoảng cách từ trọng tâm G của tam giác SAB đến
SAC
. Đáp số:
32
, ; ,
26
aa
d A SBC d G SAC
Ví dụ 6: Cho hình thoi ABCD tâm O cạnh a,
AC a
. Từ trung điểm H của AB dựng
( ),AH ABCD SH a
. Tính
;(d O SCD
và
;(d A SBC
Đáp số:
21 2 57
, ; ,
14 19
aa
d O SCD d A SBC
Ví dụ 7: Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
0;0;0 , ;0;0 ; 0; ;0A B a D a
,
' 0;0;Ab
với
,0ab
, M là trung điểm CC’.
a) Tính
'BDA M
V
b) Tìm tỉ số
a
b
để
( ' ) ( )A BD MBD
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 19
Ví dụ 8: Cho tứ diện OABC có các cạnh OA, OB, OC vuông góc với nhau từng đôi một. Gọi
,,
lần lượt là các góc hợp bởi các mặt phẳng (OAB), (OBC), (OCA) với mặt phẳng (ABC).
Bằng phương pháp toạ độ, chứng minh rằng:
a) Tam giác ABC có ba góc nhọn
b) b)
1coscoscos
222
Ví dụ 9. Cho hình chóp
.S ABCD
có ABCD là hình chữ nhật,
, 2 ,AD a AB a
,SD a
2,SB a SBD ABCD
. Tính
.S ABCD
V
và
,d A SBC
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 20
CHỦ ĐỀ 3. MẶT CẦU VÀ CÁC BÀI TOÁN LIÊN QUAN
VẤN ĐỀ 1. Viết phương trình mặt cầu
Phương pháp: Muốn viết phương trình mặt cầu ta cần xác định tâm và bán kính của nó
2
Rczbyax:R)S(I,
222
(1)
0d2cz2by2axzyx:R)S(I,
222
(2) (
0dcbavôùi
222
)
Tâm I(a ; b ; c) và
dcbaR
222
Các trường hợp cơ bản:
TH1: Mặt cầu tâm I đi qua A. Lúc đó bán kính là R=IA
TH2 : Viết phương trình mặt cầu đường kính AB
Tâm I là trung điểm AB
Bán kính R=IA
TH 3: Mặt cầu ngoại tiếp tứ diện ABCD
Bước 1: Giả sử mặt cầu có phương trình:
2 2 2
x y z 2ax 2by 2cz d 0
Bước 2: Vì A,B,C,D mc(S) nên ta thiết lập được hệ 4 phương trình 4 ẩn, giải hệ ta được
a,b,c,d
TH 4: Mặt cầu đi qua A,B,C và có tâm
()I
Bước 1: Giả sử mặt cầu có phương trình:
2 2 2
x y z 2ax 2by 2cz d 0
Bước 2: Vì A,B,C mc(S) và I thuộc mặt phẳng
()
nên ta thiết lập được hệ 4 phương
trình 4 ẩn, giải hệ ta được a, b, c, d
Ví dụ 1: Cho
1;0; 3 ; 1;2; 1AB
. Viết phương trình mặt cầu (S)
a) Có đường kính AB
b) Có tâm
I Oy
và đi qua hai điểm A, B
Đáp số:
2 2 2
2 2 2
) 1 2 3; ) 1 11a x y z b x y z
Ví dụ 2: Viết phương trình mặt cầu (S) đi qua ba điểm
1;2;4 ; 1; 3; 1 ; 2;2; 3A B C
và có
tâm
()I Oxy
. Đáp số:
2 2 2
( ): 4 2 21 0S x y z x y
Ví dụ 3: Cho 4 điểm
1;5;3 ; 4;2; 5 ; 5;5; 1 ; 1;2;4A B C D
a) Viết
1
()S
đi qua A, B, C và có tâm
(Ox )Iz
b) Viết
2
()S
đi qua A, B, C, D
Đáp số:
2 2 2 2 2 2
22 2 147
) 0; ) 4 2 19 0
5 5 5
a x y z x y b x y z x y z
Ví dụ 4: Lập phương trình mặt cầu đi qua ba điểm
2;1;1 ; 1;1;0 ; 0;2;4A B C
và
5R
.
Đáp số:
2 2 2 2 2 2
12
4 38 32 8
: 2 4 0; 0
9 9 9 3
S x y z y z S x y z x y z
VẤN ĐỀ 2. Vị trí tương đối của mặt phẳng và mặt cầu
Phương pháp: Cho
2
Rczbyax:(S)
222
và : Ax + By + Cz + D = 0
Gọi d = d(I,) : khỏang cách từ tâm mc(S) đến mp :
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 21
TH 1: d > R : (S) =
TH 2: d = R : tiếp xúc (S) tại H (H: tiếp điểm, : tiếp diện)
Tìm tiếp điểm H (là hình chiếu của tâm I trên mp
)
Bước 1 : Viết phương trình đường thẳng (d) qua I và vuông góc mp . Ta có
na
d
Bước 2 : Tọa độ H là nghiệm của hpt : (d) và ()
TH 3: d < R : cắt (S) theo đường tròn có pt
2
0DCzByAx :
Rczbyax:(S)
222
Tìm bán kính r và tâm H của đường tròn:
Bán kính
),(
22
IdRr
Tìm tâm H ( là hchiếu của tâm I trên mp)
Chú ý: Cách tìm giao điểm của đường thẳng và mặt cầu
tazz
tayy
taxx
d
3o
2o
1o
:
(1) và
2
Rczbyax:(S)
222
(2)
Bước 1 : thay phương trình (1) vào pt (2), giải tìm t,
Bước 2 : Thay t vào (1) được tọa độ giao điểm
Các trường hợp cơ bản :
TH 1 : Mặt cầu tâm I tiếp xúc mp :
222
..
)(
CBA
D
I
zC
I
yB
S
I
A.x
)d(I, R
I taâmcaàu maët Pt
TH 2: Viết phương trình mặt phẳng tiếp xúc (S) và
Bước 1: Mặt phẳng vuông góc nên có :
),,( CBAan
.
Do đó : Ax + By + Cz + D = 0 ( A,B, C đã biết)
Bước 2: Để tìm D ta sử dụng thêm giải thiết d(I , ) = R
Ví dụ 1: DB B2006. Viết phương trình mặt cầu
(0;0;0); 0;0;4 ; (2;0;0)O A B
và tiếp xúc với
( ):2 5 0P x y z
. Đáp số:
2 2 2
( ): 1 1 2 6S x y z
Ví dụ 2: Viết phương trình mặt cầu (S) có tâm thuộc trục tung và tiếp xúc với hai mặt phẳng
( ):2 3 5 0; ( ):2 3 11 0x y z x y z

Đáp số:
2
22
32
3
7
x y z
Ví dụ 3: Cho
1;0; 1 ; 1;2;1 ; 0;2;0A B C
a) Viết phương trình mặt cầu đi qua O, A, B, C
b) Gọi G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng vuông góc với
OG
và tiếp xúc với (S).
Đáp số:
2
22
32
) 3 ; ) 2 3 10 0
7
a x y z b x y
Ví dụ 4: Viết phương trình mặt cầu
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 22
a) Có tâm
(2; 1;4)I
và tiếp xúc với
(Ox )y
b) Có tâm
(0;0;0)O
và tiếp xúc với mặt cầu tâm
(3; 2;4)J
và có bán kính
'1R
Đáp số:
2 2 2
22
2 2 2 2 2 2
12
) ( ): 2 1 4 16
) ( ): 29 1 ; ( ): 29 1
a S x y z
b S x y z S x y z
Ví dụ 4: Lập phương trình mặt cầu có bán kính bằng 2 và tiếp xú với
(Ox )y
tại M(3;1;0)
Đáp số:
12
3;1; 2 ; 3;1;2II
Ví dụ 5: Cho
1;2;3 ; 3;5;4 ; 3;0;5A B C
a) Lập phương trình mặt phẳng qua A, B, C
b) Lập phương trình mặt cầu nhận đường tròn ngoại tiếp tam giác ABC làm đường tròn lớn.
Hướng dẫn:
2 2 2
39 89 81 667
) :4 5 13 0; ( ):
7 14 14 14
a ABC x y z S x y z
Ví dụ 7: Cho
1 1 2
2;1; 3 ;( ): 2 3 0;( ): 2 9 0;M P x y z P x y z
a) Viết phương trình mặt cầu tiếp xúc với (P1) tại
1
M
và tiếp xúc với
2
()P
b) Viết phương trình mặt cầu tiếp xúc với
1
()P
tại
1
M
và cắt
2
()P
theo thiết diện là
đường tròn lớn.
Đáp số:
2 2 2 2 2 2
) ( ): 3 2 1 6; ) ( ): 4 3 1 24a S x y z b S x y z
BÀI TẬP ÁP DỤNG
Bài 1. Cho
1
2;5;0M
và hai mặt phẳng
12
( ):3 2 4 0; : 3 2 1 0P x y z P x y z
a) Viết phương trình mặt cầu tiếp xúc với
1
()P
tại
1
M
và tiếp xúc với
2
()P
b) Viết phương trình mặt cầu tiếp xúc với
1
()P
tại
1
M
và cắt
2
()P
theo thiết diện là
đường tròn lớn.
c) Viết phương trình mặt cầu tiếp xúc với
1
()P
tại
1
M
và cắt
2
()P
theo thiết diện là
đường tròn có bán kính
21
2
r
Hướng dẫn
a)
22
2 2 2 2
12
11 2 56
( ): 4 9 2 56; ( ): 4
3 3 9
S x y z S x y z
b)
2 2 2
( ): 8 1 2 56S x y z
c)
2 2 2
15 29 7 686
( ):
3 3 3 9
S x y z
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 23
Bài 2. Cho
2 2 2
( ):2 3 2 3 0; ( ): 8 8 7 68P x y z S x y z
a) Xác định vị trí tương đối của (P) và (S)
b) Viết phương trình mặt phẳng song song với (P) và tiếp xúc với (S)
c) Viết phương trình mặt phẳng song song với (P) và cắt mặt cầu theo thiết diện là
đường tròn lớn
d) Viết phương trình mặt phẳng song song với (P) và cắt mặt cầu theo thiết diện là
đường tròn có bán kính
51r
e) Viết phương trình mặt cầu (S’) đối xứng với (S) qua (P).
Đáp số:
12
2 2 2
)2 3 2 20 0; 2 3 2 88 0
)( ):2 3 2 54 0
)( ):2 3 2 37 0; ( ):2 3 2 71 0;
) 4 10 5 68
b x y z x y z
c Q x y z
d Q x y z Q x y z
e x y z
Bài 3. Cho
22
2
( ):2 2 5 0; ( ): 3 4 9P x y z S x y z
a) Chứng tỏ (P) tiếp xúc với (S). Tìm tọa độ tiếp điểm
b) Viết phương trình mặt phẳng song song với (P) và tiếp xúc với (S)
c) Viết phương trình mặt phẳng song song với (P) và cắt mặt cầu theo thiết diện là
đường tròn lớn
d) Viết phương trình mặt cầu (S’) đối xứng với (S) qua (P).
Đáp số:
22
2
) 1;1;2 ; )( ):2 2 23 0; ):2 2 14 0; ) 1 2 9a M b Q x y z c x y z d x y z
Bài 4. Cho
22
2
( ): 2 3 10 0; ( ): 2 2 56P x y z S x y z
a) Chứng tỏ (P) cắt (S) theo thiết diện là đường tròn. Tìm tọa độ tâm và bán kính đường
tròn
b) Viết phương trình mặt phẳng song song với (P) và tiếp xúc với (S)
c) Viết phương trình mặt phẳng song song với (P) và cắt mặt cầu theo thiết diện là
đường tròn lớn.
d) Viết phương trình mặt cầu (S’) đối xứng với (S) qua (P).
Đáp số:
12
2 2 2
) 3;2;1 ; 42 ; )( ): 2 3 32 0; ( ): 2 3 2 3 24 0;
)2 2 3 4 0; ) 2 3 18 0; )( '): 4 4 4 56
a J r b Q x y z Q x y z x y z
c x y z d x y z e S x y z
Bài 5. Cho
2 2 2
( ): 2 2 2 6 0S x y z x y z
. Viết phương trình mặt phẳng song song với
( ): 2 1 0x y z
và cắt (S) theo thiết diện là đường tròn (C) có
3S
.
Đáp số:
12
: 2 2 0; : 2 10 0x y z x y z

Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 24
Bài 6. Cho
2 2 2
( ): 2 2 2 6 0S x y z x y z
.
a) Viết phương trình mặt phẳng đi qua
4;0;0 ; 0;0;8AB
và tiếp xúc với (S)
b) Viết phương trình mặt phẳng qua
2;1;1 ; 1;1;0CD
và cắt (S) theo thiết diện là đường
tròn (C) có
Đáp số:
a)
12
( ):2 2 8 0; ( ):8 4 32 0;x y z x y z

b)
12
( ): 0; ( ): 5 6 0;x y z x y z

Bài 7. Lập phương trình mặt cầu đi qua
1;0;0 ; 0;1;0 ; 0;3;2A B C
và cắt
( ):2 2 0P x y z
theo thiết diện là đường tròn có bán kính bằng 1.
Đáp số:
2 2 2 2 2 2
12
( ): 2 2 4 1 0;( ): 8 8 2 7 0;S x y z x y z S x y z x y z
Bài 8. Cho
2 2 2
( ): 5 3 3 37;( ):2 2 1 0S x y z P x y z
a) Chứng tỏ (P) cắt (S) theo giao tuyến là một đường tròn (C). Xác định tâm và bán kính của
(C)
b) Lập phương trình mặt cầu chứa (C) và
Có tâm thuộc
( ): 9 0Q x y z
Đi qua
4;2; 2A
Tiếp xúc với
( ):3 7 0Q x y
Đáp số:
(1;1; 1)
) ( ):
1
H
aC
r
2 2 2
1
)
: 6 2 10 2 0
b
S x y z x y z
LUYỆN TẬP PHƯƠNG TRÌNH MẶT CẦU
Bài 1. Cho bốn điểm A(2;-1;6), B(-3;-1;-4), C(5;-1;0), D(1;2;1).
a) Tính bán kính đường tròn nội tiếp tam giác ABC và khoảng cách từ D tới (ABC)
b) Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD
Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 25
) Baùn kính cuûa ñöôøng troøn ngoaïi tieáp ABC laø r =
.Ñeå yù: . 0 vuoâng taïi C
2
3
30
r= 5. Khoaûng caùch töø D tôùi (ABC) laø d(D,(ABC))= ;
65
1
,
6
ABC
ABCD
ABC
ABCD
S
a
p
AB BC CA
p AC BC ABC
V
S
V AB AC

22
22
22
2 2 2
. . :3
) Goïi I(x;y;z) laø taâm ñöôøng troøn ngoaïi tieáp töù giaùc ABCD:
1
2
13 1525
IA=IAB=IC=ID . Baùn kính .
3 36
1
Caùch2: Goïi(S):
AD ÑS
b
x
IA IB
IA IC y R IC
IA ID
z
x y z





 2ax 2 2 0
Thay toïa ñoä A,B, C, D vaøo (S) ta ñöôïc heä phöông trình 4 aån a,b,c,d
by cz d
BTTT: Cho 4 điểm A(0;1;0);B(2;3;1);C(-2;2;2);D(1;-1;2)
a) Chứng minh rằng tứ diện ABCD vuông tại A
b) Viết phương trình mặt cầu ngoại tiếp tứ diện
Hướng dẫn và đáp số:
2 2 2
)chöùng minh AB, AC, AD ñoâi moät vuoâng goùc nhau
1 3 5 27
)
2 2 2 4
a
b x y z
Bài 2. Cho hình lăng trụ tam giác ABC.A’B’C’ với A(-1;6;-1), B(-4;6;2), C(-1;3;2), A’(5;12;5)
a) Chứng minh rằng hình lăng tụ đã cho là hình lăng trụ đều và tính thể của nó
b) Tìm toạ độ của tâm đường tròn ngoại tiếp tam giác A’B’C’ và viết phương trình của mặt
cầu ngoại tiếp hình lăng trụ ABC.A’B’C’
Hướng dẫn:
laø tam giaùc ñeàu
)
' ( )
)Vì tam giaùc ABC laø tam giaùc ñeàu neân taâm truøng vôùi troïng taâm G,
G(-2;5;1) laø troïng taâm cuûa ABC
Goïi G' laø troïng tam cuûa tam giaùc A'B'C', ta c
ABC
a ycbt
AA ABC
b
où
' ' '(4;11;7).Hình laêng truï ABC.A'B'C' laø hình laêng truï ñeàu neân (S)
ngoaïi tieáp hình laêng truï naøy coù taâm laø trung ñieåm I(1;8;4) cuûa GG', R=IA= 33
GG AA G
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 26
Bài 3. ĐHCĐ 2005 B . Trong không gian với hệ tọa độ Oxyz cho hình lăng trụ đứng ABC.A1B1C1
với A(0;-3;0), B(4;0;0), C(0;3;0), B1(4;0;4).
a) Tìm tọa độ các đỉnh A1, C1. Viết phương trình mặt cầu có tâm là A và tiếp xúc với mặt phẳng
(BCC1B1).
b) Gọi M là trung điểm của A1B1. Viết phương trình mặt phẳng (P) đi qua hai điểm A, M và song
song với BC. Mặt phẳng (P) cắt đường thẳng A1C1 tại điểm N. Tính độ dài MN.
Bài 4. Cho phương trình
2 2 2 2
2( 1) 4 2 6 1 0 (1)x y z m x my z m
Xác định m để phương trình (1) là phương trình của mặt cầu. Khi đó, tìm m để bán kính của mặt
cầu đạt giá trị lớn nhất.
Hướng dẫn:
2 2 2
2
2
max
(1) laø phöông trình maët caàu A 0 1 3
ñoù: R= 2 3
Xeùt haøm soá f(m)=-m 2 3, ( 1;3)
2 khi m=1
B C D m
Khi m m
mm
R
Bài 5. Cho mặt phẳng (P) và mặt cầu (S) có phương trình lần lượt là:
2 2 2
2 3 4 0; 6 2 2 3 0x y z x y z x y z
. Lập phương trình mặt phẳng
()
song song với (P) và tiếp xúc với (S).
Hướng dẫn:
( ) // (P) neân ( ) coù daïng 2 - -3 0 (D 4).
( ) tieáp xuùc vôùi (S) d(I,( ))=R D=24 hoaëc D=-4
x y z D



Bài 6. Lập phương trình mặt cầu (S) có tâm I thuộc mặt phẳng (Oyz) và đi qua A(0;0;4), B(2;1;3),
C(0;2;6)
Hướng dẫn:
Maët caàu (S) ñi qua A,B,C coù taâm I thuoäc caùc maët phaúng trung tröïc ( )
cuûa AB vaø maët phaúng trung tröïc ( ) cuûa AC
( ): 2 - 1 0; ( ): -6 0
2
Toïa ñoä I laø nghieäm cuûa heä phöông trình:
x y x y z
xy

- 1 0
57
-6 0 0; ;
72
0
x
y z I
z




BTTT:Lập phương trình mặt cầu (S) có tâm I thuộc mặt phẳng
( ):2 3 0x y z
và đi qua
A(-3;6;1), B(2;3;-3), C(-6;2;0)
Đáp số:
2 2 2
39 51 57 4651
( ):
10 10 10 100
S x y z
Bài 7. Lập phương trình mặt cầu (S) tiếp xúc với
( ): 3 0Qx
và đi qua A(1;2;-1), B(-1;0;3),
C(3;-2;1)
Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 27
( ) ñi qua A,B,C neân taâm I cuûa (S) thuoäc maët phaúng trung tröïc ( ) cuûa
AB vaø maët phaúng trung tröïc ( ) cuûa AC
( ): -2 1 0; ( ): -2 -2 0.
2 1 0
Do ñoù I thuoäc ñöôøng thaúng :
22
S
x y z x y z
x y z
x y z

0
3 2 2
: 1 . ; 1 ; vaø d ;( )
3 2 2
xt
t
y t I I t t t I Q IA
t
zt


Bài 8. ĐHCĐ 2004 K.D Trong không gian với hệ toạ độ Oxyz cho ba điểm A(2;0;1), B(1;0;0),
C(1;1;1) và mặt phẳng (P) : x + y + z – 2 = 0. Viết phương trình mặt cầu đi qua ba điểm A, B, C và
có tâm thuộc mặt phẳng (P).
Hướng dẫn:
2 2 2
; ; laø taâm maët caàu (S).
()
IA IB IC
I x y z
Ip

BTTT: Lập phương trình mặt cầu (S) tiếp xúc với
( ):2 2 12 0x y z
và đi qua A(1;2;-1),
32 41 83 9 38
; ; ; ; ; 1
9 9 9 5 5
BC

Đáp số:
2 2 2
1
2 2 2
2
( ): 2 4 5 49;
156 103 149 519841
( ):
5 5 20 400
S x y z
S x y z
Bài 9. ĐHCĐ 2009 A Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P):
2 2 4 0x y z
và mặt cầu (S):
2 2 2
2 4 6 11 0x y z x y z
. Chứng minh rằng mặt
phẳng (P) cắt mặt cầu (S) theo một đường tròn. Xác định toạ độ tâm và bán kính của đường tròn
đó.
BTTT. Trong hệ trục tọa độ Oxy cho đường tròn (C) có phương trình
2 2 2
2 2 3 5
2 2 1 0
x y z
x y z
. Tìm tâm và bán kính
Bài 10. Cho 4 điểm A(1;2;1);B(2;0;-1);C(1;3;-4);D(0;-2;2). Chứng minh rằng tập hợp những điểm M
thỏa mãn :
2 2 2 2
4MA MB MC MD
là một mặt cầu. Viết phương trình mặt cầu đó.
Hướng dẫn:
2 2 2
( ; ; ).( ): 4 3 12 334M x y z S x y z
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 28
CHỦ ĐỀ 4. ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN
A. CƠ SỞ LÝ THUYẾT
1. Vectơ chỉ phương của đường thẳng:
0u
được gọi là vtcp của đường thẳng
d
nếu giá của
u
song song hoặc trùng với
d
2. Các dạng phương trình đường thẳng:
Phương trình tham số của đường thẳng: (d) qua M(xo ;yo ;zo) có vtcp
a
= (a1;a2;a3)
PTTS:
Rt;
tazz
tayy
taxx
(d)
3o
2o
1o
:
PTCT:
0
:


23
oo
1
z - z
x x y y
(d)
a a a
PT tổng quát của (d) là giao tuyến của 2 mp 1 và 2
0 DzBxA
0 DzBxA
(d)
2222
1111
Cy
Cy
:
. Lúc đó véctơ chỉ phương
22
11
22
11
22
11
,,
BA
BA
AC
AC
CB
CB
a
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
VẤN ĐỀ 1. Viết phương trình đường thẳng
Phương pháp chung:
Tìm một điểm trên d và một vtcp của d
Tìm 2 mặt phẳng cùng đi qua d thì d là giao tuyến của 2 mặt phẳng
Các trường hợp cơ bản:
TH 1: Đường thẳng (d) đi qua A,B:
ABaVtcp
hayBquaA
d
d
)(
)(
TH 2: Đường thẳng (d) qua A và song song ():
a
d
a vtcp neân )( // (d) Vì
qua
A
d )(
TH 3 : Đường thẳng (d) qua A và vuông góc mp:
n
d
a vtcp neân )( (d) Vì
qua
A
d)(
TH 4 : Đường thẳng (d) qua A và vuông góc (d1),(d2):
]
d
a ,
d
a [ avtcp
qua
1 2
)(
A
d
Một số lưu ý:
Nếu
1
d
qua A và cắt
2
d
thì
1
d
nằm trong mặt phẳng đi qua A và chứa
2
d
Nếu
1
d
qua A và vuông góc với
2
d
thì
1
d
nằm trong mặt phẳng đi qua A và vuông góc
với
2
d
Nếu
d
qua A và song song với
()
thì
d
chứa trong mặt phẳng đi qua A và song song
với
()
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 29
Ví dụ 1 : Cho
12
: ; ( ):2 3 6 0
1 4 1
x y z
d x y z

. Viết phương trình đường thẳng
đi qua giao điểm A của d và
()
và song song với
13
': 3
2
xt
d y t
zt

Đáp số:
1
:2
2
xt
yt
zt

Ví dụ 2: Cho
2;0; 3 ; 4; 2; 1AB
và mặt phẳng
( ): 2 4 0P x y z
Viết phương trình đường thẳng
d
chứa trong (P) sao cho d cách đều A và B
Đáp số:
34
: 6 3
2
xt
yt
zt

Ví dụ 3: Cho
1;4;2 ; 1;2;4AB
và mặt phẳng
1
( ): 2
2
xt
yt
zt

a) Viết phương trình đường thẳng đi qua trọng tâm G của
OAB
và
()OAB
b) Tìm
M 
sao cho
22
MA MB
nhỏ nhất
Đáp số:
2
) : 2 ; ) 1;0;4
2
xt
a d y t b M
zt

Ví dụ 4: DB B2009. Cho
1;0; 1 ; 2;3; 1 ; 1;3;1A B C
. Viết phương trình tham số của đường
thẳng qua trực tâm
ABC
và vuông góc với
()ABC
.
Đáp số:
6
10
:2
3
3
3
2
xt
yt
zt

Ví dụ 5: ĐHA 2011. Cho
2;0;1 ; 0; 2;3AB
. Tìm
( ):2 4 0M P x y z
sao cho
3MA MB
. Đáp số:
1
6 4 12
0;1;3 ; ; ;
7 7 7
MM



Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 30
Ví dụ 6: Cho
2;1;0 ; 0;1;2 ; 0;0;1A B C
. Tìm
( ): 2 0M P x y z
sao cho
MA MB
và
MC
nhỏ nhất. Đáp số:
11
; 2;
22
M



Dạng 1. Viết phương trình đường thẳng
(
()P
hoặc
/ / ( )P
) qua điểm A và vuông góc với
đường thẳng d
Phương pháp:
Ví dụ 1: Cho
13
: ;( ):2 5 3 8 0; 3; 4;1
2 1 3
x y z
d P x y z A

a) Viết phương trình đường thẳng
1
qua A, nằm trên (P) và
d
b) Viết phương trình
1
qua A, song song với
Oxy
và
d
Hướng dẫn:
12
3
3 4 1
) : ; ) : 4 2
9 6 4
1
xt
x y z
a b y t
z

Ví dụ 2: Cho
1 4 1
: ;( ): 2 2 9 0
1 6 4
x y z
d x y z

a) Tìm
Id
sao cho
;( ) 2dI
b) Tìm
()Ad

. Viết phương trình đường thẳng đi qua A, chứa trong
()
và vuông
góc với
d
Hướng dẫn:
(3; 7;1)
) ;( ) 2 ; ) : 1
( 3;5;7)
4
xt
I
a d I b y
I
zt

Dạng 2. Viết phương trình đường thẳng
qua A, vuông góc với
1
d
và cắt
2
d
Phương pháp:
Cách 1:
Bước 1: Chuyển d2 về dạng tham số
Bước 2: Giả sử d cắt d2 tại B,
2
Bd
toạ độ B có chứa tham số
Bước 3: d vuông góc với d1
1
d
AB u
Cách 2:
Viết phương trình mặt phẳng (P) qua A và vuông góc với d1.
Viết phương trình mặt phẳng (Q) chứa A và d2.
Khi đó
= (P) (Q).
Ví dụ 1: Cho
12
1
12
: ; :
3 1 1
1
x
x y z
d d y t
zt



Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 31
Viết phương trình đường thẳng
qua
0;1;1A
, vuông góc
1
d
và cắt
2
d
Hướng dẫn:
:1
12
xt
yt
zt


Ví dụ 2: Cho
32
:1
14
xt
d y t
zt

. Viết phương trình đường thẳng
qua
0;1;1A
, vuông góc và
cắt
d
Hướng dẫn:
43
: 2 2
4
xt
yt
zt

Ví dụ 3: Cho d là giao tuyến của
:5 2 0; : 2 1 0x y z x y z

. Viết phương
trình đường thẳng
qua
2; 1;0A
, vuông góc và cắt
d
.
Hướng dẫn:
22
:1
xt
y
zt


Dạng 3. Viết phương trình đường thẳng
qua A, song song với (P) và cắt d
Phương pháp
Ví dụ 1: Viết phương trình chính tắc của đường thẳng
đi qua
3; 1;4A
, cắt trục Oy và song
song với
( ):2 0P x y
Hướng dẫn:
3 1 4
:
3 6 4
x y z
Ví dụ 2: Viết phương trình chinhd tắc của đường thẳng
đi qua
3; 2; 4A 
, cắt
2 4 1
:
3 2 2
x y z
d

và song song với
( ):2 0P x y
Hướng dẫn:
3 2 4
:
2 4 7
x y z
Dạng 4. Viết phương trình đường thẳng d nằm trong mặt phẳng (P) và cắt cả hai đường thẳng d1,
d2
Phương pháp: Tìm các giao điểm A = d1 (P), B = d2 (P). Khi đó d chính là đường thẳng AB.
Ví dụ: Viết phương trình tham số của đường thẳng nằm trong mặt phẳng
20( ):P y z
và cắt
cả hai
12
2
1
42
1 1 4
1
: , :
xt
x y z
d d y t
z

Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 32
VẤN ĐỀ 2. Vị trí tương đối của 2 đường thẳng trong không gian
Phương pháp:
1
d
qua M có vtcp
1
d
u
;
2
d
qua N có vtcp
2
d
u
1
d
chéo
2
d
12
, . 0


dd
u u MN
(không đồng phẳng)
1
d
,
2
d
đồng phẳng
12
, . 0


dd
u u MN
1
d
,
2
d
cắt nhau
12
,0


dd
uu
và
12
, . 0


dd
u u MN
1
d
,
2
d
song song nhau
12
,0


dd
uu
và
1
,0


d
u MN
1
d
,
2
d
trùng nhau
12
,0


dd
uu
và
1
,0


d
u MN
Ví dụ 1 : Cho
12
1 2 '
: 2 ; :
1 3 1 '
x mt x m t
d y m t d y mt
z m t z m t





. Tìm m để
1
d
chéo
2
d
Đáp số:
2
1
4
m
m

Ví dụ 2 : Cho
4;2;2 ; 0;0;7AB
và
3 6 1
:
2 2 1
x y z
d

a) Chứng minh d và AB cùng thuộc một mặt phẳng
b) Tìm
Cd
sao cho tam giác ABC cân tại A
Hướng dẫn:
) , . 0; ) 1;8;2 ; 9;0; 2
d
a AB u BM b C C



Ví dụ 3: Cho
12
1 1 3
: ; : 1
3 2 2
32
xt
x y z
d d y t
zt
a) Tìm giao điểm của
12
,dd
b) Viết phương trình mặt phẳng chứa
12
,dd
.
Hướng dẫn:
) 2;3;1 ; )( ):6 8 11 0a I b x y z
Dạng 1. Viết phương trình đường thẳng đi qua điểm M và cắt cả hai đường thẳng
12
,dd
Phương pháp
Cách 1:
Bước 1: Chuyển d1 và d2 về dạng tham số
Bước 2: Giả sử d cắt d1 và d2 lần lượt tại A và B
Bước 3: Ba điểm A,B,M thẳng hàng
,AB AM
cùng phương
,0AB AM



Cách 2: Gọi (P) =
1
( , )Md
, (Q) =
2
( , )Md
. Khi đó d = (P) (Q). Do đó, một VTCP của d có thể chọn
là
PQ
a n n,


.
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 33
Ví dụ 1: Cho
1; 1;1A
và hai đường thẳng
12
12
23
: ; :
1 2 1
3
xt
x y z
d y t d
zt



a) Chứng minh
1
d
chéo
2
d
b) Viết phương trình đường thẳng qua A và cắt cả
12
,dd
Đáp số:
1 1 1
:
6 1 7
x y z
d

Dạng 2. Viết phương trình đường thẳng d song song với đường thẳng
và cắt hai đường thẳng
12
,dd
Phương pháp
Bước 1: Chuyển d1 và d2 về dạng tham số
Bước 2: Giả sử d cắt d1 và d2 lần lượt tại A và B
Bước 3: d //
nên
/ / ; 0AB u AB u




Cách 2: Viết phương trình mặt phẳng (P) chứa và d1, mặt phẳng (Q) chứa và d2. Khi đó d = (P)
(Q).
Chú ý: d vuông góc với (P) và cắt hai đường thẳng
12
,dd
thì ta làm tương tự. Cụ thể
Bước 1: chuyển d1 và d2 về dạng tham số
Bước 2: Giả sử d cắt d1 và d2 lần lượt tại A và B
Bước 3: d vuông góc với (P) nên
( ) ( )
/ / ; 0
PP
AB n AB n



Ví dụ 1: Viết phương trình đường thẳng
/ /Ox
và cắt cả hai đường thẳng
12
1 2 1 1
: ; :
1 2 3 1 3 2
x y z x y z
dd
Đáp số:
8
:
5
7
5
xt
y
z

Ví dụ 2. A2007. Cho
12
12
12
: , : 1
2 1 1
3
xt
x y z
d d y t
z

a) Chứng minh
1
d
chéo
2
d
b) Viết phương trình đường thẳng
( ):7 4 0P x y z
và cắt hai đường thẳng
12
,dd
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 34
Đáp số:
27
:
14
xt
yt
zt


Dạng 3. Viết phương trình đường vuông góc chung d của hai đường thẳng chéo nhau
12
,dd
Phương pháp
Cách 1:
Bước 1: Chuyển d1 và d2 về dạng tham số (t1,t2)
Bước 2: Lấy
1 1 1
12
22
2
I IJ
;.
I
IJ
J d u t
I d J d
J d t
u

.
Bước 3: d chính là IJ
Cách 2:
Vì d d1 và d d2 nên một VTCP của d có thể là:
12
dd
a a a,


.
Lập phương trình mặt phẳng (P) chứa d và d1, bằng cách:
o Lấy một điểm A trên d1.
o Một VTPT của (P) có thể là:
1
Pd
n a a,


.
Tương tự lập phương trình mặt phẳng (Q) chứa d và d2.
Khi đó d = (P)
(Q).
Ví dụ 1: Cho
12
10
: 0 , : 4 2 '
5 5 3 '
x t x
d y d y t
z t z t





a) Chứng minh
1
d
chéo
2
d
b) Viết phương trình đường vuông góc chung của
1
d
và
2
d
. Suy ra khoảng cách giữa
12
,dd
Hướng dẫn:
12
42
) : ; ; 2 17
2 3 2
x y z
b d d d d

Ví dụ 2: Cho
12
1 2 2 '
: 2 , : '
2'
x t x t
d y t d y t
z t z t






a) Chứng minh
12
,dd
chéo nhau và vuông góc nhau
b) Viết phương trình đường vuông góc chung của
12
,dd
Hướng dẫn:
32
) : ;
1 5 2
x y z
bd


VẤN ĐỀ 3. Khoảng cách từ một điểm đến một đường thẳng và khoảng cách giữa hai đường
thẳng chéo nhau
Dạng 1. Khoảng cách từ một điểm đến một đường thẳng
Phương pháp:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 35
Ví dụ 1: B2003. Cho
2;0;0 ; 0;0;8 ; 0;6;0A B AC
. Tính khoảng cách từ trung điểm I của
BC đến OA. Đáp số:
5d
Ví dụ 2: A2009. Cho mặt phẳng và hai đường thẳng có phương trình
1
19
( ): 2 2 1 0; : ;
1 1 6
x y z
P x y x

2
1 3 1
:
2 1 2
x y z
Tìm
12
: ;( ) ;( )M d M d M P
.
Đáp số:
12
18 53 3
0;1; 3 ; ; ;
35 35 35
MM



Ví dụ 3: D2010. Cho
12
3
21
: ; :
2 1 2
xt
x y z
yt
zt


. Tìm
12
: ; 1M d M
Đáp số:
12
4;1;1 ; 7;4;4MM
Dạng 2. Khoảng cách giữa hai đường thẳng chéo nhau
Phương pháp:
12
;d d d
Ví dụ 1: Cho
1;0;0 ; 1;1;0 ; 0;1;0 ; 0;0;2A B C D
. Tính
,d AC BD
. Đáp số:
1
2
d
Ví dụ 2: Cho
12
13
24
: ; : 2
3 2 2
12
xt
x y z
d d y t
zt


a) Chứng minh
12
,dd
chéo nhau. Tính
12
,d d d
b) Với A, B cố định thuộc
d
sao cho
117AB
. Khi C di động trên d’. Tìm giá trị nhỏ nhất
của
ABC
S
Hướng dẫn:
1 2 min
39
) , 13; )
2
a d d d b S
xảy ra khi
CH MN
Dạng 3. Ứng dụng tọa độ giải toán không gian
Ví dụ 1: Cho lăng trụ
. ' ' 'ABC A B C
có đáy ABC vuông cân tại B,
AA' 2,a BA BC a
.
Gọi M là trung điểm của BC. Tính
,'d AM B C
Đáp số:
,'
7
a
d AM B C
Ví dụ 2: Cho hình lăng trụ đứng ABC.A’B’C’ có tất cả các cạnh đều bằng
a
, M là trung điểm của
AA’. Chứng minh
'MB CB
và
,'d MB B C
.
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 36
Đáp số:
30
,'
10
a
d MB B C
Ví dụ 3: A2012. Cho hình chóp
.S ABC
có đáy ABC là tam giác đều cạnh a. Hính chiếu vuông góc
của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA=2HB. Góc giữa đường thẳng
SC và mặt phẳng (ABC) bằng 60
0
. Tính thể tích khối chóp S.ABC và tính khoảng cách giữa hai
đường thẳng SA và BC.
VẤN ĐỀ 4. Các bài toán liên quan giữa đường thẳng và mặt phẳng
Phương pháp:
Các trường hợp cơ bản
TH 1: () đi qua một điểm M và một đường thẳng (d) không chứa M:
Trên (d) lấy điểm A và VTCP
u
.
Một VTPT của () là:
,n AM u


TH 2: () đi qua một điểm M và vuông góc với một đường thẳng (d):
VTCP
u
của đường thẳng (d) là một VTPT của ().
TH 3: () đi qua 2 đường thẳng cắt nhau
12
,dd
Xác định các VTCP
12
,uu
của các đường thẳng
12
,dd
Một VTPT của () là:
12
,n u u


.
Lấy một điểm M thuộc
1
d
hoặc
2
d
M ().
TH 4: () chứa đường thẳng
1
d
và song song với đường thẳng
2
d
(
12
,dd
chéo nhau):
Xác định các VTCP
12
,uu
của các đường thẳng
12
,dd
.
Một VTPT của () là:
12
,n u u


.
Lấy một điểm M thuộc
1
d
M ().
TH 5: () đi qua điểm M và song song với hai đường thẳng chéo nhau
12
,dd
:
Xác định các VTCP
12
,uu
của các đường thẳng
12
,dd
.
Một VTPT của () là:
12
,n u u


.
TH 6: () đi qua một đường thẳng (d) và vuông góc với một mặt phẳng ():
Xác định VTCP
u
của (d) và VTPT
n
của ().
Một VTPT của () là:
,n u n


.
Lấy một điểm M thuộc d M ().
Ví dụ 1: Viết phương trình mặt phẳng qua
0; 1;3A
và chứa
12
:
1 2 2
x y z
d


Đáp số:
30yz
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 37
Ví dụ 2: Cho
12
1
11
0;1;2 , : ; : 1 2
2 1 1
2
xt
x y z
A d d y t
zt



a) Viết phương trình
()
qua A và song song với
12
,dd
b) Tìm
12
,M d N d
sao cho
,,A M N
thẳng hàng
Dạng 1. Đường thẳng song song với mặt phẳng
Ví dụ 1: D2009. Cho
2;1;0 ; 1;1;2 ; 1;1;0A B C
. Tìm D trên AB sao cho
/ /( ): 20 0CD x y z
. Đáp số:
3;1; 2D
Ví dụ 2: DB B2007. Cho hai đường thẳng
1 3 5 5
: ; ':
2 3 2 6 4 5
x y z x y z
dd

và mặt
phẳng
( ): 2 2 1 0x y z
a) Viết phương trình mặt phẳng chứa d và vuông góc với
()
b) Tìm
,'M d N d
sao cho
/ /( )MN
và khoảng cách từ MN đến
()
bằng 2.
Ví dụ 3: Cho hai đường thẳng
12
2 1 2 1
: ; :
2 3 4 1 1 2
x y z x y z
. Viết phương trình
mặt phẳng (P) chứa
1
và song song
2
. Đáp số:
20xz
Ví dụ 4: Cho đường thẳng
1 1 2
:
2 1 3
x y z
d

và
( ): 1 0P x y z
. Lập phương trình
chính tắc
đi qua A(1;1;-2) song song với (P) và vuông góc với d.
Đáp số:
112
2 1 3
x y z


Ví dụ 5: Cho
12
: ; ( ): 3 2 2 0
1 2 1
x y z
d P x y z

a) Viết phương trình mặt phẳng
()
chứa d và vuông góc với (P)
b) Viết phương trình
qua M(2;2;4), song song với (P) và cắt d.
Đáp số:
2 2 4
) ( ): 1 0; ) :
1 1 1
x y z
a x y z b
Ví dụ 6: Cho hai đường thẳng
12
1
31
: 1 ; :
1 2 1
2
xt
x y z
yt
z


a) Viết phương trình mặt phẳng chứa
1
và song song
2
b) Xác định
12
,AB
sao cho AB nhỏ nhất.
Hướng dẫn:
)( ): 2 0;
) AB nhoû nhaát laø ñoaïn vuoâng goùc chung A 1; 1;2 ; 3;1;0
a P x y z
b AB B
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 38
Dạng 2. Hình chiếu vuông góc của một điểm lên mặt phẳng
Phương pháp: Cho điểm M và mặt phẳng
()
. Tìm toạ độ hình chiếu H của M lên mặt phẳng
()
Bước 1: Lập phương trình tham số của đường thẳng MH (đường thẳng MH có vtcp
u
trùng với vtpt
n
của
()
Bước 2: Thay x, y, z trong phương trình tham số của đường thẳng MH vào phương trình
()
để tính t rồi suy ra toạ độ H.
Ví dụ 1: Cho
3;5; 5 , 5; 3;7 , ( ): 0A B P x y z
a) Tìm giao điểm I của AB và (P)
b) Tìm M thuộc (P) sao cho
22
MA MB
nhỏ nhất
Hướng dẫn:
) 1;3; 2 ; ) (0;0;0)a I b M
Ví dụ 2: Cho
22
1;2; 1 ; : ;( ):2 1 0
1 3 3
x y z
A d P x y z

a) Tìm điểm B đối xứng với A qua (P)
b) Viết phương trình đường thẳng qua A, cắt
d
và song song với (P)
Hướng dẫn:
1 2 1
) 3;0;1 ; )
2 9 5
x y z
a B b

Ví dụ 3: DB A2007. Cho
1;3; 2 ; 3;7; 18 ,( ): 2 1 0A B P x y z
a) Viết phương trình mặt phẳng chứa BC và vuông góc với (P)
b) Tìm
( ):M P MA MB
ngắn nhất
Đáp số:
)( ):2 5 11 0; ) 2;2; 3a x y z b M
Ví dụ 4: DB D2004. Cho
2;0;0 ; 2;2;0 ; 0;0;A B S m
a) Khi
2m
tìm C đối xứng với O qua (SAB)
b) Gọi H là hình chiếu vuông góc của O lên SA. Chứng minh
2,
OBH
Sm
Hướng dẫn:
42
22
18
) 2;0;2 ; ) , 2 2,
2
8 16
OBH
mm
a C b S OH OB m
mm



BÀI TẬP ÁP DỤNG:
Bài 1. Cho điểm A(3;1;1), B(7;3;9) và
()
: x+y+z+3=0. Tìm điểm M trên
()
sao cho
MA MB
đạt giá trị nhỏ nhất.
Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 39
Goïi I laø trung ñieåm cuûa AB, I coá ñinh.
2 2 .
Vaäy ñaït giaù trò nhoû nhaát MI nhoû nhaát (M thuoäc ( ), I coá ñònh)
M laø hình chieáu vuoâng goùc c
MA MB MI MA MB MI
MA MB

uûa I treân ( ).... : M(0;-3;0)ÑS
Bài 2. Cho 3 điểm A(-2;1;6), B(-4;-4;7), C(-3;0;-1) và
()
: 2x-y-z-5=0. Tìm điểm M tthuộc
()
sao
cho
MA MB MC
ngắn nhất.
Hướng dẫn:
Goïi G laø trung troïng taâm cuûa tam giaùc ABC, ta coù G(-3;-1;4) vaø
3 3 .
Vaäy ngaén nhaát MI ngaén nhaát (M thuoäc ( ) vaø
MA MB MC MG MA MB MC MG
MA MB MC
G coá ñònh)
M laø hình chieáu vuoâng goùc cuûa G treân ( ).... : M(1;-3;0)ÑS
Bài 3. Cho 4 điểm A(-5;2;0), B(-8;-1;-1), C(1;1;-5), D(-3;-2;2) và
()
: 4x-y-2z-8=0. Tìm điểm M
tthuộc
()
sao cho
MA MB MC MD
ngắn nhất.
Hướng dẫn:
15
Goïi G laø trung troïng taâm cuûa töù giaùc ABCD, ta coù G(- ;0;-1) vaø
4
4 4 .
Vaäy ngaén nhaát
MA MB MC MD MG MA MB MC MD MG
MA MB MC MD
MG ngaén nhaát (M thuoäc ( ) vaø G coá ñònh)
1
M laø hình chieáu vuoâng goùc cuûa G treân ( ).... : M( ;-1;-3)
4
ÑS
Bài 4. Cho mặt phẳng
( ):2 3 0x y z
và hai điểm A(0;0;-3), B(9;15;12). Tìm điểm M thuộc
()
sao cho :
a) MA+MB ngắn nhất
b) | MA-MB| dài nhất
Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 40
)A vaø B khaùc phía so vôùi ( ):
MA+MB AB( Khoâng ñoåi)
MA+MB ngaén nhaát M ôû treân ñoaïn thaúng AB maø M ( ) neân M laø giao ñieåm
cuûa ñoaïn thaúng AB vôùi ( )..... : (3;5;2)
)A' laø ñieåm ñoái xö
a
ÑS M
b

ùng cuûa A qua ( ), ta coù:
' ' .
"=" xaûy ra M ôû treân ñöôøng thaúng AB, maø M ( ) neân M=A'B ( ).
Vaäy max ' ..... ( 17; 11; 6)
MA MB MA MB A B
Daáu
MA MB A B M

Bài 5. Cho mặt phẳng
( ): 3 19 0x y z
và hai điểm A(-2;0;1), B(-7;-5;3). Tìm điểm M
thuộc
()
sao cho :
a) MA+MB ngắn nhất
b) | MA-MB| dài nhất
Hướng dẫn:
A vaø B cuøng phía so vôùi ( ):
a) MA+MB ngaén nhaát
- Goïi A' laø ñieåm ñoái xöùng cuûa A qua ( ), H laø hình chieáu vuoâng goùc cuûa A treân ( )
vaø H(0;6;-1) A'(2;12;-3).M=A'B ( ).... : (3;5;2)
)
ÑS M
b MA


daøi nhaát
Vaäy max ..... : (3;5; 1)
MB
MA MB AB
MA MB AB ÑS M

BTTT:
Bài 1. Cho mặt phẳng
( ): 3 3 11 0x y z
và hai điểm A(3;-4;5), B(3;3;-3). Tìm điểm M
thuộc
()
sao cho : |MA-MB| lớn nhất.
Hướng dẫn và đáp số:




31 5 31
A vaø B khaùc phía so vôùi ( ). M ; ;
7 7 7
Bài 2. Cho mặt phẳng
( ):2 1 0x y z
và hai điểm A(-1;3;-2), B(-9;4;0). Tìm điểm K thuộc
()
sao cho : AK + BK đạt giá trị nhỏ nhất
Dạng 3. Hình chiếu vuông góc của một đường thẳng lên mặt phẳng
Phương pháp: Cho sẵn đường thẳng d và
()
Cách 1:
Bước 1: Tìm giao điểm A của d và
()
Bước 2: lấy
Bd
, rồi tìm toạ độ của điểm H, H là hình chiếu vuông của B lên
()
Bước 3: Viết phương trình của đường thẳng AH ( đường này đi qua điêm A hoặc H và có
vtcp
u AH
. Đường thẳng AH chính là hình chiếu của đường thẳng d trên
()
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 41
Đặc biệt: Nếu d //
()
thì lấy
Ad
. Tìm H là hình chiếu vuông góc của A trên
()
. Khi đó, gọi d’
là hình chiếu vuông góc của d trên
()
, ta có d’ // d ( Đường thẳng d’ đi qua H và có vtcp
u
)
Cách 2: Lập phương trình mặt phẳng
()
chứa d và vuông góc với mặt phẳng
()
bằng .
Khi đó
( ) ( )d


. Chuyển d về dạng tham số
Ví dụ 1: Cho
2; 1;3 ; 3;0;2 ; ( ): 2 7 0A B P x y z
. Viết phương trình hình chiếu của
AB
lên (P). Đáp số:
2 1 2
4 1 2
x y z

Ví dụ 2: Cho
1 7 3
: ; :3 2 0
2 1 4
x y z
d x y z
a) Tính
,( )dd
b) Viết phương trình hình chiếu vuông góc của d lên
()
Hướng dẫn:
4 5 2
) 14; ) :
2 1 4
x y z
a d b
Ví dụ 3. Viết phương trình hình chiếu vuông góc của đường thẳng
12
: 2 3
3
xt
d y t
zt


trên mỗi mặt
phẳng tọa độ.
Hướng dẫn:
* Hình chieáu vuoâng goùc cuûa d treân (Oxy)
Ñöôøng thaúng d caét (Oxy) taïi A(-5;-11;0). Laáy B(1;-2;3) d, hình chieáu vuoâng goùc
cuûa B treân (Oxy) laø H(1;-2;0). Hình chieáu cuûa d treân (Oxy) chín
12
h laø AH: 2 3
0
0 1 2
Töôngtöï: Hình chieáu cuûa d laàn löôït treân (Oyz) vaø (Ozx): 2 3 ; 0
33
xt
yt
z
x x t
y t y
z t z t






Ví dụ 4: Viết phương trình hình chiếu vuông góc của đường thẳng
52
: 10
2
xt
d y t
zt


trên mặt
phẳng:
3 4 3 0x y z
Hướng dẫn:
. 0 / /( ) hoaëc d ( ). A d nhöng A ( ). Do ñoù:d // ( )
H laø hình chieáu cuûa A treân ( ) H(-1;-2;-2)
1 2 2
Hình chieáu cuûa d treân ( ) laø:
2 1 2
n u d Ñieåm
x y z

Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 42
BÀI TẬP ÁP DỤNG
Bài 1. Viết phương trình hình chiếu vuông góc của đường thẳng
7
3
2
:2
2
xt
d y t
zt



trên mặt phẳng:
2 2 2 0x y z
Hướng dẫn:
7
d caét ( ) taïi A(2;1;1). Laáy B ;0;0 vaø goïi H laø hình chieáu vuoâng goùc cuûa B
2
22
7 1 1
treân ( ) H ; ; . Hình chieáu cuûa d treân ( ) laø AH: 1 2
2 3 3
1
d
xt
yt
zt









Bài 2. Cho mặt phẳng
( ): 3 3 2 0x y z
và hai đường thẳng
12
15
43
: ; : 2
2 1 2
3
xt
x y z
d d y t
zt


. Viết phương trình hình chiếu theo phương d2 của
đường thẳng d1 trên
()
Hướng dẫn:
2
21
d caét ( ) taïi A(-2;-1;1).Laáy B(-4;0;3) thuoäc d vaø goïi H laø hình chieáu theo phöông d
cuûa B treân( ) H(1;1;0). thaúng AH laø hình chieáu theo phöông d cuûa d
23
AH: 1 2
1
Ñöôøng
xt
yt
zt

BTTT: Cho mặt phẳng
( ): 3 0x y z
và hai đường thẳng

12
3 1 1 7 3 9
: ; :
7 2 3 1 2 1
x y z x y z
a) Viết phương trình hình chiếu của
2
theo phương
1
lên
()
b) Tìm trên mặt phẳng
()
điểm M sao cho
12
MM MM
nhỏ nhất. Biết M1(3;1;1);
M2(7;3;9)
Bài 5. Cho điểm A(-1;2;1), đường thẳng
1
: 4 2
23
xt
d y t
zt


và
( ): 2 3 6 0P x y z
a) Viết phương trình mặt phẳng (Q) đi qua d và A
b) Gọi
là hình chiếu vuông góc của d trên (P). Viết phương trình của đường thẳng
Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 43
24
)( ):4 2 4 0; ) :
1 2 1
x y z
a Q x y z b

Dạng 4. Hình chiếu của một điểm lên đường thẳng
Phương pháp: Cho sẵn điểm M và đường thẳng
. Tìm tọa độ điểm H (H là hình chiếu vuông
góc của M trên
).
Bước 1: Lấy H(...,...,...)
(tọa độ điểm H chính là phương trình tham số của
)
Bước 2: Tìm tọa độ của
MH
theo t. H là hình chiếu vuông góc của M trên
. 0( laø vtcp cuûa )MH u u
. Tìm t rồi suy ta tọa độ H.
Chú ý:
( , )d M MH
Ví dụ 1: Cho
12
: 2 ; ( ):2 2 1 0
3
xt
d y t P x y z
zt

a) Tìm tọa độ
Md
sao cho
( ,( )) 3d M P
b) Gọi K là điểm đối xứng của I(2;-1;3) qua đường thẳng d. Hãy xác định tọa độ K
Đáp số:
12
) 21, 8,30 ; 15;10; 24 ; ) 4;3;3a M M b K
Ví dụ 2: D2006. Cho
1
2 2 3
1;2;3 ; :
2 1 1
x y z
Ad

và
2
1 1 1
:
1 2 1
x y z
d

a) Tìm A’ đối xứng với A qua
1
d
b) Viết phương trình đường thẳng
qua A, vuông góc
1
d
và cắt
2
d
Ví dụ 3: A2008. Cho
12
2;5;3 ; :
2 1 2
x y z
Ad


a) Tìm hình chiếu vuông góc của A trên
d
b) Viết phương trình
()
chứa d sao cho
ax
,( )
m
dA
Hướng dẫn:
) 3;1;4 ; ) ( ): 4 3 0a H b x y z
BÀI TẬP ÁP DỤNG
Bài 1. Cho 3 điểm A(-1;3;2); B(4;0;-3);C(5;-1;4). Tìm tọa độ hình chiếu vuông góc của A trên đường
thẳng BC và viết phương trình mặt cầu tâm A, tiếp xúc với đường thẳng BC.
Hướng dẫn:
2 2 2
4
231 27 36
: ... ; ;
51 51 51
37
taâm A
760
( ): ( ): 1 3 2
17
R=AH
xt
BC y t H
zt
S S x y z




Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 44
Bài 2. Tìm điểm M1 đối xứng với điểm M(2;-1;-5) qua đường thẳng
2 3 1
:
2 1 1
x y z
Hướng dẫn:
Tìm toïa ñoä hình chieáu H cuûa M leân ñöôøng thaúng .
. 0........ (0; 2; 2).
laø trung ñieåm cuûa MM'. Söû duïng coâng thöùc trung ñieåm '(-2;-3;1)
MH u MH u H
HM

Bài 3. Cho 3 điểm A(4;1;-28); B(4;-9;2);C(10;2;-10) và đường thẳng
92
:
43
xt
d y t
zt


.
Tìm điểm M thuộc d sao cho
MA MB MC
đạt giá trị nhỏ nhất
Hướng dẫn:
3 , (6; 2; 12) laø troïng taâm cuûa ABC
3 . Vaäy ñaït giaù trò nhoû nhaát
MG nhoû nhaát (G coá ñònh vaø M d) M laø hình chieáu
MA MB MC MG G
MA MB MC MG MA MB MC
vuoâng goùc cuûa G leân d
..........ÑS: M(5;2;-10)
BTTT: Cho 3 điểm A(2;0;1); B(2;-1;0);C(1;0;1) và đường thẳng
:2
3
xt
d y t
zt
.
a) Tìm điểm M thuộc d sao cho
MA MB MC
đạt giá trị nhỏ nhất
b) Tính thể tích hình chóp OABC
Bài 4. Cho đường thẳng


11
:
3 2 1
x y z
d
và hai điểm A(3;0;2) và B(1;2;1).
a) Tìm điểm I trên d sao cho
IA IB
có độ dài nhỏ nhất
b) Kẻ AA’, BB’ vuông góc với d. Tính độ dài AA’
Bài 5. Cho điểm A(-2;1;-3) và đường thẳng
7 2 1
:
2 2 1
x y z
a) Tìm tọa độ hình chiếu vuông góc của A lên
b) Viết phương trình
()
chứa
và khoảng cách từ A đến
()
lớn nhất
Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 45
) (3; 2;1)
) Goïi K laø hình chieáu vuoâng goùc cuûa A treân ( ) ( laø maët phaúng chöùa ), t
coù AK AH (khoâng ñoåi) d(A,( )) AH.
Vaäy, d(A,( )) lôùn nhaát (baèng AH) K H
( ) di qua H coù vtcp
aH
b
AH


. : 5 3 4 25 0ÑS x y z
Bài 6. Cho 4 điểm A(-4;4;0); B(2;0;4);C(1;2;-1);D(7;-2;3). Chứng minh rằng
a) Bốn điểm A,B,C,D cùng nằm trên một mặt phẳng
b) Tìm khoảng cách từ C đến đường thẳng (AB)
c) Tìm M thuộc (AB) sao cho MC+MD đạt giá trị nhỏ nhất
LUYỆN TẬP PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Bài 1. Cho
()
: 3x-4y+z-3=0 và hai đường thẳng
12
53
1 4 1
: 1 ; :
1 2 4
82
xt
x y z
d y t d
zt
. Lập phương trình đường thẳng
nằm trong
()
và cắt cả (d1) và (d2).
Hướng dẫn: Hình vẽ
1
2
12
( ) (1; 1; 4);
( ) (0; 2; 5);
Ñöôøng thaúng naèm trong ( ),caét caû d , laø ñöôøng thaúng ñi qua AB.
114
:
1 1 1
dA
dB
d
x y z
Bài 2. Cho đường thẳng
12
: ; ( ): 2 0
2 2 3
x y z
P x y z

. Lập phương trình đường
thẳng d nằm trong (P), cắt và vuông góc với
.
Hướng dẫn: Hình vẽ
()
()
( ) ( 1; 2;1). Goïi laø vtcp cuûa d. Ta coù:
; (5; 5;0)
1
naèm trong (P) vaø caét neân d ñi qua A. d: 2
1
P
P
P A a
au
a u n
an
xt
d y t
z


BTTT:
Cho đường thẳng
1 2 2
: ; ( ): 2 2 0
2 1 3
x y z
P x y z
. Lập phương trình đường
thẳng d nằm trong (P), cắt và vuông góc với
.
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 46
Bài 3. Cho đường thẳng
23
: 7 ; ( ): 3 4 2 0
34
xt
d t t P x y z
zt

. Lập phương trình đường
thẳng
đi qua điểm
0
( 1;4;0)M
, song song với (P) và cắt d.
Hướng dẫn:Hình vẽ
0
00
ÑieåmM (P).
Goïi laø ñöôøng thaúng ñi qua M ( 1;4;0) caét d taïi ñieåm M(-2+3t;7-t;3-4t).
//(P) . 0 1
14
:
2 2 1
M M n M M n t
x y z


BTTT: Lập phương trình đường thẳng
đi qua điểm
0
( 1;4;0)M
cắt
1
:
2 1 1
x y z
d

và
song song với
( ): 3 1 0P x y z
Bài 3. Lập phương trình đường vuông góc chung của hai đường thẳng
'
22
1 4 4
: 3 3 ; :
3 2 1
45
xt
x y z
d y t d
zt


.
Hướng dẫn:
''
Laáy I d,laáy J d'. IJ laø ñöôøng vuoâng goùc chung cuûa d vaø d'
.0
1
.
1
.0
1
Phöông trình :
1 1 1
dd
dd
IJ u IJ u
t
t
IJ u IJ u
x y z
IJ







BTTT: Viết phương trình đường vuông góc chung của hai đường thẳng
12
2 4 8 6 10
: vaø :
1 1 2 2 1 1
x y z x y z

a) Tính khoảng cách giữa
12
vaø
b) Viết phương trình đường vuông góc chung của
12
vaø
Bài 4. Lập phương trình đường thẳng đi qua điểm M(-4;-5;3) và cắt cả hai đường thẳng
12
22
1 3 2
: ; : 1 3
3 2 1
15
xt
x y z
d d y t
zt



Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 47
1 2 1
2
Giaû söû caét d taïi A vaø caét d taïi B.Ñöôøng thaúng ñi qua M vaø caét d
taïi vaø caét d taïi B A,B,M thaúng haøng cuøng phöông
4
; 0 ' 0.Luùc ñoù :
3
A AB AM
xy
AB AM t t




53
21
z
BTTT: Lập phương trình
đi qua M(1;2;-1) và cắt cả hai đường thẳng
12
30
11
: ; :
2 1 1
0
x y z
x y z
yz


Bài 5. Cho đường thẳng
3 1 2
: ; ( ):2 5 4 0
4 3 5
x y z
d P x y z
. Lập phương trình
đường thẳng
đi qua A(2;-2;1), song song với (P) và vuông góc với d.
cắt hay không cắt d?
Hướng dẫn:
Ñieåm ( )
/ /( )
, ( 28; 14;14)
22
hoaëc (2;1; 1). : 2
1
3 1 2
4 3 5
22
Giaûi heä:
2
1
Heä voâ nghieäm, vaäy vuoâng goùc vôùi d
AP
P a n
a n u
d
au
xt
a y t
zt
x y z
xt
yt
zt







nhöng khoâng caét d
BTTT: Viết phương trình đường thẳng
qua M(1;1;1) song song với
( ): 2 1 0P x y z
và
vuông góc với
21
:
1 2 3
x y z
d


Bài 6. Viết phương trình đường thẳng
vuông góc với mặt phẳng
( ): 2 1 0x y z
và cắt
đường thẳng
1
1 1 2
:
2 1 1
x y z
và
1
2
:
12
xt
yt
zt

Bài 7. Cho điểm A(1-2m;m
2
-2;2m) và hai mặt phẳng
12
( ):2 3 1 0;( ): 2 2 5 0x y z x y z

a) Xác định m để điểm A thuộc giao tuyến của
12
( ); ( )

b) Với những giá trị nào của m thì A không thuộc
1
()
và
2
()
. Trong trường hợp này, viết
phương trình đường thẳng
đi qua A và song song với cả hai mặt phẳng
1
()
và
2
()
.
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 48
Hướng dẫn:
1
12
2
12
12
2
)1
1
) ( ) vaø A ( ) 3
4
song song vôùi caû hai ( ) ( ) , ( 4;3;5)
1 2 4
Vaäy, phöông trình : 2 3 vôùi
25
am
m
b A m
m
un
vaø u n n
un
x m t
m
y m y
z m t








1
3
4
m
m

Bài 8. Cho hai đường thẳng
12
12
1 1 2
: ; :
2 1 1
43
xt
x y z
yt
zt

a) Chứng minh
12
vaø cheùo nhau
b) Viết phương trình đường
thẳng đi qua M(1;2;-3) và cắt các đường thẳng
12
vaø 
Bài 9. Cho hai đường thẳng
12
1 3 0
: 2 ; :
2
x t x
y t y t
z t z t





a) Chứng minh
12
vaø cheùo nhau
. Tính khoảng cách giữa
12
vaø 
b) Viết phương trình đường
thẳng đi qua M(2;-1;3) vuông góc với
12
vaø caét 
c) Viết phương trình đường thẳng d vuông góc với mặt phẳng
( ):2 3 1 0x y z
và
cắt các đường thẳng
12
vaø 
Bài 10. Cho đường thẳng
1 1 1
: vaø maët phaúng ( ): -3 0
2 3 1
x y z
x y z
a) Viết phương trình hình chiếu vuông góc d của đường thẳng
trên mặt phẳng
()
b) Viết phương trình hình chiếu song song theo phương
21
:
1 1 2
x y z
m


của đường
thẳng
trên mặt phẳng
()
Hướng dẫn: Xem phương pháp giải ở mục “ Hình Chiếu”
Bài 11. Cho đường thẳng
1
:1
1
xt
y
zt



và mặt phẳng
( ):2 3 0x y z
. Viết phương trình
đường thẳng d nằm trong
()
, vuông góc với
và cắt đường thẳng
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 49
Bài 12. Cho hai đường thẳng
12
13
74
: ; : 2
2 5 3
2
xt
x y z
d d y t
zt

Chứng minh d1 cắt d2. Viết phương trình mặt phẳng chứa d1 và d2
Hướng dẫn:
12
12
12
12
12
,0
) vaø khoâng cuøng phöông ñoàng thôøi ba vecto
,0
vaø , ñoàng phaúng
b) = , 11;7;19 . ( ):11 7 16 27 0
uu
a u u
u u AB
u u AB
n u u x y z






BTTT: Cho hai đường thẳng
12
1 1 2
: 1 5 ; : 1 3
1 3 1
x t x t
y t y t
z t z t





a) Chứng minh
12
vaø 
cắt nhau.
b) Viết phương trình mặt phẳng
()
chứa hai đường thẳng
12
vaø 
Bài 13. Cho hai đường thẳng
15
3 4 1
: 5 7 ; ':
1 2 4
33
xt
x y z
d y t d
zt


a) Chứng minh
d vaø d'
chéo nhau
b) Lập phương trình mặt phẳng cách đều hai đường thẳng d và d’
Hướng dẫn:
12
'
12
) , 0
1
( ) coù vtpt ;
( )/ / ,
17
)
,( ) ( ',( ))
,( ) ,( )
9
( ) coù vtpt (2; 1; 1) vaø ñi qua trung ñieåm I 2; ;2 cuûa
2
a u u AB
n u u
dd
b
d d d d
d A d B
n AB











Bài 14. Tìm a để đường thẳng
2
11
31
: 4 caét vaø vuoâng goùc vôùi ñöôøng thaúng d':
2 1 3
5 2 1
x a t
x y z
d y at
z a t

Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 50
12
5
d vaø d' vuoâng goùc nhau . 0 1 hoaëc
2
u u a a
12
12
Vôùi a=-1: , . 0 vaø d' caét nhau
5
+Vôùi a=- : , . 0 vaø d' cheùo nhau
2
u u AB d
u u AB d





Vậy, với a=-1 thì 2 đường thẳng đã cho cắt nhau
Bài 15. Tìm m (m nguyên dương) để hai đường thẳng
2
12
72
1 3 2
: ; : 1 3
3 2 2
x m t
x y z
d d y m t
z m t



cắt nhau. Trong trường hợp này, viết phương
trình mặt phẳng qua
12
vaø dd
Hướng dẫn:
12
1 2 1 2
, 0 khoâng cuøng phöông.Hai ñöôøng thaúng caét nhau
3
, , ñoàng phaúng , . 0
11
()
4
( ):8 7 5 4 0
uu
m
u u AB u u AB
m loaïi
x y z






Bài 16. Cho đường thẳng
2
: 1 vaø ( ):3 2 5 0
35
xt
d y m mt x y z
z m m t
. Tìm m để
đường thẳng d thuộc
()
. trong trường hợp này, viết phương trình
()
qua d và vuông góc với
()
Hướng dẫn:
Ñöôøng thaúng d thuoäc ( ) 2. Vaø khi ñoù: ( ): 2 4 1 0
()
un
m x y z
A


Bài 17. Cho đường thẳng
22
12
: 4 3 vaø ( ): 2 3 5 0
3
x m t
d y m m t x y z
zt

. Tìm m để
đường thẳng d song song với
()
. Trong trường hợp này, tính khoảng cách giữa d và
()
Hướng dẫn:
8
Ñöôøng thaúng d song song ( ) 2. Vaø khi ñoù: d ,( )
()
14
un
md
A


Bài 18. Tìm m để đường thẳng
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 51
2
12
12
2
: 3 3 song song hoaëc truøng vôùi ñöôøng thaúng d : 6 2
12
32
x m mt
xt
d y t y m t
zt
z mt



. Trong
trường hợp
12
//dd
, viết phương trình mặt phẳng đi qua
1
d
và
2
d
Hướng dẫn:
12
1 2 1 2 1 2
12
2( vôùi gt naøy thì / / )
/ / hoaëc , 0
1( vôùi gt naøy thì )
( ): 2 3 3 0
m d d
d d d d u u
m d d
yz



Bài 18. Cho 3 điểm A(-2;2;1), B(1;2;-2);C(2;1;2). Viết phương trình tham số đường thẳng
vuông
góc với (ABC) và đi qua trực tâm của tam giác ABC
Chứng minh rằng tồn tại điểm S thuộc đường thẳng
5 1 1
:
2 3 1
x y z
d


sao cho S.ABC là
hình chóp đều.
Hướng dẫn:
Ta ñeå yù raèng ABC ñeàu tröïc taâm cuûa tam giaùc truøng vôùi troïng taâm cuûa tam giaùc
1
3
5
: 5 laø truïc ñöôøng troøn ngoaïi tieáp ABC
3
1
3
) ( 1; 5; 1),roõ raøng
xt
yt
zt
b S d S S G



Bài 19. Tính khoảng cách giữa hai đường thẳng
12
33
24
: 1 3 :
1 1 3
29
xt
x y z
d y t d
zt


Hướng dẫn:
1 2 1 2
Ñeå : / / , , 30yù d d d d d
Bài 20. Tìm điểm I thuộc đường thẳng
1
:1
x
d y t
zt


và cách đường thẳng
3 1 7
':
2 1 2
x y z
d

một khoảng bằng 3.
Bài 21. Cho hai đường thẳng
12
3 1 3
: ; ':
1 4 2
3
xt
x y z
yt
zt

Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 52
a) Chứng minh
vaø ' cheùo nhau. Tính khoaûng caùch giöõa vaø '
b) Trên
lấy đoạn AB=4 và trên
'
lấy đoạn CD=3. Tính thể tích của khối tứ diện ABCD
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 53
VẤN ĐỀ 5. Các bài toán liên quan giữa đường thẳng và mặt cầu
Ví dụ 1. Lập phương trình mặt cầu có tâm I(2;3;-1) và cắt đường thẳng
12
:
2 1 2
x y z
tại 2
điểm A và B sao cho AB=16.
Hướng dẫn:
2 2 2 2
2 2 2
8
Goïi H laø trung ñieåm cuûa AB, ta coù
( , )
64 . Vôùi IH laø khoaûng caùch töø I ñeán AB
641
:( ): 2 3 1
9
HA HB
IH IH d I
R AH IH IH
ÑS S x y z

ĐHCĐ 2010 A –NC. Trong không gian tọa độ Oxyz, cho điểm A(0; 0; 2) và đường thẳng
2 2 3
:
2 3 2
x y z
. Tính khoảng cách từ A đến . Viết phương trình mặt cầu tâm A, cắt tại
hai điểm B và C sao cho BC = 8.
BTTT: Trong không gian Oxyz cho đường thẳng
1
:1
2
1
xt
d y t
zt

và mặt cầu
2 2 2
( ): 4 6 0S x y z x y m
. Tìm m để d cắt (S) tại 2 điểm M,N sao cho MN=8
Hướng dẫn:
(S): I(-2; 3; 0);
R IN 13 m
, với m < 13.
Dựng
IH MN MH HN 4
22
IH IN HN 13 m 16 m 3
, m < -3.
222
2 2 2
[AI; u]
3 6 6 81
h 3.
u
9
2 1 2


IH = h
m 3 3 m 3 9
m 12
(thoã)
Bài 2. Lập phương trình mặt cầu (S) có tâm nằm trên đường thẳng
11
:
2 1 2
x y z
d


và tiếp
xúc với
( ): 2 5 0; ( ):2 2 0x y z x y z

.
Hướng dẫn:
Goïi I laø taâm (S) I(2t;1+t;-1+2t).
4
(S) tieáp xuùc vôùi ( ) vaø ( ) R=d(I;( ))=d(I;( )) hoaëc t=-2
3
t
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 54
BTTT: . Lập phương trình mặt cầu (S) có tâm nằm trên đường thẳng
33
:2
12
xt
d y t
zt


và tiếp xúc
với
( ): 2 2 2 0; ( ):2 2 4 0x y z x y z

.
Đáp số:
2 2 2
2 2 2
12 18 13 16
( ):
5 5 5 25
12 30 19 16
( ):
11 11 11 25
S x y z
S x y z
Bài 3. Cho mặt cầu
2 2 2
( ): 10 2 26 113 0S x y z x y z
và hai đường thẳng
12
73
5 1 13
: ; : 1 2
2 3 2
8
xt
x y z
yt
z
. Viết phương trình (P) tiếp xúc với (S) và song
song với cả
12
vaø 
Hướng dẫn:
12
12
( ) song song vôùi neân , (4,6,5)
205
( ): 4 6 5 0.Maët khaùc: d ,( )
103
p
P vaø n u u
D
P x y z D I P R
D




Bài 4. Cho đường thẳng
12
: ; ( ):2 2 2 0
3 1 1
x y z
d x y z

Lập phương trình mặt cầu (S) có tâm nằm trên d, bán kính bằng 1 và tiếp xúc với
()
Hướng dẫn:
Goïi I laø taâm (S) I(1+3t;-2+t;t).
1
(S) tieáp xuùc vôùi ( ) R=d(I;( ))=1 hoaëc t=-1
5
t

Bài 5. Trong không gian cho (P) và mặt cầu (S) có phương trình lần lượt là
2 2 2 2
(P):2x 2y z m 3m 0 ; (S): (x 1) (y 1) (z 1) 9
.
Tìm m để (P) tiếp xúc với (S). Tìm toạ độ tiếp điểm
Hướng dẫn:
(P) tieáp xuùc vôùi (S) d(I,(P))=R m=2 hoaëc m=-5
Toïa ñoä giao ñieåm cuûa ñöôøng thaúng ñi qua I vaø vuoâng goùc vôùi(P)
laø tieáp ñieåm cuûa (P) vaø (S). : (3;1;2)ÑS M

Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 55
Bài 6. Viết phương trình mặt cầu (S) có bán kính nhỏ nhất và tiếp xúc với hai đường thẳng
12
54
1
: 1 3 ; :
2 1 1
3
xt
x y z
d y t d
z

Hướng dẫn:
1 2 1 2
1
1
2
2
Goïi IJ laø ñoaïn vuoâng goùc chung cuûa d vaø d (I d ,J d )
( ) coù baùn kính nhoû nhaát vaø tieáp xuùc vôùi hai ñöôøng thaúng d
vaø d laø maët caàu coù ñöôøng kính IJ. Ta coù:
S
IJ d IJ
IJ d

1
2
2
22
.0
1
'1
.0
1 29
( ): 2 2
24
u
t
t
IJ u
S x y z






Bài 7. Viết phương trình mặt cầu có tâm ở trên đường thẳng
2 6 4
:
1 3 2
x y z
d


và tiếp
xúc
12
2
21
: vaø d :
2 2 1
23
xt
x y z
d y t
zt

Hướng dẫn:
1 2 1 2
2 2 2
Goïi I laø taâm maët caàu I 2 ;6 3 ; 4 2
Maët caàu tieáp xuùc vôùi d vaø d neân d I,(d ) (I,d
1. Luùc ñoù: (S): 1 3 2 18
t t t
dR
t x y z

Bài 8. Cho mặt cầu (S) có tâm I(2;0;-1) và tiếp xúc với đường thẳng
2
:2
12
xt
y a t
z a t

. Xác định a
để mặt cầu (S) có bán kính nhỏ nhất
Hướng dẫn:
2
min
( ) tieáp xuùc vôùi ñöôøng thaúng neân R=d ;
3 12 20 8 2 2
2
6 6 3 3
SI
aa
R R a


Bài 9. Viết phương tình mặt cầu (S) có tâm I(-4;1;1) và cắt mặt phẳng
( ): 2 2 1 0x y z
theo giao tuyến là một đường tròn có bán kính bằng
22
Hướng dẫn:
2 2 2
Deãdaøngnhaän thaáy: ,( ) 2 2 1 2 2 3R d I R R
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 56
Bài 10. Viết phương tình mặt cầu (S) có tâm I(-4;1;1) và cắt đường thẳng
1 1 1
:
2 1 2
x y z
tại hai điểm A và b sao cho tam giác IAB vuông
Hướng dẫn:
Tam giaùc IAB caân taïi I. Maët khaùc theo giaû thieát noù laø tam giaùc vuoâng. Do ñoù
40
tam giaùc IAB vuoâng caân taïi I. Vaäy R=IA=IB= 2 ,
3
dI
Bài 11. Cho đường thẳng
12
7 3 9 3 1 1
: ; :
1 2 1 7 2 3
x y z x y z

a) Tìm các điểm A thuộc
1
, B thuộc
2
sao cho AB là đoạn vuông góc chung của
1
và
2
b) Viết phương trình mặt cầu (S) tiếp xúc với đường thẳng
1
tại A và
2
tại B.
Hướng dẫn:
1
2
1
2
1
.0
0
a)
'0
.0
)Maët caàu (S) tieáp xuùc vôùi . 0 tai A vaø taïi B neân coù taâm I thuoäc maët
phaúng vuoâng goùc vôùi ñöôøng thaúng taïi A vaø
u BA
t
t
u BA
b u BA


2
12
12
taïi B.
Vì AB laø ñoaïn vuoâng goùc chung cuûa vaø neân AB thuoäc maët phaúng ( ).
Töông töï AB thuoäc maët phaúng ( ). vaø khoâng cuøng phöông, do ñoù ( ) khoâng



2 2 2
song song vôùi ( ) AB=( ) ( ) I AB.( ) qua AB I laø trung ñieåm cuûa AB.
(S): 5 2 5 21
S
x y z
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 57
CHỦ ĐỀ 5. GÓC TRONG KHÔNG GIAN
PHƯƠNG PHÁP
1. Góc giữa hai đường thẳng
Cho hai đường thẳng d1, d2 lần lượt có các VTCP
12
aa,
.
Góc giữa d1, d2 bằng hoặc bù với góc giữa
12
aa,
.
12
12
12
aa
aa
aa
.
cos ,
.
2. Góc giữa một đường thẳng và một mặt phẳng
Cho đường thẳng d có VTCP
1 2 3
a a a a( ; ; )
và mặt phẳng (
) có VTPT
n A B C( ; ; )
.
Góc giữa đường thẳng d và mặt phẳng (
) bằng góc giữa đường thẳng d với hình chiếu d
của nó
trên (
).
1 2 3
2 2 2 2 2 2
1 2 3
Aa Ba Ca
d
A B C a a a
sin ,( )
.

VẤN ĐỀ 1. Góc và các bài toán liên quan
Ví dụ 1. Cho ba đường thẳng (d1), (d2), (d3) có phương trình :
R
tz
ty
tx
d
t
32
42
1
:
1
,
012
034
:
2
zyx
zyx
d
;
1
5
1
1
3
:
3
zyx
d
a) Xác định cosin góc giữa (d1),(d2).
b) Lập phương trình đường thẳng (d) song song với (d3) đồng thời cắt cả (d1),(d2).
Ví dụ 2. Cho đường thẳng (d) và mặt phẳng (P) có phương trình
1
3
2
4
1
3
:
zyx
d
và
(P):2x+y+z-1=0
a) Xác định số đo góc giữa đường thẳng (d) và mặt phẳng (P) .
b) Tìm toạ độ giao điểm A của đường thẳng (d) và mặt phẳng (P).
c) Lập phương trình tổng quát của đường thẳng (d1) đi qua A vuông góc với (d) và nằm
trong mặt phẳng (P).
Ví dụ 3: Tìm
k
để đường thẳng
1
:2
12
xt
d y kt
zt

và
( ): 3 5 0xz
có số đo góc bằng
0
45
.
Đáp số:
0k
Ví dụ 4: Cho điểm
3; 5;1A
đường thẳng
: 6 2
1
xt
d y t
zt

và
( ):2 2 5 0x y z
. Lập
phương trình đường thẳng
đi qua A, cắt d và hợp với
()
một góc
0
45
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 58
Ví dụ 5: Cho điểm
3; 1; 3A 
đường thẳng
1
:2
4
xt
d y t
z



. Lập phương trình đường thẳng
đi qua A, cắt và hợp với d một góc
0
60
.
Ví du 6: Trong không gian, cho
1 2 2 1
: ; :
1 1 1 2 1 1
x y z x y z
d

. Viết phương trình
mặt phẳng (P) chứa d và tạo với
một góc
0
30
VẤN ĐỀ 2 . Sử dụng tọa độ giải toán hình học không gian
Ví dụ 1 : A2008. Cho lăng trụ
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông tại A,
, 3,AA' 2 .AB a AC a a
Hình chiếu A’ lên (ABC) là trung điểm H của BC. Tính
'.A ABC
V
và
AA', ' 'BC
.
Ví dụ 2: B2008. Cho
.S ABCD
có đáy ABCD là hình vuông cạnh 2a, SA=a,
3SB a
,
SAB ABCD
. Gọi M, N là trung điểm của AB và BC. Tính
.S BMDN
V
và
cos ,SM DN
.
Ví dụ 3 : Cho hình lăng trụ
. ' ' 'ABC A B C
, đáy
0
, 2 , 120AB a AC a BAC
. Gọi M là trung
điểm của BB’,
( ) ( ' ')MAC MA C
. Tính
. ' ' 'ABC A B C
V
và
os , ' 'c MAC BCC B
Ví dụ 4 : B2001. Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a.
a) Tính khoảng cách giữa hai đường thẳng chéo nhau BA’ và DB’
b) Gọi M, N, P lần lượt là trung điểm của BB’, CD, A’D’. Tính góc của hai đường thẳng MP
và NC’.
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 59
CHỦ ĐỀ 6. MỘT SỐ PHƯƠNG PHÁP GIẢI TOÁN CỰC TRỊ HÌNH HỌC KHÔNG GIAN
VẤN ĐỀ 1. Giải toán cực trị hình học bằng cách sử dụng bất đẳng thức hình học
Phương pháp: Ta thường sử dụng các bất đẳng thức hình học sau
1) Bất đằng thức tam giác: Với ba điểm
,,A B C
ta có:
AB BC AC
, dấu “=” xảy ra
,,A B C
thẳng hàng và
B
nằm giữa
,AC
;
AB AC BC
, dấu “=” xảy ra
,,A B C
thẳng hàng và
A
nằm ngoài
,BC
;
|AB-AC| < BC
AB+BC > AC
|AB-BC|=BC
AB+BC=AC
A
B
C
A
C
A
B
B
2) Bất đẳng thức giữa đường xiên và đường vuông góc: Nếu H là hình chiếu vuông góc của điểm
A lên mặt phẳng (P) (hoặc đường thẳng d),
M
là điểm bất kì trên
()P
(hoặc
d
) thì
AM AH
.
Dấu “=” xảy ra khi
MH
AM
≥
AH
d
AM
≥
AH
P
A
H
M
A
H
M
Ví dụ 1: Trong không gian
Oxyz
cho hai điểm
5; 2;6 ; 3; 2;1AB
và mặt phẳng
( ):2 2 6 0x y z
. Tìm điểm
()MP
sao cho
a)
MA MB
nhỏ nhất. b)
MA MB
lớn nhất
Lời giải: Đặt
2 2 6,,F x y z x y z
, ta có
5 2 6 3 2 0, , . , ,FF
nên
,AB
nằm cùng
phía so với
()P
.
a) Gọi
'A
là điểm đối xứng của A qua
()P
. Lúc đó
'MA MA
.
Ta có:
''MA MB MA MB A B
. Dấu “=” xảy ra khi
M
là giao điểm của
'AB
với
()P
.
Gọi
là đường thẳng đi qua
A
và vuông góc với
()P
52
2
62
:
xt
yt
zt


. Gọi
H
là tọa độ giao
điểm của
với
()P
( H là trung điểm của AA’). Suy ra
1 1 2 3 2 2; ; ' ; ;HA
. Phương
trình đường thẳng
36
24
23
':
xt
A B y t
zt

.
Ta có
21 14 5
11 11 11
A'B (P) M ; ;M



Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 60
b) Vì A và B cùng phía so với (P) nên với mọi
()MP
ta luôn có
MA MB AB
, đẳng thức
xảy ra khi
()M AB P
.
Phương trình đường thẳng
52
17 3
22
77
65
: ; ;
xt
AB y M
zt





Ví dụ 2: Trong không gian
Oxyz
cho hai điểm
1;1;0 ; 2;1;1AB
và đường thẳng
12
2 1 1
:
x y z
d


. Viết phương trình đường thẳng
đi qua A,
d
sao cho khoảng cách
từ B đến đường thẳng
nhỏ nhất.
Lời giải:
nằm trong mặt phẳng
()P
đi qua A và vuông góc với
d
.
Ta có
2 3 0( ):P x y z
. Gọi H, K lần lượt là hình chiếu vuông góc của B trên (P) và trên
.
Ta có
,d B BK BH
. Dấu “=” xảy ra khi
KH
. Vậy đường thẳng
cần tìm là đường
thẳng AH. Gọi
'd
là đường thẳng đi qua B và song song với d thì
2 1 1
2 1 1
':
x y z
d

. H là
giao điểm của d’ và (P) nên
11
1
22
;;H



. Từ đó,
1
1:
x
yt
yt
VẤN ĐỀ 2. Giải toán cực trị bằng phương pháp hàm số hoặc bằng cách sử dụng bất đẳng thức đại
số
Phương pháp
Ta thường dùng phương pháp hàm số để tìm giá trị lớn nhất, giá trị nhỏ nhất của một yếu
tố nếu yếu tố đó được tính bởi một biểu thức phụ thuộc một biến số
Ta thường dùng các bất đẳng thức đại số để tìm GTLN, GTNN của một yếu tố nếu yếu tố
đó được tính bởi một biểu thức phụ thuộc một hoặc nhiều biến số
Ví dụ 3. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
2 0 0 111; ; ; ; ;AM
. Giả sử (P)
là mặt phẳng thay đổi nhưng luôn đi qua đường thẳng AM và cắt các trụ Oy, Oz lần lượt tại các
điểm
0 0 0 0 0 0; ; , ; ; , ,B b C c b c
. Chứng minh rằng
2
bc
bc
và tìm
,bc
sao cho
diện tích tam giác
ABC
nhỏ nhất.
Lời giải: mặt phẳng (P) có phương trình
1
2
( ):
x y z
P
bc
. Vì
111; ; ( )MP
nên
1 1 1
1
22
bc
bc
bc
. Ta có
2 0 2 0 2 2; ; , ; ; , , ; ;AB b AC c AB AC bc c b


2 2 2 2
11
4
22
,
ABC
S AB AC b c b c


. Áp dụng bất đẳng thức Cosi ta có
22
2b c bc
. Dấu “=” xảy ra
bc
. Mặt khác ta cung có
2b c bc
mà
2
bc
bc
nên
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 61
2 16
2
bc
bc bc
. Dấu “=” xảy ra
4bc
. Từ đó ta suy ra
2 2 2
11
4 2 16 8 16 4 6
22
. . .
ABC
S b c bc
. Dấu “=” xảy ra
4bc
.
Vậy Min
46
ABC
S
, đạt được khi
4bc
Ví dụ 4. Trong không gian
Oxyz
cho đường thẳng
1
1 2 1
:
x y z
và ba điểm
3 2 1 1 2 1; ; , ; ;AB
. Tìm
M
thuộc
sao cho
MA MB
nhỏ nhất
Lời giải: Vì
2 1 3 2 2 2 1 2 2; ; , ; ; , ; ;M M t t t AM t t t BM t t t
Ta có
2 2 2 2
22
3 6 7 6 7
6 18 17 6 6 5 6 6
2 2 2 2
MA MB t t t t t t
Áp dụng bất đẳng thức
22
2 2 2 2
a b c d a c b d
, đẳng thức xảy ra khi
ac
bd
, ta có
22
3 6 6 7
6 6 2 38
2 2 2
MA MB t t
Đẳng thức xảy ra khi
3 6 6 1
66
2 2 2
t t t
. Vậy
11
1
22
;;M



Ví dụ 5. Trong không gian cho điểm
1 11;;A
và đường thẳng
11
2 1 1
:
x y z
. Viết
phương trình mặt phẳng
()
chứa hai điểm
111 1 2 1; ; , ; ;MN
và tạo với đường thẳng
một góc lớn nhất.
Lời giải: Giả sử
0( ):ax by cz d
. Gọi
,( )
. Vì
, ( )MN
nên
3
0
2
2 2 2 3 0
2 0 1
2
. Ta ñöôïc ( ):
db
a b c d
ax by b a z b
a b c d
c a b


Ta có
22
22
2
22
4 2 2
1 12 36
5 4 8
6
6 4 4 2
.
sin
.
nu
a b b a
b ab b
b ab a
nu
a b b a


Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 62
Nếu
3
0
2
sin ,a
với
0,a
đặt
,
b
tt
a

. Xét hàm số
2
2
12 36
5 4 8
()
tt
ft
tt


ta tìm
được
5 53
89
max ( )f t f




. Do đó
5
8
ax ax
sin
mm
b
a
, chọn
58,ba
Vậy phương trình mặt phẳng
16 10 11 15 0( ): x y z
VẤN ĐỀ 3. Giải toán cực trị bằng phương pháp ứng dụng tâm tỉ cự
Phương pháp: Xuất phát từ việc khai thác bài toán sau
Cho n điểm
12
, ,...,
n
A A A
với n số
12
, ,...,
n
k k k
mà
12
0...
n
k k k k
. Lúc đó ta có các tính
chất sau
Có duy nhất một điểm
G
sao cho
1 1 2 2
0...
nn
k GA k GA k GA
, điểm G như vậy gọi là
tâm tỉ cự của hệ điểm
i
A
, gắn với các hệ số
i
k
. Trong trường hợp các hệ số
i
k
bằng nhau ( và
do đó ta có thể xem các
i
k
đều bằng 1) thì G gọi là trọng tâm của hệ điểm
i
A
.
Nếu G là tâm tỉ cự thì mọi điểm O bất kì ta có
1 1 2 2
1
...
nn
OG k OA k OA k OA
k
Dạng 1. Cực trị độ dài vectơ
Xét bài toán tổng quát : Cho n điểm
12
, ,...,
n
A A A
với n số
12
, ,...,
n
k k k
mà
12
0...
n
k k k k
và đường thẳng d hoặc mặt phẳng (P). Tìm M ở trên d hoặc trên (P) sao
cho
1 1 2 2
...
mm
k MA k MA k MA
nhỏ nhất.
Cách giải :
Bước 1: Gọi I là điểm thỏa mãn
1 1 2 2
0...
mm
k IA k IA k IA
Bước 2: Áp dụng qua tắc 3 điểm biến đổi
1 1 2 2 1 2
... ... .
m m n
k MA k MA k MA k k k MI k MI
Bước 3: Tìm độ dài nhỏ nhất của vectơ
MI
xảy ra khi M ở vị trí nào.
Ví dụ 1 : Trong không gian Oxyz cho hai điểm
3;1;1 ; 7;3;9AB
và
( ): 3 0x y z
. Tìm
()M
sao cho
MA MB
nhỏ nhất. Đáp số :
0; 3;0M
Ví dụ 2 : Trong không gian Oxyz cho hai điểm
3;4; 1 ; 5;3; 2 ; 3; 1;2 ; 1;1;4A B C D
Tìm
M trong không gian sao cho
MA MB MC MD
nhỏ nhất. Đáp số :
1 7 3
;;
244
M



Ví dụ 3 : Trong không gian Oxyz cho hai điểm
1;2;3 ; 1;0; 3 ; 2; 3; 1A B C
và
1 1 1
:
2 3 1
x y z
. Tìm
M 
sao cho
75MA MB MC
lớn nhất.
Đáp số :
31 29 5
;;
7 7 7
M



Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 63
Dạng 2. Cực trị độ dài bình phương vô hướng của vectơ
Xét bài toán tổng quát : Cho n giác
12
...
n
A A A
với n số
12
, ,...,
n
k k k
mà
12
0...
n
k k k k
và đường thẳng d hoặc mặt phẳng (P). Tìm M ở trên d hoặc trên (P) sao cho
2 2 2
1 1 2 2
...
nn
S k MA k MA k MA
nhỏ nhất.
Cách giải :
Bước 1: Gọi I là điểm thỏa mãn
1 1 2 2
0...
mm
k IA k IA k IA
. Từ đây ta tìm được điểm
I
Bước 2: Áp dụng qua tắc 3 điểm biến đổi
2 2 2 2 2 2 2
1 1 2 2 1 1 2 2
... ...
n n n n
S k MA k MA k MA kMI k IA k IA k IA
.
Bước 3: Do
0k
Vậy để
2 2 2
1 1 2 2
...
nn
S k MA k MA k MA
đạt giá trị nhỏ nhất thì ta
xác định vị trí M cần tìm
Chú ý: Bài toán tìm GTLN cũng hoàn toàn làm tương tự
Ví dụ 1 : Trong không gian Oxyz cho hai điểm
1;2; 1 ; 3;1; 2 ; 1; 2;1A B C
và
( ): 2 0x y z
. Tìm
()M
sao cho
2 2 2
MA MB MC
lớn nhất. Đáp số :
2; 2; 2M 
Ví dụ 2 : Trong không gian Oxyz cho hai điểm
1;1;1 ; 0;1;2 ; 2;0;1A B C
và
( ): 1 0x y z
. Tìm
()M
sao cho
2 2 2
2MA MB MC
nhỏ nhất.
Đáp số :
3 3 1
;;
2 4 4
M




Ví dụ 3 : Trong không gian Oxyz cho hai điểm
1;2;3 ; 1;0; 3 ; 2; 3; 1A B C
và
( ):2 2 1 0x y z
. Tìm
()M
sao cho
2 2 2
3 4 6MA MB MC
nhỏ nhất.
Đáp số :
11;25;1M
Dạng 3. Cực trị dựa vào tính chất hình học
Phương pháp :
Ví dụ 1 : Cho hai điểm A(-1;6;6); B(3;-2;4)
a) Tìm điểm M thuộc (Oxy) sao cho MA+MB nhỏ nhất
b) Tìm điểm N thuộc (Oyz) sao cho
NA NB
nhỏ nhất
Hướng dẫn và đáp số:
) vaø z cuøng daáu neân hai ñieåm A vaø B cuøng moät phía ñoái vôùi (Oxy)
76
: ; ;0
55
) vaø x cuøng daáu neân hai ñieåm A vaø B hai phía khaùc nhau ñoái vôùi (Oyz)
: 0;10;7
AB
AB
az
ÑS M
bx
ÑS N



Ví dụ 2: Trong không gian Oxyz cho hai điểm
5; 2;6 ; 3; 2;1AB
và
( ):2 2 6 0x y z
.
Tìm
()M
sao cho
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 64
a)
MA MB
nhỏ nhất.
b)
MA MB
lớn nhất
Ví dụ 3: Trong Oxyz cho đường thẳng
1
:
1 2 1
x y z
và ba điểm
3;2; 1 ; 3; 2;1AB
. Tìm
M 
sao cho
MA MB
nhỏ nhất. Đáp số:
Ví dụ 4: Trong không gian
Oxyz
cho điểm
1; 1;1A
và đường thẳng
có phương trình
11
2 1 1
x y z

và mặt phẳng
( ):2 2 1 0P x y z
a) Viết phương trình mặt phẳng (Q) chứa đường thẳng
và khoảng cách từ A đến (Q) lớn
nhất
b) Viết phương trình mặt phẳng
()R
chứa
và tạo với
()P
một góc nhỏ nhất.
c) Viết phương trình mặt phẳng
()
chứa hai điểm
1;1;1 , 1;2; 1MN
và tạo với đường
thẳng
một góc lớn nhất.
Đáp số:
) ( ):2 3 1 0; ) ( ):10 7 13 3 0; )( ):16 10 11 15 0a Q x y z b R x y z c x y z
Ví dụ 5: Lập phương trình đường thẳng
d
đi qua
0; 1;2A
và cắt đường thẳng
12
':
2 1 1
x y z
d


sao cho
a) Khoảng cách từ
(2;1;1)B
đến đường thẳng
d
là lớn nhất, nhỏ nhất
b) Khoảng cách giữa
d
và
5
:
2 2 1
x y z
là lớn nhất
Đáp số:
1 2 1 2
) : ; ) :
1 1 1 29 41 4
x y z x y z
a d b d
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 65
PHỤ LỤC
PHỤ LỤC 1. MỘT SỐ BÀI TẬP RÈN LUYỆN HÌNH HỌC GIẢI TÍCH TRƯỚC KHI THI
Bài 1. Trong không gian Oxyz, viết phương trình mặt phẳng (P) chứa đường thẳng (d) :
x y 2 0
2x z 6 0
sao cho giao tuyến của mặt phẳng (P) và mặt cầu (S) :
2 2 2
x y z 2x 2y 2z 1 0
là đường tròn có bán kính r = 1.
Hướng dẫn:
Mặt phẳng (P) chứa (d) có dạng: m(x – y – 2) + n(2x – z – 6) = 0
(P): (m 2n)x my nz 2m 6n 0
Mặt cầu (S) có tâm I(-1; 1; -1), bán kính R = 2.
(P) cắt (S) theo một đường tròn giao tiếp (C) có bán kính r = 1
22
d(I; P) R r 3
2 2 2
m 2n m n 2m 6n
3
(m 2n) m n

22
4m 7n 3. 2m 5n 4m.n
22
5m 22m.n 17n 0
. Cho
2
17
n 1 5m 22m 17 0 m 1 hay m
5
Vậy, có 2 mặt phẳng (P):
1
2
(P ): x y z 4 0
(P ): 7x 17y 5z 4 0
Bài 2. Trong không gian Oxyz cho A(0; 1; 0), B(2; 2; 2), C(-2; 3; 1) và đường thẳng
x 1 y 2 z 3
2 1 2

a)
b) Tìm điểm N thu
Hướng dẫn:
a) Phương trình tham số của (
):
x 1 2t
y 2 t
z 3 2t


Ta có
M ( ) M(1 2t; 2 t; 3 2t)
AB (2; 1; 2), AC ( 2; 2;1)
[AB; AC] ( 3; 6; 6) 3(1; 2; 2) 3.n
, với
n (1; 2; 2)
Phương trình mp (ABC) qua A với pháp vectơ
n
: (ABC): x + 2y – 2z – 2 = 0.
2 2 2
ABC
1 1 9
S [AB; AC] ( 3) ( 6) 6 .
2 2 2
Đường cao MH của tứ diện MABC là khoảng từ M đến (ABC):
1 2t 2( 2 t) 2(3 2t) 2 4t 11
MH d(M(ABC))
3
1 4 4

Thể tích tứ diện MABC bằng 3
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 66
4t 11
19
V . . 3
3 2 3
5 17
4t 11 6 t hay t .
44
Vậy, có 2 điểm M cần tìm là:
3 3 1 15 9 11
M ; ; hay M ; ;
2 4 2 2 4 2
b)
N ( ) N(1 2t; 2 t; 3 2t)
22
ABN
1 1 2 3 2
S [NA; NB] 32t 128t 146 (4t 8) 9
2 2 2 2
ABN
32
maxS 4t 8 0 t 2.
2
Vậy, điểm N cần tìm là N(-3; 0; 1).
Bài 3. Trong không gian Oxyz cho đường thẳng (d) và mặt cầu (S):
2 2 2
2x 2y z 1 0
(d): ; (S):x y z 4x 6y m 0
x 2y 2z 4 0
Tìm m để (d) cắt (S) tại hai điểm M, N sao cho MN = 8.
Hướng dẫn:
Mặt cầu (S):
2 2 2
(x 2) (y 3) z 13 m
có tâm I(-2; 3; 0), bán kính
R IN 13 m
, với
m < 13.
Dựng
IH MN MH HN 4
22
IH IN HN 13 m 16 m 3
,
Phương trình tham số của đường thẳng (d):
xt
1
y 1 t
2
z 1 t

(d) có vectơ chỉ phương
11
u 1; ; 1 (2; 1; 2)
22


và đi qua điểm A(0; 1; -1)
AI ( 2; 2; 1); [AI; u] (3; 6; 6)
Khoảng cách h từ I đến đường thẳng (d):
222
2 2 2
[AI; u]
3 6 6 81
h 3.
u
9
2 1 2


Ta có: IH = h
m 3 3 m 3 9
m 12
(thỏa điều kiện)
Vậy, giá trị cần tìm: m = -12.
Bài 4. – y + z – 5 = 0. Viết phương trình mặt phẳng
có thể tích bằng
36
125
.
Hướng dẫn: Phương trình mặt phẳng (xOy): z = 0
m(2x – y + z – 5) – nz = 0
(P): 2mx my (m n)z 5m 0
Giao điểm A, B, C của (P) và 3 trục Ox, Oy, Oz lần lượt có tọa độ:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 67
5 5m
A ; 0; 0 , B(0; 5; 0), C 0; 0;
2 m n
Thể tích tứ diện OABC bằng
125
36
1 1 5 5m 125
V .OA.OB.OC . .5.
6 6 2 m n 36
m n 3m m 1, n 2
m n 3 m
m n 3m m 1, n 4



Vậy, có 2 phương trình mặt phẳng (P):
1
2
(P ): 2x y 3z 5 0 (m 1; n 2)
(P ): 2x y 3z 5 0 (m 1; n 4)
Bài 5. Trong không gian Oxyz, tìm trên Ox điểm A cách đều đường thẳng
(d) :
2
2z
2
y
1
1x
– y – 2z = 0.
Hướng dẫn: Gọi A(a; 0; 0)
Ox
.
2 2 2
2a 2a
d(A; )
3
2 1 2

0
M (1; 0; 2)
và có vectơ chỉ phương
u (1; 2; 2)
Đặt
01
M M u
01
AM M
01
2
0
AM M
01
[AM ; u]
2.S
8a 24a 36
d(A; )
M M u 3

2
2 2 2
2
2a
8a 24a 36
4a 8a 24a 36 4a 24a 36 0
33
4(a 3) 0 a 3.

Vậy, có một điểm: A(3; 0; 0).
Bài 6. Trong không gian với hệ tọa độ vuông góc Oxyz cho mặt phẳng (P) và mặt cầu (S):
(P):
2 2 2 2
2x 2y z m 3m 0 ; (S): (x 1) (y 1) (z 1) 9
.
Tìm m để (P) tiếp xúc (S). Với m tìm được xác định tọa độ tiếp điểm.
Hướng dẫn:
Ta có:
2
(P): 2x 2y z m 3m 0
;
2 2 2
(S): (x 1) (y 1) (x 1) 9
có tâm I(1; -1; 1) và
bán kính R = 3.
(P) tiếp xúc (S)
d[I, (P)] R
2
2
2 2 2
m2
2.1 2.( 1) 1.1 m 3m
3 m 3m 1 9
m5
2 2 1


Vậy, (P) tiếp xúc (S) khi m = -5 hay m = 2, khi đó (P): 2x + 2y + z – 10 = 0
Đường thẳng (d) qua I và vuông góc với (P) có phương trình:
x 1 y 1 z 1
2 2 1

Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 68
Tọa độ tiếp điểm là nghiệm của hệ:
x3
2x 2y z 10 0
y1
x 1 y 1 z 1
z2
2 2 1


Vậy, tọa độ tiếp điểm M(3; 1; 2).
Bài 7. Trong không gian oxyz cho hai đường thẳng:
(d1) :
4z
ty
t2x
; (d2) :
012z3y4x4
03yx
Chứng minh (d1) và (d2) chéo nhau. Viết phương trình mặt cầu (S) có đường kính là đoạn vuông
góc chung của (d1) và (d2).
Hướng dẫn:
(d1) đi qua điểm A(0; 0; 4) và có vectơ chỉ phương
1
u (2;1; 0)
(d2) đi qua điểm B(3; 0; 0) và có vectơ chỉ phương
2
u (3; 3; 0)
AB (3; 0; 4)
;
1 2 1 2
AB.[u ; u ] 36 0 AB, u , u
không đồng phẳng.
Vậy, (d1) và (d2) chéo nhau.
(d2) có phương trình tham số:
/
/
x 3 t
yt
z0


.
Gọi MN là đường vuông góc chung của (d1) và (d2)
1
M (d ) M(2t; t; 4)
,
//
2
N (d ) N(3 t ; t ; 0)
//
MN (3 t 2t; t t; 4)
Ta có:
//
/
1
//
2
MN u 2(3 t 2) (t t) 0 M(2; 1; 4)
t1
N(2; 1; 0)
t1
3 t 2t (t t) 0
MN u

Tọa độ trung điểm I của MN: I(2; 1; 2), bán kính
1
R MN 2.
2

Vậy, phương trình mặt cầu (S):
2 2 2
(x 2) (y 1) (z 2) 4.
Bài 8. Trong không gian Oxyz cho 2 đường thẳng: (d1) :
t26z
t4y
tx
; và (d2) :
1'tz
6't3y
'tx
Gọi K là hình chiếu vuông góc của điểm I(1; -1; 1) trên (d2). Tìm phương trình tham số của đường
thẳng qua K vuông góc với (d1) và cắt (d1).
Hướng dẫn:
(d1) có vectơ chỉ phương
1
u (1; 1; 2)
; (d2) có vectơ chỉ phương
2
u (1; 3; 1)
/ / / / / /
2
K (d ) K(t ; 3t 6; t 1) IK (t 1; 3t 5; t 2)
/ / / /
2
18 18 12 7
IK u t 1 9t 15 t 2 0 t K ; ;
11 11 11 11



Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 69
1) tại
1
H(t; 4 t; 6 2t), (H (d ))
18 56 59
HK t; t; 2t
11 11 11


1
18 56 118 26
HK u t t 4t 0 t
11 11 11 11
30 7 1
HK 4; ; (44; 30; 7).
11 11 11


18
x 44
11
12
y 30
11
7
z7
11
.
Bài 9. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
: 2 2z + 5 = 0; Q : 2 2z -13 = 0.P x y x y
Viết phương trình của mặt cầu (S) đi qua gốc tọa độ O, qua điểm A(5;2;1) và tiếp xúc với cả hai
mặt phẳng (P) và (Q).
Hướng dẫn:
Bài 1.
Gọi I(a;b;c) là tâm và R là bán kính của mặt cầu (S). Từ giả thiết ta có:
, , ,
,,
OI AI
OI AI d I P d I Q OI d I P
d I P d I Q
Ta có:
2 2 2
2 2 2 2 2
5 2 1
10 4 2 30 (1)
OI AI OI AI a b c a b c
a b c
2
2 2 2 2 2 2
| 2 2 5|
, 9 2 2 5 (2)
3
a b c
OI d I P a b c a b c a b c
| 2 2 5| | 2 2 13 |
,,
33
2 2 5 2 2 13( )
2 2 4 (3)
2 2 5 2 2 13
a b c a b c
d I P d I Q
a b c a b c
a b c
a b c a b c
lo¹i
Từ (1) và (3) suy ra:
17 11 11 4a
; (4)
3 6 3
a
bc
Từ (2) và (3) suy ra:
2 2 2
9 (5)a b c
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 70
Thế (4) vào (5) và thu gọn ta được:
2 221 658 0aa
Như vậy
2a
hoặc
658
221
a
.Suy ra: I(2;2;1) và R = 3 hoặc
658 46 67
;;
221 221 221
I



và R= 3
Vậy có hai mặt cầu thỏa mãn yêu cầu với phương trình lần lượt là:
2 2 2
2 2 1 9x y z
và
2 2 2
658 46 67
9
221 221 221
x y z
Bài 10. Trong không gian với hệ trục Oxyz cho mặt cầu (S) có phương trình
2 2 2
2 4 6 11 0x y z x y z
và mặt phẳng (
):2x + 2y - z + 17 = 0. Viết phương trình mặt
phẳng (
) song song với (
) và cắt (S) theo giao tuyến là đường tròn có chu vi bằng 6.
Hướng dẫn:
Do () // () nên () có phương trình 2x + 2y – z + D = 0 (D
17)
Mặt cầu (S) có tâm I(1; -2; 3), bán kính R = 5
Đường tròn có chu vi 6 nên có bán kính r = 3.
Khoảng cách từ I tới () là h =
2 2 2 2
5 3 4Rr
Do đó
2 2 2
2.1 2( 2) 3
7
4 5 12
17 (lo¹i)
2 2 ( 1)
D
D
D
D

Vậy () có phương trình 2x + 2y – z - 7 = 0
Bài 11. Trong không gian Oxyz, tìm trên Ox điểm A cách đều đường thẳng
(d) :
12
1 2 2
x y z

và mặt phẳng (
) : 2x – y – 2z = 0.
Hướng dẫn: Gọi A(a; 0; 0)
Ox
.
Khoảng cách từ A đến mặt phẳng (
) :
2 2 2
22
( ; )
3
2 1 2
aa
dA


(
) qua
0
(1; 0; 2)M
và có vectơ chỉ phương
(1; 2; 2)u
Đặt
01
M M u
. Do đó: d(A;
) là đường cao vẽ từ A trong tam giác
01
AM M
01
2
0
01
[ ; ]
2.
8 24 36
( ; )
3
AM M
AM u
S
aa
dA
MM
u

Theo giả thiết: d(A;
) = d(A;
)
2
2 2 2
2
2
8 24 36
4 8 24 36 4 24 36 0
33
4( 3) 0 3.
a
aa
a a a a a
aa

Vậy, có một điểm A(3; 0; 0).
Bài 12. Trong không gian với hệ tọa độ Oxyz .Viết phương trình (P) qua O , vuông góc với mặt
phẳng (Q) :
0x y z
và cách điểm M(1;2;
1
) một khoảng bằng
2
.
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 71
Hướng dẫn: Phương trình mặt phẳng (P) qua O nên có dạng : Ax + By + Cz = 0 với
2 2 2
0A B C
Vì (P)
(Q) nên 1.A+1.B+1.C = 0
A+B+C = 0
C A B
(1)
Theo đề :
d(M;(P)) =
2
2 2 2 2
2 2 2
2
2 ( 2 ) 2( )
A B C
A B C A B C
A B C


(2)
Thay (1) vào (2) , ta được : 8AB+5
2
8
0 0 hay B =
5
A
BB
(1)
0 . Cho 1, 1B C A A C
thì (P) :
0xz
8
B =
5
A
. Chọn A = 5 , B =
1
(1)
3C
thì (P) :
5 8 3 0x y z
Bài 13. Cho điểm A(10; 2; -1) và đường thẳng d có phương trình
11
2 1 3
x y z

. Lập phương
trình mặt phẳng (P) đi qua A, song song với d và khoảng cách từ d tới (P) là lớn nhất.
Hướng dẫn:
Gọi H là hình chiếu của A trên d, mặt phẳng (P) đi qua A và (P)//d, khi đó khoảng cách giữa d và
(P) là khoảng cách từ H đến (P).
G.sử điểm I là hình chiếu của H lên (P), ta có
AH HI
=> HI lớn nhất khi
AI
Vậy (P) cần tìm là mặt phẳng đi qua A và nhận
AH
làm véc tơ pháp tuyến.
(1 2 ; ;1 3 )H d H t t t
vì H là hình chiếu của A trên d nên
. 0 ( (2;1;3)AH d AH u u
là véc tơ chỉ phương của d)
(3;1;4) ( 7; 1;5)H AH
Vậy (P): 7(x – 10) + (y – 2) – 5(z + 1) = 0
7x + y -5z -77 = 0
Bài 14. Trong không gian với hệ tọa độ Oxyz, cho điểm A ( 3 ; - 1 ; 1 ) , đường thẳng
và mp ( P)
lần lượt có phương trình
2
:
1 2 2
x y z
, ( P ) : x – y + z - 5 = 0 .
Viết phương trình tham số của đường thẳng d thỏa các điều kiện :đi qua A , nằm trong ( P) và hợp
với đường thẳng
một góc 45
0
.
Hướng dẫn:
Gọi
,,
dP
u u n
lần lươt là các vtcp của đt d , đt
và vtpt của mp ( P).
Đặt
2 2 2
( ; ; ), ( 0)
d
u a b c a b c
. Vì d nằm trong ( P) nên ta có :
Pd
nu
=> a – b + c = 0 b = a + c ( 1 ).
Theo gt : góc giữa 2 đt bằng 45
0
Góc giữa 2 vtcp bằng 45
0
.
2 2 2 2
2 2 2
22
2
2( 2 ) 9( ) (2)
2
.3
a b c
a b c a b c
a b c


Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 72
Thay (1) vào ( 2) ta có :
2
0
14 30 0
15
7
c
c ac
a
c

* Với c = 0 : chọn a = b = 1 . Ta có ptts của d là : x = 3 + t ; y = - 1 – t ; z = 1
* Với c = - 15a / 7 . chọn a = 7 , c = - 15 , b = -8 . ta có ptts của d là :
37
: 1 8
1 15
xt
d y t
zt


Bài 15. Trong không gian oxyz cho hai đường thẳng d1 :
1 1 2
x y z

; d2
12
1
xt
yt
zt

và điểm M(1;2;3).
1.Viết phương trình mặt phẳng chứa M và d1 ; Tìm M
’
đối xứng với M qua d2.
2.Tìm
12
;A d B d
sao cho AB ngắn nhất .
Hướng dẫn:
Trong không gian oxyz cho hai đường thẳng d1 :
1 1 2
x y z

; d2
12
1
xt
yt
zt

và điểm M(1;2;3).
1.Viết phương trình mặt phẳng chứa M và d1 ; Tìm M
’
đối xứng với M qua d2.
+ Phương trình mặt phẳng chứa M và d1 …. Là (P) x + y – z = 0
+ Mp(Q) qua M và vuông góc với d2 có pt 2x – y - z + 3 = 0
+ Tìm được giao của d2 với mp(Q) là H(-1 ;0 ;1)
…
Điểm đối xứng M
’
của M qua d2 là M
’
(-3 ;-2 ;-1)
2.Tìm
12
;A d B d
sao cho AB ngắn nhất .
Gọi A(t;t;2t) và B(-1-2t1 ;-t1 ;1+t1) AB ngắn nhất khi nó là đoạn vuông góc chung của hai đường
thẳng d1 và d2 .
1
2
.0
.0
AB v
AB v
…….
tọa độ của
3 3 6
;;
35 35 35
A



và
1 17 18
;;
35 35 35
B




Bài 16. Trong không gian với hệ toạ độ Oxyz ,cho điểm I(1;5;0) và hai đường thẳng
1
:4
12
xt
yt
zt
;
2
2
:
1 3 3
x y z

1. Viết phương trình tham số của đường thẳng d đi qua điểm I và cắt cả hai đường thẳng
1
và
2
2. Viết phương trình mặt phẳng(
) qua điểm I , song song với
1
và
2
Hướng dẫn:
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 73
I(1;5;0) ,
1
:4
12
xt
yt
zt
2
2
:
1 3 3
x y z

1
có vtcp
1
(1; 1;2)u
;và
1
đi qua điểm M
1
(0;4; 1)
2
có vtcp
2
(1; 3; 3)u 
;
2
đi qua điểm
2
(0;2;0)M
mp(P)chứa
1
và điểm I có vtpt
11
, (3; 1; 2)n M I u


p/t mp(P) : 3x –y - 2z + 2 = 0
Tương tự mp(Q) chứa
2
và điểm I có vtpt
'
n
(3;-1;2)
p/t mp(Q) : 3x - y + 2z + 2 = 0
*Vì đường thẳng d qua I , cắt
1
và
2
, nên d = (P)
(Q)
đường thẳng d có vtcp
'
,
d
u n n



= (1;3;0); d đi qua điểm I(1;5;0)
Nên p/t tham số của d là
1
53
0
xt
yt
z


*mp(
) qua điểm I và song song với
1
và
2
nên (
) có vtpt
n
=
12
,uu


=(9;5;-2)
p/t (
) : 9x + 5y -2z – 34 = 0
Bài 17. Trong không gian với hệ trục toạ độ Oxyz cho 4 điểm A( 1; -1; 2), B( 1; 3; 2), C( 4; 3; 2), D( 4;
-1; 2) và mặt phẳng (P) có phương trình:
20x y z
. Gọi A’là hình chiêú của A lên mặt
phẳng Oxy. Gọi ( S) là mặt cầu đi qua 4 điểm A’, B, C, D. Xác định toạ độ tâm và bán kính của
đường tròn (C) là giao của (P) và (S).
Hướng dẫn:
Dễ thấy A’ ( 1; -1; 0)
* Giả sử phương trình mặt cầu ( S) đi qua A’, B, C, D là:
0dcba,0dcz2by2ax2zyx
222222
Vì
SD,C,B,'A
nên ta có hệ:
1d
1c
1b
2
5
a
021dc4b2a8
029dc4b6a8
014dc4b6a2
02db2a2
Vậy mặt cầu ( S) có phương trình:
01225
222
zyxzyx
(S) có tâm
1;1;
2
5
I
, bán kính
2
29
R
+) Gọi H là hình chiếu của I lên (P). H là tâm của đường tròn ( C)
+) Gọi ( d) là đường thẳng đi qua I và vuông góc với (P).
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 74
(d) có vectơ chỉ phương là:
1;1;1n
Suy ra phương trình của d:
t1;t1;t
2
5
H
t1z
t1y
t2/5x
Do
)P(dH
nên:
6
5
t
2
5
t302t1t1t
2
5
6
1
;
6
1
;
3
5
H
Bà 18. Trong không gian với hệ trục toạ độ Oxyz cho
: 2 5 0P x y z
và đường thẳng
3
( ): 1 3
2
x
d y z
, điểm A( -2; 3; 4). Gọi
là đường thẳng nằm trên (P) đi qua giao điểm
của ( d) và (P) đồng thời vuông góc với d. Tìm trên
điểm M sao cho khoảng cách AM ngắn nhất.
Hướng dẫn:
Chuyển phương trình d về dạng tham số ta được:
3
1
32
tz
ty
tx
Gọi I là giao điểm của (d) và (P)
3;1;32 tttI
Do
4;0;1105)3()1(232 IttttPI
* (d) có vectơ chỉ phương là
)1;1;2(a
, mp( P) có vectơ pháp tuyến là
1;2;1 n
3;3;3n,a
. Gọi
u
là vectơ chỉ phương của
1;1;1u
u4z
uy
u1x
:
. Vì
u4;u;u1MM
,
u;3u;u1AM
AM ngắn nhất
AM
0u.1)3u(1)u1(10u.AMuAM
3
4
u
. Vậy
3
16
;
3
4
;
3
7
M
Bài 19. Cho mặt phẳng
( ): 2 0x y z
và các điểm A(1;2;-1), B(3;1;-2), C(1;-2;1). Tìm điểm M
thuộc mặt phẳng
()
sao cho:
a) MA+MB nhỏ nhất
b) |MA-MB| lớn nhất
c)

2 2 2
lôùn nhaátMA MB MC
d)
 nhoû nhaátMA MB MC
Đáp số:
13 4 7 11 5 1 2
) ;1; ; ) ; ;1 ; ) (2; 2; 2); ) ; ;
5 5 2 2 3 3 3
a M b M c M d M
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 75
Bài 20. Cho đường thẳng


11
:
1 1 2
x y z
d
và các điểm A(1;4;2), B(-1;2;4). Tìm điểm M thuộc
d sao cho:
a)
MA MB
nhỏ nhất
b) MA+MB nhỏ nhất
c)
22
nhoû nhaátMA MB
d)
AMB nhoû nhaát
Đáp số:










2 1 2 7
1 10 4 7 12 5 38
) 1;0;4 ; ) 1;0;4 ; ) ; ; ; ) ; ;
3 7 7 7
3 1 7 3 1 7
a M b M c M d M
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 76
PHỤ LỤC 2. GIẢI BÀI TOÁN HÌNH HỌC KHÔNG GIAN BÀNG HAI CÁCH
Bài 1. Cho hình chóp SABC có đáy ABC là tam giác đều có cạnh bằng
2a 2
, SA vuông góc với
(ABC) và SA = a. Gọi E, F lần lượt là trung điểm của cạnh AB, BC. Tính góc và khoảng cách giữa
hai đường thẳng SE và AF.
Hướng dẫn:
Cách 1: Gọi M là trung điểm của BF EM // AF
(SA; AF) (EM; AF) SEM
2 2 2 2 2
SE SA AE a 2a 3a
SE a 3
2a 2. 3
AF a 6
2

a6
EM BM MF ; BF a 2
2
2 2 2 2 2 2
SB SA AB a 8a 9a SB 3a
2 2 2 2 2 2
SF SA AF a 6a 7a SF a 7
2 2 2 2
1
SB SF 2.SM BF
2
2
2 2 2 2 2
1 15a
9a 7a 2SM .2a SM
22
. Áp dụng định lý hàm Côsin vào
22
2
2 2 2
3a 15a
3a
ES EM SM 2 2
22
cos cosSEM
2.ES.EM 2 2
a6
2. .a 3
2


o
45 .
Dựng
AK ME; AH SK.
Ta có:
a2
AK MF
2

và
AH (SME)
Vì
AF//ME d(SE; AF) d(AF; (SME)) AH.
2 2 2 2 2 2
1 1 1 1 2 3 a 3
AH
3
AH SA AK a a a
Vậy,
a3
d(SE; AF)
3
.
Cách 2:
Dựng hệ trục Axyz, với Ax, Ay, Az với A(0; 0; 0),
B(a 2; a 6; 0), C( a 2; a 6; 0), S(0; 0; a),
a 2 a 6 a 2
E ; ; 0 ; F(0; a 6; 0);M ; a 6; 0
2 2 2
.
z
a
S
A
x
E
B
M
F
y
C
C
S
F
M
B
E
K
H
A
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 77
a 2 a 6 a 2
SE ; ; a ; AF (a; a 6; 0), SM ; a 6; a
2 2 2
2
22
22
a 2 a 6
0. a 6. 0( a)
3a 2
22
cos cos(SE; AF)
2
a 6.a 3
a 3a
0 6a 0. a
22

o
45 .
2 2 2 2
a 6 a 3 a 3 a 3
[SE; SM] ; 0; ( 2; 0; 1) n,
2 2 2 2


với
n ( 2; 0;1)
Phương trình mặt phẳng (SEM) qua S với pháp vectơ
n: 2x z a 0.
Khoảng cách từ A đến (SEM):
0 0 a
a2
d(A;SEM)
3
21


Vì
AF//EM AF//(SEM) d(SE; AF) d(A; SEM)
. Vậy,
a3
d(SE; AF) .
3
Bài 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a, cạnh SA vuông
theo a.
Hướng dẫn:
Cách 1:
Ta có:
SA (ABC) SA AC.
vuông tại A có AM là trung tuyến nên
1
MA SC.
2
Ta lại có:
SA (ABC)
AB BC ( ABC vuoâng taïi B)

SB BC
(định lý 3 đường vuông góc)
tuyến nên
1
MB SC.
2
Suy ra: MA = MB tại M..
Dựng MH // SA và
HK // BC (H AC; K AB)
vì:
1
MH SA a
SA (ABC) MH (ABC)
2
BC AB HK AB 1
HK BC a
2







2 2 2 2 2 2
MK MH HK a a 2a MK a 2
S
M
C
H
B
K
A
z
S
2a
M
C
y
a5
H
B
A
K
x
a
5
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 78
2
MAB
1 1 a 2
S .MK.AB .a 2.a
2 2 2
Cách 2:
2 2 2 2 2 2
AC AB BC a 4a 5a AC a 5
Dựng
BH AC (H AC),
ta có:
22
AB a a
AH
AC
a 5 5
;
2 2 2 2
1 1 1 5
BH AB BC 4a

2a
BH
5

Dựng hệ trục tọa vuông góc Axyz, với Ax, Ay, Az đôi một vuông góc và
2a a
A(0; 0; 0), C(0; a 5; 0), S(0; 0; 2a), B ; ; 0
55



Tọa độ trung điểm M của SC là
a5
M 0; ; a
2



Ta có:
a 5 3a
MA 0; ; a MA
22


;
2a 3a 3a
MB ; ; a MB .
2
5 2 5


suy ra: MA = MB
Ta có:
22
22
a 2a
[MA; MB] ; ; a [MA; MB] a 2
55



2
2
MAB
1 1 a 2
S [MA; MB] .a 2 .
2 2 2
Bài 3. Cho hình chóp đều S.ABC, đáy ABC có cạnh bằng a, mặt bên tạo với đáy một góc bằng
oo
(0 90 )
. Tính thể tích khối hình chóp S.ABC và khoảng cách từ đỉnh A đến mặt phẳng
(SBC).
Cách 1: Gọi H là trung điểm của BC.. nên chân đường cao đỉnh S
trùng với giao điểm ba đường cao là trực tâm O Suy ra:
BC SH, BC AH,
nên
SHA 
.
Ta có:
1 a 3
OH AH .
36

SHO
vuông góc:
a3
SO HO.tg tg
6
và
HO a 3
SH
cos 6.cos


Thể tích hình chóp S.ABC:
23
ABC
1 1 a 3 a 3 a tg
V .SO.S . tg .
3 3 6 4 24
2
SBC
1 a 3
S .SH.BC
2 12.cos

.
Gọi h là khoảng cách từ A đến (SBC), ta có:
32
SBC
SBC
1 3.V a tg a 3 a 3
V .h.S h 3. : sin
3 S 24 12cos 2
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 79
Cách 2: Vì S.ABC là hình chóp đều nên chân đường cao đỉnh S
trùng với tâm O đường tròn (ABC). Gọi M là trung điểm của BC.
Ta có:
2 a 3
AO AM
33

và
a3
OM
6
AM BC, SM BC SMA
:
a3
SO OM.tg tg
6
Dựng hệ trục tọa độ Axyz, với Ax, Ay, Az đôi một vuông góc, A(0; 0; 0),
a a 3 a a 3 a 3 a 3 a 3 a 3
B ; ; 0 ,C ; ; 0 ,M 0; ; 0 , O 0; ; 0 , S 0; ; tg
2 2 2 2 2 3 3 6

Thể tích hình chóp:
3
ABC
1 a tg
V .SO.S
3 24

Ta có:
a a 3 a 3
BS ; ; tg , BC ( a; 0; 0)
2 6 6



22
a 3 a 3
[BS; BC] 0; tg ; n
66



Phương trình mặt phẳng (SBC) qua B với vectơ pháp tuyến
n:
22
a a 3 a 3 a 3
0 x tg y (z 0) 0
2 6 2 6







a3
(SBC): tg y z tg 0.
2
Khoảng cách d từ A đến (SBC):
2
a3
a3
tg .O O tg
tg
2
a3
2
d sin .
1
2
tg 1
cos

Bài 4. Cho hình lập phương ABCD . A'B'C'D' cạnh a. M, N lần lượt là trung điểm của AB và C'D'.
Tính khoảng cách từ B' đến (A'MCN).
Cách 1: Bốn tam giác vuông
/ / / /
AA M, BCM, CC N, A D N
bằng nhau (c.g.c)
//
A M MC CN NA
/
A MCN
là hình thoi.
Hai hình chóp B
/
A
/
MCN và B
/
.A
/
NC có chung đường cao vẽ từ
đỉnh B
/
và
//
A MCN A NC
S 2.S
nên:
/ / / /
B .A MCN B .A NC.
V 2.V
Mà:
/ / / / /
//
3
/
B .ANC C.A B N A B N
3
B .A MCN
1 1 1 a
V V .CC .S .a. .a.a
3 3 2 6
a
V.
3

C

M
B
x
A
z
S
O
y
D
/
A
/
B
/
C
/
D
A
B
C
M
N
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 80
Ta có:
/
/
A MCN
1
S .A C.MN,
2
với
//
A C a 3; MN BC a 2
/
2
A MCN
a6
S.
2

Gọi H là hình chiếu của B
/
trên (A
/
MCN), ta có:
/ / /
/
B .A MCN A MCN
1
V .B H.S
3
//
/
32
/
B .A MCN
A MCN
3.V
a a 6 a 6
B H 3. : .
S 3 2 3
Cách 2: Chọn hệ trục Dxyz, với Dx, Dy, Dz
đôi một vuông góc, A(a; 0; 0), B(a; a; 0), C(0; a; 0),
D(0; 0; 0), A
/
(a; 0; a), B
/
(a; a; a), C
/
(0; a; a), D
/
(0; 0; a),
aa
M a; ; 0 , N 0; ; a
22
Ta có:
/
A C ( a; a; a), MN ( a; 0; a)
/ 2 2 2 2
2
[A C; MN] (a ; 2a ; a ) a (1; 2; 1)
a .n vôùi n (1; 2;1).


Phương trình mp (A
/
MCN) qua C(0; a; 0) với pháp vectơ
n:
1(x 0) 2(y a) 1(z 0) 0
/
(A MCN): x 2y z 2a 0.
Khoảng cách d từ B
/
(a; a; a) đến mp(A
/
MCN):
a 2a a 2a
2a a 6
d.
3
1 4 1 6

Bài 5. Tính thể tích của hình chóp S.ABC, biết đáy ABC là một tam giác đều cạnh a, mặt bên
(SAB) vuô
Cách 1:Dựng
SH AB
Ta có:
(SAB) (ABC), (SAB) (ABC) AB, SH (SAB)
SH (ABC)
và SH là đường cao của hình chóp.
Dựng
HN BC, HP AC
SN BC, SP AC SPH SNH
HN = HP.
o
a3
HP HA.sin60 .
4

a3
SH HP.tg tg
4
Thể tích hình chóp
23
ABC
1 1 a 3 a 3 a
S.ABC: V .SH.S . .tg . tg
3 3 4 4 16
C
a
A
/
C
/
D
A
B
M
N
D
/
z
a
a
y
x
S
H
P
C
A
B
N
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 81
Cách 2: Dựng
SH AB
Ta có:
(SAB) (ABC), (SAB) (ABC) B, SH (SAB) SH (ABC)
Vì (SAC) và (SBC)
Dựng hệ trục tọa độ Hxyz, với Hx, Hy, Hz đôi một vuông góc,
H(0; 0; 0),
aa
A ; 0; 0 ; B ; 0; 0 ,
22
a3
C 0; ; 0 , S(0; 0; h), (h 0).
2



Phương trình mp (ABC): z = 0, với pháp vectơ
1
n (0; 0;1)
. Phương trình mp (SAC):
x y z
1
ah
a3
(SAC): 2h 3x 2hy a 3z ah 3 0
với
2
n (2h 3; 2h; a 3)
.
2 2 2 2 2
0 0 a 3
a3
cos
0 0 1. 12h 4h 3a 16h 3a

22
2
22
22
2
1 16h 3a
1 tg
cos 3a
3a tg a 3
h h tg
16 4
Thể tích hình chóp S.ABC:
23
ABC
1 1 a 3 a 3 a
V .h.S . tg . tg
3 3 4 4 16
.
Bài 6. Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với AB = AC = a, góc
o
BAC 120
cosin của góc giữa hai mặt phẳng (ABC) và (AB'I).
Hướng dẫn:
Cách 1: Gọi H là trung điểm
BC AH BC.
a
AH
2
và
a3
BH BC a 3
2
.
//
IB C
vuông có:
22
/ 2 / 2 / / 2 2
a 13a
IB IC B C 3a
44
22
2 2 2 2
a 5a
AI IC AC a
44
z
h
S
B
C
A
x
H
a
2
a3
2
y
A
/
B
/
C
/
A
B
C
30
o
H
I
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Page 82
Ta có:
22
2 / 2 2 / 2
5a 13a
AI AB 2a IB
44
(AB
/
là đường chéo của hình vuông AA
/
B
/
B cạnh
a).
/
I vuông tại A.
Ta có:
/
2
/
AB I
1 1 a 5 a 10
S .AI.AB . .a 2
2 2 2 4
;
2
ABC
1 1 a a 3
S .AH.BC . .a 3
2 2 2 4
/
I), theo công thức chiếu, ta có:
/
22
ABC
AB I
S
a 3 a 10 30
cos :
S 4 4 10
Cách 2: Gọi H là trung điểm BC
AH BC
a
AH
2

và
a3
BH BC a 3
2
Dựng hệ trục Axyz, với Ax, Ay, Az đôi một vuông góc,
A(0; 0; 0),
/ / /
a 3 a a 3 a a 3 a a 3 a
B ; ; 0 , C ; ; 0 , A (0; 0; a), B ; ; a , C ; ; a ,
2 2 2 2 2 2 2 2
a 3 a a
I ; ;
2 2 2





/
a 3 a a 3 a a
AB ; ; a , AI ; ;
2 2 2 2 2
Ta có:
2 2 2
/
a 3 a 3 a a a 3a a 2a
AB .AI . . a. 0
2 2 2 2 2 4 4 4



/
AB AI.
/
I vuông tại A.
Phương trình mp(ABC): z = 0 có pháp vectơ
1
n (0; 0; 1)
mp (AB
/
I) có cặp vectơ chỉ phương
/
AB , AI
, nên có pháp vectơ:
2 2 2 2 2
/
2
a 3a 3 2a 3 a a
[AB ; AI] ; ; (1; 3 3; 2 3) .n
4 4 4 4 4


với
2
n (1; 3 3; 2 3)
.
/
I), ta có:
0 0 2 3
2 3 30
cos .
10
0 0 1. 1 27 12 40

60
o
B
/
A
/
C
/
z
a
B
C
A
H
I
y
z
| 1/83
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRUNG TÂM LUYỆN THI VÀ GIA SƯ CHẤT LƯỢNG CAO
SĐT: 01234332133. ĐC: Phòng 5, dãy 22 Tập thể xã tắc.TP HUẾ
Biên soạn: Ths. Trần Đình Cư KĨ THUẬT GIẢI NHANH
 Dành cho học sinh luyện thi THPT Quốc Gia.
 Bồi dưỡng học sinh giỏi 10, 11, 12.
 Giáo viên giảng dạy, dạy thêm và luyện thi Quốc gia
TÀI LIỆU DÀNH TẶNG
HỌC SINH LỚP TOÁN THẦY CƯ
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. MỤC LỤC
CHỦ ĐỀ 1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN ..................................................... 3
VẤN ĐỀ 1. Các bài toán điển hình thường gặp .............................................................. 5
VẤN ĐỀ 2. Ứng dụng tọa độ giải toán hình học không gian........................................... 9
CHỦ ĐỀ 2. MẶT PHẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN ............................... 10
VẤN ĐỀ 1. Viết phương trình mặt phẳng ................................................................ 11
VẤN ĐỀ 2. Vị trí tương đối của hai mặt phẳng ............................................................ 14
VẤN ĐỀ 3. Khoảng cách từ một điểm đến một mặt phẳng, khoảng cách giữa hai mặt
phẳng song song. Hính chiếu và điểm đối xứng ............................................................. 16
VẤN ĐỀ 4. Góc của hai mặt phẳng............................................................................... 17
VẤN ĐỀ 5. Ứng dụng giải toán hình học không gian ................................................... 18
CHỦ ĐỀ 3. MẶT CẦU VÀ CÁC BÀI TOÁN LIÊN QUAN ..................................... 20
VẤN ĐỀ 1. Viết phương trình mặt cầu ........................................................................ 20
VẤN ĐỀ 2. Vị trí tương đối của mặt phẳng và mặt cầu................................................ 20
CHỦ ĐỀ 4. ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN ........................ 28
VẤN ĐỀ 1. Viết phương trình đường thẳng .................................................................. 28
Dạng 1. Viết phương trình đường thẳng (   (P) hoặc / / (P) ) qua điểm A và
vuông góc với đường thẳng d ..................................................................................... 30
Dạng 2. Viết phương trình đường thẳng qua A, vuông góc với d d
1 và cắt 2 ........ 30
Dạng 3. Viết phương trình đường thẳng qua A, song song với (P) và cắt d ......... 31
Dạng 4. Viết phương trình đường thẳng d nằm trong mặt phẳng (P) và cắt cả hai
đường thẳng d1, d2...................................................................................................... 31
VẤN ĐỀ 2. Vị trí tương đối của 2 đường thẳng trong không gian ........................ 32
Dạng 1. Viết phương trình đường thẳng đi qua điểm M và cắt cả hai đường thẳng d ,d 1
2 .......................................................................................................................... 32
Dạng 2. Viết phương trình đường thẳng d song song với đường thẳng và cắt hai
đường thẳng d ,d 1
2 ..................................................................................................... 33
Dạng 3. Viết phương trình đường vuông góc chung d của hai đường thẳng chéo nhau
................................................................................................................................... 34
VẤN ĐỀ 3. Khoảng cách từ một điểm đến một đường thẳng và khoảng cách
giữa hai đường thẳng chéo nhau ............................................................................... 34
Dạng 1. Khoảng cách từ một điểm đến một đường thẳng .......................................... 34
Dạng 2. Khoảng cách giữa hai đường thẳng chéo nhau ............................................. 35
Dạng 3. Ứng dụng tọa độ giải toán không gian ......................................................... 35
VẤN ĐỀ 4. Các bài toán liên quan giữa đường thẳng và mặt phẳng ............................ 36
Dạng 1. Đường thẳng song song với mặt phẳng ....................................................... 37
Dạng 2. Hình chiếu vuông góc của một điểm lên mặt phẳng ..................................... 38
Dạng 3. Hình chiếu vuông góc của một đường thẳng lên mặt phẳng ........................ 40
Dạng 4. Hình chiếu của một điểm lên đường thẳng .................................................. 43
VẤN ĐỀ 5. Các bài toán liên quan giữa đường thẳng và mặt cầu ................................. 53 Page 1
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
CHỦ ĐỀ 5. GÓC TRONG KHÔNG GIAN ............................................................... 57
VẤN ĐỀ 1. Góc và các bài toán liên quan ................................................................ 57
VẤN ĐỀ 2 . Sử dụng tọa độ giải toán hình học không gian ........................................... 58
CHỦ ĐỀ 6. MỘT SỐ PHƯƠNG PHÁP GIẢI TOÁN CỰC TRỊ HÌNH HỌC
KHÔNG GIAN ............................................................................................................... 59
VẤN ĐỀ 1. Giải toán cực trị hình học bằng cách sử dụng bất đẳng thức hình học ....... 59
VẤN ĐỀ 2. Giải toán cực trị bằng phương pháp hàm số hoặc bằng cách sử dụng bất
đẳng thức đại số ............................................................................................................. 60
VẤN ĐỀ 3. Giải toán cực trị bằng phương pháp ứng dụng tâm tỉ cự .................. 62
Dạng 1. Cực trị độ dài vectơ...................................................................................... 62
Dạng 2. Cực trị độ dài bình phương vô hướng của vectơ .......................................... 63
Dạng 3. Cực trị dựa vào tính chất hình học ............................................................... 63
PHỤ LỤC ......................................................................................................................... 65
PHỤ LỤC 1. MỘT SỐ BÀI TẬP RÈN LUYỆN HÌNH HỌC GIẢI TÍCH TRƯỚC KHI
THI ................................................................................................................................ 65
PHỤ LỤC 2. GIẢI BÀI TOÁN HÌNH HỌC KHÔNG GIAN BÀNG HAI CÁCH ...... 76 Page 2
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
CHỦ ĐỀ 1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
A. CƠ SỞ LÝ THUYẾT
1. AB  (x x ,y y ,z z ) B A B A B A
2. AB AB  x x y y z z B A 2
B A2  B A2
3. a b  a b ,a b ,a b 1 1 2 2 3 3 
4. k.a  ka ,ka ,ka 1 2 3  2 2 2
5. a  a a a 1 2 3 a b 1 1 6. a b
  a b 2 2 a b  3 3
7. a.b a .b a .b a .b |
a | . | b | cosa,b 1 1 2 2 3 3 a a a      1 2 3 8. a / /b a k.b a,b  0      b b b 1 2 3 9. a  b  .
a b  0  a .b a .b a .b  0 1 1 2 2 3 3  a a a a a a  2 3 3 1 1 2 10. [a,b]   , ,   b b b b b b   2 3 3 1 1 2  Trong không gian (Ox )
yz cho Ax ;y ;z ;Bx ;y ;z ; Cx ;y ;z A A A B B B C C C  . Ta có:
AB  x x ;y y ;z z B A B A B A
AB AB  x x y y z z B A 2
B A2  B A2  x x A B x   I 2   y y
I là trung điểm của AB thì A By I 2   z z A B z   I 2  
x x x A B Cx G 3  
y y y
G là trọng tâm của tam giác ABC thì A B Cy G 3  
z z z A B C z   G 3  Page 3
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Tính chất tích có hướng
1. a,b    , b a    
2. a,b  a . b .sin   a,b
3.a,b  a;a,b  b    
Ứng dụng của tích có hướng    1. , a , b c đồng phẳng , a b .c  0   1   
2. Diện tích tam giác ABC: S AB, AC 2     
3. Diện tích hình bình hành ABCD: S AB, AD   1   
4. Thể tích tứ diện ABCD: V
AB, AC .AD 6     
5. Thể tích hình hộp ABC .
D A'B'C'D': V A , B AC .AA'   Page 4
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
VẤN ĐỀ 1. Các bài toán điển hình thường gặp
Ví dụ 1: a  1; ;
m 2;b  m  2;2; 
1 ;c  0;m 2;2
a) Tìm m để a b b) Tìm m để , a , b c đồng phẳng
c) Tìm m để a b c 4 2
ĐS: a) m   ; b)m   ; c)m  6   3 3 3 5
Ví dụ 2: Tìm x, y để ba điểm A 2
 ;0;2;B1;2;3;C ;
x y 3;7 thẳng hàng
ĐS: x  13, y  13
Ví dụ 3. Cho tam giác ABC có A(1;2;1), B(5;3;4); C(8;-3;2)
a) Chứng minh rằng ABC vuông 2 2 2
b) Tìm điểm M sao cho MA MB MC nhoû nhaát Hướng dẫn a) A . B BC  0 b)M( ; x y, )
z ...; x  4,y  4  ,z  1 
Ví dụ 4. Cho 3 điểm A(1;-1;2), B(2;1;0); C(0;1;-1). Tìm điểm M thuộc trục Oz sao cho 2 2 2
MA MB MC nhoû nhaát 1
Hướng dẫn: M(0; 0;t);...,t  3
BTTT: Cho 3 điểm A(1;-1;2), B(-1;2;0); C(3;-1;0). Tìm điểm M thuộc trục Oz sao cho 2 2 2
MA MB MC nhoû nhaát 1
Hướng dẫn: M(0; 0;t);...,t  3
Ví dụ 5. Cho 3 điểm A(1;-1;1), B(2;1;-2); C(0;0;1). Tìm tọa độ trực tâm của ABC Hướng dẫn: AH BCAH.BC  0      5 4 8  BH AC
 BH.AC  0 .ÑS : H ; ;  9 9 9     
BC, AC,CH ñoàng phaúng
CH.BC; AC  0    
BTTT: Cho 3 điểm A(4;-2;-1), B(1;4;-1); C(1;-2;-7). Tìm tọa độ trực tâm của ABC .
Đáp số: H(3;-1;-2)
Ví dụ 6. Cho 2 điểm A(1;2;-1), B(-2;1;3). Tìm M thuộc trục Ox sao cho A
MB có diện tích nhỏ nhất. 1 1 2 1   
Hướng dẫn M( ; t 0;0).S AM; AB
17t  2t  75,....t   AMB  2   2 17 Page 5
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Ví dụ 7. Cho tam giác ABC có A(-1;0;2), B(0;4;3); C(-2;1;2). Tính độ dài đường phân giác trong AD
của tam giác ABC, D BC . Hướng dẫn: DB AB
k roài suy ra DB  kDC. Suy ra toïa ñoä cuûa D, sau ñoù tính DA. DC AC  3 7 9  3 6 ÑS : D  ; ;  AD   2 4 4    4
BTTT: Cho tam giác ABC có A(1;2;-1), B(2;-1;3); C(-4;7;5). Tính độ dài đường phân giác trong góc B.  17 26  Đáp số:  ; ;7  3 3   
Ví dụ 8. Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC biết A(0;0;-2), B(1;-4;1); C(2;2;-1) Hướng dẫn:  2 2 IA IBIA IB IC      2 2  59 14 13    IA IC ÑS : I ; ;   A ;
B AC;MA ñoàng phaúng   30 15 30  A ; B AC.MA  0    1 5 
BTTT: Cho điểm M  2 ; x 3  ; x  2x  2 2
 và tam giác ABC với A(1;1;3), B(0;5;2);C(-1;3;4).  
a) Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC
b) Chứng minh rằng với mọi x  0 , đường thẳng MI vuông góc với (ABC) Hướng dẫn:
a)Tam giaùc ABC vuoâng taïi C  taâm laø trung ñieåm cuûa AB
MI.AB  0 b)
MI.AC  0
Ví dụ 9. Cho 4 điểm A(-2;2;-1); B(-3;-2;-4); C(5;1;2); D  Oxz. 37
Tìm D biết DA=DB và VABCD 6 . Hướng dẫn: D (O ) xz neân D(x;0;z). 37 2 2 V 
 15x  29z  35  37; DA DB DA DB x  3z  10 ABCD 6 ÑS : D( 1  ;0; 3  ) hoaëc D( 4  ;0; 2)  Ví dụ 10.
a) Cho hai điểm A(1;2;-1); B(4;3;5). Xác định M thuộc Ox sao cho M cách đều A và B
b) Cho hai điểm A(-4;-1;2); B(3;5;-1). Tìm C biết trung điểm của AC thuộc Oy và trung điểm của BC thuộc (Oxz) Page 6
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. Hướng dẫn: a)M(0;0;4) b)C( ; a ;
b c)....ÑS : a  4;b  5  ;c  2
Ví dụ 11. Cho 4 điểm A(1;2;4); B(2;-1;0); C(-2;3;-1); M( ; x ; y )
z ABC. Tìm hệ thức liên hệ
giữa x, y, z. Tìm tọa độ D biết ABCD là hình bình hành và diện tích hình bình hành ABCD. Hướng dẫn:
M ABC  A ;
B AC.AM  0  19x 17y  8z  29  0   D( 1  ;0; 5  );S  714 ABCD
Ví dụ 12. Cho tứ diện ABCD, có A(2;3;1); B(1;1;-2); C(2;1;0); D(0;-1;2). Đường cao AH. Tìm tọa độ chân đường cao Hướng dẫn: AH BC   3 1  AH BD .....H 3; ;  2 2    
BC;BD.BH  0  
Ví dụ 13. Cho 3 điểm A(3;2;-5); B(-2;1;-3); C(5;1;-1).
a) Chứng minh rằng ABC nhọn
b) Tìm điểm D thuộc (xOy) sao cho tứ diện ABCD là tứ diện trực tâm ( có các cặp cạnh đối vuông góc với nhau) Hướng dẫn:
a)*Chöùng minh A, B, C laø ba ñænh cuûa tam giaùc 2 2 2 2 2 2 2 2 2
* Chöùng minh AB  BC CA , AB CA BC ,BC CA AB b)D(x; ; y 0) A .
B AC; AD  0      
Ñieàu kieän ABCD laø töù dieän tröïc taâm 31 19  A . B CD  0 .....D ; ;0  7 7     A . B BD  0  
Ví dụ 14. Tam giác ABC có các đỉnh A, B, C lần lượt thuộc các trục Ox, Oy, Oz và có trọng tâm
G(1;2;-1). Tính diện tích tam giác đó. Hướng dẫn: x  3 ( A ; x 0;0);B(0; ;
y 0);C(0;0;z).G laø troïng taâm cuûa tam giaùc ABC neân y  7 z  3   3V 27 OABC S
(h laø khoaûng caùch töø O ñeán (ABC))  ABC h 2
Ví dụ 15. Cho ba điểm A(2;0;0), B(1;1;2), C(3;-1;1). Page 7
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
a) Chứng minh rằng tam giác ABC là một tam giác vuông
b) Biết ABC.A’B’C’ là một hình lăng trụ đứng có các cạnh bên AA’, BB’, CC’ và A’ ở trên mặt
phẳng Oyz. Tìm tọa độ của A’,B’,C’
Hướng dẫn và đáp số a) A
BC laø tam giaùc vuoâng taïi A
b)A'Oyz  A'(0; ; m p)
ABC.A'B'C' laø hình laêng truï ñöùng neân AB
AA'.AB  0 m  2  AA'       ........B'( 1  ; 1  ;2)vaø C'(1; 3  ;1) AC
AA'.AC  0 p  0
Ví dụ 16. Cho hình hộp ABCD.A’B’C’D’ có A(1;2;-1); C(3;-4;1), B’(2;-1;3)., D’(0;3;5)
a) Tính tọa độ các đỉnh của hình hộp
b) Tính thể tích hình hộp
Hướng dẫn và đáp số:
a)AC coù trung ñieåm I(2;-1;0). B'D' coù trung ñieåm laø I'(1;1;4); A'(x;y;z).
AA'  II '  A'(0;4;3);BB'  II '  B(3; 3  ; 1  ) C '(2; 2  ;5);D(1;1;1;) b)V
AA'.AB, AD  6
ABCD.A'B'C'D'  
BTTT: Cho hình hộp ABCD.A’B’C’D’ có A(1;0;1); B’(2;1;1), C(4;5;-5),
D’(1;-1;1). Tính tọa độ các đỉnh của hình hộp. Đáp số:  7 3   3 5   5 9   5 3  B 3; ; ;D 2; ; ; A' 0; ; ;C' 3; ; ;
 2 2  2 2  2 2  2 2        
Ví dụ 17. Cho 3 điểm A(2;-1;-4); B(-2;3;-4), C(2;m+1;-8)
a) Tìm m để tam giác ABC là tam giác đều
b) Với giá trị m tìm được, hãy xác định tọa độ điểm S thuộc (Oyz) sao cho S.ABC là hình chóp đều.
Đáp số: a) m=2; b) S(0;1;-6) Page 8
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
VẤN ĐỀ 2. Ứng dụng tọa độ giải toán hình học không gian Bài 1. Cho .
S ABCD có ABCD là hình chữ nhật với AB  , a AD  2 ,
a SA  (ABCD), góc giữa a 3
SB với mặt phẳng (ABCD) bằng 600. Lấy M S , A AM V
2 , (BCM) cắt SD tại N. Tính S.BCNM . Bài 2. Cho .
S ABCD có ABCD là hình vuông cạnh bằng , a S
AD đều, SAD  ABCD.
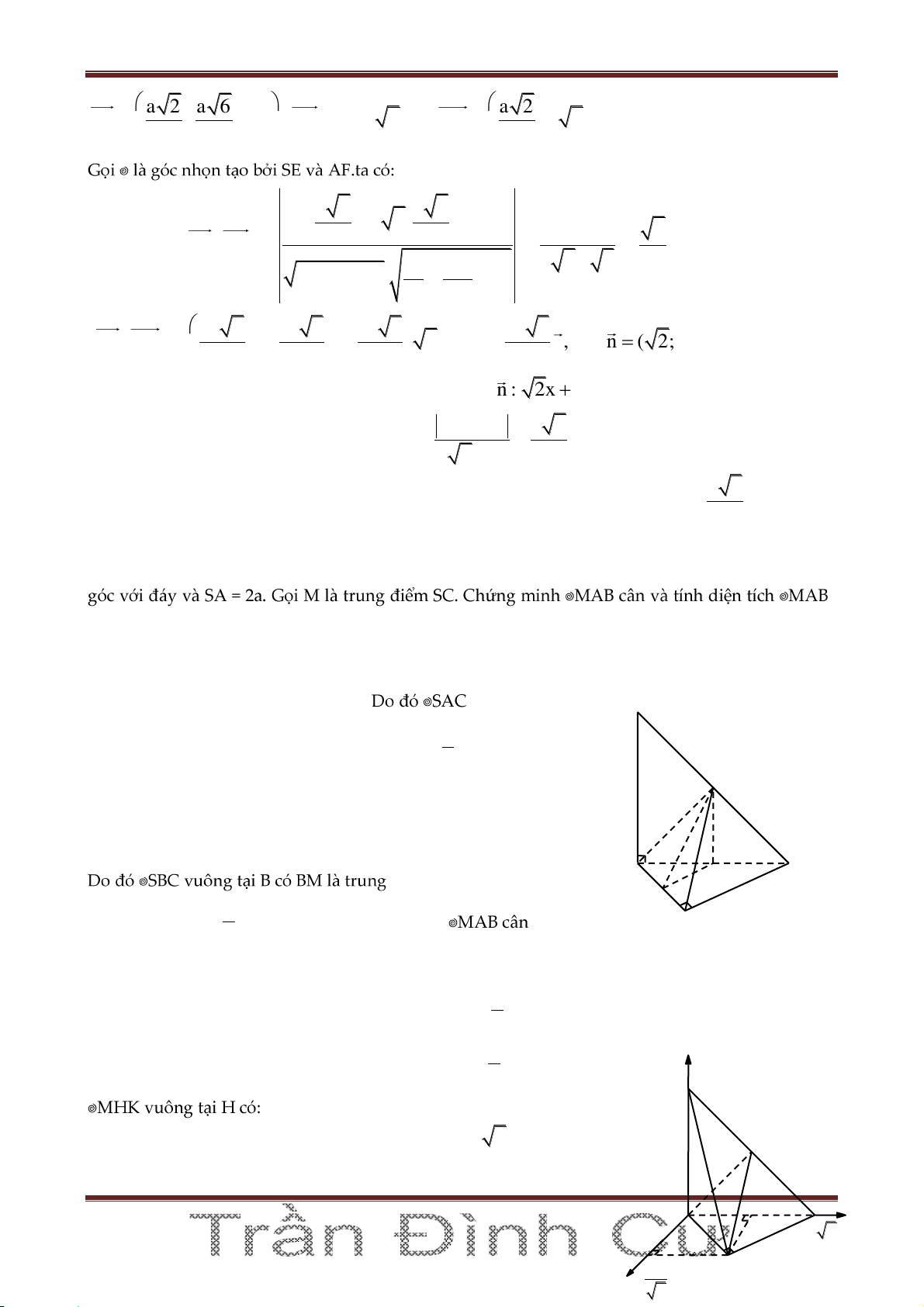
Gọi M, N, P lần lượt là trung điểm của SB, BC, CD. Chứng minh AM BP và VCMNP . Bài 3. Cho .
S ABC có SA  ABC , tam giác ABC vuông tại B, AB  ,
a BD SA  2a . Gọi M
là trung điểm của SC. Chứng minh A
MB cân tại M. Tính SAMB.
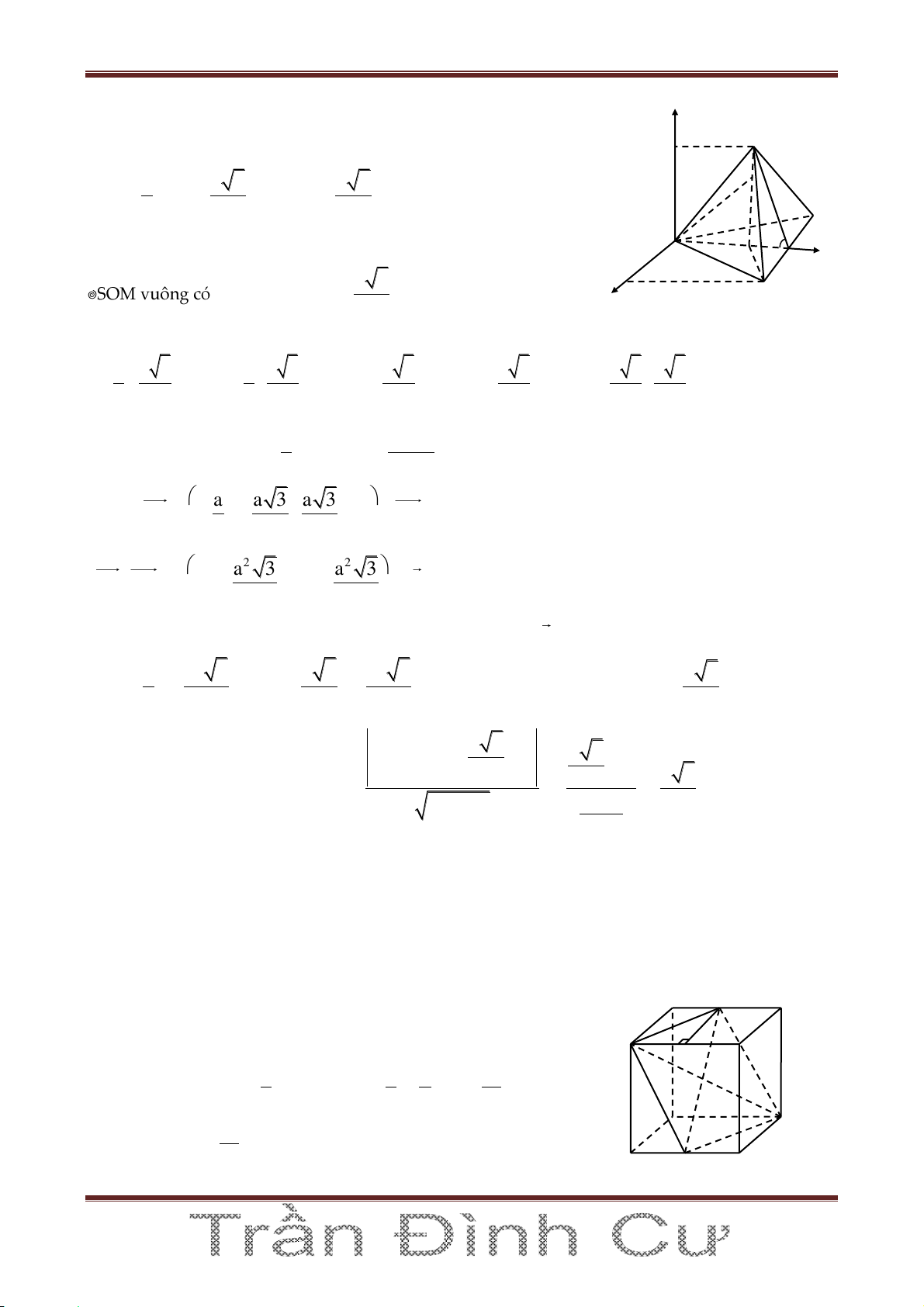
Bài 4. Cho lăng trụ đứng AB .
C A'B'C' có đáy là tam giác vuông, AB AC  , a AA'  a 2 .
Gọi M, N lần lượt là trung điểm của AA’, BC’. Chứng minh MN là đường vuông góc chung của
AA’ và BC’. Tính VM.A'BC' 0
Bài 5. Cho lăng trụ đứng ABC .
D A'B'C'D' có đáy ABCD là hình bình thoi cạnh a, BAD  60 .
Gọi M, N theo thứ tự là trung điểm của AA’, CC’. Chứng minh bốn điểm B’, M, D, N cùng thuộc
một mặt phẳng. Tính AA’ theo a để B’MDN là hình vuông.
Bài 6. D2010. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, cạnh bên SA=a; AC
hình chiếu vuông góc của đỉnh S trên (ABCD) là điểm H thuộc AC, AH  4 . Gọi CM là đường
cao của tam giác SAC. Chứng minh M là trung điểm của SA và tính thể tích khối tứ diện SMBC theo a Page 9
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
CHỦ ĐỀ 2. MẶT PHẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN
A. CƠ SỞ LÝ THUYẾT
1. Vectơ pháp tuyến của mp: Vectơ n  0 được gọi là véctơ pháp tuyến của  nếu giá của n
vuông góc với ( )
2. Cặp véctơ chỉ phương của mp: Cho hai vectơ a,b không cùng phương và khác 0 . Nếu giá
của a,b song song hoặc nằm trên ( ) thì a,b được gọ là cặp vectơ chỉ phương của ( ) . Lúc n   , a b đó:  
3. Phương trình mặt phẳng: Có dạng Ax By Cz D  0 với n   ; A ;
B C là vectơ pháp
tuyến của mặt phẳng.
 Phương trinh mặt phẳng ( ) đi qua điểm M x ; y ; z và có vectơ pháp tuyến 0  0 0 0  n   ; A ;
B C sẽ có dạng Ax x B y y C z z  0 0   0   0  x y z
 Phương trình mặt phẳng đi qua A(a,0,0) B(0,b,0) ; C(0,0,c) có dạng    1 a b c
 Phương trình các mặt phẳng tọa độ
(Oyz) : x = 0 ; (Oxz) : y = 0 ; (Oxy) : z = 0
4. Vị trí tương đối của hai mp (1) và (2) :
( ) : A x B y C z D  0 Cho hai mặt phẳng 1 1 1 1
( ) : A x B y C z D  0 2 2 2 2
  caét   A : B : C A : B : C 1 1 1 2 2 2  A B C D 1 1 1 1  //      A B C D 2 2 2 2  A B C D 1 1 1 1        A B C D 2 2 2 2
     A A B B C C  0 1 2 1 2 1 2
5. Khoảng cách từ một điểm đến mặt phẳng
Ax By Cz D
Cho M(x ; y ; z )      o o o 0 0 0 và ( ) : Ax By Cz D
0 . Lúc đó d(M,)  2 A  2 B  2 C Page 10
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. n .n
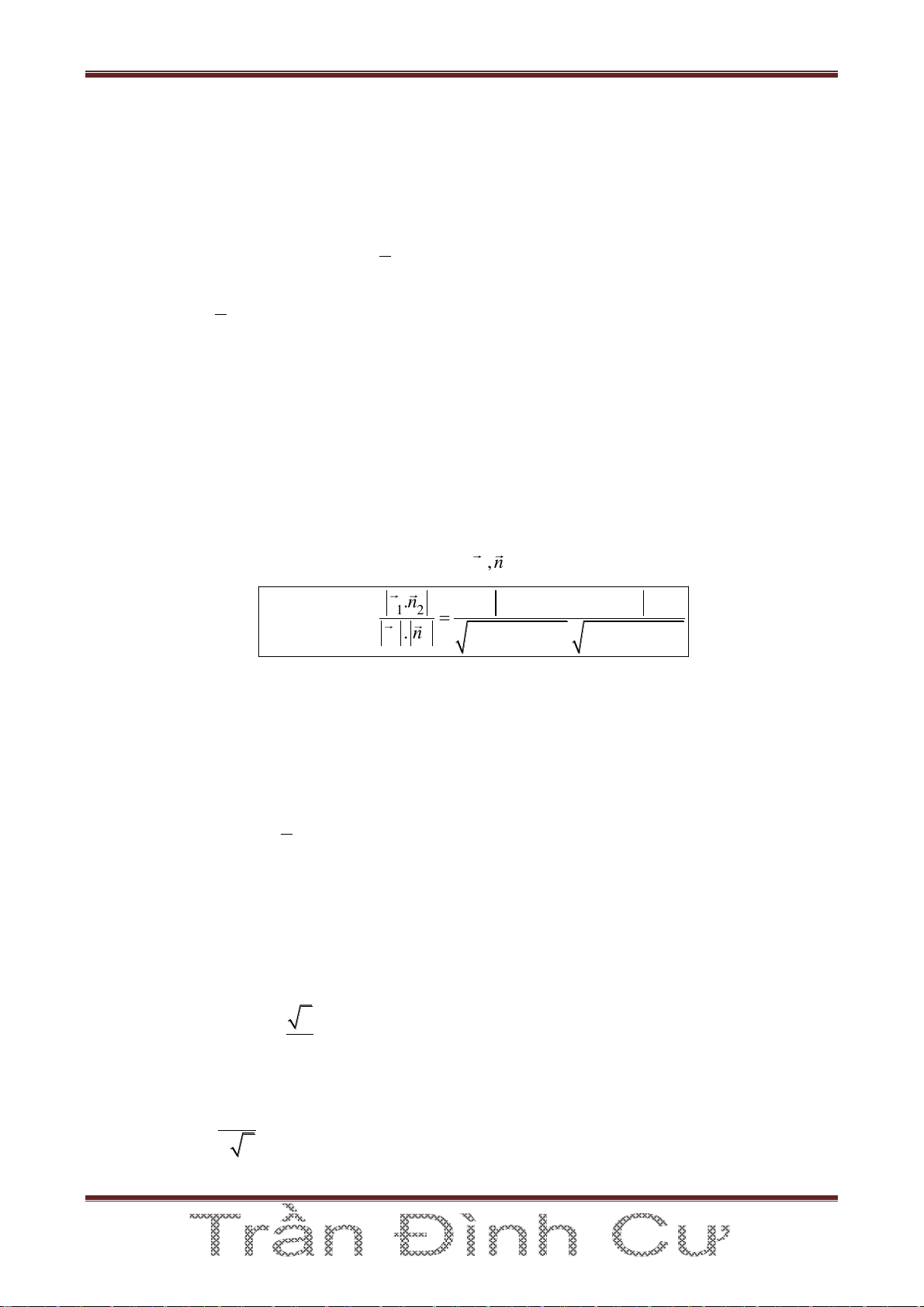
6. Góc giữa hai mặt phẳng :   cos  ( , )  n . n  
VẤN ĐỀ 1. Viết phương trình mặt phẳng
Phương pháp chung: Để lập phương trình mặt phẳng () ta cần xác định một điểm thuộc () và một VTPT của nó.
TH 1: () đi qua điểm M x ; y ; z có VTPT n   A; B;C  : 0 0 0 
(): Ax x B y y C z z  0 0   0   0 
n  a,b
TH 2: () đi qua điểm M x ; y ; z có cặp VTCP a,b . Khi đó một VTPT của () là . 0 0 0 
TH 3: () đi qua điểm M x ; y ; z và song song với (): Ax + By + Cz + D = 0: 0 0 0 
(): Ax x B y y C z z  0 0   0   0 
TH 4: () đi qua 3 điểm không thẳng hàng A, B, C:   
Khi đó ta có thể xác định một VTPT của () là: n AB, AC   x y z
TH 5: Phương trình mặt phẳng đi qua A(a,0,0) B(0,b,0) ; C(0,0,c) có dạng    1 a b c
TH 6: () đi qua điểm M và vuông góc với hai mặt phẳng cắt nhau (), ():
 Xác định các VTPT n ,n   của () và ().   
Một VTPT của () là: n ,n     .
Ví dụ 1. Trong mỗi trường hợp sau, viết phương trình mặt phẳng
a) Đi qua ba điểm A(-1;2;3),B(2;-4;3),C(4;5;6)
b) Đi qua điểm M(1;2;-2) và vuông góc với trục Oy
c) Đi qua điểm M(1;3;-2) và vuông góc với đường thẳng BC với B(0;2;-3), C(1;-4;1)
d) Đi qua M(1;3;-2) và song song với () : 2x y  3z  4  0
e) Đi qua điểm A(3;1;-1),B(2;-1;4) và vuông góc với mặt phẳng 2x-y+3z+4=0
f) Đi qua điểm M(2;-1;2), song song với Oy và vuông góc với mặt phẳng 2x y  3z  4  0 .
g) Đi qua điểm M(-2;3;1) và vuông góc với hai mặt phẳng Page 11
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
() : 2x y  2z  5  0;
() : 3x  2y z 3  0
h) Đi qua A1;1;  1 ;B5;3; 
1 và song song với trục Oz
i) Mặt phẳng trung trực ( ) của đoạn thẳng AB, biết A 1  ;2;  1 ;B 5  ;3;2
Ví dụ 2. Viết phương trình mặt phẳng ( ) trong mỗi trường hợp sau: a) Đi qua điểm M(2;1;-1) và qua giao tuyến của hai mặt phẳng
x y z  4  0; 3x y z 1 0
b) Qua giao tuyến của hai mặt phẳng y  2z  4  0; x y z  3  0 đồng thời song song
với mặt phẳng x y z  2  0
c) Qua giao tuyến của hai mặt phẳng 3x y z  2  0; x  4y  5  0 đồng thời vuông góc
với mặt phẳng 2x z  7  0
Ví dụ 3. Cho điểm H(-1;4;2). Mặt phẳng ( ) đi qua H và cắt các trục toạ độ tại A, B, C (không
trùng với O). Biết H là trực tâm của tam giác ABC. Viết phương trình mặt phẳng ( ) Hướng dẫn: OH AB chöùng minh:  OH  (ABC) OH BC
()  (ABC) :Qua H vaø nhaän OH laøm vtpt
() : x  4y  2z  21
BTTT: Viết phương trình ( ) đi qya H(2;1;1) và cắt các trục tọa độ tại các điểm , A , B C sao cho
H là trục tâm của tam giác ABC. Đáp số: 2x y z  6  0
Ví dụ 4. Cho mặt phẳng ( ) đi qua điểm M(-4;1;-3) và cắt ba trục toạ độ Ox, Oy, Oz tại A,B,C
(Khác O). Biết M là trọng tâm của tam giác ABC. Viết phương trình của mặt phẳng ( ) Hướng dẫn:
Goïi A(a;0;0);B(0;b;0);C(0;0;c).
Phöông trình maët phaúng (): x y z    1. a b c a  0  0 4    3   0  b  0 M laø troïng taâm cuûa A  BC neân 1    a  12
 ,b  3,c  9 3   0  0 3  c     3
BTTT: Viết phương trình ( ) đi qua G 1;2;3 và cắt các trục tọa độ tại các điểm A, B, C sao cho
G là trọng tâm của tam giác ABC. Đáp số: 6x  3y  2z 18  0
Ví dụ 5. Cho điểm M(4;1;2). Gọi (P) là mặt phẳng qua M và cắt các tia Ox, Oy, Oz theo chiều
dương lần lượt tại A,B,C. Viết phương trình của (P) khi khối tứ diện OABC có thể tích nhỏ nhất. Hướng dẫn: Page 12
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. Goïi ( A ; a 0;0);B(0; ;
b 0);C(0;0;c). (a  0,b  0,c  0)
Phöông trình maët phaúng (P): x y z    1. a b c 4 1 2
(P) ñi qua ñieåm M(4;1;2) neân    1. (1) a b c 1 1 V  . OA . OB OC abc (2) OABC 6 6 4 1 2
Theo baát ñaúng thöùc Cauchy, ta coù: 4 1 2    3 3 . . (3) a b c a b c 8 4 1 2 1 Töø (1),(2),(3)  3 3
V  36. Ñaúng thöùc xaûy ra     6V a b c 3
a  12;b  3;c  6
BTTT: Viết phương trình mặt phẳng đi qua điểm M(1;1;1) cắt các trục Ox, Oy, Oz tại A, B, C sao
cho thể tích của OABC có giá trị nhỏ nhất. Đáp số: x y z  3  0
Ví dụ 6. Trong không gian Oxyz cho mặt phẳng () : 2x y x  5  0 . Viết phương trình mặt
phẳng (P) qua giao tuyến ( ) và mặt phẳng (xOy) và (P) tạo với 3 mặt phẳng tọa độ một tứ diện 125 có thể tích bằng 36 Hướng dẫn: Phương trình (xOy): z = 0
m(2x – y + z – 5) – nz = 0  (P) : 2mx  my  (m  n)z  5m  0  5   5m 
(P) cắt Ox, Oy, Oz lần lượt là A
; 0; 0 , B(0;  5; 0), C 0; 0;   2     m n    1 1 5 5m 125 m  1, n  2 V  .OA.OB.OC  . .5.   6 6 2 m  n 36  m  1, n  4 
Vậy có 2 mặt phẳng (P):
(P ) : 2x  y  3z  5  0 (m  1; n  2) 1
(P ): 2x y 3z 5  0 (m 1; n  4  )  2
Ví dụ 7. Viết phương trình mặt phẳng ( ) đi qua điểm M (1;2; 4), 0
cắt các trục tọa độ Ox, Oy,
Oz lần lượt tại các điểm A,B,C sao cho OA=OB=OC  0 Hướng dẫn: Page 13
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
( ) : ax  
1  by  2  cz  4  2 0,a  2 b  2 c  0 (1)
 ax  by cz a  2b  4c
a  2b  4c
  a  2b  4c
( ) caét Ox, Oy, Oz laàn löôït A ;0;0;B0; ;0;  2   2  
a  2b  4c C 0;0; vôùi a+2b+4c    0.  2  Ta coù: OA=OB=OC  2 2 2 OA =OB =OC  2 a  2 b  2 cNeáu , a ,
b c cuøng daáu thì a b c
vaø (1) trôû thaønh x y z - 7  0
Neáu a,b cuøng daáu
vaø khaùc daáu vôùi c thì a b  -c
vaø (1)trôû thaønh x y - z 1  0
Neáu a,c cuøng daáu
vaø khaùc daáu vôùi b thì a c  -b
vaø (1)trôû thaønh x - y z -3  0
Neáu c,b cuøng daáu
vaø khaùc daáu vôùi a thì -a b c
vaø (1)trô ûthaønh - x y z -5  0
Ví dụ 8. Cho A0;1;2;B2; 2  ;  1 ;C 2  ;0;  1
a) Viết phương trình mặt phẳng đi qua A, B, C
b) Tìm M () : 2x  2y z  3  0 sao cho MA=MB=MC Đáp số: )
a ABC: x  2y  4z  6  0; ) b M 2;3; 7  
BTTT: Cho A0;0;3;B2;0; 
1 ; và (P): 3x 8y  7z 1  0 . Tìm C (P) sao cho tam giác   ABC đều.
ĐS: C     2 2 1 2; 2; 3 ; C  ; ;  3 3 3  
Ví dụ 9. Viết phương trình mặt phẳng ( ) đi qua điểm M 4; 1  ; 
1 và cắt các tia Ox,Oy,Oz lần
lượt tại A, B, C sao cho OA  2OB  3OC
ĐS: x  2y  3z  5  0
Ví dụ 10. Cho hai điểm A(-1;3;2), B(2;3;-1) và () : 2x y  3z  5  0 . Tìm điểm C thuộc ( ) sao cho tam giác ABC đều.
VẤN ĐỀ 2. Vị trí tương đối của hai mặt phẳng
Phương pháp:
( ) : A x B y C z D  0 Cho hai mặt phẳng 1 1 1 1
( ) : A x B y C z D  0 2 2 2 2
  caét   A : B : C A : B : C 1 1 1 2 2 2  A B C D 1 1 1 1  //      A B C D 2 2 2 2  A B C D 1 1 1 1        A B C D 2 2 2 2
   A A B B C C  0 1 2 1 2 1 2
Ví dụ 1: Cho hai mặt phẳng (P) : x y z  2  0;( )
Q : 2x 3y z  2  0
a) Chứng tỏ (P)  ( )
Q . Chỉ ra phương trình giao tuyến d của (P) và (Q) Page 14
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
b) Lập phương trình mặt phẳng (R) chứa d và qua M(1;2;3).
Đáp số: b) 7x 13y  3z 10  0
Ví dụ 2: Cho ba mặt phẳng (P) : x y z  2  0;( )
Q : x 3y z  2  0;( )
R : 4y z 2  0
a) Chứng tỏ (P) và (R) cắt nhau theo giao tuyến (d)
b) Lập phương trình mặt phẳng (T) chứa d và song song với (Q)
Đáp số: b) x  3y z  0
Ví dụ 3: Cho hai mặt phẳng () : 2x y  2z 1  0; ( ) : x  2y z  0
a) Chứng tỏ ( ),( ) cắt nhau theo giao tuyến d
b) Lập phương trình mặt phẳng ( ) chứa d và cắt các trục tọa độ theo thứ tự các điểm M, N, 1 P sao cho VOMNP 6
Đáp số: b) x y z 1  0
Ví dụ 4: Xác định k và m để ba mặt phẳng sau đây cùng đi qua một đường thẳng :
5x ky  4z m  0; 3x  7y z 3  0; x  9y  2z  5  0 Hướng dẫn:
Goïi  laø giao tuyeán cuûa 2 maët phaúng 3x-7y+z-3=0; x-9y-2z+5=0  1 18   31 9  Laáy A ;0; ; B ; ;0    7 7  10 10      i
Ñ eåm A,B thuoäc : 5x+ky+4z+m=0  k=-5;m=-11
Ví dụ 5: Xác định m để ba mặt phẳng sau đây đôi một cùng vuông góc với nhau, tìm giao điểm
chung của 3 mặt phẳng đó.
(P) : 5x ky  4z m  0;
(Q) :3x  7y z  3  0;
(R) : x  9y  2z  5  0 Hướng dẫn: n .n  0 P Q
Ba maët phaúng ñoâi moät vuoâng goùc nhau 
 n .n  0  m  1 P Rn .n  0  R Q
Goïi I(x;y;z) laø nghieäm chung cuûa 3 maët phaúng, toïa ñoä I laø nghieäm cuûa heä 3 phöông
trình ba maët phaúng treân. I(1;2;3)
BTTT:Xác định m để ba mặt phẳng sau đây đôi một cùng vuông góc với nhau, tìm giao điểm
chung của 3 mặt phẳng đó.
(P) : x y z  6  0;
(Q) :mx  2y z m 1  0; Đáp số: I(1;2;3)
(R) : mx  m  
1 y z  2m  0 Page 15
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
VẤN ĐỀ 3. Khoảng cách từ một điểm đến một mặt phẳng, khoảng cách giữa hai mặt phẳng song
song. Hính chiếu và điểm đối xứng Phương pháp
 Khoảng cách từ điểm M0(x0; y0; z0) đến mặt phẳng (): Ax + By + Cz + D = 0
Ax By Cz D d M ,() 0 0 0  0 2 2 2
A B C
Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì trên mặt phẳng
này đến mặt phẳng kia.
Chú ý: Nếu hai mặt phẳng không song song thì khoảng cách giữa chúng bằng 0.  
MH, n cuøng phöông
Điểm H là hình chiếu của điểm M trên (P) H (P)
Điểm M đối xứng với điểm M qua (P) MM  2MH
Ví dụ 1: Cho (P) :6x  2y z 1  0; ( )
Q : 6x  2y z 3  0 . Tính khoảng cách giữa (P) và (Q).
Ví dụ 2: Viết phương trình tổng quát của (P) cách (Q) một khoảng k  14 với ( )
Q : 3x y  2x 3  0.
Ví dụ 3: Viết phương trình mặt phẳng () / /( ) : x  2y  2z  5  0 và cách ( A 2; 1  ;4) một khoảng k  4
Ví dụ 4:Tìm M Ox và cách đều hai mặt phẳng ( ),( ) với () : x  2y  2z 1  0 và
() : 2x  2y z  5  0.
Ví dụ 5: Tìm M Oy và cách đều N 1; 4  ; 2
  và (): x y z 14  0.
Ví dụ 6: Cho A1;1; 
1 . Tìm M Oz sao cho MA  3d  , A (Oxy)
Ví dụ 7: Cho (P) : x y  5z 14  0; M(1; 4  ; 2  )
a) Tính d(M,(P))
b) Tìm tọa độ hình chiếu của M trên (P). Từ đó suy ra tọa độ M’ là điểm đối xứng của M trên (P). BÀI TẬP ÁP DỤNG
Bài 1. Cho hai mặt phẳng () : 2x y  2z  4  0; () : 4
x  2y  4z  9  0
a) Tính d , 
b) Viết phương trình mặt phẳng (P) cách đều hai mặt phẳng ( ),( ) 1 17 Đáp số: a) ;
b)2x y  2z   0 6 4
Bài 2. B2009. Cho A1;2;  1 ;B 2  ;1;3;C2; 1  ;  1 ;D0;3; 
1 . Viết phương trình mặt phẳng
() qua A, B và d C,()  d , D ()
Đáp số: ( ) : 4x  2y  7z 15  0; ( ) : 2x  3z  5  0; 1 2 Page 16
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Bài 3. Cho A1;2; 
1 ;B0;4;0;C0;0;4; . Viết Phương trình mặt phẳng () chứa đường
thẳng OA và cách đều hai điểm B, C.
Đáp số: ( ) : 3x y z  0; ( ) : x y z  0; 1 2
Bài 4. B2010. Cho A1;0;0;B0; ;
b 0;C0;0;c, ,
b c  0 và (P) : y z 1  0. Xác định b, c 1
biết (ABC)  (P) và d( ; O (ABC))  3. 1
Đáp số: b c  2
Bài 5. Cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là những số dương thay đổi sao cho 2 2 2
a b c  3. Xác định a, b, c để khoảng cách từ O đến (ABC) lớn nhất
Đáp số: a b c  1
VẤN ĐỀ 4. Góc của hai mặt phẳng Phương pháp
Cho hai mặt phẳng (), () có phương trình:
(): A x B y C z D  0 1 1 1 1
(): A x B y C z D  0 2 2 2 2
Góc giữa (), () bằng hoặc bù với góc giữa hai VTPT n , n . 1 2 n n
A A B B C C cos(),() . 1 2 1 2 1 2 1 2   n . n 2 2 2 2 2 2 1 2
A B C . A B C 1 1 1 2 2 2 Chú ý:  0  (),() 0 0  90 .
 ()  ( )  A A B B C C  0 1 2 1 2 1 2
Ví dụ 1: Viết phương trình mặt phẳng ( ) đi qua A3;0;0, C 0;0; 
1 và cắt trục tung tại điểm 7 B sao cho A
BC có S  2
Ví dụ 2: Viết phương trình mặt phẳng ( ) đi qua A0;0;3, C 0;0; 
1 , cắt trục hoành tại điểm
B và ( ) tạo với (Oxy) một góc 300.
Ví dụ 3: Viết phương trình mặt phẳng (P) đi qua A3;0;0,B2;1;0 và tạo với (Oxy) một góc 0 60 . 6
Hướng dẫn: (P) : x y z  3  0 3
Ví dụ 4: Cho ( ) : x  2y  3z  6  0; ( ) :m  
1 x  m  2y  4m 6  0. Tìm m để  P Q  5 cos ( ),( )  2 7 Page 17
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. 7
Hướng dẫn: m  1
 ; m   2
mx  2y mz 12  0 
Ví dụ 5: Tìm m để góc giữa hai mặt phẳng sau bằng  : x my z  7  0  0    45
VẤN ĐỀ 5. Ứng dụng giải toán hình học không gian a 6
Ví dụ 1: A2003. Cho hình chóp .
S ABC có tam giác ABC đều cạnh a, SA  , SA  (ABC). 2 a 2 Tính d  , A (SBC).
Đáp số: d  2 Ví dụ 2: B2004. Cho . S ABC 0 ,SA  3 ,
a SA  (ABC), AB BC  2 , a ABC 120 . Tính d  , A (SBC) 3a .
Đáp số: d  2
Ví dụ 3: A2007. Cho lăng trụ đứng AB .
C A'B'C' có AB  , a AC  2 , a AA'  2a 5, 0
BAC  120 . M là trung điểm của CC’. Chứng minh: MB MA' và d  ,
A (A'BM. a
Đáp số: d A A BM  5 ,( '  3
Ví dụ 4: DB A2003. Cho lăng trụ đứng AB .
C A'B'C' có A
BC cân AB AC a BB'  , a 0
BAC  120 . I là trung điểm của CC’. Chứng minh: A
B'I vuông và tính
cos(ABC),(AB'I). Đáp số: ABC AB I  30 cos ( ),( ' )  10
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA a 3 ,
SA  ABCD.Tính d ,
A SBC và khoảng cách từ trọng tâm G của tam giác SAB đến SACa 3 a 2 .
Đáp số: d  ,
A SBC  ;
d G,SAC  2 6
Ví dụ 6: Cho hình thoi ABCD tâm O cạnh a, AC a . Từ trung điểm H của AB dựng
AH  (ABCD),SH a. Tính d  ;(
O SCD và d ;( A SBCa 21 2a 57
Đáp số: d O,SCD  ; d  ,
A SBC  14 19
Ví dụ 7: Cho hình hộp chữ nhật ABC .
D A'B'C'D' có A0;0;0,B ;
a 0;0;D0; ; a 0,
A'0;0;b với ,
a b  0, M là trung điểm CC’.
a) Tính VBDA'M a b) Tìm tỉ số A BD MBD b để ( ' ) ( ) Page 18
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Ví dụ 8: Cho tứ diện OABC có các cạnh OA, OB, OC vuông góc với nhau từng đôi một. Gọi
, , lần lượt là các góc hợp bởi các mặt phẳng (OAB), (OBC), (OCA) với mặt phẳng (ABC).
Bằng phương pháp toạ độ, chứng minh rằng:
a) Tam giác ABC có ba góc nhọn
b) b) cos2   cos2   cos2   1
Ví dụ 9. Cho hình chóp .
S ABCD có ABCD là hình chữ nhật, AD  , a AB  2 , a SD  , a SB  2 ,
a SBD  ABCD. Tính V d  , A SBC S.ABCD và  Page 19
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
CHỦ ĐỀ 3. MẶT CẦU VÀ CÁC BÀI TOÁN LIÊN QUAN
VẤN ĐỀ 1. Viết phương trình mặt cầu
Phương pháp: Muốn viết phương trình mặt cầu ta cần xác định tâm và bán kính của nó
 S(I,R) : x  a2  y  b2  z  c2 2  R (1)
 S(I,R) : x2  y2  z2  2ax  2by  2cz  d  0 (2) ( vôùi a2 b2  c2  d  0 ) 2 2 2
Tâm I(a ; b ; c) và R a  b  c  d
Các trường hợp cơ bản:
TH1: Mặt cầu tâm I đi qua A. Lúc đó bán kính là R=IA
TH2 : Viết phương trình mặt cầu đường kính AB
 Tâm I là trung điểm AB  Bán kính R=IA
TH 3: Mặt cầu ngoại tiếp tứ diện ABCD 2 2 2
 Bước 1: Giả sử mặt cầu có phương trình: x  y  z  2ax  2by  2cz d  0
 Bước 2: Vì A,B,C,D  mc(S) nên ta thiết lập được hệ 4 phương trình 4 ẩn, giải hệ ta được a,b,c,d I ()
TH 4: Mặt cầu đi qua A,B,C và có tâm 2 2 2
 Bước 1: Giả sử mặt cầu có phương trình: x  y  z  2ax  2by  2cz d  0
 Bước 2: Vì A,B,C  mc(S) và I thuộc mặt phẳng ( ) nên ta thiết lập được hệ 4 phương
trình 4 ẩn, giải hệ ta được a, b, c, d
Ví dụ 1: Cho A 1  ;0; 3  ;B1;2; 
1 . Viết phương trình mặt cầu (S) a) Có đường kính AB
b) Có tâm I Oy và đi qua hai điểm A, B 2 2 2 2 2 2 Đáp số: )
a x  y  
1  z  2  3; )
b x  y   1  z  11
Ví dụ 2: Viết phương trình mặt cầu (S) đi qua ba điểm A1;2;4;B1; 3  ;  1 ; C2;2; 3   và có 2 2 2
tâm I (Oxy) .
Đáp số: (S) : x y z  4x  2y  21  0
Ví dụ 3: Cho 4 điểm A1;5;3;B4;2; 5  ;C5;5;  1 ;D1;2;4 a) Viết (S ) I z
1 đi qua A, B, C và có tâm (Ox ) b) Viết (S ) 2 đi qua A, B, C, D 2 2 2 22 2 147 2 2 2
Đáp số: a) x y z x y
 0; b) x y z x  4y  2z 19  0 5 5 5
Ví dụ 4: Lập phương trình mặt cầu đi qua ba điểm A2;1; 
1 ;B1;1;0; C0;2;4 và R  5. 2 2 2 2 2 2 4 38 32 8
Đáp số: S :x y z  2y  4z  0; S x y z x y z   0 1   2 9 9 9 3
VẤN ĐỀ 2. Vị trí tương đối của mặt phẳng và mặt cầu 2 2 2
Phương pháp: Cho (S) : x   a  y   b  z   2
c  R và  : Ax + By + Cz + D = 0
Gọi d = d(I,) : khỏang cách từ tâm mc(S) đến mp : Page 20
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
TH 1: d > R : (S)   = 
TH 2: d = R :  tiếp xúc (S) tại H (H: tiếp điểm, : tiếp diện)
Tìm tiếp điểm H (là hình chiếu của tâm I trên mp)
 Bước 1 : Viết phương trình đường thẳng (d) qua I và vuông góc mp . Ta có a nd
 Bước 2 : Tọa độ H là nghiệm của hpt : (d) và ()
(S): x  a2  y  b2  z  c2  2 R
TH 3: d < R :  cắt (S) theo đường tròn có pt   Ax :  By  Cz  D  0
Tìm bán kính r và tâm H của đường tròn:  Bán kính 2 2 r  R d (I,)
 Tìm tâm H ( là hchiếu của tâm I trên mp)
Chú ý: Cách tìm giao điểm của đường thẳng và mặt cầu x  xo  a t 1  d : 2 2 2 y  y
(S) : x  a  y b  z  c  o  a2t (1) và       2 R (2)  z  zo  a3t
 Bước 1 : thay phương trình (1) vào pt (2), giải tìm t,
 Bước 2 : Thay t vào (1) được tọa độ giao điểm
Các trường hợp cơ bản : m Pt aët c aàu taâm I
TH 1 : Mặt cầu tâm I tiếp xúc mp : (S ) A.x  . B y
C.z D I I I  R d (I, )  2 2 2 AB C
TH 2: Viết phương trình mặt phẳng  tiếp xúc (S) và  
 Bước 1: Mặt phẳng  vuông góc  nên có : n a  ( , A , B C)  .
Do đó  : Ax + By + Cz + D = 0 ( A,B, C đã biết)
 Bước 2: Để tìm D ta sử dụng thêm giải thiết d(I ,  ) = R
Ví dụ 1: DB B2006. Viết phương trình mặt cầu (0
O ;0;0); A0;0;4; (
B 2;0;0) và tiếp xúc với
(P) : 2x y z  5  0 2 2 2 .
Đáp số: (S) : x   1  y  
1  z 2  6
Ví dụ 2: Viết phương trình mặt cầu (S) có tâm thuộc trục tung và tiếp xúc với hai mặt phẳng
(): 2x y 3z 5  0; (): 2 x y 3  z 1  1 0
Đáp số: x  y  2 2 2 32 3  z  7
Ví dụ 3: Cho A1;0;  1 ;B1;2;  1 ;C0;2;0
a) Viết phương trình mặt cầu đi qua O, A, B, C
b) Gọi G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng vuông góc với OG và tiếp xúc với (S). Đáp số:
a x  y  2 2 2 32 ) 3  z  ; )
b x  2y  3  10  0 7
Ví dụ 4: Viết phương trình mặt cầu Page 21
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. a) Có tâm I (2; 1
 ;4) và tiếp xúc với (Oxy) b) Có tâm (0
O ;0;0) và tiếp xúc với mặt cầu tâm J(3; 2
 ;4) và có bán kính R' 1 Đáp số:
a) (S) : x  22  y  2
1  z  42 16
b) (S ) : x y z   29  2
1 ; (S ) : x y z   29  2 2 2 2 2 2 2 1 1 2
Ví dụ 4: Lập phương trình mặt cầu có bán kính bằng 2 và tiếp xú với (Oxy) tại M(3;1;0)
Đáp số: I 3;1; 2  ; I 3;1;2 1   2 
Ví dụ 5: Cho A1;2;3;B3;5;4;C 3;0;5
a) Lập phương trình mặt phẳng qua A, B, C
b) Lập phương trình mặt cầu nhận đường tròn ngoại tiếp tam giác ABC làm đường tròn lớn. 2 2 2  39   89   81 667
Hướng dẫn: a)  ABC :4x y  5z 13  0; (S) : x   y   z    7   14   14        14
Ví dụ 7: Cho M 2;1; 3
 ;(P ) : x y  2z  3  0;(P ) : x y  2z  9  0; 1   1 2
a) Viết phương trình mặt cầu tiếp xúc với (P M (P ) 1) tại 1 và tiếp xúc với 2
b) Viết phương trình mặt cầu tiếp xúc với (P ) M (P ) 1 tại 1 và cắt 2 theo thiết diện là đường tròn lớn. 2 2 2 2 2 2 Đáp số: )
a (S) : x 3 y 2  z   1  6; )
b (S) : x  4  y 3  z   1  24 BÀI TẬP ÁP DỤNG
Bài 1. Cho M 2;5; 0
(P ) : 3x  2y z  4  0; P : x 3y  2z 1  0 1   và hai mặt phẳng 1  2
a) Viết phương trình mặt cầu tiếp xúc với (P ) M (P ) 1 tại 1 và tiếp xúc với 2
b) Viết phương trình mặt cầu tiếp xúc với (P ) M (P ) 1 tại 1 và cắt 2 theo thiết diện là đường tròn lớn.
c) Viết phương trình mặt cầu tiếp xúc với (P ) M (P ) 1 tại 1 và cắt 2 theo thiết diện là 21
đường tròn có bán kính r  2 Hướng dẫn 2 2 2 2 2 2  11  2  56
a) (S ) : x  4
y  9  z  2  56; (S ) : x  4  y   z   1       2    3   3     9 2 2 2
b) (S) :  x  8  y  
1  z  2  56 2 2 2  15   29   7  686 c) (S) : x   y   z    3   3   3        9 Page 22
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. 2 2 2
Bài 2. Cho (P) : 2x  3y  2z  3  0; (S) : x  8  y  8  z  7  68
a) Xác định vị trí tương đối của (P) và (S)
b) Viết phương trình mặt phẳng song song với (P) và tiếp xúc với (S)
c) Viết phương trình mặt phẳng song song với (P) và cắt mặt cầu theo thiết diện là đường tròn lớn
d) Viết phương trình mặt phẳng song song với (P) và cắt mặt cầu theo thiết diện là
đường tròn có bán kính r  51
e) Viết phương trình mặt cầu (S’) đối xứng với (S) qua (P). Đáp số:
b)2x  3y  2z  20  0; 2x  3y  2z  88  0
c)(Q) :2x  3y  2z  54  0
d)(Q ) :2x  3y  2z  37  0; (Q ) :2x  3y  2z  71  0; 1 2
e)x  42  y 102  z  52  68 2 2 2
Bài 3. Cho (P) : 2x y  2z  5  0; (S) : x  3  y  z  4  9
a) Chứng tỏ (P) tiếp xúc với (S). Tìm tọa độ tiếp điểm
b) Viết phương trình mặt phẳng song song với (P) và tiếp xúc với (S)
c) Viết phương trình mặt phẳng song song với (P) và cắt mặt cầu theo thiết diện là đường tròn lớn
d) Viết phương trình mặt cầu (S’) đối xứng với (S) qua (P). Đáp số: a M
b Q x y z  c x y z  d x  2 y 2 2 ) 1;1;2 ; )( ) :2 2 23 0; ):2 2 14 0; ) 1 2  z  9 2 2 2
Bài 4. Cho (P) : x  2y  3z 10  0; (S) : x  2  y  z  2  56
a) Chứng tỏ (P) cắt (S) theo thiết diện là đường tròn. Tìm tọa độ tâm và bán kính đường tròn
b) Viết phương trình mặt phẳng song song với (P) và tiếp xúc với (S)
c) Viết phương trình mặt phẳng song song với (P) và cắt mặt cầu theo thiết diện là đường tròn lớn.
d) Viết phương trình mặt cầu (S’) đối xứng với (S) qua (P). Đáp số: a)J 3;2 
;1 ;r  42 ; b)(Q ) :x  2y  3z  32  0; (Q ) :x  2y  3z x  2y  3z  24  0; 1 2
c)2x  2y  3z  4  0; d) x  2y  3z 18  0; )
e (S') : x  42  y  42  z  42  56 2 2 2
Bài 5. Cho (S) : x y z  2x  2y  2z  6  0 . Viết phương trình mặt phẳng song song với
() : x  2y z 1  0 và cắt (S) theo thiết diện là đường tròn (C) có S  3 .
Đáp số:  : x  2y z  2  0;
 : x  2y z 10  0 1   2 Page 23
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. 2 2 2
Bài 6. Cho (S) : x y z  2x  2y  2z  6  0 .
a) Viết phương trình mặt phẳng đi qua A4;0;0;B0;0;8 và tiếp xúc với (S)
b) Viết phương trình mặt phẳng qua C 2;1; 
1 ;D1;1;0 và cắt (S) theo thiết diện là đường
tròn (C) có S  6 Đáp số:
a) ( ) : 2x  2y z  8  0; ( ) : 8x y  4z  32  0; 1 2
b) ( ) : x y z  0; ( ) : x  5y z  6  0; 1 2
Bài 7. Lập phương trình mặt cầu đi qua
A1;0;0;B0;1;0;C0;3;2 và cắt
(P) : 2x  2y z  0 theo thiết diện là đường tròn có bán kính bằng 1. 2 2 2 2 2 2
Đáp số: (S ) : x y z  2x  2y  4z 1  0;(S ) : x y z  8x  8y  2z  7  0; 1 2 2 2 2
Bài 8. Cho (S) : x  5  y  3  z  3  37;(P) : 2x y  2z 1  0
a) Chứng tỏ (P) cắt (S) theo giao tuyến là một đường tròn (C). Xác định tâm và bán kính của (C)
b) Lập phương trình mặt cầu chứa (C) và  Có tâm thuộc ( )
Q : x y z  9  0  Đi qua A4;2; 2    Tiếp xúc với ( )
Q : 3x y  7  0 Đáp số: H(1;1; 1  )
a) (C) : r   1 b) S  2 2 2
: x y z  6x  2y 10z  2  0 1  
LUYỆN TẬP PHƯƠNG TRÌNH MẶT CẦU
Bài 1. Cho bốn điểm A(2;-1;6), B(-3;-1;-4), C(5;-1;0), D(1;2;1).
a) Tính bán kính đường tròn nội tiếp tam giác ABC và khoảng cách từ D tới (ABC)
b) Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD Hướng dẫn: Page 24
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. S
a) Baùn kính cuûa ñöôøng troøn ngoaïi tieáp AB  C laø r = ABC p
AB BC CA p
.Ñeå yù: AC.BC  0  ABC vuoâng taïi C 2 30 3V r=
 5. Khoaûng caùch töø D tôùi (ABC) laø d(D,(ABC))= ABCD ; 6 5 SABC 1 V
 AB, AC.AD . ÑS : 3 ABCD 6  
b) Goïi I(x;y;z) laø taâm ñöôøng troøn ngoaïi tieáp töù giaùc ABCD:  1 x    2 2  2 IA IB   2 2  13 1525
IA=IAB=IC=ID  IA IC  y   . Baùn kính R IC  . 3 36  2 2 IA ID    z  1   2 2 2
Caùch2: Goïi(S) : x y z  2ax  2by  2cz d  0
Thay toïa ñoä A,B, C, D vaøo (S) ta ñöôïc heä phöông trình 4 aån a,b,c,d
BTTT: Cho 4 điểm A(0;1;0);B(2;3;1);C(-2;2;2);D(1;-1;2)
a) Chứng minh rằng tứ diện ABCD vuông tại A
b) Viết phương trình mặt cầu ngoại tiếp tứ diện
Hướng dẫn và đáp số:
a)chöùng minh AB, AC, AD ñoâi moät vuoâng goùc nhau 2 2 2  1   3   5  27 b) x   y   z    2   2   2        4
Bài 2. Cho hình lăng trụ tam giác ABC.A’B’C’ với A(-1;6;-1), B(-4;6;2), C(-1;3;2), A’(5;12;5)
a) Chứng minh rằng hình lăng tụ đã cho là hình lăng trụ đều và tính thể của nó
b) Tìm toạ độ của tâm đường tròn ngoại tiếp tam giác A’B’C’ và viết phương trình của mặt
cầu ngoại tiếp hình lăng trụ ABC.A’B’C’ Hướng dẫn: A
BC laø tam giaùc ñeàu
a)ycbt  AA'(ABC)
b)Vì tam giaùc ABC laø tam giaùc ñeàu neân taâm truøng vôùi troïng taâm G,
G(-2;5;1) laø troïng taâm cuûa ABC
Goïi G' laø troïng tam cuûa tam giaùc A'B'C', ta coù
GG'  AA'  G'(4;11;7).Hình laêng truï ABC.A'B'C' laø hình laêng truï ñeàu neân (S)
ngoaïi tieáp hình laêng truï naøy coù taâm laø trung ñieåm I(1;8;4) cuûa GG', R=IA= 33 Page 25
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Bài 3. ĐHCĐ 2005 B . Trong không gian với hệ tọa độ Oxyz cho hình lăng trụ đứng ABC.A1B1C1
với A(0;-3;0), B(4;0;0), C(0;3;0), B1(4;0;4).
a) Tìm tọa độ các đỉnh A1, C1. Viết phương trình mặt cầu có tâm là A và tiếp xúc với mặt phẳng (BCC1B1).
b) Gọi M là trung điểm của A1B1. Viết phương trình mặt phẳng (P) đi qua hai điểm A, M và song
song với BC. Mặt phẳng (P) cắt đường thẳng A1C1 tại điểm N. Tính độ dài MN. 2 2 2 2
Bài 4. Cho phương trình x y z  2(m 1)x  4my  2z  6m 1  0 (1)
Xác định m để phương trình (1) là phương trình của mặt cầu. Khi đó, tìm m để bán kính của mặt
cầu đạt giá trị lớn nhất. Hướng dẫn: 2 2 2
(1) laø phöông trình maët caàu  A  B C D  0  1   m  3 2
Khi ñoù: R= m  2m  3 2
Xeùt haøm soá f(m)=-m  2m  3,m ( 1  ;3) R  2 khi m=1 max
Bài 5. Cho mặt phẳng (P) và mặt cầu (S) có phương trình lần lượt là: 2 2 2
2x y 3z  4  0; x y z  6x  2y  2z  3  0 . Lập phương trình mặt phẳng ()
song song với (P) và tiếp xúc với (S). Hướng dẫn:
() // (P) neân () coù daïng 2x - y -3z D  0 (D  4).
() tieáp xuùc vôùi (S)  d(I,())=R  D=24 hoaëc D=-4
Bài 6. Lập phương trình mặt cầu (S) có tâm I thuộc mặt phẳng (Oyz) và đi qua A(0;0;4), B(2;1;3), C(0;2;6) Hướng dẫn:
Maët caàu (S) ñi qua A,B,C coù taâm I thuoäc caùc maët phaúng trung tröïc ()
cuûa AB vaø maët phaúng trung tröïc ( ) cuûa AC
() : 2x y - x 1  0; () : y z -6  0
2x y - x 1  0   
Toïa ñoä I laø nghieäm cuûa heä phöông trình: 5 7
y z -6  0  I 0; ;    7 2  z  0  
BTTT:Lập phương trình mặt cầu (S) có tâm I thuộc mặt phẳng () : 2x y z  3  0 và đi qua
A(-3;6;1), B(2;3;-3), C(-6;2;0) 2 2 2  39   51  57  4651
Đáp số: (S) : x   y   z    10   10   10        100
Bài 7. Lập phương trình mặt cầu (S) tiếp xúc với ( )
Q : x  3  0 và đi qua A(1;2;-1), B(-1;0;3), C(3;-2;1) Hướng dẫn: Page 26
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
(S) ñi qua A,B,C neân taâm I cuûa (S) thuoäc maët phaúng trung tröïc () cuûa
AB vaø maët phaúng trung tröïc ( ) cuûa AC
() : x y -2z 1  0; () : x -2y z -2  0.
x y  2z 1  0
Do ñoù I thuoäc ñöôøng thaúng  : x2yz2 0 x t    
  y    t I   I t   t t I Q t 3 2 2 : 1 .
; 1 ; vaø d ;( )  IA      t  3  2 2 z t
Bài 8. ĐHCĐ 2004 K.D Trong không gian với hệ toạ độ Oxyz cho ba điểm A(2;0;1), B(1;0;0),
C(1;1;1) và mặt phẳng (P) : x + y + z – 2 = 0. Viết phương trình mặt cầu đi qua ba điểm A, B, C và
có tâm thuộc mặt phẳng (P).
IA IB IC
Hướng dẫn: I x y z 2 2 2
; ; laø taâm maët caàu (S).  I (p)
BTTT: Lập phương trình mặt cầu (S) tiếp xúc với () : 2x  2y z 12  0 và đi qua A(1;2;-1),  32 41 83   9 38  B ; ; ;C  ; ; 1   9 9 9   5 5      Đáp số:
(S ) : x  22  y  42  z  52  49; 1 2 2 2  156   103   149  519841 (S ) : x   y   z   2  5   5   20        400
Bài 9. ĐHCĐ 2009 A Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P):
2x  2y z  4  0 2 2 2
và mặt cầu (S): x y z  2x  4y  6z 11  0 . Chứng minh rằng mặt
phẳng (P) cắt mặt cầu (S) theo một đường tròn. Xác định toạ độ tâm và bán kính của đường tròn đó.
BTTT. Trong hệ trục tọa độ Oxy cho đường tròn (C) có phương trình
x  2 y  2 z 2 2 2 3  5  . Tìm tâm và bán kính
x  2y  2z 1  0
Bài 10. Cho 4 điểm A(1;2;1);B(2;0;-1);C(1;3;-4);D(0;-2;2). Chứng minh rằng tập hợp những điểm M 2 2 2 2
thỏa mãn : MA MB MC  4MD là một mặt cầu. Viết phương trình mặt cầu đó. 2 2 2
Hướng dẫn: M( ; x ; y )
z .(S) : x  4 y 3 z 12  334 Page 27
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
CHỦ ĐỀ 4. ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN
A. CƠ SỞ LÝ THUYẾT
1. Vectơ chỉ phương của đường thẳng: u  0 được gọi là vtcp của đường thẳng d nếu giá của u
song song hoặc trùng với d
2. Các dạng phương trình đường thẳng:
Phương trình tham số của đường thẳng: (d) qua M(xo ;yo ;zo) có vtcp a = (a1;a2;a3) x  x  a t o 1  PTTS: (d) 
:y  y  a t ; t R o 2 z  z  a t  o 3 x  x y  y z - z  o o 0 PTCT: (d) :   a a a 2 3 1
PT tổng quát của (d) là giao tuyến của 2 mp 1 và 2 A x  B  B C C A A B
y C z  D  0 (d) 1 1 1 1 1 1 : 1 1 1 1
. Lúc đó véctơ chỉ phương a   , , 
A x  B y C z  D  0 B C C A A B 2 2 2 2  2 2 2 2 2 2 
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
VẤN ĐỀ 1. Viết phương trình đường thẳng
Phương pháp chung:
 Tìm một điểm trên d và một vtcp của d
 Tìm 2 mặt phẳng cùng đi qua d thì d là giao tuyến của 2 mặt phẳng
Các trường hợp cơ bản: quaA (hayB)
TH 1: Đường thẳng (d) đi qua A,B: (d ) Vtcp a AB d qua A
TH 2: Đường thẳng (d) qua A và song song (): (d )   ( Vì d ) ( //  n ) eân v tc p a  a d  qua A
TH 3 : Đường thẳng (d) qua A và vuông góc mp: (d )   ( Vì d )   ( n ) eân v tcp a  n d  qua A
TH 4 : Đường thẳng (d) qua A và vuông góc (d    1),(d2): (d ) vtcp a  a [ a , ] d1 d2 Một số lưu ý:  Nếu d d d d
1 qua A và cắt 2 thì 1 nằm trong mặt phẳng đi qua A và chứa 2  Nếu d d d
1 qua A và vuông góc với 2 thì 1 nằm trong mặt phẳng đi qua A và vuông góc với d2
 Nếu d qua A và song song với ( ) thì d chứa trong mặt phẳng đi qua A và song song với ( ) Page 28
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. x 1 y  2 z
Ví dụ 1 : Cho d :  
; () : 2x y  3z  6  0 1 4 1 
. Viết phương trình đường thẳng x  1   3t  
đi qua giao điểm A của d và ( ) và song song với d ' : y  3   t z  2  t  x  1 t
Đáp số:  : y  2   t z  2t
Ví dụ 2: Cho A2;0; 3  ;B4; 2  ; 
1 và mặt phẳng (P): x y  2z  4  0
Viết phương trình đường thẳng d chứa trong (P) sao cho d cách đều A và B x  3   4t
Đáp số:  : y  6   3t z  2  t  x  1 t
Ví dụ 3: Cho A1;4;2;B 1
 ;2;4 và mặt phẳng (): y  2   t z  2t
a) Viết phương trình đường thẳng đi qua trọng tâm G của OAB  và  (OAB) 2 2
b) Tìm M  sao cho MA MB nhỏ nhất x  2t
Đáp số: a) d : y  2  t ; b)M  1  ;0;4 z  2  t
Ví dụ 4: DB B2009. Cho A1;0;  1 ;B2;3;  1 ;C1;3; 
1 . Viết phương trình tham số của đường
thẳng qua trực tâm A
BC và vuông góc với (ABC).  x  6  t   10
Đáp số:  : y   2t 3   3 z    3t  2
Ví dụ 5: ĐHA 2011. Cho A2;0;  1 ;B0; 2
 ;3. Tìm M (P):2x y z  4  0 sao cho  6 4 12 
MA MB  3.
Đáp số: M 0;1;3 ; M  ; ; 1    7 7 7    Page 29
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Ví dụ 6: Cho A2;1;0;B0;1;2;C 0;0; 
1 . Tìm M (P): x y z  2  0 sao cho   MA 1 1
MB và MC nhỏ nhất. Đáp số: M ; 2  ;  2 2   
Dạng 1. Viết phương trình đường thẳng (   (P) hoặc / / (P) ) qua điểm A và vuông góc với
đường thẳng d Phương pháp: x 1 y z  3
Ví dụ 1: Cho d :  
;(P) : 2x  5y  3z  8  0; A3; 4  ;  1 2 1  3
a) Viết phương trình đường thẳng   1 qua A, nằm trên (P) và d b) Viết phương trình  Oxy  1 qua A, song song với  và d Hướng dẫn: x  3  t
x  3 y  4 z 1 a) : ; b) :      y  4   2t 1 2 9 6 4  z 1 
x 1 y  4 z 1
Ví dụ 2: Cho d :  
;() : 2x y  2z  9  0 1  6 4 
a) Tìm I d sao cho d I;()  2
b) Tìm A d  ( ) . Viết phương trình đường thẳng đi qua A, chứa trong ( ) và vuông góc với d Hướng dẫn: x t   a d I   I(3; 7;1) ) ;( ) 2 ; b) :      y  1  I( 3  ;5;7) z  4  t
Dạng 2. Viết phương trình đường thẳng qua A, vuông góc với d d
1 và cắt 2 Phương pháp: Cách 1:
 Bước 1: Chuyển d2 về dạng tham số
 Bước 2: Giả sử d cắt d2 tại B, Bd  2
toạ độ B có chứa tham số
 Bước 3: d vuông góc với d1  AB u 1 d
Cách 2:
 Viết phương trình mặt phẳng (P) qua A và vuông góc với d1.
 Viết phương trình mặt phẳng (Q) chứa A và d2. Khi đó  = (P)  (Q). x  1 
x 1 y  2 z
Ví dụ 1: Cho d : 
 ; d : y t 1 2 3 1 1 z 1 tPage 30
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Viết phương trình đường thẳng  qua A0;1;  1 , vuông góc d d 1 và cắt 2 x  t
Hướng dẫn:  : y  1 t z 1 2t  x  3   2t
Ví dụ 2: Cho d : y  1 t
. Viết phương trình đường thẳng  qua A0;1;  1 , vuông góc và z  1   4t  cắt d x  4   3t
Hướng dẫn:  : y  2   2t z  4  t
Ví dụ 3: Cho d là giao tuyến của   : 5x y z  2  0;  : x y  2z 1  0 . Viết phương
trình đường thẳng  qua A2; 1
 ;0, vuông góc và cắt d .
x  2  2t
Hướng dẫn:  : y  1  z  t
Dạng 3. Viết phương trình đường thẳng qua A, song song với (P) và cắt d Phương pháp
Ví dụ 1: Viết phương trình chính tắc của đường thẳng  đi qua A3; 1
 ;4 , cắt trục Oy và song
song với (P) : 2x y  0
x  3 y 1 z  4 Hướng dẫn:  :   3  6 4
Ví dụ 2: Viết phương trình chinhd tắc của đường thẳng  đi qua A3; 2  ; 4  , cắt
x  2 y  4 z 1 d :   P x y  3 2  2 và song song với ( ) : 2 0
x  3 y  2 z  4 Hướng dẫn:  :   2 4  7
Dạng 4. Viết phương trình đường thẳng d nằm trong mặt phẳng (P) và cắt cả hai đường thẳng d1, d2
Phương pháp: Tìm các giao điểm A = d1  (P), B = d2  (P). Khi đó d chính là đường thẳng AB.
Ví dụ: Viết phương trình tham số của đường thẳng nằm trong mặt phẳng (P) : y  2z  0 và cắt x  2  t x 1 y z  cả hai d :
  , d : y  4  2t 1 2 1  1 4 z 1 Page 31
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
VẤN ĐỀ 2. Vị trí tương đối của 2 đường thẳng trong không gian
Phương pháp: d u d u
1 qua M có vtcp d ; 2 qua N có vtcp d 1 2  d d
u u MN  1 chéo 2  , . 0  (không đồng phẳng) 1 d d2   d d
u u MN  1 , 2 đồng phẳng  , . 0  1 d d2   d du u  
u u MN  1 , 2 cắt nhau  , 0  và , . 0 1 d d2   1 d d2   d du u      1 , 2 song song nhau  , 0  và , 0 1 d d2   1 d u MN   d du u      1 , 2 trùng nhau  , 0  và , 0 1 d d2   1 d u MN  x  1 mt
x m  2t'  
Ví dụ 1 : Cho d : y m  2t
; d : y mt d d 1 2
. Tìm m để 1 chéo 2
z 1 m 3t    
z  1 m t'   m  2  Đáp số:  1 m    4
x  3 y  6 z 1
Ví dụ 2 : Cho A4;2;2;B0;0;7 và d :   2  2 1
a) Chứng minh d và AB cùng thuộc một mặt phẳng
b) Tìm C d sao cho tam giác ABC cân tại A Hướng dẫn: ) a A ,
B u .BM  0; )
b C1;8;2; C9;0; 2  d    x t
x 1 y 1 z  3 
Ví dụ 3: Cho d :  
; d : y 1 t 1 2 3 2 2  z  3   2t
a) Tìm giao điểm của d , d 1 2
b) Viết phương trình mặt phẳng chứa d , d 1 2 . Hướng dẫn: ) a I 2;3;  1 ; )
b () : 6x 8y z 11  0
Dạng 1. Viết phương trình đường thẳng đi qua điểm M và cắt cả hai đường thẳng d ,d 1 2 Phương pháp Cách 1:
 Bước 1: Chuyển d1 và d2 về dạng tham số
 Bước 2: Giả sử d cắt d1 và d2 lần lượt tại A và B
 Bước 3: Ba điểm A,B,M thẳng hàng  A ,
B AM cùng phương   A , B AM   0  
Cách 2: Gọi (P) = (M,d ), (Q) = (M, d ) . Khi đó d = (P)  (Q). Do đó, một VTCP của d có thể chọn 1 2
là a   P n , Q n  . Page 32
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. x  1 2t
x  2 y  3 z
Ví dụ 1: Cho A1; 1  ; 
1 và hai đường thẳng d : y t ; d :   1 2 1 2  1 z  3 t  a) Chứng minh d d 1 chéo 2
b) Viết phương trình đường thẳng qua A và cắt cả d ,d 1 2
x 1 y 1 z 1 Đáp số: d :   6 1 7 
Dạng 2. Viết phương trình đường thẳng d song song với đường thẳng và cắt hai đường thẳng d ,d 1 2 Phương pháp
Bước 1: Chuyển d1 và d2 về dạng tham số
Bước 2: Giả sử d cắt d1 và d2 lần lượt tại A và B
Bước 3: d //  nên AB / / u  A ; B u   0    
Cách 2: Viết phương trình mặt phẳng (P) chứa  và d1, mặt phẳng (Q) chứa  và d2. Khi đó d = (P)  (Q).
Chú ý: d vuông góc với (P) và cắt hai đường thẳng d ,d 1
2 thì ta làm tương tự. Cụ thể
 Bước 1: chuyển d1 và d2 về dạng tham số
 Bước 2: Giả sử d cắt d1 và d2 lần lượt tại A và B
 Bước 3: d vuông góc với (P) nên AB / /     ( n ) A ; B  ( n ) 0 P P
Ví dụ 1: Viết phương trình đường thẳng  / /Ox và cắt cả hai đường thẳng x y z 1
x  2 y 1 z 1 d :   ; d :   1 2 1 2 3 1  3 2  x t   8
Đáp số:  : y   5   7 z    5 x  1   2t x y 1 z  2 
Ví dụ 2. A2007. Cho d :  
, d : y 1 t 1 2 2 1  1 z  3  a) Chứng minh d d 1 chéo 2
b) Viết phương trình đường thẳng   (P) : 7x y  4z  0 và cắt hai đường thẳng d ,d 1 2 Page 33
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
x  2  7t
Đáp số:  : y t z  1   4t
Dạng 3. Viết phương trình đường vuông góc chung d của hai đường thẳng chéo nhau d ,d 1 2 Phương pháp Cách 1:
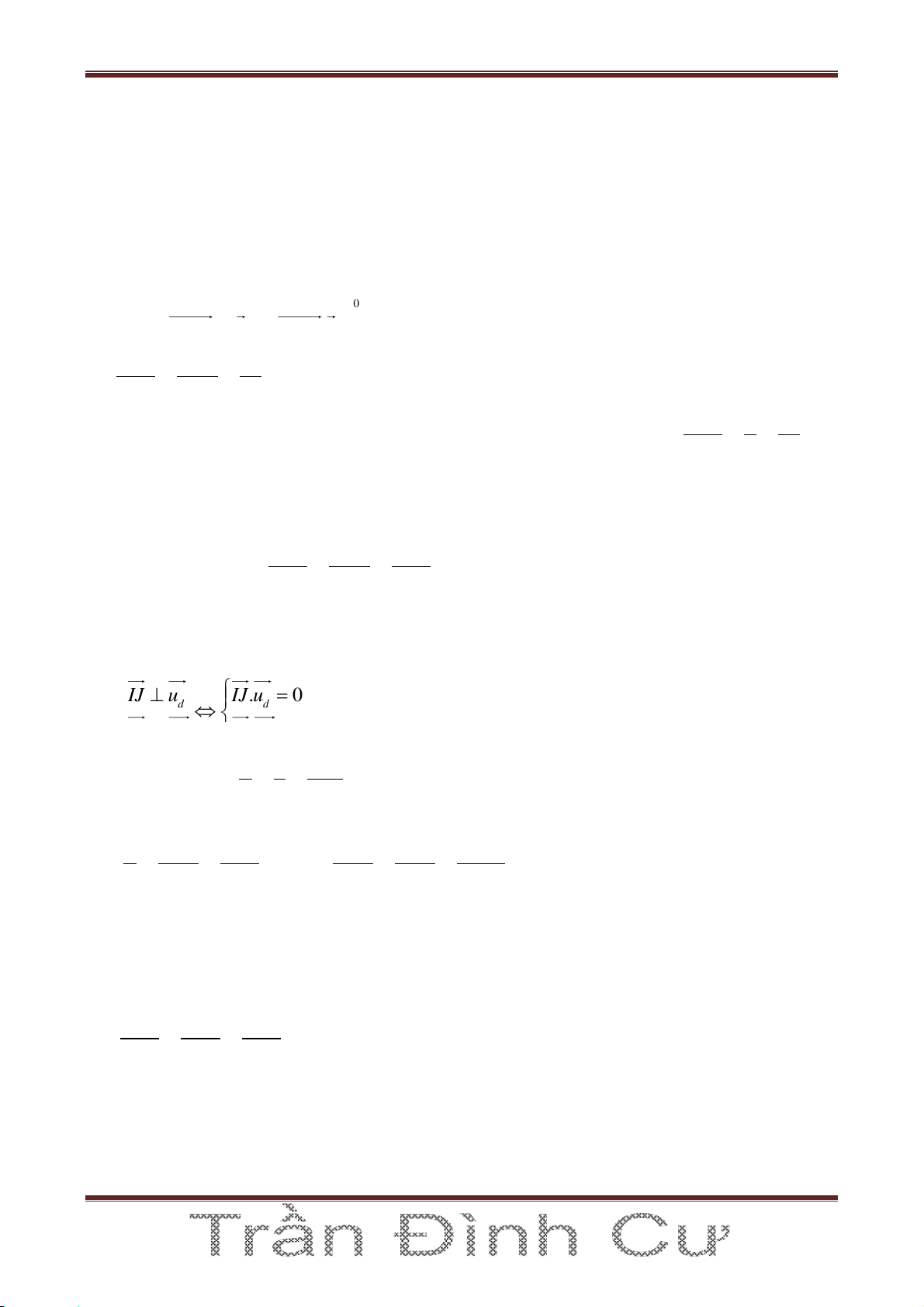
 Bước 1: Chuyển d1 và d2 về dạng tham số (t1,t2) IJ d IJ  u t   Bước 2: Lấy 1 1 1 I       1 d ; J d2.  . IJ d  2 IJ  t u   2 2
 Bước 3: d chính là IJ  Cách 2:  Vì d  d
a  a ,a
1 và d  d2 nên một VTCP của d có thể là: d d   . 1 2
 Lập phương trình mặt phẳng (P) chứa d và d1, bằng cách:
o Lấy một điểm A trên d1.
o Một VTPT của (P) có thể là: P
n  a, d a    . 1
 Tương tự lập phương trình mặt phẳng (Q) chứa d và d2.
Khi đó d = (P) (Q).x  1 tx  0  
Ví dụ 1: Cho d : y  0
, d : y  4  2t' 1 2 z 5 t     z  5  3t'   a) Chứng minh d d 1 chéo 2
b) Viết phương trình đường vuông góc chung của d d d ,d
1 và 2 . Suy ra khoảng cách giữa 1 2
x  4 y z  2
Hướng dẫn: b) d :   ;
d d ;d  2 17 1 2  2  3 2 x  1 tx  2   2t'  
Ví dụ 2: Cho d : y  2  t , d : y  t ' 1 2 z 2t   z t'  
a) Chứng minh d ,d 1
2 chéo nhau và vuông góc nhau
b) Viết phương trình đường vuông góc chung của d ,d 1 2
x y  3 z  2
Hướng dẫn: b) d :   ; 1 5 2
VẤN ĐỀ 3. Khoảng cách từ một điểm đến một đường thẳng và khoảng cách giữa hai đường thẳng chéo nhau
Dạng 1. Khoảng cách từ một điểm đến một đường thẳng Phương pháp: Page 34
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Ví dụ 1: B2003. Cho A2;0;0;B0;0;8; AC  0;6;0 . Tính khoảng cách từ trung điểm I của BC đến OA.
Đáp số: d  5
Ví dụ 2: A2009. Cho mặt phẳng và hai đường thẳng có phương trình x 1 y z  9 (P) : x
x 1 y  3 z 1
 2y  2x 1  0; :   ;  :   1 1 1 6 2 2 1 2 
Tìm M   :d M;( )  d M;(P) 1  2   .  18 53 3 
Đáp số: M 0;1; 3  ; M ; ; 1   235 35 35   x  3  t
x  2 y 1 z
Ví dụ 3: D2010. Cho  : y t ;  :  
M  : d M; 1 1 2 2 1 2 . Tìm 1  2  z t
Đáp số: M 4;1;1 ; M 7;4;4 1   2 
Dạng 2. Khoảng cách giữa hai đường thẳng chéo nhau
Phương pháp:
d d ;d  1 2  1
Ví dụ 1: Cho A1;0;0;B1;1;0;C 0;1;0; D0;0;2 . Tính d AC,BD . Đáp số: d 2 x  1 3t x  2 y z  4 
Ví dụ 2: Cho d :  
; d : y  2  t 1 2 3 2  2 z  1   2t
a) Chứng minh d ,d d d ,d 1 2 chéo nhau. Tính  1 2
b) Với A, B cố định thuộc d sao cho AB  117 . Khi C di động trên d’. Tìm giá trị nhỏ nhất của SABC Hướng dẫn: a d  39 ) d ,d  13; b)S   1 2  min
2 xảy ra khi CH MN
Dạng 3. Ứng dụng tọa độ giải toán không gian
Ví dụ 1: Cho lăng trụ AB .
C A'B'C' có đáy ABC vuông cân tại B, AA'  a 2,BA BC a .
Gọi M là trung điểm của BC. Tính d AM,B'Ca
Đáp số: d AM,B'C  7
Ví dụ 2: Cho hình lăng trụ đứng ABC.A’B’C’ có tất cả các cạnh đều bằng a , M là trung điểm của
AA’. Chứng minh MB CB' và d M , B B'C . Page 35
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. a
Đáp số: d MB B C 30 , '  10
Ví dụ 3: A2012. Cho hình chóp .
S ABC có đáy ABC là tam giác đều cạnh a. Hính chiếu vuông góc
của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA=2HB. Góc giữa đường thẳng
SC và mặt phẳng (ABC) bằng 600. Tính thể tích khối chóp S.ABC và tính khoảng cách giữa hai đường thẳng SA và BC.
VẤN ĐỀ 4. Các bài toán liên quan giữa đường thẳng và mặt phẳng
Phương pháp:
Các trường hợp cơ bản
TH 1: () đi qua một điểm M và một đường thẳng (d) không chứa M:
 Trên (d) lấy điểm A và VTCP u .    
Một VTPT của () là: n AM,u  
TH 2: () đi qua một điểm M và vuông góc với một đường thẳng (d):
VTCP u của đường thẳng (d) là một VTPT của ().
TH 3: () đi qua 2 đường thẳng cắt nhau d ,d 1 2
 Xác định các VTCP u ,u d ,d 1
2 của các đường thẳng 1 2    
Một VTPT của () là: n u ,u 1 2   .
 Lấy một điểm M thuộc d d 1 hoặc 2  M  ().
TH 4: () chứa đường thẳng d d d ,d
1 và song song với đường thẳng 2 ( 1 2 chéo nhau):
 Xác định các VTCP u ,u d ,d 1
2 của các đường thẳng 1 2 .    
Một VTPT của () là: n u ,u 1 2   .
 Lấy một điểm M thuộc d1  M  ().
TH 5: () đi qua điểm M và song song với hai đường thẳng chéo nhau d ,d 1 2 :
 Xác định các VTCP u ,u d ,d 1
2 của các đường thẳng 1 2 .    
Một VTPT của () là: n u ,u 1 2   .
TH 6: () đi qua một đường thẳng (d) và vuông góc với một mặt phẳng ():
 Xác định VTCP u của (d) và VTPT n của ().    
Một VTPT của () là: n , u n   .
 Lấy một điểm M thuộc d  M  (). x 1 y z  2
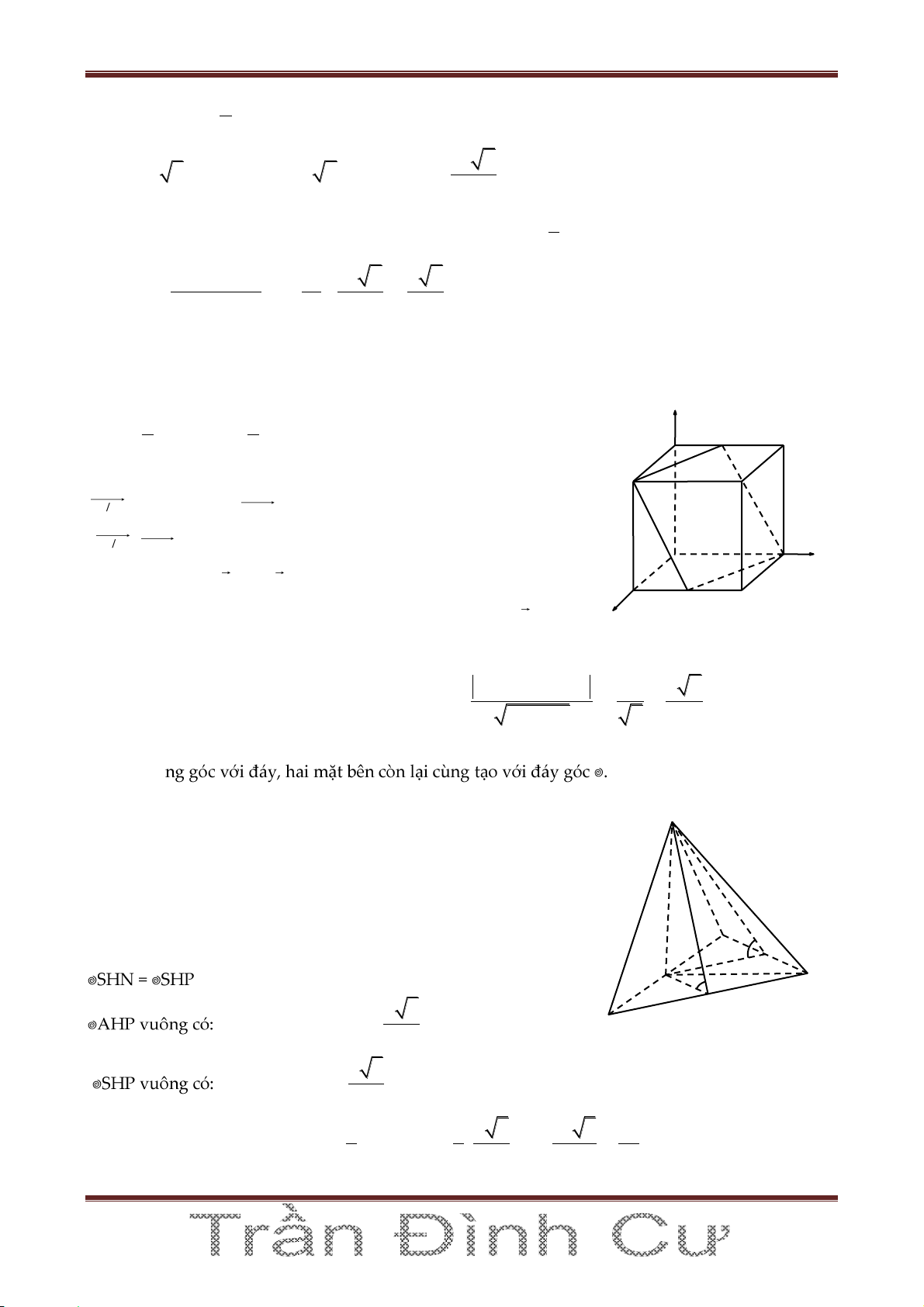
Ví dụ 1: Viết phương trình mặt phẳng qua A0; 1
 ;3 và chứa d :   1 2 2 
Đáp số: y z  3  0 Page 36
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. x  1 t x y 1 z 1 
Ví dụ 2: Cho A0;1;2, d :   ; d : y  1   2t 1 2 2 1 1  z  2  t
a) Viết phương trình ( ) qua A và song song với d ,d 1 2
b) Tìm M d , N d A M N 1 2 sao cho , , thẳng hàng
Dạng 1. Đường thẳng song song với mặt phẳng Ví dụ 1: D2009. Cho
A2;1;0;B1;1;2;C1;1;0 . Tìm D trên AB sao cho
CD / /(): x y z  20  0.
Đáp số: D 3;1; 2  
x 1 y  3 z
x  5 y z  5
Ví dụ 2: DB B2007. Cho hai đường thẳng d :   ; d ' :   2 3  2 6 4 5  và mặt
phẳng () : x  2y  2z 1  0
a) Viết phương trình mặt phẳng chứa d và vuông góc với ( )
b) Tìm M d, N d ' sao cho MN / /( ) và khoảng cách từ MN đến ( ) bằng 2. x y  2 z
x 1 y  2 z 1
Ví dụ 3: Cho hai đường thẳng  :   ;  :   1 2 2 3 4 1 1 2 . Viết phương trình mặt phẳng (P) chứa   x z  1 và song song 2 . Đáp số: 2 0
x 1 y 1 z  2
Ví dụ 4: Cho đường thẳng d :  
P x y z   2 1 3 và ( ) : 1 0 . Lập phương trình
chính tắc  đi qua A(1;1;-2) song song với (P) và vuông góc với d.
x 1 y 1 z  2 Đáp số:   2 1  3  x y 1 z  2
Ví dụ 5: Cho d :  
; (P) : x  3y  2z  2  0 1 2 1
a) Viết phương trình mặt phẳng ( ) chứa d và vuông góc với (P)
b) Viết phương trình  qua M(2;2;4), song song với (P) và cắt d.
x  2 y  2 z  4
Đáp số: a) ( ) : x y z 1  0; ) b  :   1 1  1 x  1 t
x  3 y 1 z
Ví dụ 6: Cho hai đường thẳng  : y  1   t;  :   1 2 1  2 1 z  2 
a) Viết phương trình mặt phẳng chứa   1 và song song 2
b) Xác định A   , B   1 2 sao cho AB nhỏ nhất. Hướng dẫn:
a)(P) : x y z  2  0;
b) AB nhoû nhaát  AB laø ñoaïn vuoâng goùc chung  A1; 1
 ;2;B3;1;0 Page 37
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Dạng 2. Hình chiếu vuông góc của một điểm lên mặt phẳng
Phương pháp: Cho điểm M và mặt phẳng ( ) . Tìm toạ độ hình chiếu H của M lên mặt phẳng ()
Bước 1: Lập phương trình tham số của đường thẳng MH (đường thẳng MH có vtcp u
trùng với vtpt n của ( )
Bước 2: Thay x, y, z trong phương trình tham số của đường thẳng MH vào phương trình
() để tính t rồi suy ra toạ độ H.
Ví dụ 1: Cho A 3  ;5; 5  ,B5; 3
 ;7, (P): x y z  0
a) Tìm giao điểm I của AB và (P) 2 2
b) Tìm M thuộc (P) sao cho MA MB nhỏ nhất Hướng dẫn: ) a I  1  ;3; 2  ; ) b M(0;0;0) x y z
Ví dụ 2: Cho A   2 2 1;2; 1 ; d :  
;(P) : 2x y z 1  0 1 3 3
a) Tìm điểm B đối xứng với A qua (P)
b) Viết phương trình đường thẳng qua A, cắt d và song song với (P) x y z
Hướng dẫn: a B   1 2 1 ) 3;0;1 ; b)   2 9  5 
Ví dụ 3: DB A2007. Cho A 1  ;3; 2  ;B 3  ;7; 1
 8,(P): 2x y z 1 0
a) Viết phương trình mặt phẳng chứa BC và vuông góc với (P)
b) Tìm M (P) : MA MB ngắn nhất Đáp số: )
a () :2x  5y z 11  0; ) b M 2;2; 3  
Ví dụ 4: DB D2004. Cho A2;0;0; B2;2;0;S0;0;m
a) Khi m  2 tìm C đối xứng với O qua (SAB)
b) Gọi H là hình chiếu vuông góc của O lên SA. Chứng minh S  2, mOBH Hướng dẫn:   4 2 1 m  8 ) 2;0;2 ; )   ,   2 m a C b S OH OB  2, mOBH 2 2 2   m  8m 16 BÀI TẬP ÁP DỤNG:
Bài 1. Cho điểm A(3;1;1), B(7;3;9) và ( ) : x+y+z+3=0. Tìm điểm M trên ( ) sao cho MA MB
đạt giá trị nhỏ nhất. Hướng dẫn: Page 38
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Goïi I laø trung ñieåm cuûa AB, I coá ñinh.
MA MB  2MI MA MB  2MI.
Vaäy MA MB ñaït giaù trò nhoû nhaát  MI nhoû nhaát (M thuoäc (), I coá ñònh)
 M laø hình chieáu vuoâng goùc cuûa I treân ()....ÑS : M(0;-3;0)
Bài 2. Cho 3 điểm A(-2;1;6), B(-4;-4;7), C(-3;0;-1) và ( ) : 2x-y-z-5=0. Tìm điểm M tthuộc ( ) sao
cho MA MB MC ngắn nhất. Hướng dẫn:
Goïi G laø trung troïng taâm cuûa tam giaùc ABC, ta coù G(-3;-1;4) vaø
MA MB MC  3MG MA MB MC  3MG.
Vaäy MA MB MC ngaén nhaát  MI ngaén nhaát (M thuoä  c ( ) vaø G coá ñònh)
 M laø hình chieáu vuoâng goùc cuûa G treâ 
n ( )....ÑS : M(1;-3;0)
Bài 3. Cho 4 điểm A(-5;2;0), B(-8;-1;-1), C(1;1;-5), D(-3;-2;2) và ( ) : 4x-y-2z-8=0. Tìm điểm M
tthuộc ( ) sao cho MA MB MC MD ngắn nhất. Hướng dẫn: 15
Goïi G laø trung troïng taâm cuûa töù giaùc ABCD, ta coù G(- ;0;-1) vaø 4
MA MB MC MD  4MG MA MB MC MD  4MG.
Vaäy MA MB MC MD ngaén nhaát
 MG ngaén nhaát (M thuoäc  ( ) vaø G coá ñònh) 1
M laø hình chieáu vuoâng goùc cuûa G treân  ( )....ÑS : M( ;-1;-3) 4
Bài 4. Cho mặt phẳng () : 2x y  3z  0 và hai điểm A(0;0;-3), B(9;15;12). Tìm điểm M thuộc () sao cho : a) MA+MB ngắn nhất b) | MA-MB| dài nhất Hướng dẫn: Page 39
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
a)A vaø B khaùc phía so vôùi (): MA+MB  AB( Khoâng ñoåi)
MA+MB ngaén nhaát  M ôû treân ñoaïn thaúng AB maø M() neân M laø giao ñieåm
cuûa ñoaïn thaúng AB vôùi ().....ÑS : M(3;5;2)
b)A' laø ñieåm ñoái xöùng cuûa A qua (), ta coù:
MA MB MA' MB A' . B
Daáu "=" xaûy ra  M ôû treân ñöôøng thaúng AB, maø M() neân M=A'B ().
Vaäy max MA MB A' .. B ...M( 17  ; 11  ; 6  )
Bài 5. Cho mặt phẳng () : x  3y z 19  0 và hai điểm A(-2;0;1), B(-7;-5;3). Tìm điểm M thuộc ( ) sao cho : a) MA+MB ngắn nhất b) | MA-MB| dài nhất Hướng dẫn:
A vaø B cuøng phía so vôùi (): a) MA+MB ngaén nhaát
- Goïi A' laø ñieåm ñoái xöùng cuûa A qua (), H laø hình chieáu vuoâng goùc cuûa A treân ()
vaø H(0;6;-1)  A'(2;12;-3).M=A'B ()....ÑS : M(3;5;2)
b) MA MB daøi nhaát
MA MB AB
Vaäy max MA MB A ..
B ...ÑS : M(3;5; 1  ) BTTT:
Bài 1. Cho mặt phẳng 
( ) : x 3y  3z 11  0 và hai điểm A(3;-4;5), B(3;3;-3). Tìm điểm M
thuộc ( ) sao cho : |MA-MB| lớn nhất.
Hướng dẫn và đáp số:
A vaø B khaùc phía so vôùi   31 5 31 ( ). M  ;  ;   7 7 7
Bài 2. Cho mặt phẳng 
( ) : 2x y z 1 0 và hai điểm A(-1;3;-2), B(-9;4;0). Tìm điểm K thuộc
() sao cho : AK + BK đạt giá trị nhỏ nhất
Dạng 3. Hình chiếu vuông góc của một đường thẳng lên mặt phẳng
Phương pháp: Cho sẵn đường thẳng d và ( ) Cách 1:
 Bước 1: Tìm giao điểm A của d và ()
 Bước 2: lấy Bd , rồi tìm toạ độ của điểm H, H là hình chiếu vuông của B lên ()
 Bước 3: Viết phương trình của đường thẳng AH ( đường này đi qua điêm A hoặc H và có
vtcp u AH . Đường thẳng AH chính là hình chiếu của đường thẳng d trên ( ) Page 40
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Đặc biệt: Nếu d // ( ) thì lấy Ad . Tìm H là hình chiếu vuông góc của A trên ( ) . Khi đó, gọi d’
là hình chiếu vuông góc của d trên ( ) , ta có d’ // d ( Đường thẳng d’ đi qua H và có vtcp u )
Cách 2: Lập phương trình mặt phẳng ( ) chứa d và vuông góc với mặt phẳng ( ) bằng .
Khi đó d  ( )  ( ). Chuyển d về dạng tham số
Ví dụ 1: Cho A2; 1
 ;3;B3;0;2; (P): x 2y z 7  0. Viết phương trình hình chiếu của AB
x  2 y 1 z  2 lên (P). Đáp số:   4 1 2 
x 1 y  7 z  3
Ví dụ 2: Cho d :  
;  :3x 2y z  0 2 1 4
a) Tính d d,()
b) Viết phương trình hình chiếu vuông góc của d lên ( )
x  4 y  5 z  2
Hướng dẫn: a) d  14; ) b  :   2 1 4 x  1 2t
Ví dụ 3. Viết phương trình hình chiếu vuông góc của đường thẳng d : y  2
  3t trên mỗi mặt z  3 t  phẳng tọa độ. Hướng dẫn:
* Hình chieáu vuoâng goùc cuûa d treân (Oxy)
Ñöôøng thaúng d caét (Oxy) taïi A(-5;-11;0). Laáy B(1;-2;3)d, hình chieáu vuoâng goùc x  1 2t
cuûa B treân (Oxy) laø H(1;-2;0). Hình chieáu cuûa d treân (Oxy) chính laø AH:y  2   3tz  0  x  0 x  1 2t
Töôngtöï: Hình chieáu cuûa d laàn löôït treân (Oyz) vaø (Ozx):y 2 3t;    y  0 z 3 t    z  3  t  
x  5  2t
Ví dụ 4: Viết phương trình hình chiếu vuông góc của đường thẳng d : y  10   t trên mặt z  2  t
phẳng: 3x  4y z  3  0 Hướng dẫn: .
n u  0  d / /() hoaëc d  ().ÑieåmA d nhöng A (). Do ñoù:d // ()
H laø hình chieáu cuûa A treân ()  H(-1;-2;-2)
x 1 y  2 z  2
Hình chieáu cuûa d treân () laø:   2 1 2  Page 41
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. BÀI TẬP ÁP DỤNG  7 x   3t  2 
Bài 1. Viết phương trình hình chiếu vuông góc của đường thẳng d : y  2
t trên mặt phẳng: z  2  t  
x  2y  2z  2  0 Hướng dẫn:  7 
d caét () taïi A(2;1;1). Laáy B ;0;0  d vaø goïi H laø hình chieáu vuoâng goùc cuûa B  2   
x  2  2t  7 1 1  treân () H ;
; . Hình chieáu cuûa d treân () laø AH:     y  1 2t  2 3 3  z 1 tBài 2. Cho mặt phẳng
(): x 3y 3z  2  0 và hai đường thẳng x  1   5t
x  4 y z  3 d : ; d :    y  2  t 1 2 2  1 2
. Viết phương trình hình chiếu theo phương d2 của z  3  t  đường thẳng d  1 trên ( ) Hướng dẫn:
d caét () taïi A(-2;-1;1).Laáy B(-4;0;3) thuoäc d vaø goïi H laø hình chieáu theo phöông d 2
cuûa B treân()  H(1;1;0).Ñöôøngthaúng AH laø hình chieáu theo phöông d cuûa d 2 1 x  2   3t AH:y  1   2tz 1 t
BTTT: Cho mặt phẳng 
( ) :x y z  3  0 và hai đường thẳng
x  3 y 1 z 1
x  7 y  3 z  9  :   ;  :   1  2 7 2 3 1 2 1
a) Viết phương trình hình chiếu của 2 theo phương 1 lên  ( )
b) Tìm trên mặt phẳng 
( ) điểm M sao cho MM MM 1
2 nhỏ nhất. Biết M1(3;1;1); M2(7;3;9) x  1 t
Bài 5. Cho điểm A(-1;2;1), đường thẳng d :  y  4  2t và ( )
P : x  2y  3z  6  0 z  2   3t
a) Viết phương trình mặt phẳng (Q) đi qua d và A
b) Gọi  là hình chiếu vuông góc của d trên (P). Viết phương trình của đường thẳng  Hướng dẫn: Page 42
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. x  2 y  4 z
a) (Q) :4x y  2z  4  0; ) b  :   1 2 1 
Dạng 4. Hình chiếu của một điểm lên đường thẳng
Phương pháp: Cho sẵn điểm M và đường thẳng  . Tìm tọa độ điểm H (H là hình chiếu vuông
góc của M trên  ).
Bước 1: Lấy H(...,...,...)  (tọa độ điểm H chính là phương trình tham số của  )
Bước 2: Tìm tọa độ của MH theo t. H là hình chiếu vuông góc của M trên 
MH.u  0( u laø vtcp cuûa ). Tìm t rồi suy ta tọa độ H.
Chú ý: d(M, )   MH x  1 2t
Ví dụ 1: Cho d : y  2  t ; (P) : 2x y  2z 1  0 z  3t
a) Tìm tọa độ M d sao cho d(M,(P))  3
b) Gọi K là điểm đối xứng của I(2;-1;3) qua đường thẳng d. Hãy xác định tọa độ K Đáp số: ) a M 21, 8  ,30 ;M 1  5;10; 2  4 ; ) b K 4;3;3 1   2   
x  2 y  2 z  3
x 1 y 1 z 1
Ví dụ 2: D2006. Cho A1;2;3;d :   d :   1 2 1  1 và 2 1  2 1
a) Tìm A’ đối xứng với A qua d1
b) Viết phương trình đường thẳng  qua A, vuông góc d d 1 và cắt 2 x y z
Ví dụ 3: A2008. Cho A  1 2 2;5;3 ;d :   2 1 2
a) Tìm hình chiếu vuông góc của A trên d
b) Viết phương trình ( ) chứa d sao cho d  , A () ax m Hướng dẫn: ) a H 3;1;4; )
b () : x  4y z 3  0 BÀI TẬP ÁP DỤNG
Bài 1. Cho 3 điểm A(-1;3;2); B(4;0;-3);C(5;-1;4). Tìm tọa độ hình chiếu vuông góc của A trên đường
thẳng BC và viết phương trình mặt cầu tâm A, tiếp xúc với đường thẳng BC. Hướng dẫn: x  4  t   231 27 36 
BC : y  t ...H ; ;    51 51 51  z  3   7t   taâm A S
S x  2  y  2  z  2 760 ( ) : ( ) : 1 3 2  R=AH 17 Page 43
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. Bài 2. Tìm điểm M1 đối xứng với điểm M(2;-1;-5) qua đường thẳng
x  2 y  3 z 1  :   2 1  1 Hướng dẫn:
Tìm toïa ñoä hình chieáu H cuûa M leân ñöôøng thaúng . 
MH u MH.u  0........H(0; 2  ; 2)  .  
H laø trung ñieåm cuûa MM'. Söû duïng coâng thöùc trung ñieåm  ' M (-2;-3;1)
x  9  2t
Bài 3. Cho 3 điểm A(4;1;-28); B(4;-9;2);C(10;2;-10) và đường thẳng d : y  t . z  4   3t
Tìm điểm M thuộc d sao cho MA MB MC đạt giá trị nhỏ nhất Hướng dẫn:
MA MB MC  3MG, G(6;2;12) laø troïng taâm cuûa  ABC
MA MB MC  3MG. Vaäy MA MB MC ñaït giaù trò nhoû nhaát
 MG nhoû nhaát (G coá ñònh vaø M d)  M laø hình chieáu vuoâng goùc cuûa G leân d ..........ÑS: M(5;2;-10) x t
BTTT: Cho 3 điểm A(2;0;1); B(2;-1;0);C(1;0;1) và đường thẳng d : y  2t . z   3t
a) Tìm điểm M thuộc d sao cho MA MB MC đạt giá trị nhỏ nhất
b) Tính thể tích hình chóp OABC x 1 y z 1
Bài 4. Cho đường thẳng d :   3 2
1 và hai điểm A(3;0;2) và B(1;2;1).
a) Tìm điểm I trên d sao cho IA IB có độ dài nhỏ nhất
b) Kẻ AA’, BB’ vuông góc với d. Tính độ dài AA’
x  7 y  2 z 1
Bài 5. Cho điểm A(-2;1;-3) và đường thẳng  :   2 2 1 
a) Tìm tọa độ hình chiếu vuông góc của A lên 
b) Viết phương trình ( ) chứa  và khoảng cách từ A đến ( ) lớn nhất Hướng dẫn: Page 44
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. a)H(3; 2  ;1)
b) Goïi K laø hình chieáu vuoâng goùc cuûa A treân () ( laø maët phaúng chöùa ), t
coù AK  AH (khoâng ñoåi)  d(A,())  AH.
Vaäy, d(A,()) lôùn nhaát (baèng AH)  K  H
() di qua H coù vtcp AH.
ÑS : 5x  3y  4z  25  0
Bài 6. Cho 4 điểm A(-4;4;0); B(2;0;4);C(1;2;-1);D(7;-2;3). Chứng minh rằng
a) Bốn điểm A,B,C,D cùng nằm trên một mặt phẳng
b) Tìm khoảng cách từ C đến đường thẳng (AB)
c) Tìm M thuộc (AB) sao cho MC+MD đạt giá trị nhỏ nhất
LUYỆN TẬP PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Bài 1. Cho ( ) : 3x-4y+z-3=0 và hai đường thẳng x  5   3t
x 1 y  4 z 1
d : y 1 t ;d :   1 2 1 2 4
 . Lập phương trình đường thẳng  nằm trong z  8   2t
() và cắt cả (d1) và (d2).
Hướng dẫn: Hình vẽ d  ()  ( A 1; 1  ; 4);  1
d  ()  B(0; 2  ; 5  ); 2
Ñöôøng thaúng  naèm trong (),caét caû d ,d laø ñöôøng thaúng ñi qua AB. 1 2
x 1 y 1 z  4 :    1 1 1 x 1 y z  2
Bài 2. Cho đường thẳng  :  
; (P) : x y z  2  0 2 2 3 
. Lập phương trình đường
thẳng d nằm trong (P), cắt và vuông góc với  .
Hướng dẫn: Hình vẽ   (P)  ( A 1  ; 2
 ;1). Goïi a laø vtcp cuûa d. Ta coù: a u   
a  u ;n   (5; 5  ;0)  (P) a n     (P) x  1   t
d naèm trong (P) vaø caét neân d ñi qua A. d:  y  2   tz 1  BTTT:
x 1 y  2 z  2 Cho đường thẳng  :  
; (P) : x  2y z  2  0 2 1  3
. Lập phương trình đường
thẳng d nằm trong (P), cắt và vuông góc với  . Page 45
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. x  2   3t
Bài 3. Cho đường thẳng d : t  7  t
; (P) : x  3y  4z  2  0 . Lập phương trình đường z  3 4t
thẳng  đi qua điểm M ( 1  ;4;0) 0
, song song với (P) và cắt d.
Hướng dẫn:Hình vẽ Ñieåm M  (P).
Goïi  laø ñöôøng thaúng ñi qua M ( 1
 ;4;0) caét d taïi ñieåm M(-2+3t;7-t;3-4t). 0
//(P)  M M n M M.n  0  t  1 0 0 x 1 y  4  : z   2 2 1  x 1 y z
BTTT: Lập phương trình đường thẳng  đi qua điểm M ( 1  ;4;0) d :   0 cắt 2 1 1  và
song song với (P) : x  3y z 1  0
Bài 3. Lập phương trình đường vuông góc chung của hai đường thẳng
x  2  2t  '
x 1 y  4 z  4
d : y  3 3t ; d :   3 2  1  . z  4   5tHướng dẫn:
Laáy I d,laáy Jd'. IJ laø ñöôøng vuoâng goùc chung cuûa d vaø d' IJ u IJ.u  0 t d d 1       . IJ u  IJ.u  0 t  1  d '  d ' x y z 1
Phöông trình IJ :   1 1 1
BTTT: Viết phương trình đường vuông góc chung của hai đường thẳng
x y  2 z  4
x  8 y  6 z 10  :   vaø  :   1 2 1 1  2 2 1 1 
a) Tính khoảng cách giữa  vaø  1 2
b) Viết phương trình đường vuông góc chung của  vaø  1 2
Bài 4. Lập phương trình đường thẳng đi qua điểm M(-4;-5;3) và cắt cả hai đường thẳng
x  2  2t
x 1 y  3 z  2 d : ; d :    y  1   3t 1 2 3 2  1  z 15tHướng dẫn: Page 46
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Giaû söû  caét d taïi A vaø caét d taïi B.Ñöôøng thaúng  ñi qua M vaø caét d 1 2 1
taïi A vaø caét d taïi B  A,B,M thaúng haøng  AB cuøng phöông AM 2 x  4  5 z  3   ;
  0   '  0.Luùc ñoù  : y AB AM t t     3  2  1
BTTT: Lập phương trình  đi qua M(1;2;-1) và cắt cả hai đường thẳng
x 1 y 1 z
x y z  3  0  :   ;  : 1 2 2 1 1   y z  0
x  3 y 1 z  2
Bài 5. Cho đường thẳng d :  
; (P) : 2x  5y z  4  0 4 3  5 . Lập phương trình
đường thẳng  đi qua A(2;-2;1), song song với (P) và vuông góc với d.  cắt hay không cắt d? Hướng dẫn: Ñieåm A (P)  / /(P) a n     a   , n u  ( 2  8; 1  4;14)   d a u  
x  2  2t
hoaëc a (2;1; 1). :     y  2   tz 1 t
x  3 y 1 z  2    4 3  5 
Giaûi heä: x  2  2t  y  2   t
z  1 t
Heä voâ nghieäm, vaäy  vuoâng goùc vôùi d nhöng khoâng caét d
BTTT: Viết phương trình đường thẳng  qua M(1;1;1) song song với (P) : x  2y z 1  0 và x  2 y z 1 vuông góc với d :   1 2  3
Bài 6. Viết phương trình đường thẳng  vuông góc với mặt phẳng () : x  2y z 1  0 và cắt x  2  t
x 1 y 1 z  2  đường thẳng  :  
 : y  t 1 2 1 1  và 1 z  1   2tBài 7. Cho điểm A(1-2m;m2-2;2m) và hai mặt phẳng
( ) : 2x y  3z 1  0;( ) : x  2y  2z  5  0 1 2
a) Xác định m để điểm A thuộc giao tuyến của ( ); ( ) 1 2
b) Với những giá trị nào của m thì A không thuộc ( ) ( ) 1 và
2 . Trong trường hợp này, viết
phương trình đường thẳng  đi qua A và song song với cả hai mặt phẳng ( ) ( ) 1 và 2 . Page 47
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. Hướng dẫn: a)m  1  m  1 
b) A ( ) vaø A ( )     m  3 1 2 m  4  u n   1
 song song vôùi caû hai ( ) vaø ( )   
u  n ,n   ( 4  ;3;5) 1 2   1 2 u n     2
x  1 2m  4tm  1   2 Vaäy, phöông trình :  
y m  2  3y vôùi m  3
z  2m  5t   m  4  x  1   2t
x 1 y 1 z  2
Bài 8. Cho hai đường thẳng  : y t ;  :   1 2 2 1 1 z  4 3t
a) Chứng minh  vaø  cheùo nhau 1 2
b) Viết phương trình đường  thẳng đi qua M(1;2;-3) và cắt các đường thẳng  vaø  1 2 x  1 3tx  0  
Bài 9. Cho hai đường thẳng  : y  2t ;  : y t 1 2 z t   z  2   t  
a) Chứng minh  vaø  cheùo nhau  vaø  1 2
. Tính khoảng cách giữa 1 2
b) Viết phương trình đường  thẳng đi qua M(2;-1;3) vuông góc với  vaø caét  1 2
c) Viết phương trình đường thẳng d vuông góc với mặt phẳng ( ) : 2x y  3z 1  0 và
cắt các đường thẳng  vaø  1 2
Bài 10. Cho đường thẳng
x 1 y 1 z 1  :  
vaø maët phaúng () : x y z -3  0 2 3 1 
a) Viết phương trình hình chiếu vuông góc d của đường thẳng  trên mặt phẳng ( ) x  2 y z 1
b) Viết phương trình hình chiếu song song theo phương m :   1  1 2 của đường
thẳng  trên mặt phẳng ( )
Hướng dẫn: Xem phương pháp giải ở mục “ Hình Chiếu” x  1 t
Bài 11. Cho đường thẳng  : y  1
và mặt phẳng () : 2x y  3z  0 . Viết phương trình z 1 t
đường thẳng d nằm trong ( ) , vuông góc với  và cắt đường thẳng  Page 48
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. x  1   3t
x y  7 z  4 
Bài 12. Cho hai đường thẳng d :  
; d : y  2t 1 2 2 5 3  z  2   t
Chứng minh d1 cắt d2. Viết phương trình mặt phẳng chứa d1 và d2 Hướng dẫn:
u ,u   0 1 2 a)  
u vaø u khoâng cuøng phöông ñoàng thôøi ba vecto 1 2 
u ,u AB  0 1 2  
u vaø u , AB ñoàng phaúng 1 2
b)n = u ,u   11;7;19 . ():11x  7y 16z  27  0  1 2     x  1 tx  1 2t  
BTTT: Cho hai đường thẳng  : y 1 5t;
 : y 1 3t 1 2 z 1 3t    z  1 t   a) Chứng minh  vaø  1 2 cắt nhau.
b) Viết phương trình mặt phẳng ( ) chứa hai đường thẳng  vaø  1 2 x  1 5t
x  3 y  4 z 1
Bài 13. Cho hai đường thẳng d : y   5 7t; d ' :   1 2  4 z 3 3t
a) Chứng minh d vaø d' chéo nhau
b) Lập phương trình mặt phẳng cách đều hai đường thẳng d và d’ Hướng dẫn:
a)u ,u AB  0 1 2   '  1 (
 )/ /d,d (
 ) coù vtpt n  u ;u  1 2 b)    d  d,()  17  d(d ',()) d   ,
A ()  d B,()  9 
 () coù vtpt n  (2; 1  ; 1
 ) vaø ñi qua trung ñieåm I 2; ;2 cuûa AB  2   
Bài 14. Tìm a để đường thẳng x     2 1 a   1 t  x  3 y 1 :   4 
caét vaø vuoâng goùc vôùi ñöôøng thaúng d': z d y at   
z    a  2 1 3 5 2 1 t  Hướng dẫn: Page 49
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. 5
d vaø d' vuoâng goùc nhau  u .u  0  a  1  hoaëc a   1 2 2
 Vôùi a=-1: u ,u .AB  0  d vaø d' caét nhau 1 2   5
+Vôùi a=- : u ,u .AB  0  d vaø d' cheùo nhau 1 2 2  
Vậy, với a=-1 thì 2 đường thẳng đã cho cắt nhau Bài 15. Tìm m (m nguyên dương) để hai đường thẳng 2
x m  7  2t
x 1 y  3 z  2  d :  
; d : y m 13t 1 2 3  2 2 
cắt nhau. Trong trường hợp này, viết phương
z m t
trình mặt phẳng qua d vaø d 1 2 Hướng dẫn:
u ,u   0  khoâng cuøng phöông.Hai ñöôøng thaúng caét nhau 1 2   m  3 
u ,u ,AB ñoàng phaúng  u ,u .AB  0   1 2 1 2 11    m  (loaïi)  4
() : 8x  7y  5z  4  0 x t 
Bài 16. Cho đường thẳng d : y m 1 mt vaø
() : 3x  2y z  5  0 . Tìm m để
z m 3   2m 5t
đường thẳng d thuộc ( ) . trong trường hợp này, viết phương trình ( ) qua d và vuông góc với () Hướng dẫn:
Ñöôøng thaúng d thuoäc () u n    m  2
 . Vaø khi ñoù: ( ) : 2x y  4z 1  0 A()
x m 1 2t  2 2
Bài 17. Cho đường thẳng d : y m  4  m  3t vaø
() : 2x  3y z  5  0 . Tìm m để z 3t
đường thẳng d song song với ( ) . Trong trường hợp này, tính khoảng cách giữa d và ( ) Hướng dẫn: u n     m  d   8
Ñöôøng thaúng d song song ( ) 2. Vaø khi ñoù: d ,( )  A() 14
Bài 18. Tìm m để đường thẳng Page 50
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. x  2  t
x  1 2m mt   2
d : y  3
  3t song song hoaëc truøng vôùi ñöôøng thaúng d : y  6
  m  2 t 1 2   . Trong z 1 2t      z   3   2mt
trường hợp d / / d d d 1
2 , viết phương trình mặt phẳng đi qua 1 và 2 Hướng dẫn: m  2
 ( vôùi gt naøy thì d / / d ) 1 2
d / / d hoaëc d d  u ,u   0  1 2 1 2 1 2    m  1
 ( vôùi gt naøy thì d d )  1 2
() : 2y  3z  3  0
Bài 18. Cho 3 điểm A(-2;2;1), B(1;2;-2);C(2;1;2). Viết phương trình tham số đường thẳng  vuông
góc với (ABC) và đi qua trực tâm của tam giác ABC
x  5 y 1 z 1
Chứng minh rằng tồn tại điểm S thuộc đường thẳng d :   2 3  1  sao cho S.ABC là hình chóp đều. Hướng dẫn: Ta ñeå yù raèng A
 BC ñeàu  tröïc taâm cuûa tam giaùc truøng vôùi troïng taâm cuûa tam giaùc  1 x   t  3   5 :
 y   5t  laø truïc ñöôøng troøn ngoaïi tieáp ABC 3   1 z   t   3
b)S    d S( 1  ; 5  ; 1
 ),roõ raøng S G
Bài 19. Tính khoảng cách giữa hai đường thẳng x  3   3t
x  2 y z  4
d : y 13t d :   1 2 1  1 3  z  2   9t
Hướng dẫn: Ñeå yù : d / /d , d d ,d  30 1 2  1 2 x  1  
Bài 20. Tìm điểm I thuộc đường thẳng
d : y  1 t và cách đường thẳng z t
x  3 y 1 z  7 d ' :   2 1 2 một khoảng bằng 3. x  1   2t
x  3 y 1 z  3
Bài 21. Cho hai đường thẳng  : y  t ; ' :   1  4 2 z  3 tPage 51
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. a) Chứng minh  vaø '
 cheùo nhau. Tính khoaûng caùch giöõa  vaø ' 
b) Trên  lấy đoạn AB=4 và trên  ' lấy đoạn CD=3. Tính thể tích của khối tứ diện ABCD Page 52
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
VẤN ĐỀ 5. Các bài toán liên quan giữa đường thẳng và mặt cầu x y 1 z  2
Ví dụ 1. Lập phương trình mặt cầu có tâm I(2;3;-1) và cắt đường thẳng  :   2 1 2  tại 2
điểm A và B sao cho AB=16. Hướng dẫn:
HA HB  8
Goïi H laø trung ñieåm cuûa AB, ta coù IH   IH d(I,) 2 2 2 2
R AH IH  64  IH . Vôùi IH laø khoaûng caùch töø I ñeán AB
ÑS S x  2  y  2  z  2 641 :( ) : 2 3 1  9
ĐHCĐ 2010 A –NC. Trong không gian tọa độ Oxyz, cho điểm A(0; 0; 2) và đường thẳng x  2 y  2 z  3  :  
. Tính khoảng cách từ A đến . Viết phương trình mặt cầu tâm A, cắt  tại 2 3 2
hai điểm B và C sao cho BC = 8. x t   1
BTTT: Trong không gian Oxyz cho đường thẳng d : y  1 t 2 và mặt cầu  z  1   t  2 2 2
(S) : x y z  4x  6y m  0. Tìm m để d cắt (S) tại 2 điểm M,N sao cho MN=8 Hướng dẫn:
(S): I(-2; 3; 0); R  IN  13  m , với m < 13.
Dựng IH  MN  MH  HN  4 2 2
 IH  IN  HN  13  m 16  m  3 , m < -3. [AI; u] 2 2 2 3  6  6 81 h     3. 2 2 2 u 2 1  2 9 IH = h 
m  3  3   m  3  9  m  1  2 (thoã) x y 1 z 1
Bài 2. Lập phương trình mặt cầu (S) có tâm nằm trên đường thẳng d :   2 1 2 và tiếp
xúc với () : x y  2z  5  0; ( ) : 2x y z  2  0 . Hướng dẫn:
Goïi I laø taâm (S)  I(2t;1+t;-1+2t). 4
(S) tieáp xuùc vôùi () vaø ( )  R=d(I;())=d(I;( ))  t  hoaëc t=-2 3 Page 53
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
x  3  3t
BTTT: . Lập phương trình mặt cầu (S) có tâm nằm trên đường thẳng d : y  2  t và tiếp xúc z  1   2t
với () : x  2y  2z  2  0; ( ) : 2x y  2z  4  0 . Đáp số: 2 2 2   12   18   13  16 (S) : x   y   z    5   5   5         25  2 2 2   12   30   19  16 (S) : x   y   z       11     11     11  25 2 2 2
Bài 3. Cho mặt cầu (S) : x y z 10x  2y  26z 113  0 và hai đường thẳng x  7   3t
x  5 y 1 z 13 : ; :      y  1   2t 1 2 2 3  2
. Viết phương trình (P) tiếp xúc với (S) và song z  8  song với cả  vaø  1 2 Hướng dẫn:
(P) song song vôùi  vaø  neân n  u ,u   (4,6,5) 1 2 p  1 2    P
x y z D  I P D 205 ( ) : 4 6 5
0.Maët khaùc: d ,( )  R  D  103 
x 1 y  2 z
Bài 4. Cho đường thẳng d : 
 ; () : 2x y  2z  2  0 3 1 1
Lập phương trình mặt cầu (S) có tâm nằm trên d, bán kính bằng 1 và tiếp xúc với ( ) Hướng dẫn:
Goïi I laø taâm (S)  I(1+3t;-2+t;t). 1
(S) tieáp xuùc vôùi ()  R=d(I;())=1  t  hoaëc t=-1 5
Bài 5. Trong không gian cho (P) và mặt cầu (S) có phương trình lần lượt là 2 2 2 2
(P) : 2x  2y  z  m  3m  0 ;
(S) : (x 1)  (y 1)  (z 1)  9 .
Tìm m để (P) tiếp xúc với (S). Tìm toạ độ tiếp điểm Hướng dẫn:
(P) tieáp xuùc vôùi (S)  d(I,(P))=R  m=2 hoaëc m=-5
Toïa ñoä giao ñieåm cuûa ñöôøng thaúng ñi qua I vaø vuoâng goùc vôùi(P)
laø tieáp ñieåm cuûa (P) vaø (S). ÑS : M(3;1;2) Page 54
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Bài 6. Viết phương trình mặt cầu (S) có bán kính nhỏ nhất và tiếp xúc với hai đường thẳng
x  5  4tx y 1 :   1   3 ; : z d y t d   1 2 2 1 1  z  3  Hướng dẫn:
Goïi IJ laø ñoaïn vuoâng goùc chung cuûa d vaø d (I d ,J d ) 1 2 1 2
(S) coù baùn kính nhoû nhaát vaø tieáp xuùc vôùi hai ñöôøng thaúng d1 IJ d
IJ.u  0 t  1 1 
vaø d laø maët caàu coù ñöôøng kính IJ. Ta coù:   1   2  IJ d  IJ.u  0 t'  1  2  2 2  1  S x   
y  2 z 2 29 ( ) : 2 2    2  4
x  2 y  6 z  4
Bài 7. Viết phương trình mặt cầu có tâm ở trên đường thẳng d :   1  3  2 và tiếp x  2   t x  2 y z 1  xúc d :  
vaø d : y  t 1 2 2 2 1 z  2   3tHướng dẫn:
Goïi I laø taâm maët caàu  I2  ;t6 3 ;t 4   2t
Maët caàu tieáp xuùc vôùi d vaø d neân d I,(d )  d (I,d  R 1 2  1   2
t  1. Luùc ñoù: (S):x  2
1  y 32  z  22 18 x  2  t
Bài 8. Cho mặt cầu (S) có tâm I(2;0;-1) và tiếp xúc với đường thẳng  : y a  2  t . Xác định a
z a 1 2t
để mặt cầu (S) có bán kính nhỏ nhất Hướng dẫn:
(S) tieáp xuùc vôùi ñöôøng thaúng  neân R=dI; 2 3a 12a  20 8 2 2 R     R   a  2 min 6 6 3 3
Bài 9. Viết phương tình mặt cầu (S) có tâm I(-4;1;1) và cắt mặt phẳng () : x  2y  2z 1  0
theo giao tuyến là một đường tròn có bán kính bằng 2 2 Hướng dẫn: 2 2
R d I   2 Deãdaøngnhaän thaáy:
,( )  2 2  R 1  2 2  R  3 Page 55
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
x 1 y 1 z 1
Bài 10. Viết phương tình mặt cầu (S) có tâm I(-4;1;1) và cắt đường thẳng  :   2 1 2
tại hai điểm A và b sao cho tam giác IAB vuông Hướng dẫn:
Tam giaùc IAB caân taïi I. Maët khaùc theo giaû thieát noù laø tam giaùc vuoâng. Do ñoù d I  40
tam giaùc IAB vuoâng caân taïi I. Vaäy R=IA=IB= 2 ,  3
x  7 y  3 z  9
x  3 y 1 z 1
Bài 11. Cho đường thẳng  :   ;  :   1 2 1 2 1  7  2 3
a) Tìm các điểm A thuộc    1 , B thuộc
2 sao cho AB là đoạn vuông góc chung của 1 và 2
b) Viết phương trình mặt cầu (S) tiếp xúc với đường thẳng   1 tại A và 2 tại B. Hướng dẫn: u .BA  0   t  0 1 a)   u .BA  0 t'  0   2
b)Maët caàu (S) tieáp xuùc vôùi u .BA  0 tai A vaø  taïi B neân coù taâm I thuoäc maët 1  2
phaúng   vuoâng goùc vôùi ñöôøng thaúng  taïi A vaø  taïi B. 1 2
Vì AB laø ñoaïn vuoâng goùc chung cuûa  vaø  neân AB thuoäc maët phaúng (). 1 2
Töông töï AB thuoäc maët phaúng ( ).  vaø  khoâng cuøng phöông, do ñoù () khoâng 1 2
song song vôùi ( )  AB=()( )  I AB.(S) qua AB  I laø trung ñieåm cuûa AB.
(S):x  52  y  22  z  52  21 Page 56
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
CHỦ ĐỀ 5. GÓC TRONG KHÔNG GIAN PHƯƠNG PHÁP
1. Góc giữa hai đường thẳng
Cho hai đường thẳng d a ,a
1, d2 lần lượt có các VTCP . 1 2 Góc giữa d a ,a
1, d2 bằng hoặc bù với góc giữa . 1 2 a a . cosa ,a  1 2  1 2 a . a 1 2
2. Góc giữa một đường thẳng và một mặt phẳng
Cho đường thẳng d có VTCP a  (a ; a ; a ) và mặt phẳng () có VTPT n  (A; B;C) . 1 2 3
Góc giữa đường thẳng d và mặt phẳng () bằng góc giữa đường thẳng d với hình chiếu d của nó trên ().   sind,() Aa Ba Ca 1 2 3  2 2 2 2 2 2
A B C . a a a 1 2 3
VẤN ĐỀ 1. Góc và các bài toán liên quan
Ví dụ 1. Cho ba đường thẳng (d1), (d2), (d3) có phương trình : x t 1  
x y  4z  3  0 x y 1 z  5 d : , d  ; d   3  : 2  : 1
y  2  t 4 t  R  2
x y z 1  0 3 1 1 z  2  t  3
a) Xác định cosin góc giữa (d1),(d2).
b) Lập phương trình đường thẳng (d) song song với (d3) đồng thời cắt cả (d1),(d2). x  3 y  4 z  3
Ví dụ 2. Cho đường thẳng (d) và mặt phẳng (P) có phương trình d :   và 1 2 1 (P):2x+y+z-1=0
a) Xác định số đo góc giữa đường thẳng (d) và mặt phẳng (P) .
b) Tìm toạ độ giao điểm A của đường thẳng (d) và mặt phẳng (P).
c) Lập phương trình tổng quát của đường thẳng (d1) đi qua A vuông góc với (d) và nằm trong mặt phẳng (P). x  1 t  0
Ví dụ 3: Tìm k để đường thẳng d : y  2
  kt và () : x 3z  5  0 có số đo góc bằng 45 . z  1   2t
Đáp số: k  0 x t
Ví dụ 4: Cho điểm A3; 5  ; 
1 đường thẳng d : y  6  2t và (): 2x y 2z  5  0. Lập z 1 t  0
phương trình đường thẳng  đi qua A, cắt d và hợp với ( ) một góc 45 Page 57
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. x  1 t
Ví dụ 5: Cho điểm A3; 1  ; 3
  đường thẳng d : y  2  t . Lập phương trình đường thẳng  z  4   0
đi qua A, cắt và hợp với d một góc 60 .
x 1 y  2 z x y  2 z 1
Ví du 6: Trong không gian, cho d :   ;  :   1 1  1 2 1 1  . Viết phương trình 0
mặt phẳng (P) chứa d và tạo với  một góc 30
VẤN ĐỀ 2 . Sử dụng tọa độ giải toán hình học không gian
Ví dụ 1 : A2008. Cho lăng trụ AB .
C A'B'C' có đáy ABC là tam giác vuông tại A, AB  ,
a AC a 3,AA'  2 .
a Hình chiếu A’ lên (ABC) là trung điểm H của BC. Tính VA'.ABC và AA',B'C'.
Ví dụ 2: B2008. Cho .
S ABCD có đáy ABCD là hình vuông cạnh 2a, SA=a, SB a 3 ,
SAB ABCD. Gọi M, N là trung điểm của AB và BC. Tính V cos SM,DN S.BMDN và  . 0
Ví dụ 3 : Cho hình lăng trụ AB .
C A'B'C', đáy AB  , a AC  2 ,
a BAC 120 . Gọi M là trung
điểm của BB’, (MAC)  (MA'C '). Tính V o
c s MAC , BCC'B' 
ABC.A'B'C ' và    
Ví dụ 4 : B2001. Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a.
a) Tính khoảng cách giữa hai đường thẳng chéo nhau BA’ và DB’
b) Gọi M, N, P lần lượt là trung điểm của BB’, CD, A’D’. Tính góc của hai đường thẳng MP và NC’. Page 58
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
CHỦ ĐỀ 6. MỘT SỐ PHƯƠNG PHÁP GIẢI TOÁN CỰC TRỊ HÌNH HỌC KHÔNG GIAN
VẤN ĐỀ 1. Giải toán cực trị hình học bằng cách sử dụng bất đẳng thức hình học
Phương pháp: Ta thường sử dụng các bất đẳng thức hình học sau
1) Bất đằng thức tam giác: Với ba điểm , A , B C ta có: 
AB BC AC , dấu “=” xảy ra  , A ,
B C thẳng hàng và B nằm giữa , A C ; 
AB AC BC , dấu “=” xảy ra  , A ,
B C thẳng hàng và A nằm ngoài , B C ; C B B A B A C A AB+BC > AC AB+BC=AC |AB-BC|=BC |AB-AC| < BC
2) Bất đẳng thức giữa đường xiên và đường vuông góc: Nếu H là hình chiếu vuông góc của điểm
A lên mặt phẳng (P) (hoặc đường thẳng d), M là điểm bất kì trên (P) (hoặc d ) thì AM AH .
Dấu “=” xảy ra khi M H A A d H AM ≥ AH P M H AM ≥ AH M
Ví dụ 1: Trong không gian Oxyz cho hai điểm A5; 2  ;6; B3; 2  ;  1 và mặt phẳng
(): 2x y  2z 6  0 . Tìm điểm M (P) sao cho
a) MA MB nhỏ nhất.
b) MA MB lớn nhất
Lời giải: Đặt F x,y,z  2x y  2z  6, ta có F 5, 2  ,6.F3, 2  ,  0 nên , A B nằm cùng phía so với (P) .
a) Gọi A ' là điểm đối xứng của A qua (P) . Lúc đó MA MA' .
Ta có: MA MB MA' MB A' B . Dấu “=” xảy ra khi M là giao điểm của A' B với (P) .
x  5  2t
Gọi  là đường thẳng đi qua A và vuông góc với (P)   : y  2
  t . Gọi H là tọa độ giao
z  6  2t
điểm của  với (P) ( H là trung điểm của AA’). Suy ra H 1; 1  ;2  A' 3  ;2; 2  . Phương x  3   6t
trình đường thẳng A ' B : y  2  4t . z  2   3t   21 14 5 
Ta có M  A'B  (P)  M ; ;    11 11 11 Page 59
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
b) Vì A và B cùng phía so với (P) nên với mọi M (P) ta luôn có MA MB AB , đẳng thức
xảy ra khi M AB  (P).
x  5  2t  17 3 
Phương trình đường thẳng AB : y  2   M ; 2  ;     7 7 z   6  5t
Ví dụ 2: Trong không gian Oxyz cho hai điểm A1;1;0; B2;1;  1 và đường thẳng 1 2 : x y z d   
 . Viết phương trình đường thẳng  đi qua A,   d sao cho khoảng cách 2 1 1
từ B đến đường thẳng  nhỏ nhất.
Lời giải: nằm trong mặt phẳng (P) đi qua A và vuông góc với d .
Ta có (P) : 2x y z  3  0 . Gọi H, K lần lượt là hình chiếu vuông góc của B trên (P) và trên  . Ta có d  ,
B   BK BH . Dấu “=” xảy ra khi K H . Vậy đường thẳng  cần tìm là đường 2 1 1
thẳng AH. Gọi d ' là đường thẳng đi qua B và song song với d thì ' : x y z d      . H là 2 1 1 x  1  1 1  
giao điểm của d’ và (P) nên H 1; ; 
 . Từ đó,  : y  1 t  2 2  y t
VẤN ĐỀ 2. Giải toán cực trị bằng phương pháp hàm số hoặc bằng cách sử dụng bất đẳng thức đại số Phương pháp
 Ta thường dùng phương pháp hàm số để tìm giá trị lớn nhất, giá trị nhỏ nhất của một yếu
tố nếu yếu tố đó được tính bởi một biểu thức phụ thuộc một biến số
 Ta thường dùng các bất đẳng thức đại số để tìm GTLN, GTNN của một yếu tố nếu yếu tố
đó được tính bởi một biểu thức phụ thuộc một hoặc nhiều biến số
Ví dụ 3. Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A2;0;0; M 1 1 ; ;  1 . Giả sử (P)
là mặt phẳng thay đổi nhưng luôn đi qua đường thẳng AM và cắt các trụ Oy, Oz lần lượt tại các bc điểm B0; ;
b 0, C0;0;c, b  0,c  0. Chứng minh rằng b c  và tìm , b c sao cho 2
diện tích tam giác ABC nhỏ nhất.
Lời giải: mặt phẳng (P) có phương trình ( ) : x y z P
   1. Vì M 11 ; ;  1 (P) nên 2 b c 1 1 1 bc
  1 b c        . Ta có AB
 2; ;b0,AC  2;0;c, A ,BAC  b ;c2 ;c2b 2 b c 2   1 1 2 2 S  A , B AC 
b c  4 b c ABC  
 2 2 . Áp dụng bất đẳng thức Cosi ta có 2 2 bc 2 2
b c  2bc . Dấu “=” xảy ra  b c. Mặt khác ta cung có b c  2 bc mà b c  nên 2 Page 60
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
bc  2 bc bc 16. Dấu “=” xảy ra  b c  4. Từ đó ta suy ra 2 1 1 2 2 2 Sb c  4 2 . .bc  16  8 1 . 6  4 6  b c ABC . Dấu “=” xảy ra 4 . 2 2 Vậy Min S  4 6  b c ABC  , đạt được khi 4 1
Ví dụ 4. Trong không gian Oxyz cho đường thẳng : x y z     1 2 1  và ba điểm A3;2;  1 , B1; 2  ; 
1 . Tìm M thuộc  sao cho MA MB nhỏ nhất
Lời giải: Vì M    M  ; t 2t 1
;  t,AM  t 3;2t  2; t
  2,BM  t 1;2t  2; t   Ta có 2 2 2 2  3 6   7   6   7  2 2
MA MB  6t 18t 17  6t  6t  5    6t       6t       2   2   2   2          2 2
Áp dụng bất đẳng thức 2 2 2 2
a b c d  a c  b d , đẳng thức xảy ra khi a c 2 2      3 6 6 7
MA MB    t t       b d , ta có 6 6 2 38  2 2   2      3 6 6 1  1 1  Đẳng thức xảy ra khi
 6t  6t
t  . Vậy M 1 ; ;   2 2 2  2 2  1 1
Ví dụ 5. Trong không gian cho điểm A1; 1  ; 
1 và đường thẳng  : x y z   2 1 1  . Viết
phương trình mặt phẳng () chứa hai điểm M 1 1 ; ;  1 , N  1  ;2; 
1 và tạo với đường thẳng  một góc lớn nhất.
Lời giải: Giả sử ( )
 : ax by cz d  0. Gọi   ,() . Vì M,N ( )  nên  3 d   b
a b c d  0  2   
. Ta ñöôïc () : 2ax  2by  b  2az 3b  0
a  2b c d  0 1
c  a b  2 n .u 2 2 
4a  2b b  2a 1
b 12ab  36b Ta có sin     n . u
b ab a
6 4a  4b  b  2a 2 2 2 2 2 6 5 4 8 Page 61
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. 3 b 2 12  36
Nếu a  0  sin  
, với a  0, đặt t  ,t  . Xét hàm số ( ) t t f t  ta tìm 2 a 2 5t  4t  8  5  53 b 5
được max f (t)  f    . Do đó   sin
  , chọn b  5,a  8  a m x a m x 8  9 a 8
Vậy phương trình mặt phẳng ( )
 :16x 10y 11z 15  0
VẤN ĐỀ 3. Giải toán cực trị bằng phương pháp ứng dụng tâm tỉ cự
Phương pháp: Xuất phát từ việc khai thác bài toán sau
Cho n điểm A , A ,..., A với n số k ,k ,...,k mà k k  ...  k k  0 . Lúc đó ta có các tính 1 2 n 1 2 n 1 2 n chất sau
 Có duy nhất một điểm G sao cho k GA k GA  ...  k GA  0 , điểm G như vậy gọi là 1 1 2 2 n n
tâm tỉ cự của hệ điểm A k k
i , gắn với các hệ số i . Trong trường hợp các hệ số i bằng nhau ( và
do đó ta có thể xem các k A
i đều bằng 1) thì G gọi là trọng tâm của hệ điểm i . 1
 Nếu G là tâm tỉ cự thì mọi điểm O bất kì ta có OG  k OA k OA ... k OA 1 1 2 2 n n k
Dạng 1. Cực trị độ dài vectơ
Xét bài toán tổng quát : Cho n điểm
A , A ,..., A với n số k ,k ,...,k mà 1 2 n 1 2 n
k k  ... k k  0 và đường thẳng d hoặc mặt phẳng (P). Tìm M ở trên d hoặc trên (P) sao 1 2 n
cho k MA k MA  ...  k MA nhỏ nhất. 1 1 2 2 m m Cách giải :
Bước 1: Gọi I là điểm thỏa mãn k IA k IA  ...  k IA  0 1 1 2 2 m m
Bước 2: Áp dụng qua tắc 3 điểm biến đổi
k MA k MA  ... k MA k k  ... k MI k .MI 1 1 2 2 m m  1 2 n
Bước 3: Tìm độ dài nhỏ nhất của vectơ MI xảy ra khi M ở vị trí nào.
Ví dụ 1 : Trong không gian Oxyz cho hai điểm A3;1; 
1 ; B7;3;9 và (): x y z3  0. Tìm
M () sao cho MA MB nhỏ nhất.
Đáp số : M 0;3;0
Ví dụ 2 : Trong không gian Oxyz cho hai điểm A3;4;  1 ; B 5  ;3; 2  ;C3; 1
 ;2;D1;1;4 Tìm  1 7 3 
M trong không gian sao cho MA MB MC MD nhỏ nhất. Đáp số : M ; ;  2 4 4   
Ví dụ 3 : Trong không gian Oxyz cho hai điểm A1;2;3; B 1  ;0; 3  ;C2; 3  ;  1 và
x 1 y 1 z 1  :  
MA MB MC 2 3 1
 . Tìm M  sao cho 7 5 lớn nhất.  31 29 5 Đáp số : M ; ;  7 7 7   Page 62
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Dạng 2. Cực trị độ dài bình phương vô hướng của vectơ
Xét bài toán tổng quát : Cho n giác A A ...A với n số k ,k ,...,k mà k k  ...  k k  0 1 2 n 1 2 n 1 2 n
và đường thẳng d hoặc mặt phẳng (P). Tìm M ở trên d hoặc trên (P) sao cho 2 2 2
S k MA k MA  ... k MA nhỏ nhất. 1 1 2 2 n n Cách giải :
Bước 1: Gọi I là điểm thỏa mãn k IA k IA  ...  k IA  0 . Từ đây ta tìm được điểm 1 1 2 2 m m I
Bước 2: Áp dụng qua tắc 3 điểm biến đổi 2 2 2 2 2 2 2
S k MA k MA  ... k MA kMI k IA k IA  ... k IA . 1 1 2 2 n n 1 1 2 2 n n
Bước 3: Do k  0 Vậy để 2 2 2
S k MA k MA  ... k MA đạt giá trị nhỏ nhất thì ta 1 1 2 2 n n
xác định vị trí M cần tìm
Chú ý: Bài toán tìm GTLN cũng hoàn toàn làm tương tự
Ví dụ 1 : Trong không gian Oxyz cho hai điểm A1;2;  1 ; B3;1; 2  ;C1; 2  ;  1 và
(): x y  2z  0 2 2 2
. Tìm M ( ) sao cho MA MB MC lớn nhất. Đáp số : M 2; 2  ;2
Ví dụ 2 : Trong không gian Oxyz cho hai điểm A1;1; 
1 ; B0;1;2;C 2  ;0;  1 và
(): x y z 1 0 2 2 2
. Tìm M ( ) sao cho 2MA MB MC nhỏ nhất.  3  3 1  Đáp số : M ; ;  2 4 4   
Ví dụ 3 : Trong không gian Oxyz cho hai điểm A1;2;3; B 1  ;0; 3  ;C2; 3  ;  1 và
(): 2x y 2z 1 0 2 2 2
. Tìm M ( ) sao cho 3MA  4MB  6MC nhỏ nhất.
Đáp số : M  1  1;25;  1
Dạng 3. Cực trị dựa vào tính chất hình học
Phương pháp :
Ví dụ 1 : Cho hai điểm A(-1;6;6); B(3;-2;4)
a) Tìm điểm M thuộc (Oxy) sao cho MA+MB nhỏ nhất
b) Tìm điểm N thuộc (Oyz) sao cho NA NB nhỏ nhất
Hướng dẫn và đáp số:
a)z vaø z cuøng daáu neân hai ñieåm A vaø B cuøng moät phía ñoái vôùi (Oxy) A B  7 6  ÑS : M ; ;0  5 5   
b) x vaø x cuøng daáu neân hai ñieåm A vaø B hai phía khaùc nhau ñoái vôùi (Oyz) A B
ÑS : N 0;10;7
Ví dụ 2: Trong không gian Oxyz cho hai điểm A5; 2  ;6; B3; 2  ; 
1 và (): 2x y  2z 6  0 .
Tìm M ( ) sao cho Page 63
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
a) MA MB nhỏ nhất. b)
MA MB lớn nhất x y z 1
Ví dụ 3: Trong Oxyz cho đường thẳng  :   A 3;2; 1  ; B 3; 2  ;1 1 2 1  và ba điểm    . Tìm
M  sao cho MAMB nhỏ nhất. Đáp số:
Ví dụ 4: Trong không gian Oxyz cho điểm A1; 1  ; 
1 và đường thẳng  có phương trình x 1 y z 1   P
x y z   2 1 1  và mặt phẳng ( ): 2 2 1 0
a) Viết phương trình mặt phẳng (Q) chứa đường thẳng  và khoảng cách từ A đến (Q) lớn nhất
b) Viết phương trình mặt phẳng (R) chứa  và tạo với (P) một góc nhỏ nhất.
c) Viết phương trình mặt phẳng ( ) chứa hai điểm M 1;1;  1 ,N  1  ;2;  1 và tạo với đường
thẳng  một góc lớn nhất. Đáp số: ) a ( )
Q : 2x y 3z 1 0; ) b ( )
R :10x 7y 13z 3  0; )
c ():16x 10y 11z 15  0
Ví dụ 5: Lập phương trình đường thẳng d đi qua A0; 1
 ;2 và cắt đường thẳng x 1 y z  2 d ' :   2 1 1  sao cho a) Khoảng cách từ (
B 2;1;1) đến đường thẳng d là lớn nhất, nhỏ nhất x  5 y z
b) Khoảng cách giữa d và  :   2 2  1 là lớn nhất Đáp số: x y 1 z  2 x y 1 z  2 ) a d :   ; ) b d :   1  1 1  29 4  1 4 Page 64
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. PHỤ LỤC
PHỤ LỤC 1. MỘT SỐ BÀI TẬP RÈN LUYỆN HÌNH HỌC GIẢI TÍCH TRƯỚC KHI THI
Bài 1. Trong không gian Oxyz, viết phương trình mặt phẳng (P) chứa đường thẳng (d) : x  y  2  0 
sao cho giao tuyến của mặt phẳng (P) và mặt cầu (S) : 2x  z  6  0 2 2 2
x  y  z  2x  2y  2z 1  0 là đường tròn có bán kính r = 1. Hướng dẫn:
Mặt phẳng (P) chứa (d) có dạng: m(x – y – 2) + n(2x – z – 6) = 0
 (P) : (m  2n)x  my  nz  2m  6n  0
Mặt cầu (S) có tâm I(-1; 1; -1), bán kính R = 2.
(P) cắt (S) theo một đường tròn giao tiếp (C) có bán kính r = 1 2 2  d(I; P)  R  r  3
m  2n  m  n  2m  6n   3 2 2  4
 m  7n  3. 2m  5n  4m.n 2 2 2 (m  2n)  m  n 2 2  5m  22m.n 17n  0 2 17
. Cho n  1  5m  22m  17  0  m  1  hay m   5
(P ) : x  y  z  4  0 1
Vậy, có 2 mặt phẳng (P): (P ): 7x 17y  5z  4  0  2
Bài 2. Trong không gian Oxyz cho A(0; 1; 0), B(2; 2; 2), C(-2; 3; 1) và đường thẳng x 1 y  2 z  3   2 1  2 a) b) Tìm điểm N thu Hướng dẫn: x  1 2t 
a) Phương trình tham số của (  ): y  2   t z  3 2t  Ta có M( )
  M(1 2t;  2  t; 3 2t) AB  (2; 1; 2), AC  ( 2  ; 2;1) [AB; AC]  ( 3  ;  6; 6)  3  (1; 2;  2)  3
 .n, với n  (1; 2;  2)
Phương trình mp (ABC) qua A với pháp vectơ n : (ABC): x + 2y – 2z – 2 = 0. 1 1 2 2 2 9 S  [AB; AC]  ( 3  )  ( 6  )  6  . ABC 2 2 2
Đường cao MH của tứ diện MABC là khoảng từ M đến (ABC): 1 2t  2( 2
  t)  2(3  2t)  2 4  t 11 MH  d(M(ABC))   1  4  4 3
Thể tích tứ diện MABC bằng 3 Page 65
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. 1 9 4t 11 5 17  V  . .
 3  4t 11  6  t   hay t   . 3 2 3 4 4  3 3 1   15 9 11
Vậy, có 2 điểm M cần tìm là: M  ;  ; hay M  ; ;  2 4 2  2 4 2      b) N ( )
  N(1 2t;  2  t; 3 2t) 1 1 2 2 2 3 2 S  [NA; NB]  32t 128t 146  (4t  8)  9  ABN 2 2 2 2 3 2  maxS   4t  8  0  t  2  . ABN 2
Vậy, điểm N cần tìm là N(-3; 0; 1).
Bài 3. Trong không gian Oxyz cho đường thẳng (d) và mặt cầu (S): 2  x  2y  z 1  0 2 2 2 (d) : ;
(S) :x  y  z  4x  6y  m  0 x  2y  2z  4  0
Tìm m để (d) cắt (S) tại hai điểm M, N sao cho MN = 8. Hướng dẫn: 2 2 2
Mặt cầu (S): (x  2)  (y  3)  z  13  m có tâm I(-2; 3; 0), bán kính R  IN  13  m , với m < 13. 2 2
Dựng IH  MN  MH  HN  4  IH 
IN  HN  13 m 16  m 3 , x  t  1
Phương trình tham số của đường thẳng (d): y  1 t 2  z  1   t   1  1
(d) có vectơ chỉ phương u  1; ; 1  (2; 1; 2)  2 
và đi qua điểm A(0; 1; -1)   2 AI  ( 2
 ; 2; 1); [AI; u]  (3; 6;  6) [AI; u] 2 2 2 3  6  6 81
Khoảng cách h từ I đến đường thẳng (d): h     3. 2 2 2 u 2 1  2 9 Ta có: IH = h 
m  3  3   m  3  9  m  1  2 (thỏa điều kiện)
Vậy, giá trị cần tìm: m = -12. Bài 4.
– y + z – 5 = 0. Viết phương trình mặt phẳng 125 có thể tích bằng 36 .
Hướng dẫn: Phương trình mặt phẳng (xOy): z = 0 
m(2x – y + z – 5) – nz = 0  (P) : 2mx  my  (m  n)z  5m  0
 Giao điểm A, B, C của (P) và 3 trục Ox, Oy, Oz lần lượt có tọa độ: Page 66
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.  5   5m  A
; 0; 0 , B(0;  5; 0), C 0; 0;   2     m n   
 Thể tích tứ diện OABC bằng 125 1 1 5 5m 125  V  .OA.OB.OC  . .5.  36 6 6 2 m  n 36 m  n  3m m  1, n  2  m  n  3 m    m n 3m     m  1, n  4 
(P ) : 2x  y  3z  5  0 (m  1; n  2) 1
Vậy, có 2 phương trình mặt phẳng (P):
(P ): 2x y 3z 5  0 (m 1; n  4  )  2
Bài 5. Trong không gian Oxyz, tìm trên Ox điểm A cách đều đường thẳng x 1 y z  2 (d) :   1 2 2 – y – 2z = 0.
Hướng dẫn: Gọi A(a; 0; 0)  Ox . 2a 2a d(A; )   2 2 2 2 1  2 3 M (1; 0;  2)  0
và có vectơ chỉ phương u (1; 2; 2) Đặt M M  u AM M 0 1 0 1 2.S [AM ; u] 2 AM M 0 8a  24a  36 0 1  d(A; )    M M u 3 0 1 2 2a 8a  24a  36 2 2 2  
 4a  8a  24a  36  4a  24a  36  0 3 3 2
 4(a  3)  0  a  3.
Vậy, có một điểm: A(3; 0; 0).
Bài 6. Trong không gian với hệ tọa độ vuông góc Oxyz cho mặt phẳng (P) và mặt cầu (S): 2 2 2 2
(P): 2x  2y  z  m  3m  0 ;
(S) : (x 1)  (y 1)  (z 1)  9.
Tìm m để (P) tiếp xúc (S). Với m tìm được xác định tọa độ tiếp điểm. Hướng dẫn: 2 2 2 2
Ta có: (P) : 2x  2y  z  m  3m  0 ; (S) : (x  1)  (y  1)  (x 1)  9 có tâm I(1; -1; 1) và bán kính R = 3.
(P) tiếp xúc (S)  d[I, (P)]  R 2 2.1 2.( 1  ) 1.1 m  3m  2 m  2 
 3  m  3m 1  9   2 2 2 2  2 1 m  5 
Vậy, (P) tiếp xúc (S) khi m = -5 hay m = 2, khi đó (P): 2x + 2y + z – 10 = 0 x 1 y 1 z 1
Đường thẳng (d) qua I và vuông góc với (P) có phương trình:   2 2 1 Page 67
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. 2x  2y  z 10  0 x  3  
Tọa độ tiếp điểm là nghiệm của hệ: x 1 y 1 z 1  y  1    2 2 1  z  2
Vậy, tọa độ tiếp điểm M(3; 1; 2).
Bài 7. Trong không gian oxyz cho hai đường thẳng: x 2t  x  y 30 (d y  t 1) :  ; (d2) :   4x  4y  z 3 120 z 4
Chứng minh (d1) và (d2) chéo nhau. Viết phương trình mặt cầu (S) có đường kính là đoạn vuông
góc chung của (d1) và (d2). Hướng dẫn: (d 
1) đi qua điểm A(0; 0; 4) và có vectơ chỉ phương 1 u (2; 1; 0) (d u  (3;  3; 0)
2) đi qua điểm B(3; 0; 0) và có vectơ chỉ phương 2 AB  (3; 0;  4); AB. 1 [u ; 2 u ]  36  0  AB, 1 u , 2 u không đồng phẳng.
Vậy, (d1) và (d2) chéo nhau. / x  3  t  / (d y  t
2) có phương trình tham số: . z  0 
Gọi MN là đường vuông góc chung của (d1) và (d2) M  (d )  M(2t; t; 4) / /
N  (d )  N(3 t ;  t ; 0) / /
 MN  (3 t  2t;  t  t;  4) 1 , 2 / / / MN  1 u 2
 (3 t  2) (t  t)  0 t  1  M(2; 1; 4) Ta có:        / / MN  u 3
  t  2t  (t  t)  0 t  1 N(2; 1; 0) 2 1
Tọa độ trung điểm I của MN: I(2; 1; 2), bán kính R  MN  2. 2 2 2 2
Vậy, phương trình mặt cầu (S): (x  2)  (y 1)  (z  2)  4. x  t x  t'  
Bài 8. Trong không gian Oxyz cho 2 đường thẳng: (d y  4  t y  t 3 '6 1) :  ; và (d2) :    z  6  2t z  t' 1
Gọi K là hình chiếu vuông góc của điểm I(1; -1; 1) trên (d2). Tìm phương trình tham số của đường
thẳng qua K vuông góc với (d1) và cắt (d1). Hướng dẫn: (d  u  (1; 3; 1) 1) có vectơ chỉ phương 1 u
(1; 1; 2); (d2) có vectơ chỉ phương 2 / / / / / / K (
 d )  K(t ; 3t  6; t 1)  IK  (t 1; 3t  5; t  2) 2 / / / / 18 18 12 7 IK u 
 2  t 1 9t 15  t  2  0  t   K ;  ; 11  11 11 11   Page 68
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
H(t; 4  t; 6  2t), (H(d )) 1) tại 1 18 56 59 HK t; t; 2t         11 11 11    18 56 118 26 HK  1 u   t   t   4t  0  t   11 11 11 11  30 7  1  HK  4;  ;   (44;  30;  7).  11 11   11  18 x   44  11   12 y    30 11 .   7 z   7  11
Bài 9. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
P: x 2y 2z + 5 = 0;Q: x 2y 2z -13 = 0.
Viết phương trình của mặt cầu (S) đi qua gốc tọa độ O, qua điểm A(5;2;1) và tiếp xúc với cả hai mặt phẳng (P) và (Q). Hướng dẫn: Bài 1.
Gọi I(a;b;c) là tâm và R là bán kính của mặt cầu (S). Từ giả thiết ta có: OI AI
OI AI d I,P dI,Q O    
  I d I,P  d
 I,P  d I,Q Ta có:
OI AI OI AI a b c  a  2  b  2  c  2 2 2 2 2 2 5 2 1
 10a  4b  2c  30 (1)
OI d I P
| a  2b  2c  5 | ,
a b c
 9a b c   a  2b  2c  52 2 2 2 2 2 2 (2) 3
d I P  dI Q | a  2b 2c  5| | a  2b 2c 13| , ,   3 3
a  2b  2c  5  a  2b  2c 13 ( lo¹i) 
a  2b  2c  4 (3) 
a  2b  2c  5  a  2b  2c 13 17 11a 11 4a
Từ (1) và (3) suy ra: b ; c     (4) 3 6 3 2 2 2
Từ (2) và (3) suy ra: a b c  9 (5) Page 69
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Thế (4) vào (5) và thu gọn ta được: a  2221a  658  0 658  658 46 67 
Như vậy a  2 hoặc a I ; ;
221 .Suy ra: I(2;2;1) và R = 3 hoặc  221 221 221 và R= 3  
Vậy có hai mặt cầu thỏa mãn yêu cầu với phương trình lần lượt là: 2 2 2 x  658   46   67 
 2  y  2  z  2 2 2 1  9 và x   y   z   9  221  221  221      
Bài 10. Trong không gian với hệ trục Oxyz cho mặt cầu (S) có phương trình 2 2 2
x y z  2x  4y  6z 11  0 và mặt phẳng ():2x + 2y - z + 17 = 0. Viết phương trình mặt
phẳng () song song với () và cắt (S) theo giao tuyến là đường tròn có chu vi bằng 6. Hướng dẫn:
Do () // () nên () có phương trình 2x + 2y – z + D = 0 (D  17)
Mặt cầu (S) có tâm I(1; -2; 3), bán kính R = 5
Đường tròn có chu vi 6 nên có bán kính r = 3. 2 2 2 2
Khoảng cách từ I tới () là h = R r  5  3  4 2.1 2( 2  )  3  DD  7  Do đó  4  5
  D  12   2 2 2 2  2  ( 1  ) D  17 (lo¹i)
Vậy () có phương trình 2x + 2y – z - 7 = 0
Bài 11. Trong không gian Oxyz, tìm trên Ox điểm A cách đều đường thẳng x 1 y z  2 (d) :   1 2
2 và mặt phẳng ( ) : 2x – y – 2z = 0.
Hướng dẫn: Gọi A(a; 0; 0)  Ox . 2a 2a
Khoảng cách từ A đến mặt phẳng ( ) : d( ; A )   2 2 2 3 2 1  2
(  ) qua M (1; 0;  2) u  0
và có vectơ chỉ phương (1; 2; 2) Đặt M M u AM M 0 1
. Do đó: d(A;  ) là đường cao vẽ từ A trong tam giác 0 1 2.S [AM ; u] 2 AM M 0
8a  24a  36 0 1  d( ; A )    M M u 3 0 1
Theo giả thiết: d(A;  ) = d(A;  ) 2 2a
8a  24a  36 2 2 2  
 4a  8a  24a  36  4a  24a  36  0 3 3 2
 4(a  3)  0  a  3. Vậy, có một điểm A(3; 0; 0).
Bài 12. Trong không gian với hệ tọa độ Oxyz .Viết phương trình (P) qua O , vuông góc với mặt
phẳng (Q) : x y z  0 và cách điểm M(1;2; 1
 ) một khoảng bằng 2 . Page 70
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Hướng dẫn: Phương trình mặt phẳng (P) qua O nên có dạng : Ax + By + Cz = 0 với 2 2 2
A B C  0
Vì (P)  (Q) nên 1.A+1.B+1.C = 0  A+B+C = 0  C  A B (1) Theo đề :
A  2B C d(M;(P)) = 2 2 2 2 2 
 2  (A  2B C)  2(A B C ) (2) 2 2 2
A B C 2 8A
Thay (1) vào (2) , ta được : 8AB+5 B  0  B  0 hay B =  5 (1)
B  0 C  A . Cho A  1,C  1
 thì (P) : x z  0 8A  B =  C
x y z  5 . Chọn A = 5 , B = 1  (1) 3 thì (P) : 5 8 3 0 x 1 y z 1
Bài 13. Cho điểm A(10; 2; -1) và đường thẳng d có phương trình   2 1 3 . Lập phương
trình mặt phẳng (P) đi qua A, song song với d và khoảng cách từ d tới (P) là lớn nhất. Hướng dẫn:
Gọi H là hình chiếu của A trên d, mặt phẳng (P) đi qua A và (P)//d, khi đó khoảng cách giữa d và
(P) là khoảng cách từ H đến (P).
G.sử điểm I là hình chiếu của H lên (P), ta có AH HI => HI lớn nhất khi A I
Vậy (P) cần tìm là mặt phẳng đi qua A và nhận AH làm véc tơ pháp tuyến.
H d H(1 2 ;t ;t1 3t)vì H là hình chiếu của A trên d nên
AH d AH.u  0 (u  (2;1;3) là véc tơ chỉ phương của d)  H(3;1;4)  AH( 7  ; 1  ;5)
Vậy (P): 7(x – 10) + (y – 2) – 5(z + 1) = 0  7x + y -5z -77 = 0
Bài 14. Trong không gian với hệ tọa độ Oxyz, cho điểm A ( 3 ; - 1 ; 1 ) , đường thẳng  và mp ( P) x y  2 z
lần lượt có phương trình  :   1 2
2 , ( P ) : x – y + z - 5 = 0 .
Viết phương trình tham số của đường thẳng d thỏa các điều kiện :đi qua A , nằm trong ( P) và hợp
với đường thẳng  một góc 450. Hướng dẫn: Gọi u , u , n d
P lần lươt là các vtcp của đt d , đt  và vtpt của mp ( P). 2 2 2 Đặt u  ( ; a ;
b c), (a b c  0) n u d
. Vì d nằm trong ( P) nên ta có : P d
=> a – b + c = 0  b = a + c ( 1 ).
Theo gt : góc giữa 2 đt bằng 450  Góc giữa 2 vtcp bằng 450 .
a  2b  2c 2  2 2 2 2 
 2(a  2b c)  9(a b c ) (2) 2 2 2
a b c 2 .3 Page 71
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. c  0 2 
Thay (1) vào ( 2) ta có : 14c  30ac  0  15ac    7
* Với c = 0 : chọn a = b = 1 . Ta có ptts của d là : x = 3 + t ; y = - 1 – t ; z = 1
x  3  7t
* Với c = - 15a / 7 . chọn a = 7 , c = - 15 , b = -8 . ta có ptts của d là : d : y  1   8t z 115t  x  1   2t x y z
Bài 15. Trong không gian oxyz cho hai đường thẳng d   y t 1 : 1 1 2 ; d2 z 1 t  và điểm M(1;2;3).
1.Viết phương trình mặt phẳng chứa M và d1 ; Tìm M’ đối xứng với M qua d2.
2.Tìm A d ; B d 1 2 sao cho AB ngắn nhất . Hướng dẫn: x  1   2t x y z
Trong không gian oxyz cho hai đường thẳng d   y t 1 : 1 1 2 ; d2 z 1 t  và điểm M(1;2;3).
1.Viết phương trình mặt phẳng chứa M và d1 ; Tìm M’ đối xứng với M qua d2.
+ Phương trình mặt phẳng chứa M và d1 …. Là (P) x + y – z = 0
+ Mp(Q) qua M và vuông góc với d2 có pt 2x – y - z + 3 = 0
+ Tìm được giao của d2 với mp(Q) là H(-1 ;0 ;1)
…  Điểm đối xứng M’ của M qua d2 là M’(-3 ;-2 ;-1)
2.Tìm A d ; B d 1 2 sao cho AB ngắn nhất .
Gọi A(t;t;2t) và B(-1-2t1 ;-t1 ;1+t1) AB ngắn nhất khi nó là đoạn vuông góc chung của hai đường thẳng d1 và d2 . A . B v  0  3 3 6   1  1  7 18   1 
…….  tọa độ của A ; ;   và B ; ;   A . B v  0   35 35 35   35 35 35  2
Bài 16. Trong không gian với hệ toạ độ Oxyz ,cho điểm I(1;5;0) và hai đường thẳng x tx y  2 z
 : y  4  t  :   1 ; 2  1 3  3  z  1   2t
1. Viết phương trình tham số của đường thẳng d đi qua điểm I và cắt cả hai đường thẳng   1 và 2
2. Viết phương trình mặt phẳng( ) qua điểm I , song song với   1 và 2 Hướng dẫn: Page 72
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. x tx y  2 z
I(1;5;0) ,  : y  4  t  :   1 2  1 3  3  z  1   2t   u (1; 1  ;2)  (0;4; 1  ) 1 có vtcp 1 ;và 1 đi qua điểm M1  u (1; 3  ; 3  )  M (0;2;0) 2 có vtcp 2 ; 2 đi qua điểm 2     mp(P)chứa  n M I,u  (3; 1  ; 2  ) 1 và điểm I có vtpt 1 1  
p/t mp(P) : 3x –y - 2z + 2 = 0 ' Tương tự mp(Q) chứa  n 2 và điểm I có vtpt (3;-1;2)
p/t mp(Q) : 3x - y + 2z + 2 = 0
*Vì đường thẳng d qua I , cắt   1 và 2 , nên d = (P)  (Q)   ' 
đường thẳng d có vtcp u  , n n d 
 = (1;3;0); d đi qua điểm I(1;5;0) x  1 t
Nên p/t tham số của d là y  5  3t z  0 
*mp( ) qua điểm I và song song với     1 và
2 nên ( ) có vtpt n = u , u 1 2   =(9;5;-2)
 p/t ( ) : 9x + 5y -2z – 34 = 0
Bài 17. Trong không gian với hệ trục toạ độ Oxyz cho 4 điểm A( 1; -1; 2), B( 1; 3; 2), C( 4; 3; 2), D( 4;
-1; 2) và mặt phẳng (P) có phương trình: x y z  2  0 . Gọi A’là hình chiêú của A lên mặt
phẳng Oxy. Gọi ( S) là mặt cầu đi qua 4 điểm A’, B, C, D. Xác định toạ độ tâm và bán kính của
đường tròn (C) là giao của (P) và (S). Hướng dẫn: Dễ thấy A’ ( 1; -1; 0)
* Giả sử phương trình mặt cầu ( S) đi qua A’, B, C, D là: x2  y2  z2  ax 2  2by  cz 2  d  , 0
a2 b2 c2 d 0   a 2  2b  d  2  5 0 a    2  a
2  6b  4c  d  14  0  Vì ' A , , B ,
C D S nên ta có hệ:   b  1  a
8  6b  4c  d  29  0 c    1 a
8  2b  4c  d  21    0 d  1
Vậy mặt cầu ( S) có phương trình: 2 2 2
x y z  5x  2y  2z 1  0  5  29 (S) có tâm I 1 ; 1 ;  , bán kính R   2  2
+) Gọi H là hình chiếu của I lên (P). H là tâm của đường tròn ( C)
+) Gọi ( d) là đường thẳng đi qua I và vuông góc với (P). Page 73
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
(d) có vectơ chỉ phương là: n 1 ; 1 ; 1 x  5/ 2  t   5 
Suy ra phương trình của d: y  1  t
 H  t 1; t 1; t   2  z  1 t 5 5 5  5 1 1  Do H  d (P) nên:
 t 1 t 1 t  2  0  t 3  
 t    H ; ;  2 2 6  3 6 6 
Bà 18. Trong không gian với hệ trục toạ độ Oxyz cho P : x  2y z  5  0 và đường thẳng x  3 (d) :
y 1  z  3 2
, điểm A( -2; 3; 4). Gọi  là đường thẳng nằm trên (P) đi qua giao điểm
của ( d) và (P) đồng thời vuông góc với d. Tìm trên  điểm M sao cho khoảng cách AM ngắn nhất. Hướng dẫn:
x  2t  3 
Chuyển phương trình d về dạng tham số ta được: y t 1  z t  3
Gọi I là giao điểm của (d) và (P)  I 2t  ; 3 t  ; 1 t   3
Do I  P  2t  3  ( 2 t  ) 1  (t  )
3  5  0  t  1  I  4 ; 0 ; 1 
* (d) có vectơ chỉ phương là a( ) 1 ; 1 ; 2
, mp( P) có vectơ pháp tuyến là  n ; 2 ; 1   1   ,an   3 ; 3 ; 3
. Gọi u là vectơ chỉ phương của    u  1 ; 1 ; 1 x  1  u    : y  u . Vì M     M 1  ; u 4 ; u  u,   AM 1  ; u u  ; 3 u  z  4  u
AM ngắn nhất  AM    AM  u  u . AM  0   1 ( 1  ) u  ( 1 u  ) 3  u . 1  0 4    7 4 16  u  . Vậy M ; ;  3  3 3 3 
Bài 19. Cho mặt phẳng 
( ) : x y  2z  0 và các điểm A(1;2;-1), B(3;1;-2), C(1;-2;1). Tìm điểm M thuộc mặt phẳng  ( ) sao cho: a) MA+MB nhỏ nhất b) |MA-MB| lớn nhất 2 2 2
c) MA MB MC lôùn nhaát
d) MA MB MC nhoû nhaát Đáp số: 13 4   7 11   5 1 2  a)M ;1; ; ) b M
; ;1 ; c)M(2;2;2); d)M ; ;        5 5   2 2   3 3 3  Page 74
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
x 1 y 1 z
Bài 20. Cho đường thẳng d :   1 1
2 và các điểm A(1;4;2), B(-1;2;4). Tìm điểm M thuộc d sao cho:
a) MA MB nhỏ nhất b) MA+MB nhỏ nhất 2 2
c) MA MB nhoû nhaát d) AMB nhoû nhaát Đáp số:  2 1 2 7      a M  1 10 4 7 12 5 38 )
1;0;4; b)M 1;0;4     ; c)M ; ; ; d)M ; ;  3 7 7 7 3 1 7 3 1 7                 Page 75
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
PHỤ LỤC 2. GIẢI BÀI TOÁN HÌNH HỌC KHÔNG GIAN BÀNG HAI CÁCH
Bài 1. Cho hình chóp SABC có đáy ABC là tam giác đều có cạnh bằng 2a 2 , SA vuông góc với
(ABC) và SA = a. Gọi E, F lần lượt là trung điểm của cạnh AB, BC. Tính góc và khoảng cách giữa
hai đường thẳng SE và AF. Hướng dẫn:
Cách 1: Gọi M là trung điểm của BF  EM // AF S
 (SA; AF)  (EM; AF)  SEM 2 2 2 2 2
SE  SA  AE  a  2a  3a  SE  a 3 H A 2a 2. 3 C AF   a 6 2 K F a 6 E  EM  BM  MF  ; BF  a 2 M 2 B 2 2 2 2 2 2
SB  SA  AB  a  8a  9a  SB  3a 2 2 2 2 2 2
SF  SA  AF  a  6a  7a  SF  a 7 2 2 2 2 1 2 SB 1 15a  SF  2.SM  BF 2 2 2 2 2
 9a  7a  2SM  .2a  SM  2 2 2
. Áp dụng định lý hàm Côsin vào 2 2 2 3a 15a 2 2 2 3a ES EM SM     2 2 2 2 cos  cosSEM      o    45 . 2.ES.EM a 6 2 2 2. .a 3 2 a 2
Dựng AK  ME; AH  SK. Ta có: AK  MF   2 và AH (SME)
Vì AF // ME  d(SE; AF)  d(AF; (SME)) AH. 1 1 1 1 2 3 a 3       AH  2 2 2 2 2 2 AH SA AK a a a 3 a 3 Vậy, d(SE; AF)  3 . z a S Cách 2:
Dựng hệ trục Axyz, với Ax, Ay, Az với A(0; 0; 0),
B(a 2; a 6; 0), C(a 2; a 6; 0), S(0; 0; a), C  a 2 a 6   a 2  E .  ; ; 0; F(0; a 6; 0);M ; a 6; 0 A  2 2   2      x F E y M B Page 76
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.  a 2 a 6   a 2  SE   ;
;  a; AF  (a; a 6; 0), SM   ; a 6;  a 2 2 2      a 2 a 6 0.  a 6. 0(a) 2 3a 2 2 2 cos  cos(SE; AF)    o    45 . 2 2 a 3a a 6.a 3 2 2 2 0  6a  0.   a 2 2 2 2 2 2  a 6 a 3  a 3 a 3 [SE; SM]   ; 0;   ( 2; 0; 1)  n,   2 2  2 2 với n ( 2; 0; 1)
Phương trình mặt phẳng (SEM) qua S với pháp vectơ n : 2x  z  a  0. 0  0  a a 2
Khoảng cách từ A đến (SEM): d(A;SEM)   2 1 3 a 3
Vì AF // EM  AF //(SEM)  d(SE; AF)  d(A; SEM) . Vậy, d(SE; AF)  . 3
Bài 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a, cạnh SA vuông theo a. Hướng dẫn: Cách 1:
Ta có: SA  (ABC)  SA  AC. S 1
vuông tại A có AM là trung tuyến nên MA  SC. 2 S  A  (ABC) M Ta lại có:  AB  BC ( A  BC vuoâng taïi B)
 SB  BC (định lý 3 đường vuông góc) C A H 1 K tuyến nên MB  SC. 2 Suy ra: MA = MB  tại M.. B
Dựng MH // SA và HK // BC (H  AC; K  AB)  1 MH  SA  a SA  (ABC) MH  (ABC)  2 vì:     BC AB HK AB    1 HK  BC  a z  2 S 2a 2 2 2 2 2 2
MK  MH  HK  a  a  2a  MK  a 2 M A H Page 77 C y a 5 K x a B 5
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. 2 1 1 a 2 S  .MK.AB  .a 2.a  MAB 2 2 2 2 2 2 2 2 2 Cách 2:
AC  AB  BC  a  4a  5a  AC  a 5 2 2 AB a a
Dựng BH  AC (H  AC), ta có: AH    AC ; a 5 5 1 1 1 5 2a     BH  2 2 2 2 BH AB BC 4a 5
Dựng hệ trục tọa vuông góc Axyz, với Ax, Ay, Az đôi một vuông góc và  2a a
A(0; 0; 0), C(0; a 5; 0), S(0; 0; 2a), B ; ; 0  5 5     a 5 
Tọa độ trung điểm M của SC là M  0; ; a 2     a 5  3a  2a 3a  3a Ta có: MA   0; ; a  MA  MB   ; ; a  MB .  2  2 ;  5 2 5    2 suy ra: MA = MB  2 2  a 2a  2 2 Ta có: [MA; MB]   ;  ; a   [MA; MB]  a 2  5 5  2 1 1 2 a 2 S  [MA; MB]  .a 2  . MAB 2 2 2
Bài 3. Cho hình chóp đều S.ABC, đáy ABC có cạnh bằng a, mặt bên tạo với đáy một góc bằng o o
(0    90 ). Tính thể tích khối hình chóp S.ABC và khoảng cách từ đỉnh A đến mặt phẳng (SBC).
Cách 1: Gọi H là trung điểm của BC..
nên chân đường cao đỉnh S
trùng với giao điểm ba đường cao là trực tâm O Suy ra:
BC  SH, BC AH, nên SHA   . 1 a 3 Ta có: OH  AH  . 3 6 a 3 S HO a 3
 HO vuông góc: SO  HO.tg  tg SH   6 và cos 6.cos 2 3 1 1 a 3 a 3 a tg
Thể tích hình chóp S.ABC: V  .SO.S  . tg .   ABC 3 3 6 4 24 2 1 a 3 S  .SH.BC  SBC 2 12.cos .
Gọi h là khoảng cách từ A đến (SBC), ta có: 3 2 1 3.V a tg a 3 a 3 V  .h.S  h   3. :  sin SBC 3 S 24 12cos 2 SBC Page 78
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Cách 2: Vì S.ABC là hình chóp đều nên chân đường cao đỉnh S z
trùng với tâm O đường tròn (ABC). Gọi M là trung điểm của BC. S Ta có: 2 a 3 AO a 3  AM  OM  3 3 và 6 C
AM  BC, SM  BC  SMA   A  O M y a 3 : SO  OM.tg  tg B 6 x
Dựng hệ trục tọa độ Axyz, với Ax, Ay, Az đôi một vuông góc, A(0; 0; 0),
 a a 3   a a 3   a 3   a 3   a 3 a 3  B ; ; 0,C ; ; 0,M0; ; 0, O0; ; 0, S0; ; tg  2 2   2 2   2   3   3 6            3 1 a tg Thể tích hình chóp: V  .SO.S  ABC 3 24  a a 3 a 3  Ta có: BS    ;  ; tg, BC  (a; 0; 0) 2 6 6   2 2  a 3 a 3  [BS; BC]  0;  tg ;     n 6 6  
Phương trình mặt phẳng (SBC) qua B với vectơ pháp tuyến n : 2 2  a  a 3  a 3  a 3 0 x a 3   tg    y   
(z  0)  0  (SBC) : tg y   z  tg  0. 2 6  2    6   2 a 3 tg .  O O  tg a 3 tg 2  a 3 2
Khoảng cách d từ A đến (SBC): d    sin .  2 1 tg  1 2 cos
Bài 4. Cho hình lập phương ABCD . A'B'C'D' cạnh a. M, N lần lượt là trung điểm của AB và C'D'.
Tính khoảng cách từ B' đến (A'MCN). / / / /
Cách 1: Bốn tam giác vuông AA M, BCM, CC N, A D N bằng nhau (c.g.c) / /  A M  MC  CN  NA /  A MCN là hình thoi.
Hai hình chóp B/A/MCN và B/.A/NC có chung đường cao vẽ từ D/ N C/ đỉnh B/ và S  2.S V  2.V / / A MCN A NC nên: / / / / B .A MCN B .A NC. Mà: A/ B/ 3 1 / 1 1 a V  V  .CC .S  .a. .a.a  / / / / / B .ANC C.A B N A B N 3 3 2 6 D C 3 a  V  . / / B .A MCN 3 A B M Page 79
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. 1 / Ta có: S  .A C.MN, / A MCN 2 với 2 / / a 6
A C  a 3; MN  BC  a 2  S  . / A MCN 2 1 /
Gọi H là hình chiếu của B/ trên (A/MCN), ta có: V  .B H.S / / / B .A MCN A MCN 3 3 2 3.V / / / a a 6 a 6 B .A MCN  B H   3. :  . S 3 2 3 / A MCN
Cách 2: Chọn hệ trục Dxyz, với Dx, Dy, Dz đôi một vuông góc, A(a; 0; 0), B(a; a; 0), C(0; a; 0),
D(0; 0; 0), A/(a; 0; a), B/(a; a; a), C/(0; a; a), D/(0; 0; a),  a   a z M a; ; 0 , N 0; ; a  D/ 2   2  N C/     a Ta có: A/ / A C  ( a  ; a; a), MN  ( a  ; 0; a) / 2 2 2 2
[A C; MN]  (a ; 2a ; a )  a (1; 2; 1) D C a y 2
a .n vôùi n  (1; 2; 1). A a M B
Phương trình mp (A/MCN) qua C(0; a; 0) với pháp vectơ n : x
1(x  0)  2(y  a) 1(z  0)  0 /
 (A MCN) : x  2y  z  2a  0. a  2a  a  2a 2a a 6
Khoảng cách d từ B/(a; a; a) đến mp(A/MCN): d    . 1 4 1 6 3
Bài 5. Tính thể tích của hình chóp S.ABC, biết đáy ABC là một tam giác đều cạnh a, mặt bên (SAB) vuô
Cách 1:Dựng SH  AB S Ta có:
(SAB)  (ABC), (SAB)(ABC) AB, SH  (SAB)
 SH  (ABC) và SH là đường cao của hình chóp. Dựng HN  BC, HP  AC B
 SN  BC, SP  AC  SPH  SNH   N H HN = HP.  C P o a 3 HP  HA.sin60  . 4 A a 3 SH  HP.tg  tg 4 2 3 1 1 a 3 a 3 a
Thể tích hình chóp S.ABC : V  .SH.S  . .tg .   tg ABC 3 3 4 4 16 Page 80
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế.
Cách 2: Dựng SH  AB
Ta có: (SAB)  (ABC), (SAB)  (ABC)  B, SH  (SAB)  SH  (ABC) Vì (SAC) và (SBC)
Dựng hệ trục tọa độ Hxyz, với Hx, Hy, Hz đôi một vuông góc, H(0; 0; 0),  a   a A ; 0; 0 ; B ; 0; 0  ,  2   2      z  a 3  C0; ; 0, S(0; 0; h), (h  0). h S 2  
Phương trình mp (ABC): z = 0, với pháp vectơ 1
n  (0; 0;1) . Phương trình mp (SAC): B x y z    1 a a 3 h C H a 3
 (SAC) : 2h 3x  2hy  a 3z  ah 3  0 y A 2 a
với n2  (2h 3; 2h; a 3) . 2 x 0  0  a 3 a 3 cos   2 2 2 2 2
0  0 1. 12h  4h  3a 16h  3a 2 2 1 2 16h  3a   1 tg   2 2 cos  3a 2 2 2 3a tg  a 3  h   h  tg 16 4 2 3 1 1 a 3 a 3 a
Thể tích hình chóp S.ABC: V  .h.S  . tg .   tg ABC 3 3 4 4 16 .
Bài 6. Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với AB = AC = a, góc o BAC 120
cosin của góc giữa hai mặt phẳng (ABC) và (AB'I). Hướng dẫn:
Cách 1: Gọi H là trung điểm BC  AH  BC. a  AH  B/ C/ 2 và a 3 BH   BC  a 3 / / I  B C A/ 2 . vuông có: I 2 2 / 2 / 2 / / 2 a 2 13a IB  IC  B C   3a  4 4 H B 30o C 2 2 2 2 2 a 2 5a AI  IC  AC   a  4 4 A Page 81
Bài giảng Hình Học Giải tích Không gian.
Ths. Trần Đình Cư. SĐT: 01234332133. Luyện thi và gia sư chất lượng cao Môn Toán, TP Huế. 2 2 2 / 2 5a 2 13a / 2 Ta có: AI  AB   2a   IB 4 4
(AB/ là đường chéo của hình vuông AA/B/B cạnh a). /I vuông tại A. 2 1 2 / 1 a 5 a 10 1 1 a a 3 Ta có: S  .AI.AB  . .a 2  S  .AH.BC  . .a 3  / AB I 2 2 2 4 ; ABC 2 2 2 4
/I), theo công thức chiếu, ta có: 2 2 S a 3 a 10 30 ABC cos   :  S 4 4 10 / AB I C/ z
Cách 2: Gọi H là trung điểm BC  AH  BC A/ a B/ I a a 3  AH  BH   BC  a 3 2 và 2 C
Dựng hệ trục Axyz, với Ax, Ay, Az đôi một vuông góc, A A(0; 0; 0), 60o H y z B  a 3 a   a 3 a      / / a 3 a / a 3 a B ; ; 0, C  ; ; 0, A (0; 0; a), B  ; ; a, C   ; ; a,  2 2   2 2   2 2   2 2           a 3 a a  I  ; ;   2 2 2    /  a 3 a   a 3 a a  AB   ; ; a, AI   ; ; 2 2 2 2 2      2 2 2 / a 3  a 3  a a a 3a a 2a Ta có: AB .AI  .   .  a.      0 2 2 2 2 2 4 4 4   /  AB  AI. /I vuông tại A.
Phương trình mp(ABC): z = 0 có pháp vectơ n  (0; 0; 1) 1 /
mp (AB/I) có cặp vectơ chỉ phương AB , AI , nên có pháp vectơ: 2 2 2 2 2 /  a 3a 3 2a 3  a a [AB ; AI]   ;  ;    (1; 3 3;  2 3)   .n2 4 4 4 4 4   với n  (1; 3 3;  2 3) 2 . /I), ta có: 0  0  2 3 2 3 30 cos    . 0  0 1. 1 27 12 40 10 Page 82