Lời giải bài tập tích phân bội ba | Giải tích 2 | Đại học Bách Khoa Hà Nội
Lời giải bài tập tích phân bội ba | Giải tích 2 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!
Môn: Giải tích 2 40 tài liệu
Trường: Đại học Bách Khoa Hà Nội 2.8 K tài liệu
Tác giả:
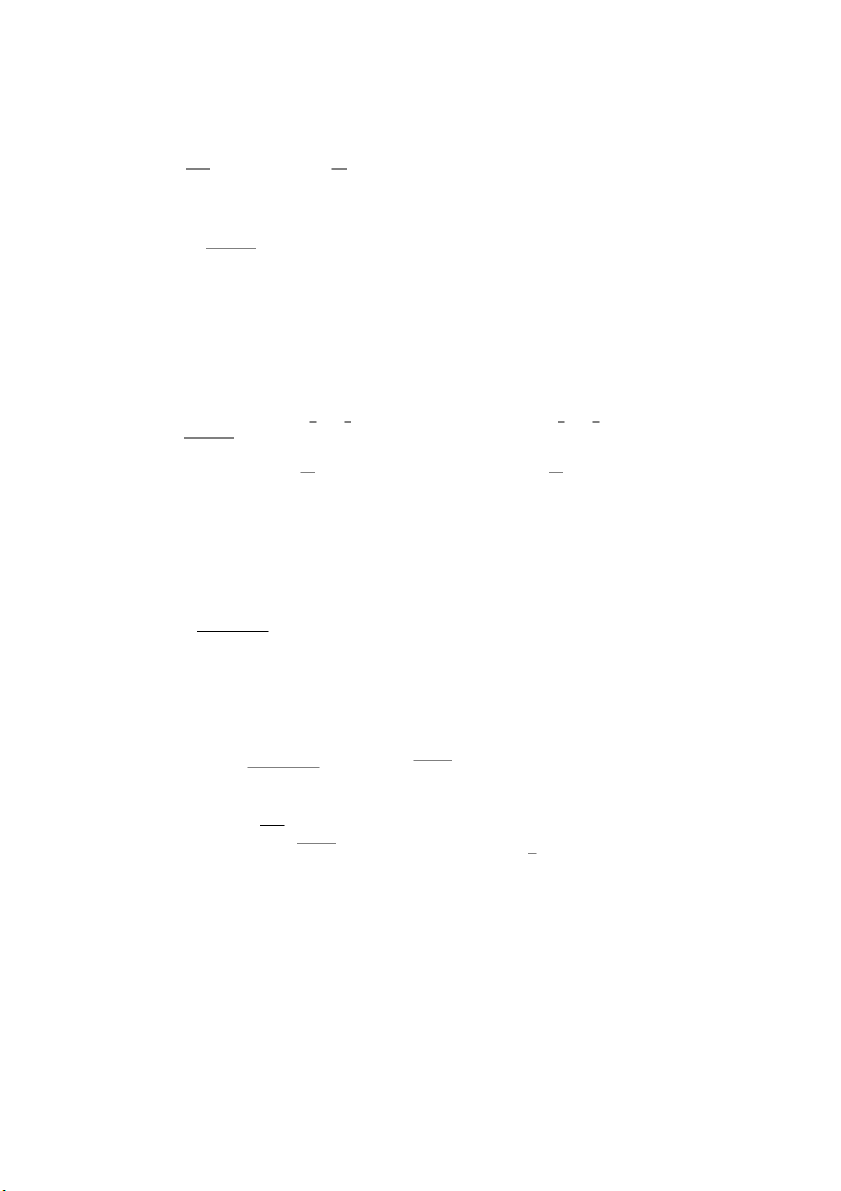
Preview text:
LỜI GIẢI BÀI TẬP TÍCH PHÂN BỘI BA
Câu 1: Tính các tích phân b i ba sau ộ Gi i ả : 0 ≤ 𝑥 ≤ 1/4
𝑎) ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧, (𝑉) { 𝑥 ≤ 𝑦 ≤ 2𝑥 𝑉
0 ≤ 𝑧 ≤ √1 − 𝑥2 − 𝑦2 1 1 4 2𝑥 √1−𝑥2−𝑦2 4
2𝑥 1 √1 − 𝑥2 − 𝑦2
∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫
𝑧𝑑𝑧 = ∫ 𝑑𝑥 ∫ ( 2𝑧2| ) 𝑑𝑦 𝑉 0 𝑥 0 0 𝑥 0 1 1 4 2𝑥 4 1 10 = 1 43
2 ∫ 𝑑𝑥 ∫ (1 − 𝑥2 − 𝑦2)𝑑𝑦 = 2 ∫ (𝑥 − 3 𝑥3) 𝑑𝑥 = 3072 0 𝑥 0
𝑏) ∭ 𝑥2𝑦3𝑑𝑥𝑑𝑦𝑑𝑧 , (𝑉 :
) 1 ≤ 𝑥 ≤ 2, 2 ≤ 𝑦 ≤ 3, 3 ≤ 𝑧 ≤ 4 𝑉 2 3 4 2 3 2 65 455
∭ 𝑥2𝑦3𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫ 𝑥2𝑦3𝑑𝑧 = ∫ 𝑑𝑥 ∫ 𝑥2𝑦3𝑑𝑦 = ∫ 4 𝑥2𝑑𝑥 = 12 𝑉 1 2 3 1 2 1
𝑐) ∭ 𝑥𝑦𝑧𝑑𝑥𝑑𝑦𝑑𝑧, (𝑉): 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ √1 − 𝑥2, 0 ≤ 𝑧 ≤ √𝑥2 + 𝑦2 𝑉 1 √1−𝑥2 √𝑥2+𝑦2 1 √1−𝑥2
∭ 𝑥𝑦𝑧𝑑𝑥𝑑𝑦𝑑𝑧 𝑥(𝑥2 + 𝑦2)𝑦
= ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫ 𝑥𝑦𝑧 𝑑𝑧 = ∫ 𝑑𝑥 ∫ 2 𝑑𝑦 𝑉 0 0 0 0 0
1 𝑥2(1 − 𝑥2) (1 − 𝑥2)2 = ∫ [ 1 4 + 8 ] . 𝑥𝑑𝑥 = 24 0
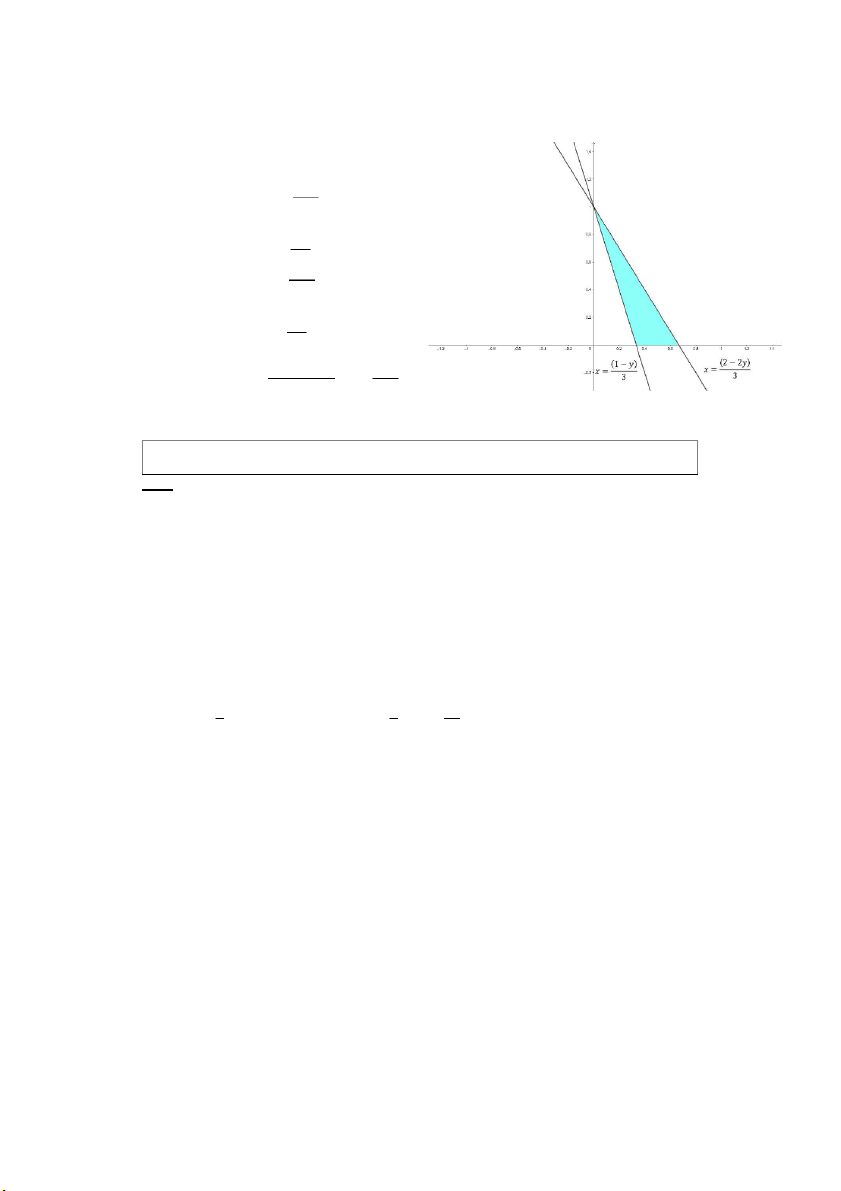
𝑑) ∭ 𝑥𝑑𝑥𝑑𝑦𝑑𝑧 , 𝑉: 3𝑥 + 𝑦 ≥ 1, 3𝑥 + 2𝑦 ≤ 2, 𝑦 ≥ 0, 0 ≤ 𝑧 ≤ 1 − 𝑥 − 𝑦 𝑉
Xét hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷 xác định bởi 3𝑥 + 𝑦 ≥ 1, 3𝑥 + 2𝑦 ≤ 2, 𝑦 ≥ 0 PHAM THANH TUNG
⇒ 𝐷: {(1 − 𝑦)/3 ≤ 𝑥 ≤ (2 − 2𝑦)/3 0 ≤ 𝑦 ≤ 1 2−2𝑦 1 3 1−𝑥−𝑦
⇒ ∭ 𝑥𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝑦 ∫ 𝑑𝑥 ∫ 𝑥𝑑𝑧 𝑉 0 1−𝑦 0 3 2−2𝑦 1 3
= ∫ 𝑑𝑦 ∫ 𝑥(1 − 𝑥 − 𝑦)𝑑𝑥 0 1−𝑦 3 1 13(𝑦 − 1)3 −13 = ∫ 162 𝑑𝑦 = 638 0
Câu 2: Tính các tích phân b i ba sau: ộ Gi i ả :
𝑎) ∭(−𝑥 + 2𝑦)𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 g ới hạn bởi 1 i
≤ −𝑥 + 2𝑦 ≤ 2, −1 ≤ 2𝑥 + 𝑦 + 𝑧 ≤ 2, 0 ≤ 𝑧 ≤ 3 𝑉 𝑢 = −𝑥 + 2𝑦 𝑢′ ′ ′ 𝑥 𝑢𝑦 𝑢𝑧 −1 2 0
Đặt {𝑣 = 2𝑥 + 𝑦 + 𝑧 ⇒ 𝐽−1 = | 𝑣′ ′ ′ 𝑥
𝑣𝑦 𝑣𝑧| = | 2 1 1| = −5 ⇒ 𝐽 = −1/5 𝑤 = 𝑧 𝑤′ ′ ′ 𝑥 𝑤𝑦 𝑤𝑧 0 0 1 1 ≤ 𝑢 ≤ 2
Miền 𝑉 trong tọa độ mới 𝑂𝑢𝑣𝑤 là 𝑉𝑢𝑣𝑤 : { −1 ≤ 𝑣 ≤ 2 0 ≤ 𝑤 ≤ 3 3 2 2 1 ⇒ 𝐼 = ∭ 1 27
5 𝑢𝑑𝑢𝑑𝑣𝑑𝑤= ∫ 𝑑𝑤 ∫ 𝑑𝑣 ∫ 5 𝑢𝑑𝑢 = 10 𝑉𝑢𝑣𝑤 0 −1 1
𝑏) ∭(2𝑥 + 3𝑦)𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 g ới hạn 𝑥 i
+ 𝑦 + 𝑧 = ±3 , 𝑥 + 2𝑦 − 𝑧 = ±1 , 𝑥 + 4𝑦 + 𝑧 = ±2 𝑉 𝑢 = 𝑥 + 𝑦 + 𝑧 𝑢′ ′ ′ 𝑥 𝑢𝑦 𝑢𝑧 1 1 1 Đặ ′ ′ ′
t {𝑣 = 𝑥 + 2𝑦 − 𝑧 ⇒ 𝐽−1 = |𝑣𝑥
𝑣𝑦 𝑣𝑧 | = |1 2 −1| = 6 ⇒ 𝐽 = 1/6 𝑤 = 𝑥 + 4𝑦 + 𝑧 𝑤′ ′ ′ 1 4 1 𝑥 𝑤𝑦 𝑤𝑧 PHAM THANH TUNG −3 ≤ 𝑢 ≤ 3
Miền 𝑉 trong tọa độ mới 𝑂𝑢𝑣𝑤 là 𝑉𝑢𝑣𝑤 : { −1 ≤ 𝑣 ≤ 1 −2 ≤ 𝑤 ≤ 2 2 1 3 2 1 1 ⇒ 𝐼 = ∭ 1 1
6 (𝑢 + 𝑣)𝑑𝑢𝑑𝑣𝑑𝑤= ∫ 𝑑𝑤 ∫ 𝑑𝑣 ∫ 6 (𝑢 + 𝑣)𝑑𝑢 = ∫ 𝑑𝑤 ∫ 6 (0 + 6𝑣)𝑑𝑣 = 0 𝑉𝑢𝑣𝑤 −2 −1 −3 −2 −1
𝑐) ∭(4𝑥2𝑦 − 3𝑥𝑦𝑧)𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉: 1 ≤ 𝑥 ≤ 2,0 ≤ 𝑥𝑦 ≤ 2,0 ≤ 𝑧 ≤ 2 𝑉 𝑢 = 𝑥 𝑢′ ′ ′ 𝑥 𝑢𝑦 𝑢𝑧 1 0 0 Đặ ′ ′ ′
t {𝑣 = 𝑥𝑦 ⇒ 𝐽−1 = |𝑣𝑥
𝑣𝑦 𝑣𝑧 | = | 𝑦 𝑥 0| = 𝑥 ⇒ 𝐽 = 1/𝑥 = 1/𝑢 𝑤 = 𝑧 𝑤′ ′ ′ 𝑥 𝑤𝑦 𝑤𝑧 0 0 1 1 ≤ 𝑢 ≤ 2
Miền 𝑉 trong tọa độ mới 𝑂𝑢𝑣𝑤 là 𝑉𝑢𝑣𝑤 : { 0 ≤ 𝑣 ≤ 2 0 ≤ 𝑤 ≤ 2 2 2 2 1 ⇒ 𝐼 = ∭ 3𝑣𝑤
𝑢 (4𝑢𝑣 − 3𝑣𝑤)𝑑𝑢𝑑𝑣𝑑𝑤= ∫ 𝑑𝑤 ∫ 𝑑𝑣 ∫ (4𝑣 − 𝑢 ) 𝑑𝑢 𝑉𝑢𝑣𝑤 0 0 1 2 2 2
= ∫ 𝑑𝑤 ∫(4𝑣 − 3 ln 2 . 𝑣𝑤)𝑑𝑣= ∫(8 − 6 ln 2 . 𝑤)𝑑𝑤 = 16 − 12 ln 2 0 0 0
𝑑) ∭(3𝑥2 + 2𝑦 + 𝑧)𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉: |𝑥 − 𝑦| ≤ 1, |𝑦 − 𝑧| ≤ 1, |𝑧 + 𝑥| ≤ 1 𝑉 𝑢 = 𝑥 − 𝑦 𝑢′ ′ ′ 𝑥 𝑢𝑦 𝑢𝑧 1 −1 0 Đặ ′ ′ ′
t { 𝑣 = 𝑦 − 𝑧 ⇒ 𝐽−1 = | 𝑣𝑥
𝑣𝑦 𝑣𝑧| = | 0 1 −1| = 2 ⇒ 𝐽 = 1/2 𝑤 = 𝑧 + 𝑥 𝑤′ ′ ′ 𝑥 𝑤𝑦 𝑤𝑧 1 0 1 |𝑢| ≤ 1 −1 ≤ 𝑢 ≤ 1
Miền 𝑉 trong tọa độ mới 𝑂𝑢𝑣𝑤 là 𝑉𝑢𝑣𝑤 : { |𝑣| ≤ 1 ⇔ {−1 ≤ 𝑣 ≤ 1 |𝑤| ≤ 1 −1 ≤ 𝑤 ≤ 1 𝑢 = 𝑥 − 𝑦 𝑥 = (𝑢 + 𝑣 + 𝑤)/2
Ta có: { 𝑣 = 𝑦 − 𝑧 ⇒ { 𝑦 = (𝑣 + 𝑤 − 𝑢)/2 𝑤 = 𝑧 + 𝑥
𝑧 = (𝑤 − 𝑢 − 𝑣)/2 PHAM THANH TUNG 1 3 (𝑤 − 𝑢 − 𝑣)
⇒ 𝐼 = ∭ 2[4(𝑢 + 𝑣 + 𝑤)2 + (𝑣 + 𝑤 − 𝑢) + 2 ] 𝑑𝑢𝑑𝑣𝑑𝑤 𝑉𝑢𝑣𝑤 1 1 1 1 3 3 1 3
= 2 ∫𝑑𝑤 ∫𝑑𝑣 ∫[4(𝑢2 + 𝑣2 + 𝑢2 + 2𝑢𝑣 + 2𝑢𝑤 + 2𝑣𝑤) +2𝑤 + 2𝑣 − 2𝑢]𝑑𝑢 = 3 −1 −1 −1
Câu 3: Tính các tích phân b i ba sau: ộ Gi i ả :
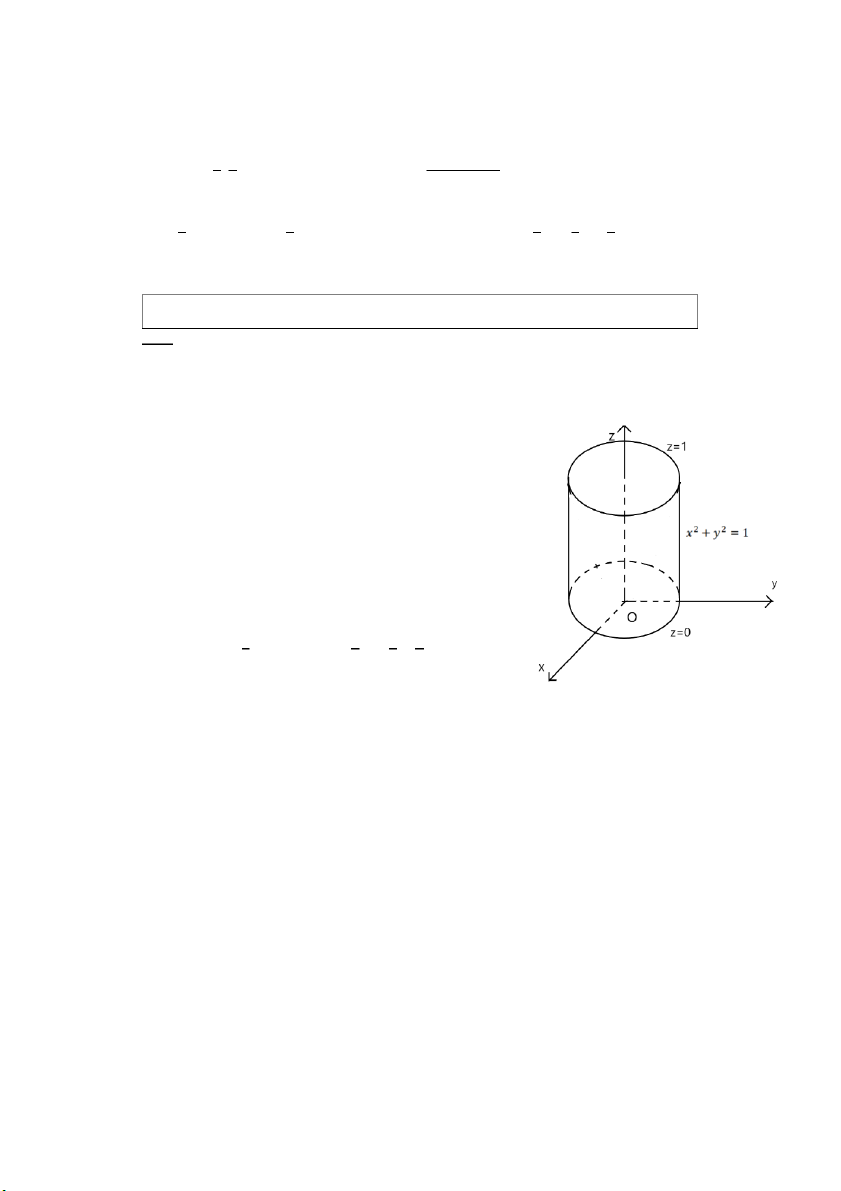
𝑎) ∭(𝑥2 + 𝑦2)𝑧2𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 đ ợc ư g ới hạn b i
ởi 𝑥2 + 𝑦2 = 1, 𝑧 = 0, 𝑧 = 1. 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧 0 ≤ 𝑟 ≤ 1
Miền 𝑉 trong tọa độ trụ là 𝑉: {0 ≤ 𝜑 ≤ 2𝜋 0 ≤ 𝑧 ≤ 1 2𝜋 1 1
⇒ ∭(𝑥2 + 𝑦2)𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑∫ 𝑑𝑟 ∫ 𝑟2𝑧. 𝑟𝑑𝑧 𝑉 0 0 0 2𝜋 1 1 1 𝜋 = 1
2 ∫ 𝑑𝜑 ∫ 𝑟3𝑑𝑟 = 2 . 2𝜋. 4 = 4 0 0
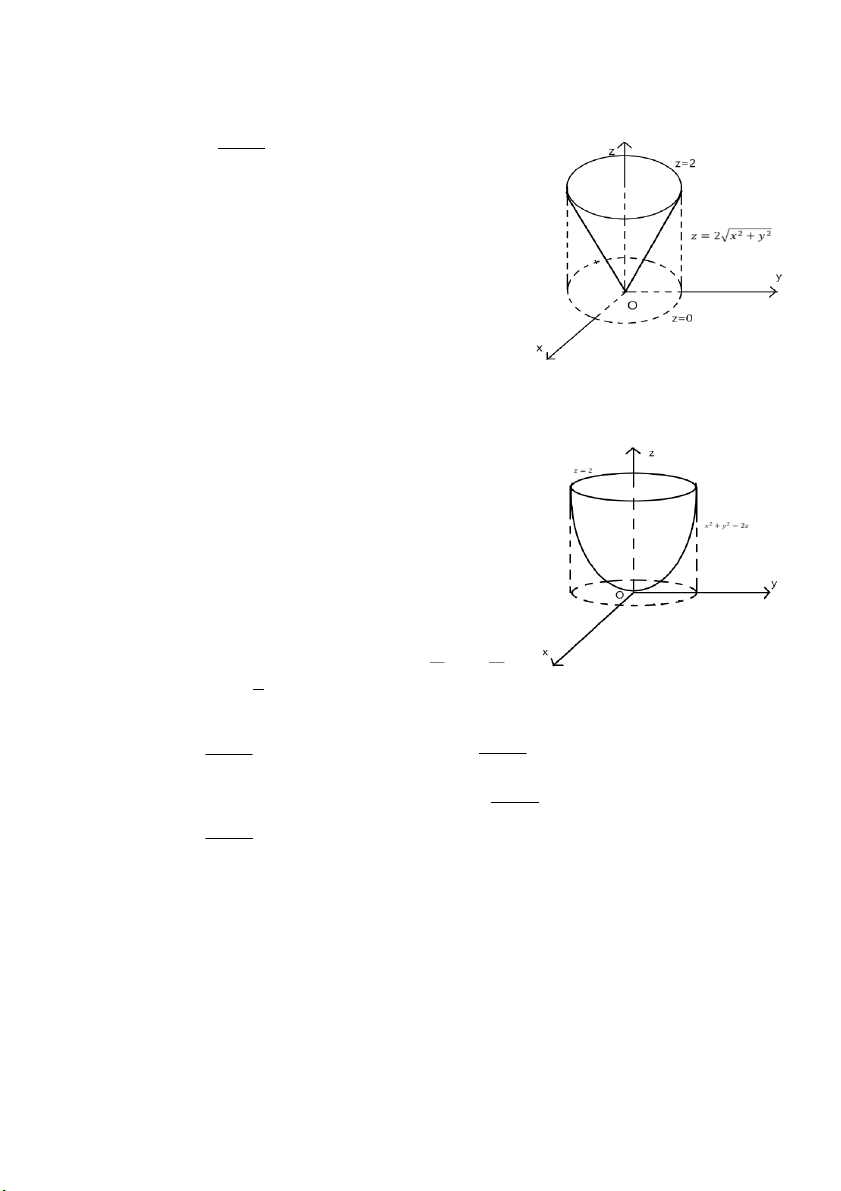
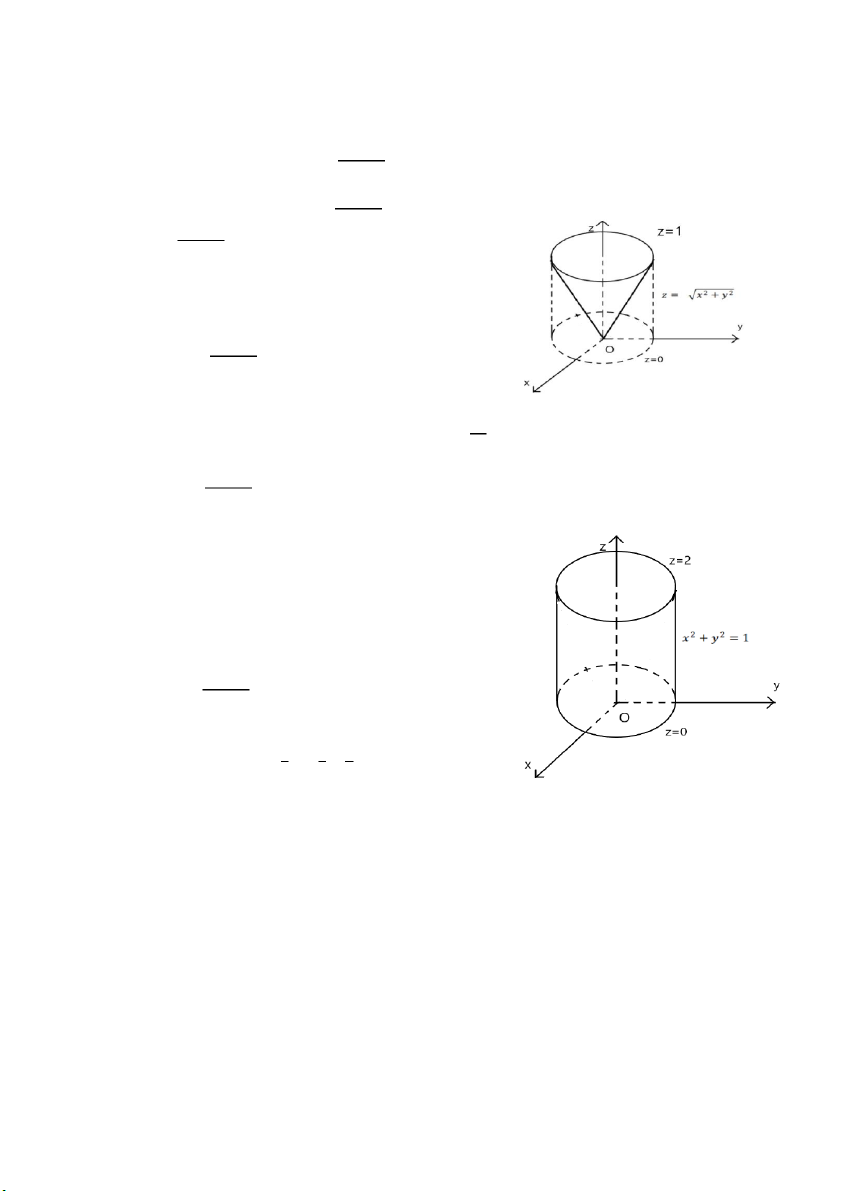
𝑏) ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 g ới hạn bởi 𝑧 i
2 = 4(𝑥2 + 𝑦2),𝑧 = 2. 𝑉
Xét giao tuyến của hai mặt 𝑧2 = 4(𝑥2 + 𝑦2), 𝑧 = 2
⇒ 4(𝑥2 + 𝑦2) = 4 ⇔ 𝑥2 + 𝑦2 = 1
⇒ Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là: 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑
Đặt {𝑦 = 𝑟 sin𝜑 , 𝐽 = 𝑟 PHAM THANH TUNG 2𝑟 ≤ 𝑧 ≤ 2
Miền 𝑉: {2√𝑥2 + 𝑦2 ≤ 𝑧 ≤ 2 ⇔ { 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝐷: { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 2 2𝜋 1
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑧. 𝑟𝑑𝑧 = ∫ 𝑑𝜑 ∫(2 − 2𝑟2). 𝑟𝑑𝑟= 𝜋 0 0 2𝑟 0 0
𝑐) ∭(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 g ới hạn bởi 𝑥 i 2 + 𝑦2 = 2𝑧, 𝑧 = 2 𝑉
Xét giao tuyến hai mặt 𝑥2 + 𝑦2 = 2𝑧 và 𝑧 = 2 ⇒ 𝑥2 + 𝑦2 = 4
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 4 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧 Miền 𝑉: { 𝐷: 𝑥2 + 𝑦2 ≤ 4
(𝑥2 + 𝑦2)/2 ≤ 𝑧 ≤ 2 ⇔ {𝐷: { 0 ≤ 𝑟 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋 𝑟2/2 ≤ 𝑧 ≤ 2 2𝜋 2 2 2𝜋 2 𝑟2 16
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑟2. 𝑟𝑑𝑧 = ∫ 𝑑𝜑∫ 𝑟3 (2 − 2 )𝑑𝑟 = 3 𝜋 0 0 𝑟2 0 0 2
𝑑) ∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 , 𝑉 đ ợc ư g ới hạn bởi 𝑦 i
= −√4𝑥 − 𝑥2, 𝑦 = 0, 𝑧 = 0, 𝑧 = 4 𝑉
Hình chiếu 𝐷 của 𝑉 lên 𝑂𝑥𝑦 giới hạn b ng ởi các đườ
𝑦 = −√4𝑥 − 𝑥2, 𝑦 = 0
⇒ 𝐷: − √4𝑥 − 𝑥2 ≤ 𝑦 ≤ 0 ⇔ {(𝑥 − 2)2 + 𝑦2 ≤ 4 𝑦 ≤ 0 ⇔ {𝑥2 + 𝑦2 ≤ 4𝑥 𝑦 ≤ 0 PHAM THANH TUNG 𝑥 = 𝑟 cos 𝜑 0 ≤ 𝑟 ≤ 4 cos 𝜑 Đặ −𝜋
t { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 ⇒ Miền 𝑉: {𝐷: 𝑥2 + 𝑦2 ≤ 4𝑥, 𝑦 ≤ 0 ≤ 𝜑 ≤ 0 𝑧 = 𝑧 0 ≤ 𝑧 ≤ 4 ⇔ { 20≤𝑧 ≤4 0 4 cos 𝜑 4 0 4 cos 𝜑 8 0
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ 𝑑𝑟∫ 𝑧. 𝑟. 𝑟𝑑𝑧 = 8 ∫ 𝑑𝜑 ∫ 𝑟2𝑑𝑟 = 3 ∫(4cos𝜑)3𝑑𝜑 −𝜋 0 0 −𝜋 0 −𝜋 2 2 2 0 0 0 512 512 512 = = = 1024
3 ∫(cos 𝜑)2. cos 𝜑 𝑑𝜑
3 ∫[1 − (sin 𝜑)2]𝑑(sin 𝜑) 3 ∫(1 − 𝑢2)𝑑𝑢= 9 −𝜋 −𝜋 −1 2 2
𝑒) ∭ 𝑥𝑑𝑥𝑑𝑦𝑑𝑧 , 𝑉 đ ợc
ư giới hạn bởi 𝑧 = 0, 𝑧 = 𝑦2, 𝑥 = 2𝑦2, 𝑥 = 1 + 𝑦2 𝑉
Hình chiếu 𝐷 của 𝑉 lên 𝑂𝑥𝑦 được giới hạn bởi 𝑥 = 2𝑦2, 𝑥 = 1 + 𝑦2
⇒ 𝐷: {2𝑦2 ≤ 𝑥 ≤ 1 + 𝑦2 −1 ≤ 𝑦 ≤ 1 0 ≤ 𝑧 ≤ 𝑦2
Ta có: { 𝐷: {2𝑦2 ≤ 𝑥 ≤ 1 + 𝑦2 −1 ≤ 𝑦 ≤ 1 𝑦2 1 1+𝑦2 𝑦2 1 1+𝑦2
⇒ 𝐼 = ∬ 𝑑𝑥𝑑𝑦∫ 𝑥𝑑𝑧 = ∫ 𝑑𝑦 ∫ 𝑑𝑥 ∫ 𝑥𝑑𝑧 = ∫ 𝑑𝑦 ∫ 𝑥𝑦2𝑑𝑥 𝐷 0 −1 2𝑦2 0 −1 2𝑦2 PHAM THANH TUNG 1 1 = ∫ 32
2 [(1 + 𝑦2)2 − (2𝑦2)2]. 𝑦2𝑑𝑦= 105 −1
𝑓) ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 , 𝑉 xác định bởi 𝑥2 + 𝑦2 ≤ 1, 𝑦2 + 𝑧2 ≤ 4, 𝑧 ≥ 0 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1
Miền 𝑉: {0 ≤ 𝑧 ≤ √4 − 𝑦2 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑
0 ≤ 𝑧 ≤ √4 − (𝑟 sin 𝜑)2
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 ⇒ 𝑉: { 0 ≤ 𝑟 ≤ 1 𝑧 = 𝑧 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 √4−(𝑟 sin𝜑)2 1 2𝜋 1
∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫
𝑧. 𝑟𝑑𝑧 = 2∫ 𝑑𝜑 ∫[4 − (𝑟sin𝜑)2].𝑟𝑑𝑟 𝑉 0 0 0 0 0 2𝜋 1 1 15𝜋 15𝜋 = 1
2 ∫ [2 − 4 (sin 𝜑)2] 𝑑𝜑 = 2 . 4 = 8 0
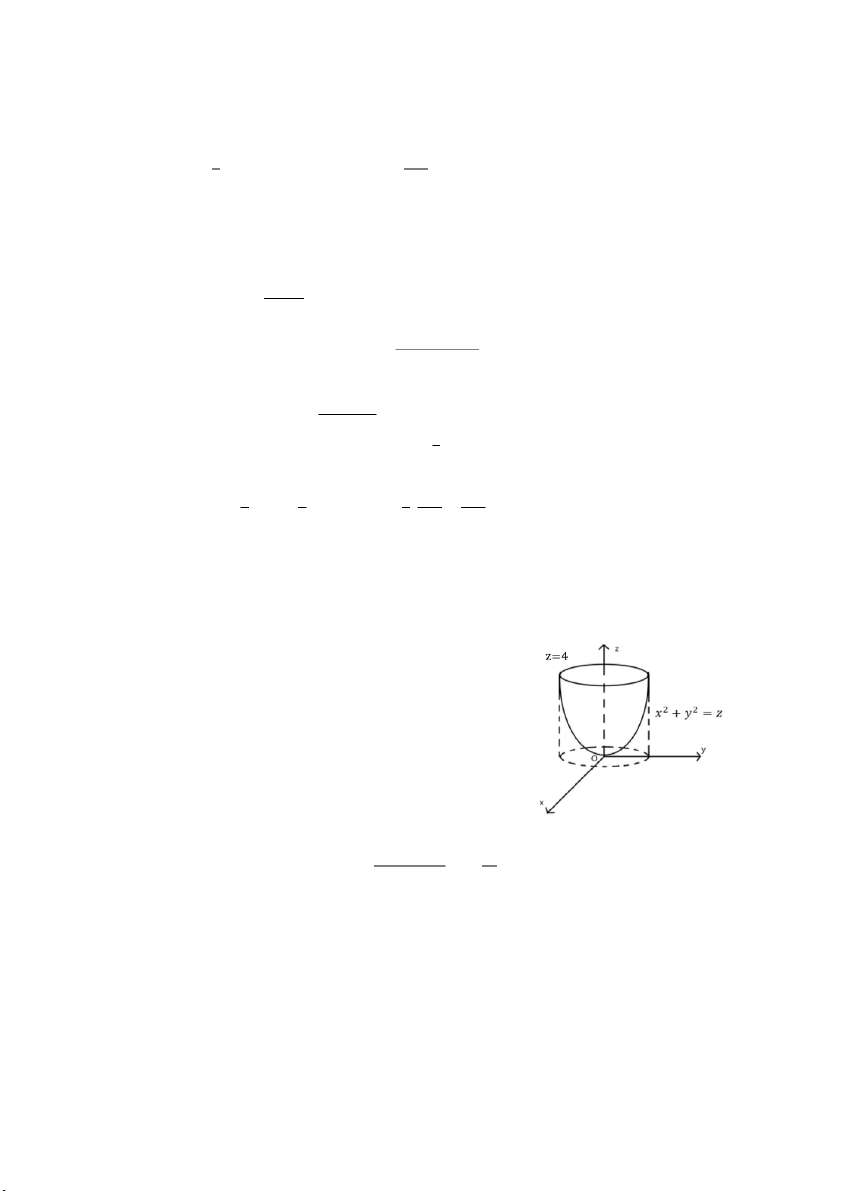
𝑔) ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 g ới hạn bởi 𝑥 i 2 + 𝑦2 = 𝑧, 𝑧 = 4 𝑉
Xét giao tuyến hai mặt 𝑥2 + 𝑦2 = 𝑧 và 𝑧 = 4 ⇒ 𝑥2 + 𝑦2 = 4
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 4 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧
Miền 𝑉: { 𝐷: 𝑥2 + 𝑦2 ≤ 4
(𝑥2 + 𝑦2) ≤ 𝑧 ≤ 4 ⇔ {𝐷: { 0 ≤ 𝑟 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋 𝑟2 ≤ 𝑧 ≤ 4 2𝜋 2 4 2𝜋 2 ( ⇒ 𝐼 = ∫ 𝑑𝜑 16 − 𝑟4). 𝑟
∫ 𝑑𝑟 ∫ 𝑧. 𝑟𝑑𝑧 = ∫ 𝑑𝜑 64 ∫ 2 𝑑𝑟 = 3 𝜋 0 0 𝑟2 0 0 PHAM THANH TUNG
ℎ) ∭(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧, (𝑉): √𝑥2 + 𝑦2 ≤ 𝑧 ≤ 1. 𝑉
Xét giao tuyến của hai mặt 𝑧 = √𝑥2 + 𝑦2, 𝑧 = 1
⇒ √𝑥2 + 𝑦2 = 1 ⇔ 𝑥2 + 𝑦2 = 1
⇒ Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là: 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧 𝑟 ≤ 𝑧 ≤ 2
Miền 𝑉: {√𝑥2 + 𝑦2 ≤ 𝑧 ≤ 1 ⇔ { 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝐷: { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 2 2𝜋 1 3𝜋
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑟2. 𝑟𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑟3(2 − 𝑟)𝑑𝑟 = 5 0 0 𝑟 0 0
𝑖) ∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 , 𝑉 g ới hạn bởi 𝑥 i
2 + 𝑦2 = 1, 𝑧 = 0, 𝑧 = 2 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧 0 ≤ 𝑟 ≤ 1
Miền 𝑉 trong tọa độ trụ là 𝑉: {0 ≤ 𝜑 ≤ 2𝜋 0 ≤ 𝑧 ≤ 2 2𝜋 1 2
⇒ ∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟∫ 𝑧. 𝑟. 𝑟𝑑𝑧 𝑉 0 0 0 2𝜋 1 1 1 𝜋
= 2 ∫ 𝑑𝜑 ∫ 𝑟2𝑑𝑟 = 2.2𝜋. 3 =3 0 0 PHAM THANH TUNG
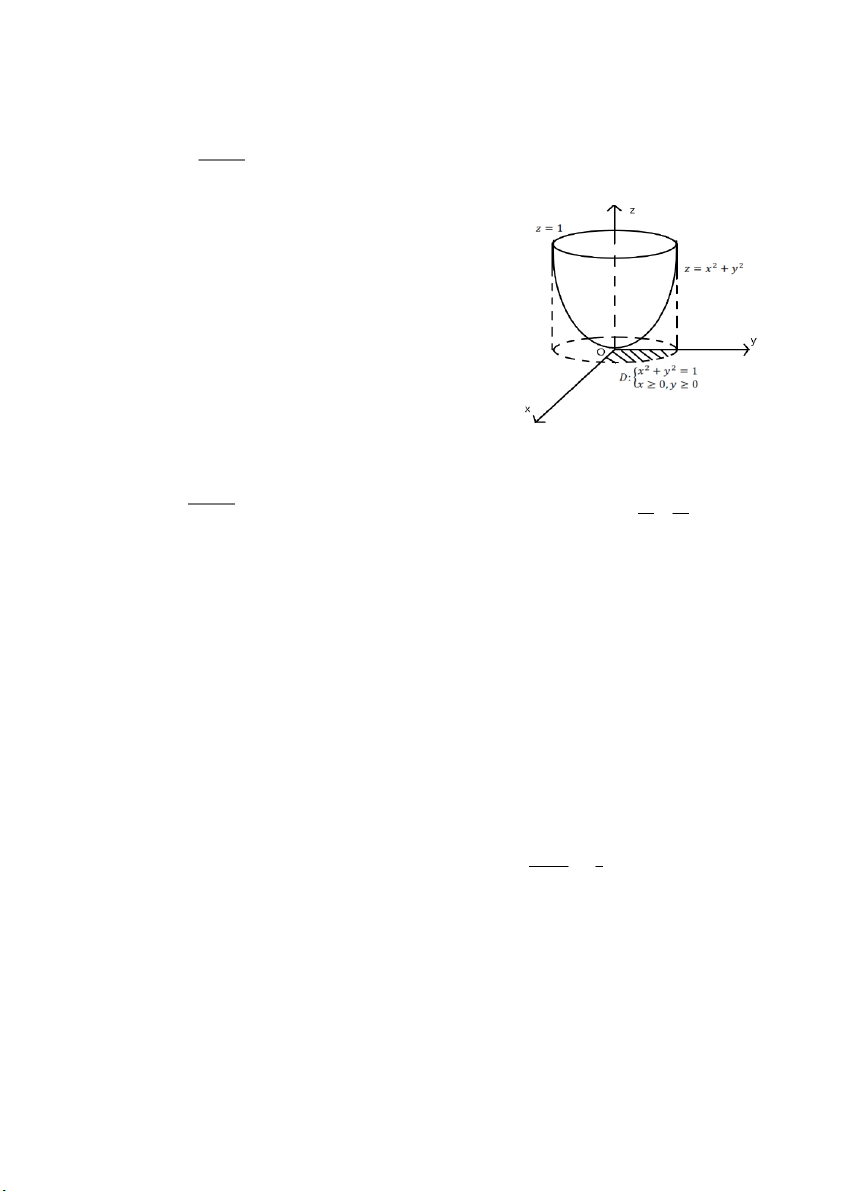
𝑗) ∭ √3𝑥2 + 𝑦2 𝑑𝑥𝑑𝑦𝑑𝑧, (𝑉): 𝑥2 + 𝑦2 ≤ 𝑧 ≤ 1, 𝑥 ≥ 0, 𝑦 ≥ 0 𝑉
Xét giao tuyến của hai mặt 𝑧 = 𝑥2 + 𝑦2, 𝑧 = 1 ⇒ 𝑥2 + 𝑦2 = 1
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: {𝑥2 + 𝑦2 ≤ 1 𝑥 ≥ 0, 𝑦 ≥ 0 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧 𝑥2 + 𝑦2 ≤ 𝑧 ≤ 1
Miền 𝑉: { 𝐷:{𝑥2 + 𝑦2 = 1 𝑥 ≥ 0, 𝑦 ≥ 0 𝑟2 ≤ 𝑧 ≤ 1
Miền 𝑉 trong tọa độ trụ 𝑉: { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 𝜋/2 2𝜋 1 1 2𝜋 1 9 9𝜋 ∭ √
3 𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫𝑑𝑟 ∫𝑟2/3.𝑟𝑑𝑧 = ∫ 𝑑𝜑 ∫(1 − 𝑟2)𝑟5/3𝑑𝑟 = 2𝜋. 56 = 28 𝑉 0 0 𝑟2 0 0
𝑘) ∭(𝑥2 + 𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 g ới hạn bởi 𝑥 i = 𝑦2 + 4𝑧2, 𝑥 = 4 𝑉
Xét giao tuyến của hai mặt 𝑥 = 𝑦2 + 4𝑧2, 𝑥 = 4 ⇒ 𝑦2 + 4𝑧2 = 4
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑦2 + 4𝑧2 ≤ 4 𝑦 = 𝑟 cos 𝜑
Đặt {𝑧 = (𝑟 sin 𝜑)/2, 𝐽 = 𝑟/2 𝑥 = 𝑥 𝑟2 ≤ 𝑥 ≤ 1
Miền 𝑉: {𝑦2 + 4𝑧2 ≤ 𝑥 ≤ 4
𝐷: 𝑦2 + 4𝑧2 ≤ 4 ⇒ Miền 𝑉 trong tọa độ trụ 𝑉: { 0 ≤ 𝑟 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 2 1 𝑟 sin 𝜑 2 𝑟
∭(𝑥2 + 𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ [𝑥2 + (𝑟 cos 𝜑)2 + ( 2 ) ].2𝑑𝑥 𝑉 0 0 𝑟2 PHAM THANH TUNG 2𝜋 2 1 − 𝑟6 𝑟 sin𝜑 2 𝑟 −85𝜋
= ∫ 𝑑𝜑 ∫ [ 3 + (1 − 𝑟2)(𝑟cos𝜑)2 + (1 − 𝑟2)( 2 ) ].2𝑑𝑟 = 6 0 0
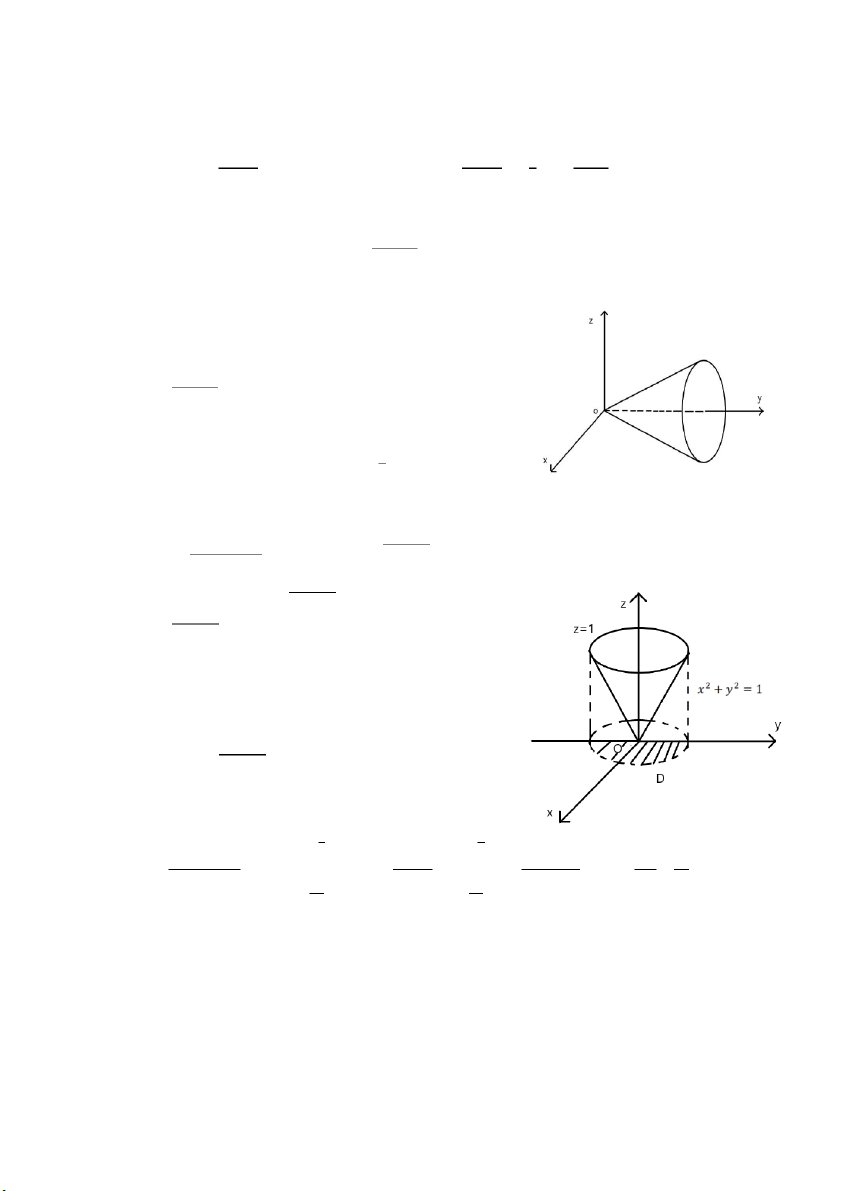
𝑙) ∭ 𝑦𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 g ới hạn bởi 𝑦 i = √𝑥2 + 𝑧2, 𝑦 = 2 𝑉 Hình chiếu c a mi ủ
ền 𝑉 lên 𝑂𝑥𝑧 là 𝐷: 𝑥2 + 𝑧2 ≤ 4 𝑧 = 𝑟 cos 𝜑
Đặt {𝑥 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑦 = 𝑦 𝑟 ≤ 𝑦 ≤ 2
𝑉: {√𝑥2 + 𝑧2 ≤ 𝑦 ≤ 2 ⇔ {0 ≤ 𝜑 ≤ 2𝜋 𝐷: 𝑥2 + 𝑧2 ≤ 4 0 ≤ 𝑟 ≤ 2 2𝜋 2 2 2𝜋 2 1
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑦. 𝑟𝑑𝑦= ∫ 𝑑𝜑 ∫ 2(4 − 𝑟2).𝑟𝑑𝑟= 4𝜋 0 0 𝑟 0 0 𝑧3
𝑚) ∭1 + 𝑥2 + 𝑦2 𝑑𝑥𝑑𝑦𝑑𝑧,𝑉:𝑥 ≥ 0,√𝑥2 + 𝑦2 ≤ 𝑧 ≤ 1 𝑉
Xét giao tuyến của 𝑧 = √𝑥2 + 𝑦2 và 𝑧 = 1
⇒ √𝑥2 + 𝑦2 = 1 ⇔ 𝑥2 + 𝑦2 = 1
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: {𝑥2 + 𝑦2 ≤ 1 𝑥 ≥ 0 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧 𝑟 ≤ 𝑧 ≤ 1
Miền 𝑉: { √𝑥2 + 𝑦2 ≤ 𝑧 ≤ 1
⇔ { −𝜋/2 ≤ 𝜑 ≤ 𝜋/2
𝐷: 𝑥2 + 𝑦2 ≤ 1, 𝑥 ≥ 0 0 ≤ 𝑟 ≤ 1 𝜋 𝜋 2 1 1 2 1 𝑧3 𝑟5 1 ∭ 𝑧3. 𝑟 ∫ ln 2 1 + 𝑥
𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 = ∫ 𝑑𝜑 2 + 𝑦2
∫ 𝑑𝑟∫ 1 + 𝑟2𝑑𝑧
4(1 + 𝑟2) 𝑑𝑟 = 𝜋 ( 8 − 16) 𝑉 −𝜋 0 𝑟 −𝜋 0 2 2 PHAM THANH TUNG
𝑛) ∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 g ới hạn bởi 𝑥 i
2 + 𝑦2 = 2𝑥, 𝑧 = 0,𝑧 = 2 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 2𝑥 𝑥 = 𝑟 cos 𝜑 0 ≤ 𝑧 ≤ 2
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 ⇒ 𝑉: { 0 ≤ 𝑧 ≤ 2 2
⇔ {−𝜋/2 ≤ 𝜑 ≤ 𝜋/2 𝑧 = 𝑧 𝐷: 𝑥2 + 𝑦 ≤ 2𝑥 0 ≤ 𝑟 ≤ 2 cos 𝜑 𝜋 𝜋 2 2cos 𝜑 2 2 2 cos𝜑
∭ 𝑧√𝑥2 + 𝑦2 𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑧. 𝑟. 𝑟𝑑𝑧 = ∫ 𝑑𝜑 ∫ 2𝑟2𝑑𝑟 𝑉 −𝜋 0 0 −𝜋 0 2 2 𝜋 𝜋 𝜋 2 2 2 16 16 16 = = = 3 ∫(cos 𝜑)3𝑑𝜑
3 ∫(cos 𝜑)2. cos 𝜑 𝑑𝜑
3 ∫[1 − (sin 𝜑)2] 𝑑(sin 𝜑) −𝜋 −𝜋 −𝜋 2 2 2 16 1 = 64
3 ∫(1 − 𝑢2) 𝑑𝑢 = 9 −1
𝑜) ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 , 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 6, 𝑧 ≥ 𝑥2 + 𝑦2 𝑉
Xét giao tuyến của 𝑥2 + 𝑦2 + 𝑧2 = 6, 𝑧 = 𝑥2 + 𝑦2
⇒ 𝑥2 + 𝑦2 + (𝑥2 + 𝑦2)2 = 6 ⇔ 𝑥2 + 𝑦2 = 2
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 2 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧
Miền 𝑉: {𝑥2 + 𝑦2 ≤ 𝑧 ≤ √6 − 𝑥2 − 𝑦2 𝐷: 𝑥2 + 𝑦2 ≤ 2
𝑟2 ≤ 𝑧 ≤ √6 − 𝑟2
Miền 𝑉 trong tọa độ trụ 𝑉: { 0 ≤ 𝑟 ≤ √2 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 √2 √6−𝑟2 2𝜋 √2 1 11
∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑧. 𝑟𝑑𝑧 =
∫ (6 − 𝑟2 − 𝑟4). 𝑟𝑑𝑟 2 ∫ 𝑑𝜑 = 3 𝜋 𝑉 0 0 𝑟2 0 0 PHAM THANH TUNG
𝑝) ∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 , 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 4, 𝑧 ≥ 0 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 4
Miền 𝑉: {0 ≤ 𝑧 ≤ √4 − 𝑥2 − 𝑦2 𝐷: 𝑥2 + 𝑦2 ≤ 4 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧 0 ≤ 𝑧 ≤ √4 − 𝑟2
Miền 𝑉 trong tọa độ trụ 𝑉: { 0 ≤ 𝑟 ≤ 2 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 2 √4−𝑟2
∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑧. 𝑟. 𝑟𝑑𝑧 𝑉 0 0 0 2𝜋 2 1 64
=2∫ 𝑑𝜑∫(4 − 𝑟2)𝑟2𝑑𝑟 = 15𝜋 0 0
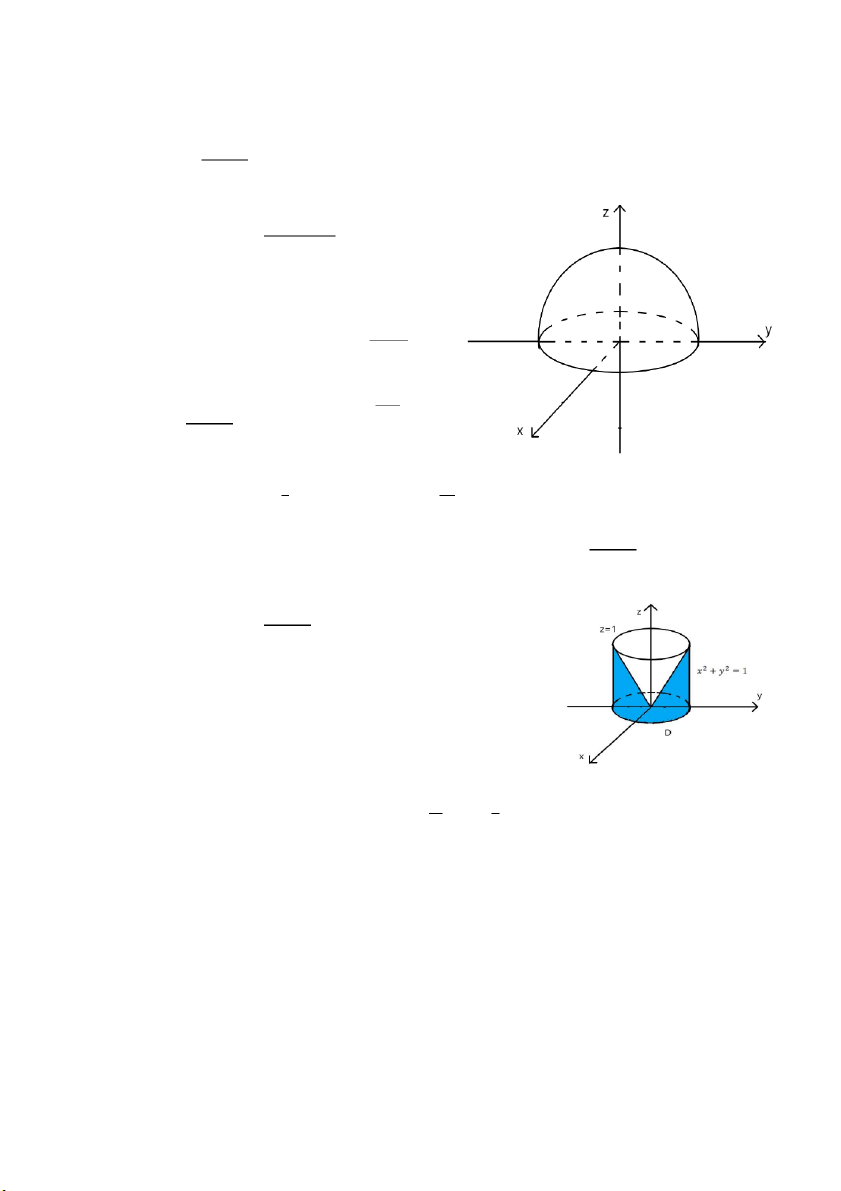
𝑞) ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉 là m ền nằm trong i
trụ 𝑥2 + 𝑦2 = 1, giới hạn bởi 𝑧 = √𝑥2 + 𝑦2, 𝑧 = 0 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 (𝑉 là miền màu xanh)
Miền 𝑉: {0 ≤ 𝑧 ≤ √𝑥2 + 𝑦2 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧 0 ≤ 𝑧 ≤ 𝑟
Miền 𝑉 trong tọa độ trụ 𝑉: { 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 𝑟 2𝜋 1 𝑟2 𝜋
∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑧. 𝑟𝑑𝑧 = ∫ 𝑑𝜑 ∫ 2 .𝑟𝑑𝑟 =4 𝑉 0 0 0 0 0 PHAM THANH TUNG
Câu 4: Tính các tích phân b i ba sau: ộ Gi i ả :
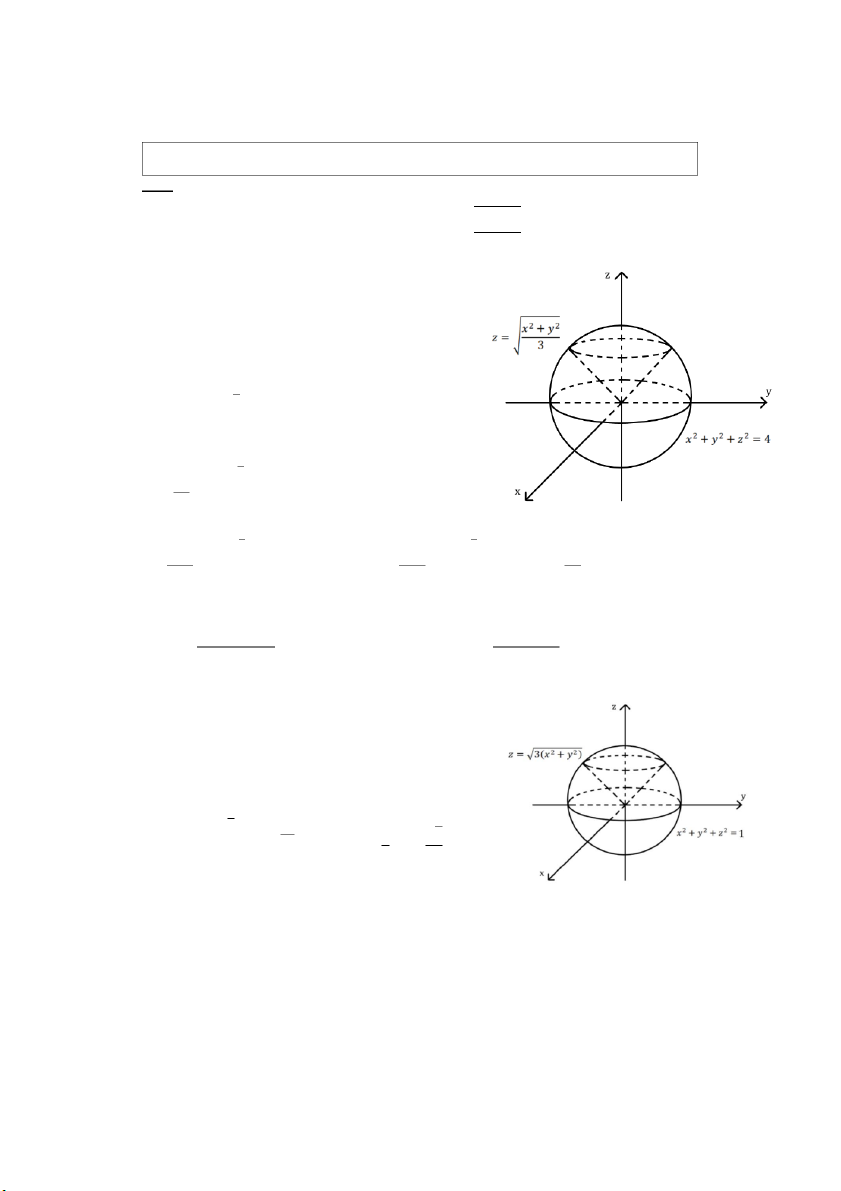
𝑎) ∭(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧, (𝑉): 𝑥2 + 𝑦2 + 𝑧2 ≤ 4, 𝑧 ≥ √𝑥2 + 𝑦2 3 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 2
Miền 𝑉 trong tọa độ cầu là 𝑉: {0 ≤ 𝜃 ≤ 𝜋/3 0 ≤ 𝜑 ≤ 2𝜋 𝜋 2𝜋 3 2
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫ 𝑟2(sin 𝜃)2. 𝑟2 sin 𝜃 𝑑𝑟 0 0 0 𝜋 2𝜋 3 32
= 5 ∫ 𝑑𝜑∫(sin𝜃)2.sin𝜃𝑑𝜃 0 0 𝜋 1 2𝜋 2𝜋 −32 3 2 = −32 8𝜋
5 ∫ 𝑑𝜑 ∫[1 − (cos 𝜃)2]𝑑(cos 𝜃)= 5 ∫ 𝑑𝜑∫(1 − 𝑢2)𝑑𝑢 = 3 0 0 0 1
𝑏) ∭ √𝑥2 + 𝑦2 + 𝑧2 𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 1, 𝑧 ≥ √3(𝑥2 + 𝑦2) 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 1
Miền 𝑉 trong tọa độ cầu là 𝑉: {0 ≤ 𝜃 ≤ 𝜋/6 0 ≤ 𝜑 ≤ 2𝜋 𝜋 2𝜋 6 1 𝜋
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫ √𝑟2. 𝑟2 sin 𝜃 𝑑𝑟 = √3 2 (1 − 2 ) 0 0 0 PHAM THANH TUNG
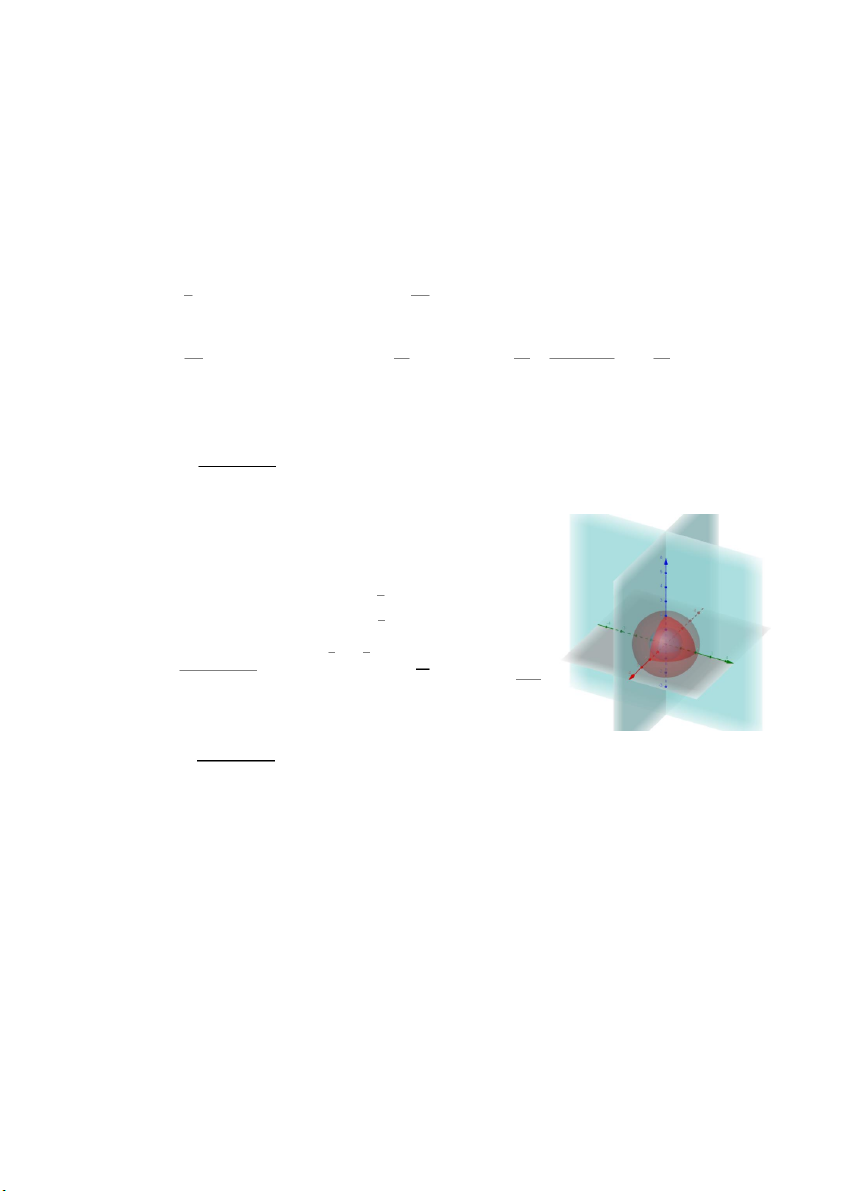
𝑐) ∭ 𝑥𝑦𝑧𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 1, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0. 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑 0 ≤ 𝑟 ≤ 1
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃. Miền 𝑉 trong tọa độ cầu là 𝑉: {0 ≤ 𝜃 ≤ 𝜋/2 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝜑 ≤ 𝜋/2 𝜋 𝜋 2 2 1
∭ 𝑥𝑦𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝜃∫ 𝑟3(sin 𝜃)2 cos 𝜃 sin𝜑 cos 𝜑 . 𝑟2 sin 𝜃 𝑑𝑟 𝑉 0 0 0 𝜋 𝜋 𝜋 𝜋 1 2 2 2 2 = 1
6 ∫ 𝑑𝜑 ∫(sin 𝜃)3 cos 𝜃 sin 𝜑 cos 𝜑 𝑑𝜃= 6 ∫ 𝑑𝜑∫(sin 𝜃)3 sin 𝜑 cos 𝜑 𝑑(sin 𝜃) 0 0 0 0 𝜋 𝜋 2 1 2 1 1 1
= 6∫𝑑𝜑∫𝑢3sin𝜑 cos𝜑 𝑑𝑢 = 24∫ sin𝜑cos𝜑 𝑑𝜑 = 48 0 0 0
𝑑) ∭(𝑥2 + 𝑦)𝑑𝑥𝑑𝑦𝑑𝑧, (𝑉): 𝑥2 + 𝑦2 + 𝑧2 ≤ 1 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 1
Miền 𝑉 trong tọa độ cầu là 𝑉: { 0 ≤ 𝜃 ≤ 𝜋 0 ≤ 𝜑 ≤ 2𝜋 PHAM THANH TUNG {
Miền 𝑉 đối xứng qua mặt 𝑂𝑥𝑧
Hàm 𝑓(𝑥, 𝑦, 𝑧) = 𝑦 l hàm lẻ à
với biến 𝑦 ⇒ ∭ 𝑦𝑑𝑥𝑑𝑦𝑑𝑧= 0 𝑉 2𝜋 𝜋 1
∭(𝑥2 + 𝑦)𝑑𝑥𝑑𝑦𝑑𝑧 = ∭ 𝑥2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑∫ 𝑑𝜃 ∫ 𝑟2(sin 𝜃)2(cos 𝜑)2. 𝑟2 sin 𝜃 𝑑𝑟 𝑉 𝑉 0 0 0 2𝜋 𝜋 2𝜋 𝜋 1 = −1
5 ∫ 𝑑𝜑∫(sin 𝜃)2 sin 𝜃 (cos 𝜑)2𝑑𝜃= 5 ∫ 𝑑𝜑 ∫[1 − (cos 𝜃)2] (cos 𝜑)2𝑑(cos 𝜃) 0 0 0 0 2𝜋 0 2𝜋 2𝜋 −1 2 2 1 + cos 2𝜑 2𝜋 = 2
5 ∫ 𝑑𝜑 ∫[1 − 𝑢 ] (cos 𝜑)2𝑑𝑢= 15 ∫ (cos 𝜑)2𝑑𝜑= = 15 ∫ 2 𝑑𝜑 15 0 1 0 0
𝑒) ∭ √𝑥2 + 𝑦2 + 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 , (𝑉): 1 ≤ 𝑥2 + 𝑦2 + 𝑧2 ≤ 4, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0. 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 1 ≤ 𝑟 ≤ 2 0 ≤ 𝜃 ≤ 𝜋
Miền 𝑉 trong tọa độ cầu là 𝑉: { 2 0 ≤ 𝜑 ≤ 𝜋2 𝜋 𝜋 2 2 2 15𝜋
∭ √𝑥2 + 𝑦2 + 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫ √𝑟2.𝑟2 sin 𝜃 𝑑𝑟 = 6 𝑉 0 0 1
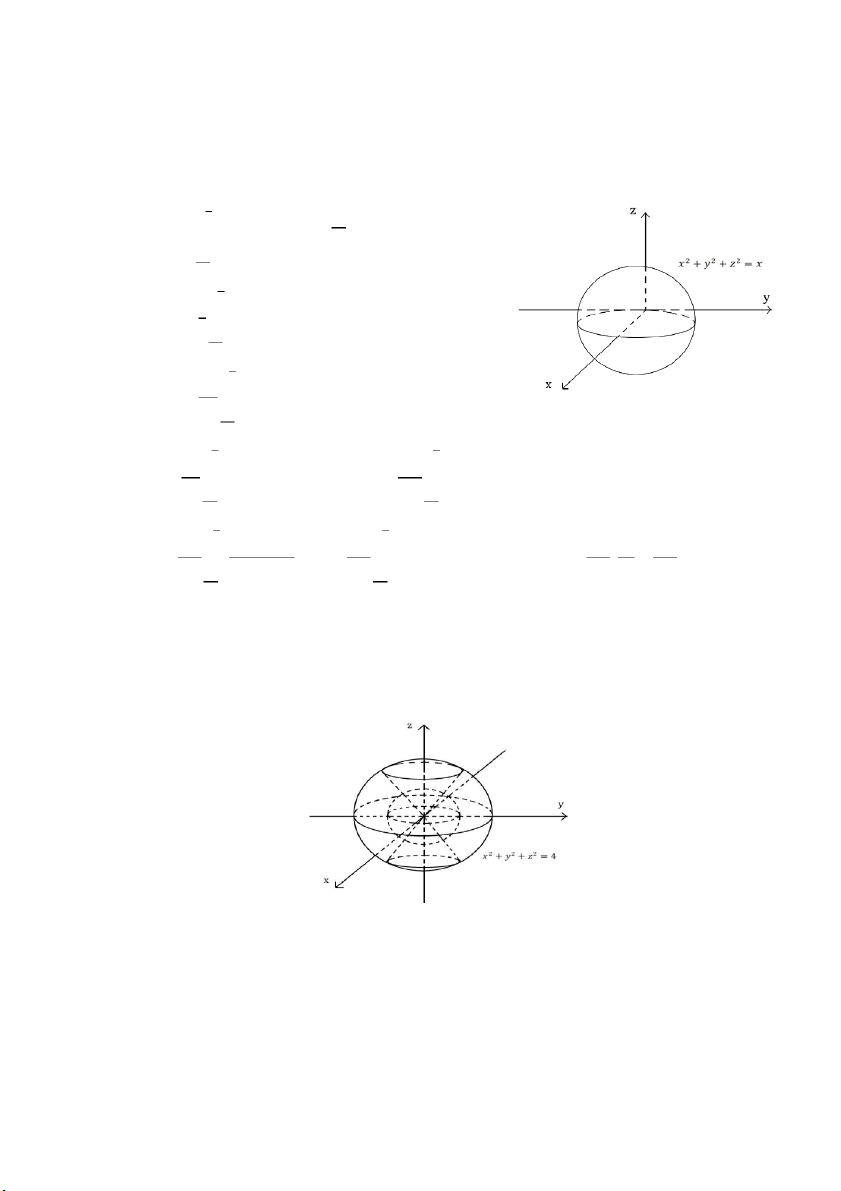
𝑓) ∭ √𝑥2 + 𝑦2 + 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 , (𝑉): 𝑥2 + 𝑦2 + 𝑧2 ≤ 𝑥 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 PHAM THANH TUNG
0 ≤ 𝑟 ≤ sin 𝜃 cos 𝜑
Miền 𝑉 trong tọa độ cầu là 𝑉: { 0 ≤ 𝜃 ≤ 𝜋 −𝜋/2 ≤ 𝜑 ≤ 𝜋/2 𝜋 2 𝜋 sin𝜃 cos 𝜑
⇒ 𝐼 = ∫ 𝑑𝜑∫ 𝑑𝜃 ∫
√𝑟2.𝑟2 sin 𝜃 𝑑𝑟 −𝜋 0 0 2 𝜋 2 𝜋 1
= 4 ∫𝑑𝜑∫(sin𝜃 cos𝜑)4sin𝜃 𝑑𝜃 −𝜋 0 2 𝜋 2 𝜋 −1
= 4 ∫𝑑𝜑 ∫(cos𝜑)4[1 − (cos𝜃)2]4𝑑(cos𝜃) −𝜋 0 2 𝜋 𝜋 2 −1 2 −1 = 64
4 ∫(cos 𝜑)4𝑑𝜑∫ (1 − 𝑢2)4𝑑𝑢= 315 ∫[(cos 𝜑)2]2𝑑𝜑 −𝜋 1 −𝜋 2 2 𝜋 𝜋 2 2 64 1 + cos 2𝜑 2 16 16 3𝜋 8𝜋 = 315 ∫( 2 ) 𝑑𝜑 = =
315 ∫[1 + 2 cos 2𝜑 + (cos 2𝜑)2]𝑑𝜑 315 . 2 = 105 −𝜋 −𝜋 2 2
𝑔) ∭(𝑥 + 𝑦 + 𝑧)2𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉: 1 ≤ 𝑥2 + 𝑦2 + 𝑧2 ≤ 4 , 𝑥2 + 𝑦2 ≤ 𝑧2 𝑉 PHAM THANH TUNG
∭(𝑥 + 𝑦 + 𝑧)2𝑑𝑥𝑑𝑦𝑑𝑧 = ∭(𝑥2 + 𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 + ∭(2𝑥𝑦 + 2𝑦𝑧 + 2𝑥𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑉 𝑉
𝑓(𝑥, 𝑦, 𝑧) = 2𝑥𝑦, 𝑔(𝑥, 𝑦, 𝑧) = 2𝑥𝑧 lẻ với biến 𝑥 − {
ℎ(𝑥, 𝑦, 𝑧) = 2𝑦𝑧 lẻ với biến 𝑦
⇒ ∭(2𝑥𝑦 + 2𝑦𝑧 + 2𝑥𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 = 0
Miền 𝑉 đối xứng qua 𝑂𝑦𝑧 v 𝑂 à 𝑥𝑧 𝑉
− {(𝑥2 + 𝑦2 + 𝑧2) chẵn với biến 𝑧
Miền 𝑉 đối xứng qua 𝑂𝑥𝑦
⇒ ∭(𝑥2 + 𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 = 2 ∭(𝑥2 + 𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑉+
Với 𝑉+: 1 ≤ 𝑥2 + 𝑦2 + 𝑧2 ≤ 4 , √𝑥2 + 𝑦2 ≤ 𝑧 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 1 ≤ 𝑟 ≤ 2
Miền 𝑉 trong tọa độ cầu là 𝑉: {0 ≤ 𝜃 ≤ 𝜋/4 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 𝜋 2
∭(𝑥 + 𝑦 + 𝑧)2𝑑𝑥𝑑𝑦𝑑𝑧 = 2 ∫ 𝑑𝜑 ∫ 𝑑𝜃∫ 𝑟2. 𝑟2 sin 𝜃 𝑑𝑟 248𝜋 = 5 𝑉 0 0 1 𝑦2 𝑧2
ℎ) ∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉: 𝑥2 + 4 + 9 ≤ 4,𝑦 ≥ 0,𝑧 ≥ 0 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 2𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −6𝑟2 sin 𝜃 𝑧 = 3𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 2
Miền 𝑉 trong tọa độ cầu suy rộng là 𝑉: { 0 ≤ 𝜃 ≤ 𝜋2 0 ≤ 𝜑 ≤ 𝜋 𝜋 𝜋 𝜋 2 2 𝜋 2
∭ 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝜃∫ 3𝑟 cos 𝜃 . 6𝑟2 sin 𝜃 𝑑𝑟 = 72 ∫ 𝑑𝜑 ∫ cos 𝜃 . sin 𝜃 𝑑𝜃 = 36𝜋 𝑉 0 0 0 0 0 PHAM THANH TUNG 𝑥2 + 𝑦2 𝑧2 𝑧2 𝑖) ∭ ( 𝑥2 + 𝑦2 4
+ 9 )𝑑𝑥𝑑𝑦𝑑𝑧 ,(𝑉): 4 + 9 ≤ 1 𝑉 𝑥 = 2𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 2𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −12𝑟2 sin 𝜃 𝑧 = 3𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 1
Miền 𝑉 trong tọa độ cầu suy rộng là 𝑉: { 0 ≤ 𝜃 ≤ 𝜋 0 ≤ 𝜑 ≤ 2𝜋 𝜋 𝜋 2𝜋 3 2 384 2𝜋 3
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ 𝑑𝜃∫ 𝑟2. 12𝑟2 sin 𝜃 𝑑𝑟 = 5 ∫ 𝑑𝜑 ∫sin𝜃 𝑑𝜃 0 0 0 0 0 384 = 5 𝜋
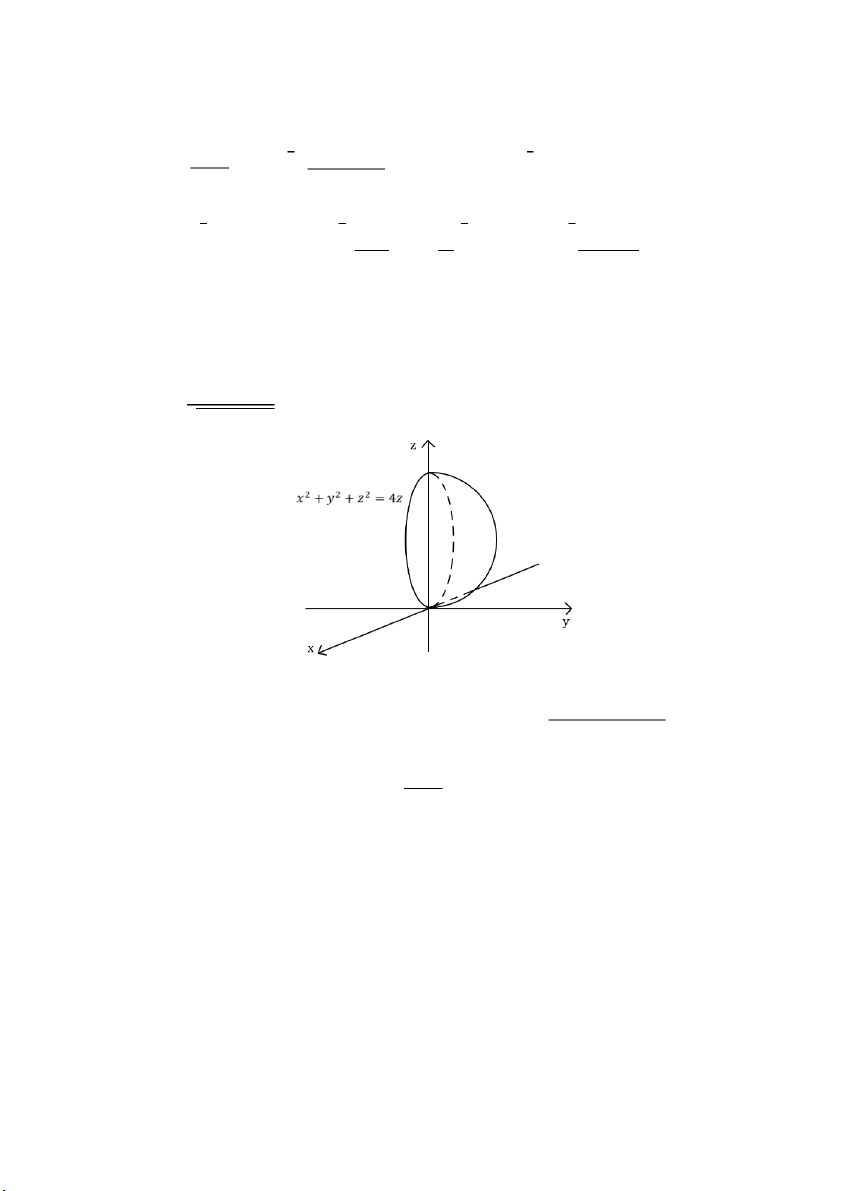
𝑗) ∭(4𝑧 − 𝑥2 − 𝑦2 − 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧, (𝑉): 𝑥2 + 𝑦2 + 𝑧2 ≤ 4𝑧 𝑉
Miền 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 4𝑧 ⇔ 𝑥2 + 𝑦2 + (𝑧 − 2)2 ≤ 4 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 2 + 𝑟 cos𝜃 0 ≤ 𝑟 ≤ 2
Miền 𝑉 trong tọa độ cầu suy rộng là 𝑉: { 0 ≤ 𝜃 ≤ 𝜋 0 ≤ 𝜑 ≤ 2𝜋
⇒ 𝐼 = ∭ √4 − 𝑥2 − (𝑧2 − 4𝑧 + 4) − 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 = ∭ √4 − [𝑥2 + 𝑦2 + (𝑧 − 2)2]𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑉 2𝜋 𝜋 2
= ∫ 𝑑𝜑 ∫ 𝑑𝜃∫ √4 − 𝑟2. 𝑟2 sin 𝜃 𝑑𝑟 0 0 0
Đặt 𝑟 = 2 sin 𝑡 ⇒ 𝑑𝑟 = 2 cos 𝑡 𝑑𝑡 𝑟 2 0 𝑡 𝜋 0 2 PHAM THANH TUNG 𝜋 𝜋 2 2 2
⇒ ∫ √4 − 𝑟2. 𝑟2𝑑𝑟 = ∫ 4
√ − 4(sin 𝑡)2. 4(sin 𝑡)2. 2 cos 𝑡𝑑𝑡 = ∫ 2 cos 𝑡 . 4(sin 𝑡)2. 2 cos 𝑡𝑑𝑡 0 0 0 𝜋 𝜋 𝜋 𝜋 2 2 sin2𝑡 2 16 2 2 1 − cos4𝑡
= 16 ∫(sin 𝑡 cos 𝑡)2𝑑𝑡= 16 ∫ ( 2 ) 𝑑𝑡 = 4 ∫(sin2𝑡)2𝑑𝑡 = 4∫ 2 𝑑𝑡 = 𝜋 0 0 0 0 2𝜋 𝜋
⇒ ∭(4𝑧 − 𝑥2 − 𝑦2 − 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 = 𝜋 ∫ 𝑑𝜑 ∫ sin 𝜃 𝑑𝜃 = 4𝜋2 𝑉 0 0 𝑦2 𝑘) ∭
𝑑𝑥𝑑𝑦𝑑𝑧 , (𝑉): 𝑥2 + 𝑦2 + 𝑧2 ≤ 4𝑧, 𝑦 ≥ 0 √4𝑧 − 𝑥2 − 𝑧2 𝑉
Miền 𝑉: {𝑥2 + 𝑦2 + 𝑧2 ≤ 4𝑧 𝑦 ≥ 0
⇔ {𝑦2 ≤ −𝑥2 − 𝑧2 + 4𝑧 𝑦 ≥ 0 ⇔ 0 ≤ 𝑦 ≤ 4
√ − [𝑥2 + (𝑧 − 2)2]
Hình chiếu của 𝑉 lên 𝑂𝑥𝑧 là 𝐷: 𝑥2 + (𝑧 − 2)2 ≤ 4 𝑧 = 2 + cos 𝜑 0 ≤ 𝑦 ≤ √4 − 𝑟2
Đặt { 𝑥 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 ⇒ 𝑉: { 0 ≤ 𝑟 ≤ 2 𝑧 = 𝑧 0 ≤ 𝜑 ≤ 2𝜋 PHAM THANH TUNG √4−𝑟2 𝑦2 2𝜋 2 2𝜋 2 ∭ 𝑦2 1
𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑∫ 𝑑𝑟 ∫ . 𝑟𝑑𝑦 = ∫(4 − 𝑟2)𝑟𝑑𝑟 √4𝑧 − 𝑥2 − 𝑧2 √4 − 𝑟2 3 ∫ 𝑑𝜑 𝑉 0 0 0 0 0 8𝜋 = 3
𝑙) ∭(2𝑦 − 𝑧)2𝑑𝑥𝑑𝑦𝑑𝑧, (𝑉): 𝑥2 + 𝑦2 + 𝑧2 ≤ 1 𝑉
𝐼 = ∭(4𝑦2 − 4𝑦𝑧 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 = ∭(4𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧+ ∭(−4𝑦𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑉 𝑉
{𝑓(𝑥, 𝑦, 𝑧) = −4𝑦𝑧 là hàm lẻ với biến 𝑦
Miền 𝑉 đối xứng qua 𝑂𝑥𝑧
⇒ ∭(−4𝑦𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 = 0 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 1
Miền 𝑉 trong tọa độ cầu là 𝑉: { 0 ≤ 𝜃 ≤ 𝜋 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 𝜋 1
𝐼 = ∭(4𝑦2 + 𝑧2)𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫[4(𝑟 sin 𝜃 sin 𝜑)2 + (𝑟 cos 𝜃)2]𝑟2 sin 𝜃 𝑑𝑟 𝑉 0 0 0 2𝜋 𝜋 2𝜋 4 1 16 2 4
= ∫ 𝑑𝜑∫ [5(sin𝜃 sin𝜑)2 +5(cos𝜃)2 ]sin𝜃 𝑑𝜃= ∫ [15(sin𝜑)2 +15]𝑑𝜑 = 3𝜋 0 0 0
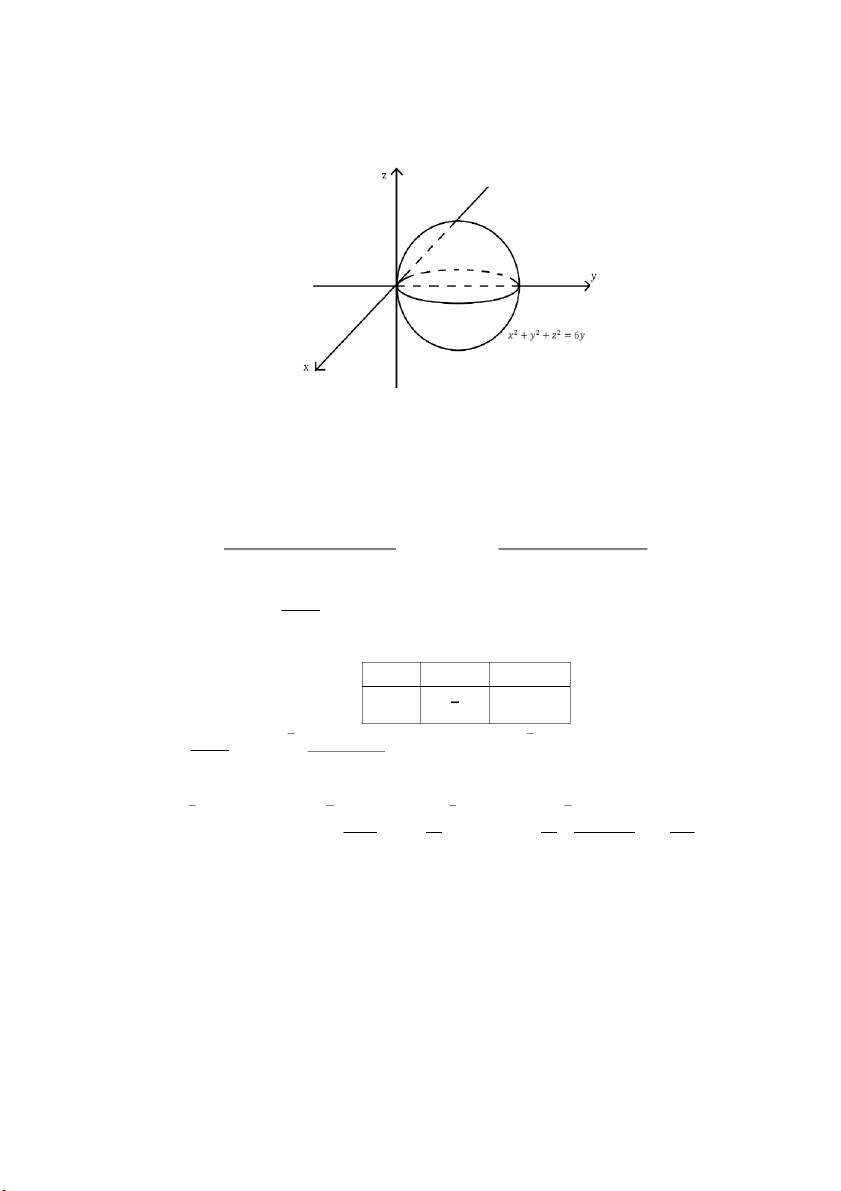
𝑚) ∭ √6𝑦 − 𝑥2 − 𝑦2 − 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 , 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 6𝑦 𝑉
Miền 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 6𝑦 ⇔ 𝑥2 + (𝑦 − 3)2 + 𝑧2 ≤ 9 PHAM THANH TUNG 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 3 + 𝑟 sin 𝜃 sin 𝜑, 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 3
Miền 𝑉 trong tọa độ cầu suy rộng là 𝑉: { 0 ≤ 𝜃 ≤ 𝜋 0 ≤ 𝜑 ≤ 2𝜋 ⇒ 𝐼 = ∭ 9
√ − 𝑥2 − (𝑦2 − 6𝑦 + 9) − 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 = ∭ 9
√ − [𝑥2 + (𝑦 − 3)2 + 𝑧2]𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑉 2𝜋 𝜋 3
= ∫ 𝑑𝜑 ∫ 𝑑𝜃∫ √9 − 𝑟2. 𝑟2 sin 𝜃 𝑑𝑟 0 0 0
Đặt 𝑟 = 3 sin 𝑡 ⇒ 𝑑𝑟 = 3 cos 𝑡 𝑑𝑡 𝑟 3 0 𝑡 𝜋 0 2 𝜋 𝜋 3 2 2
⇒ ∫ √9 − 𝑟2. 𝑟2𝑑𝑟 = ∫ 9
√ − 9(sin 𝑡)2. 9(sin 𝑡)2. 3 cos 𝑡𝑑𝑡 = ∫ 3 cos 𝑡 . 9(sin 𝑡)2. 3 cos 𝑡𝑑𝑡 0 0 0 𝜋 𝜋 𝜋 𝜋 2 2 sin2𝑡 2 81 2 81 2 81𝜋
= 81 ∫(sin 𝑡 cos 𝑡)2𝑑𝑡= 81 ∫ ( 1 − cos 4𝑡
2 ) 𝑑𝑡 = 4 ∫(sin 2𝑡)2𝑑𝑡 = = 4 ∫ 2 𝑑𝑡 16 0 0 0 0 PHAM THANH TUNG 2𝜋 𝜋 81𝜋 ⇒ 𝐼 = ∫ sin 𝜃 𝑑𝜃 81 16 ∫ 𝑑𝜑 = 4 𝜋2 0 0
𝑛) ∭ 𝑒√𝑥2+𝑦2+𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 , (𝑉): 𝑥2 + 𝑦2 + 𝑧2 ≤ 4, 𝑥 ≥ 0, 𝑧 ≥ 0 𝑉 𝑥 = 𝑟 sin 𝜃 cos 𝜑
Đặt {𝑦 = 𝑟 sin 𝜃 sin 𝜑 , 𝐽 = −𝑟2 sin 𝜃 𝑧 = 𝑟 cos 𝜃 0 ≤ 𝑟 ≤ 2
Miền 𝑉 trong tọa độ cầu suy rộng là 𝑉: { 0 ≤ 𝜃 ≤ 𝜋/2 −𝜋/2 ≤ 𝜑 ≤ 𝜋/2 𝜋 𝜋 𝜋 𝜋 2 2 2 2 2
∭ 𝑒√𝑥2+𝑦2+𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫ 𝑒𝑟. 𝑟2 sin 𝜃 𝑑𝑟 = (2𝑒2 − 2) ∫ 𝑑𝜑∫ sin 𝜃 𝑑𝜃 𝑉 −𝜋 0 0 −𝜋 0 2 2 = (2𝑒2 − 2)𝜋 2
(Sử dụng tích phân từng phân để tính ∫ 𝑒𝑟. 𝑟2𝑑𝑟 ) 0
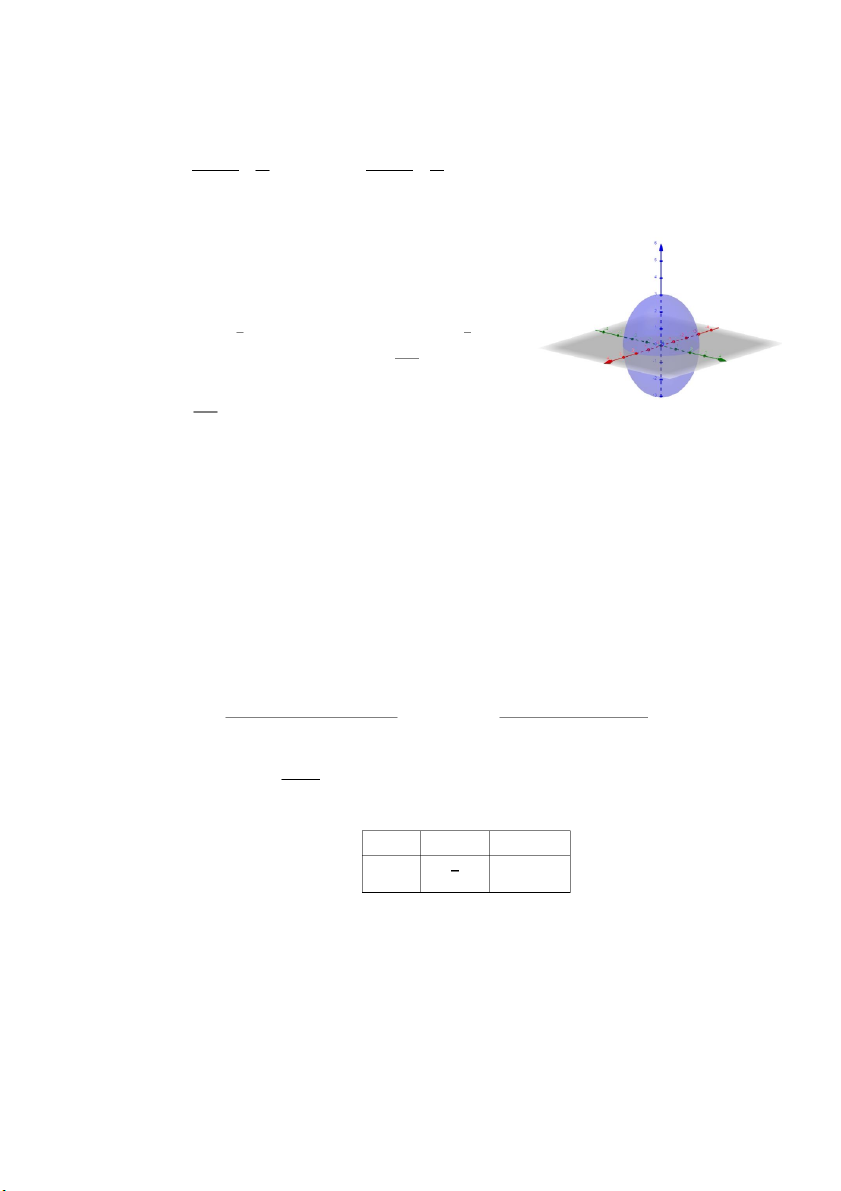
𝑜) ∭ √1 − 𝑥2 − 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 , (𝑉): 𝑥2 + 𝑦2 + 𝑧2 ≤ 1, 𝑧 ≥ 0. 𝑉
Hình chiếu của 𝑉 lên 𝑂𝑥𝑦 là 𝐷: 𝑥2 + 𝑦2 ≤ 1 𝑥 = 𝑟 cos 𝜑
Đặt { 𝑦 = 𝑟 sin 𝜑 , 𝐽 = 𝑟 𝑧 = 𝑧 2 2 0 < 𝑧 ≤ 1 √ − 𝑟2 ⇒ 𝑉: {0 ≤ 𝑧 ≤ 1 √ − 𝑥 − 𝑦 ⇔ { 𝐷: 𝑥2 + 𝑦2 ≤ 1 0 ≤ 𝑟 ≤ 1 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 1 √1−𝑟2 2𝜋 1 𝜋
⇒ 𝐼 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ √1 − 𝑟2. 𝑟𝑑𝑧 = ∫ 𝑑𝜑∫(1 − 𝑟2). 𝑟𝑑𝑟 = 2 0 0 0 0 0 PHAM THANH TUNG Hình vẽ minh h a ọ 5𝑥2 − 3𝑦2 + 𝑧2 + 4 𝑝) ∭ 𝑥
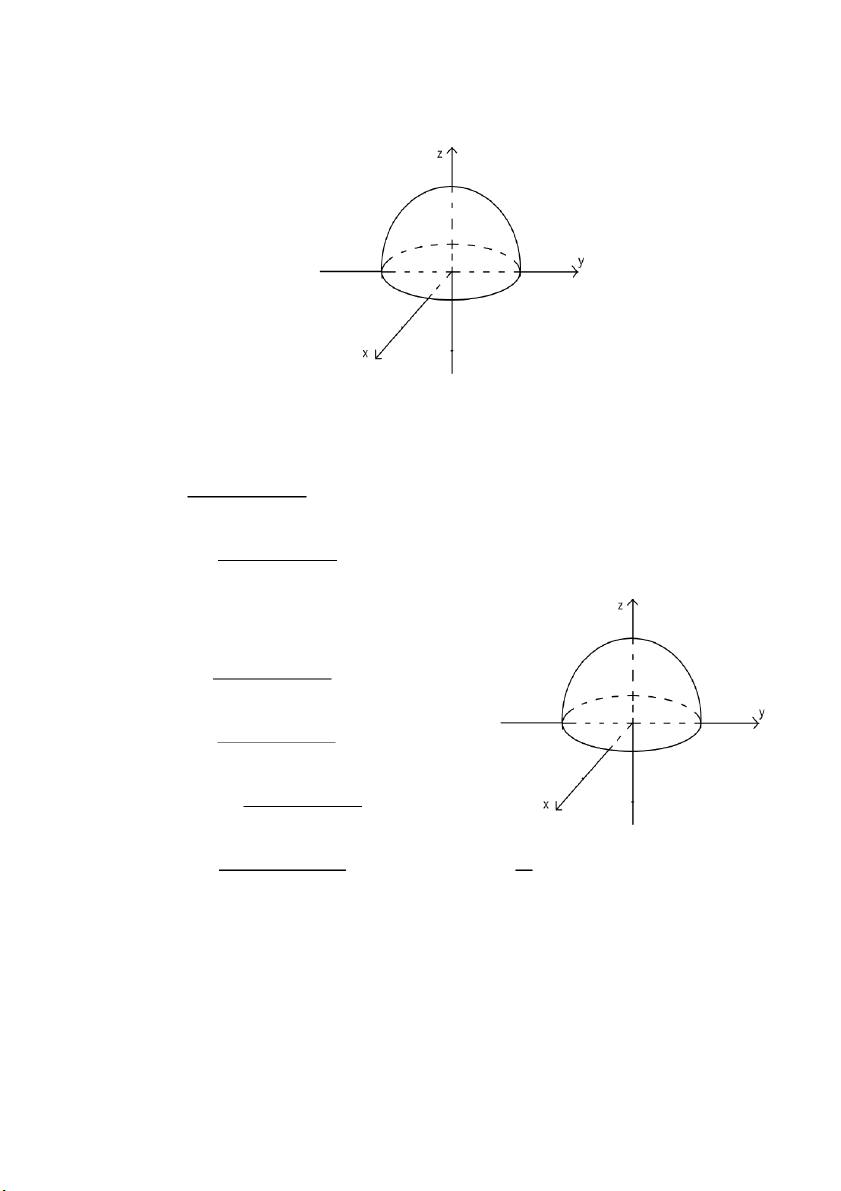
𝑑𝑥𝑑𝑦𝑑𝑧, 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 1, 𝑧 ≥ 0 2 + 𝑦2 + 𝑧2 + 4 𝑉 5𝑥2 − 3𝑦2 + 𝑧2 + 4
Đặ𝑡 𝐼 = ∭ 𝑥2 + 𝑦2 + 𝑧2 + 4 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
Đổi vai trò của 𝑥, 𝑦
⇒ Miền 𝑉 không thay đổi, 𝑉: 𝑥2 + 𝑦2 + 𝑧2 ≤ 1, 𝑧 ≥ 0 5𝑦2 − 3𝑥2 + 𝑧2 + 4
⇒ 𝐼 = ∭ 𝑥2 + 𝑦2 + 𝑧2 + 4 𝑉 5𝑥2 − 3𝑦2 + 𝑧2 + 4 ⇒ 2𝐼 = ∭
𝑥2 + 𝑦2 + 𝑧2 + 4 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 5𝑦2 − 3𝑥2 + 𝑧2 + 4
+ ∭ 𝑥2 + 𝑦2 + 𝑧2 + 4 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 2𝑥2 + 2𝑦2 + 2𝑧2 + 8 = ∭ 4𝜋
𝑥2 + 𝑦2 + 𝑧2 + 4 𝑑𝑥𝑑𝑦𝑑𝑧 = 2 ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = 3 𝑉 𝑉 PHAM THANH TUNG 2𝜋 ⇒ 𝐼 = 3 (𝑦 − 1)2
𝑞) ∭𝑥2 +𝑦2 +𝑧2 +3𝑑𝑥𝑑𝑦𝑑𝑧 ,(𝑉):𝑥2 +𝑦2 +𝑧2 ≤ 1 𝑉 (𝑦 − 1)2
Đặ𝑡 𝐼 = ∭𝑥2 + 𝑦2 + 𝑧2 + 3𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 𝑦2 + 2𝑦 + 1 𝑦2 + 1 2𝑦𝑑𝑥𝑑𝑦𝑑𝑧
𝐼 = ∭𝑥2 + 𝑦2 + 𝑧2 + 3𝑑𝑥𝑑𝑦𝑑𝑧 = ∭𝑥2 + 𝑦2 + 𝑧2 + 3 𝑑𝑥𝑑𝑦𝑑𝑧 + ∭ 𝑥2 + 𝑦2 + 𝑧2 + 3 𝑉 𝑉 𝑉 2𝑦 2𝑦
{ 𝑥2 + 𝑦2 + 𝑧2 + 3 lẻ với biến 𝑦 ⇒ ∭ = 0 2 2 𝑑𝑥𝑑𝑦𝑑𝑧
Miền 𝑉 đối xứng qua 𝑂𝑥𝑧 𝑥2 + 𝑦 + 𝑧 + 3 𝑉 𝑦2 + 1
⇒ 𝐼 = ∭ 𝑥2 + 𝑦2 + 𝑧2 + 3 𝑑𝑥𝑑𝑦𝑑𝑧 (1) 𝑉
Đổi vai trò của 𝑥, 𝑦 miền 𝑉 không thay đổi 𝑥2 + 1
⇒ 𝐼 = ∭ 𝑥2 +𝑦2 +𝑧2 +3 𝑑𝑥𝑑𝑦𝑑𝑧 (2) 𝑉
Đổi vai trò của 𝑦, 𝑧 miền 𝑉 không thay đổi PHAM THANH TUNG 𝑧2 + 1 ⇒ 𝐼 = ∭ ( 𝑥 𝑑𝑥𝑑𝑦𝑑𝑧 3) 2 + 𝑦2 + 𝑧2 + 3 𝑉 ( 𝑥2 + 𝑦2 + 𝑧2 + 3 4 1) + (2) + (3) ⇒ 3𝐼 = ∭ 4
𝑥2 + 𝑦2 + 𝑧2 + 3 𝑑𝑥𝑑𝑦𝑑𝑧 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 = 3 𝜋 ⇒ 𝐼 = 9 𝜋 𝑉 𝑉 PHAM THANH TUNG
TÀI LIỆU THAM KHẢO :
− Bài giảng môn Giải tích II, thầy Bùi Xuân Diệu.
− Bài tập giải sẵn Giải tích 2 (Tóm tắt lý thuyết và chọn lọc), thầy Trần Bình.
− Bài tập Toán học cao cấp, tập hai: Giải tích, GS.TS Nguyễn Đình Trí (chủ
biên), PGS.TS. Trần Việt Dũng, PGS.TS. Trần Xuân Hiền, PGS.TS Nguyễn Xuân Thảo.
− Bộ đề cương Giải tích II, Viện Toán ứng dụng và Tin học.
− Bộ đề thi Giữa kì và Cuối kì môn Giải tích II Trường ĐH Bách Khoa Hà Nội.
Tài liệu được biên soạn dựa trên kinh nghiệm cá nhân, dù đã rất cố gắng nhưng
chắc chắn vẫn sẽ tồn tại các lỗi sai tính toán, lỗi đánh máy, …mọi ý kiến góp ý
bạn đọc vui lòng gửi qua link fb “fb.com/tungg810” để mình có thể kiểm tra,
hoàn thiện bộ tài liệu. Xin chân thành cảm ơn! PHAM THANH TUNG